Empirical Study on the Influence of Different Mathematical Methods (Algebraic Formula Method and Newton Sum Method) on ChatGPT (AI) Competence in Solving Quadratic Root Functions

Preprint

Article

Empirical Study on the Influence of Different Mathematical Methods (Algebraic Formula Method and Newton Sum Method) on ChatGPT (AI) Competence in Solving Quadratic Root Functions

Altmetrics

Downloads

107

Views

Comments

Peter Chew^*

This version is not peer-reviewed

This preprints belongs to the Topic

Education for Sustainable Development and Science Teaching

Submitted:

21 October 2023

Posted:

23 October 2023

You are already at the latest version

Alerts

Abstract

Introduction: This empirical study investigates the impact of two distinct mathematical problem-solving methods – the Algebraic Formula Method and the Newton Sum Method – on enhancing ChatGPT's competence in effectively solving quadratic root functions. The integration of Artificial Intelligence (AI) into mathematical problem-solving has paved the way for innovative approaches. In this study, we delve into the Algebraic Formula Method and the Newton Sum Method, essential techniques for solving quadratic root functions. We aim to showcase the profound influence of these methods on ChatGPT's capacity to excel in solving quadratic equations. Evidence Through concrete evidence, we demonstrate ChatGPT's adept utilization of the Newton Sum Method for quadratic root function calculations. While ChatGPT can compute quadratic root functions of the form α^15 + β^15 using this method, its proficiency in using algebraic formula methods typically extends only up to α^4 + β^4. This marked discrepancy underscores the pivotal role that different methods play in amplifying the AI system's mathematical capabilities Result The results of this study provide concrete evidence of ChatGPT's superior utilization of the Newton Sum Method for calculating quadratic root functions. The model adeptly computes expressions of the form α^15 + β^15 using this method, while its proficiency using algebraic formula methods is generally limited to α^4 + β^4. This striking discrepancy underscores the transformative impact that different methods can have on elevating the AI system's mathematical prowess. Conclusion :Pushing Boundaries: Pioneering Novel Maths Approaches for Overcoming Limitations in AIThis study serves as an illuminating testament to the significance of pioneering innovative methodologies, rules, theorems, or formulas to surmount the current limitations in AI systems like ChatGPT. These innovative pursuits hold the key to unlocking the untapped potential that lies within, propelling AI systems to greater heights of proficiency. In essence, they offer a strategic pathway towards expanding the capabilities of AI and pushing the boundaries of what can be achieved. Discussion The outcomes derived from this study underscore the significant influence wielded by the method selection in augmenting the mathematical competencies of ChatGPT. Particularly noteworthy is the application of the Newton Sum Method, which surfaces as a compelling exemplar. This method serves as a pivotal conduit through which the model surpasses its prior constraints, allowing it to venture into the realm of calculations entailing higher exponents. Implications and Future Research: These findings not only contribute to AI's mathematical competencies but also emphasize the need for pioneering new methods, rules, theorems, or formulas to further enhance AI systems like ChatGPT. Future research could explore the development of novel mathematical techniques tailored to AI systems, thus expanding their capabilities across diverse problem-solving domains.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

This empirical study investigates the impact of two distinct mathematical problem-solving methods – the Algebraic Formula Method and the Newton Sum Method – on enhancing ChatGPT's competence in effectively solving quadratic root functions.

1.1. ChatGPT¹

Introducing ChatGPT

We’ve trained a model called ChatGPT which interacts in a conversational way. The dialogue format makes it possible for ChatGPT to answer follow up questions, admit its mistakes, challenge incorrect premises, and reject inappropriate requests.

Introducing ChatGPT Plus

We’re launching a pilot subscription plan for ChatGPT, a conversational AI that can chat with you, answer follow-up questions, and challenge incorrect assumptions.

{C h a t G P T}^{2}

knowledge is still limited to 2021 data, which means it can't answer current questions.

1.2. Knowledge Is Power: Why the Future Is not just about the tech³

If we are to rely on machine intelligence, we need to understand the two types of knowledge.

Understanding knowledge means we can distinguish where we want machines to do the mundane work and where we want humans to perform intuitive tasks. Such an approach will be as beneficial for business as for education. As virtual and physical worlds become increasingly interdependent, knowledge – and how we manage it – will become the secret ingredient to manage the situation. And thrive.

Virtual technologies are swiftly becoming intertwined with our physical world, and companies need to adapt. But that doesn’t simply mean replacing humans with robots or relying on artificial intelligence (AI) to make all of our decisions. This is because technology, though powerful, is just part of the equation. In fact, human intelligence will be one of the most valuable assets in today's Fourth Industrial Revolution (FIR), and companies may flounder if they fail to strike the right balance of automated technology and human insights.

1.3. Algebra Formula

1.3.1. The following functions are some symmetric function of a quadratic’s roots

\frac{1}{α} + \frac{1}{β}

\frac{α + β}{α β}

α^{2} + β^{2}

(α + α)^{2}

- 2

c) α (- β)^{2}

(α + β)^{2}

- 4

α, β

d) α^{3} + β^{3}

(α + β) [(α + β)^{2} - 3 α β]

α^{4} + β^{4}

(α^{2} + β^{2})^{2}

- 2

α^{2} β^{2}

= =

[(α + β)^{2}

- 2

α β]^{2}

- 2

(α β)^{2}

1.3.2. The following functions are asymmetric function of a quadratic’s roots

a) α - β

\pm \sqrt{(α + α)^{2} - 4 α β}

b) α^{2} - β^{2}

\pm (+) \sqrt{(α + β)^{2} - 4 α β}

c) α^{3} - α^{3}

\pm \sqrt{(α + α)^{2} - 4 α β} [(α + β)^{2} - α β] .

α^{4} - β^{4}

(α^{2} - β^{2}) (α^{2} + β^{2})

\pm [(+) \sqrt{(α + β)^{2} - 4 α β}

]

[(α + β)^{2}

- 2

α β]^{2}

- 2

(α β)^{2}]

Note: Student need to remember above Algebra Formula if they use Veda's theorem method for Construct New Quadratic Equation.

1.4. Newton Sum (Newton's Identities)⁴

Newton's identities, also known as Newton-Girard formulae, is an efficient way to find the power sum of roots of polynomials without actually finding the roots. If

x_{1}, x_{2}, \dots . . x_{n}

are the roots of a polynomial equation, then Newton's identities are used to find the summations like

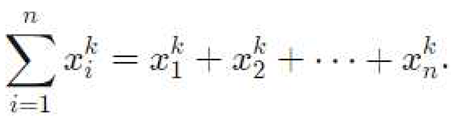
It is mainly used in conjunction with Vieta's formula while working with the (complex) roots (say

a_{1}, a_{2}, \dots . . a_{k}

) of a

k^{t h}

degree polynomial. The main idea is that the elementary symmetric polynomials form an algebraic basis to produce all symmetric polynomials. Newton's identity gives us the calculation via a recurrence relation with known coefficients.

Newton's Identities for a Quadratic Polynomial

Suppose that you have a quadratic polynomial P(x) with (complex) roots

α_{1}

and

α_{2}

. Now, you are asked to find the value of

{α_{1}}^{2} + {α_{2}}^{2}

. This seems very easy since you can use Vieta's formula along with the identity

{(a + b)}^{2}

a^{2}

b^{2}

+ 2ab to find the required result. But what if you need to find

({α_{1}}^{10} + {α_{2}}^{10})

? This would take a while if you were to simply use algebraic manipulations. But there's a clever way, using Newton's sums.

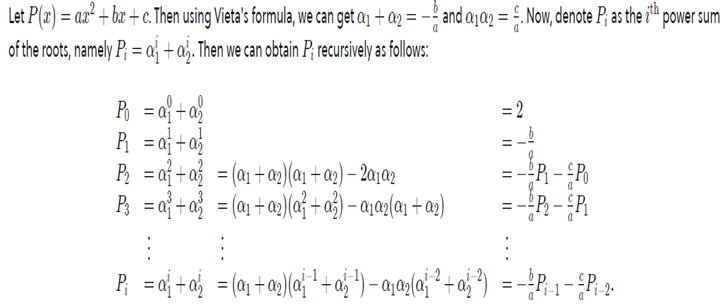
This is a linear recurrence relation that gives us the

i^{t h}

power sum. Note that solving this recurrence to get a closed-form solution is equivalent to finding the roots of the quadratic polynomial.

1.5. The French Mathematician, ${V i e t a}^{5}$

François Viète ( Latin: Franciscus Vieta; 1540 – 23 February 1603)

The French mathematician Veda established the relationship between the equation root and the coefficient in 1615. Veda's theorem states that if α and β are two roots of the quadratic equation a

x^{2} + b x + c = 0

and a ≠ 0.

Then, The sum of the two roots, α+β= -

\frac{b}{a}

, The product of the two roots, αβ=

\frac{c}{a} .

Prove α + β = -

\frac{b}{a} a n d

αβ =

\frac{c}{a}

If α and β are two roots of the quadratic equation a

x^{2} + b x + c = 0

and a ≠ 0.

Then α

= \frac{- b + \sqrt{b^{2} - 4 a c}}{2 a}

, β

= \frac{- b - \sqrt{b^{2} - 4 a c}}{2 a}

So, α + β

= \frac{- b + \sqrt{b^{2} - 4 a c}}{2 a} + \frac{- b - \sqrt{b^{2} - 4 a c}}{2 a}

= \frac{- 2 b}{2 a}

=

\frac{b}{a}

α β

= \frac{- b + \sqrt{b^{2} - 4 a c}}{2 a} \times \frac{- b - \sqrt{b^{2} - 4 a c}}{2 a}

\frac{(- b)^{2} - {(\sqrt{b^{2} - 4 a c})}^{2}}{(2 a)^{2}} = \frac{\begin{matrix} b^{2} - {(b}^{2} - 4 a c) \end{matrix}}{4 a^{2}} = \frac{4 a c}{4 a^{2}} = \frac{c}{a}

2. Evidence

Through concrete evidence, we demonstrate ChatGPT's adept utilization of the Newton Sum Method for quadratic root function calculations. While ChatGPT can compute quadratic root functions of the form α^15 + β^15 using this method, its proficiency in using algebraic formula methods typically extends only up to α^4 + β^4. This marked discrepancy underscores the pivotal role that different methods play in amplifying the AI system's mathematical capabilities

2.1. Algebraic Formula Methods. Using Chat ${G P T}^{6}$

for Calculate

2.1.1. If the roots of the equation x² - 3x + 2 $=$ 0 are α and β, find $α^{2} + β^{2}$

2.1.2. Algebra Formula, Using Chat GPT for Calculate

If the roots of the equation x² - 3x + 2

=

0 are α and β, find

α^{3} + β^{3}

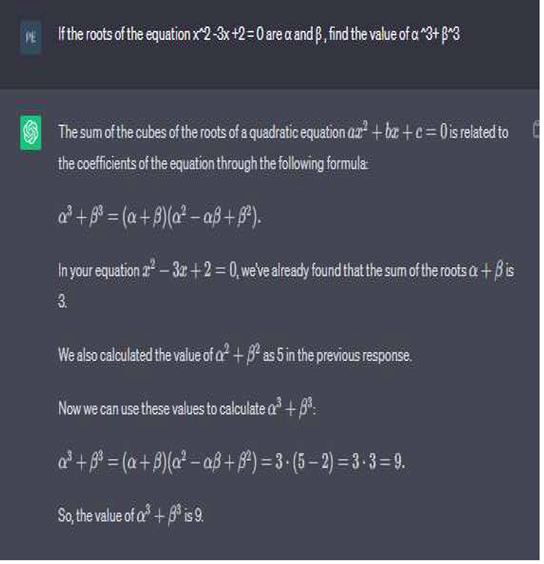
2.1.3. Algebra Formula, Using Chat GPT for Calculate

If the roots of the equation x² - 3x + 2

=

0 are α and β, find

α^{4} + β^{4}

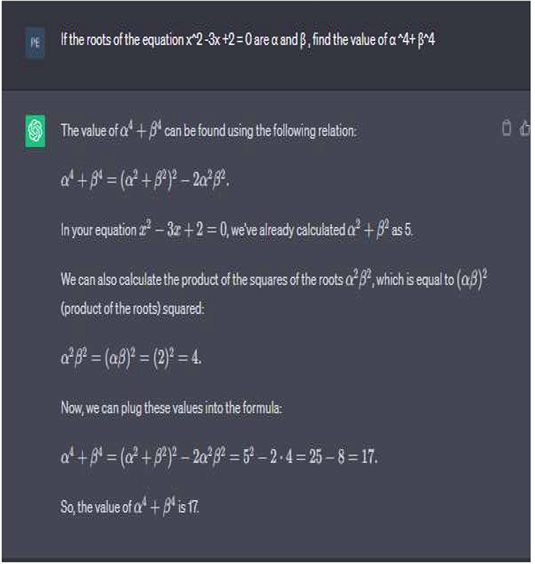
2.1.4. Algebra Formula, Using Chat GPT for Calculate

If the roots of the equation x² - 3x + 2

=

0 are α and β, find

α^{5} + β^{5}

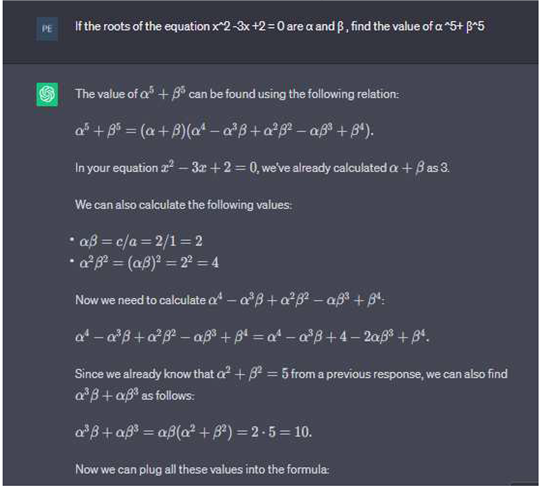
When employing the Algebraic Formula, ChatGPT faces limitations in delivering conclusive solutions for problems like α^5 + β^5, owing to the intricate nature of the solutions.. As we see Chat GPT Reply: At this point, finding the exact value of

β^{2}

and subsequently

α^{5} + β^{5}

becomes more complex and likely involves solving a higher-degree equation for β. The process becomes intricate and might not lead to a simple numerical result. In general, the expressions involving higher powers of the roots can become quite involved, and finding specific numerical values can be complex.

2.2. Newton sum Methods. Using Chat GPT for Calculate

2.2.1. If the roots of the equation x^2 - 3x + 2 = 0 are α and β, find the value of α^2 + β^2 using Newton sum . Sk = α^k + β^k = -a_(k-1) * S_(k-1) - a_(k-2) * S_(k-2)

2.2.2. Newton Sum, Using Chat GPT for Calculate

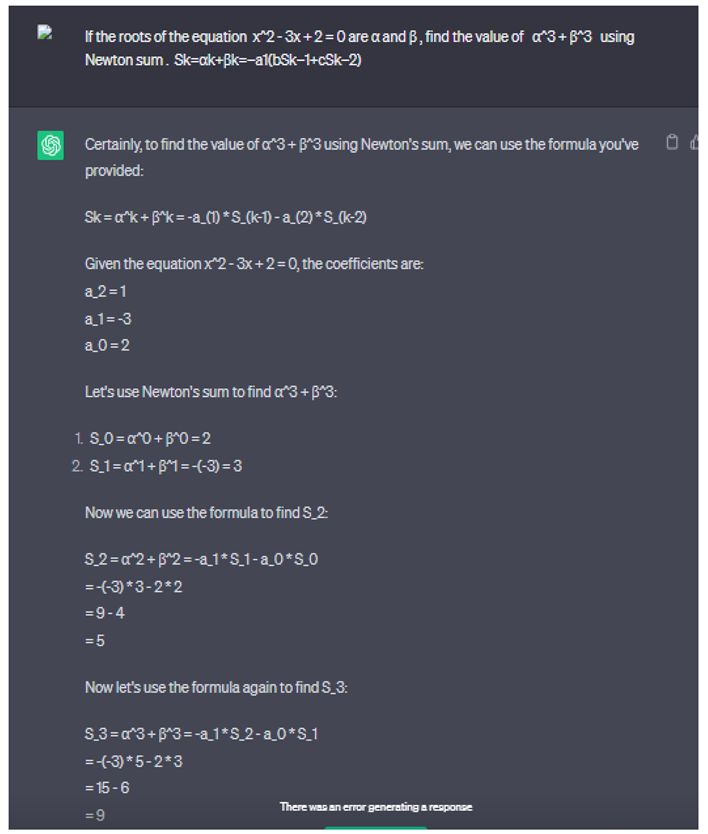
If the roots of the equation x^2 - 3x + 2 = 0 are α and β, find the value of α^3 + β^3 using Newton sum . Sk=αk+βk=−a1(bSk−1+cSk−2)

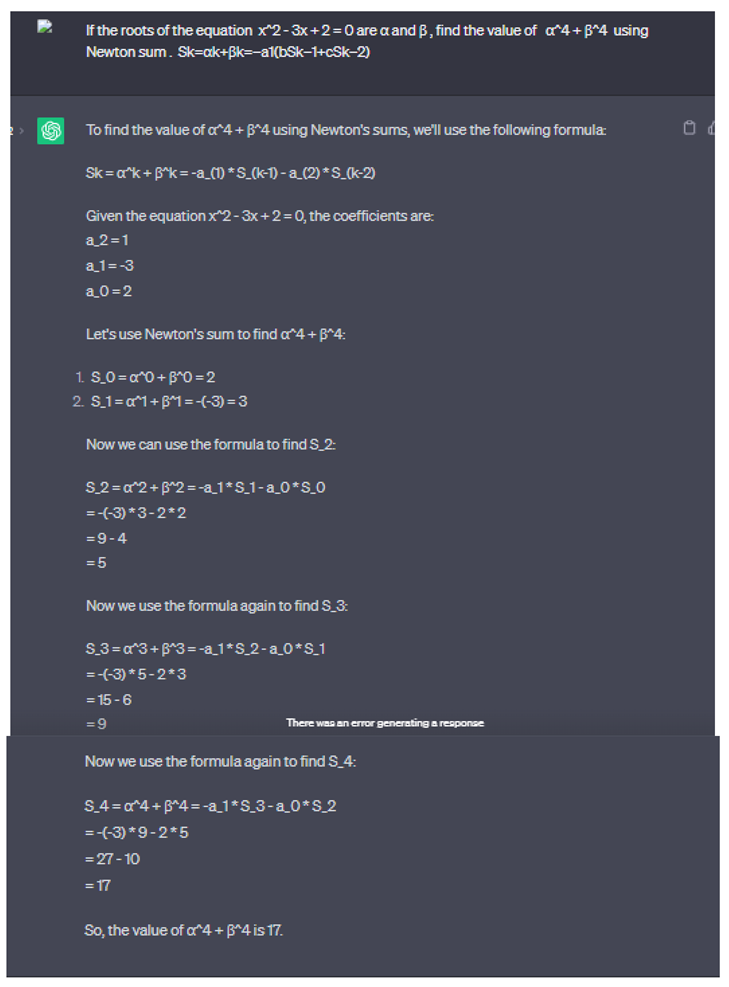
2.2.3. Newton Sum, Using Chat GPT for Calculate

If the roots of the equation x^2 - 3x + 2 = 0 are α and β, find the value of α^4 + β^4 using Newton sum . Sk=αk+βk=−a1(bSk−1+cSk−2)

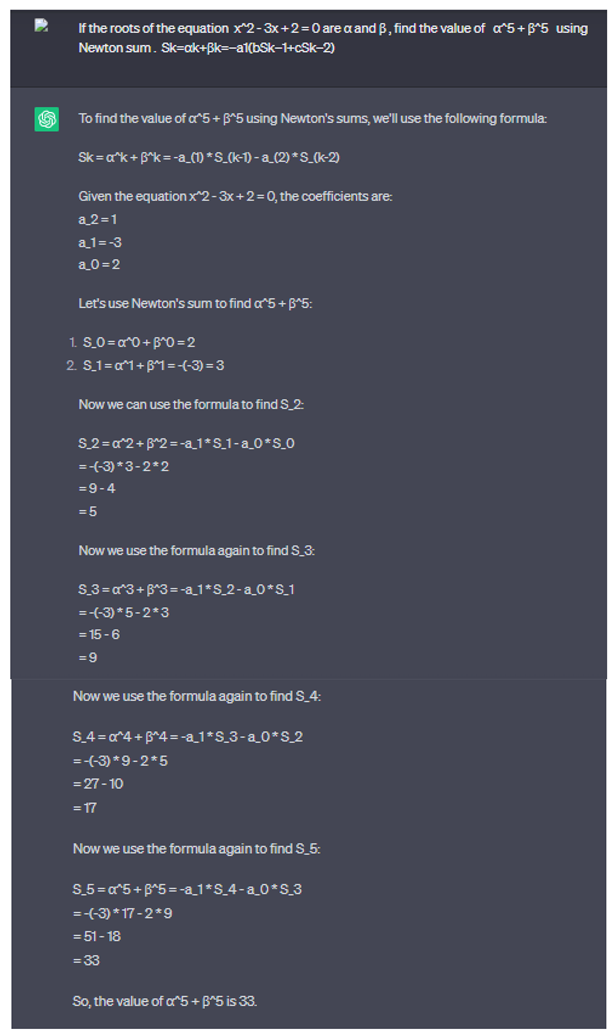
2.2.4. Newton Sum, Using Chat GPT for Calculate

If the roots of the equation x^2 - 3x + 2 = 0 are α and β, find the value of α^5 + β^5 using Newton sum . Sk=αk+βk=−a1(bSk−1+cSk−2)

2.2.5. Newton Sum, Using Chat GPT for Calculate

If the roots of the equation x^2 - 3x + 2 = 0 are α and β, find the value of α^6 + β^6 using Newton sum . Sk=αk+βk=−a1(bSk−1+cSk−2).

2.2.6. Newton Sum, Using Chat GPT for Calculate

If the roots of the equation x^2 - 3x + 2 = 0 are α and β, find the value of α^7 + β^7 using Newton sum . Sk=αk+βk=−a1(bSk−1+cSk−2).

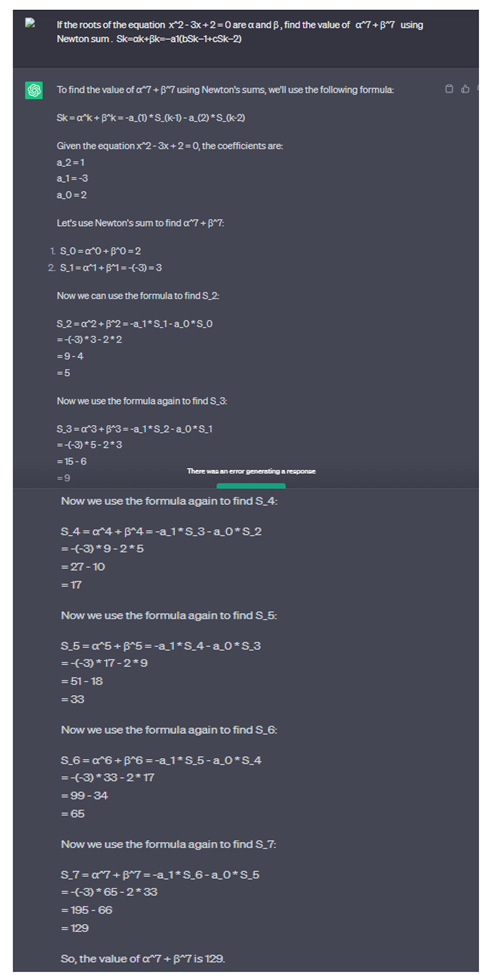
2.2.7. Newton Sum, Using Chat GPT for Calculate

If the roots of the equation x^2 - 3x + 2 = 0 are α and β, find the value of α^8 + β^8 using Newton sum . Sk=αk+βk=−a1(bSk−1+cSk−2).

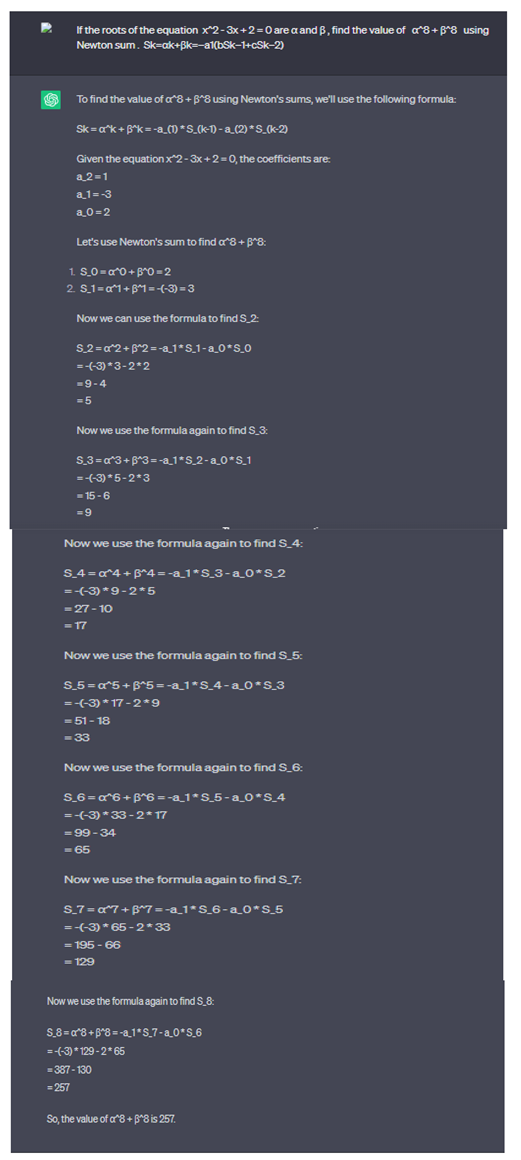
2.2.8. Newton Sum, Using Chat GPT for Calculate

If the roots of the equation x^2 - 3x + 2 = 0 are α and β, find the value of α^9 + β^9 using Newton sum . Sk=αk+βk=−a1(bSk−1+cSk−2).

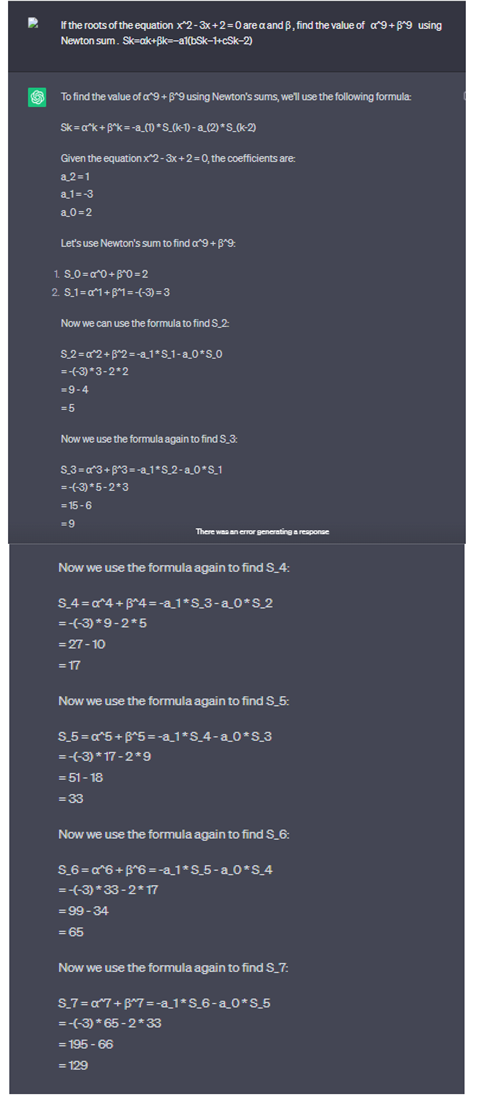
2.2.9. Newton Sum, Using Chat GPT for Calculate

If the roots of the equation x^2 - 3x + 2 = 0 are α and β, find the value of α^10 + β^10 using Newton sum . Sk=αk+βk=−a1(bSk−1+cSk−2).

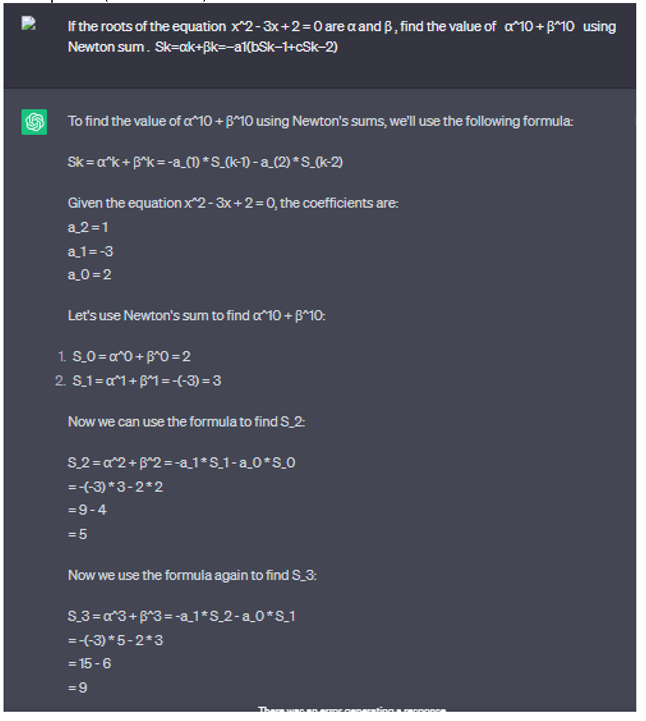
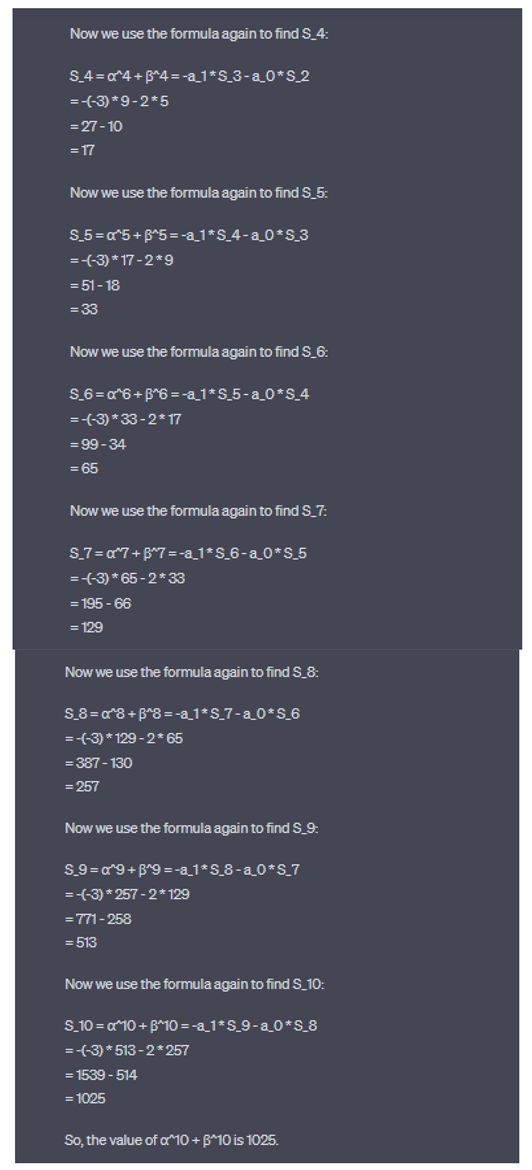
2.2.10. Newton Sum, Using Chat GPT for Calculate

If the roots of the equation x^2 - 3x + 2 = 0 are α and β, find the value of α^11 + β^11 using Newton sum . Sk=αk+βk=−a1(bSk−1+cSk−2).

2.2.11. Newton Sum, Using Chat GPT for Calculate

If the roots of the equation x^2 - 3x + 2 = 0 are α and β, find the value of α^12 + β^12 using Newton sum . Sk=αk+βk=−a1(bSk−1+cSk−2).

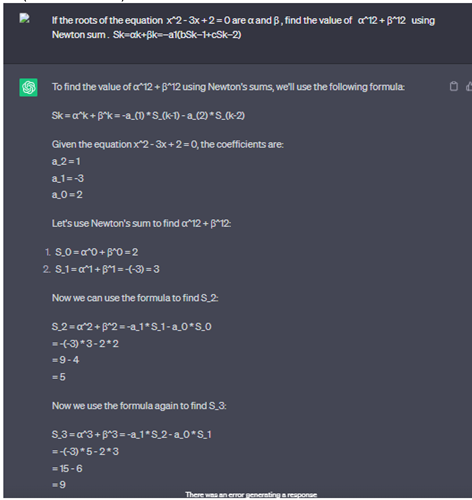
2.2.12. Newton Sum, Using Chat GPT for Calculate

If the roots of the equation x^2 - 3x + 2 = 0 are α and β, find the value of α^13 + β^13 using Newton sum . Sk=αk+βk=−a1(bSk−1+cSk−2).

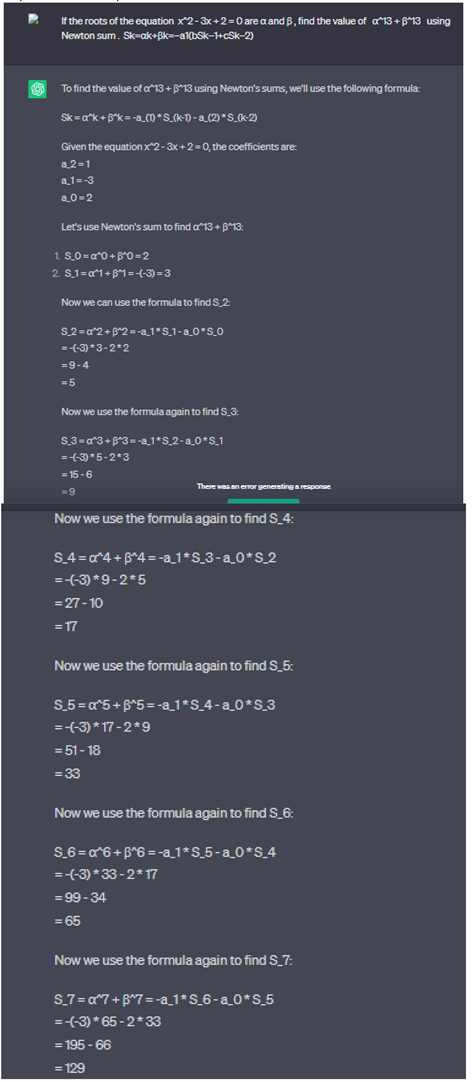
2.2.13. Newton Sum, Using Chat GPT for Calculate

If the roots of the equation x^2 - 3x + 2 = 0 are α and β, find the value of α^14 + β^14 using Newton sum . Sk=αk+βk=−a1(bSk−1+cSk−2).

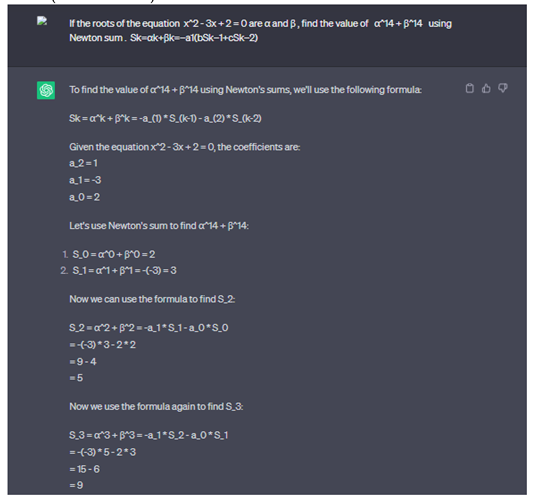
2.2.14. Newton Sum, Using Chat GPT for Calculate

If the roots of the equation x^2 - 3x + 2 = 0 are α and β, find the value of α^15 + β^15 using Newton sum . Sk=αk+βk=−a1(bSk−1+cSk−2).

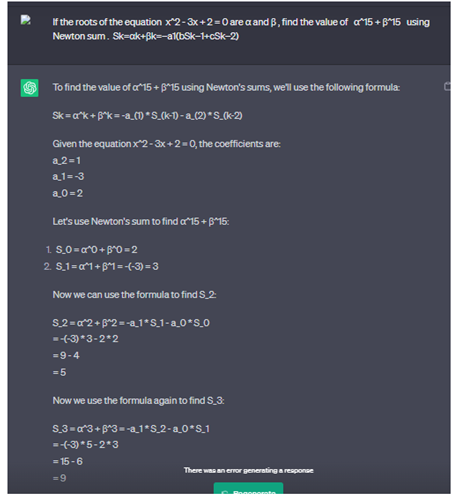
2.2.15. Newton Sum, Using Chat GPT for Calculate

If the roots of the equation x^2 - 3x + 2 = 0 are α and β, find the value of α^28 + β^28 .

3. Results

The results of this study provide concrete evidence of ChatGPT's superior utilization of the Newton Sum Method for calculating quadratic root functions. The model adeptly computes expressions of the form α^15 + β^15 using this method, while its proficiency using algebraic formula methods is generally limited to α^4 + β^4. This striking discrepancy underscores the transformative impact that different methods can have on elevating the AI system's mathematical prowess.

In the realm of quadratic root function calculations, the Newton Sum Method emerges as a powerful tool compare Algebra Formula method, enabling AI systems like α^15 + β^15 which can not be solve by Algebra formula method. However, a noteworthy facet emerges as ChatGPT encounters challenges in yielding definitive solutions for expressions such as α^28 + β^28. The intricate nature of these solutions proves to be a stumbling block, leading to limitations in the scope of deliverable conclusions.

The core reason behind these limitations lies in the inherent methodology of the Newton Sum calculation technique. Rooted in historical calculations, this method relies on previous results to determine the current outcome. As a consequence, when confronted with higher-order quadratic root function calculations like α^28 + β^28, the computational process undergoes a transformation into a labyrinthine endeavour, entailing increased intricacy and time consumption.

Engaging with this limitation, ChatGPT offers a comprehensive strategy: "We'll need to calculate S26 and S25 using the same recursive formula. Continuing this process, we'll eventually calculate S27, and then we can calculate S28 using the formula above. However, this recursive process can become quite complex and time-consuming for higher values of k. If you're looking for a more efficient method, you might consider using a mathematical software or programming language that can handle symbolic computations."

4. Conclusion

Pushing Boundaries: Pioneering Novel Maths Approaches for Overcoming Limitations in AI

This study serves as an illuminating testament to the significance of pioneering innovative methodologies, rules, theorems, or formulas to surmount the current limitations in AI systems like ChatGPT. These innovative pursuits hold the key to unlocking the untapped potential that lies within, propelling AI systems to greater heights of proficiency. In essence, they offer a strategic pathway towards expanding the capabilities of AI and pushing the boundaries of what can be achieved.

In the broader panorama of AI's evolutionary trajectory, these findings resonate as a resonant call to action. They invite researchers, developers, and practitioners to seize the opportunity and embark on a transformative journey. The limitations encountered today are not mere roadblocks but stepping stones towards a more capable AI landscape. As the digital realm continues to evolve, the pursuit of novel methodologies becomes an integral part of this evolutionary symphony.

These findings cast a compelling vision for future research endeavours. They beckon researchers to embark on audacious explorations into uncharted territories. This involves delving deep into the unexplored realm of novel mathematical techniques, intricately tailored to accommodate the unique characteristics of AI systems. Such an endeavour, though challenging, promises to be transformative. The resulting synergy between innovative mathematics and advanced AI systems holds the potential to reshape the technological landscape.

In conclusion, this study resonates as a clarion call to innovation, urging stakeholders to embrace the challenge and forge ahead. The limitations encountered today are the building blocks of progress. The pioneering of novel methodologies is not only an aspiration but a necessity to shape the future of AI. As we stand at the precipice of an AI-powered future, the beckoning of uncharted territories invites us to create a new paradigm, where the potential of AI systems is truly unleashed and their impact resonates across the technological landscape.

5. Discussion

The results obtained from this study strongly emphasize the substantial impact that the choice of method holds in bolstering the mathematical proficiencies of ChatGPT. One method that particularly stands out is the application of the Newton Sum Method, which emerges as a compelling and illustrative example.

This method acts as a pivotal gateway, enabling the model to transcend its previous limitations and boldly explore the domain of calculations involving higher exponents. This significant breakthrough not only showcases the Newton Sum Method's efficacy but also highlights its pivotal role in pushing the boundaries of ChatGPT's mathematical capabilities.

6. Implications and Future Research

The discoveries unearthed by this study carry a dual impact, contributing not solely to the advancement of AI's mathematical competencies but also underscoring the imperative of forging ahead with innovation. These findings serve as a clarion call for the exploration and creation of pioneering methodologies, novel rules, inventive theorems, and groundbreaking formulas. The aim is clear: to propel AI systems like ChatGPT to even greater heights of proficiency and utility.

Looking ahead, the vista of future research beckons. A promising avenue lies in the exploration and refinement of novel mathematical techniques that are expressly tailored to the unique demands of AI systems. This deliberate alignment holds the potential to significantly expand the purview of AI's capabilities, allowing them to permeate a diverse spectrum of problem-solving domains.

In essence, this study isn't merely a snapshot of AI's current capabilities; it's a catalyst for future innovation. It reinforces the idea that as AI continues its evolution, it must continue to push boundaries, to delve into uncharted territories, and to chart new courses of advancement. By embracing this ethos, researchers can fuel the ongoing transformation of AI from a tool of the present into an even more formidable force in the future, reshaping the way we approach complex problem-solving across a multitude of domains.

References

Introducing ChatGPT. OpenAI . https://openai.com/blog/chatgpt.
Matt G. Southern OpenAI’s ChatGPT Update Brings Improved Accuracy. Search Engine Journal. January 10, 2023. https://www.searchenginejournal.com/openai-chatgpt-update/476116/#close.
James Lin,Knowledge is power: why the future is not just about the tech . World Economy Forum Jan 25, 2021 https://www.weforum.org/agenda/2021/01/knowledge-is-power-why-the-future-is-not-just-about-the-tech/.
Prasun Biswas et all . Newton's Identities. BRILLIANT. https://brilliant.org/wiki/newtons-identities/.
François Viète . Wikipedia https://en.wikipedia.org/wiki/Fran%C3%A7ois_Vi%C3%A8te.
Chat GPT. https://chat.openai.com/?model=text-davinci-002-render-sha.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Empirical Study on the Influence of Different Mathematical Methods (Algebraic Formula Method and Newton Sum Method) on ChatGPT (AI) Competence in Solving Quadratic Root Functions

Abstract

1. Introduction

1.1. ChatGPT1

Introducing ChatGPT

Introducing ChatGPT Plus

1.2. Knowledge Is Power: Why the Future Is not just about the tech3

1.3. Algebra Formula

1.3.1. The following functions are some symmetric function of a quadratic’s roots

1.3.2. The following functions are asymmetric function of a quadratic’s roots

1.4. Newton Sum (Newton's Identities)4

1.5. The French Mathematician, V i e t a 5

2. Evidence

2.1. Algebraic Formula Methods. Using Chat G P T 6

2.1.1. If the roots of the equation x2 - 3x + 2 = 0 are α and β, find α 2 + β 2

2.1.2. Algebra Formula, Using Chat GPT for Calculate

2.1.3. Algebra Formula, Using Chat GPT for Calculate

2.1.4. Algebra Formula, Using Chat GPT for Calculate

2.2. Newton sum Methods. Using Chat GPT for Calculate

2.2.1. If the roots of the equation x^2 - 3x + 2 = 0 are α and β, find the value of α^2 + β^2 using Newton sum . Sk = α^k + β^k = -a_(k-1) * S_(k-1) - a_(k-2) * S_(k-2)

2.2.2. Newton Sum, Using Chat GPT for Calculate

2.2.3. Newton Sum, Using Chat GPT for Calculate

2.2.4. Newton Sum, Using Chat GPT for Calculate

2.2.5. Newton Sum, Using Chat GPT for Calculate

2.2.6. Newton Sum, Using Chat GPT for Calculate

2.2.7. Newton Sum, Using Chat GPT for Calculate

2.2.8. Newton Sum, Using Chat GPT for Calculate

2.2.9. Newton Sum, Using Chat GPT for Calculate

2.2.10. Newton Sum, Using Chat GPT for Calculate

2.2.11. Newton Sum, Using Chat GPT for Calculate

2.2.12. Newton Sum, Using Chat GPT for Calculate

2.2.13. Newton Sum, Using Chat GPT for Calculate

2.2.14. Newton Sum, Using Chat GPT for Calculate

2.2.15. Newton Sum, Using Chat GPT for Calculate

3. Results

4. Conclusion

Pushing Boundaries: Pioneering Novel Maths Approaches for Overcoming Limitations in AI

5. Discussion

6. Implications and Future Research

References

MDPI Initiatives

Important Links

Subscribe

1.1. ChatGPT¹

1.2. Knowledge Is Power: Why the Future Is not just about the tech³

1.4. Newton Sum (Newton's Identities)⁴

1.5. The French Mathematician, ${V i e t a}^{5}$

2.1. Algebraic Formula Methods. Using Chat ${G P T}^{6}$

2.1.1. If the roots of the equation x² - 3x + 2 $=$ 0 are α and β, find $α^{2} + β^{2}$