Prerpints.org logo
Preprint
Article

Water Entry: A Classical Naval Hydrodynamics Problem Enhanced with the Heat and Mass Transfer, and Applied in an Immersion Quenching Simulation

Altmetrics

Downloads

106

Views

44

Comments

0

Submitted:

20 October 2023

Posted:

23 October 2023

You are already at the latest version

Alerts
Abstract
The computational model that is able to estimate the temperature distribution inside a solid specimen during the film boiling phase of immersion quenching (water entry) process has been presented in paper, and it is based on the prescribed initial temperatures of the solid specimen and the liquid quenchant. In addition, the turbulence effects have to be considered using the assumed turbulence kinetic energy value, i.e., the “frozen turbulence” approach, that remains constant thorough the simulation. The studied material is nickel alloy, Inconel 600, for which the extensive experimental data is available. The work has been carried out using ANSYS Fluent computational fluid dynamics software and the methods for solution of Stefan problem by Eulerian two fluid VOF model.. A satisfactory agreement between the experimental and the calculated data has been achieved, yielding thereby the computationally obtained data that fits to a great extent to the prescribed error band of ± 10 % during the estimated film boiling phase of the immersion quenching process itself.
Keywords: 
Subject: Engineering  -   Marine Engineering

1. Introduction

TIn naval hydrodynamics, the water entry is an interesting phenomenon from the viewpoint of investigation of hydrodynamic loads on floating bodies when they are being immersed into liquid medium. These studies usually focus on wedges-like objects, spheres and horizontal cylinders. The analytical solutions from Wagner and Von Kármán exist to this end; both being presented in the PhD thesis by Toso [1]. In numerical simulation of such a phenomena, two distinct approaches may be found with respect of the way the body is immersed: a free fall, and a constant velocity drop-down; both approaches being applied in Kleefsman et al. [2], whilst the latter has been, although in a fully Lagrangian manner, solved in Bašić et al. [3]. Within the studies focused on free fall, further two modeling approaches are used in regard of computation of drop-down velocity, i. e., from accounting the forces that act on a falling body: the 6- degrees of freedom (DOF) and the computation of velocity upon a previous time step. More recently, the former approach has been adopted within the parametric study of a 3D sphere impacting the free surface of water in Yu et al. [4], being noted in the recent theoretical exposure in Lu et al. [5].
Apart from the aforementioned isothermal water entry studies, we shall outline the studies with immersion of heated solids into liquid mediums. To this end, in a study by Li et al. [6], the stability of vapor-liquid interface was studied for different degrees of subcooling and/or wall superheats. Still being in the context of naval hydrodynamics is the application of so-called air lubrication systems (ALS), but using water vapor as a medium instead of air bubbles. In that sense is the study by Jetly et al. [7], wherein the influence of vapor film formation around a sphere on flow hydrodynamics was examined during water entry of heated sphere in a liquid FC-72 medium using experimental investigation. The influence of Leidenfrost effect within the framework of water entry, i.e., the formation of vapor blanked around a spherical body on flow enhancement during immersion of a heated sphere in liquid, has been discussed from the theoretical point of view in Gylys et al. [8]. The authors evaluated the energy consumption required in realization of such cases.
However, a study that encompass the water entry and immersion of a heated cylindrical body, investigating thereby also the temperature evolution inside the material (conjugate heat transfer, CHT) together with incorporating the phase change phenomena that occurs in the liquid phase, using numerical simulation technique and, at least when a mass transfer process is considered, basic principles approach, has not been found in the open literature.
On the other hand, the temperature field investigations within solid bodies usually involve the inverse heat transfer analysis (IHTA) models that require previously obtained experimental data in order to make estimates of the heat transfer characteristics during the immersion quenching process. In this regard, the IHTA of the Inconel 600 probe is presented in the PhD thesis by Felde [9]. Since only one temperature is measured, that is, at the center of the probe, only the heat transfer coefficient in the immediate vicinity of that axial point (at the radius of that axial point) may be obtained, hc(r, T), where index c denotes the central point of a specimen, r is the position vector, and T is the absolute temperature in degrees Kelvin. The obtained heat transfer coefficient values may either compose steep and/or linear distribution. The IHTA has also been used in a study by Demirel [10]. The author coupled it with finite element method (FEM) in order to predict the temperature evolution in a solid material; it is clearly shown by the author how the heat transfer coefficient estimated by the IHTA refers to a specific, local, zone of the material in question. An investigation on temperature-time distributions during quenching of a nickel Inconel 600 alloy has been reported in Landek et al. [11]. The authors, among other data, have also shown the temperature and the heat transfer coefficient calculations using an analytical expression and inverse heat transfer analysis, respectively. Only the temperature in a geometric center of a probe was evaluated experimentally using a K type thermocouple; whilst the surface temperature has been calculated on a basis of transient heat conduction analytical model. In addition, two distinct approaches were used in estimation of temperature, and thus the time; distributions of the heat transfer coefficient; the one proposed by the authors, and the one obtained by the ivfSmartQuench system commercial software. Speaking in terms of the aforementioned software, the ivfSmartQuench system, it is the standardized method for estimation of quenching power of liquids and is explained in more detail in Troell et al. [12]. Furthermore, the fundamentals of the IHTA together with the examples in a realistic quenching application using computational software are described in the paper.
Furthermore, in Landek [13], the influence of thermal effusivity, b   =   ρ s c s λ s , , a material ability to transfer the heat into the surrounding medium has been studied; however, in the framework of the spray quenching processes. It was observed in a PhD thesis by Tenzer [14], that the Leidenfrost temperature decreases with the increase in thermal effusivity, also within the context of spray quenching. A recent study by Jagga and Vanapalli [15] reveals how the standard boiling modes are only valid in the case of high thermal effusivity materials, whilst in the opposite situation the materials may exhibit different behavior. Its value in calculation of Leidenfrost temperature in the case of forced convection film boiling has been reported in [16]. As can be concluded from the above mentioned studies that dealt with the phenomena in solid, that is, the quenching studies, the heat transfer coefficient has been selected as an input parameter, determined using previously conducted experiment and an inverse heat transfer analysis. Thus, a temperature field inside the material is obtained and can be supplemented to further analysis (stress and strain analysis).
A main goal of the present research is to establish a conjunction between the two distinct approaches; that is, to encompass an immersion process (usually isothermal) with conjugate heat transfer study (mostly without moving boundaries), incorporating thereby the phase change and turbulence phenomena that occur in the liquid phase. With this conjunction a novel numerical approach is proposed that alleviates the experimental input of cooling curve recorded in a solid specimen and provides sufficiently accurate results for temperatures and heat transfer coefficients on the specimen surface using only initial temperature of the solid and a quenchant medium.

2. Materials and Methods

2.1. Description of the quenching experiment

Specimen used in all cooling tests was a temperature probe made of Inconel 600 alloy according to the ISO 9950:1995 norm. The diameter of the probe is 12.5 mm, and the length is 60 mm. A type K thermocouple is installed in the center of the probe. The temperature is monitored in the central point of the specimen, i.e., 30 mm above the bottom surface. Before the experiment, the probe is cooled and heated in an electric furnace at 855 °C for 10 min. Before the beginning of immersion, the probe is uniformly heated to the temperature of the furnace, and during transfer from the furnace to the receptacle above the container with water, the center of the probe may cool down to 850 °C. The specimen is initially placed 170 mm above the free surface of water, and is manually immersed into the quenchant medium; a 0.13 m/s constant velocity translatory motion of the specimen may be assumed in the model according to estimation in [17]. In doing so a steel rod is connected to the specimen's top horizontal surface. This steel rod has been neglected in the present numerical study for the sake of simplicity.; The temperature acquisition starts when temperature at the measuring location reaches approximately 850 °C. The immersion stops when the bottom surface of the specimen is 260 mm below the free surface of the water. The thermoelement is expected to register the radial temperature change before the axial one, due to small radial thickness in comparison to the axial one, i.e., the distance from the thermocouple to the cylinder bottom surface.
The snapshots of the solid specimen immersion quenching is shown in Figure 1. The studied specimen is heated to a predefined high temperature 855 °C in a small laboratory furnace, and then dipped down to a quiescent liquid that has been previously heated until the temperature of ca. 52 ℃ is reached. Please note the vapor bubble formation beneath the horizontal bottom surface, and at the cylindrical surface of the specimen.
From immersion snapshots one can identify the advancement of the temperature in a bottom-up fashion in the axial direction, and from the outer side to the inner part of the body in the radial direction. Thus behavior featuring the existence of significant temperature gradients with respect to space in the solid object, i.e., the cooling case with a large Biot number (Bi → +∞).

2.2. Mathematical modeling of an immersion process

2.2.1. The Eulerian two-fluid VOF model

In the Eulerian two-fluid VOF model applied here, the mass, momentum, and energy conservation equations are defined on a per-phase basis, that is, for each phase involved in computation, a separate set of governing equations is being solved. The communication between the sets of the governing equations is established via the source terms that describe the interphase transfer between the phases. The description on the mathematical model underlying the selected approach is available in [18], while the generalities and application of the mesh motion has been tackled in [19]. Turbulent flow characteristics, associated with the flow studied herein, is extensively described in the recent paper by Cukrov et al. [20]. In order to establish a linear translatory motion of a solid specimen, an arbitrary Lagrangian-Eulerian (ALE) scheme is used for conduction of the motion of the computational mesh in conjunction with the constant velocity in the downward direction and the remeshing technique. Therefore, the transport equation for a general scalar, ɸ, would read:
d d t ∫ V       ρ ϕ d V + ∫ ∂ V       ρ ϕ u → − u → g ⋅ d A → = ∫ ∂ V       Γ ∇ ϕ ⋅ d A → + ∫ V       S ϕ d V
where the first term on the l.h.s. in Eq. (1) represents the rate of change of the dependent scalar variable ɸ in a cell volume that is changing its dimensions; the second term is the advection flux of a general scalar across the cell volume's face, and is the term that accounts for the motion of the solid boundary, u → g , together with the motion of the fluid with the velocity u → ; whilst on the r.h.s. of the equation are the diffusion flux across the cell face, and the source term, respectively. Hence, the governing equation for all the dependent variables in the case of mesh motion involves the velocity of the moving zone. The volumetric rate of change, i.e., the change in the cell volume with respect to time has to satisfy the so-called volume conservation law, also known as space conservation law that may be expressed as:
d V d t = ∑ i n f       u → g , i ⋅ A i →
where n f is the number of cell faces that compose the surface of a computational cell; u → g , i is the velocity component in the normal direction to the i-th face of the cell; whilst A → i is the area of the i-th face of the computational cell subjected to the mesh motion. The historical evolution of the approach together with its mathematical foundations has been addressed in dipping study by Aubram [21].

2.2.2. Geometry domains

The test case is designed as shown in Figure 2. Two distinct fluid zones, namely vapor and a liquid zone, are present in the domain, together with one cell zone occupied by a solid. The computational domain is designed as an axis-symmetric and of dimensions 100 mm in radius and 960 mm in height, divided into two continua: fluid and a solid continuum; the fluid part thereby contains vapor and water medium, whilst the solid material is made of Inconel 600 alloy and its material properties are discussed in the forthcoming section. The material properties of the liquid and a vapor phase are defined based on the interface temperature as in [18]; hence, a thermal equilibrium is assumed at the interface, that is, the interface is kept at the saturation temperature due to macroscopic scale of the studied film boiling phenomena. Furthermore, one may also need to distinguish between two types of interfaces that are present during the water entry of a heated cylinder: the free surface and the interface. The free surface of water relates to a large-scale interface between two bulk mediums; whilst the interface is designated as the surface between the two phases in a phase change process, that is, between the vapor phase, generated in boiling process, and a bulk liquid phase.
The solid continuum is of dimensions 6.25 mm radius and 60 mm height, and occupies a zone on a symmetry axis as shown in Figure 2. These physical properties, namely: density, ρ s , thermal conductivity, λ s , and specific heat capacity, c s , assigned to the solid part are those of Inconel 600, nickel alloy used in the experiment from Landek et al. [11], and were taken from the properties listed in a Hännoschöck [22]; however, due to strong temperature dependence of thermal conductivity and the specific heat capacity, these values were approximated using piecewise-linear segments according to data listed in [22]. Thus, four different points: 200 ℃, 400 ℃, 600 ℃, and 800 ℃, were taken in approximation of specific heat capacities; whilst five points were used in extraction of thermal conductivity data: 200 ℃, 400 ℃, 600 ℃, 800 ℃, and 900 ℃. The values of thermal properties between these temperatures are determined by linear interpolation.
The initial distributions of volume fraction (both liquid and vapor), TKE (liquid only) and temperature are imposed in the computational domain together with the zero-velocity field in a manner similar as before, using the Define-init user defined function. Figure 2 depicts the initial vapor and liquid fields, i.e., the respective volume fraction distributions, while dashed lines outline the two interface zones; first one being as in the former case, used in order to induce the mass transfer and specify the laminar zone in an initial vapor layer, the so-called “Interface zone 1”; whilst the second one is used for turbulence modeling purposes, i. e., the TKE value, that may calculated by the procedure similar to those in validation part, is imposed only in these cells, the so-called “Interface zone 2”. In order to prevent the occurrence of the mass transfer between two bulk phases, vapor and a liquid, the complete domain, with the exception of a single cell layer adjacent to the specimen wall, is set to 60 ℃. Otherwise, due to the existence of temperature and volume fraction gradients at the interface, a mass transfer would take place.

2.3. Generating a finite volume mesh

As was noted before, the solid body is immersed using 130 mm/s velocity in the downward direction; thus, invoking the necessity to treat the problem as the moving boundary problem, since the specimen boundary changes its position with respect to certain part of the performed numerical simulation. This is accomplished via the “interface zone 2”, shown in Figure 2, which moves at a constant speed downward, embracing thereby all the subset zones: “interface zone 1”, and the solid zone. The motion is established for initial ~2 s, that is determined by the known distance that is to be passed by the bottom horizontal surface of the specimen.
The hybrid mesh composed of both the triangular and quadrilateral cells is used in the present numerical simulation, as depicted in Figure 3.
The computational mesh is composed of 254 cells that consist of the solid part, contributing to, in total, 10354 initial cells that compose the whole computational mesh, generated using GMSH open source mesh generator [23], that was also applied in structural ship analysis in Grubišić et al. [24]. This mesh size is not constant during the computation; yet it is increased due to remeshing procedure. The mesh is designed as a hybrid mesh, since it is composed of both the isotropic triangular and quadrilateral finite volumes. The mesh is by purpose designed to have a jump in cell height in transition from quadrilateral to triangular cells in order to impose the stringent conditions that are to appear in the industrial practice. This has been found in the one in the PhD thesis by Yoshikawa [25], wherein it is applied in the wind tunnel study. This, however, would mean that the continuum surface stress (CSS) model should be applied to model the surface tension, due to its robustness in handling coarse meshes as noted in the review by Kharangate and Mudawar [26]. However, within this research, the continuum surface model (CSF) by Brackbill et al. [27], as in the previous study on stable film boiling in [20]. The usage of triangular cells is now mandatory due to remeshing technique that is used for immersion of a solid object into liquid medium.

2.4. Turbulence modeling

In the former subsection it has been outlined that the turbulence kinetic energy (TKE) is specified in the region outside the near wall adjacent zone consisted of one-cell layer, that may be denoted as „interface region 1”, but being thereby limited in the outer region with the boundary of „interface region 2” according to Figure 4.
The turbulence kinetic energy levels in the case of pool film boiling may be found to be similar to ones in the case of wave flow, according to results obtained in the preceding chapter; a detailed Smoothed Particle Hydrodynamics (SPH) case of the wave flow is given in Makris et al. [28]; whilst the former (TKE values in pool film boiling studied herein) has been obtained merely using a parametric study, that was lately justified with a computational model, the latter (field TKE distributions) were confirmed with a detailed numerical simulations.

2.5. Solution procedure

Firstly, ten iterations with a very small-time step were used for initialization. A stabilized bi-conjugate gradient method was switched in order to establish a stable computation; this has been addressed in the documentation as a stability measure in the case of convergence problems. It is noteworthy that, after the initialization has been carried out, the interpolation method is changed from the default least squares cell based to Green-Gauss node based, according to recommendation in the official documentation regarding the computations that involve triangular and/or tetrahedral meshes. The dipping of a solid specimen has been solved predominantly using 1e-4 s. The temperature is limited to a lower-level value of 333.15 K, thus mimicking the Newton-Raphson numerical nonlinear equation system solution method, wherein a solution interval needs to be assumed [29]. This is due to some unphysical temperatures below the minimum temperature that were observed in the simulation.

3. Results and discussion

The temperatures were sampled in a vicinity of a specimen's center, a volume-weighted average value in two cells in the immediate neighborhood of the specimen center was used due to mesh motion, i.e., the axial coordinate of a specimen's cell center is being changed thorough the simulation, in particular during the immersion process, say, the initial ~ 2 s. The obtained temperature distribution exhibits the slope shown in Figure 5, and a fairly good agreement with the experimental data, with approximate ± 10 % error.
Furthermore, it is obvious that this error band covers the majority of the data before an inflection point of the experimental curve is reached; this can be deduced from the prescribed 10 % error band and the auxiliary plot of the experimental data in Figure 6. It should be noted that the experimental data has been tracked after the temperature in the specimen's center has reached 849.9 ℃ [17].
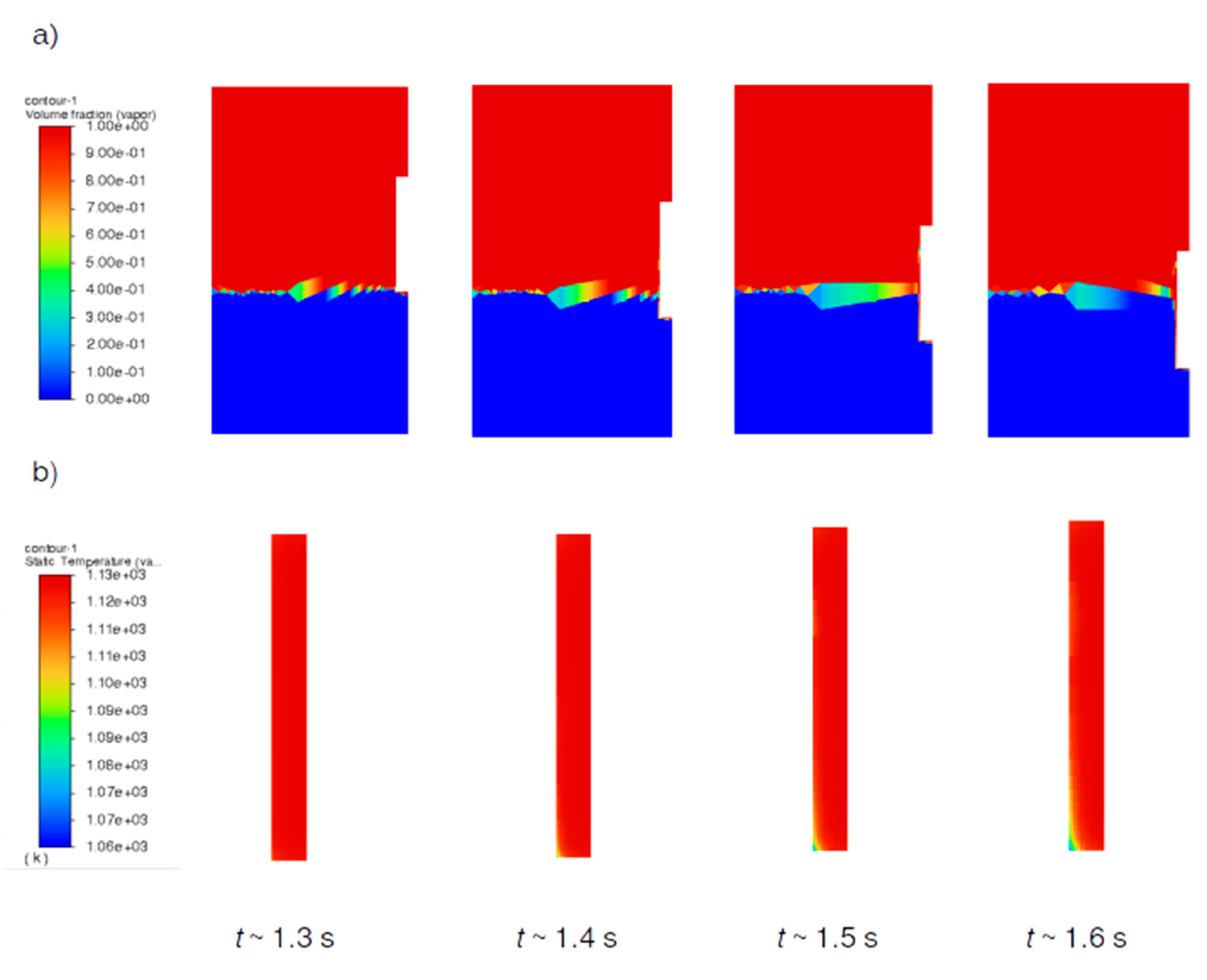
It is noteworthy that the experimentally based plot in Figure 6 is calculated from the inverse heat transfer analysis; hence it is supposed that it has its own computational errors that should be taken into consideration. The Figure 7 represents the temporal distribution of the vapor phase (Figure 7a) and the temperature field in a solid specimen, Figure 7b. The explosion of the vapor phase is noticeable from the change in vapor volume fraction at the liquid free surface, Figure 7a, whilst the temperature distribution shows the evolution of the cooling from the bottom surface up to the radial and longitudinal directions as shown in Figure 7b.
This confirms that using the Eulerian two-fluid method is able to accurately predict the temperature distribution in a solid material during film boiling mode of immersion quenching process.

4. Conclusions and future work perspectives

The numerical simulation setup required for calculation of temperature field in a solid specimen during the film boiling phase of immersion quenching process has been presented in this paper. The context of this immersion process may be inherited from naval hydrodynamics application within the framework of water entry problems, in the sense that a cylinder water entry has been studied first. Additionally, this case, among others, also involves heat and mass transfer in contrast to the classical water entry problem, in conjunction with CHT.
Furthermore, the computational results of the numerical simulation of immersion quenching process have been carried out. The expected outcomes, i. e., the temperature distribution with respect to time in the specimen center and on its surface were obtained and compared to experimental (central temperatures) and experiment related, calculated, values (surface temperatures). A satisfactory agreement has been achieved, yielding thereby the data that fits to a great extent to the prescribed error band of ± 10 %.
It was also shown that the method provides the detailed inspection in the flow fields as well as in the solid temperature distribution, that confirms that using the Eulerian two-fluid model one may obtain the accurate field distribution of the temperature evolution in a solid material, based on known initial temperatures of the solid specimen and quenchant medium.
In addition, the further refinement of the applied TKE value would provide a more accurate result, but, since we want, to a great extent, the model that is based on the basic principles and the derivatives thereof, fine tuning was found as an inappropriate approach in the context of the present study. Further theoretical treatises are needed in order to obtain a more comprehensive approach in further modeling of TKE. For example, a study by Takamatsu et al. [31] deals with stability analysis of the vapor film thickness in the case of subcooled film boiling around a horizontal wire.
In conclusion, using this approach is available to tackle the skin resistance reduction via the vapor phase, that in contrast to standard air phase used in air lubrication systems (ALS) used in naval hydrodynamics, posses the better thermophysical properties in a sense of heat rejection (for example, the specific heat capacity of air can be taken as the value at 0 oC 1.005 kJ/kg/K, while in the case of superheated vapor it has the value 1.93 kJ/kg/K). Thus, the boiling flow, which has been limited to the high resolution meshes, if tackled using DNS of interface motion, or empiricism, when modeled using the Eulerian two-fluid models, can now be modeled at a moderate computational cost using the approach proposed within this work.
Moreover, as a subset of this approach, the general (isothermal) naval hydrodynamics problems may be tackled with the anisotropic drag model applied in the momentum equations in the present approach. Thus, a detailed computational meshes, as in the study in [32], may be tackled with moderate computational cost, that is, with lower resolution meshes as is proven in a standard interface tracking case in [33]. The authors have shown the application of two-fluid model in the bubble rise case, and have proven that by the appropriate momentum transfer modeling the standard VOF case can be successfully resolved on a coarser grid. Furthermore, since the approach shown in the present paper uses asymptotic behavior of the two-fluid model, that is, the limiting case when the two-fluid model behaves as the one-fluid model (the equality of velocities at the interface shown in [18], there may be no need for the involvement of empiricism in the model.
Finally, we can conclude that by application of this approach we are step forward to application of naval hydrodynamics CFD practices in everyday use in the industry due to moderate computational cost associated with it.

Author Contributions

Conceptualization, A.C. and D.L.; methodology, A.C.; software, I.B.; validation, A.C.; formal analysis, A.C.; investigation, A.C.; resources, I.B.; data curation, D.L.; writing—original draft preparation, A.C.; writing—review and editing, Y.S., D.L.; visualization, A.C.; supervision, I.B.; project administration, B.N.; funding acquisition, I.B., B.N.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data are available upon request from the corresponding author.

Acknowledgments

The inputs from Dr. Kai Zhang, Zhangjiang Laboratory, Shanghai, PR China, have been acknowledged. Furthermore, the help received by Ms. Izabela Martinez in conducting the experiment and reproducing the data has been also gratefully acknowledged.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Toso, N.R.S. Contribution to the Modelling and Simulation of Aircraft Structures Impacting on Water. Beitrag zur Modellierung und Simulation von Luftfahrtstrukturen beim Wasseraufprall 2009. [CrossRef]
  2. Kleefsman, K.M.T.; Fekken, G.; Veldman, A.E.P.; Iwanowski, B.; Buchner, B. A Volume-of-Fluid Based Simulation Method for Wave Impact Problems. Journal of Computational Physics 2005, 206, 363–393. [CrossRef]
  3. Bašić, J.; Degiuli, N.; Werner, A. Simulation of Water Entry and Exit of a Circular Cylinder Using the ISPH Method. Transactions of FAMENA 2014, 38, 45–62.
  4. Yu, P.; Shen, C.; Zhen, C.; Tang, H.; Wang, T. Parametric Study on the Free-Fall Water Entry of a Sphere by Using the RANS Method. Journal of Marine Science and Engineering 2019, 7. [CrossRef]
  5. Lu, Y.; Del Buono, A.; Xiao, T.; Iafrati, A.; Xu, J.; Deng, S.; Chen, J. Parametric Study on the Water Impacting of a Free-Falling Symmetric Wedge Based on the Extended von Karman’s Momentum Theory. Ocean Engineering 2023, 271, 113773. [CrossRef]
  6. Li, J.-C.; Wei, Y.-J.; Wang, C.; Xia, W.-X. Cavity Formation during Water Entry of Heated Spheres. Chinese Phys. B 2018, 27, 094703. [CrossRef]
  7. Jetly, A.; Vakarelski, I.U.; Yang, Z.; Thoroddsen, S.T. Giant Drag Reduction on Leidenfrost Spheres Evaluated from Extended Free-Fall Trajectories. Experimental Thermal and Fluid Science 2019, 102, 181–188. [CrossRef]
  8. Gylys, J.; Skvorčinskienė, R.; Paukštaitis, L. Peculiarities of the Leidenfrost Effect Application for Drag Force Reduction. Mechanics 2014, 20, 266–273. [CrossRef]
  9. Felde, I. Új Módszer Acélok Edzéséhez Használatos Hűtőközegek Hűtőképességének Minősítésére. PhD értekezés, Miskolci Egyetem. Műszaki Anyagtudományi Kar. Kerpely Antal Anyagtudományok és technológiák Doktori Iskola, 2007.
  10. Demirel, C. Experimentelle Untersuchung und Simulation des Abschreckprozesses von bauteilähnlichen Geometrien aus G-AlSi7Mg. 2009.
  11. Landek, D.; Župan, J.; Filetin, T. A Prediction of Quenching Parameters Using Inverse Analysis. Matls. Perf. Charact. 2014, 3, 229–241. [CrossRef]
  12. Troell, E.; Kristoffersen, H.; Bodin, J.; Segerberg, S.; Felde, I. Unique Software Bridges the Gap between Cooling Curves and the Result of Hardening∗. 2007, 62, 110–115. [CrossRef]
  13. Landek, D. Models and Algorithms for Computer-Aided Planning of Induction Hardening Process. PhD Thesis, 2005.
  14. Tenzer, F.M. Heat Transfer during Transient Spray Cooling: An Experimental and Analytical Study. Ph.D. Thesis, Technische Universität: Darmstadt, 2020.
  15. Jagga, S.; Vanapalli, S. Cool-down Time of a Polypropylene Vial Quenched in Liquid Nitrogen. International Communications in Heat and Mass Transfer 2020, 118, 104821. [CrossRef]
  16. Afify, M.; Gentile, D.; Llory, M. Courbes d’ébullition en convection forcée. Deuxième partie : Effets paramétriques et corrélations. La Houille Blanche 1986, 72, 463–474. [CrossRef]
  17. Župan, J.; Landek, D.; Filetin, T. Cooling Characteristics of Water Based Nanofluids with Agitation. Materials Performance and Characterization 2014, 3, 326–336.
  18. Cukrov, A.; Sato, Y.; Boras, I.; Ničeno, B. A Solution to Stefan Problem Using Eulerian Two-Fluid VOF Model. Brodogradnja : Teorija i praksa brodogradnje i pomorske tehnike 2021, 72, 141–164. [CrossRef]
  19. Zhu, H.J.; Lin, Y.H.; Xie, L.H. FLUENT Fluid Analysis and Simulation Practical Tutorial. People’s Posts and Telecommunications Press 2010, 112–122.
  20. Cukrov, A.; Sato, Y.; Boras, I.; Ničeno, B. Film Boiling around a Finite Size Cylindrical Specimen—A Transient Conjugate Heat Transfer Approach. Applied Sciences 2023, 13. [CrossRef]
  21. Aubram, D. An Arbitrary Lagrangian-Eulerian Method for Penetration into Sand at Finite Deformation; 2014; ISBN 978-3-8440-2507-1.
  22. Hannoschöck, N. Wärmeleitung und -transport: Grundlagen der Wärme- und Stoffübertragung; Springer Berlin Heidelberg: Berlin, Heidelberg, 2018; ISBN 978-3-662-57571-0.
  23. Geuzaine, C.; Remacle, J.-F. Gmsh: A 3-D Finite Element Mesh Generator with Built-in Pre- and Post-Processing Facilities. International Journal for Numerical Methods in Engineering 2009, 79, 1309–1331. [CrossRef]
  24. Grubišić, L.; Lacmanović, D.; Tambača, J. Preconditioning the Quad Dominant Mesh Generator for Ship Structural Analysis. Algorithms 2022, 15. [CrossRef]
  25. Yoshikawa, M. A Study on Wind Load Estimation of High-Rise Buildings by Unstructured Grid LES, 2016.
  26. Kharangate, C.R.; Mudawar, I. Review of Computational Studies on Boiling and Condensation. International Journal of Heat and Mass Transfer 2017, 108, 1164–1196. [CrossRef]
  27. Brackbill, J.U.; Kothe, D.B.; Zemach, C. A Continuum Method for Modeling Surface Tension. Journal of Computational Physics 1992, 100, 335–354. [CrossRef]
  28. Makris, C.V.; Memos, C.D.; Krestenitis, Y.N. Numerical Modeling of Surf Zone Dynamics under Weakly Plunging Breakers with SPH Method. Ocean Modelling 2016, 98, 12–35. [CrossRef]
  29. Čančarević, M. Približno rješavanje nelinearnih sustava ( Newton - Raphsonova metoda ). Poučak : časopis za metodiku i nastavu matematike 2010, 11, 64–72.
  30. Rohatgi, A. Webplotdigitizer: Version 4.5 2021.
  31. Takamatsu, H.; Yamashiro, H.; Honda, H. Theoretical Analysis of the Stability of Vapor Film in Subcooled Film Boiling on a Horizontal Wire. Heat Transfer - Japanese Research 1997, 26, 219–235. [CrossRef]
  32. Degiuli, N.; Farkas, A.; Martić, I.; Zeman, I.; Ruggiero, V.; Vasiljević, V. Numerical and Experimental Assessment of the Total Resistance of a Yacht. Brodogradnja: Teorija i praksa brodogradnje i pomorske tehnike 2021, 72, 61–80.
  33. Gauss, F.; Lucas, D.; Krepper, E. Grid Studies for the Simulation of Resolved Structures in an Eulerian Two-Fluid Framework. Nuclear Engineering and Design 2016, 305, 371–377. [CrossRef]
Preprints 88340 g001
Figure 1. The water entry of a Inconel 600 nickel alloy during the immersion of the specimen quenching in a quiescent liquid-water pool at the initial pool temperature of ca. 52 ℃: (a) immediately before the immersion; (b) after the top of the body has been immersed; (c) later on during the immersion quenching process.
Figure 1. The water entry of a Inconel 600 nickel alloy during the immersion of the specimen quenching in a quiescent liquid-water pool at the initial pool temperature of ca. 52 ℃: (a) immediately before the immersion; (b) after the top of the body has been immersed; (c) later on during the immersion quenching process.
Preprints 88340 g001
Preprints 88340 g002
Figure 2. An overview of the computational domain with the selected boundary conditions; a "Coupled" boundary condition that is prescribed boundary condition is omitted from the sketch for the sake of clarity. All the dimensions are expressed in mm.
Figure 2. An overview of the computational domain with the selected boundary conditions; a "Coupled" boundary condition that is prescribed boundary condition is omitted from the sketch for the sake of clarity. All the dimensions are expressed in mm.
Preprints 88340 g002
Preprints 88340 g003
Figure 3. A view on computational mesh: (a) the area in the vicinity of the specimen; (b) a broader view.
Figure 3. A view on computational mesh: (a) the area in the vicinity of the specimen; (b) a broader view.
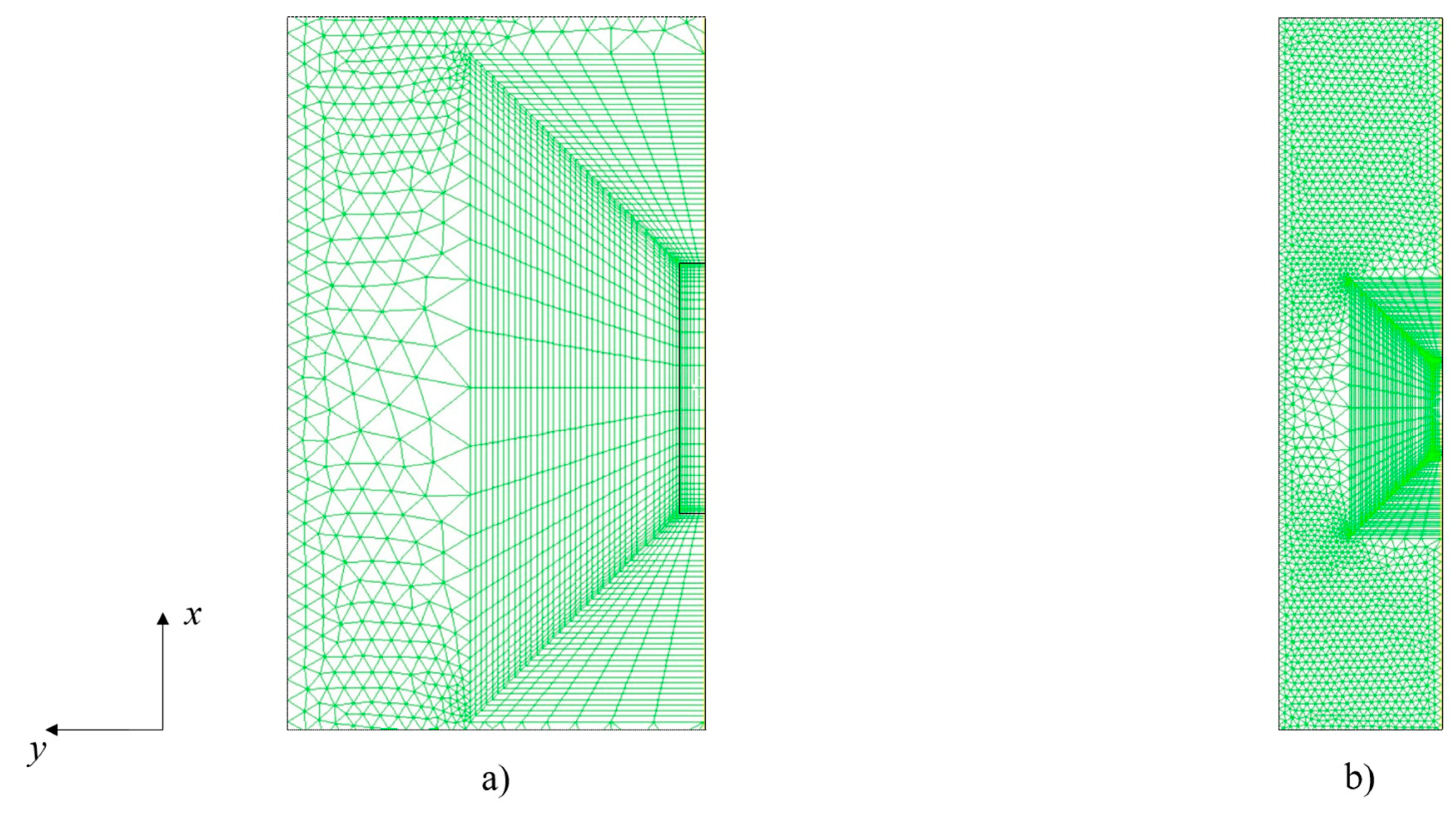
Preprints 88340 g003
Preprints 88340 g004
Figure 4. The initial TKE distribution in the analyzed case.
Figure 4. The initial TKE distribution in the analyzed case.
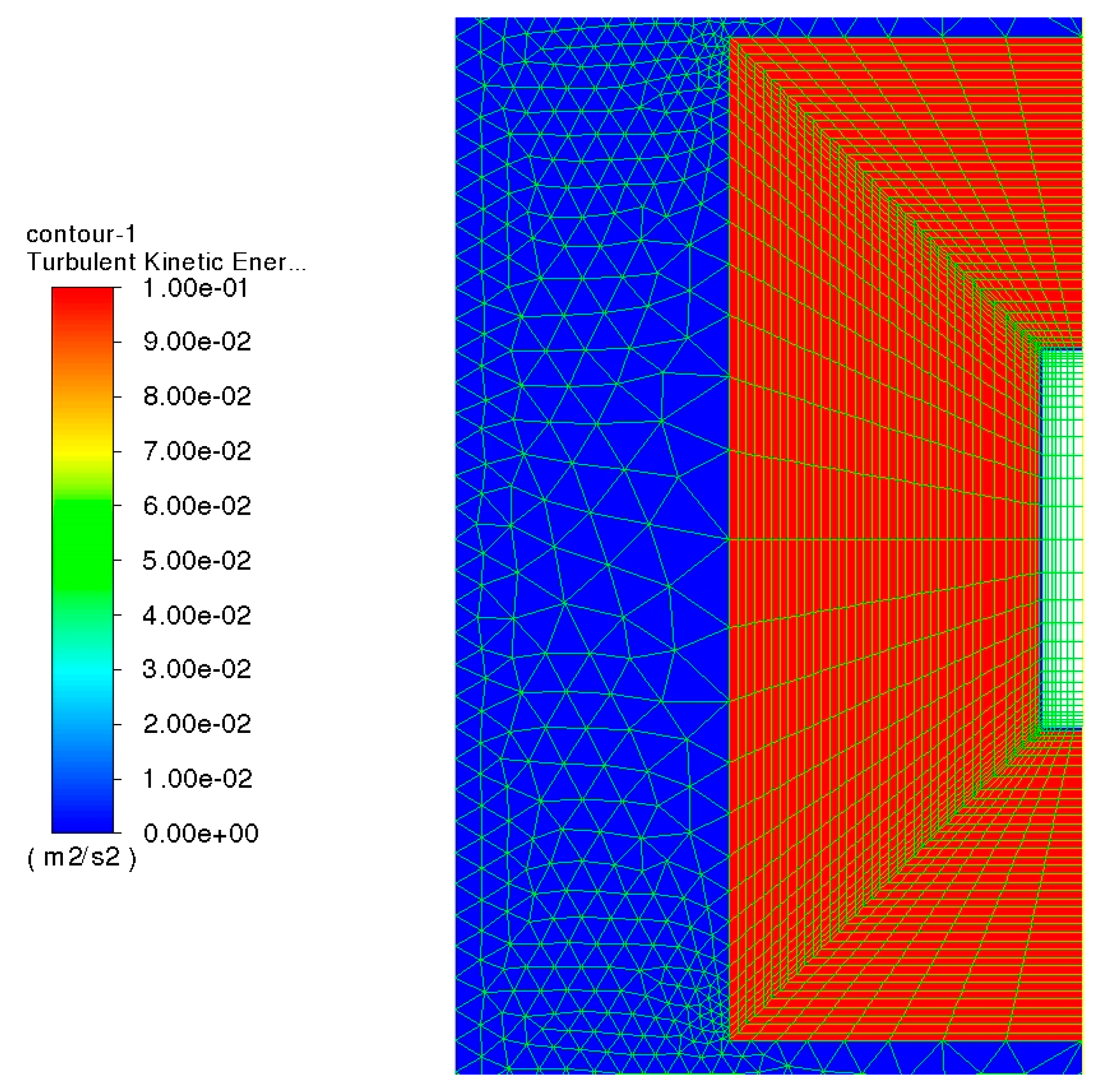
Preprints 88340 g004
Preprints 88340 g005
Figure 5. Comparison of the computational result in the vicinity of the specimen center with the data available from the experiment in Landek et al. [11]; extracted using [30].The dashed lines represent 10 % discrepancy from the experimental data. is a figure. Schemes follow the same formatting.
Figure 5. Comparison of the computational result in the vicinity of the specimen center with the data available from the experiment in Landek et al. [11]; extracted using [30].The dashed lines represent 10 % discrepancy from the experimental data. is a figure. Schemes follow the same formatting.
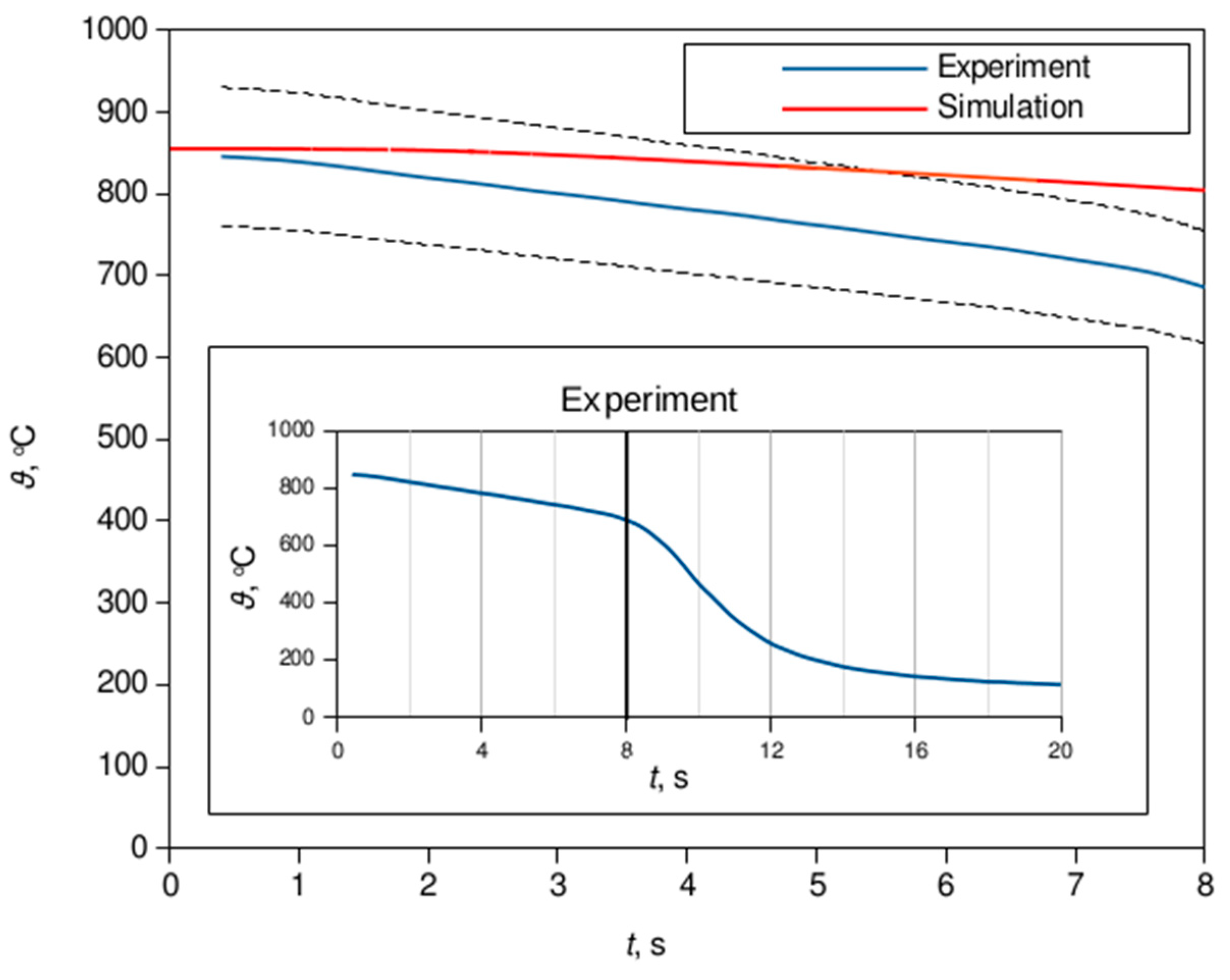
Preprints 88340 g005
Preprints 88340 g006
Figure 6. Comparison of the surface temperature obtained using the data from the experiment in Landek et al. [11] and the simulation data. The dashed lines denote 10 % discrepancy from the published data.
Figure 6. Comparison of the surface temperature obtained using the data from the experiment in Landek et al. [11] and the simulation data. The dashed lines denote 10 % discrepancy from the published data.
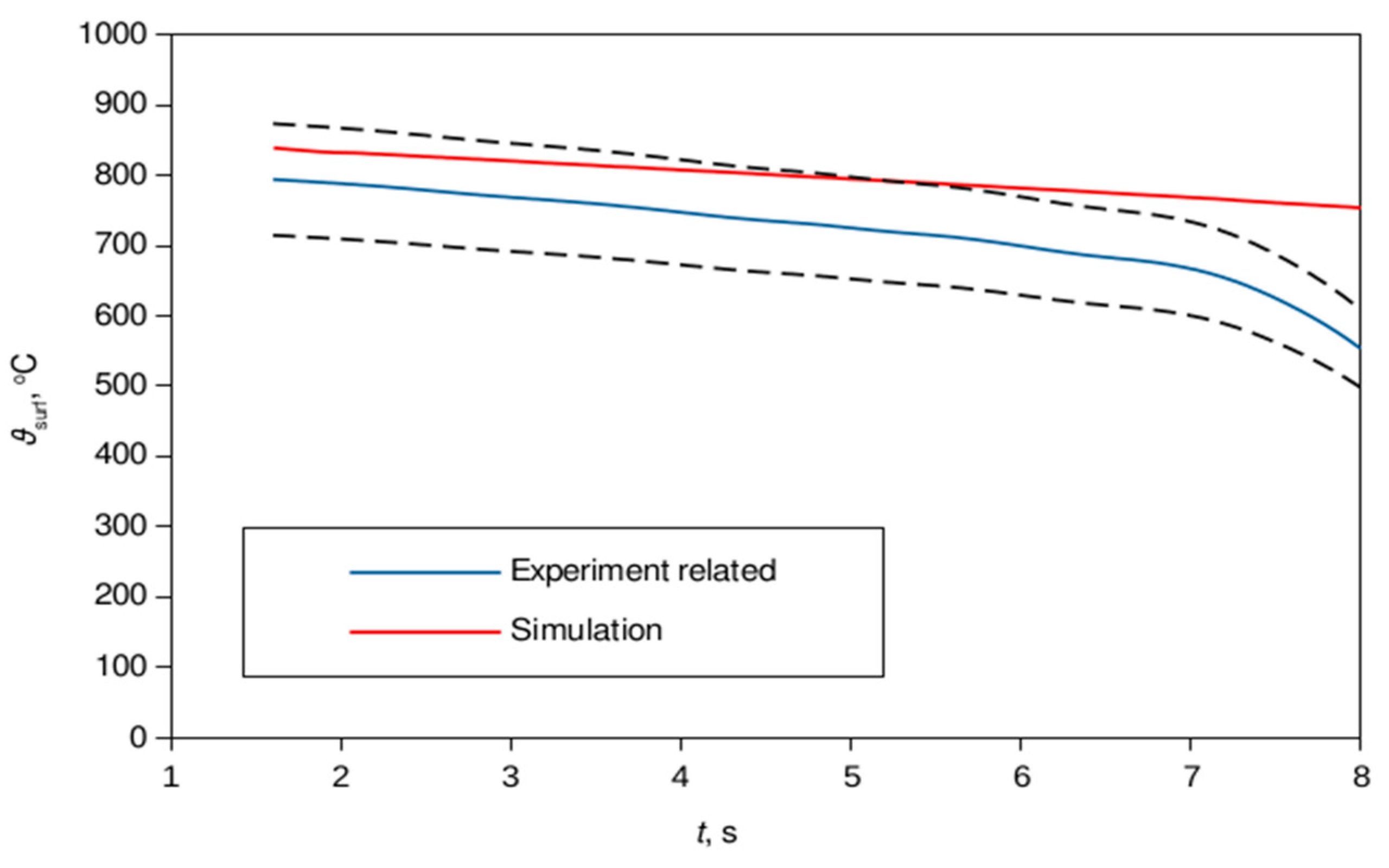
Preprints 88340 g006
Preprints 88340 g007
Figure 7. The volume fraction field evolution in time (a) together with the spatial temperature distribution in degrees Kelvin in solid (b), both being addressed during the water entry, i.e., the immersion process.
Figure 7. The volume fraction field evolution in time (a) together with the spatial temperature distribution in degrees Kelvin in solid (b), both being addressed during the water entry, i.e., the immersion process.
Preprints 88340 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated