Preprint
Article
Power Distribution Systems Vulnerability by Regions Caused by Electrical Discharges
This version is not peer-reviewed.
Submitted:
20 October 2023
Posted:
23 October 2023
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
Energy supply interruptions or blackouts caused by faults in power distribution feeders entail several damages to power utilities and consumer units: financial losses, damage to power distribution reliability, power quality deterioration, etc. Most studies in the specialized literature concerning faults in power distribution systems present methodologies for detecting, classifying, and locating faults after their occurrence. In contrast, this study aims to prevent faults by estimating the city regions whose power grid is most vulnerable to them. This work incorporates the geographic space study to prevent faults in the distribution power grid through a spatial data analysis using local variables that increase the fault risk in feeders in some city regions. Geographically weighted spatial analysis is applied to data aggregated by regions to produce thematic maps with the city regions whose feeders are more vulnerable to failures. Spatial data analysis is developed in QGIS and R programming environments. It is applied in real data of electrical discharges in a medium-sized city with approximately 200,000 inhabitants. In this study, we highlight a moderate positive correlation between electrical discharge density and the percentage of faults in transformers by regions in the central and western areas of the city under study.
Keywords:
Subject:
Engineering - Electrical and Electronic Engineering1. Introduction
Energy supply interruptions (ESI) or faults are events associated with the operational process of power distribution systems (PDS) [1]. They are classified into two categories: temporary and permanent. Transient faults occur in a very short time (in the order of milliseconds). After this, PDS is automatically restored. On the other hand, there is no electrical system restoration in the presence of a permanent fault. In this case, PDS returns to its nominal operating conditions after the fault location and removal [2].
ESI entails substantial financial losses for power utilities and consumer units (CU) that share the same distribution power grid. In this sense, electrical discharges represent a relevant cause of ESI; furthermore, they are associated with damage to electrical equipment [3]. With the energy market development, the energy supply with quality and reliability become a relevant factor for the power grid operators [4]. Thus, ESI depreciates the PDS indices of quality and reliability[5], where fault events represent 80% to 90% of the time without energy supply to CUs [6].
In this context, there are several factors associated with ESI: (i) adverse weather conditions, (ii) fires, (iii) tree vegetation close to the overhead power distribution, (iv) human failures, and (v) equipment failures (due manufacturing defect, lack of maintenance or obsolescence) [2,7].
The National Electrical System Operator (ONS) presented a statistical resume of the main factors responsible for faults in Brazilian power grids, as shown in Table 1. Adverse weather conditions such as electrical discharges, heavy rains, storms, and wind gusts are the main ESI causes, with approximately 30% participation [7].
Additionally, Table 1 shows the reasons associated with ESI, representing an average among Brazilian cities. In this sense, consider a town on the northeast coast of Brazil, where wind gusts are the main reason for faults in distribution feeders. On the other hand, they are not associated with ESI for another city in the central region with different weather conditions of coastal towns. Therefore, various factors cause ESI in other areas. Thus, incorporating spatial data analysis (SDA) helps understand which factors are relevant to a city region becoming more vulnerable to ESI.
To the best of the authors' knowledge, most studies in the specialized literature prioritize fault detection and location after their occurrence. For example, in [8], fault detection and classification were performed considering various fault scenarios involving generation and distribution units. On the other hand, estimating regions in which the power grid distribution is more vulnerable to failures provides crucial information for planning measures to avoid inconveniences and additional costs arising after steady-state faults occur.
Reducing the time of ESI is essential for improving the power quality in PDS [9]. In this context, estimating regions vulnerable to failures assists in decision-making and identifying critical areas that must be prioritized for replacing damaged equipment. Thus, the power supply with more excellent quality and reliability is ensured.
In this sense, this study aims to incorporate the analysis of geographic space for estimating city regions whose utility grid is more vulnerable to failures. It is assumed that some local factors or variables interfere with the utility grid, making it more vulnerable to failures. These local factors or variables are shown in Table 1: adverse weather conditions such as electrical discharges, tree vegetation, and fires.
In this context, geographic information systems (GIS) are essential to SDA to estimate regions vulnerable to faults. They are used in managing, planning, and controlling power grids. They comprise geoprocessing tools for collecting, storing, analyzing, and displaying geographic data. GIS application enables the power grid visualization, which is affected by local factors that belong to the region where it is located, as well as the other power utilities assets, such as substations, transformers, and protection equipment [10,11].
According to [12], the first step in SDA is to perform an exploratory analysis of spatial or georeferenced data. Exploratory analysis consists of the graphical representation of data available on thematic maps or heatmaps and incorporating descriptive statistics metrics considering the geographic space.
Thus, this study performs a geographically weighted exploratory analysis (GWEA) on geographic data from a Brazilian city. Crucial for this study are the georeferenced data and the weighting matrix. In the former, georeferenced data are those whose geographical coordinates of the phenomenon under investigation are known. In the latter, the weighting matrix represents the urban zone's neighborhood structure because it allows for characterizing the influence among small regions or census tracts (CTs).
Therefore, the first step of SDA with aggregated data in small regions or CTs is performed in this study: GWEA. It is performed based on a local factor or variable frequently associated with faults in PDS: electrical discharges. It is evaluated whether these local variables become the utility grid in some city regions more vulnerable to failures. Therefore, GWEA is applied to data aggregated by small areas to produce thematic maps with the city regions whose feeders are more susceptible to failures.
1.1. Literature Review
A fault incidence matrix method was introduced in [4] to evaluate the reliability of a medium voltage distribution grid. The authors presented a reliability calculation unit called M-Segment-N-tie-switch (MSNT), which included several distribution grid structures; thus, the method became applicable for different system operating conditions. Each MSNT was associated with a matrix of power supply path obtained by inversing the node branch incidence matrix. Subsequently, it was used to obtain the fault incidence matrix. The reliability indices for each system load were calculated, where the fault incidence matrix and the vectors of fault events characteristics were applied. The technique improved the reliability efficiency, as it avoided some procedures such as the fault events enumeration and the repetitive search of the fault influence range. Furthermore, the technique is intuitive and enables sensitivity analysis and system vulnerability identification.
In [13], a GIS-based tool for spatial analysis in PDS. The authors applied spatial analysis techniques such as inverse distance weighting, slope, and contour maps. The load flow results were the input data for the ArcGIS, where several maps were produced to analyze the dynamic behavior of the PDS. The results showed that any disturbances occurring in the PDS were detected and controlled in real-time through the GIS application.
Chen and Kezunovic [14] proposed a fuzzy logic-based tool for the predictive analysis of ESI. The authors highlighted the extreme climate impacts and their risk to the electrical system operation. Fuzzy logic was introduced to process weather information. Wind speeds and gusts were input parameters, whereas the fuzzy inference system provides an alert level as output. A risk map was produced from the vulnerability results and performed via GIS. Risk results were shown as power-cut probability maps. Weather forecasts and operational data belonging to the system improved the decision-making process.
In [5], a data mining-based tool was proposed to determine the fault probability. The technique was based on the Naive Bayes model, incorporating weather information, assets, and outage history. Feeder sections were classified according to their fault probability via GIS.
Zhou et al. [1] presented a methodology for assessing and managing fault risk in PDS with distributed generation. An island partitioning strategy was proposed to improve accuracy and speed in the evaluation process. The best managing strategy was calculated by applying an improved genetic algorithm.
Monte Carlo simulation (MCS) was introduced by Goerdin, Smit, and Mehairjan [15] for fault risk analysis in PDS. A decision-making framework based on fault risk was built from the MCS results to guide asset management processes. The study performed the faults prediction with a focus on medium voltage cables and failures in cable joints.
Muñoz and García [16] presented a GIS-based tool for analyzing the impacts of floods on the PDS. The technique applies flood risk analysis and calculation of reliability indices for PDS.
In [17], a strategy for analyzing the vulnerability of geographically correlated faults was proposed. The authors introduced a DC power flow and a cascade fault model. The detection of areas most vulnerable to faults was performed through the application of a network survival analysis and from data obtained via GIS.
A study of impacts on energy supply was presented in [18]. The authors introduced an analysis of extreme weather events that directly affect Indonesia's electrical system. In this sense, electrical discharges represent an essential cause of ESI in high-voltage transmission lines.
A method for forecasting vulnerability to faults in PDS was proposed in [19]. Piping and cables on the verge of failure were identified. The authors applied geospatial data, georeferenced faults clustering, and machine learning. The system components were classified according to the number of failures attributed to them. This way, a ranking list was created where equipment with a high probability of failure occupied the first places.
1.2. Contributions
This study presents a method for estimating vulnerable regions to faults. The highlights of the proposed approach are described below.
- (1)
- Incorporation of geographic space to the problem of estimating regions vulnerable to failures in PDS.
- (2)
- Accomplishing GWEA by regions from local variables associated with faults and electrical discharges.
1.2. Paper Structure
This study follows in Section 2 with the relationship between ESI and electrical discharges. Section 3 shows an overview of exploratory spatial data analysis (ESDA) (Section 3.1), spatial analysis with data aggregated by regions (Section 3.2), neighborhood structure with data aggregated by areas (Section 3.2.1), and GWEA (Section 3.2.2). Section 4 shows a case study of the implementation of GWEA in a Brazilian city. Section 4.1 and 4.2 present a case study description. In Section 4.3, an ESDA is performed, where the variables electrical discharge density (Section 4.3.1) and the number of faults in distribution transformers by regions (Section 4.3.2) are presented. Section 4.3.3 offers the geographically weighted (GW) statistical summary considering the neighborhood structure and weighting among areas. Finally, Section 5 shows the conclusions of this study.
2. Energy Supply Interruptions: Electrical Discharges
Overhead distribution grids are susceptible to ESI due to adverse weather conditions such as electrical discharges, rains, storms, and wind gusts. Numerous electrical discharge protection measures, such as lightning rod installations, have been implemented, improving the insulation level. However, ESI caused by electrical discharges is significant according to operational experience [20]. They contribute significantly to both temporary and permanent interruptions [21].
Electrical discharges occur directly and indirectly in transmission and distribution lines. Direct events, the most dangerous, happen when an electrical discharge directly strikes the line. They are usually studied for transmission lines. On the other hand, indirect events, whose frequency is higher, are classified as occurring in regions where the power grid is close to the ground. These events are critical for distribution systems since they are characterized by a low critical flashover voltage [22].
3. Spatial Data Analysis
SDA aims to measure properties and relationships considering the phenomenon of spatial location. In this way, the geographic space is incorporated into the study; thus, there is a visual perception via spatial distribution of the problem under analysis [24].
3.1. Exploratory Spatial Data Analysis
ESDA is a graphical presentation of georeferenced data on thematic maps or heatmaps. ESDA is a set of techniques to describe and explore spatial or georeferenced data [25]. In this context, a series of metrics derived from descriptive statistics are incorporated; thus, one can identify spatial patterns and formulate hypotheses related to data distribution in geographic space [24,26]. ESDA is the first step towards a study in SDA.
3.2. Spatial Analysis with Data Aggregated by Regions
This study is associated with SDA with data aggregated by regions. It consists of methods that allow the analysis of georeferenced data whose location is associated with areas delimited by polygons. It is applied to address events aggregated by municipalities, neighborhoods, or CTs, where the exact location of events is unavailable; however, an aggregated value by area is available. The data aggregated visualization by regions is usually performed through thematic maps with the phenomenon spatial pattern under study [12,27].
With data aggregated by areas, SDA allows the use of public information by the Brazilian Institute of Geography and Statistics (IBGE). IBGE does not disclose the private data of the individuals interviewed for confidentiality reasons. These data are grouped into small areas or polygons called CTs, whose area is a function of population density: CTs with higher population density have a smaller area, and vice versa.
3.2.1. Weighting Matrix
Studies in the specialized literature that apply SDA techniques commonly belong to epidemiology, botany, criminology, and mineral resources prospecting. In these fields of study, there is a typical neighborhood structure based on spatial proximity or Euclidean distance among the centroids of areas; closer areas have more significant influence than more distant areas [28]. This neighborhood structure based on spatial proximity among areas is applied in our study, too. Numerous other neighborhood structures are based on spatial proximity among areas evaluated in [29].
In this context, a spatial weighting matrix (SWM) is formed by weights , where the degree of spatial relationship or spatial dependence between the variables observed in the areas and is estimated. SWM is an essential tool for GW modeling. Three key elements must be considered for SWM building: distance type, kernel function, and bandwidth [30,31].
The SWM is a symmetric matrix built for a set of areas , where from each element the spatial relationship or spatial dependence between the variables observed in and areas are estimated.
Figure 2 shows an illustrative example to obtaining weighting matrix. In Figure 2a, there is a city with five CTs (, , , and ); on the other hand, in Figure 2b, there is a weighting matrix for a city with CTs and whose obtaining rule is according to (1). The CT has borders in common with two other CTs: and . Therefore, the total number of borders CTs for is equal to two. Thus, the weighting matrix elements, (weighting between and ) and (weighting between and ) are equal to according to (1). Others CTs do not have borders in common with ( and for example); therefore, they have zero weighting: and .
3.2.2. Geographically Weighted Statistics Metrics
Geographically weighted models (GWMs) are techniques belonging to non-stationary spatial statistics, which incorporate local spatial relationships into their structure intuitively and explicitly [30,32]. Its application is suitable for situations where the spatial data needs to be better described by a global model since it enables the estimation and mapping of each location in the geographic space under study. GWMs’ outputs are commonly mapped to provide a helpful tool that usually precedes a more sophisticated statistical analysis [29].
Spatial weighting functions are crucial elements in GW modeling, whose objective is quantifying the spatial relationship or spatial dependence between the observed variables via SWM [30].
In this context, in our study, the SWM elements are obtained via Gaussian kernel application in (2) and shown in Figure 3. It is a monotonic decreasing function of the distance among centroids of areas and . These functions have a parameter for the bandwidth, which controls their decay rate [27,30].
For example, Figure 3 shows [30] the most conventional kernel function or weighting function: the Gaussian kernel. It is obtained using (2) with an arbitrary bandwidth .
Where represents the distance between the centroids of areas and . and is the bandwidth parameter.
A GW local summary statistic can be obtained from a spatial data set. Therefore, from the attributes and at any point , the following metrics can be obtained through (3)–(6): mean GW, standard deviation GW, Pearson's correlation coefficient GW and covariance GW, respectively [29,33].
Where is an element of SWM .
4. Results and Discussion
In this study, the spatial regression terminology is applied where there is a dependent or study variable whose distribution in geographic space is partially explained by a set of independent or explanatory variables. In our study, the dependent variable consists of a percentage of damaged distribution transformers that resulted in steady-state failures.
According to [34], the power utility of Paraná State, Brazil (COPEL) presented an annual failure rate in distribution transformers of 1.2%, where electric discharges caused 30% of these occurrences.
In this sense, the independent or explanatory variable analyzed is the surface density of electric discharges per km². They are associated with faults in distribution feeders. It is worth pointing out that all transformers and all-electric discharges in the city under study are georeferenced; their geographic coordinates are known, making it possible to apply SDA.
4.1. Case Study in a Brazilian City
This work performs an exploratory spatial data analysis to evaluate how electric discharges influence some city regions more vulnerable to steady-state faults. In this sense, Figure 4 shows an overview of the main steps of our study: (1) acquisition of georeferenced data (damaged distribution transformers and electric discharges), (2) exploratory analysis of spatial data, and (3) the results are shown in thematic maps.
The power utility applied in the simulations has a real feeder located in São Paulo State, Brazil. The simulations use QGIS and R software version 4.1.2 (R Core Team, 2015). R is a programming language and free statistical and graphical computing software. It contains many libraries or packages for numerical analysis, such as the GWmodel applied in this study. Unlike QGIS, R was not initially created as a GIS; however, it can perform functions like a GIS.
All simulations in this study are applied on a computer with an Intel Core i7 processor, 1.8 – 2.3 GHz, and 16 GB of RAM.
4.2. Database Description
In this section, the variable electrical discharge density () and the percentage of permanent faults in distribution transformers by regions () are evaluated; therefore, electrical discharges can make some city regions more vulnerable to faults. and are variables obtained in small areas called CTs. CTs release the public demographic census data produced by IBGE, because individual data are confidential.
Consider a of the city under analysis with , where corresponds to the number of CTs. The dependent or study variable is shown in (7). It is obtained from the ratio between the number of permanent faults per that caused faults in power distribution transformers and the total number of transformers in represented by . represents a probability of faults in transformer per . Thus, the number of failures in transformers by is approximately proportional to its total number of transformers. Noteworthy that the faults in our study are associated with transformers because they are georeferenced.
Independent or explanatory variable is represented by the surface density of electrical discharges () and it is obtained in (8). It is the ratio between the number of electrical discharges and the area per km². variable obtained is more effective than the total number of electrical discharges by CTs, because the number of electrical discharges that reach a CT is approximately proportional to its area.
Figure 5 shows the main reasons that caused 9,266 ESIs during more than one minute in a Brazilian city over four years. According to Figure 1 and Figure 5, weather conditions are the leading causes of interruptions in the utility grid. Figure 5 shows that meteorological conditions such as wind gusts and electrical discharges accounted for 21.9% of ESI.
However, it is worth noting that Figure 5 shows numerical values from the power utility database without a refined treatment. Thus, technicians in the field identified the percentages associated with the factors responsible for ESI without further investigation. For example, the leading causes of ESI were “equipment failures,” with an occurrence of 44.7%. However, this is a “black box” because equipment failures can be caused by numerous factors such as equipment obsolescence, adverse weather conditions (rains, wind gusts, electrical discharges), overload, clandestine connections, or human failures. In this sense, the overview of the numerous factors responsible for ESI is more important than the numerical values shown in Figure 5.
4.3. Exploratory Spatial Data Analysis
4.3.1. Electrical Discharges
Electrical discharges occasionally reach the utility grid, and consequently, they cause disturbances and ESI. Figure 6 shows a monthly distribution of 2,036 electrical discharges that came the city under study over four years. Table 2 shows some descriptive statistics metrics by CTs. From Table 2, each CT is reached between one and two electrical discharges by year on average. However, a single CT was the target of 40 electrical discharges in 2011.
Figure 7a–d show the heatmaps obtained via Gaussian kernel density considering the electrical discharge distribution for the years 2009, 2010, 2011, and 2012, respectively. Gaussian kernel is based on electrical discharge clustering based on a predefined distance called bandwidth. Therefore, CTs with high concentrations of electrical discharges (indicated by red regions) have high Gaussian kernel values. In 2010, the maximum Gaussian kernel value corresponds to approximately half of the value observed in other years, for example. Therefore, this variation indicates a heterogeneous distribution of electrical discharges over the years.
variable considers the total area of each CT in km². In many cases, the number of electrical discharges in a CT is proportional to its area. Figure 8a–d show thematic maps for over the years 2009, 2010, 2011 and 2012, respectively. The numbers in parentheses indicate the CTs whose is in the designated range. For example, in Figure 8a, which corresponds to in 2009, it is observed that 41 CTs have with a value between 2 and 6 electrical discharges per km². Most of these CTs belong to city’s periphery and they are represented in light green.
According to Figure 8, has a similar pattern for all years analyzed. CTs with high belong to the central regions and move towards the center-southeast and center-northwest of the city. There is an exception in Figure 8b. According to Table 2, 2010 is an atypical year (outlier) with few rains and electrical discharges. The regions with high (central, northwest, and southeast) are more densely urbanized and have many elevated structures such as buildings, antennas, and tree vegetation that attract electrical discharges. On the other hand, CTs located on the city’s periphery and, therefore, close to rural areas show reduced . These CTs contain extensive flat areas with open fields.
4.3.2. Number of Faults in Transformers by Regions
The number of faults in transformers is the dependent or study variable. This work covers 3,794 interruptions caused by distribution transformer failures. This approach is adopted because transformers are georeferenced, and this is a condition for using SDA techniques.
Table 3 shows metrics of descriptive statistics applied to the annual number of interruptions by CTs caused by faults in power distribution transformers from 2009 to 2012. There were three yearly interruptions by CT on average. However, there were 42 interruptions in a single CT caused by transformer failures in 2009.
Figure 9a–d show the heatmaps where the interruptions in distribution transformers occurred in 2009, 2010, 2011, and 2012 are represented. The main objective is to visualize the high concentration of interruptions in transformers in some city areas. The heatmaps for all years have a similar pattern with high fault concentration in the city’s central region. This region has a high population density and, therefore, has many transformers. Figure 9c shows the heatmap for the year 2011, with warm areas in center-southeast direction. Finally, Figure 9d shows the heatmap for the year 2012, where there is a significant cluster of distribution transformer faults in the western, center, and southeast regions.
In this sense, Figure 10a–d show thematic maps for dependent variable for the years 2009, 2010, 2011, and 2012, respectively. The maps visually represent interruptions, considering the total number of transformers installed in each CT. There is a contrast between Figure 9 and Figure 10. Figure 9 shows a fault distribution pattern with a significant concentration in the central region. On the other hand, Figure 10 shows a variation in trends over the years studied.
Noteworthy, Figure 10 has information in parentheses with the total number of CTs whose is within of the indicated range. For example, Figure 10a has 86 CTs with , where most of CTs have in that range for all years evaluated.
In Figure 10a, there are 64 CTs with high . Most are in the southeast, west, and north regions. In Figure 10b, there are 80 CTs with high . The southeast and west regions remain with some CTs with high and other CTs appear in the northwest region. Figure 10c has the largest number of CTs with high being 93 CTs. Southeast, west, and northwest regions remain with many CTs with high and other CTs appear in the northeast and central regions. Lastly, Figure 10d has the smallest number of CTs with high : there are 41 CTs where the majority are in the east, west and northwest regions. Certainly, in 2012, the distributor performed maintenance or replacement of many damaged transformers located in CTs with many faults.
According to Figure 10, there are some CTs with high located in peripheral city’s regions. On the other hand, these regions have low in the Figure 8. Therefore, a preliminary assessment indicates that there are possibly other local variables that influence the high in these regions.
In this context, peripheral regions close to rural regions are fire targets. However, we cannot conclude that is high in peripheral regions of the city due to fires. Further studies should confirm or refute that hypothesis.
4.3.3. Geographically Weighted Summary Statistics
This section presents thematic maps as the result of applying the GW metrics in (3)-(6). The neighborhood structure among nth CTs influences these GW metrics. The neighborhood structure is represented by the weighting matrix which is constructed from Gaussian kernel in (2) and represented in Figure 3.
Neighborhood structure in this study follows Tobler's notion of spatial dependence, which states the first law of geography where all things are similar; however, things closer look more than distant things [28] .
In this sense, the weighting assigned by the Gaussian kernel is inversely proportional to the Euclidean distance between the CT centroids. Thus, as the distance between CTs and is reduced, the weighting between them increases. The elements belong to weighting matrix and it represent the neighborhood structure in an urban area of Brazilian city with CTs.
Therefore, if a CT has a high number of electrical discharges, it is likely that nearby CTs will show this same characteristic. On the other hand, if a CT has feeders with many ESI, nearby CTs are expected to have this same problem because they share the same power grid. Therefore, the neighborhood structure based on Euclidean distance among CTs is suitable for estimating areas vulnerable to faults.
Figure 11a–d show the GW standard deviation for the independent variable for the years 2009, 2010, 2011 and 2012, respectively. Figure 11a,c show high local variability for the central and southeastern regions. Figure 11b shows high local variability for the central-east region. Finally, Figure 11d shows high local variability for the central-eastern region. High local variability indicates that there are nearby CTs that present very different values. As shown in Figure 11, it is worth highlighting the high local variability in regions around the central area. It contains buildings and tree vegetation that attract electrical discharges.
On the other hand, Figure 12a–d show the GW standard deviation for the dependent variable for the years 2009, 2010, 2011 and 2012, respectively. Figure 12a shows high local variability for the northern regions. Figure 12b shows high local variability for the southeast region, and finally, Figure 12c,d show high local variability for the southeast and northwest regions. It is worth highlighting, there is a change in regions with greater local variability that is more pronounced for than over the years. Field teams work continuously to maintain and replace damaged transformers; therefore, there is greater variation in than by CTs over the years.
Lastly, Figure 13a–d show local correlation GW between the dependent variable and the independent variable for the years 2009 to 2012, respectively. There is a non-stationary relationship between and variables with GW local correlation moderate in the central (Figure 13a,d) and west (Figure 13b,c) regions.
The positive correlation means that, in these regions, and are directly proportional variables. Therefore, there is a first numerical indication that electrical discharges are associated with ESI in power grid transformers in these regions.
The non-stationary relationship between and indicates that a global spatial regression model would not be suitable for estimating regions vulnerable to faults; on the other hand, a local regression model would be better suited to represent non-stationarity at the local level.
It is worth highlighting that GWEA is performed with an adaptive bandwidth where the influence of 45 closest CTs is considered for the analysis of each CT. This closest CT value corresponds to 15% of the total CTs in the city under study [29].
5. Conclusions
In this study, a crucial step was performed that precedes the estimating of census tracts (CTs) vulnerable to faults: the geographically weighted (GW) exploratory spatial data analysis (ESDA). Essential for this analysis was the availability of georeferenced real data: the dependent variable number faults in distribution transformers () by census tracts (CTs) and the independent or explanatory variable electrical discharges density ().
ESDA was performed using GW statistics metrics with visual presentation of variables in the city’s geographic space. GW statistics summary demonstrated the spatial variability between and variables.
The GW correlation showed a moderate positive correlation between and in the central (in 2009 and 2012) and in west (in 2010 and 2011) regions. Therefore, the electrical discharges are associated with the power grid faults in these regions.
ESDA performed in this study was vital for implementing more sophisticated mathematical models in future studies to estimate regions vulnerable to faults. Furthermore, incorporating other variables, such as tree vegetation, will provide greater robustness to future analysis.
Author Contributions
Conceptualization, A.S.S., L.T.F., methodology, A.S.S. and L.T.F.; software, A.S.S. and L.T.F.; validation, A.S.S., L.T.F., M.L.M.L., and C.R.M.; formal analysis, A.S.S., L.T.F., M.L.M.L., and C.R.M.; investigation, A.S.S.; resources, C.R.M.; data curation, A.S.S.; writing—original draft preparation, A.S.S. and L.T.F.; writing—review and editing, A.S.S., L.T.F., M.L.M.L., and C.R.M.; visualization, A.S.S.; supervision, C.R.M.; project administration, C.R.M.; funding acquisition, C.R.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Coordination for the Improvement of Higher Education Personnel (CAPES), Financing Code 001, and the National Council for Scientific and Technological Development (CNPq) Agency – Brazil.
Data Availability Statement
Confidential data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Q. Zhou, X. Li, J. Liao, and T. Xiong, “Power failure risk assessment and management based on stochastic line failures in distribution network including distributed generation,” IEEJ Transactions on Electrical and Electronic Engineering, vol. 13, no. 9, pp. 1303–1312, Sep. 2018. [CrossRef]
- S. S. Gururajapathy, H. Mokhlis, and H. A. Illias, “Fault location and detection techniques in power distribution systems with distributed generation: A review,” Renewable and Sustainable Energy Reviews, vol. 74. Elsevier Ltd, pp. 949–958, 2017. [CrossRef]
- P. N. Mikropoulos and T. E. Tsovilis, “Statistical Method for the Evaluation of the Lightning Performance of Overhead Distribution Lines,” IEEE Transactions on Dielectrics and Electrical Insulation, vol. 20, pp. 202–211, 2013. [CrossRef]
- C. Wang, T. Zhang, F. Luo, P. Li, and L. Yao, “Fault incidence matrix based reliability evaluation method for complex distribution system,” IEEE Transactions on Power Systems, vol. 33, no. 6, pp. 6736–6745, Nov. 2018. [CrossRef]
- J. B. Leite, J. R. S. Mantovani, T. Dokic, Q. Y. Chen, and M. Kezunovic, “Failure Probability Metric by Machine Learning for Online Risk Assessment in Distribution Networks,” in 2017 IEEE PES Innovative Smart Grid Technologies Conference-Latin America (ISGT Latin America), Quito, Ecuador, 2017, pp. 1–6.
- F. A. Souza, M. F. Castoldi, and A. Goedtel, “A cascade perceptron and Kohonen network approach to fault location in rural distribution feeders,” Applied Soft Computing, vol. 96, p. 106627, 2020. [CrossRef]
- National Electric System Operator, “Supply Quality,” ONS. (In Portuguese).
- da S. Santos, L. T. Faria, M. L. M. Lopes, A. D. P. Lotufo, and C. R. Minussi, “Efficient Methodology for Detection and Classification of Short-Circuit Faults in Distribution Systems with Distributed Generation,” Sensors, vol. 22, no. 23, Dec. 2022. [CrossRef]
- J. Yuan and Z. Jiao, “Faulty feeder detection based on image recognition of current waveform superposition in distribution networks,” Appl Soft Comput, vol. 130, p. 109663, 2022. [CrossRef]
- A.-S. A. AL-Sakkaf and B. M. AL-Ramadan, “Applications of GIS in Electrical Power System,” Dhahran, 2013, pp. 1–6.
- M. Shafiullah, S. M. Rahman, Md. G. Mortoja, and B. Al-Ramadan, “Role of spatial analysis technology in power system industry: An overview,” Renewable and Sustainable Energy Reviews, vol. 2016, pp. 584–595, 66AD. [CrossRef]
- G. Câmara, M. S. Carvalho, O. G. Cruz, and V. Correa, Spatial analysis of areas. Brasília, Brazil, 2004. (In Portuguese).
- Abdulrahman and • Ghadir Radman, “Power system spatial analysis and visualization using geographic information system (GIS),” Spatial Information Research, vol. 28, pp. 101–112, 2019. [CrossRef]
- C. Chen and M. Kezunovic, “Fuzzy Logic Approach to Predictive Risk Analysis in Distribution Outage Management,” IEEE Trans Smart Grid, vol. 7, pp. 2827–2836, 2016. [CrossRef]
- S. A. V. Goerdin, J. J. Smit, and R. P. Y. Mehairjan, “Monte Carlo simulation applied to support risk-based decision making in electricity distribution networks,” in 2015 IEEE Eindhoven PowerTech, PowerTech 2015, Institute of Electrical and Electronics Engineers Inc., Aug. 2015. [CrossRef]
- D. S. Muñoz and J. L. D. Garcia, “GIS-based tool development for flooding impact assessment on,” J Clean Prod, vol. 320, p. 128793, 2021, doi: 10.1016. [CrossRef]
- Bernstein, D. Bienstock, D. Hay, M. Uzunoglu, and G. Zussman, “Power Grid Vulnerability toGeographically Correlated Failures –Analysis and Control Implications,” in IEEE INFOCOM 2014-IEEE conference on computer communications, IEEE, 2014, pp. 2634–2642.
- Handayani, T. Filatova, and Y. Krozer, “The vulnerability of the power sector to climate variability and change: Evidence from Indonesia,” Energies (Basel), vol. 12, no. 19, Sep. 2019. [CrossRef]
- K. Mortensen, H. R. Shaker, and C. T. Veje, “Relative fault vulnerability prediction for energy distribution networks,” Appl Energy, vol. 322, pp. 119449–119449, Jan. 2022. [CrossRef]
- Y. Xu, C. Tong, M. Xiang, T. Wang, J. Xu, and J. Zheng, “Lightning risk estimation and preventive control method for power distribution networks referring to the indeterminacy of wind power and photovoltaic,” Electric Power Systems Research, vol. 214, p. 108896, 2023. [CrossRef]
- P. Sestasombut and A. Ngaopitakkul, “Evaluation of a direct lightning strike to the 24 kV distribution lines in Thailand,” Energies (Basel), vol. 12, no. 16, Aug. 2019. [CrossRef]
- D. Mestriner, R. A. R. de Moura, R. Procopio, and M. A. de O. Schroeder, “Impact of grounding modeling on lightning-induced voltages evaluation in distribution lines,” Applied Sciences (Switzerland), vol. 11, no. 7, Apr. 2021. [CrossRef]
- T. Miyazaki and S. Okabe, “Field analysis of the occurrence of distribution-line faults caused by lightning effects,” IEEE Trans Electromagn Compat, vol. 53, no. 1, pp. 114–121, Feb. 2011. [CrossRef]
- S. Druck, M. S. Carvalho, G. Câmara, and A. M. V. Monteiro, Spatial analysis of geographic data. 2004. (In Portuguese).
- J. Le Gallo and C. Ertur, “Exploratory spatial data analysis of the distribution of regional per capita GDP in Europe, 1980–1995,” Papers in regional science, vol. 82, pp. 175–202, 2003. [CrossRef]
- R. Haining, Spatial data analysis: theory and practice, vol. 1. Cambrigdge University Press, 2003.
- T. Faria, J. D. Melo, and A. Padilha-Feltrin, “Spatial-Temporal Estimation for Nontechnical Losses,” IEEE Transactions on Power Delivery, vol. 31, pp. 362–369, 2016. [CrossRef]
- W. R. Tobler, “Cellular geography,” Philosophy in geography, pp. 379–386, 1979.
- R. S. Bivand, E. Pebesma, and V. Gómez-Rubio, Applied Spatial Data Analysis with R, vol. 10. Springer, 2013. [Online]. Available: http://www.springer.com/series/6991.
- Gollini, B. Lu, M. Charlton, C. Brunsdon, and P. Harris, “GWmodel: An R Package for Exploring Spatial Heterogeneity Using Geographically Weighted Models,” JSS Journal of Statistical Software, vol. 63, pp. 1–52, 2015, [Online]. Available: http://www.jstatsoft.org/.
- C. Brunsdon, A. S. Fotheringham, and M. E. Charlton, “Geographically weighted regression a method for exploring spatial nonstationarity,” Geographical analysis, vol. 28, pp. 281–298, 1996. [CrossRef]
- S. Fotheringham, C. Brunsdon, and M. Charlton, Geographically weighted regression: the analysis of spatially varying relationships. JOHN WILEY & SONS, 2002.
- Dykes and C. Brunsdon, “Geographically weighted visualization: interactive graphics for scale-varying exploratory analysis,” IEEE Trans Vis Comput Graph, vol. 13, no. 6, pp. 1161–1168, 2007. [CrossRef]
- K. Kuster, S. L. F. Santos, A. Piantini, A. E. Lazzaretti, L. G. Mello, and C. L. S. Pinto, “An Improved Methodology for Evaluation of Lightning Effects on Distribution Networks,” in 2017 International Symposium on Lightning Protection (XIV SIPDA, IEEE, 2017, pp. 261–267. [CrossRef]
Figure 1.
Disturbances caused by electrical discharges between 2012 and 2022 in Brazil [7].
Figure 1.
Disturbances caused by electrical discharges between 2012 and 2022 in Brazil [7].
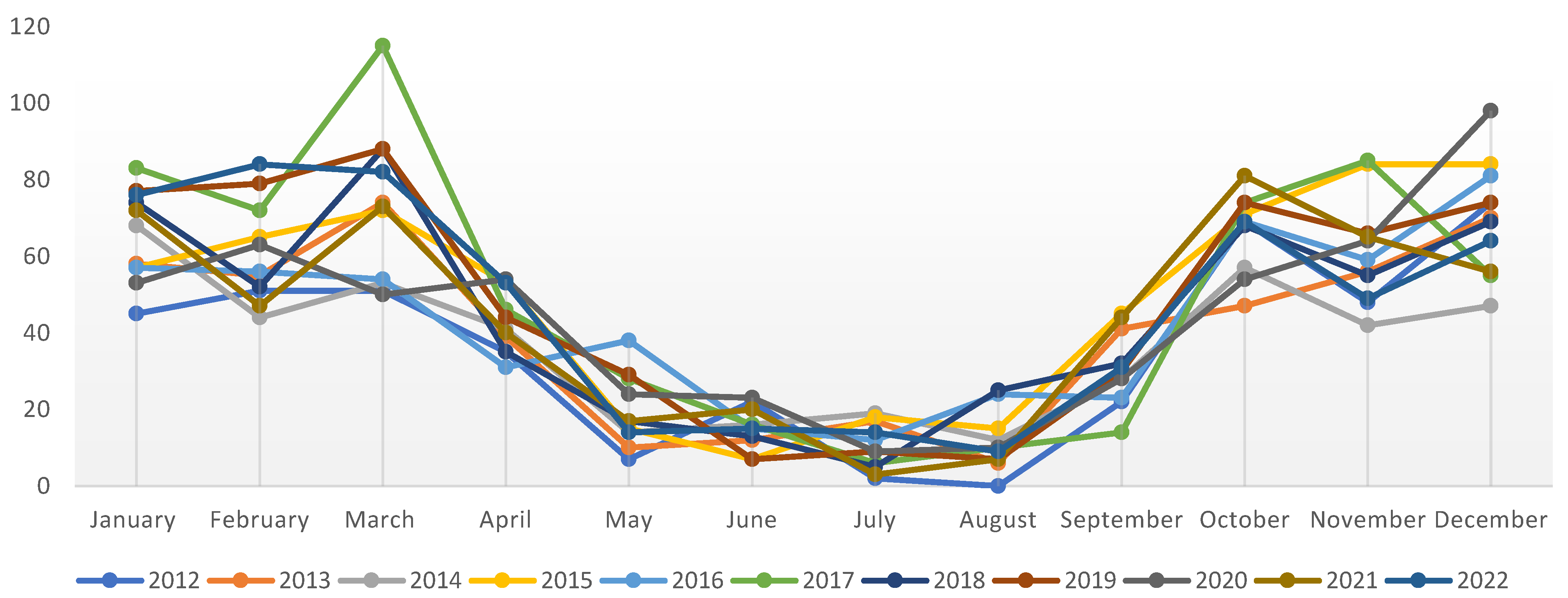
Figure 2.
An illustrative example of constructing a weighting matrix: (a) five census tracts of the city under study; (b) corresponding weighting matrix.
Figure 2.
An illustrative example of constructing a weighting matrix: (a) five census tracts of the city under study; (b) corresponding weighting matrix.
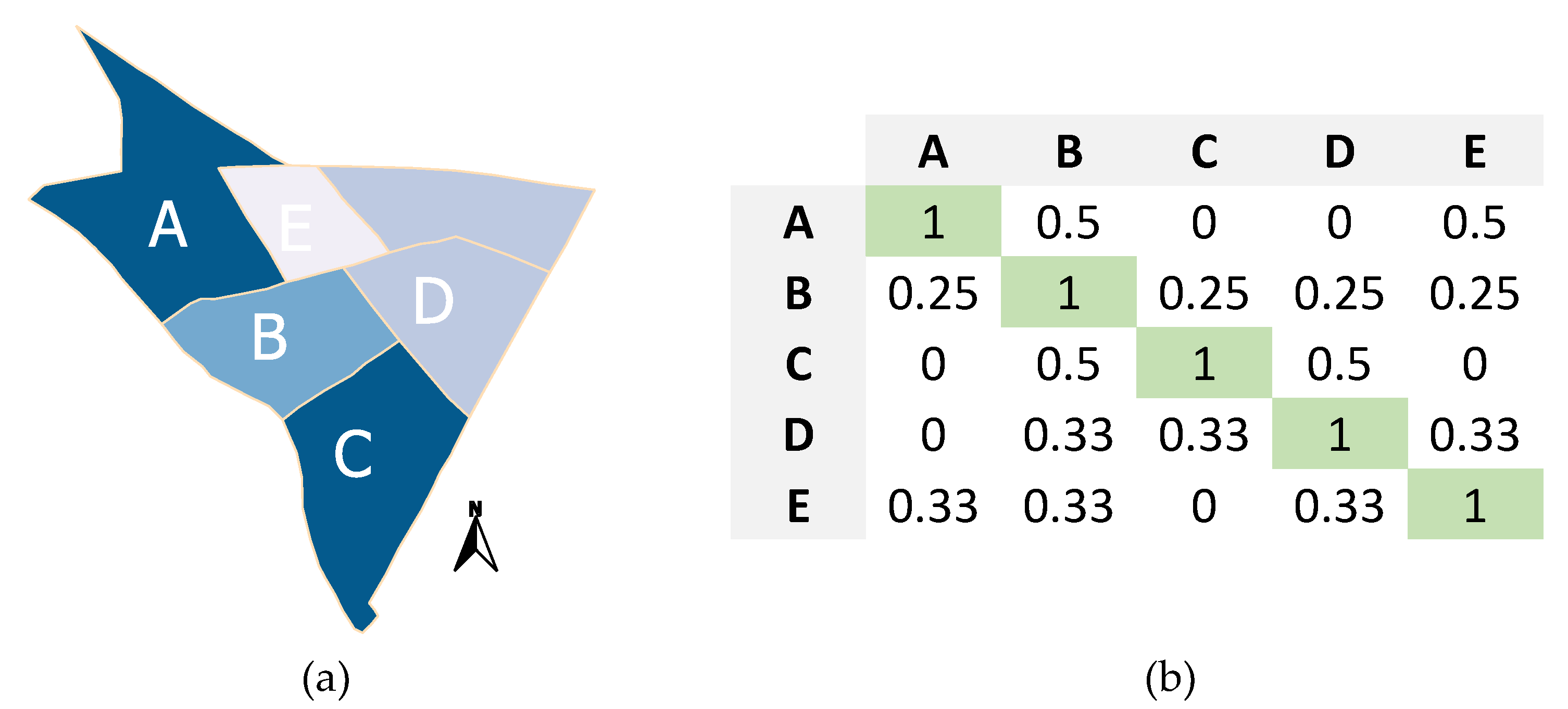
Figure 3.
Gaussian kernel function with bandwidth b=1000.
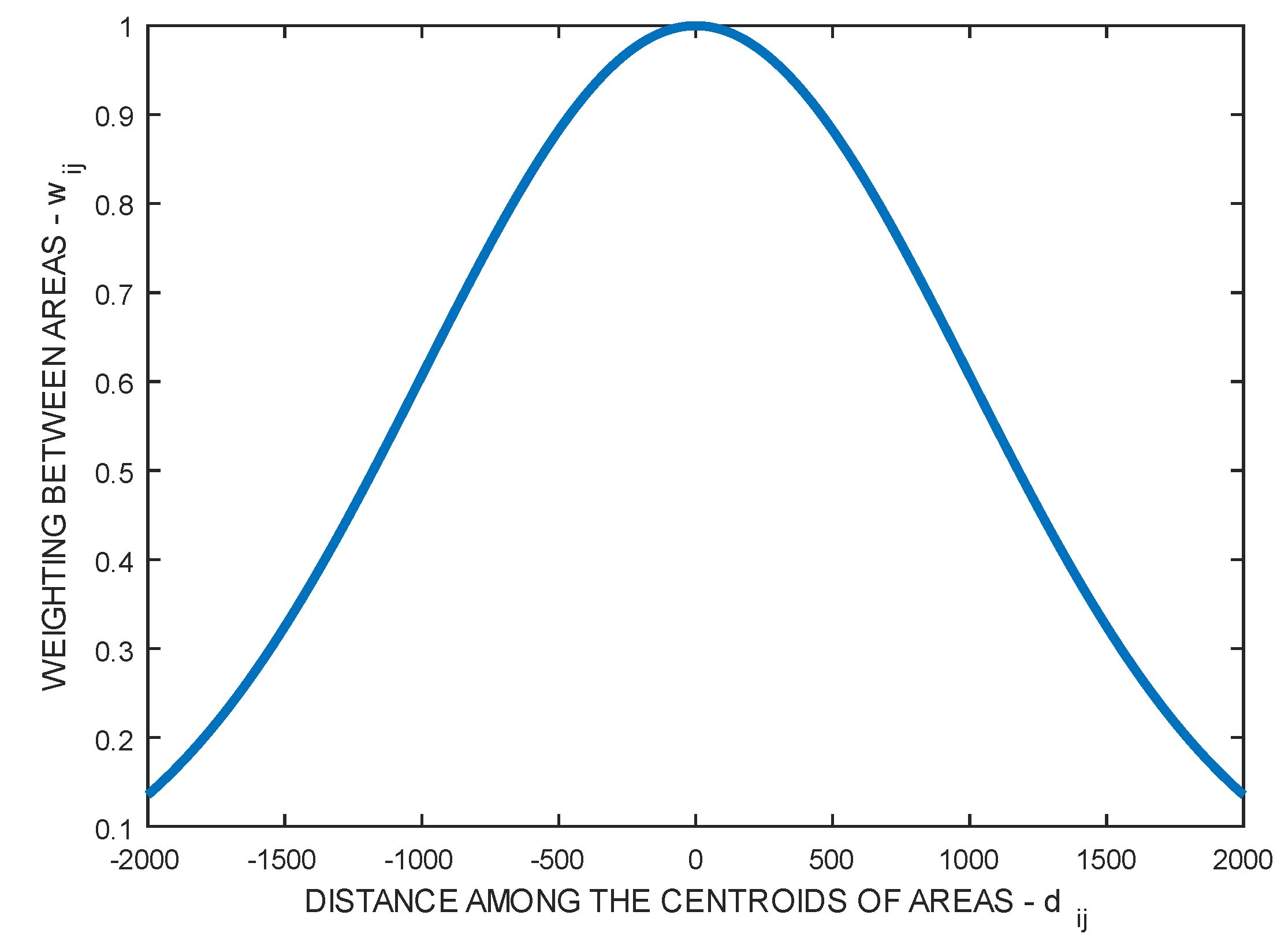
Figure 4.
Overview of an exploratory analysis of spatial data.
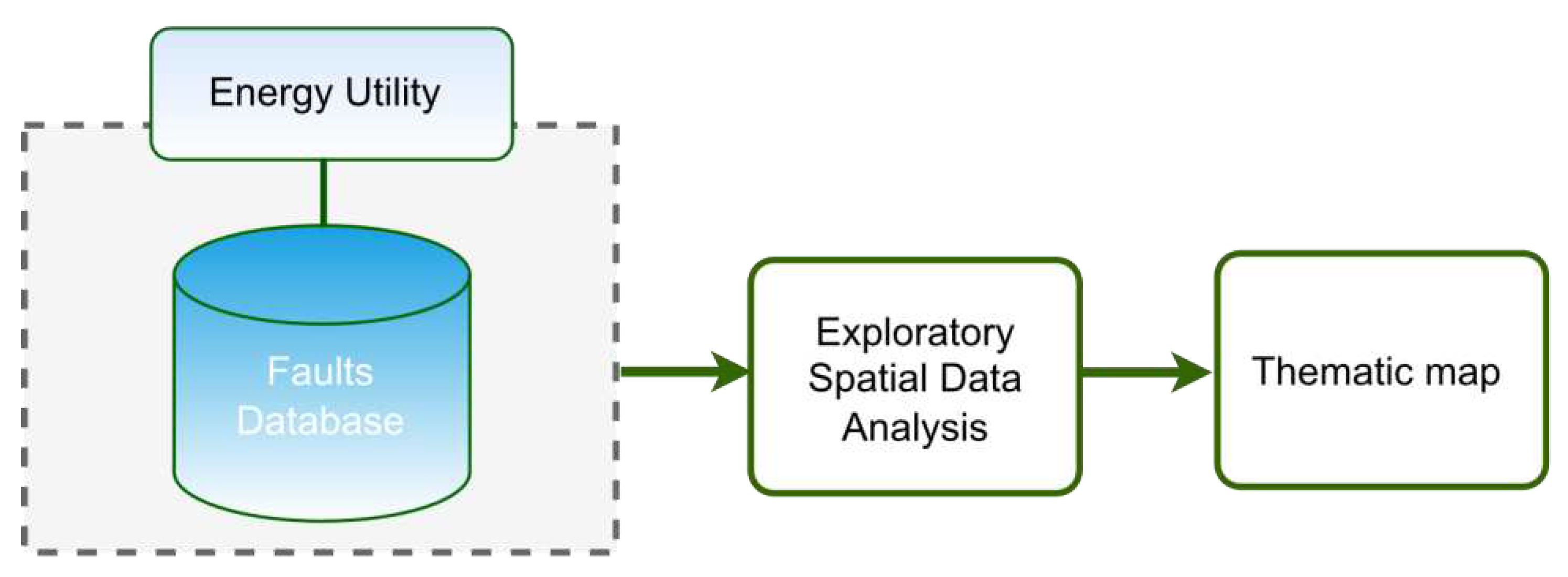
Figure 5.
Main factors that caused permanent faults in a Brazilian city.
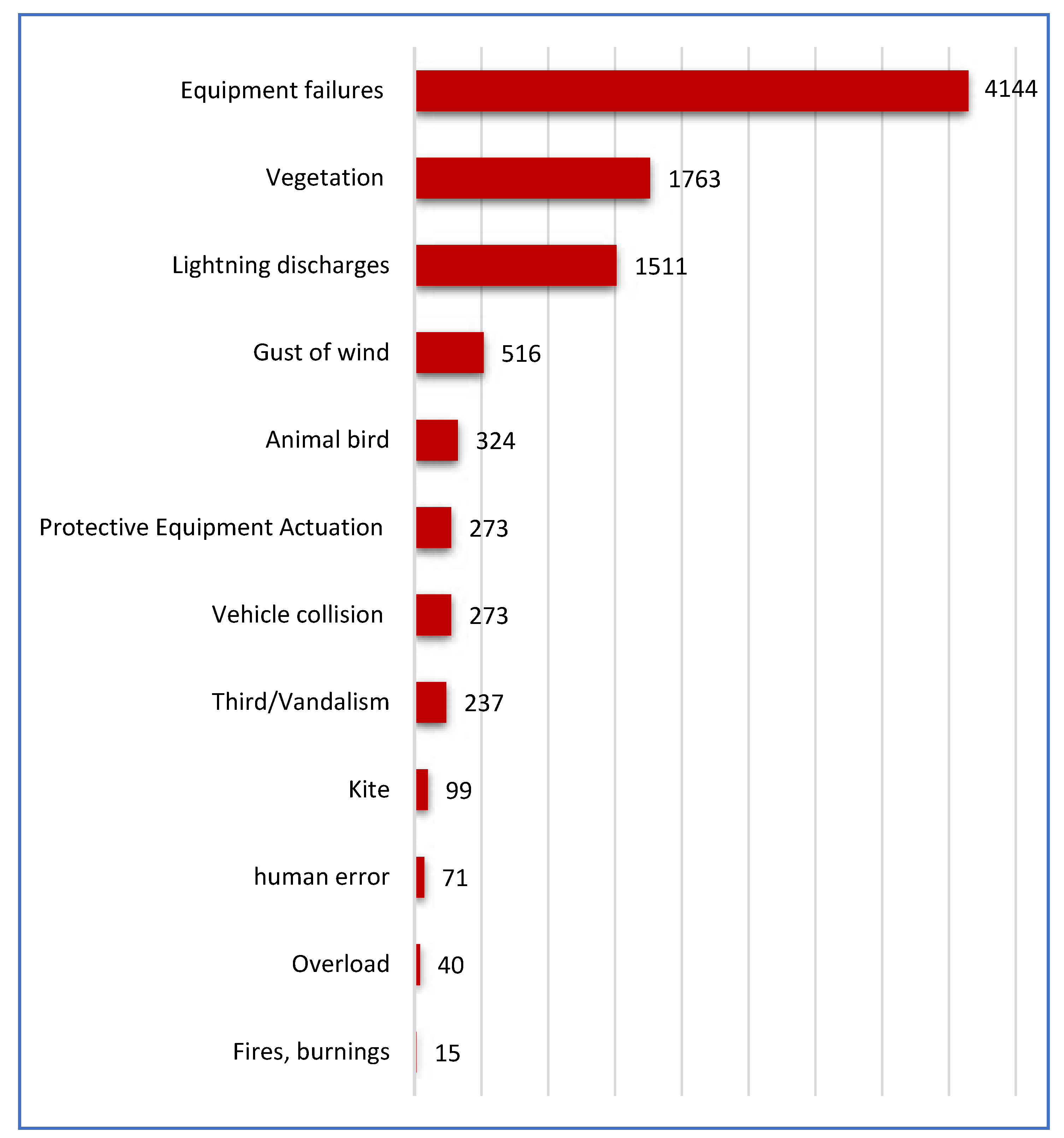
Figure 6.
Monthly distribution of electrical discharges.
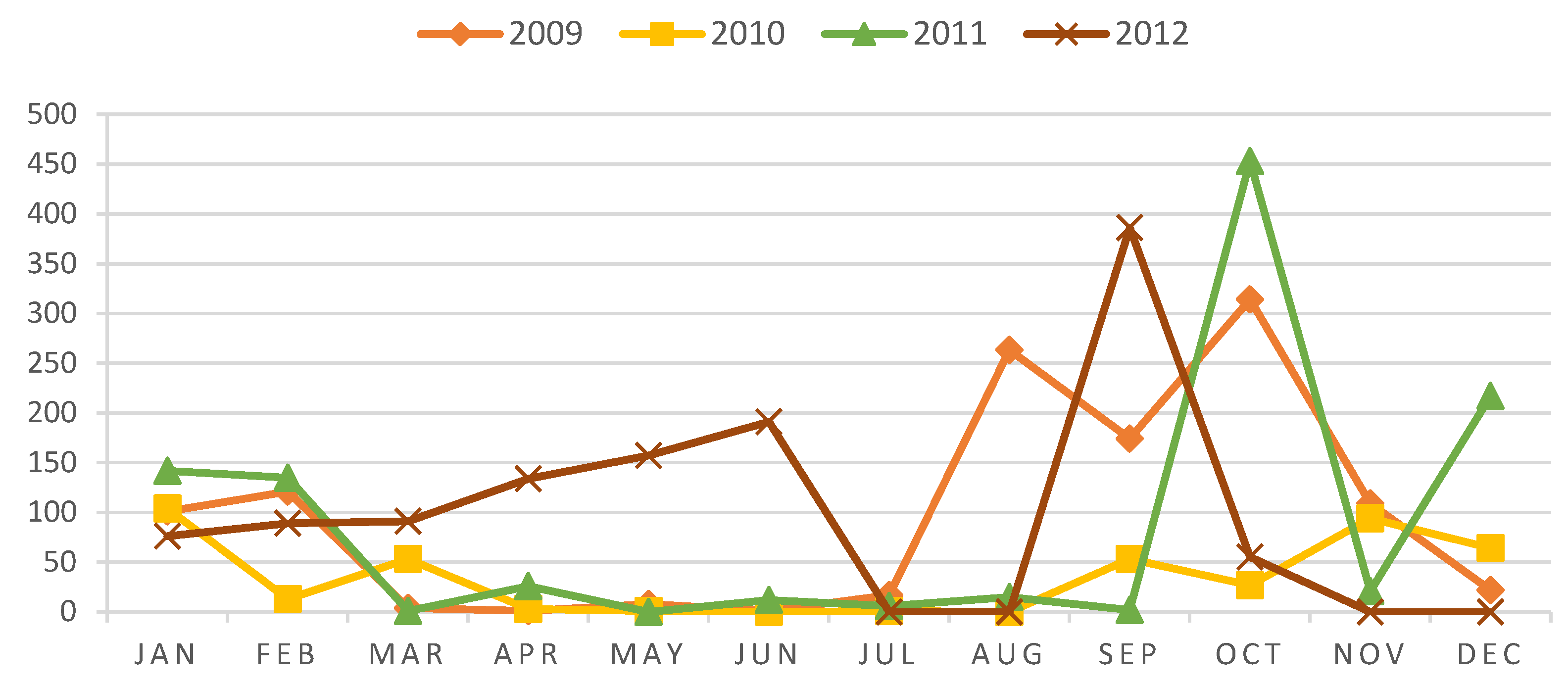
Figure 7.
Heatmap considering electric discharge distribution by census tracts for the years: (a) 2009, (b) 2010, (c) 2011, and (d) 2012.
Figure 7.
Heatmap considering electric discharge distribution by census tracts for the years: (a) 2009, (b) 2010, (c) 2011, and (d) 2012.
Figure 8.
Electrical discharges density by census tracts for the years of 2009 (a), 2010 (b), 2011 (c) and 2012 (d).
Figure 8.
Electrical discharges density by census tracts for the years of 2009 (a), 2010 (b), 2011 (c) and 2012 (d).
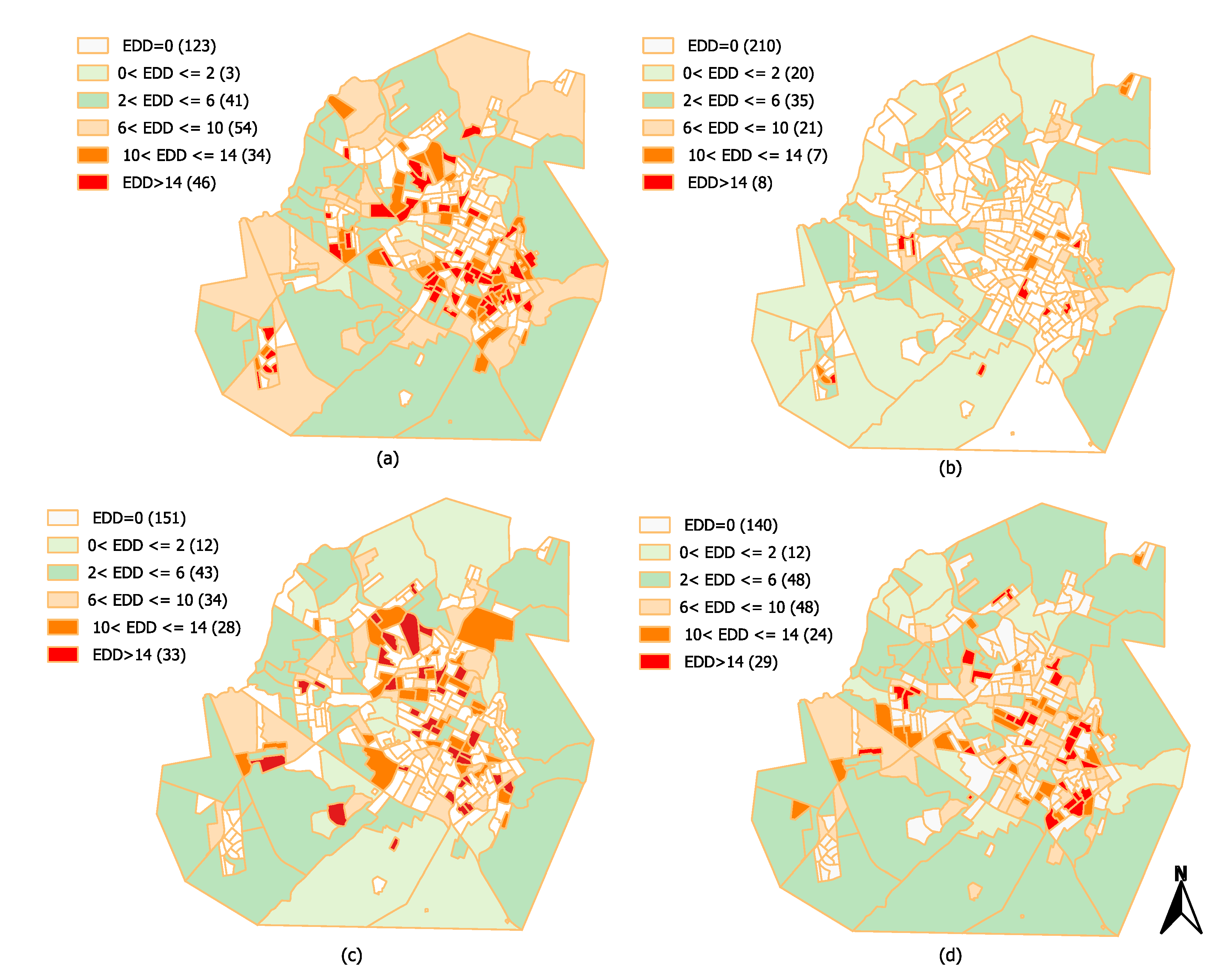
Figure 9.
Heatmap considering faults in transformers by census tracts in urban areas for the years 2009 (a), 2010 (b), 2011 (c), and 2012 (d).
Figure 9.
Heatmap considering faults in transformers by census tracts in urban areas for the years 2009 (a), 2010 (b), 2011 (c), and 2012 (d).
Figure 10.
Percentage of faults in transformers () by census tracts for the years 2009 (a), 2010 (b), 2011 (c) and 2012 (d).
Figure 10.
Percentage of faults in transformers () by census tracts for the years 2009 (a), 2010 (b), 2011 (c) and 2012 (d).
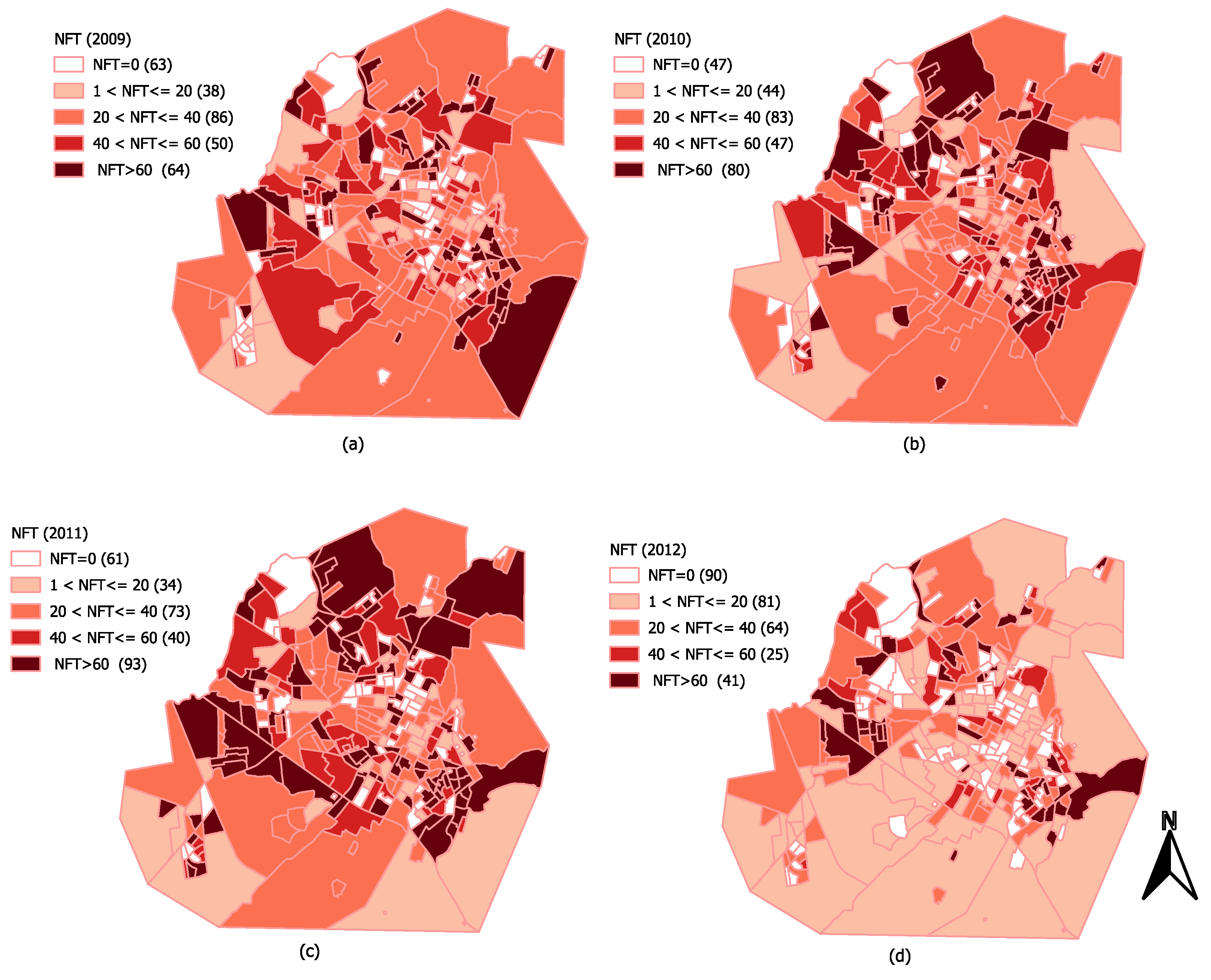
Figure 11.
GW standard deviation for electrical discharges density for the years 2009 (a), 2010 (b), 2011 (c) and 2012 (d).
Figure 11.
GW standard deviation for electrical discharges density for the years 2009 (a), 2010 (b), 2011 (c) and 2012 (d).
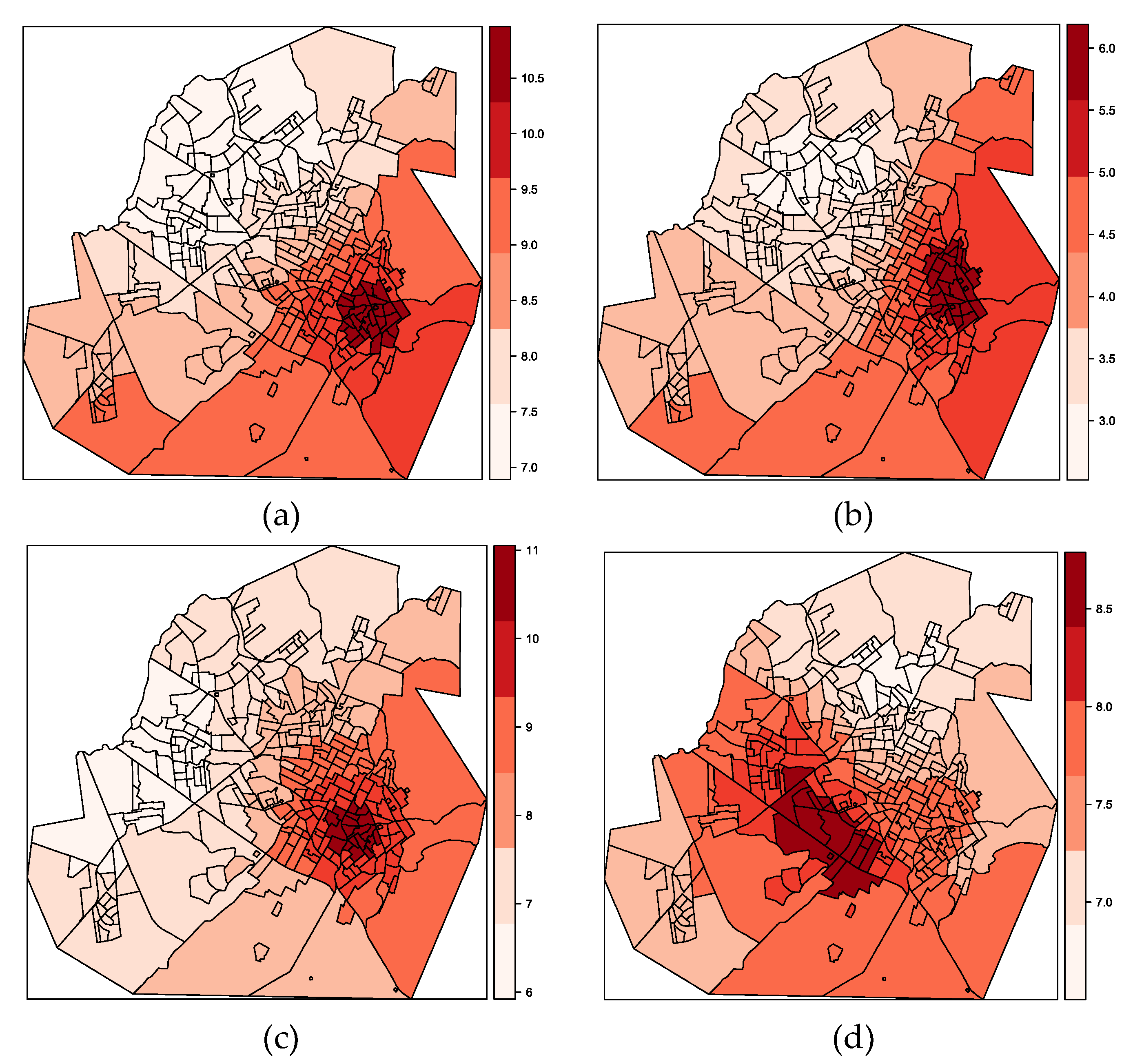
Figure 12.
GW standard deviation for the percentage of faults in transformers by CTs for the years 2009 (a), 2010 (b), 2011 (c) and 2012 (d).
Figure 12.
GW standard deviation for the percentage of faults in transformers by CTs for the years 2009 (a), 2010 (b), 2011 (c) and 2012 (d).
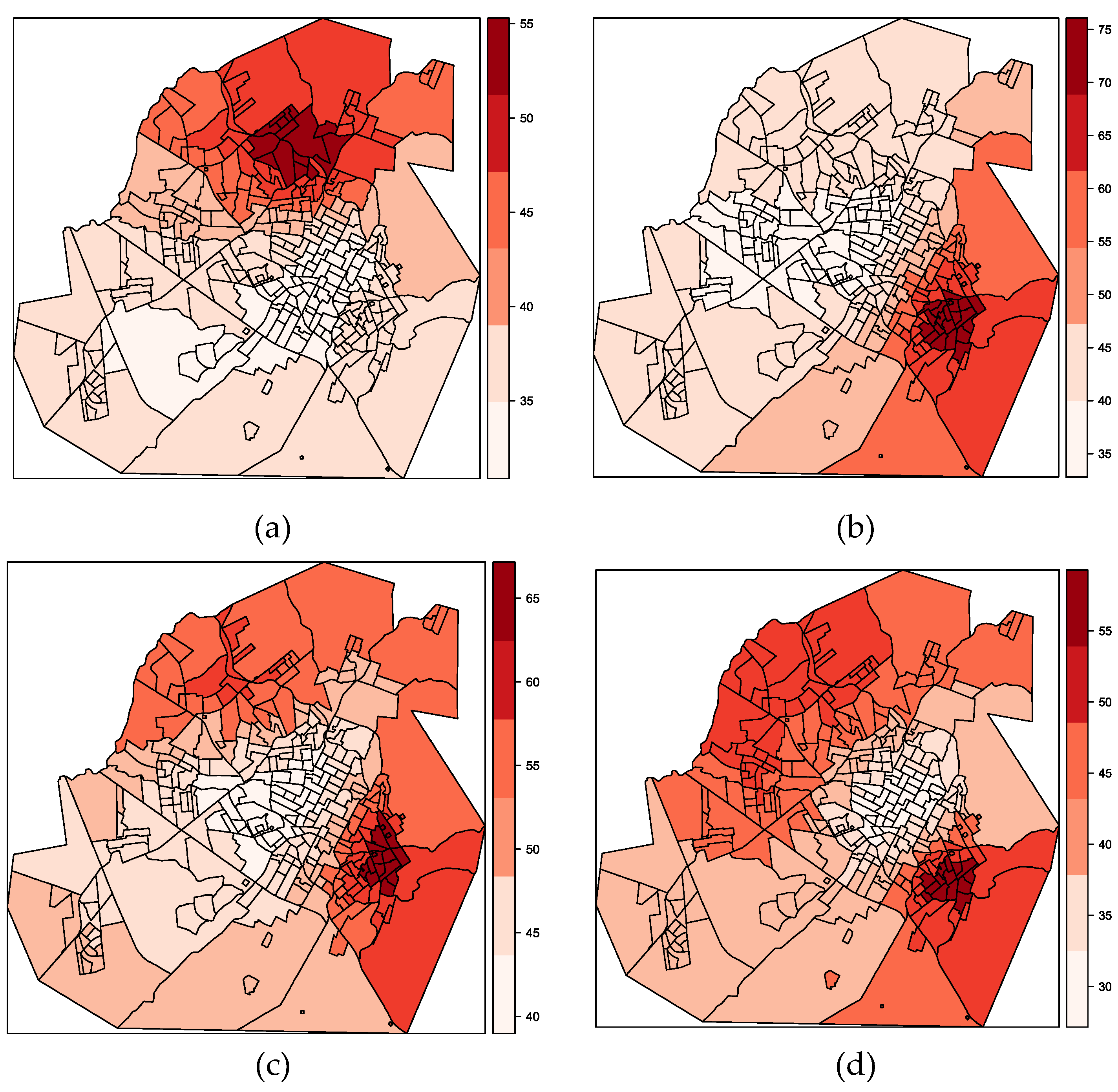
Figure 13.
GW local correlation between and for the years 2009 (a), 2010 (b), 2011 (c) and 2012 (d).
Figure 13.
GW local correlation between and for the years 2009 (a), 2010 (b), 2011 (c) and 2012 (d).
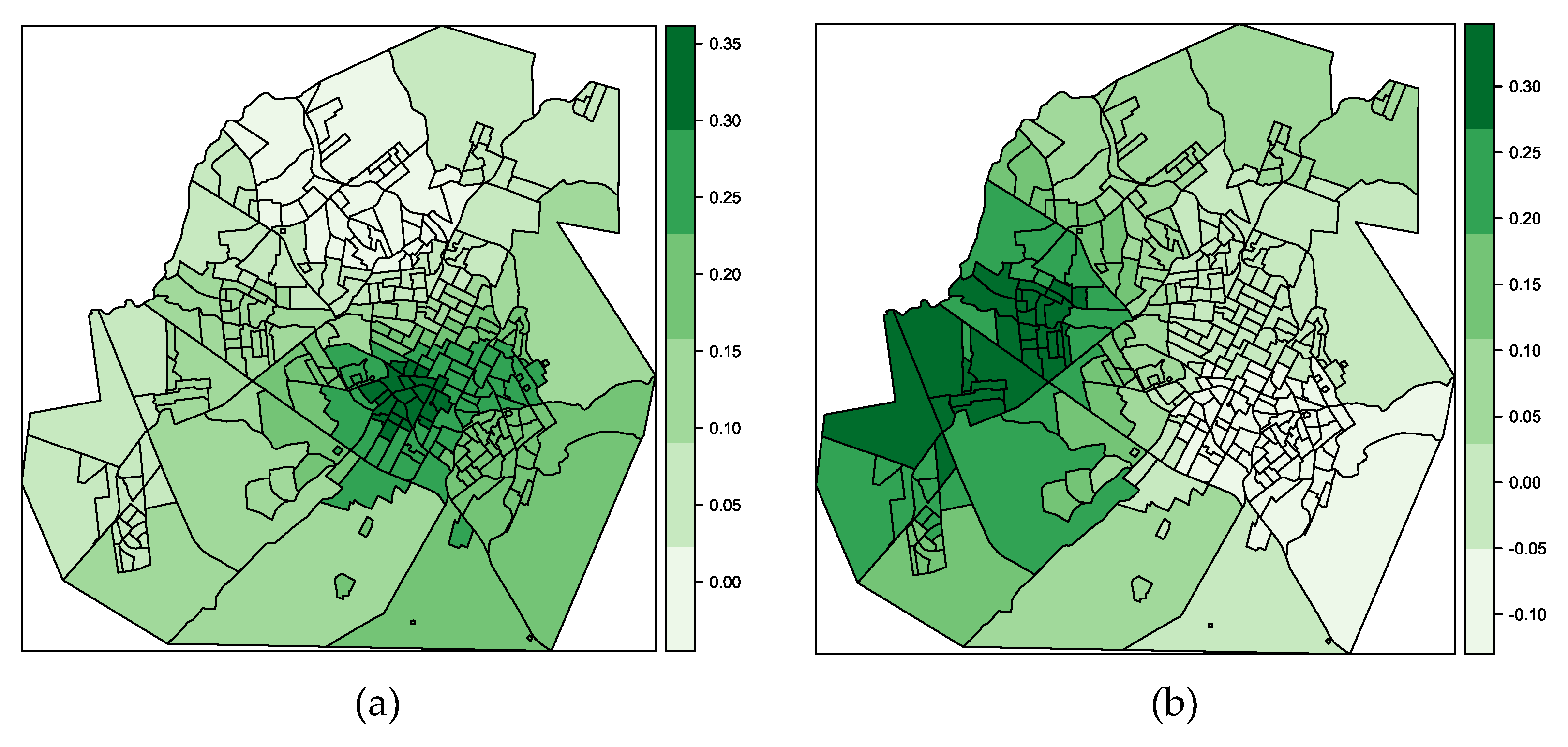
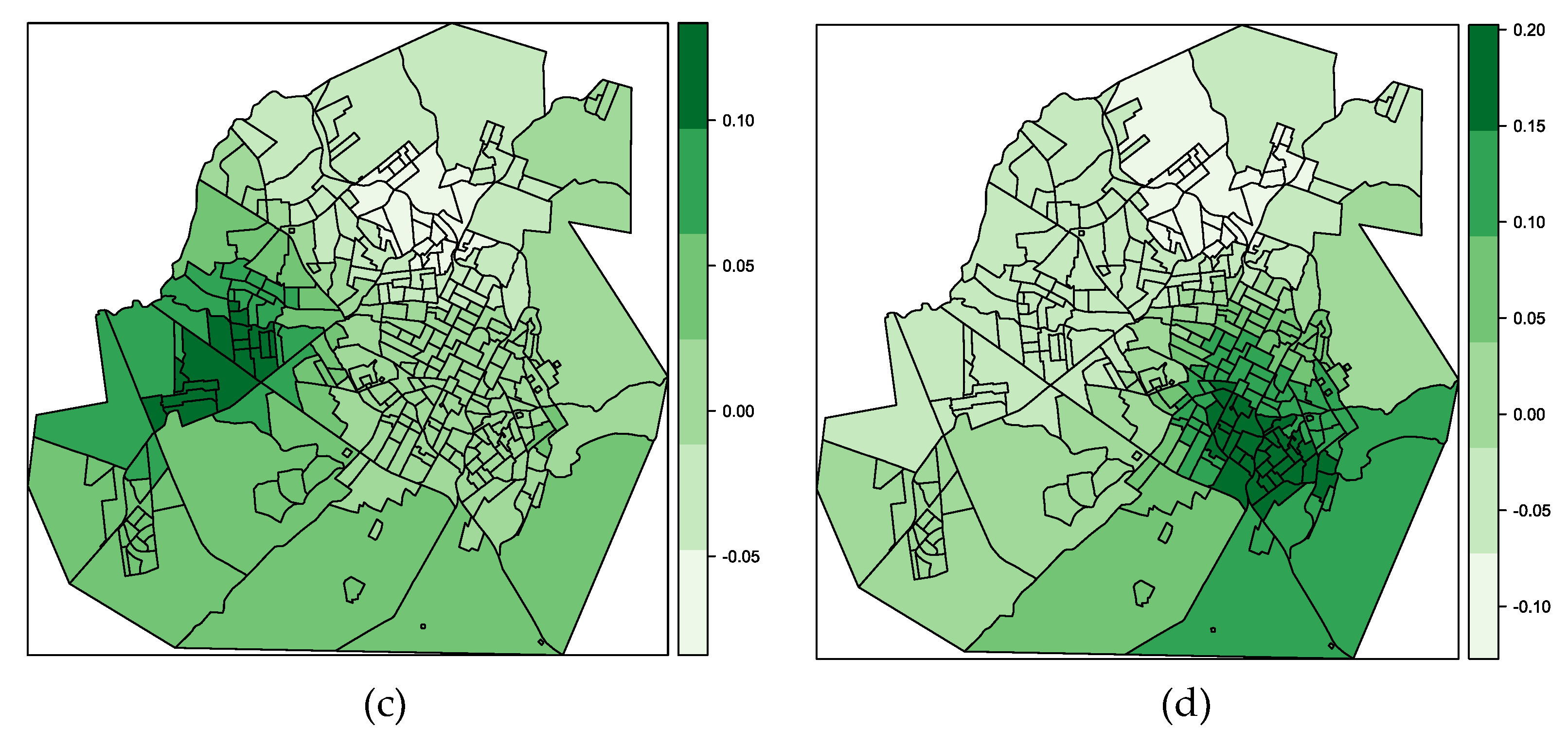
Table 1.
Table 1. Main causes of disturbances in Brazilian power grids.
| Fault Reasons | Number of Annual Faults | |||||
|---|---|---|---|---|---|---|
| 2020 | % | 2021 | % | 2022 | % | |
| Adverse Weather Conditions | 708 | 29.75% | 704 | 29.82% | 743 | 35.01% |
| Fires | 587 | 24.66% | 633 | 26.81% | 250 | 11.80% |
| Equipment Failures | 144 | 6.05% | 167 | 7.10% | 127 | 6.00% |
| Tree Vegetation | 135 | 5.67% | 87 | 3.70% | 97 | 4.60% |
| Human Failures | 109 | 4.58% | 141 | 6.00% | 136 | 6.41% |
1 (ONS)
Table 2.
Statistical summary of electric discharges by census tracts.
| Parameters | Evaluated years | |||
|---|---|---|---|---|
| 2009 | 2010 | 2011 | 2012 | |
| Maximum | 39 | 26 | 40 | 39 |
| Minimum | 0 | 0 | 0 | 0 |
| Average | 2.35 | 0.79 | 1.82 | 1.80 |
| Standard deviation | 5.78 | 2.52 | 4.55 | 5.03 |
| Total number | 707 | 239 | 548 | 542 |
Table 3.
Statistical summary for the number of interruptions in transformers by census tracts.
| Parameters | Evaluated years | |||
|---|---|---|---|---|
| 2009 | 2010 | 2011 | 2012 | |
| Maximum | 42 | 21 | 27 | 13 |
| Minimum | 0 | 0 | 0 | 0 |
| Average | 3.14 | 3.55 | 3.83 | 2.08 |
| Standard deviation | 4.08 | 3.63 | 4.28 | 2.35 |
| Total number | 946 | 1069 | 1153 | 626 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated






