A Flexible FPGA-Based Stochastic Decoder for 5G LDPC codes

Sivarama Prasad Tera; Rajesh Alantattil; Roy Paily

doi:10.20944/preprints202310.1472.v1

Submitted:

21 October 2023

Posted:

24 October 2023

You are already at the latest version

Abstract

Iterative Stochastic decoding is an alternative to standard fixed-point decoding of Low-density parity check codes (LDPC) to reduce inter-node routing. In this paper, we propose a Flexible Field-Programmable Gate Array (FPGA)-Based Stochastic decoding (SD) hardware architecture for LDPC codes in the Fifth-Generation (5G) New Radio (NR) Standard that supports decoding of set of various code rates. This decoder’s runtime flexibility is desirable to switch a better performing code rate automatically based on the channel conditions without the extra time needed for reprogramming of FPGA. An offline design method is implemented to generate the hardware description language (HDL) code description of the decoder for the required code-rate set, which is further synthesized and integrated into the Xilinx Kintex-7 series FPGA board to determine the hardware resource utilisation and processing throughput. The Synopsys design tools were employed during both the simulation and synthesis stages, in combination with TSMC 65-nm CMOS standard cell technology, to facilitate comparative analysis. Compared with state-of-the-art designs, the proposed architecture reduces hardware utilization by up to 26% and achieved energy efficiency by 52%.

Keywords:

5G NR standard

;

Error correcting codes

;

Low-density parity check codes (LDPC)

;

Stochastic decoding (SD)

;

Field-Programmable Gate Array (FPGA).

Subject:

Engineering - Electrical and Electronic Engineering

1. Introduction

Low-density parity check codes (LDPC) [1] have become one of the essential channel codes in many communication standards, such as DVB-S2 [2], IEEE 802.11 (WiFi) [3], and IEEE 802.16e (WiMax) [4], including Fifth-Generation (5G) wireless technology [5], because of their higher error correction capabilities close to Shannon’s limit [6,7]. In 5G New Radio (NR) specifications, Quasi-Cyclic (QC) LDPC codes are selected as the channel coding scheme for data channels to achieve high throughput and low latency [8]. These QC LDPC codes have adopted two Base Graph Matrices (BGMs):

H_{b 1}

and

H_{b 2}

, and fifty one lifting sizes or expansion factors

z_{c}

to support various code rates [8]. The

H_{b 1}

has the dimension of 46 block rows and 68 block columns, and it supports code rates ranging from 1/3 to 8/9. The

H_{b 2}

has a dimension of 42 block rows and 52 block columns which supports code rates from 1/5 to 2/3.

The runtime flexibility of the decoder is desirable for the decoding received messages associated with different BGMs of the multiple code rates at the runtime [9]. Hence the decoder dynamically switches between a given set of LDPC code rates having diverse BGMs. This decoder has various commercial applications, such as switching to a better performing code rate automatically based on the channel conditions [10], without the extra time needed for reprogramming of FPGA. Another application is eliminating the re-synthesis of FPGA to test the performance of different code rates.

The specifications of 5G NR show that the BGM

H_{b 1}

can support a vast range of code rates from 1/3 to 8/9. The irregular degrees and diverse connections within these BGMs create a more complex routing network using traditional FPGA-based fixed-point LDPC decoders based on the Sum product algorithm (SPA) [11] and Min sum algorithm [12]. This problem is further aggravated by using multi-bit, wide-channel Logarithmic-Likelihood Ratio (LLR) messages in the decoder, which require high FPGA resources. One alternative solution is converting the channel probability values corresponding to their respective channel LLRs into stochastic bit sequence representation in Stochastic decoding (SD) [13]. This conversion helps each stochastic bit sequence need a single wire to exchange extrinsic values in a bit-wise manner between the nodes, rather than the W-wires needed for multi-bit wide LLR in conventional decoders. It significantly helps to reduce the inter-node routing complexity of the decoder [14]. The single bit-wise computations in Stochastic variable node (SVN) and Stochastic check node (SCN) units require simple logic units for the implementation. These Stochastic LDPC decoders provide error correction capability comparable to traditional fixed-point decoders [15]. The number of node-interconnects (I) of a decoder is calculated from (1) to determine the routing complexity [16].

I = 2 \times N \times e_{l} \times w_{v}

(1)

N is codeword length,

e_{l}

is extrinsic message length, and

w_{v}

is column weight. For instance, 1/3-rate codeword length

N = 3808

LDPC code having average column weight

w_{v} = 4.56

is decoded using SPA and SD. The number of node-interconnects required for SPA and SD are 138916 and 34729, respectively. The number of node-interconnects in SD is reduced by four times due to extrinsic message length

e_{l}

= 1 for SD, whereas at least

e_{l}

= 4 for fixed-point LDPC decoders using SPA.

Our Contributions:

This work’s main contribution is to propose a new partially parallel decoder architecture for Bit-wise Stochastic decoding for 5G NR standard LDPC codes. This architecture has been designed for code word length N = 3808, having code rates $R =$ 1/3, 2/5, 1/2, 2/3, 3/4, 5/6, and 8/9 for BGM1.
Our proposed automated design flow procedure enables this flexibility in design. It creates an optimal FPGA-based Stochastic LDPC decoder design for any selected code rate set. This approach helps to reduce the time needed to design hand-coded interconnections in Hardware Description Language (HDL).

This paper is structured as follows. Section 2 introduces the basic concepts of Stochastic decoding and its Algorithm. Section 3 focuses on constructing BGM of 5G NR standard QC LDPC codes suitable for Stochastic decoders. Section 4 provides architecture details. Design flow is discussed in Section 5. Section 6 discusses Simulation results. Finally, the conclusion is noted in Section 7.

2. Preliminaries

2.1. Stochastic bit sequence generation

A Stochastic approach to LDPC decoding was introduced in [17]. This decoding process converts the received channel probability values into a Stochastic bit sequence equivalent. In general, the LLR of the s-th symbol

x_{s}

of a code word is found from the s-th received channel symbol

y_{s}

at

S V N_{s}

, which is represented as

L_{c h, v_{s}}

. By considering the Binary Phase-Shift Keying (BPSK) modulation over Additive White Gaussian noise (AWGN) channel with zero mean and variance

σ^{2}

, the channel LLR computed as

L_{c h, v_{s}} = 2 \times y_{s} / σ^{2}

. The channel probability is also known as the intrinsic message, calculated as

P_{c h, v_{s}} = P (x_{s} = 1 / y_{s}) = [\frac{e x p (L_{c h, v_{s}})}{e x p (L_{c h, v_{s}}) + 1}]

(2)

The

P_{c h, v_{s}}

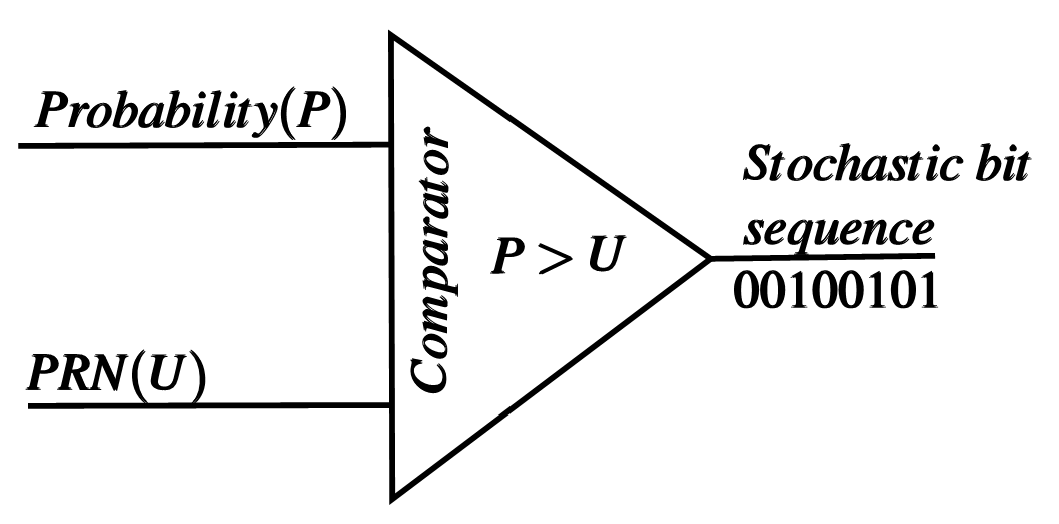
value is represented with W binary symbols and compared with W-bit Pseudo-Random Number (PRN)

U \in [0, 1]

of the Comparator[18], which varies with every clock cycle to generate the equivalent Stochastic bit sequence of length

f = 8

as shown in Figure 1. For example,

P_{c h, v_{s}} = 0.3125

is represented as

W = 4

-bit fractional binary symbols

P = 0101

. At each clock cycle, a PRN generator based on Linear Feedback Shift Register (LFSR) [19] produces a new

W = 4

-bit PRN U. Suppose

P > U

, the Comparator output at that clock cycle is 1 and otherwise 0. As shown in Table 1, after eight clock cycles, the Comparator output is 00100101, which is the Stochastic bit sequence belonging to

P_{c h, v_{s}} = 0.3125

. This sequence has a mean value of

3 / 8

, close to

P_{c h, v_{s}} = 0.3125

[20].

2.2. Stochastic decoding algorithmic description

A binary

(N, K)

LDPC code in 5G is characterized by the null space of Parity Check Matrix (PCM) H with dimension

M \times N

over GF(2). The PCM is also visualized graphically as a bipartite Tanner graph [21,22]. A set of M Parity or Check nodes of the Tanner graph representing the rows of H, and a set of N Bit or Variable nodes of the Tanner graph representing the columns of H. In Stochastic decoding of LDPC code, the Stochastic bit sequence of the channel probability values corresponds to their respective channel LLRs exchanged iteratively bitwise between the SCNs and the SVNs until the desirable codeword is found or reaches the maximum iteration limit [23]. To illustrate the simplification of the decoding process, a degree-3 SCN and a degree-3 SVN are adopted. Both SCN and SVN elements perform the bitwise Modulo-2 arithmetic operations in SD. The steps are shown in the following:

1) Initialization: Once the channel probability values are reached at SVNs, compare the W-bit fractional binary equivalent sequence of

P_{c h, v n_{j}}

with W-bit PRN U and initialize generated stochastic bit sequence to its corresponding SVNs

v n_{j}

.

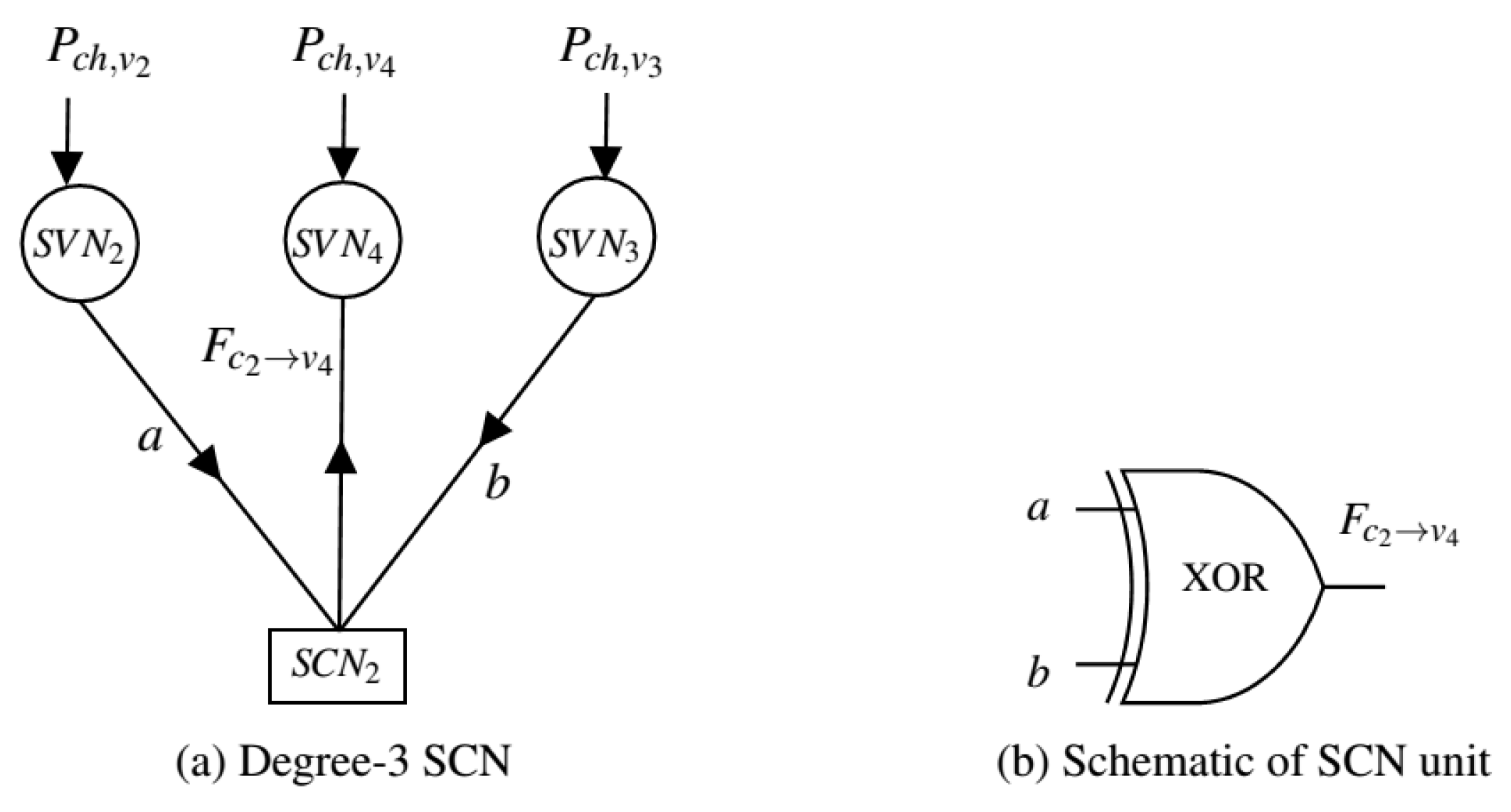
2) SCN update: As shown in Figure 2, the

{S C N}_{2}

is connected to three SVNs

{S V N}_{2}

,

{S V N}_{3}

, and

{S V N}_{4}

. The arriving SCN to SVN single-bit extrinsic message for node

{S V N}_{4}

is computed as

F_{c_{2} \to v_{4}} = a . (1 - b) + b . (1 - a)

(3)

Here a is the single-bit of stochastic bit sequence

{a [k]}

,

k = 0, \dots, f - 1

, belonging to its

P_{c h, v_{2}}

, which has been received message from

{S V N}_{2}

to

{S C N}_{2}

in previous clock cycle and b is the single-bit of stochastic sequence

{b [k]}

, belonging to its

P_{c h, v_{3}}

, which has been received message from

{S V N}_{3}

to

{S C N}_{2}

in a previous clock cycle.

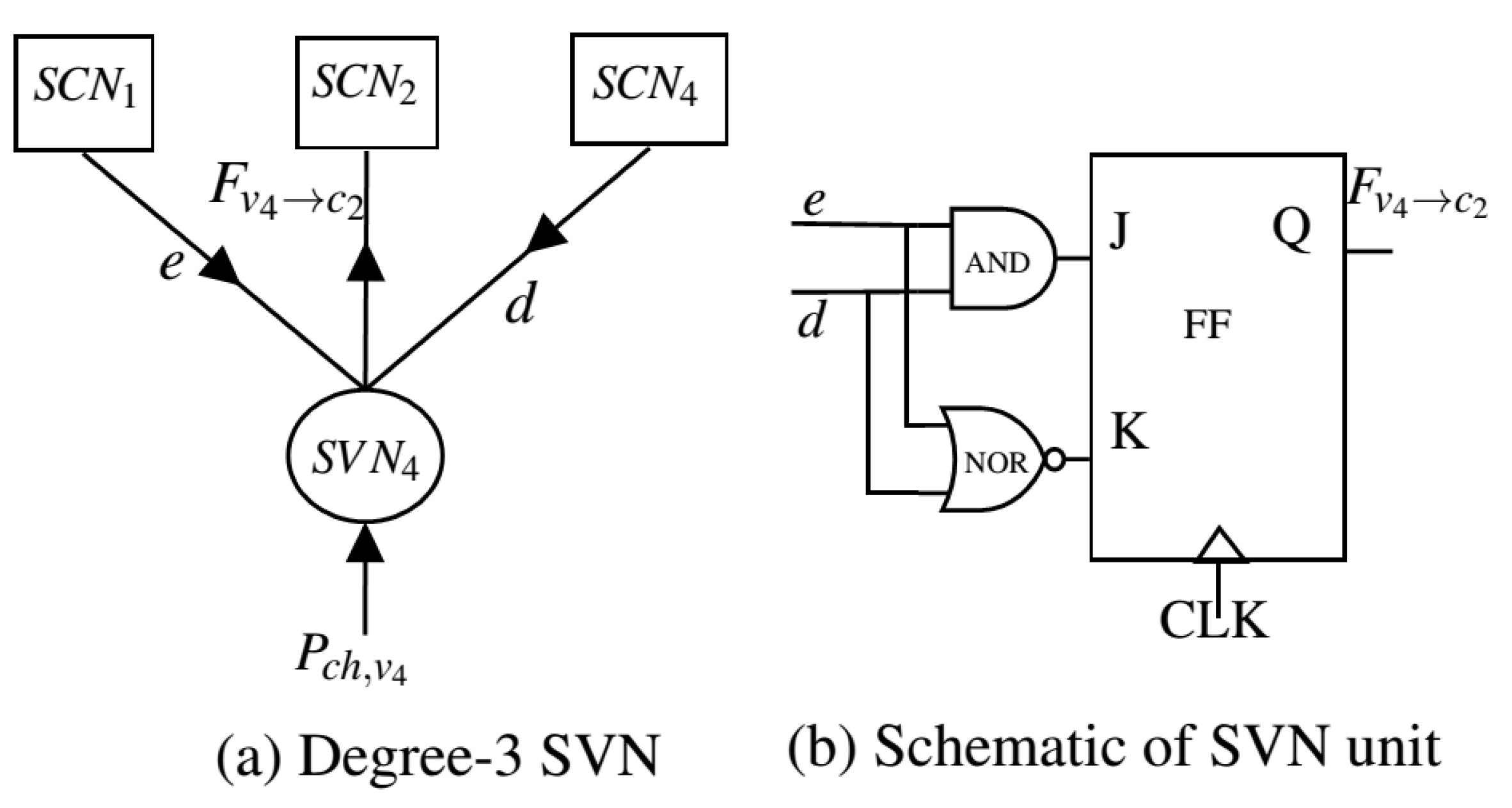
3) SVN update: In Figure 3, the

S V N_{4}

is connected to three SCNs

S C N_{1}

,

S C N_{2}

, and

S C N_{4}

. The arriving SVN to SCN single-bit extrinsic message for node

{S C N}_{2}

is computed as

F_{v_{4} \to c_{2}} = \frac{e . d}{e . d + (1 - e) . (1 - d)}

(4)

Here e is the single-bit of stochastic bit sequence

{e [k]}

, belonging to the received message from

{S C N}_{1}

to

{S V N}_{4}

in the previous clock cycle and d is the single-bit of stochastic bit sequence

{d [k]}

, belonging to the received message from

{S C N}_{4}

to

{S V N}_{4}

in a previous clock cycle.

4) Termination: This iterative process will stop if it reaches the maximum Decoding cycles (DC) limit or all parity check equations are satisfied.

3. Construction of BGM in 5G NR standard

The PCM H is represented and constructed from its BGM

H_{b}

[24]. The

H_{b}

has dimension

m_{b} \times n_{b}

, where

M = m_{b} \times z_{c}

and

N = n_{b} \times z_{c}

. The entries of

H_{b}

are expanded with

z_{c} \times z_{c}

square sub-matrix in H, where

z_{c}

is known as the lifting size or expansion factor. The entry value `-1’ of

H_{b}

is replaced by a zero matrix of dimension

z_{c} \times z_{c}

in H, and the value `0’ is replaced by the Identity matrix of dimension

z_{c} \times z_{c}

, and another non `-1’ entry value

1 \leq S_{i, j} \leq z_{c}

, also known as shift value, is replaced by circulant permutation matrix

I (S_{i, j})

. The subscripts

i, j

represent the row index and column index of the entry. The sub-matrix

I (S_{i, j})

is obtained by each row of the identity matrix having a right-shift value of

S_{i, j}

positions. The value of

S_{i, j}

is calculated from the function (5). The value of

V_{i, j}

is obtained from Tables 5.3.2-2, and 5.3.2-3 of 5G-NR standard specification 3GPP TS 38.212 [8] according to the selected BGM and the set index

i_{L S}

.

In this paper, we constructed BGM

H_{b 1}

of

(N, K)

LDPC code having a message or information block length

K = 1232

and code rate

R = K / N = 1 / 3

. The five steps are listed below for constructing the

H_{b 1}

having

k_{b}

as the length of message block columns. The terms

k_{b}

of

H_{b 1}

and K of H are related as

K = k_{b} \times z_{c}

.

Selection from the two BGMs: As per the specification of 3GPP TS 38.212 [8], since the code rate $R \geq 1 / 4$ , BGM1 is selected.
Calculate the value $k_{b}$ after selecting BGM: From the specification of 3GPP TS 38.212 [8], the BGM1 has $k_{b}$ = 22.
Find the expansion factor $z_{c}$ : The selection of the minimum $z_{c}$ from Table 5.3.2-1 [8], such that $k_{b} \times z_{c} \geq K$ . For given $K = 1232$ , $k_{b}$ = 22, $z_{c}$ is calculated as $1232 / 22 = 56$ .
Selection of set index $i_{L S}$ : After $z_{c}$ is determined, the suitable shift coefficient matrix set from Table 5.3.2-1 [8] must be selected. Since $z_{c} = 56$ , the set index $i_{L S}$ = 3 is considered.
Compute the BGM entry values: Utilize the function (5) to determine the entry values $S_{i, j}$ by means of the modular $z_{c}$ operation.

$S_{i, j} = f (V_{i, j}, z_{c}) = \{\begin{matrix} - 1, & if V_{i, j} = - 1; \\ m o d (V_{i, j}, z_{c}), & else \end{matrix}$

(5)
Construction of the PCM H: Substitute each entry of the BGM by the corresponding circulant permutation matrix or zero matrix of size $z_{c} \times z_{c}$ in H.

From the Step 5, first entry

h_{0, 0}

of

H_{b 1}

is calculated using

m o d (V_{0, 0}, z_{c})

= mod (223, 56) = 55, where the selected

V_{0, 0} = 223

value obtained from Table 5.3.2-2 [8], which correspond to row index

i = 0

, column index

j = 0

under set index

i_{L S} = 3

. Similarly, the remaining entry values are calculated by using a function (5) and

V_{i, j}

values obtained from Table 5.3.2-2 [8] based entry’s row and column indexes. The Table 2 shows calculations of the corresponding values of few entries of

H_{b 1}

. The constructed

H_{b 1}

has dimension of

46 \times 68

. The BGM

H_{b 1}

is shown in Table 4.

In order to achieve the desired information lengths and rate adaptation in 5G NR QC-LDPC codes, a process of shortening and puncturing is carried out. The characteristics of the BGM1 are described in the Table 3.

Table 3. Parameters of BGM1.

Characteristics	BGM1 ( $H_{b 1}$ )
Number block columns ( $n_{b}$ )	68
Number block rows ( $m_{b}$ )	46
Number edges	316
Column weights ( $w_{v}$ )	1 to 30
Row weights ( $w_{c}$ )	3 to 19
Base code rate	1/3

Table 4. Base Graph Matrix

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	......	65	66	67
0	55	16	38	35	-1	18	10	-1	-1	0	37	48	21	47	-1	14	14	-1	29	30	48	25	1	0	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
1	29	-1	45	39	46	7	-1	45	21	31	-1	38	37	-1	23	9	6	26	-1	31	-1	19	0	0	0	-1	-1	-1	-1	-1	......	-1	-1	-1
2	39	35	31	-1	8	12	18	39	41	9	14	-1	-1	21	46	21	-1	30	5	55	34	-1	-1	-1	0	0	-1	-1	-1	-1	......	-1	-1	-1
3	33	18	-1	53	5	-1	45	30	16	-1	34	43	45	35	13	-1	40	18	43	-1	30	46	1	-1	-1	0	-1	-1	-1	-1	......	-1	-1	-1
4	2	10	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	0	-1	-1	-1	......	-1	-1	-1
5	52	3	-1	30	-1	-1	-1	-1	-1	-1	-1	-1	24	-1	-1	-1	14	-1	-1	-1	-1	18	41	-1	-1	-1	-1	0	-1	-1	......	-1	-1	-1
6	46	-1	-1	-1	-1	-1	7	-1	-1	-1	-1	21	-1	7	-1	-1	-1	51	24	-1	4	-1	-1	-1	-1	-1	-1	-1	0	-1	......	-1	-1	-1
7	17	20	-1	-1	48	-1	-1	44	38	-1	-1	-1	-1	-1	46	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	0	......	-1	-1	-1
8	33	39	-1	4	-1	-1	-1	-1	-1	-1	-1	-1	49	-1	-1	-1	36	-1	-1	39	-1	2	44	-1	33	-1	-1	-1	-1	-1	......	-1	-1	-1
9	9	37	-1	-1	-1	-1	-1	-1	-1	-1	45	49	-1	33	-1	-1	-1	17	53	-1	50	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
10	-1	26	53	-1	6	-1	-1	19	26	-1	-1	-1	-1	-1	47	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
11	52	11	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	2	-1	-1	-1	35	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
12	30	7	-1	-1	-1	-1	-1	-1	-1	-1	24	3	-1	28	-1	-1	-1	-1	14	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
13	25	-1	-1	0	-1	-1	-1	16	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	49	-1	-1	22	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
14	14	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	7	-1	-1	43	23	51	-1	-1	-1	43	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
15	34	8	-1	-1	-1	-1	-1	-1	-1	-1	19	-1	-1	41	-1	-1	-1	-1	41	-1	-1	-1	-1	-1	-1	25	-1	-1	-1	-1	......	-1	-1	-1
16	-1	42	-1	52	-1	-1	-1	-1	-1	-1	-1	43	-1	-1	-1	-1	-1	-1	-1	-1	21	-1	45	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
17	0	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	54	-1	32	7	-1	-1	-1	4	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
18	-1	31	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	54	32	-1	-1	-1	-1	31	18	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
19	8	6	-1	-1	-1	-1	-1	47	30	-1	8	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
20	49	-1	-1	42	-1	-1	-1	-1	-1	9	-1	46	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	15	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
21	-1	24	-1	-1	-1	19	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	52	-1	-1	-1	50	50	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
22	53	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	0	3	-1	-1	-1	36	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
23	-1	32	35	-1	-1	-1	-1	-1	-1	-1	0	-1	-1	-1	-1	-1	-1	-1	10	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
24	49	-1	-1	45	8	-1	-1	-1	-1	-1	-1	25	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	12	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
25	-1	1	-1	-1	-1	-1	54	9	-1	-1	-1	-1	-1	-1	25	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
26	51	-1	8	-1	44	-1	-1	-1	-1	15	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
27	-1	40	-1	-1	-1	-1	29	-1	6	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
28	34	-1	-1	-1	41	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	49	-1	2	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
29	-1	38	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	11	-1	-1	-1	53	-1	-1	2	-1	-1	-1	12	-1	-1	-1	-1	......	-1	-1	-1
30	34	-1	-1	-1	-1	-1	-1	-1	-1	-1	18	-1	-1	42	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
31	-1	7	-1	-1	-1	-1	-1	49	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	9	-1	-1	16	-1	-1	-1	-1	......	-1	-1	-1
32	24	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	41	-1	2	-1	-1	-1	-1	-1	-1	-1	-1	-1	30	-1	-1	-1	-1	-1	......	-1	-1	-1
33	-1	2	49	-1	-1	-1	-1	-1	-1	-1	-1	49	-1	-1	-1	-1	-1	-1	-1	-1	-1	25	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
34	26	-1	-1	-1	-1	-1	-1	18	-1	-1	-1	-1	-1	-1	-1	12	-1	38	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
35	-1	24	-1	-1	-1	-1	5	-1	-1	-1	-1	-1	26	-1	-1	-1	-1	-1	-1	-1	-1	-1	19	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
36	54	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	45	0	-1	-1	6	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
37	-1	25	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	27	-1	-1	-1	-1	-1	-1	-1	-1	-1	26	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
38	11	-1	-1	-1	-1	-1	-1	-1	-1	34	17	-1	10	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
39	-1	12	-1	21	-1	-1	-1	49	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	2	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
40	11	-1	-1	-1	-1	-1	-1	-1	45	-1	-1	-1	-1	-1	-1	-1	-1	40	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
41	-1	23	-1	47	-1	-1	-1	-1	-1	4	-1	-1	-1	-1	-1	-1	-1	-1	55	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
42	2	-1	-1	-1	35	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	22	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
43	-1	38	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	22	-1	22	-1	-1	-1	-1	-1	-1	49	-1	-1	-1	-1	......	-1	-1	-1
44	28	-1	-1	-1	-1	-1	-1	4	-1	9	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	12	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1
45	-1	16	-1	-1	-1	-1	9	-1	-1	-1	29	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	......	-1	-1	-1

4. Proposed architecture

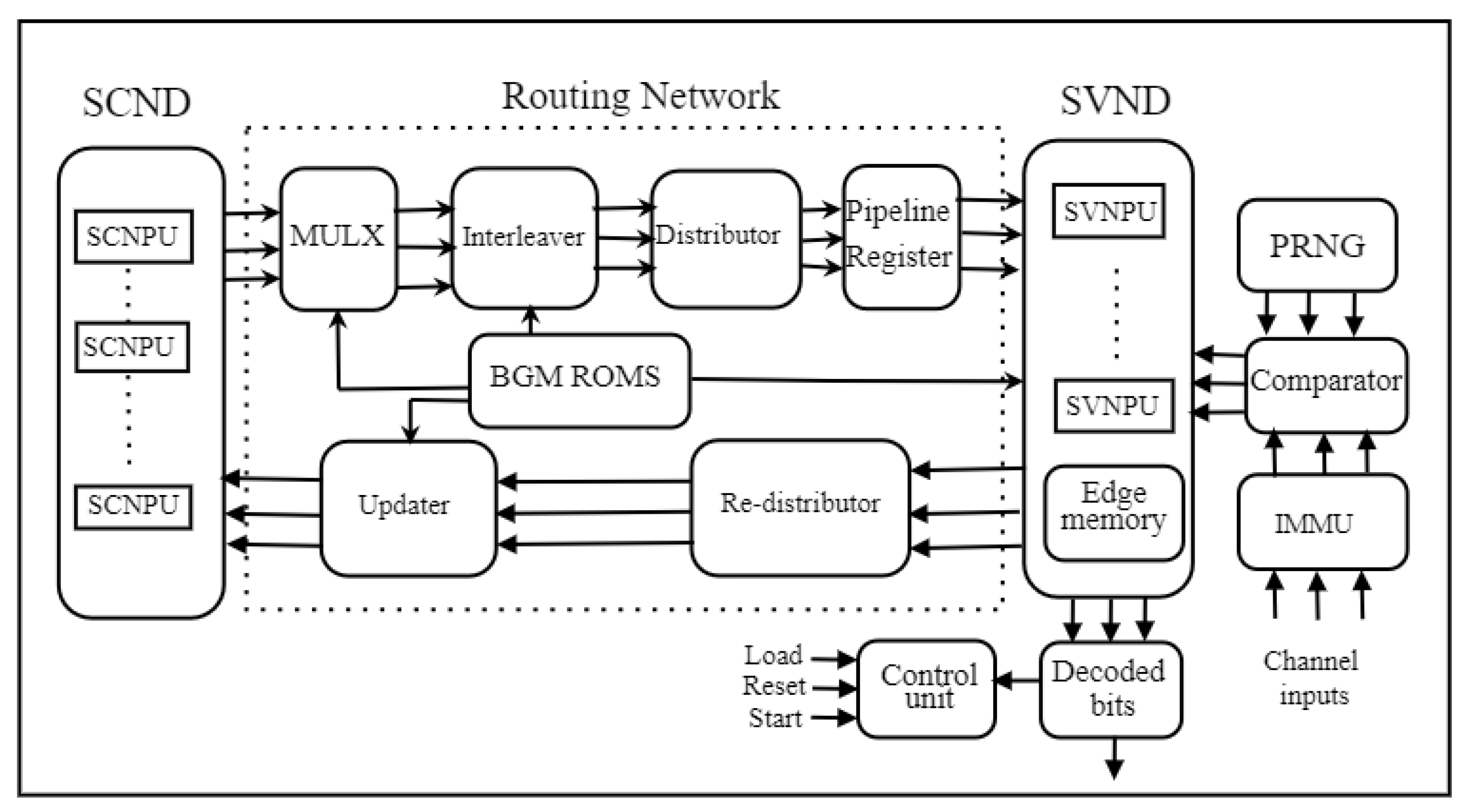
The suggested FPGA-based partially parallel Stochastic decoder’s top-level design presents in this section. It has runtime flexibility and the capability of decoding the received messages corresponding to the set of seven code rates

R =

1/3, 2/5, 1/2, 2/3, 3/4, 5/6, and 8/9 of codeword length N = 3808 QC LDPC code compliant to 5G NR standard. Initially, the architecture determines the maximum matrix dimensions, such as the number of block columns

N_{B} = 68

, the number of block rows

M_{B} = 46

, lifting size

Z_{c} = 56

, column-weight

W_{v} = 30

, and row-weight

W_{c} = 19

, for this decoder from the supported code rate set. The architecture comprises various basic modules such as Stochastic Variable Node Decoder (SVND), Stochastic Check Node Decoder (SCND), BGM Read-Only Memory (ROM), Controller unit, Intrinsic Message Memory Unit (IMMU), and Routing network between modules SVND and SCND. These modules of the design are explained in the following subsections.

4.1. Layered decoding schedule

In partially-parallel architectures, only a few SVNs and SCNs are instantiated simultaneously. Figure 4 shows the proposed architecture that connects the SCND to the SVND. The SCND consists of M D Flip-Flops, used as memories to store updated SCN messages received from SVND. Here, M is the total number of SCNs of the Tanner graph of the decoded LDPC code. The architecture adopted Shuffled iterative decoding [25], in which the total number of block-columns of the BGM is subdivided into vertical layers, each layer consists of one block column of BGM or

η_{v}

columns of the PCM, where

η_{v}

is the SVN parallelism factor, these columns are mapped as SVNs of the Tanner graph of the decoded LDPC code. Before the next vertical layer is processed, the SVNs of each layer are processed in parallel, and the results are used to update the connected SCNs. Using this scheduling, the 3808 columns of the 1/3-rate codeword length

N = 3808

LDPC code PCM are divided into

N_{B} = 68

vertical layers, each layer consists of

η_{v} = 56

columns. Accordingly, the proposed decoder has a SVND, which comprises

η_{v} = 56

Stochastic variable node processing units (SVNPU), which function based on SVN update. These units process a layer of

η_{v} = 56

columns of the PCM during each clock cycle, with these updated values being written back to SCND immediately. Hence each Decoding cycle (DC) require

τ_{D} = N_{B} = 68

clock cycles. Each DC creates one new bit in each stochastic bit sequence.

4.2. BGM ROMs

It is possible to regulate the routing and shifting of intrinsic and extrinsic messages between the routing network, SVNPUs and SCNPUs by employing a set of ROM blocks that hold the location and shift values of non `-1’ entries of each BGM in a hardware-optimized form: the three ROMs, namely ROM1-location, ROM2-shift, and ROM3-weight. Firstly, the row indices of all non `-1’ entries within each block column of BGM are represented by the values in the ROM1-location. Second, ROM2-shift saves the shift value difference between each non `-1’ entry in each block column and the previous non `-1’ entry in the same block row. This value can be determined at design time and saved as described. Lastly, each block column of BGM’s weight is stored in the ROM3-weight. For the proposed architecture, all three ROMs contain

N_{b} = 68

locations, each with

W_{v} = 30

values i.e.,

N_{b} \times W_{v} = 2040

locations.

4.3. Routing network

The Routing network carries the single-bit SCN to SVN messages from the SCND registers to the

η_{v} = 56

SVNPUs in the SVND, which are updated and sent back to the SCND. This routing network combines separate modules called Multiplexer (MULX), Interleaver, Distributor, Re-distributor, and Updater. The functions of these blocks are explained later in this section. The maximum number of SCN to SVN message inputs needed for any SVNPU at any time is

W_{v}

= 30, the maximum number of non `-1’ entries in any block column within the allowed code rate set.

4.3.1. Multiplexer

Using the row-index values kept in the ROM1-location, the MULX unit chooses

W_{v} = 30

blocks of

Z_{c} = 56

bits from the SCND. However, instead of connecting each input to each output, this module requires fewer hardware resources by adopting the method of storing ROM1-location row index values in ascending order [27]. For instance, the block column of any BGM has weight

w_{v}

, such that

w_{v} \leq W_{v}

. Out of the total

W_{v}

values of ROM1-location arranged with top

w_{v}

block row indices of the non `-1’ entries in that block column in ascending order, while remaining

W_{v} - w_{v}

values are empty data. The multiplexer designed to support the seven LDPC BGMs of the allowed code rate set having maximum column weight

W_{v} = 30

requires 210 connections. By using this method [27], the number of connections decreased to 39%.

4.3.2. Interleaver

The

W_{v} = 30

MULX output blocks from the SCND are cyclically shifted by

W_{v} = 30

parallel Barrel Shifters in the Interleaver module based on shift values stored in ROM2-shift. Before being read by the SVND, a group of

η_{v} = 56

messages of sub matrix must be converted from a row-centric to a column-centric representation based on the corresponding shift value in BGM

H_{b 1}

by a Barrel shifter. Each Barrel shifter has

Z_{c} = 56

inputs and outputs because the shift value can be any integer between 0 and

Z_{c} = 56

. The hardware description language (HDL) used for the BSs integrated with the proposed flexible decoder architecture is customised for the supported BGMs during the design phase. The choice of multiplexer input for every BGM is influenced by the expansion factor

Z_{c} = 56

value linked to the corresponding BGM, based on the cyclic shift decomposition algorithm mentioned in [26].

4.3.3. Distributor and Re-distributor

The distributor takes

W_{v}

= 30 blocks of

η_{v} = 56

bits from SCND and performs a rearrangement process to form

η_{v} = 56

blocks of

W_{v}

= 30 bits. The pipeline registers may optionally latch these blocks before the SVND processes them. After undergoing SVND processing, the resulting

η_{v} = 56

blocks of

W_{v}

= 30 bits are again subjected to a similar rearrangement process by the Re-distributor to form

W_{v}

= 30 blocks of

η_{v} = 56

bits.

4.3.4. Pipeline registers

Stochastic layered decoding involves binary operations, causing each layer’s message updates to either alter or leave prior layer updates unchanged. The decoding schedule needs to store updates from each previous layer before moving on to the next. Adding a single pipeline stage to the suggested architecture can sometimes improve BER performance without negatively impacting the decoding process. In some BGMs, a column-wise permutation occurs, allowing for column-orthogonality in block columns. Adding a pipeline stage during the data path does not negatively impact decoding performance when processed in this order [27]. If a permutation is not found, introducing a few

τ

vacant stall layers among non-orthogonal columns can be developed. Finding the necessary minimum values of

τ

for each BGM and adding this supplementary pipeline stage is advantageous. Decreased block rows while keeping block columns constant can enhance coding rate. Simulations show that high-rate codes require more

τ

vacant stall layers among non-orthogonal columns compared to low-rate codes.

4.3.5. Updater

Using the values from the ROM1-location, this component transfers these

W_{v}

= 30 blocks of

η_{v} = 56

bits back into the SCND at the proper location. Moreover, the ROM3-weight is utilized in this case to guarantee that just the most recent

W_{v}

values are written, removing any potential interference from non `-1’ entries or "don’t care" data. As D-Flip Flops are being used to implement the SCND, each layer can be written right away.

4.4. Stochastic variable node decoder (SVND)

The SVND module contains

η_{v} = 56

parallel Stochastic variable node processing units (SVNPU). These SVNPUs can process one block column of the BGM

H_{b 1}

. Hence each SVNPU process one column of the PCM. Each SVNPU has multiple inputs and outputs equal to

W_{v} + 1

, where

W_{v}

is the highest column weight among the supported BGM code-rate set. The extra input and output are utilized, respectively, for channel-intrinsic messages and the estimation of the decoded bit. It is essential to consider that this largest number of inputs and outputs must be taken into account to guarantee that each SVNPU can decode any arbitrary column-weight column in the code-rate set. The SVND accepts the maximum SVN weight

W_{v} = 30

input bits from the connected SCNs, and an intrinsic bit from the Intrinsic Message Memory unit (IMMU). By considering such values, SVND implements the SVN update operation and the updated extrinsic values sent to the corresponding SCNPUs.

4.4.1. Stochastic variable node processing unit (SVNPU)

In this Stochastic architecture, the chance of SVNPU output being in the Hold state increases as inputs of SVNPU increase [20]. The SVNPU forces the current output to continuously repeat the previous output over a certain period when the two input bits of the SVNPU are not equal, known as the Hold state of SVNPU [23]. Due to this state, the decoder is unable to make correct decisions. It interrupts the decoder convergence and its Bit Error Rate (BER) performance degradation. Hence, the architecture of high column-weight SVNPU is built using low-weight sub-nodes with memory blocks; typically,

w_{v} \leq 4

sub-nodes are employed.

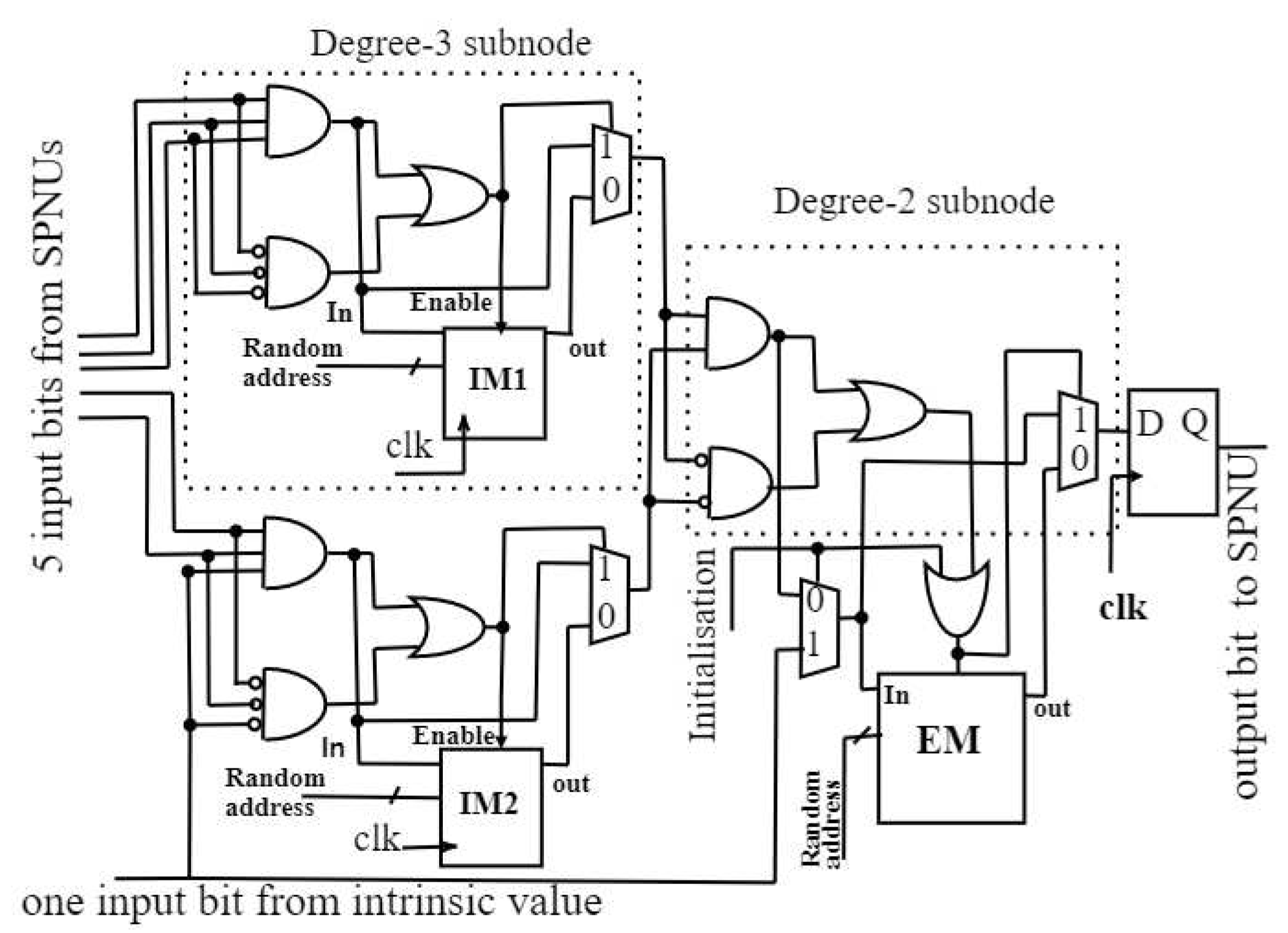
As shown in Figure 5, the column-weight

w_{v} = 6

SVNPU is constructed using two column -weight

w_{v} = 3

and one

w_{v} = 2

sub-nodes. The memory blocks are Internal memory (IM) which has a length of

I = 2

bits for each sub-node, and Edge memory (EM) has a length of

E = 64

bits at the output edge. The critical role of EMs and IMs is to minimize the correlation produced by the Hold state in a stochastic sequence and disrupt the correlation of stochastic sequence by randomizing stochastic bits [28]. We used a dual-tree design [27] to build a high column-weight SVNPU that would be flexible enough to handle any active inputs and outputs up to the maximum

λ = W_{v} + 1

, which is a power of 2. For instance, column weight

W_{v} = 30

of SVNPU has

λ = 32

inputs and outputs. As a result, the adopted SVNPU dual-tree design requires a total of

S = 3 \times λ - 6 = 90

sub-nodes. Two significant components, summing and combining, each with

t = {log}_{2} (λ) - 1 = 4

stages, make up the dual-tree structure.

4.5. Control unit

The Control unit of the decoder manages internal and external control signals, including to stop or proceed with the iterative decoding. A new group of

η_{v} \times w

- bit intrinsic probabilities may need to be loaded into the IMMU, and this can be indicated by the LOAD signal. The decoder must decode a new frame, and all modules must be reset to their default conditions using the RESET signal. The ability of the proposed architecture to swap the current BGM to decode the message contained in the IMMU during a single clock cycle is one of its essential characteristics. The supporting BGMs are parameterized in ROMs at compile-time to enable this flexibility level. The process of decoding is started and maintained by the START signal. As long as this signal is active, the decoder will keep doing iterative decoding; the decoding operation is stopped once it does.

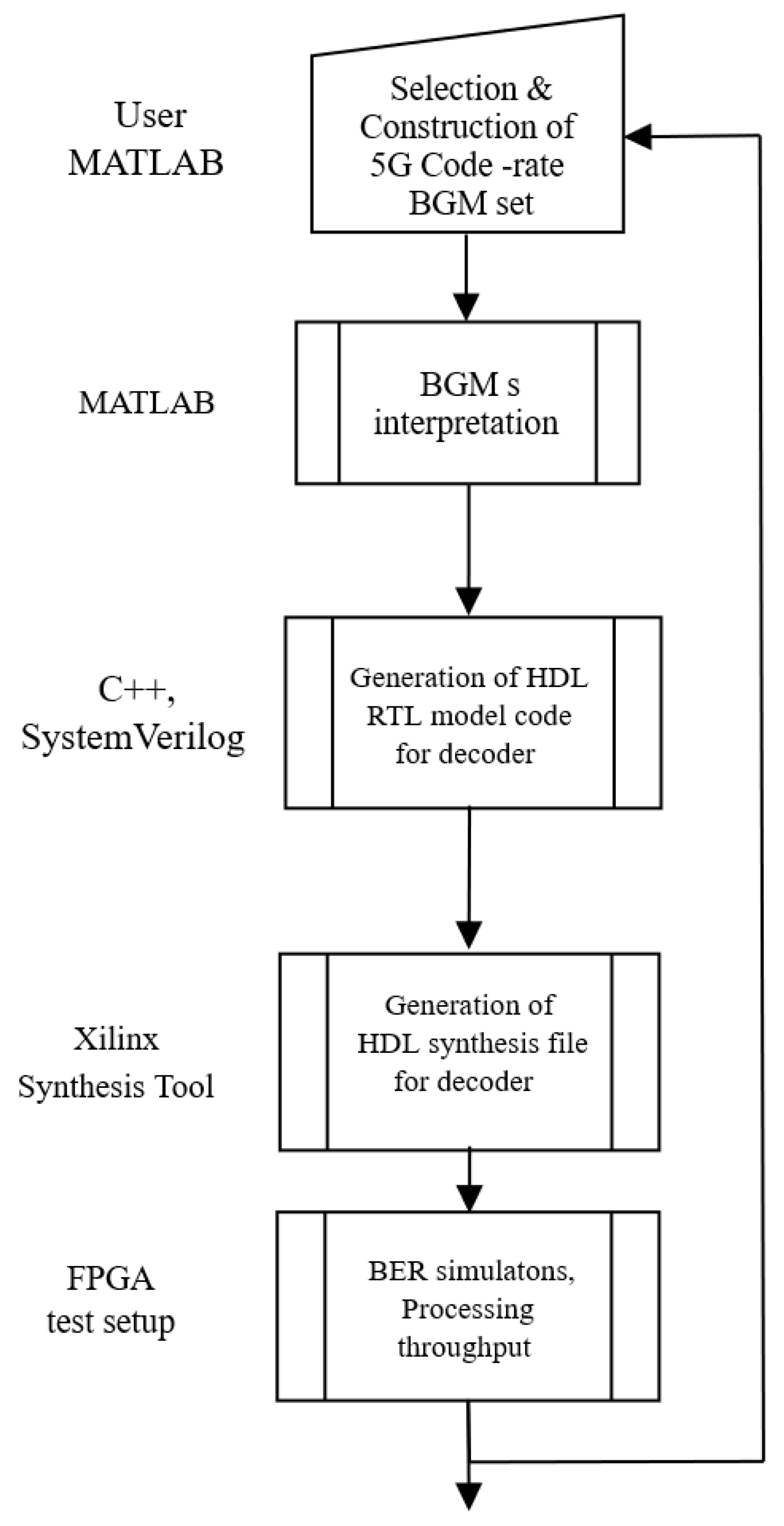
5. Design flow

This section outlines the suggested design flow, which enables the automated flexibility in design and creates an optimal FPGA-based Stochastic LDPC decoder for a selected set of 5G QC LDPC codes. The flow chart in Figure 6 depicts the design flow. In the first step, the Construction of the required code-rate BGM set is based on the user inputs like message length, code rate, and lifting sizes of the 5G LDPC code. The second step has two tasks: Determining the decoder’s parameters, such as the maximum of the matrix dimensions and weights, namely

N_{b}

,

M_{b}

,

Z_{c}

,

W_{v}

, and

W_{c}

, respectively, which describe the chosen set of supported BGMs. Based on lifting size

Z_{c}

, it is possible to determine the parallelism factor

η_{v}

from these. For

N = 3808

LDPC code-rate set, the maximum values are

N_{b} = 68

,

M_{b} = 46

,

Z_{c} = 56

,

W_{v} = 30

, and

W_{c} = 19

. Another task is extracting the positions and shift values of the non `-1’ entries in each BGM and arranging them consistent with the ROMs. Considering the parameters derived in the earlier step, the design flow utilizes High-Level Synthesis (HLS) tool [29] to produce the Hardware Description Language (HDL) SystemVerilog code for the suggested architecture written in the High-level language C++. After the Register Transfer Level (RTL) modelling of the decoder, it is synthesized using Xilinx Synthesis Tool to measure the hardware requirements of the decoder. The Bit Error Rate (BER) simulations have been implemented on the FPGA test setup.

6. Implementation results and discussion

6.1. Approach

After the offline design method is completed, the HDL code description of the decoder for the required code-rate set is generated, which is further synthesized and integrated into the Xilinx Kintex-7 XC7K160T series FPGA board to determine the hardware resource utilisation and processing throughput. An additional parameter that is measured is the transmission energy efficiency of the synthesized decoder in terms of the channel’s signal-to-noise power ratio per bit

E_{b} / N_{o}

at a required BER of

10^{- 6}

for each target BGM. Simulations are carried out to evaluate the transmission energy efficiency of the synthesized decoder. The simulations entail a minimum of 100 frame errors per BER measurement and a maximum of 600 DCs per frame.

The intrinsic channel LLRs serve as input to the decoder module of the FPGA board, which is received via the RS232 port of the computer. In order to facilitate communication with the computer, an RS232 transceiver module has been designed. The MATLAB environment in the computer is utilised to send and receive the same set of decoded LLRs after completing the decoding process on FPGA. Subsequently, MATLAB compares the input and output LLRs of FPGA and estimates the BER performance.

6.2. Results

In order to analyse the performance of the proposed decoder, we consider three parameters: BER performance, Hardware utilisation, and Processing throughput.

6.2.1. BER performance

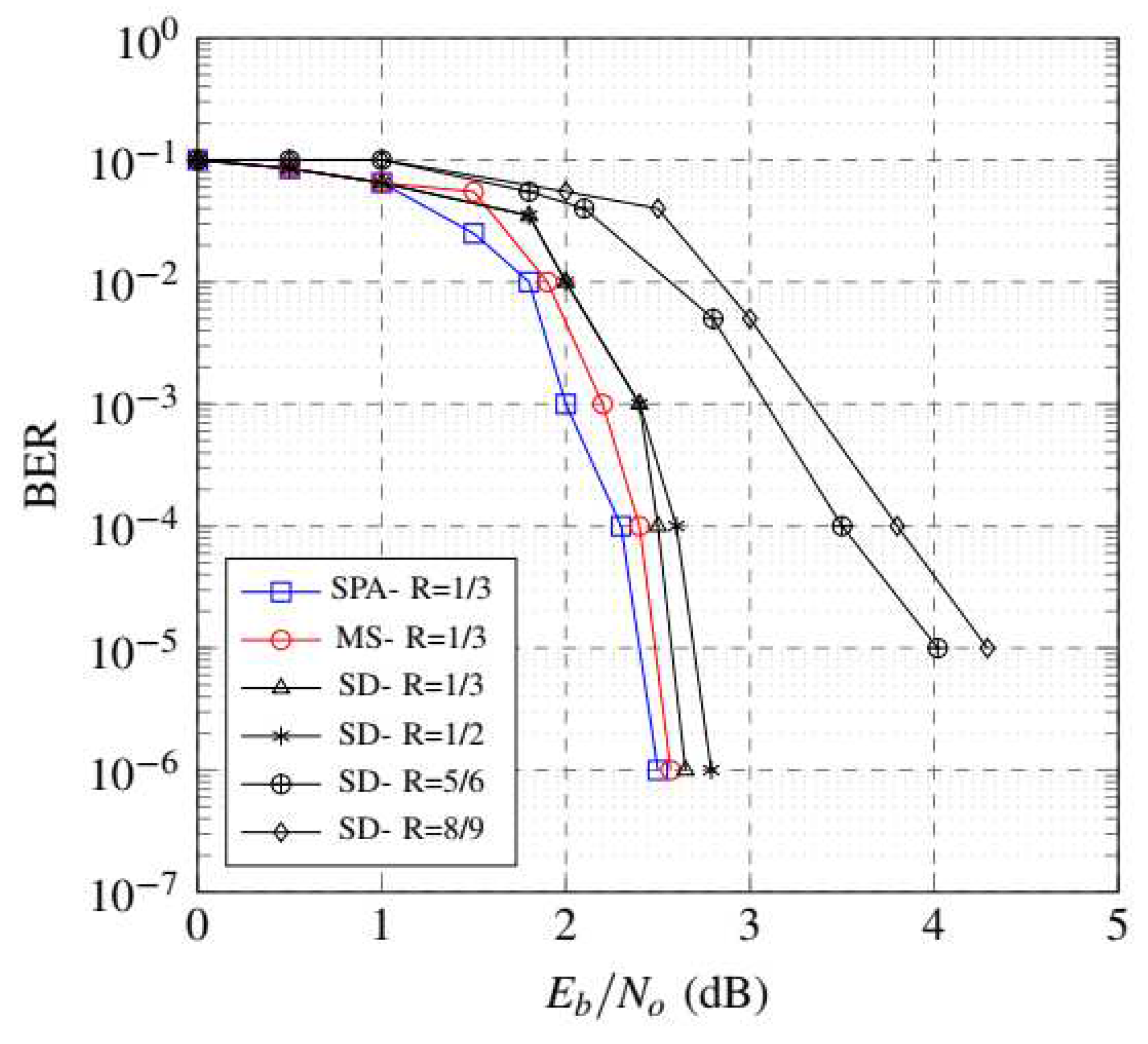
Figure 7 shows BER performance of the proposed decoder which delivers BER =

10^{- 6}

at 2.65 dB of

E_{b} / N_{o}

for block length of 3808 with base code rate of 1/3. It has been observed that SD provides approximately nearer error correction performance compared with the conventional Sum-product (SPA) and Min-sum (MS) algorithms. Notably, decoding iterations of SD require more clock cycles than conventional designs. Additionally, it has been observed that applying noise-dependent scaling of 0.86 [28] to the received channel probabilities improves performance for lower code rates such as 1/3 and 2/5. Conversely, this performance declines for higher code rates such as 5/6 and 8/9.

6.2.2. Hardware utilisation

The proposed design’s advantage lies in the significant reduction of decoder complexity. Table 5 compares the suggested design and the min-sum-based decoder architectures, indicating that the former requires less hardware by approximately 37%. A crucial parameter that affects the decoder’s area and routing complexity is the number of interconnecting wires between its nodes. In this regard, the suggested design outperforms the Min-sum-based decoder by requiring 34729 fewer interconnect wires. Other parameters of the suggested design are comparable to those of the Min-sum-based decoder. The results in Table 6 indicate that the increase in coding rate significantly impacts the SD decoder’s decoded processing throughput. However, at the same time, it negatively affects the error correction performance.

6.2.3. Processing throughput

The proposed architecture requires a reduction in hardware resources, although at a considerably lower processing throughput expense. This lower throughput of Stochastic decoders is due to the high number of Decoding cycles (DC) needed to reach a correct code word. Due to the high number of DCs and partially parallel decoder architecture, the problem is made worse by the fact that each DC requires many clock cycles, which reduces decoding throughput. The SD architecture requires maximum 620 DCs per frame, and each decoding cycle necessitates 68 clock cycles for code length

N = 3808

. Table 5 compares both designs and concludes that the processing throughput of the SD design is about 38% lower than that of the Min-sum design. Table 6 demonstrates that an increase in code rate results in a concurrent increase in processing throughput.

6.3. Comparative analysis

To facilitate a comparative analysis, the Verilog hardware description language (HDL) was employed to model the architecture. It was subsequently subjected to simulation to verify its functionality using a test pattern generated from a C++ simulator. The design functions were verified successfully, following which the architecture was synthesized while adhering to suitable time and area constraints. The Synopsys design tools were employed during both the simulation and synthesis stages, in combination with TSMC 65-nm CMOS standard cell technology. The results obtained post-synthesis are presented in Table 7. Specifically, the proposed SD architecture occupies an area of 1.10

m m^{2}

and achieves a throughput of 1.12 Gbps, while the power consumption is 410 mW.

The comparison of the proposed SD with other LDPC decoders is provided in Table 7, considering implementation and performance. The proposed design has been shown to reduce the decoder architecture’s complexity significantly. These designs exhibit varying implementation parameters, including code length and decoding algorithms such as Combined Min-Sum (CMS) and Normalised Min-Sum (NMS). Compared to the reported decoders, the proposed architecture exhibits area efficiency by 26% compared to [31] while delivering energy efficiency by 52% compared to [32].

7. Conclusions

In this paper, we constructed BGM of QC LDPC code of 5G NR standard. We presented Stochastic decoding to LDPC codes as a hardware-efficient alternative to SPA and MS -based LDPC decoders. From simulations, it has been observed that with the inclusion of features like Scaling and Edge memory, Stochastic decoding performs almost nearer to SPA-based LDPC decoder in terms of BER performance.

References

R. G. Gallager, “Low-density parity-check codes.” IRE Transactions on information theory 8, no. 1 (1962): 21-28.
ETSI, “ETSI EN 302 307 v1.3.1 Digital Video Broadcasting (DVB); Second generation,” 2013.
IEEE 802.11n-2009, “Standard for Information technology-Local and metropolitan area networks-Specific requirements-Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications,” 2009.
IEEE 802.16-2004, “Standard for Local and Metropolitan Area Networks - Part 16: Air Interface for Fixed Broadband Wireless Access Systems,” 2004.
3GPP, “R1-1611081 Final Report,” in 3GPP TSG RAN WG1 Meeting 86bis, Lisbon, Portugal, Oct 2016, pp. 83-89.
D. J. C. MacKay and R. M. Neal, “Near Shannon limit performance of low-density parity-check codes,” Electronics Letters, vol. 32, no. 18, pp. 1645–1646, Aug. 1996.
Chung, Sae-Young, G. David Forney, Thomas J. Richardson, and Rudiger Urbanke. “On the design of low-density parity-check codes within 0.0045 dB of the Shannon limit.” IEEE Communications letters 5, no. 2 (2001): 58-60.
Ad-Hoc chair (Nokia). Chairman’s Notes of Agenda Item 7.1.4. Channel Coding. 3GPP TSG RAN WG1 Meeting AH 2, R1-1711982 (2017), /: Online: https.
P. Hailes, L. P. Hailes, L. Xu, R. G. Maunder, B. M. Al-Hashimi and L. Hanzo, “A Flexible FPGA-Based Quasi-Cyclic LDPC Decoder,” in IEEE Access, vol. 5, pp. 20965-20984, 2017.
C. Zhang, Z. C. Zhang, Z. Wang, J. Sha, L. Li and J. Lin, “Flexible LDPC Decoder Design for Multigigabit-per-Second Applications,” in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 57, no. 1, pp. 116-124, Jan. 2010.
Kschischang, Frank R., Brendan J. Frey, and H-A. Loeliger. “Factor graphs and the sum-product algorithm.” IEEE Transactions on information theory vol.47, no. 2 (2001): 498-519.
Angarita, Fabian, Javier Valls, Vicenc Almenar, and Vicente Torres. “Reduced-complexity min-sum algorithm for decoding LDPC codes with low error-floor.” IEEE Transactions on Circuits and Systems I: Regular Papers 61, no. 7 (2014): 2150-2158.
V. C. Gaudet and A. C. Rapley, “Iterative decoding using stochastic computation,” in Electronics Letters, vol. 39, no. 3, pp. 299–301, 2003.
J. P. Hayes, “Introduction to Stochastic Computing and its Challenges,” in Proceedings of the 52nd Annual Design Automation Conference, San Francisco, CA, USA, Jun 2015, pp. 2-4.
Lee, Xin-Ru, Chih-Lung Chen, Hsie-Chia Chang, and Chen-Yi Lee, “A 7.92 Gb/s 437.2 mW Stochastic LDPC Decoder Chip for IEEE 802.15.3c Applications,” in IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 62, no. 2, pp. 507-516, Feb. 2015.
Chandrasetty, Vikram, and Sayed Mahfuzul Aziz. “ Resource efficient LDPC decoders: from algorithms to hardware architectures”. Academic Press.
Gross, Warren J., Vincent C. Gaudet, and Aaron Milner. “Stochastic implementation of LDPC decoders.” in Conference Record of the Thirty-Ninth Asilomar Conference on Signals, Systems, and Computers, 2005, pp. 713-717, IEEE.
D. Zhang and H. Li, “A Stochastic-Based FPGA Controller for an Induction Motor Drive With Integrated Neural Network Algorithms,” in IEEE Transactions on Industrial Electronics, vol. 55, no. 2, pp. 551-561, Feb. 2008.
Dinu, A., M. N. Cirstea, and M. McCormick. “Stochastic implementation of motor controllers.” In Industrial Electronics, 2002. ISIE 2002. Proceedings of the 2002 IEEE International Symposium on, vol. 2, pp. 639-644. IEEE, 2002.
S. S. Tehrani, Shie Mannor, and W. J. Gross, “ Fully Parallel Stochastic LDPC decoders,” IEEE Transactions on Signal Processing, vol.56, no.11, Nov.2008.
R. M. Tanner, “A recursive approach to low complexity codes,” IEEE Transactions on Information Theory, vol. 27, no. 5, pp. 533–547, 1981.
Wiberg, Niclas. “Codes and decoding on general graphs.” Citeseer (1996).
Winstead, Chris, Vincent C. Gaudet, Anthony Rapley, and Christian Schlegel. “Stochastic iterative decoders.” In Proceedings. International Symposium on Information Theory, 2005. ISIT 2005., pp. 1116-1120, IEEE, 2005.
Fossorier, Marc PC. “Quasi cyclic low-density parity-check codes from circulant permutation matrices.” IEEE Transactions on information theory, vol. 50, no. 8, pp. 1788–1793, Aug. 2004.
Juntan Zhang and M. P., C. Fossorier, “Shuffled iterative decoding,” IEEE Transactions on Communications, vol. 53, no. 2, pp. 209-213, Feb. 2005.
Y. Jung, Y. Y. Jung, Y. Jung, S. Lee, and J. Kim, “Low-complexity multi-way and re-configurable cyclic shift network of QC-LDPC decoder for Wi-Fi/WIMAX applications,” IEEE Transactions on Consumer Electronics, vol. 59, no. 3, pp. 467-475, 2013.
Peter Hailes, “Design and implementation of flexible FPGA-based LDPC decoders,” UNIVERSITY OF SOUTHAMPTON, 2018.
S. Sharifi Tehrani, W. J. S. Sharifi Tehrani, W. J. Gross and S. Mannor, “Stochastic decoding of LDPC codes,” IEEE Communications Letters, vol. 10, no. 10, pp. 716-718, Oct. 2006.
R. Nane et al, “ A Survey and Evaluation of FPGA High-Level Synthesis Tools,” IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 35, no. 10, pp. 1591-1604, Oct. 2016.
Xilinx. 7 Series FPGA Configurable Logic Block User Guide—UG474. 2014.
Thi Bao Nguyen, Tram, Tuy Nguyen Tan, and Hanho Lee, “ Low-complexity high-throughput QC-LDPC decoder for 5G new radio wireless communication.,” Electronics 10, no. 4 (2021): 516.
Zhang, Kai, Xinming Huang, and Zhongfeng Wang, “ High-throughput layered decoder implementation for quasi-cyclic LDPC codes,” IEEE Journal on Selected Areas in Communications, 2009 ;27(6) : 985-94. 28 July.

Figure 1. Schematic of Comparator.

Figure 2. SCN and its implementation unit.

Figure 3. SVN and its implementation unit.

Figure 4. Block diagram of the proposed Stochastic decoder.

Figure 5. Block diagram of SVNPU with high

w_{v} = 6

[20].

Figure 5. Block diagram of SVNPU with high

w_{v} = 6

[20].

Figure 6. Flow chart for Offline design and implementation of the proposed decoder.

Figure 7. BER plot of various algorithms and code rates for N = 3808.

Table 1. Example of Stochastic bit sequence generation.

Clock cycle(k)	U	$u (r e a l v a l u e)$	comparator output( $P > U$ )
0	1101	0.8125	0
1	0111	0.4375	0
2	0011	0.1875	1
3	0110	0.375	0
4	1001	0.5625	0
5	0010	0.125	1
6	1100	0.75	0
7	0100	0.25	1

Table 2. Calculation of the entry values of

H_{b 1}

.

Table 2. Calculation of the entry values of

H_{b 1}

.

Entry of $H_{b 1}$	$V_{i, j}$	$m o d (V_{i, j}, z_{c})$	Corresponding values
$h_{0, 0}$	$V_{0, 0} = 223$	$m o d (223, 56)$	55
$h_{0, 1}$	$V_{0, 1} = 16$	$m o d (16, 56)$	16
$h_{0, 2}$	$V_{0, 2} = 94$	$m o d (94, 56)$	38
$h_{0, 3}$	$V_{0, 3} = 91$	$m o d (91, 56)$	35
$h_{0, 4}$	$V_{0, 4} = - 1$	$m o d (- 1, 56)$	-1
$h_{0, 5}$	$V_{0, 5} = 74$	$m o d (74, 56)$	18
$h_{0, 6}$	$V_{0, 6} = 10$	$m o d (10, 56)$	10
$h_{0, 7}$	$V_{0, 7} = - 1$	$m o d (- 1, 56)$	-1
$h_{0, 8}$	$V_{0, 8} = - 1$	$m o d (- 1, 56)$	-1
$h_{0, 9}$	$V_{0, 9} = 0$	$m o d (0, 56)$	0

Table 5. FPGA Implementation results.

Standard	5G	5G
Code length	3808	3808
Base Code rate	1/3	1/3
Sub-matrix size	56	56
Implementation	Kintex-7 FPGA	Kintex-7 FPGA
Decoding algorithm	Stochastic Decoding	Min-Sum
Scheduling	Column-layered	Row-layered
No.of interconnects	34729	138916
Intrinsic message width	8-bit	4-bit
Extrinsic message width	1-bit serial	4-bit
LUTs	8,278	12,962
Slice Registers	1,767	2,041
DCs or Itrs	≈ 620 DCs	15
Avg. throughput	≈ 953 Mbps	1.5 Gbps
$E_{b} / N_{o}$ at BER= $10^{- 6}$	2.65dB	2.57dB

Table 6. SD results of various code rates of

N =

3808.

Table 6. SD results of various code rates of

N =

3808.

Active Code-rate	No.of clock cycles per DC	LUTs(k)	Slice registers(k)	Throughput(Mbps)	$E_{b} / N_{o}$ at BER= $10^{- 6}$	No.of DC per frame
1/3	68	8.2	1.7	953.4	2.65dB	620
2/5	68	8.2	1.7	964.3	2.69dB	530
1/2	68	8.2	1.9	1100.9	2.79dB	450
2/3	68	8.2	1.9	1189.3	3.28dB	430
3/4	68	8.2	1.9	1240.5	3.87dB	400
5/6	68	8.2	1.9	1267.6	4.02dB	360
8/9	68	8.2	1.9	1298.2	4.29dB	330

Table 7. Comparative results.

Design	Proposed	[31]	[32]
Standard	5G-NR	5G-NR	802.16e
Code length	3808	3808	2304
Base code rate	1/3	1/3	1/2
Decoding algorithm	SD	CMS	NMS
Scheduling	Column-layered	Row-layered	Row- layered
Extrinsic message width	1-bit	4-bit	4-bit
Sub-matrix size	56	56	96
DCs or Itrs	620	10	10
Area ( $m m^{2}$ )	1.10	1.49	2.9
Throughput (Gbps)	1.12	3.04	2.20
Power (mW)	410	259	870

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

A Flexible FPGA-Based Stochastic Decoder for 5G LDPC codes

Abstract

Keywords:

Subject:

1. Introduction

2. Preliminaries

2.1. Stochastic bit sequence generation

2.2. Stochastic decoding algorithmic description

3. Construction of BGM in 5G NR standard

4. Proposed architecture

4.1. Layered decoding schedule

4.2. BGM ROMs

4.3. Routing network

4.3.1. Multiplexer

4.3.2. Interleaver

4.3.3. Distributor and Re-distributor

4.3.4. Pipeline registers

4.3.5. Updater

4.4. Stochastic variable node decoder (SVND)

4.4.1. Stochastic variable node processing unit (SVNPU)

4.5. Control unit

5. Design flow

6. Implementation results and discussion

6.1. Approach

6.2. Results

6.2.1. BER performance

6.2.2. Hardware utilisation

6.2.3. Processing throughput

6.3. Comparative analysis

7. Conclusions

References

MDPI Initiatives

Important Links

Subscribe