Prerpints.org logo
Preprint
Article

Qualitative Analysis of Rlc Circuit Described by Hilfer Derivative with Numerical Treatment Using the Lagrange Polynomial Method

This version is not peer-reviewed.

Submitted:

07 October 2023

Posted:

24 October 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
In this paper, existence and stability results of non-local integro-differential equation with Hilfer derivative of order ω∈(1,2) have been investigated. In this derivative is applied in RLC circuit equation of various fractional order. To proposed problem the existence solutions are derived using Schaefer’s fixed point theorem and the Banach contraction principle is using for uniqueness results. To demonstrate the effectiveness and applicability of our theoretical conclusions and two-step Lagrange polynomial interpolation were used to solve four numerical results.
Keywords: 
Subject: 
Computer Science and Mathematics  -   Applied Mathematics

1. Introduction

Very recently, fractional differential equations(FDE’s) have gained much attention due to extensive applications of these equations in the mathematical modeling of physics, engineering, biological phenomena and viscoelasticity. Fractional derivatives(FD’s) are well-known for their utility in describing memory and heredity qualities of numerous materials and processes that integer order derivatives cannot. A variety of issues in a various of sectors can be solved. Material science, physics, wave propagation, and signal processing are all described by fractional calculus. processing, identification of systems, and so forth. FDE’s are a type of differential equation that has a fractional derivative. During the last three decades, it has grown in significance. The subject of applied mathematics known as differential equations has grown in popularity [1,2,3,4,5]. Hilfer proposed a generalized Riemann-Liouville(R-L) fractional derivative. Hilfer fractional derivative, which includes R-L fractional derivative and Caputo FD (see [6,7,8,9,10,11,12,13,14]).
Fractional derivatives present a host of advantages over their traditional counterparts. Firstly, they incorporate memory, a fundamental feature in non-integer type differential equations. This attribute makes fractional derivatives superior in accurately describing physical systems compared to classical derivatives [15,16,17,18]. Additionally, fractional derivatives facilitate the generation of a wide range of diffusion processes, including super-diffusion, hyper diffusion, and ballistic diffusion, offering a rich field of study for those interested in these phenomena [19].
The advent of fractional derivatives has spurred the development of numerous novel mathematical models, particularly in the realm of electrical circuits. Recent research has prominently featured various formulations of fractional electrical circuits, as extensively documented in references [15,20,21,22]. In the studies detailed in [23,24,25,26,27], we delve into the modeling of fractional RL and RC circuits. The fractional LC circuit, initially introduced in [25], further expands the repertoire of available models. Central to the investigation of fractional electrical circuits are the pursuit of both numerical and analytical solutions, which constitute the cornerstone of these studies [26,27].
In [25], the AB derivative is employed by the authors to explore numerical solutions for fractional RL and RC circuits. Aguilar et al., in [19], propose solutions for non-integer order electrical RC, LC, and RL circuits using the Mittag–Leffler fractional derivative. Rawdan et al., in [26], discuss about the fractional-order RL and LC circuits, suggesting a comparative analysis with conventional electrical circuits. Further descriptions of electrical RC and LC circuits in terms of fractional derivatives are provided by Aguilar et al. and Sene et al. in [28,29,30]. Additionally, Aguilar et al., in their paper [29], delve into research on fractional electrical circuits characterized by a non-integer derivative with a regular Kernel.
Integer order integro-differential equations find the applications in various domains of science and engineering, including circuit analysis. According to Kirchhoff’s second law, the total voltage drop across a closed loop is equal to the applied voltage, denoted as E(t). This principle essentially stems from the law of energy conservation. Consequently, an RLC circuit equation is
L d d t I ( t ) + R I ( t ) + 1 C ∫ 0 t I ( s ) d s = E ( t ) .
Table 1. Notations.
Table 1. Notations.
Paramter Notation Parameter Notation
I ( t ) Current V ( t ) charge at t
E ( t ) supplied source (volt) C Capacitance (farad)
R Resistance (ohms) t time
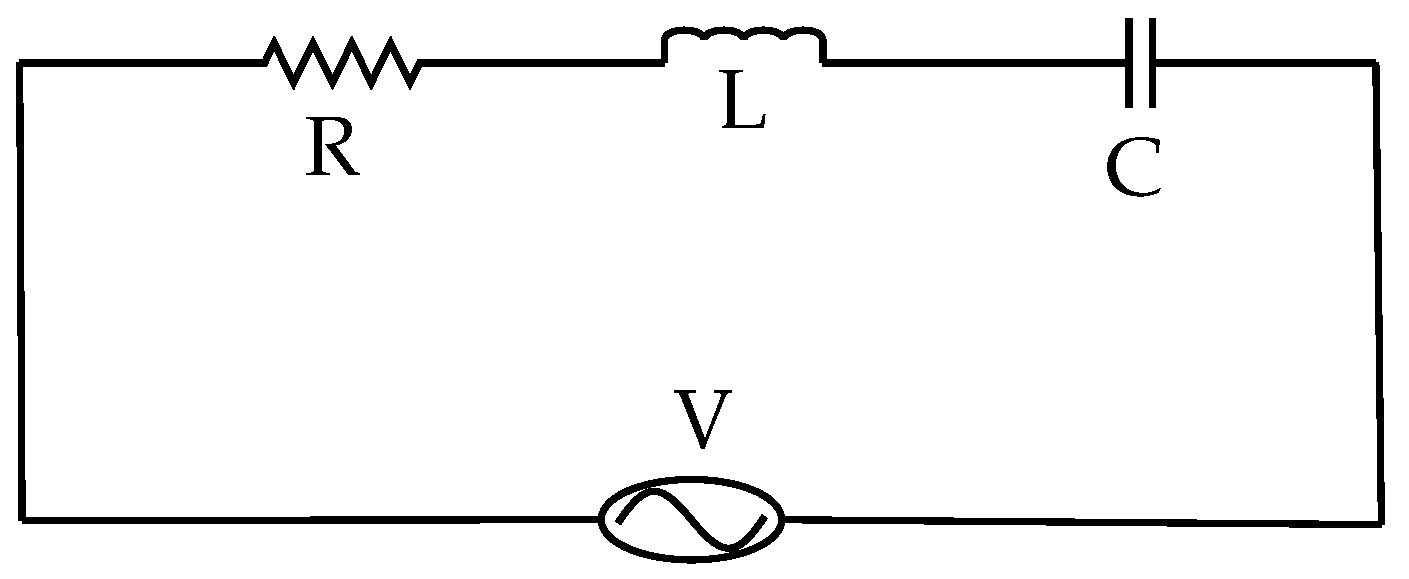
The RLC circuit serves as a fundamental component in the assembly of more intricate electrical circuits and networks. Illustrated in Figure Section 1, it comprises a resistor with a resistance of R ohms, an inductor with an inductance of L henries, and a capacitor with a capacitance of C farads, all arranged in series with an electromotive force source (like a battery or a generator) providing a voltage of E(t) volts at time t.
In [31] Uroosa Arshad et al are investigate the fractional order RLC derivative using three numerical methodology of the system is
D 2 α I ( t ) + 1 L C I ( t ) = E ( t ) L D α V ( t ) + 1 C R V ( t ) = E ( t ) R D α I ( t ) + R L I ( t ) = E ( t ) L .
In [32], Malarvizhi et al. discussed about the transient analysis of RLC circuit in RK4 order method. In [33], Gomez-Aguilar et al. studied the electrical circuit RC and RL for Atangana Beleanu Caputo(ABC) fractional bi-order system
A B C D β V ( t ) = δ E ( t ) − δ V .
The main objective of the current work is introduce the new type of fractional derivative of RLC circuit equation with nonlocal boundary value problem
D ω , τ I ( t ) = E ( t ) L − R L I ( t ) − 1 CL ∫ 0 t I ( s ) d s , y ( a ) = 0 , y ( b ) = ∑ j = 1 k ϱ j I ν j y ζ j , ν j > 0 , ϱ j ∈ R , ζ j ∈ [ a , b ] .
The primary contribution of this endeavor can be outlined as follows:
  • The solution Hilfer Fractional Integro Differential Equations of RLC circuit equation (HFIDE’s) has been achieved through the application of fixed point theory, establishing both the existence, uniqueness and stability of the results and investigated.
  • In recently [33] Gomez-Aguilar et al. studied the Atangana Beleanu Caputo fractional derivative is applied in RLC circuit equation.
  • We apply the novel hypothesis to verify the existence, uniqueness and Ulam Hyers stability of the solution for RLC circuit equation, although (3) involving integro system. Additionally, we illustrate numerical results using the two step Lagrangian polynomial approach, validating the theoretical outcome.
  • Examine the RLC equation of HFIDE’s with nonlocal boundary value problem to investigate and validate the results, and effectively implement in real-world scenarios.
The following is an overview of the paper’s structure: Section 2, contains a list of preliminary concepts that are applicable to our problem and will be helpful in the sections that follow. The uniqueness results for Hilfer derivatives of boundary value problem are discussed in Section 3. The results of Ulam stability are studied in Section 4. Then we discuss the example that was illustrated in Section 5.

2. Auxiliary Results

This section provides the study’s essential definitions, as well as other fundamental results and lemmas.
Let Y = C [ J , R ] be the space of all continuous function form J into R with norm | | v | | = max | v ( t ) | , t ∈ J . Obviously Y is a Banach space under this norm and hence the product also Banach space with norm | | ( v , w ) | | = | | v | | + | | w | | .
Definition 2.1 
([10] Caputo fractional derivative). The Caputo derivative of order q for the function g : J → R is defined as
c D ω g ( x ) = 1 Γ ( p − ω ) ∫ a x g ( p ) ( s ) ( x − s ) ω + 1 − p d s = I p − ω g ( p ) ( x ) , x > 0 , p − 1 < ω < p .
Definition 2.2 
([10] Riemann-Liouville Integral). The R-L fractional integral of order ω > 0 function is defined as
I a ω g ( x ) = 1 Γ ( p − ω ) ∫ a x g ( s ) ( x − s ) p − ω − 1 d s , p − 1 < ω < p .
Definition 2.3 
([10] Riemann-Liouville Derivative). The R-L FD of order ω > 0 of a continuous function is defined by
RL D ω g ( t ) = D p I p − ω g ( t ) , = 1 Γ ( p − ω ) d p d t p ∫ a t g ( s ) ( t − s ) p − ω − 1 d s , p − 1 < ω < p .
By a new theory of the FD which had been proposed by [3]. The FD of generalized R-L is defined as:
Definition 2.4 
([10] Hilfer Derivative). The generalized R-L FD of order ω and parameter τ of a function is described by
H D ω , τ g ( x ) = I τ ( p − ω ) D p I ( 1 − τ ) ( p − ω ) g ( x ) ,
where ω ∈ ( p − 1 , p ) , τ ∈ [ 0 , 1 ] , x > a , D = d d x .
Remark 2.1 
([10]). From Definition 2.4, we observe that:
  • The operator H D ω , τ can be written as
    H D ω , τ = I τ ( 1 − ω ) D I ( 1 − γ ) = I τ ( 1 − ω ) D γ , γ = ω + τ − τ ω ;
  • The Hilfer fractional derivative can be interpolate between R-L derivative ( τ = 0 ) and Caputo derivative ( τ = 1 ) as
    H D ω , τ = D I ( 1 − ω ) = D ω , if τ = 0 ; I ( 1 − ω ) D = C D ω , if τ = 1 .
Lemma 2.2 
([10]). If 1 < ω ≤ 2 . Then
I ω D ω g ( t ) = g ( t ) − I 1 − ω g ( a ) Γ ( ω ) ( t − a ) ω − 1 − I 2 − ω g ( a ) Γ ( ω − 1 ) ( t − a ) ω − 2 .

3. Main Results

These following assumptions are required to conclude the below results.
( A 1 ) The function g : [ a , b ] × Y × Y → Y is completely continuous and there exists a function μ ∈ L ′ ( J , R ) such that
| g ( t , x , y ) | ≤ μ ( t ) , ∀ t ∈ J = [ a , b ] , x , y ∈ Y .
( A 2 ) f is continuous function and there exists a constant L 1 , L 2 > 0 such that
| g ( t , x 1 , y 1 ) − g ( t , x 2 , y 2 ) | ≤ L 1 | x 1 − x 2 | + L 2 | y 1 − y 2 |
( A 3 ) There exists a constant M > 0 such that
| f ( t , s , x 1 ) − f ( t , s , x 2 ) | ≤ M | x 1 − x 2 |

Problem Formulation

Let us consider the general structure of Hilfer fractional order RLC circuit integro differential equation with nonlocal boundary value problem
H D ω , τ y ( t ) = g ( t , y ( t ) , H ( y ( s ) ) ) , t ∈ [ a , b ]
y ( a ) = 0 , y ( b ) = ∑ j = 1 k ϱ j I ν j y ζ j , ν j > 0 , ϱ j ∈ R , ζ j ∈ [ a , b ]
where   H D ω , τ is the Hilfer FD of order ω ∈ ( 1 , 2 ) , & parameter τ ∈ [ 0 , 1 ] , I ν j is the R-L fractional integral of order ν j > 0 , ζ j ∈ [ a , b ] , a ≥ 0 and ϱ j ∈ R , j = 1 , … , k .
g ( t , y ( t ) , ∫ a t f ( t , s , y ( s ) d s ) = E ( t ) L − R L I ( t ) − 1 CL ∫ 0 t I ( s ) d s and then H ( y ( s ) ) = ∫ a t f ( t , s , y ( s ) ) d s .
Using some fixed point theorems, the existence and uniqueness results are established. For (4) - (5), we employ Banach’s fixed point theorem and Schaefer’s fixed point theorem for uniqueness and existence results.
Lemma 3.1. 
For g ∈ C ( [ a , b ] , R ) is a solution of the boundary value problem
H D ω , τ y ( t ) = g ( t , y ( t ) , H y ( s ) ) , t ∈ J
y ( a ) = 0 , y ( b ) = ∑ j = 1 k ϱ j I ν j y ζ j , ν j > 0 , ϱ j ∈ R , ζ j ∈ [ a , b ] ,
satisfies the following equation
y ( t ) = ( t − a ) σ − 1 Φ Γ ( σ ) I ω g ( s , y ( s ) , H y ( s ) ) ( b ) − ∑ j = 1 k ϱ j I ω + ν j g ( s , y ( s ) , H y ( s ) ) ( ζ j )
+ I ω g ( s , y ( s ) , H y ( s ) ) ( t ) ,
where
Φ = ∑ j = 1 k ϱ j ( ζ j − a ) σ − ν j − 1 Γ ( σ + ν j ) − ( b − a ) σ − 1 Γ ( σ ) ≠ 0 ,
where j = 1 , 2 , 3 , . . . , k , 1 < ω < 2 , σ = ω + τ − ω τ .
Proof. 
The equation (6) can be written as
I τ ( 2 − ω ) D 2 I ( 1 − τ ) ( 2 − τ ) y ( t ) = g ( t )
As a results of determining the ω order integral of the related inequality, we obtain
I ω I τ ( 2 − ω ) D 2 I ( 1 − τ ) ( 2 − τ ) y ( t ) = I ω g ( t )
Indeed
I ω I τ ( 2 − ω ) D 2 I ( 1 − τ ) ( 2 − τ ) y ( t ) = I σ D 2 I 2 − σ y ( t ) = I σ R L D σ y ( t ) .
and therefore
I σ R L D σ y ( t ) = I ω g ( t ) .
By using equation (2.2) and setting I 2 − ω g ( a ) = c 1 , I 1 − ω g ( a ) = c 2 , Then
y ( t ) = c 2 Γ ( σ ) ( t − a ) σ − 1 + c 1 Γ ( σ − 1 ) ( t − a ) σ − 2 + I ω g ( t , y ( t ) , H y ( t ) ) .
By the condition y ( a ) = 0 , we obtain c 1 = 0 . Then we get
y ( t ) = c 2 Γ ( σ ) ( t − a ) σ − 1 + I ω g ( t , y ( t ) , H y ( t ) )
and
∑ j = 1 k ϱ j I ν j y ( ζ j ) = c 2 ∑ j = 1 k ϱ j ( ζ j − a ) σ + ν j − 1 Γ ( σ + ν j ) + ∑ j = 1 k ϱ j I ω + ν j g ( s , y ( s ) , H y ( s ) ) ( ζ j ) .
From our condition, by using (14), then
c 2 ∑ j = 1 k ϱ j ( ζ j − a ) σ + ν j − 1 Γ ( σ + ν j ) − ( t − a ) σ − 1 Γ ( σ ) = I ω g ( s , y ( s ) , H y ( s ) ) ( b ) − ∑ j = 1 k ϱ j I ω + ν j g ( s , y ( s ) , H y ( s ) ) ( ζ j )
from which we get
c 2 = 1 Φ I ω g ( s , y ( s ) , H y ( s ) ) ( b ) − ∑ j = 1 k ϱ j I ω + ν j g ( s , y ( s ) , H y ( s ) ) ( ζ j )
Substituting the value of c 1 and c 2 in (12), we obtain the solution (8). This completes the proof. □
Theorem 3.2. 
Assume that ( A 1 ) holds. Then (4)-(5) has at least one solution on [ a , b ] .
Proof. 
The proof of the theorem follows like this.
Let C = C 1 − σ [ J , Y ] , examine the operator P : C → C defined by
( P y ) ( t ) = ( t − a ) σ − 1 Φ Γ ( σ ) I ω g ( s , y ( s ) , H y ( s ) ) ( b ) − ( t − a ) σ − 1 Φ Γ ( σ ) ∑ j = 1 k ϱ j I ω + ν j g ( s , y ( s ) , H y ( s ) ) ( ζ ) + I ω g ( s , y ( s ) , H y ( s ) ) ( t )
we have to prove that the operator P is continuous and completely continuous.
Step:1 Let us prove that P is continuous
We take y n be a sequence then such that y n → y ∈ C . ∀ t ∈ J
| ( t − a ) 1 − σ ( ( P y n ) ( t ) − ( P y ) ( t ) ) | = | 1 Φ Γ ( σ ) [ 1 Γ ( ω ) ∫ a t ( b − s ) ω − 1 g ( s , y n ( s ) , H y n ( s ) ) − g ( s , y ( s ) , H y ( s ) ) d s − ∑ j = 1 k ϱ j 1 Γ ( ω + ζ j ) ∫ a t ( ζ j − s ) ω + ζ j − 1 g ( s , y n ( s ) , H y n ( s ) ) − g ( s , y ( s ) , H y ( s ) ) d s ] + ( t − a ) 1 − σ Γ ( ω ) ∫ a t ( t − s ) ω − 1 g ( s , y n ( s ) , H y n ( s ) ) − g ( s , y ( s ) , H y ( s ) ) d s | ≤ 1 | Φ | Γ ( σ ) [ 1 Γ ( ω ) ∫ a t ( b − s ) ω − 1 | g ( s , y n ( s ) , H y n ( s ) ) − g ( s , y ( s ) , H y ( s ) ) | d s − ∑ j = 1 k | ϱ j | 1 Γ ( ω + ζ j ) ∫ a t ( ζ j − s ) ω + ζ j − 1 | g ( s , y n ( s ) , H y n ( s ) ) − g ( s , y ( s ) , H y ( s ) ) | d s ] + ( t − a ) 1 − σ Γ ( ω ) ∫ a t ( t − s ) ω − 1 | g ( s , y n ( s ) , H y n ( s ) ) − g ( s , y ( s ) , H y ( s ) ) | d s ≤ 1 ∥ Φ ∥ Γ ( σ ) [ ( b − s ) ω Γ ( ω + 1 ) ∥ g ( s , y n ( s ) , H y n ( s ) ) − g ( s , y ( s ) , H y ( s ) ) ∥ C − ∑ j = 1 k ∥ ϱ j ∥ ( ζ j − s ) ω + ζ j Γ ( ω + ζ j + 1 ) ∥ g ( s , y n ( s ) , H y n ( s ) ) − g ( s , y ( s ) , H y ( s ) ) ∥ C ] + ( t − s ) ω ( t − a ) σ − 1 Γ ( ω + 1 ) ∥ g ( s , y n ( s ) , H y n ( s ) ) − g ( s , y ( s ) , H y ( s ) ) ∥ C
Since the function g is a continuous function, we have
∥ ( t − a ) 1 − σ ( ( P y n ) ( t ) − ( P y ) ( t ) ) ∥ ≤ 1 ∥ Φ ∥ Γ ( σ ) [ ( b − s ) ω Γ ( ω + 1 ) ∥ g ( . , y n ( . ) , H y n ( . ) ) − g ( . , y ( . ) , H y ( . ) ) ∥ C − ∑ j = 1 k ∥ ϱ j ∥ ( ζ j − s ) ω + ζ j Γ ( ω + ζ j + 1 ) ∥ g ( . , y n ( . ) , H y n ( . ) ) − g ( . , y ( . ) , H y ( . ) ) ∥ C ] + ( t − s ) ω ( t − a ) σ − 1 Γ ( ω + 1 ) ∥ g ( . , y n ( . ) , H y n ( . ) ) − g ( . , y ( . ) , H y ( . ) ) ∥ C → 0 as n → ∞
Step:2  P : bounded sets → bounded sets ∈ C
Let q > 0 . ∃ + v e constant.
l such that y ∈ B q = { y in C : ∥ y ∥ ≤ q } , we have ∥ P y ∥ C ≤ l
| ( t − a ) 1 − σ ( P y ) ( t ) | ≤ 1 | Φ | Γ ( σ ) [ 1 Γ ( ω ) ∫ a t ( b − s ) ω − 1 | g ( s , y ( s ) , H y ( s ) ) | d s − ∑ j = 1 k | ϱ j | 1 Γ ( ω + ζ j ) ∫ a t ( ζ j − s ) ω + ζ j − 1 | g ( s , y ( s ) , H y ( s ) ) | d s ] + ( t − a ) 1 − σ Γ ( ω ) ∫ a t ( t − s ) ω − 1 | g ( s , y ( s ) , H y ( s ) ) | d s ≤ 1 | Φ | Γ ( σ ) [ 1 Γ ( ω ) ∫ a t ( b − s ) ω − 1 | μ ( s ) | d s − ∑ j = 1 k | ϱ j | 1 Γ ( ω + ζ j ) ∫ a t ( ω ζ j − s ) ω + ζ j − 1 | μ ( s ) | d s ] + ( t − a ) 1 − σ Γ ( ω ) ∫ a t ( t − s ) ω − 1 | μ ( s ) | d s ≤ ∥ μ ( s ) ∥ C | Φ | Γ ( σ ) ( b − s ) ω Γ ( ω + 1 ) − ∑ j = 1 k | ϱ j | ( ζ j − s ) ω + ζ j Γ ( ω + ζ j + 1 ) + ( t − s ) ω ( t − a ) 1 − σ Γ ( ω + 1 )
Step:3  P : bounded sets to equicontinuous set of C.
Then we take a ≤ t 1 , t 2 ≤ b , t 1 < t 2 , B q be a bounded set of C as mentioned above, & y ∈ B q ,
| ( t 2 − a ) 1 − σ ( P y ) ( t 2 ) − ( t 1 − a ) 1 − σ ( P y ) ( t 1 ) | ≤ 1 ∣ Φ ∣ Γ ( σ ) [ 1 Γ ( ω ) ∫ a t 2 ( b − s ) ω − 1 | g ( s , y ( s ) , H y ( s ) ) | d s − ∑ j = 1 k ∣ ϱ j ∣ Γ ( ω + ζ j ) ∫ a t 2 ( ζ j − s ) ω + ζ j | g ( s , y ( s ) , H y ( s ) ) | d s ] + ( t 2 − a ) σ − 1 Γ ( ω ) ∫ a t 2 ( t 2 − s ) ω − 1 | g ( s , y ( s ) , H y ( s ) ) | d s − 1 ∣ Φ ∣ Γ ( σ ) [ 1 Γ ( ω ) ∫ a t 1 ( b − s ) ω − 1 | g ( s , y ( s ) , H y ( s ) ) | d s + ∑ j = 1 k ∣ ϱ j ∣ Γ ( ω + ζ j ) ∫ a t 1 ( ζ j − s ) ω + ζ j | g ( s , y ( s ) , H y ( s ) ) | d s ] − ( t 1 − a ) σ − 1 Γ ( ω ) ∫ a t 1 ( t 1 − s ) ω − 1 | g ( s , y ( s ) , H y ( s ) ) | d s
≤ | g ( s , y ( s ) , H y ( s ) ) | ∣ Φ ∣ Γ ( σ ) Γ ( ω ) ∫ a t 2 ( b − s ) ω − 1 d s − ∫ a t 1 ( b − s ) ω − 1 d s − ∑ j = 1 k ∣ ϱ j ∣ | g ( s , y ( s ) , H y ( s ) ) | ∣ Φ ∣ Γ ( σ ) Γ ( ω + ζ j ) ∫ a t 2 ( ζ j − s ) ω + ζ j − 1 d s − ∫ a t 1 ( ζ j − s ) ω − 1 d s + | g ( s , y ( s ) , H y ( s ) ) | ( t 2 − a ) σ − 1 Γ ( ω ) ∫ t 1 t 2 ( t 2 − t 1 ) ω − 1 d s ≤ ∥ μ ∥ C ∣ Φ ∣ Γ ( σ ) Γ ( ω ) ∫ a t 2 ( b − s ) ω − 1 d s − ∫ a t 1 ( b − s ) ω − 1 d s − ∑ j = 1 k ∣ ϱ j ∣ ∥ μ ∥ C ∣ Φ ∣ Γ ( σ ) Γ ( ω + ζ j ) ∫ a t 2 ( ζ j − s ) ω + ζ j − 1 d s − ∫ a t 1 ( ζ j − s ) ω − 1 d s + ∥ μ ∥ C ( t 2 − a ) σ − 1 Γ ( ω ) ∫ t 1 t 2 ( t 2 − t 1 ) ω − 1 d s
As t 2 → t 1 , The R.H.S. of the inequality above approaches 0. We can deduce that P : C → C is continuous and completely continuous as a combination of above steps and the Arzela-Ascoli theorem.
Step:4 A priori bounds.
Let is take Φ = { y ∈ C : Y = ϱ ( P ( y ) ) ; ϱ ∈ ( 0 , 1 ) } is bounded set.
If y ∈ Φ , y = ϱ ( P ( y ) ) for some ϱ ∈ ( 0 , 1 ) . Thus ∀ t ∈ [ a , b ] . Then
y ( t ) = ϱ [ ( t − a ) σ − 1 Φ Γ ( σ ) I ω g ( s , y ( s ) , H y ( s ) ) ( b ) + ( t − a ) σ − 1 Φ Γ ( σ ) ∑ j = 1 k ϱ j I ω + ν j g ( s , y ( s ) , H y ( s ) ) ( ζ ) + I ω g ( s , y ( s ) , H y ( s ) ) ( t ) ]
This implies by ( A 2 ) that ∀ t ∈ [ a , b ] , Then
| y ( t ) ( t − a ) 1 − σ | ≤ | ( t − a ) 1 − σ ( P y ) ( t ) | ≤ 1 ∣ Φ ∣ Γ ( σ ) [ 1 Γ ( ω ) ∫ a t ( b − s ) ω − 1 | g ( s , y ( s ) , H y ( s ) ) | d s − ∑ j = 1 k | ϱ j | 1 Γ ( ω + ζ j ) ∫ a t ( ζ j − s ) ω + ζ j − 1 | g ( s , y ( s ) , H y ( s ) ) | d s ] + ( t − a ) 1 − σ Γ ( ω ) ∫ a t ( t − s ) ω − 1 | g ( s , y ( s ) , H y ( s ) ) | d s
≤ 1 ∣ Φ ∣ Γ ( σ ) [ 1 Γ ( ω ) ∫ a t ( b − s ) ω − 1 | μ ( s ) | d s − ∑ j = 1 k | ϱ j | 1 Γ ( ω + ζ j ) ∫ a t ( ζ j − s ) ω + ζ j − 1 | μ ( s ) | d s ] + ( t − a ) 1 − σ Γ ( ω ) ∫ a t ( t − s ) ω − 1 | μ ( s ) | d s ≤ 1 ∣ Φ ∣ Γ ( σ ) ( b − s ) ω Γ ( ω + 1 ) ∥ μ ( s ) ∥ C − ∑ j = 1 k | ϱ j | ( ζ j − s ) ω Γ ( ω + ζ j + 1 ) ∥ μ ( s ) ∥ C + ( t − a ) 1 − σ ( t − s ) ω Γ ( ω + 1 ) ∥ μ ( s ) ∥ C ≤ ℜ
that ∥ μ ( s ) ∥ C ≤ ℜ .
Therefore the set Φ is bounded. We derive that P is a fixed point then it is a solution of (4)-(5) as an outcome of Schaefer’s Fixed point theorem. □
The above theorem we have to proved the existence results. Now we have to shown that the uniqueness results by using the Banach contraction principles.
Theorem 3.3. 
Suppose that the conditions ( A 2 ) , ( A 3 ) and following inequality holds
( L 1 + L 2 M ) ( b − a ) ω + σ − 1 ∣ Φ ∣ Γ ( σ ) Γ ( ω + 1 ) + ( b − a ) ω + σ − 1 ∣ Φ ∣ Γ ( σ ) ∑ i = 0 m ∣ ϱ j ∣ ( ζ j − a ) ω + ζ j Γ ( ω + ν j + 1 ) + ( b − a ) ω Γ ( ω + 1 ) < 1
Then (4)-(5) has a unique solution on J.
Proof. 
Let us define the operator P to transform (4)-(5) into a fixed point problem
( P y ) ( t ) = ( t − a ) σ − 1 Φ Γ ( σ ) I ω g ( s , y ( s ) , H y ( s ) ) ( b ) + ( t − a ) σ − 1 Φ Γ ( σ ) ∑ j = 1 k ϱ j I ω + ν j g ( s , y ( s ) , H y ( s ) ) ( ζ ) + I ω g ( s , y ( s ) , H y ( s ) ) ( t ) | ( P y ) ( t ) | ≤ ( t − a ) σ − 1 Φ Γ ( σ ) I ω | g ( s , y ( s ) , H y ( s ) ) | ( b ) + ( t − a ) σ − 1 Φ Γ ( σ ) ∑ j = 1 k ϱ j I ω + ν j | g ( s , y ( s ) , H y ( s ) ) | ( ζ ) + I ω | g ( s , y ( s ) , H y ( s ) ) | ( t ) | ( P y ) ( t ) − ( P x ) ( t ) | ≤ ( b − a ) σ − 1 Φ Γ ( σ ) I ω | g ( s , y ( s ) , H y ( s ) ) − g ( s , x ( s ) , H x ( s ) ) | ( b ) + ( b − a ) σ − 1 Φ Γ ( σ ) ∑ j = 1 k ϱ j I ω + ν j | g ( s , y ( s ) , H y ( s ) ) − g ( s , x ( s ) , H x ( s ) ) | ( ζ ) + I ω | g ( s , y ( s ) , H y ( s ) ) − g ( s , x ( s ) , H x ( s ) ) | ( t )
≤ ( L 1 + L 2 M ) | y ( s ) − x ( s ) | [ ( b − a ) ω + σ − 1 ∣ Φ ∣ Γ ( σ ) Γ ( ω + 1 ) + ( b − a ) ω + σ − 1 ∣ Φ ∣ Γ ( σ ) ∑ i = 0 m ∣ ϱ j ∣ ( ζ j − a ) ω + ζ j Γ ( ω + ν j + 1 ) + ( t − a ) ω Γ ( ω + 1 ) ]
Thus
∥ ( P y ) ( t ) − ( P x ) ( t ) ∥ ≤ ( L 1 + L 2 M ) [ ( b − a ) ω + σ − 1 ∣ Φ ∣ Γ ( σ ) Γ ( ω + 1 ) + ( b − a ) ω + σ − 1 ∣ Φ ∣ Γ ( σ ) ∑ i = 0 m ∣ ϱ j ∣ ( ζ j − a ) ω + ζ j Γ ( ω + ν j + 1 ) + ( b − a ) ω Γ ( ω + 1 ) ] ∥ y − x ∥ ∞
From (17), the operator P is contraction. By the Banach contraction principle P has a fixed point, which proves the uniqueness of the problem (4)-(5). □

4. Ulam Stability(US) Results

Ulam first mentioned the stability of functional equations in a lecture at the University of Wisconsin in 1940. In the instance of Banach spaces, Hyers provided the first response to Ulam’s question in 1941. Ulam-Hyers stability(UHS) is the name given to this sort of stability [34,35,36,37,38]. By considering variables, Rassias [39] proposed a surprising generalization of the UHS of maps in 1978. When we substitute the FE with an inequality that acts as a perturbation of the form, we have the concept of stability for a FE. Some researchers proposed US for FDEs with Caputo and R-L derivatives. [39,40,41,42] provide further historical details as well as recent advancements in such stabilities.
The US of IDEs with Hilfer fractional derivatives(4)-(5) are discussed in this section.
Definition 4.1 
([11]). The equation (4)-(5) is U-HS if ∃ C f > 0 , it is real number then such that ∀ ϵ > 0 and for all solution z ∈ C 1 − σ σ [ a , b ] of the variation
| D 1 + ω , τ z ( t ) − g ( t , z ( t ) , H z ( t ) ) | ≤ ϵ , t ∈ ( 0 , T ]
∃ x ∈ C 1 − σ σ [ J ] of equation (4)-(5) then
∣ z ( t ) − y ( t ) ∣ ≤ c g ϵ , t ∈ J
Definition 4.2 
([11]). The equation (4)-(5) is generalized UHS if
∃ ψ g ∈ C R + , R + , ψ g ( 0 ) = 0 , such that for all solution z ∈ C 1 − σ σ ( J ) of the variation
| D 0 + ω , τ z ( t ) − g t , z ( t ) , H z ( t ) | ≤ ϵ , t ∈ ( 0 , T ]
Therefore the solution is exist y ∈ C 1 − σ σ ( J ) of the equation (4)-(5) then
∣ z ( t ) − y ( t ) ∣ ≤ ψ g ( ϵ ) , t ∈ ( 0 , T ]
Definition 4.3 
([11]). The equation (4)-(5) is Ulam-Hyers-Rassias stable(UHRS) with ν ∈ C [ a , b ] , R + if ∃ c g > 0 such that ∀ ϵ > 0 and for all solution z ∈ C 1 − σ σ ( [ a , b ] ) of the variation
| D 0 + ω , τ z ( t ) − g t , z ( t ) , H z ( t ) | ≤ ϵ ν ( t ) , t ∈ ( 0 , T ]
Therefore the solution is exist y ∈ C 1 − σ σ ( [ a , b ] ) of (4)-(5) with
∣ z ( t ) − y ( t ) ∣ ≤ c g , ν ϵ ν ( t ) , t ∈ ( 0 , T ]
Definition 4.4 
([11]). (4)-(5) is generalized UHRS with ν ∈ C J , R + if ∃ C g , ν > 0 such that for all solution z ∈ C 1 − σ σ ( J ) of the variation
| D 0 + ω , τ z ( t ) − g t , z ( t ) , H z ( t ) | ≤ ν ( t ) , t ∈ ( 0 , T ]
Therefore the solution is exists y ∈ C 1 − σ σ ( J ) of (4)-(5) then
∣ z ( t ) − y ( t ) ∣ ≤ c g , ν ν ( t ) , t ∈ ( 0 , T ]
Remark 4.1 
([11]). A function z ∈ C 1 − σ σ ( [ a , b ] ) is a solution of the variation
| D 0 + ω , τ z ( t ) − g t , z ( t ) , H z ( t ) | ≤ ϵ , t ∈ ( 0 , T ]
iff there ∃ a function g ∈ C 1 − σ σ ( [ a , b ] ) such that
  • ∣ g ( t ) ∣ ≤ ϵ , 0 < t ≤ T
  • D 0 + ω , τ z ( t ) = g t , z ( t ) , H z ( t ) + g ( t ) , 0 < t ≤ T
Remark 4.2 
([11]). It is clearly that,
  • Definition ( 4 . 1 ) ⇒ Definition ( 4 . 2 )
  • Definition ( 4 . 3 ) ⇒ Definition ( 4 . 4 ) .
Theorem 4.3. 
Assume that ( A 1 ) and (17) are satisfied, the following problem (4)-(5) is UHS.
Proof. 
Let ϵ > 0 and then z ∈ C 1 − σ σ [ a , b ] be a function. Then satiate the variation (18) and let y ∈ C 1 − σ σ [ a , b ] be a unique solution given system
H D ω , τ y ( t ) = g ( t , y ( t ) , ∫ a t g ( t , s , y ( s ) ) d s ) , t ∈ [ a , b ] , 1 < ω < 2 , 0 ≤ τ ≤ 1 y ( a ) = 0 , y ( b ) = ∑ j = 1 k ϱ j I ν j x ζ j , ν j > 0 , ϱ j ∈ R , ζ j ∈ [ a , b ]
where 1 < ω < 2 and parameter 0 ≤ τ ≤ 1 .
| z ( t ) − ( b − a ) σ − 1 Φ Γ ( σ ) I ω g ( s , z ( s ) , H z ( s ) ) ( b ) + ( b − a ) σ − 1 Φ Γ ( σ ) ∑ j = 1 k ϱ j I ω + ν j g ( s , z ( s ) , H z ( s ) ) ( ζ ) − I ω g ( s , z ( s ) , H z ( s ) ) ( t ) | ≤ ϵ t ω Γ ( ω + 1 ) ≤ ϵ T ω Γ ( ω + 1 )
we have for any t ∈ ( 0 , T ]
| z ( t ) − y ( t ) | ≤ | z ( t ) − ( b − a ) σ − 1 Φ Γ ( σ ) I ω g ( s , y ( s ) , H y ( s ) ) ( b ) + ( b − a ) σ − 1 Φ Γ ( σ ) ∑ j = 1 k ϱ j I ω + ν j g ( s , y ( s ) , H y ( s ) ) ( ζ ) − I ω g ( s , y ( s ) , H y ( s ) ) ( t ) | ≤ | z ( t ) − ( b − a ) σ − 1 Φ Γ ( σ ) I ω g ( s , z ( s ) , H z ( s ) ) ( b ) + ( b − a ) σ − 1 Φ Γ ( σ ) ∑ j = 1 k ϱ j I ω + ν j g ( s , z ( s ) , H z ( s ) ) ( ζ ) − I ω g ( s , z ( s ) , H z ( s ) ) ( t ) | + | ( b − a ) σ − 1 Φ Γ ( σ ) I ω g ( s , z ( s ) , H z ( s ) ) − g ( s , y ( s ) , H y ( s ) ) ( b ) − ( b − a ) σ − 1 Φ Γ ( σ ) ∑ j = 1 k ϱ j I ω + ν j g ( s , z ( s ) , H z ( s ) ) − g ( s , y ( s ) , H y ( s ) ) ( ζ ) + I ω g ( s , z ( s ) , H z ( s ) ) − g ( s , y ( s ) , H y ( s ) ) ( t ) | ≤ ϵ T ω Γ ( ω + 1 ) + ( L 1 + L 2 M )
( ( b − a ) ω + σ − 1 ∣ Φ ∣ Γ ( σ ) Γ ( ω + 1 ) + ( b − a ) ω + σ − 1 ∣ Φ ∣ Γ ( σ ) ∑ i = 0 m ∣ ϱ j ∣ ( ζ j − a ) ω + ζ j Γ ( ω + ν j + 1 ) + ( b − a ) ω Γ ( ω + 1 ) ) | z ( t ) − y ( t ) | ≤ ϵ T ω Γ ( ω + 1 ) + K | z ( t ) − y ( t ) | ≤ ϵ T ω ( 1 − K ) Γ ( ω + 1 ) | z ( t ) − y ( t ) | ≤ c g . ϵ
where K = ( L 1 + L 2 M ) ( b − a ) ω + σ − 1 ∣ Φ ∣ Γ ( σ ) Γ ( ω + 1 ) + ( b − a ) ω + σ − 1 ∣ Φ ∣ Γ ( σ ) ∑ i = 0 m ∣ ϱ j ∣ ( ζ j − a ) ω + ζ j Γ ( ω + ν j + 1 ) + ( b − a ) ω Γ ( ω + 1 ) Thus the equation(4)-(5) is UHS. □
Theorem 4.4. 
Assume that ( A 1 ) , ( A 2 ) , ( A 3 ) and (17) hold. Then ∃ ν ∈ C 1 − σ [ J ] it is an increasing function and ∃ ς ν > 0 then for any t ∈ [ a , b ] .
| z ( t ) − y ( t ) | ≤ ς ν φ ( t ) .
Therefore (4)-(5) has UHRS.
Proof. 
Let z ∈ C 1 − σ σ [ a , b ] be a solution of the variation (20) and let x ∈ C 1 − σ σ [ a , b ] be the unique solution of given system
H D ω , τ y ( t ) = g ( t , y ( t ) , ∫ a t g ( t , s , y ( s ) ) d s ) , t ∈ [ a , b ] y ( a ) = 0 , y ( b ) = ∑ j = 1 k ϱ j I ν j x ζ j , ν j > 0 , ϱ j ∈ R , ζ j ∈ [ a , b ]
where 1 < ω < 2 and parameter 0 ≤ τ ≤ 1 .
We obtain the equation (20), we get the following
y ( t ) = ( t − a ) σ − 1 Φ Γ ( σ ) I ω g ( s , y ( s ) , H y ( s ) ) ( b ) − ( t − a ) σ − 1 Φ Γ ( σ ) ∑ j = 1 k ϱ j I ω + ν j g ( s , y ( s ) , H y ( s ) ) ( ζ ) + I ω g ( s , y ( s ) , H y ( s ) ) ( t )
By integrating the variation (20), then
| z ( t ) − ( b − a ) σ − 1 Φ Γ ( σ ) I ω g ( s , z ( s ) , H z ( s ) ) ( b ) + ( b − a ) σ − 1 Φ Γ ( σ ) ∑ j = 1 k ϱ j I ω + ν j g ( s , z ( s ) , H z ( s ) ) ( ζ ) − I ω g ( s , z ( s ) , H z ( s ) ) ( t ) | ≤ ϵ ς ν φ ( t )
Then any 0 < t ≤ T
| z ( t ) − y ( t ) | ≤ | z ( t ) − ( b − a ) σ − 1 Φ Γ ( σ ) I ω g ( s , y ( s ) , H y ( s ) ) ( b ) + ( b − a ) σ − 1 Φ Γ ( σ ) ∑ j = 1 k ϱ j I ω + ν j g ( s , y ( s ) , H y ( s ) ) ( ζ ) − I ω g ( s , y ( s ) , H y ( s ) ) ( t ) | ≤ | z ( t ) − ( b − a ) σ − 1 Φ Γ ( σ ) I ω g ( s , z ( s ) , H z ( s ) ) ( b ) + ( b − a ) σ − 1 Φ Γ ( σ ) ∑ j = 1 k ϱ j I ω + ν j g ( s , z ( s ) , H z ( s ) ) ( ζ ) − I ω g ( s , z ( s ) , H z ( s ) ) ( t ) | + | ( b − a ) σ − 1 Φ Γ ( σ ) I ω g ( s , z ( s ) , H z ( s ) ) − g ( s , y ( s ) , H y ( s ) ) ( b ) − ( b − a ) σ − 1 Φ Γ ( σ ) ∑ j = 1 k ϱ j I ω + ν j g ( s , z ( s ) , H z ( s ) ) − g ( s , y ( s ) , H y ( s ) ) ( ζ ) + I ω g ( s , z ( s ) , H z ( s ) ) − g ( s , y ( s ) , H y ( s ) ) ( t ) |
≤ ϵ ς ν φ ( t ) + ( L 1 + L 2 M ) ( ( b − a ) ω + σ − 1 ∣ Φ ∣ Γ ( σ ) Γ ( ω + 1 ) + ( b − a ) ω + σ − 1 ∣ Φ ∣ Γ ( σ ) ∑ i = 0 m ∣ ϱ j ∣ ( ζ j − a ) ω + ζ j Γ ( ω + ν j + 1 ) + ( b − a ) ω Γ ( ω + 1 ) ) | z ( t ) − y ( t ) | ≤ ϵ ς ν φ ( t ) + K | z ( t ) − y ( t ) | ≤ ϵ ς ν φ ( t ) ( 1 − K ) Γ ( ω ) | z ( t ) − y ( t ) | ≤ c g , ν ϵ ν ( t )
Thus, the equation (4)-(5) is UHRS. □

5. Example

Example 5.1. 
Consider the nonlocal BVP’s by using Hilfer FIDE’s of the form
H D ω , τ y ( t ) = cos 2 t ( e − t + 2 ) 2 ∣ y ( t ) ∣ + 1 2 ∫ 0 t e − 1 / 2 y ( s ) d s , t ∈ [ 3 10 , 13 10 ] y ( 3 10 ) = 0 , y ( 13 10 ) = 17 50 I 13 15 y ( 23 50 ) + 21 50 I 37 100 y ( 91 100 ) + 3 25 I 41 100 y ( 4 5 )
Where ω = 6 5 , τ = 1 5 , σ = 7 4 , a = 3 10 , b = 13 10 , ϱ 1 = 17 50 , ϱ 2 = 21 50 , ϱ 3 = 3 25 , ν 1 = 13 15 , ν 2 = 37 100 , ν 3 = 41 100 , ζ 1 = 23 50 , ζ 2 = 91 100 , ζ 3 = 4 5 , L 1 = L 2 = 1 9 , M = 1 8
Hence the assumption ( A 2 ) , ( A 3 ) hold.
We check the condition
( L 1 + L 2 M ) [ ( b − a ) ω + σ − 1 ∣ Φ ∣ Γ ( σ ) Γ ( ω + 1 ) + ( b − a ) ω + σ − 1 ∣ Φ ∣ Γ ( σ ) ∑ i = 0 m ∣ ϱ j ∣ ( ζ j − a ) ω + ζ j Γ ( ω + ν j + 1 ) + ( b − a ) ω Γ ( ω + 1 ) ] < 1 ≈ 0.7347 .
Hence, the problem (22) has a unique solution on [ 3 10 , 13 10 ] .
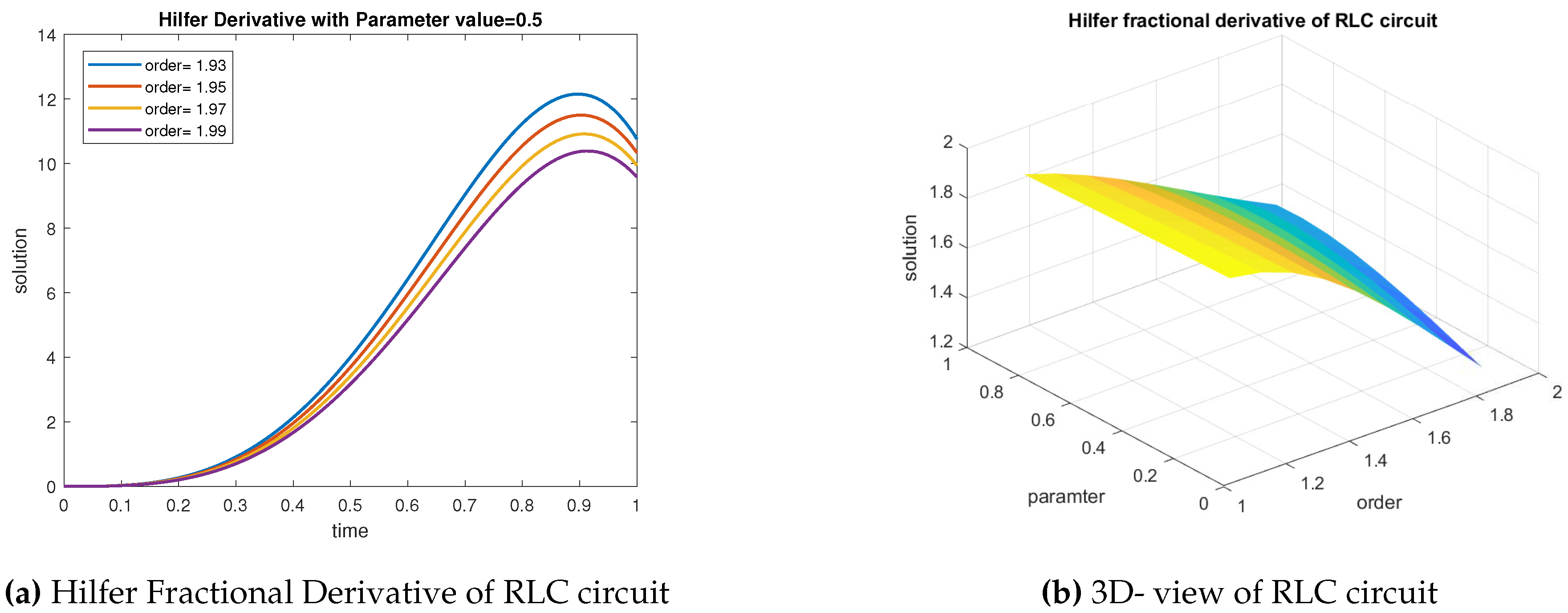
Example 5.2. 
Examine the RLC circuit equation of Hilfer fractional differential equation of the form
H D ω , τ I ( t ) = E 0 L − R L I ( t ) − 1 CL ∫ 0 t I ( s ) d s , t ∈ [ 0 , 1 ] y ( 0 ) = 0 , y ( 1 ) = 0.34 I 0.87 y ( 0.46 ) + 0.42 I 0.37 y ( 0.91 ) + 0.12 I 0.41 y ( 0.8 ) .
RLC circuits are commonly used in filter design, where they can be configured as low-pass, high-pass, band-pass, or band-stop filters. These filters are crucial in signal processing, telecommunications, and audio electronics. It is used in tuned circuits, which are employed in radio receivers to select a particular frequency from a mixture of signals. This is essential for tuning in to specific radio stations. It can be used in control systems for tasks such as damping oscillations and stabilizing feedback loops.
In Figure 1a various fractional order with fix the parameter value at 0 . 5 for RLC circuit equation. Figure 1b represent the 3 dimensional view of RLC with circuit elements are R = 4 , I = 2 , C = 5 , E 0 = 10 .
Example 5.3. 
Consider the following integro-differential equation of Hilfer fractional differential equation of the form
H D ω , τ y ( t ) = cos 2 ( t ) ( e − t + 2 ) 2 + 1 2 e − 1 / 2 ∫ 0 t y ( s ) d s , t ∈ [ 0 , 5 ] , y ( 0 ) = 0 , y ( 5 ) = 0.34 I 0.87 y ( 0.46 ) + 0.42 I 0.37 y ( 0.91 ) + 0.12 I 0.41 y ( 0.8 ) .
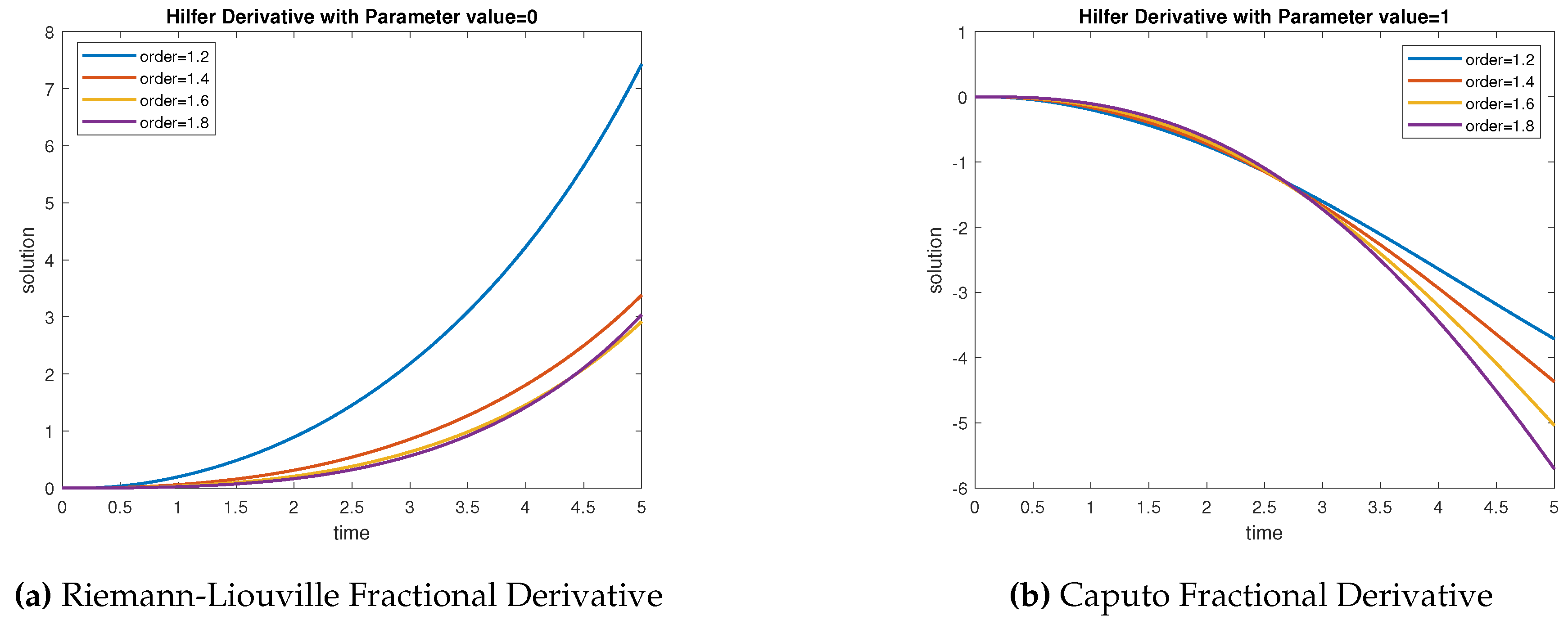
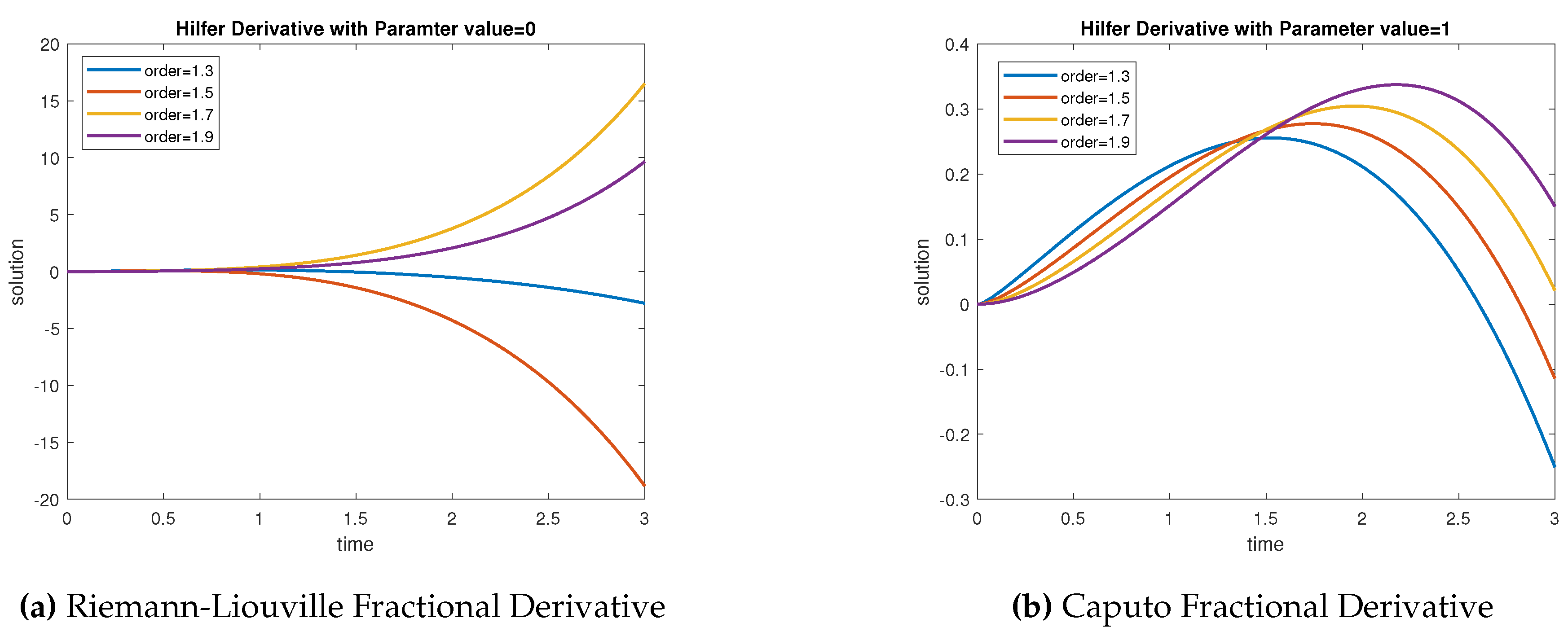
In this figures, its clearly revealed the significant of fractional order derivatives. In order to show the significant of fractional order derivative, the output responses of the consider systems respectively with respect to Riemann-Liouville, Caputo and Hilfer derivative graphically represent in Figure 2, Figure 3 and Figure 4.
Notably, In Figure 2a, for distinct values of order ω , ( ω = 1 . 2 , 1 . 4 , 1 . 6 , 1 . 8 ) with the parameter τ = 0 is plotted. Similarly, for τ = 1 is plotted in Figure 2b. In Figure 3a, is picturise for τ = 0 . 9 . In Figure 3b, it should be noted that Hilfer fractional order derivative is defined for the value of τ lies between 0 and 1, this is 0 < τ < 1 .
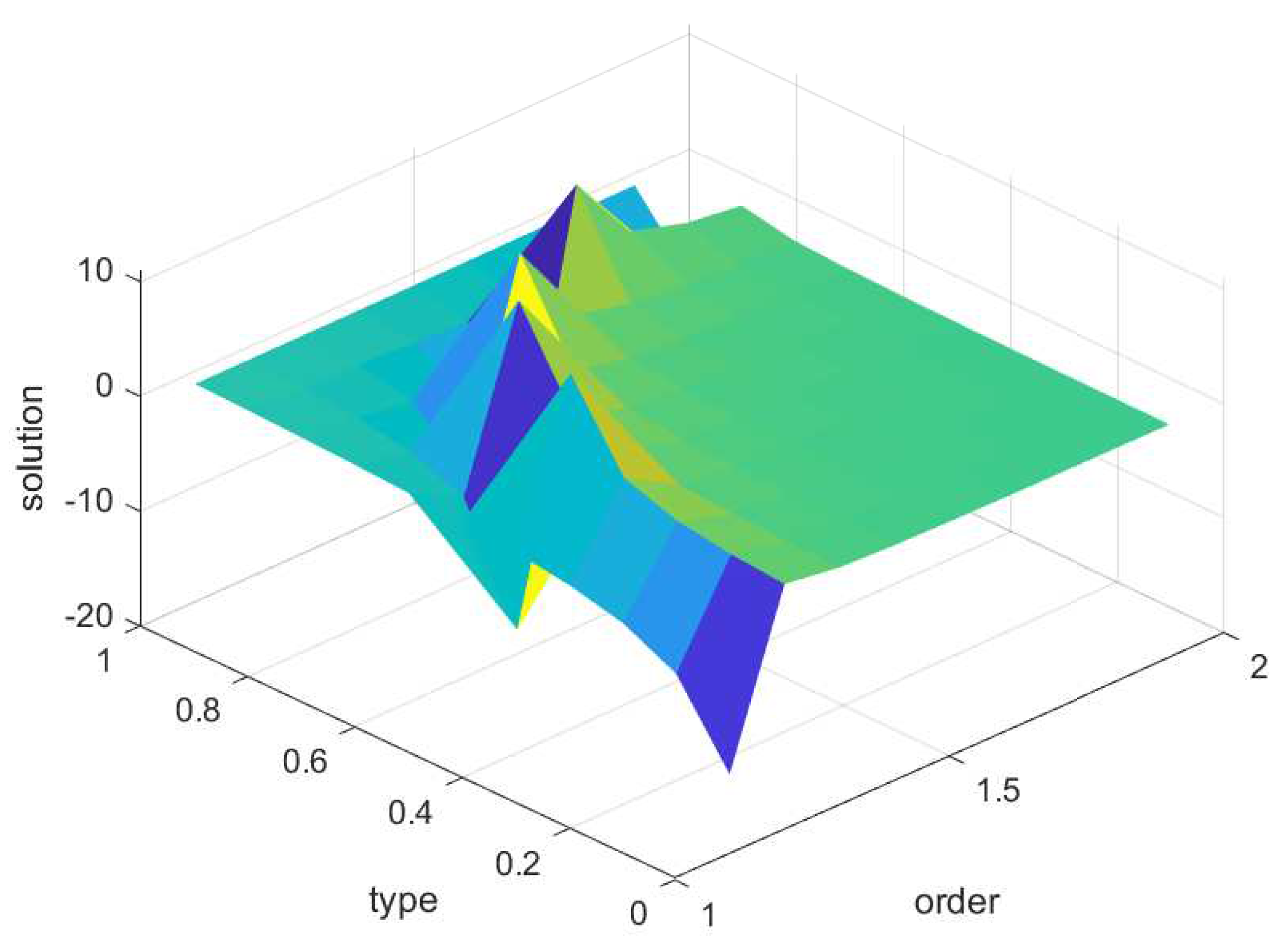
In additional to this, a 3D plot with respect to the order ω , parameter τ and y ( t ) is given in Figure 4. This figure, clearly picturised the the impact of order ω and parameter τ for obtaining the solution of the considered systems. Overall from the simulation result, the robustness of the developed methodology is validated.
The solution representation is modified when we change the order and parameter. One of the main benefits of our problem of non-local integro differential boundary value problems is that, while this change’s small size of order and parameter values, it can have a major effect when applied to a real-world problem.
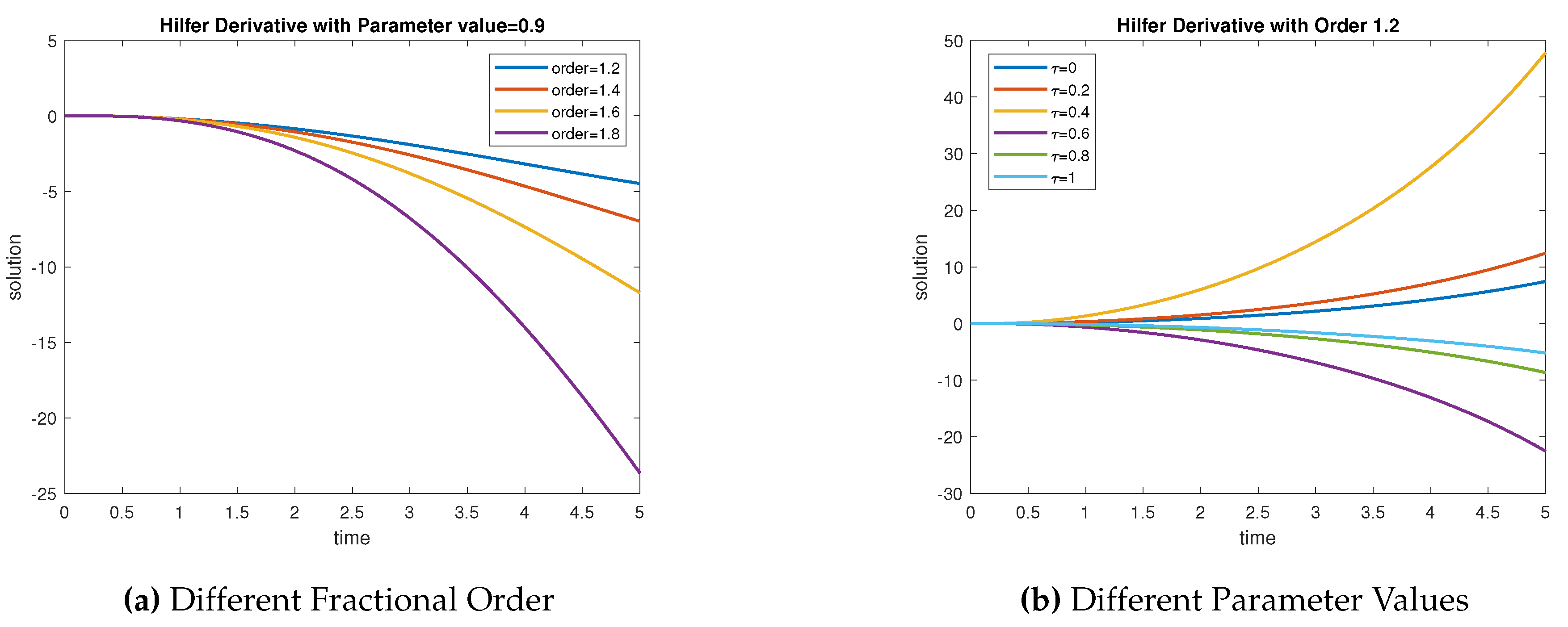
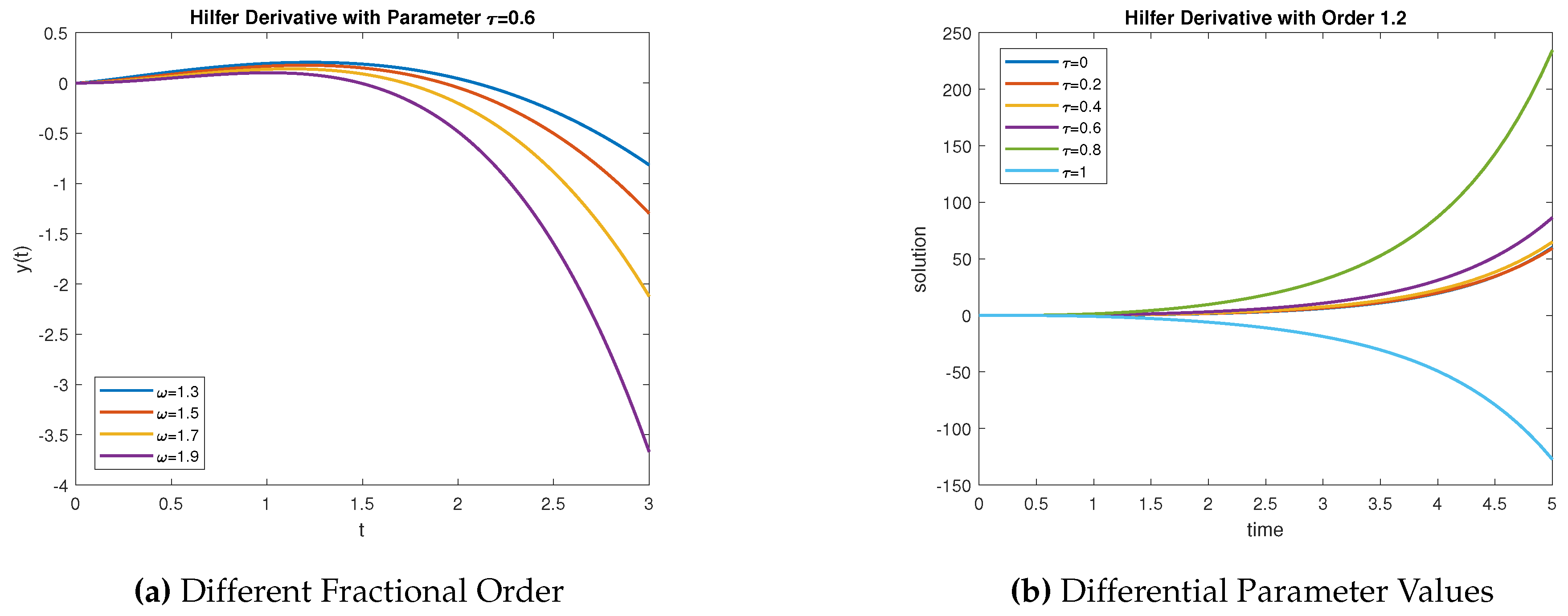
Example 5.4. 
Consider the following non-local boundary value problem with integro-differential equation of Hilfer fractional differential equation of the form
H D ω , τ y ( t ) = 4 4 t + 7 ( y 2 ( t ) 1 + | y ( t ) | + 2 3 ) + 1 2 e − 1 / 2 ∫ 0 t y ( s ) d s , t ∈ [ 0 , 3 ] , y ( 0 ) = 0 , y ( 3 ) = 0.8 I 0.75 y ( 0.5 ) + 0.5 I 0.85 y ( 0.75 ) + 0.48 I 0.54 y ( 0.25 ) .
In Figure 5a, let us assume different values of the order ω = 1 . 2 , 1 . 4 , 1 . 6 , 1 . 8 with parameter τ = 0 . It becomes the Riemann–Liouville derivative. In Figure 5b, let us assume different values of the order ω = 1 . 2 , 1 . 4 , 1 . 6 , 1 . 8 with parameter τ = 1 which is the Caputo derivative. In Figure 6a, let us take different fractional orders and assume the parameter value τ = 0 . 6 . It is called the Hilfer derivative.
In Figure 6b, let us assume fractional order ω = 1 . 2 with different parameter values. If in this figure take τ = 1 and τ = 0 then it is referred to as the Caputo derivative and R-L derivative respectively. And the remaining parameter values are called as the Hilfer derivative.

Conclusion

In this paper, we have investigated the RLC circuit equation for existence and uniqueness results by using Schaefer’s fixed point theorem and Banach contraction principle. The stability results for RLC equation of Hilfer fractional integro differential equations with non-local boundary value problems are investigated. Finally, the numerical examples are provided. In the future, uniqueness and stability results in the system of ( k , ψ ) -Hilfer fractional derivatives of some multi-point boundary conditions with computational accuracy can be investigated.

References

  1. Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. Journal of Mathematical Analysis and Applications 2002, 265, 229–248. [Google Scholar] [CrossRef]
  2. Gupta, V.; Dabas, J.; Fečkan, M. Existence results of solutions for impulsive fractional differential equations. Nonautonomous Dynamical Systems 2018, 5, 35–51. [Google Scholar]
  3. Hilfer, R. Applications of fractional calculus in physics; World scientific, 2000.
  4. Podlubny, I. Fractional differential equations, mathematics in science and engineering, 1999.
  5. Zhou, Y. Zhou, Y. Basic theory of fractional differential equationsWorld Scientific Publishing Co. Pte. Ltd., Hackensack, NJ 2014.
  6. Ahmad, B.; Nieto, J.J. Riemann-Liouville fractional integro-differential equations with fractional nonlocal integral boundary conditions. Boundary Value Problems 2011, 2011, 1–9. [Google Scholar] [CrossRef]
  7. Borisut, P.; Kumam, P.; Ahmed, I.; Jirakitpuwapat, W. Existence and uniqueness for ψ-Hilfer fractional differential equation with nonlocal multi-point condition. Mathematical Methods in the Applied Sciences 2021, 44, 2506–2520. [Google Scholar] [CrossRef]
  8. Furati, K.M.; Kassim, M.D.; others. Existence and uniqueness for a problem involving Hilfer fractional derivative. Computers & Mathematics with Applications 2012, 64, 1616–1626. [Google Scholar]
  9. Gu, H.; Trujillo, J.J. Existence of mild solution for evolution equation with Hilfer fractional derivative. Applied Mathematics and Computation 2015, 257, 344–354. [Google Scholar] [CrossRef]
  10. Asawasamrit, S.; Kijjathanakorn, A.; Ntouyas, S.K.; Tariboon, J. Nonlocal boundary value problems for Hilfer fractional differential equations. Bulletin of the Korean Mathematical Society 2018, 55, 1639–1657. [Google Scholar]
  11. Vivek, D.; M Elsayed, E.; Kanagarajan, K. Nonlocal Initial Value Problems For Nonlinear Neutral Pantograph Equations With Hilfer-Hadamard Fractional Derivative. Information Sciences Letters 2021, 10, 13. [Google Scholar]
  12. Wang, J.; Zhang, Y. Nonlocal initial value problems for differential equations with Hilfer fractional derivative. Applied Mathematics and Computation 2015, 266, 850–859. [Google Scholar]
  13. Gholami, Y. Existence and uniqueness criteria for the higher-order Hilfer fractional boundary value problems at resonance. Advances in Difference Equations 2020, 2020, 1–25. [Google Scholar]
  14. Naveen, S.; Srilekha, R.; Suganya, S.; Parthiban, V. Controllability of damped dynamical systems modelled by Hilfer fractional derivatives. Journal of Taibah University for Science 2022, 16, 1254–1263. [Google Scholar] [CrossRef]
  15. Owolabi, K.M. NUMERICAL ANALYSIS AND PATTERN FORMATION PROCESS FOR SPACE-FRACTIONAL SUPERDIFFUSIVE SYSTEMS. Discrete & Continuous Dynamical Systems-Series S 2019, 12. [Google Scholar]
  16. Gómez-Aguilar, J. Fundamental solutions to electrical circuits of non-integer order via fractional derivatives with and without singular kernels. The European Physical Journal Plus 2018, 133, 197. [Google Scholar] [CrossRef]
  17. Sabir, Z.; Saoud, S.; Raja, M.A.Z.; Wahab, H.A.; Arbi, A. Heuristic computing technique for numerical solutions of nonlinear fourth order Emden–Fowler equation. Mathematics and Computers in Simulation 2020, 178, 534–548. [Google Scholar] [CrossRef]
  18. Sabir, Z.; Raja, M.A.Z.; Arbi, A.; Altamirano, G.C.; Cao, J. Neuro-swarms intelligent computing using Gudermannian kernel for solving a class of second order Lane-Emden singular nonlinear model. AIMS Math 2021, 6, 2468–2485. [Google Scholar] [CrossRef]
  19. Gómez-Aguilar, J.; Atangana, A. New insight in fractional differentiation: power, exponential decay and Mittag-Leffler laws and applications. The European Physical Journal Plus 2017, 132, 1–21. [Google Scholar] [CrossRef]
  20. Sene, N.; Abdelmalek, K. Analysis of the fractional diffusion equations described by Atangana-Baleanu-Caputo fractional derivative. Chaos, Solitons & Fractals 2019, 127, 158–164. [Google Scholar]
  21. AGUILAR, J.F.G. Behavior characteristics of a cap-resistor, memcapacitor, and a memristor from the response obtained of RC and RL electrical circuits described by fractional differential equations. Turkish Journal of Electrical Engineering and Computer Sciences 2016, 24, 1421–1433. [Google Scholar] [CrossRef]
  22. Morales-Delgado, V.F.; Gómez-Aguilar, J.F.; Taneco-Hernández, M.A.; Escobar-Jiménez, R.F. Fractional operator without singular kernel: applications to linear electrical circuits. International Journal of Circuit Theory and Applications 2018, 46, 2394–2419. [Google Scholar] [CrossRef]
  23. Morales-Delgado, V.; Gómez-Aguilar, J.; Taneco-Hernandez, M. Analytical solutions of electrical circuits described by fractional conformable derivatives in Liouville-Caputo sense. AEU-International Journal of Electronics and Communications 2018, 85, 108–117. [Google Scholar]
  24. Gómez-Aguilar, J.; Escobar-Jiménez, R.; Olivares-Peregrino, V.; Taneco-Hernandez, M.; Guerrero-Ramírez, G. Electrical circuits RC and RL involving fractional operators with bi-order. Advances in mechanical engineering 2017, 9, 1687814017707132. [Google Scholar]
  25. Gómez-Aguilar, J.F.; Atangana, A.; Morales-Delgado, V.F. Electrical circuits RC, LC, and RL described by Atangana–Baleanu fractional derivatives. International Journal of Circuit Theory and Applications 2017, 45, 1514–1533. [Google Scholar] [CrossRef]
  26. Radwan, A.G.; Salama, K.N. Fractional-order RC and RL circuits. Circuits, Systems, and Signal Processing 2012, 31, 1901–1915. [Google Scholar] [CrossRef]
  27. Sene, N.; Gómez-Aguilar, J. Analytical solutions of electrical circuits considering certain generalized fractional derivatives. The European Physical Journal Plus 2019, 134, 260. [Google Scholar] [CrossRef]
  28. Sene, N. Fractional input stability for electrical circuits described by the Riemann-Liouville and the Caputo fractional derivatives. Aims Math 2019, 4, 147–165. [Google Scholar] [CrossRef]
  29. Gómez-Aguilar, J.; Córdova-Fraga, T.; Escalante-Martínez, J.; Calderón-Ramón, C.; Escobar-Jiménez, R. Electrical circuits described by a fractional derivative with regular kernel. Revista mexicana de física 2016, 62, 144–154. [Google Scholar]
  30. Francisco, G.A.J.; Juan, R.G.; Manuel, G.C.; Roberto, R.H.J. Fractional RC and LC electrical circuits. Ingeniería, Investigación y Tecnología 2014, 15, 311–319. [Google Scholar] [CrossRef]
  31. Arshad, U.; Sultana, M.; Ali, A.H.; Bazighifan, O.; Al-Moneef, A.A.; Nonlaopon, K. Numerical solutions of fractional-order electrical rlc circuit equations via three numerical techniques. Mathematics 2022, 10, 3071. [Google Scholar] [CrossRef]
  32. Malarvizhi, M.; Karunanithi, S.; Gajalakshmi, N. Numerical Analysis Using RK-4 In Transient Analysis Of RLC Circuit. Advances in Mathematics: Scientific Journal 2020, 9, 6115–6124. [Google Scholar]
  33. Gómez-Aguilar, J.; Escobar-Jiménez, R.; Olivares-Peregrino, V.; Taneco-Hernandez, M.; Guerrero-Ramírez, G. Electrical circuits RC and RL involving fractional operators with bi-order. Advances in mechanical engineering 2017, 9, 1687814017707132. [Google Scholar] [CrossRef]
  34. Abbas, S.; Benchohra, M.; Sivasundaram, S. Dynamics and Ulam stability for Hilfer type fractional differential equations. Nonlinear Studies 2016, 23. [Google Scholar]
  35. András, S.; Kolumbán, J.J. On the Ulam–Hyers stability of first order differential systems with nonlocal initial conditions. Nonlinear Analysis: Theory, Methods & Applications 2013, 82, 1–11. [Google Scholar]
  36. Harikrishnan, S.; Kanagarajan, K.; Vivek, D. SOME EXISTENCE AND STABILITY RESULTS FOR INTEGRO-DIFFERENTIAL EQUATION BY HILFER-KATUGAMPOLA FRACTIONAL DERIVATIVE. Palestine Journal of Mathematics 2020, 9. [Google Scholar]
  37. Sudsutad, W.; Thaiprayoon, C.; Ntouyas, S.K. Existence and stability results for ψ-Hilfer fractional integro-differential equation with mixed nonlocal boundary conditions. AIMS Math 2021, 6, 4119–4141. [Google Scholar] [CrossRef]
  38. Wang, J.; Zhou, Y.; Medveď, M. Existence and stability of fractional differential equations with Hadamard derivative. Topological Methods in Nonlinear Analysis 2013, 41, 113–133. [Google Scholar]
  39. Rus, I.A. Ulam stabilities of ordinary differential equations in a Banach space. Carpathian Journal of Mathematics 2010, pp. 103–107.
  40. Ibrahim, R.W. Generalized Ulam-Hyers stability for fractional differential equations. International Journal of mathematics 2012, 23, 1250056. [Google Scholar] [CrossRef]
  41. Pachpatte, D.B. Existence and stability of some nonlinear ψ-Hilfer partial fractional differential equation. Partial Differential Equations in Applied Mathematics 2021, 3, 100032. [Google Scholar] [CrossRef]
  42. Wang, J.; Lv, L.; Zhou, Y. New concepts and results in stability of fractional differential equations. Communications in Nonlinear Science and Numerical Simulation 2012, 17, 2530–2538. [Google Scholar] [CrossRef]
Preprints 87152 g001
Figure 1. Diagram of a series RLC circuit.
Figure 1. Diagram of a series RLC circuit.
Preprints 87152 g001
Preprints 87152 g002
Figure 2. RLC circuit equation with Hilfer fractional derivative of parameters R = 4 , I = 2 , C = 5 , E 0 = 10 .
Figure 2. RLC circuit equation with Hilfer fractional derivative of parameters R = 4 , I = 2 , C = 5 , E 0 = 10 .
Preprints 87152 g002
Preprints 87152 g003
Figure 3. Different fractional order of R-L and Caputo Derivative.
Figure 3. Different fractional order of R-L and Caputo Derivative.
Preprints 87152 g003
Preprints 87152 g004
Figure 4. Hilfer Fractional Derivative.
Figure 4. Hilfer Fractional Derivative.
Preprints 87152 g004
Preprints 87152 g005
Figure 5. 3D-View of Hilfer Derivative of Different Orders and Parameter at t = 2 . 5 .
Figure 5. 3D-View of Hilfer Derivative of Different Orders and Parameter at t = 2 . 5 .
Preprints 87152 g005
Preprints 87152 g006
Figure 6. Different Fractional order of R-L and Caputo Derivative.
Figure 6. Different Fractional order of R-L and Caputo Derivative.
Preprints 87152 g006
Preprints 87152 g007
Figure 7. Hilfer Fractional Derivative.
Figure 7. Hilfer Fractional Derivative.
Preprints 87152 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated