Preprint
Article
An Efficient Plug-and-Play Post-Training Pruning Strategy in Large Language Models
Altmetrics
Downloads
563
Views
434
Comments
0
This version is not peer-reviewed
Submitted:
23 October 2023
Posted:
24 October 2023
Read the latest preprint version here
Alerts
Abstract
With the rapid growth of large language models (LLMs), there is increasing demand for memory and computation for LLMs. Recent efforts on post-training pruning of LLMs aim to reduce the model size and computation, yet the performance is still sub-optimal. In this paper, we present a plug-and-play solution for post-training pruning of LLMs. The proposed solution has two innovative components: 1) **Relative Importance and Activations** (RIA), a new pruning metric that jointly considers the weight and activations efficiently on LLMs; and 2) **Channel Permutation**, a new approach to maximally preserve important weights under N:M sparsity. The proposed two components can be readily combined to further enhance the N:M structuredly pruned LLMs. Our empirical experiments show that RIA alone can already surpass all existing post-training pruning methods on prevalent LLMs, e.g., LLaMA ranging from 7B to 65B. Furthermore, N:M structured pruning with channel permutation can even outperform the original LLaMA2 70B on zero-shot tasks, together with practical speed-up on specific hardware.
Keywords:
Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning
1. Introduction
Recent research on Large Language Models (LLMs) has garnered significant interest. These LLMs, characterized by their vast number of parameters, have exhibited remarkable proficiency across a wide range of tasks. However, deploying such models poses challenges due to their substantial size, computational demands, and execution time. To address this, several methods for network compression have been explored, including model quantization (Frantar et al. 2022; Lin et al. 2023; Xiao et al. 2023) which is the most popular and mature method, and network sparsity (Frantar and Alistarh 2023; Hassibi et al. 1993; LeCun et al. 1989; Mocanu et al. 2018; Sun et al. 2023).
Unlike quantization techniques, which adjust the precision of weights or activations to compress the network, network sparsity primarily targets the elimination of redundant or useless weights within models. Despite its potential, the exploration of sparsity in LLMs remains somewhat limited. Generally, there are three primary ways to induce sparsity in neural networks: 1) sparse training (Evci et al. 2020; Hoang et al. 2022; Lee et al. 2018; Mocanu et al. 2018; Sanh et al. 2020; Yuan et al. 2021; Zhang et al. 2023); 2) pruning-aware training (Han et al. 2015; Liu et al. 2021); and 3) post-training pruning (PTP) (Frantar and Alistarh 2023; Hassibi et al. 1993; Li and Louri 2021; Sun et al. 2023). However, both sparse training and during-training pruning require multiple rounds of iterative training, which is computationally costly and time-consuming, especially for LLMs. Therefore, one-shot PTP on a well-pre-trained model represents a more reasonable approach for LLMs.
The primary challenge associated with post-training pruning lies in the substantial performance degradation compared to dense models. Current methods, like SparseGPT (Frantar and Alistarh 2023) and Wanda (Sun et al. 2023), exhibit promising results in unstructured pruning. Nonetheless, to achieve practical speed-up, it is favored to conduct N:M structured pruning, which can be supported on specific hardware with sparse matrix multiplications Mishra et al. (2021). These prior methods Frantar and Alistarh (2023); Sun et al. (2023) under the N:M sparsity suffer from significant performance drops, thereby restricting their applications in practice. Recently, (Pool and Yu 2021) has introduced an input channel permutation method using the greedy search, which can boost the performance under the N:M sparsity. However, the greedy search is time-consuming on LLMs and thus can be hardly applied.
In this paper, we introduce a plug-and-play post-training pruning method for LLMs. Specifically, the method comprises two key components. First, we introduce Relative Importance and Activation (RIA), a new pruning metric for LLM pruning. We show that prior pruning metrics Frantar and Alistarh (2023); Sun et al. (2023) tend to prune away entire channels of network weights, which is undesired for neither unstructured nor N:M structured pruning. Instead, RIA jointly considers the input and output channels of weight, together with the activation information, and it turns out to effectively mitigate such issues. Second, we also consider a better way to turn LLMs into N:M sparsity. Unlike existing methods that directly convert the weight matrix to N:M sparsity, we propose channel permutation to properly permute the weight channels so as to maximally preserve the important weights under N:M structures. Finally, the proposed RIA and channel permutation can be readily combined, leading to an efficient and plug-and-play approach for the real-world acceleration of sparse LLMs inference.
Extensive evaluation on open-sourced LLMs (e.g., LLaMA (Touvron et al. 2023), LLaMA-2 (Touvron et al. 2023), and OPT (Zhang et al. 2022)) demonstrates that RIA outperforms SOTA one-shot post-training pruning (PTP) methods in both unstructured sparsity and N:M sparsity scenario. Additionally, channel permutation can be efficiently scaled to LLMs with over 70B parameters within 2 hours, yet recover a lot of the performance drop caused by N:M constraint and even outperforms 3 out of 5 datasets in comparison to the dense models involved in the article. By employing RIA and channel permutation, LLMs can undergo a smooth transition into N:M constraints. This ensures compatibility with hardware requirements while maintaining the performance of the pruned model intact.
2. Related work
Post-Training Pruning. PTP methods trace their roots to OBD (LeCun et al. 1989), which employs the Hessian Matrix for weight pruning. OBS (Hassibi et al. 1993) further refines the approach by adjusting remaining weights to minimize loss changes during pruning. The advent of Large Language Models (LLMs) has sparked interest in leveraging the Hessian Matrix for pruning, exemplified by works like AdaPrune (Li and Louri 2021) and Iterative Adaprune (Frantar and Alistarh 2022) targeting BERT (Devlin et al. 2018). However, weight reconstruction via Hessian Matrix inverse incurs substantial computational complexity, at . SparseGPT (Frantar and Alistarh 2023) reduces this complexity to , while Wanda (Sun et al. 2023) leverages input activations for efficient one-shot PTP with reduced pruning time and comparable performance to SparseGPT. Our proposed method, Relative Importance and Activations (RIA) inherits the time-saving advantages of Wanda while simultaneously enhancing the performance of the pruned LLMs.
N:M Sparsity. Recently, NVIDIA has introduced N:M constraint sparsity (Mishra et al. 2021) as a method to compress neural network models while preserving hardware efficiency. This N:M sparsity constraint stipulates that at least N out of every contiguous M element must be set to zero, thereby accelerating matrix-multiply-accumulate instructions. For instance, a 2:4 constraint ratio results in 50% sparsity, effectively doubling the model’s inference speed when utilizing the NVIDIA Ampere GPU architecture. However, directly applying SOTA unstructured pruning methods to meet the N:M sparsity often leads to a noticeable decline in performance, as demonstrated in Table 5. Some approaches (Hubara et al. 2021; Zhang et al. 2022; Zhou et al. 2021) suggest fine-tuning pruned models to recover capacity, but this is prohibitively expensive for Large Language Models (LLMs).
Matrix Permutation. N:M sparsity primarily targets the application of sparsity in the input channel dimension. (Pool and Yu 2021) presents a permutation method to identify the optimal permutation of input channels through an exhaustive greedy search and an escape phase to navigate local minima. However, this greedy approach becomes impractically time-consuming when applied to LLMs due to their extensive linear layers. In this study, we leverage the specific characteristics of LLMs and propose a Channel Permutation strategy. This approach transforms the permutation problem into a well-known combinatorial optimization problem, the linear sum assignment (LSA). We efficiently solve this problem using the Hungarian algorithm, resulting in a significant reduction in computation time.
3. LLM Pruning with Relative Importance and Activations
3.1. Post-training Pruning: Preliminaries
Post-training pruning (PTP) typically starts from the pre-trained network, removes redundant parameters, and does not need end-to-end fine-tuning. Unlike training-based pruning methods (Mocanu et al. 2018; Sanh et al. 2020; Zhang et al. 2023), PTP is fast, resource-saving, and therefore preferred for compressing LLMs (Frantar and Alistarh 2023; Sun et al. 2023). PTP is currently prevalent in unstructured pruning and N:M structured pruning, which is also the main focus of this paper. It is less applied in structured pruning due to a larger performance drop.
A common approach to achieve PTP is layer-wise pruning, i.e., minimizing the discrepancy square error between the dense and pruned model layer-by-layer recursively. Specifically, we denote the input of the l-th linear layer as , and weight , where r and c represents the number of output and input channels respectively. Our primary goal is to find the pruning mask that minimizes the distance error between the original and pruned layer. Therefore, the objective can be formally expressed as follows:
where k represents the number of remaining weights determined by the pruning ratio, and is the -norm (i.e., the number of non-zero elements). To solve in Equation 1, there are various pruning metrics, e.g., magnitude-based pruning that mask the weight below a certain threshold. Nonetheless, we show that these prior pruning metrics have intrinsic drawbacks, as discussed in the following section. Optionally, the weight in Equation 1 can also be reconstructed via closed-form updates (Frantar and Alistarh 2023); see Appendix B for more discussions.
3.2. Relative Importance: A New Pruning Metric
We present relative importance (dubbed as RI), a new metric for LLM pruning. We find that prevalent PTP methods tend to suffer from channel corruption, i,e., the entire input or output channel is pruned away, which severely downgrades the LLMs similar to structured pruning. To illustrate this, Figure 1 shows a linear layer with . Magnitude-based pruning with 50% unstructured sparsity will corrupt , i,e, the 4-th output channel. In practice, we find similar issues also exist in other prevalent pruning metrics, e.g., Wanda (Sun et al. 2023) prunes around 600 channels pruned out of 5120 channels, with more than 10% channels corrupted. Given that well-trained LLMs contain unique information in the input and output channels, it is critical to avoid channel corruption in post-training pruning.
Figure 1.
An example of Relative Importance. The connection at position 44 will be removed based on global network magnitude, however, it is retained when evaluated for its significance within relative connections.
Figure 1.
An example of Relative Importance. The connection at position 44 will be removed based on global network magnitude, however, it is retained when evaluated for its significance within relative connections.
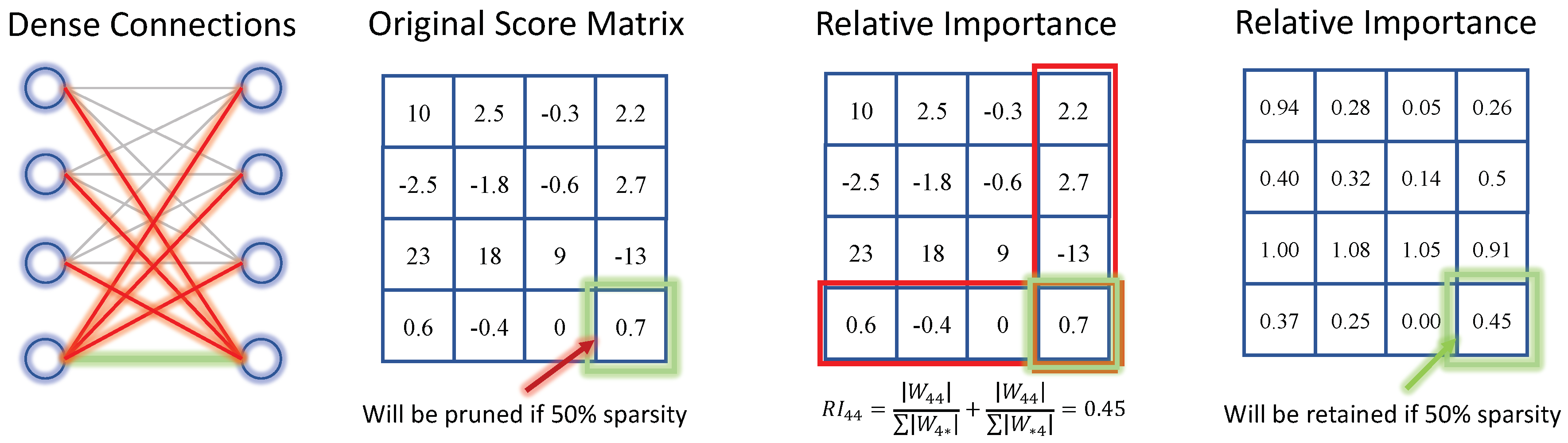
To mitigate such issues, the proposed relative importance (RI) aims to re-evaluate the importance of each weight element based on all connections that originate from the input neuron i or lead to the output neuron j. Specifically, the relative importance for can be calculated as:
where sums over the absolute values of input channel j, and similarly for the sum of oinputput channels i. The resulting score offers insight into the relative importance of weight in the context of its connections to neurons i and j.
3.3. Incorporating Activations into Relative Importance
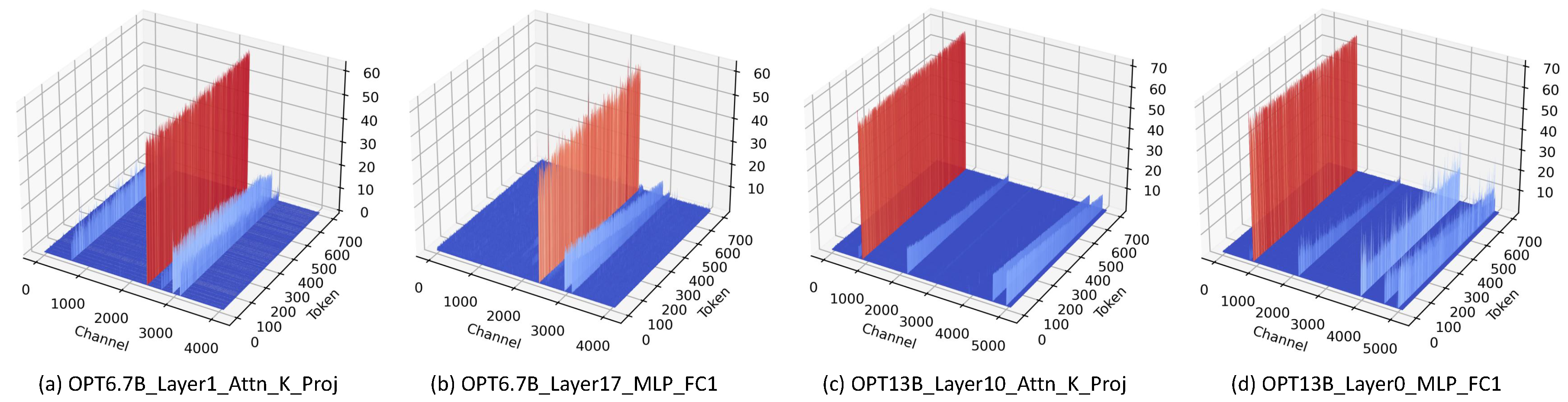
The proposed relative importance can be further combined with activations to better assess the weight significance, dubbed as relative importance and activation (RIA). Recent findings (Xiao et al. 2023) show that the occurrence of activation outliers has become a well-known issue in quantizing LLMs. Our visualizations on LLaMA-7B and LLaMA-13B also confirm these outliers; see Figure A1 and Figure A2 for details.
Moreover, we find that activation outliers persist regardless of the dataset or parts of the model. To see this, we calculate the Spearman’s Rank Correlation Coefficient of activations between different datasets. From Figure 2, it can be found that pair-wise correlations of activations exhibit positive values and similar trends across different layers and Transformer modules.
Built upon Equation 2, for each element , RIA further combines -norm of activations as follows:
where a power factor a is introduced to control the strength of activations. Our empirical results show that works generally well for different LLMs and datasets.
4. Turning into N:M Sparsity
This section studies how to turn LLMs into N:M sparsity with the pruning metric. N:M sparsity is usually favored by post-training pruning given its practical speed-up on specific hardware. Unlike existing solutions that directly convert to the N:M format, we propose channel permutation, a new approach that better leverages the pruning metrics by efficiently permuting the weight channels. Channel permutation can work seamlessly with the RIA metric in Section 3, as well as other prevalent methods such as (Frantar and Alistarh 2023; Sun et al. 2023).
4.1. N:M Structured Pruning: Formulation
We begin by revisiting unstructured PTP in Equation 1. Without loss of generality, we denote the weight importance score as , which can be either RIA or other pruning metrics. It is an NP-hard problem (Frantar and Alistarh 2023) to find the optimal in Equation 1. A common surrogate is to maximize the sum of retained weight importance scores as follows:
Similarly, for N:M sparsity, every N out of M contiguous elements is zero along each output channel, and the objective is re-formulated as:
A simple solution to Equation 5 in existing works (Frantar and Alistarh 2023; Sun et al. 2023) is directly setting the mask of top N elements in to 1, and 0 otherwise. Nonetheless, this usually leads to sub-optimal solutions. As illustrated in Figure 3, some input channels with similar scores, either large or small, might get stuck in the same weight block . As a consequence, some large weights might be pruned by mistake while small weights might be preserved instead.
4.2. Channel Permutation for Improved N:M Sparsity
To address the aforementioned challenge, we present a new channel permutation (CP) approach that gives better N:M structures. Note that permuting the input channels of weight can lead to different importance scores . We thus introduce an additional column permutation matrix for , such that the sum of retained weight importance can be further maximized:
For ease of presentation in the following, we denote the block of the weight matrix as , where and K is the number of blocks. N:M pruning thus occurs row-wisely within each block, i.e., only n values are preserved out of m elements for . Based on the notation, the proposed channel permutation mainly includes the following two steps.
- Step 1:
- Heuristic Channel Allocation.
We first calculate the sum of weight importance for each input channel. These channels are then sorted to be allocated in K blocks. To maximally retain the important channels in each block with N:M sparsity, we use a heuristic allocation strategy. Given K blocks, we alternatively allocate every top-K input channel into each block, and this process is repeated for m times until all channels are allocated. An example is illustrated in Figure 3. Given 8 input channels and 4 output channels, there are 2 blocks under 2:4 sparsity. The top-1 and and top-2 channels are allocated to block 1 and block 2, and similarly for the rest input channels. Given such a heuristic channel allocation strategy, it can be found that there is a significant enhancement in the sum of retained weight importance scores compared to direct N:M pruning.
- Step 2:
- Linear Sum Assignment.
In the next, we show the heuristic allocation strategy can be further refined. The refining process can be formulated as a linear sum assignment (LSA) problem, which can be efficiently solved by the Hungarian algorithm Kuhn (1955). To see this, we can take out one allocated channel from each block, and thus there are K channels to be filled back to K blocks. It is thus a traditional linear sum assignment problem to find a better one-by-one matching between the K channels and K blocks, such that the weight importance sum in Equation 6 can be further improved. From Figure 3, LSA further improves the score sum by , with the top-1 and top-2, top-3 and top-4 channels swapped from the heuristic channel allocation.
- Remarks.
Note that the permutation of weight matrices does not affect the output of LLMs. For dense layers, the input activations need to be simultaneously permuted, which can be done by permuting the output channels of the previous layer. The exception lies in the residual connection, which can be done with an efficient permutation operator. More details on implementing channel permutation and Hungarian algorithm are listed in Appendix C.
5. Experiments
5.1. Setup
We evaluate the proposed approach on three popular LLMs: LLaMA 7B-65B (Touvron et al. 2023), LLaMA2 7B-70B (Touvron et al. 2023), and OPT 1.3B-13B (Zhang et al. 2022). We use the public checkpoint of the involved models in the HuggingFace Transformers library 1. We utilize 3 NVIDIA A100 GPUs each equipped with 80GB memory. For each model under consideration, we apply uniform pruning to all linear layers, with the exception of embeddings and the head. Specifically, in each self-attention module, there are four linear layers, while each MLP module contains three linear layers for LLaMA model families and two for OPT. All the evaluations are conducted with the same code to make sure the comparison is fair.
- Tasks and Metrics.
We mainly evaluate language modeling and zero-shot classification. Our initial assessment of language modeling involves a comprehensive evaluation of perplexity (PPL), where lower values indicate better performance. This evaluation is conducted on the test set of Wikitext2 (Merity et al. 2016). For further evaluation, we also conduct experiments on zero-shot classification to assess the ability of the sparse model to correctly classify objects or data points into categories it has never seen during training across five common-sense datasets: Hellaswag, BoolQ, ARC-Challenge, MNLI, and RTE, in comparison to the performance of the dense model. We run the experiments with the public GitHub benchmark EleutherAI/lm-evaluation-harness (Gao et al. 2021).
- Baselines.
For unstructured pruning, we compare with: 1) magnitude pruning (Zhu and Gupta 2017), the most prevalent pruning approach; and two more recent state-of-the-art works on LLM pruning: 2) SparseGPT (Frantar and Alistarh 2023) and 3) Wanda (Sun et al. 2023). These methods can be evaluated both on unstructured pruning and N:M structured pruning in the following sections.
- Calibration Data.
We employ 128 samples from the C4 dataset (Raffel et al. 2019) for all models, and each sample contains 2048 tokens. This also aligns with the settings in baseline methods for a fair comparison. Note that we also discuss the choice of calibration data across different datasets, and more details can be found in Appendix A.
5.2. Unstructured Pruning
- Main Results.
As highlighted in Table 1, RIA consistently outperforms Wanda and SparseGPT across all scenarios. Notably, our method achieves a 50% improvement in preventing performance drop of the Dense model in comparison to Sparsegpt (16% in LLaMA and LLaMA2 model family), and 17% improvement in preventing performance drop in comparison to Wanda (13% in LLaMA and LLaMA2 model family). It is essential to note that as the model size increases, the performance gap between models pruned by RIA and the original dense models diminishes significantly.
- Ablation Studies.
To thoroughly evaluate the influence of each element within our RIA equation, we undertook an ablation test, with the outcomes presented in Table 2. We disassembled our formula into several distinct components for closer scrutiny: : weight magnitude; : weight magnitude normalized by the input channels; : weight magnitude normalized by the output channels; RI: stands for relative importance which is the combination of and ; and and combines relative importance with input activations with different values of a.
As illustrated in Table 2, normalizing the weight magnitude through either input or output channels offers a substantial performance boost over merely considering weight magnitude. Interestingly, utilizing Relative Importance alone can match or, in instances like LLaMA-30B, even outperform SparseGPT. A distinguishing feature of Relative Importance is its reliance solely on weight information, eliminating the need for calibration data. In contrast, both Wanda and SparseGPT necessitate calibration data to derive input activations or Hessian matrices. The table also showcases enhancements brought about by the other equation components of RIA.
Sparsity. In Figure 4(a), we examine the effects of varying sparsity levels, ranging from 0.1 to 0.6, on the performance of the LLaMA 65b model. The PPL curves clearly demonstrate that Magnitude pruning is particularly sensitive to increased sparsity levels, with a 60% sparsity level resulting in significant model degradation. In contrast, the SparseGPT, Wanda, and RIA models exhibit more robust performance across all tested sparsity levels, with RIA (green) consistently outperforming the others at every level of sparsity.
Calibration data. SparseGPT, Wanda, and RIA all require calibration data for obtaining either input activations or the Hessian matrix. To assess the robustness of our algorithm concerning the calibration data, we conducted a sensitivity test involving variations in the type of calibration datasets and the number of calibration samples. The influence of calibration datasets is presented in Table A1. Our aim here is to assess the impact of the number of calibration samples.
As illustrated in Figure 4(b), an example of the LLaMA30B model, SparseGPT appears to rely on a larger number of calibration samples, while both Wanda and RIA demonstrate robust performance across varying sample sizes. Notably, RIA consistently outperforms the other methods in all cases.
Zero-shot performance. In Table 3, we present the zero-shot performance of unstructured 50% sparsity of the models pruned with magnitude, Wanda, sparsegpt, and RIA on LLaMA2-70b model. We report the average performance across these datasets in the last column. As shown in the table, RIA gets the best performance on 3/5 datasets and also achieves the best average performance across the 5 datasets.
5.3. N:M Structured Pruning
While RIA aims to explore the upper bounds of performance achievable through one-shot PTP methods, combining it with the N:M constraint seeks the real inference speed by aligning with the present GPU hardware environment. In this subsection, we assess how Channel Permutation (CP) can enhance the performance of one-shot PTP when incorporated with the N:M constraint.
- Main Results.
In this comparison, we assess the performance of unstructured 50% sparsity, 2:4 constraint sparsity, and 4:8 constraint sparsity for Magnitude, Wanda, SparseGPT, and RIA. Additionally, we provide the performance results when applying Channel Permutation (CP) to each of these methods. Direct using step 1 of CP (CP w/o LSA) is also displayed in the table, serving as an ablation test in comparison to the complete one. We present the Perplexity of each pruned model on the Wikitext2 dataset, maintaining the same settings as in Section 5.1.
As presented in Table 4, RIA consistently delivers superior performance across all semi-structured sparsity patterns when employing one-shot PTP. Importantly, when utilizing merely CP, every method—with the exception of Magnitude—already exhibits a significant improvement in performance. With the incorperation of LSA, the performance is further improved. This highlights our motivation to group the input channels based on their sorted indices, ensuring that similar scaling channels don’t end up in the same block.
Zero-shot Performance. In Table 5, we present the zero-shot performance of the N:M constraint models pruned using RIA and Wanda. The table’s last column also provides the average performance across these datasets. As the table indicates, while there’s a performance decline on the Hellaswag and ARC-C datasets, the case of RIA (2:4+CP) performs even surpasses the dense model with a large amplitude on BoolQ, MNLI, and RTE datasets. This highlights the observation that large language models can be prone to overfitting, resulting in an abundance of redundant, unnecessary, or potentially harmful elements. It’s noteworthy that with the incorporation of CP, there’s a remarkable improvement in performance for both Wanda and RIA.
5.4. Running time analysis
- Pruning and permutation running time.
We present the actual running times of each algorithm on the largest model involved in this article, LLaMA2-70b. The relative complexity analysis can be found in Appendix D.
- Pruning time. We test each algorithm with 128 calibration data. For SparseGPT, the pruning time amounts to 5756 seconds (approximately 1.5 hours). In contrast, Wanda and RIA demonstrate significantly reduced runtimes, with times of approximately 611 seconds (approximately 10 minutes) and 627 seconds (approximately 10 minutes)
- Channel permutation time. For a comparative analysis of execution duration, we present the processing time of a single matrix constructed using our algorithm for the N:M sparsity. This is compared against the greedy method and its variants, which employ escaping strategies to circumvent getting trapped in local minima, as discussed in (Pool and Yu 2021). The results for different dimensions are provided in Table A3.
Inference acceleration. We assess the inference acceleration offered by sparsity in Large Language Models (LLMs). In a manner akin to SparseGPT (Frantar and Alistarh 2023), we present data for both the unstructured sparsity and 2:4 sparsity acceleration on CPU and GPU relative to the dense model across various components. For CPU-based inference, the torch. sparse package is employed to manage the sparse matrix and execute sparse matrix multiplication. Our observations indicate an inference speed acceleration ranging between 1.8× and 2.0×. In addition, we evaluate the speed acceleration observed on the GPU when applying a 2:4 constraint. Theoretically, employing an N:M sparsity can yield up to a 2× speedup when contrasted with dense models. We conducted tests on the Nvidia Tesla A100, utilizing the cuSPARSELt library for Sparse Matrix-Matrix Multiplication (SpMM) (Mishra et al. 2021) with N:M sparse matrices. For unstructured sparsity, we treated it as a dense matrix and assessed the actual inference speed. Comprehensive acceleration metrics for each module are outlined in Table 6 and the acceleration of each layer is about 1.6×. It’s worth mentioning that the overall speed enhancement for the entire model might be slightly reduced due to inherent overhead factors.
6. Discussion
Based on the results presented in Section 5, it is evident that after applying channel permutation, the performance of N:M constraint models significantly improves in comparison to executing N:M sparsity directly. This improvement can be demonstrated through empirical observations made within Large Language Models (LLMs). As shown in Figure 5, pruning with 50% unstructured sparsity versus direct N:M constraint sparsity (2:4 in the figure) produces distinct variances in the distribution of input channels’ retained degree. The N:M constraint, by its nature, results in a more uniform pruning pattern. With an example of the first row of Figure 3, when directly pruning with 2:4 constraint sparsity, if the input channels with universally larger scores get stuck in the same block, some of the weights will be “wrongly" pruned. Conversely, the block with universally smaller scaling scores will “wrongly" preserve some weights. One diminishes while the other grows, resulting in a more uniform pruning, a smaller variance of retained degree distribution of input channels, and therefore a lower total sum scores after pruning. In contrast, unstructured pruning takes on a broader perspective, pruning weights within their global context. This expansive methodology inherently introduces more variability, leading to a larger variance in the retained degree of input channels after pruning. The channel permutation method proposed in this article tackles this challenge smoothly by distributing similar scaling input channels into different blocks, allowing weights that should be retained to be preserved as much as possible. The post-channel-permutation distribution (2:4 + CP) of input channels’ retained degrees can be seen in Figure 5, closely mirroring the results of unstructured pruning.
7. Conclusion
In this article, we have introduced two novel methods, RIA and Channel Permutation, that together establish an effective plug-and-play pipeline for post-training pruning and inference acceleration of large language models. RIA incorporates Relative Importance and the feature of input activations that create a criterion to prune the weights of LLMs. Through extensive experiments on prominent LLMs like LLaMA, LLaMA2, and OPT across varying model sizes, we have demonstrated that RIA consistently outperforms existing SOTA one-shot pruning techniques SparseGPT and Wanda, which sets a new benchmark for post-training pruning performance. Furthermore, Channel Permutation successfully reduces the performance drop when adapting the model to N:M constraint by reframing the input channel permutation problem as a combinatorial optimization task and solving it efficiently with the Hungarian algorithm. Together, RIA and Channel Permutation form a seamless "plug-and-play" method, enabling effective one-shot post-training pruning for all current large language models. Furthermore, this method is hardware-friendly, ensuring enhanced inference acceleration.
Appendix A. Sensitivity test on calibration datasets
Table A1.
Assessing across various calibration and evaluation datasets. (LLaMA2-13B)
| Eval. dataset | PTB | wikitext2 | c4 | ||||||
| Calib. dataset | wikitext2 | c4 | PTB | wikitext2 | c4 | PTB | wikitext2 | c4 | PTB |
| Magnitude | 146.35 | 6.83 | 9.38 | ||||||
| Wanda | 68.49 | 69.70 | 63.58 | 5.85 | 5.97 | 5.89 | 8.43 | 8.30 | 8.25 |
| SparseGPT | 72.94 | 72.31 | 59.10 | 5.69 | 6.03 | 5.90 | 8.50 | 8.22 | 8.30 |
| RIA | 67.58 | 68.69 | 67.88 | 5.75 | 5.83 | 5.83 | 8.07 | 8.03 | 8.08 |
Figure 2 illustrates that different datasets exhibit varying data distributions, which in turn impact the input activations. Consequently, we conducted experiments employing different calibration datasets to evaluate the robustness of the pruned model. Specifically, we utilized three different datasets—Wikitext2, C4, and PTB (Marcus et al. 1993)—with 128 samples, each containing 2048 tokens, for calibration purposes, and evaluated the performance on Wikitext2. RIA is compared with Wanda and SparseGPT, with the results summarized in Table A1. RIA surpasses other algorithms in the majority of scenarios, with the exception of when using identical calibration and evaluation datasets for PTB and wikitext2. This exception can be primarily attributed to the weight reconstruction process. A distribution that is more congruent tends to yield enhanced performance through reconstruction. We therefore explored integrating the reconstruction approach with both Wanda and RIA in Appendix B. Furthermore, looking at the results across different calibration datasets, the results of RIA are more stable which indicates that RIA is more robust to the calibration data.
Appendix B. Weight Reconstruction
Following the approach of OBS (Hassibi et al. 1993), which replaces the fine-tuning process with weight reconstruction using calibration data, this method has gained traction in LLMs post-pruning as an alternative to fine-tuning and retraining. SparseGPT (Frantar and Alistarh 2023) extends this idea by permitting partial updates, thereby reducing computational complexity. The specific formula for this is detailed in (Frantar and Alistarh 2023). This weight reconstruction technique is essentially a tool embraced by all PTP methods that revise the objective function of equation 1 to A1.
In this formulation, represents the weight matrix after undergoing the reconstruction process. In this section, we evaluate Wanda and RIA based on their adoption of weight reconstruction and juxtapose their performance with that of SparseGPT. Our findings are presented in Table A2. We omit the results from PTB as their PPLs are excessively high, rendering them of no reference value. It’s evident that RIA+rec outperforms other reconstruction-based algorithms. However, except for wikitext2 is used both for calibration and evaluation, the reconstruction does not appear to enhance performance. Therefore, we have chosen not to employ this weight reconstruction approach in our main text.
Table A2.
Assessing the post-training pruning methods with weight reconstruction. (LLaMA13B)
| wikitext2 | c4 | |||||
| wikitext2 | c4 | PTB | wikitext2 | c4 | PTB | |
| Magnitude | 6.38 | 9.38 | ||||
| Magnitude + rec | 5.84 | 6.07 | 6.17 | 8.48 | 8.30 | 8.62 |
| Wanda | 5.85 | 5.97 | 5.89 | 8.43 | 8.30 | 8.25 |
| Wanda+rec | 5.70 | 6.00 | 5.91 | 8.57 | 8.29 | 8.35 |
| SparseGPT | 5.69 | 6.03 | 5.90 | 8.50 | 8.22 | 8.30 |
| RIA | 5.75 | 5.83 | 5.83 | 8.07 | 8.03 | 8.08 |
| RIA+rec | 5.57 | 5.86 | 5.83 | 8.20 | 8.03 | 8.21 |
Appendix C. Implementation Details of Channel Permutation
From a perspective of computational efficiency, directly implementing permutation on input vectors introduces extra runtime overhead for extracting the permuted index and applying it to the input vectors. However, an alternative approach can be considered. Given that each input serves as the output of the preceding layer, we can permute the output channels of the previous layers’ weights to serve as the permuted index for the next layers’ input channels. This eliminates the need to permute the input index separately, resulting in time savings.
However, two key considerations must be taken into account:
a) For the Q, K, and V projection layers within a single module, they must be treated as a unified matrix, concatenating them into a single entity that shares the same input channel indices. This ensures that the input index permutation remains identical across these layers, avoiding the need for additional permutations. In the case of LLaMA, the MLP module presents a similar scenario, as it contains parallel layers, namely, down_proj and gate_proj, which also need to be concatenated into a single matrix.
b) Another important factor to note is that when dealing with models featuring residual connections, this strategy cannot be applied. This is due to the fact that inputs in such modules also originate from the previous module. As a result, permutations must be applied to the input activations at the beginning of each module. However, this process doesn’t significantly impact execution time. In fact, we’ve modified the RMS normalization layer — which typically follows the Residual connection — using Triton (Tillet et al. 2019). This ensures the output channel indices of this layer align with the input indices of the subsequent layers. In our tests, the time taken for this adjustment is negligible.
Figure A1.
Outliers in LLaMA-7B and LLaMA-13B.
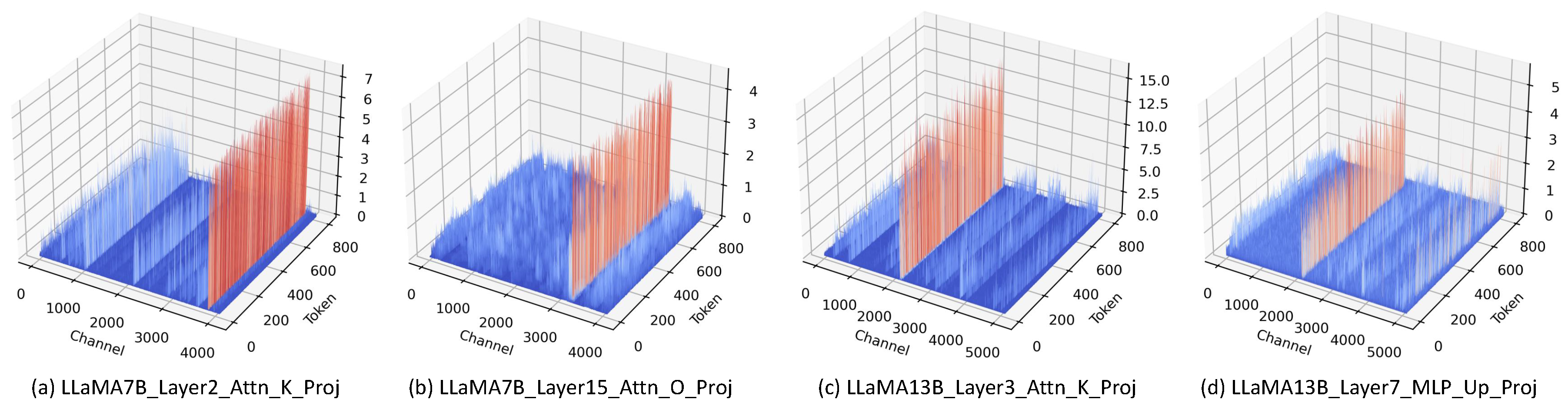
Figure A2.
Outliers in opt-6.7B and opt-13B.
Appendix D. Complexity analysis of RIA and Channel Permutation
RIA. We provide a summary of the computational complexity of various Post-Training Pruning (PTP) algorithms. For SparseGPT, the time complexity is approximately (Frantar and Alistarh 2023), whereas both RIA and Wanda exhibit similar time complexities of approximately (Sun et al. 2023).
Table A3.
Permutation time (seconds) for Greedy algorithm and Channel Permutation
| Greedy | 252.1 | 495.4 | 818.7 | 1563.6 |
| Greedy + 100 escapes | 845.3 | 1349.1 | 1896.4 | 3592.3 |
| Channel Permutation | 6.2 | 8.1 | 11.5 | 15.3 |
Channel Permutation The process of channel reallocation to obtain the sorted input channel indices is straightforward. Computation of the score matrix S involves determining the outcome of placing each objection into every box and summing the results while processing the 2:4 constraint within each block. Consequently, the time complexity for this computation is , where represents the computational complexity for the N:M constraint within each block. The time complexity of the Hungarian algorithm is .
The greedy method (Pool and Yu 2021) is challenging to implement in LLMs due to its prohibitive running time, as shown in Table A3. We conducted only a single experiment for performance comparison on LLaMA2-13b, which took us 3 days. We tested the greedy method with 100 escape iterations to handle the permutation, the PPL on wikitext2 with a permuted 2:4 constraint is 8.01 which is just comparable to our CP method (7.99). However, the CP’s execution time was just 30 minutes, making it possible to be applied in the LLMs.
Appendix E. Hungarian Algorithm
Given a bipartite graph with N left vertices and N right vertices, depicted by matrix , where represents the weight between the left vertex i and the right vertex j, the algorithm aims to identify the ideal matching that minimizes the aggregate weight. This goal is captured in the subsequent objective function:
In this Equation, is a binary determinant that showcases whether the left vertex i is paired with the right vertex j. In our scenario, the initial first group of input indices is treated as vertex i, with the incomplete boxes acting as vertex j. This transition into an LSA problem is seamlessly facilitated by the Hungarian algorithm, which subsequently derives the optimal permutation. After rearranging the first indices of the blocks, we apply the same procedure to the subsequent groups in sequence.
References
- Devlin, Jacob, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2018. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805.
- Evci, Utku, Trevor Gale, Jacob Menick, Pablo Samuel Castro, and Erich Elsen. 2020. Rigging the lottery: Making all tickets winners. In International Conference on Machine Learning, pp. 2943–2952. PMLR.
- Frantar, Elias and Dan Alistarh. 2022. Spdy: Accurate pruning with speedup guarantees. In International Conference on Machine Learning, pp. 6726–6743. PMLR.
- Frantar, Elias and Dan Alistarh. 2023. Sparsegpt: Massive language models can be accurately pruned in one-shot.
- Frantar, Elias, Saleh Ashkboos, Torsten Hoefler, and Dan Alistarh. 2022. Gptq: Accurate post-training quantization for generative pre-trained transformers. arXiv preprint arXiv:2210.17323.
- Gao, Leo, Jonathan Tow, Stella Biderman, Sid Black, Anthony DiPofi, Charles Foster, Laurence Golding, Jeffrey Hsu, Kyle McDonell, Niklas Muennighoff, Jason Phang, Laria Reynolds, Eric Tang, Anish Thite, Ben Wang, Kevin Wang, and Andy Zou. 2021, September. A framework for few-shot language model evaluation. [CrossRef]
- Han, Song, Jeff Pool, John Tran, and William Dally. 2015. Learning both weights and connections for efficient neural network. Advances in neural information processing systems 28. [CrossRef]
- Hassibi, Babak, David G Stork, and Gregory J Wolff. 1993. Optimal brain surgeon and general network pruning. In IEEE international conference on neural networks, pp. 293–299. IEEE. [CrossRef]
- Hoang, Duc NM, Shiwei Liu, Radu Marculescu, and Zhangyang Wang. 2022. Revisiting pruning at initialization through the lens of ramanujan graph. In The Eleventh International Conference on Learning Representations.
- Hubara, Itay, Brian Chmiel, Moshe Island, Ron Banner, Joseph Naor, and Daniel Soudry. 2021. Accelerated sparse neural training: A provable and efficient method to find n: m transposable masks. Advances in neural information processing systems 34, 21099–21111. [CrossRef]
- Kuhn, Harold W. 1955. The hungarian method for the assignment problem. Naval Research Logistics Quarterly 2(1-2), 83–97. [CrossRef]
- LeCun, Yann, John Denker, and Sara Solla. 1989. Optimal brain damage. Advances in neural information processing systems 2.
- Lee, Namhoon, Thalaiyasingam Ajanthan, and Philip HS Torr. 2018. Snip: Single-shot network pruning based on connection sensitivity. arXiv preprint arXiv:1810.02340.
- Li, Jiajun and Ahmed Louri. 2021. Adaprune: An accelerator-aware pruning technique for sustainable cnn accelerators. IEEE Transactions on Sustainable Computing 7(1), 47–60. [CrossRef]
- Lin, Ji, Jiaming Tang, Haotian Tang, Shang Yang, Xingyu Dang, and Song Han. 2023. Awq: Activation-aware weight quantization for llm compression and acceleration. arXiv preprint arXiv:2306.00978.
- Liu, Shiwei, Tianlong Chen, Xiaohan Chen, Zahra Atashgahi, Lu Yin, Huanyu Kou, Li Shen, Mykola Pechenizkiy, Zhangyang Wang, and Decebal Constantin Mocanu. 2021. Sparse training via boosting pruning plasticity with neuroregeneration. Advances in Neural Information Processing Systems 34, 9908–9922.
- Marcus, Mitchell P., Beatrice Santorini, and Mary Ann Marcinkiewicz. 1993. Building a large annotated corpus of English: The Penn Treebank. Computational Linguistics 19(2), 313–330. [CrossRef]
- Merity, Stephen, Caiming Xiong, James Bradbury, and Richard Socher. 2016. Pointer sentinel mixture models.
- Mishra, Asit, Jorge Albericio Latorre, Jeff Pool, Darko Stosic, Dusan Stosic, Ganesh Venkatesh, Chong Yu, and Paulius Micikevicius. 2021. Accelerating sparse deep neural networks. arXiv preprint arXiv:2104.08378.
- Mocanu, Decebal Constantin, Elena Mocanu, Peter Stone, Phuong H Nguyen, Madeleine Gibescu, and Antonio Liotta. 2018. Scalable training of artificial neural networks with adaptive sparse connectivity inspired by network science. Nature communications 9(1), 2383. [CrossRef]
- Pool, Jeff and Chong Yu. 2021. Channel permutations for n: M sparsity. Advances in neural information processing systems 34, 13316–13327.
- Raffel, Colin, Noam Shazeer, Adam Roberts, Katherine Lee, Sharan Narang, Michael Matena, Yanqi Zhou, Wei Li, and Peter J. Liu. 2019. Exploring the limits of transfer learning with a unified text-to-text transformer. arXiv e-prints.
- Sanh, Victor, Thomas Wolf, and Alexander Rush. 2020. Movement pruning: Adaptive sparsity by fine-tuning. Advances in Neural Information Processing Systems 33, 20378–20389.
- Sun, Mingjie, Zhuang Liu, Anna Bair, and J Zico Kolter. 2023. A simple and effective pruning approach for large language models. arXiv preprint arXiv:2306.11695.
- Tillet, Philippe, Hsiang-Tsung Kung, and David Cox. 2019. Triton: an intermediate language and compiler for tiled neural network computations. In Proceedings of the 3rd ACM SIGPLAN International Workshop on Machine Learning and Programming Languages, pp. 10–19.
- Touvron, Hugo, Thibaut Lavril, Gautier Izacard, Xavier Martinet, Marie-Anne Lachaux, Timothée Lacroix, Baptiste Rozière, Naman Goyal, Eric Hambro, Faisal Azhar, et al. 2023. Llama: Open and efficient foundation language models. arXiv preprint arXiv:2302.13971.
- Touvron, Hugo, Louis Martin, Kevin Stone, Peter Albert, Amjad Almahairi, Yasmine Babaei, Nikolay Bashlykov, Soumya Batra, Prajjwal Bhargava, Shruti Bhosale, et al. 2023. Llama 2: Open foundation and fine-tuned chat models. arXiv preprint arXiv:2307.09288.
- Xiao, Guangxuan, Ji Lin, Mickael Seznec, Hao Wu, Julien Demouth, and Song Han. 2023. Smoothquant: Accurate and efficient post-training quantization for large language models. In International Conference on Machine Learning, pp. 38087–38099. PMLR.
- Yuan, Geng, Xiaolong Ma, Wei Niu, Zhengang Li, Zhenglun Kong, Ning Liu, Yifan Gong, Zheng Zhan, Chaoyang He, Qing Jin, et al. 2021. Mest: Accurate and fast memory-economic sparse training framework on the edge. Advances in Neural Information Processing Systems 34, 20838–20850.
- Zhang, Susan, Stephen Roller, Naman Goyal, Mikel Artetxe, Moya Chen, Shuohui Chen, Christopher Dewan, Mona Diab, Xian Li, Xi Victoria Lin, et al. 2022. Opt: Open pre-trained transformer language models. arXiv preprint arXiv:2205.01068.
- Zhang, Yuxin, Mingbao Lin, Zhihang Lin, Yiting Luo, Ke Li, Fei Chao, Yongjian Wu, and Rongrong Ji. 2022. Learning best combination for efficient n: M sparsity. Advances in Neural Information Processing Systems 35, 941–953.
- Zhang, Y, J Zhao, W Wu, A Muscoloni, and CV Cannistraci. 2023. Epitopological sparse ultra-deep learning: A brain-network topological theory carves communities in sparse and percolated hyperbolic anns.
- Zhou, Aojun, Yukun Ma, Junnan Zhu, Jianbo Liu, Zhijie Zhang, Kun Yuan, Wenxiu Sun, and Hongsheng Li. 2021. Learning n: m fine-grained structured sparse neural networks from scratch. arXiv preprint arXiv:2102.04010.
- Zhu, Michael and Suyog Gupta. 2017. To prune, or not to prune: exploring the efficacy of pruning for model compression. arXiv preprint arXiv:1710.01878.
| 1 |
https://huggingface.co/meta-llama, https://huggingface.co/facebook |
Figure 2.
Spearman’s Rank correlation of LLaMA2-13B activations from Wikitext2, C4, and PTB, each with 128 samples. Note that the Q, K, and V layers all share the same input activations. Similarly, the Up and Gate layers also receive identical input activations.
Figure 2.
Spearman’s Rank correlation of LLaMA2-13B activations from Wikitext2, C4, and PTB, each with 128 samples. Note that the Q, K, and V layers all share the same input activations. Similarly, the Up and Gate layers also receive identical input activations.
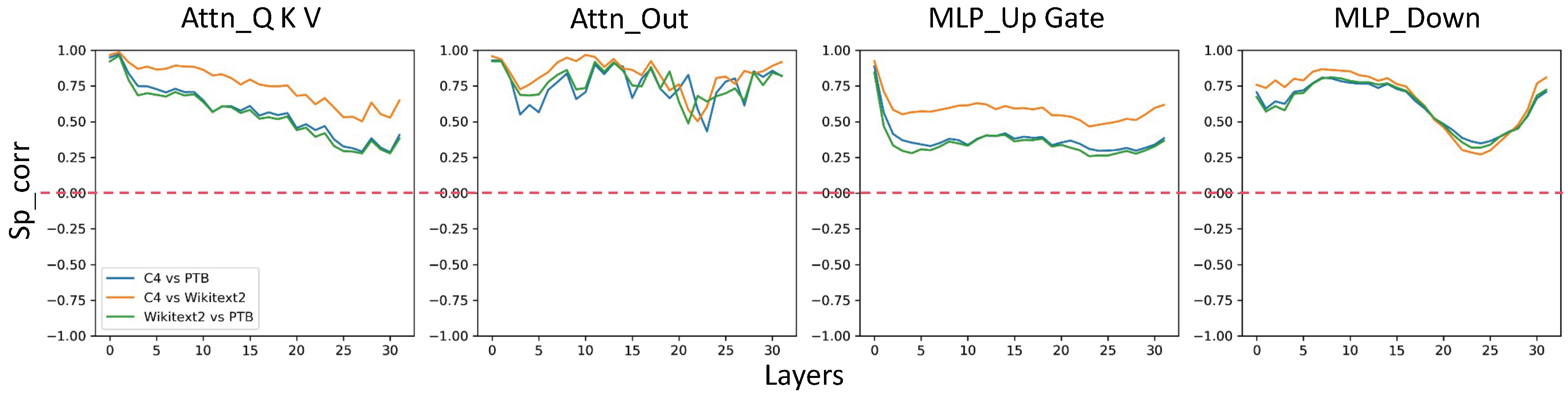
Figure 3.
Illustration of Channel Permutation. Given a score matrix assigned by various criteria, directly processing it with 2:4 sparse results in a total sum of the retained score being 85.7. However, by using channel permutation, we could get a final total sum of score 104.9 which aligns with the unstructured pruning — representing the global optimum.
Figure 3.
Illustration of Channel Permutation. Given a score matrix assigned by various criteria, directly processing it with 2:4 sparse results in a total sum of the retained score being 85.7. However, by using channel permutation, we could get a final total sum of score 104.9 which aligns with the unstructured pruning — representing the global optimum.
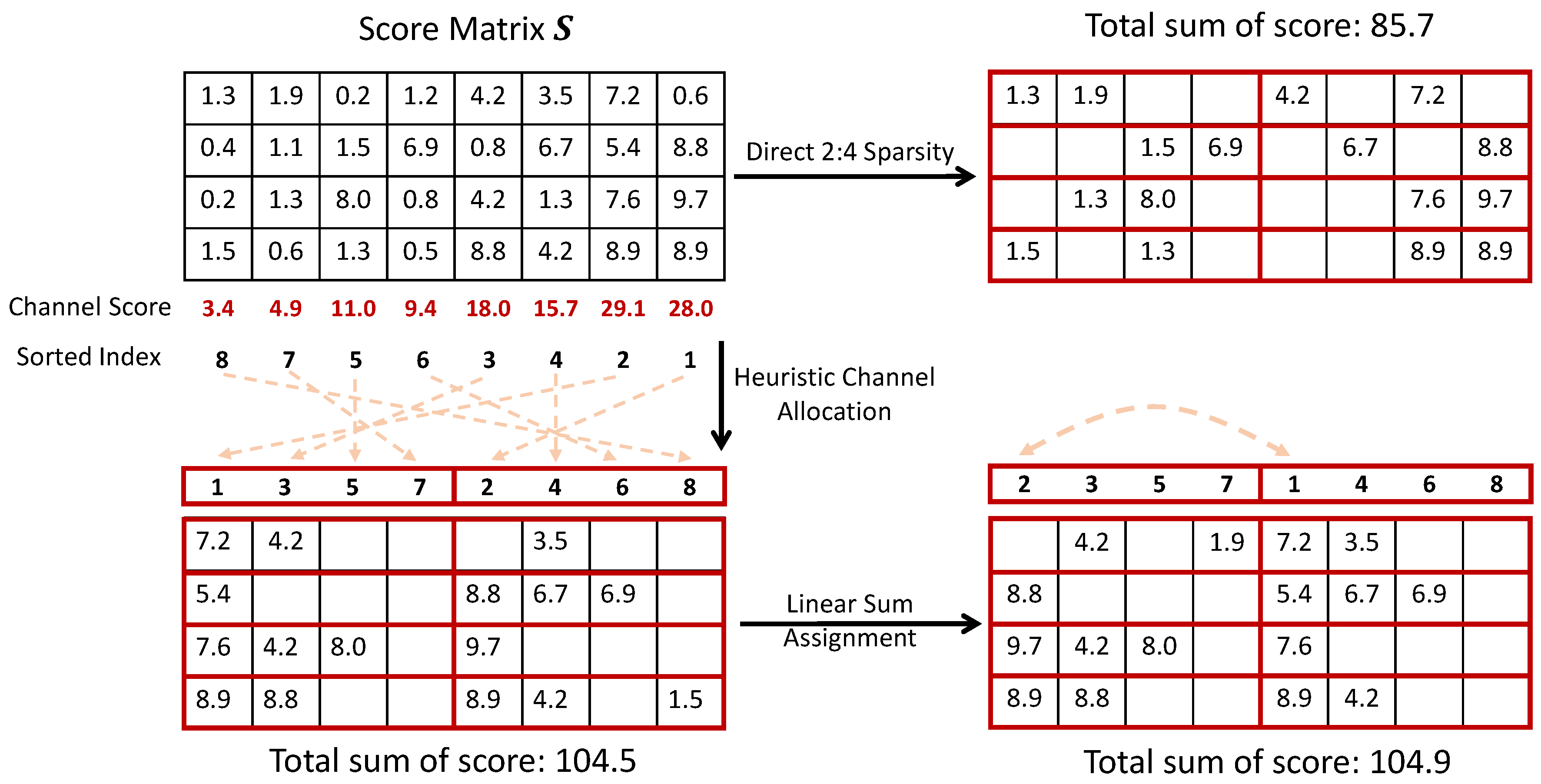
Figure 4.
Sensitivity Evaluation on Sparsity and number of calibration samples (nsamples).
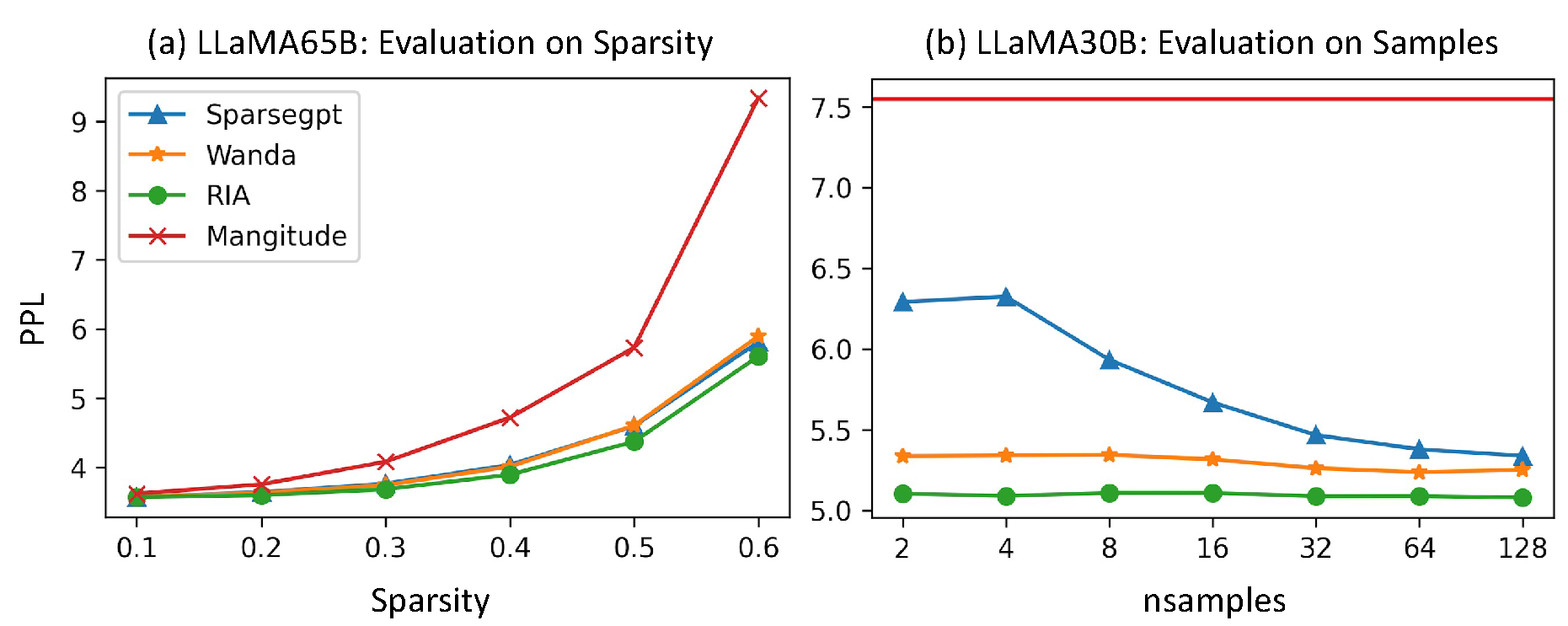
Figure 5.
The degree distribution for input channels after pruning.
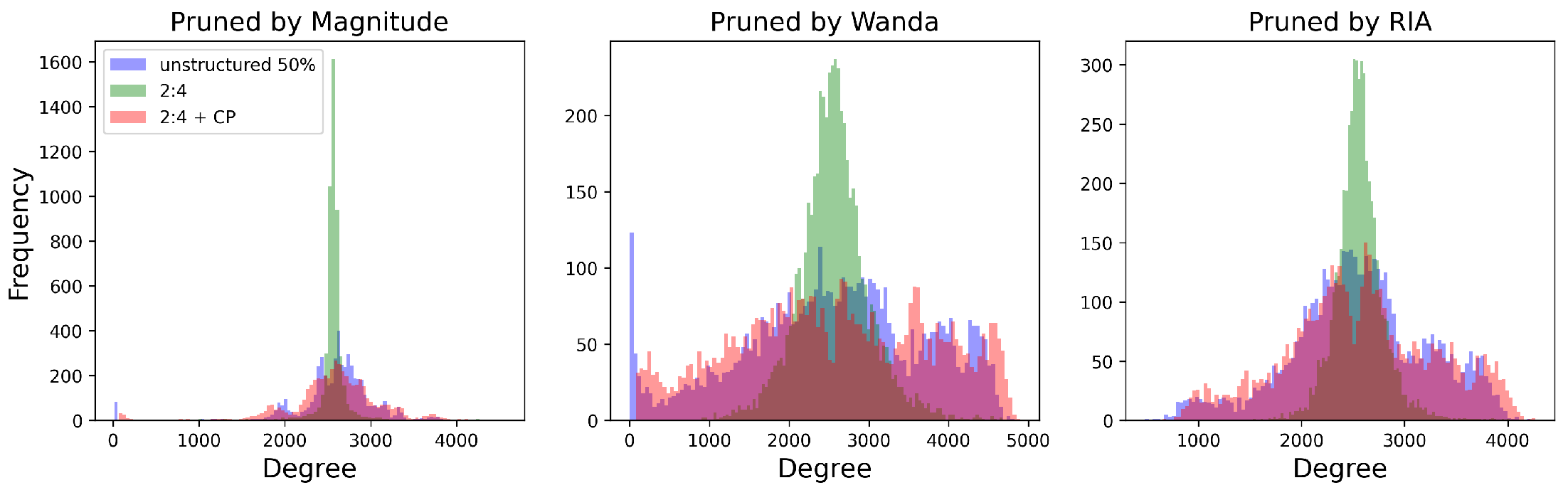
Table 1.
Perplexity results on Wikitext2. We produce the one-shot Post-Training pruning methods with 50% unstructured sparsity on LLaMA, LLaMA2 and OPT models.
Table 1.
Perplexity results on Wikitext2. We produce the one-shot Post-Training pruning methods with 50% unstructured sparsity on LLaMA, LLaMA2 and OPT models.
| Method | LLaMA 7b | LLaMA 13b | LLaMA 30b | LLaMA 65b | LLaMA2 7b | LLaMA2 13b | LLaMA2 70b | OPT 1.3b | OPT 13b |
| Dense | 5.68 | 5.09 | 4.77 | 3.56 | 5.47 | 4.88 | 3.32 | 14.62 | 10.13 |
| Magnitude | 17.28 | 20.22 | 7.54 | 5.90 | 16.02 | 6.83 | 5.36 | 1712 | 11561 |
| Wanda | 7.26 | 6.15 | 5.24 | 4.57 | 6.92 | 5.99 | 4.22 | 18.41 | 11.92 |
| SparseGPT | 7.24 | 6.20 | 5.32 | 4.57 | 6.99 | 6.10 | 4.25 | 27.00 | 11.18 |
| RIA (Ours) | 7.12 | 6.08 | 5.08 | 4.38 | 6.81 | 5.83 | 4.11 | 18.08 | 11.05 |
Table 2.
Ablation Studies of RIA on LLaMA-13B and LLaMA-30B models.
| LLaMA-13B | LLaMA-30B | |
| 20.22 | 7.55 | |
| 11.97 | 6.73 | |
| 7.80 | 5.55 | |
| 6.57 | 5.27 | |
| 6.14 | 5.13 | |
| 6.08 | 5.08 |
Table 3.
LLaMA2-70B: Zero-Shot Performance of the model with unstructured 50% sparsity compared to the dense model. Bold values denote the best performance across all the post-training pruning methods. An asterisk (“*") signifies performance surpassing that of the dense method.
Table 3.
LLaMA2-70B: Zero-Shot Performance of the model with unstructured 50% sparsity compared to the dense model. Bold values denote the best performance across all the post-training pruning methods. An asterisk (“*") signifies performance surpassing that of the dense method.
| Method | Hellaswag | BoolQ | ARC-C | MNLI | RTE | AVG |
| Dense | 64.77 | 83.70 | 54.44 | 45.81 | 67.87 | 63.32 |
| magnitude | 60.58 | 71.10 | 49.32 | 32.80 | 60.65 | 54.89 |
| wanda | 62.70 | 83.27 | 52.50 | 43.19 | 70.84 * | 62.50 |
| sparsegpt | 62.36 | 84.26 * | 53.07 | 40.29 | 70.76 * | 62.15 |
| RIA | 63.22 | 84.77 * | 52.56 | 42.80 | 71.48 * | 62.97 |
Table 4.
Unstructured sparsity and semi-structured sparsity results on Wikitext2. We highlight the best performance among all methods within the same sparsity pattern in bold.
Table 4.
Unstructured sparsity and semi-structured sparsity results on Wikitext2. We highlight the best performance among all methods within the same sparsity pattern in bold.
| Method | Unstructured 50% | 2:4 | 2:4+CP w/o LSA | 2:4+CP | 4:8 | 4:8+CP | |
| LLaMA2-13b (Dense 4.88) |
Magnitude | 6.83 | 8.74 | 8.89 | 8.72 | 7.32 | 7.52 |
| Wanda | 5.99 | 9.00 | 8.79 | 8.60 | 7.00 | 6.73 | |
| SparseGPT | 6.10 | 8.77 | 8.61 | 8.53 | 7.01 | 6.70 | |
| RIA (Ours) | 5.83 | 8.41 | 8.03 | 7.97 | 6.74 | 6.33 | |
| LLaMA2-70b (Dense 3.32) |
Magnitude | 5.36 | 6.76 | 6.77 | 6.73 | 5.89 | 6.03 |
| Wanda | 4.23 | 5.48 | 5.29 | 5.29 | 4.77 | 4.65 | |
| SparseGPT | 4.25 | 5.68 | 5.37 | 5.34 | 4.91 | 4.76 | |
| RIA (Ours) | 4.11 | 5.36 | 5.18 | 5.11 | 4.68 | 4.46 |
Table 5.
LLaMA2-70B: Zero-Shot Performance of N:M constraint model comparing to the dense model. Bold values denote the best performance across all N:M constraint models. An asterisk (“*") signifies performance surpassing that of the dense method.
Table 5.
LLaMA2-70B: Zero-Shot Performance of N:M constraint model comparing to the dense model. Bold values denote the best performance across all N:M constraint models. An asterisk (“*") signifies performance surpassing that of the dense method.
| Method | Hellaswag | BoolQ | ARC-C | MNLI | RTE | AVG |
| Dense | 64.77 | 83.70 | 54.44 | 45.81 | 67.87 | 63.32 |
| Wanda (2:4) | 57.35 | 81.44 | 46.01 | 37.69 | 68.59 * | 58.22 |
| Wanda (2:4+CP) | 59.37 | 84.50 * | 48.55 | 43.09 | 66.43 | 60.39 |
| Wanda (4:8+CP) | 60.86 | 82.73 | 49.94 | 40.15 | 67.87 | 60.51 |
| RIA (2:4) | 57.13 | 82.78 | 46.76 | 37.39 | 69.31 * | 58.68 |
| RIA (2:4+CP) | 58.48 | 85.14 * | 49.15 | 49.08 * | 68.95 * | 62.16 |
| RIA (4:8+CP) | 60.44 | 83.58 | 50.43 | 48.69 * | 70.04 * | 62.64 |
Table 6.
LLaMA2-13B: Inference time of different sparsity patterns
| Method | Q/K/V/Out | Up/Gate | Down |
| unstructured 50% (CPU) | 1.91× | 1.84× | 1.80× |
| 2:4 (CPU) | 1.91× | 1.84× | 1.80× |
| unstructured 50% (GPU) | 0.98× | 0.98× | 0.97× |
| 2:4 (GPU) | 1.64× | 1.65× | 1.62× |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







