A Charging Planning Method for Shared Electric Vehicles with the Collaboration of Mobile and Fixed Facilities

Preprint

Article

A Charging Planning Method for Shared Electric Vehicles with the Collaboration of Mobile and Fixed Facilities

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

21 October 2023

Posted:

24 October 2023

You are already at the latest version

Alerts

Abstract

Facing the charging difficulties of free-floating shared electric vehicle and the high cost of mobile charging for single demand, this article proposes a collaborative charging planning method based on the complementary advantages of fixed charging stations and mobile charging vehicles, which can charge shared electric vehicles more efficiently and reduce the charging cost at the same time. A bi-level programming model for fixed and mobile cooperative charging is constructed. The upper level of the model is the minimization model of system charging total cost, seeking the optimal charging scheme and the number of mobile charging vehicles. The lower model is a fixed and mobile cooperative charging path planning model, which calculates the optimal routes for mobile charging vehicles and the shared electric vehicles that need to be transferred to the fixed charging station. The example results show that the cost of the proposed fixed-mobile cooperative charging scheme is reduced by 12.6% compared with the pure fixed charging scheme and 14.9% compared with the pure mobile charging scheme

Keywords:

Subject: Engineering - Transportation Science and Technology

1. Introduction

With the development of electric vehicles, a new charging model for electric vehicles is starting to gain attention. Contrary to the fixed charging mode, in this new model, we can install a charger on a movable object, and then send the charger to serve the electric vehicle (EV) on demand. From the customers' point of view, they can call for the charging service once they park their EVs at any location they want, which means that the charging activity will not affect their schedules. This kind of charging mode is referred to as "mobile charging" [1], and a conceptual illustration is given in Figure 1. In practice, some companies have started to provide mobile charging services. Scholars also have achieved some results in the field of mobile charging scheduling. For example, Huang et al. [2] designed a mobile charging service model based on the "nearest-work-next" rule. Cui et al. [3] modeled the mobile charging system as a vehicle routing problem and formulated it with a mixed-integer linear program. Tang et al. [4] established a simulation-based optimization framework for simulating and verifying the mobile charging system's design and operation.

Free-floating shared vehicles [5,6] have developed rapidly in recent years and are favored by users due to their convenient rental and unrestricted parking spaces. However, free-floating shared vehicles are usually parked at locations without charging piles, and it is too costly to manually transfer Shared Electric Vehicles (SEVs) to charging stations for charging and it is difficult to charge the SEVs without sufficient power to reach fixed charging stations. Mobile charging services have flexible working characteristics. Mobile charging vehicles (MCVs) can arrive at the request location to provide charging services based on the request information, or they can choose a certain fixed location and charge multiple SEVs in the vicinity of that location. For SEV operators, choosing MCVs to their parking locations for charging can resolve the charging difficulties.

At the same time, the users of free-floating shared electric vehicle present significant tidal and regularity during their daily trips, and a cluster distribution in some popular places. Given that operators need to replenish power for SEVs in a timely manner to ensure that they can serve more users, the introduction of MCVs, which gives full play to the advantages of cluster distribution of SEVs and reduces charging costs, becomes a charging choice that operators can prioritize. Due to the high cost of MCV charging, operators need to further think about how to combine the original fixed charging mode with the new mobile charging mode, and rationalize the arrangement of different MCVs to serve different clusters of SEVs, so as to provide charging services for SEVs in a more flexible and low-cost way.

The main proposed problem of this paper is as follows:

(1) Can mobile charging services be introduced to solve the problem of difficult and costly charging of free-floating shared electric vehicle?

(2) How can operators plan flexible mobile charging vehicles and low-cost fixed charging stations to get the most economical charging scheme?

(3) How can operators efficiently arrange the moving path of charging SEVs in the two types of charging with the power distribution and location distribution characteristics of free-flowing shared electric vehicles?

Existing studies on free-floating SEVs mainly include the dispatch of free-floating SEVs and the relocation of charging stations. Weikl and Bogenberger [7] developed an intra-region SEV relocation model and an inter-region SEV relocation model for a free-floating car-sharing system that mixes conventional and electric vehicles, which considers the charging of electric vehicles and the refueling of conventional vehicles. They concluded that free-floating car sharing systems not only enable operators to increase their profits but also reduce the average idle time at the end of each trip. Folkestad [8] proposed a model optimizing free-floating SEV charging and repositioning to maximize revenues and orders, where the repositioning of free-floating SEVs is performed by employees. Kypriadis[3] study the optimal repositioning problem for free-floating SEVs with one and multiple employees to minimize the walking cost of the employees. Roni [9] study the relationship between the number of charging stations and the free-floating SEV idle time. They constructed an integer model to jointly optimize the resetting of charging stations and the allocation of SEVs to charging stations. Based on millions of data from free-floating internal combustion engine vehicle leases, Cocca [10] developed a discrete event tracking driving simulator to optimize the location of SEV charging stations, and based on the study of charging station locations, a data-driven optimization method is proposed to simultaneously optimize the location of charging stations, and the number of chargers.

Existing research on EV charging is mainly based on fixed charging mode, setting charging thresholds, developing charging cycles and performing vehicle scheduling.

Boyaci [11] constructed a multi-objective mixed-integer linear programming model to determine the optimal number of vehicles and the location and number of stations for a one-way shared electric vehicle system, but the charging process was not explicitly modeled [6]. Brandstätter investigate the problem of strategic planning levels for a one-way shared vehicle system that employs electric vehicles to maximize the revenue of the shared vehicle system without exceeding the budget by identifying the optimal location of charging stations among the alternative charging station set to determine the location of the optimal charging station and to determine the number of electric vehicles needed to maximize the benefits of the car sharing system.

Zhao [12] applied spatio-temporal networks for the first time in the field of one-way sharing electric vehicles to describe the problem of scheduling and employee dispatching of electric vehicles, they considered the limitation of electric vehicle power, assumed that the charging process and the discharging process are linear, and tracked in detail the changes in the power level of 130 electric vehicles by modeling the charging and discharging processes.

Huang [13] developed a mixed-integer nonlinear programming model to determine the allocation of one-way shared electric vehicles in a specified area, which was divided into two parts: decision level and operation level, where the decision level was used to determine the number of vehicles required for operation and the capacity of the stations, and the operation level determined the scheduling of vehicles. In a subsequent study comparing operator-based and user-based vehicle scheduling, Huang [14] used the same continuous distribution to model changes in vehicle power.

Xu and Meng [15] maximized the operational revenue of shared electric vehicle companies by determining the number of electric vehicle vehicles; they assumed that the vehicles can be charged at all the stations they pass through, and that the charging process of electric vehicles is a nonlinear function of time, and provided a detailed description of the power change and charging time. When determining the number of vehicles to be operated, whether the vehicles are charged or not, the charging time and the vehicle scheduling are considered together optimally. Gambella [16] equalize the regional distribution of electric vehicles by means of a scheduler performing scheduling tasks on the vehicles, explicitly considering the consumption of electric vehicle batteries and the charging process.

Research on mobile charging mainly focuses on how to reasonably arrange the scheduling of mobile charging vehicles and path optimization. Qi [17] proposed an optimal path selection method for mobile charging vehicles and solved it using an improved genetic algorithm, in which traffic information such as road congestion, road class, and road length were considered in path selection. When an EV arrives at a station where the charging piles are fully occupied, it needs to wait for a longer time to perform charging operations, Atmaja and Mirdanies [18] considered the use of mobile charging vehicles to provide additional charging capacity to charging overloaded stations and designed a strategy for scheduling mobile charging vehicles in the network. In order to solve the problem of difficult charging of electric vehicles, Bao [19] studied the reasonable distribution of mobile charging vehicles as well as the scheduling optimization, they firstly determined the number of mobile charging vehicles needed in the service area as well as the initial location, and then, with the goal of the shortest time to service the demand, they established a scheduling model of mobile charging vehicles. Huang [20] proposes that using mobile charging to replenish EVs can compensate for the lack of charging infrastructure coverage, and describes a strategy for mobile charging to serve the nearest users, where each charging vehicle will serve the next spatially closest EV after completing its current charging needs. Tang [21] argues that mobile charging can improve the convenience of charging for electric vehicle users, and its first attempt to propose a two-tier simulation-based model to describe the planning and operational aspects of mobile charging systems.

With the popularity of shared electric vehicles and the rise of mobile charging, the optimization problem of MCV in mobile charging mode has become a hot research topic. Already the related research on shared electric vehicles has achieved more results in path optimization and vehicle deployment, but the research on the introduction of MCV currently has the following shortcomings.

(1) MCV is flexible and costly, while fixed charging is economic and needs to rely on manual transfer of SEV to complete charging. Literature search indicates that there is no published investigation on how to match the two charging facilities to get the most economical and efficient charging scheme.

(2) Existing studies on MCVs mainly target one-to-one charging needs, and such charging service has relatively high costs and low efficiency. The cluster distribution characteristics of free-mobile SEVs make it possible to utilize MCVs for multi-user parallel charging, and the research on matching MCVs with SEV clusters needs to be carried out in depth.

(3) On one hand, there is manual transfer SEV path planning based on the location of fixed charging stations, and on the other hand, there is MCV path planning considering SEV clusters. The coordination of fixed and mobile charging planning is worth studying based on the power distribution characteristics and positional characteristics of SEVs.

2. Methodology

2.1. Scenario Description

Supposed that MCVs are purchased by the SEV operator, there is known that the set of SEV cluster nodes C = {1, 2, ...}, the set of charging stations F = {1, 2, ...}, where the numbers in parentheses represent cluster node numbers and charging station numbers respectively, and N-1 denotes the total number of nodes in the SEV cluster. As shown in Figure 2, the dispatched MCVs all start from site 0, travel to the customer node to provide charging service, and return to site N after completing the assigned charging scheme. In fact, MCV depot 0 and N are the same location. Each SEV cluster node can contain multiple SEVs with different charging needs and idle time windows. One or more SEVs parked at the same SEV cluster node with overlapping time windows may be charged by a MCV simultaneously or sequentially, with the charging routes indicated by black arrows. When the MVC does not have enough power to provide charging service or returns to site N, the MVC can be replenished by charging at the site or charging station. In addition, SEVs can be charged by fixed charging with a human driver transferring to a charging station. This kind of charging route is indicated by a red arrow.

Due to the limited battery capacity of MCVs and the limitation of the idle time window of SEVs, the selected SEVs of the same SEV cluster node can be charged by MCVs simultaneously or sequentially. A set K= {1, 2, ⋯, N-1} of virtual SEV cluster nodes is defined, where the numbers represent the SEV virtual numbers. By setting K, SEVs parked at the same SEV cluster node are assigned to be on top of different virtual cluster nodes, and the travel distance between virtual SEV cluster nodes corresponding to the same SEV cluster node is 0. With this setup, each SEV in the SEV cluster node is set up as a virtual node, so that the SEVs can be numbered independently. Similar to the setting K of the virtual SEV cluster nodes, the setting F' of the virtual charging stations is also defined based on the set F of charging stations, where the distance between the virtual charging station nodes corresponding to the same charging station is 0. Each virtual charging station node in F' can be accessed at most once, and the setting of F' makes the number of times each charging station is accessed in fixed or mobile charging modes easy to calculate. Based on the above scenario, the optimal charging scheme and path optimization are investigated by coordinating mobile charging and fixed charging.

2.2. Assumptions and Variables

The following hypotheses are made in response to the research questions:

Speed and power consumption rate are constant. SEV or MCV traveling time is equal to the distance between nodes divided by the speed, and the travelling power consumed between nodes is equal to the distance between nodes multiplied by the power consumption rate.
The period of the charging scheme is fixed.
The charging service time of each SEV is fixed.
The SEV charging threshold is a fixed value. SEVs with the power below this threshold send charging demand, and SEVs with power below the demand of being able to reach the nearest fixed charging station will stop their service to wait for MCV charging.

Table 1. List of parameters used in this paper.

Parameter	Define
$f_{m}$	Number of mobile charging vehicles (veh)
$β_{1}$	Charging price (RMB/KWH)
$β_{2}$	Depreciation cost per MCV (RMB)
$β_{3}$	Initial price of manually transferring SEV to fixed charging station (RMB)
$β_{4}$	Mileage price per kilometer when manually transferring SEVs (RMB/km)
$i, j$	virtual node
$x_{i j k}^{m}$	$x_{i j k}^{m} \in \{0, 1\}$ , indicates whether the virtual SEV node k is charged by MCV. $x_{i j k}^{m} = 1$ , indicates that SEV k is charged by MCV.
$x_{i j k}^{s}$	$x_{i j k}^{s} \in \{0, 1\}$ , indicates whether the virtual SEV node k is charged in a fixed mode or not.
$h$	Power consumption per kilometer of MCV (KWH/h)
$q_{k}^{m}$	Charging demand for virtual SEV node k, which is handled by a mobile charging vehicle (KWH).
$q_{k}^{s}$	Charging demand for virtual SEV node k, which is covered by a fixed charging station (KWH).
$P$	Battery capacity of SEV (KWH)
$p_{i k}$	Electricity of SEV node k (KWH)
$y_{i}$	The remaining power when MVC reaches at node i (KWH)
$Q$	Battery capacity of MVC (KWH)
$Y_{i}$	Charging quantity of MVC at fixed charging stations. $i \in V' \cup \{0\}$ (KWH)
$d_{i j}$	Path distance between nodes (i, j) (km)
$τ_{i}$	Time to start services for SEV on the virtual client node
$e_{i}$	Start time of service time window
$l_{i}$	End time of service time window
$t_{i j}$	The travel time of a road segment, which is related to the distance of segment $d_{i j}$ and the fixed speed of MCV (min).
$t_{i}$	The time that a mobile charging vehicle spends on charging a shared electric vehicle at node $i$ (min)
M	The length of the longest link in the path set L (km)
$s_{i j}$	$s_{i j}$ ∈{0,1}, indicates whether the charging services at the virtual SEV cluster nodes can be performed at the same time.

2.3. The Bi-Level Programming Model for Cooperative Charging

In order to address the charging scheme issues raised above, a bi-level programming model for fixed and mobile cooperative charging is constructed. The upper model is the minimization model of system charging total cost, seeking the optimal charging scheme and the number of mobile charging vehicles. The lower model is a fixed and mobile cooperative charging path planning model, which calculates the optimal routes for mobile charging vehicles and the shared electric vehicles that need to be transferred to the fixed charging station.

2.3.1. The Upper Model

From the operator's point of view, the upper level of the bi-level programming model focuses on the charging cost issue with the aim of deriving the optimal charging scheme and the number of MCVs to be dispatched. The objective of the upper model is to minimize the total system charging cost. The total system charging cost consists of the following two components: mobile charging cost and fixed charging cost.

(1) Mobile charging cost

The cost of mobile charging is made up of the following components.

1) Vehicle Use Cost. MCV purchase cost is translated into depreciation cost for a single trip with reference to the current tolling model, as in Formula (1).

C_{1}^{m} = β_{2} f_{m}

(1)

2) Time window penalty cost. If the MCV arrives earlier than the time window, it has to wait and pay the corresponding early arrival penalty cost

p_{e}

. If the MCV arrives later than the time window then there is a penalty cost for late arrival

p_{l}

. Time window violations in each service path are penalized by calculating only the time window violation on the first virtual SEV cluster node, instead of calculating the idle time window violation on the entire path. The time window penalty is defined as in Formula (2).

\begin{array}{l} C_{2}^{} = \sum_{i \in V} W (t_{i}) \\ W (t_{i}) = \{\begin{array}{l} p_{e} (e_{i} - t_{i}) & , t_{i} < e_{i} \\ 0 & , e_{i} < t_{i} < l_{i} \\ p_{l} (t_{i} - l_{i}) & , t_{i} > l_{i} \end{array} \end{array}

(2)

3) Charging cost. It consists of the traveling power cost and charging cost of MCV. Traveling power cost indicates the cost of power consumed by MCV during movement. Charging cost contains the cost consumed by MCV in fixed charging station and the cost consumed for charging SEV, as in Formulas (3) and (4).

C_{3}^{m} = β_{_{1}}^{} (\sum_{k \in K_{M}} d_{i j} x_{i j k}^{m} h + \sum_{k \in K_{M}} q_{k}^{m})

(3)

q_{k}^{m} = P - p_{i k}, \forall i \in K, \forall k \in K_{M}

(4)

(2) Fixed charging cost

Fixed charging cost is made up of the following components.

1) Labor cost. It refers to the cost consumed by manually driving SEVs to fixed charging station, which consists of initial cost and mileage cost, as in Formula (5).

C_{1}^{s} = \sum_{k \in K_{S}} β_{3} x_{i j k}^{s} + \sum_{k \in K_{S}} d_{i j} x_{i j k}^{s} β_{4}

(5)

2) Charging cost. It is the cost of SEV charging at a fixed charging station, as in Formulas (6) and (7).

In summary, the upper level of the bi-level programming model is Formula (8).

C_{3}^{s} = β_{_{1}}^{} \sum_{k \in K_{S}} q_{k}^{s}

(6)

q_{k}^{s} = P - p_{i k} + h d_{i j}, \forall i \in K, \forall k \in K_{S}

(7)

\min Y = β_{_{1}}^{} (\sum_{k \in K_{M}} d_{i j} x_{i j k}^{m} h + \sum_{k \in K_{M}} q_{k}^{s} + \sum_{k \in K_{S}} q_{k}^{m}) + \sum_{k \in K_{S}} d_{i j} x_{i j k}^{s} β_{4} + β_{2} f_{m} + \sum_{k \in K_{S}} β_{3} x_{i j k}^{s} + \sum_{i \in V} W (t_{i})

(8)

2.3.2. The Lower Model

The lower level of the bi-level programming model is a path planning model for cooperative charging by fixed and mobile modes. The purpose is to find the optimal routes for MCVs and SEVs based on the charging scheme from the upper model, minimizing the path planning cost, as in Formula (9).

\min Z = β_{1} (\sum_{i \in V^{'} \cup {0}, j \in V^{'} \cup {N}, i \neq j, k \in K_{M}} d_{i j} x_{i j k}^{m} h + \sum_{i \in K, k \in K_{s}} q_{i k}^{s} + \sum_{i \in K, k \in K_{M}} q_{i k}^{m}) + \sum_{i \in V^{'}, j \in F^{'}, i \neq j, k \in K_{s}} d_{i j} x_{i j k}^{s} β_{4} + \sum_{i \in V} W (t_{i})

(9)

There are some constraints of the lower model as follows.

1) Charge mode constraint

Classifying SEVs below the charge level into either fixed or mobile charging modes, Formula

\sum_{j \in V^{'} \cup {N}, i \neq j, k \in K_{M}} x_{i j k} + \sum_{j \in V^{'} \cup {N}, i \neq j, k \in K_{S}} x_{i j k} = 1, \forall i \in K

(10)

(10) ensures that all SEVs below the charge threshold are charged in one of these methods:

2) Vehicle equilibrium constraint

\sum_{j \in V^{'} \cup {N}, i \neq j, k \in K} x_{j i k} = \sum_{j \in V^{'} \cup {0}, i \neq j, k \in K} x_{i j k}, \forall i \in V^{'}

(11)

Formula (11) indicates that the total number of vehicles in any two nodes, except for the depot, remains constant, ensuring that the total number of MCV and SEV vehicles does not change.

3) Time window constraint

e_{i} ⩽ τ_{i} ⩽ l_{i}, \forall i \in V^{'} \cup {0, N}

(12)

Formula (12) ensures that the charging services provided by the MCVs are counted from the beginning of the time window.

4) Fixed charging station constraint

\sum_{j \in V^{'} \cup {N}, i \neq j} x_{i j} ⩽ 1, \forall i \in F^{'}

(13)

Since each visit to a charging station node generates a new virtual charging station node, Formula (13) is proposed to ensure that each virtual charging station node is visited at most once.

p_{i k} - h d_{i j} x_{i k} + P (1 - x_{i j k}^{s}) \geq 0, \forall i \in V', \forall j \in F', i \neq j, \forall k \in K_{S}

(14)

Formula (14) ensures that the power of the SEV leaving the virtual node can reach the fixed charging station.

τ_{i} + t_{i j} x_{i j k}^{s} + α s_{i j} - l_{0} (1 - x_{i j k}^{s}) ⩽ τ_{j}, \forall i \in K, \forall j \in V^{'}, i \neq j, k \in K_{S}

(15)

Formula (15) ensures the temporal feasibility of SEVs leaving the links of SEV virtual cluster nodes and virtual charging station nodes.

p_{i k} \leq h d_{i j}, \forall i \in K, \forall j \in F', k \in K_{M}

(16)

The current power level of the electric vehicle is judged, and it is classified into the mobile charging scheme when the power is not enough to reach the fixed charging station.

5) Related constraints of mobile charging mode

x_{i j k}^{m} q_{j} ⩽ y_{j} ⩽ y_{i} - h d_{i j} x_{i j k}^{m} - q_{i} x_{i j k}^{m} + Q (1 - x_{i j k}^{m}), \forall i \in K, \forall j \in V^{'} \cup {N}, i \neq j, k \in K_{M}

(17)

x_{i j k}^{m} q_{j} ⩽ y_{j} ⩽ Y_{i} - h d_{i j} x_{i j k}^{m} + Q (1 - x_{i j k}^{m}), \forall i \in F^{'} \cup {0}, \forall j \in V^{'} \cup {N}, i \neq j, k \in K_{M}

(18)

y_{i} ⩽ Y_{i} ⩽ Q, \forall i \in F^{'} \cup {0}

(19)

Formulas (17) and (18) ensure that the power state of the MCVs leaving the virtual customer node, the virtual charging node, and the starting point satisfy the subsequent services, respectively, and Formula (19) puts a limit on the MCV power. Formula (18) is the MCV's power relationship between two nodes, in case

x_{i j k}^{m} = 1

. The left-hand side constraint ensures that the remaining power of the MVC to reach node

j

is not less than the charging demand of node

j

, and the right-hand side constraint ensures that the remaining power of the MVC

y_{j}

to reach node

j

is greater than the sum of the power demand and trip consumption at the two nodes of

(i, j)

τ_{0} + t_{0 j} x_{_{0 j k}}^{m} - l_{0} (1 - x_{_{0 j}}^{m}) ⩽ τ_{j}, \forall j \in V^{'} \cup {N}, k \in K_{M}

(20)

τ_{i} + t_{i j} x_{_{i j k}}^{m} + α t_{i} - l_{0} (1 - x_{_{i j k}}^{m}) ⩽ τ_{j}, \forall i \in K, \forall j \in V^{'} \cup {N}, i \neq j, k \in K_{M}

(21)

τ_{i} + t_{i j} x_{_{i j k}}^{m} + g (Y_{i} - y_{i}) - (l_{0} + g Q) (1 - x_{_{i j k}}^{m}) ⩽ τ_{j}, \forall i \in F^{'}, \forall j \in V^{'} \cup {N}, i \neq j, k \in K_{M}

(22)

Formulas (20), (21), and (22) ensure the temporal feasibility of the linking of MCVs leaving depot 0, SEV virtual cluster nodes, and virtual charging station nodes respectively.

In order to ensure that the MCV can simultaneously charge multiple SEVs at the same time without exceeding the limit on the number of their simultaneous charging, the parallel mobile charging constraint is proposed as follows.

\frac{d_{i j} x_{i j k}^{m}}{M} ⩽ s_{i j} ⩽ K d_{i j} x_{i j k}^{m} + \frac{d_{i j}}{M}, \forall i \in K, \forall j \in V^{'} \cup {N}, i \neq j, k \in K_{M}

(23)

\min \{x_{i j k}^{m}, 1 - s_{i j}, \max \{\frac{τ_{i} + α - τ_{j}}{E}, 0\}\} ⩽ R_{i j}, \forall i \in V^{'} \cup {0}, \forall j \in V^{'} \cup {N}, i \neq j, k \in K_{M}

(24)

Φ_{j} = \max \{(Φ_{i} + R_{i j}) R_{i j}, 1\}, \forall i \in V^{'} \cup {0}, \forall j \in C^{'}, i \neq j

(25)

0 ⩽ Φ_{i} ⩽ H, \forall i \in V^{'} \cup {0, N}

(26)

Formula (23) ensures that the services of two nodes in close proximity can be performed simultaneously or sequentially by the same MCV, while the charging services of two virtual nodes located farther apart can only be performed sequentially. Formula (24) is used to determine whether the two SEVs located at virtual nodes and are simultaneously charged by the same MCV. Formula (25) records the number of SEVs being simultaneously charged by the MCVs. Formula (26) ensures that the number of SEVs being simultaneously charged by one MCV does not exceed the number limit.

2.4. GASA Algorithm

Given that the solved fixed-mobile cooperative path planning problems are NP-hard problems, solving such problems using exact algorithms consumes a long time and it is difficult to obtain the global optimal solution. Liu [] combined the advantages of genetic algorithm and simulated annealing algorithm and proposed Genetic-Simulated Annealing Algorithm (GASA) for solving the bi-level programming model, GASA has stronger search capability and efficiency, and it can obtain the global optimal solution.

For the given fixed and mobile cooperative charging bi-level programming model, the overall bi-level programming model is solved using the GASA algorithm, and the lower level of the Bi-level programming model is solved using the genetic algorithm. The solution ideas are as follows.

Step.1 Set the genetic parameters: population size

N

, crossover probability

P_{c}

, mutation probability

P_{m}

, and evolutionary generation

g

. Set the simulated annealing parameters and perform binary coding on the feasible solutions.

Step.2 Given an initial charging scheme population

{(x_{i j k}^{m (g)}, x_{i j k}^{s (g)})}_{N}

g = 0

；

Step.3 Calculate the fitness function values (The upper level of the Bi-level programming model objective function value) for the individuals in the population:

(1) Set the initial solution under the individual charging scheme with iteration number n=0. The initial solution is obtained by continuously constructing the feasible route.

(2) Calculation of broad charging costs

Y

(3) Using genetic algorithms to find optimal populations

(x_{i j k}^{m (g)}, x_{i j k}^{s (g)}, f_{m}^{(g)})

；

(4) The output population

(x_{i j k}^{m (g)}, x_{i j k}^{s (g)}, f_{m}^{(g)})

is substituted into the upper model to find the value of the fitness function.

Step.4 Genetic operations such as replication, crossover and mutation are performed on the population based on the value of the fitness function to obtain a new charging scheme population

{(x_{i j k}^{m (g + 1)^{'}}, x_{i j k}^{s (g + 1)^{'}}, f_{m}^{(g + 1)'})}_{N}

Step.5 Perform a simulated annealing operation on the individuals in the population to obtain the charging scheme population

{(x_{i j k}^{m (g + 1)}, x_{i j k}^{s (g + 1)}, f_{m}^{(g + 1)})}_{N}

;

Step.6 Execute Step.3 for the individuals in the population of charging scheme

{(x_{i j k}^{m (g)}, x_{i j k}^{s (g)}, f_{m}^{(g)})}_{N}

to get the value of fitness function, determine whether it is equal to the maximum number of evolutionary generations, otherwise, set

g = g + 1

, and transfer to Step.4 to continue solving. If it is, output the result, and the individual with the largest fitness in the population is the optimal solution.

3. Numerical Example

From the perspective of SEV operator, MCVs are purchased by SEV operator. Based on the known information of parking points, idle time windows, and charging demand of SEVs, the key issue is to develop a fixed and mobile cooperative charging scheme and arrange the number of MCVs based on the layout of SEV charging clusters and fixed charging stations within a charging cycle, so as to efficiently charge SEVs that are below the power threshold and to reduce the charging cost.

3.1. Data Source

The study is based on the operation data of a large-scale shared electric vehicle enterprise in Nanjing, China, and the data used mainly include order data, vehicle data, and location data of stations. Part of the vehicle information is extracted from the data, including location, parking time, electricity and other information. The time window is set according to the parking time, and the shared electric vehicles whose electricity is lower than the charging electricity threshold are selected as the object of example analysis.

In order to simplify the problem, the involved shared electric vehicle parking points are set as virtual nodes with the same location as the original nodes. Using, charging station points, the coordinate information, time window, service time and electricity of the shared cars are shown in Table 2 and Table 3. Where 0 denotes the MCV station and 51-54 denote the fixed charging stations.

3.2. Parameter Setting

The charging scheme cycle is set to 5 hours, the charging threshold is set to 40%, and the charging service time per SEV for MCVs is set to be fixed and equal to 20 minutes, whereas the fixed charging station has a charging time of 60 minutes for the SEVs, and the charging time for the MCVs is determined by subsequent charging demand and mileage traveled. Assuming a battery capacity of 50

k w h

for SEVs and 800

k w h

for MCVs, both traveling at a speed of 30

k m / h

, and a consumption rate of 0.2

k w h / k m

during the trip, the fixed charging station charges a rate of 1

R M B / k w h

and the MCV charging price at MCV stations is 0.5

R M B / k w h

. For MCVs, the initial price is 100

R M B

, for fixed charging mode, the initial price is 10

R M B

, and the mileage price is 0.8

R M B / k m

. Parameters in the penalty function is

p_{e} = p_{l} = 300 R M B / h

3.3. Calculation Result

Using the Matlab programming, the problem is solved to obtain the charging scheme as shown in Table 4, which consists of vehicle charging mode division, number of MCVs, and driving path. Charging mode division means that each charging SEV will be divided into fixed or mobile mode for charging. The number of MCVs refers to the optimal number of MCVs dispatched in order to ensure that charging demand is met and charging cost is reduced. The optimal charging path is shown in Figure 3, and the traveling path includes the charging path of MCVs, and SEVs to fixed charging stations for charging and return paths.

3.4. Analysis of Results

3.4.1. The Impact of Different Charging Modes on the Cost of Charging Schemes

In order to compare the charging schemes with different charging modes and verify the practicality of the cooperative charging model, the proposed model is compared with the conventional charging model. In the fixed charging scheme, the SEVs with enough power to reach the nearest fixed charging station will be transferred to the station for charging by people, while the SEVs that do not have enough power to reach the fixed charging station will be classified into the mobile charging scheme and be charged by the MCVs. While in the mobile charging scheme, all SEVs rely on MCVs for charging, considering parallel mobile charging constraints. The resultant calculation is shown in Figure 4.

As can be seen in Figure.4, the proposed fixed and mobile cooperative charging scheme spends the least charging cost among the three schemes, which is reduced by 12.6% compared to the fixed charging scheme and 14.9% compared to the mobile charging scheme. The results prove the effectiveness of the planning method. In this example, the total cost of mobile charging scheme is 4.1% higher than that of fixed charging scheme, mainly because MCV depots are generally not located in the city center area. In order to complete all the charging requirements within the charging cycle and avoid the time-window penalties, more MVCs would be needed and dispatched for charging SEVs, and charging the SEVs that are too remote would greatly increase the charging costs.

3.4.2. Sensitivity Analysis

There are many factors that have an impact on charging paths and charging schemes, and charging price, MCV charging performance, and time window penalty cost are selected for sensitivity analysis.

(1) Charging price

A sensitivity analysis is performed for the three charging schemes as the charging price changes. It can be seen in Figure 5 that the costs of three schemes increase with the charging price, with the lowest total charging cost for the fixed and mobile cooperative charging scheme. When the charging price is low, the total cost of the pure mobile charging scheme is higher than that of the fixed charging scheme. But after the price rises to a certain level, the cost of electricity consumed by the SEV driving mileage of the fixed charging scheme begins to increase rapidly, which leads to the total cost of the fixed charging scheme being higher than that of the mobile charging scheme.

(2) MCV charging performance

In the fixed and mobile cooperative charging mode, the charging schemes are calculated with different MCV charging capacities and service time, and the results are shown in Table 5 and Table 6.

As can be seen from Table 5, the total charging cost is related to the battery capacity of MCV. When the battery capacity of MCV reaches a certain level, no more vehicles can be served for the limitation of time window. Moreover, due to the increasing depreciation cost of MCV, the total cost of charging increases. From Table 6, the total cost of charging is positively correlated with the MCV charging service time. When the charging efficiency is improved, the cost of charging will decrease. Therefore, SEV companies need to choose MCVs with appropriate charging capacity when operating, or even use a combination of MCVs with different charging capacity to reduce charging costs.

(3) Time window penalty cost

The charging schemes are calculated with different time window penalty costs and the results are shown in Table 7.

From Table 7, it can be seen that when the penalty cost increases, in order to reduce the impact of the time window penalty, the operator will reduce the number of SEVs served by MCVs, and more SEVs will be assigned to fixed charging stations for charging. When the cost of the time window penalty is high to a certain extent, the operator will put more MCVs in the charging program to ensure that charging demand can be met without receiving penalty.

4. Conclusions

In order to solve the charging difficulties caused by free flow SEVs parked at will, and the high cost caused by single charging demand of MCVs, based on the complementary advantages of fixed charging and mobile charging, a bi-level programming model of fixed and mobile cooperative charging is proposed, and the best charging scheme and the number of required MCVS are obtained. Compared with the traditional charging path planning model, the model proposed in this paper has the following innovations.

(1) MCVs serving the single charging demands will lead to high charging cost. In this article, MCVs are introduced to serve multiple SEVs and the parallel mobile charging service are used in the free-mobile SEV charging, which expand the service scope and reduces the charging cost of MCVs.

(2) Utilizing the complementary advantages of fixed charging mode and MCVs, we propose a bi-level programming model for fixed and mobile cooperative charging, and solve the model using the GASA algorithm to derive the optimal charging scheme and the number of required MCVs, which solves the problems of charging difficulties for free-floating SEV.

(3) In order to solve the charging path problem of MCVs and SEVs, a fixed-mobile cooperative charging path planning model and related constraints are proposed to calculate the optimal paths for MCVs and SEVs to be transferred to a fixed charging station for charging.

In this article, some results have been achieved in the study of the path planning problem of shared electric vehicles and mobile charging vehicles, but there are still some shortcomings:

(1) In practice, fixed charging stations often face the problem of charging queues, which leads to an increase in the cost of fixed charging stations. This article does not consider the problem of queuing at fixed charging stations, and the impact caused by queuing can be considered in subsequent studies.

(2) The road network and the setting during driving are ideal, and the traffic information such as the degree of road congestion and road class can be taken into account to calculate the driving time and power consumption on different roads in the path selection in future.

Author Contributions

Conceptualization, Q. L. and Z. Y.; methodology, Z. Y. and Q. L.; writing—original draft preparation, Z. Y.; writing—review and editing, H. J.; funding acquisition, Q. L. and H. J. All authors have read and agreed to the published version of the manuscript.

Funding

This research is funded by the Humanities and Social Science Fund of Ministry of Education of People’s Republic of China [grant number 20YJCZH115] and Science and Technology Development Project of Jilin Province under Grant 20230203127SF.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Ciociola et al., UMAP: Urban mobility analysis platform to harvest car sharing data, 2017 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computed, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation, Aug. 2017, pp. 1–8.
S. Schmöller, S. Weikl, J. Müller, and K. Bogenberger, Empirical analysis of free-floating carsharing usage: The Munich and Berlin case, Transportation Research Part C: Emerging Technologies, vol. 56, Jul. 2015, 34–51. [CrossRef]
Stead, D. Relationships between transport emissions and travel patterns in Britain. Transport Policy, 1999, 6, 247–258. [CrossRef]
Richardson, B.C. Sustainable transport: Analysis frameworks. J. Transport Policy, 2005, 13, 29–39. [CrossRef]
Lefèvre, B. Long-term energy consumptions of urban transportation: A prospective simulation of “transport–land uses” policies in Bangalore. Energy Policy, 2009, 37, 940–953. [CrossRef]
Santos, G. et al, A. Part I: Externalities and economic policies in road transport. Research in Transportation Economics, 2010, 28, 2–45. [CrossRef]
Eriksson, L., Nordlund, A.M., Garvill, J. Expected car use reduction in response to structural travel demand management measures. Transportation Research Part F, 2010, 13, 329–342. [CrossRef]
Habibian, M., Kermanshah, M. Exploring the role of transportation demand management policies’ interactions. Scientia Iranica A, 2011, 18, 1037–1044. [CrossRef]
De Palma, A., Lindsey, R. Traffic congestion pricing methodologies and technologies. Transportation Research Part C 2011, 19, 1377–1399. [CrossRef]
Lautso, K., Spiekermann, K., Wegener, M. Propolis: Planning and Research of Policies for Land Use and Transport for Increasing Urban Sustainability, 2013.
Santos, G., Behrendt, H., Teytelboym, A. Part II: Policy instruments for sustainable road transport. Research in Transportation Economics, 2010, 28, 46–91. [CrossRef]
Ong, H.C., Mahlia, T.M.I., Masjuki, H.H. A review on emissions and mitigation strategies for road transport in Malaysia. Renewable and Sustainable Energy Reviews, 2011, 15, 3516–3522. [CrossRef]
Henderson J V. Road congestion: A reconsideration of pricing theory. Journal of Urban Economics, 1974, 1(3): 346-365. [CrossRef]
Friesz T L, Bernstein D, Kydes N. Dynamic congestion pricing in disequilibrium. Networks ＆ Spatial Economics, 2004, 4(2): 181-202. [CrossRef]
Yang F. Day to Day dynamic optimal tolls with elastic demand. Transportation Research Board 87th Annual Meeting, 2008.
Nagurney A. Congested urban transportation networks and emission paradoxes. Transportation Research Part D: Transportation and Environment, 2000, 5: 145–151. [CrossRef]
Sharma S, Mishra S. A study on effect on GHG emissions by addition of transit mode in existing road network and optimal emission pricing models for reducing carbon footprints. Transportation Research Board 92th Annual Meeting, January 2013.
Johansson O. Optimal road-pricing: simultaneous treatment of time losses, increased fuel consumption, and emissions. Transportation Research Part D: Transportation and Environment, 1997, 2: 77–87. [CrossRef]
Zhang Haozhi, Gao Ziyou, Zhang Bei. Optimization Model and Solution Algorithm of Urban Traffic Integrated Network Design under Environmental Objectives. Chinese Journal of Civil Engineering, 2006, 39(11): 114-119.
Zhang Kai. Estimation and Pricing of urban Road network traffic pollution emission. Dalian University of Technology, 2016.
Wang C, Study on Characteristics and Prediction of Vehicle exhaust Emission in Shandong Province based on COPERT model. Ocean University of China, 2015.
He Xiaoyun, Study on Characteristics of vehicle exhaust pollution in Hangzhou City based on COPERT Model. Environmental Control and Pollution, 2018, 02: 193-197.
Yu Lei, Wang Hongtu et al. Comparison of MOBILE and COPERT emission Models Based on PEMS. Transportation system engineering information, 2011, 03: 176-181.
Xie Shaodong, Song Xiangyu, Shen Xinhua. Calculation of vehicle emission Factors in China by COPERT III Model. Environmental Science, 2006, 27(3): 415-419.
Liu Weiming, Jiang Shan. Research on Solving Algorithm of Two-layer Programming Model Based on Hybrid Optimization Strategy. Chinese Journal of Civil Engineering, 2003, 07: 27-32.
Xiong Wei. Research on Traffic Allocation Model and its Algorithm considering emissions. Wuhan University of Technology, 2008.
Chen, L., Zhang, L. Congestion pricing model and algorithm based on Bi-level programming model. J. Beijing Uni. of Tech. 2006, 6, 526–528.
Xing, L. Study on the Theory of Road Congestion Pricing. Master’s Thesis, Jilin University, Changchun, China, 2 June 2007.
Goh, M. Congestion management and electronic road pricing in Singapore. Journal of Transport Geography 2002, 10, 29–38. [CrossRef]
Atkinson, R.W. et al. The impact of the congestion charging scheme on ambient air pollution concentrations in London. Atmospheric Environment, 2009, 43, 5493–5500. [CrossRef]
Eliasson, J., Hultkrantz, L., Nerhagen, L., Rosqvist, L.S. The Stockholm congestion-charging trial 2006: Overview of effects. Transp. Res. Part A 2009, 43, 240–250. [CrossRef]
Ferrari, P. Road Pricing and Users’ Surplus. Transport Policy 2005, 12, 477–487. [CrossRef]
Farrella, S., Saleh, W. Road-user charging and the modelling of revenue allocation. Transport Policy 2005, 12, 431-442.
Small, K.A. Using the revenues from congestion pricing. Transportation 1992, 19, 359–381. [CrossRef]
Hau, T.D. Congestion Pricing and Road Investment. In Road Pricing, Traffic Congestion and the Environment: Issues of Efficiency and Social Feasibility, by Button, K.J. and Verhoef, E.T.; Edward Elgar Publishing Limited: Cheltenham, England, 1998, Chapter 3, pp. 39-78.

Figure 1. Concepts of fixed charging and mobile charging.

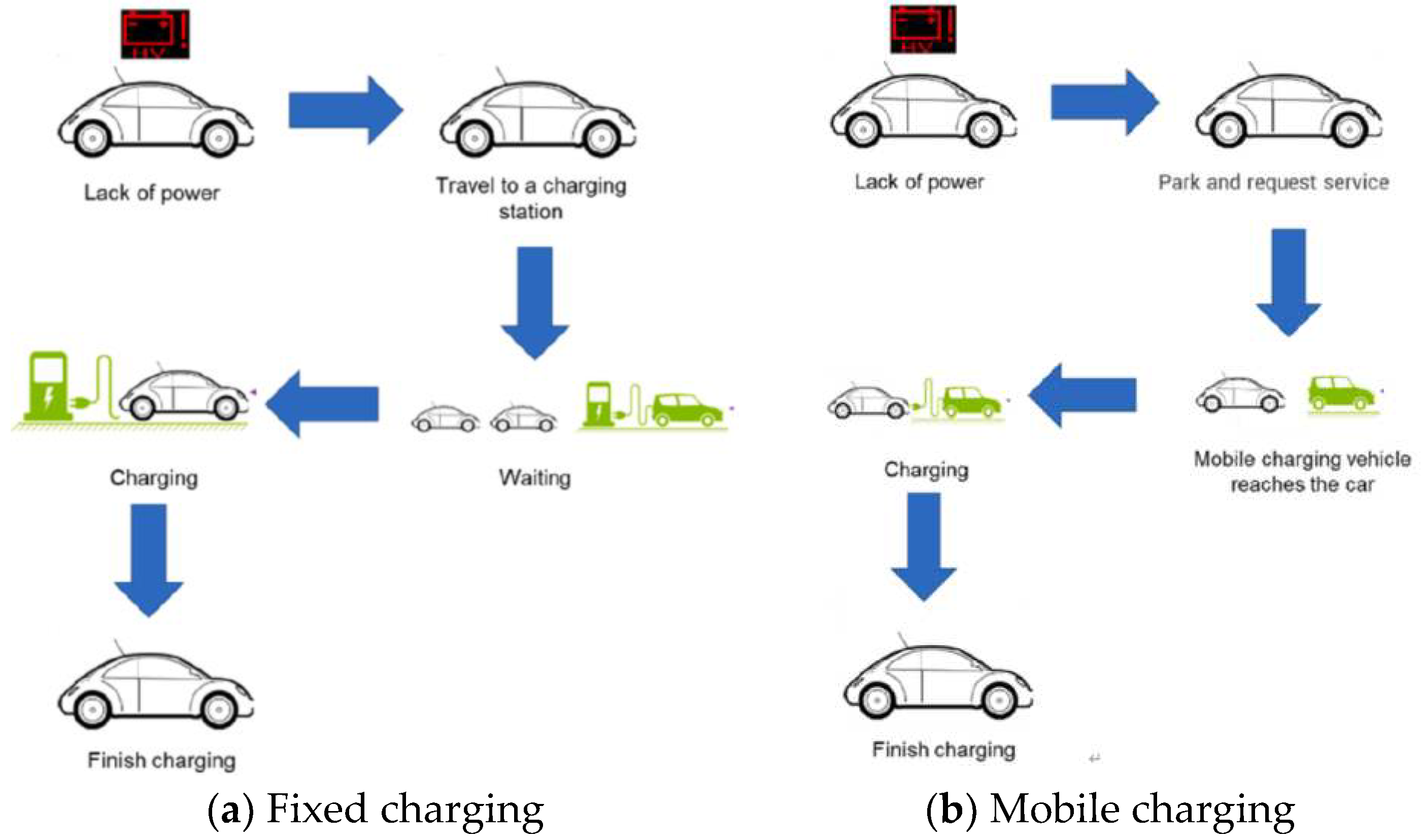
Figure 2. Scenario description.

Figure 3. The path planning results for fixed and mobile co-charging.

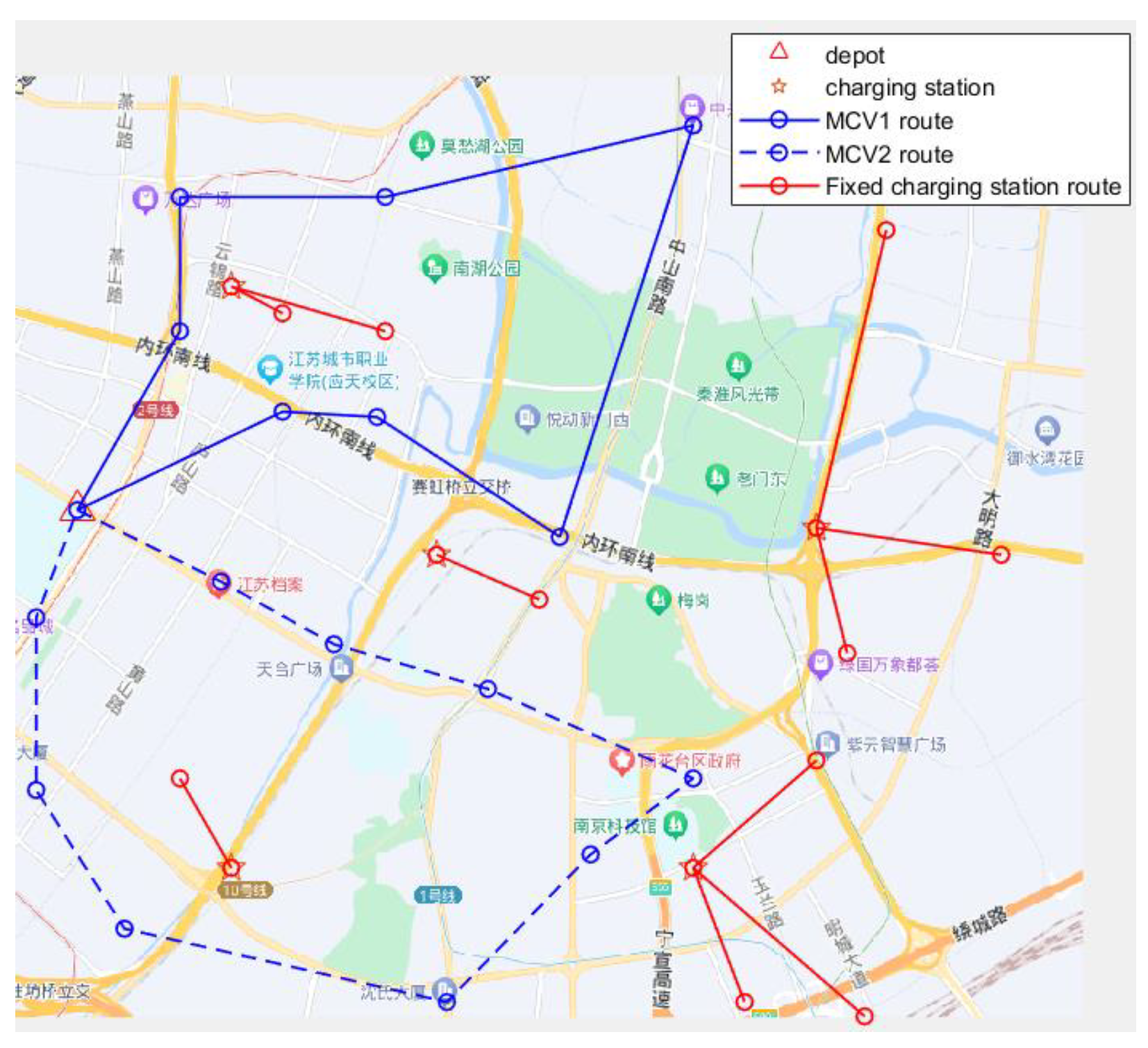
Figure 4. The comparison of charging costs by solution.

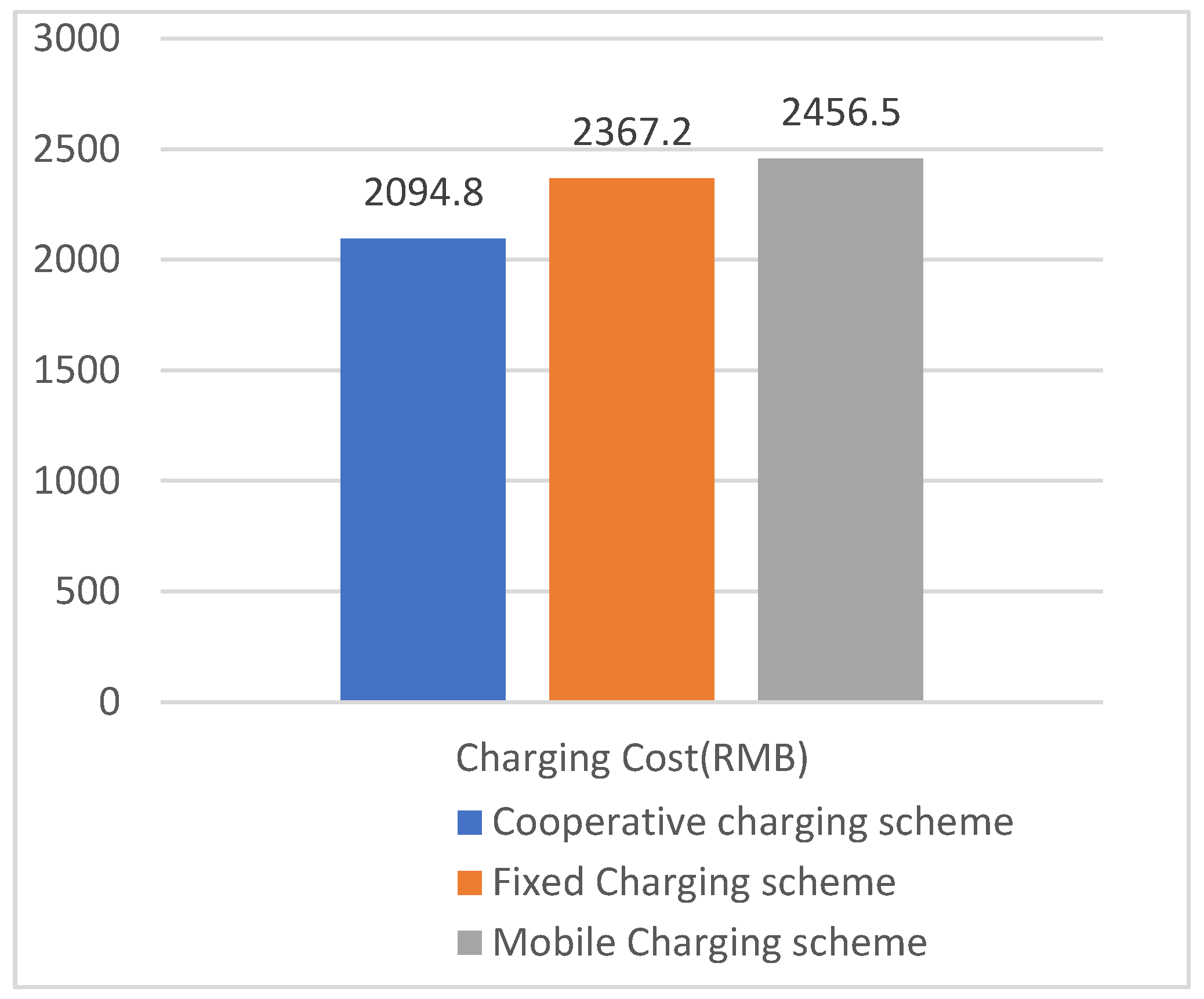
Figure 5. The impact of charging price.

Table 2. Information of SEVs.

SEV (id)	Latitude	Longitude	Time window (min)		Electricity (%)
1	118.385968	32.705249	211	247	0.32
2	118.170446	32.688855	50	90	0.27
3	118.238767	32.952442	59	79	0.18
4	118.003842	32.81767	103	133	0.23
5	118.093071	32.641006	35	61	0.34
6	118.057605	32.860424	190	208	0.20
……	……	……	……	……	……
39	118.235922	32.8217	30	160	0.31
40	118.281175	32.938024	35	150	0.35
41	118.346757	32.704077	20	90	0.08

Table 3. Information of fixed charging stations.

SEV (id)	Latitude	Longitude
0	118.374992	32.674618	300
51	118.015484	32.871561	300
52	118.19667	32.618216	300
53	118.217592	32.871277	300
54	118.281175	32.938024	300

Table 4. Calculation results.

	Mobile charging mode	Fixed charging mode
SEV (id)	1、2、3、4、7、9、12、13、14、15、16、17、18、19、20、21、22、23、24、25、26、29、31、32、34、35、37、38、39、40、41	5、6、8、10、11、27、28、30、33、36
Number of vehicles	31	10
Charging Path	MCV1:0-(4,31)-(20,21)-16-26-(19,32)-17-(13,14)-(7,34)-(40,41)-0$$$MCV2:0-25-(1,2,3,15,37)-9-(12,29,38)-(18,39)-35-(22,23,24)-0	5-51-5、6-51-6、8-51-8、$$$10-52-10、11-52-11、27-52-27、28-53-28、30-54-30、36-55-36
Total cost of charging (RMB)	2094.8

Table 5. The impact of MCV charging capacity.

MCV battery capacity	Depreciation cost (RMB)	Number of MCVs	Number of SEVs in mobile charging	Number of SEVs in fixed charging	Total system cost (RMB)
600KWH	80	3	37	4	2155.7
800KWH	100	2	31	10	2094.8
1000KWH	130	2	32	9	2046.5
1200KWH	160	2	32	9	2067.3

Table 6. The impact of MCV charging service time.

MCV charging service time	Depreciation cost (RMB)	Number of MCVs	Number of SEVs in mobile charging	Number of SEVs in fixed charging	Total system cost (RMB)
10min	150	2	35	10	2056.3
20min	100	2	24	13	2094.8
30min	80	3	31	6	2227.5

Table 7. The impact of Time Window Penalty Cost.

Time Window Penalty Cost	Number of MCVs	Number of SEVs in mobile charging	Number of SEVs in fixed charging	Total system cost (RMB)
150RMB/h	2	30	7	1976.3
300RMB/h	2	24	13	2094.8
600RMB/h	3	31	6	2323.5

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Charging Planning Method for Shared Electric Vehicles with the Collaboration of Mobile and Fixed Facilities

Abstract

1. Introduction

2. Methodology

2.1. Scenario Description

2.2. Assumptions and Variables

2.3. The Bi-Level Programming Model for Cooperative Charging

2.3.1. The Upper Model

2.3.2. The Lower Model

2.4. GASA Algorithm

3. Numerical Example

3.1. Data Source

3.2. Parameter Setting

3.3. Calculation Result

3.4. Analysis of Results

3.4.1. The Impact of Different Charging Modes on the Cost of Charging Schemes

3.4.2. Sensitivity Analysis

4. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe