Prerpints.org logo
Preprint
Article

A Novel Real Time Robust Controller of a Four-Wheel Independent Steering System for EV using Neural Networks and Fuzzy Logic

Altmetrics

Downloads

82

Views

21

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 October 2023

Posted:

24 October 2023

You are already at the latest version

Alerts
Abstract
This paper presents a novel real time control strategy on four-wheel independent steering system for electric vehicle with stepper motors using neural networks combined with fuzzy logic. The control of the four wheels is based on a variation of Hopfield Neural Network (VHNN) method, in which the input is the error of each steering motor and the output is processed by a hyperbolic tangent function (HTF) feeding the fuzzy logic controller (FLC), which ultimately drives the stepper motor. The whole system is made up of the four aforementioned blocks where they work in sync and inseparable from each other with the common goal of driving all the steering stepper motors at the same time. Simulation results demonstrate that the proposed control method has strong robustness and practicability under different angles and speeds.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Electric vehicles are becoming increasingly popular as a solution to reduce environmental pollutants and mitigate climate change. One of the challenges of electrification is the integration of the Brushless Direct Current (BLDC) electric motors into the wheels to have direct transmission to all four wheels without the interference of intermediate gears and other friction parts that reduce efficiency. In addition, Steer-by-Wire (SBW) technology is an important innovation in the steering system, as it eliminates any mechanical connection between the steering wheel and the driving wheels.
Hence, it is essential to focus on investigating a control strategy that maximizes the benefits offered by the four-wheel independent steering system. Several researchers have made significant contributions to the design and control of four-wheel independent steering systems for electric vehicles. Furukawa et al. [1] aims to identify key components of 4WS technology in vehicle dynamics and control techniques, offering an overview and perspective on the related research areas. Shibahata et al. [2] describe the development of a vehicle with four-wheel steering, in which the rear wheels can be controlled electronically, and the side-slip angle at the vehicle's center of gravity is maintained at zero, improving the basic dynamic properties of the vehicle. Sano et al. [3] develop a controller that achieves a zero sideslip angle at steady state. Hongyu et al. [4] propose an optimization control method based on the coincidence degree of steering centers to improve driving performance and address issues such as tire wear and unharmonious vehicle movement. In reference [5], the authors introduce a new algorithm for optimal Ackermann angle allocation at full speed, aiming to enhance steering stability and reduce tire wear. Also, Yin et al. [6] focus on global yaw moment generation and develop a torque distribution control system for four-wheel independent-drive electric vehicles (4WIDEVs), considering tire usage and the efficiency of yaw moment generation for improved vehicle stability and handling performance. In references [7] and [8], the authors utilize fuzzy control theory to establish fuzzy controllers that determine the rear wheel steering angle based on the influence of the front wheel steering angle and speed, effectively reducing sideslip angle, yaw rate, and roll angle peaks. Furthermore, Tian et al. [9] investigate the skid steering and differential steering of four-wheel independent-drive electric vehicles, particularly in cases of steering failure. In reference [10], the authors develop a fuzzy logic controller that integrates the driver's steering input with the four-wheel steering system, achieving zero body sideslip angle and ensuring a quick response of the yaw rate. Haytham et al. [11] design an optimally-tuned PID controller for steering control of a four-wheel steering vehicle using a genetic algorithm. Moreover, Ariff et al. [12] propose a four-wheel-active steering system with a model following control structure that enhances the vehicle's dynamic behavior using feed-forward and feedback compensation strategies based on the driver's steering intention and vehicle state feedback errors. Also, Khan et al. [13] investigate a robust differential steering control system for an independent four-wheel drive electric vehicle using the robust H∞ control methodology. Finally, Zhou et al. [14] propose a multi-mode optimal decision control system based on the vehicle's linear 2-DOF dynamic model, aiming to improve vehicle performance under different working conditions.
To address these challenges, this paper proposes a novel real-time robust controller for a four-wheel independent steering system for electric vehicles with stepper motors using neural networks and fuzzy logic. The proposed control system is not centralized, which offers several advantages, such as better stability and reduced complexity. In the proposed system, the motion of each motor is done taking under consideration the position of the other motors, making it more stable and robust. By optimizing the control strategy, the system achieves smoother and more coordinated steering motions, resulting in improved vehicle handling and reduced stress on the tires [4,5].
Neural networks and fuzzy logic are both powerful tools used in control systems to tackle complex problems and make intelligent decisions. It's worth noting that neural networks and fuzzy logic are not mutually exclusive and can be used together in hybrid systems to harness their respective advantages and address complex control problems more comprehensively [16]. While the specific system in question may not heavily rely on data-driven learning, the neural networks can still be utilized for tasks such as motor control or mapping sensor inputs to desired steering outputs. Furthermore, by using a neural network, the computational power required by the fuzzy logic algorithm is greatly simplified as clearly shown in the corresponding section below.
Numerical simulations are conducted using the Matlab/Simulink platform to evaluate the control system’s performance. The proposed control method was tested through simulation tests that introduced random wheel position errors into a neural network that it based on the idea of the Hopfield networks. The weights of the neural network were chosen so that each wheel contributed equally to the error calculation. Tests were carried out with different activation functions in the neural network, and the optimal behavior in the error calculation was achieved with the Tan-sigmoid (sigmoid) function, with a dead point of 0 and a large relative error tending to -1 and small relative error tending to 1. The error was then converted from the range (-1,1) to the range (0,1) and fed into a simple fuzzy logic algorithm that commands the selector of each motor.
In comparison with other papers, this proposed control system offers several advantages. For instance, it is more stable and robust due to the fact that the motion of each motor is being done while ‘listening to’ the position of the other motors. Additionally, the proposed method simplifies the computational power required by the fuzzy logic algorithm, using a neural network. Compared to other centralized control systems, the proposed control method offers greater stability, improved efficiency, and reduced complexity. Overall, the results of the simulation tests demonstrate that the proposed control system can achieve optimal simultaneous driving of the motors, while adhering to the control rules for different angles and speeds of the vehicle, demonstrating high robustness and practicality.
In conclusion, the proposed real-time robust controller is a significant step forward in the field of electric vehicle control systems. The novel features of this control method offer several advantages compared to existing systems and provide high stability, efficiency, and practicality.
The rest of the article is organized as follows. The four-wheel steering geometry theory and calculation for each wheel is introduced in Section 2. The mathematical modelling of a hybrid stepper motor and the parameters of the stepper motor under consideration are illustrated in Section 3. The real time control strategy on four-wheel independent steering system for electric vehicle with stepper motors using neural networks combined with fuzzy logic are proposed in Section 4. Simulation results and analysis are carried out in Section 5, followed by the conclusion in Section 6.

2. Steering Geometry Calculations

In 4-wheel steering vehicles, the relation (k) of rear to front wheels steering angles (δrear and δfront respectively), depends on the vehicle speed (U) and is given by the diagram of Figure 1. [3]
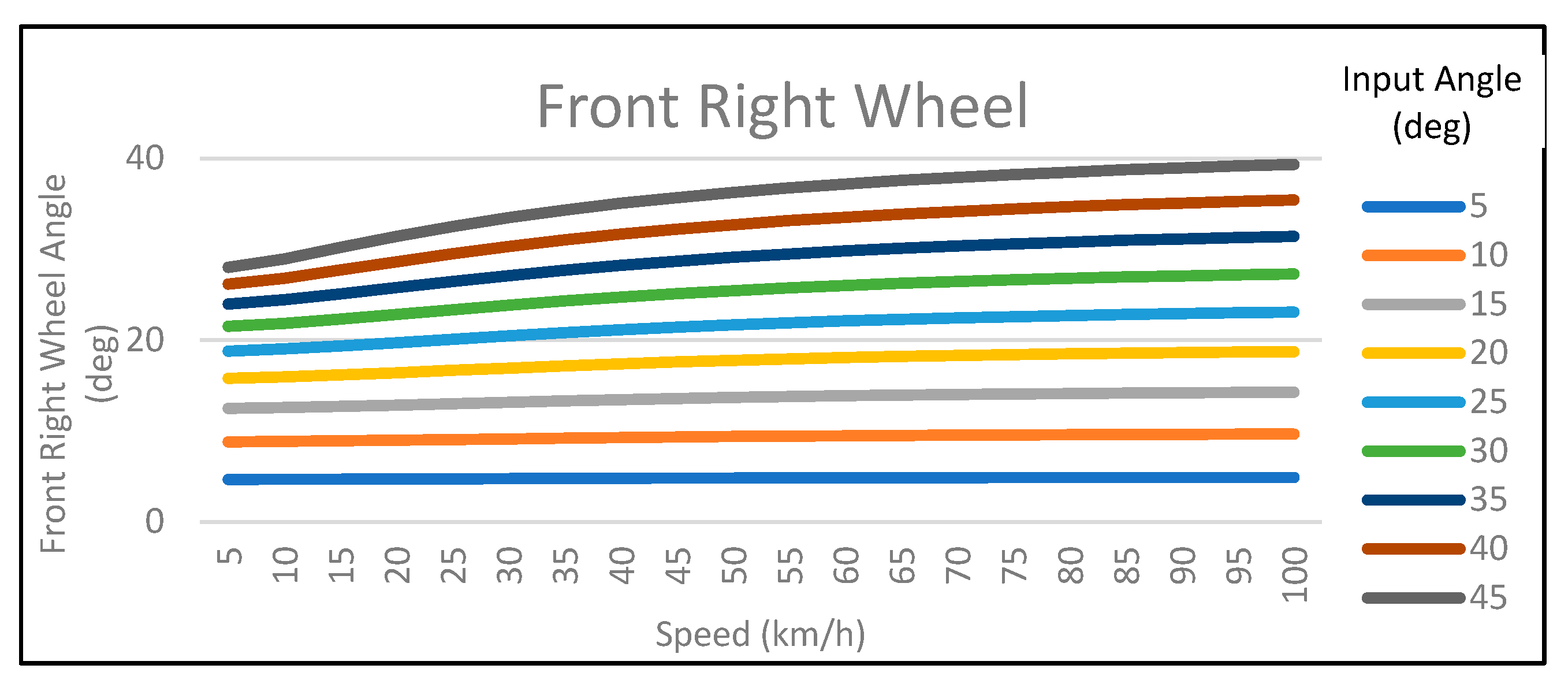
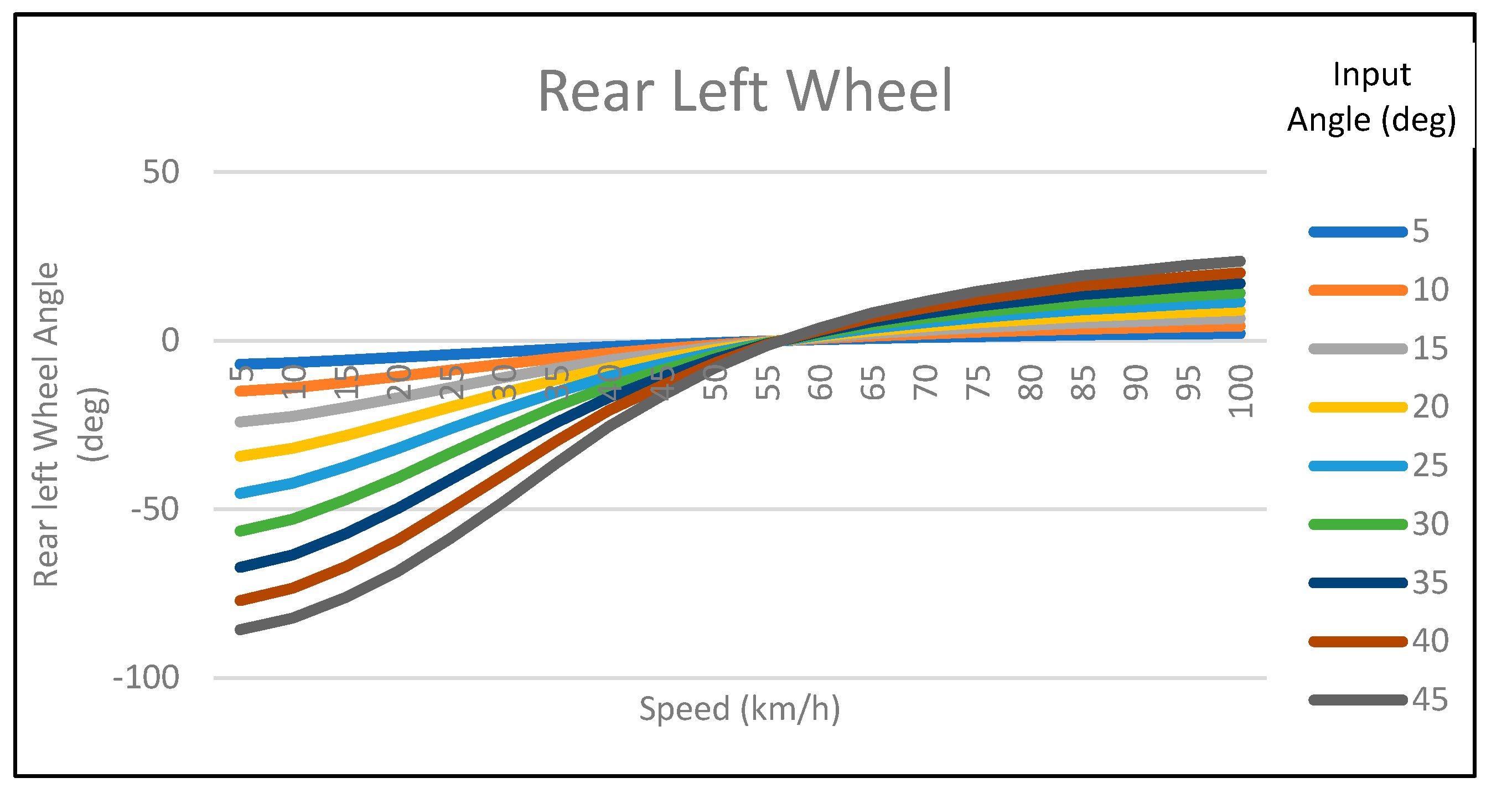
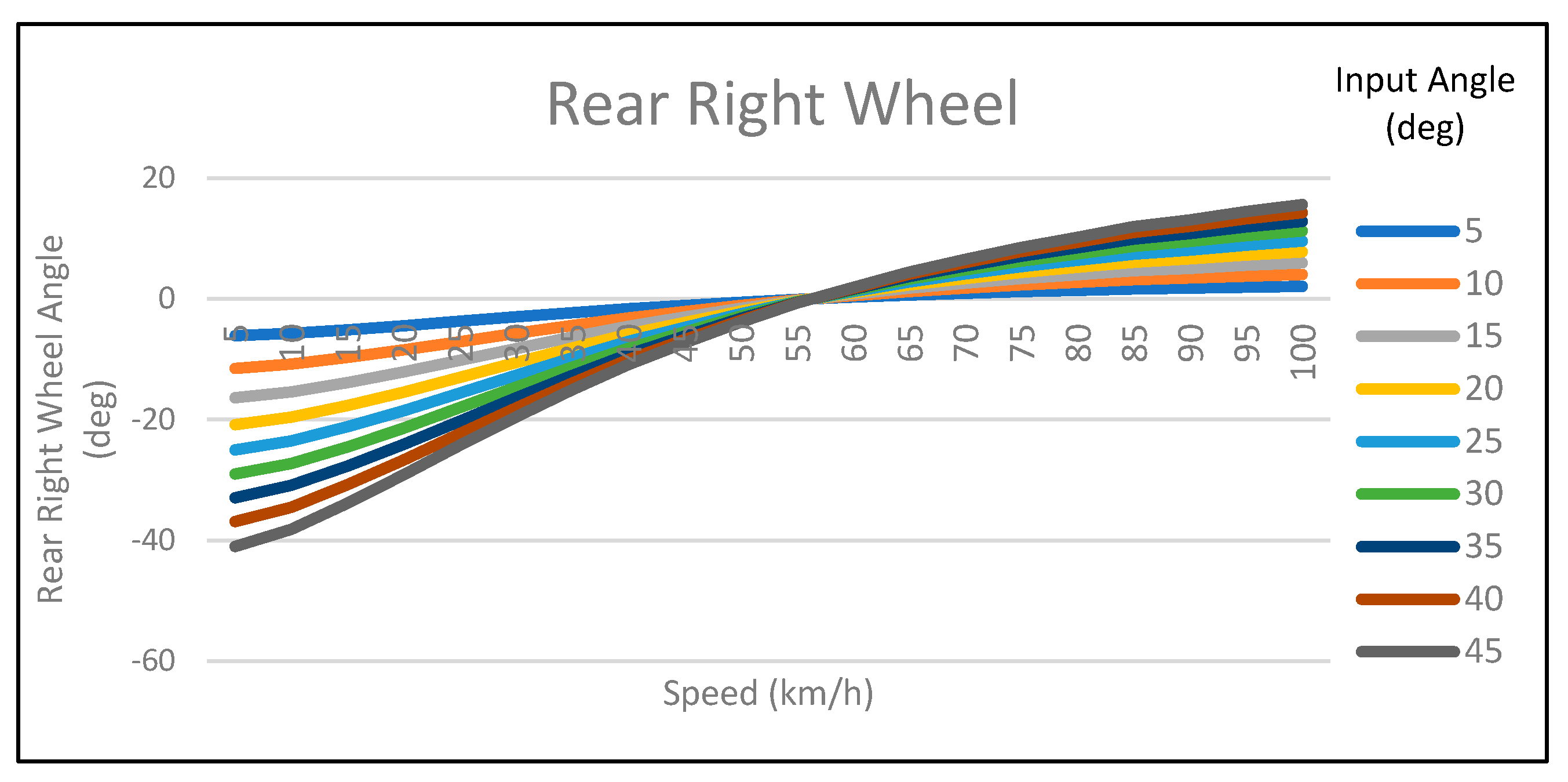
At low speed, rear wheels are steered in the opposite direction in comparison to the ones in the front. At high speed, the front and rear wheels turn in the same direction.
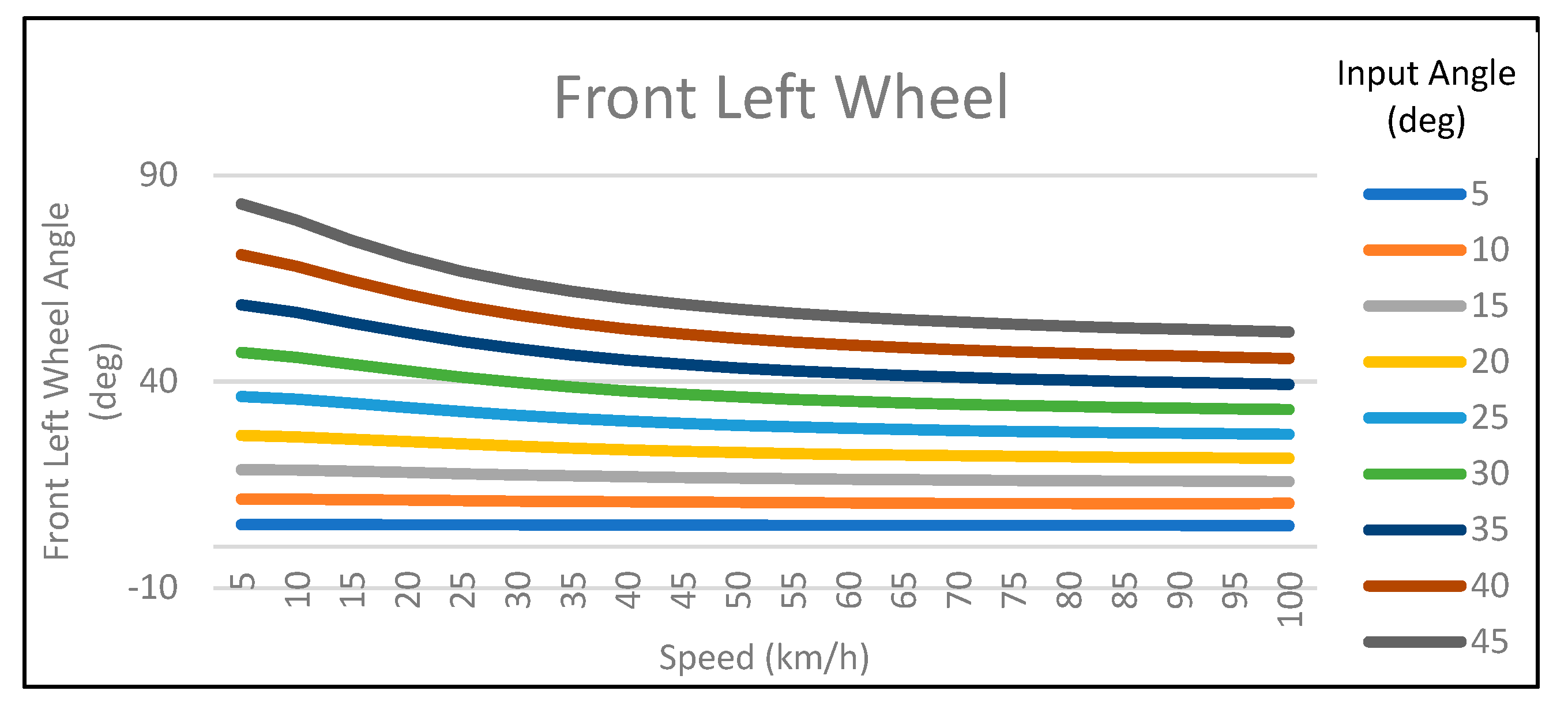
The entry angle, given by the vehicle driver or by the software in the case of autonomous driving, is considered as the central angle of the front axle (δfront). During normal driving (not in cases of parking or zero turn) the entry angle varies between -45° ≤ δfront ≤ 45°. Following, there are four graphs (Figure 2, Figure 3, Figure 4 and Figure 5) that illustrate the angle of each wheel, depending on the speed of the vehicle and the angle of the steering command [15].

3. Mathematical modelling of a Hybrid Stepper Motor

Hybrid stepper motors are a variant of modern permanent magnet motors with two phases, phase A and phase B, which are perpendicular to each other and thus their mutual inductance is zero [8]. Eqns (1) and (2) represent the basic electrical equations of the hybrid stepper motor:
u a = R i a + L d i a d t − K m ω sin ⁡ ( N θ )
u b = R i b + L d i b d t − K m ω cos ⁡ ( N θ )
where ia and ib are the currents of phases A and B (A), ua and ub are the phase voltages (V), R is the phase resistance (Ω), L is the phase inductance (H), Km is the torque constant (V·s/rad), ω is the angular velocity (rad/s), θ is the mechanical rotor position (rad), and N is the rotor number teeth.
The mechanical equations of the hybrid stepper motor are expressed by eqns (3) and (4).
K m ( − i a sin ⁡ N θ + i b cos ⁡ N θ − T L = J d ω d t + K v ω
ω = d θ d t
where Kv is the coefficient of viscous friction (N·m·s/rad), J is the system inertia (kg·m2), and TL is the load torque (N·m).
The parameters of hybrid stepper motor used for the simulation are given in Table 1.

4. Controller Design Strategy

The hybrid stepper motor controller is responsible for the simultaneous rotation of all wheels to their final position according to the central command of the vehicle's steering. The requirement in such a system is the interaction of all the wheels with each other and, by extension, of course, with the central command. Consequently, during operation each wheel must rotate at the angle to which it is assigned, but also it must “listen” to the state of the other wheels.
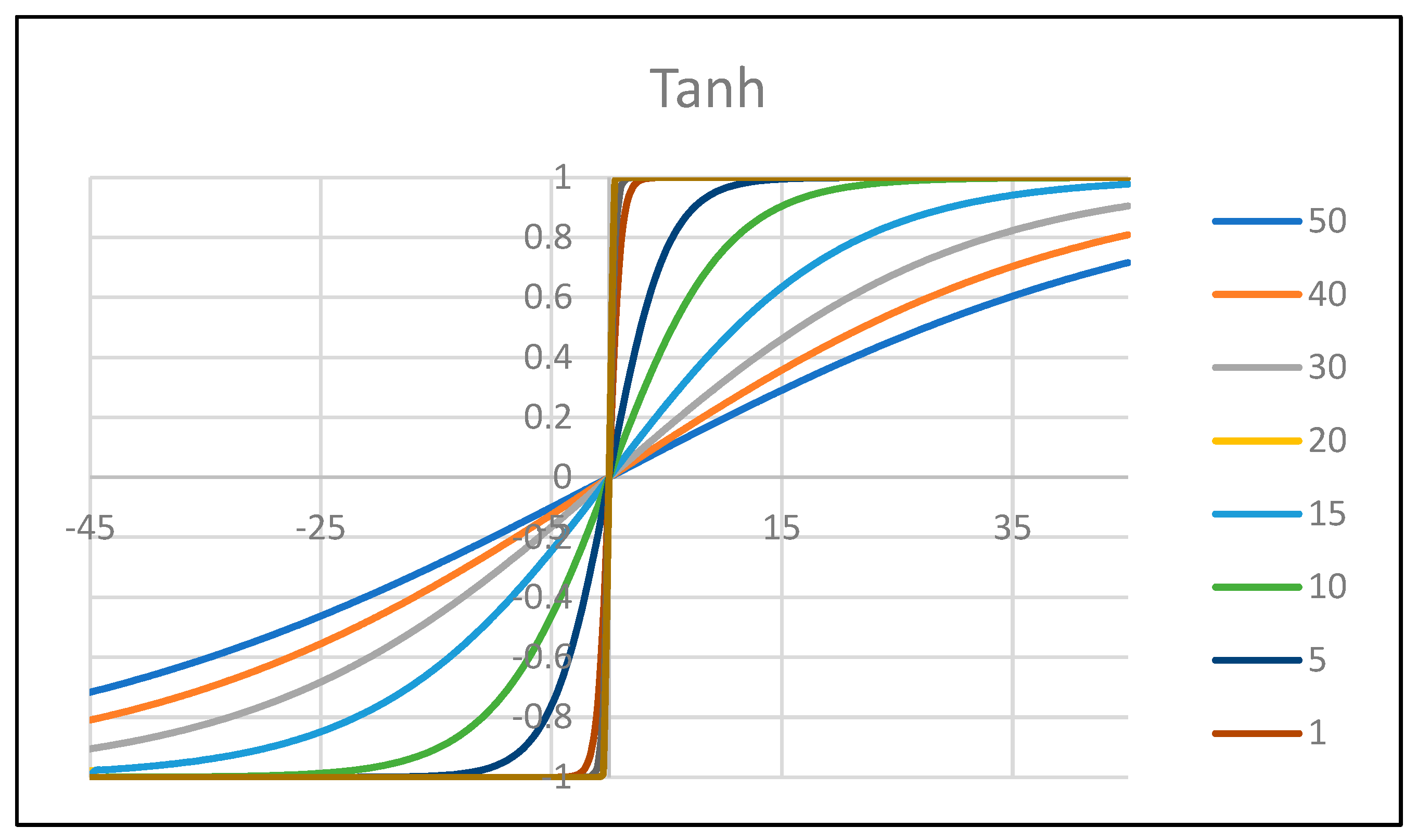
The control system presented in the paper combines techniques derived from the fields of neural networks and fuzzy logic. One important component of neural networks is the activation function, which maps the input to a non-linear output that is used to determine the level of activation of the neuron. Here, the hyperbolic tangent function is used as the activation function in the neural network in order to classify the error values into a range between -1 and 1. Furthermore, by means of the coefficient k of the hyperbolic tangent, the slope of the function is varied, as shown in Figure 6.
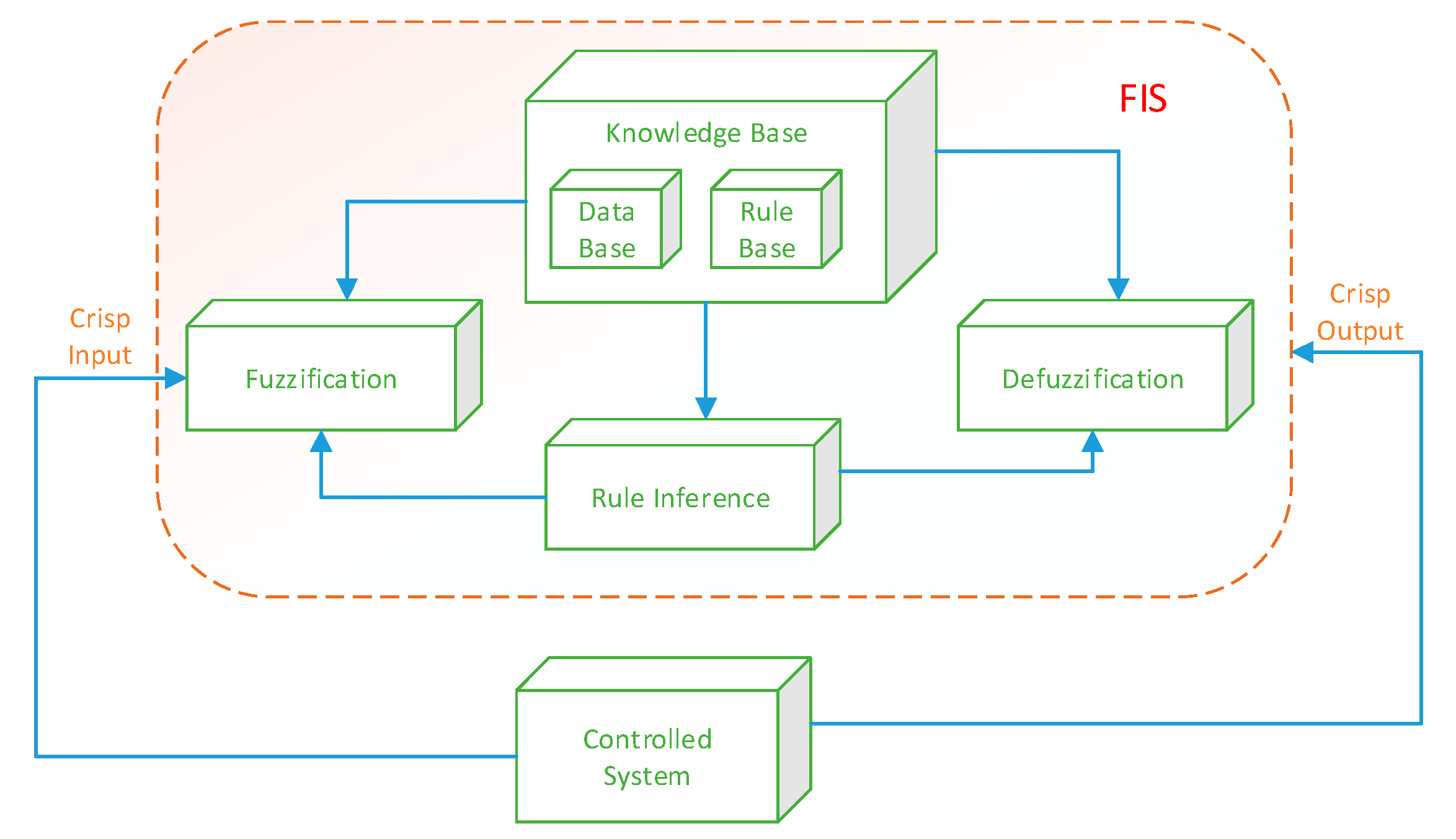
Fuzzy logic, on the other hand, relies on the concepts of fuzzification and defuzzification to deal with imprecision of the data. Fuzzification involves mapping continuous input values to a set of fuzzy values or membership functions that describe the degree of membership of the input to each fuzzy set. In this paper, the position error is fuzzified to enable the system to deal with imprecision of the data. The resulting fuzzy sets are then used to determine the degree of activation of each rule in the rule base.
Defuzzification is the process of mapping fuzzy values to a crisp value that can be used to control the system. In this work, the output of the fuzzy logic function is defuzzified using the Mamdani method, which involves combining the outputs of all the activated rules using a weighted average. The resulting crisp value is used to control the stepper motor and ensure that each wheel rotates at the angle to which it is assigned, while also “listening” to the state of the other wheels.
Preprints 86749 g007
Figure 7. Fuzzy Logic Process
Figure 7. Fuzzy Logic Process
Preprints 86749 g007
Overall, the combination of neural networks and fuzzy logic enables the control system to operate in a complex and uncertain environment, where the inputs and outputs are imprecise and the relationships between them are non-linear. The activation function in the neural network provides a non-linear mapping of the input that can capture the complex relationships between the input and output, while the fuzzy logic function provides a set of rules that can deal with the imprecision and uncertainty of the data. The use of defuzzification, using the Mamdani method, ensures that the resulting crisp value can be used to control the system and ensure the simultaneous rotation of all wheels to their final position according to the central command of the vehicle's steering.
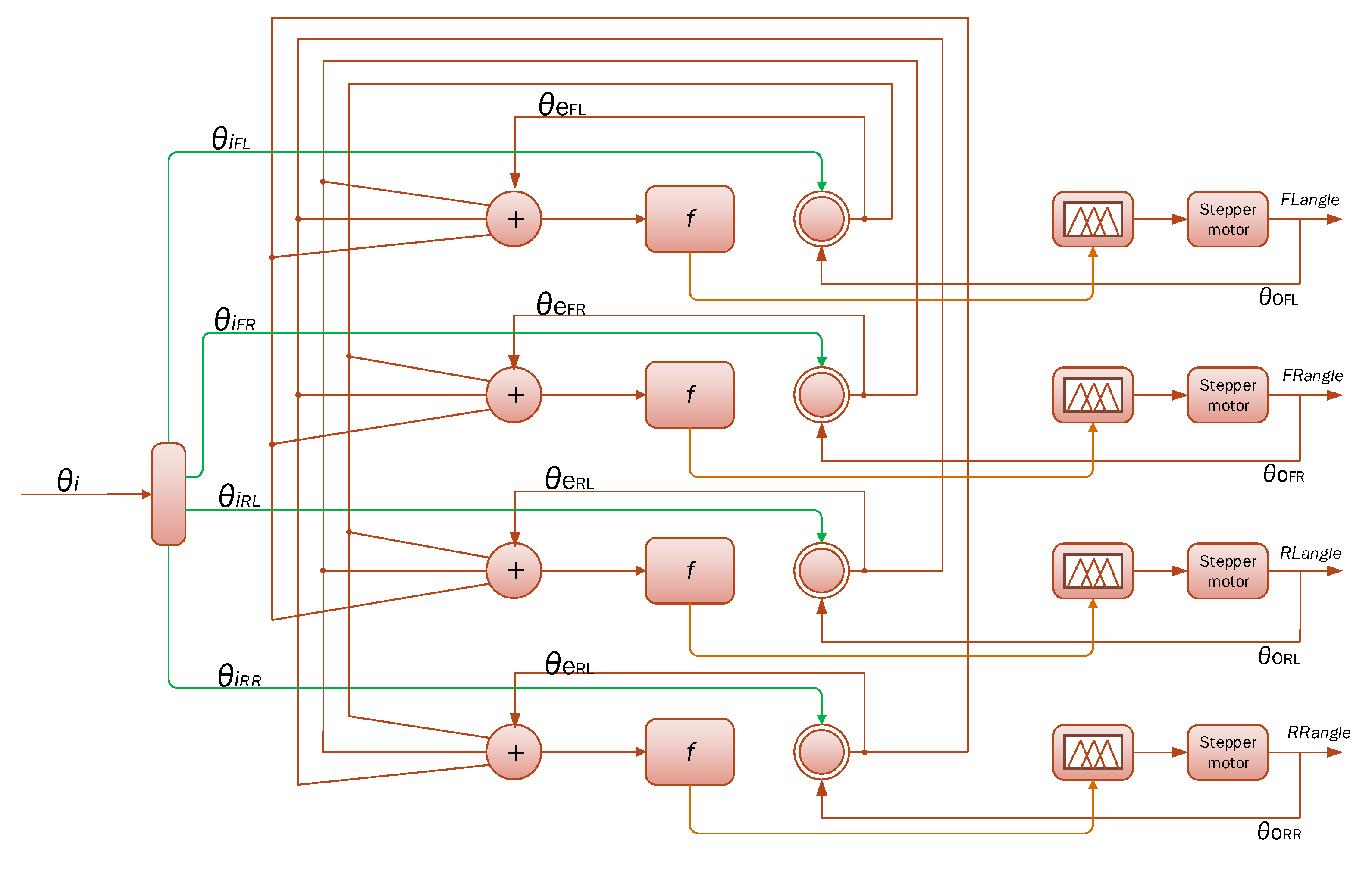
In more detail, the control strategy is as follows: The vehicle steering command θi is sent to all the motor controllers, where it converts the vehicle angle to the wheel angle (θiFL, θiFR, θiRL, θiRR). The desired angle of each wheel (θiFL, θiFR, θiRL, θiRR) is then compared with the output of the corresponding stepper motor (θoFL, θoFR, θoRL, θoRR) and the error (θeFL, θeFR, θeRL, θeRR) is obtained.
The resulting error is fed back to all the neural networks and the error of the motor of interest is multiplied by 1 while the resulting errors of the other motors are multiplied by -1/3 (in order to take under consideration the average error derived from the other controllers). Thereinafter, the result is fed into the hyperbolic tangent function f(error) (5). The coefficient k was chosen by considering Figure 6 and the desired response of the fuzzy logic control. As it can be seen in Figure 6 for low values of k the tanh function becomes stiff and the error fed in the fuzzy logic control for small angle errors tends to have a stiff response (i.e. for small angle errors feed the maximum allowed value of error in the fuzzy logic unit), while for higher values of coefficient k the error fed to the fuzzy logic control presents better controllability. However, if the value of k is too high the desired response is very slow. Therefore, the value of k should be chosen carefully. In the following results k = 5 was chosen considering Figure 6 and the abovementioned “restrictions”.
f e r r o r = e k x − e − k x e − k x + e k x   , − 1 < f ( e r r o r ) < 1
The result of f(error), which varies due to the nature of the function between -1 and 1, is fed into MAP(ferror) (6) and the function is adjusted to the limits between 0 and 1.
M A P f e r r o r = f e r r o r + 1 2 , 0 < M A P ( f e r r o r ) < 1
Preprints 86749 g008
Figure 8. Control Block Diagram
Figure 8. Control Block Diagram
Preprints 86749 g008
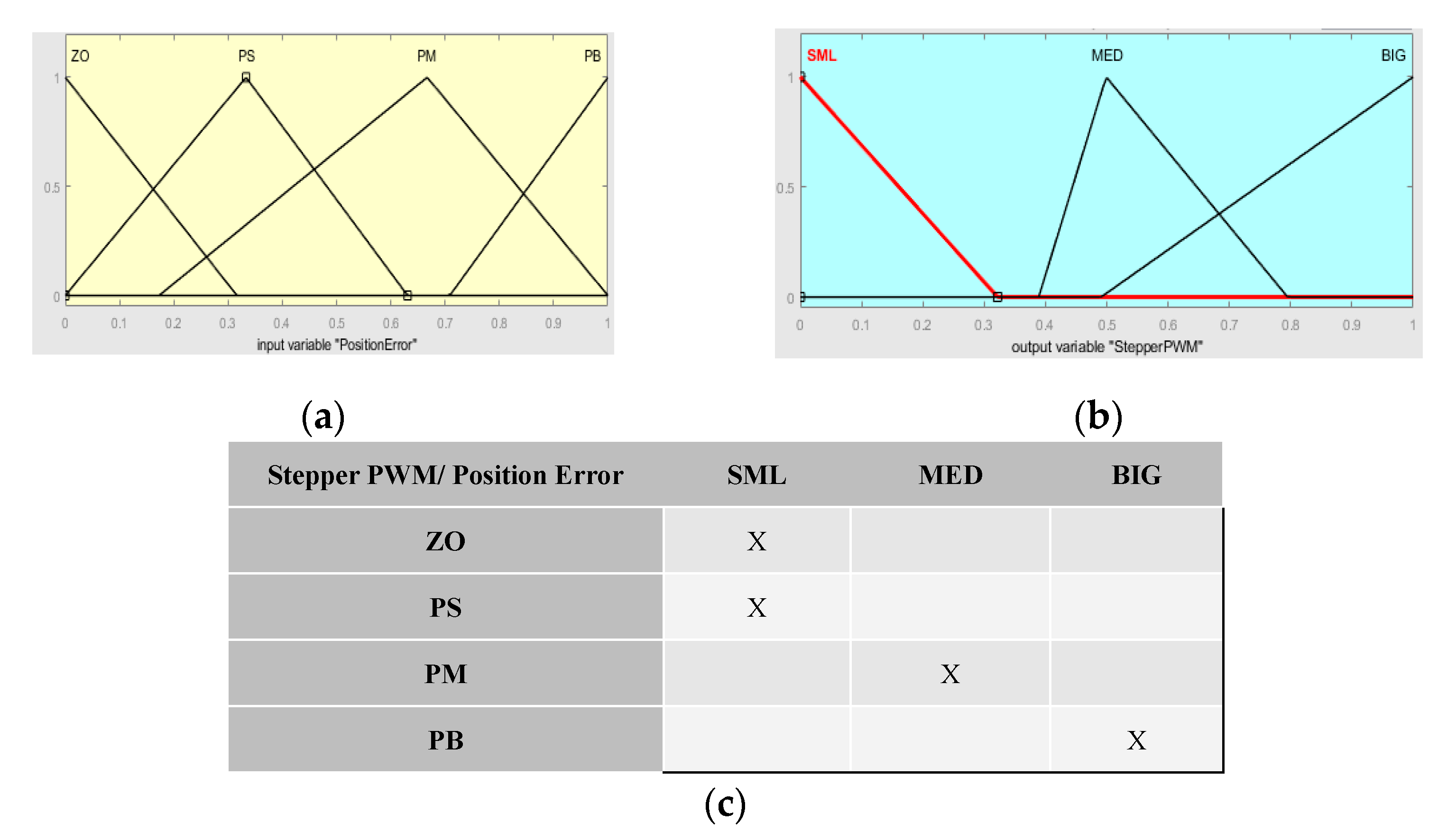
The output of MAP(ferror) then feeds the simple fuzzy logic function, where the input (PositionError) and output (StepperPWM) membership functions and rule base for the Stepper motor control are shown in Figure 9a–c. The PositionError and StepperPWM are normalized from 0 to 1.
It is noted that in the above fuzzy logic function, the control is only performed for positive wheel angle. This is because in the case of negative angles, the corresponding positive output (StepperPWM) is used by digitally driving the wheel in the negative direction.

5. Simulation and Results

The proposed control method aims to achieve a specific angle for each wheel simultaneously, indicating a desired motion. For the purposes of this research and in order to verify the proposed control method indicative representative combinations of address and velocity are selected. These values are shown in Table 2.
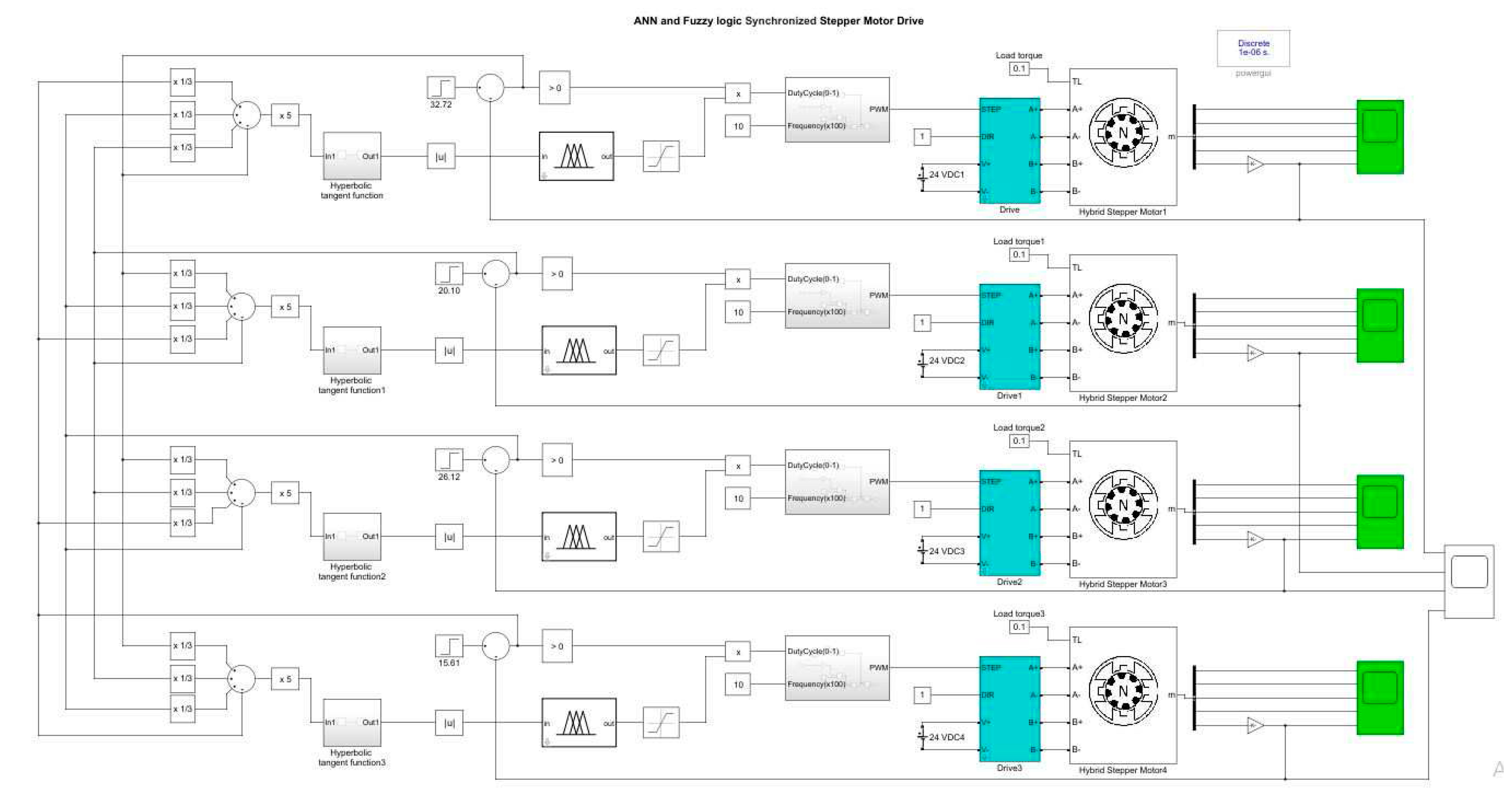
The model was developed in Matlab/Simulink simulation software in order to confirm the theoretical hypothesis.
Preprints 86749 g010
Figure 10. Βlock diagram of the proposed four stepper motor steering scheme in Matlab/Simulink platform.
Figure 10. Βlock diagram of the proposed four stepper motor steering scheme in Matlab/Simulink platform.
Preprints 86749 g010
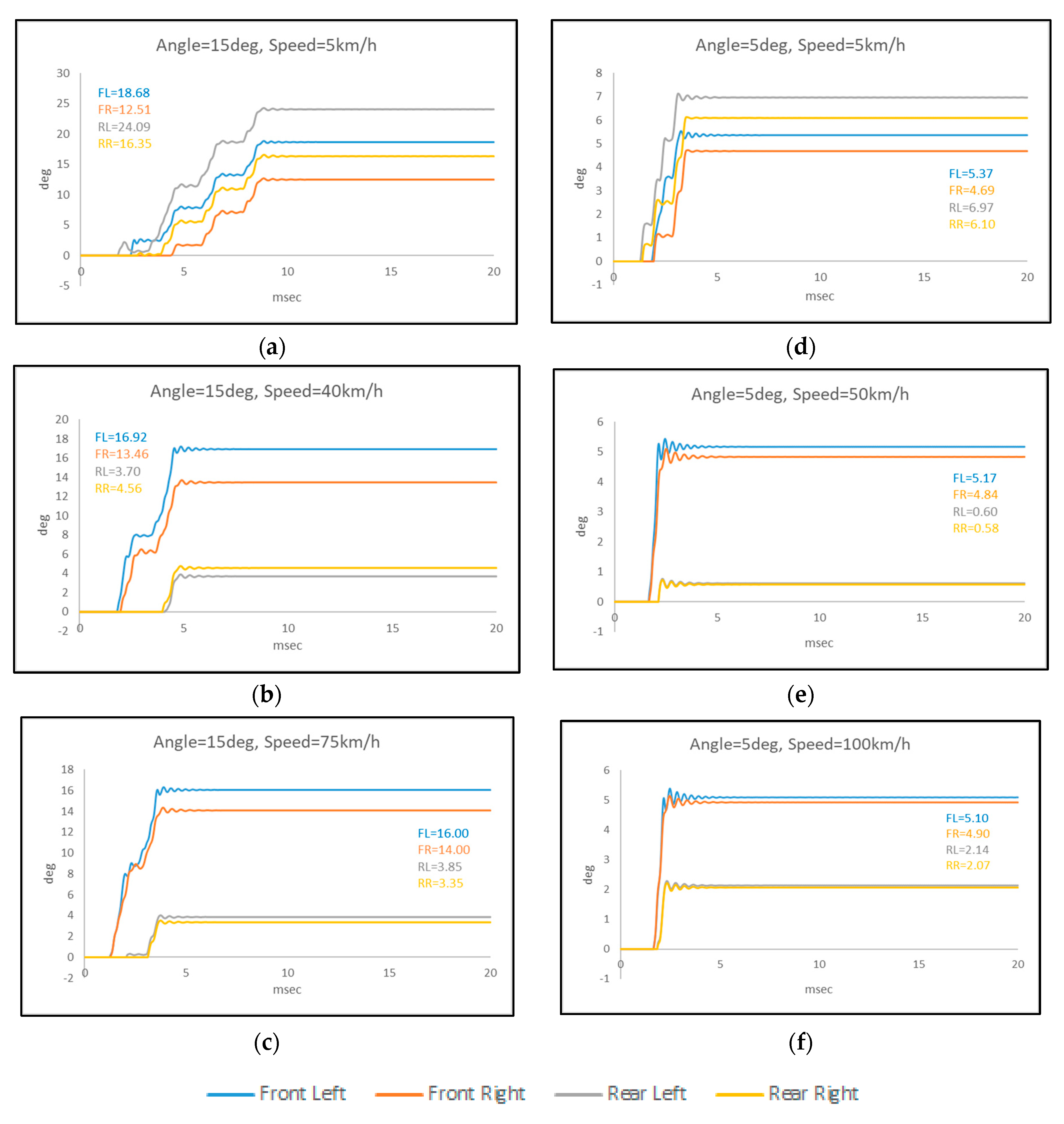
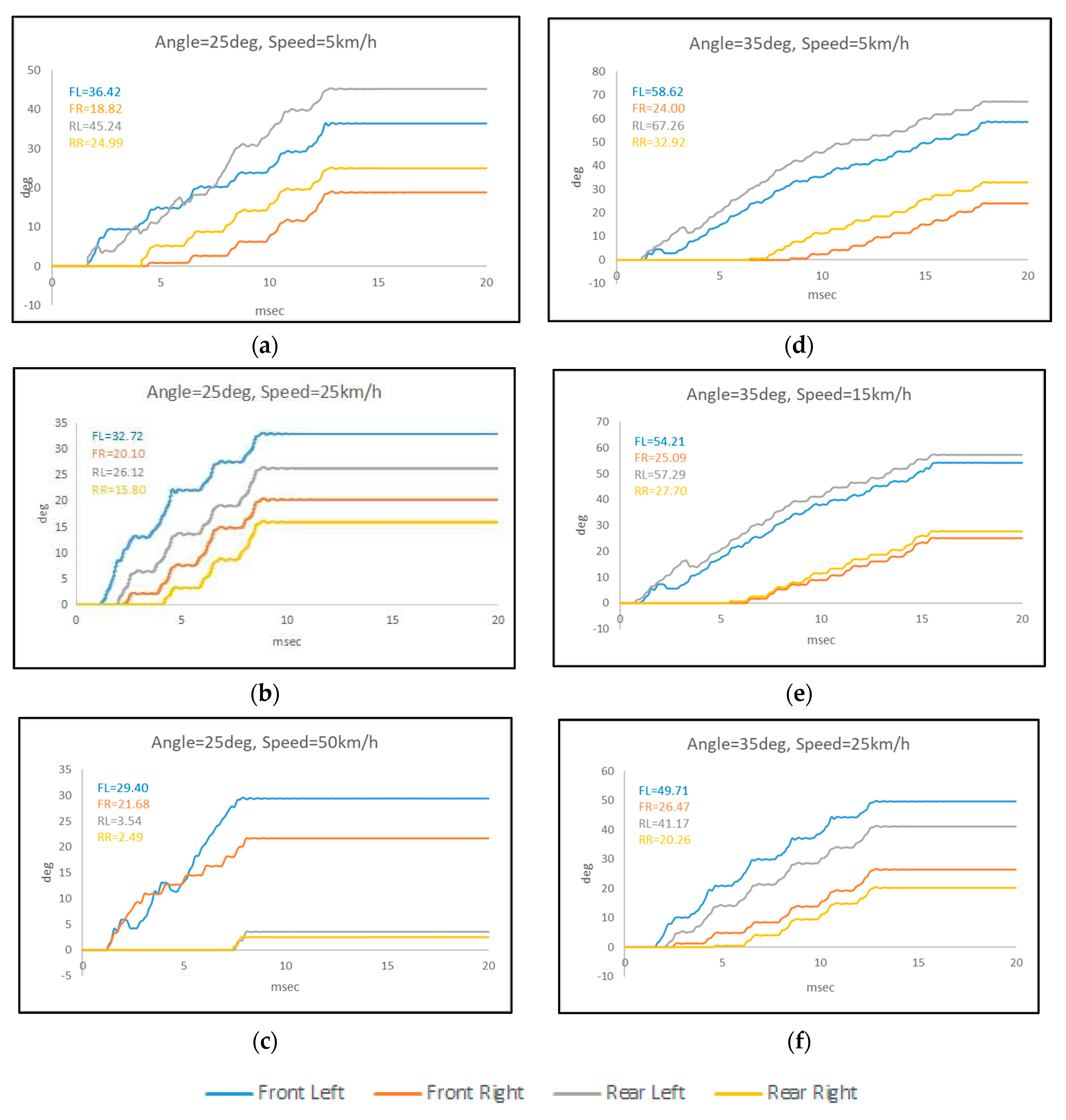
The step response results depicted in Figure 11 and Figure 12 provide insights into the system's behavior under constant load conditions (0.1Nm) on each motor. Analyzing these figures allows for an evaluation of how well the control method maintains the desired angles for each wheel.
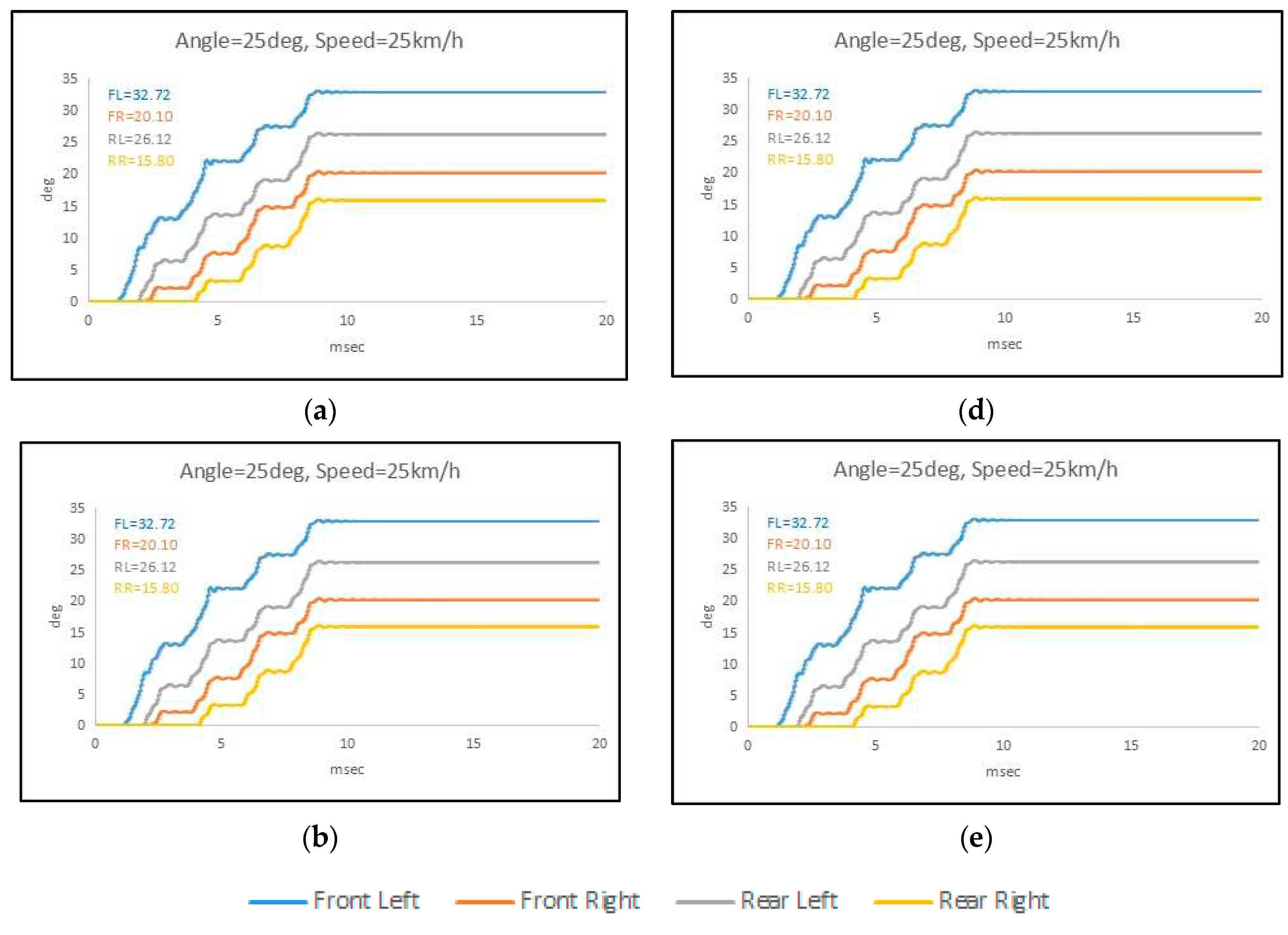
Figure 13 introduces a more challenging scenario, where the control system is tested under difficult conditions. By keeping the entry angle and speed constant (25deg-25km/h) while varying the load on one wheel, the performance of the control system can be assessed when faced with different loads. This analysis provides a better understanding of the control system's robustness and its ability to maintain the desired wheel angles despite external disturbances.
Overall, the research aims to provide a comprehensive evaluation of the proposed control method. By simulating various scenarios and assessing the control response, insights can be gained into the system's behavior, its ability to achieve simultaneous wheel angles, and its robustness under different operating conditions. These findings can potentially contribute to the development of more effective control strategies for multi-wheel systems.

6. Conclusions

This paper presents a real-time robust controller for a four-wheel independent steering system in electric vehicles. By integrating neural networks and fuzzy logic, and adopting a decentralized control approach, the proposed method offers significant advantages in terms of stability, efficiency, and practicality. The simulation results provide promising evidence of the synchronization capability of stepper motor rotations, regardless of input variations and load conditions, distinguishing it from existing systems.
Furthermore, the proposed control system brings numerous benefits. It ensures precise and accurate steering control, guaranteeing high stability. It also optimizes energy consumption, resulting in enhanced overall efficiency for the four-wheel independent steering system. Given its practicality, this approach holds potential for real-world applications in electric vehicles.
To validate the effectiveness of the proposed method, comprehensive simulation tests were conducted. These tests intentionally introduced random wheel position errors and variations in motor characteristics. The successful outcomes of these simulations demonstrate the system's robustness and synchronization capabilities.
The next crucial step involves verifying the findings through experimental tests. Implementing the proposed control scheme in a physical system will enable researchers to assess its performance under real-world conditions. By conducting these experimental tests, empirical evidence to support the viability and effectiveness of the developed controller would be gathered.
In conclusion, the paper's findings highlight the potential of the proposed control scheme and its ability to enhance the control of four-wheel independent steering systems in electric vehicles. The combination of neural networks, fuzzy logic, and decentralization provides notable advantages in terms of stability, efficiency, and practicality. The simulation results lay a solid foundation, while the forthcoming experimental tests will further validate the capabilities of the proposed controller in real-world scenarios.

References

  1. Furukawa, Y.; Yuhara, N.; Sano, S.; Takeda, H.; Matsushita, Y. A Review of Four-Wheel Steering Studies from the Viewpoint of Vehicle Dynamics and Control. Vehicle System Dynamics 1989, 18, 151–186. [Google Scholar] [CrossRef]
  2. Shibahata, Y.; Irie, N.; Itoh, H.; Nakamura, K. The Development of an Experimental Four-Wheel-Steering Vehicle. SAE Transactions 1986, 95, 862–869. [Google Scholar]
  3. Sano, S.; Furukawa, Y.; Shiraishi, S. Four Wheel Steering System with Rear Wheel Steer Angle Controlled as a Function of Steering Wheel Angle.; February 1 1986; p. 860625.
  4. Zheng, H.; Yang, S.; Li, B. Optimization Control for 4WIS Electric Vehicle Based on the Coincidence Degree of Wheel Steering Centers. SAE Int. J. Veh. Dyn., Stab., and NVH 2018, 2, 169–184. [Google Scholar] [CrossRef]
  5. Chen, H.; Chen, S.; Zhou, R.; Huang, X.; Zhu, S. Research on Four-wheel Independent Steering Intelligent Control Strategy Based on Minimum Load. Concurrency Computat Pract Exper 2021, 33. [Google Scholar] [CrossRef]
  6. Yin, D.; Wang, J.; Du, J.; Chen, G.; Hu, J.-S. A New Torque Distribution Control for Four-Wheel Independent-Drive Electric Vehicles. Actuators 2021, 10, 122. [Google Scholar] [CrossRef]
  7. Cao, Y.; Qiao, M. Application of Fuzzy Control in Four Wheel Steering Control System. In Proceedings of the 2017 International Conference on Advanced Mechatronic Systems (ICAMechS); IEEE: Xiamen, December, 2017; pp. 62–66. [Google Scholar]
  8. Hakima, A.; Ameli, S. Designing a Fuzzy Logic Controller to Adjust the Angle of Tires in Four Wheel Steering Vehicles. In Proceedings of the 2010 11th International Conference on Control Automation Robotics & Vision; December 2010; pp. 2208–2213.
  9. Tian, J.; Tong, J.; Luo, S. Differential Steering Control of Four-Wheel Independent-Drive Electric Vehicles. Energies 2018, 11, 2892. [Google Scholar] [CrossRef]
  10. Özatay, E. Fuzzy Logic Control of Four-Wheel Steering System. Master Thesis, Middle East Technical University, 2003.
  11. Haytham, A.; Elhalwagy, Y.Z.; Wassal, A.; Darwish, N.M. Modeling and Simulation of Four-Wheel Steering Unmanned Ground Vehicles Using a PID Controller. In Proceedings of the 2014 International Conference on Engineering and Technology (ICET); IEEE: Cairo, Egypt, April, 2014; pp. 1–8. [Google Scholar]
  12. Vehicle Engineering I-Kohza Malaysia Japan International Institute of Technology University Teknologi Malaysia 54100JalanSemarak, Kuala Lumpur, Malaysia; Ariff, M.H.M.; Zamzuri, H.; Nordin, M.A.M.; Yahya, W.J.; Mazlan, S.A.; Rahman, M.A.A.; Vehicle Engineering I-Kohza Malaysia Japan International Institute of Technology University Teknologi Malaysia 54100JalanSemarak, Kuala Lumpur, Malaysia OPTIMAL CONTROL STRATEGY FOR LOW SPEED AND HIGH SPEED FOUR-WHEEL-ACTIVE STEERING VEHICLE. J. Mech. Eng. Sci. 2015, 8, 1516–1528. [CrossRef]
  13. Khan, M.A.; Aftab, M.F.; Ahmed, E.; Youn, I. Robust Differential Steering Control System for an Independent Four Wheel Drive Electric Vehicle. Int.J Automot. Technol. 2019, 20, 87–97. [Google Scholar] [CrossRef]
  14. Zhou, P.; Ren, C.; Meng, L.; Chen, Y.; Nan, Y. Study on the Multi-Mode Optimal Control of Four-Wheel Steering Vehicle. Applied Sciences 2022, 12, 7037. [Google Scholar] [CrossRef]
  15. Kosmidis, A.N.; Ioannidis, G.Ch.; Vokas, G.A.; Psomopoulos, C.S. Analysis and Simulation of Four-Wheel Independent Steering Control for Electric Vehicles.; Athens, Greece, 2020; p. 020046.
  16. Pham, Duc-Anh, and Seung-Hun Han. Design of Combined Neural Network and Fuzzy Logic Controller for Marine Rescue Drone Trajectory-Tracking. Journal of Marine Science and Engineering 2022, 10, 1716. [Google Scholar] [CrossRef]
Preprints 86749 g001
Figure 1. k ratio in relation with vehicle speed.
Figure 1. k ratio in relation with vehicle speed.
Preprints 86749 g001
Preprints 86749 g002
Figure 2. Front Left Wheel Angle
Figure 2. Front Left Wheel Angle
Preprints 86749 g002
Preprints 86749 g003
Figure 3. Front Right Wheel Angle
Figure 3. Front Right Wheel Angle
Preprints 86749 g003
Preprints 86749 g004
Figure 4. Rear Left Wheel Angle
Figure 4. Rear Left Wheel Angle
Preprints 86749 g004
Preprints 86749 g005
Figure 5. Rear Right Wheel Angle
Figure 5. Rear Right Wheel Angle
Preprints 86749 g005
Preprints 86749 g006
Figure 6. Tangent function according to k value
Figure 6. Tangent function according to k value
Preprints 86749 g006
Preprints 86749 g009
Figure 9. (a) Input variable “PossitionError”; (b) Output variable “StepperPWM”; (c) Rule Base Control
Figure 9. (a) Input variable “PossitionError”; (b) Output variable “StepperPWM”; (c) Rule Base Control
Preprints 86749 g009
Preprints 86749 g011
Figure 11. (a) Step response at 5deg-5km/h; (b) Step response at 5deg-50km/h; (c) Step response at 5deg-100km/h; (d) Step response at 15deg-5km/h; (e) Step response at 15deg-40km/h; (f) Step response at 15deg-75km/h;.
Figure 11. (a) Step response at 5deg-5km/h; (b) Step response at 5deg-50km/h; (c) Step response at 5deg-100km/h; (d) Step response at 15deg-5km/h; (e) Step response at 15deg-40km/h; (f) Step response at 15deg-75km/h;.
Preprints 86749 g011
Preprints 86749 g012
Figure 12. (a) Step response at 25deg-5km/h; (b) Step response at 25deg-25km/h; (c) Step response at 25deg-50km/h; (d) Step response at 35deg-5km/h; (e) Step response at 35deg-15km/h; (f) Step response at 35deg-25km/h;.
Figure 12. (a) Step response at 25deg-5km/h; (b) Step response at 25deg-25km/h; (c) Step response at 25deg-50km/h; (d) Step response at 35deg-5km/h; (e) Step response at 35deg-15km/h; (f) Step response at 35deg-25km/h;.
Preprints 86749 g012
Preprints 86749 g013
Figure 13. (a) Step response at 25deg-25km/h – Front Left Motor overloaded x3; (b) Step response at 25deg-25km/h – Rear Left Motor overloaded x3; (c) Step response at 25deg-25km/h – Front Right Motor overloaded x3; (d) Step response at 25deg-25km/h – Rear Right Motor overloaded x3;.
Figure 13. (a) Step response at 25deg-25km/h – Front Left Motor overloaded x3; (b) Step response at 25deg-25km/h – Rear Left Motor overloaded x3; (c) Step response at 25deg-25km/h – Front Right Motor overloaded x3; (d) Step response at 25deg-25km/h – Rear Right Motor overloaded x3;.
Preprints 86749 g013
Table 1. Stepper Motor Parameters
Table 1. Stepper Motor Parameters
Number of phases 2
Winding Inductance (H) 1.4e-3
Winding resistance (Ohm) 0.7
Step angle (degree) 1.8
Maximum Flux Linkage (Vs) 0.005
Maximum Detent Torque (N.m) 0.002
Total inertia (kg.m.m) 1.2e-7
Total friction (N.m.s) 1e-7*1000
Table 2. Simulation Test Parameters
Table 2. Simulation Test Parameters
Input Angle
(deg)		 Vehicle Speed
(km/h)		 Front Left
angle (deg)		 Front Rear
angle (deg)		 Rear Left
angle (deg)		 Rear Right
angle (deg)
5 5 5,36 4,69 -6,97 -6,10
5 50 5,17 4,84 -0,61 -0,57
5 100 5,09 4,92 2,13 2,06
15 5 18,68 12,51 -24,09 -16,35
15 40 16,92 13,46 -3,70 -4,57
15 75 16,05 14,08 3,85 3,35
25 5 36,42 18,82 -45,24 -24,99
25 15 34,72 19,36 -37,43 -21,21
25 25 32,72 20,10 -26,12 -15,61
35 5 58,62 24,00 -67,25 -32,92
35 15 54,21 25,09 -57,27 -27,71
35 25 49,71 26,47 -41,17 -20,26
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated