Prerpints.org logo
Preprint
Article

Processing Accuracy of Microwave Photonic Signal Processors Based on Microcombs as a Function of Different Input Signal Waveforms

Altmetrics

Downloads

106

Views

21

Comments

0

This version is not peer-reviewed

Submitted:

24 October 2023

Posted:

24 October 2023

You are already at the latest version

Alerts
Abstract
Microwave photonic (MWP) signal processors, which process microwave signals based on photonic technologies, bring advantages intrinsic to photonics such as low loss, large processing bandwidth, and strong immunity to electromagnetic interference. Optical microcombs can offer a large number of wavelength channels and compact device footprints, which make them powerful multi-wavelength sources for MWP signal processors to realize a variety of processing functions. In this paper, we experimentally demonstrate the capability of microcomb-based MWP signal processors to handle diverse input signal waveforms. In addition, we quantify the processing accuracy for different input signal waveforms, including Gaussian, triangle, parabolic, super Gaussian, and nearly square waveforms. Finally, we analyze the factors contributing to the difference in the processing accuracy among the different input waveforms, and our theoretical analysis well elucidates the experimental results. These results provide a guidance for microcomb-based MWP signal processors when processing microwave signals of various waveforms.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Microwave signal processors have found wide applications in telecommunication and radar systems [1,2,3,4]. Traditional microwave signal processors relying on electronic devices exhibit significant loss and strong crosstalk when handling high-frequency microwave signals, which make them suffer from limited operation bandwidths. To overcome this restriction, microwave photonic (MWP) signal processors that perform signal processing functions based on MWP technologies have attracted great interests [3,4,5,6].
A variety of MWP signal processors have been demonstrated by exploiting different optical filtering modules to process microwave signals modulated onto a single optical carrier [7,8,9,10,11,12,13,14,15,16,17]. Although these approaches feature high performance in achieving specific processing functions, they face limitations in their reconfigurability to realize diverse processing functions based on a single system. On the contrary, in MWP signal processors implemented based on the transversal filter structure [18], input microwave signals are modulated onto multiple optical carriers with adjustable time delays and tap weights before summing via photodetection. This enables a high reconfigurability to achieve various processing functions without changing any hardware [2,18].
For MWP signal processors implemented by the transversal filter systems, a large number of taps, or the wavelength channels provided by multi-wavelength optical sources, is required to improve their performance. Compared to other multi-wavelength optical sources, such as discrete laser arrays [19,20,21], fibre Bragg grating arrays [22,23,24], laser frequency combs generated by electro-optic (EO) modulation [25,26,27], and mode-locked fiber lasers [28,29], optical microcombs can provide a large number of wavelength channels by using compact micro-scale resonators [3,4,30]. They are also with the ability to offer broad Nyquist zones, which allow for large processing bandwidths [4,31,32]. With these advantages, a variety of signal processing functions have been successfully demonstrated using microcomb-based MWP signal processors, such as differentiation [33], integration [34], Hilbert transform [35], arbitrary waveform generation [36], and convolutional processing [37,38].
Although a range of signal processing functions have been realized, they only used Gaussian input waveforms for demonstrations, while the ability to handle various input signal waveforms is essential for practical applications. In this paper, we experimentally demonstrate the capability of microcomb-based MWP signal processors for dealing with various input signal waveforms. We investigate the processing accuracy of different input waveforms, including Gaussian, triangle, parabolic, super Gaussian, and nearly square waveforms. We also perform theoretical analysis and discuss the reasons for the difference in the processing accuracy among the different input waveforms. These results offer a valuable guide for microcomb-based MWP signal processors to handle microwave signals with different waveforms.

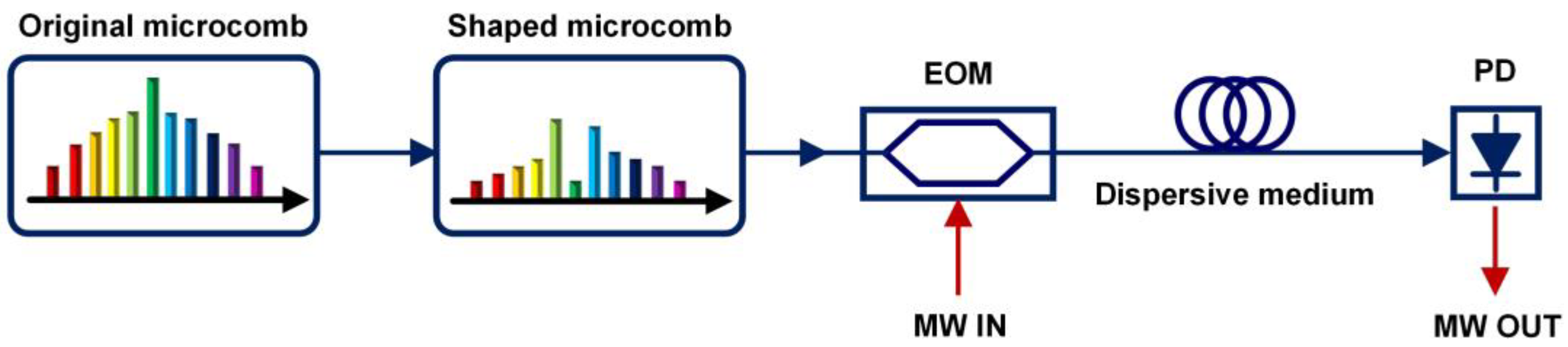
2. Microcomb-based MWP signal processors

MWP signal processors based on the transversal filter are implemented based on MWP technologies, which can overcome the electrical bandwidth bottleneck by providing a substantially increased processing bandwidth. A MWP transversal signal processor has a high reconfigurability in terms of its spectral transfer function, which can be expressed as [4]
H ( ω ) = ∑ M - 1 n = 0 a n e - j ω n Δ T ,
where ω is the angular frequency of the input microwave signal to be processed, M is the tap number, an (n = 0, 1, 2, …, M-1) is the tap coefficient of the nth tap, and ΔT is the time delay between adjacent taps. By properly designing the various tap coefficients an (n = 0, 1, 2, …, M-1), different signal processing functions can be realized by using a single system without changing the hardware.
Figure 1 shows the schematic of a microcomb-based MWP signal processor. An optical microcomb is used to generate multiple wavelength channels that act as discrete taps for the transversal signal processor. The generated optical microcomb is spectrally shaped according to the designed tap coefficients an (n = 0, 1, 2, …, M-1). Next, all of the wavelength channels of the shaped optical microcomb are imprinted with the input microwave signal via an electro-optic modulator (IM), leading to the generation of multiple microwave replicas. Following this, the modulated optical signals transmit through a dispersive medium to introduce time delays ∆T, which progressively separate the microwave replicas. Finally, the delayed replicas are summed upon photodetection via a photodetector.

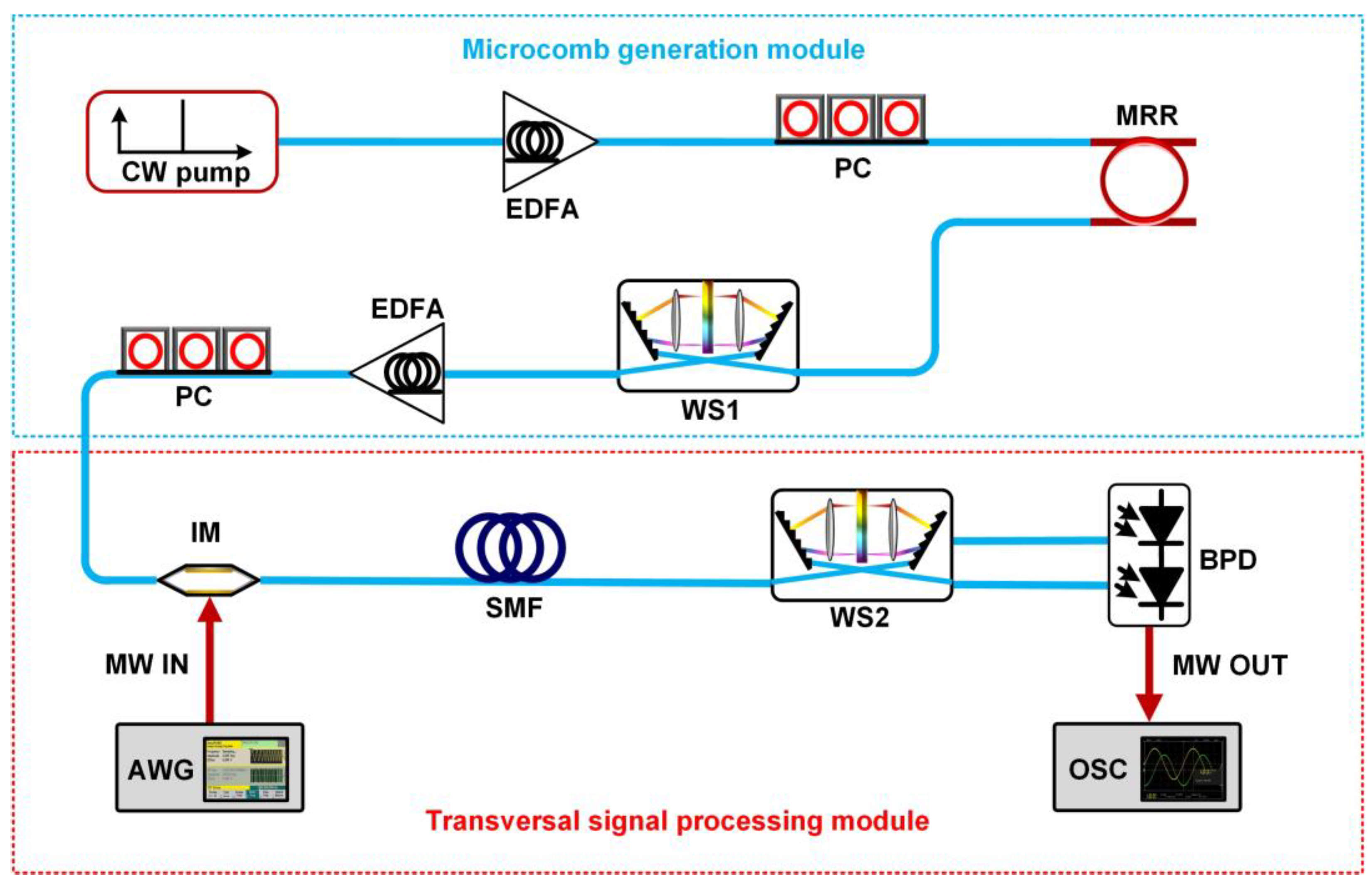
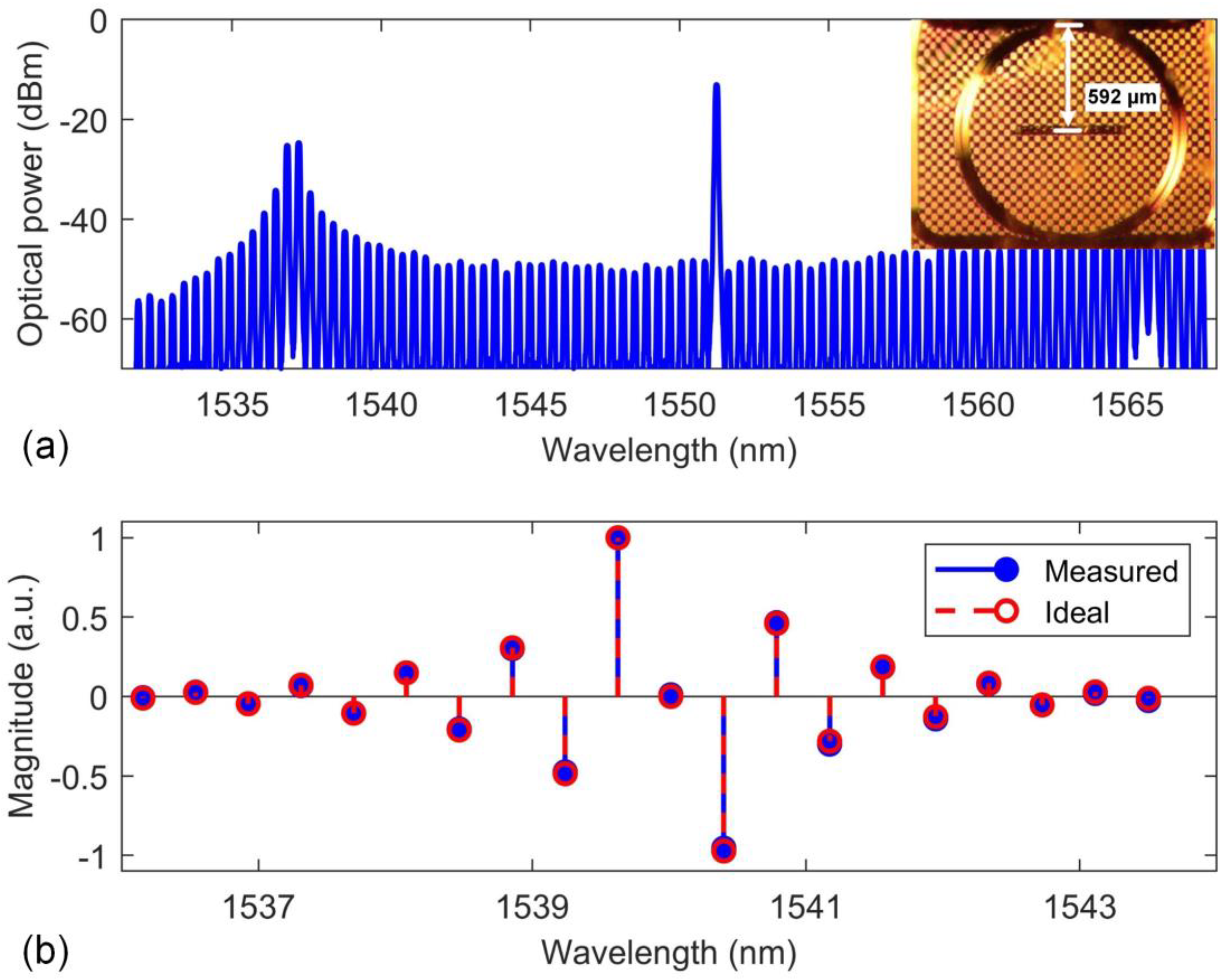
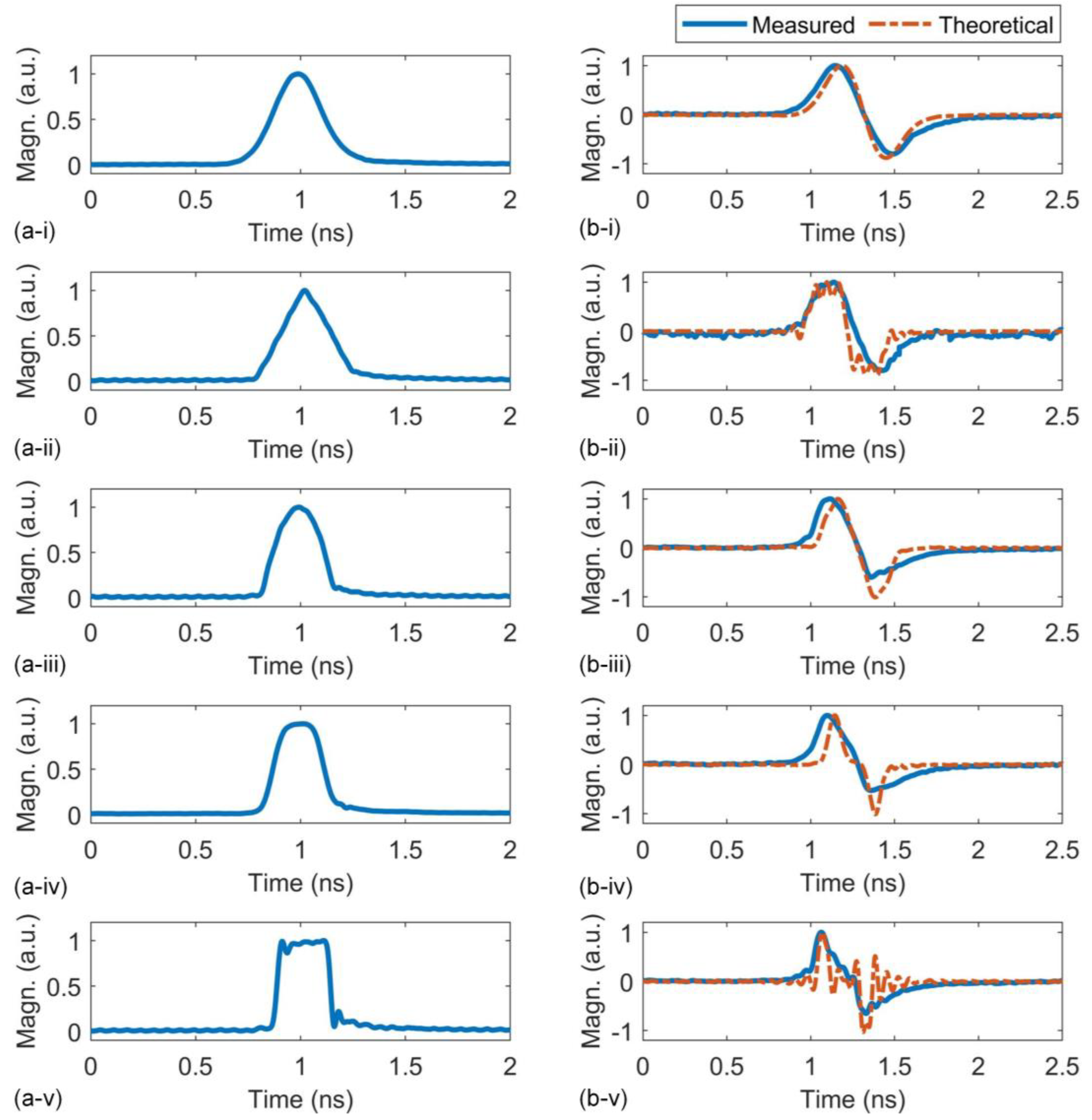
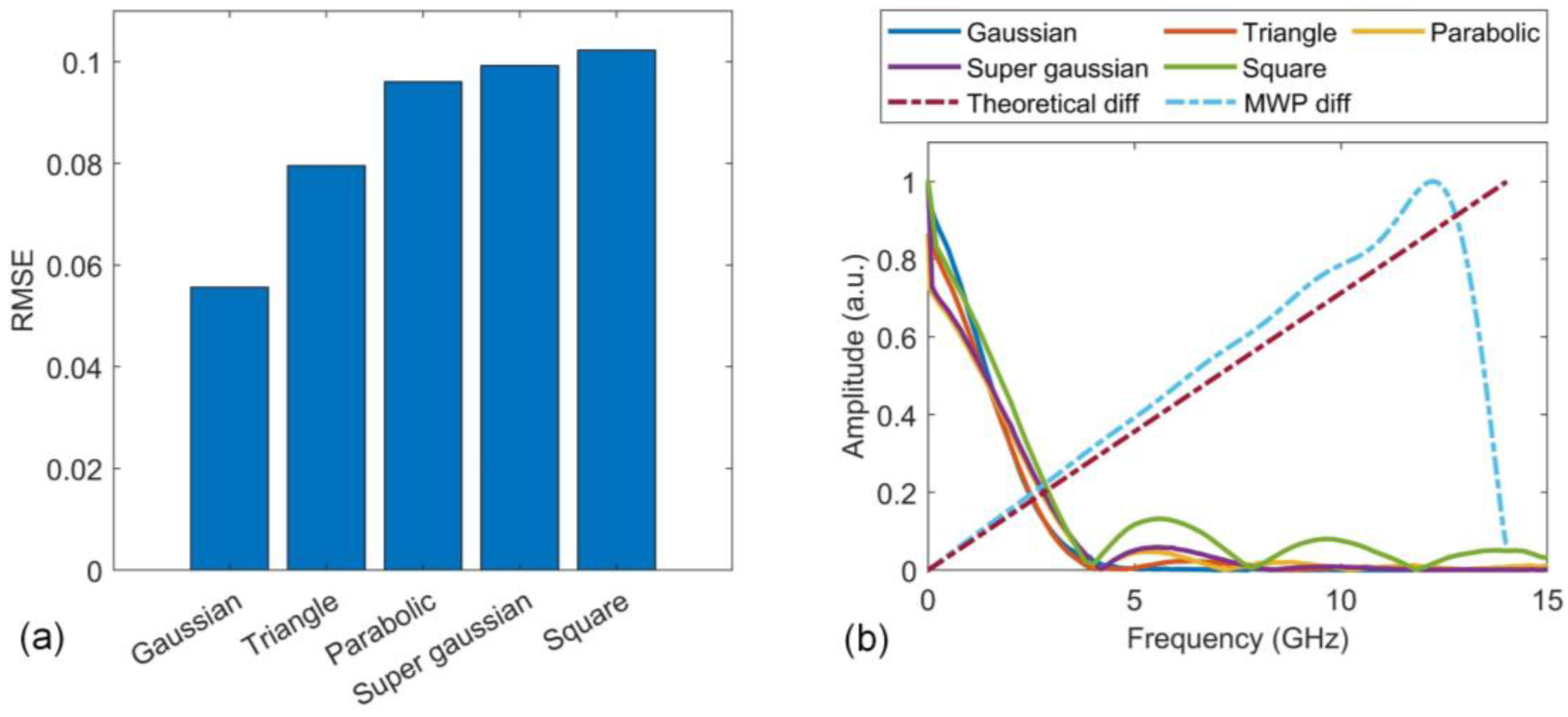
3. Experimental results

In our experimental demonstration, we implemented the microcomb-based MWP signal processors based on the setup shown in Figure 2, which consisted of a microcomb generation module and a transversal signal processing module. In the microcomb generation module, the optical microcomb was generated by a microring resonator (MRR) made from high-index doped silica glass [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106]. The high-index doped silica glass offers attractive material properties for microcomb generation, including ultra-low linear loss (~0.06 dB/cm), a moderate nonlinear parameter (~233 W-1 · km-1), and a negligible nonlinear loss even at extremely high intensities (~25 GW · cm-2) [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106]. The MRR had a quality factor of ~1.5 × 106. A continuous-wave (CW) light was amplified to ~32.1 dBm by an erbium-doped fibre amplifier (EDFA) and used to pump the MRR. The polarization of the CW pump was adjusted to TE polarization, which aligned with a TE-polarized resonance of the MRR at ~1551.23 nm. When the pump power of the CW laser was sufficient high and its wavelength was swept across the MRR’s resonance at ~1551.23 nm, optical parametric oscillation occurred, resulting in the generation of a palm-like soliton crystal microcomb [40,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106], as shown in Figure 3(a). The MRR was designed to have a radius of ~592 μm, which corresponded to a comb spacing of ~0.4 nm or ~49 GHz. In our experimental demonstration, 20 comb lines were employed to as discrete taps. The initially generated microcomb exhibited non-uniform power distributions among the comb lines and so it was shaped by the first waveshaper (WS1, Finisar) to flatten the comb lines. This was done to achieve a higher signal-to-noise ratio and reduce the required loss control range for the second waveshaper in the transversal signal processing module, which further shaped the comb lines according to the designed tap coefficients.
In the transversal signal processing module, the shaped microcomb was modulated by the input microwave signal via an intensity modulator (IM) (iXblue). The input microwave signal was multicast onto different wavelength channels, resulting in the generation of multiple microwave replicas. Next, the microwave replicas were transmitted through a spool of single mode fibre (SMF), which served as the dispersive medium that introduced a time delay between adjacent wavelength channels, i.e., ∆T in Eq. (1). The time delay ∆T can be further expressed as [4]
  Δ T = L   ×   D 2   ×   Δ λ
where L is the fibre length, D2 is the second-order dispersion parameter, and ∆λ is the comb spacing. In our experiments, these parameters were L = ~5.124 km, D2 = ~17.4 ps/nm/km, and ∆λ = ~0.4 nm, which resulted in a time delay ∆T = ~ 35.7 ps.
After passing the dispersive medium, the comb lines were spectrally shaped by the second waveshaper (WS2, Finisar) according to the designed tap coefficients an (n = 0, 1, 2, …, M-1). Finally, the delayed microwave replicas were summed upon photodetection via a balanced photodetector (BPD, Finisar). The BPD separated the wavelength channels into two categories according to the sign of tap coefficients, achieving both positive and negative tap coefficients.
We took the first-order differentiation as an example to investigate the influence of different input signal waveforms on the processing accuracy of microcomb-based MWP signal processors. The spectral transfer function of the first-order differentiation can be described by [3]
  H ( ω )   = j ω ,
where j = - 1 , and ω is the angular frequency. The ideal tap coefficients were calculated by performing an inverse Fourier transform of Eq. (3), and the results is shown in Figure 3(b). For comparison, the measured tap coefficients after spectral shaping of the comb lines are also shown. As can be seen, the measured tap coefficients closely matched with the ideal tap coefficients, indicating the achievement of effective spectral shaping.
We selected five different temporal waveforms for the input microwave signal, including Gaussian, triangle, parabolic, super Gaussian, and nearly square waveforms. The input microwave signals were generated by an arbitrary waveform generator (AWG, Keysight). According to the Nyquist sampling theorem, the sampling rate of a continuous-time bandwidth-limited signal needs to exceed twice its maximum frequency component to avoid aliasing. This constraint sets an upper threshold for the bandwidth of the input microwave signal to be processed, which should not surpass half of the microcomb’s comb spacing, i.e., ~24.5 GHz. On the other hand, the FSR of the RF spectral response (FSRRF) of the differentiator was inversely related to the time delay (Eq. (2)) 1/∆T = ~28 GHz. Therefore, the operation bandwidth of the signal processor is given by fOB = ½ FSRRF = ~14 GHz, which sets another limitation for the maximum bandwidth of the input microwave signal. Considering these factors, in our experiments we employed input microwave signals with a full width at half maximum (FWHM) of ~0.2 ns (Figure 4(a)) and the primary frequency components resided within 14 GHz.
The signal processing results are shown in Figure 4(b), which were measured by a high-speed real-time oscilloscope (OSC, Keysight). The theoretical outputs are also shown for comparison, which were calculated based on Eqs. (1) ‒ (3). To facilitate a fair comparison, we used the recorded waveforms generated by the AWG as the input signal waveforms to calculate the theoretical outputs. As can be seen, all the measured outputs match with their corresponding theoretical outputs. Nevertheless, different input waveforms exhibit differences in the discrepancies between them. The Gaussian input waveform shows the lowest discrepancies, whereas the nearly square waveform displays the highest.
To quantify the processing accuracy of the processing results, the concept of root mean square error (RMSE) is introduced , which is defined as [30]
R M S E = ∑ i   = 1 k Y i - y i 2 k
where Y1, Y2, …, Yk are the values of theoretical processing results, y1, y2, …, yk are values of measured output waveforms.
Figure 5(a) shows the RMSEs between the measured output waveforms and the theoretical processing results for different input signal waveforms. The Gaussian and nearly square waveforms have the lowest and highest RMSE values, showing agreement with the results in Figure 4(b).
To analyze the reason for the differences in the processing accuracy for different waveforms, we further plot the amplitude frequency response of the processor and a theoretical differentiator in Figure 5(b), together with the spectra of input signals with different waveforms. It can be seen that the deviations between the response of the transversal signal processor and the theoretical differentiator become more significant in the high-frequency range. On the other hand, the nearly square waveform contains greater high-frequency components than other waveforms, which results in a reduction in its processing accuracy. In contrast, the Gaussian waveform has the least high-frequency components, enabling the highest level of processing accuracy.
Based on the above results, it can be seen that the processing accuracy varies for different input signal waveforms, even when performing the same processing function. The processing accuracy improves when there is better overlap between the high-intensity frequency components of the input signal and the low-error region of the MWP processor’s response spectrum. These results have implications for a wide range of linear and nonlinear photonic devices. [107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153]

4. Conclusion

In summary, we experimentally demonstrate that microcomb-based MWP signal processors are capable of processing microwave signals with different temporal waveforms. We characterize the processing accuracy for different input signal waveforms, including Gaussian, triangle, parabolic, super Gaussian, and nearly square waveforms. We find that the difference in the processing accuracy for various input waveforms is mainly resulting from the difference in their frequency components, as well as their overlap with the processor’s frequency response that exhibit different degrees of deviation from the ideal response. These results provide a useful guidance for microcomb-based MWP signal processors to process microwave signals with various waveforms.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Capmany, J., and Novak, D.: ‘Microwave photonics combines two worlds’, Nat. Photonics, 2007, 1, (6), pp. 319-330. [CrossRef]
  2. Yao, J.: ‘Microwave Photonics’, Journal of Lightwave Technology, 2009, 27, (3), pp. 314-335.
  3. Wu, J.Y., Xu, X.Y., Nguyen, T.G., Chu, S.T., Little, B.E., Morandotti, R., Mitchell, A., and Moss, D.J.: ‘RF Photonics: An Optical Microcombs' Perspective’, Ieee Journal of Selected Topics in Quantum Electronics, 2018, 24, (4), pp. 20.
  4. Sun, Y., Wu, J., Tan, M., Xu, X., Li, Y., Morandotti, R., Mitchell, A., and Moss, D.J.: ‘Applications of optical microcombs’, Adv. Opt. Photon., 2023, 15, (1), pp. 86-175.
  5. Marpaung, D., Yao, J., and Capmany, J.: ‘Integrated microwave photonics’, Nat. Photonics, 2019, 13, (2), pp. 80-90.
  6. Capmany, J., Mora, J., Gasulla, I., Sancho, J., Lloret, J., and Sales, S.: ‘Microwave Photonic Signal Processing’, Journal of Lightwave Technology, 2013, 31, (4), pp. 571-586. [CrossRef]
  7. Liu, W., Li, M., Guzzon, R.S., Norberg, E.J., Parker, J.S., Lu, M., Coldren, L.A., and Yao, J.: ‘A fully reconfigurable photonic integrated signal processor’, Nat. Photonics, 2016, 10, (3), pp. 190-195. [CrossRef]
  8. Ferrera, M., Park, Y., Razzari, L., Little, B.E., Chu, S.T., Morandotti, R., Moss, D.J., and Azaña, J.: ‘On-chip CMOS-compatible all-optical integrator’, Nat. Commun., 2010, 1, (1), pp. 29. [CrossRef]
  9. Yao, J., and Zhang, W.: ‘Fully reconfigurable waveguide Bragg gratings for programmable photonic signal processing’, Journal of Lightwave Technology, 2019, 38, (2), pp. 202-214. [CrossRef]
  10. Zhang, W., and Yao, J.: ‘Photonic integrated field-programmable disk array signal processor’, Nat. Commun., 2020, 11, (1), pp. 1-9. [CrossRef]
  11. Berger, N.K., Levit, B., Fischer, B., Kulishov, M., Plant, D.V., and Azaña, J.: ‘Temporal differentiation of optical signals using a phase-shifted fiber Bragg grating’, Opt. Express, 2007, 15, (2), pp. 371-381. [CrossRef]
  12. Rutkowska, K.A., Duchesne, D., Strain, M.J., Morandotti, R., Sorel, M., and Azaña, J.: ‘Ultrafast all-optical temporal differentiators based on CMOS-compatible integrated-waveguide Bragg gratings’, Opt. Express, 2011, 19, (20), pp. 19514-19522. [CrossRef]
  13. Liu, F., Wang, T., Qiang, L., Ye, T., Zhang, Z., Qiu, M., and Su, Y.: ‘Compact optical temporal differentiator based on silicon microring resonator’, Opt. Express, 2008, 16, (20), pp. 15880-15886. [CrossRef]
  14. Wu, J., Cao, P., Hu, X., Jiang, X., Pan, T., Yang, Y., Qiu, C., Tremblay, C., and Su, Y.: ‘Compact tunable silicon photonic differential-equation solver for general linear time-invariant systems’, Opt. Express, 2014, 22, (21), pp. 26254-26264. [CrossRef]
  15. Wu, J., Liu, B., Peng, J., Mao, J., Jiang, X., Qiu, C., Tremblay, C., and Su, Y.: ‘On-Chip Tunable Second-Order Differential-Equation Solver Based on a Silicon Photonic Mode-Split Microresonator’, Journal of Lightwave Technology, 2015, 33, (17), pp. 3542-3549. [CrossRef]
  16. Zheng, A., Dong, J., Zhou, L., Xiao, X., Yang, Q., Zhang, X., and Chen, J.: ‘Fractional-order photonic differentiator using an on-chip microring resonator’, Opt. Lett., 2014, 39, (21), pp. 6355-6358. [CrossRef]
  17. Zheng, A., Yang, T., Xiao, X., Yang, Q., Zhang, X., and Dong, J.: ‘Tunable fractional-order differentiator using an electrically tuned silicon-on-isolator Mach-Zehnder interferometer’, Opt. Express, 2014, 22, (15), pp. 18232-18237. [CrossRef]
  18. Capmany, J., Ortega, B., Pastor, D., and Sales, S.: ‘Discrete-time optical processing of microwave signals’, Journal of Lightwave Technology, 2005, 23, (2), pp. 702-723. [CrossRef]
  19. Mansoori, S., and Mitchell, A.: ‘RF transversal filter using an AOTF’, IEEE Photonics Technology Letters, 2004, 16, (3), pp. 879-881.
  20. Zhang, J., and Yao, J.: ‘Photonic true-time delay beamforming using a switch-controlled wavelength-dependent recirculating loop’, Journal of Lightwave Technology, 2016, 34, (16), pp. 3923-3929. [CrossRef]
  21. Zhang, L., Li, M., Shi, N., Zhu, X., Sun, S., Tang, J., Li, W., and Zhu, N.: ‘Photonic true time delay beamforming technique with ultra-fast beam scanning’, Opt. Express, 2017, 25, (13), pp. 14524-14532. [CrossRef]
  22. Yu, G., Zhang, W., and Williams, J.: ‘High-performance microwave transversal filter using fiber Bragg grating arrays’, IEEE Photonics Technology Letters, 2000, 12, (9), pp. 1183-1185. [CrossRef]
  23. Hunter, D.B. , Minasian, R.A., and Krug, P.A.: ‘Tunable optical transversal filter based on chirped gratings’, in Editor (Ed.)^(Eds.): ‘Book Tunable optical transversal filter based on chirped gratings’ (Institution of Engineering and Technology, 1995, edn.), pp. 2205-2207.
  24. Liu, Y., Yao, J., and Yang, J.: ‘Wideband true-time-delay unit for phased array beamforming using discrete-chirped fiber grating prism’, Optics Communications, 2002, 207, (1-6), pp. 177-187. [CrossRef]
  25. Supradeepa, V.R., Long, C.M., Wu, R., Ferdous, F., Hamidi, E., Leaird, D.E., and Weiner, A.M.: ‘Comb-based radiofrequency photonic filters with rapid tunability and high selectivity’, Nat. Photonics, 2012, 6, (3), pp. 186-194.
  26. Hamidi, E., Leaird, D.E., and Weiner, A.M.: ‘Tunable Programmable Microwave Photonic Filters Based on an Optical Frequency Comb’, IEEE Transactions on Microwave Theory and Techniques, 2010, 58, (11), pp. 3269-3278. [CrossRef]
  27. Metcalf, A.J., Kim, H.J., Leaird, D.E., Jaramillo Villegas, J.A., McKinzie, K.A., Lal, V., Hosseini, A., Hoefler, G.E., Kish, F., and Weiner, A.M.: ‘Integrated line-by-line optical pulse shaper for high-fidelity and rapidly reconfigurable RF-filtering’, Opt. Express, 2016, 24, (21), pp. 23925-23940. [CrossRef]
  28. Ortigosa-Blanch, A., Mora, J., Capmany, J., Ortega, B., and Pastor, D.: ‘Tunable radio-frequency photonic filter based on an actively mode-locked fiber laser’, Opt. Lett., 2006, 31, (6), pp. 709-711. [CrossRef]
  29. Maram, R., Onori, D., Azaña, J., and Chen, L.R.: ‘Discretely programmable microwave photonic filter based on temporal Talbot effects’, Opt. Express, 2019, 27, (10), pp. 14381-14391. [CrossRef]
  30. Yang Sun, Jiayang Wu, Yang Li, Mengxi Tan, Xingyuan Xu, Sai Chu, Brent Little, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Quantifying the Accuracy of Microcomb-based Photonic RF Transversal Signal Processors”, IEEE Journal of Selected Topics in Quantum Electronics 29 no. 6, pp. 1-17, Art no. 7500317 (2023). [CrossRef]
  31. Pasquazi, A., Peccianti, M., Razzari, L., Moss, D.J., Coen, S., Erkintalo, M., Chembo, Y.K., Hansson, T., Wabnitz, S., and Del’Haye, P.: ‘Micro-combs: A novel generation of optical sources’, Physics Reports, 2018, 729, pp. 1-81. [CrossRef]
  32. Xu, X., Tan, M., Wu, J., Morandotti, R., Mitchell, A., and Moss, D.J.: ‘Microcomb-Based Photonic RF Signal Processing’, IEEE Photonics Technology Letters, 2019, 31, (23), pp. 1854-1857. [CrossRef]
  33. Xu, X., Wu, J., Shoeiby, M., Nguyen, T.G., Chu, S.T., Little, B.E., Morandotti, R., Mitchell, A., and Moss, D.J.: ‘Reconfigurable broadband microwave photonic intensity differentiator based on an integrated optical frequency comb source’, APL Phontonics, 2017, 2, (9), pp. 096104. [CrossRef]
  34. Xu, X., Tan, M., Wu, J., Boes, A., Corcoran, B., Nguyen, T.G., Chu, S.T., Little, B.E., Morandotti, R., Mitchell, A., and Moss, D.J.: ‘Photonic RF and Microwave Integrator Based on a Transversal Filter With Soliton Crystal Microcombs’, IEEE Trans. Circuits Syst. II-Express Briefs, 2020, 67, (12), pp. 3582-3586. [CrossRef]
  35. Tan, M., Xu, X., Corcoran, B., Wu, J., Boes, A., Nguyen, T.G., Chu, S.T., Little, B.E., Morandotti, R., Mitchell, A., and Moss, D.J.: ‘Microwave and RF Photonic Fractional Hilbert Transformer Based on a 50 GHz Kerr Micro-Comb’, Journal of Lightwave Technology, 2019, 37, (24), pp. 6097-6104. [CrossRef]
  36. Wang, B., Yang, Z., Sun, S., and Yi, X.: ‘Radio-frequency line-by-line Fourier synthesis based on optical soliton microcombs’, Photonics Res., 2022, 10, (4), pp. 932-938. [CrossRef]
  37. Xu, X., Tan, M., Corcoran, B., Wu, J., Boes, A., Nguyen, T.G., Chu, S.T., Little, B.E., Hicks, D.G., Morandotti, R., Mitchell, A., and Moss, D.J.: ‘11 TOPS photonic convolutional accelerator for optical neural networks’, Nature, 2021, 589, (7840), pp. 44-51. [CrossRef]
  38. Feldmann, J., Youngblood, N., Karpov, M., Gehring, H., Li, X., Stappers, M., Le Gallo, M., Fu, X., Lukashchuk, A., Raja, A.S., Liu, J., Wright, C.D., Sebastian, A., Kippenberg, T.J., Pernice, W.H.P., and Bhaskaran, H.: ‘Parallel convolutional processing using an integrated photonic tensor core’, Nature, 2021, 589, (7840), pp. 52-58. [CrossRef]
  39. Razzari, L., Duchesne, D., Ferrera, M., Morandotti, R., Chu, S., Little, B.E., and Moss, D.J.: ‘CMOS-compatible integrated optical hyper-parametric oscillator’, Nat. Photonics, 2010, 4, (1), pp. 41-45. [CrossRef]
  40. Pasquazi, et al., “Sub-picosecond phase-sensitive optical pulse characterization on a chip”, Nature Photonics, vol. 5, no. 10, pp. 618-623 (2011). [CrossRef]
  41. Bao, C., et al., "Direct soliton generation in microresonators", Opt. Lett, 42, 2519 (2017). [CrossRef]
  42. M.Ferrera et al., “CMOS compatible integrated all-optical RF spectrum analyzer”, Optics Express, vol. 22, no. 18, 21488 - 21498 (2014).
  43. M. Kues, et al., “Passively modelocked laser with an ultra-narrow spectral width”, Nature Photonics, vol. 11, no. 3, pp. 159, 2017. [CrossRef]
  44. L. Razzari, et al., “CMOS-compatible integrated optical hyper-parametric oscillator,” Nature Photonics, vol. 4, no. 1, pp. 41-45, 2010. [CrossRef]
  45. M. Ferrera, et al., “Low-power continuous-wave nonlinear optics in doped silica glass integrated waveguide structures,” Nature Photonics, vol. 2, no. 12, pp. 737-740, 2008. [CrossRef]
  46. M.Ferrera et al.“On-Chip ultra-fast 1st and 2nd order CMOS compatible all-optical integration”, Opt. Express, vol. 19, (23) 23153-23161 (2011).
  47. D. Duchesne, M. Peccianti, M. R. E. Lamont, et al., “Supercontinuum generation in a high index doped silica glass spiral waveguide,” Optics Express, vol. 18, no, 2, pp. 923-930, 2010. [CrossRef]
  48. H Bao, L Olivieri, M Rowley, ST Chu, BE Little, R Morandotti, DJ Moss, et al., “Turing patterns in a fiber laser with a nested microresonator: Robust and controllable microcomb generation”, Physical Review Research 2 (2), 023395 (2020). [CrossRef]
  49. M. Ferrera, et al., “On-chip CMOS-compatible all-optical integrator”, Nature Communications, vol. 1, Article 29, 2010. [CrossRef]
  50. A Pasquazi, et al., “All-optical wavelength conversion in an integrated ring resonator,” Optics Express, vol. 18, no. 4, pp. 3858-3863, 2010.
  51. Pasquazi, Y. Park, J. Azana, et al., “Efficient wavelength conversion and net parametric gain via Four Wave Mixing in a high index doped silica waveguide,” Optics Express, vol. 18, no. 8, pp. 7634-7641 (2010).
  52. M. Peccianti, M. Ferrera, L. Razzari, et al., “Subpicosecond optical pulse compression via an integrated nonlinear chirper,” Optics Express, vol. 18, no. 8, pp. 7625-7633 (2010). [CrossRef]
  53. Little, B. E. et al., “Very high-order microring resonator filters for WDM applications”, IEEE Photonics Technol. Lett. 16, 2263–2265 (2004). [CrossRef]
  54. M. Ferrera et al., “Low Power CW Parametric Mixing in a Low Dispersion High Index Doped Silica Glass Micro-Ring Resonator with Q-factor > 1 Million”, Optics Express, vol.17, no. 16, pp. 14098–14103 (2009).
  55. M. Peccianti, et al., “Demonstration of an ultrafast nonlinear microcavity modelocked laser”, Nature Communications, vol. 3, pp. 765, 2012.
  56. Pasquazi, et al., “Self-locked optical parametric oscillation in a CMOS compatible microring resonator: a route to robust optical frequency comb generation on a chip,” Optics Express, vol. 21, no. 11, pp. 13333-13341 (2013).
  57. Pasquazi, et al., “Stable, dual mode, high repetition rate mode-locked laser based on a microring resonator,” Optics Express, vol. 20, no. 24, pp. 27355-27362, 2012.
  58. Pasquazi, A. et al. Micro-combs: a novel generation of optical sources. Physics Reports 729, 1-81 (2018). [CrossRef]
  59. Moss, D. J. et al., “New CMOS-compatible platforms based on silicon nitride and Hydex for nonlinear optics”, Nature photonics 7, 597 (2013). [CrossRef]
  60. H. Bao, et al., Laser cavity-soliton microcombs, Nature Photonics, vol. 13, no. 6, pp. 384-389 (2019). [CrossRef]
  61. Antonio Cutrona, Maxwell Rowley, Debayan Das, Luana Olivieri, Luke Peters, Sai T. Chu, Brent L. Little, Roberto Morandotti, David J. Moss, Juan Sebastian Totero Gongora, Marco Peccianti, Alessia Pasquazi, “High Conversion Efficiency in Laser Cavity-Soliton Microcombs”, Optics Express Vol. 30, Issue 22, 39816-39825 (2022). [CrossRef]
  62. M.Rowley, P.Hanzard, A.Cutrona, H.Bao, S.Chu, B.Little, R.Morandotti, D. J. Moss, G. Oppo, J. Gongora, M. Peccianti and A. Pasquazi, “Self-emergence of robust solitons in a micro-cavity”, Nature 608 (7922) 303–309 (2022).
  63. Cutrona, M. Rowley, A. Bendahmane, V. Cecconi,L. Peters, L. Olivieri, B. E. Little, S. T. Chu, S. Stivala, R. Morandotti, D. J. Moss, J. S. Totero-Gongora, M. Peccianti, A. Pasquazi, “Nonlocal bonding of a soliton and a blue-detuned state in a microcomb laser”, Nature Communications Physics 6, 259 (2023). [CrossRef]
  64. Cutrona, M. Rowley, A. Bendahmane, V. Cecconi,L. Peters, L. Olivieri, B. E. Little, S. T. Chu, S. Stivala, R. Morandotti, D. J. Moss, J. S. Totero-Gongora, M. Peccianti, A. Pasquazi, “Stability Properties of Laser Cavity-Solitons for Metrological Applications”, Applied Physics Letters 122 (12) 121104 (2023). [CrossRef]
  65. Kues, M. et al. “Quantum optical microcombs”, Nature Photonics 13, (3) 170-179 (2019). [CrossRef]
  66. Reimer, L. Caspani, M. Clerici, et al., “Integrated frequency comb source of heralded single photons,” Optics Express, vol. 22, no. 6, pp. 6535-6546, 2014.
  67. Reimer, et al., “Cross-polarized photon-pair generation and bi-chromatically pumped optical parametric oscillation on a chip”, Nature Communications, vol. 6, Article 8236 (2015). [CrossRef]
  68. L. Caspani, C. Reimer, M. Kues, et al., “Multifrequency sources of quantum correlated photon pairs on-chip: a path toward integrated Quantum Frequency Combs,” Nanophotonics, vol. 5, no. 2, pp. 351-362 (2016). [CrossRef]
  69. C Reimer et al., “Generation of multiphoton entangled quantum states by means of integrated frequency combs,” Science 351 (6278) 1176-1180, (2016). [CrossRef]
  70. M. Kues, et al., “On-chip generation of high-dimensional entangled quantum states and their coherent control”, Nature, vol. 546, no. 7660, pp. 622-626, 2017. [CrossRef]
  71. P. Roztocki et al., “Practical system for the generation of pulsed quantum frequency combs,” Optics Express, vol. 25, no. 16, pp. 18940-18949 ( 2017). [CrossRef]
  72. Y. Zhang, et al., “Induced photon correlations through superposition of two four-wave mixing processes in integrated cavities”, Laser and Photonics Reviews, vol. 14, no. 7, pp. 2000128 (2020). [CrossRef]
  73. Reimer, et al., “High-dimensional one-way quantum processing implemented on d-level cluster states”, Nature Physics, vol. 15, no.2, pp. 148–153, 2019. [CrossRef]
  74. P.Roztocki et al., “Complex quantum state generation and coherent control based on integrated frequency combs”, Journal of Lightwave Technology 37 (2) 338-347 (2019).
  75. S. Sciara et al., “Generation and Processing of Complex Photon States with Quantum Frequency Combs”, IEEE Photonics Technology Letters 31 (23) 1862-1865 (2019). [CrossRef]
  76. Stefania Sciara, Piotr Roztocki, Bennet Fisher, Christian Reimer, Luis Romero Cortez, William J. Munro, David J. Moss, Alfonso C. Cino, Lucia Caspani, Michael Kues, J. Azana, and Roberto Morandotti, “Scalable and effective multilevel entangled photon states: A promising tool to boost quantum technologies”, Nanophotonics 10 (18), 4447–4465 (2021). [CrossRef]
  77. L. Caspani, C. Reimer, M. Kues, et al., “Multifrequency sources of quantum correlated photon pairs on-chip: a path toward integrated Quantum Frequency Combs,” Nanophotonics, vol. 5, no. 2, pp. 351-362, 2016. [CrossRef]
  78. Xu, X., Tan, M., Wu, J., Nguyen, T.G., Chu, S.T., Little, B.E., Morandotti, R., Mitchell, A., and Moss, D.J.: ‘Advanced Adaptive Photonic RF Filters with 80 Taps Based on an Integrated Optical Micro-Comb Source’, Journal of Lightwave Technology, 2019, 37, (4), pp. 1288-1295. [CrossRef]
  79. Xu, X., et al., Photonic microwave true time delays for phased array antennas using a 49 GHz FSR integrated micro-comb source, Photonics Research, 6, B30-B36 (2018). [CrossRef]
  80. X. Xu, et al., “High performance RF filters via bandwidth scaling with Kerr micro-combs,” APL Photonics, vol. 4 (2) 026102. 2019. [CrossRef]
  81. M. Tan, et al., “RF and microwave fractional differentiator based on photonics”, IEEE Transactions on Circuits and Systems: Express Briefs, vol. 67, no.11, pp. 2767-2771, 2020. [CrossRef]
  82. M. Tan, et al., “Photonic RF arbitrary waveform generator based on a soliton crystal micro-comb source”, Journal of Lightwave Technology, vol. 38, no. 22, pp. 6221-6226 (2020). [CrossRef]
  83. M. Tan, X. Xu, J. Wu, R. Morandotti, A. Mitchell, and D. J. Moss, “RF and microwave high bandwidth signal processing based on Kerr Micro-combs”, Advances in Physics X, VOL. 6, NO. 1, 1838946 (2021). [CrossRef]
  84. X. Xu, et al., “Advanced RF and microwave functions based on an integrated optical frequency comb source,” Opt. Express, vol. 26 (3) 2569 (2018). [CrossRef]
  85. M. Tan, X. M. Tan, X. Xu, J. Wu, B. Corcoran, A. Boes, T. G. Nguyen, S. T. Chu, B. E. Little, R.Morandotti, A. Lowery, A. Mitchell, and D. J. Moss, “"Highly Versatile Broadband RF Photonic Fractional Hilbert Transformer Based on a Kerr Soliton Crystal Microcomb”, Journal of Lightwave Technology vol. 39 (24) 7581-7587 (2021). [CrossRef]
  86. Wu, J. et al. RF Photonics: An Optical Microcombs’ Perspective. IEEE Journal of Selected Topics in Quantum Electronics Vol. 24, 6101020, 1-20 (2018).
  87. T. G. Nguyen et al., “Integrated frequency comb source-based Hilbert transformer for wideband microwave photonic phase analysis,” Opt. Express, vol. 23, no. 17, pp. 22087-22097 (2015). [CrossRef]
  88. X. Xu, et al., “Broadband RF channelizer based on an integrated optical frequency Kerr comb source,” Journal of Lightwave Technology, vol. 36, no. 19, pp. 4519-4526 (2018). [CrossRef]
  89. X. Xu, et al., “Continuously tunable orthogonally polarized RF optical single sideband generator based on micro-ring resonators,” Journal of Optics, vol. 20, no. 11, 115701 (2018). [CrossRef]
  90. X. Xu, et al., “Orthogonally polarized RF optical single sideband generation and dual-channel equalization based on an integrated microring resonator,” Journal of Lightwave Technology, vol. 36, no. 20, pp. 4808-4818 (2018). [CrossRef]
  91. X. Xu, et al., “Photonic RF phase-encoded signal generation with a microcomb source”, J. Lightwave Technology, vol. 38, no. 7, 1722-1727, (2020). [CrossRef]
  92. X. Xu, et al., Broadband microwave frequency conversion based on an integrated optical micro-comb source”, Journal of Lightwave Technology, vol. 38 no. 2, pp. 332-338 (2020). [CrossRef]
  93. M. Tan, et al., “Photonic RF and microwave filters based on 49GHz and 200GHz Kerr microcombs”, Optics Comm. vol. 465,125563 (2020). [CrossRef]
  94. X. Xu, et al., “Broadband photonic RF channelizer with 90 channels based on a soliton crystal microcomb”, Journal of Lightwave Technology, Vol. 38, no. 18, 5116 – 5121 (2020). [CrossRef]
  95. M. Tan et al, “Orthogonally polarized Photonic Radio Frequency single sideband generation with integrated micro-ring resonators”, IOP Journal of Semiconductors, Vol. 42 (4), 041305 (2021). [CrossRef]
  96. Mengxi Tan, X. Xu, J. Wu, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, and David J. Moss, “Photonic Radio Frequency Channelizers based on Kerr Optical Micro-combs”, IOP Journal of Semiconductors Vol. 42 (4), 041302 (2021). [CrossRef]
  97. B Corcoran, et al., “Ultra-dense optical data transmission over standard fiber with a single chip source”, Nature Communications, vol. 11, Article: 2568, (2020).
  98. X. Xu et al, “Photonic perceptron based on a Kerr microcomb for scalable high speed optical neural networks”, Laser and Photonics Reviews, vol. 14, no. 8, 2000070 (2020). [CrossRef]
  99. X. Xu et al., “Neuromorphic computing based on wavelength-division multiplexing”, 28 IEEE Journal of Selected Topics in Quantum Electronics Vol. 29 Issue: 2, Article 7400112 (2023). [CrossRef]
  100. Yang Sun, Jiayang Wu, Mengxi Tan, Xingyuan Xu, Yang Li, Roberto Morandotti, Arnan Mitchell, and David Moss, “Applications of optical micro-combs”, Advances in Optics and Photonics 15 (1) 86-175 (2023). [CrossRef]
  101. Yunping Bai, Xingyuan Xu,1, Mengxi Tan, Yang Sun, Yang Li, Jiayang Wu, Roberto Morandotti, Arnan Mitchell, Kun Xu, and David J. Moss, “Photonic multiplexing techniques for neuromorphic computing”, Nanophotonics 12 (5): 795–817 (2023). [CrossRef]
  102. Chawaphon Prayoonyong, Andreas Boes, Xingyuan Xu, Mengxi Tan, Sai T. Chu, Brent E. Little, Roberto Morandotti, Arnan Mitchell, David J. Moss, and Bill Corcoran, “Frequency comb distillation for optical superchannel transmission”, Journal of Lightwave Technology 39 (23) 7383-7392 (2021). [CrossRef]
  103. Mengxi Tan, Xingyuan Xu, Jiayang Wu, Bill Corcoran, Andreas Boes, Thach G. Nguyen, Sai T. Chu, Brent E. Little, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Integral order photonic RF signal processors based on a soliton crystal micro-comb source”, IOP Journal of Optics 23 (11) 125701 (2021). [CrossRef]
  104. Yang Sun, Jiayang Wu, Yang Li, Xingyuan Xu, Guanghui Ren, Mengxi Tan, Sai Tak Chu, Brent E. Little, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Performance analysis of microcomb-based microwave photonic transversal signal processors with experimental errors”, Journal of Lightwave Technology Vol. 41 Special Issue on Microwave Photonics (2023).
  105. Mengxi Tan, Xingyuan Xu, Andreas Boes, Bill Corcoran, Thach G. Nguyen, Sai T. Chu, Brent E. Little, Roberto Morandotti, Jiayang Wu, Arnan Mitchell, and David J. Moss, “Photonic signal processor for real-time video image processing at 17 Tb/s”, Communications Engineering Vol. 2 (2023).
  106. Mengxi Tan, Xingyuan Xu, Jiayang Wu, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Photonic RF and microwave filters based on 49GHz and 200GHz Kerr microcombs”, Optics Communications, 465, Article: 125563 (2020). [CrossRef]
  107. Yuning Zhang, Jiayang Wu, Yang Qu, Yunyi Yang, Linnan Jia, Baohua Jia, and David J. Moss, “Enhanced supercontinuum generated in SiN waveguides coated with GO films”, Advanced Materials Technologies 8 (1) 2201796 (2023). [CrossRef]
  108. Yuning Zhang, Jiayang Wu, Linnan Jia, Yang Qu, Baohua Jia, and David J. Moss, “Graphene oxide for nonlinear integrated photonics”, Laser and Photonics Reviews 17 2200512 (2023). [CrossRef]
  109. Jiayang Wu, H. Lin, D. J. Moss, T.K. Loh, Baohua Jia, “Graphene oxide: new opportunities for electronics, photonics, and optoelectronics”, Nature Reviews Chemistry 7 (3) 162–183 (2023). [CrossRef]
  110. Yang Qu, Jiayang Wu, Yuning Zhang, Yunyi Yang, Linnan Jia, Baohua Jia, and David J. Moss, “Photo thermal tuning in GO-coated integrated waveguides”, Micromachines 13 1194 (2022). [CrossRef]
  111. Yuning Zhang, Jiayang Wu, Yunyi Yang, Yang Qu, Houssein El Dirani, Romain Crochemore, Corrado Sciancalepore, Pierre Demongodin, Christian Grillet, Christelle Monat, Baohua Jia, and David J. Moss, “Enhanced self-phase modulation in silicon nitride waveguides integrated with 2D graphene oxide films”, IEEE Journal of Selected Topics in Quantum Electronics 29 (1) 5100413 (2023). [CrossRef]
  112. Yuning Zhang, Jiayang Wu, Yunyi Yang, Yang Qu, Linnan Jia, Baohua Jia, and David J. Moss, “Enhanced spectral broadening of femtosecond optical pulses in silicon nanowires integrated with 2D graphene oxide films”, Micromachines 13 756 (2022). [CrossRef]
  113. Linnan Jia, Jiayang Wu, Yuning Zhang, Yang Qu, Baohua Jia, Zhigang Chen, and David J. Moss, “Fabrication Technologies for the On-Chip Integration of 2D Materials”, Small: Methods 6, 2101435 (2022). [CrossRef]
  114. Yuning Zhang, Jiayang Wu, Yang Qu, Linnan Jia, Baohua Jia, and David J. Moss, “Design and optimization of four-wave mixing in microring resonators integrated with 2D graphene oxide films”, Journal of Lightwave Technology 39 (20) 6553-6562 (2021).
  115. Yuning Zhang, Jiayang Wu, Yang Qu, Linnan Jia, Baohua Jia, and David J. Moss, “Optimizing the Kerr nonlinear optical performance of silicon waveguides integrated with 2D graphene oxide films”, Journal of Lightwave Technology 39 (14) 4671-4683 (2021). [CrossRef]
  116. Yang Qu, Jiayang Wu, Yuning Zhang, Yao Liang, Baohua Jia, and David J. Moss, “Analysis of four-wave mixing in silicon nitride waveguides integrated with 2D layered graphene oxide films”, Journal of Lightwave Technology 39 (9) 2902-2910 (2021). [CrossRef]
  117. Jiayang Wu, Linnan Jia, Yuning Zhang, Yang Qu, Baohua Jia, and David J. Moss,“ Graphene oxide: versatile films for flat optics to nonlinear photonic chips”, Advanced Materials 33 (3) 2006415, pp.1-29 (2021). [CrossRef]
  118. Y. Qu, J. Wu, Y. Zhang, L. Jia, Y. Yang, X. Xu, S. T. Chu, B. E. Little, R. Morandotti, B. Jia, and D. J. Moss, “Graphene oxide for enhanced optical nonlinear performance in CMOS compatible integrated devices”, Paper No. 11688-30, PW21O-OE109-36, 2D Photonic Materials and Devices IV, SPIE Photonics West, San Francisco CA March 6-11 (2021). 6 March 2583.
  119. Yang Qu, Jiayang Wu, Yunyi Yang, Yuning Zhang, Yao Liang, Houssein El Dirani, Romain Crochemore, Pierre Demongodin, Corrado Sciancalepore, Christian Grillet, Christelle Monat, Baohua Jia, and David J. Moss, “Enhanced nonlinear four-wave mixing in silicon nitride waveguides integrated with 2D layered graphene oxide films”, Advanced Optical Materials vol. 8 (21) 2001048 (2020). [CrossRef]
  120. Yuning Zhang, Yang Qu, Jiayang Wu, Linnan Jia, Yunyi Yang, Xingyuan Xu, Baohua Jia, and David J. Moss, “Enhanced Kerr nonlinearity and nonlinear figure of merit in silicon nanowires integrated with 2D graphene oxide films”, ACS Applied Materials and Interfaces vol. 12 (29) 33094−33103 June 29 (2020). [CrossRef]
  121. iayang Wu, Yunyi Yang, Yang Qu, Yuning Zhang, Linnan Jia, Xingyuan Xu, Sai T. Chu, Brent E. Little, Roberto Morandotti, Baohua Jia,* and David J. Moss*, “Enhanced nonlinear four-wave mixing in microring resonators integrated with layered graphene oxide films”, Small vol. 16 (16) 1906563 April 23 (2020). 23 April. [CrossRef]
  122. Jiayang Wu, Yunyi Yang, Yang Qu, Xingyuan Xu, Yao Liang, Sai T. Chu, Brent E. Little, Roberto Morandotti, Baohua Jia, and David J. Moss, “Graphene oxide waveguide polarizers and polarization selective micro-ring resonators”, Paper 11282-29, SPIE Photonics West, San Francisco, CA, 4 - 7 February (2020). [CrossRef]
  123. Jiayang Wu, Yunyi Yang, Yang Qu, Xingyuan Xu, Yao Liang, Sai T. Chu, Brent E. Little, Roberto Morandotti, Baohua Jia, and David J. Moss, “Graphene oxide waveguide polarizers and polarization selective micro-ring resonators”, Laser and Photonics Reviews vol. 13 (9) 1900056 (2019). [CrossRef]
  124. Yunyi Yang, Jiayang Wu, Xingyuan Xu, Sai T. Chu, Brent E. Little, Roberto Morandotti, Baohua Jia, and David J. Moss, “Enhanced four-wave mixing in graphene oxide coated waveguides”, Applied Physics Letters Photonics vol. 3 120803 (2018). [CrossRef]
  125. Linnan Jia, Yang Qu, Jiayang Wu, Yuning Zhang, Yunyi Yang, Baohua Jia, and David J. Moss, “Third-order optical nonlinearities of 2D materials at telecommunications wavelengths”, Micromachines (MDPI) 14, 307 (2023). [CrossRef]
  126. Hamed Arianfard, Saulius Juodkazis, David J. Moss, and Jiayang Wu, “Sagnac interference in integrated photonics”, Applied Physics Reviews vol. 10 (1) 011309 (2023). [CrossRef]
  127. Hamed Arianfard, Jiayang Wu, Saulius Juodkazis, and David J. Moss, “Optical analogs of Rabi splitting in integrated waveguide-coupled resonators”, Advanced Physics Research 2 (2023). [CrossRef]
  128. Hamed Arianfard, Jiayang Wu, Saulius Juodkazis, and David J. Moss, “Spectral shaping based on optical waveguides with advanced Sagnac loop reflectors”, Paper PW22O-OE201-20, SPIE-Opto, Integrated Optics: Devices, Materials, and Technologies XXVI, SPIE Photonics West, San Francisco CA January 22 - 27 (2022). 22 January. [CrossRef]
  129. Hamed Arianfard, Jiayang Wu, Saulius Juodkazis, David J. Moss, “Spectral Shaping Based on Integrated Coupled Sagnac Loop Reflectors Formed by a Self-Coupled Wire Waveguide”, IEEE Photonics Technology Letters vol. 33 (13) 680-683 (2021). [CrossRef]
  130. Hamed Arianfard, Jiayang Wu, Saulius Juodkazis and David J. Moss, “Three Waveguide Coupled Sagnac Loop Reflectors for Advanced Spectral Engineering”, Journal of Lightwave Technology vol. 39 (11) 3478-3487 (2021). [CrossRef]
  131. Hamed Arianfard, Jiayang Wu, Saulius Juodkazis and David J. Moss, “Advanced Multi-Functional Integrated Photonic Filters based on Coupled Sagnac Loop Reflectors”, Journal of Lightwave Technology vol. 39 Issue: 5, pp.1400-1408 (2021). [CrossRef]
  132. Hamed Arianfard, Jiayang Wu, Saulius Juodkazis and David J. Moss, “Advanced multi-functional integrated photonic filters based on coupled Sagnac loop reflectors”, Paper 11691-4, PW21O-OE203-44, Silicon Photonics XVI, SPIE Photonics West, San Francisco CA March 6-11 (2021).
  133. Jiayang Wu, Tania Moein, Xingyuan Xu, and David J. Moss, “Advanced photonic filters via cascaded Sagnac loop reflector resonators in silicon-on-insulator integrated nanowires”, Applied Physics Letters Photonics vol. 3 046102 (2018). [CrossRef]
  134. Jiayang Wu, Tania Moein, Xingyuan Xu, Guanghui Ren, Arnan Mitchell, and David J. Moss, “Micro-ring resonator quality factor enhancement via an integrated Fabry-Perot cavity”, Applied Physics Letters Photonics vol. 2 056103 (2017). [CrossRef]
  135. Linnan Jia, Dandan Cui, Jiayang Wu, Haifeng Feng, Tieshan Yang, Yunyi Yang, Yi Du, Weichang Hao, Baohua Jia, David J. Moss, “BiOBr nanoflakes with strong nonlinear optical properties towards hybrid integrated photonic devices”, Applied Physics Letters Photonics vol. 4 090802 (2019). [CrossRef]
  136. Linnan Jia, Jiayang Wu, Yunyi Yang, Yi Du, Baohua Jia, David J. Moss, “Large Third-Order Optical Kerr Nonlinearity in Nanometer-Thick PdSe2 2D Dichalcogenide Films: Implications for Nonlinear Photonic Devices”, ACS Applied Nano Materials vol. 3 (7) 6876–6883 (2020). [CrossRef]
  137. E.D Ghahramani, DJ Moss, JE Sipe, “Full-band-structure calculation of first-, second-, and third-harmonic optical response coefficients of ZnSe, ZnTe, and CdTe”, Physical Review B 43 (12), 9700 (1991). [CrossRef]
  138. C Grillet, C Smith, D Freeman, S Madden, B Luther-Davies, EC Magi, ... “Efficient coupling to chalcogenide glass photonic crystal waveguides via silica optical fiber nanowires”, Optics Express vol. 14 (3), 1070-1078 (2006). [CrossRef]
  139. S Tomljenovic-Hanic, MJ Steel, CM de Sterke, DJ Moss, “High-Q cavities in photosensitive photonic crystals” Optics Letters vol. 32 (5), 542-544 (2007).
  140. M Ferrera et al., “On-Chip ultra-fast 1st and 2nd order CMOS compatible all-optical integration”, Optics Express vol. 19 (23), 23153-23161 (2011).
  141. VG Ta’eed et al., “Error free all optical wavelength conversion in highly nonlinear As-Se chalcogenide glass fiber”, Optics Express vol. 14 (22), 10371-10376 (2006). [CrossRef]
  142. M Rochette, L Fu, V Ta'eed, DJ Moss, BJ Eggleton, “2R optical regeneration: an all-optical solution for BER improvement”, IEEE Journal of Selected Topics in Quantum Electronics vol. 12 (4), 736-744 (2006). [CrossRef]
  143. TD Vo, et al., “Silicon-chip-based real-time dispersion monitoring for 640 Gbit/s DPSK signals”, Journal of Lightwave Technology vol. 29 (12), 1790-1796 (2011). [CrossRef]
  144. C Monat, C Grillet, B Corcoran, DJ Moss, BJ Eggleton, TP White, ..., et al., “Investigation of phase matching for third-harmonic generation in silicon slow light photonic crystal waveguides using Fourier optics”, Optics Express 18 (7), 6831-6840 (2010).
  145. L Carletti, P Ma, Y Yu, B Luther-Davies, D Hudson, C Monat, .... , et al., “Nonlinear optical response of low loss silicon germanium waveguides in the mid-infrared”, Optics Express 23 (7), 8261-8271 (2015).
  146. E Ghahramani, DJ Moss, JE Sipe, “Second-harmonic generation in odd-period, strained, (Si(Ge/Si superlattices and at Si/Ge interfaces”, Physical Review Letters 64 (23), 2815 (1990).
  147. MD Pelusi, F Luan, E Magi, MRE Lamont, DJ Moss, BJ Eggleton, ... et al., “High bit rate all-optical signal processing in a fiber photonic wire”, Optics Express 16 (15), 11506-11512 (2008).
  148. M Shokooh-Saremi, VG Ta'Eed, NJ Baker, ICM Littler, DJ Moss, ... et al., “High-performance Bragg gratings in chalcogenide rib waveguides written with a modified Sagnac interferometer”, JOSA B 23 (7), 1323-1331 (2006).
  149. MRE Lamont, VG Ta'eed, MAF Roelens, DJ Moss, BJ Eggleton, DY Choi, ... et al., “Error-free wavelength conversion via cross-phase modulation in 5cm of As2S3 chalcogenide glass rib waveguide”, Electronics Letters 43 (17), 945-947 (2007).
  150. M Ferrera, Y Park, L Razzari, BE Little, ST Chu, R Morandotti, DJ Moss, ... et al., “All-optical 1st and 2nd order integration on a chip”, Optics Express 19 (23), 23153-23161 (2011).
  151. C Grillet, C Monat, CLC Smith, BJ Eggleton, DJ Moss, S Frédérick, ... et al., “Nanowire coupling to photonic crystal nanocavities for single photon sources”, Optics Express 15 (3), 1267-1276 (2007).
  152. VG Ta'Eed, MRE Lamont, DJ Moss, BJ Eggleton, DY Choi, S Madden, ... et al., “All optical wavelength conversion via cross phase modulation in chalcogenide glass rib waveguides”, Optics Express 14 (23), 11242-11247 (2006).
  153. TM Monro, D Moss, M Bazylenko, CM De Sterke, L Poladian, “Observation of self-trapping of light in a self-written channel in a photosensitive glass”, Physical Review Letters 80 (18), 4072 (1998). [CrossRef]
Preprints 88580 g001
Figure 1. Schematic diagram of a microcomb-based microwave photonic (MWP) signal processor. EOM: electro-optic modulator. MW: microwave. PD: photodetector.
Figure 1. Schematic diagram of a microcomb-based microwave photonic (MWP) signal processor. EOM: electro-optic modulator. MW: microwave. PD: photodetector.
Preprints 88580 g001
Preprints 88580 g002
Figure 2. Experimental schematic of a microcomb-based MWP signal processor. CW pump: continuous-wave pump. EDFA: erbium-doped fibre amplifier. PC: polarization controller. MRR: microring resonator. WS: wave shaper. IM: intensity modulator. MW: microwave. BPD: balanced photodetector. SMF: single-mode fibre. AWG: arbitrary waveform generator. OSC: oscilloscope.
Figure 2. Experimental schematic of a microcomb-based MWP signal processor. CW pump: continuous-wave pump. EDFA: erbium-doped fibre amplifier. PC: polarization controller. MRR: microring resonator. WS: wave shaper. IM: intensity modulator. MW: microwave. BPD: balanced photodetector. SMF: single-mode fibre. AWG: arbitrary waveform generator. OSC: oscilloscope.
Preprints 88580 g002
Preprints 88580 g003
Figure 3. (a) Optical spectrum of soliton crystal microcomb generated by a MRR made from high-index doped silica glass. Inset shows a microscope image of the MRR. (b) Ideal and measured tap coefficients after optical spectral shaping.
Figure 3. (a) Optical spectrum of soliton crystal microcomb generated by a MRR made from high-index doped silica glass. Inset shows a microscope image of the MRR. (b) Ideal and measured tap coefficients after optical spectral shaping.
Preprints 88580 g003
Preprints 88580 g004
Figure 4. (a) Measured input microwave signal waveforms of (i) Gaussian, (ii) triangle, (iii) parabolic, (iv) super Gaussian, and (v) nearly square waveforms with full width at half maximum (FWHM) of ~0.2 ns. (b) Measured output waveforms from the MWP signal processor that performs first-order differentiation. The theoretical output results are also shown for comparison.
Figure 4. (a) Measured input microwave signal waveforms of (i) Gaussian, (ii) triangle, (iii) parabolic, (iv) super Gaussian, and (v) nearly square waveforms with full width at half maximum (FWHM) of ~0.2 ns. (b) Measured output waveforms from the MWP signal processor that performs first-order differentiation. The theoretical output results are also shown for comparison.
Preprints 88580 g004
Preprints 88580 g005
Figure 5. (a) RMSEs between theoretical differentiation results and the processor’s output waveforms for different input microwave signal waveforms in Figure 4. (b) Amplitude frequency response of theoretical differentiation and the processor, together with the amplitude spectra of different input microwave signals including with Gaussian, triangle, parabolic, super Gaussian, and nearly square waveforms shown in Figure 4(a).
Figure 5. (a) RMSEs between theoretical differentiation results and the processor’s output waveforms for different input microwave signal waveforms in Figure 4. (b) Amplitude frequency response of theoretical differentiation and the processor, together with the amplitude spectra of different input microwave signals including with Gaussian, triangle, parabolic, super Gaussian, and nearly square waveforms shown in Figure 4(a).
Preprints 88580 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated