Preprint
Article
Robust Machine Learning Framework for Modeling the Compressive Strength of SFRC–Database Compilation, Predictive Analysis, and Empirical Verification
Altmetrics
Downloads
70
Views
33
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
24 October 2023
Posted:
25 October 2023
You are already at the latest version
Alerts
Abstract
Abstract: In recent years, the construction engineering sector has undergone a transformative shift towards the integration of machine learning (ML) techniques, particularly in predicting the properties of steel fiber-reinforced concrete (SFRC). Despite the theoretical sophistication of existing models, a persistent challenge remains – their opacity, lacking transparency and real-world relevance for practi-tioners. To address this gap and advance our current understanding, this study employs the extra gradient (XG) Boosting algorithm, crafting a comprehensive ap-proach. Grounded in a meticulously curated database drawn from 43 seminal pub-lications, encompassing 420 distinct records, this research focuses predominantly on three primary fiber types: crimped, hooked, and mil-cut. Complemented by hands-on experimentation involving 20 diverse SFRC mixtures, this empirical campaign is further illuminated through the strategic use of Partial Dependence Plots (PDPs), revealing intricate relationships between input parameters and con-sequent compressive strength. A pivotal revelation of this research lies in the identification of optimal SFRC formulations, offering tangible insights for real-world applications. The developed ML model stands out not only for its sophistication but also its tangible accuracy, evidenced by exemplary performance against inde-pendent datasets, boasting a commendable mean target-prediction ratio of 99%. To bridge the theory-practice gap, we introduce a user-friendly digital interface, thri-ughly designed to guide professionals in optimizing and accurately predicting the compressive strength of SFRC. This research thus contributes to the construction and civil engineering sectors by enhancing predictive capabilities and refining mix designs, fostering innovation, and addressing the evolving needs of the industry.
Keywords:
Subject: Engineering - Civil Engineering
1. Introduction
Today, the world consumes 14 billion cubic meters of concrete annually, equating to approximately 4.4 tons per individual [1]. Despite its popularity, concrete has some inherent difficulties that limit its use under harsh weather conditions and in modern architectural designs. A major drawback of concrete is its relatively low tensile strength. Reinforced concrete (RC) structures are traditionally designed without considering this property, constituting approximately 6 to 12% of the normal concrete’ compressive strength (CS) [2,3,4]. Using discrete, randomly distributed, and discontinuous steel fibers in concrete reinforces the mix to mitigate problems [5,6,7]. This type of composite material is known as steel fiber-reinforced concrete (SFRC). Consequently, RC members can be enhanced in crack resistance by using this easy-to-manufacture and highly effective technology [8].
Concrete stands out as the foremost building material employed extensively across the global construction industry, thanks to its unparalleled attributes of durability, strength, and sustainability [9,10,11]. Within this context, Steel Fiber Reinforced Concrete (SFRC), fortified with short discrete fibers as mass reinforcement, emerges as a highly efficient cement-based composite capable of mitigating, to a considerable extent, the inherent brittleness of plain concrete [12]. The incorporation of fibers into concrete represents a pivotal enhancement, notably augmenting its strength, toughness, crack resistance, and tension performance. This transformative effect occurs because the haphazardly distributed fibers adeptly curtail the unstable propagation of cracks, operating both at the micro and macro levels [13]. Remarkably, SFRC exhibits a phenomenon known as strain-softening behavior, persisting even after the emergence of macro-cracks—a testament to the significant crack control offered by these fibers [14]. The introduction of steel fiber reinforcement into concrete goes a step further, markedly elevating its ductility and toughness. This outcome is primarily attributed to the introduction of supplementary fracture mechanisms and the energy expended in overcoming the interlocking and adhesion forces between the fibers and the cementitious matrix [15]. Assessing the enhancement of the ultimate properties necessitates mechanical tests and can only be determined upon reaching the conclusion of the loading phase. Recent developments have underscored the utility of acoustic emission as a means to evaluate the performance of SFRC beams [16]. Additionally, it's worth noting that the formation of macro-cracks can potentially lead to the corrosion of steel reinforcement. Therefore, the reduction in crack width, achieved through the presence of fibers, assumes paramount importance in enhancing the durability of Reinforced Concrete (RC) structural elements [17]. Furthermore, compelling evidence suggests that the inclusion of steel fibers may reduce the need for conventional steel shear reinforcement. This conclusion is drawn from a comprehensive array of tests and analyses conducted by the authors and other esteemed researchers in the field [18,19,20].
The SFRC was patented by Bernard in 1874 for strengthening concrete in tension, using steel splinters to achieve this purpose [21]. In the ensuing years, this exploration has led to many studies being conducted on its microstructure [22,23], flowability and SFRC’s behavior under tension [24,25], durability [26,27,28], strength under extreme and cyclic loadings [28,29,30]. In recent years, several new types of fibers have been proposed as reinforcements for the SFRC, along with the use of magnetic fields to align the steel fibers during casting [30,31], and microscale numerical analyses have been published to illustrate the fundamental failure mechanism of SFRC under varying external loads [32,33]. According to these studies, SFRC has substantially different strength and elasticity properties than traditional concrete. For the post-cracking response, the SFRC is positively influenced by the high tensile resistance and elasticity that results in a crack-bridging mechanism. Hence, this composite material has excellent behavior under tension and shear loadings. A large extent of mechanical property variability is, however, a result of material heterogeneity. A steel fiber reinforcement can prevent macrocrack propagation in concrete, but the resulting SFRC may be less flowable than its conventional equivalent. The quality reduction is likely caused by the interference between aggregates and fibers [33].
A design-oriented formulation for the key mechanical properties of SFRCs is necessary for the calculation of their key performance characteristics to facilitate their successful implementation in practical applications. Further, the existing models, however, tend to be either insufficiently accurate or lack physical relevance. In the literature, there have been several studies [34,35,36] proposing linear empirical formulas for predicting SFRC mechanical properties. There is a general consensus that fiber dosage and water-binder ratio play the greatest role in determining SFRC behavior. A composite material mixing theory indicates that SFRC properties strongly correlate with matrix and steel fiber elastic properties. This theoretical background has been used as a foundation for the development of various empirical models [37]. In spite of the fact that some of the currently available empirical models are capable of accurately predicting the results of a small number of tests [7,38], the development and implementation of comprehensive and robust models are still in the early stages of development.
Machine learning (ML) and ML interpretability algorithms find extensive application in various aspects of structural engineering. These applications span a wide spectrum of areas within structural engineering, encompassing: structural analysis and design, structural health monitoring and damage detection, fire resistance of structures, resistance of structural members under various loads, andthe characterization of mechanical properties and mix design of concrete [39]. As an illustration of the capabilities of these techniques, Zheng et al. [40] successfully employed a YOLO-v5 model to detect surface cracks on wind turbines. Similarly, Cardellicchio et al. [41] leveraged ML to facilitate the recognition and interpretation of defects for the purpose of risk management in heritage bridge preservation.
The use of machine learning (ML) to model the SFRC's mechanical properties has become increasingly popular over the last few years. In this context, the back-propagation Artificial Neural Network (ANN) approach has been utilized to calculate the SFRC's CS by Açikgenç et al. [38]. Their study used the aggregate size at maximum, fiber dosage, length, and size, as well as fiber length and size, as input variables. In a similar manner, Awolusi et al. [42] used an ANN method to predict the flowability, CS, and splitting strength of SFRC. In addition, Karahan [43] used multiple nonlinear regression techniques in conjunction with ANN to predict the long-term strength of SFRC containing varying levels of fly ash. While these closed-source databases may be able to provide accurate estimates of SFRC mechanical properties, their limitations remain a concern. There have been criticisms of these models for their deficiencies, which include a lack of a physical mechanism illustration and a lack of an application tool. Recently, Pakzad et al. [7] have employed various data-driven machine-learning algorithms to predict the CS of SFRC. Sensitivity and parametric analyses were performed to demonstrate the capabilities of ML algorithms in their study.
In this study, we present solutions to the above-mentioned by focusing on the CS of SFRC-containing mono-fibrous (crimped, hooked, and mil-cut) systems. The research has been completed in several phases to achieve the goal. First, a comprehensive database of 420 records collected from 43 published studies was compiled and refined to establish a representative sample population. The second component of this research involves constructing and evaluating a numerical model that uses a state-of-the-art ML technique (XG Boost). A third aspect of the study involved narrowly focused experiments designed to verify the developed model using 30 SFRC mixes. Fourth, the model parameters were ranked according to their importance, and partial dependence plots were constructed to visualize their relationships. An intuitive graphical user interface was developed to enhance the model's applicability.
ML has seen increased application in modeling SFRC properties. However, many current ML models for this purpose are "black boxes" that lack transparency and physical relevance, and also present implementation challenges. Moreover, globally, there is significant consumption of concrete, which, despite its popularity, has inherent limitations, including its relatively low tensile strength. The necessity to improve the transparency, relevance, and implement-ability of ML models for SFRC properties, combined with the global demand for more durable and versatile concrete solutions, drives this research. Existing models for predicting and optimizing SFRC properties using ML lack transparency, do not have a clear physical basis, and are challenging to implement in practical scenarios. This study introduces an innovative approach that utilizes the extreme gradient (XG) Boosting algorithm for predicting and optimizing the CS of SFRC. The approach is grounded in a comprehensive database, which is a compilation from 43 publications, and is validated through extensive experimental studies. The ML model developed in this research not only promises superior predictive capabilities against independent experimental data but also introduces a user-friendly interface, paving the way for more accessible and efficient predictions and optimizations in the realm of SFRC. This study represents a transformative effort within the construction industry landscape. Although ML techniques have gained prominence in predicting material properties, a significant challenge endures—the lack of transparency and practical relevance in existing models. To address this challenge and enhance real-world applicability, this research adopts a meticulous approach, leveraging the XG Boosting algorithm. Furthermore, the investigation gains clarity through the application of Partial Dependence Plots (PDPs), which reveal intricate connections between input parameters and the CS of SFRC. Of utmost importance, the current study uncovers optimal SFRC formulations, offering practical insights into the most effective combinations of fibers for real-world applications.
2. Methodological approach
2.1. Background
The Extreme Gradient Booting (XG Boost) algorithm is a collective ML method that integrates a gradient boosting algorithm with decision trees to convert training data into a regression model suitable to classify new data [44]. Due to Friedman et al.'s [45] introduction of the gradient-boosting methodology, Chen et al. [46] developed an algorithm designed to enhance the performance of the gradient-boosting methodology. In comparison to gradient boosting, the XG Boost algorithm can be distinguished from gradient boosting by several advantages, such as efficient tree partitioning, shorter nodes, randomized with Newton-Raphson boosting, and multi-objective optimization [47]. In recent years, it has become a very popular programming language because of its inclusion in Python and its use in several Kaggle [48] competitions. The model has demonstrated excellent predictive capabilities in identifying a person's medical condition [49], forecasting the effects of the COVID-19 pandemic [50], and predicting a company's probability of bankruptcy [51].
2.2. XG boost algorithm development
In Figure 1, a conceptual diagram illustrates the steps involved in the preparation of an XG Boost algorithm, while the following equations provide a detailed formulation of the algorithm. It is noteworthy that Python [52] for coding was used.
In this study, the database of the SFRC involves variables with and the model’s output, , where M and N equal 420 and 12, respectively. Here, the first step involves the creation of a model’s output constant (initial) value [] using Eq. (1). In the following step, evaluate the scores () and canvases () by employing Eqs. (2)–(3), respectively. This step involves all nodes (– ) having weak responses. As a result, the multi-objective condition [Eq. (4)] can be solved using the training set , as a basis for fitting the base learner (tree). The model is then iteratively enhanced in accordance with Eq. (5), following a process of optimization. The final results are then evaluated using Eq. (6) following the calibration of the model. In Eq. (1)–(6), is a loss function that behaves differently depending on differentiability, and is the learners' rate of progress. It is important to note that, as part of the XG Boost single tree analysis, is continually evaluated during the modeling process of each node to determine the node that will result in the highest gain over time. When features in are split into subsets, it is possible to create an additional regression tree. The accuracy of the model is calculated after adding up each predictor's score to determine the total score for the model.
2.3. Indicators of prediction performance
As a means of testing the accuracy of the developed models about the test observations of the characteristic CS of SFRC, four performance metrics [Eqs. (7)–(10)] were calculated in this study. In these formulas, , , and are the tested, calculated, and mean of tested SFRC’s CS, respectively.
3. Data collection, characteristics, and handling
3.1. Data compilation
In this study, the primary focus was on the 28d CS of SFRC with three types of mono-fibrous systems (crimped, hooked, and mil-cut) as a response to the SFRC ingredients and their characteristics. In total, the unprocessed population of the study consists of 422 datasets collected from 43 independent reports that were published between the period of 1994–2021. The careful selection of these reports was guided by a comprehensive evaluation of accessibility, data richness, and alignment with research objectives in order to ensure the robustness and relevance of the datasets. As listed in Table 1 and Table 2, the variables in the study are coded according to the database's inputs (X) and output (y). Moreover, Table 3 provides a summary of the collected datasets that were used in the study.
3.2. Data wrangling and statistical analysis
3.2.1. Treatment of outliers
Statistically significant outliers are data points that deviate from the norm, which indicates there could be an anomaly in the data [95]. It is common practice in regression analysis to deal with outliers as the first factor, which can significantly impact the outcome [96]. Several factors can contribute to detecting an outlier in a given data set; these include errors in measurement, mistakes made in capturing data, and signals detected in newly acquired data. In statistical models and analyses, outliers pose a challenge, particularly when the data involved in the analysis is excessive [97,98]. However, outliers present an exciting opportunity for exploring new possibilities. It is possible to identify outliers using various methods based on the type of data being analyzed and the type of outlier being sought. Furthermore, these methods can detect emerging phenomena or anomalous behavior. Some methods, such as Chauvenet's criteria and Grubb's test, are available for identifying outliers that use averages and standard deviations and assume a normal data distribution [48].
The variables included in the study were analyzed using descriptive statistics according to the method described in [99] to identify any outliers. Here, Grubb's test was used during preprocessing to detect outliers, errors, and even distributions in the data by checking them for outliers, errors, and odd distributions. For this purpose, we used the p-test of the hypothesis (with a 5% significance level), where the null hypothesis is that all data values come from the same normal population and the alternative hypothesis is that the largest or smallest data value is an outlier. It is noteworthy that further critical analysis of the data is an essential measure for determining the weaknesses of the approach to enhance its effectiveness. This analysis has been carried out via bivariate boxplots, confirming the datasets’ regularity. An evaluation of the rationality of the datasets has been conducted using bivariate boxplots (Figure 2), which indicated the rationality of the datasets for further regression analysis. This figure provides an informative summary of the distribution characteristics (e.g., median, interquartile range, outlier, and skewness) of model variables, making them valuable tools for data exploration
3.2.2. Data descriptive statistics and visualization
After cleaning up the database, two outliers were removed [(i) MPa, and (ii) mm], thus leaving 420 observations available for developing the AI model. A summary of the statistical information obtained from the refined database after removing outliers is presented in Table 5, while Figure 3 displays their graphical visualization. The figure demonstrates that the distribution of the majority of these variables is well-suited for applications in machine learning.
4. Results and discussion
4.1. Features and label relations
In the current study, a Pearson correlation constant (Eq. 11) was calculated during data preprocessing to assess the linear correlation between the model variables. A constant with a value between -1 and 1 is always present in this equation [100]. In this equation, is the number of records , ) is the number feature–label set having an average value of . In a linear relationship between two random variables, the constant represents the average degree of variability of the linear relationship. The resulting correlation constant coefficients for the features–label relations are presented in Figure 4. As shown in the figure, cement, HRWR contents, and fiber tensile strength (i.e., , , and ) had the largest positive impact on SFRC CS. The results obtained here are consistent with those of Ayan et al. [101], in which it was shown that the type and amount of binder and the volume fraction of steel fiber had the most significant impact on SFRC compression strength. In contrast, increasing the proportions of water-binder ratio, water and coarse aggregates (i.e., , , and ) would likely reduce CS. The finding can be explained by poor microstructural properties and packing densities resulting from increased water-binder ratio and coarse aggregate contents [102]. Furthermore, a comprehensive examination of the data depicted in Figure 4 explains that variables X6 (fine aggregate content) and X11 (diameter of fiber) will likely exert minimal influence on the CS of SFRC. Given their negligible impact, these specific variables have been thoughtfully excluded from subsequent analyses and modeling.
4.2. Development and performance of the initial model
The default hyperparameters (Table 6) were used as a starting point for the development of the model (Model-0). It is worth noting that only the fine-tuned hyperparameters are included in this table. The prediction performance measures for this benchmark model are listed in Table 6. The initial model's performance indicators for the test data were lower than those for the training data. Based on this finding, it appears that the initial model was prone to overfitting. Therefore, a multi-objective optimization process was used to fine-tune the default hyperparameters to maximize the model's performance.
4.3. Fine-tuned model
In the present study, hyperparameters (Table 6) most affecting the model's performance, were optimized by trial and error to achieve the best accuracy. In the pursuit of refining the model's default hyperparameters, we adopted a multi-objective optimization strategy that combines aspects of both random search and grid search. At each iteration of the approach, we methodically documented the model's performance, facilitating the identification of an optimal configuration that effectively balances diverse performance objectives, encompassing the scores for both training and testing data. The favorable result was achieved using a multitarget optimization technique based on Pareto's [103] frontier approach. Figure 5 depicts the results of this multi-objective optimization process. The optimized model exhibited adequate prediction performance with scores of 0.966 and 0.879 (Table 7) for training and testing data. As presented in Figure 6, the model-target results were close to the ±95%, and ±85% accuracy ranges for both training and testing results, respectively. Additionaly, the error of the predictions by the constructed model are rarely exceeds ±30%. The model seems to be able to make accurate predictions for the database used during the modeling process. The next stage of the study involved a narrowly focused experimental campaign to verify the accuracy of the proposed ML model. The following section provides details of the experimental programs.
4.4. Experimental verification
4.4.1. Materials
Ordinary Portland cement (OPC) type I (according to ASTM C 150) was used to prepare the SF-HSC, which was sourced from a local plant. This cement is estimated to have a median particle size of 13 microns. An analysis of the physicochemical properties of the OPC used is provided in Table 8, and the distribution of its grain size is shown in Figure 7. In addition, this figure illustrates a photograph obtained by scanning electron microscopy (SEM) of the OPC. This figure illustrates that OPC particles have several features, including polyangular shapes, asymmetrical distribution, and sizes ranging from 1 to 20 µm.
The desired workability of the concrete mixes was successfully achieved through the application of a modified polycarboxylic ether polymer high-range water-reducing (HRWR, commercially known as MasterGlenium 51). This HRWR contains 36% dry powder and has a relative density of 1.1, according to the manufacturer. To determine the amount of HRWR to be added to the concrete mix, we divided the dry extract (D.E.) by the cement weight. Optimum concrete workability for this mix has been achieved by optimizing this ratio.
Additionally, all concrete mixes were prepared with coarse aggregates (Ag) whose maximum aggregate size is 10 mm. Figure 8 displays the particle size curves of the aggregates used in this study..
Three different hook-ended steel fibers were used in the production of SFRCs. A steel fiber of three different lengths and diameters was used. A summary of the physicomechanical properties of steel fibers used is given in Table 9.
The present study involved the preparation and testing of 20 concrete mixes using three different water-cement ratios (0.25, 0.35, and 0.45), three types of fiber (Table 9), and four levels of fiber dosage (0.0, 0.5, 1.0, and 1.5). Table 10 summarizes the proportions of these mixes, including the amount of steel fibers included in each one. Here, the letters U, H, and N denote concrete that contains a water-cement ratio of 0.25, 0.35, and 0.45, respectively. Thus, the “U-F1-0.5” mix means that it was prepared with water–cement ratio of 0.25, steel fiber type "F1" at a dosage of 0.5 percent (vol.). A noteworthy feature of the control mixes is that the slump (as a workability measure) was set to 100 ±25 mm and measured according to ASTM C143.
4.4.2. Methods
4.4.2.1. Preparation of the test specimens
This study was carried out by stirring a variety of aggregates in a typical concrete mixer for a few minutes, with the associated absorption water being introduced simultaneously. In the following, cement was mixed in a dry state for a few minutes. The HRWR was mixed with water for two minutes, then re-mixed with the aggregates for three minutes, followed by another three minutes without mixing before the final mixing of two minutes was conducted. A concrete mixture was eventually poured into different molds in accordance with the specimen size and the mixer was turned off. In the case of the SFRC mixes the fibers were introduced into the concrete mixture after the concrete mixture had been prepared and mixed well for five minutes so that the fibers were dispersed well within the concrete mixture.
A series of 100 (dia.) × 200 (ht.) mm concrete cylinder specimens were cast in rigid plastic molds to evaluate the CS of the concrete. To maintain moist conditions, the specimens were covered with plastic sheets after excess material was removed from the mold's surface. In this study, the specimens were demolded after 24 h and cured at 22 ± 2 °C and a relative humidity of 100%. Test specimens were kept in this condition until the time of testing. A total of three specimens were cast for each type of test as well as for each mix. For the CS specimens, tests were conducted after seven and 28 days. As a result of the study, we calculated and presented average strength results for the three specimens.
4.4.2.2. Detail of testing
The cylindrical specimens are coated with sulfur mortar before conducting the uniaxial compression test to ensure the load is evenly distributed across the top and bottom surfaces. An assessment of the 7d and 28d CSs of cement-based materials was performed in this study according to ASTM C39 specifications. A ToniTech universal testing machine equipped with a 3000 kN load capacity (Figure 9) was utilized to carry out this test. The samples were attached to two linear variable displacement transducers (LVDTs) and a compressometer ring at approximately 100 mm, the height of the center of the samples, to measure in-plane and transverse strains. The test was conducted under displacement-controlled conditions with a rate of 2.5×10-3 mm/s. The compressed test was performed on two or three duplicate samples, and the mean result was reported to ensure its reliability.
4.4.3. Test and model results
The observed and calculated CS of the studied SFRC mixes is listed in Table 11. The developed ML model yielded reasonable predictions. The mean and COV of the tested-to-predicted results were about 0.99 and 9%, respectively. A demonstration of this superior predictive capability is shown in Figure 10. In this figure, the predicted and tested data points show a low error rate of less than 10% in most cases.
5. Model implementation
5.1. Feature ranking
In this research, two [(Gini index [104] and SHapley Additive exPlanations (SHAP)] techniques have been used to assess the significance of the model's features. The practice of analyzing features based on Gini coefficients has proven to be more effective in detecting the significance of features with unique values [105]. The results of this analysis are shown in Figure 11.
The SHAP approach unveiled that the model's most influential variables are X9, X4, X5, X7, and X8, while the Gini index indicates that the importance factors include X7, X5, X3, X4, X9, and X13. Consequently, both approaches concur that the key parameters influencing the CS of SFRC are X9 (high-range water reducer content), X4 (cement content), X5 (water-binder ratio), and X7 (gravel content). It can be seen from Figure 11 (a) that a high value of the cement increases the strength and vice versa at low content. The two methods also were consistent about the rank for other variables [i.e., coarse aggregate content () and fiber type ( and )]. Interestingly, these results are consistent to some extent with those reported in 4.1. This conclusion is made because the Pearson correlation constant analysis also showed that the most significant features are X5, X4, and X9.
5.2. Partial dependence plots
This study conducted a partial dependence analysis for each independent variable employed in the ML model. Figure 9 shows the PDPs of the CS of SFRC in response to different predictors, except the dummy ones. The figure suggests the optimum water content () and HRWR () are in the range of 100–150 and more than 10–20 kg/m3 to maximize the CS and strength notably decreases as the content increases. Further, the strength will likely increase as the cement content () increase. Also, the ideal content for coarse aggregate () content is perhaps 900–1100 kg/m3. Moreover, the results in the figure suggested that the best fibrous combination that has a tensile strength () of about 1000 MPa, dosage () of around 1.0%, and length () of 40–50 mm. As expected, Figure 12 also illustrated that the CS decreased as the water–binder ratio () increases.
5.3. Graphical user interface development
In this study, we provide an intuitive graphical user interface (GUI) for interacting with the developed XG Boost model. Python and Gradio [106] have been used to implement sliding control systems that allow input values to be limited to minimums and maximums (Table 5). Figure 13 shows three main components: input features with slider controls, output results, and SHAP-based explanations. The model produces SFRC's strength and the concrete class ("normal strength" if it has a strength lower than 60 MPa, otherwise "high strength concrete").
6. Conclusions, implications, and future research
This study involved the compilation and refinement of an extensive database, comprising 420 entries sourced from 43 scholarly publications. We conducted experimental analyses on 20 different SFRC mixtures to assess the predictive accuracy of the constructed model. Furthermore, we employed PDPs to elucidate the relationships between the model's input variables and its outcomes. The significance of these input variables within the model was also explored. To enhance the model's usability, we developed a user-friendly graphical interface. It is worth noting that the research specifically focused on three distinct fiber types: crimped, hooked, and mil-cut. Therefore, the findings may not be directly applicable to SFRCs with alternative fiber types or mixtures. Additionally, while the model consistently performed well with experimental data, its effectiveness may vary under different conditions or when using different raw materials. Regarding the research findings:
1.The analysis, including Pearson correlations, Gini indices, and SHAP analyses, highlighted that the most significant factors influencing the CS of SFRC were the cement and HRWR contents, as well as the fiber tensile strength-water-binder ratio. Notably, increasing the proportion of water and coarse aggregates is likely to reduce the compressive strength of the concrete.
2. We utilized the Pareto frontier multi-criterion method to develop an optimized version of the standard XG Boost model. Based on training and testing datasets, the optimized model demonstrated satisfactory predictive performance, achieving scores of 0.97 and 0.88, respectively.
3. The developed ML model consistently exhibited superior predictive capability when tested against independent experimental data conducted by the authors, with average and COV values of the tested-predicted results at 0.99 and 6%, respectively.
4. Through the application of PDPs, we determined that the optimal water and HRWR contents for achieving maximum CS are in the range of 100–150 kg/m³ and 10–20 kg/m³, respectively. Similarly, for coarse aggregates, ideal contents fall in the ranges of 900–1100 kg/m³. Additionally, the most effective fibrous combination exhibited a tensile strength of 1000 MPa, a diameter length of 40–50 mm, and a dosage of about 1.0%.
The adoption of ML techniques, particularly the XG Boosting methodology, offers the construction and civil engineering sectors an enhanced predictive toolset for determining the CS of SFRC. This research not only elucidates optimal SFRC formulations, pinpointing effective fiber combinations but also facilitates the development of concrete with superior strength and durability. In future investigations, it would be valuable to compare the predictive competence of the current numerical model against existing empirical and analytical frameworks. Additionally, the inclusion of data on ultra-high-performance concrete could enhance the model's universality. Addressing the size effect might benefit from the incorporation of a conversion factor as an input variable for various types of test samples, effectively contributing to handling this aspect of the study. While our present research offers a robust database, there is a compelling case for expanding this repository by incorporating newer studies and a wider array of SFRC mix variations, ensuring it remains at the forefront of technological progress. Despite the current study's reliance on the XG Boosting technique, exploring alternative ML schemes (e.g., neural networks or stacked ensemble alogrithms) may reveal novel perspectives and enhance predictive accuracy. Beyond immediate CS predictions, there is a growing need to investigate the enduring resilience of SFRC in diverse scenarios. In an era emphasizing ecological responsibility, future research should critically assess the environmental implications of various SFRC formulations, including aspects such as lifecycle assessments, carbon emissions, and potential for recycling.
Acknowledgments
The authors extend their appreciation to Researcher Supporting Project number (RSPD2023R692), King Saud University, Riyadh, Kingdom of Saudi Arabia.
References
- Bennett, B.; Visintin, P.; Xie, T. Global Warming Potential of Recycled Aggregate Concrete with Supplementary Cementitious Materials. Journal of Building Engineering 2022, 52, 104394. [CrossRef]
- Sepulveda, B.D.G.; Visintin, P.; Oehlers, D.J. Fatigue Bond-Slip Properties of Steel Reinforcing Bars Embedded in UHPFRC: Extraction and Development of an Accumulated Damage Law. Case Studies in Construction Materials 2022, 17, e01370. [CrossRef]
- Abbas, Y.M.; Fares, G.; Iqbal Khan, M. Depth-Dependent Flexural Behavior of Plain and Bar-Reinforced Ultra-High-Performance Hybrid Fiber-Reinforced Concrete –Analytical, Numerical, and Uncertainty Modeling. Structures 2023, 52, 723–741. [CrossRef]
- Abellan-Garcia, J.; Fernández, J.; Khan, M.I.; Abbas, Y.M.; Carrillo, J. Uniaxial Tensile Ductility Behavior of Ultrahigh-Performance Concrete Based on the Mixture Design – Partial Dependence Approach. Cem Concr Compos 2023, 140, 105060. [CrossRef]
- Abbas, Y.M.; Iqbal Khan, M. Fiber–Matrix Interactions in Fiber-Reinforced Concrete: A Review. Arab J Sci Eng 2016, 41, 1183–1198. [CrossRef]
- Qin, Y.; Su, J.; Cao, J.; Liu, R. Investigation of Orientation Coefficient on Meso-Damage Evolution of Steel Fiber-Reinforced Cement Composites. Eng Fract Mech 2023, 284, 109210. [CrossRef]
- Pakzad, S.S.; Roshan, N.; Ghalehnovi, M. Comparison of Various Machine Learning Algorithms Used for Compressive Strength Prediction of Steel Fiber-Reinforced Concrete. Sci Rep 2023, 13, 3646. [CrossRef]
- Wang, Y.; Jin, H.; Demartino, C.; Chen, W.; Yu, Y. Mechanical Properties of SFRC: Database Construction and Model Prediction. Case Studies in Construction Materials 2022, 17, e01484. [CrossRef]
- Khan, M.I.; Abbas, Y.M. Intelligent Data-Driven Compressive Strength Prediction and Optimization of Reactive Powder Concrete Using Multiple Ensemble-Based Machine Learning Approach. Constr Build Mater 2023, 404, 133148. [CrossRef]
- Abbas, Y.M.; Fares, G.; Khan, M.I. Impact of Hot Weather Conditions on the Performance of Supplementary Cementitious Materials Concrete. Sustainability 2023, 15, 8393. [CrossRef]
- Abbas, Y.M.; Hussain, L.A.; Khan, M.I. Constitutive Compressive Stress–Strain Behavior of Hybrid Steel-PVA High-Performance Fiber-Reinforced Concrete. Journal of Materials in Civil Engineering 2022, 34. [CrossRef]
- Guerini, V.; Conforti, A.; Plizzari, G.; Kawashima, S. Influence of Steel and Macro-Synthetic Fibers on Concrete Properties. Fibers 2018, 6, 47. [CrossRef]
- Ortiz Navas, F.; Navarro-Gregori, J.; Leiva Herdocia, G.; Serna, P.; Cuenca, E. An Experimental Study on the Shear Behaviour of Reinforced Concrete Beams with Macro-Synthetic Fibres. Constr Build Mater 2018, 169, 888–899. [CrossRef]
- Bajpai, A.; Wetzel, B.; Klingler, A.; Friedrich, K. Mechanical Properties and Fracture Behavior of High-performance Epoxy Nanocomposites Modified with Block Polymer and Core–Shell Rubber Particles. J Appl Polym Sci 2020, 137. [CrossRef]
- Mujalli, M.A.; Dirar, S.; Mushtaha, E.; Hussien, A.; Maksoud, A. Evaluation of the Tensile Characteristics and Bond Behaviour of Steel Fibre-Reinforced Concrete: An Overview. Fibers 2022, 10, 104. [CrossRef]
- Mpalaskas, A.C.; Matikas, T.E.; Aggelis, D.G.; Alver, N. Acoustic Emission for Evaluating the Reinforcement Effectiveness in Steel Fiber Reinforced Concrete. Applied Sciences 2021, 11, 3850. [CrossRef]
- Hollý, I.; Bilčík, J. Effect of Chloride-Induced Steel Corrosion on Working Life of Concrete Structures. Solid State Phenomena 2018, 272, 226–231. [CrossRef]
- Abbas, Y.M.; Tuken, A.; Siddiqui, N.A. Improving the Structural Behavior of Shear-Deficient RC Deep Beams Using Steel Fibers: Experimental, Numerical and Probabilistic Approach. Journal of Building Engineering 2022, 46, 103711. [CrossRef]
- Cucchiara, C.; La Mendola, L.; Papia, M. Effectiveness of Stirrups and Steel Fibres as Shear Reinforcement. Cem Concr Compos 2004. [CrossRef]
- Tarawneh, A.; Almasabha, G.; Alawadi, R.; Tarawneh, M. Innovative and Reliable Model for Shear Strength of Steel Fibers Reinforced Concrete Beams. Structures 2021, 32, 1015–1025. [CrossRef]
- Lantsoght, E.O.L. How Do Steel Fibers Improve the Shear Capacity of Reinforced Concrete Beams without Stirrups? Compos B Eng 2019, 175, 107079. [CrossRef]
- Wang, X.H.; Jacobsen, S.; He, J.Y.; Zhang, Z.L.; Lee, S.F.; Lein, H.L. Application of Nanoindentation Testing to Study of the Interfacial Transition Zone in Steel Fiber Reinforced Mortar. Cem Concr Res 2009, 39, 701–715. [CrossRef]
- Lu, J.; Liu, J.; Fan, X.; Wan, X.; Gao, J.; Zhang, J.; Li, P. Study on the Mechanical Properties and Microstructure of Fiber-Reinforced Concrete Subjected to Sulfate Erosion. Arab J Sci Eng 2022, 47, 13639–13653. [CrossRef]
- Guojie; W. Chuanlin; J. ZHANG; L. Zeping; T. ZHANG; Y. ZHANG Influence of Steel Fiber Shape on the Performance of High-Performance Concrete. 复合材料学报, 2021; 38, 4313–4324.
- Wu, X.; Ding, F.; Xiang, P.; Wang, Y.; Yu, Z.; Liu, C. Multiaxial Damage Ratio Strength Criteria for Fiber-Reinforced Concrete. J Eng Mech 2022, 148. [CrossRef]
- Frazão, C.; Camões, A.; Barros, J.; Gonçalves, D. Durability of Steel Fiber Reinforced Self-Compacting Concrete. Constr Build Mater 2015, 80, 155–166. [CrossRef]
- Liu, C.; Hunag, X.; Wu, Y.-Y.; Deng, X.; Zheng, Z.; Yang, B. Studies on Mechanical Properties and Durability of Steel Fiber Reinforced Concrete Incorporating Graphene Oxide. Cem Concr Compos 2022, 130, 104508. [CrossRef]
- Parvez, A.; Foster, S.J. Fatigue of Steel-Fibre-Reinforced Concrete Prestressed Railway Sleepers. Eng Struct 2017, 141, 241–250. [CrossRef]
- Jin, L.; Zhang, R.; Dou, G.; Du, X. Fire Resistance of Steel Fiber Reinforced Concrete Beams after Low-Velocity Impact Loading. Fire Saf J 2018, 98, 24–37. [CrossRef]
- Liang, X.; Wu, C. Investigation on Thermal Conductivity of Steel Fiber Reinforced Concrete Using Mesoscale Modeling. Int J Thermophys 2018, 39, 142. [CrossRef]
- Qing, L.; Zhang, H.; Niu, C.; Mu, R.; Li, M. Preparation and Fracture Behavior of Annularly Aligned Steel Fiber Reinforced Cementitious Composite: Experiment and Simulation. Journal of Building Engineering 2023, 67, 106019. [CrossRef]
- Zhang, J.; Liu, X.; Wu, Z.; Yu, H.; Fang, Q. Fracture Properties of Steel Fiber Reinforced Concrete: Size Effect Study via Mesoscale Modelling Approach. Eng Fract Mech 2022, 260, 108193. [CrossRef]
- Yu, Y.; Zhao, X.-Y.; Xu, J.-J.; Wang, S.-C.; Xie, T.-Y. Evaluation of Shear Capacity of Steel Fiber Reinforced Concrete Beams without Stirrups Using Artificial Intelligence Models. Materials 2022, 15, 2407. [CrossRef]
- Abbass, W.; Khan, M.I.; Mourad, S. Evaluation of Mechanical Properties of Steel Fiber Reinforced Concrete with Different Strengths of Concrete. Constr Build Mater 2018, 168, 556–569. [CrossRef]
- Bai M; Niu DT; Jiang L; Miao Y. Research on Improving the Mechanical Properties and Microstructure of Concrete with Steel Fiber. Chinese.] Bull. Chin. Ceram. Soc. 2013, 32, 2084–2089.
- H. Chang; P. Shen; F. Gu Analysis of the Influence Law of Steel Fiber on Concrete Thermal Conductivity and Pressure Strength. Concrete 2021, 4, 67–69.
- Y. Wang Steel Fiber Reinforced Concrete Durability in the Atmospheric Environmental Based on Multi-Factor Effects. Doctoral dissertation, Xi’an University of Architecture and Technology, 2011.
- Açikgenç, M.; Ulaş, M.; Alyamaç, K.E. Using an Artificial Neural Network to Predict Mix Compositions of Steel Fiber-Reinforced Concrete. Arab J Sci Eng 2015, 40, 407–419. [CrossRef]
- Thai, H.-T. Machine Learning for Structural Engineering: A State-of-the-Art Review. Structures 2022, 38, 448–491. [CrossRef]
- Zheng, Y.; Liu, Y.; Wei, T.; Jiang, D.; Wang, M. Wind Turbine Blades Surface Crack-Detection Algorithm Based on Improved YOLO-v5 Model. J Electron Imaging 2023, 32. [CrossRef]
- Cardellicchio, A.; Ruggieri, S.; Nettis, A.; Renò, V.; Uva, G. Physical Interpretation of Machine Learning-Based Recognition of Defects for the Risk Management of Existing Bridge Heritage. Eng Fail Anal 2023, 149, 107237. [CrossRef]
- Awolusi, T.F.; Oke, O.L.; Akinkurolere, O.O.; Sojobi, A.O.; Aluko, O.G. Performance Comparison of Neural Network Training Algorithms in the Modeling Properties of Steel Fiber Reinforced Concrete. Heliyon 2019, 5, e01115. [CrossRef]
- Karahan, O.; Tanyildizi, H.; Atis, C.D. An Artificial Neural Network Approach for Prediction of Long-Term Strength Properties of Steel Fiber Reinforced Concrete Containing Fly Ash. Journal of Zhejiang University-SCIENCE A 2008, 9, 1514–1523. [CrossRef]
- Rathakrishnan, V.; Bt. Beddu, S.; Ahmed, A.N. Predicting Compressive Strength of High-Performance Concrete with High Volume Ground Granulated Blast-Furnace Slag Replacement Using Boosting Machine Learning Algorithms. Sci Rep 2022, 12, 9539. [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive Logistic Regression: A Statistical View of Boosting (With Discussion and a Rejoinder by the Authors). The Annals of Statistics 2000, 28. [CrossRef]
- T. Chen; C. Guestrin Xgboost: A Scalable Tree Boosting System. In Proceedings of the Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining; 2016; pp. 785–794.
- Wikipedia contributors XGBoost Available online: https://en.wikipedia.org/wiki/XGBoost (accessed on 29 August 2022).
- Wikiedia contributors Outlier Available online: https://en.wikipedia.org/wiki/Outlier (accessed on 20 October 2023).
- Kivrak, M.; Guldogan, E.; Colak, C. Prediction of Death Status on the Course of Treatment in SARS-COV-2 Patients with Deep Learning and Machine Learning Methods. Comput Methods Programs Biomed 2021, 201, 105951. [CrossRef]
- Xu, H.; Wang, H.; Yuan, C.; Zhai, Q.; Tian, X.; Wu, L.; Mi, Y. Identifying Diseases That Cause Psychological Trauma and Social Avoidance by GCN-Xgboost. BMC Bioinformatics 2020, 21, 504. [CrossRef]
- Carmona, P.; Dwekat, A.; Mardawi, Z. No More Black Boxes! Explaining the Predictions of a Machine Learning XGBoost Classifier Algorithm in Business Failure. Res Int Bus Finance 2022, 61, 101649. [CrossRef]
- G.V. Rossum; J.F. Drake Python Reference Manual; Centrum voor Wiskunde en Informatica : Amsterdam, 1995;
- M. Yalcin Optimization and Performance Based Design of Steel Fiber Reinforced Concretes, Istanb. Tech. Univ., 1994.
- Nili, M.; Afroughsabet, V. Combined Effect of Silica Fume and Steel Fibers on the Impact Resistance and Mechanical Properties of Concrete. Int J Impact Eng 2010, 37, 879–886. [CrossRef]
- Nguyen-Minh, L.; Rovňák, M.; Tran-Quoc, T.; Nguyenkim, K. Punching Shear Resistance of Steel Fiber Reinforced Concrete Flat Slabs. Procedia Eng 2011, 14, 1830–1837. [CrossRef]
- Ibrahim, I.S.; Che Bakar, M.B. Effects on Mechanical Properties of Industrialised Steel Fibres Addition to Normal Weight Concrete. Procedia Eng 2011, 14, 2616–2626. [CrossRef]
- Eren, Ö.; Marar, K. Effects of Limestone Crusher Dust and Steel Fibers on Concrete. Constr Build Mater 2009, 23, 981–988. [CrossRef]
- Şahin, Y.; Köksal, F. The Influences of Matrix and Steel Fibre Tensile Strengths on the Fracture Energy of High-Strength Concrete. Constr Build Mater 2011, 25, 1801–1806. [CrossRef]
- Buratti, N.; Mazzotti, C.; Savoia, M. Post-Cracking Behaviour of Steel and Macro-Synthetic Fibre-Reinforced Concretes. Constr Build Mater 2011, 25, 2713–2722. [CrossRef]
- Lau, A.; Anson, M. Effect of High Temperatures on High Performance Steel Fibre Reinforced Concrete. Cem Concr Res 2006, 36, 1698–1707. [CrossRef]
- Shakya, K.; Watanabe, K.; Matsumoto, K.; Niwa, J. Application of Steel Fibers in Beam–Column Joints of Rigid-Framed Railway Bridges to Reduce Longitudinal and Shear Rebars. Constr Build Mater 2012, 27, 482–489. [CrossRef]
- Soulioti, D. V.; Barkoula, N.M.; Paipetis, A.; Matikas, T.E. Effects of Fibre Geometry and Volume Fraction on the Flexural Behaviour of Steel-Fibre Reinforced Concrete. Strain 2011, 47. [CrossRef]
- Ünal, O.; Demir, F.; Uygunoğlu, T. Fuzzy Logic Approach to Predict Stress–Strain Curves of Steel Fiber-Reinforced Concretes in Compression. Build Environ 2007, 42, 3589–3595. [CrossRef]
- Carmona, S.; Aguado, A.; Molins, C. Characterization of the Properties of Steel Fiber Reinforced Concrete by Means of the Generalized Barcelona Test. Constr Build Mater 2013, 48, 592–600. [CrossRef]
- Cantin, R.; Pigeon, M. Deicer Salt Scaling Resistance of Steel-Fiber-Reinforced Concrete. Cem Concr Res 1996, 26, 1639–1648. [CrossRef]
- Pigeon, M.; Cantin, R. Flexural Properties of Steel Fiber-Reinforced Concretes at Low Temperatures. Cem Concr Compos 1998, 20, 365–375. [CrossRef]
- Z.X. C Experimental Study on Constitutive Relation of Steel Fiber Reinforced Concrete under Uniaxial Compresion, Zhengzhou University, 2017.
- J.Y. Chen The Study of the Effect of Aggregate Size and the Steel Fiber’s Length on the Fracture Property of SFRC, Zhengzhou University, 2016.
- C.C. Li Study on Mechanical Properties and Relationship of Steel Fiber Reinforced Concrete Cubic and Cylindrical Specimen, Zhengzhou University, 2016.
- J. Yue; Y. Xia; H. Fang Experimental Study on Fracture Mechanism and Tension Damage Constitutive Relationship of Steel Fiber Reinforced Concrete. China Civ. Eng. J 2021, 54, 93–106.
- Y. Yang Effect of Fiber Dosage and Bond Length on Pullout Mechanical Property Study, Guangzhou University, 2015.
- Zhang L J. Mixture Design and Performance Calculation Method of Steel Fiber Recycled Concrete, Zhengzhou University, 2016.
- L. Liao Study on the Optimisation of Steel Fiber Reinforced Concrete, Taiyuan Technology University, 2011.
- C.Y. Fan Study on Mechanical Properties of Hybrid Steel Fiber Reinforced Concrete, Zhengzhou University, 2017.
- W.W. Yang Experimental Study on Mechanical Properties and Durability of Fiber Reinforced Concrete, Shandong University, 2012.
- B. Raja Rajeshwari; M. Sivakumar Influence of Coarse Aggregate Properties on Specific Fracture Energy of Steel Fiber Reinforced Self Compacting Concrete. Advances in concrete construction 2020, 9, 173–181.
- C. Gao Experimental Research on Mechanical Properties of Concrete and Reinfroced Oncrete after High Temperature, Yangzhou University, 2013.
- H.Q. Cheng Experimental Research on Adherence Property of Fresh Fiber Reinforced Concrete to Old Concrete, Zhengzhou University, 2007.
- J. Liu Study on the Relationship between Pressure and Tensile Properties of Steel Fiber Reinforced Recycled Concrete, Zhengzhou University, 2016.
- Z.Y. Ma An Experimental Study on the Properties of Steel Fiber Reinforced Concrete at Early Ages, Beijing Technology University, 2003.
- Q. Li; Y. Fang; C. Y L Experimental Study on Mechanical Properties of Concrete with Adding Steel Fiber at Early Age. Concrete 2020, 6, 102–105.
- T.Y. Zhu The Mechanical Properties of Steel Fiber-Reinforced Concrete at Low Fiber Content, Zhengzhou University, 2011.
- L.L. Niu; S.P. Zhang; Y.X. Wei Effect of Fiber Dosage on the Mechanical Property of SFRC. China Concrete and Cement Products 2019, 3.
- H.X. Peng Experimental Research of Steel Fiber Reinforced Concrete on Speed-Repairing the Airport Pavement, Beijing Technology University, 2002.
- M. Gul; A. Bashir; J.A. Naqash Study of Modulus of Elasticity of Steel Fiber Reinforced Concrete. Int. J. Eng. Adv. Technol 2014, 3, 304–309.
- F. Minelli; A. Conforti; E. Cuenca; G. Plizzari Are Steel Fibres Able to Mitigate or Eliminate Size Effect in Shear? Materials and structures 2014, 459–473.
- Conforti, A.; Minelli, F.; Plizzari, G.A. Wide-Shallow Beams with and without Steel Fibres: A Peculiar Behaviour in Shear and Flexure. Compos B Eng 2013, 51, 282–290. [CrossRef]
- Cuenca, E. On Shear Behavior of Structural Elements Made of Steel Fiber Reinforced Concrete; Springer International Publishing: Cham, 2015; ISBN 978-3-319-13685-1.
- Characterization and Modelling of SFRC Elements, Universitat Politècnica de Catalunya, 2013.
- Facconi, L.; Minelli, F. Behavior of Lightly Reinforced Fiber Reinforced Concrete Panels under Pure Shear Loading. Eng Struct 2020, 202, 109879. [CrossRef]
- Conforti, A.; Zerbino, R.; Plizzari, G.A. Influence of Steel, Glass and Polymer Fibers on the Cracking Behavior of Reinforced Concrete Beams under Flexure. Structural Concrete 2019, 20, 133–143. [CrossRef]
- Tiberti, G.; Minelli, F.; Plizzari, G. Cracking Behavior in Reinforced Concrete Members with Steel Fibers: A Comprehensive Experimental Study. Cem Concr Res 2015, 68, 24–34. [CrossRef]
- Committee, A. 318 Building Code Requirements for Structural Concrete (ACI 318-19) and Commentary.; American Concrete Institute, 2022.
- Wu, B.; Yu, Y.; Chen, Z.; Zhao, X. Shape Effect on Compressive Mechanical Properties of Compound Concrete Containing Demolished Concrete Lumps. Constr Build Mater 2018, 187, 50–64. [CrossRef]
- Aggarwal, C.C. An Introduction to Outlier Analysis. In Outlier Analysis; Springer International Publishing: Cham, 2017; pp. 1–34.
- Atkinson, A.; Riani, M. Robust Diagnostic Regression Analysis; Springer New York: New York, NY, 2000; ISBN 978-1-4612-7027-0.
- Pimentel, M.A.F.; Clifton, D.A.; Clifton, L.; Tarassenko, L. A Review of Novelty Detection. Signal Processing 2014, 99, 215–249. [CrossRef]
- Zimek, A.; Schubert, E.; Kriegel, H. A Survey on Unsupervised Outlier Detection in High-dimensional Numerical Data. Statistical Analysis and Data Mining: The ASA Data Science Journal 2012, 5, 363–387. [CrossRef]
- Khan, M.I.; Abbas, Y.M. Robust Extreme Gradient Boosting Regression Model for Compressive Strength Prediction of Blast Furnace Slag and Fly Ash Concrete. Mater Today Commun 2023, 35, 105793. [CrossRef]
- Wikipedia contributors Pearson Correlation Coefficient Available online: https://en.wikipedia.org/wiki/Pearson_correlation_coefficient (accessed on 20 October 2023).
- Ayan, E.; Saatçioğlu, Ö.; Turanli, L. Parameter Optimization on Compressive Strength of Steel Fiber Reinforced High Strength Concrete. Constr Build Mater 2011, 25, 2837–2844. [CrossRef]
- Yu, J.; Zhang, B.; Chen, W.; He, J. Experimental and Multi-Scale Numerical Investigation of Ultra-High Performance Fiber Reinforced Concrete (UHPFRC) with Different Coarse Aggregate Content and Fiber Volume Fraction. Constr Build Mater 2020, 260, 120444. [CrossRef]
- V. Pareto Cours d’économie Politique; Librairie Droz, 1964;
- Hastie, T.; Friedman, J.; Tibshirani, R. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer New York: New York, NY, 2001; ISBN 978-1-4899-0519-2.
- Gong, J.; Chu, S.; Mehta, R.K.; McGaughey, A.J.H. XGBoost Model for Electrocaloric Temperature Change Prediction in Ceramics. NPJ Comput Mater 2022, 8, 140. [CrossRef]
- A. Abid; A. Abdalla; A. Abid; D. Khan; A. Alfozan; J. Zou Gradio: Hassle-Free Sharing and Testing of Ml Models in the Wild. arXiv preprint arXiv 2019.
Figure 1.
XG Boost methodology.
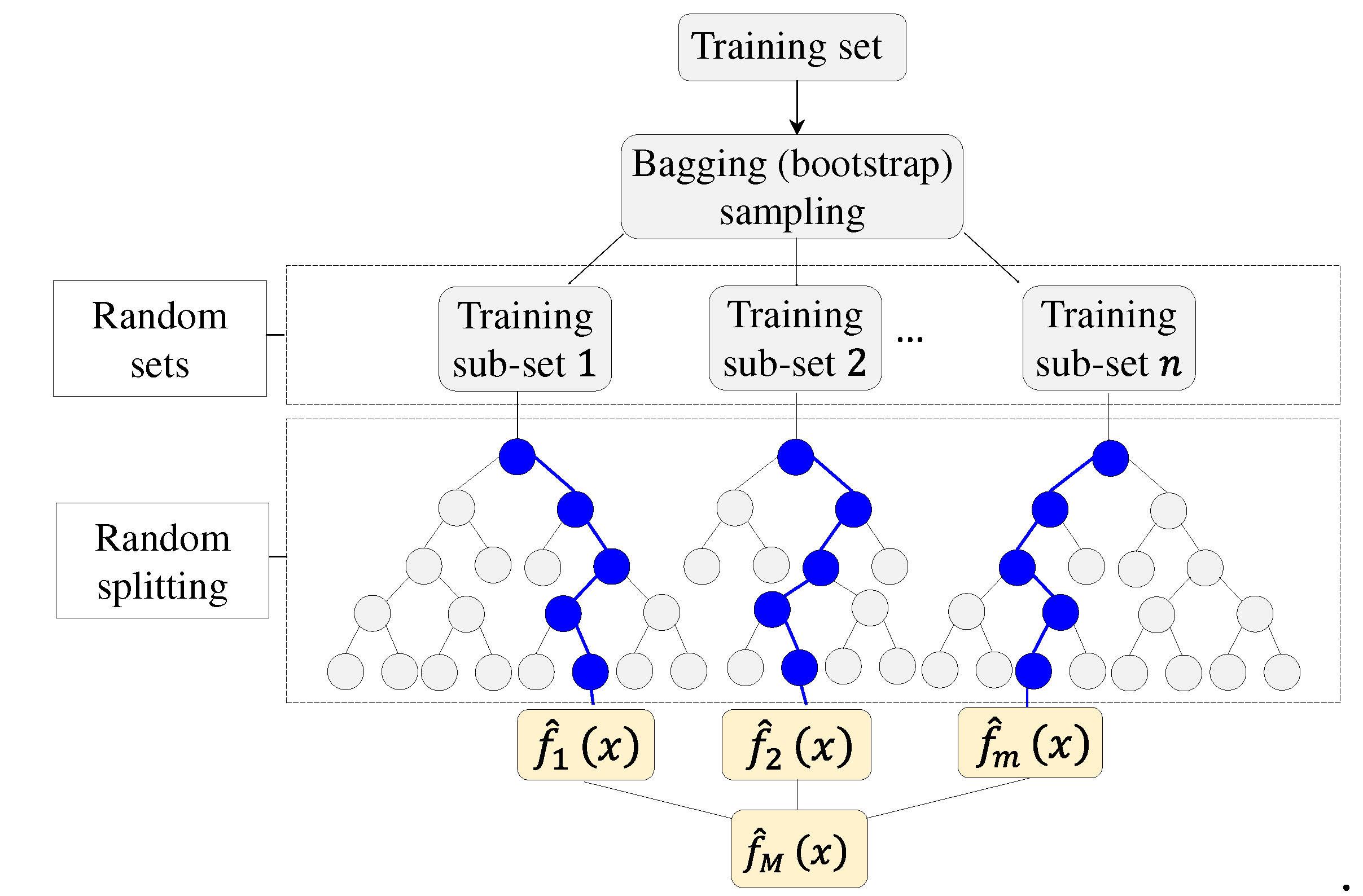
Figure 2.
Boxplots of the model variables.
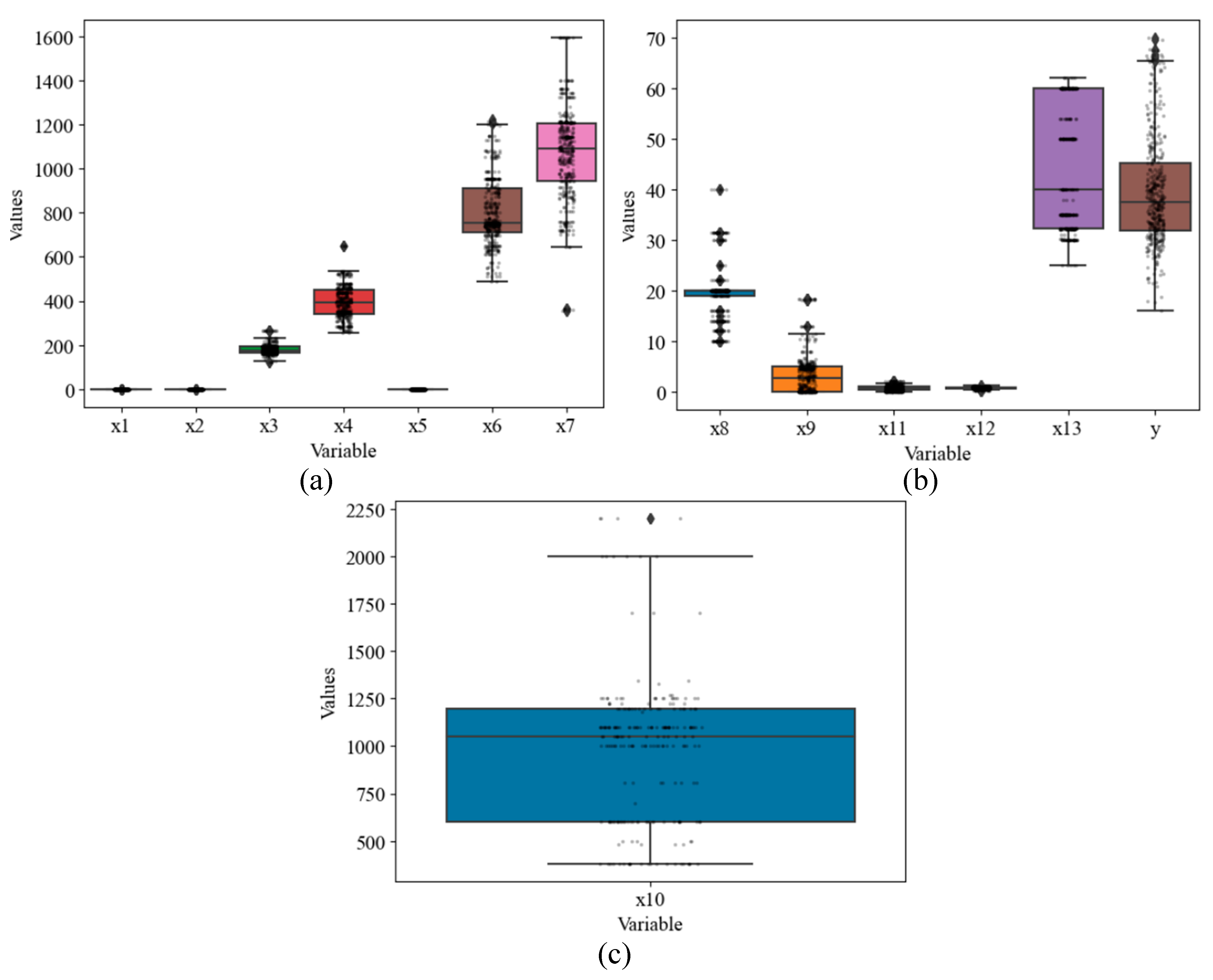
Figure 3.
A graphic depiction of a model's variables.
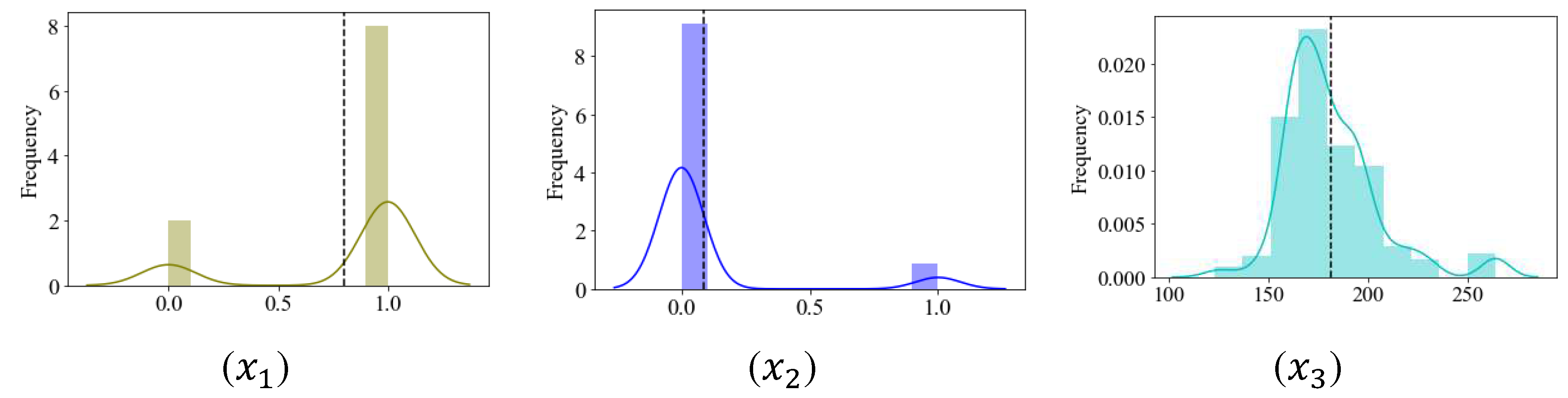
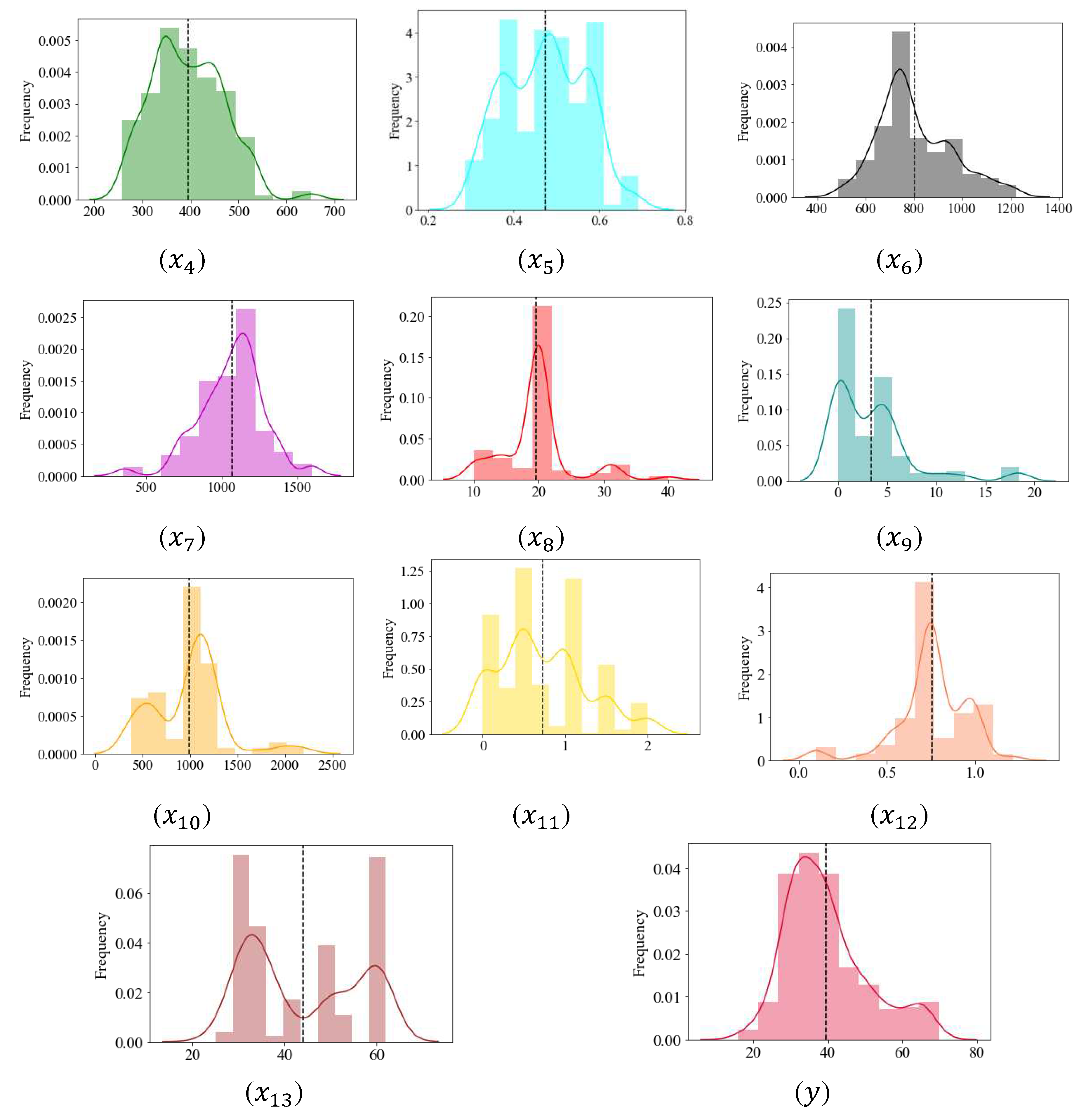
Figure 4.
(a) Pearson’s encoded matrix, and (b) linear correlations between features and label.
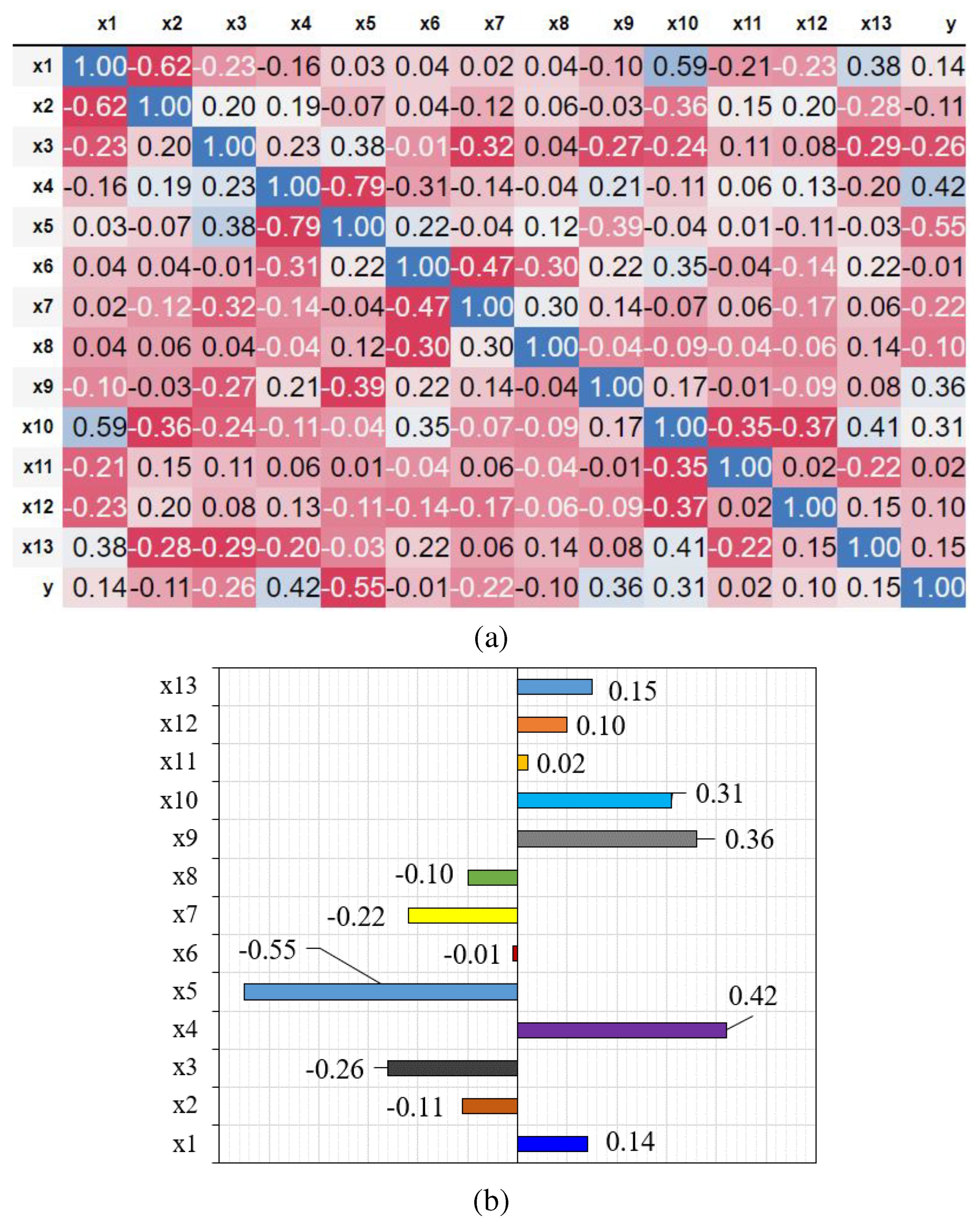
Figure 5.
Pareto frontier-based model’s multi-objective optimization.
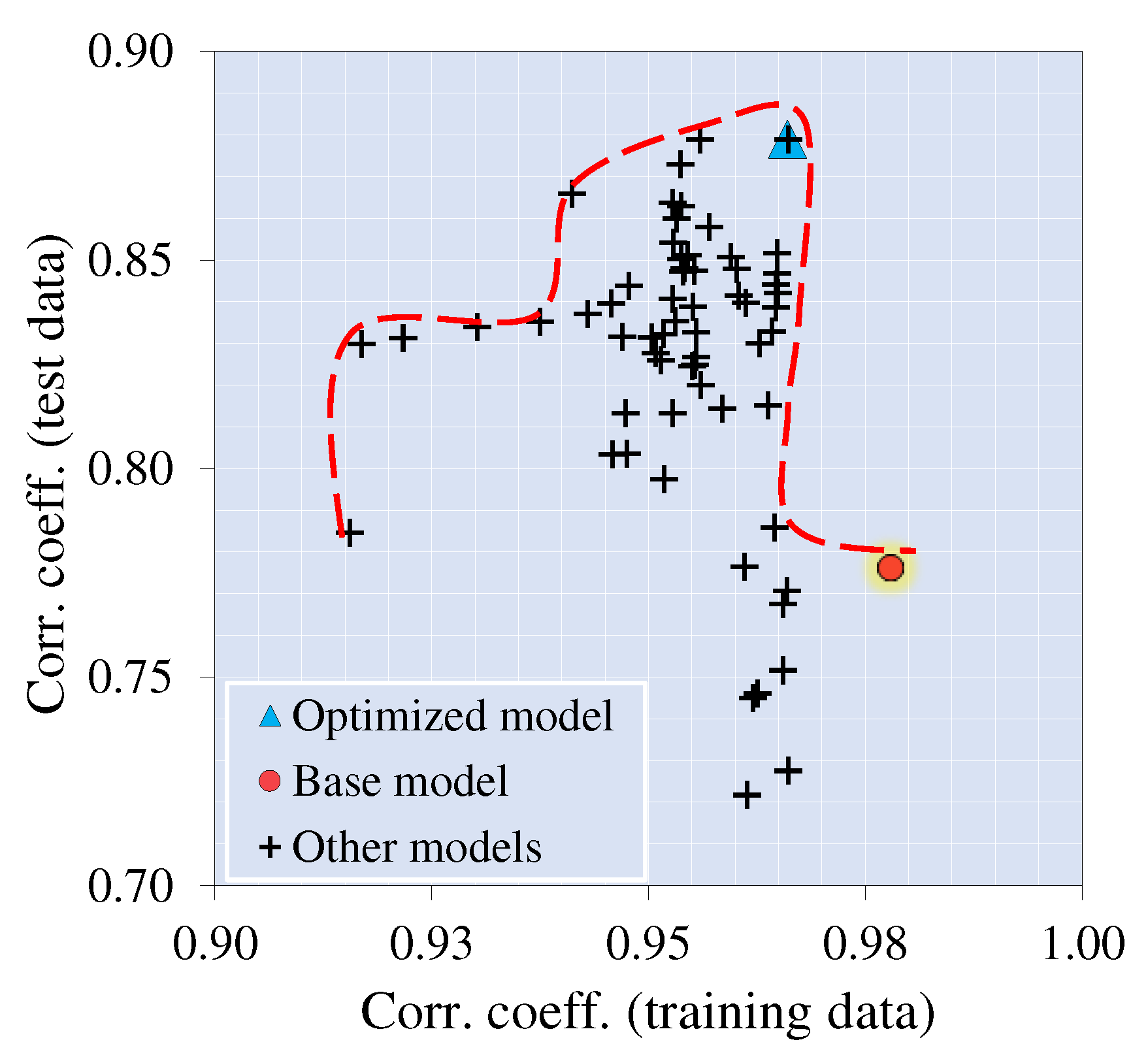
Figure 6.
Predicted vs. target results for the: (a) training, and (b) testing data.
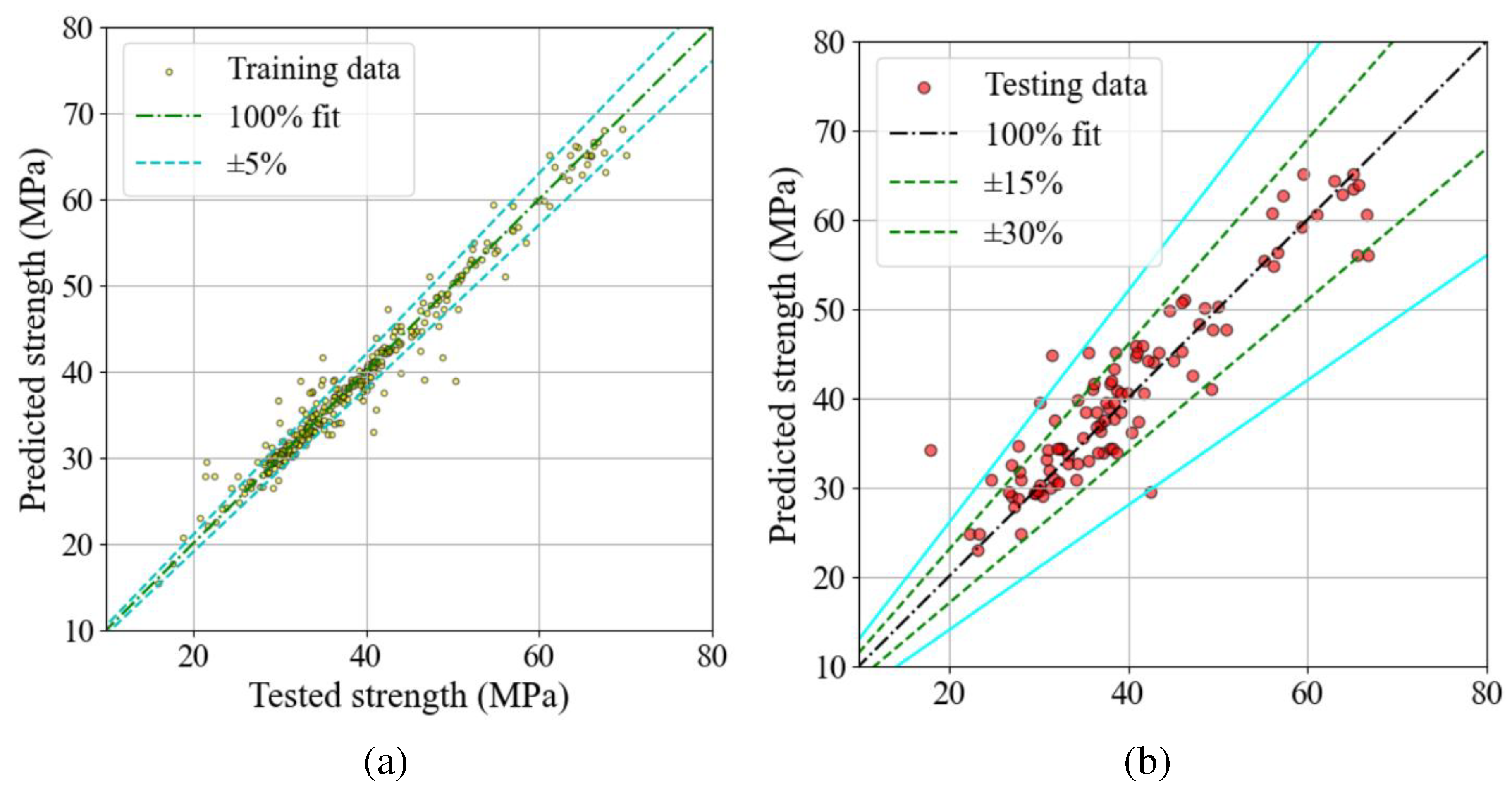
Figure 7.
SEM analysis and particle size curves for the used OPC.
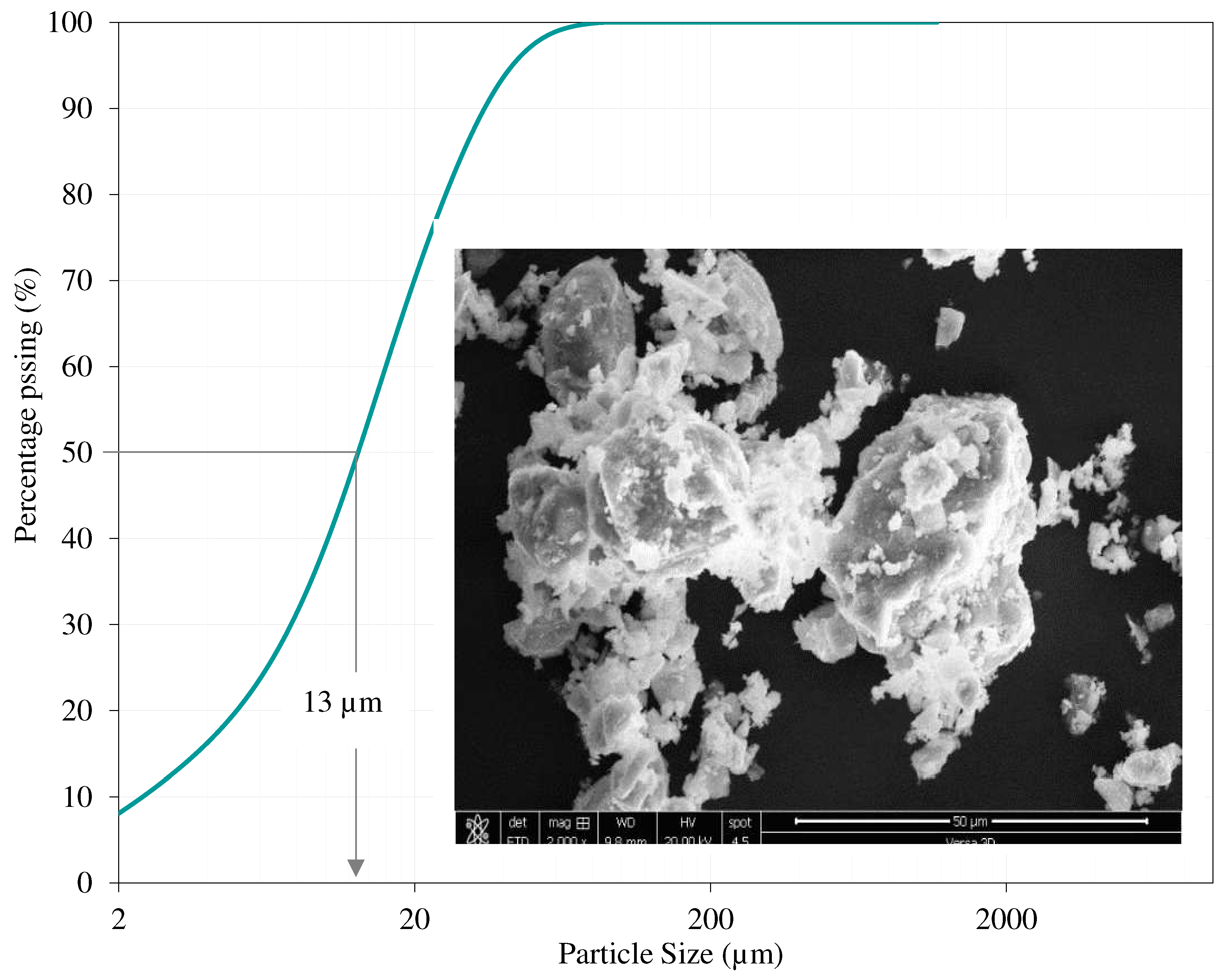
Figure 8.
Particle size curves for various aggregates.

Figure 9.
The uniaxial compression test: (a) representatives’ diagram and (b) detailed setup.

Figure 10.
Predicted vs. target results for experimental verification data.
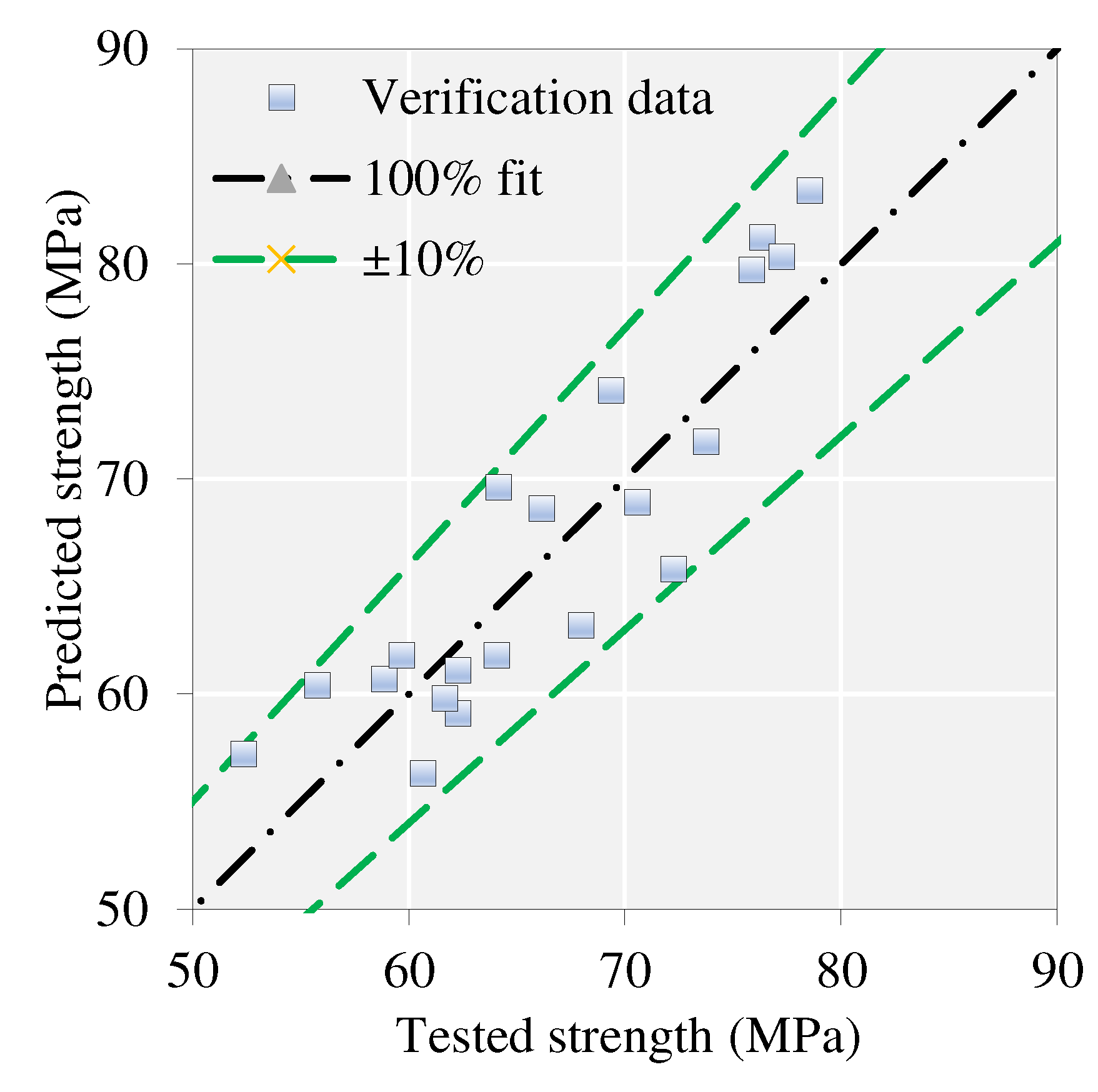
Figure 11.
Variable significance by: (a SHAP value, and (b) Gini index methods.
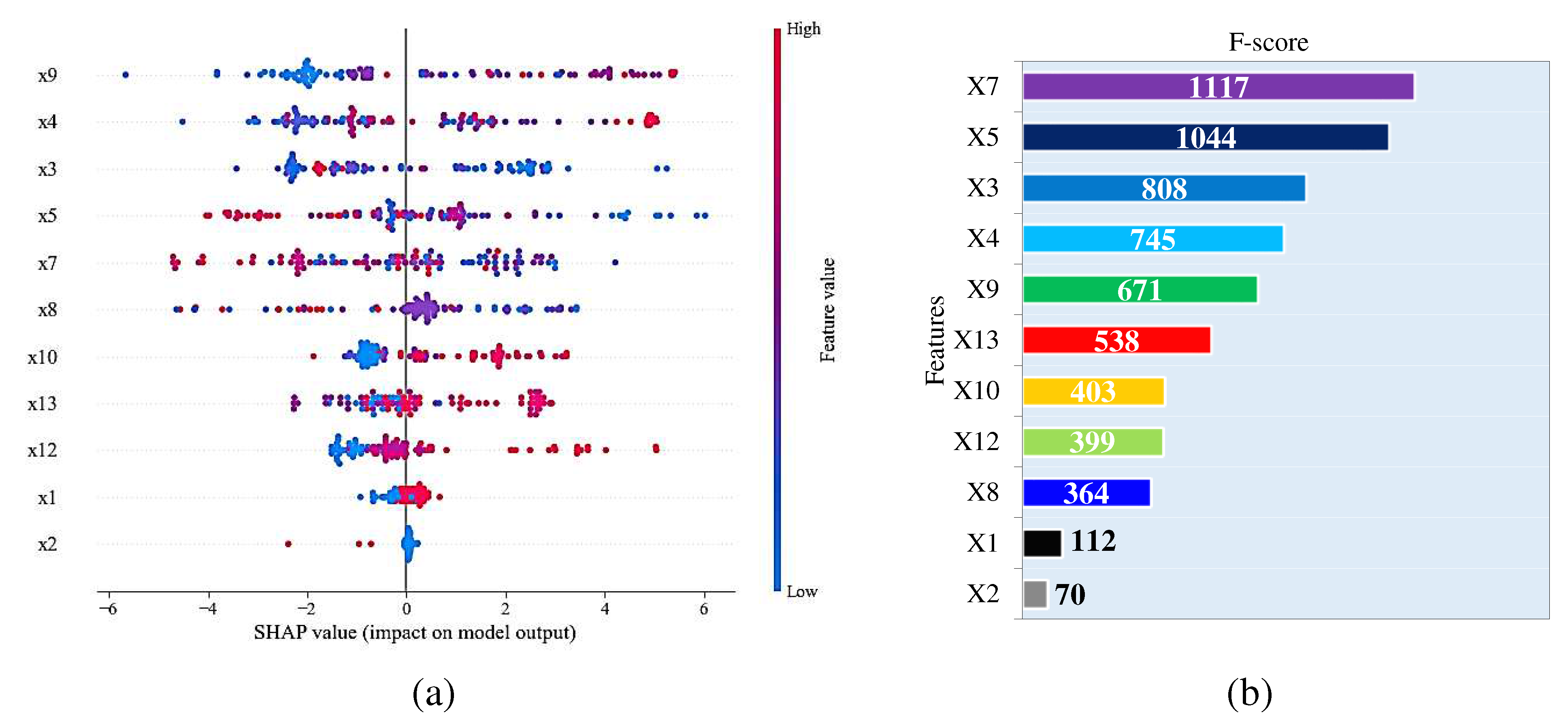
Figure 12.
Compressive strength of SFRC partial dependence plots.
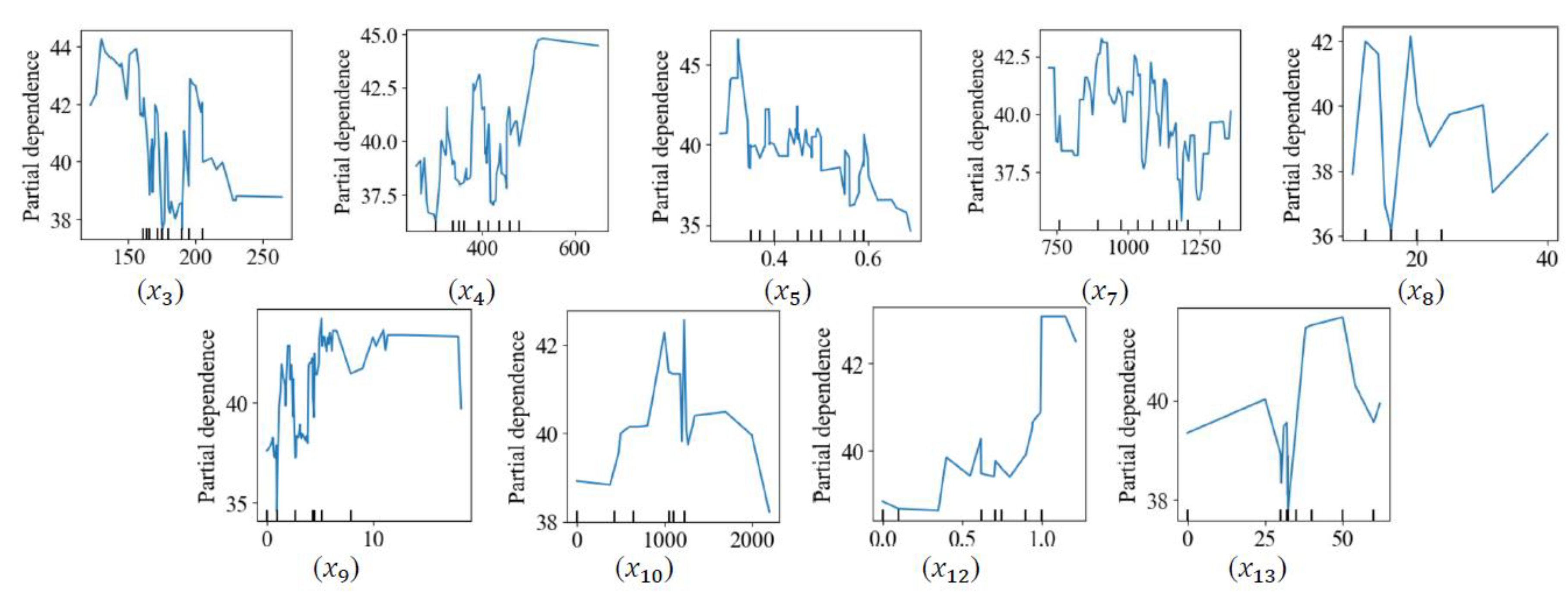
Figure 13.
A GUI for predicting the compressive strength of SFRC using the XG Boost model.
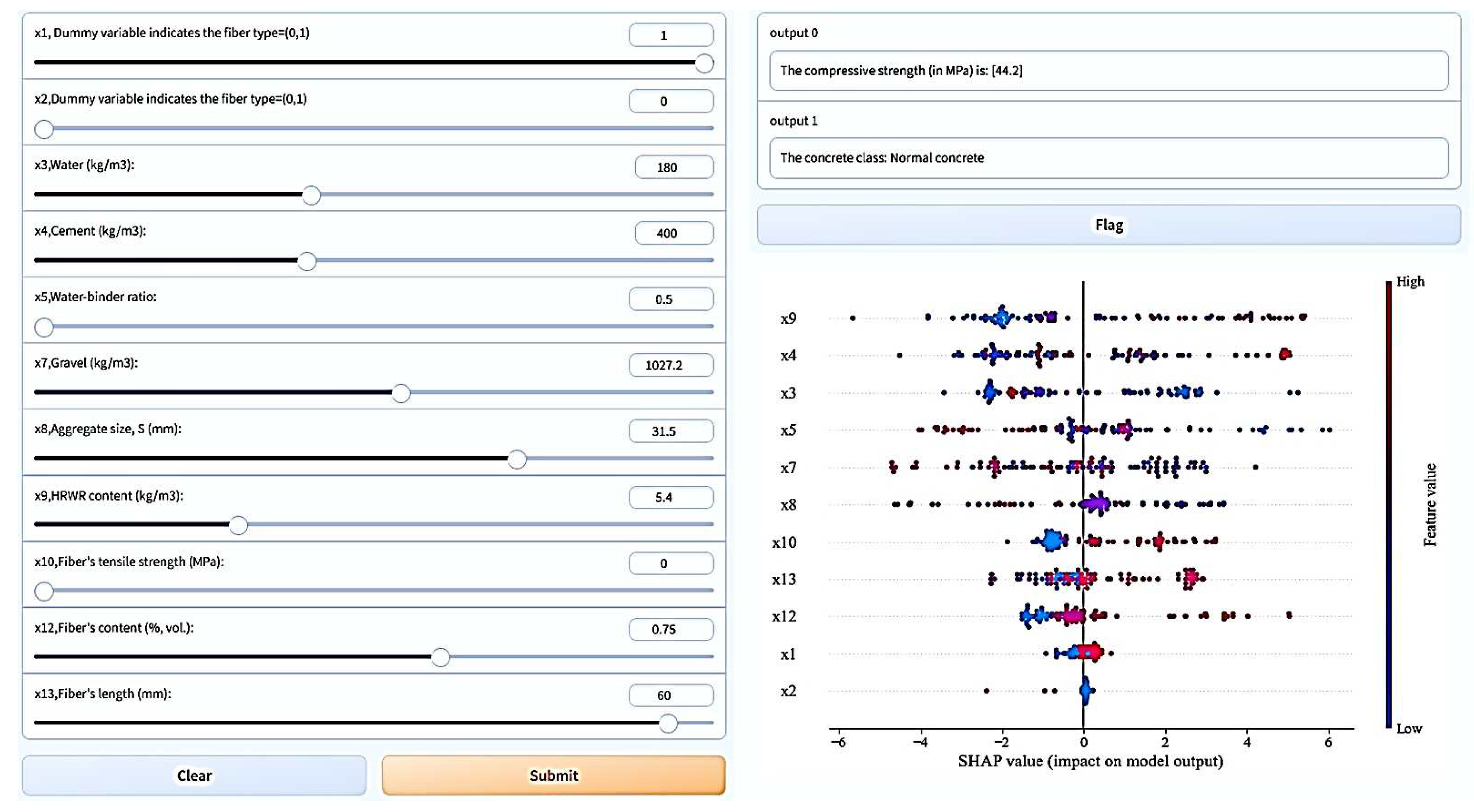
Table 1.
Coding system used for the dummy variables.
| Fiber type | Hooked | Mil-cut | Crimped |
|---|---|---|---|
| 1 | 0 | 0 | |
| 0 | 1 | 0 |
Table 2.
Coding system used for other variables.
| variable | Unit | Description | variable | Unit | Description |
|---|---|---|---|---|---|
| kg/m3 | Water content | kg/m3 | HRWR content | ||
| Cement content | MPa | Tensile strength of the fiber | |||
| –– | water-binder ratio | mm | Diameter of the fiber | ||
| kg/m3 | Fine aggregate content | %, vol. | Dosage of the fiber | ||
| Coarse aggregate content | mm | Length of the fiber | |||
| mm | Maximum aggregate size | MPa | 28d CS of the SFRC |
Note. HRWR: high-range water reduction superplasticizer.
Table 3.
Summary of the collected CS database of SFRC.
| Ref. | Data-sets | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [53] | 17 | 1 | 0 | 180–192.5 | 280–400 | 0.5|0.6|0.7 | 713.8–762.6 | 1027.2–1097.4 | 31.5 | 3.4–6.6 | –– | 0.19–0.64 | 0.55–0.9 | 30–60 | 29.7–46.7 |
| [54] | 12 | 1 | 0 | 162–177 | 354–450 | 0.4|0.5 | 893–920 | 858–887 | 19 | 2.3–6.5 | 1050 | 0–1 | 0.75 | 60 | 31.5–53.3 |
| [55] | 4 | 1 | 0 | 181.2 | 453 | 0.4 | 624 | 1242 | 22 | 1 | 1100 | 0–0.8 | 0.75 | 60 | 21.7–25.3 |
| [56] | 5 | 1 | 0 | 230.2 | 338 | 0.7 | 1049.2 | 760 | 10 | 0.7 | –– | 0–1.25 | 0.75 | 60 | 25.6–28.1 |
| [57] | 40 | 1 | 0 | 175 | 350 | 0.5 | 952.2 | 1321.2–1398.8 | 20 | 4.5 | 1100–1250 | 0–1.5 | 0–1.5 | 50–60 | 17.9–40.8 |
| [58] | 14 | 1 | 0 | 178–179 | 325–396 | 0.4|0.6 | 842–891 | 913–965 | 19 | 0.9–1.4 | 1050–2000 | 0–1 | 0.71–0.75 | 60 | 47.2–61.1 |
| [59] | 2 | 1 | 0 | 175.6 | 351 | 0.5 | 914.8 | 994.7 | 22 | 2.7 | –– | 0.26–0.45 | 1 | 50 | 33.3–33.4 |
| [60] | 5 | 1 | 0 | 205–398 | 311–458 | 0.6|0.7 | 408–665 | 1156–1407 | 20 | 3.1–7.3 | 1700 | 0–1 | 0.4 | 25 | 31.2–88.0 |
| [61] | 2 | 1 | 0 | 169.8–177.6 | 283–296 | 0.6 | 705–838 | 968–1071 | 10 | 2.8–3.3 | –– | 1–1.5 | 0.62 | 30 | 23.3–30.0 |
| [62] | 7 | 1 | 0 | 220 | 440 | 0.5 | 1193–1225 | 356–366 | 10 | 3–4 | –– | 0–1.5 | 0.75 | 25–31 | 35.1–43.8 |
| [63] | 8 | 1 | 0 | 191.2–191.6 | 324 | 0.6 | 1052.8–1064.2 | 750.0–758.3 | 22 | 3.2 | 1200 | 0.19–0.76 | 0.5–0.75 | 30–60 | 34.0–48.0 |
| [64] | 2 | 1 | 0 | 185 | 410 | 0.5 | 915 | 866 | 20 | 2–4 | 1100 | 0.5–1.0 | 1 | 50 | 50.0–52.0 |
| [65] | 10 | 0|1 | 0 | 150–168 | 341–429 | 0.3|0.4|0.5 | 800 | 975 | 14 | 2.8–11 | –– | 0.51 | 1 | 54–60 | 40.9–67.6 |
| [66] | 18 | 1 | 0 | 123–167 | 325–439 | 0.6 | 741–885 | 846–998 | 14 | 0.5–11.4 | –– | 0.48–0.75 | 1 | 54–60 | 38.2–69.6 |
| [36] | 6 | 1 | 0 | 195 | 342 | 0.3|0.5|0.6 | 701 | 1143 | 20 | 10.3 | –– | 0–1.5 | 0.75 | 30 | 24.6–30.6 |
| [67] | 23 | 1 | 0 | 164–185 | 308.3–529.1 | 0.3|0.6 | 639.3–763.9 | 928.6–1232.7 | 20 | 0–5.8 | 600–1000 | 0-2 | 0.55–0.75 | 35 | 26.7–65.4 |
| [68] | 32 | 1 | 0 | 172–195 | 336–521 | 0.6 | 652–750 | 1080–1145 | 10–40 | 0–5.2 | 1100 | 0-1 | 0.75 | 30–60 | 25.8–67.4 |
| [69] | 21 | 0|1 | 0 | 166 | 286 | 0.4 | 739 | 1170–1259 | 20 | 0–0.6 | 600 | 0–2 | 0.75 | 30–40 | 28.0–33.0 |
| [35] | 5 | 0 | 0 | 165 | 367 | 0.3|0.4|0.5 | 702–765 | 1053–1146 | 16 | 2.2 | 380 | 0–2 | 0.5 | 30 | 26.8–31.0 |
| [70] | 12 | 1 | 0 | 195–200 | 415–651 | 0.4|0.7 | 527–610 | 1022–1182 | 20 | 0 | 1000 | 0–1.5 | 0.75 | 32 | 30.9–58.5 |
| [71] | 6 | 1 | 0 | 185 | 268–524 | 0.4|0.5|0.6 | 488–725 | 1056–1185 | 31.5 | 0 | 1000 | 0–0.63 | 1 | 50 | 16.0–34.4 |
| [72] | 22 | 0|1 | 0|1 | 172–196 | 321–475 | 0.4|0.5 | 622.8–886.0 | 960–1171 | 20 | 0–4.5 | –– | 0–2 | 0.75–0.94 | 32.3–62 | 26.6–43.6 |
| [73] | 6 | 1 | 0 | 156–165 | 312–381 | 0.6 | 817–1200 | 700–1214 | 20 | 2.2–5.3 | 1000 | 0.38–0.77 | 1 | 50 | 63.9–67.5 |
| [74] | 13 | 0|1 | 0 | 264 | 480 | 0.4 | 716.5–769.1 | 895.1–989.5 | 20 | 0 | 380–500 | 0–2 | 0.9–1.2 | 30.2–32.3 | 27.7–34.3 |
| [75] | 4 | 1 | 0 | 175 | 461 | 0.4 | 512 | 1252 | 10 | 0 | 600 | 0–1.5 | 1.0 | 35 | 28.5–31.4 |
| [76] | 2 | 1 | 0 | 160 | 400 | 0.4|0.6 | 750 | 1140 | 20 | 8 | 1700 | 0–0.5 | 0.5 | 30 | 42.7–45.1 |
| [77] | 2 | 1 | 0 | 230 | 535 | 0.5 | 556 | 1079 | 16 | 0 | 1345 | 0–1.0 | 0.6 | 30 | 36.5–41.1 |
| [37] | 2 | 0 | 0 | 165 | 300–471 | 0.4 | 690–760 | 1038–1140 | 20 | 1.8–2.8 | 380 | 1 | 0.5 | 30 | 23.8–39.0 |
| [78] | 18 | 0 | 1 | 195–228 | 361–475 | 0.4 | 630–875 | 715–1180 | 20 | 0 | 380 | 0–2 | 0.94 | 32.2 | 28.1–34.1 |
| [79] | 2 | 1 | 0 | 166 | 415 | 0.4 | 838.6 | 1024.9 | 20 | 0 | 1345 | 0–1 | 0.55 | 35 | 40.8–42.6 |
| [80] | 5 | 0 | 1 | 161 | 460 | 0.4 | 1150 | 1048.8 | 20 | 18.4 | 808.6 | 0–1 | 0.8 | 32 | 30.0–40.6 |
| [81] | 4 | 0 | 1 | 215.5 | 480 | 0.4 | 825 | 880 | 25 | 8 | –– | 0–0.51 | 0.5 | 38 | 40.6–49.3 |
| [82] | 16 | 0|1 | 0|1 | 160–200 | 258–513 | 0.4|0.5|0.6 | 540–868 | 1012–1283 | 20 | 0 | 500–1325 | 0–0.7 | 0.55–1.15 | 32–50 | 27.0–47.0 |
| [83] | 5 | 1 | 0 | 172 | 400 | 0.4 | 730 | 1046–1100 | 15 | 0 | –– | 0 | 0.8 | 32 | 27.7–37.0 |
| [84] | 10 | 0 | 0 | 161.0–167.7 | 453.3–460.0 | 0.4 | 699.2 | 1594.2 | 20 | 18.1–18.4 | 808.6 | 0–1.6 | 0.8 | 32–40 | 43.5–56.0 |
| [85] | 28 | 1 | 0 | 161.7 | 437 | 0.4 | 756 | 1210 | 20 | 1.3–6.1 | –– | 0–1.5 | 0.7 | 35–50 | 31.8–50.3 |
| [86] | 3 | 1 | 0 | 168.1 | 410 | 0.4 | 1073 | 645 | 16 | 4.1–5.7 | 1100 | 0–1 | 0.8 | 50 | 32.1–38.7 |
| [87] | 3 | 1 | 0 | 167.7 | 390 | 0.4 | 1075 | 758 | 16 | 2.3–3.1 | 1100 | 0–1.45 | 0.8 | 50 | 36.9–40.5 |
| [88] | 9 | 1 | 0 | 198–205 | 440–460 | 0.4|0.5 | 924–985 | 721–846 | 12 | 11.1–12.8 | 1225 | 0.76 | 0.62 | 40 | 52.4–70.0 |
| [89] | 5 | 1 | 0 | 165 | 300 | 0.6 | 1128.8 | 806.3 | 16 | 2.5 | 1050–1100 | 0–0.5 | 0.55–0.75 | 35–60 | 17.6–29.2 |
| [90] | 6 | 1 | 0 | 190 | 380 | 0.6 | 1082.0 | 742.0 | 12 | 0.0–2.4 | 2200 | 0–0.63 | 0.35 | 30 | 21.6–43.92 |
| [91] | 3 | 1 | 0 | 169.1 | 412.4 | 0.4 | 927.8 | 890.7 | 12 | 0.0 | 1100 | 0–0.63 | 1 | 50 | 40.1–41.6 |
| [92] | 3 | 1 | 0 | 188.0 | 400.0 | 0.5 | 610.0 | 1132.0 | 10 | 3.3 | 1270 | 0–1 | 0.62 | 30 | 36.4–40.5 |
| Tot. | 422 | 0|1 | 0|1 | 123–398 | 258–651 | 0.3–0.7 | 408–1225 | 356.0–1594.2 | 10–40 | 0.0–18.4 | 380–2200 | 0–2 | 0.1–1.2 | 25–62 | 16–88 |
Note. In this table, is rounded to one decimal place.The datasets for the current study were derived from the comprehensive database compiled by Wang et al. [8], which served as a basis for the present study. Their study focused on the mechanical characteristics of normal and high-strength SFRC mixtures that only contained Portland cement (type I), natural aggregate, and a single type of steel fiber. A further aspect of ensuring the integrity of the compressive data has been achieved by considering the test specimen cylindrical with a diameter of 150 and a height of 300 mm. As a result, the conversion factors in Table 4 were applied to ensure consistency in the test results.
Table 4.
Data consistency conversion factors.
| Specimen type | Conversion factor | Source | Note |
|---|---|---|---|
| Cubic | 0.80 | ACI 318 [93] | Below 60 MPa strength |
| Cubic | 0.90 | ACI 318 [93] | Above 60 MPa strength |
| Prismatic | 0.96 | Wu et al. [94] | –– |
Table 5.
Descriptive statistics of the processed datasets.
| Variable | Mean | StDev | Minimum | Q1 | Median | Q3 | Maximum |
|---|---|---|---|---|---|---|---|
| 0.8012 | 0.3997 | 0.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| 0.0865 | 0.2814 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | |
| 181.19 | 23.62 | 123.00 | 165.00 | 175.00 | 192.50 | 264.00 | |
| 394.97 | 74.01 | 258.00 | 342.00 | 392.00 | 450.00 | 651.00 | |
| 0.472 | 9.23 | 0.285 | 0.390 | 0.4800 | 0.550 | 0.690 | |
| 804.05 | 152.58 | 488.00 | 713.00 | 756.00 | 911.00 | 1225.00 | |
| 1067.6 | 210.6 | 356.0 | 945.0 | 1088.6 | 1206.3 | 1594.2 | |
| 19.542 | 5.218 | 10.000 | 19.000 | 20.000 | 20.000 | 40.000 | |
| 3.451 | 4.131 | 0.000 | 0.000 | 2.750 | 4.963 | 18.400 | |
| 989.4 | 378.5 | 380.0 | 600.0 | 1050.0 | 1200.0 | 2200.0 | |
| 0.7246 | 0.5377 | 0.0000 | 0.3840 | 0.5780 | 1.0000 | 2.0000 | |
| 0.7553 | 0.1970 | 0.1000 | 0.7000 | 0.7500 | 0.9000 | 1.2150 | |
| 44.015 | 12.178 | 25.000 | 32.300 | 40.000 | 60.000 | 62.000 | |
| 39.677 | 11.034 | 16.000 | 31.800 | 37.418 | 45.358 | 70.000 |
Table 6.
XG Boost hyperparameters for the initial and fine-tuned models.
| Hyperparameter | Role | Range | Default value (Model-0) | Optimized value (Model-1) |
|---|---|---|---|---|
| max_depth | Tree Maximum Depth: Modifying this parameter to higher values results in a more intricate model, increasing the risk of overfitting. | 6 | 52 | |
| n_estimators | This hyperparameter dictates the quantity of boosting iterations or trees incorporated within the ensemble. | 100 | 325 | |
| learning_rate | step size shrinkage employed during updates is intended to mitigate overfitting | 0–1 | 0 | 0.2 |
| colsample_bytree | The subsample ratio of columns determines the proportion of features used when constructing each tree. | 0–1 | 1 | 0.1 |
| subsample | Subsample ratio of training instance (e.g., 0.5 indicates 50% of data used prior to growing trees). | >0–1 | 1 | 0.5 |
| reg_alpha | L1 regularization (increasing its value makes the model more conservative). | –– | 0 | 0.01 |
| reg_lambda | L2 regularization (increasing its value makes the model more conservative). | –– | 1 | 10 |
| gamma | Regularization parameter for tree pruning that specifies the minimum loss reduction required to make a split. | 0 | 0.1 |
Table 7.
Performance metrics of the initial and fine-tuned models.
| Performance indicator | Model-0 | Model-1 | ||
|---|---|---|---|---|
| Training set | Testing set | Training set | Testing set | |
| 0.742 | 3.541 | 1.239 | 2.797 | |
| 2.576 | 28.413 | 4.008 | 16.997 | |
| 1.605 | 5.330 | 2.002 | 3.933 | |
| 0.978 | 0.776 | 0.966 | 0.879 | |
Table 8.
The physicochemical properties of the used OPC.
| Oxide composition (%) | L.O.I. (%) | Specific gravity | Fineness (m2/kg) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| SiO2 | Al2O3 | Fe2O3 | CaO | MgO | Na2Oeq | SO3 | |||
| 20.20 | 5.49 | 4.12 | 65.43 | 0.71 | 0.26 | 2.61 | 1.38 | 3.14 | 373 |
Table 9.
Properties of the used steel fibers.
| Fiber | Length (mm) |
Diameter (mm) |
Aspect ratio | Young’s Modulus (GPa) |
Tensile strength (MPa) |
|
|---|---|---|---|---|---|---|
| shape | ID | |||||
 |
F1 | 40 | 0.62 | 65 | 210 | 1250 |
| F2 | 50 | 0.62 | 80 | |||
| F3 | 60 | 0.75 | 80 | |||
Table 10.
Test features and response.
| Model’s input variables | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | ID | ||||||||||||||||
| 1 | H-F1-0.5 | 1 | 0 | 157.5 | 450 | 0.35 | 716 | 1053 | 10 | 0.68 | 1250 | 0.62 | 0.5 | 65 | 69.4 | 74.1 | 0.937 |
| 2 | N-F1-0.5 | 1 | 0 | 157.5 | 350 | 0.45 | 798 | 1078 | 10 | 0.42 | 1250 | 0.62 | 0.5 | 65 | 60.7 | 56.3 | 1.078 |
| 3 | H-F1-1.0 | 1 | 0 | 157.5 | 450 | 0.35 | 716 | 1053 | 10 | 0.68 | 1250 | 0.62 | 1.0 | 65 | 72.3 | 65.8 | 1.099 |
| 4 | N-F1-1.0 | 1 | 0 | 157.5 | 350 | 0.45 | 798 | 1078 | 10 | 0.42 | 1250 | 0.62 | 1.0 | 65 | 64.1 | 61.8 | 1.037 |
| 5 | H-F1-1.5 | 1 | 0 | 157.5 | 450 | 0.35 | 716 | 1053 | 10 | 0.68 | 1250 | 0.62 | 1.5 | 65 | 75.9 | 79.7 | 0.952 |
| 6 | N-F1-1.5 | 1 | 0 | 157.5 | 350 | 0.45 | 798 | 1078 | 10 | 0.42 | 1250 | 0.62 | 1.5 | 65 | 62.3 | 59.1 | 1.054 |
| 7 | H-F2-0.5 | 1 | 0 | 157.5 | 450 | 0.35 | 716 | 1053 | 10 | 0.68 | 1250 | 0.62 | 0.5 | 80 | 73.8 | 71.7 | 1.029 |
| 8 | N-F2-0.5 | 1 | 0 | 157.5 | 350 | 0.45 | 798 | 1078 | 10 | 0.42 | 1250 | 0.62 | 0.5 | 80 | 55.8 | 60.4 | 0.924 |
| 9 | H-F2-1.0 | 1 | 0 | 157.5 | 450 | 0.35 | 716 | 1053 | 10 | 0.68 | 1250 | 0.62 | 1.0 | 80 | 76.4 | 81.2 | 0.941 |
| 10 | N-F2-1.0 | 1 | 0 | 157.5 | 350 | 0.45 | 798 | 1078 | 10 | 0.42 | 1250 | 0.62 | 1.0 | 80 | 62.3 | 61.1 | 1.020 |
| 11 | H-F2-1.5 | 1 | 0 | 157.5 | 450 | 0.35 | 716 | 1053 | 10 | 0.68 | 1250 | 0.62 | 1.5 | 80 | 77.3 | 80.3 | 0.963 |
| 12 | N-F2-1.5 | 1 | 0 | 157.5 | 350 | 0.45 | 798 | 1078 | 10 | 0.42 | 1250 | 0.62 | 1.5 | 80 | 64.2 | 69.6 | 0.922 |
| 13 | H-F3-0.5 | 1 | 0 | 157.5 | 450 | 0.35 | 716 | 1053 | 10 | 0.68 | 1250 | 0.75 | 0.5 | 80 | 68.0 | 63.2 | 1.076 |
| 14 | N-F3-0.5 | 1 | 0 | 157.5 | 350 | 0.45 | 798 | 1078 | 10 | 0.42 | 1250 | 0.75 | 0.5 | 80 | 58.9 | 60.7 | 0.970 |
| 15 | H-F3-1.0 | 1 | 0 | 157.5 | 450 | 0.35 | 716 | 1053 | 10 | 0.68 | 1250 | 0.75 | 1.0 | 80 | 70.6 | 68.9 | 1.025 |
| 16 | N-F3-1.0 | 1 | 0 | 157.5 | 350 | 0.45 | 798 | 1078 | 10 | 0.42 | 1250 | 0.75 | 1.0 | 80 | 59.7 | 61.8 | 0.966 |
| 17 | H-F3-1.5 | 1 | 0 | 157.5 | 450 | 0.35 | 716 | 1053 | 10 | 0.68 | 1250 | 0.75 | 1.5 | 80 | 78.6 | 83.4 | 0.942 |
| 18 | N-F3-1.5 | 1 | 0 | 157.5 | 350 | 0.45 | 798 | 1078 | 10 | 0.42 | 1250 | 0.75 | 1.5 | 80 | 66.2 | 68.6 | 0.965 |
| 19 | H-CTRL | 1 | 0 | 157.5 | 450 | 0.35 | 716 | 1053 | 10 | 0.68 | –– | –– | –– | –– | 61.7 | 59.8 | 1.032 |
| 20 | N-CTRL | 1 | 0 | 157.5 | 350 | 0.45 | 798 | 1078 | 10 | 0.42 | –– | –– | –– | –– | 52.4 | 57.2 | 0.916 |
| 0.992 | |||||||||||||||||
| 0.058 | |||||||||||||||||
| CV | 0.059 | ||||||||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







