Prerpints.org logo
Preprint
Article

A Three-Dimensional Time-Dependent Model of the Degradation Caused by Chromium Poisoning in a Solid Oxide Fuel Cell Stack

Altmetrics

Downloads

127

Views

76

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

24 October 2023

Posted:

25 October 2023

You are already at the latest version

Alerts
Abstract
Chromium poisoning strongly influences the performance of solid oxide fuel cell (SOFC) stacks. A three-dimensional, time-dependent, computational fluid dynamics model of a single channel of a F10 SOFC stack in Forschungszentrum Jülich GmbH is developed to investigate chromium poisoning for different stack designs, temperatures and absolute air humidities. The model takes into account both chemical and electrochemical mechanisms of chromium poisoning and is able to predict the spatial distribution of SrCrO4 and Cr2O3. The voltage degradation over 100 kh can be simulated quantitatively. According to the simulation results, chromium poisoning is almost eliminated by the application of the protective coating fabricated by the atmospheric plasma-spraying (APS) technology. Besides, with the help of the APS protective coating, operating a SOFC stack with less dehumidified air at 650 oC is possible according to the simulation.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

Solid oxide fuel cells (SOFCs) are a promising future power supply technology due to their high efficiency, fuel flexibility, low exhaust emissions and ability to be coupled with the heating sectors [1,2]. Currently, the mainstream material of the interconnects is steel. The metal interconnect (MIC) provides strong support and satisfying conductivity at the intermediate temperature, but it is found that the volatile chromium species CrO2(OH)2 and CrO3 can be released by the oxide scale, (e.g., Cr2O3) formed on the surface of MIC, via the following reactions
2 C r 2 O 3 ( s ) + 3 O 2 ( g ) + 4 H 2 O ( g ) ⇄ 4 C r O 2 ( O H ) 2 ( g )
2 C r 2 O 3 ( s ) + 3 O 2 ( g ) ⇄ 4 C r O 3 ( g )
The gaseous chromium species lead to a drastic degradation in the air electrode through chromium poisoning [3,4,5] that has to be mitigated [6]. Numerical modelling can be a helpful assistance in studying chromium poisoning, as it can quantitatively predict the voltage degradation under different operation conditions and stack designs. However, only limited models of chromium poisoning can be found in the current literature. A representative work comes from reference [7], which performed a one-dimensional time-dependent simulation and studied the triple-phase-boundary (TPB) and voltage evolution due to chromium poisoning in the composite air electrode (La,Sr)MnO3/ZrO2−Y2O3 (LSM/YSZ). A Butler-Volmer expression was used to predict the decrease of TPB as a result of chromium deposition. In other words, the model only considers chromium poisoning based on electrochemical reactions. The model was later extended to three dimensions [8]. The TPB was found more likely to be degraded at the interface between the air electrode and the electrolyte (AEL/EELC). A similar model was applied to study the local degradation in a 18-cells SOFC stack [9]. It was shown that chromium poisoning was the dominant degradation in the last period of operation.
Although the above models could be used to study chromium poisoning and hence simulate the voltage degradation, they were designed for LSM/YSZ air electrodes and only considered electrochemical chromium poisoning. The state-of-art air electrode consists of a mixed ionic and electronic conductor, La0.58Sr0.4Co0.2Fe0.8O3-δ (LSCF), which exhibits a different scenario of degradation owing to chromium poisoning. For example, the formation of strontium chromate on the surface of air electrodes made by LSCF was widely observed after fuel cell operation [4,10,11]. More importantly, strontium chromate was probably generated via chemical reactions due to several findings: 1) SrO segregation on the surface of LSCF was observed at the high temperature [12,13], 2) It was found that SrO could react with gaseous chromium species to produce strontium chromate based on thermodynamic calculations [14], and 3) strontium chromate was found on the surface of LSCF under the open-circuit-voltage condition [11]. The formation of strontium chromate should not be ignored in the model as it not only lowers the conductivity, but also decreases the reactive area of the air electrode.
Another drawback in the above models is that the effect of the protective coating on the inner surface of air channels is missing. However, the protective coating exists in a real SOFC stack and an inferior protective coating surely leads to more severe chromium poisoning. For example, it has been shown that [15,16] a SOFC stack with a protective coating prepared by wet-powder-spraying (WPS) was more strongly degraded by chromium poisoning than one with a protective coating prepared by atmospheric plasma-spraying (APS), as the former had a higher porosity whereas the latter provided a fairly dense coating.
To improve the understanding of chromium poisoning in a real SOFC stack, a physical model coupling both electrochemical reactions and chemical reactions is useful. In this study, a three-dimensional computational fluid dynamics (CFD) model of a single channel of a F10 SOFC stack in Forschungszentrum Jülich GmbH (FZJ) considering chromium poisoning on the air electrode side has been developed to investigate the degradation of the F10 SOFC stack [17] performance. The voltage degradation due to decreasing reactive area during 100 kh of operation is simulated. The effects of temperature, the partial pressure of the steam in the air inlet and different protective coatings on chromium poisoning are discussed.

2. Geometry of the model

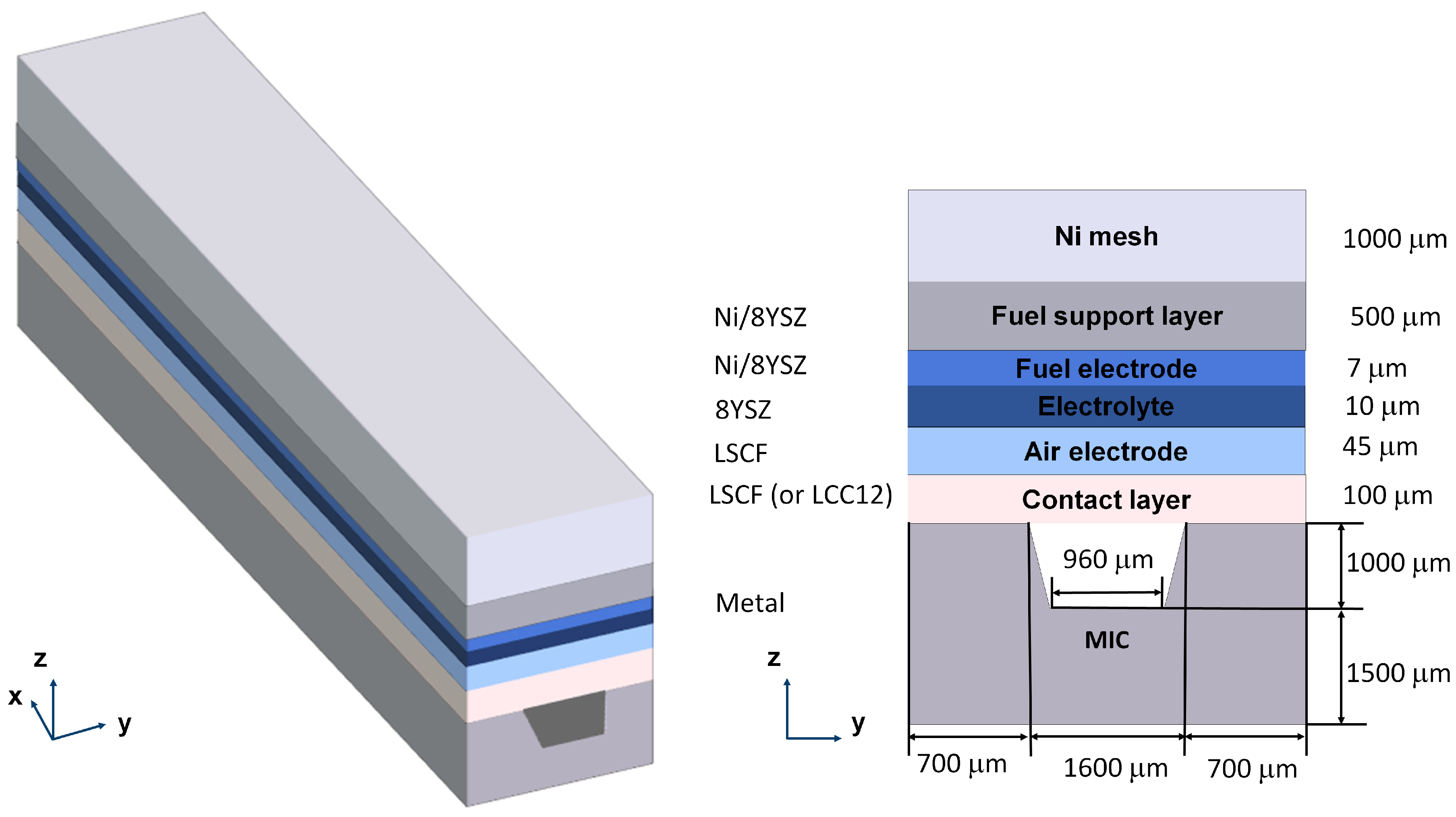
The model considers one channel of the F10 SOFC stack in FZJ. The geometry is shown in Figure 1, whose details can be found in reference [18]. On the fuel side, a Ni mesh is chosen as the gas distributor. A thick fuel electrode support layer provides the necessary mechanical strength for the cell. A thin fuel electrode is applied where the electrochemical reaction takes place. Both the fuel electrode and the support layer are made of Ni/8 mol % ZrO2−Y2O3 (8YSZ). On the air side, LSCF is chosen as the material for the air electrode. There is a contact layer (CL) between the MIC and the air electrode (AEL). It can be made of LSCF or La0.97Mn0.4Co0.3Cu0.3O3-δ (LCC12). Unlike LSCF, LCC12 serves additionally as the chromium getter since it can absorb chromium gaseous species by forming a stable Mn-Cr spinel phase [16]. Besides, there is no strontium segregation inside LCC12.
Additionally, there should be a protective coating on the inner surface of the air channel in a real SOFC stack to prevent chromium poisoning. It is simplified as a thin surface (no volume) in the model due to the computational cost, and its influence on chromium poisoning is considered in the boundary condition for the mass transport of chromium gaseous species. Details can be found in Section 3.2.

3. Numerical model

The numerical model in this work is the extension of the previous work, where a steady-state model is developed [18,19]. By adding a degradation model of chromium poisoning, the model becomes time-dependent. Only the governing equations and parameters related to chromium poisoning are present in this work. Information about the steady-state model and parameters of the material properties, such as the conductivity and porosity of the electrodes, can be found in the reference [18].

3.1. Assumptions

There are three important assumptions for the model regarding the chromium poisoning. First, chromium poisoning is only considered on the air side. In principle, it can happen on the fuel side as well. However, it was demonstrated that chromium poisoning insignificantly affected the degradation of the fuel electrode in the fuel cell mode owing to a rather low partial pressure of chromium gaseous species [20]. Secondly, only CrO2(OH)2 is considered for chromium poisoning. Thermodynamic calculations pointed out that even in the case of low water partial pressure (e.g., ∼ 0.1% atm), CrO2(OH)2 is dominant over CrO3 at the typical operation temperature of the SOFC stacks considered here (600 ∼ 800 °C) [3]. Thirdly, the degradation only arises from the decreasing reactive area of LSCF due to chromium deposition processes. Other factors that can also lead to degradation, such as fractures of material and lowered conductivity due to the formation of secondary phases, are currently not considered in the model.

3.2. Mass transport of CrO2(OH)2

The mass transport of CrO2(OH)2 is governed by
∂ ( c Y CrOH ) ∂ t + ∇ · ( c U → Y CrOH ) + ∇ · N → CrOH = S o u r c e mole , CrOH
where c is the molar density of the air, Y CrOH is the molar fraction of CrO2(OH)2 in the air, U → is the velocity of the air that is solved from the momentum transport equation [18], N → CrOH is the molar diffusion flux of CrO2(OH)2 and S o u r c e mole , CrOH is the source term of moles of CrO2(OH)2, which is related with the adsorption of CrO2(OH)2 on the LSCF surface and its definition can be found in Appendix A. Fick’s law [21,22] is used to solve the molar flux, given by the following equation
N → CrOH = − D CrOH , air ∇ ( c Y CrOH )
where D CrOH , air is the diffusion coefficient of CrO2(OH)2 in the air.
In order to solve Equation (3), the boundary condition of Y CrOH needs to be determined. It is assumed that CrO2(OH)2 only originates from the inner surface of the air channel according to the reaction (1). Followed by the reference [23,24], the reaction (1) reaches the thermal equilibrium on the inner surface of the air channel and therefore the molar fraction of CrO2(OH)2 at the surface of an air channel without any coatings, Y CrOH , uncoated , can be calculated as
Y CrOH , uncoated = ( K CrOH · Y H 2 O 4 · Y O 2 3 ) 0.25
where K CrOH is the thermal equilibrium constant of reaction (1), Y H 2 O is the molar fraction of H2O in the air and Y O 2 is the molar fraction of the O2 in the air. According to the database summarized by Ebbinghaus [25], K CrOH is
K CrOH = 10 − 12262 / T [ K ] − 5.2
where T is the temperature. It should be noted that Equation (5) is valid for surfaces without any coatings. However, in a real FZJ SOFC stack, there is usually a protective coating on the inner surface of the air channel preventing chromium poisoning. To consider the protecting effect, the surface-averaged molar fraction, Y CrOH , is used. For each mesh grid, the surface-average molar fraction at the channel surface is calculated by including the porosity of the protective coating, ε coating , i , to Equation (5) as follows:
Y CrOH = A uncoated Y CrOH , uncoated A = ε coating , i · ( K CrOH · Y H 2 O 4 · Y O 2 3 ) 0 . 25
where A is the surface area of the whole mesh surface, A uncoated is the uncoated surface area and i refers to the technique for fabricating the coating.

3.3. The kinetic model of chromium poisoning

When chromium gaseous species are adsorbed on LSCF surface, the reactive surface decreases and consequently it is more difficult for oxygen being adsorbed and having the electrochemical reaction on LSCF surface. To model the process, a kinetic model that can predict the free adsorption area on LSCF is needed. This section will introduce the Langmuir model to describe the adsorption and desorption first. Then electrochemical and chemical reactions are considered for the adsorbate to calculate surface coverage of free adsorption sites.
Based on the Langmuir model [26,27], when gas molecules are adsorbed on the surface of LSCF, the change of the surface coverage can be described by
d Θ i d t = k a , i Θ free − k d , i Θ i
where Θ i is the surface coverage of the adsorbate i, k a , i is the adsorption rate of i, Θ free is the free surface coverage that can be adsorbed and k d , i is the desorption rate of i. k a , i can be obtained through Langmuir–Hertz equation [28] as follows
k a , i = S i P i Γ LSCF 2 π M i R T
where S i is the sticking coefficient of the gas i, P i is the partial pressure of the gas i, Γ LSCF is the density of the adsorption sites on LSCF particles, M i is the molar mass of the species i, R is the universal gas constant. k d , i generally can be calculated via [28]
k d , i = k a , i exp Δ G ads , i R T
where Δ G ads , i is the Gibbs free energy change in case species i being adsorbed on the LSCF surface.
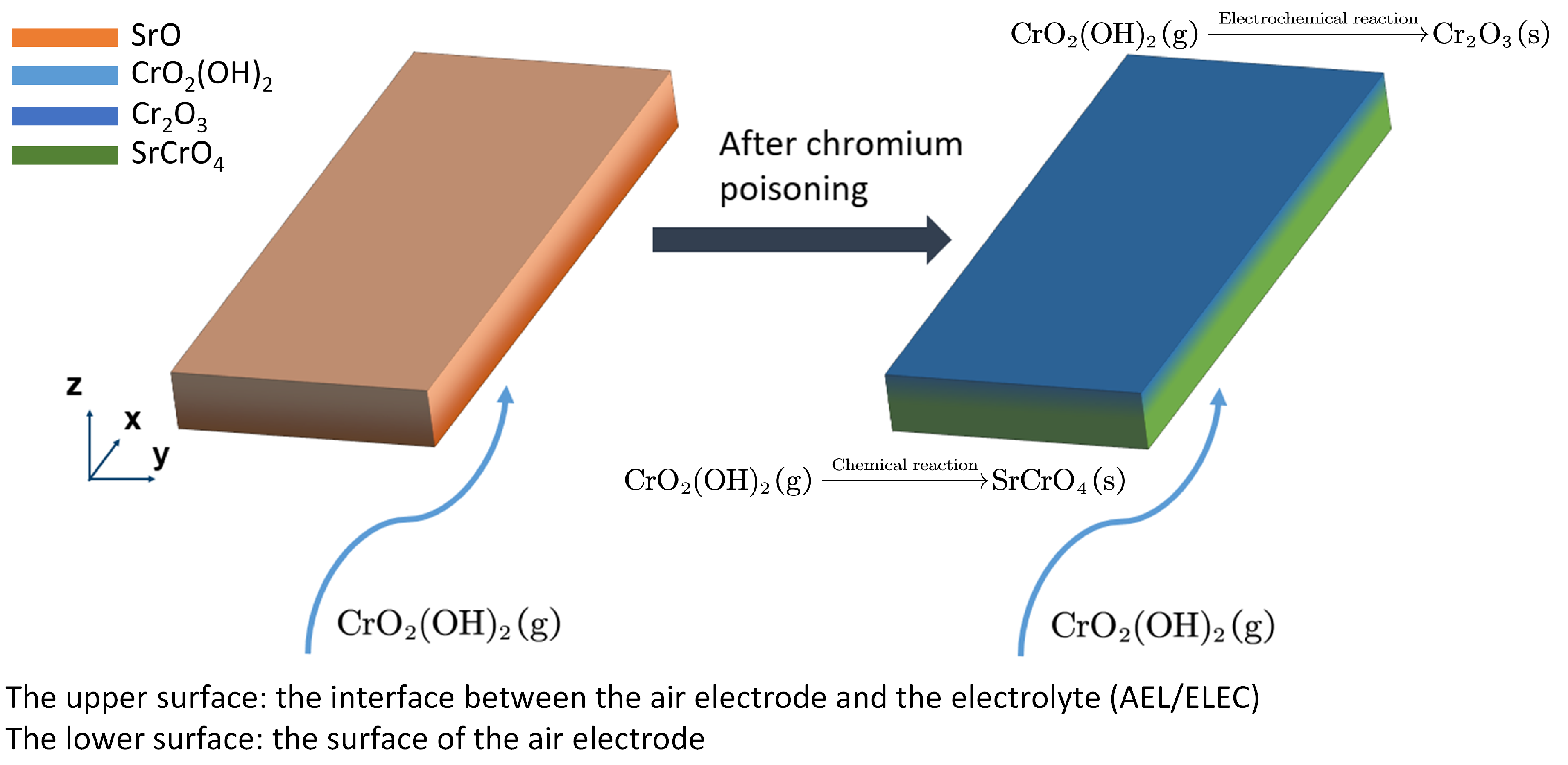
In addition to adsorption and desorption between the gas and the surface of LSCF, there exists two reactions related to chromium poisoning. Figure 2 illustrates how chromium poisoning takes place inside the AEL made of LSCF. At the surface of the AEL, due to strontium segregation (see the left figure in Figure 2), the chemical reaction generating SrCrO4 is dominating, which happens on the LSCF surface via [29]
C r O 2 ( O H ) 2 ( L S C F ) + S r O ( L S C F ) ⇄ k chemCr S r C r O 4 ( LSCF ) + H 2 O ( LSCF ) Δ G SrCrO 4
where k chemCr and Δ G SrCrO 4 are the rate of the surface coverage change due to the reaction and the Gibbs free energy change of the reaction (11), respectively. The method of determining Δ G SrCrO 4 is given in Appendix B.
As CrO2(OH)2 diffuses deeper towards AEL/ELEC, the overpotential gradually decreases (to be more negative) which is likely to result in the electrochemical reaction being nonnegligible [3], as shown in the right figure in Figure 2. The electrochemical reaction is
C r O 2 ( O H ) 2 ( LSCF ) + 3 e − → k chemCr 0.5 C r 2 O 3 ( LSCF ) + 1.5 O 2 − ( LSCF ) + H 2 O ( LSCF )
where k eleChemCr is the rate of the surface coverage change due to the reaction (12). Similar to the reference [7,8], a Bulter-Volmer type expression is employed to describe k eleChemCr :
k eleChemCr = k eleChemCr , 0 P CrO 2 OH 2 0 . 5 / P H 2 O 0 . 5 2 sinh 3 F 2 R T η air
where η air is the overpotential in the AEL. k eleChemCr , 0 is chosen as -5 × 10 − 8 s − 1 in the model.
Considering all these processes and assuming the chemical reaction (11) obeys the thermal equilibrium, the kinetic model for chromium poisoning is summarized as follows:
d Θ H 2 O d t = k a , H 2 O Θ free − k d , H 2 O Θ H 2 O + k chemCr Θ CrOH Θ SrO + k eleChemCr Θ C r O H
d Θ S r O d t = − k chemCr Θ CrOH Θ SrO
d Θ S r C r O 4 d t = k chemCr Θ CrOH Θ SrO
d Θ C r O H d t = k a , C r O H Θ free − k d , C r O H Θ C r O H − k chemCr Θ CrOH Θ SrO − k eleChemCr Θ C r O H
d Θ C r 2 O 3 d t = 0.5 k eleChemCr Θ CrOH
Θ H 2 O + Θ S r O + Θ S r C r O 4 + Θ C r O H + Θ C r 2 O 3 + Θ f r e e = 1
K S r C r O 4 = Θ S r C r O 4 Θ H 2 O Θ SrO Θ CrOH
where the subscript "H2O", "SrO", "SrCrO4", "CrOH" and "Cr2O3" denote the chemical species of H2O, SrO, SrCrO4, CrO2(OH)2 and Cr2O3, respectively. K SrCrO 4 is the thermal equilibrium constant of reaction (11), defined as K SrCrO 4 = exp − Δ G SrCrO 4 R T . k chemCr can be obtained from the Equation (20) by getting the time derivatives at the both side of the equation as follows:
d Θ SrCrO 4 Θ H 2 O d t = K SrCrO 4 d Θ CrOH Θ SrO d t → k chemCr = K SrCrO 4 k a , CrOH Θ free Θ SrO − k d , CrOH + k eleChemCr Θ SrO Θ CrOH d e n − Θ SrCrO 4 k eleChemCr Θ CrOH − k d , H 2 O Θ H 2 O + k a , H 2 O Θ free d e n
where d e n is
d e n = Θ C r O H Θ SrO Θ H 2 O + Θ SrCrO 4 Θ C r O H Θ SrO + K SrCrO 4 Θ SrO 2 Θ C r O H + K SrCrO 4 Θ SrO Θ CrOH 2
Oxygen can only be adsorbed and have eletrochemical reactions on Θ free . It is supposed that the reaction current density in the AEL, i v , air , is proportional to Θ free [7,28], i v , air can be rewritten as follows:
i v , air = Θ free η air R air exp ( E a , air R T ) a O 2 − 0 . 25
Equation (23) is based on the definition of i v , air in reference [18], where more details can be found.
Parameters used in the model can be found in Table C1.

4. Numerical setting

The simulation is carried out with the help of openFuelCell2 [19], which has been coupled into an open-source library, OpenFOAM. Discretization of the time derivative is achieved by the Backward Euler method. The IDA package in SUNDIALS [30,31] was used to solve Equations (14) ∼ (19).
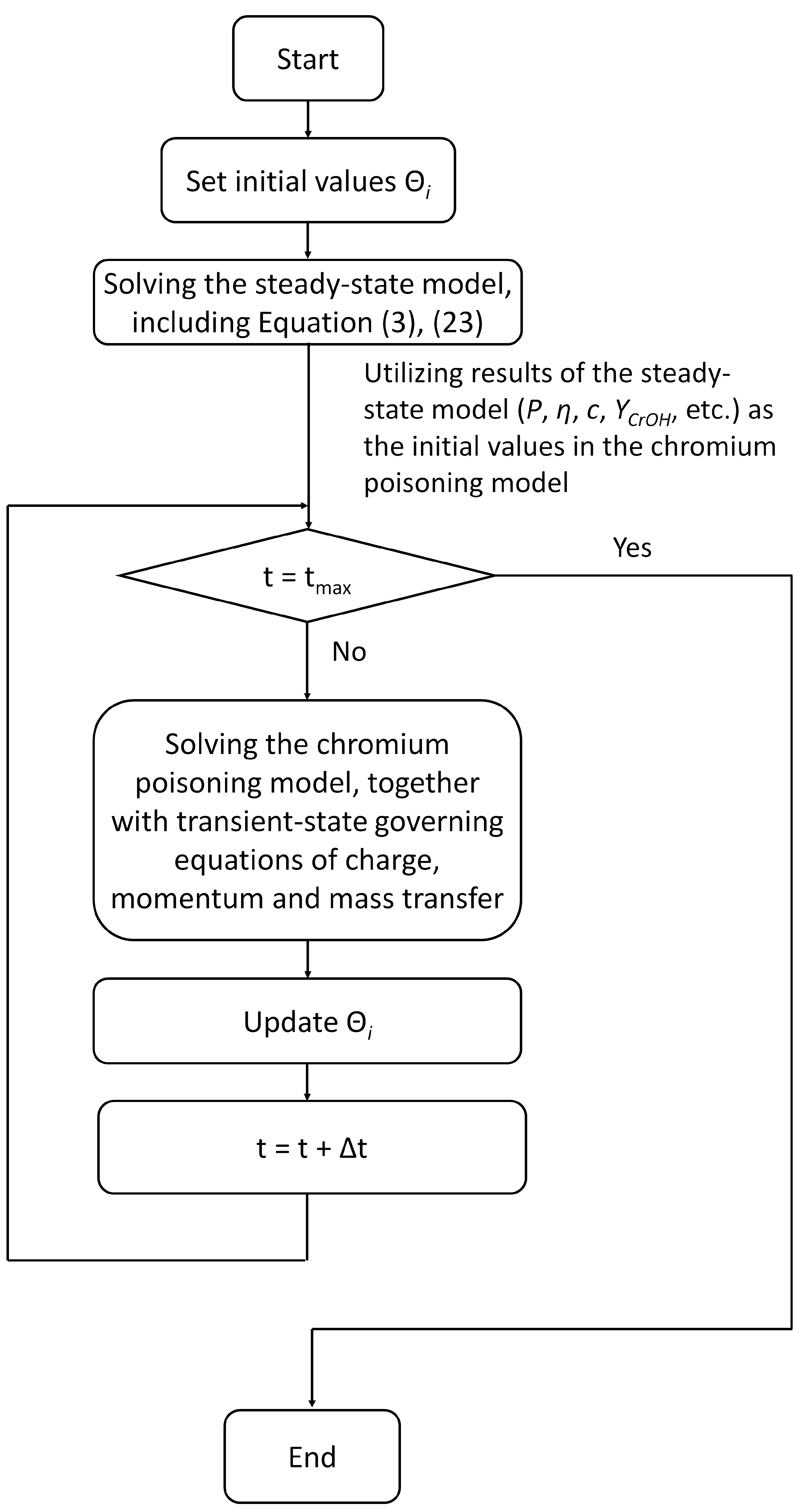
Figure 3 illustrates the procedures of numerical calculation in this work:
  • Set initial values of Θ H 2 O , Θ SrO , Θ SrCrO 4 , Θ CrOH and Θ Cr 2 O 3 . Details can be found in Appendix D and Appendix E.
  • Conduct the steady-state simulation based on the reference [18].
  • Obtain the results of steady-state simulation [18] and set them as the initial values for the time-dependent chromium poisoning simulation.
  • Set t max . t max is equal to the time period of the steady operation of the SOFC stack.
  • Conduct the chromium poisoning simulation. The chromium poisoning model is solved with other transient-state governing equations [18] of charge, momentum and mass transfer.
  • Repeat step 5 until the time reaches t max .
Table 1 presents the governing equations of the chromium poisoning model and computational domains where corresponding governing equations are applied. It should be noted that governing equations of the chromium deposition are solely valid for the components made of LSCF.
All simulations are carried out on a single core of a computer (CentOS 9) with CPU i7-9700K and 32 GB RAM.

5. Results

5.1. Validation

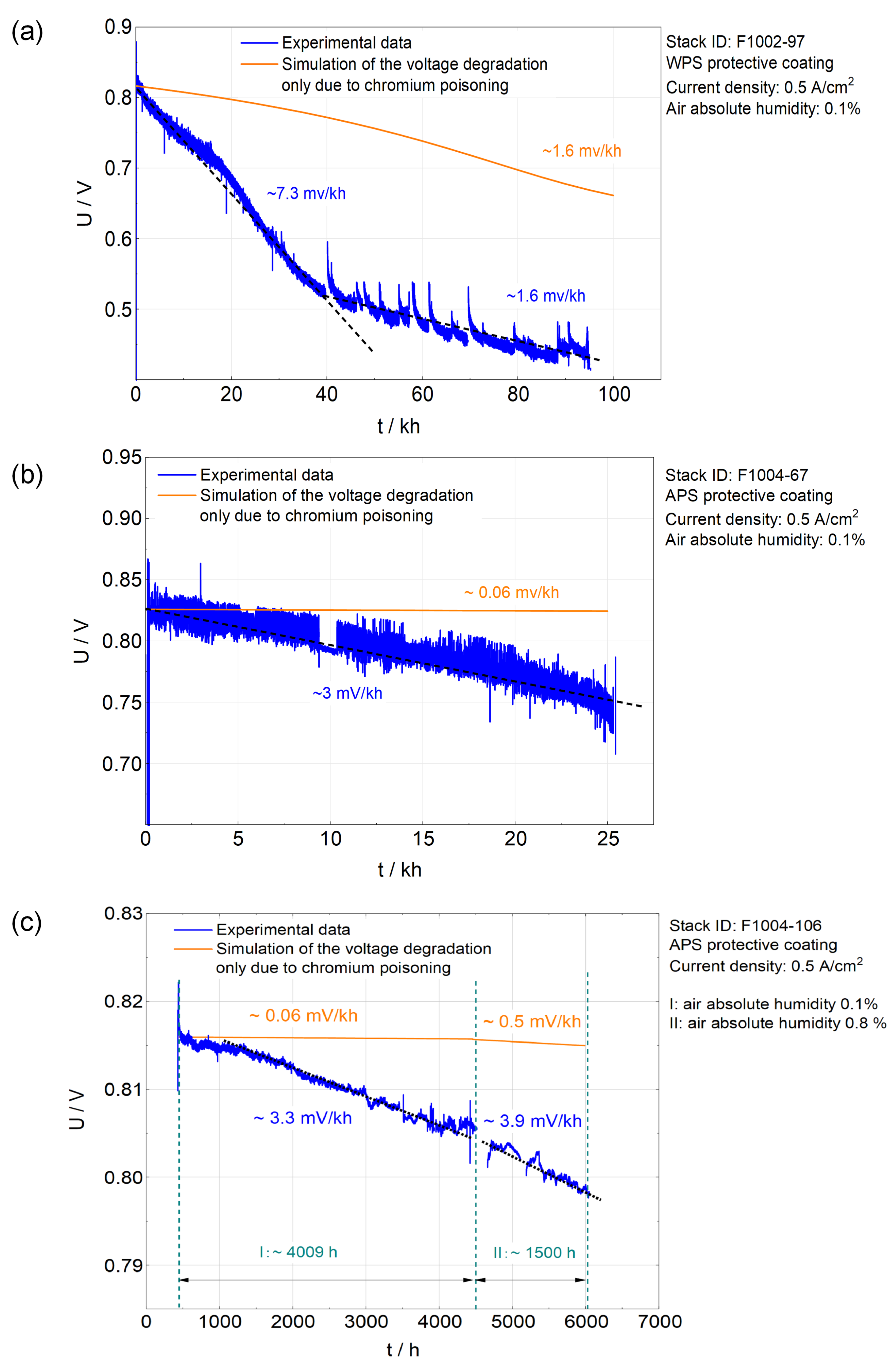
When validating the model, it should be noticed that the model in this work considers the decreasing reactive area of LSCF owing to chromium poisoning as the only degradation mechanism. Table 2 presents three stacks used for validation, where stack designs (e.g., materials of CLs and fabrication techniques for protective coatings) and operation conditions are given. Three corresponding simulations are carried out, Ut-curves of which are shown in Figure 4.
F1002-97, with LCC12 as the CL and the WPS coating as the protective coating, was operated over ∼ 100 kh. Since the WPS technique can not generate a dense coating, LCC12 that can adsorb CrO2(OH)2 is used as the CL to reduce chromium poisoning in the AEL. However, the degradation rate of F1002-97 was still notably higher than the other two stacks, using the APS protective coating. As shown in Figure 4(a), the simulation points out that the degradation solely owing to chromium poisoning causes a degradation rate of ∼ 1.6 mV/kh. The increasing specific-area-resistance (ASR) after 100 kh operation can thus be calculated as ∼ 320 m Ω cm 2 . Fang et al. [5] obtained the increasing ASR due to polarization in the AEL as ∼ 310 m Ω cm 2 by analyzing IV-curves and electrochemical impedance spectroscopy (EIS), which was close to the present simulation results. It is reasonable to compare the above two values. Chromium poisoning is believed to be the dominating degradation mechanism that increases the polarization in the AEL, because chromate contributed to the majority of the impurity in the AEL of F1002-97 [10].
F1004-67, with LSCF as the CL and APS coating as the protective coating, was operated for roughly 25 kh. The APS technique produces a suffiently dense coating that LCC12 as the CL is not needed. Thanks to the APS protective coating, the degradation rate decreased drastically. According to the simulation given in Figure 4(b), chromium poisoning is obviously suppressed as the simulated degradation rate is just ∼ 0.06 mV/kh. Experimental findings also support this conclusion. From a post-characterization, Menzler et al. [16] found a tiny amount of chromate in a similar SOFC stack with protective coating prepared by APS and operated for 36 kh. 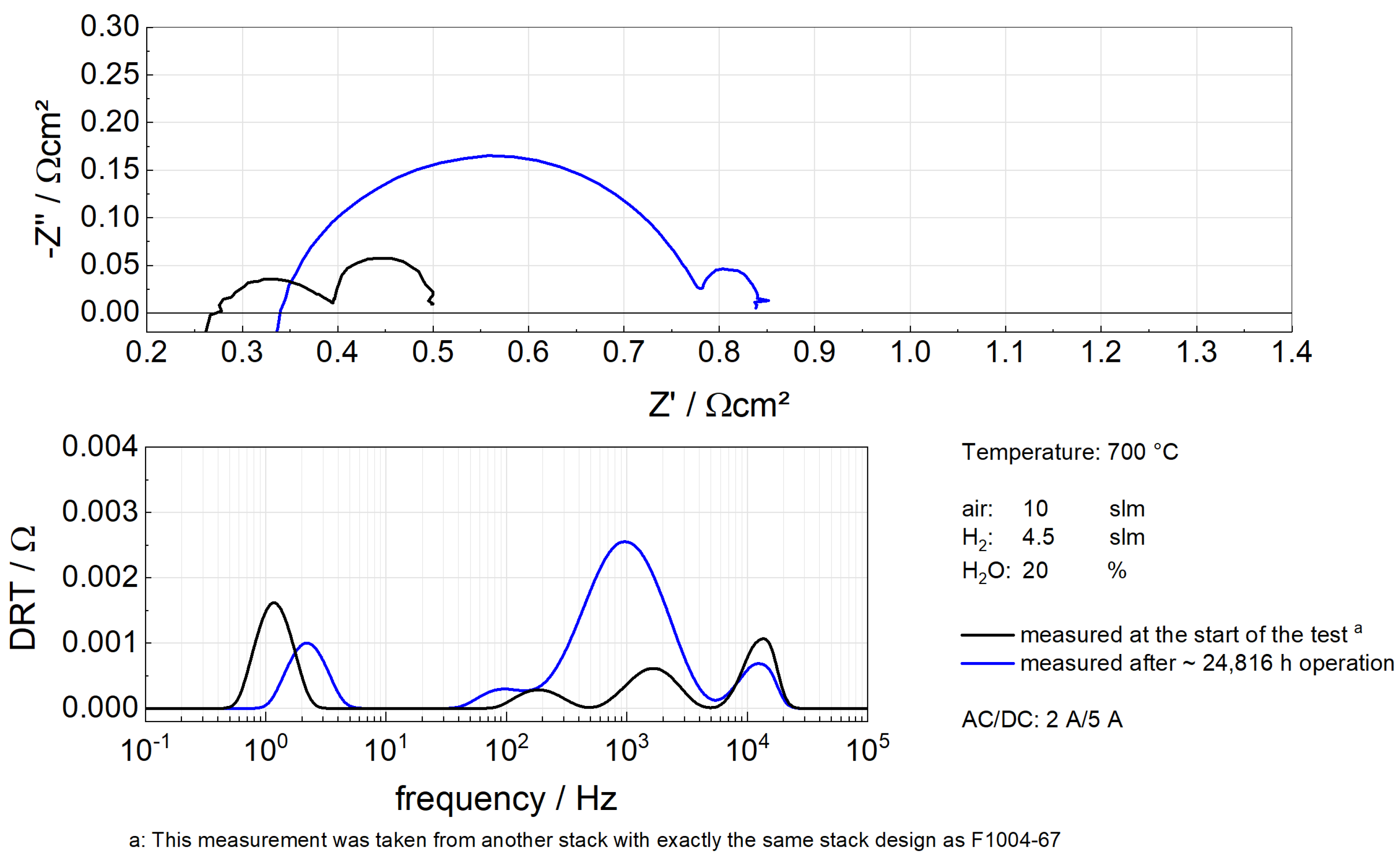It was concluded that the application of the APS protective coating could almost solve the issue of chromium poisoning [15,16]. In addition, EIS was carried out on the stack F1004-67 with 20% humidified hydrogen at 700 °C. Figure 5 shows Nyquist plots and distribution of relaxation times (DRT) for F1004-67. From the Nyquist plots, it can be seen that degradation mainly arose from the increasing polarization. Besides, the DRT suggests that the polarization was dominated by the degradation in the fuel electrode, which according to previous research is characterized by the third peak (around 1 kHz) in the DRT plot [5,33,34]. In contrast, it is clearly found that the polarization in the AEL, represented by the second peak (around 100 Hz) in the DRT plot [5,33,34], contributed slightly to the total polarization as the peak barely changed. Therefore, a conclusion could be reached that chromium poisoning was inconspicuous in the stack F1004-67.
F1004-106 had the same stack design as F1004-67, but it was operated under ambient air for ∼ 2190 h. The validation here only considers 1500 h of operation with ambient air because a progressive degradation with unknown cause happened after the replacement of gas valves (in the last operation period of 690 h) [32]. The absolute humidity of the ambient air was calculated by using the database from [35] and the calculator from [36]. The simulation from Figure 4(c) shows a small change in the absolute values (∼ 0.44 mV/kh) of degradation rates before and after ambient air is used. A similar observation is found from the experimentally measured Ut-curves (the blue curve) in Figure 4(c). Moreover, Fang et al. [32] proposed the same conclusion by analyzing EIS data of F1004-106 (the F1 stack in reference [32]).
In brief, the model agrees well with experimental findings for different stack designs and absolute humidities in the inlet air.
Preprints 88632 g005
Figure 5. EIS analysis of F1004-67. EIS was measured by a Zahner IM6 workstation. The upper figure is the Nyquist plot while the lower figure is the DRT plot produced by the Matlab toolbox DRTTOOLS [37].
Figure 5. EIS analysis of F1004-67. EIS was measured by a Zahner IM6 workstation. The upper figure is the Nyquist plot while the lower figure is the DRT plot produced by the Matlab toolbox DRTTOOLS [37].
Preprints 88632 g005

5.2. Simulation results of F1002-97

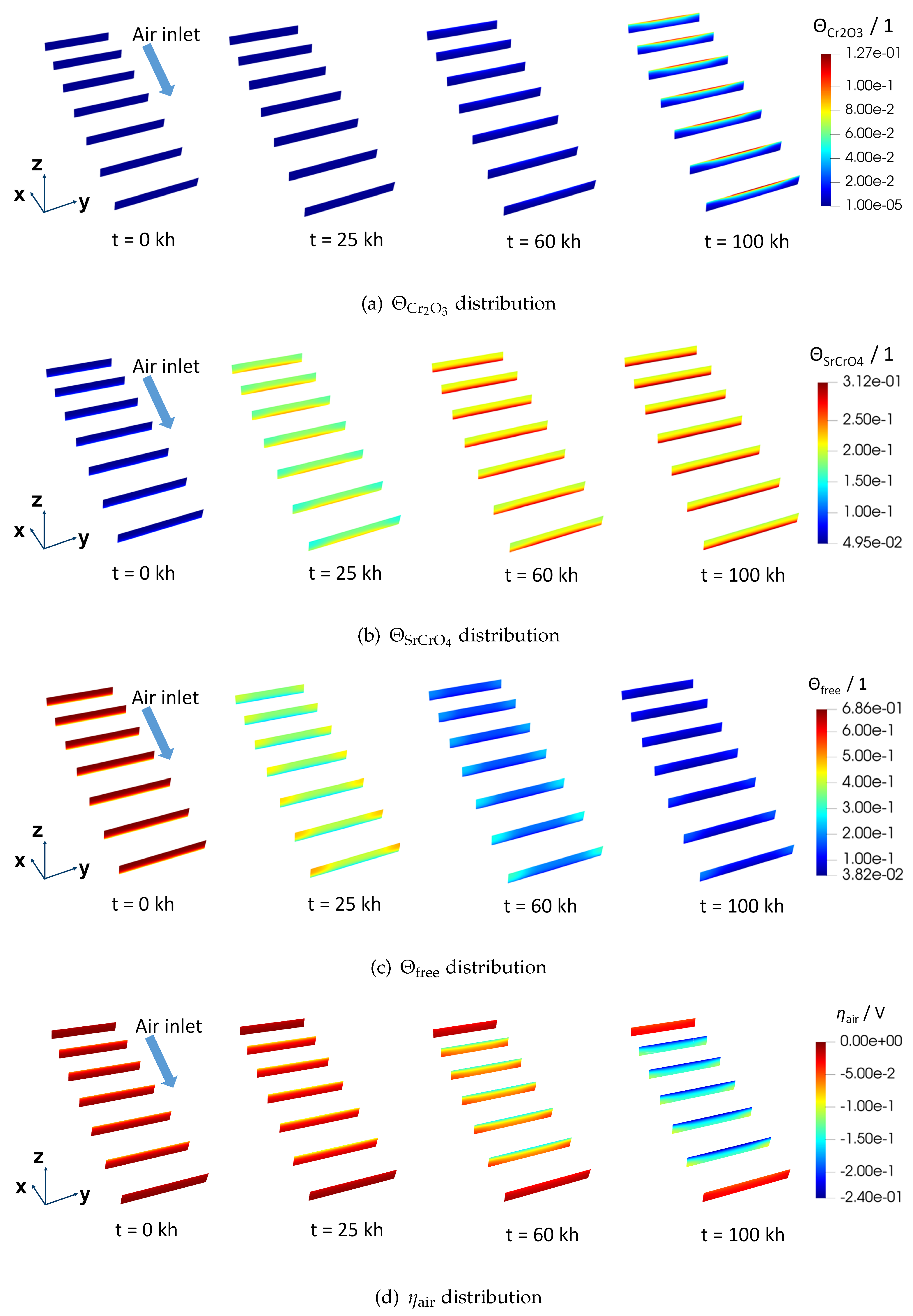
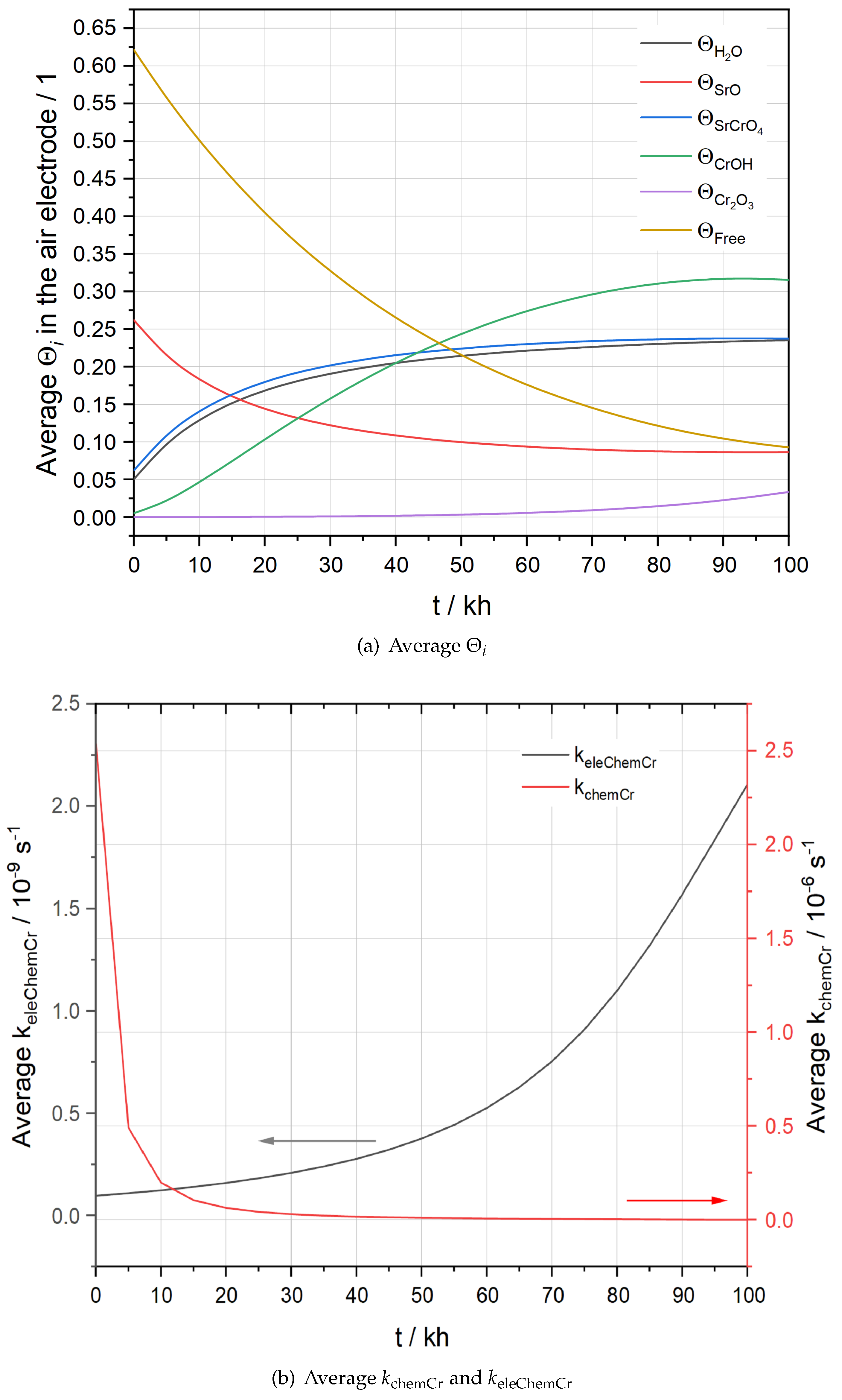
Simulation results of F1002-97 are present here to illustrate chromium poisoning. Figure 6 gives the spatial distribution of physical variables inside the AEL. Figure 7 presents the evolution of average k chemCr , k eleChemCr and Θ i inside the AEL over 100 kh.
According to Figure 6(a), Θ Cr 2 O 3 barely exists inside the AEL before 25 kh. The same result can be more clearly found in Figure 7(a), where average Θ Cr 2 O 3 is close to zero. This is because at the start of the operation, η air is not high as there is still sufficient free surface, Θ free , for oxygen reduction reaction. As time goes by, η air becomes more negative due to chromium deposition and hence k eleChemCr increases exponentially as presented in Figure 7(b), which can be explained by using a Butler-Volmer type expression for k eleChemCr . At the end of the simulation, the highest Θ Cr 2 O 3 is found at the AEL/EELC where the lowest η air locates as shown in Figure 6(d). From Figure 7(a), the average Θ Cr 2 O 3 after 100 kh in the AEL is around 0.03, which is small. However, the segregation of Cr2O3 on AEL/ELEC, which leads to ∼ 0.17 Θ Cr 2 O 3 locally, may still cause a nonnegligible ohmic resistance since a low electrical conducting layer is likely to form.
The distribution of Θ SrCrO 4 is shown in Figure 6(b). Unlike Θ Cr 2 O 3 , Θ SrCrO 4 tends to segregate on the surface of the AEL, which is consistent with the experimental observation from reference [4,10,11]. Plus, in opposition to the evolution trend of Θ Cr 2 O 3 , Θ SrCrO 4 increases quickly within the first 25 kh while it hardly changes after 60 kh. The trend is more distinctly illustrated by the evolution of the average Θ SrCrO 4 shown in Figure 7(a). This can be explained by the assumption that reaction (11) obeys the thermal equilibrium. When the operation starts, a high k chemCr should be observed as a tiny amount of Θ SrCrO 4 and Θ H 2 O exists on the LSCF surface. With increasing Θ SrCrO 4 and Θ H 2 O , due to k chemCr being constrained by the thermal equilibrium, a fast attenuation of k chemCr happens, as shown in Figure 7(b).
The spatial evolution of Θ free is given in Figure 6(c). Similar to Θ SrCrO 4 , Θ free decreases quickly at the beginning of 25 kh, probably due to the fast adsorption of CrO2(OH)2 at the initial stage as shown in Figure 7(a). Consequently, η air decreases as governed by Equation (23). In addition, the simulation shows the highest Θ free is found above the rib and close to AEL/ELEC. Advanced surface characterization is needed to further validate this distribution. At 100 kh, as a result of a rather low Θ free , η air roughly decreases by a factor of four in comparison with the initial state, as shown in Figure 6(d). At the air inlet and air outlet, η air is not much influenced by the chromium poisoning. The probable explanation is that electrochemical reactions mainly take place at the centre of the air electrode in the situation where the counter-flow field for the fuel and air is applied.
Preprints 88632 g006
Figure 6. Spatial distribution of physical variables in the AEL of F1002-97 (a) Θ Cr 2 O 3 , (b) Θ SrCrO 4 , (c) Θ free and (d) η air . Slices are in the y-z plane and uniformly distributed across the whole AEL. The first and the last slices are at the boundary faces of the geometry. The geometry is scaled according to (x,y,z) = (0.1, 1, 10).
Figure 6. Spatial distribution of physical variables in the AEL of F1002-97 (a) Θ Cr 2 O 3 , (b) Θ SrCrO 4 , (c) Θ free and (d) η air . Slices are in the y-z plane and uniformly distributed across the whole AEL. The first and the last slices are at the boundary faces of the geometry. The geometry is scaled according to (x,y,z) = (0.1, 1, 10).
Preprints 88632 g006
Preprints 88632 g007
Figure 7. Evolution of average (a) Θ i and (b) k chemCr and k eleChemCr in the AEL of the stack F1002-97.
Figure 7. Evolution of average (a) Θ i and (b) k chemCr and k eleChemCr in the AEL of the stack F1002-97.
Preprints 88632 g007

5.3. Effects of temperatures and humidities on chromium poisoning

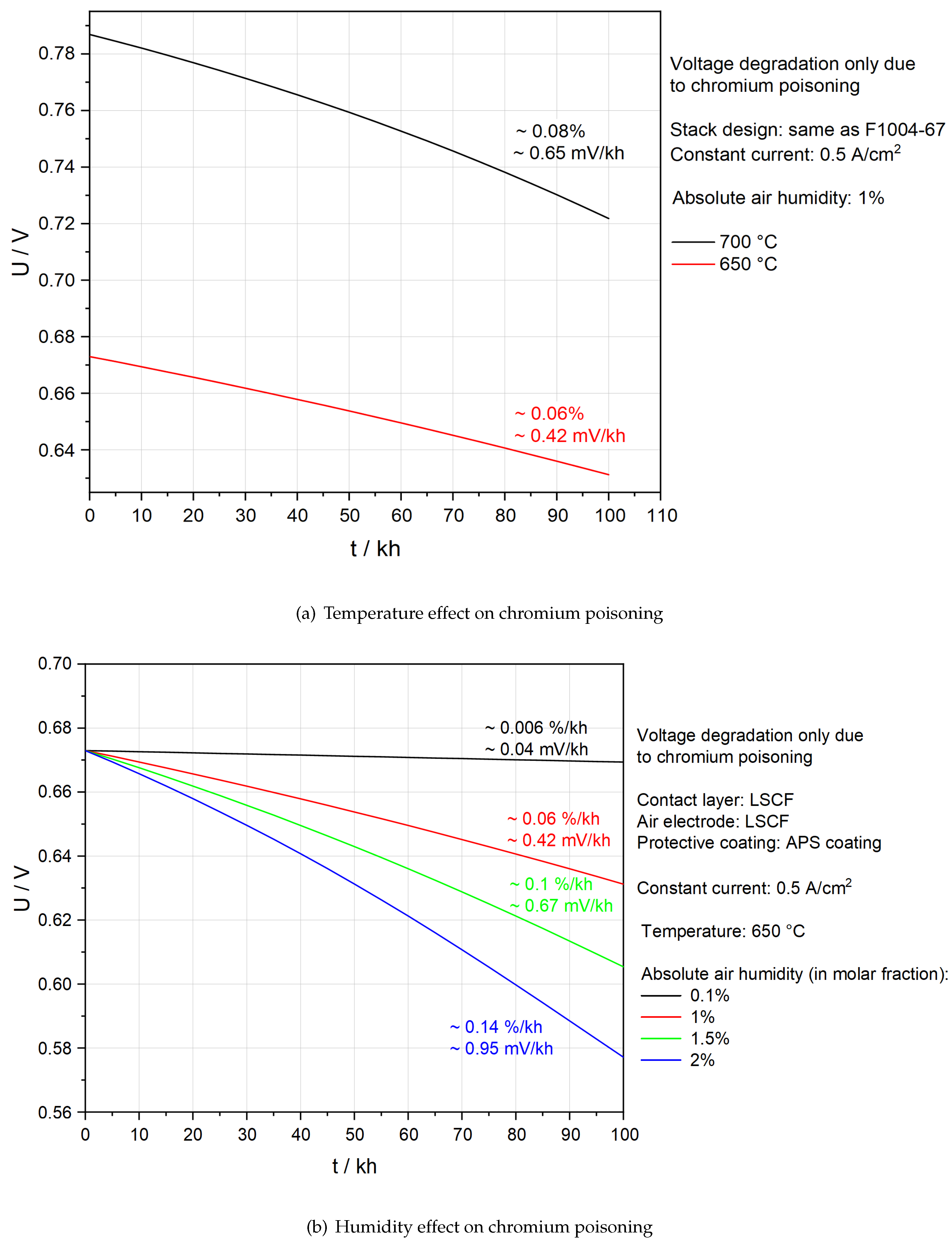
Figure 4(b) and 4(c) demonstrate that with the help of APS protective coatings, SOFC stacks suffer little from chromium poisoning. It is thus significant to see whether the above stack designs can also efficiently prevent chromium poisoning at lower temperatures and ambient air.
Figure 8(a) studies the influence of temperature on chromium poisoning. A lower temperature leads to a smaller degradation rate owing to slower adsorption kinetics. However, it also leads to a lower voltage because conductivity decreases. To maintain the required power output, the active area needs to be larger and the number of layers in stacks should be increased. Unfortunately, both strategies lead to a challenge of the mechanical strength of the stack. Economic analysis, system-level simulation and solid mechanics modelling are needed to further demonstrate the feasibility of lowering the operation temperature.
Figure 8(b) compares Ut-curves under different absolute humidities in the air at 650 °C. The aim is to determine whether it is possible to save energy for the dehumidification of the air by maintaining an acceptable degradation rate. First of all, 2 % humidity is undoubtedly not feasible because the degradation rate due to chromium poisoning is already ∼ 0.14 %/kh. The total degradation rate in an actual SOFC stack is likely to be above the target, 0.3 %/kh [38], if other degradation processes are involved. Secondly, 1.5 % humidity is also not recommended as there is a tendency for progressive degradation after 80 kh. A humidity of around 1% could be more promising, as less energy is required for dehumidification of the air, no progressive degradation is observed and the degradation rate is low even though it is ten times higher compared to the case of 0.1 % humidity.

6. Discussion

6.1. One channel model representing the chromium poisoning in the whole SOFC stack

Due to computational cost, this work only considers the single channel of a SOFC stack to study chromium poisoning. Previously, it has been proven that this simplification is already sufficient to provide accurate predictions of IV-curves [18]. For the simulation of chromium poisoning, it is worthwhile to discuss further whether the simplification is acceptable to provide reliable results. Three variables are discussed here, temperature, pressure and the origin of CrO2(OH)2 since they directly influence governing equations of chromium poisoning. The SOFC stacks considered in this work were tested inside ovens. Thanks to the heat radiation, based on the temperature measured from thermocouples in the stack, it was found that the spatial variation of temperature across the whole stack during the steady operation was slight (10 ∼ 15 °C). Hence, the temperature field in the single channel is expected to be similar to that in the SOFC stack (reactive parts). Unlike temperature, the spatial distribution of pressure is difficult to measure, and usually it is obtained through numerical calculations. The simulation on the single cell stack (i.e., the geometry in reality) of F1004-67 found the range of pressure on the air side is 100 kPa ∼ 100.473 kPa [39], indicating the pressure is uniformly distributed. As for the origin of CrO2(OH)2, the model in this work assumes that CrO2(OH)2 solely comes from the internal surface of the channel via reaction (1). In principle reaction (1) could also occur on the metal frames’ surface. However, internal experiments indicate the impact of metal frames is neglectable for at least 3 kh.
In brief, although there could be some deviations, the accuracy of the single channel model on chromium poisoning is likely acceptable. Hence, its simulation results can be compared with experimental findings on the stack level.

6.2. The stack design

In this work, two stack designs are compared regarding the performance degradation due to chromium poisoning. The first employs the APS protective coating and LSCF as the CL (F1004-67). As a result of a quite dense protective coating, chromium poisoning is almost neglectable. Degradation in the stack F1004-67 arose from other processes according to post-test analysis, such as gas leakage, nickel agglomeration, manganese diffusion, increasing ohmic resistance and contact loss due to the formation of secondary phases. The second utilizes a protective coating prepared by WPS and LCC12 as the CL (F1002-97). Since the WPS protective coating has a relatively high porosity, LCC12 that can adsorb CrO2(OH)2 was chosen as the CL. Although the adsorption rate of CrO2(OH)2 by LCC12 is two orders of magnitude higher than that of LSCF (see definitions of S o u r c e mole , CrOH LCC 12 and S o u r c e mole , CrOH LSCF in Appendix A), this stack design is unable to prevent chromium poisoning efficiently, as shown in Figure 4(a). However, WPS technology is cheaper than APS technology. If WPS protective coatings need to be applied after considering the costs, fabrication should be optimized to lower its porosity.

6.3. Operation under higher air absolute humidity and lower temperature

As shown in Figure 8, based on the current model and only from the perspective of the degradation rate, there is a potential to lower the operation temperature to 650 °C and increase absolute air humidity to 1 %, if the APS protective coating is applied. However, it remains uncertain whether it is worthwhile to make such changes in future. The present model may underestimate the degradation due to chromium poisoning as it ignores the influence of the insulation phase SrCrO4. 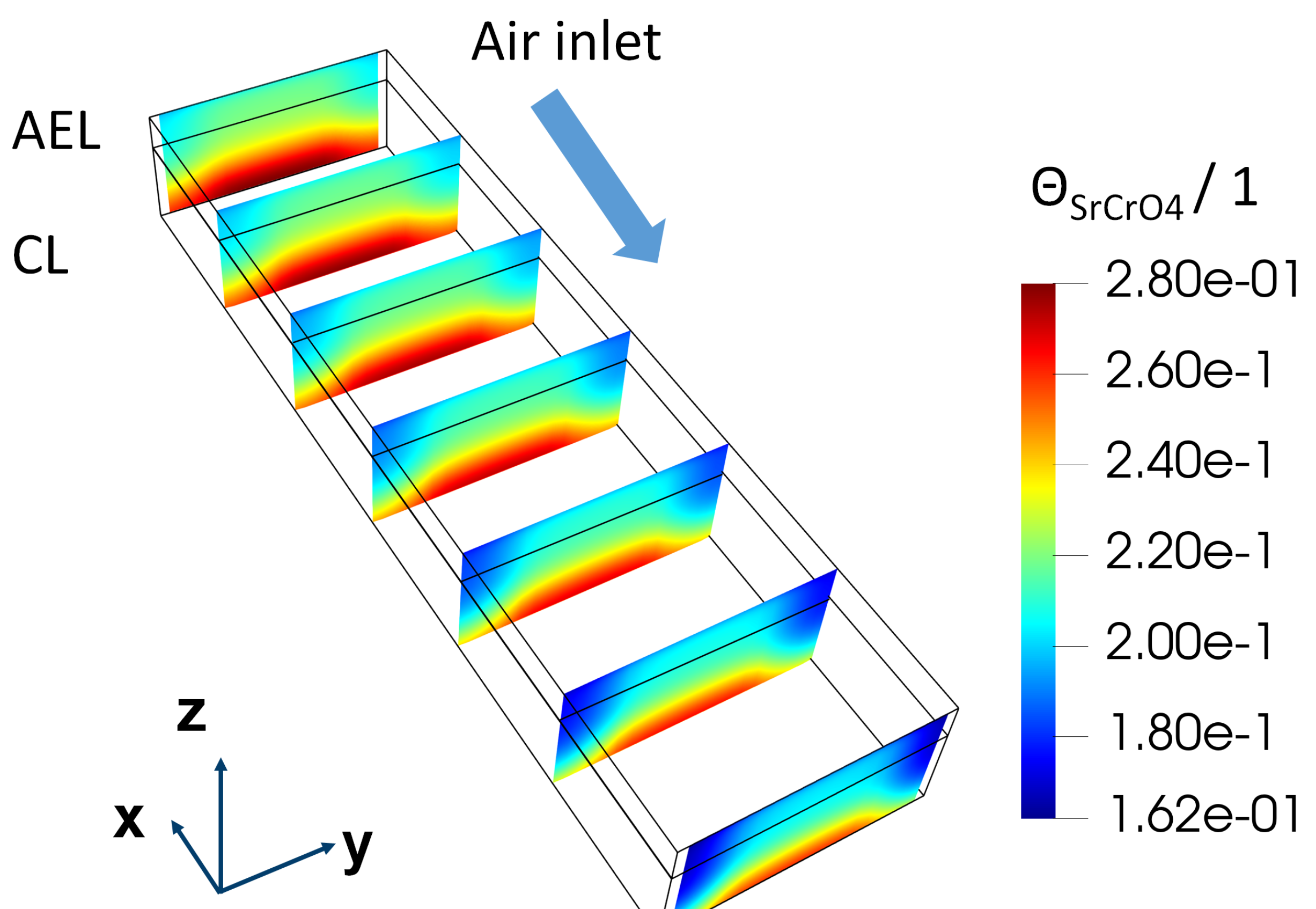Figure 9 shows the distribution of Θ SrCrO 4 inside the AEL and the CL under the above-mentioned operation conditions and stack designs. After 100 kh operation, a clear gathering of Θ SrCrO 4 on the surface of the CL can be found. ∼ 0.28 surface coverage of the insulation phase could lead to substantial ohmic resistance. A more sophisticated model is therefore needed to understand the increase of ohmic resistance.

7. Conclusion

A three-dimensional CFD model of a single channel in a Jülich F10 SOFC stack is proposed, taking into account one of the most important degradation process, chromium poisoning. The numerical simulation is capable of predicting voltage degradation during 100 kh of operating time. The model is able to predict the reduction of free adsorption sites on LSCF during chromium poisoning and the polarization degradation due to that reduction. The model is supported by comparing simulation results with experimentally measured voltage degradation and EIS data. The model can be used to study chromium poisoning under different temperatures, absolute humidity and stack designs. Based on the simulation results, three important conclusions are drawn:
  • With APS protective coating, chromium poisoning in the SOFC stack is almost solved.
  • Lower temperatures and less moisture in the inlet air mitigate chromium poisoning.
  • It should be possible to operate a SOFC stack with 1 % humidified air at 650 °C, if APS protective coating is applied.
As a result of the segregation of Θ SrCrO 4 and Θ SrCrO 4 , an increasing ohmic resistance due to chromium poisoning is expected. However, the influence of the decrease in conductivity is not considered in this model. Incorporating the decreasing conductivity into the model will produce a more reliable prediction of the performance of SOFC stacks and will be considered in future. In addition, some kinetic parameters are assumed in the present model, such as sticking coefficients and the prefactor of k eleChemCr . These parameters need to be experimentally measured or theoretically calculated for the numerical model to provide a more precise prediction of the degradation of chromium poisoning.

Author Contributions

Conceptualization, S.Y.; data curation, S.Y.; investigation, S.Y.; methodology, S.Y. and S.Z.; project administration, D.S. and F.K.; supervision, D.S. and R.-A.E.; visualization, S.Y.; writing the original draft, S.Y.; writing—review and editing, S.Z., D.S., R.P., R.-A.E., F.K. and S.Y.. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the German Federal Ministry of Education and Research (BMBF) grant numbers FKZ 03SF0621A.

Acknowledgments

The authors would like to thank all their colleagues engaged in SOC development at Jülich.

Conflicts of Interest

The authors have no conflicts of interest to declare. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

Appendix A. Definition of S mole , CrOH

The source term, S o u r c e mole , CrOH , used in Equation (3) is given as follows:
S o u r c e mole , CrOH = S o u r c e mole , CrOH LCC 12 + S o u r c e mole , CrOH LSCF
where S o u r c e mole , CrOH LCC 12 and S o u r c e mole , CrOH LSCF are the source terms that are non-zero only when the calculation domain is made of LCC12 and LSCF respectively. In other words, S o u r c e mole , CrOH LCC 12 is defined as follows (when WPS protective coating is used) [40]:
S o u r c e mole , CrOH LCC 12 = − 5 . 7 × 10 − 6 [ mol m − 3 s − 1 ] if the calculation domain is made of LCC 12. 0 Other situations
Similarly, when CrO2(OH)2 diffuses into the component made of LSCF, it can be adsorbed on the LSCF surface as shown in Equation (8). Inside the domain made of LSCF, S o u r c e mole , CrOH LSCF could be obtained by
S o u r c e mole , CrOH LSCF = − ( k a , CrOH Θ free − k d , CrOH Θ CrOH ) · Γ LSCF · N LSCF A LSCF / V mesh
where N LSCF is the number of LSCF particles in the local mesh, A LSCF is the surface area of one LSCF particle and V mesh is the volume of the local mesh. N LSCF can be expanded as
N LSCF = V LSCF , tot / V LSCF
where V LSCF , tot and V LSCF are the total volume of LSCF particles in the local mesh and the volume of one LSCF particle. The relation between V LSCF , tot and V mesh is
V LSCF , tot = ( 1 − ε ael ) V mesh
where ε ael is the porosity of the AEL. After combining Equation (A3) ∼ (A5), S o u r c e mole , CrOH LSCF can be obtained by
S o u r c e mole , CrOH LSCF = − ( 1 − ε ael ) ( k a , CrOH Θ free if the calculation domain − k d , CrOH Θ CrOH ) Γ LSCF a LSCF is made of LSCF . 0 Other situations
where a LSCF ( A LSCF / V LSCF ) is the specific area of LSCF particles, whose value can be found in Appendix C.
Table B1. Parameters used for calculating Δ G SrCrO 4
Table B1. Parameters used for calculating Δ G SrCrO 4
Value Reference Comment
/ kJ mol − 1
Δ G ads , CrOH -370 [42] The value is adjusted as the value in the reference is actually for CrO3 adsorbed on LSCF.
Δ G SrO segregation -41.5 [43] The data is for the case of LSM where the surface coverage of Sr is increased from 0.25 to 0.5.
Δ G des , H 2 O 127.4 [44]
Table C1. Parameters used in the model
Table C1. Parameters used in the model
Properties Values
Porosity of the AEL (ael) 0.45 [45]
Specific area of the LSCF particles ( a LSCF ) 2.84 × 10 6 m − 1 [45]
Porosity of WPS protective coating ( ε coating , WPS ) 0.45 [46]
Porosity of APS protective coating ( ε coating , APS ) 0.03 [47]
Diffusion coefficient of CrO2(OH)2 ( D CrOH , air ) 1 × 10 − 4 m 2 s − 1 [48]
Density of adsorption sites ( Γ LSCF ) 1.1 × 10 − 5 mol m − 2 [49]
Sticking coefficient of CrO2(OH)2 ( S CrOH ) 1 × 10 − 4 exp − 75 [ kJ mol − 1 ] R T 1
Sticking coefficient of H2O ( S H 2 O ) 0 2 [50]
1 Sticking coefficient can be written as an Arrhenius expression [27].
2 It was demonstrated that there was little interaction between LSCF and H2O when temperature is above 500 °C [50].

Appendix B. Calculation of ΔG SrCrO 4

The following reaction
C r O 2 ( O H ) 2 ( g ) + S r O ( s ) ⇄ SrCrO 4 ( s ) + H 2 O ( g ) Δ G SrCrO 4 0
has a Gibbs free energy change Δ G SrCrO 4 0 which is [41]:
Δ G SrCrO 4 0 = 0 . 04713 [ 1 / K ] · T − 338 . 81232 [ kJ mol − 1 ]
where T is the temperature. However, it is Δ G SrCrO 4 of the reaction (11) happening on the LSCF surface that needs to be determined. This work uses a similar method provided by the reference [28] to calculate Δ G SrCrO 4 . The reaction (A7) consists of the following processes:
  • Adsorption of CrO2(OH)2 on the LSCF surface ( Δ G ads , CrOH )
  • SrO segregation on LSCF surface ( Δ G SrO segregation )
  • Formation of SrCrO4 ( Δ G SrCrO 4 0 )
  • Desorption of H2O from the LSCF surface ( Δ G des , H 2 O )
As a result, Δ G SrCrO 4 can be written as
Δ G SrCrO 4 = Δ G SrCrO 4 0 − Δ G ads , CrOH − Δ G SrO segregation − Δ G des , H 2 O
The data of Gibbs free energy can be found in Table B1.
Table D1. Initial values of Θ SrO in the model
Table D1. Initial values of Θ SrO in the model
Stack design Boundary value [13] Distribution
function 1
LSCF as the CL Θ SrO = 0.21 at AEL / EELC 0.47 at surface of CL a ( z − b ) 4 + 0.21
LCC12 as the CL Θ SrO = 0.21 at AEL / EELC 0.47 at surface of AEL a ( z − b ) 4 + 0.21
1z is the z-coordinate in the model. a and b are constants that need to be calculated according to the boundary values.
Table E1. Initial values of Θ CrOH , Θ H 2 O , Θ Cr 2 O 3 and Θ SrCrO 4 in the model
Table E1. Initial values of Θ CrOH , Θ H 2 O , Θ Cr 2 O 3 and Θ SrCrO 4 in the model
Initial value / 1 Comment
Θ CrOH 5 × 10 − 3 Assumed value
Θ H 2 O 5 × 10 − 2 Assumed value
Θ Cr 2 O 3 1 × 10 − 5 Assumed value
Θ SrCrO 4 K SrCrO 4 Θ CrOH Θ SrO Θ H 2 O 1 Obtained according to the thermal equilibrium
1 Θ SrO is calculated according to Appendix D.

Appendix C. Parameters used in the model

Parameters used in the model is given in Table C1. S CrOH is the parameter that no reference can be found in the literature. The value is fitted according to experimental results.

Appendix D. Initial values of Θ SrO in the model

The initial value of Θ SrO for two stack designs, LSCF as the CL or LCC12 as the CL, is shown in Table D1. It is assumed that if the CL is made of LCC12, SrO segregation only happens in the AEL. In contrast, if the CL is made of LSCF, SrO segregation happens across both CL and AEL and the maximum segregation is at the surface of the CL.
The distribution function Θ SrO = f ( z ) can not be found in the literature. It is therefore assumed f ( z ) is a quartic function as given in Table D1. The constants a and b can be determined by boundary values.

Appendix E. Initial values of Θ CrOH , Θ H 2 O , Θ Cr 2 O 3 and Θ SrCrO 4 in the model

The initial values of Θ CrOH , Θ H 2 O , Θ Cr 2 O 3 and Θ SrCrO 4 are shown in Table E1. The model in this work focuses on the period of the steady operation of SOFC stacks. Before the start of the steady operation, stacks go through being heated up, sealant-joining process, initial characterization of IV-curves and EIS, etc, where operation conditions keeps varying. Consequently, assumed values are used as knowing the exact initial values is very hard. The Initial value of Θ Cr 2 O 3 is a pure assumed value. The initial values of Θ CrOH and Θ H 2 O are determined based on the same model’s simulation results of two processes: 1) the heating up process at the speed of 1 K/min from 20 °C to 350 °C and 2 K/min from 350 °C to 850 °C (all with 1 % humidified air) and 2) the sealant-joining process, 15 h under 850 °C with 1 % humidified air and 85 h under 850 °C with 0.1 % humidified air.

References

  1. Zarabi Golkhatmi, S.; Asghar, M.I.; Lund, P.D. A review on solid oxide fuel cell durability: Latest progress, mechanisms, and study tools. Renewable and Sustainable Energy Reviews 2022, 161, 112339. [CrossRef]
  2. Li, W.; Wang, Y.; Liu, W. A review of solid oxide fuel cell application. IOP Conference Series: Earth and Environmental Science 2020, 619, 012012. [CrossRef]
  3. Zhou, L.; Mason, J.H.; Li, W.; Liu, X. Comprehensive review of chromium deposition and poisoning of solid oxide fuel cells (SOFCs) cathode materials. Renewable and Sustainable Energy Reviews 2020, 134, 110320. [CrossRef]
  4. Horita, T. Chromium poisoning for prolonged lifetime of electrodes in solid oxide fuel cells - Review. Ceramics International 2021, 47, 7293–7306. [CrossRef]
  5. Fang, Q.; Blum, L.; Stolten, D. Electrochemical Performance and Degradation Analysis of an SOFC Short Stack Following Operation of More than 100,000 Hours. Journal of The Electrochemical Society 2019, 166, F1320–F1325. [CrossRef]
  6. Vora, S.D.; Lundberg, W.L.; Pierre, J.F. Overview of U.S. Department of Energy Office of Fossil Energy’s Solid Oxide Fuel Cell Program. ECS Transactions 2017, 78, 3. [CrossRef]
  7. Nakajo, A.; Tanasini, P.; Diethelm, S.; herle, J.V.; Favrat, D. Electrochemical Model of Solid Oxide Fuel Cell for Simulation at the Stack Scale II: Implementation of Degradation Processes. Journal of The Electrochemical Society 2011, 158, B1102. [CrossRef]
  8. Miyoshi, K.; Iwai, H.; Kishimoto, M.; Saito, M.; Yoshida, H. Chromium poisoning in (La,Sr)MnO3 cathode: Three-dimensional simulation of a solid oxide fuel cell. Journal of Power Sources 2016, 326, 331–340. [CrossRef]
  9. Babaie Rizvandi, O.; Miao, X.Y.; Frandsen, H.L. Multiscale modeling of degradation of full solid oxide fuel cell stacks. International Journal of Hydrogen Energy 2021, 46, 27709–27730. [CrossRef]
  10. Menzler, N.H.; Sebold, D.; Sohn, Y.J.; Zischke, S. Post-test characterization of a solid oxide fuel cell after more than 10 years of stack testing. Journal of Power Sources 2020, 478, 228770. [CrossRef]
  11. Jiang, S.P.; Chen, X. Chromium deposition and poisoning of cathodes of solid oxide fuel cells – A review. International Journal of Hydrogen Energy 2014, 39, 505–531. [CrossRef]
  12. Koo, B.; Kim, K.; Kim, J.K.; Kwon, H.; Han, J.W.; Jung, W. Sr Segregation in Perovskite Oxides: Why It Happens and How It Exists. Joule 2018, 2, 1476–1499. [CrossRef]
  13. Türk, H.; Götsch, T.; Schmidt, F.P.; Hammud, A.; Ivanov, D.; de Haart, L.G.J.B.; Vinke, I.C.; Eichel, R.A.; Schlögl, R.; Reuter, K.; Knop-Gericke, A.; Lunkenbein, T.; Scheurer, C. Sr Surface Enrichment in Solid Oxide Cells – Approaching the Limits of EDX Analysis by Multivariate Statistical Analysis and Simulations. ChemCatChem 2022, 14, e202200300, [https://chemistry-europe.onlinelibrary.wiley.com/doi/pdf/10.1002/cctc.202200300]. [CrossRef]
  14. Yin, X.; Bencze, L.; Motalov, V.; Spatschek, R.; Singheiser, L. Thermodynamic perspective of Sr-related degradation issues in SOFCs. International Journal of Applied Ceramic Technology 2018, 15, 380–390. [CrossRef]
  15. Blum, L.; Fang, Q.; Groß-Barsnick, S.M.; de Haart, L.B.; Malzbender, J.; Menzler, N.H.; Quadakkers, W.J. Long-term operation of solid oxide fuel cells and preliminary findings on accelerated testing. International Journal of Hydrogen Energy 2020, 45, 8955–8964. [CrossRef]
  16. Menzler, N.H.; Sebold, D.; Guillon, O. Post-test characterization of a solid oxide fuel cell stack operated for more than 30,000 hours: The cell. Journal of Power Sources 2018, 374, 69–76. [CrossRef]
  17. Steinberger-Wilckens, R.; De Haart, L.; Vinke, I.; Blum, L.; Cramer, A.; Remmel, J.; Blass, G.; Tietz, F.; Quadakkers, W. Recent Results of Stack Development at Forschungszentrum Jülich. Fuel Cell Technologies: State and Perspectives; Sammes, N.; Smirnova, A.; Vasylyev, O., Eds.; Springer Netherlands: Dordrecht, 2005; pp. 123–134.
  18. Yu, S.; Zhang, S.; Schäfer, D.; Peters, R.; Kunz, F.; Eichel, R.A. Numerical Modeling and Simulation of the Solid Oxide Cell Stacks and Metal Interconnect Oxidation with OpenFOAM. Energies 2023, 16. [CrossRef]
  19. Zhang, S.; Hess, S.; Marschall, H.; Reimer, U.; Beale, S.B.; Lehnert, W. openFuelCell2: A New Computational Tool for Fuel Cells, Electrolyzers, and other Electrochemical Devices and Processes, In press.
  20. Hilpert, K.; Das, D.; Miller, M.; Peck, D.H.; Weiß, R. Chromium Vapor Species over Solid Oxide Fuel Cell Interconnect Materials and Their Potential for Degradation Processes. Journal of The Electrochemical Society 1996, 143, 3642. [CrossRef]
  21. Ni, M.; Leung, M.K.H.; Leung, D.Y.C. A modeling study on concentration overpotentials of a reversible solid oxide fuel cell. Journal of Power Sources 2006, 163, 460–466. [CrossRef]
  22. Ni, M. Computational fluid dynamics modeling of a solid oxide electrolyzer cell for hydrogen production. International Journal of Hydrogen Energy 2009, 34, 7795–7806. [CrossRef]
  23. Opila, E.J. Volatility of Common Protective Oxides in High-Temperature Water Vapor: Current Understanding and Unanswered Questions. High Temperature Corrosion and Protection of Materials 6. Trans Tech Publications Ltd, 2004, Vol. 461, Materials Science Forum, pp. 765–774. [CrossRef]
  24. Wuillemin, Z. Experimental and modeling investigations on local performance and local degradation in solid oxide fuel cells. PhD thesis, École Polytechnique Fédérale de Lausanne, 2009.
  25. Ebbinghaus, B.B. Thermodynamics of gas phase chromium species: The chromium oxides, the chromium oxyhydroxides, and volatility calculations in waste incineration processes. Combustion and Flame 1993, 93, 119–137. [CrossRef]
  26. Foo, K.; Hameed, B. Insights into the modeling of adsorption isotherm systems. Chemical Engineering Journal 2010, 156, 2–10. [CrossRef]
  27. Chorkendorff, I.; Niemantsverdriet, J. Concepts of Modern Catalysis and Kinetics, 3 ed.; Wiley-VCH: Germany, 2017.
  28. Kröll, L.; de Haart, L.G.J.; Vinke, I.; Eichel, R.A. Degradation Mechanisms in Solid-Oxide Fuel and Electrolyzer Cells: Analytical Description of Nickel Agglomeration in a Ni/YSZ Electrode. Phys. Rev. Appl. 2017, 7, 044007. [CrossRef]
  29. Beez, A.; Schiemann, K.; Menzler, N.H.; Bram, M. Accelerated Testing of Chromium Poisoning of Sr-Containing Mixed Conducting Solid Oxide Cell Air Electrodes. Frontiers in Energy Research 2018, 6. [CrossRef]
  30. Hindmarsh, A.C.; Brown, P.N.; Grant, K.E.; Lee, S.L.; Serban, R.; Shumaker, D.E.; Woodward, C.S. SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Transactions on Mathematical Software (TOMS) 2005, 31, 363–396. [CrossRef]
  31. Gardner, D.J.; Reynolds, D.R.; Woodward, C.S.; Balos, C.J. Enabling new flexibility in the SUNDIALS suite of nonlinear and differential/algebraic equation solvers. ACM Transactions on Mathematical Software (TOMS) 2022. [CrossRef]
  32. Fang, Q.; Menzler, N.H.; Blum, L. Degradation Analysis of Long-Term Solid Oxide Fuel Cell Stacks with Respect to Chromium Poisoning in La0.58Sr0.4Co0.2Fe0.8O3- and La0.6Sr0.4CoO3- in Cathodes. Journal of The Electrochemical Society 2021, 168, 104505. [CrossRef]
  33. Yan, Y.; Fang, Q.; Blum, L.; Lehnert, W. Performance and degradation of an SOEC stack with different cell components. Electrochimica Acta 2017, 258, 1254–1261. [CrossRef]
  34. Caliandro, P.; Nakajo, A.; Diethelm, S.; Van herle, J. Model-assisted identification of solid oxide cell elementary processes by electrochemical impedance spectroscopy measurements. Journal of Power Sources 2019, 436, 226838. https://doi.org/https://doi.org/10.1016/j.jpowsour.2019.226838.
  35. Weather data in Jülich from December 2019 to February 2020. https://www.timeanddate.com/weather/germany/juelich/historic?month=3&year=2020. Accessed: 2023-02-01.
  36. Calculator of the absolute humidity. https://www.omnicalculator.com/physics/absolute-humidity. Accessed: 2023-02-01.
  37. Wan, T.H.; Saccoccio, M.; Chen, C.; Ciucci, F. Influence of the Discretization Methods on the Distribution of Relaxation Times Deconvolution: Implementing Radial Basis Functions with DRTtools. Electrochimica Acta 2015, 184, 483–499. [CrossRef]
  38. Whiston, M.M.; Azevedo, I.M.; Litster, S.; Samaras, C.; Whitefoot, K.S.; Whitacre, J.F. Meeting U.S. Solid Oxide Fuel Cell Targets. Joule 2019, 3, 2060–2065. [CrossRef]
  39. Zhang, S.; Shangzhe Yu, R.P.; Schäfer, D.; Beale, S.B.; Kunz, F.; Eichel, R.A. Simple and Complex Solid Oxide Cell Stack Models: A Comparison. Applications in Energy and Combustion Science To be submitted.
  40. Haart, L.G.J.B.D.; Beale, S.B.; Deja, R.; Dittrich, L.; Duyster, T.; Fang, Q.; Foit, S.; Gross-Barsnick, S.; Margaritis, N.; de Haart, U.; Hoven, I.; Kruse, N.; Lenser, C.; Ma, Q.; Menzler, N.H.; Naumenko, D.; Nohl, M.; Peters, R.; Sebold, D.; Thaler, F.; Tiedemann, W.; Unachukwu, I.; Varghese, B.A.; Vibhu, V.; Vinke, I.; Wolf, S.E.; Zhang, S.; Zurek, J.; Blum, L. Forschungszentrum Jülich – Current Activities in SOC Development. ECS Transactions 2021, 103, 299. [CrossRef]
  41. Qiu, P.; Lin, J.; Lei, L.; Yuan, Z.; Jia, L.; Li, J.; Chen, F. Evaluation of Cr-Tolerance of the Sr2Fe1.5Mo0.5O6- Cathode for Solid Oxide Fuel Cells. ACS Applied Energy Materials 2019, 2, 7619–7627. [CrossRef]
  42. Niu, Y.; Zhou, Y.; Lv, W.; Chen, Y.; Zhang, Y.; Zhang, W.; Luo, Z.; Kane, N.; Ding, Y.; Soule, L.; Liu, Y.; He, W.; Liu, M. Enhancing Oxygen Reduction Activity and Cr Tolerance of Solid Oxide Fuel Cell Cathodes by a Multiphase Catalyst Coating. Advanced Functional Materials 2021, 31, 2100034. [CrossRef]
  43. Yang, J.; Polfus, J.M.; Li, Z.; Tuller, H.L.; Yildiz, B. Role of Adsorbate Coverage on the Oxygen Dissociation Rate on Sr-Doped LaMnO3 Surfaces in the Presence of H2O and CO2. Chemistry of Materials 2020, 32, 5483–5492. [CrossRef]
  44. Zhou, Y.; Zhang, W.; Kane, N.; Luo, Z.; Pei, K.; Sasaki, K.; Choi, Y.; Chen, Y.; Ding, D.; Liu, M. An Efficient Bifunctional Air Electrode for Reversible Protonic Ceramic Electrochemical Cells. Advanced Functional Materials 2021, 31, 2105386, [https://onlinelibrary.wiley.com/doi/pdf/10.1002/adfm.202105386]. [CrossRef]
  45. Joos, J. Microstructural Characterisation, Modelling and Simulation of Solid Oxide Fuel Cell Cathodes. PhD thesis, Karlsruher Institut für Technologie (KIT), 2017. [CrossRef]
  46. Ruder, A.; Buchkremer, H.P.; Jansen, H.; Malléner, W.; Stöver, D. Wet powder spraying—a process for the production of coatings. Surface and Coatings Technology 1992, 53, 71–74. [CrossRef]
  47. Grünwald, N.; Lhuissier, P.; Salvo, L.; Villanova, J.; Menzler, N.H.; Guillon, O.; Martin, C.L.; Vaßen, R. In situ investigation of atmospheric plasma-sprayed Mn–Co–Fe–O by synchrotron X-ray nano-tomography. Journal of Materials Science 2020, 55, 12725–12736. [CrossRef]
  48. Stenzel, A.; Fähsing, D.; Schütze, M.; Galetz, M.C. Volatilization kinetics of chromium oxide, manganese oxide, and manganese chromium spinel at high temperatures in environments containing water vapor. Materials and Corrosion 2019, 70, 1426–1438, [https://onlinelibrary.wiley.com/doi/pdf/10.1002/maco.201810655]. [CrossRef]
  49. Effori, E.; Laurencin, J.; Silva, E.D.R.; Hubert, M.; David, T.; Petitjean, M.; Geneste, G.; Dessemond, L.; Siebert, E. An Elementary Kinetic Model for the LSCF and LSCF-CGO Electrodes of Solid Oxide Cells: Impact of Operating Conditions and Degradation on the Electrode Response. Journal of The Electrochemical Society 2021, 168, 044520. [CrossRef]
  50. Huang, Y.L.; Pellegrinelli, C.; Wachsman, E.D. Fundamental Impact of Humidity on SOFC Cathode ORR. Journal of The Electrochemical Society 2015, 163, F171. [CrossRef]
Preprints 88632 g001
Figure 1. A schematic of the geometry of the model. The left figure is the geometry in three dimensions and the right figure is the geometry in the cross-section of y z plane.
Figure 1. A schematic of the geometry of the model. The left figure is the geometry in three dimensions and the right figure is the geometry in the cross-section of y z plane.
Preprints 88632 g001
Preprints 88632 g002
Figure 2. The schematic of chromium poisoning inside the AEL. The left figure shows the distribution of SrO and the right figure shows the distribution of Cr2O3 and SrCrO4 in the AEL. A darker color indicates a higher amount of chemical species.
Figure 2. The schematic of chromium poisoning inside the AEL. The left figure shows the distribution of SrO and the right figure shows the distribution of Cr2O3 and SrCrO4 in the AEL. A darker color indicates a higher amount of chemical species.
Preprints 88632 g002
Preprints 88632 g003
Figure 3. Procedures in the numerical calculation.
Figure 3. Procedures in the numerical calculation.
Preprints 88632 g003
Preprints 88632 g004
Figure 4. Comparing simulation results of Ut-curves with experimental data of (a) F1002-97, (b) F1004-67 and (c) F1004-106. The air absolute humidities are the molar fractions of water in the air. Inserted orange and blue numbers are absolute degradation rates (mV/kh) calculated from simulations and experimental data respectively.
Figure 4. Comparing simulation results of Ut-curves with experimental data of (a) F1002-97, (b) F1004-67 and (c) F1004-106. The air absolute humidities are the molar fractions of water in the air. Inserted orange and blue numbers are absolute degradation rates (mV/kh) calculated from simulations and experimental data respectively.
Preprints 88632 g004
Preprints 88632 g008
Figure 8. Parametric study of (a) the temperature effect and (b) the humidity effect on chromium poisoning. The inserted numbers are overall absolute degradation rates (mV/kh) and relative degradation rates (%/kh).
Figure 8. Parametric study of (a) the temperature effect and (b) the humidity effect on chromium poisoning. The inserted numbers are overall absolute degradation rates (mV/kh) and relative degradation rates (%/kh).
Preprints 88632 g008
Preprints 88632 g009
Figure 9. Simulation of the spatial distribution of Θ SrCrO 4 in the AEL and the CL after 100 kh operation. The stack design is the same as F1004-67. The temperature is 650 °C and absolute air humidity is 1 %. Slices are in the y-z plane and uniformly distributed across the whole AEL. The first and the last slices are at the boundary faces of the geometry. The geometry is scaled according to (x,y,z) = (0.1, 1, 10).
Figure 9. Simulation of the spatial distribution of Θ SrCrO 4 in the AEL and the CL after 100 kh operation. The stack design is the same as F1004-67. The temperature is 650 °C and absolute air humidity is 1 %. Slices are in the y-z plane and uniformly distributed across the whole AEL. The first and the last slices are at the boundary faces of the geometry. The geometry is scaled according to (x,y,z) = (0.1, 1, 10).
Preprints 88632 g009
Table 1. Governing equations and computational domains of the chromium poisoning model
Table 1. Governing equations and computational domains of the chromium poisoning model
Physical process Governing equation Computational domain
Mass transport of CrO2(OH)2 Equation (3) Air channel, CL and AEL
Chromium deposition Equation (14) ∼ (19), (23) Domain made of LSCF
Table 2. Stack designs and operation conditions of SOFC stacks
Table 2. Stack designs and operation conditions of SOFC stacks
F1002-97 1 F1004-67 2 F1004-106 3
Stack design CL LCC12 LSCF LSCF
Protective coating WPS APS APS
Operation conditions Temperature 4 720 °C 730 °C 720 °C
Current density 0.5 Acm − 2 0.5 Acm − 2 0.5 Acm − 2
Time 100 kh 25 kh 5509 h
Fuel mass flow 1.18 × 10 − 7 kg/s 1.15 × 10 − 7 kg/s 1.15 × 10 − 7 kg/s
Molar ratio in fuel H2/H2O 79/21 80/20 80/20
Air mass flow 1.9 × 10 − 6 kg/s 1.18 × 10 − 6 kg/s 1.18 × 10 − 6 kg/s
Molar ratio in air O2/N2 21/79 21/79 21/79
Absolute humidity 0.1% 0.1% ∼4009 h 0.1%
in inlet air ∼1500 h 0.8%
Details of experimental information can be found in reference [5].
Details of experimental information can be found in reference [18].
Details of experimental information can be found in reference [32].
The temperature is measured by the thermocouple, which was inserted ∼ 10 mm-deep into the intermediate interconnector (details can be found in reference [5]).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated