Efficient Formulation for Vendor–Buyer System Considering Optimal Allocation Fraction of Green Production

Preprint

Article

Efficient Formulation for Vendor–Buyer System Considering Optimal Allocation Fraction of Green Production

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Adel A. Alamri^*

This version is not peer-reviewed

Submitted:

24 October 2023

Posted:

25 October 2023

You are already at the latest version

Alerts

Abstract

The classical joint economic lot-sizing (JELS) policy in a single-vendor single-buyer system generates an equal production quantity in all cycles, where the input parameters remain static indefinitely. In this paper, a new two-echelon supply chain inventory model is developed involving a hybrid production system that simultaneously focuses on green and regular production methods with optimal allocation fraction of green and regular productions. Unlike the classical mathematical formulation, each cycle is independent from the previous one, and consequently, the input parameters can be adjusted to be responsive to the dynamic nature of demand rate and price fluctuation. A rigorous heuristic approach is used to derive a global optimal solution for a joint hybrid production system. The model accounts for carbon emissions from production and storage activities related to green and regular produced items along with transportation activity under a multi-level emission-taxing scheme. The results emphasize the significant impact of green production on emissions. That is, the higher the allocation fraction of green production the lower the total amount of emissions generated by the system, i.e., the system becoming more sustainable. Adopting a hybrid production method not only decreases the greenhouse gas (GHG) emissions dramatically, but also reduces the per unit time total cost when compared with regular production. One of the main findings is that the total system cost generated by the base closed-form formula of the proposed model is considerably lower than that of the existing literature i.e., 33.59% (16.13%) lower in the first cycle (subsequent cycles) when the regular production method is assumed. Moreover, the optimal production rate generated by the proposed model is the one that minimizes the emissions production function. Illustrative examples and special cases that reflect different realistic situations are compared to outline managerial insights.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

Nowadays, global warming and environmental change emerge as a challenge facing governments and the United Nations (UN). This can be attributed to the dramatic increase in greenhouse gas (GHG) over the last decade with a rate of increase, almost twice as that recorded for the last three decades [1]. The impact of such increase has forced governments to design regulations to limit GHG emissions omitted into the environment. Carbon emission reduction regulations may comprise carbon tax, carbon offset, carbon caps, or carbon cap-and-trade policies. These polices have been established by the UN and the European Union (EU) to reflect the 2030 Agenda for Sustainable Development Goals (SDGs) [2]. In response to the regulations, several countries made a commitment to limit GHG emissions. Manufacturing and transportation are among the biggest sectors in the world that contribute to GHG emissions [3]. For, example, 29% of total GHG emissions in the U.S. is omitted by transportation activities, which is recognized as the largest sector that generates GHG emissions [4]. To comply with the GHG emissions policies established by the governments, the manufacturers need to focus on sustainable development of logistics systems that minimize overall emissions. In this regard, adopting green technology is one of the most effective strategies to reduce carbon dioxide (CO₂) emissions in their supply chain activities [5,6]. Implementing green technology leads to green production that reflects environmentally friendly inventions. The aim is to use renewable energy, reduce energy use, generate lower emissions, and emphasize awareness of health and safety concerns. Although green production reduces GHG emissions dramatically when compared with the regular production, it may result in higher operating costs [7–9]. Therefore, it is perhaps more cost effective if the manufacturer uses a hybrid production system that combines green and regular productions. This entails a mechanism that balances green and regular production activities considering operating costs.

Supply chain management (SCM) aims to decrease costs and enhances coordination between supply chain members. One of the main objectives of such coordination is to achieve economic balance among supply chain entities. This can be attained by sharing accurate and timely information towards effective use of recourses. In the classical two-level supply chain consisting of a vendor and a buyer, the lot sizing strategy is optimized independently. Whereas a joint economic lot sizing (JELS) refines traditional independent inventory control methods for a joint strategy that simultaneously determines optimal production quantity and the number of shipments per time interval [10–13]. It has been introduced by many researchers to show that a joint production and inventory policy is a key determinant in carbon emission reduction [14–16]. The Vendor-Managed Inventory (VMI) represents a two-echelon supply chain system that involves information sharing between the vendor and the buyer. Through collaborative relationship, the vendor adjusts the production-inventory policy to replenish multiple lot sizes to the buyer subject to the buyer’s information related to demand and stock-level. Sustainable supply chain cooperation between a vendor and a buyer emerges as an opportunity beyond cost-sharing efficiency. In the VMI systems, a collaborative relationship may lead to a more profitable joint policy, carbon emissions reduction, inventory cost reduction, and logistic flexibility. This partnership also implies that economic, social interests, and environmental aspects are nested inside each other, i.e., the system becoming more sustainable [17–19]. The highlights of this manuscript are summarized below:

A two-echelon supply chain inventory model is developed for a VMI system. The developed model considers a hybrid production system involving green and regular production methods with optimal allocation fraction of green and regular productions. The proposed model accounts for carbon emissions omitted from production and storage activities related to green and regular produced items along with transportation activity. The cost function includes penalty charge for exceeding the permissible emissions limits, however, the system earns revenue by selling excess quota in the case that the total emissions generated by the system is less than that of the emission cap, which reflects the cap-and-trade policy. The mathematical formulation considers that the initial on-hand inventory of the buyer is zero in the first-time interval, which can be attributed to the fact that no items have been produced yet. Therefore, two models are developed. The first model reflects the mathematical formulation of the first cycle, whereas the second considers subsequent cycles. Each cycle is independent from the previous one, and consequently, the input parameters can be adjusted to be responsive to the dynamic nature of demand rate and price fluctuation. Results show that the base closed-form formula of the proposed model generates optimal results with considerable total system cost reduction when compared with the existing literature. The optimal production rate generated by the proposed model is the one that minimizes the emission production function. That is, it generates the lowest emission possible when compared with the existing literature. For subsequent cycles, production process starts at the time needed to produce and deliver the first lot size. Such displacement in time prevents keeping items at the vendor’s warehouse for extra time that is associated with the consumption of the last lot that has been delivered to the buyer from previous cycle.

2. Literature Review

The first approach that formulate a joint inventory model was introduced by Goyal [20]. The author investigated the vendor production-inventory policy assuming instantaneous production rate, where a lot-for-lot (LFL) policy is considered for delivering the lot sizes to the buyer. Banerjee [13] considered the model of Goyal [20] under the assumption of a finite production rate. Wahab et al. [21] proposed inventory models considering emissions costs from transportation activity. The models determine the optimal production quantity and shipments frequency for imperfect quality items. Hua et al. [22] investigated the model for carbon footprints along with carbon emissions trading. They examined the effects of carbon taxes, carbon cap, and carbon trade on total cost, order quantity, and carbon emissions. Wangsa [23] examined the JELS model considering industrial and transport emissions under penalties and incentives. Ben-Daya and Hariga [24] investigated the model where the lead time is a function of the lot size quantity. Hariga et al. [25] evaluated the effect of carbon emissions in a multistage supply chain of a cold item during storage and transportation activities. Gautam et al. [26] studied the model, where the carbon emission is caused by transportation activity. Halat and Hafezalkotob [27] considered a multi-stage green supply chain inventory model under four different types of carbon regulations. They examined the effect of coordinated and non-coordinated structures on inventory cost and carbon emissions. Khouja and Mehrez [28] investigated the case when the unit production cost is a function of the production rate. They assumed that the increase of the production rate deteriorates the quality of the production process. Eiamkanchanalai and Banerjee [29] considered the case when the unit production cost is a quadratic function of the production rate in a single-level inventory model. Ghosh et al. [30] considered strict carbon cap policy on a multi-echelon supply chain inventory model. They considered emissions related to production, inventory, and transportation activities. Saga et al. [31] investigated the model for imperfect production processes and inspection errors. The carbon emissions are related to energy generated from transportation and production activities, where incentive and penalty policy are assumed for carbon emission reduction. Huang et al. [32] investigated the effect of green technology on a two-echelon supply chain with carbon emissions related to production, transportation, and storage activities along with carbon taxes, limited total carbon emissions, and cap-and-trade policies.

Chen et al. [33] provided conditions to reducing emission by modifying order quantities. They discussed factors affecting emission reduction and cost increase. Kumar and Uthayakumar [34] considered five different stock control policies for unequal shipments to the buyer. The cost function comprises taxes and penalties to reducing emission from production. Zanoni et al. [35] presented a JELS model with consignment stock (CS) agreement considering emissions taxes, penalty costs, and an emission-trading scheme. Jaber et al. [36] examined the effect of carbon emissions on the JELS inventory models. They accounted for carbon taxes and penalties, where the production rate is assumed as a function of the rate of the carbon emission. Turken et al. [37] considered various environmental regulations in a multiple buyers-single vendor inventory model. Bazan et al. [38] proposed two models that investigate emissions costs from transportation activity along with energy used for production. The first model underlies the traditional coordination strategy and the second underlies CS agreement strategy.

Astanti et al. [39] considered a VMI model for imperfect quality items and deterioration. The model is associated with carbon emissions related to transportation and production operations. Malik and Kim [40] investigated the model considering defect from production operation, where the production rate is a function of the carbon emission. Jauhari et al. [41] proposed a VMI model for a hybrid production system involving green and regular productions. They assumed carbon emissions related to transportation, storage, and production activities.

The above-cited references are directly relevant to the proposed model. However, the effects of carbon emission reduction on the JELS models have been extended in several ways. Many researchers have accounted for cases that are not limited to, deterministic and stochastic demand, imperfect quality items related to production process, equal or unequal shipments policies, and deterioration [42–55]. For more details on the mathematical modeling of the JELS and the related research (see [6,10]). Recently, Alamri [56] pointed out that the classical formulation of the joint VMI system assumed an infinite planning horizon and ignored the fact that the inventory level at the buyer’s warehouse is zero in the first cycle since the production process has not yet started. The author rectified the model of Jaber et al. [36] and provided a closed-form formula that generates considerably lower total cost. Two models were developed involving carbon emissions from production, storage, and transportation activities. The first model formulates the total cost function for the first cycle, whereas the second formulates the function of subsequent cycles. The author also showed that ignorance of the physical transportation cost does not affect the optimal production quantity. Table 1 below depicts and compares the proposed model with some related previously published works.

Table 1. A comparison between the proposed model with respect to some selected previous studies.

No	Authors	First cycle	Adjustable parameters	Adjustable production rate	Hybrid production	Emissions	Carbon regulations
1	Wahab et al. [21]	$\times$	$\times$	$\times$	$\times$	Transportation	Carbon tax
2	Hariga et al. [25]	$\times$	$\times$	$\times$	$\times$	Storage, Transportation	Carbon tax
3	Jaber et al. [36]	$\times$	$\times$	$\sqrt$	$\times$	Production	Carbon tax, Penalty
4	Bazan et al. [38]	$\times$	$\times$	$\sqrt$	$\times$	Production, Transportation	Carbon tax, Penalty
5	Kumar and Uthayakumar [34]	$\times$	$\times$	$\times$	$\times$	Production	Carbon tax, Penalty
6	Zanoni et al. [35]	$\times$	$\times$	$\times$	$\times$	Production	Carbon tax, Penalty
7	Konur [57]	$\times$	$\times$	$\times$	$\times$	Transportation	Carbon cap
8	Astanti et al. [39]	$\times$	$\times$	$\times$	$\times$	Production, Transportation	Carbon tax
9	Malik and Kim [40]	$\times$	$\times$	$\sqrt$	$\times$	Production
10	Bouchery [58]	$\times$	$\times$	$\sqrt$	$\times$	Transportation
11	Jauhari et al. [41]	$\times$	$\times$	$\sqrt$	$\sqrt$	Production, Transportation, Storage	Carbon tax
13	Alamri [56]	$\sqrt$	$\sqrt$	$\times$	$\times$	Production, Transportation, Storage	Carbon tax,Carbon cap
14	Proposed model	$\sqrt$	$\sqrt$	$\sqrt$	$\sqrt$	Production, Transportation, Storage	Carbon tax, Carbon cap, Penalty

3. Research Contribution

The mathematical formulation of the classical JELS inventory model generates an equal production quantity in all cycles. This can be attributed to the fact that the formulation assumes an infinite planning horizon. Such assumption suggests a static production process that is associated with a fixed multiplier in all cycles including the first cycle. However, the initial on-hand inventory of the buyer is zero in the first-time interval since no items have been produced yet. This necessitates a production policy that distinguishes the first cycle from subsequent cycles. Therefore, two mathematical formulations that reflect the behavior of the first and subsequent cycles are needed. The first mathematical formulation derives distinct optimal solution for the first cycle, while the other generates distinct optimal solution for subsequent cycles. Therefore, each subsequent cycle can be associated with its distinct input parameters to ensure that it is independent from the previous one. It is worth noting here that such consideration overcomes the implicit assumption associated with the classical formulation that input parameters remain static indefinitely. This is so, because the classical formulation assumes that the production process for subsequent cycles begins to generate the same lot sizes equal that of the last lot that has been produced in previous cycle, which represents the initial on-hand inventory of the buyer. Accordingly, if the situation warrants and the decision-maker obliged to deviate from the current policy, then the optimal production quantity as the classical formulation would then suggest cannot be considered as the optimal quantity for subsequent cycles.

The proposed model considers the abovementioned issues and, therefore, allowing for the adjustment of the input parameters for any subsequent cycle. This also guarantees that the model remains viable and keeps generating optimal results for subsequent cycles subjected to the desirable adjustment of the input parameters. In practice, input parameters encounter adjustment due to many realistic situations. Such adjustment may occur because of external competitiveness and/or internal challenges or as a response to the dynamic nature of demand rate and/or price fluctuation. Moreover, implementing of a new policy due to acquiring new knowledge, periodic review applications, and machine maintenance scheduling activities may trigger situations that force the decision-maker to consider a suitable adjustment of the input parameters [59,60].

In this paper, we propose a VMI inventory model that investigates the effect of carbon emissions together with the implementation of green technology. The developed model considers a hybrid production system that simultaneously focuses on green and regular production methods with optimal allocation fraction of green and regular productions. In this model, emissions are released from production and storage activities related to green and regular produced items along with transportation activity. The carbon emissions are relatively associated with carbon taxes and penalties for exceeding the allowable emissions limits. The model also assumes that the system earns revenue by selling excess quota in the case that the total emission generated by the system is less than that of the emission cap, which reflects the cap-and-trade policy. Unlike traditional modeling, hybrid production implies simultaneous production fractions associated with green and regular productions, where each is associated with its distinct released emission level. In this case, the demand is satisfied from a collection of green and regular produced items. This method enables decision-maker to trade-off between the production cost and emissions. For subsequent cycles, the production process starts at the time needed to produce and deliver the first lot size. Such displacement in time prevents keeping items at the vendor’s warehouse for extra time that is associated with the consumption of the last lot that has been delivered to the buyer.

Transportation service that is associated with inventory mathematical modeling is either the Truck Load (TL) or Less than Truck Load (LTL) services. An TL service applies such that the cost incurs for the whole truck [57,61,62]. Whereas an LTL service refers to the case when the cost is paid per unit of item that is transported. To entice manufacturers, logistics companies often offer the option for utilizing both LT and LTL services. Therefore, the decision-maker needs to allocate the fraction based on the capacity of the truck that renders LT transportation service or a mixed services of LT and LTL minimizes the transportation cost. That said, the allocation fraction is associated with a positive integer multiplier representing the number of trucks (TL) required for each shipment along with the remaining quantity that needs to be transported by (LTL) service. The remainder of this paper is organized as follows:

In section 4, the cost components related to the joint hybrid production system are presented to formulate the first and subsequent cycles. Illustrative examples and special cases that reflect the application of the joint model are given in Section 5. Section 6 represents model overview and managerial insights. In Section 7, the concluding remarks and further research are provided. Finally, the holding cost functions related to the joint hybrid model are given in Appendix A, whereas the solution procedure for the first and subsequent cycles are given in Appendix B.

4. Formulation of the Joint Model

4.1. Notations

The list of notations used to develop the joint hybrid inventory system are given in Table 2 below:

Table 2. List of notations used to develop the hybrid green and regular production joint model.

$z$	$(z = g, r)$ $g$ $denotes green production and r$ denotes regular production
$k$	$(k = 1, s)$ $1$ refers to the first cycle and $s$ refers to the subsequent cycles
$d$	Buyer’s demand rate (units/unit time)
$t_{k}$	The time to produce $q_{k}$ units
$t_{l}$	The lead time (order point) to deliver the order quantity of size $q_{k}$
$T_{k}$	The time to consume $q_{k}$ units
$T_{s k}$	Cycle time
$T_{s - 1}$	The time to consume $q_{s - 1}$ units
$t_{d}$	The idle time before commencing the production process for subsequent cycles
$E_{e}$	CO₂ emissions from electricity (ton CO₂/kWh)
$E_{w b}$	Buyer’s energy consummation for keeping items in storage (kWh/unit/unit time)
$E_{w z}$	Vendor’s energy consummation for keeping items in storage (kWh/unit/unit time)
$e_{b k}$	CO₂ emissions generated by the buyer’s facility (ton CO₂/unit)
$E_{b}$	Buyer’s CO₂ emissions tax ($/ton CO₂)
$v_{c}$	The truck capacity (units/truck)
$v_{t}$	Fixed transportation cost per truck ($/truck)
$c_{t}$	Fixed transportation cost per unit ($/unit), where $\frac{v_{t}}{v_{c}} < c_{t}$
$T_{w}$	Product’s weight (ton/unit)
$T_{f}$	Distance from the freight to the vendor (km)
$T_{v}$	Distance from the vendor to the buyer (km)
$f_{e}$	The amount of fuel consumed by an empty truck (liters/km)
$f$	The amount of fuel consumed by a truckload (liters/km/ton)
$v_{v}$	Variable transportation cost associated with fuel consumption ($/liter)
$E_{T}$	CO₂ emissions from truck fuel (ton CO₂/liter)
$E_{z k}$	CO₂ emissions generated by the vendor’s facility (ton CO₂/unit)
$E_{s k}$	The total amount of CO₂ emissions (ton CO₂/unit), where $E_{s k} = e_{b k} + E_{z k}$
$E_{l i}$	CO₂ emissions limit $i$ (ton CO₂/unit time)
$E_{p i}$	CO₂ emissions penalty that the system incurs for exceeding emissions limit $i$ ($ /unit time)
$E_{c}$	CO₂ emissions cap (ton CO₂), where $E_{c} = E_{l 1}$
$E_{v z}$	Vendor’s CO₂ emissions tax ($/ton CO₂)
$E_{v}$	Vendor’s CO₂ emissions revenue earned for selling excess quota ($/ton CO₂)
$E_{v T}$	Vendor’s CO₂ emissions tax for transportation ($ /ton CO₂)
$a_{z}$	CO₂ emissions function parameter for production (kg CO₂ $\cdot$ unit time²/unit³)
$b_{z}$	CO₂ emissions function parameter for production (kg CO₂ $\cdot$ unit time/unit²)
$c_{z}$	CO₂ emissions function parameter for production (kg CO₂/unit)
$E_{m z}$	The per unit time cost to run the machine independent of production rate ($/unit time)
$E_{p z}$	The increase in unit machining cost associated with the increase of one unit in production rate ($ $\cdot$ unit time/unit²);
$S_{b}$	Buyer’s ordering cost
$S_{z}$	Vendor’s set-up cost
$h_{z}$	Vendor’s holding cost

Decision variables:
$λ$	Vendor’s coordination multiplier, where $λ \geq 1$ and integer
$ξ$	Vendor’s allocation fraction of green production, where $0 \leq ζ \leq 1$
$p_{z}$	Production rate (units/unit time), where $p_{m i n} \leq p_{z} \leq p_{m a x}$
$q_{k}$	Order quantity (units/unit time), where $q_{k} = q_{g k} + q_{r k}$
$n$	Number of trucks required to deliver $q_{k}$ , where $n \geq 0$ and integer

4.2. Assumptions

The following assumptions have been considered:

A single item is manufactured by a combination of green and regular production methods.
The demand rate is satisfied from a collection of green and regular produced items.
Any order size of $q_{k}$ placed at time $t_{l}$ arrives the buyer just prior to the depletion of the on-hand inventory of that same period. In the first period of the first cycle, the buyer’s initial inventory is zero because no items have been manufactured yet. Accordingly, the vendor delivers the first lot size, $q_{1}$ once it has been accumulated from green and regular produced items by time $t_{1}$ and, will reach the buyer after a transportation time $t_{l}$ . Therefore, shortages are allowed in the first period of the first cycle and fully backordered by time $t_{1} + t_{l}$ . Thus, we restrict that $p_{1} (T_{1} - t_{l}) \geq 2 d T_{1}$ in the first cycle, i.e., the second replenishment will reach the buyer before the depletion of the on-hand inventory of the first period, i.e., no later than time $T_{1}$ .

4.3. The Mathematical Formulation of the Joint Model

Figures 1 and 2 depict, respectively, inventory variation of the proposed joint model for a tow-echelon supply chain consisting of a vendor and a buyer for the first and subsequent cycles. At the beginning of the first cycle, the production process of green and regular produced items starts at a rate

p_{z k}

. At time

t_{1}

, the vendor delivers the first lot of size

q_{1}

units that have been accumulated from green and regular produced items. This quantity satisfies demand and shortages that has been accumulated during time

t_{1} + t_{l}

. As can been seen from Figures 1 and 2, holding cost are applied for

λ

lots for both the vendor and the buyer. This is so, because the vendor must deliver two lots by time

T_{1}

to avoid shortages for the second period. Therefore, the first lot that has been replenished at time

t_{1}

reaches the buyer at time

t_{1} + t_{l}

to satisfy demand and shortages. Whereas the second reaches the buyer just before the inventory level becomes zero, i.e., by time

T_{1}

. In the subsequent cycles, the production process starts at time

t_{d} = T_{s - 1} - t_{s} - t_{l}

. That is, the production time is displaced until the time required to produce and deliver the first lot.

Figure 1. Inventory variation for a coordinated two-echelon supply chain in the first cycle

T_{s 1}

Figure 1. Inventory variation for a coordinated two-echelon supply chain in the first cycle

T_{s 1}

Figure 2. Inventory variation for a coordinated two-echelon supply chain in the subsequent cycles

T_{s s}

Figure 2. Inventory variation for a coordinated two-echelon supply chain in the subsequent cycles

T_{s s}

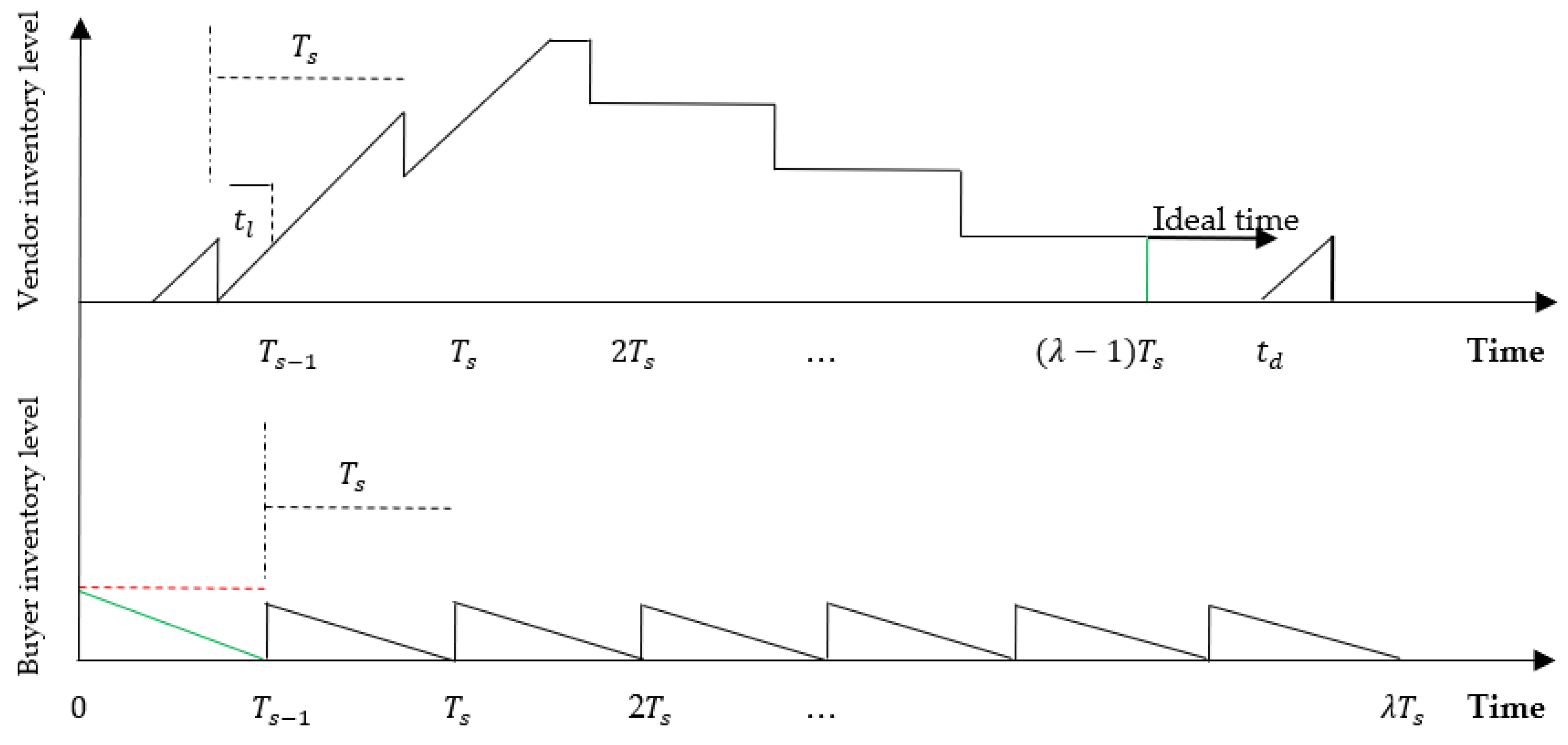
Figure 3 represents the direct and indirect CO₂ emissions generated by the buyer and the vendor activities. The buyer experiences direct CO₂ emissions, which are related to amount of GHG emissions generated for keeping items in storage. Whereas the vendor experiences both direct and indirect CO₂ emissions. The direct CO₂ emissions occur due to production and storge activities for both green and regular produced items. The vender is responsible for transportation activity, which is associated with direct and indirect CO₂ emissions. The direct CO₂ emissions related to transportation involves product’s weight. Whereas the indirect CO₂ emissions related to transportation includes shipments frequency, distance travelled from freight to vendor, distance travelled from vendor to buyer, and fuel consumption.

Figure 3. Classification of CO₂ emissions of the joint hybrid model for the vendor and the buyer.

4.3.1. The Mathematical Formulation of the First Cycle

The per unit time holding cost function (see Appendix A) for the base model depicted by Figure 1 (first cycle) is given by:

W_{s 1} = \frac{h_{b} d^{2} {t_{l}}^{2}}{2 λ q_{1}} + \frac{h_{b} q_{1} d}{2 λ} [\frac{d}{p^{2}} - \frac{2}{p} + \frac{λ}{d}] + \frac{h_{b}}{2 λ} [\frac{2 d^{2} t_{l}}{p} - 2 d t_{l}] + \frac{h_{v} q_{1}}{2 λ} [\frac{2 d}{p} + λ^{2} (1 - \frac{d}{p}) - λ] - \frac{h_{v} (λ - 1) d t_{l}}{λ} .

(1)

Below we introduce the relevant elements related to the inventory model with environmental effect:

In addition to the holding cost that is applied for the buyer’s base model represented by the first three terms of Equation (1), the buyer incurs an ordering cost per lot size. The buyer also encounters a cost related to the emissions generated during inventory storage of items because of warehousing activities, which depends on the buyer’s inventory level [27,39,58,63]. Considering the above and Equation (1), the per unit time total cost function for the buyer in the first cycle is given by:

W_{E b 1} = \frac{S_{b} d}{q_{1}} + \frac{(h_{b} + E_{b} E_{e} E_{w b}) d^{2} {t_{l}}^{2}}{2 λ q_{1}} + \frac{(h_{b} + E_{b} E_{e} E_{w b}) q_{1} d}{2 λ} [\frac{d}{p^{2}} - \frac{2}{p} + \frac{λ}{d}] + \frac{(h_{b} + E_{b} E_{e} E_{w b})}{2 λ} [\frac{2 d^{2} t_{l}}{p} - 2 d t_{l}] .

(2)

The CO₂ emissions generated by the buyer is given by:

e_{b 1} = \frac{E_{e} E_{w b} d^{2} {t_{l}}^{2}}{2 λ q_{1}} + \frac{E_{e} E_{w b} q_{1} d}{2 λ} [\frac{d}{p^{2}} - \frac{2}{p} + \frac{λ}{d}] + \frac{E_{e} E_{w b}}{2 λ} [\frac{2 d^{2} t_{l}}{p} - 2 d t_{l}] .

(3)

Similarly, in addition to the holding cost that is applied for the vendor’s base model, the vendor incurs a set-up cost as well as the following transportation and carbon emissions costs:

As that of the buyer, the vendor also incurs a cost related to the emissions generated during inventory storages, which depend on the vendor’s inventory levels of green and regular produced items.

Transportation is associated with direct and indirect carbon emissions. The direct emission level underlies the wight of the product transferred to the buyer. The indirect emission level underlies the shipments frequency, distance travelled from freight to vendor, distance travelled from vendor to buyer, and fuel consumption [58]. Transportation is also associated with a cost for delivering each lot size to the buyer. In this regard, the vendor may deliver each lot size using a combination of LTL and TL services. Hence, let

∆ = \frac{v_{t}}{c_{t}} < v_{c}

represents the quantity with identical transportation cost by either service. In addition, let

δ = (\frac{q_{1}}{v_{c}} - n)

denotes the portion of truck capacity that needs to be delivered using either TL or LTL. If

δ v_{c} \leq ∆

, then it is more cost effective for the vendor to use a combination of LTL and TL services, i.e.,

v_{t} n + (\frac{q_{1}}{v_{c}} - n) v_{c} c_{t}

. Alternatively, if

δ v_{c} \geq ∆

then it is more beneficial for the vendor to use TL service, i.e.,

v_{t} (n + 1)

trucks. Accordingly, we set

\emptyset = 1

if the TL service is utilized and

\emptyset = 0

if a mixed policy of LTL and TL services is implemented. Therefore, the physical and emissions transportation costs per unit time for the vendor are given by:

\frac{\emptyset v_{t} (n + 1) d}{q_{1}} + \frac{(1 - \emptyset) ((v_{t} - v_{c} c_{t}) n + c_{t} q_{1}) d}{q_{1}} + (v_{v} + E_{v T} E_{T}) d (\frac{{T_{f} f}_{e}}{q_{1}} + T_{v} T_{w} f) .

(4)

The vendor has two production options, i.e., green, and regular production, where each generates distinct emission level. In this case,

ζ q_{1}

is produced by the green production method with a production rate

ξ p = p_{g}

and the rest, i.e.,

(1 - ζ) q_{1}

is produced by the regular production method with a production rate

(1 - ζ) p = p_{r}

. This implies that the first lot size

q_{1}

, is delivered to the buyer once both quantities accumulate the sum of

q_{1}

units, i.e., at time

\frac{q_{1}}{p}

. Accordingly, the mathematical modeling of the duration time for holding inventories in storage for both methods is identical with that of the base model except that each method is associated with its distinct input parameters.

The production costs associated with the green production are higher than those of the regular one. This can be attribute to the fact that the green production is equipped with machine tools that are based on green technology, and consequently,

E_{m g} (E_{p g}) > E_{m r} (E_{p r})

. Here, we assume that

E_{m z} (E_{p z})

decreases (increases) as production rate increases (decreases). For example, the more items that are accomplished by the worker, the lower the wage per unit time is paid by the company. Similarly, as the production rate increases, tools and rework cost increase due to the increase off defective items resulting from tool wear [64]. Therefore, the production costs per unit time are, respectively, given by:

(\frac{E_{m g}}{p_{g}} + E_{p g} p_{g}) ζ d

(5)

(\frac{E_{m r}}{p_{r}} + E_{p r} p_{r}) (1 - ζ) d

(6)

Carbon emission released from production is represented by a function that links the production rate with the rate of emission [36,38]. However, the vendor invests in the green production facility aiming to reduce CO₂ emissions. Therefore, the vendor reaps the benefit of such investment that renders produced items greener, and consequently, the vendor reduces the cost incurred for emissions. The emissions costs for green and regular productions per unit time are, respectively, given by:

E_{v g} (a_{g} {p_{g}}^{2} - b_{g} p_{g} + c_{g}) ζ d

(7)

E_{v r} (a_{r} {p_{r}}^{2} - b_{r} p_{r} + c_{r}) (1 - ζ) d

(8)

According to Fandel [65] and Narita [66], machines constructed for green production generate a lower level of emission due to the use of green technology, and consequently,

a_{g} < a_{r}, c_{g} < c_{r}, a n d b_{g} > b_{r}

. Thus, the CO₂ emissions generated by the green and regular facilities are, respectively, given by:

E_{g 1} = \frac{{E_{e} E}_{w g} ζ q_{1}}{2 λ} [\frac{2 d}{p} + λ^{2} (1 - \frac{d}{p}) - λ] - \frac{ζ (λ - 1) {E_{e} E}_{w g} d t_{l}}{λ} + E_{T} d (\frac{{T_{f} f}_{e}}{q_{1}} + T_{v} T_{w} f) + (a_{g} ζ^{2} p^{2} - b_{g} ζ p + c_{g}) ζ d .

(9)

E_{r 1} = \frac{{E_{e} E}_{w r} (1 - ζ) q_{1}}{2 λ} [\frac{2 d}{p} + λ^{2} (1 - \frac{d}{p}) - λ] - \frac{(1 - ζ) (λ - 1) {E_{e} E}_{w r} d t_{l}}{λ} + (a_{r} {(1 - ζ)}^{2} p^{2} - b_{r} (1 - ζ) p + c_{r}) (1 - ζ) d .

(10)

Note that the emissions related to transportation applies only once, therefore it is included either for

E_{g 1}

E_{r 1}

In addition, the joint system either earns revenue from selling excess quota or incurs a penalty cost for exceeding the allowable limits [36,38]. The penalty cost is given by:

\sum_{i = 1}^{k} Y_{i} E_{p i},

(11)

where

Y_{i} = 1

, if

E_{s 1} > E_{l i} (i = 1, 2, \dots, k),

and

Y_{i} = 0

, otherwise, where

E_{p i} < E_{p i + 1}

The cap-and-trade regulations is given by:

E_{R} = E_{v} α (E_{c} - E_{s 1}),

(12)

where

α = 1

, if

E_{s 1} < E_{c}

and

α = 0

, otherwise.

Now, considering the above and Equation (1), the total cost functions per unit time for the vendor in the first cycle for green and regular productions are, respectively, given by:

W_{E g 1} = \frac{S_{g} d}{λ q_{1}} + \frac{(h_{g} + E_{v g} {E_{e} E}_{w g}) ζ q_{1}}{2 λ} [\frac{2 d}{p} + λ^{2} (1 - \frac{d}{p}) - λ] - \frac{ζ (λ - 1) (h_{g} + E_{v g} {E_{e} E}_{w g}) d t_{l}}{λ} + \frac{(1 - \emptyset) ((v_{t} - v_{c} c_{t}) n + c_{t} q_{1}) d}{q_{1}} + \frac{\emptyset v_{t} (n + 1) d}{q_{1}} + (v_{v} + E_{v T} E_{T}) d (\frac{{T_{f} f}_{e}}{q_{1}} + T_{v} T_{w} f) + (\frac{E_{m g}}{p} + E_{p g} ζ^{2} p) d + E_{v g} (a_{g} ζ^{2} p^{2} - b_{g} ζ p + c_{g}) ζ d + \sum_{i = 1}^{k} Y_{i} E_{p i} + E_{v} α (E_{c} - E_{s 1}) .

(13)

W_{E r 1} = \frac{S_{r} d}{λ q_{1}} + \frac{(h_{r} + E_{v r} {E_{e} E}_{w r}) (1 - ζ) q_{1}}{2 λ} [\frac{2 d}{p} + λ^{2} (1 - \frac{d}{p}) - λ] - \frac{(1 - ζ) (λ - 1) (h_{r} + E_{v r} {E_{e} E}_{w r}) d t_{l}}{λ} + (\frac{E_{m r}}{p} + E_{p r} {(1 - ζ)}^{2} p) d + E_{v r} (a_{r} {(1 - ζ)}^{2} p^{2} - b_{r} (1 - ζ) p + c_{r}) (1 - ζ) d .

(14)

Note that the physical and emissions transportation costs, cap-and-trade revenue, and penalty cost apply only once, therefore they are included either for

W_{E g 1}

W_{E r 1}

. Therefore, the per unit time total joint cost function in the first cycle considering Equations (2), (13) and (14) is given by:

W_{E s 1} = \frac{S_{b} d}{q_{1}} + \frac{(S_{g} + S_{r}) d}{λ q_{1}} + \frac{(h_{b} + E_{b} E_{e} E_{w b}) d}{2 λ} (\frac{d {t_{l}}^{2}}{q_{1}} + q_{1} [\frac{d}{p^{2}} - \frac{2}{p} + \frac{λ}{d}] + [\frac{2 d t_{l}}{p} - 2 t_{l}]) + \frac{[(h_{g} + E_{v g} {E_{e} E}_{w g}) ζ q_{1} + (h_{r} + E_{v r} {E_{e} E}_{w r}) (1 - ζ) q_{1}]}{2 λ} [\frac{2 d}{p} + λ^{2} (1 - \frac{d}{p}) - λ] - \frac{[ζ (h_{g} + E_{v g} {E_{e} E}_{w g}) + (1 - ζ) (h_{r} + E_{v r} {E_{e} E}_{w r})] (λ - 1) d t_{l}}{λ} + \frac{\emptyset v_{t} (n + 1) d}{q_{1}} + \frac{(1 - \emptyset) ((v_{t} - v_{c} c_{t}) n + c_{t} q_{1}) d}{q_{1}} + (v_{v} + E_{v T} E_{T}) d (\frac{{T_{f} f}_{e}}{q_{1}} + T_{v} T_{w} f) + (\frac{E_{m g}}{p} + E_{p g} ζ^{2} p) d + (\frac{E_{m r}}{p} + E_{p r} {(1 - ζ)}^{2} p) d + E_{v g} (a_{g} ζ^{2} p^{2} - b_{g} ζ p + c_{g}) ζ d + E_{v r} (a_{r} {(1 - ζ)}^{2} p^{2} - b_{r} (1 - ζ) p + c_{r}) (1 - ζ) d + \sum_{i = 1}^{k} Y_{i} E_{p i} + E_{v} α (E_{s 1} - E_{c}) .

(15)

For simplicity, let

S_{g} + S_{r} = c 1, h_{b} + E_{b} E_{e} E_{w b} = c 2, h_{g} + E_{v g} {E_{e} E}_{w g} = c 3, h_{r} + E_{v r} {E_{e} E}_{w r} = c 4, a n d v_{v} + E_{v T} E_{T} = c 5

. Thus, Equation (15) can be rewritten as:

W_{E s 1} = \frac{S_{b} d}{q_{1}} + \frac{c 1 d}{λ q_{1}} + \frac{c 2 d}{2 λ} (\frac{d {t_{l}}^{2}}{q_{1}} + q_{1} [\frac{d}{p^{2}} - \frac{2}{p} + \frac{λ}{d}] + [\frac{2 d t_{l}}{p} - 2 t_{l}]) + \frac{[c 3 ζ q_{1} + c 4 (1 - ζ) q_{1}]}{2 λ} [\frac{2 d}{p} + λ^{2} (1 - \frac{d}{p}) - λ] - \frac{[ζ c 3 + (1 - ζ) c 4] (λ - 1) d t_{l}}{λ} + \frac{\emptyset v_{t} (n + 1) d}{q_{1}} + \frac{(1 - \emptyset) ((v_{t} - v_{c} c_{t}) n + c_{t} q_{1}) d}{q_{1}} + c 5 d (\frac{{T_{f} f}_{e}}{q_{1}} + T_{v} T_{w} f) + (\frac{E_{m g}}{p} + E_{p g} ζ^{2} p) d + (\frac{E_{m r}}{p} + E_{p r} {(1 - ζ)}^{2} p) d + E_{v g} (a_{g} ζ^{2} p^{2} - b_{g} ζ p + c_{g}) ζ d + E_{v r} (a_{r} {(1 - ζ)}^{2} p^{2} - b_{r} (1 - ζ) p + c_{r}) (1 - ζ) d + \sum_{i = 1}^{k} Y_{i} E_{p i} + E_{v} α (E_{c} - E_{s 1}) .

(16)

4.3.2. The Mathematical Formulation of the Subsequent Cycles

The per unit time holding cost function (see Appendix A) for the base model depicted by Figure 2 (subsequent cycles) is given by:

W_{s s} = \frac{h_{b} q_{s}}{2} + \frac{h_{v} q_{s}}{2} [\frac{d}{p} + (λ - 1) (1 - \frac{d}{p})] .

(17)

Therefore, by a similar above-discussed approach for the first cycle, the per unit time total joint cost function for subsequent cycles is given by:

W_{E s s} = \frac{S_{b} d}{q_{s}} + \frac{c 1 d}{λ q_{s}} + \frac{c 2 q_{s}}{2} + \frac{[c 3 ζ q_{s} + c 4 (1 - ζ) q_{s}]}{2} [\frac{d}{p} + (λ - 1) (1 - \frac{d}{p})] + \frac{\emptyset v_{t} (n + 1) d}{q_{s}} + \frac{(1 - \emptyset) ((v_{t} - v_{c} c_{t}) n + c_{t} q_{s}) d}{q_{s}} + c 5 d (\frac{{T_{f} f}_{e}}{q_{s}} + T_{v} T_{w} f) + (\frac{E_{m g}}{p} + E_{p g} ζ^{2} p) d + (\frac{E_{m r}}{p} + E_{p r} {(1 - ζ)}^{2} p) d + E_{v g} (a_{g} ζ^{2} p^{2} - b_{g} ζ p + c_{g}) ζ d + E_{v r} (a_{r} {(1 - ζ)}^{2} p^{2} - b_{r} (1 - ζ) p + c_{r}) (1 - ζ) d + \sum_{i = 1}^{k} Y_{i} E_{p i} + E_{v} α (E_{c} - E_{s s}) .

(18)

From Equation (18) we note that the CO₂ emissions generated by the buyer in subsequent cycles is:

e_{b s} = \frac{E_{e} E_{w b} q_{s}}{2} .

(19)

From Equation (18), the CO₂ emissions generated by the green and regular facilities in subsequent cycles are, respectively, given by:

E_{g s} = \frac{{E_{e} E}_{w g} ζ q_{s}}{2} [\frac{d}{p} + (λ - 1) (1 - \frac{d}{p})] + E_{T} d (\frac{{T_{f} f}_{e}}{q_{1}} + T_{v} T_{w} f) + (a_{g} ζ^{2} p^{2} - b_{g} ζ p + c_{g}) ζ d .

(20)

E_{r s} = \frac{{E_{e} E}_{w r} (1 - ζ) q_{s}}{2} [\frac{d}{p} + (λ - 1) (1 - \frac{d}{p})] + (a_{r} {(1 - ζ)}^{2} p^{2} - b_{r} (1 - ζ) p + c_{r}) (1 - ζ) d .

(21)

Our goal is to minimize

W_{E s 1} (W_{E s s})

given by Equations (16) and (18) subject to integer values of

λ a n d n

Therefore, the goal is to solve the following optimization problem.

W_{E S 1} (W_{E S S}) = \{\begin{matrix} minimize W_{E s 1} (W_{E s s}) given by Equations 16 (18) \\ subject to ∆ < v_{c}, (\frac{q_{1} (q_{s})}{v_{c}} - n) \geq 0, n \geq 0, λ \geq 1, \\ \emptyset = \{\begin{matrix} 1 i f (\frac{q_{1} (q_{s})}{v_{c}} - n) v_{c} \geq ∆ \\ 0 else \end{matrix} \\ 0 \leq ζ \leq 1 \\ p_{m i n} \leq p \leq p_{m a x} \\ n and λ intiger values \end{matrix}\} .

(22)

From Equations (A.51) and (A.52) (see Appendix B),

W_{E s 1, m i n}

and

W_{E s 1, m i n}

are, respectively, given by Equations (23) and (24) below:

W_{E s 1, m i n} = \frac{\sqrt{d (2 λ (S_{b} + c 5 {T_{f} f}_{e}) + 2 c 1 + c 2 d {t_{l}}^{2}) (c 2 [\frac{d^{2}}{p^{2}} - \frac{2 d}{p} + λ] + [c 3 ζ + c 4 (1 - ζ)] [\frac{2 d}{p} + λ^{2} (1 - \frac{d}{p}) - λ])}}{λ} + \frac{c_{2}}{2 λ} [\frac{2 d^{2} t_{l}}{p} - 2 d t_{l 1}] - \frac{[ζ c 3 + (1 - ζ) c 4] (λ - 1) d t_{l}}{λ} + c 5 d T_{v} T_{w} f + (\frac{E_{m g}}{p} + E_{p g} ζ^{2} p) d + (\frac{E_{m r}}{p} + E_{p r} {(1 - ζ)}^{2} p) d + E_{v g} (a_{g} ζ^{2} p^{2} - b_{g} ζ p + c_{g}) ζ d + E_{v r} (a_{r} {(1 - ζ)}^{2} p^{2} - b_{r} (1 - ζ) p + c_{r}) (1 - ζ) d + \sum_{i = 1}^{k} Y_{i} E_{p i} + E_{v} α (E_{c} - E_{s 1}) .

(23)

W_{E s s, m i n} = \sqrt{\frac{2 d (λ (S_{b} + c 5 {T_{f} f}_{e}) + c 1) [c 2 + [c 3 ζ + c 4 (1 - ζ)] [\frac{d}{p} + (λ - 1) (1 - \frac{d}{p})]]}{λ}} + c 5 d T_{v} T_{w} f + (\frac{E_{m g}}{p} + E_{p g} ζ^{2} p) d + (\frac{E_{m r}}{p} + E_{p r} {(1 - ζ)}^{2} p) d + E_{v g} (a_{g} ζ^{2} p^{2} - b_{g} ζ p + c_{g}) ζ d + E_{v r} (a_{r} {(1 - ζ)}^{2} p^{2} - b_{r} (1 - ζ) p + c_{r}) (1 - ζ) d + \sum_{i = 1}^{k} Y_{i} E_{p i} + E_{v} α (E_{c} - E_{s s}) .

(24)

As can be seen, Equations (23) and (24) still depend on

p

and

ζ

, therefore, no closed form formulation have been found for

p

and

ζ

. Thus, their optimal values can be obtained using numerical search from which Equations (23) and (24) are minimized subject to

p_{m i n} \leq p \leq p_{m a x}

and

0 \leq ζ \leq 1

. Then, from Equations A.49 (A.50) (see Appendix B) we can find

\frac{q_{1}}{v_{c}} (\frac{q_{s}}{v_{c}})

, if

δ v_{c} \geq ∆

, then we set

\emptyset = 1

in Equations 16 (18). Otherwise, i.e.,

δ v_{c} < ∆

, then we set

\emptyset = 0

in Equations 16 (18). Note that

\frac{q_{1}}{v_{c}} (\frac{q_{s}}{v_{c}})

represents the integer value of

n

plus the fraction

δ

5. Numerical Examples

In this section, we present examples and special cases to illustrate the application of the proposed model in different sittings. The problems

W_{E S 1} a n d W_{E S S}

have been coded in MATLAB for the set of input parameters that are listed in Tables 3 and 4 below. Table 3 shows the input parameters illustrating the application of the proposed model, whereas Table 4 represents the emissions penalties schedule for exceeding allowable limits.

Table 3. Input parameters for Example 1.

$E_{m g}$	$E_{m r}$	$E_{p g}$	$E_{p r}$	$E_{v g}$	$E_{v r}$
2500	2000	0.0008	0.0004	1.6	2
USD/month	USD/month	USD $\cdot$ month /unit²	USD $\cdot$ month /unit²	USD/ton CO₂	USD/ton CO₂
$E_{T}$	$f$	$f_{e}$	$T_{w}$	$E_{v T}$	$v_{v}$
0.0026	0.064	0.32	0.01	2	0.75
ton CO₂/liter	liters/km/ton	liters/km	ton/unit	USD/ton CO₂	USD/liter
$T_{f}$	$T_{v}$	$E_{c}$	$h_{g}$	$h_{r}$	$h_{b}$
80	300	400	5	4	3
km	km	ton CO₂/month	USD/unit/month	USD/unit/month	USD/unit/month
$t_{l}$	$E_{b}$	$E_{v}$	$d$	$p_{m a x}$	$p_{m i n}$
0.08	2	2	1000	4000	1200
month	USD/ton CO₂	USD/ton CO₂	units/month	units/month	units/month
$S_{g}$	$S_{r}$	$S_{b}$	$v_{t}$	$v_{c}$	$c_{t}$
1200	800	400	500	300	2
USD/set-up	USD/set-up	USD/order	USD/truck	units/truck	USD/unit
$a_{g}$	$b_{g}$	$c_{g}$	$a_{r}$	$b_{r}$	$c_{r}$
0.0000003	0.0012	1.4	0.0000005	0.0008	1.5
ton CO₂ $\cdot$ month ²/unit³	ton CO₂ $\cdot$ month /unit²	ton CO₂/unit	ton CO₂ $\cdot$ month ²/unit³	ton CO₂ $\cdot$ month /unit²	ton CO₂/unit
$E_{w b}$	$E_{w g}$	$E_{w r}$	$E_{e}$
1.44	1	1.44	0.0005
kWh/unit/month	kWh/unit/month	kWh/unit/month	ton CO₂/kWh

Table 4. CO₂ emissions penalties scheme.

$i$	$E_{l i}$ (ton CO₂/unit time)	Penalty scheme	$E_{p i}$ (USD /unit time)
1	400	$E_{s k} < E_{c} = E_{l 1}$	0
2	500	$E_{l 1} \leq E_{s k} < E_{l 2}$	500
3	600	$E_{l 2} \leq E_{s k} < E_{l 3}$	1000
4	700	$E_{l 3} \leq E_{s k} < E_{l 4}$	1500
5	800	$E_{l 4} \leq E_{s k} < E_{l 5}$	2000
6	800	$E_{s k} \geq E_{l 6}$	2500

5.1. Example 1

In this example, we consider the set of values that are presented in Tables 3 and 4 to observe the behavior of the system.

Table 5 depicts the effect of the hybrid production system on the first and subsequent cycles and summarizes the optimal values of

ξ_{k}^{*}, p_{k}^{*}, q_{k}^{*}, λ_{k}^{*}, n_{k}^{*}, E_{s k}^{*}, a n d W_{s k}^{*}

Table 5. Optimal results for a hybrid production system for example 1.

First cycle	$ξ_{1}^{*}$	$p_{1}^{*}$	$q_{1}^{*}$	$λ_{1}^{*}$	$n_{1}^{*}$	$E_{s 1}^{*}$	$W_{S 1}^{*}$	Mixed strategy
	0.686	2635.15	755.76	2	2	516.74	12,163.86	$\sqrt$
Subsequent cycles	$ξ_{s}^{*}$	$p_{s}^{*}$	$q_{s}^{*}$	$λ_{s}^{*}$	$n_{s}^{*}$	$E_{s s}^{*}$	$W_{s s}^{*}$
	0.647	3427.72	1053.79	1	3	586.39	13,197.82	$\sqrt$

In the first cycle, the optimal production quantity of green and regular items is

q_{1}^{*} = 755.76 u n i t s

, which satisfies demand and shortages that have been accumulated in the first period, with

λ_{1}^{*} = 2

. The optimal production rate is

p_{1}^{*} = 2635.15 u n i t s

, with

ξ_{1}^{*} = 0.686

(68.6%) that comes from green production facility and the remaining fraction is produced in the regular production facility. Note that the demand is satisfied from a collection of green and regular produced items. From Equation (A.49),

\frac{q_{1}^{*}}{v_{c}} = \frac{755.76}{300} = 2.5192 \Rightarrow n_{1}^{*} = 2

, where

∆ = \frac{v_{t}}{c_{t}} = \frac{500}{2} = 250 u n i t s < v_{c} = 300 u n i t s .

This is so, since

δ = (\frac{q_{1}^{*}}{v_{c}} - n_{1}^{*}) = 0.5192 < \frac{∆}{c_{v}} = \frac{v_{t}}{{c_{v} c}_{t}} = \frac{500}{300 \times 2} = 0.833

. Therefore,

0.5192

indicates the fraction of truck capacity that needs to be transported by LTL service. In this case,

δ v_{c} = 0.5192 \times 300 = 155.76 < ∆ = \frac{v_{t}}{c_{t}} = 250 ⟹ v_{t} n + (\frac{q_{1}^{*}}{v_{c}} - n) v_{c} c_{t}

. That is, we set

\emptyset = 0

and

n_{1}^{*} = 2

in Equation (16). The total cost per month is

W_{s 1}^{*} = U S D 12,163.86

, with GHG emissions being generated due to production, storage, and transportation activities equals to

E_{s 1}^{*} = 516.74 t o n {C O}_{2}

. The vast majority (71.82%) of the emissions is related to regular production activities (

E_{r 1} = 371.11 t o n {C O}_{2}

) even though less than 32% of the production quantity has been produced in the regular facility. Note that this amount does not include emissions related to transportation activity (recall Equation (10)). The amount of GHG emissions related to green production is

E_{g 1} = 145.46 t o n {C O}_{2}

, with

0.587 t o n {C O}_{2}

being released due to transportation activity. Whereas the emissions related to storage activity of green and regular produced items at both warehouses are negligible, i.e.,

0.06 t o n {C O}_{2}

and

0.024 t o n {C O}_{2}

, respectively. The emissions related to keeping items at the buyer’s warehouse is

e_{b 1} = 0.172 t o n {C O}_{2}

. Note that

p_{1}^{*} (T_{1} - t_{l}) \geq 2 d T_{1}

, i.e.,

p_{1}^{*} (T_{1} - t_{l}) = 2635.15 \times (\frac{755.76}{1000} - 0.08) = 1780.7 > 2 q_{1}^{*} = 1511.5

In subsequent cycles, the optimal production quantity of green and regular items is

q_{s}^{*} =

1053.79

u n i t s

, which satisfies demand in the first period, with

λ_{s}^{*} = 1

and

ξ_{s}^{*} = 0.647

. That is, 64.7% of the demand is satisfied from green production and the remaining quantity is fulfilled from regular production with a production rate equals to

p_{s}^{*} = 3427.72 u n i t s

. From Equation (A.50), we have

\frac{q_{s}^{*}}{v_{c}} = \frac{1053.79}{300} = 3.5126

. Thus,

n_{s}^{*} = 3 a n d δ = (\frac{q_{s}^{*}}{v_{c}} - n_{s}^{*}) = 0.5126 < 0.833

, which represents the fraction of truck capacity that needs to be transported by LTL service. Therefore,

δ v_{c} = 0.5126 \times 300 = 153.79 < ∆ = \frac{v_{t}}{c_{t}} = 250 ⟹ v_{t} n + (\frac{q_{s}^{*}}{v_{c}} - n) v_{c} c_{t}

, from which we set

\emptyset = 0

and

n_{s}^{*} = 3

in Equation (18). The total cost per month is

W_{s s}^{*} = U S D 13,197.82

, with GHG emissions being generated from production, storage, and transportation activities equals to

E_{s s}^{*} = 586.39 t o n {C O}_{2}

. The GHG emissions associated with regular production activities is

E_{r s} = 447.02 t o n {C O}_{2}

, which represents 76.25% of the total emissions released into the environment. As that of the first cycle, this amount does not comprise emissions related to transportation activity (recall Equation (21)). The amount of GHG emissions related to green production is

E_{g s} = 138.99 t o n {C O}_{2}

, with

0.562 t o n {C O}_{2}

being generated from transportation activity. The amount of GHG emissions associated with keeping items in storage at both warehouses are

0.10 t o n {C O}_{2}

and 0.066

t o n {C O}_{2}

, for green and regular produced items, respectively. Whereas the emissions related to keeping items at the buyer’s warehouse is

e_{b s} = 0.379 t o n {C O}_{2}

. The system incurs penalties costs for exceeding the emissions allowance limit (

E_{c} = 400 t o n {C O}_{2}

), which occurs in both the first and subsequent cycles. That is,

Y_{1} = Y_{2} = Y_{3} = 1 \Rightarrow \sum_{i = 1}^{3} Y_{i} E_{p i} = U S D 1500

(recall Table 4).

Note that

T_{s - 1} = T_{1} \neq T_{s}

, i.e., the second cycle behaves differently and, therefore, it is independent form the first cycle. That is, the proposed model ensures that

T_{s - 1} \neq T_{s}

holds for subsequent cycles, which implies that the input parameters can be adjusted in any cycle. However,

T_{s - 1} = T_{s}

if the input parameters remain identical for the subsequent cycle (e.g., the third cycle). This also can be observed in both, the mathematical formulation and Figure 1 and Figure 2. That is, the associated costs of the last lot that has been delivered to the buyer from the previous cycle (the first lot that appears (shaded) for subsequent cycle for illustrative purposes only) are ignored in cycle

T_{s s}

but are considered in cycle

T_{s s - 1}

(the same previous cycle) (Alamri [56]). Note also that the constraint

p_{s}^{*} (T_{1} - t_{l 1}) \geq 2 d T_{1}

does not apply for subsequent cycles. In this case, the constraint

p_{s}^{*} \geq (1 + t_{l}) d

is sufficient.

Note that if the emission cap increased from its current allowance limit (

E_{c} = 400 t o n {C O}_{2}

), to

E_{c} = 1000 t o n {C O}_{2}

, then the cap-and-trade regulations is applied, and the system earns revenue by selling excess quota. This revenue is set equal to

E_{v} (E_{c} - E_{s 1}) = 2 (1000 - 516.74) = 2 (483.26) = U S D 966.52

. Note that in this case, the system also does not incur a cost applies for penalty charge. Therefore,

W_{s 1}^{E_{c} = 1000} = 12,163.86 - 1500 - 966.52 = U S D 9697.3

, where the first term refers to the total cost of the first cycle of example 1 and the second term represents the penalty charge, whereas the third term refers to the revenue gained by selling excess quota. The same applies for subsequent cycles if the allowance limit increases from

E_{c} = 400 t o n {C O}_{2}

E_{c} = 1000 t o n {C O}_{2}

It is worth noting here that the beginning of production time for subsequent cycles is displaced, i.e., the re-start-up production time is

t_{d} = T_{s - 1} - t_{s} - t_{l} = \frac{755.76}{1000} - \frac{1053.79}{3427.72} - 0.08 = 0.368 m o n t h \approx 11 d a y s

. This is key in the mathematical formulation and has two main roles. The first one stems from the fact that this displacement reduces the holding cost. That is, it prevents keeping items at the vendor’s warehouse for extra time that is associated with the consumption of the last lot that has been delivered to the buyer. The second ensures each subsequent cycle is independent from the previous one. Therefore, allowing for the adjustment of the input parameters for any subsequent cycle as a response to the dynamic nature of demand and/or price fluctuation. The latter also guarantees that the model remains viable and keeps generating optimal results for subsequent cycles subjected to the desirable adjustment of the input parameters. Further discussion related to this point is given in the next example.

5.2. Example 2

In this example, we observe the behavior of the system if the demand rate increases in the third cycle from 1000 units to 1200 units. The rest of the input parameters remain as that listed in Table 3 and Table 4. Such adjustment is important since the demand rate or any other input parameters are subject to adjustment due to many realistic situations. Moreover, such adjustment constitutes evidence that the proposed model remains as a viable solution and continues to generate optimal values that reflect the adjustment that might occur for subsequent cycles. Table 6 shows the behavior of the optimal values of

ξ_{k}^{*}, p_{k}^{*}, q_{k}^{*}, λ_{k}^{*}, n_{k}^{*}, E_{s k}^{*}, a n d W_{s k}^{*}

when the demand rate increases in the third cycle from 1000 units to 1200 units. Note that the fourth raw of Table 6 represents the optimal values that were already derived for the subsequent cycles in Example 1, which now, is referred to as the second cycle.

Table 6. Optimal results for example 1 when the demand rate increased to 1200 units in the third cycle.

First cycle	$ξ_{1}^{*}$	$p_{1}^{*}$	$q_{1}^{*}$	$λ_{1}^{*}$	$n_{1}^{*}$	$E_{s 1}^{*}$	$W_{S 1}^{*}$	Mixed strategy
	0.686	2635.15	755.76	2	2	516.74	12,163.86	$\sqrt$
Second cycle	$ξ_{2}^{*}$	$p_{2}^{*}$	$q_{2}^{*}$	$λ_{2}^{*}$	$n_{2}^{*}$	$E_{s 2}^{*}$	$W_{s 2}^{*}$
	0.647	3427.72	1053.79	1	3	586.39	13,197.82	$\sqrt$
Subsequent cycles	$ξ_{s}^{*}$	$p_{s}^{*}$	$q_{s}^{*}$	$λ_{s}^{*}$	$n_{s}^{*}$	$E_{s s}^{*}$	$W_{s s}^{*}$
	0.654	3102.41	667.01	2	2	663.81	16,776.23	$\sqrt$

A comparison between the results in Table 6 reveals that increasing the demand rate decreases both the optimal production quantity and the production rate. However, increasing the demand rate slightly increases the proportion of green production, i.e., it increased from

ξ_{2}^{*} = 0.647

ξ_{s}^{*} = 0.654

. The optimal production quantity is

q_{s}^{*} = 667.01 u n i t s

, which is lower than that of the second cycle. The total cost per month is

W_{s s}^{*} = U S D 16,776.23

, which can be attributed to the fact that,

Y_{1} = Y_{2} = Y_{3} = Y_{4} = 1 \Rightarrow \sum_{i = 1}^{4} Y_{i} E_{p i} = U S D 3000

(Table 2). That is, the system encounters an additional penalty charge of

U S D 1500

. The system also experiences an extra cost associated with the increase in the amount of emissions generated by the system compared with that of the second cycle. It is worth noting here that the production rate decreased from

p_{2}^{*} = 3427.72

p_{s}^{*} = 3102.41

even though the emissions increased from

E_{s 2}^{*} = 586.39

E_{s s}^{*} = 663.81

. This result is consistent with the finding in Alamri [56], i.e., the amount of GHG emissions generated by the system increases (decreases) as the demand rate increases (decreases). That is, fixing the production rate and increasing (decreasing) the demand rate increases (decreases) the amount of GHG emissions generated by the system. Note that the production rate that minimizes the emission production function is that of

p_{g}^{\circ} = \frac{b_{g}}{2 a_{g} ζ}

and

p_{r}^{\circ} = \frac{b_{r}}{2 a_{r} (1 - ζ)}

. Given the input parameters of Table 3, then

p_{g}^{\circ} = 2989.5 a n d p_{r}^{\circ} = 2416.9

. Therefore, any deviation from

p_{g}^{\circ} a n d p_{r}^{\circ}

, i.e., increasing (decreasing)

p_{g}^{\circ} a n d p_{r}^{\circ}

increases the emissions generated by each production function. Note that from Table 6, we have

p_{g s}^{*} = ξ_{s}^{*} p_{s}^{*} = 2029 a n d p_{r s}^{*} = (1 - ξ_{s}^{*}) p_{s}^{*} = 1073.4

. On the other hand, Equations (16) and (18) indicate that the demand rate is linked with each production function. In this case, increasing (decreasing) the demand rate increases (decreases) the emissions generated by the system, which is reflected in this example (Example 2). Therefore, we can deduce that the lower the demand rate the lower the emissions, which implies fewer multiple penalties charge associated with the boundaries of emissions (Table 4).

As can be seen, the proposed model is a viable solution and generates optimal values that reflect the adjustment of the demand rate, i.e., the validity and robustness of our model are ascertained.

5.3. Example 3

In this example, we repeat example 1 to investigate the behavior of the model in different settings for sensitivity analysis purposes subject to the set of values as listed in Table 3 and Table 4. Namely, the direct input parameters that affect the behavior of the model are considered and the results are summarized in Table 7 below.

Table 7. Sensitivity analysis for optimal results for a hybrid production system in different settings.

Parameter	First cycle	$ξ_{1}^{*}$	$p_{1}^{*}$	$q_{1}^{*}$	$λ_{1}^{*}$	$n_{1}^{*}$	$E_{s 1}^{*}$	$W_{S 1}^{*}$	Mixed strategy
$h_{r} = h_{g} = 4$		0.697	2644.95	789.51	2	2	503.01	12,037.37	$\sqrt$
	Subsequent cycles	$ξ_{s}^{*}$	$p_{s}^{*}$	$q_{s}^{*}$	$λ_{s}^{*}$	$n_{s}^{*}$	$E_{s s}^{*}$	$W_{s s}^{*}$
		0.666	3083.21	636.70	2	2	537.83	13,000.38	$\sqrt$
$S_{r} = S_{g} = 800$	First cycle	$ξ_{1}^{*}$	$p_{1}^{*}$	$q_{1}^{*}$	$λ_{1}^{*}$	$n_{1}^{*}$	$E_{s 1}^{*}$	$W_{S 1}^{*}$	Mixed strategy
		0.648	3221.85	1189.00	1	4	566.89	12,213.34	$\times$
	Subsequent cycles	$ξ_{s}^{*}$	$p_{s}^{*}$	$q_{s}^{*}$	$λ_{s}^{*}$	$n_{s}^{*}$	$E_{s s}^{*}$	$W_{s s}^{*}$
		0.648	3403.90	961.65	1	3	582.27	12,773.99	$\sqrt$
$d = 900$	First cycle	$ξ_{1}^{*}$	$p_{1}^{*}$	$q_{1}^{*}$	$λ_{1}^{*}$	$n_{1}^{*}$	$E_{s 1}^{*}$	$W_{S 1}^{*}$	Mixed strategy
		0.655	3166.62	1235.95	1	4	499.75	9,862.99	$\sqrt$
	Subsequent cycles	$ξ_{s}^{*}$	$p_{s}^{*}$	$q_{s}^{*}$	$λ_{s}^{*}$	$n_{s}^{*}$	$E_{s s}^{*}$	$W_{s s}^{*}$
		0.647	3423.41	1015.44	1	3	526.92	12,323.63	$\sqrt$
$p_{m g} = p_{m g} = 2000$	First cycle	$ξ_{1}^{*}$	$p_{1}^{*}$	$q_{1}^{*}$	$λ_{1}^{*}$	$n_{1}^{*}$	$E_{s 1}^{*}$	$W_{S 1}^{*}$	Mixed strategy
		0.701	2476.57	767.30	2	2	508.67	11,968.41	$\sqrt$
	Subsequent cycles	$ξ_{s}^{*}$	$p_{s}^{*}$	$q_{s}^{*}$	$λ_{s}^{*}$	$n_{s}^{*}$	$E_{s s}^{*}$	$W_{s s}^{*}$
		0.649	3367.31	1050.79	1	3	577.90	13,050.79	$\sqrt$

Table 7 shows that the model behaves as expected in all cases. For instance, when the vendor allocates equal holding costs for the green and regular produced items, i.e.,

h_{r} = h_{g} = 4

, then the model generates grater quantity in the first cycle than that of example 1, which is associated with lower total minimum cost. For subsequent cycles, both the total minimum cost per month and the optimal production quantity are lower than those of example 1. The total amount of GHG emissions generated by the system in both the first and subsequent cycles are lower than those of example 1. The production rate is higher (lower) in the first cycle (subsequent cycles) than that of example 1. The allocation fraction of green production in both the first and subsequent cycles is higher than that of example 1. For equal set-up costs, i.e.,

S_{r} = S_{g} = 800

, the per unit time total minimum cost, total amount of GHG emissions, production rate, and the optimal production quantity in the first cycle (subsequent cycles) are higher (lower) than those of example 1. The allocation fraction of green production in the first cycle is lower than that of example 1 and slightly increases in subsequent cycles.

Decreasing the demand rate from 1000 units to 900 units decreases the total minimum cost per month and total amount of GHG emissions in the first and subsequent cycles. The optimal production quantity and the production rate increase (decrease) in the first cycle (subsequent cycles) compared with those of example 1. The allocation fraction of green production decreases in the first cycle and remains identical in subsequent cycles when compared with that of example 1. Finally, when the per unit time costs to run the machine independent of production rate are equal, i.e.,

p_{m g} = p_{m r} = 2000

, the model behaves differently. In particular, the per unit time total minimum cost, total amount of GHG emissions, and production rate in the first and subsequent cycles are lower than those of example 1. Whereas the allocation fraction of green production in the first and subsequent cycles is higher than that of example 1. The optimal production quantity in the first cycle (subsequent cycles) is higher (lower) than that of example 1.

As can be seen from the results obtained in Table 5, Table 6 and Table 7, the total amount of emissions generated by the system increases (decreases) with demand rate. Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 depict and compare the behavior of the model on the optimal production quantity, the amount of CO₂ emissions released by the system, the per unit time total cost, production rate, and the allocation fraction of green production for the joint system in different settings.

5.4. Example 4

In this example, we investigate the behavior of the model for regular production option to observe the advantageous associated with the hybrid production scenario and how much saving the system may gain if a hybrid production option is considered. In this case we set

p_{m g} = S_{g} = ζ = 0

in Equations (16) and (18) where the rest of the input parameters remain as that listed in Table 3 and Table 4. Table 8 depicts the behavior of the model for regular production option.

Table 8. Optimal results for regular production scenario for example 1 when

p_{m g} = ζ = 0

Table 8. Optimal results for regular production scenario for example 1 when

p_{m g} = ζ = 0

First cycle	$p_{1}^{*}$	$q_{1}^{*}$	$λ_{1}^{*}$	$n_{1}^{*}$	$E_{s 1}^{*}$	$W_{S 1}^{*}$	Mixed strategy	Saving due to hybrid production
	2000.00	652.06	2	2	1900.08	19,745.98	$\sqrt$	38.40%
Subsequent cycles	$p_{s}^{*}$	$q_{s}^{*}$	$λ_{s}^{*}$	$n_{s}^{*}$	$E_{s s}^{*}$	$W_{s s}^{*}$
	1200.00	385.46	4	1	1261.00	19,765.70	$\sqrt$	33.23%

A comparison between Table 5 and Table 8 indicates that adopting a hybrid production mode decreases the GHG emissions dramatically, which in turn reduces the per unit time total cost by 38.40% (33.23%) in the first cycle (subsequent cycles). From Table 8 we can see that the production rate and the optimal production quantity are less than those of hybrid production (Table 5). The total cost per month is

W_{s 1}^{*} = U S D 19,745.98

in the first cycle and

W_{s s}^{*} = U S D 19,765.70

in the subsequent cycles, which can be attributed to the fact that,

Y_{1} = Y_{2} = Y_{3} = Y_{4} = Y_{5} = Y_{6} = 1 \Rightarrow \sum_{i = 1}^{6} Y_{i} E_{p i} = U S D 7500

(Table 4). That is, the system encounters an additional penalty charge of

U S D 6000

in all cycles due to the dramatic increase of GHG emissions generated by the regular production. The GHG emissions related to storage and transportation activities are negligible, i.e.,

0.74 t o n {C O}_{2}

and 0.81

t o n {C O}_{2}

in the first cycle and subsequent cycles, respectively. Figure 9 and Figure 10 show and compare the behavior of the model on the optimal production quantity, the amount of CO₂ emissions released by the system, the per unit time total cost, and production rate, with respect to hybrid and regular production options.

5.5. Example 5

In this example, we compare our model for the regular production scenario with the existing literature. In particular, the models of Jaber et al. [36] and Bazan et al. [38] since they have been extensively adopted by many researchers in the field. Therefore, only the input parameters that were considered by [36,38] have been addressed for comparison purposes and the rest of the values have been omitted from our regular model. The input parameters as that of example 3 (page 76) in Jaber et al. [36] are:

E_{v r} = 18, E_{c} = 220, a_{r} = 0.0000003, b_{r} = 0.0012, c_{r} = 1.4, S_{b} = 400, S_{r} = 1200, d = 1000, h_{r} = 60 a n d h_{b} = 30

. Table 9 represents CO₂ emissions penalties scheme similar to that suggested by Jaber et al. [36].

Table 9. CO₂ emissions penalties scheme for comparison example.

$i$	$E_{l i}$ (ton CO₂/unit time)	Penalty scheme	$E_{p i}$ (USD /unit time)
1	220	$E_{s k} < E_{c} = E_{l 1}$	0
2	330	$E_{l 1} \leq E_{s k} < E_{l 2}$	1000
3	440	$E_{l 2} \leq E_{s k} < E_{l 3}$	2000
4	550	$E_{l 3} \leq E_{s k} < E_{l 4}$	3000
5	600	$E_{l 4} \leq E_{s k} < E_{l 5}$	4000
6	600	$E_{s k} \geq E_{l 6}$	5000

The per unit time total cost functions that are presented for comparison purposes are, respectively, given by:

W_{s 1}^{*} = \frac{\sqrt{2 d (λ S_{b} + S_{r}) (h_{b} [\frac{d^{2}}{p^{2}} - \frac{2 d}{p} + λ] + h_{r} [\frac{2 d}{p} + λ^{2} (1 - \frac{d}{p}) - λ])}}{λ} + E_{v r} (a_{r} p^{2} - b_{r} p + c_{r}) d + \sum_{i = 1}^{k} Y_{i} E_{p i} .

(25)

W_{s s}^{*} = \sqrt{\frac{2 d (λ S_{b} + S_{r}) [h_{b} + h_{r} [\frac{d}{p} + (λ - 1) (1 - \frac{d}{p})]]}{λ}} + E_{v r} (a_{r} p^{2} - b_{r} p + c_{r}) d + \sum_{i = 1}^{k} Y_{i} E_{p i} .

(26)

W^{J^{*}} = W^{B^{*}} = \sqrt{2 d (λ S_{b} + S_{r}) [h_{r} (1 - \frac{d}{p} + \frac{1}{λ}) + \frac{h_{b}}{λ}]} + E_{v r} (a_{r} p^{2} - b_{r} p + c_{r}) d + \sum_{i = 1}^{k} Y_{i} E_{p i} .

(27)

Equation (25) represents the model of the regular production in the first cycle, which is a modified version of Equation (23). Note that the lead time, i.e.,

t_{l} = 0

as this time is not considered by Jaber et al. [36] and Bazan et al. [38]. Similarly, Equation (26) represents the model of the regular production in the subsequent cycles, which is a modified version of Equation (24). Equation (27) represents the models of Jaber et al. [36] and Bazan et al. [38]. It is clear to deduce that only the first term of Equations (25), (26), and (27) affects the optimal production quantity. In addition, the first term of Equations (25) and (26), is identical with that of Alamri [56], from which we conclude that the work of Alamri [56] constitutes a special case of our proposed model.

Now, by implementing the values determined above in Equations (25), (26), and (27), we obtain the following results:

The per unit time total minimum cost generated by Equation (27) is

W^{J^{*}} = W^{B^{*}} = U S D 20,289.54

with a production rate equals to

p_{J}^{*} =

p_{B}^{*} = 1741.8

when

λ^{J^{*}} = λ^{B^{*}} = 3

. The amount of GHG emissions generated is

E_{J}^{*} = E_{B}^{*} = 220 t o n {C O}_{2}

. Therefore, no penalty charge is imposed though the emissions tax is

U S D 3960

. These results are identical with that of Jaber et al. [36] and Bazan et al. [38]. The per unit time total minimum cost generated by Equation (25) is

W_{s 1}^{*} = U S D 13,474.21

with an optimal production rate quals to

p_{1}^{*} = 2000

when

λ_{1}^{*} = 2

. The amount of GHG emissions generated by our regular production model is

E_{r 1}^{*} = 200 t o n {C O}_{2}

. Similarly, no penalty charge is imposed though the emissions tax is

U S D 3600

. Note that the production rate that minimizes the emissions production function is that of

p_{r}^{\circ} = \frac{b_{r}}{2 a_{r}} = 2000 = p_{1}^{*}

(recall example 2). The optimal production quantity is

q_{1}^{*} = 202.55

, from which

p_{1}^{*} (T_{1} - 0) = 2000 \times (202.55 / 1000) = 2 d T_{1} = 2 q_{1}^{*} = 405.1

. For subsequent cycles, the minimum total cost generated by Equation (26) is

W_{s 1}^{*} = U S D 17,016.41

with an optimal production rate quals to

p_{s}^{*} = 2000

when

λ_{s}^{*} = 2

and

q_{s}^{*} = 149.07

. The amount of GHG emissions is identical with that of the first cycle, i.e.,

E_{r s}^{*} = 200 t o n {C O}_{2}

with no penalty charge is imposed and the system incurs an emissions tax of

U S D 3600

. As that of the first cycle, the production rate that minimizes the emissions production function is that of

p_{r}^{\circ} = \frac{b_{r}}{2 a_{r}} = 2000 = p_{s}^{*}

As illustrated above, our model generates an optimal production quantity with a dramatic cost reduction. That is, in the first cycle the cost generated by our model is less than that of Jaber et al. [36] and Bazan et al. [38] by

33.59 % (\frac{20,289.54 - 13,474.21}{20,289.54}) \times 100 = 33.59

. For subsequent cycles, Equation (26) generates an optimal production quantity with a cost less than that of Jaber et al. [36] and Bazan et al. [38] by

16.13 % (\frac{20,289.54 - 17,016.41}{20,289.54}) \times 100 = 16.13

. This, indeed, constitutes a considerable saving and may interest both practitioners and researchers. Therefore, our model achieves three main features: (1) The proposed model generates optimal results associated with lower minimum total system cost; (2) The initial on-hand inventory at the buyer’s warehouse is zero in the first cycle, which reflects real-life settings and implies that the subsequent cycle is independent from the first one. Moreover, each subsequent cycle can be associated with its distinct input parameters to ensure that it is independent from the previous one (see also Example 2). This is key in the mathematical formulation, which implies that the input parameters can be adjusted for subsequent cycles; (3) The optimal production rate generated by our model is the one that minimizes the emissions production function. That is, the model generates the lowest emissions possible when compared with the existing literature.

6. Summary of implications and managerial insights

Unlike the classical JELS inventory model that generates an equal production quantity in all cycles, the proposed model distinguishes the first cycle from subsequent cycles.
Two mathematical models that reflect the behavior of the first and subsequent cycles are developed. The first model derives distinct optimal solution for the first cycle, while the other generates distinct optimal solution for subsequent cycles.
The initial on-hand inventory of the buyer is zero in the first-time interval since no items have been produced yet.
Each subsequent cycle can be associated with its distinct input parameters to ensure that it is independent from the previous one.
The proposed model allowing for the adjustment of the input parameters for any subsequent cycle.
The model remains viable and keeps generating optimal results for subsequent cycles subjected to the desirable adjustment of the input parameters as a response to the dynamic nature of demand rate and/or price fluctuation. Such adjustment may also reflect situations such as implementing of a new policy due to acquiring new knowledge, periodic review applications, or machine maintenance scheduling activities that may force decision-maker to consider a suitable adjustment of the input parameters.
The developed model considers a hybrid production system that simultaneously focuses on green and regular production methods with optimal allocation fraction of green and regular productions.
The proposed model enables decision-maker to utilize a mixed transportation policy that combines LT and LTL services, which reduces transportation cost.
The demand is satisfied from a collection of green and regular produced items.
The proposed model enables decision-maker to trade-off between the production cost and emissions.
For subsequent cycles, production process starts at the time needed to produce and deliver the first lot size. Therefore, prevents keeping items at the vendor’s warehouse for extra time that is associated with the consumption of the last lot that has been delivered to the buyer, which implies further cost reduction.
Emissions are released from production and storage activities related to green and regular produced items along with transportation activity.
The carbon emissions are relatively associated with carbon taxes and penalties for exceeding the allowable emissions limits. However, the system earns revenue by selling excess quota in the case that the total emissions generated by the system is less than that of the emission cap, which reflects the cap-and-trade policy.
The base closed-form formula of the proposed model produces optimal results with considerable total system cost reduction, i.e., 33.59% (16.13%) in the first cycle (subsequent cycles) when compared with existing literature.
The optimal production rate generated by the proposed model is the one that minimizes the emissions production function. That is, it generates the lowest emissions possible when compared with the existing literature.
Adopting a hybrid production method decreases the GHG emissions dramatically, which in turn reduces the per unit time total cost by 38.40% (33.23%) in the first cycle (subsequent cycles) when compared with regular production.
The results indicate that the total amount of emissions generated by the system increases (decreases) with demand rate.

7. Conclusion and Further Research

This study developed a VMI model for a JELS policy under a multi-level emission-taxing scheme. Two mathematical formulations that reflect the behavior of the first and subsequent cycles are developed. This implies that each model generates distinct optimal solution associated with distinct fixed multiplier in all cycles to ensure that each cycle is independent from the previous one. Therefore, the model for subsequent cycles remains viable and keeps generating optimal results subjected to the desirable adjustment of the input parameters. Such adjustment is a response to the real-life settings that may reflect situations such as the dynamic nature of demand rate and/or price fluctuation, implementing of a new policy due to acquiring new knowledge, periodic review applications, or machine maintenance scheduling activities that may force decision-maker to consider a suitable adjustment of the input parameters.

This study investigated the effect of carbon emissions together with the implementation of green technology. The developed model considers a hybrid production system that simultaneously focuses on green and regular production methods with optimal allocation fraction of green and regular productions. In this model, emissions are released from production and storage activities related to green and regular produced items along with transportation activity. The carbon emissions are relatively associated with carbon taxes and penalties for exceeding the allowable emissions limits. The model also assumes that the system earns revenue by selling excess quota in the case that the total emissions generated by the system is less than that of the emission cap, which reflects the cap-and-trade policy. Hybrid production implies simultaneous production fractions associated with green and regular productions, where each is associated with its distinct released emissions level. In this case, the demand is satisfied from a collection of green and regular produced items.

This study enables decision-maker to trade-off between the production cost and emissions. For subsequent cycles, production process starts at the time needed to produce and deliver the first lot size, i.e., it prevents keeping items at the vendor’s warehouse for extra time that is associated with the consumption of the last lot that has been delivered to the buyer, which implies further cost reduction. In addition, the system reaps further cost reduction by utilizing a mixed transportation policy that combines LT and LTL services.

Illustrative examples emphasized the significant impact of the first cycle on the optimal results, i.e., the first cycle is associated with distinct optimal values. The viability, validity, and robustness of the proposed model are ascertained, where the optimal values are divergent for the case that the input parameters are adjusted. Sensitivity analysis is evaluated in different realist situations to highlight some important opportunities that may interest decision-makers. The results emphasized the significant impact of the demand rate on the total amount of emissions generated by the system, which increases (decreases) with demand rate. The results also emphasized the significant impact of green production on emissions. That is, the higher the allocation fraction of green production the lower the total amount of emissions generated by the system, i.e., the system becoming more sustainable. One of the main findings is that the total system cost generated by the base closed-form formula of the proposed model is considerably lower than that of the existing literature, i.e., 33.59% (16.13%) lower in the first cycle (subsequent cycles) when the regular production method is assumed. Moreover, the optimal production rate generated by the proposed model is the one that minimizes the emissions production function. That is, it generates the lowest emissions possible when compared with the existing literature. Adopting a hybrid production method not only decreases the GHG emissions dramatically, but also reduces the per unit time total cost by 38.40% (33.23%) in the first cycle (subsequent cycles) when compared with regular production.

Further research may include the formulation of imperfect quality items in the production process where each lot size is subjected to a 100 per cent inspection. Extending the model accounting for general functions of time of demand and deterioration rates is another interesting line of further research. The formulation of a closed-loop supply chain model involving manufacturing, remanufacturing, along with transportation under GHG emissions is also possible. Furthermore, it seems plausible to consider the formulation of single-vendor multi-buyers inventory model along with different emissions trading schemes. Finally, the proposed mathematical formulation can be further adopted to rectify existing VMI models or accounting for further inquiry related to VMI mathematical modeling.

Funding

This research received no external funding.

Conflicts of Interest

The author declares no conflict of interest.

Appendix A

Below we formulate the average inventory functions for the joint model.

First cycle (Figure 1)

Buyer’s average inventory function.

As can be seen from figure 1, the vendor delivers the first lot size,

q_{1} = d T_{1}

once it has been accumulated from green and regular produced items by time

t_{1}

and, will reach the buyer after a transportation time

t_{l}

Note that shortages are allowed in the first period of the first cycle and fully backordered by time

t_{1} + t_{l}

. In this case, the maximum inventory level for the buyer is

(T_{1} - t_{1} - t_{l}) d

units, where

(T_{1} - t_{1} - t_{l}) = \frac{q_{1}}{d} - \frac{q_{1}}{p} - t_{l}

In the first period, the buyer’s average inventory function is given by:

\frac{{q_{1}}^{2}}{2} [1 - \frac{d}{p} - \frac{d t_{l}}{q_{1}}] [\frac{1}{d} - \frac{1}{p} - \frac{t_{l}}{q_{1}}] = \frac{{q_{1}}^{2}}{2} [\frac{1}{d} - \frac{2}{p} - \frac{2 t_{l}}{q_{1}} + \frac{d}{p^{2}} + \frac{2 d t_{l}}{p q_{1}} + \frac{d {t_{l}}^{2}}{{q_{1}}^{2}}]

Figure 1 indicates that the buyer’s initial inventory level is zero and the last lot produced by the vendor represents the last lot consumed by the buyer. Therefore, we have

T_{s 1} = λ T_{1} = \frac{λ q_{1}}{d} .

(A.1)

From Equation (A.1) and Figure 1, the average inventory function for the remaining lots is given by:

\frac{(λ - 1) {q_{1}}^{2}}{2 d}

Therefore, the buyer average inventory function is given by:

\frac{{q_{1}}^{2}}{2} [\frac{d}{p^{2}} - \frac{2}{p} + \frac{λ}{d}] + \frac{q_{1}}{2} [\frac{2 d t_{l}}{p} - 2 t_{l}] + \frac{d {t_{l}}^{2}}{2}

From which, the per unit time holding cost function is given by:

\frac{h_{b} q_{1} d}{2 λ} [\frac{d}{p^{2}} - \frac{2}{p} + \frac{λ}{d}] + \frac{h_{b}}{2 λ} [\frac{2 d^{2} t_{l}}{p} - 2 d t_{l}] + \frac{h_{b} d^{2} {t_{l}}^{2}}{2 λ q_{1}} .

(A.2)

Note that Equation (A.2) is identical with that of Alamri [56].

Vendor’s average inventory function.

From Figure 1, the average inventory function for green production is given as follows:

λ = 1 \Rightarrow \frac{ζ q_{1}}{2} \frac{q_{1}}{p} = \frac{ζ {q_{1}}^{2}}{2 p} .

λ = 2 \Rightarrow \frac{ζ q_{1}}{2} \frac{q_{1}}{p} + \frac{ζ q_{1}}{2} \frac{q_{1}}{p} + ζ q_{1} [\frac{q_{1}}{d} - \frac{2 q_{1}}{p} - t_{l}] .

λ = 3 \Rightarrow \frac{ζ q_{1}}{2} \frac{q_{1}}{p} + \frac{ζ q_{1}}{2} \frac{q_{1}}{p} + ζ q_{1} [\frac{q_{1}}{d} - \frac{2 q_{1}}{p} - t_{l}] + \frac{ζ q_{1}}{2} \frac{q_{1}}{p} + ζ q_{1} [\frac{{2 q}_{1}}{d} - \frac{3 q_{1}}{p} - t_{l}] .

⋮

λ = λ \Rightarrow \frac{{ζ q_{1}}^{2}}{2} [\frac{2}{p} + λ^{2} (\frac{1}{d} - \frac{1}{p}) - \frac{λ}{d}] - ζ q_{1} (λ - 1) t_{l}

(A.3)

Therefore, the per unit time holding cost function for green production is given by:

\frac{h_{g} ζ q_{1}}{2 λ} [\frac{2 d}{p} + λ^{2} (1 - \frac{d}{p}) - λ] - \frac{h_{g} ζ (λ - 1) d t_{l}}{λ} .

(A.4)

Similarly, the per unit time holding cost function for regular production is given by:

\frac{h_{r} (1 - ζ) q_{1}}{2 λ} [\frac{2 d}{p} + λ^{2} (1 - \frac{d}{p}) - λ] - \frac{h_{r} (1 - ζ) (λ - 1) d t_{l}}{λ} .

(A.5)

Note that for

ζ = 0

, Equations (A.4) and (A.5) reduce to that of Alamri [56].

Subsequent cycles (Figure 2)

Buyer’s average inventory function.

As can be seen from Figure 2, the buyer average inventory function is that of the EOQ. Therefore, the per unit time holding cost function is given by:

\frac{h_{b} q_{s}}{2} .

Vendor’s average inventory function.

From Figure 2, the average inventory function for green production is given as follows:

λ = 1 \Rightarrow \frac{ζ q_{s}}{2} \frac{q_{s}}{p} = \frac{{ζ q_{s}}^{2}}{2 p} .

λ = 2 \Rightarrow \frac{ζ q_{s}}{2} \frac{q_{s}}{p} + \frac{ζ q_{1}}{2} \frac{q_{s}}{p} + ζ q_{s} [\frac{q_{s}}{d} - \frac{q_{s}}{p}] .

λ = 3 \Rightarrow \frac{ζ q_{s}}{2} \frac{q_{s}}{p} + \frac{ζ q_{s}}{2} \frac{q_{s}}{p} + ζ q_{s} [\frac{q_{s}}{d} - \frac{q_{s}}{p}] + \frac{ζ q_{s}}{2} \frac{q_{s}}{p} + ζ q_{s} [\frac{{2 q}_{s}}{d} - \frac{2 q_{s}}{p}] .

⋮

λ = λ \Rightarrow \frac{{λ ζ q_{s}}^{2}}{2 d} [\frac{d}{p} + (λ - 1) (1 - \frac{d}{p})]

(A.6)

Therefore, the per unit time holding cost function for green production is given by:

\frac{h_{g} ζ q_{s}}{2} [\frac{d}{p} + (λ - 1) (1 - \frac{d}{p})]

(A.7)

Similarly, the per unit time holding cost function for regular production is given by:

\frac{h_{g} (1 - ζ) q_{s}}{2} [\frac{d}{p} + (λ - 1) (1 - \frac{d}{p})] .

(A.8)

Note that for

ζ = 0

, Equations (A.7) and (A.8) reduce to that of Alamri [56].

Appendix B

The goal here is to derive the solution procedure that render

W_{E S 1} (W_{E S S})

achieves the unique and global optimal solution.

Solution Procedure

According to Alamri [56], ignoring the physical transportation cost does not affect the optimal production quantity, therefore, Equations (16) and (18) can be rewritten as:

W_{E s 1, m i n} = \frac{S_{b} d}{q_{1}} + \frac{c 1 d}{λ q_{1}} + \frac{c 2 d}{2 λ} (\frac{d {t_{l}}^{2}}{q_{1}} + q_{1} [\frac{d}{p^{2}} - \frac{2}{p} + \frac{λ}{d}] + [\frac{2 d t_{l}}{p} - 2 t_{l}]) + \frac{[c 3 ζ q_{1} + c 4 (1 - ζ) q_{1}]}{2 λ} [\frac{2 d}{p} + λ^{2} (1 - \frac{d}{p}) - λ] - \frac{[ζ c 3 + (1 - ζ) c 4] (λ - 1) d t_{l}}{λ} + c 5 d (\frac{{T_{f} f}_{e}}{q_{1}} + T_{v} T_{w} f) + (\frac{E_{m g}}{p} + E_{p g} ζ^{2} p) d + (\frac{E_{m r}}{p} + E_{p r} {(1 - ζ)}^{2} p) d + E_{v g} (a_{g} ζ^{2} p^{2} - b_{g} ζ p + c_{g}) ζ d + E_{v r} (a_{r} {(1 - ζ)}^{2} p^{2} - b_{r} (1 - ζ) p + c_{r}) (1 - ζ) d + \sum_{i = 1}^{k} Y_{i} E_{p i} + E_{v} α (E_{c} - E_{s 1}) .

(A.9)

W_{E s s, m i n} = \frac{S_{b} d}{q_{s}} + \frac{c 1 d}{λ q_{s}} + \frac{c 2 q_{s}}{2} + \frac{[c 3 ζ q_{s} + c 4 (1 - ζ) q_{s}]}{2} [\frac{d}{p} + (λ - 1) (1 - \frac{d}{p})] + c 5 d (\frac{{T_{f} f}_{e}}{q_{s}} + T_{v} T_{w} f) + (\frac{E_{m g}}{p} + E_{p g} ζ^{2} p) d + (\frac{E_{m r}}{p} + E_{p r} {(1 - ζ)}^{2} p) d + E_{v g} (a_{g} ζ^{2} p^{2} - b_{g} ζ p + c_{g}) ζ d + E_{v r} (a_{r} {(1 - ζ)}^{2} p^{2} - b_{r} (1 - ζ) p + c_{r}) (1 - ζ) d + \sum_{i = 1}^{k} Y_{i} E_{p i} + E_{v} α (E_{c} - E_{s s}) .

(A.10)

Any existing solution of

W_{E s 1, m i n} (W_{E s s, m i n})

is a minimizing solution to

W_{E S 1} (W_{E S S})

if its Hessian matrix

H_{s 1} (H_{s s})

is positive definite calculated at any critical point

(q_{k}^{*}, λ_{k}^{*}, p_{k}^{*}, ζ_{k}^{*})

H_{s 1} (H_{s s})

given by Equation A.11 (A.12) below:

H_{s 1} = (\begin{matrix} \frac{\partial^{2} W_{E s 1}}{\partial^{2} q_{1}} & \frac{\partial^{2} W_{E s 1}}{\partial q_{1} \partial λ} & \begin{matrix} \frac{\partial^{2} W_{E s 1}}{\partial q_{1} \partial p} & \frac{\partial^{2} W_{E s 1}}{\partial q_{1} \partial ζ} \end{matrix} \\ \frac{\partial^{2} W_{E s 1}}{\partial λ \partial q_{1}} & \frac{\partial^{2} W_{E s 1}}{\partial^{2} λ} & \begin{matrix} \frac{\partial^{2} W_{E s 1}}{\partial λ \partial p} & \frac{\partial^{2} W_{E s 1}}{\partial λ \partial ζ} \end{matrix} \\ \begin{matrix} \frac{\partial^{2} W_{E s 1}}{\partial p \partial q_{1}} \\ \frac{\partial^{2} W_{E s 1}}{\partial ζ \partial q_{1}} \end{matrix} & \begin{matrix} \frac{\partial^{2} W_{E s 1}}{\partial p \partial λ} \\ \frac{\partial^{2} W_{E s 1}}{\partial ζ \partial λ} \end{matrix} & \begin{matrix} \begin{matrix} \frac{\partial^{2} W_{E s 1}}{\partial^{2} p} \\ \frac{\partial^{2} W_{E s 1}}{\partial ζ \partial p} \end{matrix} & \begin{matrix} \frac{\partial^{2} W_{E s 1}}{\partial p \partial ζ} \\ \frac{\partial^{2} W_{E s 1}}{\partial^{2} ζ} \end{matrix} \end{matrix} \end{matrix}),

(A.11)

H_{s s} = (\begin{matrix} \frac{\partial^{2} W_{E s s}}{\partial^{2} q_{s}} & \frac{\partial^{2} W_{E s s}}{\partial q_{s} \partial λ} & \begin{matrix} \frac{\partial^{2} W_{E s s}}{\partial q_{s} \partial p} & \frac{\partial^{2} W_{E s s}}{\partial q_{s} \partial ζ} \end{matrix} \\ \frac{\partial^{2} W_{E s s}}{\partial λ \partial q_{s}} & \frac{\partial^{2} W_{E s s}}{\partial^{2} λ} & \begin{matrix} \frac{\partial^{2} W_{E s s}}{\partial λ \partial p} & \frac{\partial^{2} W_{E s s}}{\partial λ \partial ζ} \end{matrix} \\ \begin{matrix} \frac{\partial^{2} W_{E s s}}{\partial p \partial q_{s}} \\ \frac{\partial^{2} W_{E s s}}{\partial ζ \partial q_{s}} \end{matrix} & \begin{matrix} \frac{\partial^{2} W_{E s s}}{\partial p \partial λ} \\ \frac{\partial^{2} W_{E s s}}{\partial ζ \partial λ} \end{matrix} & \begin{matrix} \begin{matrix} \frac{\partial^{2} W_{E s s}}{\partial^{2} p} \\ \frac{\partial^{2} W_{E s s}}{\partial ζ \partial p} \end{matrix} & \begin{matrix} \frac{\partial^{2} W_{E s s}}{\partial p \partial ζ} \\ \frac{\partial^{2} W_{E s s}}{\partial^{2} ζ} \end{matrix} \end{matrix} \end{matrix}),

(A.12)

where

\frac{\partial^{2} W_{E s 1}}{\partial^{2} q_{1}} = \frac{2 S_{b} d}{{q_{1}}^{3}} + \frac{2 c 1 d}{λ {q_{1}}^{3}} + \frac{c 2 d^{2} {t_{l}}^{2}}{λ {q_{1}}^{3}} + \frac{2 c 5 d {T_{f} f}_{e}}{{q_{1}}^{3}} .

(A.13)

\frac{\partial^{2} W_{E s 1}}{\partial^{2} p} = \frac{c 2 d}{λ} [\frac{3 q_{1} d}{p^{7}} + \frac{2 d t_{l}}{p^{3}} - \frac{2 q_{1}}{p^{3}}] + \frac{[c 3 ζ q_{1} + c 4 (1 - ζ) q_{1}] d}{2 λ} [\frac{4}{p^{3}} - \frac{{2 λ}^{2}}{p^{3}}] + \frac{2 E_{m g} d}{p^{3}} + \frac{2 E_{m r} d}{p^{3}} + 2 {E_{v g} a}_{g} ζ^{3} d + 2 E_{v r} a_{r} {(1 - ζ)}^{3} d .

(A.14)

\frac{\partial^{2} W_{E s 1}}{\partial^{2} λ} = \frac{2 c 1 d}{λ^{3} q_{1}} + \frac{c 2 d}{λ^{3}} (\frac{d {t_{l}}^{2}}{q_{1}} + q_{1} [\frac{d}{p^{2}} - \frac{2}{p}] + [\frac{2 d t_{l}}{p} - 2 t_{l}]) + \frac{2 [c 3 ζ q_{1} + c 4 (1 - ζ) q_{1}] d}{λ^{3} p} + \frac{2 [ζ c 3 + (1 - ζ) c 4] d t_{l}}{λ^{3}} .

(A.15)

\frac{\partial^{2} W_{E s 1}}{\partial^{2} ζ} = 2 d p (E_{p g} + E_{p r}) + 2 E_{v g} d p (3 a_{g} ζ p - b_{g}) + {2 E}_{v r} d p (3 a_{r} (1 - ζ) p - b_{r}) .

(A.16)

\frac{\partial^{2} W_{E s 1}}{\partial q_{1} \partial p} = \frac{\partial^{2} W_{E s 1}}{\partial p \partial q_{1}} = \frac{c 2 d}{λ} [\frac{1}{p^{2}} - \frac{d}{p^{3}}] + \frac{[c 3 ζ + c 4 (1 - ζ)] d}{2 λ} [\frac{λ^{2}}{p^{2}} - \frac{2}{p^{2}}] .

(A.17)

\frac{\partial^{2} W_{E s 1}}{\partial q_{1} \partial λ} = \frac{\partial^{2} W_{E s 1}}{\partial λ \partial q_{1}} = \frac{c 1 d}{λ^{2} {q_{1}}^{2}} + \frac{c 2 d}{2 λ^{2}} (\frac{d {t_{l}}^{2}}{{q_{1}}^{2}} - [\frac{d}{p^{2}} - \frac{2}{p}]) - \frac{[c 3 ζ + c 4 (1 - ζ)] d}{λ^{2} p} + \frac{[c 3 ζ + c 4 (1 - ζ)]}{2} (1 - \frac{d}{p}) .

(A.18)

\frac{\partial^{2} W_{E s 1}}{\partial q_{1} \partial ζ} = \frac{\partial^{2} W_{E s 1}}{\partial ζ \partial q_{1}} = \frac{[c 3 - c 4]}{2 λ} [\frac{2 d}{p} + λ^{2} (1 - \frac{d}{p}) - λ] .

(A.19)

\frac{\partial^{2} W_{E s 1}}{\partial p \partial λ} = \frac{\partial^{2} W_{E s 1}}{\partial λ \partial p} = \frac{- c 2 d}{λ^{2}} [\frac{q_{1}}{p^{2}} - \frac{q_{1} d}{p^{3}} - \frac{d t_{l}}{p^{2}}] + \frac{[c 3 ζ q_{1} + c 4 (1 - ζ) q_{1}] d}{2 p^{2}} + \frac{[c 3 ζ q_{1} + c 4 (1 - ζ) q_{1}] d}{p^{2} λ^{2}} .

(A.20)

\frac{\partial^{2} W_{E s 1}}{\partial p \partial ζ} = \frac{\partial^{2} W_{E s 1}}{\partial ζ \partial p} = \frac{[c 3 q_{1} - c 4 q_{1}] d}{2 λ} [\frac{λ^{2}}{p^{2}} - \frac{2}{p^{2}}] + 2 d (E_{p g} ζ - E_{p r} (1 - ζ)) + 2 E_{v g} d (3 a_{g} ζ^{2} p - b_{g} ζ) - {2 E}_{v r} d (3 {(1 - ζ)}^{2} p - b_{r} (1 - ζ)) .

(A.21)

\frac{\partial^{2} W_{E s 1}}{\partial λ \partial ζ} = \frac{\partial^{2} W_{E S 1}}{\partial ζ \partial λ} = - \frac{[c 3 q_{1} - c 4 q_{1}] d}{λ^{2} p} + \frac{[c 3 q_{1} - c 4 q_{1}]}{2} (1 - \frac{d}{p}) - \frac{[c 3 - c 4] d t_{l}}{λ^{2}} .

(A.22)

Equation

(A . 13) > 0

, if only the first two terms of Equation (A.14) are considered, then Equation

(A . 14) > 0

λ = 1

. Recall that

p_{1} > d

and

c 1 ≫ c 2

, then Equation

(A . 15) > 0

. Note that

3 a_{g} ζ p - b_{g} > 0

and

3 a_{r} (1 - ζ) p - b_{r} > 0

, from which Equation

(A . 16) > 0

Similarly, for

H_{s s}

we have

\frac{\partial^{2} W_{E s s}}{\partial^{2} q_{s}} = \frac{2 S_{b} d}{{q_{s}}^{3}} + \frac{2 c 1 d}{λ {q_{s}}^{3}} + \frac{2 c 5 {{d T}_{f} f}_{e}}{{q_{s}}^{3}} .

(A.23)

\frac{\partial^{2} W_{E s s}}{\partial^{2} p} = \frac{[c 3 ζ q_{s} + c 4 (1 - ζ) q_{s}] d}{2} [\frac{2}{p^{3}} - \frac{2 (λ - 1)}{p^{3}}] + \frac{2 E_{m g} d}{p^{3}} + \frac{2 E_{m r} d}{p^{3}} + 2 {E_{v g} a}_{g} ζ^{3} d + 2 E_{v r} a_{r} {(1 - ζ)}^{3} d .

(A.24)

\frac{\partial^{2} W_{E s s}}{\partial^{2} λ} = \frac{2 c 1 d}{λ^{3} q_{s}} .

(A.25)

\frac{\partial^{2} W_{E s s}}{\partial^{2} ζ} = 2 d p (E_{p g} + E_{p r}) + 2 E_{v g} d p (3 a_{g} ζ p - b_{g}) + {2 E}_{v r} d p (3 a_{r} (1 - ζ) p - b_{r}) .

(A.26)

\frac{\partial^{2} W_{E s s}}{\partial q_{s} \partial p} = \frac{\partial^{2} W_{E s s}}{\partial p \partial q_{s}} = \frac{[c 3 ζ + c 4 (1 - ζ)] d}{2} [\frac{(λ - 1)}{p^{2}} - \frac{1}{p^{2}}] .

(A.27)

\frac{\partial^{2} W_{E s s}}{\partial q_{s} \partial λ} = \frac{\partial^{2} W_{E s s}}{\partial λ \partial q_{s}} = \frac{c 1 d}{λ^{2} {q_{s}}^{2}} + \frac{[c 3 ζ + c 4 (1 - ζ)]}{2} (1 - \frac{d}{p}) .

(A.28)

\frac{\partial^{2} W_{E s s}}{\partial q_{s} \partial ζ} = \frac{\partial^{2} W_{E s s}}{\partial ζ \partial q_{s}} = \frac{[c 3 - c 4]}{2} [\frac{d}{p} + (λ - 1) (1 - \frac{d}{p})] .

(A.29)

\frac{\partial^{2} W_{E s s}}{\partial p \partial λ} = \frac{\partial^{2} W_{E s s}}{\partial λ \partial p} = \frac{[c 3 ζ q_{s} + c 4 (1 - ζ) q_{s}] d}{2 p^{2}} .

(A.30)

\frac{\partial^{2} W_{E s s}}{\partial p \partial ζ} = \frac{\partial^{2} W_{E s s}}{\partial ζ \partial p} = \frac{[c 3 q_{s} - c 4 q_{s}] d}{2} [\frac{(λ - 1)}{p^{2}} - \frac{1}{p^{2}}] + 2 d (E_{p g} ζ - E_{p r} (1 - ζ)) + {2 E}_{v g} d (3 a_{g} ζ^{2} p - b_{g} ζ) - {2 E}_{v r} d (3 a_{r} {(1 - ζ)}^{2} p - b_{r} (1 - ζ)) .

(A.31)

\frac{\partial^{2} W_{E S s}}{\partial λ \partial ζ} = \frac{\partial^{2} W_{E S s}}{\partial ζ \partial λ} = \frac{[c 3 q_{s} - c 4 q_{s}]}{2} (1 - \frac{d}{p}) .

(A.32)

Equations

(A . 23) a n d (A . 25) > 0

, if only the first term of Equation (

A . 24

) is considered, then Equation

(A . 24) > 0

λ = 1

. Recall that

3 a_{g} ζ p - b_{g} > 0

and

3 a_{r} (1 - ζ) p - b_{r} > 0

, from which Equation

(A . 26) > 0

Moreover, by Stewart [67], Balkhi and Benkherouf [68], Emet [69], and Alamri [70], the symmetric matrix

H_{s 1} (H_{s s})

is positive definite if

\frac{\partial^{2} W_{E s 1}}{\partial^{2} q_{1}} > |\frac{\partial^{2} W_{E s 1}}{\partial q_{1} \partial λ}| + |\frac{\partial^{2} W_{E s 1}}{\partial q_{1} \partial p}| + |\frac{\partial^{2} W_{E s 1}}{\partial q_{1} \partial ζ}|,

(A.33)

\frac{\partial^{2} W_{E s 1}}{\partial^{2} λ} > |\frac{\partial^{2} W_{E s 1}}{\partial λ \partial q_{1}}| + |\frac{\partial^{2} W_{E s 1}}{\partial λ \partial p}| + |\frac{\partial^{2} W_{E s 1}}{\partial λ \partial ζ}|,

(A.34)

\frac{\partial^{2} W_{E s 1}}{\partial^{2} p} > |\frac{\partial^{2} W_{E s 1}}{\partial p \partial q_{1}}| + |\frac{\partial^{2} W_{E s 1}}{\partial p \partial λ}| + |\frac{\partial^{2} W_{E s 1}}{\partial p \partial ζ}|,

(A.35)

\frac{\partial^{2} W_{E s 1}}{\partial^{2} ζ} > |\frac{\partial^{2} W_{E s 1}}{\partial ζ \partial q_{1}}| + |\frac{\partial^{2} W_{E s 1}}{\partial ζ \partial λ}| + |\frac{\partial^{2} W_{E s 1}}{\partial ζ \partial p}|,

(A.36)

Similarly,

\frac{\partial^{2} W_{E s s}}{\partial^{2} q_{s}} > |\frac{\partial^{2} W_{E s s}}{\partial q_{s} \partial λ}| + |\frac{\partial^{2} W_{E s s}}{\partial q_{s} \partial p}| + |\frac{\partial^{2} W_{E s s}}{\partial q_{s} \partial ζ}|,

(A.37)

\frac{\partial^{2} W_{E s s}}{\partial^{2} λ} > |\frac{\partial^{2} W_{E s s}}{\partial λ \partial q_{s}}| + |\frac{\partial^{2} W_{E s s}}{\partial λ \partial p}| + |\frac{\partial^{2} W_{E s s}}{\partial λ \partial ζ}|,

(A.38)

\frac{\partial^{2} W_{E s s}}{\partial^{2} p} > |\frac{\partial^{2} W_{E s s}}{\partial p \partial q_{s}}| + |\frac{\partial^{2} W_{E s s}}{\partial p \partial λ}| + |\frac{\partial^{2} W_{E s s}}{\partial p \partial ζ}|,

(A.39)

\frac{\partial^{2} W_{E s s}}{\partial^{2} ζ} > |\frac{\partial^{2} W_{E s s}}{\partial ζ \partial q_{s}}| + |\frac{\partial^{2} W_{E s s}}{\partial ζ \partial λ}| + |\frac{\partial^{2} W_{E s s}}{\partial ζ \partial p}|,

(A.40)

Therefore, if conditions A.33-A.36 (A.37-A.40) hold, then they constitute the sufficient conditions under which the Hessian matrix

H_{s 1} (H_{s s})

is positive definite.

Thus, any existing solution of

W_{E s 1, m i n} (W_{E s s, m i n})

for which conditions A.33-A.36 (A.37-A.40) hold is the unique and global optimal solution to

W_{E S 1} (W_{E S S})

The necessary conditions for the minimum cost for

W_{E s 1, m i n}

are:

\frac{\partial W_{E s 1}}{\partial q_{1}} = - \frac{S_{b} d}{{q_{1}}^{2}} - \frac{c 1 d}{λ {q_{1}}^{2}} - \frac{c 2 d^{2} {t_{l}}^{2}}{2 λ {q_{1}}^{2}} + \frac{c 2 d}{2 λ} [\frac{d}{p^{2}} - \frac{2}{p} + \frac{λ}{d}] + \frac{[c 3 ζ + c 4 (1 - ζ)]}{2 λ} [\frac{2 d}{p} + λ^{2} (1 - \frac{d}{p}) - λ] - \frac{c 5 d {T_{f} f}_{e}}{{q_{1}}^{2}} = 0 .

(A.41)

\frac{\partial W_{E s 1}}{\partial p} = \frac{c 2 d}{λ} [\frac{q_{1}}{p^{2}} - \frac{q_{1} d}{p^{3}} - \frac{d t_{l}}{p^{2}}] + \frac{[c 3 ζ q_{1} + c 4 (1 - ζ) q_{1}] d}{2 λ} [\frac{λ^{2}}{p^{2}} - \frac{2}{p^{2}}] + (E_{p g} ζ^{2} - \frac{E_{m g}}{p^{2}}) d + (E_{p r} {(1 - ζ)}^{2} - \frac{E_{m r}}{p^{2}}) d + E_{v g} (2 a_{g} ζ^{2} p - b_{g} ζ) ζ d + E_{v r} (2 a_{r} {(1 - ζ)}^{2} p - b_{r} (1 - ζ)) (1 - ζ) d = 0 .

(A.42)

\frac{\partial W_{E s 1}}{\partial λ} = - \frac{c 1 d}{λ^{2} q_{1}} - \frac{c 2 d}{2 λ^{2}} (\frac{d {t_{l}}^{2}}{q_{1}} + q_{1} [\frac{d}{p^{2}} - \frac{2}{p}] + [\frac{2 d t_{l}}{p} - 2 t_{l}]) - \frac{[c 3 ζ q_{1} + c 4 (1 - ζ) q_{1}] d}{λ^{2} p} + \frac{[c 3 ζ q_{1} + c 4 (1 - ζ) q_{1}]}{2} (1 - \frac{d}{p}) - \frac{[ζ c 3 + (1 - ζ) c 4] d t_{l}}{λ^{2}} = 0 .

(A.43)

\frac{\partial W_{E s 1}}{\partial ζ} = \frac{[c 3 q_{1} - c 4 q_{1}]}{2 λ} [\frac{2 d}{p} + λ^{2} (1 - \frac{d}{p}) - λ] - \frac{[c 3 - c 4] (λ - 1) d t_{l}}{λ} + 2 d E_{p g} ζ p - 2 d E_{p r} (1 - ζ) p + E_{v g} d ((2 a_{g} ζ p^{2} - b_{g} p) ζ + (a_{g} ζ^{2} p^{2} - b_{g} ζ p + c_{g})) - E_{v r} d ((2 a_{r} (1 - ζ) p^{2} - b_{r} p) (1 - ζ) + (a_{r} {(1 - ζ)}^{2} p^{2} - b_{r} (1 - ζ) p + c_{r})) = 0 .

(A.44)

Similarly, the necessary conditions for the minimum cost for

W_{E s s, m i n}

are:

\frac{\partial W_{E s s}}{\partial q_{s}} = - \frac{S_{b} d}{{q_{s}}^{2}} - \frac{c 1 d}{λ {q_{s}}^{2}} + \frac{c 2}{2} + \frac{[c 3 ζ + c 4 (1 - ζ)]}{2} [\frac{d}{p} + (λ - 1) (1 - \frac{d}{p})] - \frac{c 5 d {T_{f} f}_{e}}{{q_{s}}^{2}} = 0 .

(A.45)

\frac{\partial W_{E s s}}{\partial p} = \frac{[c 3 ζ q_{s} + c 4 (1 - ζ) q_{s}] d}{2} [\frac{(λ - 1)}{p^{2}} - \frac{1}{p^{2}}] + (E_{p g} ζ^{2} - \frac{E_{m g}}{p^{2}}) d + (E_{p r} {(1 - ζ)}^{2} - \frac{E_{m r}}{p^{2}}) d + E_{v g} (2 a_{g} ζ^{2} p - b_{g} ζ) ζ d + E_{v r} (2 a_{r} {(1 - ζ)}^{2} p - b_{r} (1 - ζ)) (1 - ζ) d = 0 .

(A.46)

\frac{\partial W_{E s s}}{\partial λ} = - \frac{c 1 d}{λ^{2} q_{s}} + \frac{[c 3 ζ q_{s} + c 4 (1 - ζ) q_{s}]}{2} (1 - \frac{d}{p}) = 0 .

(A.47)

\frac{\partial W_{E s s}}{\partial ζ} = \frac{[c 3 q_{s} - c 4 q_{s}]}{2} [\frac{d}{p} + (λ - 1) (1 - \frac{d}{p})] + 2 d E_{p g} ζ p - 2 d E_{p r} (1 - ζ) p + E_{v g} d ((2 a_{g} ζ p^{2} - b_{g} p) ζ + (a_{g} ζ^{2} p^{2} - b_{g} ζ p + c_{g})) - E_{v r} d ((2 a_{r} (1 - ζ) p^{2} - b_{r} p) (1 - ζ) + (a_{r} {(1 - ζ)}^{2} p^{2} - b_{r} (1 - ζ) p + c_{r})) = 0 .

(A.48)

From which we have

\frac{\partial W_{E s 1}}{\partial q_{1}} = 0 \Rightarrow q_{1} = \sqrt{\frac{d (2 λ (S_{b} + c 5 {T_{f} f}_{e}) + 2 c 1 + c 2 d {t_{l}}^{2})}{c 2 [\frac{d^{2}}{p^{2}} - \frac{2 d}{p} + λ] + [c 3 ζ + c 4 (1 - ζ)] [\frac{2 d}{p} + λ^{2} (1 - \frac{d}{p}) - λ]}} .

(A.49)

\frac{\partial W_{E s s}}{\partial q_{s}} = 0 \Rightarrow q_{s} = \sqrt{\frac{2 d (λ (S_{b} + c 5 {T_{f} f}_{e}) + c 1)}{λ [c 2 + [c 3 ζ + c 4 (1 - ζ)] [\frac{d}{p} + (λ - 1) (1 - \frac{d}{p})]]}} .

(A.50)

Hence, from Equations (A.49) and (A.50),

W_{E s 1, m i n}

and

W_{E s 1, m i n}

are, respectively, given by Equations (A.51) and (A.52) below:

W_{E s 1, m i n} = \frac{\sqrt{d (2 λ (S_{b} + c 5 {T_{f} f}_{e}) + 2 c 1 + c 2 d {t_{l}}^{2}) (c 2 [\frac{d^{2}}{p^{2}} - \frac{2 d}{p} + λ] + [c 3 ζ + c 4 (1 - ζ)] [\frac{2 d}{p} + λ^{2} (1 - \frac{d}{p}) - λ])}}{λ} + \frac{c_{2}}{2 λ} [\frac{2 d^{2} t_{l}}{p} - 2 d t_{l 1}] - \frac{[ζ c 3 + (1 - ζ) c 4] (λ - 1) d t_{l}}{λ} + c 5 d T_{v} T_{w} f + (\frac{E_{m g}}{p} + E_{p g} ζ^{2} p) d + (\frac{E_{m r}}{p} + E_{p r} {(1 - ζ)}^{2} p) d + E_{v g} (a_{g} ζ^{2} p^{2} - b_{g} ζ p + c_{g}) ζ d + E_{v r} (a_{r} {(1 - ζ)}^{2} p^{2} - b_{r} (1 - ζ) p + c_{r}) (1 - ζ) d + \sum_{i = 1}^{k} Y_{i} E_{p i} + E_{v} α (E_{c} - E_{s 1}) .

(A.51)

W_{E s s, m i n} = \sqrt{\frac{2 d (λ (S_{b} + c 5 {T_{f} f}_{e}) + c 1) [c 2 + [c 3 ζ + c 4 (1 - ζ)] [\frac{d}{p} + (λ - 1) (1 - \frac{d}{p})]]}{λ}} + c 5 d T_{v} T_{w} f + (\frac{E_{m g}}{p} + E_{p g} ζ^{2} p) d + (\frac{E_{m r}}{p} + E_{p r} {(1 - ζ)}^{2} p) d + E_{v g} (a_{g} ζ^{2} p^{2} - b_{g} ζ p + c_{g}) ζ d + E_{v r} (a_{r} {(1 - ζ)}^{2} p^{2} - b_{r} (1 - ζ) p + c_{r}) (1 - ζ) d + \sum_{i = 1}^{k} Y_{i} E_{p i} + E_{v} α (E_{c} - E_{s s}) .

(A.52)

The minimum and maximum values for

λ

can be found by setting the first partial derivative of Equations (A.51) and (A.52) with respect to

λ

equals to zero, where infeasible values of

λ

are omitted to get:

λ = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}

where

a, b a n d c

, are respectively, given by:

a = 6 d (S_{b} + c 5 {T_{f} f}_{e}) [c 3 ζ + c 4 (1 - ζ)] (1 - \frac{d}{p}),

b = 2 [2 d (S_{b} + c 5 {T_{f} f}_{e}) (c 2 - [ζ c 3 + (1 - ζ) c 4]) + {[ζ c 3 + (1 - ζ) c 4]}^{2} d^{2} {t_{l}}^{2} + d [ζ c 3 + (1 - ζ) c 4] (2 c 1 + c 2 d {t_{l}}^{2}) (1 - \frac{d}{p})],

c = 2 d (S_{b} + c 5 {T_{f} f}_{e}) ([\frac{c 2 d^{2}}{p^{2}} - \frac{2 c 2 d}{p}] + [\frac{2 [c 3 ζ + c 4 (1 - ζ)] d}{p}]) + d (2 c 1 + c 2 d {t_{l}}^{2}) (c 2 - [ζ c 3 + (1 - ζ) c 4]) - 2 {[ζ c 3 + (1 - ζ) c 4]}^{2} d^{2} {t_{l}}^{2} - ([\frac{2 {c_{2} d}^{2} t_{l}}{p} - 2 c_{2} d t_{l 1}]) [ζ c 3 + (1 - ζ) c 4] d t_{l},

For the first cycle, and

λ = \pm \frac{\sqrt{(- [c 3 ζ + c 4 (1 - ζ)] (S_{b} + c_{5} T_{f} f_{e}) c_{1} (d - p) (2 d [c 3 ζ + c 4 (1 - ζ)] + (c_{2} - [c 3 ζ + c 4 (1 - ζ)]) p))}}{[c 3 ζ + c 4 (1 - ζ)] (S_{b} + c_{5} T_{f} f_{e}) (d - p)} .

For the subsequent cycles.

References

Wang, X.J.; Choi, S.H. Impacts of Carbon Emission Reduction Mechanisms on Uncertain Make-To-Order Manufacturing. Int J Prod Res 2016, 54, 3311–3328, doi:10.1080/00207543.2015.1106606. [CrossRef]
Benjaafar, S.; Li, Y.; Daskin, M. Carbon Footprint and the Management of Supply Chains: Insights from Simple Models. IEEE transactions on automation science and engineering 2012, 10, 99–116. [CrossRef]
Pachauri, R.K.; Reisinger, A. Climate Change 2007: Synthesis Report. Contribution of Working Groups I, II and III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Climate Change 2007. Working Groups I, II and III to the Fourth Assessment 2007.
EPA. Carbon Pollution from Transportation. U.S. Environmental Protection Agency; 2022. Available online: https://www.epa.gov/transportation-air-pollution-and-climate-change/carbon-pollution-transportation#transportation.
Damert, M.; Feng, Y.; Zhu, Q.; Baumgartner, R.J. Motivating Low-Carbon Initiatives among Suppliers: The Role of Risk and Opportunity Perception. Resour Conserv Recycl 2018, 136, 276–286. [CrossRef]
Das, C.; Jharkharia, S. Low Carbon Supply Chain: A State-of-the-Art Literature Review. Journal of Manufacturing Technology Management 2018, 29, 398–428. [CrossRef]
Phouratsamay, S.-L.; Cheng, T.C.E. The Single-Item Lot-Sizing Problem with Two Production Modes, Inventory Bounds, and Periodic Carbon Emissions Capacity. Operations Research Letters 2019, 47, 339–343. [CrossRef]
Gong, X.; Zhou, S.X. Optimal Production Planning with Emissions Trading. Oper Res 2013, 61, 908–924. [CrossRef]
Hong, Z.; Chu, C.; Yu, Y. Dual-Mode Production Planning for Manufacturing with Emission Constraints. Eur J Oper Res 2016, 251, 96–106. [CrossRef]
Utama, D.M.; Santoso, I.; Hendrawan, Y.; Dania, W.A.P. Integrated Procurement-Production Inventory Model in Supply Chain: A Systematic Review. Operations Research Perspectives 2022, 100221. [CrossRef]
Devy, N.L.; Ai, T.J.; Astanti, R.D. A Joint Replenishment Inventory Model with Lost Sales. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing, 2018; Vol. 337, p. 12018.
Dong, Y.; Xu, K. A Supply Chain Model of Vendor Managed Inventory. Transp Res E Logist Transp Rev 2002, 38, 75–95. [CrossRef]
Banerjee, A. A Joint Economic-lot-size Model for Purchaser and Vendor. Decision sciences 1986, 17, 292–311. [CrossRef]
Schaefer, B.; Konur, D. Economic and Environmental Considerations in a Continuous Review Inventory Control System with Integrated Transportation Decisions. Transp Res E Logist Transp Rev 2015, 80, 142–165. [CrossRef]
Hovelaque, V.; Bironneau, L. The Carbon-Constrained EOQ Model with Carbon Emission Dependent Demand. Int J Prod Econ 2015, 164, 285–291. [CrossRef]
Bouchery, Y.; Ghaffari, A.; Jemai, Z.; Dallery, Y. Including Sustainability Criteria into Inventory Models. Eur J Oper Res 2012, 222, 229–240. [CrossRef]
Gunasekaran, A.; Irani, Z.; Papadopoulos, T. Modelling and Analysis of Sustainable Operations Management: Certain Investigations for Research and Applications. Journal of the Operational Research Society 2014, 65, 806–823. [CrossRef]
Taleizadeh, A.A.; Soleymanfar, V.R.; Govindan, K. Sustainable Economic Production Quantity Models for Inventory Systems with Shortage. J Clean Prod 2018, 174, 1011–1020. [CrossRef]
Montabon, F.; Pagell, M.; Wu, Z. Making Sustainability Sustainable. Journal of Supply Chain Management 2016, 52, 11–27. [CrossRef]
Goyal, S.K. An Integrated Inventory Model for a Single Supplier-Single Customer Problem. The International Journal of Production Research 1977, 15, 107–111. [CrossRef]
Wahab, M.I.M.; Mamun, S.M.H.; Ongkunaruk, P. EOQ Models for a Coordinated Two-Level International Supply Chain Considering Imperfect Items and Environmental Impact. Int J Prod Econ 2011, 134, 151–158. [CrossRef]
Hua, G.; Cheng, T.C.E.; Wang, S. Managing Carbon Footprints in Inventory Management. Int J Prod Econ 2011, 132, 178–185. [CrossRef]
Wangsa, I. Greenhouse Gas Penalty and Incentive Policies for a Joint Economic Lot Size Model with Industrial and Transport Emissions. International Journal of Industrial Engineering Computations 2017, 8, 453–480. [CrossRef]
Ben-Daya, M.; Hariga, M. Integrated Single Vendor Single Buyer Model with Stochastic Demand and Variable Lead Time. Int J Prod Econ 2004, 92, 75–80. [CrossRef]
Hariga, M.; As’ ad, R.; Shamayleh, A. Integrated Economic and Environmental Models for a Multi Stage Cold Supply Chain under Carbon Tax Regulation. J Clean Prod 2017, 166, 1357–1371. [CrossRef]
Gautam, P.; Kishore, A.; Khanna, A.; Jaggi, C.K. Strategic Defect Management for a Sustainable Green Supply Chain. J Clean Prod 2019, 233, 226–241. [CrossRef]
Halat, K.; Hafezalkotob, A. Modeling Carbon Regulation Policies in Inventory Decisions of a Multi-Stage Green Supply Chain: A Game Theory Approach. Comput Ind Eng 2019, 128, 807–830. [CrossRef]
Khouja, M.; Mehrez, A. An Economic Production Lot Size Model with Imperfect Quality and Variable Production Rate. Journal of the Operational Research Society 1994, 45, 1405–1417. [CrossRef]
Eiamkanchanalai, S.; Banerjee, A. Production Lot Sizing with Variable Production Rate and Explicit Idle Capacity Cost. Int J Prod Econ 1999, 59, 251–259. [CrossRef]
Ghosh, A.; Jha, J.K.; Sarmah, S.P. Optimal Lot-Sizing under Strict Carbon Cap Policy Considering Stochastic Demand. Appl Math Model 2017, 44, 688–704. [CrossRef]
Saga, R.S.; Jauhari, W.A.; Laksono, P.W.; Dwicahyani, A.R. Investigating Carbon Emissions in a Production-Inventory Model under Imperfect Production, Inspection Errors and Service-Level Constraint. International Journal of Logistics Systems and Management 2019, 34, 29–55. [CrossRef]
Huang, Y.-S.; Fang, C.-C.; Lin, Y.-A. Inventory Management in Supply Chains with Consideration of Logistics, Green Investment and Different Carbon Emissions Policies. Comput Ind Eng 2020, 139, 106207. [CrossRef]
Chen, X.; Benjaafar, S.; Elomri, A. The Carbon-Constrained EOQ. Operations Research Letters 2013, 41, 172–179. [CrossRef]
Ganesh Kumar, M.; Uthayakumar, R. Modelling on Vendor-Managed Inventory Policies with Equal and Unequal Shipments under GHG Emission-Trading Scheme. Int J Prod Res 2019, 57, 3362–3381. [CrossRef]
Zanoni, S.; Mazzoldi, L.; Jaber, M.Y. Vendor-Managed Inventory with Consignment Stock Agreement for Single Vendor–Single Buyer under the Emission-Trading Scheme. Int J Prod Res 2014, 52, 20–31. [CrossRef]
Jaber, M.Y.; Glock, C.H.; El Saadany, A.M.A. Supply Chain Coordination with Emissions Reduction Incentives. Int J Prod Res 2013, 51, 69–82. [CrossRef]
Turken, N.; Geda, A.; Takasi, V.D.G. The Impact of Co-Location in Emissions Regulation Clusters on Traditional and Vendor Managed Supply Chain Inventory Decisions. Ann Oper Res 2021, 1–50. [CrossRef]
Bazan, E.; Jaber, M.Y.; Zanoni, S. Supply Chain Models with Greenhouse Gases Emissions, Energy Usage and Different Coordination Decisions. Appl Math Model 2015, 39, 5131–5151. [CrossRef]
Astanti, R.D.; Daryanto, Y.; Dewa, P.K. Low-Carbon Supply Chain Model under a Vendor-Managed Inventory Partnership and Carbon Cap-and-Trade Policy. Journal of Open Innovation: Technology, Market, and Complexity 2022, 8, 30. [CrossRef]
Malik, A.I.; Kim, B.S. A Constrained Production System Involving Production Flexibility and Carbon Emissions. Mathematics 2020, 8, 275. [CrossRef]
Jauhari, W.A.; Pujawan, I.N.; Suef, M.; Govindan, K. Low Carbon Inventory Model for Vendor‒buyer System with Hybrid Production and Adjustable Production Rate under Stochastic Demand. Appl Math Model 2022, 108, 840–868. [CrossRef]
Sarkar, B.; Saren, S. Product Inspection Policy for an Imperfect Production System with Inspection Errors and Warranty Cost. Eur J Oper Res 2016, 248, 263–271. [CrossRef]
Rad, M.A.; Khoshalhan, F.; Glock, C.H. Optimal Production and Distribution Policies for a Two-Stage Supply Chain with Imperfect Items and Price-and Advertisement-Sensitive Demand: A Note. Appl Math Model 2018, 57, 625–632. [CrossRef]
Kim, M.-S.; Kim, J.-S.; Sarkar, B.; Sarkar, M.; Iqbal, M.W. An Improved Way to Calculate Imperfect Items during Long-Run Production in an Integrated Inventory Model with Backorders. J Manuf Syst 2018, 47, 153–167. [CrossRef]
De Giovanni, P.; Karray, S.; Martín-Herrán, G. Vendor Management Inventory with Consignment Contracts and the Benefits of Cooperative Advertising. Eur J Oper Res 2019, 272, 465–480. [CrossRef]
Phan, D.A.; Vo, T.L.H.; Lai, A.N.; Nguyen, T.L.A. Coordinating Contracts for VMI Systems under Manufacturer-CSR and Retailer-Marketing Efforts. Int J Prod Econ 2019, 211, 98–118. [CrossRef]
Ben-Daya, M.; As’ ad, R.; Nabi, K.A. A Single-Vendor Multi-Buyer Production Remanufacturing Inventory System under a Centralized Consignment Arrangement. Comput Ind Eng 2019, 135, 10–27. [CrossRef]
Tarhini, H.; Karam, M.; Jaber, M.Y. An Integrated Single-Vendor Multi-Buyer Production Inventory Model with Transshipments between Buyers. Int J Prod Econ 2020, 225, 107568. [CrossRef]
Dey, O.; Giri, B.C. A New Approach to Deal with Learning in Inspection in an Integrated Vendor-Buyer Model with Imperfect Production Process. Comput Ind Eng 2019, 131, 515–523. [CrossRef]
Giri, B.C.; Chakraborty, A.; Maiti, T. Consignment Stock Policy with Unequal Shipments and Process Unreliability for a Two-Level Supply Chain. Int J Prod Res 2017, 55, 2489–2505. [CrossRef]
Jauhari, W.A.; Sofiana, A.; Kurdhi, N.A.; Laksono, P.W. An Integrated Inventory Model for Supplier-Manufacturer-Retailer System with Imperfect Quality and Inspection Errors. International Journal of Logistics Systems and Management 2016, 24, 383–407. [CrossRef]
Khan, M.; Hussain, M.; Cárdenas-Barrón, L.E. Learning and Screening Errors in an EPQ Inventory Model for Supply Chains with Stochastic Lead Time Demands. Int J Prod Res 2017, 55, 4816–4832. [CrossRef]
Pal, S.; Mahapatra, G.S. A Manufacturing-Oriented Supply Chain Model for Imperfect Quality with Inspection Errors, Stochastic Demand under Rework and Shortages. Comput Ind Eng 2017, 106, 299–314. [CrossRef]
Tiwari, S.; Kazemi, N.; Modak, N.M.; Cárdenas-Barrón, L.E.; Sarkar, S. The Effect of Human Errors on an Integrated Stochastic Supply Chain Model with Setup Cost Reduction and Backorder Price Discount. Int J Prod Econ 2020, 226, 107643. [CrossRef]
Jaggi, C.K.; Tiwari, S.; Shafi, A.A. Effect of Deterioration on Two-Warehouse Inventory Model with Imperfect Quality. Comput Ind Eng 2015, 88, 378–385. [CrossRef]
Alamri, A.A. Carbon Emissions Effect on Vendor-Managed Inventory System Considering Displaced Re-Start-Up Production Time. 2023, 7, 67, doi:10.3390/logistics7040067. [CrossRef]
Konur, D. Carbon Constrained Integrated Inventory Control and Truckload Transportation with Heterogeneous Freight Trucks. Int J Prod Econ 2014, 153, 268–279. [CrossRef]
Bouchery, Y.; Ghaffari, A.; Jemai, Z.; Tan, T. Impact of Coordination on Costs and Carbon Emissions for a Two-Echelon Serial Economic Order Quantity Problem. Eur J Oper Res 2017, 260, 520–533. [CrossRef]
Alamri, A.A. A Sustainable Closed-Loop Supply Chains Inventory Model Considering Optimal Number of Remanufacturing Times. Sustainability 2023, 15. [CrossRef]
Alamri, A.A. Exploring the Effect of the First Cycle on the Economic Production Quantity Repair and Waste Disposal Model. Appl Math Model 2021, 89, 519–540, doi:https://doi.org/10.1016/j.apm.2020.06.073. [CrossRef]
Lippman, S.A. Economic Order Quantities and Multiple Set-up Costs. Manage Sci 1971, 18, 39–47. [CrossRef]
Venkatachalam, S.; Narayanan, A. Efficient Formulation and Heuristics for Multi-Item Single Source Ordering Problem with Transportation Cost. Int J Prod Res 2016, 54, 4087–4103. [CrossRef]
Kazemi, N.; Abdul-Rashid, S.H.; Ghazilla, R.A.R.; Shekarian, E.; Zanoni, S. Economic Order Quantity Models for Items with Imperfect Quality and Emission Considerations. International Journal of Systems Science: Operations & Logistics 2018, 5, 99–115. [CrossRef]
Khouja, M.; Mehrez, A. Economic Production Lot Size Model with Variable Production Rate and Imperfect Quality. Journal of the Operational Research Society 1994, 45, 1405–1417. [CrossRef]
Fandel, G. Production and Cost Theory. Berlin: Springer 1991, 10, 973–978.
Narita, H. Environmental Burden Analyzer for Machine Tool Operations and Its Application. Manufacturing system 2012, 247–260.
Stewart, G.W. Introduction to Matrix Computations, Acad 1973.
Balkhi, Z.T.; Benkherouf, L. A Production Lot Size Inventory Model for Deteriorating Items and Arbitrary Production and Demand Rates. Eur J Oper Res 1996, 92, 302–309. [CrossRef]
Emet, S. An Mixed Integer Approach for Optimizing Production Planning. In Proceedings of the Proceedings of the 13th WSEAS international conference on Applied mathematics; 2008; pp. 361–364.
Alamri, A.A. Theory and Methodology on the Global Optimal Solution to a General Reverse Logistics Inventory Model for Deteriorating Items and Time-Varying Rates. Comput Ind Eng 2011, 60, doi:10.1016/j.cie.2010.11.005. [CrossRef]

Figure 4. The behavior of the optimal production quantity in deferent settings.

Figure 5. The behavior of CO₂ emissions in deferent settings.

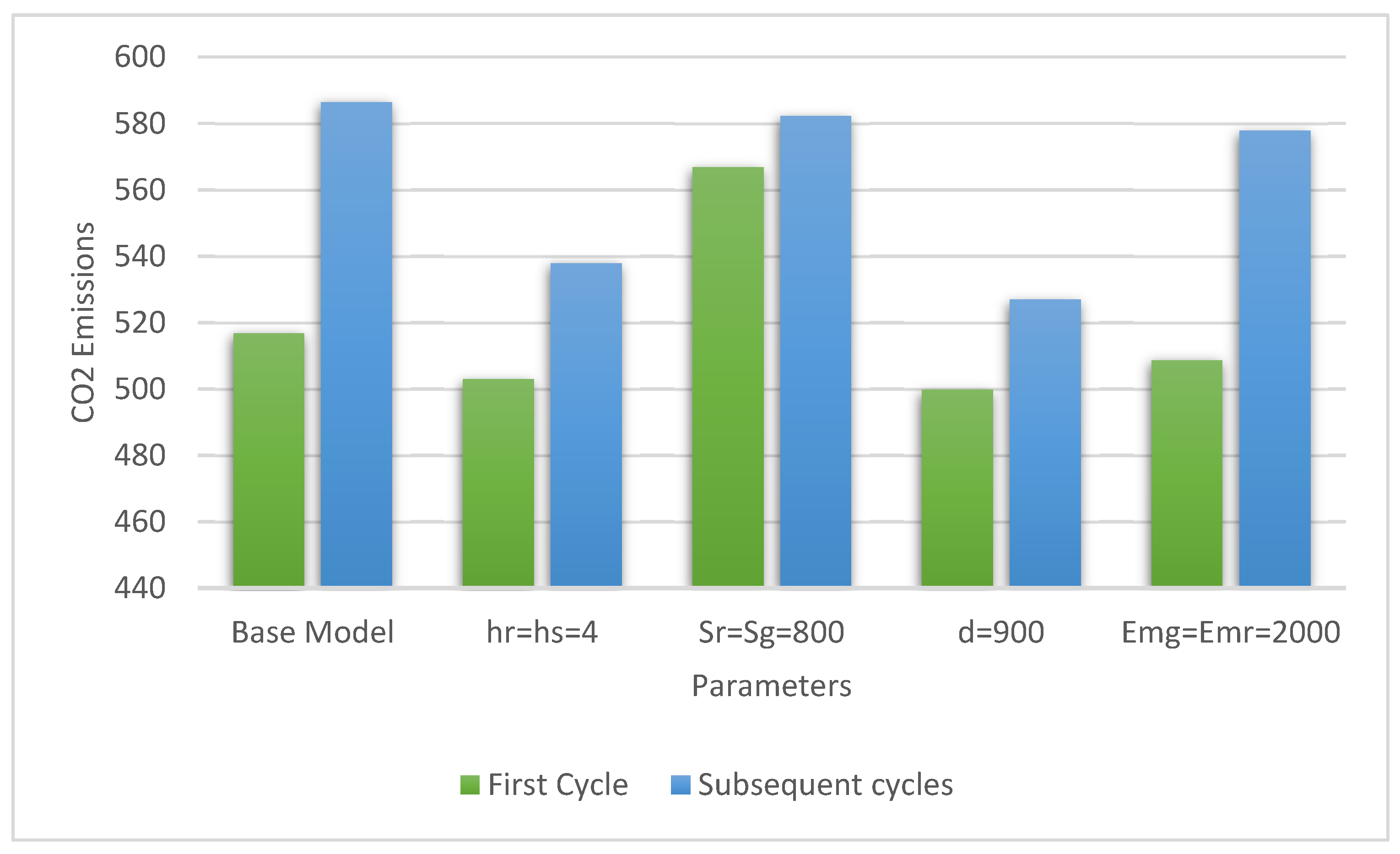
Figure 6. The behavior of the minimum total cost per unit time in deferent settings.

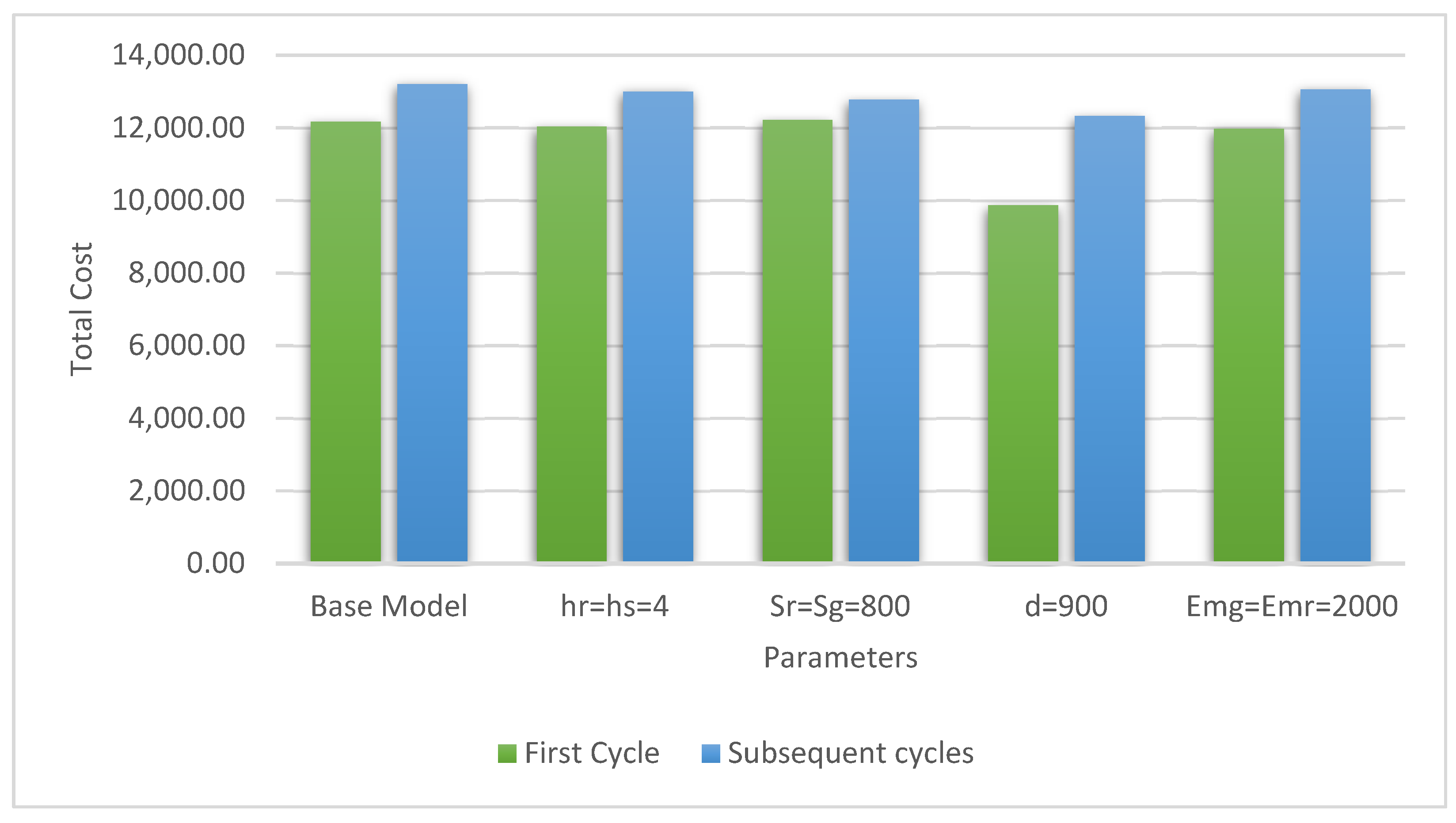
Figure 7. The behavior of the optimal production rate in deferent settings.

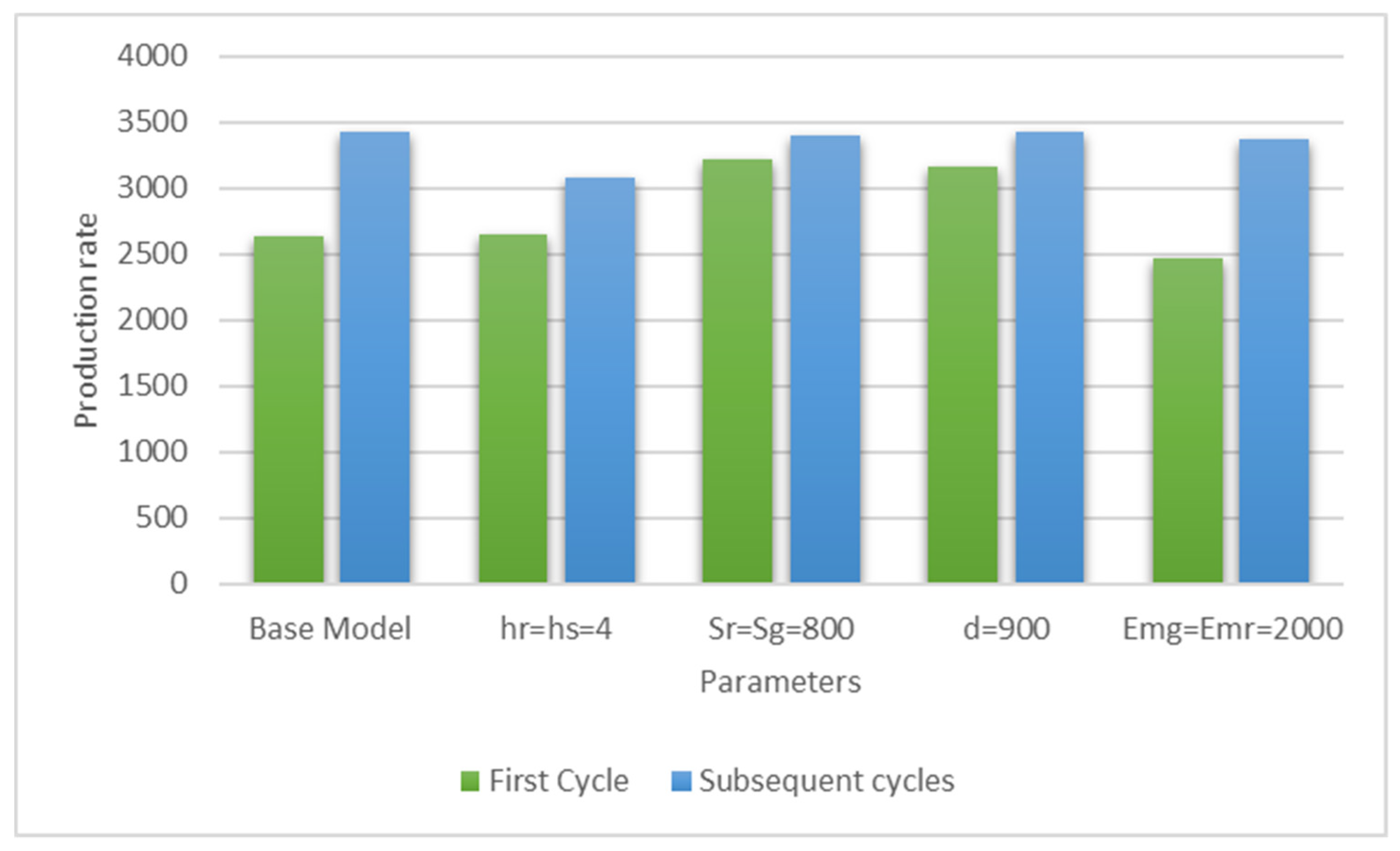
Figure 8. The behavior of the optimal allocation fraction of green production in deferent settings.

Figure 9. A comparison of the optimal produced quantity, production rate, and carbon emissions with respect to hybrid and regular production methods.

Figure 10. A comparison of the optimal total cost of the system with respect to hybrid and regular roduction methods.

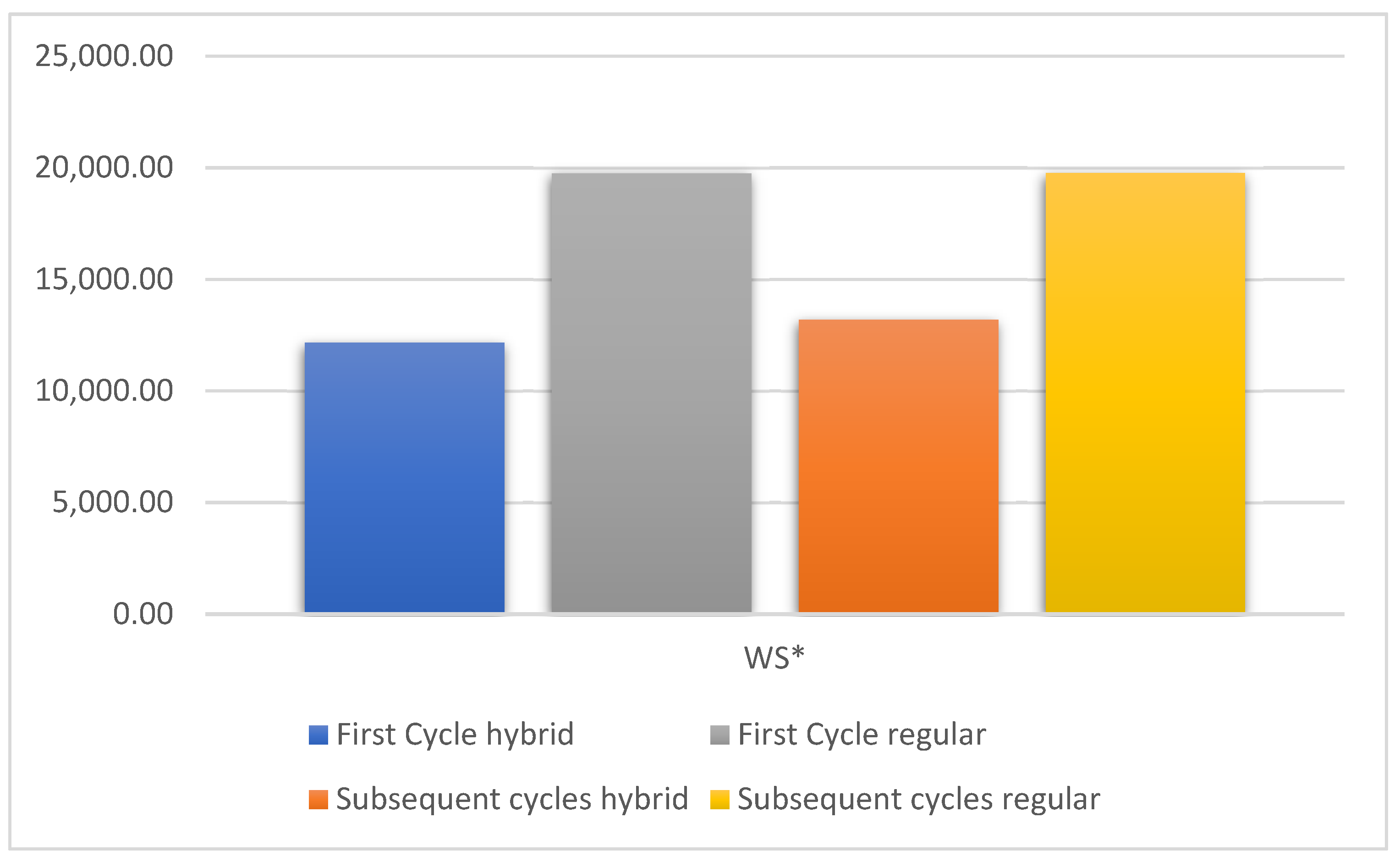
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Efficient Formulation for Vendor–Buyer System Considering Optimal Allocation Fraction of Green Production

Abstract

1. Introduction

2. Literature Review

3. Research Contribution

4. Formulation of the Joint Model

4.1. Notations

4.2. Assumptions

4.3. The Mathematical Formulation of the Joint Model

4.3.1. The Mathematical Formulation of the First Cycle

4.3.2. The Mathematical Formulation of the Subsequent Cycles

5. Numerical Examples

5.1. Example 1

5.2. Example 2

5.3. Example 3

5.4. Example 4

5.5. Example 5

6. Summary of implications and managerial insights

7. Conclusion and Further Research

Funding

Conflicts of Interest

Appendix A

Appendix B

References

MDPI Initiatives

Important Links

Subscribe