Preprint
Article
Scalable Retrieval of Similar Landscapes in Optical Satellite Imagery Using Unsupervised Representation Learning
This version is not peer-reviewed.
Submitted:
24 October 2023
Posted:
25 October 2023
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
Global Earth Observation (EO) is becoming increasingly important in understanding and addressing critical aspects of life on our planet about environmental issues, natural disasters, sustainable development and others. EO plays a key role in making informed decisions on applying or reforming land use, responding to disasters, shaping climate adaptation policies etc. EO is also becoming a useful tool for helping professionals make the most profitable decisions, e.g., in real estate or the investment sector. Finding similarities in landscapes may provide useful information regarding applying contiguous policies, taking alike decisions or learning from best practices on events and happenings that have already occurred in similar landscapes in the past. However, current applications of similar landscape retrieval are limited by moderate performance and the need for time-consuming and costly annotations. We propose splitting the similar landscape retrieval task into a set of smaller tasks that aim at identifying individual concepts inherent to satellite images. Our approach relies on several models trained with Unsupervised Representation Learning (URL) on Google Earth images to identify these concepts. We show the efficacy of matching individual concepts for tackling the task of retrieving similar landscape(s) to a user-selected satellite image with a proof-of-concept application of the proposed approach on the geographical territory of the Republic of Cyprus. Our results demonstrate the efficacy of breaking up the landscape similarity task into individual concepts closely related to remote sensing instead of trying to capture all concepts and image semantics with a single model like a single RGB semantics model.
Keywords:
Earth Observation; Landscape Similarity; Image Retrieval; Satellite Images; Unsupervised Learning
Subject:
Computer Science and Mathematics - Artificial Intelligence and Machine Learning1. Introduction
A growing amount of remotely sensed images and environmental data retrieved from in-situ sensors are made available to scientists, policymakers and stakeholders, allowing them to make critical decisions on important aspects of the planet’s future (e.g., environmental policies). This growing accumulation of data renders the need to better process and exploit this abundant big data. Satellite imagery is becoming increasingly available at unprecedented spatial and temporal resolution, allowing more sophisticated tasks to be tackled and more interesting analyses to be conducted. Meanwhile, the environmental disturbance and the endangerment of ecosystems caused by human actions magnify the need to better understand, process, and analyze landscapes. Analyzing landscapes and identifying similar ones will support better policy-making and decision-making and may reveal relations or features between landscapes located far away from each other that were never realized before. For example, retrieving landscapes like a user-selected landscape may provide useful information regarding applying alike policies or taking contiguous measures against events that have already occurred to the initial landscape e.g., wildfires, contagious diseases, earthquakes, flooding, war-related actions, pollution and contamination etc. Likewise, other predicted events or associations may relate to imminent overcrowding, near-future land cover or land use change of some kind, or even certain deterioration risks like vegetation wilting or water stress of crops due to prolonged heat and drought. Besides similarities and associations based on environmental aspects, landscape similarity could also associate geographical areas in various contexts. For example, the image retrieval engine could associate landscapes based on economic-related factors like land price inflation/deflation tendency, property estimation and risk/vulnerability analysis, making it a useful tool for real estate professionals or investors, as well as insurance companies.
Early works in quantifying landscape similarity in the optical remote sensing field relied on landscape metrics; much of the work toward this direction was conducted in the context of Land Use/Land Change (LULC) research [1,2,3,4]. Initially, partly because the resolution of available satellite images was very low and since feature extraction techniques based on advanced image processing and computer vision methods, such as Deep Learning (DL), were yet to be developed and refined, several works [5,6,7] used distribution statistics (first- and second-order statistical summaries) as landscape similarity metrics (LMs). These simple LMs proved to be effective when Euclidean Distance was used to compute the similarity between two landscapes. Such approaches led to the development of FRAGSTATS [8], a very popular spatial pattern analysis program for categorical mapping. Besides FRAGSTATS, many contemporary spatial analysis software uses similar metrics [9]. Besides their effectiveness and ease of use on low-resolution satellite imagery, first and second-order landscape statistics are not suitable for high-resolution imagery because they do not capture the semantics of the image and do not comprise a robust methodology to identify high-level image/landscape similarities. Image statistics constitute a signature that may be used to identify similar depictions in a more general sense, e.g., the depiction of a pasture, an urban area, an industrial area, etc. However, such simple statistics cannot go beyond very distinct image features. The image statistics based LMs can be used in various formulations to construct the representation vector of a landscape which is then used to compute the similarity measure with other landscapes. An assessment of the performance of such different formulations was studied by Niesterowicz and Stepinski [10].
In recent years, in the era of big data and DL, image retrieval has focused on the extraction of features from deep convolutional layers. Shi et al [11] proposed a simple but effective method called Strong-Response-Stack-Contribution (SRSC) that facilitates the construction of better representations by focusing on a suitable Region Of Interest (ROI). Similarly, Chen et al [12] proposed the identification of an ROI in the image that is then used to extract a set of features from the fully connected layer of the model. Another interesting approach by Babenko et al [13] proposed aggregating the local features to form new powerful global descriptors. Finally, a nice survey on DL-driven remote sensing image scene understanding, including scene retrieval, was published by Gu et al [14].
In this work, we present a proof-of-concept application of landscape similarity matching with URL. Following the DL paradigm, we learn the features of landscapes depicted in Google Earth satellite images using the island of Cyprus as our case study [15], by training a model in an unsupervised manner (without using any annotations/labels) and then identifying the most similar landscapes to a user query by computing representations’ distances. Our approach refrains from using any labels at all by taking advantage of the knowledge gained from learning to identify self-sustained concepts that are essential to remote sensing imagery, e.g., the road network, the buildings and the trees’ configuration or particularly notable or unique characteristics regarding depicted surfaces, textures, or shapes. Learning the arrangement of the objects requires the use of additional DL models that extract the concepts’ information from the satellite images. However, once these models are trained, developing any similarity model is achieved with URL without the need for expensive annotations. A similar work by Aksoy et al [16] uses a large-scale benchmark archive called the BigEarthNet [17] consisting of Sentinel-1 and Sentinel-2 satellite images from 10 European countries and a web application (EarthQube) for image retrieval. EarthQube uses a deep hashing algorithm named metric-learning-based deep hashing network (MiLaN) [18] to implement similar image retrieval. MiLaN was trained with the triplet loss function [19] to learn a metric space where similar images are mapped close to each other while dissimilar images are mapped far from each other. While MiLan is effective in retrieving similar landscapes, it requires extremely heavy labeling since the images must be annotated with multiple labels to facilitate the triplet loss in calculating an appropriate metric space.
In contrast to related work, the contribution of our work is the proposal of a new method for landscape similarity matching from optical satellite imagery based on the URL technique, which does not require heavy data annotation. A key finding, discussed and demonstrated in Section 3, is the efficacy of breaking up the landscape similarity task into individual concepts closely related to remote sensing instead of trying to capture all concepts and image semantics with a single model like a single RGB semantics model.
2. Materials and Methods
Defining what makes two optical satellite images similar or not is not a precise scientific challenge. There are several aspects of the satellite images that comprise what humans perceive as similarities between two satellite images of different landscapes, e.g., the colors, the shapes of the buildings, the tree configuration, the texture of the surfaces, the high-level semantics of the depicted landscape etc. The most popular similarity metrics used for image retrieval rely on either identifying common structures in the images (e.g., based on trivial image statistics or LMs) or comparing the query image’s embedding against the embeddings of the images stored in a database (based on distance calculation metrics). While the former approach usually matches images based on sparse but highly distinct similarities such as textures and common structural components, it often fails to capture whether two images are similar in the broader sense, e.g., they share the same high-level semantics. Likewise, image embeddings tend to match broader concepts encapsulated in a high-dimensional vector but may ignore sparse but distinct features shared by two images, especially when the images do not have many high-level concepts in common. Also, image similarity depends on the content of the images and the image domain: when quantifying the similarity between two images, we tend to match different domain aspects for closed-caption photography than for satellite imagery.
To face the challenge of measuring the similarity between two satellite images, we propose to divide the similarity identification problem into four smaller (sub)tasks that are closely related to remotely sensed optical imagery:
- the task of finding landscapes with a similar road network.
- the task of finding landscapes containing similar buildings’ configuration.
- the task of matching the trees’ configuration in the query image.
- the task of matching the high-level semantics of the query image.
The first three concepts (roads, buildings, trees) comprise dominant components of satellite images that occupy a huge portion of the image semantics and monopolize the observer’s interest. The high-level semantics-matching task complements the operation of the dominant components and is particularly useful when the landscape contains no or very few roads, buildings or trees. By breaking the task into smaller subtasks, it is also possible to apply weighting to each task and thus control its influence on the outcome. For example, a user might be more interested in the similarity of the road network instead of the trees’ arrangement in the area. In this case, the calculated road network similarity should get a higher weight than the trees’ arrangement similarity. Likewise, another user might only consider two of the applicable similarity aspects and ignore the remaining one. The details of applying weights to the similarity concepts are presented in Section 2.3.
The following subsections present the DL models and methodologies used for learning appropriate representations to implement the similarity metrics, explain the embedding database details, and describe the image retrieval process.
2.1. Similarity Models and Algorithms
Our approach uses URL to discover the underlying data clusters, apply data groupings and identify hidden pattern associations without requiring labels of any kind. In contrast to Supervised Learning (SL), where the model is trained on a set of annotated/labeled data, URL aims at discovering patterns and structure in unlabeled data, clustering similar data points together and extracting data features in an unsupervised manner. URL has numerous applications in computer vision and natural language processing, especially in AI applications for which data labeling is costly and time-consuming. We use four different DL models trained with URL, one for each similarity aspect we explore (roads, buildings, trees, and general image semantics).
2.1.1. Unsupervised Representation Learning and the Barlow Twins Algorithm
Many of the algorithms implementing URL are based on Contrastive Learning (CL) [20], which is about training a model to distinguish between pairs of similar and dissimilar patterns. Simple Contrastive Learning of Representations (SimCLR) [21] is one of the most popular URL algorithms that use different views of the same data points to map similar inputs to nearby points in the feature space and dissimilar inputs to distant points. The technique of using different views of the same data with contrastive learning is used by many URL algorithms besides SimCLR like Momentum Contrast (MoCo) [22], Bootstrap Your Own Latent (BYOL) [23], the Barlow Twins model [24] and the Simple Siamese model (SimSiam) [25]. MoCo incorporates a momentum-based update that smoothens the representation space and improves training stability. BYOL trains a model to predict the features of a different view of a data point given another different view of the same data point. The Barlow Twins (BT) model also uses different views of the same data points to reduce the correlation (redundancy) between the different dimensions of the representations. To reduce the redundancy between the learned representations, the BT model computes the cross-correlation matrix of the output features along the batch dimension of size . This strategy makes the model learn meaningful representations that contain discriminative domain features. The loss function of the model is defined as
The first term of the loss is the invariance term trying to equate the diagonal terms of the cross-correlation matrix to 1 and thus make the embeddings invariant to the augmentations applied. The second term is the redundancy reduction term that pushes the off-diagonal terms of the matrix towards 0 and thus de-correlates the embeddings of non-similar images. The hyper-parameter λ controls the effect of the second term on the overall loss function. By generating normalized representations, the Barlow Twins model allows direct application of the cosine similarity metric to the embeddings and thus the derivation of an intuitive metric for identifying patterns of similar semantic content.
The BT algorithm, like every other URL algorithm, uses augmentations to produce different views of the data points. URL algorithms often use the same or a very similar augmentation queue to the one proposed by [21] to create different views for every data point: color jitter (brightness, contrast, saturation and hue), random gray scaling, resizing-cropping and random horizontal flipping. In particular, the BT algorithm achieves state-of-the-art results in image classification benchmarks and, very importantly, it is not as sensitive to the batch size used during training as other URL methods. The BT algorithm is also less sensitive to the number of negative examples required for every data point to obtain satisfactory results in contrast to other methods. These advantages also contribute to more stable training and render the BT model suitable for our case because of memory constraints imposed by using large-sized satellite patches in the training set. Specifically, we use satellite patches of size depicting a reasonable area of a landscape, thus capturing an adequate portion of the region’s semantics. Such a large patch size limits the use of large training batches due to memory constraints, making the BT algorithm a good fit for the current study.
2.1.2. Using Unsupervised Representation Learning to Develop Similarity Models
We use four ResNet34 [26] models trained with URL on hundreds of thousands of Google Earth images of Cyprus. During inference, we consider the cosine distance between the embedding of the query image (the landscape selected by the user) and the embeddings of every image in the database and the top-K images with the smallest distance to the user query are returned.
We use Google Earth images for our image retrieval application because they provide high spatial resolution (~30 cm/pixel), they are relatively easy to acquire and they are (fairly) frequently updated (i.e., every 4-6 months). The satellite images used in this study were acquired in June 2022 and span the southern part of the island of Cyprus. The images are split into patches of size pixels, providing nearly million patches in total. We use of the patches for training the URL models with the BT algorithm and 20% of the patches for test purposes (visual inspection of the similarity between retrieved images during inference). In all four models, the backbone is a ResNet34 architecture outputting a multidimensional normalized representation for every input satellite patch.
As described in Section 2.1.1, the BT algorithm is used for training models on outputting similar embeddings for similar inputs and dissimilar embeddings for dissimilar inputs, according to a certain concept each time. As mentioned above, we use four concepts that are dominant in remotely sensed optical images: road networks, buildings’ arrangement, trees’ arrangement and general image semantics. Each model builds a feature space for the concept it is exposed to and learns how to combine the emerging domain patterns to calculate the embedding of an input. Since the models’ training objective function minimizes the cosine similarity between the embeddings of similar images, the model learns to map images of similar appearance to feature space areas that are in proximity in terms of cosine similarity. However, examining the overall similarity of two images by considering various aspects of them requires some modifications to the way the original BT algorithm creates the different views of the data points (see Section 2.1.3). For example, the roads’ similarity model should get as input a binary mask representing the road network depicted in the image. The buildings’ similarity model should get as input a binary mask showing the buildings in the image while the trees’ similarity model should get as input a binary mask representing the trees in the image. The semantics similarity model accepts RGB images as input and complements the similarity models that do inference based on binary masks of the main concepts (roads, buildings, trees). The roads’ mask is extracted from a Geographic Information System (GIS) road network layer of the island of Cyprus. The buildings’ mask is extracted from a GIS layer created by the authors with an AI segmentation model they developed that identifies the contours of buildings depicted in Google Earth images [27]. Finally, the trees’ mask is extracted from a GIS layer created by the authors with an AI tree detection model they developed to count trees in satellite images [28,29]. Figure 1 shows an example of a Google Earth image and its concepts’ masks extracted using the GIS layers empowered by the AI models mentioned above. Figure 2 shows the data flow of the proposed approach for landscape-similarity matching.
When assessing whether two images are similar or not (or calculating the similarity between two images) our approach examines the three concepts’ masks in pairs and computes a similarity score for each pair. In addition to these scores, our approach also computes a similarity score for the two RGB images and combines all four scores into a final similarity measure. We note that in practice our approach does not use the developed AI detection models (building and tree detection AI models) for inferring the binary maps of each patch because this would be very costly. Instead, the AI detection models were used to create two GIS layers, one for buildings and one for trees, which are used for fast extraction of the binary masks each time a new patch is processed.
Figure 3 shows the process of inferring the similarity score of two concept masks and the training process of the model. During training, the two masks are created from the same image, one being the actual concept mask of the image and the other being a modified version of it. Retrieving the most similar image to a certain selected image (the query image) requires computing the similarity score between the query and all the images in the database and then selecting the image in the database that has the smallest distance to the query image. This procedure can be very inefficient and time-consuming if not implemented correctly and is discussed in detail in Section 2.2.
In the following sections we present the four models of our approach, one for each similarity concept we considered and described above. We also discuss how the models are trained i.e., how the different concepts’ views are created for each model and how they are used to train the models.
2.1.3. Creating the Training Data for the Road Network Similarity Model
We apply the BT algorithm to train a ResNet34 model to output similar embeddings for alike road network masks. Specifically, the embeddings of two similar road network masks should be close to each other while the embeddings of two dissimilar road network masks should be far from each other.
The conventional augmentations used by the SimCLR, the BT algorithm and many other URL algorithms are not suitable in our case because the input to the model is a binary mask and not an RGB image. Having a binary mask as input to the model renders the color jitter augmentations (brightness, contrast, saturation and hue) useless. Furthermore, since we aim at training a model on a concept that sources from the entirety of the input image and not from certain regions only, we also do not use resizing and cropping. We create pairs of similar road network masks by modifying a certain binary mask with morphological operations, translation and rotations of multiples of . First, the mask goes through 10 dilation/erosion steps of random intensity and kernel sizes. The dilation steps enlarge and expand the active areas of the mask making them wider, while erosion reduces the size of the active mask areas and gradually diminishes them. Then, the mask is horizontally translated (shifted) in either direction by a random number of pixels (-20 to +20 pixels). Finally, the mask is rotated by an angle of or with a probability of 0.3 for each rotating angle (the probability of not rotating the mask is 0.1). The pseudocode for creating pairs of similar road network masks to train the model is shown in Table 1.
2.1.4. Creating the Training Data for the Buildings’ Layout Similarity Model
Like the road network model (and the models of all the concepts we examine), the buildings’ layout similarity model is a ResNet34 network trained with the BT algorithm. The data used to train the buildings’ layout similarity model is generated by an augmentation scheme that is tailored to the features of the buildings’ layout masks. As shown in Table 2, we create the bounding boxes containing the buildings in a mask (each bounding box encloses one building) and then we randomly translate each of the bounding boxes by pixels. Then, the resulting mask is modified via 10 steps of random erosion/dilation operations with kernels of random size. Finally, the mask is randomly rotated by an angle of or . In contrast to the road network model’s augmentation process, the no-rotate probability ( rotation) is equal to the probability of rotating by any other angle. This strategy gives better results because the building masks inherently have more variation than the road masks and we compensate for the road masks’ lower variance by applying more rotations.
2.1.5. Creating the Training Data for the Trees’ Arrangement Similarity Model
The augmentation process used in feeding the trees’ arrangement similarity model with similar pairs of masks is the same as the augmentation process of the buildings’ layout similarity model (Table 2) with the only difference being the use of a random translation of pixels instead of pixels. Tree masks usually contain many more objects than building masks and thus they inherently possess a higher variation canceling out the need to vary them significantly.
2.1.6. Creating the Training Data for the RGB Similarity Model
The RGB similarity model captures more general similarities than the ones captured by the models that process binary masks of certain concepts. Since the model’s input is an RGB image, the augmentation process generating similar image pairs follows the same conventional augmentation queue as proposed by SimCLR, creating different views of a certain RGB image.
In this case, the augmentation queue is shown in Table 3 and includes a resize/crop augmentation followed by a left-to-right flip, a color jitter augmentation and finally a color-dropping step.
2.1.5. Implementation details
We use a training batch size of and Mixed Floating Point (FP16) precision to reduce the memory requirements and speed up the training. For all four similarity concepts we use an embedding size of 256. To train the model we use eight RTX A5000 GPUs and the Adam [30] optimizer with a fixed learning rate of and a weight decay of .
2.2. Similar Landscape Retrieval Process
The image retrieval process relies on the embeddings provided by the similarity models. Assuming a region of interest (e.g., the area of a city, a country or a broader region on Earth), the satellite imagery acquisition from this region is kept in storage and their details (file path and geographical coordinates) are stored in a MySQL database [31] for fast information retrieval. Also, the embedding of each satellite image is precomputed and stored in a Milvus vector database [32]. When we want to match a place found in the region of interest to other places in the region, we compare the embedding of the query satellite image with the embeddings stored in the vector database. The entries with the most similar embeddings are returned while their coordinates and info about the file paths of the corresponding satellite images are retrieved from the MySQL database.
The use of a vector database is crucial for making the solution scalable. Even in case studies covering small regions of interest, like this study in which we focus only on the southern part of the island of Cyprus, the number of satellite images is large ( and can easily explode to an unmanageable size when considering a large country, a continent or even the whole planet. Refraining from using a vector database but finding the most similar place in the region by calculating the similarity of a query comparing with every image in the database instead, imposes a limit to the size of the studied region. The problem emanates from the accumulating computational cost of calculating the similarity between the query image and every image in the database in a naive way (applying the similarity formula sequentially for all possible embeddings and then choosing the one with the closest value). This simple image retrieval process has a complexity of , where is the number of the images in the database, which makes it very inefficient for huge . Precomputing the cosine similarity of every image in the database with every other image in the database and thus making the similarity measures readily available during inference is also impractical for a substantial number of images because the complexity of such an approach is . Furthermore, for each future image added to the database, similarity computations are needed, which reduces the scalability of the “precomputed similarities” strategy.
2.2.1. Vector Databases
Vector databases offer optimized storage and querying capabilities for embeddings in contrast to traditional scalar-based databases. Working with vector embeddings imposes challenges on real-time analysis, scalability and performance that traditional scalar-based databases cannot address properly. High-dimensional indexing databases add significant capabilities to modern AI systems like information retrieval and long-term memory and play a crucial role in managing and retrieving information from large datasets with complex structures, enabling applications that require efficient similarity-based querying and analysis. Vector databases commonly use methods like tree-based structures [33], graph-based indexing [34] and hashing techniques [35,36] to organize and search the data efficiently. They often support distance metrics such as Euclidean distance, cosine similarity, Jaccard similarity [37], and more, allowing users to define the notion of similarity that best suits their data domain.
Milvus is an open-source vector database built for similarity search and analytics. It supports a variety of distance metrics and indexing methods. It is particularly well-suited for applications involving machine learning, computer vision, natural language processing, and other tasks/challenges that deal with complex data types represented as vectors. Milvus is designed to scale horizontally, meaning it can handle growing datasets and increasing query loads by distributing data across multiple nodes or servers, which makes it suitable for large-scale applications. Furthermore, it addresses the challenges of efficiently managing and querying high-dimensional data, providing developers and researchers with a powerful tool for building applications that rely on similarity search and analysis.
2.2.2. The Landscape Retrieval Pipeline
The landscape retrieval system is built around three main components: the map service, the MySQL database and the Milvus vector database. As described above, all satellite images ( patches) of the ROI are kept in storage and their information is maintained in a table in the MySQL database. The Milvus vector database stores the embeddings of all satellite patches using the same IDs as in the MySQL database and performs the embeddings’ similarity-matching operation. Figure 4 shows the image retrieval pipeline, the components of the system and their interaction.
The identification of similar landscapes based on a query image starts with the interaction with an online map service that allows the user to select a certain location of her choice contained in an ROI. Next, the map service translates the selected coordinates to a file path which is used to query the MySQL database to get the ID of the query image. Then, the ID is used to retrieve the embedding of the query image from the vector database. After the query embedding is available, an embedding similarity search is conducted to find the ID(s) of the image(s) with the most similar embedding(s). Finally, the retrieved ID (s) is/are matched in the MySQL database and the details of the results (file path, coordinates) are returned to the user.
2.3. Tuning the Importance of the Similarity Aspects
As shown in Figure 2, the similarity aspects’ embeddings (road network, buildings’ layout, trees’ arrangement and the general RGB semantics) are concatenated into a single embedding that holds all the representations of the individual aspects together. The individual embeddings are normalized and thus calculating the dot product between two embeddings is equivalent to calculating the cosine similarity between them. Assuming the similarity aspects embeddings , , and for the road network, the buildings’ layout, the trees’ arrangement and the general RGB semantics respectively, and being the size of the embeddings, then the concatenated embeddings are of the form . Since all embeddings are normalized, it holds that . To make a certain similarity concept more important during a similarity search, we only need to multiply the embedding of the certain concept with a scalar . This is true because of the homogeneity property of the norm of a vector , i.e., = . Since we want to keep the stored embeddings (in the vector database) unmodified (normalized) and apply similarity-concept weighting of any magnitude at any time, we choose to apply the importance scaling to the query embeddings or , each corresponding to one of the similarity concepts. Of course, one can apply an importance scaling to more than one query embedding at the same time. A similarity measurement between a query landscape embedding ] and a candidate entry in the database is as follows:
with DP representing the dot product operation. Using the importance scaling scheme and assuming four scaling factors for the query embeddings such as , , and , the dot product (DP) of the similarity check comprises four terms: with each term holding the dot product of one of the four concepts. This result shows that each aspect contributes to the overall result with a quantity that is scaled by the weight of the specific concept embedding. Controlling the significance of each of the concepts examined is very useful especially when the query landscape is complex and the similarity between itself and the candidate landscapes is not immediately evident and is thus difficult to quantify.
3. Results
We apply the proposed landscape similarity algorithm to retrieve similar landscapes to areas located in the southern part of the island of Cyprus, which is used as our case study. To avoid the trivial case of getting nearby or neighboring coordinates as a result, we increase the number of the candidate landscapes returned by the similarity search and choose the first one in the returned similarity ranking that is located at least one kilometer away from the query landscape. We use the simplest experimental setup by assigning the same importance to all similarity aspects, i.e., no scaling is applied to the query embeddings. We follow the pipeline described in Figure 4, i.e., choose a landscape from a Google Earth region and use its coordinates to get the file path of the saved image via a dictionary created during the training of the models. Both the map and the dictionary that links the coordinates of a landscape to the storage location of its satellite image comprise the map service shown in Figure 4; in a commercial application the map service could be a web service incorporating the map and the mapping dictionary. The file path is used in a MySQL query that retrieves the ID of the landscape the user selects. This ID is also kept in the vector database and is thus used to retrieve the embedding of the query landscape. Then, the vector database searches for the k-most similar landscapes to the query embedding and the first entry from the ranked results whose coordinates are at least one kilometer away from the query’s coordinates is selected. In our experiments, we used k=10. Figure 5 shows the results of several landscape similarity searches, picking the best match from the top 10 matches retrieved. From the examples visualized in Figure 5, the reader may observe that the similarity decision is affected by the shape of the road network, the arrangement of the trees and the shapes and placement of the buildings in the query image. The results suggest that the algorithm considers all the similarity concepts and returns an outcome that constitutes a reasonable compromise between them: even when there is a much better match for each of the concepts separately, the algorithm returns a landscape that generally satisfies the specifications imposed by all binary masks and the RGB semantics’ model. This is demonstrated even more clearly in Figure 6, which shows the best matches per individual concept inferred using the cosine similarity of each concept embedding individually instead of the concatenated concept which is illustrated in Figure 2. The returned landscape computed by considering the concatenated embeddings’ vector corresponds to neither of the individual masks. On the contrary, the returned landscape’s concept masks are on par (in terms of similarity) with the masks of the best matches in a way that balances the overall similarity between the individual concepts to achieve a reasonable compromise driven by the cosine similarity metric. An effective way to perturb the consistency of returning a landscape that balances the matching of the individual concepts is to apply a weight to the concept embeddings as described in section 2.3. By doing so, the returned landscape focuses more on a certain concept depending on the magnitude of the weight applied to the specific concept. The results also suggest that the algorithm returns landscapes of similar classes, i.e., an urban landscape is returned when the query landscape is urban, or a rural landscape is returned when the query landscape is rural. This consistency was evident throughout our experiments.
The results also demonstrate the efficacy of breaking up the landscape similarity task into individual concepts closely related to remote sensing instead of trying to capture all concepts and image semantics with a single model like a single RGB semantics model. Using only one such model and refraining from using the proposed individual concept-matching approach does not capture the essence of landscape similarity, despite that single models trained with URL algorithms are effective with closed-caption imagery containing objects, persons and sceneries at smaller scales, e.g., with datasets like the ImageNet [38]. A model trained with URL on RGB images captures useful content structures, semantics, and texture/color characteristics, which is impossible to achieve with the binary masks alone. Specifically, the use of the RGB semantics model in the proposed approach is essential for capturing the characteristics of large surfaces in optical satellite imagery, which adds a particularly useful dimension to the problem of identifying landscape similarity. However, while the RGB semantics model provides useful insights, it is not sufficient on its own to tackle the problem. The RGB semantics’ model captures the textures and colors of the query image but neglects the arrangement of the objects captured by the models trained with binary masks. Throughout our experimentation, the returned landscape was rarely the same as the best match of the RGB semantics’ model, but its textures and colors were heavily determined by it. This behavior is highly desired because the individual concepts complement each other and act synergically to identify the best match for a certain query. Finally, these results suggest that a multi-concept approach is a better fit than a single-model (single-concept) approach for identifying landscape similarity.
4. Discussion
Breaking down the task of retrieving similar landscapes to domain-specific concepts is a strategy like how humans perceive similarity between two optical satellite images: some concepts are dominant and tend to overthrow the prevailing of other concepts. For example, the trees’ arrangement might be of less importance than how large buildings are scattered in an image and the texture of a large field might be unimportant when the layout of the road network and the layout of the buildings of two images match. This hierarchical concepts’ importance cannot be exploited when a single model is used, and no individual concepts are identified. Of course, this hierarchy can be modified according to the preferences of the user and the application requirements (Section 2.3 on tuning the importance of the similarity aspects).
In this work, we demonstrate a proof-of-concept application of the proposed approach based on satellite images of the southern part of Cyprus. The approach could easily scale up without significant performance concerns to larger countries or even greater geographic areas like continents. At such scales, inferred outcomes based on landscape similarity could be very impactful. For example, similar landscapes to a flooded area combined with additional information like altitude, slope and soil type could indicate a high flood risk. Similar trees’ arrangement to populated areas that suffered from wildfires may indicate a substantial risk of fire spreading. Landscape similarity and especially road network similarity to areas of deadly car accidents might help policymakers understand the landscape conditions causing the accidents. This could then be correlated with speed limits in various locations or regions, to better shape safer and convenient speed limits. We can imagine applications also in the real estate domain, where potential buyers create a draft drawing (could be a binary mask) of the ideal setting of their home (e.g., concerning trees, road network, buildings) and then the best matches of landscapes having properties under sale are returned. An obvious match would be when the buyer looks for a property at a cul-de-sac, while this info is not listed in the candidate properties’ features. In the same context, landscape similarity inference (especially when reinforced with additional data) could support the buildup of knowledge regarding environmental aspects.
4.1. Limitations
While the proposed approach achieves reasonable results, there are some important limitations regarding its implementation. First, the results have been assessed based on human observation and not based on some quantitative performance metric. We plan to experiment with and propose meaningful metrics that could be used in this research area, to be able to set the baseline for comparisons of research efforts. Based on human observation and assessment alone, this process needs to be formalized by inviting various users, preferably experts in satellite imagery or landscape planning, to give scores to the landscape matching performed by different algorithms/approaches.
Further, to determine the most similar landscape to a query, the proposed approach uses four DL models that are individually trained to perform different tasks. This inherently means that the errors of the models accumulate when they collectively contribute to the final decision. Since the Google Earth satellite images of Cyprus are often blurry, noisy and of lower quality than other parts of the world (e.g., major, more densely populated regions on Earth), creating the datasets for the building and the tree masks to train the similarity models is hard and prοne to errors. For similar reasons, the RGB semantics’ model is also prοne to errors. Furthermore, the road network GIS layer contains errors too and this also contributes to the overall matching uncertainty.
4.2. Future Work
The problem of low-quality satellite images of regions on Earth that are not visited by satellites very often to support the build of good-quality satellite imagery may be considered as an opportunity for significant results’ improvement when the approach is applied to regions for which high-quality optical satellite imagery is available. In future work, we will apply our method to such areas and compare the results with the case of Cyprus.
A straight-forward next step would be to include other similarity concepts beyond buildings, trees and roads, such as swimming pools and industrial units (which already play a role in the landscape matching process, see Figure 5), railways, airports, sports outdoor fields, agricultural fields, parks, etc. This would require significant effort because the AI models creating the binary masks of those ROIs detected need to be developed beforehand.
Moreover, we intend to experiment with different weighting of each similarity concept, to understand the impact of different weights on the results. When embracing more similarity concepts, such as the ones suggested above, understanding the significance of each similarity concept would give insights into how humans define similarity in images, in particular landscapes visible from space.
Further, our intention is also to experiment with images beyond optical satellite imagery. We aim to investigate landscape similarity when multispectral or hyperspectral satellite imagery is available, creating binary masks for certain bands beyond the optical/RGB at which important indicators for pollution/contamination, crops’ growth or water stress, etc. are evident. This will allow us to match landscapes with similar characteristics and learn lessons about actions taken, e.g., to mitigate or avoid pollution, ensure food security, adapt to climate change, etc.
Finally, combining landscape similarity with multiple modalities (e.g., in-situ field sensors and geospatial information) could be an exciting research field. Examples include better development of species distribution modeling, understanding the abundance of wildlife and biodiversity in regions with similar landscapes and micro-climate, deciding on the most appropriate speed limit on roads with certain characteristics, valorizing properties more accurately, etc.
5. Conclusion
Identifying similarities in landscapes provides useful insights that can shape better policies or lead to better decisions by stakeholders in different application domains. Since the existing applications of similar landscape retrieval are limited by moderate performance and the need for time-consuming and costly annotations, this paper proposes a method that involves splitting the similar landscape retrieval task into a set of smaller tasks that aim at identifying individual concepts inherent to optical satellite images. Our approach relies on several models trained with Unsupervised Representation Learning (URL) on Google Earth images to identify these concepts. We have demonstrated the efficacy of matching individual concepts for tackling the task of retrieving similar landscape(s) to a user-selected satellite image with a proof-of-concept application of the proposed approach on the southern part of the island of Cyprus. Our results indicated the efficacy of breaking up the landscape similarity task into individual concepts closely related to remote sensing instead of trying to capture all concepts and image semantics with a single model like a single RGB semantics model. Our method has certain limitations but at the same time, there is potential for future work which can lead to significant new insights in this emerging research field.
Author Contributions
Conceptualization, S.K.; methodology, S.K.; software, S.K.; validation, S.K.; formal analysis, S.K. and A.K.; investigation, S.K.; resources, C.P.; data curation, C.P.; writing—original draft preparation, S.K.; writing—review and editing, A.K.; visualization, S.K.; supervision, A.K.; project administration, A.K.; funding acquisition, A.K.; All authors have read and agreed to the published version of the manuscript.
Funding
This project has received funding from the European Union’s Horizon 2020 Research and Innovation Programme under Grant Agreement No 739578 and the Government of the Republic of Cyprus through the Deputy Ministry of Research, Innovation and Digital Policy.
Data Availability Statement
Data sharing is not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saponaro, M.; Tarantino, E. LULC Classification Performance of Supervised and Unsupervised Algorithms on UAV-Orthomosaics. In Proceedings of the Computational Science and Its Applications - ICCSA 2022 Workshops - Malaga, Spain, July 4-7, 2022, Proceedings, Part III; Gervasi, O., Murgante, B., Misra, S., Rocha, A.M.A.C., Garau, C., Eds.; Springer, 2022; 13379, pp. 311–326. [Google Scholar]
- Balarabe, A.T.; Jordanov, I. LULC Image Classification with Convolutional Neural Network. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2021, Brussels, Belgium, July 11-16, 2021; IEEE, 2021; pp. 5985–5988.
- Çavur, M.; Kemeç, S.; Nabdel, L.; Düzgün, H.S. An Evaluation of Land Use Land Cover (LULC) Classification for Urban Applications with Quickbird and WorldView2 Data. In Proceedings of the Joint Urban Remote Sensing Event, JURSE 2015, Lausanne, Switzerland, March 30 - April 1, 2015; IEEE, 2015; pp. 1–4.
- Dong, S.; Guo, H.; Chen, Z.; Pan, Y.; Gao, B. Spatial Stratification Method for the Sampling Design of LULC Classification Accuracy Assessment: A Case Study in Beijing, China. Remote Sens 2022, 14, 865. [Google Scholar] [CrossRef]
- Cushman, S.A.; McGarigal, K.; Neel, M.C. Parsimony in Landscape Metrics: Strength, Universality, and Consistency. Ecol. Indic. 2008, 8, 691–703. [Google Scholar] [CrossRef]
- Cardille, J.A.; Lambois, M. From the Redwood Forest to the Gulf Stream Waters: Human Signature Nearly Ubiquitous in Representative US Landscapes. Front. Ecol. Environ. 2010, 8, 130–134. [Google Scholar] [CrossRef]
- Partington, K.; Cardille, J.A. Uncovering Dominant Land-Cover Patterns of Quebec: Representative Landscapes, Spatial Clusters, and Fences. Land 2013, 2, 756–773. [Google Scholar] [CrossRef]
- McGarigal, K. FRAGSTATS: Spatial Pattern Analysis Program for Quantifying Landscape Structure; US Department of Agriculture, Forest Service, Pacific Northwest Research Station, 1995; Vol. 351;
- Bassuk, N.L.; Universite, A.; Jean, M.; Universite, C.; Bibliography, A. On Using Landscape Metrics for Landscape Similarity Search. Landsc Urban Plan 2015, 117, 1–12. [Google Scholar]
- Niesterowicz, J.; Stepinski, T.F. On Using Landscape Metrics for Landscape Similarity Search. Ecol. Indic. 2016, 64, 20–30. [Google Scholar] [CrossRef]
- Shi, X.; Qian, X. Exploring Spatial and Channel Contribution for Object Based Image Retrieval. Knowl Based Syst 2019, 186. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, Z.; Pan, Z.; Yang, C.-N. Instance Retrieval Using Region of Interest Based Cnn Features. J. New Media 2019, 1, 87. [Google Scholar] [CrossRef]
- Babenko, A.; Lempitsky, V. Aggregating Local Deep Features for Image Retrieval. In Proceedings of the Proceedings of the IEEE international conference on computer vision; 2015. pp. 1269–1277.
- Gu, Y.; Wang, Y.; Li, Y. A Survey on Deep Learning-Driven Remote Sensing Image Scene Understanding: Scene Classification, Scene Retrieval and Scene-Guided Object Detection. Appl. Sci. 2019, 9, 2110. [Google Scholar] [CrossRef]
- Google Earth 9.194, G. Cyprus GE Satellite Images. Available online: https://earth.google.com (accessed on 1 September 2023).
- Aksoy, A.K.; Dushev, P.; Zacharatou, E.T.; Hemsen, H.; Charfuelan, M.; Quiané-Ruiz, J.-A.; Demir, B.; Markl, V. Satellite Image Search in AgoraEO. ArXiv Prepr. ArXiv220810830 2022. [Google Scholar] [CrossRef]
- Sumbul, G.; Charfuelan, M.; Demir, B.; Markl, V. Bigearthnet: A Large-Scale Benchmark Archive for Remote Sensing Image Understanding. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium; IEEE; 2019; pp. 5901–5904. [Google Scholar]
- Roy, S.; Sangineto, E.; Demir, B.; Sebe, N. Metric-Learning-Based Deep Hashing Network for Content-Based Retrieval of Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2020, 18, 226–230. [Google Scholar] [CrossRef]
- Hoffer, E.; Ailon, N. Deep Metric Learning Using Triplet Network. In Proceedings of the Similarity-Based Pattern Recognition: Third International Workshop, SIMBAD 2015, Copenhagen, Denmark, October 12-14, 2015. Proceedings 3; Springer, 2015; pp. 84–92.
- Chopra, S.; Hadsell, R.; LeCun, Y. Learning a Similarity Metric Discriminatively, with Application to Face Verification. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05); IEEE, 2005; Vol. 1; pp. 539–546. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A Simple Framework for Contrastive Learning of Visual Representations. In Proceedings of the International conference on machine learning; PMLR; 2020; pp. 1597–1607. [Google Scholar]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum Contrast for Unsupervised Visual Representation Learning. In Proceedings of the Proceedings of the IEEE/CVF conference on computer vision and pattern recognition; 2020; pp. 9729–9738.
- Grill, J.-B.; Strub, F.; Altché, F.; Tallec, C.; Richemond, P.H.; Buchatskaya, E.; Doersch, C.; Pires, B.Á.; Guo, Z.; Azar, M.G.; et al. Bootstrap Your Own Latent - A New Approach to Self-Supervised Learning. In Proceedings of the Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, December 6-12, 2020, virtual; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.-F., Lin, H.-T., Eds.; 2020. [Google Scholar]
- Zbontar, J.; Jing, L.; Misra, I.; LeCun, Y.; Deny, S. Barlow Twins: Self-Supervised Learning via Redundancy Reduction. In Proceedings of the International Conference on Machine Learning; PMLR; 2021; pp. 12310–12320. [Google Scholar]
- Chen, X.; He, K. Exploring Simple Siamese Representation Learning. In Proceedings of the Proceedings of the IEEE/CVF conference on computer vision and pattern recognition; 2021; pp. 15750–15758.
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. CoRR, 1512. [Google Scholar]
- Periopsis Ltd Estimating the Area of Buildings from Satellite Images. Available online: https://www.periopsis.com/blog/building-finder/ (accessed on 12 October 2023).
- Periopsis Ltd Tree Counting. Available online: https://www.periopsis.com/blog/tree-counter/ (accessed on 12 October 2023).
- Pervasive Real-World Computing for Sustainability (SuPerWorld) Cyprus TreeMapper: Detection of All Trees around Cyprus. Available online: https://superworld.cyens.org.cy/product2.html (accessed on 12 October 2023).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings; Bengio, Y., LeCun, Y., Eds.; 2015. [Google Scholar]
- MySQL 8.0 MySQL Relational Databases. Available online: www.mysql.com (accessed on 1 September 2023).
- Milvus 2.3 Milvus: Vector Database Built for Scalable Similarity Search. Available online: www.milvus.io (accessed on 1 September 2023).
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. (Eds.) Introduction to Algorithms, Third Edition; 3rd ed.; The MIT Press, 2009; ISBN 0-262-03384-4.
- Yan, X.; Yu, P.S.; Han, J. Graph Indexing: A Frequent Structure-Based Approach. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Paris, France, June 13-18, 2004; Weikum, G., Deßloch, A.C.K. andStefan, Eds.; ACM, 2004; pp. 335–346.
- Knuth, D.E. The Art of Computer Programming: Fundamental Algorithms; 3rd ed.; Addison Wesley: Reading, Massachusetts, 1997; Volume 1, ISBN 0-201-89683-4. [Google Scholar]
- Aggarwal, K.; Verma, H.K. Hash_RC6 — Variable Length Hash Algorithm Using RC6. In Proceedings of the 2015 International Conference on Advances in Computer Engineering and Applications; 2015; pp. 450–456. [Google Scholar]
- Zijdenbos, A.P.; Dawant, B.M.; Margolin, R.A.; Palmer, A.C. Morphometric Analysis of White Matter Lesions in MR Images: Method and Validation. IEEE Trans. Med. Imaging 1994, 13 4, 716–724. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; E, H.G. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS); Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc. 2012; pp. 1097–1105. [Google Scholar]
Figure 1.
To determine the similarity between two satellite images, we examine three major concepts that are paramount in landscape similarity determination: the road network, the buildings’ surfaces, and the trees’ arrangement. These concepts are represented as binary masks extracted from GIS layers. The buildings and trees GIS layers were created by the authors based on AI segmentation models they developed. From left to right: the original RGB satellite image, the binary mask of the road network, the binary mask of the buildings’ surfaces and the binary mask of the trees’ foliage.
Figure 1.
To determine the similarity between two satellite images, we examine three major concepts that are paramount in landscape similarity determination: the road network, the buildings’ surfaces, and the trees’ arrangement. These concepts are represented as binary masks extracted from GIS layers. The buildings and trees GIS layers were created by the authors based on AI segmentation models they developed. From left to right: the original RGB satellite image, the binary mask of the road network, the binary mask of the buildings’ surfaces and the binary mask of the trees’ foliage.

Figure 2.
The data flow of the proposed landscape-similarity identification approach. For the case study described in this paper we considered the southern part of the island of Cyprus, which we split into about 4 million satellite images (patches). A GIS road network layer provides the road network binary map, a building detection DL model extracts the buildings’ layout binary map and a tree detection DL model extracts the trees’ layout binary map. Furthermore, a DL model provides an embedding that encodes the general semantics of an RGB patch. Each binary mask type (roads, buildings, trees) goes through an augmentation process to train a similarity model with URL. The embeddings calculated by the similarity models are concatenated with the RGB embeddings to construct the final embedding of each satellite patch. All individual embeddings used in the proposed approach (roads, buildings, trees and RGB semantics) are normalized.
Figure 2.
The data flow of the proposed landscape-similarity identification approach. For the case study described in this paper we considered the southern part of the island of Cyprus, which we split into about 4 million satellite images (patches). A GIS road network layer provides the road network binary map, a building detection DL model extracts the buildings’ layout binary map and a tree detection DL model extracts the trees’ layout binary map. Furthermore, a DL model provides an embedding that encodes the general semantics of an RGB patch. Each binary mask type (roads, buildings, trees) goes through an augmentation process to train a similarity model with URL. The embeddings calculated by the similarity models are concatenated with the RGB embeddings to construct the final embedding of each satellite patch. All individual embeddings used in the proposed approach (roads, buildings, trees and RGB semantics) are normalized.
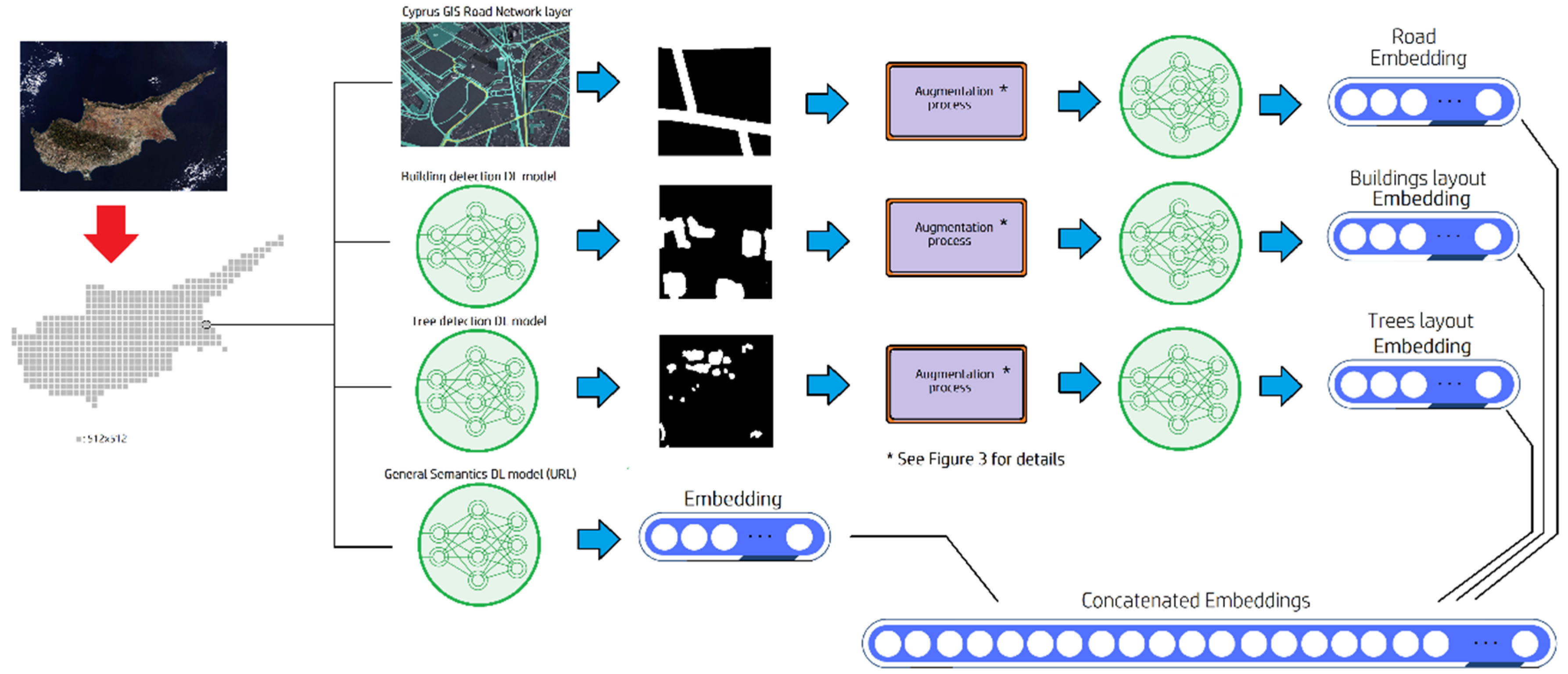
Figure 3.
Training and inferring concepts’ similarity based on the Barlow Twins algorithm. The example relates to the road network concept, but the processes generalize to the other similarity concepts (buildings, trees) or any other similarity concept that might be defined in future works. (a) Training with similar masks: An input image is used to create two views of the concept of the input image . The two views and pass through the model whose weights are adapted so that the cross-correlation matrix of the two output embeddings has a diagonal with values 1 and every off-diagonal element is zero. (b) Inference with dissimilar masks: the concepts’ masks extracted from two different images and pass through the model to get the intermediate representations and their cosine similarity is computed. Their cosine similarity should be low indicating dissimilarity. (c) Inference with similar masks: the concepts’ masks m1 and m2 are extracted from two similar images and the cosine similarity between their intermediate representations obtained from the model is computed. The cosine similarity should be high, thus indicating the masks’ similarity.
Figure 3.
Training and inferring concepts’ similarity based on the Barlow Twins algorithm. The example relates to the road network concept, but the processes generalize to the other similarity concepts (buildings, trees) or any other similarity concept that might be defined in future works. (a) Training with similar masks: An input image is used to create two views of the concept of the input image . The two views and pass through the model whose weights are adapted so that the cross-correlation matrix of the two output embeddings has a diagonal with values 1 and every off-diagonal element is zero. (b) Inference with dissimilar masks: the concepts’ masks extracted from two different images and pass through the model to get the intermediate representations and their cosine similarity is computed. Their cosine similarity should be low indicating dissimilarity. (c) Inference with similar masks: the concepts’ masks m1 and m2 are extracted from two similar images and the cosine similarity between their intermediate representations obtained from the model is computed. The cosine similarity should be high, thus indicating the masks’ similarity.
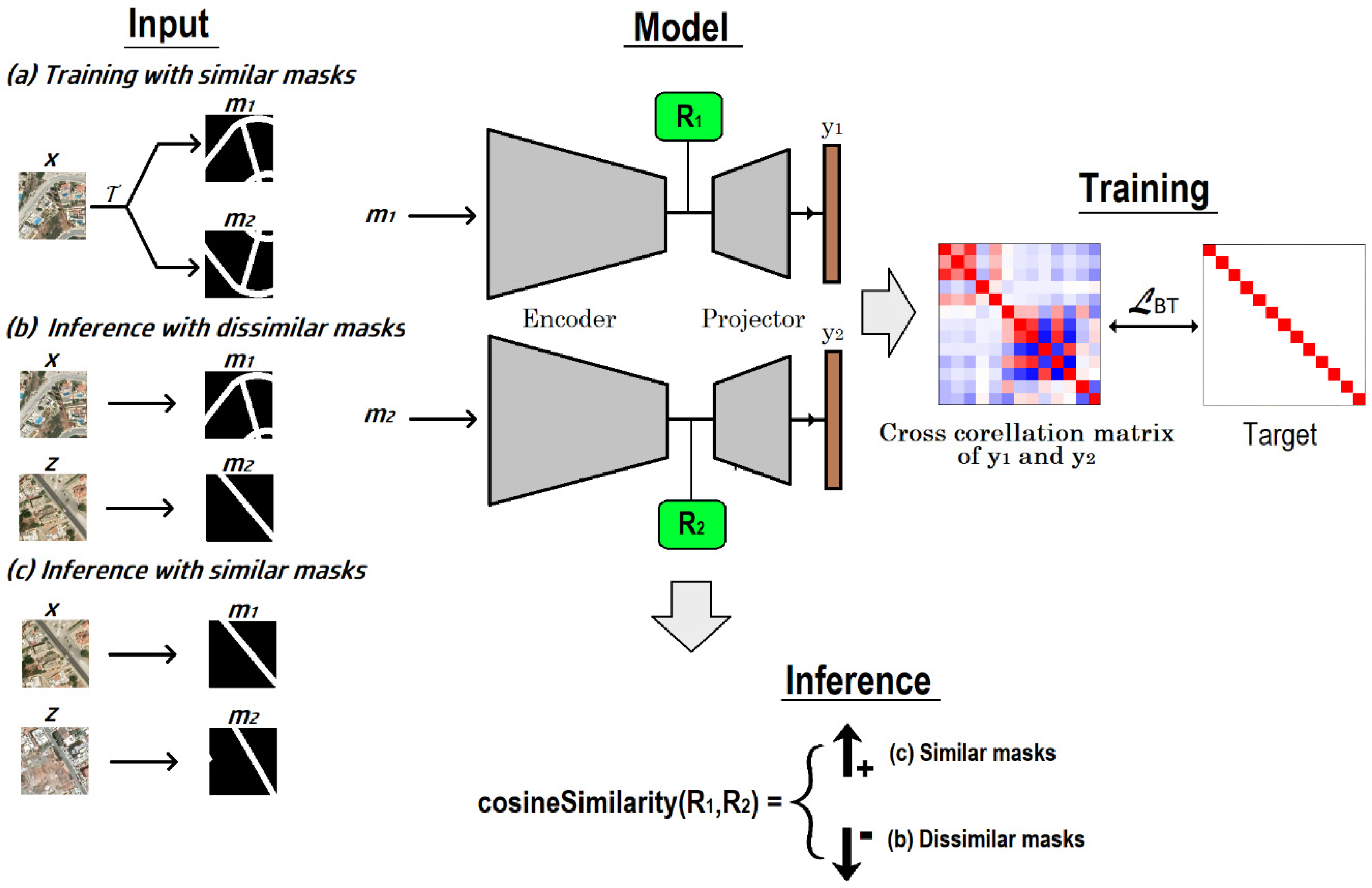
Figure 4.
The retrieval pipeline: A map service handles the user’s query and returns the information of the user-selected area which is used to retrieve the area ID from the MySQL database. The ID of the query image is used to retrieve the query image embedding from the Milvus vector database which is then used in the similarity search. The similarity search returns the ID(s) of the most similar landscape(s) in the vector database. Finally, the information associated with the ID(s) returned by the similarity search is retrieved from the MySQL database.
Figure 4.
The retrieval pipeline: A map service handles the user’s query and returns the information of the user-selected area which is used to retrieve the area ID from the MySQL database. The ID of the query image is used to retrieve the query image embedding from the Milvus vector database which is then used in the similarity search. The similarity search returns the ID(s) of the most similar landscape(s) in the vector database. Finally, the information associated with the ID(s) returned by the similarity search is retrieved from the MySQL database.
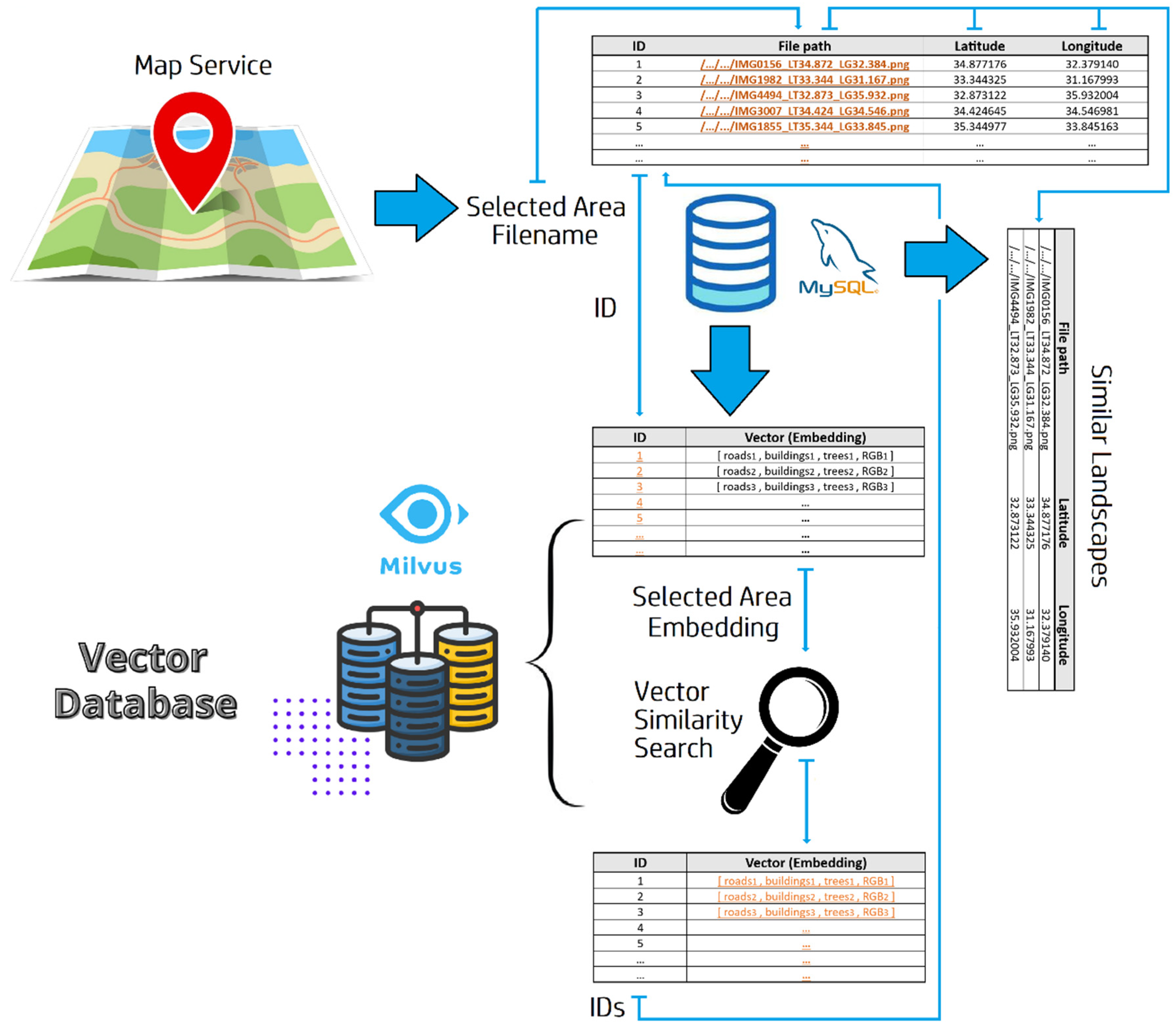
Figure 5.
The results of several landscape similarity searches. In each pair, the left satellite image is the query image and the right image is the output of the similarity search algorithm for the most similar image. The coordinates (longitude, latitude) of each satellite image are shown below the images.
Figure 5.
The results of several landscape similarity searches. In each pair, the left satellite image is the query image and the right image is the output of the similarity search algorithm for the most similar image. The coordinates (longitude, latitude) of each satellite image are shown below the images.



Figure 6.
Six examples of queries, binary images and outputs. Each query group is visualized in two rows. The first row contains the query RGB (leftmost image), the binary images of the concepts of the query image (roads, buildings, trees) and the output of the approach (the RGB corresponding to the result of the similarity search); the second row of each group contains the best RGB match (returned by the RGB model alone) and the best matches for the 3 concepts (as indicated by the concepts’ models individually: the road network, the buildings and the trees models); The approach outputs a matching decision that combines the similarities detected without fully adopting either of the individual concepts’ matches. The fact that the output landscapes look more like the query images than the best RGB matches alone, suggests that breaking up the similarity search task into individual concepts is beneficial. The similarity search algorithm outputs a decision that rarely corresponds to either of the best matches of the individual concepts.
Figure 6.
Six examples of queries, binary images and outputs. Each query group is visualized in two rows. The first row contains the query RGB (leftmost image), the binary images of the concepts of the query image (roads, buildings, trees) and the output of the approach (the RGB corresponding to the result of the similarity search); the second row of each group contains the best RGB match (returned by the RGB model alone) and the best matches for the 3 concepts (as indicated by the concepts’ models individually: the road network, the buildings and the trees models); The approach outputs a matching decision that combines the similarities detected without fully adopting either of the individual concepts’ matches. The fact that the output landscapes look more like the query images than the best RGB matches alone, suggests that breaking up the similarity search task into individual concepts is beneficial. The similarity search algorithm outputs a decision that rarely corresponds to either of the best matches of the individual concepts.


Table 1.
The pseudocode for feeding the road network similarity model with pairs of similar road masks during training.
Table 1.
The pseudocode for feeding the road network similarity model with pairs of similar road masks during training.
|
Input: Binary mask of the road network Output: A binary mask similar to ( is a modification of ) |
|
### 10 Erosion/Dilation steps for i =1…10 do: kernelSize = randInteger(3,9) # random kernel size between 3 and 9 kernel = rectKernel(kernelSize) # rectangle kernel if rand() < 0.5: = erode(,kernel, iterations = 1) else: = dilate(,kernel,iterations = 1) ### Randomly Translate = RandomlyTranslate( # Randomly translate mask ( ### Rotate by with probabilities [0.1, 0.3, 0.3, 0.3] respectively angle = randomchoice([0,90,180,270], p=[0.1,0.3,0.3,0.3]) = rotate(,angle) return |
Table 2.
The pseudocode for feeding the buildings’ layout similarity model with pairs of similar building masks during training.
Table 2.
The pseudocode for feeding the buildings’ layout similarity model with pairs of similar building masks during training.
|
Input: Binary mask of the buildings’ layout Output: A binary mask similar to ( is a modification of ) |
|
### Randomly translate individual buildings in the image bboxes = Mask2bbs ## buildings are contained in bboxes for bb in bboxes: RandomlyTranslate( #Translate the content of each bb ( ### 10 Erosion/Dilation steps for i =1…10 do: kernelSize = randint(3,9) # random kernel size between 3 and 9 kernel = rectKernel(kernelSize) # rectangle kernel if rand() < 0.5: = erode(,kernel, iterations = 1) else: = dilate(,kernel,iterations = 1) ### Rotate by with probabilities [0.25, 0.25, 0.25, 0.25] respectively angle = randomchoice([0,90,180,270], p=[0.25, 0.25, 0.25, 0.25]) = rotate(,angle) return |
Table 3.
The pseudocode of the augmentation process that feeds the RGB similarity model with pairs of similar RGBs during training.
Table 3.
The pseudocode of the augmentation process that feeds the RGB similarity model with pairs of similar RGBs during training.
|
Input: RGB image Output: RGB image similar to ( is a modification of ) |
|
### Random Crop and Scale ### Final RGB size = ### Scale range = [0.2, 1.0], Aspect ratio = [0.75, 1.25] RandomResize(, [0.2, 1.0], [0.75, 1.25]) RandomCrop(, [512,512]) ### Horizontal Flip with p=0.5 HFlip(0.5) ### Apply Color Jitter (brightness=0.8, contrast=0.8, saturation=0.8, hue=0.8) with p=0.75 RandomColorJitter(, [0.8, 0.8, 0.8, 0.8], 0.75) ### Convert to grayscale with p=0.2 Grayscale( 0.2) return |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Downloads
97
Views
38
Comments
0
Subscription
Notify me about updates to this article or when a peer-reviewed version is published.
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated






