Prerpints.org logo
Preprint
Review

Nonequilibrium Dynamics in Conservation Biology: Scales, Attractors and Critical Points

Altmetrics

Downloads

565

Views

751

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 October 2023

Posted:

26 October 2023

You are already at the latest version

Alerts
Abstract
Preserving and restoring biodiversity is becoming a great challenge as we face a world where planetary boundaries will likely be crossed over the following decades. Such challenge needs to consider multiple scales of complexity, both in space and time. A common thread in most cases is the presence of nonlinear phenomena generating shifts among alternative states. These breaking points imply a new perception of risk and different management strategies. A broad range of phenomena affect the preservation of healthy communities and constrain the ways to deal with conservation, from local features associated with habitat loss or facilitation to mesoscale or global network-level ecological complexity and the role played by extreme events. How are these scales connected? How can the emergent properties associated with ecosystem dynamics be exploited? Here a synthesis of ideas is presented, with a complex systems view of the different scales involved, the emergent phenomena separating them, and the universal properties that allow defining simple models on each scale.
Keywords: 
Subject: Biology and Life Sciences  -   Ecology, Evolution, Behavior and Systematics
In a mechanical system the parts shaped the whole 
while in an organic system the whole shaped the parts. 
Alexander von Humboldt 

1. Introduction

The future of our biosphere is likely to be decided within this century. Potential paths to sustainable growth are to some extent in conflict with ongoing human population growth, overexploitation of resources and the resulting impacts on climate. Different studies suggest that decisive actions might be required within the next few decades (Solé and Levin, 2022). Because of its relevance, biodiversity emerges here as the cornerstone of any relevant path to Earth stewardship (Chapin et al., 2022). What are the right and effective ways of dealing with conservation? Alternatives range over a very vast landscape of possibilities, from the expansion of protected areas to ecosystem bioengineering. No matter what kind of path is followed, we need to deal with the complex nature of ecosystems and the biosphere (Levin ,1998; Brown et al., 2002; Green et al., 2005; Solé and Bascompte, 2012; Oro and Martinez-Abrain, 2023; Riva et al., 2023). In this context, an obvious problem is the presence of multiple scales that we naturally appreciate when looking at ecosystems organization and how they appear to be somewhat disconnected. Information concerning genomic-level description of species or communities might be very useful to map genetic diversity, but will tell little about population fluctuations and their responses to environmental challenges. Species-level properties, on the other hand, will not be enough to explain the spatiotemporal properties of communities (Levin, 1992; Levin et al., 1997). One obvious example is pattern formation in drylands, where large-scale patterns (sometimes highly regular) arise from short-scale interactions among individual plants.
Such scales are, all of them, relevant to our understanding of the biosphere and the threads associated to climate change (Peñuelas et al., 2013). Genomics can play a leading role in conservation efforts (Breed et al., 2019) while data-driven monitoring of global ecosystems by means of remote sensing can help define a resilience index (Lenton et al., 2022). However, against the traditional views of physics and biology, each scale is not reducible (in mechanistic terms) to the properties of the lower levels. This is at the core of the concept of emergence, which percolates complexity in living systems (Solé and Bascompte, 2012; Levin, 1999). At the heart of this complexity lies a common thread: the presence of nonlinear thresholds that can trigger sudden and profound shifts among alternative states within ecosystems. These tipping points represent critical junctures where small changes in environmental conditions lead to disproportionately significant and irreversible consequences (Scheffer et al., 2001; Lenton et al., 2008; Scheffer, 2009; Dakos et al., 2019). Recognising the existence and implications of these tipping points demands a paradigm shift in our perception of risk and calls for innovative and adaptable management strategies (Suding and Hobbs, 2009).
Different factors influence the preservation of healthy communities and how we approach conservation efforts. From the local level, challenges arise from habitat loss, fragmentation, and the disruption of ecological interactions. Concurrently, at larger scales, the intricate web of ecological complexities and the influence of extreme events further compound the conservation landscape. Understanding the linkages among these diverse scales is crucial to crafting effective conservation practices.
In this paper I present several key ideas and case studies that illustrate the presence of emergent phenomena in ecosystems with relevant implications for biological conservation. This is not a systematic overview nor a collection of examples, some of which are shown in Figure 1a–f. Instead, our aim is to clarify the nature of some universal properties that appear to be common to a broad range of situations. As part of the analysis, I want to show why (and how) very simple models can be helpful to answer crucial questions about the nature of nonlinear behaviour and how they pervade habitat degradation, extinction or defaunation dynamics. Three main topics will be explored in terms of the simple mathematical models that can account for their dynamics. All have important consequences to our potential to preserve biodiversity and define conservation strategies. Specifically, I have chosen these: (a) habitat loss and fragmentation, (b) facilitation and (c) criticality and forest fire dynamics. These three case studies, and the mathematical models used to make sense of them, illustrate the need of theory as a robust approach to the different scales involved and their origins.
A common feature of complex systems is the presence of negative and positive feedbacks (DeAangelis and Waterhouse, 1987). Both kind of feedbacks (or the combination of them) introduce the nonlinearities that determine the stability of the system and the emergence of complex dynamics. Typically, highly stable states allow fluctuations to be kept at bay thus allowing a robust homeostatic state despite the noise. This was one of the key contributions of cybernetics: how feedback control creates stability. The former have a rather different role. They involve interactions that enhance growth and as such are amplifiers of fluctuations. Their relevance in science is illustrated by their presence in different fields, from neuroscience to Earth sciences.
Negative feedbacks are easily identified in the classical models of population growth. This is the case of the so called logistic growth model, where a single-species population expands by reproduction while competition for available, finite resources, limits further growth (Case,1999). It is such an implicit limitation what describes the negative feedback: as soon as population size starts to be comparable with the maximum population size achievable, further growth starts to be inhibited and a slowdown in growth rates will be inevitable. The presence of negative feedback is behind part of the ability of ecosystems to respond homeostatically to external changes. But the interaction of growth and death can also generate thresholds that separate two "phases" associates to community persistence and extinction, respectively.
Positive feedbacks, on the other hand, are a natural consequence of mutualistic interactions. As will be shown below, these positive exchanges are responsible for the presence of multiple alternative states (May, 1977). Oftentimes, a stable population can suddenly jump into a degraded state under small variations of parameters (Scheffer et al., 2001). Finally, the spatial dimension naturally introduces further levels of complexity and new emergent properties (Levin, 1992; Rietkerk and Van de Koppel, 2008). Positive and negative exchanges can, under dispersal, generate stable self-organised spatial structures far beyond the short scale of local interactions (Margalef, 1968; 1979; Nicolis and Prigogine, 1989; Bascompte and Solé, 1995; Solé and Bascompte, 1998; Murray, 2003) but also highly dynamical states, such as forest fires, which act as global herbivores (Bond and Keeley, 2005). All these examples share a common feature that has significant implications to conservation and engineering practices. On the one hand, universal phenomena pervade their nature and deeply constrain their emergence. On the other, this universality is what makes possible to predict future scenarios of change as well as the potential impacts of interventions.

2. Ecological Attractors

As Robert May aptly noted, simple mathematical models can exhibit highly intricate dynamics (May, 1976). As will be shown in the following examples, the nonlinear dynamics of complex ecosystems might be properly captured by seemingly simplistic models. Prior to delving into our illustrative examples, let us provide a concise overview of essential definitions and properties that will be utilised here and will help to follow the logic of simple models and their unexpected predictions. Readers already acquainted with these concepts can readily proceed to the subsequent section.
The most elementary class of mathematical models encompasses one-dimensional population models, where the fraction of individuals denoted as x follows a dynamic equation:
d x d t = f μ ( x )
In this equation, the rate of change of our population, denoted by the derivative d x / d t , is determined by a population-dependent function f μ ( x ) . The subscript μ serves as a reminder that all processes typically rely on one or more parameters. Occasionally, continuous variations in these parameters can give rise to discontinuous changes in x.
Two fundamental concepts, straightforward yet pivotal to our analysis, will be employed below. The first is the notion of an equilibrium (or fixed) point. We designate a fixed point x * as a population value for which
d x d t x * = 0
The underlying idea is that, when the population reaches this value, it remains unchanged. However, the nature of this equilibrium can vary widely. This distinction is often depicted through a mechanical analogy, as illustrated in Figure 1g–j. Equilibrium points can be likened to marbles positioned in an abstract landscape that somewhat represents potential available states of the given ecosystem. Under a given set of conditions (where parameters are fixed) we will observe the state of the community (defined by some variables) as located at the bottom of one valley ( S 1 in Figure 1g). As parameters change (such as increased aridity, acidity or reduced precipitation) the landscape is deformed and the original state becomes unstable and a new alternative state is reached in a catastrophic way ( I → j ).
In a general scenario, with several dimensions involved, the underlying landscape will be much more complex, as illustrated in (Figure 1k). Here several stable attractors are shown (1,2,3). A given initial condition within the basin of a given valley (such as 4) will roll down towards the stable state 1. Moreover, we also display another state (5) that could be stable: if we place a marble here, it might be that it remains there. But any slight perturbation will break the balance either towards 1 or 2. This constitutes an unstable fixed point. A distinct yet noteworthy (and vital, as explained later) case is that of marginal fixed points. These arise when perturbing x * with a slight displacement simply transitions the state to another (analogous to a flat landscape). Determining whether a fixed point is stable, unstable, or marginal is a key consideration.
There are two ways in which we can answer this question. One is to determine the stability of x * is to find the sign of the derivative of the growth function f μ ( x ) against x and evaluated at the given x * . In other words, calculate the parameter:
λ ( x * ) = d f μ ( x ) d x x *
which is a real number. It can be shown (see appendix) that a given, small deviation y from equilibrium (i.e., pushing the system slightly away from x * to a new state x * + y ) will evolve in time following
y ( t ) ∼ e λ t
if λ < 0 , the fixed point will be stable (since x → 0 ) while λ > 0 indicates an unstable (since y will grow). Marginal points are characterised by a zero value.
One final component of this short review of simple dynamical systems concerns the mechanical analogy described above. Although the qualitative picture is a compelling one, a rigorous mathematical definition of this landscape would be desirable. Although there is no general result for dynamical systems with dimension two or larger, it is possible to write down a well-defined expression for the so called potential function V ( x ) . Specifically, the system is said to derive from a potential function V ( S ) (Strogatz, 1994; Solé, 2011) if we can write the dynamical system as:
d x d t = − d V d x
From the previous equation, it can be shown (see appendix) that the potential reads:
V ( x ) = − ∫ x f μ ( x ) d x .
One of the main messages gathered from the study of emergent phenomena is that complex dynamics can be captured by very simple models. More importantly, there are several fundamental properties that behave in universal ways. Many of the key results developed within theoretical models of species extinction are connected with (or equivalent to) well-established models of the physics of strongly interacting systems (Chopard and Droz, 1998). This is in fact one of the most relevant domains of statistical physics, where the concept of universality is central to our understanding of complexity (Sethna, 2021). In a nutshell, nonlinear systems with strongly interacting parts will typically exhibit low-dimensional dynamics as a few degrees of freedom dominate the macroscopic patterns (Haken, 1975, 1980; Nicolis and Prigogine, 1989; Gutenkunst et al., 2007). This is the basis of our success from using simple mathematical models displaying emergent behaviour.

3. Habitat Loss and Extinction Thresholds

Habitat destruction has been long recognised as one of the most impactful sources of biodiversity loss (Laurance, 2010; Haddad et al., 2015). It provides a first example of the relevance of simple models allowing to understand the presence of threshold phenomena. As we will see, despite the apparently simple nature of the process, some of the implications of this class of models is sometimes unexpected and contrary to linear thinking.
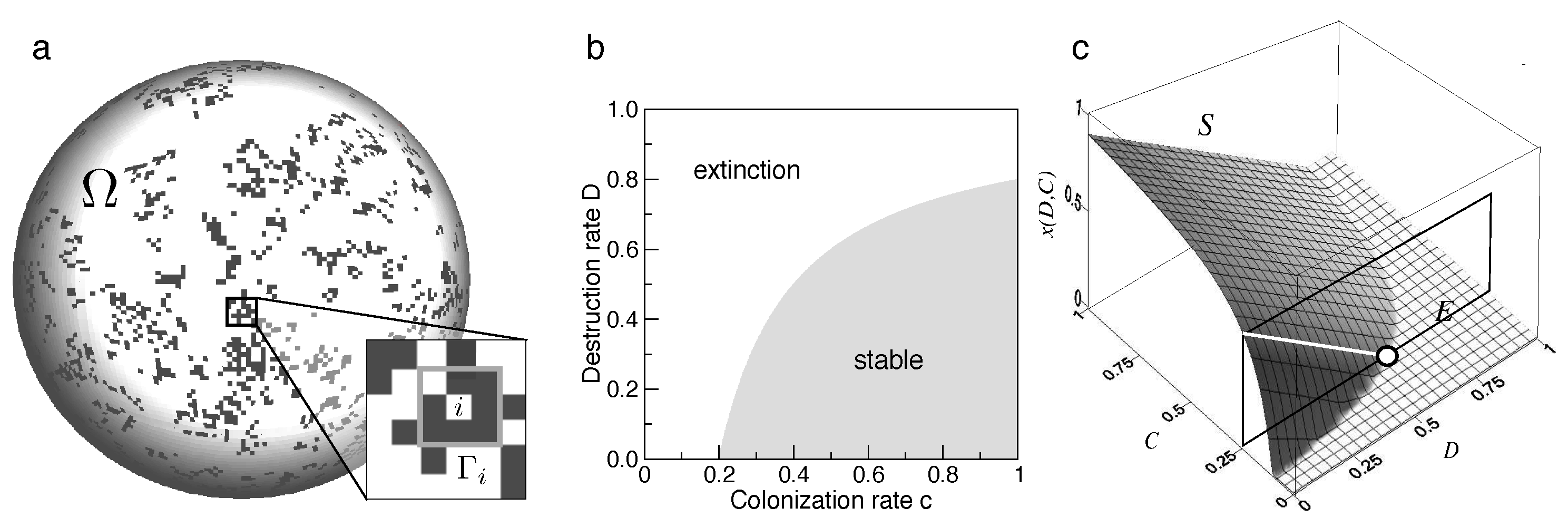
A very simple approach to habitat loss is provided by an extension of Levins metapopulation model (Levins, 1969). In the original formulation, a given finite habitat is considered as made of a collection of connected patches. The connectivity is defined by accessibility through dispersal: two local patches are connected if they can access each other by means of the movement of individuals. One given patch might contain one or many individuals, or be empty. If 1 ≥ x ≥ 0 is the fraction of occupied habitat, Levins model reads:
d x d t = c x ( 1 − x ) − e x .
Here a set μ = { c , e } of two parameters are involved. One is the probability c that a given empty patch is colonised by an occupied one, while e is the probability that a site experiences an extinction event. We can easily describe these two conflicting rates in terms of probabilities of colonisation and decay on a given abstract habitat, as shown in Figure 2a, where occupied and empty patches are indicated as filled and empty squares, respectively. A crucial consequence of this model Is that there are thresholds to extinction. Since the fixed points obtained from d x / d t = 0 are x 0 * = 0 (extinction) and x 1 * = 1 − e / c , it is easy to see that the second (nontrivial) point x 1 * > 0 only if e < c . How is this model extended to incorporate habitat loss?
Habitat loss can be easily introduced by means of a single parameter D that gives the fraction of patches that have been destroyed and cannot be colonised. In its simplest form, we just need to extract D from the available habitat, which now will be 1 − D − x . It is easy to see that this corresponds to a slightly different equation, namely:
d x d t = c x ( 1 − D − x ) − e x
The new fixed points are now x * = 0 and
x * = 1 − D − e c
It can be shown that extinction will occur if λ ( x * = 0 ) < 0 which gives a threshold:
D > D c = 1 − e c
which is our first key, relevant result. It is summarised in Figure 2b, where we plot the so called phase space of our model on the ( D , C ) plane. The shaded area corresponds to the parameter combinations allowing for a stable metapopulation, whereas the white area is the "phase" where extinction is expected.
When we plot x * against both c and D, we can see that, for a fixed colonisation, x * decreases from x * ( D = 0 ) = 1 − e / c in a linear fashion (white line) until it reaches extinction at the corresponding threshold value of destruction. And here comes a fundamental result. Once the critical threshold has been reached, there is still a potential available habitat given by 1 − D . The linear view would have predicted that a smaller, but nevertheless non-zero fraction of patches should be occupied. However, and this is a consequence of the original Levins model, the species-specific parameters c and e are also important and impose boundaries to metapopulation persistence. The take-home message is clear: even if some significant part of a landscape remains suitable for a given species, once we cross the minimal requirements imposed by the previous model, persistence is not an option. Mounting evidence has shown how habitat loss can trigger the extinction of endangered species. Examples include, among others, the Northern Spotted Owl (Lande, 1987) that has become a canonical example of how a few key parameters associated to dispersal and demography allow defining the critical conditions for survival.
Another important property of these thresholds is the presence of a marked increase of fluctuations as we approach D c . Some further analysis of the model can help to show that this phenomenon must be expected. Consider our original Equation (8) for our metapopulation model and suppose that we start from a very small metapopulation size, i.e., x ≪ 1 . In that case, the model becomes much simpler:
d x d t x ≪ 1 ∼ c D c − D x
which can be solved to give a dynamical Equation of x close to criticality:
x ( t ) = x 0 e c D c − D t
How long it takes, from a given x 0 , to reach extinction? The time T ( ϵ , D ) needed to achieve this can be found from the last equation. By replacing t = T ( ϵ , D ) and the final state x ( T ( ϵ , D ) ) = ϵ we obtain
T ( ϵ , D ) = ln ( ϵ / x 0 ) c D c − D ∼ ( D c − D ) − 1
This result has an enormous implications. It tells us that the relaxation time to equilibrium diverges close to the critical point. In practical terms, it means that, because the marble is rolling now on a rather flat valley, population size can fluctuate with a high variance. The exact number of individuals becomes less predictable while the time required to achieve extinction can be very long. This is in fact a well-known result from the statistical physics of phase transitions and is known as critical slowing down (Solé, 2011; Ganghi et al., 1998). It is a universal property of systems that display continuous phase transitions where conflicting tendencies between order and disorder are present.
What are the implications of these long transients? One is that we can actually use this feature to detect so called warning signals: as we get close to a critical points where some undesirable shift can occur, we should observe that population time series should display increasing variance (Scheffer et al., 2009; Clement and Ozgui, 2018). Another consequence (to be discussed in the next section) is that high variances might translate into confusing results concerning the outcome of habitat loss. Although this process should in principle correlate with biodiversity decays, some studies have pointed out that the opposite might sometimes be observed. Here long-term fluctuations might obscure the predicted decay and be a byproduct of the slowing down close to threshold points. In this context, generalisations of the previous model can be derived, including a S-species competitive community. This is the case for the following model (Solé et al., 2004):
d x i d t = c i x i 1 − D − ∑ j = 1 S x j − ϕ ( c i ) x i
with I = 1 , . . . , S and ϕ ( c i ) introduces a trade-off between colonisation and extinction so that c / e is the same for all species. Using e i = ϕ ( c i ) = α c i , this deterministic, quasi-neutral model behaves in similar ways as the single-species scenario, with all species getting extinct for D c = 1 − α . However, the spatially-extended counterpart displays a maximum of species diversity, as measured by Shannon’s entropy, right on that point. This is an important problem that needs to be investigated. Additionally, other models involving a ranked structure of competitors shows that extinction can occur in a delayed manner: even when given thresholds have already been crossed, it can take a long interval to observe the final demise of a given species (Tilman et al., 1994). As pointed out by some researchers, this poses a challenge to biological conservation policies (Kussaari et al., 2009).
A final but not less important phenomenon needs to be considered. Our model so far is a mean field model: we completely ignore the existence of local interactions. This is not a minor matter. The introduction of space in an explicit fashion can generate novel phenomena, from stable regular patterns to complex waves (Murray, 2003). These are emergent properties: they are system-level phenomena out of local, microscopic interactions, but cannot be reduced to the lower-level components (Artime and De Domenico, 2022).
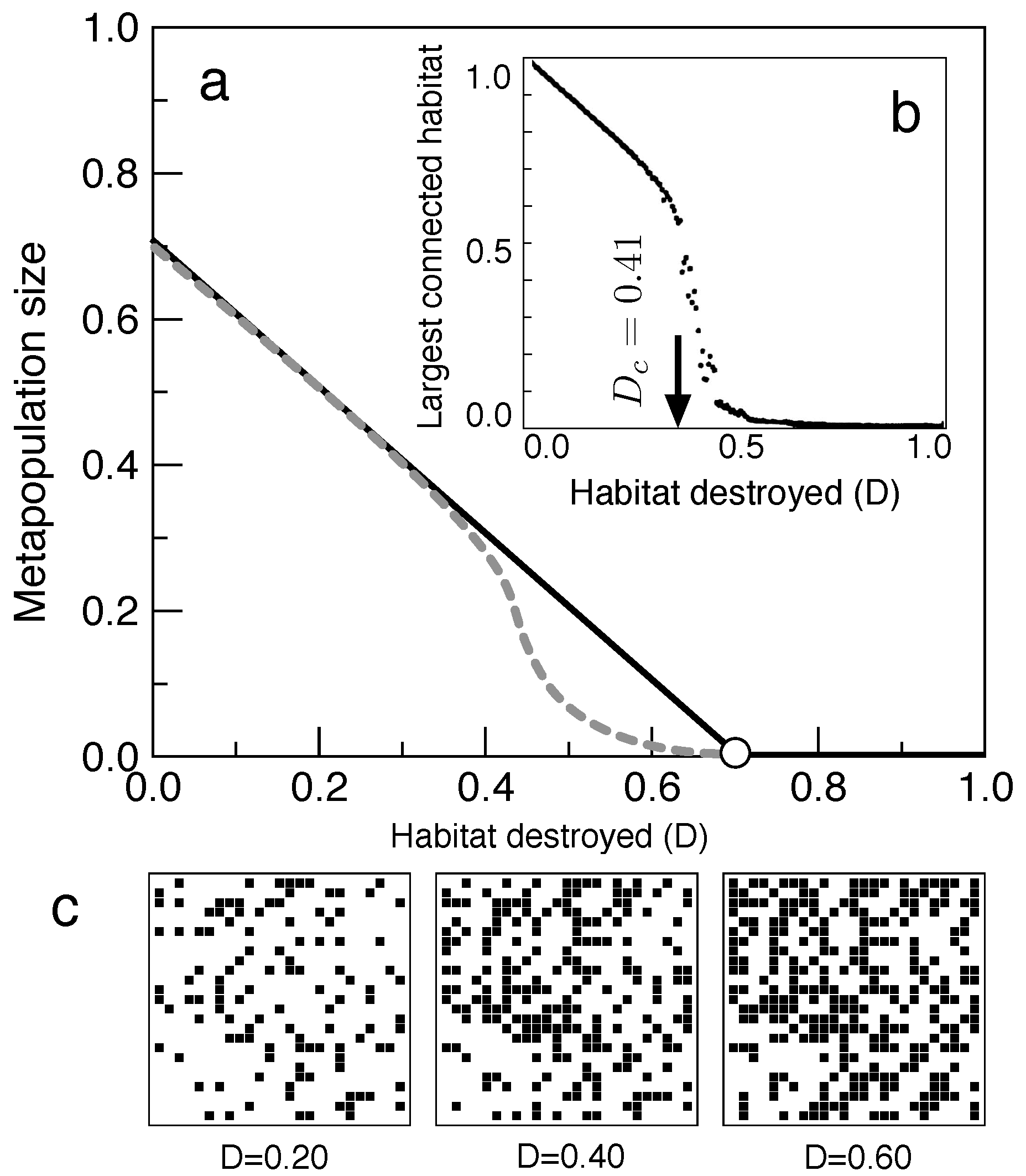
It was shown in the early times of spatial ecology that introducing space in an explicit manner can deeply modify the expectations from well-mixed systems (Durrett and Levin, 1994; Bascompte and Solé, 1995). In Figure 3a–c we show what happens when space is taken into account. To build such a spatial model, as the one outlined in Figure 2a for the Levins model, we consider a set of probabilistic rules of patch colonisation and extinction (see Bascompte and Solé 1997 for a detailed explanation). In a nutshell, a given empty site i ∈ Ω can be colonised, with probability c, by any of the occupied sites in the neighbourhood Γ i (Figure 2a, zoomed area). Similarly, an occupied site can get extinct with a probability e.
The metapopulation occupancy resulting from these set of rules is shown in Figure 3a for different habitat destruction values using a 100 lattice (gray curve) and compared with the theoretical prediction from Levins model (black line). A marked difference is observed: the occupied habitat becomes much less than the one expected from the well-mixed one. What is going on? We will be back to this when we explore the problem of percolation, but let us advance that an emergent phenomenon occurs at a given destruction threshold, indicated in Figure 3b, where we plots the size of the largest connected set of patches for each value of D. Despite the smooth character of the increased habitat loss (depicted in Figure 3c for three D values), a phase transition takes place at D ≈ 0.4 . The system becomes fragmented afterwards, becoming broken in multiple patches. Because of this phenomenon, different isolated clusters of healthy habitat will sustain disconnected metapopulations, that will be more and more affected by fluctuations. This combination of smaller domains and persistence thresholds translates into the observed displacement of the extinction threshold.
Field observations and theoretical models have been instrumental in developing a conservation strategy to fight the effects of habitat fragmentation. In order to recover the connectivity required to increase the effective habitat size (as would be defined by the largest connected habitat) is to design biological corridors (Anderson and Jenkins, 2006; Pimm and Jenkins, 2019). Using models allow to address the problem of optimal reserve design, often using concepts of graph theory (Williams et al., 2005; Niebuhr et al., 2015; Rocha et al., 2021) particularly within the context of future climate change scenarios (McGuire et al., 2016).

4. Facilitation and Tipping Points

In the previous section we have considered models where species responses are somewhat isolated from the rest of the community. This is the case of Levins model and its extensions to habitat loss scenarios. In those models, the predicted critical point that separates a stable metapopulation from its demise applies to a case study where only one species is present. Single-species metapopulation models that address the conditions for extinction in a given landscape have received much attention (Hanski, 1999). However, this cannot be a satisfactory picture if we deal with species interactions, which can introduce new kinds of nonlinearities. To explore their impact, let us now consider a simple, but extremely important phenomenon known as facilitation, that is very relevant in dryland ecosystems (Rietkerk and van de Koppel 1997, Scanlon et al. 2007, Kéfi et al., 2007a-b, Solé 2007) where warming, steady declines in rainfall and increased grazing are likely to promote a sudden shift from a vegetated ("Green") to a desert state (Solé, 2017). The analysis and modelling of spatial patterning in semiarid habitats consistently supports the suggestion that rapid shifts might occur in a near future (Kéfi et al. 2007a-b, Solé 2011).
Facilitation refers to positive (cooperative) interactions between individuals that confer benefits upon at least one of the participating entities (Brooker et al. 2008). A particularly relevant instance encompasses instances where one organism enhances the local environment, rendering it more conducive for another, irrespective of whether they belong to the same species or not. This affirmative influence can manifest directly, such as through shading mechanisms that alleviate water or nutrient stress, or indirectly, like the removal of competitors or the deterrence of predators (Bruno et al. 2003).
In order to push forward the idea that the addition of qualitative properties to a given ecological model leads to new emergent dynamics, I will use as a case study a straightforward extension of the previous habitat fragmentation models including facilitation in its simplest form (Sardanyes et al., 2019). With this simple model, we will be able to address several important questions: What implications does habitat destruction bear on an ecological system that incorporates facilitation? How does this impact interact with the nonlinear attributes associated with facilitation?
Let us start with some complexity and see how can can reduce an initial multispecies model to a single-variable model. Consider the available space as a finite resource that we assume (for convenience) normalized to one. Let us also assume that part of this habitat has been lost due to habitat destruction. Those affected areas (either by the presence of barren soil or contaminated patches) are no longer amenable for colonization. Consider a population of S species where abundances are indicated as x 1 , x 2 , . . . , x S . Let us assume that they display both competition and cooperation. The model now involves multiple dimensions (species diversity) and reads:
d x i d t = ∑ j = 1 S c i j x i x j 1 − D − ∑ w = 1 S x k − e i x i ,
Here c i j stands for the mutual help (facilitation) that a given plant species j provides to the individuals belonging to species i. The cooperaive nature of facilitation is introduced by the cross-interaction terms x i x j indicating that both populations are needed to allow growth. As with Levins model, the amount of available area is limited to a maximum 1 − D . This is a high-dimensional system with many variables, but relevant results can be obtained if we consider a homogeneous parameter set. If c i j = c , e i = e for all species, then we have:
d x i d t = c x i ∑ j = 1 S x j 1 − D − ∑ w = 1 S x k − e i x i ,
Now assuming that, since all species are parametrically identical, and indicating by x = ∑ i x i the total population, we expect x k ∼ x / S . We can now write:
d x i d t = 1 S d x d t = c x S x ( 1 − D − x ) − e x S ,
Finally, the mathematical model describing the metapopulation occupancy can be written as follows:
d x d t = c x 2 ( 1 − D − x ) − e x ,
If e = D = 0 , this model reduces to a simple logistic growth model where the population would eventually occupy the whole area.
The model is almost the same as Levins model with habitat loss, with just a nonlinear term x 2 . But this linear term, indicating that interactions among individuals are taken into account, changes everything. Using the steady state condition:
d x d t { c , D , e } = c x 2 ( 1 − D − x ) − e x = 0
for a given parameter combination { c , D , e } , three possible fixed points are found, namely x 0 * = 0 and the pair
x ± * = 1 2 1 − D ± ( 1 − D ) 2 − 4 r ,
where r ≡ e / c . These possible states are summarized in the bifurcation diagram shown in Figure 3a. The upper branch x + * is a stable state (while x − * is unstable) and as we can see, increasing levels of destruction gradually reduce the size of the vegetation cover. However, (and here comes a big point) there is a critical threshold:
D c = 1 − 2 r .
associated with a catastrophic shift. For D > D c the two equilibria x ± * do not exist in the biologically-meaningful domain, and the system faces extinction in a discontinuous manner. Using a spatially extended version of this model, we can observe a replacement process between two community states, namely C R → C D . After a given transient, the slight increase in D has produced a dramatic outcome.
We can use again the potential function to visualize the system’s dynamics against changing levels of habitat loss. The potential function now reads:
V ( x ) = − c x 2 − r 2 + 1 − D 3 x − 1 4 x 2
and is displayed in Figure 3b for several values of habitat destruction D. For D < D c (solid lines) two wells are found, corresponding to the two alternative stable states ( x 0 * and x + * ) resulting in bistability, that will be achieved depending on the initial conditions. As we can appreciate, once the D c state is crossed, a rapid roll down of the marble will take place towards the only available state, located at the bottom of the desert state valley. But in this case, by contrast with Levins model, where we could consider a recovery strategy based on restoring habitat quality and available patches, another important phenomenon is present: there is an irreversible change, and improvements in habitat availability will not allow the system for getting back to the vegetated state again. In order to do so, restoration can only occur if we add the adequate amount of individual plants in order to put urselves above the unstable point x − * . Otherwise, the dynamics drives us again back to the zero-vegetation state. The implications of this phenomenon are obvious: any restoration effort once we cross the threshold is likely to require great investments and active efforts, which can have staggering costs.
One could argue that a realistic approach to drylands needs to consider many other variables beyond vegetation cover. Such a multivariate formulation has been developed, based on the concept of multifunctionality (MF). As implicit in the term, MF encapsulates multiple ecosystem functions. Using remote sensing and field data (Berdugo et al., 2017) a picture of global drylands emerges that gives aupport to the alternative state scenario depicted by our simple model. However, there are several potential thresholds associated to drylands degradation. In this context, a global analysis comprising 5 × 10 4 data points spanning different scales (from individuals to ecosystems) revealed three well-defined shifts (Berdugo et al, 2020) resulting from increasing aridity levels. In Figure 4d we summarize these results and the corresponding interpretation in terms of potential functions. As aridity α is increased, the thresholds include:
1.
For α = 0.54 , a decay in photosynthetic activity and nitrogen storage that result from the shrinkage of leaf area. The shift is observable in particular as a marked reduction in plant productivity.
2.
For α = 0.7 , a deep weakening of plant-soil interactions occurs, with a soil disruption involving a shift from stress-tolerant communities (STC) towards infertile shrublands (US). These transition has been studied within the context of shrub encroachment in arid grasslands, and is known to involve a sudden transition (D’Odorico et al., 2012; 2013).
3.
As we approach α = 0.8 we get back to the green-desert transition with a systemic breakdown. The shift is marked by drastic reductions in plant cover as well as changes in leaf traits associated with stress avoidance.
Can our understanding of these tipping points and their underlying emergent patterns be exploited to prevent them from occurring? This is largely an open question, but theoretical models suggest that their nonlinear properties could be exploited to avoid undesirable shifts. Using tools from statistical physics, it has been shown that changes in the patterns of fluctuations or dispersal could change the nature of the transition from discontinuous to continuous (Vila Martin et al., 2015). Similarly, using synthetic biology it would be possible to modify the dynamics of the microbiome of soil crusts in drylands (Belnap and Lange, 2001; Pointing and Belnap, 2012), creating synthetic soil crusts that could push away catastrophic shifts (Vidiella et al., 2020).
Finally, we should mention that drylands models also predict the presence of ghosts associated to the very long transient times to collapse close to tipping points. By making small-scale, regular interventions, these ghost dynamics can be exploited (even beyond the critical point) to maintain the vegetated state (Vidiella et al., 2018). In all these cases, it is important to point out that interventions are aimed at enhancing bottom-up properties of communities, such as biodiversity, by contrast with standard, top-down engineering (Solé, 2015; Solé and Levin, 2022).

5. Percolation: What Makes A System

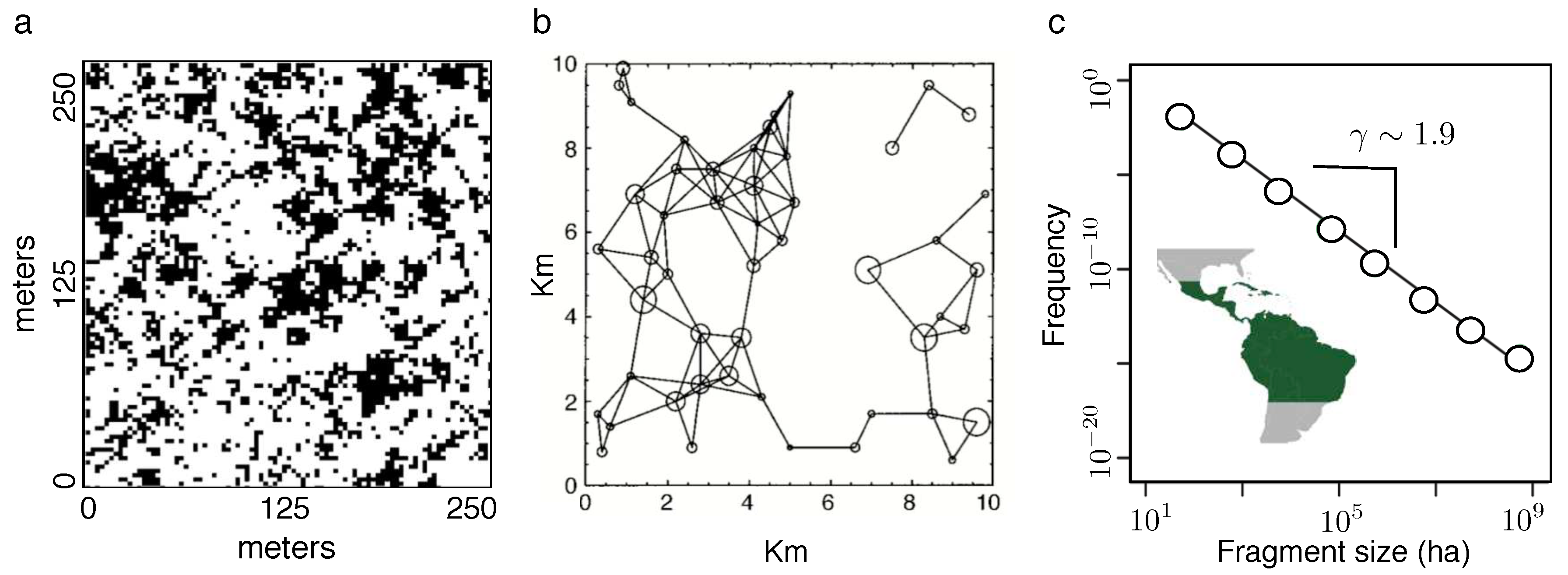
Ecology is one of the few sciences where the systems-level view has played a central role since the early beginnings of the discipline (Odum, 1983; Wulf, 2015). Several common threads, such as space, hierarchy, information or network structure have a long tradition. But one could ask a naive question: what defines a "system"? (Keller, 2005). It might seem a rather vague question, perhaps leading (as it occurs with many fundamental questions) to qualitative answers and little predictive power. But here too, there is a powerful concept that provides an answer with deep implications for biodiversity conservation. Before we present the theoretical framework, let us consider three different case studies spanning three very different time scales, as shown in Figure 5a–c.
The first example is a spatial set of patches obtained from the canopy tree plot from Barro Colorado Island (Welden et al., 1991; Hubbell et al., 1999). The map contains a 250 × 250 meters domain where black squares (with a 5 × 5 meters width) indicate locations of a gap in the canopy, indicating a height smaller than h c = 15 meters (Figure 5a). This pattern changes over time, given the highly dynamic nature of the gap formation process (Brokaw, 1985; Whitmore, 1990; Scnitzer and Carson, 2001; Wright, 2002), but its statistical properties remain the same. As we can appreciate, clusters of canopy points are highly heterogeneous. In fact, if we look at the frequency of clusters of size s, it is found that it follows a power law distribution (Solé and Manrubia, 1995), namely:
P ( s ) = 1 Z s − γ
where γ ∼ 1.8 is the so called scaling exponent and
Z = ∫ s 0 s m s − γ d s
a normalization constant, defined from the minimum gap size s 0 to the maximum observed ( s m ). Additionally, the spatial organization of this area has been shown to display a fractal structure: if we zoom over this plot, the same pattern looks the same on different scales1. How do these scale-free structures emerge? One potential explanation of the patterns behind the BCI data is a critical state. An example would be the critical habitat loss D c depicted in Levins model. As we already discussed abpve, at the critical point several unexpected phenomena occur and available evidence strongly suggests that the rainforest might live close to criticality (see Schlicht and Iwasa, 2004).
The second example, which works on a spatial scale of Kilometres, is also tied to the problem of habitat connectivity in a heterogeneous landscape. The plot in Figure 5b shows a number of suitable habitat areas where a given species can thrive. If individuals of a given species are able to move from one patch to another, we say that these two sites (open circles in our plot) are connected. Formally speaking, two sites S i and S j will be connected if their Euclidean distance d i j is lower than the characteristic dispersal distance d c of the species under consideration (here the Northern Spotted Owl). This threshold condition is all we need to build the landscape connectivity graph G = ( S , A ) , defined as the set of nodes S and a n × n matrix A (the adjacency matrix) where a i j = 1 if the pair { S i , S j } is connected through dispersal. The key problem addressed by this graph is to measure the total number of connected sites. The graph shown here is a special one, obtained when the critical distance is d c = 1500 . Below this value, the graph is disconnected into many separated sites. For d > d c becomes hyperconnected. Right on d = d c , a sudden jump in the number of connected sites occurs. This threshold provides a powerful tool to predict the conditions for species persistence (Gardner et al., 1987; Urban and Keith, 2001; Keith et al., 1997).
Our third case study involves a global survey of 130 million forest fragments from three continents (Taubert et al., 2018). This study revealed two important things. The first was the presence of a robust scaling law in the size distribution of forest fragments. Specifically, it was found that it scales as described by Equation (20), now with a scaling exponent γ ≈ 2 (see Figure 5c for the Americas set).
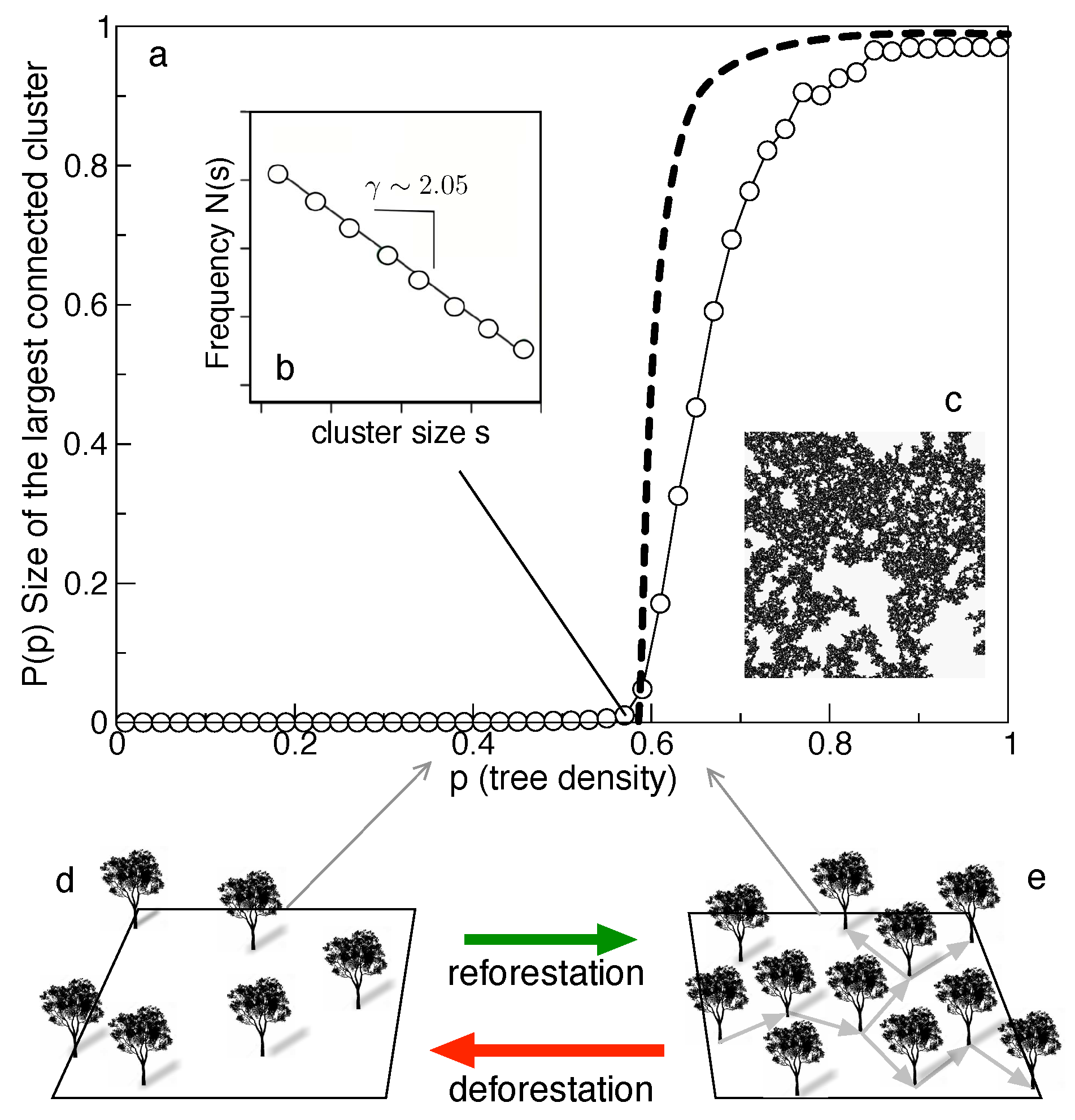
The three examples described above share the a threshold condition that is associated to the problem of percolation (Stauffer and Aharony, 2018; Christensen and Moloney, 2005). Percolation is not only the simplest example of a phase transition. It perfectly illustrates the idea that universal patterns emerge close to critical points and that they have crucial implications to fundamental features of very diverse types of systems. In fact, percolation defines a threshold condition that allows us to sharply separate a connected, coherent system from a set of many disconnected parts. In other words, percolation is at the core of what defines a complex system. The idea itself is very simple, and is fully illustrated by a two-dimensional toy model.
Consider a lattice Ω initially made of L × L empty sites. Let us now introduce "trees" by choosing random sites. A given empty site will be occupied by a tree with probability p. We want to define a measure of connectivity that tells us something about how easy is to move from one tree to its neighbours. As before, we will consider the four nearest sites as the neighbourhood of a given site. Using this definition, we can count the size of connected clusters. For small p values, we cannot expect to observe large patches of connected trees, while for large p we should be able to move across the whole landscape jumping from tree to tree. What about intermediate values? To address this question, let us define P ( p , ∞ ) , i.e., the fraction of sites that belong to the largest connected cluster. This quantity tells us how much of the trees in our lattice belong to a single system, and compare it with the size of the whole lattice. When we plot this fraction against the occupation probability p, a rather unexpected result emerges, as shown in Figure 6a. Instead of a continuous increase, two well-defined phases are observed. The two phases are separated through a well-defined critical point p c ∼ 0.59 . For very large L, it can be shown that P ( p , ∞ ) behaves as
P ( p , ∞ ) ∼ ( p − p c ) β
for p > p c (and zero for p < p c ) with β ≈ 1.16 .
If we measure the number of clusters of different size s, a power law distribution is obtained (Figure 6b) and the structure of the largest connected cluster is very complex, defining a fractal object (Figure 6c). The distribution is very similar to the one reported in (Taubert et al., 2018). This likely indicates that the observed forest fragmentation pattern is close to criticality. As deforestation proceeds, we should expect the system to cross the critical point, thus moving from an essentially connected system to a disconnected one (Figure 6d,e). What is the importance of these findings? Since deforestation rates and future estimates can be determined (within some bounds), the model provides an estimated time window to reach the transition to p c .
Using different versions of the percolation model, the authors forecast for the America’s (where deforestation and reforestation rates are estimated) these time window would be around 2050. For each continent, estimated of expected deforestation and planned or required reforestation allow to exploit the robust theoretical predictions while guiding mitigation plans. In this case, by contrast with the transition to extinction in levin’s or facilitation models) there is a reversibility intrinsic to the nature of the percolation threshold. If reforestation is performed close to p c and within a time scale where fragmentation might not cause major population effects, recovery of connected landscapes can be achieved.

6. Fires and Ecological Time Asymmetries

Our last example deals with the long-time recognised existence of a separation of time scales in ecological dynamics. It has been known since a long time ago that slow-dynamical regimes are sometimes followed by sudden changes occurring in a very short time scale (Levin, 2000). These have been traditionally connected to the presence of multiple states separated by breakpoints (May, 1977). Our case study here is fire, which is known to be a very important environmental factor in many biomes. It was so long before the ascent of our species, but has become heavily influenced by human activity through the Anthropocene (Bowman et al., 2011; Hantson et al., 2015).
Fire is one particularly relevant example of this separation between slow and fast time scales that departs from our previous examples. It is connected with a phenomenon that, despite its global impacts, is seldom found in textbooks of conservation ecology (Bond and Keeley, 2005). Along with soil properties and environmental factors, fire has played a major role in shaping ecological communities (Bond et al., 2005), by acting as a "global herbivore". Fires fully illustrate the importance and implications of the asymmetry that pervades them. As the Catalan ecologist Ramon Margalef once said: "A forest needs one hundred years to get built, but burns in one day". But this only reveals one aspect of fires. They are self-organized, highly dynamical systems, coevolving with diverse range of species that became adapted to fire regimes.
What makes forest fires different? The answer needs to be found in the way they occur and how their emergence interacts with vegetation. Because they need vegetation cover to spread, a process of forest growth is first required, which takes a long time, while the effects are -in comparison- almost instantaneous. Since fires can get started anytime at some location and spread until they run out of fuel, what kind of dynamical state results from this dynamics? One important clue to answer this question is provided by fire size distributions. If s indicates the size of a given fire event, it has been shown (Pueyo, 2007) that the frequency of fires of size s follows a power law distribution (Figure 7a), which we have already described within the context of forest fragments i.e.,
P ( s ) = 1 Z s − β
where the normalization constant reads
Z = 1 β − 1 s 0 − β + 1
Here s 0 is the minimum forest fire size (usually in units of area) and we assume that largest fire sizes s m are such that s m ≫ s 0 . As it occurs with other systems exhibiting power laws, the distribution has no characteristic scale (there are no "typical" fires with some expected, average size). While fires will be typically small, very large ones with scales close to the system’s size, are expected to occur. Since we have seen in previous examples that power laws are expected close to critical points, one could ask: what is the parameter that we need to tune in this case? The answer is that there is no tuning: the system self-organizes itself to criticality (Muñoz, 2018). The concept of selforganized criticality (SOC) was first proposed by Danish physicist Per Bak (Bak et al., 1987; Bak and Chen, 1991; Bak, 2013; Jensen, 1998) and is a keystone in our understanding of criticality in ecology and evolution (Solé et al., 1999; Levin, 1999). The intuitive example is provided by a sandpile: if we slowly add grains of sand to a surface (one by one), a sandpile if slowly formed with an increasing slope. At the beginning, the grains fall down and their behaviours is capture by standard physics. However, once the pile reaches a given critical slope, a collective process starts to unfold: one grain can trigger an avalanche. Most of the time, these avalanches are small, involving just a few grains, but very large (and fast) avalanches will also occur. The self-similar pattern of avalanches is an emergent phenomenon resulting from the constant driving followed by reset events.
A simple cellular automaton model (Chopard and Droz, 1998) of fire propagation in a virtual forest illustrates the idea within our context. Consider the so called Forest Fire Model (Bak et al., 1990, Drossel and Schawbl, 1992a, 1992b; Clar et al., 1996) where a discrete description of fire spreading is applied to the states of each site on a two-dimensional lattice Ω . Each site r ∈ Ω can be in three possible states, namely S ( r ) ∈ Σ = { E , T , F } , where E denotes an empty cell, T a tree cell and F a fire cell. The state of the system will be updated by means of three probabilistic events, namely: (1) spontaneous burning of a tree, i.e., a transition T → F at a rate f, leading to a burning site (fire cell); (2) growth of new trees from empty sites, i.e., with a probability p we have E → T . (3) The last rule allows fire propagation: if a given tree has a burning neighbour, it burns too. This means a (deterministic) transition T → F .
Despite its simplicity, the FFM exhibits a very complex behaviour. In particular, for p , f ≪ 1 and f ≪ p the dynamics of fire propagation exhibits a self-organized critical (SOC) state that includes extreme events. An example of the time series generated by the model is displayed in Figure 7b,c. While fires have a marked bursting dynamics, tree cover reveals a continuous growth pattern followed by a reset that correlates with fire peaks. One snapshot of the model is also shown in Figure 7d, associated with a peak in the fire spreading. Trees, fires and empty sites are indicated as green, yellow and black colours, respectively.
Despite of its simplicity, versions of the FFM and variations of it have been successfully adapted to model the statistical patterns of the actual fires (Pueyo, 2007). In this context, it has been shown that the observed exponents in woodland forests depart from those predicted by the FFM. In particular, the sudden appearance of trees in random locations is clearly unrealistic. In fact, it has been shown that the accumulation of fuel after previous fires plays a key role. This qualitatively relevant observation can be easily incorporated (Pueyo, 2007) by a simple rule that accounts for fuel increase. This is done by introducing a propagation rate that would suddenly decay after fire and then slowly increasing. The resulting model (which also takes into account environmental factors) successfully accounts for the observed statistical patterns. Importantly, in this case the observed exponent can change in different geographic locations due to the influence of weather (Pueyo, 2007; Hantson et al., 2014).
The work by these authors reveals that forest fire dynamics combines features of the SOC mechanism (the separation of time scales) along with heterogeneities associated to fuel accumulation, which plays a role of an actual tunable parameter. By looking all these factors, a global map of fire size distribution can be obtained, with different areas marked by a characteristic, estimated exponent β (Hantson et al, 2014). Since this parameter is affected by climate change, it offers a unique possibility predict the future impacts of global warming on fire sizes.

7. Discussion

The preservation and restoration of biodiversity stand as formidable challenges in an increasingly interconnected world. As we face the looming threat of crossing planetary boundaries in the coming decades, it becomes imperative to address these challenges with a comprehensive and multiscale approach. Biodiversity conservation necessitates considering the intricate interplay of multiple scales of complexity, and embrace theoretical models as a powerful approximation to reality. Such reality often departs from the linear intuition, and makes difficult to create a narrative that fits our intuitions. Since the success of conservation policies is not only a matter of good science science but also public understanding, this is not a minor problem.
Delving into the emergent properties arising from ecosystem dynamics offers valuable insights into developing successful conservation strategies. By identifying these emergent phenomena, which differentiate the various scales involved, we can design targeted interventions that tackle conservation challenges more efficiently. Moreover, uncovering the universal properties that underpin ecosystem dynamics allows us to develop simple yet powerful models for each scale, aiding in the formulation of evidence-based policies and management decisions. In this paper I have summarised a few well-established models that share a common simplicity in their formulation. This simplicity, however, does not mean that they fall short in explaining observed patterns. Instead, simple models of nonlinear systems can fully capture their crucial properties.
A summary of the models presented here, the underlying case studies and their relationships is provided in Figure 8. From bottom ti top, the different kinds of predicted transitions described by the previous models and the mathematical models are displayed. This scheme also helps emphasising the idea that the introduction of extra rules can generate novel, emergent phenomena. When dealing with single-species studies (a,b), species are considered as isolated entities whose populations change as a consequence of a balance between dispersal (immigration) and extinction. In these models, intra-specific competition is the dominant interaction, although the estimated rates are of course somehow coarse-graining interspecific traits. If habitat loss is introduced (c,d), an extra parameter D modifies the previous transitions, but have a common continuous behaviour until extinction occurs at a given critical habitat destruction level.
If an extra layer of complexity associated with species interactions (beyond competition) is introduced, the nature of the transition dramatically changes. Here we have considered facilitation (e) where local interactions have a cooperative nature that translates into a quadratic growth term. This means that increasing changes in the key parameter (habitat destruction) trigger a catastrophic shift after the threshold level is reached. Finally, on a very large scale (f) the process of habitat loss requires a model that takes space into account in an explicit manner. In this case, percolation is the conceptual framework that provides robust predictors for fragmentation thresholds. Each of these models is able to guide conservation efforts at a given scale, but cannot be extrapolated as we move to the next level. Each level of complexity is irreducible. The selection of the models and associated case studies showcased here is based on their deliberate simplicity. This choice serves as a demonstration of the efficacy of well-defined models. Due to their straightforward nature, these models enable us to methodically analyze the significance of various variables and ascertain their relative importance, or lack thereof. These models can also be expanded upon to encompass additional aspects of population dynamics and their interaction with the environment, as demonstrated by Bauch et al. (2016), Weinberger et al. (2017), and Farahbakhsh et al. (2022).
A notable example pertains to the issue of habitat fragmentation arising as a consequence of agricultural expansion. In the work by Bengochea Paz et al. (2022), the authors present a model that intertwines agricultural expansion with human population growth. The latter is dependent on the former, leading to increased habitat loss and fragmentation. Consequently, this results in the depletion of ecosystem services provided by these fragmented habitat patches and a decrease in overall productivity. This, in turn, can drive land managers to further expand crop areas, exacerbating habitat loss. This feedback loop eventually pushes the system towards a state of percolation. The model’s predictions indicate a transition from sustainable states to a phase of collapse. The precise boundary between these two phases hinges on the delicate balance between land use under intensive agriculture and the rate at which demographic changes occur.
Embracing a complex systems view empowers us to approach biodiversity preservation with greater foresight, acknowledging the complex web of dependencies and feedback loops that sustain life on Earth. In such a world, where the fate of our planet hangs in the balance, it is vital to integrate sound scientific knowledge, forward-thinking management strategies, and global cooperation to safeguard and restore biodiversity. Such integration will require a collective effort across disciplines where our understanding of different scales will benefit from the universal patterns displayed by simple models of ecological complexity.

Acknowledgments

The author thanks the members of the complex systems Lab for useful discussions. This work was funded by a grant AGAUR FI-SDUR 2020 and by the Santa Fe Institute.

Appendix A. Potentials

A very common metaphor of a stable ecological state considers a physical analogy, where a marble (representing population size) is located at the bottom of a valley Holling1973,Scheffer2009,Sole2011 . If perturbed, the marble will move around but eventually will settle back to the bottom state again. In contrast, a marble located on a peak in this landscape might stay there but the slightest perturbation makes it to run away: the peak corresponds to an unstable state. Is there a way to define this landscape in some rigorous mathematical way? For a one-dimensional dynamical system defined as d S / d t = f ( S ) where f and its derivative are continuous. The system is said to derive from a potential function V ( S ) (Strogatz, 1994; Scheffer 2008; Solé, 2011) if we can write the dynamical system as:
d x d t = − d V d x
i.e., when the changes in the state of the system obey a gradient response: the steeper the derivative in the right hand side, the larger the damping in the opposite direction. If we move away from x * towards x * + Δ x (where Δ x is small) the change in the potential with s will be
Δ V Δ x = V ( x * + Δ x ) − V ( x * ) Δ x
If Δ V > 0 means that the potential grows (we are in a valley) and thus, from (6) the right hand side of (5) is negative: growth is inhibited. The opposite occurs if we are in an unstable point. From the previous equation, it is easy to see that
V ( x ) = − ∫ d x d t d x = − ∫ f ( x ) d x
At a given x * , using the previous definitions (equations (1) and (3)), the first derivative is
d V ( x ) d x x * = − f ( x * )
and the second derivative reads
d 2 V ( x ) d x 2 x * = − λ ( x * ) ,
respectively. The first derivative is zero (as it should be for an extremum of the function) and the second will be positive (negative) if the point is stable (unstable), consistently with a minimum (maximum) of the potential.

References

  1. Anderson, A.B. and Jenkins, C.N., 2006. Applying nature’s design: corridors as a strategy for biodiversity conservation. Columbia University Press.
  2. Artime, O. and De Domenico, M. From the origin of life to pandemics: Emergent phenomena in complex systems. Philosophical Transactions of the Royal Society A 2022, 380, 20200410. [Google Scholar] [CrossRef] [PubMed]
  3. Azaele, S. , Suweis, S., Grilli, J., Volkov, I., Banavar, J. R., and Maritan, A. Statistical mechanics of ecological systems: Neutral theory and beyond. Rev. Mod. Phys. 2016, 88, 035003. [Google Scholar] [CrossRef]
  4. Bak, P. , Tang, C. and Wiesenfeld, K. Self-organized criticality: An explanation of the 1/f noise. Physical review letters 1987, 59, 381. [Google Scholar] [CrossRef] [PubMed]
  5. Bak, P. , Chen, K. and Tang, C. A forest-fire model and some thoughts on turbulence. Physics letters A 1990, 147, 297–300. [Google Scholar] [CrossRef]
  6. Bak, P. and Chen, K. Self-organized criticality. Scientific American 1991, 264, 46–53. [Google Scholar] [CrossRef]
  7. Bak, P. , 2013. How nature works: the science of self-organized criticality. Springer, New York.
  8. Barnosky, A.D. et al. Approaching a state of shift in Earth’s biosphere. Nature 2012, 486, 52–58. [Google Scholar] [CrossRef] [PubMed]
  9. Barnosky, A.D. and Hadly, E.A. (2016) Tipping point for planet Earth: how close are we to the edge?. St. Martin’s Press, New York, NY, USA.
  10. Bascompte, J. and Solé, R.V. Rethinking complexity: modelling spatiotemporal dynamics in ecology. Trends in Ecology and Evolution 1995, 10, 361–366. [Google Scholar] [CrossRef] [PubMed]
  11. Bascompte, J. and Solé, R.V. (). Habitat fragmentation and extinction thresholds in spatially explicit models. J. Anim. Ecol. 1996, 65, 465–473. [Google Scholar] [CrossRef]
  12. Bauch, C.T. , Sigdel, R., Pharaon, J. and Anand, M. Early warning signals of regime shifts in coupled human?environment systems. Proc. Natl. Acad. Sci. USA 2016, 13, 14560–14567. [Google Scholar] [CrossRef]
  13. Farahbakhsh, I. , Bauch, C. And Anand, M. 2022. Modelling coupled human-environment complexity and its implications for the future of the biosphere.
  14. Belnap, J. and Lange, O.L. ed., 2001. Biological soil crusts: structure, function, and management. Springer, Berlin.
  15. Bengochea Paz, D. , Henderson, K. and Loreau, M. Habitat percolation transition undermines sustainability in social?ecological agricultural systems. Ecology Letters 2022, 25, 163–176. [Google Scholar] [CrossRef]
  16. Berdugo, M. , Kéfi, S., Soliveres, S., Maestre, F. Plant spatial patterns identify alternative ecosystem multifunctionality states in global drylands. Nature Ecol. Evol. 2017, 1, 1–7. [Google Scholar]
  17. Berdugo, M. , Delgado-Baquerizo, M., Soliveres, S. et al. Global ecosystem thresholds driven by aridity. Science 2020, 367, 787–790. [Google Scholar] [CrossRef] [PubMed]
  18. Bond, W.J. et al. The global distribution of ecosystems in a world without fire. New Phytol 2005, 165, 525–538. [Google Scholar] [CrossRef]
  19. Bond, W.J. and Keeley, J.E. Fire as a global ?herbivore?: the ecology and evolution of flammable ecosystems. Trends in ecology and evolution 2005, 20, 387–394. [Google Scholar] [CrossRef]
  20. Breed, M.F. , Harrison, P.A., Blyth, C., et al. The potential of genomics for restoring ecosystems and biodiversity. Nature Reviews Genetics 2019, 20, 615–628. [Google Scholar] [CrossRef] [PubMed]
  21. Brokaw, N.V. Gap?phase regeneration in a tropical forest. Ecology 1985, 66, 682–687. [Google Scholar] [CrossRef]
  22. Brooker RW, Maestre FT, Callaway RM et al. Facilitation in plant communities: the past, the present, and the future. J. Ecol. 2008, 96, 18–34. [CrossRef]
  23. Brown, J.H. , Gupta, V.K., Li, B.L., Milne, B.T., Restrepo, C. and West, G.B. The fractal nature of nature: power laws, ecological complexity and biodiversity. Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences 2002, 357, 619–626. [Google Scholar] [CrossRef]
  24. Bruno, J. F. , Stachowicz, J. J. and Bertness, M. D. Inclusion of facilitation into ecological theory. Trends Ecology and Evolution 2003, 18, 119–125. [Google Scholar] [CrossRef]
  25. Case, T.J., 1999. Illustrated guide to theoretical ecology. Oxford U. Press.
  26. Chapin III, F.S. , Weber, E.U., Bennett, E.M. et al. Earth stewardship: Shaping a sustainable future through interacting policy and norm shifts. Ambio 2022, 51, 1907–1920. [Google Scholar] [CrossRef]
  27. Chopard, B., and Droz, M. (1998). Cellular automata. Springer, Berlin.
  28. Clar, S. , Drossel, B. and Schwabl, F. Forest fires and other examples of self-organized criticality. Journal of Physics: Condensed Matter 1996, 8, 6803. [Google Scholar]
  29. Christensen, K. and Moloney, N.R., 2005. Complexity and criticality (Vol. 1). World Scientific Publishing Company.
  30. Dai L, Voselen D, Korolev KS, Gore J. Resilience before a tipping point leading to a population collapse. Science 2012, 336, 1175–1177. [Google Scholar] [CrossRef] [PubMed]
  31. Dakos, V. , Matthews, B., Hendry, A.P., Levine, J., Loeuille, N., Norberg, J., Nosil, P., Scheffer, M. and De Meester, L. Ecosystem tipping points in an evolving world. Nature ecology and evolution 2019, 3, 355–362. [Google Scholar] [CrossRef] [PubMed]
  32. DeAngelis, D.L. and Waterhouse, J.C. Equilibrium and nonequilibrium concepts in ecological models. Ecological monographs 1987, 57, 1–21. [Google Scholar] [CrossRef]
  33. D’Odorico, P. , Okin, G.S. and Bestelmeyer, B.T. A synthetic review of feedbacks and drivers of shrub encroachment in arid grasslands. Ecohydrology 2012, 5, 520–530. [Google Scholar] [CrossRef]
  34. D’Odorico, P. , Bhattachan, A., Davis, K.F., Ravi, S. and Runyan, C.W. Global desertification: Drivers and feedbacks. Advances in water resources 2013, 51, 326–344. [Google Scholar] [CrossRef]
  35. Drossel, B. and Schwabl, F. Self-organized critical forest-fire model. Physical review letters 1992, 69, 1629. [Google Scholar] [CrossRef]
  36. Drossel, B. and Schwabl, F. Self-organized criticality in a forest-fire model. Physica A: Statistical Mechanics and its Applications 1992, 191, 47–50. [Google Scholar] [CrossRef]
  37. Durrett, R. and Levin, S. The importance of being discrete (and spatial). Theoretical population biology 1994, 46, 363–394. [Google Scholar] [CrossRef]
  38. Foley, J.A. , Coe, M.T., Scheffer, M. and Wang, G. Regime shifts in the Sahara and Sahel: interactions between ecological and climatic systems in Northern Africa. Ecosystems 2003, 6, 524–539. [Google Scholar] [CrossRef]
  39. Gardner, R.H. , Milne, B.T., Turnei, M.G. and O’Neill, R.V. Neutral models for the analysis of broad-scale landscape pattern. Landscape ecology 1987, 1, 19–28. [Google Scholar] [CrossRef]
  40. Green, J.L. , Hastings, A., Arzberger, P., Ayala, F.J., Cottingham, K.L., Cuddington, K., Davis, F., Dunne, J.A., Fortin, M.J., Gerber, L. and Neubert, M. Complexity in ecology and conservation: mathematical, statistical, and computational challenges. BioScience 2005, 55, 501–510. [Google Scholar] [CrossRef]
  41. Gutenkunst, R.N. , Waterfall, J.J., Casey, F.P., Brown, K.S., Myers, C.R. and Sethna, J.P. Universally sloppy parameter sensitivities in systems biology models. PLoS computational biology 2007, 3, e189. [Google Scholar] [CrossRef] [PubMed]
  42. Haddad, N.M. , Brudvig, L.A., Clobert, J., Davies, K.F., Gonzalez, A., Holt, R.D., Lovejoy, T.E., Sexton, J.O., Austin, M.P., Collins, C.D. and Cook, W.M. Habitat fragmentation and its lasting impact on Earth?s ecosystems. Science advances 2015, 1, e1500052. [Google Scholar] [CrossRef] [PubMed]
  43. Haken, H. Cooperative phenomena in systems far from thermal equilibrium and in nonphysical systems. Reviews of modern physics 1975, 47, 67. [Google Scholar] [CrossRef]
  44. Haken, H. Synergetics: are cooperative phenomena governed by universal principles? Naturwissenschaften, 1980; 67, 121–128. [Google Scholar]
  45. Hanski, I. (1999). Metapopulation Ecology. Oxford U. Press, Oxford, UK.
  46. Hantson, S. , Pueyo, S. and Chuvieco, E. Global fire size distribution is driven by human impact and climate. Global Ecology and Biogeography 2015, 24, 77–86. [Google Scholar] [CrossRef]
  47. Hubbell, S.P. , Foster, R.B., O’Brien, S.T., Harms, K.E., Condit, R., Wechsler, B., Wright, S.J. and De Lao, S.L. Light-gap disturbances, recruitment limitation, and tree diversity in a neotropical forest. Science 1999, 283, 554–557. [Google Scholar] [CrossRef] [PubMed]
  48. Jensen, H.J. 1998. Self-organized criticality: emergent complex behavior in physical and biological systems. Cambridge university press.
  49. Kéfi, S. , Rietkerk, M., van Baalen, M. and Loreau, M. Local facilitation, bistability and transitions in arid ecosystems. Theor. Po Biol. 2007, 71, 367–379. [Google Scholar] [CrossRef] [PubMed]
  50. Kéfi, S. , Rietkerk, M, Alados C.L., Pueyo, Y., Papanastasis, V.P., ElAich, A., Ruiter et al. and Loreau, M. Spatial vegetation patterns and imminent desertification in Mediterranean arid ecosystems. Nature 2007, 449, 213–217. [Google Scholar] [CrossRef]
  51. Keitt, T.H. , Urban, D.L. and Milne, B.T., 1997. Detecting critical scales in fragmented landscapes. Conservation ecology, 1.
  52. Keller, E.F. Ecosystems, organisms, and machines. BioScience 2005, 55, 1069–1074. [Google Scholar] [CrossRef]
  53. Kuussaari, M. , Bommarco, R., Heikkinen, R.K., Helm, A., Krauss, J., Lindborg, R., Ockinger, E., Partel, M., Pino, J., Rodá, F. and Stefanescu, C. Extinction debt: a challenge for biodiversity conservation. Trends in ecology and evolution 2009, 24, 564–571. [Google Scholar] [CrossRef] [PubMed]
  54. Lande, R. Extinction thresholds in demographic models of territorial populations. The American Naturalist 1987, 130, 624–635. [Google Scholar] [CrossRef]
  55. Laurance, W.F. Habitat destruction: death by a thousand cuts. Conservation biology for all 2010, 1, 73–88. [Google Scholar]
  56. Lenton, T.M. et al. Tipping elements in the Earths climate system. Proc. Natl. Acad. Sci. USA 2008, 105, 1786–1793. [Google Scholar] [CrossRef] [PubMed]
  57. Lenton, T.M. , Buxton, J.E., Armstrong McKay, D.I., et al. A resilience sensing system for the biosphere. Philosophical Transactions of the Royal Society B 2022, 377, 20210383. [Google Scholar] [CrossRef]
  58. Levin, S.A. The problem of pattern and scale in ecology: the Robert H. MacArthur award lecture. Ecology 1992, 73, 1943–1967. [Google Scholar] [CrossRef]
  59. Levin, S.A. 1999. Fragile dominion: complexity and the commons. Reading, MA: Perseus Books.
  60. Levin, S.A. Multiple scales and the maintenance of biodiversity. Ecosystems 2000, 3, 498–506. [Google Scholar] [CrossRef]
  61. Levins, R. Some demographic and genetic consequences of environmental heterogeneity for biological control. Bulletin of the ESA 1969, 15, 237–240. [Google Scholar] [CrossRef]
  62. Maestre, F.T. , Delgado-Baquerizo, M., Jeffries, T.C. et al. Increasing aridity reduces soil microbial diversity and abundance in global drylands. Proc. Natl. Acad. Sci. USA 2015, 112, 15684–15689. [Google Scholar] [CrossRef]
  63. Manrubia, S.C. and Solé, R. Self-organized criticality in rainforest dynamics. Chaos, Solitons and Fractals 1996, 7, 523–541. [Google Scholar] [CrossRef]
  64. Margalef, R. 1968. Perspectives in ecological theory. University of Chicago Press.
  65. Margalef, R. , 1979. The organization of space. Oikos, 152-159.
  66. Martin, P.V. , Bonachela, J.A., Levin, S.A. and Muñoz, M.A. Eluding catastrophic shifts. Proc. Natl. Acad. Sci. USA 2015, 112, E1828–E1836. [Google Scholar]
  67. May, R.M. Thresholds and breakpoints in ecosystems with a multiplicity of stable states. Nature 1977, 269, 471–477. [Google Scholar] [CrossRef]
  68. McGuire, J.L. , Lawler, J.J., McRae, B.H., Nuñez, T.A. and Theobald, D.M. Achieving climate connectivity in a fragmented landscape. Proc. Natl. Acad. Sci. USA 2016, 113, 7195–7200. [Google Scholar] [CrossRef] [PubMed]
  69. Muñoz, M.A. Colloquium: Criticality and dynamical scaling in living systems. Reviews of Modern Physics 2018, 90, 031001. [Google Scholar] [CrossRef]
  70. Murray, J.D. , 2003. Mathematical Biology: II: Spatial Models and Biomedical Applications (Vol. 3). New York: springer.
  71. Nicolis, G. and Prigogine, I., 1989. Exploring complexity: An introduction. Wiley, New York.
  72. Niebuhr, B.B. , Wosniack, M.E., Santos, M.C., Raposo, E.P., Viswanathan, G.M., Da Luz, M.G. and Pie, M.R. Survival in patchy landscapes: the interplay between dispersal, habitat loss and fragmentation. Scientific reports 2015, 5, 11898. [Google Scholar] [CrossRef] [PubMed]
  73. Odum, H.T. 1983. Systems Ecology; an introduction. Wiley, New York.
  74. Oro, D. and Martinez-Abrain, A. Ecological non-equilibrium and biological conservation. Biological Conservation 2023, 286, 110258. [Google Scholar] [CrossRef]
  75. Peñuelas, J. , Sardans, J., Estiarte, M. et al. Evidence of current impact of climate change on life: a walk from genes to the biosphere. Global change biology, 2013; 19, 2303–2338. [Google Scholar]
  76. Pigolotti, S. , Cencini, M., Molina, D. and Muñoz, M.A. Stochastic spatial models in ecology: a statistical physics approach. J. Stat. Phys. 2018, 172, 44–73. [Google Scholar] [CrossRef]
  77. Pimm, S.L. , 1991. The balance of nature?: ecological issues in the conservation of species and communities. University of Chicago Press.
  78. Pimm, S.L. and Jenkins, C.N. Connecting Habitats to Prevent Species Extinctions Conservation biologists are creating links between forest fragments where the most animals with small ranges live. American Scientist 2019, 107, 162–169. [Google Scholar]
  79. Pointing, S.B. and Belnap, J. Microbial colonization and controls in dryland systems. Nature Reviews Microbiology 2012, 10, 551–562. [Google Scholar] [CrossRef]
  80. Pueyo, S. Self-organised criticality and the response of wildland fires to climate change. Climatic Change 2007, 82, 131–161. [Google Scholar] [CrossRef]
  81. Rietkerk, M. and Van de Koppel, J. Alternate stable states and threshold effects in semi-arid grazing systems. OIKOS 1997, 79, 69–76. [Google Scholar] [CrossRef]
  82. Rietkerk, M. and Van de Koppel, J. Regular pattern formation in real ecosystems. Trends in ecology evolution 2008, 23, 169–175. [Google Scholar] [CrossRef] [PubMed]
  83. Riva, F. , Graco-Roza, C., Daskalova, G.N., Hudgins, E.J., Lewthwaite, J.M., Newman, E.A., Ryo, M. and Mammola, S. Toward a cohesive understanding of ecological complexity. Science Advances 2023, 9, eabq4207. [Google Scholar] [CrossRef] [PubMed]
  84. Rocha, E.G.D. , Brigatti, E., Niebuhr, B.B., Ribeiro, M.C. and Vieira, M.V. Dispersal movement through fragmented landscapes: the role of stepping stones and perceptual range. Landscape Ecology 2021, 36, 3249–3267. [Google Scholar] [CrossRef]
  85. Rockström, J. et al. Planetary boundaries: exploring the safe operating for humanity. Ecology and Society 2009, 14, 32. [Google Scholar] [CrossRef]
  86. Scanlon, T.M. , Caylor, K.K., Levin, S.A. and Rodriguez-Iturbe, I. Positive feedbacks promote power-law clustering of Kalahari vegetation. Nature 2007, 449, 209–212. [Google Scholar] [CrossRef] [PubMed]
  87. Scheffer, M. , Carpenter, S., Foley, J.A., Folke, C. and Walker, B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [Google Scholar] [CrossRef]
  88. Scheffer, M. (2009). Critical transitions in nature and society. Princeton U. Press, Princeton, NJ, USA.
  89. Scheffer, M. , Carpenter S., Foley J.A., Folke C., Walker B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [Google Scholar] [CrossRef] [PubMed]
  90. Schlicht, R. and Iwasa, Y. Forest gap dynamics and the Ising model. Journal of theoretical Biology 2004, 230, 65–75. [Google Scholar] [CrossRef] [PubMed]
  91. Schnitzer, S.A. and Carson, W.P. Treefall gaps and the maintenance of species diversity in a tropical forest. Ecology 2001, 82, 913–919. [Google Scholar] [CrossRef]
  92. Sethna, J.P. , 2021. Statistical mechanics: entropy, order parameters, and complexity (Vol. 14). Oxford University Press.
  93. Solé, R. and Manrubia, S.C. Are rainforests self-organized in a critical state? Journal of Theoretical Biology 1995, 173, 31–40. [Google Scholar] [CrossRef]
  94. Solé, R. , Manrubia, S., Luque, B., Delgado, J. and Bascompte, J., 1996. Phase transitions and complex systems: Simple, nonlinear models capture complex systems at the edge of chaos.
  95. Solé, R. and Bascompte, J., 1998. Emergent phenomena in spatially extended model ecosystems. In: Bascompte, J. and Solé, R., Modeling spatiotemporal dynamics in ecology, pp 7-25.
  96. Solé, R. , Manrubia, S.C., Benton, M., Kauffman, S. and Bak, P. Criticality and scaling in evolutionary ecology. Trends in ecology and evolution 1999, 14, 156–160. [Google Scholar] [CrossRef] [PubMed]
  97. Solé, R. , Alonso, D. and McKane, A. Self-organized inestability in complex ecosystems. Phil. Trans. R. Soc. Lond. B 2002, 357, 667–681. [Google Scholar] [CrossRef] [PubMed]
  98. Solé, R. Scaling laws in the drier. Nature 2007, 449, 151–153. [Google Scholar] [CrossRef]
  99. Solé, R. (2011). Phase transitions. Princeton U. Press, Princeton, NJ, USA, 134-147.
  100. Solé, R. and Bascompte, J., 2012. Self-Organization in Complex Ecosystems. Princeton University Press.
  101. Solé, R. Bioengineering the biosphere? Ecological Complexity 2015, 22, 40–49. [Google Scholar] [CrossRef]
  102. Solé, R. And Levin, S. Ecological complexity and the biosphere: the next 30 years. Phil. Trans. R. Soc. Lond. B, 2022; 77, 20210376. [Google Scholar]
  103. Stauffer, D. and Aharony, A., 2018. Introduction to percolation theory. CRC press.
  104. Strogatz, S.H., 1994. Nonlinear dynamics and chaos. Perseus Books. New York.
  105. Suding, K.N. and Hobbs, R.J. Threshold models in restoration and conservation: a developing framework. Trends in ecology evolution 2009, 24, 271–279. [Google Scholar] [CrossRef]
  106. Tilman, D. , May, R.M., Lehman, C.L. and Nowak, M.A. Habitat destruction and the extinction debt. Nature 1994, 371, 65–66. [Google Scholar] [CrossRef]
  107. Urban, D. and Keitt, T. Landscape connectivity: a graph?theoretic perspective. Ecology 2001, 82, 1205–1218. [Google Scholar] [CrossRef]
  108. Vidiella, B. , Sardanyes, J. and Solé, R. Exploiting delayed transitions to sustain semiarid ecosystems after catastrophic shifts. Journal of The Royal Society Interface 2018, 15, 20180083. [Google Scholar] [CrossRef]
  109. Vidiella, B. , Sardanyes, J. and Solé, R. Synthetic soil crusts against green-desert transitions: a spatial model. Royal Society open science, 2020; 7, 200161. [Google Scholar]
  110. Villa Martin P, Bonachela JA, Levin SA, Muñoz MAEluding catastrophic shifts. Proceedings of the National Academy of Sciences. 2015, 112, E1828-36.
  111. Weinberger, V.P. , Quiñinao, C. and Marquet, P.A. Innovation and the growth of human population. Philosophical Transactions of the Royal Society B: Biological Sciences 2017, 372, 20160415. [Google Scholar] [CrossRef] [PubMed]
  112. Weissmann, H. and Shnerb, N.M. Stochastic desertification. Europhys. Lett. 2014; 106, 28004. [Google Scholar]
  113. Weissmann, H. , Kent, R., Michael, Y. and Shnerb, N.M. Empirical analysis of vegetation dynamics and the possibility of a catastrophic desertification transition. PloS ONE 2017, 12, e0189058. [Google Scholar] [CrossRef] [PubMed]
  114. Welden, C.W. , Hewett, S.W., Hubbell, S.P. and Foster, R.B. Sapling survival, growth, and recruitment: relationship to canopy height in a neotropical forest. Ecology 1991, 72, 35–50. [Google Scholar] [CrossRef]
  115. Whitmore, T.C. 1990. An introduction to tropical rain forests. Clarendon Press.
  116. Williams, J.C. , ReVelle, C.S. and Levin, S.A. Spatial attributes and reserve design models: a review. Environmental Modeling and Assessment 2005, 10, 163–181. [Google Scholar] [CrossRef]
  117. Windus, A. and Jensen, H.J. Phase transitions in a lattice population model. J. Phys. A 2007, 40, 2287. [Google Scholar] [CrossRef]
  118. Wright, J.S. Plant diversity in tropical forests: a review of mechanisms of species coexistence. Oecologia 2002, 130, 1–14. [Google Scholar] [CrossRef]
  119. Wulf, A. 2015. The invention of nature: Alexander von Humboldt’s new world. Knopf. New York.
1
More precisely, they can be described in terms of a Multifractal, see (Manrubia and Solé, 1996).
Preprints 88125 g001
Figure 1. Thresholds, scales and nonlinearities in conservation. Understanding how species respond to environmental changes requires a multi scale picture where each scale has novel features. The preservation of some species, such as (a) the Northern Spotted Owl is a canonic case study of how habitat loss can trigger extinction when some critical conditions are met. Studies involving forest fragments (b) have revealed that space itself has an important role in defining thresholds that respond to universal patterns. As species interactions are added, the nature of the transitions also changes, as it occurs with facilitation dynamics among plants in drylands (c) where shifts between states are tied to the nonlinear nature of cooperative exchanges. When dealing with ecosystem-level scales, where multiple species are considered, the architecture of interaction networks (d) becomes relevant, potentially leading to cascades of extinction. Finally, asymmetries in ecology are of extreme importance: a forest might need 50 years or a century to become mature (e) but it burns in one day (f). All these case studies share a common thread: they can be described (up to some detail) by means of transitions among ecological attractors that can be imagined as marbles on a landscape (g-k). Stable states, here indicated as S 1 and S 2 , correspond to marbles sitting at the bottom of valleys in the potential function V ( x ) . A given system might start at S 1 (g) and, because of changes in a given parameter, the landscape changes in such a way that the S 1 valley becomes first shallow (h) and then disappears (i). A new state is then reached (j) and this occurs in a discontinuous fashion. In general, the landscape can be more complex (k) with multiple valleys (1,2,3) that can be reached from initial conditions within the valley domain (4) that sometimes define the boundaries between unstable states (5).
Figure 1. Thresholds, scales and nonlinearities in conservation. Understanding how species respond to environmental changes requires a multi scale picture where each scale has novel features. The preservation of some species, such as (a) the Northern Spotted Owl is a canonic case study of how habitat loss can trigger extinction when some critical conditions are met. Studies involving forest fragments (b) have revealed that space itself has an important role in defining thresholds that respond to universal patterns. As species interactions are added, the nature of the transitions also changes, as it occurs with facilitation dynamics among plants in drylands (c) where shifts between states are tied to the nonlinear nature of cooperative exchanges. When dealing with ecosystem-level scales, where multiple species are considered, the architecture of interaction networks (d) becomes relevant, potentially leading to cascades of extinction. Finally, asymmetries in ecology are of extreme importance: a forest might need 50 years or a century to become mature (e) but it burns in one day (f). All these case studies share a common thread: they can be described (up to some detail) by means of transitions among ecological attractors that can be imagined as marbles on a landscape (g-k). Stable states, here indicated as S 1 and S 2 , correspond to marbles sitting at the bottom of valleys in the potential function V ( x ) . A given system might start at S 1 (g) and, because of changes in a given parameter, the landscape changes in such a way that the S 1 valley becomes first shallow (h) and then disappears (i). A new state is then reached (j) and this occurs in a discontinuous fashion. In general, the landscape can be more complex (k) with multiple valleys (1,2,3) that can be reached from initial conditions within the valley domain (4) that sometimes define the boundaries between unstable states (5).
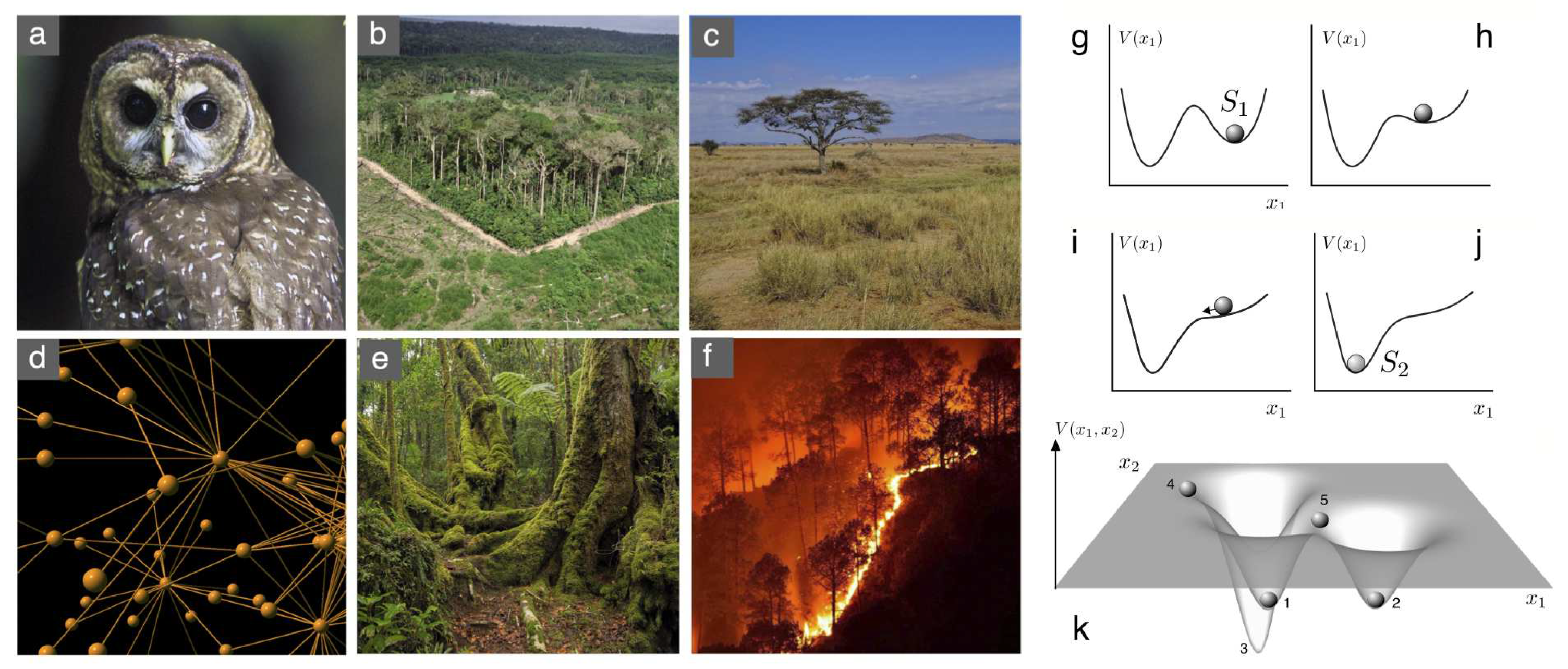
Preprints 88125 g001
Preprints 88125 g002
Figure 2. Persistence and extinction in Levin’s metapopulation model with habitat loss. In (a) the discrete picture of the spatial Levins metapopulation is shown: on a two-dimensional domain Ω , two kinds of patches exist: occupied (filled squares) and empty (open squares). Each site (zoomed area) i ∈ Ω is surrounded by a set Γ i of nearest neighbours that can colonize the central site, each one with a probability c. Moreover, each occupied site can become empty with probability e. this and (b) we display two complementary views of the model behaviour as a function of both colonization (c) and fragmentation (D) rates. A well-critical oundary D c = 1 − e / c separates stable populations from extinction. In (c) we show three snapshots of a discrete implementation on a two-dimensional model on a lattice, where each square is a site.
Figure 2. Persistence and extinction in Levin’s metapopulation model with habitat loss. In (a) the discrete picture of the spatial Levins metapopulation is shown: on a two-dimensional domain Ω , two kinds of patches exist: occupied (filled squares) and empty (open squares). Each site (zoomed area) i ∈ Ω is surrounded by a set Γ i of nearest neighbours that can colonize the central site, each one with a probability c. Moreover, each occupied site can become empty with probability e. this and (b) we display two complementary views of the model behaviour as a function of both colonization (c) and fragmentation (D) rates. A well-critical oundary D c = 1 − e / c separates stable populations from extinction. In (c) we show three snapshots of a discrete implementation on a two-dimensional model on a lattice, where each square is a site.
Preprints 88125 g002
Preprints 88125 g003
Figure 3. Spatial effects in Levins model with habitat loss and fragmentation. In (a) the observed metapopulation size (fraction of occupied patches) is shown in grey for a 100 × 100 lattice using c = 0.3 and e = 0.1 , which predicts (from Levins extended model, black line) a critical destriction rate D c ≈ 0.67 . A marked deviation occurs in the spatial version, suggesting that spatial correlations play a role. Such effects are captured by looking at the size of the largest connected cluster (b), which defines an effective habitat size. Although the landscape is constructed using a linear destruction process, (see three snapshots in (c)) an abrupt transition occurs at another destruction level D * ≈ 0.40 .
Figure 3. Spatial effects in Levins model with habitat loss and fragmentation. In (a) the observed metapopulation size (fraction of occupied patches) is shown in grey for a 100 × 100 lattice using c = 0.3 and e = 0.1 , which predicts (from Levins extended model, black line) a critical destriction rate D c ≈ 0.67 . A marked deviation occurs in the spatial version, suggesting that spatial correlations play a role. Such effects are captured by looking at the size of the largest connected cluster (b), which defines an effective habitat size. Although the landscape is constructed using a linear destruction process, (see three snapshots in (c)) an abrupt transition occurs at another destruction level D * ≈ 0.40 .
Preprints 88125 g003
Preprints 88125 g004
Figure 4. Tipping points in a facilitation model including habitat loss and linear mortality associated to environmental stress (such as increasing aridification). By solving the model (18) it is possible to find the different potential stable states under different parameter values. In (a) such states are represented in a bifurcation diagram, where we plot the stable states x * against the level of habitat loss D. Here, stable and unstable states are indicated by means of continuous and dashed lines, respectively. A tipping point is present at D c = 1 − 2 e / c ≈ 0.314 (using c = 0.85 and e = 0.1 ) . This is a catastrophic shift separating the upper state associated to the vegetated community C R from the desert state C D , which we represent (centre) by means of two spatial snapshots of the corresponding cellular automaton model. In (c) the potential function (Equation (20)) is displayed for several values of D. In (d) we summarise the results from (Berdugo et al., 2020) on global drylands that reveal three different aridity levels where marked shifts occur. These include a decline in plant productivity and cover, a second phase of disrupted plant-soil interactions and a last one involving a systemic breakdown leading to a green-desert transition. The last two shifts might be described in terms of sudden transitions among stable states (see Berdugo et al., 2022).
Figure 4. Tipping points in a facilitation model including habitat loss and linear mortality associated to environmental stress (such as increasing aridification). By solving the model (18) it is possible to find the different potential stable states under different parameter values. In (a) such states are represented in a bifurcation diagram, where we plot the stable states x * against the level of habitat loss D. Here, stable and unstable states are indicated by means of continuous and dashed lines, respectively. A tipping point is present at D c = 1 − 2 e / c ≈ 0.314 (using c = 0.85 and e = 0.1 ) . This is a catastrophic shift separating the upper state associated to the vegetated community C R from the desert state C D , which we represent (centre) by means of two spatial snapshots of the corresponding cellular automaton model. In (c) the potential function (Equation (20)) is displayed for several values of D. In (d) we summarise the results from (Berdugo et al., 2020) on global drylands that reveal three different aridity levels where marked shifts occur. These include a decline in plant productivity and cover, a second phase of disrupted plant-soil interactions and a last one involving a systemic breakdown leading to a green-desert transition. The last two shifts might be described in terms of sudden transitions among stable states (see Berdugo et al., 2022).
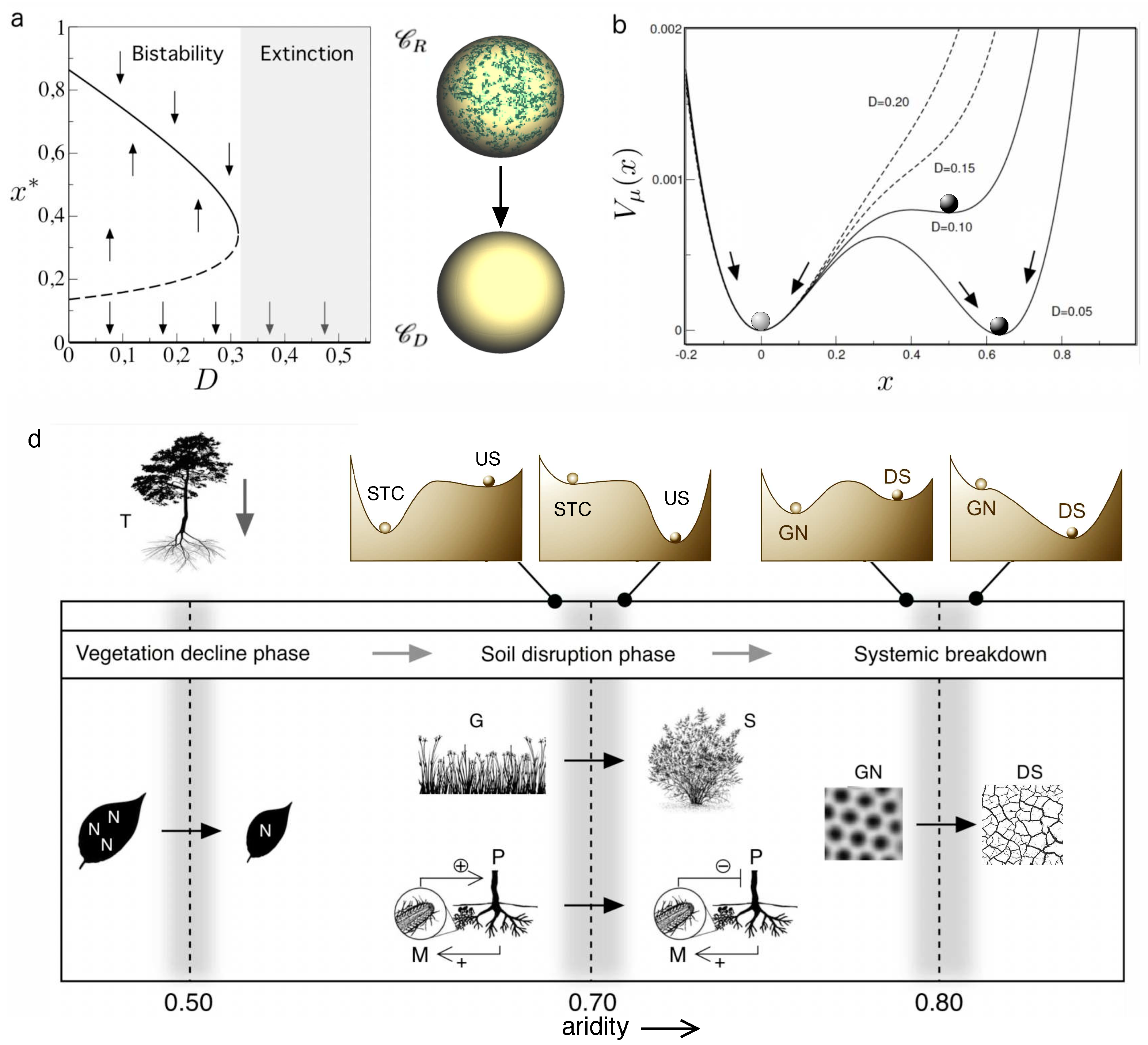
Preprints 88125 g004
Preprints 88125 g005
Figure 5. Complexity and criticality in spatially extended ecosystems. In these plots we show three scales of ecosystem organization where scaling phenomena and critical thresholds are at work. From left to right: (a) a canopy gap plots from the Barro Colorado island, where black square indicate gaps defined as canopy height lower than 10 m; the gaps are the result of a complex dynamical state associated with the growth and fall of trees, which is influenced by the presence of local gaps; (b) a connectivity graph linking suitable habitat locations for the Northern Spotted Owl (Keith et al., 1999) and (c) a large-scale analysis of clusters of habitat loss in tropical forests (Taubert et al., 2018). In the case, the statistical distribution of the number of forest fragments N ( s ) (in area units of size s) displays a power law behaviour, with N ( s ) ∼ s − 1.9 .
Figure 5. Complexity and criticality in spatially extended ecosystems. In these plots we show three scales of ecosystem organization where scaling phenomena and critical thresholds are at work. From left to right: (a) a canopy gap plots from the Barro Colorado island, where black square indicate gaps defined as canopy height lower than 10 m; the gaps are the result of a complex dynamical state associated with the growth and fall of trees, which is influenced by the presence of local gaps; (b) a connectivity graph linking suitable habitat locations for the Northern Spotted Owl (Keith et al., 1999) and (c) a large-scale analysis of clusters of habitat loss in tropical forests (Taubert et al., 2018). In the case, the statistical distribution of the number of forest fragments N ( s ) (in area units of size s) displays a power law behaviour, with N ( s ) ∼ s − 1.9 .
Preprints 88125 g005
Preprints 88125 g006
Figure 6. Universal patterns in percolation. Using a standard 2D model, increasing occupation probabilities p are used to determine the fraction of sites P ( p , ∞ that belong to the largest cluster (here we use a L = 150 lattice and average over R = 300 replicas). A marked transition (a) is found for p ∼ 0.59 and, right on this point, a power law distribution of cluster sizes P ( s ) ∼ s − γ with γ ∼ 2 , as shown in (b). The largest cluster is displayed in (c), where we can appreciate a fractal organization. The thick dashes line indicates the predicted transition from an infinite lattice. Crossing the critical point due to deforestation (d,e) implies a loss of connectivity. While supercritical forests (f), with p > p c , allow finding paths connecting large groups of trees over long distances (grey arrows), the subcritical phase ( p < p c ) is made of disconnected patches.
Figure 6. Universal patterns in percolation. Using a standard 2D model, increasing occupation probabilities p are used to determine the fraction of sites P ( p , ∞ that belong to the largest cluster (here we use a L = 150 lattice and average over R = 300 replicas). A marked transition (a) is found for p ∼ 0.59 and, right on this point, a power law distribution of cluster sizes P ( s ) ∼ s − γ with γ ∼ 2 , as shown in (b). The largest cluster is displayed in (c), where we can appreciate a fractal organization. The thick dashes line indicates the predicted transition from an infinite lattice. Crossing the critical point due to deforestation (d,e) implies a loss of connectivity. While supercritical forests (f), with p > p c , allow finding paths connecting large groups of trees over long distances (grey arrows), the subcritical phase ( p < p c ) is made of disconnected patches.
Preprints 88125 g006
Preprints 88125 g007
Figure 7. Complex dynamics of forest fires. The statistical distribution of fire sizes (in Ha) follows a power law, as shown in (a) for wildland fire size distribution in the AlbertaÕs Forest Protection Area (Canada, adapted from Pueyo, 2007). A simple discrete simulation is obtained from a forest fire model (FFM) where bursting dynamics of fires is obtained (b) along with a growth and reset pattern of tree growth (c). In (d) a snapshot of the model is shown for a 30 × 30 lattice at t = 2842 , associated to a peak in fire size ad the onset of a rapid decline in tree cover. Here black, green and yellow sites indicate empty (ashes), tree and fire states, respectively.
Figure 7. Complex dynamics of forest fires. The statistical distribution of fire sizes (in Ha) follows a power law, as shown in (a) for wildland fire size distribution in the AlbertaÕs Forest Protection Area (Canada, adapted from Pueyo, 2007). A simple discrete simulation is obtained from a forest fire model (FFM) where bursting dynamics of fires is obtained (b) along with a growth and reset pattern of tree growth (c). In (d) a snapshot of the model is shown for a 30 × 30 lattice at t = 2842 , associated to a peak in fire size ad the onset of a rapid decline in tree cover. Here black, green and yellow sites indicate empty (ashes), tree and fire states, respectively.
Preprints 88125 g007
Preprints 88125 g008
Figure 8. Scales, thresholds and emergence in biological conservation. We represent here four levels of description associated to relevant problems discussed in the paper (left column), the relevant dynamical behaviour behind potential threshold phenomena (central column) and the basic model components relevant to each case (right column). From bottom to top, we have: (a,b) metapopulations in healthy habitats associated to species-level studies where the balance between colonisation and extinction, as described by Levins model, define the conditions for survival within a infraspecific competition context. (c,d) the consequences of habitat loss and fragmentation, as illustrated by the patchy deforestation patterns in Warwickshire (here dark areas are remaining forest canopy in 400 AD and 1086, respectively), (e) species interactions beyond competition, as illustrated by facilitation in drylands that introduced a square non-linearity responsible for the presence of catastrophic shifts and (f) global patterns of habitat fragmentation that can be captured by a percolation model. The black arrow indicates the current trend of deforestation that might end up in crossing the percolation threshold p c , leading to a transition from connected to disconnected forest cover.
Figure 8. Scales, thresholds and emergence in biological conservation. We represent here four levels of description associated to relevant problems discussed in the paper (left column), the relevant dynamical behaviour behind potential threshold phenomena (central column) and the basic model components relevant to each case (right column). From bottom to top, we have: (a,b) metapopulations in healthy habitats associated to species-level studies where the balance between colonisation and extinction, as described by Levins model, define the conditions for survival within a infraspecific competition context. (c,d) the consequences of habitat loss and fragmentation, as illustrated by the patchy deforestation patterns in Warwickshire (here dark areas are remaining forest canopy in 400 AD and 1086, respectively), (e) species interactions beyond competition, as illustrated by facilitation in drylands that introduced a square non-linearity responsible for the presence of catastrophic shifts and (f) global patterns of habitat fragmentation that can be captured by a percolation model. The black arrow indicates the current trend of deforestation that might end up in crossing the percolation threshold p c , leading to a transition from connected to disconnected forest cover.
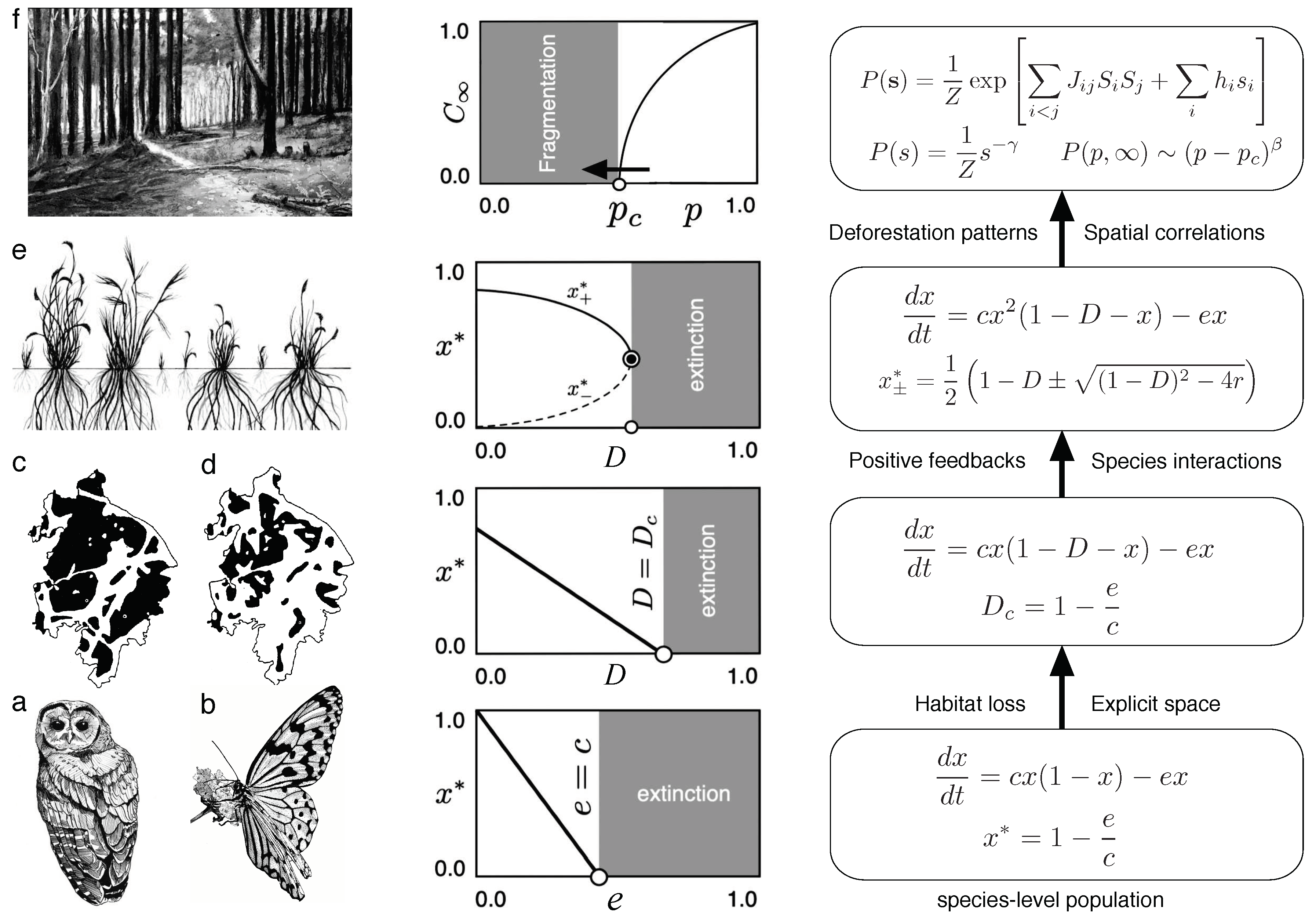
Preprints 88125 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated