Preprint

Article

Monothetic Genera are the Cast-Iron Building Blocks of Evolution

Altmetrics

Downloads

107

Views

Comments

Supplementary Material

supplementary.xlsx (12.57KB )

Richard Zander^*

This version is not peer-reviewed

Submitted:

24 October 2023

Posted:

25 October 2023

You are already at the latest version

Alerts

Abstract

Detailed evaluation is provided for the likelihood statistics intrinsic to interlocking Sequential Bayes analysis, which allows estimation of evidential support for dendrograms charting the macroevolution of taxa. It involves complexity functions, such as fractal evolution, to generate well-supported evolutionary trees. Required are data on trait changes from ancestral species to descendant species, which is facilitated by reduction of large genera to monothetic groups (one ancestral species each), most conveniently named as separate genera. Assigning each species one Shannon informational bit per new trait, then adding the traits as sequential Bayesian analysis (each posterior probability used as the prior for the next iteration of Bayes Formula), then interpretation with an odds chart, provides a posterior probability that the ancestor-descendant order is correct, that is, entirely follows evolutionary theory involving adaptation and rarity of total trait reversals. The key fact is that the most recently acquired traits of the ancestral species are selectively inviolate and passed on without change to each descendant species. The details of sequential Bayesian analysis were clarified by calculation of likelihood ratios and Bayes factors that compare optimal models with the next most likely model. Such analysis demonstrated that the optimum arrangement of ancestor and descendant species leads to high support values for fitting evolutionary theory, comparable to statistical support levels reported for molecular evolutionary trees. The fact that phylogenetic analysis does not offer an ancestor-descendant model in is found to be conducive of precision at the expense of accuracy, and leads to wrong ancestor-free models with likelihoods explaining data at high credible levels. The number of advanced traits in the outgroup as a Bayesian prior greatly enhances posterior probability. The method is simple, free of special computer analysis, and well-suited to standard taxonomic practice.

Keywords:

Subject: Biology and Life Sciences - Ecology, Evolution, Behavior and Systematics

1. Introduction

Complexity analysis (Abel, 2009; Bennet, 2010; Binning, 1989; Doebeli & Ipolatov, 2014; Ferriere & Fox, 1995; Gershenson, 2004; Hilborn, 2000; Ito & Gunji, 1994; Kaneko & Tsuda, 2000; Kondepudi et al., 2020; Lewin, 1999; Liu & Bassler, 2006; Mesarovic et al., 2004; Packard, 1988; Prigogine, 1978) includes chaos theory, dissipative structure, fractal self-similarity, and self-organization aspects of evolutionary analysis. Complexity is not the overwhelming diversity of data on the natural world, but comprises the emergent processes that sustain and constrain that data, presenting taxonomists with species and higher taxa. Given the past range and substance of research on complexity, it is surprising that there have been few (Notale et al., 2000; Lv et al, 2014) direct applications to biodiversity study, one of the most informationally complex fields of scientific endeavor.

Complexity functions, e.g. the edge of chaos, fractal evolution, and logistic map (Ito & Gunji, 1994; Kauffman, 1993, 2000; Lewin, 1999; Nicolis & Prigogine, 1989; Packard, 1988; Pimm, 1984; Schroeder, 1991), are not deduced from axioms or rounded up by reductionist techniques, but are emergent phenomena in the mesocosm. An important recent paper developing the use of complexity analyses in the study of the natural environment is that of Wong et al. (2023), who propose the ubiquity in macro- and microcosmic systems of selection on functional information in a complexity context. They asserted that functional information must increase with degree of function, from zero for no function (or minimal function) to a maximum value corresponding to the number of Shannon informational bits that are both necessary and sufficient to specify any system configuration. Functional information must have three critical characteristics: (1) there is multiple interacting components, (2) elements occur in combinatorically large numbers of different configurations, and (3) selection processes differentially support configurations that display useful functions. These strictures apply well to the present paper, which similarly uses Shannon information bits to specify model condigurations.

Zander’s (2023) complexity-based evaluation of the evolutionary relationships of certain groups of mosses in the West Indies and adjacent Middle America led to the following conclusions:

(1) Extant ancestral species are commonly able to be identified as such;

(2) Monothetic genera (those with one ancestral species) are identifiable;

(3) Evolutionary diagrams (caulograms) connecting series of genera composed of an ancestral and a few descendant species may show up to four or five levels of extant ancestry;

(4) Monothetic genera are fractal in that the new traits of the shared ancestral species are not modified in speciation but are gifted to the descendants, whose new traits are modifications of presently non-adaptive traits of distant ancestral species;

(5) Newly evolved species of descendants in monothetic genera are about the same number per genus, while average number of newly evolved traits in a monothetic genus is also the same, with 4 being the magic number at the edge of chaos across scales;

(6) Monothetic genera surviving robustly at the edge-of-chaos can be distinguished by NK-analysis in random Boolean network theory from those that are more likely to go extinct or be reduced to solitary species, or which are likely to be fragmented by global perturbations;

(7) Fractal genera are less likely to exceed the edge of chaos because identical shared ancestral traits provide phyletic constraint; and

(8) Taxa are real things in nature that exist over millions of years through geologic ages, geographic space, and elapsed time, and can be treated as responding to much the same functional processes in complexity studies of biodiversity.

Interlocking Sequential Bayes is a way to judge likelihood support for the order of a series of elements, and has been used for taxonomic study by Zander (e.g. 2013, 2016, 2018, 2019, 2021a,b, 2023). In the present paper, we want to know how well the data fit evolutionary theory (e.g., Barraclough, 2010; Gould, 2002; Pianka, 2000; and standard works such as that of Grant, 1985), in particular, how well traits of taxa support different orderings of ancestor and descendant species. Evolutionary theory is, of course, complex, but most simply, as here applied, ancestor-descendant order is expected to reflect reasonable interpretation of adaptations (Mayr, 1983) involving reduction and elaboration, given Darwinian gradualism (no or few major jumps in numbers of trait combinations, as in natura non facit saltus). Analytic methods include outgroup comparison, in which species of a group may be ordered assuming that a related group, the outgroup, shares traits very similar to those of the ancestor of the ingroup, and these shared traits are primitive or plesiomorphic in cladistic terms. A second method is ingroup comparison such that species with rare or unusual traits are more probably derived than primitive, and are those of advanced descendant species.

The simplest model for analysis of trait changes is the monothetic genus consisting of one ancestral species and its direct descendant species. Van Valen (1973) early pointed out that ancestral species were both extant and common. Ancestral species are mostly ignored in modern taxonomic work because: (1) classical taxonomy commonly assigns species to polythetic genera and relegates trait changes to the intellectual domain of evolutionists, (2) systematics in the cladistic context focuses on clustering taxa by relative degree of shared ancestry, without identifying particular species as ancestors, i.e., all species are terminal on a cladogram, and (3) molecular systematics depends on relative degree of shared apparently non-expressed and randomly fixed molecular sequences, and simply maps expressed traits to the molecular cladogram assumed to track expressed-trait evolution.

The monothetic group is most easily dealt with if named as a separate genus, but for convenience a subgenus or section may be used. The work of Zander (2023) summarizes several papers dealing with monothetic genera and trait changes between ancestral species and descendants, and also between ancestral monothetic genera and descendant monothetic genera.

Zander (2023a) found that monothetic genera in the groups studied (in the moss families Pottiaceae and Streptotrichaceae) were usually of four descendant species, and each species in the genus had usually four traits. The genera were fractal, being self-similar across scale. The constraint around the number four (actually averaging about 3.6) was explained using NK-analysis with a random Boolean network model (Gershenson, 2004; Kauffman, 1993: 218; McKelvey, 1999). The number four was interpreted as the optimal edge of chaos (Packard, 1988) for interactions of competition and mutualism for each genus for survival across geologic time. This includes major perturbations, such as boloid impacts at the KT boundary, the late Cretaceous and early Eocene temperature maxima, and Pleistocene glaciations, and less catastrophic climate change such as Milankovitch events and minor volcanism (Behrensmeyer, 1992; Bender, 2013).

Trait changes were grouped as the novon, the set of new traits of a descendant species, and the ancestron, the set of traits of the ancestral species. The immediate ancestron is critical, defined as the set of new traits provided to the ancestral species by its own ancestral species. Of importance is that the immediate ancestron is passed on as an identical set to all descendant species. The characters used as sources of new traits (character state changes) in descendants are apparently those older and less important traits in the trail of characters of the ancestral species. The fact of this latency of the advanced traits of the ancestor is the stabilizing concept for fractal evolution, and becomes the solid evolutionary substance of a monothetic genus.

This latency of the immediate ancestron is the key to the fractal nature of a genus, and provides a clue to the natural-selection-based process supporting survival through adaptation. The immediate ancestron ensures that a descendant species is equipped with tested traits for local or sympatric (Artzy-Randrup & Kondrashov, 2006) and peripatric survival and the novon is a probe into a constantly changing environment including speciation that is allopatric in geography and time. The species is not, then, the central actor in evolution, it is the monothetic genus that is a tiny, working Spaceship Earth, one of an integrated fleet of lineages comprising the ecosphere in space-time.

A series of connected monothetic genera is a stem-taxon dendrogram called a caulogram Zander (2023a,b), and is obtained with Shannon-Turing analysis. This method assigns each newly evolved trait one informational bit, which is given a probability using an odds table (Table 1). The bits may be added because they are exponents and of similar distribution and thus conjugate priors (Etz, 2019). Treating the bits of the posterior of an ancestor as the prior of the next is entirely equivalent to concatenating instances of Bayes’ formula, thus we have sequential Bayes. The method (Good, 2011) was pioneered by A. Turing in breaking German codes during World War 2, but is now used (Zander, 2013, 2018, 2021a,b) with Shannon informational bits rather than decibans. The essential statistical process in the present paper consists of the monothetic genus of one ancestor, one or more descendant species, and an outgroup species, and the three elements are rendered as a minimum sequential Bayesian posterior probability (min SBPP), the outgroup providing the prior. A more detailed explanation is given by Zander (2023a).

The Bayes Formula combines a prior probability with a likelihood (Bernardo & Smith, 1994; Winkler, 1972). The prior may be well conceived, or a flat prior of 0.50. The likelihood is the actual data (flips of coins, numbers of traits). The prior is the initial estimate of the chance that that the model explains the data. The likelihood is the chance that the data explains the model, i.e. that the model is supported by the data. A posterior distribution (a distribution between 0.00 and 1.00) is arranged by combining the prior and likelihood with a normalizing factor. The answer obtained by the Formula is the Bayesian posterior probability (BPP). Sequential Bayes analysis uses the posterior probability of one instance of the Bayes’ formula as the prior of the next instance. Any Bayesian statistics manual or treatments on the Web will provide well-illustrated explanations of the use of Bayes’ formula in statistics.

A caulogram presents series of monothetic genera with species arranged as best representing evolutionary theory. Because it was found (Zander, 2023a) that the advanced traits of the ancestral species are donated entire to each and every immediate descendant species (i.e., as the latency of the immediate ancestron), there are very few instances where the optimal arrangement of ancestral and descendant species must include exceptions to theory, such as surprising reversals or non-parsimonious trait changes. One assumes there need be a minimum of two correlated new traits to identify a population as a distinct species, otherwise one new trait may be a simple mutation that does not imply a degree of genetic isolation.

2. Materials and Methods

We will use likelihood ratios (L.R.) to investigate the details of interlocking Shannon-Turing analysis, which is based on sequential Bayesian analysis. When a prior is known, we will call these ratios Bayes factors (B.F.), a minor terminology glitch following the literature. Consider a monothetic genus of four descendants each with a minimum two traits. If we assign one positive informational bit to a new trait, and add them within a monothetic genus of optimal one ancestor and four descendants, then the evolutionary theory identifying those four as descendants would be supported by eight traits (four descendants each with two bits). An odds table (see Table 1) would assign Bayesian support as posterior probability (BPP) at 0.996, or 250:1 that this is correct, or far more likely than any alternative. Were there trait changes contrary to evolutionary theory, such as a reversal, then a minus bit would be added, lowering the bit count but this is rare in studies of actual monothetic genera that best follow evolutionary theory.

The series of monothetic genera comprising a caulogram is then supported by a series of sets of traits whose existence, if following evolutionary theory, provides each other with support as part of a model reflecting evolutionary theory. Together they form an evolutionary model supported sometimes by as much as six standard deviations (six sigma), 29 or more bits. It may seem far-fetched that a particular model of evolution is considered to be wrong only once out of 500 million times that it is generated (Table 2). Six sigma is reached because the accumulating priors of sequential Bayes narrow down the area of distribution in which the likelihood calculations can be found. Essentially, what this means is that monothetic genera, when concatenated, fully reflect evolutionary theory in respect to fixed trait changes between progenitor and descendant species, given the data and theory. If expressed-trait evolution were neutral and fixed randomly, this would not be the case.

Table 1 may be used to determine the probabilities of positive and negative bits. Both likelihood ratio (L.R.) and Bayes factors (B.F.) can be calculated there from bit ranges between 1 and 16, or –1 and –16, or the spreadsheet may be used (Zander, 2023b) for ranges to plus or minus 32. The likelihood ratio formula is about the same as the Bayes factor formula. The latter simply involves the addition of positive bits reflecting the number of new advanced traits given the ancestor (by its own ancestor, the outgroup). These positive bits of the ancestor are added to the bits of each descendant. This is the prior.

The Bayes’ formula calculates the probability of one model (the optimum or A > B) compared to the probability of the best of alternative models (whichever has the smallest number of negative bits for a descendant switching places with the optimum ancestor, say B > A). This is clarified in Figure 1 and Figure 2. It uses fractions based on odds ratios, see Table 1. Thus, the formula (1), which is the basis of Table 1:

L.R.. or B.F. = (2^p / 1+2^p ) / ((2^-q ) / (1+2^-q))

(1)

Where p = bits supporting A > B, and q = bits refuting A > B, reflecting reversals.

Innumerate botanists (those lacking mathematical skills) may easily navigate this formula by using the “x^y” key in an scientific calculator. The “x^y” key does not work with negative exponents unless you press the “+/-“ key after entering the exponent number, not before. A number to a negative exponent is simply the reciprocal (divide into 1) of the number to the same but positive exponent. See formula (2).

L.R.. or B.F. are also = (2^p / 1+2^p ) / ((1/2^q ) / (1+1/2^q))

(2)

Remember to press the “=” key when dealing with multiple parentheses to finalize the calculation in the parentheses before dealing with the next set of parentheses, as only the last two numbers entered are addressed.

When there are long branching lines of monothetic genera, the bits of all descendant species are added (Etz, 2019) fully across the dendrogram because any one determination of ancestor-descendant status supports any other in the lineage, both backwards and forwards. The totaled numbers of bits in a dendrogram can be associated with various levels of standard deviation or sigma. Table 2 shows bit strength needed for up to 6 sigma, a standard measure of confidence for industry easily comparable to the 1.00 Bayesian posterior probabilities used in molecular phylogenetics for statistical certainty, given the data. Standard deviations are generally associated with frequentist statistics, not Bayesian, but the posterior distribution of the latter can be converted by normalization and rescaling to an approximation of a probability density.

In examining the relationship between ancestral and descendant species, interlocking sequential Bayes (Zander 2023: 16) is considered an example of likelihood ratio analysis when one monothetic (one ancestor) genus alone is examined. It is called a Bayes Factor analysis (Garcia-Donato & Chen, 1979; Kass & Raftery, 1995) when an outgroup species is included, or the equivalent of an outgroup being two monothetic genera concatenated in a lineage.

Likelihood is a measure of support of a particular model by the available data, that is, how likely are the data given the model. Example: the probability of a fair coin coming up heads is 0.5; the likelihood of a particular coin being fair and coming up heads is the data of 25 heads and 30 tails, or 25/30, or 0.46). In other words, the data, not the concept, is the likelihood. The likelihood ratio is the probability of one model (the best one) being correct divided by the probability of the second best model being correct.

The Bayesian formula has two parts, one is the likelihood (the actual data) and the other is the prior (reflecting previous knowledge of probability of the model, or if none, then 0.50 probability). If there are two concatenated monothetic genera, then the first is the prior of the second. Bit values for the first may be added to those of the second giving logically the same result as does the Bayes formula (formula 3), and the likelihood is then called the Bayes factor.

P(model|data) = P(model) × P(data|model) / P(data)

(3)

In Bayes’ formula the probability of the model given the data (here the particular evolutionary diagram) equals the prior (probability of the model) times the probability of the data given the model (the likelihood), that divided by the probability of the data (a normalizing function that scales the value between zero and one. In short, the posterior probability equals the likelihood times the prior divided by the normalization constant. The posterior probability, P(model/data), is the how likely the model is given the data. The likelihood, P(data|model), is the probability of seeing the data given the evidence. The normalizing constant is unnecessary if the prior and likelihood are conjugate priors, that is, having the same statistical distributions. One can then use Bayes’ Rule, that the posterior is proportional to the likelihood multiplied by the prior (Etz, 2015), to simplify calculations. This is done in sequential Bayes. Bayesian statistical analysis is difficult and mind-bending in logical and mathematical complexity, and has always been a battleground between Fisherian, Neyman-Pearson and Bayesian schools of statistics (Gigerenzer et al., 1989).

Likelihoods are determined by the probability of the theoretically optimal, most likely (highest bit count) model arrangement of species in a monthetic genus divided by that of the second most probable model (switching the least dissimilar immediate descendant species with the ancestor). Since the most probable model has a probability that reaches 0.99 with as few as 7 bits, the number of bits in the alternative model determines the L.R. or B.F. Likelihood ratios are much the same as Bayes’ Factors, except that the latter compares posterior probabilities by dividing the larger probability by the smaller.

Given that the ancestral species in the above likelihood examples are all part of a series of Bayes’ formulas, they are already posterior probabilities, and standard charts (Table 3) (Jeffrey1961; Kass & Rafftery 1995) of the significance of levels of Bayes’ Factor support are useful. All species in the monothetic genus, including the descendant species, have the same immediate ancestron, so the status of the conceived ancestral species as truly ancestral is largely based on likelihoods internal to the monothetic genus with a very high composite maximum likelihood for the genus.

The aim of this paper is to investigate the details of of Shannon-Turing analysis in terms of likelihood ratios and Bayes factors. Shannon-Turing analysis is simply described as assigning each new trait of a descendant species one informational bit, then adding these (exponents of 2) to match operationally the Bayes’ formula, both within a monothetic genus and between genera. The details are in the likelihood ratios, not previously addressed. Bits matching evolutionary theory are positive, bits contrary to theory are negative (Table 1).

3. Results

Example 1. Likelihood (Figures 1-1 and 2-1) Table 4

If there were one ancestral species and one descendant, then there are two hypotheses, or models, either A generates B, or B generates A, say A > B or B > A. (The symbol > means generates through speciation.) Given that A > B fits theory (A is a generalist species, and B has rare or specialized traits and or unusual habitat), then given the minimum of 4 traits per species, A > B rates +4 bits, and B > A gets –4 bits. Positive fur bits, by the odds table, is 0.941 BPP or 16 to 1, and –4 bits is 0.059 BPP or 1:16. The likelihood ratio that the evolutionary order A > B is a better model of evolution than B > A is then the probability of A > B divided by the probability that B > A. This is 0.941 / 0.0.588. Thus A > B is 16 times as likely as B > A, with 16 being the L.R. (Figures 1-1 and 2-1). The determination of which is ancestor depends on a context of many related species for evaluating which is theoretically more generalist, most unspecialized, least adapted compared to other species having the same immediate ancestron. For this and all examples, a table is given to facilitate understanding of the calculations (Table 4).

Example 2. Bayesian, that is, with outgroup as prior (Figures 1-2 and 2-2) Table 5.

Switching descendant and ancestor is an analytic scenario is more clear if there is an outgroup such as a closely related group, ideally a species to ancestral the ancestral species in the monothetic genus. Call this outgroup species X, belonging to a possible penultimate monothetic genus X > (N, O, P, Q). If both A and B would be about as advanced in relation to the more distant ancestral species X, then there is no relevant evolutionary information. The descendant species must be advanced in relation to both its ancestor A and the ancestor’s ancestor X for a well-supported order of evolution. A caulogram as an evolutionary tree is then essentially a concatenation of prior and likelihood comprising the Bayes formula. This is technically a second-order Markov chain decision tree. The context of the ancestor X of the immediate ancestor A becomes more important when there are more than one descendant species, and the problem is to determine how much more likely they are than their immediate ancestor to be the descendants than for one of them to be the actual ancestral species.

An example caulogram with one ancestor, one descendant and an outgroup, all species with 4 new traits is presented in Figures 1-2 and 2-2. Because there is an outgroup as a Bayesian prior, we call the result a B.F. The effect of the outgroup is strong, increasing the B.F. of the model in Figures 1-2 and 2-2 from 16 to 250. Because there is a prior to focus the likelihoods into a posterior distribution of likelihoods, we can say this model has a Bayes Factor of 250.

Example 3. One ancestor and four descendants, with outgroup Table 6

Consider there being one ancestral species and four descendant species, or A> (B, C, D, E), as is the optimal case, judged from NK-analysis with random Boolean network models (Zander, 2023a), and an outgroup X. Descendants B, C D and E are all advanced against the more generalist ancestral species A. They have traits mostly not found in the ancestor’s ancestor X, and they have unusual or specialized features or odd habitats.

For this example, each descendant species has 2 traits that are new, not found in the ancestor, and the ancestor has 2 traits not found in outgroup X. Then we assign one bit per new trait in each of the four descendants, and add the bits. The sum of 8 bits (2 bits for traits in each descendant from A, plus the prior of 2 bits for each) yields 0.99998, a very strong support for the configuration of A > (B, C, D, E) and 2 bits. Again, assuming only one ancestral species, then if we try B as ancestor for all four other species (the descendant species are all equally distant from A in numbers of new traits, then we have two reversals from X > B, plus two reversals for B > A, and no information for B > C, B > D or B >E. There is no information when the negative bits from the prior on the false, alternative ancestor B are added to the two positive bits from B > any descendant not the true ancestor. Calculating the likelihood of the optimum A > (B, C, D, E) comes down to the fraction of the likelihood probabilities of the two alternative models, probability of 16 bits divided by probability of –4 bits, or 17 times as likely.

Example 4. Five species per monothetic genus with four advanced traits per species, plus outgroup (Figures 1-3 and 2-3) Table 7

This is the same as Example 3, but with 4 bits per species, the optimal edge-of-chaos numbers (Zander, 2023a). For the scenario of 1-ancestor, 4-descendant, 4 traits (bits) per species, plus X as outgroup, there are 4 bits from the outgroup-to-ancestor transition (as minimum sequential Bayesian Posterior Probability) added to each ancestor-descendant lineage of 4 bits. Thus, four descendants each given 4 + 4 or 8 bits each, or 32 bits per monothetic genus (A > (B, C, D, E). The likelihood is 1.00 for this optimal model, from the spreadsheet (Zander, 2023b).

Because all descendants have the same number of new traits, any one descendant can represent the ancestor in the alternative, next most-likely model. Consider X > B > (A, C, D, E). For the outgroup, X > B yields –4 bits because the “ingroup” of (A, C, D, E) refutes this order of speciation. Then, B > A is another reversal of –4 bits, then we have –8 bits for B > A. In addition, B > C or D or E requires reversal of 4 bits in B before B can give rise to C, D, or E and afterwards add 4 bits (because then C, D, and E are then advanced), thus B > (C, D or E) is zero bits. The bit count for X > B > (A, C, D, E) is then –8 bits. The probability is 0.004.

Given that sequential Bayes uses outgroups as priors, the likelihood ratios for all determinations using outgroups, which is most of them, are actually Bayes Factors. The chart (Table 3) of Bayes Factors by Jeffries (1961) and Kass and Raftery (1995) is pertinent.

All other configurations reflecting exchanging a descendant with the optimal ancestral species give the same probability of the alternative model. The Bayes factor comparing the optimal caulogram X > A > (B,C,D, E) against the alternative X > B > (A, C, D, E) is then 1 / 0.004, or 257. A B.F. of 257 is, by Table 3, decisive (Jeffries, 1961). This is very strong support (Kass & Raftery, 1995).

Example 5. The above model but with a secondary ancestor as alternative

The reader can work out that an alternative (to Example 4) model configuration of X > B > A > (C, D, E) has the same bit value as the alternative with all descendants immediate on A. Although certainly (C, D, E) are direct descendants of A at four times plus 4, this does not support B being the ancestor of A, and –4 may be added to plus 4 to get, as in the alternative of Example 4, zero. Given that X > B > A > (C, D, E) is not a real alternative to X > B > (A, C, D, E) inasmuch as four trait changes are needed to transform B into an acceptable ancestor, and that exact trait combination is the same as that of A, this configuration is a superfluous alternative.

Example 6. Model with descendants having different numbers of new traits. Table 8

The above models all had descendants with the same number of new traits (bits). Consider the above model (Example 4) of five species per monothetic genus with four advanced traits per species, plus outgroup (Figures 1-3 and 2-3) (Table 7). Suppose descendants had 2, 3, 4 and 5 bits each instead of each having 4 bits. Then the descendant species with the least number of bits, say B has only 2 bits, would be the one chosen to switch with the true ancestor for the most likely alternative model. When deciding trait change differences between a false ancestor and a descendant, say B > C, we subtract the number of trait changes as reversals needed to change the false ancestor B into the true ancestor A, the add the bits of the descendant reflecting its distance from B as the new A. For B > C, we subtract 2 bits from B to make it the equivalent of A, then add the difference from A to C, 3 bits, plus of course the outgroup of minus 4. See Table 8, which demonstrates the bit count,

Likelihood ratio and Bayes factors given above are largely determined by bits assigned to alternative model, e.g., B > A. This is true when the optimal A > B model has likelihoods of 0.99 or greater, which obtains when the optimal model has 7 or more bits (summed new traits of ancestor over outgroup and descendants over immediate ancestor). Tale 9 gives ranges of L.R. and B.F. for various bits of alternative models.

Example 7. A test case from nature. Table 10.

The interlocking Shannon-Turing analysis may have its internal Bayes factors further clarified with an actual monothetic genus in the moss family Pottiaceae. Taoinoa R. H. Zander is a small genus of six moss species endemic to the West Indies and adjacent Central America and Mexico. Trait details are given by Zander (2023). Five species were investigated using the present bit-summing method. The species involved are assigned a letter and number of bits reflecting its number of newly evolved traits:

X (outgroup) is Neotrichostomum crispulum (Buch) R. H. Zander

A (putative progenitor species) is Tainoa pygmaega (E. B. Bartram) R. H. Zander 3 bits

B is T. sinaloensis (E. B. Bartram R. H. Zander 5 bits

C is C. T. subangustifolia (Thér.) R. H. Zander 3 bits

D is T. subcucullata (R. S. Willliams) R. H. Zander 4 bits

E. is T. bartramiana (Steere) R. H. Zander 3 bits

The evolutionary formula for the above monothetic genus Tainoa is X > A > (B, C, (D > E)), as given by Zander (2023a).

The analysis is the same as for Figure 2-3, except for the bit count and one descendant (E) is a secondary ancestor to its own descendant (D). The evolutional transition from X to A is +3 bits. This number is added to each of the three immediate descendants (B, C and D) as per minimum sequential Bayesian posterior probability (min SBPP), which adds bits from two concatenated species as prior and likelihood.

Summing the bits assigned to X > A > B, plus X > A > C, D plus X > A > D is 21. To this is added A (new outgroup) > D > E or 10 bits. The sum is 31, as given in Table 10. The probability that A > (B, C, (D > E)) is essentially 1.00 (statistical certainty). In words, species A is very well supported as ancestral to the remaining species by its A’s strong distinction and yet close similarity to the outgroup X, while the other species are removed from this relationship by advanced traits numbering 3 to 5. Interestingly, in the case of secondary ancestor D, first ancestor A becomes the prior for D > E, and X no longer contributes the immediate ancestron. Secondary ancestors apparently serve to distance their own descendants from the phyletic constraint of the outgroup, and probably signal a genus changing through selection its immediate ancestron, which is no longer of survial advantage. An example of such a transitioning genus is Anoectangium Hedw., with two secondary ancestral species (Zander, 2019b).

To generate a Bayes factor for the above monothetic genus A > (B, C, (D > E)), the probability of the most probable alternative model is needed. The alternative model is selected as the descendant most similar to the ancestral species A by having least number of advanced traits. This is species C, with 3 advanced traits, or3 bits. Switching C with A in the evolutionary tree to get the alternative model X > C > (A, B, (D > E)) allows the calculations summarized in Table 10.

The alternative evolutionary order X > C gives –3 bits to reflect advanced traits coming before ancestral traits and thus equivalent to reversals. So, we subtract 3 bits from all positive bits of the descendants, excepting E, for which X is not the prior, see Table 10. Total is –8 bits. Total of optimal model is 31 bits, probability 1.00 (statistical certainty).The probability of minus 8 bits is (from the spreadsheet) is 0.004, and the B.F. is then 250, strong support for the optimal model of A > (B, C, (D > E)), given outgroup X.

4. Discussion

Likelihood is the chance of the data given the model, that is, the probability of getting the particular distribution of traits given that the evolutionary diagram is correct. Likelihood is a particular chance, for that singular data set, of probability on a curve in which that data probably occurs, and the prior determines the area of the curve in which the likelihood must fall.

Likelihood assumes the model—the evolutionary diagram—is correct. Computerized cladistics and likelihood or Bayesian phylogenetic analyses provide only cladograms as models, where no species are singled out as ancestral to others, and relative shared ancestry is the only important measure of evolutionary distance. Evolutionary systematics holds, on the contrary, that the model must reflect ancestor-descendant relationships as determined by studies that establish the premises of evolutionary theory. Appropriate theory (Artzy-Randrup & Kondrashov, 2006; Barraclough, 2010; Lewontin, 1978; Mayr, 1983; Schneider, 2000) involves adaptation, chance of reversals, rarity and specialization of traits, saltational changes, and other elements used in generating optimal evolutionary trees.

Bayesian analysis uses likelihood and a prior probability from previously obtained data that supports the likelihood and provides a range within which the likelihood value exists. A flat prior is one of 0.50, where there is either no previous data or the data is equivocal. In sequential Bayes methodology using Shannon-Turing analysis, the result of one Bayesian analysis is used as the prior of the next. Flat priors, then, in the studies cited in the present paper occur only in outgroups at the very base of a caulogram where no prior species is used for analysis. Such outgroups are, however, not randomly chosen but are in all cases associated with species in their proper genus as assigned by prior taxonomic study, and are thus gifted with a Bayesian prior certainly larger than 0.50. Thus, the number of flat priors that indicate that the model is wrong or just random—that that therefore the order of the evolutionary diagram is incorrect—is zero, which fully supports the evolutionary theory that was examined for generating the optimal model.

In the study of Zander (2023a) there were no flat priors in evaluation of three genera with 11 species with 44 critical trait changes in one study, and five genera with 19 species with 64 critical traits changes in another. The same is true for the previous study of the Streptotrichaceae of seven genera, 28 species, and 113 trait changes. Thus, there has been no refutation of the theory used to generate positive and negative Shannon informational bits among the models of species generation for 58 species.

In addition, the numbers of possible alternative models are kept low if monothetic genera are analyzed alone, which is possible because immediate ancestrons, i.e., advanced traits of the ancestral species, are shared exactly among descendant species. Consider the above analysis of X > A > (B,C,D, E), with 1 ancestor, 4 descendants and 4 traits per species, plus outgroup (Figures 1-3, 2-3, and Table 7. The L.R. of 257, established for this model, is rather stable against all likely alternative models, of which there are only twice as many as there are descendants. On the other hand, reversals of four traits in a species must be a rare thing, and essentially impossible following the arguments concerning non-reversibility of traits in reconstructing an entire species in the context of Dollo parsimony (Gould, 1970). It is possible that there are no acceptable alternative models if any of the true descendant species have reversals in the minimum of two advanced traits here required to delineate a species (one trait does not satisfactorily imply genetic isolation and unique adaptation to the environment).

Let us speculate, however, and consider a possible minimum evolutionary model to be one with 2 bits per species (two new traits). Consider the case of the above Example 3, with 1 ancestor, 4 descendants, plus outgroup with each species of 2 bits per species. The optimal model of X > A > (B, C, D, E) has a likelihood probability of +2 from the outgroup, and +2 from each descendant. In this case, each descendant has 4 bits, yielding 16 bits for A > (B, C, D, E). The probability of the optimum model is then 0.9999847. The probability of the alternative model of X > B > (A, C, D, E) is simply –2 bits plus –2, or –4, or 0.059, because positive and negative cancel out for B > C or D or E. Dividing the probabilities provides a Bayes factor of 17 for the optimal model against the alternative model with a 2-bit reversal for B > A. Thus, even for the most probable alternative reversal scenario (involving 2-trait reversals) for the simplest model of evolution, given Dollo parsimony, the evidence of B.F. of 17 for the optimal evolutionary order of A > (B, C, D, E) remains substantial to strong (Table 2).

If there are indeed only two possible models, then an approximate probability distribution might be had by adding the two alternative probabilities, 0.9990847 and 0.059, this equaling 1.05847. Then, we divide this into 1 to get a conversion factor, which is 0.9443007. Multiplying the optimal probability by the normalizing conversion factor yields 0.94421, a quite high probability density for the optimal edge-of-chaos 5-species monothetic genus with minimal 2 traits per species, plus outgroup. This is the estimated very minimum probabilistic support for the optimally configured monothetic genus, which may be considered a cast-iron building block of evolution and operationally the fundamental evolutionary structure (Zander, 2023).

Comparison with molecular phylogenetics

Evolutionary analysis using likelihood and Bayesian Markov chain Monte Carlo methods are common in modern phylogenetic analysis. The difference between likelihood and probability is, again, that likelihood asks of two or more models: which best explains the data. Probability asks which model is best explained by the data. Bayesian analysis uses the prior as a probability of where the likelihood may be in a distribution of likelihoods. In phylogenetics, including maximum parsimony, only cladograms are offered as models that explain the data, and quite precise results can be obtained if the data were fairly homogenized, i.e., no difference between ancestral species and their descendants. Phylogenetic software provides no choice of stem-taxa evolutionary trees (ancestor-descendant caulograms) that might best explain the data.

Because likelihood requires accurate evolutionary theory upon which to gauge relative probabilities of the data given a model, theory is critical. There are problems with the theory that phylogenetic analysis uses:

(1) Most salient of the problems is that ancestral species are judged extinct, and all extant ancestral species are to be placed terminal on branches of a cladogram. Yet ancestral species are common (Van Valen, 1973), as I have demonstrated repeatedly in past studies.

(2) With molecular data it is presupposed in phylogenetics that ancestral species either continue mutating or go extinct, but the possibility exists that various populations of the ancestral species remain in isolation after generation of descendant species. When this occurs, then the ancestral morphospecies may appear in many places on a molecular cladogram. Modern practice is to name these as “cryptic” species. The fact that cryptic species do occur, perhaps modified somewhat by microevolution, demonstrates that when speciation happens, there are two molecular variants of the same morphotype, and both can survive to the present. The massive naming of new molecular or quasi-molecular species and higher taxa is unjustified.

(3) Morphological dendrograms are deprecated in phylogenetics. This is because non-parametric bootstrapping (Felsenstein, 1985) has apparently once demonstrated that morphological study is of low coherence and reliability. However, such bootstrapping was done on data sets that already combined well duplicated information into single traits, i.e. essentially descriptions of species, and subsampling data already digested into species descriptions eliminated the duplication required for surviving subsampling to achieve high bootstrap values.

(4) Elimination of genera and families is now rampant as generated by cladist taxonomists following the principle of strict monophyly. For instance, the moss genus Pleurochaete (Pottiaceae) was sunk into Tortella by Grundmann et al. (2006) because embedded in the Tortella cladogram, but should be continued to be recognized because it does not share the same immediate ancestron as the closest monothetic group in Tortella. A definition of a genus as those species sharing an immediate ancestron is effective and productive, and supports the thesis of Wong et al. (2023) that multi-scale complexity is closely associated with selection on functionality.

That molecular phylogeny continues to attract researchers is astonishing, and may be attributed to the cachet of obscure and dense statistics associated with “black-box” computerized analysis and the exciting prospect of DNA models. It is common that likelihood and Bayesian phylogenetic analyses demonstrate high probabilities of the data given the model, but, lacking an ancestral dimension, if the model is faulty. The mathematical exercises in the present paper may seem messy and tedious compared with the results of phylogenetic software, but they may be accomplished with a scientific hand calculator and are conceptually basic, operationally simple, and based on well-conceived evolutionary theory.

5. Conclusions

Complexity entails envisioning new, over-arching processes not easily derived from known physics, and analogic conceptions can clothe poorly understood trends and biases in nature with form and function. Sets of monothetic genera may be analogically linked together as strongly coherent and well-fitting jigsaw puzzle pieces. The illustration locked in place on the analogous jigsaw puzzle is that of evolutionary theory regarding adaptive speciation. Complexity analysis of evolution, given the power of the latency of the immediate ancestron (advanced traits of ancestral species transferred entire to descendant species), is also like solving a maze, a NP-complete (nondeterinistic polynomial-time-complete) problem (Garey & Johnson, 1979; Poundstone, 1988: 164), by exploring all paths at once to find the exit. Analogically this may be accomplished either by modeling the maze as branching tube, flooding with a hose and sending a cork through, or as stream channels and following the fastest flow in a boat. The flood is the immediate ancestron.

The present environmental crisis needs advice from the systematic community. The public funds our large multi-million-specimen herbaria and faunal collections. Molecular cladograms cannot help predict the edge-of-chaos actions of nature. Ancestor-descendant cladograms based on actual trait changes that probably reflect adaptations to environmental perturbations can. Lineages are multimillion-year data sets, and expressed trait changes might be mapped as adaptations to major perturbations such as changes in global temperature and extinction events in the past.

The critical fact enabling ease of likelihood and Bayes factor analysis is the observation (Zander, 2023) that the traits of the descendant are not derived from the important traits of the ancestor but from older, long-established traits in the train of characters of the ancestor. In other words, the new traits of the ancestral species are preserved in the descendant species, and the new traits of the descendant species are modified character states that the ancestral species apparently no longer needs for differential survival. This allows statistical analysis that more accurately evaluates the coherence of the resulting evolutionary relationships with full respect for modern, hard-won evolutionary theory.

The obtained high likelihood ratios and Bayes factors for edge-of-chaos models justifies use of Shannon-Turing analysis in interlocking sequential Bayes in concatenating progenitor and descendant species of monothetic genera into well-supported evolutionary trees (caulograms), thus supporting the several past studies reviewed by Zander (2023).

Wong et al. (2023) have raised the role of complexity analysis into importance at micro-, meso- and macrocosmic levels, emphasizing selection on functional attributes as primary in sustaining and constraining evolving systems. The present study focuses on one complexity function, the latency of the immediate ancestron, which is hypothesized as extensible across scales by fractal evolution throughout evolving life. Newton established that physical laws are valid and potent beyond our sublunar envelope. It is likely that the latency of the immediate ancestron and similar emergent complex functions are universal, inevitable, and common to a myriad of Gaia ecospheres surfing the edge of chaos on the shores of the interstellar sea.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Spreadsheet for Likelihood Ratios or Bayes Factors for Interlocking Sequential Bayes Analysis.

Funding

No funding supported this work.

Acknowledgments

The Missouri Botanical is saluted as it continues to support major research in biodiversity studies.

References

Abel, D. 2009. The capabilities of chaos and complexity. Int. J. Mol. Sci. 10: 247–291. Epub 2009 Jan 9. [CrossRef]
Artzy-Randrup, Y. & A. S. Kondrashov. 2006. Sympatric speciation under incompatibility selection. PNAS 103: 11619–11624.
Barraclough, T. G. 2010. Evolving entities: Towards a unified framework for understanding diversity at the species and higher levels. Phil. Trans. Roy. Soc. B 365: 1801–1813.
Behrensmeyer, A. K. Terrestrial Ecosystems through Time. Chicago University Press, Chicago.
Beneder, M. L. 2013. Paleoclimate. Princeton University Press, Princeton.
Bennett, K. 2010. The chaos theory of evolution. New Scientist 13 Oct. 2010 https://www.newscientist.com/article/mg20827821-000-the-chaos-theory-of-evolution/ Viewed 30 June 2022.
Bernardo, J. M. & A. F. M. Smith. 1994. Bayesian Theory. John Wiley & Sons, New York.
Binning, G. 1989. The fractal structure of evolution. Physica D: Nonlinear Phenomena 38: 32–36.
Etz, A. 2015. Understanding Bayes: Updating priors via the likelihood. The Etz-Files. URL:.
10. https://alexanderetz.com/2015/07/25/understanding-bayes-updating-priors-via-the-likelihood/ Viewed 12 Oct. 2023.
Doebeli, M. & I. Ipolatov. 2014. Chaos and unpredictability in evolution. Evolution 68: 1365–1373.
Felsenstein, J. 1985. Confidence limits on phylogenies: An approach using the bootstrap. Evolution 39: 783-791.
Ferriere, R. & G. A. Fox. 1995. Chaos and evolution. Trends Ecol. Evol. 10: 480–485.
García-Donato, G. & M.-H. Chen. 2005. Calibrating Bayes factor under prior predictive distributions. Statistica Sinica 15: 359–380.
Garey, M. R. & D. S. Johnson. 1979. Computers and Intractability: Guide to the theory of NP-Completeness. W. H. Freeman: New York.
Gershenson, C. 2004. Introduction to random Boolean networks. Pp. 160–1733in M. Bedau, P. Husbands, T. Hutton, S. Kumar& H. Suzuki (editors.) Workshop and Tutorial Proceedings, Ninth International Conference on the Simulation and Synthesis of Living Systems (ALife IX). Also arXiv:nlin/0408006 https://arxiv.org/abs/nlin–/0408006 Viewed 14 Nov. 2022.
Gershenson, C. 2012. Guiding the self-organization of random Boolean networks. Theory Biosci. 131(3):181-91. [CrossRef]
Gigerenzer, G., Z. Swijtink, T. Porter, L. Daston, J. Beatty & L. Krüger. 1989. The Empire of Chance. Cambridge Univ. Press, Cambridge.
Gould, S. J. 1970. Dollo on Dollo’s Law: irreversibility and the status of evolutionary laws. J. Hist. Biol. 3: 189–212.
Gould, S. J. 2002. The Structure of Evolutionary Theory. Belknap Press of Harvard University Press, Cambridge.
Grant, V. 1985. The Evolutionary Process. Columbia University Press, New York.
Grundmann, M., H. Schneider, S. J. Russell & J. C. Vogel. 2006. Phylogenetic relationships of the moss genus Pleurochaete Lindb. (Bryales: Pottiaceae) based on chloroplast and nuclear genomic markers. Organisms, Diversity & Evolution 6: 33–45.
Hilborn, R. C. 2000. Chaos and Nonlinear Dynamics. 2nd ed. Oxford University Press, Oxford, U.K.
Ito, K. & Y. P. Gunji. 1994. Self-organization of living systems towards criticality at the edge of chaos. 33: 17–24.
Jeffreys, H. 1961. The Theory of Probability. Third edition. Oxford University Press, Oxford.
Kass R. E. & Raftery A. E. 1995. Bayes factors. Journal of the American Statistics Association 90: 773–795l.
Kaneko, K. & I. Tsuda. 2000. Complex Systems. Chaos and Beyond, A Constructive Approach with Applications in the Life Sciences. Springer, New York.
Kauffman, S. A. 1969. Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theoret. Biol. 22: 437–467.
Kauffman, S. A. 1993. The Origins of Order, Self-Organization and Selection in Evolution. Oxford University Press, New York.
Kauffman, S. A. 1995. Escaping the Red Queen effect. McKinsey Quarterly 1(Winter): 118–129. Gale Academic OneFile, link.gale.com/apps/–doc/A17177226/AONE?u=anon~a591d228&sid=googleScholar&xid=b661ce56. Accessed 24 Aug. 2021.
Kauffman, S. A. 2000. Investigations. Oxford University Press, Oxford.
Niklas, K. 2016. Plant Evolution: An Introdution to the History of Life. University of Chicago Press, Chicago.
Kondepudi, D. K., B. De Bari & J. A. Dixon. 2020. Dissipative structures, organisms and evolution. Entropy 22(11), 1305; 1–19; https:/–/doi.org/10.3390/e22111305 Viewed 30 June 2022.
Lewin, R. 1999. Complexity: Life at the Edge of Chaos. 2nd ed. University of Chicago Press, Chicago.
Lewontin, R. 1978. Adaptation. Scientific America 239(3): 213–230.
Liu, M. & K. E. Bassler. 2006. Emergent criticality from coevolution in random Boolean networks. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 74(4 Pt 1):041910. Epub 2006 Oct 17. PMID: 17155099. [CrossRef]
Lloyd, E. A. & S. J. Gould. 1993. Species selection on variability. PNAS 90: 595–599.
Lv, X., Y. Wu & B. Ma. 2014. The fractal dimension of the tree of life. PeerJ Preprints 23 Jan. 2014. https://peerj.com/preprints/198/ Viewed 30 June 2022.
McKelvey, B. 1999. Self-organization, complexity catastrophe, and microstate models at the edge of chaos. Pp. 279–307 in J. A. C. Baum & B. McKelvey (editors), Variations in Organization Science: In Honor of Donald T. Campbell. SAGE, Thousand Oaks.
Mayr, E. 1983. How to carry out the adaptationist program? Amer. Nat. 121: 324–334.
Mesarovic, M. D., S. N. Sreenath & J. D. Keene. 2004. Search for organizing principles: understanding in systems biology. Syst. Biol. (Stevenage) 1: 19–27. [CrossRef]
Nicolis, G. & I. Prigogine. 1989. Exploring Complexity: An Introduction. W. JH. Freeman and Company, New York.
Nottale, L., J. Chalime & P. Grou. 2000. On the fractal structure of evolutionary trees. Pp. 247–258 in E. G. Losa, T. Merlini, T. Nonnenmacher & E. Weibel (editors). Fractals in Biology and Medicine, Vol. III. Birkhäuser Verlag, Basel, Switzerland.
Packard, N. H. 1988. Adaptation towards the Edge of Chaos. University of Illinois at Urbana-Champaign, Center for Complex Systems Research. Urbana, Illinois.
Pacrat, D. 2013. Help describing decibans? LessWrong URL https://www.lesswrong.com/posts/hPR4jF8jJaQrJSyyZ/help-describing-decibans Accessed May 20, 2021. (As “DataPacRat”).
Pimm, S. 1984. The complexity and stability of ecosystems. Nature, 307: 321–326.
Poundstone, W. 1988. Labyrinths of Reason. Doubleday, Anchor Books: New York.
Prigogine, I. 1978. Time, structure and fluctuations. Science 201: 777–785.
49. Raschka,j S. 2023. Machine learning FAQ. What is the difference between likelihood and probability? AI Magazine Blog. Ahead of AI. URL: https://sebastianraschka.com/faq/docs/probability-vs-likelihood.html Viewed 12 Oct. 2023.
50. Schneider. C. J. 2000. Natural selection and speciation. PNAS 97: 12398–12399.
Schroeder, M. 1991. Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. W. H. Freeman and Company, New York.
Van Valen, L. 1973. A new evolutionary law. Evol. Theory 1: 1–30.
Winkler, R. L. 1972. An Introduction to Bayesian Inference and Decision. Holt, Rinehart and Winston, Inc., N.Y.
Wong, M. L., C. E. Cleland, D. Arend Jr., S. Bartlett, H. J. Cleaves II, H. Demarest, A. Prabhu, J. I. Lunine & R. M. Hazen. 2023. On the roles of function and selection in evolving systems. PNAS 120(43): e2310223120. Viewed 17 Oct. 2023. [CrossRef]
Zander, R. H. 2013. Framework for Post-Phylogenetic Systematics. Zetetic Publications, St. Louis, U.S.A.
Zander, R. H. 2016. Macrosystematics of Didymodon sensu lato (Pottiaceae, Bryophyta) using an analytic key and information theory. Ukr. Bot. J. 73: 319–333.
Zander, R. H. 2018. Macro evolutionary Systematics of Streptotrichaceae of the Bryophyta and Application to Ecosystem Thermodynamic Stability. Edition 2. Zetetic Publications, St. Louis.
Zander R.H. 2019a. Macro evolutionary versus molecular analysis: Systematics of the Didymodon segregates Aithobryum, Exobryum and Fuscobryum (Pottiaceae, Bryophyta). Hattoria 10: 1–38.
Zander, R. H. 2019b. Macro evolutionary evaluation methods extended, consolidated, and exemplified with Anoectangium (Pottiaceae) in North America and the Himalayas. Ann. Missouri Bot. Gard. 104: 324–338.
Zander, R. H. 2021a. Evolutionary leverage of dissilient genera of Pleuroweisieae (Pottiaceae) evaluated with Shannon-Turing analysis. Hattoria 12: 9–25.
Zander, R. H. 2021b. Synopsis of Ozobryum (Pottiaceae, Bryophyta), and sequential Bayes evaluation of genus integrity. Ann. Missouri Bot. Garden 106: 458–468.
Zander, R. H. 2023a. Fractal Evolution, Complexity and Systematics. Zetetic Publications, St. Louis.
Zander, R. H. 2023b. Spreadsheet for Likelihood Ratios in Interlocking Sequential Bayesian Analysis. Res Botanica Technical Report 2023-10-02.

Figure 1. Elements of analysis of trait changes in a theory-based model monothetic genus and a least different alternative model for likelihood ratio calculation. Each double lump is a species with colors representing its novon and immediate ancestron. 1. Two species in a genus. Each species is composed of two critical sets of traits, a novon of most recent new traits (yellow), and an immediate ancestron composed of the ancestor’s new traits (blue). The descendant’s immediate ancestron is the same as the ancestor’s novon (blue). The alternative model is simply switching ancestor with descendant, and considering trait changes contrary to theory as reversals. 2. Two species in a genus plus an outgroup species. There are two sets of trait reversals in the alternative model, between outgroup and descendant switched with ancestor, and between descendant and switched ancestor. Green shows traits shared by outgroup and ancestor of monothetic genus. 3. Edge-of-chaos optimal five-species genus with outgroup. Blue denotes ancestor’s novon shared by all four descendants. Trait changes occur at every change in color, all in line with evolutionary theory. Alternative model switches ancestor with one of descendants (they all have same number of traits) and there are trait reversals non-parsimoniously contrary to evolutionary theory between outgroup and false ancestor and between false ancestor and true ancestor. Negative trait changes between false ancestor and other descendants due to outgroup refutation are countered by positive trait changes between false ancestor after reversal to match the optimal true ancestor and true descendants.

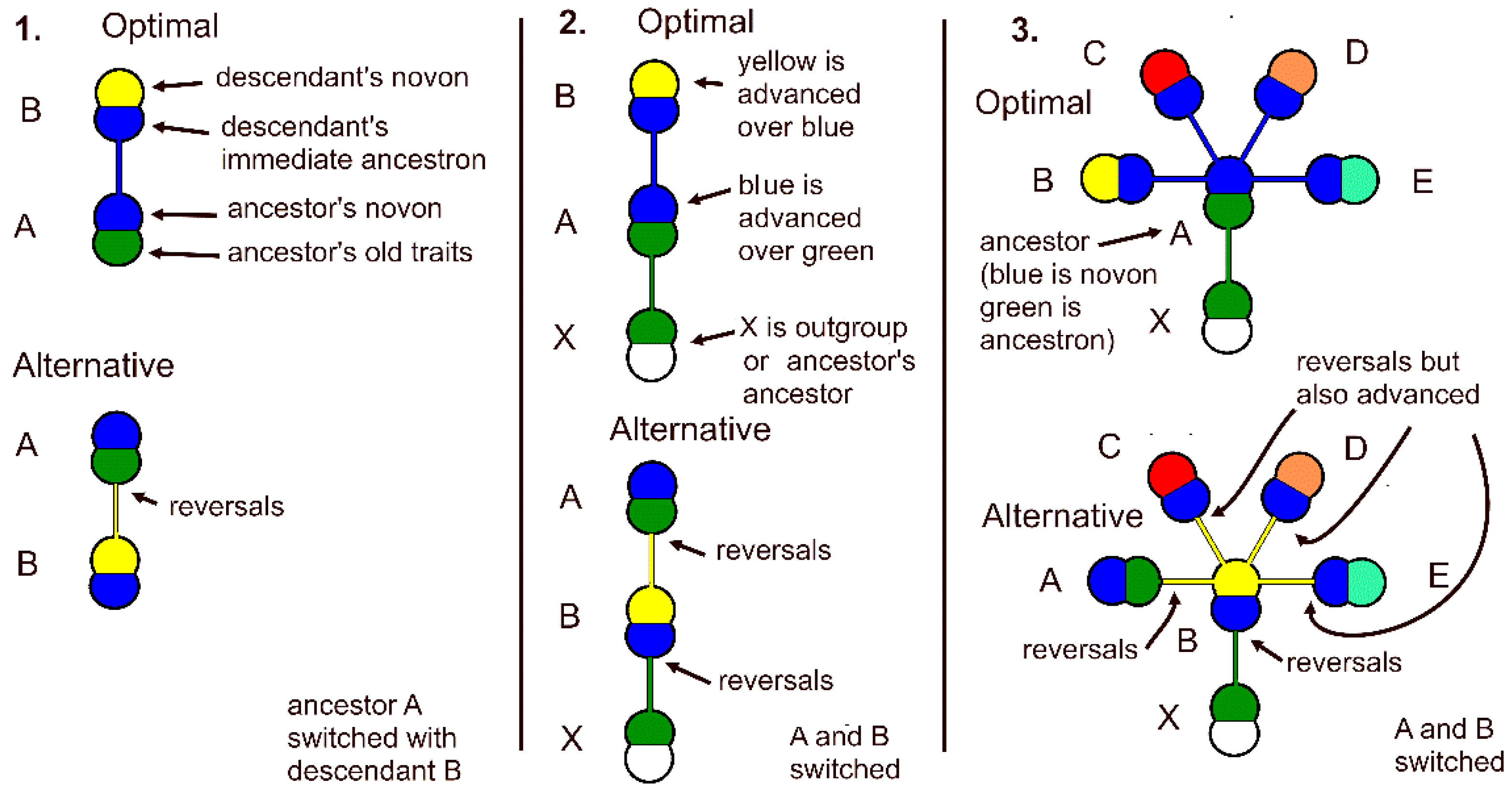
Figure 2. Positive and negative trait changes in optimal and alternative models of monothetic genus, with all species shaving four traits in the novon. 1. Two species. Optimal model has +4 bits supporting the model. Alternative model has 4 reversals from false ancestor to true ancestor, or –4 bits. Likelihood ratio is likelihood of +4 divided by likelihood of –4 bits, or 16 (Table 1). 2. Two species in a genus plus an outgroup species. Optimal model has + 4 bits from outgroup supporting ancestor, and +4 bits from true ancestor and true descendant. By sequential Bayes, ancestor-descendant relationship totals +8 bits. Alternative has –4 bits from outgroup to false ancestor, which adds negatively to –4 bits from false ancestor to true ancestor, totaling –8 bits. L.R. = 250. 3. Edge-of-chaos optimal five-species genus with outgroup. Optimal model adds informational bits from theory-based trait changes from outgroup to ancestor, which is added to each descendant receiving support from the ancestor (+4 bits) plus the outgroup (+4 bits) or +8 bits, totaling +32 bits. L.R. = 257. (L.R. is likelihood ratio; B.F. is Bayes factor.).

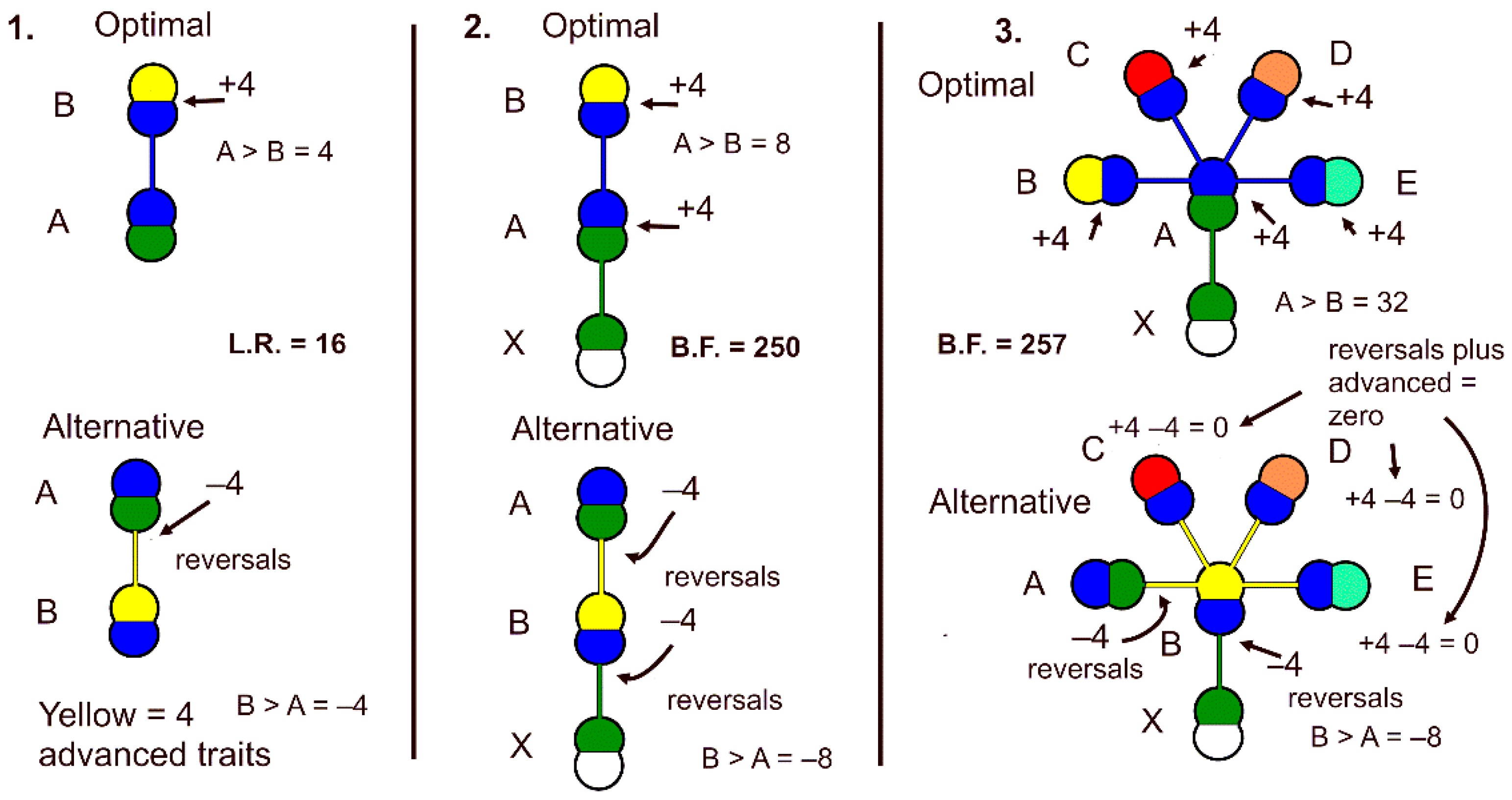
Table 1. Shannon informational bits, odds, and probabilities. Analyses assign one bit per theoretically advanced trait, a negative bit for a reversal, and no bits for no information pertinent to evolutionary theory involving outgroup selection, and rarity or specialization of traits. Each bit is a power of two; value is the decimal equivalent; odds ratio compares the success of a model over an alternative model; fraction is a value converted from odds ratio; probability is the fraction in decimal form. A number with a negative exponent is the reciprocal of the corresponding number with a positive exponent. Zero bits has a decimal value of zero, an odds ratio of 1:1, a fraction of 1/2, and a probability of 0.500. See spreadsheet (Zander, 2023b) for other figures through plus or minus 32 bits.

Bits-Positive	1	2	3	4	5	6	7	8
Value	2	4	8	16	32	64	128	256
Odds ratio	2:1	4:1	8:1	16:1	32:1	64:1	128:1	256:1
Fraction	2/3	4/5	8/9	16/17	32/33	64/65	128/129	256/257
Probability	0.667	0.800	0.889	0.941	0.970	0.985	0.992	0.996
Bits-Positive	9	10	11	12	13	14	15	16
Value	512	1024	2048	4048	8096	16192	32768	65536
Odds ratio	512:1	1024:1	2048:1	4048:1	8096:1	16192:1	32768:1	65536:1
Fraction	512/513	1024/1025	2048/2049	4048/4049	8096/8097	16192/16193	32768/32769	65536/65537
Probability	0.99805	0.99902	0.9995	0.99975	0.999876	0.999938	0.9999695	0.9999847

Bits-Negative	-1	-2	-3	-4	-5	-6	-7	-8
Value	0.500	0.250	0.125	0.063	0.031	0.016	0.008	0.004
Odds ratio	1:2	1:4	1:8	1:16	1:32	1:64	1:128	1:256
Fraction	1/3	1/5	1/9	1/17	1/33	1/65	1/129	1/257
Probability	0.333	0.200	0.111	0.059	0.030	0.015	0.007	0.004
Bits-Negative	-9	-10	-11	-12	-13	-14	-15	-16
Value	0.002	0.001	0.0005	0.000025	0.0000124	0.00006	0.000031	0.000015
Odds ratio	1:512	1:1024	1:2048	1:4048	1:8096	1:16192	1:32768	1:65536
Fraction	1/513	1/1025	1/2049	1/4049	1/8097	1/16193	1/32769	1/65537
Probability	0.00195	0.00098	0.00049	0.000025	0.000124	0.000062	0.000031	0.000015

Table 2. Standard deviations (sigmas) 1 through 6, with odds ratio and Shannon information bits needed to represent the Bayesian posterior probability area of the distribution. From Pacrat (2013).

Sigmas	Bits in distribution	Odds ratio, approx.	BPP %
1	0–1.7	3:1	to 66.7
2	1.7+–4.3	20:1	to 95.2
3	4.3+–8.7	400:1	to 99.0
4	8.7+–14	16,000:1	to 99.993
5	14.0+–20.7	1.5 mn:1	to 99.99994
6	20.7+–29.0	500mn:1	to 99.999998

Table 3. Interpretations of support for Bayes factors. The present paper considers Bayes factors to be the same as likelihoods when calculating ratios of optimum versus alternative models.

Jeffries (1961) support	B.F. Range	Kass & Raftery (1995) support	B.F. Range
substantial	3 to 10	positive	3 to 20
strong	10 to 100	strong	20 to 150
decisive	more than 100	very strong	More than 150

Table 4. Likelihood ratio of one ancestral species (A) and one descendant (B), two new traits per speciation, no outgroup (no prior). L.R. = 16. Because there is no prior, we call the result a L.R.

Optimal	A > B	Total bits	Likelihood
	+4	+4	0.941
Alternative	B > A
	– 4	– 4	0.0588

Table 5. Example caulogram with one ancestor, one descendant and an outgroup, all species with 4 new traits. B.F. = 250.

Optimal	X>A ₊ A > B	Total bits	Probability
	+4 +4	+8	0.996
Alternative	X > B + B > A
	–4 –4	–8	0.004

Table 6. Example of 1 ancestor, four descendants, and an outgroup, all species have two new traits (2 bits). Because there is a prior (X > A), we say B.F. = 17. (not illustrated).

Optimum	X > A ₊ A > B	X > A ₊ A > C	X > A ₊ A > D	X > A ₊ A > E	Total bits	Probability
	+2 +2	+2 +2	+2 +2	+2 +2	16	0.99998
Alternative	X > B ₊ B > A	X > B ₊ B > C	X > B ₊ B > D	X > B ₊ B > E
	–2 –2	–2 +2	–2 +2	–2 +2	–4	0.059

Table 7. Example of 1 ancestor, four descendants, and an outgroup, all species have four new traits (4bits). Because there is a prior (X > A), we say B.F. = 257 instead of L.R.

Optimum	X > A ₊ A > B	X > A ₊ A > C	X > A ₊ A > D	X > A ₊ A > E	Total bits	Probability (from spreadsheet)
	+4 +4	+4 +4	+4 +4	+4 +4	32	1.00
Alternative	X > B ₊ B > A	X > B ₊ B > C	X > B ₊ B > D	X > B ₊ B > E
	–4 –4	–4 +4	–4 +4	–4 +4	–8	0.00389

Table 8. Example of 1 ancestor, four descendants, and an outgroup, all descendant species have different numbers of new traits, outgroup has 4 bits. Because there is a prior (X > A), we say B.F. = 4096, quite different from that of all descendants having equal numbers of new traits because the positive bits of descendants do not cancel out the negative bits of the outgroup, which are overwhelming.

Optimum	X > A ₊ A > B	X > A ₊ A > C	X > A ₊ A > D	X > A ₊ A > E	Total bits	Probability (from spreadsheet)
	+4 +2	+4 +3	+4 +4	+4 +5	30	1.00
Alternative	X > B ₊ B > A	X > B ₊ B > C	X > B ₊ B > D	X > B ₊ B > E
	–4 –2	–4 +1	–4 +2	–4 +3	–12	0.000244

Table 9. Likelihood ratios or Bayes factors for various bits of alternative models when optimal model has probability near 1.0 or 7 or more bits.

Bits of alternative model	L.R. or B.F. for optimal model of 7 or more bits.
2	4.9–5
3	8.9–9
4	16.9–17
5	32.7–33
6	64.5–65
7	128–129
8	255–257
9	509–513
10	1017–1025
11	2033–2049
12	4065–4097

Table 10. Example for Tainoa genus, with T. angustifolia (C) as alternative ancestor. B.F. is 250.

Optimum	X > A ₊ A > B	X > A ₊ A > C	X > A ₊ A > D	X > A ₊ D > E	Total bits	Probability (from spreadsheet)
	+3 +5	+3 +3	+3 +4	+3 +4+3	31	1.00
Alternative	X > C ₊ C > A	X > C ₊ C > B	X > C ₊ C > D	X > B ₊ D > E
	–3 –3	–3 +5–3	–3 +4 –3	–2 +3	–8	0.004

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.