Preprint
Article
Is Short-Term Memory Made of Two Processing Units? Clues from Italian and English Literatures Down Several Centuries
Altmetrics
Downloads
72
Views
17
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
25 October 2023
Posted:
25 October 2023
You are already at the latest version
Alerts
Abstract
We propose that the short−term memory (STM), when processing a sentence, uses two uncorrelated processing units in series. The clues for conjecturing this model emerge from studying many novels of the Italian and English Literatures. This simple model, referring to the surface of language, seems to describe mathematically the input-output characteristics of a complex mental process involved in a reading/writing a sentence. We show that there are no significant mathematical/statistical differences between the two literary corpora by considering deep-language variables and linguistic communication channels, therefore, the surface mathematical structure of alphabetical languages is very deeply rooted in human mind, independently of the language used. The first processing unit is linked to the number of words between two contiguous interpunctions, variable Ip, approximately ranging in Miller’s 7±2 range; the second unit is linked to the number of Ip’s contained in a sentence, variable MF, ranging approximately from 1 to 6. The overall capacity required to process fully of a sentence ranges from 8.3 to 61.23 words, values that can be converted into time by assuming a reading speed, giving the range 2.64~19.54 seconds for fast-reading and 5.3~30.1 seconds for average reader. Since a sentence conveys meaning, the surface features we have found might be the starting point to arrive at an Information Theory that includes meaning.
Keywords:
Subject: Computer Science and Mathematics - Information Systems
1. Short-term memory capacity can be estimated from literary texts
The aim of this paper is to propose that the short−term memory (STM) – which refers to the ability to remember a small number of items for a short period of time - is likely made by two consecutive (in series) and uncorrelated processing units with similar capacity. The clues for conjecturing this model emerge from studying many novels of the Italian and English Literatures. Although simple, because only the surface structure of texts is considered, the model seems to describe mathematically the input-output characteristics of a complex mental process, largely unknown.
To model a two-unit STM processing, we further develop our previous studies based on a parameter called the “word interval”, indicated by , given by the number of words between any two contiguous interpunctions [1,2,3,4,5,6,7,8]. The term “interval” arises by noting that does measure an “interval” - expressed in words - which can be transformed into time through a reading speed [9], as shown in [1].
The parameter varies in the same range of the STM capacity, given by Miller’s law [10], a range that includes 95% of cases. As discussed in [1], the two ranges are deeply related because interpunctions organize small portions of more complex arguments (which make a sentence) in short chunks of text, which represent the natural STM input (see [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31], a sample of the many papers appeared in the literature, and also the discussion in Ref. [1]). It is interesting to recall that , drawn against the number of words per sentence, , approaches a horizontal asymptote as increases [1,2,3]. The writer, therefore, maybe unconsciously, introduces interpunctions as sentences get longer because he/she acts also as a reader, therefore limiting approximately in Miller’s range.
The presence of interpunctions in a sentence and its length in words are, very likely, the tangible consequence of two consecutive processing units necessary to deliver the meaning of the sentence, the first of which we have already studied with regard to and the linguistic I-channel [1,2,3,4,5,6,7,8].
A two-unit STM processing can be justified, at least empirically, according to how a human mind is thought to memorize “chunks” of information in the STM. When we start reading a sentence, the mind tries to predict its full meaning from what it has already read and only when an in-sentence interpunction is found (i.e., comma, colon, semicolon), it can partially understand the text, whose full meaning is finally revealed when a final interpunction (question mark, exclamation mark, full-stop) is found. This first processing therefore is revealed by , the second processing is revealed by and by the number of word intervals contained in the sentence, the latter indicated by [1,2,3,4,5,6,7,8].
The longer and more twisted a sentence is, the longer the ideas remain deferred until the mind can establish its meaning from all its words, with the result that the text is less readable. The readability can be measured by the universal readability index which includes the two-unit STM processing [6].
In synthesis, in the present paper we conjecture that in reading a full sentence humans engage a second STM capacity – quantitatively measured by - which works in series with the first STM – quantitatively measured by . We refer to the second STM capacity as the “extended” STM (E-STM) capacity. The modeling of the STM capacity with has never been considered in the literature [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31] before our paper in 2019 [1]. The number , of contained in a sentence studied previously in I-channels [4], is now associated with the E-STM.
The E-STM should not be confused with the intermediate memory [32,33], not to mention the long-term memory. It should be also clear that the E-STM is not modelled by studying neuronal activity, but from counting words and interpunctions, whose effects hundreds of writers - both modern and classic - and millions of people have experienced through reading.
The stochastic variables , , , and the number of characters per word, , are loosely termed deep-language variables considered in this paper, following our general statistical theory on alphabetical languages and its linguistic channels, developed in a series of papers [1,2,3,4,5,6,7,8]. These parameters refer, of course, to the “surface” structure of texts, not to the “deep” structure mentioned in cognitive theory.
These variables allow to perform “experiments” with ancient or modern readers by studying the literary works read. These “experiments” have revealed unexpected similarity and dependence between texts, because the deep−language variables may be not consciously controlled by writers. Moreover, the linear linguistic channels present in texts can further assess, by a sort of “fine tuning”, how much two texts are mathematically similar.
In the present paper, we base our study on a large data base of texts (novels) belonging to the Italian Literature spanning seven centuries [1], and to the English Literature spanning four centuries [5]. In References [1,5], the reader can find the list of novels considered in the present paper with their full statistics on the linguistic variables recalled above.
We will show, in the following sections, that the two literary corpora can be merged to study the surface structure of texts, therefore, they make a reliable data set from which the size of the two STM capacities can be conjectured.
After this introduction, Section 2 recalls the deep-language parameters and show some interesting relationships between them, applied to the Italian and English Literatures; Section 3 recalls the nature of linguistic communication channels present in texts; Section 4 shows relationships with a universal readability index; Section 5 models the two STM processing units in series and Section 6 concludes and proposes future work.
2. Deep-language parameters and their relationships
Let us consider a literary work (e.g., a novel) and its subdivision in disjoint blocks of text long enough to give reliable average values, such as chapters, as we have done in References [1,2,3,4,5,6,7,8]. Let be the number of sentences contained in a text block, the number of words contained in the sentences, the number of characters contained in the words and the number of punctuation marks (interpunctions) contained in the sentences. All other alphanumeric symbols have been deleted, thus leaving only words and interpunctions. The four deep-language variables are defined as [1]:
Notice that Equation (4) can be written also as:
As recalled above, gives the number of word intervals contained in a sentence.
The relationships between these linguistic variables show very interesting and fundamental features of texts, practically indistinguishable in the two literatures, as we show next.
2.1. Sentences versus words
Figure 1 shows the scatterplot of sentences per chapter, , versus words per chapter, , for the Italian Literature - blue circles, 1260 chapters - and the English Literature - red circles, 1114 chapters - for a total of 2374 samples. Table 1 reports slopes and correlation coefficients of the two regression lines drawn in Figure 1. There are no significant differences between the two literary corpora therefore underlining the fact that the mathematical surface structure of alphabetical languages - a creation of human mind - is very deeply rooted in humans, independently of the particular language used. This issue will be further discussed by considering the theory of linguistic channels in Section 3.
2.2. Interpunctions versus sentences
Figure 2 shows the scatterplot of interpunctions, , versus sentences, , for the Italian and the English literatures. Table 2 reports slopes and correlation coefficients of the two regression lines drawn in Figure 2. The two literary corpora almost coincide – as far as the slope is concerned - as if the samples were extracted from the same data base. This issue will be further discussed by considering the theory of linguistic channels in Section 3.
2.3. Words per sentence versus word interval per sentence
Figure 3 shows the scatterplot of words per sentence, , versus word intervals per sentence, . It is interesting to notice a tight similar linear relationship in both literatures, see slopes and correlation coefficients in Table 3. This issue will be further discussed by considering the theory of linguistic channels in Section 3.
The linear relationship shown in Figure 3 states that as a sentence gets longer writers introduce more , regardless of the length of . This seems to be a different mechanism - compared to that concerning the words that build up - that writers use to convey the full meaning of a sentence. We think that describes another STM processing beyond that described by and uncorrelated with it, as it can be deduced from the findings reported in the next sub-sections.
2.4. Word intervals versus words per sentence
Figure 4 shows the scatterplot of word interval, , versus words per sentence, , for the Italian Literature (blue circles) and the English Literature (red circles). The magenta lines refer to Miller’s law range (95% of samples). The black curve models the best-fit relating to for all samples shown in Figure 4, as done in [1,2], given by:
As discussed in [1,2,3,4] and recalled above, Equation (6) models the saturation of as increases. Italian and English texts show no significant differences, therefore underlining a general behavior of human readers/writers, independent of language.
In equation (6), and . It is striking to notice that Miller’s range – which, as recalled, refers to 95% of samples - contains about 95% of all samples of shown in the ordinate scale of Figure 4 (precisely in the range from 4.8 to 8.6, see Section 2.6 below) and that the horizontal asymptote () is just Miller’s range center value.
Defined the error , between the experimental datum and that given by Eq. (6), the average error is for Italian and for English, with standard deviation and , respectively. Therefore, the two literary corpora are very similarly scattered around the black curve given by Eq. (6),
In conclusion, the two literary corpora, for the purpose of the present study, can be merged together and the findings obtained reinforce the conjecture that does describe the STM capacity defined by Millers’ Law.
2.5. Word intervals per sentence versus word intervals
Figure 5 shows the scatterplot of word intervals per sentence, , versus word intervals, . The correlation coefficient is in the Italian Literature, and in the English Literature, values which practically state that the two linguistic variables are uncorrelated. The decorrelation between and strongly suggests the presence of two processing units acting independently of one another, a model we discuss further in Section 5.
In the next sub-section, dealing with linguistic communication channels, we reinforce the fact that the two literary corpora can be merged together, therefore, the can give a homogeneous data base of alphabetical texts sharing a common surface mathematical structure from which two STM processing units can be modelled.
2.6. Probability distributions
In the previous sub-sections, we have noticed that there are no significant differences between the statistical features of Italian and English novels, therefore we are allowed to merge the two literary corpora for estimating the probability distributions of the deep-language variables. These are shown in Figure 6, Figure 7 and Figure 8, respectively for , and . These probability distributions can be modelled with a three-parameter log-normal probability density function, as done for Italian Literature for in Ref. [1], given by the general expression (natural logs):
In Eq. (7), and are, respectively, the average value and standard deviation. These constants are obtained as follows. Given the linear average value and the linear standard deviation of the random variable , the standard deviation and the average value of the random variable of a three−parameter log−normal probability density function, defined for , are given by [34]:
3. Linguistic communication channels in texts
To study the chaotic data that emerge in any language, the theory developed in Reference [2] compares a text (the reference, or input text, written in a language) to another text (output text, “cross‒channel”, written in any language) or to itself (“self‒channel”), with a complex communication channel ‒ made of several parallel single channels, two of which were explicitly considered in [2,4,5,7] ‒ in which both input and output are affected by “noise”, i.e. by diverse scattering of the data around a mean linear relationship, namely a regression line, as those shown in Figure 1, Figure 2 and Figure 3 above.
In Reference [3] we have applied the theory of linguistic channels to show how an author shapes a character speaking to diverse audiences by diversifying and adjusting (“fine tuning”) two important linguistic communication channels, namely the Sentences channel (S‒channel) and the Interpunctions channel (I‒channel). The S‒channel links of the output text to of the input text, for the same number of words. The I‒channel links (i.e., the number of ) of the output text to of the input text, for the same number of sentences.
In Reference [5] we have further developed the theory of linguistic channels by applying it to Charles Dickens’ novels and to other novels of the English Literature (the same literary corpus considered in the present paper) and found, for example, that this author was very likely affected by King James’ New Testament.
In S‒channels the number of sentences of two texts is compared for the same number of words, therefore, they describe how many sentences the writer of text (output) uses to convey a meaning, compared to the writer of text (input) ‒ who may convey, of course, a diverse meaning ‒ by using the same number of words. Simply stated, it is about how a writer shapes his/her style for communicating the full meaning of a sentence with a given number of words available, therefore it is more linked to author’s style. These channels are those described by the scatterplots and regression lines - shown in Figure 1 - in which we get rid of the independent variable .
In I‒channels the number of word intervals of two texts is compared for the same number of sentences, therefore, they describe how many short texts make a full sentence. Since is connected to the STM capacity (Miller’s Law) and is linked –in our present conjecture - to the E-STM, I‒channels are more related to how the human mind processes information than to authors’ style. These channels are those described by the scatterplots and regression lines - shown in Figure 2 - in which we get rid of the independent variable .
In the present paper, for the first time, we consider linguistic channels which compare of two texts for the same number of , therefore also these channels are connected with the E-STM, as they are a kind on “inverse” channels of the I-channels. These channels are those described by the scatterplots and regression lines - shown in Figure 3 - in which we get rid of the independent variable . We refer to these channels as the -channels.
Recall that regression lines, however, consider and describe only one aspect of the linear relationship, namely that concerning (conditional) mean values. They do not consider the scattering of data, which may not be similar when two regression lines almost coincide, as Figure 1, Figure 2 and Figure 3 show. The theory of linguistic channels, on the contrary, by considering both slopes and correlation coefficients, provides a reliable tool to fully compare two sets of data.
To apply the theory of linguistic channels [2,3], we need the slope and the correlation coefficient of the regression line between: (a) and to study S‒channels (Figure 1); (b) and to study I‒channels (Figure 2); (c) and to study -channels (Figure 3), values listed in Table 1, Table 2 and Table 3.
In synthesis, the theory calculates the slope and the correlation coefficient of the regression line between the same linguistic parameters by linking the input k (independent variable) to the output j (dependent variable) of the virtual scatterplot in the three linguistic channels mentioned above.
The similarity of the two data sets (regression lines and correlation coefficients) are synthetically measured by the theoretical signal-to-noise ratio (dB) [2]. First, the noise-to-signal ratio , in linear units, is calculated from:
Secondly, from Equation (7), the total signal−to−noise ratio is given (in dB) by:
Notice that when a text is compared to itself , because , .
Table 6 shows the results when Italian is the input language and English the output language ; Table 7 shows the results when English is the input language and Italian is the output language .
- (a)
- The slopes are very close to unity, implying, therefore, that the two languages are very similar in average values (i.e., the regression line).
- (b)
- The correlation coefficients are very close to 1, implying, therefore, that data scattering is very small.
- (c)
- (d)
In other words, the “fine tuning” done through the three linguistic channels strongly reinforces the conclusion that the two literary corpora are “extracted” from the same data set, from the same “book”, whose “text” is interweaved in a universal surface mathematical structure that human mind imposes to alphabetical languages. The next section further reinforces this conclusion when text readability is considered.
4. Relationships with a universal readability index
In Reference [6], we have proposed a universal readability index which includes the STM capacity, modelled by , applicable to to any alphabetical language, given by:
With
In Equation (12) the E-STM is also indirectly present with the variable of Equation (13). Notice that a text readability increases (text more readable) as increases.
The observation that differences between readability indices give more insight than absolute values has justified the development of Equation (9).
By using Eqs. (10) and (11), the average value of any language is forced to be equal to that found in Italian, namely . In doing so, if it is of interest, can be linked to the number of years of schooling in Italy [1,6].
There are two arguments in favor of Equation (14), the first is that affects a readability formula much less than [1]. The second is that is a parameter typical of a language which, if not scaled, would bias without really quantifying the change in reading difficulty of readers, who are accustomed to reading, in their language, shorter or longer words, on the average, than those found in Italian. This scaling, therefore, avoids changing only because in a language, on the average, words are shorter or longer than in Italian.
Figure 9 shows the histogram of . The mean value is (practically the peak), the standard deviation is and the 95% range is .
Figure 10 shows the scatterplot of versus in the Italian and English Literatures. There are no significant differences between the two languages, therefore we can merge all samples. The vertical black lines are drawn at the mean value and at the values exceeded with probability (and (The range includes, therefore, 95% of the samples and it corresponds to Miller’s range (Table 5).
Figure 11 shows the scatterplot of versus . The vertical black lines are drawn at the mean value and at the values exceeded with probability (and (The range includes 95% of the merged samples corresponding to Miller’s range (Table 5). The horizontal green lines refer to (95% range ).
Figure 12 shows the scatterplot of versus . The vertical black lines are drawn at the mean value and at the values exceeded with probability (and (The range includes, therefore, 95% of the samples and it corresponds to Miller’s range (Table 5). The horizontal green lines refer to (95% range ).
In all cases, we can observe that , as expected, is inversely proportional to the deep-language variable involved in the STM processing. In other words, the larger is the independent variable, the lower is the readability index.
5. Two STM processing units in series
From the findings reported in the previous sections, we are justified to conjecture that the STM elaborates information with two processing units, regaedless of language, author, time and audience. The model seems to be universally valid, at least according to how this largely unknown surface processing is seen through the lens of the most learned writings, down several centuries. The main reasons to propose this conjecture are the following.
According to Figure 5, and are decorrelated. This suggests the presence of two processing units working with different, although similar, “protocols”, the first capable of processing approximately items (Miller’s law) – capacity measured by - and the second capable of processing items – capacity measured by .
Figure 13 shows how these two capacities are related at equal probability exceeded. We can see that the relationship is approximately linear in the range of ( of ).
Figure 14 shows the ideal flow-chart of the two STM units that process a sentence. After the previous sentence (not shown), a new sentence starts: The words , ,… are stored in the first buffer, with capacity given by a number approximately in Miller’s range, until an interpunction is introduced to fix the length of . The word interval is then stored in the E-STM buffer up to items, from about 1 to 6, until the sentence ends. The two buffers are afterwards cleared and a new sentence can start.
Let us calculate the overall capacity required by the full processing described in Figure 14. If we consider the 95% range in both processing units (Table 5) we get words and words.
We can roughly estimate the time necessary to complete the cycle of a sentence, by converting the capacity expressed in words into a time interval required to read them by assuming a reading speed, such as 188 words for Italian, or very similar values for other languages [9]. Notice, however, that this reading speed refers to a fast reading reader not to a common reader of novels, whose pace can be slower, down to approximately 90 words per minute [35]. Now, reading 188 words in 1 minute gives 2.6 and 19.5 seconds, respectively, values that become 5.3 and 30.1 seconds when reading 90 words per minute, very well contained in experimental findings concerning the STM processing [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31].
6. Conclusion
We have shown that during a sentence, the alphabetical text is processed by the short-term memory (STM) with two uncorrelated processing units in series, with similar capacity. The clues for conjecturing this model has emerged by considering many novels belonging to the Italian and English Literatures.
We have shown that there are no significant mathematical/statistical differences between the two literary corpora by considering deep-language variables and linguistic communication channels. This finding underlines the fact that the mathematical surface structure of alphabetical languages - a creation of human mind - is very deeply rooted in humans, independently of the particular language used, therefore we have merged the two literary corpora in one data set and obtained universal results.
The first processing unit is linked to the number of words between two contiguous interpunctions, variable indicated by, approximately ranging in Miller’s law range; the second unit is linked to the number of’s contained in a sentence, variable indicated by and referred to as the extended STM, or E-STM, ranging approximately from 1 to 6.
We have recalled that a two-unit STM processing can be empirically justified according to how a human mind is thought to memorize “chunks” of information contained in a sentence. Although simple and related to the surface of language, the model seems to describe mathematically the input-output characteristics of a complex mental process, largely unknown.
The overall capacity required by the full processing of a sentence ranges from to words, values that can be converted into time by assuming a reading speed. This conversion gives the range seconds for a fast-reading reader and seconds for a common reader of novels, values well supported by experiments reported in the literature.
A sentence conveys meaning, therefore, the surface features we have found might be the starting point to arrive at an Information Theory that includes meaning.
Future work should be done on ancient readers of Greek and Latin Literatures to assess whether their STM processing was, very likely, similar to that discussed in the present paper.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The author wishes to thank the many scholars who, with great care and love, maintain digital texts available to readers and scholars of different academic disciplines, such as Perseus Digital Library and Project Gutenberg.
Conflicts of Interest
The author declares no conflict of interest.
References
- Matricciani, E. Deep Language Statistics of Italian throughout Seven Centuries of Literature and Empirical Connections with Miller’s 7 ∓ 2 Law and Short–Term Memory. Open Journal of Statistics 2019, 9, 373–406. [CrossRef]
- Matricciani, E. A Statistical Theory of Language Translation Based on Communication Theory. Open Journal of Statistics. 2020, 10, 936–997. [CrossRef]
- Matricciani, E. Linguistic Mathematical Relationships Saved or Lost in Translating Texts: Extension of the Statistical Theory of Translation and Its Application to the New Testament. Information 2022, 13, 20. [CrossRef]
- Matricciani, E. Multiple Communication Channels in Literary Texts. Open Journal of Statistics 2022, 12, 486–520. [CrossRef]
- Matricciani, E. Capacity of Linguistic Communication Channels in Literary Texts: Application to Charles Dickens’ Novels. Information 2023, 14, 68. [CrossRef]
- Matricciani, E. Readability Indices Do Not Say It All on a Text Readability. Analytics 2023, 2, 296-314. [CrossRef]
- Matricciani, E. Linguistic Communication Channels Reveal Connections between Texts: The New Testament and Greek Literature. Information 2023, 14, 405. [CrossRef]
- Matricciani, E. Short-Term Memory Capacity across Time and Language Estimated from Ancient and Modern Literary Texts. Study-Case: New Testament Translations. Open Journal of Statistics, 2023, 13, 379-403. [CrossRef]
- Trauzettel−Klosinski, S., K. Dietz, K. Standardized Assessment of Reading Performance:The New International Reading Speed Texts IreST, IOVS 2012, 5452−5461. [CrossRef]
- Miller, G.A. The Magical Number Seven, Plus or Minus Two. Some Limits on Our Capacity for Processing Information, 1955, Psychological Review, 343−352. [CrossRef]
- Atkinson, R.C., Shiffrin, R.M., The Control of Short-Term Memory, 1971, Scientific American, 225, 2, 82-91.
- Baddeley, A.D., Thomson, N., Buchanan, M., Word Length and the Structure of Short−Term Memory, Journal of Verbal Learning and Verbal Behavior, 1975, 14, 575−589. [CrossRef]
- Mandler G, Shebo, B.J. Subitizing: An Analysis of Its Componenti Processes, Journal of Experimental Psychology: General, 1982, III(1), 1−22. [CrossRef]
- Cowan, N., The magical number 4 in short−term memory: A reconsideration of mental storage capacity, Behavioral and Brain Sciences, 2000, 87−114. [CrossRef]
- Muter, P. The nature of forgetting from short−term memory, Behavioral and Brain Sciences, 2000, 24, 134. [CrossRef]
- Grondin, S. A temporal account of the limited processing capacity, Behavioral and Brain Sciences, 2000, 24, 122−123. [CrossRef]
- Pothos, E.M., Joula, P., Linguistic structure and short−term memory, Behavioral and Brain Sciences, 2000, 138−139.
- Bachelder, B.L. The Magical Number 4 = 7: Span Theory on Capacity Limitations. Behavioral and Brain Sciences 2001, 24, 116-117. [CrossRef]
- Conway, A.R.A., Cowan, N., Michael F. Bunting, M.F., Therriaulta, D.J., Minkoff, S.R.B., A latent variable analysis of working memory capacity, short−term memory capacity, processing speed, and general fluid intelligence, Intelligence, 2002, 163−183. [CrossRef]
- Saaty, T.L., Ozdemir, M.S., Why the Magic Number Seven Plus or Minus Two, Mathematical and Computer Modelling, 2003, 233−244. [CrossRef]
- Chen, Z. and Cowan, N. Chunk Limits and Length Limits in Immediate Recall: A Reconciliation. Journal of Experimental Psychology, Learning, Memory, and Cognition, 2005, 3, 1235-1249. [CrossRef]
- Richardson, J.T.E, Measures of short-term memory: A historical review, 2007, Cortex, 43, 5, 635-650. [CrossRef]
- Mathy, F., Feldman, J. What’s magic about magic numbers? Chunking and data compression in short−term memory, Cognition, 2012, 346−362. [CrossRef]
- Barrouillest, P., Camos, V., As Time Goes By: Temporal Constraints in Working Memory, Current Directions in Psychological Science, 2012, 413−419. [CrossRef]
- Mathy, F. and Feldman, J. What’s Magic about Magic Numbers? Chunking and Data Compression in Short-Term Memory. Cognition, 2012, 122, 346-362. [CrossRef]
- Gignac, G.E. The Magical Numbers 7 and 4 Are Resistant to the Flynn Effect: No Evidence for Increases in Forward or Backward Recall across 85 Years of Data. Intelligence, 2015, 48, 85-95. [CrossRef]
- Jones, G, Macken, B., Questioning short−term memory and its measurements: Why digit span measures long−term associative learning, Cognition, 2015, 1−13. [CrossRef]
- Chekaf, M., Cowan, N., Mathy, F., Chunk formation in immediate memory and how it relates to data compression, Cognition, 2016, 155, 96−107. [CrossRef]
- Norris, D., Short-Term Memory and Long-Term Memory Are Still Different, 2017, Psychological Bulletin, 143, 9, 992–1009. [CrossRef]
- Hayashi, K., Takahashi, N., The Relationship between Phonological Short-Term Memory and Vocabulary Acquisition in Japanese Young Children. Open Journal of Modern Linguistics, 2020, 132-160. [CrossRef]
- Islam, M., Sarkar, A., Hossain, M., Ahmed, M., Ferdous, A. Prediction of Attention and Short-Term Memory Loss by EEG Workload Estimation. Journal of Biosciences and Medicines, 2023, 304-318. [CrossRef]
- Rosenzweig, M.R., Bennett, E.L., Colombo, P.J., Lee, Peter, D.W. Short-term, intermediate-term and Long-term memories, Behavioral Brain Research, 1993, 57, 2, 193-198. [CrossRef]
- Kaminski, J Intermediate-Term Memory as a Bridge between Working and Long-Term Memory, The Journal of Neuroscience, 2017, 37(20), 5045–5047. [CrossRef]
- Bury, K.V. (1975), Statistical Models in Applied Science, 1975, New York, John Wiley.
- Matricciani, E.; De Caro, L. Jesus Christ’s Speeches in Maria Valtorta’s Mystical Writings: Setting, Topics, Duration and Deep-Language Mathematical Analysis. J 2020, 3, 100-123. [CrossRef]
Figure 1.
Scatterplot of sentences versus words . Italian Literature: blue circles and blue regression line; English Literature: red circles and red regression line. Samples refer to chapters, 1260 in the Italian Literature, 1114 in the English Literature; total: 2374. The blue and red lines are the regression lines with slope and correlation coefficient reported in Table 1.
Figure 1.
Scatterplot of sentences versus words . Italian Literature: blue circles and blue regression line; English Literature: red circles and red regression line. Samples refer to chapters, 1260 in the Italian Literature, 1114 in the English Literature; total: 2374. The blue and red lines are the regression lines with slope and correlation coefficient reported in Table 1.
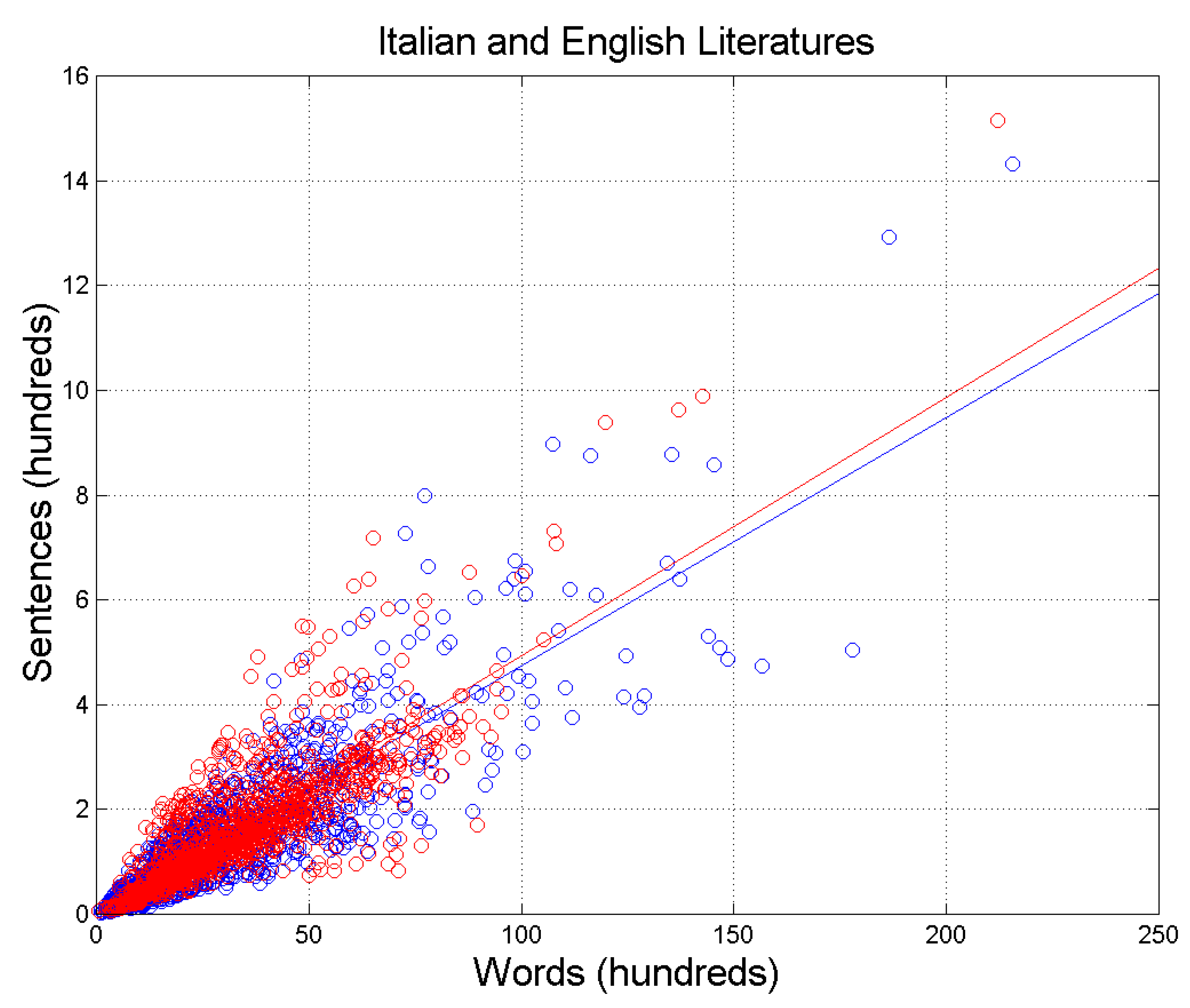
Figure 2.
Scatterplot of interpunctions versus sentences . Italian Literature: blue circles and blue regression line; English Literature: red circles and red regression line. The blue and red lines are the regression lines with slope and correlation coefficient reported in Table 2.
Figure 2.
Scatterplot of interpunctions versus sentences . Italian Literature: blue circles and blue regression line; English Literature: red circles and red regression line. The blue and red lines are the regression lines with slope and correlation coefficient reported in Table 2.
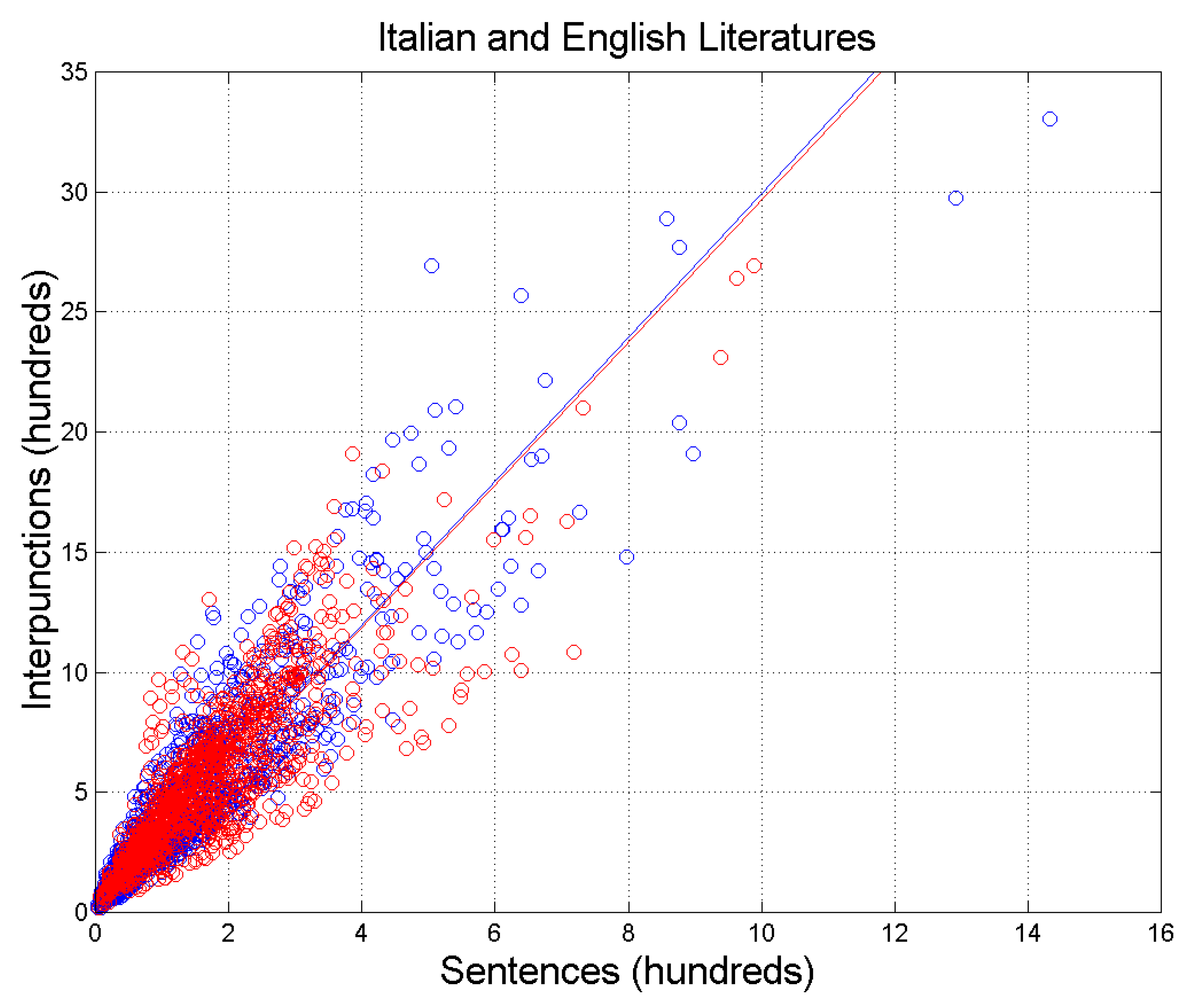
Figure 3.
Scatterplot of versus . Italian Literature: blue circles and blue regression line; English Literature: red circles and red regression line. The blue and red lines are the regression lines with slope and correlation coefficient reported in Table 3.
Figure 3.
Scatterplot of versus . Italian Literature: blue circles and blue regression line; English Literature: red circles and red regression line. The blue and red lines are the regression lines with slope and correlation coefficient reported in Table 3.
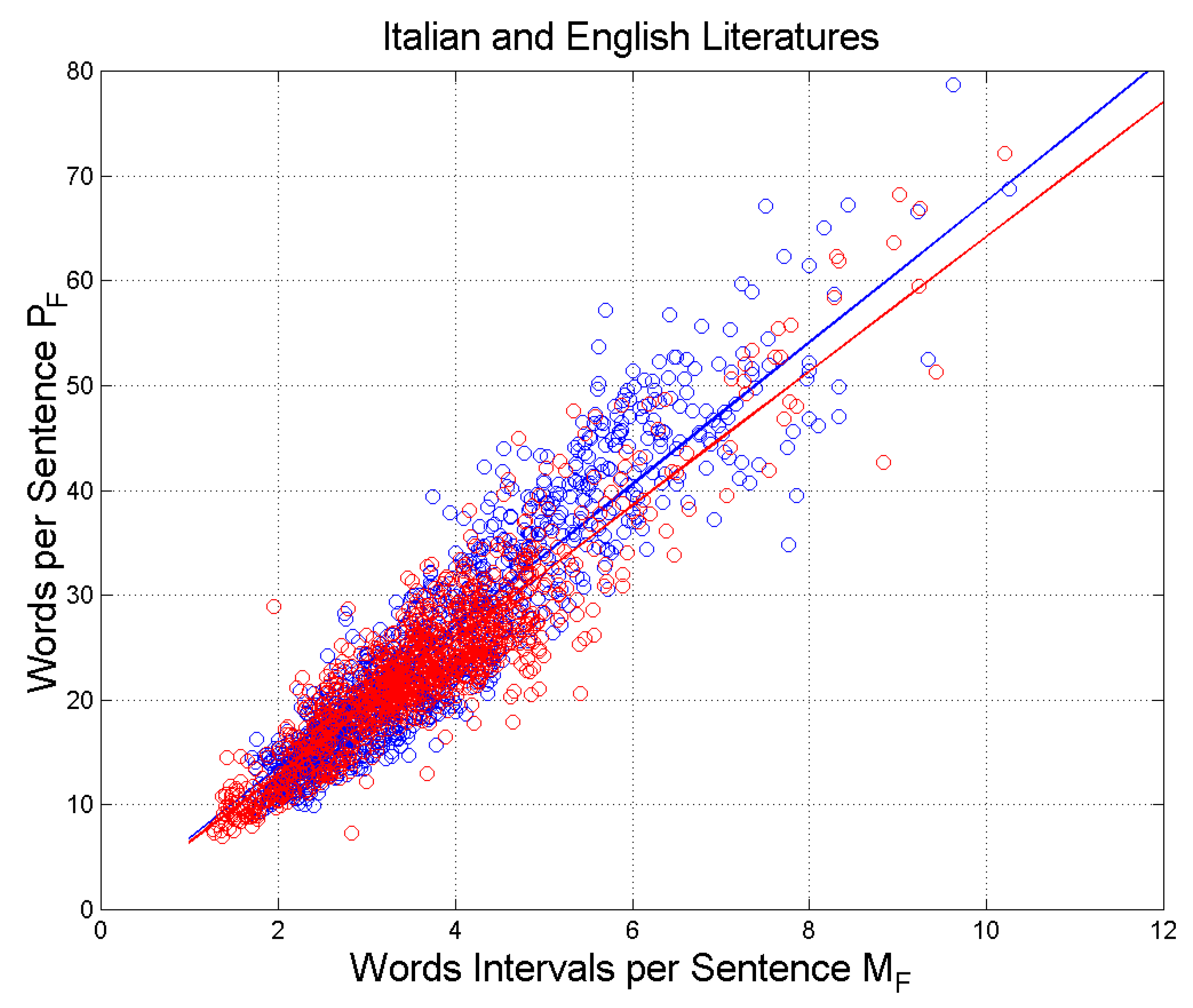
Figure 4.
Scatterplot of versus . Italian Literature: blue circles; English Literature: red circles. The black curve is given by Equation (6) and it is the best-fit curve to all samples. The magenta lines refer to Miller’s law range of STM capacity.
Figure 4.
Scatterplot of versus . Italian Literature: blue circles; English Literature: red circles. The black curve is given by Equation (6) and it is the best-fit curve to all samples. The magenta lines refer to Miller’s law range of STM capacity.
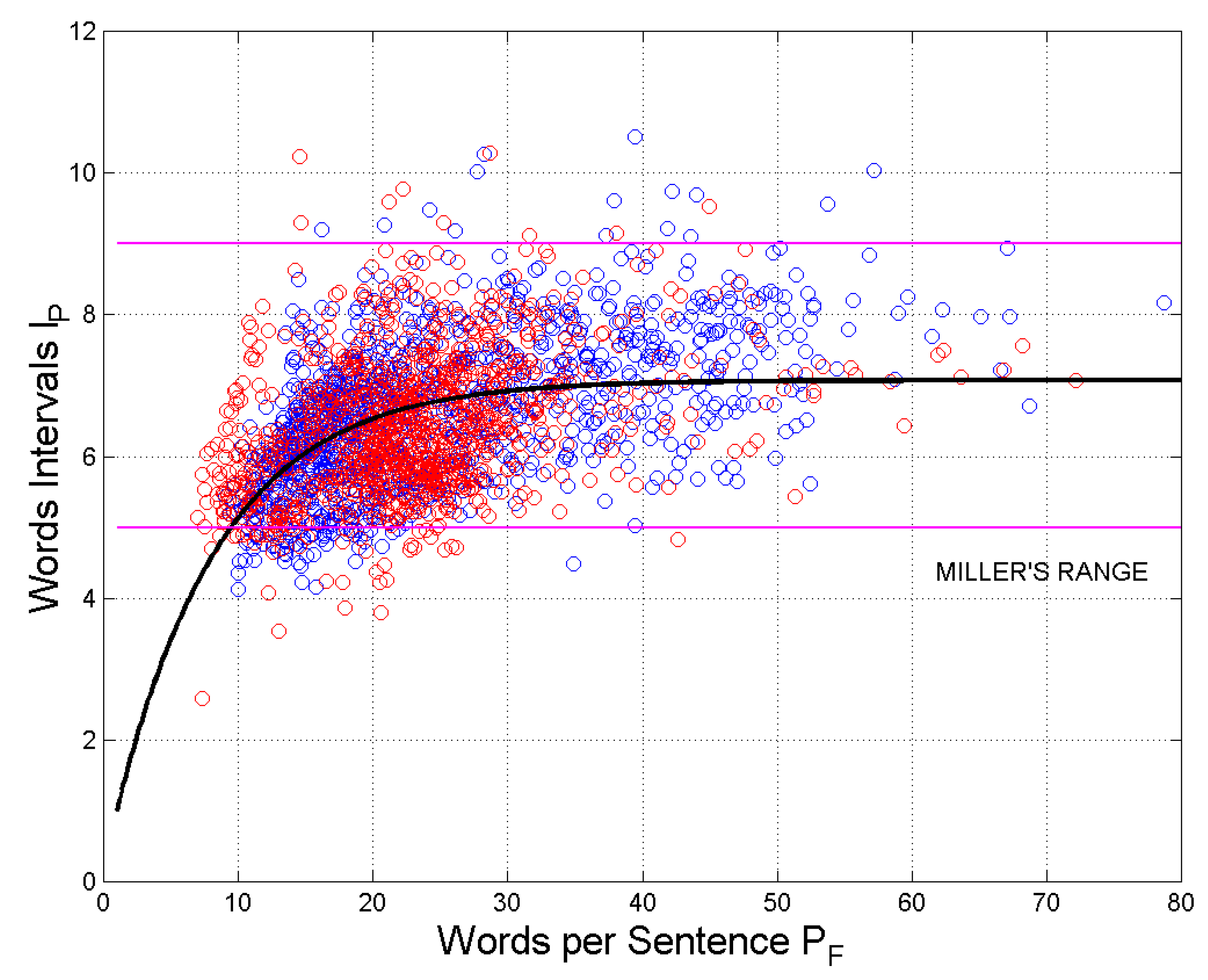
Figure 5.
Scatterplot of versus . Italian Literature: blue circles; English Literature: red circles. Correlation coefficient for Italian, and for English.
Figure 5.
Scatterplot of versus . Italian Literature: blue circles; English Literature: red circles. Correlation coefficient for Italian, and for English.
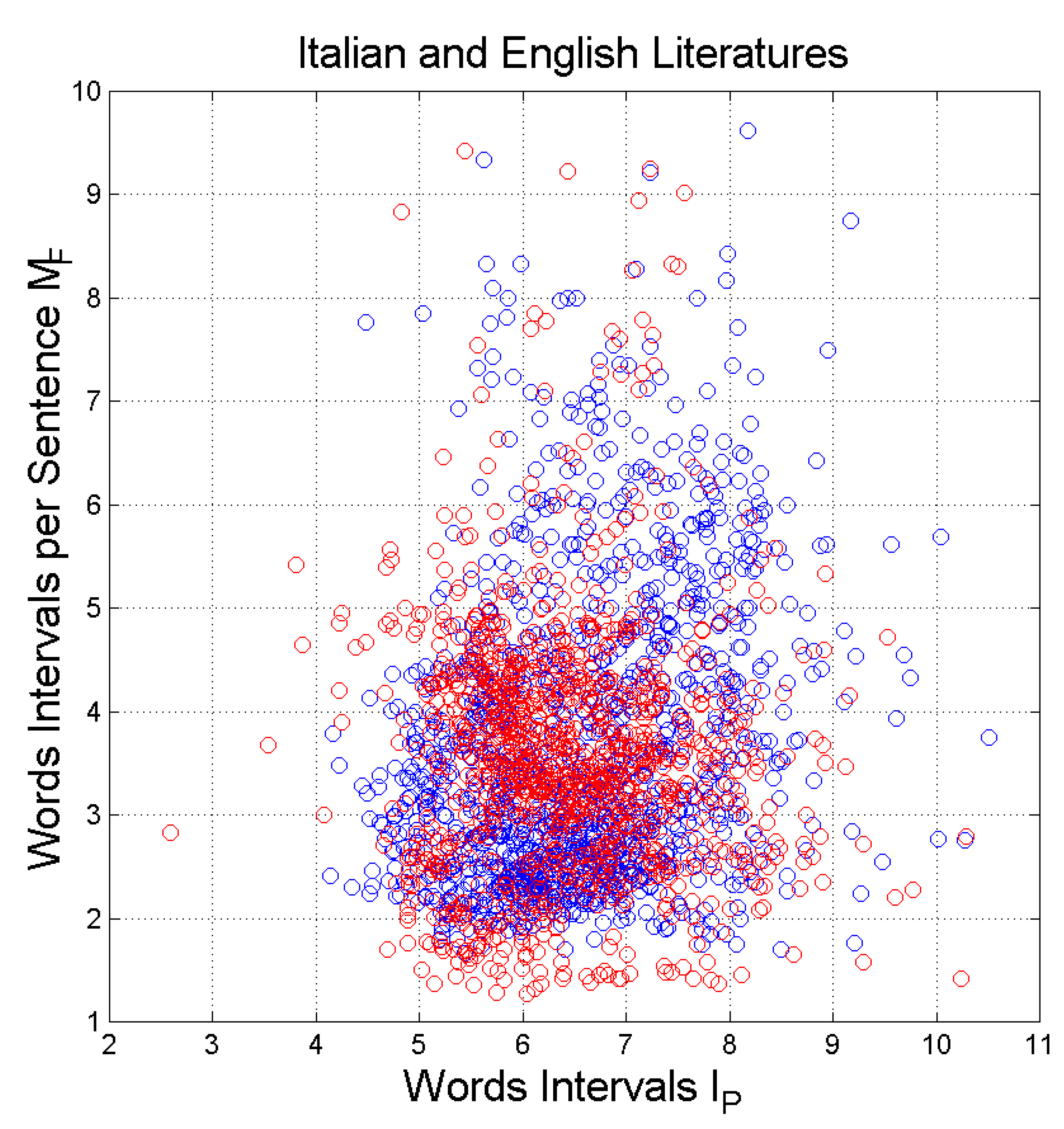
Figure 6.
Histogram and log-normal probability modelling of .
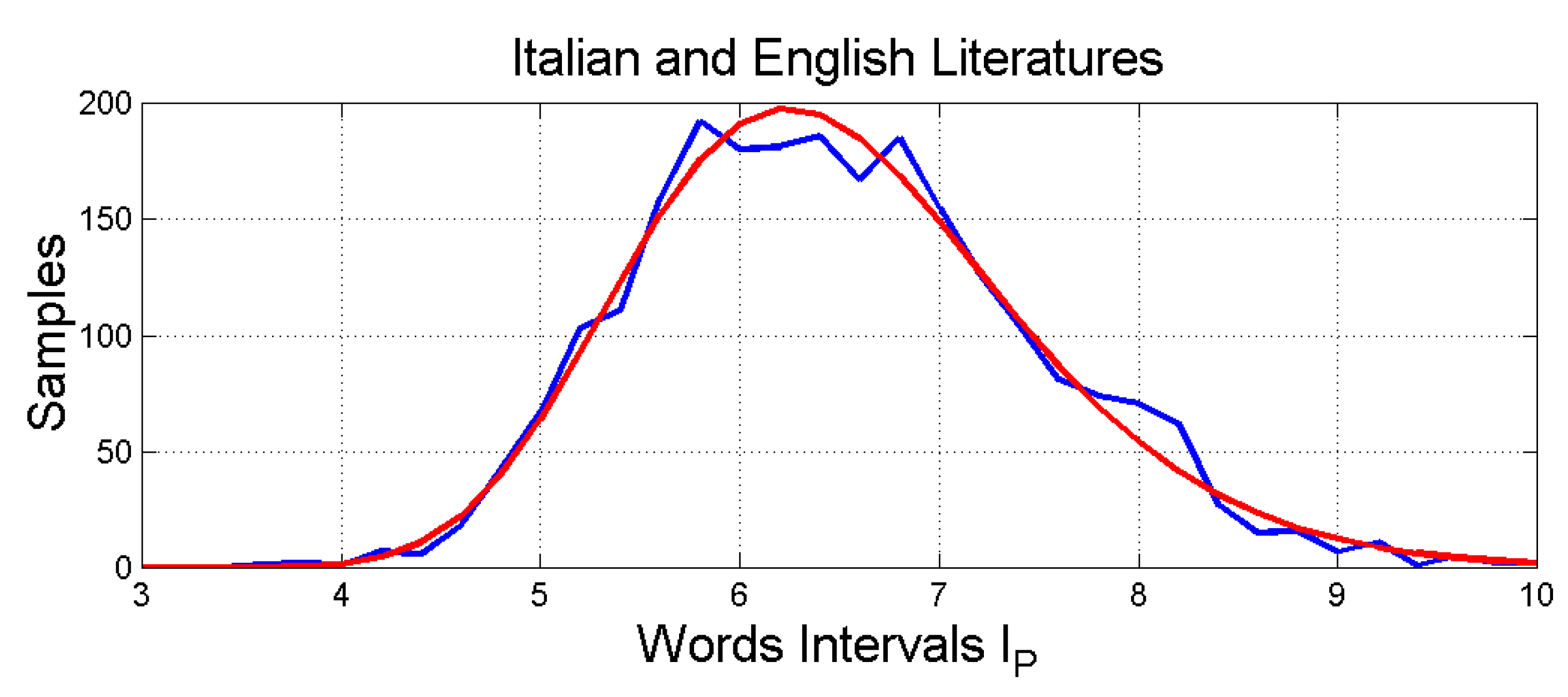
Figure 7.
Histogram and log-normal probability modelling of .
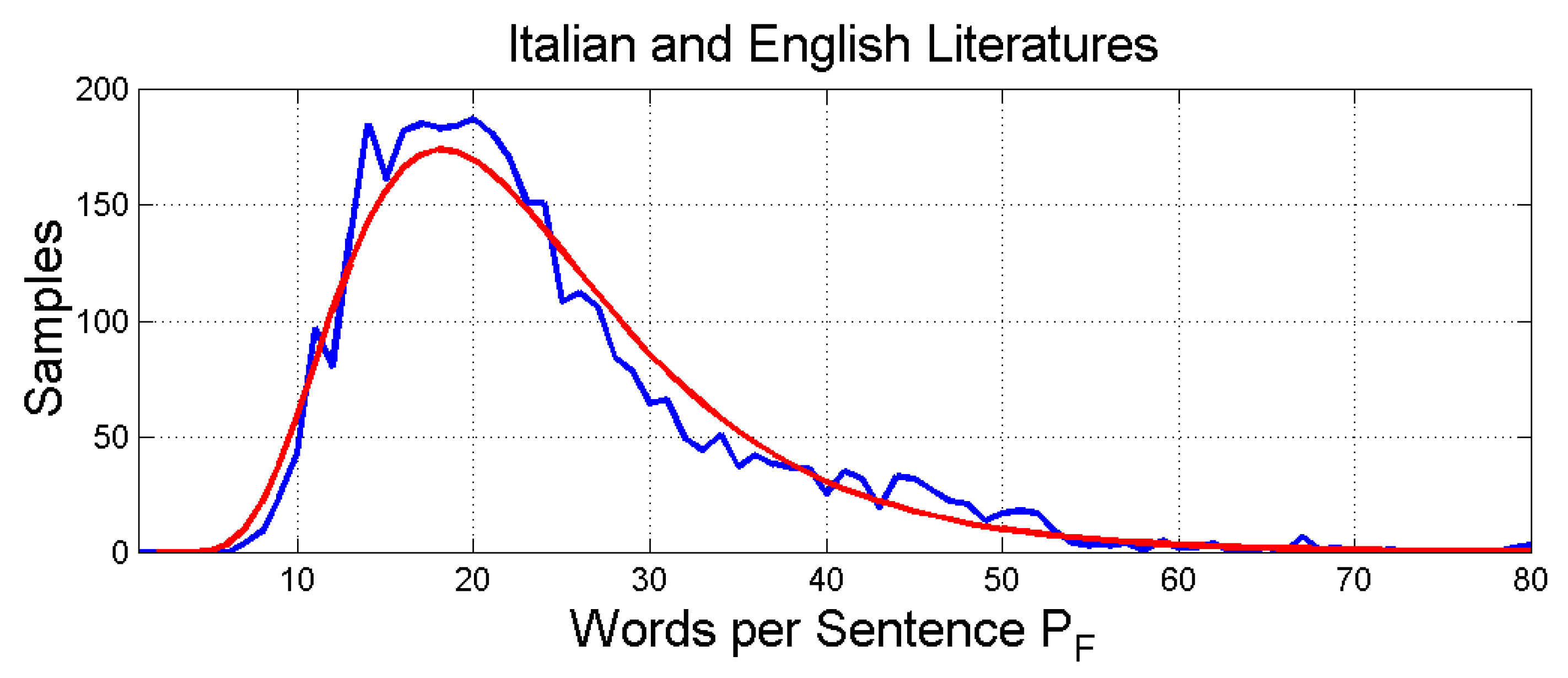
Figure 8.
Histogram and log-normal probability modelling of.
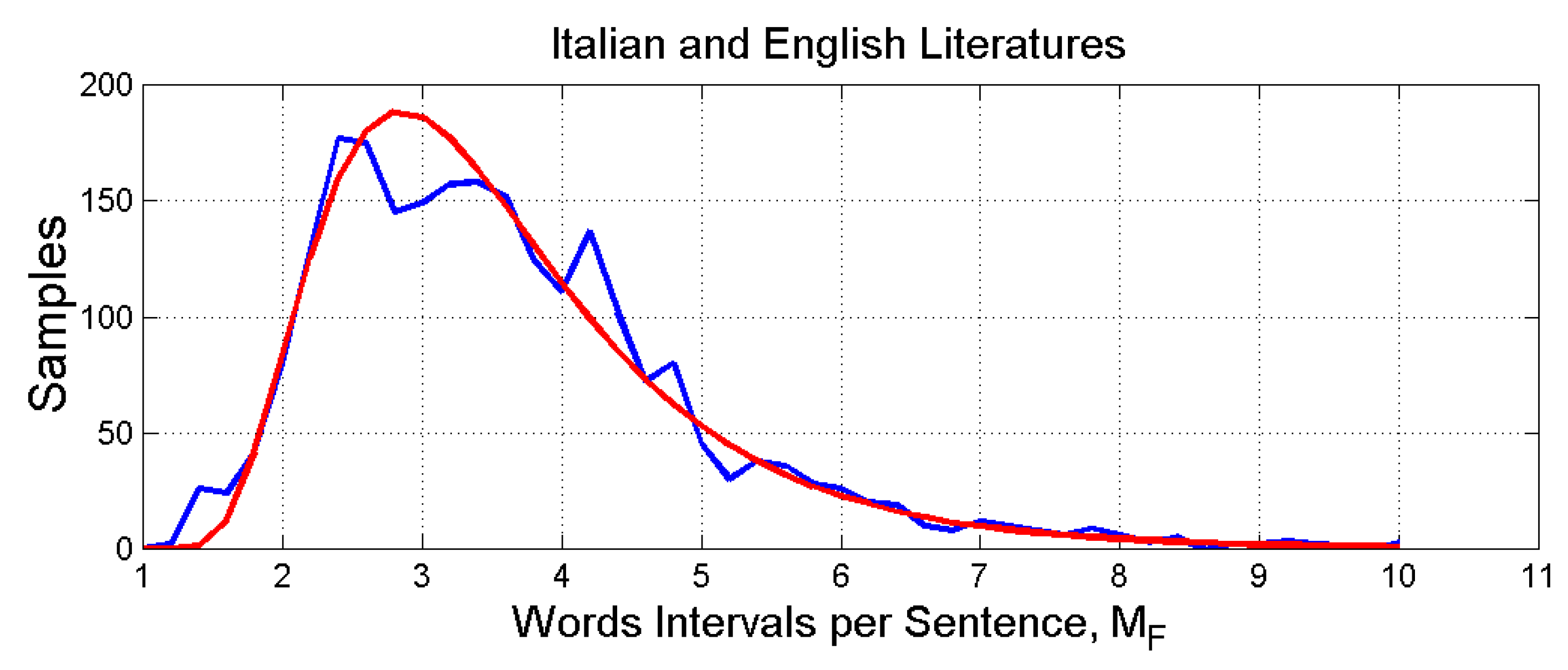
Figure 9.
Histogram of . The mean value is (peak), the standard deviation is and the 95% range is .
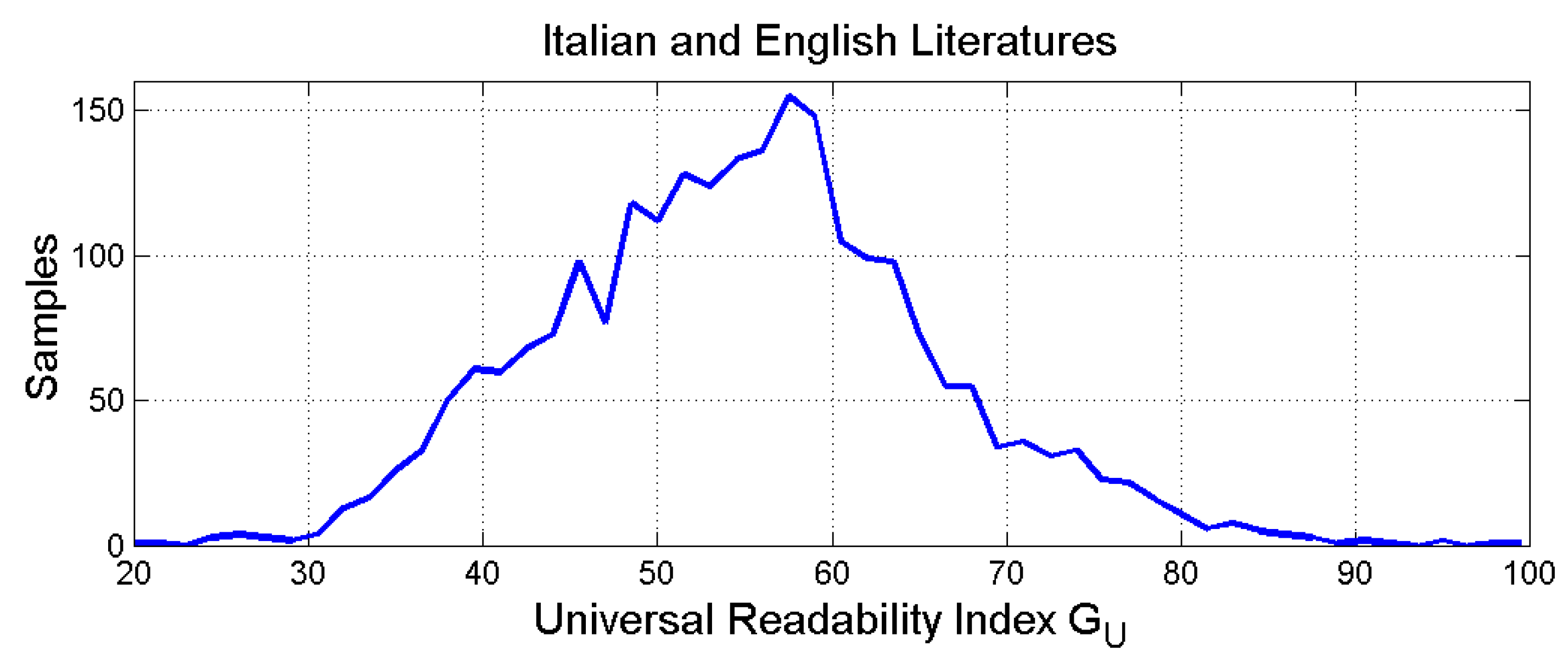
Figure 10.
Scatterplot of the universal readability index versus the word interval . Italian Literature: blue circles; English Literature: red circles. The vertical black lines are drawn at the mean value and at the values is exceeded with probability 0.025 (and 0.975 (The range includes 95% of the samples, therefore, it corresponds to Miller’s range . The horizontal green lines refer to (95% range ).
Figure 10.
Scatterplot of the universal readability index versus the word interval . Italian Literature: blue circles; English Literature: red circles. The vertical black lines are drawn at the mean value and at the values is exceeded with probability 0.025 (and 0.975 (The range includes 95% of the samples, therefore, it corresponds to Miller’s range . The horizontal green lines refer to (95% range ).
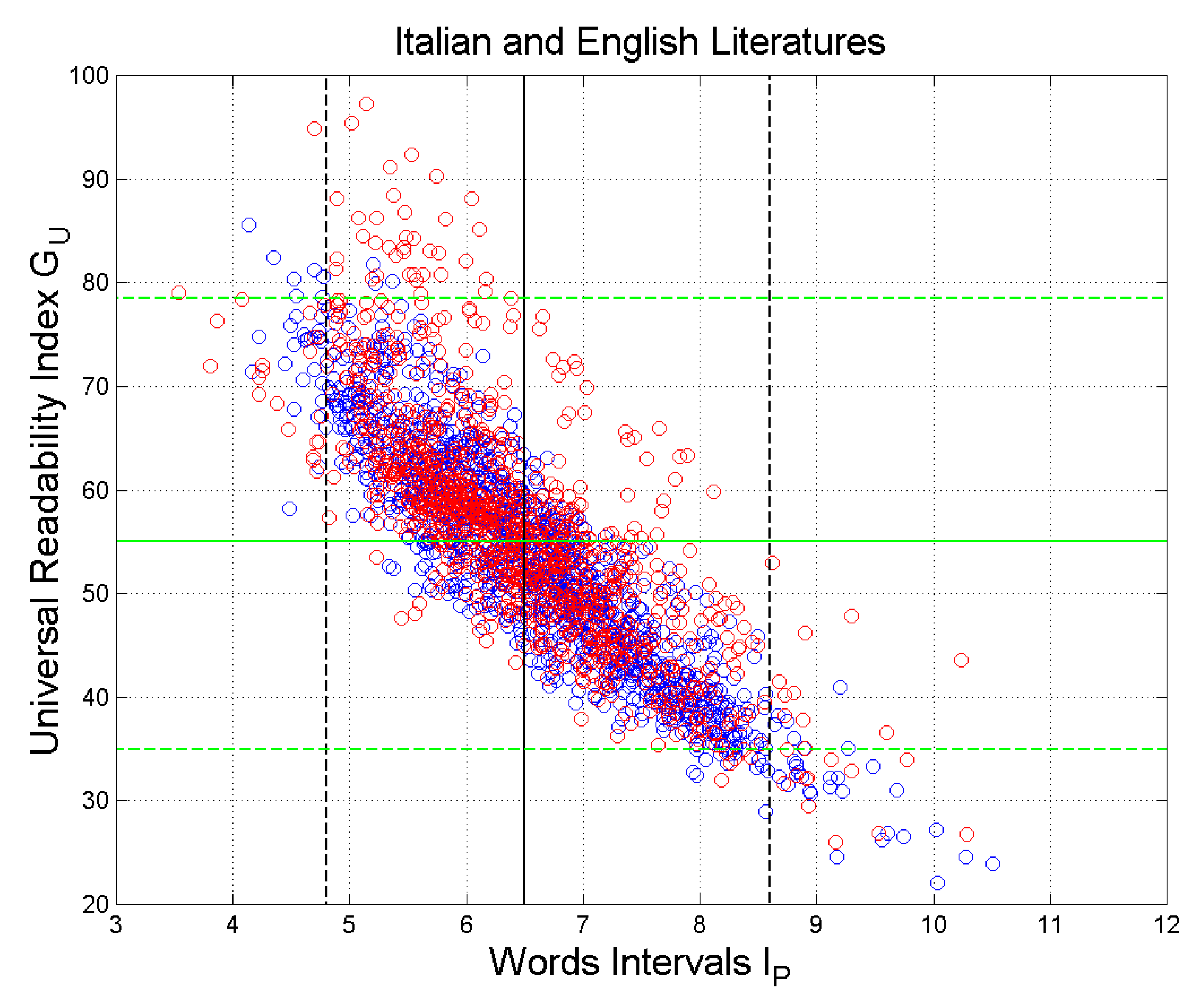
Figure 11.
Scatterplot of the universal readability index versus the words per sentence s . Italian Literature: blue circles and blue regression line; English Literature: red circles and red regression line. The vertical black lines are drawn at the mean value and at the values exceeded with probability (and (The range includes 95% of the samples, therefore, it corresponds to Miller’s range of . The horizontal green lines refer to (95% range ).
Figure 11.
Scatterplot of the universal readability index versus the words per sentence s . Italian Literature: blue circles and blue regression line; English Literature: red circles and red regression line. The vertical black lines are drawn at the mean value and at the values exceeded with probability (and (The range includes 95% of the samples, therefore, it corresponds to Miller’s range of . The horizontal green lines refer to (95% range ).
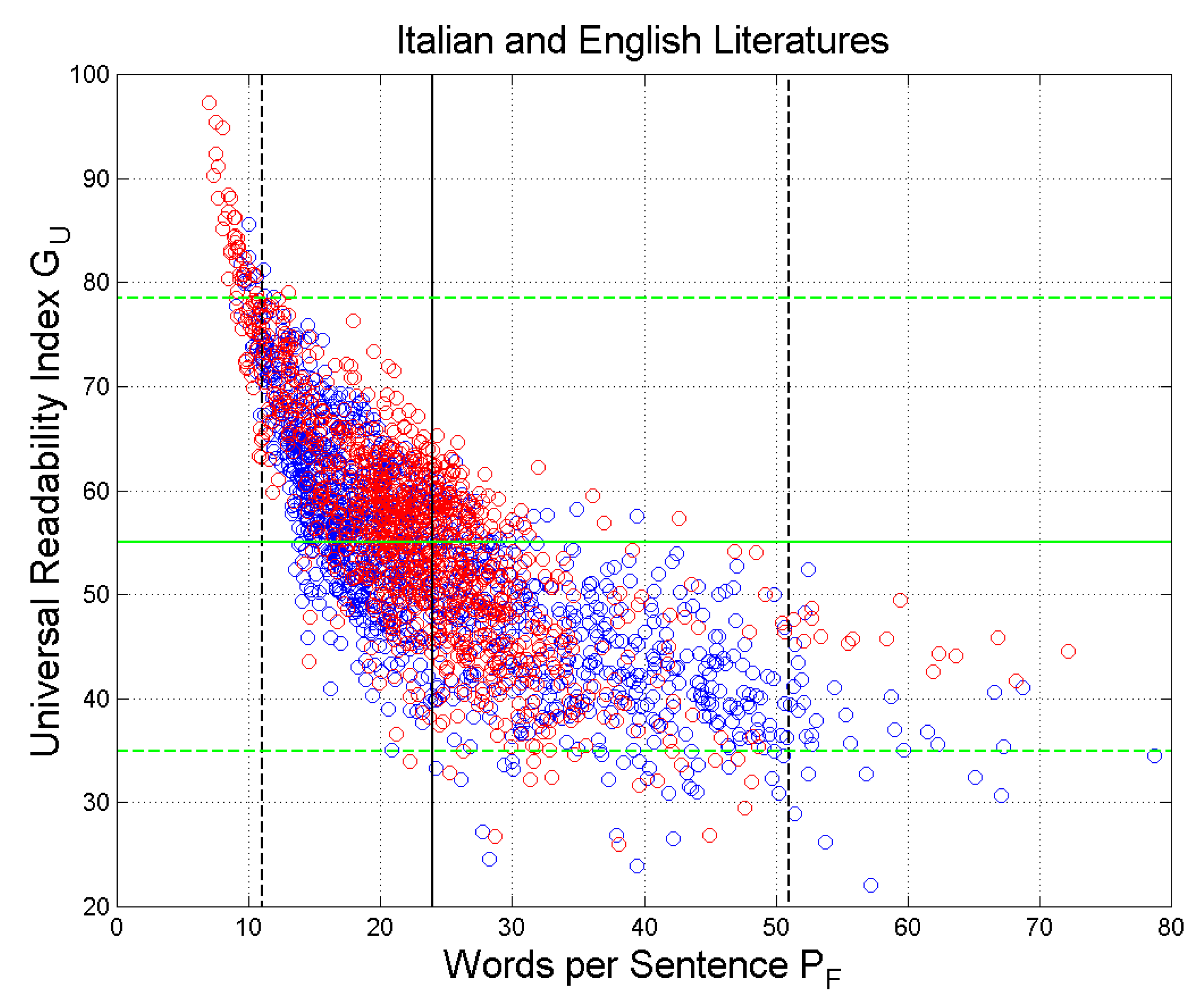
Figure 12.
Scatterplot of the universal readability index versus the word intervals . Italian Literature: blue circles and blue regression line; English Literature: red circles and red regression line. The vertical black lines are drawn at the mean value and at the values exceeded with probability 0.025 (and 0.975 (The range includes 95% of the samples, therefore, it corresponds to Miller’s range. The horizontal green lines refer to (95% range ).
Figure 12.
Scatterplot of the universal readability index versus the word intervals . Italian Literature: blue circles and blue regression line; English Literature: red circles and red regression line. The vertical black lines are drawn at the mean value and at the values exceeded with probability 0.025 (and 0.975 (The range includes 95% of the samples, therefore, it corresponds to Miller’s range. The horizontal green lines refer to (95% range ).
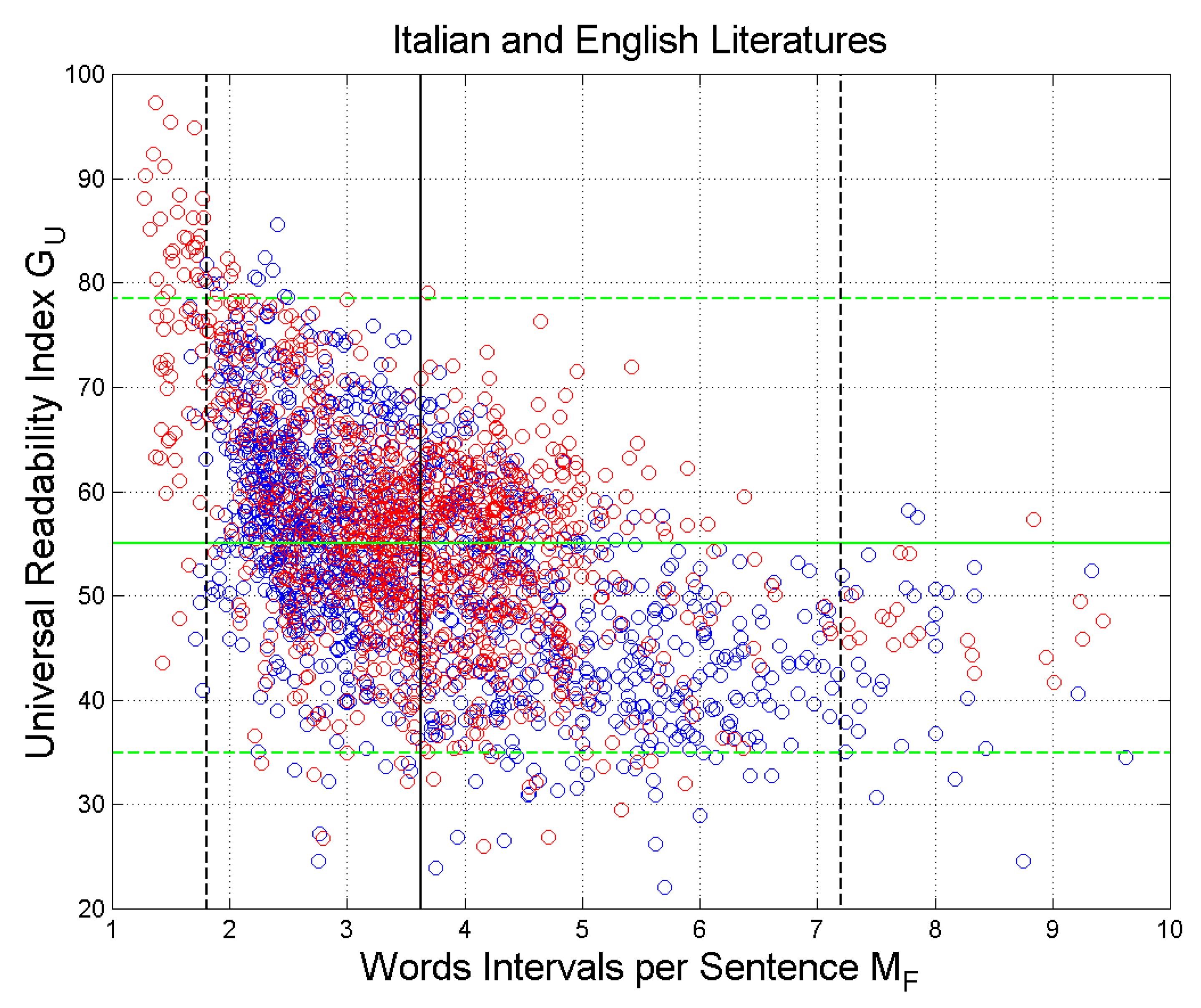
Figure 13.
Capacity of the second STM processing unit, versus capacity of the first STM processing unit, calculated at equal probability exceeded.
Figure 13.
Capacity of the second STM processing unit, versus capacity of the first STM processing unit, calculated at equal probability exceeded.
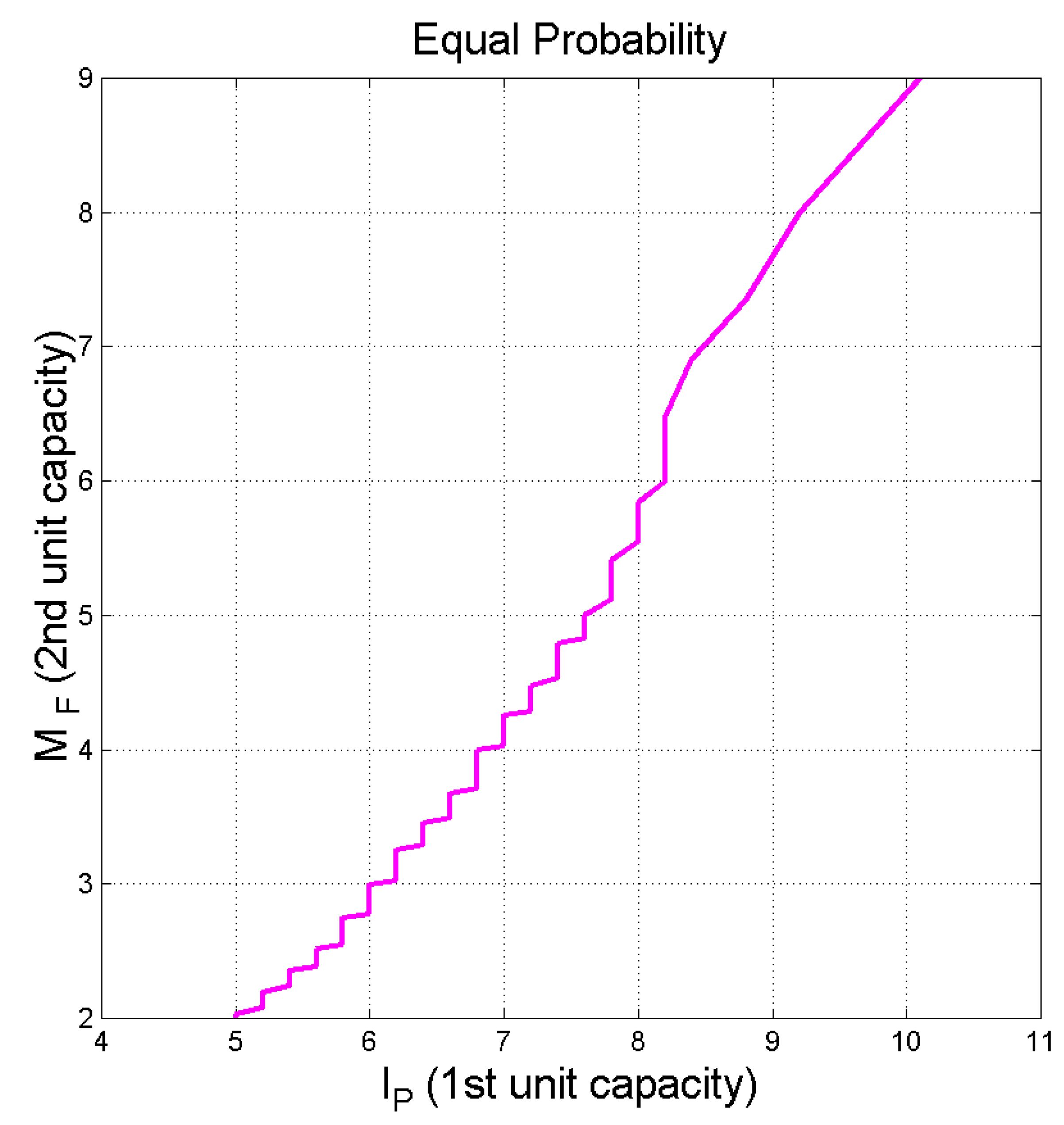
Figure 14.
Flow-chart of the two processing units that make a sentence. The words , ,… are stored in the first buffer up to items, approximately in Miller’s range, until an interpunction is introduced to fix the length of . The word interval is then stored in the E-STM buffer up to items, from about 1 to 6 items, until the sentence ends.
Figure 14.
Flow-chart of the two processing units that make a sentence. The words , ,… are stored in the first buffer up to items, approximately in Miller’s range, until an interpunction is introduced to fix the length of . The word interval is then stored in the E-STM buffer up to items, from about 1 to 6 items, until the sentence ends.
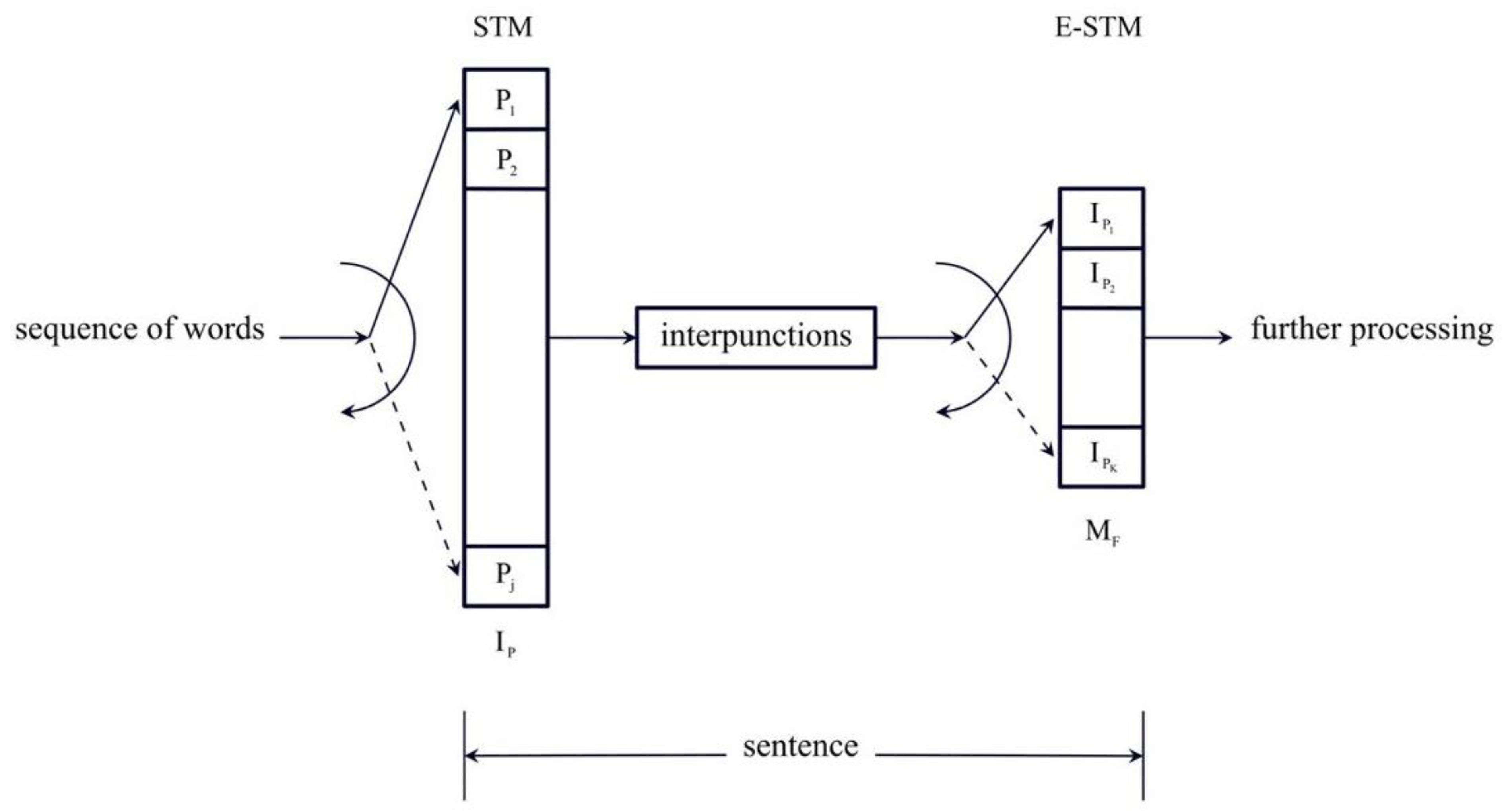
Table 1.
Slope and correlation coefficient of versus of the regression lines drawn in Figure 1.
Table 1.
Slope and correlation coefficient of versus of the regression lines drawn in Figure 1.
| Italian | 0.0474 | 0.877 |
| English | 0.0493 | 0.819 |
Table 2.
Slope and correlation coefficient of interpunctions per chapter, , versus sentences per chapter, , of the regression lines drawn in Figure 2.
Table 2.
Slope and correlation coefficient of interpunctions per chapter, , versus sentences per chapter, , of the regression lines drawn in Figure 2.
| Italian | 2.994 | 0.913 |
| English | 2.969 | 0.853 |
Table 3.
Slope and correlation coefficient of versus of the regression lines drawn in Figure 3.
Table 3.
Slope and correlation coefficient of versus of the regression lines drawn in Figure 3.
| Italian | 6.763 | 0.937 |
| English | 6.421 | 0.914 |
Table 4.
Average value and standard deviation of of the indicated variables and the average value and standard deviation of the error defined as the difference between the number of experimental samples and that predicted by the log-normal model.
Table 4.
Average value and standard deviation of of the indicated variables and the average value and standard deviation of the error defined as the difference between the number of experimental samples and that predicted by the log-normal model.
| Average error | Standard deviation of error | |||
| 0.002 | 56.92 | |||
| 0.049 | 12.44 | |||
| 0.126 | 12.72 |
Table 5.
Linear mean, standard deviation and 95% probability range (Miller’s range) of the indicated variables.
Table 5.
Linear mean, standard deviation and 95% probability range (Miller’s range) of the indicated variables.
| Mean | Standard Deviation | Miller’s Range (95%) | |
Table 6.
Slope and correlation coefficient of the regression line between the same linguistic parameter of the two languages and the signal-to-noise ratio (dB) in the linguistic channel. Input channel: Italian; Output channel: English.
Table 6.
Slope and correlation coefficient of the regression line between the same linguistic parameter of the two languages and the signal-to-noise ratio (dB) in the linguistic channel. Input channel: Italian; Output channel: English.
| S-channel | versus | 1.040 | 0.994 | 18.37 |
| I-channel | versus | 0.992 | 0.992 | 17.80 |
| E-channel | versus | 0.949 | 0.998 | 22.18 |
Table 7.
Slope and correlation coefficient of the regression line between the same linguistic parameter of the two languages and the signal-to-noise ratio (dB) in the linguistic channel. Input channel: English; Output channel: Italian.
Table 7.
Slope and correlation coefficient of the regression line between the same linguistic parameter of the two languages and the signal-to-noise ratio (dB) in the linguistic channel. Input channel: English; Output channel: Italian.
| S-channel | versus | 0.962 | 0.994 | 19.01 |
| I-channel | versus | 1.009 | 0.992 | 17.65 |
| E-channel | versus | 1.053 | 0.998 | 21.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






