1. Introduction
Tensors are high-dimensional arrays that have many applications in science and engineering, including in image, video and signal processing, computer vision, and network analysis [
11,
12,
16,
17,
18,
19,
20,
26]. A new t-product based on third-order tensors proposed by Kilmer et al [
1,
2]. When using high-dimensional data, t-product shows a greater potential value than matricization, see [
2,
6,
11,
12,
21,
22,
24,
25,
27]. The t-product has been found to have special value in many application fields, including image deblurring problems [
1,
6,
11,
12], image and video compression [
26], facial recognition problems [
2], etc.
In this paper, we consider the solution of large minimization problems of the form
The Frobenius norm of singular tube of
rapidly attenuates to zero with the increase of the index number. In particular,
has ill-determined tubal rank. Many of its singular tubes are nonvanishing with tiny Frobenius norm of different orders of magnitude. Problems (
1) with such a tensor is called the tensor discrete linear ill-posed problems. They arise from the restoration of color image and video, see e.g., [
1,
11,
12]. Throughout this paper, the operation ∗ represents tensor t-product and
denotes the tensor Frobenius norm or the spectral matrix norm.
We assume that the observed tensor
is polluted by an error tensor
, i.e.,
where
is an unknown and unavailable error-free tensor related to
.
is determined by
, where
represents the explicit solution of problems (
1) that is to be found. We assume that the upper bound of the Frobenius norm of
is known, i.e,
Straightforward solution of (
1) is usually meanless to get an approximation of
because of the illposeness of
and the error
will be amplified severely. We use Tikhonov regularization to reduce this effect in this paper and replace (
1) with penalty least-squares problems
where
is a regularization parameter. We assume that
where
denotes the null space of
,
is the identity tensor and
is a lateral slice whose elements are all zero. The normal equation of minimization problem (
4) is
then
is the unique solution of the Tikhonov minimization problem (
4) under the assumption (
5).
There are many techniques to determine the regularization parameter
, such as the L-curve criterion, generalized cross validation (GCV), and the discrepancy principle. We refer to [
4,
5,
8,
9,
10] for more details. In this paper, the discrepancy principle is extended to tensors based on t-product and is employed to determine a suitable
in (
4). The solution
of (
4) satisfies
where
is usually a user-specified constant and is independent of
in (
3). When
is smaller enough, and
approaches 0, result in
. For more details on the discrepancy principle, see e.g., [
7].
In this paper, we also consider the expansion of minimization problem (
1) of the form
where
,
.
There are many methods for solving large-scale discrete linear ill-posed problems (
1). Recently, a tensor Golub- Kahan bidiagonalization method [
11] and a GMRES method [
12] were introduced for solving large-scale linear ill-posed problems (
4). The randomized tensor singular value decomposition (rt-SVD) method in [
3] was presented for computing super large data sets, and has prospects in image data compression and analysis. Ugwu and Reichel [
23] proposed a new random tensor singular value decomposition (R-tSVD), which improves the truncated tensor singular value decomposition (T-tSVD) in [
1]. Kilmer et al. [
2] presented a tensor Conjugate-Gradient (t-CG) method for tensor linear systems
corresponding to the least-squares problems. The regularization parameter in the t-CG method is user-specified. In this paper, we further discuss the automatical determinization of suitable regularization parameters of the tCG method by the discrepancy principle. The proposed method is called the tCG method with automatical determination of regularization parameters (auto-tCG). We also present a truncated auto-tCG method (auto-ttCG) to improve the auto-tCG method by reducing the computation. At last, a preprocessed version of the auto-ttCG method is proposed, which is abbreviated as auto-ttpCG.
The rest of this paper is organized as follows.
Section 2 introduces some symbols and preliminary knowledge that will be used in the context.
Section 3 presents the auto-tCG, auto-ttCG and auto-ttpCG methods for solving the minimization problems (
4) and (
9).
Section 4 gives several examples on image and video restoration and
Section 5 draws some conclusions.
2. Preliminaries
This section gives some notations and definitions, and briefly summarizes some results that will be used later. For a third-order tensor
,
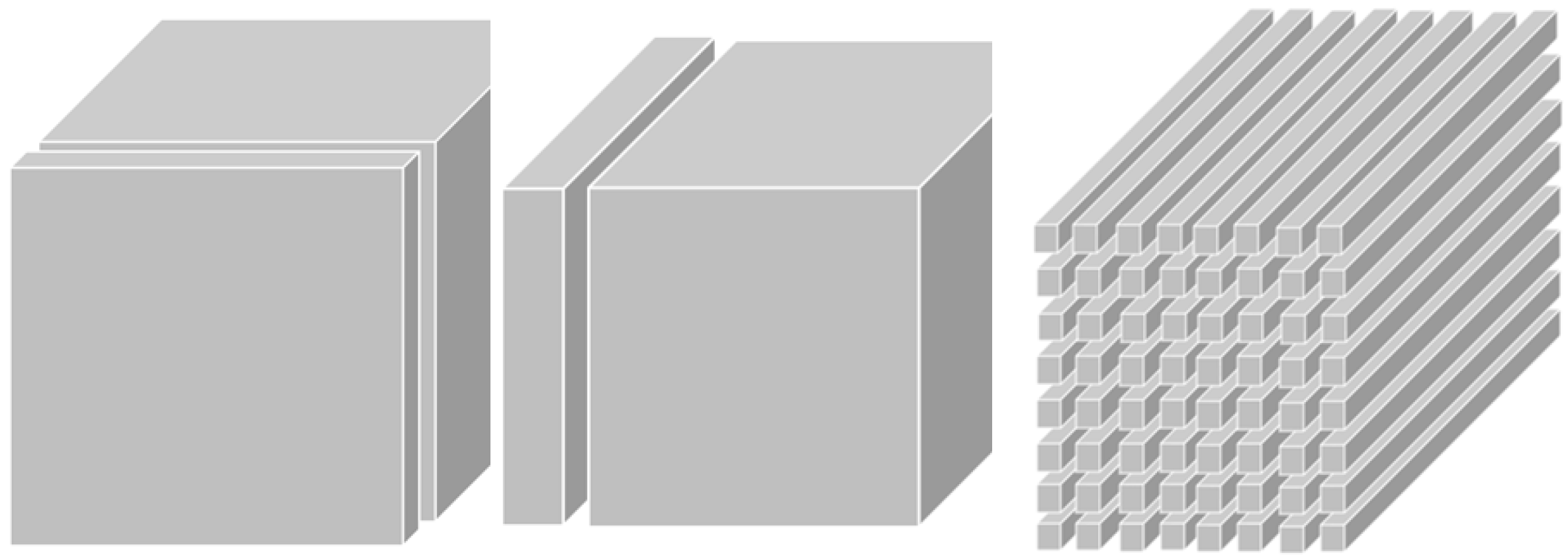
Figure 1 shows the frontal slices
, lateral slices
and tube fibers
. We abbreviate
for simplication. An
matrix is obtained by the operator
, whereas the operator
folds this matrix back to the tensor
, i.e.,
Definition 1.
Let , then a block-circulant matrix of is denoted by , i.e.,
Definition 2. ([1]) Given two tensors and , the t-product is defined as
where .
The following remarks will be used in
Section 3.
Remark 1. ([14]) For suitable tensors and , it holds that
(1). .
(2). .
(3). .
Let
be an n-by-n unitary discrete Fourier transform matrix, i.e,
where
, then we get the tensor
generated by using FFT along each tube of
, i.e,
where ⊗ is the Kronecker product,
is the conjugate transposition of
and
denetes the frontal slices of
. Thus the t-product of
and
in (
10) can be expressed by
and (
10) is reformulated as
It is easy to calculate (
12) in MATLAB.
For a non-zero tensor
, we can decompose it in the form
where
is a normalized tensor; see, e.g., [
6] and
is a tube scalar. Algorithm 1 summarizes the decomposition in (
14).
|
Algorithm 1 Normalization |
|
Input: is a nonzero tensor |
|
Output:, with ,
|
|
fft(,[ ],3) |
|
for
do
|
| ( is a vector) |
| if then
|
|
|
| else
|
| ; ; ;
|
| end if
|
| end for |
|
ifft(,[ ],3); ifft(,[ ],3) |
Given a tensor
, the singular value decomposition (tSVD) of
is expressed as
where
and
are orthogonal under t-product,
is an upper triangular tensor with the singular tubes
satisfying
The operators
and
[
13] are expressed by
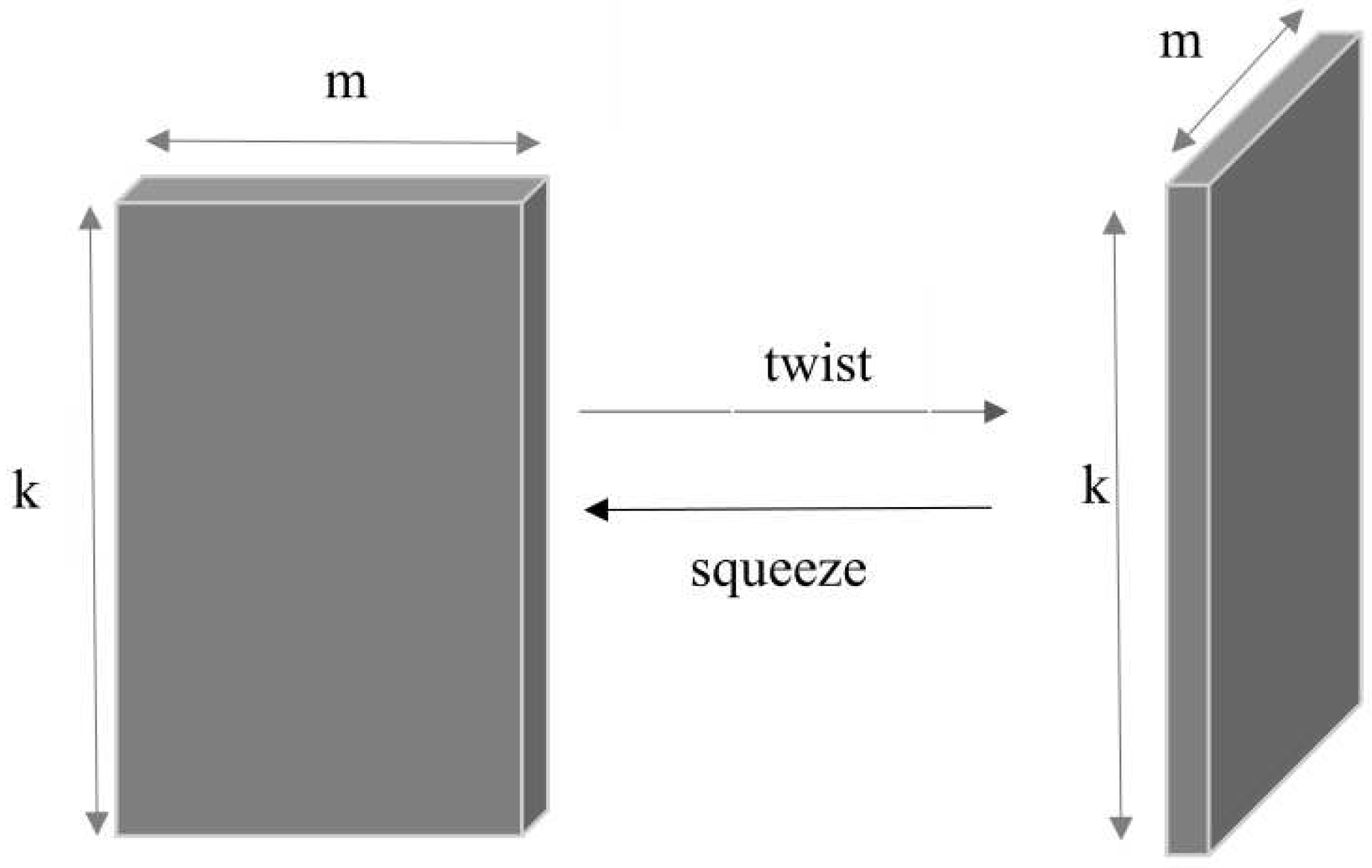
Figure 2 illustrates the transformation between a matrix and a tensor column by using
and
. Generally, the operators
and
are defined for a third-order tensor to make it squeezed or twisted. For a tensor
with
,
means that all side slices of
are squeezed and stacked as front slices of
, the operator
is the reverse operation of
. Thus
. We refer to
Table 1 for more notations and definitions.
4. Numerical Examples
This section presents three examples to show the application of Algorithms 2, 3 and 5 on the restoration of image and video. All calculations are performed in MATLAB R2018a on computers with intel core i7 and 16GB ram.
Suppose
is the
k-th approximate solution to the minimization problem (
9). The quality of the approximate solution
is defined by
the relative error
and
the signal-to-noise ratio (SNR)
where
denotes the uncontaminated data tensor and
is the average gray-level of
. The observed data
in (
9) is contaminated by a "noise" tensor
, i.e.,
.
is determined as follows. Let
be the
th transverse slice of
, whose entries are scaled and normally distributed with a mean of zero, i.e.,
where the data of
is generated according to N(0, 1).
Example 4.1 This example considers the restoration of the blurred and noised
cameraman image with the size of
. For the operator
, its front slices
are generated by using the MATLAB function
blur, i.e.,
with
,
and
. The condition numbers of
are
, while he condition numbers of the remaining slices are infinite. Let
denote the original undaminated
cameraman image. The operator
converts
into tensor column
for storage. The noised tensor
is generated by (
36) with different noise level
. The blurred and noisy images are generated by
.
The auto-tCG, auto-ttCG and auto-ttpCG methods are used to solve the tensor discrete linear ill-posed problems (
1). The discrepancy principle is employed to determine a suitable regularization parameter by using
with
and
. We set
in (
8).
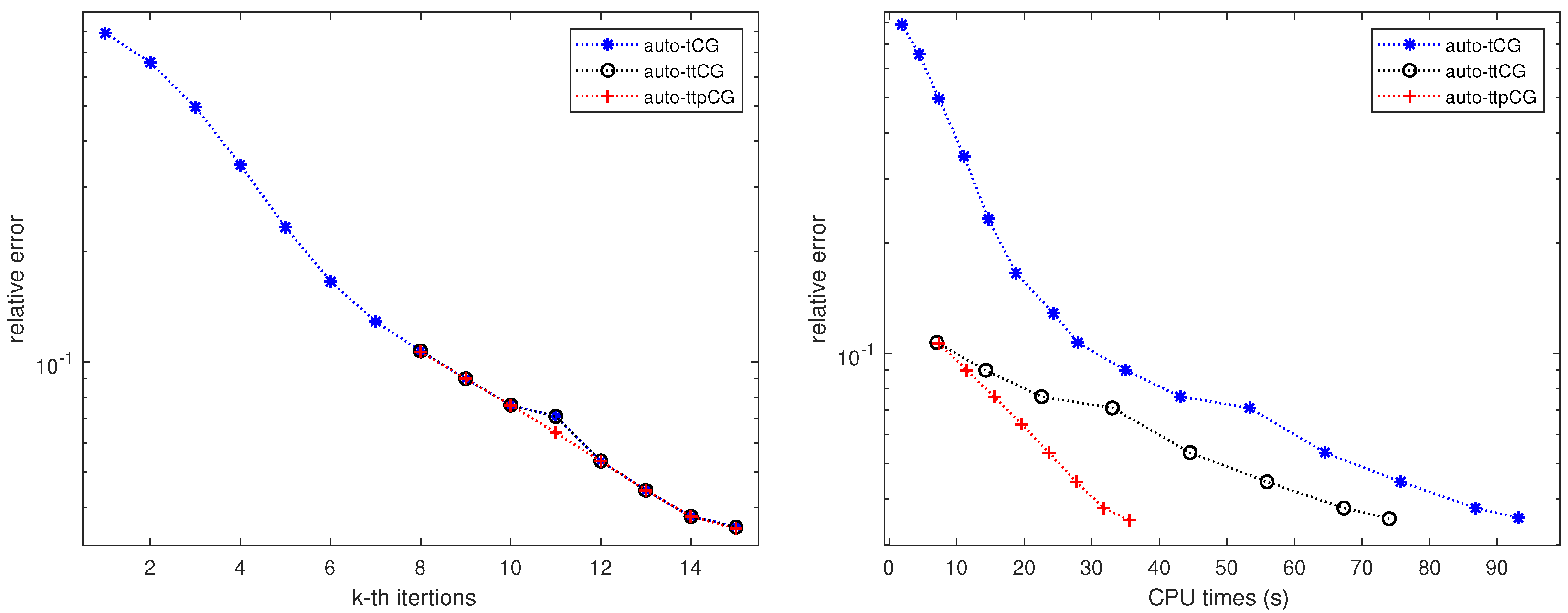
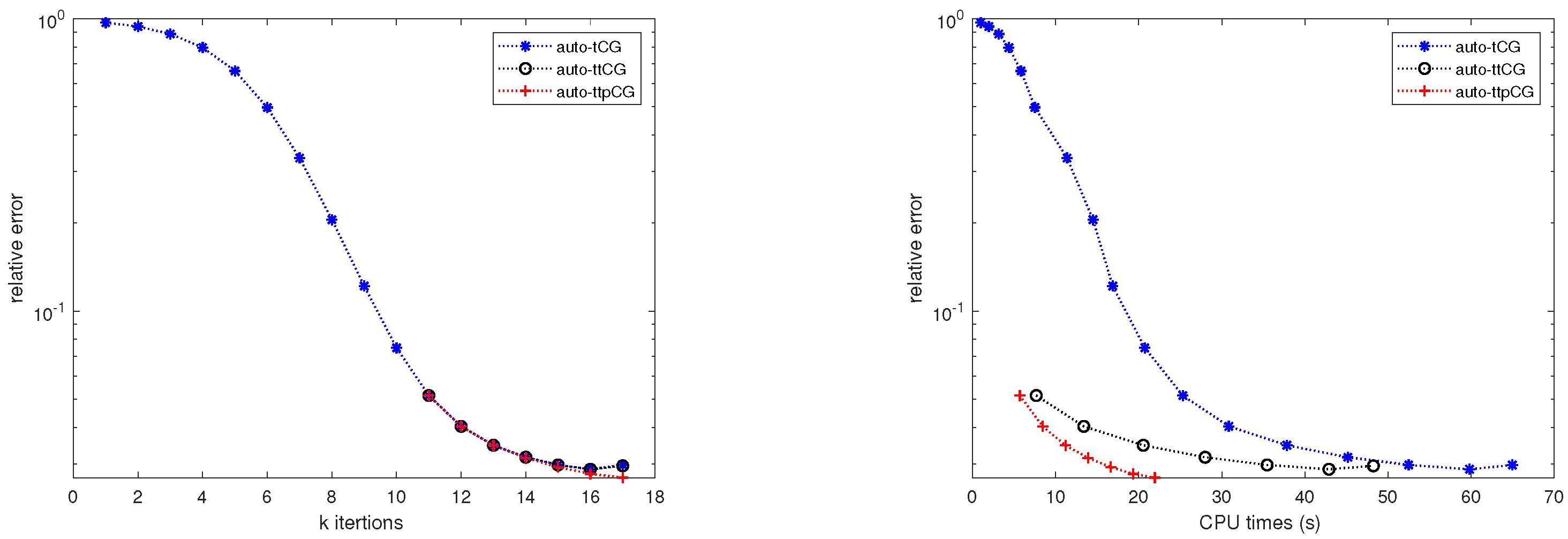
Figure 3 shows the convergence of relative errors verus (a) the iteration number
k and (b) the CPU time for the auto-tCG, auto-ttCG and auto-ttpCG methods with the noise level
corresponding in the
Table 2. The iteration process is terminated when the discrepancy principle is satisfied. From
Figure 3 (a), we can see that the auto-ttCG and auto-ttpCG methods do not need to solve the normal equation for all
. This shows that the auto-ttCG and auto-ttpCG methods improve the auto-tCG method by the condition (
24).
Figure 3 (b) shows that the auto-ttpCG method converges fastest among three methods.
Table 2 lists the regularization parameter, the iteration number, the relative error, SNR and the CPU time of the optimal solution obtained by using the auto-tCG, auto-ttCG and auto-ttpCG methods with different noise levels
. It can be seen from
Table 2 that the auto-ttpCG method has the lowest relative error, highest SNR and the least CPU time for different noise level.
Figure 4 shows the reconstructed images obtained by using the auto-tCG, auto-ttCG and auto-ttpCG methods on the blurred and noised image with the noise level
in
Table 2. From
Figure 4 we can see that the restored image by the auto-ttpCG method looks a bit better than others but the least CPU time.
Example 4.2 This example shows the restoration of a blurred
color image by Algorithms 2, 3 and 5. The original
image
is stored as a tensor
through the MATLAB function
. We set
and band=12, and get
by
Then
, and the condition number of other tensor slices of
is infinite. The noise tensor
is defined by (
36). The blurred and noised tensor is derived by
, which is shown in Figure 6 (a).
We set the color image
to be divided into multiple lateral slices and independently process each slice through (
1) by using the auto-tCG, auto-ttCG and auto-ttpCG methods.
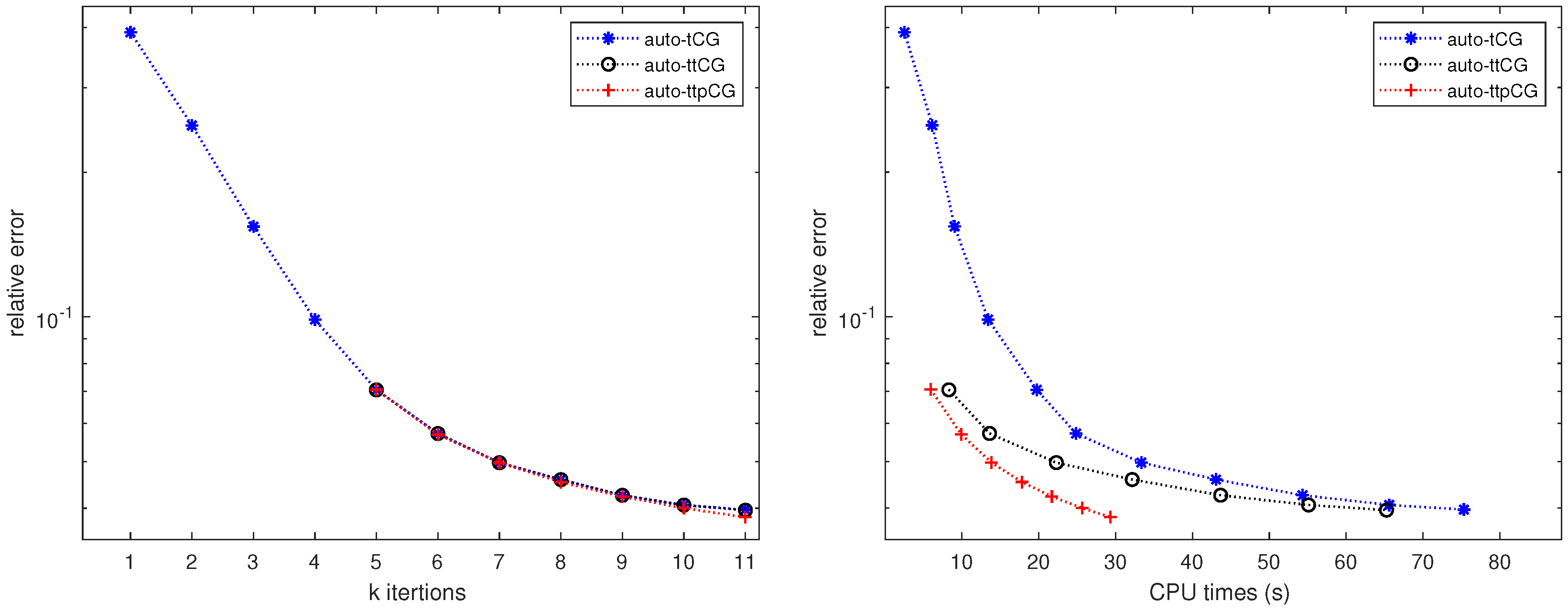
Figure 5 shows the convergence of relative errors verus (a) the iteration number
k and (b) the CPU time for the auto-tCG, auto-ttCG and auto-ttpCG methods when dealing with the first tensor lateral slice
of
with
. Similar results can be derived as that in Example 5.1 from
Figure 5. We can see that the auto-ttCG and auto-ttpCG methods need less iterations than the auto-tCG method from
Figure 5 (a) and the auto-ttpCG method converges fastest among all methods from
Figure 5 (b).
Table 3 lists the relative error, SNR and the CPU time of the optimal solution obtained by using the auto-tCG, auto-ttCG and auto-ttpCG methods with different noise levels
. The results are very similar to that in
Table 2 for different noise level.
Table 3.
Example 4.2: Comparison of relative error, SNR, and CPU time between the auto-tCG, auto-ttCG and auto-ttpCG methods with different noise level .
Table 3.
Example 4.2: Comparison of relative error, SNR, and CPU time between the auto-tCG, auto-ttCG and auto-ttpCG methods with different noise level .
| Noise level |
Method |
Relative error |
SNR |
time (secs) |
|
auto-tCG |
5.90e-02 |
14.62 |
314.73 |
| auto-ttCG |
5.90e-02 |
14.62 |
262.81 |
| auto-ttpCG |
5.43e-02 |
15.37 |
103.41 |
|
auto-tCG |
7.64e-02 |
12.37 |
117.48 |
| auto-ttCG |
7.48e-02 |
12.55 |
62.01 |
| auto-ttpCG |
7.01e-02 |
13.13 |
54.85 |
Figure 6 shows the recovered images by the auto-tCG, auto-ttCG and auto-ttpCG methods corresponding to the results with noise level
. The results are very similar to that in
Figure 6.
Figure 6.
Example 4.2: (a) The blurred and noised
Lena image and reconstructed images by (b) the auto-tCG method, (c) the auto-ttCG and (d) the auto-ttpCG method according to the noise level
in
Table 3.
Figure 6.
Example 4.2: (a) The blurred and noised
Lena image and reconstructed images by (b) the auto-tCG method, (c) the auto-ttCG and (d) the auto-ttpCG method according to the noise level
in
Table 3.
Example 4.3 (
Video) We recover the first 10 consecutive frames of blurred and noised
Rhinos video from MATLAB. Each frame has
pixels. We store 10 pollution- and noise-free frames of the original video in the tensor
. Let
z be defined by (
37) with
,
and
. The coefficient tensor
is defined as follows:
The condition number of the frontal slices of
is
, and the condition number of the remaining frontal sections of
is infinite. The suitable regularization parameter is determined by using the discrepancy principle with
. The blurred- and noised tensor
is generated by
with
being defined by (
36).
Figure 7 shows the convergence of relative errors verus the iteration number
k and relative errors verus the CPU time for the auto-tCG, auto-ttCG and auto-ttpCG methods when the second frame of the video with
is restored. Very similar results can be derived from
Figure 7 to that in Example 5.1.
Table 4 displays the relative error, SNR and the CPU time of the optimal solution obtained by using the auto-tCG, auto-ttCG and auto-ttpCG methods for the second frame with different noise levels
. We can see that the auto-ttpCG method has the largest SNR and the lowest CPU time for different noise level
.
Figure 8 shows the original video, blurred and noised video, and the recovered video of the second frame of the video for the auto-tCG, auto-ttCG and the auto-ttpCG methods with noise level
corresponding to the results in
Table 4. The recovered frame by the auto-ttpCG method looks best among all recovered frames.