Study on the Mechanism of Gas Intrusion and Its Transportation in Wellbore Under Shut-In Conditions

This paper presents a comprehensive study based on multiphase seepage and wellbore multiphase flow theories. It establishes a gas intrusion rate calculation model that considers various factors including formation pore permeability, bottomhole pressure difference, drilling fluid rheology, and surface tension. Experiments were conducted to investigate the gas intrusion mechanism under shut-in conditions, and the experimental results were employed to validate the reliability of the proposed gas intrusion rate calculation method. Furthermore, the research explores the transportation rates of single bubbles and bubble clusters in drilling fluid under shut-in conditions. Meanwhile, empirical expressions were derived for the drag coefficient for single bubbles and bubble clusters in the wellbore. These expressions can be used to calculate gas transportation rates for various equivalent radii of single bubbles and bubble clusters. Additionally, a method was developed for calculating the rising velocity of bubble clusters in water based on experimental results. The study reveals that the average bubble size in the bubble cluster is significantly smaller than the size of the single bubble generated from the orifice. When the viscosity of the drilling fluid is low, the bubble cluster transportation velocity exhibits a positive correlation with the average bubble diameter. When the average bubble diameter exceeds 1 mm, the bubble velocity no longer varies with the change in the bubble cluster diameter. The initial bubble size of intrusive gas, the transportation speed of intrusive gas in the wellbore, the gas intrusion rate, and variations of the wellbore pressure after gas intrusion were analyzed. The research results provide theoretical support for wellbore pressure prediction and pressure control under shutdown conditions.

Keywords:

Subject: Engineering - Mining and Mineral Processing

1. Introduction

As oil and gas exploration extends into deep and ultra-deep formations, the geological structures encountered during the drilling of oil and gas wellbores become notably complex. Studies show that various factors can lead to the intrusion of formation fluids into these wellbores. In the process of offshore drilling, if gas invasion and overflow are not detected in time, a blowout can rapidly occur. Influx fluids tend to have a high pressure; a gas kick is much more detrimental than a liquid kick due to gas expansion and, as a result, has a higher variation in pressure [1]. To ensure the safety of drilling operations and facilitate the rapid progress of drilling, the development of a precise model for gas intrusion rates and bubble transportation is of significant importance. Such a model can provide the foundation for predicting wellbore pressure dynamics.

The mechanisms responsible for gas intrusion into the wellbore can be categorized into three classes: differential pressure gas intrusion, diffusion gas intrusion, and gas intrusion driven by gravity displacement. The present study focuses on the most common mechanism, which is differential pressure gas intrusion. The majority of gas intrusion models based on differential pressure gas intrusion have been developed using the percolation theory. Numerous investigations have considered various factors influencing pressure differential gas intrusion. For instance, Rommetveit [2] conducted field experiments to investigate the impact of diverse factors on gas intrusion. Moreover, Stefan and Samuel [3] focused on the pore pressure and permeability of the formation in the prediction model.

To enhance the accuracy of multiphase flow models and simulate gas intrusion accurately, numerous investigations have been conducted focusing on gas bubble migration. Gas migration is a crucial process in gas-liquid two-phase flows, and is also a theoretical and fundamental problem in wellbore during well drilling. Studies show that the mechanisms governing gas migration are closely related to factors such as drilling conditions, drilling fluid properties, and gas intrusion into the wellbore. Davies and Taylor [4] proposed a predictive expression for gas slip velocity in various flow types such as Taylor bubbles, segmented plug flow, and churning flow within vertical round tube flow. Harmathy [5] performed experiments and derived an empirical expression for estimating bubble rising velocity in stationary liquids. Wallis [6] studied the flow of gas bubbles in stationary liquids in a round tube and modified the empirical expression proposed by Harmathy for single bubbles. Mendelson, Fan, and Tamiyama [7] introduced different models for the rising velocity of gases in non-Newtonian fluids under various experimental conditions. In recent years, extensive investigations have been carried out focusing on bubble-rising behavior, employing advanced experimental equipment and numerical simulation techniques. For instance, Tai Wang et al. [8] studied the fusion of two bubbles along the same axis, revealing that bubbles do not fuse when the surface tension is high. Conversely, it was found that bubbles are prone to fragmentation when the surface tension is very small. Liu Yipeng et al. [9] combined the theory of flow transformation with experiments and developed a predictive expression for the formation position of Taylor bubbles in cryogenic pipelines. Krzan et al. [10] performed comprehensive experiments and demonstrated that the addition of a small quantity of ionic surfactant can effectively reduce the rising rate of bubbles in organic solutions. Furthermore, Azzopardi et al. [11] experimentally investigated the rising of large bubbles in highly viscous liquids and established a model for periodic oscillation of the free liquid surface induced by gas lift. Keshavarzi et al. [12] experimentally analyzed the interface deformation during the rise of individual bubbles and validated the theoretical models of VOF and CLSVOF. Cano-Lozano et al. [13] correlated the Rastello bubble linear rise model with the Clift bubble curve rise model, yielding a correlation equation applicable to the calculation of bubble rise velocities for a wide range of bubble diameters and liquid properties. Xiao Kang Yan [14] conducted numerous experiments using a high-speed video system and proposed an equation for predicting the drag coefficient. Khodayar [15] investigated the dynamics of rising bubbles on vertical walls under different wettability conditions, discovering that bubbles with contact angles less than 90° move faster than bubbles with contact angles more than 90°. Du Jingyu [16] found that bubble lift-off diameter is arranged to be related to wall superheat, latent heat, liquid velocity, fluid properties, bulk liquid subcooling, etc. Francesca [17] examined the effects of density and viscosity on the behavior of bubble populations in turbulent channels, highlighting the influence of viscosity in fracture and agglomeration. He Hongbin [18] used numerical simulations to investigate the effects of initial bubble diameter, horizontal spacing and arrangement on the kinematic state of three parallel bubbles.

Recently, investigating gas intrusion in conjunction with engineering challenges has become a research hot topic. However, the majority of studies have focused on gas intrusion during normal drilling, and a few comprehensive investigations are related to wells. This gap is especially more pronounced in deep-water oil and gas fields with long distances from offshore, often exceeding 300 km. During these offshore operations, which may also involve lengthy equipment maintenance periods due to severe weather conditions, gas can intrude into the wellbore and subsequently accumulate at the wellhead. Over time, this accumulation poses a significant risk to open-well operations [19]. In the case of pressure differential gas intrusion under well shut-in conditions, the behavior of gas-liquid two-phase flow within the wellbore differs from other conditions where gas intrusion occurs. This may be because the drilling fluid cannot flow back out from the wellhead. Studies show that the initial characteristics of the invading gas bubbles and their rising velocity within the wellbore are influenced by a variety of factors, including surface tension, rheological properties, density of the drilling fluid under well shut-in conditions, reservoir properties, and the pressure difference between the reservoir and the wellbore bottom. It is worth noting that the rise speed of intrusion gas bubbles within the wellbore is an important parameter for calculating the wellbore pressure and the total gas intrusion volume. A review of the literature indicates that although numerous investigations have been conducted in the field of wellbore drilling and gas intrusion, further research is required in areas such as analyzing the influence of surface tension, rheological characteristics, density of drilling fluids, reservoir properties, and pressure difference between the reservoir and the wellbore bottom on the size of intrusion gas bubbles and flow patterns of individual and cluster bubble within the wellbore. Aiming at addressing this shortcoming, the present study investigates the gas intrusion mechanism when gas enters the wellbore due to pressure differences during well shutdown. This investigation considers various formation properties, drilling fluid characteristics, and pressure difference conditions between formation and wellbore. The study focuses on the initial size of bubbles, the transportation speed of the intruding gas within the wellbore, and changes in gas intrusion rates. The findings of this article are expected to provide theoretical support for predicting and controlling wellbore pressure under shutdown conditions.

2. Visualization of gas intrusion

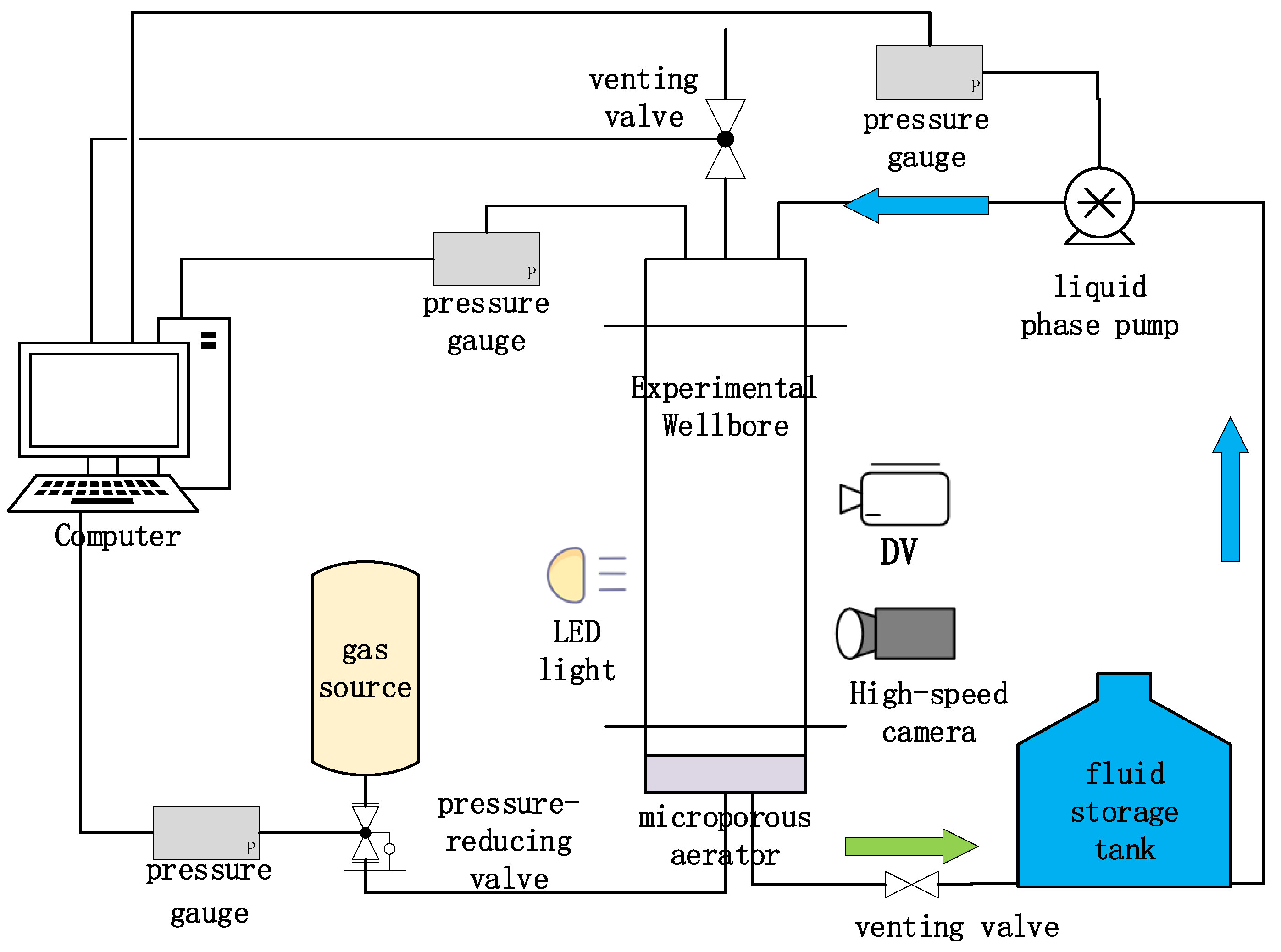
2.1. Experimental system

Schematic of the experimental setup is shown in Figure 1. The experimental setup for simulating gas intrusion under well shutdown conditions consists of a stratigraphic system, an experimental wellbore system, and a data acquisition system.

The stratigraphic system consists of a gas source, a pressure-reducing valve, a pressure gauge, a microporous aerator (92 mm diameter, 80 mesh screen), and several valves. During the experiment, gas passes through the microporous aerator and is transported upward in the wellbore in the form of bubble clusters.

The main structure of the experimental wellbore system is constructed from Plexiglas with an inner diameter of 150 mm, a wall thickness of 10 mm, a height of 1000 mm, and a pressure resistance of 5 MPa. The bottom center of the wellbore is connected to the stratigraphic system, and the side of the wellbore is equipped with a drain hole for discharging the experimental solution. Meanwhile, a scale is provided within the wellbore and on walls to calibrate the size of air bubbles and the void ratio of the wellbore. The upper part of the wellbore is equipped with a manometer, a liquid injection hole, and an air vent hole.

The data acquisition system includes a pressure acquisition module and an image acquisition module. The former module consists of a pressure gauge at the gas source and a manometer at the top of the wellbore, which measures the pressure and transmits the collected data to the computer. The latter module consists of a high-speed camera (OLYMPUS I-Speed 3, Japan), a DV, and a computer. The high-speed camera has a maximum frame rate of 2000 fps and a pixel accuracy of 13 μm.

2.2. Experimental materials

Xanthan gum (XC) is a commonly used viscosity enhancer for drilling fluids, and. In the present study, deionized water and aqueous solutions with various concentrations of Xanthan gum are utilized to simulate drilling fluids in the experiments. The experimental process considered the influence of liquid phase rheology on the gas intrusion speed and the size of the intruding bubbles, while the effects of gas dissolution on the intrusion are ignored. Furthermore, nitrogen was used as the experimental gas phase. The rheological test results of the experimental solutions with various concentrations are shown in Figure 2.

The solution rheology was fitted using a power law function with the specific parameters shown in Table 1.

2.3. Experimental procedure

The experiments are divided into the simulation of gas intrusion into the wellbore under shut-in conditions and the simulation of intruded gas transportation velocity in the wellbore under shut-in conditions. Prior to the experiment, instruments were calibrated, the connection joints between instruments and pipelines were sealed, and the gas tightness test was conducted across the experimental loop. To minimize the experimental errors, each test was repeated five times and the average data was recorded. The main experimental procedures are as follows:

(1) Simulation of gas intrusion into the wellbore under shut-in conditions

This part of the test consists of six parts as the following:

① Connect the experimental device and check its gas tightness;

② Inject the experimental solution to the liquid surface at a height of 70 cm, the upper part of the air is at atmospheric pressure;

③ Close the top exhaust valve of the wellbore, adjust the decompression valve in the system to the set pressure, open the ball valve injecting the formation gas into the wellbore, record variations of the gas pressure within the wellbore using a manometer and record the gas intrusion into the wellbore using a high-speed camera. Furthermore, record the size and rising speed of bubbles, as well as the gas level in the gas intrusion using DV;

④ When the pressure in the upper part of the wellbore is stabilized, close the ball valves between the injection system and the wellbore, and open the venting valve at the top of the wellbore to exhaust the accumulated gas;

⑤ Repeat steps ③ and ④ for 5 times and record the data;

⑥ Adjust the pressure of the formation simulation system, and repeat the steps ③-⑤ to study gas intrusion under different pressure conditions. After completion of the experiment, open the drain valve at the bottom of the wellbore, drain the experimental solution, and inject deionized water to inflate and clean the wellbore 3-5 times; Replace the experimental solution and repeat steps ③-⑥ to simulate gas intrusion under various pressure differences.

(2) Obtaining intrusive gas transportation velocity within the wellbore under shut-in conditions

Bubble cluster transport velocity experiments were conducted using various solutions under shut-in conditions, following the same experimental procedure as described in the experiment (1). Subsequently, the microporous aerator was replaced with a 0.5 mm diameter nozzle, and experiments were conducted to measure the transport velocity of individual bubbles under various solution properties. The measurement of bubble speed involves the following steps:

①Time measurement: Set the shooting rate of the high-speed camera to 1000 fps;

② Coordinate conversion: There is a scale within the wellbore, and the interval between every two scales along the horizontal direction is 1 mm. In the vertical direction, the heights of the scale lines are as follows: The ordinary scale line is 3 mm, the secondary scale line every 5 mm is 4 mm, and the main scale line every 10 mm is 5 mm. This scale is used to convert pixel coordinates to mm-scale coordinates, thereby eliminating the “convex lens” effect on the bubble geometry within the circular wellbore;

③Measurement of bubble geometric features: Utilize the Edit-Draw function in Image Pro Plus software to trace the outline of the selected bubble. Then use the count size function to determine parameters at the center of the bubble, including horizontal and vertical coordinates (X, Y), maximum radius (Rmax), and minimum radius (Rmin). Additionally, the Measure function was employed to directly measure the geometric features of the bubble;

④ Bubble rising speed measurement: While observing the movement of bubbles in the camera, select a bubble in the i^th frame, measure its geometric features (X1, Y1, R1max, and R1min), record its geometric features in the i+n^th frame (X2, Y2, R2max, and R2min), and calculate the average rising speed of bubbles over the test period using the following expression:

u_{z} = \frac{Y_{2} - Y_{1}}{Δ t} = \frac{Y_{2} - Y_{1}}{0.001 n}

(2-1)

3. Results and Analysis

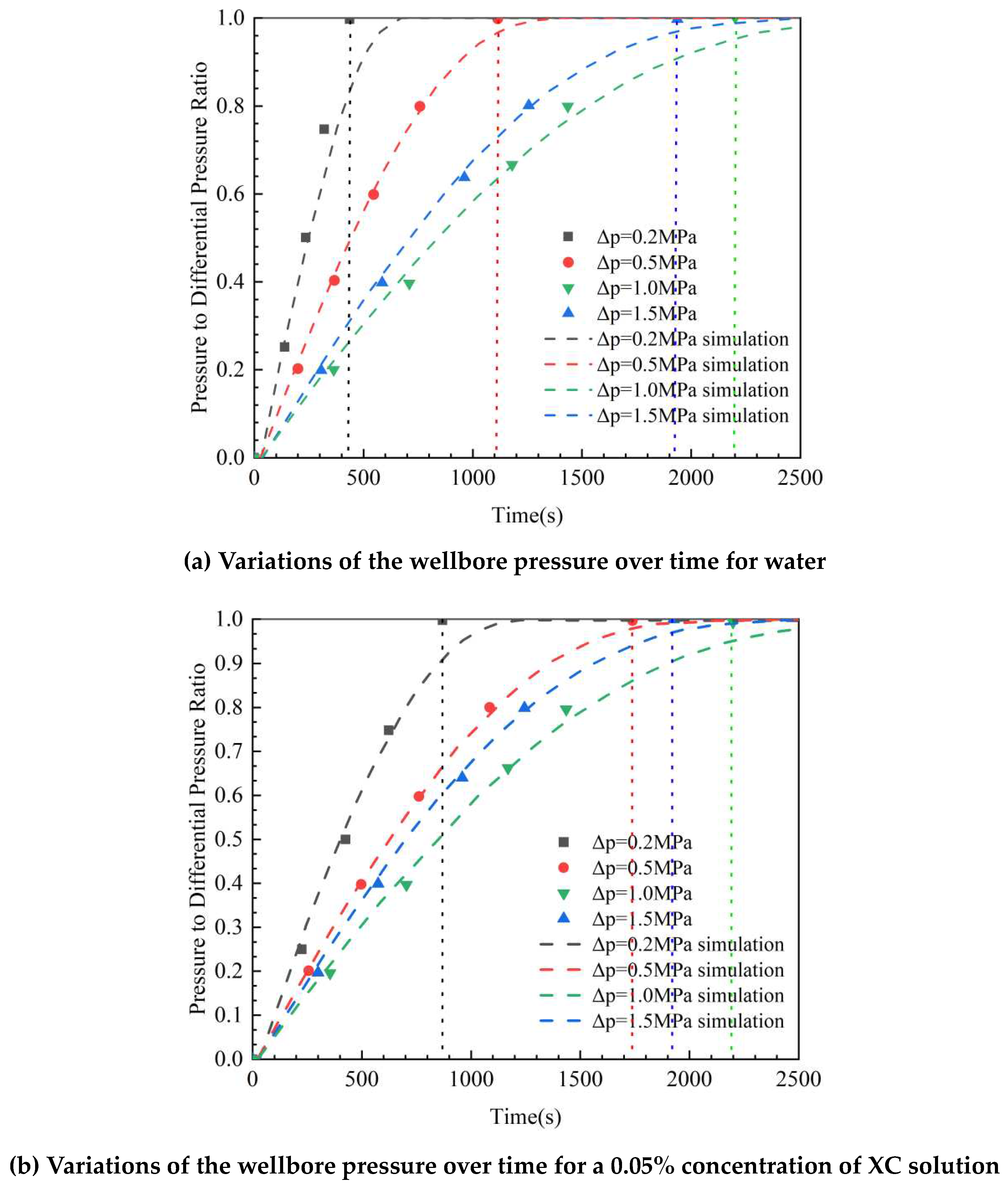
3.1. Simulation of gas intrusion into the wellbore under shutdown conditions

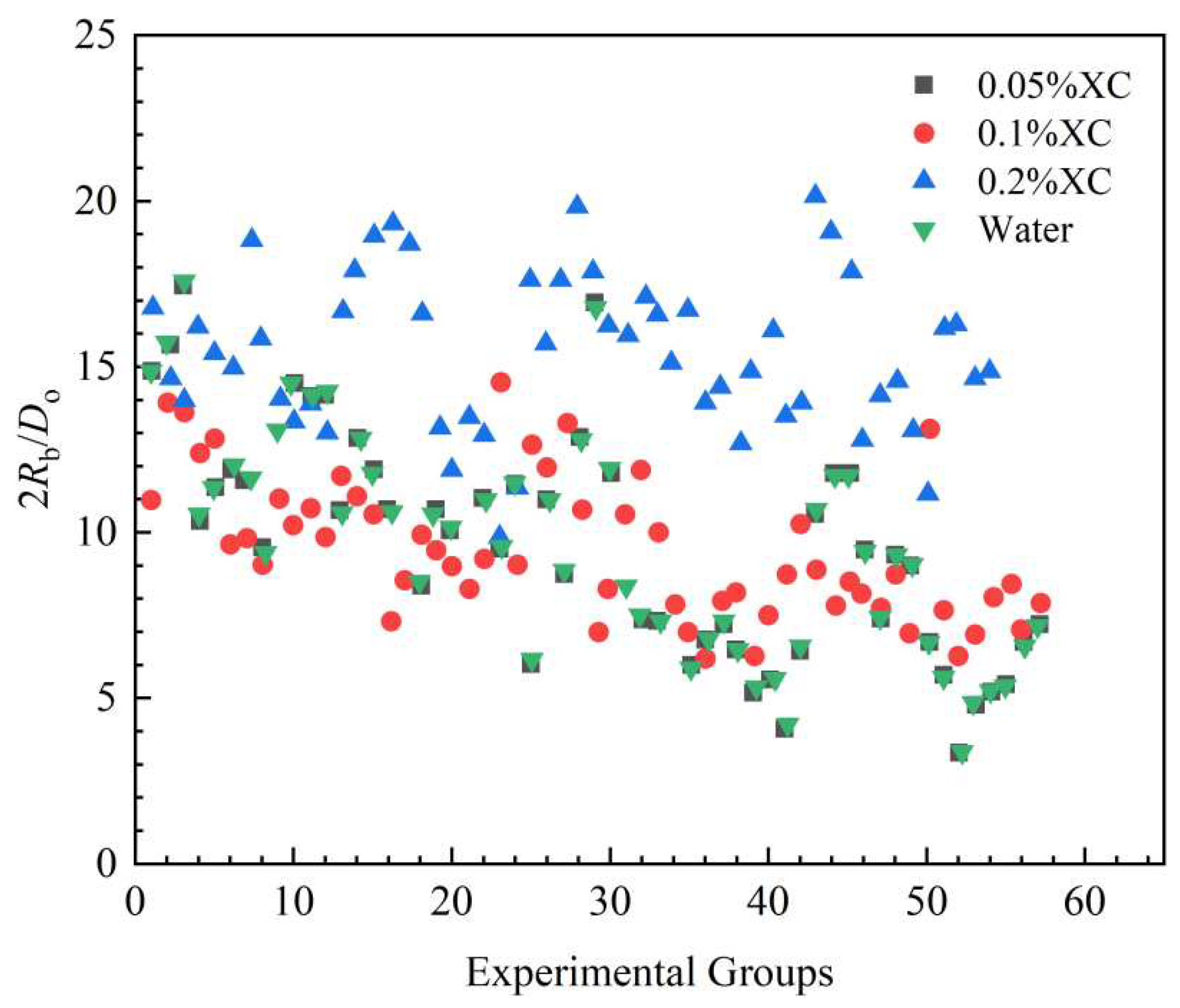
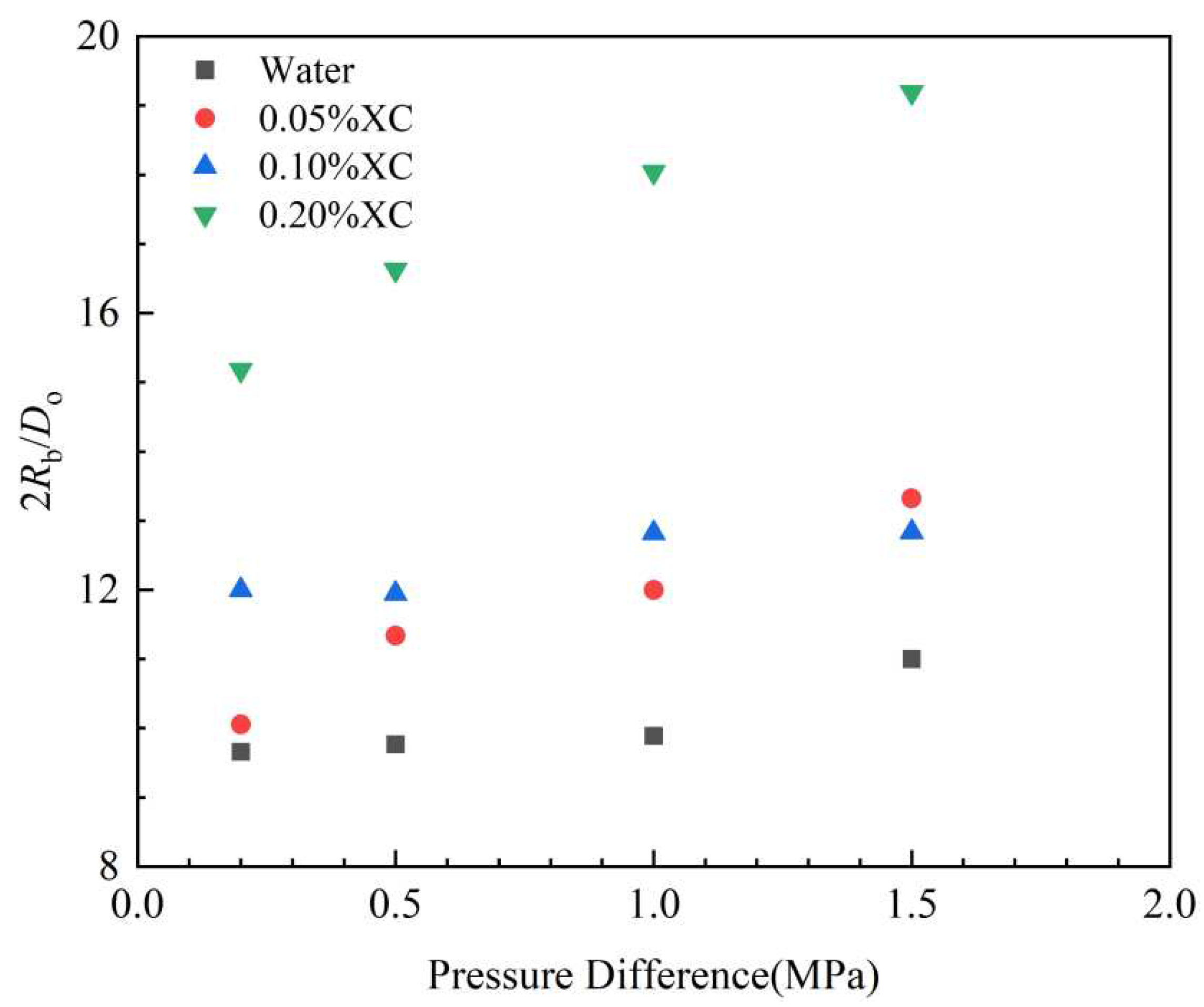
3.1.1. Variations of the intrusion bubble size

The pore diameter of the microporous aerator is 0.178 mm, corresponding to the dimensionless bubble size (2R_b/D_o). The experimental results are shown in Figure 3. It is observed that when the viscosity of the drilling fluid is low, the initial size of intruding bubbles is mainly affected by the surface tension at the orifice when the bubbles are dislodged. Moreover, Figure 3 indicates that there is a positive correlation between the size of intruding bubbles and the viscosity of the liquid phase. The average sizes of bubbles in the 0.05% concentration of the XC solution and in the aqueous solution are nearly identical. However, the size of bubbles in the 0.05% concentration of the XC solution is significantly smaller than that observed in the 0.1% and 0.2% concentrations of the XC solution. In summary, the bubble size in the 0.05% XC solution is significantly smaller than that in the 0.1% and 0.2% XC solutions.

Figure 4 indicates that the average dimensionless diameter of gas bubbles is affected by the pressure difference. More specifically, the larger the pressure difference between the formation and the wellbore, the larger the average size of intruding gas bubbles. This phenomenon may be attributed to the substantial pressure difference between the formation and the wellbore caused by the gas intrusion into the wellbore. Consequently, the gas seepage rate increases, intruding gas bubbles expand, and the average size of bubbles increases when they detach from the borehole.

3.1.2. Modeling gas intrusion rate under shut-in well conditions

When a well is shut down after an overflow and the formation pressure exceeds the bottomhole pressure, the formation fluid intrudes into the wellbore due to the pressure difference. The flow behavior can be described using Darcy’s law. Since the gas intrusion into the wellbore is an unsteady planar radial seepage process, the unsteady gas intrusion binomial flow equation is employed to describe the seepage process [20].

p_{e}^{2} - p_{w}^{2} = (\frac{μ_{g} Z}{π k h} \frac{p_{a} T}{Z_{a} T_{a}} \ln \frac{r_{e}}{r_{w}}) Q_{g} + \frac{α ρ_{a}}{2 π^{2} h^{2}} \frac{p_{a} Z T}{Z_{a} T_{a}} (\frac{1}{r_{w}} - \frac{1}{r_{e}}) Q_{g}^{2}

(3-1)

Where p_e is formation pressure, Pa; p_w is the bottomhole pressure, Pa; μ_g is the average gas viscosity, Pa·s; Z is the gas compression factor at the temperature and pressure of the formation; k is the formation permeability, m²; h is the thickness of the open gas layer, m; p_a is the pressure of the standard atmosphere, Pa; T is the formation temperature, K; Z_a is the gas compression factor under the standard conditions; T_a is the temperature under the standard conditions, K; r_e is the effective gas intrusion radius, m; r_w is the bottomhole radius, m; Q_g is the gas intrusion flow rate under standard conditions, m³/s; α is the coefficient of inertial drag caused by turbulence; ρ_a is the gas density under standard conditions, g/m³.

With continuous gas intrusion into the wellbore, the wellbore pressure gradually increases and the pressure difference between the formation and the wellbore gradually decreases. As a result, the gas intrusion rate gradually decreases. The total volume of the intruded gas under standard conditions can be obtained using the following expression:

Δ V_{g} = \int_{0}^{t_{1}} Q_{g} (t) d t

(3-2)

Based on Equation (3-1), the gas intrusion rate is related to the bottomhole pressure [20]:

A = (\frac{μ_{g} Z}{π K h} \frac{p_{a} T}{Z_{a} T_{a}} \ln \frac{r_{e}}{r_{w}})

(3-3)

B = \frac{α ρ_{a}}{2 π^{2} h^{2}} \frac{p_{a} Z T}{Z_{a} T_{a}} (\frac{1}{r_{w}} - \frac{1}{r_{e}})

(3-4)

Q_{g} = \frac{\sqrt{A^{2} + 4 B (p_{e}^{2} - p_{w}^{2} (t))} - A}{2 B}

(3-5)

The total gas intrusion volume under standard conditions can be obtained through the following expression:

Δ V_{g, b} = \int_{0}^{t_{1}} \frac{\sqrt{A^{2} + 4 B (p_{e}^{2} - p_{w}^{2} (t))} - A}{2 B} d t

(3-6)

Where t₁ is the total intrusion time from the onset of gas intrusion to its cessation, s.

Equation (3-6) indicates that the total gas intrusion is related to the wellbore pressure, which is affected by numerous factors such as gas rising speed. Therefore, calculating the total gas intrusion requires the establishment of a model for calculating the gas transport velocity. Ignoring the effects of gas expansion on the wellbore pressure, the wellbore pressure is only related to the amount of gas intrusion into the wellbore. In the experiments, the volume of the upper part of the wellbore is denoted as V₀, and the temperature is maintained at 290 K. Ignoring the temperature change caused by variations in the pressure, instantaneous wellbore pressure can be calculated using the following expression:

p_{w} (t) = \frac{P_{a} Z T_{s}}{V_{0} Z_{a} T_{a}} (\frac{Z_{a} T_{a}}{Z_{s} T_{s}} V_{0} + Δ V_{g, b})

(3-7)

Where T_s is the experimental temperature, K; Z_s is the gas compression factor at 0.1 MPa and experimental temperature.

p_{w} (t) = \frac{P_{a} Z T_{s}}{Z_{a} T_{a}} (\frac{Z_{a} T_{a}}{Z_{s} T_{s}} V_{0} + \int_{0}^{t_{1}} \frac{\sqrt{A^{2} + 4 B (p_{e}^{2} - p_{w}^{2} (t))} - A}{2 B} d t)

(3-8)

Equation (3-8) can be rewritten in the form below:

p_{w} (t) = \frac{Z}{Z_{s}} P_{a} + \frac{P_{a} T_{s}}{V_{0} Z_{a} T_{a}} \sum_{i = 1}^{N} \frac{Z \sqrt{A^{2} + 4 B (p_{e}^{2} - p_{w}^{2} (\frac{i}{N} t_{1}))} - A}{2 B} \frac{i}{N} t_{1}

(3-9)

Figure 5 illustrates the distribution of wellbore pressure over time, calculated using Equation (3-9). It is observed that the highest wellbore pressure is obtained for water, 0.05% concentration of XC solution, 0.1% concentration of XC solution and 0.2% concentration of XC solution.

Figure 5 indicates that the model prediction results align with the experimental results. The results show that as the negative pressure difference between the formation and the wellbore increases, the duration from the initiation of gas intrusion to its cessation extends. Meanwhile, as the solution viscosity increases, the time required to reach equilibrium between wellbore pressure and formation pressure after gas intrusion shortens. When considering the changes in the initial size of gas bubbles from invading gases in the wellbore due to variations in solution viscosity, it is inferred that the larger the solution viscosity, the larger the initial size of gas bubbles from invading gases in the wellbore. Consequently, this results in a shorter time for invading gases to reach the upper section of the wellbore, thereby rapidly increasing the wellbore pressure.

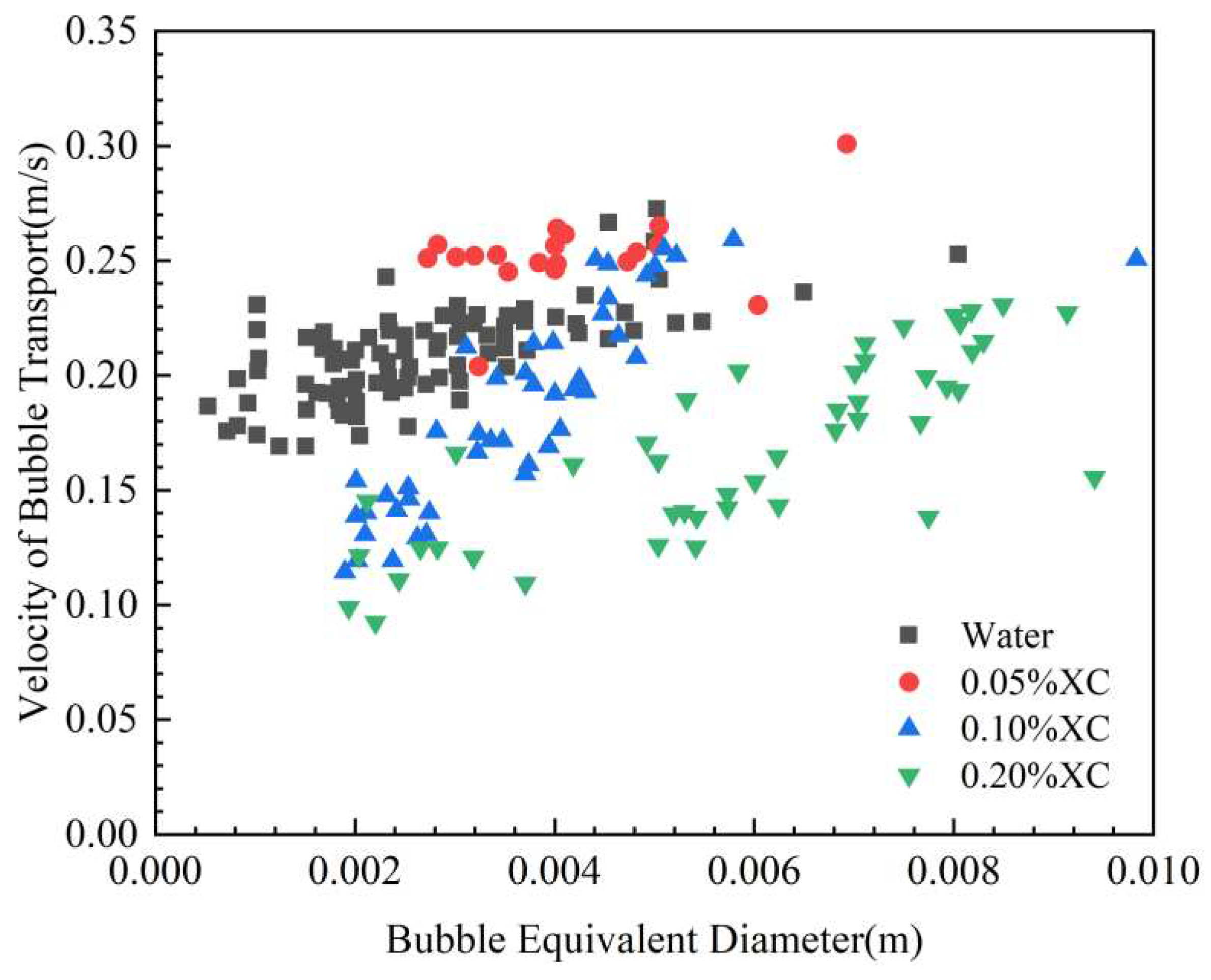
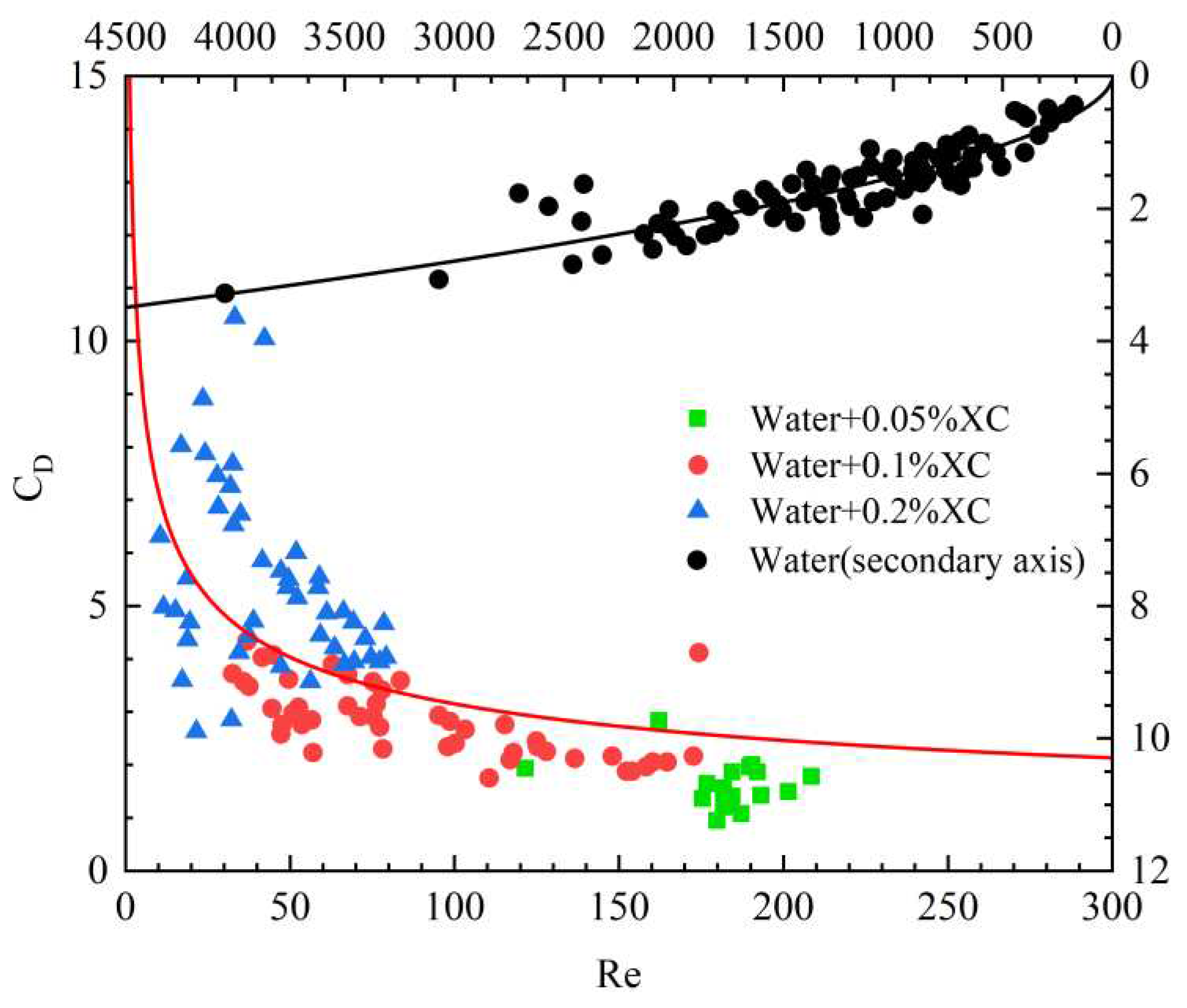
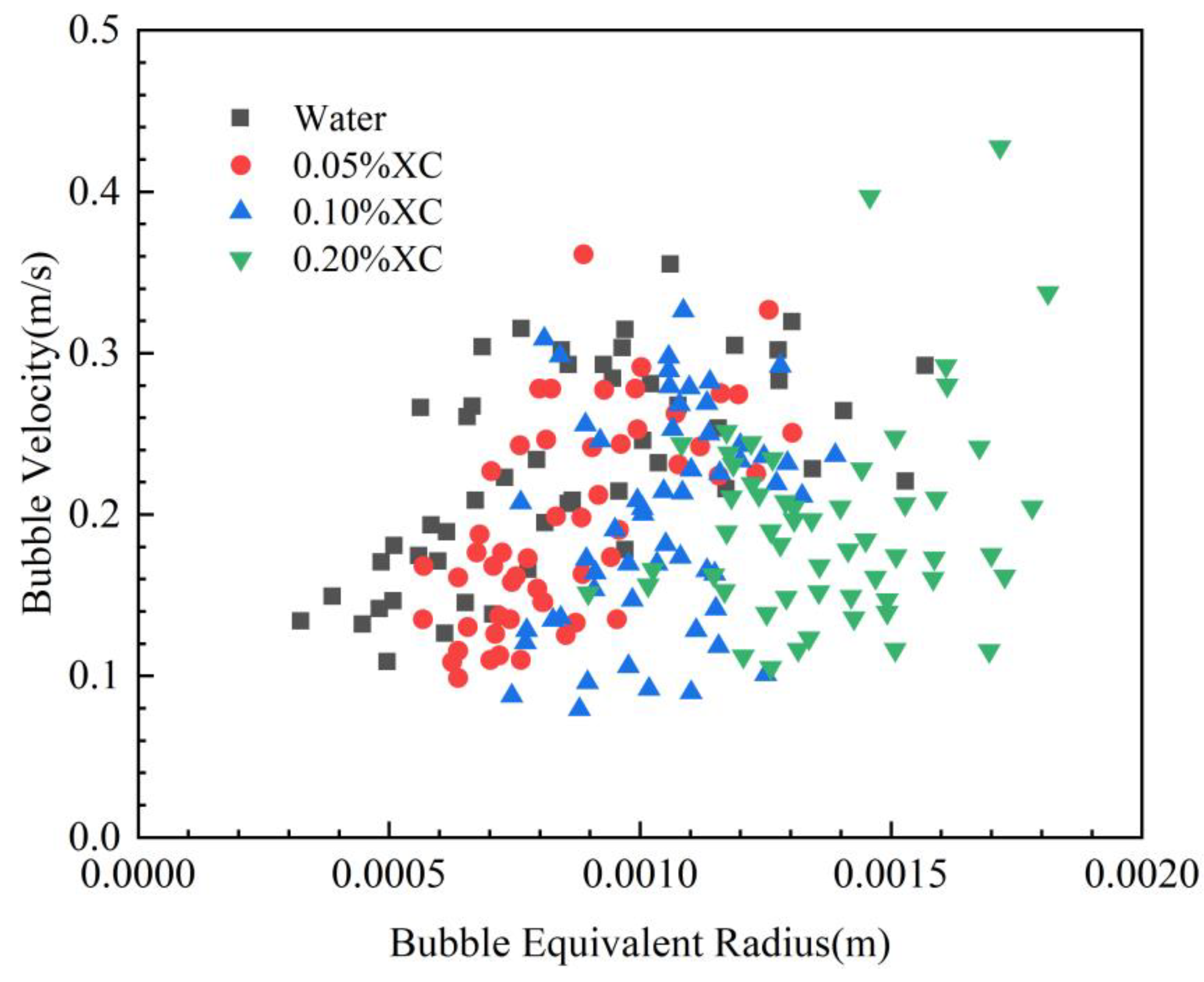
3.2. Simulation of intrusive gas transportation velocity in wellbore under shut-in conditions

3.2.1. Single bubble transport experiment

In this section, it is intended to investigate the transportation velocity of individual bubbles in experimental solutions. Variations of the transportation velocity of individual bubbles with the geometry of bubbles in different solutions are shown in Figure 6. It is found that when the viscosity of the solution is low, bubbles injected through the orifice are prone to rupture during the ascent, resulting in smaller average equivalent diameter of bubbles in low-viscosity solutions. In the case of water and a 0.05% concentration of XC solution, the bubble speed changes slightly, and the change in bubble speed with increasing bubble equivalent radius is small. However, as solution viscosity increases, the range of bubble equivalent diameter expands. Concurrently, variations of the bubble speed with respect to changes in bubble equivalent radius change also increase.

When the equivalent radius of bubbles is small, it experiences resistance from the viscous solution, causing slower bubble ascent. Consequently, the higher the solution viscosity, the slower the bubble rise. On the other hand, as the bubble equivalent radius increases, the bubble rise rate also increases. In this case, bubbles are affected by both viscous forces and buoyancy, which affect the bubble transport speed. Furthermore, when the solution viscosity increases, the equivalent radius of individual bubbles generated at the orifice increases. Consequently, the rise rate of bubbles increases and the buoyant force that pushes bubbles upward becomes more dominant than the viscous force. As a result, bubbles may exceed the transport speed of gas in low-viscosity fluids. The buoyancy force pushes the bubble upward more than the viscous force, resulting in a bubble upward velocity that may exceed the gas transport velocity in lower viscosity fluids. In order to gain a deeper understanding of single bubble transport velocity, the experimental results are analyzed as shown in Figure 7.

Since the Reynolds number for bubble transport in water is much larger than that in the XC solution [17], the experimental data in water are represented using the sub-coordinate axes (the left numerical axis is the vertical axis, and the upper numerical axis is the horizontal axis), and the red solid line in the figure is the fitted model of the drag force coefficient method with the Reynolds number in the xanthan gum solution, while the black solid line is the fitted model of the drag force coefficient method with the Reynolds number in the water, in which the. The intrinsic model for the XC solution follows a power-law model, and its parameters are provided in Table 1, with the Reynolds number defined as:

Re = \frac{2 ρ u_{z} R_{b}}{K {\dot{γ}}^{n - 1}} = \frac{ρ u_{z} R_{b}}{K {(\frac{u_{z}}{R_{b}})}^{n - 1}} = \frac{ρ u_{z} R_{b}^{2 - n}}{K u_{z}^{n - 1}}

(3-10)

The drag force coefficient C_D is defined as [21]:

C_{D} = \frac{8 g (ρ_{l} - ρ_{g}) R_{b}}{3 ρ_{l} u_{z}^{2}}

(3-11)

An empirical relationship between the drag force coefficient and Reynolds number for bubbles in water and XC solution is derived by fitting the experimental data:

C_{D, X C} = \frac{22.136 \pm 3.88}{{Re}^{0.432 \pm 0.046}}

(3-12)

The empirical relationship for the drag force coefficient in water is as follows:

C_{D, w} = (0.0292 \pm 0.004) {Re}^{0.568 \pm 0.029}

(3-13)

3.2.2. Experiments on the transport of bubble populations

When gas intrudes into the wellbore due to the pressure difference between the formation and the bottom of the well, the gas typically passes through the porous medium in the form of a bubble cluster. It is worth noting that the transport speed of the bubble cluster differs from that of an individual bubble. This section intends to experimentally investigate the transport speed of bubble clusters in the wellbore under various gas intrusion conditions.

Compared with single bubbles injected through an orifice, intruding gas bubbles in porous media exhibit a smaller average size. The maximum equivalent bubble radius observed in the experiments for the bubble cluster is 1.81 mm, as shown in Table 2 and Figure 8. However, it should be indicated that the gas rise velocity in the bubble cluster is typically greater than that of a single bubble of the same size.

In contrast to the positive correlation between the rise velocity of individual bubbles and their equivalent radius, the gas transport velocity within a bubble cluster exhibits a positive correlation with the equivalent radius of bubbles when the viscosity of the liquid phase is low. However, when the viscosity is high, no correlation is detected between the gas transport velocity and the equivalent radius of bubbles. In order to investigate the transportation velocity of the bubble cluster in the wellbore, a dimensionless analysis of the bubble cluster transportation velocity is carried out.

The following relationship between the bubble Reynolds number and the drag coefficient during bubble rise is established through fitting based on experimental results shown in Figure 9.

C_{D, X C} = (27.12 \pm 3.7) {Re}^{- 0.955 \pm 0.045}

(3-14)

Figure 10 reveals that the bubble cluster transport velocity in the water is related to its equivalent radius. The bubble cluster transport velocity in water can be calculated using the following expressions:

u_{z} = 2.5 \sqrt{g R_{b}} R_{b} \leq 1 m m

(3-15)

u_{z} = 0.26 m / s R_{b} \geq 1 m m

(3-16)

4. Conclusions

The present study incorporates the theories of multiphase seepage and multiphase flow in the wellbore to investigate gas intrusion into the wellbore induced by differential pressure after well shutdown. In this regard, a model is established for calculating the rate of gas intrusion, considering various parameters including the porosity of the formation, permeability of the formation, pressure difference between the formation and the wellbore, rheology of the drilling fluid, and the surface tension. The experimental results were utilized to validate the feasibility of the prediction model for the initial size of gas bubbles and the calculation method for gas intrusion rates. The findings reveal that ignoring the change in wellbore pressure caused by the upward movement of gas, the lower the viscosity of the drilling fluid, the longer the time for the wellbore pressure to reach equilibrium with the formation pressure. Additionally, the larger the pressure difference between the formation and the wellbore during gas intrusion, the longer the time for the wellbore pressure to reach equilibrium with the formation pressure. The initial size of the gas intruding into the wellbore and the rate of gas intrusion are crucial factors for calculating the transportation speed of the intruding gas within the wellbore and the changes in the wellbore pressure due to gas intrusion.

Based on the experimental results, empirical expressions were established to predict the drag coefficient of single bubbles and bubble clusters flowing in the wellbore. These expressions can be used to calculate the gas transport velocity for different equivalent radii of single bubbles and the average equivalent radius of bubble clusters. Additionally, the calculation method for the rise velocity of bubble clusters in water was derived based on experimental results. The findings indicate that in both water and a 0.05% concentration of XC solution, changes in bubble velocity are negligible. Moreover, the change in bubble velocity with respect to bubble equivalent radius is also small. As the solution viscosity increases from 0.1% to 0.2% concentration of the XC solution, the range of bubble equivalent diameters expands. Simultaneously, the magnitude of change in bubble velocity with bubble equivalent radius also increases. The equivalent radius of bubbles within a bubble cluster is significantly smaller than the equivalent radius of single bubbles generated by the orifice. When the viscosity of the drilling fluid is low, the transportation speed of bubble clusters exhibits a positive correlation with the average bubble diameter. However, when the average bubble diameter exceeds 1 mm, the bubble cluster transportation speed no longer changes with variations in bubble diameter. On the other hand, when the viscosity of drilling fluid is high, there is no apparent relationship between the transportation velocity of bubble clusters and bubble equivalent radius. This observation is of great significance when considering the influence of drilling fluid on the bubble transport velocity in multiphase flow modeling.

Acknowledgments

The authors acknowledge the support from the National Natural Science Foundation (52004315, U21B2069), Natural Science Foundation of Shandong Province (ZR2020QE113).

References

Yin H, Si M, Li Q, Zhang J, Dai L. Kick Risk Forecasting and Evaluating During Drilling Based on Autoregressive Integrated Moving Average Model. Energies. 2019, 12(18): 3540. [CrossRef]
Rommetveit R, Vefring E H. Comparison of results from an advanced gas kick simulator with surface and downhole data from scale gas kick experiments in an inclined well. SPE 22558, 1991. [CrossRef]
Stefan M, Samuel G, Azar J. Modeling of pressure buildup on a kicking well and its practical application. Permian Basin Oil and Gas Recovery Conference, 1996. [CrossRef]
Davies R M, Taylor G. The mechanics of large bubbles rising through extended liquids and through liquids in tubes. Dynamics of Curved Fronts, 1988, 200(1062): 377-392. [CrossRef]
Harmathy T Z. Velocity of large drops and bubbles in media of infinite or restricted extent. Aiche Journal, 1960, 6(2): 281-288. [CrossRef]
Wallis G B. One dimensional two-phase flows. International Journal of Multiphase Flow, 1969(1-2): 97-112. [CrossRef]
Fan W Y. Study of Bubble Behaviors and Flow Field around Moving Bubble in Non-Newtonian Fluid. Tianjin: Tianjin University, 2008.
Wang T, Li H X, Li Y. Numerical Investigation on Coaxial Coalescence of Two Gas Bubbles. Journal of Xi’an Jiaotong University, 2013, 47(07): 1-6.
Liu Y P, Wang P Y, Lin S N. Correlation of Position of Taylor Bubble Formation in Cryogenic Tube. Journal of Shanghai Jiaotong University, 2013,47(10): 1509- 1514, 1519.
Krzan M, Lotfi M, Kovalchuk V I, et al. Influence of β-lactoglobulin and its surfactant mixtures on velocity of the rising bubbles. Colloids & Surfaces A Physicochemical & Engineering Aspects, 2014, 460: 361-368. [CrossRef]
Azzopardi B J, Pioli L, Abdulkareem L A. The properties of large bubbles rising in very viscous liquids in vertical columns. International Journal of Multiphase Flow, 2014, 67: 160-173. [CrossRef]
Keshavarzi G, Pawell R S, Barber T J, et al. Transient analysis of a single rising bubble used for numerical validation for multiphase flow. Chemical Engineering Science, 2014, 112(12): 25-34. [CrossRef]
Cano-Lozano J C, Bolaños-Jiménez R, Gutiérrez-Montes C, et al. The use of volume of fluid technique to analyze multiphase flows: specific case of bubble rising in still liquids. Applied Mathematical Modeling, 2015, 39(12): 3290-3305. [CrossRef]
Yan X, Zheng K, Jia Y, et al. Drag Coefficient Prediction of a Single Bubble Rising in Liquids.Industrial & Engineering Chemistry Research, 2018, 57(15): 5385-5393. [CrossRef]
Khodayar J, Davoudian S H. Surface Wettability Effect on the Rising of a Bubble Attached to a Vertical Wall. International Journal of Multiphase Flow, 2018, 109:178-190. [CrossRef]
Du J, Zhao C, Bo H, Ren X. The Modeling of Bubble Lift-Off Diameter in Vertical Subcooled Boiling Flow. Energies. 2022, 15(18): 6857. [CrossRef]
Mangani F, Soligo G. Influence of density and viscosity on deformation, breakage, and coalescence of bubbles in turbulence. Physical Review Fluids, 2022,7(5):34. [CrossRef]
He H, Liu Z, Ji J, Li S. Analysis of Interaction and Flow Pattern of Multiple Bubbles in Shear-Thinning Viscoelastic Fluids. Energies. 2023, 16(14): 5345. [CrossRef]
Guo Y L. Study on Gas Invasion Mechanism and Wellbore Pressure during Well Shut-in in Deepwater Drilling. Qingdao: China University of Petroleum, 2018.
Jianguo Zhang, Dianfa Du, Jian Hou. Seepage mechanics of oil and gas reservoirs. Second edition. Dongying: China University of Petroleum Press, 2009. (In Chinese).
Sun B, Guo Y, Wang Z, et al. Experimental study on the drag coefficient of single bubbles rising in static non-Newtonian fluids in wellbore. Journal of Natural Gas Science and Engineering, 2015, 26(07): 867-872. [CrossRef]

Figure 1. Schematic of gas intrusion test system.

Figure 2. The rheology properties of experiment solutions.

Figure 3. Distribution of dimensionless bubble diameter.

Figure 4. The distribution of dimensionless bubble diameter against pressure difference.

Figure 5. Variations of the wellbore pressure during gas intrusion for various concentrations of XC solution.

Figure 6. Velocity distribution of a single bubble versus equivalent bubble radius.

Figure 7. The drag coefficient for various Reynolds numbers.

Figure 8. Velocity distribution of bubbles against equivalent bubble radius.

Figure 9. The distribution of the drag coefficient for various Re numbers.

Figure 10. The velocity of a bubble cluster in water.

Table 1. Properties of experimental materials.

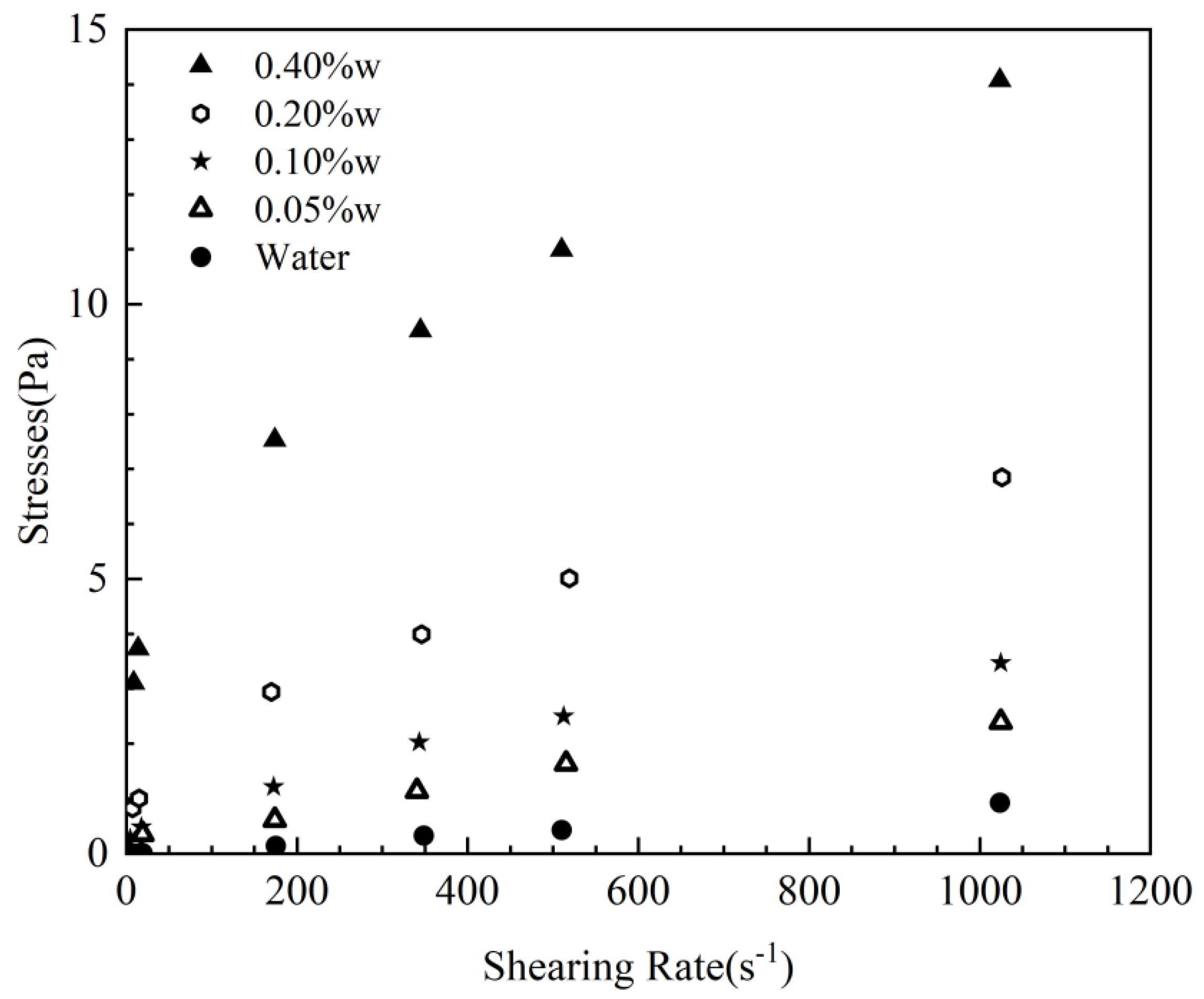
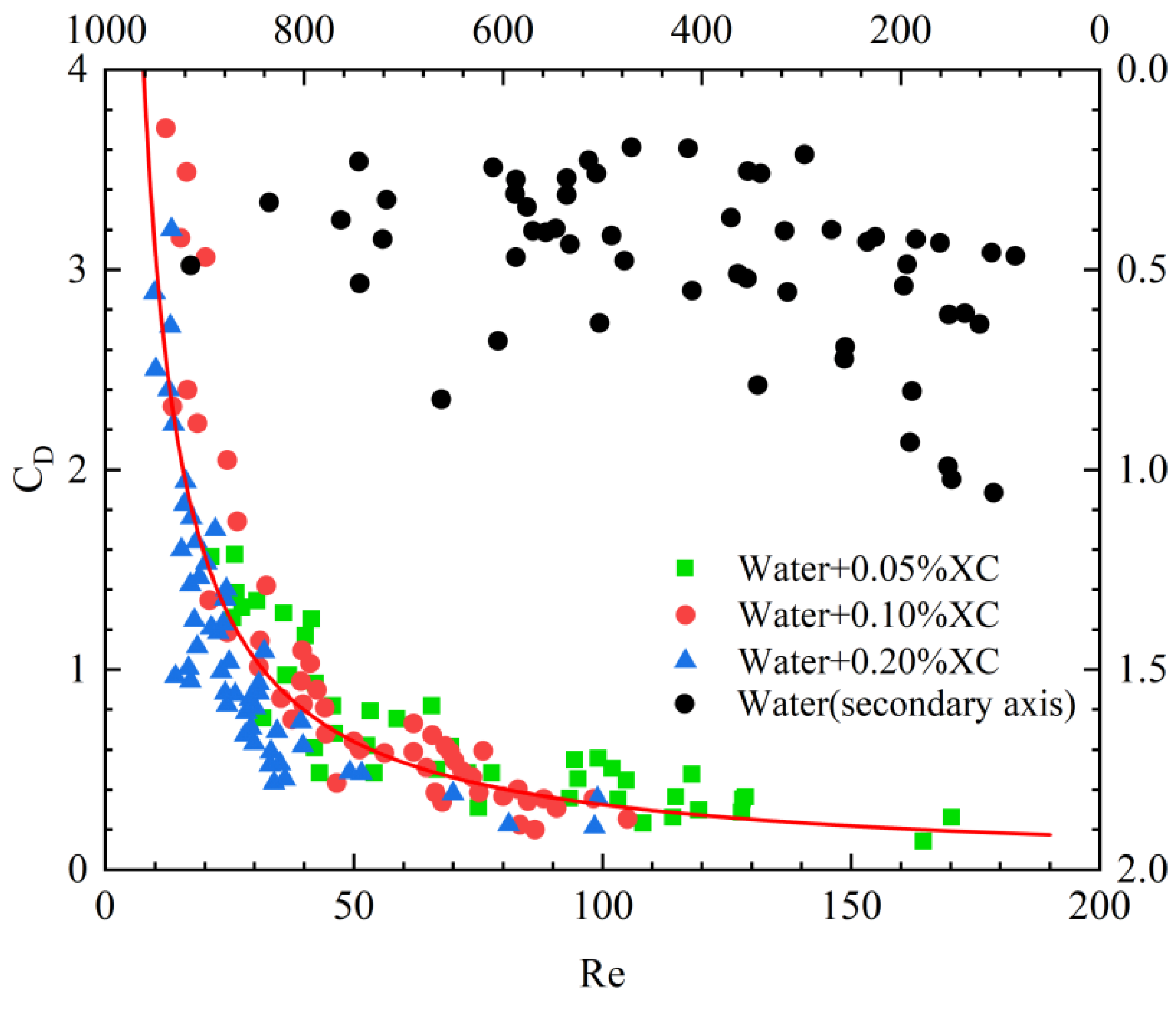
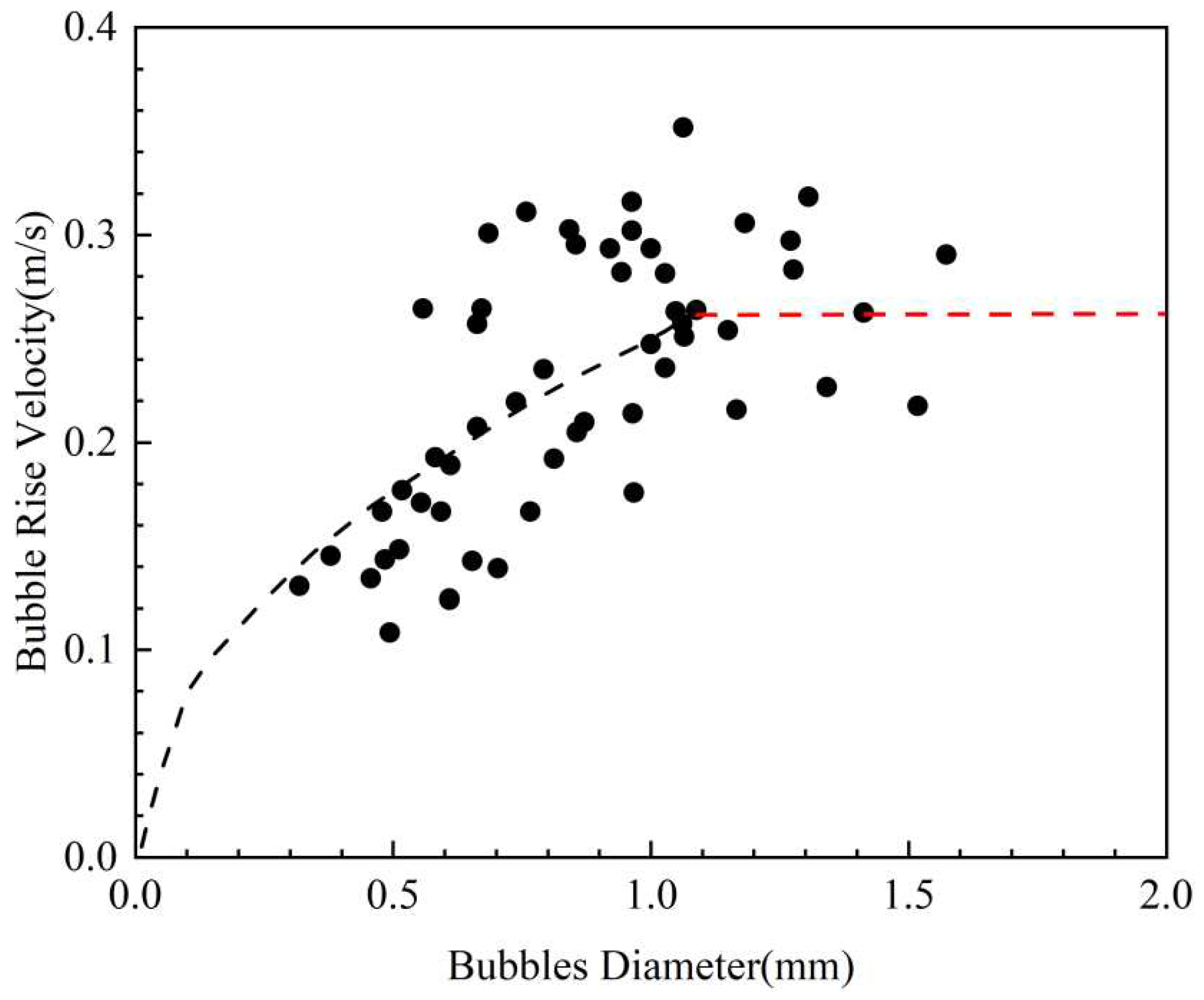
Type	Consistency factor K (Pa·s^-n)	Fluidity index n	Density (kg·m^-3)	Surface tension (N·m^-1)
Water	0.01	1	1000	72.35
0.05%XC	0.07224	0.51458	1000	73.67
0.1%XC	0.12377	0.48544	1000	74.24
0.2%XC	0.34337	0.43297	1000	75.05
0.4%XC	1.28381	0.34793	1000	76.75

Table 2. Range of bubble velocity and equivalent radius.

Type	Range of bubble equivalent radius (mm)		Bubble velocity range (mm/s)
Type	Single-bubble	Bubble group	Single-bubble	Bubble group
Water	0.5-8	0.32-1.6	170-267	110-330
0.05%XC	2.7-6.9	0.56-1.29	213-303	100-360
0.1%XC	2-9.8	0.74-1.43	116-259	77.9-321
0.2%XC	1.9-9.4	0.89-1.81	95-231	106-428

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer