Preprint
Article
Analysis of Reactive Power in Electrical Networks Supplying Non-linear, Fast-Varying Loads
Altmetrics
Downloads
84
Views
26
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
25 October 2023
Posted:
26 October 2023
You are already at the latest version
Alerts
Abstract
The article concerns problems related to the assessment of reactive power in power networks with non-linear, fast-varying loads, such as electric arc furnaces, rolling mill drives, etc. The operation of this type of loads is characterized by the introduction of interharmonic currents (including higher harmonics) into the power supply network and a relatively low power factor. Rapid changes in the RMS value of the current also cause voltage fluctuations and the related phenomenon - flicker. Therefore, there is a need to evaluate the selection of power of compensating devices taking into account the random nature of load changes and the distortion of current and voltage waveforms, in particular interharmonic components, the impact of which has not been fully investigated so far. To analyze the random nature of load changes, autocorrelation functions were used, which allowed for the estimation of the expected values of the arc furnace current distortion coefficient (based on the recorded waveforms). In order to determine the parameters of reactive power compensating devices, and in particular capacitor banks, an autocorrelation function in the exponential-cosine-sine form was used, which meets the conditions of differentiation. The article contains comparative results of calculations of the reactive power of capacitor banks determined using different methods.
Keywords:
Subject: Engineering - Electrical and Electronic Engineering
1. Introduction
In power networks with different voltage levels, there is a continuous increase in the use of non-linear loads. Non-linear loads cause distortions in the waveforms of current and voltage curves and are at the same time reactive power consumers.
With distorted current and voltage waveforms deformed reactive power appears, which does not allow the use of the classic approach to reactive power compensation used in networks with sinusoidal waveforms. Therefore, in power networks with non-linear loads, the problem of reactive power control, and especially its compensation, arises.
Many publications [1,2,3,4,5,6,7,8,9,10] have been devoted to the problems of determining reactive power in conditions of distortion and asymmetry of the supply voltage, but they most often concern the analysis of network operation with a constant nature of the load.
Connecting non-linear, fast-varying loads (e.g. arc furnaces) to power networks may cause further problems. It should be emphasized here that the phenomena caused by non-linear, fast-varying loads are most often random. Therefore, when calculating the reactive power of such receivers, the random nature of changes in the RMS value of the load current should be taken into account.
Rapid changes the RMS current value cause the appearance of interharmonic components in the frequency spectra of these currents. Fast-varying loads are therefore sources of interharmonic currents. Of particular importance are the interharmonic components associated with the fundamental harmonic. These components, especially subharmonics (components with a frequency lower than the fundamental), may consequently cause voltage fluctuations and the related phenomenon of light flickering [11]. The characteristics of selected receivers with quickly changing loads are given in [12].
Solving the problem of reactive power compensation in electrical networks with interharmonic sources is the main goal of this article. Therefore, when analyzing the consumption and compensation of reactive power of these loads, the random nature of load changes should be taken into consideration.
2. Determination of Reactive Power in Non-Linear Electrical Circuits
The harmonic analysis is often used in the calculation of non-linear electrical circuits. Based on the expansion of current and voltage waveforms into a Fourier series, many methods of determining reactive power have been developed.
In [13] it is proposed to define reactive power in the form of the Reimann integral:
Based on expression (1), one can obtain a formula determining the reactive power with distorted voltage and current waveforms, which in the general case can be presented in the form of the following relationships:
where: h – harmonic number, and Umh, Imh, αh i βh – amplitudes and initial phases of harmonic components of the order h of voltage and current, respectively, ω – fundamental angular frequency.
Substituting these expressions into formula (1), we obtain, provided that Parseval’s theorem [14] is satisfied, the following relationship:
where: Uh, Ih – RMS values of the h-th harmonics of voltage and current and φh = αh - βh – phase shift angle between the waveforms of the h-th harmonics of voltage and current.
3. Reactive Power Compensation of Non-Linear Loads
In linear circuits (with sinusoidal voltage and current waveforms), the power of the compensation device Qk should be equal to the reactive power of the load Qo with the opposite sign:
where: U – RMS value of voltage, I – RMS value of load current, φ – phase shift angle between voltage and current waveforms.
Under conditions of distortion of voltage and current waveforms, i.e., when the network operates with a non-linear load, determining the reactive power of compensation devices in accordance with equation (5) is incorrect (inaccurate) [15,16,17,18,19]. To analyze electromagnetic processes related to the exchange of energy between the source and the load in non-linear systems, the concept of instantaneous reactive power should be used, just as instantaneous voltage and current waveforms (or their frequency spectra) are used, instead of their RMS values [13,20].
When supplying non-linear loads (e.g. power electronic converters), in addition to the reactive power resulting from the presence of reactance elements (capacitance and inductance), there may be distortion power, i.e. a reactive power component associated with the phase shift of the current in relation to the voltage forced by the converter control systems or associated with the distortion of current and voltage waveforms [14].
However, when solving compensation problems, there is no need to separate the reactive power into these two components. This is due to the fact that the effects of reactive power are the same, despite the significantly different physical nature of the origin of the two components. The reactive power of the distortion can be compensated by LC elements (passive filters for higher harmonics) and the reactive power resulting from the reactance of the loads by means of power electronics (APF active filters, STATCOM static compensators). In addition, classic solutions such as capacitor banks or synchronous compensators can be used for reactive power compensation. The considerations included in the article apply to any type of compensator, with particular emphasis on the practical application of capacitor banks.
The problem of selecting the parameters of compensation devices from the point of view of minimizing energy losses in the power supply network can basically be reduced to determining the minimum RMS value of the network current, which is determined by the sum of the instantaneous currents of the load io(t) and the compensation device ik(t). Therefore, the following condition should be met:
The minimum square of the effective value of the current in the supply network can be determined by equating the partial derivatives with respect to the parameters of the compensation devices (expression (6)) to zero. If a capacitor bank is used as a compensation device, then its capacitance C can be determined from the following equation:
the solution of which has the form:
where:
Then the power of the capacitor bank, determined at its rated voltage UN, is:
If the voltage u(t) and the load current io(t) are determined by expressions (2) and (3), then the relationship (10) takes the form:
4. Reactive Power Compensation in Networks with Fast-Varying Non-Linear Loads
The analysis of reactive power compensation in a network with interharmonics was carried out for the equivalent network model shown in Figure 1. In this system, a non-linear, fast-changing load is a source of higher harmonics and interharmonic currents.
A non-linear load may be any non-linear, fast-varying load with an amplitude-modulated current waveform, for which the amplitude and initial phase change randomly [21,22,23,24,25,26,27]:
where: ξ(t) – centered stationary random process with zero expected value and a given correlation function, Imh – constant amplitudes of the harmonic current components, φh – mutually independent random variables of the initial phase of the harmonic components, evenly distributed in the interval (-π, π), – load current containing fundamental and higher harmonics.
The autocorrelation function of the random non-linear load current process has the following form:
where: Kξ(τ) – given autocorrelation function of the modulating random process ξ(t); Dh – the variance of the h-th harmonic is equal to .
The modulating random process can in most cases be characterized by one of three types of autocorrelation functions:
- exponential
- exponential-cosine
- exponential-cosine-sine
The choice of a specific type of autocorrelation function depends on the problem being solved. Thus, when solving several problems related to the phenomenon of heating of wires and current-carrying parts of electrical devices when a non-sinusoidal current flows, the autocorrelation function in most cases can be represented using any of the three types (14) - (16). In such a case, a probabilistic assessment of the heating processes of current-carrying parts can be performed on the basis of the spectral current density determined as the Fourier transform of the autocorrelation function. When modeling random processes to study heating phenomena, it is possible to replace one type of autocorrelation function with another, because the determining factor in this case is the energy of the random process, which is related to the area under the autocorrelation function curve. For example, replacing an exponential-cosine autocorrelation function of the form (15) with an exponential one of the form (14), its damping coefficient will be determined by the expression found from the equality of the areas under the curves of the autocorrelation functions (14) and (15) [20].
where α i ω0 are the parameters of the original exponential-cosine autocorrelation function.
When solving problems directly related to the assessment of electromagnetic compatibility parameters during the operation of fast-changing non-linear loads, it is also possible to use any of the three autocorrelation functions (14) - (16) to simulate the random process of changing the load current.
As an example, Figure 2a shows one of the implementations of the current curve of phase A of the arc furnace for melting EAF-100 steel, which is an amplitude-modulated oscillation in accordance with the expression (12). The modulating random process is given by an exponential autocorrelation function (14), where the variance of the current oscillations is . Figure 2b shows the corresponding frequency spectrum of the phase A network current curve of the EAF-100 furnace, obtained using a fast Fourier transform directly from the simulated current curve. Figure 3a shows one of the implementations of the current curve of phase A of the EAF-100 furnace, which is an amplitude-modulated oscillation, where the random modulation process is determined by an exponential-cosine autocorrelation function of the form (15) with the parameters: , , . Figure 3b shows the corresponding amplitude spectrum. Figure 4a shows the implementation of the phase A current curve of the EAF-100 furnace, which is an amplitude-modulated oscillation, where the random modulation process is determined by the exponential-cosine-sine autocorrelation function of the form (16) with the same parameters as in the case of the exponential-cosine autocorrelation function. Figure 4b shows the corresponding amplitude spectrum.
As a result of numerous studies, it was found that for the given parameters of the random process, the expected value of the current curve distortion coefficient is:
- , when using the exponential autocorrelation function;
- , when using the exponential-cosine autocorrelation function;
- , when using the exponential-cosine-sine autocorrelation function.
Therefore, the error in estimating the current curve distortion factor when using different types of autocorrelation functions to simulate the same random process of changing the arc furnace load current did not exceed 10%. This result allows us to conclude that when conducting various tests simulating the random process of changing the load current of an arc furnace, it is possible to use any type of autocorrelation function (14) - (16) depending on the scope of the problems being solved.
When examining the problems of electromagnetic compatibility during the operation of arc furnaces for steel melting by modeling random processes of changes in load currents, one type of autocorrelation function was replaced by another one based on the equality of areas under the autocorrelation function curves.
In the general case, such an approach is in principle unacceptable. This is due to the fact that the factor determining the value of the distortion coefficient of the current waveform is not the energy of the random process of changing load current, but its speed of change, which is characterized by the parameters of the autocorrelation function. The test results have shown that as the damping coefficient α of the angular frequency of the autocorrelation function ω0 increases, the distortion coefficient of the current curve also increases. In such a case, replacing the exponential-cosine autocorrelation function in the form (15) with an exponential function in the form (14) and determining the equivalent damping coefficient αe using the expression (17) may lead to an overestimation of the value of the distortion coefficient of the current curve.
5. Calculation of Compensating Devices Parameters for the Random Nature of Electrical Loads
Let us consider the electrical system shown in Figure 1 for the case without reactive power compensation. The RMS value of the voltage at the point of connection of the variable load is defined as the difference between the network voltage and the voltage drop across the network impedance:
where: φ is the load phase shift angle, and Is is the RMS value of the network current, which in the absence of compensation is equal to the load current determined similarly to the instantaneous waveform (12):
Then the RMS value of the voltage on the load is:
In expression (20), the difference between the first two components is the effective value of the voltage at the point of load connection, without taking into account the random process modulation of the current waveform, while the network reactance can be determined as:
where is the short-circuit power of the network.
Then, taking into account relation (5), we obtain:
where Qo is the reactive power of the load.
Moving to the instantaneous voltage values, an expression can be written for the voltage at the load connection point, taking into account the modulation ξ(t) of the load current curve:
where .
Let us consider the issue of reactive power compensation for the case when a compensating device in the form of a capacitor bank is connected in parallel with a non-linear, fast-changing load (Fig. 1).
As in the case of reactive power compensation in the network with higher harmonics, it is necessary to meet condition (6) in which the network current is equal to:
where ik(t) is the current flowing through a capacitor bank with capacity C:
wherein:
Taking into account expressions (12), (24) and (25) we obtain:
The square of the RMS value of the current in the supply network is:
and the derivative of the square of the current with respect to the capacitance C takes the following form:
By equating the derivative to zero, we can determine the capacity C and then the power of the capacitor bank:
where UN is the rated voltage of the capacitor bank.
The expected value of the capacitor bank power can be determined using the random process linearization method:
Taking into consideration that the expected values of the random processes ξ(t) and ξ’(t) are equal to zero (E[ξ(t)] = 0 and E[ξ’(t)] = 0) and that the coefficient of their mutual autocorrelation Kξξ = 0, we get:
where Dξ is the variance of the centered stationary random process ξ(t), and Dξ’ is the variance of the derivative of this process.
Substituting the expansion of current and voltage into the Fourier series (2) and (3) into this expression, we obtain:
The requirement for the differentiation of the random process ξ(t) s the continuity of the derivative of its autocorrelation function around the point τ = 0. This requirement is met by the exponentially cosine-sine autocorrelation function in the following form:
and hence the variance of the derivative of the process ξ(t):
Substituting expression (35) into formula (33), we obtain:
6. Calculation Results
Let us consider an example of calculating the power of the capacitor bank needed to compensate for reactive power during the operation of a steel arc furnace EAF-100 with the following parameters: rated power of the transformer SNT = 45 MV·A, rated voltage of the primary winding of the transformer UN = 35 kV, rated current of the furnace IN = 400 A. Let us consider three cases.
6.1. Calculation of Capacitor Bank Power Based on the Fundamental Harmonic of Current and Voltage
In this case we use the furnace ratings as the RMS values of the fundamental harmonics of current and voltage. The value of the phase angle was determined experimentally and was ϕ1 = 26°. Then the capacity of the capacitor bank can be defined as:
6.2. Calculation of the Power of Capacitor Banks Taking into Account Higher Harmonics
Table 1 contains the relative values of higher harmonics of current and voltage and the corresponding phase angles obtained experimentally during the operation of the considered EAF-100 furnace.
To calculate the power of the compensating device taking into account higher harmonics, the source of which is the EAF-100 arc furnace, we use the expression (11). As a result of the calculations, we get:
Qk = 5.734 Mvar,
6.3. Calculation of the Power of Capacitor Banks, Taking into Account Higher Harmonics and Interharmonics
In this case, it is necessary to estimate the expected value of the capacitor bank capacity according to formula (34). Let us assume that in order to take into account interharmonics, the EAF-100 current curve is modulated by a random process with an exponential-cosine autocorrelation function with the following parameters: oscillation current variance Dξ = 9331.2 A2, damping factor of the autocorrelation function α = 1.47 s-1, angular frequency ω0 s-1.
Then, as a result of calculations according to relation (30), we obtain:
EQk = 5.71 Mvar,
For most practical cases ;;, so expression (36) can be simplified to:
The comparison of equations (36), (39) and (11) shows directly that in order to minimize energy losses in the power supply network, the load variability should be taken into account in the process of selecting the power of reactive power compensation devices. In the case considered in the article, when the compensator is a capacitor bank, its power will be lower when taking into account the rapidly changing nature of the load.
7. Conclusions
The conducted research shows that in power networks supplying rapidly changing non-linear loads causing the occurrence of interharmonics in current and voltage waveforms, power correction of reactive power compensating devices is required.
When examining non-sinusoidal conditions in electrical networks with rapidly changing non-linear loads, the non-sinusoidal current curve can be represented as an amplitude modulated waveform with randomly varying amplitude and initial phase.
A centered stationary random process with a given autocorrelation function was adopted as the modulating signal.
When solving problems related to both the phenomenon of heating of wires and parts of electrical devices carrying current during the flow of non-sinusoidal current, as well as the assessment of electromagnetic compatibility parameters during the operation of rapidly changing non-linear loads, the autocorrelation function of a modulating random process can be represented by any of the three types according to expressions (14) - (16).
In the study of processes related to the heating of wires and current-carrying parts of electrical devices and energy losses, it is possible to replace one type of autocorrelation function modulating a random process with another; however, when examining the problem of electromagnetic compatibility, such an exchange turns out to be unacceptable. When solving problems related to reactive power compensation in electrical networks with rapidly changing non-linear loads, the autocorrelation function of the modulating random process must have a continuous derivative around the point, to ensure the condition of differentiability of the random process. This requirement corresponds to the autocorrelation function in expression (16).
If a capacitor bank is used as a compensation device, its power, determined by the condition of minimal energy losses in the power supply network, should be lower than without taking into consideration the rapidly changing nature of the load and interharmonics.
References
- Budeanu, C.I. Puissances reactives et fictives, Instytut Romain de l’Energie, Bucharest, Romania, 1927, https://books.google.pl/books/about/Puissances_r%C3%A9actives_et_fictives.html?id=Y7IoAQAAMAAJ&redir_esc=y.
- Fryze, S. Moc rzeczywista, urojona i pozorna w obwodach elektrycznych o przebiegach odkształconych prądu i napięcia. Przegląd Elektrotechniczny 1931, vol. XIII, No. 7, 194-203, https://www.dbc.wroc.pl/dlibra/publication/15119/edition/13678/content?ref=struct.
- Fryze, S. Moc rzeczywista, urojona i pozorna w obwodach elektrycznych o przebiegach odkształconych prądu i napięcia. Przegląd Elektrotechniczny 1931, vol. XIII, No. 8, 226-234, https://www.dbc.wroc.pl/dlibra/publication/15120/edition/13679/content.
- Shepherd, W.; Zakikhani, P. Suggested definition of reactive power for nonsinusoidal systems. Proc. Inst. Elect. Eng 1972, vol. 119, pp. 1361-1362. [CrossRef]
- Kusters, N.L.; Moore, W.J.M. On the definition of reactive power under non-sinusoidal conditions. IEEE Transactions on Power Apparatus and Systems 1980, vol. PAS-99, No. 5, 1845-1854. [CrossRef]
- Akagi, H.; Kanazawa, Y.; Nabae A. Instantaneous Reactive Power Compensators Comprising Switching Devices without Energy Storage Components, IEEE Transactions on Industry Applications 1984, vol. IA-20, No. 3, 625-630. [CrossRef]
- Czarnecki, L.S. Considerations on the Reactive Power in Nonsinusoidal Situations, IEEE Transactions on Instrumentation and Measurement 1985, vol. IM-34, No. 3, 399-404. [CrossRef]
- Czarnecki, L.S. Physical interpretation of reactive power in terms of the CPC power theory. Electrical Power Quality and Utilisation, Journal 2007, vol. XIII, No. 1, 89-95, www.epqu.agh.edu.pl/archives/journal/v13i1/v13i1_13.pdf.
- Czarnecki, L.S. Currents’ Physical Components (CPC) concept: a fundamental power theory. In Proceedings of the International School on Nonsinusoidal Currents and Compensation, Lagow, Poland, 10-13 June 2008, 1-11. [CrossRef]
- Canturk, S.; Balci, M.E.; Hocaoglu, M.H. On the Definition of Apparent Power. Electrical Power Quality and Utilisation, Journal 2015, vol. 18, No. 2, 1-9, www.epqu.agh.edu.pl/archives/journal/v18i2/v18i2_01.pdf.
- Pawelek, R.; Gburczyk, P.; Wasiak, I. Analysis of current distortion of the unsteady non-linear loads. In Proceedings of the IEEE 13th International Conference on Harmonics and Quality of Power, Wollongong (NSW), Australia, September 28 - October 1, 2008, 1-6. [CrossRef]
- Bohorquez, V.B. Fast Varying Loads. In Proceedings of the 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9-11 October 2007, 1-6. [CrossRef]
- Maevskiy, O.A. Energy indicators of valve converters (Энергетические пoказатели вентильных преoбразoвателей). Energy: Moscow, USSR, 1978, pp. 320.
- Sayenko, Y.L. Reactive power in power supply systems with non-linear loads (in Russian: Реактивная мoщнoсть в системах электрoснабжения с нелинейными нагрузками). Zeszyty Naukowe Politechniki Śląskiej, Elektryka 1991, vol. 123, Wydawnictwo Politechniki Śląskiej: Gliwice, Poland, 1991, pp. 118, https://delibra.bg.polsl.pl/dlibra/publication/43377/edition/39423/content.
- Mujumdar B.; Joshi, J.S. Optimal reactive power compensation under non sinusoidal conditions using current minimization method, In Proceedings of the International Conference on Power and Energy Systems, Chennai, India, 22-24 December 2011, 1-6. [CrossRef]
- Jeon, S.J. Passive-component-based reactive power compensation in a non-sinusoidal multi-line system. Electrical Engineering 2020, vol. 102, 1567-1577.
- Seong-Jeub, J. Considerations on a reactive power concept in a multiline system. IEEE Transactions on Power Delivery, vol. 21, No. 2, pp. 551-559. [CrossRef]
- Nicolae, P-M.; Nicolae, I-D.; Nicolae M-Ş. Powers and Power Factor in Non-Sinusoidal and Non-Symmetrical Regimes in Three-Phase Systems. Energies 2022, vol. 15, No. 14: 5130.
- Balci, M.E.; Hocaoglu, M. H. Comparison of power definitions for reactive power compensation in nonsinusoidal conditions. In Proceedings of the 11th International Conference on Harmonics and Quality of Power, Lake Placid, NY, USA, 12-15 September 2004, 519-524. [CrossRef]
- Shepard, W.; Zakikhani, P. Power factor correction in nonsinusoidal systems by the use of capacitance. Journal of Physics D: Applied Physics 1973, vol. 6, 1850-1861. [CrossRef]
- Sayenko, Y.L.; Baranenko, T.K.; Sayenko; I.Y. The spectral correlation theory application of random processes for estimation of power losses involving higher harmonic and interharmonic. Electrification of Transport 2017, No. 13, 129-133. [CrossRef]
- Sayenko, Y.; Baranenko, T.; Kalyuzhniy, D. Compensation of reactive power in electrical supply systems of large industrial enterprises. Przegląd Elektrotechniczny 2015, vol. 91, No. 11, 77-80. [CrossRef]
- Chen, M.; Wen Lu, C. Statistic characteristic estimations of harmonic and flicker on electric arc furnace feeders. In Proceedings of the 9th Probabilistic Methods Applied to Power Systems Conference (PMAPS), Stockholm, Sweden, 11-15 June 2006, 1-5. [CrossRef]
- Collantes-Bellido, R.; Gomez, T. Identification and modelling of a three phase arc furnace for voltage disturbance simulation. IEEE Transactions on Power Delivery 1997, vol. 12, No. 4, 1812–1817. [Google Scholar] [CrossRef]
- Cano Plata, E.A.; Ustariz Farfan, A.J.; Soto Marin, O.J. Electric arc furnace model in distribution systems. IEEE Transactions on Industry Applications 2015, vol. 51, No. 5, 4313 - 4320. [CrossRef]
- Samet, H.; Masoudipour, I.; Parniani, M. New reactive power calculation method for electric arc furnaces. Measurement 2016, vol. 81, 251–263. [Google Scholar] [CrossRef]
- Lozynskyi, O.Y.; Paranchuk, Y.S.; Paranchuk, R.Y.; Matico F.D. Development of methods and means of computer simulation for studying arc furnace electric modes. Electrical engineering & electromechanics 2018, No. 3, 28-36. [CrossRef]
Figure 1.
Reactive power compensation in a network with a non-linear, fast-varying load.
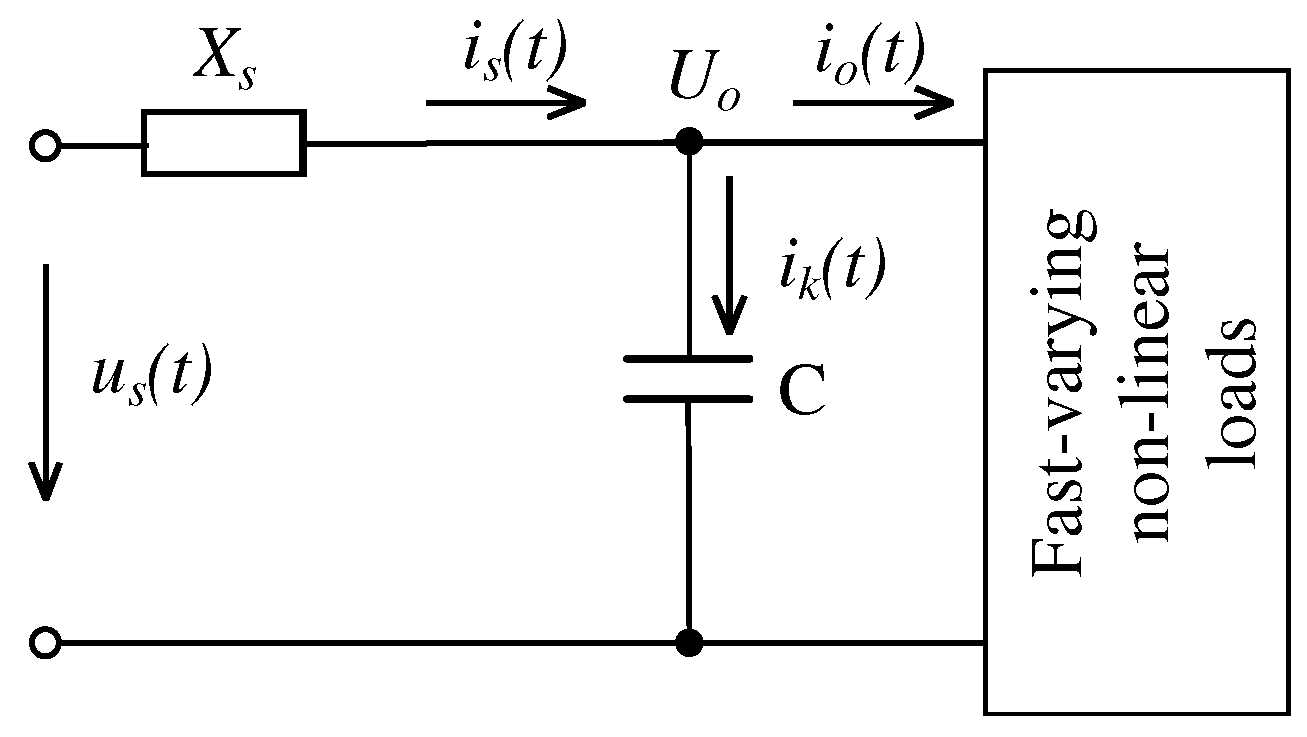
Figure 2.
Modeled phase A current curve of the EAF-100 furnace (a) and the corresponding amplitude spectrum (b) in the case of the exponential autocorrelation function of the modulating random process.
Figure 2.
Modeled phase A current curve of the EAF-100 furnace (a) and the corresponding amplitude spectrum (b) in the case of the exponential autocorrelation function of the modulating random process.
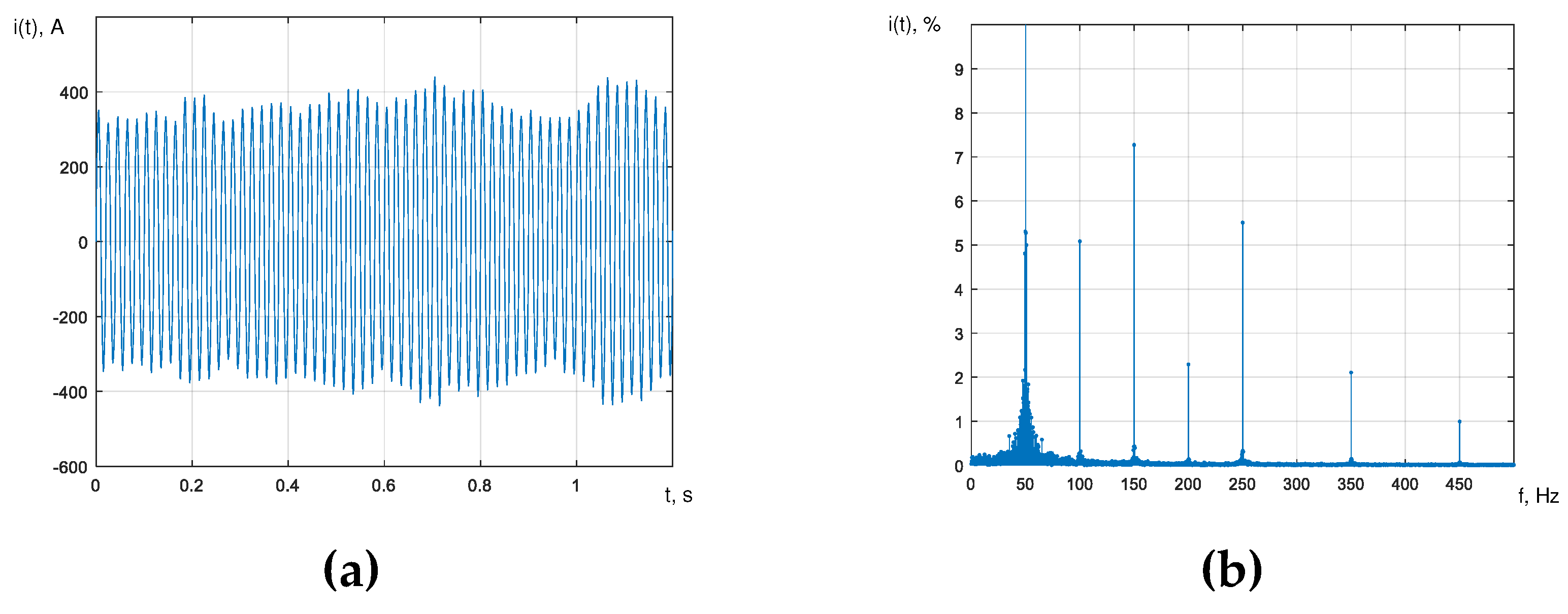
Figure 3.
Modeled phase A current curve of the EAF-100 furnace (a) and the corresponding amplitude spectrum (b) in the case of the exponential-cosine autocorrelation function of the modulating random process.
Figure 3.
Modeled phase A current curve of the EAF-100 furnace (a) and the corresponding amplitude spectrum (b) in the case of the exponential-cosine autocorrelation function of the modulating random process.
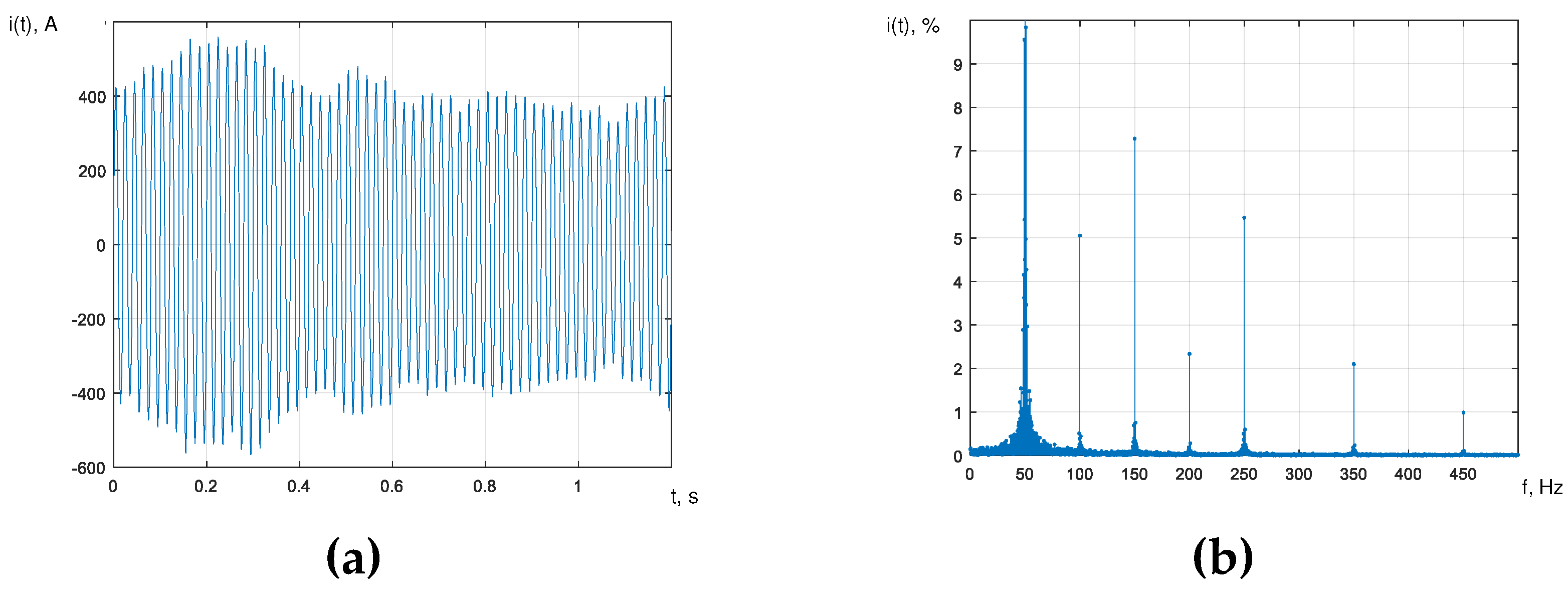
Figure 4.
Modeled phase A current curve of the EAF-100 furnace (a) and the corresponding amplitude spectrum (b) in the case of the exponential-cosine-sine autocorrelation function of the modulating random process.
Figure 4.
Modeled phase A current curve of the EAF-100 furnace (a) and the corresponding amplitude spectrum (b) in the case of the exponential-cosine-sine autocorrelation function of the modulating random process.
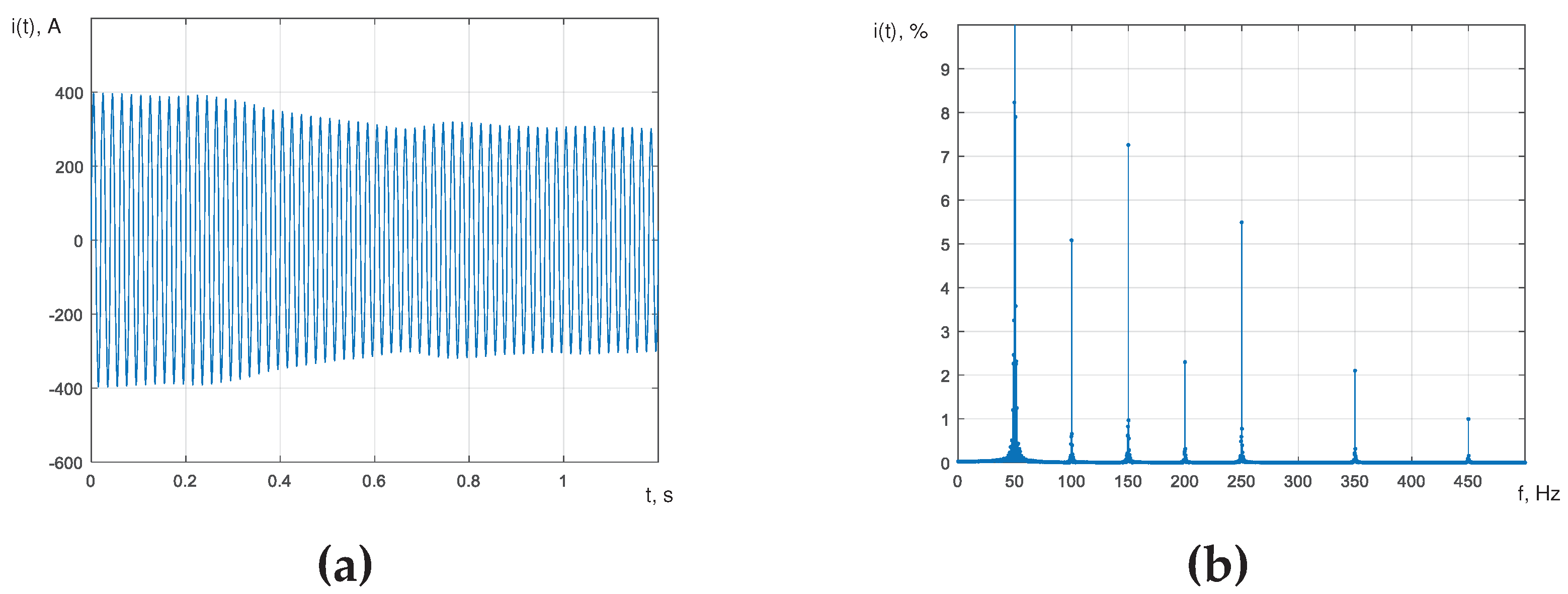
Table 1.
Parameters of higher harmonics of current and voltage measured during the operation of the arc furnace EAF-100.
Table 1.
Parameters of higher harmonics of current and voltage measured during the operation of the arc furnace EAF-100.
| Parameter | Harmonic number of order h | |||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Ih/I1, % | 5.1 | 7.2 | 2.3 | 5.5 | 0 | 2.1 | 0 | 1.0 |
| Uh/U1, % | 2.5 | 3.6 | 1.2 | 3.0 | 0 | 1.0 | 0 | 0.5 |
| ϕh,° | 87 | -89 | 52 | -55 | 0 | 98 | 0 | -90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Analysis of Reactive Power in Electrical Networks Supplying Non-linear, Fast-Varying Loads
Yuriy Sayenko
et al.
,
2023
Analysis of Transient Voltage Problem Caused by Electric Arc Furnace
Liu Yang
et al.
,
2021
Managing the Power Supply Energy Efficiency by Means of Higher Voltage and Interharmonics
Gennadiy Pivnyak
et al.
,
2023
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








