Bifurcations Associated with Three-Phase Polynomial Dynamical Systems and Complete Description of Symmetry Relations Using Discriminant Criterion

Preprint

Article

Bifurcations Associated with Three-Phase Polynomial Dynamical Systems and Complete Description of Symmetry Relations Using Discriminant Criterion

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Yury Shestopalov^*

,Azizaga Shakhverdiev,Sergey V. Arefiev

Yury Shestopalov^*

,Azizaga Shakhverdiev,Sergey V. Arefiev

This version is not peer-reviewed

Submitted:

26 October 2023

Posted:

26 October 2023

You are already at the latest version

Alerts

Abstract

The behaviour and bifurcations of solutions to three-dimensional (three-phase) quadratic polynomial dynamical systems (DSs) are considered. The integrability in elementary functions is proved for a class of autonomous polynomial DSs. The occurrence of bifurcations of the type twisted fold is discovered on the basis and within the frames of the elements of the developed DS qualitative theory. The discriminant criterion applied originally to two-phase quadratic polynomial DSs is extended to three-phase DSs investigated in terms of their coefficient matrices. Specific classes of D- and S-vectors are introduced and complete description of the symmetry relations inherent to the DS coefficient matrices is performed using the discriminant criterion.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

Analysis of bifurcations in polynomial dynamical systems (DSs) consitutes a classical problem of the qualitative theory of DSs and differential equations and catastrophe theory and has been a subject of intense studies [1,2,3,4,5]. The main attention has been paid to nonautonomous polynomial DSs where many characteristic bifurcation types have been identified including equilibriums, sinks, saddles, limit cycles. Autonomous polynomial DSs investigated in these studies, especially the case of two dimensions, are non-integrable and characterized by ’mixed’ right-hand sides involving second-order polynomials in two variables.

In this regard, a complete investigation of particular families of DSs, and first of all quadratic polynomial DSs, which reveals all possible singular points and solutions is of definite interest, both theoretically and from the viewpoint of various applications. A specific interest here is towards identifying particular parameter DS families that admit complete description of all their singular points and bifurcations.

In this work, an integrable family of three-dimensional (three-phase) polynomial quadratic DSs is identified and considered. We show, as an extension of a similar study performed in [6] for two-dimensional polynomial quadratic DSs, that one can carry out complete investigation of singularities and in this manner create a complete qualitative theory in the three-phase case as well. Two-dimensional integrable polynomial quadratic DSs considered in [6,7] preserve certain clear types of symmetry; all characterisic cases are summarized in [6] as collections of curves on the phase planes. The symmetry is governed by the occurrence of a finite number of integrable combinations of the DS solutions; all of them are described and vizualized in [6]. We extend in the paper this finding to the 3D-case and demonstrate that there is finitely many integrable combinations of the three-phase DS solutions which can be fully classified by three parameters applying the so-called discriminant criterium. However, this number (which we have determined) is huge, much greater than in the 2D-case. In spite of a broad variety of such combinations, we state the absence of many bifurcations and critical modes known for autonomous and nonautonomous polynomial DSs, like limit circles. On the other hand, we report a specific type of bifurcation characteristic for the DSs under consideration, stating a conjecture that the three-dimensional polynomial quadratic DSs have only this very bifurcation type.

As it is known from the theory of two-phase filtration, when oil is displaced by water in reservoir conditions, an unstable front zone is formed, at which water saturation has a triple value and changes discontinuously, which in turn leads to water breakthrough to oil producing wells. The model and solution of this problem is proposed in [8,9,10,11,12,13] as well as various applications of the proposed technique. In the case of three-phase filtration, the gas phase is involved in the process, which significantly complicates the solution of the problem, since gas behaves the same way as water and breaks through to the producing wells even more actively. As a result, all this leads to premature breakthrough of gas and water to the producing oil wells and, consequently, to the reduction of oil recovery and oil production stimulation. At present there are no theoretical mathematical solutions to this complex and important problem of oil science.

In a model of regulating and monitoring the process of waterflooding and the development of an oil or gas field, the considered three-dimensional autonomous polynomial DSs (system (42) in the tex below) describe [8,10,13] the change in time, at a given interval

t \in (t_{0}, t_{1}), t_{0} \geq 0,

and under predetermined constant values of the problem parameters

a_{i j}

i, j = 1, 2, 3,

the accumulated oil flow rate, x(t), water, y(t), and gas, z(t) corresponding to the three phases: oil, water, and gas. In practice, the accumulated and current well rates are known, which makes it possible to determine the coefficients of the polynomials entering DSs as constant values over a given interval. The discriminants of the growth model for each phase: for oil (

D_{o}

), gas (

D_{g}

), and water (

D_{w}

), are used as appropriate control parameters.

The particular form of three-dimensional autonomous polynomial DSs with ’separated’ variables (as (42)) is dictated by the results of long-standing observations and monitoring of oil and gas fields and huge amount of the registered, experimental and measurement data [7,11,18].

The present paper proposes a new approach to create qualitative theory and describe singularities and bifurcations of the DSs under study on the basis of the growth model from catastrophe theory [18,19,20,21]. The model has been equipped with new tools that enable one to classify all possible solution types into equivalence classes defined in terms of the so-called discriminant (D-) vectors.

With a certain combination of values and signs of discriminants for oil, water and gas and using the technique developed in this work, it is possible to formulate criteria that allow predicting the breakthrough of water and gas into oil producing wells.

Performing qualitative analysis of three-dimensional DSs addressed in the paper we describe specific scenarios for modeling of the concrete processes under study. The results obtained are summarized in a compact form of a matrix and a criterion that employs D- and S-vectors and enables one to identify all possible different types of stable and unstable solutions and their singularities governed in the end by the signs of the polynomials’ discriminants.

2. A Family of Polynomial Dynamical Systems

2.1. Matrix Representation of Polynomial Dynamical Systems

In order to propose and apply a general matrix framework for polynomial DSs and in this manner to identify the place of the anzats treated in this study consider the second- and third-order (two- and three-dimensional) polynomial DSs that inolve quasi-polynomials (QPs); the DSs of this class can be written in the general form containing all quadratic terms

\{\begin{matrix} \dot{x} = a_{0} + a_{1} x + a_{2} y + a_{3} x^{2} + a_{4} y^{2} + a_{5} x y, \\ \dot{y} = b_{0} + b_{1} x + b_{2} y + b_{3} x^{2} + b_{4} y^{2} + b_{5} x y, \end{matrix}

(1)

\{\begin{matrix} \dot{x} = a_{0} + a_{1} x + a_{2} y + a_{3} z + a_{4} x^{2} + a_{5} y^{2} + a_{6} z^{2} + a_{7} x y + a_{7} x z + a_{9} y z, \\ \dot{y} = b_{0} + b_{1} x + b_{2} y + b_{3} z + b_{4} x^{2} + b_{5} y^{2} + b_{6} z^{2} + b_{7} x y + b_{8} x z + b_{9} y z, \\ \dot{z} = c_{0} + c_{1} x + c_{2} y + c_{3} z + c_{4} x^{2} + c_{5} y^{2} + c_{6} z^{2} + c_{7} x y + c_{8} x z + c_{9} y z, \end{matrix}

(2)

where dot denotes differentiation with respect to time.

In view of the technique developed in this work, it is convenient to introduce the coefficient 2 x 5 or 3 x 9 matrices associated with DS (1) or (2),

\begin{matrix} A^{(2)} = [\begin{matrix} a_{0} & a_{1} & \dots & a_{5} \\ b_{0} & b_{1} & \dots & b_{5} \end{matrix}], A^{(3)} = [\begin{matrix} a_{0} & a_{1} & \dots & a_{9} \\ b_{0} & b_{1} & \dots & b_{9} \\ c_{0} & c_{1} & \dots & c_{9} \end{matrix}] . \end{matrix}

(3)

Different sets of real coefficients

a, b

a, b, c

that enter matrices (3) govern qualitative behaviour of solutions and the occurrence and character of singularities and bifurcations. Note that generally all these DSs are non-integrable.

A well-known particular case of (1) constitutes linear homogeneous two-dimensional DSs that admit a matrix representation employing a square matrix

\{\begin{matrix} \dot{x} = a_{1} x + a_{2} y, \\ \dot{y} = b_{1} x + b_{2} y, \end{matrix} o r \dot{x} = A x, A = [\begin{matrix} a_{1} & a_{2} \\ b_{1} & b_{2} \end{matrix}]

(4)

(because the number of unknowns equals the number of equations). All their bifurcation types (critical modes) at the origin are identified and classified in terms of the eigenvalues

λ_{1}, λ_{2}

of the DS coefficient (real-valued) matrix A; more precisely, by the combination of their signs (or of the signs of their imaginary parts if they are complex) and zero values

λ_{1, 2} > 0

λ_{1, 2} < 0

λ_{1} > 0, λ_{2} < 0

λ_{1} = 0, λ_{2} \neq 0

etc (node (source, sink), saddle, focus, center etc). Every such combination naturally gives rise to a class of equivalence on the set

R^{4}

of square

2 \times 2

matrices with real entries characterized by the unique combination of signs of eigenvalues or their real and imaginary parts. Limiting ourselves to the set

R^{4, r e}

of matrices having real nonzero eigenvalues one may identify three such classes (without separating the cases of double roots) denoting them by the ’sign’ vectors

s_{1} = [+ +]

s_{2} = [- -]

, and

s_{3} = [- +]

. Each class has its particular type of bifurcation at the origin (source, sink, saddle).

One can create general qualitative theory for the DSs described by (4). However, it is not possible to create any general qualitative theory for the whole DS class described by (1) or (2). Therefore, a common practice is that researchers (beginning from Hilbert and Poincare) specify certain sub-classes of quadratic polynomial DSs, mainly in 2D, which are amenable to qualitative analysis. The present study is on this track and picks up a certain sub-class which can be fully investigated as a family of integrable DSs.

In [2,5] a detailed qualitative investigation is performed of two-dimensional polynomial DSs and a long list of the relevant publications can be found. A global bifurcation theory of such systems is presented, including particularly the issues connected with solution to the famous Hilbert’s Sixteenth Problem concerning the determination of the maximum number and relative position of limit cycles. In this respect, certain specific families of two-dimensional polynomial DSs (1) are identified. Particularly, give examples of their so-called canonical forms [5] with ’mixed’ variables accepted in the literature

\{\begin{matrix} \dot{x} = - y - α y^{2} - x y, \\ \dot{y} = x + (λ + β + γ) y + a x^{2} + c γ y^{2} + (α + β + γ) x y, \end{matrix}

(5)

with

\begin{matrix} a_{0} = a_{1} = a_{3} = 0, a_{2} = - 1, a_{4} = - α, a_{5} = - 1, \\ b_{0} = 0, b_{1} = 1, b_{2} = λ + β + γ, b_{3} = a, b_{4} = c γ, b_{5} = α + β + γ, \end{matrix}

(6)

and the coefficient matrix

\begin{matrix} A^{(2)} = [\begin{matrix} 0 & 0 & - 1 & 0 & - α & - 1 \\ 0 & 1 & λ + β + γ & a & c γ & α + β + γ \end{matrix}], \end{matrix}

(7)

\{\begin{matrix} \dot{x} = - y - ν y^{2}, ν = 0, 1, \\ \dot{y} = x + (λ + β + γ) y + a x^{2} + c γ y^{2} + (β + γ) x y, \end{matrix}

(8)

in (1) with

\begin{matrix} a_{0} = a_{1} = a_{3} = a_{5} = 0, a_{2} = - 1, a_{4} = - ν, \\ b_{0} = 0, b_{1} = 1, b_{2} = λ + β + γ, b_{3} = a, b_{4} = c γ, b_{5} = β + γ, \end{matrix}

(9)

in (1) and the coefficient matrix

\begin{matrix} A^{(2)} = [\begin{matrix} 0 & 0 & - 1 & 0 & - ν & 0 \\ 0 & 1 & λ + β + γ & a & c γ & β + γ \end{matrix}], \end{matrix}

(10)

\{\begin{matrix} \dot{x} = - y + ν y^{2}, ν = 0, 1, \\ \dot{y} = x + (λ + β) y + a x^{2} + c y^{2} + β x y \end{matrix}

(11)

in (1) and the coefficient matrices

\begin{matrix} A_{ν = 0}^{(2)} = [\begin{matrix} 0 & 0 & - 1 & 0 & 0 & 0 \\ 0 & 1 & λ + β & a & c & β \end{matrix}], A_{ν = 1}^{(2)} = [\begin{matrix} 0 & 0 & - 1 & 0 & 1 & 0 \\ 0 & 1 & λ + β & a & c & β \end{matrix}] . \end{matrix}

(12)

There is a number of other forms employing different sets of real coefficients

a, b, c

characterized each by specific properties of bufircations.

The volume of research and quantity of publication dealing with qualitative analysis of quadratic two-dimensional polynomial DSs may be characterized as enormous; however, many problems remain unsolved. Exemplify the classification of the number and character of finite singularities reported for these systems; particularly for (11) it is established that there may be one saddle and three antisaddles, three saddles and one antisaddle, two saddles and two antisaddles etc depending on the parameter sets involved.

Qualitative analysis of quadratic three-dimensional polynomial DSs (2) is less developed; the amount of the obtained results could be hardly compared with that achieved for two-dimensional polynomial DSs. Note in this way a class of the T-systems of the form

\{\begin{matrix} \dot{x} = y - x, \\ \dot{y} = m x - x z, \\ \dot{z} = - n z + x y \end{matrix}

(13)

and the coefficient matrix composed according to (3)

\begin{matrix} A^{(3)} = [\begin{matrix} 0 & 1 & - 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & m & 0 & 0 & 0 & 0 & 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & - n & 0 & 0 & 0 & 1 & 0 & 0 \end{matrix}] . \end{matrix}

(14)

The DSs belonging to the class of T-systems are studied in [22] (we also refer to the references therein), where, among all, the pitchfork and Hopf bifurcations occurring in the T-system are reported as well as the influence of the symmetry of the system on its dynamics. Seemingly simple, these systems require the elaboration of advanced mathematical tools within the frames the singular perturbation and geometric singular perturbation theory [23].

The latter has become a driving force: in our studies, we address, as well as in this one, a particular integrable family of quadratic autonomous three-dimensional polynomial DSs with ’separated’ variables and free terms

\{\begin{matrix} \dot{x} = a_{0} + a_{1} x + a_{4} x^{2}, \\ \dot{y} = b_{0} + b_{2} y + b_{5} y^{2}, \\ \dot{z} = c_{0} + c_{3} z + c_{6} z^{2} . \end{matrix}

(15)

with the coefficient matrix (3)

\begin{matrix} A^{(3)} = [\begin{matrix} a_{0} & a_{1} & 0 & 0 & a_{4} & 0 & 0 & 0 & 0 & 0 \\ b_{0} & 0 & b_{2} & 0 & 0 & b_{5} & 0 & 0 & 0 & 0 \\ c_{0} & 0 & 0 & c_{3} & 0 & 0 & c_{6} & 0 & 0 & 0 \end{matrix}] . \end{matrix}

(16)

Representation (15) where the number of terms on the right-hand side equals the number of dependent variables enables one to write the corresponding DS in a compact quadratic-matrix form which will be done below in this section. In view of this, it is convenient to rearrange the coefficient matrix of (15) to the symmetric

3 \times 3

form

\begin{matrix} A^{(3)} = [\begin{matrix} a_{0} & a_{1} & a_{4} \\ b_{0} & b_{2} & b_{5} \\ c_{0} & c_{3} & c_{6} \end{matrix}] = {∥a_{k j}∥}_{k, j = 1, 2, 3} . \end{matrix}

(17)

Here we see a formal similarity between the DS classes described by (4) and (15), (17) (partly because in both cases the number of the equation terms equals the number of equations yielding square DS coefficient matrices). In our analysis we extend this similarity and introduce and describe the equivalence classes using the ’sign’ S-vectors on the set of

3 \times 3

coefficient matrices.

Investigation of the DS (15) may be, among all, the first step towards analysis of more complicated polynomial DSs with ’mixed’ variables as in (2). Here, the sets of nine real coefficients

a, b, c

in (15) govern qualitative behaviour of solutions; however, as we show, many important properties are governed by actually three decisive parameters. Namely, there is a finite number of integrable combinations of solutions to (15) and, remarkably, they all can be fully classified by three parameters, the discriminants of the polynomial entering DSs using the discriminant criterium [6,7].

The proposed matrix representation of polynomial DSs is among all definitely a useful tool of saving information about the DS in a compact form. Indeed, as we see from (5)–(12) and (13), many known kinds of DSs can be described using this compact matrix anzats.

A conjecture is that there are deep specific relations between the structure of the coefficient matrix (its rank, symmetry) and qualitative properties of a polynomial DS. In this study we confirm this statement for a specific integrable family of such DSs.

2.2. Discriminant Criterion and Matrix Representation of 3D Polynomial Dynamical Systems

The discriminant criterion employs introduction of the D-vectors which is based on the following general anzats: A DS coefficient matrix can be represented, as well as any

3 \times 3

matrix, in the form of a column of raw vectors

\begin{matrix} A^{(3)} = [\begin{matrix} a_{0} & a_{1} & a_{4} \\ b_{0} & b_{2} & b_{5} \\ c_{0} & c_{3} & c_{6} \end{matrix}] = {∥a_{k j}∥}_{k, j = 1, 2, 3} = [\begin{matrix} {a^{'}}_{1} \\ {a^{'}}_{2} \\ {a^{'}}_{3} \end{matrix}] . \end{matrix}

(18)

Let

f (x, y, z) :

R^{3} \to

R denote a smooth real-valued function of three variables. An f-vector

F^{(3)}

associated with function f and matrix (18) can be defined as a ’3D vector-valued functional’ according to

\begin{matrix} F^{(3)} = [\begin{matrix} f ({a^{'}}_{1}) \\ f ({a^{'}}_{2}) \\ f ({a^{'}}_{3}) \end{matrix}] . \end{matrix}

(19)

A concrete form of f is dictated by specific needs of analysis.

Particularly, we define f-vectors of the DS coefficient matrices as the discriminant (D-) column vector; simultaneously we define the (S-) row vector of the discriminant signs associated with the DS coefficient matrix (17):

\begin{matrix} D^{(3)} = D^{(3)} (A^{(3)}) = [\begin{matrix} D_{1} \\ D_{2} \\ D_{3} \end{matrix}], S^{(3)} = S^{(3)} (A^{(3)}) = [s i g n D_{1}, s i g n D_{2}, s i g n D_{3}] . \end{matrix}

(20)

S-vectors may be equally represented as sets of the three ordered numbers

- 1, 0, 1

, so that, for example,

\begin{matrix} S^{(3)} = [+ 0 -] = [1 0 - 1] i f D_{1} > 0, D_{2} = 0, D_{3} < 0 . \end{matrix}

The quantities

{D = D}_{i} = {a_{i 2}}^{2} - 4 a_{i 1} a_{i 3}

in (20) specifying the concrete form of f are the discriminants of the quadratic trinomials

P_{i}

entering the ith row of system (42); they are considered each as a real-valued function of three variables

a_{i 1}, a_{i 2}, a_{i 3}

i = 1, 2, 3

, with the range being the set of all real numbers.

Generally an f-vector (19) and particularly a D-vector (20) is an aggregate quantity (a ’vector-valued functional’) describing in a compact form certain important properties of a

3 \times 3

matrix or particularly the DS coefficient matrix and in this manner the DS itself, including its symmetries, bifurcations and singular points. The corresponding S-vector in its turn is an informative three-symbol description of a (set of) D-vector specifying characteristic classes of these vectors and yelding much less information than the D-vector: the range of D-vectors is the same as that of three-dimensional vectors with real components while the range of S-vectors is the set of three symbols (or three numbers

- 1, 0, 1

). S-vectors form a set denoted by S³ which contains a finite number of elements (this number is determined in the next section).

D-vectors (20) may be naturally considered as elements of a three-dimensional space R³ and a subset of D-vectors corresponding to an S-vector in (20) composed by a particular triple of signs will be a particular set of R³. Namely: the first, second, etc octants of R³ correspond to S-vectors

[+ + +]

[- + +]

, etc; the coordinate planes in R³ correspond to S-vectors

[\pm \pm 0]

[\pm 0 \pm]

[0 \pm \pm]

; and the coordinate axes in R³ correspond to S-vectors

[\pm 0 0]

[0 \pm 0]

[0 0 \pm]

etc.

We can define now the following sets and relations (mappings, denoted by

< >

) that couple these sets:

\begin{matrix} Set of polynomial DSs (15) \sim Set R^{9} of their coefficient matrices (17) < R^{9} \to R^{3} > \end{matrix}

(21)

\begin{matrix} Set R^{3} of D - vectors (20) < R^{3} \to S^{3} > Set of S - vectors (20) . \end{matrix}

(22)

Application of the discriminant criterion means that, on the first step, we assign to a coefficient matrix (17) the discriminant D-vector and to the latter the S-vector of the discriminant signs (20). On the second step, one establishes classes of equivalence (invariance, symmetry) on the sets of the DS coefficient matrices and DS general solutions and the D-vectors in terms, respectively, of the D- or S-vectors (this issue is addressed in the next section). On the third step, analysis is performed of the DS qualitative behavior within a chosen equivalence class including the occurrence and character of bifurcations, as well as specific analysis of the transitions between classes (when one of the discriminants changes the sign).

Exemplify the relations between particular coefficient matrix families and its D- and S-vectors which, as will be shown below, govern qualitative properties of the corresponding DS solutions.

Identity and ’anti-identity’ matrices:

\begin{matrix} A^{(3)} = I^{(3)} = [\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}], {I^{'}}^{(3)} = [\begin{matrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{matrix}], \end{matrix}

(23)

\begin{matrix} D^{(3)} (I^{(3)}) = D^{(3)} ({I^{'}}^{(3)}) = [\begin{matrix} 0 \\ 1 \\ 0 \end{matrix}], S^{(3)} = [0 + 0], \end{matrix}

Diagonal and ’anti-diagonal’ matrices:

\begin{matrix} A^{(3)} = [\begin{matrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & c \end{matrix}], {A^{'}}^{(3)} = [\begin{matrix} 0 & 0 & a \\ 0 & b & 0 \\ c & 0 & 0 \end{matrix}], \end{matrix}

(24)

\begin{matrix} D^{(3)} (A^{(3)}) = D^{(3)} ({A^{'}}^{(3)}) = [\begin{matrix} 0 \\ b^{2} \\ 0 \end{matrix}], S^{(3)} = [0 + 0] . \end{matrix}

Upper- (lower-) triangular matrix:

\begin{matrix} A^{(3)} = [\begin{matrix} a & b & c \\ 0 & d & e \\ 0 & 0 & f \end{matrix}], D^{(3)} = [\begin{matrix} b^{2} - 4 a c \\ d^{2} \\ 0 \end{matrix}], S^{(3)} = [\pm + 0]; \end{matrix}

(25)

\begin{matrix} A^{(3)} = [\begin{matrix} f & 0 & 0 \\ e & d & 0 \\ a & b & c \end{matrix}], D^{(3)} = [\begin{matrix} 0 \\ d^{2} \\ b^{2} - 4 a c \end{matrix}], S^{(3)} = [0 + \pm] . \end{matrix}

(26)

Symmetric matrix:

\begin{matrix} A^{(3)} = [\begin{matrix} a & b & c \\ b & d & e \\ c & e & f \end{matrix}], D^{(3)} = [\begin{matrix} b^{2} - 4 a c \\ d^{2} - 4 b e \\ e^{2} - 4 c f \end{matrix}], S^{(3)} = [\pm \pm \pm] . \end{matrix}

(27)

One may continue this list for other particular matrix families.

We see that for matrices (23)–(24), the D- and S-vectors are invariant w.r.t. interchange (permutation) of the first and third raws, creating in this manner a definite symmetry (and the invariance or equivalence classes). This issue is discussed in more detail in the next section.

Next, according to relations (21) and (22) and between subsets of the space R³ of D- and S-vectors, the D- and S-vectors may be treated as quantities establishing classes of equivalence (invariance, symmetry) on the sets of (i) the DS coefficient matrices and DS general solutions in terms of the D- or S-vectors (when each D-vector corresponds to a particular subset of the DS coefficient matrices and each S-vector corresponds to a particular subset of D-vectors) and (ii) the D-vectors in terms of the S-vectors using relations (22). There are finitely many equivalence classes specified by condition (ii) and they are described in the next section.

Whether the DS coefficient matrix (17) belongs to a certain equivalence class determines the presence and nature (type) of singular points and bifurcations of the corresponding polynomial DS (15). This is a crucial reason to introduce D- and S-vectors and investigate quadratic polynomial DSs in terms of the equivalence classes (symmetry relations) defined using these vector quantities.

2.3. Symmetry Relations on the Sets of Coefficient Matrices and D-Vectors

D-vectors possess definite symmetry relations; namely, representing coefficient matrix (17) as a triple (raw) of column vectors,

\begin{matrix} A^{(3)} = {∥a_{k j}∥}_{k, j = 1, 2, 3} = [a_{1} a_{2} a_{3}] \end{matrix}

(28)

we can write a D-vector with components (20) as

\begin{matrix} D^{(3)} = D^{(3)} (a_{1}, a_{2}, a_{3}) = {∥{a_{i 2}}^{2} - 4 a_{i 1} a_{i 3}∥}_{i = 1, 2, 3} = a_{2}^{2} - 4 a_{1} a_{3} \end{matrix}

(29)

and deduce that

and the following symmetry relations hold

\begin{matrix} D^{(3)} (a_{1}, a_{2}, a_{3}) = D^{(3)} (a_{1}, - a_{2}, a_{3}), D^{(3)} (a_{1}, a_{2}, a_{3}) = D^{(3)} (a_{3}, a_{2}, a_{1}) . \end{matrix}

(33)

The same symmetry relations (33) hold for S-vectors (D- and S-vectors are invariant. w.r.t. the sign of the central column and interchange of the side columns).

We see that for the matrices satisfying (30)–(32), the D- and S-vectors are the same; i.e. they are invariant w.r.t. any interchange (permutation) of the matrix raws creating in this manner definite symmetries (and the invariance or equivalence classes).

It is reasonable to introduce and consider a subset of coefficient matrices (17) of the form

\begin{matrix} A^{(3)} = [\begin{matrix} a & 2 b & 1 \\ c & 2 d & 1 \\ e & 2 f & 1 \end{matrix}] = [a_{1} 2 a_{2} 1], \end{matrix}

(34)

with the D-vectors

\begin{matrix} D^{(3)} = D^{(3)} (a_{1}, a_{2}, 1) = a_{2}^{2} - a_{1} = [\begin{matrix} b^{2} - a \\ d^{2} - c \\ f^{2} - e \end{matrix}] \end{matrix}

(35)

corresponding to DSs (15) with reduced polynomials having nonzero quadratic terms. Unlike (17) which is a nine-parameter matrix set, coefficient matrices (34) constitute a six-parameter subset of

3 \times 3

matrices. The following conditions hold that specify the subsets of the equivalence classes of matrices (34):

A case which may important is the set of degenerate coefficient matrices (34) having the forms

\begin{matrix} [α \cdot 1 2 a_{2} 1] = [\begin{matrix} α & 2 b & 1 \\ α & 2 d & 1 \\ α & 2 f & 1 \end{matrix}], [a_{1} β \cdot 1 1] = [\begin{matrix} a & β & 1 \\ c & β & 1 \\ e & β & 1 \end{matrix}] o r [a_{1} γ \cdot a_{1} 1] = [\begin{matrix} a & γ a & 1 \\ c & γ c & 1 \\ e & γ e & 1 \end{matrix}] . \end{matrix}

(39)

For these coefficient matrices the conditions (36) -(38) that specify belonging to the equivalence classes governed by the corresponding S-vectors may be greatly simplified; e.g.

\begin{matrix} D^{(3)} (α \cdot 1, 2 a_{2}, 1) : α < 0 \to S^{(3)} = [+ + +] . \end{matrix}

(40)

Many more symmetry (equivalence, invariance) relations may be discovered and described for the set of D-vectors. Their complete description goes far beyond the scope of the present study and may be a subject of a great number of future works performed by other researchers.

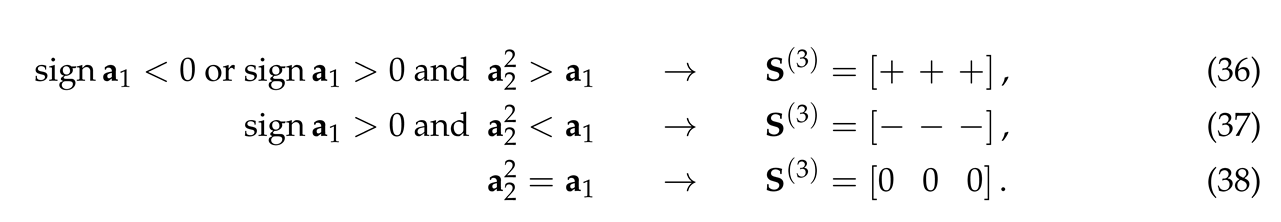
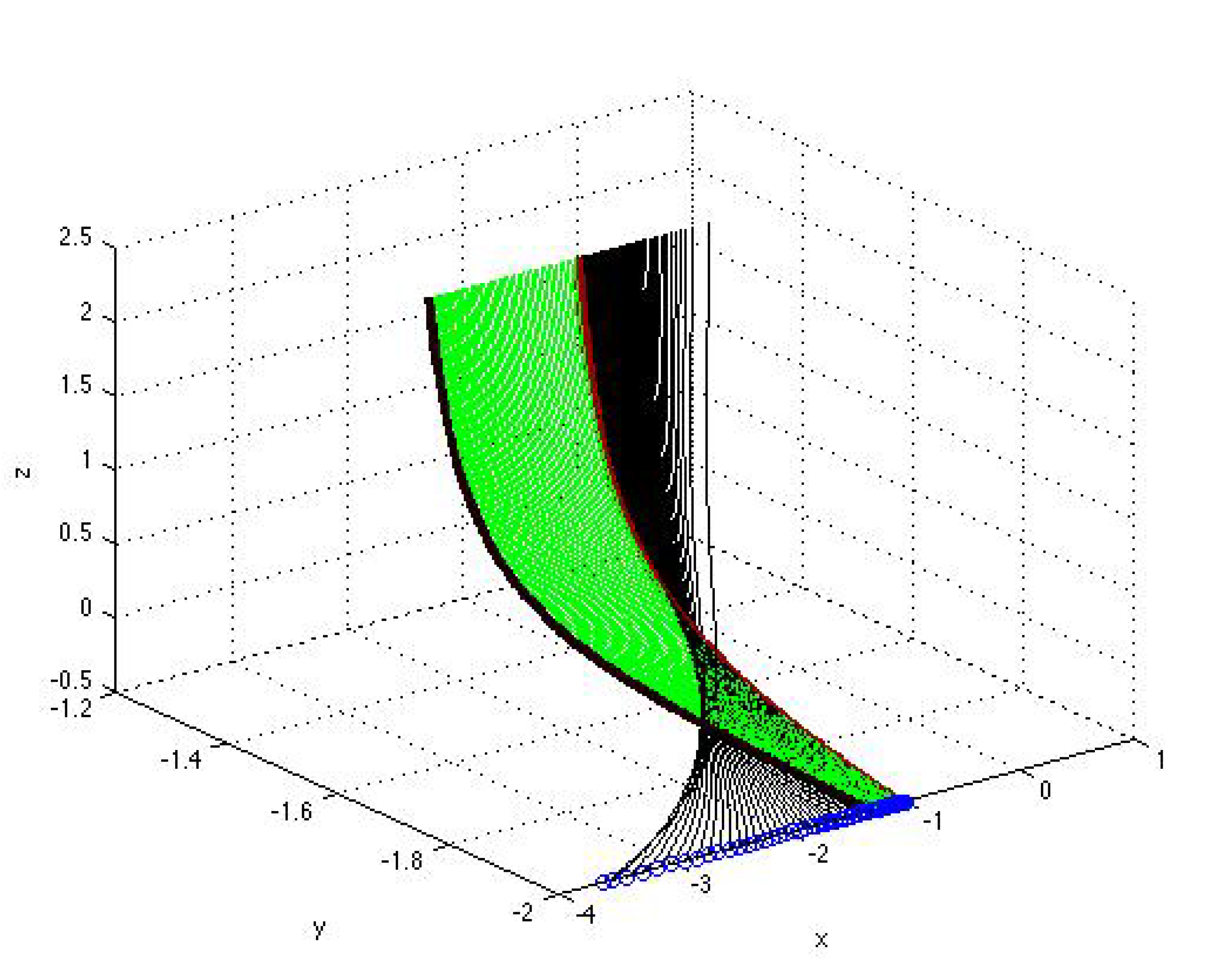
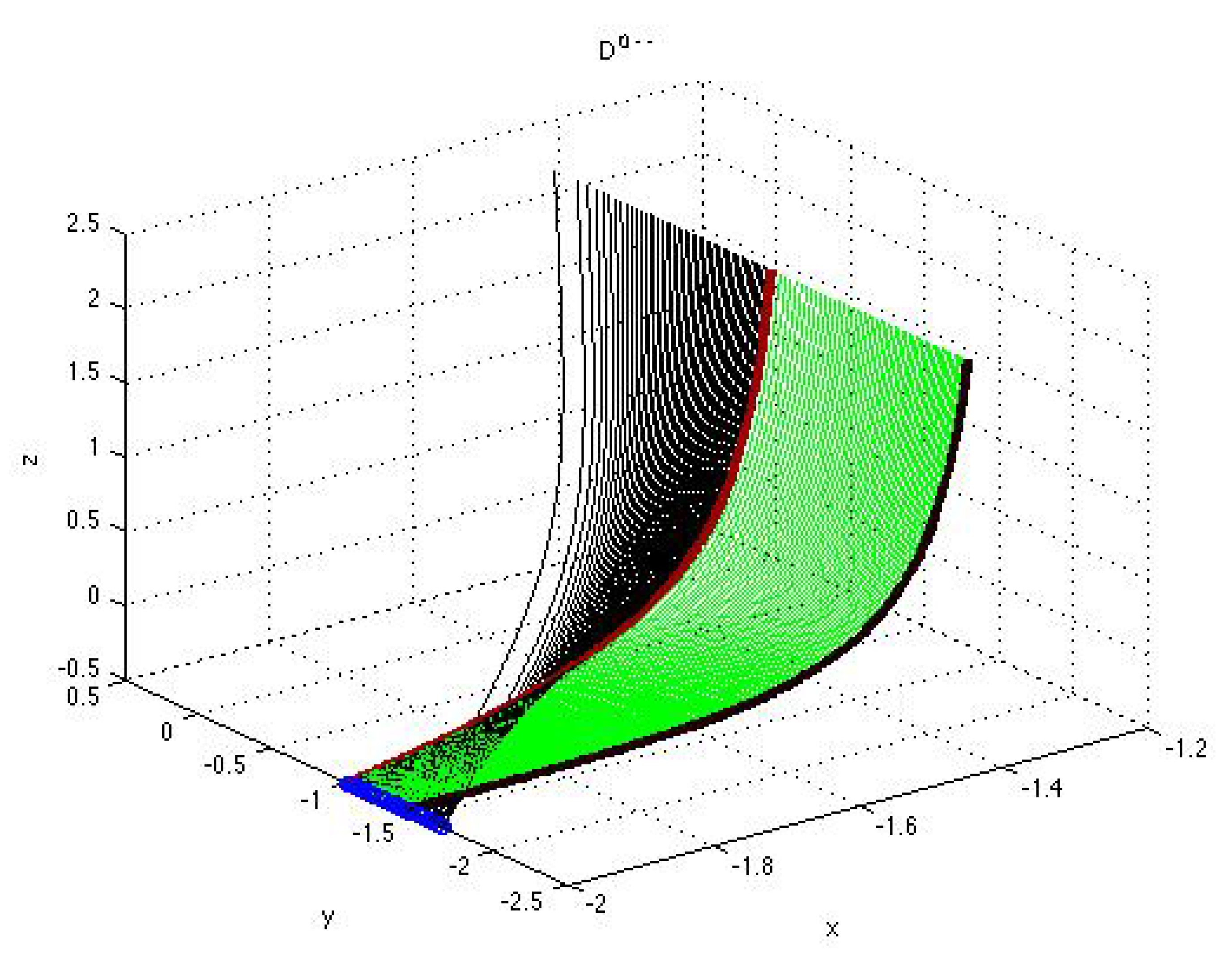
3. Classification of Solutions to Autonomous Polynomial Equations

3.1. Representations of Autonomous and Integrable Polynomial Dynamical Systems

In view of integrability of (15) for arbitray set of its nine parameters (coefficients)

a, b, c

we propose and develop a method of analysis of singularities and bifurcations based on direct investigation of its explicitly obtained general solutions and solutions to initial-value problems (rather than on the methods employing general bifurcation theory, characteristic DS polynomials and the like). This technique of the ’direct’ DS qualitative analysis has proved to be a good complement to general methods of analysis.

Following [6,7] present a brief description of a family of autonomous DSs written in the compact vector form as

\dot{x} = F (x), x, F \in R^{n},

where

R^{n}

denotes n-dimensional vector space. A sub-family of autonomous DSs for which vector-functions

F

are QPs, namely, finite sums of monomials containing powers of the dependent variables that can be real numbers are exemplified in (1)–(15).

Autonomous symmetric n-dimensional polynomial DSs form a class of autonomous DSs,

\frac{d x_{k}}{d t} = \sum_{i, j = 1}^{n} A_{k}^{i j} x_{i} (t) x_{j} (t), k = 1, 2, \dots, n,

involving symmetric polynomials in n variables of degree two with equal-index quadratic terms (

i = j

), where

A_{k}^{i j} = A_{k}^{j i}

are given real numbers and

x = [x_{1} (t), x_{2} (t), \dots, x_{n} (t)];

below, when convenient, we will a use the notation

x = [x, y, z]

in the 3D case under an assumption that

R^{3}

is equipped with a Cartesian coordinate system.

There are several families of algebraically integrable autonomous polynomial DSs mentioned in Introduction. In general, however, autonomous polynomial DSs are not integrable. Note that such DSs containing solely equal-index quadratic terms with the nonzero

A_{k}^{k k} = a_{1 k}

(

k = 1, 2, \dots, n)

and the rest of

A_{k}^{i j} = 0

consitute a sub-family of degenerate autonomous polynomial DSs as in (15) and are algebraically integrable in elementary functions.

Autonomous n-dimensional polynomial DSs which are generally nonsymmetric and where (each) ith component of

F

is a polynomial of degree

N_{i}

in one variable

x_{i}, i = 1, 2, \dots, n,

with real coefficients can be represented as

\dot{x} = P (x), or \frac{d x_{i}}{d t} = P_{i} (x_{i}), P_{i} (s) = \sum_{j = 1}^{N_{i} + 1} a_{j i} s^{N_{i} - j + 1}, i = 1, 2, \dots, n,

(41)

where

a_{j i}

are given real numbers. To every DS of the type (41) the vector of the polynomial dimensions

\bar{N} = {\{N_{i}\}}_{i = 1}^{n}

can be assigned as well as the number

N = \sum_{i = 1}^{n} N_{i}

, the DS total order. Autonomous n-of dimensional polynomial DSs (41) are algebraically integrable in elementary functions; the corresponding statements are proved in Appendix A.

DSs (41) of the dimension

n = 3

with

\bar{N} = [2, 2, 2]

and total order 6,

\dot{x} = P (x), or \frac{d x_{k}}{d t} = P_{k} (x_{k}), P_{k} (s) = \sum_{j = 1}^{3} a_{k j} s^{j - 1}, k = 1, 2, 3

(42)

(this form is equivalent to (15) with matrix (17) having the entries

a_{11} = a_{0}

a_{12} = a_{1}

a_{13} = a_{4}

a_{21} = b_{0}

a_{22} = b_{2}

a_{23} = b_{5}

, and

a_{31} = c_{0}

a_{32} = c_{3}

a_{33} = c_{6}

) are generally nonsymmetric, each component of

F

is a polynomial of degree two (with real coefficients) in one variable

x_{j}, j = 1, 2, 3

As follows from Theorem 1 in Appendix A, DSs (15) are algebraically integrable in elementary functions. In other words, DSs (2) with coefficient matrices (16) are algebraically integrable.

The sets of solutions to (42) (or (15)) are described in the next section.

Obtaining general solution to DSs (42) is based on

(a) factorization of the polynomials

P_{i} (s)

on the right-hand side of DS (15), (41), or (42) to a product of irreducible polynomials performed in Appendix A,

(b) subsequent representation of functions

{P_{i} (s)}^{- 1}

as partial fraction decomposition, and

All steps (a)—(c) can be accomplished explicitly for polynomials of degree two ending up with general solution to the corresponding three-dimensional polynomial DSs.

In this paper we investigate qualitatively the behavior of the solutions to DS (42). With this purpose we make use of the DS coefficient matrices and divide the DS family under study into the equivalence classes using the specially defined discriminant vectors. Based on this framework, we introduce and identify the particular bifurcations using the proposed methods of analysis of polynomial quadratic DSs. We employ the characteristic property inherent just to quadratic three-dimensional DSs: solutions

x = x (t)

to these DSs and particularly to (42) are curves in

R^{3}

parametrized by time t.

We consider the properties of the general solution of each of the equations in the system using the example of the equation

\dot{x} = f (x),

and solutions of the Cauchy problem

\dot{x} = f (x)

x (0) = q_{0}

(of the quadratic polynomial DS) on the phase plane x, t depending on the problem parameters.

3.2. General Solutions to Autonomous Second-Order Polynomial Equations

The general solutions of the autonomous polynomial equation

\dot{x} = f (x), f (x) = a x^{2} + b x + c,

is obtained for all possible factorization cases (with respect to the signs of the discriminants) and combinations of the polynomial coefficients in the system. The discriminants of polynomials (namely, their signs) are the defining parameters that control the essential properties of solutions specify their complete classification.

(a) $a = 0$ ; $\dot{x} = f (x)$ is a first-order linear equation with constant coefficients and its solutions $x (t) = {\frac{1}{b} (- c + C e}^{t}), b \neq 0,$ are differentiable monotone functions on the whole line.

In what follows we will consider the equations with $a \neq 0 .$
(b)D> 0; there are three families of the general solution

${x (t; C) = x}_{1} + \frac{\sqrt{D}}{a} \frac{1}{- 1 + C e^{- \sqrt{D} t}}, x_{1, 2} = - x_{0} \pm \frac{\sqrt{D}}{2 a}, x_{0} = \frac{b}{2 a}, D = b^{2} - 4 a c,$

of the equation $\dot{x} = f (x)$ :

Family U, $C > 0$ : solutions $x (t; C) = x_{U} (t; C)$ are unstable, since they

(i) have a “movable” singularity with $t = t^{*} (C) = \frac{ln C}{\sqrt{D}}$ ,

(ii) are monotonically increasing functions on the whole line for $t \neq t^{*}$ since $\frac{d x (t; C)}{d t} = \sqrt{D} \frac{C e^{- \sqrt{D} t}}{{(C e^{- \sqrt{D} t} - 1)}^{2}} > 0$ for C> 0,

(iii) satisfy the condition $x (t; C) > x_{2}, x < t^{*}, x (t; C) < x_{1}, x > t^{*},$ and

(iv) have two horizontal asymptotes $x = x_{1} or x = x_{2}$ ; these solutions are not bounded on the whole line (the latter means instability).

Family S, $C > 0$ : solutions $x (t; C) = x_{S} (t; C)$ are stable since they have no singularities, are monotonically decreasing $(\frac{d x (t; C)}{d t} < 0)$ and bounded functions on the whole line, satisfying the condition $x_{1} < x (t; C) < x_{2}$ , and have two asymptotes $x = x_{1} and x = x_{2}$ (the last condition written in the form of limits (A1) means stability).

Family T, : $x = x_{1}$ and $x = x_{2}$ are stationary solutions of the equation $\dot{x} = f (x)$ satisfying the initial conditions $x (0) = x_{1} o r x (0) = x_{2},$ and the first corresponds to $C = 0$ in ${x (t; C) = x}_{1} + \frac{\sqrt{D}}{a} \frac{1}{- 1 + C e^{- \sqrt{D} t}}$ .

Stationary solutions $x = x_{1}$ and $x = x_{2}$ are ’nonisolated’, so that in every neighborhood of each of these solutions there are infinitely many ’non-singular’ solutions $x_{U} (t; C)$ or $x_{S} (t; C)$ from families U or S:

$\forall ε > 0 \exists B > 0, C \neq 0 : |x_{U} (t; C) - x_{1, 2}| < ε, |t| > B or |x_{S} (t; C) - x_{1, 2}| < ε, |t| > B,$

and an arbitrarily small change of the parameter $q_{0}$ in the initial condition $x (0) = q_{0} = x_{1}$ or $x (0) = q_{0} = x_{2}$ translates the stationary solution $x = x_{1}$ or $x = x_{2}$ to one of the stable or unstable solutions from the families S or U.
(c), $D = 0$ : all solutions

$x (t; C) = - \frac{1}{a} (\frac{b}{2} + \frac{1}{t - C})$

are unstable since they have a “moving” singularity at $t = C,$ are monotonically increasing or decreasing (depending on the sign of a) functions for $t \neq C$ are not bounded on the whole line (the latter means instability) and have the asymptote $x = {- x}_{0}$ . Stationary solutions $x = {- x}_{0}$ are special in the sense that in any neighborhood there are infinitely many ’non-singular’ solutions $x (t; C)$ .
(d), $D < 0$ : all solutions

$x (t; C) = - x_{0} + \frac{\sqrt{- D}}{2 a} tan \frac{\sqrt{- D}}{2} (t + C), D < 0,$

are unstable since they have “movable” singularities for $t = t_{n}^{*} (C) = \frac{2}{\sqrt{- D}} (\frac{π}{2} (2 n + 1) - C),$ $n = 0, \pm 1, \pm 2, \dots,$ are monotonically increasing or decreasing (depending on the sign of parameter a) functions for $t \neq t_{n}^{*} (C)$ because, for example,

$\frac{d x (t; C)}{d t} = \frac{(- D)}{4 a} \frac{1}{{(cos \frac{\sqrt{- D}}{2} (t + C))}^{2}} > 0$

for $C > 0$ , $D < 0$ , and $a > 0$ and are not bounded on the whole line (the latter means instability).

In case (d) there are no solutions that are special in the same sense as stationary solutions in case (b).

3.3. Equivalence Classes of D-Vectors and General Solutions to Autonomous Polynomial Equation Systems

Summarize all possible combinations of general solutions to DS (42) of dimension three identifying eight solution sets

D^{+ + +}

D^{+ + -}

D^{+ - +}

D^{+ - -}

D^{- + +}

D^{- + -}

D^{- - +}

, and

D^{- - -}

governed by all possible combinations of the nonzero discriminant signs. We identify as well 27 solution to DS (42) of dimension three as sets D^pmz, where p, m and z denote plus, minus, or zero and

p m z

is any of their combinations including those with two or three repetitions, corresponding to all possible combinations of the zero and nonzero discriminant signs.

A set D^pmz with a fixed combination

p m z

of signs is the equivalence class (defined in terms of S-vectors) in the sense that all its elements have the same S-vector S^pmz.

These solution sets are presented below in the convenient form of matrices (47) and (48).

In what follows we will consider the equations in system (42) with

a_{i 1} \neq 0

i = 1, 2, 3 .

and make use of the function families

g^{+} (t; D, C, a) = \frac{\sqrt{D}}{a} \frac{1}{- 1 + C e^{- \sqrt{D} t}}, D > 0,

g^{0} (t; C, a, b) = - \frac{1}{a} (\frac{b}{2} + \frac{1}{t - C}), D = 0,

(43)

g^{-} (t; D, C, a) = \frac{\sqrt{- D}}{2 a} tan \frac{\sqrt{- D}}{2} (t + C), D < 0,

where C is an arbitrary constant, specifying componentwise the general solutions of (42) for the respective signs of the discriminants

{D = D}_{i} = {a_{i 2}}^{2} - 4 a_{i 1} a_{i 3}

of polynomials

P_{i}

in system (42),

i = 1, 2, 3

3.4. Description of All Possible solution Combinations in Terms of Discriminants

In view of (43) and the relation between the coefficient matrix (17) and vectors (20), introduce the eight vector-functions

g⁺⁺⁺=[

g^{+} (t; D_{1}, C_{1}, a_{11}), g^{+} (t; D_{2}, C_{2}, a_{21}), g^{+} (t; D_{3}, C_{3}, a_{31})],

⋯⋯,

g⁻⁻⁻=[

g^{-} (t; D_{1}, C_{1}, a_{11}), g^{-} (t; D_{2}, C_{2}, a_{21}), g^{-} (t; D_{3}, C_{3}, a_{31})],

corresponding to the respective solution sets D⁺⁺⁺, ..., D⁻⁻⁻, so that the upper indices are the S-vectors that indicate the respective equivalence classes; the solution sets are formed by the vector-functions

x^{+ + +} = x_{1} + g^{+ + +}, or \{\begin{matrix} {x (t; C_{1}) = x}_{1} + \frac{\sqrt{D_{1}}}{a_{11}} \frac{1}{- 1 + C_{1} e^{- \sqrt{D_{1}} t}}, \\ {y (t; C_{2}) = y}_{1} + \frac{\sqrt{D_{2}}}{a_{21}} \frac{1}{- 1 + C_{2} e^{- \sqrt{D_{2}} t}}, \\ {z (t; C_{3}) = z}_{1} + \frac{\sqrt{D_{3}}}{a_{31}} \frac{1}{- 1 + C_{3} e^{- \sqrt{D_{3}} t}}, \end{matrix}

(44)

\dots \dots

x^{- - -} = x_{1} + g^{- - -}, or \{\begin{matrix} {x (t; C_{1}) = x}_{1} + \frac{\sqrt{- D_{1}}}{2 a} tan \frac{\sqrt{- D_{1}}}{2} (t + C_{1}), \\ {y (t; C_{2}) = y}_{1} + \frac{\sqrt{- D_{2}}}{2 a} tan \frac{\sqrt{- D_{2}}}{2} (t + C_{2}), \\ {z (t; C_{3}) = z}_{1} + \frac{\sqrt{- D_{3}}}{2 a} tan \frac{\sqrt{- D_{3}}}{2} (t + C_{3}); \end{matrix}

(45)

here

\begin{matrix} x_{1, 2} (D_{1}) & = & - x_{0} \pm \frac{\sqrt{D_{1}}}{2 a_{11}}, x_{0} = \frac{a_{12}}{2 a_{11}}, \\ y_{1, 2} (D_{2}) & = & - y_{0} \pm \frac{\sqrt{D_{2}}}{2 a_{21}}, y_{0} = \frac{a_{22}}{2 a_{21}}, \\ z_{1, 2} (D_{3}) & = & - z_{0} \pm \frac{\sqrt{D_{3}}}{2 a_{31}}, z_{0} = \frac{a_{32}}{2 a_{31}} \end{matrix}

(46)

a_{i 1} \neq 0

and

D_{i} > 0

i = 1, 2, 3

Figure 1. Surface

X_{D_{1}}^{- 0 -} \cup X_{D_{1}}^{+ 0 -}

formed by the parametrized curves

x (t; D_{1}) = x_{1} + g^{- 0 -}

(black),

C_{1} = - 1

- 4 < D_{1} < 0

, and

x (t; D_{1}) = x_{1} + g^{+ 0 -}, 0 \leq t \leq 1.3

(green),

0 < D_{1} < 4

, with

a_{11} = a_{13} = a_{21} = 1

and

a_{22} = 2

given by (43)–(46) corresponding to the solutions from the sets

D^{- 0 -}

and

D^{+ 0 -}

.The explicit formulas (A22)–(A26) for the parametrized components are in Appendix A.

Figure 1. Surface

X_{D_{1}}^{- 0 -} \cup X_{D_{1}}^{+ 0 -}

formed by the parametrized curves

x (t; D_{1}) = x_{1} + g^{- 0 -}

(black),

C_{1} = - 1

- 4 < D_{1} < 0

, and

x (t; D_{1}) = x_{1} + g^{+ 0 -}, 0 \leq t \leq 1.3

(green),

0 < D_{1} < 4

, with

a_{11} = a_{13} = a_{21} = 1

and

a_{22} = 2

given by (43)–(46) corresponding to the solutions from the sets

D^{- 0 -}

and

D^{+ 0 -}

.The explicit formulas (A22)–(A26) for the parametrized components are in Appendix A.

The matrix

\begin{matrix} G^{(+ -)} = [\begin{matrix} g^{+ + +} & g^{+ - +} & g^{+ + -} \\ g^{+ - -} & g^{- - -} \\ g^{- + +} & g^{- - +} & g^{- + -} \end{matrix}] \end{matrix}

(47)

associated with DS (42) comprises all possible eight solution sets of system (42) corresponding to all possible combinations of the solution components having nonzero determinants and characterized by their S-vectors. Empty entries may be replaced by zeros.

Figure 2. Surface

X_{D_{1}}^{- 0 -} \cup X_{D_{1}}^{+ 0 -}

formed by the parametrized curves

x (t; D_{1}) = x_{1} + g^{- 0 -}

(right, black),

- 4 < D_{1} < 0

, and

x (t; D_{1}) = x_{1} + g^{+ 0 -}, 0 \leq t \leq 1.3

(left, blue),

0 < D_{1} < 4

, with

a_{11} = a_{13} = a_{21} = 1

and

a_{22} = 2

given by (43)–(46) corresponding to the solutions from the sets

D^{- 0 -}

and

D^{+ 0 -}

. The explicit formulas (A16)–(A21) for the parametrized components are in Appendix A.

Figure 2. Surface

X_{D_{1}}^{- 0 -} \cup X_{D_{1}}^{+ 0 -}

formed by the parametrized curves

x (t; D_{1}) = x_{1} + g^{- 0 -}

(right, black),

- 4 < D_{1} < 0

, and

x (t; D_{1}) = x_{1} + g^{+ 0 -}, 0 \leq t \leq 1.3

(left, blue),

0 < D_{1} < 4

, with

a_{11} = a_{13} = a_{21} = 1

and

a_{22} = 2

given by (43)–(46) corresponding to the solutions from the sets

D^{- 0 -}

and

D^{+ 0 -}

. The explicit formulas (A16)–(A21) for the parametrized components are in Appendix A.

The matrix

\begin{matrix} G^{(+ - 0)} = [\begin{matrix} g^{+ + +} & g^{+ + -} & g^{+ - -} & g^{+ - +} & g^{+ + 0} & g^{+ - 0} \\ g^{- + +} & g^{- + -} & g^{- - -} & g^{- - +} & g^{- + 0} & g^{- - 0} \\ g^{00 +} & g^{00 -} & g^{000} \\ g^{+ 00} & g^{- 00} & g^{0 + 0} \\ g^{0 - 0} & g^{+ 0 +} & g^{0 + +} \\ g^{- 0 +} & g^{0 + -} & g^{+ 0 -} & g^{0 - +} & g^{- 0 -} & g^{0 - -} \end{matrix}] \end{matrix}

(48)

comprises all possible 27 solution sets of system (42) corresponding to all possible combinations with nonzero and zero determinants and characterized by their S-vectors. Empty entries in (48) may be replaced by zeros.

Figure 3. Surface

X_{D_{1}}^{- 0 -} \cup X_{D_{1}}^{+ 0 -}

formed by the parametrized curves

x (t; D_{1}) = x_{1} + g^{- 0 -}

(black),

C_{1} = - 1.3

- 4 < D_{1} < 0

, and

x (t; D_{1}) = x_{1} + g^{+ 0 -}, 0 \leq t \leq 1.3

(green),

0 < D_{1} < 4

, with

a_{11} = a_{13} = a_{21} = 1

and

a_{22} = 2

given by (43)–(46) corresponding to the solutions from the sets

D^{- 0 -}

and

D^{+ 0 -}

Figure 3. Surface

X_{D_{1}}^{- 0 -} \cup X_{D_{1}}^{+ 0 -}

formed by the parametrized curves

x (t; D_{1}) = x_{1} + g^{- 0 -}

(black),

C_{1} = - 1.3

- 4 < D_{1} < 0

, and

x (t; D_{1}) = x_{1} + g^{+ 0 -}, 0 \leq t \leq 1.3

(green),

0 < D_{1} < 4

, with

a_{11} = a_{13} = a_{21} = 1

and

a_{22} = 2

given by (43)–(46) corresponding to the solutions from the sets

D^{- 0 -}

and

D^{+ 0 -}

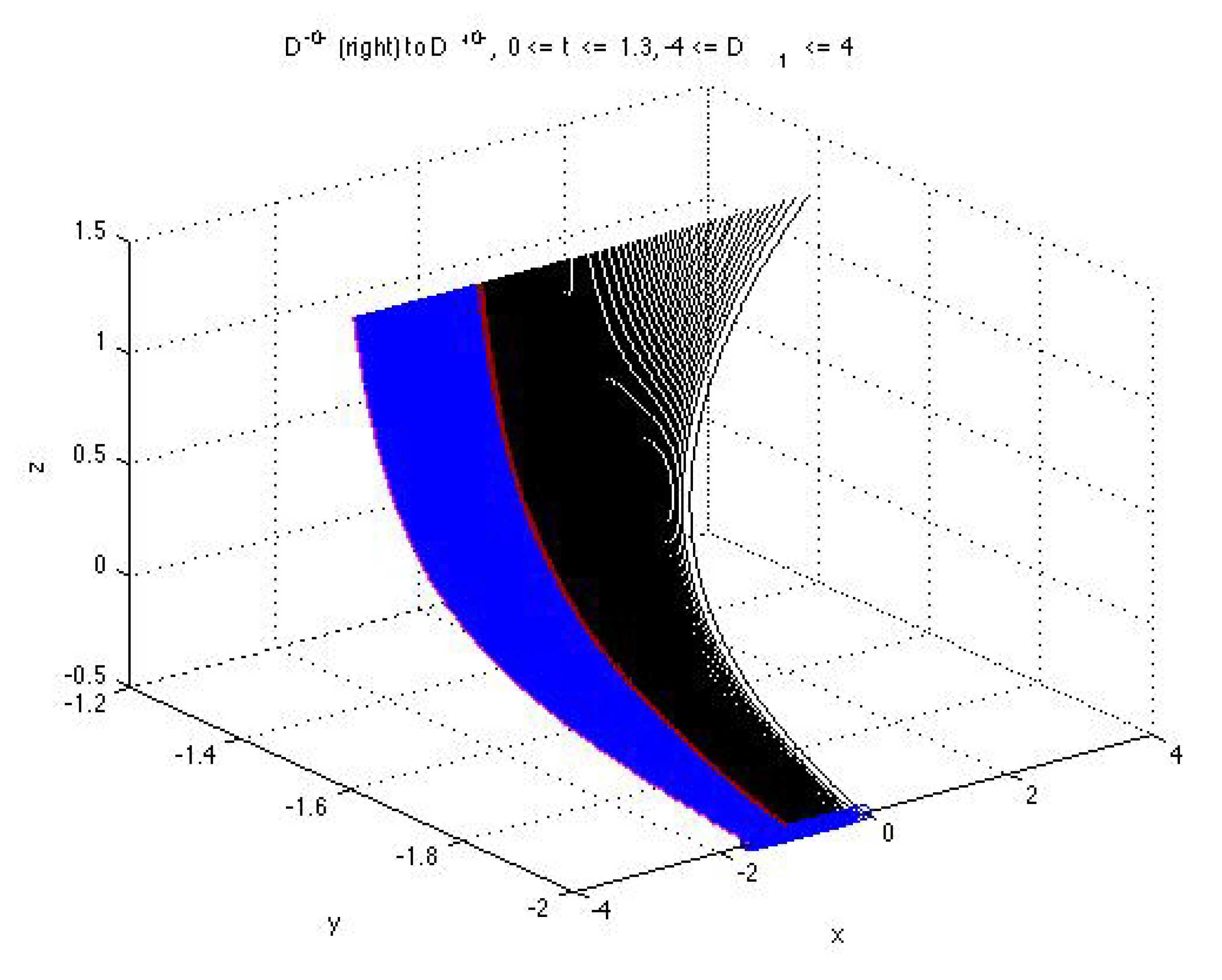
3.5. Analysis of Solutions to Cauchy Problems

Solutions to the Cauchy problems, e.g. to

\dot{x} = P_{1} (x)

x (0) = q_{0},

x (t; C_{1}^{0, +}) = x_{1} + g^{+} (t; D_{1}, C_{1}^{0, +}, a_{11}) = x_{1} + \frac{\sqrt{D_{1}}}{a_{11}} \frac{1}{- 1 + C_{1}^{0, +} e^{- \sqrt{D_{1}} t}},

C_{1}^{0, +} = 1 + \frac{a_{11}}{\sqrt{D_{1}}} \frac{1}{q_{0} - x_{1}}

for

D_{1} > 0

and

x (t; C_{1}^{0, -}) = - x_{0} + g^{-} (t; D_{1}, C_{1}^{0, -}, a_{11}) = - x_{0} + \frac{\sqrt{- D_{1}}}{2 a_{11}} tan \frac{\sqrt{- D_{1}}}{2} (t + C_{1}^{0, -}),

C_{1}^{0, -} = \frac{2}{\sqrt{- D_{1}}} arctan [\frac{2 a_{11}}{\sqrt{- D_{1}}} (q_{0} + x_{0})], C_{1}^{0, -} \neq \frac{π}{2} + π n, n = 0, \pm 1, \pm 2, \dots,

for

D_{1} < 0,

so that the solution to

\dot{x} = P (x), x (0) = q^{0}, q^{0} = [q_{1}^{0}, q_{2}^{0}, q_{3}^{0}],

can be written for different solution sets D⁺⁺⁺, ..., D⁻⁻⁻, as

x = x_{1} + g^{+ + +}, or \{\begin{matrix} x (t; C_{1}^{0, +}) = x_{1} + \frac{\sqrt{D_{1}}}{a_{11}} \frac{1}{- 1 + C_{1}^{0, +} e^{- \sqrt{D_{1}} t}}, \\ y (t; C_{2}^{0, +}) = y_{1} + \frac{\sqrt{D_{2}}}{a_{21}} \frac{1}{- 1 + C_{2}^{0, +} e^{- \sqrt{D_{2}} t}}, \\ z (t; C_{3}^{0, +}) = z_{1} + \frac{\sqrt{D_{3}}}{a_{31}} \frac{1}{- 1 + C_{3}^{0, +} e^{- \sqrt{D_{3}} t}}, \end{matrix}

C_{i}^{0, +} = 1 + \frac{a_{i 1}}{\sqrt{D_{i}}} \frac{1}{q_{i}^{0} - x^{(i)}},

for D⁺⁺⁺ etc, where

i = 1, 2, 3,

{x^{(1)} = x}_{1}, {x^{(2)} = y}_{1}, {x^{(3)} = z}_{1} .

Figure 4. Surface

X_{D_{1}}^{0 - -} \cup X_{D_{1}}^{+ 0 -}

formed by the parametrized curves

x (t; D_{1}) = x_{1} + g^{0 - -}

(black),

C_{1} = - 1

- 4 < D_{1} < 0

, and

x (t; D_{1}) = x_{1} + g^{+ 0 -}, 0 \leq t \leq 1.3

(green),

0 < D_{1} < 4

, with

a_{11} = a_{13} = a_{21} = 1

and

a_{22} = 2

given by (43)–(46) corresponding to the solutions from the sets

D^{0 - -}

and

D^{+ 0 -}

Figure 4. Surface

X_{D_{1}}^{0 - -} \cup X_{D_{1}}^{+ 0 -}

formed by the parametrized curves

x (t; D_{1}) = x_{1} + g^{0 - -}

(black),

C_{1} = - 1

- 4 < D_{1} < 0

, and

x (t; D_{1}) = x_{1} + g^{+ 0 -}, 0 \leq t \leq 1.3

(green),

0 < D_{1} < 4

, with

a_{11} = a_{13} = a_{21} = 1

and

a_{22} = 2

given by (43)–(46) corresponding to the solutions from the sets

D^{0 - -}

and

D^{+ 0 -}

4. Analysis of Bifurcations

Families of vector-functions (44)

x^{. . .} (t; C; D)

of the type (44) with

C = [C_{1}, C_{2}, C_{3}] \in C \subset

R³ and

D = [D_{1}, D_{2}, D_{3}] \in D \subset

R³, where C, D, and ... denote, respectively, certain 3D sets (or domains) and any combination of three signs +, − and 0, specify each a 3D-surface

X_{Ψ}^{. . .}

formed by the corresponding curves

x^{. . .} (t; .)

parametrized by

t \in [T_{0}, T_{1}], T_{0} \geq 0

and constructed for different values of one (the rest being fixed) real parameter

Ψ = D_{j}

Ψ = C_{j}

j = 1, 2, 3

X_{Ψ}^{. . .} = \{x^{. . .} (t; Ψ), t \in [T_{0}, T_{1}], Ψ \in [Ψ_{0}, Ψ_{1}]\}

Figure 5. Surface

X_{D_{1}}^{- 0 -}

formed by the parametrized curves

x (t; D_{1}) = x_{1} + g^{- 0 -}

0 \leq t \leq 1.45, - 2 \leq D_{1} < 0

a_{11} = a_{13} = 1

given by (43)–(46) corresponding to the solutions from the set

D^{- 0 -}

Figure 5. Surface

X_{D_{1}}^{- 0 -}

formed by the parametrized curves

x (t; D_{1}) = x_{1} + g^{- 0 -}

0 \leq t \leq 1.45, - 2 \leq D_{1} < 0

a_{11} = a_{13} = 1

given by (43)–(46) corresponding to the solutions from the set

D^{- 0 -}

We investigate particularly the occurrence of bifurcations for the combined surfaces

X_{Ψ = D_{1}}^{- 0 -} \cup X_{Ψ = D_{1}}^{+ - 0}

when the discriminant of one (or two) component varies.

Figure 6. Enlarged fragment of the projection on the

(x, y)

-plane of the surface presented in Figure 4 close to the point of bifuraction associated with the stationary solution

y = - 1

of the second component in system (51) (graphs of the parametrized curves

x (t) = x_{1} + g^{0 - -}

(black),

C_{1} = - 1

- 4 < D_{1} < 0

, and

x (t) = x_{1} + g^{+ 0 -}, 0 \leq t \leq 1.3

(green),

0 < D_{1} < 4

, with

a_{11} = a_{13} = a_{21} = 1

and

a_{22} = 2

given by (43)–(46) corresponding to the solutions from the sets

D^{0 - -}

and

D^{+ 0 -}

Figure 6. Enlarged fragment of the projection on the

(x, y)

-plane of the surface presented in Figure 4 close to the point of bifuraction associated with the stationary solution

y = - 1

of the second component in system (51) (graphs of the parametrized curves

x (t) = x_{1} + g^{0 - -}

(black),

C_{1} = - 1

- 4 < D_{1} < 0

, and

x (t) = x_{1} + g^{+ 0 -}, 0 \leq t \leq 1.3

(green),

0 < D_{1} < 4

, with

a_{11} = a_{13} = a_{21} = 1

and

a_{22} = 2

given by (43)–(46) corresponding to the solutions from the sets

D^{0 - -}

and

D^{+ 0 -}

Figure 7. Graphs of the parametrized curves

x (t; D_{1}) = x_{1} + g^{- 0 -}

(black),

C_{1} = - 1

C_{2} = - 0.04

- 4 < D_{1} < 0

, and

x (t; D_{1}) = x_{1} + g^{+ 0 -}, 0 \leq t \leq 1.4

(yellow),

0 < D_{1} < 4

, with

a_{11} = a_{13} = a_{21} = 1

and

a_{22} = 2

given by (43)–(46) corresponding to the solutions from the sets

D^{- 0 -}

and

D^{+ 0 -}

Figure 7. Graphs of the parametrized curves

x (t; D_{1}) = x_{1} + g^{- 0 -}

(black),

C_{1} = - 1

C_{2} = - 0.04

- 4 < D_{1} < 0

, and

x (t; D_{1}) = x_{1} + g^{+ 0 -}, 0 \leq t \leq 1.4

(yellow),

0 < D_{1} < 4

, with

a_{11} = a_{13} = a_{21} = 1

and

a_{22} = 2

given by (43)–(46) corresponding to the solutions from the sets

D^{- 0 -}

and

D^{+ 0 -}

We have, according to (43),

\begin{matrix} {lim}_{D_{1} \to + 0} [- x_{0} \pm \frac{\sqrt{D_{1}}}{2 a_{11}} + g^{+} (t; D_{1}, C, a_{11})] & = & - x_{0}, \end{matrix}

(49)

\begin{matrix} {lim}_{D_{1} \to - 0} [- x_{0} + g^{-} (t; D_{1}, C, a_{11})] & = & - x_{0}, \end{matrix}

(50)

uniformly with respect to

t \in [t_{0}, T_{0}], t_{0} \geq 0

. (49) and (50) mean that there is no bifurcation associated with the transition

D^{- 0 -} \to

D^{+ 0 -}

as illustrated by Figure 2.

Figure 8. Enlarged fragment of the surface close to the point of bifuraction associated with the stationary solution

y = - 1

of the second and third components in system (51) (graphs of the parametrized curves

x (t; D_{1}) = x_{1} + g^{- 00}

(black),

C_{1} = - 1

- 4 < D_{1} < 0

C_{2} = 1.6

C_{3} = 2

, and

x (t; D_{1}) = x_{1} + g^{+ 00}, 0 \leq t \leq 1.5

(yellow),

0 < D_{1} < 4

, with

a_{11} = a_{13} = a_{21} = 1

and

a_{22} = 2

given by (43)–(46) corresponding to the solutions from the sets

D^{- 00}

and

D^{+ 00}

Figure 8. Enlarged fragment of the surface close to the point of bifuraction associated with the stationary solution

y = - 1

of the second and third components in system (51) (graphs of the parametrized curves

x (t; D_{1}) = x_{1} + g^{- 00}

(black),

C_{1} = - 1

- 4 < D_{1} < 0

C_{2} = 1.6

C_{3} = 2

, and

x (t; D_{1}) = x_{1} + g^{+ 00}, 0 \leq t \leq 1.5

(yellow),

0 < D_{1} < 4

, with

a_{11} = a_{13} = a_{21} = 1

and

a_{22} = 2

given by (43)–(46) corresponding to the solutions from the sets

D^{- 00}

and

D^{+ 00}

Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 illustrate the formation of a bifuraction of the type twisted fold (a ’cusp’). This bifuraction occurs with variation of discriminant

D_{1}

of a single (first or second) solution component within single family

D^{- 0 -}

D^{0 - -}

at certain values of constant

C_{1}

(namely, at

C_{1} = - 1, - 1.3

) when the first and third (or the second and third) components (independent of variable

D_{1}

) are bounded in a closed interval

t \in [0, T_{0}]

where the parametrization is applied.

A twisted fold manifests itself as a ’rotation’ caused by a varied

D_{1} \in (- 4, 0)

of a 3D-surface formed by the curves

x^{- 0 -} (t; D_{1})

x^{0 - -} (t; D_{1})

parametrized by

t \in [T_{0}, T_{1}], T_{0} \geq 0

, with fixed vector

C = [C_{1}, C_{2}, C_{3}]

and

D = [D_{1}, D_{2}, D_{3}]

with constant

D_{2}

and

D_{3}

and varied

D_{1}

. The ’rotation’ takes place around a point of equilibrium where all the curves

x^{- 0 -} (t; D_{1})

x^{0 - -} (t; D_{1})

with different

D_{1} \in (- 4, 0)

merge at a certain

t \in [T_{0}, T_{1}]

Figure 9. Graph of the initial condition

x (0) = \frac{\sqrt{D_{1} + 4}}{2} - \frac{\sqrt{- D_{1}}}{2} tan \frac{\sqrt{- D_{1}}}{2}

D_{1} \in (- 4, 0]

of the first component of the solution (A22), (A23) from the set

D^{- 0 -}

presented in Figure 1.

Figure 9. Graph of the initial condition

x (0) = \frac{\sqrt{D_{1} + 4}}{2} - \frac{\sqrt{- D_{1}}}{2} tan \frac{\sqrt{- D_{1}}}{2}

D_{1} \in (- 4, 0]

of the first component of the solution (A22), (A23) from the set

D^{- 0 -}

presented in Figure 1.

Figure 10. Graphs of the parametrized curves

x (t) = x_{1} + g^{- - -}

0 \leq t \leq 2, - 4 \leq D_{1}, D_{3} < 0

a_{11} = a_{13} = 1

a_{22} = a_{32} = 2

C_{j} = - 1

j = 1, 2, 3

, given by (43)–(46) corresponding to the solutions from the set

D^{- - -}

with two variable components.

Figure 10. Graphs of the parametrized curves

x (t) = x_{1} + g^{- - -}

0 \leq t \leq 2, - 4 \leq D_{1}, D_{3} < 0

a_{11} = a_{13} = 1

a_{22} = a_{32} = 2

C_{j} = - 1

j = 1, 2, 3

, given by (43)–(46) corresponding to the solutions from the set

D^{- - -}

with two variable components.

To understand the nature of the observed bifurcation consider system (42) corresponding to families

D^{\mp 0 -}

and the cases involving the specific values of parameters (coefficients of the trinomials in (42)) illustrated by Figure 3 and Figure 5

\{\begin{matrix} \dot{x} = {(x - \frac{1}{2} \sqrt{D_{1} + 4})}^{2} - \frac{1}{4} D_{1}, \\ \dot{y} = {(y + 1)}^{2}, \\ \dot{z} = {(z - \frac{1}{2})}^{2} + \frac{3}{4}, \end{matrix}

(51)

where

D_{1} < 0

and

D_{1} > 0

are, respectively, for

D^{- 0 -}

and

D^{+ 0 -}

. The second component in (51) has the degenerate stationary solution

y = - 1

while the first and third components preserve the (positive) sign when parameter

D_{1}

varies. Figure 9 displays the initial condition

x (0) = \frac{\sqrt{D_{1} + 4}}{2} - \frac{\sqrt{- D_{1}}}{2} tan \frac{\sqrt{- D_{1}}}{2}

D_{1} \in (- 4, 0]

of the first component of the solution (A22), (A23) from the set

D^{- 0 -}

presented in Figure 1. We see that the initial condition changes sign as

D_{1} < 0

increases which causes twist of the curves, contrary to the surface

X_{D_{1}}^{- 0 -} \cup X_{D_{1}}^{+ 0 -}

in Figure 2 where the solutions from the sets

D^{- 0 -}

and

D^{+ 0 -}

are given by (A16)–(A21) and the initial condition

x (0) = \frac{\sqrt{D_{1} + 4}}{2}

for the first component considered vs

D_{1} \in (- 4, 0]

does not change sign and the solution curves in both sets

D^{- 0 -}

and

D^{+ 0 -}

preserve the same shape.

Figure 11. Graphs of the parametrized curves

x (t) = x_{1} + g^{- + -}

(right) and

x (t) = x_{1} + g^{+ + -}, 0 \leq t \leq 1.3, - 4 \leq D_{1} \leq 6

a_{11} = a_{13} = 1

given by (43)–(46) corresponding to the solutions from the sets

D^{- + -}

and

D^{+ + -}

Figure 11. Graphs of the parametrized curves

x (t) = x_{1} + g^{- + -}

(right) and

x (t) = x_{1} + g^{+ + -}, 0 \leq t \leq 1.3, - 4 \leq D_{1} \leq 6

a_{11} = a_{13} = 1

given by (43)–(46) corresponding to the solutions from the sets

D^{- + -}

and

D^{+ + -}

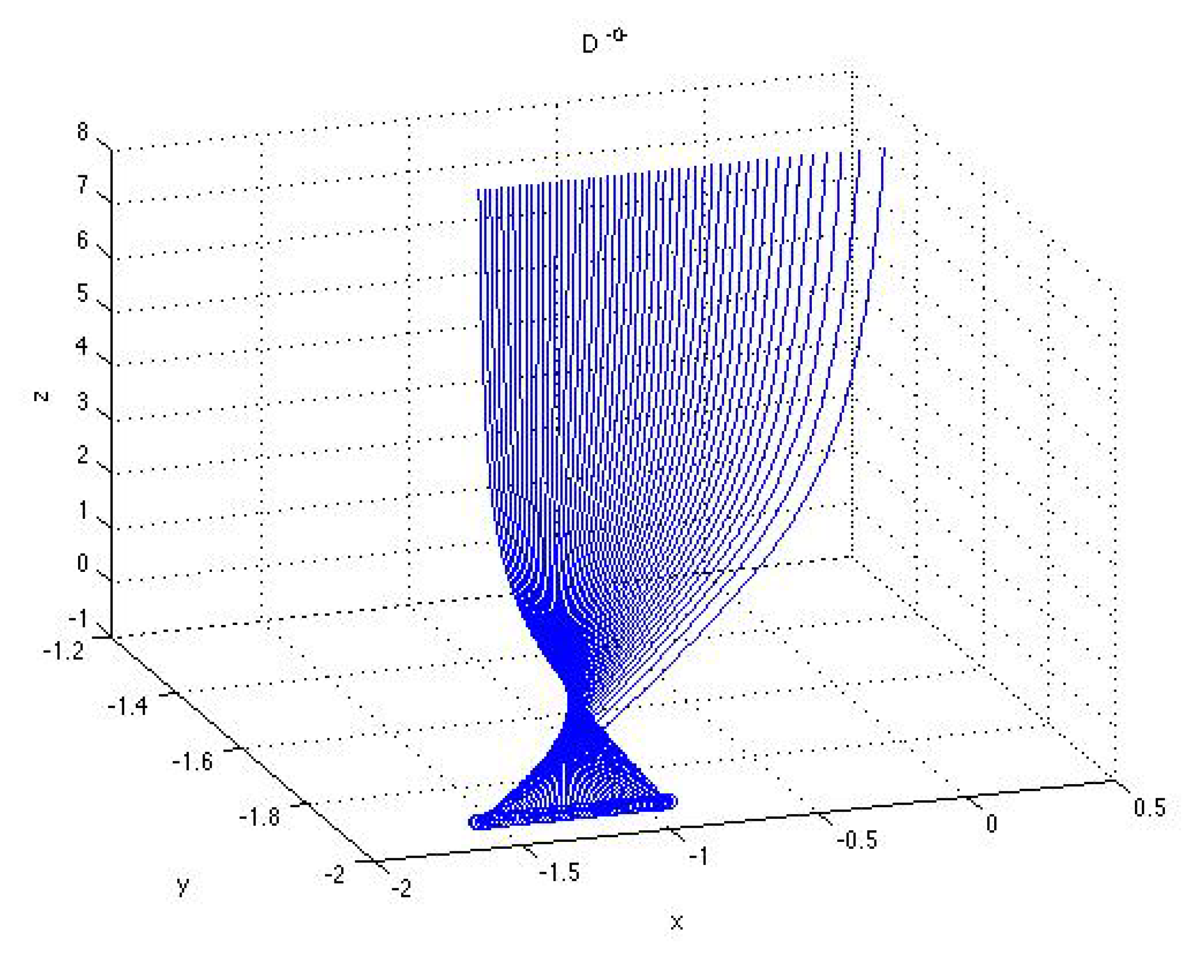
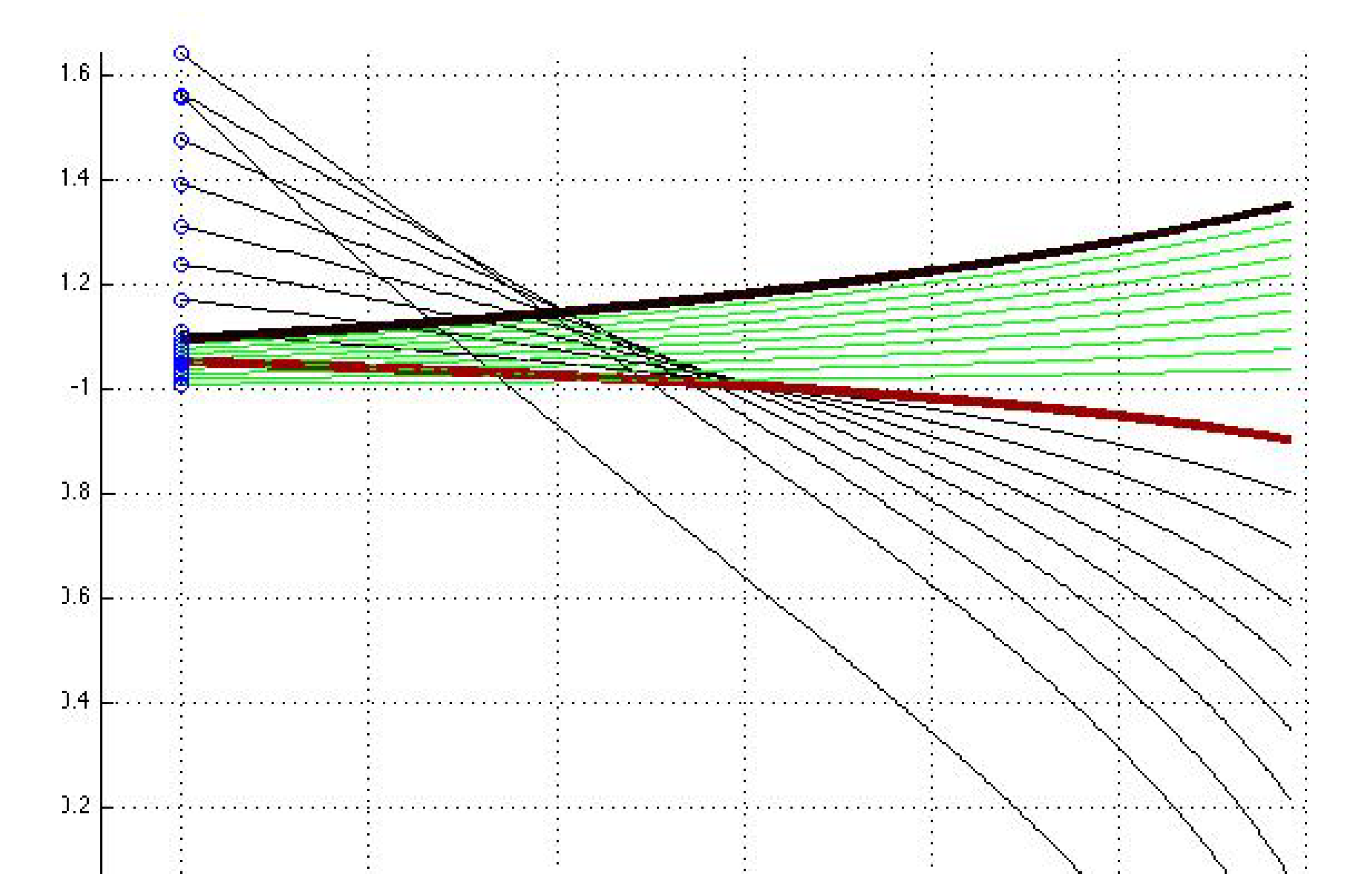
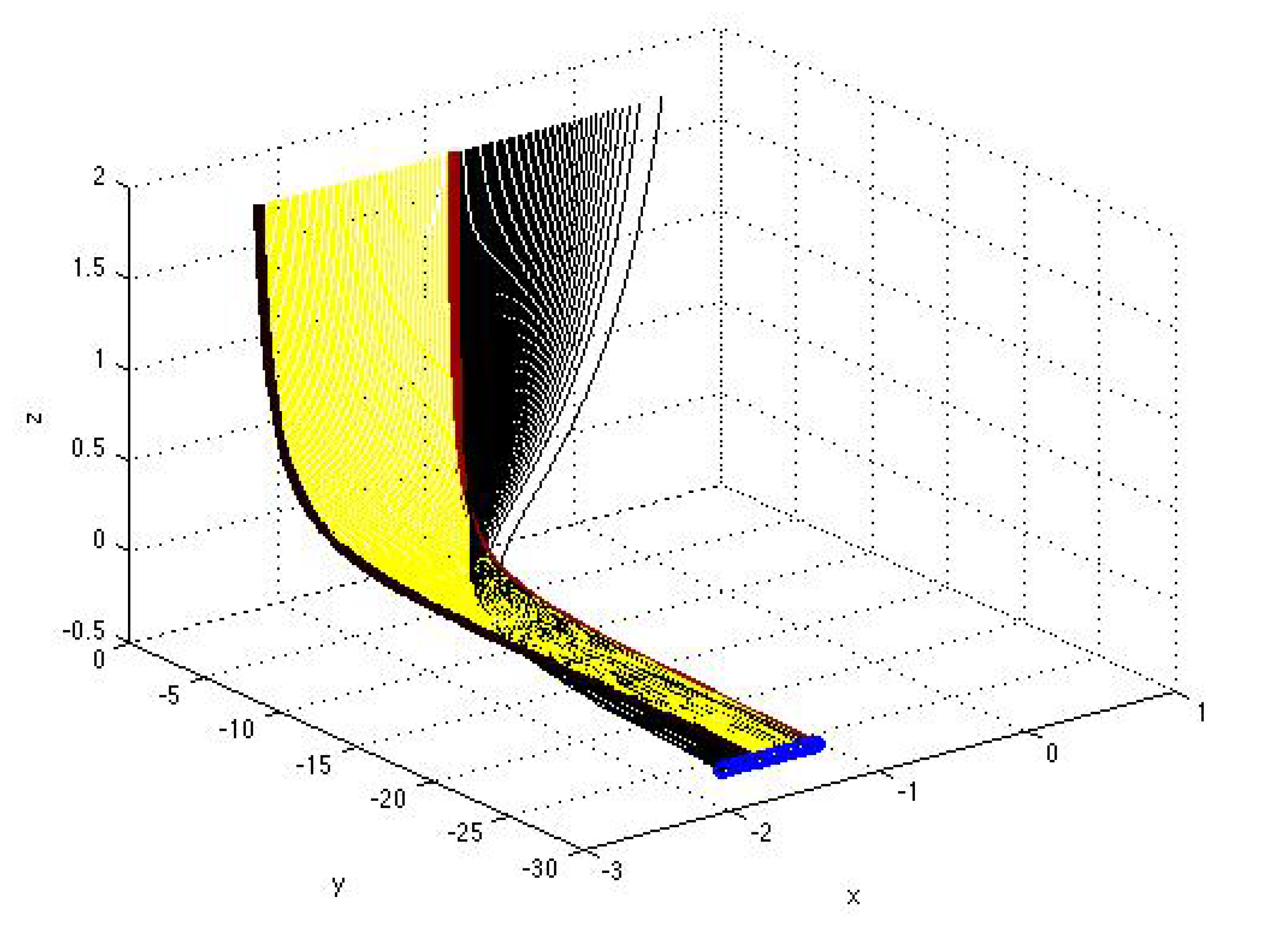
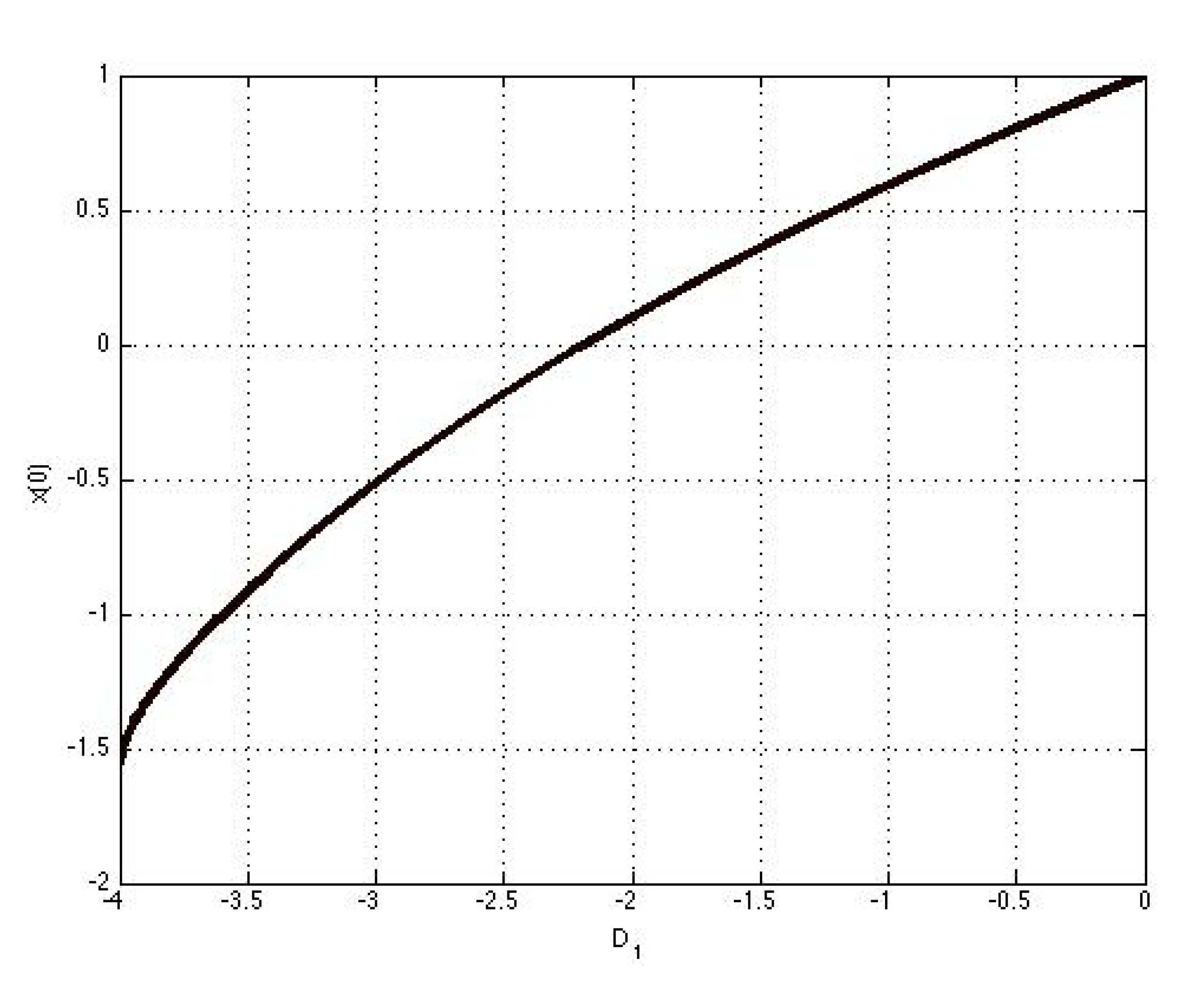
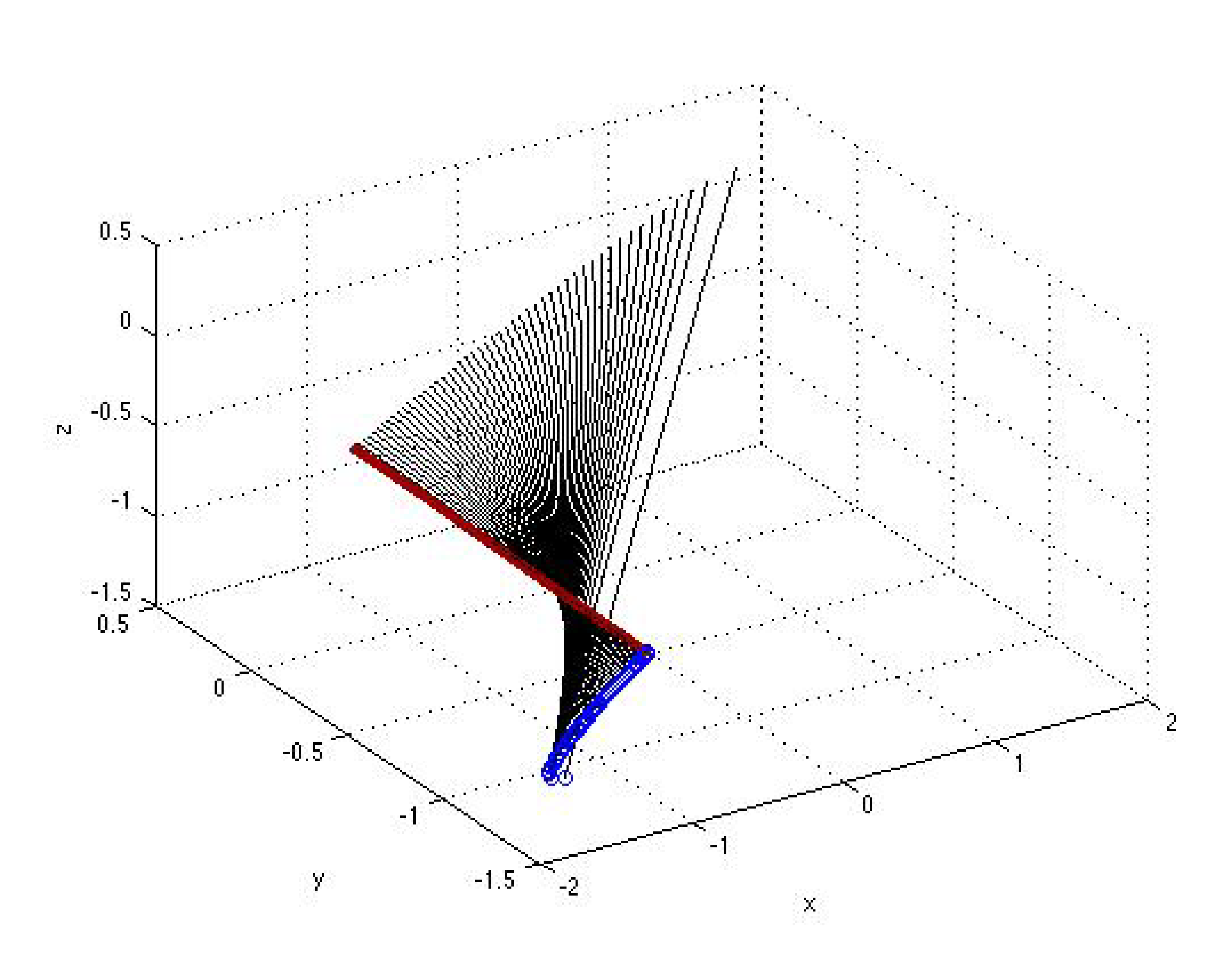
5. Conclusion

We have extended the discriminant criterion applied originally to two-phase quadratic polynomial DSs to three-phase DSs investigated in terms of their coefficient matrices. Based in this criterion and the established integrability in elementary functions for the considered class of autonomous polynomial DSs, we have proposed a general approach to qualitative analysis of these DSs. Specific classes of D- and S-vectors have been introduced which enable one to classify the DS solutions depending on the discriminant signs. Complete description of the symmetry relations inherent to the DS coefficient matrices has been performed using the discriminant criterion. The DS solution properties have been investigated in terms of two-parameter surfaces. The behaviour and bifurcations of solutions to three-dimensional quadratic polynomial DSs have been considered. The occurrence of bifurcations of the type twisted fold has been discovered on the basis and within the frames of the developed DS qualitative theory.

Based on the results of the study, we have made the following conclusion: whether the DS coefficient matrix belongs to a particular equivalence class determines the presence and nature (type) of singular points and bifurcations of the corresponding polynomial DS.

As far as the application of the developed approach and technique to regulating and monitoring the waterflooding and the development of oil or gas fields is concerned, the proposed approach enables one to simulate the consequences of instable behavior of the displacement front. Using the results of this work, engineers and practitioners will be able to predict natural abrupt variations in water saturation and dependent well exploatation parameters using the analysis of the growth model employing three-phase quadratic polynomial DSs.

The results and findings reported in this study make it possibile to carry out systematic optimization of non-stationary waterflooding and the prospect of enhanced oil recovery, as well as to control reduction in the amount of water that is not efficiently injected and withdrawn.

Appendix A

Appendix A.1. Autonomous Polynomial Dynamical Systems Integrable in Elementary Functions

A polynomial

P_{i} (x)

of degree

N_{i} \geq 2

(

i = 1, 2, \dots, n

) with real coefficients can be uniquely factorized and represented as

P_{i} (x) = Π_{s = 1}^{m_{i}} {(x - x_{s}^{(i)})}^{k_{s}^{(i)}} Π_{t = 1}^{n_{i}} {(r_{t}^{(i)})}^{p_{t}^{(i)}},

(A1)

where

\sum_{s = 1}^{m_{i}} k_{s}^{(i)} + 2 \sum_{t = 1}^{n_{i}} p_{t}^{(i)} = N_{i}

m_{i}, n_{i} \geq 0

, and

r_{s}^{(i)} (x) = a_{s, 1}^{(i)} x^{2} + a_{s, 2}^{(i)} x + a_{s, 3}^{(i)} = a_{s, 1}^{(i)} [{(x + x_{s, 0}^{(i)})}^{2} - \frac{D_{s}^{(i)}}{4 {(a_{s, 1}^{(i)})}^{2}}] (a_{s, 1}^{(i)} \neq 0)

(A2)

are irreducible quadratic trinomials with

x_{s, 0}^{(i)} = \frac{a_{s, 2}^{(i)}}{2 a_{s, 1}^{(i)}}

and the discriminants

D_{s}^{(i)} = {(a_{s, 2}^{(i)})}^{2} - 4 a_{s, 1}^{(i)} a_{s, 3}^{(i)} < 0, s = 1, 2, \dots, n_{i}, i = 1, 2, \dots, n .

(A3)

A rational function

Q_{i} (x) = P_{i}^{- 1} (x)

can be uniquely decomposed [17] into partial fractions,

Q_{i} (x) = \sum_{s = 1}^{m_{i}} \sum_{j = 1}^{k_{s}^{(i)}} \frac{A_{s j}^{(i)}}{{(x - x_{s}^{(i)})}^{j}} + \sum_{t = 1}^{n_{i}} \sum_{j = 1}^{p_{t}^{(i)}} \frac{B_{t j}^{(i)} x + C_{t j}^{(i)}}{{(r_{t}^{(i)})}^{j}}

(A4)

where

A_{s j}^{(i)}

B_{t j}^{(i)}

, and

C_{t j}^{(i)}

are uniquely determined real numbers.

Lemma A1.

Each term in (A4) is integrable in elementary functions

Proof.

Verification of the statement is obvious for the terms entering the first double sum in (A4).

Consider the terms entering the second double sum in (A4). To prove the required integrability it is sufficient to calculate two indefinite integrals

I_{j}^{(1)} (x) = \int \frac{x d x}{r^{j} (x)} a n d I_{j}^{(2)} (x) = \int \frac{d x}{r^{j} (x)}, r (x) = a x^{2} + b x + c,

(A5)

with integer

j \geq 1

and

D = b^{2} - 4 a c < 0

. For the first integral, we have

\begin{matrix} I_{j}^{(1)} (x) & = & \int \frac{x d x}{{[a ({(x + x_{0})}^{2} - \frac{D}{4 a^{2}})]}^{j}} = \\ = & - \frac{1}{2 a^{j} (j - 1)} \frac{1}{{[{(x + x_{0})}^{2} - \frac{D}{4 a^{2}}]}^{j - 1}} - \frac{x_{0}}{a^{j}} I_{j}^{(2)} (x) \end{matrix}

(A6)

for

j \geq 2

and

\begin{matrix} I_{1}^{(1)} (x) & = & \frac{1}{a} \int \frac{x d x}{[{(x + x_{0})}^{2} - \frac{D}{4 a^{2}}]} = \end{matrix}

(A7)

\begin{matrix} = & \frac{1}{2 a} ln [{(x + x_{0})}^{2} - \frac{D}{4 a^{2}}] - \frac{x_{0}}{a} I_{1}^{(2)} (x) = \\ = & \frac{1}{2 a} ln [{(x + x_{0})}^{2} - \frac{D}{4 a^{2}}] - \frac{2 x_{0}}{\sqrt{- D}} {tan}^{- 1} [\frac{2 a (x + x_{0})}{\sqrt{- D}}] + C \end{matrix}

(A8)

for

j = 1

. For the second integral, we have for

j \geq 2

\begin{matrix} I_{j}^{(2)} (x) = - \frac{2 a x + b}{(j - 1) D r^{j - 1} (x)} - \frac{2 a (2 j - 3)}{(j - 1) D} I_{j - 1}^{(2)} (x) . \end{matrix}

(A9)

This is actually a first-order inhomogeneous difference equation which can be written in a compact form

\begin{matrix} I_{j}^{(2)} = α_{j - 1} I_{j - 1}^{(2)} + β_{j - 1}, j = 2, 3, \dots, I_{1}^{(2)} = \frac{2 a}{\sqrt{- D}} {tan}^{- 1} [\frac{2 a (x + x_{0})}{\sqrt{- D}}], \end{matrix}

(A10)

The solution to (A10) is

\begin{matrix} I_{j}^{(2)} = \sum_{s = 1}^{j} β_{j - s} Π_{t = 1}^{s} α_{j - t + 1} + I_{1}^{(2)} Π_{t = 1}^{j} α_{t}, \end{matrix}

(A11)

where

\begin{matrix} α_{j - 1} = - \frac{2 a x + b}{(j - 1) D r^{j - 1} (x)}, β_{j - 1} = - \frac{2 a (2 j - 3)}{(j - 1) D} . \end{matrix}

(A12)

Thus, both

I_{j}^{(1)}

and

I_{j}^{(2)}

are expressed in elementary functions using (A11) and (A12). The indefinite integral

\int Q_{i} (x) d x = \sum_{s = 1}^{m_{i}} \sum_{j = 1}^{k_{s}^{(i)}} A_{s j}^{(i)} q_{j, s}^{(i)} (x) + T_{i} (x),

(A13)

where

q_{j, s}^{(i)} (x) = \{\begin{matrix} - \frac{1}{(j - 1) {(x - x_{s}^{(i)})}^{j - 1}}, & j \geq 2, \\ ln |x - x_{s}^{(i)}|, & j = 1, \end{matrix}

(A14)

and

T_{i} (x)

is a linear combination of

I_{j}^{(1)}

and

I_{j}^{(2)}

which proves the lemma. □

Theorem A1.

DSs (41) (and (42)) are integrable in elementary functions.

Proof.

Each particular row equation in (41) written as

\begin{matrix} \frac{d x}{d t} & = & P_{i} (x), P_{i} (x) = \sum_{j = 1}^{N_{i} + 1} a_{j i} x^{N_{i} - j + 1} = \\ = & a_{1 i} x^{N_{i}} + a_{2 i} x^{N_{i} - 1} + \dots + a_{N_{i}, i} x + a_{N_{i} + 1, i} (i = 1, 2, \dots, n) \end{matrix}

(A15)

yields a rational function

Q_{i} (x) = P_{i}^{- 1} (x)

which is uniquely decomposed into partial fractions (A4) and is therefore integrable in elementary functions according to Lemma A1.

□

Appendix A.2. Examples with Bifurcations

Parametrized curves

x (t; D_{1}) = x_{1} + g^{- 0 -}

- 4 < D_{1} < 0

, and

x (t; D_{1}) = x_{1} + g^{+ 0 -}

0 < D_{1} < 4

for

0 \leq t \leq 1.3

, forming surface

X_{D_{1}}^{- 0 -} \cup X_{D_{1}}^{+ 0 -}

corresponding to the solutions from the sets

D^{- 0 -}

and

D^{+ 0 -}

displayed in Figure 2

x^{- 0 -} = x_{1} + g^{- 0 -} =

(A16)

\{\begin{matrix} x (t; C_{1} = 0) = - x_{0} + g^{-} (t; D_{1}, C_{1} = 0, 1) \\ y (t; C_{2}) = g^{0} (t; C_{2} = - 1, a_{21}, a_{22}), \\ z (t; C_{3}) = - z_{0} + g^{-} (t; D_{3} = - 3, C_{3} = 0, 1), \end{matrix} =

(A17)

= \{\begin{matrix} \frac{\sqrt{D_{1} + 4 a_{11} a_{13}}}{2 a_{11}} + \frac{\sqrt{- D_{1}}}{2 a_{11}} tan (\frac{\sqrt{- D_{1}}}{2} t), \\ - \frac{1}{a_{21}} (\frac{a_{22}}{2} + \frac{1}{t - C_{2}}), \\ \frac{\sqrt{D_{3} + 4 a_{31} a_{33}}}{2 a_{31}} + \frac{\sqrt{- D_{3}}}{2 a_{31}} tan (\frac{\sqrt{- D_{3}}}{2} t), \end{matrix} = \{\begin{matrix} \frac{1}{2} \sqrt{D_{1} + 4} + \frac{\sqrt{- D_{1}}}{2} tan (\frac{\sqrt{- D_{1}}}{2} t), \\ - 1 - \frac{1}{t + 1}, \\ \frac{1}{2} + \frac{\sqrt{3}}{2} tan (\frac{\sqrt{3}}{2} t) . \end{matrix}

(A18)

x^{+ 0 -} = x_{1} + g^{+ 0 -} =

(A19)

\{\begin{matrix} x (t; C_{1} = - 1) = x_{1} + \frac{\sqrt{D_{1}}}{a_{11}} \frac{1}{- 1 + C_{1} e^{- \sqrt{D_{1}} t}}, \\ y (t; C_{2}) = g^{0} (t; C_{2} = - 1, a_{21}, a_{22}), \\ z (t; C_{3}) = - z_{0} + g^{-} (t; D_{3} = - 3, C_{3} = 0, 1), \end{matrix} =

(A20)

= \{\begin{matrix} \frac{\sqrt{D_{1} + 4 a_{11} a_{13}}}{2 a_{11}} + \frac{\sqrt{D_{1}}}{2 a_{11}} + \frac{\sqrt{D_{1}}}{a_{11}} \frac{1}{- 1 + C_{1} e^{- \sqrt{D_{1}} t}}, \\ - \frac{1}{a_{21}} (\frac{a_{22}}{2} + \frac{1}{t - C_{2}}), \\ \frac{\sqrt{D_{3} + 4 a_{31} a_{33}}}{2 a_{31}} + \frac{\sqrt{- D_{3}}}{2 a_{31}} tan (\frac{\sqrt{- D_{3}}}{2} t), \end{matrix} = \{\begin{matrix} \frac{1}{2} \sqrt{D_{1} + 4} - \frac{\sqrt{D_{1}}}{1 + e^{- \sqrt{D_{1}} t}}, \\ - 1 - \frac{1}{t + 1}, \\ \frac{1}{2} + \frac{\sqrt{3}}{2} tan (\frac{\sqrt{3}}{2} t) . \end{matrix}

(A21)

Parametrized curves

x (t; D_{1}) = x_{1} + g^{- 0 -}

C_{1} = - 1

- 4 < D_{1} < 0

, and

x (t; D_{1}) = x_{1} + g^{+ 0 -}

0 < D_{1} < 4

, for

0 \leq t \leq 1.3

with

a_{11} = a_{13} = a_{21} = 1

and

a_{22} = 2

forming surface

X_{D_{1}}^{- 0 -} \cup X_{D_{1}}^{+ 0 -}

corresponding to the solutions from the sets

D^{- 0 -}

and

D^{+ 0 -}

displayed in Figure 1

x^{- 0 -} = x_{1} + g^{- 0 -} =

(A22)

\{\begin{matrix} x (t; C_{1} = - 1) = - x_{0} + g^{-} (t; D_{1}, C_{1} = - 1, 1) \\ y (t; C_{2}) = g^{0} (t; C_{2} = - 1, a_{21}, a_{22}), \\ z (t; C_{3}) = - z_{0} + g^{-} (t; D_{3} = - 3, C_{3} = 0, 1), \end{matrix} =

(A23)

= \{\begin{matrix} \frac{\sqrt{D_{1} + 4 a_{11} a_{13}}}{2 a_{11}} + \frac{\sqrt{- D_{1}}}{2 a_{11}} tan (\frac{\sqrt{- D_{1}}}{2} (t - 1)), \\ - \frac{1}{a_{21}} (\frac{a_{22}}{2} + \frac{1}{t - C_{2}}), \\ \frac{\sqrt{D_{3} + 4 a_{31} a_{33}}}{2 a_{31}} + \frac{\sqrt{- D_{3}}}{2 a_{31}} tan (\frac{\sqrt{- D_{3}}}{2} t), \end{matrix} = \{\begin{matrix} \frac{1}{2} \sqrt{D_{1} + 4} + \frac{\sqrt{- D_{1}}}{2} tan (\frac{\sqrt{- D_{1}}}{2} (t - 1)), \\ - 1 - \frac{1}{t + 1}, \\ \frac{1}{2} + \frac{\sqrt{3}}{2} tan (\frac{\sqrt{3}}{2} t), \end{matrix}

x^{+ 0 -} = x_{1} + g^{+ 0 -} =

(A24)

= \{\begin{matrix} x (t; C_{1} = - 1) = x_{1} + \frac{\sqrt{D_{1}}}{a_{11}} \frac{1}{- 1 + C_{1} e^{- \sqrt{D_{1}} t}}, \\ y (t; C_{2}) = g^{0} (t; C_{2} = - 1, a_{21}, a_{22}), \\ z (t; C_{3}) = - z_{0} + g^{-} (t; D_{3} = - 3, C_{3} = 0, 1), \end{matrix} =

(A25)

= \{\begin{matrix} \frac{\sqrt{D_{1} + 4 a_{11} a_{13}}}{2 a_{11}} + \frac{\sqrt{D_{1}}}{2 a_{11}} + \frac{\sqrt{D_{1}}}{a_{11}} \frac{1}{- 1 + C_{1} e^{- \sqrt{D_{1}} t}}, \\ - \frac{1}{a_{21}} (\frac{a_{22}}{2} + \frac{1}{t - C_{2}}), \\ \frac{\sqrt{D_{3} + 4 a_{31} a_{33}}}{2 a_{31}} + \frac{\sqrt{- D_{3}}}{2 a_{31}} tan (\frac{\sqrt{- D_{3}}}{2} t), \end{matrix} = \{\begin{matrix} \frac{1}{2} \sqrt{D_{1} + 4} - \frac{\sqrt{D_{1}}}{1 + e^{- \sqrt{D_{1}} t}}, \\ - 1 - \frac{1}{t + 1}, \\ \frac{1}{2} + \frac{\sqrt{3}}{2} tan (\frac{\sqrt{3}}{2} t) . \end{matrix}

(A26)

References

V. A. Gaiko, Global bifurcations and chaos in polynomial dynamical systems, 2003 International Conference Physics and Control. Proceedings, St. Petersburg, Russia, 2003, vol.2, pp.670–674. [CrossRef]
Valery, A. Gaiko, Global Bifurcation Theory and Hilbert’s Sixteenth Problem, Book Series: Mathematics and its Applications, Vol. 562, Kluwer, Boston, 2003.
Albert Luo, Polynomial Functional Dynamical Systems, E-book. Springer International Publishing, 2022.
Bautin, N.N. , Leontovich, E.A.: Methods and Examples of the Qualitative Analysis of Dynamical Systems in a Plane. Nauka, Moscow (1990).
V. A. Gaiko, On Global Bifurcation Theory of Polynomial Dynamical Systems and Its Applications, 2000. [CrossRef]
Y. V. Shestopalov, A. Kh. Y. V. Shestopalov, A. Kh. Shakhverdiev, Qualitative theory of two-dimensional polynomial dynamical systems, Symmetry, 13:10 (2021), pp. 1884–1899. [CrossRef]
A. Kh. Shakhverdiev and Yu. V. Shestopalov, Qualitative analysis of quadratic polynomial dynamical systems associated with the modeling and monitoring of oil fields, Lobachevskii J. Math., 40:10 (2019), pp. 44-50. [CrossRef]
A. Kh., Shakhverdiev. Some conceptual aspects of systematic optimization of oil field development. Oil Industry 2017, 58–63. [Google Scholar]
I. Buckley and M. C., Leverett. Mechanism of Fluid Displacement in Sands. Trans. AIME 1942, 146, 107–119. [Google Scholar] [CrossRef]
A. Kh. Shakhverdiev, System optimization of non-stationary flooding for the purpose of increasing oil recovery, Petroleum Engineering (2019), pp.44–49. [CrossRef]
A. Kh. Shakhverdiev, S. V. A. Kh. Shakhverdiev, S. V. Arefiev, A. V. Denisov, R. R. Yunusov, Method for restoring the optimal mode of operation of the reservoir-well system, taking into account the instability of the displacement front, Oil Industry, 6 (2020), pp. 52–57. [CrossRef]
A. Kh. Shakhverdiev, S. V. A. Kh. Shakhverdiev, S. V. Arefiev, The concept of monitoring and optimization of oil reservoirs waterflooding under the conditions of displacement front instability, Oil Industry, 11 (2021), pp. 104–109. [CrossRef]
A. Kh., Shakhverdiev. Once again about oil recovery factor. Neftyanoe Khozyaystvo 2014, 1, 44–48. [Google Scholar]
J. M. T. Thomson, Instabilities and Catastrophes in Science and Engineering, J. Wiley and Sons, New York, 1982.
L. Brenig and A., Goriely. Universal canonical forms for time-continuous dynamical systems. Phys. Rev. 1989, A40, 4119–4125. [Google Scholar] [CrossRef] [PubMed]
<italic>V.M. Buchstaber, S. V.M. Buchstaber, S. Konstantinou-Rizos, A.V. Mikhailov Recent developments in integrable systems and related topics of mathematical physics, Springer Proc. Math. Stat., 273 (2018), Springer, Cham.
William T. Bradley and William J., Cook. Two Proofs of the Existence and Uniqueness of the Partial Fraction Decomposition. International Mathematical Forum 2012, 7, 1517–1535. [Google Scholar]
A. Kh. Shakhverdiev, Y. V. A. Kh. Shakhverdiev, Y. V. Shestopalov, I. E. Mandrik, S. V. Arefiev, Alternative concept of monitoring and optimization water flooding of oil reservoirs in the conditions of instability of the displacement front, Petroleum Engineering, 12 (2019), pp. 118–123. [CrossRef]
A. Kh. Shakhverdiev, System optimization of non-stationary water flooding for IOR/EOR. Oil industry 2019, 1, 44–50.
F. Craig Forrest Jr., The Reservoir Engineering Aspects of Waterflooding Society of Petroleum Engineers of AIME, New York, 1971.
L.P. Dake, The practice of reservoir engineering - Shell Internationale Petroleum Maatschappij B.V., The Hague, The Netherlands, 2001.
Dana Constantinescu, On the Bifurcations of a 3D Symmetric Dynamical System, Symmetry 15:4 ( 2023), pp. 923–935.
Fenichel, N. Geometric Singular Perturbations Theory for Ordinary Differential Equations. J. Differ. Eq. 1979, 31, 53–98. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Bifurcations Associated with Three-Phase Polynomial Dynamical Systems and Complete Description of Symmetry Relations Using Discriminant Criterion

Abstract

1. Introduction

2. A Family of Polynomial Dynamical Systems

2.1. Matrix Representation of Polynomial Dynamical Systems

2.2. Discriminant Criterion and Matrix Representation of 3D Polynomial Dynamical Systems

2.3. Symmetry Relations on the Sets of Coefficient Matrices and D-Vectors

3. Classification of Solutions to Autonomous Polynomial Equations

3.1. Representations of Autonomous and Integrable Polynomial Dynamical Systems

3.2. General Solutions to Autonomous Second-Order Polynomial Equations

3.3. Equivalence Classes of D-Vectors and General Solutions to Autonomous Polynomial Equation Systems

3.4. Description of All Possible solution Combinations in Terms of Discriminants

3.5. Analysis of Solutions to Cauchy Problems

4. Analysis of Bifurcations

5. Conclusion

Appendix A

Appendix A.1. Autonomous Polynomial Dynamical Systems Integrable in Elementary Functions

Appendix A.2. Examples with Bifurcations

References

MDPI Initiatives

Important Links

Subscribe