Enhancing Thermo-Acoustic Waste Heat Recovery through Machine Learning: A Comparative Analysis of ANN-PSO, ANFIS, and ANN Models

Preprint

Article

Enhancing Thermo-Acoustic Waste Heat Recovery through Machine Learning: A Comparative Analysis of ANN-PSO, ANFIS, and ANN Models

Altmetrics

Downloads

108

Views

Comments

A peer-reviewed article of this preprint also exists.

Miniyenkosi Ngcukayitobi,

Lagouge Kwanda Tartibu^*

,Flávio Bannwart

Miniyenkosi Ngcukayitobi,

Lagouge Kwanda Tartibu^*

,Flávio Bannwart

This version is not peer-reviewed

Submitted:

25 October 2023

Posted:

27 October 2023

You are already at the latest version

Alerts

Abstract

Waste heat recovery stands out as a promising technique to tackle both energy shortages and environmental pollution. Currently, this valuable resource, generated from processes like fuel combustion or chemical reactions, is often dissipated into the environment, despite its potential to significantly contribute to the economy. To harness this untapped potential, a travelling-wave thermo-acoustic generator has been designed and subjected to comprehensive experimental analysis. Fifty-two data corresponding to different working conditions of the system were extracted to build ANN, ANFIS and ANN-PSO models. Evaluation of performance metrics reveals that the ANN-PSO model demonstrates the highest predictive accuracy (R^2=0.9959), particularly in relation to output voltage. This research demonstrates the potential of machine learning techniques for the analysis of thermo-acoustic systems. By doing so, it is possible to get an insight into nonlinearities inherent to thermo-acoustic systems. This advancement empowers researchers to forecast the performance characteristics of alternative configurations with a heightened level of precision.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

Artificial Intelligence (AI) has captivated researchers worldwide, particularly in various engineering disciplines and thermal science. It can be defined as the development of a computer system capable of performing tasks that traditionally required human intelligence, including decision-making, pattern recognition, and speed identification. AI encompasses a broad spectrum of technologies such as deep learning (DL), natural language processing (NLP), and machine learning (ML). In the realm of thermo-acoustic systems research, AI models have found application in tasks ranging from parameter selection and optimization to output prediction [1].

An Artificial Neural Network (ANN) is a collection of interconnected components designed to process data and mimic the cognitive processes of the human brain. It comprises linked layers of neurons [1]. Data is transmitted through the network from layer to layer via connections or synapses, each characterized by its own strength or weight [1]. To establish the necessary correlation between the network's output and input, values must be determined for both the activation function and connection weights. This entire process is referred to as supervised training [1]. When implemented in a computer, ANNs are not pre-programmed to perform specific tasks. Instead, they undergo training to learn patterns from provided inputs and associated data. Once the training phase is complete, new patterns can be presented for classification or prediction [1,2]. ANNs have the capability to learn patterns autonomously from various sources, including data from physical models, real-world systems, computer programs, and more. They are adept at handling numerous inputs and generating outputs suitable for further processing or analysis by designers. Developed as an extension of mathematical models of neural biology, ANNs operate on the premise that information processing takes place within elements known as neurons [2]. Signals are transmitted through neurons via connection links, and each neuron employs an activation function (typically nonlinear with respect to its net input) to determine its output signals [2]. One of the key strengths of ANNs lies in their ability to acquire knowledge from examples, making them proficient problem solvers with notable advantages, particularly in learning and discerning the underlying relationships between inputs and outputs without explicit consideration of physical principles [3].

Particle Swarm Optimization (PSO) stands as an intelligent stochastic optimization technique conceived by Eberhart and Kennedy in 1995 [4]. This method delves into the search space of a given problem to pinpoint the crucial structural parameters essential for optimizing a defined objective or critical target [4]. Rooted in the concept of swarm intelligence, PSO draws inspiration from the collective behavior observed in various creatures, insects, and animals, leveraging this insight to craft algorithms for tackling real-world challenges. The PSO algorithm has gained substantial traction in the realm of computational intelligence and has demonstrated successful applications across a diverse range of research problems and optimization scenarios [4]. Regarded as one of the preeminent and widely recognized algorithms in the literature of computational intelligence, optimization, and metaheuristics, PSO has made significant inroads in fields spanning engineering and science [4]. The essence of PSO lies in the dynamic interplay and communication among a group of interconnected particles or individuals. They interact, link, and communicate with one another, employing gradients or search directions to enhance their collective exploration of the solution space [4]. Within the PSO algorithm, established particles traverse the search space in pursuit of the global optimum. Throughout the iterative process, each particle updates its position based on its previous experiences and knowledge, as well as information gleaned from the surrounding search context. The trajectory of particle movement holds paramount importance, as effective communication plays a pivotal role in guiding the navigation process [4].

The Adaptive Neuro Fuzzy Inference System (ANFIS) is a sophisticated technique that seamlessly integrates neural networks (NN) and fuzzy systems [5]. Its versatile application has spanned various realms of time series research, including forecasting chaotic time series through the implementation of ANFIS based on singular spectrum analysis [5], as well as fuzzy time series forecasting, and the prediction of chaotic time series using an enhanced ANFIS approach [5]. Additionally, ANFIS has been instrumental in devising innovative methods for forecasting trends in oil prices, predicting financial volatility, and projecting stock returns [5]. Within the ANFIS framework, the neural network's hidden nodes and the components of the fuzzy system are equally pivotal. The architecture comprises five fixed layers, encompassing fuzzification (Lay-er-1), the fuzzy inference system (Layer-2 and Layer-3), defuzzification (Layer-4), and aggregation (Layer-5) [5]. This structured approach harmoniously combines the strengths of both neural networks and fuzzy logic. Soft computing techniques play a crucial role in providing approximate solutions to intricate problems [6]. In contemporary times, these methods find widespread application across diverse disciplines, serving various objectives including optimization, prediction, and design. Notably, soft computing methods have seen extensive utilization in the design and analysis of complex systems such as Stirling engines, travelling-wave thermo-acoustic generators, and thermo-acoustic refrigerators [6]. Among the dominant intelligent approaches applied to thermo-acoustic systems are ANFIS, Genetic Algorithms (GA), Particle Swarm Optimization, Fuzzy Logic, and Artificial Neural Networks (ANN) [6].

Thermo-acoustics is a field that investigates the interplay between heat transfer and acoustics [7]. In thermo-acoustic systems, there exists a dual functionality: they can either utilize acoustic work to facilitate the transfer of heat from a low-temperature medium to a high-temperature one, or they can harness thermal energy to generate acoustic work [7]. These systems are broadly categorized into two types: heat pumps, which function as refrigerators or coolers, and prime movers, which operate as heat engines. Specifically, a heat pump employs acoustic power to move heat from a lower temperature level to a higher one, while heat engines convert heat power into acoustic power. In practical terms, heat pumps are engineered to maintain the temperature of a designated space above that of its surroundings, while refrigerators are designed to keep the temperature of a given space below that of the surrounding environment [7]. Figure 1 provides a visual representation of the conversion processes intrinsic to thermo-acoustic engines and refrigerators.

Ngcukayitobi and Tartibu [8] conducted an experimental investigation on a four-stage travelling-wave thermo-acoustic generator, utilizing an audio loudspeaker as a sound-to-electricity converter. Their findings demonstrate that the four-stage travelling-wave thermo-acoustic system achieves resonance more rapidly and demands comparatively lower heat input to generate a sound wave, subsequently favoring a higher voltage inducted at the loudspeaker terminals [8]. Their model achieved a peak output voltage of 4.218 V, as measured at the loudspeaker terminals [8]. This voltage output of 4.218 V should suffice for charging mobile phones in remote areas of developing nations. Furthermore, the onset temperature of approximately 200℃ aligns with certain practical energy sources. In 2017, Bi et al. [9] pioneered the development of a novel travelling-wave thermo-acoustic electric generator, comprising a multi-stage travelling-wave thermo-acoustic heat engine equipped with linear alternators. The engines in their prototype are interlinked by slender resonance tubes, a crucial design element for generating an efficient travelling-wave within the regenerator [9]. At the terminus of each of these slim resonance tubes, an alternator was integrated as a bypass. Through rigorous testing of the prototype, they achieved impressive results: a peak electric power output of 4.69 KW, accompanied by a thermal-to-electric efficiency of 15.6%. Furthermore, they attained a maximum thermal-to-electric efficiency of 18.4%, producing an electric power output of 3.46 KW, all under 6 MPa of pressurized helium [9]. It's worth noting that they maintained consistent cooling and heating temperatures at 25℃ and 650℃, respectively.

Wu et al. [10] designed and investigated a 1 kW travelling-wave thermo-acoustic electrical generator. In their initial trials, these researchers achieved a preliminary electric power output of 638 W at a frequency of 74 Hz. Through meticulous analysis, they unveiled a crucial acoustic impedance coupling relationship between the alternator and the engine using a numerical approach. Leveraging their numerical insights, they successfully reduced the operating frequency in their experiments from 74 Hz to 64 Hz by introducing a 4.5% mole fraction of argon gas into the system. This adjustment led to a remarkable improvement, resulting in a maximum electric power output of 1043 W with a thermal-to-electric efficiency of 17.7%. Additionally, they attained a peak thermal-to-electric efficiency of 19.8%, yielding an electric power output of 970 W.

Wu et al. [11] designed and constructed a solar-powered travelling-wave thermo-acoustic electricity generator. This innovative system comprised a solar dish for concentrating sunlight, coupled with a pool boiler-type heat receiver to effectively transfer solar energy to the engine. In their experimental setup, cartridge heaters were employed to provide the necessary heating energy. Through their efforts, they achieved notable results: a peak electric power output of 481 W and a maximum thermal-to-electric efficiency of 15%, operating under 3.5 MPa of pressurized helium at a frequency of 74 Hz. In their solar-powered experiments, they achieved a maximum electric power output of approximately 200 W.

The integration of Artificial Intelligence (AI) techniques into research pertaining to thermo-acoustic systems has garnered significant attention. This AI-driven approach has found wide-ranging applications across various industrial sectors, renewable energy challenges, and engineering disciplines. Machesa et al. [12] conducted a comprehensive study on a thermo-acoustic refrigerator, employing Artificial Intelligence (AI) techniques. They employed different methodologies, including an Adaptive Neuro-Fuzzy Inference System (ANFIS), an Artificial Neural Network (ANN) trained using Particle Swarm Optimization (ANN-PSO), and a standalone Artificial Neural Network to predict the oscillatory heat transfer coefficient within the heat exchangers of the thermo-acoustic system. Their evaluation criteria encompassed metrics such as Mean Square Error (MSE) and regression analysis to gauge the models' performance and accuracy [12]. Their findings demonstrate that predicting the oscillatory heat transfer coefficient holds promise for enhancing the performance of thermo-acoustic refrigeration systems. Furthermore, Toghyani et al. [13] introduced an Imperialist Competitive Algorithm and a hybrid ANN-PSO approach to investigate the nonlinear correlations between experimental input variables—such as working medium temperature, fuel mass flow rate, and speed—and output parameters, namely power and torque. The outcomes presented by these researchers indicated that the hybrid ANN-PSO method outperformed the ANN-ICA combination. Additionally, Toghyani et al. [13] identified key performance indicators, namely torque and output power, for evaluating Stirling engines. Duan et al. [14] conducted a multi-objective optimization study employing Particle Swarm Optimization (PSO) to enhance thermal efficiency, output power, and minimize cycle irreversibility parameters. Their efforts resulted in a remarkable 15% boost in output power.

2. Motivation of the study

While considerable progress has been achieved in advancing efficient thermo-acoustic systems and employing numerical simulations for performance prediction, the persistent challenge lies in addressing the nonlinearity inherent in the operation of these devices. Nonlinearity in thermo-acoustic systems pertains to the non-proportional relationships between various physical parameters, such as pressure, temperature, and velocity. This complexity makes it challenging to formulate mathematical models. Additionally, the temperature-dependent nature of medium properties like density, speed of sound, and thermal conductivity introduces further nonlinearity, as alterations in temperature lead to corresponding changes in these properties, subsequently influencing the behavior of acoustic waves. Comprehending and quantifying these nonlinearities is paramount for accurately modelling and controlling thermo-acoustic systems. Such an understanding can give rise to phenomena like hysteresis, limit cycles, and chaotic behavior, all of which carry substantial practical implications in domains like combustion engines, thermo-acoustic refrigeration, and other heat-driven systems. This study makes a significant contribution to the modelling of travelling-wave thermo-acoustic systems by developing machine learning models capable of predicting configurations that were not explicitly measured during experimental investigations. This not only streamlines the experimental process, reducing time consumption, but also presents an alternative modelling approach for the thermo-acoustic research community.

This research study advocates for the adoption of soft computing techniques to forecast output voltages for both single-stage and multi-stage thermo-acoustic generators. The key input parameters considered are the temperature differential across each engine stage and the number of stages. In this context, the output voltage serves as the primary performance metric for both single-stage and multi-stage setups. The chosen techniques for output voltage prediction encompass Artificial Neural Net-works (ANN), Adaptive Neuro-Fuzzy Inference Systems (ANFIS), and ANN optimized through Particle Swarm Optimization (PSO). Soft computing techniques are recommended for their proficiency in analyzing data and discerning intricate patterns that may elude human perception. Consequently, they promise more precise predictions compared to conventional rule-based systems.

3. Proposed Approaches

This section outlines the methodologies employed for data acquisition and the machine learning techniques utilized in forecasting the output voltage of the travel-ling-wave air-filled thermo-acoustic electric generator.

3.1. Design of a thermo-acoustic generator

In the pursuit of developing a multi-stage thermo-acoustic generator, the initial phase involves the fabrication of three pivotal components: the cold heat exchangers, regenerators, and hot heat exchangers. Both the cold and hot heat exchangers were meticulously crafted using copper strips, each measuring 100 mm in length, which were then seamlessly joined through a soldering technique to form a square configuration. Subsequently, these assemblies were drilled and carefully positioned over the cartridge heaters and copper pipes within the regenerator tube. For optimal performance, honeycomb ceramic was chosen as the material of choice for this design owing to its commendable attributes such as excellent thermal conductivity, ready availability, and low thermal conductivity, as highlighted in reference [15]. The honeycomb ceramic utilized possessed a Cell Per Square Inch (CPSI) rating of 400, and was precisely tailored to dimensions of 85 mm by 95 mm before being snugly fitted into the regenerator tube. It is worth noting that honeycomb ceramic finds wide-ranging applications as catalyst supports and particulate filters for controlling vehicular emissions. The construction and assembly of the multi-stage travelling-wave thermo-acoustic generator are visually elucidated in Fig. 4 and Fig. 5. The experimental phase was carried out under ambient atmospheric pressure and room temperature conditions to facilitate the measurement of key parameters including output voltage, onset time, working fluid velocity, and temperature differentials (∆T) across each stage of the engine.

Figure 2: Thermo-acoustic core.

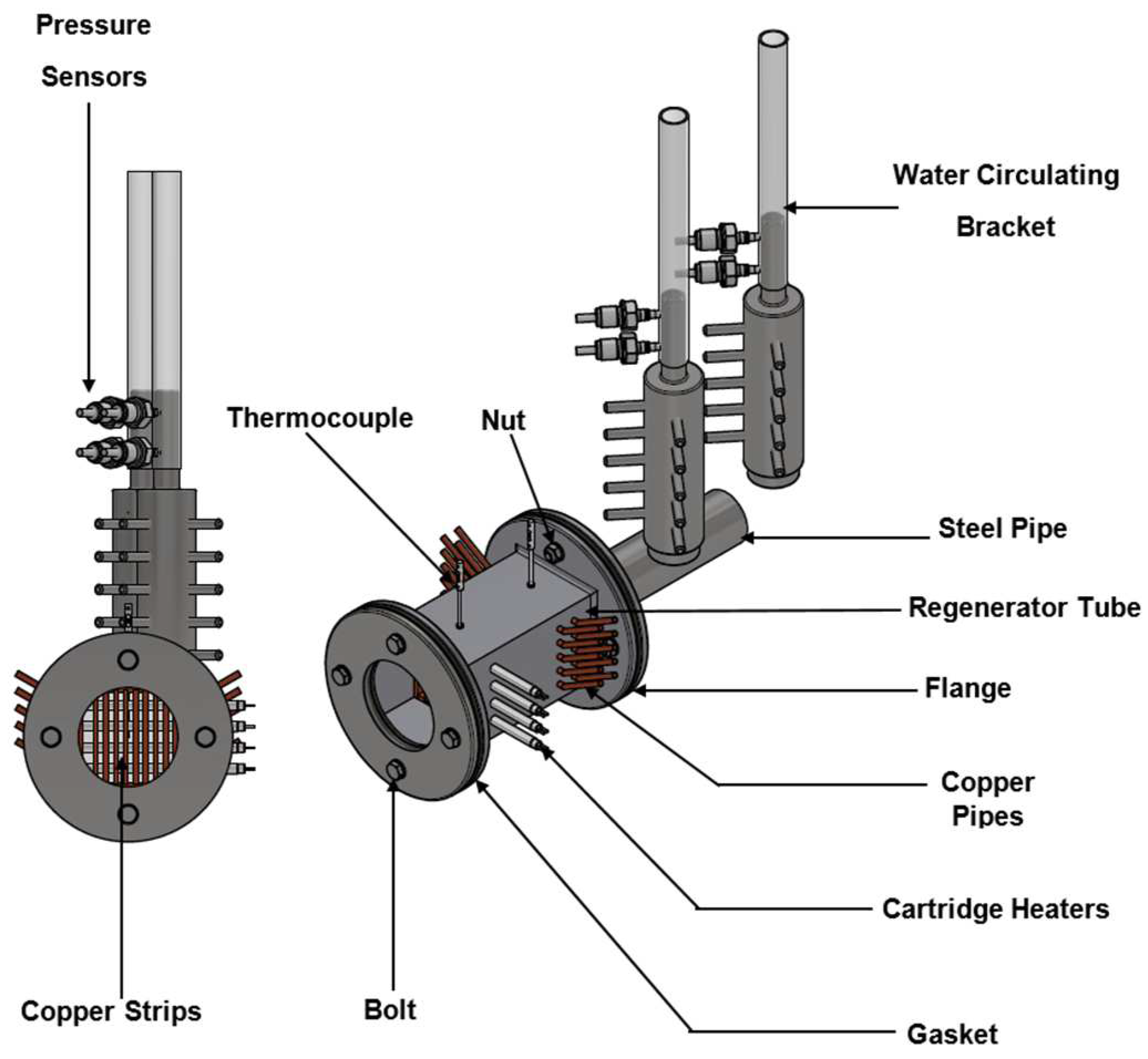
Figure 3: Travelling-wave Thermo-acoustic Electricity Generator.

3.2. Temperature Measurements

In this research study, the effectiveness of thermo-acoustic device in generating electricity for thermo-acoustic generator system is primarily assessed by the temperature difference across the regenerator units. This crucial parameter is typically measured using K-type thermocouple temperature sensors, chosen for their adherence to IEC 584 standards and class 1 tolerance for utmost accuracy [16]. These sensors boast a robust construction, featuring a stainless steel 310 probe sheath and a PFA insulated lead. The mineral insulated flexible probe sheath allows for bending and customization to suit a wide array of applications. Additionally, the thermocouple is equipped with a single element insulated hot junction to reduce electrical interference, and it has a plain pot seal with a temperature rating of up to 200℃ [16]. According to RS components, these specific thermocouples accommodate a temperature range from -40℃ to 1100℃ [16]. Their accuracy is within ±2.5℃ [16]. Typical applications for these miner-al insulated type-K thermocouple probes encompass heat exchangers, heat treatment and annealing furnaces, brick and cement kilns, power stations, food thermometers, thermostats, vehicle diagnostics, and laboratory settings [16].

The experiments were conducted at room temperature for both single-stage and multiple-stage travelling-wave thermo-acoustic generators. The experimental cycle commenced by running the cold water tap in the ambient heat exchangers for both single-stage and multiple-stage thermo-acoustic systems. Subsequently, electric power was supplied to the system through a variable transformer and a set of cartridge heaters. The input voltage, ranging from 115 V to 200 V, was measured using a digital multi-meter to ensure uniform electric power distribution across all engine stages. The temperature difference (∆T) across each engine stage was recorded by two K-type thermocouples, which were positioned on the cold and hot sides of the regenerator units. These thermocouples were then connected to the data acquisition device (DAQ), which, in turn, was linked to the computer for data capture. The onset temperature difference, defined as the minimum temperature required for the thermo-acoustic engines to generate sound, was recorded across each engine stage. Three sets of experiments were conducted, and the results were averaged to minimize measurement errors. Following each experimental run, the engines were allowed to cool down with cold water and a damp cloth for approximately 30 minutes and then left for about 2 hours. Finally, a digital multilevel meter was employed to measure the generated output voltage for both single-stage and multiple-stage setups. The results presented in this research study for onset temperature across engine stages and output voltage were obtained from three experimental trials and averaged to reduce measurement uncertainties. The experimental setup for temperature measurement is depicted in Figure 4.

3.3. Artificial Neural Network (ANN)

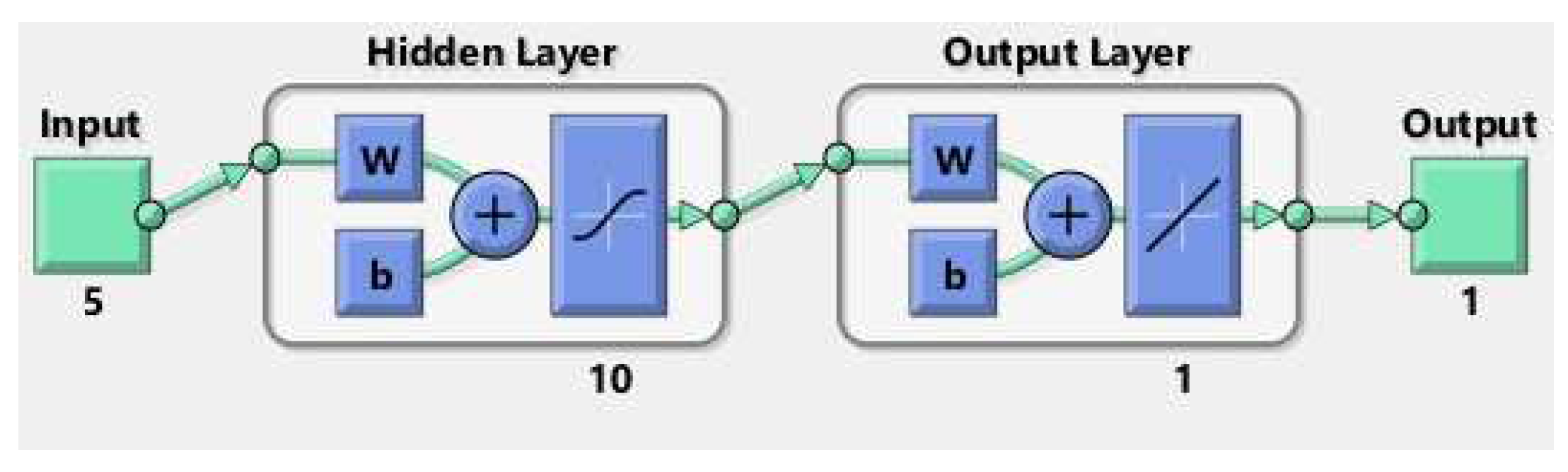
Artificial neural network (ANN) models were developed using MATLAB software. Parametric analysis was performed to identify the configuration of the model that yield the best results. This was achieved by adjusting the number of neurons in the hidden layers iteratively. The neural fitting app facilitated network training, data selection, and performance evaluation based on mean square error and regression analysis. For this study, a two-layer feed-forward network with a linear target neuron and sigmoid hidden neurons was employed to fit fifty-two (52) datasets derived from di-verse configurations of travelling-wave thermo-acoustic systems. The Leven-berg-Marquardt backpropagation algorithm was chosen for training due to its efficiency in processing data[17]. To ensure robust evaluation, the dataset was partitioned into three subsets: 37 samples (70%) for training, 5 samples (10%) for validation, and 10 samples (20%) for testing purposes. The input parameters for the ANN prediction were the onset temperature difference across each engine stage and the number of engine stages. The architecture of the neural network models, as depicted in Fig. 5, outlines the configurations utilized in predicting output voltage for both multiple-stage and single-stage thermo-acoustic generators. The prediction error (Pe) and average prediction error (APe) were computed using the equations provided in reference [17].

P e % = ⃒ \frac{P r e d i c t e d r e s u l t s - E x p e r i m e n t a l r e s u l t s}{E x p e r i m e n t a l r e s u l t s} ⃒

(1)

A P e % = \frac{\sum_{i - 1}^{n} - p r e d i c t i o n e r r o r %}{n}

(2)

Figure 5: ANN Structure (Predicting Output Voltage).

3.4. Adaptive Neuro Fuzzy-Inference System (ANFIS)

The experimental data was partitioned into training and testing sets to assess the predictive accuracy of the output voltage using the ANFIS model. The testing set comprised the minimum and maximum values (20%) of the experimental data, while the training set consisted of 80% of the data for network training. The input variables for the network were defined as the onset temperature difference across each engine stage and the number of engine stages, whereas the output voltage represented the target variable. This data partitioning ensured a distinct separation between the testing and training phases. The ANFIS model was trained over 1000 epochs for optimal performance.

3.5. Hybrid ANN-PSO

The hybrid Artificial Neural Network-Particle Swarm Optimization (ANN-PSO) approach aims to enhance the predictive performance of the output voltage in travelling-wave thermo-acoustic generators. To implement this technique, the ANN model has been integrated with Particle Swarm Optimization (PSO). A total of fifty-two (52) data points were generated for both single-stage and multiple-stage thermo-acoustic systems. These data were then divided into two sets: one for training and the other for testing. Specifically, forty-two (42) data points were utilized for training the hybrid ANN-PSO model, while ten (10) were reserved for testing the models. The PSO parameters, including the number of neurons in the hidden layer (n), swarm size population (N), and values of the acceleration factors (

C_{1}

and

C_{2}

), were systematically adjusted. Multiple runs were conducted, exploring various combinations of these parameters to ensure the development of a robust network. Throughout this research study, seven different neuron counts (ranging from 5 to 11), diverse swarm sizes spanning from 15 to 420, and acceleration factors (

C_{1}

and

C_{2}

) in the range of 1 to 3 were considered for predicting the output voltage for both single-stage and multiple-stage engines. The number of iterations was uniformly set to 1000.

4. Results and Discussion

This section presents the experimental results for both single-stage and multiple-stage travelling-wave thermo-acoustic generators. A dataset comprising fifty-two (52) data points was employed in constructing the ANN, ANN-PSO, and ANFIS models. The analysis focused on the onset temperature difference across each engine stage and the number of engine stages to assess the thermo-acoustic system's performance. The output voltage served as the primary performance metric for evaluating the thermo-acoustic device. The experimental data for both single-stage and multiple-stage thermo-acoustic systems is outlined in Table 1.

4.1. Comparison of a temperature difference of a four-stage configuration

The four-stage travelling-wave thermo-acoustic system underwent an experi-mental investigation, focusing on the analysis of temperature differentials across each engine stage. Heat was concurrently supplied to all engine stages, ranging from 200 V to 120 V. It was observed that despite the visual similarity in design, the engine stages were not identical, leading to distinct temperature differentials. The graphical repre-sentation in Figure 6 clearly illustrates that the second engine exhibited the lowest on-set temperature difference.

4.2. ANN Model Prediction

The ANN model was employed to predict the output voltage for both single-stage and multiple-stage configurations. The training process involved adjusting the number of hidden neurons, ranging from two to fourteen, and conducting three iterations. This endeavor aimed to identify the optimal ANN architecture that minimizes the deviation between experimental data and predicted values of output voltage. The discrepancies between the model's predictions and the experimental data were calculated and subsequently plotted against the number of neurons in the hidden layers, as illustrated in Figure 7. Figure 7 reveals that the average prediction error was minimized when employing ten (10) neurons. Consequently, the most effective network configurations for accurately predicting output voltage were those featuring ten (10) hidden neurons. Specifically, the output voltage network necessitates five input nodes and one output neuron, denoted as a 5-10-1 configuration. The regression analysis, as depicted in Figure 8, highlights the robust performance of the model. Both the training and validation phases demonstrate high regression values of 0.99864, while the testing phase exhibits a slightly lower yet commendable value of 0.99496. This underscores the efficacy of the proposed ANN model in accurately predicting the output voltage for both single-stage and multiple-stage engines. Figure 8 showcases the model's proficiency in generating reliable responses for any new input data within the scope of our study.

The experimental data was compared with the results predicted by the Artificial Neural Network (ANN) model, and this comparison is visually depicted in Figure 9. The analysis reveals a notable alignment between the experimental and mod-el-predicted data, with the most significant deviation being only 23.45%. These results underscore the effectiveness of the proposed model. This research suggests that it is possible to estimate the performance of both single-stage and multiple-stage configurations that were not specifically examined in the experiments, thereby reducing the need for time-consuming experimental trials.

4.3. ANFIS Model Prediction

The experimental data for both single-stage and multiple-stage engines were compared with the predictions generated by the ANFIS model, and the results have been visually represented in Figure 10. Upon careful examination of the graphical representation, it is evident that the trends in the experimental results for both single-stage and multiple-stage engines closely align with the output predictions generated by the ANFIS model. This observed agreement is further substantiated by the high regression test value of 0.9921, as demonstrated in Figure 11. Furthermore, Figure 12 provides a comprehensive 3-dimensional surface plot illustrating the correlation between the temperature difference across each engine stage and the corresponding output voltage. This plot serves to visually elucidate the intricate relationship between these variables.

4.4. Analysis of ANN-PSO Models

Table 2 below displays the results of the ANN-PSO hybrid model for each configuration in terms of training and testing. The superior training and testing values are indicated in bold for clarity.

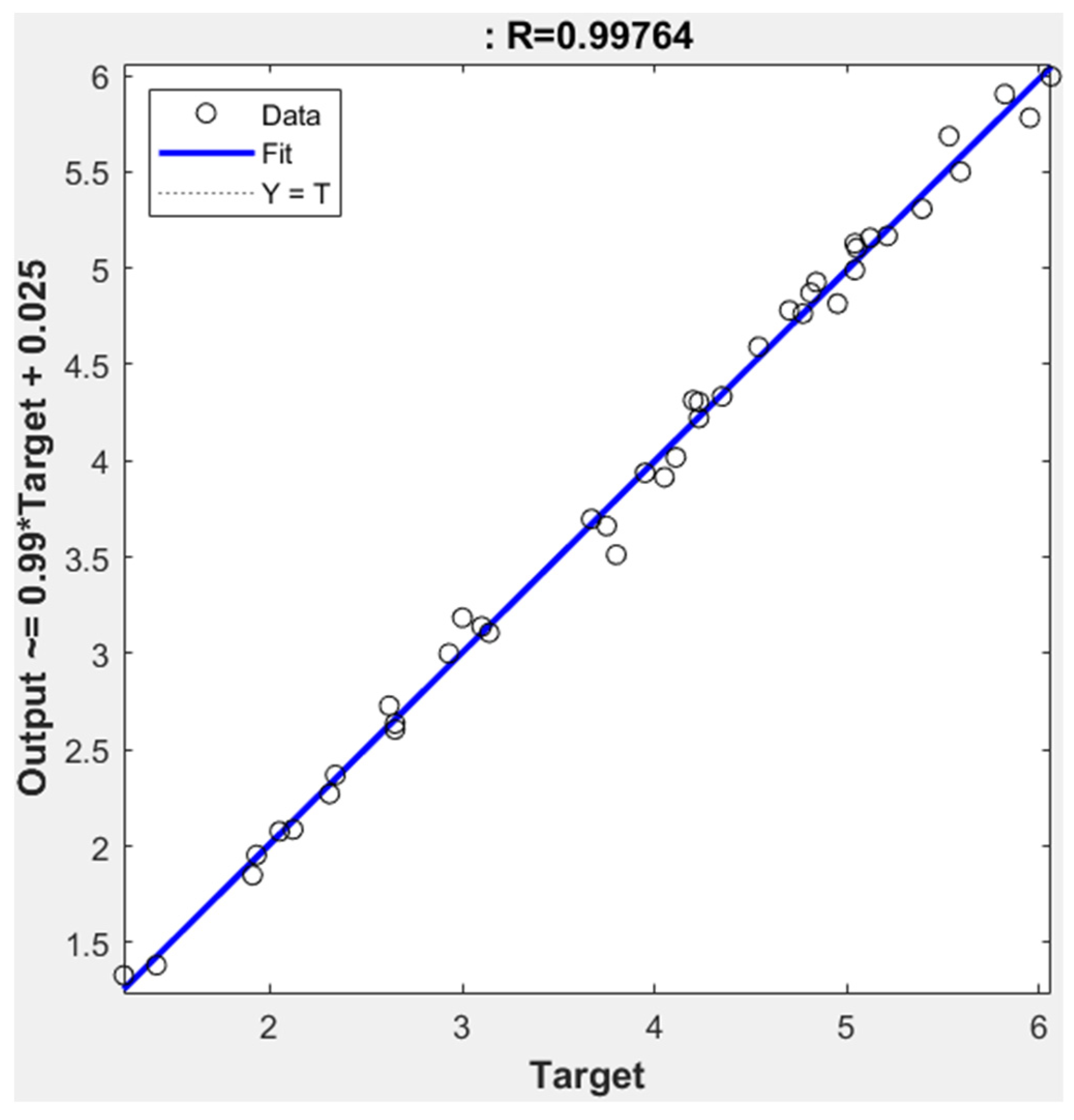
Based on the findings outlined in Table 2, it is evident that the best training outcomes, considering output voltage, were achieved for both single-stage and multiple-stage engines when employing a swarm population size of 200, utilizing 10 neurons, and setting acceleration factors (

C_{1}

and

C_{2}

) to 1 and 2.75 respectively. The corresponding mean square error (MSE) and training regression values were calculated at 0.0082 and 0.99764, as illustrated in Fig. 13. For the best testing results, a swarm population size of four hundred (400), eight (8) neurons, and acceleration factors of 1 and 2.25 (

C_{1}

and

C_{1}

) proved optimal. The resulting testing R² value stood at an impressive

0.9959

, as depicted in Figure 14. The comparison between experimental data and predictions generated by the ANN-PSO model was meticulously undertaken and visually represented in Fig. 15. It is noteworthy that the observed output voltage closely aligns with the predictions derived from the ANN-PSO model, substantiated by a testing regression (R²) of 0.9971 and a maximum discrepancy of only 21.66%, as demonstrated in Figure 15.

Figure 13: Training Response of the Best Performance Network for Output Voltage.

4.5. Comparison of results for ANN-PSO, ANFIS, and ANN

The performance of three models, namely ANN-PSO, ANN, and ANFIS, was assessed based on their mean squared error (MSE) and regression values (

R^{2}

), as summarized in Table 3. The results presented therein reveal that the ANN-PSO model exhibited the highest regression test value (

R^{2}

) of 0.9959, followed closely by the ANN model with a regression test value of 0.99496. The ANFIS model, while still commendable, demonstrated a slightly lower regression test value of 0.9921. Upon analyzing Figure 16 and Figure 17, it is evident that the predicted values generated by all three models (ANN-PSO, ANN, and ANFIS) closely align with the experimental data (target). This congruence is further corroborated by the deviation graph depicted in Figure 17. Notably, the ANFIS model exhibited the highest deviation at 36.38%, followed by the ANN model with a deviation of 23.45%. The ANN-PSO model, on the other hand, demonstrated the lowest deviation at 22.20%.

5. Conclusions

This study introduces a novel approach employing machine learning techniques to predict the output voltage of both single-stage and multi-stage thermo-acoustic systems. Specifically, three models were investigated: an Artificial Neural Network trained by Particle Swarm Optimization (ANN-PSO), Adaptive Neuro-Fuzzy Inference System (ANFIS), and a conventional Artificial Neural Network. To validate these models, a travelling-wave thermo-acoustic system was meticulously constructed and subjected to comprehensive experimental analysis. The dataset comprised fifty-two data points, encompassing variations in temperature differentials across each engine stage and the number of engine stages. The output voltage served as a pivotal metric for evaluating thermo-acoustic generator performance. Upon scrutiny of performance metrics, it was discerned that the ANN-PSO model demonstrated the highest predictive accuracy, with an impressive coefficient of determination (

R^{2} = 0.9959

). The application of these machine learning techniques underscores their potential in significantly reducing the number of required experimental configurations. Consequently, this enables researchers to estimate the performance attributes of other configurations with a heightened degree of precision. The findings of this study suggest that machine learning approaches offer an efficient alternative to the conventional experimentation process, thereby circumventing the need for protracted trials. To enhance the robustness of these machine learning models, it is recommended to scale up the prototype, thereby generating a more extensive dataset amenable for the development of resilient models. This research stands to contribute to the thermo-acoustic research community by ushering in a more streamlined and effective modelling approach.

Data Availability Statement

The data for this study is available upon request from the corresponding authors, for the purposes of replication, validation, and further research inquiries. This availability adheres to pertinent ethical and legal considerations. To obtain access to the dataset, please reach out to one of the authors.

Acknowledgments

This work was supported by the University of Johannesburg research funds.

Conflicts of Interest

The authors declare that there is no conflict of interest.

References

B. Radian, Artificial intelligence techniques for solar energy and photovoltaic applications. Robotics, concepts, methodologies, tools, and application, IGI Global, 2014 1661-1720.
L. Fausett, Fundamentals of neural networks. Architectures, algorithms, and application. Pearson; 1st edition (December 19, 1993), ISBN-10: 0133341860, pp.9-20.Author 1, A.; Author 2, B. Book Title, 3rd ed.; Publisher: Publisher Location, Country, 2008; pp. 154–196.
A. Rahman, X. Zhang, Prediction of acoustic-wave parameters of thermo-acoustic prime mover through Artificial Neural Network technique: practical approach for thermo-acoustics. Journal of thermal science and engineering progress, 8 (2018) 257-268.
M. Okwu, LK. Tartibu, Metaheuristic Optimization: Nature-Inspired Algorithms Swarm and Computational Intelligence, Theory and Applications. Studies in Computational Intelligence, Vol 927, ISBN 978-3-030-61111-8 (eBook).
A. Tarno, A. Rusgiyono, Sugito, Adaptive Neuro Fuzzy Inference System (ANFIS) approach for modeling paddy production data in Central Java. Journal of Physics: Conf. Series 1217 (2019) 012083. [CrossRef]
S. Zare, A.R. Tavakolpour-saleh, A. Aghahosseini, M.H. Sangdani, R. Mirshekari, Design and Optimization of Stirling Engines Using Soft Computing Methods: A review. Journal of Applied Energy, vol.283 (2021) 116258.
M.E.H. Tijani, J.C.H. Zeegers, A.T.A.M. De Waele, the optimal stack spacing for thermo-acoustic refrigeration. Journal of Acoustic Society of America, Vol. 112, Issue.1, pp. 128 -23. July 2002. [CrossRef]
M. Ngcukayitobi, L.K. Tartibu, Construction, testing and performance analysis of a multi-stage travelling-wave thermo-acoustic generator. International Journal of Green Energy. February 2023. [CrossRef]
T. Bi, Z. Wu, G. Yu, E. Luo, W. Dai. Development of a 5 kW traveling-wave thermo-acoustic electric generator. Applied Energy, vol. 185, pp. 1355-1361, 2016.
Z. Wu, L. Zhang, W. Dai, E. Luo, Investigation on a 1 kW travelling-wave thermo-acoustic electrical generator. Applied Energy, vol. 124, pp.140-147, 2014.
Z. Wu, W. Dai, M. Man, E. Luo, A solar-powered travelling-wave thermo-acoustic electricity generator. Solar Energy, vol. 86. pp. 2376 – 2382, 2012.
M. Machesa, L.K Tartibu, M. Okwu, Prediction of the oscillatory heat transfer coefficient in thermos-acoustic refrigerators. Sustainability, vol. 13, issue.17, 9509. August 2021. [CrossRef]
Toghyani S, Ahmadi MH, Kasaeian A, Mohammadi AH (2016) Artificial neural network, ANN-PSO and ANN-ICA for modelling the Stirling engine. Int J Ambient Energy 37(5):456–468.
C. Duan, X. Wang, S. Shu, C. Jing, H. Chang, Thermodynamic Design of Stirling Engine Using multi-objective Particle Swarm Optimization Algorthm. Energy Convers Manage, vol. 84, pp.88-96, 2014.
M.EH. Tijani, J.C.H. Zeegers, A.T.AM. De Waele ATAM, Design of thermo-acoustic refrigerators. Cryogenics, Vol. 42, pp. 49–57. [CrossRef]
RS component thermocouples and sensors. RS PRO Type K Thermocouple 150mm Length, 6mm Diameter. https://docs.rsonline.com/bd9d/A700000007350778.pdf.
A. Rahman, X. Zhang, Prediction of acoustic-wave parameters of thermo-acoustic prime mover through Artificial Neural Network technique: practical approach for thermo-acoustics. Journal of thermal science and engineering progress, 8 (2018) 257-268.

Figure 1: Thermo-acoustic Conversion Processes.

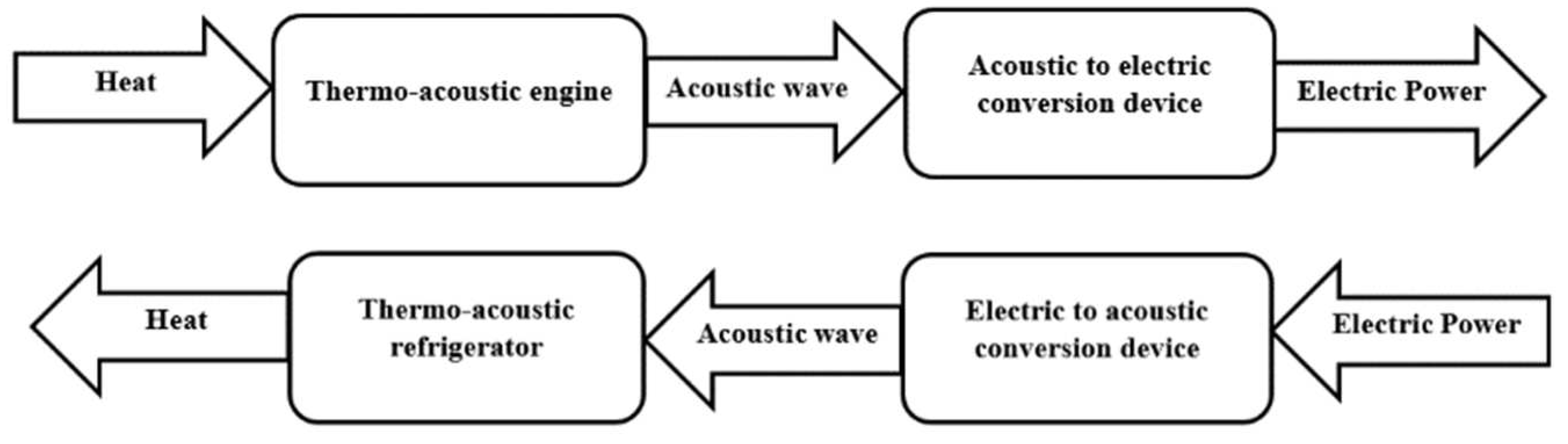
Figure 4: Experimental Setup for Temperature Measurements.

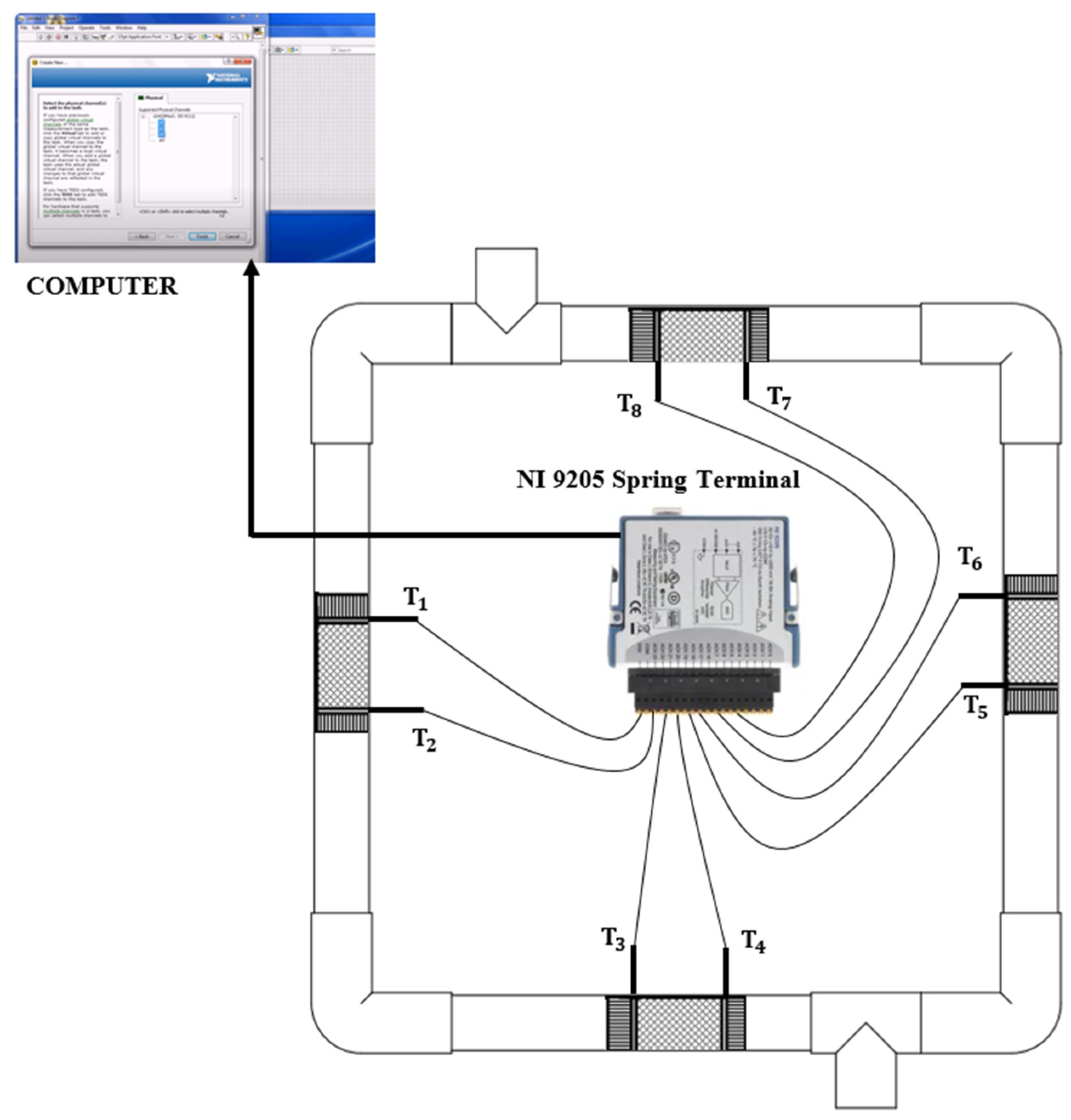
Figure 6: Temperaturer Difference for Four-stage Configuration.

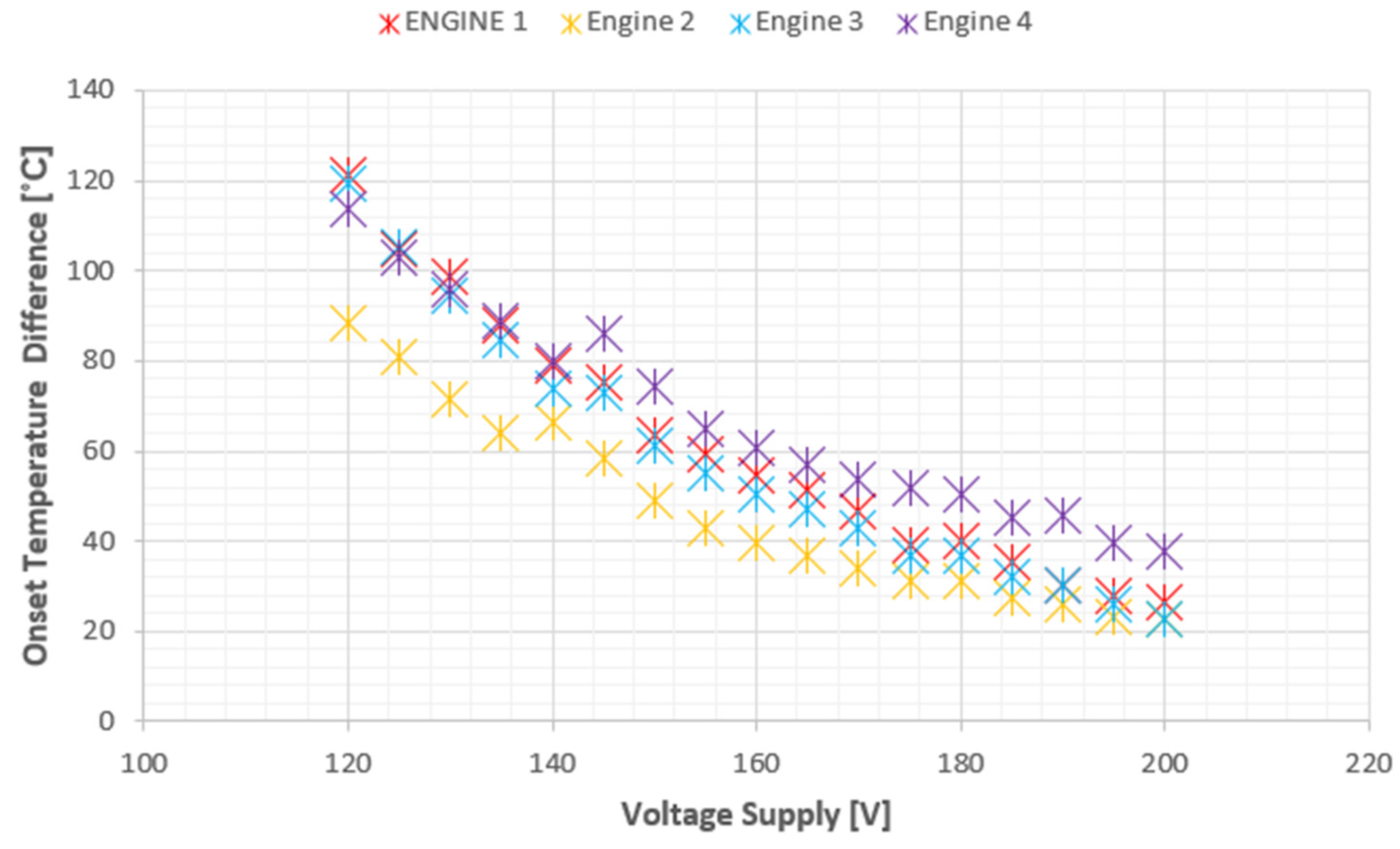
Figure 7: Average Prediction Error of Output Voltage [%] VS Number of Hidden Neurons.

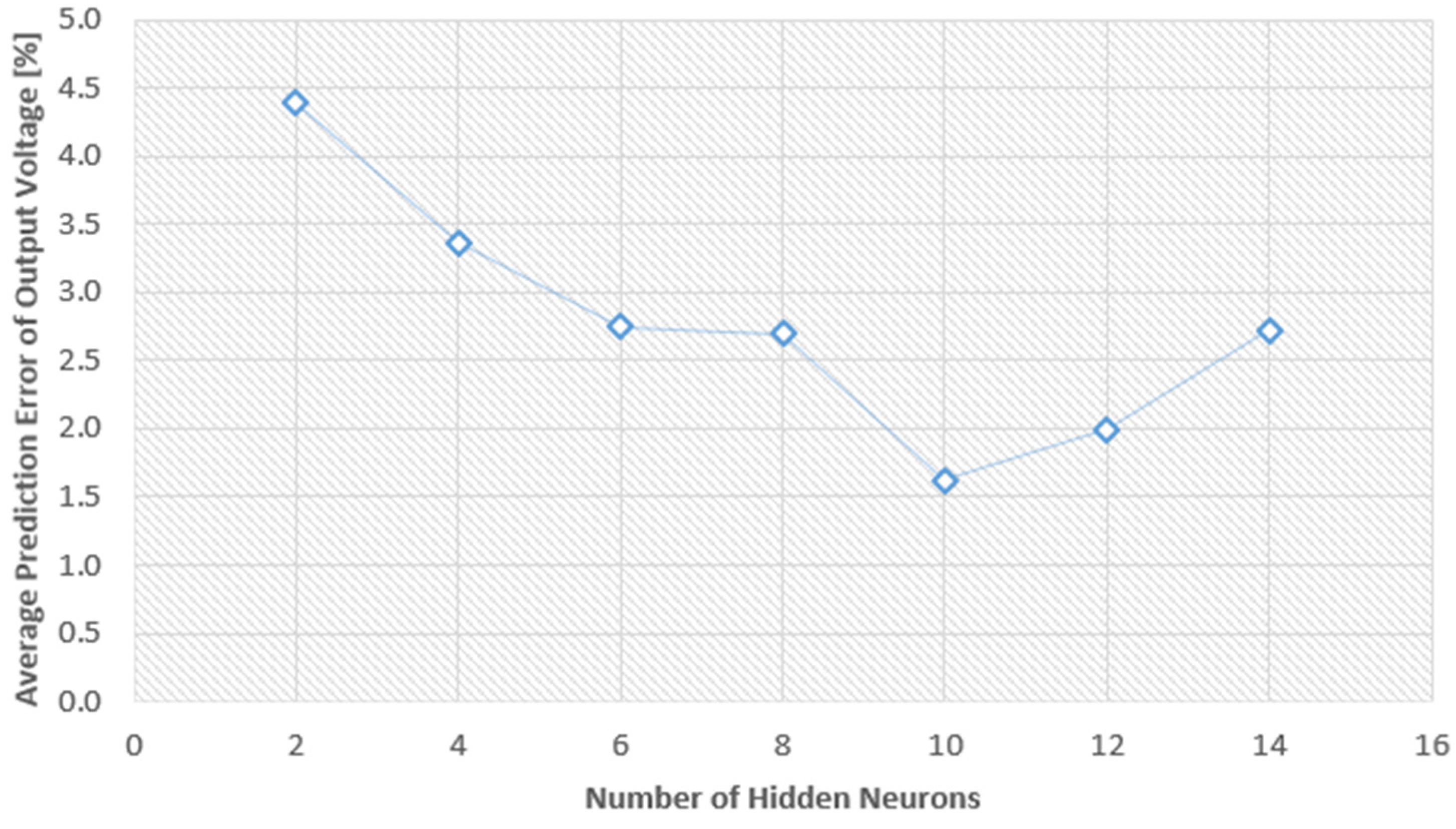
Figure 8: Regression Plot for Validation, Testing, and Training Phases (Output Voltage).

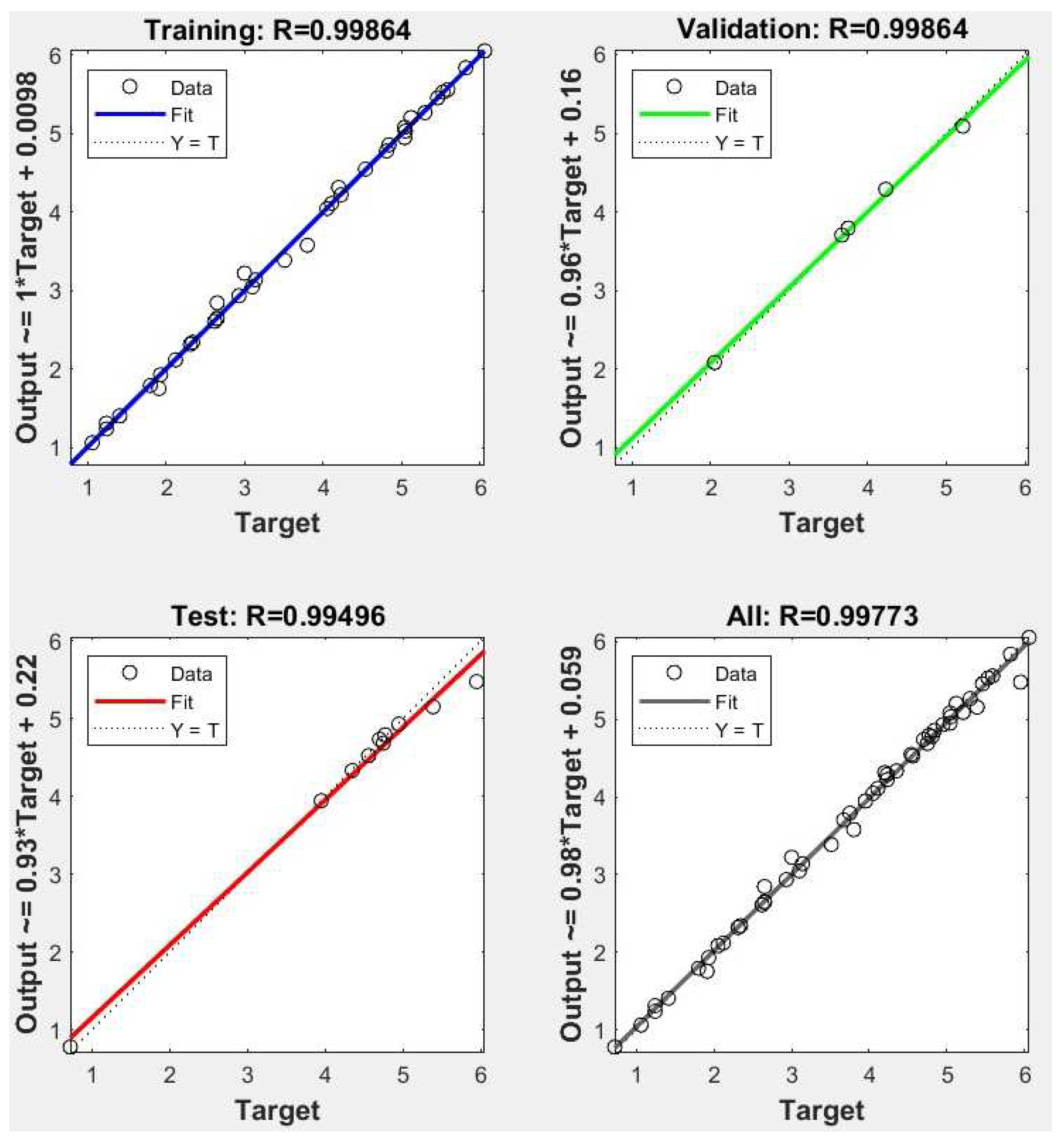
Figure 9: ANN Prediction VS Output Parameters/Output Voltage.

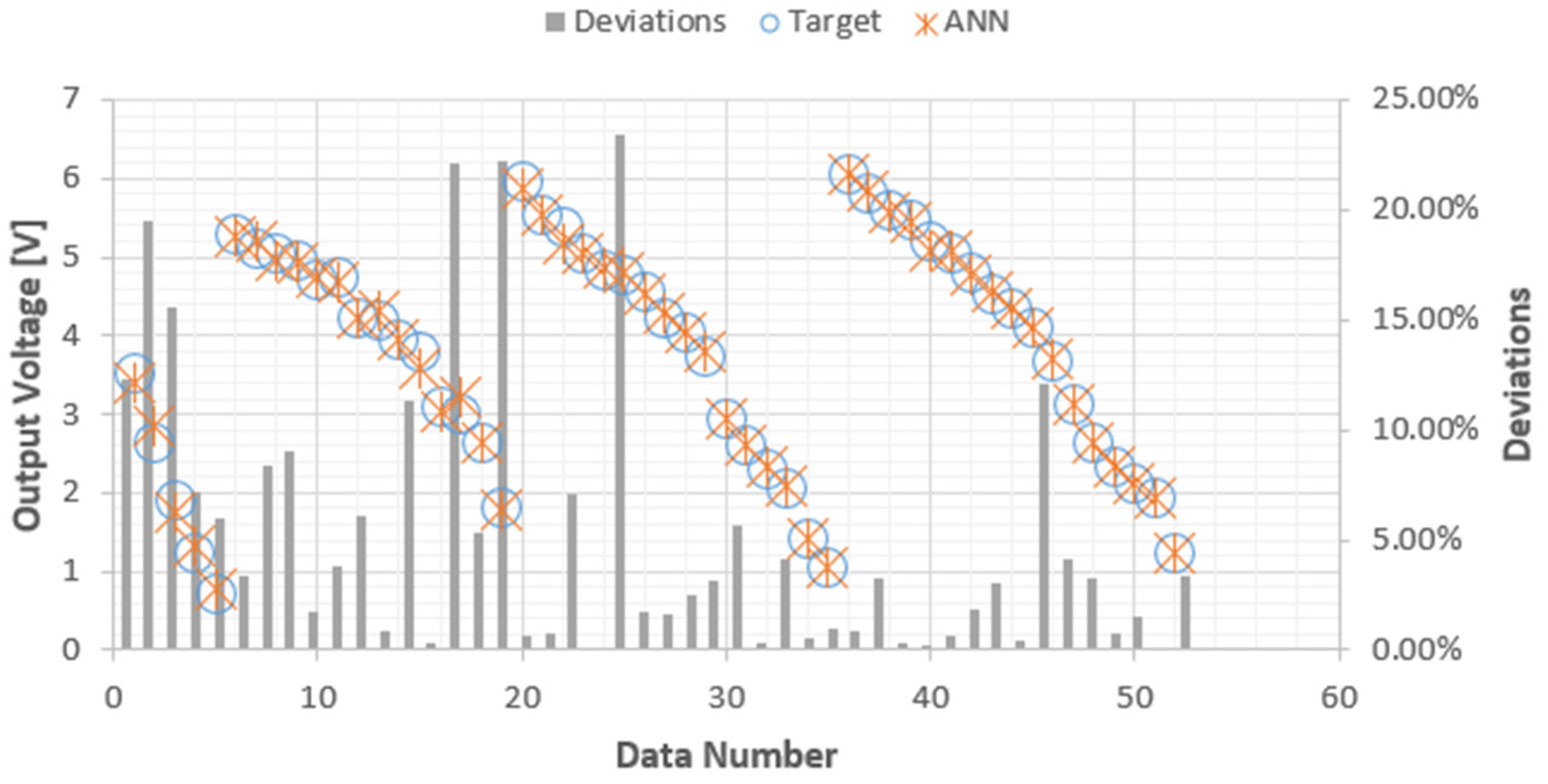
Figure 10: ANFIS Prediction VS Output Parameters (Output Voltage).

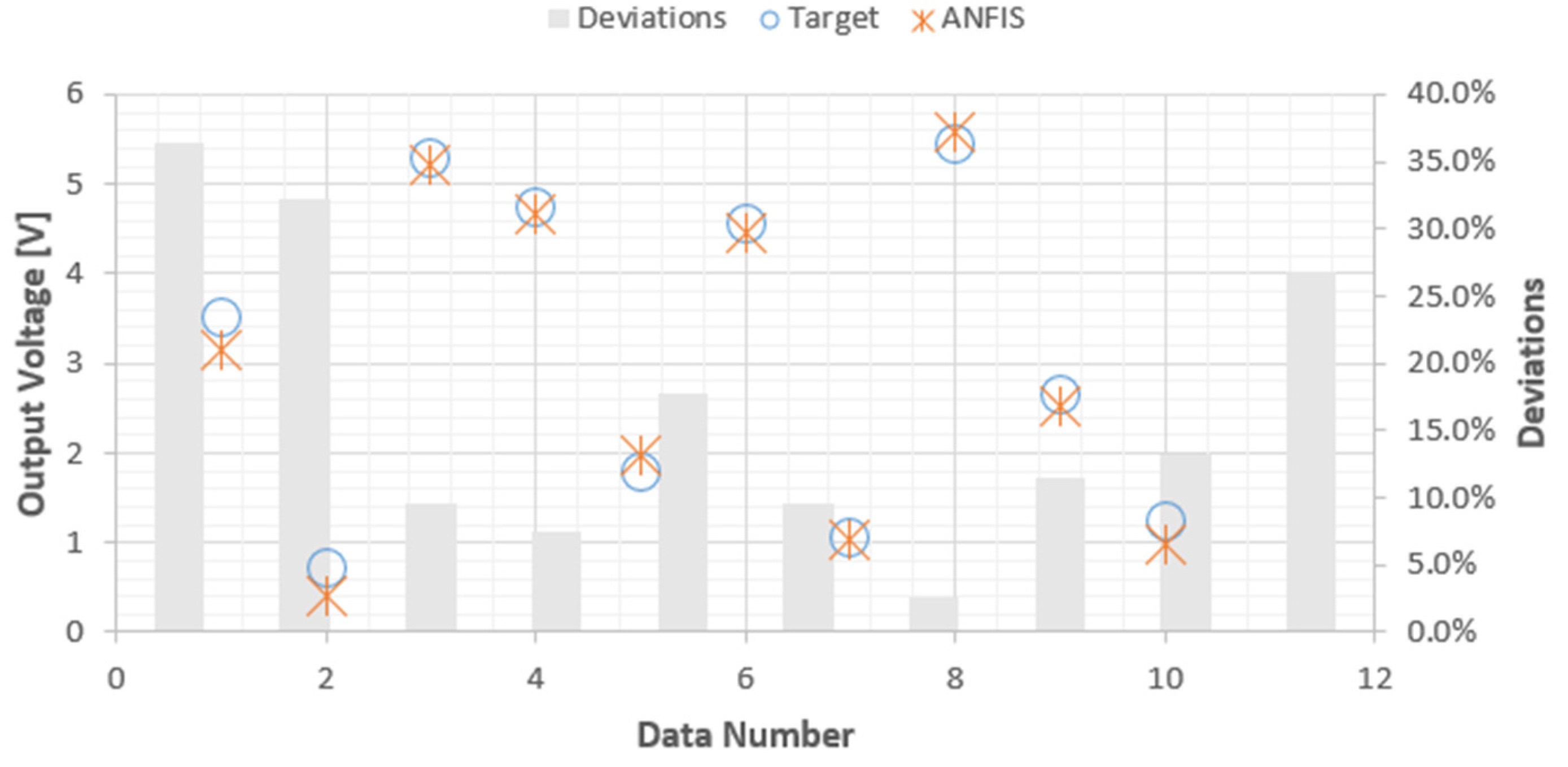
Figure 11: ANFIS Regression Plot (Output Voltage Test Values).

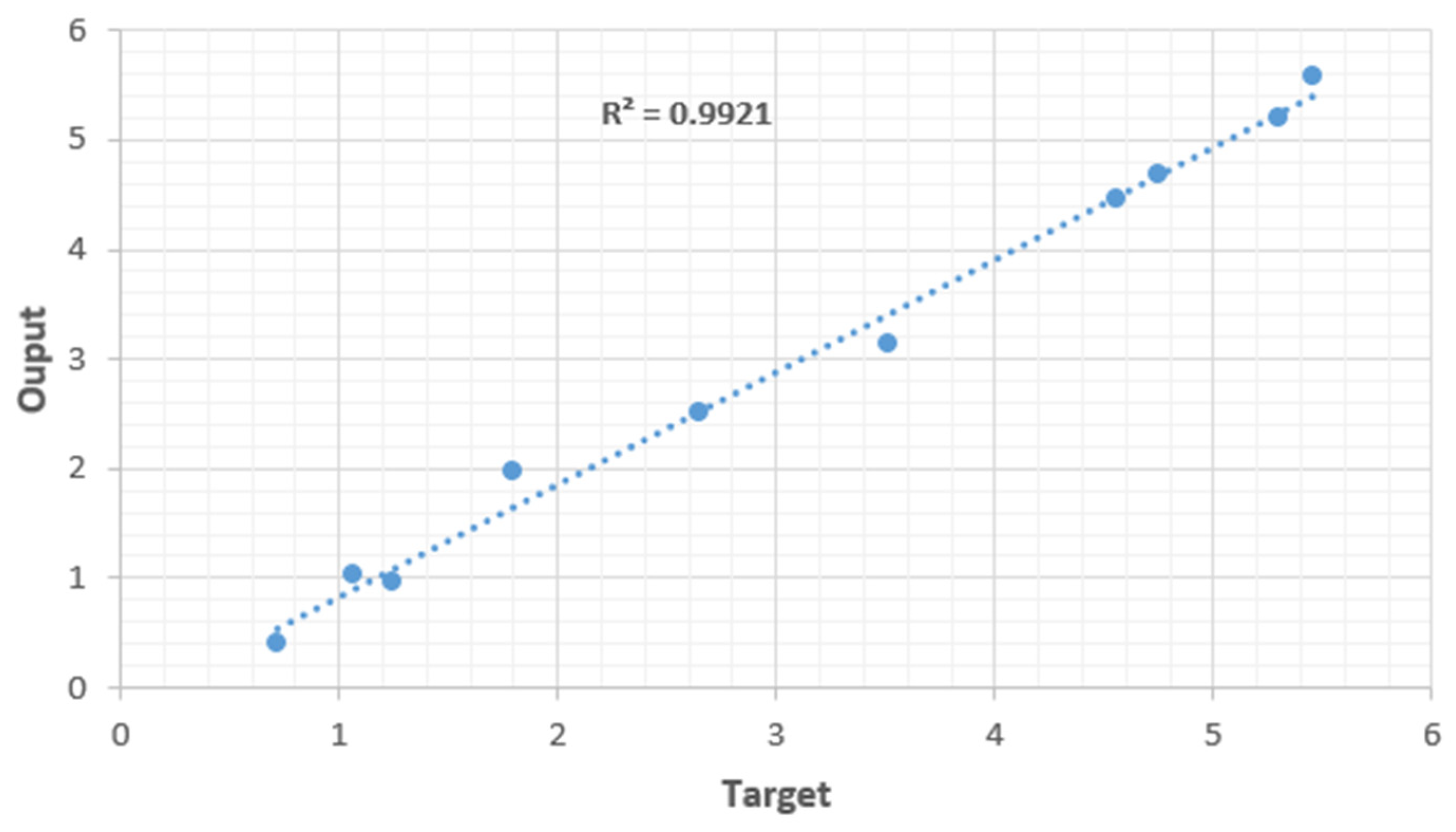
Figure 12: ANFIS 3D Surface Plot for Output Input Correlation.

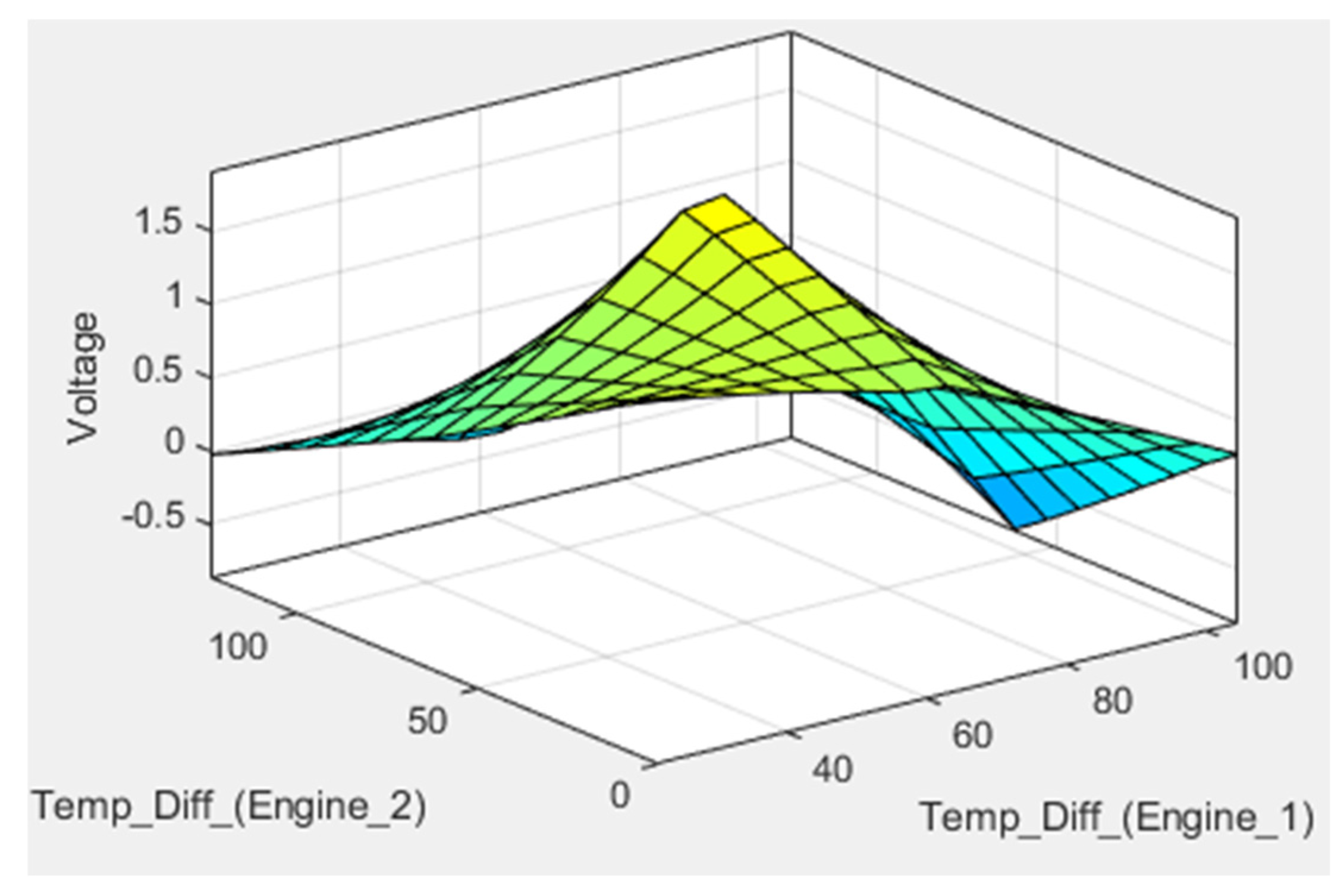
Figure 14: Testing Response of the Best Performance Network for Output Voltage.

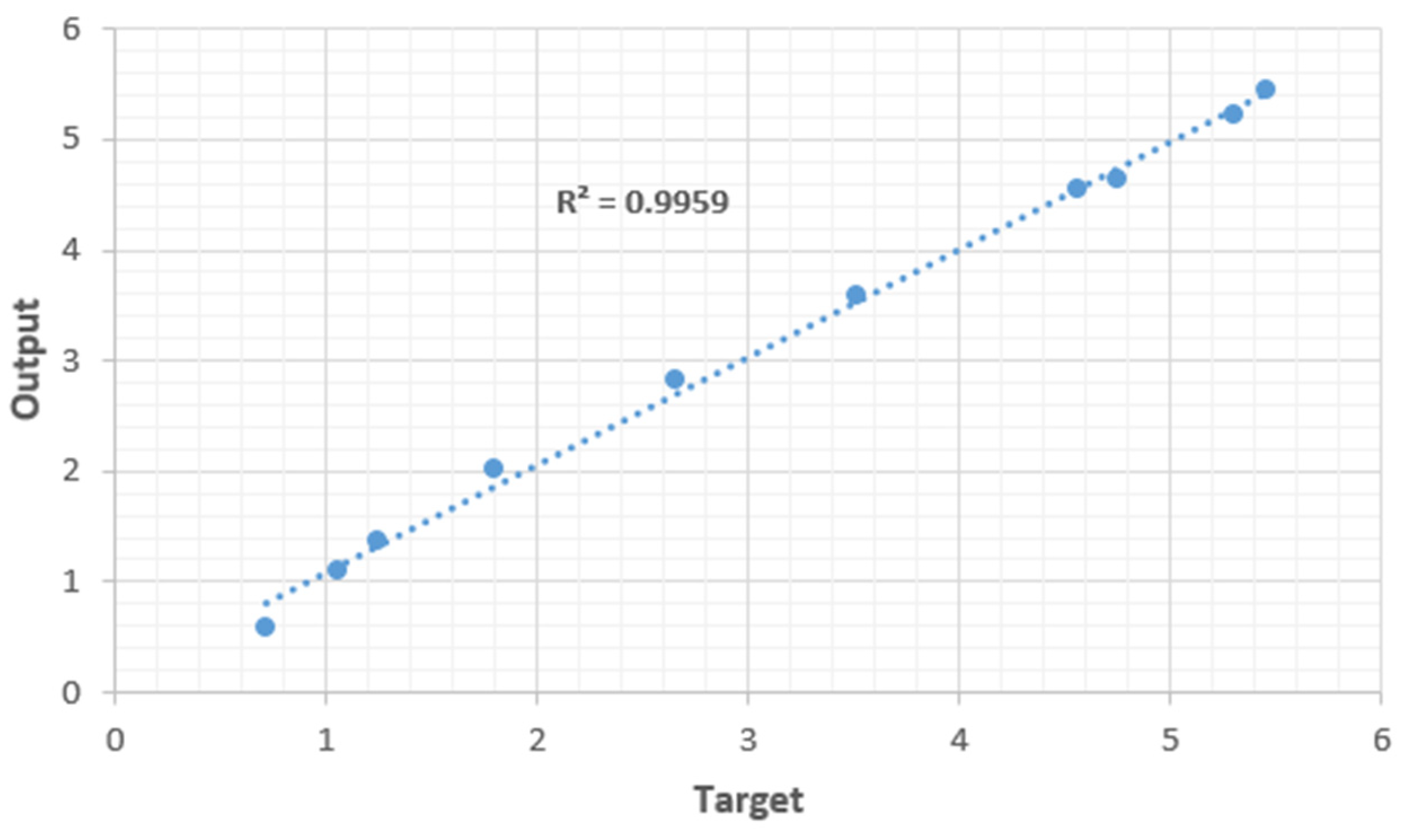
Figure 15: ANN-PSO Prediction vs Output Parameters/ Output Voltage.

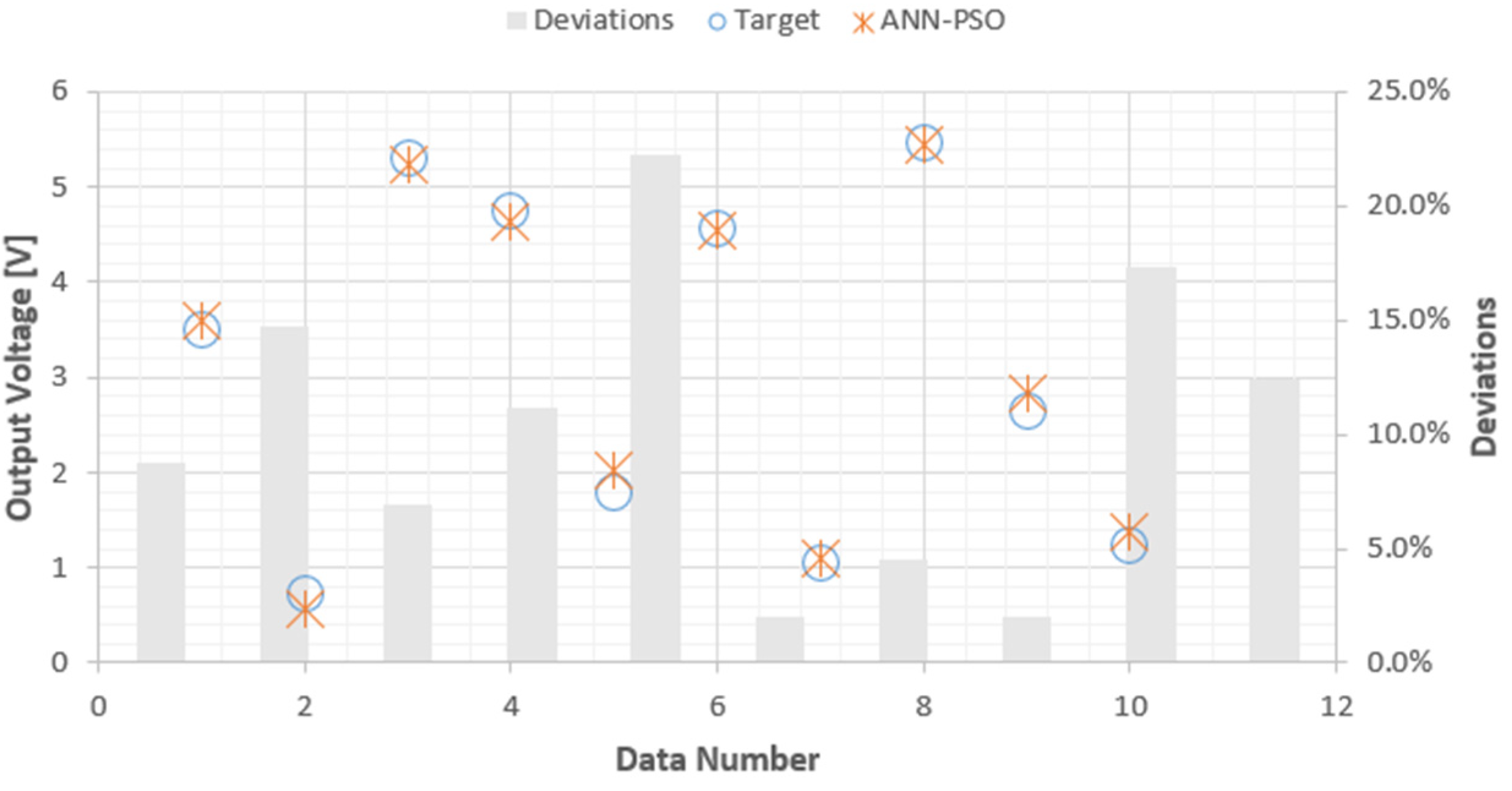
Figure 16: Results Comparison for Output Voltage.

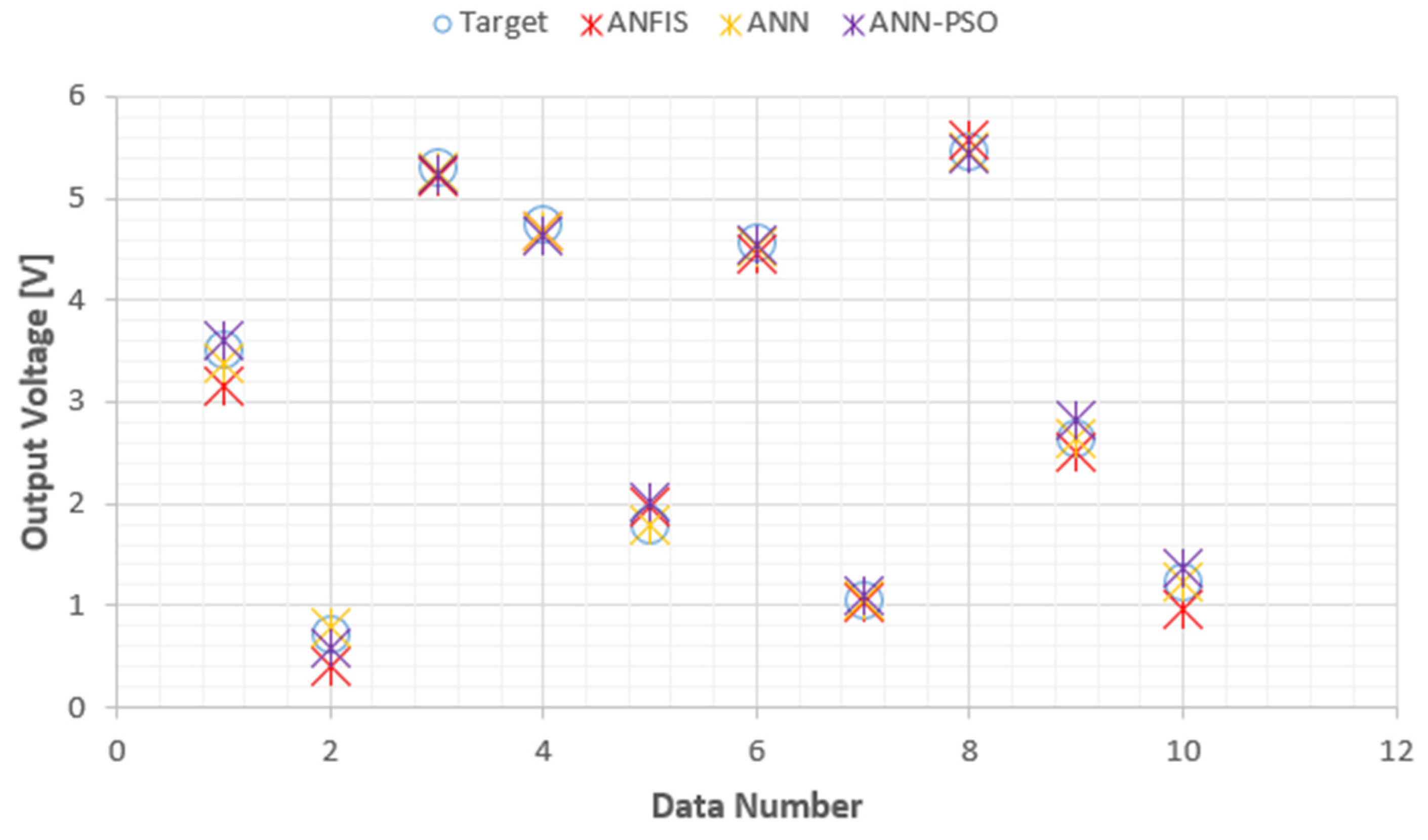
Figure 17: Deviations Between Target and Output from ANN-PSO, ANFIS, AND ANN/ Output Voltage.

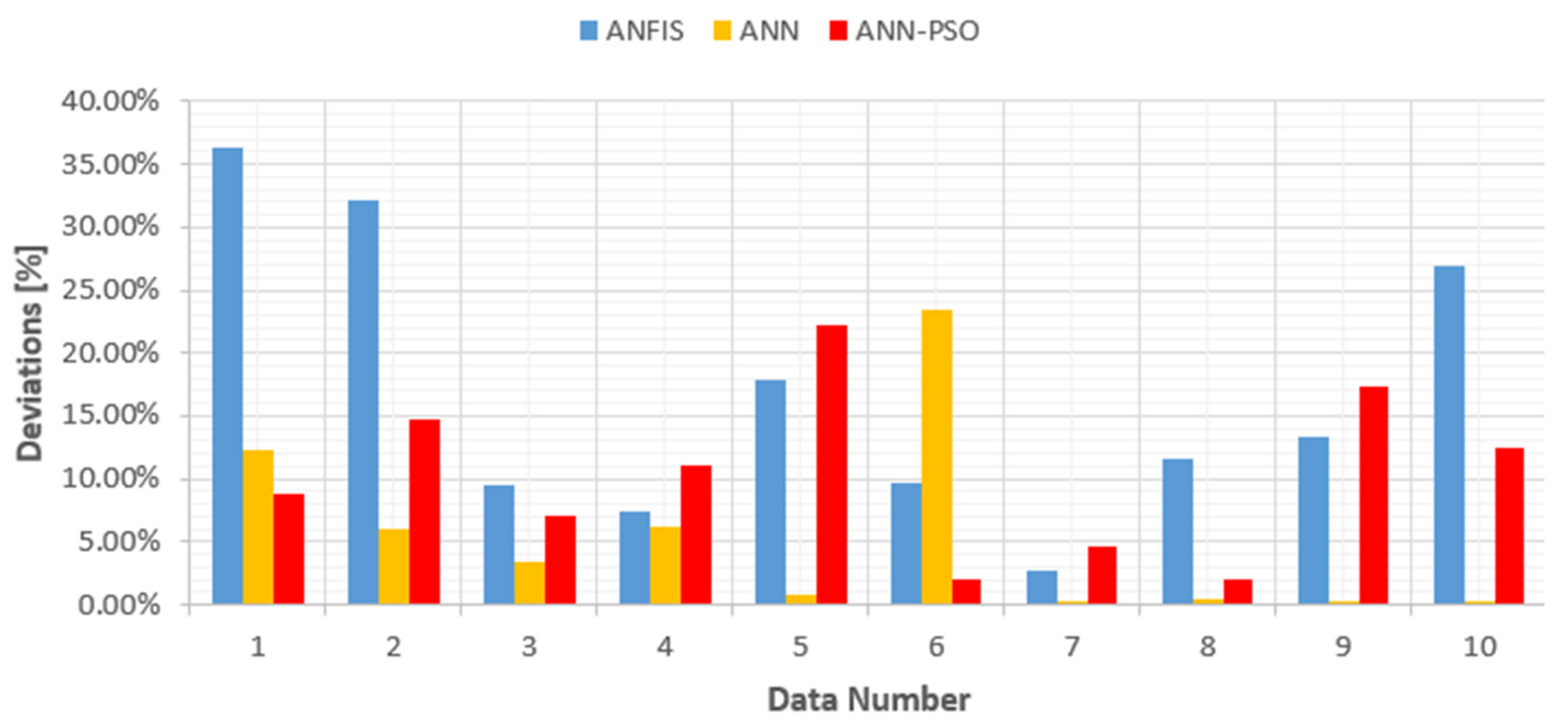
Table 1: Experimental Data for Travelling-wave Thermo-acoustic Generator.

$Stage 1 Onset Temp Diff [℃]$	$Stage 2 Onset Temp Diff [℃]$	$Stage 3 Onset Temp Diff [℃]$	$Stage 4 Onset Temp Diff [℃]$	No of Engine Stages	Output Voltage [V]
36.37	0	0	0	1	3.51
39.09	0	0	0	1	2.65
46.92	0	0	0	1	1.91
51.56	0	0	0	1	1.24
58.24	0	0	0	1	0.72
21.47	18.85	0	0	2	5.3
21.18	20.17	0	0	2	5.12
24.27	24.03	0	0	2	5.04
27.38	23.36	0	0	2	4.95
27.93	26.99	0	0	2	4.7
30.25	27.25	0	0	2	4.75
35.78	34.78	0	0	2	4.23
35.76	32.97	0	0	2	4.2
41.88	38.4	0	0	2	3.95
48.95	43.34	0	0	2	3.8
54.56	54.8	0	0	2	3.1
54.23	49.3	0	0	2	3
64.19	59.41	0	0	2	2.65
73.35	60.98	0	0	2	1.8
29.71	29.09	39.18	0	3	5.95
31.27	30.36	44.48	0	3	5.53
33.64	35.58	52.64	0	3	5.39
36.4	38.87	56.51	0	3	5.05
37.93	41.81	58.6	0	3	4.84
41.86	46.23	61.32	0	3	4.77
45.3	51.73	66.14	0	3	4.56
47.95	56.34	70.47	0	3	4.23
51.77	61.81	75.42	0	3	4.05
58.25	67.41	81.78	0	3	3.75
59.92	74.6	87.45	0	3	2.93
66.42	81.23	91.63	0	3	2.62
75.54	92.04	99.36	0	3	2.31
91.47	107.33	111.72	0	3	2.05
98.28	123.41	118.25	0	3	1.41
111.55	141.72	130.25	0	3	1.06
26.29	22.62	22.66	37.61	4	6.06
27.85	23.07	26.21	39.72	4	5.82
30.4	26.21	30.39	45.68	4	5.59
35.62	27.52	32.11	45.33	4	5.46
39.92	31.14	37.03	50.35	4	5.21
39.23	31.18	36.98	51.86	4	5.04
46.79	34.15	42.68	53.81	4	4.81
51.13	36.7	47.05	57.08	4	4.54
54.55	39.53	50.59	60.83	4	4.35
59.5	42.91	55.22	65.14	4	4.11
63.66	49.04	60.98	74.44	4	3.67
75.49	58.25	72.85	85.92	4	3.14
79.06	66.16	73.96	79.91	4	2.65
88.12	64.06	84.78	88.83	4	2.34
98.61	71.28	94.54	95.82	4	2.12
104.81	80.76	105.31	102.96	4	1.93
121.23	88.21	119.23	113.8	4	1.24

Table 2: Analysis of ANN-PSO Model for Output Voltage.

Number of neurons	Swarm population size	Acceleration factors $C_{1}$ $C_{2}$		$Training R^{2}$	MSE	$Testing R^{2}$
5	10	2.25	2	0.98675	0.0459	0.9124
5	20	2.25	2	0.99070	0.0323	0.8843
5	50	1.5	2.25	0.99456	0.0189	0.9439
5	100	1	2.75	0.99519	0.0167	0.9481
5	200	1.5	2	0.99599	0.0139	0.9840
5	400	1.5	2	0.99590	0.0142	0.9714
6	10	1	3	0.99553	0.0155	0.9232
6	20	2	2.25	0.98119	0.0663	0.9190
6	50	1	2.5	0.99587	0.0143	0.9743
6	100	1	2.5	0.99633	0.0128	0.8290
6	200	1	2.75	0.99617	0.0133	0.9200
6	400	1	2.25	0.99505	0.0172	0.9661
7	10	1.5	2.5	0.99522	0.0166	0.9478
7	20	1	2.75	0.99563	0.0152	0.9544
7	50	1	2.5	0.99519	0.0167	0.9640
7	100	1	2.5	0.99386	0.0213	0.9566
7	200	1.5	2.25	0.99365	0.0220	0.9811
7	400	2	2	0.99442	0.0194	0.9497
8	10	1	2.75	0.99499	0.0174	0.9871
8	20	1	2.5	0.99563	0.0152	0.9391
8	50	1.5	2.25	0.99551	0.0156	0.9630
8	100	1	2.5	0.99741	0.0090	0.9740
8	200	1	2.75	0.99762	0.0083	0.9844
8	400	1	2.25	0.99522	0.0026	0.9959
9	10	1	2.75	0.98904	0.0380	0.8716
9	20	1	3	0.99618	0.0133	0.9667
9	50	1.5	2.25	0.99408	0.0206	0.9697
9	100	2	2	0.99362	0.0222	0.9559
9	200	1.5	2.25	0.99533	0.0162	0.9593
9	400	1	2.5	0.99704	0.0103	0.9796
10	10	1	2.75	0.99485	0.0179	0.9406
10	20	1.5	2.5	0.99470	0.0184	0.9480
10	50	1.5	2.5	0.99656	0.0120	0.9555
10	100	1	2.75	0.99645	0.0123	0.9459
10	200	1	2.75	0.99764	0.0082	0.9717
10	400	1.5	2.5	0.99419	0.0202	0.9738

Table 3: Performance Results of ANN-PSO, ANN, AND ANFIS Models.

Output Voltage
	$R^{2}$ (Training or Testing)	MSE (Training or Testing)
ANN-PSO	0.99764/0.9959	0.0026/-
ANN	0.99864/0.99496	5.89257e-3/2.87704e-2
ANFIS	0.9981/0.9921	0.0574524/0.0574534

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Enhancing Thermo-Acoustic Waste Heat Recovery through Machine Learning: A Comparative Analysis of ANN-PSO, ANFIS, and ANN Models

Abstract

1. Introduction

2. Motivation of the study

3. Proposed Approaches

3.1. Design of a thermo-acoustic generator

3.2. Temperature Measurements

3.3. Artificial Neural Network (ANN)

3.4. Adaptive Neuro Fuzzy-Inference System (ANFIS)

3.5. Hybrid ANN-PSO

4. Results and Discussion

4.1. Comparison of a temperature difference of a four-stage configuration

4.2. ANN Model Prediction

4.3. ANFIS Model Prediction

4.4. Analysis of ANN-PSO Models

4.5. Comparison of results for ANN-PSO, ANFIS, and ANN

5. Conclusions

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe