Preprint
Review
Surfactants as Performance-Enhancing Additives in Supercapacitor Electrolyte Solutions – An Overview
Altmetrics
Downloads
93
Views
31
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
26 October 2023
Posted:
30 October 2023
You are already at the latest version
Alerts
Abstract
Wetting of the surface area of an electrode materials as complete as possible is desirable to achieve optimum specific capacity of an electrode material. Keeping this surface area utilized even at high current densities and even when inside of pores is required for high capacitance reten¬tion. The addition of surfactants at very small concentration to aqueous supercapacitor electro¬lyte solutions has been suggested as a way to improved performance in terms of capacitance, ca¬pacitance retention at increased current density and higher stability. Effects are pronounced with car¬bon materials used in electro-chemical double layer capacitors, they are also observed with re¬dox materials. Causes of the observed improvements and mode of operation of the added surfac¬tants seem to need further investigations; they are inconclusive beyond the obvious statement of in¬creased wetting. Reported examples and the current state of understanding are reviewed.
Keywords:
Subject: Chemistry and Materials Science - Electrochemistry
1. Introduction
Supercapacitors (for the sometimes confusing usage of their names, trademarks etc. see [1,2]) are devices in electrical engineering and electronics accepting and delivering extremely high currents, i.e. high power, like a large conventional capacitor. They store electric energy by separating electric charges across electrochemical interfaces at the boundary between an ionically conducting phase, the electrolyte or electrolyte solution, and an electronically conducting phase, the electrode. Two such interfaces or electrodes joined together by the common ionically conducting phase form the complete device. This operating principle characteristic of a supercapacitor of the electrochemical double layer capacitor type (EDLC-type) is sketched schematically in Figure 1 and compared with the operation of a rechargeable secondary battery. Different from the conventional capacitor the extremely large surface areas of the participating electrodes the amount of stored charge and thus of stored energy is much larger for a supercapacitor.
The cell voltage of a supercapacitor is limited by the stability of the ionically conducting phase; too high voltages will result in electrolytic decomposition of the solvent or the electrolyte. With a water-based electrolyte solution, this limits the cell voltage to values in the range of 1.2 V, sometimes higher values are claimed because said decomposition may be extremely slow at one or both electrodes because of e.g. kinetic hindrances. With organic-based solvents, larger values are possible. Relationships between properties of the employed materials and the considered range of possible electrode potentials and cell voltages have been critically examined [3]. Too large values may result in overoxidation of the electrode material at the positive electrode (sometimes slightly confusingly called cathode) [4].
Because the amount of stored energy depends on the amount of stored charge and the electrode potentials/cell voltage associated with this charge separation larger amounts of stored energy are possible preferably, by storing larger amounts of charge; the accessible potentials and voltages are limited as described. The charge per unit area of a typical electrochemical interface (the double layer) and voltage difference (i.e. electrode potential) can be expressed in terms of an interfacial capacitance. Taking the Helmholtz-model [5] and the common equation for a parallel-plate condenser
with permittivity ε = 6 F·m-1 and distance d = 300 pm a value C = 18 μF·cm-2 is calculated as the capacitance. The capacitance of the electrochemical double layer CDL can subsequently be considered either in differential form [6,7]:
or in integral form:
with the electrode potential E, the electrode potential of zero charge Epzc and q = ΔQ. They are related to each other according to:
The value calculated above is very close to a frequently mentioned value of 20 μF·cm-2 for a perfectly smooth metal surface in contact with a moderately concentrated aqueous electrolyte solution. This value may not be adequate for carbon materials. Randin and Yeager examined various high-pressure stress-annealed pyrolytic graphite’s SAPGs. The basal plane showed Cdiff = 3 μF·cm-2 [14,15]. This small value was attributed to the space charge region inside the SAPG, not to the electrochemical double layer (see also [16]). With boronated SAPG values depending on the identity of the electrolyte were slightly higher [17]. Edge-oriented SAPG showed values of Cdiff = 50 - 70 μF·cm-2 [18]. Respective values for highly oriented pyrolytic graphite HOPG and natural graphite crystals were much smaller, respectively [19]. Less well-oriented ordinary pyrolytic graphite showed Cdiff = 16 μF·cm-2 for the polished basal plane [14]. Values reported elsewhere for ordinary pyrolytic graphite OPG varied significantly [20]. Given the large variations of structures in carbon [21] a wide range of maximum values of Cdiff per m2 of surface area and in turn per gram of material may be expected [22]. An attempt to close the gap between surface areas determined with the Brunauer–Emmett–Teller (BET)-method without/with support by density functional theory (DFT) as well as other approaches taking into account further effects like structural changes during processing of a carbon material into an actual electrode and the double layer capacitance has been reported [23], a capacitance of 0.1 F per m2 effective surface area (which may differ considerably from BET-surface area) was tentatively concluded. Some of these authors reported exactly the same value earlier [24]. Gagnon reported exactly this value much earlier from a study of carbon blacks of various BET-surface areas in contact with a concentrated solution of KOH [25]. A further complication in establishing any correlation was added by a study of Wen et al. [26]. CDL per BET-surface area growing with increasing pore size was attributed to growing utilization of said surface area.
A larger storage capability, i.e. a larger capacitance, can accordingly be achieved by a larger interfacial area. The use of highly porous materials as electrodes is thus the central idea in the technical development of the supercapacitor [1]. Larger surface areas can be achieved mainly by utilizing ever-smaller pores meaning the use of more porous materials. At this step, further aspects of interfacial science come into play: Such surface inside ever-smaller pores must be accessible for the ionically conducting phase. Surface tension, capillary forces, viscosity and wetting are of growing importance. Initial fears that pores with too small openings would be inaccessible for electrolyte solutions, in particular for solvated ions therein needed for charge storage turned out to be partially incorrect. Starting with early observations [27] in subsequent studies evidence of at least partial desolvation was reported [28,29,30,31,32]; this extended the range of useful pores to smaller values than initially expected. However, accessibility of internal pore surface is not all that is needed for materials surface utilization. An electrochemical double layer must be established; in addition, for the surface to become an electrochemically active surface area [5,33] it must come into contact with the electrode (solution): it must be wetted. Moreover – last but not least – ionic movement into and out of even tiny pores must proceed at a rate compatible with large electric currents typical of a supercapacitor. With ever-smaller pore openings, conceivable interactions between moving ions and the electrochemical double layer on the walls of the pore mouth may become influential.
Possibly not all surface of a material in a supercapacitor electrode, whether it is an activated carbon (AC), a chalcogenide or any other redox-active material showing pseudocapacitive behavior, is immediately wetted and is sufficiently hydrophilic. This depends very much on materials properties of phases, the solid and the liquid one. Wetting of carbon materials has been discussed before (in the context of fuel cell technology and later of supercapacitors) [34]. Some carbons (e.g. carbon black, acetylene black) are highly hydrophobic, some (many activated carbons, some graphitic materials) are more or less hydrophilic. Hydrophilicity of carbon surfaces can be increased by creation of surface functional groups containing oxygen. In a typical study carbon fibers created from polyacrylonitrile were exposed to oxygen at elevated temperatures [35]. An increase of Cdiff of only a few percent was noticed, but the Faradaic current presumably due to surface redox reactions resulting in a pseudocapacitive behavior increased by several orders of magnitude. Thus the overall increase of capacitance (about 25 %) of a complete device was attributed mostly to redox processes but only a very small fraction to increased utilized because wetted surface area. Unfortunately such oxidative treatment may contribute to faster self-discharge of devices [36] and faster ageing [37].
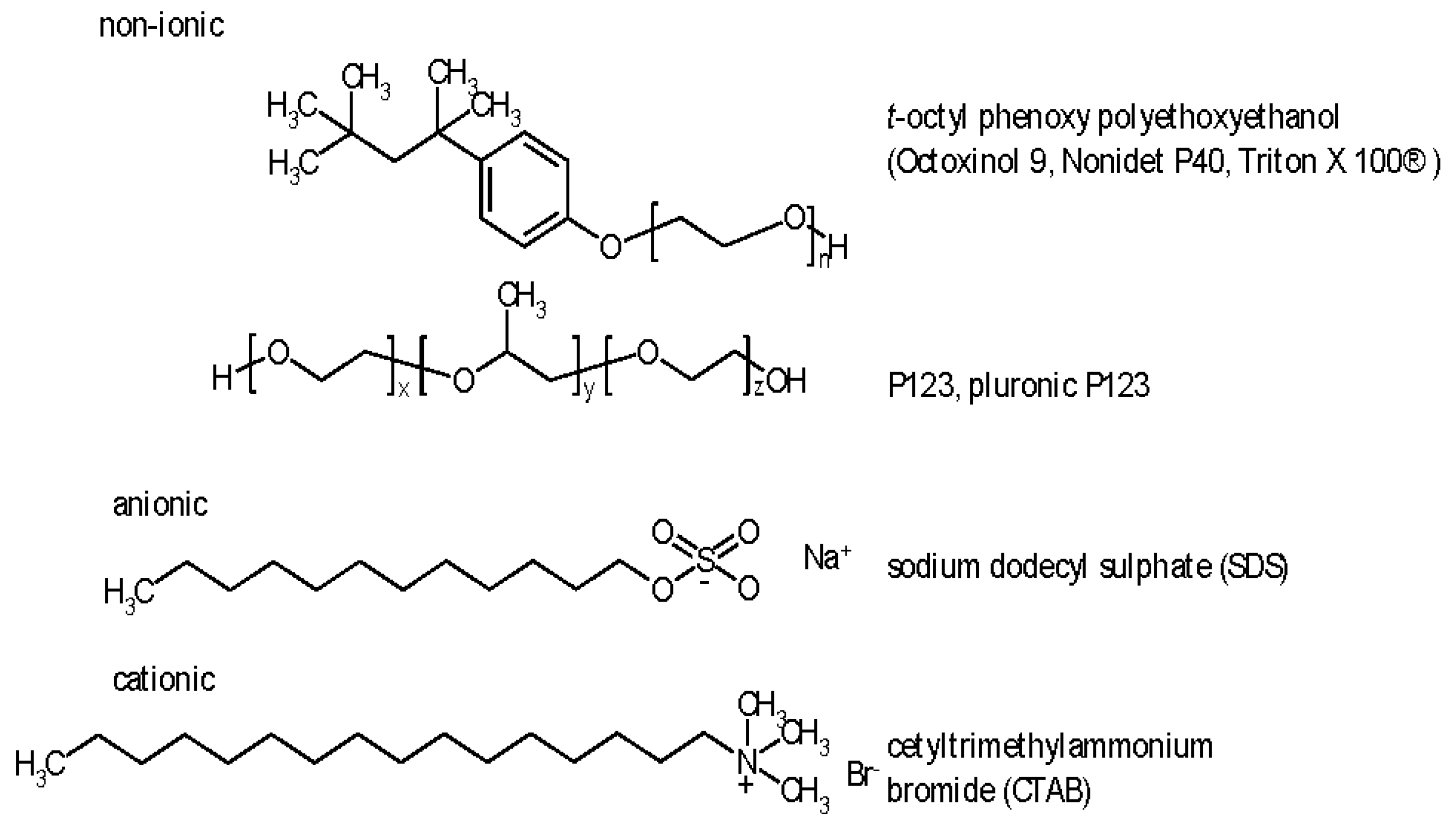
Nevertheless wetting behavior beyond surface properties and pore size considerations was never ignored. For improved wetting of a material’s surface surfactants may be helpful, their use has been established in various fields and industries for a long time [38,39]. Surfactants of interest in the present context can be classified into non-ionic, cationic and anionic ones. Typical examples and some frequently encountered compounds are depicted in Figure 2. Generally they contain a hydrophilic section/end containing heteroatoms like oxygen and a hydrophobic section with aliphatic or aromatic CH-building blocks. The molecular sizes range from about 0.5 to 2 nm.
The same considerations regarding porosity and wetting apply to redox-active materials showing pseudocapacitive behavior as proposed first by Conway et al. [40,41,42,43,44] as well as plain battery electrode materials. The particular behavior of some of this materials showing in CVs a response to a changing electrode potential closely resembling that of a capacitor has resulted in the designation by Gileadi and Conway [41] as pseudocapacitive behavior, for an update see [45]. An earlier use of the term “pseudo-capacity” by Grahame [46] refers to redox processes at the mercury electrode/aqueous electrolyte solution interface with reduction and subsequent oxidation of cadmium/cadmium ions, i.e. involving solutions species different from the suggestion by Gileadi and Conway involving redox reactions of surface-attached species.
Complete wetting of the surface area of a carbon or any other supercapacitor electrode material may be impeded by insufficient hydrophilicity or presence of surface area inside of pores with openings too small for electrolyte solution to get inside because of surface tension [47]. To improve this situation surfactants [38,39] improving wetting by reducing the surface tension of the electrolyte solution and/or reducing surface hydrophobicity [48] have been added to aqueous electrolyte solutions. Presumably the first study of surfactant effects has been reported with surfactant-treated carbon materials (no surfactant addition to the electrolyte solution) [49]. The studied materials were soaked in solutions of unspecified surfactants and dried. Enhanced wetting was easily verified visibly. Apparently and not very surprisingly, some surfactant was trapped in the porous electrode material and got transferred into the device. No experimental results suggesting specific effects of surfactant molecules adsorbed on the electrode material surface were reported. Considering the already mentioned size of surfactant molecules they may be too large to enter into very small pores, they may actually block openings of very small pores resulting in a negative effect on capacitance [50,51,52,53,54].
Most reports on the addition of surfactants into electrolyte solutions (including those inspected within this report) deal with aqueous electrolyte solutions, they will be in the focus of interest in the following sections. Nonaqueous solutions have been studied frequently because they permit a wider cell voltage window of operation. Basically the same considerations apply there also, but now with an inverted perspective: Instead of wetting with an aqueous phase now wetting with a nonaqueous phase is required. Instead of hydrophilic surfaces, hydrophobic surfaces are of interest. Accordingly, hydrophobisation of (instead of hydrophylisation) of surfaces is an option to increase better “wetting” of a surface. Other surfactants than those shown in a representative selection in Figure 1 may be effective. Better hydrophobisation by vinyltrimethoxysilane than with sodium oleate has been reported with a carbon aerogel (both as prepared and activated) as electrode material [55,56]. The same benefits (higher specific capacitance, better capacitance retention with increased current density and lower electric series resistance ESR of a complete cell) achieved with surfactant treatment as observed before with aqueous solutions were found. Different from surfactant addition to the electrolyte solution in this example modification of the carbon surface by grafting (i.e. chemical attachment via covalent bonding) of the surfactant was achieved. Less pronounced effects were achieved by adsorptive treatment of a carbon aerogel with sodium oleate [57]. Another option of surfactant use has been examined in studies of ACs vacuum-impregnated with fluorinated surfactants [58]. Moderate performance improvements (higher capacitance, better stability) were best with a cationic surfactant.
2. The systems
Effects of surfactant addition to aqueous electrolyte solutions in contact with carbonaceous supercapacitor electrode materials will be examined in the following section; in the section thereafter, effects with other redox-active electrode materials are inspected. Because in a substantial number of publications surfactants are used in other ways or play other roles in supercapacitors, in particular in preparation of the electrode materials, these further applications will be summarized briefly in a final section.
2.1. With carbonaceous supercapacitor electrode materials
Fic et al. [59,60,61] examined the effect of various surfactants including t-octyl phenoxy polyethoxyethanol (Triton X-100), tetrapropylammonium bromide (TPAB), sodium dodecyl sulphate (SDS) and further surfactants added at 5 mM concentration into the 6 M KOH electrolyte solution in a symmetric supercapacitor of the EDLC-type with AC electrodes. Higher surfactant concentrations were inefficient because of micelle formation. Best improvements including enhanced capacitance at higher current density, i.e., major improvement of capacitance retention with growing current density, slower self-discharge (of a complete device in terms of e.g. cell voltage or a single electrode in terms of electrode potential) and increased stability were found with non-ionic Triton X-100. The reported main effect of surfactant addition was a reduction of surface tension of the aqueous phase enabling penetrating pores of smaller diameters than possible without surfactant addition. Polarity of the surfactant affected their influence on observed capacitance values. However, these statements appear to be slightly inconclusive.
Upon closer inspection, further details emerge. At lowest current density, addition of any surfactant did not show an increase of specific capacitance (see e.g. Figure 1 in ref. [59] and Figure 4 in ref. [60]). Accordingly a simple wetting enhancement is not the full explanation – if any explanation at all because it should have resulted in higher values of specific capacitance even at lowest scan rates. The significantly improved capacitance retention with the studied AC electrode material suggests instead better utilization of inner pore surface area than without added surfactant. Thus the surfactant – whether adsorbed on the carbon surface or dissolved in the electrolyte solution – seems to accelerate ion transport. This points in particular at improved ion passage through pore openings somehow supported by the added surfactant. Whether ion channels formed by surfactant molecules (see [62]) accelerate ion transport is currently only a speculation. In a study of layered 2D-nanomaterials hydrophilic and ionophobic surfaces generated by corresponding surface treatment in particular by attachment of suitable functional groups could drastically reduce ion diffusion resistance [63]. Similar considerations with ionic liquids as electrolyte taking into account the different properties of these materials have been reported with conclusions pointing into the same direction [64]. Addition of a surfactant to the electrolyte solutions and subsequent adsorption on the carbon surface may have a similar effect in terms of increased hydrophilicity. Effects of surfactants on ionophobicity are hard to estimate, in addition the size of the surfactant molecules must be considered with respect to pore sizes. Given the determined morphological data of the AC used in [60] as previously reported in [65] such effect may be conceivable when the surfactant molecules are adsorbed flat or strongly tilted on the carbon surface.
Somewhat surprisingly, the effect of surfactant molecules possibly displacing water molecules in the electrochemical double on the specific double layer capacity has not been considered. Elsewhere in studies of the adsorption of aliphatic alcohols (being somewhat related to surfactant molecules) with different chain lengths on a polycrystalline gold electrode a significant decrease of the specific double layer capacitance was observed, particularly pronounced at maximum coverage [66,67]. With increasing chain length of the studied alcohols the capacitance continuously decreased. A perpendicular adsorption of the alcohol molecules was concluded. With the surfactant molecules employed in the studies reviewed here such orientation is highly likely. Adsorption studies of these surfactants on carbon or the electrode material inspected below are not reported, thus the degree of coverage and any decrease of specific capacitance remains unknown; more research works still needs to be carried out to investigate the underlying mechanism in the future.
2.2. With redox-active supercapacitor electrode materials
Tremendous power densities have been achieved with EDLC so far whereas energy densities are still disappointingly low [68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88]. Metal oxides employed as active materials in supercapacitor electrodes to overcome this limitation have been examined only very infrequently with surfactants added into the electrolyte solution. To the fundamentally different surface compositions of carbon-based materials used in ECDL supercapacitors and metal oxides used in redox capacitors the different charge storage mechanisms – ion accumulation vs. superficial redox reactions add a further dimension of properties and behavior. Composites of metal oxides with carbon materials or intrinsically conducting polymers as a further class of redox-active materials may cause further differences in properties and behavior [89,90]. These differences may result in different effects of added surfactants. Presumably, the concentration of added surfactant should again be kept below the critical micelle concentration (CMC), in particular to avoid blocking of pores by micelles [50,51,52,53,54]. Following, results obtained with these three classes of materials will be inspected.
Wang et al. have examined the influence of SDS, Triton X-100 and P123 (poly(ethylene glycol)-block-poly (propylene glycol)-block-poly(ethylene glycol)) added at 5 mM concentration to an aqueous electrolyte solution of 2 M LiNO3 on the properties of manganese ferrite MnFe2O4 suggested as supercapacitor electrode material [91]. Highest capacitance increase by 36.8 % was found with SDS. This was attributed to “enhanced lithium ion penetration” as already suggested elsewhere [92]. At a moderate current density of 0.5 A·g-1 82 % of the initial capacitance were retained after 1000 cycles. Capacitance retention with increasing current was markedly improved in particular with SDS. Surfactant concentrations above 5 mM (e.g. 10 mM with SDS) resulted in a decrease of capacitance because of micelle formation impeding ion movement and because of diminished efficiency of the surfactant, which is now presumably in part assembled in micelles instead of being active at the solution/carbon interface. Improved capacitance retention at higher current densities was also noted, again with SDS showing the most pronounced effect. Different from a previous report by Wu and Kuo [93] the CV response showed a pronounced pseudocapacitive shape, no current peak due to a redox process of the ferrite was found. The absence of plateaus in the galvanostatic charge/discharge curves confirms this conclusion. Quite notably self-discharge – which is an inherent problem possibly limiting the use of supercapacitors for long-term energy storage – is significantly slowed down with added SDS. During 1000 cycles capacitance losses again depended on the added surfactant with Triton X-100 and P123 performing slightly better. Co(OH)2 on nickel foil was prepared by electroreduction of Co(NO3)2 in an aqueous solution [94]. Reduction of nitrate anions yielded nitrite and hydroxyl ions, the latter formed the expected precipitate of sheet-like Co(OH)2. Addition of 0.05 % Triton X-100 yielded significant increases in storage capability as well as in stability. The effect of representative surfactants from the three classes presented above with electrodes made from a specific type of α-NiOH)2 and MgCo2O4 has been reported [95]. With the former oxide beneficial effects in terms of greater capacitance, better capacitance retention with increased current density and higher stability were noticed whereas the latter mixed oxide did not show any improvement. From these results, the surfactants appear to work in different ways; the working mode may also be completely different.
Ghasemi and Ahmadi have compared the effects of added Triton X-100, SDS and cetyltrimethylammonium bromide (CTAB) on the performance of a composite of reduced graphene oxide and Fe3O4 [96]. The capacitance of 154 F·g-1 at a current density of 1 A·g-1 was increased upon addition of Triton X-100 to the electrolyte solution to 236 F·g-1, after 500 cycles a capacity retention of 97 % was observed. Without added surfactant, the losses amounted to 13 %. For practical applications, such retention would be demanded after 105 to 106 cycles. Beneficial effects of the other ionic surfactants were less pronounced. How the presence of surfactant shall accelerate charge carrier transport along the electrolyte/electrode interface is not explained; attribution of this claim to an earlier report [6060] wherein such claim is not made doesn’t help. Possibly an explanation along the line of reasoning presented above may be applicable.
Surfactants have been incorporated into polypyrrole during oxidative chemical polymerization of pyrrole monomers [97]. The ionic surfactant acts reportedly as counterion in the oxidized polymer. Neither the function of the surfactant nor the improvement achieved when comparing the performance of this polymer with polypyrrole formed with other counter anions was explained.
2.3. Other uses of surfactants related to supercapacitors
The vast majority of publications related to surfactants and supercapacitor electrode materials deals with either the use of surfactants during synthesis and electrode preparation [98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152] (for an overview see [153]) or explicitly claim a surfactant-free process [154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170]. During synthesis surfactants served as soft templates, by increasing wettability of reactants [171] or for controlling particle morphology, pore size distribution and surface area [172,173,174]. In electrode preparation they helped again by increasing wettability of electrode constituents. Further uses of surfactants have been mentioned. Tan et al. have coated a polyelectrolyte-ferrocenyl surfactant complex on carbon paper for use as a supercapacitor electrode [175]. Anionic surfactant ionic liquids mixed with ordinary ionic liquids have been suggested for use in supercapacitors to increase surface utilization sometimes impeded with ionic liquids by their viscosity [176]. Capacitance value increases with addition of 10 wt.% of a surfactant-ionic liquid are attributed to improved pore accessibility. With larger size of the surfactant-ionic liquid pore blocking was observed during extended operation. At elevated temperatures the decreased viscosity resulted in increased ionic conductivity supporting high current performance. Surfactants have been used as “pillars” in layered compounds to facilitate movement of ions into and out of interlayer spaces during intercalation and deintercalation processes [177]. Intercalation has been named here as a third charge storage process beyond the two well-established ones commonly discussed with supercapacitors (Ion accumulation possibly including adsorption in double layer charge in EDLC devices and redox processes in redox capacitors). This suggestions appears rather unneeded because intercalation itself is not an electrochemical process, it just indicates the mode of storage of species and their location. Consequently this “third mechanism” has not received further attention. The use of surfactants in flow capacitors has been proposed [178].
3. Conclusions
Addition of surfactants to electrolyte solutions results in faster and better wetting of electrode surfaces and may thus increase the electrochemically active surface are and thus the interfacial capacitance. This is generally observed with carbonaceous materials for EDLC-type supercapacitors, in case of redox materials the increase of capacitance is not always observed. In addition to higher capacitance better capacitance retention with increasing current density. This cannot be explained by invoking the already mentioned larger capacitance, it must instead be based on faster charge transport and lower effective electrolyte resistance. Explanations are inconclusive based on the reported examples – when this question is addressed at all.
4. Trends and Perspectives
Addition of surfactants to electrolyte solutions in supercapacitors provides performance improvements in particular with carbonaceous materials and aqueous electrolyte solutions in EDLC devices. Given the pronounced interest in devices with aqueous solutions (because of higher safety, cheaper materials and production, lower internal resistance but also lower cell voltage) more systematic investigations of the most efficient surfactant and the optimum concentration are needed. For a required deeper understanding of the effects surfactants apparently have, further fundamental studies of wetting behavior and transport parameters are suggested.
Author Contributions
Conceptualization, writing X.C. and R.H.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
Preparation of this communication has been supported in various ways by the Alexander von Humboldt-Foundation, Deutscher Akademischer Austauschdienst, Fonds der Chemischen Industrie, Deutsche Forschungsgemeinschaft, National Basic Research Program of China, and Natural Science Foundation of China. It includes results obtained within a research project at St. Petersburg State University supported by grant № 26455158.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dubal, D.P.; Wu, Y.P.; Holze, R. Supercapacitors: from the Leyden jar to electric busses. Chemtexts 2016, 2, 13. [CrossRef]
- Khorate, A.; Kadam, A.V. An overview of patents and recent development in flexible supercapacitors. J. Energy Storage 2022, 52, 104887. [CrossRef]
- Peljo, P.; Girault, H.H. Electrochemical potential window of battery electrolytes: The HOMO-LUMO misconception. Energy Environ. Sci. 2018,11, 2306. [CrossRef]
- Holze, R. Overoxidation of Intrinsically Conducting Polymers. Polymers 2022, 14, 1584. [CrossRef]
- Xie, X.; Holze, R. Electrode Kinetic Data: Geometric vs. Real Surface Area. Batteries, 2022, 8, 146. [CrossRef]
- Vielstich, W.; Schmickler, W. Elektrochemie II: Kinetik elektrochemischer Systeme, Haase, R., Ed., Steinkopff: Darmstadt, 1976.
- Gileadi, E.; Kirowa-Eisner, E.; Penciner, J. Interfacial Electrochemistry, Addison Wesley: London, 1975.
- Holze, R.; Schneider, J.; Hamann, C.H. Eine neue Methode zur Untersuchung der Elektrosorption reaktiver Verbindungen. Ber. Bunsenges. Phys. Chem. 1988, 92, 1319-1325. [CrossRef]
- Doss, K.S.G.; Kalyanasundaram, A. Effect of surface active substances on the capacity of the electric double layer. Proc. Indian Acad. Sci. 1952, 35A, 27-33. [CrossRef]
- Breyer, B.; Hacobian, S. Tensammetry: A Method of Investigating Surface Phenomena by AC Current Measurements. Aust. J. Sci. Res. Ser. A 1952, 5, 500-520. [CrossRef]
- Plambeck, J.A. Electroanalytical chemistry, Wiley: New York, 1982.
- Holze, R. Landolt-Börnstein: Numerical Data and Functional Relationships in Science and Technology, New Series, Group IV: Physical Chemistry, Volume 9: Electrochemistry, Subvolume A: Electrochemical Thermodynamics and Kinetics, Martienssen W, Lechner MD, Eds., Springer: Berlin, 2007.
- Jehring, H. Elektrosorptionsanalyse mit der Wechselstrompolarographie. Akademie-Verlag: Berlin, 1975.
- Randin, J.P.; Yeager, E. Differential Capacitance Study of Stress-Annealed Pyrolytic Graphite Electrodes. J. Electrochem. Soc. 1971, 118, 711-714. [CrossRef]
- Randin, J.P.; Yeager, E. Differential capacitance study on the basal plane of stress-annealed pyrolytic graphite. J. Electroanal. Chem. 1972, 36, 257-276. [CrossRef]
- Gerischer, H. An Interpretation of the Double-Layer Capacity of Graphite-Electrodes in Relation to the Density of States at the Fermi Level. J. Phys. Chem. 1985, 89, 4249-4251. [CrossRef]
- Randin, J.P.; Yeager, E. Effect of boron addition on the differential capacitance of stress-annealed pyrolytic graphite. J. Electroanal. Chem. 1974, 54, 93-100. [CrossRef]
- Randin, J.P.; Yeager, E. Differential capacitance study on the edge orientation of pyrolytic graphite and glassy carbon electrodes, J. Electroanal. Chem. 58 (1975) 313-322. [CrossRef]
- Velicky, M.; Toth, P.S.; Woods, C.R.; Novoselov, K.S.; Dryfe, R.A.W. Electrochemistry of the Basal Plane versus Edge Plane of Graphite Revisited. J. Phys. Chem. C 2019, 123, 11677-11685. [CrossRef]
- Bauer, H.H.; Spritzer, M.S.; Elving, P.J. Double-Layer capacity at a pyrolytic graphite disk electrode. J. Electroanal. Chem. 1968, 17, 299-306. [CrossRef]
- Krüger, A. Neue Kohlenstoffmaterialien, Teubner-Verlag, Wiesbaden 2007.
- Kinoshita, K. Carbon: Electrochemical and Physicochemical Properties, WILEY, New York 1988.
- Lobato, B.; Suarez, L.; Guardia, L.; Centeno, T.A. Capacitance and surface of carbons in supercapacitors. Carbon 2017, 122, 434-445. [CrossRef]
- Stoeckli, F.; Centeno, T.A. Optimization of the characterization of porous carbons for supercapacitors, J. Mater. Chem. A 2013, 1, 6865-6873. [CrossRef]
- Gagnon, E.G. Triangular voltage sweep method for determining double-layer capacity of porous-electrodes 4. Porous carbon in potassium hydroxide. J. Electrochem. Soc. 1975, 122, 521-525. [CrossRef]
- Wen, Y.H.; Cao, G.P.; Cheng, J.; Yang, Y.S. Relationship between electrolyte ion and double-layer capacitance of carbon electrode. Acta Phys. Chim. Sin. 2005, 21, 494-498.
- Chmiola, J. Pore-size ion-size correlations for carbon supercapacitors, PhD-thesis Drexel University, 2009.
- Largeot, C.; Portet, C.; Chmiola, J.; Taberna, P.L.; Gogotsi, Y.; Simon, P. Relation between the ion size and pore size for an electric double-layer capacitor. J. Am. Chem. Soc. 2008, 130, 2730. [CrossRef]
- Feng, G.; Qiao, R.; Huang, J.; Sumpter, B.G.; Meunier, V. Ion distribution in electrified micropores and its role in the anomalous enhancement of capacitance. ACS Nano 2010, 4, 2382. [CrossRef]
- Ania, C.O.; Pernak, J.; Stefaniak, F.; Raymundo-Piñero, E.; Béguin, F. Polarization-induced distortion of ions in the pores of carbon electrodes for electrochemical capacitors. Carbon, 2009, 47, 3158. [CrossRef]
- Chmiola, J.; Yushin, G.; Gogotsi, Y.; Portet, C.; Simon, P.; Taberna, P.L. Anomalous increase in carbon capacitance at pore sizes less than 1 nanometer. Science, 2006, 313, 1760. [CrossRef]
- Chmiola, J.; Largeot, C.; Taberna, P.L.; Simon, P.; Gogotsi, Y. Desolvation of ions in subnanometer pores and its effect on capacitance and double-layer theory. Angew. Chem. Int. Ed. 2008, 47, 3392. [CrossRef]
- Xie, X.; Holze, R. Meaning and Determination of Electrode Surface Area. Available online: URL https://encyclopedia.pub/ entry/41569 (accessed on 02.05.2023).
- Kinoshita, K. Carbon: Electrochemical and Physicochemical Properties. WILEY: New York, 1988.
- Hsieh, C.T.; Teng, H. Influence of oxygen treatment on electric double-layer capacitance of activated carbon fabrics. Carbon 2002, 40, 667-674. [CrossRef]
- Wu, Y.; Holze, R. Self-discharge in supercapacitors: Causes, effects and therapies: An overview. Electrochem. Energy Technol. 2021, 7, 1-37. [CrossRef]
- X. Chen, Y. Wu, R. HolzeAg(e)ing and Degradation of Supercapacitors: Causes, Mechanisms, Models and Countermeasures. Molecules 2023, 28, 5028. [CrossRef]
- Rosen, M.J. Surfactants and interfacial phenomena. Wiley: New York 1989.
- Rosen, M.J.; Kunjappu, J.T. Surfactants and interfacial phenomena 4th edn., John Wiley and Sons: Hoboken, 2012.
- Conway, B.E.; Birss, V.; Wojtowicz, J. The role and utilization of pseudocapacitance for energy storage by supercapacitors. J. Power Sources, 1997, 66, 1. [CrossRef]
- Conway, B.E.; Gileadi, E.; Kinetic Theory of Pseudo-Capacitance and Electrode Reactions at Appreciable Surface Coverage. Trans. Faraday Soc. 1962, 58, 2493. [CrossRef]
- Conway, B.E. Transition from "Supercapacitor" to "Battery" behavior in electrochemical energy storage. J. Electrochem. Soc. 1991, 138, 1539. [CrossRef]
- Dubal, D.P.; Holze, R. Synthesis, properties, and performance of nanostructured metal oxides for supercapacitors. Pure Appl. Chem. 2014, 86, 611. [CrossRef]
- Dubal, D.P.; Chodankar, N.R.; Gomez-Romero, P.; Kim, D.H. Fundamentals of Binary Metal Oxide-Based Supercapacitors in: Metal Oxides in Supercapacitors (D.P. Dubal, P. Gomez-Romero eds.) Elsevier, Amsterdam 2017, p. 79-98. [CrossRef]
- Holze, R. From current peaks to waves and capacitive currents-on the origins of capacitor-like electrode behavior. J. Solid State Electr. 2017, 21, 2601‒2607. [CrossRef]
- Grahame, D.C. Properties of the Electrical Double Layer at a Mercury Surface. I. Methods of Measurement and Interpretation of Results. J. Am. Chem. Soc. 1941, 63, 1207-1215. [CrossRef]
- Szubzda, B.; Szmaja, A.; Halama, A. Influence of structure and wettability of supercapacitor electrodes carbon materials on their electrochemical properties in water and organic solutions. Electrochim. Acta 2012, 86, 255-259. [CrossRef]
- Trasatti, S. Progress in the Understanding of the Structure of the Metal Electrode/Solution Interface. Evolution of the Concept of Hydrophilicity. Croat. Chem. Acta, 1987, 60, 357-370.
- Yoshida, A.; Tanahashi, I.; Nishino, A.; Effect of concentration of surface acidic functional groups on electric double-layer properties of activated carbon fibers. Carbon 1990, 28, 611-615. [CrossRef]
- Gu, W.; Yushin, G.; Review of nanostructured carbon materials for electrochemical capacitor applications: Advantages and limitations of activated carbon, carbide-derived carbon, zeolite-templated carbon, carbon aerogels, carbon nanotubes, onion-like carbon, and graphene. WIREs Energy Environ. 2014, 3, 424-473. [CrossRef]
- Robson, R.J.; Dennis, E.A. The size, shape, and hydration of nonionic surfactant micelles. Triton X-100. J. Phys. Chem. 1977, 81 1075-1078. [CrossRef]
- Le, T.T.Y.; Hussain, S.; Lin, S.Y. A study on the determination of the critical micelle concentration of surfactant solutions using contact angle data. J. Mol. Liq. 2019, 294, 111582. [CrossRef]
- Hunter, R.J. Foundations of colloid science. Oxford University Press: Oxford, 2001.
- Bard, A.J.; Inzelt, G.; Scholz, F. Electrochemical Dictionary 2edn,. Springer-Verlag: Heidelberg, 2012. [CrossRef]
- Fang, B.; Binder, L. Enhanced surface hydrophobisation for improved performance of carbon aerogel electrochemical capacitor. Electrochim. Acta 2007, 52, 6916-6921. [CrossRef]
- Fang, B.; Binder, L. A modified activated carbon aerogel for high-energy storage in electric double layer capacitors. J. Power Sources 2006, 163, 616-622. [CrossRef]
- Wei, Y.Z.; Fang, B.; Iwasa, S.; Kumagai, M. A novel electrode material for electric double-layer capacitors. J. Power Sources 2005, 141, 386-391. [CrossRef]
- He, T.; Ren, X.; Cai, K.; Wei, Y.; Sun, S. Electrochemical performance of activated carbon treated by vacuum impregnation using fluorinated surfactant. Mater. Technol. 2013, 28, 364-369. [CrossRef]
- Fic, K.; Lota, G.; Frackowiak, E. Effect of surfactants on capacitance properties of carbon electrodes 2011, Mater. Res. Soc. Symp. Proc. 1333. [CrossRef]
- Fic, K.; Lota, G.; Frackowiak, E. Effect of surfactants on capacitance properties of carbon electrodes. Electrochim. Acta 2012, 60, 206-212. [CrossRef]
- Fic, K.; Lota, G.; Frackowiak, E. Electrochemical properties of supercapacitors operating in aqueous electrolyte with surfactants. Electrochim. Acta 2010, 55, 7484-7488. [CrossRef]
- Matile S, Som A, Sord N‚Recent synthetic ion channels and pores. Tetrahedron 2004, 60, 6405-6435. [CrossRef]
- Bo, Z.; Huang, Z.; Zheng, Z.; Chen, Y.; Yan, J.; Cen, K.; Yang, H.; Ostrikov, K. Accelerated ion transport and charging dynamics in more ionophobic sub-nanometer channels. Energy Stor. Mater. 2023, 59, 102797. [CrossRef]
- Kondrat, S.; Wu, P.; Qiao, R.; Kornyshev, A.A. Accelerating charging dynamics in subnanometre pores. Nature Mater. 2014, 13, 387-393. [CrossRef]
- Lota, G.; Centeno, T.A.; Frackowiak, E.; Stoeckli, F. Improvement of the structural and chemical properties of a commercial activated carbon for its application in electrochemical capacitors. Electrochim.Acta 2008, 53, 2210-2216. [CrossRef]
- Holze, R.; Bełtowska-Brzezinska, M. On the adsorption of aliphatic alcohols on gold. Electrochim. Acta 1985, 30, 937-939. [CrossRef]
- Holze, R.; Bełtowska-Brzezinska, M. On the adsorption of aliphatic alcohols on gold Part II. J. Electroanal. Chem. 1986, 201, 387-396. [CrossRef]
- Kurc, B.; Pigłowska, M.; Rymaniak, Ł; Fuć, P. Modern nanocomposites and hybrids as electrode materials used in energy carriers. Nanomaterials 2021, 11, 1-45. [CrossRef]
- Poonam; Sharma, K.; Arora, A.; Tripathi, S.K. Review of supercapacitors: Materials and devices. J.Energy Storage 2019, 21, 801‒825. [CrossRef]
- Chakraborty, S.; Mary, N.L. Review-An Overview on Supercapacitors and Its Applications. J. Electrochem. Soc. 2022, 169, 020552. [CrossRef]
- Dhandapani, E.; Thangarasu, S.; Ramesh, S.; Ramesh, K.; Vasudevan, R.; Duraisamy, N. Recent development and prospective of carbonaceous material, conducting polymer and their composite electrode materials for supercapacitor-A review. J. Energy Storage 2022, 52, 104937. [CrossRef]
- Patel, K.K.; Singhal, T.; Pandey, V.; Sumangala, T.P.; Sreekanth, M.S. Evolution and recent developments of high performance electrode material for supercapacitors: A review. J. Energy Storage 2021, 44, 103366. [CrossRef]
- Abdel Maksoud, M.I.A.; Fahim, R.A.; Shalan, A.E.; Elkodous, M.A.; Olojede, S.O.; Osman, A.I.; Farrell, C.; Al-Muhtaseb, A.H.; Awed, A.S. Advanced materials and technologies for supercapacitors used in energy conversion and storage: a review, Environm. Chem. Lett. 2021, 19, 375‒439. [CrossRef]
- Bigdeloo, M.; Kowsari, E.; Ehsani, A.; Chinnappan, A.; Ramakrishna, S.; Ali Akbari, R. Review on innovative sustainable nanomaterials to enhance the performance of supercapacitors. J. Energy Storage 2021, 37, 102474. [CrossRef]
- Forouzandeh, P.; Kumaravel, V.; Pillai, S.C. Electrode Materials for Supercapacitors: A Review of Recent Advances. Catalysts 2020, 10, 969. [CrossRef]
- Li, Z.; Xu, K.; Pan, Y. Recent development of Supercapacitor Electrode Based on Carbon Materials. Nanotechnol. Rev. 2019, 8, 35‒49. [CrossRef]
- Miller, E.E.; Hua, Y.; Tezel, F.H. Materials for energy storage: Review of electrode materials and methods of increasing capacitance for supercapacitors. J. Energy Storage 2018, 20, 30‒40. [CrossRef]
- Suriyakumar, S.; Bhardwaj, P.; Grace, A.N.; Stephan, A.M. Role of Polymers in Enhancing the Performance of Electrochemical Supercapacitors: A Review. Batteries&Supercaps 2021, 4, 571‒584. [CrossRef]
- Kiamahalleh, M.V.; Zein, S.H.S.; Najafpour, G.; Abd Sata, S.; Buniran, S. Multiwalled carbon nanotubes based nanocomposites for supercapacitors: A review of electrode materials. Nano 2012, 7, 12300022. [CrossRef]
- Dubal, D.P.; Wu, Y.; Holze, R. Supercapacitors as fast storage systems for electric energy. Bunsen-Magazin 2015, 17, 216‒227.
- Shukla, A.K.; Sampath, S.; Vijayamohanan, K. Electrochemical supercapacitors: Energy storage beyond batteries. Curr. Sci. 2000, 79, 1656‒1661.
- Dubal, D.P.; Wu, Y.P.; Holze, R. Supercapacitors: from the Leyden jar to electric busses. ChemTexts 2016, 2, 13. [CrossRef]
- Yu, A.; Chabot, V.; Zhang, J. Electrochemical Supercapacitors for Energy Storage and Delivery - Fundamentals and Applications, CRC Press: Boca Raton, 2013.
- Inamuddin, Ahmer, M.F.; Asiri, A.M.; Zaidi, S. Electrochemical Capacitors in: Materials Research Foundations, Materials Research Forum LLC: Millersville, 2018; Volume 26.
- Stevic, Z. Supercapacitor Design and Applications. ExLi4EvA2016 2016.
- Miller, J.M. Ultracapacitor Applications, The Institution of Engineering and Technology: London, 2011.
- Shaikh, N.S.; Ubale, S.B.; Mane, V.J.; Shaikh, J.S.; Lokhande, V.C.; Praserthdam, S.; Lokhande, C.D.; Kanjanaboos, P. Novel electrodes for supercapacitor: Conducting polymers, metal oxides, chalcogenides, carbides, nitrides, MXenes, and their composites with graphene. J. Alloys Compd. 2022, 893, 161998. [CrossRef]
- Beguin, F.; Frackowiak, E. Supercapacitors, Wiley-VCH: Weinheim, 2013.
- Holze, R. Composites and Copolymers Containing Redox-Active Molecules and Intrinsically Conducting Polymers as Active Masses for Supercapacitor Electrodes-An Introduction. Polymers 2020, 12, 1835. [CrossRef]
- Ul Hoque, Md.I.; Holze, R. Intrinsically Conducting Polymer Composites as Active Masses in Supercapacitors. Polymers 2023, 15, 730. [CrossRef]
- Wang, B.; Guo, P.; Bi, H.; Li, Q.; Zhang, G.; Wang, R.; Liu, J.; Zhao, X.S. Electrocapacitive properties of MnFe2O4 electrodes in aqueous LiNO3 electrolyte with surfactants. Int. J. Electrochem. Sci. 2013, 8, 8966-8977. [CrossRef]
- Goddard, E.D.; Ananthapadmanabhan, K.P. Interactions of Surfactants with Polymers and Protein.s CRC Press: Boca Raton, 1993.
- Kuo S L, Wu N L. Electrochemical capacitor of MnFe2O4 with NaCl electrolyte. Electrochem. Solid-State Lett. 2005, 8, A495-A499. [CrossRef]
- Aydin, A.; Patat, S.; Ulgen, A.; Sahan, H.; Fatma; Dokan, K.; Veziroglu, S. Synthesis, characterization and improvement of α-Co(OH)2 for supercapacitor applications 2014 International Conference on Optimization of Electrical and Electronic Equipment, OPTIM 2014, 1087-1091. [CrossRef]
- Ge, Y.; Roscher, J.; Holze, R.; Increased capacitance of metal oxide-based supercapacitor electrodes caused by surfactant addition to the electrolyte solution. J. Nanosci. Nanotechnol. 2020, 20, 7544-7552. [CrossRef]
- Ghasemi, S.; Ahmadi, F. Effect of surfactant on the electrochemical performance of graphene/iron oxide electrode for supercapacitor. J.Power Sources 2015, 289, 129-137. [CrossRef]
- Malik, R.; Lata, S.; Malik, R.S. Electrochemical behavior of composite electrode based on sulphonated polymeric surfactant (SPEEK/PSS) incorporated polypyrrole for supercapacitor. J. Electroanal. Chem. 2019, 835, 48-59. [CrossRef]
- Sumboja, A.; Foo, C.Y.; Yan, J.; Yan, C.; Gupta, R.K.; Lee, P.S. Significant electrochemical stability of manganese dioxide/polyaniline coaxial nanowires by self-terminated double surfactant polymerization for pseudocapacitor electrode. J. Mater. Chem. 2012, 22, 23921-23928. [CrossRef]
- Zhang, K.; Mao, L.; Zhang, L.L.; On Chan, H.S.; Zhao, X.S.; Wu, J. Surfactant-intercalated, chemically reduced graphene oxide for high performance supercapacitor electrodes. J. Mater. Chem. 2011, 21, 7302-7307. [CrossRef]
- Chen, X.; Kierzek, K.; Jiang, Z.; Chen, H.; Tang, T.; Wojtoniszak, M.; Kalenczuk, R.J.; Chu, P.K.; Borowiak-Palen, E. Synthesis, growth mechanism, and electrochemical properties of hollow mesoporous carbon spheres with controlled diameter J. Phys. Chem. C 2011, 115, 17717-17724. [CrossRef]
- Chen, X.; Cendrowski, K.; Srenscek-Nazzal, J.; Rümmeli, M.; Kalenczuk, R.J.; Chen, H.; Chu, P.K.; Borowiak-Palen, E.; Fabrication method of parallel mesoporous carbon nanotubes. Coll. Surf. A 2011, 377, 150-155. [CrossRef]
- Chen, X.; Kierzek, K.; Kalenczuk, R.J.; Mijowska, E.; Jiang, Z.; Tang, T. New synthesis method of sword-sheath structured carbon nanotubes. 2012 2012 International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale, 3M-NANO 2012 - Conference Proceedings, 297-300. [CrossRef]
- Chen, X.; Kierzek, K.; Wenelska, K.; Cendrowski, K.; Gong, J.; Wen, X.; Tang, T.; Chu, P.K.; Mijowska, E. Electrochemical characteristics of discrete, uniform, and monodispersed hollow mesoporous carbon spheres in double-layered supercapacitors. Chem. Asian J. 2013, 8, 2627-2633. [CrossRef]
- Wilgosz, K.; Chen, X.; Kierzek, K.; Machnikowski, J.; Kalenczuk, R.J.; Mijowska, E. Template method synthesis of mesoporous carbon spheres and its applications as supercapacitors. Nanoscale Res. Lett. 2012, 7, 269. [CrossRef]
- Kong, L.B.; Lu, C.; Liu, M.C.; Luo, Y.C.; Kang, L. Effect of surfactant on the morphology and capacitive performance of porous NiCo2O4. J. Solid State Electr. 2013, 17, 1463-1471. [CrossRef]
- Fang, B.; Wei, Y.Z.; Suzuki, K.; Kumagai, M.; Surface modification of carbonaceous materials for EDLCs application. Electrochim. Acta 2005, 50, 3616-3621. [CrossRef]
- Fang, B.; Wei, Y.Z.; Kumagai, M. Modified carbon materials for high-rate EDLCs application. J. Power Sources 2006, 155 487-491. [CrossRef]
- Dettlaff, A.; Wilamowska, M. Electrochemical synthesis and characterization of nanocomposites based on poly(3,4-ethylenedioxythiophene) and functionalized carbon nanotubes. Synth. Met. 2016, 212, 31-43. [CrossRef]
- Liu, P.; Wang, X.; Li, H.; Facile preparation of string-like composite of hollow PPy nanospheres decorated on the carbon nanotubes. Synth. Met. 2014, 189 173-176. [CrossRef]
- Alshahrie, A.; Ansari, M.O. High Performance Supercapacitor Applications and DC Electrical Conductivity Retention on Surfactant Immobilized Macroporous Ternary Polypyrrole/Graphitic-C3N4@Graphene Nanocomposite. Electron. Mater. Lett. 2019, 15, 238-246. [CrossRef]
- Zhang, L.L.; Zhao, S.; Tian, X.N.; Zhao, X.S. Layered graphene oxide nanostructures with sandwiched conducting polymers as supercapacitor electrodes. Langmuir 2010, 26, 17624-17628. [CrossRef]
- Meng, Q.; Wang, K.; Guo, W.; Fang, J.; Wei, Z.; She, X. Thread-like supercapacitors based on one-step spun nanocomposite yarns. Small 2014, 10, 3187-3193. [CrossRef]
- Athira, A.R.; Deepthi, S.; Xavier, T.S. Impact of an anionic surfactant on the enhancement of the capacitance characteristics of polyaniline-wrapped graphene oxide hybrid composite. Bull. Mater. Sci. 2021, 44, 178. [CrossRef]
- Ma, Z.; Zhao, J.; Fan, Y.; Qin, X.; Shao, G.; High surface area of crystalline/amorphous ultrathin MnO2 nanosheets electrode for high-performance flexible micro-supercapacitors. J. Alloys Compd. 2022, 920, 166012. [CrossRef]
- Maheswari, N.; Muralidharan, G. Supercapacitor Behavior of Cerium Oxide Nanoparticles in Neutral Aqueous Electrolytes. Energy Fuels 2015, 29, 8246-8253. [CrossRef]
- Yuan, R.; Li, H.; Zhang, X.; Zhu, H.; Zhao, J.; Chen, R. Facile one-pot solvothermal synthesis of bifunctional chrysanthemum-like cobalt-manganese oxides for supercapacitor and degradation of pollutants. J. Energy Storage 2020, 29, 101300. [CrossRef]
- Yoon, S.; Oh, S.M.; Lee, C. Direct template synthesis of mesoporous carbon and its application to supercapacitor electrodes. Mater. Res. Bull. 2009, 44, 1663-1669. [CrossRef]
- Idisi, D.O.; Oke, J.A.; Bello, I.T. Graphene oxide/Au nanoparticles: Synthesis, properties, and application: A mini-review., Int. J. Energy Res. 2021, 45, 19772-19788. [CrossRef]
- Díez, N.; Sevill,a M.; Fuertes, A.B. Dense (non-hollow) carbon nanospheres: synthesis and electrochemical energy applications. Mater. Today Nano 2021, 16, 100147. [CrossRef]
- Castro-Gutiérrez, J.; Díez, N.; Sevill,a M.; Izquierdo, M.T.; Celzard, A.; Fierro, V. Model carbon materials derived from tannin to assess the importance of pore connectivity in supercapacitors. Renew. Sustain. Energy Rev. 2021, 151, 111600. [CrossRef]
- Jia, S.; Guo, Q.; Shen, M.; Gao, Q.; Wang, K. Controlled synthesis of carbon spheres via the modulation of the hydrophobic length of fatty aldehyde for supercapacitors. Coll. Surf. A 2022, 636, 128064. [CrossRef]
- Kim, Y.S.; Sohn, J.S.; Ju, H.R.; Inamdar, A.I.; Im, H.; Kim, H. Effect of surfactants on PANI morphologies and supercapacitive properties. J. Kor. Phys. Soc. 2012, 60, 1767-1771. [CrossRef]
- Wickramaarachchi, K.; Minakshi, M. Status on electrodeposited manganese dioxide and biowaste carbon for hybrid capacitors: The case of high-quality oxide composites, mechanisms, and prospects. J. Energy Storage 2022, 56, 106099. [CrossRef]
- Zhang, X.; Wang, X.;, Jiang, L.; Wu, H.; Wu, C.; Su, J. Effect of aqueous electrolytes on the electrochemical behaviors of supercapacitors based on hierarchically porous carbons. J. Power Sources 2012, 216, 290-296. [CrossRef]
- Zhang, X.; Wang, X.; Su, J.; Wang, X.; Jiang, L.; Wu, H.; Wu, C.; The effects of surfactant template concentration on the supercapacitive behaviors of hierarchically porous carbons. J. Power Sources 2012, 199, 402-408. [CrossRef]
- Reiman, K.H.; Brace, K.M.; Gordon-Smith, T.J.; Nandhakumar, I.; Attard, G.S.; Owen, J.R. Lithium insertion into TiO2 from aqueous solution - Facilitated by nanostructure. Electrochem. Commun. 2006, 8, 517-522. [CrossRef]
- Yang, L.; Wu, W.; Ohki, Y.; Feng, Y.; Li, S.; Enhanced conductivity of polyaniline in the presence of nonionic amphiphilic polymers and their diverse morphologies. J. Appl. Polym. Sci. 2017, 134, 45547. [CrossRef]
- Zhang, L.; Zheng, W.; Jiu, H.; Ni, C.; Chang, J.; Qi, G. The synthesis ofNiO and NiCo2O4 nanosheets by a new method and their excellent capacitive performance for asymmetric supercapacitor. Electrochim. Acta 2016, 215, 212-222. [CrossRef]
- Liu, A.; Lv, Y.; Mu, J.; Guo, Z.; Pei, Z.; Zhang, X.; Bai, Y.; Xie, H.; Che, H. Facile synthesis of hollow Ni0.2Mn0.8O1.5 twin microspheres for electrochemical energy storage. J. Appl. Electrochem. 2018, 48, 15-26. [CrossRef]
- Krishnan, S.G.; Harilal, M.; Yar, A.; Vijayan, B.L.; Dennis, J.O.; Yusoff, M.M.; Jose, R. Critical influence of reduced graphene oxide mediated binding of M (M = Mg, Mn) with Co ions, chemical stability and charge storability enhancements of spinal-type hierarchical MCo2O4 nanostructures Electrochim. Acta 2017, 243, 119-128. [CrossRef]
- Patra, S.; Munichandraiah, N. Supercapacitor studies of electrochemically deposited PEDOT on stainless steel substrate. J. Appl. Polym. Sci. 2007, 106, 1160-1171. [CrossRef]
- Zhang, H.; Wang, Y.; Wang, C. Influence of surfactant on the capacitive performance of manganese dioxide prepared at different temperatures. Energy Convers.Management 2013, 74, 286-292. [CrossRef]
- Kim, Y.S.; Sohn, J.S.; Ju, H.R.; Inamdar, A.I.; Im, H.; Kim, H. Effect of surfactants on PANI morphologies and supercapacitive properties. J. Kor. Phys. Soc. 2012, 60 ,1767-1771. [CrossRef]
- Kathuroju, P.K.; Nagaraju, J. Supercapacitor studies on globular polypyrrole microstructures developed by a facile electrochemical route. Micro Nano Lett. 2011, 6, 1002-1006. [CrossRef]
- Lin, Y.; Zhang, H.; Liao, H.; Zhao, Y.; Li, K. A physically crosslinked, self-healing hydrogel electrolyte for nano-wire PANI flexible supercapacitors. Chem. Eng. J. 2019, 367, 139-148. [CrossRef]
- Cui, L.; Huang, L.; Ji, M.; Wang, Y.; Shi, H.; Zuo, Y.; Kang, S. High-performance MgCo2O4 nanocone arrays grown on three-dimensional nickel foams: Preparation and application as binder-free electrode for pseudo-supercapacitor. J. Power Sources 2016, 333, 118-124. [CrossRef]
- Sharma, A.K.; Chaudhary, G.; Bhardwaj, P.; Kaushal, I.; Duhan, S. Studies on Metal Doped Polyaniline-Carbon Nanotubes Composites for High Performance Supercapacitor. Curr. Anal. Chem. 2017, 13, 277-284. [CrossRef]
- Singu, B.S.; Palaniappan, S.; Yoon, K.R. Polyaniline-nickel oxide nanocomposites for supercapacitor. J. Appl. Electrochem. 2016, 46, 1039-1047. [CrossRef]
- Saranya, S.; Selvan, R.K.; Priyadharsini, N. Synthesis and characterization of polyaniline/MnWO4 nanocomposites as electrodes for pseudocapacitors. Appl. Surf. Sci. 2012, 258, 4881-4887. [CrossRef]
- Zou, B.; Gong, S.; Wang, Y.; Liu, X. Tungsten Oxide and Polyaniline Composite Fabricated by Surfactant-Templated Electrodeposition and Its Use in Supercapacitors. J. Nanomater. 2014, 2014, 813120. [CrossRef]
- Sidhu, N.K.; Rastogi, A.C. Vertically aligned ZnO nanorod core-polypyrrole conducting polymer sheath and nanotube arrays for electrochemical supercapacitor energy storage. Nanoscale Res.Lett. 2014, 9, 453. [CrossRef]
- Shanmugavadivel, M.; Violet Dhayabaran, V.; Subramanian, M. Fabrication of a Novel Polymer Nanohybrid Electrode Material PANI-BaMnO3 for High Power Supercapacitor Application. Port. Electrochim. Acta 2017, 35, 225-232. [CrossRef]
- Sen, P.; De, A. Electrochemical performances of poly(3,4-ethylenedioxythiophene)-NiFe2O4 nanocomposite as electrode for supercapacitor. Electrochim. Acta 2010, 55, 4677-4684. [CrossRef]
- Krishnan, S.G.; Harilal, M.; Misnon, I.I.; Reddy, M.V.; Adams, S.; Jose, R. Effect of processing parameters on the charge storage properties of MgCo2O4 electrodes. Ceram. Int. 2017, 43, 12270-12279. [CrossRef]
- Singu, B.S.; Male, U.; Srinivasan, P:; Pabba, S. Use of surfactant in aniline polymerization with TiO2 to PANI-TiO2 for supercapacitor performance. J. Solid State Electr. 2014, 18, 1995-2003. [CrossRef]
- Qian, A.; Zhuo, K.; Shin, M.S.; Chun, W.W.; Choi, B.N.; Chung, C.H. Surfactant Effects on the Morphology and Pseudocapacitive Behavior of V2O5·H2O. ChemSusChem 2015, 8, 2399-2406. [CrossRef]
- Zhao, W.; Wang, W.; Peng, J.; Chen, T.; Jin, B.; Liu, S.; Huang, W.; Zhao, Q. Wrinkled two-dimensional ultrathin Cu(ii)-porphyrin framework nanosheets hybridized with polypyrrole for flexible all-solid-state supercapacitors. Dalton Trans. 2019, 48, 9631-9638. [CrossRef]
- Jeong, G.H.; Lee, I.; Kang, J.G.; Lee, H.; Yoon, S.; Kim, S.W. Mesoporous hollow carbons on graphene and their electrochemical properties. RSC Adv. 2015, 5, 73119-73125. [CrossRef]
- Patra, S.; Munichandraiah, N. Supercapacitor studies of electrochemically deposited PEDOT on stainless steel substrate. J. Appl. Polym. Sci. 2007, 106, 1160-1171. [CrossRef]
- Zhang, H.; Wang, Y.; Wang, C. Influence of surfactant on the capacitive performance of manganese dioxide prepared at different temperatures. Energy Convers. Managem. 2013, 74, 286-292. [CrossRef]
- Devaraj, S.; Munichandraiah, N.; The effect of nonionic surfactant Triton X-100 during electrochemical deposition of MnO2 on its capacitance properties. J. Electrochem. Soc. 2007, 154, A901-A909. [CrossRef]
- Kathuroju, P.K.; Nagaraju, J,.;Supercapacitor studies on globular polypyrrole microstructures developed by a facile electrochemical route. Micro Nano Lett. 2011, 6, 1002-1006. [CrossRef]
- Ying, J.Y.; Mehnert, C.P.; Wong, M.S.; Synthesis and applications of supramolecular-templated mesoporous materials. Angew. Chem. Int. Ed. 1999, 38, 56-77. [CrossRef]
- Peng, H.; Ma, G.; Sun, K.; Mu, J.; Wang, H.; Lei, Z. High-performance supercapacitor based on multi-structural CuS@polypyrrole composites prepared by in situ oxidative polymerization. J. Mater. Chem. A 2014, 2, 3303-3307. [CrossRef]
- Nagaraju, P.; Vasudevan, R.; Alsalme, A.; Alghamdi, A.; Arivanandhan, M.; Jayavel, R. Surfactant-Free Synthesis of Nb2O5 Nanoparticles Anchored Graphene Nanocomposites with Enhanced Electrochemical Performance for Supercapacitor Electrodes. Nanomaterials 2020, 10, 160. [CrossRef]
- Guo, N.; Lin, Y.; Cui, Y.; Su, S.; Dai, H.; Yang, J.; Zhu, X. Effect of MWCNTs additive on preservation stability of rGO powder. J. Mater. Sci. Mater. Electron. 2022, 33, 6766-6779. [CrossRef]
- Huo, W.C.; Liu, X.L.; Yuan, Y.S.; Li, N.; Lan, T.; Liu, X.Y.; Zhang, Y.X. Facile synthesis of manganese cobalt oxide/nickel cobalt oxide composites for high-performance supercapacitors. Front. Chem. 2019, 7, 661. [CrossRef]
- Vijayakumar, S.; Nagamuthu, S.; Lee, S.H.; Ryu, K.S. Porous thin layered nanosheets assembled ZnCo2O4 grown on Ni-foam as an efficient electrode material for hybrid supercapacitor applications. Int. J. Hydrogen Energy 2017, 42, 3122-3129. [CrossRef]
- Du, H.; Li, Y.; Ding, F.; Zhao, J.; Zhang, X.; Li, Y.; Zhao, R.; Cao, M.; Yu, T.; Xu, X. Boosting the capacitance of NiCo2O4 hierarchical structures on nickel foam in supercapacitors. Int. J. Hydrogen Energy 2018, 43, 15348-15357. [CrossRef]
- Aghazadeh, M.; Golikand, A.N.; Ghaemi, M. Synthesis, characterization, and electrochemical properties of ultrafine beta- Ni(OH)2 nanoparticles. Int. J. Hydrogen Energy 2011, 36, 8674-8679. [CrossRef]
- Li, J.; Wei, M.; Chu, W.; Wang, N. High-stable alpha-phase NiCo double hydroxide microspheres via microwave synthesis for supercapacitor electrode materials. Chem. Eng. J. 2017, 316, 277-287. [CrossRef]
- Naveen, A.N.; Selladurai, S. Fabrication and performance evaluation of symmetrical supercapacitor based on manganese oxide nanorods-PANI composite. Mater. Sci. Semicon. Proc. 2015, 40, 468-478. [CrossRef]
- Yao, W.; Zhou, H.; Lu, Y. Synthesis and property of novel MnO2@polypyrrole coaxial nanotubes as electrode material for supercapacitors. J. Power Sources 2013, 241, 359-366. [CrossRef]
- Jiang, F.; Li, W.; Zou, R.; Liu, Q.; Xu, K.; An, L.; Hu, J. MoO3/PANI coaxial heterostructure nanobelts by in situ polymerization for high performance supercapacitors. Nano Energy 2014, 7, 72-79. [CrossRef]
- Nie, G.; Lu, X.; Zhu, Y.; Chi, M.; Gao, M.; Chen, S.; Wang, C. Reactive Template Synthesis of Inorganic/Organic VO2@ Polyaniline Coaxial Nanobelts for High-Performance Supercapacitors. ChemElectroChem 2017, 4, 1095-1100. [CrossRef]
- Wang, S.; Wang, Z.; Wang, Y.; Chen, J.; Chen, Z.; Chen, Y.; Fu, J. Environmentally friendly room temperature synthesis of hierarchical porous alpha-Ni(OH)2 nanosheets for supercapacitor and catalysis applications. Green Chem. 2019, 21, 5960-5968. [CrossRef]
- Nagaraju, P.; Arivanandhan, M.; Alsalme, A.; Alghamdi, A.; Jayavel, R. Enhanced electrochemical performance of α-MoO3/graphene nanocomposites prepared by an in situ microwave irradiation technique for energy storage applications. RSC Adv. 2020, 10, 22836-22847. [CrossRef]
- Zheng, X.; Han, Z.; Yang, W.; Qu, F.; Liu, B.; Wu, X. 3D Co3O4@MnO2 heterostructures grown on a flexible substrate and their applications in supercapacitor electrodes and photocatalysts. Dalton Trans. 2016, 45, 16850-16858. [CrossRef]
- Liu, Y.; Teng, X.; Mi, Y.; Chen, Z. A new architecture design of Ni-Co LDH-based pseudocapacitors. J. Mater. Chem. A 2017, 5, 24407-24415. [CrossRef]
- Anothumakkool, B.; Soni, R.; Bhange, S.N.; Kurungot, S. Novel scalable synthesis of highly conducting and robust PEDOT paper for a high performance flexible solid supercapacitor. Energy Environ.Sci. 2015, 8, 1339-1347. [CrossRef]
- Pech, D.; Brunet, M.; Taberna, P.L.; Simon, P.; Fabre, N.; Mesnilgrente, F.; Conedera, V.; Durou, H. Elaboration of a microstructured inkjet-printed carbon electrochemical capacitor. J. Power Sources 2010, 195, 1266-1269. [CrossRef]
- Yang, X.H.; Wang, Y.G.; Xiong, H.M.; Xia, Y.Y. Interfacial synthesis of porous MnO2 and its application in electrochemical capacitor. Electrochim. Acta 2007, 53, 752-757. [CrossRef]
- Hsu, C.T.; Hu, C.C. Synthesis and characterization of mesoporous spinel NiCo2O4 using surfactant-assembled dispersion for asymmetric supercapacitors. J. Power Sources 2013, 242, 662-671. [CrossRef]
- Devaraj, S.; Munichandraiah, N. The effect of nonionic surfactant triton X-100 during electrochemical deposition of MnO2 on its capacitance properties. J. Electrochem. Soc. 2007, 154, A901-A909. [CrossRef]
- Tan, G.; Cheng, Z.; Qiu, Y.; Huang, W.; Fan, H.; Ren, B. Supercapacitors based on polyelectrolyte/ferrocenyl-surfactant complexes with high rate capability. RSC Adv. 2016, 6, 31632-31638. [CrossRef]
- Xu, N.; Klein, J.M.; Huang, P.; Alwusaydi, H.A.; Mann, E.K.; Gurkan, B.E. Improved accessibility of porous carbon electrodes with surfactant ionic liquids for supercapacitors. J. Appl. Electrochem. 2019, 49, 151-162. [CrossRef]
- Lin, Y.; Xie, X.; Wang, X.; Zhang, B.; Li, C.; Wang, H.; Wang, L. Understanding the enhancement of electrochemical properties of NiCo layered double hydroxides via functional pillared effect: an insight into dual charge storage mechanisms. Electrochimica Acta, 2017, 246, 406-414. [CrossRef]
- Lee, J.; Weingarth, D.; Grobelsek, I.; Presser, V. Use of surfactants for continuous operation of aqueous electrochemical flow capacitors. Energy Technol. 2016, 4, 75-84. [CrossRef]
Figure 1.
Schematic principles of operation of supercaps and secondary batteries.
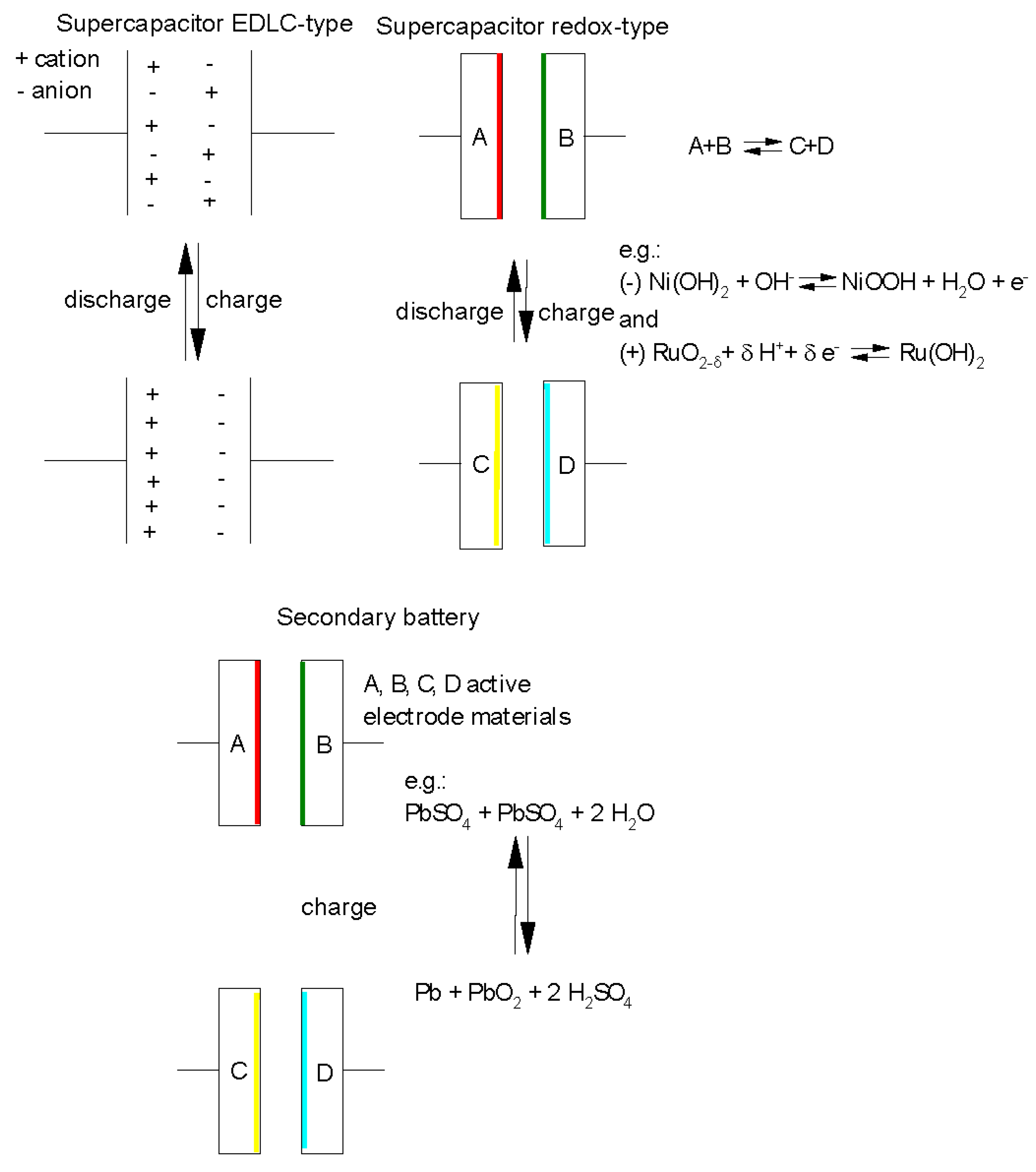
Figure 2.
Molecular formulas, systematical names, tradenames and acronyms of representative surfactants.
Figure 2.
Molecular formulas, systematical names, tradenames and acronyms of representative surfactants.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






