Prerpints.org logo
Preprint
Article

Cloud Characteristics and Their Effects on Solar Irradiance According to the ICON Model, CLOUDNET and BSRN Observations

Altmetrics

Downloads

101

Views

45

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

26 October 2023

Posted:

27 October 2023

You are already at the latest version

Alerts
Abstract
We investigated the liquid water path and global solar irradiance at ground (Q) according to the ICON model, CLOUDNET measurements in Lindenberg, Munich, Jülich, and BSRN observations in Lindenberg. The liquid water path is underestimated, while global irradiance is overestimated. The lower liquid water path is due to liquid water content underestimation practically in all atmosphere layers and lower frequency of liquid clouds occurrence compare to observations. The latter is partly associated with a reduced model’ sensitivity to the cloud condensation nuclei (CCN). An increase in CCN from 250 cm-3 (typical background value for the region of interest) to 1700 cm-3 (characteristic of polluted continental clouds) leads to an increase in grid-scale liquid water path by 40% and a decrease in Q under overcast conditions by 12%. However, we also showed that liquid water path is not a key factor of Q overestimation. The main factor is an inaccurate description of the cloud spatial structure, where the correct prediction of the direct to global irradiance ratio as a spatial characteristic of clouds plays the most important role compared to standard cloud fraction.
Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

Solar irradiance is one of the most important meteorological characteristics, which significantly affects temperature regime of the atmosphere and underlying surface [1]. The quality of solar irradiance prediction is determined by a set of atmospheric parameters. The cloudiness is still one of the most difficult issues of successful numerical forecasting of solar irradiance due to its large scale of spatial and temporal inhomogeneity and their optical and microphysical properties [2, 3]. For example, the difference of solar irradiance forecast between a “more cloudy” and “less cloudy” atmospheric condition can reach hundreds of W/m2 [4].
The solar irradiance forecast is directly related to the accuracy of the cloud macro- and microphysical properties. Bulk microphysical schemes are mainly focused on the precipitation forecast than on the detailed prediction of cloud macrophysical properties. The effect of inaccurate forecast of liquid water path and size of cloud particles on the cloud-radiation interaction is shown in many studies. Sotiropoulou et al. [5] showed the effect of cloud parametrization scheme on the summer Arctic clouds and global solar irradiance in the ECMWF (European Centre for Medium-Range Weather Forecasts) model. The study [6] focused on the overestimation of WRF (Weather Research and Forecasting model) simulated liquid water path by a factor of 1.1-1.6 in case of high cloud condensation nuclei content. Dipu et al. [7] found an underestimation of liquid water path in the COSMO (COnsortium of Small-Scale MOdelling) mesoscale model with two-moment microphysical scheme in comparison with satellite observations.
Today, the development of mesoscale numerical weather prediction (NWP) models is taking place with the account of cloud-aerosol interaction processes. Accounting of cloud condensation nuclei (CCN) impact on the liquid water content and on the effective radius of cloud droplets in NWP models contributes to the successful evaluation of cloud structure [8]. On the other hand, the operational numerical weather prediction models still work with the bulk microphysical schemes, which use the saturation adjustment approach [9]. The saturation adjustment approach contributes to a lower sensitivity of cloud particle size distribution to CCN content compared to the bin microphysical schemes [10]. Wang et al. [11] found a lower simulated liquid water content due to low condensation rate and high evaporation rate in the bulk scheme compared to the bin scheme.
The global irradiance forecast also depends on simulated cloud fraction. The breakthrough of recent decades in the field of weather prediction has not helped to solve many difficulties related to measurement and forecasting of cloud fraction [12]. The diagnostic and prognostic approaches are used in numerical weather prediction models for cloud fraction. Diagnostic schemes are based on parametrizations of cloud fraction at each model level using relative humidity or cloud water content [13]. Prognostic schemes suggest an evaluation of cloud fraction with deployed consideration of cloud sources and sinks [14]. Computationally inexpensive but highly efficient diagnostic schemes are widely spread in numerical weather prediction models. However, their physical basis is not able to take into account for all the variety of cloud processes [15] providing cloud fraction and solar irradiance errors.
This paper presents a comparative study of liquid water path according to the ICON model and ground-based and satellite measurements as well as the analysis of the CCN number concentration effect on the liquid water path forecast. We also analyze the influence of cloud spatial structure on solar irradiance prediction. The work is structured by sections as follows. Section 2 provides a brief description of the ICON model and the ecRad radiation scheme, as well as measurement data and operating procedures. Section 3 describes the most important results of the analysis of ICON model experiments together with ground-based and satellite observations. Conclusions and critical evaluation of the results are presented in Section 4 and Section 5.

2. Model and Methods

2.1. ICON Model Configuration

The ICON (ICOsahedral Nonhydrostatic model) is a non–hydrostatic model of weather and climate forecasting [16]. Its implementation (ICON-Ru model) operates in the Hydrometeorological Research Center of Russia [17]. A certain configuration of the model was used to perform numerical experiments. In particular, the characteristics of grid-scale clouds in the model are determined by a two-moment microphysical scheme [18]. The nucleation of cloud droplets is represented by the Segal-Khain scheme [19]. The scheme uses the specified number concentration of cloud condensation nuclei, parameters of aerosol size distribution and grid-scale vertical velocity at the cloud base. As a result, the scheme calculates the profile of particles, which are available for the condensation in the presence of an appropriate amount of excess water vapor. Warm cloud processes are described according to [18, 20]. Ice nucleation processes are presented according to [21, 22].
We used the diagnostic scheme of the subgrid-scale liquid and ice water content and cloud fraction. The scheme is based on the division of sub-grid clouds into stratiform and convective components. The detailed description of sub-grid cloud scheme is shown in [23]. The specific liquid water content of the subgrid-scale stratiform clouds is assumed to be 0.5 % of the saturation specific humidity. The convective subgrid-scale specific liquid and ice water contents are 1% of the saturation specific humidity, but not less than 0.2 g/kg. The cloud fraction at each model level is assumed equal to one if there is grid-scale liquid and/or ice water content at the level. If there is no grid-scale cloud fraction, the subgrid-scale convective (Nsgs,con) and/or stratiform (Nsgs,strat) clouds are calculated. Nsgs,con is a function of the geometric thickness of the convective cloud (H, m):
N s g s , c o n = m i n 1 , m a x 0.05,0.35 ∗ H / 5000
Nsgs,strat is calculated based on the total specific moisture content in gaseous, solid and liquid form (qtot), saturation specific humidity (qsat), atmospheric pressure at the model level (p) and at the surface (ps):
N s g s , s t r a t = m a x 0 , m i n 1 , q t o t q s a t − 0.95 − 0.8 ∗ p / p s 1 − p / p s 1 + 3 p p s − 0.5 1 − 0.95 − 0.8 ∗ p / p s 1 − p / p s 1 + 3 p p s − 0.5 .
The final value of the subgrid-scale cloud fraction is calculated from the stratiform and convective components as:
N s g s = N s g s , s t r a t + N s g s , c o n 1 − N s g s , s t r a t .
Additionally, a correction is applied for the upper troposphere ice cloud fraction and the type of atmospheric stratification [23]. This scheme is also operational in the COSMO-Ru model (COnsortium of Small-scale MOdeling, Russian realization).
Radiative processes in ICON are represented by the ecRad scheme with McICA solver (Monte Carlo Independent Column Approximation) [24, 25]. We used the optical properties of liquid clouds according to SOCRATES (Suite of Community Radiation Codes based on Edwards & Slingo 1996) [26] and according to [27, 28] for ice clouds. The McICA solver was applied in numerical experiments due to its highest computational efficiency among those presented in the ecRad scheme. Cloud overlap is described by an exponential-random scheme [29].

2.2. Experimental Data

Experimental data include both satellite and ground-based measurements. Observations of the CLOUDNET ground–based measurement network [30, 31] at the sites in Lindenberg [32], Jülich [33] and Munich were used for characterizing the cloud parameters. The retrievals of liquid water path (LWP) are based on brightness temperature measured by a two-channel microwave radiometer (MWR), with the additional calibration for clear sky cases and validation by lidar data [34]. The liquid water content is retrieved based on the LWP data in the adiabatic approximation. Taking into account the uncertainties, we considered liquid water path higher 30 g/m2 [34]. The upper limit of MWR-retrieved LWP was set equal to 800 g/m2 to restrict the analysis to non-precipitating clouds following [35].
Additionally, we used cloud characteristics retrievals from MODIS (MODerate resolution Imaging Spectroradiometer; Collection 6.1 Level 2, LAADS DAAC system, https://ladsweb.modaps.eosdis.nasa.gov; accessed on 14 October 2023) spectroradiometer [36] for the domain of numerical experiments. The MODIS algorithm of cloud characteristics retrievals above snowless surface is based on measurements at two wavelengths: 2.1 microns – in the water absorption spectrum, and 650 nm – outside the absorption spectrum, where the surface reflectivity is minimized [37]. The satellite-based LWP is calculated according to cloud optical thickness and cloud droplet effective radius retrievals [37]. We used the pixels with MODIS measurement errors of liquid water path and cloud optical thickness less than 20%. This threshold was taken according to the uncertainty of MODIS retrievals [36].
The study used measurements of the 3-hourly low level cloud fraction at the Lindenberg site from the database of the Hydrometeorological Research Center of Russia, as well as hourly observations of the total cloud fraction (https://rp5.ru/Weather_archive_in_Lindenberg, accessed on 14 October 2023).
We also used high-precision measurements of global and diffuse solar irradiance at ground from the Lindenberg BSRN site (Baseline Surface Radiation Network; https://bsrn.awi.de; accessed on 14 October 2023) and direct radiation at horizontal surface, calculated as the difference between them.
Some additional information on measurements, their spatial and temporal resolutions, as well as statistical characteristics are shown in Table 1. The measurement uncertainties of cloud parameters are presented in the form of average measurement errors given for each moment of observations by data developers [30, 36]. Measurement errors of BSRN data are provided in accordance with network standards [38]. Given in the Table 1, BSRN data belongs to cases with a Sun elevation of more than 15°, and half of the sample is in the range of Sun elevation from 28° to 49°.
The statistical characteristics of clouds in Table 1 show that observations lie in the range of typical values of cloud characteristics in middle latitudes [31, 34, 39]. The liquid water path in 91% of cases does not exceed 400 g/m2, which corresponds to non-precipitation clouds [40]. The liquid water content in 80% of cases is in the range from 0.01 to 0.5 g/m3. The cloud optical thickness according to the MODIS data does not exceed 20 in 75% of cases, which corresponds to typical values in middle latitudes [41, 42]. The observation cases under consideration include both liquid clouds and mixed-phase clouds. In mixed-phase clouds, the ice water content exceeds 0.012 g/m3 in no more than 25% of cases (see Table 1).

2.3. Experiment Design

Numerical experiments were made over the territory of Europe for domains with a grid spacing of 4.4, 2.2 and 1.1 km and 90 vertical levels. We analyzed the ICON results with a grid spacing of 1.1 km (Figure 1). The model was initialized using the data of global version of the ICON model with a grid spacing of 13 km. Boundary conditions were provided with a 3 h time step. The experiments were performed for 32 selected days during warm (snowless) period of 2021 (7 - spring days, 19 - summer days, 6 - autumn days) with a lead time of 36 hours. Limiting the study to a warm period avoids large errors associated with the uncertainty of surface albedo evaluation. The choice of the numerical experiments region is determined by the availability of both radar and satellite cloud observations. The forecast started at 12 UTC of the previous day relative to the selected one. Only the last 24 hours of the forecast were analyzed to avoid the spin-up period. The selection of days for numerical experiments was carried out according to cloud and radiation measurements at the Lindenberg site with the most complete dataset and under a number of measuring conditions of stratiform clouds at solar elevation higher 15°, without precipitation (less 0.5 mm per day) and a good quality of observations marked by the corresponding labels. By excluding the situations with precipitation from the analysis, we avoid its influence on cloud droplet distribution, as well as on low quality of measurements in conditions with raindrops at the domes of instruments [35, 43]. The BSRN, CLOUDNET and ICON data were averaged with hourly resolution. The nearest neighbor method was used for comparisons of model grid data with point observations [44]. We took into account only non-zero simulated and observed values of the liquid water content, the liquid water path, the cloud optical thickness and the number concentration of cloud droplets in the analysis.
Observations and retrievals of cloud droplets number concentrations (Nd) are associated with many methodological assumptions, instrumental limitations and uncertainties [45, 46] as well as the aerosol contribution to cloud condensation nuclei (CCN). Therefore, the range of Nd values over the European territory is very wide [47, 48]. The typical Nd is about 200-300 cm-3 according to [49, 50] or ~100-500 cm-3 according to [51]. We used Nd retrievals according to the satellite 1 km resolution MODIS data following the methodology described in [52], taking into account the restrictions on solar elevation, instrument zenith angle, cloud phase, number of cloud layers, cloud optical thickness and cloud droplet effective radius. To filter the pixels with precipitation, we additionally applied the restriction on cloud droplet effective radius less 18 μm [53].
We used the method [54] (Equation 4) for the droplet concentration (Nd, cm-3) retrievals with the application of the liquid cloud optical thickness (COTliq) and liquid water path (LWP):
N d = k 1 C O T l i q 3 L W P − 2.5 10 − 6
where k1 is equal to 157.216 kg5/2m-8. The average obtained Nd is 245±25 cm-3 with daily Nd varying from 109 to 472 cm-3 for the selected 32 days. Thus, the obtained Nd is close to the typical values in Europe.
The most accurate estimates of the CCN content and its nucleation activity can be obtained using specific experiments [55]. However, such approach is too detailed for the task of weather forecasting. The application of the background CCN content is more appropriate for weather prediction tasks. Based on the analysis given in [56, 57], we can assume that the satellite-derived number concentrations of cloud droplets (Nd) equals to minimum CCN (CCNmin) at the cloud base.
Thus, we can apply the obtained Nd values as an estimate of the observed minimum CCN at the cloud base. The default CCN value in the ICON model, equal to 250 cm-3, is very close to the average satellite-obtained value of 245 cm-3. As a result, the number concentration of cloud condensation nuclei (NCCN) was set to 250 cm-3 in the two-moment microphysical scheme. We should also note that, in the model, not all of the CCN can be activated as cloud drops inside the cloud [19]. This effect is discussed below, in Section 3.

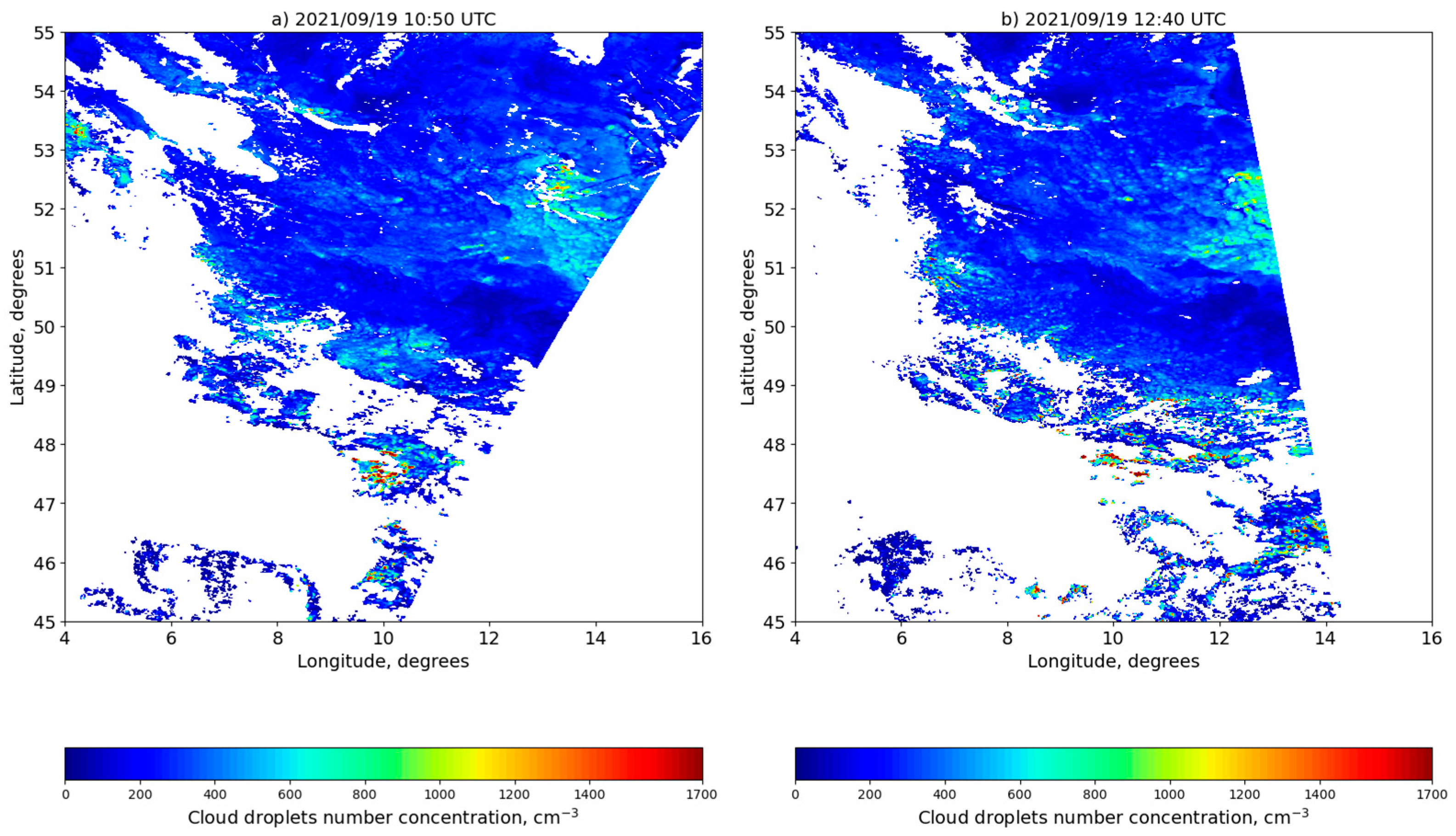
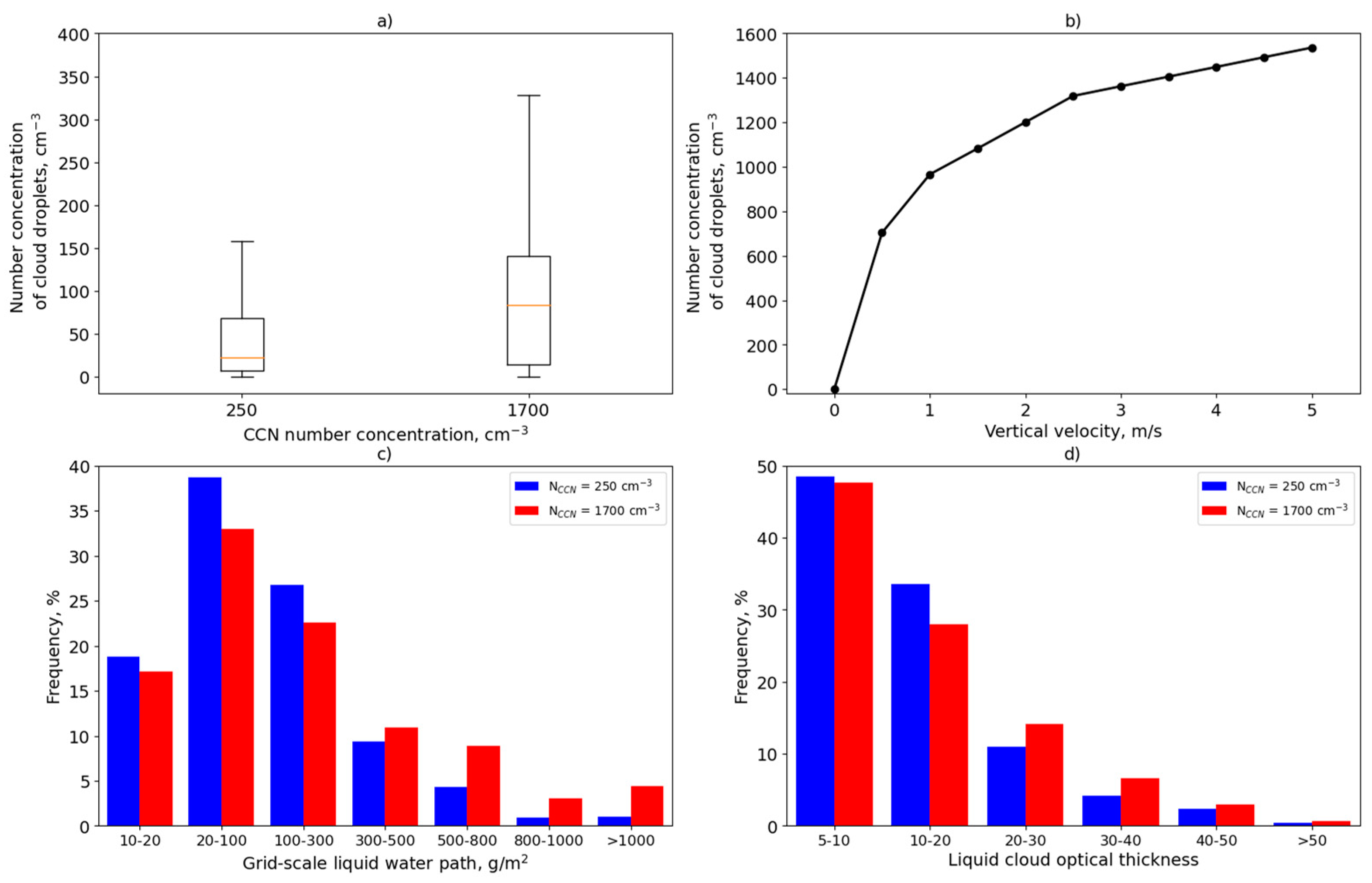
3. Results

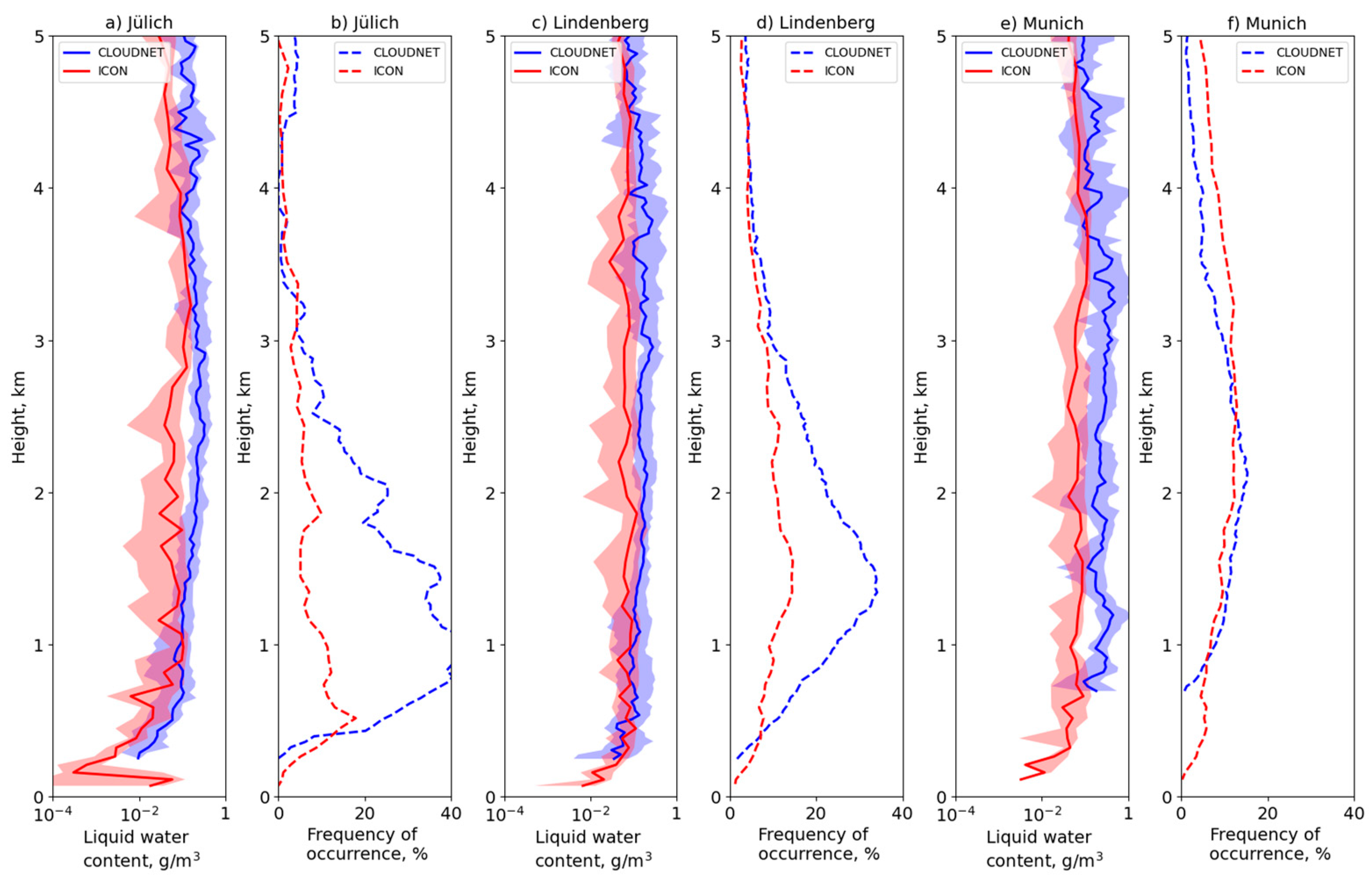
3.1. Liquid Water Content

Figure 2 shows the medians of CLOUDNET observed liquid water content, ICON simulated grid-scale liquid water content (Figure 2a, c, e) and its frequency of occurrence (Figure 2b, d, f) in Munich, Lindenberg and Jülich. The frequency of occurrence of observed and simulated liquid water content was calculated for the values greater than 10-6 g/m3.
Table 2 presents the main statistical parameters of the liquid water path according to hourly average measurements and modelling in Jülich, Lindenberg and Munich. For ICON simulations both the grid-scale and the total (grid-scale and subgrid-scale) LWP are shown. Vertical cloud structure is well reproduced by ICON, but there is a slight underestimation of liquid water content throughout the profile. As a result, the simulated grid-scale liquid water path (LWP) is on average underestimated relative to CLOUDNET observations by 68±17 g/m2. The accounting of subgrid-scale liquid water content leads to the liquid water path increase. However, the total liquid water path is still underestimated by 59±16 g/m2. In addition, model results provide lower frequency of LWC in Lindenberg and Jülich (Figure 2b, d). A better agreement of model LWC frequency of occurrence over Munich (Figure 2f) could be attributed to a successfully forecast of sub-inversion clouds by the ICON model there and, to some extent, much smaller statistics. However, the LWP is underestimated at all CLOUDNET sites, and its interquartile range is lower in Lindenberg and Munich (see Table 2).
All these differences may be associated with the following:
(1) Insufficient concentration of cloud condensation nuclei for droplets nucleation and liquid water content growth in conditions with CCN=250 cm-3;
(2) Too intensive formation of ice crystals, which can lead to a decrease the excess specific humidity required for the cloud droplet nucleation;
(3) Too intensive processes of autoconversion and accretion, leading to the transition of cloud water mass into precipitation;
(4) The problems with the saturation adjustment scheme, influencing on the deficiency of specific humidity to activate condensation nuclei.
Satellite data provides Nd values that correspond to the cloud base level. ICON model provides height-resolved Nd values. To bring ICON results closer to MODIS estimates of Nd (see Section 2.3), we considered hourly average vertically maximum simulated number concentrations of cloud droplets. The maximum cloud droplets number concentration in the model can be not only near cloud base. So, we do not limit the simulated Nd and choose the maximum value in each profile. However, even in this case, no more than 25% of the whole ICON sample accounted for Nd concentrations is above 77 cm-3. The Nd interquartile range of ICON results is 63 cm-3 with a median of 29 cm-3. The ice water content is also higher than the simulated one (not shown), so no intensive nucleation and growth of ice crystals are observed. For considering the influence of autoconversion and accretion processes on LWP, we compared the measured liquid water path with simulated liquid and rain water path (LWP+RWP). Even taking into account raindrops, the simulated LWP is generally underestimated by 17±13 g/m2. This approach does not show enhanced autoconversion and accretion as the principal reason of LWP underestimation. We assume that this mechanism could be important, but there is no observation-based experimental data for proving the level of this process. Therefore, we rely on observational data and the conclusions shown above.
The simulated liquid water content may be less than the observed LWC due to inaccurate prediction of the water vapor path, since water vapor is the main source of the cloud droplet nucleation and growth. However, according to studies of the ICON model [58, 59], this characteristic is predicted quite accurately.
Thus, one of the reasons of the model lower liquid water content and its occurrence may be the saturation adjustment scheme, which is the most important regulator of all microphysical processes. Saturation adjustment leads to a lower condensation and to a higher evaporation rates of droplets in the bulk scheme relative to the spectral microphysical scheme. The work [11] showed that the saturation adjustment contributes to lower LWC for situations of strato-cumulus clouds. Khain and Pinsky [3] also showed negative effect of saturation adjustment on the diffusion growth of cloud particles in different cloud types. Unfortunately, we cannot consider this issue in more detail, since this requires a mixed-phase spectral microphysical scheme, which is more close to the real physics of clouds [10] compared to saturation adjustment scheme used in the ICON model. The liquid water path underestimation in some cases could be due to the low specified CCN of 250 cm-3, hence, we conducted a numerical experiment with a higher content of cloud condensation nuclei. Based on satellite measurements and upper-air sounding data, we chose September 19, 2021 as the day with the most uniform clouds over the simulation domain. Figure 3 shows MODIS retrievals of cloud droplet number concentrations at the cloud base according to the method (Equation 4) with the average Nd of 258 cm-3. We carried out a numerical experiment with high CCN of 1700 cm-3, since this value is typical for the continental or polluted clouds [19, 55, 60].
Figure 4a shows box plots of simulated cloud droplet number concentration over the CLOUDNET sites with cloud condensation nuclei 250 and 1700 cm-3. The whole four-dimension (height-field-time) simulated Nd was taken into account to compare results of specified CCNs. The cloud droplet number concentration increases by 94±20 cm-3 (65%) with this CCN growth. Median (interquartile range) values of Nd are 22 (62) cm-3 and 84 (127) cm-3 for CCN=250 cm-3 and CCN=1700 cm-3, respectively.
Considering vertically maximum ICON simulated number concentrations of cloud droplets, median Nd increases from 23 cm-3 with NCCN 250 cm-3 to 89 cm-3 with NCCN 1700 cm-3. Thus, not all of ССN were activated in the model.
Vertical velocity (W) is an important factor in the cloud droplet nucleation [53, 61]. Kretzschmar et al. [62] showed that one of the reasons for the low Nd and liquid water content in ICON may be an unsufficient W, providing lower CCN activation in the parametrization. Figure 4b illustrates the dependence of cloud droplet concentration on vertical velocity in the Segal-Khain scheme [19] for CCN of 1700 cm-3. At low vertical velocities, less than half of the CCN can be available for nucleation. The maximum value of the simulated grid-scale vertical velocity at levels near the cloud base for September 19, 2021 was 0.9 m/s at CLOUDNET sites. Thus, the CCN concentration was actually in the range from 140 cm-3 to 900 cm-3 at the simulated vertical velocities instead of the specified 1700 cm-3. The CCN content of 140 cm-3 corresponds to the minimum permissible vertical velocity of 0.1 m/s in the cloud droplet nucleation scheme. However, in our experiments the simulated Nd is significantly less than the satellite-derived Nd. This indicates low intensity of cloud droplet nucleation and the contribution of the saturation adjustment scheme together with other microphysical processes, for example, evaporation, to the resulting Nd and LWP values.
In general, an increase in the concentration of cloud condensation nuclei contributed to an increase in the grid-scale liquid water path over the modeling domain (Figure 4c). Following [63], Figure 4c shows only grid-scale liquid water path of more than 10 g/m2. With the growth of cloud condensation nuclei, there is a shift in the distribution of liquid water path towards higher values. The grid-scale liquid water path increased by an average of 118±2 g/m2 (40%). As a result, the liquid clouds have become more optically thick (Figure 4d, the cases with liquid cloud optical thickness of more than 5 are shown). However, taking into account the subgrid-scale clouds, the effect of CCN on the cloud optical thickness is less pronounced. Liquid cloud optical thickness increased by an average of 1 (8%). In order to determine the effect of CCN on the simulated global irradiance at ground, we considered cases of overcast conditions with a solar elevation of at least 25° and liquid cloud optical thickness of more than 5. Under these conditions, the CCN increase from 250 cm-3 to 1700 cm-3 provides the solar irradiance decrease by 9 W/m2 (12%).

3.2. Cloud Optical Thickness and Shortwave Irradiance at Ground

Cloud optical thickness and the cloud fraction are the most important factors in the cloudy atmosphere, which determine the global solar irradiance at ground. Cloud optical thickness is determined by a liquid water content and effective radius of cloud droplets [64].
In order to exclude the influence of errors in the scheme of clouds optical properties evaluation in the ecRad scheme on the cloud-radiation interaction, we compared the liquid cloud optical thickness (COTliq) according to MODIS and ICON data. We consider the cases with LWP successful prediction, when the absolute error of the simulated LWP was less than 15% (391770 pixels) compared to the MODIS LWP. In this case the median liquid cloud optical thickness and its interquartile range, shown in brackets, are 13.3 (12) and 13.5 (11) according to MODIS and ICON, respectively. The average error of simulated COTliq is +0.04±0.03 (0.02%). If considering all cases, regardless the quality of the simulated cloud water (8642685 pixels), the ICON cloud water path (liquid and ice phases) is on average 52±0.1 g/m2 lower relative to the MODIS retrievals. As a result, the cloud optical thickness is underestimated by 4±0.01 (24%). Hence, the cloud optical thickness is predicted with sufficient accuracy if liquid water path is successfully estimated.
The cloud fraction is a more difficult for evaluation from both numerical forecasting and observations [65]. Standard verification approaches are not suitable for cloud fraction analysis, therefore other, more sophisticated methods and measurement data are required [66, 67]. Therefore, we analyzed not only cloud fraction, but also considered another characteristic – the ratio (R) of direct radiation at horizontal surface to global solar irradiance using hourly average data. This value can be considered as an analogue of the cloud fraction after the application of hourly average procedure [68]. The hourly R values actually characterizes the proportion of gaps in the clouds.
According to the BSRN observations in cloudy conditions, ICON simulated hourly global irradiance at ground is overestimated on average by 46±15 W/m2 (18%). At the same time, the simulated R is overestimated by 0,13±0,02. Figure 5 shows the hourly average values of global irradiance (Q), liquid water path (LWP) and R averaged over the R intervals according to measurements (Figure 5a) and according to measurements and simulations (Figure 5b). The results of ICON simulations are presented using CCN number concentration of 250 cm-3. In addition, low level cloud fraction (CLCL, dotted lines) and total cloud fraction (CLCT, crosses) are also shown.
According to the ICON numerical experiments, R values are higher than the observed ones (Figure 5a). For overcast situations (Robs is equal to 0), average Rsim=0.2±0.04. As a result, simulated global irradiance is higher than the measured one: 263±33 W/m2 and 162±13 W/m2, respectively. At different averaging intervals (horizontally), the Robs grows much faster relative to the simulated R (see Figure 5a). If we rank the cases based on both the measured and simulated R, the differences between simulated and measured global irradiance decrease (Figure 5b). Note, that the simulated liquid water path is underestimated compared to the CLOUDNET observations for all considered R intervals (Figure 5a, b). Thus, improving the quality of the forecast of the R contributes to reducing the error of solar irradiance evaluation even with a general underestimation of the liquid water path.
The total cloud fraction according to the ICON estimates generally corresponds to the observations (Figure 5a, b), while a more pronounced decrease in the measured CLCLs is observed compared to the simulated values. The model CLCLs are overestimated almost everywhere. However, even at higher model CLCLs we observe the overestimating of Q. In addition, the sensitivity of global solar irradiance to cloud fraction is generally less pronounced than its sensitivity to R (see Figure 5). The linear correlation coefficients of CLCL and Q are -0.26 and -0.23, while the correlation coefficients between R and Q are 0.78 and 0.86 according to measurement and simulation data, respectively.
Preprints 88865 g005
Figure 5. Global solar irradiance (Q), liquid water path (LWP), low level cloud fraction (CLCL), total cloud fraction (CLCT), and the R ratio according to simulations (Rsim) and observations (Robs) as a function of R according to measurements (a, 214 cases) and for consistent R values according to simulations and measurements (b, 84 cases). Lindenberg site. Simulations with CCN 250 cm-3. The solar elevation is above 25°. Confidence intervals are represented by a fill for R and lines for the other variables.
Figure 5. Global solar irradiance (Q), liquid water path (LWP), low level cloud fraction (CLCL), total cloud fraction (CLCT), and the R ratio according to simulations (Rsim) and observations (Robs) as a function of R according to measurements (a, 214 cases) and for consistent R values according to simulations and measurements (b, 84 cases). Lindenberg site. Simulations with CCN 250 cm-3. The solar elevation is above 25°. Confidence intervals are represented by a fill for R and lines for the other variables.
Preprints 88865 g005
Hence, the error in R is the main factor determining the overestimation of simulated global irradiance. This could be observed due to inaccurate overlapping procedure between the layers. For example, Kawai et al. [69] showed the effect of the overlapping scheme on the cloud albedo without changing the total cloud cover in the MRI-ESM2 climate model. Even with the observed liquid water path underestimation, an accurate forecast of R leads to an improvement in the global irradiance prediction. It should be noted that the penetration of direct radiation through the gaps may provide a significant contribution to global solar irradiance and, hence, air temperature. The effect of the liquid water path underestimation on solar radiation is less pronounced, since the sensitivity of global irradiance to cloud optical thickness becomes lower with the increase in COT [70], which is also noted as an "accumulation effect" [71]. The quality of cloud fraction forecast at each model level is directly related to the quality of cloud moisture forecast (see Section 2.1). This means that the underestimation of cloud moisture may also contribute to the modeling of less cloudy conditions.
The forecast of broken clouds is known to be the weakest points of cloud cover forecast [72]. The errors in cloud fraction prediction are noted in the studies concerning many numerical weather prediction and climate forecasting models [12, 15, 67, 73-75]. The main reasons for inaccuracies in the cloud fraction forecast include the errors in the structure of simulated convective clouds, liquid water content of stratiform clouds and clouds frequency of occurrence in general. Errors of solar irradiance prediction, besides cloud cover schemes, depend on the cloud overlap assumption, which is a difficult task both in modeling and observations [76, 77]. Many forecasting centers try to reduce the systematic errors in cloud fraction prediction in postprocessing, in particular, using neural networks [78, 79]. At the moment, the new ICON diagnostic cloud fraction scheme is developing [80]. The scheme is generally corresponded to the global trend of complicating microphysical processes by considering a whole complex of physical cloud mechanisms [81].

4. Discussion

We found an underestimation of simulated liquid water path relative to observations at three CLOUDNET sites (Lindenberg, Jülich and Munich). The main possible reasons of this underestimation are the uncertainties in cloud droplet nucleation and saturation adjustment scheme. Khain et al. [10] showed that the saturation adjustment scheme leads to decreasing the sensitivity of microphysical processes to aerosol in bulk schemes. Khain et al. [82] found a good sensitivity in the ICON two-moment bulk scheme to the cloud condensation nuclei content relative to the spectral scheme. However, Khain et al. [82] concluded that the saturation adjustment scheme still should be substituted in the future. With the implementation of a mixed-phase spectral scheme into the ICON model, a more detailed assessment of the saturation adjustment scheme’ effect on the cloud properties will be possible (https://www.cosmo-model.org/content/tasks/priorityProjects/caiir/default.htm, accessed on 14 October 2023).
The model’ cloud condensation nuclei was set to the default value of 250 cm-3. Using MODIS observations and following the method described in [54], we demonstrated that the default CCN content of 250 cm-3 is typical background value over Europe with daily variations of MODIS-derived Nd from 100 to 500 cm-3 on selected days. We chose the CCN number concentration of 1700 cm-3 which corresponds to the polluted continental clouds according to [19] as an upper limit for an additional numerical experiment. As a result, the cloud droplet number concentration and grid-scale liquid water path increase by an average of 65% and 40%, respectively. The changes in cloud structure provided the decreasing solar irradiance at ground by an average of 12% in overcast conditions with solar elevation above 25° and cloud optical thickness more than 5. The obtained effects of cloud condensation nuclei growth promote to reducing prediction errors in the liquid water path and solar irradiance at ground.
Another reason of LWP underestimation may be in significant low nucleation intensity of cloud droplets due to small vertical velocity in the Segal-Khain scheme, which have been also obtained in our study. At a vertical velocity of 1 m/s, when CCN was set equal to 1700 cm-3, no more than 60% CCN are activated. Our results concerning cloud-aerosol interaction are in the line with the studies [11, 63, 83] for other models and geographical regions. In the absence of vertical velocity observations, we cannot state the underestimation of simulated vertical velocity. However, Tonttila et al. [84] found an underestimation of vertical velocity variability at the cloud base in the AROME model with 2.5 km grid spacing. Malavelle et al. [85] showed the positive impact of subgrid-scale vertical velocity on the CCN activation in the Unified Model with 1 km horizontal grid spacing. By taking into account for the subgrid-scale vertical velocity, the errors might be significantly reduced in the cloud droplets nucleation scheme of kilometer-scale models [83, 86]. Anyway, this issue is a good point for future research.
We found a sufficient accuracy of cloud optical thickness with successful liquid water path prediction in comparison with MODIS data. In broken cloud conditions the liquid water content prediction uncertainty may be one of the reasons for the cloud fraction prediction error [87]. In the case of the ICON model, this may also happen due to the saturation adjustment scheme, as well as the nucleation scheme of cloud droplets due to its reduced sensitivity to CCN content as was discussed above for lower ICON liquid water path. Thus, Van Weverberg and Morcette [87] show that the prognostic and diagnostic cloud fraction schemes have the errors of a general nature. We plan to conduct a more detailed analysis of this assumption in the future.
To assess the influence of clouds spatial inhomogeneity, the R (ratio of direct to global solar radiation) was considered. R parameter is an analogue of the cloud fraction regarding cloud spatial heterogeneity, but, in contrast with cloud fraction, R is based on high-precision 10-minutes observations. We showed that global solar irradiance is more sensitive to the prediction of R than to the liquid water path or cloud fraction forecast. A successful R prediction significantly improves the forecast of solar irradiance compared to cloud fraction parameter. Cloud fraction prediction errors may be related to the choice of a cloud overlap scheme and scheme’s approximations in general [29, 66]. 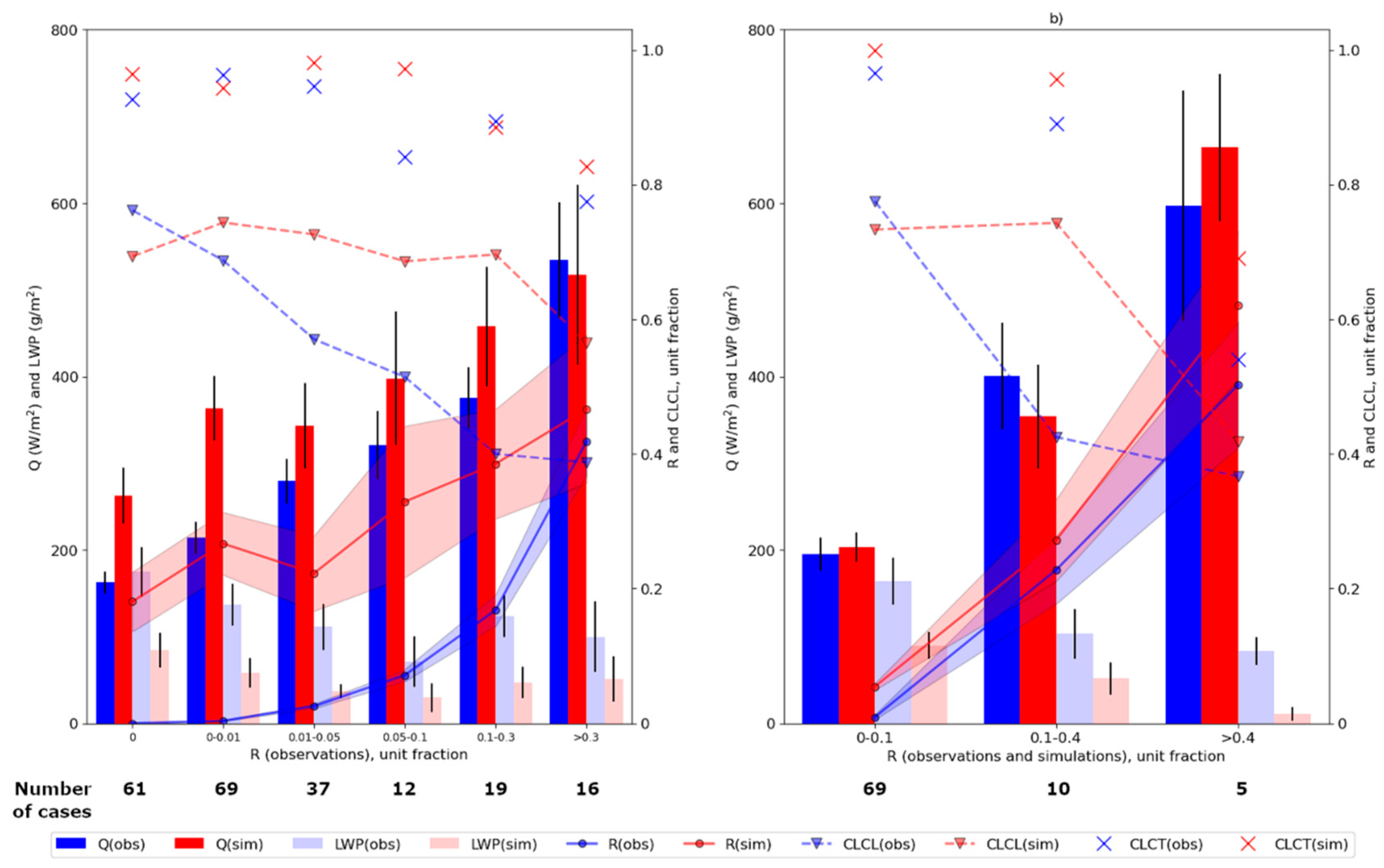Since observations and studies of cloud overlap still have some difficulties and uncertainties [76], the issue of successful cloud overlap forecasting is still open in numerical weather prediction.

5. Conclusions

This study provides a joint detailed research of cloud moisture and solar irradiance at ground according to the ICON numerical weather prediction model, CLOUDNET ground-based network of cloud characteristics at the three sites (Lindenberg, Jülich and Munich), BSRN high-precision ground-based radiation network in Lindenberg and MODIS observations of cloud characteristics. The main conclusions are the following:
Comparison of ICON and CLOUDNET data showed an underestimation of simulated grid-scale liquid water content. Taking into account the subgrid-scale component of clouds, the average liquid water path is still underestimated by 59±16 g/m2.
The CCN growth from 250 cm-3 to 1700 cm-3 led to an increase of cloud droplet number concentration by an average of 94±20 cm-3 (65%), providing the increase in the grid-scale liquid water path and cloud optical thickness by 118±2 g/m2 (40%) and by 1 (8%), respectively. This led to a decrease in solar irradiance at ground by an average of 9 W/m2 (12%) in overcast conditions. The obtained CCN effects contribute to reducing errors in the liquid water path prediction and solar irradiance at ground.
We obtained a sufficient accuracy of cloud optical thickness forecast using SOCRATES parametrization of ecRad scheme [26] with successful liquid water path prediction in comparison the with MODIS data.
The solar irradiance at ground is on average overestimated compared to the BSRN observations. We showed that global irradiance values are more sensitive to the prediction of R (ratio of direct to global solar irradiance) than to the liquid water path and cloud fraction forecast. A successful R prediction significantly improves the forecast of solar irradiance.

Author Contributions

Conceptualization, methodology, formal analysis, investigation, validation, writing—original draft preparation, writing—review and editing – J.S., N.C. and M.S.; software, J.S.; resources, M.S.; data curation, J.S.; visualization, J.S.; supervision, N.C. and M.S.; project administration, N.C.; funding acquisition, N.C. All authors have read and agreed to the published version of the manuscript.

Funding

The research was supported by the grant of Ministry of Science and Higher Education of the Russian Federation (project number 075–15–2021–574) and fulfilled at the Lomonosov Moscow State University under the Development Program of the MSU Interdisciplinary Scientific and Educational School “Future Planet and Global Environmental Change”. The configuration of ecRad radiative scheme in the ICON was carried out within Roshydromet Research Work number AAAA-20-120021490079-3.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The results presented in this manuscript were created based on the MODIS dataset available at (https://ladsweb.modaps.eosdis.nasa.gov; accessed on 14 October 2023); CLOUDNET observations available at (CLU, 2023); BSRN observations at Lindenberg Meteorological Observatory, available at (https://bsrn.awi.de; accessed on 14 October 2023) on request. We used numerical weather prediction realization of ICON model version 2.6.5 (https://code.mpimet.mpg.de/projects/iconpublic/wiki/How%20to%20obtain%20the%20model%20code; accessed on 14 October 2023). The ecRad radiative transfer scheme is available at (https://github.com/ecmwf-ifs/ecrad; accessed on 14 October 2023). The detailed description of methods is shown in Section 2. Figures were created with Python version 3.10.2 – available at (https://www.python.org; accessed on 14 October 2023).

Acknowledgments

We are very grateful to the staff of the Lindenberg Meteorological Observatory, the Jülich Observatory and the Munich supersite for the providing cloud and radiative data.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Mauder, M.; Foken, T.; Cuxart, J. Surface-Energy-Balance Closure over Land A Review. Boundary-Layer Meteorology 2020, 177, 395–426. [Google Scholar] [CrossRef]
  2. Marshak, A.; Davis, A.B. 3D Radiative Transfer in Cloudy Atmospheres. Springer-Verlag: Berlin Heidenberg, Germany, 2005: 686 pp.
  3. Khain, A. P.; Pinsky, M. Physical Processes in Clouds and Cloud Modeling. Cambridge University Press: Cambridge, UK, 2005: 626 pp. [CrossRef]
  4. Haiden, T.; Forbes, R.M.; Ahlgrimm, M.; Bozzo, A. The skill of ECMWF cloudiness forecast. ECMWF Newsletter 2015, 143, 1–7. (https://www.researchgate.net/profile/Thomas-Haiden/publication/292989145_The_skill_of_ECMWF_cloudiness_forecasts/links/56b497e608ae922e6c020100/The-skill-of-ECMWF-cloudiness-forecasts.pdf; accessed on 14 October 2023).[. [Google Scholar]
  5. Sotiropoulou, G.; Sedlar, J.; Forbes, R.; Tjernström, M. Summer Arctic clouds in the ECMWF forecast model: an evaluation of cloud parametrization schemes. Quarterly Journal of the Royal Meteorological Society 2016, 142, 387–400. [Google Scholar] [CrossRef]
  6. Tuccella, P.; Curci, G.; Grell, G. A.; Visconti, G.; Crumeyrolle, S.; Schwarzenboeck, A.; et al. A new chemistry option in WRF-Chem v. 3.4 for the simulation of direct and indirect aerosol effects VBS: evaluation against IMPACT-EUCAARI data. Geoscientific Model Development 2015, 8, 2749–2776. [Google Scholar] [CrossRef]
  7. Dipu, S.; Quaas, J.; Wolke, R.; Stoll, J.; Mühlbauer, A.; Sourdeval, O.; et al. Implementation of aerosol-cloud interactions in the regional atmosphere-aerosol model COSMO-MUSCAT(5.0) and evaluation using satellite data. Geoscientific Model Development 2017, 10, 2231–2246. [Google Scholar] [CrossRef]
  8. Muskatel, H.B.; Blahak, U.; Khain, P.; Levi, Y.; Fu, Q. Parametrizations of liquid and ice clouds’ optical properties in operational numerical weather prediction models. Atmosphere 2021, 12, 89. [Google Scholar] [CrossRef]
  9. Tao. , W.-K.; Simpson, J.; McCumber, M. An Ice-Water Saturation Adjustment. Monthly Weather Review 1989, 117, 231–235. [Google Scholar] [CrossRef]
  10. Khain, A.; Beheng, K. D.; Heymsfield, A.; Korolev, A.; Krichak, S. O.; Levin, Z.; et al. Representation of microphysical processes in cloud-resolving models: Spectral (bin) microphysics versus bulk parametrization. Reviews of Geophysics 2015, 53, 247–322. [Google Scholar] [CrossRef]
  11. Wang, Y.; Fan, J.; Zhang, R.; Leung, L. R.; Franklin, C. Improving bulk microphysics parametrizations in simulations of aerosol effects. Journal of Geophysical Research: Atmospheres 2013, 118, 5361–5379. [Google Scholar] [CrossRef]
  12. Haiden, T.; Trentmann, J. Verification of cloudiness and radiation forecasts in the greater Alpine region. Meteorologische Zeitschrift 2016, 25, 3–15. [Google Scholar] [CrossRef]
  13. Sundqvist, H.; Berge, E.; Kristjansson, J. E. Condensation and Cloud Parametrization Studies with a Mesoscale Numerical Weather Prediction Model. Monthly Weather Review 1989, 117, 1641–1657. [Google Scholar] [CrossRef]
  14. Tiedke, M. Representation of Clouds in Large-Scale Models. Monthly Weather Review 1993, 121, 3040–3061. [Google Scholar] [CrossRef]
  15. Ma, Z.; Liu, Q.; Zhao, C.; Shen, X.; Wang, Y.; Jiang, J. H.; et al. Application and Evaluation of an Explicit Prognostic Cloud-Cover Scheme in GRAPES Global Forecast System. Journal of Advances in Modeling Earth Systems 2018, 10, 652–667. [Google Scholar] [CrossRef]
  16. Zängl, G.; Reinert, D.; Ripodas, P.; Baldauf, M. The ICON (ICOsahedral Non-hydrostatic) modelling framework of DWD and MPI-M: Description of the non-hydrostatic dynamical core. Quarterly Journal of the Royal Meteorological Society 2015, 141, 563–579. [Google Scholar] [CrossRef]
  17. Rivin, G. S.; Rozinkina I., A. Astakhova, E. D.; Blinov, D. V.; Bundel, A. Yu.; Kirsanov, A. A.; et al. COSMO-Ru high-resolution short-range numerical weather prediction system: its development and applications. Hydrometeorological research and forecasts 2019, 374, 37–53. In Russian. (https://method.meteorf.ru/publ/tr/tr374/03.pdf; accessed on 14 October 2023). [Google Scholar] [CrossRef]
  18. Seifert, A.; Beheng, K. D. A two-moment cloud microphysics parameterization for mixed-phase clouds. Part 1: Model description. Meteorology and atmospheric physics 2006, 92, 45–66. [Google Scholar] [CrossRef]
  19. Segal, Y.; Khain, A. Dependence of droplet concentration on aerosol conditions in different cloud types: Application to droplet concentration parameterization of aerosol conditions. Journal of Geophysical Research: Atmospheres 2006, 111. [Google Scholar] [CrossRef]
  20. Seifert, A. On the parametrization of evaporation of raindrops as simulated by a one-dimensional rainshaft model. Journal of the Atmospheric Sciences 2008, 65, 3608–3619. [Google Scholar] [CrossRef]
  21. Kärcher, B.; Hendricks, J.; Lohmann, U. Physically based parameterization of cirrus cloud formation for use in global atmospheric models. Journal of Geophysical Research: Atmospheres 2006, 111. [Google Scholar] [CrossRef]
  22. Phillips, V. T. J.; DeMott, P. J.; Andronache, C. An Empirical Parametrization of Heterogeneous Ice Nucleation for Multiple Chemical Species of Aerosol. Journal of Atmospheric Sciences 2008, 65, 2757–2783. [Google Scholar] [CrossRef]
  23. Doms, G.; Foerstner, J.; Heise, E.; Herzog, H.-J.; Mironov, D.; Raschendorfer, M.; et al. A Description of the Nonhydrostatic Regional COSMO-Model. Part II: Physical Parametrizations (COSMO 6.0). Deutscher Wetterdienst: Offenbach, Germany, 2021: 171 pp. [CrossRef]
  24. Hogan, R. J.; Bozzo, A. ECRAD: A new radiation scheme for the IFS. ECMWF Technical Memoranda 2016, 787. (https://www.ecmwf.int/sites/default/files/elibrary/2016/16901-ecrad-new-radiation-scheme-ifs.pdf; accessed on 14 October 2023). [Google Scholar]
  25. Pincus, R.; Barker, H. W.; Morcrette, J. J. A fast, flexible, approximate technique for computing radiative transfer in inhomogeneous cloud fields. Journal of Geophysical Research: Atmospheres 2003, 108. [Google Scholar] [CrossRef]
  26. Edwards, J. M.; Slingo, A. Studies with a flexible new radiation code. I: Choosing a configuration for a large-scale model. Quarterly Journal of the Meteorological Society 1996, 122, 689–719. [Google Scholar] [CrossRef]
  27. Fu, Q. An accurate parametrization of the solar radiative properties of сirrus clouds for climate models. Journal of Climate 1996, 9, 2058–2082. [Google Scholar] [CrossRef]
  28. Fu, Q.; Yang, P.; Sun, W. B. An accurate parameterization of the infrared radiative properties of cirrus clouds for climate models. Journal of Climate 1998, 11, 2223–2237. [Google Scholar] [CrossRef]
  29. Hogan, R. J.; Illingworth, A. J. Deriving cloud overlap statistics from radar. Journal of the Atmospheric Sciences 2000, 126, 2903–2909. [Google Scholar] [CrossRef]
  30. CLU. Cloud profiling products: Classification, Liquid water content, Categorize; cloud profiling measurements: Microwave radiometer; 2021-03-01 to 2021-10-31; from Jülich, Lindenberg, Munich. Generated by the cloud profiling unit of the ACTRIS Data Centre, 14 October 2023. Available online: https://hdl.handle.net/21.12.132/2.117b713d7c04494e (accessed on 14 October 2023).
  31. Illingworth, A. J.; Hogan, R. J.; O’Connor, E. J.; Bouniol, D.; Brooks, M. E.; Delanoea, J.; et al. Cloudnet: Continuous evaluation of cloud profiles in seven operational models using ground-based observations. Bulletin of the American Meteorological Society 2007, 88, 883–898. [Google Scholar] [CrossRef]
  32. Görsdorf, U.; Lehmann, V.; Bauer-Pfundstein, M.; Peters, G.; Vavriv, D.; Vinogradov, V.; Volkov, V. A 35-GHz Polarimetric Doppler Radar for Long-Term Observations of Cloud Parameters – Description of System and Data Processing. Journal of Atmospheric and Oceanic Technology 2015, 32, 675–690. [Google Scholar] [CrossRef]
  33. Löhnert, U.; Scheween, J.H.; Acquistapace, C.; Ebell, K.; Maahn, M.; Barrera-Verdejo, M.; et al. JOYCE: Jülich observatory for cloud evolution. Bulletin of the American Meteorological Society 2015, 96, 1157–1174. [Google Scholar] [CrossRef]
  34. Gaussiat, N.; Hogan, R. J.; Illingworth, A. J. Accurate liquid water path retrieval from low-cost microwave radiometers using additional information from a lidar ceilometer and operational forecast models. Journal of Atmospheric and Oceanic Technology 2007, 24, 1562–1575. [Google Scholar] [CrossRef]
  35. Roebeling, R. A.; Deneke, H. M.; Feijt, A. J. Validation of cloud liquid water path retrievals from SEVIRI using one year of CloudNET observations. J. Appl. Meteorol. And Climatol. 2007, 47, 206–222. [Google Scholar] [CrossRef]
  36. Platnick, S.; Meyer, K.G.; King, M.D.; Wind, G.; Amarasinghe, N.; Marchant, B.; et al. The MODIS cloud optical and microphysical products: Collection 6 updates and examples from Terra and Aqua. IEEE Trans. Geosci. Remote Sens 2016, 55, 502–525. [Google Scholar] [CrossRef]
  37. Platnick, S.; King, M. D.; Ackerman, S. A.; Menzel, W. P.; Baum, B. A.; Riedi, J. C.; Frey, R. A. The MODIS cloud products: Algorithms and examples from Terra. IEEE Trans. Geosci. Remote Sens. 2003, 41, 459–473. [Google Scholar] [CrossRef]
  38. McArthur, L. J. B. World Climate Research Programme-Baseline Surface Radiation Network (BSRN)-Operations Manual Version 2.1. WMO/TD 2005, 1274. (https://epic.awi.de/id/eprint/45991/1/McArthur.pdf; accessed on 14 October 2023). [Google Scholar]
  39. Gultepe, I.; Isaac, G. A. Liquid water content and temperature relationship from aircraft observations and its applicability to GCMs. Journal of Climate 1997, 11, 446–452. [Google Scholar] [CrossRef]
  40. Löhnert, U.; Crewell, S.; Simmer, C.; Macke, A. Profiling cloud liquid water combining active and passive microwave measurements with cloud model statistics. Journal of Atmospheric and Oceanic Technology 2001, 18, 1354–1366. [Google Scholar] [CrossRef]
  41. Tselioudis, G.; Rossow, W.B.; Rind, D. Global patterns of cloud optical thickness variation with temperature. Journal of Climate 1992, 5, 1484–1495. [Google Scholar] [CrossRef]
  42. Lau, Ng.-Ch.; Crane, M.W. A satellite view of the synoptic-scale organization of cloud properties in Midlatitude and tropical circulation systems. Monthly Weather Review 1995, 123, 1984–2006. [Google Scholar] [CrossRef]
  43. Hogan, R.J.; Illingworth, A.J.; O’Connor, E.J.; Bouniol, D.; Brooks, M.E.; Delanoea, J.; et al. Cloudnet: Evaluation of model clouds using ground-based observations. In Proceedings of the ECMWF Workshop on Parametrization of clouds in large-scale models, Reading, 13-15. (https://www.ecmwf.int/sites/default/files/elibrary/2007/9929-cloudnet-evaluation-model-clouds-using-ground-based-observations.pdf; accessed on 14 October 2023). 2006. [Google Scholar]
  44. Fix, E.; Hodges, J. L. Discriminatory analysis, nonparametric estimation: consistency properties. US Air Force School of Aviation Medicine 1951, 4, 21–49. [Google Scholar] [CrossRef]
  45. Merk, D.; Deneke, H.; Pospichal, B.; Seifert, P. Investigation of the adiabatic assumption for estimating cloud micro- and macrophysical properties from satellite and ground observations. Atmospheric Chemistry and Physics 2016, 16, 933–952. [Google Scholar] [CrossRef]
  46. Gupta, S.; McFarququhar, G. M.; O’Brien, J. R.; Poellot, M. R.; Delene, D. J.; Chang, I.; et al. In situ and satellite-based estimates of cloud properties and aerosol-cloud interactions over the southeast Atlantic Ocean. Atmospheric Chemistry and Physics 2022, 22, 12923–12943. [Google Scholar] [CrossRef]
  47. Hande, L.B.; Engler, C.; Hoose, C.; Tegen, I. Parameterizing cloud condensation nuclei concentrations during HOPE. Atmospheric Chemistry and Physics 2016, 16, 12059–12079. [Google Scholar] [CrossRef]
  48. Paramonov, M.; Kerminen, V.-M.; Gysel, M.; Aalto, P.P.; Andreae, M.O.; Asmi, E.; et al. A synthesis of cloud condensation nuclei counter (CCNC) measurements within the EUCAARI network. Atmospheric Chemistry and Physics 2015, 15, 12211–12229. [Google Scholar] [CrossRef]
  49. Li, J.; Jian, B.; Huang, J.; Hu, Y.; Zhao, C.; Kawamoto, K.; et al. Long-term variation of cloud droplet number concentrations from Space-based Lidar. Remote Sens. Environ. 2018, 213, 144–161. [Google Scholar] [CrossRef]
  50. Quaas, J.; Boucher, O.; Lohmann, U. Constraining the total aerosol indirect effect in the LMDZ and ECHAM4 GCMs using MODIS satellite data. Atmospheric Chemistry and Physics 2006, 6, 947–955. [Google Scholar] [CrossRef]
  51. Fanourgakis, G. S.; Kanakidou, M.; Nenes, A.; Bauer, S. E.; Bergman, T.; Carslaw, K. S.; et al. Evaluation of global simulations of aerosol particle and cloud condensation nuclei number, with implications for cloud droplet formation. Atmospheric Chemistry and Physics 2019, 19, 8591–8617. [Google Scholar] [CrossRef] [PubMed]
  52. Shuvalova, J.; Chubarova, N.; Shatunova, M. Impact of cloud condensation nuclei reduction on cloud characteristics and solar radiation during COVID-19 lockdown 2020 in Moscow. Atmosphere 2022, 13, 1710. [Google Scholar] [CrossRef]
  53. Rosenfeld, D.; Zheng, Y.; Hashimshoni, E.; Poehlker, M.L.; Jefferson, A.; Poehlker, C.; et al. Satellite retrieval of cloud condensation nuclei concentrations by using clouds as CCN chambers. Proceedings of the National Academy of Sciences 2016, 113, 5828–5834. [Google Scholar] [CrossRef] [PubMed]
  54. McComiskey, A.; Feingold, G.; Frisch, A.S.; Turner, D.D.; Miller, M.A.; Chiu, J.C.; et al. An assessment of aerosol-cloud interactions in marine stratus clouds based on surface remote sensing. J. Geophys. Res. Atmos. 2009, 114, D09203. [Google Scholar] [CrossRef]
  55. Mikhailov, E. F.; Ivanova O., A.; Vlasenko, S. S.; Nebos’ko, E. Yu.; Ryshkevich, T. I. Cloud Condensation Nuclei Activity of the Aitken Mode Particles near St. Petersburg, Russia. Izvestiya, Atmospheric and Oceanic Physics 2017, 53, 326–333. [Google Scholar] [CrossRef]
  56. Quaas, J.; Arola, A.; Cairns, B.; Christensen, M.; Deneke, H.; et al. Constraining the Twomey effect from satellite observations: issues and perspectives. Atmospheric Chemistry and Physics 2020, 20, 15079–15099. [Google Scholar] [CrossRef]
  57. Painemal, D.; Chang, F.-L.; Ferrare, R.; Burton, S.; Li, Z.; et al. Reducing uncertainties in satellite estimates of aerosol-cloud interactions over the subtropical ocean by integrating vertically resolved aerosol observations. Atmospheric Chemistry and Physics 2020, 20, 7167–7177. [Google Scholar] [CrossRef]
  58. Steinke, S.; Eikenberg, S.; Loehnert, U.; Dick, G.; Klocke, D.; Di Girolamo, P.; Crewell, S. . Assessment of small-scale integrated water vapour variability during HOPE. Atmospheric Chemistry and Physics 2015, 15, 2675–2692. [Google Scholar] [CrossRef]
  59. Kiszler, T.; Ebell, K.; Schemann, V. A Performance Baseline for the Representation of Clouds and Humidity in Cloud-Resolving ICON-LEM Simulations in the Arctic. Journal of Advances in Modeling Earth Systems 2023, 15, 1–14. [Google Scholar] [CrossRef]
  60. Schmale, J.; Henning, S.; Henzing, B.; Keskinen, H.; Sellegri, K.; Ovadnevaite, J.; et al. Collocated observations of cloud condensation nuclei, particle size distributions, and chemical composition. Scientific data 2017, 4, 1–27. [Google Scholar] [CrossRef]
  61. Twomey, S. The nuclei of natural cloud formation. Part II: The supersaturation in natural clouds and the variation of cloud droplet concentration. Geofisica pura e applicata 1959, 43, 243–249. [Google Scholar] [CrossRef]
  62. Kretzschmar, J.; Stapf, J.; Klocke, D.; Wendisch, M.; Quaas, J. Employing airborne radiation and cloud microphysics observations to improve cloud representation in ICON at kilometer-scale resolution in the Arctic. Atmospheric Chemistry and Physics 2020, 20, 13145–13165. [Google Scholar] [CrossRef]
  63. Costa-Suros, M.; Sourdeval, O.; Acquistapace, C.; Baars, H.; Henken, C. C.; Genz, C.; et al. Detection and attribution of aerosol-cloud interactions in large-domain large-eddy simulations with the ICOsahedral Non-hydrostatic model. Atmospheric Chemistry and Physics 2020, 20, 5657–5678. [Google Scholar] [CrossRef]
  64. Wood, R. Relationships between optical depth, liquid water path, droplet concentration, and effective radius in adiabatic layer cloud, University of Washington, 2006. (https://atmos.uw.edu/~robwood/papers/chilean_plume/optical_depth_relations.pdf; accessed on 14 October 2023). 14 October.
  65. Mittermaier, M. A critical assessment of surface cloud observations and their use for verifying cloud forecasts. Quarterly Journal of the Royal Meteorological Society 2012, 138, 1794–1807. [Google Scholar] [CrossRef]
  66. Hogan, R. J.; O’Connor, E. J.; Illingworth, A. J. Verification of cloud-fraction forecasts. Quarterly Journal of the Royal Meteorological Society 2009, 135, 1494–1511. [Google Scholar] [CrossRef]
  67. Morcette, C. J.; O’Connor, E. J.; Petch, J. C. Evaluation of two cloud parametrization schemes using ARM and Cloud-Net observations. Quarterly Journal of the Royal Meteorological Society 2012, 138, 964–979. [Google Scholar] [CrossRef]
  68. Mullammaa, Y. R.; Sulev, M. A.; Pyldmaa, V. K.; Ohvril, H. A.; Niylisk, H. J.; Allenov, M. I.; et al. Stochastic structure of cloud and radiation fields. NASA TT F-822, Studies in atmospheric physics, AN ESR, Institute of Physics and Astronomy, 1975, 18, (https://archive.org/details/nasa_techdoc_19760004517; accessed on 14 October 2023). [Google Scholar]
  69. Kawai, H.; Yukimoto, S.; Koshiro, T.; Oshima, N.; Tanaka, T.; Yoshimura, H.; Nagasawa, R. Significant improvement of cloud representation in the global climate model MRI-ESM2. Geoscientific Model Development 2019, 12, 2875–2897. [Google Scholar] [CrossRef]
  70. Tarasova, T.; Chubarova, N. On the calculation of optical thickness of extended low and middle clouds using measurements of solar radiation in three solar spectrum ranges on the Earth’s surface. Izvestiya Atmospheric and Oceanic Physics 1994, 30, 253–257. (https://istina.msu.ru/publications/article/376715/; accessed on 14 October 2023). [Google Scholar]
  71. Crewell, S.; Simmer, C.; Feijt, A.; van Meijgaard, E. CLIWA-NET: BALTEX BRIDGE Cloud Liquid Water Network. Internat. BALTEX Secretariat, 2003. (https://baltex-research.eu/publications/SSG_minutes_diverse/BALTEX_NO26.pdf; accessed on 14 October 2023). 14 October.
  72. Teixeira, J. Cloud Fraction and Relative Humidity in a Prognostic Cloud Fraction Scheme. Monthly Weather Review 2001, 129, 1750–1753. [Google Scholar] [CrossRef]
  73. Shimpo, A.; Kanamitsu, M.; Iacobellis, S.F. Comparison of Four Cloud Schemes in Simulating the Seasonal Mean Field Forced by the Observed Sea Surface Temperature. Monthly Weather Review 2008, 136, 2557–2575. [Google Scholar] [CrossRef]
  74. Park, R.-S.; Chae, J.-H.; Hong, S.-Y. A revised prognostic cloud fraction scheme in a global forecasting system. Monthly Weather Review 2016, 144, 1219–1229. [Google Scholar] [CrossRef]
  75. Schaefer, S.; Hogan, R.; Rieger, D.; Koehler, M.; Ahlgrimm, M.; Ukkonen, P. Improvements in radiation, gas and cloud parametrization in ICON with ecRad. ICCARUS 2023. Book of Abstracts, 2023, 23. (https://go.dwd-nextcloud.de/index.php/s/cGZw9B35N8W8njF ?dir=undefinedpath=%2FTuesdayopenfile=68207; accessed on 14 October 2023).
  76. Park, S.; Bretherton, C.S.; Rasch, P.J. Integrating cloud processes in the Community Atmosphere Model, Version 5. Journal of Climate 2014, 27, 6821–6856. [Google Scholar] [CrossRef]
  77. Li, J.; Huang, J.; Wang, T.; Lv, Q.; Jin, H. A global survey of cloud overlap based on CALIPSO and CloudSat measurements. Atmospheric Chemistry and Physics 2015, 15, 519–536. [Google Scholar] [CrossRef]
  78. Dupuy, F.; Mestre, O.; Serrurier, M.; Burda, K.V.; Zamo, M.; Citlali, N.; et al.; 2021 ARPEGE Cloud Cover Forecast Postprocessing with Convolutional Neural Network. Weather and Forecasting 2021, 36, 567–586. [Google Scholar] [CrossRef]
  79. Baran, A.; Lerch, S.; El Ayari, M.; Baran, S. Machine learning for total cloud cover prediction. Neural Computing and Applications 2021, 33, 2605–2620. [Google Scholar] [CrossRef]
  80. Prill, F.; Reinert, D.; Rieger, D.; Zängl, G. ICON Tutorial. Working with the ICON Model, Deutscher Wetterdienst: Offenbach, Germany, 2023: 272 pp. [CrossRef]
  81. Muench, S.; Lohmann, U. Developing a Cloud Scheme With Prognostic Cloud Fraction and Two Moment Microphysics for ECHAM-HAM. Journal of Advances in Modeling Earth Systems 2020, 12, 1–37. [Google Scholar] [CrossRef]
  82. Khain, P.; Shpund, J.; Levi. , Y.; Khain, A. Warm-phase spectral-bin microphysics in ICON: reasons of sensitivity to aerosols. Atmospheric Research 2022, 279, 106388. [Google Scholar] [CrossRef]
  83. Rothenberg, D.; Avramov, A.; Wang, C. On the representation of aerosol activation and its influence on model-derived estimated of the aerosol indirect effect. Atmospheric Chemistry and Physics 2018, 18, 7961–7983. [Google Scholar] [CrossRef]
  84. Tontilla, J.; O’Connor, E.J.; Niemelae, S.; Raeisaenen, P.; Jaervinen, H. Cloud base vertical velocity statistics: a comparison between an atmospheric mesoscale model and remote sensing observations. Atmospheric Chemistry and Physics 2011, 11, 9207–9218. [Google Scholar] [CrossRef]
  85. Malavelle, F. F.; Haywood, J. M.; Field, P. R.; Hill, A. A.; Abel, S. J.; Lock, A. P.; et al. A method to represent subgrid-scale updraft velocity in kilometer-scale models: Implication for aerosol activation. Journal of Geophysical Research: Atmospheres 2014, 119, 4149–4173. [Google Scholar] [CrossRef]
  86. Khain, A.; Pokrovsky, A.; Pinsky, M.; Seifert, A.; Phillips, V. Simulation of effects of atmospheric aerosols on deep turbulent convective clouds using a spectral microphysics mixed-phase cumulus cloud model. Part I: Model description and possible applications. Journal of the Atmospheric Sciences 2004, 124, 2963–2982. [Google Scholar] [CrossRef]
  87. Van Weverberg, K.; Morcette C., J. Sensitivity of cloud-radiative effects to cloud fraction parametrizations in tropical, midlatitude, and arctic kilometer-scale simulations. Quarterly Journal of the Royal Meteorological Society 2022, 148, 2563–2586. [Google Scholar] [CrossRef]
Preprints 88865 g001
Figure 1. The domain of the ICON simulations with 1.1 km grid spacing and CLOUDNET sites. The figure was created using Google Earth Pro.
Figure 1. The domain of the ICON simulations with 1.1 km grid spacing and CLOUDNET sites. The figure was created using Google Earth Pro.
Preprints 88865 g001
Preprints 88865 g002
Figure 2. The median grid-scale liquid water content (a, c, e) and its frequency of occurrence (b, d, f) according to CLOUDNET measurements and ICON simulations in Lindenberg (c, d), Jülich (a, b), Munich (e, f). The interquartile range is shown by filling. The LWC medians were obtained using hourly average datasets.
Figure 2. The median grid-scale liquid water content (a, c, e) and its frequency of occurrence (b, d, f) according to CLOUDNET measurements and ICON simulations in Lindenberg (c, d), Jülich (a, b), Munich (e, f). The interquartile range is shown by filling. The LWC medians were obtained using hourly average datasets.
Preprints 88865 g002
Preprints 88865 g003
Figure 3. Cloud droplets number concentrations over the simulation domain at 10:50 h UTC (a) and 12:40 h UTC (b) on September 19, 2021. Calculations from MODIS data with 1 km grid spacing using method (Equation 4).
Figure 3. Cloud droplets number concentrations over the simulation domain at 10:50 h UTC (a) and 12:40 h UTC (b) on September 19, 2021. Calculations from MODIS data with 1 km grid spacing using method (Equation 4).
Preprints 88865 g003
Preprints 88865 g004
Figure 4. Effects of an CCN increase, case September 19, 2021: a) Box plots of simulated cloud droplet concentrations at CCN 250 and 1700 cm-3 at CLOUDNET sites; b) The dependence of the concentration of cloud droplets on the vertical velocity at the cloud base in the Segal-Khain scheme at CCN 1700 cm-3 [19]; c) Histograms of grid-scale liquid water path at CCN 250 and 1700 cm-3 for the entire modeling area; d) Histograms of cloud optical thickness at CCN 250 and 1700 cm-3 for the entire modeling area.
Figure 4. Effects of an CCN increase, case September 19, 2021: a) Box plots of simulated cloud droplet concentrations at CCN 250 and 1700 cm-3 at CLOUDNET sites; b) The dependence of the concentration of cloud droplets on the vertical velocity at the cloud base in the Segal-Khain scheme at CCN 1700 cm-3 [19]; c) Histograms of grid-scale liquid water path at CCN 250 and 1700 cm-3 for the entire modeling area; d) Histograms of cloud optical thickness at CCN 250 and 1700 cm-3 for the entire modeling area.
Preprints 88865 g004
Table 1. Measurement data and their main characteristics.
Table 1. Measurement data and their main characteristics.
Source Data spatial and temporal resolution Name Quantiles Number Measurement error
25% 50% 75%
CLOUDNET 30 sec Liquid water content (LWC), g/m3 0.04 0.10 0.24 116206 1.7 dBZ
Liquid water path (LWP), g/m2 57 106 219 3670 48 g/m2
Ice water content, g/m3 0.0008 0.004 0.012 93008 1.7 dBZ
MODIS 5 min,
1 km		 LWP, g/m2 46 99 208 622 335 910 19%
Droplets effective radius (Reff), um 11 15 23 8%
Cloud optical thickness (COT) 5 10 20 9%
BSRN 10 min Global solar irradiance (Q), W/m2 140 225 350 2123 2% (5 W/m2)
Diffuse solar irradiance (D), W/m2 129 191 287 2% (3 W/m2)
Table 2. Median, interquartile range and average values of synchronized hourly average liquid water path data according to CLOUDNET observations and ICON simulations. Jülich, Lindenberg and Munich stations.
Table 2. Median, interquartile range and average values of synchronized hourly average liquid water path data according to CLOUDNET observations and ICON simulations. Jülich, Lindenberg and Munich stations.
Median value / interquartile range / average value, g/m2
Liquid water path source Jülich Lindenberg Munich All sites
CLOUDNET 106 / 152 / 151 89 / 112 / 127 118 / 202 / 215 102 / 139 / 147
ICON grid-scale 21 / 129 / 92 32 / 76 / 65 89 / 99 / 107 35 / 101 / 79
ICON total 53 / 157 / 108 53 / 67 / 69 93 / 81 / 112 61 / 85 / 88
Number of cases 121 201 53 375
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated