Prerpints.org logo
Preprint
Article

Predicting Road Traffic Collisions Using a Two-Layer Ensemble Machine Learning Algorithm.

Altmetrics

Downloads

120

Views

177

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

26 October 2023

Posted:

27 October 2023

Read the latest preprint version here

Alerts
Abstract
Road collisions are among the world’s critical issues causing many casualties, deaths, and economic losses. To deal with this scenario, precise analysis is required. In this paper, we use Machine Learning (ML) techniques to assess and predict road traffic collisions. An ensemble machine learning model with two layers was developed to analyze simulation data from the driving simulator. The first (base) layer integrates supervised learning techniques namely, k- Nearest Neighbors (k-NN) AdaBoost, Naive Bayes (NB), and Decision Trees (DT). The second layer predicts road collisions by combining the base layer outputs by employing the stacking ensemble method using logistic regression as a meta-classifier. The data for this study were imbalanced; therefore, we performed a SMOTE resampling strategy to handle the dataset imbalance. To simplify the model, the PSO algorithm was used to select the most important features in our dataset. The two-layer ensemble model proposed had the best outcomes with an accuracy of 88%, F1 score of 83%, and an AUC of 86% as compared with k-NN, DT, NB, and AdaBoost.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

A World Health Organization (WHO 2018) research report revealed that Kenya was one of the world’s worst collisions recorded, accounting for a fatality rate of 27.8 per 100,000, population [1]. Accordingly, the city of Nairobi recorded the highest share of the total road crashes in Kenya. In addition, road traffic collisions in Nairobi Kenya are a cause of significant losses of human life and economic resources. According to the National Transport and Safety Authority (NTSA) Report 2022, 4,690 people lost their lives to road collisions between January 1 and December 13 in 2022. Additionally, the report notes that pedestrians and riders are dying at much higher rates because of car collisions from time to time in Kenya. The UN's initiative, "The Global Goals for Sustainable Development (2020)," presents the following recommendations to solve this issue in numerical three: to cut the number of people killed and injured worldwide in traffic collisions in half by 2030. As a result, research into building prediction models (PMs) and traffic collision prevention is critical to meeting this objective for sustainable development to improve road safety policies and to reduce fatalities on roads, by developing a crash prediction model using machine learning algorithms to predict road collisions and their patterns. To predict road collisions, ML techniques have been applied to primary and secondary road collision datasets.
Supervised classification methods are widely used ML approaches that attempt to explain the dependent variable in terms of the independent variables [2]. Various ML algorithms have been successfully used to extract usable information from huge and complicated data sets containing road traffic collisions, weather patterns, and so on. Classification techniques are widely used in traffic collision analysis, to develop classifiers that can predict road traffic collisions and their trends.
There's been an increased level of interest worldwide over the last few years in investigating road traffic collisions, particularly in analyzing and modeling collision data to improve understanding and assessment of the causes and impacts of these collisions [3]. In this study, we perform accident analysis, by applying a two-layer ensemble method using logistic regression as a meta-classifier, and the four most popular supervised machine learning algorithms: NB, k-NN, DT, and AdaBoost, because of their proven accuracy in this field.

2. Materials and Methods

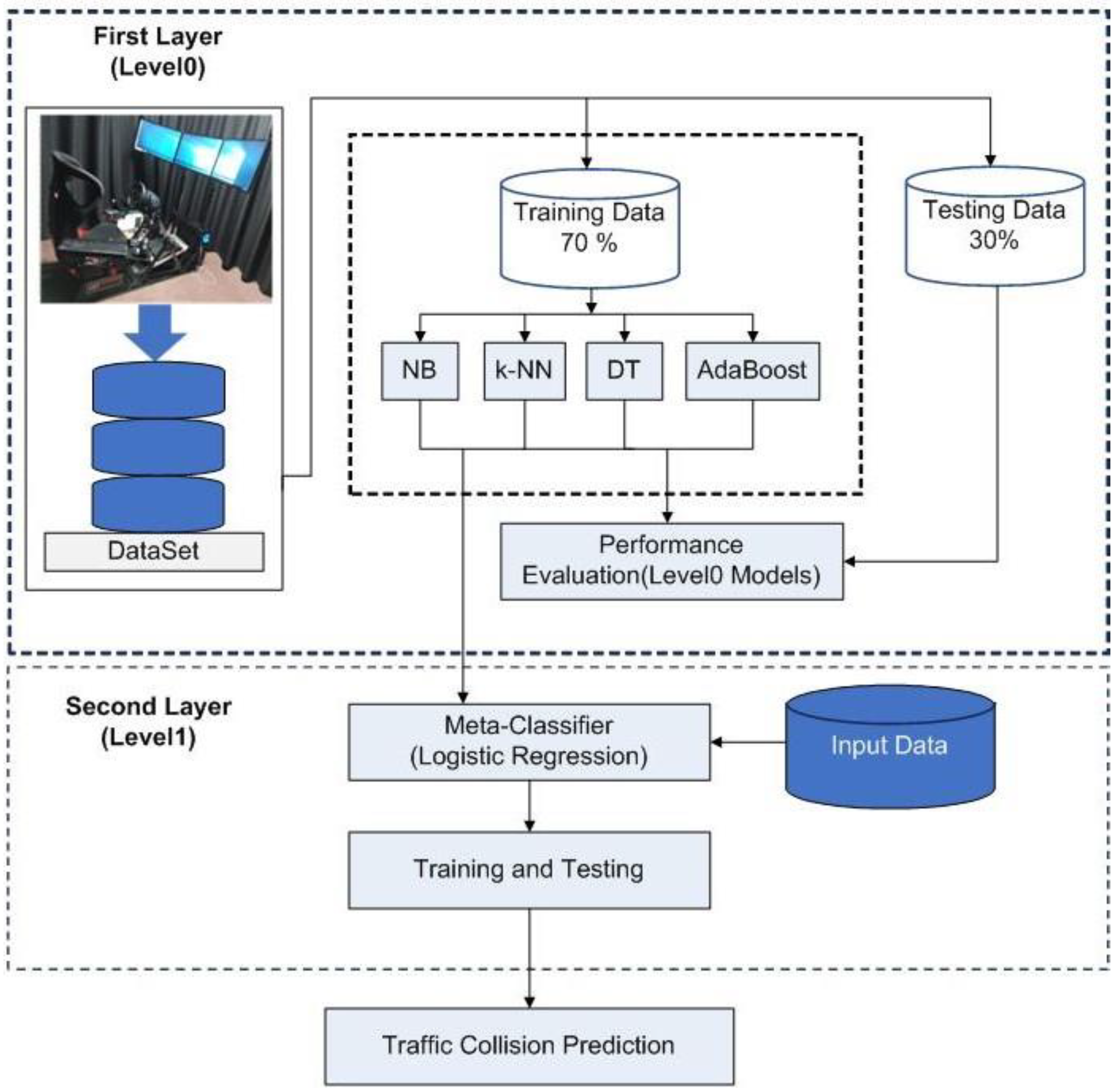
In this study, we developed an ensemble model with two layers using four base classifiers and a meta-classifier that integrates the base layer models to improve the performance. The four supervised ML algorithms employed to predict road collisions and their patterns are k-NN, DT, AdaBoost, and Naïve Bayes. Subsequently, the logistic regression was integrated as a meta-classifier in the second layer of the model by integrating the outputs of the four first layer models. The research methodology has been structured into the following steps: data collection, data preprocessing, building a classification model, and performance evaluation of the model.

2.1. Study Population and Data Description

A driving simulator was used to collect data for this study. It is very dangerous to conduct trials in the real world environment, driving simulator provides an excellent tool for collecting data in a safe environment [11]. The 3.5km Mbagathi way in Nairobi, Kenya was modelled in the driving simulator at Strathmore University Business School, Institute of healthcare management. The simulations included 80 participants with more than two years of driving experience, who drove through the various simulated roadway scenarios [12]. Weather, the speed limit, lane width, and road layout served as the primary determinants of the scenarios. The driving simulator has a driving seat, a powerful simulation computer, 3 screens that display the driving scenarios, an observer screen, a 7” Tablet that displays the speedometer, a steering wheel, a clutch, a gear stick, an accelerator, and brakes. The simulations were based on 2 scenarios that included before treatment and after treatment.
Preprints 88830 g001
Figure 1. A participant driving on the simulated road scenario at Strathmore University.
Figure 1. A participant driving on the simulated road scenario at Strathmore University.
Preprints 88830 g001
Preprints 88830 g002
Figure 2. The proposed Two-layer ensemble model.
Figure 2. The proposed Two-layer ensemble model.
Preprints 88830 g002

2.2. Data Preprocessing

The data with 15 features were loaded into the panda data frame object to facilitate various preprocessing procedures. Firstly, the data set was normalized using 15 features, after which missing values were discovered in some of the fields. Since the missing values would affect the performance of the model, we replaced the blank and null feature values by applying the mean value of that feature column. The mean values that were used to fill the missing feature records presented no extreme value that could have affected the mean.

2.2.1. Feature Selection

Feature selection is a critical factor in obtaining an accurate prediction. Using all the features leads to an inefficient model, as the number of features increases, models struggle for accuracy hence reducing model performance [13]. In this study, we used Sklearn, a Python library to select the features. To obtain the most important features for this study, we employed four algorithms: particle swarm optimization (PSO), univariate feature selection, recursive feature elimination, and feature importance.
  • Particle swarm optimization (PSO) algorithm: This technique works by searching for the optimal subset of features. It locates the minimum of a function by creating several ‘particles. These particles store their best position as well as the global position. It is this combination of local and global information that gives rise to ‘swarm intelligence’ [14]. In our study we implemented XGBoost and linear regression algorithms to select the best features.
  • Recursive feature elimination: This technique works by selecting the optimal subset of features for estimation by reducing 0 to N features iteratively. The best subset is then chosen based on the model's accuracy, cross-validation score, or Roc-Auc curve.
  • Univariate feature selection: This approach works by selecting the optimal features using the univariate statistical tests. It might be considered a stage in the estimator's preprocessing process. In our study, we implemented the chi-squared statistical test using the SelectKBest method.
  • Feature importance: It works by classifying and evaluating each attribute to create splits. Decision tree models that are developed on ensembles, for example, extra trees and random forests can be used to rank the relevance of certain features. In our study, we employed the extra trees classifier for feature selection.
After performing the feature selection algorithms, we selected the top six features as shown in Table 1 based on the selected features algorithms.
Three techniques, namely univariate, recursive elimination method and feature importance had the top six common features, while the PSO algorithm had four common features with the other three techniques. For this study, we employed the PSO feature selection method because the performance of the model was not affected when evaluating the model using the features selected by the other three techniques.

2.3. Building the Two-Layer Ensemble Model

We evaluated the performance of machine learning approaches, by splitting the dataset in the ration of ratio of 70% training dataset and 30% testing dataset. In our research, we employed four well-known classification algorithms previously used to predict road traffic collisions and the stacking ensemble method to predict road traffic collisions. Stacking is an ensemble method for integrating numerous models with a meta-classifier [15]. Following the development of the base models, the four base models (level-0) – k-NN, AdaBoost, DT, and Naïve Bayes were integrated using a stacking framework for road collision prediction. We selected the four base models because of their proven diversity in predicting road collisions. In the second layer, Logistic regression, was employed as a meta-classifier to classify road collisions from the outputs of the base models. A 10-fold cross-validation technique was used to evaluate how well the models predicted traffic collisions [16]. The following section expounds on the four supervised machine-learning techniques and the stacking method employed for our study.
(i) Naïve Bayesian Classifier (NBC): This algorithm employs the theorem of Bayes. It works by estimating the probability of various classes based on a variety of features and allocates the new class to the class with the highest probability. In our study, Gaussian NB was chosen because the feature set contains continuous variables. The NB is represented by the following formular.
P H E = P E H ∗ P H P E
where P(H|E) is the posterior probability of the hypothesis given that the evidence is true, P(E|H) is likelihood of the evidence given that the hypothesis is true, P(H) is prior probability of the hypothesis, and P(E) is prior probability that the evidence is true. The posterior probability is mainly the probability of ′ H ′ being true given that ′ E ′ is true [17].
(ii) k-Nearest Neighbors (k-NN): This method can be considered a voting system, where the majority class determines the class label of a new data point among its nearest neighbor [18]. It then analyzes datasets, calculates the distance function and similarities between them, and groups them based on k values. In our study, the k value was obtained by performing several tests with values ranging from 1 to 50, and the prediction performance was compared to the k value. We plotted the accuracies for both training and test datasets as shown in figure 3. The performance of k-NN shows a drop in both the test and training datasets after adding neighbors, the drop continues for both until a point where they converge. The test dataset improves with an increase in the number of neighbors from iteration 33 until they converge with the training dataset at neighbor 42. In the proposed model, we set the k value at 42 as this yielded the best results and Euclidean distance was selected as distance function.
The distance between the clusters is used to classify new input data, and the closest cluster is allocated. The following formula illustrates the k-NN approach.
  d x , y = ∑ i = 1 n ( y i − x i ) 2    
where x   , y , is the two points in n-space, n is the number of input samples, and y i ,   x i   is the distance vectors starting from the original point.
(iii) Decision Trees (DT): This methodology is a nonparametric supervised learning method for classification and regression. The goal is to build a model that predicts the target variable's value by learning simple decision rules based on data attributes [19]. This is shown by the mathematical formula below.
E n t r o p y : ∑   i = 1 − p ∗ l o g 2 p i
E n t r o p y S = − p + l o g 2 p + − p - l o g 2 p −
Given S is the sample of training examples, and p+ is the proportion of the positive training examples while p− is the proportion of the negative training examples. DT has an overfitting problem, and to overcome it, we used pruning technique to remove splits with little information gained. This simplifies the DT and eliminates the problem of overfitting. In our study, increasing the tree depth in early stages results in a corresponding improved performance for training dataset and reduced performance in test dataset. As the tree depth grows, a corresponding improvement is noted on both training and test dataset up to the depth of 4. Depth 5 reveals that the model overfits the training dataset at the expense of the test dataset. as shown in figure 4 below. In our study we set the maximum tree depth at 4.
(iv) Adaptive Boosting (AdaBoost): AdaBoost is a classification method that calls a given weak learner algorithm repeatedly in a number of rounds. In the training dataset, each instance is weighed, and overall errors are calculated. More weight is given when it is difficult to predict, and less weight is given when it is simple to predict [20]. The AdaBoost approach has a weight that is represented as a vector for each weak learner. The input samples are illustrated in the equation 5 as follows:
W e i g h t , w i = 1 n
where wi is the i’th training instance weight and n is the number of the training instances.
(v) Stacking ensemble method: Stacking is a method of integrating predictions from various machine learning models on the same dataset, such as bagging and boosting. The stacking technique's architecture consists of two or more models, known as base models or level-0, and meta-models that combine the predictions of the base models, known as level-1 models [21]. For our study, stacking was selected because the employed models are often distinct and fit on the same dataset, then a single model is trained to integrate the outputs of the base as best as possible. In our study, we implemented logistic regression as meta-model to provide a seamless interpretation of the base models' predictions.

2.4. Validation and Performance Measurement

We performed some steps in our experiment to develop the accident prediction model. The first step was to partition the dataset in the ratio of 70% training and 30% testing data. The accuracy was assessed using a 10-fold cross-validation technique in the second stage. The entire dataset was divided into 10 subsets at random, where each subset was used as testing data along with the other nine subsets. Our dataset was imbalanced and therefore we performed a SMOTE resampling strategy to handle the data imbalance. The SMOTE algorithm develops synthetic positive cases to enhance the proportion of the minority class [22]. Our data had 76% instances of no collision and 24% instances of collision as shown in figure 5.
The dataset before SMOTE is illustrated in Figure 6 as a scatter plot with many points spread for the majority class and a small number of points scattered for the minority class majority class, 0 represents No collisions and 1 represents collisions.
The transformed dataset was balanced after SMOTE as shown in the scatter plot figure 7 below.
The crash prediction model's performance was evaluated using the classification report that included computed values of accuracy, precision, recall and F1 score of the algorithms. Our model suffered from underfitting because of using the outputs of the base layer model in the second layer, and to overcome the problem of underfitting in our model, some input features from Table 1 that were used in base layer models were reduced and used together with the output of the base layer models. The reason for this approach was to improve the model. Logistic regression was used to train the level-1 input features as a meta-classifier. The test data set was then used to evaluate the two-layer ensemble model. The model with the highest values of the metrics was considered the best prediction model.
The data generated by the confusion matrix was used to test each model's performance metric. The outcomes of the initial and predicted classifications generated by a classification model comprise the confusion matrix (CM) [23]. Table 2 shows a representation of a confusion matrix.
The confusion matrix layout shown above displays the actual classes in the rows and the predicted class observations in the columns.
The following defines each entity in CM.
In TN, the entities that are originally negative are appropriately classified as negative.
In FN, the entities that are originally positive are wrongly classified as negative.
In TP, the entities that are originally positive are appropriately classified as positive.
In FP, the entities that are originally negative are incorrectly classified as positive.
The observations of the confusion matrix for every model were used to calculate the following performance metrics and evaluate model performance based on these metrics:
Accuracy: represents the percentage of the total number of instances that were correctly classified, as shown by the equation below:
A c c u r a c y   A C = T P + T N T P + T N + F P + F N
Recall: represents the percentage of positive events that were correctly classified as shown by the following equation:
        R e c a l l   R = T P T P + T N
Precision: the percentage of correctly predicted positive instances, shown by the equation below:
P r e c i s i o n   P = T P T P + P
F1- Measure: the performance of the model is measured using the F1 measure that represents the harmonic mean of the Recall and Precision. Its value is in the range of 0 to 1, with 1 denoting the best model and 0 denoting the poorest model. The F1 equation is represented by the equation below:
      F 1 = 2 ∗ R ∗ P R + P
Error rate: represents the frequency of miscalculation of the predictions depicted as represented by the equation below.
E r r o r r a t e E R = 1 − A c c u r a c y

3. Results

3.1. Results of the Classification before SMOTE

Since we are predicting the occurrence of a road traffic collision or not, our problem is a binary classification. In this study the data sample from the driver simulation was split into 30% train data and 70% test data. The model's predictive performance on the test dataset was evaluated by comparing accuracy, precision, and F1 score. The effectiveness of each algorithm has been determined from the simulation driver data by employing AdaBoost, DT, NB, and k-NN as base models using the same selected feature set, then employed the stacking ensemble method using logistic regression as a meta classifier to improve on the model’s accuracy. We performed two scenarios where one was without SMOTE, and the second scenario was with SMOTE. Before pruning DT and setting the k value for k-NN, Decision trees achieves the highest accuracy of 87%, followed by Two-layer ensemble with 85%, Naïve Bayes with 83%, AdaBoost and k-NN achieves a similar score of 79% as illustrated in Table 3 before SMOTE technique.
The robustness of the ML model is largely assessed and validated using the area under the receiver operator curve (AUC). When the AUC is higher than 0.7, the developed model is said to have good predictive power. Before SMOTE, the Two-layer ensemble had an area of about 0.87%, followed by NB algorithm at 0.83%, AdaBoost 0.82%, k-NN 0.8%, and DT with 0.77% as shown in Figure 8. The experiment was done before implementing pruning on DT and setting the k value on k-NN.

3.2. Results of the Classification after SMOTE

The AUC scenarios were also compared, one without any resampling technique and one with a resampling strategy applied. However, after SMOTE resampling strategy, pruning DT due to overfitting, and setting the k value for k-NN, NB had an improved AUC of about 0.86%, AdaBoost remained unchanged while a decrease was noted in the Two-layer ensemble, DT and k-NN as shown in figure 9.
Overall, among all the base models, the recall value was improved on AdaBoost and the proposed two-layer ensemble when applying SMOTE, while a decrease was noted on DT and k-NN, and NB as shown in Table 4. The precision of the model after applying SMOTE was reduced on DT, k-NN, NB, AdaBoost and the two-layer ensemble model. Based on F1 score, a noticeable increase is noted on the two-layer ensemble model and AdaBoost, while the same was reduced on NB, DT, and k-NN. NB and AdaBoost achieve the highest accuracies of 81% and 79% respectively, followed by DT at 77% while k-NN achieves the lowest accuracy of 72% among the base models as shown in Table 4 after SMOTE. The overall accuracy performance, the two-layer ensemble model achieves of 85% accuracy.

4. Discussion

Accuracy is a measure of the effectiveness of a single algorithm, but relying solely on accuracy as a measure of performance index can lead to erroneous conclusions as the model may be biased towards specific collision classes. To solve this limitation in our study, other performance measurement metrics such as recall, F1 score, and precision were evaluated. These performance indicators demonstrate the performance of individual collisions and allow better insights for the model. The outcomes of the "no collisions" and "with collisions" performance measurements are shown in Table 5 and Table 6, respectively.
The definition of precision and recall states that the optimum model is one that optimizes both performance measurements. F1 score is also a good performance indicator because it interprets model performance using both precision and recall. In our study, all the models performed well for no collision, while k-NN, DT and AdaBoost performed poorly for collisions. The two-layer ensemble and NB performed well for collisions as shown in Table 5 and Table 6.
After evaluating the model using the stacking ensemble method with reduced features, there was a significant improvement in the predictive performance of the models. Table 7 shows the classification accuracy of each model. The two-layer ensemble achieved the highest accuracy of 0.88%, NB had 0.81%, DT 0.81%, AdaBoost 0.79%, while k-NN achieved the lowest score of 0.65%.
Among the base models, NB had the best F1 score performance while k-NN had the lowest. Overall, the best F1 score was achieved by the two-layer ensemble model. Similarly, the proposed two-layer ensemble model had the best recall, while NB had the best recall among the base models, AdaBoost and DT had similar scores, k-NN had the lowest recall score. The two-layer ensemble model had superior precision when compared with the other models, as shown in Table 7. The objective of the ensemble method was to predict road collisions by utilizing a minimal feature set which may be acquired within a short period from the collision scene. Based on this prediction, policy makers, road constructors and health facilities would be able to predict road traffic collisions at any given site hence put all the necessary measures required to avert collisions and save lives. The improved two-layer ensemble model demonstrates that it is the most effective method for predicting road collisions.

5. Conclusion

Our research highlights the importance of ML techniques in prediction of road traffic collisions by employing a two-layer ensemble method based on dataset from driving simulator. The employed method: two-layer ensemble was created by combining k-NN, DT, AdaBoost, NB, and Logistic regression in the two levels. With the unique combination of the ML classifiers, the two-layer ensemble method achieved a remarkable accuracy of 88% in a 10-fold cross-validation. Since traffic collisions are random, a model that can predict road traffic collisions within a short time by using a few input features is required, the two-layer ensemble model can then be used to predict road collisions. We recommend the two-layer ensemble method for predicting road collisions and their patterns. Based on the simulated crash data in this study, we highly advocate a common road collision data collection format to be used by traffic and policy enforcers worldwide. The use of computer science techniques like machine learning for predicting road collisions is found to be more accurate and effective hence if a common data collection methodology is applied, the actual collisions data model can produce more realistic results making the application, transferability, and validation of these models easy. For future work, we propose performing sensitivity analysis to select the best features, then employing the two-layer ensemble model and recent techniques such as CNN, D-RNN to predict road collisions as well as performing cross validation and ablation study.

6. Patents

No patents resulting from the work reported in this manuscript.

Author Contributions

The authors confirm contributions to the paper as follows: study conception and design: James Oduor Oyoo, Kennedy Ogada Odhiambo, Jael Sanyanda Wekesa; methodology and data collection: James Oduor Oyoo, Kennedy Ogada Odhiambo, Jael Sanyanda Wekesa, findings analysis and interpretation: James Oduor Oyoo, Kennedy Ogada Odhiambo, Jael Sanyanda Wekesa; draft manuscript preparation: James Oduor Oyoo, Jael Sanyanda Wekesa, Kennedy Ogada Odhiambo ; manuscript revision: Kennedy Ogada Odhiambo, Jael Sanyanda Wekesa, James Oduor Oyoo.

Funding

This research received no external funding.

Data Availability Statement

The datasets analyzed during the current study are available from the corresponding author upon a reasonable request.

Acknowledgments

We would also like to thank the NTSA, Kenha, KURA, Annette Murunga, Kevin Otieno, Institute of Healthcare Management- Strathmore University Business School for their support during scenario modelling and development.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. World Health Organization, Global status report on road safety 2018. Geneva: World Health Organization, 2018. Accessed: Jul. 13, 2023. [Online]. Available: https://apps.who.int/iris/handle/10665/276462.
  2. R. E. Al Mamlook, A. Ali, R. A. Hasan, and H. A. Mohamed Kazim, “Machine Learning to Predict the Freeway Traffic Accidents-Based Driving Simulation,” in 2019 IEEE National Aerospace and Electronics Conference (NAECON), Dayton, OH, USA: IEEE, Jul. 2019, pp. 630–634. [CrossRef]
  3. H. S. Park, Y. W. Park, O. H. Kwon, and S. H. Park, “Applying Clustered KNN Algorithm for Short-Term Travel Speed Prediction and Reduced Speed Detection on Urban Arterial Road Work Zones,” J. Adv. Transp., vol. 2022, pp. 1–11, Feb. 2022. [CrossRef]
  4. T. Bokaba, W. Doorsamy, and B. S. Paul, “Comparative Study of Machine Learning Classifiers for Modelling Road Traffic Accidents,” Appl. Sci., vol. 12, no. 2, p. 828, Jan. 2022. [CrossRef]
  5. K. Sefrioui Boujemaa, I. Berrada, K. Fardousse, O. Naggar, and F. Bourzeix, “Toward Road Safety Recommender Systems: Formal Concepts and Technical Basics,” IEEE Trans. Intell. Transp. Syst., vol. 23, no. 6, pp. 5211–5230, Jun. 2022. [CrossRef]
  6. Md. F. Labib, A. S. Rifat, Md. M. Hossain, A. K. Das, and F. Nawrine, “Road Accident Analysis and Prediction of Accident Severity by Using Machine Learning in Bangladesh,” in 2019 7th International Conference on Smart Computing & Communications (ICSCC), Sarawak, Malaysia, Malaysia: IEEE, Jun. 2019, pp. 1–5. [CrossRef]
  7. R. E. AlMamlook, K. M. Kwayu, M. R. Alkasisbeh, and A. A. Frefer, “Comparison of Machine Learning Algorithms for Predicting Traffic Accident Severity,” in 2019 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT), Amman, Jordan: IEEE, Apr. 2019, pp. 272–276. [CrossRef]
  8. J. Xiao, “SVM and KNN ensemble learning for traffic incident detection,” Phys. Stat. Mech. Its Appl., vol. 517, pp. 29–35, Mar. 2019. [CrossRef]
  9. K. Santos, J. P. Dias, and C. Amado, “A literature review of machine learning algorithms for crash injury severity prediction,” J. Safety Res., vol. 80, pp. 254–269, Feb. 2022. [CrossRef]
  10. M. Zheng et al., “Traffic Accident’s Severity Prediction: A Deep-Learning Approach-Based CNN Network,” IEEE Access, vol. 7, pp. 39897–39910, 2019. [CrossRef]
  11. W. Xiao, X. Luo, and S. Xie, “Feature semantic space-based sim2real decision model,” Appl. Intell., Jun. 2022. [CrossRef]
  12. U. Dahmen, T. Osterloh, and J. Roßmann, “Structured validation of AI-based systems by virtual testing in simulated test scenarios,” Appl. Intell., vol. 53, no. 15, pp. 18910–18924, Aug. 2023. [CrossRef]
  13. K. Zhao, Z. Xu, M. Yan, T. Zhang, D. Yang, and W. Li, “A comprehensive investigation of the impact of feature selection techniques on crashing fault residence prediction models,” Inf. Softw. Technol., vol. 139, p. 106652, Nov. 2021. [CrossRef]
  14. Y. Cao, G. Liu, J. Sun, D. P. Bavirisetti, and G. Xiao, “PSO-Stacking improved ensemble model for campus building energy consumption forecasting based on priority feature selection,” J. Build. Eng., vol. 72, p. 106589, Aug. 2023. [CrossRef]
  15. M. Ameksa, H. Mousannif, H. Al Moatassime, and Z. Elamrani Abou Elassad, “Crash Prediction using Ensemble Methods,” in Proceedings of the 2nd International Conference on Big Data, Modelling and Machine Learning, Kenitra, Morocco: SCITEPRESS - Science and Technology Publications, 2021, pp. 211–215. [CrossRef]
  16. A. Seraj et al., “Cross-validation,” in Handbook of Hydroinformatics, Elsevier, 2023, pp. 89–105. [CrossRef]
  17. “Rish, Irina. (2001). An Empirical Study of the Naïve Bayes Classifier. IJCAI 2001 Work Empir Methods Artif Intell. 3.”.
  18. L. Liu and M. T. Özsu, Eds., “k-Nearest Neighbor Classification,” in Encyclopedia of Database Systems, Boston, MA: Springer US, 2009, pp. 1590–1590. [CrossRef]
  19. P. Abdullah and T. Sipos, “Drivers’ Behavior and Traffic Accident Analysis Using Decision Tree Method,” Sustainability, vol. 14, no. 18, p. 11339, Sep. 2022. [CrossRef]
  20. H. Zhao, H. Yu, D. Li, T. Mao, and H. Zhu, “Vehicle Accident Risk Prediction Based on AdaBoost-SO in VANETs,” IEEE Access, vol. 7, pp. 14549–14557, 2019. [CrossRef]
  21. U. Masoor, N. T. Ratrout, S. M. Rahman, and K. Assi, “Crash Severity Prediction Using Two-Layer Ensemble Machine Learning Model for Proactive Emergency Management,” IEEE Access, vol. 8, pp. 210750–210762, 2020. [CrossRef]
  22. P. Wu, X. Meng, and L. Song, “A novel ensemble learning method for crash prediction using road geometric alignments and traffic data,” J. Transp. Saf. Secur., vol. 12, no. 9, pp. 1128–1146, Oct. 2020. [CrossRef]
  23. A. Theissler, M. Thomas, M. Burch, and F. Gerschner, “ConfusionVis: Comparative evaluation and selection of multi-class classifiers based on confusion matrices,” Knowl. -Based Syst., vol. 247, p. 108651, Jul. 2022. [CrossRef]
Preprints 88830 g003
Figure 3. Line plot illustrating k-NN accuracy on train and test datasets at different neighbors.
Figure 3. Line plot illustrating k-NN accuracy on train and test datasets at different neighbors.
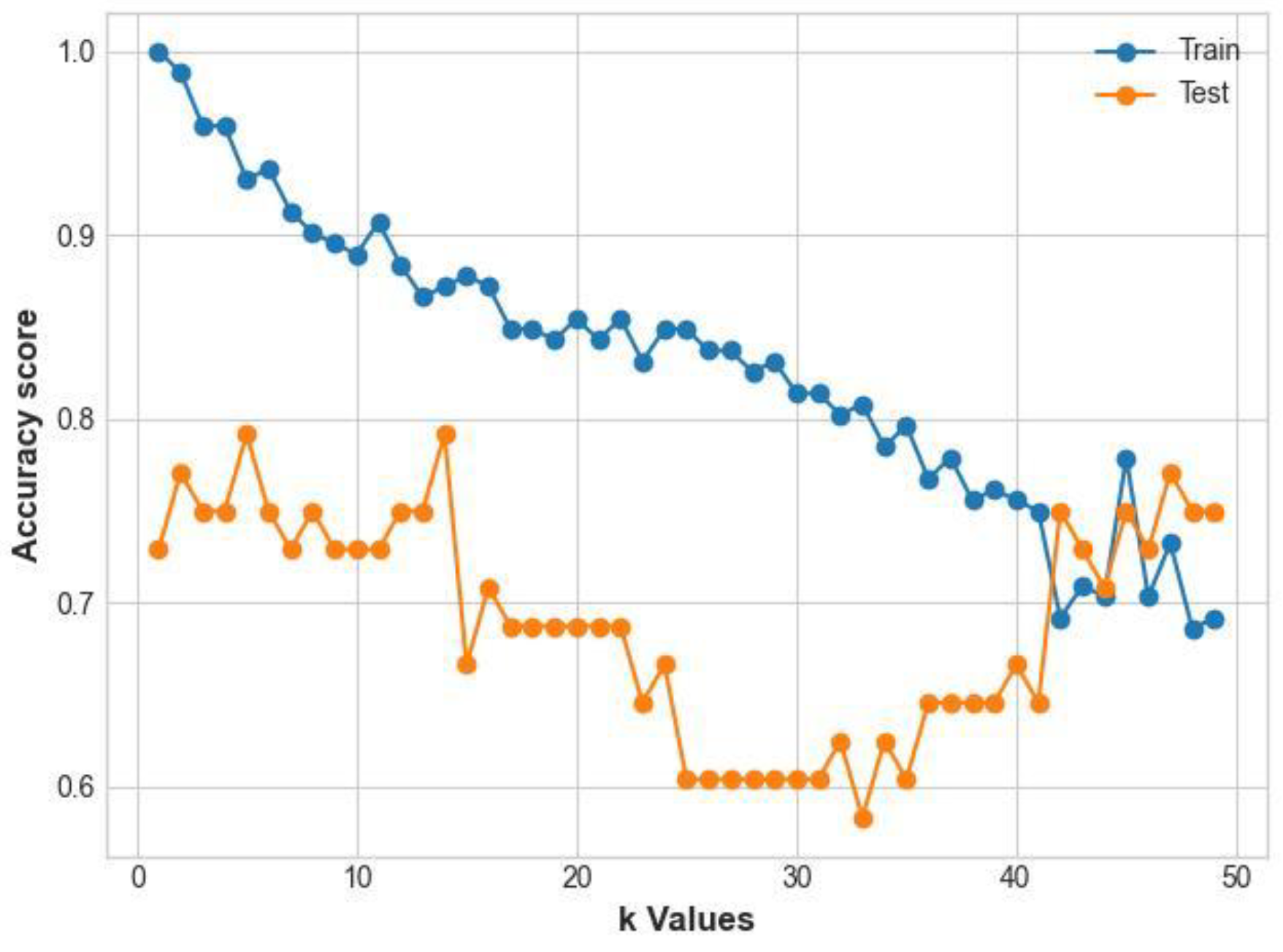
Preprints 88830 g003
Preprints 88830 g004
Figure 4. Line plot illustrates DT accuracy on train and test datasets at different tree depths.
Figure 4. Line plot illustrates DT accuracy on train and test datasets at different tree depths.
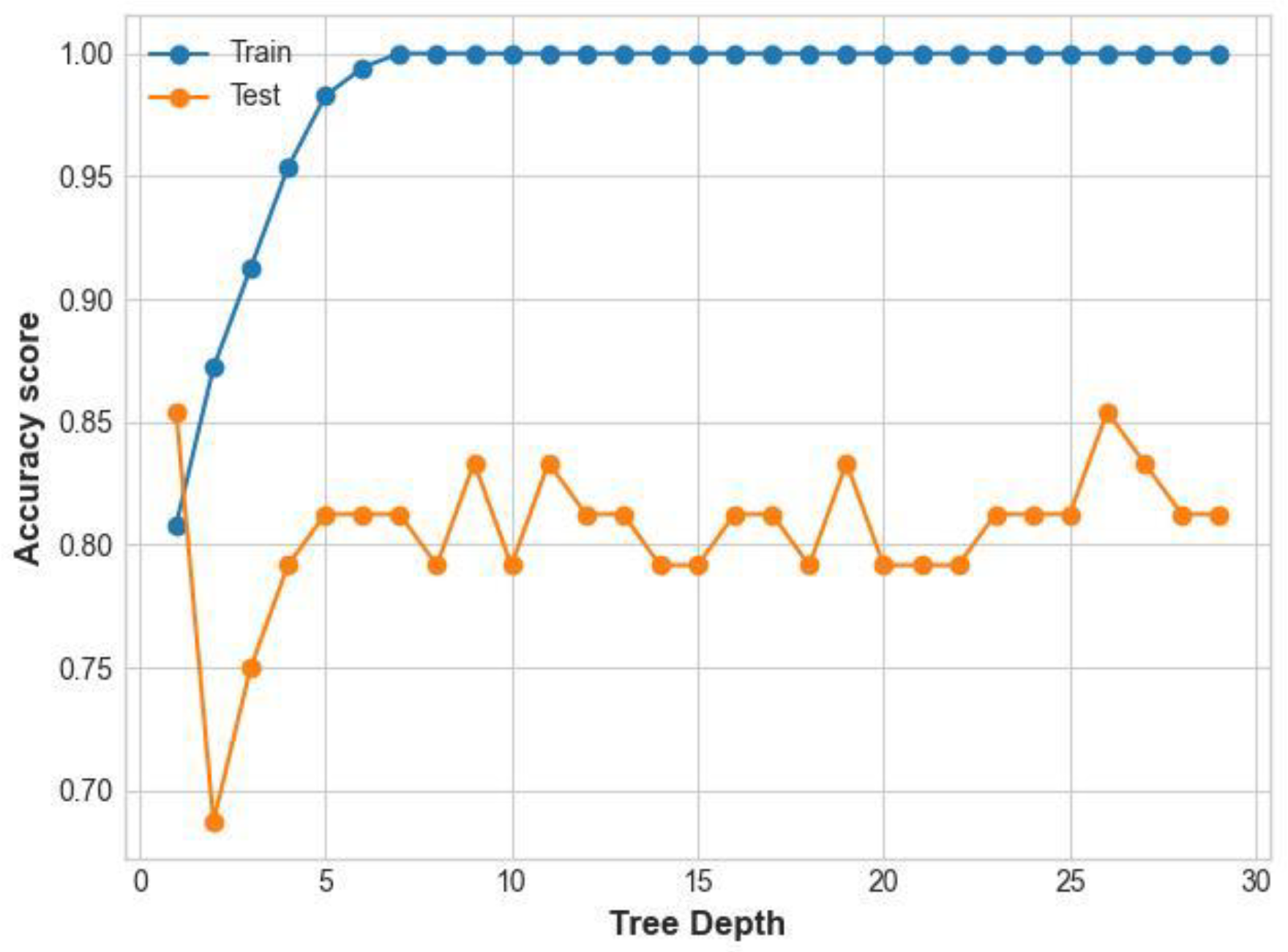
Preprints 88830 g004
Preprints 88830 g005
Figure 5. SMOTE methodology diagram.
Figure 5. SMOTE methodology diagram.
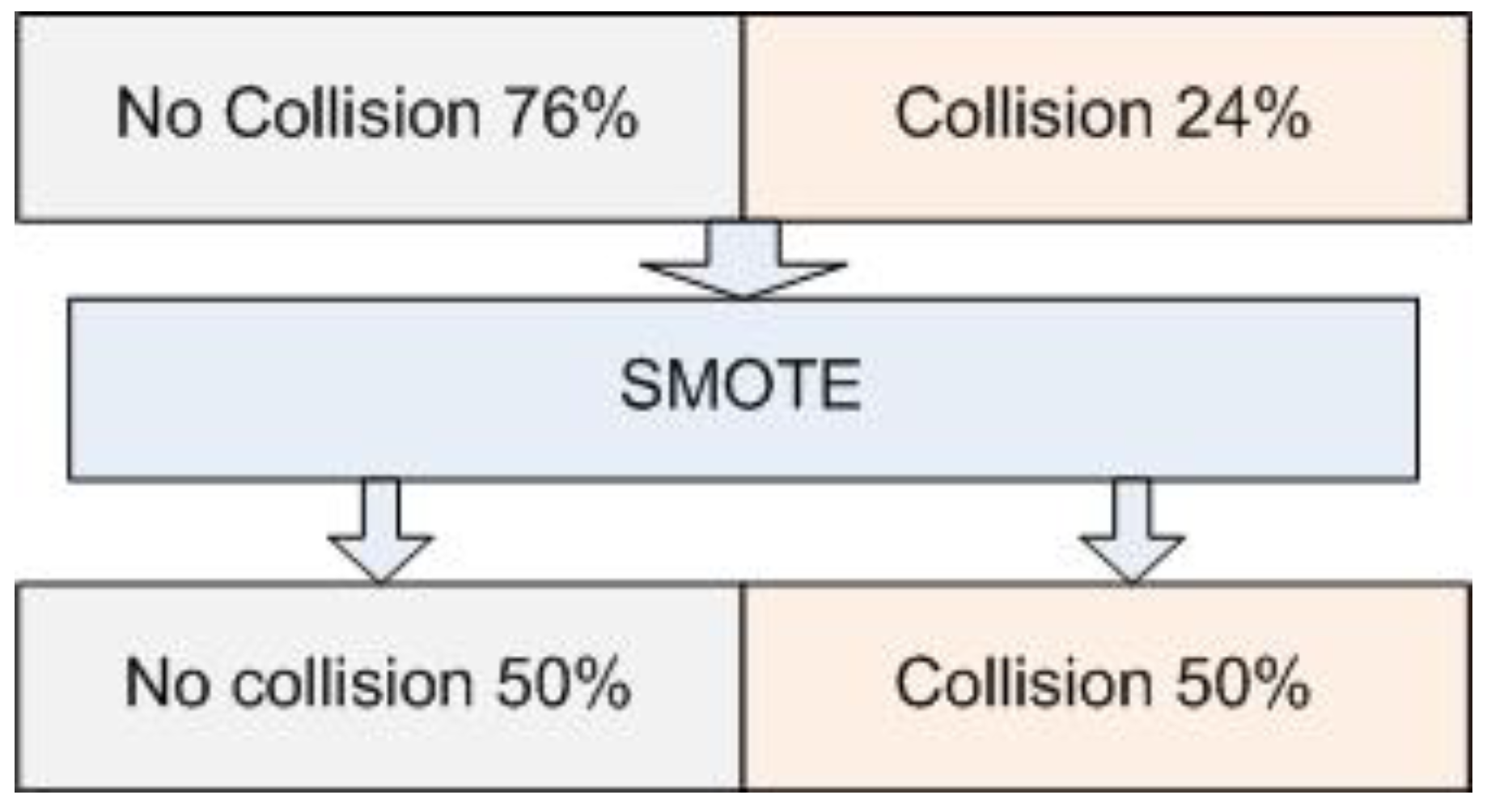
Preprints 88830 g005
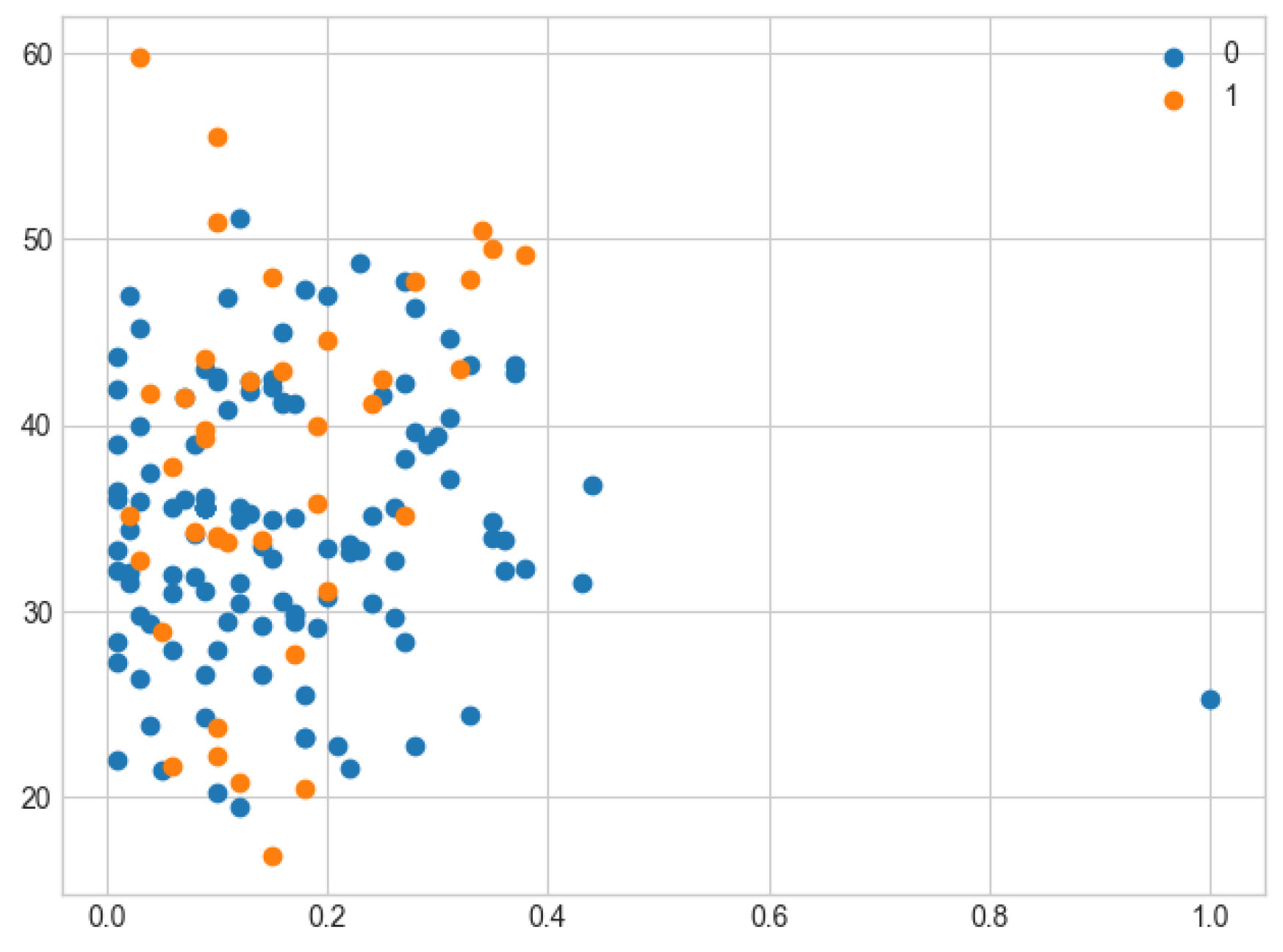
Preprints 88830 g006
Figure 6. Scatter plot of imbalanced dataset before SMOTE.
Figure 6. Scatter plot of imbalanced dataset before SMOTE.
Preprints 88830 g006
Preprints 88830 g007
Figure 7. Scatter plot of the balanced dataset after SMOTE.
Figure 7. Scatter plot of the balanced dataset after SMOTE.
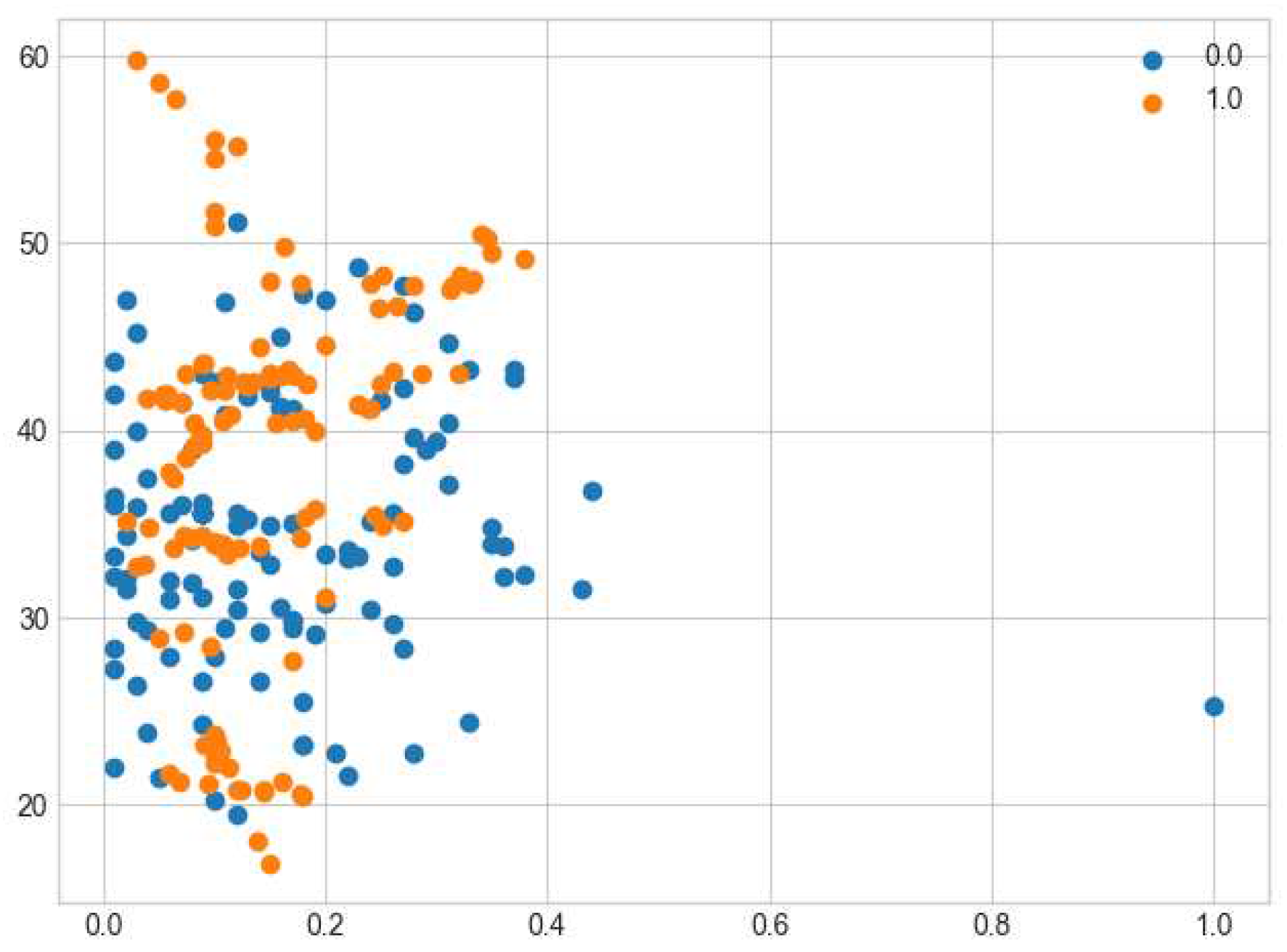
Preprints 88830 g007
Preprints 88830 g008
Figure 8. Comparison of the Area Under the Curve (ROC) for the models before SMOTE.
Figure 8. Comparison of the Area Under the Curve (ROC) for the models before SMOTE.
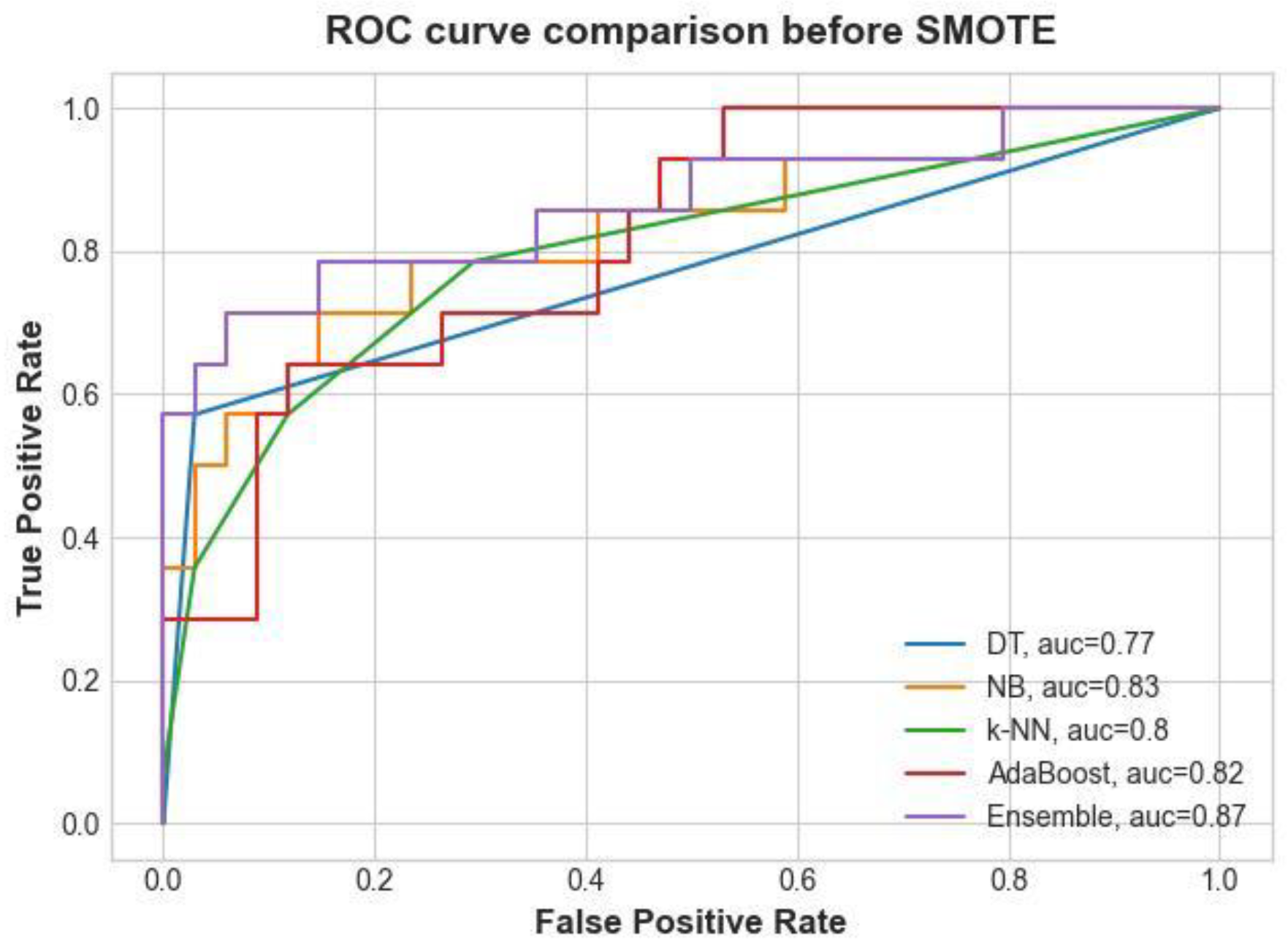
Preprints 88830 g008
Preprints 88830 g009
Figure 9. Comparison of the Area Under the Curve (ROC) for the models after SMOTE.
Figure 9. Comparison of the Area Under the Curve (ROC) for the models after SMOTE.
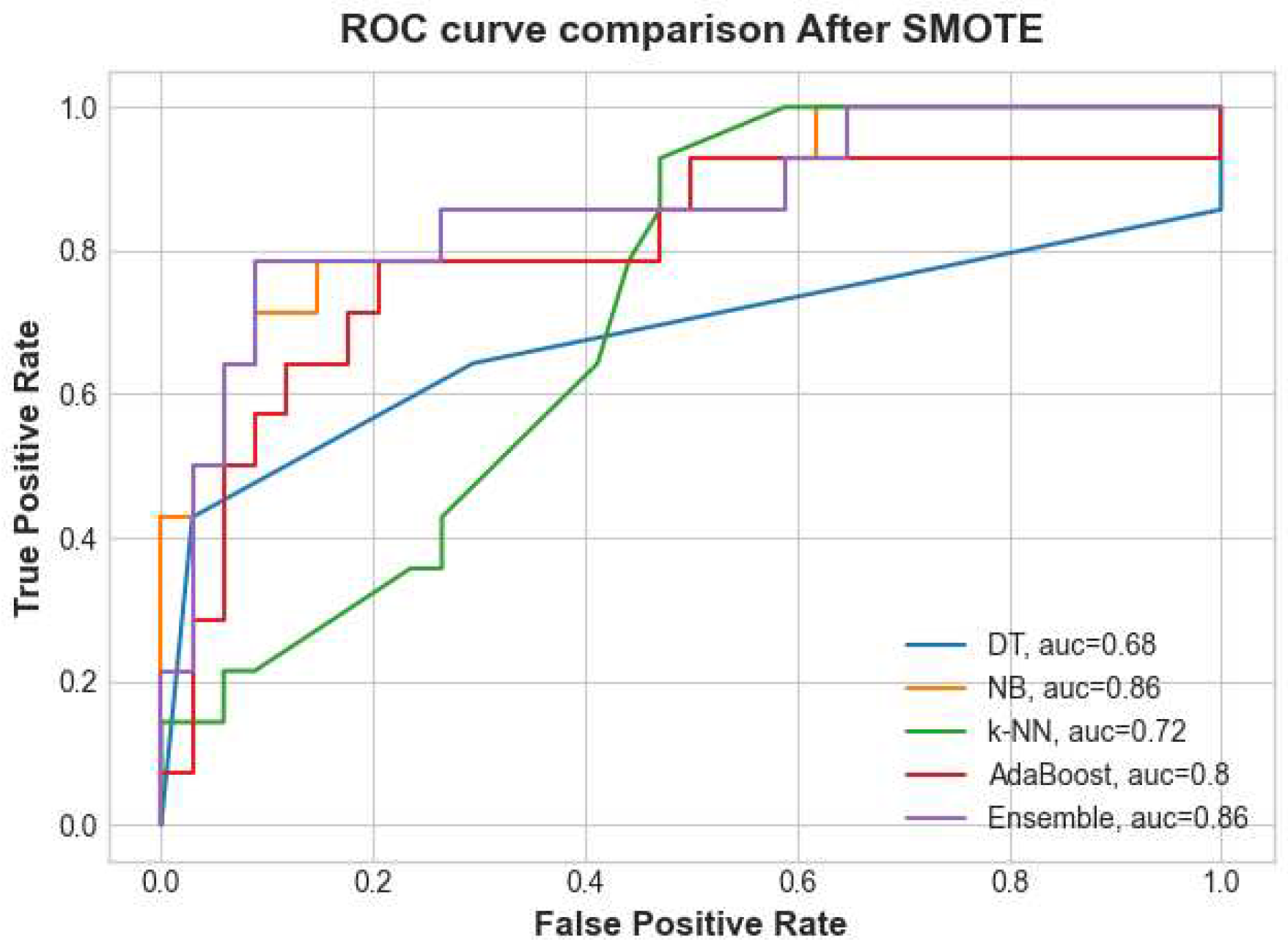
Preprints 88830 g009
Table 1. Features having a strong relationship with road collisions.
Table 1. Features having a strong relationship with road collisions.
Univariate feature Selection Recursive Elimination method Feature importance Particle swarm optimization (PSO)
Lane gap Lane gap Lane gap Lane gap
Speed Speed Speed Speed
Brake Brake Brake Brake
Education level Education level Education level Driver Experience
Driver Experience Driver Experience Driver Experience Surface condition
Drivers’ Age Drivers’ Age Drivers’ Age Gender
Table 2. The architecture of the Confusion Matrix.
Table 2. The architecture of the Confusion Matrix.
Total instances Predicted
Negative Positive

Actual		 Negative

Positive		 True Negative (TN) False Positive (FP)
False Negative (TN True Positive (TP)
Table 3. Results before performing SMOTE Analysis.
Table 3. Results before performing SMOTE Analysis.
Model Accuracy Precision Recall F1 Score
AdaBoost 0.79±0.11 0.76±0.13 0.71±0.12 0.72±0.14
k-NN 0.79±0.08 0.81±0.41 0.66±0.19 0.68±0.25
DT 0.85±0.12 0.87±0.27 0.77±0.22 0.80±0.19
NB 0.83±0.05 0.82±0.20 0.76±0.18 0.78±0.10
Two-Layer Ensemble 0.83±0.06 0.91±0.25 0.75±0.19 0.79±0.11
Table 4. Results after SMOTE Analysis for models.
Table 4. Results after SMOTE Analysis for models.
Model Accuracy Precision Recall F1Score
AdaBoost 0.79±0.09 0.75±0.12 0.73±0.13 0.74±0.08
k-NN 0.72±0.13 0.66±0.12 0.64±0.08 0.65±0.06
DT 0.77±0.08 0.69±0.90 0.68±0.08 0.68±0.10
NB 0.81±0.06 0.72±0.10 0.73±0.12 0.73±0.07
Two-Layer Ensemble 0.85±0.08 0.86±0.09 0.82±0.09 0.83±0.08
Table 5. Outcomes of the models for no collisions.
Table 5. Outcomes of the models for no collisions.
Model Precision Recall F1 Score
k-NN 0.79 0.97 0.87
Decision Trees 0.83 0.86 0.85
AdaBoost 0.83 0.86 0.85
Naïve Bayes 0.85 0.94 0.90
Two-Layer Ensemble 0.87 0.97 0.92
Table 6. Outcomes of the models for collisions.
Table 6. Outcomes of the models for collisions.
Model Precision Recall F1 Score
k-NN 0.80 0.31 0.44
Decision Trees 0.58 0.54 0.56
AdaBoost 0.58 0.54 0.56
Naïve Bayes 0.80 0.62 0.70
Two-Layer Ensemble 0.89 0.62 0.73
Table 7. Outcomes of the models.
Table 7. Outcomes of the models.
Model Accuracy Precision Recall F1 Score
k-NN 0.65±0.09 0.56±0.12 0.56±0.10 0.56±0.09
Decision Trees 0.81±0.74 0.83±0.12 0.70±0.78 0.73±0.72
AdaBoost 0.79±0.08 0.76±0.10 0.71±0.10 0.72±0.09
Naïve Bayes 0.81±0.10 0.77±0.12 0.76±0.11 0.77±0.09
Two-Layer Ensemble 0.88±0.08 0.86±0.09 0.83±0.11 0.84±0.79
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated