Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

Network-Independent Grid Synchronous Stability Boundary and Spontaneous Synchronization

Yu Yuan  *

Submitted:

10 January 2024

Posted:

10 January 2024

Read the latest preprint version here

Abstract
Spontaneous synchronization on complex networks is widespread in the real world. These synchronization behaviors are believed to be closely related to the network topology. However, it is difficult to obtain complete information in reality. Therefore, a network-independent analysis path is needed. In this study, a synchronized stability boundary equation is derived which is system- and disturbance-independent and applicable to arbitrarily coupled grids. The results also imply that spontaneous synchronization on a network may be network independent. These conclusions provide new research paths for network synchronization and analyze the synchronization stability of grids in a unified way.
Keywords: 
Complex network
;  
spontaneous synchronization
;  
synchronous stability boundary
Subject: 
Physical Sciences  -   Other

Introduction

The study of synchronization began with Huygens. With the rise of the study of collective behavior on complex systems, spontaneous synchronization in coupled systems has attracted public attention1. Synchronization in complex systems is widespread in the real world 1,2, e.g., the aggregation of flocks of birds and schools of fish, the flashing of fireflies, the synchronization of generators.
Currently, it is widely believed that network topology is closely related to spontaneous synchronization2. In order to analyze these spontaneous synchronization behaviors, the interactions between individuals are first simplified into a coupled complex network, and then studied using the knowledge of network synchronization. However, this is actually difficult to do3. Realistic interactions are often invisible, which may lead to incorrect network topologies. The complexity and nonlinearity of real networks can also make topological information incomplete. Therefore, the appropriate solution is to construct a network-independent synchronization analysis path that identifies the collective synchronization and which individuals are not in this collective only by the behavior of each individual in the system. This can be verified by the results of the study of real grids.
Synchronization is a prerequisite for the normal operation of a power grid4. Large power systems are complex coupled systems where uncertainties5 and nonlinearities coexist. To analyze the stability of these systems, researchers have developed numerous insightful discriminatory methods1,6–10, including finding stability region boundary11–13 and describing the synchronization of generators using the spontaneous synchronization conditions of complex networks2.
Finding the stability boundary of a system is an important fundamental problem12,14,15. The stable boundary is the union of unstable equilibrium points16. When an operating point is outside the boundary, the corresponding system is desynchronized13. The synchronous stability boundary, which is a core concept of grid stability, is closely related to many issues17–19. Therefore, studying synchronous stability boundary has a significant impact on the development of power systems. For decades, scientists and engineers have wanted to find an analytical equation to describe the boundary11,12,20. On the other hand, the reasonableness of this assumption, which directly equates the spontaneous synchronization with the synchronization stability, has been questioned7,21 and challenges remain in applying it to real networks1. One way to clarify this debate is to obtain evidence of spontaneous synchronization through traditional power system research methods. However, such results are rarely reported7.
Here, an equation is derived and visualized to describe the stability boundary of the power system in a unified way. This equation proves that the synchronization stability boundary is independent of the network and disturbances. Furthermore, simulation results from realistic networks demonstrate that spontaneous synchronization occurs at the boundary. This result may also hint that synchronization condition on the network may be independent of the network. This allows for the construction of another analytical approach to network synchronization. In this case, for potential scenarios where it is difficult to construct a network model, the study demonstrates the success of directly determining synchronization on the real network. Determining the stability of a coupled grid containing n generators requires only n pairs of variables. These variables have a clear physical meaning and are easily accessible. Other fields may be able to ignore the effects of the network when discussing synchronization and only change the specific form of the synchronization conditions.
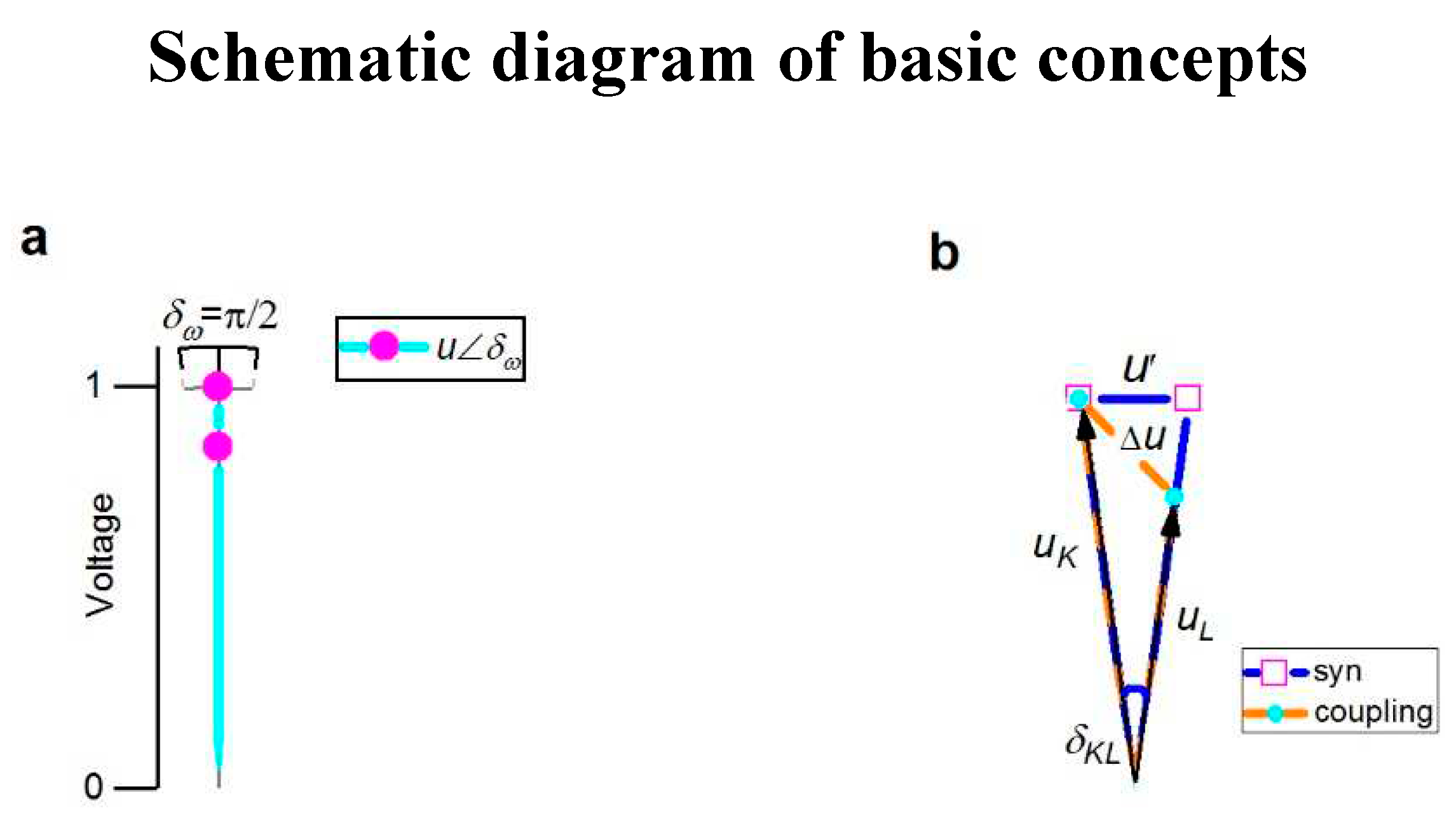
Preprints 95982 g001
Figure 1. Schematic diagram of the power system operating coordinate system （ U , δ ω ) .
Figure 1. Schematic diagram of the power system operating coordinate system （ U , δ ω ) .
Preprints 95982 g001
The generator variables are selected from the port bus voltage per unit U and the rotor speed per unit ω , U ∈ [ 0 ， + ∞ ） ， ω ∈ （ − ∞ ， + ∞ ） . The coordinates of ω are transformed: δ ω = 2 arctan ( ω ) , δ ω ∈ ( − π , π ) , where δ ω is the angle of rotation rate. The angle of rotation rate of the ith generator δ ω i is abbreviated as δ i in the following. Note: δ ω is not the power angle.
a. Synchronised system operation before disturbance, ω 1 = ω 2 = ⋯ = ω n = 1 and δ i = 2 arctan ( ω i ) = π 2 , i = 1 , 2 , ⋯ , n . The magenta dot indicates the operating point of the generator: （ U , δ ω ) .
b. The angle of rotation rate of the subsystems differ after the disturbance. u K , u L are the per unit voltage of the port bus of the Kth and Lth generators, respectively, δ K L = | δ K − δ L | ≥ 0 is the difference in the angle of rotation rate between the Kth and Lth generators. Δ u is defined as the coupling potential difference between generators Kth and Lth (yellow dotted line between Cyan dots). Correspondingly, u ′ is constructed to describe the synchronous potential difference between generators Kth and Lth (solid blue line between magenta square dots). The set of points where | u ′ | = | Δ u | is the synchronous stability boundary (see Methods for details: Derivation of the boundary equations).

Materials and Methods

Extensive interconnections between generators would make stability analysis very difficult(see Extended Figure 1). To solve this problem, the concept of a meta-generator is introduced here. At moment t, the instantaneous values of the n generators system （ u ′ i ( t ) , δ ′ i ( t ) ) , i ∈ ( 1 , 2 , ... , n ) are arranged in descending order by δ ω , relabelled, and then reconstituted as the n meta-generator system （ u i ( t ) , δ i ( t ) ) , i ∈ ( 1 , 2 , ... , n ) .
The essence of the connection between the meta-generators and the original generators is the permutation: S = ( δ ′ 1 δ ′ 2 ... δ ′ i δ ′ i + 1 ... δ ′ n δ 1 δ 2 ... δ i + 1 δ i ... δ n ) . When the condition δ ′ i + 1 ( t ) > δ ′ i ( t ) holds, （ u i + 1 ( t ) , δ i + 1 ( t ) ) = （ u ′ i ( t ) , δ ′ i ( t ) ) , （ u i ( t ) , δ i ( t ) ) = （ u ′ i + 1 ( t ) , δ ′ i + 1 ( t ) ) .
Define the distribution matrix H, where H i ′ j is the share of the i'th generator in the jth meta-generator in period T.

Data sources and experimental procedures

In this study, the IEEE 39-BUS and IEEE 9-BUS models (Extended Figure 4,5,6) were used. The two models are simulated separately using a simulation software package. Here, the fault was set as a three-phase short circuit to ground. The disturbed operating point of each generator was calculated. To observe the movement pattern of the disturbed operating points, no parameters were set for the control elements .
In advance, the fault location was fixed, and the fault duration Δ t was set. This experiment simulated the rotation rate ω ′ i ( t ) and port bus voltage u ′ i ( t ) of the ith generator after different disturbances. Then, the angle of rotation rate of the ith generator δ i ( t ) was calculated. Δ t was increased in a fixed step length and u ′ i ( t ) , δ i ( t ) were calculated again until the system was destabilised. The faulty position was replaced, and the above steps were repeated.
Subsequently, （ u ′ i ( t ) , δ ′ i ( t ) ) , i ∈ ( 1 , 2 , ... , n ) was arranged and relabelled as （ u i ( t ) , δ i ( t ) ) , i ∈ ( 1 , 2 , ... , n ) . This was then averaged as follows:
The mean of （ u i ( t ) , δ i ( t ) ) , i ∈ ( 1 , 2 , ... , n ) over [ 0 , T ] was found: u i = 1 T ∫ 0 T u i ( τ ) d τ and δ K L = 1 T ∫ 0 T δ K L ( τ ) d τ = 1 T ∫ 0 T | δ K ( τ ) − δ L ( τ ) | d τ = 1 T ∫ 0 T δ K ( τ ) − δ L ( τ ) d τ = δ K − δ L .
The mean of （ u i ( t ) , δ i ( t ) ) , i ∈ ( 1 , 2 , ... , n ) over [ T m , T m + d T ] was also found: δ i ( t m ) = 1 d T ∫ T m T m + d T δ i ( τ ) d τ , U i ( t m ) = 1 d T ∫ T m T m + d T U i ( τ ) d τ , δ k l ( t m ) = δ k ( t m ) − δ l ( t m ) . There are several definitions of mean, and the simplest, i.e., the arithmetic mean, was used here.
This work added adjacent meta-generator data ( u K , u L , δ K L ) and ( u K ( t m ) , u L ( t m ) , δ K L ( t m ) ) to the coordinate system u K − u L − δ K L to assess the system stability (Figure 2.b) and time intervals of instability ( T m , T m + d T ) (Figure 2.d).
An expression was fitted with Δ t as the independent variable and u K , u L , δ K , δ L , δ K L as the dependent variable (Figure 3). CCT and UEP were then calculated.
Near the boundary, σ ( δ i ) , δ i , u i was calculated at a finer scale.

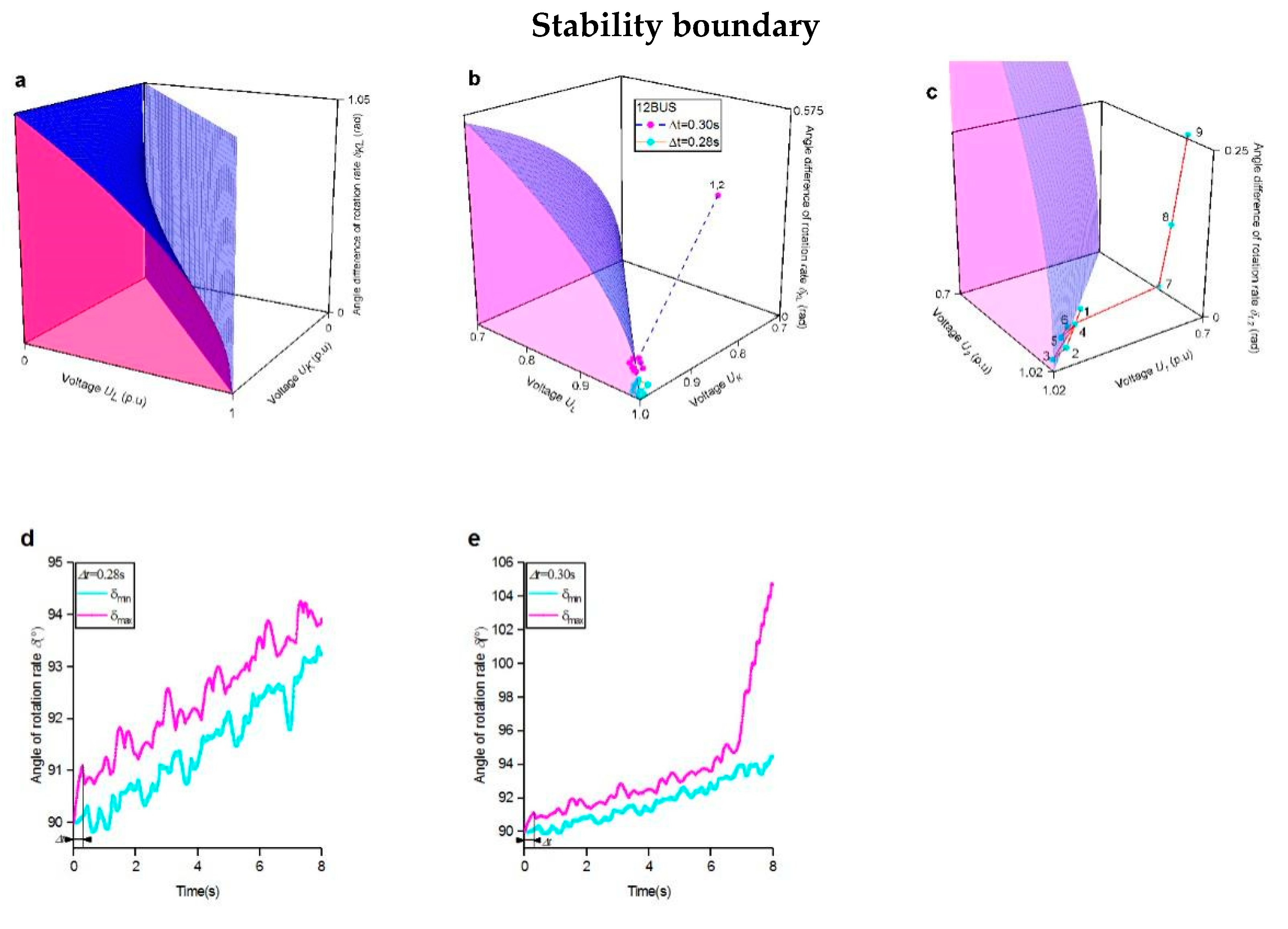
Derivation of the boundary equation

As shown in Figure 1, Δ u = u k 2 + u l 2 − 2 u k u l cos δ k l , u ′ = 2 u k 2 ( 1 − cos δ k l ) .
Following the form of power in electricity P = U 2 R , the coupling power P Δ u = | Δ u | 2 | Z K L | is defined to characterise the coupling between the meta-generators. To describe the energy required for the generator to maintain synchronous stability, the synchronous power is constructed: P u ′ = | u ′ | 2 | Z K L | . Z K L is the impedance between the Kth and Lth meta-generators.
When the system is synchronized, the meta-generators are not in balance and are still coupled ( δ K L = 0 , u ′ = 0 , Δ u = u K − u L ≠ 0 ). When the system is disturbed, δ K L increases from 0, u ′ increases from 0, and Δ u changes. When the coupling power between the two meta-generators is sufficient to provide synchronous power, i.e., | P u ′ | ≤ | P Δ u | , the system is synchronous and stable. Conversely, when | P u ′ | > | P Δ u | , there is not enough coupling power to maintain synchronization, and the system is unstable. It is observed that | P u ′ | | P Δ u | = 1 ⇔ | u ′ | | Δ u | = 1 .
In summary, f ( u K , u L , δ K L ) = | u ′ | | Δ u | = 1 is the system stability boundary equation. When | u ′ | | Δ u | < 1 , the system is stable. When | u ′ | | Δ u | > 1 , the system is unstable. Geometrically, f ( u K , u L , δ K L ) = 1 describes a curved surface that, together with ( 0 , u L , δ K L ) , ( u K , 0 , δ K L ) , ( u K , u L , 0 ) , encloses a stable domain. In summary, the boundary equation | u K | = | u L | ∪ | u L | | u K | = 2 cos δ K L − 1 can be found, where | u K | ≥ | u L | ≥ 0 , δ K L ∈ [ 0 , π 3 ] . The coordinate system u K − u L − δ K L is established, and the boundary is visualized(Figure 2).

Fitting of operating points to trajectories

The intersection of the disturbed trajectory with the stability boundary is the unstable equilibrium point (UEP), and the failure time of the operating point along the disturbed trajectory to reach the UEP is the CCT. To calculate these important results, it is necessary to fit the disturbed trajectory to the kinematic expression in the （ u , δ ω ) coordinate system. The variables of the operating point obtained from the simulation are fed into commercial software to fit the expression of the disturbed operating point.

Operating point behaviour on the boundary

d δ K L d ( Δ t ) is the derivative of δ K L of the meta-generators with respect to Δ t . Near the boundary, the derivative of d δ K L d ( Δ t ) of the partial meta-generators changes from positive to negative (Figure 3). For this unusual phenomenon, on a finer scale, （ u i ( t ) , δ i ( t ) ) , i ∈ ( 1 , 2 , ... , n ) is calculated sequentially for different Δ t . The standard deviation of δ i is calculated separately (Figure.4): σ ( δ i ) = ∑ i = 1 n ( δ i − μ ( δ i ) ) 2 n , μ ( δ i ) = ∑ i = 1 n δ i n .

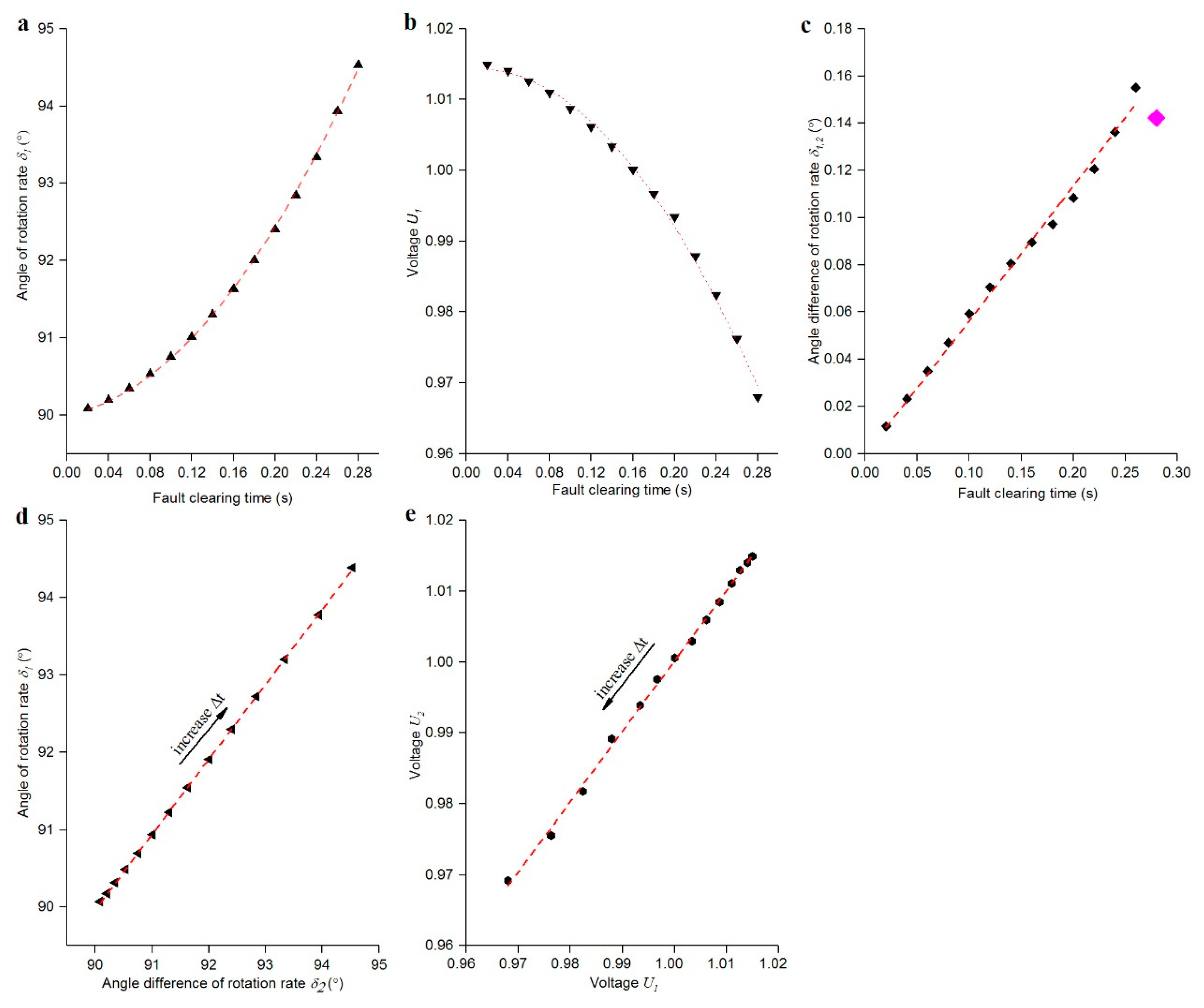
Result and discuss

Preprints 95982 g002
Figure 2. Stability boundary.
Figure 2. Stability boundary.
Preprints 95982 g002
a. Visualisation of the stable boundary. The stability boundary (blue surface) and ( 0 , u l , δ k l ) , ( u k , 0 , δ k l ) , ( u k , u l , 0 ) (pink surface) together enclose the stability domain. The boundary equation is | u k | = | u l | ∪ | u l | | u k | = 2 cos δ k l − 1 (see Methods for details: Derivation of the boundary equations). For visualisation purposes, the radian system is used for δ k l in the figure.
b and c are the results of the 12BUS three-phase short circuit to ground simulation, respectively. The system is stable at Δ t = 0.28 s , unstable at Δ t = 0.3 s , and unstable in ( 6 s , 7 s ) .
d. Boundary stability results for the 12BUS three-phase short circuit to ground, where Δ t is the duration of the fault. The positions of all operating points at Δ t = 0.28 s and Δ t = 0.3 s are indicated by cyan and magenta dots, respectively. The plane | u l | = | u k | perpendicular to u k − u l is not shown. At Δ t = 0.28 s , all the operating points are clustered together. However, Δ t = 0.3 s , the operating points are far away from the other points and outside the boundary.
e. The instability process of Multiswing for the 12BUS three-phase ground fault, where Δ t = 0.3 s . Numbers 1 to 9 indicate period T m after the fault, and d T = 1 s (see Methods for details). The system is destabilised in the time interval ( 6 s , 7 s ) (Figure 2). The diagram shows the operating points of the meta-generators 1 and 2. The operating point crosses the boundary at the time of instability, and δ k l rapidly increases after the voltage changes .
Regarding the synchronization stability, one different assumption,which appears parallel to the Kuramoto model1, than before 19: the system requires the synchronous power P u ′ = | u ′ | 2 | Z K L | to maintain synchronous stability, and the synchronous power is provided by the coupling power P Δ u = | Δ u | 2 | Z K L | within the system, Z K L is the impedance between the Kth and Lth meta-generators. (see Supplementary Materials for details).
u K = u L ∪ u L u K = 2 cos δ K L − 1 , u K > u L ≥ 0 , δ K L ∈ 0 , π 3
Eq.1 is the analytical equation for the synchronous stability boundary. Specifically, when δ K L > 0 , the set where | u L | = | u K | is the isolated stability domain. There has been previous research on the isolated domain11. Since it is very difficult to always maintain | u L | = | u K | after a disturbance of the system, this situation is not discussed in this paper.
In contrast to previous reports2,11,12, here, The synchronous stability boundary described by Eq.1 is independent of the network topology, system parameters, perturbations and the number of the subsystem. It is an inherent property of the grid systems. Regardless of the changes in the network structure and component parameters, it is only the operating points of the system that change rather than the stability boundary. This feature increases the applicability of the boundary equation to different grid systems and allows the stability of multimachine systems to be analyzed even in scenarios where the topology and parameters are not clear22, such as in a black box situation. Thus, the synchronization stability of the grid can be analyzed in a uniform way. This has been validated on different standard arithmetic models (see Figure 2 and Extended Figure 4). Eq.1 is also suitable for identifying the stability of a power system with multiple swings23 and showing the time interval of instability(as in Figure 2.c and e).
Eq.1 has a variant as follows:
δ K I c r = arccos 1 − u K − u L 2 u L
When | u K | , | u L | are sufficiently close24, the stability margin of the Kth and Lth generator angle rate difference δ K L c r also tends to 0. This indicates that the system may already be in a critical state during normal operation. In this case, even if the difference in the values between δ K and δ L is small, it takes only a very small perturbation to make the system unstable25,26. This may explain why some systems with very small speed differences are more likely to lose synchronization than those with much larger speed differences.
Placing the calculated or measured operating points in the coordinate system u K − u L − δ K L can help directly determine whether the system is stable. A system is considered unstable as long as at least one point ( u K , u L , δ K L ) is outside the boundary Figure 2.b) and far from the other operating points ( σ Δ t ( δ i ) > > σ Δ t − ε ( δ i ) , 0 < ε < Δ t , where Δ t is the fault duration) (Figure 2.b and Figure 4.a). To determine the stability of a power system of n generators, only n pairs of variables u i , δ i , i ∈ ( 1 , 2 , ... , n ) are needed, which are physically meaningful and easily obtainable.
As one of the concepts closely related to stability, intentional isolation is an effective way of avoiding widespread blackouts following instability27. Identifying coherent generators is a prerequisite for building intentional islands28. Information regarding the coherence meta-generator groups can be obtained directly from the graph. That is, the partial synchronization of multiple generators, such as chimeric states29–31, can also be identified with a stable boundary. m operating points outside the boundary indicate that the n meta-generators are sequentially divided into m+1 coherent groups.

Disturbed trajectory and parameters

To understand the behavior of the power system after a disturbance and to calculate the CCT and UEP, it is necessary to study the perturbation trajectories consisting of running points.
Preprints 95982 g003
Figure 3. Fitting results for perturbed trajectories of a 12BUS trajectory of disturbed operating points after a three-phase short circuit to ground fault. In the expressions, (i) denotes the ith meta-generator, and i = 1 , · · · , k , l , · · · , n . The subscripts u and ω denote the coefficients of the meta-generators at u i − Δ t and δ i − Δ t , respectively. Δ T ′ is the starting fault duration at which self-organised behaviour occurs at the disturbed operating point. To make it easier to show the details, δ k l in the picture uses the angle system.( d ( Δ t ) = 0.02 s ).
Figure 3. Fitting results for perturbed trajectories of a 12BUS trajectory of disturbed operating points after a three-phase short circuit to ground fault. In the expressions, (i) denotes the ith meta-generator, and i = 1 , · · · , k , l , · · · , n . The subscripts u and ω denote the coefficients of the meta-generators at u i − Δ t and δ i − Δ t , respectively. Δ T ′ is the starting fault duration at which self-organised behaviour occurs at the disturbed operating point. To make it easier to show the details, δ k l in the picture uses the angle system.( d ( Δ t ) = 0.02 s ).
Preprints 95982 g003
a. The projection of the disturbed trajectory in the δ 1 − Δ t plane, fitted using the equation δ i = a ω ( i ) 2 * Δ t 2 + b ω ( i ) * Δ t + c ω ( i ) , Δ t ∈ 0 , Δ T ′ .
b. The projection of the disturbed trajectory in the u 1 − Δ t plane, fitted using the equation u i = a u ( i ) 2 * Δ t 2 + b u ( i ) * Δ t + c u ( i ) , Δ t ∈ 0 , Δ T ′ .
c. The projection of the disturbed trajectory in the δ 1 , 2 − Δ t plane, fitted using the equation δ k l = δ k − δ l = a k l * Δ t 2 + b k l * Δ t , Δ t ∈ 0 , Δ T ′ . Notably, δ 1 , 2 descended at Δ t = 0.28 s .
d. The projection of the disturbed trajectory in the δ 1 − δ 2 plane, fitted using the equation δ k = a δ * δ l + b δ , Δ t ∈ 0 , Δ T ′ ,where δ k > δ l , a δ > 1 .
e. The projection of the disturbed trajectory in the u 1 − u 2 plane, fitted using the equation u k = a v * u l + b v , Δ t ∈ 0 , Δ T ′ .
Figure 3.a and 3.b show that the operating points move with a uniformly variable speed before the system becomes unstable.
Contrary to intuition32, δ 12 suddenly dropped at Δ t = 0.28 s (Figure 3.c). This anomaly suggested that the system appears to have a tendency to maintain its own stability.
Figure 3.d and E show that the perturbed trajectories of the subsystems of the coupled system are linearly correlated in the stability domain. This indicates that for a determined power grid, each perturbed trajectory has the same T ′ i , T ′ i being the global invariant of the system. The effects of perturbations are global, reflecting the challenges of controlling the stability of complex systems33–35.
When a high degree of accuracy of the results is not needed, a K L = 0 . The following expression can be derived:
Δ T ′ = 2 b K L − a δ − 1 b ω ( i ) a δ − 1 a ω ( i ) , i = 2 , 3 , … , n
This can be used to easily and quickly check the stability margin of the system after a disturbance36. By approximating Δ T ′ as the CCT20,36, the coordinates of the critical stable operating point ( u K c r , u L c r , δ K L c r ) and critical rate of the meta-generator l in the current system can also be estimated37.
u i c r = a u ( i ) 2 Δ T ′ 2 + b u ( i ) Δ T ′ + c u ( i ) δ K I c r = b K I Δ T ′ , Δ t ∈ 0 , Δ T ′ δ L c r = arccos u K − u L 2 u K − b δ a δ − 1 = a ω ( L ) 2 Δ T ′ 2 + b ω ( L ) Δ T ′ + c ω ( L ) ω L c r = tan δ L c r 2
In summary, the CCT and UEP can be calculated using only information about the rotation rate10, but considering only a single information source may result in more errors. Theoretically, using Δ T ′ directly as the CCT would also lead to a conservative result.
The current power system is receiving an increasing number of renewable energy sources. These sources are connected to the power grid via inverters, which may change the inertia of the system38–40, complicating the coefficients. This issue should be further studied.
On a finer scale, the operating points near the stability boundary exhibit unusual behavior (Figure 4).
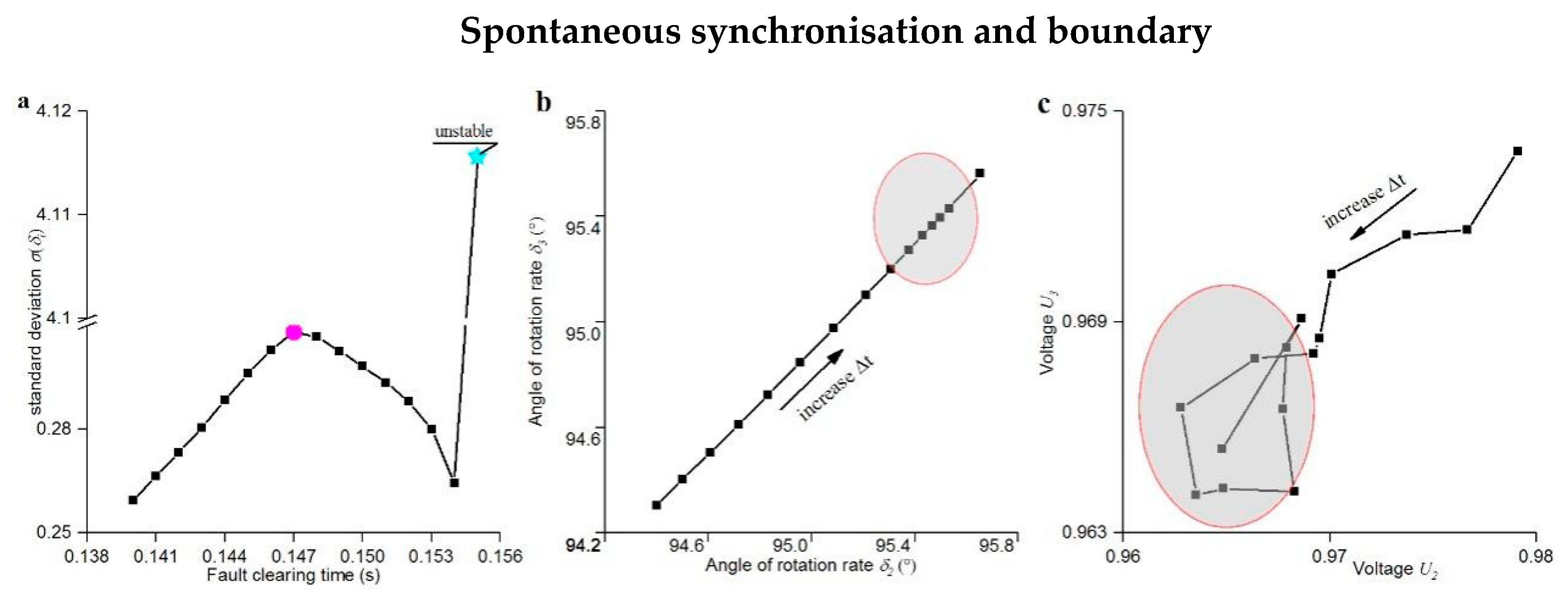
Preprints 95982 g004
Figure 4. Boundary effects of the 18bus three-phase short circuit to ground fault, with increased fault duration Δ t from 0.140s to 0.154s ( d ( Δ t ) = 0.001 s ), and the trajectory of the disturbed operating point near the boundary. The arrow shows the direction of increase of Δ t . The simulation result showed instability at Δ t =0.155s.
Figure 4. Boundary effects of the 18bus three-phase short circuit to ground fault, with increased fault duration Δ t from 0.140s to 0.154s ( d ( Δ t ) = 0.001 s ), and the trajectory of the disturbed operating point near the boundary. The arrow shows the direction of increase of Δ t . The simulation result showed instability at Δ t =0.155s.
Preprints 95982 g004
a. σ ( δ i ) is the standard deviation of δ. σ ( δ i ) started to fall at 0.147s and rose by 1300% at 0.155s when the system became unstable.
b. In the δ 1 − δ 2 plane, operating points appeared to cross the barrier before they reached the boundary. The elliptical area marks the position of the barrier. From 0.147s onwards the interval between operating points decreased in the direction of increasing Δ t (shaded area).
c. In the u 1 − u 2 plane, the graph is a critical state local attractor, which appears simultaneously with the synchronous barrier. The ellipse indicates the position of the attractor. The graph of the trajectory of the operating point from 0.147s onwards is shown as an attractor (in the shaded area).
As the stability boundary is approached, the perturbed trajectories of the operating points become interesting. The system self-organized and moved toward synchronous evolution41.
The decrease in σ ( δ i ) from the highest point indicated a tendency for the system to maintain its own stability before destabilizing and to spontaneously lead the velocities of the subsystems to the mean value. This may be the spontaneous synchronization effect caused by the coupling of the systems (Figure 4). Spontaneous synchronization is precisely a self-organizing behavior, i.e., a phenomenon whereby initially unsynchronized coupled subsystems evolve toward synchronization6,42. Spontaneous synchronization seems to occur near the synchronization stability boundary (Extended Figure 7). For coupled network systems, this strong correlation indicates that the location where spontaneous synchronization occurs is also determined in u K − u L − δ K L by Eq.12,41. This may indicate that the mechanism of spontaneous synchronization is not necessarily related to the network topology, i.e., synchronization on the network may be independent of the network43–45. This will challenge the traditional perception of synchronization in networks. At the same time, the correlation may also indicate that physically, the synchronous stability boundary may originate from spontaneous synchronisation effects.
The generators spontaneously exchanged energy through coupling to synchronize and stabilize the system. This caused the coefficients in the fitted representation to change, which was reflected in the disturbed trajectory. When the conditions were correct ( d 2 δ L d ( Δ t ) 2 = a ω ( i ) < 0 and a δ is constant), a wonderful structure emerges from the trajectory of the operating points. Due to the constraint δ K = a δ * δ L + b δ , Δ t ∈ ( 0 , Δ T ′ ] and the same Δ T ′ , the perturbed trajectories of all meta-generators simultaneously exhibit this structure. Although the phenomenon of self-organization of synchronization is often used directly to explain the synchronous operation of generators, this structure has rarely been reported in the past. The synchronous barrier and the cycle were the results of the self-organizing behavior in the δ K − δ L and u K − u L planes, respectively (Figure 4). The perturbed trajectory of the generator shows the same result at the same time (Extended Figure 3), proving that this is not caused by a substitution effect but by the emergent nature of the system at the boundary
After the operating point crosses the potential barrier, σ ( δ i ) rises sharply (Figure 4 and Extended Figure 7) , and the system is no longer synchronized.
The behavior of the running point near the boundary is very complex. For example, it does not always result in the formation of a synchronous potential barrier (see Extended Fig 6). The reasons for this difference, or rather, the specific conditions for the formation of this particular structure of synchronized barrier and more information awaits further research.

Conclusions

In this study, a graceful stabilizing boundary equation that accurately describes an ideal synchronous stabilizing boundary is derived. Since the physical quantities in the equation are independent of the network, it is universally applicable to almost any power network. Therefore, the synchronization stability of the grid can be analyzed in a uniform way. It is also shown in a seminal way that the mechanism of synchronization may not be linked to the network topology and parameters. The experimental data are derived from simulations of the IEEE standard arithmetic models. The self-organizing behavior at the operating point demonstrates the existence of spontaneous synchronization on the boundary of the synchronization stability domain, which helps to confirm the argument that spontaneous synchronization is directly equivalent to synchronization stability. Additionally, the self-organizing behavior suggests the existence of a new explanation for the origin of the grid synchronous stability boundary. The concise mathematical tools, simple and universal methods, and ability to assess synchronization stability by simply monitoring the voltage and angular velocity provide great convenience for engineering applications. It is also demonstrated that synchronous stability studies of other coupled systems without clear network details can be performed by finding the correct parameters to directly derive the stability boundary while eliminating the need to construct elaborate network models. Thus, synchronization stability analyses in other disciplines may be able to directly apply the assumption made in the manuscript, with the exact form of Eq.1 depending on the form of the synchronous power and the coupling power in each discipline. Finally, the behavior of the real system's operating points near the boundary is still very complex. It is still difficult to accurately predict these results, such as the specific conditions and duration of the occurrence of synchronous barrier structures, which require further exploration.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Data Availability Statement

All the data that support the findings of this study are available at Figshare (DOI:10.6084/m9.figshare.23585961).

Conflicts of Interest

The author declare no conflicts of interest.

References

  1. Koronovskii: A. A.: Moskalenko, O. I. & Hramov, A. E. synchronization in complex networks. Tech. Phys. Lett. 38, 924–927 (2012). [CrossRef]
  2. Dörfler, F., Chertkov, M. & Bullo, F. Synchronization in complex oscillator networks and smart grids. Proc. Natl. Acad. Sci. U. S. A. 110, 2005–2010 (2013). [CrossRef]
  3. Linyuan, L. L. & Zhou, T. Link prediction in complex networks: A survey. Phys. A Stat. Mech. its Appl. 390, 1150–1170 (2011). [CrossRef]
  4. Molnar, F., Nishikawa, T. & Motter, A. E. Asymmetry underlies stability in power grids. Nat. Commun. 12, 1–9 (2021). [CrossRef]
  5. Martínez, I., Messina, A. R. & Vittal, V. Normal form analysis of complex system models: A structure-preserving approach. IEEE Trans. Power Syst. 22, 1908–1915 (2007). [CrossRef]
  6. Zhu, L. & Hill, D. J. Synchronization of Kuramoto Oscillators: A Regional Stability Framework. IEEE Trans. Automat. Contr. 65, 5070–5082 (2020). [CrossRef]
  7. Casals, M. R. et al. Knowing power grids and understanding complexity science. Int. J. Crit. Infrastructures 11, 4 (2015). [CrossRef]
  8. Gurrala, G., Dimitrovski, A., Pannala, S., Simunovic, S. & Starke, M. Parareal in Time for Fast Power System Dynamic Simulations. IEEE Trans. Power Syst. 31, 1820–1830 (2016). [CrossRef]
  9. Gurrala, G. et al. Large Multi-Machine Power System Simulations Using Multi-Stage Adomian Decomposition. IEEE Trans. Power Syst. 32, 3594–3606 (2017). [CrossRef]
  10. Wang, B., Fang, B., Wang, Y., Liu, H. & Liu, Y. Power System Transient Stability Assessment Based on Big Data and the Core Vector Machine. IEEE Trans. Smart Grid 7, 2561–2570 (2016). [CrossRef]
  11. Yu, Y., Liu, Y., Qin, C. & Yang, T. Theory and Method of Power System Integrated Security Region Irrelevant to Operation States: An Introduction. Engineering 6, 754–777 (2020). [CrossRef]
  12. Yang, P., Liu, F., Wei, W. & Wang, Z. Approaching the Transient Stability Boundary of a Power System: Theory and Applications. IEEE Trans. Autom. Sci. Eng. 1–12 (2022). [CrossRef]
  13. Al-Ammar, E. A. & El-Kady, M. A. Application of operating security regions in power systems. IEEE PES Transm. Distrib. Conf. Expo. Smart Solut. a Chang. World (2010). [CrossRef]
  14. Kundur, P. et al. Definition and classification of power system stability. IEEE Trans. Power Syst. 19, 1387–1401 (2004).
  15. Student Member, B. B. & Senior Member, G. A. On the nature of unstable equilibrium points in power systems. IEEE Trans. Power Syst. 8, 738–745 (1993). [CrossRef]
  16. Chiang, H. D., Wu, F. F. & Varaiya, P. P. A BCU Method for Direct Analysis of Power System Transient Stability. IEEE Trans. Power Syst. 9, 1194–1208 (1994). [CrossRef]
  17. Shubhanga, K. N. & Kulkarni, A. M. Application of Structure Preserving Energy Margin Sensitivity to Determime the Effectiveness of Shunt and Serles FACTS Devices. IEEE Power Eng. Rev. 22, 57 (2002). [CrossRef]
  18. Bhui, P. & Senroy, N. Real-Time Prediction and Control of Transient Stability Using Transient Energy Function. IEEE Trans. Power Syst. 32, 923–934 (2017). [CrossRef]
  19. Al Marhoon, H. H., Leevongwat, I. & Rastgoufard, P. A fast search algorithm for Critical Clearing Time for power systems transient stability analysis. 2014 Clemson Univ. Power Syst. Conf. PSC 2014 (2014). [CrossRef]
  20. Rimorov, D., Wang, X., Kamwa, I. & Joos, G. An approach to constructing analytical energy function for synchronous generator models with subtransient dynamics. IEEE Trans. Power Syst. 33, 5958–5967 (2018). [CrossRef]
  21. Cuadra, L., Salcedo-Sanz, S., Del Ser, J., Jiménez-Fernández, S. & Geem, Z. W. A critical review of robustness in power grids using complex networks concepts. Energies 8, 9211–9265 (2015). [CrossRef]
  22. Zhou, J. et al. Large-Scale Power System Robust Stability Analysis Based on Value Set Approach. IEEE Trans. Power Syst. 32, 4012–4023 (2017). [CrossRef]
  23. Ajala, O., Dominguez-Garcia, A., Sauer, P. & Liberzon, D. A Second-Order Synchronous Machine Model for Multi-swing Stability Analysis. 51st North Am. Power Symp. NAPS 2019 (2019). [CrossRef]
  24. Karatekin, C. Z. & Uçak, C. Sensitivity analysis based on transmission line susceptances for congestion management. Electr. Power Syst. Res. 78, 1485–1493 (2008). [CrossRef]
  25. Mei, S., Ni, Y., Wang, G. & Wu, S. A study of self-organized criticality of power system under cascading failures based on AC-OPF with voltage stability margin. IEEE Trans. Power Syst. 23, 1719–1726 (2008). [CrossRef]
  26. Dobson, I., Carreras, B., Lynch, V. & Newman, D. An initial model for complex dynamics in electric power system blackouts. Proc. Hawaii Int. Conf. Syst. Sci. 51 (2001). [CrossRef]
  27. Ding, L., Gonzalez-Longatt, F. M., Wall, P. & Terzija, V. Two-step spectral clustering controlled islanding algorithm. IEEE Trans. Power Syst. 28, 75–84 (2013). [CrossRef]
  28. Znidi, F., Davarikia, H. & Rathore, H. Power Systems Transient Stability Indices: Hierarchical Clustering Based Detection of Coherent Groups Of Generators. (2021).
  29. Kuramoto, Y. & Battogtokh, D. Coexistence of Coherence and Incoherence in Nonlocally Coupled Phase Oscillators. Physics (College. Park. Md). 4, 380–385 (2002).
  30. Martens, E. A., Thutupalli, S., Fourrière, A. & Hallatschek, O. Chimera states in mechanical oscillator networks. Proc. Natl. Acad. Sci. U. S. A. 110, 10563–10567 (2013). [CrossRef]
  31. Panaggio, M. J. & Abrams, D. M. Chimera states: Coexistence of coherence and incoherence in networks of coupled oscillators. Nonlinearity 28, R67–R87 (2015). [CrossRef]
  32. Amirthalingam, K. M. & Ramachandran, R. P. Improvement of transient stability of power system using solid state circuit breaker. Am. J. Appl. Sci. 10, 563–569 (2013). [CrossRef]
  33. Liu, X., Shahidehpour, M., Cao, Y., Li, Z. & Tian, W. Risk assessment in extreme events considering the reliability of protection systems. IEEE Trans. Smart Grid 6, 1073–1081 (2015). [CrossRef]
  34. Huang, R. et al. Learning and Fast Adaptation for Grid Emergency Control via Deep Meta Reinforcement Learning. IEEE Trans. Power Syst. 37, 4168–4178 (2022). [CrossRef]
  35. Guo, M., Xu, D. & Liu, L. Design of Cooperative Output Regulators for Heterogeneous Uncertain Nonlinear Multiagent Systems. IEEE Trans. Cybern. 52, 5174–5183 (2022). [CrossRef]
  36. Roberts, L. G. W., Champneys, A. R., Bell, K. R. W. & Di Bernardo, M. Analytical Approximations of Critical Clearing Time for Parametric Analysis of Power System Transient Stability. IEEE J. Emerg. Sel. Top. Circuits Syst. 5, 465–476 (2015). [CrossRef]
  37. Owusu-Mireku, R., Chiang, H. D. & Hin, M. A Dynamic Theory-Based Method for Computing Unstable Equilibrium Points of Power Systems. IEEE Trans. Power Syst. 35, 1946–1955 (2020). [CrossRef]
  38. Sajadi, A., Kenyon, R. W. & Hodge, B. M. Synchronization in electric power networks with inherent heterogeneity up to 100% inverter-based renewable generation. Nat. Commun. 13, 1–12 (2022). [CrossRef]
  39. Sun, M. et al. On-line power system inertia calculation using wide area measurements. Int. J. Electr. Power Energy Syst. 109, 325–331 (2019). [CrossRef]
  40. Zhang, Y., Bank, J., Muljadi, E., Wan, Y. H. & Corbus, D. Angle instability detection in power systems with high-wind penetration using synchrophasor measurements. IEEE J. Emerg. Sel. Top. Power Electron. 1, 306–314 (2013). [CrossRef]
  41. Motter, A. E., Myers, S. A., Anghel, M. & Nishikawa, T. Spontaneous synchrony in power-grid networks. Nat. Phys. 9, 191–197 (2013). [CrossRef]
  42. Dörfler, F. & Bullo, F. Synchronization in complex networks of phase oscillators: A survey. Automatica 50, 1539–1564 (2014). [CrossRef]
  43. Chen, G. Searching for Best Network Topologies with Optimal Synchronizability: A Brief Review. IEEE/CAA J. Autom. Sin. 9, 573–577 (2022). [CrossRef]
  44. Li, X., Wei, W. & Zheng, Z. Promoting synchrony of power grids by restructuring network topologies. Chaos An Interdiscip. J. Nonlinear Sci. 33, 63149 (2023). [CrossRef]
  45. Zhang, Y. & Motter, A. E. Symmetry-Independent Stability Analysis of Synchronization Patterns. SIAM Rev. 62, 817–836 (2020). [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated