Prerpints.org logo
Preprint
Article

A Coupled Simulated Annealing and Particle Swarm Optimization Reliability-Based Design Optimization Strategy under Hybrid Uncertainties

Altmetrics

Downloads

98

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

23 October 2023

Posted:

30 October 2023

You are already at the latest version

Alerts
Abstract
With the engineering system becoming more and more complex, the uncertainty factors have a more and more profound influence on the reliability and security of the engineering system. In recent years, Reliability-Based Design Optimization (RBDO) has been studied extensively in complex engineering system design. The research on reliability optimization design considering stochastic uncertainty has been comprehensive and widely used. However, the reliability optimization design considering mixed uncertainty has the disadvantages of large computation and imprecise convergence. This study proposes an RBDO method based on Particle Swarm Optimization (PSO) and Simulated Annealing (SA) to overcome this challenge. In the method, PSO is used to solve the most probable point, while SA has excellent global optimization capability to acquire the global optimal solution. Finally, three examples are given to illustrate the advantages of the proposed method.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

The construction of engineering systems will inevitably be affected by complex uncertain factors [1,2,3]. Especially with the increasing complexity of engineering systems, various uncertainties will be mixed together and difficult to distinguish [4]. If these factors can’t be analyzed accurately, the reliability and security of the engineering system cannot be guaranteed [5,6,7,8]. At present, the Reliability-Based Design Optimization (RBDO) method has been widely used to improve the reliability and safety of complex mechanical systems [9]. However, with the growth of social demand, new technology should be introduced constantly to improve the development level of reliability optimization design and meet the needs of economic development for engineering [10].
RBDO takes into account the inevitable random factors in the engineering system [11,12,13,14]. It also makes the reliability of the system object within the acceptable range by optimizing the objective function [15]. RBDO is an extension of the deterministic optimization method, which is used to solve complex uncertain engineering system optimization problems, such as multi-modal function, discrete design space and non-differential problems [16,17]. In recent years, RBDO has been discussed and studied by a large number of scholars. Many algorithms as well as models have been developed to solve RBDO problems. Wang et al. [18] proposed an improved Modified Conjugate Gradient Approach (MCGA) to improve the RBDO efficiency of nonlinear functional functions. Methods Modified Conjugate Gradient Approach (CGA) and conjugate gradient method were used to search the direction of optimal design points, which improves the efficiency of RBDO. Liao et al. [19] adopted an improved double-loop calculation method to improve the computational efficiency of the RBDO model. In this method, RBDO is divided into two layers. Reliability Analysis (RA) and Deterministic Optimization (DO) are calculated step by step. However, these algorithms are mainly gradient-based algorithms and lack the ability to deal with complex and multimodal functions. Therefore, new research is carried out on RBDO based on evolutionary algorithms and heuristic algorithms. Truong et al. [20] proposed an RBDO method based on the Differential Evolution (DE) algorithm to balance local and global search using a variation strategy based on the p-best strategy. This method is very effective for RBDO of nonlinear inelastic truss structures. However, in engineering practice, uncertainty can be divided into stochastic uncertainty and cognitive uncertainty. Among them, the mixed uncertainty phenomenon is very common in today's engineering system. It is because of the existence of mixed uncertainty that the computational complexity of RBDO is greatly increased. One method is to approximate the interval variables as random variables, which simplifies the calculation but does not guarantee the accuracy of the results. To solve such problems, Du et al. [21] proposed a mixed uncertainty analysis method. Zhang et al [22]. proposed a mixed uncertainty analysis method based on probability and evidence theory to improve the efficiency of RBDO resolution. Wang et al. [23] proposed an RBDO solution strategy that relies on regulation treatment and the convex theorem. An improved genetic algorithm is used to ensure that the optimization task is reasonable and efficient.
Although many strategies have been proposed, RBDO development considering mixed uncertainty is still necessary. In this study, a method based on the particle swarm optimization algorithm and Simulated Annealing (SA) algorithm is proposed, which is mainly suitable for the analysis of RBDO problems based on mixed uncertainty. Particle Swarm Optimization (PSO) is introduced to solve the Most Probable Point (MPP), which improves the speed and efficiency of solving the RBDO model. At the same time, it is combined with the SA algorithm to search for the global optimal solution. What’s more, the paper also probes into how to improve the RBDO problem-solving method.
The rest parts of this paper include: Section. 2 summarizes the PSO algorithm and SA algorithm; Section. 3 illustrates the idea of combining the two algorithms. Section. 4 verifies and compares with other methods through examples; Section. 5 provides a summary and future work.

2. Two algorithms for optimizing the problem

2.1. Particle swarm optimization

2.1.1. Definition of Particle Swarm Optimization

PSO also known as the foraging algorithm, is a widely used meta-heuristic algorithm, which is derived from the study of bird predation behavior [24,25]. The algorithm is originally a simplified model based on swarm intelligence inspired by the regularity of bird swarm activity. Based on the observation of the activity behavior of animal clusters, the PSO algorithm makes use of the information sharing of each individual in the group, so that the movement of the whole group can evolve from disorder to order in the problem-solving space [26,27]. Finally, it can obtain the optimal solution successfully.
In PSO, the optimal solution is generated by reducing the distance between each search individual and the target point [28]. Under this goal, the position of the particle varies depending on two factors: the velocity of the particle and the current position of the particle. During the search for the optimal solution, the velocity of the particle and the current position of the particle are constantly changing. The value of velocity is determined by the particle with the optimal current position and the particle with the optimal global position. Its mathematical expression is
V k + 1 = w V k + c 1 r 1 p b e s t − X k + c 2 r 2 g b e s t − X k X k + 1 = X k + V k + 1
where V k represents the particle velocity of k iterations; X k represents the particle position of k iterations; w represents inertia weight; p b e s t represents the optimal value of the particle at its current position; g b e s t represents the global optimal value; c 1 , c 2 respectively represent individual learning coefficient and global learning coefficient; r is a random value between 0 and 1, called the learning rate.
In the process of iteration, speed boundary detection should be carried out after each speed update, that is, whether the maximum speed limit is exceeded. Generally, adopting v ( v > v max ) = v max , so as the location. The common termination conditions are reaching the set number of iterations and keeping the fitness for n times without changing [29].

2.1.2. Optimization of PSO algorithm

Equation (1), w describes the "inertia" of particles. In the early stage of iteration, the value of w should be larger to ensure the independent flight of each particle and to search the space as fully as possible. In the later stage of iteration, the value of w should be smaller and more "learned" from other particles. Similarly, c 1 and c 2 are the maximum flight steps towards individual and global extremes respectively. c 1 should be larger in the early stage, while c 2 should be larger in the late stage, to balance the local search ability and global search ability of particles. In the PSO algorithm, the parameters w , c and r jointly affect the search direction of particles. So even if other particles find a better solution, the inertia of the current particles is too large to fly to a better position quickly.
Against the deficiency of standard particle swarm algorithm, through the introduction of new mechanism and parameter optimization of adaptive changes of PSO algorithm [30]. Firstly, the parameter optimization of the PSO algorithm. As mentioned above, inertia weight w should be larger in the early stage of search and smaller in the late stage, so that particles can search the entire design space as much as possible in the early stage and more carefully in the late stage. For this optimization strategy, the inertia weight w is adjusted as follows [27]:
w k = w min + g e r − k g e r ( w max − w min )
where w k represents the inertia weight at each iteration; w min and w max respectively denote the lower and upper bounds of the inertia weight; k represents the number of current iterations; g e r represents the total number of iterations; as can be seen from the expression of w k , the value of inertia weight w k decreases monotonically, realizing the function of decreasing gradually with the process of search. Similarly, the same optimization strategy is adopted for the learning coefficient c . The expression of the optimized c 1 and c 2 is shown as follows:
c k 1 = c min + g e r − k g e r ( c max − c min ) c k 2 = c max − g e r − k g e r ( c max − c min )
where c k 1 represents the individual learning coefficient in each iteration; c k 2 represents the global learning coefficient of each iteration. In addition, the learning rate r is no longer a random value between 0 and 1, but a random variable subject to the standard normal distribution, namely r ~ ( 0 , 1 ) .
Secondly, to make the search process avoid falling into local optima and focus more on global optima, an additional method of updating particle position X and velocity V is used for reference here. The method is as follows:
X k + 1 = X k + V k + 1 E V k + 1 E = r 3 ( g b e s t − X k ) + N o r m r a n d ( 0 , 1 ) × γ k γ k = 1 − k / g e r
where the new position is calculated by the global optimal value and the random number obeying the normal distribution. r 3 is a random number between 0 and 1; N o r m r a n d ( 0 , 1 ) is a randomly generated vector conforming to the standard normal distribution; γ k is an adaptively variable step that changes the size of the random value.
As can be seen from the expression of V k + 1 E , since a random value is introduced, the probability of falling into a local optimal when updating the position can be reduced. However, the efficiency of the search will decrease accordingly in the meantime. In order to balance the two results, a new decision mechanism is introduced here:
X k + 1 = X k + V k + 1 E , r ≤ P k X k + V k + 1 , r > P k
where r is a random number between 0 and 1; P k represents the probability of the particle choosing two position updating modes. The expression is
P k = 0.2 + 0.8 k / g e r
As can be seen from the expression of P k , with the progress of iteration, the value of P k keeps increasing, which makes the probability of using V k + 1 E to update the speed of V correspondingly increase.
This mechanism for updating particle positions ensures that the particle is more focused on the global optimal value later in the search process. This improves the efficiency to some extent and reduces the probability of falling into local optimal.

2.2. Simulated annealing algorithm

2.2.1. Definition of Simulated annealing algorithm

The annealing process of a metal involves heating the metal to a sufficiently high temperature and then letting it slowly cool down to give the metal some properties it did not have before [31,32,33]. When the temperature rises, the particles inside the solid become disordered with the increase of temperature, the internal energy increases, thus the particles become unstable. The particles gradually become orderly when slowly cooled. As the energy decreases, the particles become stable [34]. The simulated annealing algorithm starts from a higher initial temperature. With the continuous decline of temperature parameters, the algorithm combines the probability jump characteristics to randomly find the global optimal solution of the objective function in the solution space.

2.2.2. Simulated annealing algorithm

The SA mechanism can avoid falling into local optimum to some extent. Different from many intelligent optimization algorithms, the SA algorithm will jump to the solution with a certain probability. Even if it finds a worse solution than the current solution in the process of local search, it can avoid falling into the local optimal [35]. This way of updating solutions requires an important judgment criterion called the Metropolis criterion:
P = 1 , E t + 1 < E t e − ( E t + 1 − E t ) k T , E t + 1 ≥ E t
where P is the probability of accepting the new solution; E t is the system energy corresponding to the current solution X t (objective function); k is the temperature drop coefficient, which is a value between 0 and 1. T indicates the initial temperature. Based on this criterion, it can be concluded that (here is to find the minimum value):
(1) When the objective function corresponding to the new solution is less than the objective function value of the current solution, it will accept the new solution. That is, the probability of accepting the new solution is 1;
(2) When the corresponding objective function of the new solution is greater than the objective function value of the current solution, the new solution will be accepted with a certain probability. When other variables are certain, the more the value of the objective function corresponding to the new solution exceeds the value of the objective function of the current solution, the smaller the probability of accepting the new solution.
The steps of the SA algorithm are as follows:
Step 1: Set the initial temperature T ; The initial solution X 0 is generated randomly and the objective function E ( X 0 ) is calculated;
Step 2: Make T = k T , k ∈ ( 0 , 1 ) ;
Step 3: Make random perturbation to the current solution X t , generate a new solution X t + 1 in its field, calculate its corresponding function value E ( X t + 1 ) . Meanwhile, judge whether to accept the new solution according to the Metropolis criterion above;
Step 4: At temperature T , iterate the disturbance and acceptance process for L times;
Step 5: Determine whether the terminal temperature is reached. If so, terminate; otherwise, return to step 2.

3. The combination of intelligent algorithms

3.1. First-order reliability method

3.1.1. First-order reliability method

The basic idea of FORM is to simplify the joint probability density function f x ( x ) and the approximate limit state function g ( x ) , primarily by performing a first-order Taylor approximation expansion at MPP [36,37,38,39]. The process of using FORM to calculate reliability includes coordinate space conversion and integral boundary approximation [40,41].
Coordinate space conversion refers to converting random variables subject to various probability distributions into variables subject to a standard normal distribution by the Rosenblatt method [42]. Suppose the random variable follows the normal distribution with mean value and standard deviation value, then the random variable transformed by the Rosenblatt method is
u = x − μ σ
The approximation of the integral boundary is an important part of FORM. Its main idea is to perform first-order Taylor expansion of the integral boundary g ( u ) = 0 to make the integral solution of failure probability easier. The first-order Taylor expansion of g ( u ) can be expressed as
g ( u ) = g ( u * ) + ∇ g ( u * ) ( u − u * ) T
where u * represents the expansion point; ∇ g ( u * ) represents the gradient of the expansion point. To reduce the precision loss caused by Taylor expansion, the MPP point on the fundamental boundary g ( u ) = 0 is expanded. Search for MPP points on integral boundary g ( u ) = 0 , that is, maximize the joint probability density:
max ∏ i = 1 n 1 2 π e − u i 2 2 s . t . g ( u ) = 0
By observing Equation (10), it can be seen that the above process is a constrained optimization problem. The deformation of Equation (10) is carried out:
∏ i = 1 n 1 2 π e − u i 2 2 2 = 1 2 π e − 1 2 ∑ i = 1 n u i 2
And,
max ∏ i = 1 n 1 2 π e − u i 2 2 2 ∼ min ∑ i = 1 n u i 2 2
Therefore, the search model of MPP points can be expressed as:
min u s . t . g ( u ) = 0
where u = u 1 2 2 + ⋯ + u n 2 2 represents the magnitude of the vector u . The above formula is solved to obtain u = u * , which is the MPP point. Let β = u * , from the perspective of two-dimensional geometry, the MPP point can be viewed as the point g ( u ) = 0 tangent to a circle centered at the origin and with radius β . According to literature, the calculation formula of reliability can be expressed as:
R = ϕ ( β )
where ϕ ( ⋅ ) represents the cumulative distribution function obeying normal distribution.
The above are the general steps of the First-order reliability analysis method. According to different solving methods, FORM can be divided into Reliability Index Approach (RIA) [37] and Performance Measure Approach (PMA) [43].

3.1.2. Reliability index method

RIA uses a reliability index instead of failure probability constraints, the mathematical model is the MPP point search model [44,45,46,47]. It can be seen that the mathematical model is an optimization problem. A variety of optimization algorithms, such as Sequential Quadratic Programming (SQP), can be used to solve the optimization model.

3.1.3. Performance measure approach

When the failure probability is 0 or 1, the corresponding reliability index will approach infinity or infinitesimal, resulting in RIA failure. At this time, PMA can be used to solve the problem. Its mathematical model is [48]:
min g ( u ) s . t . u = β t
where β t represents the target reliability index. The above model indicates that under the given reliability, if g ( u ) > 0 , it means that the solution can meet the given reliability requirements.
Through the mathematical model of RIA and PMA, it can be seen that the solution of the two ways is a reciprocal inverse process. The difference is that the feasible region of PMA is a sphere, while that of RIA is a hypersurface. In terms of computational efficiency, PMA has more advantages than RIA.

3.1.4. Reliability analysis method considering stochastic and interval uncertainties

In the above introduction to FORM, design variables are random variables that obey a normal distribution. However, in many practical engineering applications, the distribution of some random variables may not be clear [49,50,51]. The possible values of these uncertain variables are usually only in the specified interval without accurate distribution information. That is, there is interval uncertainty. When dealing with such mixed uncertainty RBDO problems, the computational complexity will be greatly increased. A simple method is to treat the interval variables as random variables to approximate the calculation. Although this method can simplify the reliability analysis, it cannot guarantee the accuracy of the results [52]. To solve such problems, Du et al. [21] proposed a kind of mixed uncertainty analysis method.
Compared with the reliability analysis considering random and interval uncertainty, some changes should be made based on the original calculation model. The transformed RIA model is directly presented here:
min u M P P ( y ) s . t . g ( u , y ) = 0 y L ≤ y ≤ y U
where y represents interval variable; y L represents the lower bound of the interval; y U is the upper bound of the interval. Similarly, the PMA mathematical model considering stochastic and interval uncertainty is:
min g ( d , u , y ) s . t . u = β t y L ≤ y ≤ y U
It can be seen that reliability analysis considering random and interval uncertainty is equivalent to adding a set of interval variables and changing the failure boundary on the basis of reliability analysis considering random uncertainty. The rest parts are the same exactly. Therefore, when there is interval uncertainty, reliability analysis using the above method will not bring about redundant calculation steps, so it will not significantly reduce the calculation efficiency.

3.1.5. MPP solution method

For FORM, the main task is to solve the MPP points. According to the mathematical models of RIA and PMA, the solution of MPP points is an optimization problem with constraints. When solving optimization problems, intelligent optimization algorithms, including PSO, do not need gradient information [53,54,55,56,57]. They can deal with discrete variable optimization problems, since they have strong global search ability [58,59]. The detailed steps of MPP point solving using the improved PSO algorithm are as follows.
When an intelligent optimization algorithm is used to solve MPP points, the probability constraint model in first-order reliability analysis can be processed by penalty function in general [60], as shown below:
min f = U + η max 0 , g ( X )
where f represents fitness; η represents the penalty factor, whose expression is:
η = 100 g ( μ )
Taking fitness f as the optimization objective, the general steps of solving MPP points by using the improved PSO algorithm are shown as follows:
Step 1: Set the initial conditions for searching MPP points, including the limit state function g ( X ) , the probability distribution function of the design variable X (a normal distribution with mean value μ and standard deviation σ and parameters of PSO algorithm, namely: population number N , the total number of iterations g e r , inertia size w and flight step length c ;
Step 2: Set the boundary conditions, including: the lower bound X L = μ − 5 σ , and upper bound X U = μ + 5 σ of the design variable and the maximum value v max = X U − X L / 100 and minimum value v min = − v max of the speed;
Step 3: Generate the initial population. The initial position X 0 = X L + r × ( X U − X L ) and initial velocity V 0 = v min + r × ( v max − v min ) of the population should be calculated. The penalty factor η should be set;
Step 4: Update local optimal value p b e s t and global optimal value g b e s t . Firstly, the design variable X was converted into the variable U , which obeyed the standard normal distribution. Then fitness f = U + η max 0 , g ( X ) was calculated. Finally, p b e s t and g b e s t were screened out;
Step 5: Update the population location. The population location updating method mentioned above was used to update all the particles;
Step 6: Check whether convergence occurs. The convergence condition can be g ( g b e s t ) < 0.001 or k = g e r . If either condition is satisfied, the iteration can be stopped and X M P P = g b e s t is output. Otherwise, do k = k + 1 and return to step (4) to continue the iteration.
The above is the method of solving MPP points by using the improved PSO.

3.2. The combination of SA and PSO algorithm

The combination of SA and PSO is as follows: PSO algorithm is used to generate a set of solutions with certain global search performance but easy to fall into the local optimal. Next, the SA algorithm is used to accept new solutions according to a certain probability to gradually jump out of the local optimal. Then the global search performance of PSO to help the global optimal solution move forward. This combination can improve the global search performance of the algorithm, but also fast convergence. The approximate steps are shown in Table 1 below:
By using this method, the advantages of a simple and efficient PSO algorithm can be brought into play. The SA algorithm can keep the original performance without expending the energy to adjust the parameters.

3.3. RBDO decoupling method

RBDO solution strategies can be divided into double-ring method, single-ring method and decoupling method [61]. The double-loop method is the most basic and direct solution strategy [62]. Its flow is a double-layer nested cycle optimization flow. What’s more, its solving efficiency is the lowest. The single-loop method is the most efficient solution strategy. However, it has problems such as low precision and difficult convergence [63]. Compared with the other two methods, the decoupling strategy is a very important RBDO method, which can give consideration to both solving accuracy and solving efficiency.
Sequence Optimization and Reliability Assessment (SORA) method is an efficient decoupling method for solving RBDO problems [64]. Based on the decoupling idea, SORA serializes the traditional two-layer nested cycle optimization process. Forming a sequential deterministic design optimization and controllability analysis process [65]. The main idea of SORA is to approximate the solution of the RBDO problem. The main method is to make the constraint gradually shift to the direction of the probability constraint, so as to quickly get the optimal solution. Its mathematical expression is
f i n d : μ X min : C ( μ X ) s . t . g i ( μ X − s i ) ≥ 0 ( i = 1 , 2 , ⋯ , m ) μ X L ≤ μ X ≤ μ X U
where s i = μ X ( k − 1 ) − x i * ( i = 1 , 2 , ⋯ , m ) is the offset vector of the i th probability constraint; 3 was the design point of the last iteration. In SORA, each iteration cycle will construct an offset vector based on the reliability analysis results of the previous iteration to move the boundary of the probability constraint. According to the constraint boundary after moving, the DO is constructed to update the optimal design scheme. The nested RBDO is decomposed into a series of reliability analyses and DO problems.

3.4. The proposed RBDO method based on the PSO and SA algorithm

The analysis optimization method proposed in this paper is a fusion of the meta-heuristic algorithm RBDO method. Its main idea is that: the SA algorithm and enhanced PSO algorithm are respectively used to perform reliability optimization and reliability analysis after decoupling. The purpose of improving the efficiency of analysis and optimization is achieved. The overall process is as follows:
Step 1: Set the probability distribution of random variables and the reliability index of the target β t ;
Step 2: Set parameters of the PSO algorithm and SA algorithm;
Step 3: Enter the optimization cycle of the SA algorithm. Select the design variable set in step (1) as the initial point to calculate the value of the objective function;
Step 4: Reliability analysis is carried out on the results obtained in step (3). The improved PSO algorithm is used to solve the MPP points, calculate the reliability index and judge its reliability. If the reliability requirements are met, this solution is output as the optimal solution. Otherwise, calculate the offset vector, update the probability constraint function and return to step (3) for a new round of reliability optimization.
The flowchart of this method is shown in Figure 1:

4. Experimental results and discussion

4.1. Example verification

In order to obtain the performance of reliability analysis by using the PSO algorithm, two mathematical examples are selected in this section for verification. The sequential quadratic programming method is selected as a comparison. The two examples are a convex function and a concave function respectively. The variables of the convex function only have random uncertainty, while those of the concave function have both random uncertainty and interval uncertainty.

4.1.1. Convex limit state function

The expression of the limit state function of this example is:
g = − e x 1 − 7 − x 2 + 10
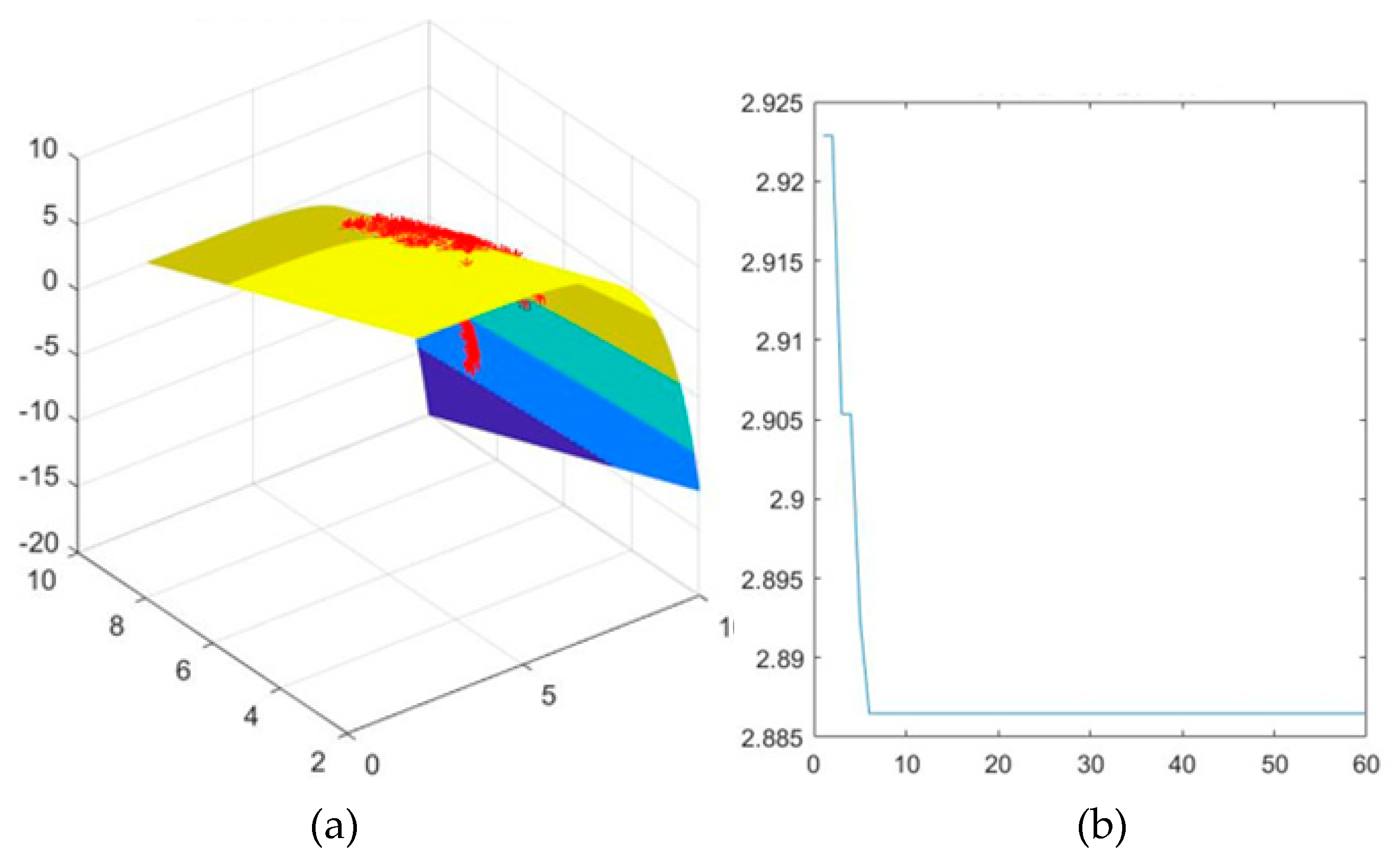
where both x 1 and x 2 have random uncertainty; x 1 ∼ N ( 6.0 , 0.8 ) , x 2 ~ N ( 6 , 0.8 ) . The limit state function is solved. Its convergence process is shown in Figure 2. The comparison of results is shown in Table 2 below:
Table 2. Reliability index of the convex function.
Table 2. Reliability index of the convex function.
Method Reliability index Error Solution time (milliseconds)
MCS 2.8445 —— 1942933
SQP 2.8782 1.2% 90
Improved PSO 2.8865 1.5% 48
It can be seen from the calculation results that the improved PSO algorithm is equivalent to the SQP algorithm in solving accuracy. However, about 50% faster than the SQP algorithm. It can be seen that the PSO algorithm has better performance in reliability analysis under stochastic uncertainty.
Preprints 88495 g002
Figure 2. Convex function iterative solution procedure. (a) State position change-Number of iterations: 60 (b) Optimal fitness evolution process.
Figure 2. Convex function iterative solution procedure. (a) State position change-Number of iterations: 60 (b) Optimal fitness evolution process.
Preprints 88495 g002

4.1.2. Concave limit state function

In this example, the limit state function can be expressed as:
g = e 0.8 x 1 − 1.2 + e 0.7 x 2 − 0.6 − 7 10
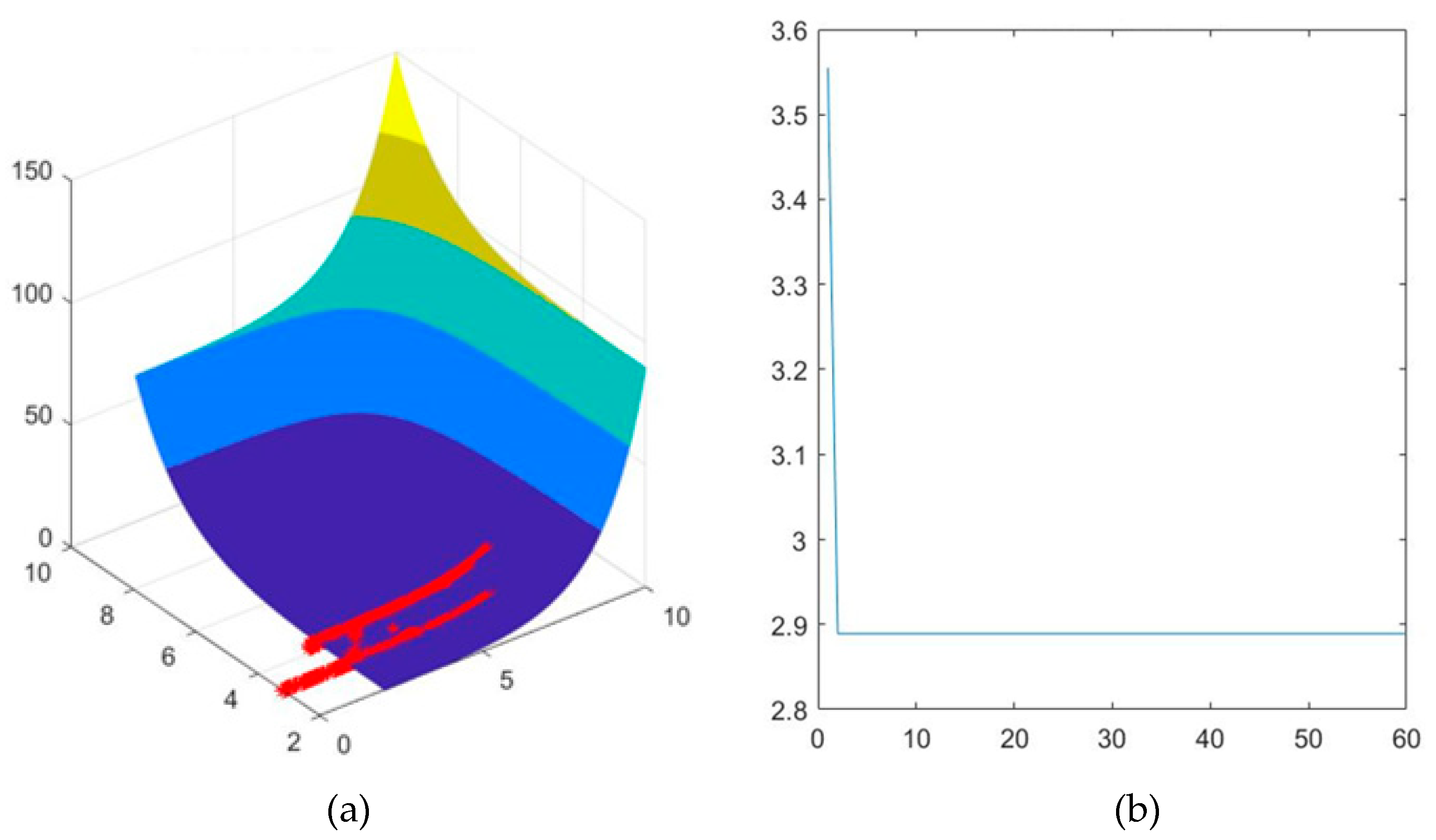
where variable x 1 has random uncertainty, x 1 ∼ N ( 4.0 , 0.8 ) ; variable x 2 has interval uncertainty, x 2 ∈ [ 3.2 , 4.2 ] . To solve this concave limit state function, the convergence process is shown in Figure 3. The comparison of results is shown in Table 3.
Table 3. Concave function reliability index.
Table 3. Concave function reliability index.
Method Reliability index Error Solution time (milliseconds)
MCS 2.9906 —— 1851967
SQP 2.1681 27.5% 83
Improved PSO 2.8891 3.4% 222
It can be seen from the table that the accuracy of PSO is about 24 % higher than that of SQP when solving the concave limit state function considering random and interval uncertainty. It can be seen that the sequential quadratic programming algorithm is not suitable for dealing with the reliability analysis problem of concave functions under mixed uncertainty. The improved PSO algorithm has good fitness when dealing with the mixed uncertainty analysis problems of convex function type and concave function type, which proves that the performance of the PSO algorithm is good enough to solve MPP points in first-order reliability analysis.
Preprints 88495 g003
Figure 3. Concave function iterative solution procedure. (a) State position change-Number of iterations: 60 (b) Optimal fitness evolution process.
Figure 3. Concave function iterative solution procedure. (a) State position change-Number of iterations: 60 (b) Optimal fitness evolution process.
Preprints 88495 g003

4.2. Mathematical example

In this section, a nonlinear mathematical example is used to verify the RBDO method of the proposed fusion meta-heuristic algorithm. The objective function of this mathematical example is the sum of two normally distributed design variables x 1 and x 2 . The constraint function consists of three nonlinear functions. The mathematical model of the optimization problem is as follows:
f i n d μ X = [ μ x 1 , μ x 2 ] min f ( μ x ) = μ x 1 + μ x 2 s . t . P r o b ( g i ( X ) ≥ 0 ) ≥ φ ( β t ) , i = 1 , 2 , 3
where β t represents the target reliability index. Its value here is β t = 3.0 ; μ x 1 and μ x 2 are the mean values of design variables x 1 and x 2 respectively. Their standard deviation σ is 0.3. The mean values range between 0 and 10, i.e.:
X ∼ N ( μ X , 0.3 2 ) 0 ≤ μ X ≤ 10
The limiting equation of state is
g 1 ( X ) = x 1 2 2 x 2 / 20 − 1 g 2 ( X ) = ( x 1 + x 2 − 5 ) 2 / 30 + ( x 1 − x 2 − 12 ) 2 / 120 − 1 g 3 ( X ) = 80 / ( x 1 2 2 + 8 x 2 + 5 ) − 1
The solution space formed by the limit state equation is shown in Figure 4.
In order to test the performance of the RBDO method of the fusion meta-heuristic algorithm proposed in this paper, the proposed method is compared with the results obtained by using the optimization algorithm SQP and the theoretical solution in the literature [66]. The results are shown in Table 4.
As can be seen from the table, the results obtained by the RBDO method combining the intelligent optimization algorithm proposed in this paper are basically consistent with those obtained by using the SQP method, which improves the solving speed by about 30%. Therefore, it can be seen that the intelligent algorithm has great advantages in solving speed.

4.3. Volume optimization of gear reducer

In the engineering example of this section, a classic case of the gear reducer is selected to optimize the reliability design. In order to verify the method presented in this paper [67,68], the original example is modified to make it a single-discipline design optimization problem considering stochastic and interval uncertainty.
The structure diagram of the gear reducer is shown in Figure 5. The optimization model has seven design variables, which are the size of each component. Among them, three variables have random uncertainty, two variables have interval uncertainty. The remaining two variables are deterministic variables. For details, see Table 5 and Table 6. In this example, the target reliability index is set as β t = 2.4 . The corresponding reliability is R = 99.18 % .
In this optimization problem, the objective is to minimize the volume V of the gear reducer, whose mathematical expression is
V = V 1 + V 2
where V 1 and V 2 represent the volume of the gear and the volume of the bearing respectively. The volume of the gear can be expressed as
V 1 = 0.7854 x 1 x 2 2 2 ( 3.3333 x 3 2 + 14.9334 x 3 − 43.0934 ) − 1.508 x 1 ( x 6 2 2 + x 7 2 2 )
The volume of the bearing can be expressed as
V 2 = 7.477 ( x 6 2 3 + x 7 2 3 ) + 0.7854 ( x 4 x 6 2 2 + x 5 x 7 2 2 )
The constraint function is the related performance index of the gear reducer, including stress, size, displacement, etc., 11 in total.
The optimization model of this problem is
f i n d X = [ x 1 , x 4 , x 5 ] min f = V 1 + V 2 s . t . P r o b ( g i ( X ) ≥ 0 ) ≥ φ ( β t ) , i = 1 , 2 , ⋯ , 11
The stress constraint function of the gear reducer performance is
g 1 = 1 − 27 / ( x 1 x 2 2 2 x 3 ) g 2 = 1 − 397.5 / ( x 1 x 2 2 2 x 3 2 2 ) g 3 = 12 − x 1 / x 2 g 4 = x 1 / x 2 − 5
The dimension constraint function is
g 5 = 1 − 1.93 x 4 2 3 / ( x 2 x 3 x 6 2 4 ) g 6 = 1 − 1.93 x 5 2 3 / ( x 2 x 3 x 7 4 ) g 7 = 1100 − A 1 / B 1 g 8 = 1 − ( 1.5 x 6 + 1.9 ) / x 4 g 9 = 1 − ( 1.1 x 7 + 1.9 ) / x 5
where A 1 = 745 x 4 / ( x 2 x 3 ) 2 + 16.9 × 10 6 ; B 1 = 0.1 x 6 2 3 .
The displacement constraint function is
g 10 = 850 − A 2 / B 2 g 11 = 40 − x 2 x 3
where A 2 = 745 x 5 / ( x 2 x 3 ) 2 + 157.5 × 10 6 , B 2 = 0.1 x 7 2 3 .
For this optimization model, the RBDO method of fusion meta-heuristic algorithm proposed in this paper is used to solve it. Meanwhile, the case where only random uncertainty is considered is calculated. The calculation results of the two uncertain cases are shown in Table 7 below.

4.4. Composite cylinder size optimization

This section further illustrates the effectiveness of the proposed method by combining cylinder size optimization cases [69]. The composite cylinder is composed of an inner cylinder and an outer cylinder. The inner diameter of the inner cylinder is a , the outer diameter is b , the inner diameter of the outer cylinder is b , the outer diameter is c . The height of the composite cylinder is 50mm. The cylinder body is subjected to a pressure of size p . The structure and initial size of the composite cylinder are shown in Figure 6.
The optimization goal of the composite cylinder is to minimize the volume of the composite cylinder while satisfying the allowable equivalent stress and tangential stress of the inner and outer cylinders. The optimization problem includes three design variables: x 1 , x 2 and x 3 , corresponding to the inner diameter a and outer diameter b of the inner cylinder and the outer diameter c of the outer cylinder respectively. There are 8 constraint conditions, among which the equivalent stress and tangential stress are all implicit expressions. The approximate mathematical expressions need to be established by finite element analysis. The optimization model of the composite cylinder is as follows:
f i n d x = ( x 1 , x 2 , x 3 ) max f = V = 12.5 π x 1 2 2 s . t . P r o b ( g i ( X ) ≥ 0 ) ≥ φ ( β t ) , i = 1 , 2 , ⋯ , 8
where β t is the target reliability index. Here β t = 2.4 .
The stress constraint and geometric constraint of the inner cylinder are
g 1 = S − S 1 g 2 = τ − τ 1 a g 3 = τ − τ 1 b g 4 = b − 1.2 a
The stress constraint and geometric constraint of the outer cylinder are
g 5 = S − S 2 g 6 = τ − τ 2 b g 7 = τ − τ 2 c g 8 = c − 1.2 b
The value range of the design variable of the composite cylinder is as follows:
31.496 ≤ a ≤ 40.64 38.1 ≤ b ≤ 50.8 30.48 ≤ c ≤ 60.96
where S and τ represent allowable equivalent stress and tangential stress respectively; S 1 and S 2 represent the maximum equivalent stress of inner cylinder and outer cylinder respectively; τ 1 a and τ 1 b represent the maximum tangential stress on inside diameter a and outside diameter b of the inner cylinder; τ 2 b and τ 2 c represent the maximum tangential stresses on inside diameters b and outside diameters c of the outer cylinder. Ansys Workbench software was used for finite element analysis. The relevant parameters of the composite cylinder are shown in Table 8.
3D modeling was carried out in Ansys Workbench. The inner diameter a of the inner cylinder, outer diameter b of the inner cylinder and outer diameter c of the outer cylinder were set as input parameters, which were used to solve the subsequent response surface. Tetrahedral elements are used to divide the grid. To ensure the number of elements and nodes on the composite cylinder wall, the cell size is set as 1mm. The displacement constraints in the direction of X, Y and Z are respectively applied to the cylinder end face of the composite cylinder. Meanwhile, the stress loading p is applied to the inner cylinder of the inner cylinder. The contact between the inner cylinder and the inner cylinder is selected as “no separation” in the “connection” option. The equivalent stress and maximum shear stress were solved respectively. The results are shown in Figure 7. The equivalent stress and maximum shear stress were set as output parameters.
According to the results of finite element analysis, the stress of the inner cylinder exceeds the maximum allowable value, so it cannot meet the use requirements at present. Its size parameters need to be further optimized. In this example, the expressions of the equivalent stress and tangential stress are approximated by polynomials. Quadratic polynomials with cross terms are selected here. The form is that the finite element analysis results show that the stress of the inner cylinder exceeds the maximum allowable value, so it cannot meet the use requirements at present. Its size parameters need to be further optimized. In this example, the expressions of equivalent stress and tangential stress are approximated by polynomials. Here, the quadratic polynomial with cross terms is selected. Its form is
F ˜ ( x ) = a 0 + ∑ i = 1 3 b i x i + ∑ i = 1 3 c i x i 2 2 + ∑ i = 1 2 ∑ j = i + 1 3 d i j x i x j + e 123 x 1 x 2 x 3
The response surface module in Ansys Workbench software is used to generate design points and calculate corresponding output values. The results are shown in Table 9.
The coefficients of the quadratic polynomial are solved in Matlab by using the above 10 groups of design points. The obtained values of each system are shown in Table 10.
By the above method, the limit state function is expressed explicitly instead of implicitly. In this problem, which has random uncertainty, their probability distribution is normal. Their standard deviation is 1% of their mean. c has interval uncertainty. Its value range is shown in Equation (36). This problem is solved. The results are shown in Table 11 below.
In order to verify the accuracy of the results, modeling and finite element analysis were conducted on the optimized composite cylinder again. The results are shown in Figure 8. It can be seen from the stress program that the maximum equivalent stress and maximum shear stress of the composite cylinder do not exceed the allowable value, which proves that the optimization scheme is feasible.

5. Conclusion

In this study, an RBDO method based on a meta-heuristic algorithm is proposed for RBDO with mixed uncertainties. The research involves: (1). Due to the high computational efficiency of the PSO algorithm, the improved PSO algorithm makes the process of solving MPP points faster and alleviates the computational burden of solving complex RBDO problems; (2). The improved PSO algorithm is combined with the SA algorithm to achieve a complete reliability optimization; (3). The double loop nesting problem of RBDO is avoided by decoupling. This method gives full play to the advantages of the two meta-heuristic algorithms and effectively improves the efficiency of solving the mixed uncertainty RBDO problem. The reliability and safety of RBDO in practical engineering applications are ensured. A mathematical example, a gear reducer volume optimization and a composite barrel size optimization problem are used to illustrate the advantages of the proposed strategy.
Mixed uncertainties are considered by the proposed method. However, in practical engineering, mixed uncertainties are very complex. Therefore, future work should be to introduce better algorithms into RBDO strategies considering mixed uncertainties.

Author Contributions

Conceptualization, S.-Y.Y., H.-T.W., Y.-H.X., Y.-Q.G., L.-D.P., J.-M.Z., X.-K.G., D.-B.M. and J.-P. W.; Methodology, S.-Y.Y., H.-T.W., Y.-H.X., Y.-Q.G., L.-D.P., J.-M.Z., X.-K.G., D.-B.M. and J.-P. W.; Validation, S.-Y.Y., H.-T.W., Y.-H.X., Y.-Q.G., L.-D.P., J.-M.Z., X.-K.G., D.-B.M. and J.-P. W.; Formal analysis, S.-Y.Y., H.-T.W., Y.-H.X., Y.-Q.G., L.-D.P., J.-M.Z., X.-K.G., D.-B.M. and J.-P. W.; Resources, S.-Y.Y., H.-T.W., Y.-H.X., Y.-Q.G., L.-D.P., J.-M.Z., X.-K.G., D.-B.M. and J.-P. W.; Writing—original draft, S.-Y.Y., H.-T.W., Y.-H.X., Y.-Q.G., L.-D.P., J.-M.Z., X.-K.G., D.-B.M. and J.-P. W.; Writing—review & editing, S.-Y.Y., H.-T.W., Y.-H.X., Y.-Q.G., L.-D.P., J.-M.Z., X.-K.G., D.-B.M. and J.-P. W.; Funding acquisition, Y.-H.X., Y.-Q.G., L.-D.P., J.-M.Z., X.-K.G. and D.-B.M.; All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (Grant No. 52175130), the Guangdong Basic and Applied Basic Research Foundation (Grant No. 2022A1515240010), and the Sichuan Science and Technology Program (Grants No. 2022YFQ0087 and 2022JDJQ0024).

Data Availability Statement

All data that support the findings of this study are included within the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zhong, Y.; Chen, Z.; Zhou, Z.; Hu, H. Uncertainty analysis and resource allocation in construction project management. Engineering Management Journal 2018, 30(4), 293-305. [CrossRef]
  2. Liao, K. W.; Kim, H.; Ha, C. Multilevel Optimization Considering Variability in Design Variables of Multidisciplinary System. In 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, Virginia, USA, 6-8 September 2006.
  3. Meng, D.; Yang, S.; He, C.; Wang, H.; Lv, Z.; Guo, Y.; Nie, P. Multidisciplinary design optimization of engineering systems under uncertainty: a review. International Journal of Structural Integrity 2022, 13(4), 565-593. [CrossRef]
  4. Liu, X.; Zhang, Y. Reliability-based design optimization for vehicle structural crashworthiness based on hybrid model. Journal of Changsha University of Science & Technology (Natural Science) 2021, 18(1), 95-101.
  5. Xue, Y.; Deng, Y. Extending set measures to orthopair fuzzy sets. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems 2022, 30(01), 63-91. [CrossRef]
  6. Zhu, S. P.; Keshtegar, B.; Bagheri, M.; Hao, P.; Trung, N. T. Novel hybrid robust method for uncertain reliability analysis using finite conjugate map. Computer Methods in Applied Mechanics and Engineering 2020, 371, 113309. [CrossRef]
  7. Bagheri, M.; Zhu, S. P.; Ben Seghier, M. E. A.; Keshtegar, B.; Trung, N. T. Hybrid intelligent method for fuzzy reliability analysis of corroded X100 steel pipelines. Engineering with computers 2021, 37(4), 2559-2573.
  8. Jiang, C.; Wang, X.; Wang, Q.; Wu W. Uncertainty quantification of natural convection of fluid in random porous media based on polynomial chaos expansion method. Journal of Changsha University of Science & Technology (Natural Science) 2019, 16(2), 62-70.
  9. Zhang, D.; Zhang, J.; Yang, M.; Wang, R.; Wu, Z. An enhanced finite step length method for structural reliability analysis and reliability-based design optimization. Structural and Multidisciplinary Optimization 2022, 65(8), 231.
  10. Meng, D.; Yang, S.; De Jesus, A. M.; Fazeres-Ferradosa, T.; Zhu, S. P. A novel hybrid adaptive Kriging and water cycle algorithm for reliability-based design and optimization strategy: Application in offshore wind turbine monopile. Computer Methods in Applied Mechanics and Engineering 2023, 412, 116083.
  11. Yang, I. T.; Hsieh, Y. H. Reliability-based design optimization with discrete design variables and non-smooth performance functions: AB-PSO algorithm. Automation in construction 2011, 20(5), 610-619. [CrossRef]
  12. Yang, M.; Zhang, D.; Wang, F.; Han, X. Efficient local adaptive Kriging approximation method with single-loop strategy for reliability-based design optimization. Computer Methods in Applied Mechanics and Engineering 2022, 390, 114462. [CrossRef]
  13. Meng, Z.; Li, G.; Wang, B. P.; Hao, P. A hybrid chaos control approach of the performance measure functions for reliability-based design optimization. Computers & Structures 2015, 146, 32-43. [CrossRef]
  14. Wang, Z.; Zhao, D.; Guan, Y. Flexible-constrained time-variant hybrid reliability-based design optimization. Structural and Multidisciplinary Optimization 2023, 66(4), 1-14.
  15. Ling, C.; Kuo, W.; Xie, M. An overview of adaptive-surrogate-model-assisted methods for reliability-based design optimization. IEEE Transactions on Reliability 2022, 60: 1-22.
  16. Zhang, D.; Shen, S.; Jiang, C.; Han, X.; Li, Q. An advanced mixed-degree cubature formula for reliability analysis. Computer Methods in Applied Mechanics and Engineering 2022, 400, 115521.
  17. Meng, Z.; Li, H.; Zeng, R.; Mirjalili, S.; Yıldız, A. R. An efficient two-stage water cycle algorithm for complex reliability-based design optimization problems. Neural Computing and Applications 2022, 34, 20993-21013. [CrossRef]
  18. Wang, Z.; Zhang, Y.; Song, Y. A modified conjugate gradient approach for reliability-based design optimization. IEEE Access 2020, 8, 16742-16749. [CrossRef]
  19. Liao, K. W.; Lu, B. C.; Yu, S. P. A Concurrent Approach for a Reliability-Based Optimization Design Problem. Journal of Advanced Mechanical Design, Systems, and Manufacturing 2012, 6(7), 1015-1030.
  20. Truong, V. H.; Kim, S. E. Reliability-based design optimization of nonlinear inelastic trusses using improved differential evolution algorithm. Advances in Engineering Software 2018, 121, 59-74. [CrossRef]
  21. Du, X. P.; Sudjianto, A.; Huang, B. Q. Reliability-based design with the mixture of random and interval variables. Journal of Mechanical Design 2005, 127(6): 1068-1076.
  22. Zhang, H.; Wang, H.; Wang, Y.; Hong, D. Incremental shifting vector and mixed uncertainty analysis method for reliability-based design optimization. Structural and Multidisciplinary Optimization 2019, 59, 2093-2109. [CrossRef]
  23. Wang, L.; Ma, Y.; Yang, Y.; Wang, X. Structural design optimization based on hybrid time-variant reliability measure under non-probabilistic convex uncertainties. Applied Mathematical Modelling 2019, 69, 330-354.
  24. Keshtegar, B.; Chakraborty, S. A hybrid self-adaptive conjugate first order reliability method for robust structural reliability analysis. Applied Mathematical Modelling 2018, 53, 319-332. [CrossRef]
  25. Mac, T. T.; Copot, C.; Tran, D. T.; De Keyser, R. A hierarchical global path planning approach for mobile robots based on multi-objective particle swarm optimization. Applied Soft Computing 2017, 59, 68-76.
  26. Li, J.; Chen, J. Solving time-variant reliability-based design optimization by PSO-t-IRS: A methodology incorporating a particle swarm optimization algorithm and an enhanced instantaneous response surface. Reliability Engineering & System Safety 2019, 191, 106580.
  27. Zhang, Y.; Liu, X.; Li C. Determining the reasonable state of cable-stayed bridges with twin towers based on multi-objective swarm optimization algorithm. Journal of Changsha University of Science & Technology (Natural Science) 2019, 16(2), 22-27.
  28. Zhu, S. P.; Keshtegar, B.; Seghier, M. E. A. B.; Zio, E.; Taylan, O. Hybrid and enhanced PSO: Novel first order reliability method-based hybrid intelligent approaches. Computer Methods in Applied Mechanics and Engineering 2022, 393, 114730. [CrossRef]
  29. Yu, S.; Wang, Z. A general decoupling approach for time-and space-variant system reliability-based design optimization. Computer Methods in Applied Mechanics and Engineering 2019, 357, 112608. [CrossRef]
  30. Wang, C.; Matthies, H. G. A comparative study of two interval-random models for hybrid uncertainty propagation analysis. Mechanical Systems and Signal Processing 2020, 136, 106531.
  31. Chopard, B.; Tomassini, M.; Chopard, B.; Tomassini, M. Simulated annealing. An introduction to metaheuristics for optimization 2018, 59-79.
  32. Wang, Z.; Liu, G.; Li, A. Three-dimensional path planning of UVAs based on simulated annealing and particle swarm optimization hybrid algorithm. In 2021 IEEE 3rd International Conference on Civil Aviation Safety and Information Technology (ICCASIT), Changsha, China, 20-22 October 2021.
  33. Abdel-Basset, M.; Ding, W.; El-Shahat, D. A hybrid Harris Hawks optimization algorithm with simulated annealing for feature selection. Artificial Intelligence Review 2021, 54, 593-637. [CrossRef]
  34. Delahaye, D.; Chaimatanan, S.; Mongeau, M. Simulated annealing: From basics to applications. Handbook of metaheuristics 2019, 1-35.
  35. Franzin, A.; Stützle, T. Revisiting simulated annealing: A component-based analysis. Computers & operations research 2019, 104, 191-206.
  36. Liu, X.; Gong, M.; Zhou, Z.; Xie, J.; Wu, W. An improved first order approximate reliability analysis method for uncertain structures based on evidence theory. Mechanics Based Design of Structures and Machines 2023, 51(7), 4137-4154.
  37. Afshari, S. S.; Enayatollahi, F.; Xu, X.; Liang, X. Machine learning-based methods in structural reliability analysis: A review. Reliability Engineering & System Safety 2022, 219, 108223.
  38. Ai, Q.; Yuan, Y.; Jiang, X.; Wang, H.; Han, C.; Huang, X.; Wang, K. Pathological diagnosis of the seepage of a mountain tunnel. Tunnelling and Underground Space Technology 2022, 128, 104657.
  39. Li, W.; Li, C.; Gao, L.; Xiao, M. Risk-based design optimization under hybrid uncertainties. Engineering with Computers 2020, 38, 2037-2049. [CrossRef]
  40. Liu, X.; Li, T.; Zhou, Z.; Hu, L. An efficient multi-objective reliability-based design optimization method for structure based on probability and interval hybrid model, Computer Methods in Applied Mechanics and Engineering 2022, 392: 114682.
  41. Luo, C.; Keshtegar, B.; Zhu, S. P.; Taylan, O.; Niu, X. P. Hybrid enhanced Monte Carlo simulation coupled with advanced machine learning approach for accurate and efficient structural reliability analysis. Computer Methods in Applied Mechanics and Engineering 2022, 388, 114218.
  42. Xin, L. I. U.; Hao, L. A. I.; Wang, X.; Song, X.; Kai, L. I. U.; Shaowei, W. U.; Zhenhua, Z. H. O. U. Aerospace Structural Reliability Analysis Method Based on Regular Vine Copula Model with the Asymmetric Tail Correlation. Aerospace Science and Technology 2023, 108670.
  43. Thakkar, A.; Lohiya, R. A survey on intrusion detection system: feature selection, model, performance measures, application perspective, challenges, and future research directions. Artificial Intelligence Review 2022, 55(1), 453-563. [CrossRef]
  44. Wang, Y. H.; Zhang, C.; Su, Y. Q.; Shang, L. Y.; Zhang, T. Structure optimization of the frame based on response surface method. International Journal of Structural Integrity 2019, 11(3), 411-425.
  45. Yang, S.; Meng, D.; Wang, H.; Chen, Z.; Xu, B. A comparative study for adaptive surrogate-model-based reliability evaluation method of automobile components. International Journal of Structural Integrity 2023, 14(3), 498-519.
  46. Meng, D.; Yang, S.; de Jesus, A. M.; Zhu, S. P. A novel Kriging-model-assisted reliability-based multidisciplinary design optimization strategy and its application in the offshore wind turbine tower. Renewable Energy 2023, 203, 407-420.
  47. Chen, J.; Zhang, X.; Jing, Z. A cooperative PSO-DP approach for the maintenance planning and RBDO of deteriorating structures. Structural and Multidisciplinary Optimization 2018, 58, 95-113.
  48. Lai, X.; Huang, J.; Zhang, Y.; Wang, C.; Zhang, X. A general methodology for reliability-based robust design optimization of computation-intensive engineering problems. Journal of Computational Design and Engineering 2022, 9(5), 2151-2169.
  49. Qiang, C.; Deng, Y. A new correlation coefficient of mass function in evidence theory and its application in fault diagnosis. Applied Intelligence 2022, 52(7), 7832-7842.
  50. Ai, Q.; Yuan, Y.; Shen, S. L.; Wang, H.; Huang, X. Investigation on inspection scheduling for the maintenance of tunnel with different degradation modes. Tunnelling and Underground Space Technology 2020, 106, 103589.
  51. Gao, J. W.; Dai, X.; Zhu, S. P.; Zhao, J. W.; Correia, J. A.; Wang, Q. Failure causes and hardening techniques of railway axles–a review from the perspective of structural integrity. Engineering Failure Analysis 2022, 106656.
  52. Yang S.; Meng, D.; Wang, H.; Yang C. A novel learning function for adaptive surrogate-model-based reliability evaluation. Phil. Trans. R. Soc A 2023, 381: 20220395. [CrossRef]
  53. Xiong, L.; Su, X.; Qian, H. Conflicting evidence combination from the perspective of networks. Information Sciences 2021, 580, 408-418.
  54. Yu, S.; Li, Y. Active learning kriging model with adaptive uniform design for time-dependent reliability analysis. IEEE Access 2021, 9, 91625-91634.
  55. Gao, X.; Su, X.; Qian, H.; Pan, X. Dependence assessment in human reliability analysis under uncertain and dynamic situations. Nuclear Engineering and Technology 2022, 54(3), 948-958.
  56. Meng, Z.; Keshtegar, B. Adaptive conjugate single-loop method for efficient reliability-based design and topology optimization. Computer Methods in Applied Mechanics and Engineering 2019, 344, 95-119.
  57. Li, W.; Xiao, M.; Garg, A.; Gao, L. A New Approach to Solve Uncertain Multidisciplinary Design Optimization based on Conditional Value at Risk. IEEE Transactions on Automation Science and Engineering 2021, 18(1), 356-368.
  58. Meng, D.; Yang, S.; Lin, T.; Wang, J.; Yang, H.; Lv, Z. RBMDO using gaussian mixture model-based second-order mean-value saddlepoint approximation. Computer Modeling in Engineering and Sciences 2022, 132(2), 553-568.
  59. Li, X. Q.; Song, L. K.; Bai, G. C. Recent advances in reliability analysis of aeroengine rotor system: a review. International Journal of Structural Integrity 2021, 13(1), 1-29.
  60. Yang, S.; Meng, D.; Guo, Y.; Nie, P.; Jesus, A. M. D. A reliability-based design and optimization strategy using a novel MPP searching method for maritime engineering structures. International Journal of Structural Integrity 2023, ahead-of-print.
  61. Pang, Y.; Lai, X.; Zhang, S.; Wang, Y.; Yang, L.; Song, X. A Kriging-assisted global reliability-based design optimization algorithm with a reliability-constrained expected improvement. Applied Mathematical Modelling 2023, 121, 611-630.
  62. Song, L. K.; Bai, G. C.; Li, X. Q.; Wen, J. A unified fatigue reliability-based design optimization framework for aircraft turbine disk. International Journal of Fatigue 2021, 152, 106422.
  63. Song, X.; Xiao, F. Combining time-series evidence: A complex network model based on a visibility graph and belief entropy. Applied Intelligence 2022, 52(9), 10706-10715.
  64. Das, S. K.; Tripathi, S.; Burnwal, A. P. Fuzzy based energy efficient multicast routing for ad-hoc network. In Proceedings of the 2015 third international conference on computer, communication, control and information technology (C3IT), Hooghly, India, 7-8 February 2015.
  65. Wang, Z.; Xiao, F.; Cao, Z. Uncertainty measurements for Pythagorean fuzzy set and their applications in multiple-criteria decision making. Soft Computing 2022, 26(19), 9937-9952.
  66. Dunn, W. L.; Shultis, J. K. Exploring monte carlo methods, 3rd ed.; Elsevier: Burlington, MA, 2012; pp. 154-196.
  67. Liang, J.; Mourelatos TU, Z. P. J. A single-Loop method for reliability-based design optimization. Proceedings of the ASME Design Engineering Technical Conference 2004, 1: 419-430.
  68. Azarm, S.; Li W. C. Multi-level design optimization using global monotonicity analysis. Journal of Mechanisms, Transmissions, and Automation in Design 1989, 111(2): 259-263.
  69. Gunawan, S.; Azarm, S.; Wu, J.; Boyars, A. Quality-assisted multi-objective multidisciplinary genetic algorithms. Aiaa Journal 2003, 41(9), 1752-1762.
Preprints 88495 g001
Figure 1. Flow chart of RBDO algorithm incorporating meta-heuristic algorithm.
Figure 1. Flow chart of RBDO algorithm incorporating meta-heuristic algorithm.
Preprints 88495 g001
Preprints 88495 g004
Figure 4. Design variable feasible domain.
Figure 4. Design variable feasible domain.
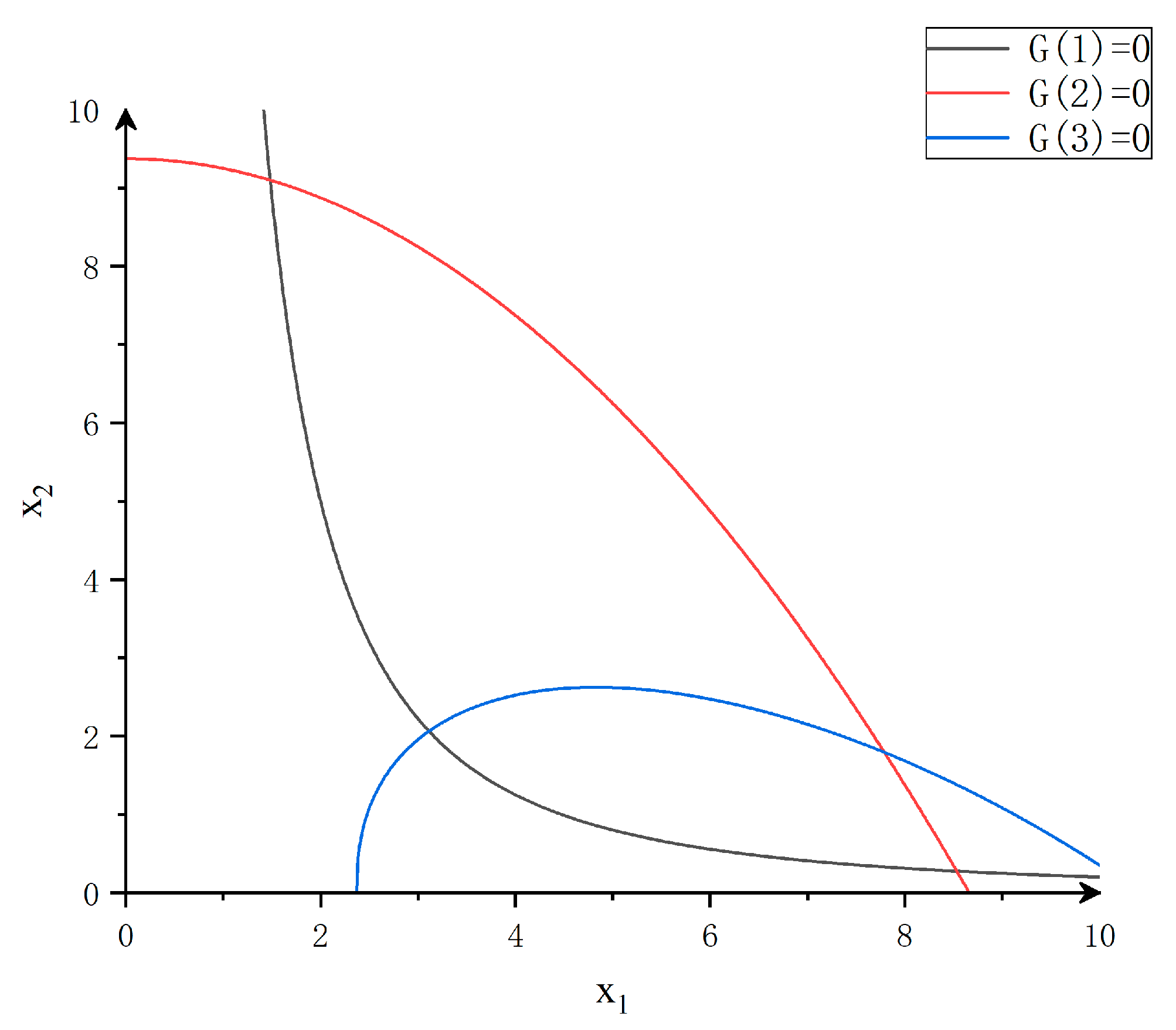
Preprints 88495 g004
Preprints 88495 g005
Figure 5. Structure diagram of gear reducer.
Figure 5. Structure diagram of gear reducer.
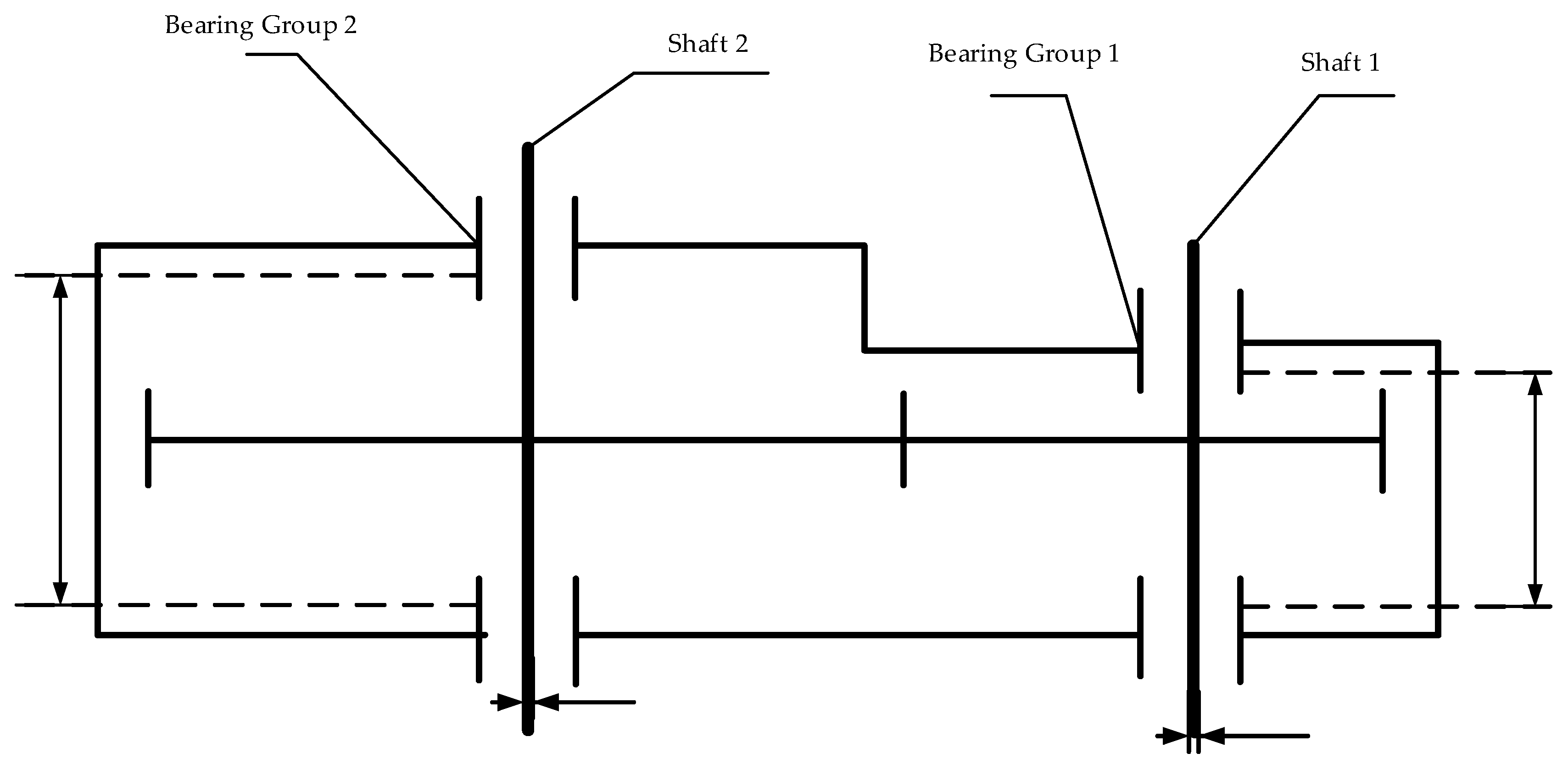
Preprints 88495 g005
Preprints 88495 g006
Figure 6. Composite cylinder structure diagram.
Figure 6. Composite cylinder structure diagram.
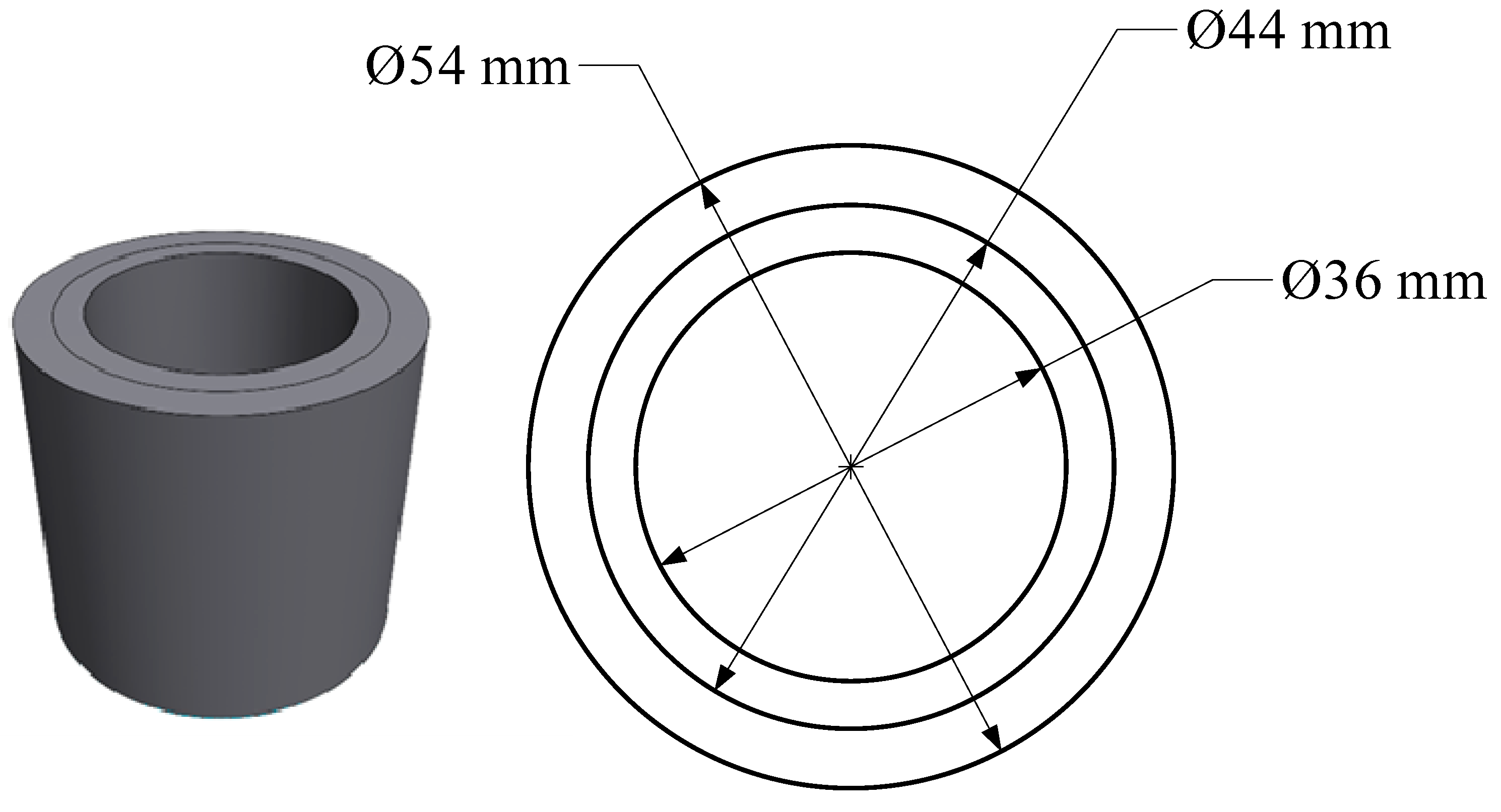
Preprints 88495 g006
Preprints 88495 g007
Figure 7. Stress nephogram of the composite cylinder. (a) Equivalent stress of inner cylinder (b) Equivalent stress of outer cylinder (c) Tangential stress on inner diameter of the inner cylinder (d) Tangential stress on outer diameter of the inner cylinder (e) Tangential stress on inner diameter of the outer cylinder (f) Tangential stress on the outer diameter of the outer cylinder.
Figure 7. Stress nephogram of the composite cylinder. (a) Equivalent stress of inner cylinder (b) Equivalent stress of outer cylinder (c) Tangential stress on inner diameter of the inner cylinder (d) Tangential stress on outer diameter of the inner cylinder (e) Tangential stress on inner diameter of the outer cylinder (f) Tangential stress on the outer diameter of the outer cylinder.
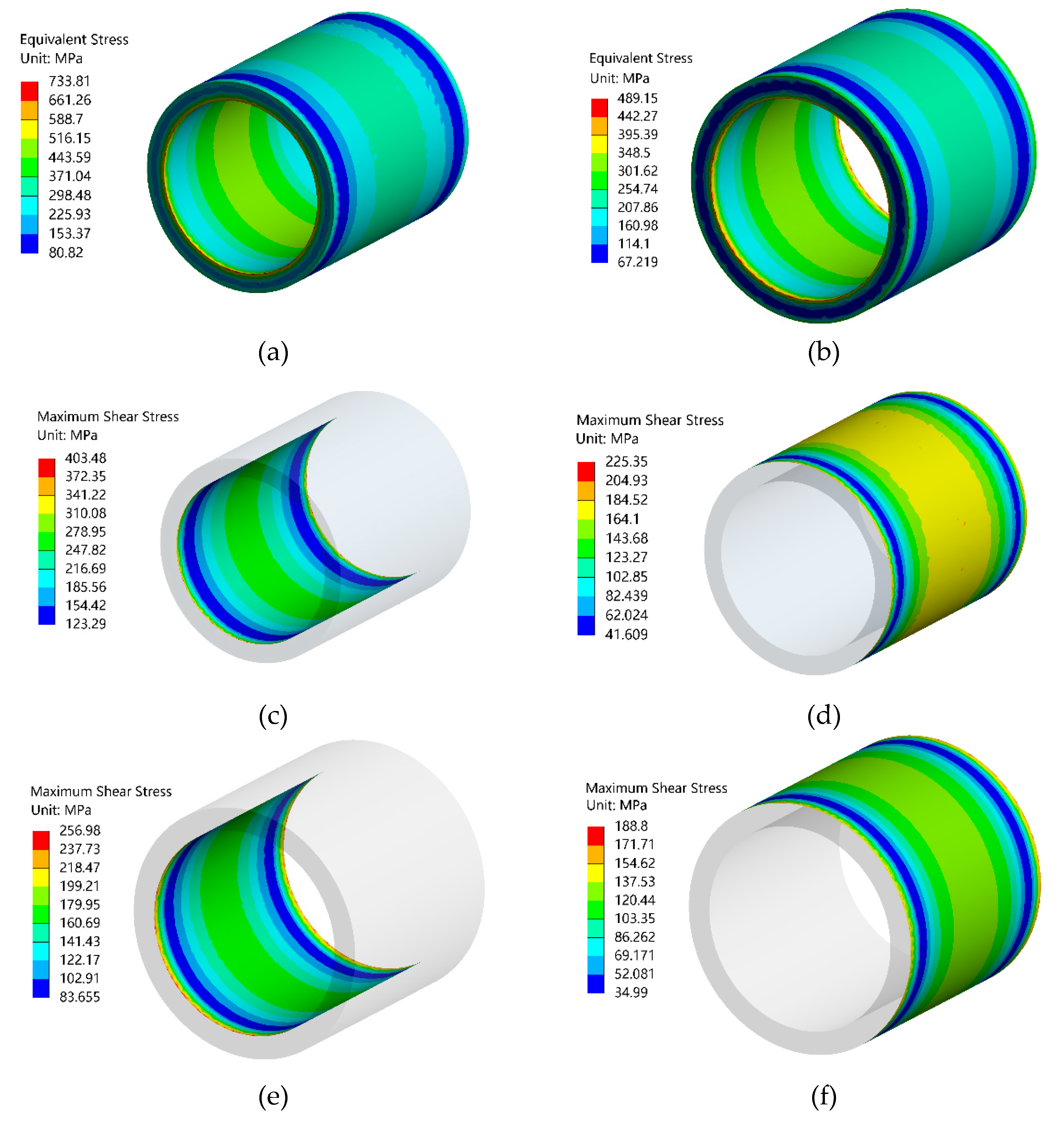
Preprints 88495 g007
Preprints 88495 g008
Figure 8. Stress nephogram of the composite cylinder after optimization. (a) Equivalent stress of inner cylinder (b) Equivalent stress of outer cylinder (c) Tangential stress on inner diameter of the inner cylinder (d) Tangential stress on outer diameter of the inner cylinder (e) Tangential stress on inner diameter of the outer cylinder (f) Tangential stress on the outer diameter of the outer cylinder.
Figure 8. Stress nephogram of the composite cylinder after optimization. (a) Equivalent stress of inner cylinder (b) Equivalent stress of outer cylinder (c) Tangential stress on inner diameter of the inner cylinder (d) Tangential stress on outer diameter of the inner cylinder (e) Tangential stress on inner diameter of the outer cylinder (f) Tangential stress on the outer diameter of the outer cylinder.
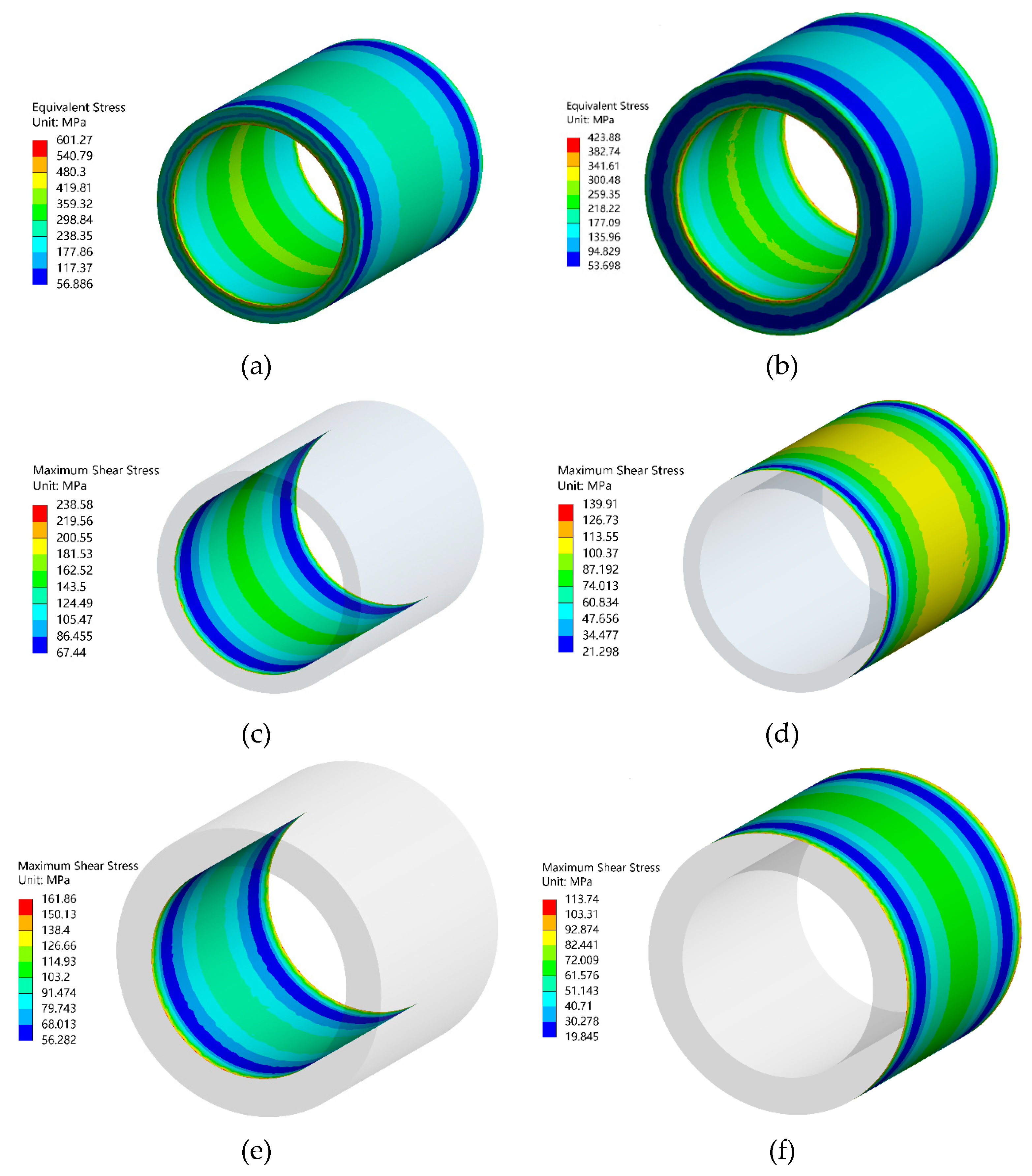
Preprints 88495 g008
Table 1. Flowchart of the SA algorithm combined with the PSO.
Table 1. Flowchart of the SA algorithm combined with the PSO.
The combination of SA and PSO
Step 1 Firstly, PSO is used to generate a set of initial solutions;
Step 2 For each particle, the value of its objective function is calculated and the current optimal solution is recorded;
Step 3 Calculate the speed of each particle, according to the speed of updating the positions of the particles in the solution space
Step 4 Using the Metropolis criterion to decide whether to accept the new position
Step 5 The particles are updated in a certain order to make the local optimal particle position move to the global optimal, which improves the global search performance of the algorithm
Step 6 Repeat steps (2) through (5) until the termination condition is reached
Table 4. Optimization result.
Table 4. Optimization result.
Method Optimal solution Error Solution time (milliseconds)
Theoretical method 6.7318 —— ——
SQP 7.4195 10.2% 319
The proposed method 7.0988 5.5% 207
Table 5. Random uncertainty description.
Table 5. Random uncertainty description.
Design variable Mean value Standard deviation Distribution type Lower bound of mean Upper bound of mean
Tooth width factor x 1 x 1 M 0.01 x 1 M Orthographic distribution 2.63 3.57
Length of shaft 1 x 4 x 4 M 0.01 x 4 M Orthographic distribution 7.31 8.29
Length of shaft 2 x 5 x 5 M 0.01 x 5 M Orthographic distribution 7.31 8.29
Table 6. Interval uncertainty description.
Table 6. Interval uncertainty description.
Design variable Upper bound of interval Lower bound of interval
Shaft 1 diameter x 6 2.93 3.87
Shaft 1 diameter x 7 5.03 5.47
Table 7. Optimization result.
Table 7. Optimization result.
Uncertainty description Optimal solution
Randomness 2773.0126
Randomness and interval 2814.9546
Table 8. Composite cylinder-related parameters.
Table 8. Composite cylinder-related parameters.
Name Symbol Value
Modulus of elasticity /Gpa E 210
Poisson’s ratio ρ 0.3
Internal pressure /Mpa p 139.7
Allowable stress /Mpa S 607.7
Allowable shear stress /Mpa τ 244.5
Table 9. Design point.
Table 9. Design point.
a b c S 1 S 2 τ 1 a τ 1 b τ 2 b τ 2 c
1 38.5 39.9 49.7 889.90 997.82 483.00 400.66 526.84 346.94
2 39.2 49.6 53.1 1069.30 518.25 578.87 273.39 273.69 180.97
3 33.0 49.5 55.5 589.82 252.57 324.35 130.22 133.18 89.94
4 39.3 43.8 58.0 792.55 528.81 441.83 281.42 279.47 186.87
5 37.1 47.6 50.4 751.12 438.64 414.24 234.62 230.51 177.81
6 32.8 39.7 52.7 605.15 391.49 337.28 195.88 207.00 135.23
7 34.2 43.1 52.3 811.37 436.74 442.53 218.96 231.57 170.05
8 36.4 49.0 56.8 881.32 430.42 483.57 201.98 226.71 155.63
9 39.7 47.5 49.7 1256.80 565.43 675.41 353.23 308.07 260.49
10 39.7 49.5 55.1 990.28 564.01 536.79 274.83 297.29 199.18
Table 10. Polynomial coefficient.
Table 10. Polynomial coefficient.
S 1 S 2 τ 1 a τ 1 b τ 2 b τ 2 c
a 0 1306319 41973.2 685669.2 116143.7 34266.6 -23063.3
b 1 -34404 -644.3 -18032.3 -2974.9 -663.4 748.8
b 2 -28761.7 -1219.7 -15093.5 -2522.8 -894.6 502.7
b 3 -24292.4 -753.5 -12764.2 -2184.7 -628.1 367.9
c 1 -5 -1.7 -3 0.8 -0.7 0.6
c 2 -10.9 0.5 -5.5 -1.1 0.01 -1.7
c 3 -9.4 -3.1 -4.7 -0.4 -1.5 0.3
d 12 761.1 18.5 399.3 65.2 16.7 -14
d 13 645.8 18.3 339 55.2 15.2 -14.6
d 23 550.9 23.7 288.7 48.9 17.5 -6.8
e 123 -14.1 -0.4 -7.4 -1.2 -0.3 0.3
Table 11. Optimization result.
Table 11. Optimization result.
Variable a b c V
Result 37.40 45.72 60.96 54929.13
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated