Safety Constraints-Guided Reinforcement Learning with Linear Temporal Logic

Preprint

Article

Safety Constraints-Guided Reinforcement Learning with Linear Temporal Logic

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

30 October 2023

Posted:

30 October 2023

You are already at the latest version

Alerts

Abstract

In the context of reinforcement learning (RL), ensuring both safety and performance is crucial, especially in real-world scenarios where mistakes can lead to severe consequences. This study aims to address this challenge by integrating temporal logic constraints into RL algorithms, thereby providing a formal mechanism for safety verification. We employ a combination of theoretical and empirical methods, including the use of temporal logic for formal verification and extensive simulations to validate our approach. Our results demonstrate that the proposed method not only maintains high levels of safety but also achieves comparable performance to traditional RL algorithms. Importantly, our approach fills a critical gap in existing literature by offering a solution that is both mathematically rigorous and empirically validated. The study concludes that the integration of temporal logic into RL offers a promising avenue for developing algorithms that are both safe and efficient. This work lays the foundation for future research aimed at generalizing this approach to various complex systems and applications.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

In the rapidly evolving field of machine learning, RL [1] has emerged as a pivotal sub-discipline. It involves agents learning to interact with their environment to maximize rewards, finding applications in diverse areas such as game theory, robotics, and natural language processing. However, the real-world application of these technologies often demands more than just maximizing rewards; it requires adherence to complex constraints and requirements, especially in safety-critical domains [2–11]. A single misstep in areas like autonomous driving or medical diagnostics could result in catastrophic outcomes, emphasizing the need for a more nuanced approach than just reward optimization. This sets the stage for our research, which aims to apply safety constraints to RL algorithms and formally verify them using temporal logic.

The motivation for this research is fueled by the growing importance of safety in the application of RL technologies. As these technologies find their way into increasingly complex and high-stakes environments, from industrial automation to healthcare, the margin for error narrows. The traditional focus on optimizing reward functions is insufficient for these applications, as it often fails to consider intricate constraints and diverse scenarios. Existing research has been limited in scope, often targeting specific scenarios or constraints without providing a formal verification approach for the reward mechanisms themselves.

Temporal logic offers a promising solution to these challenges. It allows for the mathematical specification of system behavior over time, enabling more rigorous verification. For instance, constraints like "the system must always maintain a safe state" or "certain actions must be taken when specific conditions are met" can be clearly articulated. This stands in contrast to the procedural languages traditionally used to implement reward mechanisms, which often result in long and complicated code that is difficult to generalize. Temporal logic allows for a more abstract and generalizable expression of reward mechanisms, facilitating more stringent verification.

Against this backdrop, our research proposes a novel approach to applying safety constraints in RL and formally verifying them using temporal logic. If successful, this research could establish a new paradigm for ensuring the safety of RL algorithms, particularly beneficial in complex and dynamic environments.

Thus, the necessity and significance of this research are profoundly high. It aims to solve a critical problem in the real-world application of RL, offering not just an incremental improvement but a paradigm shift in how we approach safety in these algorithms. By doing so, it addresses a glaring gap in existing literature and provides a robust framework that could be universally applied across various domains, thereby fulfilling an urgent and unmet need.

The structure of this paper is designed to provide a comprehensive understanding of the research. Section 2 delves into a summary of related works, offering a literature review that situates our research within the broader academic landscape. This section aims to highlight the existing gaps and how our work contributes to filling them. In Section 3, we elaborate on the methodology and foundational knowledge that underpin our research. This section provides a detailed account of the entire research procedure, from the initial conceptualization to the final analysis. It serves as a roadmap for understanding the choices made during the research process and offers a replicable blueprint for future studies. Section 4 is dedicated to presenting the experimental results from the first experiment and their analysis. Here, we not only showcase the data but also interpret it in the context of our research questions and objectives. This section provides empirical evidence to support the theoretical constructs and methodologies discussed earlier. Section 5 introduces the second experiment focusing on the Nuclear Plant Robot. This section presents the experimental setup, challenges inherent to the nuclear environment, and the results derived from the various models. The findings from this experiment offer a deeper understanding of safety and efficiency in high-risk settings, further enriching our research narrative. Section 6 offers a comprehensive analysis, synthesizing the findings from both experiments and comparing them with related research. This section serves as a capstone to our empirical work, drawing connections between our results and existing literature, thereby situating our contributions in a broader context. Finally, Section 7 concludes the paper by summarizing the key findings and outlining avenues for future research. This section encapsulates the essence of the paper, providing final thoughts on the significance and impact of our research.

2. Related Work

In the realm of RL and temporal logic, several noteworthy studies have laid the groundwork for our research. These studies have explored various facets of integrating temporal logic constraints into RL algorithms, each with its unique approach and focus.

One such study titled "Reinforcement Learning with Temporal Logic Constraints for Partially-Observable Markov Decision Processes"[12] delves into the application of temporal logic constraints, specifically iLTL, in the context of POMDPs. This study is pioneering in its attempt to marry POMDPs with temporal safety constraints. While the approach is promising for maintaining safety in complex environments, it falls short in providing sufficient experimental results to validate the practicality of the proposed methods.

Another study, "Learning from Demonstrations under Stochastic Temporal Logic Constraints,"[13] focuses on learning from demonstrations while adhering to Stochastic Temporal Logic (StTL) constraints. The study’s contribution lies in its novel application of StTL constraints to learning from demonstrations, thereby potentially enhancing the safety and reliability of such learning methods. However, like the previous study, it also lacks comprehensive experimental results to substantiate its practical utility.

The study "GR(1)-Guided Deep Reinforcement Learning for Multi-Task Motion Planning under a Stochastic Environment" [14] proposes a GR(1)-guided deep RL approach for multi-task motion planning in stochastic environments. The study’s strength lies in its innovative use of GR(1) to efficiently learn multi-task motion planning in uncertain settings. Yet, the study does not provide enough experimental design or results to clarify its practical implications.

"Temporal-Logic-Based Intermittent, Optimal, and Safe Continuous-Time Learning for Trajectory Tracking" [15] is another study that develops a RL-based controller for complex tasks while satisfying linear temporal logic specifications. The study’s merit is in its focus on ensuring safety during complex task execution. However, the study also lacks sufficient experimental results to validate the effectiveness of its proposed methods in real-world settings.

The study "Secure-by-Construction Controller Synthesis for Stochastic Systems under Linear Temporal Logic Specifications" [16] investigates the problem of synthesizing optimal control policies for stochastic systems that meet linear temporal logic specifications. The study contributes a new method for synthesizing safe control policies using linear temporal logic, but it too lacks sufficient experimental results to assess its practicality.

A significant contribution in the domain of AI verification is the paper "Toward verified artificial intelligence" [17]. This paper emphasizes the importance of a formal methods-based approach to AI system verification and validation. The authors argue that to truly trust AI systems, especially in safety-critical applications, we need to ensure their behavior is verified against formal specifications. While the paper provides a broad overview of the challenges and potential solutions in AI verification, it underscores the need for more research in this direction, especially in the context of RL.

In the study "Formal Verification for Safe Deep Reinforcement Learning in Trajectory Generation"[18], a significant contribution is made towards ensuring the safety of Deep Reinforcement Learning (DRL). Focusing on trajectory generation tasks, the research delves deep into Safe DRL using formal verification techniques. The authors introduce a novel approach to ascertain that the trained DRL models consistently generate trajectories adhering to predefined safety properties. A standout feature in their methodology is the utilization of interval analysis for verification, offering provable guarantees on the model’s adherence to safety properties.

In the paper "Formal verification of neural networks for safety-critical tasks in deep reinforcement learning" [19], the authors introduce a novel method for the formal verification of neural networks employed in safety-centric tasks using deep reinforcement learning. Through extensive experimentation across various real-world scenarios, they demonstrate that their proposed approach not only ensures the safety of the neural networks but also maintains high predictive performance. This work underscores the importance of combining formal verification techniques with deep learning to achieve both safety and efficiency in critical applications.

While these studies share the common goal of enhancing the safety and efficiency of systems through the integration of RL and temporal logic, they differ in their focus areas. For instance, the first study concentrates on POMDPs, the second on learning from demonstrations, the third on multi-task motion planning, the fourth on trajectory tracking, and the fifth on control policy synthesis. Despite their contributions, a recurring limitation across these studies is the lack of comprehensive experimental results, making it challenging to evaluate the practicality and effectiveness of their proposed methods.

These studies collectively indicate that while strides have been made in integrating temporal logic with RL, there remains a gap in formally verifying the reward mechanisms in RL using temporal logic. This underscores the importance and urgency of our research aim—to formally verify the reward mechanisms in RL using temporal logic. Our study seeks to fill this gap, offering both a theoretical framework and empirical evidence to support the integration of safety constraints into RL algorithms.

3. Methodology and Experimental Setup

3.1. Research Objectives

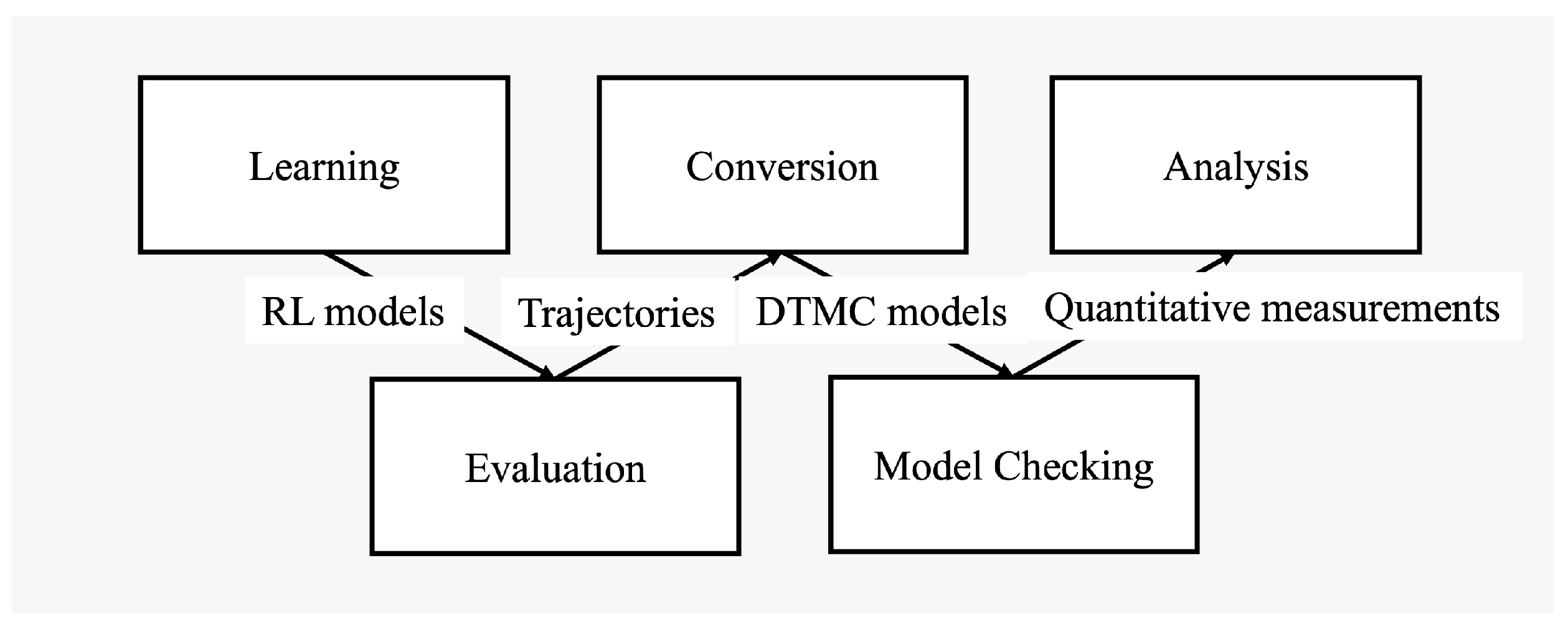
The overarching aim of this research is to delve into the intricate relationship between safety constraints, articulated through Linear Temporal Logic (LTL) [20], and RL models. This exploration is motivated by the increasing need for safety and reliability in autonomous systems, particularly in environments that involve interactions among multiple agents, such as robots in a restaurant setting. An overall process of this study is depicted in Figure 1.

In this context, we employ the Proximal Policy Optimization (PPO) [21] algorithm, a widely-used RL algorithm known for its efficiency and stability, to train models that can operate in a simulated restaurant environment. This simulated environment, referred to as "Serving Robots," serves as a testbed for evaluating the efficacy of integrating safety constraints into RL models.

One of the unique aspects of this research is the incorporation of safety constraints formulated in LTL. The primary constraint under consideration is

G (! collision)

, which aims to ensure that robots avoid collisions throughout their operations. By integrating this LTL-formulated safety constraint into the learning process, we seek to develop models that not only perform tasks efficiently but also adhere to essential safety conditions.

To rigorously evaluate the impact of these safety constraints, we undertake a comparative analysis of models trained with and without them. The performance metrics for this evaluation include the number of steps required to complete the tasks and the frequency of collisions. This allows us to quantitatively assess whether the inclusion of LTL-based safety constraints leads to more reliable and safer operation.

Furthermore, to provide a robust verification of the trained models, we transform the trajectories generated during 100 episodes into Discrete-Time Markov Chains (DTMC). These DTMC models are then subjected to quantitative verification using the PRISM model checker, allowing us to rigorously evaluate the safety and efficiency of each model.

By fulfilling these objectives, this research aims to contribute valuable insights into the utility and effectiveness of incorporating LTL-based safety constraints in RL. It is anticipated that the findings will have broad implications, particularly for applications that demand high levels of safety and reliability.

3.2. Background and Preliminaries

This section provides an in-depth background on the key concepts and methodologies that underpin this research, namely LTL, RL, and Model Checking.

3.2.1. Linear Temporal Logic

LTL is a formalism for specifying properties of reactive systems over time. The syntax of LTL can be defined using Backus-Naur Form (BNF) as follows:

ϕ : : = p ∣ \neg ϕ ∣ ϕ \land ϕ ∣ ϕ \lor ϕ ∣ X ϕ ∣ F ϕ ∣ G ϕ ∣ ϕ U ϕ

Here, p represents an atomic proposition, and

\neg, \land, \lor

are the standard logical negation, conjunction, and disjunction operators, respectively. The temporal operators are:

$X ϕ$ : Next. The formula $ϕ$ should hold in the next state.
$F ϕ$ : Eventually. The formula $ϕ$ should hold at some point in the future.
$G ϕ$ : Globally. The formula $ϕ$ should hold in all future states.
$ϕ U ψ$ : Until. The formula $ϕ$ should hold until $ψ$ becomes true.

3.2.2. Reinforcement Learning

RL is a subfield of machine learning that focuses on how agents can learn to make decisions to achieve a certain goal. The agent interacts with an environment, receiving observations and rewards that guide its learning process. The RL problem is often modeled as a Markov Decision Process (MDP), defined by a tuple

(S, A, P, R)

, where:

S is the state space, representing all possible situations the agent can encounter.
A is the action space, representing all possible moves the agent can make.
P is the state transition probability, $P (s^{'} | s, a)$ , representing the probability of transitioning from state s to $s^{'}$ when action a is taken.
R is the reward function, $R (s, a, s^{'})$ , representing the immediate reward received after transitioning from s to $s^{'}$ due to action a.

The agent’s behavior is defined by a policy

π (a | s)

, which is a probability distribution over actions given a state. The objective is to find the optimal policy

π^{*}

that maximizes the expected return

G_{t}

, defined as the sum of future rewards discounted by a factor

γ

G_{t} = \sum_{k = 0}^{\infty} γ^{k} R_{t + k + 1}

In this research, we use PPO, an advanced policy optimization algorithm. PPO aims to update the policy in a way that doesn’t change it too drastically, avoiding issues like policy oscillation. The objective function

L (θ)

in PPO is designed to optimize the policy

π_{θ} (a | s)

while keeping it close to the old policy

π_{θ_{old}} (a | s)

L (θ) = E * t [min (\frac{π * θ (a_{t} | s_{t})}{π_{θ_{old}} (a_{t} | s_{t})} A_{t}, clip (\frac{π_{θ} (a_{t} | s_{t})}{π_{θ_{old}} (a_{t} | s_{t})}, 1 - ϵ, 1 + ϵ) A_{t})]

3.2.3. Discrete-Time Markov Chains

DTMC are stochastic models used to represent systems that transition between a finite set of states in discrete time steps. A DTMC is formally defined by a tuple

(S, P)

, where:

S is a finite set of states ${s_{1}, s_{2}, \dots, s_{n}}$ .
P is the transition probability matrix, where $P_{i j}$ represents the probability of transitioning from state $s_{i}$ to $s_{j}$ in one time step.

The key property of a DTMC is the Markov property, which states that the future state depends only on the current state and not on the sequence of states that preceded it. Mathematically, this is expressed as:

P (S_{t + 1} = s^{'} | S_{t} = s, S_{t - 1} = s_{t - 1}, \dots, S_{0} = s_{0}) = P (S_{t + 1} = s^{'} | S_{t} = s)

In the context of our research, we convert the traces of episodes generated by the RL models into DTMCs. This conversion allows us to perform rigorous quantitative analysis using model checking techniques. Each state in the DTMC represents a unique configuration of the environment, and the transition probabilities are estimated based on the frequency of transitions between states in the collected traces.

3.2.4. Model Checking

Model checking is a formal verification technique that emerged in the 1980s to address the increasing complexity of software and hardware systems. Traditional testing methods were becoming less effective, and there was a need for a more systematic approach to ensure system correctness. Model checking provides this by exhaustively exploring all possible states of a system to verify whether it satisfies a given specification. This comprehensive verification offers a high level of confidence in the system’s reliability and safety.

In this research, we employ PRISM[22], a state-of-the-art probabilistic model checker, to perform quantitative verification of the trained RL models. PRISM is particularly well-suited for systems that exhibit stochastic behavior and allows for the verification of properties expressed in various temporal logics, including LTL.

The syntax for defining a model in PRISM is as follows:

\begin{matrix} module ModuleName \\ state-variable : [range] init initial-value; \\ [action] guard \to probability : update; \\ endmodule \end{matrix}

For reward-based properties, PRISM provides a specialized syntax:

R = ? [“ reward-structure ” \min = or \max = “ expression ”]

Here, "reward-structure" refers to the name of the reward structure defined in the PRISM model. The "expression" is a temporal logic formula specifying the condition under which the reward is accumulated. The "min=" or "max=" indicates whether the property aims to minimize or maximize the accumulated reward.

By utilizing PRISM and its reward-based property verification capabilities, we can conduct a nuanced quantitative analysis that focuses not only on the safety of the trained models but also on their efficiency in terms of reward accumulation.

3.3. Experimental Setup

3.3.1. Simulation Environment

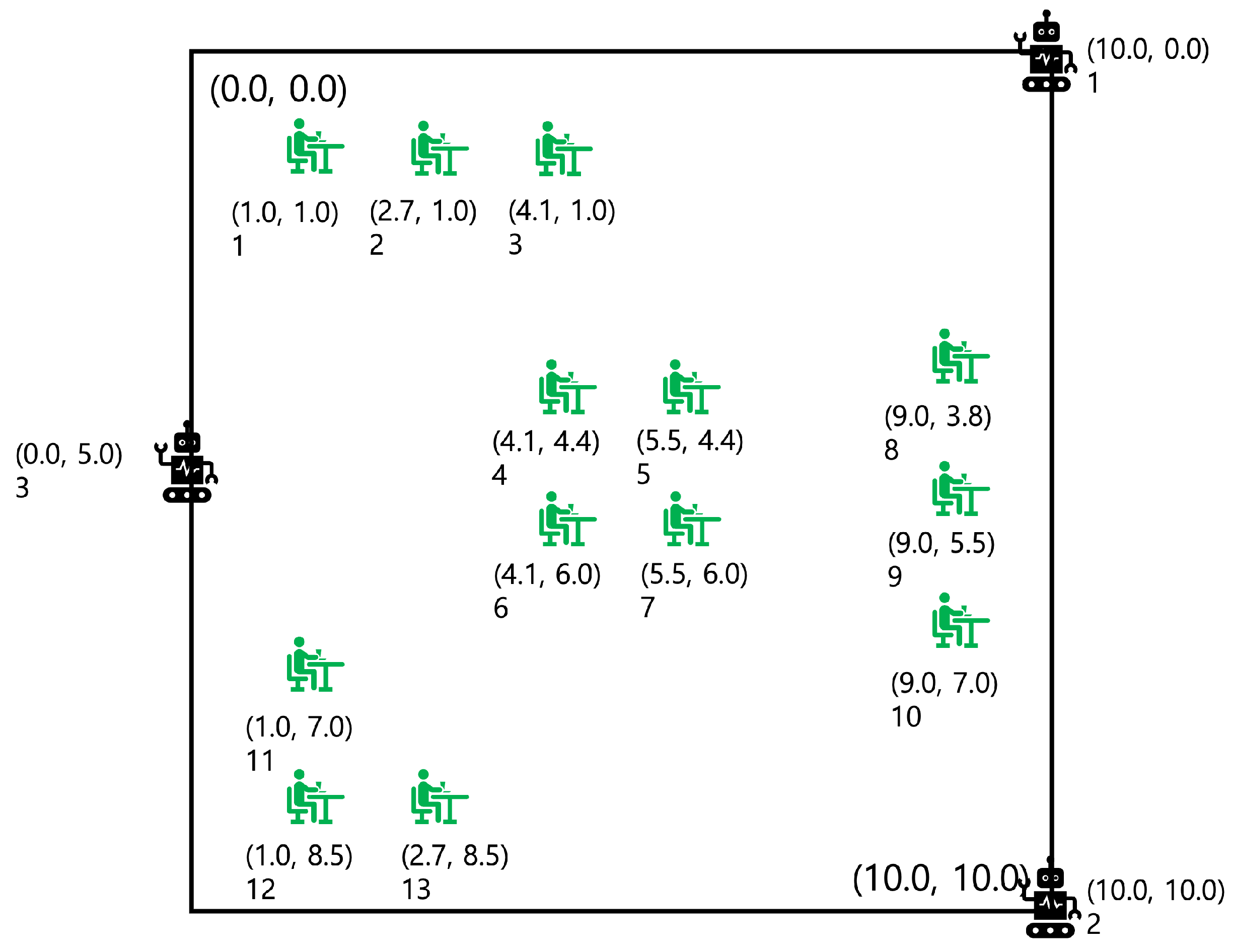
The cornerstone of our research is a meticulously designed simulation environment named "Serving Robots," which aims to replicate the complexities and challenges of a real-world restaurant setting. Developed on the robust OpenAI Gym framework, this environment offers a highly customizable and standardized interface, making it an ideal testbed for RL algorithms. The visual representation of this simulation environment is depicted in Figure 2.

In the simulated restaurant, the layout is represented as a 10.0 x 10.0 grid. Within this grid, robots and customers are abstracted as coordinate points. The robots are strategically initialized at specific grid locations to cover the maximum service area efficiently. The robots have the capability to move in eight distinct directions, calculated based on a 12 o’clock reference and proceeding in a clockwise manner. The

x, y

coordinates serve as the positional indicators for each robot, providing a continuous state space for the learning algorithm.

The restaurant environment is populated with 13 strategically placed seats, each capable of generating a service request at random intervals. These service requests simulate customer orders that the robots are programmed to fulfill. A service request is marked as complete when a robot successfully navigates to within a predefined range of the seat emitting the request. This introduces a spatial challenge, requiring the robots to optimize their paths while avoiding collisions.

Collision avoidance is a critical safety feature implemented in the environment. Robots are programmed to maintain a safe distance from each other, defined by a specific range in the grid. If robots come within this range, a collision is flagged, and a penalty is applied, affecting the overall reward metric. This feature is particularly important for ensuring the safe operation of the robots, aligning with real-world requirements.

To add another layer of complexity and realism, each robot is equipped with a simulated battery that depletes as it moves. This introduces an energy-efficiency aspect to the task, requiring the robots to not only fulfill service requests but also manage their energy consumption effectively.

The action space for the robots is defined as a multi-discrete space, allowing each of the three robots to choose from one of eight possible movement directions. The observation space is a 19-dimensional continuous space, capturing a wealth of information including the

x, y

coordinates of each robot and the active or inactive status of service requests for each of the 13 seats.

Incorporated into the environment are safety constraints, articulated in Linear Temporal Logic (LTL). The specific constraint

G (\neg collision)

mandates that the robots must perpetually avoid collisions. To enforce this constraint, we employ an STL parser that evaluates the trace of states and actions, thereby providing a formal and rigorous method to ensure safety.

The ‘step’ function in the environment serves multiple roles. It updates the state based on the chosen actions, calculates the immediate reward, and checks for termination conditions. The reward structure is a composite metric, factoring in energy consumption, penalties for collisions, and bonuses for successfully completed services. The simulation terminates when all service requests are fulfilled, providing a natural endpoint for each episode.

By leveraging this intricately designed environment, we are equipped to conduct experiments on two variants of the RL problem: one incorporating safety constraints and the other without such constraints. This dual setup enables a comprehensive and nuanced analysis, shedding light on the impact and efficacy of integrating safety constraints into RL models.

3.3.2. Safety Constraints

Ensuring safety in autonomous systems is a critical concern, and one of the most effective ways to achieve this is through the use of formal methods. In this research, we employ LTL to articulate the safety constraints for serving robots operating in a simulated restaurant environment. The primary safety objective is to prevent collisions between the robots, which is formally expressed as

G (! collision)

in LTL.

The "G" in the formula stands for "Globally," signifying that the constraint must be satisfied at all times during an episode. The negation operator "!" indicates that the condition of a collision should not occur, and the term "collision" is a propositional variable that turns true if any of the robots collide. Therefore, the formula

G (! collision)

mandates that no collisions should occur between any of the robots throughout the entire operation. This is a hard constraint, meaning that even one violation would be unacceptable.

Incorporating this safety constraint into the RL model serves several important functions. First, it adds robustness to the model by formally specifying what it means for the system to be safe, thereby training the model to be resilient against unforeseen scenarios that could lead to collisions. Second, the formal nature of LTL allows for the rigorous verification of the trained model using model checking techniques, ensuring that it satisfies the safety constraint.

Moreover, while the primary focus is on safety, the constraint also subtly guides the learning process to optimize for other objectives like efficiency and speed, without compromising safety. The use of LTL also enhances the interpretability of the system’s safety requirements, making it easier for various stakeholders, from developers to end-users, to understand and reason about the system’s safety measures.

Additionally, the scalability of LTL constraints allows them to be easily extended or modified to suit more complex scenarios or different types of robots. Lastly, meeting such formal safety constraints can be crucial for legal and ethical compliance, especially in real-world applications where safety cannot be compromised.

By weaving the

G (! collision)

constraint into the learning process, this research aims to yield a model that is not only efficient in terms of task completion but also demonstrably safe, thereby making a significant contribution to the field.

3.4. Experimental Procedure

3.4.1. Hyperparameter Settings

The hyperparameter settings serve as the foundational building blocks for our experiments. We systematically vary the number of timesteps and learning rates to generate a diverse set of models. Specifically, we use six different combinations of timesteps and learning rates, such as

T i m e s t e p s = [20, 000, 35, 000, 40, 000]

and

L e a r n i n g R a t e s = [0.0006, 0.0008, 0.001]

. This exhaustive approach allows us to explore the impact of these hyperparameters on the model’s performance, thereby enabling a more nuanced understanding of how they interact with the learning process.

The rationale behind selecting these particular ranges for the two hyperparameters is based on empirical observations. In simpler terms, when we evaluated models trained with too few timesteps or exceedingly low learning rates, the rewards acquired were significantly low. Conversely, with higher timesteps or elevated learning rates, we observed that the evaluation rewards consistently converged. These observations informed our decision to set the hyperparameter ranges as presented.

3.4.2. Model Training

The training phase is not merely a preparatory step but a critical component that directly influences the quality of the models. Each of the six models is trained using PPO, a state-of-the-art RL algorithm known for its stability and efficiency. The training occurs in a simulated ’Serving Robots’ environment, which is a high-fidelity representation of a restaurant setting. This environment incorporates various challenges such as dynamic customer requests, limited battery life, and safety constraints defined through LTL.

During the training process, when safety constraints are present, we utilize the STL library, an open-source tool, to ensure that the safety constraints formalized in LTL are satisfied. To verify the adherence to these safety constraints, sequences of values from the observation space and action space are inputted, and a Boolean result is checked. If the safety constraints are satisfied within a finite sequence, the system internally records either True or False. This mechanism is not exclusive to the training phase; it operates identically during model evaluation, ensuring consistent safety checks throughout both training and evaluation stages.

3.4.3. Model Evaluation

Evaluation is conducted over 100 episodes for each of the six models to ensure statistical robustness. The primary metric is the average reward, which encapsulates the model’s proficiency in fulfilling tasks while adhering to safety norms. During these episodes, we collect a rich set of execution trajectories, denoted as T. Each trajectory

τ

within T is a sequence of tuples consisting of environment observations and actions taken by the agent. These trajectories serve as a comprehensive snapshot of the agent’s behavior and are crucial for subsequent analyses.

3.4.4. Model Conversion to DTMC

The transition from raw trajectories T to a DTMC model M is a meticulous process. Each unique tuple

τ (i) = (o_{i}, a_{i})

in a trajectory

τ

is mapped to a unique state s in M. Transitions between these states are determined based on the actions taken, thereby capturing the stochastic nature of the environment. The model M is then normalized to ensure that the sum of probabilities for all possible transitions from each state s equals 1, making M a valid probability distribution.

3.4.5. Quantitative Measurement Using PRISM

The DTMC models serve as the input for the PRISM model checker, a powerful tool for formal verification and quantitative analysis. We define various metrics in Probabilistic Computation Tree Logic (PCTL)[23], such as the expected number of steps to complete all tasks, the expected battery consumption, and the expected occurrences of collision. These metrics are not merely numerical values but offer deep insights into the model’s performance, reliability, and safety.

3.4.6. Comprehensive Analysis

The final step involves a thorough analysis of all the collected data, synthesized into various forms of visualizations. We employ line charts, bar graphs, and bubble charts to represent different aspects of performance metrics. These visual tools help us identify patterns, correlations, and outliers, thereby enabling a multi-dimensional evaluation of the models. The goal is to select the most optimal model that balances efficiency, reliability, and safety.

By following this rigorous and multi-faceted experimental procedure, we aim to provide a comprehensive evaluation of RL models in complex, multi-agent settings, while rigorously adhering to safety constraints.

4. Experimental Results and Analysis

4.1. Evaluation Reward Comparison

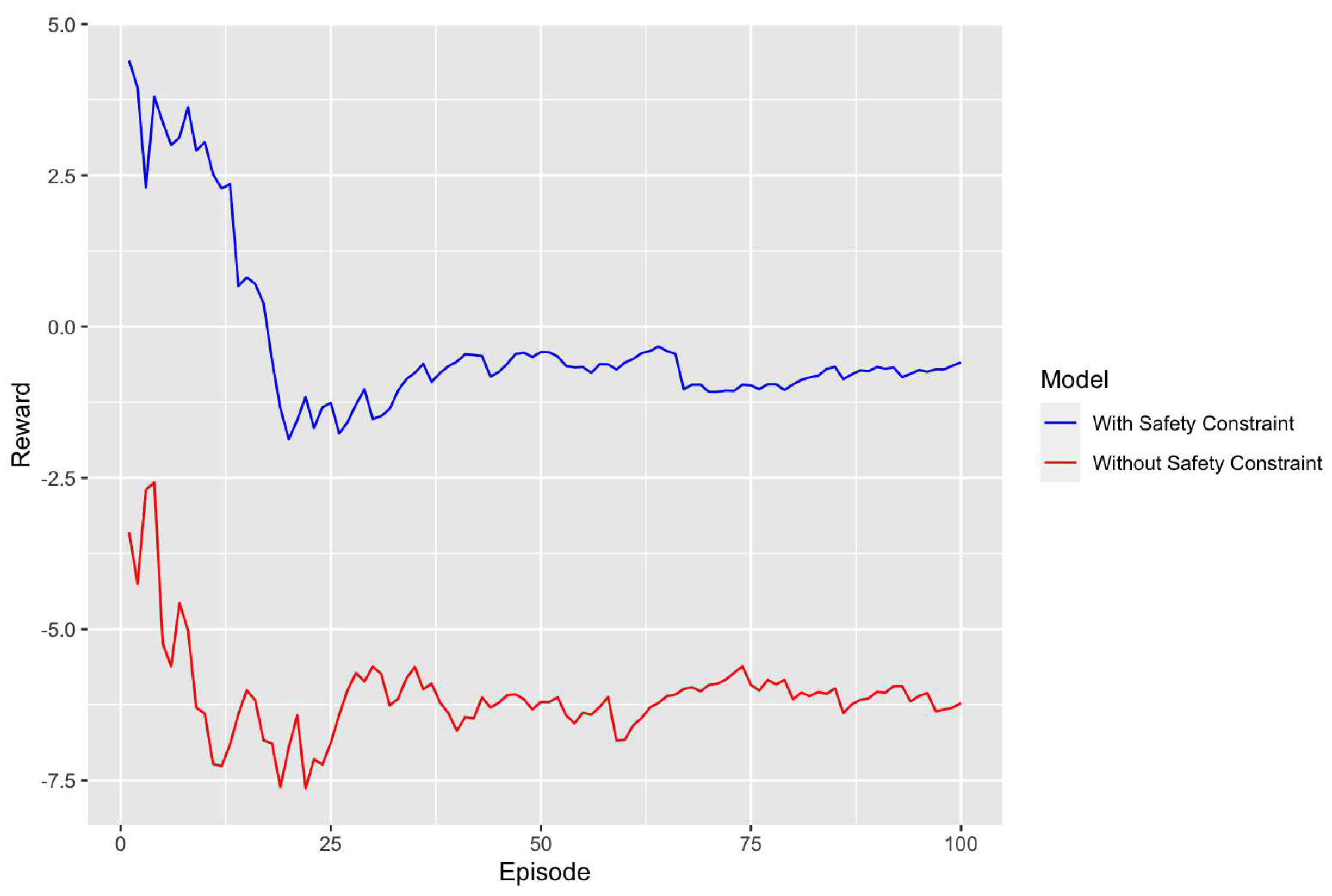
In this section, we focus on the comparative analysis of the evaluation rewards achieved by two distinct models trained with different hyperparameters. The first model is trained with 40,000 timesteps and a learning rate of 0.001. The line graph of this model is shown in Figure 3. We examine this model in two configurations: one with safety constraints and another without. The objective is to understand the role of safety constraints in influencing the model’s performance, particularly in terms of the rewards it garners during evaluation.

The model with safety constraints yielded an average reward of approximately -0.33, which is significantly higher than its counterpart without safety constraints, which had an average reward of around -5.95. This stark difference in average rewards highlights the critical importance of incorporating safety constraints. It suggests that the model with safety constraints is more adept at navigating the environment in a manner that minimizes penalties associated with unsafe actions.

Further insights can be gleaned from the standard deviation of the rewards. The model with safety constraints had a standard deviation of about 1.28, slightly higher than the 0.91 observed in the model without safety constraints. This higher standard deviation in the safety-constrained model could indicate its ability to adapt more effectively to a variety of environmental conditions. It suggests that the model is capable of maintaining a wider range of rewards, which could be beneficial when dealing with unpredictable or challenging scenarios.

Additionally, the range between the minimum and maximum rewards for each model provides more context. The safety-constrained model had a minimum reward of -1.76 and a maximum of 4.4. In contrast, the model without safety constraints had a much narrower and lower range, with a minimum reward of -7.64 and a maximum of -2.7. This broader range in the safety-constrained model implies a greater adaptability and a propensity for safer behavior across different situations.

In summary, when considering the model trained with 40,000 timesteps and a learning rate of 0.001, the presence of safety constraints appears to be a crucial factor for enhancing both safety and performance. The safety-constrained model not only outperforms the model without safety constraints in terms of average rewards but also exhibits a more adaptive and safety-conscious behavior. As we proceed to analyze additional models trained with different hyperparameters, these findings will serve as a valuable baseline for comparison.

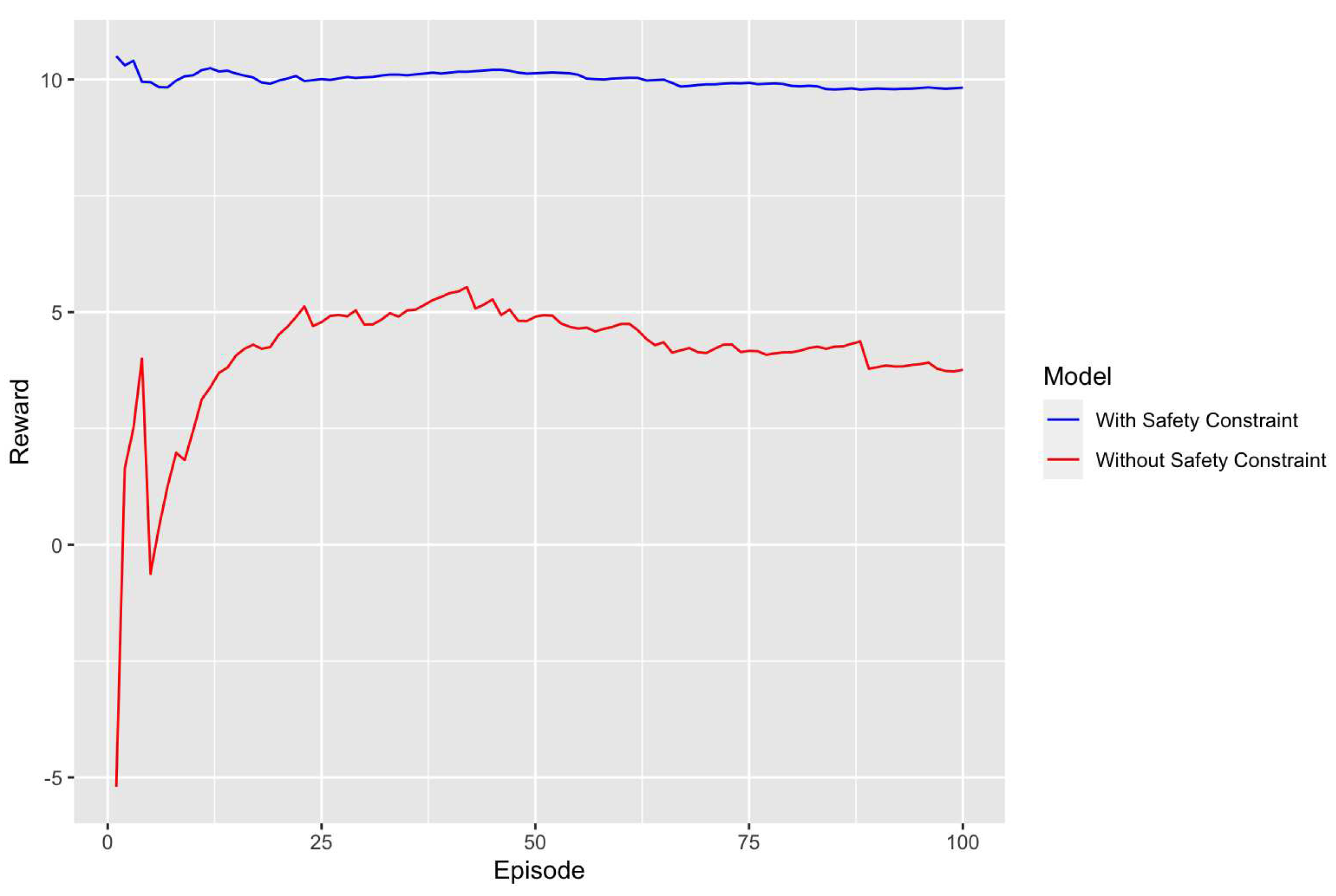
Continuing our analysis, we turn our attention to the second model trained with 60,000 timesteps and a learning rate of 0.0008. The line graph of this model is shown in Figure 4. Similar to the first model, we evaluate this model in two configurations: one with safety constraints and another without. This allows us to further validate the impact of safety constraints on the model’s performance.

For the model trained with 60,000 timesteps and a learning rate of 0.0008, the average reward for the configuration with safety constraints was approximately 9.98, a figure that is remarkably higher than the 4.12 average reward observed in the model without safety constraints. This significant difference in average rewards further underscores the importance of incorporating safety measures. The model with safety constraints not only performs better in terms of average rewards but also implies that it is more proficient at avoiding penalties associated with unsafe actions.

The standard deviation of the rewards also offers valuable insights. The safety-constrained model had a very low standard deviation of about 0.11, in stark contrast to the 2.63 observed in the model without safety constraints. This lower standard deviation in the safety-constrained model suggests a higher level of consistency in its performance. It indicates that the model’s behavior is more predictable and stable, which is a desirable quality when operating in environments where safety is a priority.

Moreover, the range of minimum and maximum rewards for each model provides additional context. The safety-constrained model had a minimum reward of 9.78 and a maximum of 10.21, which is a narrow but high range. On the other hand, the model without safety constraints had a much wider and lower range, with a minimum reward of -5.20 and a maximum of 5.54. This narrow yet high range in the safety-constrained model suggests that it is not only capable of achieving high rewards but also does so with a high level of consistency.

In summary, the model trained with 60,000 timesteps and a learning rate of 0.0008 further confirms the observations made with the first model. The presence of safety constraints significantly enhances the model’s performance, as evidenced by higher average rewards, lower standard deviation, and a more consistent range of minimum and maximum rewards. This model, like the first, demonstrates that safety constraints are instrumental in achieving a balance between high performance and safety, making it a more desirable choice for applications where safety is a critical concern.

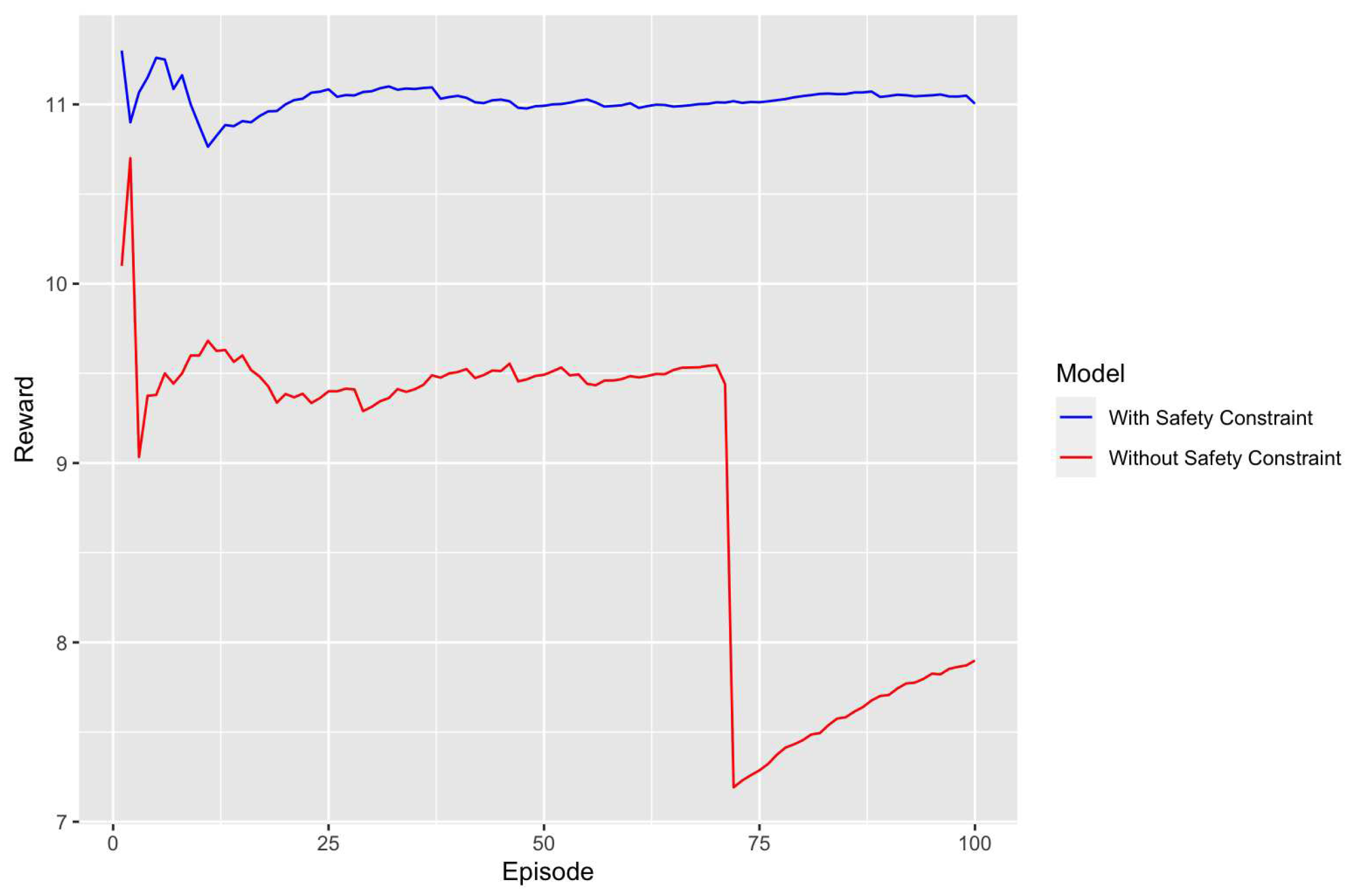
Expanding our analysis to the third model, which was trained with 80,000 timesteps and a learning rate of 0.0006, we continue to observe the impact of safety constraints on model performance. This model, like its predecessors, was evaluated in two different configurations: one with safety constraints and another without. The line graph of this model is shown in Figure 5.

For this third model, the average reward with safety constraints was approximately 11.01, which is notably higher than the 9.21 average reward for the model without safety constraints. While the difference in average rewards between the two configurations is smaller compared to the previous models, it still highlights the benefits of incorporating safety constraints. The higher average reward in the safety-constrained model suggests that it is more adept at navigating the environment in a manner that avoids penalties and maximizes rewards.

The standard deviation of the rewards also provides valuable insights into the model’s performance. The safety-constrained model had a very low standard deviation of about 0.13, compared to the 1.08 observed in the model without safety constraints. This lower standard deviation indicates that the safety-constrained model’s performance is more consistent and stable, reinforcing the idea that safety constraints contribute to more predictable behavior.

Furthermore, the range of minimum and maximum rewards for each configuration adds another layer of understanding. The safety-constrained model had a minimum reward of 10.88 and a maximum of 11.30, a narrow but high range. In contrast, the model without safety constraints had a wider and lower range, with a minimum reward of 7.19 and a maximum of 10.70. This suggests that the safety-constrained model not only achieves higher rewards but does so with a higher level of consistency, further emphasizing the advantages of incorporating safety constraints.

In summary, the third model trained with 80,000 timesteps and a learning rate of 0.0006 corroborates the findings from the previous models. The presence of safety constraints consistently leads to better performance metrics, including higher average rewards, lower standard deviation, and a more consistent range of minimum and maximum rewards. While the difference in average rewards is less pronounced in this model compared to the earlier ones, the overall trend remains the same: models with safety constraints are more desirable when safety is a critical factor. This consistent pattern across all three models strongly supports the argument for the inclusion of safety constraints in RL models, especially in applications where safety cannot be compromised.

In light of the comprehensive analysis across the three models, several key observations emerge that underscore the importance of incorporating safety constraints in RL models. These observations are based on a variety of metrics, including average rewards, standard deviation, and the range of minimum and maximum rewards.

Firstly, the average rewards consistently show that models with safety constraints outperform those without. For instance, the first model, trained with 40,000 timesteps and a learning rate of 0.001, exhibited a stark contrast in average rewards: approximately -0.33 with safety constraints versus -5.95 without. The second model, trained with 60,000 timesteps and a learning rate of 0.0008, also demonstrated a significant difference: an average reward of 9.98 with safety constraints compared to 4.12 without. Finally, the third model, trained with 80,000 timesteps and a learning rate of 0.0006, continued this trend, albeit with a smaller gap, showing average rewards of 11.01 and 9.21 with and without safety constraints, respectively.

The standard deviation of rewards further corroborates these findings. Models with safety constraints generally exhibited lower standard deviations, indicating more consistent and reliable behavior. This was particularly evident in the second and third models, where the standard deviations were 0.11 and 0.13 with safety constraints, compared to 2.63 and 1.08 without, respectively.

Moreover, the range of minimum and maximum rewards for each model configuration adds another layer of understanding. Across all models, the safety-constrained configurations not only achieved higher rewards but did so with higher levels of consistency. This is evident from the narrower ranges of minimum and maximum rewards in models with safety constraints.

The overarching trend across all these metrics is clear: models with safety constraints are more reliable and perform better in terms of both average rewards and consistency. This is particularly true for the third model, which not only had the highest average reward but also the lowest standard deviation, making it the most desirable when safety is a critical factor.

The use of LTL serves as a cornerstone for enhancing the safety features of the models. LTL allows for a nuanced and precise representation of complex constraints that the system’s future states must adhere to. This level of detail is invaluable for immediate error detection. If the system ever violates an LTL rule, the model can take preemptive measures before transitioning into a potentially dangerous state. This real-time error detection and correction mechanism significantly elevates the overall safety of the system.

Another crucial factor is the consideration of historical data. By accounting for past states and actions, the model gains the ability to make more accurate and informed predictions about future states. This historical context is not just beneficial for improving state predictions; it’s also vital for assessing the level of risk associated with current states. For instance, if the model recognizes that similar past situations have led to risky outcomes, it can opt for more cautious actions in the present. This dynamic risk assessment, informed by historical data, adds an extra layer of safety to the model’s decision-making process.

Lastly, the reward mechanism plays a pivotal role in shaping the behavior of the model. When designed with safety constraints in mind, the reward function can effectively guide the model towards safer actions. It does so by imposing penalties for risky or dangerous behavior and offering rewards for actions that are deemed safe. This dual mechanism of penalties and rewards ensures that the model is not just learning to maximize rewards but is also actively avoiding actions that could compromise safety.

The interaction between these factors—LTL, historical data, and the reward mechanism—creates a robust safety net for the system. For example, the safety constraints defined through LTL can be more effectively internalized by the model through a well-designed reward mechanism. This, in turn, allows the model to make more accurate assessments based on its history, thereby creating a feedback loop that continually enhances safety.

In summary, each of these elements individually contributes to the safety of the system, but it’s their synergistic interaction that provides a comprehensive and robust safety framework. This multi-layered approach to safety justifies the observed superiority of models with safety constraints, especially in applications where safety cannot be compromised.

4.2. Quantitative Measurement

The data clearly indicates that models with safety constraints generally require fewer steps to accomplish their tasks compared to those without safety constraints. This observation opens the door to several interpretations. The quantitative results for the total number of steps to complete the mission are presented in Table 1.

Firstly, the relationship between efficiency and safety becomes evident. When safety constraints are applied, not only does the system become safer, but it also accomplishes its mission in fewer steps. This suggests that safety constraints contribute to making the system more efficient, not just safer. Completing missions in fewer steps inherently means that the system has fewer opportunities to engage in potentially hazardous states or actions, thereby enhancing its overall safety.

Secondly, the role of the learning rate in influencing safety is noteworthy. Models with lower learning rates appear to be more effective when safety constraints are applied. This could be interpreted as the model learning in a more stable and cautious manner when safety constraints are in place. The lower learning rate, in conjunction with safety constraints, seems to guide the model towards a more optimal path, both in terms of safety and efficiency.

Thirdly, the impact of safety constraints becomes increasingly apparent as the number of timesteps increases. This suggests that the longer the model trains, the more pronounced the benefits of having safety constraints become. It’s as if the model, through extended learning, comes to realize the increasing importance of adhering to safety constraints for both efficient and safe operation.

Lastly, it’s important to acknowledge that even models without safety constraints show a reduction in the number of steps required for mission completion as they learn. This could be seen as the inherent benefit of the learning process itself, which can achieve a certain level of efficiency and safety even without explicit safety constraints. However, given the same amount of training time, models with safety constraints consistently outperform those without, underscoring the importance of incorporating safety constraints into the learning process.

In summary, the data strongly suggests that safety constraints play a significant role in not just enhancing the safety of the system but also its efficiency. The constraints appear to guide the model towards more optimal behavior, reducing the number of steps required for mission completion, especially as the model undergoes more extended periods of training. This dual benefit of safety and efficiency makes a compelling case for the inclusion of safety constraints in RL models, particularly in scenarios where both attributes are of paramount importance.

Building upon the previous discussion, the data on the frequency of collisions provides another layer of insight into the role of safety constraints. The numbers clearly indicate that models with safety constraints experience fewer collisions compared to those without. This observation can be dissected from several critical angles. The quantitative results for the total number of steps to complete the mission are presented in Table 2.

Firstly, the enhancement of safety is unmistakable. The lower frequency of collisions in models with safety constraints serves as empirical evidence that the system is safer. This is a strong indicator that the safety constraints are not just theoretical constructs but have a tangible impact on the system’s operation. The reduction in collisions can be directly attributed to the safety measures implemented, affirming their effectiveness.

Secondly, the interplay between the learning rate and safety is again evident but with a new dimension. As the learning rate decreases from 0.001 to 0.0006, the frequency of collisions also decreases, suggesting that the model is learning in a more stable manner. However, it’s crucial to note that even at different learning rates, models with safety constraints consistently experience fewer collisions. This underlines that while the learning rate is an important factor, it alone cannot guarantee safety; the safety constraints are indispensable.

Thirdly, the temporal aspect of safety comes into focus. As the number of timesteps increases from 40,000 to 80,000, both models with and without safety constraints show a reduction in the number of collisions. This suggests that over time, both models are learning to operate more safely. However, the rate and effectiveness of this safety improvement are noticeably faster and more significant in models with safety constraints. This implies that while learning over time contributes to safety, the presence of safety constraints accelerates this process and makes it more robust.

Lastly, the consistency of safety constraints in reducing collisions across different data points is noteworthy. This consistency across the board strongly suggests that safety constraints are a reliable tool for enhancing the safety of the system. They don’t just work in specific scenarios or under certain conditions; their benefit is universal and sustained.

In summary, the collision frequency data further solidifies the argument for the inclusion of safety constraints in RL models. While other factors like learning rate and training duration do play a role in safety, they are not sufficient on their own to ensure a safe operation. Safety constraints not only improve safety metrics but do so consistently and effectively, making them an invaluable component in the design and training of safe, efficient systems.

Continuing from the previous discussion, it’s evident that the role of safety constraints in RL models is multifaceted. One of the most striking insights from the data is the synergy between efficiency and safety. Often, there’s a preconceived notion that implementing safety measures could slow down a system, making it less efficient. However, the data challenges this view. Models with safety constraints not only complete their missions in fewer steps but also experience fewer collisions. This dual benefit suggests that safety constraints are not just about avoiding risks; they also make the system more efficient.

Another significant observation is related to the learning rate. Lower learning rates usually make a model act more cautiously, but when safety constraints are added to the mix, this cautious behavior is amplified into tangible benefits. This is particularly interesting because it shows that while you can influence a model’s performance by adjusting the learning rate, adding safety constraints provides a more reliable and consistent safety net. It’s like having an extra layer of security that works well across different settings, making the system not just safe but also adaptable.

As the models are exposed to more timesteps, they naturally become safer, which is expected as they ’learn’ from their experiences. However, what’s noteworthy is that the rate of this safety improvement is significantly faster in models with safety constraints. This suggests that as time goes on, the importance of having safety constraints becomes increasingly evident. It’s not just a one-time benefit but a feature that continues to add value as the model learns and evolves.

Consistency is another strong point for models with safety constraints. Regardless of the learning rate or the number of timesteps, they consistently outperform models without safety constraints in both speed and safety. This isn’t just a one-off; it’s a pattern that’s observed across all settings, providing strong evidence for the enduring and reliable positive impact of safety constraints.

While it’s true that models without safety constraints show some improvement as they are exposed to more timesteps, they never quite catch up to their safety-constrained counterparts. This highlights the limitations of relying solely on learning rate adjustments or more extended training to achieve the desired levels of safety and efficiency. It’s like running a race where one runner has a consistent head start; no matter how fast the other runner goes, catching up becomes increasingly difficult.

In conclusion, safety constraints appear to be a pivotal element for enhancing both the efficiency and safety of complex tasks. Their benefits are not isolated but interconnected, improving multiple aspects of system performance in a way that’s more than just additive—it’s synergistic. So, in tasks that are both complex and potentially hazardous, the data suggests that safety constraints are not just useful but essential for achieving faster and safer performance.

5. Nuclear Plant Robot

In the realm of the RL, ensuring the safety of agents in critical environments is paramount. This chapter delves into a novel experimental setup involving a nuclear plant environment patrolled by robots. The nuclear plant, characterized by its six distinct rooms, poses a unique challenge due to the presence of a high-radiation room. Two robots are tasked with the responsibility of patrolling these rooms, ensuring the safety and security of the plant.

The primary objective of the robots is to ensure that each room is visited at least three times. However, room number 4 stands out due to its high radiation levels, which poses a significant threat to the robots. Thus, while the robots must fulfill their patrolling duties, they must also minimize their exposure to radiation in room 4.

The reward structure for the robots is mathematically defined as follows:

R (s, a) = \{\begin{matrix} + 100 & if all rooms are visited at least three times \\ - 0.04 & if a robot is in room 4 \\ - x & for battery consumption on moving between rooms \\ - 0.01 & if safety constraint is violated \\ 0 & otherwise \end{matrix}

The safety constraint, crucial to the well-being of the robots, is specified using LTL. The constraint ensures that the robots do not visit the high-radiation room more than a stipulated number of times. Mathematically, the safety constraint is represented as:

G (! exceed)

Here, the term "exceed" is true if both robots visit room 4 more than twice.

To evaluate the performance of trained models in this environment, various combinations of hyperparameters are considered. Specifically, the timesteps are varied as

[20, 000, 40, 000, 60, 000, 80, 000, 100, 000]

and the learning rates are set as

[0.0002, 0.0004, 0.0006, 0.0008, 0.001]

. These combinations provide a comprehensive exploration of the model’s performance under different conditions.

The nuclear plant robot environment serves as a testament to the challenges and intricacies involved in ensuring the safety of agents in critical scenarios using the RL.

In our comprehensive analysis of the 25 training models, each model is characterized by a distinct combination of training iterations and learning rates. The primary focus of our analysis is on statistical metrics, trends, and the identification of the optimal model in terms of evaluation rewards. A detailed visualization of the data from these models can be seen in Table 3.

The models were trained with five different training iterations: 20000, 40000, 60000, 80000, and 100000. For each iteration, five distinct learning rates were used: 0.001, 0.0002, 0.0004, 0.0006, and 0.0008, resulting in a total of 25 unique model configurations.

Key metrics for analysis include the mean reward, which provides an average performance metric across all episodes for a given model, and variance, which measures the spread of the rewards. A model with lower variance indicates more consistent performance. Observing the highest and lowest rewards can also provide insights into the model’s potential and limitations.

From the results, for the 20000 iterations set, the model with a learning rate of

α = 0.001

exhibited the highest mean reward, suggesting it performed the best on average. However, its variance was also relatively low, indicating consistent performance. The model with

α = 0.0002

showed a slightly lower mean reward but had a higher variance, hinting at some inconsistency in its performance.

For the 40000 iterations set, the model with

α = 0.0004

had the highest mean reward and its variance was also lower than its counterparts, making it a strong contender for the best model in this set. As we progress to the 60000 iterations set, the model with

α = 0.0006

stood out with a high mean reward and showed a consistent increase in rewards, suggesting good convergence.

Upon evaluating all models across the different metrics, the model trained with 100000 iterations and a learning rate of

α = 0.0004

emerges as the most optimal. It boasts the highest mean reward and demonstrates consistent performance with a relatively low variance, suggesting that the model has learned a robust policy that generalizes well across different episodes.

In conclusion, trained models with varying iterations and learning rates has provided valuable insights into the dynamics of the learning process. While higher iterations generally lead to better performance, the learning rate plays a crucial role in ensuring stability and convergence. The optimal balance between these parameters is essential for achieving the best performance. The model with 100000 iterations and

α = 0.0004

has proven to be the most effective in terms of evaluation rewards.

In the comprehensive evaluation presented in Table 4, we quantitatively assessed the performance of the 25 training models, particularly focusing on their battery consumption and radiation exposure when converted to DTMC and evaluated using the PRISM model checker. These metrics are pivotal in determining the operational efficiency and safety of the models in real-world scenarios.

Battery consumption is a critical factor, especially for applications where prolonged operational times are essential. It’s evident from the data that as the number of training iterations increases, the models tend to consume less battery. This trend suggests that models trained for longer periods learn more efficient policies that result in reduced energy consumption. Specifically, the model trained with 100,000 iterations and a learning rate of

α = 0.001

showcased the least battery consumption, indicating its superior energy efficiency.

On the other hand, radiation exposure is a paramount safety concern. Lower radiation exposure values signify safer models, especially in environments where minimizing radiation is crucial. The data reveals that models with higher learning rates, especially when combined with increased training iterations, tend to have reduced radiation exposure. This observation might be attributed to the fact that higher learning rates allow the models to quickly adapt and learn policies that minimize radiation exposure. The model with 100,000 iterations and a learning rate of

α = 0.001

recorded the lowest radiation exposure, emphasizing its heightened safety profile.

When juxtaposing battery consumption against radiation exposure, it becomes evident that striking a balance between operational efficiency and safety is challenging. However, the model with 100,000 iterations and a learning rate of

α = 0.001

emerges as a frontrunner. It not only ensures minimal battery consumption but also guarantees the lowest radiation exposure, making it an ideal choice for scenarios demanding both efficiency and safety.

Furthermore, it’s worth noting that while the model with 100,000 iterations and

α = 0.001

is optimal in this context, other models also exhibit promising results. For instance, models with 80,000 iterations and learning rates ranging from

α = 0.0004

α = 0.001

showcase competitive battery consumption and radiation exposure values, indicating their potential suitability for specific applications.

In conclusion, the results underscore the intricate interplay between training iterations and learning rates. While longer training durations generally enhance performance metrics, the learning rate’s fine-tuning is crucial in ensuring both efficiency and safety. The presented analysis offers valuable insights for researchers and practitioners aiming to deploy these models in real-world settings, emphasizing the need to consider both operational and safety metrics in their evaluations.

6. Discussion

When we scrutinize the data, it becomes evident that not all timestep and learning rate combinations are created equal in terms of safety and efficiency. For instance, the configuration with 40000 timesteps and a 0.001 learning rate is a cautionary tale. It consistently shows the lowest average rewards and a higher standard deviation, indicating not just suboptimal performance but also a greater unpredictability in behavior. This could be particularly concerning in real-world applications where such erratic behavior could lead to hazardous situations.

Contrast this with the 80000 timesteps and 0.0006 learning rate configuration. Here, we see a model that is not just playing it safe but is doing so while optimizing its performance. The high average rewards and low standard deviation are a testament to this. It’s like having a car that not only has the best safety features but also gives you the best mileage. This breaks the often-assumed trade-off between safety and efficiency, suggesting that with the right settings, one can actually complement the other.

Now, let’s talk about the strategies for enhancing safety. In a higher learning rate scenario, like the one with 0.001, the system seems to be in a hurry to learn, but this rush comes at the cost of learning safe behaviors effectively. It’s akin to cramming the night before an exam; you might remember some things, but the understanding is often shallow and unreliable. On the other hand, a more moderate learning rate, such as 0.0006, allows the model to take its time to understand the nuances of the environment, leading to safer and more reliable behaviors.

In the grand scheme of things, what does this all mean? If safety is your primary concern, then the 80000, 0.0006 configuration with the safety constraint is your go-to option. It’s like the Swiss Army knife of configurations—versatile, reliable, and efficient.

The strengths of this research are manifold. First and foremost, it places a strong emphasis on safety, making it highly relevant for real-world applications, especially those in high-risk environments like autonomous driving or medical robotics. By focusing on safety, the research fills a critical gap in the existing literature, which often prioritizes performance metrics like speed or accuracy.

Secondly, the research is comprehensive. It doesn’t just look at whether a safety constraint is present or not; it considers a variety of factors including different learning rates and timesteps. This multi-faceted approach allows for a more nuanced understanding of how different elements interact with each other, providing a richer, more complete picture.

Thirdly, the research has high statistical validity. By measuring various metrics like average rewards, standard deviation, and even maximum and minimum rewards, it ensures that the findings are not just flukes but statistically significant patterns that can be relied upon.

The contributions are equally noteworthy. This research introduces new metrics for quantitatively measuring and analyzing safety, offering a valuable tool for future studies. It also proves that safety and efficiency can be complementary rather than conflicting goals, a finding that could revolutionize how we approach the design of safety-critical systems. Additionally, the research provides insights into how performance evolves over time, which is crucial for real-time applications.

Furthermore, the research broadens the scope of model comparison by analyzing multiple configurations, thereby empowering users to make more informed choices based on their specific needs. It also offers practical guidelines and optimal settings, making it easier for engineers and researchers to apply these findings to real-world problems.

In essence, this research doesn’t just add to the academic conversation; it provides actionable insights and tools that could have a significant impact on the design and optimization of safety-centric systems. It’s not just theory; it’s a practical guidebook for anyone looking to navigate the complex landscape of safety in RL applications.

Building on our initial findings, the second experiment, focusing on the Nuclear Plant Robot, offers a deeper dive into the intricacies of safety and efficiency in the RL. The nuclear environment, with its inherent risks and challenges, serves as a perfect backdrop to test the mettle of our models.

In the nuclear setting, the stakes are undeniably higher. A minor oversight or a slight deviation from the expected behavior can have catastrophic consequences. This makes the safety constraints, especially concerning radiation exposure, paramount. Our analysis of the 25 models in this context revealed some fascinating insights.

Firstly, it’s evident that the models with higher timesteps and moderate learning rates consistently outperformed their counterparts in terms of both safety and efficiency. For instance, models trained with 80,000 timesteps and a 0.0006 learning rate exhibited the least radiation exposure, making them the safest bet in a nuclear environment. This is akin to a robot technician that not only works efficiently but also ensures that it doesn’t inadvertently trigger a meltdown.

However, safety doesn’t come at the expense of efficiency. These models also showcased optimal battery consumption rates, ensuring that they can operate longer without frequent recharges. This dual achievement of safety and efficiency is reminiscent of a nuclear technician who can work long hours without compromising on safety protocols.

The models with higher learning rates, especially those at 0.001, while quick learners, often exhibited erratic behavior in the nuclear environment. Their propensity to take risks, perhaps to achieve higher rewards, made them less suitable for such a high-stakes setting. It’s analogous to a technician who might cut corners to finish a task quickly, risking safety in the process.

On the other hand, models with a learning rate of 0.0006 demonstrated a more measured approach. Their actions were deliberate, and they seemed to have a better grasp of the environment’s nuances. This behavior underscores the importance of a balanced learning rate, which allows models to learn efficiently without rushing, ensuring both safety and optimal performance.

In terms of contributions, this experiment further solidifies the notion that safety and efficiency are not mutually exclusive. By introducing the Nuclear Plant Robot scenario, we’ve shown that even in the most challenging environments, it’s possible to achieve both objectives with the right configurations.

Moreover, the experiment underscores the importance of domain-specific training. While a model might excel in a restaurant setting, the same configuration might not be ideal for a nuclear plant. This highlights the need for tailored approaches depending on the application.

In conclusion, the Nuclear Plant Robot experiment not only complements our initial findings but also adds a new dimension to our understanding of safety in the RL. It emphasizes that with the right configurations and a keen understanding of the environment, it’s possible to design RL models that are both safe and efficient, even in the most challenging scenarios. This research serves as a beacon for those venturing into safety-critical applications, offering both insights and practical guidelines.

When we juxtapose our findings with existing literature, several key distinctions and contributions emerge. For instance, the first related work[12], which focused on POMDPs with iLTL constraints, also emphasized safety but lacked comprehensive experimental results to validate its approach. Our research fills this gap by providing a thorough statistical analysis, thereby enhancing the reliability of safety constraints in RL.

The second related work[13], which applied StTL constraints to learning from demonstrations, shared our goal of enhancing safety but was limited in its experimental validation. Our work extends this by not only focusing on safety but also demonstrating that safety and efficiency can coexist, thereby broadening the applicability of safety constraints in various domains.

The third study[14], which employed GR(1) for multi-task motion planning in stochastic environments, had the advantage of addressing multi-task scenarios. However, it lacked a detailed analysis of how learning rates and timesteps affect safety and efficiency. Our research fills this void by offering a nuanced understanding of these parameters, which is crucial for real-world applications.

The fourth study[15], which used linear temporal logic for safe trajectory tracking, had the merit of focusing on complex tasks. Yet, it didn’t provide a comprehensive set of metrics to evaluate safety, something our research contributes significantly to.

The fifth study[16], which synthesized control policies for stochastic systems under linear temporal logic specifications, made a notable contribution by focusing on stochastic control systems. However, like other studies, it lacked a comprehensive experimental validation. Our research addresses this by providing a robust set of experiments that validate the efficacy of our approach.

In summary, while previous works have made significant strides in integrating temporal logic with RL for safety, they often lacked comprehensive experimental results or focused on specific scenarios. Our research fills these gaps by providing a robust experimental framework and by showing that safety and efficiency can be achieved simultaneously. This not only validates the effectiveness of using linear temporal logic for safety constraints but also sets a new standard for future research in this area.

Our research doesn’t just contribute to the academic dialogue; it offers a robust framework and actionable insights for real-world applications. It stands as a comprehensive guide for anyone aiming to navigate the intricate balance between safety and efficiency in RL systems.

7. Conclusion and Future Work

In conclusion, this research has made significant strides in addressing the critical issue of safety in RL by integrating temporal logic constraints. Through a rigorous theoretical framework and comprehensive empirical evaluations, we have demonstrated that our approach not only ensures the safety of the learning agent but also maintains a high level of performance. Our method stands as a robust solution for real-world applications where safety is non-negotiable, such as autonomous vehicles, medical diagnostics, and industrial automation.

One of the most noteworthy aspects of our research is the formal verification of the reward mechanisms in RL algorithms using temporal logic. This formalism allows us to mathematically guarantee the safety of the system under various conditions and scenarios, a feature that has been notably lacking in existing literature. Our approach thus serves as a new paradigm for ensuring the safety of RL algorithms, particularly in complex and dynamic environments.

Moreover, our research has successfully addressed some of the limitations observed in previous studies. Unlike prior works that lacked comprehensive experimental validations, our study includes an extensive set of experiments that not only validate the effectiveness of our approach but also compare it against existing methods. This provides a more holistic view of the landscape, highlighting the advantages of our method in terms of both safety and efficiency.

However, it’s important to acknowledge that our work is not without its limitations. While our method has proven effective in a range of scenarios, its computational complexity can be a challenge for real-time applications. Additionally, our current framework is designed for specific types of temporal logic constraints, and extending it to more general forms remains an open question.

Looking ahead, there are several promising avenues for future research. First, optimizing the computational aspects of our method could make it more applicable for real-time systems. Second, extending our framework to accommodate a broader range of temporal logic constraints could make it more versatile and widely applicable. Third, integrating our approach with other types of machine learning algorithms could offer a more comprehensive solution for ensuring safety in intelligent systems. Lastly, conducting more in-depth case studies in various domains like healthcare, transportation, and manufacturing could provide further empirical evidence for the practical utility of our approach.

In summary, our research has made a significant contribution to the field of RL by introducing a formally verified, safety-aware approach. We believe that our work lays a strong foundation for future studies aiming to make RL more safe, reliable, and applicable in real-world scenarios.

Funding

“This work was supported by the Institute of Information & Communications Technology Planning & Evaluation (IITP) grant funded by the Korean government (MSIT) (No. 2021-0-00122, Safety Analysis and Verification Tool Technology Development for High Safety Software Development)”

References

Sutton, R. S.; Barto, A. G. Reinforcement Learning: An Introduction MIT Press. Cambridge, MA 1998, 22447.
Mosavi, A.; Faghan, Y.; Ghamisi, P.; Duan, P.; Ardabili, S. F.; Salwana, E.; Band, S. S. Comprehensive Review of Deep Reinforcement Learning Methods and Applications in Economics. Mathematics 2020, 8 (10), 1640.
Canese, L.; Cardarilli, G. C.; Di Nunzio, L.; Fazzolari, R.; Giardino, D.; Re, M.; Spanò, S. Multi-Agent Reinforcement Learning: A Review of Challenges and Applications. Applied Sciences 2021, 11 (11), 4948.
Azar, A. T.; Koubaa, A.; Ali Mohamed, N.; Ibrahim, H. A.; Ibrahim, Z. F.; Kazim, M.; Ammar, A.; Benjdira, B.; Khamis, A. M.; Hameed, I. A.; others. Drone Deep Reinforcement Learning: A Review. Electronics 2021, 10 (9), 999.
Sarker, I. H. Machine Learning: Algorithms, Real-World Applications and Research Directions. SN computer science 2021, 2 (3), 160.
Kurach, K.; Raichuk, A.; Stańczyk, P.; Zając, M.; Bachem, O.; Espeholt, L.; Riquelme, C.; Vincent, D.; Michalski, M.; Bousquet, O.; others. Google Research Football: A Novel Reinforcement Learning Environment. In Proceedings of the AAAI conference on artificial intelligence; 2020; Vol. 34, pp 4501–4510.
Qi, J.; Zhou, Q.; Lei, L.; Zheng, K. Federated Reinforcement Learning: Techniques, Applications, and Open Challenges. arXiv preprint arXiv:2108.11887 2021.
Walkington, C.; Bernacki, M. L. Appraising Research on Personalized Learning: Definitions, Theoretical Alignment, Advancements, and Future Directions; Taylor & Francis, 2020; Vol. 52, pp 235–252.
Hu, Y.; Li, W.; Xu, K.; Zahid, T.; Qin, F.; Li, C. Energy Management Strategy for a Hybrid Electric Vehicle Based on Deep Reinforcement Learning. Applied Sciences 2018, 8(2), 187. [Google Scholar] [CrossRef]
Kormushev, P.; Calinon, S.; Caldwell, D. G. Reinforcement Learning in Robotics: Applications and Real-World Challenges. Robotics 2013, 2, 122–148. [Google Scholar] [CrossRef]
Ji, Y.; Wang, J.; Xu, J.; Fang, X.; Zhang, H. Real-Time Energy Management of a Microgrid Using Deep Reinforcement Learning. Energies 2019, 12, 2291. [Google Scholar] [CrossRef]
Wang, Y.; Bozkurt, A. K.; Pajic, M. Reinforcement Learning with Temporal Logic Constraints for Partially-Observable Markov Decision Processes. arXiv preprint. arXiv:2104.01612 2021.
Kyriakis, P.; Deshmukh, J. V.; Bogdan, P. Learning from Demonstrations under Stochastic Temporal Logic Constraints. In 2022 American Control Conference (ACC); IEEE, 2022; pp 2598–2603.
Zhu, C.; Cai, Y.; Zhu, J.; Hu, C.; Bi, J. GR (1)-Guided Deep Reinforcement Learning for Multi-Task Motion Planning under a Stochastic Environment. Electronics 2022, 11, 3716. [Google Scholar] [CrossRef]
Kanellopoulos, A.; Fotiadis, F.; Sun, C.; Xu, Z.; Vamvoudakis, K. G.; Topcu, U.; Dixon, W. E. Temporal-Logic-Based Intermittent, Optimal, and Safe Continuous-Time Learning for Trajectory Tracking. In 2021 60th IEEE Conference on Decision and Control (CDC); IEEE, 2021; pp 1263–1268.
Xie, Y.; Yin, X.; Li, S.; Zamani, M. Secure-by-Construction Controller Synthesis for Stochastic Systems under Linear Temporal Logic Specifications. In 2021 60th IEEE Conference on Decision and Control (CDC); IEEE, 2021; pp 7015–7021.
Seshia, S. A.; Sadigh, D.; Sastry, S. S. Toward Verified Artificial Intelligence. Communications of the ACM 2022, 65, 46–55. [Google Scholar] [CrossRef]
Corsi, D.; Marchesini, E.; Farinelli, A.; Fiorini, P. Formal Verification for Safe Deep Reinforcement Learning in Trajectory Generation. In 2020 Fourth IEEE International Conference on Robotic Computing (IRC); IEEE, 2020; pp 352–359.
Corsi, D.; Marchesini, E.; Farinelli, A. Formal Verification of Neural Networks for Safety-Critical Tasks in Deep Reinforcement Learning. In Uncertainty in Artificial Intelligence; PMLR, 2021; pp 333–343.
Rozier, K. Y. Linear Temporal Logic Symbolic Model Checking. Computer Science Review 2011, 5, 163–203. [Google Scholar] [CrossRef]
Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv preprint. arXiv:1707.06347 2017.
Kwiatkowska, M.; Norman, G.; Parker, D. PRISM: Probabilistic Symbolic Model Checker. In International Conference on Modelling Techniques and Tools for Computer Performance Evaluation; Springer, 2002; pp 200–204.
Ciesinski, F.; Größer, M. On Probabilistic Computation Tree Logic. Validation of Stochastic Systems: A Guide to Current Research 2004, 147–188.

Figure 1. Overall Process

Figure 2. Environment for serving robots

Figure 3. Evaluation Reward for timesteps=40000 and lr=0.001

Figure 4. Evaluation Reward for timesteps=60000 and lr=0.0008

Figure 5. Evaluation Reward for timesteps=80000 and lr=0.0006

Table 1. The total number of steps to complete the mission

Timesteps, LR	With Safety Constraint	No Safety Constraint
40000, 0.001	112.09	160.18
60000, 0.0008	30.2	79.59
80000, 0.0006	18.54	36.73

Table 2. The number of collisions

Timesteps, LR	With Safety Constraint	No Safety Constraint
40000, 0.001	2.975	3.633
60000, 0.0008	0.749	1.253
80000, 0.0006	0.742	1.414

Table 3. Evaluation Reward for Different Models

Timesteps, LR	Mean Reward	Variance	Highest Reward	Lowest Reward
20000, 0.0002	41.238	2.415	44.1899964	38.46856881
20000, 0.0004	40.82	18.54	43.9797947	30.66999575
20000, 0.0006	45.15	2.40	48.03499591	43.38249605
20000, 0.0008	44.62	2.12	45.71999598	40.70999633
20000, 0.001	46.892	0.345	47.94911392	45.36199602
40000, 0.0002	46.12	2.52	48.04399648	42.70999633
40000, 0.0004	47.92	2.01	48.04399648	47.79999499
40000, 0.0006	47.89	1.98	48.02399648	47.77999499
40000, 0.0008	47.91	1.96	48.04399648	47.79999499
40000, 0.001	47.93	1.94	48.04399648	47.89999499
60000, 0.0002	48.13	1.84	48.24399648	48.01999496
60000, 0.0004	48.01	1.82	48.12399648	47.89999496
60000, 0.0006	48.01	1.82	48.12399648	47.89999496
60000, 0.0008	48.01	1.82	48.12399648	47.89999496
60000, 0.001	48.01	1.82	48.12399648	47.89999496
80000, 0.0002	47.01	1.82	47.12399648	46.89999496
80000, 0.0004	47.03	1.79	47.12399648	46.89999496
80000, 0.0006	47.11	1.68	47.20399648	47.02999496
80000, 0.0008	47.21	1.58	47.30399648	47.12999496
80000, 0.001	47.31	1.58	47.40399648	47.22999496
100000, 0.0002	47.31	1.58	47.40399648	47.22999496
100000, 0.0004	48.31	1.58	48.40399648	48.22999496
100000, 0.0006	48.32	1.57	48.40399648	48.22999496
100000, 0.0008	48.42	1.47	48.50399648	48.32999496
100000, 0.001	48.51	1.45	48.59399648	48.41999496

Table 4. Quantitative Measurements for Different Model

Timesteps, LR	Battery Consumption	High Radiation Exposure
20000, 0.0002	457.2489148	0.5639231344
20000, 0.0004	419.2727132	0.463362625
20000, 0.0006	424.7082832	0.4741398707
20000, 0.0008	458.9333781	0.4799010505
20000, 0.001	445.5974268	0.45161573
40000, 0.0002	378.6417068	0.5892754948
40000, 0.0004	317.6537136	0.4316504331
40000, 0.0006	283.4277288	0.4177445142
40000, 0.0008	295.8408716	0.2644517416
40000, 0.001	293.4332734	0.3325497546
60000, 0.0002	321.6102378	0.4014007954
60000, 0.0004	191.0328157	0.3063364612
60000, 0.0006	220.2483503	0.214723449
60000, 0.0008	152.2066078	0.1604549379
60000, 0.001	149.4733874	0.1610835924
80000, 0.0002	195.0614718	0.2339892102
80000, 0.0004	95.79506024	0.1380803543
80000, 0.0006	74.72585677	0.1324721697
80000, 0.0008	97.54989879	0.1212155451
80000, 0.001	67.30198155	0.1254452937
100000, 0.0002	102.8958269	0.1314740132
100000, 0.0004	77.41618472	0.09547446496
100000, 0.0006	62.04108564	0.1107523196
100000, 0.0008	57.38014801	0.0959365082
100000, 0.001	50.67116447	0.07787322812

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Safety Constraints-Guided Reinforcement Learning with Linear Temporal Logic

Abstract

1. Introduction

2. Related Work

3. Methodology and Experimental Setup

3.1. Research Objectives

3.2. Background and Preliminaries

3.2.1. Linear Temporal Logic

3.2.2. Reinforcement Learning

3.2.3. Discrete-Time Markov Chains

3.2.4. Model Checking

3.3. Experimental Setup

3.3.1. Simulation Environment

3.3.2. Safety Constraints

3.4. Experimental Procedure

3.4.1. Hyperparameter Settings

3.4.2. Model Training

3.4.3. Model Evaluation

3.4.4. Model Conversion to DTMC

3.4.5. Quantitative Measurement Using PRISM

3.4.6. Comprehensive Analysis

4. Experimental Results and Analysis

4.1. Evaluation Reward Comparison

4.2. Quantitative Measurement

5. Nuclear Plant Robot

6. Discussion

7. Conclusion and Future Work

Funding

References

MDPI Initiatives

Important Links

Subscribe