Prerpints.org logo
Preprint
Article

Alena Tensor and Its Possible Applications in Unification Theories

Altmetrics

Downloads

2007

Views

5588

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

24 July 2024

Posted:

29 July 2024

Read the latest preprint version here

Alerts
Abstract
Alena Tensor is a recently discovered class of energy-momentum tensors that provides mathematical framework in which, as demonstrated in previous publications, the description of a physical system in curved spacetime and its description in flat spacetime with fields are equivalent. The description of a system with electromagnetic field based on Alena Tensor can be used to reconcile physical descriptions. 1) In curvilinear description, Einstein Field Equations were obtained with Cosmological Constant related to the invariant of the electromagnetic field tensor, which can be interpreted as negative pressure of vacuum, filled with electromagnetic field. 2) In classical description for flat spacetime, three densities of four-forces were obtained: electromagnetic, gravity, and the force responsible for the Abraham-Lorentz effect (radiation reaction force). Obtained connection of Einstein tensor with gravity and radiation reaction force, after transition to curvilinear description, excludes black hole singularities. There was obtained Lagrangian density and generalized canonical four-momentum, containing electromagnetic four-potential and a term responsible for other two forces. In this description charged particles cannot remain at complete rest and should have spin, their energy results from the existence of the energy of the magnetic moment and the density of this energy is part of the Poyting four-vector. The distribution of charged matter was expressed as polarization-magnetization stress-energy tensor, what may explain why gravity is invisible in QED. 3) In quantum picture, QED Lagrangian density simplification was obtained, and the Dirac, Schrödinger and Klein-Gordon equations may be considered as approximations of the obtained quantum solution. Farther use of Alena Tensor in unification applications was also discussed.
Keywords: 
Subject: Physical Sciences  -   Theoretical Physics

1. Introduction

The history of physics is also the history of unification. The past teaches us that after the stage of research on individual phenomena and obtaining a satisfactory description of them, comes the phase of unification, in which the scattered puzzles of descriptions are put together into one whole picture, which soon turns out to also be just a part of bigger picture.
Today, modern physicists are faced with many puzzles, most of which are huge pictures, entire sections of physics, composed of hundreds of smaller parts, the existence of which we owe to thousands of outstanding scientists. The largest and most famous descriptions of physical phenomena requiring unification are, of course, General Relativity (GR) and Quantum Field Theory (QFT), however, the unification cannot be simplified to finding a theory of quantum gravity. We cannot forget about other knowledge components (so fundamental that they are easy to miss), such as Continuum Mechanics or Thermodynamics, which are also being researched in the field of unification [1,2,3]. It is also important to note that even after a quantum picture of gravity is obtained, questions about the Dark Sector will still remain open [4].
"In all the attempts at unification we encounter two distinct methodological approaches: a deductive-hypothetical and an empirical-inductive method." [5] where a good examples of the first approach are String Theory [6] and Supersymmetry [7] and the second one, Grand Unification [8] and, in a sense, the Standard Model itself. Part of the entire unification effort are dualistic theories [9], mainly adopting mentioned deductive-hypothetical approach. They are usually looking for a theoretical model in which existing descriptions can be reconciled and assume, that contradictions between existing descriptions may be apparent and in fact they are only different, equally valid ways of describing the same phenomena [10].
Considering the context of unification broadly, a dualistic solution to the puzzle may appear from a completely unexpected direction, as in the work of D. Grimmer describing topological redescription [11] and giving the possibility of changing the topology of space in a way similar to changing coordinate systems. When considering the unification of GR and Electrodynamics, unifying dualistic theory may come from a rather obvious direction [12], because it can be expected that there is a mathematical transformation between accelerated motion in flat spacetime and geodesic motion in curved spacetime for all accelerations due to known fields.
For the reasons mentioned above, it is worth taking a look at a fairly new example of dualistic approach, called Alena Tensor, using it to describe a selected physical system and discussing what new research perspectives it opens. Previous publications [13,14] have shown that Alena Tensor allows to obtain a coherent solution combining relativistic electrodynamics, QED and GR equations, so it is not just a purely theoretical, mathematical construction and seems worth further development. This method also indicates that the description of the physical system in curved spacetime and its description in flat spacetime with fields are equivalent, thanks to an appropriately constructed definition of the energy-momentum tensor which greatly facilitates further research.
In Alena Tensor approach, the metric tensor is not a property of spacetime, but only a way of describing it. The tensor of the field present in the system is responsible for all forces in flat spacetime, and thus also the field tensor defines the metric tensor for which all forces vanish and may be completely replaced by curvature in curvilinear description. According to this approach, gravity is not a body force (in the sense of Continuum Mechanics), but a side effect of existence of the energy of other, more fundamental fields (e.g. EM, Electroweak). This allows for a dualistic description (curvilinear, classical and quantum), leads to compatibility with currently used descriptions of physical systems and opens the way to many further studies.
Another and perhaps the most important reason to write this article is that the Alena Tensor is not an intuitive theory, requires some systematization and yet requires further research. Therefore, to facilitate analysis and future development all main conclusions from previous publications have been systematized and aggregated in the Appendix A.
A description of a physical theory usually begins with a description of the action and by varying it, one finds the equations of the theory, energy-momentum tensor and Lagrangians. In this case, however, such a line of reasoning would make it difficult to understand the unifying potential of this theory, which is why the action and the Lagrangian (derived in previously published papers) appear only later in the Appendix A.
When considering a curved spacetime, metrics are typically obtained from the solutions of the GR equations based on the symmetries used. In this article, the conclusions regarding the Einstein tensor will be presented in flat spacetime, which also breaks a certain accepted pattern and is not intuitive. However, such an analysis will reveal the meaning of the presented dualistic description without the need to significantly expand this article, especially since Alena Tensor by definition transforms into Einstein Field Equations in curvilinear description and the methods of analyzing GR equations are quite well known.
The main article will focus on interpretation and development of previous results for a system with electromagnetic field, and will discuss the possibilities of further development and applications of Alena Tensor to analyze problems related to the broadly understood research on the unification of physical theories.
The authors use the Einstein summation convention, metric signature ( + , − , − , − ) and commonly used notations.

2. Results

Considering the system with only electromagnetic field, where the system is described by Alena Tensor according to Appendix A, further implications arising from this description can be analyzed.
Since the least obvious element of such description is the additional four-force density f o t h present in the system (A17) in flat spacetime, it will be interpreted in first subsection of this chapter. This four-force density is negligibly small for − Λ ρ > > ϱ c 2 and as it will be shown, it appears to reproduce Abraham–Lorentz force [15] (also called the radiation reaction force).
It is also known, that the existence of magnetic moment is expected for charged particles [16,17] and it influences the value of the electromagnetic force [18,19]. It will be therefore shown in the second subsection of this chapter, that the use of the Alena Tensor leads directly to the conclusion that charged particles should have spin and the energy of the particles results from the existence of energy of magnetic moment. For this reason, the energy of charged particles will also turn out to be part of the Poynting four-vector and the previously obtained relationship between four-momentum and derived gauge of electromagnetic four-potential (A24) will be clarified.
In the last subsection of this chapter, the Alena Tensor verification method within QM will be presented and it will be demonstrated, that the Dirac, Schrödinger and Klein-Gordon equations may be considered as approximations of the obtained quantum solution. It will be also shown, that presented approach allows combining the classical and quantum descriptions of the motion of charged particles which can help in many applications.

2.1. Interpretation of the Four-Force Density f o t h

Using the notation from Appendix A, one may define relative permeability μ r and volume magnetic susceptibility χ as
μ r ≡ Λ ρ p ; χ ≡ μ r − 1 = − ϱ c 2 p
thanks to which the Alena Tensor (A6) takes the form expected for the system with electromagnetic field
T α β = ϱ U α U β − 1 μ r Υ α β
where Υ α β represents energy-momentum tensor for electromagnetic field. It now may be noticed, that there are present in the system (A17) only two four-force densities: gravitational f g r α and electromagnetic corrected by the above coefficient
f E M α + f o t h α = 1 + ϱ c 2 Λ ρ f E M α = 1 μ r f E M α
This allows for the interpretation of the applied correction to the electromagnetic force, as resulting from the existing energy density of matter. In the limit for ϱ c 2 = 0 Alena Tensor simply becomes a tensor of the electromagnetic field − T α β = Υ α β and pressure p = Λ ρ , thus Λ ρ may be actually associated with the negative pressure of a vacuum, filled with an electromagnetic field. In the limit ϱ c 2 = − Λ ρ one obtains p = 0 and forces caused by field disappear. However, this would mean infinite μ r and may be considered an unattainable limit.
Using (A32), (A34), (A36) and definition of the pressure (A5) one may also notice, that
W 0 = W p v c
which, as might be expected, relates the existence of negative pressure p (A5) in the system to the field energy c W 0 in the system. It thus also becomes possible to interpret the correction for the electromagnetic force discussed in (3) considering point-like particles, where now relative permeability μ r and derived gauge of electromagnetic four-potential q A μ (A24) are
1 μ r = W p v H ; q A μ = − μ r P μ
As one may notice from (A36), the increasing energy of an accelerated body cannot take energy from nowhere. Since energy is conserved in a closed system, this means that the m c 2 γ increases at the expense of decreasing W p v in the system. Therefore, forces resulting from W p v existence, must at some point decrease. Assuming classical relation between permeability μ = μ o μ r and permittivity ε = ε o ε r
1 c 2 = μ · ε = μ o ε o · μ r ε r
one also gets that relative permittivity ε r and the electric susceptibility χ e are
ε r ≡ 1 μ r = W p v H ; χ e ≡ ε r − 1 = ϱ c 2 Λ ρ = − m c 2 γ H
As may be seen f o t h α = χ e f E M α acts as a negative correction to four-force densities (as m c 2 γ increases at the expense of W p v ) and upholds the principle of conservation of energy. It means, that discussed f o t h reproduces Abraham–Lorentz effect.
It is therefore worth noting, that by including effects of f o t h α in the curvilinear description, non-physical effects such as black hole singularity must disappear. Four-force density associated with the Einstein tensor (accurate to a constant) in (A19), may be now expressed in flat spacetime as
∂ β G α β = f g r α + f o t h α = ∂ β χ e Υ α β
This can also be seen when analyzing solutions of (A13) in curved spacetime for the static, symmetric case, as these are smooth de Sitter solutions [20], free of singularities, however, this topic deserves to be developed in a separate article. The above interpretation also introduces new possibilities regarding the interpretation of the dark sector, which will be discussed later in the article.

2.2. Classical and Quantum Interpretation for Continuous Media in Flat Spacetime

Staying with the description for a flat spacetime with an electromagnetic field, denoting the electric and magnetic fields as E → and B → and denoting the densities of electric and magnetic energy occurring in the electromagnetic field tensor as
u E ∼ ≡ ε o E 2 2 ; u B ∼ ≡ 1 μ o B 2 2
it can be seen from (A3) that
Λ ρ = u B ∼ − u E ∼
Therefore using conclusion (A29), the relationship between magnetic energy density and the energy density of the electromagnetic field Υ 00 can be written as
B 2 μ o = Λ ρ + Υ 00 = Λ ρ p ϱ o c 2 γ 3 + γ
Thanks to the above, the four-potential of the electromagnetic field (A24) can be simplified to
ρ o A μ = − B 2 μ o γ 2 + 1 1 c 2 γ U μ
For a particle at rest, the above reduces to a scalar − 1 c B 2 2 μ o expressing (negative) classical value of magnetic energy density and zero vector, but completely stationary cases must be excluded, because they lead to B → = ∇ × A → = 0 . The above equation thus also says, that even in the absence of orbital angular momentum, the particle must vibrate or rotate and experience a magnetic field, because without the magnetic field, the entire four-potential vanishes.
Therefore, primary source of the electromagnetic field of quasi-stationary particles should be, actually, a magnetic moment caused by vorticity or spin (however, since continuous media are considered here, the term magnetization should rather be used instead of the magnetic moment). The obtained four-potential must take into account changes in magnetization caused by motion, because the magnetization itself seems to be the source of the electric field and it depends on γ , while the magnetic field depends on the rotation of the velocity (vorticity).
The source of the electric field associated with charged matter can now be represented, as reduced (compared to the classical value) magnetic energy density u B ⊙
u B ⊙ ≡ 1 μ o B 2 γ 2 + 1 = − J μ A μ = Λ ρ ϱ c 2 p = − χ Λ ρ
In the classical description, the denominator always has "2", so the difference for γ ≈ 1 is almost imperceptible for non-relativistic solutions. Perhaps this is why only the QED revealed discrepancies in the measured values of magnetic moments of particles. In the above description, the 1 + γ 2 coefficient seems to be related to some intrinsic, internal volume magnetic susceptibility of the charged matter, so one may take a closer look at this phenomenon.
It can be expected, that the energy density value preserved in the system (A27) is also conserved for the electromagnetic energy densities associated with the matter
− Λ ρ = u E ∼ − u B ∼ = u E ⊙ − u B ⊙
where according to (13), (A5) and above, electric energy density associated with matter u E ⊙ may be denoted as
u E ⊙ ≡ − Λ ρ 2 p = − μ r Λ ρ
The above leads directly to the conclusion that total electromagnetic field energy density may be expressed as electric field energy density related to charged matter and the energy density of magnetic moment. It may be seen by calculating energy density of the electromagnetic field
Υ 00 = u E ∼ + u B ∼ = u E ⊙ + 2 u B ∼ − u B ⊙ = u E ⊙ + γ 2 γ 2 + 1 B 2 μ o
In above, last component of the equation represents the classical description of the energy density of magnetic moment, where γ 2 serves as volume magnetic susceptibility.
Therefore, the electromagnetic field associated with density of charged matter will be most easily described as a propagating disturbance of magnetization and polarization, because the combination of magnetization and polarization describes such electric currents [21] and relativistic tensor can be created based on them [22]. According to classical electromagnetism rules, by decomposing electromagnetic field tensor into Polarization-Magnetization tensor M α β and Electric Displacement tensor D α β one obtains
1 μ o F α β = M α β + D α β
where M α β and D α β are related by volume magnetic susceptibility coefficient. Although the general form of the M α β and D α β equivalents for the energy-momentum tensors is unknown, one may build two symmetrical energy-momentum tensors, where a division of the stress-energy tensor of electromagnetic field will be obtained, into a tensor representing magnetization-polarization of charged matter (being the source of the field), and energy-momentum tensor representing electric energy transmission. This will also agree with results in the next section, but first one may show, that the above leads directly to obtaining the classical equivalent of quantum interpretation seen in QED.
To clarify the above statement one may multiply equation (A6) by μ r from (1) to get
Υ α β = − J α A β − μ r T α β
In above
− J α A β = γ 2 γ 2 + 1 B 2 μ o · 1 γ 2 c 2 U α U β
what gives first component, describing distribution of magnetic moment. Next, using volume magnetic susceptibility χ from (1) one may introduce the symmetric energy-momentum tensor Ω α β defined as
Ω α β ≡ J α A β + χ T α β = − 1 μ o F α γ ∂ γ A β
where last transformation of the equation comes from (A30), and where according to (A25) above yields
− Υ α β = Ω α β + T α β
Component χ T α β in eq. (20) represents classical relation between Polarization-Magnetization tensor and Electric Displacement tensor, where
− χ T 00 = u B ⊙ = 1 γ 2 + 1 B 2 μ o
so, by analogy to (12), χ T α β may be also understood as the rank two tensor potential of the electromagnetic field associated with charged matter. All that remains, is to introduce rank two tensor volume magnetic susceptibility χ α μ according to the rules of classical electrodynamics
χ α μ ≡ χ ˜ α μ + χ η α μ
defined in such a way, that
χ α μ T μ β = Ω α β → χ ˜ α μ T μ β = J α A β
where χ ˜ α μ seems to be responsible for the self-interaction, resulting in the formation of internal magnetic moments - vortex field associated with elementary particles.
Summarizing, − Ω α β may be considered as Polarization-Magnetization energy-momentum tensor, describing distribution of charged matter as a sum of rank two tensor electromagnetic potential and energy distribution related to the magnetic moment. − T α β may be considered as Electric Displacement energy-momentum tensor describing electric energy transmission.
Now, one obtains the classical picture (charged matter exchanging energy of electric field) being equivalent of the description obtained in QED (leptons exchanging bosons). Trace of Ω α β gives charged matter density where the charged matter density is described by disturbances in magnetization and polarization, experiencing only electromagnetic force, which can be seen in below
− ∂ β Ω α β = ∂ β Υ α β = f E M α ; − Ω α β η α β = ϱ c 2
and where χ α μ from (24) may be farther modeled to describe polarization and magnetization by Jones matrices, vectors [23] and symmetry groups [24], analogously as it is done in QED.
In QED picture if one substitutes (A27) for the current Lagrangian density employed in QED
L Q E D = 1 4 μ o F α β F α β = 1 2 μ o F 0 γ ∂ 0 A γ = 1 2 ψ ¯ i ℏ c 2 D − m c 2 ψ
one simplifies currently used L Q E D and may derive equations that characterize the entire system involving the electromagnetic field where leptons (described by spinors) exchange bosons. However, such a representation of matter can be treated as an equivalent of Ω α β where the description used, reveals only the density of the electromagnetic four-force (25) and four-current (A28).
From this perspective, these equations describe all the forces in the system. As was shown in (A17), four-force densities f g r α and f o t h α naturally emerge within the system as an outcome of the existence of field energy-momentum tensor present in Alena Tensor, and the resultant Lagrangian density duly incorporates this aspect. These forces are now invisible in the equations, because they have been "absorbed" by the used description of charged matter Ω α β , explained in (24) and (25). Above interpretation may thus clarify the challenging quest for identifying quantum gravity as a distinct interaction within Quantum Field Theory. It would also explain the remarkable precision of QED’s predictions, provided it indeed characterizes the complete system involving the electromagnetic field.
Since in the system under consideration, all the energy present is the result of the existence of the electromagnetic field (including the energy of charged particles), the above reasoning also leads to the possibility of interpreting the Poynting four-vector Υ 0 β in (18)
Υ 0 β = γ 2 γ 2 + 1 B 2 μ o · 1 γ c U β − μ r T 0 β
In the above, the first term is responsible for transferring the energy of magnetic moment what just desribes the movement of the density of charged matter. The second element (related to Electric Displacement energy-momentum tensor) can be associated with the transfer of the electric field energy carried by light, which using (15) and (A27) leads to the conclusion that
− μ r T 0 β = u E ⊙ , u → E ⊙
since the energy and momentum densities of photons should be equal.
This conclusion opens the way to quantum analyzes and makes it possible to provide an equivalent of the presented interpretation for point-like particles.

2.3. Classical and Quantum Interpretation for Point-Like Particles in Flat Spacetime

According to interpretation from previous section (28), canonical four-momentum H μ as the volume-integrated − T 0 β (A31) in the description for point-like particles may be associated with a photon, thus
c H μ = H , c p → H = H , H →
what yields H μ H μ = 0 . This confirms the possibility of analyzing light as energy quanta and preserves the fundamental property of equality of energy and momentum of the photon. From (A36) one may also notice, that for a complete description of the behavior of a particle in flat spacetime with an electromagnetic field, it is enough to know Lagrangian and the four-vector S μ associated with a certain rotation or spin. Unfortunately, S μ is unknown, but a quantum solution can be proposed that will shed new light on the interpretation of Quantum Mechanics.
At first, one may propose general method for quantum analysis. Using volume magnetic susceptibility χ from (1) and introducing new four-vector E μ as
q E μ ≡ W μ − χ P μ
one may notice from (A24) and (A36) that it yields
H μ − q E μ = − q A μ
Since generalized canonical four-momentum H μ is four-gradient on Hamilton’s principal function (A33), therefore, according to freedom of gauge rules, in above equation, four-vector E μ is just other gauge of A μ . Also for any other scalar α , four-vectors q E μ ± ∂ μ α and q A μ ± ∂ μ α always will be an electromagnetic four-potential.
One may thus introduce quantum wave function ψ and wave four-vector K μ related to canonical four-momentum in its simplest form equal to
ψ ≡ e − i K μ X μ ; ℏ K μ ≡ H μ
to get
i ℏ ∂ μ ψ = H μ ψ
Then, acording to (5) and (A24), one may rewrite (31) as just
i ℏ ∂ μ − q E μ ψ = μ r P μ ψ
The above equation can be tested in many different quantum applications, which will allow to definitively confirm or deny the validity of the approach proposed in the Alena Tensor theory.
One may now perform reasoning that will show, that presently used quantum equations may be considered as approximation of the above equation. Using freedom of gauge rules and conclusions (A36) and (A38), one may introduce electromagnetic four-potential − Σ μ defined in following way
Σ μ ≡ P μ + ϱ c 2 γ 2 p P β + ϱ c 2 p S μ + Y μ
what yields
H μ = Σ μ + q A μ → 2 H μ = Σ μ + q E μ
and thanks to property H μ H μ = 0 from simple calculations one gets
1 2 Σ μ Σ μ + q 2 E μ E μ = μ r 2 m 2 c 2
Introducing electric energy E E ⊙ and magnetic energy E B ⊙ associated with particle as the volume integrals of the energy densities u i from equation (14), according to (4), (13) and (15) one also gets
E E ⊙ ≡ μ r H ; E B ⊙ ≡ μ r m c 2 γ
thus
Σ μ = E E ⊙ c , p → H + E B ⊙ c 2 u → ; q A μ = − E B ⊙ c , E B ⊙ c 2 u →
Therefore by introducing vector p → m such that
p → m 2 = 1 μ r 2 Σ → 2 − q 2 E μ E μ
one may rewrite (37) as
1 2 H 2 c 2 − p → m 2 = m 2 c 2
what also shows, that with constant H also p m value is constant. Now, one may perceive the particle using the newly created quantum wave function Ψ , e.g.
Ψ ≡ e ± N μ X μ ; ℏ N μ ≡ i 2 H c , p → m
to get Klein-Gordon formulation
ℏ 2 □ + m 2 c 2 Ψ = 0
One may also consider particle by the corresponding Dirac equation derived in a classical way from above. It would also lead to conclusion that the description of a free particle may be also considered as contraction of electromagnetic four-potentials with the use of spinor representation. This also means that the non-commutativity of QM is no longer an obstacle to its unification with GR, with the use of Alena Tensor.
Finally, it can also be shown that the above leads to obtaining the equivalent of the Schrödinger equation. One may notice, that since H is volume integrated field invariant (A32), thus ∂ t H = 0 , and thus it may be seen from (A35) and (A36) that
∂ t H = ∂ t m c 2 γ + 1 γ + ∂ t L
what, according to Hamilton’s equations, yields
∂ t L = 0 → 0 = ∂ t m c 2 γ = ∂ t W p v = ∂ t μ r
Therefore, referring to (39) one may define scalar α as
α ≡ t H 2 m c 2 γ + 1 γ − E E ⊙
and the following electromagnetic four-potential − Σ ^ μ can be created
Σ ^ μ ≡ Σ μ + ∂ μ α = H 2 m c 3 γ + 1 γ , p → H + E B ⊙ c 2 u → − ∇ α
Next, from (A35) on gets
H = m c 2 γ + 1 γ + L = H 2 m c 2 γ + 1 γ − H L m c 2 γ + 1 γ
what yields, that second electromagnetic four-potential q A ^ μ is
q A ^ μ ≡ q A μ − ∂ μ α = − H L m c 3 γ + 1 γ , ∇ α − E B ⊙ c 2 u →
Now using above and (33) one obtains
H μ ψ = Σ ^ μ ψ + q A ^ μ ψ
what allows to recreate Schrödinger equation by taking zero-components of above four-vectors
i c ℏ ∂ 0 ψ = − ℏ 2 m γ + 1 γ ∇ 2 ψ + c q A ^ 0 ψ
where m γ + 1 γ may be approximated as 2m with high accuracy up to velocity u ≈ 0.4 c .
The reasoning presented in this chapter ensures high compliance with the results of Quantum Mechanics and indicates, that the currently used quantum equations for the system with only electromagnetic field may be considered as approximation of the results obtained with the use of Alena Tensor. What is also important, the quantum equations discussed above describe the entire physical system under consideration, including the electromagnetic force, gravity and the Abraham-Lorentz effect, which agrees with the conclusions from the previous chapter.
In the interpretation presented, one obtains a picture in which gravity and the Abraham-Lorentz effect, in some sense, have always been present in quantum equations. They can be made visible by expanding equation (34) using volume magnetic susceptibility χ from (1), to the form
H μ = μ r P μ + q E μ = P μ + q E μ + χ P μ
In the classical picture, according to the conclusion (A41) and (3), this leads to the existence of all three forces in the system
F α = U β ∂ β P α − ∂ α P β = 1 μ r F E M α + m c 2 ∂ α ln ( μ r ) − d ln ( μ r ) d τ P α
where in above, the component m c 2 ∂ α ln ( μ r ) − d ln ( μ r ) d τ P α agrees with conclusion (A26) describing gravity and the term χ P μ in (52) is responsible for gravity and the Abraham-Lorentz effect.

2.4. Generalization to Other Fields

To describe uncharged particles related to other fields (e.g. neutrinos), one may also consider generalizing the Alena Tensor to other fields. At this point, however, it seems necessary to introduce a classification of fields that will explain the differences in the approach to their analysis in flat, curved spacetime and in quantum perspective.
Remaining with the previous notation, one may describe the field (e.g. electroweak field) in the system by some generalized field tensor F α β γ providing more degrees of freedom, and express Alena Tensor (A1) in flat spacetime as follows
T α β = ϱ U α U β − c 2 ϱ Λ ρ + 1 Λ ρ η α β − F α δ γ F δ γ β
where
Λ ρ ≡ 1 4 F α β γ F α β γ
ξ h α β ≡ F α δ γ F δ γ β Λ ρ
ξ ≡ 4 η α β h α β
The Alena Tensor defined in this way retains most of properties described in Appendix A, however, it now describes other four-force densities in the system. Total four-force density f α can be now presented as
f α = f f u n α ≡ − ∂ β F α δ γ F δ γ β ( f u n d a m e n t a l f o r c e s ) + f g r α ≡ η α β − ξ h α β ∂ β ϱ c 2 ( r e l a t e d t o g r a v i t y ) + f s e c α ≡ ϱ c 2 Λ ρ f f u n α ( s e c o n d a r y f o r c e s )
Therefore, interactions can be classified based on their properties as:
  • fundamental interactions related to body forces f f u n α
  • gravitational (or gravity with an additional field), related to f g r α
  • secondary interactions related to four-force density f s e c α
where each of above f i α four-force density should satisfy the condition
0 = U α f i α
Taking into account the conclusions from chapter Section 2.2, it can be assumed with high probability that the Electroweak Theory describes matter in an analogous way as demonstrated in (21) for electromagnetic interactions, where now Υ α β describes the energy-momentum tensor for the electroweak interactions, and Ω α β is still a spinor based description of the matter, this time describing disturbances in the propagation of this field.
This is not so obvious for QCD, due to the strong connection of these interactions with electromagnetism, and it would certainly require further research. However, it seems that the use of Alena Tensor opens up new possibilities in the study of these interactions both in the curvilinear and classical description, as well as in the regime of QFT and QM mathematical apparatus.

3. Discussion

The properties of Alena Tensor seem promising in terms of their further development what could be used in unification theories, in modified theories of gravity [25,26] or as a method of seeking an explanation for the Dark Sector [26]. For this reason, it is worth discussing the possible use of this tool in selected applications against the background of existing research.

3.1. Dark Sector and Perspectives for Unification of Interactions

The first topic discussed will be the issue of the dark sector, for which Alena Tensor brings new interpretation possibilities. Although Dark Energy and Dark Matter are concepts closely related to the General Relativity, their analysis is also carried out e.g. from the perspective of quantum theories and quantum cosmology [27,28,29].
The use of Alena Tensor indicates that the invariant of the field tensor is responsible for the vacuum energy and the associated cosmological constant [30]. This gives a chance to solve the puzzle of the "smile of the Cheshire cat" [31] explaining the reason for the appearance of the cosmological constant in Einstein Field Equations. Since the first publication of General Relativity, this constant has appeared and disappeared in EFE like Cheshire cat from the book "Alice’s Adventures in Wonderland". Equation (A13) indicates that cosmological constant is necessary and proposes an explanation of its origin.
Above opens the way to replacing current estimates of the cosmological constant [32] with an attempt to estimate the value of the field tensor invariant. It also becomes possible to search for the expected form of the field tensor based on the experimentally measured value of its invariant, and allows to look for an answer to the question of what fields, apart from the electromagnetic field, should constitute Alena Tensor.
An example of such an approach seems to be an attempt to estimate the values of magnetic and electric fields based on available background radiation data [33] and an attempt to determine the value of the invariant of the electromagnetic field tensor. Importantly, it also seems that field invariant in general does not have to be the constant [34,35], which would be particularly important for solving the Hubble tension problem [36].
Alena Tensor also introduces the possibility of a new interpretation of the forces attributed to Dark Matter. Interpretation presented in Section 2.1 drives to conclusion that issues related to Dark Matter may also be related to e.g. Abraham–Lorentz effect and, in general, does not necessarily involve the existence of additional matter. Modified Alena Tensor may also prove helpful for analysis of Maxwell’s equations with axion modifications [37] and attempts to explain Dark Matter based on these particles [38], especially in the context of the results regarding Sigma-8 tension [39].
Analyzing the possible directions of unification of interactions, it can also be noted that the Alena Tensor allows for testing hypotheses regarding the interconnections of fields and the connections of fields with gravity. Fields defined in the way presented in chapter (Section 2.4) allow for quite a lot of freedom in adapting them to the existing division of interactions that emerged in Quantum Mechanics: electroweak, strong and gravitational interactions.
Due to the fundamental importance of electroweak interactions (fermions are the building blocks of matter), it seems that the field strength tensor constituting Alena Tensor should be related to electroweak field, where the rest interactions (strong, gravity and potentially others [40]) could be linked to f g r + f s e c four-force density. It would be also supported by conclusions from research on Double Copy Theory [41,42,43], since it can be assumed that solutions should include perturbative duality between gauge theory and gravity and thus it may be expected, that stong interactions are related to the f g r + f s e c four-force density. Also introducing additional fields beyond electromagnetism to Alena Tensor causes an additional spacetime curvature term in Einstein tensor, related to new fields. Gravity is no longer "bending of the light path" only, but becomes "bending of the bosons path of all introduced fields" which, for example, could help to some extent in explaining the strong interactions. Perhaps all this may shed new light on current work on the unification of interactions [44,45,46].
Finally, when discussing the unification of interactions, it is impossible to ignore the importance of the Higgs field [47]. The adoption of an analysis model based on the Alena Tensor creates new possibilities for relating the geometry of spacetime with a field in general [48] and even based on the simple model presented in Appendix A.3, it is possible to analyze relationships between the Higgs field and the electromagnetic field [49,50]. Additionally, due to the possibility of analyzing the system based on the proposed Lagrangian and generalized canonical four-momentum, it becomes possible to study individual classes of fields in terms of their impact on the phenomenon of symmetry breaking [51,52].
When building theoretical models, however, one should remember about the limitations related to the adopted analysis method. In curved spacetime, the curvature described by the Einstein tensor will always be related to the four-force densities f g r α + f s e c α . In flat spacetime, conditions (A23), (A27) and (A31) still seem reasonable.

3.2. Quantum Gravity

There is no universal agreement on the approach to developing quantum gravity [53] and so far research is being carried out using different methods in different directions. One of the research directions is canonical quantum gravity [54] with its attempt to quantify the canonical formulation of general relativity, the most promising example of which is Loop Quantum Gravity [55].
Work is also ongoing in the field of string theory, where M-theory [56] seems to be the leading area of research. There are also many other e.g. [57,58,59] less frequently cited studies that explore different, sometimes unusual [60] research areas.
Against the background of the above research directions, the dualistic approach represented by Alena Tensor seems very promising because it changes the research paradigm in two ways.
The first paradigm shift is that, according to the conclusions presented earlier (and in the Appendix A), in the description provided by Alena Tensor, the Einstein tensor is not exclusively related to gravity but it also describes phenomena related to four-force density f s e c α . This means a change in assumptions and a new way of perceiving prospect of unifying the remaining interactions with gravity.
The second paradigm shift results from the very nature of the dualistic approach and concerns the lack of need to search for quantization methods in curved spacetime. According to the reasoning presented in the article (and in the Appendix A), if one describes the field in flat spacetime by some field tensor and enters it into the Alena Tensor in the appropriate way, the equations in curved spacetime will naturally turn into the Einstein Field Equations.
The second paradigm shift in particular seems to be extremely important from the point of view of research on quantum gravity phenomena. It also opens new possibilities for studying quantum phenomena in a strong gravitational fields.
Current research approaches to quantum problems in a strong gravitational field each time require the construction of an appropriate model in which the obtained results can be interpreted, either through careful selection of the observer [61], or making direct use of the principle of equivalence [62], or own, specific approach [63]. It also needed consideration of the specific quantum phenomena occurring in the vicinity of very massive objects, such as the Unruh effect [64] or Hawking radiation [65]. Thanks to the dualistic approach, such research can now be conducted in flat spacetime with fields and then the results can be analyzed in curved spacetime.
One of the natural directions of research seems to be the development of a field tensor that, in curved spacetime, provides the known metrics [66] used to describe gravity, extended by the term related to secondary interactions. The development of such a field tensor seems to be the first step towards building quantum gravity, this time - contrary to the direction described in the previous chapter - from the side of the General Relativity.
Interestingly, because the use of the Alena Tensor indicates the possibility of shaping the metric tensor of spacetime using a field, it also sheds new light on research on new drives [67], including the quantum effects [68] needed to analyze them. Although many QM and QFT problems seem unsolvable [69,70] using current paradigms, such as the Planck scale problems [71], previously mentioned paradigm shifts may change this situation.
It also seems interesting to search for solutions to the problem of quantization of interactions related to the tensor (A9) in various spacetimes, thus the problem of quantization should be addressed.

3.3. Quantization

To get a full picture of the applicability of the approach based on Alena Tensor, one may consider an example of its application to gravity quantization.
One may start with a choice of proper representation of a metric g α β so that the interpretation of time in first quantization will be "natural". By "natural interpretation" of time, it is understood the approach in which, after the first quantization of Hamiltonian, one gets a proper definition of the time evolution operator in the ”Schrödinger representation”, in such a way that
U ( t , t 0 ) = e − i H · ( t − t 0 ) / ℏ
fulfill classical conditions [72]
U † ( t , t 0 ) U ( t , t 0 ) = I | ψ ( t 0 ) 〉 = U ( t 0 , t 0 ) | ψ ( t 0 ) 〉 U ( t , t 0 ) = U ( t , t 1 ) U ( t 1 , t 0 )
This means that, in general, it should be possible to incorporate the Lagrangian formalism for the Gauge fields. Therefore, for the field strength tensor
F μ ν a = ∂ μ A ν a − ∂ ν A μ a + g f a b c A μ b A ν c
one needs to define proper commutator
[ t a , t b ] = i f a b c t c
As it was show in [73] this can be done by rewriting g α β in the ( 3 + 1 ) -split in Geroch decomposition manner. This approach solves the proper initial value problem, since now spacetime can be interpreted as the evolution of space in time, with interpretation of time that is consistent with Quantum Mechanics: time as a distinguished, absolute, external, global parameter. A summary of full formalism has been presented many times, last and the modern one can be found in [74], where computation rules look as follows
γ i j , π k l = 1 2 δ i k δ j l + δ j k δ i l δ 3 x − y
The above approach makes it possible to introduce gravity into Quantum Mechanics in form of canonical quantization and couple this field with other interactions in regular manner. In such picture gravity acts as just another quantum field that could be incorporated into the Standard Model Lagrangian and interact with other fields on the same principles. The only difference is that we are bound to only one representation of the metric g α β with ( 3 + 1 ) -split Geroch decomposition. However, it may be transformed to other, more convenient coordinate systems when quantum phenomena can be negligible.
Presented approach opens a natural way to implement representation of tensor g α β into the Alena Tensor (A1) for better understanding overall interpretation of GR in the big scale. It also opens the possibility to look for a quantum gravity phenomena on the small scale, where perturbation approach as quantum as gravity interaction are on the same level of magnitude. The most promising application of this approach could be implementing this calculations to Hawking radiation phenomena on the Planck scales, as the original calculations are questioned by other authors [75,76].
New observation methods allow to look for a quantum gravity phenomenon in the present or near future data that could test the boundaries of GR in the classical approach. One of the most promising directions in the present observation is the rise of gravitational wave (GW) astronomy. It might be worth investigating the post-merge echoes that occur because of the stimulated emission of Hawking radiation after compact binary merger events involving stellar black holes. This could be a promising way to search for deviations from General Relativity and could serve as evidence for the quantum structure of black hole horizons. Present methods used to model this phenomenon in modified theories of gravity are extremely challenging in Numerical Relativity and could provide inconclusive observation interpretations [77]. The approach presented in this paper may also help obtain results without using effective model echoes within the framework of linear perturbation theory.

4. Conclusions

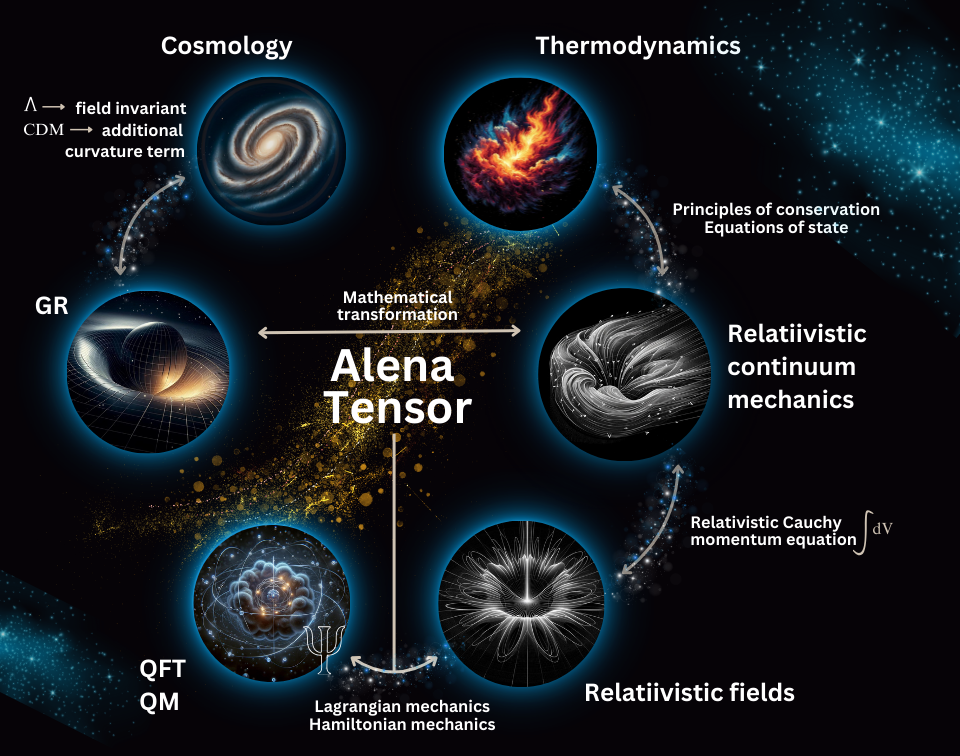
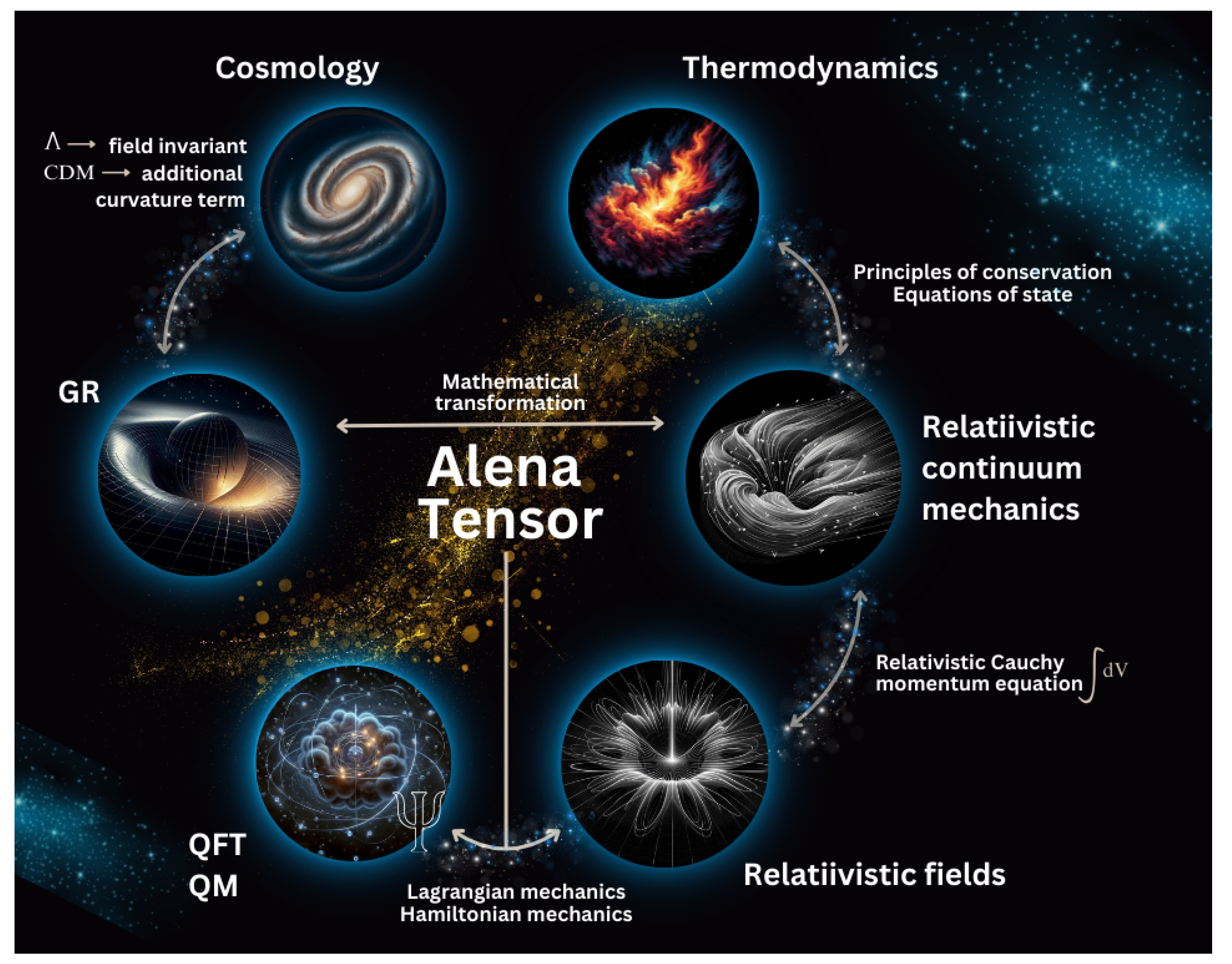
As presented in the article (and in the Appendix A), the possibility of using a new tool, Alena Tensor, seems to open up new research possibilities both in terms of searching for the relationship between QFT and GR [78], as well as in terms of connections between many phenomena previously analyzed separately: in quantum or classical description, curvilinear or in flat spacetime, or, for example, the possibility of combining the interpretation of fluid dynamics with field theory. Such an analysis may prove particularly interesting in the context of cosmology and the study of quantum phenomena in the early universe [79]. The lines of unification proposed by Alena Tensor can be visualized as in Figure 1 below.
By appropriately selecting field tensors and testing hypotheses regarding their relationship with the Einstein tensor in curved spacetime, it is possible to search for new interpretations for Dark Matter, as well as to analyze the relationships of the invariants of these field tensors with the cosmological constant. By adopting a new interpretation of the cosmological constant as an invariant of the field tensor, possibilities also open up to explain contradictory experimental data for cosmological phenomena, because the field tensor invariant does not have to be constant in time.
Due to the high flexibility of the Alena Tensor in the selection of fields, it also seems to be a good tool for testing hypotheses regarding the unification of interactions. Such research can be conducted in the regime of the QFT mathematical apparatus and, importantly, thanks to a clear interpretation of the four-divergence of the field stress-energy tensor (four-force density), obtained results would also lead to obtaining an interpretation of quantum interactions in the classical description. It could be a major milestone in combining known QFT results with the classical description of interactions.
Finally, one can also seek a quantum description of gravity in new ways, taking advantage of the paradigm shifts that Alena Tensor brings with it. This does not mean that the problems associated with quantizing fields in curved spacetime disappear and the behavior of quantum fields, when changing the metric tensor, will still require careful analysis. However, it seems that thanks to the dualistic description provided by Alena Tensor, these analysis may be much easier.
The Alena Tensor can be proven based on derived quantum equations (34) or (51), which opens the way to new experimental and theoretical research. Further research on Alena Tensor may also lead to its important transformations and generalizations, as well as to the design of experiments in terms of the sought properties that match the experimental data. And all this has a chance to bring us one step closer to the next image that will connect the previously scattered puzzles of knowledge.

5. Statements

No datasets were generated or analyzed during the current study.
During the preparation of this work the authors did not use generative AI or AI-assisted technologies, except for generating the elements of Figure 1.
Authors did not receive support from any organization for the submitted work.
Authors have no relevant financial or non-financial interests to disclose.
Both authors contributed equally.

Appendix A. Summary of Conclusions from Previous Publications about Alena Tensor

Appendix A.1. Alena Tensor and Main Definitions

This appendix summarizes the state of knowledge about Alena Tensor based on recent publications and systematizes existing conclusions in the context of further applications.
Alena Tensor is the central object of the method described in [13,14]. It is a stress-energy tensor, which can be interpreted in flat and curved spacetime. The Alena Tensor T α β has the following form
T α β = ϱ U α U β − c 2 ϱ + Λ ρ g α β − ξ h α β
Designations used:
  • g α β is a metric tensor by which the spacetime of a physical system is considered,
  • 1 / ξ ≡ 1 4 g μ ν h μ ν ,
  • ϱ ≡ ϱ o γ where ϱ o is rest mass density and γ is Lorentz gamma factor,
  • ϱ U α is four-momentum density in the system, in accordance with the postulate raised in the description to eq. (11) from publication [13],
  • h α β is the metric tensor of curved spacetime in which all motion takes place along geodesics and it is related to the field tensor, which will be explained next,
  • Λ ρ is related to the invariant of the field tensor, which will be explained next.
The field present in the system is described by some field tensor, e.g. F α β γ , which may be widely configured. To simplify the reasoning, it will be assumed that field is described by F β γ representing electromagnetic field, but the properties described here are general and apply to the field in a broader sense.
For F β γ understood as electromagnetic field tensor one gets the following relationships
h α β ≡ 2 F α δ g δ γ F β γ F α δ g δ γ F β γ g μ β F α η g η ξ F ξ μ
which provides the property h α β g μ β h α μ = 4 , and
Λ ρ ≡ 1 4 μ o F α μ g μ γ F β γ g α β
where μ o is vacuum magnetic permeability. The stress–energy tensor for electromagnetic filed, denoted as Υ α β may be thus presented in a way that relates the field to the metric tensor of curved spacetime
Υ α β ≡ Λ ρ g α β − ξ h α β = Λ ρ g α β − 1 μ o F α δ g δ γ F β γ
This connection of the field with the h α β tensor opens up wide possibilities of unification, discussed in the main article.
The pressure p in the system is equal to
p ≡ c 2 ϱ + Λ ρ
where it was shown in [14] that p is negative. This allows (A1) to be written as
T α β = ϱ U α U β − p Λ ρ Υ α β
The remaining tensors that describe the system are defined as follows
R α β ≡ 2 ϱ U α U β − p g α β
its trace R
R ≡ R α β g α β = − 2 p − 2 Λ ρ
and tensor G α β as
G α β ≡ R α β − 1 2 R ξ h α β
which allows to rewrite (A1) as
G α β − Λ ρ g α β = 2 T α β + ϱ c 2 g α β − ξ h α β
The above definitions allow to consider flat spacetime, curved spacetime, and all intermediate states, in which spacetime is partially curved and part of the motion results from the existence of residual fields. One may analyze boundary solutions: flat spacetime with fields and curved spacetime without fields.

Appendix A.2. Behavior of the System in Curved Spacetime

Considering g α β as equal to h α β one obtains that it yields ξ = 1 , therefore the whole part of Alena Tensor related to fields vanishes. It yields
T α β = ϱ U α U β
The value of tensor G α β becomes
G α β = R α β − 1 2 R h α β
and (A10) reduces to
G α β − Λ ρ h α β = 2 T α β
Therefore, in curved spacetime, R α β acts as Ricci tensor and G α β acts as Einstein curvature tensor, both with an accuracy of 4 π G c 4 constant, where cosmological constant Λ is related to the invariant of the field tensor
Λ = − 4 π G c 4 Λ ρ
where Λ ρ is negative.
Eq. (A13) can be further analyzed using known tools for considering metrics in General Relativity, taking into account the knowledge of the field tensor used to build the Alena Tensor.
Since covariant four-divergences of T α β and G α β vanish, therefore they represent curvature tensors, related to corresponding four-force densities present in flat Minkowski spacetime. For this reason it is worth to consider behavior of the system in flat Minkowski spacetime.

Appendix A.3. Behavior of the System in Flat Minkowski Spacetime

Considering g α β as equal to η α β Minkowski metric tensor, thanks to the amendment to the continuum mechanics explained in equations (13) - (21) of publication [13]
∂ α U α = − d γ d t → ∂ α ϱ U α = 0
total four-force density f α acting in the system is equal to
f α ≡ ∂ β ϱ U α U β
and for considered system, it is the sum of electromagnetic ( f E M α ), gravitational ( f g r α ) and other ( f o t h α ) four-force densities, where
f α = f E M α ≡ ∂ β Υ α β ( e l e c t r o m a g n e t i c ) + f g r α ≡ η α β − ξ h α β ∂ β ϱ c 2 ( g r a v i t a t i o n a l ) + f o t h α ≡ ϱ c 2 Λ ρ f E M α ( o t h e r )
In above, gravitational four-force density is not an interaction between bodies, but appears to result from the bending of the direction of electromagnetic field energy transport by the energy density gradient. Eq. (A17) yields
∂ β T α β = 0
and
∂ β G α β = f g r α + f o t h α
The above result shows, that when using the Alena Tensor, it should be assumed that the Einstein tensor does not describe the curvature associated with gravity alone.
Neglecting other forces (as we currently do in known solutions for GR), one actually approximately obtains metric tensors responsible for gravity alone. However, the total value of the Einstein tensor corresponds to the curvature associated with the density of the four-forces from equation (A19). This means that the above approach can be used to search for the causes of disturbances between observations and the expected motion resulting from gravitational equations, which is currently attributed entirely to Dark Matter [80].
The meaning of the four-force density f o t h α is discussed in the main article.
One may also introduce an additional tensor Π α β which turns out to play a role of deviatoric stress tensor [81]
Π α β ≡ − c 2 ϱ ξ h α β
To demonstrate this, Alena Tensor can be represented in flat Minkowski spacetime as
T α β = ϱ U α U β − p η α β − Π α β + Λ ρ ξ h α β
Now, vanishing four-divergence of the above
f α = ∂ α p + ∂ β Π α β + f E M α
express relativistic equivalence of Cauchy momentum equation (convective form) [82]. The above representation therefore allows for the analysis of the system using the tools of continuum mechanics. From this perspective, f E M appears as a body force, while the remaining forces are the effect of fluid dynamics [83] and could be modeled e.g. with help of Navier-Stokes Equations [84,85].
By imposing following condition on normalized Alena Tensor as described in [14]
0 = ∂ β T α β η μ γ T μ γ + ∂ α ln η μ γ T μ γ
one obtains further simplification. Some gauge of electromagnetic four-potential denoted as A μ may be expressed as
A μ ≡ − Λ ρ p ϱ o ρ o U μ
where ρ o denotes rest charge density in the system. It also simplifies Alena Tensor in flat Minkowski spacetime to
T α β = 1 μ o F α γ ∂ β A γ − Λ ρ η α β
and leads to the explicit form of gravitational four-force density
f g r α = ϱ d ln ( p ) d τ U μ − c 2 ∂ μ ln ( p )
Both Lagrangian density ( L ) and Hamiltonian density ( H = T 00 ) for the system appear to be related to invariant of the field tensor
L = H = Λ ρ
where it was shown in [14] that
∂ Λ ρ ∂ A α = ∂ ν ∂ Λ ρ ∂ ( ∂ ν A α ) = − J α
In above J α = ρ o γ U α is electric four-current and according to (A15) its four-divergence vanishes.
Eq. (A27) indicates, that in this solution there is no potential in the classical sense and dynamics of the system depends on itself. This is a clear analogy to main GR equation and something that should be expected from a GR-equivalent description of the system in flat spacetime.
Finally, electromagnetic field energy density Υ 00 was calculated in eq. (57) of [14] as
Υ 00 = Λ ρ p ϱ c 2 γ 2 − Λ ρ
and second representation of the stress-energy tensor was shown in eq. (38) of [14] as
T α β = p ϱ c 2 ∂ γ 1 μ o F α γ A β

Appendix A.4. Dynamics of Point-Like Particles in Flat Spacetime

It was also shown in [14], that
H β ≡ H c , p → H ≡ − 1 c ∫ T 0 β d 3 x
in flat spacetime acts as canonical four-momentum for the point-like particle, and for the system with electromagnetic field, four-divergence of H β vanishes due to the Poynting theorem. Hamiltonian for point-like particle is thus
H = − ∫ Λ ρ d 3 x
The action S (Hamilton’s principal function) for the point-like particle was derived in [14] as
− S = H β X β = m c 2 τ + ∫ p d 4 x = P β X β − m c 2 τ
where P β is four-momentum and τ is particle’s proper-time. One may denote in the above equation Pressure-Volume work (pressure potential energy) as W p v
W p v ≡ − ∫ p d 3 x
and it has positive value. Denoting F β as total four-force acting on the particle one may notice that Lagrangian L for the particle may be understood as the Lagrangian for a particle of some perfect fluid [86]
− L = 1 γ F β X β = m c 2 γ − W p v
thus it may be also analyzed from the perspective of the laws of thermodynamics.
Hamilton’s principal function (action) (A33) vanishes for the inertial system. It clearly shows that inertial systems in this approach do not exist and should be considered as some abstract idealization. Considered system without fields and forces vanishes, what, taking into account the dependence of h α β on the field tensor (A2), indicates that spacetime in this approach should be actually understood as some method to perceive the field.
According to [14], mentioned canonical four-momentum may be expressed as
H μ = P μ + W μ = − γ L c 2 U μ + S μ
where L is Lagrangian for point-like particle, S μ due to its property S μ U μ = 0 , seems to be some description of rotation or spin, and where W μ describes the transport of energy due to the field. It can be expressed in a generalized way as
W μ = X β ∂ μ P β − ∂ μ m c 2 τ
For considered system with electromagnetic field it was calculated in [14] as
W μ = q A μ + ϱ c 2 γ 2 p P β + ϱ c 2 p S μ + Y μ
where Y μ is the volume integral of the Poyinting four-vector
Y β = ∫ Υ 0 β d 3 x
and
S β = ∫ ε o Λ ρ γ c ρ o F 0 μ ∂ μ U β d 3 x
where ε o is electric vacuum permittivity.
Since in (A36) W μ is just "other gauge" of − P μ thus in the classical description for such a system occurs
F α = U β ∂ β P α − ∂ α P β = U β ∂ α W β − ∂ β W α
where U β ∂ α P β = 0 vanishes, due to the property of Minkowski metric ∂ α U β U β = 0 .

References

  1. Böhmer, C.G.; Downes, R.J. From continuum mechanics to general relativity. International Journal of Modern Physics D 2014, 23, 1442015. [Google Scholar] [CrossRef]
  2. Afonso, V.I.; Olmo, G.J.; Orazi, E.; Rubiera-García, D. Mapping nonlinear gravity into General Relativity with nonlinear electrodynamics. The European Physical Journal. C, Particles and Fields 2018, 78. [Google Scholar] [CrossRef]
  3. Shalyt-Margolin, A. The Quantum Field Theory Boundaries Applicability and Black Holes Thermodynamics. International Journal of Theoretical Physics 2021, 60, 1858–1869. [Google Scholar] [CrossRef]
  4. Abdalla, E.; Marins, A. The dark sector cosmology. International Journal of Modern Physics D 2020, 29, 2030014. [Google Scholar] [CrossRef]
  5. Goenner, H. On the History of Unified Field Theories. Living Rev. Relativ. 2004, 7. [Google Scholar] [CrossRef] [PubMed]
  6. Halverson, J.; Sung, B. Faking gauge coupling unification in string theory. Physical Review D 2022, 105, 126012. [Google Scholar] [CrossRef]
  7. Canepa, A. Searches for supersymmetry at the Large Hadron Collider. Reviews in Physics 2019, 4, 100033. [Google Scholar] [CrossRef]
  8. Rowlands, P. An approach to Grand Unification. Journal of Physics: Conference Series. IOP Publishing, 2021, Vol. 2081, p. 012010.
  9. Mahanta, M. A dualistic approach to gravitation. Annalen der Physik 1984, 496, 357–371. [Google Scholar] [CrossRef]
  10. Sanchez, N.G. The classical-quantum duality of nature including gravity. International Journal of Modern Physics D 2019, 28, 1950055. [Google Scholar] [CrossRef]
  11. Grimmer, D. Introducing the ISE Methodology: A Powerful New Tool for Topological Redescription, 2023. arXiv:physics.hist-ph/2303.04130.
  12. Torromé, R.G. Maximal acceleration geometries and spacetime curvature bounds. International Journal of Geometric Methods in Modern Physics 2020, 17, 2050060. [Google Scholar] [CrossRef]
  13. Ogonowski, P. Proposed method of combining continuum mechanics with Einstein Field Equations. International Journal of Modern Physics D 2023, 2350010, 15. [Google Scholar] [CrossRef]
  14. Ogonowski, P. Developed method: interactions and their quantum picture. Frontiers in Physics 2023, 11:1264925. [CrossRef]
  15. Polonyi, J. The Abraham–Lorentz force and electrodynamics at the classical electron radius. International Journal of Modern Physics A 2019, 34, 1950077. [Google Scholar] [CrossRef]
  16. Roberts, B.L.; Marciano, W.J. Lepton dipole moments; Vol. 20, World Scientific, 2010.
  17. Masood, S.; Mein, H. Magnetic Moment of Leptons. arXiv preprint, arXiv:1901.08569 2019.
  18. Wen, M.; Keitel, C.H.; Bauke, H. Spin-one-half particles in strong electromagnetic fields: Spin effects and radiation reaction. Physical Review A 2017, 95, 042102. [Google Scholar] [CrossRef]
  19. Wen, M.; Bauke, H.; Keitel, C.H. Identifying the Stern-Gerlach force of classical electron dynamics. Scientific reports 2016, 6, 31624. [Google Scholar] [CrossRef] [PubMed]
  20. Schleich, K.; Witt, D. Designer de Sitter spacetimes. Canadian Journal of Physics 2008, 86, 591–595. [Google Scholar] [CrossRef]
  21. Ikeda, T.N.; Sato, M. High-harmonic generation by electric polarization, spin current, and magnetization. Physical Review B 2019, 100, 214424. [Google Scholar] [CrossRef]
  22. Gonano, C.A.; Zich, R.E.; Mussetta, M. Definition for polarization P and magnetization M fully consistent with Maxwell’s equations. Progress In Electromagnetics Research B 2015, 64, 83–101. [Google Scholar] [CrossRef]
  23. Karlsson, M. The connection between polarization calculus and four-dimensional rotations, 2013, arXiv:physics.optics/1303.1836.
  24. Bașkal, S.; Kim, Y. Lorentz group in ray and polarization optics. In Mathematical Optics; CRC Press, 2018; pp. 303–340.
  25. Böhmer, C.G.; Jensko, E. A New 2D Formulation of Modified General Relativity. Fortschritte der Physik 2024, p. 2300216.
  26. Capozziello, S.; Mazumdar, A.; Meluccio, G. Can nonlocal gravity really explain dark energy? Physics of the Dark Universe 2024, 45, 101517. [Google Scholar] [CrossRef]
  27. Foster, J.W.; Kumar, S.; Safdi, B.R.; Soreq, Y. Dark Grand Unification in the axiverse: decaying axion dark matter and spontaneous baryogenesis. Journal of High Energy Physics 2022, 2022. [Google Scholar] [CrossRef]
  28. Das, S.; Sharma, M.K.; Sur, S. On the Quantum Origin of a Dark Universe. Physical Sciences Forum 2021. [Google Scholar]
  29. Ng, Y. Quantum foam, gravitational thermodynamics, and the dark sector. Journal of Physics: Conference Series 2016, 845. [Google Scholar] [CrossRef]
  30. Peebles, P.J.E.; Ratra, B. The Cosmological Constant and Dark Energy. Reviews of Modern Physics 2002, 75, 559–606. [Google Scholar] [CrossRef]
  31. Das Gupta, P. General relativity and the accelerated expansion of the universe. Resonance 2012, 17, 254–273. [Google Scholar] [CrossRef]
  32. Carlip, S. Hiding the cosmological constant. Physical review letters 2019, 123, 131302. [Google Scholar] [CrossRef] [PubMed]
  33. Lewis, A. Harmonic E / B decomposition for CMB polarization maps. Physical Review D 2003, 68, 083509. [Google Scholar] [CrossRef]
  34. Shapiro, I.L.; Sola, J.; Espana-Bonet, C.; Ruiz-Lapuente, P. Variable cosmological constant as a Planck scale effect. Physics Letters B 2003, 574, 149–155. [Google Scholar] [CrossRef]
  35. Dvali, G.; Vilenkin, A. Field theory models for variable cosmological constant. Physical Review D 2001, 64, 063509. [Google Scholar] [CrossRef]
  36. Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—a review of solutions. Classical and Quantum Gravity 2021, 38, 153001. [Google Scholar] [CrossRef]
  37. Li, T.; Zhang, R.J.; Dai, C. Solutions to axion electromagnetodynamics and new search strategies of sub-μeV axion. Journal of High Energy Physics 2022, 2023, 1–18. [Google Scholar] [CrossRef]
  38. Lee, Y.; Yang, B.; Yoon, H.; Ahn, M.; Park, H.B.; Min, B.; Kim, D.; Yoo, J. Searching for Invisible Axion Dark Matter with an 18 T Magnet Haloscope. Physical review letters 2022, 128 24, 241805. [Google Scholar] [CrossRef]
  39. Joseph, M.; Aloni, D.; Schmaltz, M.; Sivarajan, E.N.; Weiner, N. A Step in understanding the S 8 tension. Physical Review D 2023, 108, 023520. [Google Scholar] [CrossRef]
  40. Test of lepton universality in beauty-quark decays. Nature Physics 2022, 18, 277–282. [CrossRef]
  41. Díaz-Jaramillo, F.; Hohm, O.; Plefka, J. Double field theory as the double copy of Yang-Mills theory. Physical Review D 2021. [Google Scholar] [CrossRef]
  42. Spallucci, E.; Smailagic, A. Double copy of spontaneously broken Abelian gauge theory. Physics Letters B 2022. [Google Scholar] [CrossRef]
  43. Easson, D.A.; Manton, T.; Svesko, A. Sources in the Weyl Double Copy. Physical review letters 2021, 127 27, 271101. [Google Scholar] [CrossRef]
  44. Guangzhou, G. Exploration of the unification of fields. Physics Essays 2019. [Google Scholar] [CrossRef]
  45. Davighi, J.; Tooby-Smith, J. Electroweak flavour unification. Journal of High Energy Physics 2022, 2022. [Google Scholar] [CrossRef]
  46. Sarfatti, J. Unification of Einstein’s Gravity with Quantum Chromodynamics. Bulletin of the American Physical Society 2010. [Google Scholar]
  47. Lisi, A.; Smolin, L.; Speziale, S. Unification of gravity, gauge fields and Higgs bosons. Journal of Physics A: Mathematical and Theoretical 2010, 43, 445401. [Google Scholar] [CrossRef]
  48. Madore, J. The Geometry of the Higgs Field. International Journal of Geometric Methods in Modern Physics 2008, 05, 265–269. [Google Scholar] [CrossRef]
  49. Damgaard, P.H.; Heller, U.M. The U(1) Higgs model in an external electromagnetic field. Nuclear Physics 1988, 309, 625–654. [Google Scholar] [CrossRef]
  50. Nielsen, N. Higgs boson decay into two photons in an electromagnetic background field. Physical Review D 2014, 90, 016010. [Google Scholar] [CrossRef]
  51. Leder, E. Symmetry, Symmetry Breaking, and the Current View of the Dirac Monopole. 2020.
  52. Quigg, C. Spontaneous symmetry breaking as a basis of particle mass. Reports on Progress in Physics 2007, 70, 1019–1053. [Google Scholar] [CrossRef]
  53. Krasnov, K.; Percacci, R. Gravity and unification: a review. Classical and Quantum Gravity 2018, 35, 143001. [Google Scholar] [CrossRef]
  54. Thiemann, T. Canonical quantum gravity, constructive QFT, and renormalisation. Frontiers in Physics 2020, 8, 548232. [Google Scholar] [CrossRef]
  55. Ashtekar, A.; Bianchi, E. A short review of loop quantum gravity. Reports on Progress in Physics 2021, 84, 042001. [Google Scholar] [CrossRef] [PubMed]
  56. Albertini, F.; Del Zotto, M.; García Etxebarria, I.; Hosseini, S.S. Higher form symmetries and M-theory. Journal of High Energy Physics 2020, 2020, 1–46. [Google Scholar] [CrossRef]
  57. Loll, R. Quantum gravity from causal dynamical triangulations: a review. Classical and Quantum Gravity 2019, 37, 013002. [Google Scholar] [CrossRef]
  58. Fernandes, P.G.; Carrilho, P.; Clifton, T.; Mulryne, D.J. The 4D Einstein–Gauss–Bonnet theory of gravity: a review. Classical and Quantum Gravity 2022, 39, 063001. [Google Scholar] [CrossRef]
  59. Wani, S.S.; Quach, J.Q.; Faizal, M. Time Fisher information associated with fluctuations in quantum geometry. Europhysics Letters 2021, 139. [Google Scholar] [CrossRef]
  60. Epstein, H.I. Discretization and degeometrization: A new relational quantum physics and an alternate path to quantum gravity. Physics Essays 2021, 34, 429–463. [Google Scholar] [CrossRef]
  61. Augousti, A.; Gawełczyk, M.; Siwek, A.; Radosz, A. Touching ghosts: observing free fall from an infalling frame of reference into a Schwarzschild black hole. European journal of physics 2011, 33, 1. [Google Scholar] [CrossRef]
  62. Demir, D. Scattering times of quantum particles from the gravitational potential and equivalence principle violation. Physical Review A 2022, 106, 022215. [Google Scholar] [CrossRef]
  63. Pailas, T. “Time”-covariant Schrödinger equation and the canonical quantization of the Reissner–Nordström black hole. Quantum Reports 2020, 2, 414–441. [Google Scholar] [CrossRef]
  64. Chen, A. Generalized Unruh effect: A potential resolution to the black hole information paradox. Physical Review D 2023. [Google Scholar] [CrossRef]
  65. Kolobov, V.I.; Golubkov, K.; de Nova, J.R.M.; Steinhauer, J. Observation of stationary spontaneous Hawking radiation and the time evolution of an analogue black hole. Nature Physics, 2021; 1–6. [Google Scholar]
  66. Carroll, S.M. Spacetime and geometry; Cambridge University Press: London, 2019. [Google Scholar]
  67. Alcubierre, M.; Lobo, F.S. Warp drive basics. Wormholes, Warp Drives and Energy Conditions 2017, pp. 257–279.
  68. Lundblad, N.; Aveline, D.C.; Balaž, A.; Bentine, E.; Bigelow, N.P.; Boegel, P.; Efremov, M.A.; Gaaloul, N.; Meister, M.; Olshanii, M.; others. Perspective on quantum bubbles in microgravity. Quantum Science and Technology 2023, 8, 024003. [Google Scholar] [CrossRef]
  69. Tachikawa, Y. Undecidable problems in quantum field theory. International Journal of Theoretical Physics 2023, 62, 1–13. [Google Scholar] [CrossRef]
  70. Noce, C.; Romano, A. Undecidability and Quantum Mechanics. Encyclopedia 2022. [Google Scholar] [CrossRef]
  71. Diósi, L. Planck length challenges non-relativistic quantum mechanics of large masses. Journal of Physics: Conference Series 2019, 1275. [Google Scholar] [CrossRef]
  72. Sakurai, J.; Napolitano, J. Modern Quantum Mechanics; Cambridge University Press: London, 2017. [Google Scholar]
  73. Ogonowski, P.; Skindzier, P. Maxwell-like picture of General Relativity and its Planck limit, 2013, arXiv:physics.gen-ph/1301.2758].
  74. Bergstedt, V. Spacetime as a Hamiltonian Orbit and Geroch’s Theorem on the Existence of Fermions, 2020.
  75. Helfer, A.D. Do black holes radiate? Reports on Progress in Physics 2003, 66, 943–1008. [Google Scholar] [CrossRef]
  76. Brout, R.; Massar, S.; Parentani, R.; Spindel, P. Hawking radiation without trans-Planckian frequencies. Physical Review D 1995, 52, 4559–4568. [Google Scholar] [CrossRef] [PubMed]
  77. Abedi, J.; Longo Micchi, L.F.; Afshordi, N. GW190521: Search for echoes due to stimulated Hawking radiation from black holes. Phys. Rev. D 2023, 108, 044047. [Google Scholar] [CrossRef]
  78. Yang, R.Q.; Liu, H.; Zhu, S.; Luo, L.; Cai, R.G. Simulating quantum field theory in curved spacetime with quantum many-body systems. Physical Review Research 2020, 2, 023107. [Google Scholar] [CrossRef]
  79. Carloni, S.; Cianci, R.; Corradini, O.; Flachi, A.; Vignolo, S.; Vitagliano, V. Avenues of Quantum Field Theory in Curved Spacetime, Genova, 14-16 Sep 2022. Journal of Physics: Conference Series. IOP Publishing, 2023, Vol. 2531, p. 011001.
  80. Bertone, G.; Hooper, D. History of dark matter. Reviews of Modern Physics 2018, 90, 045002. [Google Scholar] [CrossRef]
  81. Surana, K.S.; Joy, A.D.; Kedari, S.R.; Nuñez, D.E.; Reddy, J.; Wongwises, S. A Nonlinear Constitutive Theory for Deviatoric Cauchy Stress Tensor for Incrompressible Viscous Fluids. 2017.
  82. Goraj, R. Transformation of the Navier-Stokes Equation to the Cauchy Momentum Equation Using a Novel Mathematical Notation. Applied Mathematics-a Journal of Chinese Universities Series B 2016, 07, 1068–1073. [Google Scholar] [CrossRef]
  83. Romatschke, P.; Romatschke, U. Relativistic fluid dynamics in and out of equilibrium: and applications to relativistic nuclear collisions; Cambridge University Press: London, 2019. [Google Scholar]
  84. Bredberg, I.; Keeler, C.; Lysov, V.; Strominger, A. From navier-stokes to einstein. Journal of High Energy Physics 2012, 2012, 1–18. [Google Scholar] [CrossRef]
  85. Lasukov, V. Cosmological and Quantum Solutions of the Navier–Stokes Equations. Russian Physics Journal 2019, 62, 778–793. [Google Scholar] [CrossRef]
  86. Manoff, S. Lagrangian theory for perfect fluids. arXiv preprint gr-qc/0303015, 2003. [Google Scholar]
Preprints 113211 g001
Figure 1. Alena Tensor framework. Source: self-made illustration created with the assistance of AI.
Figure 1. Alena Tensor framework. Source: self-made illustration created with the assistance of AI.
Preprints 113211 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated