Preprint

Article

Impact of Hydroclimatic Changes on Water Security in the Cantareira Water Production System, Brazil

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

João Rafael Bergamaschi Tercini^*

Arisvaldo Vieira Mello Júnior

João Rafael Bergamaschi Tercini^*

Arisvaldo Vieira Mello Júnior

This version is not peer-reviewed

Submitted:

27 October 2023

Posted:

30 October 2023

You are already at the latest version

Alerts

Abstract

The Cantareira Water Producer System (CWPS), which supplies water to the most populous Brazilian region, Metropolitan Region of São Paulo (MRSP), faces significant challenges due to climate change, threatening its water security. Climate change affects the hydrological cycle affecting water availability. The CWPS is vulnerable to periods of scarcity and instability due to increased climatic variability and increasing water consumption. Current water resource management systems do not consider the impacts of climate change, making it difficult to ensure water security in the future. This study analyzes the impact of climate change on the availability of CWPS using hydrological modeling approach with forecast precipitation data by CMIP6 and assessment of existing systems. The finds will provide a comprehensive understanding of the challenges faced by CWPS in the context of climate change, as well as support strategies and adaptive measures to ensure water security for MRSP.

Keywords:

Subject: Environmental and Earth Sciences - Water Science and Technology

1. Introduction

The availability of freshwater is essential for the sustainability and well-being of societies, and its efficient management becomes even more critical in the face of the challenges posed by climate change. In this context, the Cantareira Water Producer System (CWPS), which supplies the Metropolitan Region of São Paulo (MRSP), stands out as an important subject of study to understand the impacts of these changes on water security.

The CWPS is responsible for supplying water to approximately 9 million people in the MRSP. Its strategic relevance is undeniable, considering the fundamental role that water plays in socioeconomic development and quality of life. However, in recent years, the CWPS has faced significant challenges due to climate change, jeopardizing the water security of the region.

Climate change has affected the hydrological cycle and precipitation patterns worldwide, bringing direct consequences to water availability and quality. In the case of CWPS, an increase in climatic variability is observed, with extreme droughts and heavy rains becoming more frequent. This climatic variability, combined with increasing water consumption, puts CWPS in a vulnerable position, susceptible to periods of scarcity and instability in supply [1].

The operating rules of CWPS established by the current water resource management system do not consider the impacts of climate change. The hypothesis of this study was based on the idea that even with control over demands and land use in the watersheds, the current infrastructure and operating rules will not be able to ensure water security in the future, as these challenges require more complex management measures.

Computational simulations are hybrid scientific tools that allow both the reproduction of a phenomenon and intervention in its behavior. Evaluating the impact of climate change on the hydrological regime has been presented by researchers as useful techniques for addressing the problem [2,3]. Reliable information on potential changes to future hydrological conditions require knowledge of the influence of heterogeneity in soil-vegetation-atmospheric relationships [4], and basic data related to climate, topography, land cover and soil characteristics are necessary for the hydrological simulation of basins [5].

The main objective of this paper is to analyze the impact of climate change on the water security of CWPS. To achieve this goal, multidisciplinary approaches will be used, including analysis of historical climate data, hydrological modeling, and evaluation of existing water resource management systems.

2. Study Area

The study area is in Brazil and comprises a portion of the Paraíba do Sul River Basin, which flows into the Atlantic Ocean, and another portion of the Tietê River Basin, which is a tributary of the Paraná River, ultimately forming the River Plate Basin in the context of South America (Figure 1).

The study area shown in Figure 2 is a delineation of four hydrographic basins representing the CWPS: the Jaguari/Jacareí River, with its outlet at the Buenópolis fluviometric station, and the Atibaia River, with its outlet at the Valinhos Hydrometric Station, the both rivers are source of the Piracicaba River, the Juqueri River, the both a tributary of the Tietê River, with its outlet at the Paiva Castro Dam; and the Jaguari River, a tributary of the Paraíba do Sul River, with its outlet at the Jaguari Hydroelectric Plant.

The study area was further analyzed using the Digital Elevation Model (DEM) developed by [6], employing machine learning techniques to remove buildings and forests from the Copernicus DEM to produce a global elevation map with a grid spacing of 1 arc second (∼30 m). For the extraction and analysis of hydrographic information from the DEM, the TauDEM software was utilized (available at https://hydrology.usu.edu/taudem). This tool, employing flow direction methods, facilitated the delineation of contribution areas and determination of stream networks [7,8].

As described in Figure 3, the Jaguari/Jacareí basin, with its outlet being the reservoir of the same name (JAG), discharges into the downstream Buenópolis basin with its outlet at the control point of the same name (BUE). The Cachoeira and Atibainha basins, with outlets at their respective reservoirs (CAC and ATA, respectively), flow into the Atibaia basin with a control point of the same name (ATI). Subsequently, the waters proceed to the Valinhos control point (VAL), incorporating the contribution area of the same name.

As shown in Figure 2 and Figure 3, the reservoirs are interconnected by tunnels and conduits, with the main demand points being the control points, the Santa Inês Pumping Station (SIPS), and the Hydroelectric Power Plant (HPP). Table 1 presents the drainage area of the incremental basins within the study area.

3. Materials and Methods

The study’s method began with information on climate change scenarios, simulated the behavior of the CWPS for each scenario, and generated results in terms of water security indicators. Figure 4 shows the flowchart of the method.

Since the goal is to intervene in the behavior of the CWPS to achieve acceptable water security indicators, the methodology checks the sensitivity of operational variables. The chapter is divided into the presentation of the CWPS study area, description of the models and databases used for calibration and simulations.

2.1. Data

The observed meteorological data were extracted from [5], who generated a dataset of daily gridded meteorological data with a spatial resolution of 0.1° for the period from 1961 to 2020 for the entire Brazil. The information includes minimum and maximum temperatures, precipitation, solar radiation, wind speed, relative humidity, and potential evapotranspiration. Observed data from 11,473 rain gauges and 1,252 meteorological stations were used.

Simulated meteorological data were extracted from [9], who provided a dataset based on a set of 19 CMIP6 climate models with bias correction for projections over Brazilian territory, based on the SSP2-4.5 and SSP5-8.5 scenarios. The Quantile Delta Mapping approach was used to correct biases in daily time series of precipitation, maximum and minimum temperature, solar radiation, wind speed, and relative humidity. The bias-corrected dataset is available for both historical (1980-2013) and future (2015-2100) simulations at a spatial resolution of 0.25°.

The calculation of potential evapotranspiration from the climate models was processed using the PyEt library [10] employing the Hargreaves methodology [11] presented in equation 1.

E P = \frac{k}{λ} R_{a} (\frac{T_{m a x} - T_{m i n}}{2} - 17,8) \sqrt{T_{m a x} - T_{m i n}}

(1)

where k is an empirical constant, with a adopted value of 0.0135, Ra is the extraterrestrial solar radiation in MJ.m⁻²d⁻¹, λ is the latent heat of evaporation in MJ.kg⁻¹, Tmax is the maximum air temperature in °C, Tmin is the minimum air temperature in °C. The values of Ra and λ are calculated using the latitude grid values.

Discharge data from the stream gauges were obtained from the hydrological database of São Paulo State, and information about the inflow discharge of the reservoirs was obtained from the reservoir monitoring system of Brazilian National Water Agency.

The data were collected, extracted for the area of interest, and stored in a dimensional database [12]. This facilitated data aggregation for generating information and statistics. The database was built on the PostgreSQL platform, organizing information by basin, daily time basis, parameter, model, and scenario.

2.3. Evaluate climate projection models

Multicriteria decision analysis was used to evaluate climate projection models with bias correction based on the proposal by [13]. The analysis is based on comparing the precipitation from the models with observed data in the study area. The applied criteria aim to assess the overall ability of models, both with and without bias correction, to replicate the main statistics of observed data relevant to hydrological studies. The indicators include the time series (a) daily, (b) monthly, (c) annual, and (d) hydrological year (from October to September). Include average seasonality (e) day of the year, and (f) month of the year. Wet extreme about (g) day of the year, and (h) month of the year. Dry extreme of (i) day of the year, and (j) month of the year.

The performance of the ten indicators was evaluated using the modified Kling-Gupta Efficiency KGE’ coefficient initially proposed by [14] as an improvement over the Nash-Sutcliffe coefficient, and later modified by [15]. The coefficient was applied to evaluate projected precipitation in Brazil, showing satisfactory results [16]. Equation 2 shows KGE’.

K G E^{'} = 1 - \sqrt{{(r - 1)}^{2} + {(\frac{μ_{s i m}}{μ_{o b s}} - 1)}^{2} + {(\frac{σ_{s i m} . μ_{o b s}}{σ_{o b s} . μ_{s i m}} - 1)}^{2}}

(2)

Where: r (dimensionless) is the correlation coefficient, μ (mm) is the mean precipitation, σ (mm) is the standard deviation of the precipitation series, and the indices obs and sim indicate the observed and simulated series, respectively. The KGE’ varies from -∞ to 1, with 1 indicating the best fit. The KGE’ values corresponding to the selected criteria were scored according to the categories presented in Table 1 [17].

The sum of the scores for each indicator was used for ranking climate models, from highest to lowest. The maximum value is 20, where all 10 indicators are classified as high, and the minimum value is zero, where all indicators are low.

2.4. Hydrological model

The hydrological model used in this paper is based [18], a conceptual models based on some physical reasoning that represent catchment processes by several interconnected buckets, which mimic water storage and transfer within a homogeneous area. This model has been successfully applied in Brazil [19]. This deterministic model operates continuously over time and considers a daily time step. It employs a lumped approach at the watershed scale and adopts a conceptual framework incorporates linear transfer functions, considering the direct runoff, soil moisture depletion, unsaturated zone dynamics, groundwater recharge, and three linear reservoirs representing surface, soil, and aquifer retention characteristics (Figure 5).

As shown in Figure 5, a fraction of the precipitation (P in mm) is conveyed as direct runoff (DR in mm) using equation 3. This DR is routed through a linear reservoir reaching the basin outlet as routed direct runoff (RDR in mm) using equation 4.

D R = \frac{{(P - I A)}^{2}}{P - I A + S A T - R S O I L}

(3)

R D R = (1 - K D R) \times R S U R F

(4)

Where IA is initial abstraction (mm), SAT is the soil saturation capacity (mm), RSOIL is the level of the soil reservoir (mm), RSURF is the level of the surface reservoir (mm), and KDR is the direct runoff recession constant (d⁻¹).

The remaining water depth (P − DR) is subject to depletion at the potential evapotranspiration rate (PE in mm). The excess water (P – DR − PE) infiltrates into a linear reservoir that represents the upper soil horizon (unsaturated zone). Moisture is lost from this zone at an evapotranspiration rate (ER in mm) proportional to the moisture content (MC in %, shown in equation 5) and PE. The output from the unsaturated zone reservoir corresponds to the recharge (REC in mm) of the groundwater reservoir. If RSOIL exceeds the field capacity (FC in mm), REC occurs following the equation 6.

M C = \frac{R S O I L}{S A T}

(5)

R E C = (R S O I L - F C) \times M C \times C R E C

(6)

Where CREC (%) is recharge coefficient, a parameter related to the movement of water in the unsaturated soil zone, the water transferred to the groundwater reservoir regulated by this parameter. The output of the groundwater reservoir is the base flow component (BF in mm) shown in equation 7.

B F = (1 - K B F) \times R G R

(7)

Where RGR is the level of the groundwater reservoir (mm), and KBF is the base flow recession constant (d⁻¹). Runoff (RO, in m³s⁻¹) is obtained by equation 8.

R O = (R D R + B F) \times A \times 86.4

(8)

Where A is the drainage area in km². Following the above procedure, the levels in each reservoir are continuously updated for each simulation day. This calculation applies to the headwater basins. To calculate the discharge for the downstream basins, an additional method is employed to routed upstream discharge (RUD in m³s⁻¹), calculated by the routing model (McCarthy, 1938) describes in the equation 9.

{R U D}_{i} = \frac{(1 - 2 K X) {U D}_{i} + (1 + 2 K X) {U D}_{i - 1} + (2 K (1 - X) - 1) {R U D}_{i - 1}}{2 K (1 - X) + 1}

(9)

Where the RUD is routed upstream discharge (m³s⁻¹), K is the parameter to represent the time release is delayed (d) and X is the parameter referring to the reduction of the release peak in the stream. Index i is about the value on a time interval and i-1 is a previous interval value. The downstream discharge (UD in m³s⁻¹) is the sum of RO and RUD. To ensure calculation stability the channel is divided into sections to K fits within the limits shown in equation 10.

\frac{1}{2 (1 - X)} < K < \frac{1}{2 X}

(10)

The hydrological model calibration was performed using data from October 2011 to September 2019 (8 hydrological years) for the sub-basins. The choice of this period aims to cross-reference the available observed daily flow data with rainfall and evapotranspiration data in the watersheds. Unlike the traditional approach, no specific period was selected for model validation, as suggested by [20], who evaluated the performance of two conceptual hydrological models in 463 watersheds using 50 different data splitting schemes. They demonstrated that it is more robust to use the complete available dataset for calibration and skip model validation.

The parameters were optimized using the minimize function from the scipy.optimize library [21], which provides a unified interface for finding local minima of non-linear optimization problems. Within a trust region, a local model of the objective function is built based on first and second derivative information. It approximates the best point until reaching a local minimum of the original objective function. The parameters varied SAT [100, 2000], FC [30, 50], IA [2.5, 5], CREC [0, 20], KDR [0.2, 5], KBF [30, 180], K [1, 10] and X [0.25, 0.35].

The objective function was based on KGE on basins headwater basins, for better representing the volume flowing into reservoirs and downstream basins are performed Log-NSE, for better representing the limit flows at control points. The indicators NSE, R2 and PBIAS were also analyzed.

3. Results

The simulation data from the climate models were extracted and analyzed. Figure 6 shows the comparison of the accumulated rainfall for the hydrological year across different climate models, with a focus on the observed data.

The multi-criteria analysis was applied to the 38 datasets on climate models (19 bias correction and 19 row data). Table 3 shows the ranking. The model that best represents the CWPS region is GFDL-CM4 [22,23].

Given the comparison with the past, the time series composition of rainfall in the study area ranged from January 1961 to July 2020 with observed data. Starting from August 2020 until December 2100, two scenarios, SSP2-4.5 and SSP5-8.5, from the GFDL-CM4 model will be performed. Figure 7 displays the precipitation timeseries to hydrological year. The trend is towards an increase in the frequency of dry hydrological years, with two extremely dry years observed in 1968/69 (984.6 mm) and 2013/14 (1009.8 mm) within a span of 58 years. This trend progresses to five such events in an 81-year period projected in the SSP 245 scenario, occurring in 2040/41, 2048/49, 2057/58, 2071/72, and 2073/74. In the SSP 585 scenario, there are nine such events in an 81-year period, happening in 2036/37, 2045/46, 2059/60, 2079/80, 2081/82, the biennium 2084/85/86, 2089/90, and 2099/100.

Figure 8 (a) shows a trend towards a reduction in the average monthly accumulated precipitation in the projected scenarios for the last four months of the dry season, with a more pronounced change for September. The observed data indicate an average of 75.6 mm, compared to 41.3 mm in the SSP2-4.5 scenario and 33.2 mm in the SSP5-8.5 scenario. Figure 8 (b) shows a small variation in the wet semester, but a trend of less rainfall in the dry period, with an average of 350.4 mm accumulated between the months of April to September in the observed period, compared to 269.2 mm and 268 mm accumulated in the dry semester for the projected scenarios, SSP2-4.5 and SPP5-8.5, respectively. In other words, a reduction of approximately 23% in rainfall during the dry period.

The Standardized Precipitation Index (SPI) of the 6-month moving average precipitation and its respective Drought Magnitude (DM) are presented in Figure 9 calculated according to [24]. The trend of increased drought frequency is observed both in terms of intensity and the number of months classified as dry, as well as in the magnitude of the drought. Figure 10 presents the drought monitor (DM) exceedance curve for both observed data and simulated scenarios. Dry events in the study area will tend to have a higher frequency, increasing from about 30% in the analysis of observed data to 40% and 50% in the scenarios SSP2-4.5 and SSP5-8.5. In addition, the magnitude of drought, already challenging in the current CWPS configuration, was at 29.01 in the month of April 2015, and it could reach around 40 in both scenarios.

The Table 4 shows the performance indicators for each objective function used in the calibration of the hydrological model for the CWPS basins. The best results were obtained for indicators that use their own equations as objective functions to calibrate the model parameters. However, the highest values are obtained for the KGE objective function followed by Log-NSE in all basins. The correlation coefficients (R2) between observed and calculated series were higher for Log-NSE. The smallest deviations (PBIAS) occurred for the KGE objective function, with the exception of ATI and ATA basins.

Log-NSE objective functions allowed a better adjustment of minimum flows in basins without regularization of reservoirs (VAL, BUE and ATI). In these basins, flows with a probability of non-exceedance greater than the median are closer to observed flows, as shown in Figure 11.

The flows estimated by the hydrological model based on precipitation projections of the GFDL-CM4 model for the two climate scenarios (SSP2-4.5 and SSP5-8.5) are shown in Table 5. The larger angular coefficients of the regression equations of the SSP2-4.5 scenario indicate a greater ability to respond to precipitation. Higher intercept values indicate a greater contribution of the base flow and greater water availability in this scenario. The regression coefficients of the estimates were greater than 0.5 for six basins, indicating a strong correlation between variables. The estimated flows for the SSP5-8.5 scenario were lower for the 25%, 50% and 75% quartiers in all basins except the 75% quartile in the PAI basin, where there was no change. This indicates lower water availability in the SSP5-8.5 scenario, reflecting an average reduction of 16.9%, 11.8%, and 9.2% in flows corresponding to quartiers Q25, Q50, and Q75. The largest impact on minimum flows (Q25) was recorded in the VAL basin, with a reduction of 19.6%. The CAC and PAI basins showed a higher reduction in the median flow (13.4%), and the BUE basin showed the largest reduction in Q75 (12.5%).

The Table 6 shows the Frequency of non-exceedance of the ratio between precipitation and flow (P/Q) of the average of seven consecutive days. The relationship represents the degree to which precipitation deficits influence flow over the continuous seven-day period. Very low ratio values (P/Q = 0.2) tend to occur on average during 12% and 11.6% of the simulation period (2022-2100) in the scenarios SSP2-4.5 and SSP5-8.5. In this case, VAL and JPS basins showed greater sensitivity to P deficits in the SSP2-4.5 scenario, as well as JPS, CAC, PAI, and ATA basins in the SSP5-8.5. Less pronounced deficits (P/Q = 0.5) are more frequent, occurring on average 20.9% (SSP2-4.5) and 21.3% (SSP5-8.5). The JPS, CAC, PAI, and ATA basins have greater sensitivity to this level of deficit in both scenarios.

4. Discussion

Daily flow is greatly influenced by variations in soil moisture, infiltration and precipitation. The physical water characteristics of the soil influence infiltration, water storage, and aquifer recharge. These variables were adjusted in the calibration of the hydrological model by parameters such as the direct flow recession constant (KDR), the base flow recession constant (KBF), and the recharge coefficient (CREC). The intra-annual distribution of precipitation is an important condition for the performance of the hydrological model.

We selected ten indicators for a representative climate model, four for the accumulated rainfall of the time series (day, month, year, hydrological year), two for the daily and monthly seasonality, and four for the daily and monthly extremes in wet and dry periods. Of the 19 models surveyed, the GFDL-CM4 presented the best performance for the study area in terms of the modified Kling-Gupta efficiency coefficient (KGE’). According to [23], the model appears to produce a reasonable multidecadal modulation of the El Niño-Southern Oscillation due to a slight weakening of the annual cycle, relatively small biases in seasonal spatial patterns of top-of-atmosphere fluxes, surface temperature, and precipitation.

GFDL-CM4 without bias correction represents better the time series of annual and hydrological years as well as the maximum monthly precipitation than the other models. In the CWPS basins, the model represents precipitation well during the wet period (October to March) and tends to underestimate it by 23.3% during the dry period (April to September). SPI and DM indicate a higher projected drought frequency, especially for the scenario SSP5-8.5. These results are consistent with the study by [25], which identified the GFDL model for the Piracicaba River basin using the tool developed by [26].

Performance indicators indicated a satisfactory adjustment of the hydrological model calibrated to the time series observed with the objective functions KGE and log-NSE. The projected flows in the basins without a reservoir were estimated using parameters calibrated with an objective function Log-NSE, which best adjusted the minimum flows. The basins with reservoirs were simulated with parameters calibrated with KGE.

The simulated flows were strongly correlated with forecast precipitation for both climate scenarios. The SSP5-8.5 scenario indicates the lowest water availability in all basins, and VAL is the one that shows the greatest reduction in minimum flows. Considering the frequency of the average of seven consecutive days of the P/Q ratio, JPS, CAC, PAI and ATA basins show faster reactions in flows to the P deficit in both climate scenarios. For a more pronounced deficit (P/Q = 0.2), the VAL basin showed greater sensitivity in the SSP2-4.5 scenario. According to [27], basins with low P/Q values are subject to longer streamflow droughts, possibly due to lower subsurface storage.

In systems with high water demand such as the CWPS, a deficit of seven consecutive days is enough to cause operational disruptions and ultimately supply conflicts. The expected moderate (P/Q = 0.5) and severe (P/Q = 0.2) deficits are high.

5. Conclusions

It is expected that the results of this study will provide a comprehensive and well-founded understanding of the challenges faced by CWPS in the context of climate change, as well as suggest strategies and adaptive measures to ensure water security for MRSP. Understanding these impacts and identifying sustainable solutions are of utmost importance to guide decision-making and formulate public policies aimed at efficient water resource management and adaptation to climate change.

Author Contributions

Conceptualization, J.R.B.T. and A.V.M.J.; methodology, J.R.B.T. and A.V.M.J.; software, J.R.B.T.; validation, J.R.B.T. and A.V.M.J.; formal analysis, J.R.B.T. and A.V.M.J.; investigation, J.R.B.T. and A.V.M.J.; resources, J.R.B.T. and A.V.M.J.; data curation, J.R.B.T.; writing—original draft preparation, J.R.B.T. and A.V.M.J.; writing—review and editing, J.R.B.T. and A.V.M.J.; visualization, J.R.B.T. and A.V.M.J.; supervision, A.V.M.J.; funding acquisition, A.V.M.J. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data supporting this study are openly available in Hydroshare at https://www.hydroshare.org/resource/c816015d97e74be5adb984ce65f6d8e4/ (create date 25 October 2023).

Acknowledgments

In this section, you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

Conflicts of Interest

The authors declare no conflict of interest.

References

Braga, B.; Kelman, J. Facing the Challenge of Extreme Climate: The Case of Metropolitan Sao Paulo. Int J Water Resour Dev 2020, 36, 278–291. [Google Scholar] [CrossRef]
Kour, R.; Patel, N.; Krishna, A.P. Climate and Hydrological Models to Assess the Impact of Climate Change on Hydrological Regime: A Review. Arabian Journal of Geosciences 2016, 9, 544. [Google Scholar] [CrossRef]
Hakala, K.; Addor, N.; Teutschbein, C.; Vis, M.; Dakhlaoui, H.; Seibert, J. Hydrological Modeling of Climate Change Impacts. In Encyclopedia of Water; Wiley, 2019; pp. 1–20. [Google Scholar] [CrossRef]
Méllo Júnior, A.V.; Olivos, L.M.O.; Billerbeck, C.; Marcellini, S.S.; Vichete, W.D.; Pasetti, D.M.; da Silva, L.M.; Soares, G.A.S.; Tercini, J.R.B. Rainfall Runoff Balance Enhanced Model Applied to Tropical Hydrology. Water (Switzerland) 2022, 14. [Google Scholar] [CrossRef]
Xavier, A.C.; Scanlon, B.R.; King, C.W.; Alves, A.I. New Improved Brazilian Daily Weather Gridded Data (1961–2020). International Journal of Climatology 2022, 42, 8390–8404. [Google Scholar] [CrossRef]
Hawker, L.; Uhe, P.; Paulo, L.; Sosa, J.; Savage, J.; Sampson, C.; Neal, J. A 30 m Global Map of Elevation with Forests and Buildings Removed. Environmental Research Letters 2022, 17, 024016. [Google Scholar] [CrossRef]
Tesfa, T.K.; Tarboton, D.G.; Watson, D.W.; Schreuders, K.A.T.; Baker, M.E.; Wallace, R.M. Extraction of Hydrological Proximity Measures from DEMs Using Parallel Processing. Environmental Modelling & Software 2011, 26, 1696–1709. [Google Scholar] [CrossRef]
Yildirim, A.A.; Watson, D.; Tarboton, D.; Wallace, R.M. A Virtual Tile Approach to Raster-Based Calculations of Large Digital Elevation Models in a Shared-Memory System. Comput Geosci 2015, 82, 78–88. [Google Scholar] [CrossRef]
Ballarin, A.S.; Sone, J.S.; Gesualdo, G.C.; Schwamback, D.; Reis, A.; Almagro, A.; Wendland, E.C. CLIMBra—Climate Change Dataset for Brazil. Sci Data 2023, 10, 47. [Google Scholar] [CrossRef]
Vremec, M.; Collenteur, R. PyEt - a Python Package to Estimate Potential and Reference Evapotranspiration. EGU21 2021. [Google Scholar] [CrossRef]
Jensen, M.E.; Allen, R.G. Evaporation, Evapotranspiration, and Irrigation Water Requirements. Evaporation, Evapotranspiration, and Irrigation Water Requirements 2016, 1–744. [Google Scholar] [CrossRef]
Tercini, J.R.B.; Junior, A.V.M. Dimensional Database to Support Water Resources Decisions. Brazilian Journal of Development 2022, 8, 77190–77202. [Google Scholar] [CrossRef]
Billerbeck, C.; Silva, L.M.d.; Marcellini, S.S.; Méllo Junior, A. Multi-Criteria Decision Framework to Evaluate Bias Corrected Climate Change Projections in the Piracicaba River Basin. Revista Brasileira de Meteorologia 2021, 36, 339–349. [Google Scholar] [CrossRef]
Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. J Hydrol (Amst) 2009, 377, 80–91. [Google Scholar] [CrossRef]
Kling, H.; Fuchs, M.; Paulin, M. Runoff Conditions in the Upper Danube Basin under an Ensemble of Climate Change Scenarios. J Hydrol (Amst) 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
Bozzini, P.L.; Méllo Júnior, A.V. Atmospheric Model Precipitation Forecast Analysis to Support Reservoir Systems Operation. Revista Brasileira de Meteorologia 2020, 35. [Google Scholar] [CrossRef]
Irving, K.; Kuemmerlen, M.; Kiesel, J.; Kakouei, K.; Domisch, S.; Jähnig, S.C. A High-Resolution Streamflow and Hydrological Metrics Dataset for Ecological Modeling Using a Regression Model. Sci Data 2018, 5, 180224. [Google Scholar] [CrossRef] [PubMed]
Lopes, J.E.G.; Braga, B.P.F.; Conejo, J.G.L. SMAP - A Simplified Hydrological Model, Applied Modelling in Catchment Hydrology, Ed. VP Singh. In; Water Resources Publications, 1982. 1982. [Google Scholar]
Raulino, J.B.S.; Silveira, C.S.; Lima Neto, I.E. Assessment of Climate Change Impacts on Hydrology and Water Quality of Large Semi-Arid Reservoirs in Brazil. Hydrological Sciences Journal 2021, 66, 1321–1336. [Google Scholar] [CrossRef]
Shen, H.; Tolson, B.A.; Mai, J. Time to Update the Split-Sample Approach in Hydrological Model Calibration. Water Resour Res 2022, 58. [Google Scholar] [CrossRef]
Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
Adcroft, A.; Anderson, W.; Balaji, V.; Blanton, C.; Bushuk, M.; Dufour, C.O.; Dunne, J.P.; Griffies, S.M.; Hallberg, R.; Harrison, M.J.; et al. The GFDL Global Ocean and Sea Ice Model OM4.0: Model Description and Simulation Features. J Adv Model Earth Syst 2019, 11, 3167–3211. [Google Scholar] [CrossRef]
Held, I.M.; Guo, H.; Adcroft, A.; Dunne, J.P.; Horowitz, L.W.; Krasting, J.; Shevliakova, E.; Winton, M.; Zhao, M.; Bushuk, M.; et al. Structure and Performance of GFDL’s CM4.0 Climate Model. J Adv Model Earth Syst 2019, 11, 3691–3727. [Google Scholar] [CrossRef]
de Faro, G.T.C.; Garcia, J.I.B.; Oliveira, C.d.P.M.; Ramos, M.R.S. Application of Indices for Water Resource Systems Stress Assessment. Revista Brasileira de Recursos Hidricos 2019, 24. [Google Scholar] [CrossRef]
Castro, E.L.H. Avaliação Dos Impactos Das Mudanças Climáticas e Das Mudanças No Uso Da Terra Na Bacia Do Rio Piracicaba. Utilizando Modelagem Hidrológica, Universidade de São Paulo: São Carlos, 2022. [Google Scholar]
Parding, K.M.; Dobler, A.; McSweeney, C.F.; Landgren, O.A.; Benestad, R.; Erlandsen, H.B.; Mezghani, A.; Gregow, H.; Räty, O.; Viktor, E.; et al. GCMeval – An Interactive Tool for Evaluation and Selection of Climate Model Ensembles. Clim Serv 2020, 18, 100167. [Google Scholar] [CrossRef]
Odongo, R.A.; De Moel, H.; Van Loon, A.F. Propagation from Meteorological to Hydrological Drought in the Horn of Africa Using Both Standardized and Threshold-Based Indices. Natural Hazards and Earth System Sciences 2023, 23, 2365–2386. [Google Scholar] [CrossRef]

Figure 1. Location of the study area.

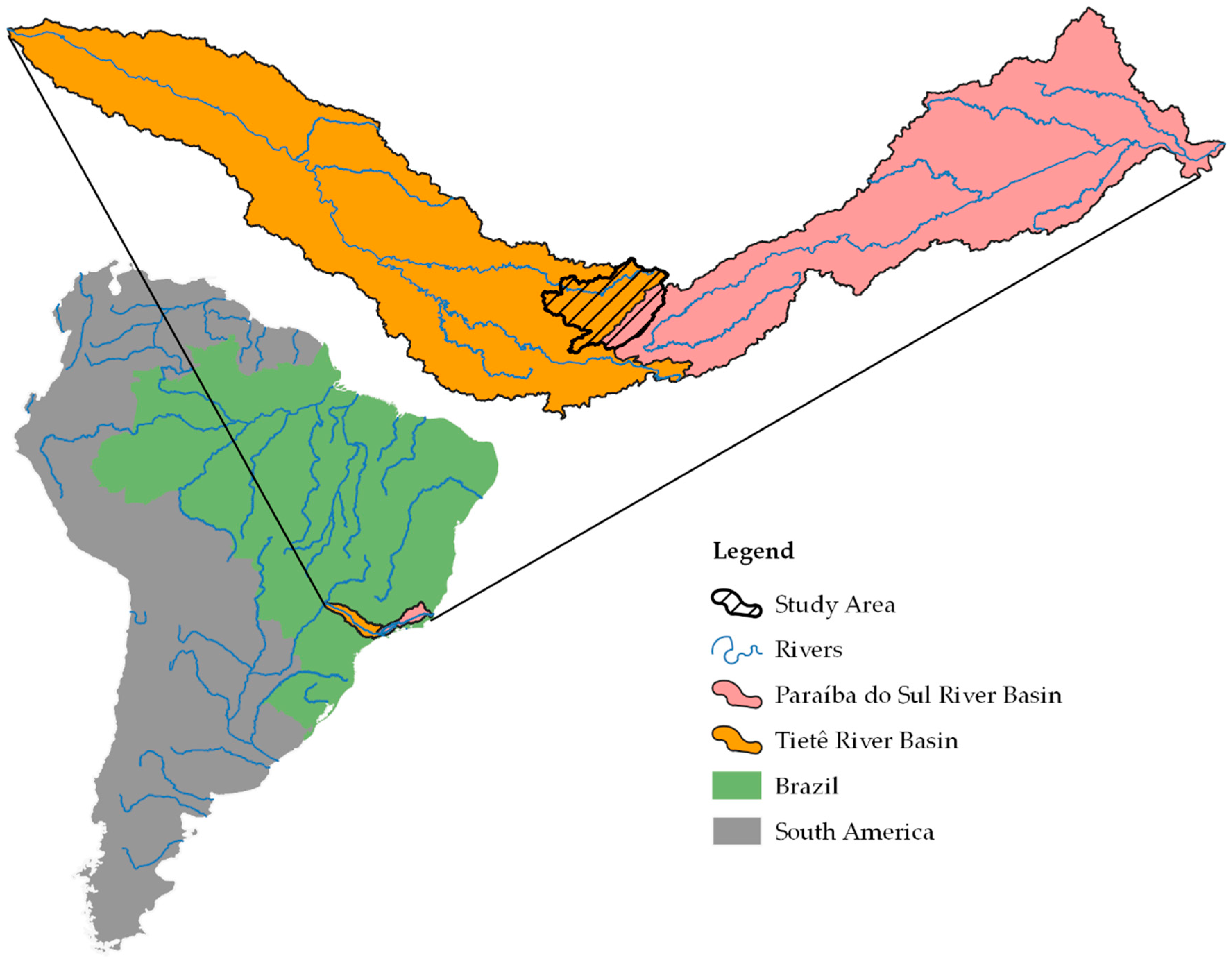
Figure 2. Map of the study area.

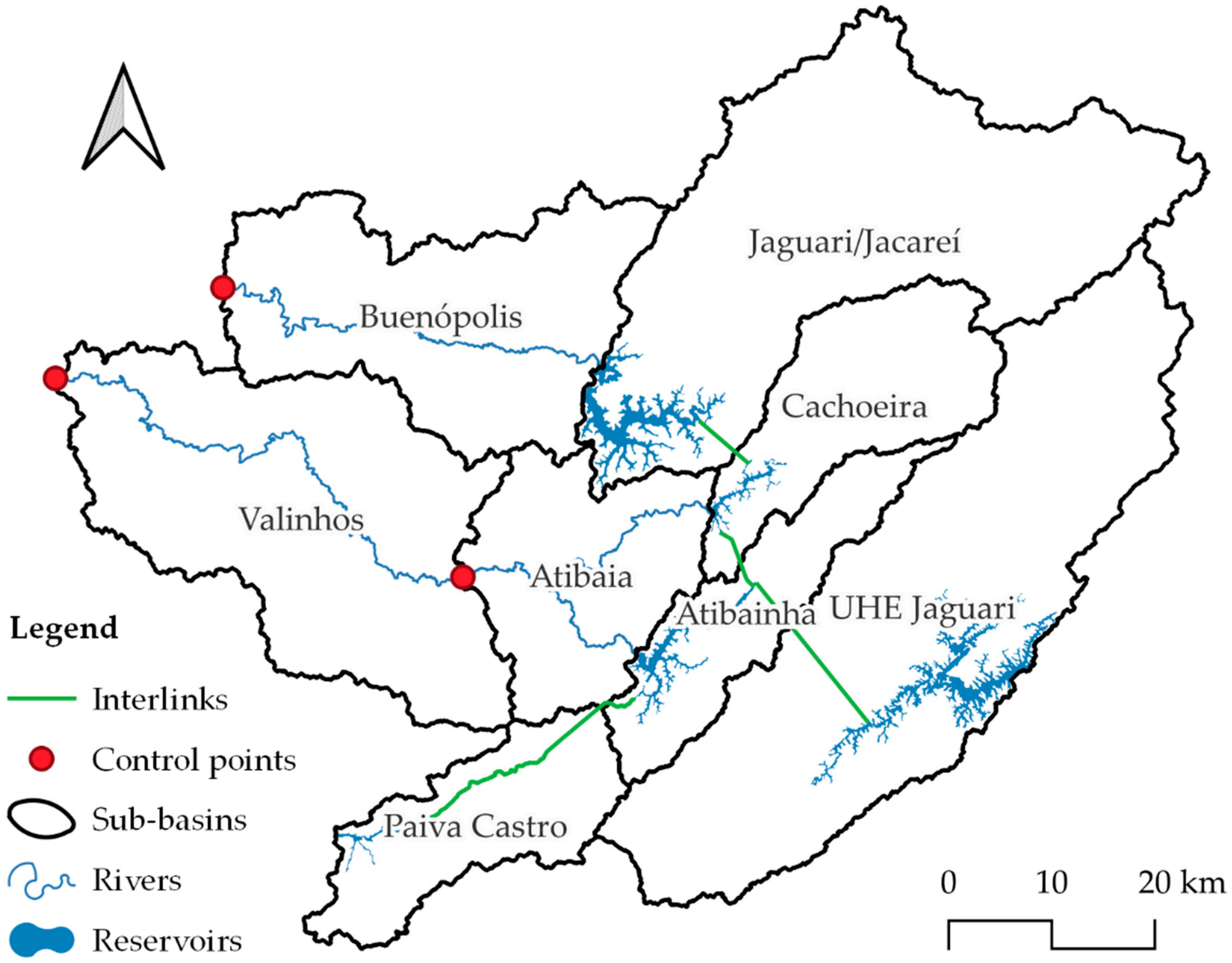
Figure 3. Schematic model of the study area.

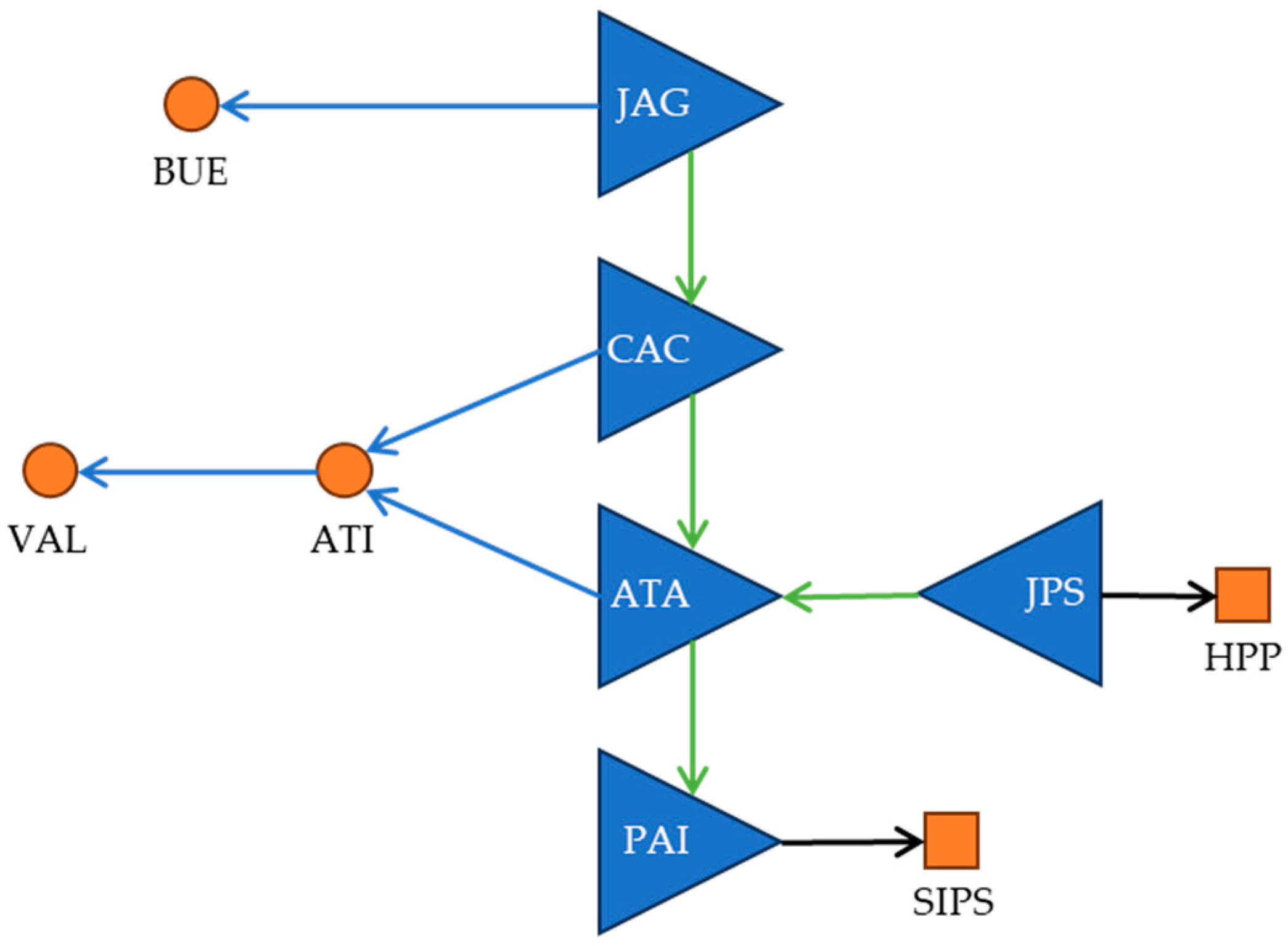
Figure 4. Flowchart of the method modelling process.

Figure 5. Hydrological model scheme.

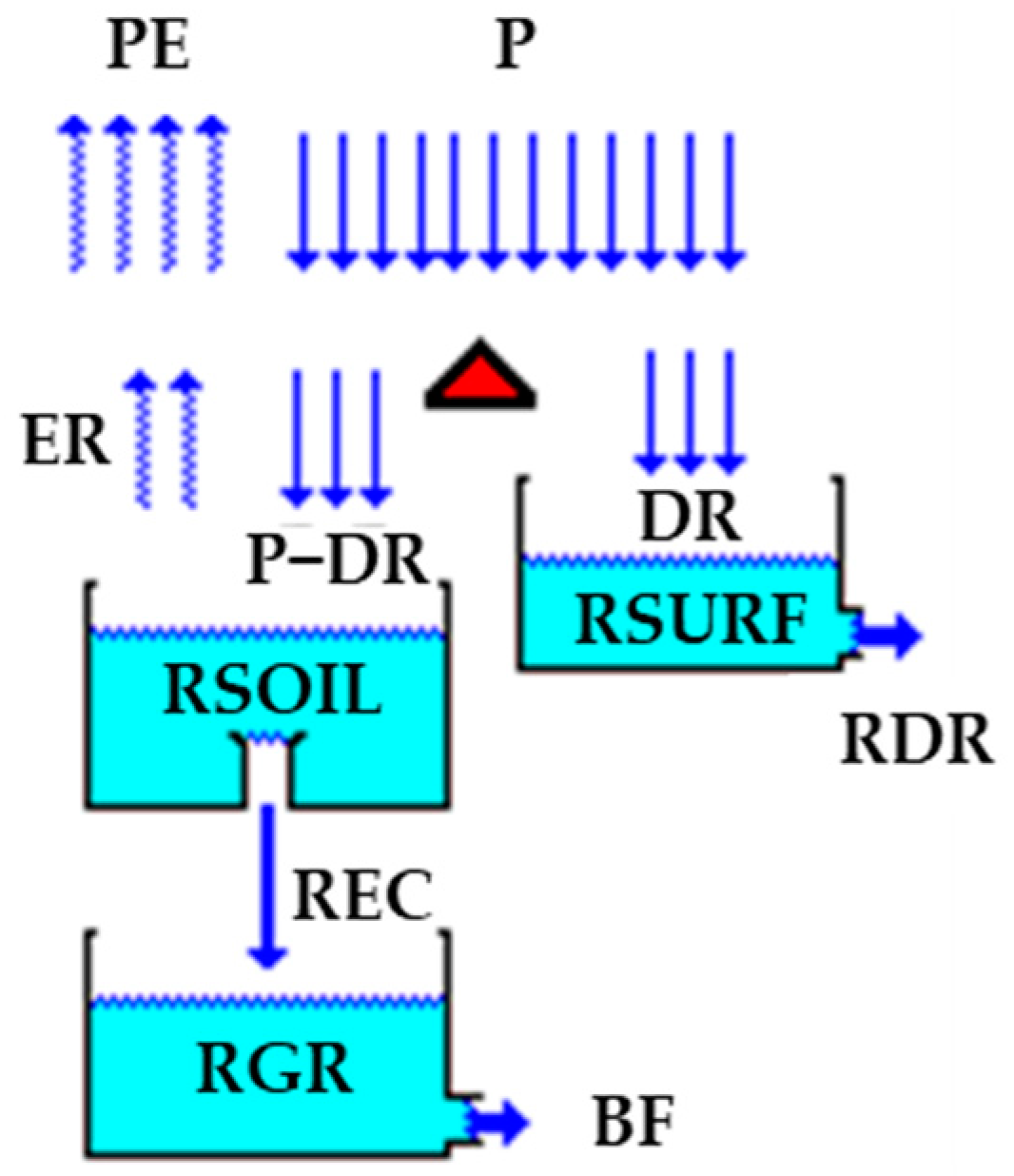
Figure 6. Timeseries of accumulated precipitation for the hydrological year from the climate models and observed data.

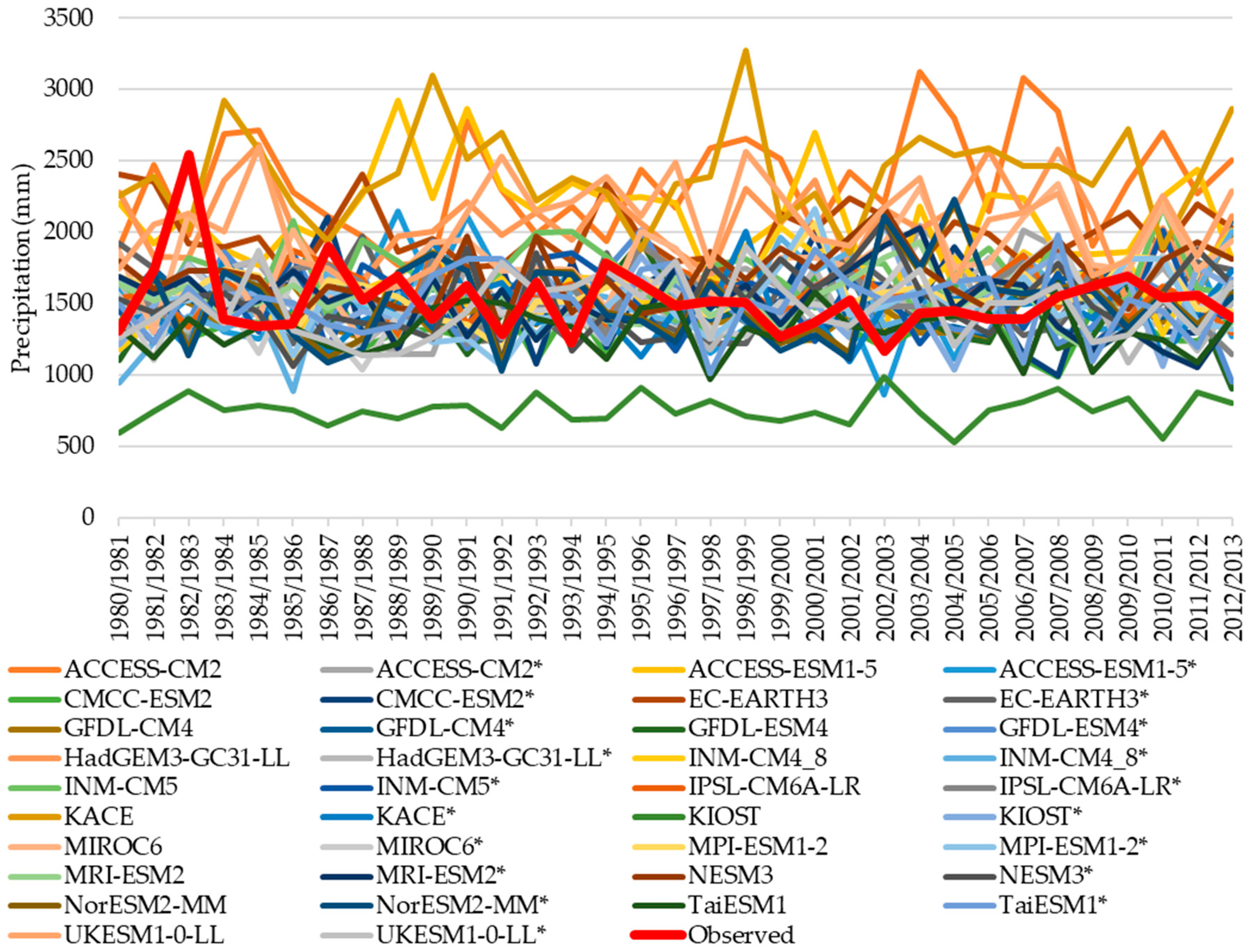
Figure 7. Timeseries of accumulated precipitation for the hydrological year from observed data and two scenarios, SSP2-4.5 and SSP5-8.5.

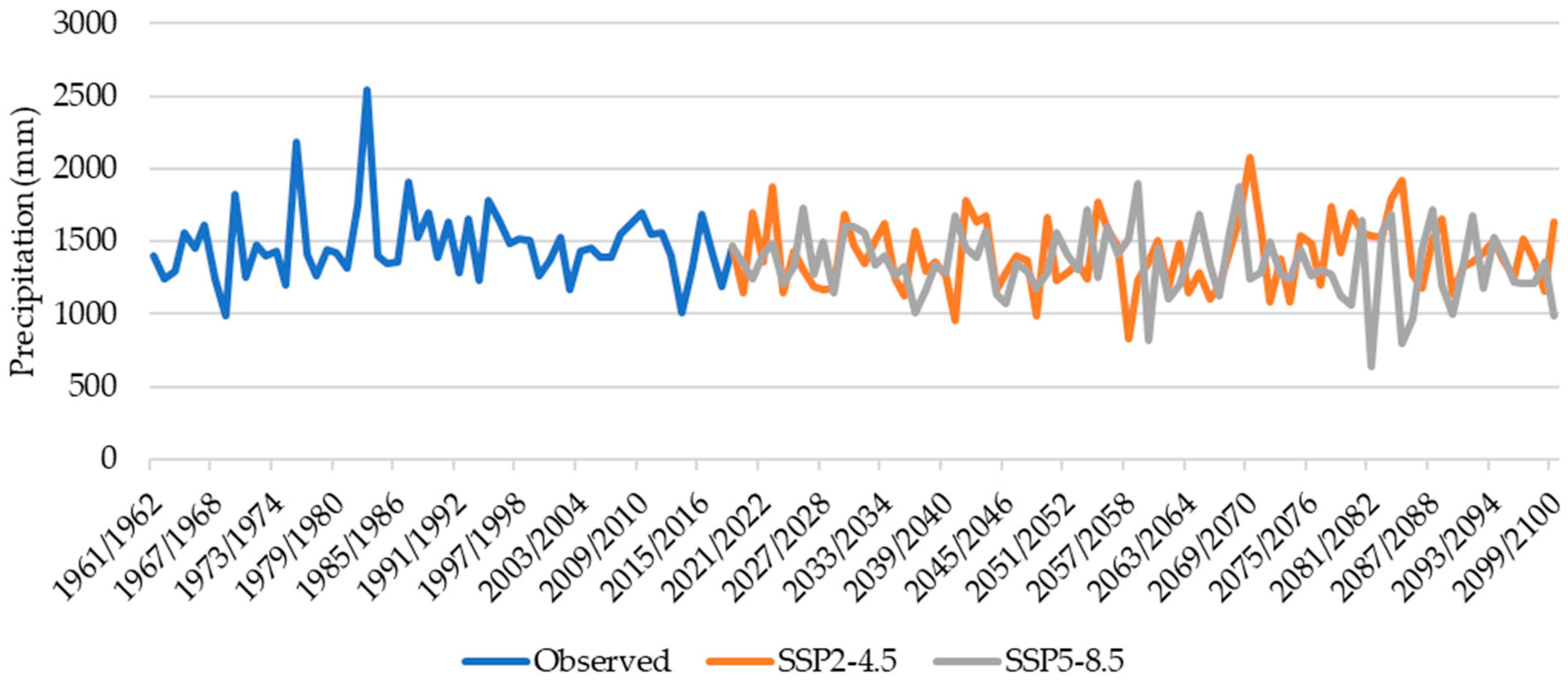
Figure 8. Seasonal trends for (a) average precipitation accumulated for the month of the year, and (b) average precipitation accumulated for the hydrologic semester from observed data and two scenarios, SSP2-4.5 and SSP5-8.5.

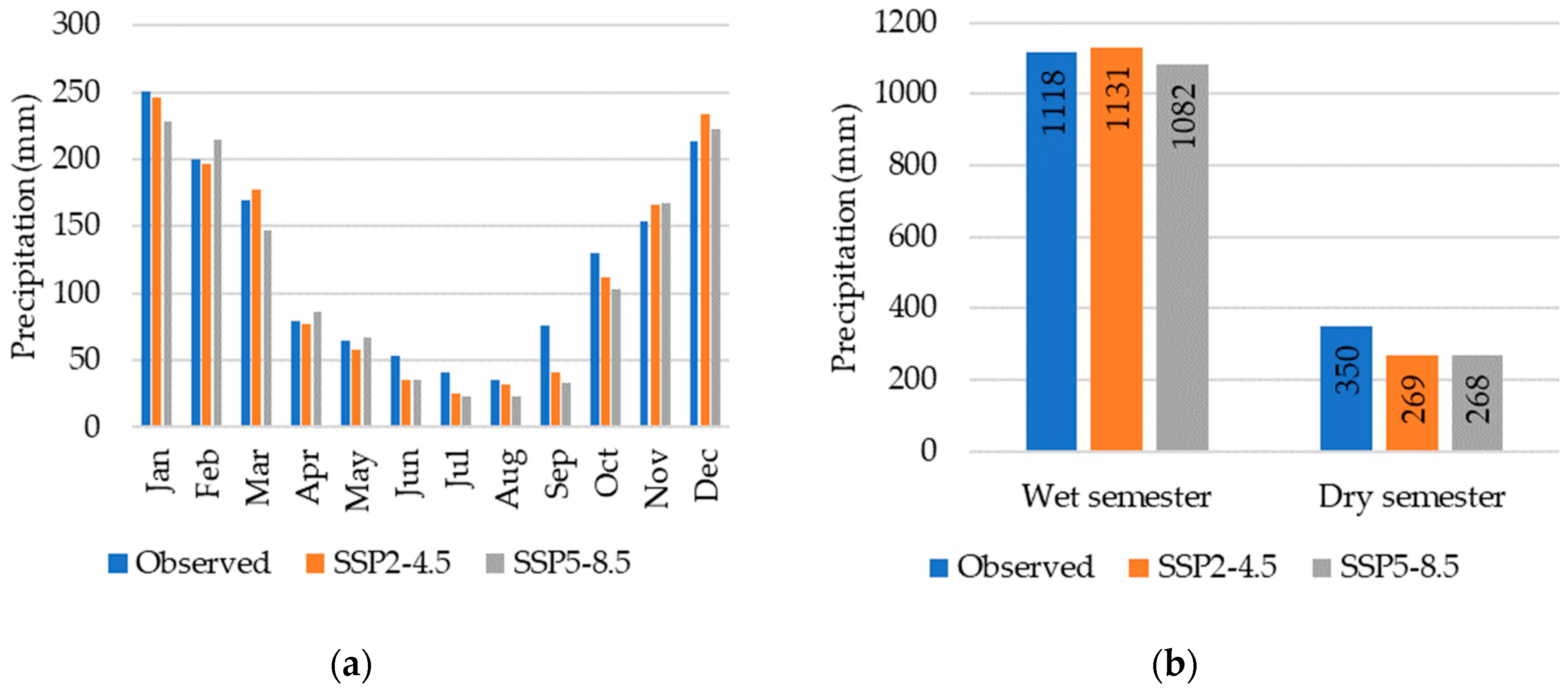
Figure 9. Average moving of the Standardized Precipitation Index (SPI) and Drought Magnitude (DM) of the observed and projected time series.

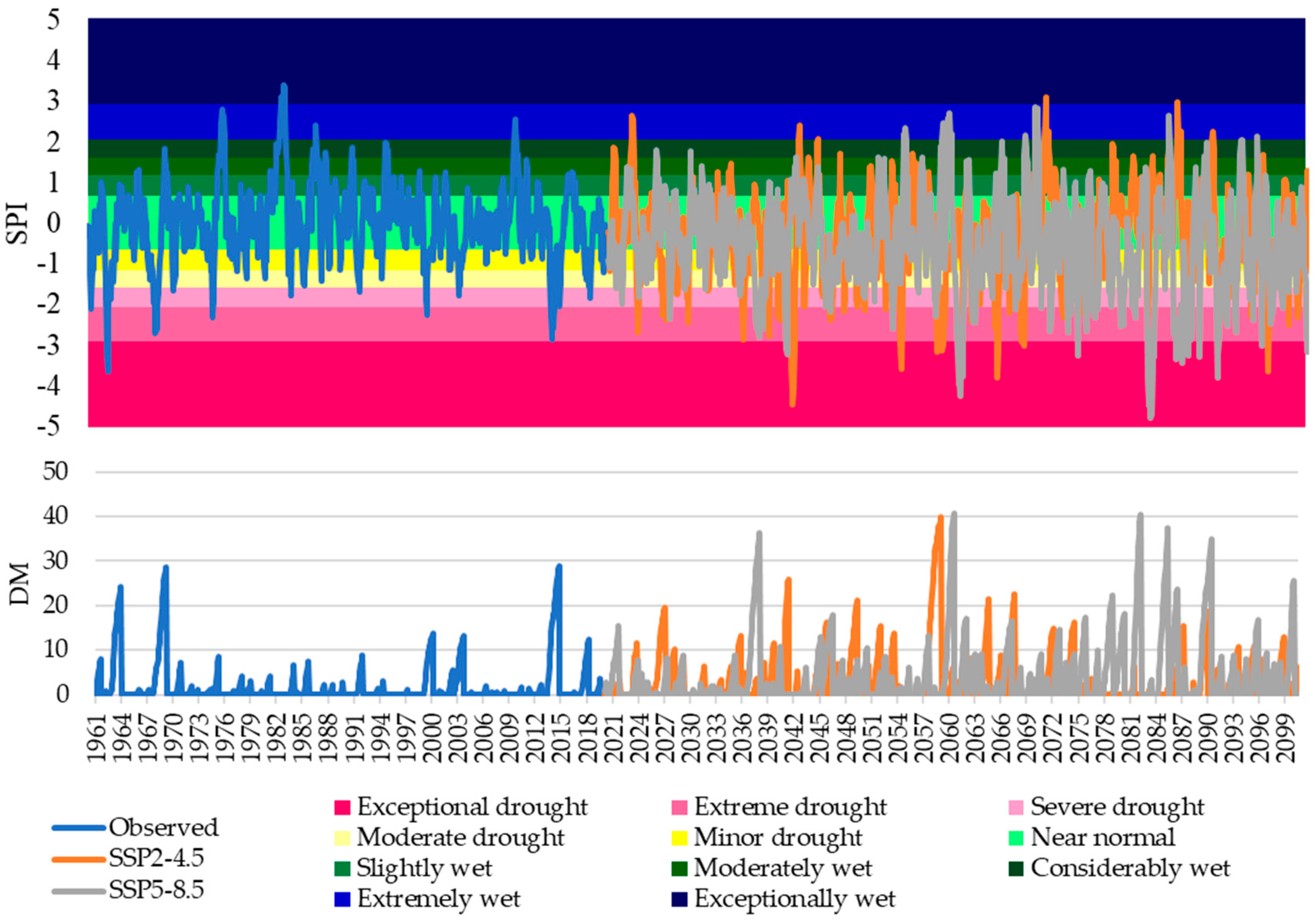
Figure 10. Drought Magnitude (DM) exceedance curves for observed and projected time series.

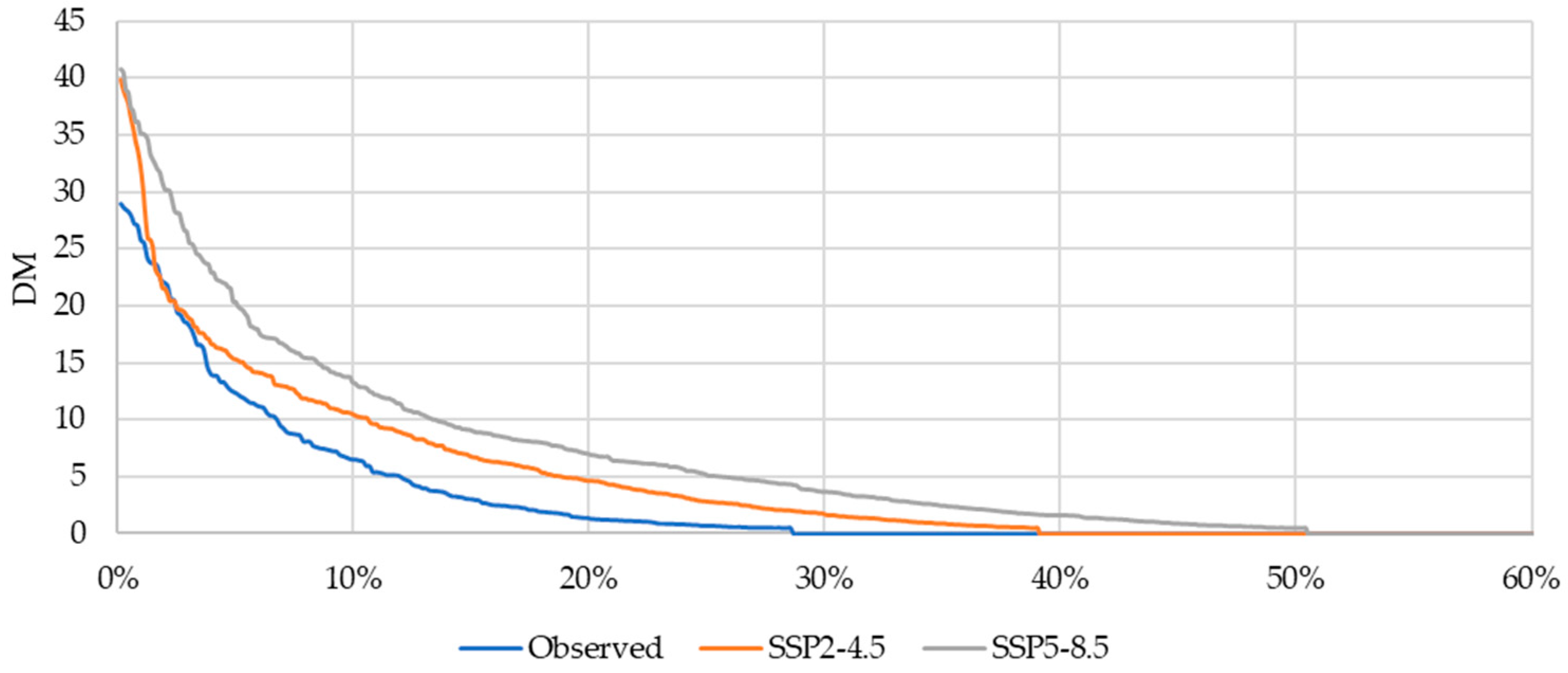
Figure 11. Frequency curves with a probability of greater than 50% of the observed and estimated flows in the calibration of basins: (a) BUE, (b) ATI and (c) VAL.

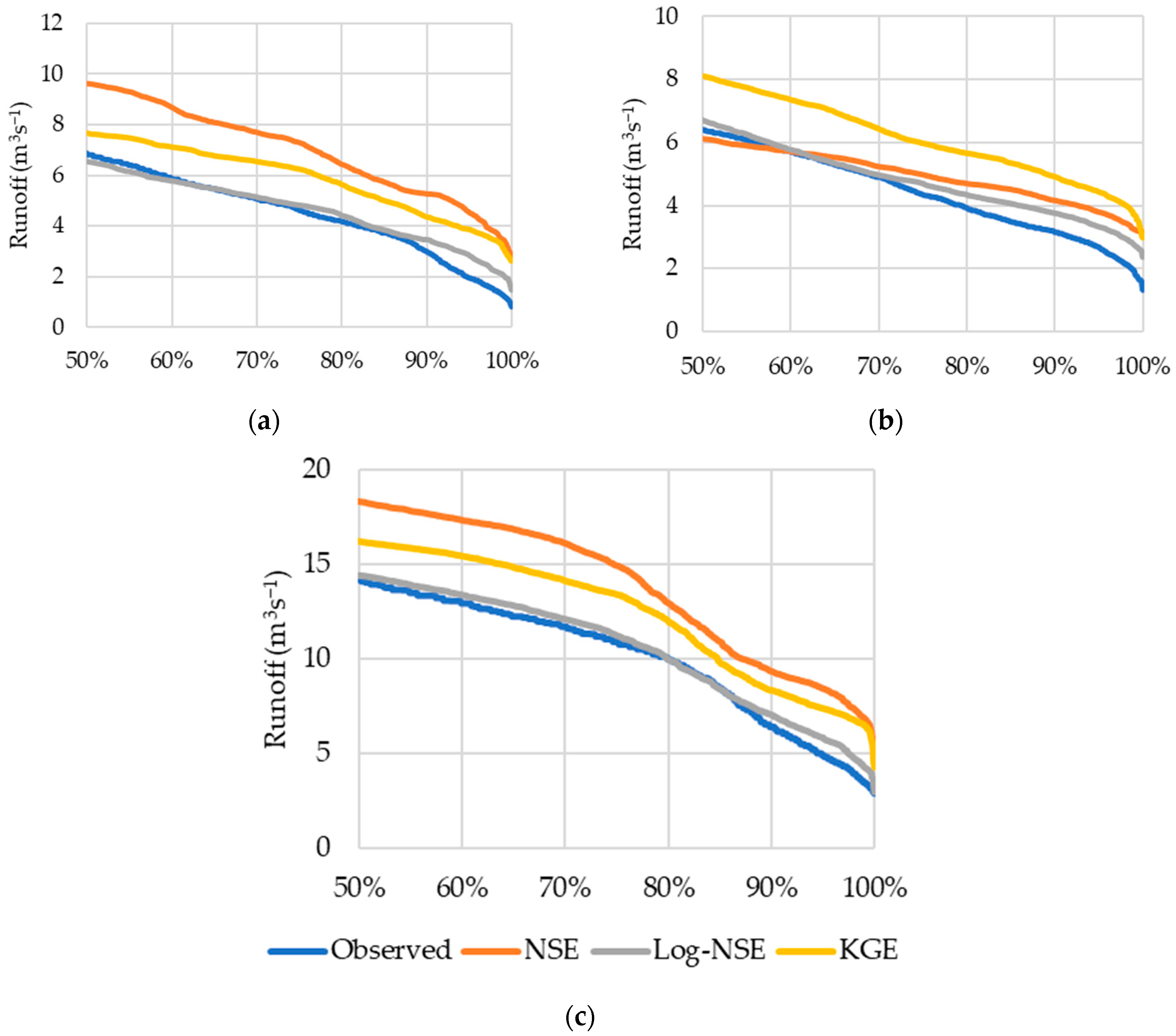
Table 1. Basin drainage area.

Basin	Abbr.	Drainage area (km²)
UHE Jaguari	JPS	1309.2
Jaguari/Jacareí	JAG	1240.6
Valinhos	VAL	982.3
Buenópolis	BUE	713.9
Atibaia	ATI	437.0
Cachoeira	CAC	392.1
Paiva Castro	PAI	337.1
Atibainha	ATA	314.3

Table 1. Score to evaluate climate projection models.

Category	Condition	Score
Low	KGE’ ≤ 0	0
Medium	0 ≥ KGE’ ≤ 0,4	1
High	KGE’ ≥ 0,4	2

Table 3. Ranking of climate projection models best evaluated to CWPS.

Dataset	Score										∑Score	∑KGE’
Dataset	a	b	c	d	e	f	g	h	i	j	∑Score	∑KGE’
GFDL-CM4	1	2	1	1	2	2	1	1	2	2	15	4,58
GFDL-ESM4	1	2	1	1	2	2	1	1	2	2	15	3,56
GFDL-CM4*	1	2	1	1	2	2	1	0	2	2	14	3,61
ACCESS-ESM1-5*	1	2	1	1	2	2	1	0	2	2	14	3,18
ACCESS-ESM1-5	1	2	0	1	2	2	1	1	2	2	14	3,02
KIOST*	1	2	1	1	2	2	1	0	2	2	14	2,91
GFDL-ESM4*	1	2	1	1	2	2	1	0	2	2	14	2,70
EC-EARTH3*	1	2	1	1	2	2	1	0	2	2	14	1,45
MPI-ESM1-2*	1	2	0	1	2	2	1	0	2	2	13	3,02
CMCC-ESM2*	1	2	1	0	2	2	1	0	2	2	13	2,33
CMCC-ESM2	1	2	1	0	2	2	1	0	2	2	13	0,19
IPSL-CM6A-LR*	1	2	1	0	2	2	1	0	2	2	13	-0,14
EC-EARTH3	1	2	1	0	2	2	1	0	2	2	13	-3,03
NESM3	1	2	0	0	2	2	1	0	2	2	12	3,65
IPSL-CM6A-LR	1	2	0	0	2	2	1	0	2	2	12	3,59
MIROC6	1	2	0	0	2	2	1	0	2	2	12	3,46
MRI-ESM2	1	2	0	0	2	2	1	0	2	2	12	3,34
MIROC6*	1	2	0	0	2	2	1	0	2	2	12	3,19
ACCESS-CM2*	1	2	0	0	2	2	1	0	2	2	12	2,85
KACE*	1	2	0	0	2	2	1	0	2	2	12	2,56
NESM3*	1	2	0	1	2	2	1	0	1	2	12	2,47
HadGEM3-GC31-LL*	1	2	0	0	2	2	1	0	2	2	12	2,28
TaiESM1	1	2	0	0	2	2	1	0	2	2	12	2,11
TaiESM1*	1	2	0	0	2	2	1	0	2	2	12	2,06
MPI-ESM1-2	1	2	0	0	2	2	1	0	2	2	12	1,48
INM-CM5	1	2	0	0	2	2	1	0	2	2	12	0,12
MRI-ESM2*	1	2	0	0	2	2	1	0	2	2	12	-0,40
UKESM1-0-LL*	1	2	0	0	2	2	1	0	1	2	11	2,77
NorESM2-MM	1	2	0	0	2	2	1	0	1	2	11	1,95
NorESM2-MM*	1	2	0	0	2	2	1	0	1	2	11	1,27
INM-CM5*	1	2	0	0	2	2	1	0	1	2	11	-0,31
INM-CM4_8	1	2	0	0	2	2	1	0	1	2	11	-1,02
UKESM1-0-LL	0	2	0	0	2	2	0	1	1	2	10	2,14
HadGEM3-GC31-LL	0	2	0	0	2	2	0	1	1	2	10	1,42
INM-CM4_8*	1	2	0	0	2	2	1	0	0	2	10	-0,01
KIOST	0	1	0	1	2	2	0	0	1	2	9	1,85
KACE	0	1	0	0	1	1	0	1	2	2	8	0,91
ACCESS-CM2	0	1	0	0	2	2	0	0	2	1	8	-3,23

^* Dataset with bias correction. Column a daily timeseries, b monthly timeseries, c annual timeseries, d hydrological year timeseries (from October to September), e average precipitation for the day of the year, and f average precipitation for the month of the year, g maximum precipitation for the day of the year, h maximum precipitation for the month of the year, i minimum precipitation for the day of the year, and j minimum precipitation for the month of the year.

Table 4. Performance indicators for the objective functions used to calibrate the hydrological model in the CWPS basins.

Performance indicator	Objective function	Basin
Performance indicator	Objective function	JPS	JAG	VAL	BUE	ATI	CAC	PAI	ATA
KGE	NSE	0.81	0.57	0.86	0.76	0.38	0.39	0.50	0.29
	Log-NSE	0.39	0.20	0.53	0.53	0.11	-0.34	0.15	-0.39
	KGE	0.83	0.71	0.90	0.83	0.68	0.53	0.62	0.51
NSE	NSE	0.67	0.45	0.84	0.71	0.23	0.24	0.35	0.31
	Log-NSE	0.16	-0.21	0.55	0.39	-0.49	-1.99	-0.82	-2.29
	KGE	0.66	0.40	0.81	0.66	0.36	0.04	0.24	-0.02
R2	NSE	0.69	0.48	0.85	0.76	0.26	0.36	0.37	0.33
	Log-NSE	0.72	0.69	0.85	0.74	0.66	0.52	0.43	0.47
	KGE	0.69	0.52	0.82	0.70	0.55	0.33	0.38	0.29
PBIAS (%)	NSE	6.72	14.73	10.44	19.32	-8.13	32.65	9.19	4.81
	Log-NSE	10.23	18.59	8.10	9.61	18.68	28.37	8.14	31.67
	KGE	4.04	6.43	2.00	4.94	18.20	17.86	3.59	15.67
Log-NSE	NSE	0.53	0.11	0.74	0.51	0.19	-0.24	-0.02	-0.07
	Log-NSE	0.69	0.64	0.89	0.78	0.60	0.35	0.22	0.40
	KGE	0.57	0.43	0.80	0.64	0.33	-0.01	0.07	0.07

Table 5. Daily flow(mm) predicted by precipitation (mm) by the GFDL-CM4 model in two climate scenarios in CWPS basins.

Basin	SSP2-4.5					SSP5-8.5
Basin	Equation (Q)	r	Q25	Q50	Q75	Equation (Q)	r	Q25	Q50	Q75
JPS	0.148P+0.990	0.67	0.88	1.14	1.52	0.141P+0.889	0.67	0.75	1.01	1.37
JAG	0.047P+0.779	0.33	0.53	0.65	0.86	0.038P+0.649	0.32	0.43	0.58	0.76
VAL	0.135P+0.813	0.53	0.46	0.69	1.17	0.125P+0.732	0.53	0.37	0.61	1.04
BUE	0.125P+0.654	0.51	0.40	0.55	0.88	0.113P+0.578	0.50	0.33	0.48	0.77
ATI	0.167P+0.866	0.58	0.48	0.67	1.35	0.155P+0.801	0.57	0.42	0.60	1.20
CAC	0.050P+0.787	0.45	0.70	0.82	0.97	0.039P+0.691	0.46	0.58	0.73	0.89
PAI	0.066P+0.842	0.56	0.81	0.93	1.10	0.054P+0.746	0.56	0.68	0.83	1.01
ATA	0.129P+0.661	0.61	0.65	0.82	1.01	0.114P+0.573	0.60	0.53	0.71	0.92

Table 6. Frequency of non-exceedance of the ratio between rainfall and flow (P/Q) of the average of seven consecutive days in the climate scenarios studied.

Basin	SSP2-4.5		SSP5-8.5
	P/Q
	0.2	0.5	0.2	0.5
JPS	14.0	25.6	14.9	26.4
JAG	10.3	20.3	10.7	20.2
VAL	18.7	18.8	10.2	19.4
BUE	8.4	17.4	9.2	17.7
ATI	9.1	18.2	10.2	19.4
CAC	12.2	22.7	12.7	23,0
PAI	12.0	22.8	12.8	23.1
ATA	11.4	21.4	12.1	21.5
Average	12.0	20.9	11.6	21.3

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer