1. Introduction

2. The Matrix Low-Rank Constrained Inpainting Model and Its Solution Algorithm

Image inpainting models based on low-rank matrix are generally as follows:

(1)

where X represents the image to be recovered (X ∈ R² grayscale value image, X ∈ R³ RGB image, grayscale value video, etc.). Θ_Ω represents the interference operator, in which the set of interference pixel positions is Ω. $\widehat{X}$ represents the optimal solution. Y represents the interfered image. ε represents the error, generally set as a small constant value matrix, such as constant 10^-14. Φ represents low-rank transformation operation. ΦX is to transform X into a matrix or tensor with low ranks, such as a low-rank matrix transformed by the similar blocks of local images, the low-rank structure matrix [1,2,4,22] transformed by the relationship of the annihilating Filter, and the low-rank matrix [7] transformed by the similarity between frames. If the videos or RGB images are treated as third-order or higher-order tensors, the rank property may come from the tensor Tucker rank [36], TT rank [26], etc. Under the interference of impulse noise, Θ_Ω operator generally has three representations.

The second is salt and pepper noise, a special case of RVIN [1],

where V_max is the maximum value of salt pepper noise and V_min is the minimum value of salt pepper noise.

The low-rank property is another form of sparsity essentially. Sparse constraints on matrices essentially minimize the zero norm of matrix elements, while low-rank constraints minimize the zero norm of singular values of the constraint matrix. The low-rank constraint on a matrix is actually the l₀ norm constraint on the singular values of the matrix, i.e. $\underset{X}{\min }rank\left(\mathsf{\Phi }X\right)⟺\underset{X}{\min }{‖\mathsf{\Phi }X‖}_0$. Since $\underset{X}{\min }{‖\mathsf{\Phi }X‖}_0$ is nonconvex, the l_p norm form $\underset{X}{\min }{‖\mathsf{\Phi }X‖}_{\mathrm{p}}$ is commonly used for convex substitution[37], where 0 ≤ p ≤ 1, ${‖\mathsf{\Phi }X‖}_{\mathrm{p}}={\displaystyle \sum _{i=1}^n}{{\sigma }_i}^p$, and σ_i are singular values of matrix ΦX of size n₁ × n₂, n = min(n₁, n₂). The special case of the l_p norm is the nuclear norm ${‖\mathsf{\Phi }X‖}_{\mathrm{*}}={\displaystyle \sum _{i=1}^n}{\sigma }_i$, which means p = 1. Whether the low-rank constraint form used can accurately convex approximation has a significant impact on the repair effect. Let ${‖\mathsf{\Phi }X‖}_p={\displaystyle \sum _i^n}{g}_p\left({\sigma }_i\right)$, where function g_p(σ_i) = ${{\sigma }_i}^p$, 0 ≤ p ≤ 1. For the l₀ and l_p norm, the function g_p(σ_i) is

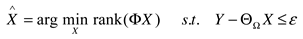
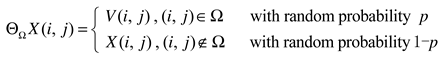
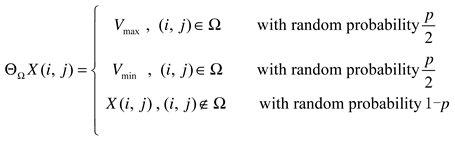
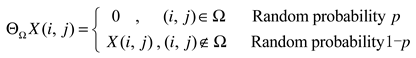
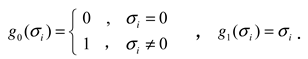
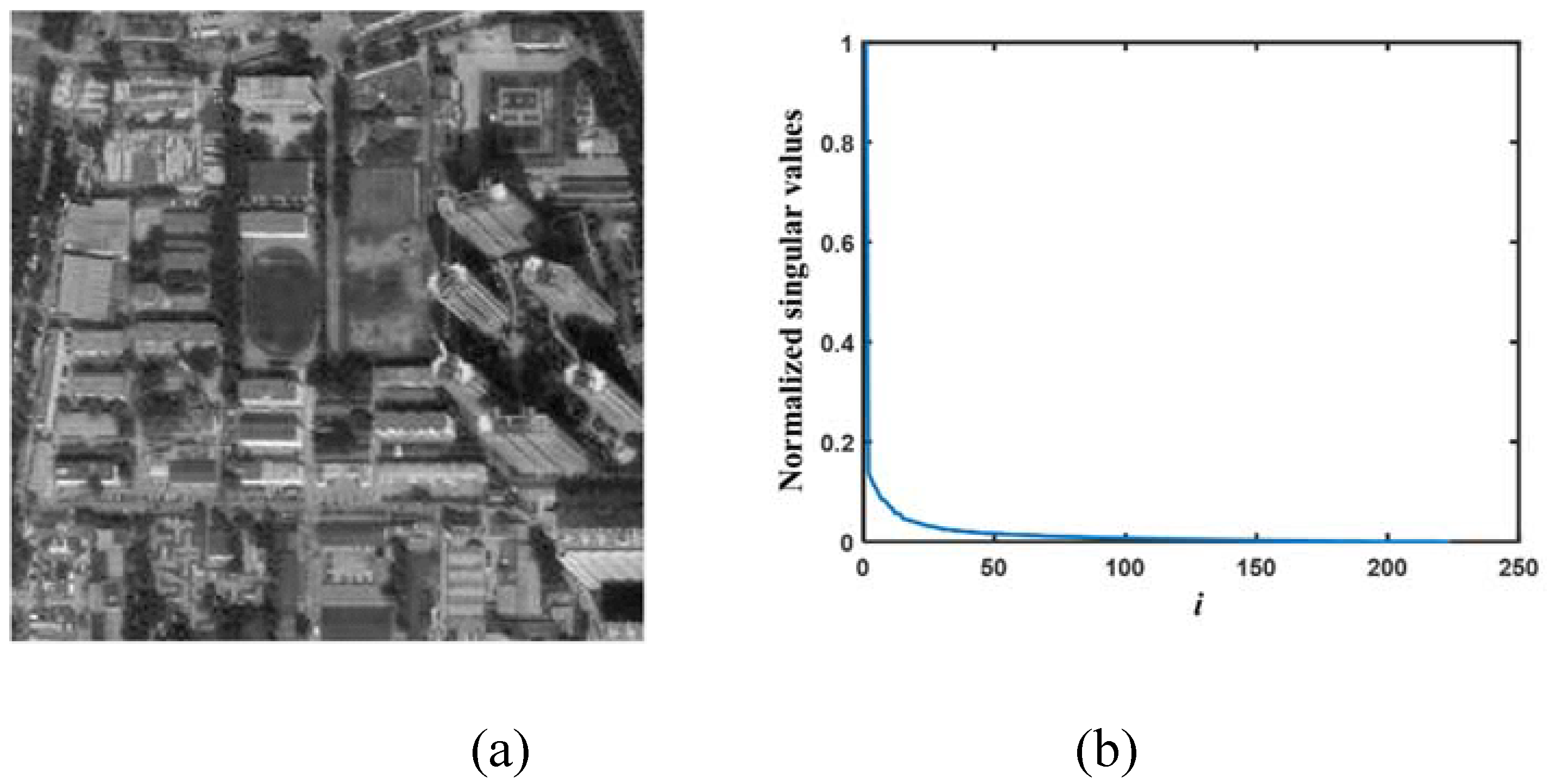
2.1. Nuclear norm ‖X‖_∗

For example, we use the minimized nuclear norm as a low rank constraint to establish an image inpainting model, as follows.

(2)

Y is the impulse interference image of size n₁ × n₂. The regularization parameter λ is introduced to convert model (2) into an unconstrained form:

(3)

Three algorithms can solve equation (3). The commonly used algorithm is the singular value shrinkage/threshold (SVT) algorithm [46].

The SVT algorithm is shown below.

First, perform singular value decomposition for Y, U∑V^H = SVD(Y), ∑ = diag( {σ_i}_1≤i≤n ), where diag( . )is the diagonal matrix operation of the elements, n = min(n₁, n₂). Then, a soft threshold operation D_λ(σ_i) = max(0, σ_i − λ) is performed on the singular values [47]. Then, set ∑_SVT = diag( {D_λ(σ_i)}_1≤i≤n ). Finally, we obtained the solution results $\widehat{X}$ = U∑_SVTV^H.

Jain P. proposed the SVP algorithm for solving model (2) problem [48]. With the development of large-scale data processing and distributed computing, the alternating direction method of multipliers (ADMM) algorithm has become the mainstream optimization algorithm [49]. When using the ADMM algorithm to solve (3), it needs to first introduce auxiliary variables Z = ΦX and residuals L to transform model (3) into multiple sub-problems for an iterative solution:

where, ρ > 0 is the introduced penalty parameter, and the SVT method is used to solve the sub problem $\hat{Z}$.

In this paper, we use the SVT algorithm, SVP algorithm, and ADMM algorithm [50,51] to solve the nuclear-norm-based image inpainting model, which corresponds to name as the SVT method, SVP method, and n_ADMM method respectively. The details of the SVT algorithm, SVP algorithm, and n_ADMM algorithm are shown in Table 1, Table 2 and Table 3 respectively.

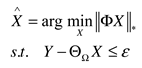
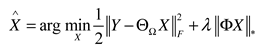
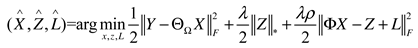
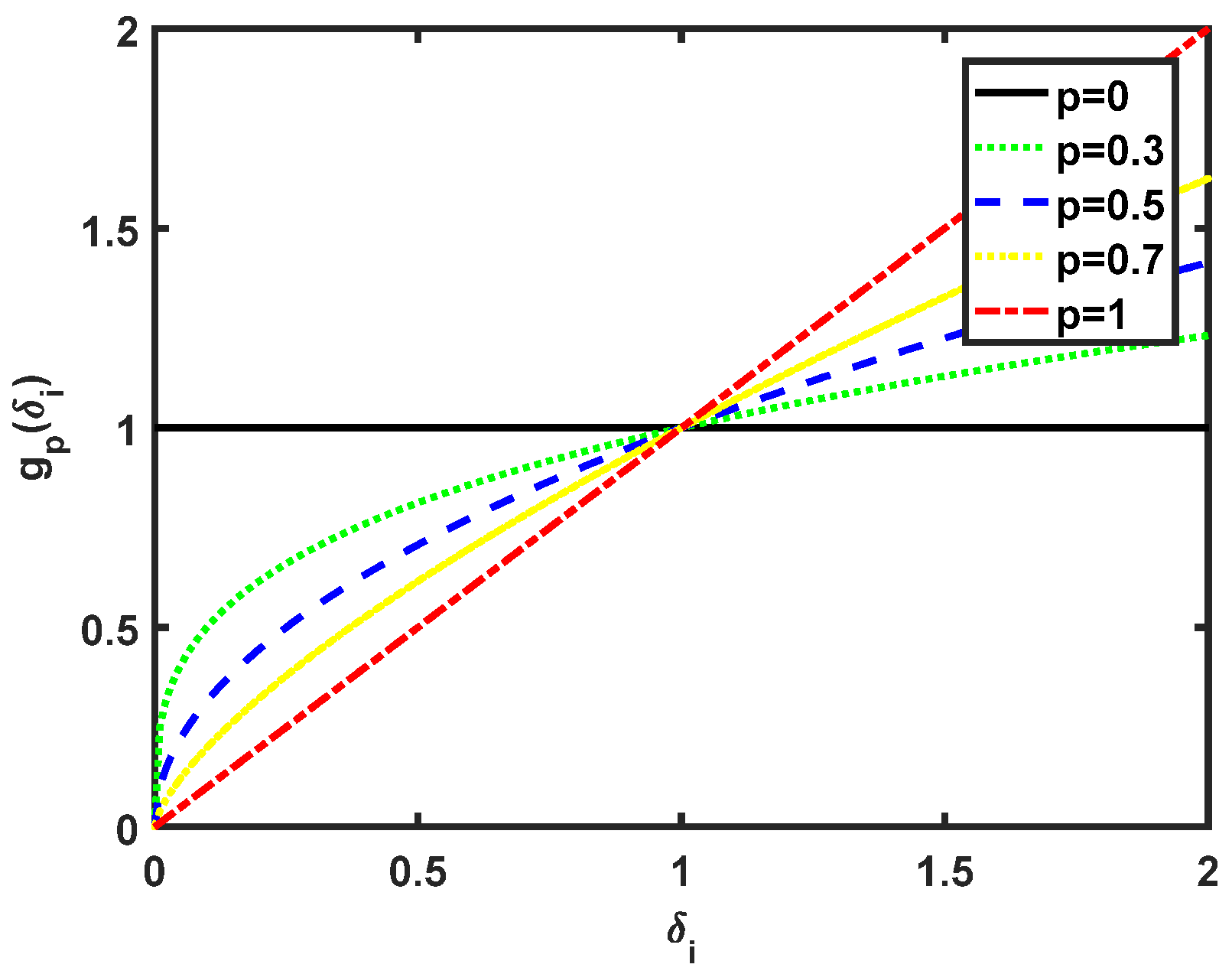
2.2. Weighted nuclear norm ${\displaystyle \sum _{i}fun({\sigma }_i)}$

The weighted nuclear norm ${\displaystyle \sum _{i}fun({\sigma }_i)}$ is a scheme that uses weighted singular value constraints to approximate l₀ constrained singular values [38,39,40,41]. It is a balanced constraint scheme that makes large singular values smaller and small singular values larger. It can be more accurate than the nuclear norm (i.e., l₁ constraints on singular values), where fun( . ) is the weighted function of each singular value σ_i of matrix ΦX, and [U, ${diag\left\{{\sigma }_i\right\}}_{{i=1:\min (n}_1,n_2)}$, V] = SVD(ΦX). We use the weighted nuclear norm as a low-rank constraint to establish an image inpainting model, as follows.

(4)

Then, we introduce the regularization parameter λ and converted model (4) into an unconstrained form:

(5)

There are many kinds of weighting functions fun( . ), and the p-norm (0<p<1) is the simplest weighting scheme, namely g_p(σ_i) = fun(σ_i). Reference [39] reviewed various weighting functions that approximate the l₀ norm of singular values, such as SCAD [52], MCP [53], Logarithm [54], Geman [55], Laplace [56,57], etc., of which the Logarithm scheme is the most classic. In the experiment part of this paper, we choose the Logarithm scheme for comparison. The weighting function in the Logarithm scheme is shown below.

(6)

where γ > 0 is a parameter that is determined based on experience.

The simplest and most direct solution for model (4) is the weighted SVT (WSVT) algorithm. Set the weight w_i = fun(σ_i), i = 1, 2, …, n, and then $\widehat{X}$ = U∑_WSVTV^H, where ∑_WSVT = diag({D_λ(w_iσ_i)}_1≤i≤n).

We use ADMM to solve the weighted nuclear norm image inpainting problem (5). We introduce auxiliary variables Z = ΦX and residuals L to transform model (5) into multiple sub-problems for iterative solution:

(7)

where ρ > 0 is the introduced penalty parameter, and the WSVT algorithm is used to solve the sub problem $\hat{Z}$. The combination of the weighted SVT algorithm and ADMM algorithm can obtain more accurate iterative estimation. We use the ADMM algorithm to solve the weighted-nuclear-norm-based image inpainting model (7), and name it WSVT_ADMM method. The details of WSVT_ADMM algorithm used to solve model (7) are shown in Table 4.

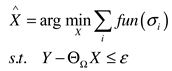
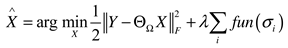
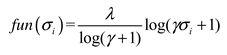
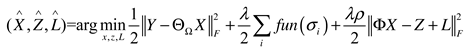
2.3. Truncated nuclear norm

In general, the singular value curve of a low-rank matrix exhibits an exponential extreme decay trend from large to small, and the singular value values sorted backward will approach 0. Therefore, the minimization of the nuclear norm is mainly to constrain the minimization of large singular values. To fully utilize the small singular values, a truncated nuclear norm minimization scheme can be used. The purpose of truncated nuclear norm minimization is to constrain the minimization of small singular values [42,43,44,45]. We use the truncated nuclear norm as a low-rank constraint to establish an image inpainting model, as follows.

(8)

where ${\mathcal{T}}_r$ is a truncation operation that extracts the first r larger diagonal elements in the diagonal matrix U^HΦXV, and ‖ΦX‖_∗ − ${\mathcal{T}}_r$(U^HΦXV) means that the first r larger diagonal elements in the diagonal matrix U^HΦXV are zeroed, and the last r smaller diagonal elements are retained [58,59]. We introduce a regularization parameter λ and converted (8) into an unconstrained form:

(9)

U, V is the truncated left and right singular value vector group matrix of ΦX. The essence of truncated nuclear norm minimization is to minimize the sum of smaller singular value elements of the constrained low-rank matrices.

The truncated-nuclear-norm-based model can be solved by APGL or ADMM algorithm. This paper combines the ADMM algorithm with the SVT algorithm to solve the truncated-nuclear-norm-based image inpainting model (9), and abbreviates it as the TSVT (Truncated SVT) algorithm. The details of the TSVT algorithm used to solve model (9) are shown in Table 5.

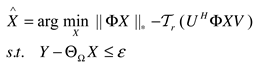
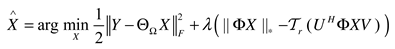
2.4. The F norm of UV matrix factorization

The process of solving the nuclear norm minimization problem involves time-consuming matrix singular value decomposition. Early Srebro N. [60] proposed the property ${‖X‖}_{*}=\underset{{UV}^H=X}{\min }\frac{1}{2}({‖U‖}_F^2+{‖V‖}_F^2)$ and proved it. Later, in many applications, the F norm of UV matrix factorization was used instead of the nuclear norm to simplify the calculation time [1,61,62,63,64]. We use the minimized F norm of UV matrix factorization as a low-rank constraint to establish an image inpainting model, as follows.

(10)

Then, we introduce the regularization parameter λ and penalty parameter ρ > 0 to convert model (10) into an unconstrained form:

(11)

where L is the residual variable. The initial values of U and V can be initialized by the LMaFit method [2,65]. The model (11) is commonly solved by the ADMM algorithm, and we name it UV_ ADMM method. The details of UV_ ADMM algorithm are shown in Table 6.

Compared with the n_ADMM method, the F-norm of UV-matrix based UV_ ADMM method avoids the time-consuming SVD in each iteration, making it more suitable for large matrix modeling with low-rank constraints. This method and the weighted nuclear norm method are commonly used in low-rank matrix constrained models.

The above model and its solving algorithm are summarized in Table 7. In addition, other algorithms that can solve the above model. For example, commonly used algorithms in sparsity-solving models. Sparsity constraint on signal refers to minimization of l₀ norm of signal elements, while low-rank constraint on signal refers to minimization of zero norms of the singular value of the signal matrix. Therefore, the optimization solution based on low-rank constraint model has a lot in common with the optimization solution based on the sparse constraint model in solving the algorithm. Iterative optimization algorithms based on sparse constraint models can be applied to optimization solutions based on matrix low-rank constraint models, such as convex relaxation algorithms, which find a sparse or low-rank approximation of signals by transforming nonconvex problems into convex problems through iterative solutions. Among them, the CG algorithm, IST algorithm [66], Split Bregman algorithm [67], and MM (major minimize) algorithm [58,68] can be flexibly changed according to different optimization models.

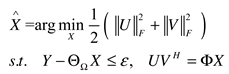
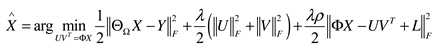
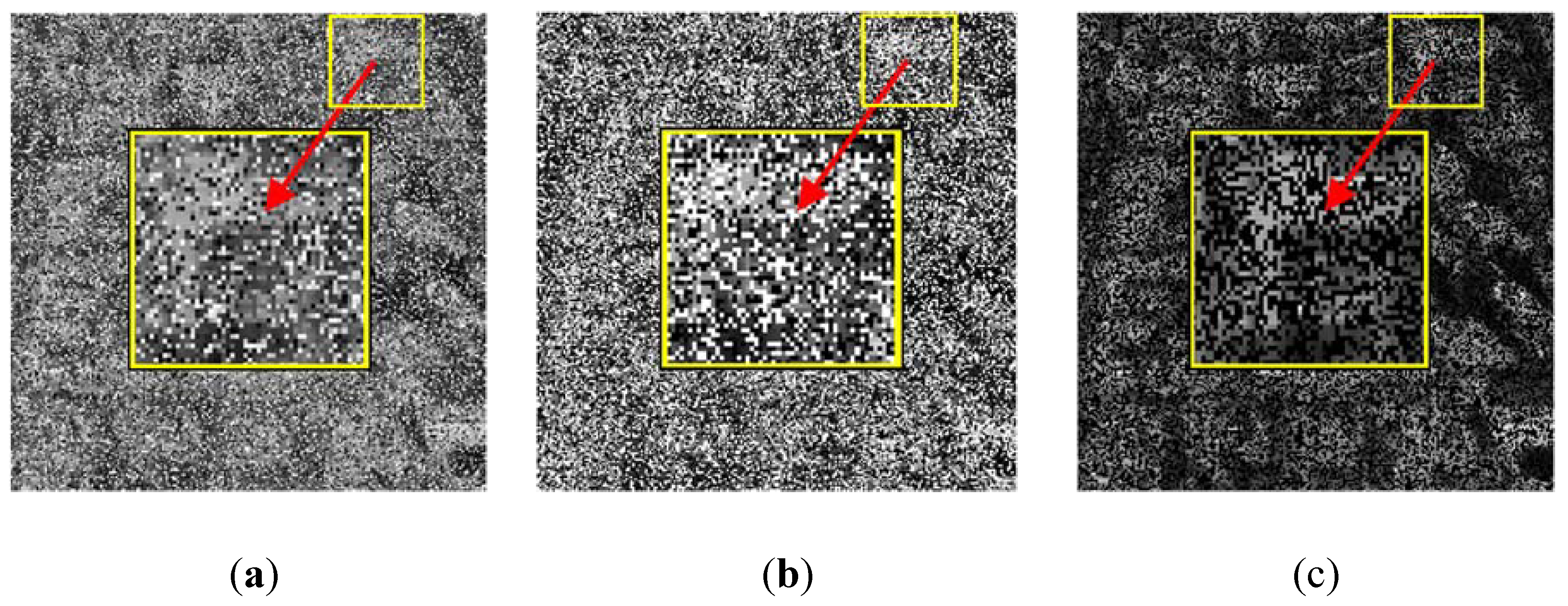
3. Comparative Experiments

4. Conclusions

References

1. Kyong, H.; Jong, C. Sparse and Low-Rank Decomposition of a Hankel Structured Matrix for Impulse Noise Removal. IEEE Trans. Image Process. 2018, 27, 1448–1461. [Google Scholar] [CrossRef]
2. Kyong, H.; Ye, J. Annihilating filterbased lowrank Hankel matrix approach for image inpainting. IEEE Trans. Image Process. 2015, 24, 3498–511. [Google Scholar] [CrossRef]
3. Balachandrasekaran, A.; Magnotta, V.; Jacob, M. Recovery of damped exponentials using structured low rank matrix completion. IEEE Trans. Med. Imaging 2017, 36, 2087–2098. [Google Scholar] [CrossRef] [PubMed]
4. Haldar, J. Low-rank modeling of local-space neighborhoods (LORAKS) for constrained MRI. IEEE Trans. Med. Imaging 2014, 33, 668–680. [Google Scholar] [CrossRef] [PubMed]
5. Ren, W.; Cao, X.; Pan, J.; et al. Image deblurring via enhanced low-rank prior. IEEE Trans. Image Process. 2016, 25, 3426–3437. [Google Scholar] [CrossRef]
6. Xu, Z.; Sun, J. Image inpainting by patch propagation using patch sparsity. IEEE Trans. Image Process. 2010, 9, 1153–1165. [Google Scholar] [CrossRef]
7. Zhao, B.; Haldar, J.; Christodoulou, A.; et al. Image reconstruction from highly undersampled (k, t)-space data with joint partial separability and sparsity constraints. IEEE Trans. Med. Imaging 2012, 31, 1809–20. [Google Scholar] [CrossRef]
8. Kyong, H.; Jong, C. Annihilating Filter-Based Low-Rank Hankel Matrix Approach for Image Inpainting. IEEE Trans. Image Process. 2018, 27, 1448–1461. [Google Scholar] [CrossRef]
9. Long, Z.; Liu, Y.; Chen, L.; et al. Low rank tensor completion for multiway visual data. Signal Process. 2019, 155, 301–316. [Google Scholar] [CrossRef]
10. Kolda, T.; Bader, B. Tensor decompositions and applications. SIAM Review 2009, 51, 455–500. [Google Scholar] [CrossRef]
11. Oseledets, I. Tensor-train decomposition. SIAM J. Scien. Comput. 2011, 33, 2295–2317. [Google Scholar] [CrossRef]
12. Shi, Q.; Cheung, M.; Lou, J. Robust Tensor SVD and Recovery With Rank Estimation. IEEE Trans. Cyber. 2022, 52, 10667–10682. [Google Scholar] [CrossRef] [PubMed]
13. Wu, F.; Li, C.; Li, Y.; Tang, N. Robust low-rank tensor completion via new regularized model with approximate SVD. Inform. Sciences 2023, 629, 646–666. [Google Scholar] [CrossRef]
14. Huang, J.; Yang, F. Compressed magnetic resonance imaging based on wavelet sparsity and nonlocal total variation. IEEE 9th International Symposium on Biomedical Imaging: From Nano to Macro, 2012, 5, 968–971. [Google Scholar] [CrossRef]
15. Zhang, X.; Chan, T. Wavelet inpainting by nonlocal total variation. Inverse Problems and Imaging 2010, 4, 191–210. [Google Scholar] [CrossRef]
16. Wang, W.; Chen, J. Adaptive rate image compressive sensing based on the hybrid sparsity estimation model. Digit. Signal Process. 2023, 139, 104079. [Google Scholar] [CrossRef]
17. Ou, Y.; Li, B.; Swamy, M. Low-rank with sparsity constraints for image denoising. Information Sciences 2023, 637, 118931. [Google Scholar] [CrossRef]
18. Lingala, S.; Hu, Y.; Dibella, E.; et al. Accelerated dynamic MRI exploiting sparsity and lowrank structure: kt SLR. IEEE Trans. Med. Imaging 2011, 30, 1042–1054. [Google Scholar] [CrossRef] [PubMed]
19. Zhang, Y.; Huang, L.; Li, Y.; Zhang, K.; Yin, C. Low-Rank and Sparse Matrix Recovery for Hyperspectral Image Reconstruction Using Bayesian Learning. Sensors 2022, 22, 343. [Google Scholar] [CrossRef] [PubMed]
20. Zhao, X.; Li, M.; Nie, T.; Han, C.; Huang, L. An Innovative Approach for Removing Stripe Noise in Infrared Images. Sensors 2023, 23, 6786. [Google Scholar] [CrossRef]
21. Tremoulheac, B.; Dikaios, N.; Atkinson, D.; et al. Dynamic MR image reconstructionseparation from undersampled (k, t)space via lowrank plus sparse prior. IEEE Trans. Med. Imaging 2014, 33, 1689–1701. [Google Scholar] [CrossRef] [PubMed]
22. Kyong, H.; Ye, J. Annihilating filter-based low-rank Hankel matrix approach for image inpainting. IEEE Trans. Image Process. 2015, 24, 3498–511. [Google Scholar] [CrossRef] [PubMed]
23. Zhao, Q.; Zhou, G.; Xie, S.; et al. Tensor ring decomposition. 2016, arXiv:1606.05535. [Google Scholar] [CrossRef]
24. Kilmer, M.; Braman, K.; Hao, N. Third-order tensors as operators on matrices: a theoretical and computational framework with applications in imaging. Siam J. Matrix Anal. A. 2013, 34, 148–172. [Google Scholar] [CrossRef]
25. Zhang, Z.; Aeron, S. Exact tensor completion using t-SVD. IEEE Trans. Signal Process. 2017, 65, 1511–1526. [Google Scholar] [CrossRef]
26. Bengua, J. Efficient tensor completion for color image and video recovery: Lowrank tensor train. IEEE Trans. Image Process. 2017, 26, 1057–7149. [Google Scholar] [CrossRef] [PubMed]
27. Ma, S.; Du, H.; Mei, W. Dynamic MR image reconstruction from highly undersampled (k, t)-space data exploiting low tensor train rank and sparse prior. IEEE Access 2020, 8, 28690–28703. [Google Scholar] [CrossRef]
28. Ma, S.; Ai, J.; Du, H.; Fang, L.; Mei, W. Recovering low-rank tensor from limited coefficients in any ortho-normal basis using tensor-singular value decomposition. IET Signal Process. 2021, 19, 162–181. [Google Scholar] [CrossRef]
29. Tang, T.; Kuang, G. SAR Image Reconstruction of Vehicle Targets Based on Tensor Decomposition. Electronics 2022, 11, 2859. [Google Scholar] [CrossRef]
30. Gross, D. Recovering low-rank matrices from few coefficients in any basis. IEEE Trans. Infor. Theory 2011, 57, 1548–1566. [Google Scholar] [CrossRef]
31. Jain P.; Oh S. Provable tensor factorization with missing data. In: Proceedings of the 27th International Conference on Neural Information Processing Systems (NIPS) 2014, 1: 1431–1439.
32. Zhang, Z.; Aeron, S. Exact tensor completion using t-SVD. IEEE Trans. Signal Process. 2017, 65, 1511–1526. [Google Scholar] [CrossRef]
33. Vetterli, M.; Marziliano, P.; Blu, T. Sampling signals with finite rate of innovation. IEEE trans. Signal Process. 2002, 50, 1417–1428. [Google Scholar] [CrossRef]
34. Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–209. [Google Scholar] [CrossRef] [PubMed]
35. Lou, Y.; Zhang, X.; Osher, S.; Bertozzi, A. Image recovery via nonlocal operators. Journal of Scientific Computing 2010, 42, 185–197. [Google Scholar] [CrossRef]
36. Filipovi, M.; Juki´, A. Tucker factorization with missing data with application to low-n-rank tensor completion. Multidim Syst. Sign. Process. 2015, 26, 677–692. [Google Scholar] [CrossRef]
37. Wang, X.; Kong, L.; Wang, L.; Yang, Z. High-Dimensional Covariance Estimation via Constrained Lq-Type Regularization. Mathematics 2023, 11, 1022. [Google Scholar] [CrossRef]
38. Candès, E.; Wakin, M.; Boyd, S. Enhancing sparsity by reweighted l1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
39. Lu, C.; Tang, J.; Yan, S.; et al. Nonconvex Nonsmooth Low-Rank Minimization via Iteratively Reweighted Nuclear Norm. IEEE Trans. Image Process. 2015, 25, 829–839. [Google Scholar] [CrossRef]
40. Zhang, J.; Lu, J.; Wang, C.; Li, S. Hyperspectral and multispectral image fusion via superpixel-based weighted nuclear norm minimization. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–12. [Google Scholar] [CrossRef]
41. Li, Z.; Yan, M.; Zeng, T.; Zhang, G. Phase retrieval from incomplete data via weighted nuclear norm minimization. Pattern Recognition. 2022, 125, 108537. [Google Scholar] [CrossRef]
42. Cao, F.; Chen, J.; Ye, H.; et al. Recovering low-rank and sparse matrix based on the truncated nuclear norm. Neural Networks 2017, 85, 10–20. [Google Scholar] [CrossRef]
43. Hu, Y.; Zhang, D.; Ye, J.; et al. Fast and accurate matrix completion via truncated nuclear norm regularization. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2117–2130. [Google Scholar] [CrossRef] [PubMed]
44. Fan, Q.; Liu, Y.; Yang, T.; Peng, H. Fast and accurate spectrum estimation via virtual coarray interpolation based on truncated nuclear norm regularization. IEEE Signal Process. Lett. 2022, 29, 169–173. [Google Scholar] [CrossRef]
45. Yadav, S.; George, N. Fast direction-of-arrival estimation via coarray interpolation based on truncated nuclear norm regularization. IEEE Trans. Circuits Syst. II, Exp. Briefs 2021, 68, 1522–1526. [Google Scholar] [CrossRef]
46. Cai, J.; Candès, E.; Shen, Z. A singular value thresholding algorithm for matrix completion. Siam J. Optimiz. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
47. Xu, J.; Fu, Y.; Xiang, Y. An edge map-guided acceleration strategy for multi-scale weighted nuclear norm minimization-based image denoising. Digit. Signal Process. 2023, 134, 103932. [Google Scholar] [CrossRef]
48. Jain P.; Meka R. Guaranteed rank minimization via singular value projection. Available online: http://arxiv.org/ abs/0909.5457, 2009. [CrossRef]
49. Stephen, B. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends in Mach. Le. 2010, 3, 1–122. [Google Scholar] [CrossRef]
50. Zhao, Q.; Lin, Y.; Wang, F. Adaptive weighting function for weighted nuclear norm based matrix/tensor completion. Int. J. Mach. Learn. Cyber. 2023. [Google Scholar] [CrossRef]
51. Liu, X.; Hao, C.; Su, Z. Image inpainting algorithm based on tensor decomposition and weighted nuclear norm. Multimed Tools Appl. 2023, 82, 3433–3458. [Google Scholar] [CrossRef]
52. Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Amer. Statist. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
53. Friedman, J. Fast sparse regression and classification. Int. J. Forecasting 2012, 28, 722–738. [Google Scholar] [CrossRef]
54. Zhang, C.-H. Nearly unbiased variable selection under minimax concave penalty. Ann. Statist. 2010, 38, 894–942. [Google Scholar] [CrossRef]
55. Geman, D.; Yang, C. Nonlinear image recovery with half-quadratic regularization. IEEE Trans. Image Process. 1995, 4, 932–946. [Google Scholar] [CrossRef] [PubMed]
56. Trzasko, J.; Manduca, A. Highly undersampled magnetic resonance image reconstruction via homotopic 0-minimization. IEEE Trans. Med. Imag. 2009, 28, 106–121. [Google Scholar] [CrossRef] [PubMed]
57. Liu, Q. A truncated nuclear norm and graph-Laplacian regularized low-rank representation method for tumor clustering and gene selection. BMC Bioinformatics. 2021, 22, 436. [Google Scholar] [CrossRef]
58. Zhang, Q.; Li, X.; Mao, H.; Huang, Z.; Xiao, Y.; Chen W., g; Xian, J.; Bi, Y. Improved sparse low-rank model via periodic overlapping group shrinkage and truncated nuclear norm for rolling bearing fault diagnosis. Measurement Sci. Technol. 2023, 34. [Google Scholar] [CrossRef]
59. Ran, J.; Bian, J.; Chen, G.; Zhang, Y.; Liu, W. A truncated nuclear norm regularization model for signal extraction from GNSS coordinate time series. Adv. Space Res. 2022, 70, 336–349. [Google Scholar] [CrossRef]
60. Signoretto M.; Cevher V.; Suykens J. An SVD-free approach to a class of structured low rank matrix optimization problems with application to system identification. In: IEEE Conference on Decision and Control, EPFL-CONF-184990, 2013.
61. Srebro N. Learning with matrix factorizations. Cambridge, MA, USA: Massachusetts Institute of Technology, 2004.
62. Recht, B.; Fazel, M.; Parrilo, P. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM review 2010, 52, 471–501. [Google Scholar] [CrossRef]
63. Ma, S.; Du, H.; Mei, W. A two-step low rank matrices approach for constrained MR image reconstruction. Magn. Reson. Imaging 2019, 60. [Google Scholar] [CrossRef]
64. Yang, G.; Zhang, L.; Wan, M. Exponential Graph Regularized Non-Negative Low-Rank Factorization for Robust Latent Representation. Mathematics 2022, 10, 4314. [Google Scholar] [CrossRef]
65. Wen, Z.; Yin, W.; Zhang, Y. Solving a low-rank factorization model for matrix completion by a nonlinear successive over-relaxation algorithm. Math. Program. Comput. 2012, 4, 333–361. [Google Scholar] [CrossRef]
66. Daubechies, I.; Defrise, M.; Mol, C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. 2004, 57, 1413–1457. [Google Scholar] [CrossRef]
67. Goldstein, T.; Osher, S. The split Bregman method for L1regularized problems. Siam J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
68. Jacobson, M.; Fessler, J. An Expanded Theoretical Treatment of IterationDependent MajorizeMinimize Algorithms. IEEE Trans. Image Process. 2007, 16, 2411–2422. [Google Scholar] [CrossRef] [PubMed]
69. Wang, Z.; Bovik, A.; Sheikh, H.; et al. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]