Preprint
Review
Characterizing and Eliminating the Inbreeding Load
Altmetrics
Downloads
112
Views
77
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
30 October 2023
Posted:
31 October 2023
You are already at the latest version
Alerts
Abstract
Authors evaluated the relevant literature related to the purging which is the interaction between selection and inbreeding where the population may get rid of its inbreeding load at least partially. The backroad of the relevant theory was given and the available methods were described both based on the conventional quantitative genetic approach (based on genealogy data) and based on the latest genomic methods. The different parameters necessary for signalling purging (highlighting those inbreeding coefficients which are not yet been widely known in animal and veterinary science) were presented together with the relevant results of the literature. The available statistical methods together with the softwares and R packages to calculate various inbreeding coefficients and to determine inbreeding depression and purging were provided. The main results of the different approaches obtained in laboratory ZOO and domesticated populations (lethal equivalents, ancestral inbreeding, Inbreeding-Purging Model, genomic approaches) were summarized and presented. Application possibilities and future prospective of purging was also discussed.
Keywords:
Subject: Biology and Life Sciences - Animal Science, Veterinary Science and Zoology
1. Introduction
Inbreeding which is the mating of related animals is [1] an inevitable consequence of selection in a closed population, especially since selecting the breeding animals is based on their estimated breeding values determined by the procedure of Best Linear Unbiased prediction (BLUP) [2,3]. The consequence of mating related animals is that the proportion of homozygous loci is getting increased to the expense of the heterozygous ones [4]. The increase in homozygosity negatively causes effects on heterozygosity which is known as individual’s genetic diversity [5]. As a result, the higher levels of inbreeding leads to the lower genetic diversity and inbreeding depression [6,7], which are two out of seven main genetic issues in the field of conservation biology [8]. It rises the importance of measurement in individual inbreeding because with such information the breeding programs can be well-designed to control the unfavourable effects on individual fitness and population dynamics due to inbreeding [7,9]. The inbreeding scales can be quantified by the inbreeding coefficient which provides the probability that the two alleles at any locus in an individual are identical by descent [10]. In the conventional approach, the inbreeding coefficients and other diversity related parameters are pedigree – based statistics [11]. Although, in recent years, the advance of technology in generating genome-wide sequencing and genotyping data allows more accurate estimation levels of homozygosity in the population, the pedigree-based analysis is contended to keep its vital role in conservation management [11]. It is well known that inbred progenies are often affected by inbreeding depression which is the reduced fitness because of lower survival, mating and/or reproduction in the progeny of related individuals compared to the progeny of unrelated animals [12]. Inbreeding depression considerably affect the survival of inbred population [13], then population size, and the eventually risk of species extinction may happen, especially for populations that are already small in size and having a closed structure. However, inbreeding depression is not limited fitness traits and it may affect any trait of interest in wild, zoo and in domesticated animal populations (e.g. [14,15,16,17,18,19,20]). In order to minimize the unfavourable effects of inbreeding standard procedures [21,22,23,24] can be applied in order to maintain long-term sustainable livestock production in the future [25]. However, under various circumstances inbreeding avoidance is simply impossible. Zoological gardens often encounter with the issue of having a captive population originated by a small number of animals where obtaining additional animals is not possible A well-known example is the Speke’s Gazelle (Gazella spekei) population in the St Louis Zoo which was founded in 1969 by one import male and two import female. In 1972 another female was imported but since then no other imports were carried out [26]. Details of the management and breeding of this population can be found in Read and Frueh [27]. As the consequence of the small population size the population experienced a severe inbreeding depression. However, Templeton and Read [26,28] developed an unorthodox breeding program based on the steps: rapidly increasing the population size, choosing inbred animals to be parents having genes from as many different ancestors as possible, producing inbred offspring with divers genetic ancestry. Templeton and Read demonstrated that after applying this breeding program the inbreeding load was halved just in a three-year long period so they concluded that inbreeding depression did not cause a unsolvable problem from the aspect of long term maintenance of a population where inbreeding cannot be avoided. Although this conclusion was debated by others and it generated an inspiring back and forth debate [29,30,31,32] the breeding program of Templeton and Read [26,28] was probably the first example where the authors deliberately used the interaction between inbreeding and selection in order to get rid of the inbreeding depression (i.e. decreasing the inbreeding load). This phenomenon is called purging [12] which so far was mostly described in laboratory conditions [33,34,35]. However, the number of available studies are much less in Zoo biology (e.g. [36]) and very few in domesticated animals (e.g. [37,38]). Therefore, the objective of this review was to summarize the characteristics of purging including the necessary parameters and methods in order to investigate and demonstrate if purging was likely to happen in a given population as neither purging nor the related parameters are not widely known neither in animal nor in veterinary science.
2. Parameters Characterizing Inbreeding Load and Purging
According to Hedrick and García-Dorado, [12] the inbreeding load is the genetic damage that is concealed in heterozygosis in the population and would be expressed in a complete homozygote. Under some simplifying assumptions (fitness multiplicative across unlinked non-epistatic loci) inbreeding load equals the rate at which fitness declines with increasing inbreeding in the absence of selection (roughly, the % of reduction in fitness expected from each 0.01 increase in F). While purging is the increased purifying selection facilitated by inbreeding as it increases the homozygosity of partially recessive deleterious variants. The related parameters are:
- Inbreeding coefficient (F) [39] is defined as the probability that the two alleles at any locus in an individual are identical by descent.
- Ancestral inbreeding coefficient (FBAL) [40] is defined as the probability that any allele in an individual has been autozygous in previous generations at least once.
- Ancestral inbreeding coefficient according to Kalinowski et al. [31] (FKAL)is defined as the probability that any allele in an individual is currently autozygous and has been autozygous in previous generations at least once.
- Kalinowski “new” inbreeding coefficient (FNEW) [31] is defined as the probability that any allele in an individual is autozygous for the first time.
- Ancestral inbreeding coefficient according to Bamung et al. [41]: Ancestral history coefficient (AHC) is defined as the number that tells how many times during pedigree segregation (gene dropping) a randomly taken allele has been in IBD status [41]
- Likelihood of genetic death (ll) [42,43] defined as the likelihood of genetic death (ie. all founders carry a recessive lethal gene).
- Ancestral inbreeding coefficient according to Hinrichs et al. [44] (FOLD) and new inbreeding (FNEW_H) according to Hinrichs et al. [44] splits the inbreeding coefficient of Wright (1922) to two part (old and new) defining an intermediate base comparing to new inbreeding to the intermediate base while the difference between the conventional inbreeding and the new inbreeding is the old inbreeding.
- Purging coefficient (d) represents the part of deleterious effect that is exposed to genetic purging due to inbreeding [45].
- Purged inbreeding coefficient (g) [45] representing the inbreeding coefficient (F) adjusted by the deleterious frequency that is expected by considering purging.
- FROH is a genomic measure of individual autozygosity defined as the proportion of the autosomal genome, in which autozygosity is derived from the assumption that very long stretches of homozygosity (ROH) can only result from inbreeding [4].
- The number of lethal equivalents (B) is defined as the number of deleterious genes per gamete that, when combined in a homozygous state, would result in the death of an individual [46,47].
The inbreeding load of the population can be characterized by the number of lethal equivalents where if it decreases over time in a given population then it signals the possibility of purging [28].
Alternatively, based on the inbreeding coefficients of (F), (FBAL), (FKAL), (AHC) and (FOLD) the possibility of purging is indicated either by the positive interaction between (F) and (FBAL) [40] or by the significantly positive effect any of the following inbreeding coefficient: (FBAL), (FKAL), (AHC) and (FOLD) on the examined trait (i.e. the possibility of purging is indicated by means of ancestral inbreeding of any type [31], [40], [41], [44]).
Concerning the purging coefficient, it signals the possibility of purging when it is significantly different from zero. In that case the purged inbreeding coefficient is significantly lower compared to the Wright inbreeding coefficient [45] (i.e. purging is indicated by the so called Inbreeding-Purging model [45]).
3. Softwares
There are several softwares calculating the conventional inbreeding coefficient (F) [48,49,50] based on the algorithm of Meuwissen and Luo, (1993) [51]. On the contrary the other inbreeding coefficients (FBAL), (FKAL), (FNEW) and (AHC) can be estimated using the GRAIN software developed by Baumung et al. [41] which was recently updated by Doekes et al. [52]. The software is based on the stochastic method of “gene dropping” [53,54] where the number of the used iteration is generally 1.000.000. Likelihood of genetic death (ll) can be calculated using the R script developed by Kennedy et al. [43].
The purging coefficient (d) and the purged inbreeding coefficient (g) can be calculated using the PURGd [55] and PurgeR [56].
The lethal equivalent can be calculated using the R script developed by Hoeck et al. [47].
After the parameters listed in the previous section are calculated they have to be evaluated where the method depends on the characteristic of the evaluated trait, If the trait has a normal distribution then the effect of inbreeding (F, FBAL, FKAL, AHC and FOLD) is determined by running a breeding value estimation procedure (animal model) [2] where the inbreeding coefficients are treated as covariates. A widely used software for performing breeding value prediction is ASREML [57]. On the contrary if the trait of interest is binomial then generalized linear mixed models (GLMM), has to be fitted using the lme4 or pedigreemm package in R [59]. If the purging coefficient and the purged inbreeding coefficients are used then the non-linear regression method has to be used in order to find the more accurate values of these coefficients (nls function, stats package of R.
4. Correlation among Inbreeding Coefficients
There are only few available studies [60,61] number of studies estimating correlation coefficients among the various inbreeding coefficients. Based on Spanish and Hungarian rabbit populations Curik et al. [60] and Piles et al. [60] both reported very high (0.97-1.00) correlation coefficients between (FBAL) and (FKAL). Piles et al. [61] also reported the possible maximum correlation coefficients (1.0) between (AHC) and (FBAL) and (AHC) and (FKAL). The conventional inbreeding coefficient showed high (0.88-0.90) correlation coefficients in both studies with all of the different ancestral inbreeding coefficients ((AHC), (FBAL) and (FKAL)). On the contrary Piles et al. [61] reported only medium correlation coefficients between the old inbreeding (FOLD) and the conventional (F) and the other ancestral type ((AHC), (FBAL) and (FKAL)) inbreeding coefficients where the reported values ranged between 0.6 and 0.7, respectively. The lowest correlations (0.0-0.40) in both studies were found among the new and ancestral inbreeding coefficients but it has to be emphasized that the calculation of the new inbreeding coefficient was different based on either [31] or [44] and consequently the estimated correlations were different in the two studies where Piles et al. [61] reported very low (0.0-0.2) values while Curik et al. [60] observed moderate (0.28-0,40) values. Similarly, the new and the conventional inbreeding coefficients showed different correlation coefficients in the two studies due to the same reason mentioned before. Again the reported values of Piles et al. [61] was low (0.2) compared to Curik et al. [60] who reported much higher values (0.67-0.73). Altogether the results indicated that the conventional, new and ancestral inbreeding coefficients are measuring different population parameters.
5. Estimates of Lethal Equivalents in Populations of Different Species
The reported values of the estimated lethal equivalent in different species is summarized in Table 1. The first study using the term lethal equivalent was that of Morton et al. [46] analysing human data collected by Sutter and Tabah [72,73] from Catholic marriage dispensations issued during 1919-1925 in two French departments (Morbihan and Loir et Cher). Two third of the families were contacted and the married couples were sorted into the groups of first cousins, 1.5 cousins, second cousins and unrelated, respectively. The same information was obtained from town clerks for a control sample of unrelated parents married during the same period and selected without regard to fertility or medical history. After determining the conventional (F) [39] the authors calculated lethal equivalents (B) from the weighted regression on (F) of the natural logarithm of the number of survivors. From Table 1. it can be seen that the calculated (B) was larger in Morbihan than in Loir et Cher and also that the (B) was smaller in the earlier life history trait of stillbirth and neonatal death compared to infant and juvenile death. In another similar human study [62] the genealogy of the Habsburg dynasty was evaluated between 1450 to 1800 covering more than 4 000 individuals along more than 20 parent-offspring generations. The analyzed period was split to two consecutive periods of 1450-1600 and 1600-1800, respectively. Mortality data were classified into two categories: infant deaths (deaths in the first year of life, excluding miscarriages and stillbirths) and child deaths (deaths between years 1–10). Only deaths attributable to natural causes were considered for the analysis. Miscarriages and stillbirths were not included in the analysis because the information on such early deaths is sometimes contradictory in the historical sources. The effect of inbreeding was evaluated both for the mother and for the progeny. The importance of treating both litter and dam inbreeding simultaneously was emphasized by Falconer [74] who noted that litter inbreeding might reduce the viability of embryos while dam inbreeding may have an effect on the fertility of the females. In this study the inbreeding coefficient of the mother did not affect either evaluated trait. According to their results they reported that the inbreeding load for child survival showed a statistically significant strong reduction corresponding to almost 80% of the inbreeding load for child survival. On the contrary for infant survival an opposite tendency was observed where the inbreeding load has been increased and this increase was very close to be significant (p=0.06). Authors concluded that the genetic basis of inbreeding depression was probably very different for infant and child survival. Nevertheless, Ceballos et al. [62] concluded that although the contribution of environmental effects to the reduction of inbreeding depression cannot be completely discarded, the reduction in inbreeding load for child survival detected in the Habsburg dynasty is in accordance with theoretical evidence from models of purging.
As already mentioned in the introduction section the captive Speke’s Gazelle population consisted of a few number of imported animals therefore avoiding the mating of related animals was not possible [26]. This population similarly to [62] also experienced a decrease of its inbreeding load in the life history trait of 30-day viability which was almost halved in a three-year long period. However, it is widely known that inbreeding depression is much stronger in harsh conditions [75]. Armbruster and Reed [75] rreviewed the current literature on the relationship between the magnitude of inbreeding depression and environmental stress and calculated haploid lethal equivalents expressed under relatively benign and stressful conditions based on data from 34 studies. Inbreeding depression increases under stress in 76% of cases, although this increase was only significant in 48% of the studies considered. Estimates of lethal equivalents were significantly greater under stressful (mean=1.45, median=1.02) than relatively benign (mean=0.85, median=0.61) conditions. This amounted to an approximately 69% increase in inbreeding depression in a stressful vs. benign environment. Based on the findings of Armbruster and Reed [75] if the environmental effects were improved during this period for the Speke’s Gazelle Zoo population [26] then it also could explain the observed decrease of (B). In studies related to different bird species [63,64,65,66,67,68] there was a clear tendency that the magnitudes of the estimated lethal equivalents increased with the age until survival was monitored. When survival rates were followed until 1-2 years or until recruitment, different authors [63,64,65,66,67,68] reported higher LE (B=3.4-6.9) compared to the study of Gruber at al. (2010) analysing the early life-stage trait of hatching rate (B=0.17).
The Soay sheep (Ovis aries), Drosophila (Drosophila melanogaster) and Killer whale (Orcinus orca) studies also followed this trend where the inbreeding load was much higher for a late life history trait. [69,70,71]. These studies are also unique from the applied methodology namely that inbreeding load based determined using genomic methods (FROH) [69-71. It has to be mentioned that the estimated lethal equivalents of the different studies listed in Table 1. were not always directly comparable as they used different methodology. According to Kennedy et al. [43], using the unstandardized version of their model the estimated effect of (F) on the survival rate at birth provides directly the number of lethal equivalents per gamete (B). Concerning the adequate methodology Grueber et al. [76] developed a model where the standardized coefficients were used to calculate lethal equivalent applying a model averaging method [77]. In a recent study, Nietlisbach et al. [78] used computer simulation in order to compare the different methods estimating (B). According to their results, exponent maximum likelihood and GLM log-link methods were unbiased while GLM logit-link method resulted overestimated LE-s especially if the true value of LE was high. On the contrary, Armstrong and Cassey [79] reanalysed the lemur dataset of Kalinowski and Hedrick (1998) [80] and they reported that the logit-linear models gave a better fit to the data than log-linear models proposed by Nietlisbach et al. [78].
6. Studies Signalling Purging Based on Ancestral Inbreeding or Inbreeding-Purging Model
The studies which are likely to observe purging are summarized in Table 2. The first comprehensive studies analysing the effect of ancestral inbreeding were performed on ZOO populations [40,81]. In these studies, many captive populations were evaluated but only a small fraction of these showed the signs of purging (one out of 25 in [40] and 14 out of 119 in [81]. Interestingly there were some contradicting results between these studies for example the Sumatran tiger population which analyzed in both studies only showed the signs of purging in the study of Ballou [40] but when it was reanalysed by Boakes et al. [81] they found no signs of purging. The two studies partly used different models as in [40] a model was defined where any fitness trait was possibly affected by the inbreeding coefficient of the litter and the inbreeding coefficient of the dam plus the interaction between the inbreeding coefficient and the ancestral inbreeding coefficient of the litter (year of birth was also included in the model). In the study of Boakes et al. [81] an alternative model was adopted from Boakes and Wang [91] where the interaction term was not used, but the inbreeding coefficient (F) of the litter and the dam and the ancestral inbreeding coefficient of the litter (FBAL) were included in the model separately. Based on computer simulations the proposed model of Boakes and Wang [91] was proved to be more advantageous in situations when when inbreeding depression is caused by mildly deleterious alleles [91]. Computer simulations indicated that purging is more likely to occur when deleterious mutations are of a large effect and when inbreeding occurs slowly and over many generations [92].
The rabbit studies [60,61] were highly adequate from this aspect as they covered 25-40 generations were the inbreeding was only slowly accumulated. For the Pannon white rabbit breed [93] it was showen that this slow increase of inbreeding level was mainly due to the applied circular mating system. However, by 2017 the Pannon white rabbit showed that more than 65% of the rabbits’ genome has already experienced inbreeding in previous generations making it less susceptible to inbreeding depression (Figure 1) [60].
This value is substantially higher than any of any examined ZOO population [81] where the populations with the highest (FBAL) were Addax (Addax nasomaculatus) and Przewalskii's horse (Equus ferus przewalskii) having mean (FBAL) values of 49.5 and 54.6%, respectively. However, it is important to note that the Pannon white rabbit population has a considerably lower inbreeding coefficient (Figure 1a, 1b) than these mentioned ZOO populations where the mean (F) values were 18.4 and 21%, respectively. It has to be emphasized that in [60] signs of purging was only detected between 1992-1997 where the litter inbreeding showed significant inbreeding depression on the survival of kits at birth while one of the ancestral inbreeding coefficients (FKAL) had a significantly positive effect. However, (FBAL) had no effect on the examined trait. Later no signs of purging were detected but inbreeding depression was also absent between 1997 and 2017 so it was concluded that the effects of new inbreeding involving several genes with large harmful effects were already purged between 1992-1997 [60]. The other rabbit study [61] was also was not fully consistent from the aspect of purging indication since these authors found the positive effects of the old inbreeding only (FOLD) on the slaughter and weaning weights respectively, while the other ancestral coefficients (FBAL, FKAL and AHC) had no effect on either trait. Concerning the cattle studies [37,38] Hinrichs et al. [37] found significantly positive effect of (FBAL) (but nonsignificant (FKAL) on birthweight signalling purging, but this finding is still not favourable as the increasing birthweight may cause problems with calving. Besides, when Hinrichs et al. [37] applied the original model of Ballou (1997) [37] then a significant positive interaction was observed between (F) and (FBAL) for birth weight and for stillbirth as well showing the possibility of purging for both traits. Calving ease, no signs of purging was found by any model. In [38] the results of (FBAL) and (FKAL) were consistent and both had positive effect on milk and protein yield of Irish Holstein-Friesian population but they did not influence other analysed traits (fat yield, calving interval, age at first calving and survival).
In case the possibility of purging is to be determined based on genealogy information then besides ancestral inbreeding the so called Inbreeding-Purging model is the other approach that can be used. The background theory was developed by García-Dorado [94] then the theory was tested on laboratory experiments using Drosophila melanogaster with different effective population sizes (between 6 and 50) [84,85]. Both studies recorded purging coefficients greater than 0 (0.02-0.30) and they concluded that in order to show purging the product of the effective population size and purging coefficient has to exceed 1 that implies that purging should be efficient for population sizes of order of a few tens and larger but purging might be inefficient against nonlethal deleterious alleles in smaller populations [84,85]. Concerning captive mammals López-Cortegano et al. [45] evaluated the genealogy of different threatened ungulate species of the Family Bovidae with different demographic histories: barbary sheep (Ammotragus lervia), Cuvier’s gazelle (Gazella cuvieri), dorcas gazelle (G. dorcas), and dama gazelle (Nanger dama). These populations had different effecting population sizes ranging between 4 (barbary sheep) and 39 (Dorcas gazelle). The study estimated purging coefficients larger than zero for all species (ranging from 0.08 to 0.48) but these estimates were only significant for the Cuvier’s gazelle and dama gazelle. Consequently, the conventional and the purged inbreeding coefficients were clearly separated for these species (Figure 2.).
The direct consequence of purging is the fitness rebound where after the initial decrease of the fitness when getting rid of the inbreeding depression the fitness of the population is increasing (Figure 3). The process is most apparent for the dama gazelle. Interestingly from the four evaluated populations the smallest and the larges populations did not show the signs of purging. The barbary sheep was too small and in this case drift overcomes purging while for the dorcas gazelle purging detection probably requires more generations [45].
In the domesticated animals according to our best understanding the only available study is [87] where the authors re-analysed the Pannon white rabbit data of Curik et al. (2020) [60]. The only other study where the ancestral inbreeding and Inbreeding-Purging model were applied for the same dataset was [86] claiming that Inbreeding-Purging Model had superior predictive characteristics compared to ancestral inbreeding predicting the future fitness of the evaluated population. The results of [87] were very similar to that of [60] finding purging signs only between 1992-1997 but not afterwards. Concerning the predicted fitness, it showed partial purging (Figure 4.) which means that after a certain period the fitness stabilized and did not show further decrease. It also confirms the conclusions of [60] that in the first period genes with large affects were purged contrary to that of the genes with mild effects.
With the advancing genomic methods, it is no wonder that when there is no pedigree available the existence of purging can also be determined using whole genome analysis [88,89,90]. These studies always compare different populations of the same species (i.e. small–isolated and large–connected Bengal tiger (P. tigris tigris) populations; [88]; island vs. mainland Kākāpō (Strigops habroptila) populations [89] and Iberian (Lynx pardinus) vs. Eurasian (Lynx lynx) lynx) populations in order to evaluate the differences and of the frequency and genomic distribution of putatively deleterious genotypes among the different populations.
7. Application Possibilities of Purging, Future Perspective
Although the purging phenomenon was investigated very extensively especially in ZOO populations [40,81] only a small fraction of these population showed the signs of purging and the observed amount of the purged inbreeding load was usually not too large. Since inbreeding can fix harmful mutations there is a general consensus in the field of animal breeding that intentional inbreeding should be avoided [25] when possible. However, in conservation genetics several studies suggested that based on different breeding designs (e.g. circular sib mating) inbreeding may be beneficial due to purging [95,96,97]. However, the efficiency of inbred mating depends on the balance between the loss of diversity, the initial decrease of fitness and the reduction of the inbreeding load [98]. Therefore, the so called application of purging should be treated with caution [99,100].
Author Contributions
Conceptualization, I.N. and T.A.N.; methodology, , I.N. and T.A.N.; software, Not Applicable; validation, , I.N. and T.A.N.; formal analysis, Not Applicable.; investigation, I.N. and T.A.N.; resources, , I.N. and T.A.N.; data curation, Not Applicable; writing—original draft preparation, , I.N. and T.A.N.; writing—review and editing, , I.N. and T.A.N.; visualization, , I.N. and T.A.N.; supervision, I.N.; project administration, Not Applicable; funding acquisition, Not Applicable. All authors have read and agreed to the published version of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Allendorf, F.W.; Funk, W.C.; Aitken, S.N; Byrne, M.; Luikart, G. Conservation and the Genomics and Populations, 3rd ed.; Publisher: Oxford University Press, Oxford, United Kingdom, 2022; pp. 1–672.
- Henderson, C.R. Best Linear Unbiased Estimation and Prediction under a selection model. Biometrics 1975, 31, 423-447. [CrossRef]
- Mehrabani-Yeganeh, H.; Gibson, J.P.; Schaeffer, L.R. Including coefficients of inbreeding in BLUP evaluation and its effect on response to selection. J. Anim. Breed. Genet. 2000, 117, 145–151. [CrossRef]
- Curik, I.; Ferencakovic, M.; Sölkner, J. Genomic dissection of inbreeding depression: A gate to new opportunities. Revista Brasileira de Zootecnia, 2017, 46, 773–782. [CrossRef]
- Schäler, J.; Krüger, B.; Thaller, G.; Hinrichs, D. Comparison of ancestral, partial, and genomic inbreeding in a local pig breed to achieve genetic diversity. Conserv. Genet. Resour., 2018, 12, 77-86. [CrossRef]
- Haig, S.; M., Ballou, J. D.; Derrickson, S. R. Management options for preserving genetic diversity: reintroduction of Guam rails to the wild. Conserv. Biol., 1990, 4, 290-300. [CrossRef]
- Zhang, Q.; Calus, M.P.; Guldbrandtsen, B.; Lund, M. S.; Sahana, G. Estimation of inbreeding using pedigree, 50k SNP chip genotypes and full sequence data in three cattle breeds. BMC Genet., 2015, 16(1), 1-11. [CrossRef]
- Frankham, R. Conservation genetics. Annu. Rev. Genetics, 1995, 29, 305-327.
- Kardos, M.; Luikart, G.; Allendorf, F.W. Measuring individual inbreeding in the age of genomics: marker-based measures are better than pedigrees. Heredity, 2015, 115(1), 63-72. [CrossRef]
- Malecot, G. (1970): Mathematics of Heredity. Publisher: Freeman & Company, Ltd. New York, US, pp. 1-88.
- Galla, S.J.; Brown, L.; Couch-Lewis (Ngāi Tahu: Te Hapū o Ngāti Wheke, Ngāti Waewae), Y., Cubrinovska, I.; Eason, D.; Gooley, R.M.; Hamilton, J.A.; Heath, J.A.; Hauser, S.S.; Latch, E.K., Matocq, M.D., Richardson, A.; Wold, J.R., Hogg, C.J., Santure, A.W.; Steeves, T.E. The relevance of pedigrees in the conservation genomics era. Mol. Ecol., 2022, 31, 41– 54.
- Hedrick, P.W.; García-Dorado, A. Understanding Inbreeding Depression, Purging, and Genetic Rescue. Trends Ecol. Evol., 2016, 31, 940-952. [CrossRef]
- Frankham, R.; Gilligan, D.M.; Morris, D.; Briscoe, D.A. Inbreeding and extinction: effects of purging. Conserv. Genet., 2001, 2, 279-284. [CrossRef]
- Crnokrak, P.; Roff; D.A, Inbreeding depression in the wild. Heredity, 1999, 83, 260-270. [CrossRef]
- Keller, L.F.; Waller, D.M. Inbreeding effects in wild populations. Trends Ecol. Evol.2002, 17, 230–241. [CrossRef]
- Leroy, G. Inbreeding depression in livestock species: review and meta-analysis. Anim. Genet., 2014, 45, 618–628. [CrossRef]
- Kardos, M.; Husby, A.; McFarlane, S. E.; Qvarnstrom, A.; Ellegren, H. Whole-genome resequencing of extreme phenotypes in collared flycatchers highlights the difficulty of detecting quantitative trait loci in natural populations. Mol. Ecol. Resour., 2016, 16, 727–741. [CrossRef]
- Doekes, H.P., Bijma, P., Windig, J.J. How depressing is inbreeding? A meta-analysis of 30 years of research on the effects of inbreeding in livestock. Genes, 2021, 12, 926. [CrossRef]
- Gutiérrez-Reinoso M.A.; Aponte P.M.; García-Herreros M.A. A review of inbreeding depression in dairy cattle: current status, emerging control strategies, and future prospects. J. Dairy Res., 2022, 28:1-10. [CrossRef]
- Vega-Trejo, R., de Boer, R.A., Fitzpatrick, J.L., Kotrschal, A. Sex-specific inbreeding depression: a meta-analysis. Ecol. Lett. 2022, 25, 1009–1026. [CrossRef]
- Sonesson, A.K.; Meuwissen, T.H.E. Mating schemes for optimum contribution selection with constrained rates of inbreeding. Genet. Sel. Evol., 2000, 32:231. [CrossRef]
- Sonesson, A.K.; Meuwissen, T.H.E. Minimization of rate of inbreeding for small populations with overlapping generations. Genet. Res. 2001, 77: 285-292. [CrossRef]
- Weigel, K. Controlling inbreeding in modern breeding programs. J. Dairy Sci. 2001, 84:E177–84. [CrossRef]
- Gebregiwergis, G.T.; Sørensen, A.C.; Henryon, M.; Meuwissen, T.H.E. Controlling coancestry and thereby future inbreeding by optimum-contribution selection using alternative genomic-relationship matrices. Front. Genet., 2020, 11, 345. [CrossRef]
- Kristensen, T.N.; Sørensen, A.C. Inbreeding–lessons from animal breeding, evolutionary biology and conservation genetics. Anim. Sci. 2005, 80, 121–33. [CrossRef]
- Templeton, A.R.; Read, B. The elimination of inbreeding depression in a captive herd of Speke’s Gazelle. In: C.M. Schonewald-Cox, S.M., MacBryde, B. and I. Thomas, editors, Genetics and conservation. Benjamin/Cummings, Menlo Park, California. 1983, p. 241-261.
- Read, B.; Frueh, R.J. Management and breeding of Speke’s gazelle, Gazella spekei, at the St. Louis Zoo, with a note on artificial insemination. — Int. Zoo Yb., 1980, 20: 99-106.
- Templeton, A.R.; Read, B. Factors eliminating inbreeding depression in a captive herd of Speke's gazelle (Gazella spekei). Zoo Biol., 1984, 3, 177-199. [CrossRef]
- Willis, K.; Wiese, R.J. Elimination of inbreeding depression from captive populations: Speke’s gazelle revisited. Zoo Biol., 1997, 16, 9–16.
- Templeton, A.R; Read, B. Elimination of inbreeding depression from a captive population of Speke’s gazelle: validity of the original statistical analysis and confirmation by permutation testing. Zoo Biol, 1998, 17:77–94. [CrossRef]
- Kalinowski, S.T.; Hedrick, P.W., Miller, P.S. Inbreeding depression in the Speke’s gazelle captive breeding program. Conserv. Biol. 2000, 14, 1375–84. [CrossRef]
- Templeton, A.R. The Speke’s gazelle breeding program as an illustration of the importance of multilocus genetic diversity in conservation biology: Response to Kalinowski et al. Conserv. Biol. 2002, 16: 1151-1155. [CrossRef]
- Bijlsma,B.; V. Putten, V. Environmental dependence of inbreeding depression and purging in Drosophila melanogaster J. Evolution. Biol.,1999, 12, 1125-1137. [CrossRef]
- Miller, P.S.; Hedrick, P.W.; Purging of inbreeding depression and fitness decline in bottlenecked populations of Drosophila melanogaster. J. Evol. Biol., 2001, 14, 595–601. [CrossRef]
- Pérez-Pereira, N., Pouso, R.; Rus, A., Vilas, A.; López-Cortegano, E., García-Dorado A., Quesada, H., Caballero, A. Long-term exhaustion of the inbreeding load in Drosophila melanogaster. Heredity, 2021, 127, 373–383. [CrossRef]
- Moreno, E.; Pérez-González, J.; Carranza, J.; Moya-Laraño, J. Better fitness in captive Cuvier’s gazelle despite inbreeding increase: evidence of purging? PloS ONE, 2015, 10:e0145111. [CrossRef]
- Hinrichs, D.; Bennewitz, J.; Wellmann, R.; Thaller, G. Estimation of ancestral inbreeding effects on stillbirth, calving ease and birthweight in German Holstein dairy cattle. J. Anim. Breed. Genet., 2015, 132, 59-67. [CrossRef]
- Mc Parland, S.; Kearney, F.; Berry, D. P. Purging of inbreeding depression within the Irish Holstein-Friesian population. Genet. Sel. Evol., 2009, 41, 1-8. [CrossRef]
- Wright, S. Coefficients of inbreeding and relationship. Am. Nat., 1922, 56, 330-338. [CrossRef]
- Ballou, J.D. Ancestral inbreeding only minimally affects inbreeding depression in mammalian populations. J. Hered., 1997, 88(3), 169-178. [CrossRef]
- Baumung, R.; Farkas, J.; Boichard, D.; Mészáros, G.; Sölkner, J.; Curik, I. GRAIN: a computer program to calculate ancestral and partial inbreeding coefficients using a gene dropping approach. J. Anim. Breed. Genet., 2015, 132, 100-108. [CrossRef]
- Slatis, H.M. An analysis of inbreeding in the European bison. Genetics, 1960, 45, 275-287. [CrossRef]
- Kennedy, E.S;, Grueber, C. E.; Duncan, R.P.; Jamieson, I.G. Severe inbreeding depression and no evidence of purging in an extremely inbred wild species—the Chatham Island black robin. Evolution, 2014, 68(4), 987-995. [CrossRef]
- Hinrichs, D.; Meuwissen, T.H.E.; Ødegard, J.; Holt, M.; Vangen, O.; Woolliams, J.A.; Analysis of inbreeding depression in the first litter size of mice in a long-term selection experiment with respect to the age of the inbreeding. Heredity, 2007, 99, 81–88. [CrossRef]
- López-Cortegano, E.; Moreno, E.; García-Dorado, A. Genetic purging in captive endangered ungulates with extremely low effective population sizes. Heredity, 2021, 127, 433-442. [CrossRef]
- Morton, N.E.; Crow, J.F.; Muller, H.J. An estimate of the mutational damage in man from data on consanguineous marriages. Proc. Natl. Acad. Sci. 1956, 42, 855–863. [CrossRef]
- Hoeck, P.E. A.; Wolak, M.E.; Switzer, R.A., Kuehler, C. M.; Lieberman, A.A. Effects of inbreeding and parental incubation on captive breeding success in Hawaiian crows. Biol. Conserv. 2015, 184, 357–364. [CrossRef]
- Boichard D. PEDIG: a fortran package for pedigree analysis suited for large populations. In Proceedings of the 7th world congress on genetics applied to livestock production: 19–23 August 2002; Montpellier. 2002, 525–8.
- Gutiérrez, J.P.; Goyache, F. A note on ENDOG: a computer program for analysing pedigree information. J. Anim. Breed. Genet., 2005, 122: 172-176. [CrossRef]
- Coster, A.; Coster, M.A. Package ‘pedigree’. R Package Version 1.4. 2010. Available online: https: //cran.r-project.org/web/packages/pedigree/index.html (accessed on 21 October 2023).
- Meuwissen, T.H.E.; Luo, Z. Computing inbreeding coefficients in large populations. Genet. Sel. Evol. 1992, 15, 24, 305–13. [CrossRef]
- Doekes, H.P.; Curik, I.; Nagy, I.; Farkas, J.; Kövér, G.; Windig, J.J. Revised calculation of Kalinowski’s ancestral and new inbreeding coefficients. Diversity, 2020, 12, 155. [CrossRef]
- MacCluer, J.W.; VandeBerg, J.L.; Read, B.; Ryder, O.A. Pedigree analysis by computer simulation. Zoo Biol., 1986, 5, 147–160. [CrossRef]
- Suwanlee, S.; Baumung, R.; Sölkner, J.; Curik, I. Evaluation of ancestral inbreeding coefficients: ballou’s formula versus gene dropping. Conserv Genet. 2007, 8, 489–95. [CrossRef]
- García-Dorado, A.; Wang, J.; López-Cortegano, E. Predictive model and software for inbreeding-purging analysis of pedigreed populations. G3, 2016, 6, 3593–3601. [CrossRef]
- López-Cortegano, E. PurgeR: Inbreeding and purging in pedigreed populations. Bioinformatics,2022, 38, 564–565. [CrossRef]
- Gilmour, A.R.; Gogel, B.J.; Cullis, B.R.; Thompson, R. ASReml User Guide Release 3.0. 2009, VSN International Ltd, Hemel Hempstead, HP1 ES, UK.
- Bates, D.; Machler, M.; Bolker, B.; Walker, S. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 2015, 67, 1–48.
- Bates, D.; Vazquez, A.I. Fit pedigree based mixed-effect models; 2014. http://pedigreemm.R-Forge.R-project.org. Accessed 22 Mar 2020.
- Curik, I.; Kover, G.; Farkas, J.; Szendrő, Z.; Romvari, R.; Sölkner, J.; Nagy, I. Inbreeding depression for kit survival at birth in a rabbit population under long-term selection. Genet. Sel. Evol., 2020, 52, 39. [CrossRef]
- Piles, M.; Sánchez, J.P.; Pascual, M.; Rodríguez-Ramilo, S.T. Inbreeding depression on growth and prolificacy traits in two lines of rabbit. J. Anim. Breed. Genet. 2023, 140, 39-48. [CrossRef]
- Ceballos, F.C.; Álvarez, G. Royal dynasties as human inbreeding laboratories: the Habsburgs. Heredity, 2013, 111, 114–21. [CrossRef]
- Jamieson, I.G.; Tracy, L.N., Fletcher, D.; Armstrong, D.P. Moderate inbreeding depression in a reintroduced population of North Island robins. Anim. Conserv. 2007, 10, 95–102. [CrossRef]
- Szulkin, M.; Garant, D.; McCleery, H.; Sheldon, B.C. Inbreeding depression along a life-history continuum in the great tit. J. Evol. Biol. 2007, 20, 1531–1543. [CrossRef]
- Laws, R.J.; Jamieson, I.G. Is lack of evidence of inbreeding depression in a threatened New Zealand robin indicative of reduced genetic load? Anim. Conserv, 2011, 14, 47-55. [CrossRef]
- Grueber, C. E.; Laws, R. J.; Nakagawa, S.; Jamieson, I.G. Inbreeding depression accumulation across life-history stages of the endangered takahe. Conserv. Biol. 2010, 24, 1617–1625. [CrossRef]
- Kennedy, E. S.; Grueber, C.E.; Duncan, R.P.; Jamieson, I.G. Severe inbreeding depression and no evidence of purging in an extremely inbred wild species - the Chatham Island black robin. Evolution 2014, 68, 987–995. [CrossRef]
- Hoeck, P.E.; Wolak, M.E.; Switzer, R.A.; Kuehler, C.M.; Lieberman, A.A. Effects of inbreeding and parental incubation on captive breeding success in Hawaiian crows. Biol. Conserv. 2015, 184, 357–364. [CrossRef]
- Stoffel, M.A.; Johnston, S.E.; Pilkington, J.G.; Pemberton, J.M.; Genetic architecture and lifetime dynamics of inbreeding depression in a wild mammal. Nat. Commun, 2021, 12, 2972. [CrossRef]
- Frankham, R. Effects of genomic homozygosity on total fitness in an invertebrate: lethal equivalent estimates for Drosophila melanogaster. Conserv. Genet. 2023, 24, 193-201. [CrossRef]
- Kardos, M.; Zhang, Y.; Parsons, K.M.; Kang, H.; Xu, X.; Liu, X.; Matkin, C.O.; Zhang, P.; Ward, E.J.; Hanson, M.B. Inbreeding depression explains killer whale population dynamics. Nat Ecol Evol. 2023, 7, 675–686. Sutter, J.;
- Tabah, L. Effets de la consanguinité et de l'endogamie. Une enquête en Morbihan et Loir-et-Cher. Population, 1952, 7, 249-266. [CrossRef]
- Tabah, L. Structure de la mortalité dans les familles consanguines. Population, 1953, 8, 511-526. [CrossRef]
- Falconer D.S. 1960. Genetics of the litter size in mice. J. Cell. Comp. Physiol. 56 (Suppl. 1) 153-167.
- Armbruster, P.; Reed, D.H. Inbreeding depression in benign and stressful environments. Heredity, 2005, 95, 235–242. [CrossRef]
- Grueber, C.E.; Nakagawa, S.; Laws, R.J.; Jamieson, I.G. Multimodel inference in ecology and evolution: challenges and solutions. J. Evol. Biol., 2011, 24, 699-711.
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach, 2nd ed. New York: Springer-Verlag; 2002.
- Nietlisbach, P.; Muff, S.; Reid, J.M.; Whitlock, M.C.; Keller, L.F. Nonequivalent lethal equivalents: Models and inbreeding metrics for unbiased estimation of inbreeding load. Evol. Appl, 2019, 12, 266–279. [CrossRef]
- Armstrong, D.P.; Cassey, P. Estimating the effect of inbreeding on survival. Anim Conserv. 2007, 10:487-92. [CrossRef]
- Kalinowski, S.T.; Hedrick, P.W. An improved method for estimating inbreeding depression in pedigrees. Zoo Biol., 1998, 17, 481-97. [CrossRef]
- Boakes, E.H.; Wang, J.; Amos, W. An investigation of inbreeding depression and purging in captive pedigreed populations. Heredity, 2007, 98, 172-182. [CrossRef]
- Lacy, R.C.; Ballou, J.D. Effectiveness of selection in reducing the genetic load in populations of Perommyscus polinotus during generations of inbreeding. Evolution, 1998, 52, 900-909. [CrossRef]
- Ács, V.; Kövér, G.; Farkas, J.; Bokor, Á.; Nagy, I. Effects of Long-Term Selection in the Border Collie Dog Breed: Inbreeding Purge of Canine Hip and Elbow Dysplasia. Animals, 2020, 10, 1743. [CrossRef]
- Bersabé, D.; García-Dorado, A. On the genetic parameter determining the efficiency of purging: An estimate for Drosophila egg-to-pupae viability.J. Evol. Biol., 2013, 26, 375–385. [CrossRef]
- López-Cortegano, E.; Vilas, A.; Caballero, A.; García-Dorado, A. Estimation of genetic purging under competitive conditions. Evolution,2016, 70, 1856–1870. [CrossRef]
- López-Cortegano, E.; Bersabé, D.; Wang, J.; García-Dorado, A. Detection of genetic purging and predictive value of purging pa- rameters estimated in pedigreed populations. Heredity,2018, 121, 38–51. [CrossRef]
- Kövér, Gy.; Curik, I.; Vostry, L.; Farkas, J.; Mezőszentgyörgyi, D.; Nagy, I. Analysis of Inbreeding Effects on Survival at Birth of Pannon White Rabbits Using the Inbreeding-Purging Model. Diversity, 2023, 15, 71. [CrossRef]
- Khan, A.; Patel. K.; Shukla, H.; Viswanathan, A.; van der Valk, T.; Borthakur, U.; Nigam, P.; Zachariah, A.; Jhala, Y.V.; Kardos, M.; Ramakrishnan, U. Genomic evidence for inbreeding depression and purging of deleterious genetic variation in Indian tigers. PNAS, 2021, 118, e2023018118. [CrossRef]
- Dussex, N.; van der Valk, T.; Morales, H.E.; Wheat, C.W.; Díez-del-Molino, D.; von Seth, J.; Foster, Y.; Kutschera, V.E.; Guschanski, K.; Rhie, A.; et al. Population genomics of the critically endangered Kākāpō. Cell Genom, 2021, 1, 100002.
- Kleinman-Ruiz, D.; Lucena-Perez, M.; Villanueva, B.; Fernández, J.; Saveljev, A.P.; Ratkiewicz, M.; Schmidt, K.; Galtier, N.; García-Dorado, A.; Godoy, J.A. Purging of deleterious burden in the endangered Iberian lynx. PNAS, 2022, 119, e2110614119. [CrossRef]
- Boakes, E.; Wang, J. A simulation study on detecting purging of inbreeding depression in captive populations. Genet Res. 2005, 86, 139–48. [CrossRef]
- Hedrick, P.W. Purging inbreeding depression and the probability of extinction: full-sib mating. Heredity, 1994, 73, 363–72. [CrossRef]
- Nagy, I.; Curik, I.; Radnai, I.; Cervantes, I.; Gyovai, P.; Baumung, R.; Farkas, J.; Szendrő, Z. Genetic diversity and population structure of the synthetic Pannon White rabbit revealed by pedigree analysis. J. Anim. Sci. 2010, 88, 1267–1275. [CrossRef]
- García-Dorado, A. Understanding and predicting the fitness decline of shrunk populations: inbreeding, purging, mutation, and standard selection. Genetics, 2012, 190, 1461–76. [CrossRef]
- Theodorou, K.; Couvet, D. The efficiency of close inbreeding to reduce genetic adaptation to captivity. Heredity, 2015, 114: 38–47. [CrossRef]
- Pérez-Pereira, N.; Caballero, A.; García-Dorado, A. Reviewing the consequences of genetic purging on the success of rescue programs. Conserv. Genet, 2022a, 23, 1–17. [CrossRef]
- Pérez-Pereira, N.; Caballero, A.; García-Dorado, A. Reviewing the consequences of genetic purging on the success of rescue programs. Conserv. Genet. 2022b, 23, 1–17. [CrossRef]
- De Cara, M.A.R.; Villanueva, B.; Toro, M.A.; Fernández, J. Purging deleterious mutations in conservation programs: Combining optimal contributions with inbred mattings. Heredity,2013, 110, 530–537. [CrossRef]
- Caballero, A.; Bravo, I.; Wang, J. The risk of forcing inbreed- ing in conservation programmes: A reply to Theodorou and Couvet. Heredity, 2017, 19, 51–53. [CrossRef]
- Ralls, K.; Sunnucks, P.; Lacy, R.C.; Frankham, R. Genetic Rescue: A Critique of the Evidence Supports Maximizing Genetic Diversity Rather than Minimizing the Introduction of Putatively Harmful Genetic Variation. Biol. Conserv., 2020, 251, 108784. [CrossRef]
Figure 1.
Evolution of the different dam and litter inbreeding coefficients of the Pannon white rabbits (Wright: a, b; Ballou: c, d; Kalinowski: e, f; Kalinowski new: g, h) [60].
Figure 1.
Evolution of the different dam and litter inbreeding coefficients of the Pannon white rabbits (Wright: a, b; Ballou: c, d; Kalinowski: e, f; Kalinowski new: g, h) [60].
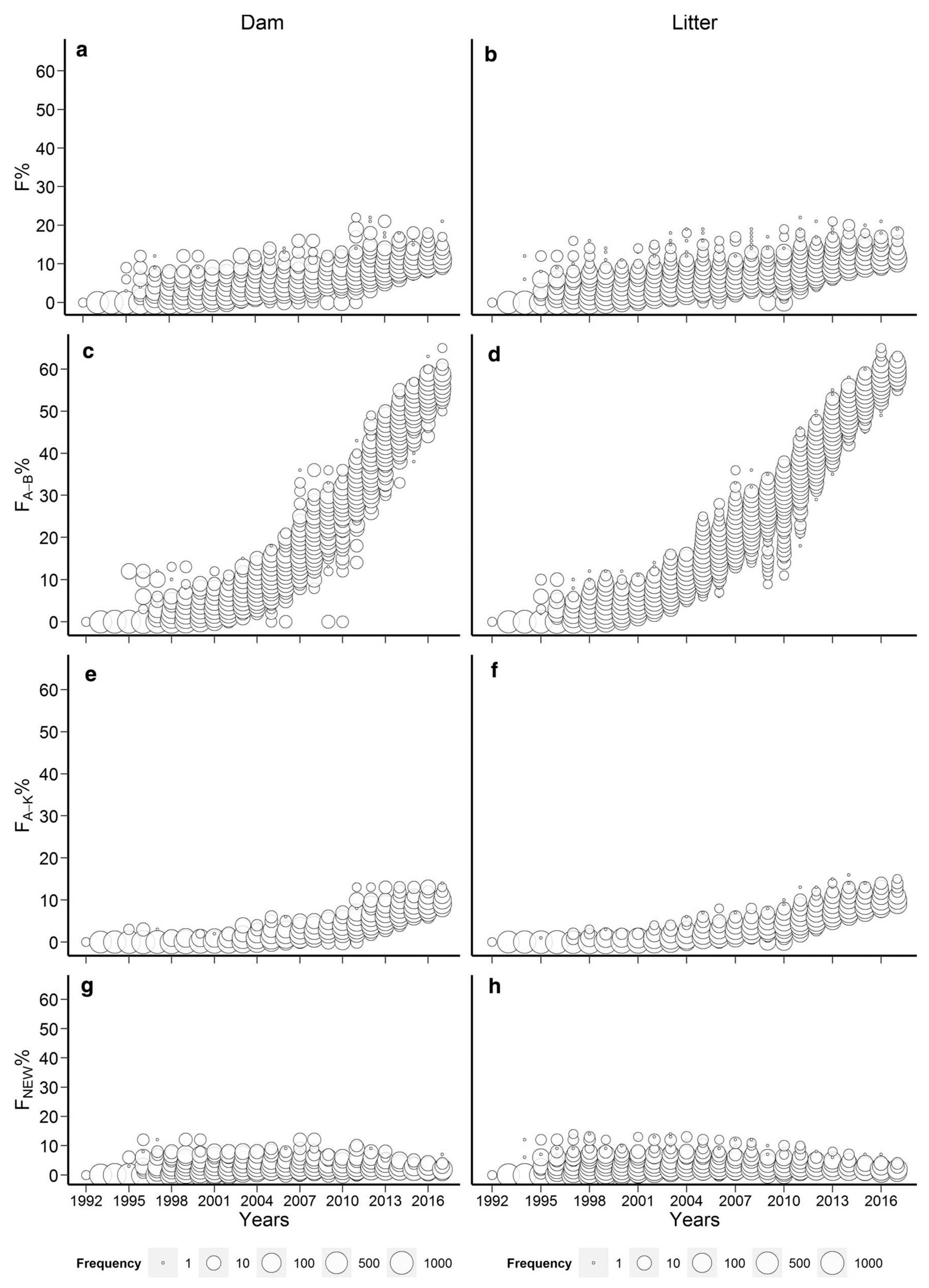
Figure 2.
Evolution of the standard (F, red) and purged (g, green) inbreeding coefficients through time. [45].
Figure 2.
Evolution of the standard (F, red) and purged (g, green) inbreeding coefficients through time. [45].
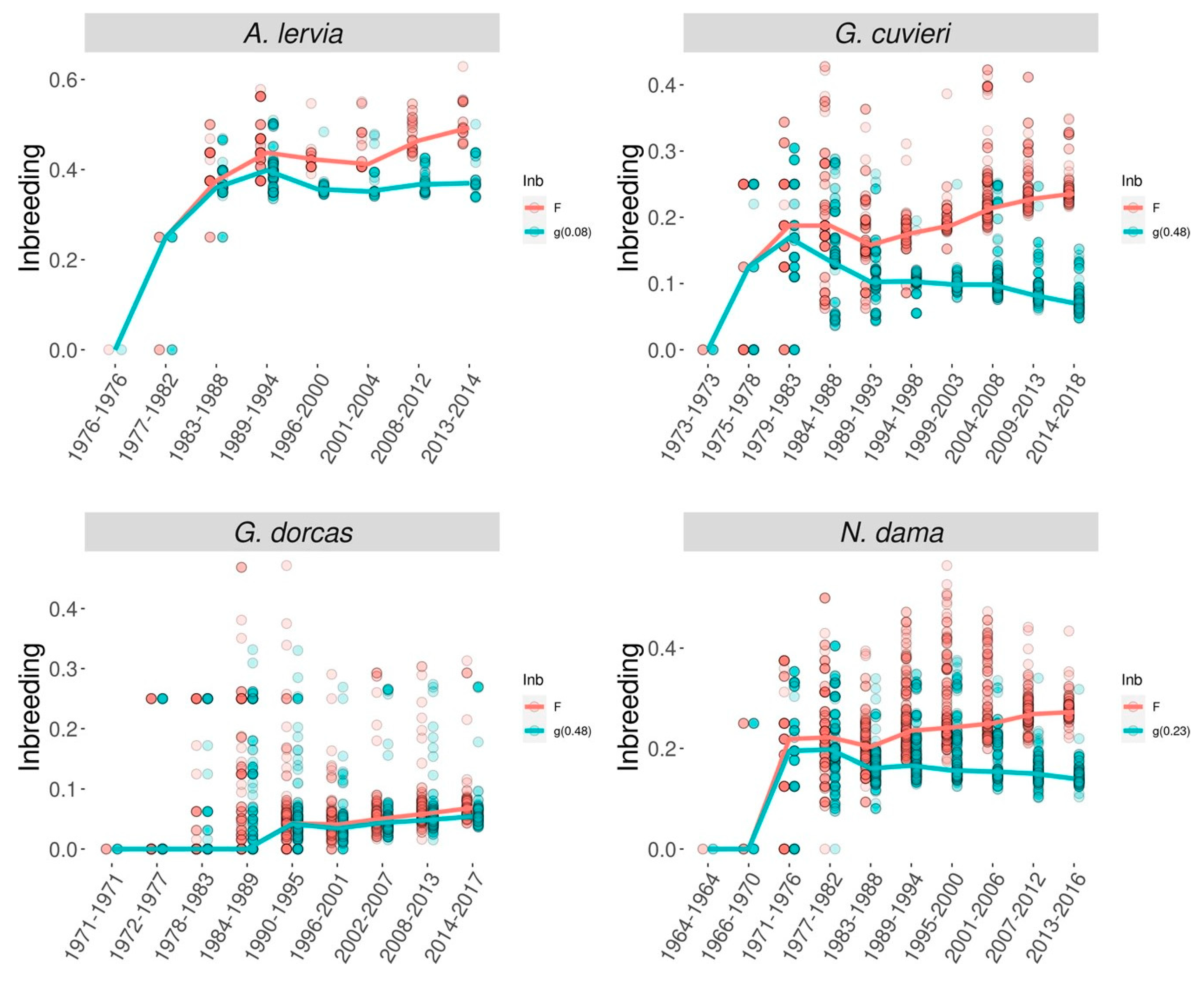
Figure 3.
Evolution of the early survival. [45].
Figure 3.
Evolution of the early survival. [45].
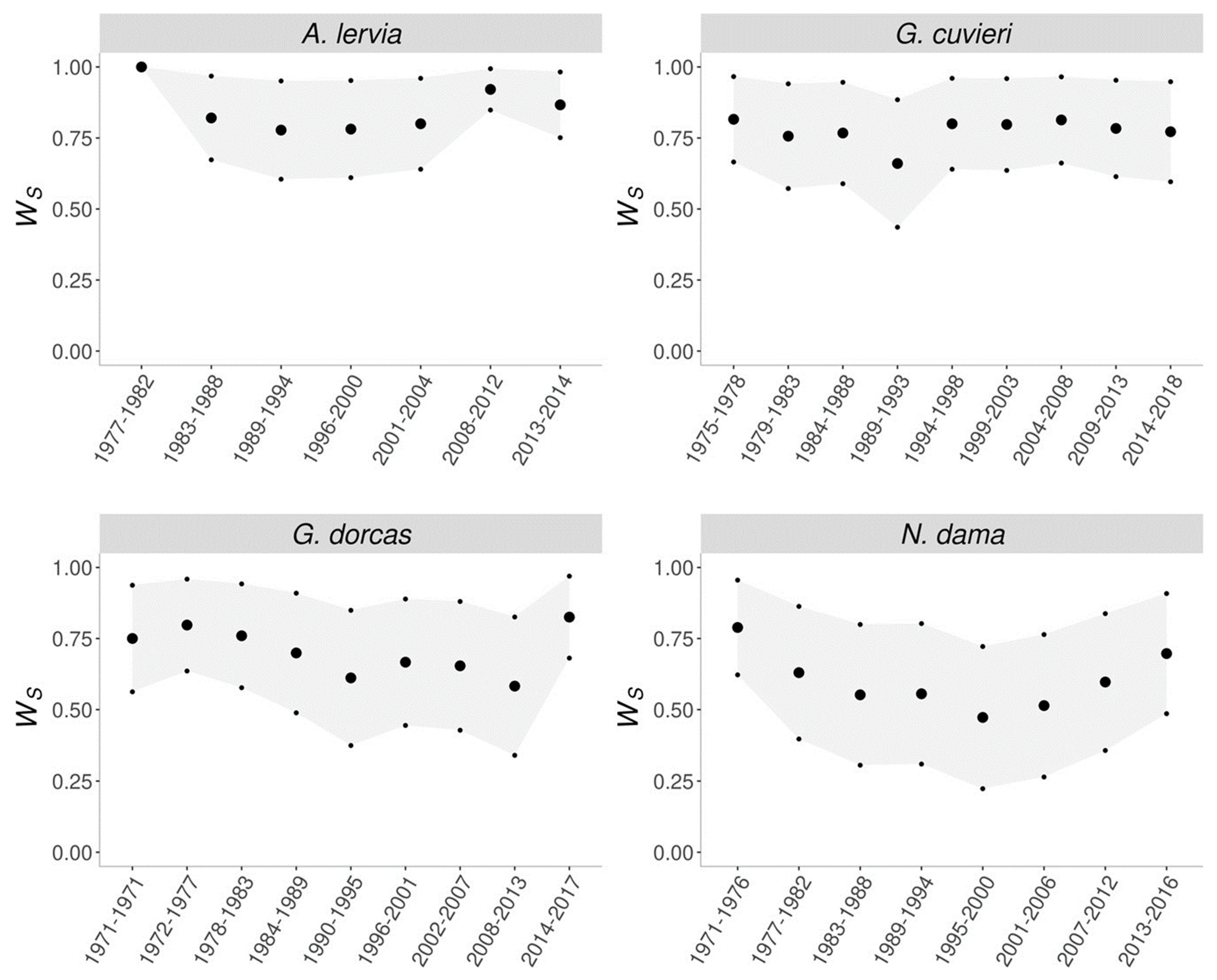
Figure 4.
The predicted fitness based on the Wright (F) and on the purged (g) inbreeding coefficients. [87].
Figure 4.
The predicted fitness based on the Wright (F) and on the purged (g) inbreeding coefficients. [87].
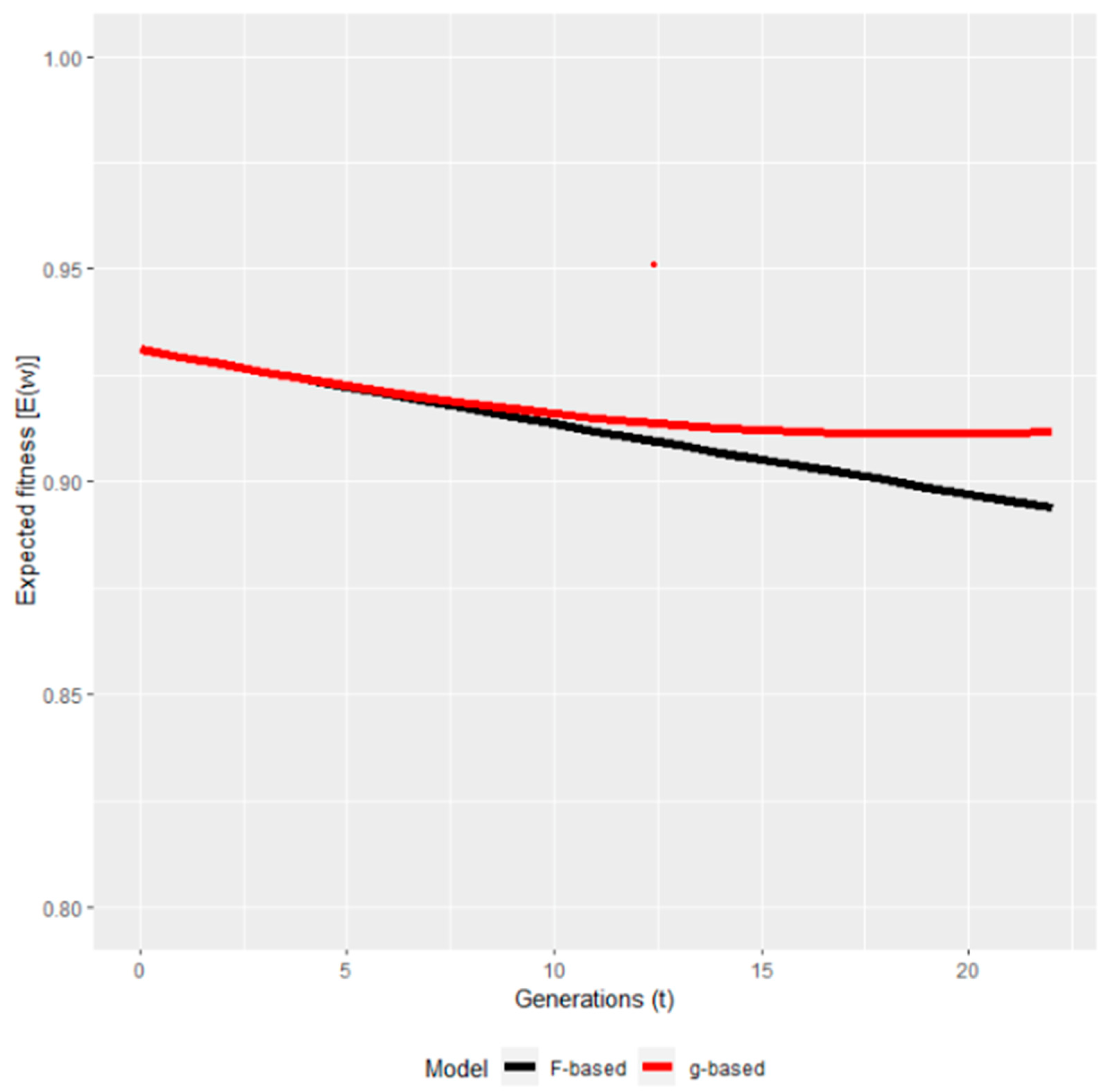
Table 1.
Haploid lethal equivalents estimated in different species.
| Species | Life history trait | Estimated lethal equivalent | Reference |
|---|---|---|---|
| Homo sapiens | Stillbirth and neonatal birth | 1.124a 0.574b |
[46] |
| Infant and juvenile death | 1.431a | ||
| 0.908b | |||
| Homo sapiens | Infant survival | 0.396c | [62] |
| 2.745d | |||
| Survival to 10 years | 4.373c | ||
| 3.674d | |||
| Speke’s Gazelle | 30-day viability | 2.97e | [26] |
| 1.59f | |||
| North Island robin | Juvenile survival | 4.14 | [63] |
| Great tit | Survival to hatching | 0.4 | [64] |
| Survival to fledging | 0.4 | ||
| Survival to recruitment | 1.3 | ||
| Survival to adulthood | 2.12 | ||
| New Zealand robin | Juvenile survival | 0.24 | [65] |
| Takahe | Hatching rate | 0.691 | [66] |
| Fledging rate | 3.339 | ||
| 2-year survival | 0.952 | ||
| Offspring recruitment | 3.383 | ||
| The Catham Island Black robin | Juvenile survival | 3.42 | [67] |
| Hawaiian crow | 2-year survival | 6.9 | [68] |
| Soay sheep | 1-year survival | 2.285 | [69] |
| Drosophila melanogaster | Total fitness | 5.04 | [70] |
| Killer whale | 1-year survival | 0.10g | [71] |
| 0.14h | |||
| 40-year survival | 2.74g | ||
| 3.74h |
aMorbihan; bLoir et Cher; c1450-1600; d1600-1800; elethal equivalent of the imported animals; flethal equivalent of the Zoo population; gmale; hfemale.
Table 2.
The observed purging cases in different species.
| Species/Breeds | Analyzed trait | Used methodology | Reference |
|---|---|---|---|
| German Holstein-Frisean | Birthweight | Ancestral inbreeding | [37] |
| Irish Holstein-Frisean | Milk yield | Ancestral inbreeding | [38] |
| Protein yield | Ancestral inbreeding | [38] | |
| Sumatran tiger | Neonatal survival rate | Ancestral inbreeding | [40] |
| Gazella cuvieri | Early survival | Inbreeding-Purging Model | [45] |
| Nanger dama | Early survival | Inbreeding-Purging Model | [45] |
| Pannon white rabbit | Survival at birth | Ancestral inbreeding | [60] |
| Prat rabbit line | Weaning weight | Ancestral inbreeding | [61] |
| Prat rabbit line | Slaughter weight | Ancestral inbreeding | [61] |
| Amur tiger | Survival to 7 days | Ancestral inbreeding | [81] |
| Black-footed ferret | Survival to 7 days | Ancestral inbreeding | [81] |
| Lesser kudu | Survival to 7 days | Ancestral inbreeding | [81] |
| Grey dorcopsis wallaby | Survival to 30 days | Ancestral inbreeding | |
| Hippopotamus | Survival to 30 days | Ancestral inbreeding | |
| Congo peafowl | Survival to 30 days | Ancestral inbreeding | [81] |
| Black-footed ferret | Survival to 30 days | Ancestral inbreeding | [81] |
| Bontebok | Survival to 30 days | Ancestral inbreeding | [81] |
| Goeldi's marmoset | Survival to 30 days | Ancestral inbreeding | [81] |
| Wied's Black-tufted-ear marmoset | Survival to 30 days | Ancestral inbreeding | [81] |
| Wyoming toad | Survival to 30 days | Ancestral inbreeding | [81] |
| Golden lion tamarin | Survival to 30 days | Ancestral inbreeding | [81] |
| Reindeer | Survival to 30 days | Ancestral inbreeding | [81] |
| Gunther's dik-dik | Survival to 30 days | Ancestral inbreeding | [81] |
| Peromyscus polinatus rhoadsi | Litter size | Ancestral inbreeding | [82] |
| Peromyscus polinatus rhoadsi | Litter weight and weaning | Ancestral inbreeding | [82] |
| Border collie dog | Hip dysplasia | Ancestral inbreeding | [83] |
| Drosophila melanogaster | Egg to pupae viability | Inbreeding-Purging Model | [84 |
| Drosophila melanogaster | Noncompetitive pupae productivity | Inbreeding-Purging Model | [85] |
| Drosophila melanogaster | Competitive productivity | Inbreeding-Purging Model | [86] |
| Pannon white rabbit | Survival at birth | Inbreeding-Purging Model | [87] |
| Indian tiger | NA | Whole genome analysis | [88] |
| Kākāpō | NA | Whole genome analysis | [89] |
| Iberian lynx | NA | Whole genome analysis | [90] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






