A Low Complexity Microwave Imaging System for Food Product Inspection through a Symmetry-Based Microwave Imaging Approach

Preprint

Article

A Low Complexity Microwave Imaging System for Food Product Inspection through a Symmetry-Based Microwave Imaging Approach

Altmetrics

Downloads

111

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

30 October 2023

Posted:

31 October 2023

You are already at the latest version

Alerts

Abstract

In food industry, there is a growing demand for cost-effective methods for inline inspection of food items able to non-invasively detect small foreign bodies which may have contaminated the product during the production process. Microwave imaging may be a valid alternative to the existing technologies, thanks to its inherently low-cost and its capability of sensing low-density contaminants. In this paper, a low-complexity microwave imaging system specifically designed to enable the inspection of a large variety of food products is presented. The system consists of two Circularly Loaded Antipodal Vivaldi Antennas, having a very large operative band, from 1 to 15 GHz, thus allowing a suitable spatial resolution for different food products from mostly fatty to high water-content ones. The antennas are arranged in such a way to collect the signal useful to exploit a recently proposed real-time microwave imaging strategy, leveraging the inherent symmetries usually characterizing food items. The system is experimentally characterized, and the achieved results compare favorably with the design specifications and the numerical simulations. Relying on these positive results, a first experimental proof of the effectiveness of the whole system is presented, which confirms its efficacy.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

In the food industry, products can be exposed to various contaminants that are potentially harmful to health. These contaminants include biological or chemical agents (such as bacteria, heavy metals, pesticides, and so forth) or solid contaminants like small fragments of glass, plastic, metal, wood, or other materials commonly used in packaging. Therefore, it is essential to monitor food items as they progress through the production chain to ensure their integrity before they reach the market [1,2]. Special attention is given to inspecting the presence of small foreign objects that may have entered the food during various production stages, especially during packaging [1].

This inspection can be done offline on selected samples or directly in-line when the product moves along the production line. The former method is less efficient and more costly because the discovery of even a single contaminated item can lead to the disposal of an entire batch, and it still does not guarantee the detection of all contaminated pieces. Therefore, in-line inspection is to be preferred.

Currently, several technologies are employed to perform this monitoring task: metal detectors, X-ray scanners, near-infrared sensors, or specialized optical cameras designed to seamlessly integrate into the production process [3,4,5,6]. However, there is still a notable rate of missed detections (false negatives). For example, metal detectors can only identify metallic objects, while X-ray technology may fall short in identifying low-density foreign materials, such as various types of plastics or fragile pieces of glass or wood. It may also pose potential risks to workers due to accidental exposure to radiation. Infrared sensors are limited by their penetration depth into the sample, and optical cameras are suitable only for transparent food and packaging. Hence, there is significant interest in exploring alternative solutions to address these limitations.

Recently, microwave imaging (MWI) has emerged as an appealing alternative to conventional diagnostic tools [6,7,8,9,10,11,12]. This approach is entirely safe, using low-intensity non-ionizing radiation, and offers good penetration depth for packaged food, making it a cost-effective and easily integrable solution for industrial production lines [11]. Of course, MWI is only applicable to food items packaged in non-metallic containers, which nonetheless, represent a significant portion of cases in food industry. These advantages have led to the recent development of dedicated MWI systems for food inspection [13,14,15,16].

In its basic configuration, an MWI system consists of a pair of antennas positioned on both sides of the conveyor belt on the production line. The system operates in bistatic mode [11] and probes the Object Under Test (OUT) at different frequencies and at different positions of the OUT while it moves along the production line (when in proximity of the system). The antennas need to be wideband [17] to ensure adequate frequency diversity necessary for reliable imaging. The antennas should be even Ultrawideband (UWB) to guarantee a good imaging resolution for a large variety of products (from mostly fatty to high water-content food), by exploiting different frequency sub-bands. To address this point, the design of the Circularly Loaded Antipodal Vivaldi Antenna (CLAVA) has been recently proposed, characterized by a broad operational band, from 1 to 15 GHz [14]. Moreover, being a printed antenna, such a solution meets the requirements of compactness and cost-effectiveness.

Regarding the image formation approach, the key requirements are a negligible computational burden to enable real-time imaging and a sufficient sensitivity, to reliably image even small foreign bodies, such as millimeter-sized inclusions. To achieve these features, the first proposed solution (hereafter referred to as the reference-based approach) is a differential approach where the imaging is performed by processing the difference between the data acquired for the OUT and those of a contaminant-free object (acquired once at the beginning and stored in memory) used as a reference [11]. However, this solution has the inconvenience that the reference object may be not identical to the OUT, or the positions at which the OUT is probed may not exactly match those at which the data of the reference object is acquired. As a result, a significant non-null differential signal may occur even in the absence of inclusions, thereby leading to a high rate of false positives. To avoid using a reference object, an alternative approach, hereafter referred to as the symmetry-based MWI approach, has been recently proposed. It is still a differential approach, but reference data are obtained from the data of the OUT itself [18,19], by exploiting the inherent “symmetries” that may characterize the OUT (a typical example of symmetric OUT is a product packaged in circular jars). The idea underlying the approach is that if the overall system, the OUT plus antenna system, exhibits certain spatial symmetries, namely does not change for rigid spatial transformations (like rotation, mirroring, and so on), the same happens for the acquired data (provided that the data are collected according to a scheme which is consistent with the considered symmetry). Therefore, as long as no inclusion is present, the difference between the “original” and “transformed” data is zero. Conversely, if an inclusion is present and its position in the OUT is such to disrupt the symmetry, the acquired data are no longer symmetric, and the difference between the original and transformed data is no longer zero. This difference can be, then, used to detect and image the inclusion. Of course, this approach works solely in the case of symmetric food items, which, however, is a common feature in practice.

Considering the above, the aim of this paper is to present a low-complexity MWI system for in-line food monitoring that exploits a pair of properly arranged CLAVAs and the symmetry-based (SB) approach to form the image. To this end, a comprehensive characterization of the CLAVA is performed, comparing the realized antenna with the designed one. Additionally, a proof-of-concept experiment is presented, to prove in simplified conditions the effectiveness of an MWI system equipped with the considered antennas and the SB approach.

The paper is organized as follows: Section 2 provides an overview of the design of CLAVA, of the basic architecture of the MWI system, and of the SB imaging approach. Then, the experimental setup (including the MWI system), build up to carry out the imaging experiment, is presented. Section 3 shows and discusses the results of both the experimental characterization of the antenna system and the imaging experiment carried out by using the system and the SB approach. Conclusions follow in Section 4.

2. Materials and Methods

2.1. Antenna Design

In order to create a device that can maintain consistent performance standards regardless of the specific food being inspected (i.e., irrespective of varying dielectric properties), the use of a UWB antenna is mandatory [20,21]. To achieve this goal, a frequency range of operation spanning from 1 GHz to 15 GHz has been considered. This range strikes an optimal balance between the achievable spatial resolution and the ability to penetrate diverse types of food materials. Furthermore, it is essential that the designed antenna meets criteria such as compactness, affordability, and resilience in the presence of other antennas within the MWI array.

The chosen antenna design adheres to the typical Antipodal Vivaldi Antenna configuration, enhanced by the incorporation of circular loads, referred to as CLAVA [14] (see Figure 1 for reference). The circular loads serve the dual purpose of extending the lower operating frequency range and enhancing the antenna's radiation characteristics, while maintaining a compact antenna size. Additionally, it is worth noting that the Vivaldi antenna is well-regarded for its directional properties, which are crucial for effectively radiating objects positioned just a few centimeters in front of the antenna.

The design methodology for the Antipodal Vivaldi Antenna was adapted from [20], with modifications to the dimensions and structure of certain elements to better meet the specific requirements at hand. For the actual project of the CLAVA, after constructing the antenna as described in [20], an optimization process was undertaken to reduce the antenna dimension, in order to enable a minimal impact on the structure of the production line. To this end, the first strategy was to choose a substrate dielectric material with high permittivity. In particular, RT/Duroid 6010LM was chosen, which has a dielectric constant of 𝜀𝑟=10.7, loss tangent 𝜏=0.0023, thickness ℎ=0.0635 𝑚𝑚, respectively; the copper thickness from which the antenna is built is 𝑡=0.017 𝑚𝑚.

The selected dimensions for the Vivaldi Antenna must obey with the following equations [20]:

L_{s u b} = \frac{c}{f_{L}} \sqrt{\frac{2}{ε_{r} + 1}}

(1)

and

W_{A N} = \frac{c}{2 f_{L}} \sqrt{\frac{2}{ε_{r}}}

(2)

where

L_{s u b}

and

W_{A N}

are respectively the length of the antenna and the opening of the flare (Figure 1), c is the speed of light,

f_{L}

is the lowest operating frequency and

ε_{r}

the dielectric permittivity of the material used for the substrate.

As mentioned above, the desired lower cutoff frequency is 1 GHz and the relative dielectric permittivity of the substrate is 𝜀_𝑟= 10.7. Substituting these values in (1) and (2), we get

L_{s u b} = 124 m m

and

W_{A N} = 45.85 m m

. However, the dimensions of this design still exceed the requirements for the intended application, making it incompatible with the fundamental design criterion: antenna compactness. To address this challenge and balance antenna size and bandwidth, we introduced two circular antipodal loads onto the radiator and ground, as illustrated in Figure 1, with radius

r = 14.78 m m

. This approach enables us to sustain a desired bandwidth while reducing the antenna's overall size [14].

The antenna parameters were optimized by way of simulations performed through CST Studio Suite (Dassault Systèmes, Vélizy-Villacoublay, France). The parameters considered in the optimization process were the substrate length

L_{s u b}

and width

W_{s u b}

, which define the antenna’s overall dimensions and affect its matching.

Additionally, the input microstrip line width

W_{f}

as well as the curvature of the ground plane to allow the transition from the input microstrip line to the balanced line feeding the antenna was optimized too. The final design foresees an antenna dimensions of

L_{s u b} = 50 m m

and

W_{s u b} = 71.56 m m

; a microstrip width of

W_{f} = 0.55 m m

, and a curvature of the lower ground section realized through a quarter ellipse with semi-axes equal to 𝑟₁=5.7 mm and 𝑟₂=13.725 mm (refer to bottom part of Figure 1).

Other details about the antenna design and the parameters optimization can be found in [14]. Two prototypes of the CLAVA antenna were realized through photolithography process, to allow performing the MWI experiments.

2.2. Basic Structure of the MWI System and Measurement Scheme

The basic architecture of the MWI system is shown in Figure 2. As anticipated, it consists of two CLAVAs positioned in front of each other on both sides of the production line. Each antenna works as both transmitter and receiver allowing one to acquire the 2 × 2 scattering matrix, S_ij i,j = 1, 2, by using a two-port Vector Network Analyzer (VNA). To increase the number of independent data available, the S_ij are acquired at 2M+1 different positions, zm = mΔ_z, m = −M,..., M, assumed by the OUT when approaching the system, having assumed as z₀ = 0 cm the position of the OUT when it is in the middle between the two antennas (as shown in Figure 2). Moreover, for each probing position, the S_ij are measured at N frequencies, say f_n, n = 1,...,N (for further details, the reader is referred to [18]).

2.3. MWI Approach

The adopted SB approach exploits the symmetries that typically characterize the OUT and the MWI system, thus avoiding the need for additional reference measurements as in the RB approach [11].

A typical case (referred to as Orthogonally Symmetry-based (OSP) approach [18]) is that depicted in Figure 3a where the OUT has circular symmetry (a quite common case in food industry) and each antenna is characterized by its own symmetry plane, which virtually splits it into two identical halves (this is quite common in antenna design, including the developed CLAVA, for which a symmetry plane is the xy-plane of Figure 1). In this case, if the two antennas are placed in front of each other with their symmetry planes coincident and orthogonal to the direction of motion (as shown in Figure 3a, where the symmetry planes coincide with the xy-plane), the overall system, observed when the OUT is at z = z_-m, appears perfectly specular to the overall system observed when the OUT is at z = z_+m (m = 1,…, M). As a result, the transmission parameters, S₂₁ and S₁₂, measured by the couple of antennas, when the OUT is respectively at z = z_-m and at z = z_+m, are equal, so that their difference is zero (below the measurement noise, in practice). However, if an inclusion is present in the OUT (see Figure 3b), such symmetry is lost, and the transmission parameters are no longer equal. Then, their difference can be used to detect and image the inclusion.

As pointed out in [18], The advantage of this approach is that the symmetry is preserved even when the OUT is not evenly spaced from the two antennas, but is slightly displaced towards one of them, as shown in Figure 3a. This happens because the displacement is along the symmetry plane. Another advantage is the use of the transmission parameters as input data of the inversion. Indeed, thanks the reciprocity, S₂₁=S₁₂, so that the antennas are exchangeable. This implies that the antennas can be even different to each other, provided that they have a same symmetry plane. A drawback of this approach is the limited number of data exploited (only the measured transmission parameters) which results in not unique imaging of the contaminant (as it will be shown in Section 3.2). In any case, the lesser challenging requirements, listed above, make this second symmetry easier to implement in practice, so that it will be the symmetry assessed in this paper through the implemented MWI system.

2.4. Numerical Green’s Function

As described in [18], the SB reconstructs the inclusion from the data by solving a linear inverse problem, where the Green’ function is the dot product between the electric fields radiated by the two antennas in the OUT (without the inclusion), evaluated at each frequency, f_n, and position, z_m. Therefore, one needs to know the Green’ function to reconstruct the inclusion from the measured data. A way to do this is by numerical simulations. Again, we have employed the CST Microwave Studio.

The adopted numerical model is depicted in Figure 4 (in the case of OUT at the position z = 0 cm). As in [18], the Green’ function was computed by placing the OUT at each of the 2M+1positions, z_m=mΔ_z (m=-M,…,M, M = 6 and Δ_z = 1 cm) and running the simulation, over the frequency band 4-7 GHz (this is the sub-band exploited in Section 3 for the imaging). The data vectors, of N*P elements, extracted from each simulation (being N = 13 the number of evenly spaced frequency samples, over the range 4-7 GHz, and P = 84054 the number of cells of the mesh in the OUT), were then organized in a rectangular matrix, of size M*N x P, relative only to the positions z_m with m = 1,…, M, representing the Green’ function used in the SB approach (see [18]).

In conclusion, it is worth noting that, while the considered model is realistic, it does not perfectly reproduce the experimental setup (see Figure 5b). Indeed, while the antennas are accurately modeled, all the other parts, such as the cable connecting the antennas to the VNA, the antenna supports and the system's workbench, are either roughly recreated or even missing in the model. Even the OUT is not perfectly modeled.

Indeed, while shape and sizes are quite faithful to the actual OUT, the food level in the jar, the jar thickness (assumed uniform and equal to 3 mm in the model) and so on, are not accurately reproduced. As well as it may be different the values of the complex relative permittivity of the different materials composing the OUT, here assumed equal to 6 for glass and equal to 3 – j 0.42 for the cream, over the whole analyzed frequency range. Indeed, these values are the ones measured for the product investigated in [11] and are averaged over the investigated frequency range. Of course, a not precise numerical model, as ours, translates into a not accurate computing of the Green’s function and so to a worsening of the imaging performance. However, a more accurate modelling is hard to achieve in practice due to the increase of the uncertainty associated with a greater number of involved parameters (both electromagnetic and geometrical). Nonetheless, a lesser accurate model was intentionally employed in order to test the robustness of the SB approach against the model uncertainties.

2.5. Measurement Setup

Figure 5 shows a picture of the realized MWI system. According to the scheme in Figure 2, the system comprises two CLAVAs placed in front of each other at a distance d_a = 15 cm (Figure 5a). The antennas are mounted parallelly to the bench, on which the overall system is placed, at a height d_p = 5 cm. To exploits the SB approach, the antennas are aligned with their symmetry planes orthogonal to the direction along which the OUT moves (red arrow in Figure 5a).

The data (scattering parameters S_ij i,j=1, 2) are measured by a two ports VNA (PNA Network Analyzer E8363C, Agilent Technologies, [10 MHz-40 GHz]) connected to the antennas through two coaxial cables.

To ensure the symmetry of the overall system, a (homogeneous) chocolate-hazelnut cream packaged in circular jar of glass (of radius 4 cm and height 10 cm) was chosen as OUT. Figure 5b shows the system with the OUT positioned in the middle between the two antennas (at the distance d_c = 4 cm from each of them).

The presence of an inclusion in the OUT was simulated by inserting in the cream a metallic sphere of

1 c m

in size, positioned at a height of about 5 cm in the jar, on the left-bottom quadrant (see Figure 6). Note that the size and the material of the inclusion are not properly the ones typically encountered in practice where the contaminant is usually smaller (around 5 mm in size) and not metallic (typically the contaminant is made of glass, plastic, or wood). This choice is justified by the preliminary nature of the presented experimental validation, whose main goal is to provide a first proof of the effectiveness of the SB approach proposed in [18,19], leaving aside any sensitivity analysis with respect to the size, material, and position of the inclusion.

The imaging experiments were carried out with and without the inclusion in the OUT in order to enable a comparison with a control case.

The movement of the OUT on the production line was reproduced by manually moving it along the direction of the arrow in Figure 5b, corresponding to the z-axis in Figure 2. The data were acquired at different positions of the OUT, ranging from -6 cm to +6 cm, with a step of 1 cm (i.e., z_m=mΔ_z, with m = -M,…, M, M =6 and Δ_z = 1 cm). ). Note that this number of measurements is consistent with the constraints arising from the typical speed of production lines and VNA acquisition rates [11]. The reference position, z₀ = 0 cm, is when the OUT is just in the middle between the two antennas (see Figure 5b). For each position, the data at N=13 frequencies, ranging from 4 to 7 GHz with a frequency step of 0.25 GHz were acquired. It is worth noting that, while the antennas are characterized in a wider band, from 1 to 15 GHz as shown in Section 3, only a sub-band was used in the imaging experiments. This choice is in part motivated by the need of limiting the detrimental effects on the symmetry of a not perfect manual alignment of the antennas, as well as a not perfect manual positioning of the OUT at the specular positions z_±m, which are surely more pronounced at higher frequencies. In addition, this choice still allows to treat the inclusion as a small scatterer and so to face the imaging problem at hand as a linear inversion problem (although the inclusion is surely not a weak scatterer).

2.6. Measurement Procedure

The measurement procedure begins with the full two-ports calibration of the VNA. As previously reported, the considered frequency range is 4-10 GHz. 1601 frequency samples were acquired, with an IF bandwidth of 1 kHz, and an incident power set to 0 dBm.

Concerning the characterization of the antennas, two sets of measurements were carried out. Firstly, the reflection coefficient at the input port of each antenna was measured with the antenna standing alone. This was done to evaluate whether the measured bandwidth (at -10 dB) matches the design specifications and the simulation results. Then, the four scattering parameters of the antenna system (see Figure 5a) were measured to assess how the reflection coefficients of the antennas change and to evaluate the levels of the transmission parameters, S₁₂ and S₂₁, which are the parameters exploited for the imaging.

Regarding the assessment of the SB approach, as already stressed, two different imaging experiments were carried out (according to the measurement scheme described in Section 2.2 and 2.3):

OUT with the inclusion inside.
OUT without inclusion.

The latter serves as control case, to check that in the absence of an inclusion, no image is produced by the SB approach. In addition, these data are used as reference data to implement the RB approach, to allow a comparison with the reconstructions achieved by the SB approach.

3. Results and Discussion

3.1. Validation of the Antenna Design

Figure 7 shows a comparison of the measured reflection coefficient of the two fabricated antennas with the simulated one. The measurements were carried out with the two antennas placed 15 cm apart from each other, in accordance with what was mentioned in section 2.5. In particular, Figure 7a shows the reflection coefficient magnitude, while Figure 7b reports the transmission coefficient ones. From the figure a good agreement can be derived between simulations and measurements. At the same time, it can be noted that, due to the limited accuracy of the manufacturing process, the two antennas have several differences, which nonetheless do not invalidate the matching, nor the transmission of the signal.

3.2. Assessment of the SB Approach

Figure 8 shows the magnitude (in dB), vs frequency, of the difference S₂₁(z_-m, f)−S₂₁(z_+m, f), measured when the OUT is positioned at z_±m = ± 1, ± 2,…, ± 6 cm along the z-axis (it is worth recalling that the antennas are mounted with their symmetry planes coincident with the xy-plane, i.e. with the plane of equation z = 0, so that the probing positions, z_±m, are specular to each other with respect to such plane). Specifically, the blue lines represent the data relative to the OUT with inclusion and are the data provided in input to the inversion algorithm implementing the SB approach. For comparison, Figure 8 also shows the same data, but relative to the OUT free of inclusion (red lines).

Note that the figure provides the difference over the frequency range 4–7 GHz, in agreement with what stated in Section 2.3.

From Figure 8, it can be noted that the blue lines dominate over the red lines. Since |S₂₁(z_-m, f)−S₂₁(z_+m, f)| can be interpreted as an indicator of the degree of symmetry of the OUT (the larger its value the lower the degree of symmetry of the OUT), this implies that in the case of the blue data, the OUT exhibits a reduced symmetry, in agreement with the presence of the inclusion. Therefore, the presence of the inclusion impairs the symmetry of the system, resulting in a remarkable difference between the transmission parameters measured at specular positions, z_±m, of the OUT along the line.

Furthermore, note that a non-null |S₂₁(z_-m, f)−S₂₁(z_+m, f)| (i.e., above the noise level, but not larger than about -35 dB) is also observed in the case of OUT free of inclusion. This suggests that the overall system is not perfectly symmetrical even when no inclusion is present in the OUT.

Such difference can arise due to several factors, including misalignment between the two antennas or between the antennas and the direction of movement, or inaccurate positioning of the OUT at the specular positions z_±m. However, such a difference is notably lower, by up to 20 dB, than the difference observed in the presence of the inclusion (as in the case z_±m = ± 1 cm). Moreover, it can be further reduced by removing (or mitigating) the sources of “asymmetry” mentioned above. This is an encouraging outcome, especially in view of the practical applications of the method, where the goal is to detect and image smaller and less contrasting inclusions.

From Figure 8 it can be also noted that the discrepancy between blue and red lines is more pronounced in the case z_±m = ± 1, ± 2 cm, gradually reducing in the other cases. This trend is coherent with the fact that at z_±m = ± 1, ± 2 cm the OUT, hence the inclusion, is closer to (and more in front of) the antennas than the other positions, thus yielding a more intense scattered signal.

For the sake of comparison, Figure 9 shows the magnitude (in dB) vs frequency of the difference between the transmission parameters measured when the OUT carries the inclusion and the ones measured when the OUT is free of inclusion (reference data). These are the data to be provided as input to the inversion algorithm implementing the RB approach. As it can be seen, a remarkable difference is observed for certain positions (above -30 dB for z=+1 cm), revealing the presence of the inclusion in the OUT, which is absent in the reference object. Once again, this difference becomes more pronounced as the OUT, along with the inclusion, approaches the antennas’ aperture and becomes progressively less significant when the OUT goes away from the antennas.

The data in Figure 8 and Figure 9 were then processed through the respective inversion algorithms to provide an image of the inclusion.

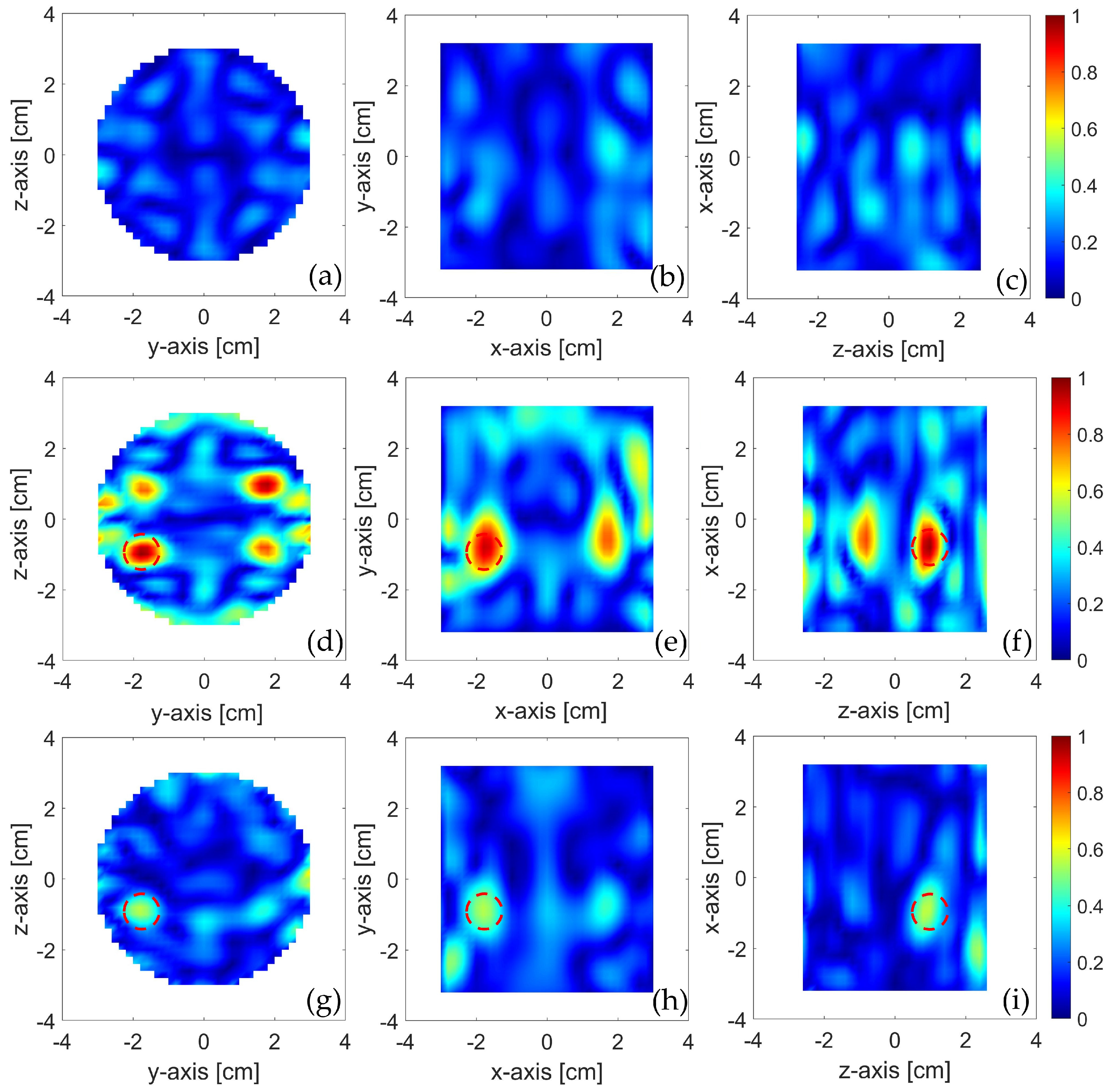
Figure 10 displays the reconstructions achieved for the magnitude of the electric contrast variation, say χ(r), due to the inclusion. Specifically, panels (a)-(c) show (in three different cut-planes) the reconstruction achieved through the SB approach, by processing the red data in Figure 8 (i.e., those relative to the OUT without inclusion); panels (d)-(f) show the reconstructions obtained by processing the blue data in Figure 8 (i.e., those relative to the OUT with inclusion). Finally, panels (g)-(i) present the reconstruction obtained by processing the data in Figure 9, through the RB approach. For the sake of comparison, all the maps were normalized to the maximum value, denoted as

{m a x}_{\underline{r}, t} | χ_{t} (\underline{r}) |

, where the subscript t indicates the type of MWI approach adopted to reconstruct χ(r), SB or RB.

From panels (a)-(c), it is noticeable that in absence of inclusion, a substantially flat map is returned, while well-localized spots emerge in panels (d)-(f), indicating the presence of the inclusion. This confirms the effectiveness of the SB approach in providing reliable results for both the possible situations: OUT with and without inclusion. An inherent inconvenience of this approach is that it does not yield a univocal image, but multiple images of the same inclusion: one at the actual position (indicated by the red dashed circles in Figure 10) and the three others at exactly specular positions with respect to the y = 0 and z = 0 planes (see panel (d)). The onset of these replicas is an unavoidable consequence of: I) the assumed symmetry along the z-axis, which does not allow to discriminate the actual position of the inclusion with respect to such axis, and II) the reciprocity, which does not allow to distinguish the reciprocal position of the inclusion concerning the antennas (hence, with respect to the y-axis). From a practical point of view, this effect results from the reduced number of data available for the imaging, as half of them are used as reference data and half of them are equal for reciprocity. Nevertheless, given that the main aim of the system would be to discriminate between OUT with and without contaminants, the presence of the ghost images is not an actual shortcoming of the procedure. Additionally, the ambiguity can be overcome by building a more sophisticated MWI system and exploiting other symmetries, involving the reflection coefficients (for more details, the reader is referred to the numerical results in [18]) or rotating the OUT by 90 degrees and repeating the measurement.

Finally, the maps in the panels (d)-(f) with those in panels (g)-(i), obtained with the RB approach, can be compared. As it can be observed, the RB approach also returns a spot just at the position of the inclusion (plus another less intense spot, arising at the specular positions with respect to the y-axis, again due to reciprocity), perfectly overlapping one of the spots in panels (d)-(f). The correspondence between the two reconstructions allows to rule out that the result in (d)-(f) is an artifact, thus further confirming the effectiveness of the SB approach investigated in this paper.

4. Conclusions

In this paper, we developed a preliminary proof of concept that involves the utilization of a MWI system based on two CLAVAs to detect contaminants in packaged food items. Additionally, we experimentally confirmed the effectiveness of an imaging approach that leverages the symmetries of both the MWI system and of the inspected object. The conducted analyses demonstrate the feasibility of the proposed system and method. In fact, as evidenced by the reconstructions and as it can be easily inferred from the scattering parameter trends, this experimental setup can detect the contaminant object inside the jar. From this point of view, the presence of "ghosts" can be sufficiently tolerated.

It is worth noticing that imaging is not a crucial aspect in the food industry. This suggests that, although imaging of contaminants can be useful, the primary focus is on the detection of anomalies or the contaminants themselves within food products. From this perspective, the proposed imaging method, such as the SB approach, appears to be sufficient to fulfill this task. The next step would be contaminant imaging. In this case, the SB approach alone is not enough, but an alternative would be to use it in conjunction with other methods, like the Parallel Symmetry Plane (PSP) method presented in [18]. It's important to emphasize that in the case under consideration, the parallel symmetry was intentionally not used because there is uncertainty about whether the jar is precisely centered between the two antennas, and therefore, the scattering parameters S₁₁/S₂₂ may not be symmetrical.

The study presented reports preliminary experimental results. This is due to several factors. Firstly, the measurements were not conducted in a controlled environment, as an anechoic chamber was not used to eliminate potential interference. The system used consists of two antennas of the same type but not perfectly identical, resulting in slightly different scattering coefficients. Furthermore, the alignment of the system cannot be considered perfect, leading to some discrepancies in measurements when the jar's position varied. To account for all these uncertainties, it was also decided to use a sphere with a diameter larger than the contaminants one would expect in a jar of hazelnut cream. Nevertheless, it's worth noting that the absence of a controlled environment may have its advantages. In an industrial setting, multiple reflections can occur during the process, potentially introducing interference that impacts the received signal at the antenna terminals.

Everything that has been done so far represents a starting point; from here on, there are several things to do. First and foremost, it is necessary to build a dedicated measurement system with high symmetry, ensuring that the antennas comprising it exhibit consistent behavior. Additionally, it is necessary to repeat the measurements in a more controlled environment. This would allow to replicate this study, not only with the proposed SB but also with PSP methods. Furthermore, by eliminating the uncertainties of the system, it would be possible to use more realistic contaminants, such as half-centimeter-long fiberglass fibers.

Author Contributions

Conceptualization, G. B., L. C., and M. C.; methodology, G. B., L. C., N. Z., S. Z., and M. C.; numerical simulation and analysis G. B., N. Z., and. S. Z.; measurements A. B., A. M. N. Z. and M. C., validation G. B., L. C., N. Z., S. Z. and M. C.; writing—original draft, G. B., L. C., S. Z. and M. C.; funding: G. B., L. C. and M. C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Italian Ministry of University and Research under the 2017 PRIN project “BEST-Food, Broadband Electromagnetic Sensing Technologies for Food Quality and Security Assessment.”, Prot. N. 20179FLH4A.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

CLAVA	Circularly Loaded Antipodal Vivaldi Antenna
MWI	MicroWave Imaging
OUT	Object Under Test
OSP	Orthogonal Symmetry Plane
PSP	Parallel Symmetry Plane
RB	Reference-Based
SB	Symmetry-Based
UWB	Ultrawideband
VNA	Vector Network Analyzer

References

Lau, O.W.; Wong, S.K. Contamination in food from packaging material. J. Chromatogr. A 2000, 882, 255–270. [Google Scholar] [CrossRef] [PubMed]
Nerín, C.; Aznar, M.; Carrizo, D. Food contamination during food process. Trends in food science & technology. 2016, 48, 63–68. [Google Scholar]
Porep, J. U.; Kammerer; D. R.; Carle, R. On-line application of near infrared (NIR) spectroscopy in food production. Trends in Food Science & Technology 2015, 46, 211–230.
Haff, R.P.; Toyofuku, N. X-ray detection of defects and contaminants in the food industry. Sens. Instrum. Food Qual. Saf. 2008, 2, 262–273. [Google Scholar] [CrossRef]
Bick, M.; Sullivan, P.; Tilbrook, D. L.; Du, J.; Gnanarajan, S.; Leslie, K. E.; Foley, C. P. A SQUID-based metal detector—comparison to coil and X-ray systems. Superconductor Science and Technology. 2015, 18, 346. [Google Scholar] [CrossRef]
Edwards, M. (Ed.). Detecting foreign bodies in food. Elsevier. 2004.
Nikolova, N.K. Introduction to Microwave Imaging, 1st ed.; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
Wu Z.; Wang. H. Microwave tomography for industrial process imaging: Example applications and experimental results. IEEE Antennas Propag. Mag. 2017, 59, 61–71. [CrossRef]
Asefi, M.; Jeffrey, I.; LoVetri, J.; Gilmore, C.; Card, P.; Paliwal, J. Grain bin monitoring via electromagnetic imaging. Comput. Electron. Agric. 2015, 119, 133–141. [Google Scholar] [CrossRef]
Vipiana, F.; Crocco, L.; Lo Vetri, J. Electromagnetic imaging and sensing for food quality and safety assessment. IEEE Antennas Propag. Mag. 2020, 62, 16–17. [Google Scholar] [CrossRef]
Vasquez, J. A. T.; Scapaticci, R.; Turvani, G.; Ricci, M.; Farina, L.; Litman, A.; Vipiana, F. Noninvasive inline food inspection via microwave imaging technology: An application example in the food industry. IEEE Antennas and Propagation Magazine. 2020, 62, 18–32. [Google Scholar] [CrossRef]
Farina, L.; Scapaticci, R.; Vasquez, J. T.; Rivero, J.; Litman, A.; Crocco, L., Vipiana, F. (2019, July). Microwave imaging technology for in-line food contamination monitoring. In 2019 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting (pp. 817-818). IEEE.
Augustin, G.; Denidni, T.A. Ultrawideband Antennas for Microwave Imaging Systems, 1st ed.; Artech House: London, UK, 2014. [Google Scholar]
Zeni, N.; Bellizzi, G.; Crocco, L.; Cavagnaro, M. (2023, March). A Compact Antipodal Vivaldi Antenna for Food Investigation. In 2023 17th European Conference on Antennas and Propagation (EuCAP) (pp. 1-4). IEEE.
Farina, L.; Scapaticci, R.; Vasquez, J. T.; Rivero, J.; Litman, A.; Vipiana, F. (2019, March). A feasibility study of a microwave imaging device for in-line food contamination monitoring. In 2019 13th European Conference on Antennas and Propagation (EuCAP) (pp. 1-2). IEEE.
Ricci, M.; Vasquez, J.A.T.; Scapaticci, R.; Crocco, L.; Vipiana, F. Multi-antenna system for in-line food imaging at microwave frequencies. IEEE Trans. Antennas Propag. 2022, 78, 7094–7105. [Google Scholar] [CrossRef]
Darwish A.; Ricci M.; Zidane F.; Vasquez JAT.; Casu MR.; Lanteri J.; Migliaccio C.; Vipiana F. Physical Contamination Detection in Food Industry Using Microwave and Machine Learning. Electronics 2022, 11, 3115. [CrossRef]
Zeni, N.; Crocco, L.; Cavagnaro, M.; Bellizzi, G. A Simple Differential Microwave Imaging Approach for In-Line Inspection of Food Products. Sensors. 2023, 23, 779. [Google Scholar] [CrossRef]
Bellizzi, G.; Crocco, L.; Cavagnaro M.; Ricci, M.; Vasquez, J. T.; Vipiana, F. (2022, March). A Simple Imaging Strategy for In-Line food Inspection via Microwave Imaging. In 2022 16th European Conference on Antennas and Propagation (EuCAP) (pp. 1-4). IEEE.
Tayebi, M.; Dastranj, A. A.; Alighanbari, A. (2019, April). Ultra Wide Band Antipodal Vivaldi Antenna with Tapered Triangular Corrugated Edges. In 2019 27th Iranian Conference on Electrical Engineering (ICEE) (pp. 1637-1642). IEEE.
Wu, Y.; Lu, J.; Liu, Y.; Yang, H. (2012, October). Modified design of the antipodal Vivaldi antenna. In ISAPE 2012 (pp. 316-319). IEEE.

Figure 1. Sketch of the layout of the designed antenna (top view).

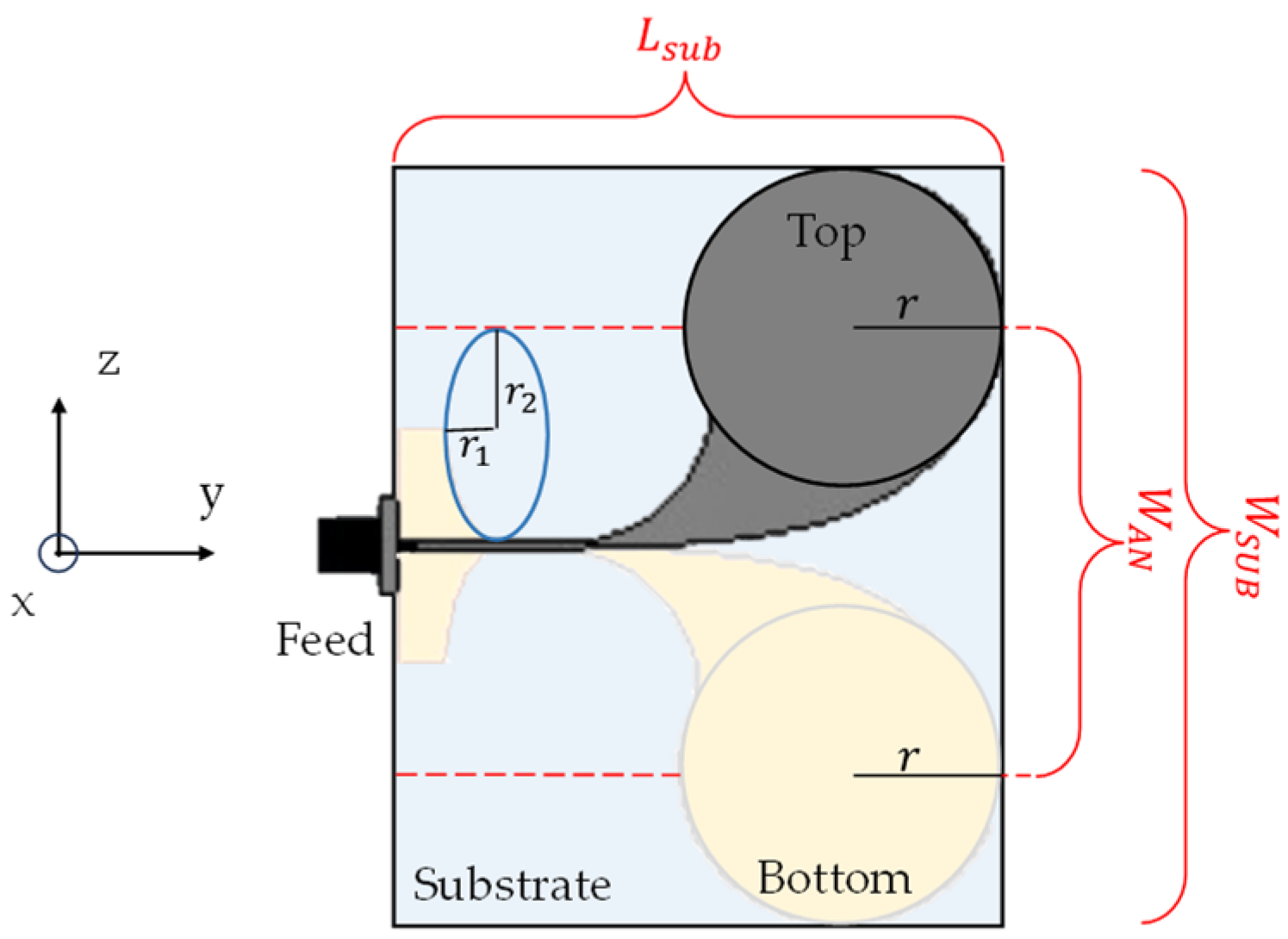
Figure 2. Sketch of the overall MWI system, OUT plus antenna system (top view).

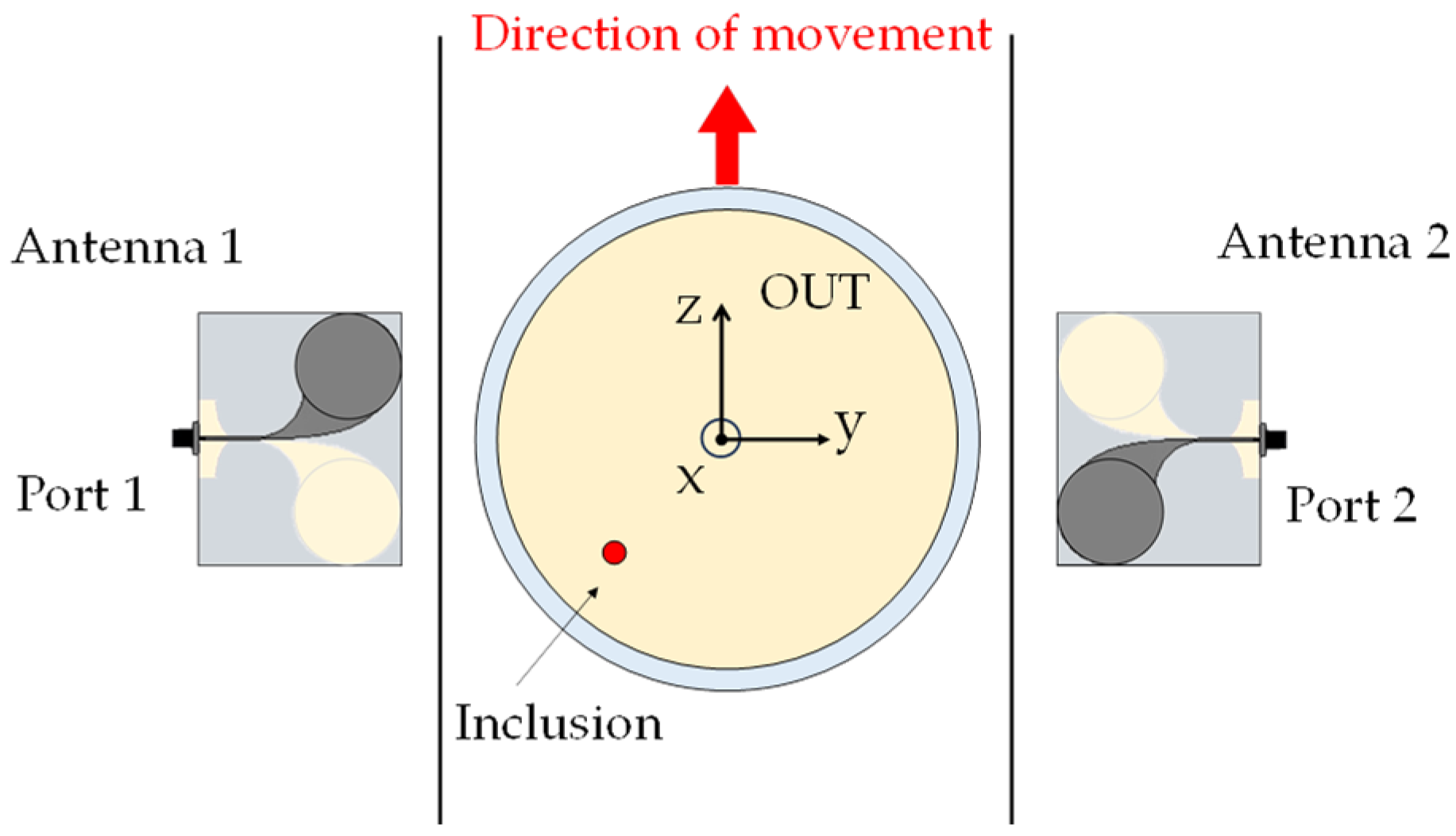
Figure 3. Schematic representation of possible symmetries of the system. System symmetric with respect to the xy-plane: (a) the system, when the OUT occupies the position z_-m, is specular to the system when the OUT occupies the position z_+m; (b) the presence of an inclusion impairs the symmetry.

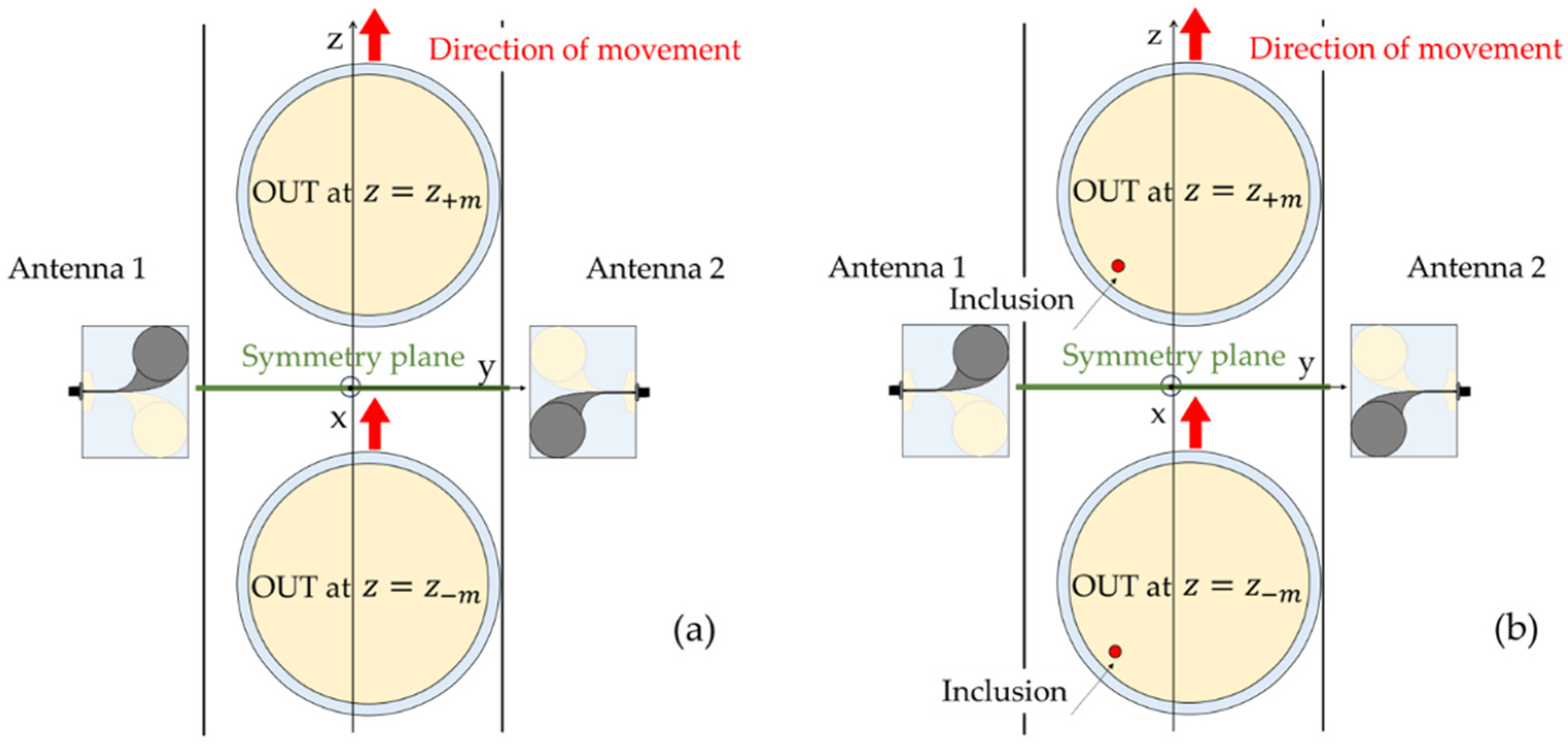
Figure 4. Numerical model of the overall system in CST Microwave Studio environment: (a) top view; (b) front view.

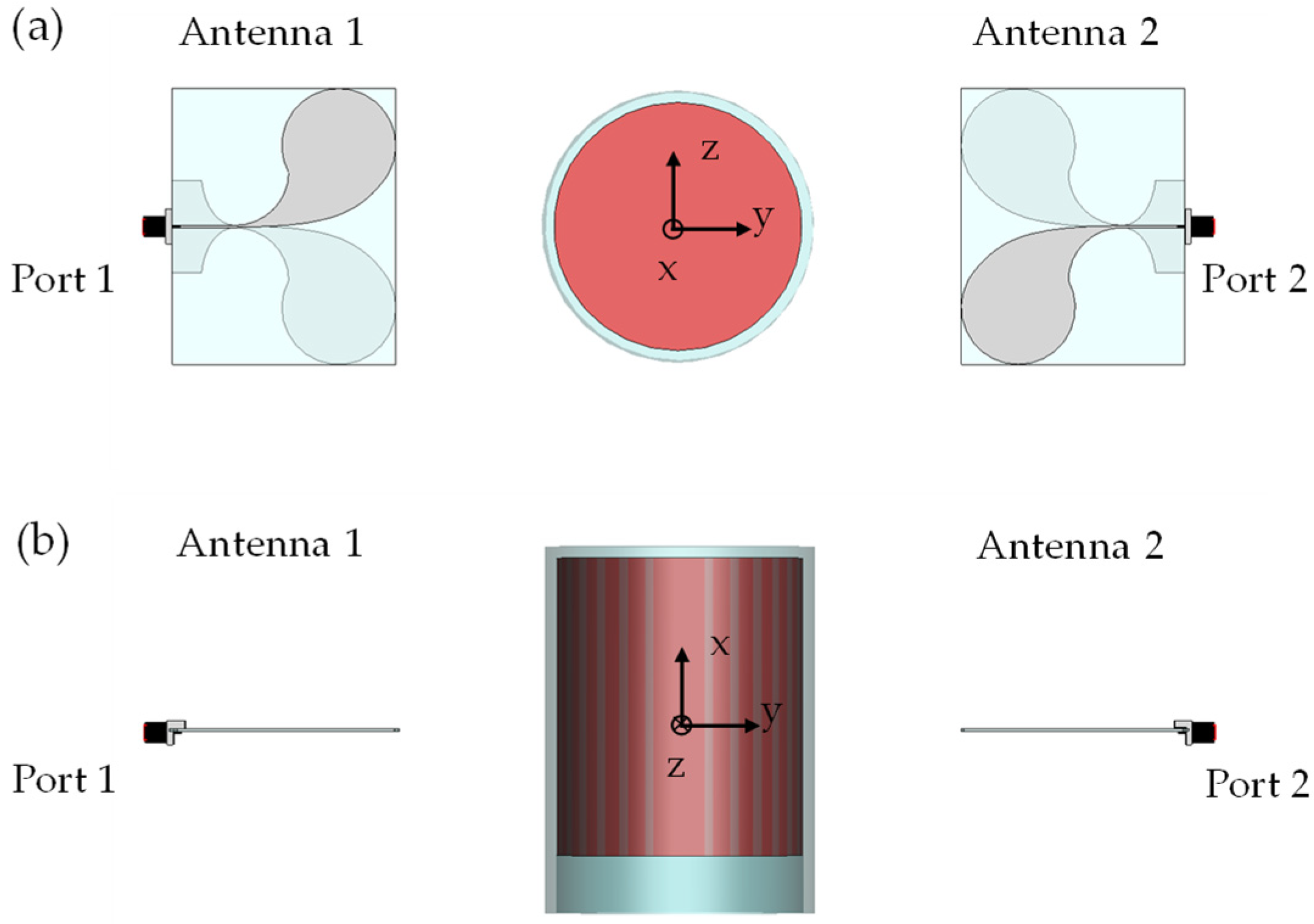
Figure 5. Experimental setup: the two CLAVAs facing each other without (a) and with (b) the OUT placed in the middle. The red arrow indicates the direction of the OUT movement.

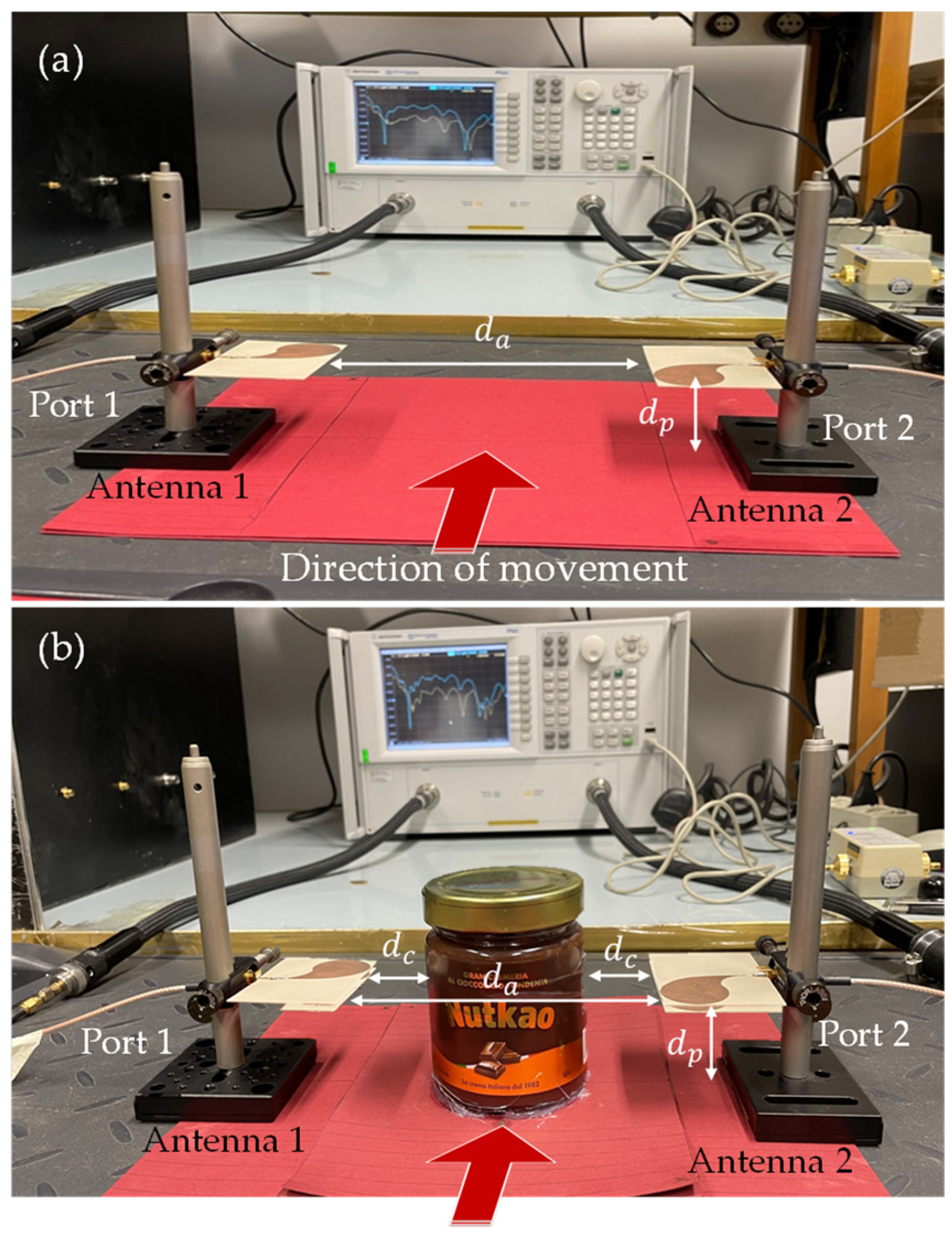
Figure 6. Positioning of the metallic inclusion inside the OUT: (a) front view; (b) top view.

Figure 7. Comparison of the measured scattering parameters with those simulated in [14]: (a) reflection coefficients magnitude vs frequency; (b) transmission coefficients magnitude vs frequency.

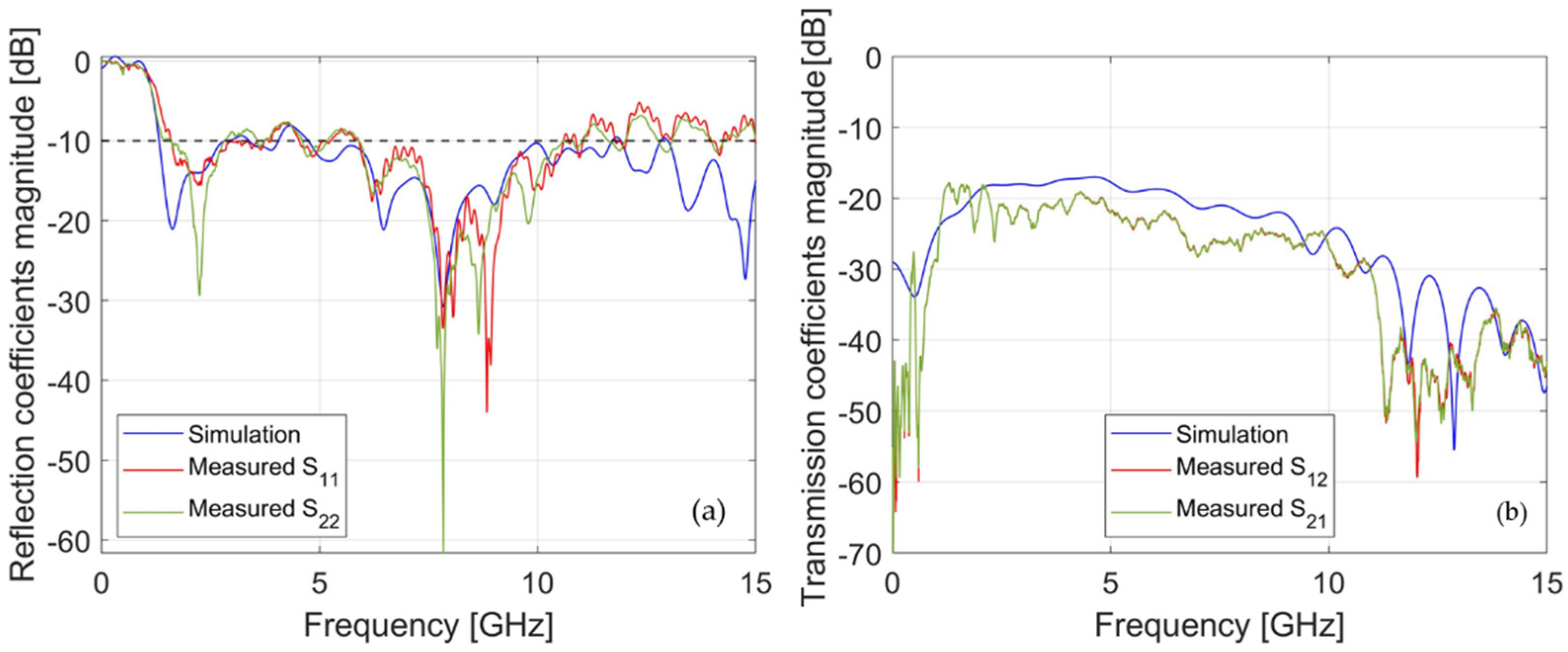
Figure 8. Magnitude (in dB), vs frequency, of the difference between the transmission parameters measured when the OUT is at z_m = ± 1, ± 2,…, ± 6 cm. (blue lines: OUT with inclusion; red lines: OUT without inclusion).

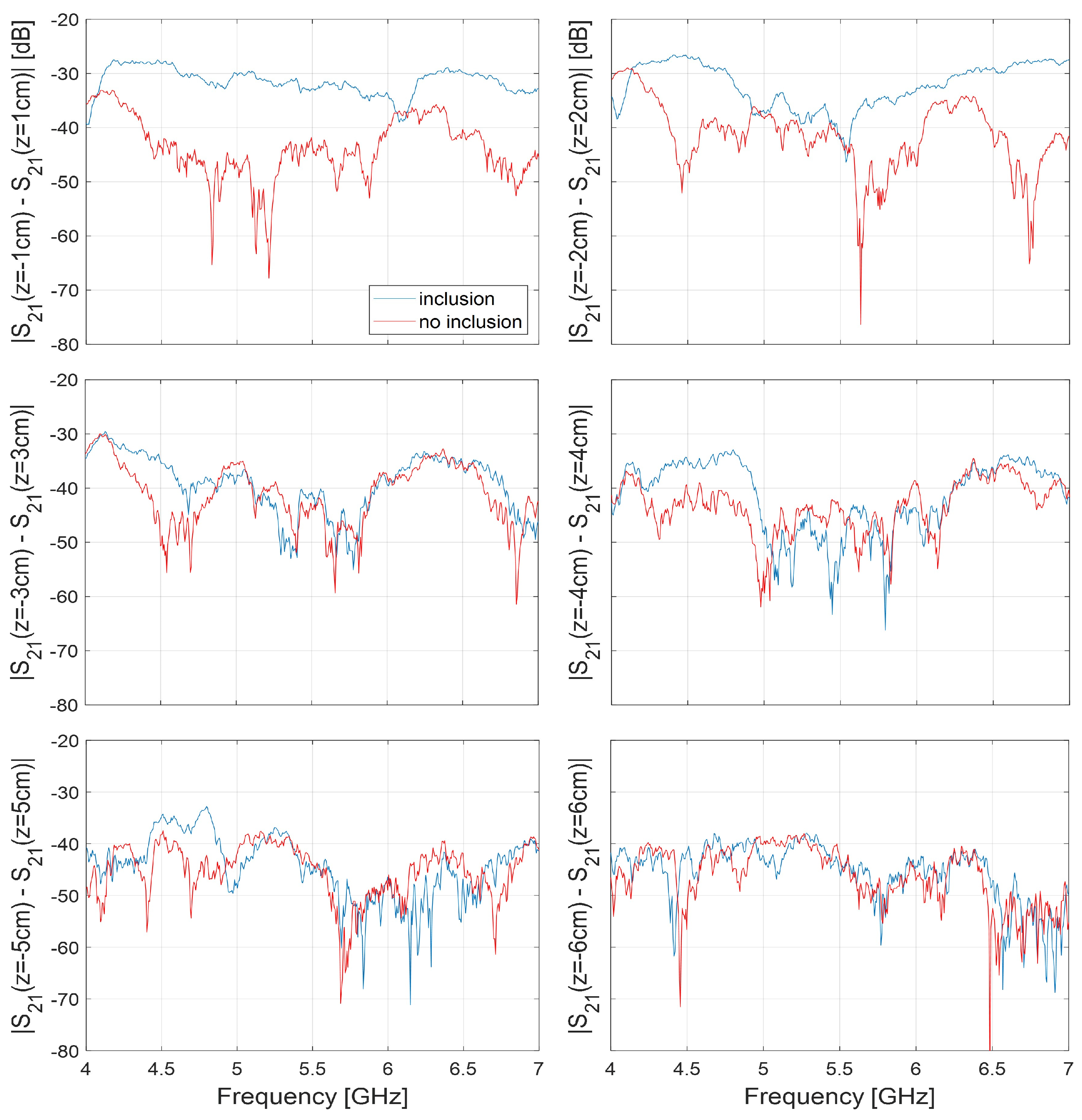
Figure 9. Magnitude (in dB), vs frequency, of the difference between the transmission parameters measured when the OUT carries the inclusion and when the OUT is free of inclusion (each line refers to a different position, z_m= -6, …, + 6 cm, of the OUT).

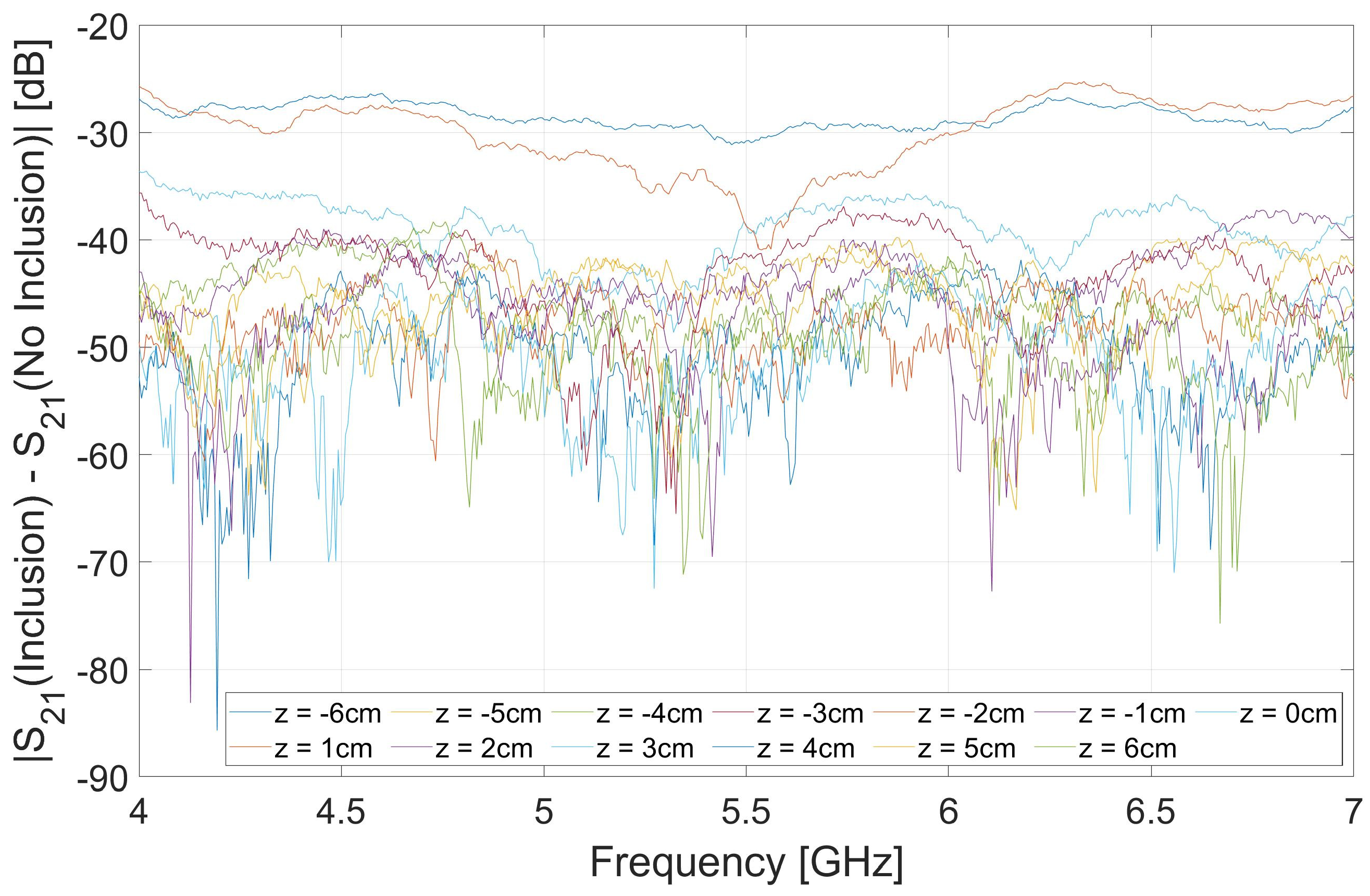
Figure 10. Reconstruction of the inclusion shown in three orthogonal cut planes crossing the center of the inclusion: (a)-(c) SB approach and OUT without inclusion; (d)-(f) SB approach and OUT with inclusion; (g)-(i) RB approach and OUT with inclusion. The dashed circles in the panels represent the inclusion.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Low Complexity Microwave Imaging System for Food Product Inspection through a Symmetry-Based Microwave Imaging Approach

Abstract

1. Introduction

2. Materials and Methods

2.1. Antenna Design

2.2. Basic Structure of the MWI System and Measurement Scheme

2.3. MWI Approach

2.4. Numerical Green’s Function

2.5. Measurement Setup

2.6. Measurement Procedure

3. Results and Discussion

3.1. Validation of the Antenna Design

3.2. Assessment of the SB Approach

4. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe