Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, Inside a Neutron

Preprint

Article

Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, Inside a Neutron

Altmetrics

Downloads

354

Views

1340

Comments

Hector Gerardo Flores^*,

Maria Isabel Gonçalves de Souza^*

Hector Gerardo Flores^*,

Maria Isabel Gonçalves de Souza^*

This version is not peer-reviewed

Submitted:

30 March 2024

Posted:

01 April 2024

You are already at the latest version

Alerts

Abstract

Here we will electrically-quantum model the neutron and proton as a three-phase alternating current electric generator, for this, we will use the theory of three-phase electric generators and vector or phasor diagrams. We will use this model to hypothesize how the quarks that form neutrons and protons with a combined mass of 10 MeV/c², can generate, through quarks-antiquarks-gluon interactions, a mass of 939.56 MeV/c² for the neutron and a mass of 938.27 MeV/c² for the proton. Using quantum mechanics and the theory of the generalization of the Boltzmann constant in curved space-time we will calculate the number of quarks-antiquarks-gluons and gravitons inside a neutron. We will also analyse βˉ decay using vector diagrams, we will calculate the tension of the string T₀ and the length of the string ℓs between quarks-antiquark and finally, we will model a black hole using a neutron equivalent model. In version 2 of this article, we will update the vector diagrams of the βˉ decay and theoretically calculate the energy of the W⁻ boson, the Z⁰ boson, and the Θ angle, Θ = arc cos (W⁻/Z⁰). We will demonstrate, through vector diagrams, that quarks-antiquarks-gluon interactions are the cause of the origin of the W⁻ boson and the Z⁰ boson. We will also demonstrate how the fine structure constant α originates. It is important to make clear, in future updates, we will describe the relationship that exists between the theory described in this paper and the Isospin theory, flavour and colour theory

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Relationship between a Three-Phase Electric Generator and the Quarks-Antiquarks-Gluons Inside a Neutron and Proton

According to Max Planck, science is not only about discoveries, but also about changing the way we think, we should not be afraid of the unknown and we must feel free to follow our curiosity. Following this premise, we are going to develop this theory.

It is important to make clear that the interpretation we use of the structure of quarks does not correspond to QCD theory, it is a personal interpretation. In other words, this theory is outside the formal theory of quarks and gluons (QCD), it is totally personal.

The main idea is to try to demystify the realm in which quark-antiquark-gluon interactions dominate, presenting an alternative theory that contributes to the formal QCD theory.

Whenever we analyse scientific literature, articles, papers, that are related to collisions of subatomic particles, we see that in the collisions of subatomic particles, pairs of particles of matter and antimatter are produced, this always happens, fulfilling the principle of conservation of energy.

Taking into account what has been stated, we are going to consider matter and antimatter to develop our theory. We are going to propose the following model for the neutron and the proton.

Here we put forward the hypothesis for a neutron, as a quark-antiquark-gluon interaction, and not as represented in the formal theory of QCD, as a quark-gluon interaction. See Figure 1

Here we put forward the hypothesis for a proton, as a quark-antiquark-gluon interaction, and not as represented in the formal theory of QCD, as a quark-gluon interaction. See Figure 2.

Before continuing, let's explain why the UU and DD dipoles do not annihilate each other.

When we developed the paper titled: Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann's Constant; at the end of the paper, we show that the up quark and down quark, with a temperature of the order of 10¹⁰ K, have a space-time contraction factor of the order of 10⁶, in other words, the space-time envelope that surrounds the quark acts as a shell, like a protection, preventing the U quark and the U antiquark from annihilating each other, the same happens with the D quark and its D antiquark. , avoiding its annihilation.

This happens only at the quark level, as matter increases in complexity, this space-time protection becomes weaker, which leads to matter-antimatter annihilation.

In Figure 3 and Figure 4; we are going to represent a three-phase generator.

If we look at Figure 3 and Figure 4, which correspond to the electrical circuit of a three-phase generator, we see that the electrical circuit of a neutron represented in Figure 1 and the electrical circuit of a proton represented in Figure 2, have an identical diagram. Basically, the difference is the following, in a three-phase generator, the pairs, XX', YY' and ZZ' have the same frequency and in the case of a proton and neutron the DD pairs have twice the frequency of the UU pairs.

In Figure 5 we are going to represent the diagram of the standard model of particle physics.

In Figure 6, it represents the characteristics of the up and down quark, we can see that the frequency of the down quark is approximately double that of the up quark.

If we rotate the rotor of a generator, this induces a variable magnetic field in the stator and this generates a three-phase sinusoidal voltage, out of phase by 120 degrees, as seen in Figure 7, that is the operating principle of a generator.

In analogy to what happens in a generator, in the proton and the neutron, the DD dipoles vibrate at approximately twice the frequency of the UU dipoles. Continuing with the analogy, the dipoles, XX', YY' and ZZ' in a generator would be analogous to the dipoles DD, DD and UU in a neutron and the dipoles DD, UU and UU in a proton.

If we consider that the voltages, VL1, VL2 and VL3 are the result of rotating the rotor, which produces a variation of the magnetic field and ends up inducing and generating the voltages in the stator, continuing with the analogy, we can say that the dipoles DD, DD and UU in a neutron and the dipoles DD, UU and UU in a proton, is the result of a variable magnetic field that is generated from the interaction of quarks and anti-quarks with gluons, precisely this mechanism makes protons and neutrons generate their mass and are self-sustaining, this is the mechanism that allows the existence of hadrons.

Let us remember that Maxwell's fourth law does not say that a variable magnetic field produces a variable electric field and thus repeats itself indefinitely, precisely through this mechanism a photon is self-sustaining, we can say that a photon has infinite life, and we can confirm this with the CMB which is the result of primordial photons.

The dipoles DD, DD and UU in a neutron and the dipoles DD, UU and UU in a proton, are also out of phase with a phase angle that we are going to determine, the nomenclature of the gluons (R, B, G) and (R, B, G) serves to remind us that the Interactions between quarks and gluons are vectors.

Taking into account the statement, in Figure 8 and Figure 9 we are going to represent the intrinsic interactions of the neutron and the proton.

Figure 8 and Figure 9 represent the interactions that exist in a neutron and a proton, divided into interaction 1 and interaction 2.

Interaction 1 represents direct interactions between quarks and antiquarks and interaction 2 represents cross interactions between quarks and antiquarks.

Next, we are going to analyse the frequency; We said that in a three-phase generator, the frequency is always the same, we also said that the frequency of the down quark is approximately double the frequency of the up quark. We are going to analyse precisely that difference in frequency and its interpretation.

The analysis that we are going to perform is important for the following reason, when we perform a vector or phasor operation that has the same frequency, we do not have problems, but what happens if we are going to perform a vector or phasor operation with operators that have different frequencies. In this analysis we are going to answer this question!!!!!!

If we analyse Figure 9 - proton, we observe that interaction 1 between quarks and antiquarks, direct interaction, are carried out at the same frequency.

Again, if we analyse Figure 9, proton, we observe that interaction 2 between quarks and antiquarks, cross interaction, in analogy with interaction 1, the frequency difference between quarks and antiquarks, does not represent a drawback in energy exchanges.

In Figure 10 we represent the energy exchanges between quarks and antiquarks and we see how the gluons act.

In blue we represent the quarks with the frequency of the Down quark and the associated gluon also in blue, when the energy exchange is carried out so that one quark becomes another quark.

In yellow we represent the quarks with the frequency of the up quark and the associated gluon also in yellow, when the energy exchange is carried out, so that one quark becomes another quark.

We can represent the statement in Figure 11. We see why the exchange of gluons so that one quark becomes another quark does not represent a problem with frequency.

Quark U B transform quarks U G through gluon exchange G B, at the up-quark frequency, yellow.

Quark D R transform quarks D B through gluon exchange R B, at the down quark frequency, blue.

Taking into account what has been analysed so far, we can propose vector or phasor operations as valid, in analogy to that of a three-phase alternating current generator, which works with a single frequency.

It is the exchange of gluons, which is carried out at the appropriate frequency, allowing one quark to become another quark; it is this mechanism that allows us to perform a vector or phasor sum, as if this entire mechanism worked at a single frequency.

2. Electrical-Quantum Modelling of the Neutron as a Three-Phase Alternating Current Electrical Generator

We are going to work with Figure 12 to create our electrical model of the neutron as a three-phase alternating current electrical generator.

The dipole DD is analogous to L1 and RR is analogous to the current flowing through L1.

The dipole DD is analogous to L2 and BB is analogous to the current flowing through L2.

The dipole UU is analogous to L3 and GG is analogous to the current flowing through L3.

We see that there are two types of interactions.

Interaction 1 or direct interaction and interaction 2 or cross interaction.

We said that down quarks have one frequency and up quarks have another frequency; Thanks to gluons, vector or phasor operations cease to be a problem, making it possible for a quark to transform into another quark, of the same frequency, thanks to the exchange of gluons. It is an amazing mechanism. We can see this mechanism in Figure 10.

In analogy to a three-phase alternating current electric generator, we are going to represent interaction 1 and interaction 2, using vectors whose resulting vector is null. In this way, we are going to simulate a neutron as a three-phase alternating current electrical generator.

In Figure 5 of the standard model, we see that the up quark has a mass of 2.2 MeV/c² and the down quark has a mass of 4.7 MeV/c².

Taking these values as reference we are going to make our vector diagram of the neutron.

Quark Down = 4.7 MeV/c²

Quark up = 2.2 MeV/c²

It is important to make it clear that all interactions are vector, although we do not represent them as such in the figures.

Interaction 1:

If we analyse Figure 13, star connection, we see that the following vector sum is null:

R(DD)R + B(DD)B + G(UU)G = 0

If we analyse Figure 13, triangle connection, we see that the following vector sum is null:

R(DD)B + B(DU)G + R(DU)G = 0

This is telling us that the net charge in interaction 1 is zero.

Interaction 2:

If we analyse Figure 14, we observe that the following vector sum is also null:

R(DD)B + R(DU)G + B(DD)R + B(DU)G + G(UD)R + G(UD)B = 0

This is telling us that the net charge in interaction 2 is zero.

Taking into account interaction 1 and interaction 2, the total net charge of the neutron is zero, as appropriate.

Knowing that the total mass of the neutron is 939.56 MeV/c², we are going to calculate the mass content in each interaction:

R(DD)R = 8.6 x 9.8486 = 84.69 MeV/c²

B(DD)B = 8.6 x 9.8486 = 84.60 MeV/c²

G(UU)G = 4.0 x 9.8486 = 39.39 MeV/c²

R(DD)B = 10.2 x 9.8486 = 100.45 MeV/c²

R(DU)G = 10.2 x 9.8486 = 100.45 MeV/c²

B(DD)R = 10.2 x 9.8486 = 100.45 MeV/c²

B(DU)G = 10.2 x 9.8486 = 100.45 MeV/c²

G(UD)R = 16.7 x 9.8486 = 164.47 MeV/c²

G(UD)B = 16.7 x 9.8486 = 164.47 MeV/c²

(2 x (8.6) + 4.0 + 4(10.2) + 2 x (16.7) = 95.4

NECF = Mn / 95.4 = (939.56 MeV/c²) / 95.4 = 9.8486 MeV/c², Neutron electromagnetic coupling factor. The value: 95.4, could have any type of units, for practical purposes we are going to leave it without units.

If we divide the electromagnetic coupling factor of the neutron NECF, by the energy 0.388 MeV/c², corresponding to unit binding energy per nucleon, we will have the approximate number of protons to which the neutron can be stably associated.

Qtyp = NECF / ∆Eα = (9.8486 MeV/c²) / (0.388 MeV/c²) = 25.38

where ∆Eα could be considered unit binding energy per nucleon.

Qtyp = 25 proton.

Where Qtyp represents the number of protons that the neutron-proton binding energy stably supports, considering the electromagnetic coupling factor of the Neutron NECF.

Let us remember that the maximum binding energy is obtained for iron, Fe (26,30), which has 26 protons and 30 neutrons and this coincides with being the most abundant element on Earth.

According to our calculation, starting at proton number 26, the neutron-proton binding energy begins to weaken.

We are going to represent these values in Figure 15:

The electrical modelling of a neutral as a three-phase alternating current electrical generator allows us to assign a mass value to interactions 1 & 2, which we represent using a phasor diagram, as shown in Figure 14. It also allows us to verify that the sum resulting vector in interactions 1 & 2 is zero, and the scalar sum is equal to 939.56 MeV/c², as appropriate.

Analysing the vector diagrams in Figure 13 and Figure 14, we see that the degrees of freedom of the vectors are practically zero, there is no possibility of deviations, the hypothesis that the charge has to be zero restricts any possibility of changes in the position of the vectors, that is, the vectors have a unique configuration, given in Figure 13 and Figure 14.

It is important to keep in mind that the relationship between the interactions of quarks, anti-quarks and gluons is vector-type, that is, each interaction will be represented by a module and an angle.

In the neutron, if we add the phasors of interaction 1 and interaction 2 vector-wise, we see that the resulting vector is zero, in other words, the net charge is zero; but if we add the module of each vector in MeV/c² scalarly, the sum gives us 939.56 MeV/c², we represent this in Figure 14 and Figure 15, which corresponds to the neutron.

Definitely, we can assure that neutrons are true generators of energy, mass and gravity; we have verified how with three quarks that add up to approximately 10 MeV/c², we can generate a mass of 939.56 MeV/c² through the interactions of quarks, anti-quarks and gluons.

2.1. Mechanism That Generates Mass in Neutrons, Calculation of the Number of Quarks-Antiquarks-Gluons Inside a Neutron

If we look at Figure 15, we see that the neutron has a mass of 939.56 MeV/c², if we add the mass of the two D Quark and the mass of the U quark it gives us approximately 10 MeV/c²; We ask ourselves, how is the mass of 929 MeV/c² generated? That is precisely what we want to answer in this section.

If we look at Figure 15, we see that we can represent the neutron by dipoles of matter and antimatter formed by quark and anti-quark. Interaction 1 can be represented by 3 dipoles and interaction 2 can be represented by 6 dipoles.

If we analyse any dipole, we see that at one end it is formed by matter and at the other end by antimatter, opposite charges of the opposite sign.

These dipoles behave like electrical antennas, if we consider that these dipoles move in one direction, they vibrate, they are polarized, they generate an electromagnetic field in analogy to the dipoles of antennas.

The variation of the electric field in the antennas produces a variation in the electric potential and this in turn produces a flow of current, thus generating an electromagnetic wave.

In analogy to dipole antennas, polarized vibrations in one direction produce a flow of gluons that carry charge, producing a current that would generate an electromagnetic field. This flow of charge-carrying gluons would be analogous to a flow of current and this would produce an electromagnetic field generated by the matter-antimatter dipole.

We know through the equation E = mc², that energy is related to mass and precisely that energy that results from gluonic exchange is the energy that generates the mass 929 MeV/c² in a neutron.

Neutron mass = 939.56 MeV/c²

2md + mu = 11.6 MeV/c²

where md is the mass of the D quark and mu is the mass of the U quark.

Gluon exchange mass = 928 MeV/c²

Using the following equations, we are going to perform the following calculations.

Equation that defines the spectrum of electromagnetic waves:

Eε = h x fε

Cε = λε x fε

Eε = h x Cε / λε

Eε = Kʙε x Tε

Kʙε = 1.38 10⁻²³ J/K

We are going to work with the bond energy that keeps the electron attached to the proton, in the hydrogen atom.

Let's assume that the binding energy is 13.6 eV:

13.6 eV = 2.17 10⁻¹⁸ Joules
E = h x f; f = E/h = 2.17 10⁻¹⁸ / 6.63 10⁻³⁴ = 0.327 10¹⁶
f = 3.2 10¹⁵ Hz
E = K x T; T = E/K = 2.17 10⁻¹⁸ / 1.38 10⁻²³
T = 1.57 10⁵ K
M(photon) = h / (λ x C)
c = λ x f; λ = c/f = 3 10⁸ / 3.210¹⁵ = 0.937 10⁻⁷
λ = 9.37 10⁻⁸ m
M(photon) = h / (λ x C) = 6.63 10⁻³⁴ / 9.37 10⁻⁸ x 3 10⁸ = 0.235 10⁻³⁴
M(photon-gluon) = 2.35 10⁻³⁵ kg

of the photon-gluon that holds the electron to the proton in the hydrogen atom.

Through this procedure we can infer the energy of the photons-gluons inside the neutron and proton.

Let's assume that in a hydrogen atom the electron is linked to the proton through the BB gluons, which are analogous to photons and can escape confinement, in addition, the rest of the gluons have colour charge other than zero, they cannot escape confinement. We can consider that in general from the point of view of energy, for the same temperature conditions all gluons (Proton and neutron) have equivalent energies of the same order.

Later, when we analyse βˉ decay, we will show that a neutron decays into a proton and if the released electron is trapped forming the hydrogen atom, we will see that the BB gluons would be the linked photons in the electromagnetic theory, that unites the proton with the electron

Using this same procedure, we are going to generalize for lower energy values until reaching the temperature of the Bose-Einstein condensate, 10⁻¹⁰ K and for higher energy values until reaching the temperature of 10²⁶ K.

Let's assume that the binding energy is 13,600 eV:

13,600 eV = 2.17 10⁻¹⁵ Joules
E = h x f; f = E/h = 2.17 10⁻¹⁵ / 6.63 10⁻³⁴ = 0.327 10¹⁹
f = 3.27 10¹⁸ Hz
E = K x T; T = E/K = 2.17 10⁻¹⁵ / 1.38 10⁻²³ = 1.57 10⁸
T = 1.57 10⁸ K
M(photon) = h / (λ x C)
c = λ x f; λ = c/f = 3 10⁸ / 3.2 10¹⁸ = 0.937 10⁻¹⁰
λ = 9.37 10⁻¹¹ m
M(photon) = h / (λ x C) = 6.63 10⁻³⁴ / 9.37 10⁻¹¹ x 3 10⁸ = 0.235 10⁻³¹
M(photon-gluon) = 2.35 10⁻³² kg

Let's assume that the binding energy is 136,000 eV:

136,000 eV = 2.17 10⁻¹⁴ Joules
E = h x f; f = E/h = 2.17 10⁻¹⁴ / 6.63 10⁻³⁴ = 0.327 10²⁰
f = 3.27 10¹⁹ Hz
E = K x T; T = E/K = 2.17 10⁻¹⁴ / 1.38 10⁻²³ = 1.57 10⁹
T = 1.57 10⁹ K
M(photon) = h / (λ x C)
c = λ x f; λ = c/f = 3 10⁸ / 3.2 10¹⁹ = 0.937 10⁻¹¹
λ = 9.37 10⁻¹² m
M(photon) = h / (λ x C) = 6.63 10⁻³⁴ / 9.37 10⁻¹² x 3 10⁸ = 0.235 10⁻³⁰
M(photon-gluon) = 2.35 10⁻³¹ kg

Let's assume that the binding energy is 1,360,000 eV:

1,360,000 eV = 2.17 10⁻¹³ Joules
E = h x f; f = E/h = 2.17 10⁻¹³ / 6.63 10⁻³⁴ = 0.327 10²¹
f = 3.27 10²⁰ Hz
E = K x T; T = E/K = 2.17 10⁻¹³ / 1.38 10⁻²³
T = 1.57 10¹⁰ K
M(photon-gluon) = h / (λ x C)
c = λ x f; λ = c/f = 3 10⁸ / 3.2 10²⁰ = 0.937 10⁻¹²
λ = 9.37 10⁻¹³ m
M(photon) = h / (λ x C) = 6.63 10⁻³⁴ / 9.37 10⁻¹³ x 3 10⁸ = 0.235 10⁻²⁹
M(photon-gluon) = 2.35 10⁻³⁰ kg

Let's assume that the binding energy is 136,000,000 eV:

136,000,000 eV = 2.17 10⁻¹¹ Joules
E = h x f; f = E/h = 2.17 10⁻¹¹ / 6.63 10⁻³⁴ = 0.327 10²³
f = 3.2 10²² Hz
E = K x T; T = E/K = 2.17 10⁻¹¹ / 1.38 10⁻²³
T = 1.57 10¹² K
M(photon-gluon) = h / (λ x C)
c = λ x f; λ = c/f = 3 10⁸ / 3.2 10²² = 0.937 10⁻¹⁴
λ = 9.37 10⁻¹⁵ m
M(photon) = h / (λ x C) = 6.63 10⁻³⁴ / 9.37 10⁻¹⁵ x 3 10⁸ = 0.235 10⁻²⁷
M(photon-gluon) = 2.35 10⁻²⁸ kg

Let's assume that the binding energy is 1,360,000,000 eV:

1,360,000,000 eV = 2.17 10⁻¹⁰ Joules
E = h x f; f = E/h = 2.17 10⁻¹⁰ / 6.63 10⁻³⁴
f = 3.2 10²³ Hz
E = K x T; T = E/K = 2.17 10⁻¹⁰ / 1.38 10⁻²³
T = 1.57 10¹³ K
M(photon-gluon) = h / (λ x C)
c = λ x f; λ = c/f = 3 10⁸ / 3.2 10²³ = 0.937 10⁻¹⁵
λ = 9.37 10⁻¹⁶ m
M(photon) = h / (λ x C) = 6.63 10⁻³⁴ / 9.37 10⁻¹⁶ x 3 10⁸
M(photon-gluon) = 2.35 10⁻²⁷ kg

Let's assume that the binding energy is 1,360,000,000,000 eV:

1,360,000,000,000.00 eV = 2.17 10⁻⁷ Joules
E = h x f; f = E/h = 2.17 10⁻⁷ / 6.63 10⁻³⁴
f = 3.2 10²⁷ Hz
E = K x T; T = E/K = 2.17 10⁻⁷ / 1.38 10⁻²³
T = 1.57 10¹⁶ K
M(photon-gluon) = h / (λ x C)
c = λ x f; λ = c/f = 3 10⁸ / 3.2 10²⁷ = 0.937 10⁻¹⁹
λ = 9.37 10⁻²⁰ m
M(photon) = h / (λ x C) = 6.63 10⁻³⁴ / 9.37 10⁻²⁰ x 3 10⁸ = 0.235 10⁻²²
M(photon-gluon) = 2.35 10⁻²³ kg

Let's assume that the binding energy is 13,600,000,000,000,000,000,000.00 eV:

13,600,000,000,000,000,000,000.00 eV = 2.17 10³ Joules
E = h x f; f = E/h = 2.17 10³ / 6.63 10⁻³⁴ = 0.327 10³⁷
f = 3.2 10³⁶ Hz
E = K x T; T = E/K = 2.17 10³ / 1.38 10⁻²³
T = 1.57 10²⁶ K
M(photon-gluon) = h / (λ x C)
c = λ x f; λ = c/f = 3 10⁸ / 3.2 10³⁶ = 0.937 10⁻²⁸
λ = 9.37 10⁻²⁹ m
M(photon) = h / (λ x C) = 6.63 10⁻³⁴ / 0.937 10⁻²⁸ x 3 10⁸ = 2.35 10⁻¹⁴
M(photon-gluon) = 2.35 10⁻¹⁴ kg

Let's assume that the binding energy is 0.000136 eV:

0.000136 eV = 2.17 10⁻²³ Joules
E = h x f; f = E/h = 2.17 10⁻²³ / 6.63 10⁻³⁴ = 0.327 10¹¹
f = 3.2 10¹⁰ Hz
E = K x T; T = E/K = 2.17 10⁻²³ / 1.38 10⁻²³
T = 1.57 K
M(photon) = h / (λ x C)
c = λ x f; λ = c/f = 3 10⁸ / 3.210¹⁰ = 0.937 10⁻²
λ = 9.37 10⁻³ m
M(photon) = h / (λ x C) = 6.63 10⁻³⁴ / 9.37 10⁻³ x 3 10⁸ = 0.235 10⁻³⁹
M(photon-gluon) = 2.35 10⁻⁴⁰ kg

Let's assume that the binding energy is 0.00000000136 eV:

0.00000000136 eV = 2.17 10⁻²⁸ Joules
E = h x f; f = E/h = 2.17 10⁻²⁸ / 6.63 10⁻³⁴ = 0.327 10⁶
f = 3.2 10⁵ Hz
E = K x T; T = E/K = 2.17 10⁻²⁸ / 1.38 10⁻²³
T = 1.57 10⁻⁵ K
M(photon) = h / (λ x C)
c = λ x f; λ = c/f = 3 10⁸ / 3.210⁵ = 0.937 10³
λ = 9.37 10² m
M(photon) = h / (λ x C) = 6.63 10⁻³⁴ / 9.37 10² x 3 10⁸ = 0.235 10⁻⁴⁴
M(photon-gluon) = 2.35 10⁻⁴⁵ kg

Let's assume that the binding energy is 0.0000000000000136 eV:

0.0000000000000136 eV = 2.17 10⁻³³ Joules
E = h x f; f = E/h = 2.17 10⁻³³ / 6.63 10⁻³⁴ = 0.327 10
f = 3.2 10⁰ Hz
E = K x T; T = E/K = 2.17 10⁻³³ / 1.38 10⁻²³
T = 1.57 10⁻¹⁰ K

This corresponds to a temperature of a Bose-Einstein condensate

M(photon) = h / (λ x C)
c = λ x f; λ = c/f = 3 10⁸ / 3.2 10⁰ = 0.937 10⁸
λ = 9.37 10⁷ m
M(photon) = h / (λ x C) = 6.63 10⁻³⁴ / 0.937 10⁸ x 3 10⁸ = 2.35 10⁻⁵⁰
M(photon-gluon) = 2.35 10⁻⁵⁰ kg

With the calculations carried out, we are going to generate the following table:

In Table 1, we observe that as the energy increases, the frequency increases, the temperature increases and consequently the mass of the gluon increases.

If we remember what we said that neutrons and protons are formed by dipoles of matter and antimatter (quark and anti-quark), which oscillate in a certain direction similar to the electric dipoles in antennas, if we analyse Table 1, we see that as the dipoles increase their vibration frequency, their energy increases, their temperature increases and the mass of the gluon also increases as predicted.

If we look at Table 1, for T = 1.57 10⁹ K, we see that the mass of the gluons is approximate to the mass of the U quark and D quark, shown in Figure 6. This is telling us that if we consider the correct temperature, the mass of the gluons will coincide with the mass of the U quark and D quark.

mu = 4.10 10ˉ³⁰ kg, T = 2.67 10¹⁰ K, see Figure 6.
md = 8.55 10ˉ³⁰ kg, T = 5.57 10¹⁰ K, see Figure 6.
Theoretically calculated gluon mass = 2.35 19ˉ³⁰ kg, T = 1.57 10¹⁰ K, see Table 1.

If we look at Table 1, we see that the mass of gluons depends on the temperature (energy); for example, for a temperature of T = 1.57 10⁵ K a gluon mass = 2.35 10⁻³⁵ kg corresponds. We can state this in the following way, if we consider that the space-time inside the neutron has a temperature of T = 1.57 10⁵ K, the minimum jump in mass existing would correspond to, gluon mass = 2.35 10⁻³⁵ kg.

Here, it is important to highlight that we are comparing the mass of the gluons with the mass of the quarks, that is, if we consider the dipole:

R(DD)R, we have, RR = DD

We are saying that the mass of the RR gluon is equal to the mass of the DD quark, in other words, the mass of the gluons is on equal footing with the mass of the quarks. We can generalize this to the dipoles of interaction 1 and interaction 2 in protons and neutrons.

From here on, we will refer to it as the quark-antiquark-gluon mass or gluon mass, In the same way, when we talk about the number of gluons, we are including quarks.

Another important consideration to take into account is the following:

The Gluons RR, BB and GG, can escape confinement. This is observed in βˉ decay. These gluons are analogous to photons, they have the same colour charge.

The Gluons RB, RG, BR, BG, GR and GB, they cannot escape confinement, they have different colour charges, they are special photons.

Taking into account the statement:

We are going to perform the following calculation:

Neutron mass = 939.56 MeV/c²
2md + mu = 11.6 MeV/c²

Number of gluons = neutron mass / unit mass of a gluon

For T = 1.57 10⁵ K:

Approximate number of gluons per neutron = 1.67 10⁻²⁷ / 2.35 10⁻³⁵
Approximate number of gluons per neutron = 0.71 10⁸
QTY g = 7.1 10⁷ = 71,000,000.00

71 million gluons in a neutron, for T = 1.57 10⁵ K.

Where QTY g, is the number of gluons inside a neutron.

When we talk about gluons, we refer to quarks-antiquarks and gluons as a whole, as long as the interaction relationship 1 & 2 is fulfilled, as shown in Figure 15.

According to Table 1, we see that the number of gluons in a neutron depends on the temperature (energy) at which the calculation is carried out.

Looking at Table 1, we see that as the temperature increases, the mass of the quark-gluons increases, for example, for a temperature of 10⁹ K, the mass of a quark-gluon is in the order 10ˉ³¹ kg. Now, for a temperature of 10¹³ K, the mass of the quark-gluons is on the order of 10ˉ²⁷ kg.

Next, we are going to calculate the quantity of quarks-antiquarks-gluons existing, in a discriminated manner, in the dipoles of the interaction 1 & 2.

Interaction 1:

QTY g INT 1: = 0.370 10ˉ²⁷ kg / 2.35 10ˉ³⁵ kg = 1.574 10⁷ Q-Gluons
Qty g R(DD)R = 0.149 10ˉ²⁷ kg / 2.35 10ˉ³⁵ kg = 0.634 10⁷ Q-Gluons
Qty g B(DD)B = 0.149 10ˉ²⁷ kg / 2.35 10ˉ³⁵ kg = 0.634 10⁷ Q-Gluons
Qty g G(UU)G = 0.069 10ˉ²⁷ kg / 2.35 10ˉ³⁵ kg = 0.293 10⁷ Q-Gluons

Interaction 2:

QTY g INT 2 = 1.300 10ˉ²⁷ kg / 2.35 10ˉ³⁵ kg = 5.531 10⁷ Q-Gluons
QTY g R(DD)B = 0.1786 10ˉ²⁷ kg / 2.35 10ˉ³⁵ = 0.760 10⁷ Q-Gluons
QTY g R(DU)G = 0.1786 10ˉ²⁷ kg / 2.35 10ˉ³⁵ = 0.760 10⁷ Q-Gluons
QTY g B(DD)R = 0.1786 10ˉ²⁷ kg / 2.35 10ˉ³⁵ = 0.760 10⁷ Q-Gluons
QTY g B(DU)G = 0.1786 10ˉ²⁷ kg / 2.35 10ˉ³⁵ = 0.760 10⁷ Q-Gluons
QTY g G(UD)R = 0.2925 10ˉ²⁷ kg / 2.35 10ˉ³⁵ = 1.244 10⁷ Q-Gluons
QTY g G(UD)B = 0.2925 10ˉ²⁷ kg / 2.35 10ˉ³⁵ = 1.244 10⁷ Q-Gluons

Where Q-Gluons, it means quarks-antiquarks-gluons.

It is very important to be clear that the mass of quark-antiquarks-gluons varies with temperature.

These calculations were carried out for a temperature T = 1.57 10⁵ K.

For T = 1.57 10¹⁰K:

Approximate number of gluons per neutron = 1.67 10⁻²⁷ / 2.35 10⁻³⁰
Approximate number of gluons per neutron = 0.71 10³
QTY g = 7.1 10² = 710

710 gluons in a neutron, for T = 1.57 10¹⁰ K.

Where QTY g, is the number of gluons inside a neutron.

For T = 1.57 10¹²K:

Approximate number of gluons per neutron = 1.67 10⁻²⁷ / 2.35 10⁻²⁸
Approximate number of gluons per neutron = 0.7 10
QTY g = 7

7 gluons in a neutron, for T = 1.57 10¹² K.

Where QTY g, is the number of gluons inside a neutron.

For T = 1.57 10¹⁶K:

Approximate number of gluons per neutron = 1.67 10⁻²⁷ / 2.35 10⁻²³
Approximate number of gluons per neutron = 0.71 10⁻⁴
In reality it is a single gluon and the parameter that interests us is the following.
1 / Approximate number of gluons per neutron = 1 / 0.71 10⁻⁴ = 1.40 10⁴
Gluon size, Gz g = 1.4 10⁴ = 14,000 times
Gz g = 1.4 10⁴

For a temperature T = 10¹⁶ K, it is a single gluon whose size has increased to 14,000 times the size of the neutron mass.

2.1.1. Calculation of the Number of Gluons by Dividing the Volume of the Neutron by the Volume of the Quark

Rn = 0.4 10ˉ¹⁵ m

Where Rn is radius of the neutron

Vn = (4/3) ᴨ R³ = (4/3) x 3.14 x (0.4 10ˉ¹⁵) ³
Vn = 0.267 10ˉ⁴⁵ m³
Rq = 0.43 10⁻¹⁸ m

Where Rq is quark radius.

Vq = (4/3) ᴨ R³ = (4/3) x 3.14 x (0.43 10⁻¹⁸) ³ =
Vq = 0.33 10⁻⁵⁴ mᶾ

Where Vq is volume of the quark

D = Vn / Vq = 0.267 10ˉ⁴⁵ m³ / Vq = 0.33 10⁻⁵⁴ mᶾ
D = 0.80 10⁹ = 8.0 10⁸
D = 80 10⁷ gluons

Where D is the number of quark-antiquarks-gluons

According to our calculations, we have:

D ≈ 10 QTY g

We said that the mass of gluons decreases with temperature, see Table 1, if we calculate the number of quarks-antiquarks-gluons for a temperature lower than T = 10⁵ K, we will achieve the equality D = QTY g.

D = QTY g

2.2. Mechanism That Generates Gravity in Neutrons, Calculation of the Number of Gravitons Inside a Neutron

From the point of view of charge, we said that interaction 1 and interaction 2 of quarks represent electric dipoles (Spin 1). We also said that these dipoles are polarized and vibrate in one direction, producing an electromagnetic field that gives rise to a flow of gluons that generates an electric current and through this mechanism we manage to produce mass in Hadrons (proton, neutron, etc).

From the point of view of mass, if we consider quark and anti-quark dipoles as point masses that vibrate, we can idealize it as a quark linked to an anti-quark by a spring (Gravitons with spin 2), these two masses vibrating together by a spring, they would produce disturbances in space-time that would propagate in the form of gravitational waves. This would be the mechanism by which gravitational waves are generated, gravitons that would propagate in space-time.

In conclusion, it is the charge and mass properties in the quark and anti-quark dipoles represented in interaction 1 and interaction 2, which produce the mass in protons and neutrons and also cause the gravitational waves (gravitons), that propagate in space-time, what we call gravity.

Neutron mass = 939.56 MeV/c²

2md + mu = 11.6 MeV/c²

where md, is the mass of the D quark and mu, is the mass of the U quark.

Using the following equations, we are going to perform the following calculations using the effective Boltzmann constant to quantize and quantify gravity.

Equation that defines the spectrum of gravitational waves:

Eɢ = h x fɢ
Cɢ = λɢ x fɢ
Eɢ = h x Cɢ / λɢ
Eɢ = Kʙɢ x Tɢ
Kʙɢ = 1.38 10⁻²³ J/K > Kв ef > 1.78 10⁻⁴³ J/K

Moon, Kʙl = 9.15 10⁻²⁶ J/K,

Where Kʙl is approximate effective Boltzmann constant of the moon.

El = Kʙl x T
El = 9.15 10⁻²⁶ x 1.6 10³ = 14.64 x 10⁻²³
El = 14.64 10⁻²³ Joules
El = h x fl; fl = El / h = 14.64 10⁻²³ / 6.63 10⁻³⁴ = 2.34 10¹¹
fl = 2.34 10¹¹ Hz
M(graviton) = h / (λl x c)
c = λl x fl; λl = c / fl = 3 10⁸ / 2.34 10¹¹ = 1.28 10⁻³
λl = 1.28 10⁻³ m
M(graviton) = h / (λl x c) = 6.63 10⁻³⁴ / 1.28 10⁻³ x 3 10⁸ = 1.72 10⁻³⁹
M(graviton)l-eff = 1.72 10⁻³⁹ kg

Earth, Kʙt = 2.68 10⁻²⁸ J/K,

Where Kʙt is approximate effective Boltzmann constant of the earth.

Et = Kʙt x T
Et = 2.68 10⁻²⁸ x 6.7 10³ = 17.95 x 10⁻²⁵
Et = 17.95 10⁻²⁵ Joules
Et = h x ft; ft = Et / h = 17.95 10⁻²⁵ / 6.63 10⁻³⁴ = 2.70 10⁹
Ft = 2.70 10⁹ Hz
M(graviton) = h / (λ x C)
c = λt x ft; λt = c/ft = 3 10⁸ / 2.70 10⁹ = 1.11 10⁻¹
λt = 11.1 10⁻¹ m
M(graviton) = h / (λt x c) = 6.63 10⁻³⁴ / 1.11 10⁻¹ x 3 10⁸
M(graviton)t-eff = 1.99 10⁻⁴¹ kg

Sun, Kʙs = 3.58 10⁻³⁷ J/K

Where Kʙs is approximate effective Boltzmann constant of the sun.

Es = Kʙs x T
Es = 3.58 10⁻³⁷ x 15 10⁶ = 53.7 x 10⁻³¹
Es = 53.7 10⁻³¹ Joules
Es = h x fs; fs = Es / h = 53.7 10⁻³¹ / 6.63 10⁻³⁴ = 8.09 10³
fs = 8.09 10³ Hz
M(graviton) = h / (λs x c)
c = λs x fs; λs = c / fs = 3 10⁸ / 8.09 10³ = 0.37 10⁵
λs = 3.7 10⁴ m
M(graviton) = 6.63 10⁻³⁴ / (3.7 10⁴ x 3 10⁸) = 0.59 10⁻⁴⁶
M(graviton)s-eff = 5.9 10⁻⁴⁷ kg

White Dwarf, Kʙe = 1.9 10⁻³⁷ J/K

Where Kʙe is approximate effective Boltzmann constant of a white dwarf star.

Ee = Kʙe x T
Ee = 1.9 10⁻³⁷ x 20 10⁶ = 38 x 10⁻³¹
Ee = 38 10⁻³¹ Joules
Ee = h x fe; fe = Ee / h = 38 10⁻³¹ / 6.63 10⁻³⁴ = 5.73 10³
fe = 5.73 10³ Hz
M(graviton) = h / (λe x c)
c = λe x fe; λe = c / fe = 3 10⁸ / 5.73 10³ = 0.52 10⁵
λe = 5.2 10⁴ m
M(graviton) = h / (λe x c) = 6.63 10⁻³⁴ / 5.2 10⁴ x 3 10⁸ = 0.425 10⁻⁴⁶
M(graviton)e-eff = 4.25 10⁻⁴⁷ kg

Neutron Star, Kʙn = 2.42 10⁻⁴² J/K

Where Kʙn is approximate effective Boltzmann constant of a neutron star.

En = Kʙn x T
En = 2.42 10⁻⁴² x 10¹² = 2.42 x 10⁻³⁰
En = 2.42 10⁻³⁰ Joules
En = h x fn; fn = En / h = 2.42 10⁻³⁰ / 6.63 10⁻³⁴ = 0.36 10⁴
fn = 3.6 10³ Hz
M(graviton) = h / (λn x c)
c = λn x fn ; λn = c / fn = 3 10⁸ / 3.6 10³ = 0.83 10⁵
λs = 8.3 10⁴ m
M(graviton) = h / (λn x c) = 6.63 10⁻³⁴ / 8.3 10⁴ x 3 10⁸ = 0.266 10⁻⁴⁶
M(graviton)n-eff = 2.66 10⁻⁴⁷ kg

Black Hole, Kʙq = 1.78 10⁻⁴³ J/K

Where Kʙq is approximate effective Boltzmann constant of a black hole.

Eq = Kʙq x T
Eq = 1.78 10⁻⁴³ x 10¹³ = 1.78 x 10⁻³⁰
Eq = 1.78 10⁻³⁰ Joules
Eq = h x fq; fq = Eq / h = 1.78 10⁻³⁰ / 6.63 10⁻³⁴ = 0.26 10⁴
fq = 2.6 10³ Hz
M(graviton) = h / (λq x c)
c = λq x fq ; λq = c / fq = 3 10⁸ / 2.6 10³ = 1.15 10⁵
λq = 1.15 10⁵ m
M(graviton) = h / (λq x c) = 6.63 10⁻³⁴ / 1.15 10⁵ x 3 10⁸ = 1.92 10⁻⁴⁷
M(graviton)q-eff = 1.92 10⁻⁴⁷ kg

Vacuum, Kʙ = 1.38 10⁻²³ J/K

Where Kʙ is approximate effective Boltzmann constant of Vacuum.

E = Kʙ x T
E = 1.38 10⁻²³ x 1.57 = 2.16 10⁻²³
E = 2.16 10⁻²³ Joules
E = h x f; f = E / h = 2.16 10⁻²³ / 6.63 10⁻³⁴ = 0.325 10¹¹
f = 3.25 10¹⁰ Hz
M(graviton) = h / (λ x c)
c = λ x f ; λ = c / f = 3 10⁸ / 3.25 10¹⁰ = 0.92 10⁻²
λq = 0.92 10⁻² m
M(graviton) = h / (λ x c) = 6.63 10⁻³⁴ / 0.92 10⁻² x 3 10⁸ = 2.40 10⁻⁴⁰
M(graviton)eff = 2.40 10⁻⁴⁰ kg

Vacuum, Kʙ = 1.38 10⁻²³ J/K

Where Kʙ is approximate effective Boltzmann constant of Vacuum.

E = Kʙ x T
E = 1.38 10⁻²³ x 1.57 10⁻⁵ = 2.16 10⁻²⁸
E = 2.16 10⁻²⁸ Joules
E = h x f; f = E / h = 2.16 10⁻²⁸ / 6.63 10⁻³⁴ = 0.325 10⁶
f = 3.25 10⁵ Hz
M(graviton) = h / (λ x c)
c = λ x f; λ = c / f = 3 10⁸ / 3.25 10⁵ = 0.92 10³
λq = 92 m
M(graviton) = h / (λ x c) = 6.63 10⁻³⁴ / 0.92 10³ x 3 10⁸ = 2.40 10⁻⁴⁵
M(graviton)eff = 2.40 10⁻⁴⁵ kg

Vacuum, Kʙ = 1.38 10⁻²³ J/K

Where Kʙ is Boltzmann constant of Vacuum.⁰Θ

E = Kʙ x T
E = 1.38 10⁻²³ x 1.57 10⁻¹⁰ = 2.16 10⁻³³
E = 2.16 10⁻³³ Joules
E = h x f; f = E / h = 2.16 10⁻³³ / 6.63 10⁻³⁴ = 0.325 10¹
f = 3.25 10⁰ Hz
M(graviton) = h / (λ x c)
c = λ x f; λ = c / f = 3 10⁸ / 3.25 10⁰ = 0.92 10⁸
λq = 9.2 10⁷ m
M(graviton) = h / (λ x c) = 6.63 10⁻³⁴ / 0.92 10⁸ x 3 10⁸ = 2.40 10⁻⁵⁰
M(graviton)eff = 2.40 10⁻⁵⁰ kg

Black Hole, Kʙq = 1.78 10⁻⁴³ J/K

Where Kʙq is approximate effective Boltzmann constant of a black hole.

Eq = Kʙq x T
Eq = 1.78 10⁻⁴³ x 1 10¹⁶ = 1.78 x 10⁻²⁷
Eq = 1.78 10⁻²⁷ Joules
Eq = h x fq; fq = Eq / h = 1.78 10⁻²⁷ / 6.63 10⁻³⁴ = 0.268 10⁷
fq = 2.6 10⁶ Hz
M(graviton) = h / (λq x c)
c = λq x fq ; λq = c / fq = 3 10⁸ / 2.6 10⁶ = 1.15 10²
λq = 1.15 10² m
M(graviton) = h / (λq x c) = 6.63 10⁻³⁴ / 1.15 10² x 3 10⁸ = 1.92 10⁻⁴⁴
M(graviton)eff = 1.92 10⁻⁴⁴ kg

Black Hole, Kʙq = 1.78 10⁻⁴³ J/K

Where Kʙq is approximate effective Boltzmann constant of a black hole.

Eq = Kʙq x T
Eq = 1.78 10⁻⁴³ x 1 10²⁶ = 1.78 10⁻¹⁷
Eq = 1.78 10⁻¹⁷ Joules
Eq = h x fq; fq = Eq / h = 1.78 10⁻¹⁷ / 6.63 10⁻³⁴ = 0.268 10¹⁷
fq = 2.6 10¹⁶ Hz
M(graviton) = h / (λq x c)
c = λq x fq ; λq = c / fq = 3 10⁸ / 2.6 10¹⁶ = 1.15 10⁻⁸
λq = 1.15 10⁻⁸ m
M(graviton) = h / (λq x c) = 6.63 10⁻³⁴ / 1.15 10⁻⁸ x 3 10⁸ = 1.92 10⁻³⁴
M(graviton)eff = 1.92 10⁻³⁴ kg

We are going to represent all these calculations in Table 2:

It is important to clarify that the mass of the calculated graviton is an effective mass or equivalent that is related to the definition that was used to calculate the effective Boltzmann constant.

If we compare Table 1 with Table 2, for low temperatures, below 1K, we observe that the mass of the gluons coincides with the mass of the gravitons. As the temperature increases, the difference between the mass of the gluons with respect to the mass of the gravitons increases, reaching the maximum difference at the temperature of 10¹³ K, in which the mass of the gluon is 10²⁰ times greater than that of graviton.

Above the temperature of 10¹³ K, the difference between the mass of the gluon and the graviton is maintained, with the mass of the gluon being 10²⁰ times greater than the mass of the graviton.

In analogy with the calculations carried out for gluons, we are going to carry out similar calculations for gravitons using the mass of the effective graviton.

For a neutron star, we have:

Let's assume the mass of the neutron for T= 10¹² K,

For T= 10¹² K,

Neutron mass = 939.56 MeV/c²
2md + mu = 11.6 MeV/c²
QTY gr = Neutron mass / unit mass of a graviton.
QTY gr = 1.67 10⁻²⁷ / 2.66 10⁻⁴⁷
QTY gr = 0.627 10²⁰
QTY gr = 6.27 10¹⁹

Where QTY gr, is number of gravitons in a neutron, for T = 10¹²K.

Why do we use the mass of the neutron, mn = 939.56 MeV/c², to calculate the number of gravitons in a neutron!

This question, in my opinion, would have 2 answers:

First answer, from the point of view of mass, if we consider quark and anti-quark dipoles as point masses that vibrate, we can idealize it as a quark linked to an anti-quark by a spring (Gravitons with spin 2), these two masses vibrating together by a spring, they would produce disturbances in space-time that would propagate in the form of gravitational waves. This would be the mechanism by which gravitational waves are generated, gravitons that would propagate in space-time.

Second answer, if we consider the Maldacena correspondence ADS = CFT, the right side of the equation, CFT, tells us that there is a mass that corresponds to the neutron and is mn = 939.56 MeV/c²; The left side tells us that there must be a gravitational mass equivalent to mn = 939.56 MeV/c², which must be equivalent to the CFT mass, for the equation ADS = CFT to be fulfilled.

These are the two answers, for which we use the mass of the neutron to calculate the number of gravitons inside a neutron.

We will calculate the number of corresponding gravitons, for interactions 1 & 2:

Interaction 1:

QTY gr INT 1: = 0.370 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ kg = 1.39 10¹⁹ Graviton
Qty gr R(DD)R = 0.149 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ kg = 0.560 10¹⁹ Graviton
Qty gr B(DD)B = 0.149 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ kg = 0.560 10¹⁹ Graviton
Qty gr G(UU)G = 0.069 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ kg = 0.259 10¹⁹ Graviton

Interaction 2:

QTY gr INT 2 = 1.300 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ kg = 4.88 10¹⁹ Graviton
QTY gr R(DD)B = 0.1786 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ = 0.671 10¹⁹ Graviton
QTY gr R(DU)G = 0.1786 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ = 0.671 10¹⁹ Graviton
QTY gr B(DD)R = 0.1786 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ = 0.671 10¹⁹ Graviton
QTY gr B(DU)G = 0.1786 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ = 0.671 10¹⁹ Graviton
QTY gr G(UD)R = 0.2925 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ = 1.109 10¹⁹ Graviton
QTY gr G(UD)B = 0.2925 10ˉ²⁷ kg / 2.66 10ˉ⁴⁷ = 1.109 10¹⁹ Graviton

It is important to make it clear that the number of gravitons calculated inside a neutron corresponds to the temperature T = 10¹² K.

If we look at Table 2, we see that as the temperature increases the mass of the graviton decreases.

For Sun, T = 15 10⁶K:

Neutron mass = 939.56 MeV/c²
2md + mu = 11.6 MeV/c²
QTY gr = Neutron mass / unit mass of a graviton.
QTY gr = 1.67 10⁻²⁷ kg / 5.9 10⁻⁴⁷ kg = 0.283 10²⁰
QTY gr = 2.83 10¹⁹

Where QTY gr, is number of gravitons in the Sun, for T = 15 10⁶ K.

For Moon, T = 1.6 10³K:

Neutron mass = 939.56 MeV/c²
2md + mu = 11.6 MeV/c²
QTY gr = Neutron mass / unit mass of a graviton.
QTY gr = 1.67 10⁻²⁷ kg / 1.72 10⁻³⁹ kg = 0.970 10¹²
QTY gr = 9.7 10¹¹

Where QTY gr, is number of gravitons in the Moon, for T = 1.6 10³ K.

3. Electrical-Quantum Modelling of the Proton as a Three-Phase Alternating Current Electrical Generator

We are going to work with Figure 16 to create our electrical model of the proton as a three-phase alternating current electrical generator.

The dipole DD is analogous to L1 and RR is analogous to the current flowing through L1.

The dipole UU is analogous to L2 and BB is analogous to the current flowing through L2.

The dipole UU is analogous to L3 and GG is analogous to the current flowing through L3.

We see that there are two types of interactions.

Interaction 1 or direct interaction and interaction 2 or cross interaction.

In analogy to a three-phase alternating current electric generator, we are going to represent interaction 1 and interaction 2, using vectors whose resulting vector is not zero. In this way we are going to simulate a proton as a three-phase alternating current electrical generator.

In Figure 5 of the standard model, we see that the up quark has a mass of 2.2 MeV/c² and the down quark has a mass of 4.7 MeV/c².

Taking these values as reference we are going to make our vector diagram of the neutral.

Quark Down = 4.7 MeV/c²

Quark up = 2.2 MeV/c²

It is important to make it clear that all interactions are vector, although we do not represent them as such in the figures.

Interaction 1:

If we analyse Figure 17, star connection, we see that the following vector sum is not null:

R(DD)R + B(UU)B + G(UU)G ≠ 0

Interaction 2:

If we analyse Figure 18, we observe that the following vector sum is not null:

R(DU)B + R(DU)G + B(UD)R + B(UU)G + G(UD)R +G(UU)B ≠ 0

From a load point of view, we have:

R(DD)R + B(UU)B + G(UU)G + R(DU)B + R(DU)G + B(UD)R + B(UU)G + G(UD)R

+ G(UU)B = 1

From the mass point of view, we have:

R(DD)R + B(UU)B + G(UU)G + R(DU)B + R(DU)G + B(UD)R + B(UU)G + G(UD)R

+ G(UU)B = 938.27 MeV/c²

Knowing that the total mass of the proton is 938.27 MeV/c², we are going to calculate the mass content in each interaction:

R(DD)R = 8.6 x 12.0720 = 103.81 MeV/c²
B(UU)B = 4.0 x 12.0720 = 48.28 MeV/c²
G(UU)G = 4.0 x 12.0720 = 48.28 MeV/c²
R(DU)B = 4.0 x 12.0720 = 48.28 MeV/c²
R(DU)G = 10.4 x 12.0720 = 125.54 MeV/c²
B(UD)R = 13.7 x 12.0720 = 165.38 MeV/c²
B(UU)G = 8.1 x 12.0720 = 97.78 MeV/c²
G(UD)R = 16.8 x 12.0720 = 202.80 MeV/c²
G(UU)B = 8.1 x 12.0720 = 97.78 MeV/c²
8.6 + 4 x (3) + 10.4 + 13.7 + 2 x (8.1) + 16.8 = 77.7

PECF = Mp ̸ 77.7 = (938.27 MeV/c²) ̸ 77.7 = 12.0720 MeV/c², Neutron electromagnetic coupling factor. The value: 77.7, could have any type of units, for practical purposes we are going to leave it without units.

If we divide the electromagnetic coupling factor of the proton PECF, by the energy 0.388 MeV/c², corresponding to unit binding energy per nucleon, we will have the approximate number of neutrons to which the proton can be stably associated.

Qtyn = PECF / ∆Eα = (12.0720 MeV/c²) / (0.388 MeV/c²) = 31.11

where ∆Eα could be considered unit binding energy per nucleon.

Qtyn = 31 neutron.

Where Qtyn represents the number of neutrons that the proton-neutron binding energy stably supports, considering the electromagnetic coupling factor of the proton PECF.

According to our calculation, starting at neutrons number 31, the proton-neutron binding energy begins to weaken.

If we consider the electromagnetic coupling factor, NECF and PECF, the maximum stability of an atomic nucleus would be achieved with a maximum number of 25 protons and a maximum number of 31 neutrons, these quantities roughly coincide with that of the iron atom Fe (26,30), a good approximation.

We are going to represent these values in Figure 19:

The electrical modelling of a proton as a three-phase alternating current electrical generator allows us to assign a mass value to interactions 1 and 2, which we represent using a vector diagram, as shown in Figure 18Figures &Figure 19.

We can assure that protons are true generators of energy, mass and gravity; We have verified how with three quarks that add up to approximately 10 MeV/c², we can generate a mass of 938.27 MeV/c² through the interactions of quarks, anti-quarks and gluons.

4. Application of the Model and Results

4.1. Analysis of βˉ Decay. Creation of Electrons, Neutrinos and Photons

Let's briefly describe β ˉ decay:

β decay represents the decay of a parent nucleus to a daughter through the emission of the beta particle. Beta decay is governed by the weak interaction.

This transition (β ˉ decay) can be characterized as:

Figure 20. β ˉ decay.

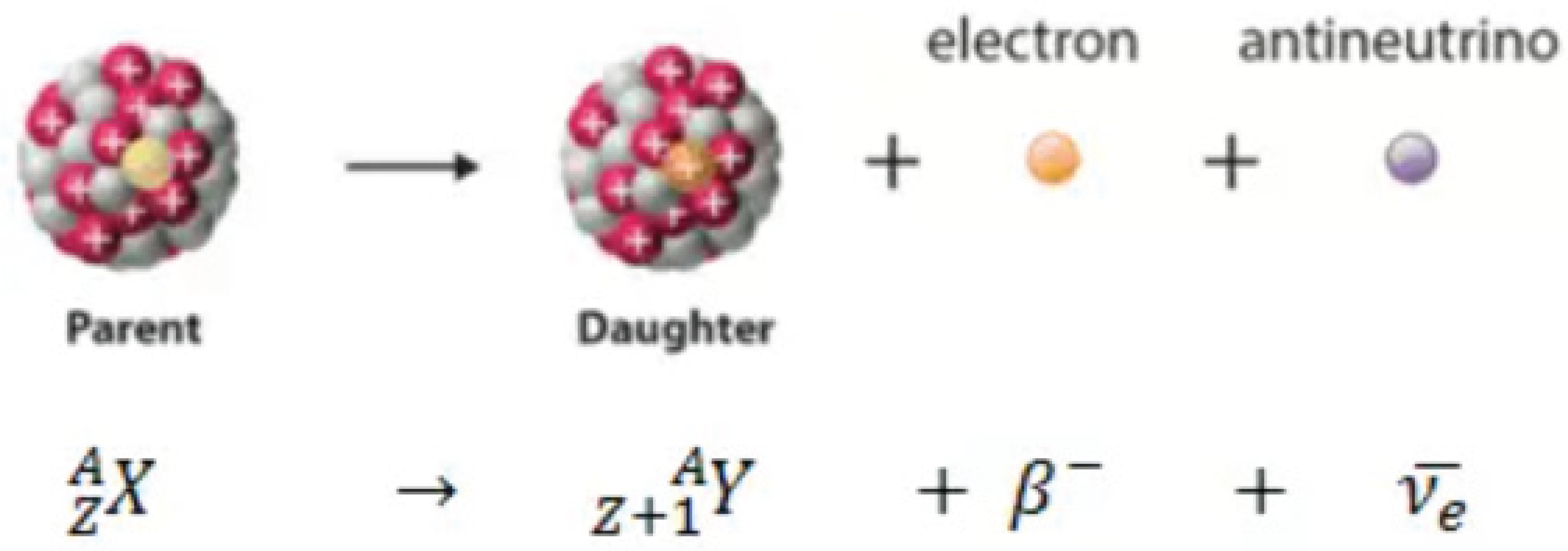
If a nucleus emits a beta particle, it loses an electron (or positron). In this case, the mass number of the daughter nucleus remains the same, but the daughter nucleus will form a different element.

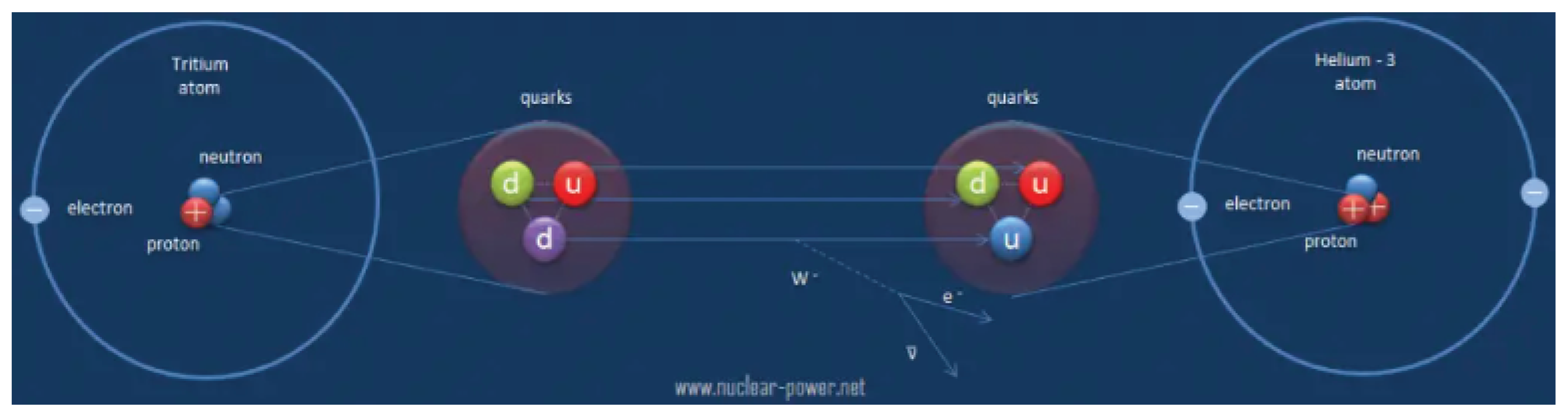
A free neutron also undergoes this type of decay. A free neutron will decay with a half-life of approximately 611 seconds (10.3 minutes) into a proton, an electron, and an antineutrino.

Figure 21. weak interaction changes one quark flavour to another.

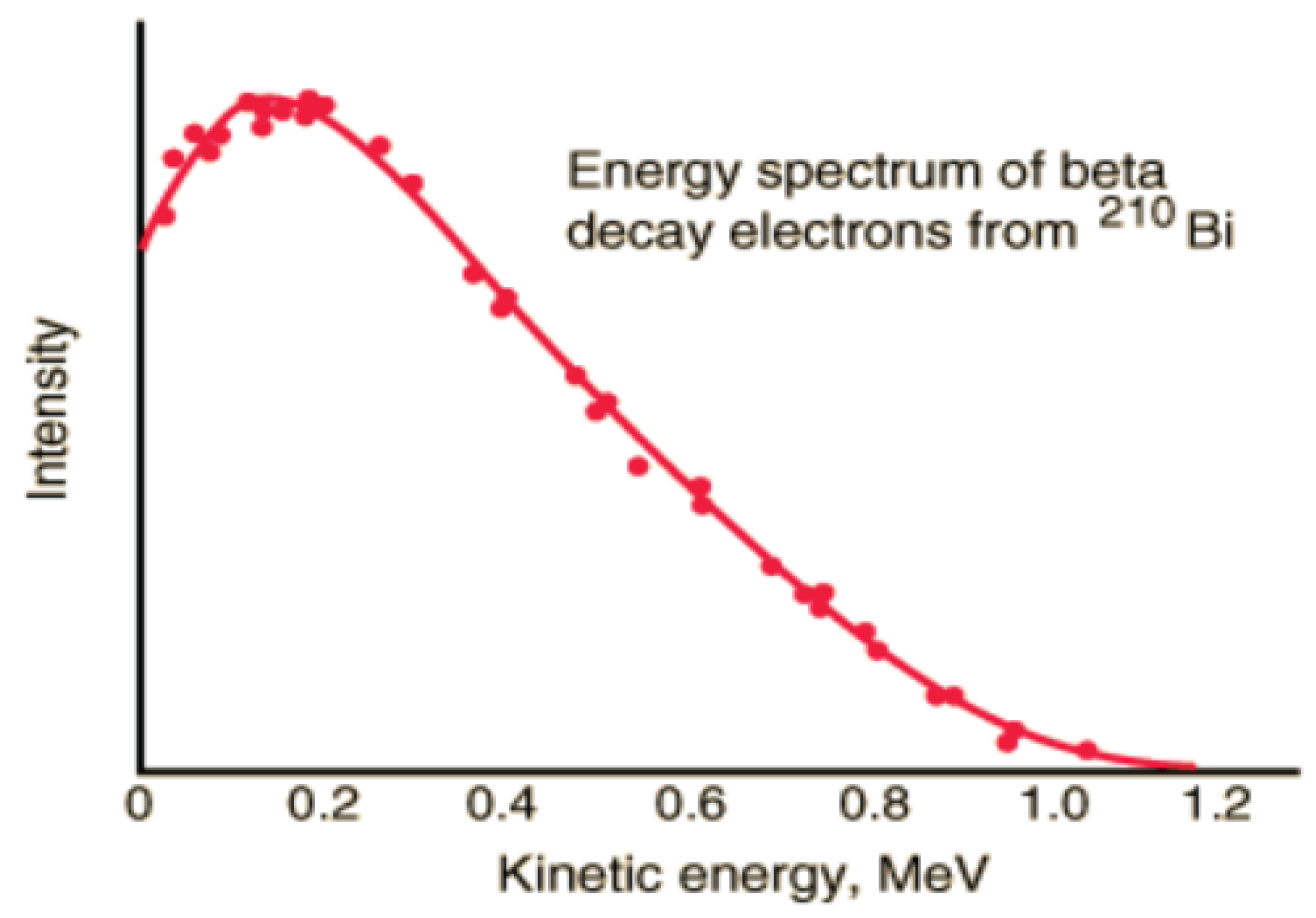
Beta decay energy spectrum

The electrons emitted in β ˉ decay have a continuous rather than discrete spectrum that seems to contradict the conservation of energy, under the current assumption that beta decay is the simple emission of an electron from a nucleus. When this was first observed, it seemed to threaten the survival of one of the most important conservation laws in physics.

In the β ˉ decay process, the antineutrino carries the missing energy and also in this process the law of conservation of energy remains valid.

Figure 22. Continuous energy spectrum of βˉ decay.

βˉ Decay – Q Value

The Q value is given by:

Q = [m father – (m Daughter + m Radiation)] c²

Figure 23. The Q value of typical β ˉ decay for Bi.

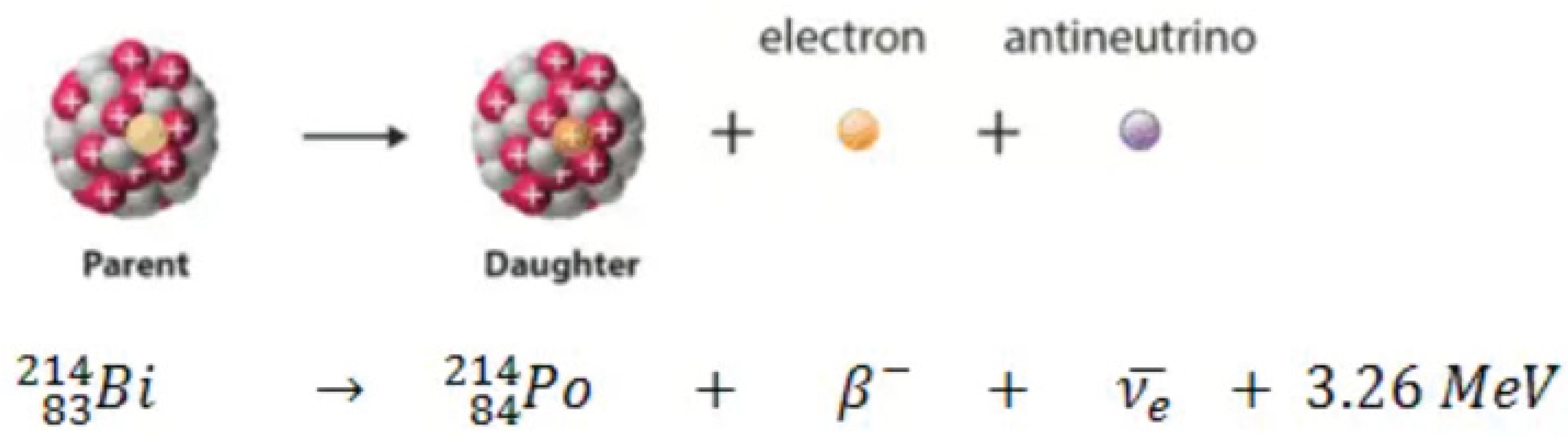
In the βˉ decay process, an electron is emitted. This emission is accompanied by antineutrino emission, which shares the energy and momentum of the decay. βˉ emission has a characteristic spectrum. This characteristic spectrum is caused by the fact that antineutrino is emitted with βˉ particle emission. The shape of this energy curve depends on what fraction of the reaction energy (Q value - the amount of energy released by the reaction) is carried by the massive particle. Therefore, βˉ particles can be emitted with any kinetic energy ranging from 0 to Q. After a βˉ decay, the daughter nucleus is often left in an excited energy state. To stabilize, it subsequently emits high-energy photons, γ rays.

Vector analysis ofβˉdecay

To analyse the mechanism of βˉ decay, using a vector diagram, we are going to use Figure 24 and Figure 25.

Let's analyse the simplest situation:

R(DD)R of the neutron, in phase with R(DD)R of the proton

B(DD)B of the neutron, in phase with B(UU)B of the proton

G(UU)G of the neutron, in phase with G(UU)G of the proton

To make the base diagram of Figure 26, We are going to use the data in Figure 24 and Figure 25 to determine the next scaling factor SF:

Scale factor:

SF = [(E MeV/c²)/ 39.39 MeV/c²] x 4

Example 1:

For G(UU)G, of the neutron.

SF = [G(UU)G / 39.39] x 4

SF = [(39.39 MeV/c²) / (39.39 MeV/c²)] x 4 = 4

For G(UU)G, of the proton.

SF = [G(UU)G / 39.39] x 4

SF = [(48.28 MeV/c²) / (39.39 MeV/c²)] x 4 = 4.90

For B(DD)B, of the neutron.

SF = [B(DD)B / 39.39] x 4

SF = [(84.69 MeV/c²) / (39.39 MeV/c²)] x 4 = 8.6

For B(UU)B, of the proton.

SF = [B(UU)B / 39.39] x 4

SF = [(48.28 MeV/c²) / (39.39 MeV/c²)] x 4 = 4.9

For R(DD)R, of the neutron.

SF = [R(DD)R / 39.39] x 4

SF = [(84.69 MeV/c²) / (39.39 MeV/c²)] x 4 = 8.6

For R(DD)R, of the proton.

SF = [R(DD)R / 39.39] x 4

SF = [(103.81 MeV/c²) / (39.39 MeV/c²)] x 4 = 10.54

In my diagram in Paint, it is represented in this scale. However, when I copy the diagram into Figure 26 it is out of scale or on a reduced scale.

It is important to highlight that the diagrams in Figure 27, Figure 28 and Figure 29, were made with this scale and all the values obtained result from using this scale.

In Figure 28, to obtain the value of En, we perform the following calculation:

En = (1 x 39.39) % 4 = 9.84 MeV/c²

En = 9.84 MeV/c²

With these examples, we can know how the values shown in Figure 30 were obtained.

If we look at Figure 27, the βˉ decay, we see that it is made up of 9 vectors: E1, E2, E3, E4, E5, E6, E7, E8 and E9. These vectors are represented in blue.

In Figure 28, we divide these vectors into three parts, which we will explain below:

En = E5 + E8

En = 9.84 MeV/c²
E5 = [R(DU)G]n → [R(DU)G]p
E8 = [G(UD)R]n → [G(UD)R]p

For E5, when the decay of [R(DU)G]n of the neutron, to [R(DU)G]p of the proton, occurs; a current of gluons RG is produced.

For E8, when the decay of [G(UD)R]n of the neutron to [G(UD)R]p of the proton occurs; a current of GR gluons is produced.

Here, we are going to hypothesize that the En energy is what gives origin to the neutrinos. Let us note that the RG and GR gluons are of different frequencies; R which is associated with the D quark, has a higher frequency than G, which is associated with the U quark.

When E5 + E8 interacts, it is like the RG and GR gluons cancel each other and the DU and UD quarks also cancel and, in this way, the resulting energy gives origin to the neutrinos, whose mass is neutral.

Ep = E1 + E3

Ep = 19.69 MeV/c²
E1 = [R(DD)R]n → [R(DD)R]p
E3 = [G(UU)G]n → [G(UU)G]p

For E1, when the decay of [R(DD)R]n of the neutron, to [R(DD)R]p of the proton, occurs; a neutral current is produced.

For E3, when the decay of [G(UU)G]n of the neutron, to [G(UU)G]p of the proton, occurs; a neutral current is produced.

Here, we are going to hypothesize that the Ep energy is what gives origin to the photons. Here it is important to highlight that the RR and GG gluons have the same frequency; RR have the frequency of the D quark and GG have the frequency of the U quark.

Ee = E2 + E4 + E6 + E7 + E9

Ee = 14.77 MeV/c²
E2 = [B(DD)B]n → [B(UU)B]p
E4 = [R(DD)B]n → [R(DU)B]p
E6 = [B(DD)R]n → [B(UD)R]p
E7 = [B(DU)G]n → [B(UU)G]p
E9 = [G(UD)B]n → [G(UU)B]p

For the vectors E2, E4, E6, E7 and E9, when the decay of neutron to proton occurs, it is observed that currents with positive and negative charges are generated.

The negative net energy of the vector Ee = 14.77 MeV/c².

Here, we are going to hypothesize that the Ee energy is what gives origin to the electron.

The emission of the energy vectors En, Ep and Ee are necessary inβˉ decay, so that the proton stabilizes and reaches its corresponding energy.

It is important to note that we speak of mass or energy interchangeably, using the equivalence E = mc².

calculation of W⁻, Z⁰andΘangle:

Experimentally the energy of βˉ decay is 0.0002[0.000194, Data provided by Don Lincoln-Fermilab)] of the total energy of the boson W⁻ = 80.360 GeV/c².

Experimental calculations:

Experimental W⁻ = 0.000194 x 80360 MeV/c²
Experimental W⁻ = 15.58 MeV/c²
Experimental Z⁰ = 0.000194 x 91190 MeV/c²
Experimental Z⁰ = 17.69 MeV/c²
W⁻/ Z⁰ = cos Θ → arc cos Θ = arc cos W⁻/Z⁰
Θ = 29⁰

Theoretical calculations that we obtain from Figure 29, βˉ decay diagram:

theoretical W⁻ = Ee = (1.5 x 39.39 MeV/c²)/ 4 = 14.77 MeV/c²
theoretical W⁻ = 14.77 MeV/c²
theoretical Z⁰ = (1.8 x 39.39 MeV/c²)/ 4 = 17.72 MeV/c²
theoretical Z⁰ = 17.72 MeV/c²
W⁻/ Z⁰ = cos Θ → arc cos Θ = arc cos W⁻/Z⁰
Θ = 33.90 ⁰
measured Θ = 35⁰

Experimentally the value calculated for W⁻ = 15.58 MeV/c²; theoretically, using our quarks-antiquarks-gluon interaction model, we have calculated W⁻ = 14.77 MeV/c². We observe that the value of W⁻ calculated experimentally is similar to the value calculated theoretically.

Experimentally the value calculated for Z⁰ = 17.69 MeV/c²; theoretically, using our quarks-antiquarks-gluon interaction model, we have calculated Z⁰ =17.72 MeV/c². We observe that the value of Z⁰ calculated experimentally is similar to the value calculated theoretically.

Experimentally the value calculated for Θ = 29⁰; theoretically, using our quarks-antiquarks-gluon interaction model, we have calculated Θ = 35⁰. We observe that the value of Θ calculated experimentally is similar to the value calculated theoretically.

We have verified theoretically, using the theory: Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, inside a Neutron; that the W⁻ and Z⁰ boson, is the resulting product of the quarks-antiquarks-gluons interactions.

The vectors E1, E2, E3, E4, E5, E6, E7, E8, and E9 that we observe in Figure 27, we are going to represent in the following Figure.

Experimental data and theoretical results:

The value of the Gamow-Teller matrix for the described decays in Table 1, they are calculated using equation (1).

(1)

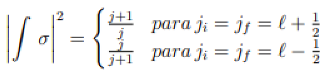
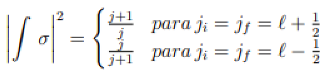
Equation (1) represents the expression of the Gamow-Teller matrix in transitions specular.

Table 1. Data for specular Transitions.

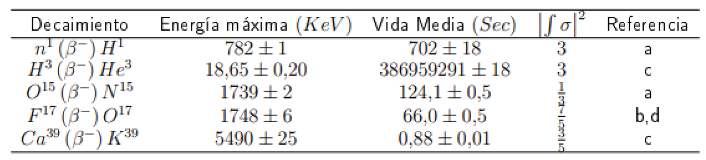
a. www.nucleide.org/DDEP_WG/DEEPdata.htm. b. L. Friedman y L. G. Smith, phys. Rev. 83, 512 (1951). c. O. C. Kistner y B. M. Rustad, Phys. Rev. 112, 1972 (1958). d. Calvin Wong, Phys. Rev. 95, 765 (1954).

Additional considerations:

Let's represent βˉdecay:

Q = [m father – (m Daughter + m Radiation)] c²

Neutron → Proton + e⁻ + ṽ + ∆E

We also said that in the Hydrogen atom, according to QED quantum electrodynamics, there is an exchange of photons between the electron and the proton.

If we carefully analyse Figure 27, B(DD)B & B(UU)B, we can affirm that the BB gluons are what keep the proton united with the electron.

In other words, what we call photons are actually BB gluons.

We are going to generalize what was stated, for this we are going to use Figure 25 which corresponds to the proton.

Interaction 1

In analogy to the BB gluon, which we consider a photon, the following gluons will also be photons.

RR = gluon = photon

BB = gluon = photon

GG = gluon = photon

the gluons RR, BB and GG, they are photons, which indicate that their interaction with the corresponding quark makes them have different phase angles. The nomenclature is telling us that they have different phase angles, i.e. RR, BB and GG, have different phase angles.

If we represent the quarks of interaction 1, in the proton as vectors (DD, UU, UU), see Figure 26, the gluons (RR, BB, GG) indicate that the vectors (DD, UU, UU) are with different phases.

These gluon-photons have the characteristic that they can escape confinement. The gluons that escape confinement are what we call photons.

It is important to highlight that in interaction 1, the gluon-photon energy exchange with the quarks takes place at the same frequency. It is the quarks that determine the frequency of the interaction.

Interaction 2:

In analogy to the BB gluon, which we consider a photon, the following gluons will also be photons.

RB = gluon = photon
RG = gluon = photon
BR = gluon = photon
BG = gluon = photon
GR = gluon = photon
GB = gluon = photon

These gluon-photons have the characteristic that they cannot escape confinement.

the gluons RB, RG, BR, BG, GR and GB, they are photons, which indicate that their interaction with the corresponding quark makes them have different phase angles.

It is important to highlight that in interaction 2, the energy exchange of the gluons-photons with the quarks, in some cases is carried out at the same frequency and in another at a different frequency. It is the quarks that determine the frequency of the interaction.

When analysing βˉ decay, considering our proposed model of neutron and proton as a three-phase electrical generator, we hypothesize that the SU(2) and SU(3) symmetry can also be reduced to the U(1) symmetry, provided that Let's consider gluons as photons.

4.2. Simple Harmonic Oscillator, String Theory and the Calculation of ℓs and T₀

In a simple harmonic oscillator, we have:

F = - k x

k = m ω²

Where K is recovery constant, m is mass and ω is angular frequency.

In string theory, we have:

ℓs = h c √α' / 2π,

Where ℓs is natural or spatial length of a string.

T₀ = 1 / α' h c,

Where T₀ is string tension.

To calculate ℓs and T₀ we are going to assume the following:

T₀ = k, this assumption is very important, it is a forced assumption.

In the following example we are going to calculate ℓs and T₀ for the following dipole R(DD)R in a proton:

R(DD)R = 103.81 MeV/c²
R(DD)R = 1.85 10⁻²⁸ Kg
ω = 2 π f = 2 x 3.14 x 1.16 10²¹ = 7.28 10²¹,

Where ω is frequency for the D quark.

ω = 7.28 10²¹ rad/s
k = m ω² = 1.85 10⁻²⁸ x (7.28 10²¹) ² = 98.03 10¹⁴ N/m
K = 98.03 10¹⁴ N/m
T₀ = k = 98.03 10¹⁴ N/m
T₀ = 1 / α' h c
α' = 1 / T₀ h c = 1 / (98.03 10¹⁴ x 6.62 10⁻³⁴ x 3 10⁸) = 1 / 1946.87 10⁻¹² = 5.13 10⁸
α' = 5.13 10⁸,

Where α' is universal regge slope.

ℓs = h c √α' / 2π
ℓs = (6.62 10⁻³⁴ x 3 10⁸ x √ 5.13 10⁸) / 2 x 3.14
ℓs = 7.16 10⁻²² m

T₀ = k = 98.03 10¹⁴ N/m
ℓs = 7.16 10⁻²² m

We calculate that the length ℓs that separates the quark from the antiquark is in the order of 10ˉ²² m.

We calculate that the tension T₀ that separates the quark from the antiquark is in the order of 10¹⁴ N/m.

We have calculated the approximate string tension T₀ and the space length ℓs for the dipole R(DD)R, with a mass of 103.81 MeV/c², formed by the DD quarks.

We wonder why the down quark and its antiparticle are not destroyed; the answer is the following:

When we developed the theory of the generalization of the Boltzmann constant in curved space-time, we used examples of how electrons, the down quark and the top quark are created; in the example of the origin of the down quark, with the frequency of the down quark we calculate the corresponding wavelength, and to calculate the diameter of the down quark we divide the wavelength λ / 2 by the contraction factor of the Boltzmann constant corresponding to the down quark temperature.

Dd = (λ/2) / fc

Where Dd is the diameter of the down quark, λ/2 is the wavelength of the down quark divided by 2 and fc is the contraction factor of the down quark that corresponds to its temperature.

For the up and down quarks, the contraction factor fc is so large on the order of 10⁶ times, similar to that of neutron stars, in other words, the gravity in the down and up quarks, is so large, that it contracts the space-time in the order of 10⁶ times, acting as a shield or protection, preventing quarks and antiquarks from annihilating each other.

Precisely, this allows us to propose our electric-quantum model of the neutron and the proton as a three-phase electric generator, as Quark-antiquark dipole pairs.

At the quark level, the contraction of space-time is so great, preventing quark-antiquark annihilation, as matter forms more complex structures, that protection disappears, allowing matter-antimatter annihilation.

Although I work on it directly in my articles, I have never mentioned it, the contraction of space-time is directly proportional to the temperature, the higher the temperature, the greater the contraction of space-time, and vice versa. The maximum contraction of space-time occurs when a black hole forms. As a black hole grows, the Planck length begins to decrease inside a black hole, to a limit at which the black hole explodes, producing the Big Bang.

We are going to perform the same calculations for the interaction 1, in a proton and we are going to show them in the Figure 31:

In Figure 31, we observe for the three quark-antiquark dipoles, interaction 1, the tension of the string T₀ is of the order of 10¹⁴ n/m and the length of the string ℓs is of the order of 10ˉ²² m

If we extrapolate the values of T₀ and ℓs, to the dipoles of interaction 2, due to the mass values that the interactions take, we conclude that the values of T₀ will be in the order of 10¹⁴ n/m and the values of ℓs They will be found in the order of 10ˉ²² m.

We are going to perform the same calculations for the interaction 1, in a neutron and we are going to show them in the Figure 32:

In Figure 32, we observe for the three quark-antiquark dipoles, interaction 1, the tension of the string T₀ is of the order of 10¹⁴ n/m and the length of the string ℓs is of the order of 10ˉ²² m

The most important thing that we can rescue or emphasize using the theory of Electrical-quantum modelling of the neutron and proton as a three-phase alternating current electrical generator, is that we can predict the typical values, that is, the order of the values for T₀ and ℓs, in the interactions 1 & 2, in the protons and neutrons.

4.3. Electrical-Quantum Modelling of the Black Hole as a Three-Phase Alternating Current Electrical Generator

Let us remember the following, in the LHC particle accelerator, it has been successfully isolated antimatter, that is, matter (-).

We will also remember, when a black hole forms, a star of more than 25 solar masses explodes in a supernova and collapses due to gravity, giving rise to a black hole of approximately 3 solar masses. It is important to note that the star loses 22 solar masses to produce a black hole of 3 solar masses.

Let's also remember the following definition of a black hole:

A black hole is a plasma of quarks and gluons, a superfluid or a super-solid, which forms a high-temperature bosonic condensate, characterized because the matter is in its state of maximum energy, that is, as a whole it behaves like an isolated quark.

This definition is in the paper: Rlc Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time.

In the definition of a black hole, we are going to highlight the word isolated quark, we could interpret this as meaning that inside a black hole there is no quarks - antiquarks - gluons interaction, only the quarks - gluons interaction exists.

With this we are proposing that inside a black hole there is no antimatter (-), that is, the interior of a black hole is made up only of matter.

Recalling again that at the LHC it was possible to isolate antimatter, that is, matter (-) and also remembering that to form a black hole a star of 25 solar masses explodes in a supernova and by gravitational collapse forms a black hole of 3 solar masses, We are wondering!!!!!!

Could it happen that the gravitational collapse process separates matter from anti-matter in analogy to what happens at the LHC?

The explosion of a supernova goes beyond chemical energy or nuclear energy; That is why we propose that a supernova when it explodes separates matter from antimatter, in other words, the black hole that remains would be made up of matter and the antimatter expands in the space-time that surrounds the black hole.

For temperatures greater than 10¹⁵ kelvin, the symmetry breaking of the electro-weak force occurs and consequently the separation of the electromagnetic force field and the weak force field; For higher temperatures, the interactions of the electromagnetic force field and those of weak force do not exist.

According to what is stated in the theory Rlc Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann's Constant in Curved Space-Time, a black hole has a temperature of 10¹³ K, that is, the supernova explosion to form a black hole produces a temperature higher than 10¹³ K, in this way, it is possible to reach at the temperature of symmetry breaking, which would mean that a black hole would form a high-temperature Bose-Einstein condensate, a single primordia atom.

Hypothesis: the disappearance of the interactions of the electromagnetic force field and the weak force field together with the gravitational collapse of a star of more than 25 solar masses due to the explosion of a supernova generates a black hole of mass (+), matter; that is, a black hole without antimatter, without mass (-).

Taking the above into account, we are going to propose the following vector model of a black hole and we are going to compare it with the vector model of a neutron.

We compare it with a neutron because we assume that the net charge of a black hole is also zero.

We are going to carry out mathematical calculations to see if we can obtain important conclusions:

We will calculate the Schwarzschild´s radius for a black hole of 3 solar masses.

M = 6 10³⁰ kg
mn = 939.56 MeV/c²
mn = 1.675 10ˉ²⁷ kg

Where mn is mass of the neutron.

Rs = 2GM / c²
Rs = (2 x 6.67 10¯¹¹ x 6 10³⁰) / 9 10¹⁶ = 80.04 10¹⁹ / 9 10¹⁶
Rs = 8.89 10³ m

Where Rs is Schwarzschild´s radius.

We will calculate the volume of a black hole of three solar masses:

V = 4/3 ᴨ R³
V = 1.33 x 3.14 x (8.89 10³) ³
V = 1.33 x 3.14 x 702.59 10⁹
V = 2934.15 10⁹

Where V is volume of the black hole.

We will calculate the volume of a neutron.

Rn = 0.4 10⁻¹⁵ m

Where Rn is radius of the neutron.

Vn = 4/3 ᴨ R³
Vn = 4/3 ᴨ R³ = 4/3 x 3.14 x (0.4 10⁻¹⁵) ³ = 0.267 10⁻⁴⁵ mᶾ, volume of the neutron.
Vn = 0.267 10⁻⁴⁵ mᶾ,

Where Vn is volume of the neutron.

We will define D, a scale factor that represents the ratio of the volume of a black hole of 3 solar masses to the volume of the neutron.

D = V / Vn

Where D is scale factor.

D = V / Vn
D = V / Vn = 2934.15 10⁹ / 0.267 10⁻⁴⁵ = 10989.34 10⁵⁴
D = 10.98 10⁵⁷

We divide the mass of the black hole by the factor D.

Mn = M/D
Mn = 6 10³⁰ kg / 10.98 10 ⁵⁷ kg
Mn = 0,54 10 ⁻²⁷ kg

If we divide Mn by mn, we obtain:

K = Mn / mn = 0.54 10⁻²⁷ / 1.67 10⁻²⁷ = 0.32
K = 0,32
Mn = 939.56 x 0.32 = 300.65 MeV/c²
Mn = 300.65 MeV/c²

Where Mn is the mass contained in a black hole, in a volume equivalent to that of the neutron.

This result that we obtained for Mn is very interesting, it is telling us that the mass content in a volume equivalent to that of a neutron inside a black hole is less than the mass of the neutron; precisely this coincides with our assumption that inside a black hole we do not have antimatter, a black hole is formed only by matter.

If the statement is true: a black hole is formed only by matter, the antimatter is expelled when the collapse of a star occurs and a supernova explosion occurs; This would explain the enigma of antimatter during the Big Bang, it would explain why the Big Bang produces matter and not antimatter.

Vector diagram corresponding to Figure 34, black hole:

Figure 33. Neutron.

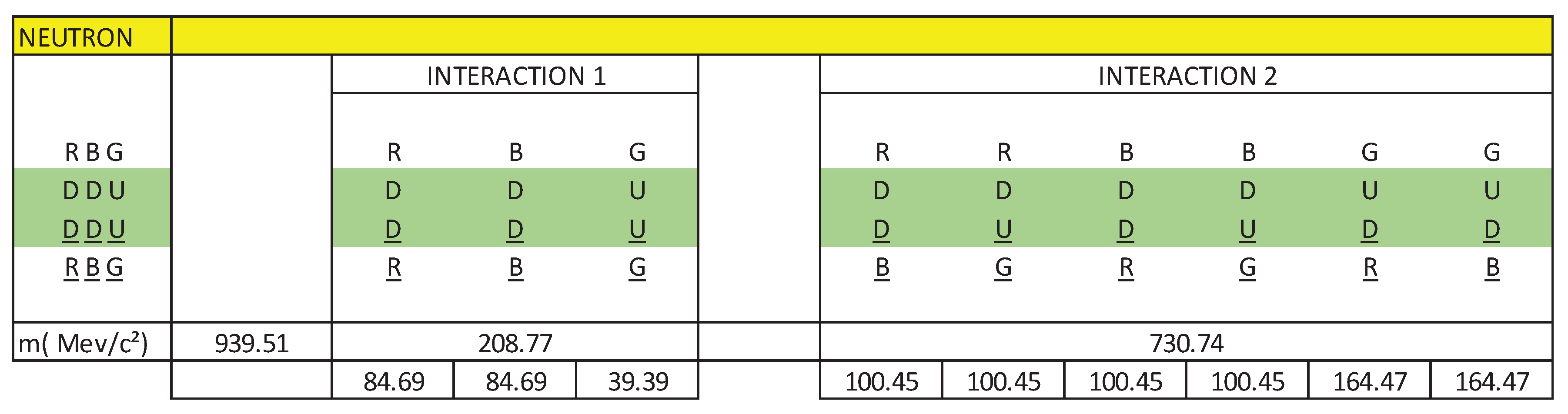
Considering the conversion factor, we calculate the value of interaction 2, for the six corresponding dipoles, which we will represent below:

R(DD)B = 28.54 MeV/c²
R(DU)G = 60.88 MeV/c²
B(DD)R = 28.54 MeV/c²
B(DU)G = 60.88 MeV/c²
G(UD)R = 60.88 MeV/c²
G(UD)B = 60.88 MeV/c²

We are going to represent these values in Figure 36:

In Figure 36, we see that the equivalent mass of the neutron inside a black hole is approximately one-third of the mass of the neutron.

We observe that the direct interaction, interaction 1, is null.

We observe that the cross interaction, interaction 2, the scalar sum is equal to 300.60 MeV/c² and the vector sum is zero

4.4. Fine Structure Constant α

In this item, we will determine the origin of the fine structure constant α.

To do this, let's remember the definition of NECF and PECF.

NECF = Mn / 95.4 = (939.56 MeV/c²) / 95.4 = 9.8486 MeV/c², Neutron electromagnetic coupling factor.

NECF = 9.8486 MeV/c²

Qtyp = NECF / ∆Eα = (9.8486 MeV/c²) / (0.388 MeV/c²) = 25.38

Qtyp = 25 proton.

Where Qtyp represents the number of protons that the neutron-proton binding energy stably supports, considering the electromagnetic coupling factor of the Neutron NECF.

According to our calculation, starting at proton number 26, the neutron-proton binding energy begins to weaken.

PECF = Mp ̸ 77.7 = (938.27 MeV/c²) ̸ 77.7 = 12.0720 MeV/c², Neutron electromagnetic coupling factor.

PECF = 12.0720 MeV/c²

Qtyn = PECF / ∆Eα = (12.0720 MeV/c²) / 0.388 MeV/c² = 31.11

Qtyn = 31 neutron.

Where Qtyn represents the number of neutrons that the proton-neutron binding energy stably supports, considering the electromagnetic coupling factor of the proton PECF.

According to our calculation, starting at neutrons number 31, the proton-neutron binding energy begins to weaken.

If we consider the electromagnetic coupling factor, NECF and PECF, the maximum binding energy is obtained for Iron (26,30), which has 26 protons and 30 neutrons; Above the number of protons and neutrons that Iron has, the binding energy begins to decrease, we can see this in Figure 37.

we are going to calculate the value of the fine structure constant α, considering NECF and PECF and then we are going to make a description of the parameters that influence NECF and PECF.

Calculation of the fine structure constant α:

∆Eα / NECF = (0.388 MeV/c²) / (9.8486 MeV/c²) = 0.0393964
∆Eα / PECF = (0.388 MeV/c²) / (12.0720 MeV/c²) = 0.0321404
α´ = (∆Eα / NECF) – (∆Eα / PECF)
α´ = 0.0393964 - 0.0321404 = 0.007256
α´ = 0.007256
1/α´ = 137.81

Where, α´ is calculated theoretical value.

α = 0.00729

Where α is calculated experimental value.

1/α = 137.17

% = {(137.81 – 137.17) / 137.17} x 100 = 0.46 %

The difference is very small considering that the calculated theoretical value is obtained from vector diagrams.

We can define the fine structure constant α, as an interaction between the electromagnetic coupling factor of the neutron and the proton. The electromagnetic coupling factor in the neutron and proton is determined by the quarks-antiquarks-gluons interaction.

It is the quarks-antiquarks-gluon interactions in the protons and neutron that determine the fine structure constant α, we can see this by analysing βˉ decay.

The electromagnetic coupling factor of the neutron and the proton is very important, it determines the configuration of baryonic matter as we know it.

∆Eα = (1 / α) x [(1 / NECF) – (1 / PECF)]

∆Eα = (1 / α) x [(PECF - NECF) / (NECF x PECF)]

Where ∆Eα is the unit binding energy per nucleon.

∆Eα = 0.388 MeV

Up to this point, we have seen how the fine structure constant is a consequence of the parameters given by the unit binding energy per nucleon ∆Eα, the electromagnetic coupling factor of the neutron NECF and the electromagnetic coupling factor of the proton PECF.

α = (∆Eα / NECF) – (∆Eα / PECF)

where α is fine structure constant.

M = Z mp + (A-Z)mn – B, B >0

Figure 37. Atomic mass number A vs binding energy per nucleon (MeV).

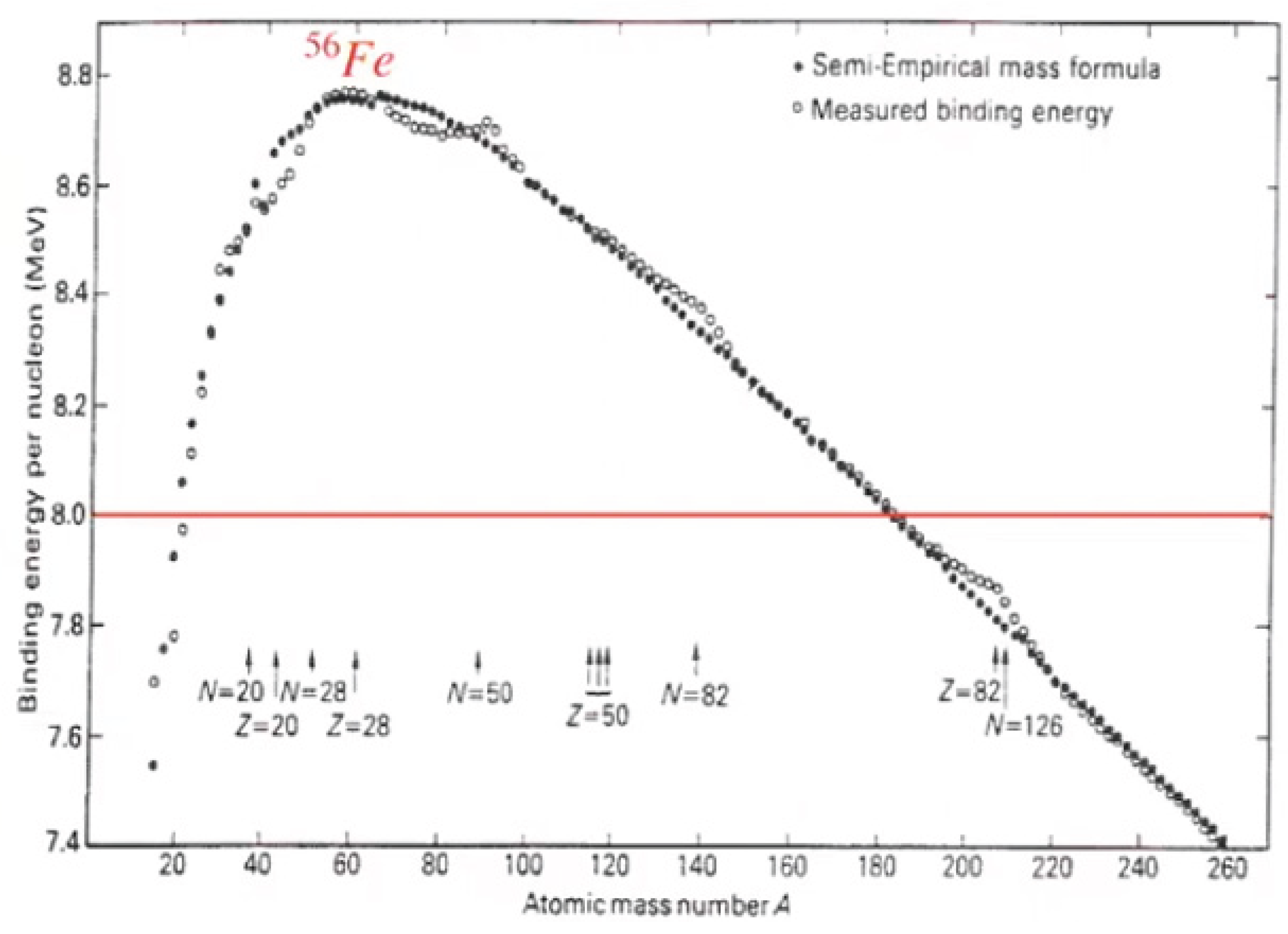
Where, B is binding energy.

The binding energy B is what makes the nucleus stable and is preferable to its parts being free.

The average binding energy, B = 8 MeV, is of the order of 1% of the energy of the mass of the proton or neutron.

The maximum binding energy is found in iron Fe (26,30), and this is consistent with it being the most stable nucleus.

For stable atomic nuclei, the strong nuclear force is greater than the electromagnetic repulsion force, for unstable atomic nuclei, the electromagnetic force begins to be relevant.

Now, we are going to give a brief description of the relationship that exists between the fine structure constant and the atomic orbitals.

As spectroscopy developed, it was observed that the fundamental orbital levels were divided into two, this led us to a much more complex atomic model, which introduced relativistic corrections, spin corrections, etc.; which allowed us to describe the atomic orbitals more precisely.

In our approximate model as a three-dimensional harmonic oscillator, the electromagnetic coupling factor of the proton and the neutron, given by the interactions of the quarks-antiquarks-gluons, is related to the following parameters:

N, No. of nodes

n, principal quantum number

L, quantum number of angular momentum.

m, quantum number of the magnetic moment.

Figure 38. Shell model, first orbitals.

The most rigorous way to take into account relativistic corrections is to pose the Dirac equation. But we won't do that now.

It is also important to mention that NECP and PECP electromagnetic coupling is also related to corrections due to relativistic and spin effects.

The most important corrections that contribute to the fine structure constant α are three, induce order corrections mc²α⁴:

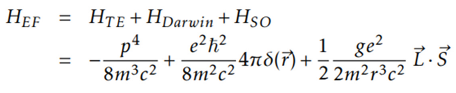
Relativistic correction in kinetic energy

The first term that we will consider in the fine structure has to do with the fact that the kinetic energy of the electron has a correction due to relativistic effects.

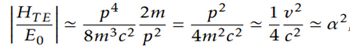
where we use that the speed v in the first orbit of the Bohr atom is v/c ≈ e² / hc. Consequently, as we already mentioned, the correction is very small compared to the 13.6 eV scale (i.e., it is about 10⁻⁴ eV, which corresponds to a typical frequency of tens of GHz, microwave).

Finite size of the electron: Darwin's term

Taking into account relativistic effects, the electron cannot be considered a point particle. Indeed, it is impossible to locate a particle of mass m below a length of the order of the Compton wavelength. The heuristic argument on which this statement is based is that to locate a particle below a length λc it is necessary to use photons that have a energy hω which is greater than that necessary to create a pair of particles (consequently, in that limit the theory for a single particle does not make sense). This length is λc = h /mc. Taking into account the above, to understand this correction, we can assume that the electron is a cloud of charge located around a certain point r of radius λc, which interacts with the electrostatic potential produced for the atom.

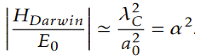
Consequently, this term also has a magnitude α² times smaller than the typical energies of E0

Spin-orbit coupling

There is a third relativistic effect that appears naturally in the Hydrogen atom. As we said, the electron has spin, and therefore has a momentum associated magnetic.

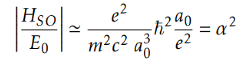
Consequently, this term also has a magnitude α² times smaller than the typical energies of E0.

We observe that the corrections given by H(TE), H(Darwin) and H(SO) are α² smaller than their original energy.

We can see through these two descriptions how the fine structure constant relates the stability of the atomic nuclei to the shell model that describes the atomic orbitals.

Summing up to conclude, it is the quarks-antiquarks-gluon interactions that determine the electromagnetic coupling factor of the neutron and the proton and this, in turn, determines the fine structure constant α; We can see this by applying the concepts in βˉ decay.

4.5. Binding Energy B

We are going to make a brief comment on the binding energy between the proton and the neutron.

We are going to need the following figures:

Figure 39. Neutron.

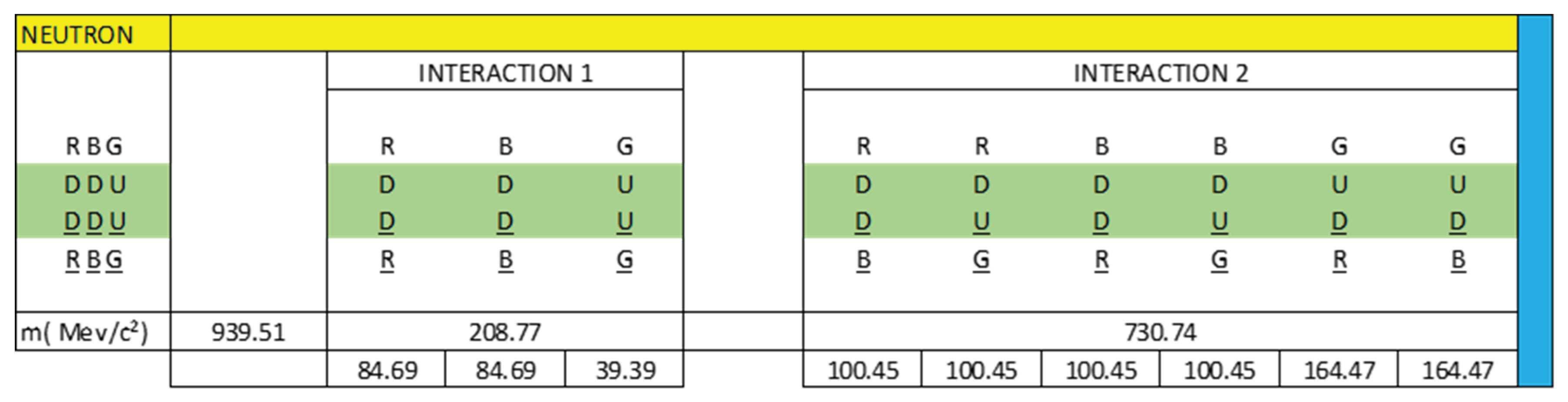
Figure 40. Proton.

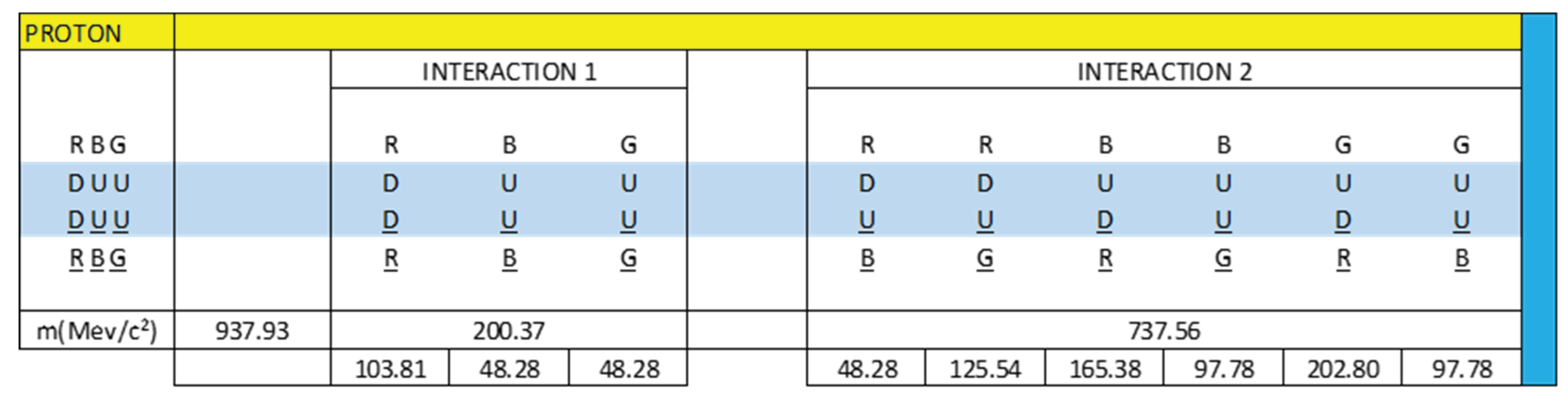
If we look at interaction 1:

(R(DD)R)n à (R(DD)R)p, these dipoles have affinity through the RR gluons, that is, through the exchange of RR gluons between the neutron and the proton, they can generate a binding energy.

If we observe beta decay, we see that the gluons in the interaction (R(DD)R)n → (R(DD)R)p, are in phase and the net interaction takes the following value:

∆(RR) = 19.12 MeV/c²

Where ∆(RR) is the binding energy between the neutron and the proton. Eventually, the exchange could also include DD quarks.

(G(UU)G)n à (G(UU)G)p, these dipoles have affinity through the GG gluons, that is, through the exchange of GG gluons between the neutron and the proton, they can generate a binding energy.

If we observe beta decay, we see that the gluons in the interaction (G(UU)G)n → (G(UU)G)p, are in phase and the net interaction takes the following value:

∆(GG) = 8.89 MeV/c²

Where ∆(GG) is the binding energy between the neutron and the proton. Eventually, the exchange could also include UU quarks.

If we look at interaction 2:

(R(DU)G)n à (R(DU)G)p, these dipoles have affinity through the RG gluons. that is, through the exchange of RG gluons between the neutron and the proton, they can generate a binding energy.

If we observe beta decay, we see that the gluons in the interaction (R(DU)G)n → (R(DU)G)p, are in phase and the net interaction takes the following value:

∆(RG) = 25.09 MeV/c²

Where ∆(RG) is the binding energy between the neutron and the proton. Eventually, the exchange could also include DU quarks.

(G(UD)R)n à (G(UD)R)p, these dipoles have affinity through the GR gluons. that is, through the exchange of GR gluons between the neutron and the proton, they can generate a binding energy.

If we observe βˉ decay, we see that the gluons in the interaction (G(UD)R)n → (G(UD)R)p, are in phase and the net interaction takes the following value:

∆(GR) = 19.69 MeV/c²

Where ∆(GR) is the binding energy between the neutron and the proton. Eventually, the exchange could also include UD quarks.

Let's remember that interactions are represented by vectors.

IEnI = E5 + E8 = ∆(GR) + ∆(RG) = 9.84 MeV/c²

IEpI = E1 + E3 = ∆(RR) + ∆(GG) = 19.69 MeV/c²

These four dipoles are what generate a binding energy between the neutron and the proton, through the exchange of quarks-gluons. Let us remember that we always talk in a generalized way about gluons, this also includes quarks.

The other five dipoles represent cross interactions in which there is no affinity between gluons, making the binding between the neutron and the proton difficult.

The 5 dipoles only become important when βˉ decay occurs.

It is important to highlight the similarity between the four dipoles described here, with the pions described in QCD.

π⁺ = UD
π⁻ = DU
π⁰ = UU or DD

7. Conclusions

Using the theory of three-phase alternating current electric generators, we have demonstrated how neutrons and protons behave as true energy generators due to quarks-antiquarks-gluon interactions. We have demonstrated how our quarks-antiquarks-gluons model, through their interactions, produces the mass for the neutron of 939.56 MeV/c² and for the proton of 938.27 MeV/c². A very important characteristic that we must emphasize is that in our theory, we consider the UU and DD dipoles, in other words, we consider antimatter in order to carry out our calculations, as shown in Figure 1 and Figure 2.

We also calculate for neutrons, using quantum mechanics and the theory of the generalization of the Boltzmann constant in curved space-time, the mass of quarks -antiquarks, gluons and gravitons in a wide temperature range ranging from 10⁻¹⁰ K to 10²⁶ K. Later we calculate the number of quarks-antiquarks-gluons inside a neutron, for a temperature of 10⁵ K, we also calculate the number of gravitons inside a neutron, for a temperature of 10¹² K. For To confirm that the calculated values are correct, we calculate the volume of the neutron and the volume of a quark and divide them, confirming that the calculated value is within the estimated order.

In Section 4.1), in version 2 of this paper, we updated the vector diagrams of the βˉ decay, this allowed us to calculate the energy of the W⁻ and Z⁰ boson and Θ angle. The theoretical value calculated for the boson W⁻ = 14.77 MeV/c², the experimental value for the boson W⁻ = 15.58 MeV/c². The theoretical value calculated for the boson Z⁰ = 17.72 MeV/c², the experimental value for the boson Z⁰ = 17.69 MeV/c². The theoretical value calculated for Θ = 35⁰, the experimental value for Θ = 29⁰.

In Section 4.2) we calculate the tension and length of the string, which exists between the UU and DD quarks inside a proton and a neutron. The values calculated for the tension of the string 10¹⁴n/m and the values calculated for the spatial length of the string 10ˉ²² m are in the order of the values calculated by scientists.

In Section 4.3) we model a black hole using the equivalent model of a neutron. We show that the equivalent mass of a neutron is one-third (1/3) of the mass of a neutron, inside of a black hole. All these calculations are under the assumption that antimatter does not exist inside a black hole, thus fulfilling the hypothesis that when a black hole disintegrates, Big Bang, produces only a universe with matter, solving the enigma of antimatter.

In Section 4.4) we have calculated the fine structure constant α.

About the authors: HECTOR GERARDO FLORES (ARGENTINA, 1971). I studied Electrical Engineering with an electronic orientation at UNT (Argentina); I worked and continue to work in oil companies looking for gas and oil for more than 25 years, as a maintenance engineer for seismic equipment in companies such as Western Atlas, Baker Hughes, Schlumberger, Geokinetics, etc. Since 2010, I study theoretical physics in a self-taught way. In the years 2020 and 2021, during the pandemic, I participated in the course and watched all the online videos of Cosmology I and Cosmology II taught by the Federal University of Santa Catarina UFSC (graduate level). MARIA ISABEL GONÇALVEZ DE SOUZA (Brazil, 1983). I studied professor of Portuguese language at the Federal University of Campina Grande and professor of pedagogy at UNOPAR University, later I did postgraduate, specialization. I am currently a qualified teacher and I work for the São Joao do Rio do Peixe Prefecture, Paraiba. I am Hector's wife and my studies served to collaborate in the formatting of his articles, corrections, etc; basically, help in the administrative part with a small emphasis in the technical part analyzing and sharing ideas.

Conflicts of Interests

The authors declares that there are no conflicts of interest.

References

Flores, H.G. Rlc Electrical Modelling of Black Hole and Early Universe. Generalization of Boltzmann’s Constant in Curved Space-Time. Preprints 2023, 2023052246. [CrossRef]
Flores, H.G.; Gonçalvez de Souza, M.I. Theory of the Generalization of the Boltzmann’s Constant in Curved Space-Time. Shannon-Boltzmann Gibbs Entropy Relation and the Effective Boltzmann’s Constant. Preprints 2023, 2023090301. [CrossRef]
GERADORES DE CORRENTE ALTERNADA. Universidad Federal Rio Grande do Norte UFRN – Apostille. Available online: https://docente.ifrn.edu.br/heliopinheiro/Disciplinas/maquinas-acionamentos-eletricos/apostila-de-maquinas-de-cc.
Eisberg Resnick, Física Cuántica.
Eyvind, H. Wichmann. Física cuántica.
Sears – Zemansky. Física Universitaria con Física Moderna Vol II.
Aula 02: circuitos Trifásicos. Universidad Federal de Parana, UFPR. Available online: https://www.eletrica.ufpr.br/sebastiao/wa_files/te344%20aula%2002%20-%20circuitos%20trifasicos_(2).pdf.
Circuitos Trifasicos. Universidad de São Paulo, USP. Available online: https://edisciplinas.usp.br/pluginfile.php/5335698/mod_resource/content/1/Slides%231.pdf.
Gabriel Vinicius Vian. Introdução à Eletrodinâmica e Cromodinâmica Quântica. UNIVERSIDADE FEDERAL DA FRONTEIRA SUL, CAMPUS REALEZA. CURSO DE FÍSICA – LICENCIATURA – 2022. Available online: https://rd.uffs.edu.br/bitstream/prefix/5440/1/VIAN.pdf.
Jefferson Taneo Shida Gonçalves. Introdução à QCD, Fundamentos e aplicações na física do LHC. Universidade Federal do Rio Grande - Instituto de Matemática, Estatística e Física. Rio Grande, 2017. Available online: https://imef.furg.br/images/stories/Monografias/Fisica_bacharelado/2017/2017-2_Jefferson_Shida.pdf.
Michelangelo L. Mangano. INTRODUCTION TO QCD. CERN, TH Division, Geneva, Switzerland. Available online: https://cds.cern.ch/record/454171/files/p41.pdf.
P. Z. Skands. Introduction to QCD. Theoretical Physics, CERN, 1211 Geneva 23, Switzerland. School of Physics & Astronomy, Monash University, Clayton VIC 3800, Australia. Updated: July, 2017. Available online: https://arxiv.org/pdf/1207.2389.pdf.
Thomas Gehrmann and Bogdan Malaescu. Precision QCD Physics at the LHC. Annual Review of Nuclear and Particle Science. Available online: https://www.annualreviews.org/docserver/fulltext/nucl/72/1/annurev-nucl-101920-014923.pdf?expires=1711222185&id=id&accname=guest&checksum=718297BFB633C2F332DE04F95BB9CFE2.

Figure 1. Electrical model of the neutron considering matter and antimatter. Where D corresponds to the D quark and D corresponds to the D antiquark. Where U corresponds to the U quark and U corresponds to the U antiquark. The gluon interaction is given by (R, B, G) and (R, B, G).

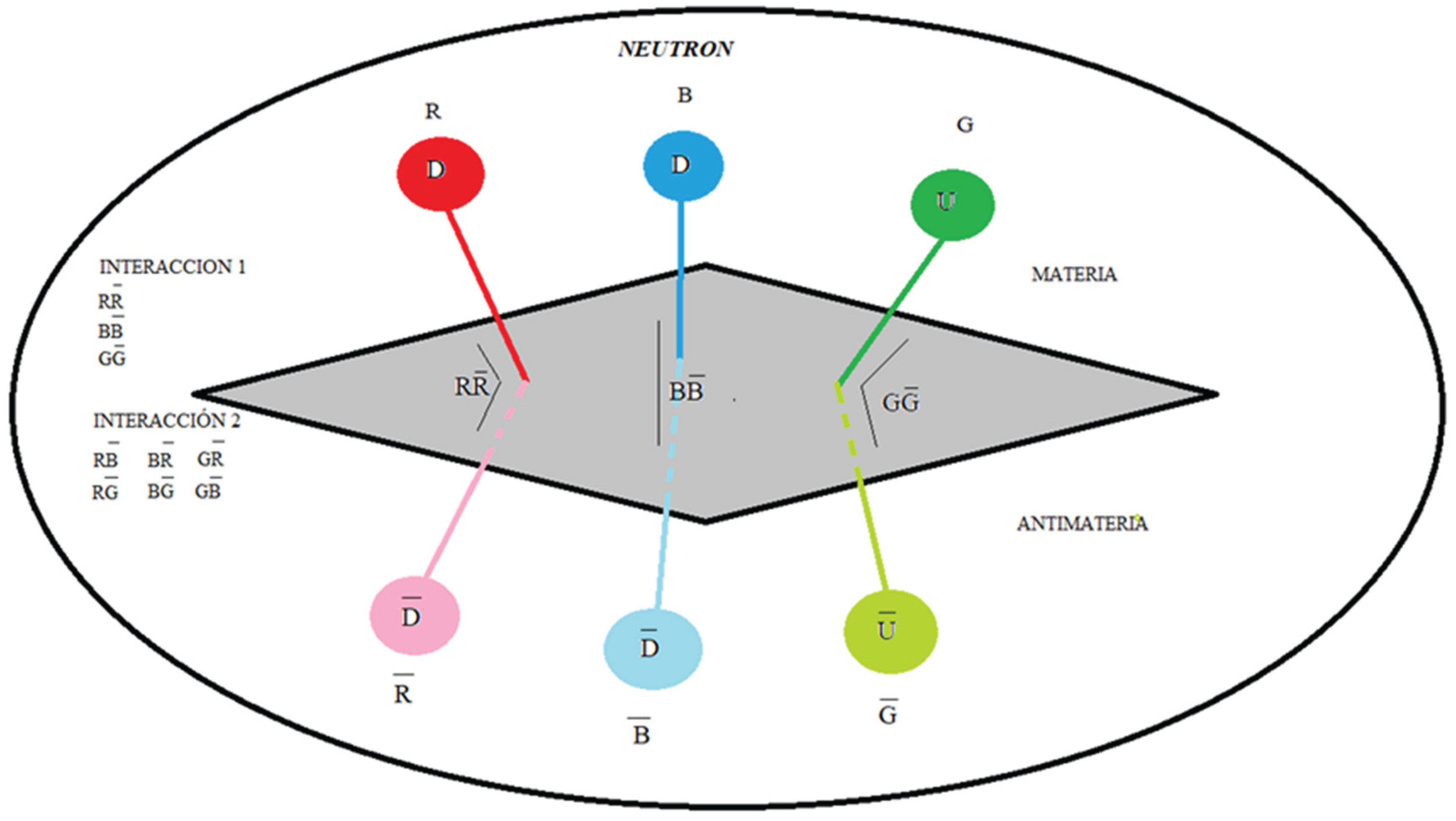
Figure 2. Electrical model of the proton considering matter and antimatter.

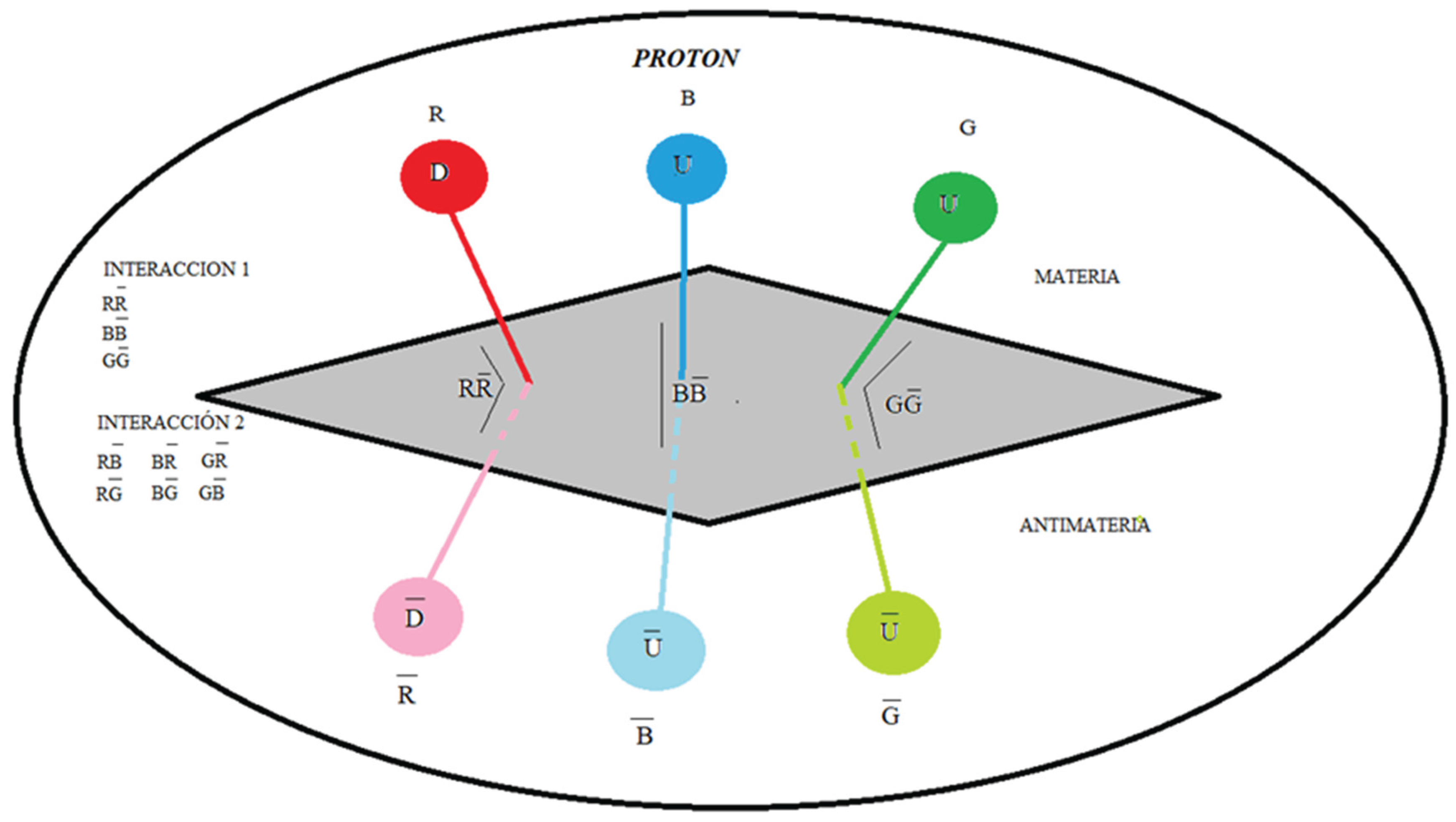
Figure 3. Three phase generator.

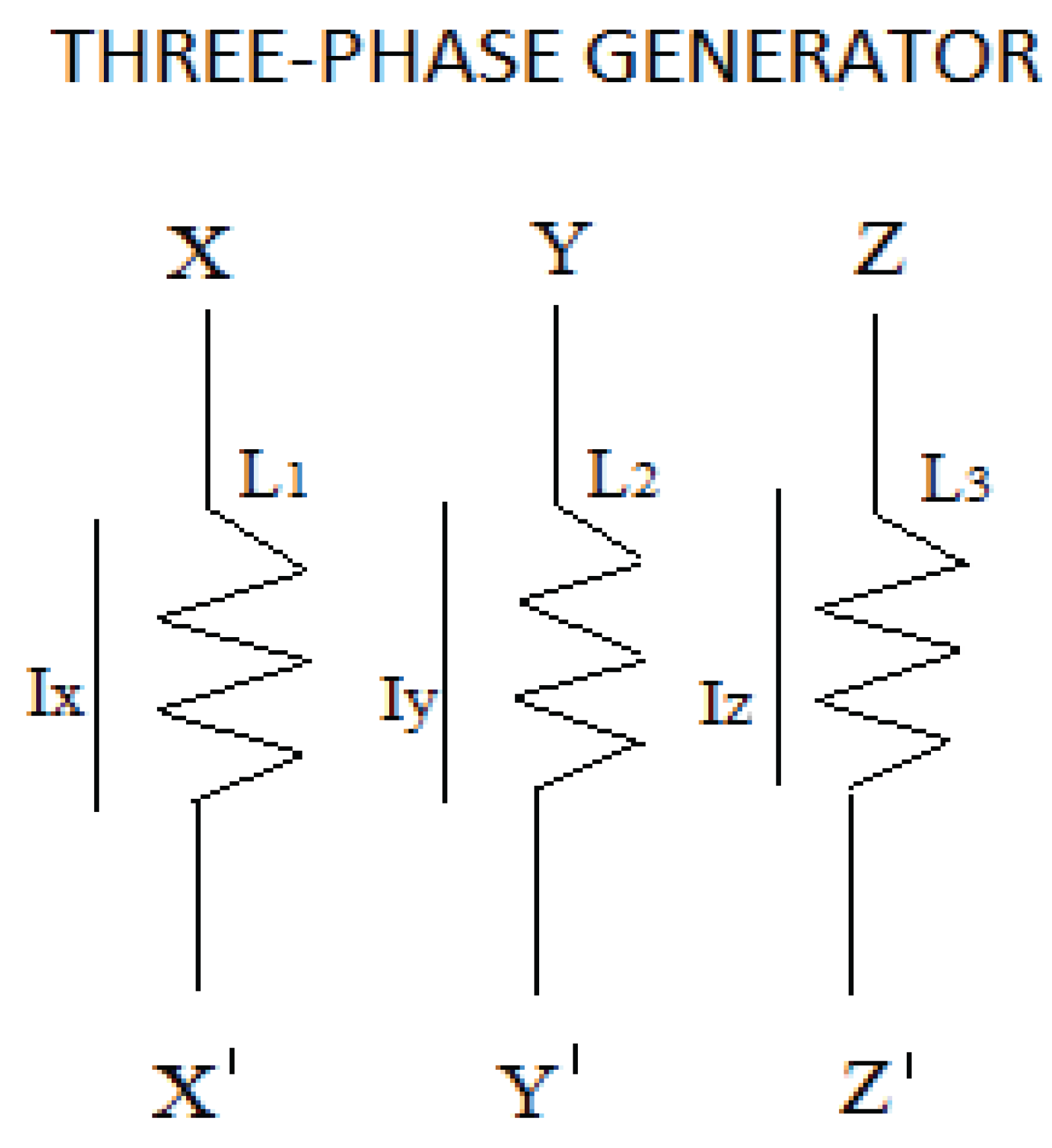
Figure 4. Three phase generator.

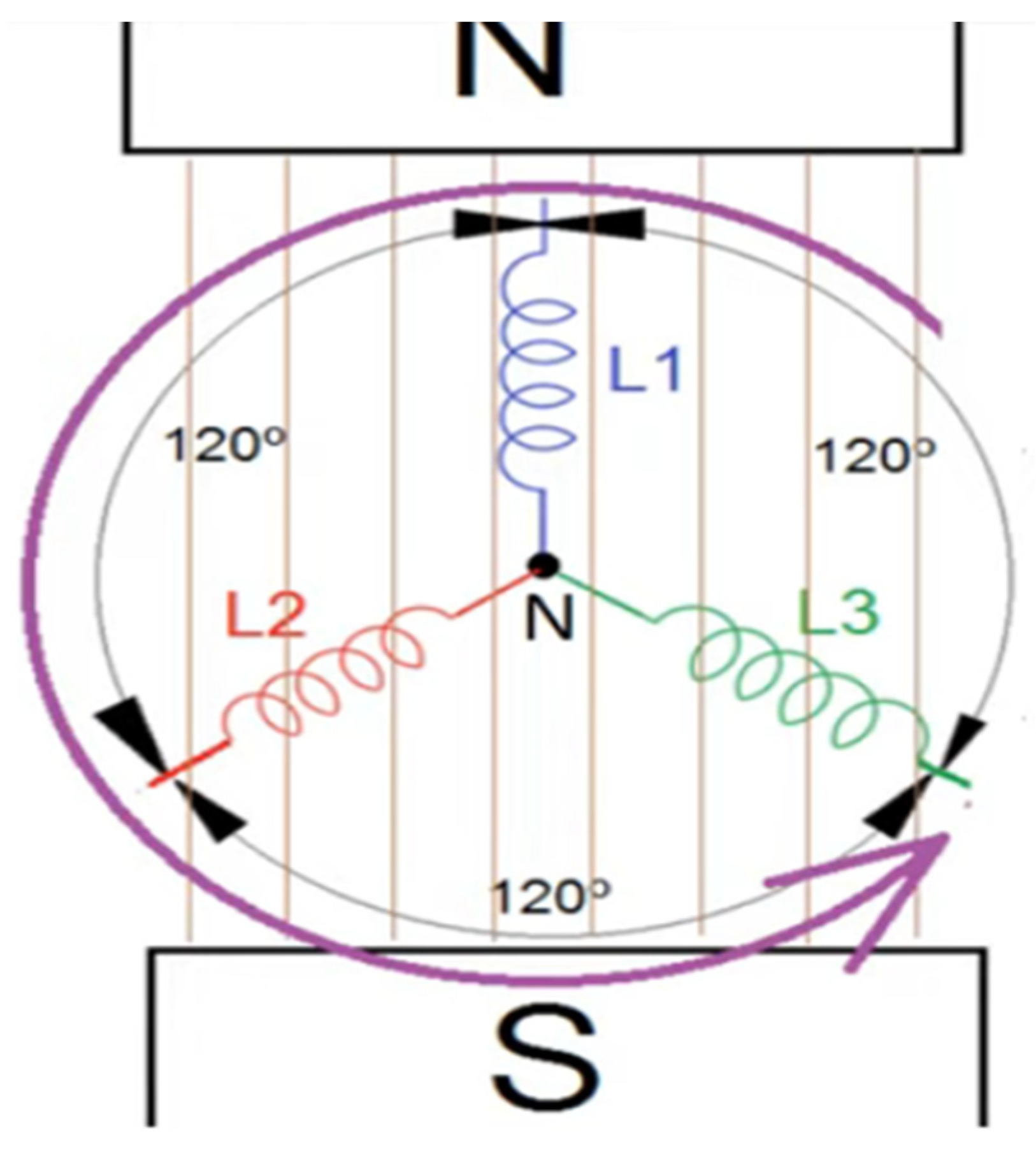
Figure 5. Standard Model.

Figure 6. Characteristics of the up and down quark.

Figure 7. Three-phase voltage generated with a phase shift of 120 degrees.

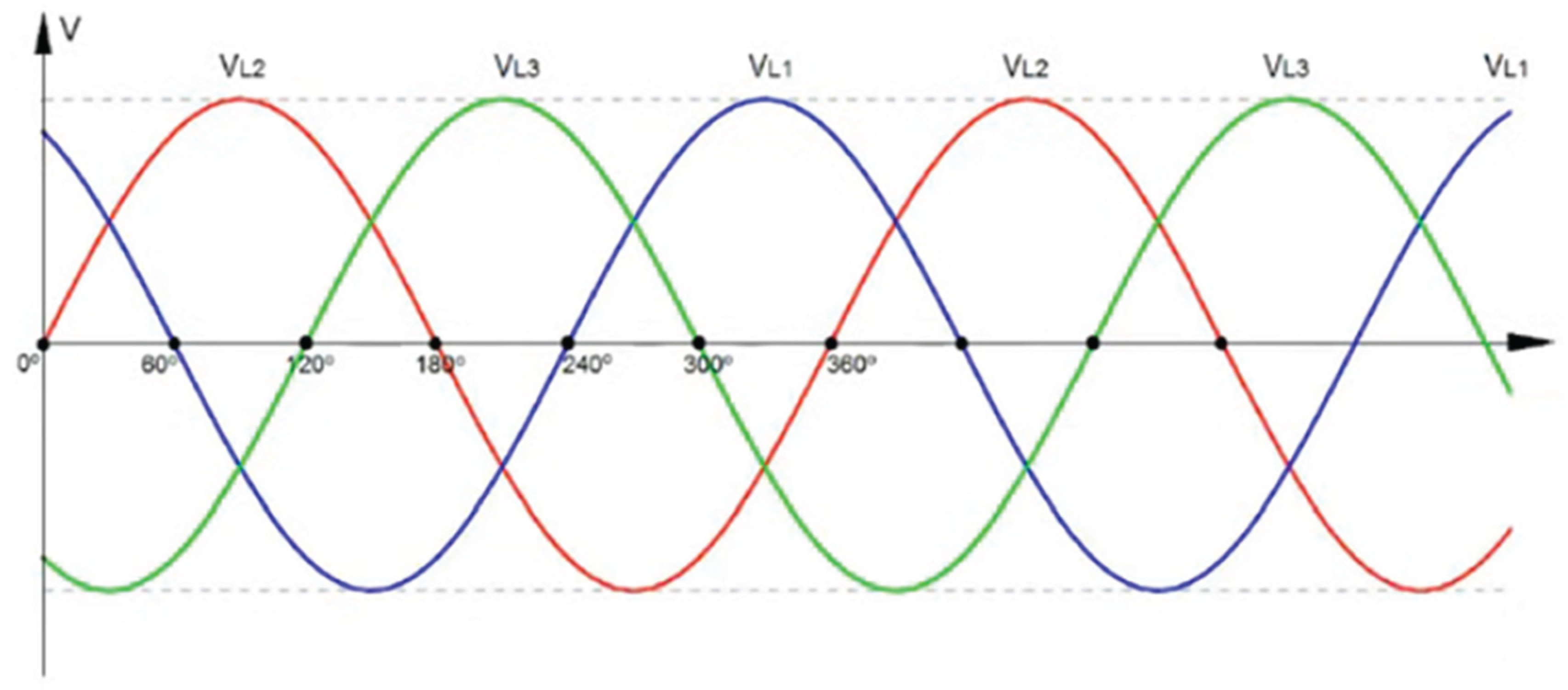
Figure 8. Neutron.

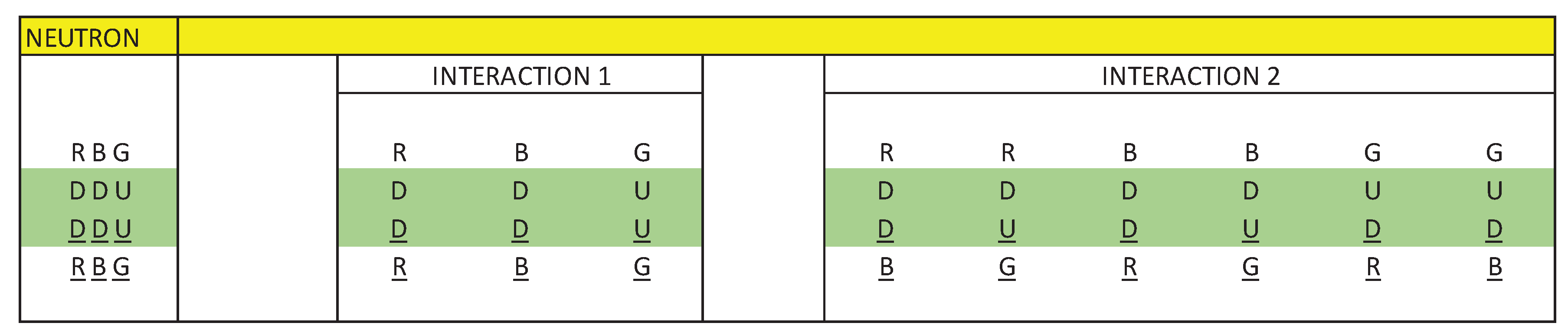
Figure 9. Proton.

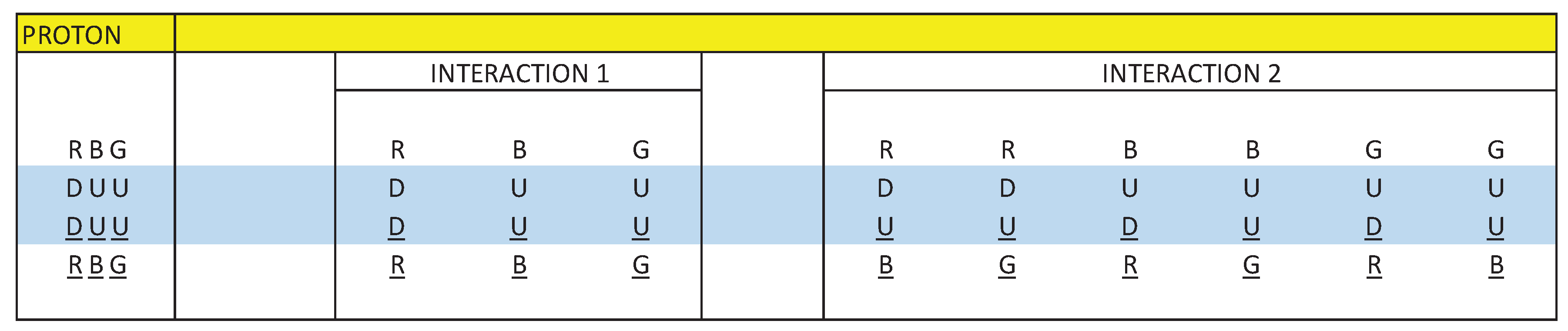
Figure 10. Cross-gluon interaction in a proton.

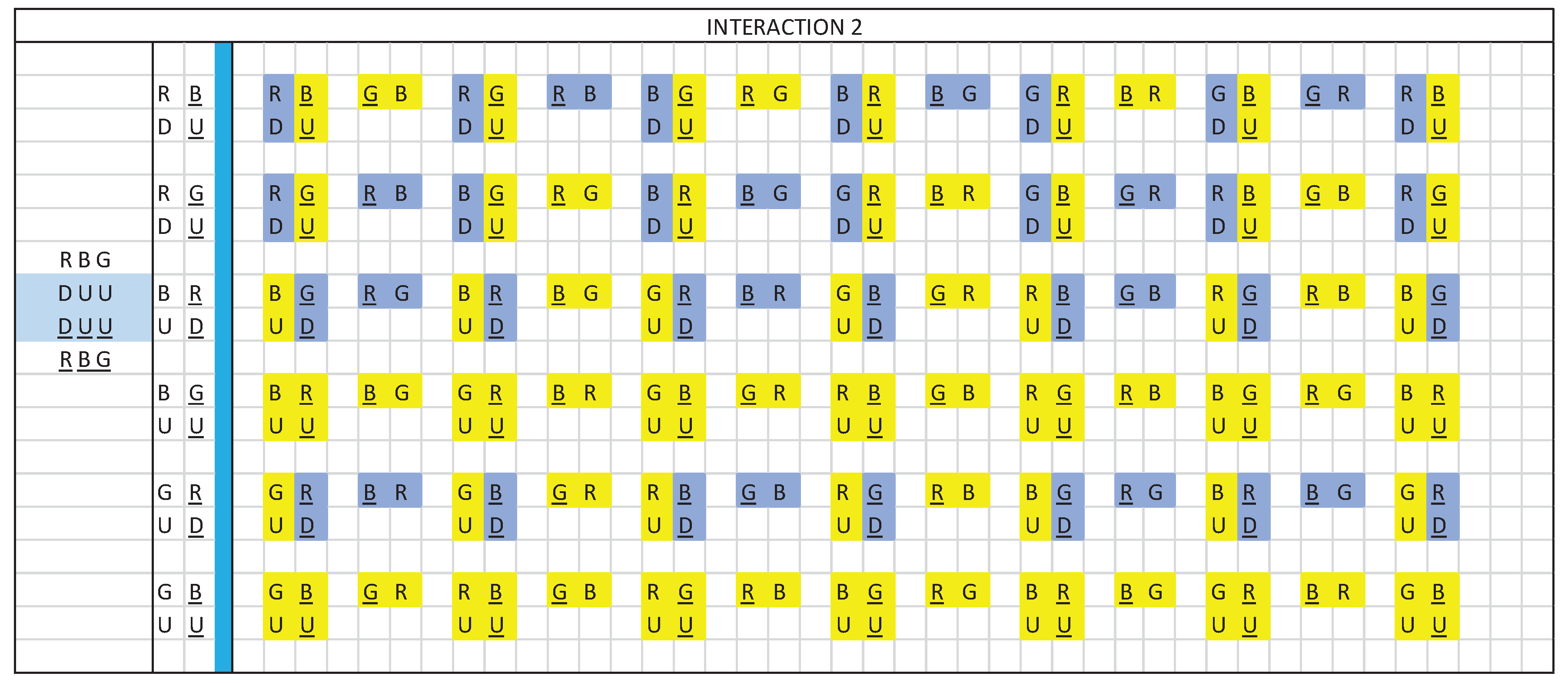
Figure 11. Represents a quark transforming into another quark through the exchange of gluons. In blue represents the frequency of the down quark and in yellow the frequency of the up quark.

Figure 12. Neutron.

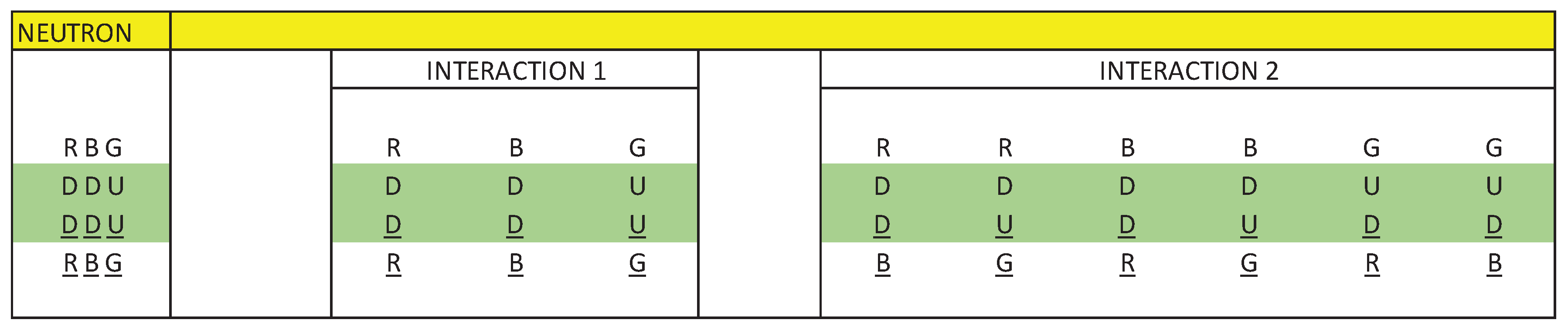
Figure 13. interaction 1 of the neutron.

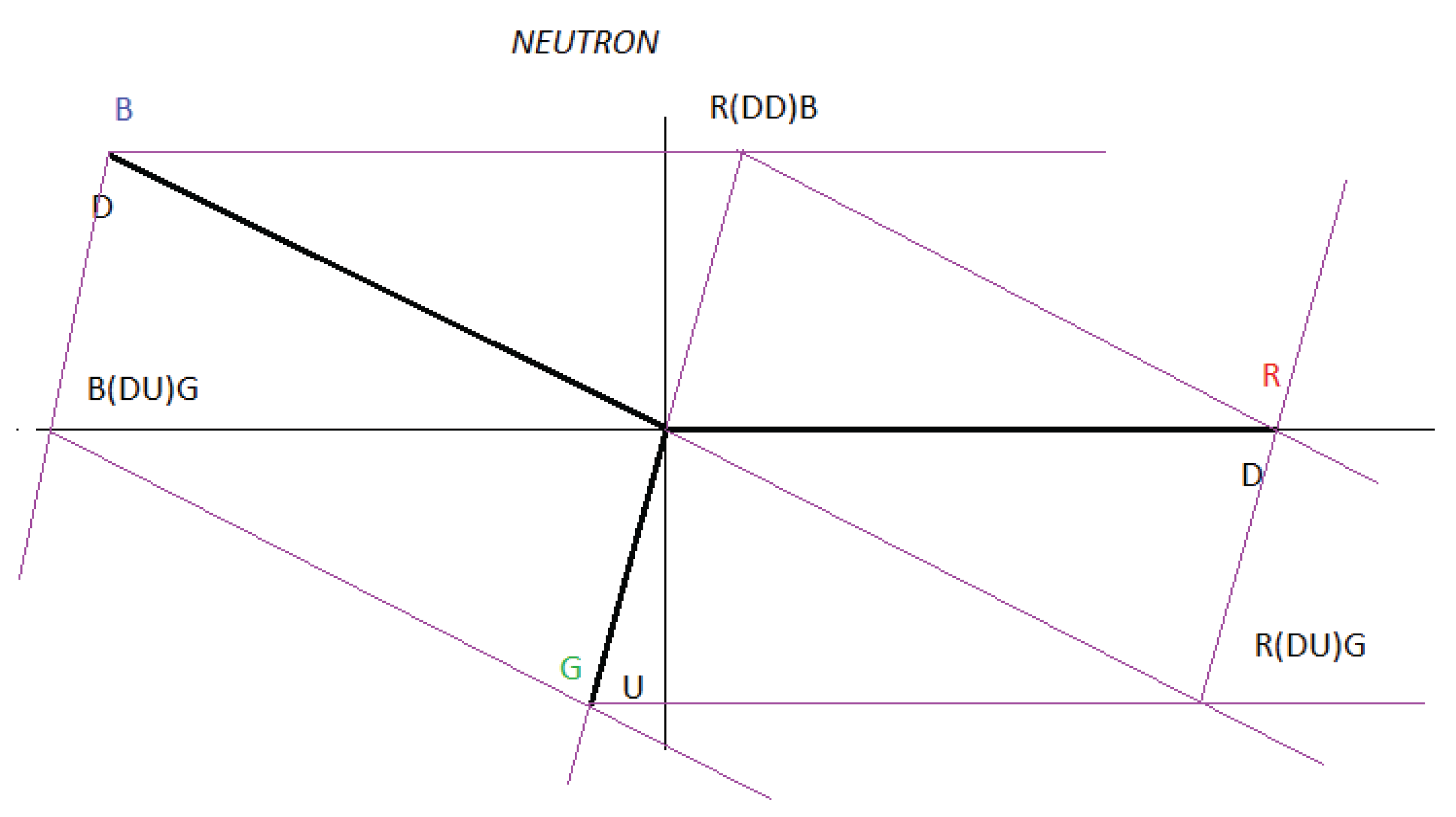
Figure 14. Interaction 1 & 2 of the neutron.

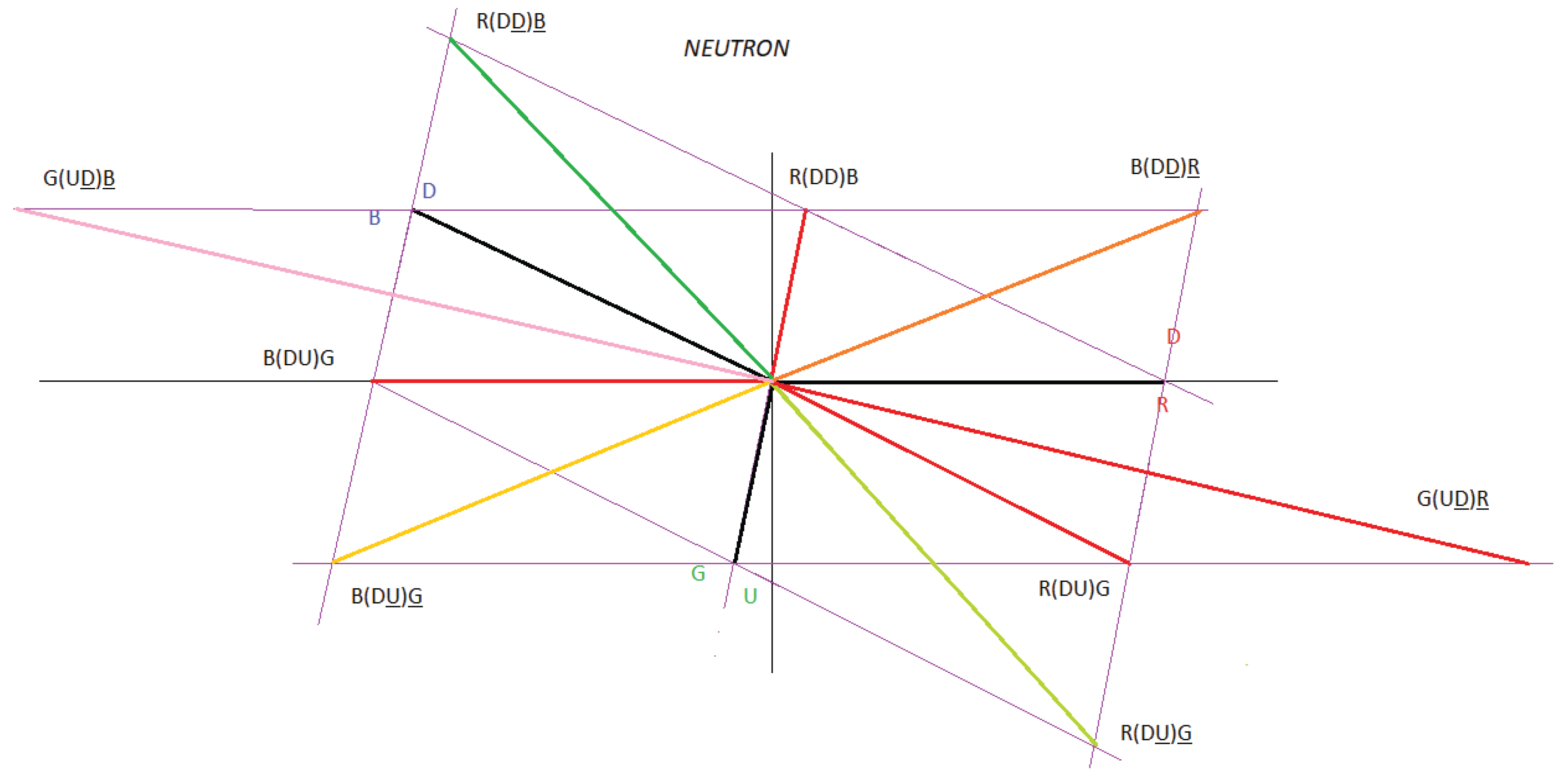
Figure 15. Mass distribution in interactions 1 & 2.

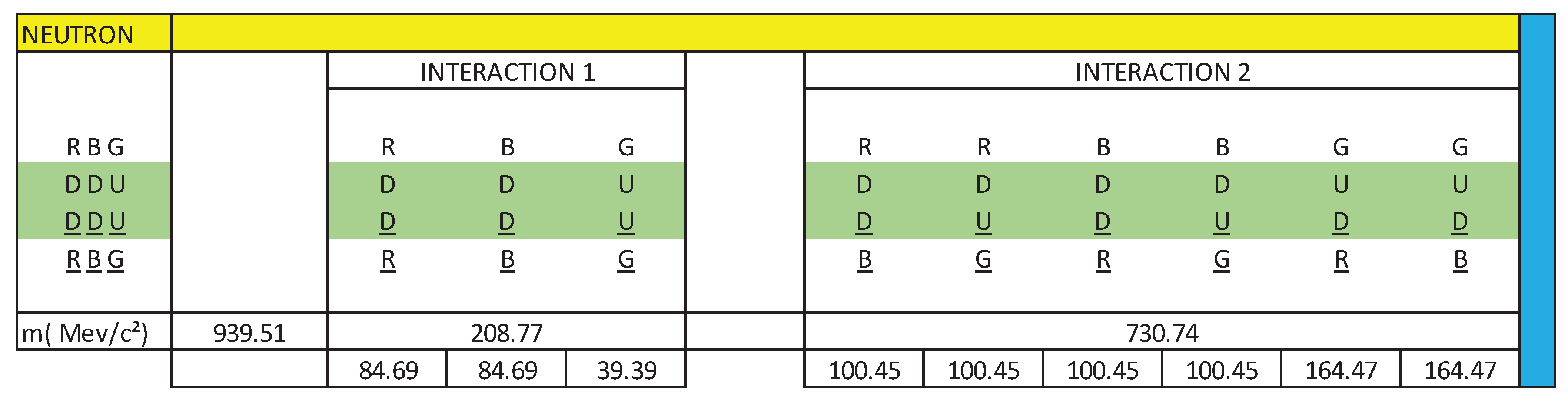
Figure 16. Proton.

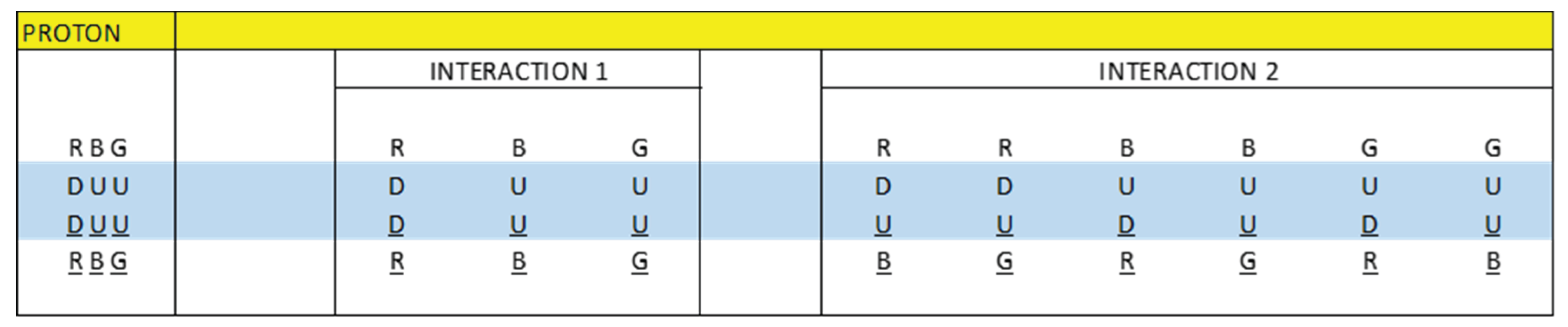
Figure 17. Proton interaction 1.

Figure 18. Interaction 1 & 2 of the proton.

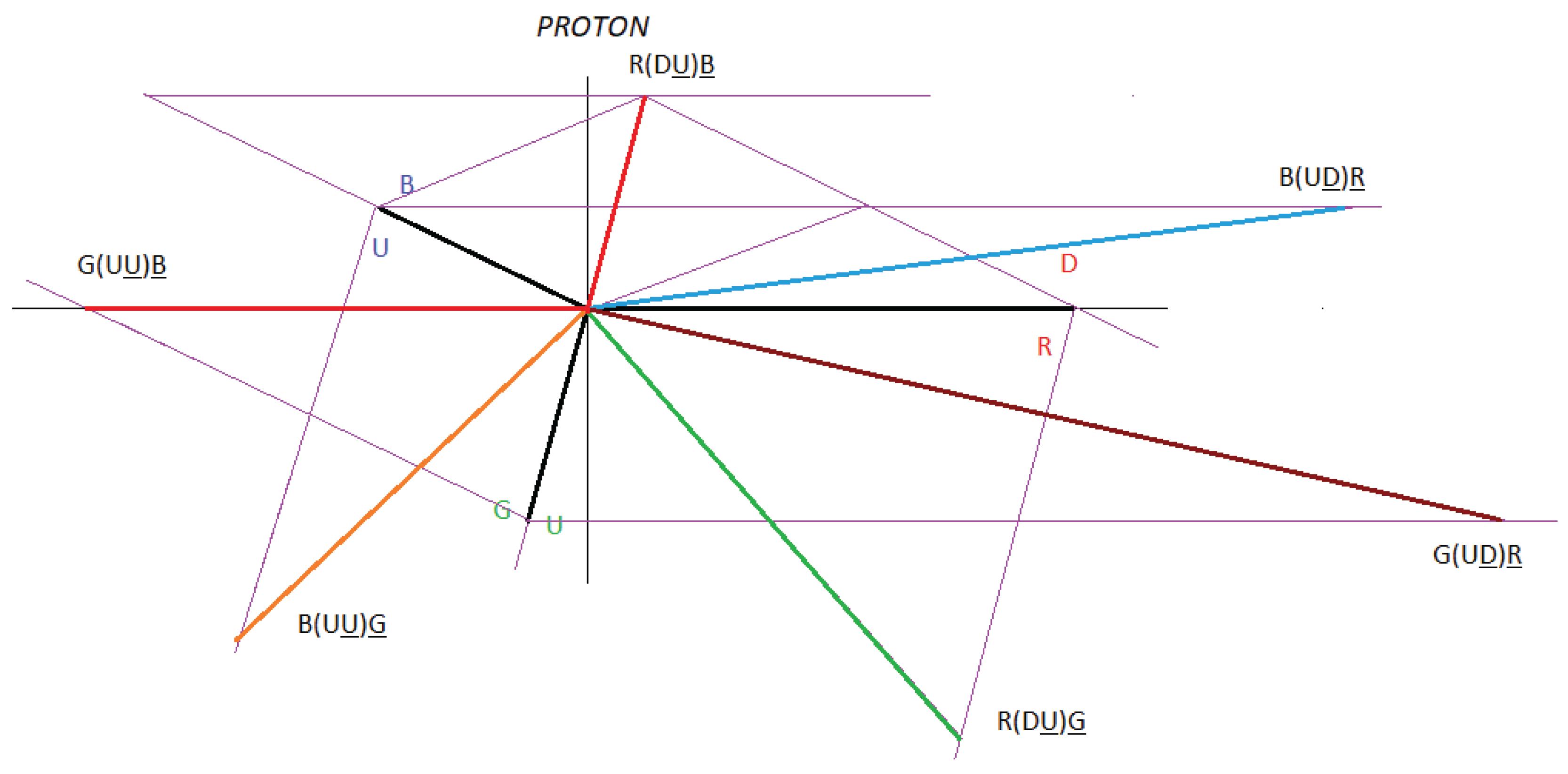
Figure 19. Mass distribution in interactions 1 & 2.

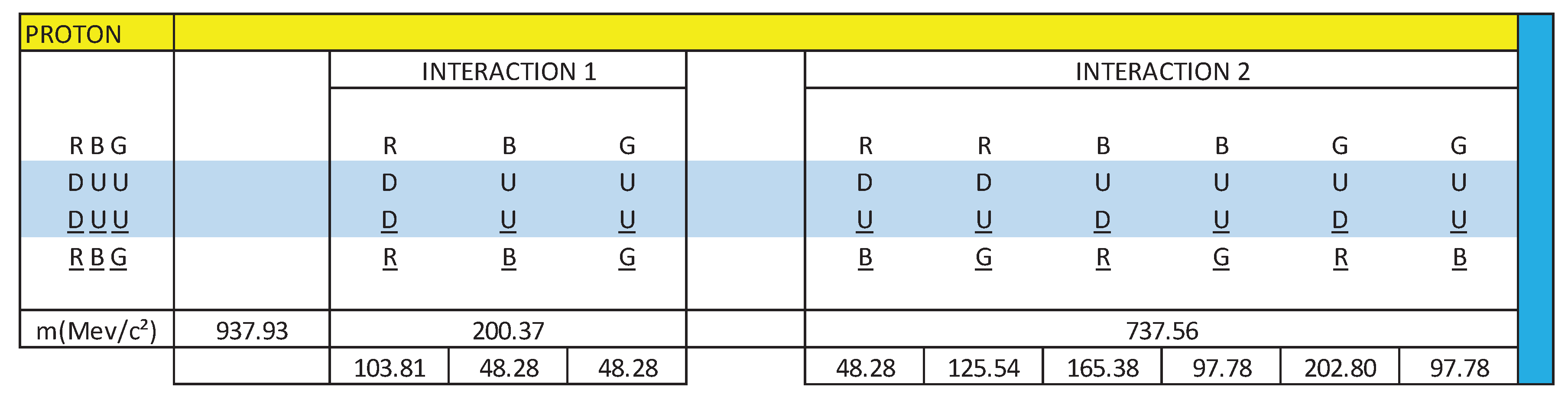
Figure 24. Neutron.

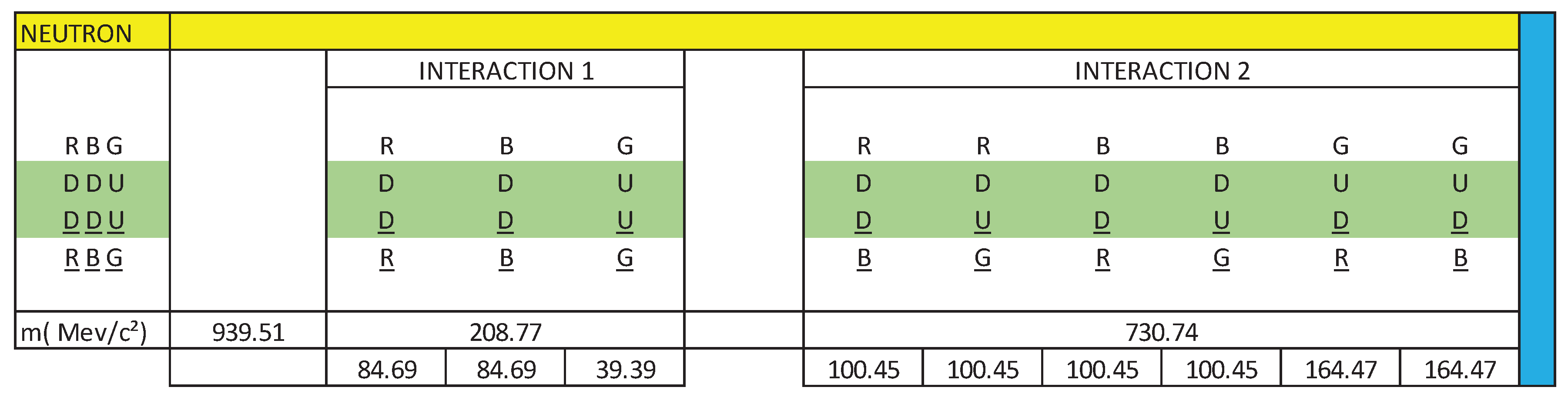
Figure 25. Proton.

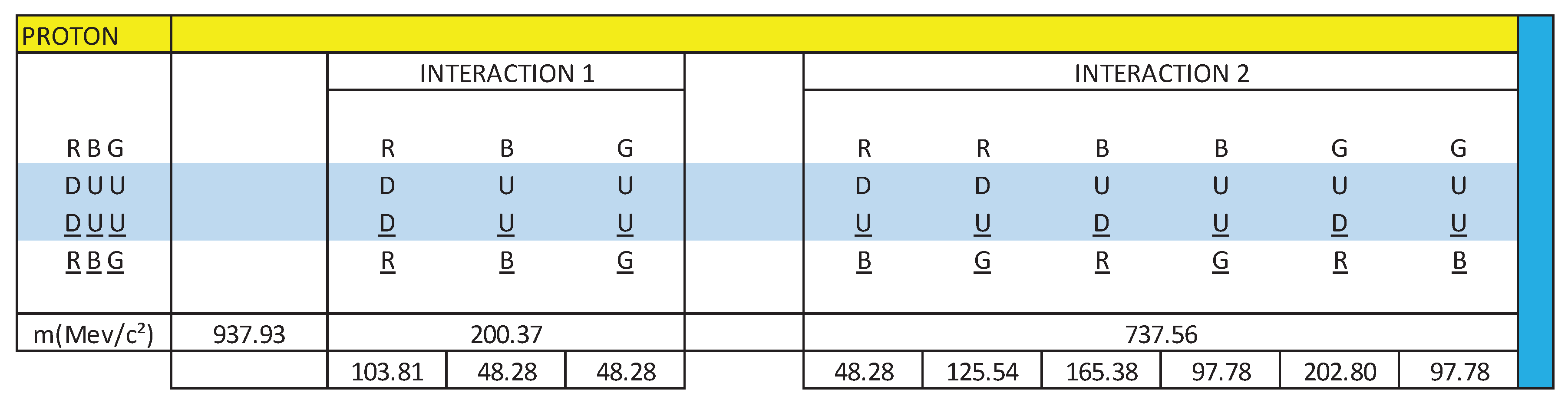
Figure 26. Vector diagram of the neutron in black and vector diagram of the proton in red.

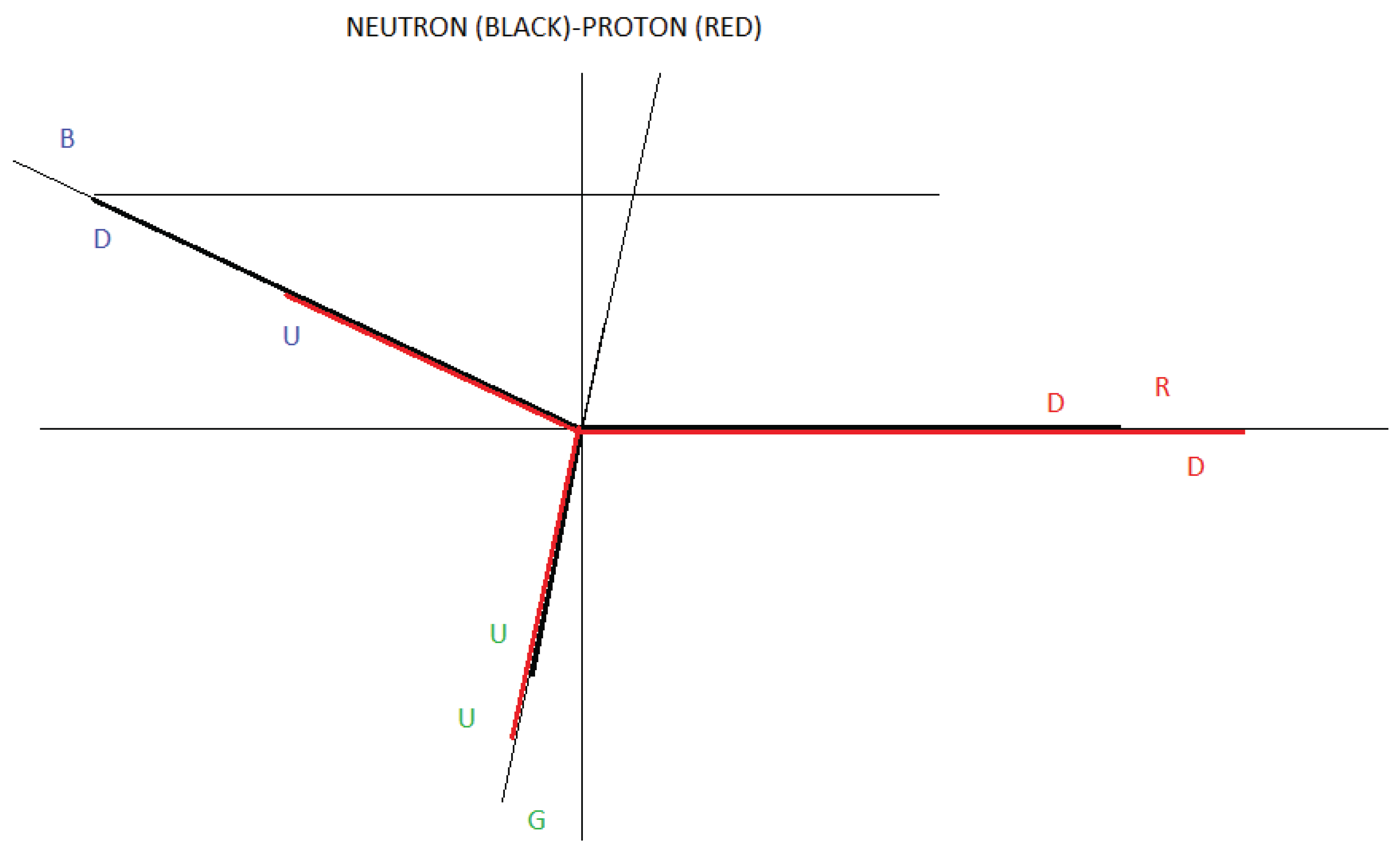
Figure 27. βˉ decay.

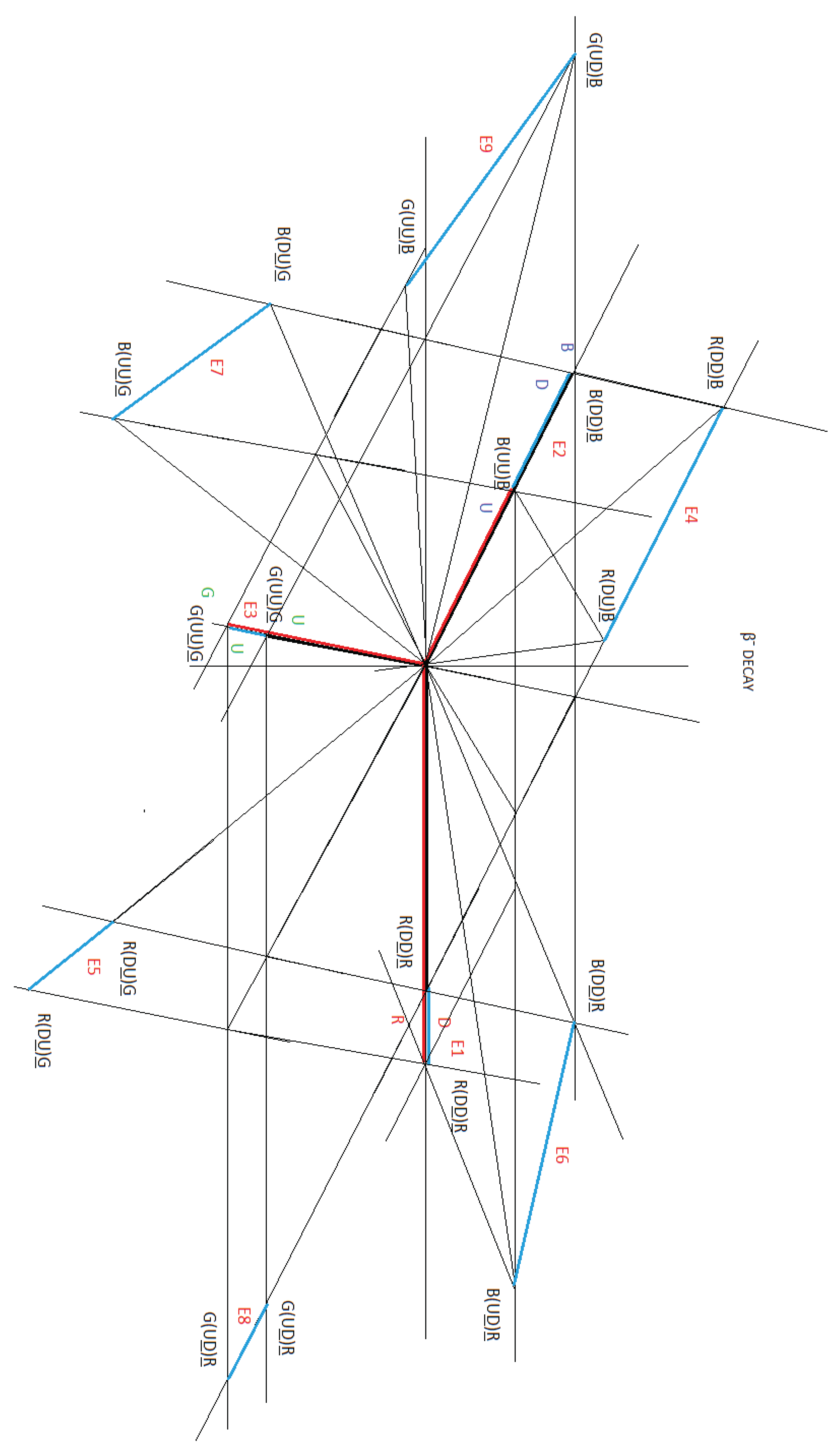
Figure 28. En in green, sum of vectors (E5 +E8) whose charge is zero, Ep in orange, sum of vectors (E1 +E3) whose charge is zero. Ee in brown, sum of vectors ( E2 + E4 + E6 + E7 + E9) with positive and negative charge.

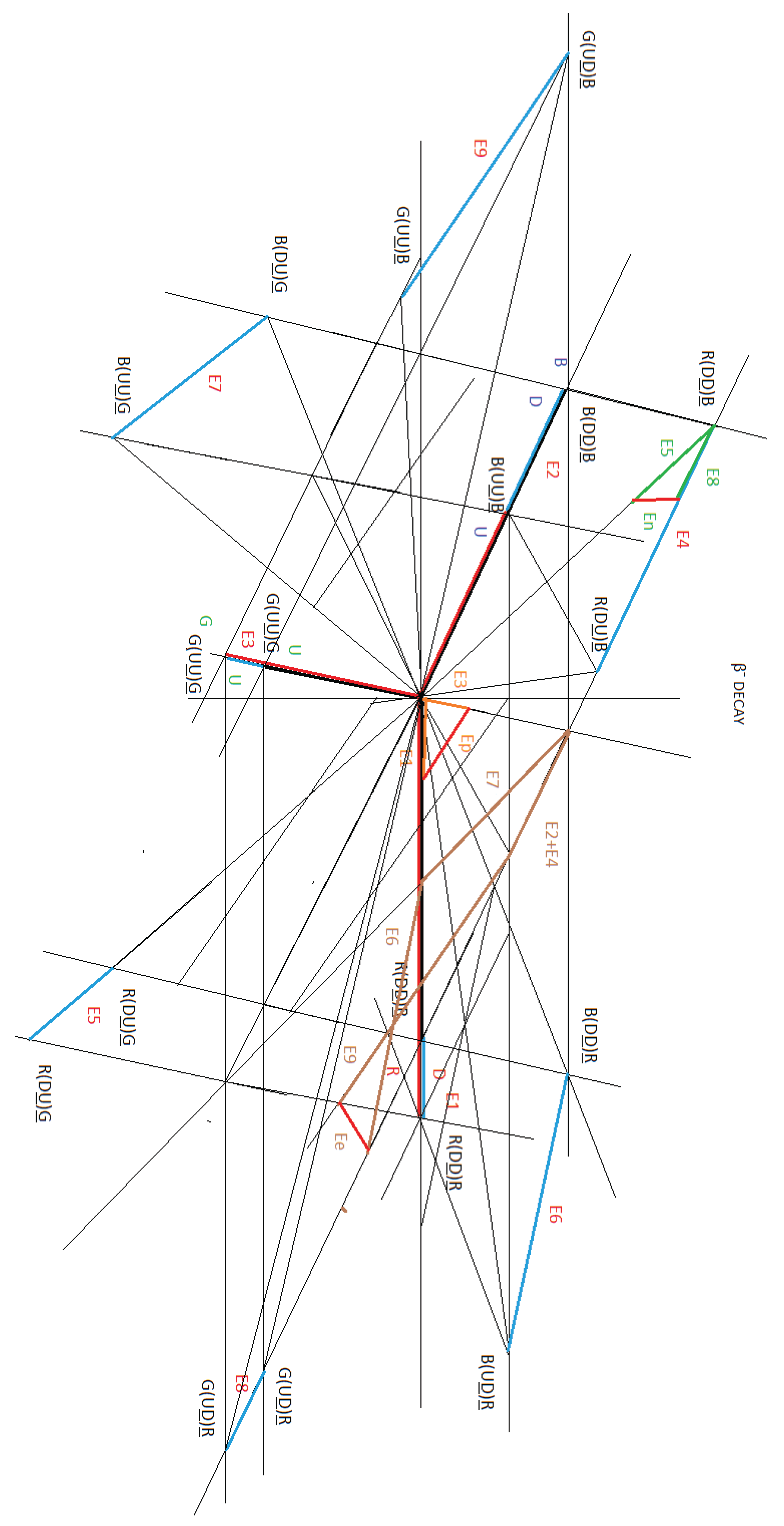
Figure 29. Diagram W⁻, Z⁰ and Θ angle.

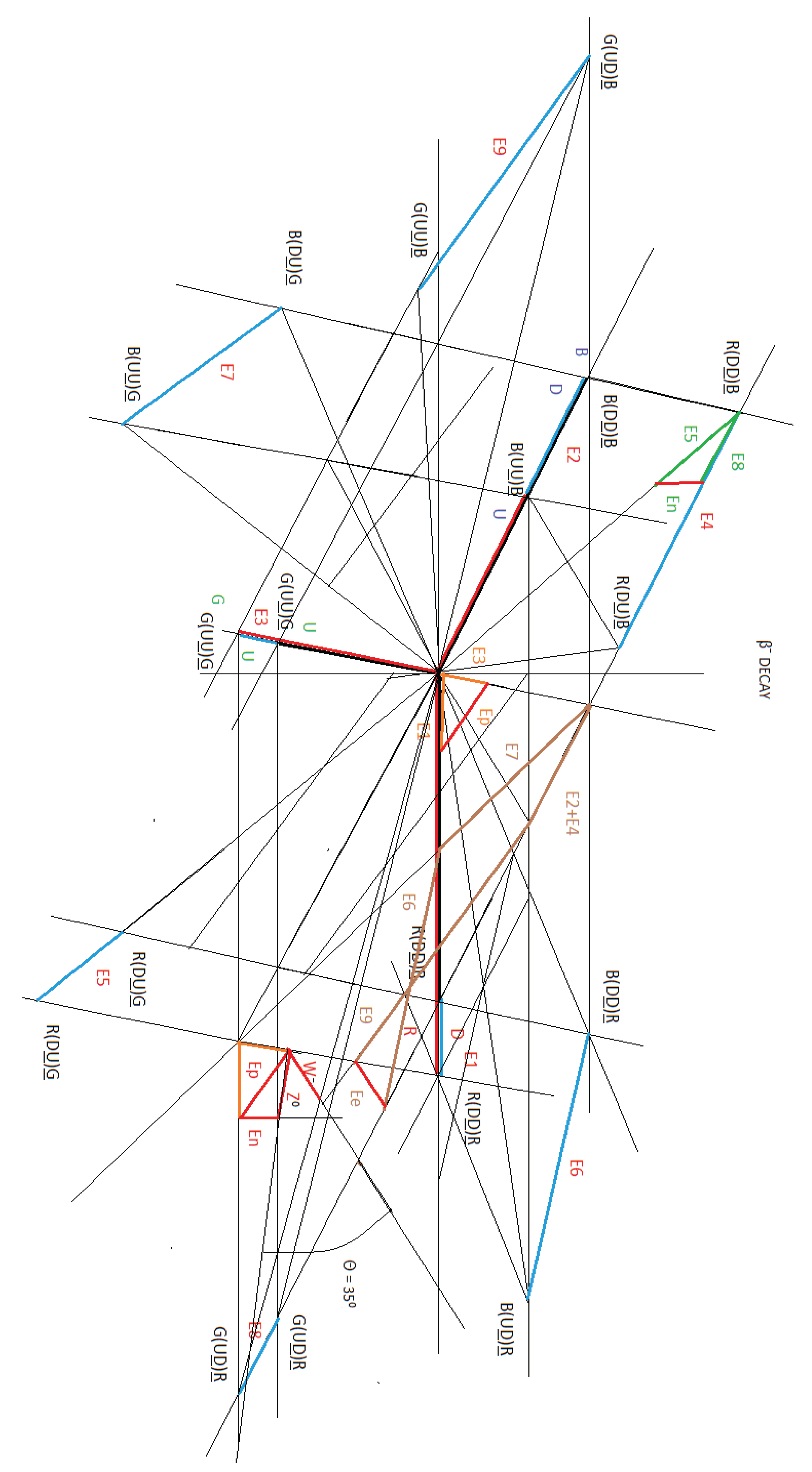
Figure 30. interactions βˉ, neutron → proton.

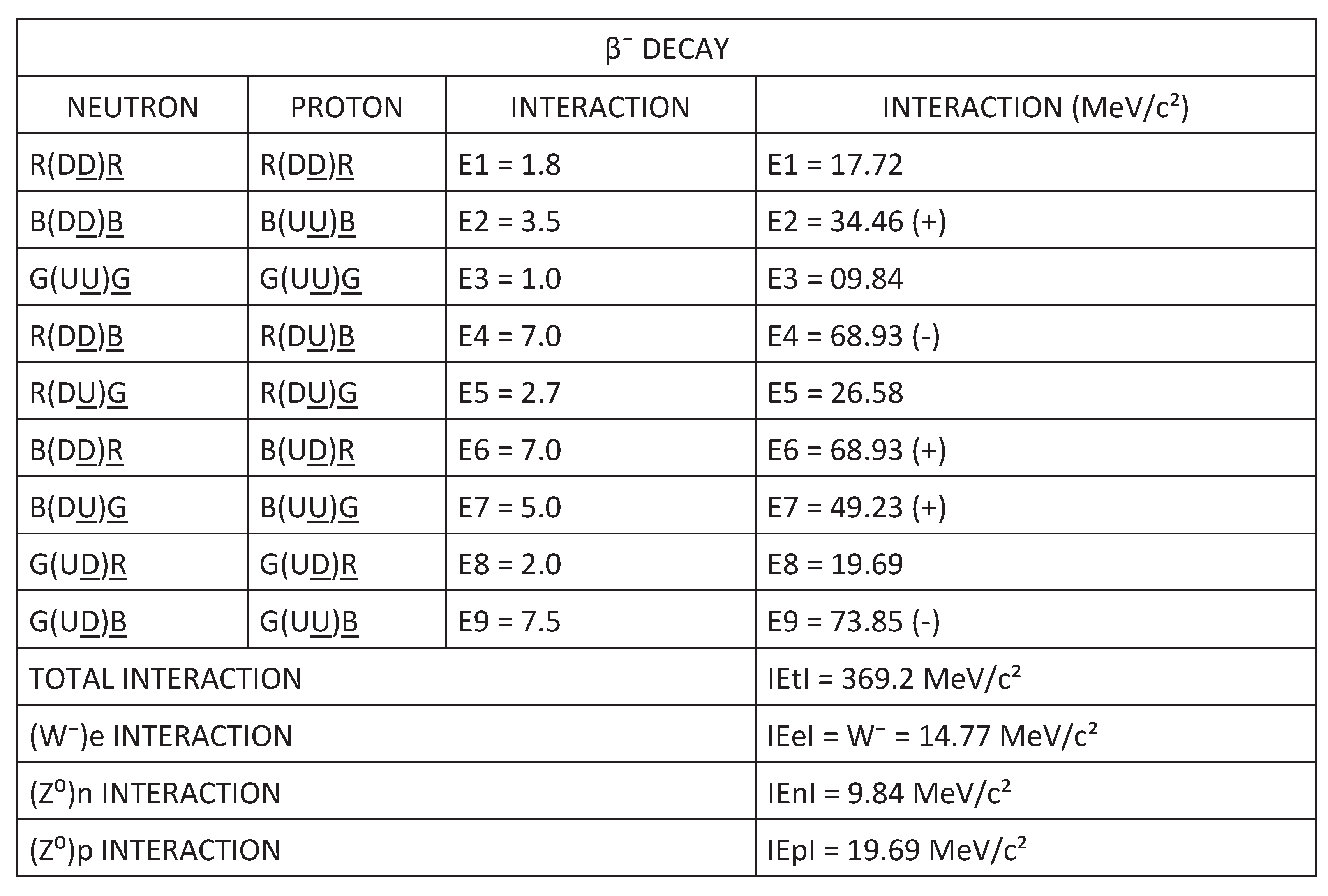
Figure 31. Representation of ℓs and T₀ of interaction 1, proton.

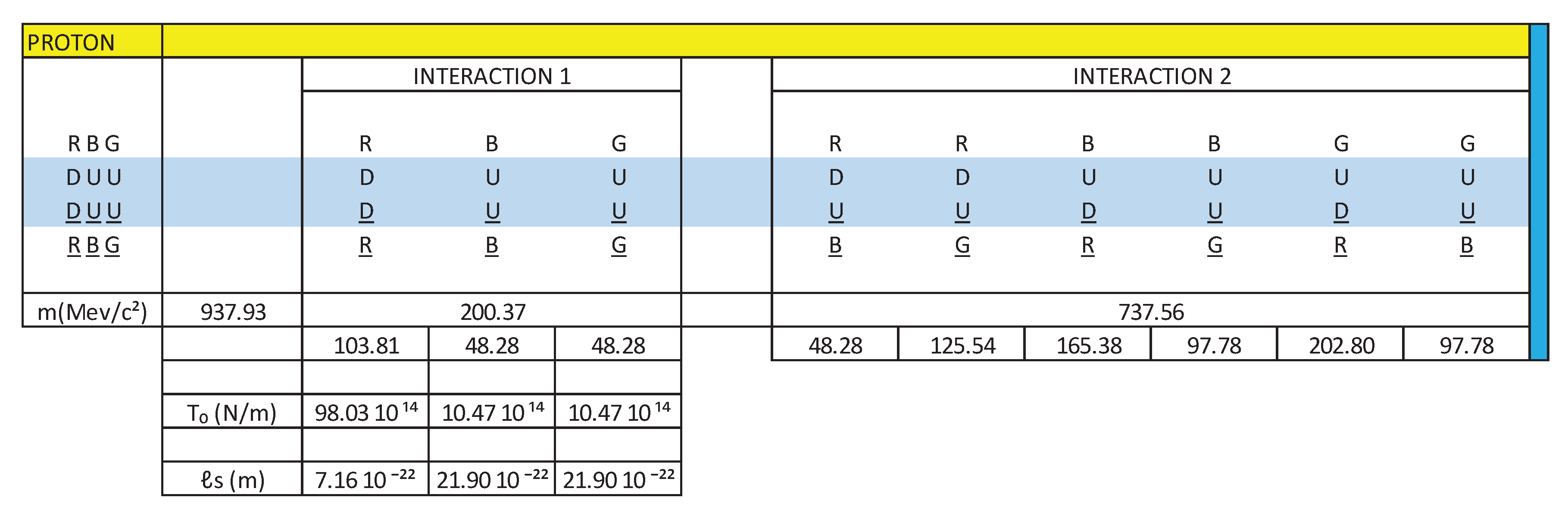
Figure 32. Representation of ℓs and T₀ of interaction 1, neutron.

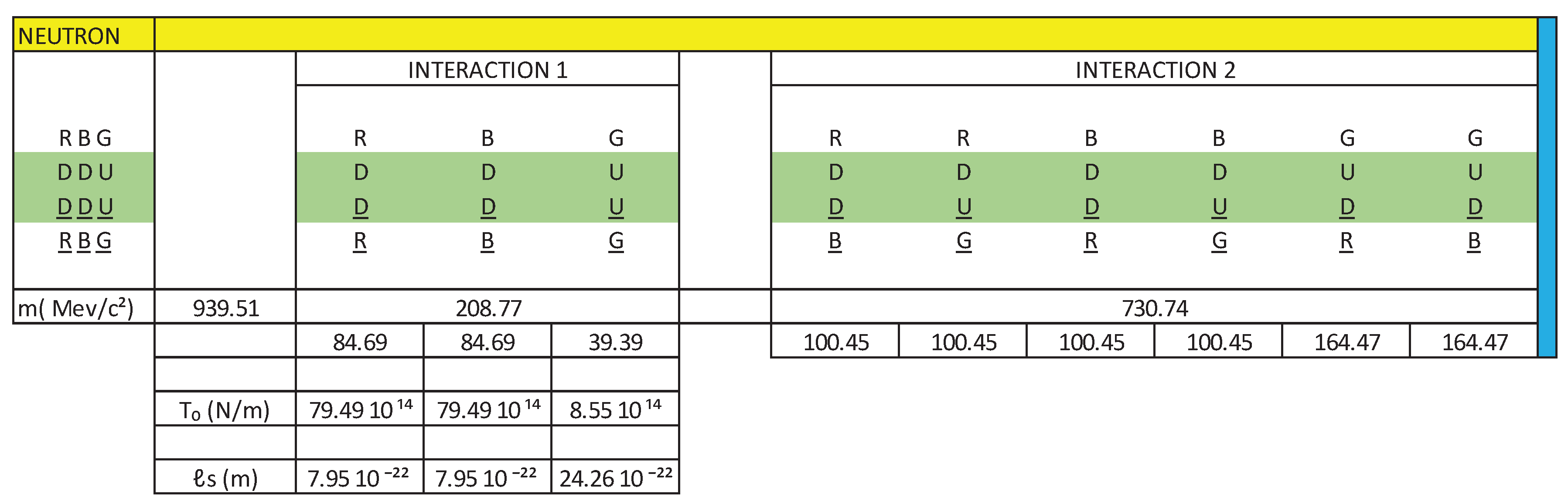
Figure 34. Equivalent Neutron / Black Hole.

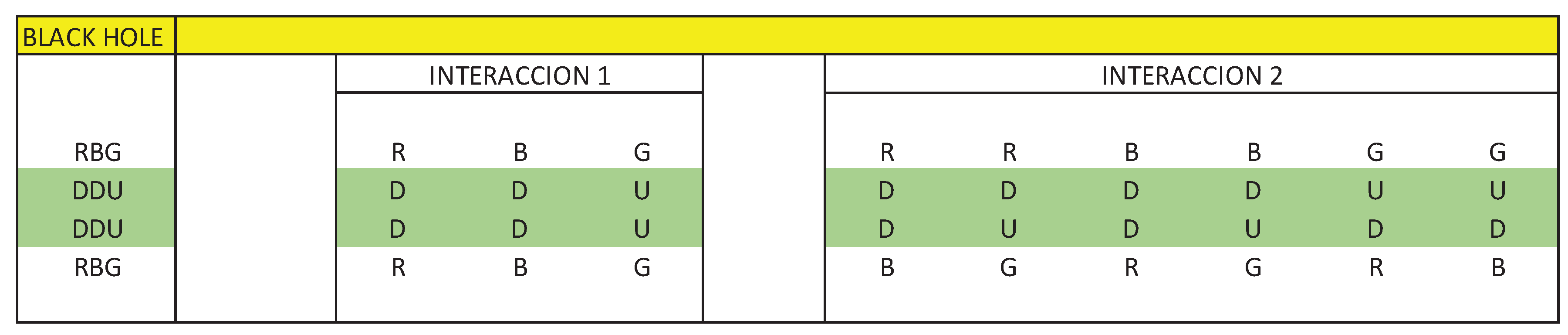
Figure 35. Vector Diagram of a Black Hole.

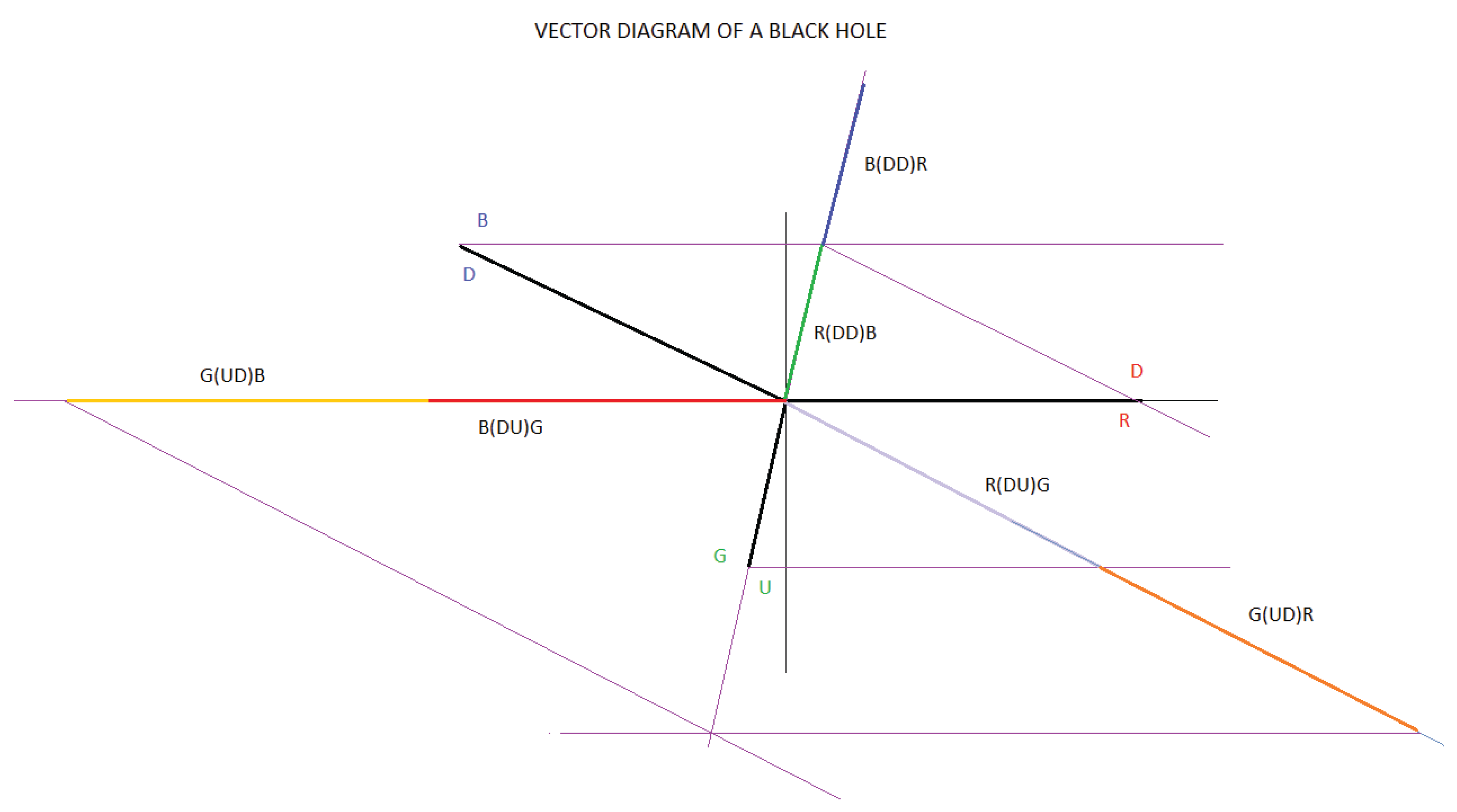
Figure 36. Equivalent Neutron/ Black Hole.

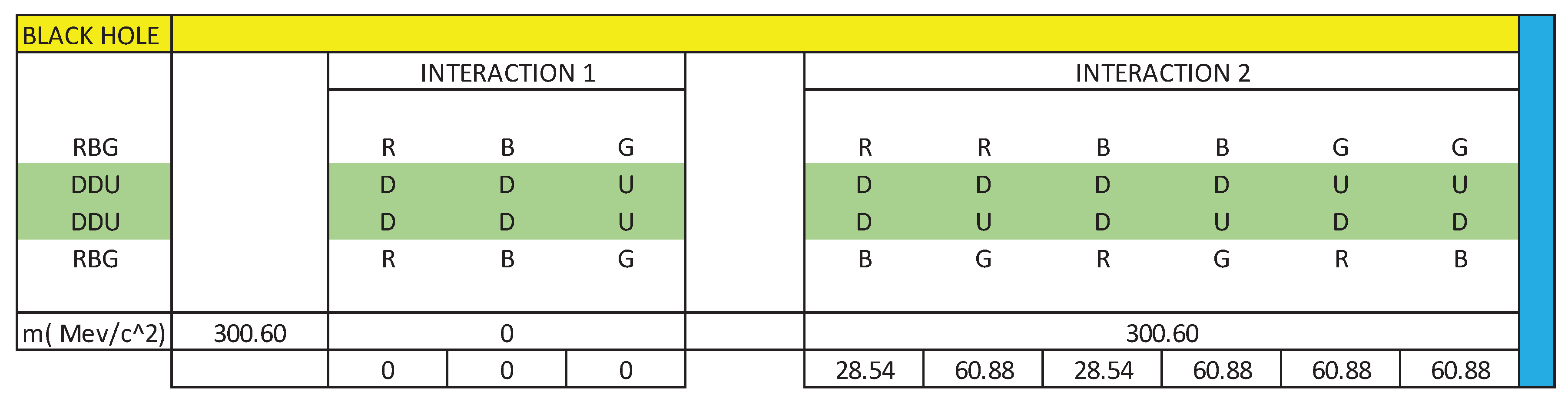
Table 1. Variation of the mass of gluons with temperature.

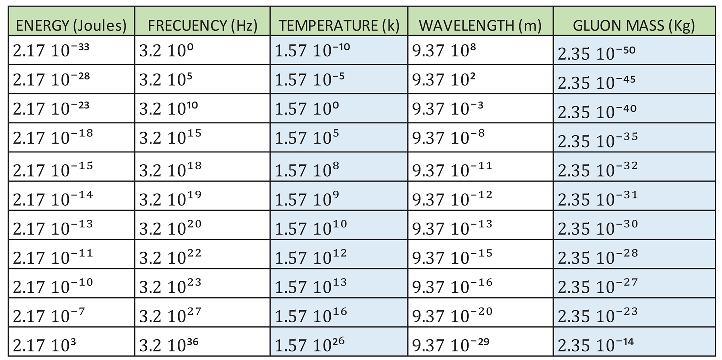
Table 2. Calculation of the mass of the graviton as a function of temperature.

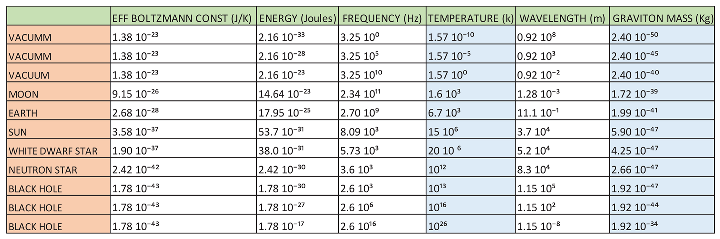
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Electrical-Quantum Modelling of the Neutron and Proton as a Three-Phase Alternating Current Electrical Generator. Determination of the Number of Quarks-Antiquarks-Gluons and Gravitons, Inside a Neutron

Abstract

1. Relationship between a Three-Phase Electric Generator and the Quarks-Antiquarks-Gluons Inside a Neutron and Proton

2. Electrical-Quantum Modelling of the Neutron as a Three-Phase Alternating Current Electrical Generator

2.1. Mechanism That Generates Mass in Neutrons, Calculation of the Number of Quarks-Antiquarks-Gluons Inside a Neutron

2.1.1. Calculation of the Number of Gluons by Dividing the Volume of the Neutron by the Volume of the Quark

2.2. Mechanism That Generates Gravity in Neutrons, Calculation of the Number of Gravitons Inside a Neutron

3. Electrical-Quantum Modelling of the Proton as a Three-Phase Alternating Current Electrical Generator

4. Application of the Model and Results

4.1. Analysis of βˉ Decay. Creation of Electrons, Neutrinos and Photons

4.2. Simple Harmonic Oscillator, String Theory and the Calculation of ℓs and T₀

4.3. Electrical-Quantum Modelling of the Black Hole as a Three-Phase Alternating Current Electrical Generator

4.4. Fine Structure Constant α

4.5. Binding Energy B

7. Conclusions

Conflicts of Interests

References

MDPI Initiatives

Important Links

Subscribe