Prerpints.org logo
Preprint
Article

CNN-Based Facial Expression Recognition with Simultaneous Consideration of Inter-class and Intra-class Variations

Altmetrics

Downloads

75

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

31 October 2023

Posted:

01 November 2023

You are already at the latest version

Alerts
Abstract
Facial expression recognition is crucial for understanding human emotions and nonverbal communication. With the growing prevalence of facial recognition technology and its various applications, accurate and efficient facial expression recognition has become a significant research area. However, most previous methods have focused on designing unique deep-learning architectures while overlooking the loss function. This study presents a new loss function that allows simultaneous consideration of inter- and intra-class variations to be applied to CNN architecture for facial expression recognition. More concretely, this loss function reduces the intra-class variations by minimizing the distances between the deep features and their corresponding class centers. It also increases the inter-class variations by maximizing the distances between deep features and their non-corresponding class centers, and the distances between different class centers. Numerical results from several benchmark facial expression databases, such as Cohn-Kanade Plus, Oulu-Casia, MMI, and FER2013, are provided to prove the capability of the proposed loss function compared with existing ones.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Facial expressions have been used as critical and natural signals to represent human emotions and intentions. Therefore, various facial expression recognition (FER) methods have been studied and applied to fields, such as virtual reality (VR) [1], human-robot interaction (HRI) [2], and advanced driver assistant systems (ADAS) [3].
Typical FER methods include three stages: (1) face component detection, (2) feature point extraction, and (3) facial expression classification. Facial-component detection involves extracting a facial region from an input image to obtain features such as the eyes and nose from the detected facial components. More recently, studies have shown that feature extraction can be classified into spatial [4,5], and temporal feature extraction [6]. Generally, the expression classifier and feature extraction are vital for the accuracy of FER. Many developments have been made to exploit facial expression (FE) classification, including the Bayesian Classifier [7], Hidden Markov Model (HMM) [8], Adaboost [9], and Support Vector Machine (SVM) [10]. Fig. 1 shows the details of the conventional FER process.
Recent developments in deep learning have achieved significant advancements in computer vision and image processing [11,12,13]. Among the deep-learning methods, the Convolutional Neural Network (CNN) has been proven capable of reducing the dependency on analytical models and preprocessing techniques by enabling “end-to-end” direct learning from input images. For example, feature extraction and recognition are jointly learned using deep-learning methods [14,15,16].
FER is highly sensitive to intra-class variation according to age and gender, illuminance, and facial pose [17]. In addition, because FER datasets are limited and small, operating a CNN to extract the salient features that represent the facial expressions from the facial image is problematic. Several methods have been explored to overcome this problem [18]. Examples of this are the transfer learning method [19] for solving the overfitting problem in training datasets, and the ensemble architectures [20] and hybrid variant input approaches [21] for extracting discriminative features. Notably, most of these approaches primarily concentrated on designing new deep-learning architectures and overlooked the loss function. Additionally, the limited training datasets remain a challenge in improving FER performance.
One method of extracting salient features from limited datasets is to change the traditional loss function of the CNN architecture to reduce the intra-class variation and increase the inter-class variation of the deep features, thereby creating discriminative features. Typically, CNN-based FER optimizes the softmax loss function, which seeks to penalize misclassified samples, encouraging the distinction of features between different classes. The softmax layer is crucial for ensuring that the learned features of various classes remain distinguishable. However, severe intra-class variation remains challenging. Advanced loss functions can be used to address this problem. Generally, advanced loss functions are divided into two categories: Angular-distance-based method (L-Softmax [22], AM-Softmax [23]), Euclidean-distance-based method (contrastive loss [24], triplet loss [25], center loss [26]).
The angular-distance-based losses have made the learned features potentially separable with a larger angular/cosine distance. These losses were reformulated based on the original softmax loss, allowing inter-class separability and intra-class compactness between learned features. However, these loss functions was difficult to converge when trained with complex datasets such as that of FER.
Furthermore, Euclidean distance-based methods have embedded the input images in the Euclidean space to decrease intra-class variation and increase inter-class variation. Contrastive and triplet losses increased memory load and training time owing to the complex recombination of training samples. Center loss updated the center by reducing the distance between the deep features and their corresponding class centers. Nevertheless, it disregarded inter-class variation, thus limiting the FER performance improvement.
To summarize, the existing loss functions for CNN-based FER have the following drawbacks: (1) difficulty in convergence with the complex training dataset, (2) the high memory consumption and training time, and (3) the disregard of inter-class similarity.
Given the above analysis, this study presents a variant loss to minimize the distance between the deep features and their corresponding class centers as well as maximize the distances of deep features with their non-corresponding class centers, and the distances between different class centers. Fig. 2 illustrates the concept of the proposed loss function. Finally, the proposed loss function was assessed on four well-known benchmark facial expression databases: the Cohn-Kanade Plus (CK+) [27], the Oulu-CASIA [28], MMI [29], and FER2013 [30] databases. The contributions of this study can be summarized as follows:
• A new loss function is proposed to simultaneously consider inter- and intra-class variations, which enables CNN-based FER methods to achieve impressive performance.
• A new loss function can be easily optimized with various CNN architectures on diverse databases to learn the discriminative power of deep features for the FER problem.
• Comprehensive experiments on benchmark databases are conducted to prove that the auxiliary CNN architectures trained with the proposed loss function performed much better than with existing loss functions.
The remainder of this paper is organized into four sections. Section II summarizes previous loss functions and auxiliary CNN architectures. Section III describes the proposed loss function that simultaneously considers intra- and inter-class variations. Section IV analyzes the simulation results, and Section V states the conclusions.

2. Related Work

2.1. Previous Loss Functions

The softmax loss is obviously good at increasing the inter-class variation but unable to decrease the intra-class variation. To tackle this problem, several loss functions have been introduced to reduce the intra-class variation. Most representatively, L-Softmax loss [22] is an improvement over the conventional softmax loss, enabling inter-class separability and intra-class compactness between learned features. With an adjustable margin value, L-softmax could determine an adaptable learning task with flexible difficulty for CNNs. It also prevented overfitting problems to leverage the powerful learning capacity of deep and wide architectures. Nevertheless, when the training dataset has various subjects, the convergence of L-Softmax will be tougher than the softmax loss. AM-Softmax loss [23] used an additive margin strategy to the target logit of softmax loss with feature and weights normalized. Although it was intuitively appealing and more interpretable than the L-Softmax [22], the selection of the margin hyperparameter was challenging.
Contrastive [24] and triplet losses [25] adopted pair training technique. In particular, the contrastive loss included negative and positive pairs. Its gradients attracted positive pairs and repelled negative ones. Whereas, triplet loss reduced the distance between an anchor and a positive sample, and increased the distance between an anchor and a negative sample of a different identity. The training procedure for these losses was still challenging owing to the selection of effective training samples. Center loss [26] decreased intra-class variations during training by penalizing the distances between deep features and their corresponding class centers. By relying solely on training CNNs with center loss, the deep features and class centers might deteriorate to zero. Moreover, the center loss was minimal, and discriminative features could not be achieved. Thus, the center loss should be jointly supervised with the softmax loss during training. However, each identity’s center doubled the memory storage of the last CNN layer.
Range loss [31] was proposed to effectively use the whole long-tailed dataset in the training procedure. The range loss was optimized jointly with softmax loss as supervisory signals to train CNNs. However, the optimization strategy could be challenging because softmax loss requires uniform distribution among all the classes, and the ability to improve inter-class differences within each mini-batch was restricted. Marginal loss [32] could decrease the intra-class variances and enlarge the inter-class distances by focusing on the marginal samples. The marginal combined with a softmax loss to jointly supervise the learning of CNN, the discriminative capacity of deep features could be greatly improved for efficient face recognition. Even so, the age variance restriction in the training data could significantly reduce the performance when there was a large year gap.
Overall, while existing loss functions achieved promising performance, there is still much room for improvement. To this end, this study proposes variant loss to minimize the distance between the deep features and their corresponding class centers as well as maximize the distances of deep features with their non-corresponding class centers and the distances between different class centers. The proposed loss function is easy to adopt in CNN-based FER methods and achieves outstanding performance.

2.2. Auxiliary CNN Architectures

Given an input image or feature, classification models predict specific labels. In this study, six popular CNN architectures are trained using various loss functions to evaluate the feasibility of the proposed loss function. First, AlexNet [33] has eight layers comprising five convolutional layers and three fully connected layers combined with dropout techniques. Its simplicity and moderate depth made its training fast.
To improve the classification performance, InceptionNet [34] was designed based on the Inception module, which aggregated four parallel branches: three convolution branches with different kernel sizes (1×1, 3×3, and 5×5) and a max-pooling branch. InceptionNet contained 22 layers, including nine Inception modules stacked on top of each other. This design increased the width of the network and adaptability to various scales.
Additionally, the deep learning networks suffer from a vanishing gradient problem that impedes accuracy. ResNet [35] was proposed to add skip connections from the input to the output of the convolutional layer to address these problems. The residual block contained two 3×3 convolutional layers, each followed by Batch Norm and ReLU activate function. ResNet-18 was selected to train with the comparative loss function in this study. Fig. 3 shows the ResNet-18 architecture, whereas ResBlock is shown in Fig. 4.
DenseNet [36] proposed dense blocks and transition layers. Dense blocks concatenated the output of the previous layer as the input of the next. In this way, a feed-forward nature could be maintained. However, the number of channels would be increased when concatenating layers. The transition was used to control the size of the features by 1×1 convolution. Moreover, the height and width of features were reduced through the average pooling layer.
Recently, MobileNetV3 [37] can be applied to mobile and embedded devices owing to its lightweight. It was based on a combination of hardware-aware network architecture search (NAS) algorithm and squeeze-and-excitation (SE) module [38]. The block-wise search algorithm (MnasNet [39]) was employed to identify global network structures, and then the layer-wise search algorithm (NetAdapt [40]) was sequentially employed to adjust individual layers. MobileNetV3 inserted the SE module to build channel-wise attention. The hard-sigmoid function was utilized to substitute the conventional sigmoid in the SE module for more efficient calculation. In addition, the hard-swish function was adopted instead of ReLU for non-linearity improvement.
Finally, ResNeSt [41] is an improved version of ResNet. It combined channel-wise attention with multi-path representation into a unified Split-Attention block. These Split-Attention blocks were stacked to follow the concept of residual learning from the ResNet model [35]. This architecture enhanced learned feature representations for multiple high-level vision tasks, including object detection, image classification, and semantic segmentation. Moreover, it was reported that ResNeSt enabled the acceleration of training with computationally efficient.

3. Proposed Method

As aforementioned, a variant loss is proposed to minimize the distance between the deep features and their corresponding class centers as well as maximize the distances of deep features with their non-corresponding class centers, and the distances between different class centers. The new loss function is expressed as follows:
L v = 1 2 ∑ i = 1 M ( ∥ F ( x i ) − c y i ∥ 2 2 + λ 1 ϵ 1 + ∑ j = 1 , j ≠ y i N ∥ F ( x i ) − c j ∥ 2 2 ) + λ 2 ϵ 2 + ∑ m ∈ N ∑ n ∈ N n ≠ m ∥ c m − c n ∥ 2 2 ,
where y i , x i ∈ R d are the ordinary label and input images of i- t h sample facial expressions, respectively; d is dimension features. F ( . ) expresses the feature extraction from the CNNs; c y i ∈ R d denotes the y i - t h class center of the deep features from the CNNs with the same label class y i . M is the number of training data in the batch size; N is the number of classes; c j , c m , and c n ∈ R d are the j- t h , m- t h , and n- t h class centers of deep features, respectively. ϵ 1 and ϵ 2 are tolerance parameters that guarantee that the denominator is higher than zero; and λ 1 , λ 2 are the hyperparameters used for balancing these loss terms.
The first term is similar to the center loss and tends to reduce the distance between the deep features and their corresponding class centers. The second and third terms tend to increase the distance between the deep features and their non-corresponding class centers and between class centers, respectively. By minimizing the proposed loss function, the intra-class variations of the deep features are reduced, whereas the inter-class variations continue to increase.
The proposed loss function is applied to the batch data in each iteration to train it with the softmax loss. The overall loss function for training the CNN is computed as the sum of the weights of the softmax and variant losses. It is expressed as follows:
L = L s + λ L v ,
where λ is a hyperparameter used for balancing the softmax and the variant losses. The overall system of the CNNs using the proposed loss is illustrated in Fig. 5.
In this method, the network parameters include CNN parameters W and the softmax loss parameters θ are updated on mini-batches. Only the gradient of L s is needed to update the softmax loss parameters θ because the L v does not affect it. The gradient of overall loss is used to update W. The gradient of L v with respect to the F ( x i ) is calculate as follows:
d L v d F ( x i ) = ( F ( x i ) − c y i ) − λ 1 ∑ j = 1 , j ≠ y i N ( F ( x i ) − c j ) ( ϵ 1 + ∑ j = 1 , j ≠ y i N ∥ F ( x i ) − c j ∥ 2 2 ) 2 − λ 2 ∑ m = y i n ∈ N n ≠ m ( c y i − c n ) − ∑ m ∈ N n = y i n ≠ m ( c m − c y i ) ( ϵ 2 + ∑ m ∈ N ∑ n ∈ N n ≠ m ∥ c m − c n ∥ 2 2 ) 2 .
In addition, the class center is calculated by averaging the features in the same class and updating in each iteration. The centers are updated as follows:
c k t + 1 = c k t + α ∇ c k ,
where α is the learning rate of class centers.
The update of the k- t h class center can be computed as a derivative of the overall loss with respect to the class center c k :
∇ c k = ∑ i = 1 M δ ( y i , k ) ( c k − F ( x i ) ) 1 + ∑ i = 1 M δ ( y i , k ) − λ 1 ∑ i = 1 M ( 1 − δ ( y i , k ) ) ( c k − F ( x i ) ) ( ϵ 1 + ∑ j = 1 , j ≠ y i N | | F ( x i ) − c j | | 2 2 ) 2 − λ 2 ∑ m ∈ N δ ( m , k ) ∑ n ∈ N n ≠ m ( c k − c n ) ( ϵ 2 + ∑ m ∈ N ∑ n ∈ N n ≠ m ∥ c m − c n ∥ 2 2 ) 2 ( 1 + ∑ m ∈ N δ ( m , k ) ) ,
where δ ( y i , k ) and δ ( m , k ) are defined as
δ ( y i , k ) = 1 ; y i = k 0 ; y i ≠ k ,
δ ( m , k ) = 1 ; m = k 0 ; m ≠ k .
CNNs can be trained utilizing standard stochastic gradient descent (SGD). The hyperparameters of CNNs contain: a batch size M, the number of training iterations T, the learning rates of the weight parameter μ , the learning rates of the class centers α , and balanced terms of the loss functions λ , λ 1 , λ 2 . First, the parameters of the CNNs are initialized W, the softmax loss parameters θ , and class center c k . In each iteration, M training images x i are passed into the CNNs to obtain the output of the last fully-connected layer F ( x i ) in each batch. The overall loss of the model and derivative of the loss functions with respect to the output of the last fully-connected layers F ( x i ) are calculated to update the parameters of the CNNs. θ is independent of the overall loss; therefore, only the softmax loss is considered. Whereas the gradient of overall loss is used to update W. The update process of W and θ are separated with difference derivatives. Finally, the derivatives of the overall loss with respect to class center c k are calculated to update the class centers c k with the learning rate of the class center α . The training process for CNNs with proposed loss is interpreted in Algorithm 1.
Algorithm 1 Training process for CNNs with proposed loss
     Input: Training images x i , batch size M, number of training iterations T, learning rates of weight parameter μ , learning rate of class centers α , hyper-parameters λ , λ 1 , λ 2 .
     Initialization: the CNNs parameters W, the softmax loss parameters θ , the class centers c k , the iteration t=0.
1:
while t ≤ T do  
2:
    Calculate the deep features, the output of the last fully-connected layers F ( x i ) of M input images in one mini-batch.  
3:
    Calculate the overall loss as in (2):   
4:
     L = L s + λ L v   
5:
    Calculate the gradients for each input i by:   
6:
     d L t d F ( x i ) t = d L s t d F ( x i ) t + λ d L v t d F ( x i ) t   
7:
    Update parameters θ by:  
8:
     θ t + 1 = θ t − μ d L t d θ t = θ t − μ d L s t d θ t   
9:
    Update parameters W by:  
10:
     W t + 1 = W t − μ d L t d W t = W t − μ ∑ i M d L t d F ( x i ) t d F ( x i ) t d W t   
11:
    Update c k for k-th class center: c k t + 1 = c k t − α ∇ c k   
12:
     t = t + 1   
13:
end while
   End of the algorithm: The CNNs parameters W, the softmax loss parameters θ

4. Experiments

4.1. Experimental Setup

The performance of the proposed method was evaluated based on four benchmark facial expression databases: three from a laboratory environment, namely, Cohn-Kanade Plus (CK+) [27], Oulu-CASIA [28], MMI [29]; and one from a wild environment, FER2013 [30]. A 10-fold cross-validation strategy was employed for model evaluation, especially focusing on scenarios with small and imbalanced datasets such as CK+, MMI, and Oulu-CASIA. Each of these databases was strictly divided into 90% as a training set and 10% allocated as a testing set. Furthermore, FER is a large-scale dataset; the training and evaluation processes were conducted on its provided datasets. Several sample images derived from these databases are illustrated in Fig. 6. The details of the databases and the number of images for each emotion are presented in Table 1.
To minimize the variations in the face scale and in-plane rotation, the face was detected and aligned from the original database using the OpenCV library with Haar–Cascade detection [42]. The aligned facial images were resized to 64×64 pixels. Moreover, intensity equalization was used to enhance the contrast in facial images. A data augmentation technique was used to overcome the restricted number of training images in the FER problem. Furthermore, the facial images were flipped, and each one and its corresponding flipped image was rotated at -15, -10, -5, 5, 10, and 15 °. The training databases were augmented 14 times using original, flipped, six-angle, and six-angle-flipped images. The rotated facial images are shown in Fig. 7.
The proposed loss function was compared with softmax, center [26], range [31], and marginal losses[32] using the same CNN architectures to demonstrate the effectiveness of the proposed loss function. The experiment was conducted in a subject-independent scenario. The CNN architectures were processed with 64 images in each batch. The training was performed using the standard SGD technique to optimize the loss functions. The hyper-parameter λ was used to balance the softmax and variant losses. λ 1 and λ 2 were utilized to balance among these losses in the variant loss, and α controlled the learning rate of the class center c k . All of these factors affect the performance of our model. In this experiment, the values λ =0.001, λ 1 =0.4, λ 2 =0.6, ϵ 1 = ϵ 2 =10e-3 were empirically selected for the proposed loss. For the center, marginal, and range losses, λ was set to 0.001. An Intel®Xeon® CPU E5-2620 v2 @ 2.10GHz ×12 48GB RAM and an NVIDIA RTX 3090 GPU were used to implement the proposed method in a Pytorch framework.

4.2. Experimental Results

1) Results on Cohn-Kanade Plus (CK+) database: The CK+ is a representative laboratory-controlled database for FER. It comprises 593 image sequences collected from 123 participants. 327 of these image sequences have one of seven emotion labels: anger, contempt, disgust, fear, happiness, sadness, and surprise, from 118 subjects. Each image sequence starts with a neutral face and ends with the peak emotion. To collect additional data, the last three frames of each sequence were collected and associated with the provided labels. Therefore, a database containing 981 experimental images was constructed. The images were primarily grayscale and digitized to a 640×490 or 640×480 resolution.
The average recognition precision of the methods based on the loss functions and CNN architectures is listed in Table 2. The accuracy of the proposed loss function was superior to that of the others for all six CNN architectures. For the same loss functions, the accuracy of ResNet was the highest, followed by those of MobileNetV3, ResNeSt, InceptionNet, AlexNet, and DenseNet. Overall, the proposed loss produced an average recognition accuracy of 94.89% for the seven expressions using the ResNet.
Table 3 presents the confusion matrix of the ResNet, which was optimized using the proposed loss function. The accuracy of the contempt, disgust, happiness, and surprise labels was significant. Notably, the happiness percentage was the highest at 99.5%, followed closely by surprise, disgust, and contempt at 98.4%, 97.7%, and 93.4%, respectively. The proportions of the anger, fear, and sadness labels were inferior to these emotions because of their visual similarity.
2) Results on Oulu-CASIA database: The Oulu-CASIA database includes 2,880 image sequences obtained from 80 participants using a visible light (VIS) imaging system under normal illumination conditions. Six emotion labels were assigned to each image sequence: anger, disgust, fear, happiness, sadness, and surprise. Like the Cohn-Kanade Plus database, the image sequence started with a neutral face and ended with the peak emotion. For each image sequence, the last three frames were collected as the peak frames of the labeled expression. The imaging hardware was operated at 25 fps with an image resolution of 320×240 pixels.
The average recognition accuracy of the methods is listed in Table 4. The performance of the proposed loss function was comparable to that of previous ones. Specifically, the proposed loss achieved an average recognition accuracy of 77.61% for the six expressions using the ResNet architectures.
Table 5 presents the confusion matrix of ResNet trained with the proposed loss function. The accuracy of the happiness and surprise labels increased, with the former achieving 92.1% and the latter gaining 84.0%. The accuracy for anger, disgust, fear, and sadness was inferior, obtained 66.2%, 70.5%, 76.3%, and 76.5%, respectively.
3) Results on MMI database: The laboratory-controlled MMI database comprises 312 image sequences collected from 30 participants. 213 image sequences were labeled with six facial expressions: anger, disgust, fear, happiness, sadness, and surprise. Moreover, 208 sequences from 30 participants were captured in frontal view. The spatial resolution was 720×576 pixels, and the videos were recorded at 24 fps. Unlike the Cohn-Kanade Plus and Oulu-CASIA databases, the MMI database features image sequences labeled by the onset-apex. Therefore, the sequences started with a neutral expression, peaked near the middle, and returned to a neutral expression. The location of the peak expression frame was not provided. Furthermore, the MMI database presented challenging conditions, particularly in the case of large interpersonal variations. Three middle frames were chosen as the peak expression frames in each image sequence to conduct a subject-independent cross-validation scenario.
Table 6 lists the average recognition accuracy of the methods. Our loss function outperformed all the other loss functions by a certain margin. Specifically, the proposed loss achieved an average recognition accuracy of 67.43% for the six expressions using the MobileNetV3 architecture.
Table 7 presents the percentages in the confusion matrix of the MobileNetV3 optimized with the proposed loss function. The accuracy for all emotions was under 80.0%, except for happiness and surprise, which obtained 89.7% and 81.3%, respectively. This may be due to the number of images in each class. An instance of this is fear, which had the fewest labels and whose accuracy was a low 31.0%. Similar results were also confirmed for the accuracy of anger, disgust, and sadness.
4) Results on FER2013 database: FER2013 is a large-scale, unconstrained database automatically collected by the Google image search API. It includes 35,887 images with a relatively low resolution of 48×48 pixels, which are labeled with one of seven emotion labels: anger, disgust, fear, happiness, sadness, surprise, and neutral. The training set comprises 28,709 examples. The public test consists of 3,589 examples; the remaining 3,589 images are used as a private test set.
Table 8 lists all the methods’ average recognition accuracy. The accuracy of the proposed loss function greatly exceeds that of the others in all CNN architectures except AlexNet. The proposed loss achieved a peak average recognition accuracy of 61.05% for the seven expressions using the ResNeSt architecture.
The confusion matrix of ResNeSt, which was trained with the proposed loss function, is present in Table 9. The happiness percentage was highest at 80.7%, followed by the surprise at 77.4%. The others obtained relatively low prediction ratios.

4.3. Training Time

The training time is essential for evaluating the computational complexity of deep learning networks with specific loss functions. This section compares the training time of the auxiliary CNN architectures with the existing and proposed loss functions. Notably, all loss functions were trained on a single GPU. Depending on the dataset and network architecture, the number of iterations was empirically set to achieve optimal convergence with the corresponding loss function. As presented in Table 10, the softmax loss trained the fastest because it only uses one term in the mathematical function, followed closely by the center and proposed loss functions. Meanwhile, the range and marginal loss functions required longer training times among the compared methods because their complex mathematical functions produced a time-consuming backpropagation process. In summary, only softmax and center loss were marginally faster than the proposed method. However, the proposed method achieved superior performance compared with these loss functions. Therefore, the proposed method is computationally efficient and meets the practical requirements.

5. Conclusions

Although loss functions can drive network learning, it has received little attention for promoting FER performance. This study presents a new loss function that allows simultaneous consideration of inter- and intra-class variations to be applied to CNN architecture for facial expression recognition. More specifically, this loss minimizes the distance between the deep features and their corresponding class centers as well as maximizes the distances of deep features with their non-corresponding class centers and the distances between different class centers. In addition, the proposed loss improves the testing accuracy of the benchmark FER database compared to several other loss functions. Overall, this study demonstrates that choosing optimal loss functions strongly affects the performance of deep learning networks, even when maintaining their architecture. We hope the proposed loss function can be applied to other high-level vision tasks.

Author Contributions

Conceptualization, methodology, T.-D.P; resources, investigation, analysis, writing-original draft, M.-T.D.; software, Q.-T.H.; validation, project administration, S.L.; supervision, writing-review and editing, M.-C.H. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by Korea Institute for Advancement of Technology (KIAT) grant funded by the Korea Government (MOTIE)(P0017011, HRD Program for Industrial Innovation). It was also supported by Industrial Technology Challenge Track of the Ministry of Trade, Industry and Energy (MOTIE) / Korea Evaluation Institute of Industrial Technology (KEIT)(20012624). It was also supported by the R&D Program of the Ministry of Trade, Industry, and Energy (MOTIE) and Korea Evaluation Institute of Industrial Technology (KEIT)(RS-2023-00232192).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Jourabloo, A.; De la Torre, F.; Saragih, J.; Wei, S.E.; Lombardi, S.; Wang, T.L.; Belko, D.; Trimble, A.; Badino, H. Robust egocentric photo-realistic facial expression transfer for virtual reality. Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., 2022, pp. 20323–20332. [CrossRef]
  2. Putro, M.D.; Nguyen, D.L.; Jo, K.H. A Fast CPU Real-Time Facial Expression Detector Using Sequential Attention Network for Human–Robot Interaction. IEEE Trans. Ind. Informat. 2022, 18, 7665–7674. [CrossRef]
  3. Xiao, H.; Li, W.; Zeng, G.; Wu, Y.; Xue, J.; Zhang, J.; Li, C.; Guo, G. On-road driver emotion recognition using facial expression. Appl. Sci. 2022, 12, 807. [CrossRef]
  4. Zhao, G.; Pietikainen, M. Dynamic texture recognition using local binary patterns with an application to facial expressions. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 915–928. [CrossRef]
  5. Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit. Ieee, 2005, Vol. 1, pp. 886–893. [CrossRef]
  6. Niese, R.; Al-Hamadi, A.; Farag, A.; Neumann, H.; Michaelis, B. Facial expression recognition based on geometric and optical flow features in colour image sequences. IET Comput. Vis. 2012, 6, 79–89. [CrossRef]
  7. Moghaddam, B.; Jebara, T.; Pentland, A. Bayesian face recognition. Pattern Recognit. 2000, 33, 1771–1782. [CrossRef]
  8. Liu, J.; Zhang, L.; Chen, X.; Niu, J. Facial landmark automatic identification from three dimensional (3D) data by using Hidden Markov Model (HMM). Int. J. Ind. Ergonom. 2017, 57, 10–22. [CrossRef]
  9. Chen, L.; Li, M.; Su, W.; Wu, M.; Hirota, K.; Pedrycz, W. Adaptive feature selection-based AdaBoost-KNN with direct optimization for dynamic emotion recognition in human–robot interaction. IEEE Trans. Emerg. Topics Comput. Intell. 2019, 5, 205–213. [CrossRef]
  10. Kotsia, I.; Pitas, I. Facial expression recognition in image sequences using geometric deformation features and support vector machines. IEEE Trans. Image Process. 2006, 16, 172–187. [CrossRef]
  11. Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6999–7019. [CrossRef]
  12. Hoang, H.A.; Yoo, M. 3ONet: 3D Detector for Occluded Object under Obstructed Conditions. IEEE Sensors Journal 2023, 23, 18879–18892. [CrossRef]
  13. Karnati, M.; Seal, A.; Bhattacharjee, D.; Yazidi, A.; Krejcar, O. Understanding deep learning techniques for recognition of human emotions using facial expressions: a comprehensive survey. IEEE Trans. Instrum. Meas 2023, 72, 1–31. [CrossRef]
  14. Villanueva, M.G.; Zavala, S.R. Deep neural network architecture: Application for facial expression recognition. IEEE Latin Amer. Trans. 2020, 18, 1311–1319. [CrossRef]
  15. Ge, H.; Zhu, Z.; Dai, Y.; Wang, B.; Wu, X. Facial expression recognition based on deep learning. Comput. Methods Programs Biomed. 2022, 215, 106621. [CrossRef]
  16. Lee, D.H.; Yoo, J.H. CNN Learning Strategy for Recognizing Facial Expressions. IEEE Access 2023, 11, 70865–70872. [CrossRef]
  17. Wu, B.F.; Lin, C.H. Adaptive feature mapping for customizing deep learning based facial expression recognition model. IEEE Access 2018, 6, 12451–12461. [CrossRef]
  18. Li, S.; Deng, W. Deep facial expression recognition: A survey. IEEE Trans. Affective Comput. 2020, 13, 1195–1215. [CrossRef]
  19. Akhand, M.; Roy, S.; Siddique, N.; Kamal, M.A.S.; Shimamura, T. Facial emotion recognition using transfer learning in the deep CNN. Electronics 2021, 10, 1036. [CrossRef]
  20. Renda, A.; Barsacchi, M.; Bechini, A.; Marcelloni, F. Comparing ensemble strategies for deep learning: An application to facial expression recognition. Expert Syst. Appl. 2019, 136, 1–11. [CrossRef]
  21. Liu, C.; Hirota, K.; Ma, J.; Jia, Z.; Dai, Y. Facial expression recognition using hybrid features of pixel and geometry. IEEE Access 2021, 9, 18876–18889. [CrossRef]
  22. Liu, W.; Wen, Y.; Yu, Z.; Yang, M. Large-margin softmax loss for convolutional neural networks. Proc. Int. Conf. Mach. Learn. 2016, 2, 507–516.
  23. Wang, F.; Cheng, J.; Liu, W.; Liu, H. Additive margin softmax for face verification. IEEE Signal Process. Lett. 2018, 25, 926–930. [CrossRef]
  24. Sun, Y.; Chen, Y.; Wang, X.; Tang, X. Deep learning face representation by joint identification-verification. Advances in neural information processing systems 2014, 27.
  25. Schroff, F.; Kalenichenko, D.; Philbin, J. Facenet: A unified embedding for face recognition and clustering. Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., 2015, pp. 815–823.
  26. Wen, Y.; Zhang, K.; Li, Z.; Qiao, Y. A discriminative feature learning approach for deep face recognition. Proc. Eur. Conf. Comput. Vis. Springer, 2016, pp. 499–515.
  27. Lucey, P.; Cohn, J.F.; Kanade, T.; Saragih, J.; Ambadar, Z.; Matthews, I. The extended cohn-kanade dataset (ck+): A complete dataset for action unit and emotion-specified expression. Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit. Workshops. IEEE, 2010, pp. 94–101.
  28. Zhao, G.; Huang, X.; Taini, M.; Li, S.Z.; PietikäInen, M. Facial expression recognition from near-infrared videos. Image Vis. Comput. 2011, 29, 607–619. [CrossRef]
  29. Pantic, M.; Valstar, M.; Rademaker, R.; Maat, L. Web-based database for facial expression analysis. Proc. IEEE Int. Conf. Multimedia Expo. IEEE, 2005, pp. 317–321.
  30. Goodfellow, I.J.; Erhan, D.; Carrier, P.L.; Courville, A.; Mirza, M.; Hamner, B.; Cukierski, W.; Tang, Y.; Thaler, D.; Lee, D.H.; others. Challenges in representation learning: A report on three machine learning contests. Neural Netw., 2015, Vol. 64, pp. 59–63. [CrossRef]
  31. Zhang, X.; Fang, Z.; Wen, Y.; Li, Z.; Qiao, Y. Range loss for deep face recognition with long-tailed training data. Proc. IEEE/CVF Int. Conf. Comput. Vis., 2017, pp. 5409–5418.
  32. Deng, J.; Zhou, Y.; Zafeiriou, S. Marginal loss for deep face recognition. Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit. Workshops, 2017, pp. 60–68.
  33. Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Proc. Adv. Neural Inf. Process. Syst, 2012, Vol. 25, pp. 1097–1105.
  34. Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., 2015, pp. 1–9.
  35. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., 2016, pp. 770–778.
  36. Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., 2017, pp. 4700–4708.
  37. Howard, A.; Sandler, M.; Chu, G.; Chen, L.C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; others. Searching for mobilenetv3. Proc. IEEE/CVF Int. Conf. Comput. Vis., 2019, pp. 1314–1324.
  38. Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., 2018, pp. 7132–7141.
  39. Tan, M.; Chen, B.; Pang, R.; Vasudevan, V.; Sandler, M.; Howard, A.; Le, Q.V. Mnasnet: Platform-aware neural architecture search for mobile. Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., 2019, pp. 2820–2828.
  40. Yang, T.J.; Howard, A.; Chen, B.; Zhang, X.; Go, A.; Sandler, M.; Sze, V.; Adam, H. Netadapt: Platform-aware neural network adaptation for mobile applications. Proc. Eur. Conf. Comput. Vis., 2018, pp. 285–300.
  41. Zhang, H.; Wu, C.; Zhang, Z.; Zhu, Y.; Lin, H.; Zhang, Z.; Sun, Y.; He, T.; Mueller, J.; Manmatha, R.; others. Resnest: Split-attention networks. Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., 2022, pp. 2736–2746.
  42. Viola, P.; Jones, M. Rapid object detection using a boosted cascade of simple features. Proc. IEEE/CVF Int. Conf. Comput. Vis. IEEE, 2001, Vol. 1, pp. 511–518.
Preprints 89259 g001
Figure 1. Pipeline of the FER system.
Figure 1. Pipeline of the FER system.
Preprints 89259 g001
Preprints 89259 g002
Figure 2. Visualization of the proposed loss for one batch image in an Euclidean space. Supposing the three classes anger, happiness, and surprise in this batch, the proposed loss aims to reduce the intra-distance d 1 and enhance the inter-distance d 2 and class distance d 3 (Best viewed in color).
Figure 2. Visualization of the proposed loss for one batch image in an Euclidean space. Supposing the three classes anger, happiness, and surprise in this batch, the proposed loss aims to reduce the intra-distance d 1 and enhance the inter-distance d 2 and class distance d 3 (Best viewed in color).
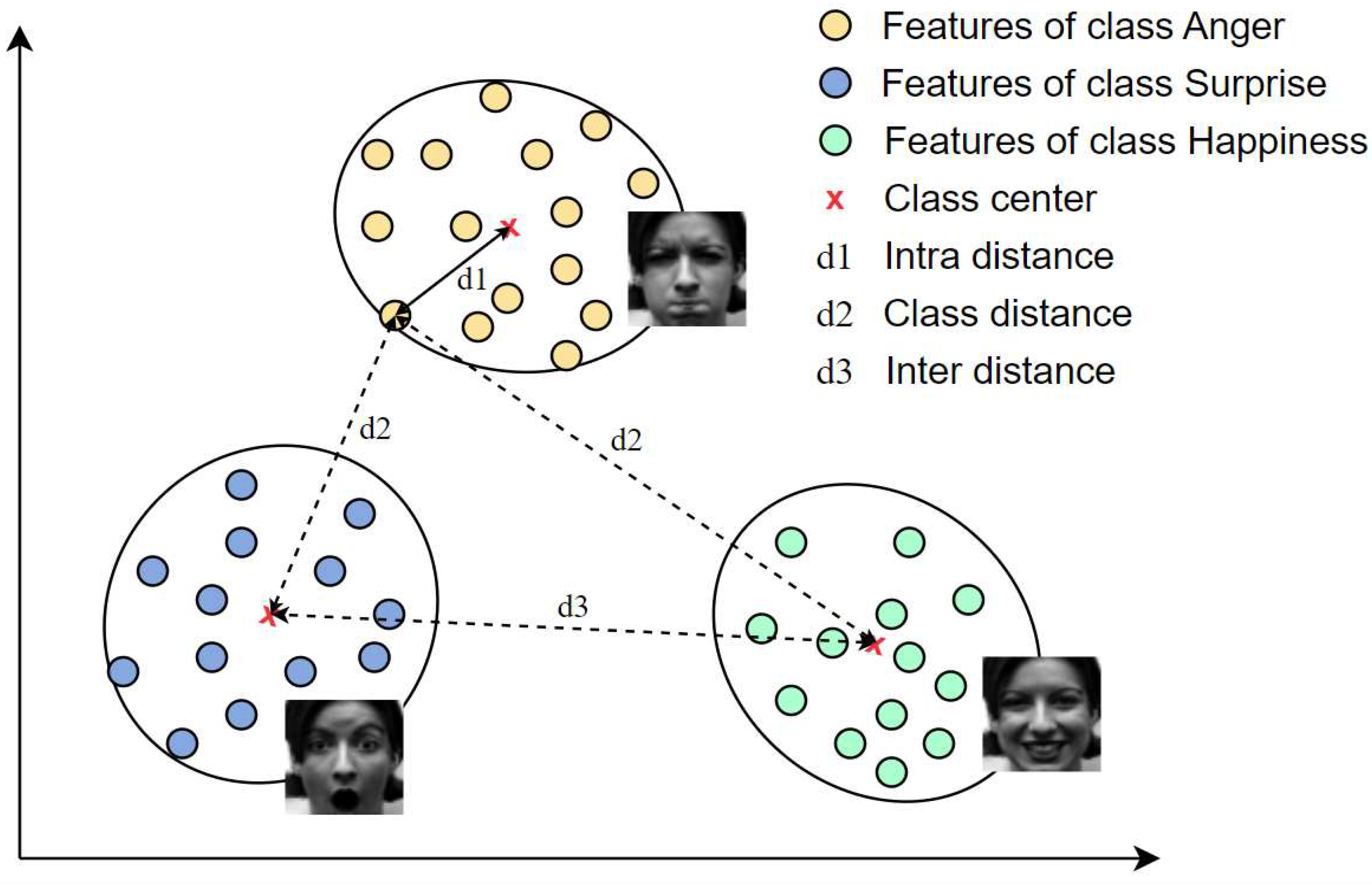
Preprints 89259 g002
Preprints 89259 g003
Figure 3. ResNet-18 architecture.
Figure 3. ResNet-18 architecture.
Preprints 89259 g003
Preprints 89259 g004
Figure 4. ResBlock architecture.
Figure 4. ResBlock architecture.
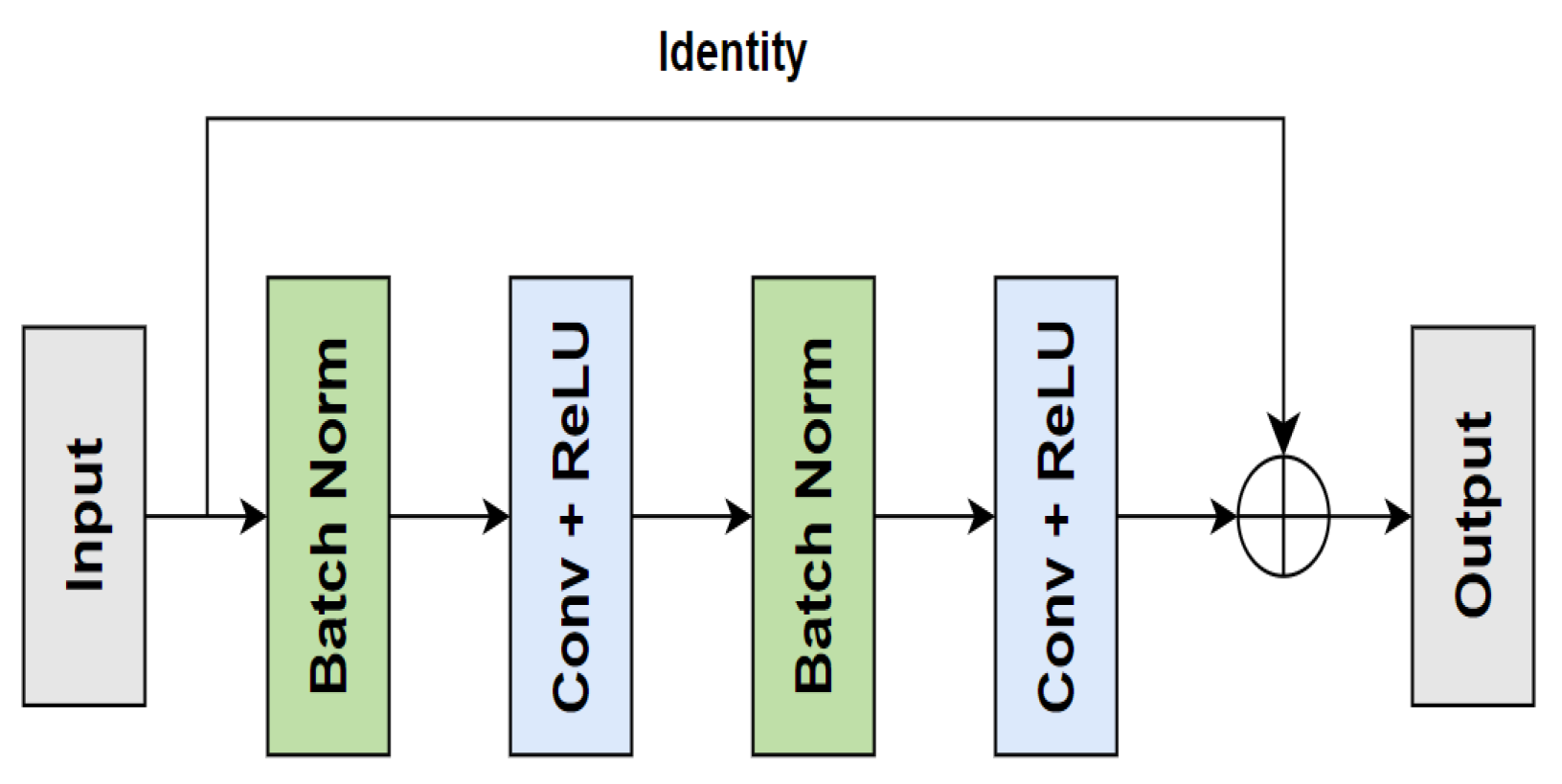
Preprints 89259 g004
Preprints 89259 g005
Figure 5. Overall system CNNs using the proposed loss.
Figure 5. Overall system CNNs using the proposed loss.
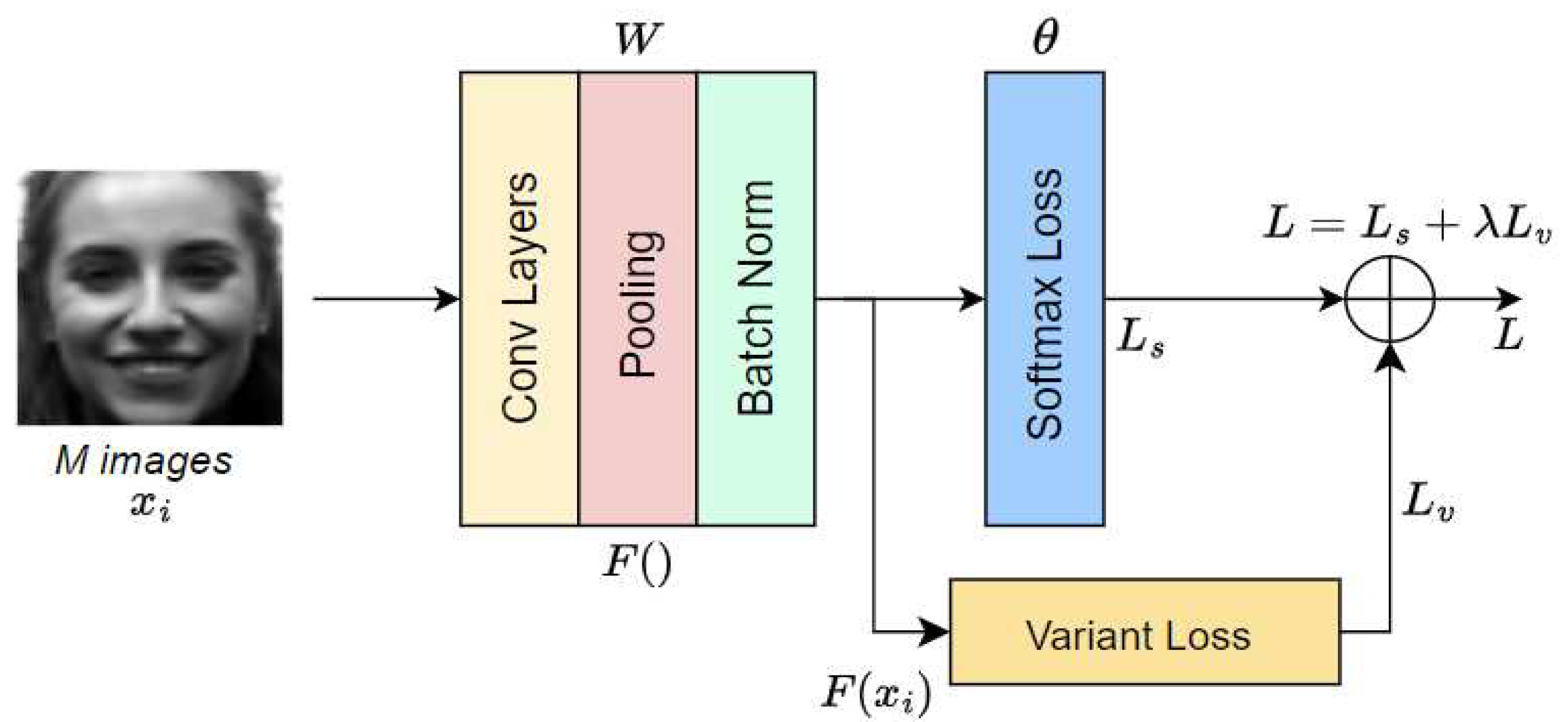
Preprints 89259 g005
Preprints 89259 g006
Figure 6. Example face images from CK+ (top), Oulu-CASIA (center), and MMI (bottom) databases. The facial expressions from left to right convey anger, contempt, disgust, fear, happiness, sadness, and surprise. The contempt images of Oulu-CASIA and MMI are null.
Figure 6. Example face images from CK+ (top), Oulu-CASIA (center), and MMI (bottom) databases. The facial expressions from left to right convey anger, contempt, disgust, fear, happiness, sadness, and surprise. The contempt images of Oulu-CASIA and MMI are null.
Preprints 89259 g006
Preprints 89259 g007
Figure 7. Example rotated images from CK+ database. The facial expressions from left to right convey anger, contempt, disgust, fear, happiness, sadness, and surprise. The rotation degrees from top to bottom are -5, -10, -15, 5, 10, 15 °.
Figure 7. Example rotated images from CK+ database. The facial expressions from left to right convey anger, contempt, disgust, fear, happiness, sadness, and surprise. The rotation degrees from top to bottom are -5, -10, -15, 5, 10, 15 °.
Preprints 89259 g007
Table 1. Number of images for each emotion: anger (An), contempt (Co), disgust (Di), fear (Fe), happiness (Ha), sadness (Sa), surprise (Su), neutral (Ne).
Table 1. Number of images for each emotion: anger (An), contempt (Co), disgust (Di), fear (Fe), happiness (Ha), sadness (Sa), surprise (Su), neutral (Ne).
An Co Di Fe Ha Sa Su Ne All
CK+ 135 54 177 75 207 84 249 - 981
Oulu 240 - 240 240 240 240 240 - 1440
MMI 99 - 96 84 126 96 123 - 624
FER2013 4953 - 547 5121 8989 6077 4002 6198 35887
Table 2. Performance comparison on the CK+ database in terms of the seven expressions.
Table 2. Performance comparison on the CK+ database in terms of the seven expressions.
Method AlexNet InceptionNet ResNet DenseNet MobileNetV3 ResNeSt
Softmax 87.38 87.18 90.65 83.68 91.60 85.58
Center 88.08 87.88 92.46 83.38 87.78 85.98
Range 90.59 88.08 91.79 85.28 91.50 88.68
Marginal 89.18 86.68 87.78 84.18 89.68 86.38
Proposed 90.79 89.18 94.89 85.98 91.90 89.28
Table 3. Confusion matrix of the ResNet optimized with the proposed loss on the CK+ database. The labels in the leftmost column and on top represent the ground truth and the prediction results, respectively.
Table 3. Confusion matrix of the ResNet optimized with the proposed loss on the CK+ database. The labels in the leftmost column and on top represent the ground truth and the prediction results, respectively.
An Co Di Fe Ha Sa Su
An 86.2% 1.4% 6.5% 0% 0% 5.1% 0.8%
Co 3.6% 93.4% 0% 1.5% 0% 1.5% 0%
Di 1.7% 0% 97.7% 0% 0.6% 0% 0%
Fe 0% 2.6% 0% 87.2% 7.6% 2.6% 0%
Ha 0% 0% 0% 0.5% 99.5% 0% 0%
Sa 7.5% 1.1% 1.1% 0% 0% 90.3% 0%
Su 0.8% 0% 0% 0.4% 0% 0.4% 98.4%
Table 4. Performance comparison on the Oulu-CASIA database in terms of the six expressions.
Table 4. Performance comparison on the Oulu-CASIA database in terms of the six expressions.
Method AlexNet InceptionNet ResNet DenseNet MobileNetV3 ResNeSt
Softmax 70.52 65.16 72.46 68.67 73.24 70.23
Center 71.95 64.09 74.96 69.09 74.89 67.23
Range 72.17 64.38 74.11 69.52 69.09 63.80
Marginal 70.24 68.09 71.88 68.67 73.74 68.95
Proposed 72.96 69.17 77.61 69.88 76.46 70.24
Table 5. Confusion matrix of the ResNet optimized with the proposed loss on the Oulu-CASIA database. The labels in the leftmost column and on top represent the ground truth and the prediction results, respectively.
Table 5. Confusion matrix of the ResNet optimized with the proposed loss on the Oulu-CASIA database. The labels in the leftmost column and on top represent the ground truth and the prediction results, respectively.
An Di Fe Ha Sa Su
An 66.2% 13.0% 6.9% 0% 13.9% 0%
Di 12.4% 70.5% 7.3% 2.6% 6.8% 0.4%
Fe 5.8% 1.3% 76.3% 5.4% 5.0% 16.3%
Ha 0% 2.1% 5.8% 92.1% 0% 0%
Sa 12.4% 3.8% 5.1% 1.7% 76.5% 0.4%
Su 1.4% 0% 11.9% 2.7% 0% 84.0%
Table 6. Performance comparison on the MMI database in terms of the six expressions.
Table 6. Performance comparison on the MMI database in terms of the six expressions.
Method AlexNet InceptionNet ResNet DenseNet MobileNetV3 ResNeSt
Softmax 57.76 53.92 61.59 60.52 61.44 54.07
Center 58.98 58.52 61.92 59.29 64.36 57.29
Range 62.67 61.75 61.13 54.68 64.20 55.76
Marginal 59.44 55.14 57.62 57.61 64.66 53.00
Proposed 63.13 63.74 65.89 61.13 67.43 58.83
Table 7. Confusion matrix of the MobileNetV3 optimized with the proposed loss on the MMI database. The labels in the leftmost column and on top represent the ground truth and prediction results, respectively.
Table 7. Confusion matrix of the MobileNetV3 optimized with the proposed loss on the MMI database. The labels in the leftmost column and on top represent the ground truth and prediction results, respectively.
An Di Fe Ha Sa Su
An 57.1% 14.3% 11.4% 3.8% 12.4% 1.0%
Di 13.0% 72.2% 2.8% 4.6% 4.6% 2.8%
Fe 11.5% 5.8% 31.0% 9.2% 11.5% 31.0%
Ha 0% 6.3% 1.6% 89.7% 0% 2.4%
Sa 14.7% 13.8% 8.8% 0% 59.8% 2.9%
Su 4.1% 0.8% 7.3% 1.6% 4.9% 81.3%
Table 8. Performance comparison on the FER2013 database in terms of the seven expressions.
Table 8. Performance comparison on the FER2013 database in terms of the seven expressions.
Method AlexNet InceptionNet ResNet DenseNet MobileNetV3 ResNeSt
Softmax 59.77 55.92 59.21 59.15 56.33 60.85
Center 58.48 57.42 56.70 59.82 50.43 60.93
Range 58.65 56.22 48.37 59.59 52.99 60.96
Marginal 59.04 57.12 57.51 58.71 56.56 59.76
Proposed 58.51 57.81 59.65 60.46 58.29 61.05
Table 9. Confusion matrix of the ResNeSt optimized with the proposed loss on the FER2013 database. The labels in the leftmost column and on top represent the ground truth and prediction results, respectively.
Table 9. Confusion matrix of the ResNeSt optimized with the proposed loss on the FER2013 database. The labels in the leftmost column and on top represent the ground truth and prediction results, respectively.
An Di Fe Ha Sa Su Ne
An 55.7% 0.4% 8.6% 6.6% 14.6% 3.2% 10.9%
Di 23.2% 46.4% 7.2% 1.8% 10.7% 3.6% 7.1%
Fe 8.9% 0.2% 42.5% 4.2% 23.4% 8.3% 12.5%
Ha 3.6% 0% 1.5% 80.7% 3.6% 2.8% 7.8%
Sa 13.6% 0.5% 11.8% 6.9% 48.5% 2.8% 15.9%
Su 4.3% 0% 7.9% 3.9% 2.4% 77.4% 4.1%
Ne 9.9% 0.2% 7.1% 8.7% 16.8% 2.3% 55.0%
Table 10. Training time (s) comparison of the auxiliary CNN architecture with different loss functions.
Table 10. Training time (s) comparison of the auxiliary CNN architecture with different loss functions.
Methods AlexNet InceptionNet DenseNet
CK+ Oulu-CASIA MMI FER2013 CK+ Oulu-CASIA MMI FER2013 CK+ Oulu-CASIA MMI FER2013
Softmax 146 142 116 150 499 497 479 1529 393 504 394 2036
Center 150 143 121 157 502 493 494 1621 418 494 400 2050
Range 2871 2937 2219 2619 3432 3265 3219 9238 2679 3231 2460 12113
Marginal 15424 15552 12149 15222 15625 15621 15513 46090 12443 15717 12372 62438
Proposed 157 156 127 163 520 518 522 1677 410 503 412 2177
Iterations 10000 10000 8000 10000 10000 10000 10000 30000 10000 10000 8000 10000
Methods ResNet MobileNetV3 ResNeSt
CK+ Oulu-CASIA MMI FER2013 CK+ Oulu-CASIA MMI FER2013 CK+ Oulu-CASIA MMI FER2013
Softmax 231 252 254 568 431 1144 1066 3215 2008 1619 2110 4108
Center 235 265 250 600 373 1055 1195 2415 2466 1779 2200 10969
Range 2361 2533 2443 5774 5247 6445 6176 14283 7368 5936 7856 64143
Marginal 11648 12632 11648 30686 12164 34076 33580 83618 37944 29172 35354 197333
Proposed 243 271 266 601 456 1072 1108 2943 2570 1780 2273 14004
Iterations 7500 8000 8000 20000 7500 20000 20000 50000 20000 15000 20000 100000
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated