Preprint
Article
Theory of Relationships between Spaces to Obtain Numerical Knowledge
Altmetrics
Downloads
200
Views
95
Comments
0
This version is not peer-reviewed
Submitted:
31 October 2023
Posted:
01 November 2023
Read the latest preprint version here
Alerts
Abstract
The theory says that number interacts with spaces based on the meaning of mathematics, this way it is possible to obtain numerical knowledge. The theory shows the possibility of using spaces relating to each other to explain the reasons why two even numbers form a pair, two odd numbers form a pair, an even and an odd number form an odd number, three odd numbers form an odd number, three even numbers form an odd number. one even, one odd and two evens form an odd, two odd and one even form a pair.
Keywords:
Subject: Computer Science and Mathematics - Mathematics
1. Introduction
The theory helps to understand the fact that formations happen, based on the meaning of mathematics that rigorously describes the real world. through representations of an element or fact that are linked to space, thus, using the relationships between spaces it is possible to understand odd and even numbers. This study presents a possible model for understanding formations.
Note: the study uses a venn diagram developed by jonh venn.
2. Math Sense
The knowledge of mathematics today is not the same as it was at the beginning of the history of mathematics, because in the trajectory of thousands of years ago there was an evolution in the knowledge of mathematics, just as in the future of mathematics thousands of years will continue to evolve its knowledge, with the aim of describing the world with rigor and precision.
The first signs of knowledge of mathematics occurred due to the need to represent elements, giving rise to mathematicswhich emerged in Ancient Egypt and the Babylonian Empire, around 3500 BC.However, in prehistoric times, human beings already used the concepts of counting and measuring. An example of the first elements to represent were stones and sheep, where each stone represented a sheep. An example if there were 15 stones and because there were also 15 sheep, in this case two stones are missing during the count and because there are also two sheep missing. This need to represent the elements in the case of sheep arose with the aim of avoiding losses of sheep, that is, avoiding losses.
The emergence of the representation of elements aims to describe the world with rigor and precision. Many people benefit from mathematics because mathematics makes everyone's life easier, as is the case of the sheep counter who, because of mathematics, did not suffer any harm.
Therefore, based on the meaning of mathematics, it is possible to state that mathematics is related to physical spaces.
3. The Use of Mathematics in Everything
Furthermore, mathematics is used in many things, such as probability, which analyzes the possibility of an event occurring. Percentage is used to compare quantities, profits, discounts and losses. Geometry is present in traffic signs, houses and buildings. The quadratic or 2-degree function is used to calculate projectile launches and motions. In trigonometry it is possible to determine the height of a given building and measure the distance between the Earth and the Moon. The proportion is applicable to decreasing or increasing quantities, an example would be the quantity of food. Set theory helps determine the number of respondents and their groups. The exponential function explains radioactive decay and ecological and sociological growth.
4. Detailed Examples of Math Usage
Example 01: A group of friends made up of 8 people go to eat at a pizzeria, where they buy 2 pizzas of 8 slices each, that is, 16 slices in total. When the two pizzas arrive, one of the friends tries to get everyone to eat the same number of slices, so the division calculation was made: if the total is 16 slices and there are 8 people to eat, each person can eat 2 slices equally each one.
In this case, the division is calculated so that none of the 8 friends eats more or less than any member of the group, the division arises to maintain equality.
Example 02:In research there is an intense presence of mathematics in his work. A survey, for example, aims to understand the profile of crime in Brazil, that is, characteristics of crime. The numbers indicate the reality of crime in Brazil: poorer regions have more violence, richer regions have less violence.
In this case, it is up to public policies to act in the poorest regions, through the implementation of opportunities for people to escape poverty. All this because numbers present information, and from that it is possible to deduce solutions.
Example 03:Mathematics is strongly linked to health, as numbers indicate information that may be contained in food products or medical tests. The information, through numbers, can tell you the ideal amount of consumption or not of this food. Additionally, medical tests can diagnose a disease. If so, numbers can help humanity stay healthy.
Example 04:The numbers can help with people's safety by showing limits for people in elevators, boats, planes and cars. The limits are known through a study with numbers. Additionally, the numbers indicate the speed limit of a means of transport.
Example 05:The existence of commerce depends on mathematics, as the product that commerce sells has a value, but the value can be changed as you seek the ideal profit from the product.
In this case, knowledge of the number is essential to know the value of a product, to obtain the desired profit.
In general, mathematics is present in everything, that is, in any physical space, because it arose from the need to describe the world with rigor and precision.
5. Even and Odd Numbers
An even number is a whole number that is divisible by 2 without a remainder (ex: 2, 4 and 6), and an odd number is a number that is not divisible by 2 without a remainder (ex: 1, 3 and 5).
6. Examples on the Formation of Even Numbers
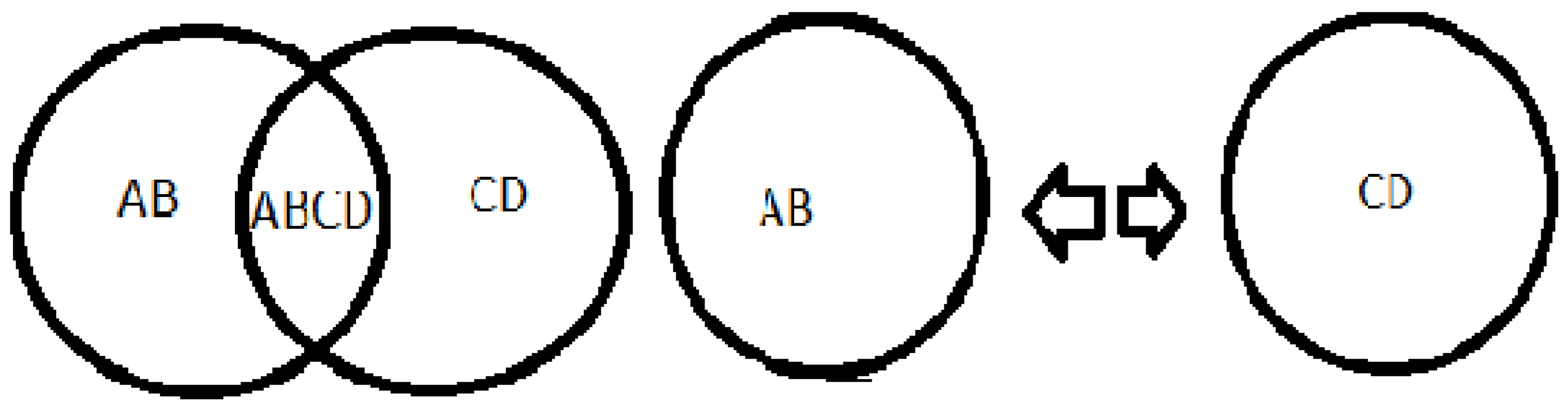
Source: prepared by the author. Table 1 Caption: imagination of space
2+8=10, the number 2 is represented by AB, as both 2 and AB are divisible by two, characterizing a pair, the same is 8 represented by CD and 10 is represented by ABCD, making it possible to divide ABCD into two parts, becoming AB and CD.
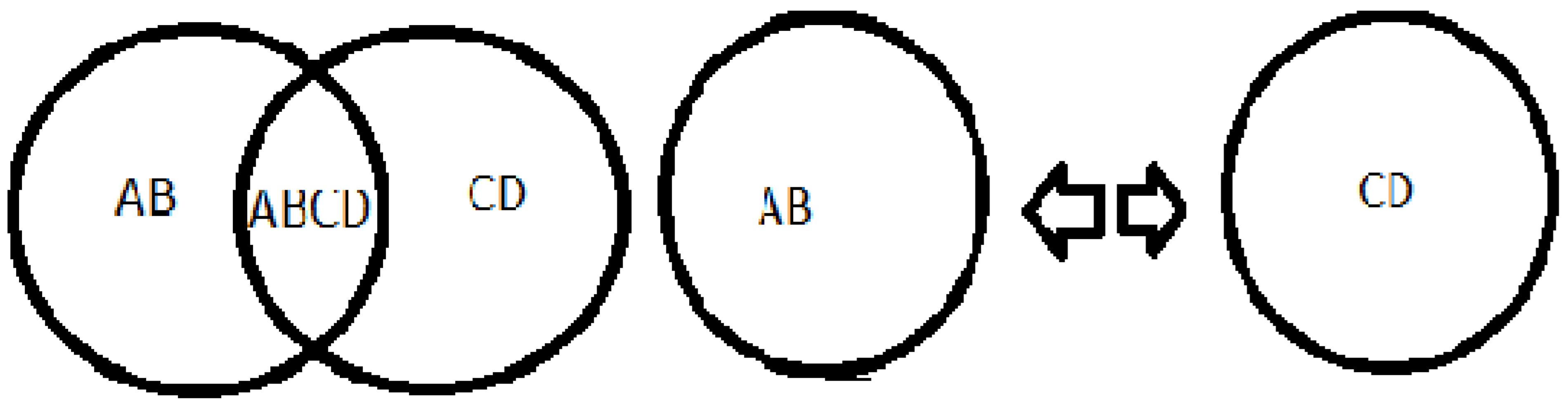
Source: prepared by the author. Table 2 Caption: imagination of space
10+4=14, the number 10 is represented by AB, as both 10 and AB are divisible by two, characterizing a pair, the same is 4 represented by CD and 14 is represented by ABCD, making it possible to divide ABCD into two parts, becoming AB and CD.
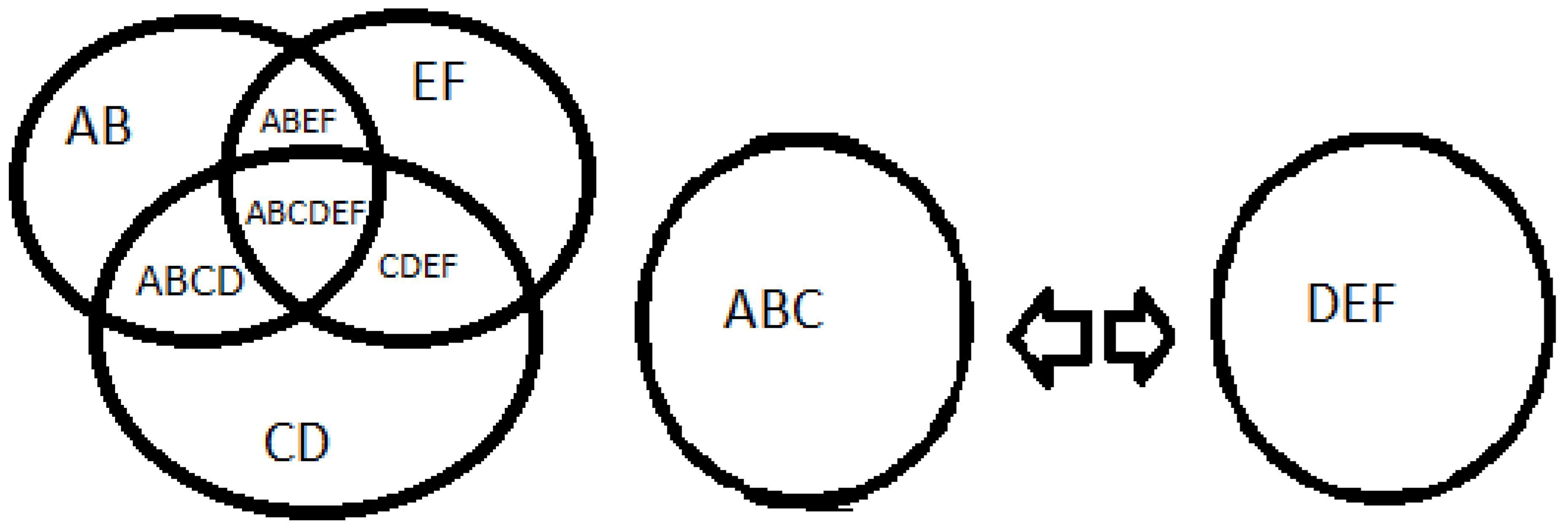
Source: prepared by the author. Table 3 Caption: imagination of space
2+10+8=20, the number 2 is an even number represented by AB, the number 10 is an even number represented by CD, the number 8 is an even number represented by EF, forming an even number 20 represented by ABCDEF and can be divided into two parts ABC and DEF.
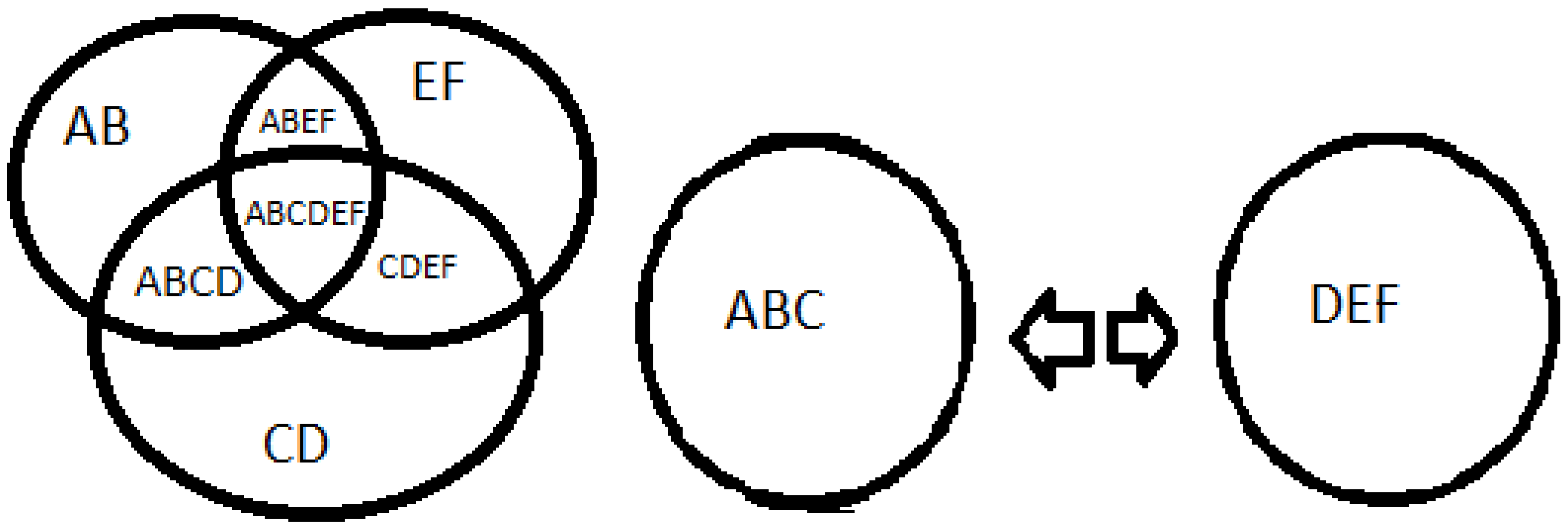
Source: prepared by the author. Table 4 Caption: imagination of space
4+12+8=24, the number 4 is an even number represented by AB, the number 12 is an even number represented by CD, the number 8 is an even number represented by EF, forming an even number 24 represented by ABCDEF and can be divided into two parts ABC and DEF.
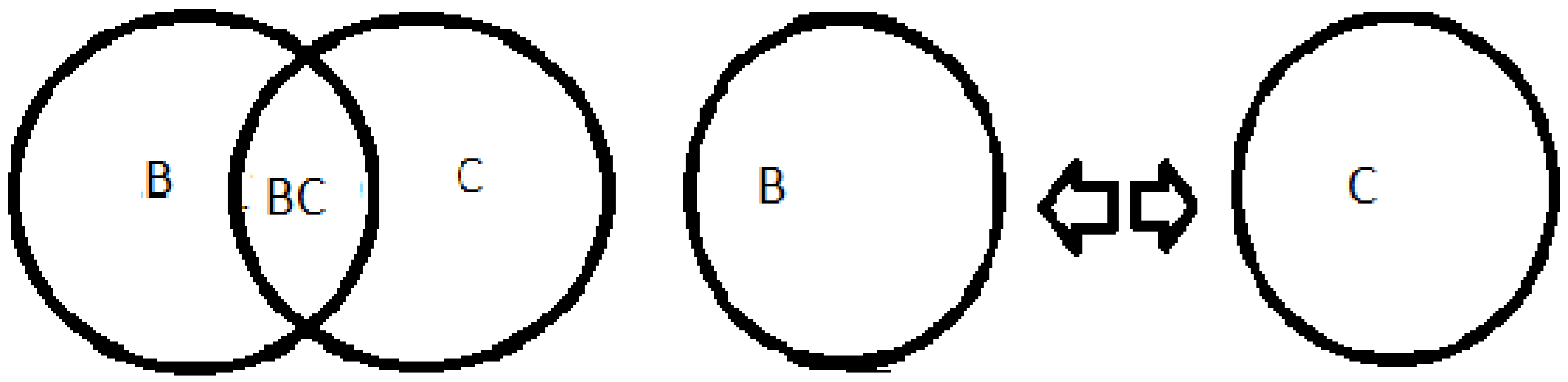
Source: prepared by the author. Table 5 Caption: imagination of space
9+1=10, 9 is odd represented by B as both 9 and B are not divisible into parts, the same is the number 1 which is odd represented by C, forming the number 10 which is even represented by BC and can be divided into B and C .
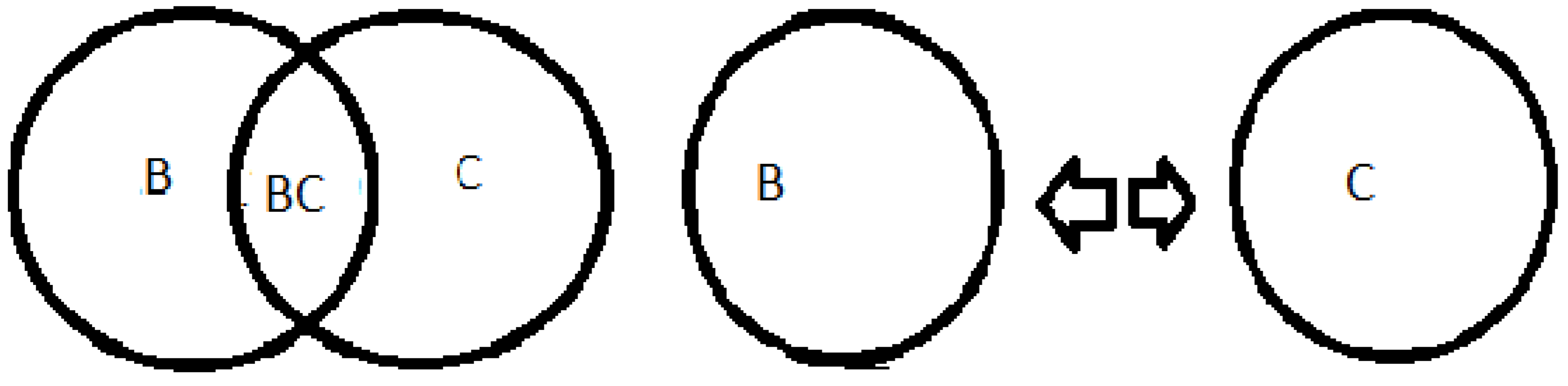
Source: prepared by the author. Table 6 Caption: imagination of space
13+5=18, 13 is odd represented by B as both 13 and B are not divisible into parts, the same is the number 5 which is odd represented by C, forming the number 18 which is even represented by BC and can be divided into B and W.
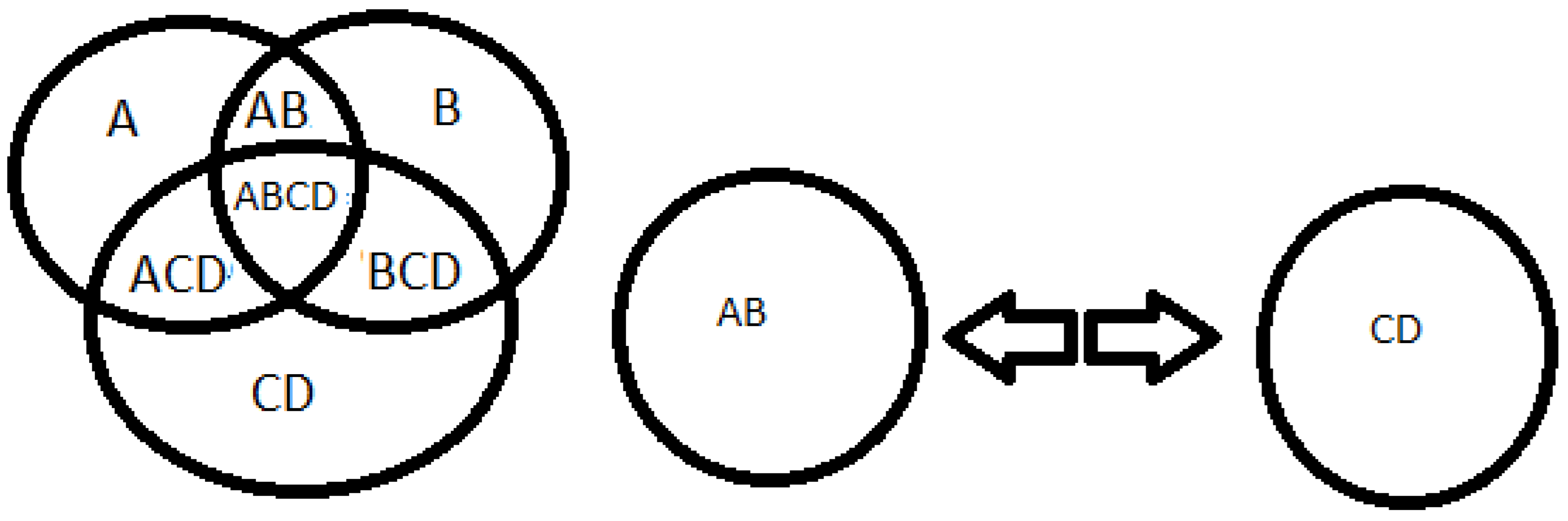
Source: prepared by the author. Table 6 Caption: imagination of space
9+5+4=18, the number 9 is odd represented by A, the number 5 is odd represented by B, the number 4 is even represented by CD, forming number 18 represented by ABCD and can be divided into AB and CD.
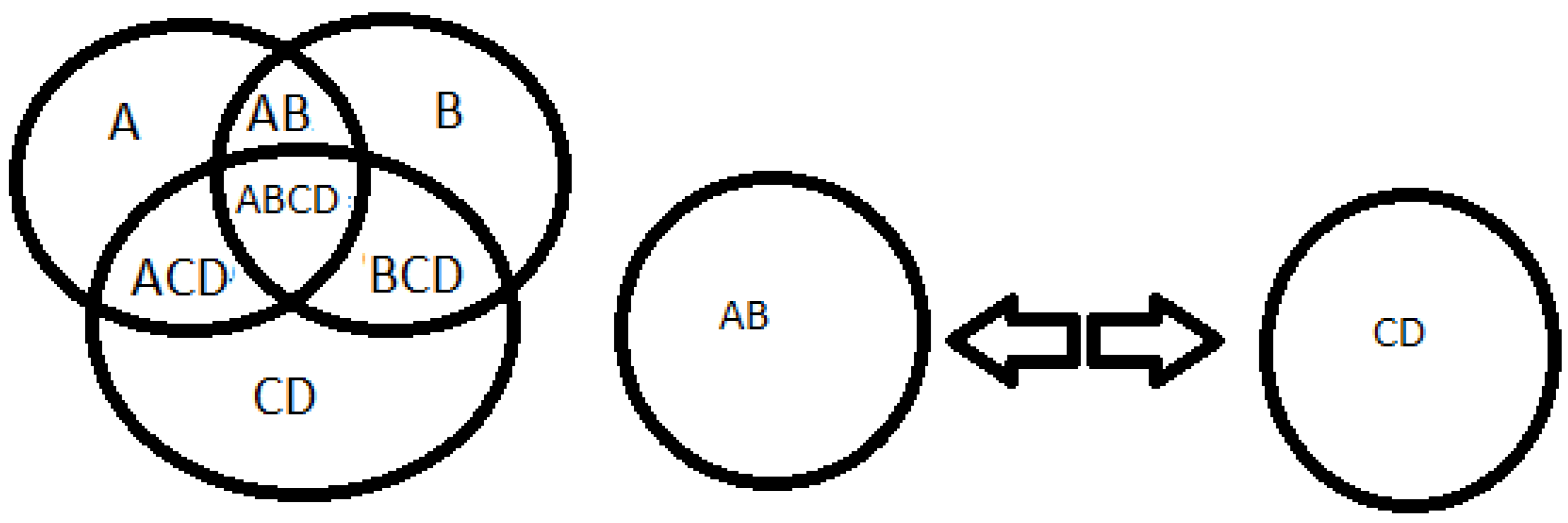
Source: prepared by the author. Table 6 Caption: imagination of space
3+7+10=20, the number 3 is odd represented by A, the number 7 is odd represented by B, the number 10 is even represented by CD, forming number 20 represented by ABCD and can be divided into AB and CD.
7. Examples on the Formation of Odd Numbers
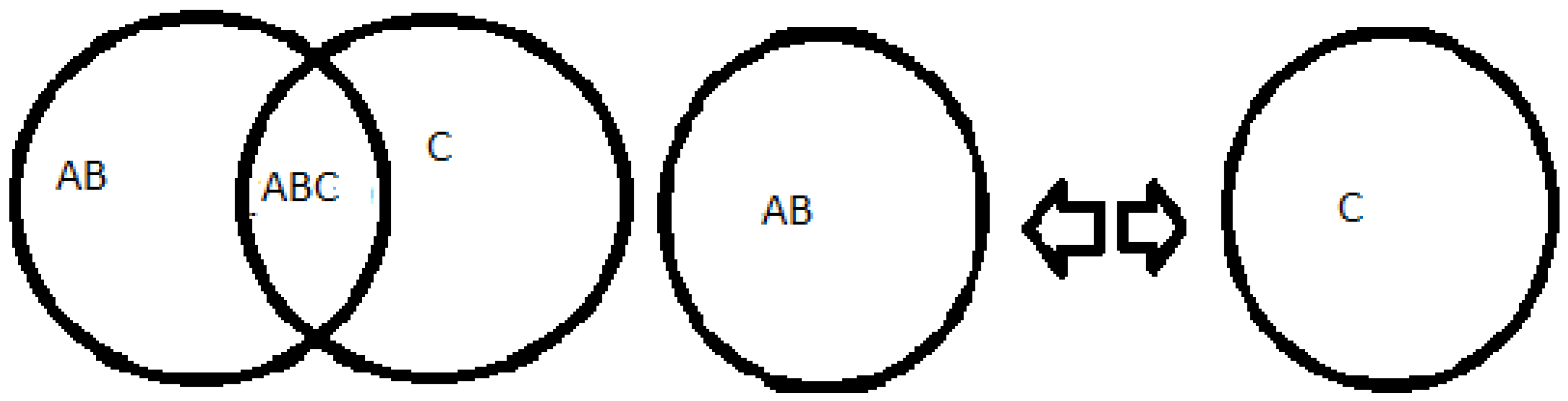
Source: prepared by the author. Table 7 Caption: imagination of space
10+3=13, the number 10 is even represented by AB, number 3 is odd represented by C, forming 13 odd represented by ABC not divisible into equal parts.

Source: prepared by the author. Table 8 Caption: imagination of space
18+5=23, the number 18 is even represented by AB, number 5 is odd represented by C, forming 23 odd represented by ABC not divisible into equal parts.
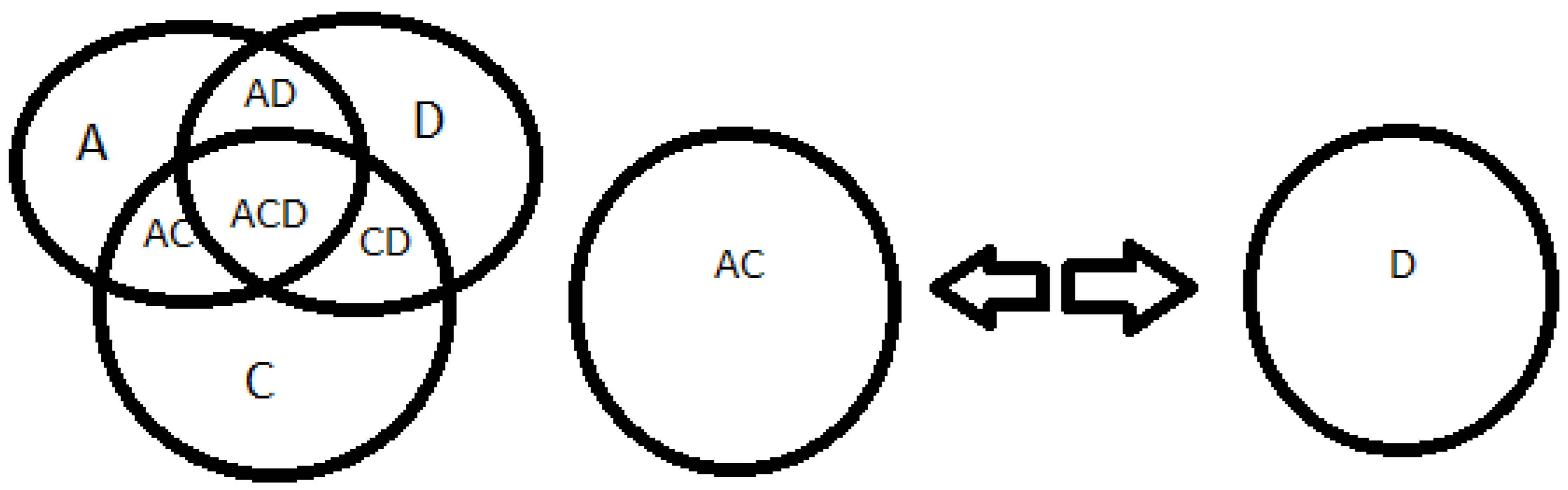
Source: prepared by the author. Table 9 Caption: imagination of space
3+7+5=15, the number 3 is odd represented by A, 7 is odd represented by C, 5 is odd represented by D, forming an odd number 25 not divisible into two parts.
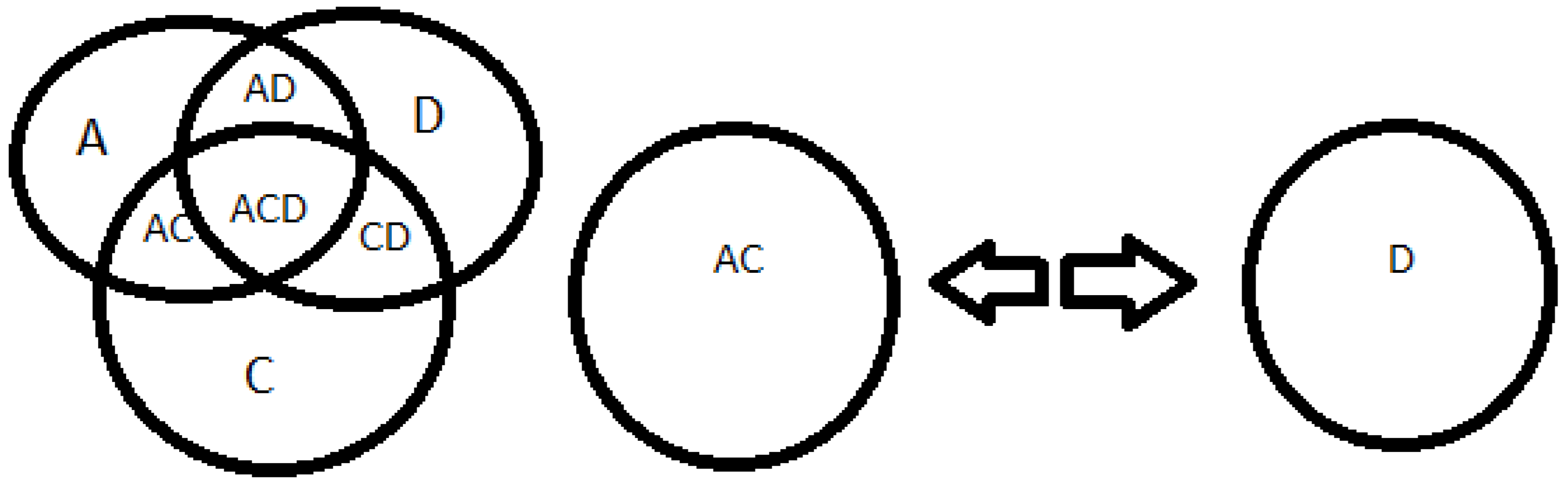
Source: prepared by the author. Table 10 Caption: imagination of space
9+13+15=37, the number 9 is odd represented by A, 13 is odd represented by C, 15 is odd represented by D, forming the number 37 which is odd represented by ACD.
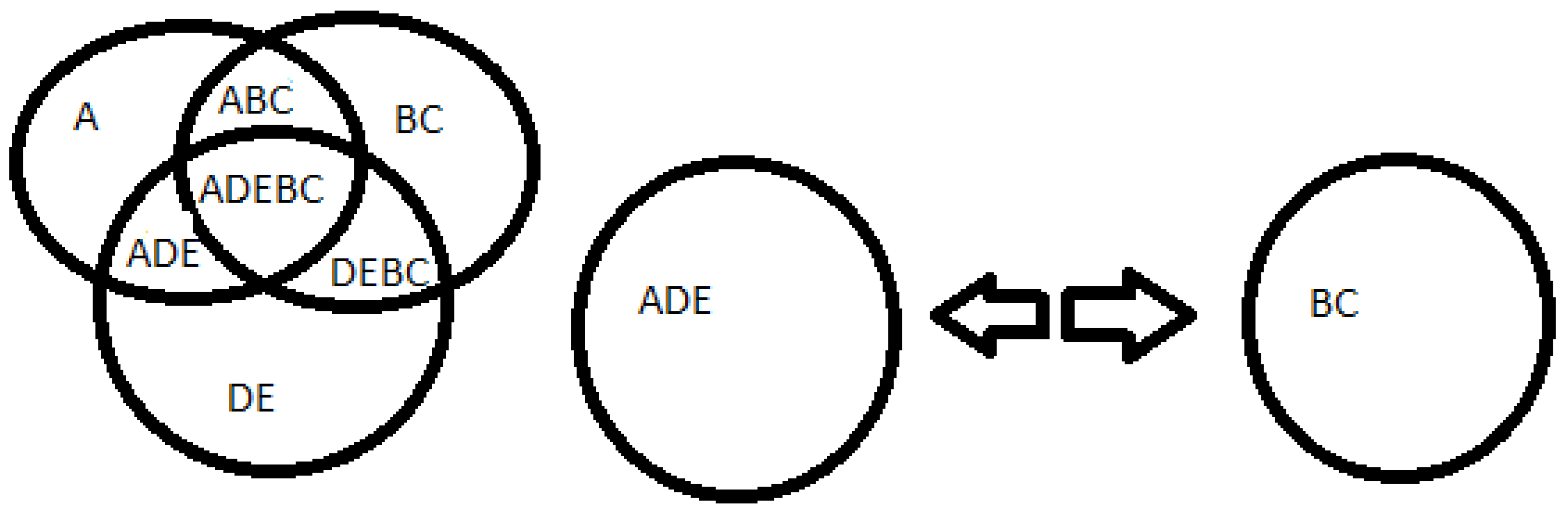
Source: prepared by the author. Table 11 Caption: imagination of space
3+10+4=17, the number 3 is odd represented by A, 10 is even represented by BC, 4 is even represented by DE, forming 17 which is odd represented by ADEBC.
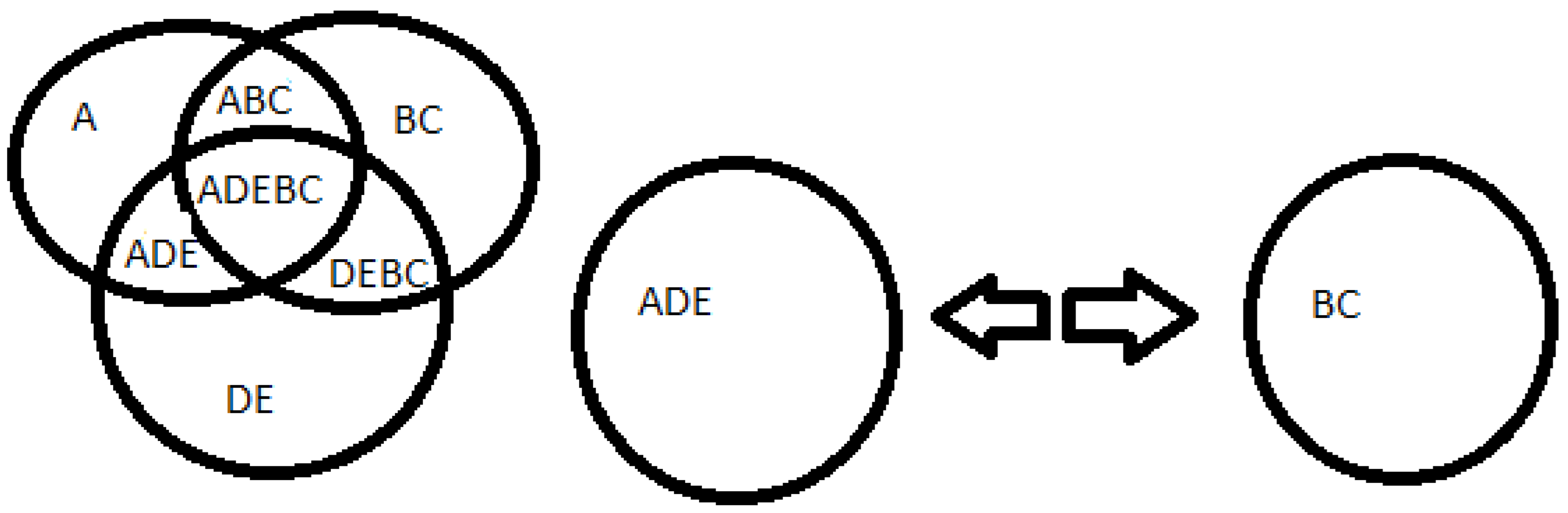
Source: prepared by the author. Table 12 Caption: imagination of space
3+8+2=13, the number 3 is odd represented by A, 8 is even represented by BC, 2 is even represented by DE, forming 13 which is odd represented by ADEBC.
8. Conclusions
Therefore, the theory that states that spaces related to each other provide numerical knowledge is observable and coherent based on the meaning of mathematics that interacts with spaces. The study aims to present a model for understanding numerical formations.
References
- How A calculation created more than 500 years ago can help you get rich – or at least save. Science-BBCNewsBrazil. August 15, 2019.
- What is mathematics? A model of reality or reality itself?Science - BBCNewsBrazil.November 17, 2019.
- Church, Gemma. The mathematical problem that can paralyze modern life. Science-BBCNewsBrazil. June 13, 2019.
- Hawking, Stephen. The universe in a nutshell. Arx, São Paulo, 216 p. April.
- 2004 Hawking, Stephen. A Brief History of Time. Intrínseco, Rio de Janeiro, 256 p. January 2015.
- TAHAN, M. The man I calculated. Rio de Janeiro, Record, 2010.
- 02 - Numbers in our daily lives - Mathematics - Teaching. Background, background. – Telecurso, Telecurso, 8 July. 2015. 11 minutes and 45 seconds. Available online: https://www.youtube.com/watch?v=6HNOg12ExEI&t=224s (accessed on 8 July 2015).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




