Preprint
Article
Influence of an Ageing Heat Treatment on the Mechanical Characteristics of Iron-Aluminium Bronze with -Transformation: Modelling and Optimization
Altmetrics
Downloads
76
Views
16
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
01 November 2023
Posted:
01 November 2023
You are already at the latest version
Alerts
Abstract
Aluminium bronzes possess a unique combination of high strength and wear and corrosion resistance in aggressive environments; thus, these alloys find wide application in marine, shipbuilding, aviation, railway, offshore platform applications and other fields. Iron-aluminium bronzes (IABs) are the cheapest and most widely used. When the aluminium content is above 9.4 wt%, IAB is biphasic (i.e. it undergoes -transformation) and can be subjected to all heat-treatment types depending on the desired operating behaviour of the bronze component. This article presents correlations (mathematical models) between the primary mechanical characteristics (yield limit, tensile strength, elongation, hardness and impact toughness) and the ageing temperature and time of quench at 920°C in water Cu-11Al-6Fe bronze, obtained using the centrifugal casting method. The microstructure evolution was evaluated depending on the ageing temperature and time changes. Overall, the research was conducted in three successive inter-related stages: a one-factor-at-a-time study, planned experiment, and optimisations. Four optimisation tasks, which have the greatest importance for practice, were formulated and solved. The defined multiobjective optimisation tasks were solved by searching for the Pareto-optimal solution approach. The decisions were made through a nondominated sorting genetic algorithm (NSGA-II) using QstatLab. The optimisation results were verified experimentally. Additional samples were made for this purpose, quenched at 920°C in water and subjected to subsequent ageing with the optimal values of the governing factors (ageing temperature and time) for the corresponding optimisation task. The comparison of the results for the mechanical characteristics with the theoretical optimisation results presents good agreement.
Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
Aluminium bronzes (Cu-Al-X, X = Fe, Ni, Mn, Be, Co, Si and Sn) possess good strength and wear and corrosion resistance in aggressive environments. Thus, these alloys find wide application in marine, shipbuilding, aviation, railway, offshore platform applications and other fields. Iron-aluminium bronzes (IABs), introduced to industry as early as 1870, are the cheapest and most widely used. The iron refines the grain, increasing its strength. Copper forms an α-solid solution with aluminium. According to the Cu-Al-5Fe equilibrium system [1], the strength and hardness of IAB cannot be improved using heat treatment if the alloy contains less than 9.4 wt% aluminium. Such an IAB is single phase (α-phase). When the aluminium content is above 9.4 wt%, IAB is biphasic (i.e. it undergoes β-transformation and can be subjected to all heat treatment types. The mechanical properties and service behaviour of IAB with β-transformation are a function of the microstructure; thus, its evolution can be controlled through appropriate heat treatment according to the specific service behaviour and requirements of this bronze.
Many researchers have investigated the correlation between the heat-treatment governing factors and the microstructure evolution and mechanical properties of complex aluminium bronzes with β-transformation. For example, detailed and systematic information is contained in the review paper in [1]. Increasing the hardness of aluminium bronzes via heat treatment is a common subject of research [2,3,4,5,6,7,8]. Other mechanical properties, which were improved through heat treatment, are the impact toughness [6] of Cu-Al-Fe-Ni and Cu-Al-Fe-Mn bronzes and the tensile strength and elongation [7] of Cu-Al-Fe-Be and Cu-Al-Fe-Ni bronzes.
The effects of various heat treatment types on the mechanical characteristics (including fatigue strength in the air) of Cu-10Al-5Fe IAB, obtained as hot-rolled bars, were studied in our previous study [9]. The types of heat treatment were Type 1: annealing at 720°C for 3 h and Type 2: heating at 920°C for 1 h and rapidly quenching in water at room temperature. Types 3 and 4 are like Type 2 but are followed by tempering at 600°C and 300°C, respectively for 3 h and then air cooling. The third type of heat treatment provides maximum impact toughness, whereas the fourth type provides maximum hardness.
However, the relationships between the heat-treatment governing factors and mechanical characteristics of the alloys are typically nonlinear. For instance, Mi et al. [7] demonstrated that the relationships between the ageing temperature (time) and some properties (hardness, extensibility and electrical resistive) of beryllium and nickel aluminium bronze are nonlinear. Therefore, the influence of the ageing temperature and time on the mechanical characteristics of IAB with β-transformation must be investigated for a broader range of variation of both variables, considering their nonlinear effects. Thus, developing mathematical models of the correlations between the ageing temperature (time) and the mechanical characteristics of IAB enables determining the optimal heat-treatment regimes, depending on the specific requirements and operational behaviour of the corresponding bronze components.
The primary goal of this study is to establish mathematical models of the leading mechanical characteristics of Cu-11Al-6Fe IAB depending on the ageing temperature and time and to conduct optimisations according to various criteria. The investigation was conducted in 10 steps. Figure 1 presents the study flow chart.
2. Materials and Methods
A chemical analysis of the IAB was performed using an optical emission spectrometer (Foundry-Master Optimum, Hitachi). Table 1 lists the composition in weight percentages.
The IAB was obtained using the centrifugal casting method (to maximise the bronze density) in the form of a tube (Figure 2a) to eliminate the effect of hot-mechanical strengthening inherent in the commercial hot-rolled bars, with the following nominal sizes: external diameter 116 mm, length 180 mm and wall thickness 13 mm. The tubes were cut via a mechanical hacksaw along their axes into 17 blanks for each tube, with nominal overall dimensions of mm (Figure 2b). Part of the blanks intended to produce tensile specimens were subjected to turning to obtain a cylindrical shape with a 12-mm diameter (Figure 2c). All blanks (except three rotary and three prismatic blanks) were heated to 920°C for 1 h and rapidly quenched in water at 20°C. The temperature of 920°C was selected based on the chemical composition of the bronze and the section of the Cu-Al-Fe equilibrium phase diagram, with a 5% Fe plane [1] (Figure 3).
The effects of the temperature and time ageing on the mechanical characteristics of the bronze were investigated in two stages: 1) scanning the factor space (in this case, a plane because there are two governing factors) using the one-factor-at-a-time method and 2) based on the results of the first stage: conducting a planned experiment, regression analyses, and optimisations. Seven ageing temperatures (20°C, 200°C, 300°C, 400°C, 500°C, 600°C, and 700°C) and four ageing times (1, 2, 3, and 4h) were used in the first stage. Three specimens were used for each experimental point, and the result was obtained as the arithmetic mean of the measurements on the three specimens. The effects of ageing temperature (time) were studied at 3 h ageing time (500°C ageing temperature). After the respective heat treatments of the cylindrical and prismatic blanks, tensile specimens (Figure 4a) and impact toughness specimens (Figure 4b) were manufactured.
The tensile tests were conducted at room temperature via a Zwick/Roell Vibrophore 100 testing machine. The impact toughness was explored using a Charpy universal impact tester (maximum impact energy: 300 J). A ZWICK/Indentec- ZHVm-S hardness tester was employed to measure the hardness using a spherical-ended indenter with a diameter of 2.5 mm, loading of 63 kg, and holding time of 10 s. The phase analysis was performed with a Bruker D8 Advance X-ray diffractometer. The Crystallography Open Database was employed to determine the peak positions. The microstructure in the specimen cross-section was observed using scanning electron microscopy (LYRA I XMU Tescan) after polishing and etching the specimens using a 20% FeCl3 solution. In addition, the energy-dispersive X-ray spectroscopy analysis was performed for the local assessment of the chemical composition at a point. Regression analyzes and optimisations were performed using QStabLab software [10].
3. Experimental Results and Discussion
3.1. Ageing temperature and time effects on mechanical characteristics: one-factor-at-a-time method
3.1.1. Effects of the ageing temperature
Figure 5 presents the nominal stress–nominal strain diagrams obtained at various ageing temperatures. The agеing temperature substantially influences the static strength and plasticity of the bronze. Information on the yield limit, tensile strength and elongation depending on the agеing temperature was obtained from these diagrams.
Figure 6 illustrates the effects of the ageing temperature on the primary mechanical characteristics. The yield limit and tensile strength (Figure 6a) exhibit a similar trend of change: they increase as the temperature increases to 350-400°C, after which they decrease. The rates of increase and decrease of the yield limit are greater than those of the tensile strength. The relative elongation characterises the material plasticity and indicates the opposite trend: the plasticity increases with an increase in the ageing temperature (Figure 6b). Figure 6c depicts the change in hardness depending on the ageing temperature. The change tendency of the hardness is analogous to that for the yield limit and tensile strength. Figure 6d presents the impact toughness change, depending on the ageing temperature. As expected, the change trend is analogous to that of the elongation and opposite the strength and hardness change trends. The four trendlines do not change their curvatures in the studied temperature interval.
3.1.2. Effects of the ageing time
Figure 7 illustrates the nominal stress–nominal strain diagrams obtained at various ageing times. A comparison with Figure 5 reveals that the influence of the agеing time within the studied time interval is significantly weaker than the effect of the agеing temperature. The influence of time agеing may be more significant for another agеing temperature. Therefore, time agеing cannot be ignored as a governing factor in the planned experiment.
Figure 8 depicts the effects of the ageing time on the primary mechanical characteristics. The yield limit indicates a weak tendency to decrease with increased time, whereas the tensile strength reaches a maximum value at about 3 h of agеing time. The elongation and hardness display an analogous trend (in a narrow variation interval) to that of the tensile strength. In contrast, the impact toughness (analogous to the yield limit) decreases with an increasing agеing time.
3.2. Microstructure evolution
Figure 9 illustrates the phase analysis outcomes. The structure after centrifugal casting is characterised by good homogeneity (Figure 10). The copper-enriched α-phase grains have an elongated shape (50–60 µm), which is characteristic of dendritic structures obtained by casting. The iron does not dissolve in copper and forms the intermetallic compound Fe3Al with aluminium (Figure 9). The Fe3Al is deposited into the copper solid solution in the form of dispersed and larger coagulated precipitates. The γ’- and β-phases are located between the α-phase grains and are observed as eutectoid zones and acicular crystals obtained by a diffusionless (martensite-like) transformation . The martensitic transformation in centrifugal casting is due to the rapid cooling, a characteristic of casting nonferrous alloys into metal moulds. The quantity of -phase (Cu3Al) and γ-phase (Cu9Al4) is significantly less than the underlying α-solid solution (Figure 9).
After quenching at 920°C in water and subsequent ageing at 20°C, a coarse-grained structure is formed (Figure 11). Dispersed martensitic-type needles are observed at the grain boundaries because of the diffusionless transformation . Dispersed zones of eutectoid breakdown are observed between the needles. The iron partially dissolves in the β-phase and separates as the intermetallic compound Fe3Al in a dispersed form.
After ageing at 200°C, an increase in acicular -grains is observed in terms of size and quantity (Figure 12) due to the inverse transformation (Figure 9) due to temperature-accelerated diffusion. The β-phase is the hardest phase of all registered phases in Figure 9: thus, the hardness as an integral mechanical characteristic of the studied bronze is significantly increased (see Figure 6c). A mechanical mixture of copper-enriched α-grains and the intermetallic compound Fe3Al is formed between the acicular β-grains. No formed α-grain boundaries are observed.
As the ageing temperature increases to 300°C, the diffusion increases, causing the partial disintegration of acicular -grains: (Figure 13). As a consequence of the coagulation of a dispersed phase of Fe3Al, relatively large grains of this intermetallic compound are observed.
After ageing at 400°C, grains are observed whose boundaries represent stripe-shaped α-subgrains, marked with a dashed green line in Figure 14. A partial tearing of the borders is noticeable in places. Temperature-induced diffusion accelerates the nucleation of the α-solid solution network and the transformation . In the rest of the -grains, the dissolved iron is separated in the form of dispersed particles of Fe3Al.
Figure 15 presents the structure after ageing at 500°C. The process of phase separation is finished. No metastable phases were found (Figure 9). Precipitated dispersed particles of Fe3Al are observed in the grains of the α-solid solution. The refinement of the stripe-like α-grains is observed because of diffusion processes, The established maximum tensile strength (see Table 5) is a consequence of the homogeneous and refined structure and dispersed particles of Fe3Al.
Figure 16 displays the structure of bronze subjected to ageing at 600°C (i.e., the heating is above the eutectoid line of 565°C; see the static diagram in Figure 3). In this region, the α-phase, -phase and are in equilibrium. All three phases are stable below the eutectoid line. Unlike the static diagram, the heating region also contains a β-phase due to an initially quenched structure (see position 2 in Figure 9). The metastable -phase is formed during air cooling, a consequence of the partial martensitic transformation , and part of the grains undergo diffusion decay . At this ageing temperature, zones form with lamellar α-subgrains (outlined with a white line).
When the ageing temperature is 700°C, conditions are created for grouping and subsequent coagulation of the coopper-enriched α-phase (Figure 17). The mechanism of clustering and growth of equiaxed α-grains is likely similar to the process occurring at lower temperature (see Figure 16). Higher temperatures accelerate the diffusion processes and cause larger grains to enlarge at the expense of smaller grains. Thus, the resulting structure is inhomogeneous with the formed zones of the coarse-grained α-phase and enclosed zones containing a mechanical mixture of partial martensitic and diffusion transformations . The partial martensitic transformation is due to the higher cooling rate in the air. The β-phase increases its degree of homogeneity (respectively expanding its solubility region) when the heating temperature increases. A study [9] found that the β-phase partially dissolves iron atoms. This reason may be why no Fe3Al peak is observed in the X-ray pattern in Figure 9.
3.3. Effect of heat treatment on mechanical characteristics: planned experiment and optimization
According to the one-factor-at-a-time experimental results, the governing factors were chosen to change as follows: and . Table 2 lists the governing factor levels. The correlation between natural and coded coordinates is
where , and are the upper, middle, and lower levels of the ith factor in natural coordinates, respectively.
The objective functions are the following mechanical characteristics: yield limit (), tensile strength (), elongation (), hardness () and impact toughness (). Figure 18 provides the experimental points in the plane of governing factors. Table 3 lists the experimental outcomes for the chosen mechanical characteristics.
An analysis of variance (ANOVA) was conducted via QStatLab [10] to investigate the significance of the governing factors. Figure 19 provides the main ANOVA effects. For all objective functions, the more significant factor is (temperature). Time has the most substantial influence on the tensile strength. The yield limit (Figure 19a) is maximum when the temperature is at the middle level and the time is at the second level (). The combination of maximum temperature and time at the middle level minimises the yield limit. The influence of the governing factors on the tensile strength is similar (Figure 19b). When the temperature and time simultaneously occupy the fourth level , the elongation is maximal (Figure 19c). The combination of the minimum time and temperature at the second level () minimises the elongation. When the temperature is at the second level and the time is at the fourth level , the hardness is maximum (Figure 19d). The minimum hardness is obtained when the temperature is maximum and the time is at the middle level . The influence of the governing factors on the impact toughness is analogous to their influence on the elongation (Figure 19e). The ANOVA predicts the influence of the governing factors only in a qualitative aspect. More accurate results are obtained after mathematically modelling the studied mechanical characteristics.
The experimental results for the mechanical characteristics were subjected to regression analyses. The significance of the regression coefficients was determined at the . Given the chosen experimental design (five levels for each factor), the approximating polynomials may be of degree 4 or lower:
where denotes the vector of the governing factors, represents the number of governing factors, and indicates the number of objective functions.
The regression analyses were performed using QStatLab [10], and Table 4 presents the regression coefficients. The magnitude (absolute value) of the coefficients in front of the dimensionless variables indicates the significance of the corresponding governing factor (variable), and the absolute value of the coefficients in front of the products of the variables indicates the significance of the interaction between the governing factors. The regression coefficients in Table 4 indicates that: 1) the ageing temperature is a much more significant factor than the ageing time, confirming the ANOVA results, and 2) the interaction between the governing factors is relatively weak, with the exception of the tensile strength.
Table 3 presents the values of the objective functions calculated using Eq. (2) for the experimental points from the plan. The comparison between the experimental results for the objective functions and those predicted by the models (at the experimental points) displays excellent agreement. Figure 20 presents a graphical visualisation of the models. The type of surfaces confirms that the ageing temperature is the more significant of the two factors. The ageing time influences the tensile strength most strongly (confirming the ANOVA results), whereas the influence is weakly expressed for the other characteristics. The factor least sensitive to the ageing time is the impact toughness.
The two primary characteristics of static strength (yield limit and tensile strength) similarly depend on the temperature. As the temperature increases, the static strength increases and reaches its maximum value between 400°C and 500°C, after which it begins to decrease at a faster rate. The behaviour of hardness is similar, but it reaches its maximum values earlier (in the interval between 250°C and 300°C) and then decreases to a minimum. The elongation and the dynamic strength (impact toughness) display similar behaviour under temperature and time changes because both characteristics have a common physical basis. The behaviour of the dynamic strength when changing the temperature is opposite that of the static strength. The maximum values of all objective functions, , and their corresponding magnitudes of the governing factors, , were found with QStatLab using the random search method with 1,000 iterations. Table 5 lists the results.
Table 5.
Maximum values of the objective functions and the corresponding governing factors.
| Objective fun ctions | Governing factors | ||
|---|---|---|---|
| Codded | Natural | ||
|
-0.19582 0.98008 |
|
431.8 | |
|
0.33077 -0.99671 |
|
812.9 | |
|
0.75517 0.41485 |
|
14.6 | |
|
-0.68099 0.39878 |
|
261.8 | |
|
0.78857 0.00032 |
|
73.65 | |
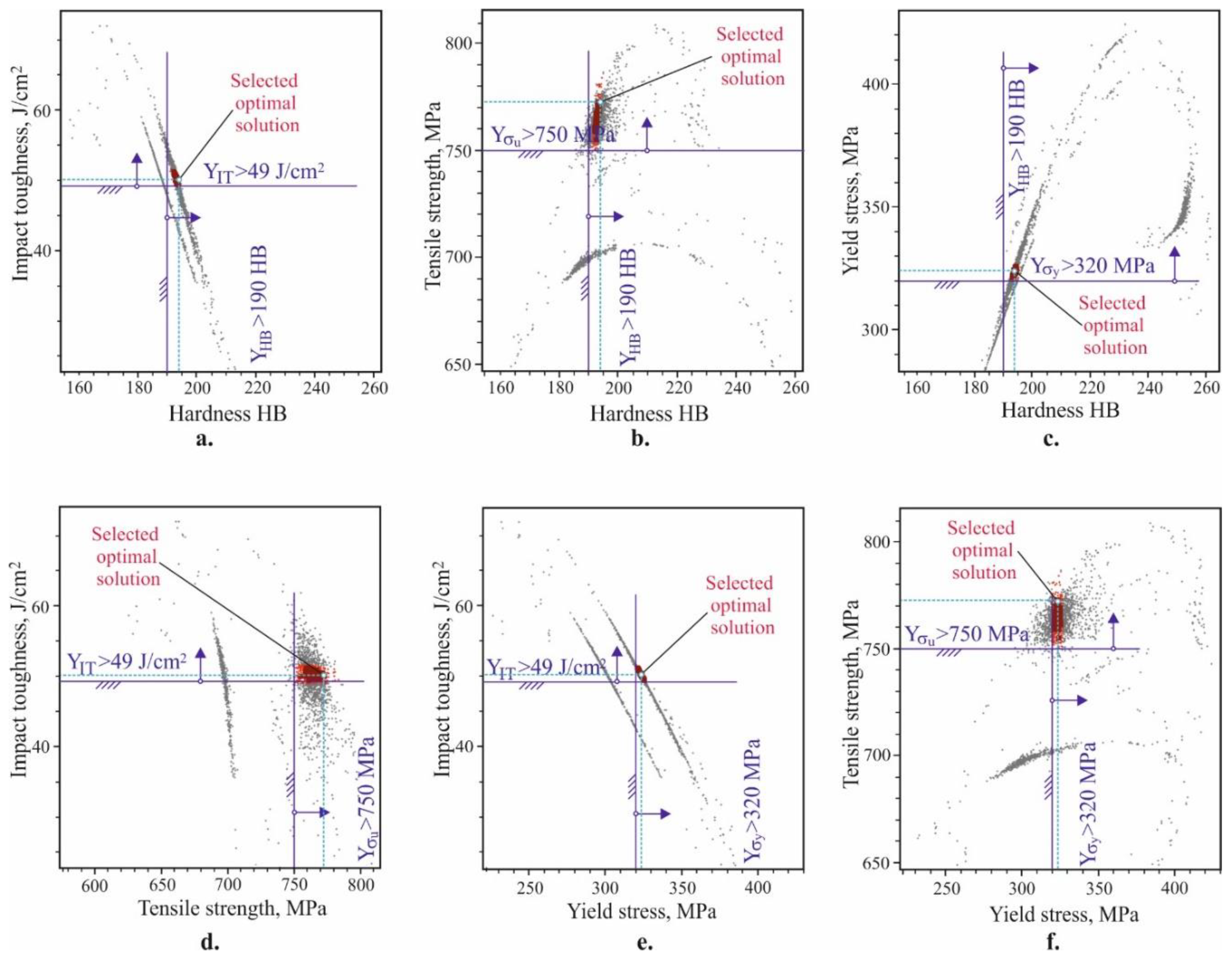
The correlations between the five objective functions were found by eliminating the governing factors for the pair of considered objective functions. These correlations are essential for setting and solving optimisation problems and for correctly defining the functional constraints. The correlations of the hardness with each of the other four mechanical characteristics were determined. Figure 21 graphically visualises the data. The dependencies of the mechanical characteristics on the hardness are nonlinear. As the hardness increases, the static strength increases up to a specific hardness value (approximately 230 HB for the yield limit and 210 HB for the tensile strength), and subsequently decreases. The elongation and dynamic strength trendlines indicates a continuous decrease when the hardness increases.
Four optimization tasks, which have the most significant importance for practice, were formulated and solved:
- 1)
- Maximum plasticity: ;
- 2)
- Maximum impact toughness (dynamic strength): ;
- 3)
-
Simultaneous high hardness and static strength: The objective function vector is,
where , and is the plane of the governing factors . The objective functions must tend to their maximum values: , , and . Based on Figure 21, the following are the functional limitations: , , and .
- 4)
-
Simultaneously high hardness, static and dynamic strength: The objective function vector is.
The objective functions must tend to their maximum values: , , , and . The following are functional limitations, according to Figure 21: , , , and .
The first two single-objective optimisation tasks require determining the largest value of the corresponding function without functional limitations and satisfying the governing factor limitations (Table 2). Table 5 lists their solution. The last two are multiobjective optimisation problems. The vector must be determined so that the objective function magnitudes to satisfy the conditions of the corresponding multi-objective optimisation task, and , , and are the compromised optimal values of the governing factors. The defined multiobjective optimisation tasks were solved by searching for the Pareto-optimal solution approach. The decision was made through the nondominated sorting genetic algorithm (NSGA-II) [11] using QstatLab. A Pareto front offering 50 compromised optimal solutions was obtained for each of the two tasks. Figure 22 and Figure 23 illustrate the Pareto front for the third and fourth optimisation problems. A compromised optimal solution is selected from each Pareto front. Table 6 contains detailed information regarding the solution results for the four optimisation tasks.
The results of the optimizations were experimentally verified. For this purpose, additional samples were manufactured for tensile and impact toughness tests, which were hardened at 920°C in water and subjected to subsequent ageing with the optimal values (Table 6) of the governing factors for the respective optimisation task. The hardness was measured on the impact toughness samples. Each experimental result was obtained as the arithmetic mean of three samples. Table 7 presents the results. The comparison with the theoretical optimisation results displays good agreement.
4. Conclusions
As outcomes of this investigation, the significant new findings concerning the ageing heat treatment of IAB with β-transformation, obtained using the centrifugal casting method, are presented below.
- The primary mechanical characteristics (yield limit, tensile strength, elongation, hardness and impact toughness) of IAB with β-transformation vary widely depending on the governing parameters of the ageing heat treatment. Therefore, they characteristics can be appropriately controlled according to the functional purpose of the corresponding bronze component. Of the two governing factors (temperature and time), the ageing temperature has a significantly greater weight. The temperature interval 640°C to 650°C maximises plasticity and dynamic strength, whereas hardness and static strength reach the maximum value in the interval of 280°C to 500°C.
Figure 23.
Generated Pareto front for fourth optimization task: a. impact toughness – hardness; b. tensile strength – hardness; c. yield stress – hardness; d. impact toughness – tensile strength; e. impact toughness – yield stress; f. tensile strength – yield stress.
Figure 23.
Generated Pareto front for fourth optimization task: a. impact toughness – hardness; b. tensile strength – hardness; c. yield stress – hardness; d. impact toughness – tensile strength; e. impact toughness – yield stress; f. tensile strength – yield stress.
- Four optimisation tasks, with the most significance in practice, were formulated and solved. Thus, the optimal (compromise optimal) values of the temperature and time and the corresponding optimal (compromise optimal) magnitudes of the mechanical characteristics for the respective optimisation task were obtained.
- The correlations of the hardness with each of the other four mechanical characteristics were determined. The dependencies of the mechanical characteristics on the hardness are nonlinear. As the hardness increases, the static strength increases up to a specific hardness value (approximately 230 HB for the yield limit and 210 HB for the tensile strength), and subsequently decrease. The elongation and dynamic strength trendlines display a continuous decrease when the hardness increases.
Author Contributions
Conceptualization, J.M.; methodology, J.M. and G.D.; software, J.M., G.D., A.A., V.D. and V.T.; validation, J.M., G.D.; formal analysis, J.M. and G.D.; investigation, A.A., V.D., Y.A., V.T., G.D., and J.M.; resources, J.M. and G.D.; data curation, J.M. and G.D.; writing—original draft preparation, J.M. and G.D.; writing—review and editing, J.M. and G.D.; visualization, J.M., G.D., and V.T.; supervision, J.M.; project administration, J.M. and G.D.; funding acquisition, J.M. and G.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Regional Development Fund within the OP “Science and Education for Smart Growth 2014–2020”, Project CoC “Smart Mechatronics, Eco- and Energy Saving Systems and Technologies”, No.BG05M2OP001-1.002-0023.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brezina, P. Heat treatment of complex aluminium bronzes. International Metals Reviews 1982, 27(2), 77–120. [Google Scholar] [CrossRef]
- Vu, A.T.; Nguyen, D.N.; Pham, X.D.; Tran, D.H.; Vuong, V.H.; Pham, M.K. Influence of strengthening phases on the microstructure and mechanical properties of CuAl9Fe4 alloy. International Journal of Scientific & Engineering Research 2018, 9, 346–351. [Google Scholar]
- Chau, M.Q.; Vu, A.T.; Le, T.S.; Mai, V.T.; Nguyen, D.N.; Doan, X.T.; Do, H.C.; Nguyen, D.T. Influence of tempering time on microstructure and mechanical properties of CuAl9Fe4 alloy. Journal of Mechanical Engineering Research and Developments 2021, 44(7), 75–85. [Google Scholar]
- Slama, P.; Dlouhy, J.; Kövér, M. Influence of heat treatment on the microstructure and mechanical properties of aluminium bronze. Materials and Technology 2014, 48(4), 599–604. [Google Scholar]
- Jain, P.; Nigam, P.K. Influence of heat treatment on microstructure and hardness of nickel aluminium bronze (Cu-10Al-5Ni-5Fe). Journal of Mechanical and Civil Engineering 2013, 4(6), 16–21. [Google Scholar] [CrossRef]
- Aaltonen, P.; Klemetti, K.; Hannien, H. Effect of tempering on corrosion and mechanical properties of cast aluminium bronzes. Scandinavian Journal of Metallurgy 1985, 14, 233–242. [Google Scholar]
- Mi, G.; Zhang, J.; Wang, H. The effect of ageing heat treatment on the mechanical properties of Cu-Al-Fe-(x) alloys. Key Engineering Materials 2011, 467-469, 257–262. [Google Scholar] [CrossRef]
- Matijevic, B.; Sushma, T.S.K.; Prathvi, B.K. Effect of heat treatment parameters on the mechanical properties and microstructure of aluminium bronze. Technical Journal 2017, 11(3), 107–110. [Google Scholar]
- Maximov, J.; Duncheva, G.; Anchev, A.; Dunchev, V.; Argirov, Y.; Todorov, V.; Mechkarova, T. Effects of heat treatment and severe surface plastic deformation on mechanical characteristics, fatigue and wear of Cu-10Al-5Fe bronze. Materials 2022, 15, 8905. [Google Scholar] [CrossRef] [PubMed]
- Vuchkov IN, Vuchkov II. QStatLab Professional, v. 5.5 – statistical quality control software. User’s Manual, Sofia, 2009.
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation 2002, 6(2), 182–197. [Google Scholar] [CrossRef]
Figure 1.
Flow chart of the study.
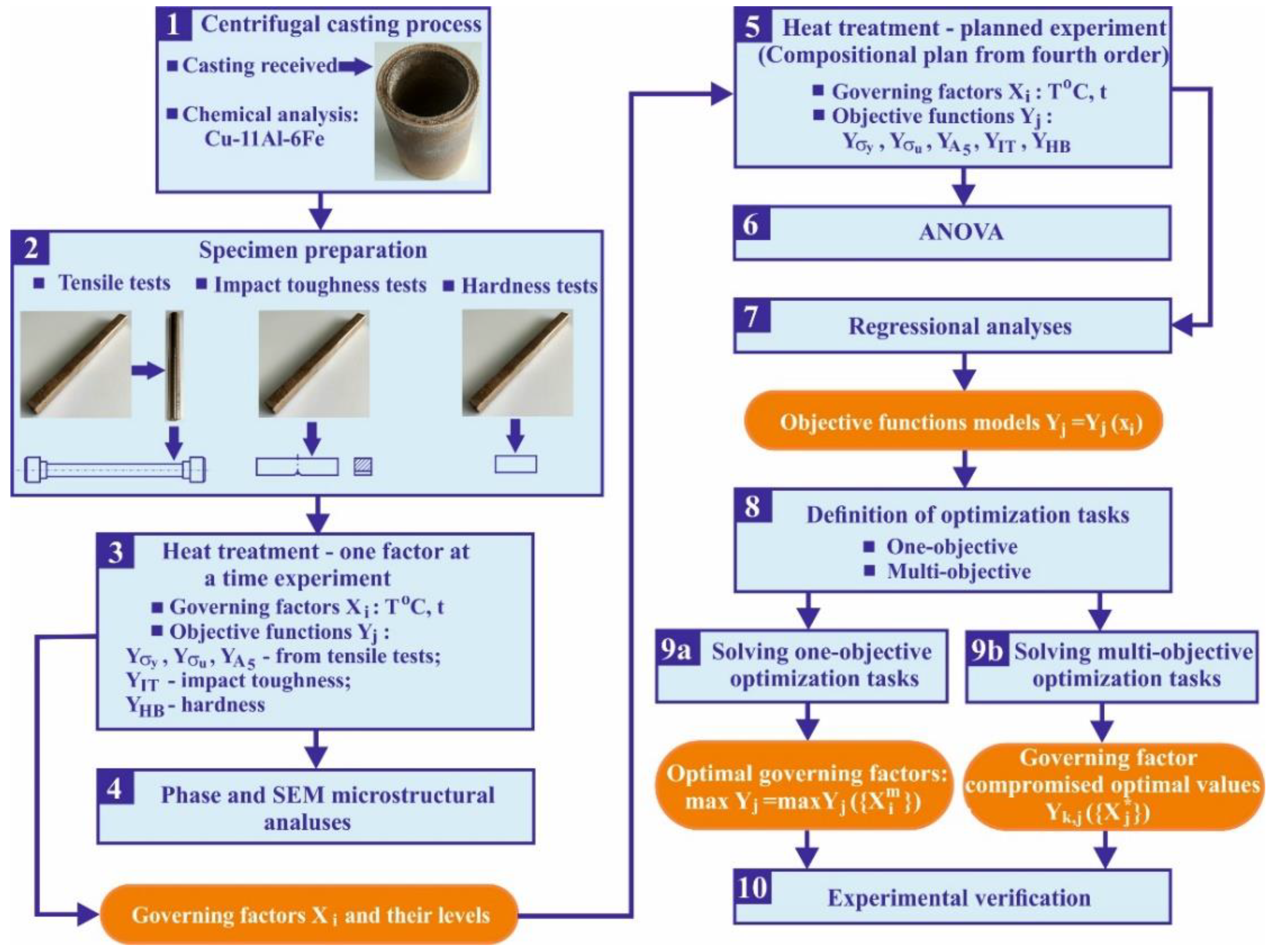
Figure 2.
Workpiece evolution for the tensile tests: a. a tube obtained via centrifugal casting; b. cutting by erosion; c. turning to produce a cylindrical shape (the sizes are in mm).
Figure 2.
Workpiece evolution for the tensile tests: a. a tube obtained via centrifugal casting; b. cutting by erosion; c. turning to produce a cylindrical shape (the sizes are in mm).

Figure 3.
A section of the Cu-Al-5Fe equilibrium phase diagram with a 5% Fe plane [1].
Figure 3.
A section of the Cu-Al-5Fe equilibrium phase diagram with a 5% Fe plane [1].
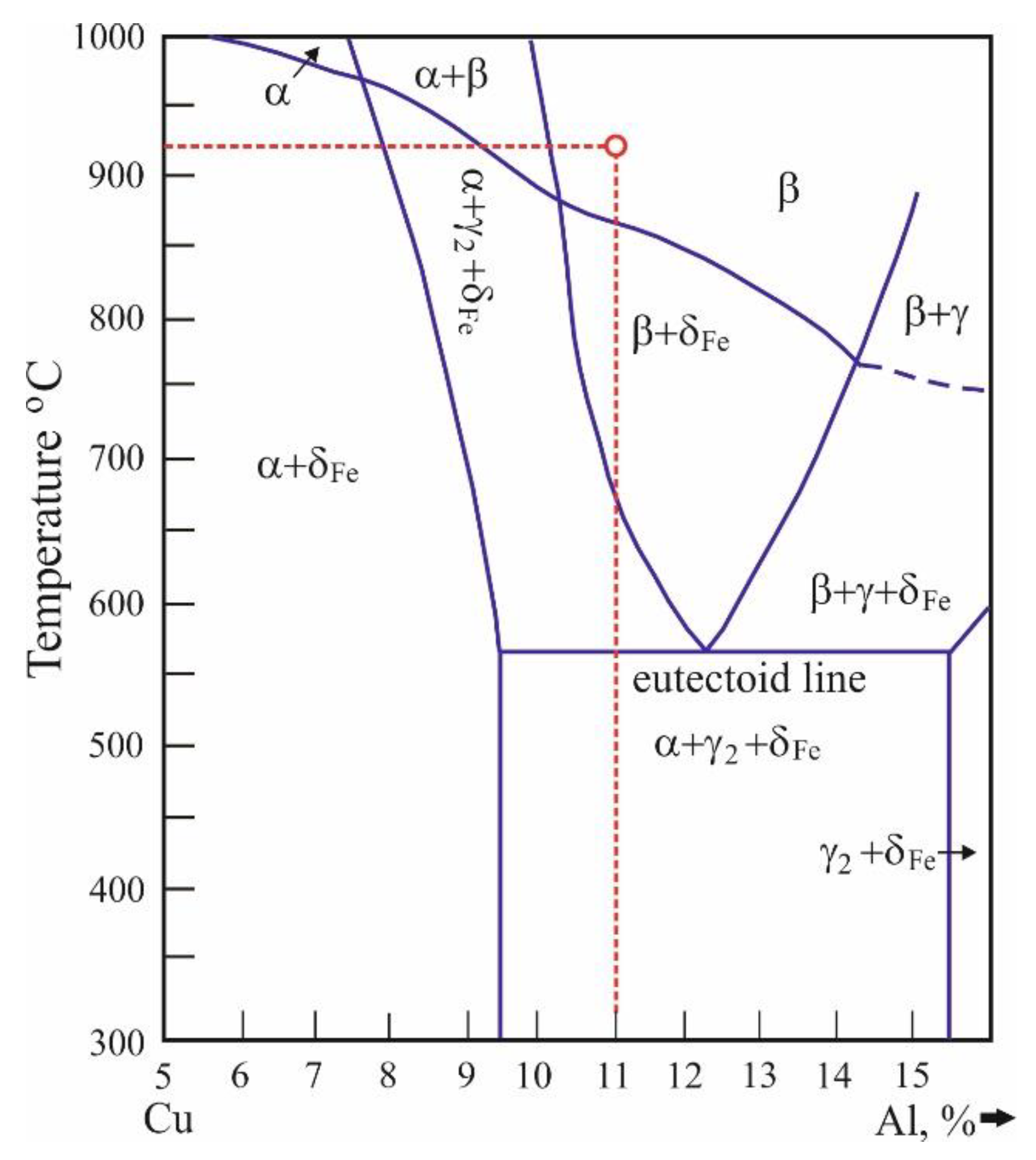
Figure 4.
Specimen geometry: (a) tensile test; b. Charpy impact toughness test.
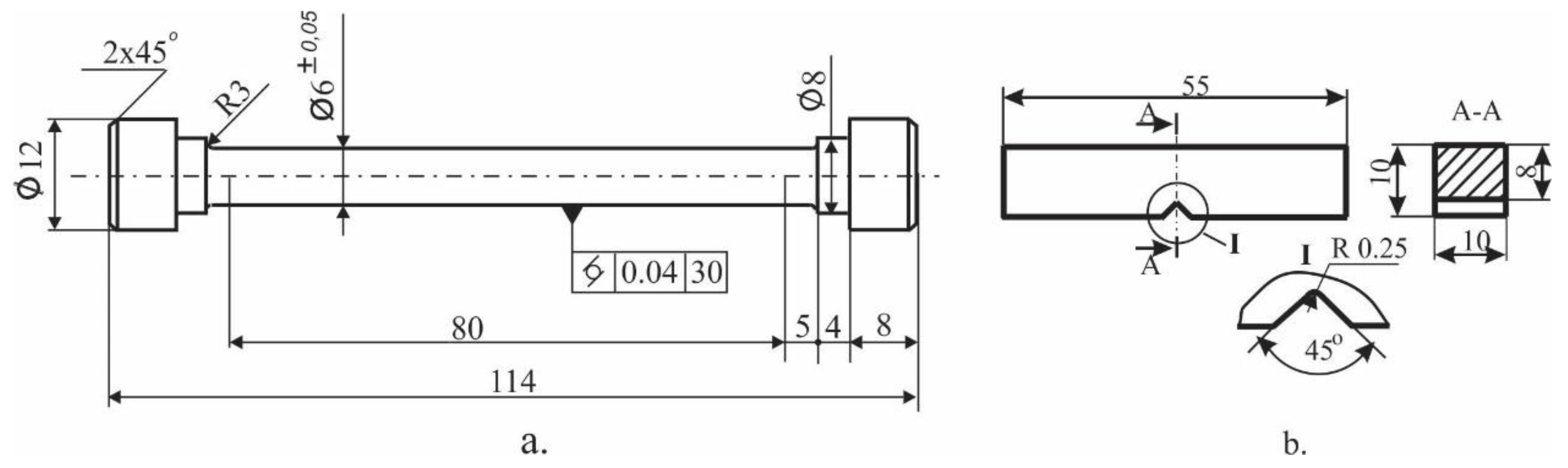
Figure 5.
Effect of ageing temperature on the nominal stress – nominal strain diagram of Cu-11Al-5Fe bronze (ageing time 3h).
Figure 5.
Effect of ageing temperature on the nominal stress – nominal strain diagram of Cu-11Al-5Fe bronze (ageing time 3h).
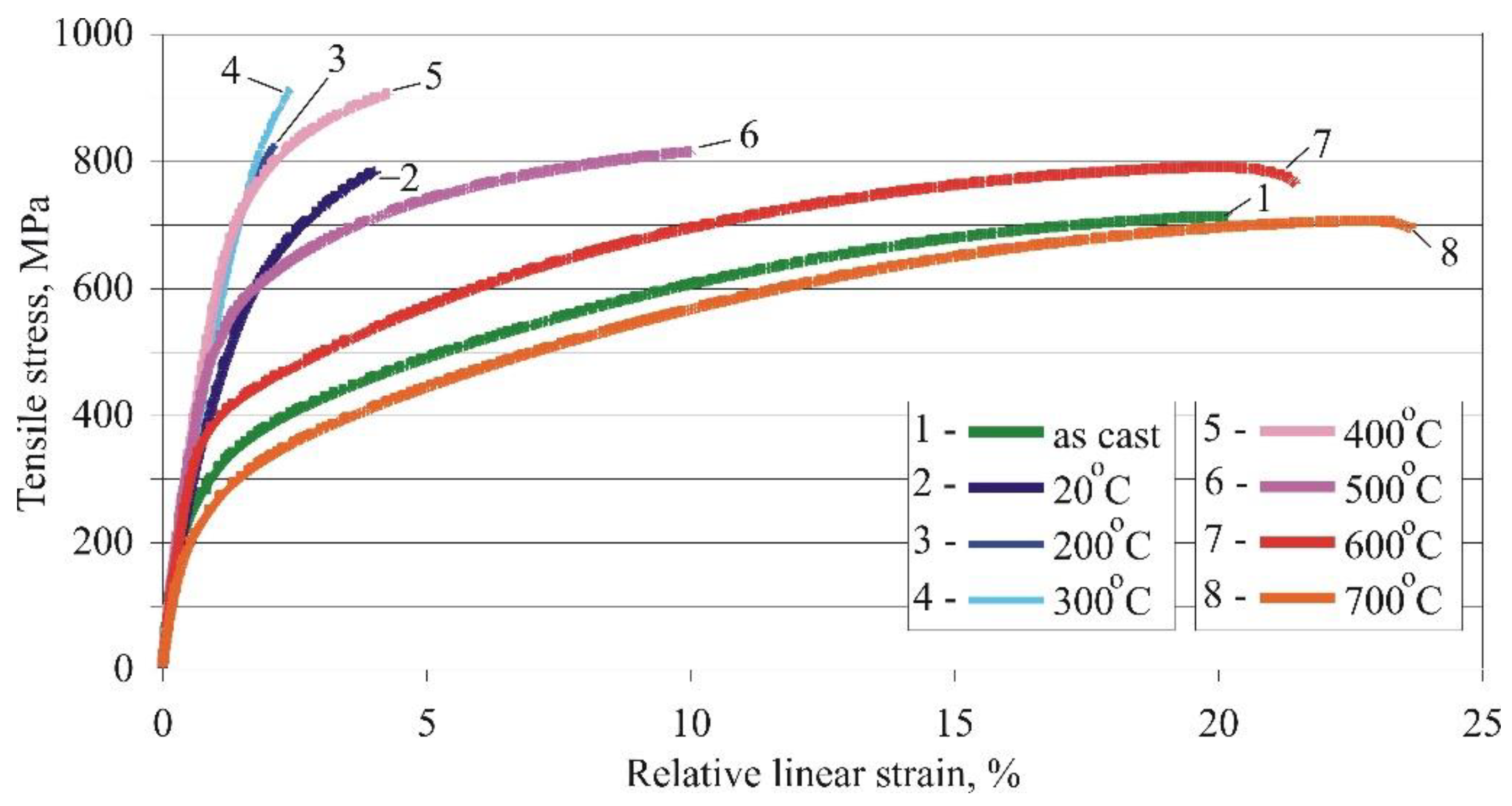
Figure 6.
Effect of ageing temperature on the main mechanical characteristics of Cu-11Al-5Fe bronze (ageing time 3h): a. yield limit and tensile tests; b. elongation; c. hardness; d. impact toughness.
Figure 6.
Effect of ageing temperature on the main mechanical characteristics of Cu-11Al-5Fe bronze (ageing time 3h): a. yield limit and tensile tests; b. elongation; c. hardness; d. impact toughness.
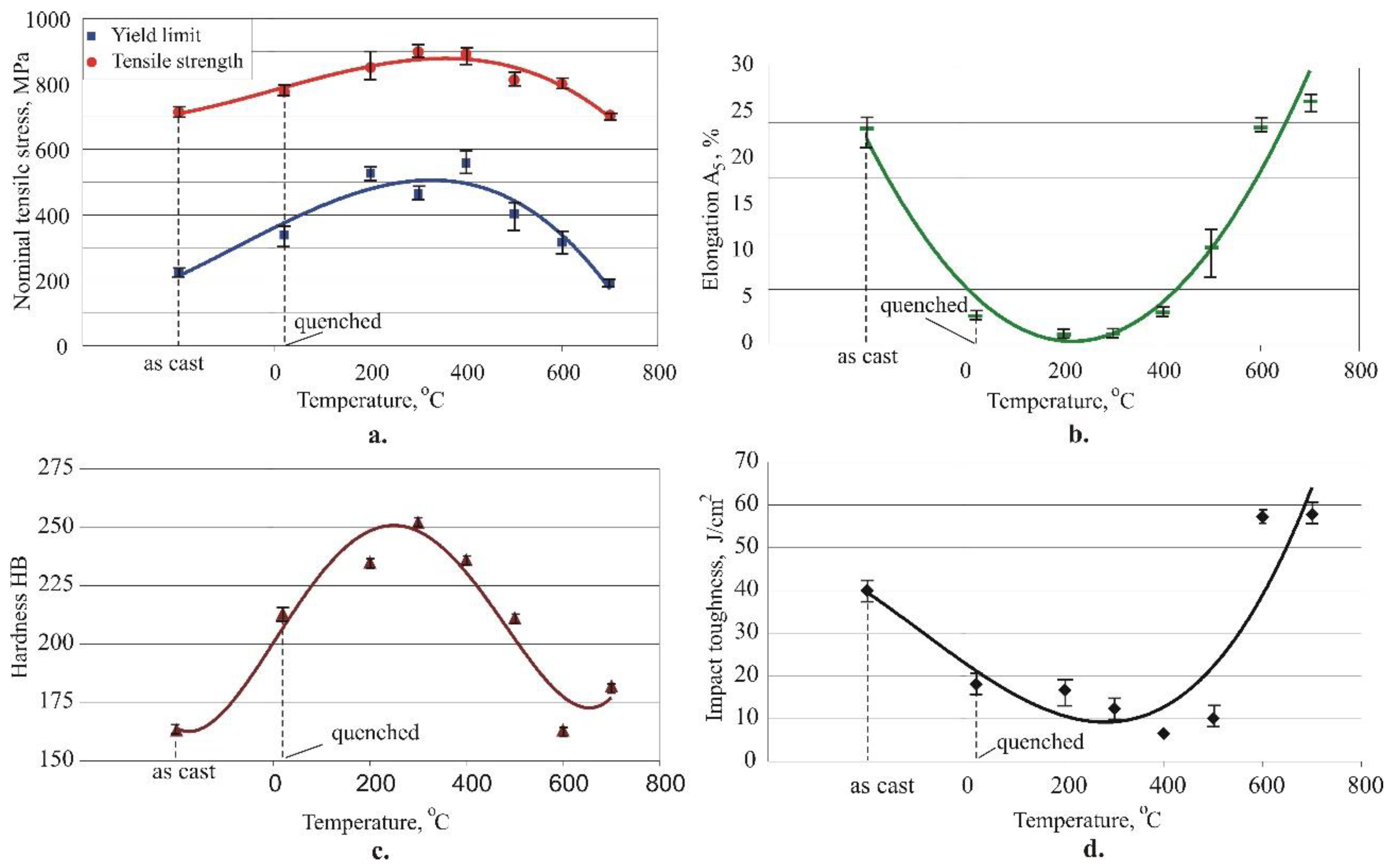
Figure 7.
Effect of ageing time on the nominal stress – nominal strain diagram of Cu-11Al-5Fe bronze (ageing temperature 500°C).
Figure 7.
Effect of ageing time on the nominal stress – nominal strain diagram of Cu-11Al-5Fe bronze (ageing temperature 500°C).
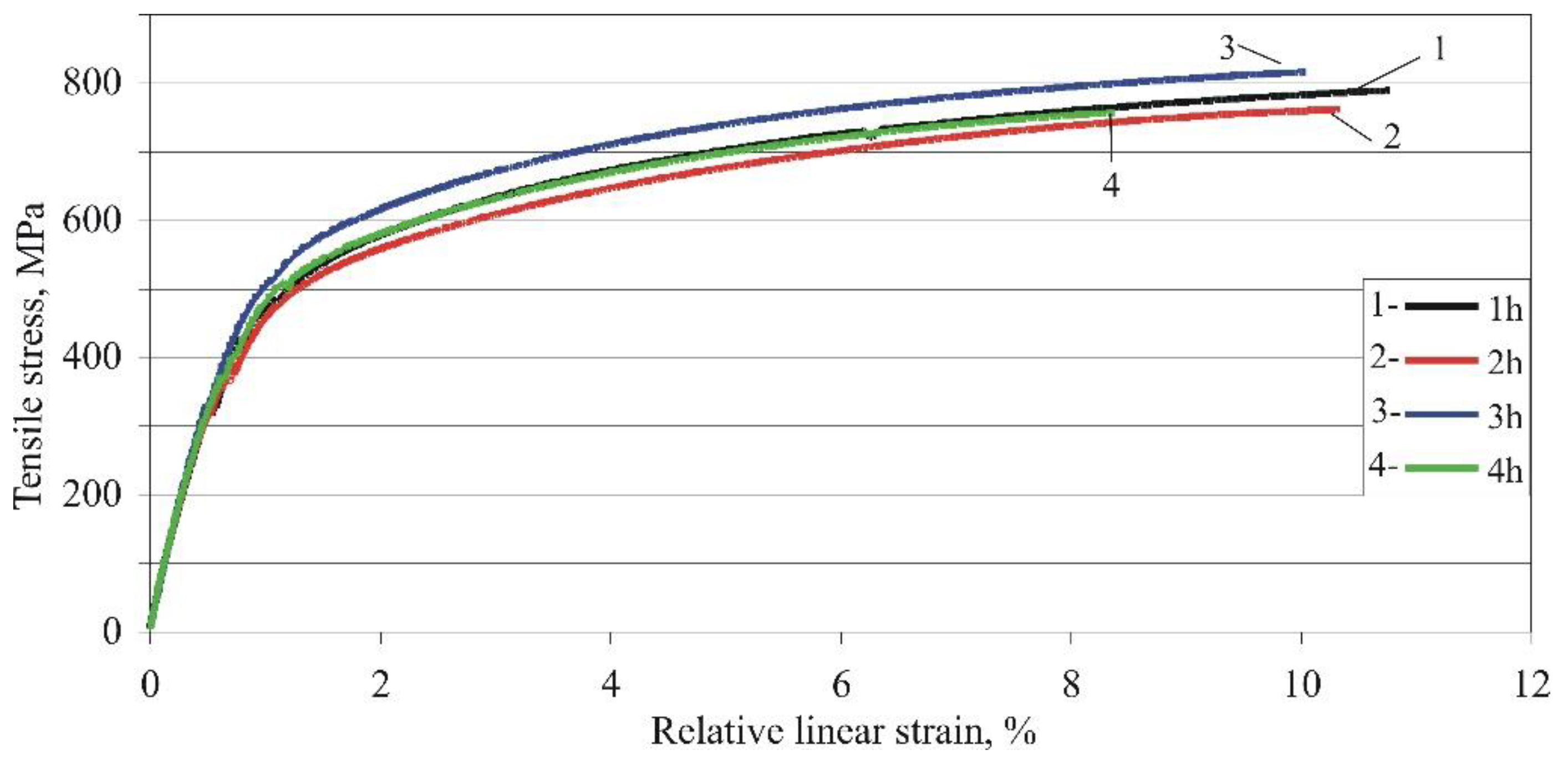
Figure 8.
Effect of ageing time on the main mechanical characteristics of Cu-11Al-5Fe bronze (ageing time 3h): a. yield limit and tensile tests; b. elongation; c. hardness; d. impact toughness.
Figure 8.
Effect of ageing time on the main mechanical characteristics of Cu-11Al-5Fe bronze (ageing time 3h): a. yield limit and tensile tests; b. elongation; c. hardness; d. impact toughness.
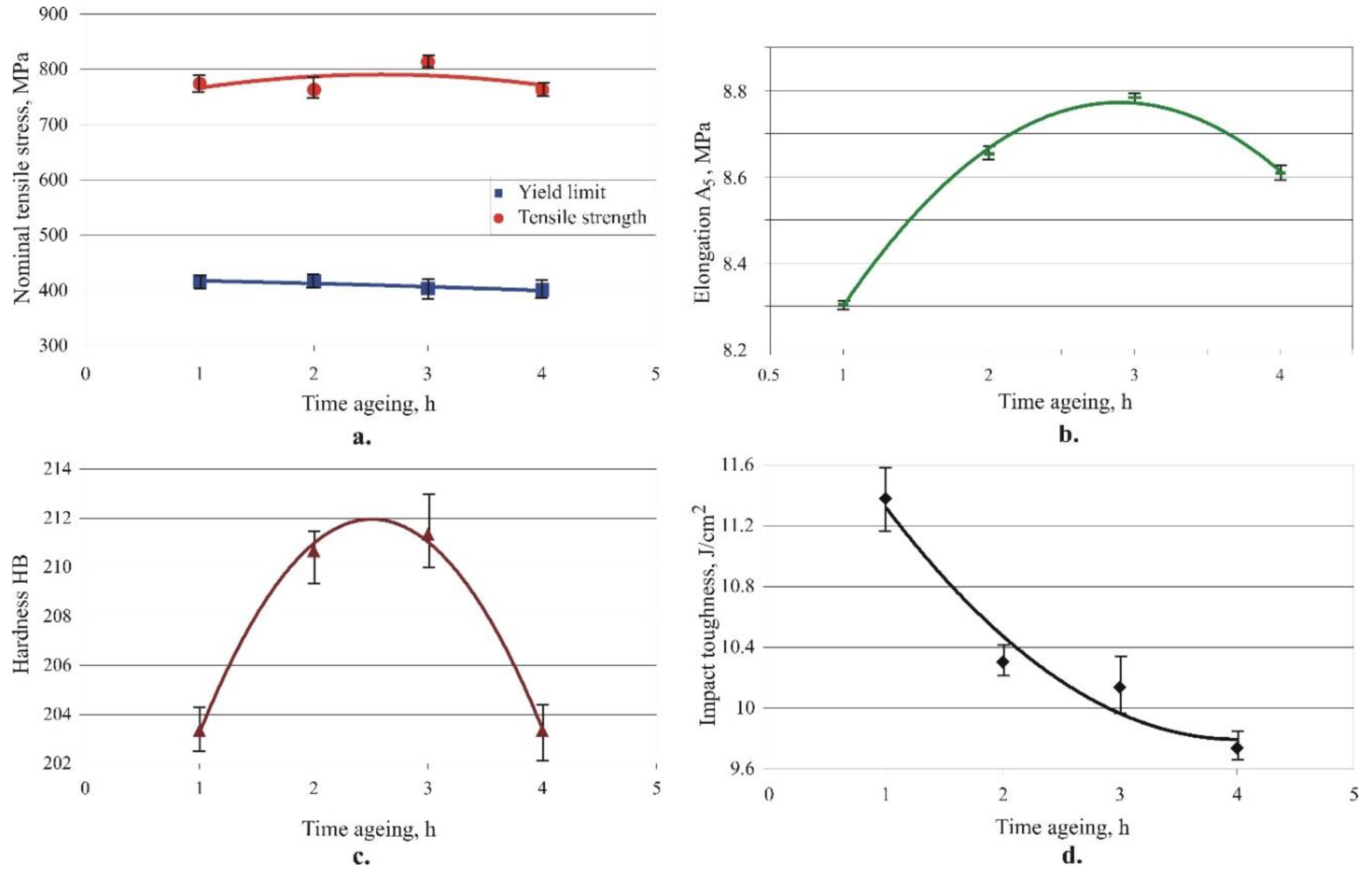
Figure 9.
Phase analysis outcomes depending on ageing temperature: 1 – as cast; 2 – ; 3 – ; 4 – ; 5 – ; 6 – ; 7 – ; 8 – .
Figure 9.
Phase analysis outcomes depending on ageing temperature: 1 – as cast; 2 – ; 3 – ; 4 – ; 5 – ; 6 – ; 7 – ; 8 – .
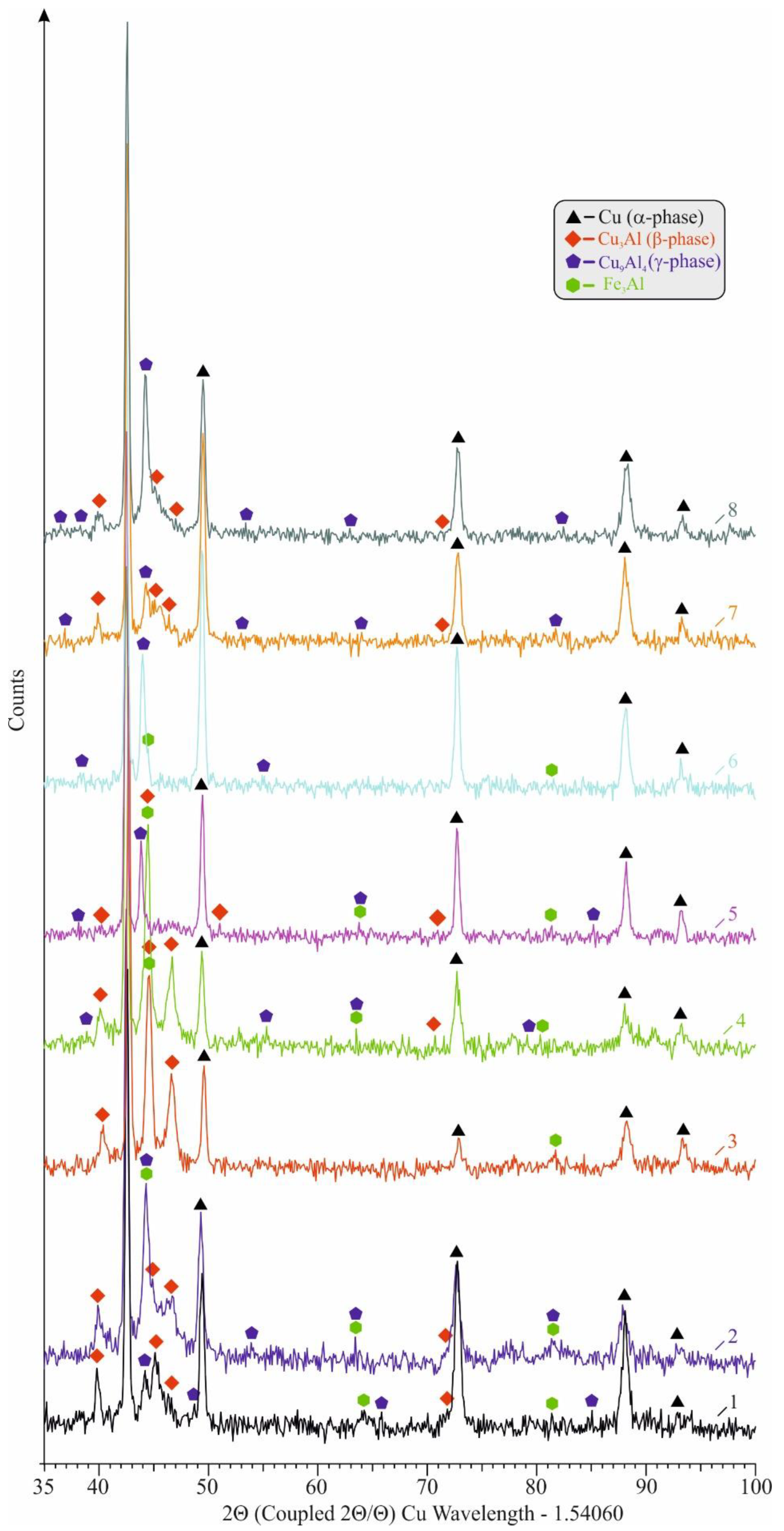
Figure 10.
Microstructure in as cast state.

Figure 11.
Microstructure at ageing temperature of 20°C.

Figure 12.
Microstructure at ageing temperature of 200°C.

Figure 13.
Microstructure at ageing temperature of 300°C.

Figure 14.
Microstructure at ageing temperature of 400°C.

Figure 15.
Microstructure at ageing temperature of 500°C.

Figure 16.
Microstructure at ageing temperature of 600°C.

Figure 17.
Microstructure at ageing temperature of 600°C.

Figure 18.
The experimental points in the governing factors plane.
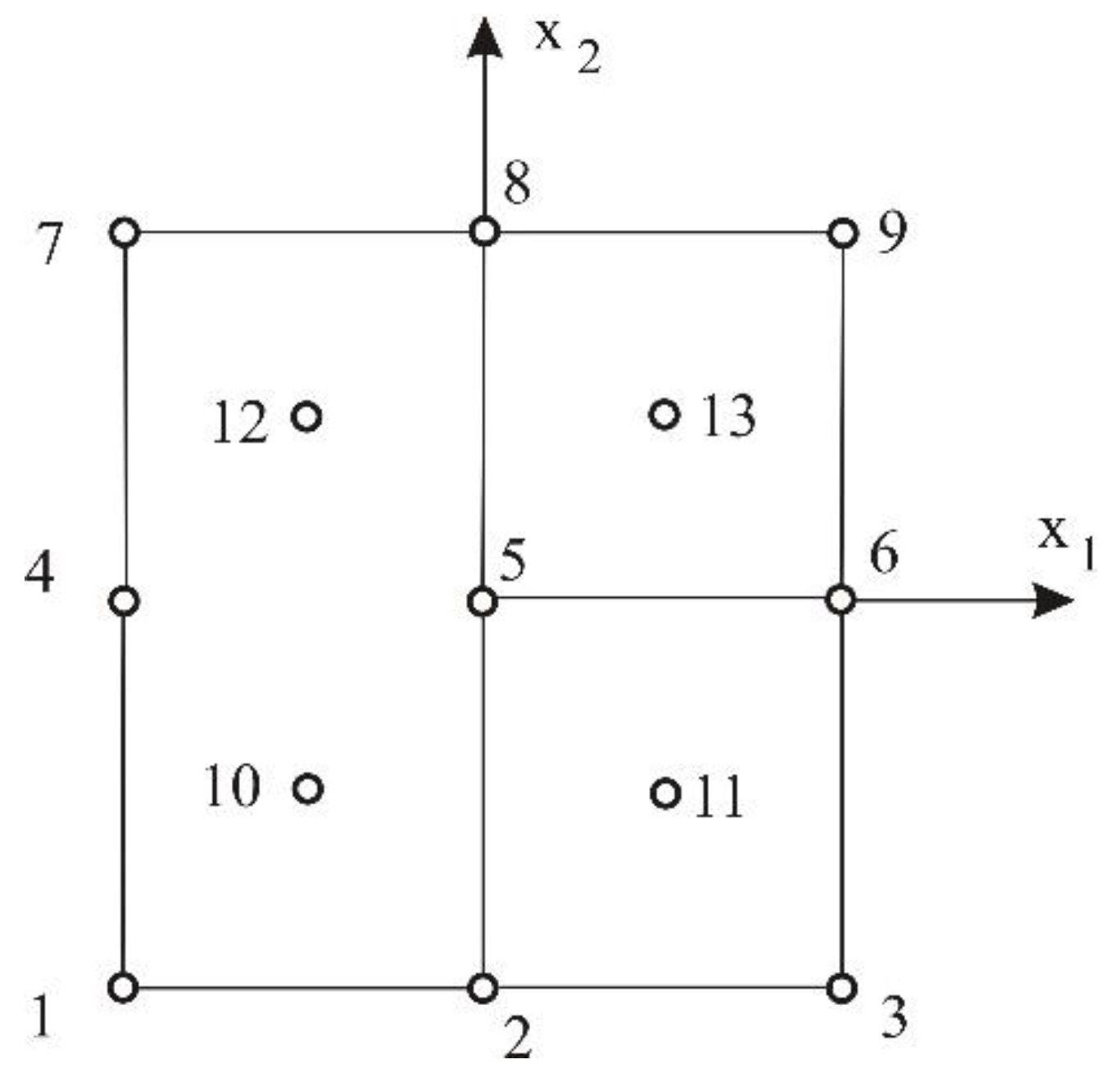
Figure 19.
ANOVA main effects: a. yield limit; b. tensile strength; c. elongation; d. hardness; e. impact toughness.
Figure 19.
ANOVA main effects: a. yield limit; b. tensile strength; c. elongation; d. hardness; e. impact toughness.
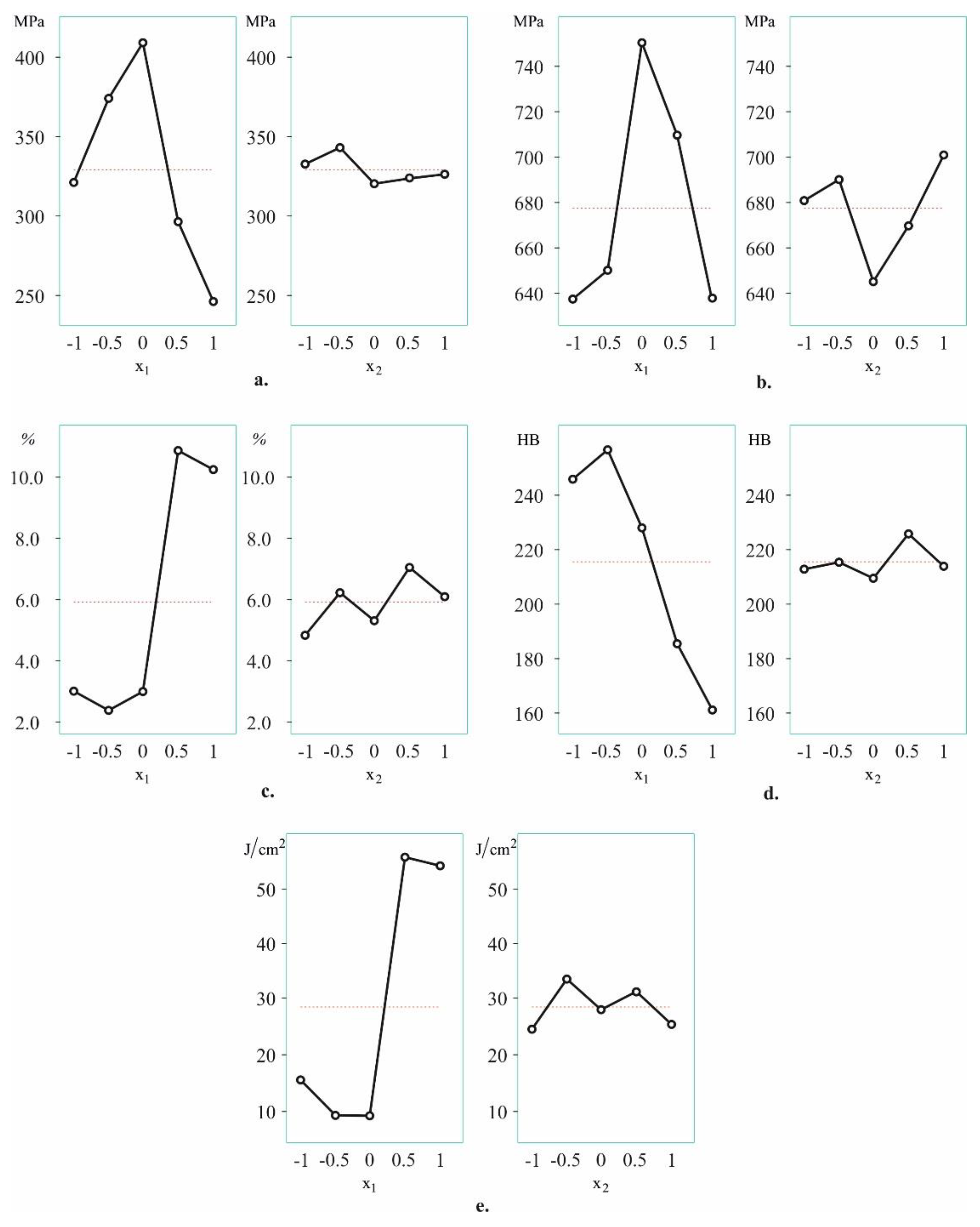
Figure 20.
Graphical visualization of the models: a. yield limit; b. tensile strength; c. hardness; d. elongation; e. impact toughness.
Figure 20.
Graphical visualization of the models: a. yield limit; b. tensile strength; c. hardness; d. elongation; e. impact toughness.
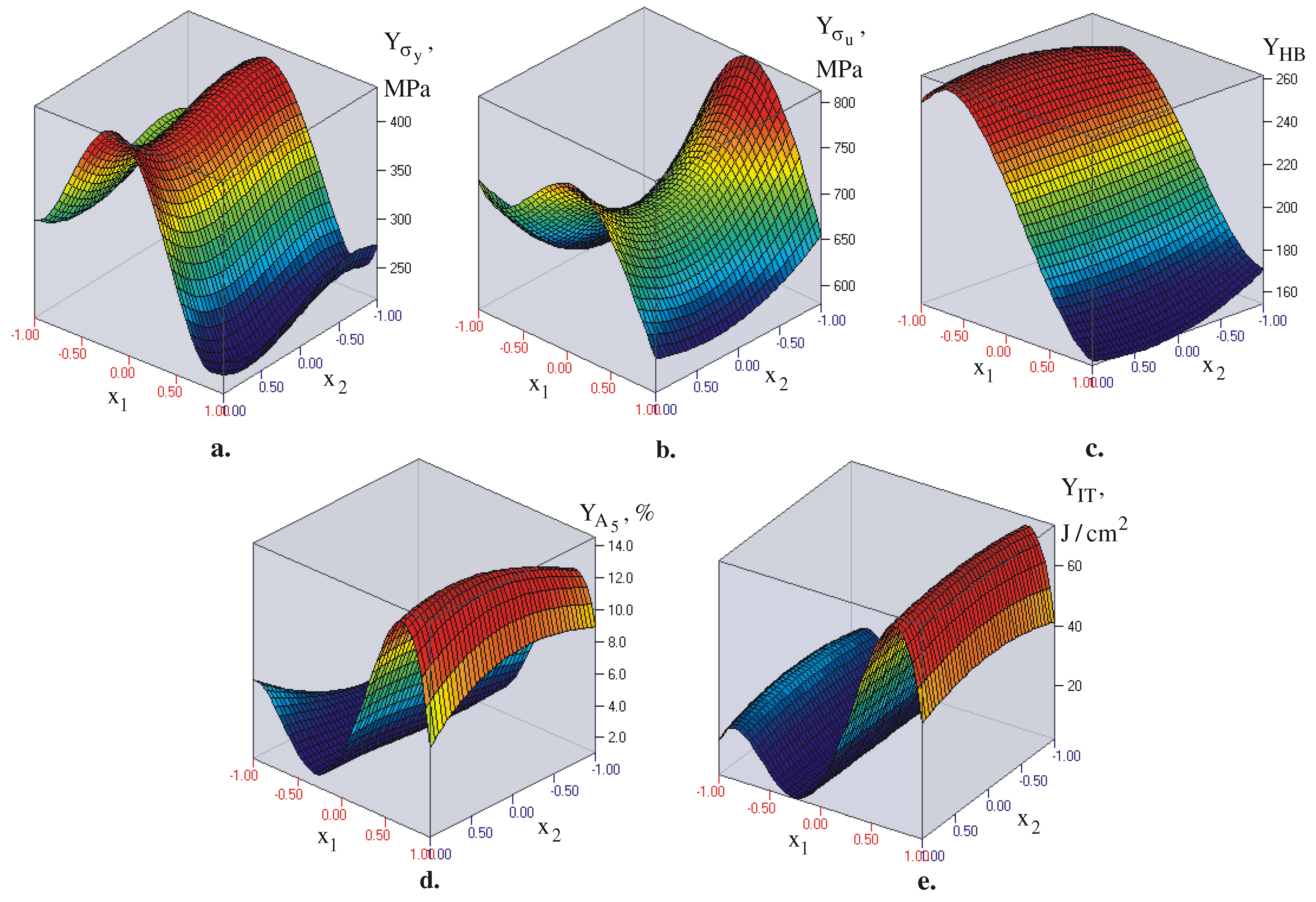
Figure 21.
Graphical visualization of the correlations between: a. yield limit and hardness; b. tensile strength and hardness; c. elongation and hardness; d. impact toughness and hardness.
Figure 21.
Graphical visualization of the correlations between: a. yield limit and hardness; b. tensile strength and hardness; c. elongation and hardness; d. impact toughness and hardness.
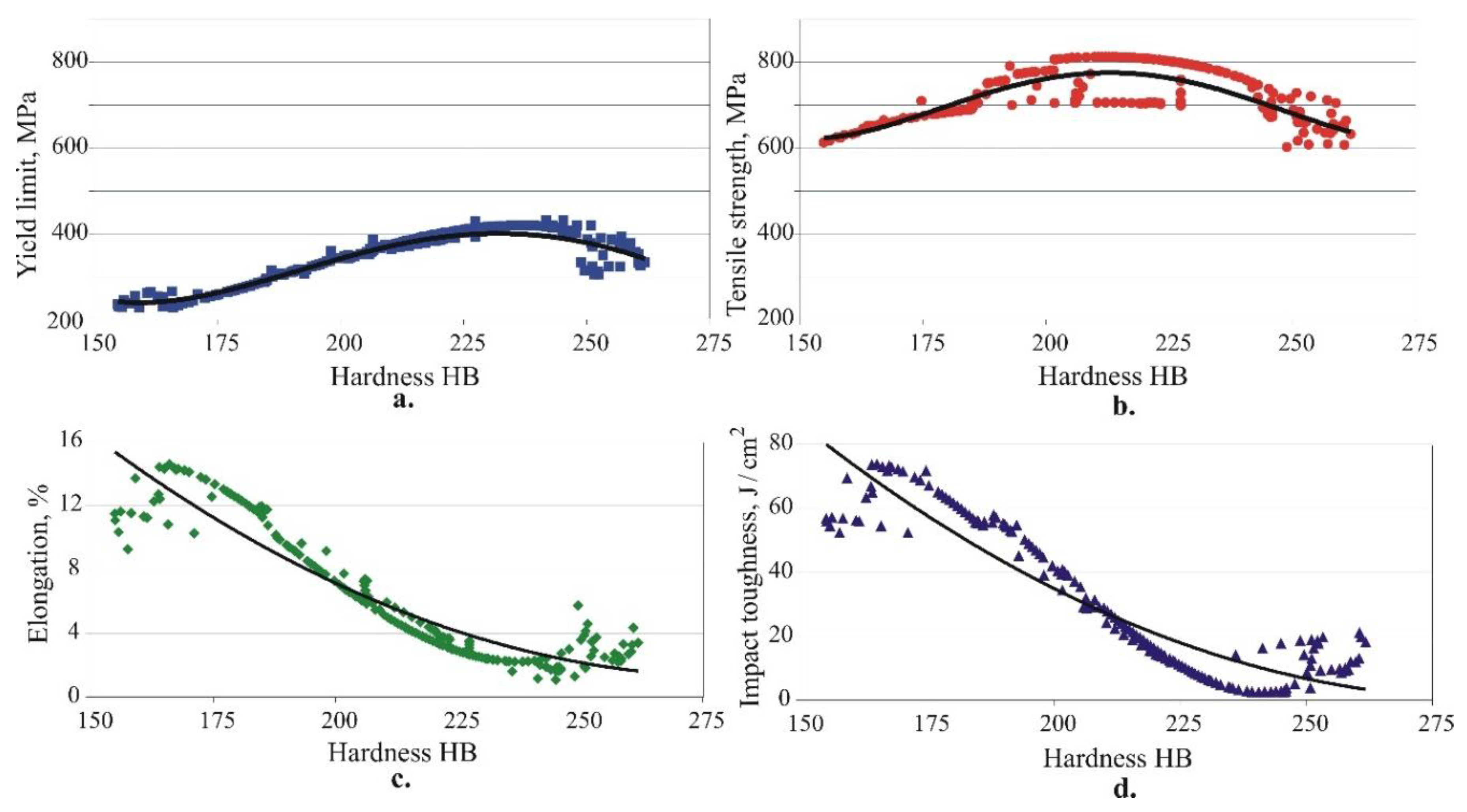
Figure 22.
Generated Pareto front for third optimization task: a. tensile strength – hardness; b. yield limit – hardness; tensile strength – yield stress.
Figure 22.
Generated Pareto front for third optimization task: a. tensile strength – hardness; b. yield limit – hardness; tensile strength – yield stress.
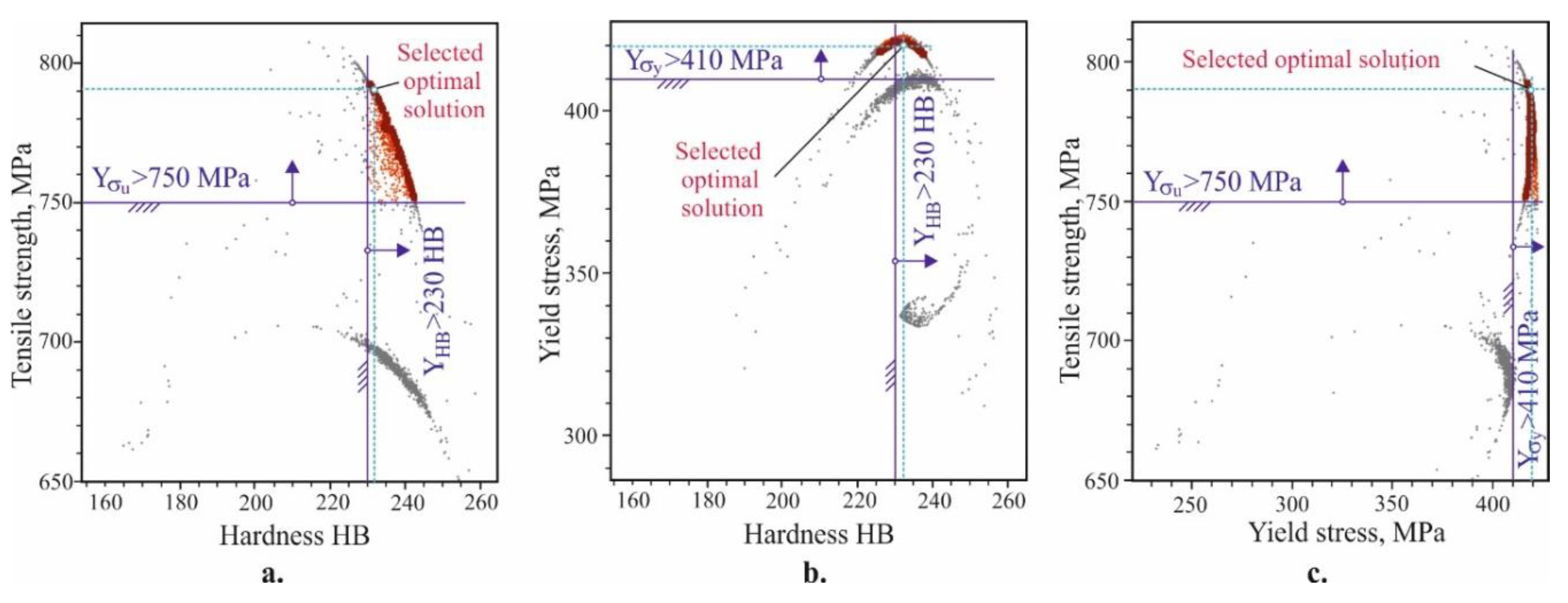
Table 1.
Chemical composition in percentages (wt.%) of the used Cu-11Al-6Fe bronze.
| Cu | Al | Fe | Mn | Ni | Pb | Zn | Si | Sn | Mg | S | Other |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 80.95 | 11.0 | 6.26 | 0. 905 | 0.391 | 0.028 | 0.280 | 0.022 | 0.071 | 0.005 | 0.010 | Balance |
Table 2.
Governing factor levels.
| Governing factors | Levels | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Natural | Codded | Natural | Coded | ||||||||||
| Ageing temperature | 200 | 325 | 450 | 575 | 700 | -1 | -0.5 | 0 | 0.5 | 1 | |||
| Ageing time | 1 | 1.75 | 2.5 | 3.25 | 4 | ||||||||
Table 3.
Experimental design and outcomes.
| № | MPa | MPa |
MPa |
MPa |
% |
% |
HB | IT |
|
|||
| 1 | -1 | -1 | 327 | 335.4 | 580.5 | 580.4 | 1.6 | 1.59 | 236 | 236.04 | 14.4 | 14.03 |
| 2 | 0 | -1 | 413 | 413 | 794.5 | 798.9 | 2.85 | 2.66 | 232 | 227.35 | 8.5 | 8.8 |
| 3 | 1 | -1 | 267 | 258.6 | 668 | 669.6 | 10.25 | 10.24 | 170 | 171.07 | 50.9 | 52.26 |
| 4 | -1 | 0 | 329.5 | 322.9 | 614.5 | 616.9 | 1.8 | 1.81 | 250 | 251.06 | 17.3 | 18.83 |
| 5 | 0 | 0 | 397 | 397 | 700 | 700 | 2.7 | 3.07 | 222 | 227.34 | 8.6 | 8.8 |
| 6 | 1 | 0 | 239.5 | 246.1 | 619.5 | 617.1 | 11.6 | 11.61 | 155 | 156.05 | 58.6 | 57.07 |
| 7 | -1 | 1 | 316.5 | 314.7 | 717.5 | 715.2 | 5.75 | 5.74 | 251 | 249.57 | 15.2 | 14.03 |
| 8 | 0 | 1 | 429.5 | 429.5 | 760.5 | 756.1 | 3.65 | 3.47 | 230 | 227.35 | 9.3 | 8.8 |
| 9 | 1 | 1 | 236 | 237.8 | 625.5 | 626.3 | 9.25 | 9.24 | 160 | 157.54 | 52.1 | 52.26 |
| 10 | -0.5 | -0.5 | 383.5 | 386.4 | 652 | 644.8 | 2.5 | 2.50 | 247 | 254.96 | 9.7 | 9.5 |
| 11 | 0.5 | -0.5 | 310.5 | 307.6 | 730.5 | 726.1 | 10.15 | 10.15 | 184 | 187.84 | 57.7 | 55.5 |
| 12 | -0.5 | 0.5 | 369 | 366.1 | 649.5 | 656.7 | 2.4 | 2.40 | 265 | 258.34 | 9.3 | 9.5 |
| 13 | 0.5 | 0.5 | 284.5 | 287.4 | 689 | 693.5 | 11.9 | 11.90 | 187 | 184.46 | 53.3 | 55.5 |
Table 4.
Coefficients of regression.
| Coefficients | Objective functions | ||||
| 397.0000 | 700.0000 | 3.0667 | 227.3488 | 8.8 | |
| -92.1944 | 78.6389 | 10.4208 | -80.9167 | 54.9611 | |
| -23.5417 | -21.3825 | 0.8375 | 0 | 0 | |
| -308.1250 | -165.4583 | 18.3639 | -23.7907 | 118.2833 | |
| 24.2500 | 77.5000 | 0 | 0 | 0 | |
| 0 | -44.5294 | 2.8958 | -6.7647 | 0 | |
| 53.7778 | -78.5555 | -5.5208 | 33.4167 | -35.8444 | |
| 31.7917 | 0 | -0.4375 | 0 | 0 | |
| -18.6250 | 44.2771 | 0.3875 | 0 | 0 | |
| 0 | 0 | -1.8625 | 8.25 | 0 | |
| 195.625 | 82.4583 | -14.7222 | 0 | -89.1333 | |
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | -4.1833 | 0 | 0 | |
| -22.1250 | -46.6250 | 0 | 0 | -4.8 | |
| 0 | 0 | 0 | 0 | 0 | |
Table 6.
Optimal compromise values of the objective functions and the corresponding governing factors.
Table 6.
Optimal compromise values of the objective functions and the corresponding governing factors.
| Optimi zation task | Optimal governing factors | ||||||
|---|---|---|---|---|---|---|---|
| Codded | Natural | ||||||
| 1 |
0.75517 0.41485 |
|
72.86 | 166.00 | 228.54 | 654.43 | |
| 2 |
0.78857 0.00032 |
|
14.3 | 165.13 | 234.7 | 652.48 | |
| 3 |
-0.1163 -1 |
2h 19min |
2.25 | 3.98 | 234.64 | 419.45 | 791.22 |
| 4 |
0.4512 -0.8375 |
1h 15min |
8.52 | 50.01 | 194.23 | 323.78 | 772.88 |
Table 7.
Experimental verification of the optimization outcomes.
| Opti-miza-tion task | Optimal values of the objective functions | |||||||||
|
, |
||||||||||
| optimiz. | experim. | optimiz. | experim. | optimiz. | experim. | optimiz. | experim. | optimiz. | experim. | |
| 1 | 14.6 | 13.8 | 72.86 | 63.4 | 166.00 | 165 | 228.54 | 249 | 654.43 | 683 |
| 2 | 14.3 | 13.1 | 73.65 | 67.0 | 165.13 | 175 | 234.7 | 258 | 652.48 | 666 |
| 3 | 2.25 | 3.4 | 3.98 | 7.2 | 234.64 | 235 | 419.45 | 407 | 791.22 | 776 |
| 4 | 8.52 | 9.7 | 50.01 | 57.4 | 194.23 | 185 | 323.78 | 314 | 772.88 | 770 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated









