Prerpints.org logo
Preprint
Article

Long-Lived Quasinormal Modes and Overtones’ Behavior of the Holonomy Corrected Black Holes

Altmetrics

Downloads

96

Views

23

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 November 2023

Posted:

02 November 2023

You are already at the latest version

Alerts
Abstract
Recently massless test scalar field perturbations of the holonomy corrected black holes [Z. Moreira et. al. Phys. Rev. D 107 (2023) 10, 104016] were studied in order to estimate quantum corrections to the quasinormal spectrum of a black hole. Here we study both the fundamental mode and overtones of scalar, electromagnetic and Dirac fields with the help of the Leaver method and higher order WKB formula with Pad\'e approximants. We observe that the overtones depend on the geometry near the event horizon, while the fundamental mode is localized near the peak of the potential barrier, what agrees with previous studies. We showed that unlike a massless field, the massive one possesses arbitrarily long lived modes. We also obtain the analytical eikonal formula for quasinormal modes and its extension beyond eikonal approximation as a series in powers of $1/\ell$, where $\ell$ is the multipole number.
Keywords: 
Subject: Physical Sciences  -   Theoretical Physics

1. Introduction

Quasinormal modes of black holes are crucial phenomena in the field of astrophysics and general relativity. These modes represent the characteristic oscillations that arise when perturbations are introduced to a black hole [1,2,3,4]. They are essential for comprehending the fundamental properties of black holes, including their mass, spin, and charge, as they manifest through the distinct frequencies and damping times of these modes.
The study of quasinormal modes is imperative for scientists as it enables a deeper examination of black hole structure and offers a means to test the predictions of Einstein’s theory of general relativity in the strong field regime. These modes serve as indispensable tools for gravitational wave astronomy, allowing for the detection and analysis of black hole mergers through the gravitational waves they emit [5,6]. Moreover, quasinormal modes are instrumental in investigating the possibility of exotic black hole solutions, including those that arise from modifications to general relativity or theories involving extra dimensions (see, for instance, [7,8,9,10,11,12,13,14] and references therein).
Furthermore, quasinormal modes provide a unique avenue to probe quantum gravity effects near black holes. In summary, quasinormal modes of black holes are pivotal in advancing our understanding of the fundamental nature of black holes, while also serving as a means to test the boundaries of quantum gravity.
A particular black hole model we are interested here is suggested in [15,16] and motivated by the holonomy corrections owing to quantum gravity. Various properties of these black holes have been recently studied in [17,18], while the first study of the quasinormal spectrum of the massless scalar and electromagnetic fields was done in [19] with the WKB and time-domain integration methods with the emphasis to the eikonal limit. A more detailed and accurate study of a test massless scalar field with the help of the lower order WKB method and Frobenius approach was done in [20].
Here we make the next step and study in details quasinormal frequencies of scalar (both massless and massive), electromagnetic and Dirac fields in the vicinity of such black holes with the help of the accurate convergent Frobenius method and check them with the higher order WKB method with Padé approximants. We will pay special attention to the two aspects of the quasinormal spectrum: arbitrary long lived modes which take place for massive fields [21,22] and overtones behavior. The overtones are important, because they are necessary to reproduce the ringdown signal not only at the late stage, but at the beginning of the ringing as well [23,24]. The massive term appears as an effective term in various higher dimensional scenarios [9,25] and when introducing magnetic fields around black holes [26,27]. Among other observations, we will show that the first few overtones deviate from their Schwarzschild limit at a smaller rate than the fundamental mode, while at sufficient high n the situation is opposite: the overtones differs from the Schwarzschild ones more than the fundamental mode n = 0 . We will show that this behavior is supported by the claim made in [28], that the overtones are determined mainly by the geometry near the event horizon, while the fundamental mode is fixed by the scattering properties near the peak of the effective potential, which is at some distance from the black hole.
The paper is organized as follows. Sec. II is devoted to the general setup related to the background metric, wave equations and boundary conditions. Sec. III is a brief summary on the methods used for finding quasinormal modes: Frobenius method and higher order WKB approach with Padé approximants. Sec. IV relates the results on numerical calculations of quasinormal modes, while Sec. V is about analytical formulas for quasinormal modes in the eikonal limit and beyond it.

2. General setup

Given a general spherically-symmetric BH with the metric
d s 2 = − A ( r ) d t 2 + B ( r ) d r 2 + r 2 ( d θ 2 + sin 2 θ d ϕ 2 ) ,
we have the following general expressions for effective potentials of scalar, electromagnetic and Dirac fields respectively:
V sc ( r ) = A ( r ) ℓ ( ℓ + 1 ) r 2 + 1 2 r d d r A ( r ) B ( r ) + A ( r ) μ 2 ,
V em ( r ) = A ( r ) ℓ ( ℓ + 1 ) r 2 ,
V D ± ( r ) = A ( r ) k ± 2 r 2 ∓ A ( r ) k ± r 2 B ( r ) ± k ± A ′ ( r ) 2 r B ( r ) ,
where the multipole numbers ℓ = 0 , 1 , 2 , 3 . . . for the scalar field, ℓ = 1 , 2 , 3 . . . for electromagnetic field, and k ± = 1 , 2 , 3 , . . . for the Dirac field. The quantity μ is the mass of the scalar field. Here the coordinate r is supposed to be a function of the “tortoise” coordinate r * via the relation
d r * = d r f ( r ) , f ( r ) ≡ A ( r ) / B ( r ) .
The general master equation for calculating quasinormal modes (QNM) ω has the form
d 2 Ψ d r * 2 + ( ω 2 − V ( r ) ) Ψ = 0
with the standard boundary conditions for the QNM problem: which are requirement of purely incoming waves at the event horizon and purely outgoing ones at infinity.
In our case the metric functions have the form [15,16]
A ( r ) = 1 − 2 M / r , B ( r ) = 1 ( 1 − r 0 / r ) A ( r ) .
Choosing M = 1 / 2 we have the normalized horizon radius r h = 1 .
The effective potentials for massless fields have the form of positive definite potential barriers with a single maximum (see Figure 1 and Figure 2), except one of the chiralities of the Dirac case, for which a negative gap near the event horizon takes places, as shown in Figure 3. However, the potential with the gap is iso-spectral with the other chirality case, so that it is sufficient to consider only one of the chiralities. The massive term adds another maximum far from the black hole as shown in Figure 1.

3. WKB and Frobenius methods for QNMs

Both used here methods are used and discussed in a great number of works. Therefore, here we will briefly summarize these methods, while further details can be found in [1,29].

3.1. Frobenius method

To acquire precise values of quasinormal modes, including overtones with ℓ < n , we will employ the Frobenius method, also known as the Leaver method [30]. The main point of the method is that the solution to the second order differential equation can be expanded into Frobenius series around the regular singular point. It is required that the coefficients in the wave equation have polynomial form, so that it can be applied to the scalar and electromagnetic fields, but not to the Dirac field in the representation we used here. The master wave-like differential equation has a regular singular point at the event horizon r = r 0 , and an irregular one at r = ∞ . Therefore, similar to the approach in [31], we introduce a novel wave function:
Ψ ( r ) = P ( r , ω ) 1 − r 0 r − i ω / F ′ ( r 0 ) y ( r ) ,
where we choose P ( r , ω ) in such a way that y ( r ) is regular in the interval r 0 ≤ r < ∞ , ensuring that Ψ ( r ) complies with the quasinormal mode boundary conditions, which require purely incoming waves at the event horizon and purely outgoing waves at infinity. Subsequently, we express y ( r ) in terms of a Frobenius series as follows:
y ( r ) = ∑ k = 0 ∞ a k 1 − r 0 r k .
In order to find the coefficients a k quickly in the above expansion we apply Gaussian elimination to the recurrence relation governing the expansion coefficients. This way the problem is simplified to a solution of an algebraic equation depending on ω . We will also use the Nollert improvement [32] in the general n-term recurrence relation form [33] in order to speed up the convergence of the procedure. When singular points of the wave-like equation are located inside the unit circle | x | < 1 , we employ integration through a series of positive real midpoints as it was suggested in [34].

3.2. WKB approach

The semi-analytic WKB approach was applied for the first time by [35] to finding of quasinormal frequencies of asymptotically flat black holes. Then, the first order formula of [35] was extended to higher orders in subsequent papers [36,37,38] and seemingly improved by using the Padé approximants [38,39].
The general form of the WKB formula can be written symbolically as an expansion around the first order, eikonal, limit [29]:
ω 2 = V 0 + A 2 ( K 2 ) + A 4 ( K 2 ) + A 6 ( K 2 ) + … − i K − 2 V 2 1 + A 3 ( K 2 ) + A 5 ( K 2 ) + A 7 ( K 2 ) + … ,
where K = n + 1 / 2 is half-integer. The corrections A k ( K 2 ) , of order k, in the eikonal formula are polynomials of K 2 with rational coefficients. The explicit form of these correction terms at various WKB orders is written in the above works [36,37,38]
These corrections are contingent upon the values of higher-order derivatives of the effective potential V ( r ) at its maximum, denoted as V j , ( j = 0 , 1 , 2 , . . . ). In order to enhance the precision of the WKB formula, we employed the aforementioned approach presented by Matyjasek and Opala [38], which utilizes Padé approximants. Specifically, we utilized the sixth-order WKB technique with m ˜ = 5 , where m ˜ signifies the corresponding polynomial degrees within the expressions for Padé approximants [29,38]. This selection provides the most accurate results in the Schwarzschild limit. Usually when the WKB frequency does not change much when one changes the WKB order or the Padé splitting, say, 5th or 6th orders with m ˜ = 4 or 5 lead to almost the same frequencies, then this WKB result is usually in a very good agreement with the precise values (see, for example, [40,41,42]). Thus, we use this "plateau of relative convergence" as an indicator of trusting to the WKB results.
However it’s crucial to emphasize that the convergence of the WKB series is purely asymptotic and the WKB method doesn’t guarantee increased precision at each order. Additionally, it does not insure the precise calculation of ℓ < n overtones, though in some cases first few such overtones could be found with reasonable accuracy. Therefore, in this context, we will employ the WKB method mainly as an additional check for the Leaver method when dealing with the fundamental mode n = 0 and also in order to find an initial guess for the frequency which is can be calculated precisely with the Leaver method.

4. Quasinormal modes

4.1. Scalar field case

Quasinormal modes for the scalar field will be considered here for both massless and massive case. As can be seen from the Table 1, Table 2 and Table 3, the frequencies obtained by the 6th order WKB with the Padé approximants are quite close to the accurate Frobenius data, keeping the error within a small fraction of one percent, except the quasi-extreme case, for which the relative error in the damping rate achieves 1 % . Results obtained by the usual 6th (here) and 3d (in [20]) orders WKB method are much less accurate, while the time-domain integration does not allow one to extract frequency with sufficient accuracy at ℓ = 0 perturbations [19]. We can see that both the real oscillation frequency and the damping rate decrease as the quantum correction parameter is increased. The damping rate is much more sensitive to the change of r 0 than the Re ( ω ) .
When the mass term μ is tuned on, the damping rate monotonically decreases, so that there is a clear indication of the arbitrarily long lived modes, called quasi-resonances (see Figure 3). The existence of such modes is not guaranteed for every background. For example, they are not allowed for the Schwarzschild-de Sitter spacetime [43].
An interesting aspect is related to the behaviour of overtones shown on Table 4: while the fundamental mode deviate from its Schwarzschild limit seemingly, by 1.6 % , the first few overtones change at a much smaller, but increasing with n rate, so that at higher n the situation becomes the opposite, i.e. the overtones deviate from their classical limits much more than the fundamental mode. This behaviour agrees with observation made in [28,44], which says that while the fundamental mode is determined by the geometry near the peak of the effective potential, the overtones are determined by the geometry in the near-horizon zone. Indeed, the effective potentials (see Figure 1, Figure 2 and Figure 3) strongly deviate from the Schwarzschild ones near the maximum, but only slightly near the horizon. Therefore, the fundamental mode deviate a lot, while the first few overtones deviate at smaller rate, though, since the phenomenon called "outburst of overtones" [28] takes place even at small deformation in the near-horizon zone, the rate of deviation increases with n, so that at sufficiently high n the frequencies differ much more from the Schwarzschild ones than the fundamental mode.

4.2. Electromagnetic field case

For electromagnetic perturbations there are some distinctions from the scalar case. First of all, Re ( ω ) monotonically increases as r 0 is increased, unlike the scalar case, for which it monotonically decreases. As ℓ = 1 is the minimal value of the multipole number now, the accuracy of the WKB method with Padé approximants is really great now as the comparison with the accurate Frobenius data on Table 5 and Table 6 shows. An important difference with the scalar case is connected to the overtones behavior and can be easily explained. The overtones deviate from the Schwarzschild values at a higher rate than the fundamental mode already starting from the first overtone, though this deviation develops slowly, because for a chosen value of the parameters the difference in the geometry near the event horizon is quite small. The effective potential as function of ris not affected by r 0 at all and the difference in geometries of the Schwarzschild and holonomy-corrected black hole is encoded in the tortoise coordinate only. For larger values of r 0 the difference of the overtones values grows much quicker with n.

4.3. Dirac field case

For the Dirac field the effective potentials does not have a polynomial form, so that we will find quasinormal modes with the 6th order WKB formula with and without Padé approximants. As for scalar and vector fields the 6th order formula with Padé approximants provided very good concordance with the precise values, we believe that the same must be for the Dirac case for which the main condition of the applicability of the WKB method ℓ > n is fulfilled for the fundamental mode. The results of calculations is shown in Table 8 and Table 9. There we can see that there is non-monotonic, but smooth change of Re ( ω ) which first grows and then decays as r 0 is increased.

5. Analytical formula for qnms in the eikonal limit and beyond

The regime of high real oscillation frequency, i.e. of high multipole numbers ℓ is hardly do be observed in the near future, because in merger of two compact objects such as black holes or neutron stars usually only a couple of first gravitational multipole numbers ( ℓ = 2 , 3 ) are excited considerably. Nevertheless, there are a number of reasons of theoretical character to study this regime. First of all, the eikonal regime corresponds to the limit of geometrical optics and it comes as no surprise that in this regime there is a correspondence between characteristics of null geodesics and eikonal quasinormal modes [45]. More exactly, the real oscillation frequency is determined by the rotation frequency of the unstable circular null geodesic1 and the damping rate is proportional to the Lyapunov exponent [45]. However, as it was shown in [49,50], this correspondence works for the WKB-like part of the spectrum and, therefore, is not always guaranteed. Thus, for example, it is not fulfilled for the gravitational perturbations in some theories with higher curvature corrections [14,51].
The other reason to treat separately the eikonal regime is that it may bring qualitatively new features of the perturbations. Thus, for example, the high ℓ modes may govern the instability, called "eikonal instability" [52,53,54,55], so that the small ℓ frequencies which are stable in such a case do not have meaning anymore: once there is one unstable mode the system is unstable.
An advantage of the eikonal regime is that it is that rare case in which quasinormal modes can be found analytically2, because the WKB method is exact in this limit. Here, using the general approach and Mathematica code shared in [58] in order to find the eikonal formula and some improvement of it via expansion beyond the eikonal limit in powers of 1 / ℓ .
The maximum of the effective potential acquires the 1 / κ 2 correction,
r m a x = 3 M + 1 κ 2 r 0 4 − M 3 + O ( 1 / κ 3 ) ,
where κ = ℓ + 1 2 . Then expansion in powers of κ gives:
ω = κ 3 3 M − i K 3 M − r 0 9 M 3 / 2 − 36 M 2 60 K 2 − 29 + 12 M r 0 79 − 156 K 2 + r 0 2 492 K 2 − 191 15552 3 M 2 κ ( 3 M − r 0 ) + O ( 1 / κ 2 ) ,
where K = n + 1 2 .
For the electromagnetic case the effective potential does not gain a r 0 correction, so that the effect is only due to the corrected tortoise coordinate. The terms beyond the eikonal approximation differs from that for the scalar field,
ω = κ 3 3 M − i K 3 M − r 0 9 M 3 / 2 − 180 M 2 12 K 2 + 23 − 12 M r 0 156 K 2 + 173 + r 0 2 492 K 2 + 241 15552 3 M 2 κ ( 3 M − r 0 ) + O ( 1 / κ 2 ) .
For the Dirac field, the maximum of the effective potential is located at
r m a x = 3 M + M ( 3 M − r 0 ) 2 κ + r 0 12 κ 2 + O ( 1 / κ 3 ) ,
while the quasinormal frequency at the first order in 1 / κ beyond the eikonal limit is
ω = κ 3 3 M − i K 3 M − r 0 9 M 3 / 2 − 36 M 2 60 K 2 + 7 − 12 M r 0 156 K 2 + 11 + r 0 2 492 K 2 + 25 15552 3 M 2 κ 3 M − r 0 + O ( 1 / κ 2 ) .
In the eikonal limit the quasinormal frequencies do not depend on the spin of the field under consideration. Comparison of the above formula in the eikonal limit with the Lyapunov exponents and rotational frequency for the null geodesics shows that the null geodesics/eikonal quasinormal modes correspondence is fulfilled in this case.

6. Conclusions

We have presented a detailed study of quasinormal modes of the holonomy corrected black holes for scalar, electromagnetic and Dirac fields, including the overtones behaviour and long-lived modes of a massive field. The quasinormal modes were computed here with two alternative methods (WKB with Padé approximants and Leaver) with excellent agreement between them in the common range of applicability. We have shown that:
  • For a nonzero mass of the field, the quasinormal modes become much longer lived and there is a clear indication of existence of arbitrarily long lived modes - quasiresonances.
  • The overtones behaviour is in concordance with observation that the higher is the overtone’s number, the more it depends on the geometry near the event horizon, while the fundamental mode depends upon the scattering near the peak of the effective potential.
  • While the third order WKB method used in earlier studies of the holonomy corrected black hole spectrum agrees well with the Leaver method only at high multipole numbers, application of the 6th order with Padé approximants provides concordance at all ℓ.
  • The analytical formula for quasinormal modes in the eikonal limit, and at some orders of 1 / ℓ beyond, was deduced and it may serve as a reasonable approximation for the lowest modes.
Outburst of overtones studied recently in a number of works also on various quantum corrected black holes [59,60] is characterized by a strong deviation already at the first few overtone numbers n. Here we observed a different picture of slow, but still increasing with n, deviation of overtones for both scalar and electromagnetic fields. In principle, the Dirac equation could be re-written using a different representation basis, so that one could reduce it to the polynomial form [61,62]. Then, the overtones behavior could analyzed for the Dirac field as well.

Acknowledgments

The author would like to acknowledge Dr. R. A. Konoplya for careful reading of the manuscript and most useful discussions. This work was supported by RUDN University research project FSSF-2023-0003.

References

  1. R. A. Konoplya and A. Zhidenko. Quasinormal modes of black holes: From astrophysics to string theory. Rev. Mod. Phys., 83:793–836, 2011. [CrossRef]
  2. Emanuele Berti, Vitor Cardoso, and Andrei O. Starinets. Quasinormal modes of black holes and black branes. Class. Quant. Grav., 26:163001, 2009. [CrossRef]
  3. Kostas D. Kokkotas and Bernd G. Schmidt. Quasinormal modes of stars and black holes. Living Rev. Rel., 2:2, 1999. [CrossRef]
  4. Hans-Peter Nollert. TOPICAL REVIEW: Quasinormal modes: the characteristic `sound’ of black holes and neutron stars. Class. Quant. Grav., 16:R159–R216, 1999.
  5. B. P. Abbott et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett., 116(6):061102, 2016. [CrossRef]
  6. B. P. Abbott et al. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett., 116(24):241103, 2016. [CrossRef]
  7. P. Kanti, R. A. Konoplya, and A. Zhidenko. Quasi-Normal Modes of Brane-Localised Standard Model Fields. II. Kerr Black Holes. Phys. Rev. D, 74:064008, 2006. [CrossRef]
  8. E. Abdalla, B. Cuadros-Melgar, A. B. Pavan, and C. Molina. Stability and thermodynamics of brane black holes. Nucl. Phys. B, 752:40–59, 2006. [CrossRef]
  9. Sanjeev S. Seahra, Chris Clarkson, and Roy Maartens. Detecting extra dimensions with gravity wave spectroscopy: the black string brane-world. Phys. Rev. Lett., 94:121302, 2005. [CrossRef]
  10. A. F. Zinhailo. Quasinormal modes of the four-dimensional black hole in Einstein–Weyl gravity. Eur. Phys. J. C, 78(12):992, 2018. [CrossRef]
  11. R. A. Konoplya, A. F. Zinhailo, and Z. Stuchlik. Quasinormal modes and Hawking radiation of black holes in cubic gravity. Phys. Rev. D, 102(4):044023, 2020. [CrossRef]
  12. Lorenzo Pierini and Leonardo Gualtieri. Quasi-normal modes of rotating black holes in Einstein-dilaton Gauss-Bonnet gravity: the first order in rotation. Phys. Rev. D, 103:124017, 2021. [CrossRef]
  13. Luciano Manfredi, Jonas Mureika, and John Moffat. Quasinormal Modes of Modified Gravity (MOG) Black Holes. Phys. Lett. B, 779:492–497, 2018. [CrossRef]
  14. R. A. Konoplya, A. F. Zinhailo, and Z. Stuchlík. Quasinormal modes, scattering, and Hawking radiation in the vicinity of an Einstein-dilaton-Gauss-Bonnet black hole. Phys. Rev. D, 99(12):124042, 2019. [CrossRef]
  15. Asier Alonso-Bardaji, David Brizuela, and Raül Vera. Nonsingular spherically symmetric black-hole model with holonomy corrections. Phys. Rev. D, 106(2):024035, 2022. [CrossRef]
  16. Asier Alonso-Bardaji, David Brizuela, and Raül Vera. An effective model for the quantum Schwarzschild black hole. Phys. Lett. B, 829:137075, 2022. [CrossRef]
  17. A. R. Soares, C. F. S. Pereira, and R. L. L. Vitória. Holonomy corrected Schwarzschild black hole lensing. 9 2023. [CrossRef]
  18. Ednaldo L. B. Junior, Francisco S. N. Lobo, Manuel E. Rodrigues, and Henrique A. Vieira. Gravitational lens effect of a holonomy corrected Schwarzschild black hole. 9 2023. [CrossRef]
  19. Guoyang Fu, Dan Zhang, Peng Liu, Xiao-Mei Kuang, and Jian-Pin Wu. Peculiar properties in quasi-normal spectra from loop quantum gravity effect. 1 2023. [CrossRef]
  20. Zeus S. Moreira, Haroldo C. D. Lima Junior, Luís C. B. Crispino, and Carlos A. R. Herdeiro. Quasinormal modes of a holonomy corrected Schwarzschild black hole. Phys. Rev. D, 107(10):104016, 2023. [CrossRef]
  21. R. A. Konoplya. Massive vector field perturbations in the Schwarzschild background: Stability and unusual quasinormal spectrum. Phys. Rev. D, 73:024009, 2006. [CrossRef]
  22. Akira Ohashi and Masa-aki Sakagami. Massive quasi-normal mode. Class. Quant. Grav., 21:3973–3984, 2004. [CrossRef]
  23. Matthew Giesler, Maximiliano Isi, Mark A. Scheel, and Saul Teukolsky. Black Hole Ringdown: The Importance of Overtones. Phys. Rev. X, 9(4):041060, 2019. [CrossRef]
  24. Naritaka Oshita. Ease of excitation of black hole ringing: Quantifying the importance of overtones by the excitation factors. Phys. Rev. D, 104(12):124032, 2021. [CrossRef]
  25. Hideki Ishihara, Masashi Kimura, Roman A. Konoplya, Keiju Murata, Jiro Soda, and Alexander Zhidenko. Evolution of perturbations of squashed Kaluza-Klein black holes: escape from instability. Phys. Rev. D, 77:084019, 2008. [CrossRef]
  26. R. A. Konoplya and R. D. B. Fontana. Quasinormal modes of black holes immersed in a strong magnetic field. Phys. Lett. B, 659:375–379, 2008. [CrossRef]
  27. R. A. Konoplya. Magnetic field creates strong superradiant instability. Phys. Lett. B, 666:283–287, 2008.
  28. R. A. Konoplya and A. Zhidenko. First few overtones probe the event horizon geometry, eprint: 2209.00679. 9 2022. [CrossRef]
  29. R. A. Konoplya, A. Zhidenko, and A. F. Zinhailo. Higher order WKB formula for quasinormal modes and grey-body factors: recipes for quick and accurate calculations. Class. Quant. Grav., 36:155002, 2019. [CrossRef]
  30. E. W. Leaver. An Analytic representation for the quasi normal modes of Kerr black holes. Proc. Roy. Soc. Lond. A, 402:285–298, 1985. [CrossRef]
  31. R. A. Konoplya and A. Zhidenko. High overtones of Schwarzschild-de Sitter quasinormal spectrum. JHEP, 06:037, 2004. [CrossRef]
  32. Hans-Peter Nollert. Quasinormal modes of Schwarzschild black holes: The determination of quasinormal frequencies with very large imaginary parts. Phys. Rev. D, 47:5253–5258, 1993. [CrossRef]
  33. Alexander Zhidenko. Massive scalar field quasi-normal modes of higher dimensional black holes. Phys. Rev. D, 74:064017, 2006. [CrossRef]
  34. Andrzej Rostworowski. Quasinormal frequencies of D-dimensional Schwarzschild black holes: Evaluation via continued fraction method. Acta Phys. Polon. B, 38:81–89, 2007. [CrossRef]
  35. Bernard F. Schutz and Clifford M. Will. Black Hole Normal Modes: A semianalytic approach. Astrophys. J. Lett., 291:L33–L36, 1985. [CrossRef]
  36. Sai Iyer and Clifford M. Will. Black Hole Normal Modes: A WKB Approach. 1. Foundations and Application of a Higher Order WKB Analysis of Potential Barrier Scattering. Phys. Rev. D, 35:3621, 1987. [CrossRef]
  37. R. A. Konoplya. Quasinormal behavior of the d-dimensional Schwarzschild black hole and higher order WKB approach. Phys. Rev. D, 68:024018, 2003. [CrossRef]
  38. Jerzy Matyjasek and Michał Opala. Quasinormal modes of black holes. The improved semianalytic approach. Phys. Rev. D, 96(2):024011, 2017. [CrossRef]
  39. Yasuyuki Hatsuda. Quasinormal modes of black holes and Borel summation. Phys. Rev. D, 101(2):024008, 2020. [CrossRef]
  40. Hideo Kodama, R. A. Konoplya, and Alexander Zhidenko. Gravitational stability of simply rotating Myers-Perry black holes: Tensorial perturbations. Phys. Rev. D, 81:044007, 2010. [CrossRef]
  41. S. V. Bolokhov. Black holes in Starobinsky-Bel-Robinson Gravity and the breakdown of quasinormal modes/null geodesics correspondence. 10 2023. [CrossRef]
  42. S. V. Bolokhov. Long lived quasinormal modes and telling oscillatory tails of the Bardeen spacetime, 10.20944/preprints202310.0517.v1. 2023. [CrossRef]
  43. R. A. Konoplya and A. V. Zhidenko. Decay of massive scalar field in a Schwarzschild background. Phys. Lett. B, 609:377–384, 2005. [CrossRef]
  44. R. A. Konoplya, A. F. Zinhailo, J. Kunz, Z. Stuchlik, and A. Zhidenko. Quasinormal ringing of regular black holes in asymptotically safe gravity: the importance of overtones. JCAP, 10:091, 2022. [CrossRef]
  45. Vitor Cardoso, Alex S. Miranda, Emanuele Berti, Helvi Witek, and Vilson T. Zanchin. Geodesic stability, Lyapunov exponents and quasinormal modes. Phys. Rev. D, 79(6):064016, 2009. [CrossRef]
  46. Che-Yu Chen, Mariam Bouhmadi-López, and Pisin Chen. Probing Palatini-type gravity theories through gravitational wave detections via quasinormal modes. Eur. Phys. J. C, 79(1):63, 2019. [CrossRef]
  47. Che-Yu Chen and Pisin Chen. Eikonal black hole ringings in generalized energy-momentum squared gravity. Phys. Rev. D, 101(6):064021, 2020. [CrossRef]
  48. Bobir Toshmatov, Zdeněk Stuchlík, Bobomurat Ahmedov, and Daniele Malafarina. Relaxations of perturbations of spacetimes in general relativity coupled to nonlinear electrodynamics. Phys. Rev. D, 99(6):064043, 2019. [CrossRef]
  49. R. A. Konoplya and Z. Stuchlík. Are eikonal quasinormal modes linked to the unstable circular null geodesics? Phys. Lett. B, 771:597–602, 2017. [CrossRef]
  50. R. A. Konoplya. Further clarification on quasinormal modes/circular null geodesics correspondence. Phys. Lett. B, 838:137674, 2023. [CrossRef]
  51. R. A. Konoplya and A. F. Zinhailo. Quasinormal modes, stability and shadows of a black hole in the 4D Einstein–Gauss–Bonnet gravity. Eur. Phys. J. C, 80(11):1049, 2020. [CrossRef]
  52. Gustavo Dotti and Reinaldo J. Gleiser. Linear stability of Einstein-Gauss-Bonnet static spacetimes. Part I. Tensor perturbations. Phys. Rev. D, 72:044018, 2005. [CrossRef]
  53. Tomohiro Takahashi. Instability of Charged Lovelock Black Holes: Vector Perturbations and Scalar Perturbations. PTEP, 2013:013E02, 2013. [CrossRef]
  54. Tomohiro Takahashi and Jiro Soda. Catastrophic Instability of Small Lovelock Black Holes. Prog. Theor. Phys., 124:711–729, 2010. [CrossRef]
  55. R. A. Konoplya and A. Zhidenko. The portrait of eikonal instability in Lovelock theories. JCAP, 05:050, 2017. [CrossRef]
  56. Maximo Banados, Claudio Teitelboim, and Jorge Zanelli. The Black hole in three-dimensional space-time. Phys. Rev. Lett., 69:1849–1851, 1992.
  57. R. A. Konoplya and A. Zhidenko. BTZ black holes with higher curvature corrections in the 3D Einstein-Lovelock gravity. Phys. Rev. D, 102(6):064004, 2020. [CrossRef]
  58. R. A. Konoplya and A. Zhidenko. Analytic expressions for quasinormal modes and grey-body factors in the eikonal limit and beyond. 9 2023. [CrossRef]
  59. R. A. Konoplya. Quasinormal modes and grey-body factors of regular black holes with a scalar hair from the Effective Field Theory. JCAP, 07:001, 2023. [CrossRef]
  60. R. A. Konoplya, Z. Stuchlik, A. Zhidenko, and A. F. Zinhailo. Quasinormal modes of renormalization group improved Dymnikova regular black holes. Phys. Rev. D, 107(10):104050, 2023. [CrossRef]
  61. Hing Tong Cho. Dirac quasinormal modes in Schwarzschild black hole space-times. Phys. Rev. D, 68:024003, 2003. [CrossRef]
  62. H. T. Cho, Alan S. Cornell, Jason Doukas, and Wade Naylor. Split fermion quasi-normal modes. Phys. Rev. D, 75:104005, 2007. [CrossRef]
1
It is also worth mentioning that and in the non-linear electrodynamics photons move not along the null geodesics, so that the terms "null geodesics" and "photons orbits" are not always interchangeable in the correspondence [46,47,48].
2
The other examples of spectral problems allowing for an exact solution of the wave equation are mostly for the 2+1 dimensional black holes, such as BTZ spacetime and its generalizations [56,57].
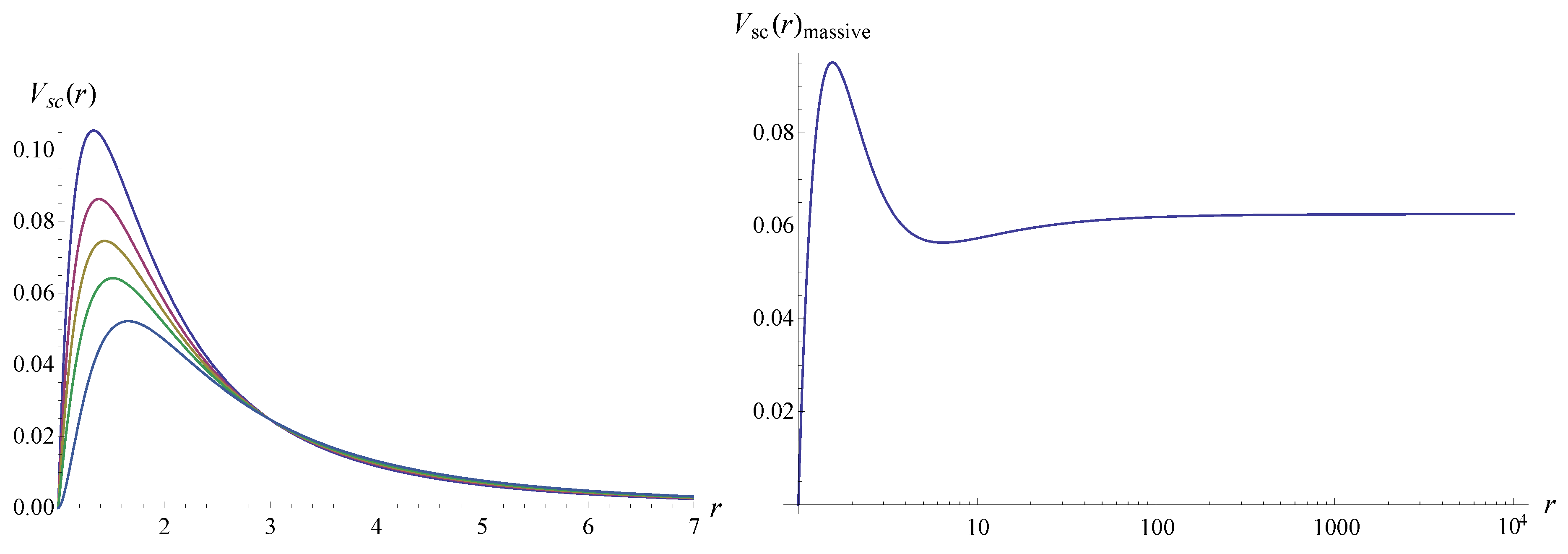
Preprints 89410 g001
Figure 1. Left panel: Effective potentials of a massless scalar field for ℓ = 0 and r 0 = 0 , 0.3 , 0.5 , 0.7 , 0.99 (from top to bottom), r h = 1 . Right panel: Effective potential of a massive scalar field for ℓ = 0 , r 0 = 0.5 , μ = 0.25 ; r h = 1 .
Figure 1. Left panel: Effective potentials of a massless scalar field for ℓ = 0 and r 0 = 0 , 0.3 , 0.5 , 0.7 , 0.99 (from top to bottom), r h = 1 . Right panel: Effective potential of a massive scalar field for ℓ = 0 , r 0 = 0.5 , μ = 0.25 ; r h = 1 .
Preprints 89410 g001
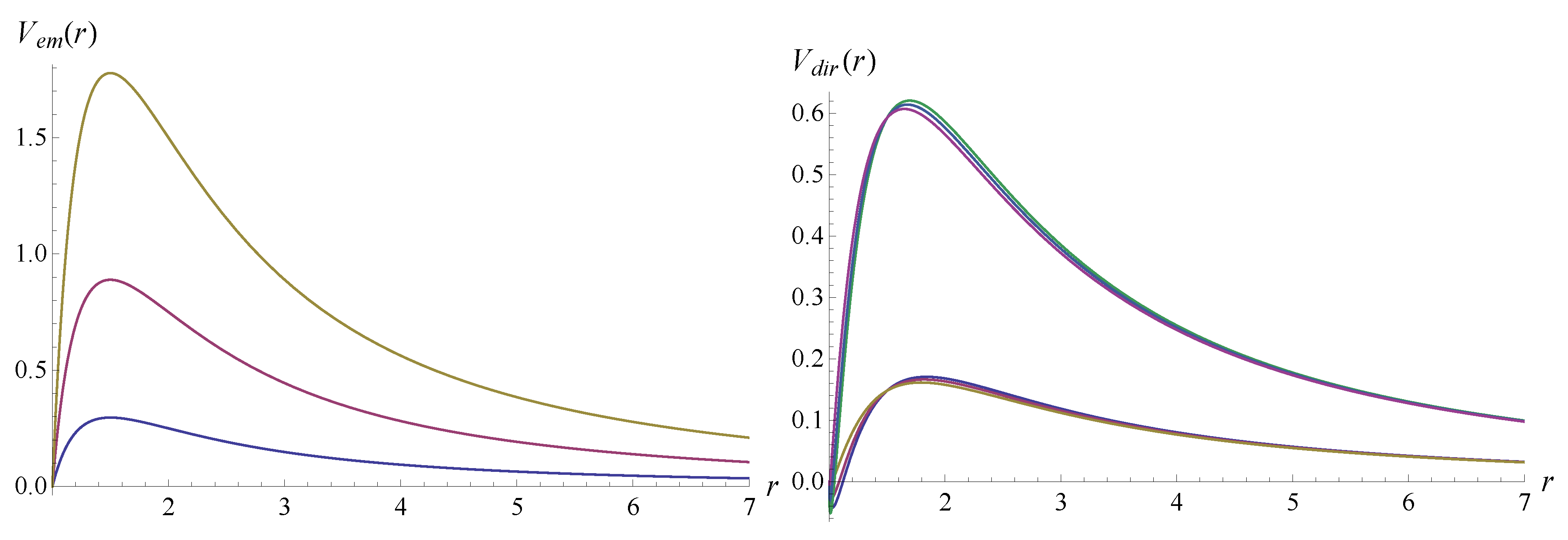
Preprints 89410 g002
Figure 2. Left panel: Effective potentials of electromagnetic field for ℓ = 1 , 2 , 3 (from bottom to top), r h = 1 . Right panel: Effective potential V D − ( r ) of the Dirac field for k = 1 (bottom bundle of curves, r 0 = 0.1 , 0.5 , 0.9 from top to bottom), and k = 2 (top bundle of curves, r 0 = 0.1 , 0.5 , 0.9 from top to bottom), r h = 1 .
Figure 2. Left panel: Effective potentials of electromagnetic field for ℓ = 1 , 2 , 3 (from bottom to top), r h = 1 . Right panel: Effective potential V D − ( r ) of the Dirac field for k = 1 (bottom bundle of curves, r 0 = 0.1 , 0.5 , 0.9 from top to bottom), and k = 2 (top bundle of curves, r 0 = 0.1 , 0.5 , 0.9 from top to bottom), r h = 1 .
Preprints 89410 g002
Preprints 89410 g003
Figure 3. The real and imaginary parts of the fundamental mode n = ℓ = 0 as functions of the mass μ , obtained by the Frobenius method for a massive scalar field.
Figure 3. The real and imaginary parts of the fundamental mode n = ℓ = 0 as functions of the mass μ , obtained by the Frobenius method for a massive scalar field.
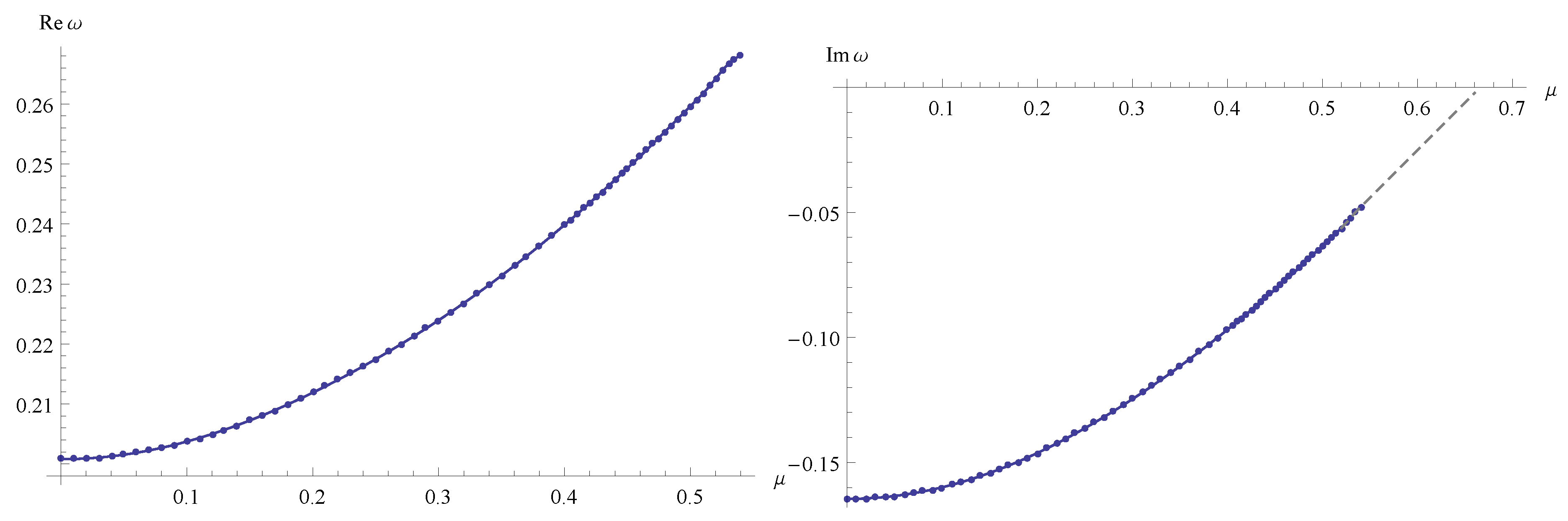
Preprints 89410 g003
Table 1. WKB QNMs of the massless scalar field for n = 0 , ℓ = 0 and various r 0 . The relative errors between the Frobenius and WKB6(Pade) data are denoted by δ Re and δ Im .
Table 1. WKB QNMs of the massless scalar field for n = 0 , ℓ = 0 and various r 0 . The relative errors between the Frobenius and WKB6(Pade) data are denoted by δ Re and δ Im .
r 0 6WKB 6WKB(Pade6) Frobenuis δ Re , % δ Im , %
0. 0.220934-0.201633 i 0.221357-0.208847 i 0.220910-0.209791 i 0.2 0.5
0.1 0.217552-0.193567 i 0.217915-0.200040 i 0.217504-0.200937 i 0.2 0.4
0.2 0.213934-0.185853 i 0.214249-0.191100 i 0.213874-0.191970 i 0.2 0.5
0.3 0.210448-0.178204 i 0.210136-0.182227 i 0.209951-0.182897 i 0.09 0.4
0.4 0.208655-0.167544 i 0.205219-0.173611 i 0.205638-0.173735 i 0.2 0.07
0.5 0.208603-0.151038 i 0.200411-0.164719 i 0.200799-0.164527 i 0.2 0.1
0.6 0.203865-0.134380 i 0.196607-0.155284 i 0.195235-0.155375 i 0.7 0.06
0.7 0.190388-0.126561 i 0.189317-0.142897 i 0.188651-0.146532 i 0.4 2.
0.8 0.177940-0.124934 i 0.179155-0.136701 i 0.180457-0.138822 i 0.7 2.
0.9 0.171056-0.122278 i 0.172101-0.132516 i 0.172187-0.133779 i 0.05 0.9
0.99 0.166036-0.118817 i 0.166942-0.128819 i 0.166989-0.130381 i 0.03 1.
Table 2. WKB QNMs of the massless scalar field for n = 0 , ℓ = 1 and various r 0 . The relative errors between the Frobenius and WKB6(Pade) data are denoted by δ Re and δ Im .
Table 2. WKB QNMs of the massless scalar field for n = 0 , ℓ = 1 and various r 0 . The relative errors between the Frobenius and WKB6(Pade) data are denoted by δ Re and δ Im .
r 0 6WKB 6WKB(Pade6) Frobenuis δ Re , % δ Im , %
0. 0.585819-0.195523 i 0.585864-0.195320 i 0.585872-0.195320 i 0.001 0.0002
0.1 0.584762-0.188491 i 0.584783-0.188359 i 0.584781-0.188354 i 0.0003 0.003
0.2 0.583633-0.181290 i 0.583644-0.181190 i 0.583630-0.181193 i 0.002 0.001
0.3 0.582424-0.173882 i 0.582414-0.173797 i 0.582405-0.173811 i 0.002 0.008
0.4 0.581117-0.166233 i 0.581089-0.166167 i 0.581087-0.166180 i 0.0003 0.008
0.5 0.579685-0.158305 i 0.579648-0.158255 i 0.579649-0.158265 i 0.0002 0.006
0.6 0.578086-0.150056 i 0.578050-0.150017 i 0.578052-0.150023 i 0.0003 0.004
0.7 0.576262-0.141436 i 0.576234-0.141402 i 0.576235-0.141405 i 0.0002 0.002
0.8 0.574121-0.132394 i 0.574107-0.132354 i 0.574273-0.131821 i 0.03 0.4
0.9 0.571523-0.122887 i 0.571527-0.122835 i 0.571522-0.122834 i 0.0008 0.0006
0.99 0.568621-0.113936 i 0.568634-0.113865 i 0.568635-0.113867 i 0.0001 0.002
Table 3. WKB QNMs of the massless scalar field for n = 0 , ℓ = 2 and various r 0 . The relative errors between the Frobenius and WKB6(Pade) data are denoted by δ Re and δ Im .
Table 3. WKB QNMs of the massless scalar field for n = 0 , ℓ = 2 and various r 0 . The relative errors between the Frobenius and WKB6(Pade) data are denoted by δ Re and δ Im .
r 0 6WKB 6WKB(Pade6) Frobenuis δ Re , % δ Im , %
0. 0.967284-0.193532 i 0.967287-0.193518 i 0.967288-0.193518 i 0.0001 0.0001
0.1 0.966641-0.186843 i 0.966643-0.186830 i 0.966644-0.186830 i 0.00007 0.0001
0.2 0.965963-0.179931 i 0.965965-0.179920 i 0.965965-0.179920 i 0.00004 0.0001
0.3 0.965243-0.172771 i 0.965244-0.172761 i 0.965244-0.172761 i 0.00002 0.0001
0.4 0.964467-0.165328 i 0.964467-0.165320 i 0.964467-0.165320 i 7 . × 10 − 6 0.0001
0.5 0.963619-0.157565 i 0.963619-0.157558 i 0.963619-0.157558 i 0.00002 0.00008
0.6 0.962675-0.149431 i 0.962675-0.149425 i 0.962675-0.149425 i 0.00003 0.00004
0.7 0.961598-0.140865 i 0.961598-0.140860 i 0.961598-0.140860 i 0.00003 0.00001
0.8 0.960332-0.131789 i 0.960332-0.131785 i 0.963197-0.130726 i 0.3 0.8
0.9 0.958783-0.122110 i 0.958784-0.122106 i 0.958783-0.122106 i 0.00002 0.00007
0.99 0.957022-0.112793 i 0.957022-0.112790 i 0.957022-0.112790 i 9 . × 10 − 6 0.00008
Table 4. QNMs of massless scalar field for the holonomy corrected BH ( r 0 = 0 . 1 ) and the Schwarzschild BH ( r 0 = 0 ) for ℓ = 0 and various overtones n. The relative difference for Re ω between these two cases is denoted by δ Re .
Table 4. QNMs of massless scalar field for the holonomy corrected BH ( r 0 = 0 . 1 ) and the Schwarzschild BH ( r 0 = 0 ) for ℓ = 0 and various overtones n. The relative difference for Re ω between these two cases is denoted by δ Re .
n Holonomy corrected BH Schwarzschild BH δ Re , %
0 0.217504-0.200937 i 0.220910-0.209791 i 1.6
1 0.172460-0.664156 i 0.172234-0.696105 i 0.1
2 0.153352-1.145927 i 0.151484-1.202157 i 1.2
3 0.143758-1.626790 i 0.140820-1.707355 i 2.0
4 0.137896-2.106328 i 0.134149-2.211264 i 2.7
5 0.133881-2.584943 i 0.129483-2.714279 i 3.3
6 0.130922-3.062923 i 0.125988-3.216683 i 3.8
7 0.128627-3.540451 i 0.123242-3.718654 i 4.2
8 0.126777-4.017645 i 0.121013-4.220307 i 4.5
9 0.125240-4.494585 i 0.119154-4.721719 i 4.9
Table 5. WKB QNMs of electromagnetic field for n = 0 , ℓ = 1 and various r 0 . The relative errors between the Frobenius and WKB6(Pade) data are denoted by δ Re and δ Im .
Table 5. WKB QNMs of electromagnetic field for n = 0 , ℓ = 1 and various r 0 . The relative errors between the Frobenius and WKB6(Pade) data are denoted by δ Re and δ Im .
r 0 6WKB 6WKB(Pade6) Frobenuis δ Re , % δ Im , %
0. 0.496383-0.185274 i 0.496509-0.184961 i 0.496527-0.184975 i 0.004 0.008
0.1 0.499896-0.179638 i 0.500019-0.179280 i 0.500035-0.179291 i 0.003 0.007
0.2 0.503368-0.173640 i 0.503482-0.173268 i 0.503496-0.173276 i 0.003 0.005
0.3 0.506777-0.167250 i 0.506879-0.166889 i 0.506890-0.166895 i 0.002 0.004
0.4 0.510100-0.160433 i 0.510186-0.160101 i 0.510195-0.160105 i 0.002 0.003
0.5 0.513301-0.153142 i 0.513371-0.152852 i 0.513377-0.152855 i 0.001 0.002
0.6 0.516331-0.145320 i 0.516383-0.145079 i 0.516387-0.145079 i 0.0007 0.0003
0.7 0.519115-0.136893 i 0.519150-0.136703 i 0.519151-0.136701 i 0.0003 0.002
0.8 0.521532-0.127774 i 0.521552-0.127634 i 0.521732-0.126988 i 0.03 0.5
0.9 0.523386-0.117876 i 0.523396-0.117779 i 0.523384-0.117771 i 0.002 0.008
0.99 0.524316-0.108278 i 0.524322-0.108206 i 0.524295-0.108205 i 0.005 0.0008
Table 6. WKB QNMs of electromagnetic field for n = 0 , ℓ = 2 and various r 0 . The relative errors between the Frobenius and WKB6(Pade) data are denoted by δ Re and δ Im .
Table 6. WKB QNMs of electromagnetic field for n = 0 , ℓ = 2 and various r 0 . The relative errors between the Frobenius and WKB6(Pade) data are denoted by δ Re and δ Im .
r 0 6WKB 6WKB(Pade6) Frobenuis δ Re , % δ Im , %
0. 0.915187-0.190022 i 0.915190-0.190009 i 0.915191-0.190009 i 0.0001 0.0001
0.1 0.917186-0.183746 i 0.917189-0.183731 i 0.917190-0.183731 i 0.0001 0.0001
0.2 0.919149-0.177203 i 0.919152-0.177188 i 0.919152-0.177188 i 0.00008 0.0001
0.3 0.921067-0.170365 i 0.921070-0.170351 i 0.921070-0.170350 i 0.00006 0.00009
0.4 0.922928-0.163195 i 0.922930-0.163182 i 0.922931-0.163182 i 0.00005 0.00008
0.5 0.924714-0.155649 i 0.924716-0.155637 i 0.924716-0.155637 i 0.00003 0.00007
0.6 0.926399-0.147669 i 0.926401-0.147660 i 0.926401-0.147659 i 0.00001 0.00007
0.7 0.927945-0.139187 i 0.927946-0.139179 i 0.927946-0.139179 i 8 . × 10 − 6 0.00007
0.8 0.929290-0.130111 i 0.929291-0.130105 i 0.930496-0.128371 i 0.1 1.
0.9 0.930333-0.120328 i 0.930333-0.120325 i 0.930332-0.120325 i 0.00009 0.00009
0.99 0.930868-0.110811 i 0.930868-0.110808 i 0.930867-0.110809 i 0.0001 0.0007
Table 7. QNMs of electromagnetic field for the holonomy corrected BH ( r 0 = 0 . 1 ) and the Schwarzschild BH ( r 0 = 0 ) for ℓ = 1 and various overtones n. The relative difference for Re ω between these two cases is denoted by δ Re .
Table 7. QNMs of electromagnetic field for the holonomy corrected BH ( r 0 = 0 . 1 ) and the Schwarzschild BH ( r 0 = 0 ) for ℓ = 1 and various overtones n. The relative difference for Re ω between these two cases is denoted by δ Re .
n Holonomy corrected BH Schwarzschild BH δ Re , %
0 0.500035-0.179291 i 0.496527-0.184975 i 0.7
1 0.439399-0.566668 i 0.429031-0.587335 i 2.4
2 0.366907-1.008246 i 0.349547-1.050375 i 4.7
3 0.313786-1.478207 i 0.292353-1.543818 i 6.8
4 0.277119-1.955922 i 0.253108-2.045101 i 8.7
5 0.250381-2.435159 i 0.224506-2.547851 i 10.3
6 0.229739-2.914343 i 0.202429-3.050533 i 11.9
7 0.213084-3.393104 i 0.184647-3.552798 i 13.3
8 0.199192-3.871396 i 0.169870-4.054612 i 14.7
9 0.187310-4.349255 i 0.157299-4.556018 i 16.0
Table 8. WKB QNMs of the Dirac field with the potential V D − ( r ) for n = 0 , k = 1 and various r 0 .
Table 8. WKB QNMs of the Dirac field with the potential V D − ( r ) for n = 0 , k = 1 and various r 0 .
k r 0 6WKB 6WKB(Pade6)
1 0. 0.366162-0.194105 i 0.365813-0.193991 i
1 0.1 0.367621-0.187362 i 0.367360-0.187224 i
1 0.2 0.369030-0.180342 i 0.368835-0.180209 i
1 0.3 0.370371-0.173012 i 0.370222-0.172915 i
1 0.4 0.371617-0.165327 i 0.371491-0.165303 i
1 0.5 0.372731-0.157236 i 0.372601-0.157325 i
1 0.6 0.373653-0.148676 i 0.373474-0.148926 i
1 0.7 0.374286-0.139579 i 0.373987-0.140027 i
1 0.8 0.374469-0.129886 i 0.373973-0.130546 i
1 0.9 0.373946-0.119604 i 0.373182-0.120470 i
1 0.99 0.372613-0.109991 i 0.371527-0.111055 i
Table 9. WKB QNMs of the Dirac field with the potential V D − ( r ) for n = 0 , k = 2 and various r 0 .
Table 9. WKB QNMs of the Dirac field with the potential V D − ( r ) for n = 0 , k = 2 and various r 0 .
k r 0 6WKB 6WKB(Pade6)
2 0. 0.760077-0.192833 i 0.760073-0.192813 i
2 0.1 0.760875-0.186255 i 0.760872-0.186238 i
2 0.2 0.761632-0.179435 i 0.761629-0.179421 i
2 0.3 0.762336-0.172344 i 0.762334-0.172332 i
2 0.4 0.762973-0.164947 i 0.762972-0.164936 i
2 0.5 0.763521-0.157200 i 0.763520-0.157189 i
2 0.6 0.763948-0.149051 i 0.763947-0.149038 i
2 0.7 0.764206-0.140433 i 0.764207-0.140417 i
2 0.8 0.764222-0.131264 i 0.764225-0.131243 i
2 0.9 0.763872-0.121451 i 0.763878-0.121422 i
2 0.99 0.763078-0.111991 i 0.763088-0.111955 i
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated