Prerpints.org logo
Preprint
Article

Adaptive Multi-source Domain Collaborative Fine-tuning for Transfer Learning

This version is not peer-reviewed.

Submitted:

02 November 2023

Posted:

02 November 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Fine-tuning is an important technique in transfer learning that has achieved significant success in tasks that lack training data. However, as it is difficult to extract effective features for single-source domain fine-tuning when the data distribution difference between the source and the target domain is large, we propose a transfer learning framework based on multi-source domain called adaptive multi-source domain collaborative fine-tuning to address this issue. This approach utilizes multiple source domain models for collaborative fine-tuning, thereby improving the model's feature extraction capability in the target task. Specifically, this approach employs an adaptive multi-source domain layer selection strategy to customize appropriate layer fine-tuning schemes for the target task among multiple source domain models. The objective is to extract more efficient features. Furthermore, a novel multi-source domain collaborative loss function is designed to facilitate the precise extraction of target data features by each source domain model. Simultaneously, it works towards minimizing the output difference among various source domain models, thereby enhancing the adaptability of the source domain model to the target data. In order to validate the effectiveness of the proposed the adaptive multi-source domain collaborative fine-tuning framework, it is analyzed and compared with the most widely used fine-tuning methods by applying them to seven publicly available visual categorization datasets commonly employed in transfer learning. Experimental results demonstrate that, in comparison with the existing fine-tuning approaches, our method not only enhances the accuracy of feature extraction in the model but also provides precise layer fine-tuning schemes for the target task, resulting in state-of-the-art performance.
Keywords: 
Subject: 
Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Transfer learning is an important machine learning technique that aims to utilize knowledge already acquired in the source domain to assist in the learning of related but different target tasks. This approach has achieved significant success in a variety of tasks for which training data is insufficient or of poor quality [1,2]. Model fine-tuning, as a commonly used transfer learning technique, effectively improves the learning performance by transferring the parameters of the pre-trained neural network (NN) model from the source domain to the target task and fine-tuning them [3,4]. Such fine-tuning techniques are already successfully used in various fields such as computer vision [5], natural language processing [6], speech recognition [7], recommendation systems [8], and medical diagnosis [9].
During the fine-tuning process, the source-domain model is usually pre-trained on a large-scale dataset (e.g., ImageNet [10]) and its parameters are replicated in the target model. In order to better adapt the model to the target task, its parameters are usually fine-tuned to improve their alignment with the target task. However, current research mostly focuses on the problem of single-source domain fine-tuning, i.e., transferring a single source-domain model for a specific target task and fine-tuning it, as shown in Figure 1. When this strategy is adopted, model performance is primarily determined by the selection of parameters during the fine-tuning process. Accordingly, parameters that are pertinent to the target task (and thus help extract features that are common to the source and the target domain) should remain unchanged, whereas those that are irrelevant or potentially detrimental to the model performance should be fine-tuned to enhance the model’s adaptive capacity. However, this requires accurate determination of the correlation between the source-domain model and the target task, which can be challenging and further complicates the selection of appropriate fine-tuning parameters. Traditional approaches for addressing this issue rely on expert experience or trial-and-error methods [2], while some researchers have implemented transfer learning by fine-tuning all layers of the model, known as full or standard fine-tuning [11,12]. Although this method is effective in improving the model performance compared to that achieved when the NN model is trained de novo, it may lead to overfitting when the source-domain model is large and the target dataset is small [13]. To mitigate this problem, some researchers proposed fine-tuning a subset of layers only [14,15,16]. However, even this strategy necessitates expert knowledge to determine which layers require fine-tuning, or this is done by trial-and-error. With the increasing scale of NN models, traditional fine-tuning methods not only become expensive but may also fail to provide precise fine-tuning schemes for the target task. Therefore, solving the problem of adaptive fine-tuning in large-scale models has become an important research focus.
In order to solve the problem that the model scale is large and the fine-tuning layer is difficult to select, optimization-based fine-tuning methods are proposed to adaptively select the layers that need to be fine-tuned [17,18], which reduces the cost of fine-tuning and improves the alignment between the source domain model and the target task. Optimization-based fine-tuning methods model the problem of selecting fine-tuning layers as an optimization problem with decision variables and iteratively optimizes to find appropriate layer fine-tuning schemes for the target task. Optimization-based methods can be further categorized into policy network and evolution optimization-based fine-tuning methods, whereby the former train an additional NN to make binary decisions for each layer in the source-domain model, thereby segregating those that need to be fine-tuned from those that do not [17,19]. While this method quickly provides suitable layer fine-tuning schemes for the target task, the optimization of policy networks based on discrete parameter training requires extensive training support. Therefore, when applying gradient descent directly, optimization can usually only be achieved by estimating approximate gradients. This, in turn, affects the accuracy of the fine-tuning schemes [20]. On the other hand, evolution optimization-based fine-tuning methods consider each fine-tuning scheme as an individual member of a population and find suitable layer fine-tuning schemes for the target task through population evolution [18,21,22]. This method avoids gradient computation and enables accurate search for fine-tuning schemes. The aforementioned arguments, however, apply to single source-domain model fine-tuning, which is suitable when the data distribution in the source and the target domain is very similar, as the crucial features of the target data can be learned and applied when learning the target task. However, when there is a significant data distribution difference between the source and the target domain, existing single-source domain fine-tuning methods often struggle to extract sufficient key feature information and experience performance degradation.
To address this shortcoming, we propose an adaptive multi-source domain collaborative fine-tuning (AMCF) framework which unifies multiple source-domain models into a single framework and fine-tunes them on the target task, thereby improving the model’s ability to extract the key features of the target task. Moreover, to determine the appropriate fine-tuning layer for multiple source-domain models, an adaptive multi-source domain layer selection strategy (AMLS) is designed. This strategy dynamically selects the layer for fine-tuning and freezing in each source-domain model based on the disparity between the target task and the source task. In addition, to mitigate the challenge posed by the variations among multiple source-domain models, which hinder the extraction of effective features for the target task, a multi-source collaborative loss function (MC-loss) is proposed. The objective of this function is to minimize the disparities in the outputs of the various source-domain models, thereby enhancing the accuracy of the features extracted by the models for the target task. The main contributions of this work are summarized below:
1) In order to enhance the feature extraction ability of the model to the target task, this paper replaces the original single model fine-tuning method by combining the collaborative fine-tuning of multiple source domains from a new perspective, which effectively improves the feature extraction ability of the model to the target task.
2) A proposed adaptive multi-source domain layer selection strategy (AMLS) aims to automatically choose the appropriate layer for fine-tuning the target task. This strategy enhances the model’s adaptability for the target task.
3) A novel transfer learning framework called adaptive multi-source domain collaborative fine-tuning (AMCF) is proposed. This framework effectively addresses the issue of a single source domain fine-tuning method struggling to extract key features from the target task when there is a significant difference in data distribution between the source and target domains. It achieves this by combining multiple source domain models to perform collaborative fine-tuning on the target task, resulting in improved model performance on the target task.
The remainder of this article is presented in four sections. Section 2 covers related work. Section 3 introduces the adaptive multi-source domain collaborative fine-tuning framework, which includes the adaptive multi-source domain layer selection strategy and the multi-source domain collaborative loss function. The experiments carried out on publicly available visual classification datasets to verify the utility of the proposed framework are presented in Section 4. This article concludes with Section 5, and offer suggestions for future work in this domain.

2. Related Work

Recently, the field of fine-tuning has experienced significant advancements, as evident from numerous publications that can be broadly categorized into those related to traditional methods and evolutionary-optimization-based methods. In the brief literature review provided below, we will focus on the work most closely related to this article.

2.1. Traditional Fine-tuning Methods

During the fine-tuning process, the selection of fine-tuning layers directly impacts the model’s performance on the target task [23]. Traditional fine-tuning methods focus on determining which layers need to be fine-tuned through expert experience and manual trial and error. In this regard, some researchers have chosen to fine-tune all layers for training on the target task, an approach known as full fine-tuning or standard fine-tuning [24,25]. For example, Dosovitskiy et al. [11] transferred a pre-trained Visual Transformer (ViT) model to multiple small-scale datasets and fine-tuned all the layers with good results. On the other hand, Raghu et al. [26] transferred a pre-trained source-domain model to the task of classifying epileptic seizure types from available electroencephalograms and fine-tuned all the model’s layer parameters, which significantly improved its performance. As a part of their work, Kornblith et al. [12] conducted extensive experiments and determined that the source-domain model accuracy when applied to the source task is strongly correlated with the accuracy transferred to the target task, highlighting the significance of source domain knowledge for the target task. However, when the amount of data related to the target task is small and the source-domain model is large, the standard fine-tuning approach tends to lead to overfitting.
To alleviate the issue of overfitting during model fine-tuning, some researchers have opted for freezing specific layers and fine-tuning only a subset of the model. For example, Basha et al. [27] effectively improved model generalizability to multiple image classification tasks by fine-tuning the last few layers of the source-domain model and freezing the remaining layers. However, this approach still requires manual setting of the number of fine-tuned layers. To address this issue, Zunair et al. [28] utilized a transfer learning technique and applied it to the Bengali digit classification problem. After conducting several experiments, these authors demonstrated that the best classification accuracy can be attained by selecting the first input layer and the last fully connected layer of the source-domain model as the fine-tuning layers. Similarly, Ghafoorian et al. [29] achieved the best performance in a transfer learning task for magnetic resonance imaging (MRI) segmentation by fine-tuning only the first six layers of the source-domain model. While these results are encouraging, as the size of convolutional neural networks (CNNs) increases, relying on manual human trial-and-error input to determine the layer parameters that need to be fine-tuned becomes time consuming and costly. Therefore, there is a need to develop automated methods for accurately selecting the layers to be fine-tuned.

2.2. Optimization-based Fine-tuning Methods

Optimization-based fine-tuning is an adaptive parameter selection method that models the fine-tuning layer selection as a combinatorial optimization problem which is solved through iterative optimization. Currently available methods based on this approach can be categorized into policy network and evolutionary optimization-based methods. The methods in the first group treat the decision of whether to fine-tune each layer parameter of the source-domain model as a binary variable and rely on an additional NN to determine a suitable fine-tuning scheme for the target task [19,30,31]. In their work focusing on image classification tasks, Guo et al. [30] utilized a recurrent gate network to make binary decisions on fine-tuning each layer during the fine-tuning process. On the other hand, Chen et al. [31] introduced a user-specific adaptive fine-tuning method (UAF) that determines which layers of the source-domain model to fine-tune for each input, whereby layer selection was accomplished using an additional policy network. To enhance model performance, Jang et al. [19] proposed a transfer learning method based on meta-learning techniques to adaptively determine which layers should be fine-tuned or frozen. Policy network-based methods are superior to traditional fine-tuning methods as they can quickly predict fine-tuning schemes suitable for the target task. While these approaches not only reduce costs but also significantly enhance the performance of fine-tuned models, this necessitates training a large number of discrete parameters. Moreover, due to the discreteness and non-differentiability of the fine-tuning parameter selection problem, directly applying gradient descent may affect the accuracy of the fine-tuning scheme [30].
These issues can be mitigated by applying the evolutionary optimization-based fine-tuning method, as it treats each fine-tuning scheme as an individual in the population. It searches for the best fine-tuning scheme through operations such as iterative population selection, crossover, and mutation. Vrbančič et al. [32] used the differential evolution algorithm to solve the combinatorial optimization problem of selecting the fine-tuning layer and determine the optimal fine-tuning scheme. Wen et al. [21] proposed a two-stage evolutionary transfer learning method to address the challenge of adapting the model structure to the target task in transfer learning. This method optimizes the selection problem of the fine-tuning layer by applying multi-objective optimization during the fine-tuning stage. Genetic algorithms have also been utilized to address the fine-tuning layer selection problem. For instance, they were adopted by Nagae et al. [18] and Mendes et al. [22] to identify effective layers suitable for fine-tuning, whereby the fine-tuning scheme was optimized using different initialization and crossover strategies. In their study, Hasan et al. [33] developed a genetic algorithm to select modules for fine-tuning in source-domain models that are typically composed of multiple modules. As shown above, the evolutionary optimization-based method eliminates the need for gradient computation and can accurately identify fine-tuning schemes that are suitable for the target task.
However, this approach is only suitable for fine-tuning a single source domain when the distribution difference between the source domain and the target domain is small. To extract more effective features for the target task, the work reported in this paper focuses on collaborative fine-tuning of multiple source-domain models, given that the learning performance when the method is applied to the target task can be further improved by jointly fine-tuning multiple source-domain models. The following section will introduce the proposed adaptive multi-source domain collaborative fine-tuning framework in detail.

3. Adaptive Multi-source Domain Collaborative Fine-tuning Framework

Most existing fine-tuning methods focus on fine-tuning individual source-domain models to the target domain. However, accurately extracting effective features from the target domain can be challenging when there is a significant difference in data distribution between the source and the target domain. We address this issue by proposing an AMCF framework for collaborative fine-tuning of multiple source-domain models, depicted in Figure 2. The AMCF framework can dynamically determine which layers should be fine-tuned and frozen for multiple source-domain models. The layers chosen for fine-tuning are updated during training, while the layers chosen for freezing retain their parameter values. The selection of fine-tuning layers is accomplished via an adaptive multi-source domain layer selection strategy (AMLS), whereby the target data is processed by each source-domain model to produce an output value. To reduce the discrepancies in output values yielded by different source-domain models, we take the average of N output values to obtain the predicted label. In fact, the core principle of the AMCF framework lies in the collaborative fine-tuning between different source-domain models. By utilizing multiple source-domain models, it is possible to extract more comprehensive features that can aid in the training of the target domain. Furthermore, by computing the difference loss between various source-domain models, the features extracted by the model can be more precise, thus enhancing the model’s performance on the target task.
The AMCF framework consists of two main components: (1) an adaptive multi-source domain layer selection strategy (AMLS) (described in Section 3.1); and (2) a multi-source collaborative loss function (MC-loss) (presented in Section 3.2).

3.1. Adaptive Multi-source Domain Layer Selection Strategy

During the fine-tuning process, certain layers in the source-domain model can extract features that are shared between the source and the target domain. These helpful network layers for the target task should be frozen, while the network layers specific to certain tasks should be fine-tuned to help the model adapt to the target task. Therefore, it is crucial to choose the right layers for fine-tuning in order to achieve optimal model performance. However, due to the large number of source-domain models, each model may have dozens or even hundreds of layers, making it difficult to efficiently select the layers that need to be fine-tuned. To address this problem, we propose an adaptive multi-source domain layer selection strategy (AMLS) that can automatically search for appropriate layer fine-tuning schemes from the vast model layers based on the differences between the target and the source domain. By employing this strategy, we can effectively identify the layers that require fine-tuning, rather than indiscriminately fine-tuning all layers, thereby enhancing the model performance on the target task.
We assume that the layers near the bottom of the source-domain model help extract shared features between the source domain and the target domain. Accordingly, we keep these layers frozen, while considering the layers closer to the top of the source-domain model (which are more susceptible to specific tasks) for fine-tuning. This is accomplished by combining the characteristics of individual models and utilizing the particle swarm optimization (PSO) algorithm to search for the optimal number of fine-tuning layers for multiple source-domain models. PSO is currently one of the most popular metaheuristic algorithms, as it is simple to implement and has strong global search capabilities [34]. When selecting fine-tuning layers for multiple source-domain models, we assume that there are N such models, denoted as { W ( 1 ) , W ( 2 ) , . . . , W ( N ) } . W ( j ) = { W 1 ( j ) , W 2 ( j ) , ⋯ , W ρ j ( j ) } represents the jth source-domain model, and W k ( j ) represents the kth layer parameters of the model W ( j ) . ρ j represents the total number of layers in model W ( j ) . The encoding form of the individuals (candidate solutions) in the problem of selecting fine-tuning layers for multiple source-domain models can be described as follows:
x i = ( x i , 1 , x i , 2 , ⋯ , x i , N )
where x i represents the ith population member, as well as the fine-tuning scheme for the corresponding layers of N models. x i , j represents the number of fine-tuned layers in the jth source domain model, and x i , j ∈ { 0 , 1 , . . . , ρ j } . Moreover, when x i , j = ρ j , it indicates that all layers of W ( j ) are fine-tuned. Conversely, when x i , j = 0 , it indicates that all layers of W ( j ) are frozen. In order to evaluate the quality of each individual, we use the classification accuracy of the target task corresponding to individual x i as the fitness value, expressed as follows:
f ( x i ) = A c c ( { W ^ ( 1 ) , W ^ ( 2 ) , ⋯ , W ^ ( N ) } ; D t )
where
W ^ ( j ) = W ( j ) − η ∂ L t o t a l ∂ W ( j ) ⊙ M ( j ) , j = 1 , 2 , ⋯ , N
M k ( j ) = 0 , k ≤ ρ j − x i , j , k = 1 , 2 , ⋯ , ρ j 1 , o t h e r
where M ( j ) = { M 1 ( j ) , M 2 ( j ) , ⋯ , M ρ j ( j ) } represents a mask matrix that corresponds one-to-one with the dimensions of model W ( j ) , which is mainly used to freeze or fine-tune parameters; W ^ ( j ) denotes the model fine-tuned by the source-domain model W ( j ) , using the mask matrix M ( j ) ; and M k ( j ) represents the mask value corresponding to all parameters W k ( j ) in the kth layer of the source-domain model W ( j ) . When M k ( j ) = 0 , it indicates that the parameters in this layer are frozen (i.e., not being fine-tuned), whereas M k ( j ) = 1 indicates that the parameters in this layer need to be fine-tuned to adapt to the target task. The value of M k ( j ) is determined by the individual x i . L t o t a l represents the multi-source domain collaborative loss function (MC-loss) proposed in this paper (as discussed in Section 3.2). A c c ( { W ^ ( 1 ) , W ^ ( 2 ) , ⋯ , W ^ ( N ) } ; D t ) represents the classification accuracy of the target task D t , which is obtained by fine-tuning the corresponding layer parameters based on individual x i in the framework of Figure 2. To reduce computational cost, the number of fine-tuning epochs for each individual is manually set to the m a x E p o c h (in this case, it is set to 5).
In the PSO, each particle has its own position (candidate solution) x i and velocity v i , which are continuously updated based on the guidance of individual historical best and the global best of the group, respectively, by applying the following expressions:
v i , d ( t + 1 ) = α * v i , d ( t ) + c 1 r 1 ( p i , d − x i , d ( t ) ) + c 2 r 2 ( p g , d − x i , d ( t ) )
x i , d ( t + 1 ) = x i , d ( t ) + v i , d ( t + 1 )
where x i , d ( t ) and v i , d ( t ) denote the position and velocity, respectively, of the ith individual in the tth generation population within the dth dimension; p i , d and p g , d respectively represent the historical optimal position of the ith individual on the dth dimension and the global optimal position of the population; r 1 and r 2 are random numbers ranging from 0 to 1; α denotes the inertia weight; and c 1 and c 2 represent the individual learning factors.
The AMLS is described in Algorithm 1. As can be seen from the presented steps, we first randomly generate a population with n individuals and initialize the velocity v = { v i , i = 1 , ⋯ , n } and the position x = { x i , i = 1 , ⋯ , n } (line 1). Each individual’s position x i represents the layer fine-tuning scheme corresponding to N source-domain models. Next, the individual best solution p i , i = 1 , ⋯ , n and the population best solution p g of n individuals are initialized respectively (line 2). Then, the masking matrix M ( k ) , k = 1 , ⋯ , N corresponding to N source-domain models is calculated based on each individual’s position information (lines 6-8), and the N source-domain models { W ( 1 ) , W ( 1 ) , ⋯ , W ( N ) } are fine-tuned m a x E p o c h times using the MC-loss function. The fitness value of each individual is calculated separately using Eq. (2), and the individual optimal position p j and the population optimal position p g are updated (lines 9-13). The current population optimal position p g is assigned to the optimal layer fine-tuning scheme x * using Eq. (5) and Eq. (6) to update the velocity and position of the individuals. After G iterations of updates, the optimal layer fine-tuning scheme x * for N source-domain models is obtained.
Algorithm 1: Adaptive multi-source domain layer selection strategy.
Input:The source-domain models W ( 1 ) , W ( 2 ) , ⋯ , W ( N ) ; target data D t ; population size n; the max iteration number G of the population.
  • Randomly generate populations with n individuals: ( v i , x i ) , i = 1 , ⋯ , n .
  • Initialize the individual optimal solution: p i = x i , i = 1 , ⋯ , n ; the population optimal
       solution: p g = x 1 .
  • for i = 1 to G do
  •      for j = 1 to n do
  •           for k = 1 to N do
  •              Calculate mask matrix M ( k ) according to x j , k using Eq. (4).
  •              Fine-tune model W ( k ) m a x E p o c h epochs on target data D t using Eq. (3).
  •          end for
  •          Calculate fitness value φ j of jth individual x j using Eq. (2).
  •          if  φ j better than p j  then
  •               p j = x j .
  •              if  φ j better than p g  then
  •                   p g = x j .
  •              end if
  •          end if
  •     end for
  •      x * = p g .
  •     Update all individual velocity v values using Eq. (5).
  •     Update all individual position x values using Eq. (6).
  • end for
Output:the optimal layer fine-tuning scheme x * .

3.2. Multi-source Collaborative Loss Function

Based on the AMLS, we can fine-tune the corresponding layers in multiple source-domain models. However, when the differences between multiple source-domain models are too large, it becomes challenging for the model to extract key feature information for the target task. Therefore, inspired by the multi-source domain adaptation method [35], we propose a multi-source domain collaborative loss (MC-loss) function to enhance the capability of multiple source-domain models in extracting crucial features for the target task. Unlike the previously reported multi-source domain adaptation methods, the method proposed in this paper does not require source domain data, as it solely relies on the pre-trained source-domain models, making its application more efficient.
In this paper, we apply the cross-entropy loss function separately to each source domain model in order to enhance the accuracy of feature extraction for multiple source domain models on the target task. In addition, when there is a significant difference in the output of the target data among multiple source domain models, it is unreasonable to treat all source domain models equally (by taking the average of the outputs), as it would lead to a decrease in the accuracy of correctly classified source domain models. Therefore, this article proposes a difference loss function that aims to minimize the discrepancy between the output of different source domain models. This loss function ensures that the outputs of the source domain models are treated equally, while also reducing the misclassification of different source domain models. The resulting multi-source collaborative loss function–a combination of the cross-entropy loss and the difference loss–can be mathematically represented as follows:
L t o t a l = ∑ k = 1 N L C E , k + β L D i f
where
L C E , k = − 1 D t ∑ i = 1 D t ∑ j = 1 C y i , j log O i , j k
L D i f = 1 D t ∑ i = 1 D t ∑ k = 1 N O i k − O ¯ i 2 2
where L C E , k represents the cross-entropy loss of model W ( k ) on the target dataset D t ; O i , j k denotes the output value of the jth dimension of the ith sample in model W ( k ) ; y i , j represents the true label of the ith sample belonging to the jth class; C is the total number of classes in the target dataset; D t represents the total number of samples in the target task; β is a hyperparameter; * 2 2 represents the 2-norm of *; L D i f denotes the difference loss between the outputs of N source-domain models; O i k represents the output of the ith sample on model W ( k ) ; and O ¯ i represents the average value of the outputs obtained by the ith sample in N source-domain models.

4. Experimental Design and Analysis of the Obtained Results

In order to verify the effectiveness of the proposed AMCF framework in solving the parameter fine-tuning problem in transfer learning, three sets of experiments were conducted. The objective of these experiments was to validate the AMLS, the MC-loss function, and the overall effectiveness of the proposed method, respectively.

4.1. Experimental Setup

In order to evaluate the effectiveness of the proposed multi-source domain collaborative fine-tuning method, we conducted extensive experiments on seven public datasets and compared the results with those obtained via currently utilized fine-tuning methods. In addition, we analyzed the effectiveness of the proposed AMLS and MC-loss function. The following three sets of experiments were performed for this purpose:
1) Experiment for establishing the effectiveness of the AMLS. The aim was to verify that the AMLS can accurately identify the layer fine-tuning scheme suitable for the target task.
2) Experiment for establishing the effectiveness of MC-loss function. Here, the goal was to verify that the MC-loss function can help multiple source-domain models learn a greater number of effective features pertaining to the target task.
3) Experiment for comparing the AMCF framework proposed here with the current state-of-the-art fine-tuning methods, including Train-From-Scratch, Standard Fine-Tuning [12], L2-SP [13], Child-Tuning [15], AdaFilter [20], and ALS [18].
Methods used in comparison: For clarity, a brief description of each method is given below.
  • Train-From-Scratch: This method trains the model anew using randomly initialized weights without applying any transfer learning methods.
  • Standard Fine-Tuning: This method fine-tunes all the parameters of the source-domain model on the target dataset [12].
  • L2-SP: This regularized fine-tuning method uses an L2 penalty in the loss function to ensure that the fine-tuned model is similar to the pre-trained model [13].
  • Child-Tuning: This method selects a child network in the source-domain model for fine-tuning through a Bernoulli distribution [15].
  • AdaFilter: This method uses a policy network to determine which filter parameters need to be fine-tuned [20].
  • ALS: This method uses a genetic algorithm to automatically select an effective update layer for transfer learning [18].
Datasets and the pre-trained models: For the comparisons, the two most widely used datasets-CIFAR-100 [36] and ImageNet [37]-served as source domain data, and Stanford Dogs [38], MIT Indoor [39], Caltech256-30, Caltech256-60 [40], Aircraft [41], UCF-101 [42], and Omniglot [43] datasets were used as the target domain data, as shown in Table 1. We used ResNet50 pre-trained on ImageNet and CIFAR-100 datasets as the two source-domain models for fine-tuning, respectively, whereby the classification accuracy of the model pre-trained on ImageNet was 75.15% (provided by the Torchvision library) and that of the model pre-trained on CIFAR-100 was 84.55%.
Implementation details: All experiments were conducted using the Pytorch framework on NVIDIA 3090 GPUs, utilizing SGD as the optimizer during training, with the weight decay and momentum set to 0.0005 and 0.9, respectively, and the initial learning rate and batch size set to 0.01 and 64, respectively. The number of fine-tuning epochs for evaluating each individual in our approach was set to 5. For the final fine-tuning, the number of epochs was set to 110, and learning rate decay was performed every 30 epochs. Each experiment was repeated five times to obtain the average classification accuracy.

4.2. Effectiveness Analysis of the Adaptive Multi-source Domain Layer Selection Strategy

In this section, we analyze the fine-tuning performance of different fine-tuning layer selection strategies to verify the effectiveness of the proposed adaptive multi-source domain layer selection (AMLS) strategy.
In this experiment, the fine-tuning performance of the AMLS is compared and analyzed with the random selection strategy, whereby the population size n was set to 10, the maximum number of population iterations G was set to 5, and the number m a x E p o c h of epochs for each individual in assessing fitness was set to 5. In the process of individual speed updating, the learning factors c 1 and c 2 were set to 1.5, and the inertia weights, α , were used in a linearly decreasing manner while remaining in the α ∈ [ 0.7 , 1.4 ] range. In the experiments with the random selection strategy, all the fine-tuning layers in the source-domain model were determined randomly. Based on the layer fine-tuning schemes obtained from the proposed strategy and the random selection strategy, we conducted 110 fine-tuning epochs on the source-domain model and evaluated its classification accuracy on each of the seven image classification datasets.
Table 2 shows the classification accuracy of the two selection strategies when applied to the test sets derived from all datasets. It is evident that the proposed AMLS achieved superior fine-tuning results on all datasets. On the other hand, the layer fine-tuned results yielded by the random selection strategy were, on average, 6% lower than those achieved with the proposed strategy, highlighting the importance of accurately selecting the layers for fine-tuning. Although making an inappropriate selection can greatly reduce the model’s performance during the fine-tuning process, the proposed strategy can accurately identify appropriate layers for fine-tuning in multiple source-domain models, effectively enhancing the model’s performance on the target task. Additionally, Figure 3 shows the number of fine-tuned layers obtained by the proposed AMLS on two source-domain models. Source-domain model 1 was trained on the CIFAR-100 dataset, while source-domain model 2 was trained on the ImageNet dataset. From the graph shown in Figure 3, it can be concluded that, even when the source domain is the same, the optimal number of fine-tuned layers will depend on the target task as well as the source-domain model.
In summary, the experimental results shown in Table 2 and Figure 3 indicate that the selection of fine-tuning layers in the source-domain model is crucial for the model performance during multi-source domain fine-tuning. The proposed AMLS can accurately identify the fine-tuning layers that are suitable for specific target tasks, thereby improving the model performance on the target task.

4.3. Effectiveness Analysis of the Multi-source Collaborative Loss Function

In this section, we report on the comparative experiments that were conducted to verify the fine-tuning effectiveness of the proposed MC-loss function when applied to the target task. For this purpose, a comparison with the cross-entropy loss function was conducted on both single-source domain and multi-source-domain models using four sets of experiments. In all experiments, the source-domain models adopted the same fine-tuning and freezing scheme (shown in Figure 3), while the hyperparameter value B was set to 0.2, and each set of experiments was trained for 110 epochs. The classification accuracy on the target task was recorded for each experiment, the details of which are outlined below.
(CE-loss, Model 1): Fine-tuning the source-domain model 1 on all target datasets using the cross-entropy loss function.
(CE-loss, Model 2): Fine-tuning the source-domain model 2 on all target datasets using the cross-entropy loss function.
(CE-loss, Model 1 and 2): The proposed multi-source domain fine-tuning framework applied for fine-tuning source-domain model 1 and source-domain model 2 using the cross-entropy loss function.
(MC-loss, Model 1 and 2): The proposed multi-source domain fine-tuning framework is applied, which involves fine-tuning source-domain model 1 and source-domain model 2 using the multi-source domain collaborative loss function.
Table 3 shows the classification accuracy achieved by the aforementioned four fine-tuning combinations on seven datasets, confirming that the multi-source domain collaborative fine-tuning method is superior to the single-source domain fine-tuning method. These results suggest that a single source-domain model can only extract limited key features for the target task, whereas collaborative fine-tuning with multiple source domains can extract more key features, leading to a significant improvement in the model performance on the target task.
These experimental results demonstrate that the MC-loss function aids in the adaptation of the source-domain model to the target task, while also minimizing differences in the extracted features. This can help the model learn more useful features, thereby significantly improving the fine-tuning performance of the model.

4.4. Comparison of the Adaptive Multi-source Collaborative Fine-tuning Method with State-of-the-art Fine-tuning Methods

In this section, we compare and analyze the proposed fine-tuning method with several popular fine-tuning methods, including Train-From-Scratch, Standard Fine-Tuning, L2-SP, Child-Tuning, AdaFilter, and ALS. The effectiveness of the proposed method is validated by applying all alternatives to seven public datasets. All methods were iterated 110 epochs and each method was applied five times to obtain the average classification accuracy and eliminate the influence of randomness. The experimental results are presented in Table 4, whereby those related to the L2-SP and AdaFilter methods were sourced from published works [13,20].
As can be seen from Table 4, the proposed multi-source domain collaborative fine-tuning method achieved the highest accuracy on all datasets. The Train-From-Scratch method achieved the lowest accuracy as it trained the target task using randomly initialized weight parameters, without employing any fine-tuning techniques. Standard Fine-Tuning, L2-SP, Child-Tuning, AdaFilter, and ALS methods are single-source domain fine-tuning techniques and utilize the source-domain model for fine-tuning. Accordingly, they greatly enhance performance compared to the Train-From-Scratch approach. However, the performance of single-source domain fine-tuning methods is limited when there is a significant difference in data distribution between the source and the target domain, as the key features extracted from a single source-domain model on the target task are limited. In contrast, the proposed multi-source domain fine-tuning method combines rich features extracted from multiple source-domain models, making the model’s predictions on the target task more accurate and effectively improving the model performance. Figure 4 shows the test accuracy curves of our method, ALS, Child-Tuning, and Standard Fine-Tuning baseline when applied to the Stanford Dogs, MIT Indoors, Caltech256-30, and Caltech256-60 datasets. The black curve represents the fine-tuning results of the proposed AMCF. It is evident that the proposed method significantly improves fine-tuning performance compared to other fine-tuning methods on all datasets. For example, after 5 epochs, our method achieves classification accuracies of 79.80%, 71.11%, 75.91%, and 80.03%, while the standard fine-tuning baseline method only achieves 67.73%, 62.61%, 69.66%, and 71.28%. Therefore, our method can match or even surpass the accuracy level of the standard fine-tuning baseline approach in fewer epochs, significantly reducing training time for new tasks, making it more suited for practical applications.
These experimental results demonstrate that the proposed AMCF effectively extracts a greater number of key features in the target task by fine-tuning multiple source-domain models. Compared to current single-source domain fine-tuning methods, it greatly enhances the fine-tuning performance, while achieving competitive results within fewer training epochs, as shown in Figure 4.

4.5. Experimental Findings

Based on the experimental results, the following conclusions can be reached: (1) multi-source domain fine-tuning is more beneficial for learning effective feature information in the target task, leading to a significant improvement in model performance; and (2) the selection of fine-tuning layers in the source-domain model is crucial for achieving optimal fine-tuning performance, and this selection varies depending on the target task. The proposed AMLS can accurately identify the appropriate layers for the target task.
While this method improves the model performance on the target task compared to single-source domain fine-tuning strategy, training multiple source-domain models can lead to slower inference speed. When there are N source-domain models, the number of parameters required for training will be approximately N times greater than that in single-source domain fine-tuning approach.

5. Conclusion

In order to mitigate the difficulty in extracting effective features through single-source domain fine-tuning when there is a significant difference in data distribution between the source domain and the target domain, we proposed a transfer learning framework called adaptive multi-source domain collaborative fine-tuning. As shown in this paper, this method effectively improves the training accuracy of the fine-tuned model on the target task by combining the collaborative fine-tuning of multiple source-domain models. In the proposed method, in order to solve the problem of accurate selection of fine-tuning layers in multi-source domain models, a multi-source domain fine-tuning layer selection strategy was designed to automatically select appropriate layers for fine-tuning in each source-domain model. Based on this strategy, a multi-source domain collaborative loss function was developed to reduce the output differences between different source-domain models, improving the accuracy of features in the model when applied to the target task. Experimental results obtained in this work show that, compared with the most widely used fine-tuning methods, the transfer learning method of multi-source domain collaborative fine-tuning strategy achieves effective and efficient knowledge transfer between multiple source-domain models and a single target task, significantly improving the training accuracy.
However, since the multi-source domain fine-tuning method combines multiple source-domain models for collaborative fine-tuning, its parameter scale is extremely large, making it difficult to execute this approach on devices with limited computational resources. Therefore, our future work will primarily focus on exploring multi-source domain collaborative fine-tuning methods that can be adopted in such contexts.

Author Contributions

Conceptualization, F.F.-J and F.L; Methodology, F.L. and Y.Y.; Software, L.Z.-L and Z.T.-T; Validation, F.L.; Formal analysis, T.H.-C; Investigation, Y.Y.; Resources, T.M.; Writing—original draft preparation, F.L.; Writing—review and editing, T.H.-C., N.Z.-Z, L.Z.-L, F.F.-J, T.M. and Z.T.-T; Supervision, F.F.-J.; Project administration, F.F.-J, T.M, L.Z.-L, F.L. and Y.Y. All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

The figures utilized to support the findings of this study are embraced in the article.

Acknowledgments

We truly thank the reviewers for the pertinent comments. This work is supported by the National Natural Science Foundation of China (62162012), the Guizhou Provincial Science and Technology Projects (QKHJCZK2022YB195, QKHJCZK2023YB143, QKHPTRCZCKJ2021007), the Natural Science Research Project of Education Department of Guizhou Province (QJJ2023061, QJJ2023012, QJJ2022015), Guizhou province pattern recognition and intelligent system key laboratory open subject (GZMUKL2022KF01, GZMUKL2022KF05), the High-Level Innovative Talent Project of Guizhou Province (QKHPTRC-GCC2023027), and the Youth Science and Technology Talent Growth Project of Guizhou Province (QJHKY2022319).

Conflicts of Interest

Declare conflicts of interest or state “The authors declare no conflict of interest.

References

  1. Pan, S. J.; Yang, Q. A Survey on Transfer Learning. IEEE Transactions on Knowledge and Data Engineering 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
  2. Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A Comprehensive Survey on Transfer Learning. Proceedings of the IEEE 2021, 109, 43–76. [Google Scholar] [CrossRef]
  3. Alhussan, A. A.; Abdelhamid, A. A.; Towfek, S. K.; Ibrahim, A.; Abualigah, L.; Khodadadi, N.; Khafaga, D. S.; Al-Otaibi, S.; Ahmed, A. E. Classification of Breast Cancer Using Transfer Learning and Advanced Al-Biruni Earth Radius Optimization. Biomimetics 2023, 8. [Google Scholar] [CrossRef]
  4. Li, H.; Fowlkes, C.; Yang, H.; Dabeer, O.; Tu, Z.; Soatto, S. Guided Recommendation for Model Fine-Tuning. 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2023; pp. 3633–3642. [Google Scholar]
  5. Dai, Z.; Cai, B.; Lin, Y.; Chen, J. Unsupervised Pre-Training for Detection Transformers. IEEE Transactions on Pattern Analysis and Machine Intelligence 2023, 45, 12772–12782. [Google Scholar] [CrossRef]
  6. Chi, Z.; Huang, H.; Liu, L.; Bai, Y.; Gao, X.; Mao, X. L. Can Pretrained English Language Models Benefit Non-English NLP Systems in Low-Resource Scenarios? IEEE/ACM Transactions on Audio, Speech, and Language Processing 2023, 1–14. [Google Scholar] [CrossRef]
  7. Chen, L. W.; Rudnicky, A. Exploring Wav2vec 2.0 Fine Tuning for Improved Speech Emotion Recognition. 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); 2023; pp. 1–5. [Google Scholar]
  8. Liao, W.; Zhang, Q.; Yuan, B.; Zhang, G.; Lu, J. Heterogeneous Multidomain Recommender System Through Adversarial Learning. IEEE Transactions on Neural Networks and Learning Systems 2022, 1–13. [Google Scholar] [CrossRef]
  9. Badawy, M.; Balaha, H. M.; Maklad, A. S.; Almars, A. M.; Elhosseini, M. A. Revolutionizing Oral Cancer Detection: An Approach Using Aquila and Gorilla Algorithms Optimized Transfer Learning-Based CNNs. Biomimetics 2023, 8. [Google Scholar] [CrossRef]
  10. Tian, J.; Dai, X.; Ma, C. Y.; He, Z.; Liu, Y. C.; Kira, Z. Trainable Projected Gradient Method for Robust Fine-Tuning. 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2023; pp. 7836–7845. [Google Scholar]
  11. Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; Uszkoreit, J.; Houlsby, N. An image is worth 16x16 words: transformers for image recognition at scale. In International Conference on Learning Representations (ICLR) 2021. [Google Scholar] [CrossRef]
  12. Kornblith, S.; Shlens, J.; Le, Q. V. Do Better ImageNet Models Transfer Better? 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2019; pp. 2656–2666. [Google Scholar]
  13. LI, X.; Grandvalet, Y.; Davoine, F. Explicit Inductive Bias for Transfer Learning with Convolutional Networks. In Proceedings of the 35th International Conference on Machine Learning 2018, pp, 2825–2834. [Google Scholar]
  14. Peters, M. E.; Ruder, S.; Smith, N. A. To Tune or Not to Tune? Adapting Pretrained Representations to Diverse Tasks. In In Proceedings of the 4th Workshop on Representation Learning for NLP 2019, pp, 7–14. [Google Scholar]
  15. Xu, R.; Luo, F.; Zhang, Z.; Tan, C.; Chang, B.; Huang, S.; Huang, F. Raise a Child in Large Language Model: Towards Effective and Generalizable Fine-tuning. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing 2021, pp, 9514–9528. [Google Scholar]
  16. Shen, Z.; Liu, Z.; Qin, J.; Savvides, M.; Cheng, K.-T. Partial Is Better Than All: Revisiting Fine-tuning Strategy for Few-shot Learning. In Proceedings of the AAAI Conference on Artificial Intelligence 2021, pp, 9594–9602. [Google Scholar] [CrossRef]
  17. Wang, W.; Chen, Y.; Ghamisi, P. Transferring CNN With Adaptive Learning for Remote Sensing Scene Classification. IEEE Transactions on Geoscience and Remote Sensing 2022, 60, 1–18. [Google Scholar] [CrossRef]
  18. Nagae, S.; Kanda, D.; Kawai, S.; Nobuhara, H. Automatic layer selection for transfer learning and quantitative evaluation of layer effectiveness. Neurocomputing 2022, 469, 151–162. [Google Scholar] [CrossRef]
  19. Jang, Y.; Lee, H.; Hwang, S. J.; Shin, J. Learning What and Where to Transfer. In Proceedings of the 36th International Conference on Machine Learning 2019, pp, 3030–3039. [Google Scholar]
  20. Guo, Y.; Li, Y.; Wang, L.; Rosing, T. Adafilter: Adaptive filter fine-tuning for deep transfer learning. In Proceedings of the AAAI Conference on Artificial Intelligence 2020, pp, 4060–4066. [Google Scholar] [CrossRef]
  21. Wen, Y. W.; Peng, S. H.; Ting, C. K. Two-Stage Evolutionary Neural Architecture Search for Transfer Learning. IEEE Transactions on Evolutionary Computation 2021, 25, 928–940. [Google Scholar] [CrossRef]
  22. Mendes, R. d. L.; Alves, A. H. d. S.; Gomes, M. d. S.; Bertarini, P. L. L.; Amaral, L. R. d. Many Layer Transfer Learning Genetic Algorithm (MLTLGA): a New Evolutionary Transfer Learning Approach Applied To Pneumonia Classification. In 2021 IEEE Congress on Evolutionary Computation (CEC) 2021, pp, 2476–2482. [Google Scholar]
  23. Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How transferable are features in deep neural networks? In Proceedings of the 27th International Conference on Neural Information Processing Systems 2014, pp, 3320–3328. [Google Scholar]
  24. Chen, M.; Radford, A.; Child, R.; Wu, J.; Jun, H.; Luan, D.; Sutskever, I. Generative pretraining from pixels. In Proceedings of the 37th International Conference on Machine Learning 2020, pp, 1691–1703. [Google Scholar]
  25. Raffel, C.; Shazeer, N.; Roberts, A.; Lee, K.; Narang, S.; Matena, M.; Zhou, Y.; Li, W.; Liu, P. J. Exploring the limits of transfer learning with a unified text-to-text transformer. The Journal of Machine Learning Research 2020, 21, 5485–5551. [Google Scholar]
  26. Raghu, S.; Sriraam, N.; Temel, Y.; Rao, S. V.; Kubben, P. L. EEG based multi-class seizure type classification using convolutional neural network and transfer learning. Neural Networks 2020, 124, 202–212. [Google Scholar] [CrossRef]
  27. Basha, S. H. S.; Vinakota, S. K.; Pulabaigari, V.; Mukherjee, S.; Dubey, S. R. AutoTune: Automatically Tuning Convolutional Neural Networks for Improved Transfer Learning. Neural Networks 2021, 133, 112–122. [Google Scholar] [CrossRef]
  28. Zunair, H.; Mohammed, N.; Momen, S. Unconventional Wisdom: A New Transfer Learning Approach Applied to Bengali Numeral Classification. In 2018 International Conference on Bangla Speech and Language Processing (ICBSLP) 2018, pp, 1–6. [Google Scholar]
  29. Ghafoorian, M.; Mehrtash, A.; Kapur, T.; Karssemeijer, N.; Marchiori, E.; Pesteie, M.; Guttmann, C. R. G.; de Leeuw, F.-E.; Tempany, C. M.; van Ginneken, B.; Fedorov, A.; Abolmaesumi, P.; Platel, B.; Wells, W. M. Transfer Learning for Domain Adaptation in MRI: Application in Brain Lesion Segmentation. In Medical Image Computing and Computer Assisted Intervention-MICCAI; 2017; pp. 516–524. [Google Scholar]
  30. Guo, Y.; Shi, H.; Kumar, A.; Grauman, K.; Rosing, T.; Feris, R. SpotTune: Transfer Learning Through Adaptive Fine-Tuning. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2019; pp. 4800–4809. [Google Scholar]
  31. Chen, L.; Yuan, F.; Yang, J.; He, X.; Li, C.; Yang, M. User-Specific Adaptive Fine-Tuning for Cross-Domain Recommendations. IEEE Transactions on Knowledge and Data Engineering 2023, 35, 3239–3252. [Google Scholar] [CrossRef]
  32. Vrbančič, G.; Podgorelec, V. Transfer Learning With Adaptive Fine-Tuning. IEEE Access 2020, 8, 196197–196211. [Google Scholar] [CrossRef]
  33. Hasana, M. M.; Ibrahim, M.; Ali, M. S. Speeding Up EfficientNet: Selecting Update Blocks of Convolutional Neural Networks using Genetic Algorithm in Transfer Learning. arXiv 2023, arXiv:00261. [Google Scholar]
  34. Zeng, N.; Wang, Z.; Liu, W.; Zhang, H.; Hone, K.; Liu, X. A Dynamic Neighborhood-Based Switching Particle Swarm Optimization Algorithm. IEEE Transactions on Cybernetics 2022, 52, 9290–9301. [Google Scholar] [CrossRef]
  35. Zhu, Y.; Zhuang, F.; Wang, D. Aligning domain-specific distribution and classifier for cross-domain classification from multiple sources. In Proceedings of the 33 AAAI Conference on Artificial Intelligence 2019, pp, 5989–5996. [Google Scholar] [CrossRef]
  36. Krizhevsky, A.; Hinton, G. Learning multiple layers of features from tiny images. Technical report 2009. [Google Scholar]
  37. Yamada, Y.; Otani, M. Does Robustness on ImageNet Transfer to Downstream Tasks? 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2022; pp. 9205–9214. [Google Scholar]
  38. Khosla, A.; Jayadevaprakash, N.; Yao, B.; Li, F.-F. Novel dataset for fine-grained image categorization: Stanford dogs. Proc. CVPR workshop on fine-grained visual categorization (FGVC) 2011. [Google Scholar]
  39. Quattoni, A.; Torralba, A. Recognizing indoor scenes. In 2009 IEEE Conference on Computer Vision and Pattern Recognition 2009, pp, 413–420. [Google Scholar]
  40. Griffin, G.; Holub, A.; Perona, P. Caltech-256 object category dataset. California Institute of Technology 2007. [Google Scholar]
  41. Maji, S.; Rahtu, E.; Kannala, J.; Blaschko, M.; Vedaldi, A. J. A. P. A. Fine-grained visual classification of aircraft. arXiv 2013, arXiv:1306.5151 2013. [Google Scholar]
  42. Bilen, H.; Fernando, B.; Gavves, E.; Vedaldi, A.; Gould, S. Dynamic Image Networks for Action Recognition. In 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2016, pp, 3034–3042. [Google Scholar]
  43. Lake, B. M.; Salakhutdinov, R.; Tenenbaum, J. B. Human-level concept learning through probabilistic program induction. Science 2015, 350, 1332–1338. [Google Scholar] [CrossRef]
Preprints 89467 g001
Figure 1. Graphical representation of the single-source domain fine-tuning process.
Figure 1. Graphical representation of the single-source domain fine-tuning process.
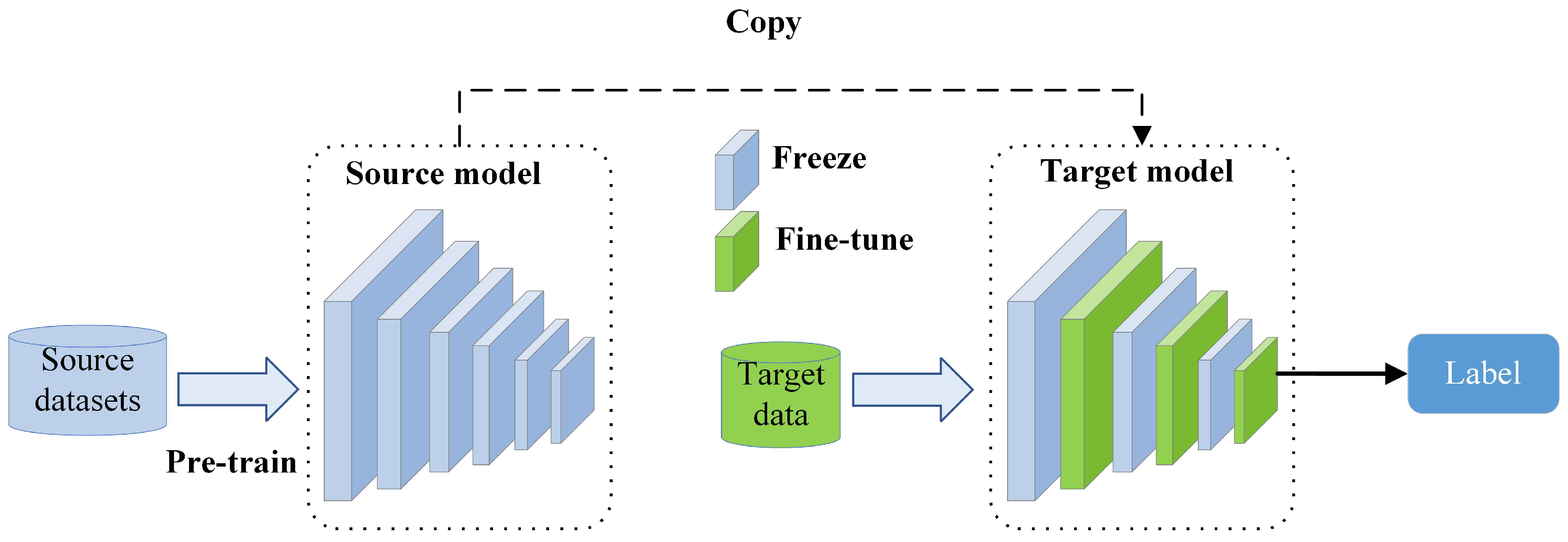
Preprints 89467 g001
Preprints 89467 g002
Figure 2. Framework diagram of the proposed adaptive multi-source domain collaborative fine-tuning (AMCF), where “AMLS” represents the proposed adaptive multi-source domain layer selection strategy, “CE loss” represents the cross-entropy loss function, and “Dif loss” represents the difference loss function.
Figure 2. Framework diagram of the proposed adaptive multi-source domain collaborative fine-tuning (AMCF), where “AMLS” represents the proposed adaptive multi-source domain layer selection strategy, “CE loss” represents the cross-entropy loss function, and “Dif loss” represents the difference loss function.
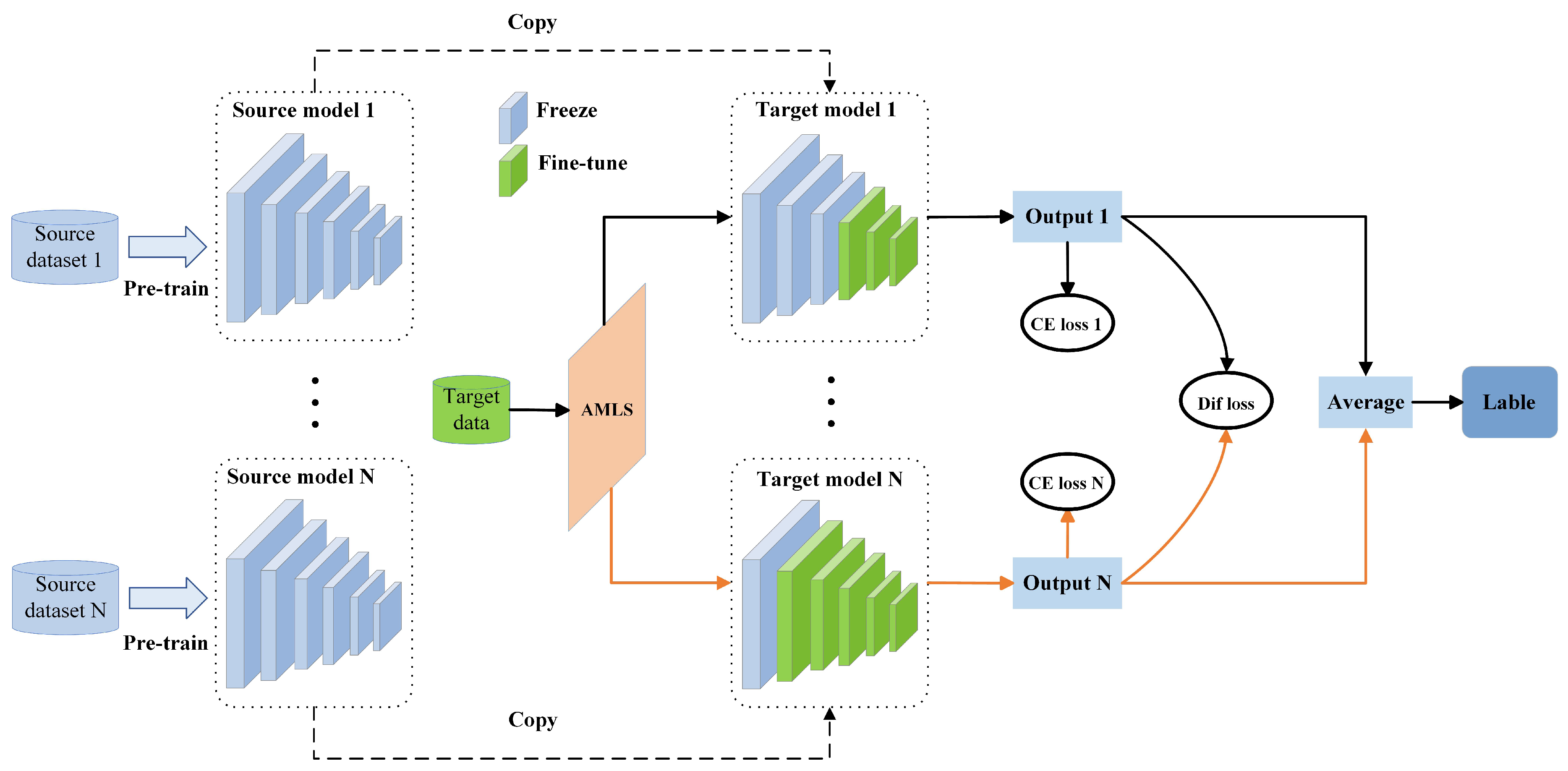
Preprints 89467 g002
Preprints 89467 g003
Figure 3. The number of fine-tuning layers obtained via each source-domain model using the AMLS.
Figure 3. The number of fine-tuning layers obtained via each source-domain model using the AMLS.
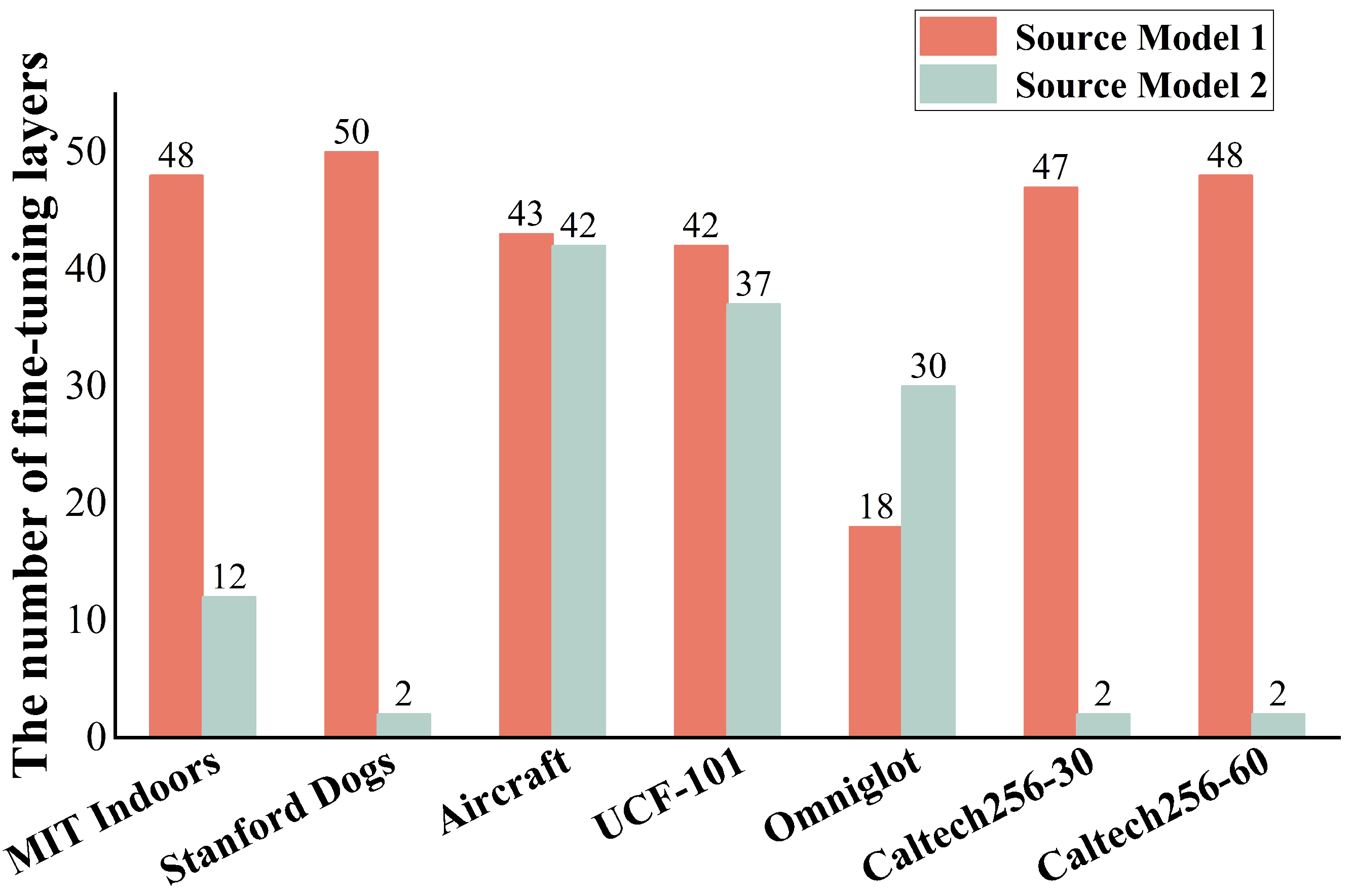
Preprints 89467 g003
Preprints 89467 g004
Figure 4. Test accuracy curve of the proposed method, ALS, Child-Tuning, and Standard Fine-Tuning baseline when applied to MIT Indoors, Stanford Dogs, Caltech256-30, and Caltech256-60 datasets.
Figure 4. Test accuracy curve of the proposed method, ALS, Child-Tuning, and Standard Fine-Tuning baseline when applied to MIT Indoors, Stanford Dogs, Caltech256-30, and Caltech256-60 datasets.
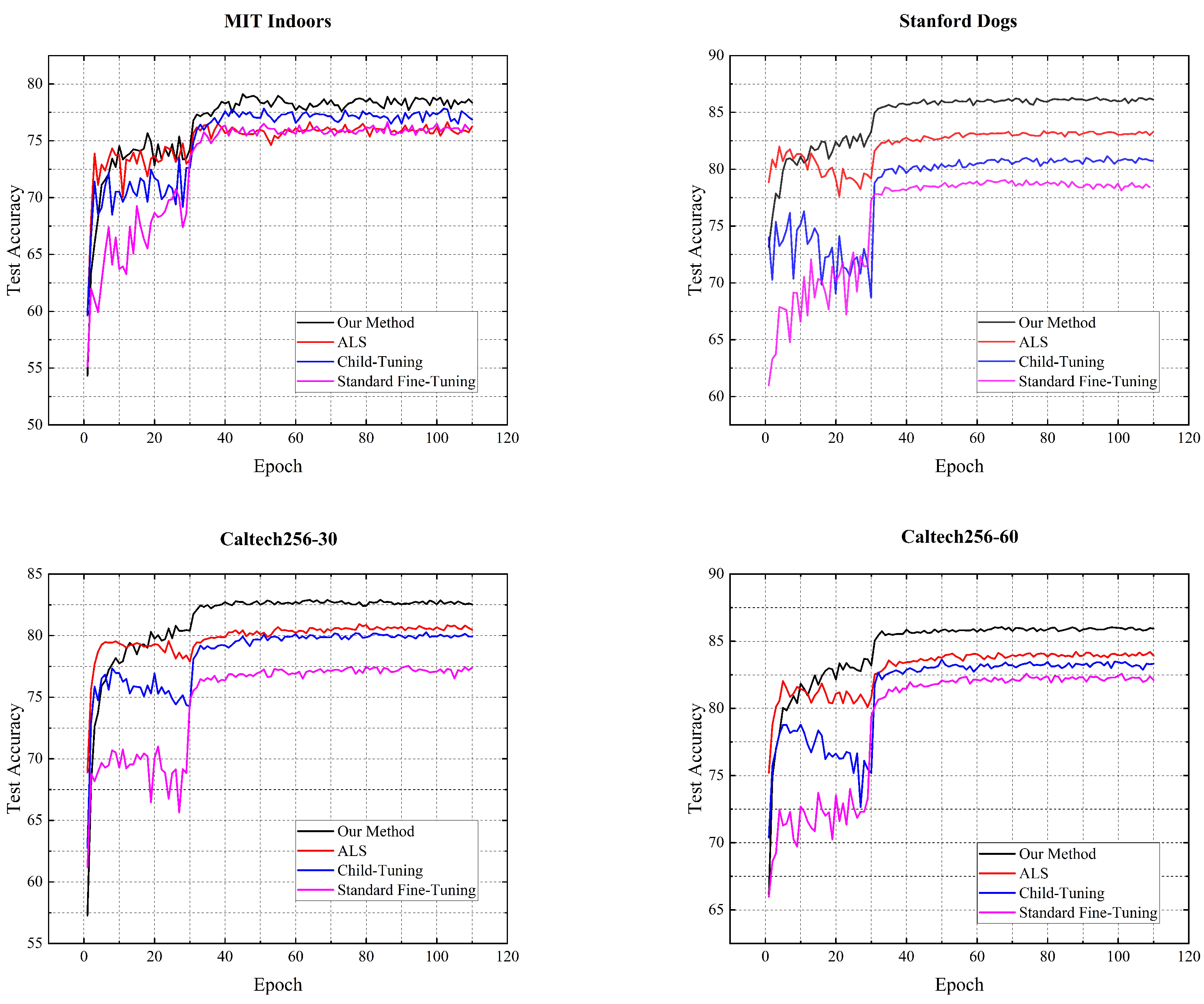
Preprints 89467 g004
Table 1. Datasets used to evaluate our method and compare it to other fine-tuning approaches.
Table 1. Datasets used to evaluate our method and compare it to other fine-tuning approaches.
Target Datasets Training Instances Evaluation Instances Classes
Stanford Dogs [38] 12000 8580 120
MIT Indoor [39] 5360 1340 67
Caltech256-30 [40] 7680 5120 256
Caltech256-60 [40] 15360 5120 256
Aircraft [41] 3334 3333 100
UCF-101 [42] 7629 1908 101
Omniglot [43] 19476 6492 1623
Table 2. Classification accuracy achieved using random selection strategy and the proposed AMLS.
Table 2. Classification accuracy achieved using random selection strategy and the proposed AMLS.
Selection Strategy MIT Indoor Stanford Dogs Caltech256-30 Caltech256-60 Aircraft UCF-101 Omniglot
Random Selection 77.91% 81.32% 77.59% 79.02% 49.50% 72.43% 85.15%
AMLS 79.10% 86.30% 82.91% 86.05% 62.31% 80.54% 87.76%
Table 3. Fine-tuning results of different loss functions on multiple source-domain models.
Table 3. Fine-tuning results of different loss functions on multiple source-domain models.
Loss Function MIT Indoor Stanford Dogs Caltech256-30 Caltech256-60 Aircraft UCF-101 Omniglot
(CE-loss, Model 1) 76.19% 84.79% 82.59% 84.65% 54.39% 76.25% 87.30%
(CE-loss, Model 2) 70.74% 75.86% 67.91% 77.16% 51.45% 76.25% 86.59%
(CE-loss, Model 1 and 2) 78.95% 85.31% 81.03% 84.86% 57.03% 78.13% 87.53%
(MC-loss, Model 1 and 2) 79.10% 86.30% 82.91% 86.05% 62.31% 80.54% 87.76%
Table 4. The proposed method is compared with the state-of-the-art method in terms of Top-1 classification accuracy.
Table 4. The proposed method is compared with the state-of-the-art method in terms of Top-1 classification accuracy.
Method MIT Indoor Stanford Dogs Caltech256-30 Caltech256-60 Aircraft UCF-101 Omniglot
Train-From-Scratch 40.82% 42.45% 25.41% 47.55% 12.12% 43.61% 84.82%
Standard Fine-Tuning [12] 76.64% 79.02% 77.53% 82.57% 56.10% 76.83% 87.21%
L2-SP [13] 76.41% 79.69% 79.33% 82.89% 56.52% 74.33% 86.92%
Child-Tuning [15] 77.83% 81.13% 80.19% 83.63% 55.92% 77.40% 87.32%
AdaFilter [20] 77.53% 82.44% 80.62% 84.31% 55.41% 76.99% 87.46%
ALS [18] 76.64% 83.34% 80.93% 84.21% 56.04% 75.78% 87.09%
Ours 79.10% 86.30% 82.91% 86.05% 62.31% 80.54% 87.76%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated