Preprint
Hypothesis
The Universal Consciousness Code Theory: Exploring the Physical Basis of Consciousness and Potential Decoding with AI Technologies
Altmetrics
Downloads
161
Views
67
Comments
0


This version is not peer-reviewed
Submitted:
02 November 2023
Posted:
02 November 2023
You are already at the latest version
Alerts
Abstract
Consciousness pervades our daily experiences, yet it remains largely unaccounted for in contemporary physics and chemistry theories. Several existing theories, such as the Integrated Information Theory (IIT), Global Workspace Theory (GWT), Electromagnetic Field Theory (EMF Theory of Consciousness), and Orchestrated Objective Reduction Theory (Orch-OR), attempt to clarify the essence of consciousness. Yet, they often encounter significant challenges. These challenges arise due to the intricate nature of our neural systems and the limitations of current measurement and computational technologies, which often prevent these theories from being rigorously mathematically described or quantitatively tested. Here we introduce a novel theory that hypothesizes consciousness as an inherent property of certain particle configurations. Specifically, when a group of particles align in a particular state, they exhibit consciousness. This relationship between particle states and conscious perceptions is governed by what we term the "universal consciousness code". And we propose a possible practical mathematical method to decipher the complex relationship between neural activities and consciousness and to test our theory using the latest artificial intelligence technologies.
Keywords:
Subject: Biology and Life Sciences - Neuroscience and Neurology
1. Introduction
Modern physics provides a remarkably precise framework for understanding the properties of particles, enabling us to describe and predict mass, energy, motion, and charge with unparalleled accuracy. This precision extends even to the smallest and largest spatial and temporal scales [1]. However, despite these advancements, a comprehensive scientific understanding of subjective consciousness, a phenomenon we encounter daily, remains elusive [2]. Given the fundamental nature of consciousness and its centrality in our daily experiences, integrating it into the framework of modern physics and expressing it through mathematical language can offer precision, predictability, and a unified understanding of this phenomenon.
Several current theories attempt to elucidate the nature of consciousness. These include the Integrated Information Theory (IIT) [3], Global Workspace Theory (GWT) [4], Electromagnetic Field Theory (EMF Theory of Consciousness) [5], and the Orchestrated Objective Reduction (Orch-OR) Theory [6]. However, many of these theories still face challenges in mathematically describing consciousness and being quantitatively validated, often due to the complexity of neural systems and the limitations of current measurement and computational methodologies.
Here we introduce a new theory for the physical basis of consciousness. Our theory suggests that consciousness emerges as an intrinsic property when specific groups of particles achieve a particular organizational state. This relationship between the states and conscious perceptions is governed by a set of principles termed the "universal consciousness codes". Furthermore, we introduce a mathematical approach that can possibly unravel the complex relationship between neural activities and consciousness and test our theory using the latest artificial intelligence technologies.
2. The Theory
2.1. Perception and consciousness
Perception can manifest in both conscious and unconscious forms [7]. For the purpose of this theory, our focus is primarily on conscious perception. Hence, "perception" mentioned in this text implies conscious perception unless stated otherwise. Traditionally, perception has been understood as the process of recognizing and interpreting sensory stimuli, such as visualizing an apple or hearing a sound. On the other hand, consciousness often includes more abstract concepts like emotions and thoughts [8]. In our theory, we propose that all forms of conscious experience, from basic sensory perceptions to complex feeling, awareness, and emotions, are manifestations of the same property of particles and they adhere to a same rule.
2.2. Physical substrate of consciousness
In our theory, consciousness is an intrinsic property of a group of particles, and we introduce the term "consciousons" for those particles. The motivation for this new terminology arises from our current limited knowledge of these particles. Within the biological neural system, these consciousons are speculated to be entities whose consciousness related activity correlates strongly with the dynamics of charged ions or neurotransmitters. It's possible that consciousons could represent a variety of particle types, but their influence on consciousness might be dominated by the interactions of charged ions or neurotransmitters in the neural system. Another consideration is that consciousons could simply be charged particles like electrons and protons, represented in our neural system as ions. For simplicity in the subsequent sections, readers can conceptualize consciousons as ions, until a clearer distinction is provided.
2.3. Origins of consciousness
We posit that consciousness emerges as an inherent property of groups of consciousons, same as other properties like mass, charge, and energy. For consciousness to manifest prominently enough to be perceived or experienced, these consciousons must be organized in specific configurations. For a toy example, if consciousons occupy spatial positions and have associated movement patterns and temporal states as depicted in Figure 1a, they will have a conscious perception of a bird. Conversely, configurations in Figure 1b, 1c, and 1d will be associated with perceptions of a specific sound, heat, or wind, respectively.
The nature of consciousness perceived is determined by the specific states in which consciousons are organized. The state in which they are organized and manifested is associated with some of their properties, possible examples include their spatial positioning, the electrical potential between them, changes in this potential, as well as the rate and pattern of these changes over both space and time. For pronounced conscious perception, these consciousons should need to occupy specific proximities or locations. The description of the relationship between their organizational state and consciousness might be simplified by viewing multiple consciousons as a unit, analogous to ions of a neuron. Rather than solely picturing them as individual particles, consciousons can be viewed as contributing to a field, similar to how electrons constitute the electromagnetic field.
The relationship between the configuration and state of a group of consciousons and the ensuing perception is governed by a Universal Consciousness Code (UCC). Different conscious perceptions or subjective experiences correspond to their unique UCCs. For instance, the perception of a bird corresponds to the state defined by the "bird" UCC, as illustrated in Figure 1a. Conversely, perceptions of a specific sound, heat, and wind are associated with the consciousons adopting states defined by their respective UCCs, showcased in Figure 1b, Figure 1c, and Figure 1d, respectively. In Figure 1, the scatter plots display the spatial configuration of consciousons, which might be in motion, with arrows indicating potential future movement. Consciousons can be grouped into two-circle units, analogous to intra- and extracellular ions of a neuron. Perceptions linked to these consciousons could be influenced by the spatial and temporal patterns of certain properties, such as the electric potential difference between the two circles of consciousons, as demonstrated in the wave graphs. The red rectangles in the graph indicate intervals where changes in electrical potential over time might shape perceptions.
This UCC concept is universal, consistent across all species and objects throughout the universe. Therefore, when we perceive a bird, the underlying direct reason isn't the physical presence of the bird but the activation of the bird's UCC within a particular region of our brain. Any group of consciousons that adopt the state defined by the bird UCC will generate the perception of a bird, regardless of the bird's physical presence or location. In our example, the bird's presence triggers electrochemical signals that activate the bird UCC. Similarly, if the bird UCC is triggered by alternative stimuli, such as high-definition virtual reality visuals or a device stimulating our brain to produce the requisite signals, the resulting perception remains that of a bird. Thus, any configuration that aligns with the "bird" UCC, irrespective of whether it's within a human, monkey, bird, or even in an isolated chamber in the void of space, will produce the perception of a bird. If two groups of organized consciousons are physically close to each other, their perceptions can be merged or combined by a specific mathematical function. Conversely, the UCC of a big or complex perception should be able to be broken down into more basic components, similar to an image can be segmented into clusters of pixels.
The “consciousness” and "perception" in this context include all forms of subjective awareness, feelings, and emotions, such as pressure, sadness, and so on. Each is defined by its unique UCC code. The ability to perceive is an inherent property of consciousons, same as their mass, energy, and charge. The behaviors of consciousons, including movement, charge, or energy, are governed by established physical laws. When consciousons come to some specific spatial and temporal states, conscious perceptions emerge. The relationship between these states and the resulting conscious perceptions is uniquely determined by the UCC.
3. Decoding the Universal Consciousness Code
UCCs represent the state of consciousons, and we can utilize mathematical vectors to represent UCCs. It's anticipated that UCCs will correlate with specific features of consciousons, possible examples including the spatial and temporal gradients of electric potential or the intensity and fluctuation of electric potential over a sustained time period. Figure 2 provides an illustrative example of vectorization of UCCs. In the example, a vector is used to represent a unit of consciousons, and each vector consists of four elements, encoding information about features potentially linked to perception. The first element denotes the difference in the number of consciousons between the inner and outer circles. The second element captures the number of peaks observed in a past time interval, while the last two elements represent the x and y spatial coordinates. To represent the UCC for all six units collectively, all six vectors can be combined through operations such as concatenation.
For a perception to be strong enough to be experienced, a large number of consciousons might be necessary, analogous to requiring the activation of thousands or even millions of neurons for specific perceptions. Additionally, the variety of possible perceptions, such as red, fast, bird, ball, hot, and so on, is vast, making the total number of UCCs huge and decoding of these UCCs challenging. However, certain strategies might alleviate the difficulty of this decoding task.
Advancements in AI technologies have given rise to deep neural network models that can handle intricate tasks. Popular models, like the Transformer [9] as of this writing, employ an embedding technique to represent model inputs [10,11]. In the context of a natural language model, an input is typically a word (though more accurately described as a token, but for simplicity's sake, we'll refer to it as a word). This word is then represented as a vector of numbers. Throughout the training process, these number values are updated to encapsulate the word's meaning, aiming to minimize the objective loss. Analogous embedding techniques for images and audios are used in their respective AI models or in multimodal AI models.
Modern AI models are often deeply layered, containing a vast number of parameters and benefitting from extensive training datasets. For instance, the GPT-3 model has 137 billion parameters, and it represents each input word (token) using a vector of 12,288 numbers [12]. They exhibit an impressive capacity for logical, intricate, and abstract ‘thinking’ similar to human capabilities. Studies suggest a significant degree of convergence in the representations and computational principles of AI models and the human brain [13,14,15,16,17,18,19,20,21,22]. For instance, studies have shown that embedding in GPT-2 model align closely with brain activity during speech and language perception [23,24], another study found that the self-supervised model of wav2vec 2.0 learned brain-like representations of audio and cortical hierarchy of speech processing [25]. Thus, it's possible that the input embeddings and the encodings in the model's upper layers capture a significant portion of the information about how our brains encode various objects, concepts, and perceptions. For instance, further investigation might reveal that specific dimensions within the AI embeddings of words, images, or audio correlate with the brain regions responsible for encoding them, in multi-modal models or even in single-modal models. Additionally, there might be other AI embedding dimensions that correspond to the frequency of action potentials associated with the concepts, or even the spatial and temporal patterns of the associated neural activity.
In intricate AI models, like the deep Transformer, the higher-layer encodings aggregate information from the lower layers. Consequently, they are likely representative of more abstract or high-level concepts. As such, the encoding within these upper layers might correspond to the UCCs associated with those particular experiences or concepts. It's worth noting, however, that these high-level encodings might not be confined to a single position within one layer. Instead, they might span multiple positions and layers.
The possibility of AI embeddings encapsulating information of UCC and the accessibility of these AI embeddings make it possible to use all kinds of mathematical techniques to study UCC. This approach may allow us to delve into the mysteries of perception and consciousness without the need for exhaustive measurement of each neuron's features and activities, a task that's currently very technologically challenging.
For instance, we can examine lower-level AI embeddings that might correspond to primary perceptions. To identify embeddings linked to more abstract experiences, we can expose the model to multiple inputs reflecting that experience and seek recurring patterns. For example, by inputting various sentences related to love, we can isolate common patterns in embeddings, potentially revealing the UCC for “love”. Techniques such as clustering might help identify shared features across perceptions, or identify perceptions with similar properties. We can also perform comparisons to identify differences between perceptions. Such insights could potentially facilitate the development of models predicting specific perceptions and enable studies exploring variations in perception across different contexts, genders, and environments.
If we manage to measure features and activities contributing to the UCCs of some specific concepts (starting perhaps with basic perceptions like recognizing a ball or sensing heat), it might be feasible to determine the mathematical transformation that maps AI embeddings to UCCs. Once we establish this mapping rule, it can be used to infer UCCs for other perceptions and conscious experiences found in the AI embedding (Figure 3), as long as they reside within the same AI space (typically indicating they're located in or have been transformed to the same AI neural network layer).
Another mathematical technique that may be helpful is alignment. If we possess data on potential features of the UCC for various perceptions but are uncertain about which features truly contribute to the UCC, we can determine the UCC associated features by identifying those that improve the alignment of the UCCs of these perceptions with their respective AI embeddings after some transformations.
4. Summary
This paper presents a novel theory aiming to elucidate the physical basis of consciousness. We propose a methodology to possibly unravel the complexities of consciousness and provide a mathematical framework for exploring and testing it using AI technologies. While the validity of the theory remains to be confirmed, it points us in two significant directions: integrating consciousness into the realm of physics and defining consciousness through mathematical language. The proposed theory holds promise for quantitative testing with current technological advancements.
References
- Griffiths, D. Introduction to Elementary particles. 2. enl. and rev. 2008.
- Koch, C. The quest for consciousness: A neurobiological approach. 2004.
- Tononi, G. An information integration theory of consciousness. BMC Neurosci 2004, 5, 42. [Google Scholar] [CrossRef]
- Baars, B.J. A Cognitive Theory of Consciousness; Cambridge University Press: 1988.
- McFadden, J. Synchronous firing and its influence on the brain's electromagnetic field: Evidence for an electromagnetic field theory of consciousness. Journal of Consciousness Studies 2002, 9, 23–50. [Google Scholar]
- Hameroff, S.; Penrose, R. Consciousness in the universe: a review of the 'Orch OR' theory. Phys Life Rev 2014, 11, 39–78. [Google Scholar] [CrossRef] [PubMed]
- Merikle, P.M.; Smilek, D.; Eastwood, J.D. Perception without awareness: perspectives from cognitive psychology. Cognition 2001, 79, 115–134. [Google Scholar] [CrossRef] [PubMed]
- Block, N. On a confusion about a function of consciousness. Behavioral and Brain Sciences 1995, 18, 227–247. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All you Need. Advances in Neural Information Processing Systems 2017, 30. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient Estimation of Word Representations in Vector Space. arXiv 2013. [Google Scholar] [CrossRef]
- Pennington, J.; Socher, R.; Manning, C.D. GloVe: Global Vectors for Word Representation. ACL Anthology 2014, 1532–1543. [Google Scholar] [CrossRef]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A. Language models are few-shot learners. Advances in neural information processing systems 2020, 33, 1877–1901. [Google Scholar]
- Li, Y.; Anumanchipalli, G.; Mohamed, A.; Lu, J.; Wu, J.; Chang, E. Dissecting neural computations of the human auditory pathway using deep neural networks for speech; 2022.
- Goldstein, A.; Zada, Z.; Buchnik, E.; Schain, M.; Price, A.; Aubrey, B.; Nastase, S.A.; Feder, A.; Emanuel, D.; Cohen, A.; et al. Shared computational principles for language processing in humans and deep language models. Nature Neuroscience 2022, 25, 369–380. [Google Scholar] [CrossRef] [PubMed]
- Antonello, R.; Turek, J.; Vo, V.; Huth, A. Low-Dimensional Structure in the Space of Language Representations is Reflected in Brain Responses. arXiv 2021. [Google Scholar] [CrossRef]
- Kietzmann, T.C.; McClure, P.; Kriegeskorte, N. Deep Neural Networks in Computational Neuroscience. In Oxford Research Encyclopedia of Neuroscience; 2019.
- Yamins, D.L.K.; DiCarlo, J.J. Using goal-driven deep learning models to understand sensory cortex. Nature Neuroscience 2016, 19, 356–365. [Google Scholar] [CrossRef] [PubMed]
- Kell, A.J.; McDermott, J.H. Deep neural network models of sensory systems: windows onto the role of task constraints. Curr Opin Neurobiol 2019, 55, 121–132. [Google Scholar] [CrossRef] [PubMed]
- Millet, J.; Dunbar, E. Do self-supervised speech models develop human-like perception biases? ACL Anthology 2022, 7591–7605. [Google Scholar] [CrossRef]
- Caucheteux, C.; King, J.-R. Brains and algorithms partially converge in natural language processing. Communications Biology 2022, 5, 134. [Google Scholar] [CrossRef]
- Gauthier, J.; Levy, R. Linking artificial and human neural representations of language. ACL Anthology 2019, 529–539. [Google Scholar] [CrossRef]
- Schrimpf, M.; Blank, I.; Tuckute, G.; Kauf, C.; Hosseini, E.A.; Kanwisher, N.; Tenenbaum, J.; Fedorenko, E. The neural architecture of language: Integrative modeling converges on predictive processing. bioRxiv 2006. [Google Scholar] [CrossRef]
- Chen, P.; He, L.; Fu, L.; Fan, L.; Chang, E.F.; Li, Y. Do self-supervised speech and language models extract similar representations as human brain? arXiv 2023. [Google Scholar] [CrossRef]
- Caucheteux, C.; Gramfort, A.; King, J.-R. GPT-2’s activations predict the degree of semantic comprehension in the human brain. bioRxiv, 2004. [Google Scholar]
- Millet, J.; Caucheteux, C.; Orhan, P.; Boubenec, Y.; Gramfort, A.; Dunbar, E.; Pallier, C.; King, J.-R. Toward a realistic model of speech processing in the brain with self-supervised learning. arXiv 2022. [Google Scholar] [CrossRef]
Figure 1.
Consciousons, when arranged or present in varying states, yield different conscious perceptions. This figure provides a basic illustration of the potential relationship between the state of consciousons and the resulting perceptions. When consciousons are in the state depicted in panel a, they have a perception of a bird. Conversely, states b, c, and d generate perceptions of a specific sound, heat, and wind, respectively. The grey spheres represent consciousons, analogous to positively charged ions within the neural system. For simplicity, the scatter plots display spatial configurations in a 2D format rather than 3D. Note that some consciousons could be in motion, and perceptions might be influenced by their trajectory and velocity. The visuals in the figure capture a snapshot of consciousons at a specific time, with arrows indicating probable movement directions shortly thereafter. Consciousons might be grouped into dual-circle units, analogous to intra- and extracellular ions in a neuron. Perceptions could relate to the spatial and temporal patterns of certain properties, for instance, the electrical potential between these circles of consciousons, depicted in the wave graph. This graph represents the fluctuation of electrical potential over time, with the black vertical line marking the moment of the snapshot. The red rectangles highlight intervals in the past where the electrical potential might influence perceptions.
Figure 1.
Consciousons, when arranged or present in varying states, yield different conscious perceptions. This figure provides a basic illustration of the potential relationship between the state of consciousons and the resulting perceptions. When consciousons are in the state depicted in panel a, they have a perception of a bird. Conversely, states b, c, and d generate perceptions of a specific sound, heat, and wind, respectively. The grey spheres represent consciousons, analogous to positively charged ions within the neural system. For simplicity, the scatter plots display spatial configurations in a 2D format rather than 3D. Note that some consciousons could be in motion, and perceptions might be influenced by their trajectory and velocity. The visuals in the figure capture a snapshot of consciousons at a specific time, with arrows indicating probable movement directions shortly thereafter. Consciousons might be grouped into dual-circle units, analogous to intra- and extracellular ions in a neuron. Perceptions could relate to the spatial and temporal patterns of certain properties, for instance, the electrical potential between these circles of consciousons, depicted in the wave graph. This graph represents the fluctuation of electrical potential over time, with the black vertical line marking the moment of the snapshot. The red rectangles highlight intervals in the past where the electrical potential might influence perceptions.
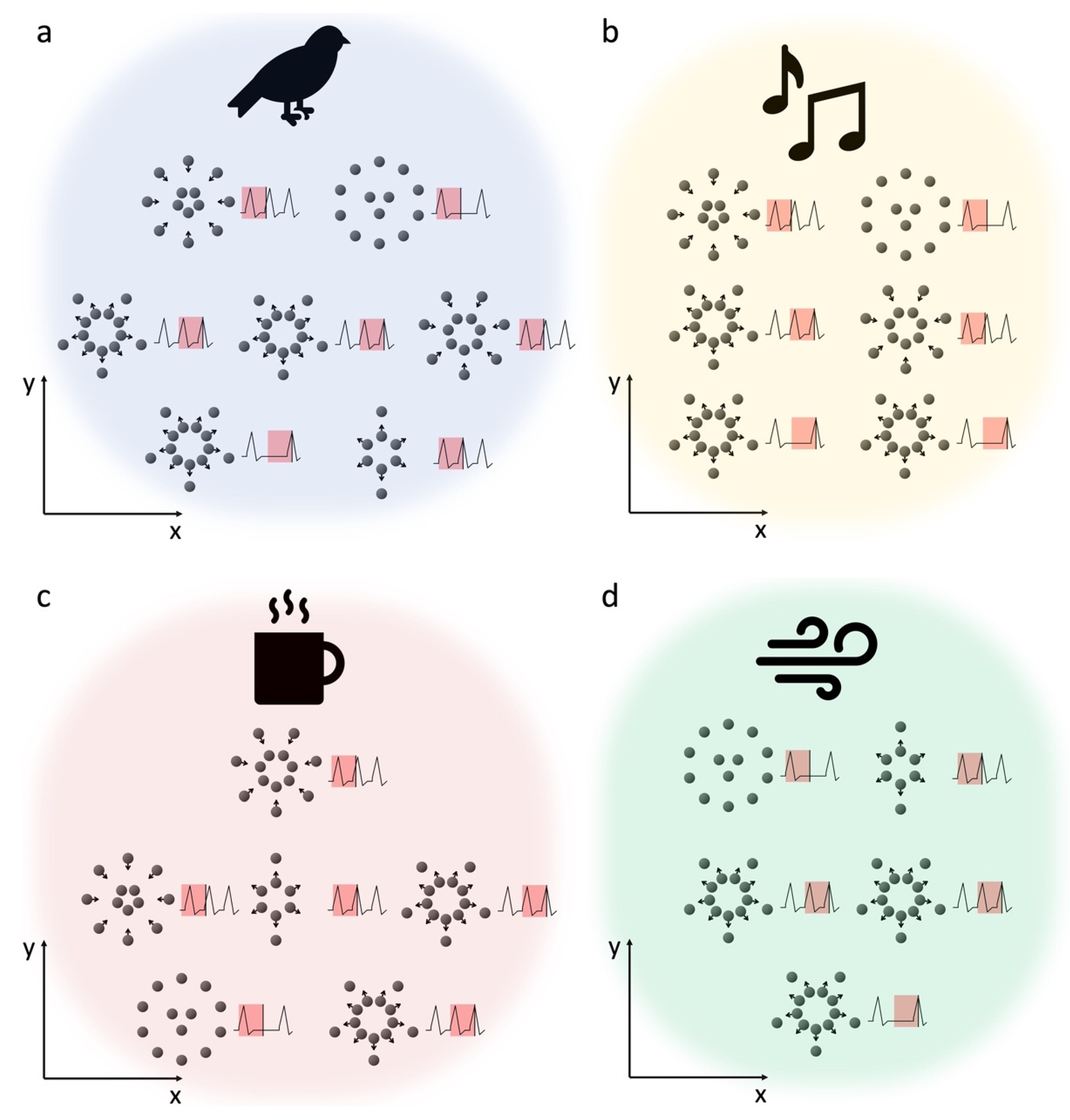
Figure 2.
UCC Representation Using Feature Vectors. The figure illustrates the UCC of a bird, where a vector is used to represent a unit of consciousons. This vector encodes information about features potentially linked to perception. In this example, each vector consists of four elements. The first element is the difference in the number of consciousons between the inner and outer circles. The second element captures the number of peaks observed in a past time interval, while the last two elements represent the x and y spatial coordinates. To represent the UCC for all six units collectively, all six vectors can be combined using operations such as concatenation.
Figure 2.
UCC Representation Using Feature Vectors. The figure illustrates the UCC of a bird, where a vector is used to represent a unit of consciousons. This vector encodes information about features potentially linked to perception. In this example, each vector consists of four elements. The first element is the difference in the number of consciousons between the inner and outer circles. The second element captures the number of peaks observed in a past time interval, while the last two elements represent the x and y spatial coordinates. To represent the UCC for all six units collectively, all six vectors can be combined using operations such as concatenation.
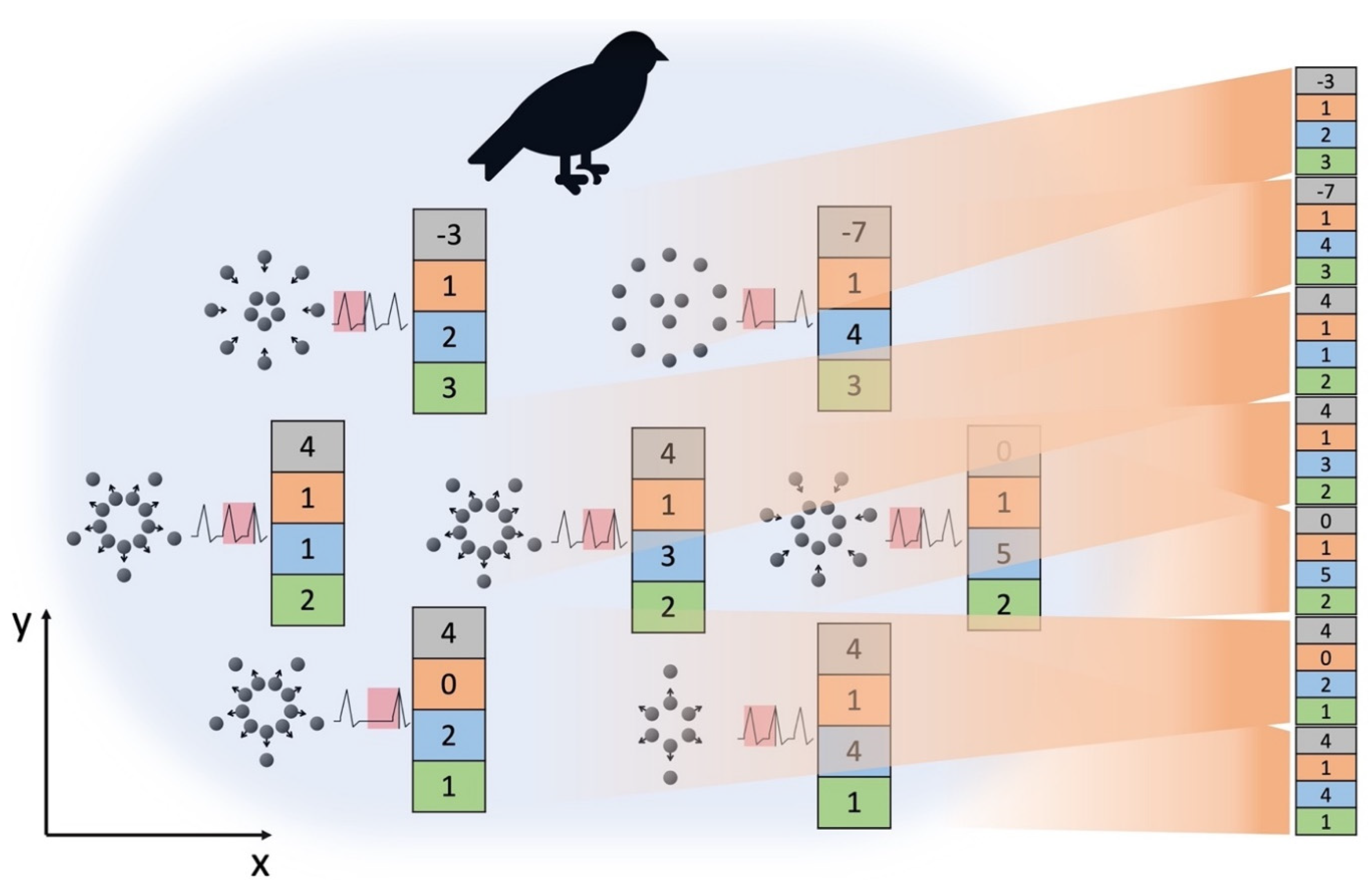
Figure 3.
Inferring UCCs Using AI Embeddings. The top panel displays colored vectors representing UCCs, potentially derived using the method from Figure 2. The bottom panel shows uncolored vectors, which are AI embeddings of corresponding perceptions. If the UCCs for certain perceptions (e.g., a bird, a specific sound, heat) can be experimentally acquired, it may be possible to establish a mathematical relationship between the AI embedding space and the UCC space. Once this relationship is understood, it can be employed to predict the UCCs of other perceptions (e.g., a bee, the taste of sweet ice cream, the experience of people dancing to music, or the sensation of love) based on their respective AI embeddings.
Figure 3.
Inferring UCCs Using AI Embeddings. The top panel displays colored vectors representing UCCs, potentially derived using the method from Figure 2. The bottom panel shows uncolored vectors, which are AI embeddings of corresponding perceptions. If the UCCs for certain perceptions (e.g., a bird, a specific sound, heat) can be experimentally acquired, it may be possible to establish a mathematical relationship between the AI embedding space and the UCC space. Once this relationship is understood, it can be employed to predict the UCCs of other perceptions (e.g., a bee, the taste of sweet ice cream, the experience of people dancing to music, or the sensation of love) based on their respective AI embeddings.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




