Prerpints.org logo
Preprint
Article

Eigenfemora – Age at Death Estimation in the Proximal Femur through an Image Processing Approach

Altmetrics

Downloads

123

Views

67

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 November 2023

Posted:

03 November 2023

You are already at the latest version

Alerts
Abstract
Estimating age at death is essential to establish a biological profile from human skeletal remains in both forensic and archeological settings. Imaging studies of skeletal age changes in adults have described metamorphosis of trabecular bone structure and bone loss in the proximal femur , as well as changes in morphology during different stages of life. This study aims to assess the utility of a digital representation of conventional X-ray films of the proximal femur for the estimation of age at death in a sample of 91 adult individuals (47 females and 44 males) of the Coimbra Identified Skeletal Collection. The proposed approach showed a root mean squared error (RMSE) of 17.32 years (and mean absolute error of 13.47 years) for females and an RMSE of 14.06 years (mean absolute error of 11.08 years) for males. The main advantage of this approach is the consistency in the feature detection and extraction, as X-ray images projected on the femora space will always produce the same set features to be analyzed for age estimation while more traditional methods rely heavily on operator experience which can lead to inconsistent age estimates among experts.
Keywords: 
Subject: Biology and Life Sciences  -   Other

1. Introduction

The assessment of age at death is an essential precondition to establish a biological profile and a necessary empirical procedure for the identification of individual skeletal remains in both forensic and archeological contexts [1,2,3]. In a forensic setting, age at death is one of the crucial biological profile parameters (i.e., biological sex, age at death, population affinities, and stature) present in the initial description of an individual, allowing investigators to narrow the pool of missing persons by excluding individuals who do not share the same physical attributes [4]. In archeological contexts, estimating age is important not only to characterize individuals, but also to ascertain the demographic profile of past populations. Physiological aging exhibits a substantial amount of variation within and between populations, which hampers the estimation of age at death in skeletal remains, particularly in adults [3,4]. No single age predictor perfectly replicates the range of factors that influence biological age; therefore, it is appropriate to use as many indicators of age and age estimation techniques as possible to evaluate age at death in adult skeletons [1,3,5,6,7].
The most common approaches to age at death estimation are based on a qualitative description of the skeletal remains, an approach highly dependent on the expert’s previous experience [8,9]. Although it is not yet a decisive issue in past population studies (even if this does not mean that efforts are not being made to overcome this issue, especially because methodological insufficiencies may be biasing the knowledge regarding past populations), the distinctive scientific and legal demands in Forensic Anthropology have prompt some at-tempts to replace this approach with quantitative methods or, at least, reinforce the expertise with the application of both analytical frameworks. Due to Daubert’s standards of admissibility, the need to quantity the results (i.e., to rephrase the expertise in terms of error rates, probabilities, or hypothesis testing) is growing [4,10,11]. While Daubert’s criteria (US federal standards specified in 1993 in Daubert vs. Merrell Dow Pharmaceuticals) applies only in the US federal courts, its standards have influence well beyond their bounds, creating the necessity to develop quantitative methods in order to decrease the subjectivity as the errors associated with the different methods must be known, and the results of the studies must be able to be replicated by different investigation teams and/or experts) and to comply with that and other admissibility criteria [4,12]. Of the two general methodological approaches commonly used in forensic anthropology or bioarcheology to estimate age at death (and excluding molecular methods), quantitative methods have the greatest potential to be developed and improved to meet these admissibility criteria. As is commonly recognized, morphological methods tend to be more subjective and their applicability tends to rely more on the expert's previous experience [10].
Age-related bone loss occurs in all populations, with age-specific bone remodeling taking place in different skeletal regions at dissimilar rates [13,14,15,16]. Trabecular bone has more surface per unit of bone volume than cortical bone, and accelerated remodeling initially stimulates a more pronounced cancellous bone loss as opposed to cortical bone loss [17]. As such, the decrease in trabecular bone begins prematurely – during early adulthood – in both sexes when compared with cortical bone loss [18]. Imaging studies of skeletal age modifications in adults have portrayed metamorphosis of bone structure, bone loss, as well as changes in gross morphology during different stages of life, e.g., [16,19,20,21,22,23,24,25,26,27,28,29,30,31]. Age-related changes in trabecular structure and bone loss are well described [32,33], and macroscopically observable features of trabecular bone in different skeletal locations have been used to develop and evaluate aging standards in adult individuals, e.g., [19,34,35,36,37,38,39].
Proximal femur bone loss has also been used to systematize standards for age at death estimation in adult skeletons [9,15,24,25,35,40,41,42]. These studies suggest that the proximal femur is reliable to estimate age at death and average to excellent results have been claimed. The internal structure of the proximal femur above de lesser trochanter comprises a slender layer of cortical bone, and a dense tessiture of cancellous bone that shapes the head, neck and greater trochanter internal system of weight bearing [43]. There are five groups of compressive and tensile trabeculae, whose spatial distribution is oriented according an optimized biomechanical pattern [25]. The trabecular architecture of the proximal femur is exposed to a significant age-related involution, with lacunae formation at the trochanter, neck and head [24,25,35,36,41]. However, qualitative visual readings of trabecular bone involution in the proximal femur are prone to intra- and inter-observer errors, being substantially affected by the previous experience of the researchers [36,37]. As such, in the present exploratory study a digital representation of conventional X-ray films of the proximal femur is produced aiming to assess the forensic value of an image processing approach for automatic feature extraction and age at death estimation of adult individuals.

2. Materials and Methods

2.1. Sample

Within the research landscape of biological anthropology, Portugal is notorious for its numerous identified skeletal collections [44]. One of the oldest and widely recognized is the Coimbra Identified Skeletal Collection (CISC) that comprises 505 skeletons (housed in the Department of Life Sciences at the University of Coimbra, Portugal). All individuals from this collection were born between 1817 and 1924, and died between 1904 and 1936. The majority was exhumed from the main Coimbra municipal cemetery, Cemitério Municipal da Conchada, during the first half of the 20th century. All the individuals were interred in shallow graves for at least 5 years and after that were usually exhumed. Available ante mortem data includes, for each individual, age at death, biological sex, cause of death, occupation, marital status, and year of death, among others [45]. In addition to the ante mortem information, this collection also has an assemblage of complementary examinations that have been carried out and curated throughout its existence, including a collection of conventional radiographies. In terms of bone representation and preservation, almost all skeletons in the collection are complete and well preserved. For the present study, all adult individuals with conventional radiographs were initially included. Subsequently, and within this group, all individuals with taphonomic modifications that greatly affected the proximal femur and/or with visible pathological conditions were excluded.
After the initial selection, the studied material included, in total, 91 plain radiographs of the left femora. The study sample is balanced for sex and age at death. Female individuals comprised 51.6% (47/91) of the sample, with recorded ages at death between 22 and 89 years (mean=51.61; SD=18.50). The 44 males (48.4%) died with ages between 21 and 86 years (mean=48.91; SD=16.20). Conventional radiographies were produced using a clinical X-ray unit (GE Medical Systems®) at the Medical Image Service in the Coimbra University Hospitals. At a focal distance of 1m, the exposure was mAseg=80-50 at kVp=30-35, according to individual bone weight and size. All bones were placed in standard anteroposterior view.

2.2. Methods

2.2.1. Acquisition and Segmentation

The first step to assess the utility of an image processing approach for automatic feature extraction and age estimation from the proximal femur was to produce a digital representation of the conventional X-ray films. All X-ray films were mounted in a light box and digitally acquired with a tripod-mounted DSLR camera (shutter speed: 6, aperture: f/5, focal length: 55 mm, automatic white balance, resolution: w [width] - 4272 by h [height] - 2848).
After image acquisition, all images were manually segmented with ImageJ software (National Institutes of Health and the Laboratory for Optical and Computational Instrumentation, University of Wisconsin) as illustrated in Figure 1. For a more precise and robust segmentation a polygon selection tool was used, and the region of interest was saved in a TIFF file of variable resolution. All subsequent analyses were conducted in the segmented regions only.
Previous approaches to age estimation from bone images or radiological images relied on the macroscopic observation or the calculation of first and second order statistics of pixel distribution [46]. The approach presented here is based on a construction of appearance-based model to code information from proximal femur images using Principal Components Analysis (PCA). PCA is frequently employed as a technique for reducing the dimensionality of extensive datasets. It achieves this by converting a large number of variables into a more concise set that retains the majority of the relevant information found in the original dataset. The specific technique employed in this study was initially developed in the field of Computer Vision and Pattern Recognition for the purpose of face detection and recognition [47].
This approach uses PCA to encode the information in a database of face images through the eigenvectors of covariance matrix of the image database. Principal Component Analysis projects the face images in a feature subspace called face space, this subspace is composed by the eigenvectors of a set of face images that encode the information from each face. The eigenvectors can be thought as features extracted from the images and can be used to compare faces in pair-wise fashion to perform face recognition; the eigenvectors or eigenfaces, as called by the Turk and Pentland [47], encode local and global features of the face but this features may not correspond to nose, eyes or mouth as perceived by humans. This approach is computationally simple and allows for the efficient learning of features of high-dimensional inputs (images) in unsupervised manner. By analogy the subspace features were labeled femora space and the extracted features eigenfemora.
In order to apply the Turk and Pentland’s PCA methodology to images, several steps were first performed to transform the proximal femur segmented images in a representation suitable for Principal Component Analysis. First, each segmented image was re-dimensioned using a bi-spline interpolation algorithm so that all images shared the same resolution of w-by-h, being w and h the half of the mean value of w (width) and h (height) of all images. Subsequently, all images were transformed to a grayscale color map and their histogram was normalized using the contrast limited adaptive histogram equalization technique (CLAHE), to enhance details of bone. At last, each image was reshaped from w-by-h matrix to a wh-by-1 vector. All image vectors were stored in a matrix D (defined as m-by-n, with m=wh), composing the database.
To produce the femora space and corresponding eigenfemora, the mean configuration of the proximal femora database was first subtracted from each femur image for purposes of normalization. Then, it was enacted a principal components analysis of the covariance matrix of the database D, defined as L=DTD instead of L=DDT (see Turk and Pentland [47] for a detailed mathematical explanation). The eigenvectors of the covariance matrix L are sorted in a descendent way according to their eigenvalues and stored in a matrix W. The femora space, a matrix S, and corresponding eigenfemora are obtained by S=DWT. The femora space contains the exact same numbers of femora used in the database X but it can be represented by a number of eigenfemora that account for a specific percentage of variation of the femora in the database D. In this case, the subspace is represented by a number of eigenfemora that account for 95% of the variation of the dataset.
The final step of this algorithmic approach is to obtain variables from each proximal femur images that can be used in subsequent statistical analysis. The features or variables that characterize each femur image are obtained by projecting the image into the femora space. The projection is performed by the matrix operation STD, this operation results in a new matrix X that is composed of features encoded by the eigenfemora for each proximal femur image projected into the femora space.

2.2.2. Age Estimation from the Femora space with K-nearest Neighbor Search

After the feature extraction phase, the variables contained in matrix X were statistically analyzed to evaluate their relationship with age at death, and the respective Spearman’s rho correlation coefficient was computed. To perform age estimation a simple k-nearest neighbor (k-nn) search procedure using a kd-tree [48] was implemented. By using this simple technique, it was applied a model-free, non-parametric and non-linear regression approach to age estimation [49]. The only assumption made by the use of this kind of approach is that age can be estimated by information of previous examples that are similar to the one the forensic expert as in hand. This age estimation procedure is simple and consists in finding, in the femora space, the k most similar proximal femora to the one being analyzed. Once the most similar femora are found, the age prediction for an unidentified set of human remains is given by calculating simple statistics such as percentiles (2.5, 50 and 97.5) for the age distribution of the most similar cases. In this manner, it is produced a prediction interval (95% prediction interval) and a point estimate of age at death (the percentile 50). In this case, weighted percentiles were calculated to ensure that the most similar case have a higher contribution to the final age estimate. The weights used are set as e-d, where d is the Euclidean distance of the similar example to the target proximal femur.
The performance of this approach was assessed using global indicators of goodness of fit [50]: root mean square error (RMSE), mean absolute error (MAE), bias, mean width of the prediction interval (MW) and coverage of the prediction interval. The root mean squared error is the square root of the average squared loss, while the mean absolute error is estimated in a comparable way utilizing the absolute instead of the squared difference between predicted and documented age. Bias, or mean bias error, is de-fined as the mean difference between the predicted age and the documented age. The pre-diction interval is a range of values that is likely to contain the value of a single new observation, with a certain level of confidence. For unbiased and realistic estimates of these parameters, the utility of this procedure was evaluated using a leave-one-out resampling strategy (also known as jackknife cross-validation). The optimal value of k, the number of femora retrieved used to estimate age at death, was also determined with the aforementioned validation strategy.
All the computational procedures were carried out with MATLAB® (MathWorks, Inc.) programming language and scientific computing environment.

3. Results

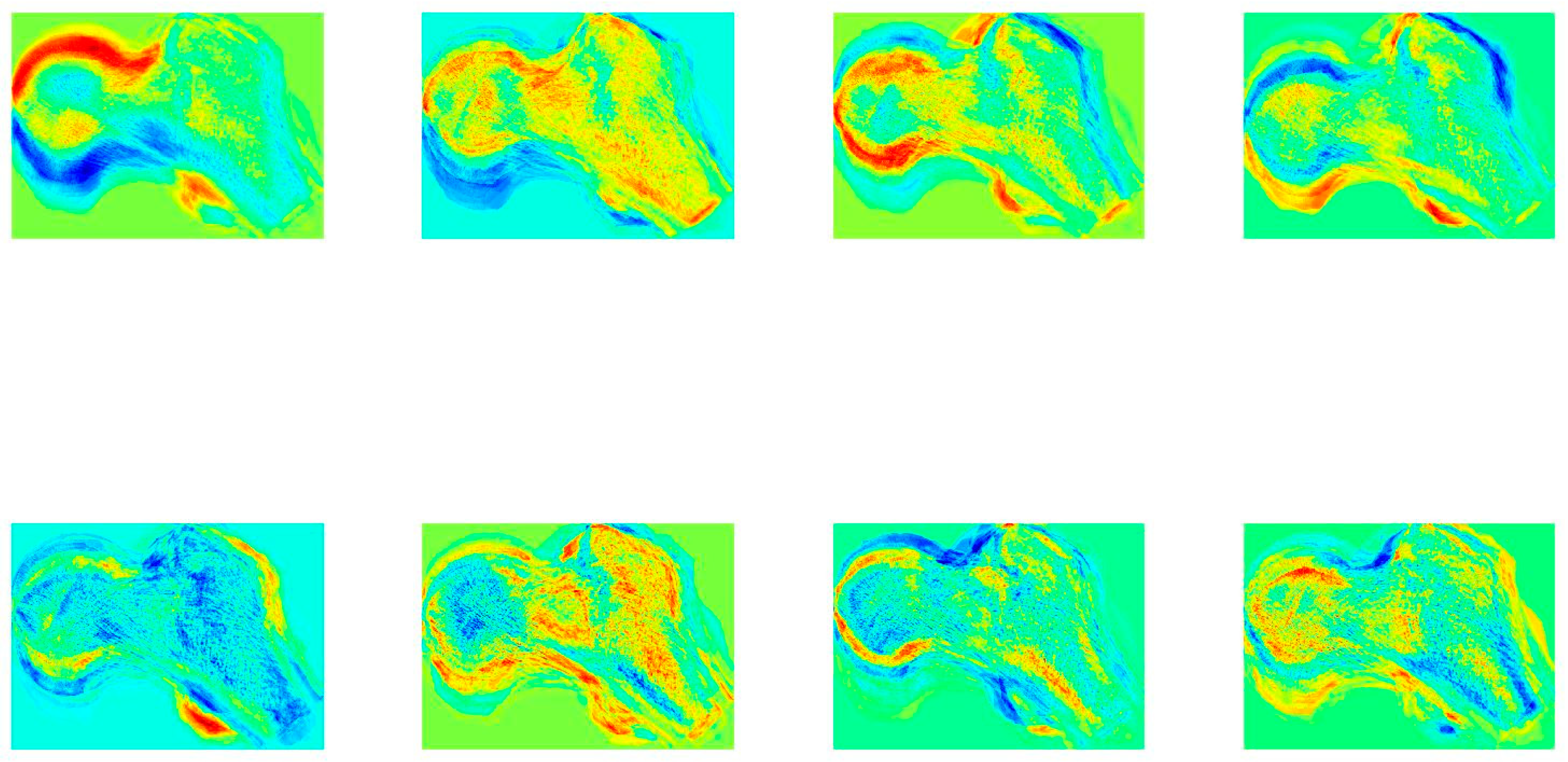
One of the advantages of the technique analyzed in this paper is that every element of the femora space, the eigenfemora, can be represented as an image itself. Figure 2 and Figure 3 illustrate some of the elements of the femora space generated for the female and male individuals present in the dataset. Each individual eigenfemur resembles a ghostly image of a proximal femur, composed of superimposed femora images. This is because each eigenfemur encodes specific information from each image of the database D. Figure 3 depicts a jet color map representation of the first eight eigenfemora for the male sample, the red color represents the region of the image that is encoded by the respective eigenfemur.
During the process of subspace generation, 95% of variation of the proximal femora was encoded in 40 female eigenfemora and in 39 eigenfemora for the male individuals. In the female sample, only the information captured by the 8th eigenfemur contained variation related to age at death (Spearman's rho=-0.4074, p-value=0.0045). In male individuals, the 1st, 4th, 5th and 6th revealed a statistically significant relationship with age at death (Spearman's rho=0.3510, Spearman's rho=-0.3127, Spearman's rho=-0.3724, Spearman's rho=0.3092; p-value=0.0195, p-value=0.038, p-value=0.0128, p-value=0.0411).
In the implemented k-nearest neighbor search procedure for age estimation, only the eigenfemora that showed statistical relationship with age at death were considered. Despite the advantages of this procedure as a non-parametric regression technique, k-nearest neighbor algorithms are very sensitive to redundant features, and since the target variable is age at death, makes sense to use only features that are related to it.
The proposed approach shows a modest success in age at death prediction for female individuals, with a relative mean standard error of 17.32 years, a mean absolute error of 13.47 years and a bias of 0.78. Generated prediction intervals only contained the known age in 83% of the cases, although they are remarkably wide (MW = 53.04 years on average). In the males’ sample, the performance was slightly better, with an RMSE of 14.06 years, a MAE of 11.08 years and a bias of 0.68. The mean width of the prediction intervals was smaller, 43.59 years, and contained the real age in 96% of the cases. The reported values are associated with k=11 for females and k=9 in males. In both sexes age at death was systematically over estimated for young individuals and under estimated for older individuals.

4. Discussion

Estimating the age of an individual at the time of death holds crucial importance in the fields of forensic anthropology and human bioarcheology; thus, enhancing the accuracy of age estimation by using different skeletal areas and statistical frameworks is pivotal to improve the chances to identify anonymous skeletal remains [9]. Involutional bone loss is an extended, gradual, and permanent process that occurs in both sexes. Significant trabecular bone loss starts in young adults of both sexes at different skeletal sites and endures throughout life with an increase of rate around menopause in females [18]. The metamorphosis of trabecular bone structure and bone loss evaluated trough radiographs has been used to develop age at death estimation methods [25,35,36,37,38,39]. The majority of these studies is based on the proximal femur trabecular structure and architecture. In fact, due to his morphology and composition, the femur is usually recovered in forensic cases. Being the bigger and one of the more robust bones of the human skeleton, its preservation is often better than other parts of skeleton [51]. In fact, the femur, and particularly the proximal region, is of paramount significance for the assessment of different parameters of the biological profile [52,53,54,55,56], including age at death [9,15,40,42,57].
Previous routines for the estimation of age through X-rays of the proximal femur were based on the visual assessment of trabecular involution, e.g., [24,35,36], a procedural framework where age assignation is inherently more subjective and dependent on the prior experience of the observer(s). Thus, the key advantage of the eigenfemora approach relates with the consistency in the feature detection and extraction, as X-ray images projected on the femora space will always produce the same set of features to be analyzed for age estimation while more traditional methods deeply rely on observer experience which can lead to inconsistent age estimates among experts [6,8,11].
In general, age at death estimation methods in both forensic and archeological contexts are still prone to substantial rates of error, being inaccurate, biased and unreliable. Thus, the results are promising but are still distant from a superlative assessment of age at death, especially if applied to a forensic case, where a narrower age at death interval is required to generate the biological profile. The age estimates produced by the implemented eigenfemora approach show a comparable error rate to the visual analysis of proximal femur trabecular structure and architecture [36], and other age estimation techniques that rely on the macroscopic analysis of the pubic symphysis and auricular surface [58,59,60]. This latter comparison is even more relevant since the pelvis is not always recovered in good preservation conditions, contrarily to the femur – the heaviest and strongest bone and, thus, frequently recovered in both forensic and archeological contexts [61].
Notwithstanding, the method presented here performs slightly worse than recent methodological routines that rely on advanced mathematical approaches, e.g., [3,7,62], including those that are also based on medical imaging of the proximal femur [9,15]. Interestingly, and contrarywise to what was observed in densitometric studies of the proximal femur, the eigenfemora approach is more accurate in the age estimation of male individuals. This highlights a potential benefit for age estimation in male individuals through the eigenfemora models when compared with age prediction through densitometry, e.g., [9,15]. In fact, bone decline with age at the proximal femur is more obvious in female individuals – and that seems to be a general trend in different populations [15,22,23,40,42]. Trabecular age-related changes are also influenced by biological sex: both sexes appear to lose a comparable volume of trabecular bone, with females tending to lose more trabeculae while males suffer more trabecular thinning with loss of trabecular elements [63,64].
The eigenfemora models show low prediction bias but there is a systematic over estimation for the young individuals and an under estimation for older individuals. This tendency was also observed in other works that evaluated age-related changes in the proximal femur [36,57], and has been identified for long as a major feature of prediction inaccuracy in different age estimation methods [65]. Claude Masset devised the term “attraction of the middle” to describe this phenomenon and associated it with the specific age distribution of the reference sample employed in creating any age estimation method. However, it has also been proposed that this error is, to some extent, a consequence of the statistical techniques, particularly linear regression, employed to predict chronological age from biological age predictors [57].
As with other age estimation techniques, biological variation inherent to structures under analysis limits the information extracted [2]. Bone loss and trabecular structure, particularly, are influenced by a plethora of individual and population factors that can hinder age assessment, including physical activity, diet, genetics, or hormonal status [9,16,57,63]. The characteristic individual and population variability in the expression of bone loss influences the accuracy and bias of methods that exploit the relationship between it and age [9]. Also, plain skeletal radiographs can only be used in an limited fashion to quantify bone density with relation to age, as demineralization only becomes visually apparent after a 30-40% or more loss of bone density [66]. This technical constraint thwarts any radiological assessment of initial stages of bone loss.
The eigenfemora approach is based on Principal Components Analysis (PCA), which is a well-established technique in the field of computer vision and image processing. Such an approach has a strong theoretical foundation and has been rigorously tested in other contexts. While deep learning methods have shown promise in various applications, they may require large amounts of data and computational resources to train and optimize the models [3,67]. In contrast, the eigenfemora approach is based on a relatively small dataset of proximal femur images. This may make it more practical and cost-effective for certain applications, particularly in forensic anthropology and archeology where resources may be limited. The eigenimage analysis offers a well-established and consistent method for image analysis in forensic age estimation, and should be seen as link to more complex methods such deep learning techniques as available data expands.
Limitations of this exploratory research study include the use of conventional radiographs (although the eigenfemora routine of analysis might be easily effected in digital radiographs) of the proximal femur and of a relatively small and population-homogeneous sample of identified skeletal remains for the survey of age-related changes in the proximal femur.

5. Final Remarks

Age estimation of adult individuals (notably older people) persists as one of the most challenging tasks in forensic anthropology expertise’s workflow, being particularly influenced by subjective analyses of age-dependent changes in the skeleton. The aim of the present exploratory study was to improve age at death assessment using a bone imaging method that is more objective than a mere visual / macroscopic inspection. The results are promising, especially in male individuals, but warrant further investigations in larger and heterogeneous samples, particularly in terms of age distribution and with different population origins. For example, it would be particularly interesting to evaluate the performance of the method in samples of elderly individuals; individuals with bone loss and osteoporosis; and individuals with pathologies that cause marked bone growth, such as diffuse idiopathic skeletal hyperostosis (DISH), or bone fragility, such as osteomalacia and Paget’s disease.

Author Contributions

Conceptualization, DN, MTF and FC; methodology, DN; software, DN; validation, DN and FC; formal analysis, DN; writing—original draft preparation, DN and FC; writing—review and editing, MTF; supervision, MTF and FC.

Funding

This work was implemented at the R&D Units Center for Functional Ecology - Science for People and the Planet (CFE), with the reference UIDB/04004/2020, and Research Centre for Anthropology and Health (CIAS), with the reference UIDB/00283/2020, both financed by the FCT/MCTES through national funds (PIDDAC).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data generated during this study are available upon request.

Acknowledgments

Eugénia Cunha and Ricardo Vicente.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Cunha, E.; Baccino, E.; Martrille, L.; Ramsthaler, F.; Prieto, J.; Schuliar, Y.; Lynnerup, N.; Cattaneo, C. The Problem of Aging Human Remains and Living Individuals: A Review. Forensic Sci. Int. 2009, 193, 1–13. [Google Scholar] [CrossRef] [PubMed]
  2. Márquez-Grant, N. An Overview of Age Estimation in Forensic Anthropology: Perspectives and Practical Considerations. Ann. Hum. Biol. 2015, 42, 306–320. [Google Scholar] [CrossRef] [PubMed]
  3. Navega, D.; Costa, E.; Cunha, E. Adult Skeletal Age-At-Death Estimation through Deep Random Neural Networks: A New Method and Its Computational Analysis. Biology (Basel). 2022, 11. [Google Scholar] [CrossRef] [PubMed]
  4. Komar, D.A.; Buikstra, J.E. Forensic Anthropology: Contemporary Theory and Practice; Oxford University Press: Oxford, 2007; ISBN 9780195300291. [Google Scholar]
  5. Xanthopoulou, P.; Valakos, E.; Youlatos, D.; Nikita, E. Assessing the Accuracy of Cranial and Pelvic Ageing Methods on Human Skeletal Remains from a Modern Greek Assemblage. Forensic Sci. Int. 2018, 286, 266.e1–266.e8. [Google Scholar] [CrossRef] [PubMed]
  6. Ubelaker, D.H.; Khosrowshahi, H. Estimation of Age in Forensic Anthropology: Historical Perspective and Recent Methodological Advances. Forensic Sci. Res. 2019, 4, 1–9. [Google Scholar] [CrossRef] [PubMed]
  7. Hens, S.M.; Godde, K. A Bayesian Approach to Estimating Age from the Auricular Surface of the Ilium in Modern American Skeletal Samples. Forensic Sci. 2022, 2, 682–695. [Google Scholar] [CrossRef]
  8. Cappella, A.; Cummaudo, M.; Arrigoni, E.; Collini, F.; Cattaneo, C. The Issue of Age Estimation in a Modern Skeletal Population: Are Even the More Modern Current Aging Methods Satisfactory for the Elderly? J. Forensic Sci. 2017, 62, 12–17. [Google Scholar] [CrossRef] [PubMed]
  9. Navega, D.; Coelho, J. d. O.; Cunha, E.; Curate, F. DXAGE: A New Method for Age at Death Estimation Based on Femoral Bone Mineral Density and Artificial Neural Networks. J. Forensic Sci. 2018, 63, 497–503. [Google Scholar] [CrossRef] [PubMed]
  10. Garvin, H.M.; Passalacqua, N. V. Current Practices by Forensic Anthropologists in Adult Skeletal Age Estimation. J. Forensic Sci. 2012, 57, 427–433. [Google Scholar] [CrossRef]
  11. Bailey, C.; Vidoli, G. Age-at-Death Estimation: Accuracy and Reliability of Common Age-Reporting Strategies in Forensic Anthropology. Forensic Sci. 2023, 3, 179–191. [Google Scholar] [CrossRef]
  12. Ousley, S.D.; Hollinger, R.E. The Pervasiveness of Daubert. In A Companion to Forensic Anthropology; Dirkmaat, D.C., Ed.; Blackwell Publishing Ltd: Chichester, 2012; pp. 654–665. ISBN 9781405191234. [Google Scholar]
  13. Shen, Y.; Huang, X.; Wu, J.; Lin, X.; Zhou, X.; Zhu, Z.; Pan, X.; Xu, J.; Qiao, J.; Zhang, T.; et al. The Global Burden of Osteoporosis, Low Bone Mass, and Its Related Fracture in 204 Countries and Territories, 1990-2019. Front. Endocrinol. (Lausanne). 2022, 13, 1–11. [Google Scholar] [CrossRef] [PubMed]
  14. Aggarwal, A.; Pal, R.; Bhadada, S.K.; Ram, S.; Garg, A.; Bhansali, A.; Singh, P.; Thakur, J.S.; Singh, T.; Sachdeva, N.; et al. Bone Mineral Density in Healthy Adult Indian Population: The Chandigarh Urban Bone Epidemiological Study (CUBES). Arch. Osteoporos. 2021, 16, 17. [Google Scholar] [CrossRef] [PubMed]
  15. Curate, F.; Navega, D.; Cunha, E.; Coelho, J. d’Oliveira DXAGE 2.0 — Adult Age at Death Estimation Using Bone Loss in the Proximal Femur and the Second Metacarpal. Int. J. Legal Med. 2022, 136, 1483–1494. [Google Scholar] [CrossRef] [PubMed]
  16. Curate, F.; Cunha, E. Femoral Cortical Bone in a Portuguese Reference Skeletal Collection. Antropol. Port. 2017, 34, 91–109. [Google Scholar] [CrossRef] [PubMed]
  17. Seeman, E. Structural Basis of Growth-Related Gain and Age-Related Loss of Bone Strength. Rheumatology 2008, 47, 2–8. [Google Scholar] [CrossRef] [PubMed]
  18. Riggs, B.L.; Melton, L.J.; Robb, R.A.; Camp, J.J.; Atkinson, E.J.; McDaniel, L.; Amin, S.; Rouleau, P.A.; Khosla, S. A Population-Based Assessment of Rates of Bone Loss at Multiple Skeletal Sites: Evidence for Substantial Trabecular Bone Loss in Young Adult Women and Men. J. Bone Miner. Res. 2008, 23, 205–214. [Google Scholar] [CrossRef] [PubMed]
  19. Schranz, D. Age Determination from the Internal Structure of the Humerus. Am. J. Phys. Anthropol. 1959, 17, 273–277. [Google Scholar] [CrossRef]
  20. Bascou, A.; Dubourg, O.; Telmon, N.; Dedouit, F.; Saint-Martin, P.; Savall, F. Age Estimation Based on Computed Tomography Exploration: A Combined Method. Int. J. Legal Med. 2021, 135, 2447–2455. [Google Scholar] [CrossRef] [PubMed]
  21. Dubourg, O.; Faruch-Bilfeld, M.; Telmon, N.; Maupoint, E.; Saint-Martin, P.; Savall, F. Correlation between Pubic Bone Mineral Density and Age from a Computed Tomography Sample. Forensic Sci. Int. 2019, 298, 345–350. [Google Scholar] [CrossRef]
  22. Paschall, A.; Ross, A.H. Biological Sex Variation in Bone Mineral Density in the Cranium and Femur. Sci. Justice 2018, 58, 287–291. [Google Scholar] [CrossRef]
  23. Dubourg, O.; Faruch-Bilfeld, M.; Telmon, N.; Savall, F.; Saint-Martin, P. Technical Note: Age Estimation by Using Pubic Bone Densitometry According to a Twofold Mode of CT Measurement. Int. J. Legal Med. 2020, 134, 2275–2281. [Google Scholar] [CrossRef]
  24. Bergot, C.; Bocquet, J.-P. Etude Systématique, En Fonction de l’âge, de l’os Spongieux et de l’os Cortical de l’humérus et Du Fémur. Bull. Mem. Soc. Anthropol. Paris 1976, 3, 215–242. [Google Scholar] [CrossRef]
  25. Szilvássy, J.; Kritscher, H. Estimation of Chronological Age in Man Based on the Spongy Structure of Long Bones. Anthropol. Anzeiger 1990, 48, 289–298. [Google Scholar] [CrossRef]
  26. Lespessailles, E.; Poupon, S.; Niamane, R.; Loiseau-Peres, S.; Derommelaere, G.; Harba, R.; Courteix, D.; Benhamou, C.L. Fractal Analysis of Trabecular Bone Texture on Calcaneus Radiographs: Effects of Age, Time since Menopause and Hormone Replacement Therapy. Osteoporos. Int. 2002, 13, 366–372. [Google Scholar] [CrossRef]
  27. Barrier, P.; Dedouit, F.; Braga, J.; Joffre, F.; Rougé, D.; Rousseau, H.; Telmon, N. Age at Death Estimation Using Multislice Computed Tomography Reconstructions of the Posterior Pelvis. J. Forensic Sci. 2009, 54, 773–778. [Google Scholar] [CrossRef] [PubMed]
  28. Ferrant, O.; Rougé-Maillart, C.; Guittet, L.; Papin, F.; Clin, B.; Fau, G.; Telmon, N. Age at Death Estimation of Adult Males Using Coxal Bone and CT Scan: A Preliminary Study. Forensic Sci. Int. 2009, 186, 14–21. [Google Scholar] [CrossRef]
  29. Curate, F.; Perinha, A.; Silva, A.M.; Cunha, E.; Umbelino, C.; Nogueira, C. Metacarpal Cortical Bone Loss and Osteoporotic Fractures in the Coimbra Identified Skeletal Collection. Int. J. Osteoarchaeol. 2019, 29, 73–81. [Google Scholar] [CrossRef]
  30. Virtama, P.; Helelä, T. Radiographic Measurements of Cortical Bone: Variations in a Normal Population between 1 and 90 Years of Age. Acta radiol. 1969, 1–268. [Google Scholar]
  31. Sinanoglu, A.; Kocasarac, H.D.; Noujeim, M. Age Estimation by an Analysis of Spheno-Occipital Synchondrosis Using Cone-Beam Computed Tomography. Leg. Med. 2016, 18, 13–19. [Google Scholar] [CrossRef] [PubMed]
  32. Turunen, M.J.; Prantner, V.; Jurvelin, J.S.; Kröger, H.; Isaksson, H. Composition and Microarchitecture of Human Trabecular Bone Change with Age and Differ between Anatomical Locations. Bone 2013, 54, 118–125. [Google Scholar] [CrossRef]
  33. Lochmüller, E.M.; Matsuura, M.; Bauer, J.; Hitzl, W.; Link, T.M.; Müller, R.; Eckstein, F. Site-Specific Deterioration of Trabecular Bone Architecture in Men and Women with Advancing Age. J. Bone Miner. Res. 2008, 23, 1964–1973. [Google Scholar] [CrossRef] [PubMed]
  34. Todd, T.W. Age Changes in the Pubic Bone. VIII. Roentgenographic Differentiation. Am. J. Phys. Anthropol. 1930, 14, 255–271. [Google Scholar] [CrossRef]
  35. Walker, R.A.; Lovejoy, C.O. Radiographic Changes in the Clavicle and Proximal Femur and Their Use in the Determination of Skeletal Age at Death. Am. J. Phys. Anthropol. 1985, 68, 67–78. [Google Scholar] [CrossRef] [PubMed]
  36. Gehring, K.D.; Haffner, H.T.; Weber, D.; Graw, M. Investigations on the Reliability of Determining an Individual’s Age from the Proximal Femur. HOMO- J. Comp. Hum. Biol. 2002, 52, 214–220. [Google Scholar] [CrossRef] [PubMed]
  37. De Froidmont, S.; Grabherr, S.; Vaucher, P.; De Cesare, M.; Egger, C.; Papageorgopoulou, C.; Roth, V.; Morand, G.; Mangin, P.; Uldin, T. Virtual Anthropology: A Comparison between the Performance of Conventional X-Ray and MDCT in Investigating the Trabecular Structure of Long Bones. Forensic Sci. Int. 2013, 225, 53–59. [Google Scholar] [CrossRef] [PubMed]
  38. Acsádi, G.Y.; Nemeskéri, J. History of Human Life Span and Mortality.; Akadémiai Kiadó: Budapest, 1970. [Google Scholar]
  39. Benito, M.; Sánchez, J.A.; Codinha, S. Age-at-Death Estimation Based on Radiological and Image Analysis Methods in Clavicle in a Current Spanish Population. Int. J. Legal Med. 2014, 128, 523–533. [Google Scholar] [CrossRef] [PubMed]
  40. Fernández Castillo, R.; López Ruiz, M.C. Assessment of Age and Sex by Means of DXA Bone Densitometry: Application in Forensic Anthropology. Forensic Sci. Int. 2011, 209, 53–58. [Google Scholar] [CrossRef]
  41. Macchiarelli, R.; Bondioli, L. Linear Densitometry and Digital Image Processing of Proximal Femur Radiographs: Implications for Archaeological and Forensic Anthropology. Am. J. Phys. Anthropol. 1994, 93, 109–122. [Google Scholar] [CrossRef]
  42. Botha, D.; Lynnerup, N.; Steyn, M. Age Estimation Using Bone Mineral Density in South Africans. Forensic Sci. Int. 2019, 297, 307–314. [Google Scholar] [CrossRef]
  43. Lu, Y.; Wang, L.; Hao, Y.; Wang, Z.; Wang, M.; Ge, S. Analysis of Trabecular Distribution of the Proximal Femur in Patients with Fragility Fractures. BMC Musculoskelet. Disord. 2013, 14. [Google Scholar] [CrossRef]
  44. Petaros, A.; Caplova, Z.; Verna, E.; Adalian, P.; Baccino, E.; de Boer, H.H.; Cunha, E.; Ekizoglu, O.; Ferreira, M.T.; Fracasso, T.; et al. Technical Note: The Forensic Anthropology Society of Europe (FASE) Map of Identified Osteological Collections. Forensic Sci. Int. 2021, 328. [Google Scholar] [CrossRef]
  45. Cunha, E.; Wasterlain, S. The Coimbra Identified Osteological Collections. In Skeletal Series in their Socioeconomic Context; Grupe, G., Peters, J., Eds.; M. Leidorf: Rahden/Westphalia, 2007. [Google Scholar]
  46. Kucheryavski, S.; Belyaev, I.; Fominykh, S. Estimation of Age in Forensic Medicine Using Multivariate Approach to Image Analysis. Chemom. Intell. Lab. Syst. 2009, 97, 39–45. [Google Scholar] [CrossRef]
  47. Matthew Turk; Alex Pentland Eigenfaces for Recognition. J. Cogn. Neurosci. 1991, 3.
  48. Bentley, J.L. Multidimensional Binary Search Trees Used for Associative Searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
  49. Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference and Prediction; Springer-Verlag New York: New York, 2009; ISBN 978-0-387-84857-0. [Google Scholar]
  50. Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Data Mining: Practical Machine Learning Tools and Techniques; Elsevier: Amsterdam, 2016; ISBN 9780128042915. [Google Scholar]
  51. Mays, S. The Archaeology of Human Bones; Routledge: London, 2021. [Google Scholar]
  52. Curate, F.; Albuquerque, A.; Ferreira, I.; Cunha, E. Sex Estimation with the Total Area of the Proximal Femur: A Densitometric Approach. Forensic Sci. Int. 2017, 275, 110–116. [Google Scholar] [CrossRef]
  53. Curate, F.; d’Oliveira Coelho, J.; Gonçalves, D.; Coelho, C.; Ferreira, M.T.; Navega, D.; Cunha, E. A Method for Sex Estimation Using the Proximal Femur. Forensic Sci. Int. 2016, 266, 579.e1–579.e7. [Google Scholar] [CrossRef]
  54. Christensen, A.M.; Leslie, W.D.; Baim, S. Ancestral Differences in Femoral Neck Axis Length : Possible Implications for Forensic Anthropological Analyses §. Forensic Sci. Int. 2014, 236, 193.e1–193.e4. [Google Scholar] [CrossRef] [PubMed]
  55. Mendonça, M.C. de Estimation of Height from the Length of Long Bones in a Portuguese Adult Population. Am. J. Phys. Anthropol. 2000, 112, 39–48. [Google Scholar] [CrossRef]
  56. Kranioti, E.F.; Vorniotakis, N.; Galiatsou, C.; Işcan, M.Y.; Michalodimitrakis, M. Sex Identification and Software Development Using Digital Femoral Head Radiographs. Forensic Sci. Int. 2009, 189. [Google Scholar] [CrossRef] [PubMed]
  57. Curate, F.; Albuquerque, A.; Cunha, E.M. Age at Death Estimation Using Bone Densitometry: Testing the Fernández Castillo and López Ruiz Method in Two Documented Skeletal Samples from Portugal. Forensic Sci. Int. 2013, 226, 296.e1–296.e6. [Google Scholar] [CrossRef]
  58. Martins, R.; Oliveira, P.E.; Schmitt, A. Estimation of Age at Death from the Pubic Symphysis and the Auricular Surface of the Ilium Using a Smoothing Procedure. Forensic Sci. Int. 2012, 219, 287.e1–287.e7. [Google Scholar] [CrossRef] [PubMed]
  59. Kotěrová, A.; Velemínská, J.; Cunha, E.; Brůžek, J. A Validation Study of the Stoyanova et Al. Method (2017) for Age-at-Death Estimation Quantifying the 3D Pubic Symphyseal Surface of Adult Males of European Populations. Int. J. Legal Med. 2019, 133, 603–612. [Google Scholar] [CrossRef] [PubMed]
  60. San Millán, M.; Rissech, C.; Turbón, D. A Test of Suchey-Brooks (Pubic Symphysis) and Buckberry-Chamberlain (Auricular Surface) Methods on an Identified Spanish Sample: Paleodemographic Implications. J. Archaeol. Sci. 2013, 40, 1743–1751. [Google Scholar] [CrossRef]
  61. White, T.; Black, M.; Folkens, P. Human Osteology; Academic Press: Amsterdam, 2012; ISBN 9780123741349. [Google Scholar]
  62. Kotěrová, A.; Navega, D.; Štepanovský, M.; Buk, Z.; Brůžek, J.; Cunha, E. Age Estimation of Adult Human Remains from Hip Bones Using Advanced Methods. Forensic Sci. Int. 2018, 287, 163–175. [Google Scholar] [CrossRef] [PubMed]
  63. MacDonald, H.M.; Nishiyama, K.K.; Kang, J.; Hanley, D.A.; Boyd, S.K. Age-Related Patterns of Trabecular and Cortical Bone Loss Differ between Sexes and Skeletal Sites: A Population-Based HR-PQCT Study. J. Bone Miner. Res. 2011, 26, 50–62. [Google Scholar] [CrossRef]
  64. Khosla, S.; Riggs, B.L.; Atkinson, E.J.; Oberg, A.L.; McDaniel, L.J.; Holets, M.; Peterson, J.M.; Melton, L.J. Effects of Sex and Age on Bone Microstructure at the Ultradistal Radius: A Population-Based Noninvasive in Vivo Assessment. J. Bone Miner. Res. 2006, 21, 124–131. [Google Scholar] [CrossRef]
  65. Masset, C. Age Estimation Based on Cranial Sutures. In Age Markers in the Human Skeleton; Iscan, M.Y., Ed.; CC Thomas: Springfield, 1989; pp. 71–103. [Google Scholar]
  66. Bonnick, S.L.; Lewis, L.A. Bone Densitometry for Technologists, Third Edition; Human Press: Tottowa, 2013; ISBN 9781461436256. [Google Scholar]
  67. d’Oliveira Coelho, J.; Curate, F.; Navega, D. Osteomics : Decision Support Systems for Forensic Anthropologists. In Statistics and Probability in Forensic Anthropology; Obertová, Z., Stewart, A., Cattaneo, C., Eds.; Academic Press: London, UK, 2020; pp. 259–273. [Google Scholar]
Preprints 89519 g001
Figure 1. Feature extraction with Principal Components Analysis – a femora space and eigenfemora approach.
Figure 1. Feature extraction with Principal Components Analysis – a femora space and eigenfemora approach.
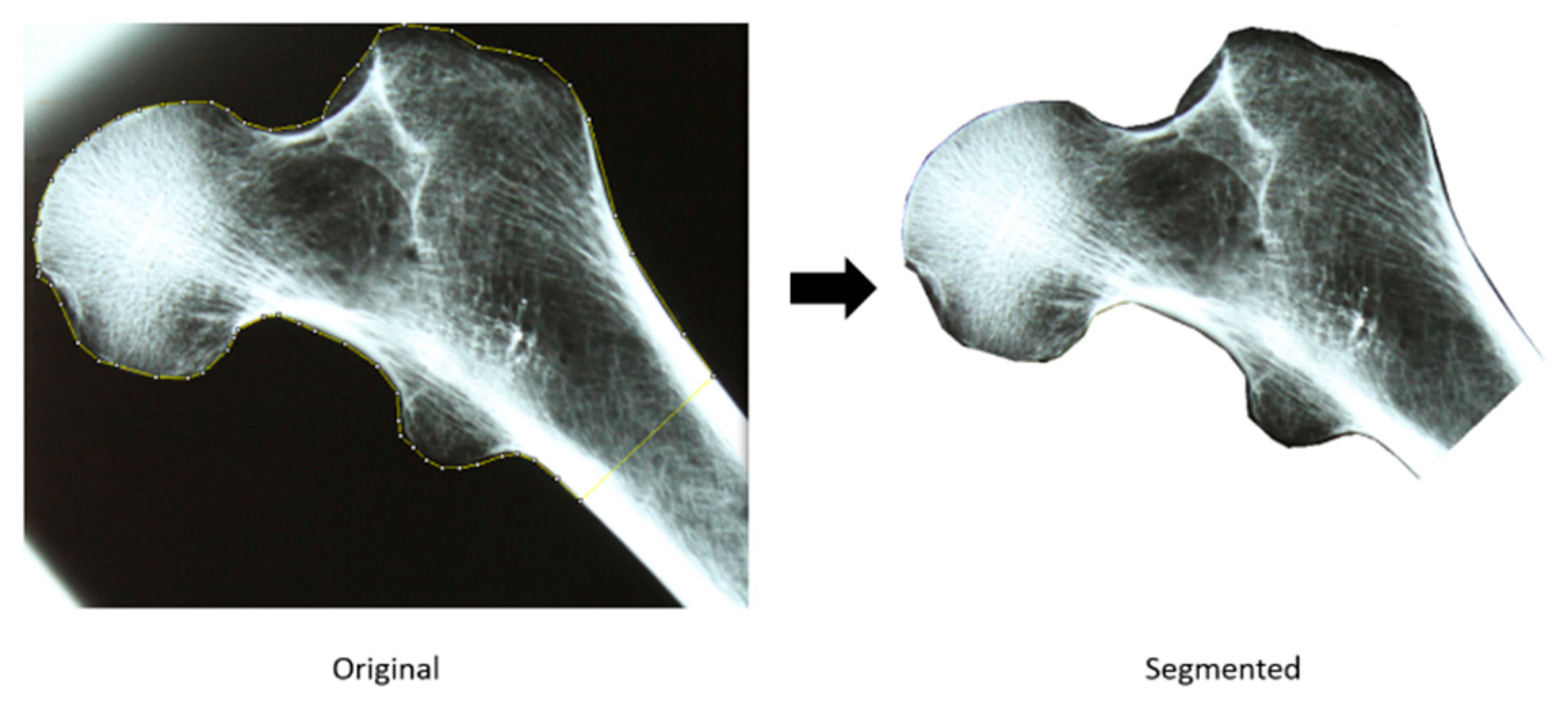
Preprints 89519 g001
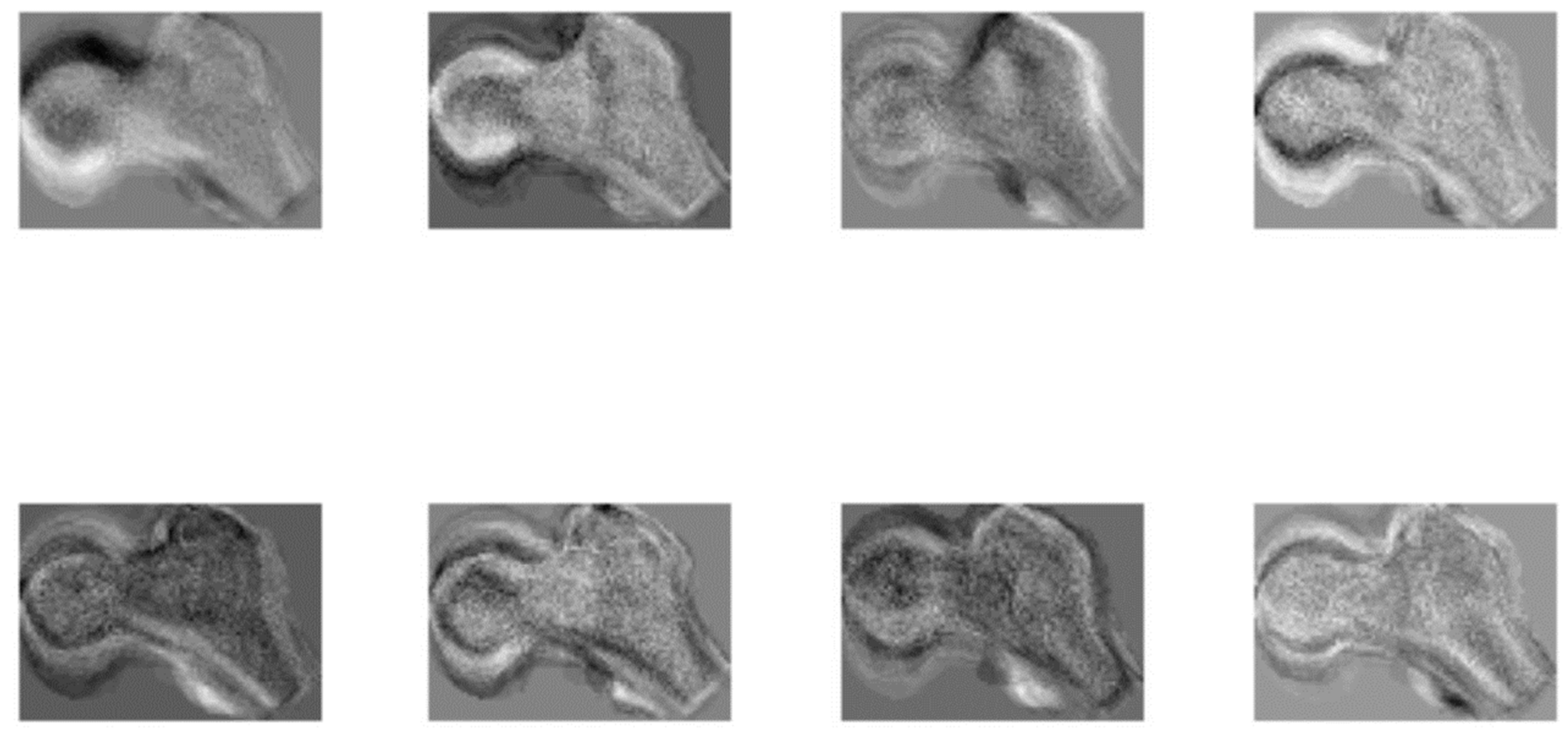
Preprints 89519 g002
Figure 2. First eight eigenfemora of the females’ sample (ordered from top left to bottom right).
Figure 2. First eight eigenfemora of the females’ sample (ordered from top left to bottom right).
Preprints 89519 g002
Preprints 89519 g003
Figure 3. Jet color map representation of the first eight eigenfemora of the males’ sample (ordered from top left to bottom right).
Figure 3. Jet color map representation of the first eight eigenfemora of the males’ sample (ordered from top left to bottom right).
Preprints 89519 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated