Prerpints.org logo
Preprint
Article

Graph Propagation Dynamics of an Epidemic Model with Heterogeneous Control Strategies on Complex Networks

Altmetrics

Downloads

133

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

02 November 2023

Posted:

03 November 2023

You are already at the latest version

Alerts
Abstract
The stability and optimal control for an SIS epidemic model with demographics and heterogeneous control strategies (immunization and quarantine) on complex networks are investigated. The epidemic threshold, disease-free and endemic equilibria are derived. Then, global asymptotical stability about the two equilibria are studied based on different methods. Furthermore, the optimal control issue about the system is also considered. We obtain the existence and uniqueness of the optimal control and optimal control tactics. Some numerical simulations were conducted to illustrate and supplement the theoretical results. Meanwhile, the effects of the combination of various immunization and quarantine schemes are studied and also compared with the optimal control strategies.
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematical and Computational Biology

1. Introduction

The prevalence and outbreak of infectious diseases is always an important issue affecting the national economy and people’s livelihood [1]. Researches on the transmission mechanism and dynamics of infectious diseases have attracted the attention of many scholars. Specifically, mathematical models have been a potent tool for forecasting the trajectory of infectious diseases and evaluating different prevention and control measures [2,3]. Through the application of optimal control theory and qualitative assessment of mathematical models, the effective management, reduction, and potential eradication of an infectious disease can be achieved. [4,5,6,7,8]. Based on different mechanisms of disease transmission, Kermack and McKendrick introduced the SIS and SIR epidemic models [9,10,11]. Subsequent to their work, a variety of epidemic models have emerged to shed light on the progression of various diseases and to offer insightful control measures.
Any research progress on the dynamics and control of epidemic transmission may have a significant impact on the prevention and control of infectious diseases, which has attracted widespread attention from scientific research [12,13]. During the transmission of infectious diseases, the infected transmission mainly occurs through the contact between susceptible and infected individuals, then quarantine has become a commonly employed strategy for controlling disease. For example, Hethcote et al. studied SIQS and SIQR epidemiology models with different incidence [14]. The Refs. [15,16,17] have also conducted qualitative analysis of mathematical models with infected isolation on the assumption of uniformly mixing population. Compared with the classics propagation models, heterogeneous networks own a better reflection with the statistical properties of real social networks. Li et al. introduced an SIQRS epidemic model based on scale-free networks, and their theoretical results indicate that the epidemic threshold is closely linked to the network’s structural characteristics [18]. Kang et al. explored how the quarantine based on node degree, as well as constant rates of birth and death, affect disease dynamics on scale-free networks by utilizing a novel deterministic model [19]. Chen et al. formulated SVIQR and SVIQS models with heterogeneous quarantine rate and immunity rate to investigate the effects of intervention methods on the behavior of infectious diseases within heterogeneous networks [12]. Cheng et al. considered a network-based SIQS model with non-monotone incidence rate and studied the global stability of equilibria [20]. Zhao et al. developed a stochastic SIQS epidemic model on scale-free networks, taking into account random fluctuations in infection rates [21]. However, those models either ignored the demographics or assumed that the recruitment of population is constant.
Consistently implementing control measures can effectively reduce the scale of infection, however, if considering the economic factors, relying solely on continuous control measures may not be sufficient to achieve optimal control goals when the disease prevalence is substantial. Therefore, A viable approach is to employ time-varying control within certain bounds to strike a balance between control objectives and the associated costs via optimal control theory. Optimal control applications in epidemic dynamics primarily concentrated on homogeneous contact networks [22,23,24,25,26,27]. Recently, many intriguing works on the optimal control of epidemics on heterogeneous networks have emerged [18,28,29,30,31,32,33,34,35]. Li et al. presented a nonlinear SIQS epidemic model on networks and explored the issue of optimal quarantine control to minimize the cost of control measures [32]. Zhang et al. examined the optimal control of an SIQRS model that includes vaccination on a network, and studied the effects of different control strategies [34]. Yang et al. investigated the stability and optimal control on treatment for SIS epidemic systems combining in directed networks [35]. However, the above results only considered the optimal control strategy for isolation and did not compare it with other forms of heterogeneous isolation strategies.
The above works provide strong theoretical supports for the prevention of infectious diseases through isolation measures. However, appropriate vaccination for susceptible individuals is also crucial for preventing and controlling infection. On the basis of above consideration, we study an SIS epidemic model with heterogeneous immune for susceptible individuals and quarantine for infected one, which also consider the demographics of individuals on heterogeneous networks. The organization of this paper is as follows. In Sect.2, we introduce an SIQS model with heterogeneous control strategies1 of individuals on complex networks and provide some description and assumptions. In Sect.3, we obtain the equilibria and basic reproduction number. The main results are showed in Sect.4, we establish uniform persistence and analyze the global stability of the disease-free and endemic equilibria of system by different mathematical methods. The optimal time-varying quarantine control for the model is considered in Sect.5. In Sect.6, some numerical simulations are conducted to illustrate and supplement the analysis results. Finally, a brief conclusion is given in Sect.7.

2. Description and formation of epidemic models

Consider a population situated on a complex network N, in which each node of N represents either an individual or an unoccupied state. Every node has three optional states: susceptible state(S), quarantined state(Q), infected state(I) [21]. We divided the population into n groups, let S k ( t ) , I k ( t ) , Q k ( t ) denote the densities of susceptible, infected and quarantine nodes (individuals) with connectivity (degree) k at time t, respectively. The mechanism of our model mainly involves three factors. The schematic diagram of the model is shown in Figure 1, the meaning of parameters is listed in Table 1.
(1) Birth and Death: Each vacant node i in the network randomly selects a neighbor. If the neighbor is a vacant node, the state of i remains unchanged. If the neighbor is a non-vacant node, the vacant node i will be activated to generate a new susceptible nodes at the birth rate b. All non-vacant nodes become vacant nodes at a natural death rate d per unit time. We assume that each non-vacant node has the same birth contact ability A (where A = 1 ) due to physiological constraints.
(2) Immunization and Quarantine ( I → Q ): At each time step, susceptible individuals with degree k are immunized with the immune rate δ k . The infected nodes with degree k will be quarantined with rate β k . The quarantined individuals will recover to susceptible node with rate η . Nodes with the same degree have identical quarantine (immunization) strategies, while those with different degrees have different strategies.
(3) SIS epidemic framework: Infection S → I : At the initial moment, randomly select some nodes as infected nodes. At each time step, the possibility that each infected node i connect to its neighboring nodes is φ ( k i ) k i , where φ ( k ) represents the infectivity of infected nodes with degree k, and φ ( k ) = k [36,37,38], φ ( k ) =A [39], φ ( k ) = k m [40], φ ( k ) = a k m 1 + b k m [41]. If an infected node i interacts with a susceptible node j along a connecting edge, node j has a possibility of being infected by i at a transmission rate λ i j . For the node with degree k, the overall transmission rate is λ ( k ) .
Recovery I → S : Each infected node reverts to being susceptible at recovery rate γ .
According to above assumption, the model is as follows,
d S k ( t ) d t = b k [ 1 − N k ( t ) ] Ψ k − d S k ( t ) − λ ( k ) ( 1 − δ k ) S k ( t ) Θ ( t ) + γ I k ( t ) + η Q k ( t ) , d I k ( t ) d t = λ ( k ) ( 1 − δ k ) S k ( t ) Θ ( t ) − ( β k + γ + d ) I k ( t ) , d Q k ( t ) d t = β k I k ( t ) − ( η + d ) Q k ( t ) .
with initial conditions 0 ≤ S k ( 0 ) , I k ( 0 ) , Q k ( 0 ) ≤ 1 , k = 1 , 2 , … , n , where Θ ( t ) = ∑ i = 1 n p ( i | k ) φ ( i ) i I i ( t ) stands for the probability that the infected contact through a link which originates from a node with degree k and points to the infected node. The Ψ k ( t ) = ∑ i = 1 n p ( i | k ) A i N i ( t ) denotes the probability that a node of degree k has a reproductive contact with an individual neighbor, the 1 i denotes the probability that an individual neighbor of vacant node with degree i. On uncorrelated networks, the likelihood is deemed to be independent of the connectedness of the originating node of the link. Thus, we note Θ ( t ) = 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) I i ( t ) , Ψ k ( t ) = 1 〈 k 〉 ∑ i = 1 n p ( i ) N i ( t ) . The average density of susceptible, infected and quarantined nodes is S ( t ) = ∑ k = 1 n S k ( t ) p ( k ) , I ( t ) = ∑ k = 1 n I k ( t ) p ( k ) , Q ( t ) = ∑ k = 1 n Q k ( t ) p ( k ) .
Let N k ( t ) denotes the density of individuals of degree k at time t, and N k = S k + I k + Q k . We develop the equation for N k as,
d N k ( t ) d t = b ( 1 − N k ) Ψ k ( t ) − d N k ( t ) .
According to Ref. [42], we get lim t → ∞ N k ( t ) = 0 when b ≤ d , no other dynamic patterns are present; when b > d , lim t → + ∞ N k ( t ) = N k ( t ) * , where N k * = b k Ψ * d + b k Ψ * , Ψ * = 1 〈 k 〉 ∑ i = 1 n i p ( i ) b Ψ * d + b i Ψ * .
Given that the original system and the limiting system exhibit identical long-term dynamic characteristics. In order to better analyze the stability of the model, we can only consider the limit system of (1) under the condition of b > d and N k * = S k ( t ) + I k ( t ) + Q k ( t ) based on the analysis of N k ( t ) . The corresponding limiting systems of model (1) are formulated as follows:
d S k ( t ) d t = b k [ 1 − N k * ] Ψ * − d S k ( t ) − λ ( k ) ( 1 − δ k ) S k ( t ) Θ ( t ) + γ I k ( t ) + η Q k ( t ) , d I k ( t ) d t = λ ( k ) ( 1 − δ k ) S k ( t ) Θ ( t ) − ( β k + γ + d ) I k ( t ) , d Q k ( t ) d t = β k I k ( t ) − ( η + d ) Q k ( t ) .
with initial conditions 0 ≤ S k ( 0 ) , I k ( 0 ) , Q k ( 0 ) ≤ N k * < 1 , k = 1 , 2 , … , n .
The following proposition shows that the state space of the solutions of system (3) is positively invariant.
Proposition 1.
If ( S k ( t ) , I k ( t ) , Q k ( t ) ) k represents a solution to the system (3) that meets the initial conditions, then 0 ≤ S k ( t ) + I k ( t ) + Q k ( t ) ≤ N k * < 1 , k ∈ N n for any t ≥ 0 , i.e., Γ is positively invariant.
Proof. 
∀ x 0 ∈ Γ . Thus, ∀ t > 0 , we have N k 0 ≥ 0 , Ψ ( 0 ) ≥ 0 .
d Ψ ( t ) d t = ( b − d ) Ψ ( t ) − b Ψ ( t ) 〈 k 〉 ∑ i i p ( i ) N i ( t ) .
We obtain that Ψ ( t ) = Ψ ( 0 ) e b − d − b 〈 k 〉 Σ i i p ( i ) N i ( t ) ≥ 0 . By N k ( t ) = S k ( t ) + I k ( t ) + Q k ( t ) and system (2), the evolution of N k ( t ) is derived by the following equation:
d N k ( t ) d t = b k [ 1 − N k ( t ) ] Ψ − d N k ( t ) ≥ − [ b k Ψ + d ] N k ( t ) .
We have N k ( t ) ≥ N k ( 0 ) e − ( b k Ψ + d ) t ≥ 0 . Then, from system (2), we also acquire
d ( 1 − N k ( t ) ) d t = − ( b k Ψ + d ) [ 1 − N k ( t ) ] + d .
Obviously, N k ( t ) < 1 , and 0 ≤ S k ( t ) + I k ( t ) + Q k ( t ) = N k ( t ) < 1 .
Then, we verify I k ≥ 0 for any k = 1 , 2 , … , n . If not, because I k ( 0 ) ≥ 0 , there is exist a j ∈ { 1 , 2 , … , n } and t 0 ≥ 0 satisfy
t 0 = inf { t | I j ( t ) = 0 , d I j ( t ) d t < 0 } .
It is evident that I j ( t 0 ) = 0 , I j ′ ( t 0 ) < 0 for any t ∈ [ 0 , t 0 ] , I j ( t ) ≥ 0 , we have
d I j ( t 0 ) d t = λ ( j ) ( 1 − δ j ) S j ( t 0 ) Θ ( t 0 ) − ( β j + γ + d ) I j ( t 0 ) = λ ( j ) ( 1 − δ j ) S j ( t 0 ) Θ ( t 0 ) < 0 .
Because of Θ ( t 0 ) = 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) I i ( t 0 ) ≥ 0 , we obtain S j ( t 0 ) < 0 . On the other hand, for any t ∈ [ 0 , t 0 ] , Q j ( 0 ) ≥ 0 , we attain
d Q j ( t ) d t = β j I j ( t ) − ( η + d ) Q j ( t ) ≥ − ( η + d ) Q j ( t ) .
That is to say Q j ( t ) ≥ Q j ( 0 ) e − ( η + d ) t ≥ 0 . When t ∈ [ 0 , t 0 ] ,
d S j ( t ) d t = b j [ 1 − N j ( t ) ] Ψ j − d S j ( t ) − λ ( j ) ( 1 − δ j ) S j ( t ) Θ ( t ) + γ I j ( t ) + η Q j ( t )   ≥ − d S j ( t ) − λ ( j ) ( 1 − δ j ) S j ( t ) Θ ( t ) .
Then, we acquire S j ( t 0 ) ≥ S j ( 0 ) e − ∫ 0 t 0 d + λ j ( 1 − δ j ) Θ ( t ) d τ ≥ 0 . It is contradictory, hence, I k ( t ) ≥ 0 , for any k and t ≥ 0 . We also can get S k ( t ) , Q k ( t ) ≥ 0 , and S k ( t ) , I k ( t ) , Q k ( t ) < 1 . That completes the proof. □

3. Equilibria and Basic Reproduction Number

In this section, the basic reproduction number R 0 is determined, which is the average number of new infections generated by a single newly infected individual throughout the entire infection period [20]. Considering the equivalent system,
d I k ( t ) d t = λ ( k ) ( 1 − δ k ) ( N k * − I k ( t ) − Q k ( t ) ) Θ ( t ) − ( β k + γ + d ) I k ( t ) , d Q k ( t ) d t = β k I k ( t ) − ( η + d ) Q k ( t ) .
Denote X is the space of functions, x = ( I 1 ( t ) , Q 1 ( t ) , … , I n ( t ) , Q n ( t ) ) ∈ X is the state space for system (4).
Γ = { x ∈ X : 0 ≤ I k ( t ) , Q k ( t ) < 1 , k = 1 , 2 , … , n } .
The Proposition 1 can show that Γ is the positive invariant for system (4). All viable steady states of system (4) are satisfied the following equation,
λ ( k ) ( 1 − δ k ) ( N k ( t ) − I k ( t ) − Q k ( t ) ) Θ ( t ) − ( β k + γ + d ) I k ( t ) = 0 , β k I k ( t ) − ( η + d ) Q k ( t ) = 0 .
In particular, there exists disease-free equilibrium of (4) E 0 = ( 0 , 0 , … , 0 ) ) , and the positive equilibrium E * = ( I k * , Q k * ) k , where E * satisfies that,
Q k * = β k η I k * , Θ * = 1 k ∑ i = 1 n φ ( i ) p ( i ) I i * , I k * = λ ( k ) ( 1 − δ k ) N k * Θ * λ ( k ) ( 1 − δ k ) ( 1 + β k η ) Θ * + β k + γ + d .
The basic reproduction number R 0 can be determined according to the following theorem.
Theorem 1.
Define the basic reproduction number
R 0 = 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) λ ( i ) ( 1 − δ i ) N i * β i + γ + d .
There always exists a disease-free equilibrium E 0 . If and only if R 0 > 1 , the system (4) has unique positive equilibrium point E * which satisfy that
Q k * = β k η I k * , Θ * = 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) I i * , I k * = λ ( k ) ( 1 − δ k ) N k * Θ * λ ( k ) ( 1 − δ k ) ( 1 + β k η ) Θ * + β k + γ + d .
Proof. 
Eq. (6) implies that
I k = λ ( k ) ( 1 − δ k ) N k Θ λ ( k ) ( 1 − δ k ) ( 1 + β k η ) Θ + β k + γ + d ,
Substituting (8) into Θ . Then we get,
Θ = 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) λ ( i ) ( 1 − δ i ) N i Θ λ ( i ) ( 1 − δ i ) ( 1 + β i η ) Θ + β i + γ + d ≜ Θ f ( Θ ) ,
where
f ( Θ ) = 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) λ ( i ) ( 1 − δ i ) N i λ ( i ) ( 1 − δ i ) ( 1 + β i η ) Θ + β i + γ + d .
Because of f ′ ( Θ ) < 0 and lim Θ → + ∞ f ( Θ ) = 0 , it is clear that Eq. (9) has the positive solution if and only if f ( 0 ) = 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) λ ( i ) ( 1 − δ i ) N i β i + γ + d > 1 . That is to say, when R 0 > 1 , Eq. (6) has unique positive solution Θ * , namely, a unique positive equilibrium point E * of system (4) exists described by equation (7) if and only if R 0 > 1 . The proof is completed. □

4. Stability Analysis for SIQS Model

4.1. Stability Analysis of Disease-Free Equilibrium

Firstly, it is proved that the disease-free equilibrium (DFE) E 0 is locally asymptotically stable by the same method in [43] by the following theorem.
Theorem 2.
If R 0 < 1 , then the DFE of system (4) is locally asymptotically stable and unstable if R 0 > 1 .
Proof. 
The Jacobian matrix of system (4) at E 0 is:
A = A 11 A 12 A 21 A 22 ,
where A 12 is the zero matrix with n order, A 21 = β k E n , A 22 = − ( η + d ) E n , E n is identity matrix, and
A 11 = ξ 1 φ 1 p 1 − ( γ + β 1 ) ξ 1 φ 2 p 2 … ξ 1 φ n p n ξ 2 φ 1 p 1 ξ 2 φ 2 p 2 − ( γ + β 2 ) … ξ 2 φ n p n ⋮ ⋮ … ⋮ ξ n φ 1 p 1 ξ n φ 2 p 2 … ξ n φ n p n − ( γ + β n ) ,
where ξ i = λ ( i ) ( 1 − δ i ) N i * 〈 k 〉 , φ i p i = φ ( i ) p ( i ) . Let y = { y 1 , y 2 , … , y n , y n + 1 , … , y 2 n } ∈ Γ .
Subsequently, the system (4) can be reformulated in a vector format as:
d y d t = A y + N ( y ) .
Let N ( y ) represent a column vector and N ( y ) ≤ 0 ,
N ( y ) = − λ ( 1 ) ( 1 − δ 1 ) ( I 1 + Q 1 ) Θ λ ( 2 ) ( 1 − δ 2 ) ( I 2 + Q 2 ) Θ ⋮ λ ( n ) ( 1 − δ n ) ( I n + Q n ) Θ 0 0 ⋮ 0 .
We consider the eigenvalues of matrix A are determined by | ρ E n − A 11 | | ρ E n − A 22 | = 0 . It is obvious that the characteristic equation has n multiple roots − ( η + d ) from | ρ E n − A 22 | = 0 . Other eigenvalues of matrix A is determined by | ρ E n − A 11 | = 0 . Through some elementary transformations, | ρ E n − A 11 | = 0 changes to
ρ − ξ 1 φ 1 p 1 + ( β 1 + γ + d ) − ξ 1 φ 2 p 2 … − ξ 1 φ n p n ξ 1 ξ 2 ( ρ + β 1 + γ + d ) ρ + ( β 2 + γ + d ) … 0 ⋮ ⋮ … ⋮ ξ 1 ξ n ( ρ + β 1 + γ + d ) 0 … ρ + ( β n + γ + d ) = 0 .
Case 1 If ρ ≠ − ( β i + γ + d ) , then we get
( ρ + β 1 + γ + d ) 1 − 1 〈 k 〉 ∑ i = 1 n λ ( i ) ( 1 − δ i ) N i * φ ( i ) p ( i ) ρ + β i + γ + d = 0 .
Note G ( ρ ) = 1 〈 k 〉 ∑ i = 1 n λ ( i ) ( 1 − δ i ) N i * φ ( i ) p ( i ) ρ + β i + γ + d . Obviously, the solutions of equation (12) are determined by G ( ρ ) = 1 . Since G ′ ( ρ ) < 0 , G ( 0 ) = R 0 , lim ρ → + ∞ G ( ρ ) = 0 , lim ρ → − ( β i + γ + d ) G ( ρ ) = ∞ , hence, when R 0 < 1 , the solutions of equation G ( ρ ) = 1 are negative. Therefore, the equation (12) only has negative solutions. Case 2 If ∏ i = 2 n ( ρ + β i + γ + d ) = 0 , since the sum of all eigenvalues is equal to the trace of the matrix. Therefore, when R 0 < 1 , ρ 1 = ξ 1 φ ( i ) p ( i ) − ( β 1 + γ + d ) < 0 , and ρ i = − ( β i + γ + d ) < 0 .
Furthermore, because N ( y ) ≤ 0 , thus d y d t ≤ A y . Since all the eigenvalues of matrix A are negative, the equilibrium point E 0 of system (4) is locally asymptotically stable when R 0 < 1 . □
Then, we get the global asymptotic stability of E 0 .
Theorem 3.
When R 0 < 1 , the disease-free equilibrium E 0 of system (4) is global asymptotic stability.
Proof. 
From system (3), we get
d Θ ( t ) d t = 1 〈 k 〉 ∑ k = 1 n φ ( k ) p ( k ) λ ( k ) ( 1 − δ k ) ( N k * − I k ( t ) − Q k ( t ) ) Θ ( t ) − ( β k + γ + d ) Θ ( t )   ≤ 1 〈 k 〉 ∑ k = 1 n φ ( k ) p ( k ) λ ( k ) ( 1 − δ k ) N k * Θ ( t ) − ( β k + γ + d ) Θ ( t )   = ( β k + γ + d ) 1 〈 k 〉 ∑ k = 1 n φ ( k ) p ( k ) λ ( k ) ( 1 − δ k ) N k * β k + γ + d − 1 Θ ( t )   = ( β k + γ + d ) ( R 0 − 1 ) Θ ( t ) .
We obtain Θ ( t ) ≤ Θ ( 0 ) e ( β k + γ + d ) ( R 0 − 1 ) t , while Θ ( t ) ≥ 0 from the Proposition 1. Therefore, if R 0 < 1 , we can acquire lim t → + ∞ Θ ( t ) = 0 , and lim t → + ∞ I k ( t ) = 0 . From the second equation of system (4), we get lim t → + ∞ Q k ( t ) = 0 . This demonstrates that E 0 of system (4) is globally stable when R 0 < 1 . The proof is finished. □

4.2. Global Stability of Endemic Equilibrium

In this section, we seek to study the conditions for the uniform persistence of the disease which is important in proving global stability of endemic equilibrium E * . The result of uniform persistence is showed in the following Lemma.
Lemma 1.
When R 0 > 1 , the system (4) is permanent, i.e., there exists ε > 0 , such that
lim t → + ∞ inf { I k ( t ) , Q k ( t ) } k = 1 n ≥ ε ,
where ( I k ( t ) , Q k ( t ) ) is any solution of system (4) satisfying (5).
Proof. 
Based on the Theorem 4.2 of [42], we need to verify that all hypotheses for system (4) are satisfied. By setting C = Γ , Condition (1) is fulfilled. Condition (2) is evidently met. For condition (3), notice that A 11 T is irreducible and a i j ≥ 0 , whenever i ≠ j , hence there exists an positive eigenvector h ˜ = ( h 1 , h 2 , . . . , h n ) of A 11 T and its corresponding eigenvalue is s ( A 11 ) ( s ( A ) = R e i λ i ), when R 0 > 1 , s ( A 11 ) > 0 . Let h n + 1 = h n + 2 = … = h 2 n = 0 , then, we note h = ( h 1 , h 2 , … , h 2 n ) , and it satisfies A T h = λ h . Let r = min 1 ≤ i ≤ n ( h i ) , for any y ∈ Γ , one has h · y ≥ r ∑ i = 1 n y i ≥ r ∑ i = 1 n y i 2 . Thus, condition (3) is verified. Since every part of N ( y ) is negative and h ≥ 0 , hence, condition (4) is satisfied. To confirm condition (5), we set G = { y ∈ Γ | h · N ( y ) = 0 } . If y ∈ G , then
∑ i = 1 n h i ( y i + y n + i ) λ ( i ) ( 1 − δ i ) Θ = 0 .
Given that every term in above sum is non-negative, one has y i = 0 for all i = 1 , 2 , … n . Therefore, the only invariant set corresponding to (11) that is contained within G is y = 0 . Condition (5) is satisfied. Hereby, all conditions are satisfied, the proof of uniform persistence is completed. □
From Lemma 1, it is clear that if R 0 > 1 , the infection will always exists. The following theorem is showed that the global stability of endemic equilibrium.
Theorem 4.
Suppose that ( I k ( t ) , Q k ( t ) ) is a solution of (4) satisfying initial condition. If R 0 > 1 , then lim t → + ∞ I k ( t ) = I k * , lim t → + ∞ Q k ( t ) = Q k * , that is to say, the endemic equilibrium E * is global attractivity.
Proof. 
Firstly, from Lemma 1 and k ∈ { 1 , 2 , … , n } , we get there exist 0 < ε ≪ 1 , such that, as t is sufficiently large, I k ≥ ε and Q k ≥ ε is satisfied. Hence, when t > 0 , we get ε 〈 φ ( k ) 〉 〈 k 〉 ≤ Θ ( t ) ≤ 〈 φ ( k ) 〉 〈 k 〉 . Then, from (4), we get
d I k ( t ) d t ≤ λ ( k ) 〈 φ ( k ) 〉 〈 k 〉 ( 1 − δ k ) ( N k * − I k ( t ) ) − ( β k + γ + d ) I k ( t ) , t > 0 .
For any given constant 0 < ε 1 < min { ε , λ ( k ) ( 1 − δ k ) 〈 φ ( k ) 〉 〈 k 〉 ( 1 − N k * ) + β k + γ + d λ ( k ) ( 1 − δ k ) 〈 φ ( k ) 〉 〈 k 〉 + β k + γ + d } , there exists a t 1 > 0 , when t > t 1 , such that
I k ( t ) ≤ A k 1 = λ ( k ) ( 1 − δ k ) 〈 φ ( k ) 〉 〈 k 〉 N k * λ ( k ) ( 1 − δ k ) 〈 φ ( k ) 〉 〈 k 〉 + β k + γ + d + ε 1 , t > t 1 .
Then, from the second equation of (4), it implies that
d Q k ( t ) d t = β k ( N k * − S k ( t ) − Q k ( t ) ) − ( η + d ) Q k ( t ) ≤ β k ( N k * − Q k ( t ) ) − ( η + d ) Q k ( t ) , t > 0 .
Hence, for any given constant 0 < ε 2 < min { 1 2 , ε 1 , η + d + β k − β k N k * η + β k } , there exists a t 2 > t 1 , such that
Q k ( t ) ≤ B k 1 = β k N k * η + d + β k , t > t 2 .
On the other hand, from the first equation of (4), it can be inferred that
d I k ( t ) d t ≥ λ ( k ) ε 〈 φ ( k ) 〉 〈 k 〉 ( 1 − δ k ) ( N k * − I k ( t ) − B k 1 ) − ( β k + γ + d ) I k ( t ) .
Hence, for any given constant 0 < ε 3 < min { 1 3 , ε 2 , λ ( k ) ( 1 − δ k ) ε 〈 φ ( k ) 〉 〈 k 〉 ( N k * − B k 1 ) λ ( k ) ( 1 − δ k ) ε 〈 φ ( k ) 〉 〈 k 〉 + β k + γ + d } , there exists a t 3 > t 2 , such that,
I k ( t ) ≥ a k 1 = λ ( k ) ( 1 − δ k ) ε 〈 φ ( k ) 〉 〈 k 〉 ( N k * − B k 1 ) λ ( k ) ( 1 − δ k ) ε 〈 φ ( k ) 〉 〈 k 〉 + β k + γ + d − ε 3 , t > t 3 .
Next, following from the second equation of system (4), we also get
d Q k ( t ) d t = β k I k ( t ) − ( η + d ) Q k ( t ) ≥ β k a k 1 − ( η + d ) Q k ( t ) .
Similarly, for any given constant 0 < ε 4 < min { 1 4 , ε 3 , β k a k 1 η + d } , there exists a t 4 > t 3 , such that
Q k ( t ) ≥ b k 1 = β k a k 1 η + d − ε 4 , t > t 4 .
Since ε i is a small constant, it follows that
0 < a k 1 ≤ I k ( t ) ≤ A k 1 < 1 , 0 < b k 1 ≤ Q k ( t ) ≤ B k 1 < 1 , t > t 4 .
and, we also get 0 < 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) a k 1 ≤ Θ ( t ) ≤ 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) A k 1 < 〈 φ ( k ) 〉 〈 k 〉 , t > t 4 . Again, by system (4), one has
d I k ( t ) d t ≤ λ ( k ) ( 1 − δ k ) ( N k * − I k ( t ) − b k 1 ) 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) A k 1 − ( β k + γ + d ) I k ( t ) , t > t 4 .
Hence, 0 < ε 5 < min { 1 5 , ε 4 , ( 1 − N k * + b k 1 ) λ ( k ) ( 1 − δ k ) 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) A k 1 + β k + γ + d λ ( k ) ( 1 − δ k ) 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) A k 1 + β k + γ + d } , there exists a t 5 > t 4 , such that,
I k ( t ) ≤ A k 2 = ( N k * − b k 1 ) λ ( k ) ( 1 − δ k ) 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) A k 1 λ ( k ) ( 1 − δ k ) 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) A k 1 + β k + γ + d + ε 5 , t > t 5 .
Thus,
d Q k ( t ) d t = β k I k ( t ) − ( η + d ) Q k ( t ) ≤ β k A k 2 − ( η + d ) Q k ( t ) , t > t 5
for any given constant 0 < ε 6 < min { 1 6 , ε 5 , η + d − β k A k 2 η + d } , there exists a t 6 > t 5 , such that,
Q k ( t ) ≤ B k 1 = min { B k 1 , β k A k 2 η + d + ε 6 } , t > t 6 .
Consequently, one obtains that
d I k ( t ) d t ≥ λ ( k ) ( 1 − δ k ) ( N k * − I k ( t ) − B k 2 ) 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) a k 1 − ( β k + γ + d ) I k ( t ) , t > t 6 .
Hence, for any given constant 0 < ε 7 < min { 1 7 , ε 6 , ( N k * − B k 2 ) λ ( k ) ( 1 − δ k ) 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) a k 1 λ ( k ) ( 1 − δ k ) 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) a k 1 + β k + γ + d } , there exists a t 7 > t 6 , such that,
I k ( t ) ≥ a k 2 = ( N k * − B k 2 ) λ ( k ) ( 1 − δ k ) 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) a k 1 λ ( k ) ( 1 − δ k ) 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) a k 1 + β k + γ + d − ε 7 , t > t 7 .
Again, one has
d Q k ( t ) d t = β k I k ( t ) − ( η + d ) Q k ( t ) ≥ β k a k 2 − ( η + d ) Q k ( t ) , t > t 7 .
for any given constant 0 < ε 8 < min { 1 8 , ε 7 , β k a k 2 η + d } , there exists a t 8 > t 7 , such that
Q k ( t ) ≥ b k 2 = max { b k 1 , β k a k 2 η + d − ε 8 } , t > t 8 .
It is clear that
0 < a k 1 < a k 2 ≤ I k ( t ) ≤ A k 2 < A k 1 < 1 , 0 < b k 1 < b k 2 ≤ Q k ( t ) ≤ B k 2 < B k 1 < 1 , t > t 8 .
Similarly, the calculation’s step m can be executed, resulting in four sequences. { A k m } , { B k m } , { a k m } , { b k m } are obtained:
I k ( t ) ≤ A k m = ( N k * − b k m − 1 ) λ ( k ) ( 1 − δ k ) 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) A k m − 1 λ ( k ) ( 1 − δ k ) 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) A i m − 1 + ( β k + γ + d ) + ε 4 m − 3 , t > t 4 m − 3 , Q k ( t ) ≤ B k m = min { B k m − 1 , β k A i m η + d + ε 4 m − 2 } , t > t 4 m − 2 , I k ( t ) ≥ a k m = ( N k * − B k m ) λ ( k ) ( 1 − δ k ) 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) a i m − 1 λ ( k ) ( 1 − δ k ) 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) a i m − 1 + ( β k + γ + d ) − ε 4 m − 1 , t > t 4 m − 1 , Q k ( t ) ≥ b k m = max { b k m − 1 , β k a k m η + d − ε 4 m } , t > t 4 m .
It is clear that
0 < a k m ≤ I k ( t ) ≤ A k m < 1 , 0 < b k m ≤ Q k ( t ) ≤ B k m < 1 , t > t 4 m .
We get { a k m } , { b k m } are monotone increasing sequences and { A k m } , { B k m } are strictly monotone decreasing sequences. It is clear that
B k m = β k A k m η + d + ε 4 m − 2 , b k m = β k a k m η + d − ε 4 m .
Since all of them are bounded monotonic sequences, the sequential limits exist. Let
lim t → + ∞ A k ( m ) ( t ) = A k , lim t → + ∞ B k ( m ) ( t ) = B k , lim t → + ∞ a k ( m ) ( t ) = a k , lim t → + ∞ b k ( m ) ( t ) = b k .
Since { ε m } satisfies that 0 < ε m < 1 m , one has ε m → 0 as m → ∞ . Therefore, from (14), as m → ∞ , we get
A k = ( N k * − b k ) λ ( k ) ( 1 − δ k ) A λ ( k ) ( 1 − δ k ) A + ( β k + γ + d ) , B k = β k A k η + d ,
a k = ( N k * − B k ) λ ( k ) ( 1 − δ k ) a λ ( k ) ( 1 − δ k ) a + ( β k + γ + d ) , b k = β k a k η + d .
where A = 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) A i , a = 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) a i Then, we get
A k = N k * ς k A ( η + d ) [ a ς k ( η + d − β k ) + ( η + d ) ( β k + γ + d ) ] H k , a k = N k * ς k a ( η + d ) [ A ς k ( η + d − β k ) + ( η + d ) ( β k + γ + d ) ] H k .
where ς k = λ ( k ) ( 1 − δ k ) , H k = ( η + d ) 2 ( ς k A + ( β k + γ + d ) ) ( ς k a + ( β k + γ + d ) ) − ς k 2 β k 2 A a . For any k, if η + d = β k , it is clear that A = a . If η + d ≠ β k , Substituting (16) into A:
A = 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) N i * ς i A ( η + d ) [ a ς i ( η + d − β i ) + ( η + d ) ( β i + γ + d ) ] H i , a = 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) N i * ς i a ( η + d ) [ A ς i ( η + d − β i ) + ( η + d ) ( β i + γ + d ) ] H i .
We get 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) ς i N i * H i ( η + d ) 2 ( β i + γ + d ) ( A − a ) = 0 . Therefore, A = a . Above all, from A = a , which is equivalent to A i = a i for any i = 1 , 2 , … , n . Then, from (13) and (14), it follows that
I k * = lim t → + ∞ I k ( t ) = A k = a k = ( N k * − b k ) λ ( k ) ( 1 − δ k ) Θ * λ ( k ) ( 1 − δ k ) Θ * + ( β k + γ + d ) ,
Q k * = lim t → + ∞ Q k ( t ) = B k = b k = β k I k * η + d .
which is consistent with Theorem 2. This completes the proof. □

5. The Optimal Control for SIQS Model

In this section, we study the optimal control for system (1). To meet the control objective and minimize control expenses at the same time, a viable approach to target epidemic outbreaks is by implementing time-varying control using optimal control theory for various infectious diseases, for example, the results in Culshaw et al. [44], Chen et al. [45] and Abboubakar et al. [46]. The aim of this section is to identify the optimal quarantine measure for controlling the transmission of diseases.
First, we introduce an time-varying control rate u k ( t ) represents the percentage of infected individuals with degree k being quarantined. Hence, system (3) can be written as
d S k ( t ) d t = b k [ 1 − N k * ] Ψ * − d S k ( t ) − λ ( k ) ( 1 − δ k ) S k ( t ) Θ ( t ) + γ I k ( t ) + η Q k ( t ) , d I k ( t ) d t = λ ( k ) ( 1 − δ k ) S k ( t ) Θ ( t ) − ( u k ( t ) + γ + d ) I k ( t ) , d Q k ( t ) d t = u k ( t ) I k ( t ) − ( η + d ) Q k ( t ) .
We note the quarantine function u ( t ) = ( u 1 ( t ) , u 2 ( t ) , . . . u n ( t ) ) are bounded, Lebesgue integrable functions. Since our aim is to reduce both the scale of infection and control strengths, we consider the following objective functional J ( u k ) associated with model in the control set Ω = { ( u 1 ( t ) , u 2 ( t ) , . . . u n ( t ) ) ∣ 0 ≤ u i ≤ 0.9 } , B k denotes a positive weight parameter. The objective (cost) functional given by
J ( u k ) = ∫ 0 T ∑ k = 1 n [ I k ( t ) + 1 2 B k u k 2 ( t ) ] d t .
The Lagrange function for optimal control problems (18) and (19) is defined as
L = ∑ i = 1 n [ I i + B i 2 u i 2 ( t ) ] .
In order to solve the optimal control problem, the existence of an optimal control must be assured. We firstly establish the existence of a solution for the control system (18) by applying the method in Refs. [45,46].
Theorem 5.
For the objective functional J ( u k ) associated with model (18) defined in Ω, there exists an optimal quarantine strategy μ * = ( μ 1 , … , μ n ) minimizing J ( u ) .
Proof. 
(i) Clearly, for any 0 ≤ t ≤ T , the Ω is an nonempty set of Lebesgue integrable functions. (ii) It is obviously that the solutions are bounded ensuring the boundedness and convexity of admissible control set. (iii) Model (18) can be written as
d Φ ( t ) d t = F ( t , Φ , u k ( t ) )
where F ( t , Φ , u k ) = ( F 1 , F 2 , … , F n ) is the right side of system (18), and Φ = ( Φ 1 , Φ 2 , … , Φ n ) T , Φ k = ( S k ( t ) , I k ( t ) , Q k ( t ) ) T . It follows that
| F ( t , Φ 1 , u k ( t ) ) − F ( t , Φ 2 , u k ( t ) ) | ≤ ∑ i | F i ( t , Φ 1 , u k ( t ) ) − F i ( t , Φ 2 , u k ( t ) ) | .
For any k ∈ N n , since | Θ 1 ( t ) − Θ 2 ( t ) | = 1 〈 k 〉 ∑ i = 1 n φ ( i ) p ( i ) | I i 1 ( t ) − I i 2 ( t ) | and the boundedness of solution, there exists a constant M 1 satisfied that | Θ 1 ( t ) − Θ 2 ( t ) | ≤ M 1 | I k 1 ( t ) − I k 2 ( t ) | . Then, There exists a positive constant M to guarantee the inequality | F k ( Φ 1 ) − F k ( Φ 2 ) | ≤ M | Φ k 1 − Φ k 2 | is satisfied. (iv) Let 0 < ξ < 1 and m k ( t ) , v k ( t ) ∈ Ω , we get L ( t , Φ , ( 1 − ξ ) m ( t ) + ξ v ( t ) ) − ( 1 − ξ ) L ( t , Φ , m ( t ) ) − ξ L ( t , Φ , v ( t ) ) = ∑ i = 1 n B i 2 ξ ( ξ − 1 ) ( v i − m i ) 2 < 0 . (v) There exist c 1 > 0 , ρ > 1 , c 2 > 0 such that L ( t , Φ , u k ( t ) ) = ∑ i = 1 n [ I i + B i 2 u i 2 ( t ) ] ≥ ∑ i = 1 n B i 2 u i 2 ( t ) ≥ B m i n 2 ∑ i = 1 n u i 2 ( t ) ≥ C 1 | u | 2 − C 2 .
By utilizing the results of Refs. [45,46], we get that there exists a optimal control μ * = ( μ 1 , ⋯ , μ n ) minimizing J ( μ ) . The proof is completed. □
The solution to the optimal control problem will be determined through Pontryagin’s minimum principle [47]. We note the Hamiltonian H as
H = ∑ i = 1 n [ I k ( t ) + 1 2 B k u k 2 ( t ) ] d t + ∑ i = 1 3 ∑ k = 1 n ω k i F k i ( t , Φ , u k ( t ) ) .
If ( Φ * , u k * ) is an optimal solution of the optimal control problem, then there exists a non-trivial vector function ω k = ( ω k 1 , ω k 2 , ω k 3 ) , k = 1 , 2 , … , n satisfying the following equalities:
d Φ ( t ) d t = ∂ H ( t , Φ * ( t ) , u k * , ω ( t ) ) ∂ ω , ∂ H ( t , Φ * ( t ) , u k * , ω ( t ) ) ∂ u k ( t ) = 0 , d ω ( t ) d t = − ∂ H ( t , Φ * ( t ) , u k * , ω ( t ) ) ∂ Φ .
It follows from the derivation above
ω * = 0 , ∂ H ∂ u k ( t ) < 0 , 0 < ω * < 0.9 , ∂ H ∂ u k ( t ) = 0 , ω * = 0.9 , ∂ H ∂ u k ( t ) > 0 .
Now the necessary conditions are implemented on the Hamiltonian H in (21) and we obtain the following results.
Theorem 6.
For a given optimal control solution μ ( t ) and the corresponding system solution S k * ( t ) , Q k * ( t ) , I k * ( t ) , there is an adjacency function ω k 1 ( t ) , ω k 2 ( t ) , ω k 3 ( t ) that satisfies the following conditions
d ω k 1 ( t ) d t = λ ( k ) ( 1 − δ k ) Θ * ( t ) [ ω k 1 ( t ) − ω k 2 ( t ) ] + d ω k 1 ( t ) − 1 , d ω k 2 ( t ) d t = λ ( k ) ( 1 − δ k ) S k * ( t ) φ ( k ) p ( k ) 〈 k 〉 ( ω k 1 ( t ) − ω k 2 ( t ) ) − γ ω k 1 ( t ) + ( u k + γ + d ) ω k 2 ( t ) − u k ω k 3 ( t ) − 1 , d ω k 3 ( t ) d t = − η ω k 1 ( t ) + ( η + d ) ω k 3 ( t ) .
with conditions ω k 1 ( T ) = ω k 2 ( T ) = ω k 3 ( T ) =0. Furthermore, the optimal control u k * = ( u 1 * , u 2 * , . . . , u n * ) is given by
u k * = min { max [ 0 , I k * ( t ) ( ω k 2 − ω k 3 ) B k ] , 0.9 }
Proof. 
We apply for the necessary conditions in the Pontryagin maximum principle with Hamiltonian function (21) to derive the adjoint variables is determined by the following equations.
d ω k 1 ( t ) d t = λ ( k ) ( 1 − δ k ) Θ * ( t ) [ ω k 1 ( t ) − ω k 2 ( t ) ] + d ω k 1 ( t ) − 1 , d ω k 2 ( t ) d t = λ ( k ) ( 1 − δ k ) S k * ( t ) φ ( k ) p ( k ) 〈 k 〉 ( ω k 1 ( t ) − ω k 2 ( t ) ) − γ ω k 1 ( t )     + ( u k + γ + d ) ω k 2 ( t ) − u k ω k 3 ( t ) − 1 , d ω k 3 ( t ) d t = − η ω k 1 ( t ) + ( η + d ) ω k 3 ( t ) .
By the optimal conditions, we have
∂ H ∂ u k ( t ) = B k u k * − ω k 2 I k * + ω k 3 I k * = 0 .
It follows that μ k * = ( ω k 2 − ω k 3 ) I k * B k . Using the property of the control space, we obtain
ω * = 0 , ( ω k 2 − ω k 3 ) I k * B k < 0 , 0 < ω * < 0.9 , ( ω k 2 − ω k 3 ) I k * B k = 0 , ω * = 0.9 , ( ω k 2 − ω k 3 ) I k * B k > 0 .
Then, we have the optimal control u k * in compact notation,
u k * = min { max [ 0 , ( ω k 2 − ω k 3 ) I k * B k ] , 0.9 }
That completes the proof. □

6. Simulations

In this section, we conducted some numerical simulations to validate and supplement our theoretical results, and to study the impact of parameters on the dynamics of disease, in order to find better control strategies. The numerical simulations include three parts, the first part is to verify the main theoretical results including the epidemic threshold and global stability. We will discuss and make some simulations to show the effectiveness of different immunity and quarantine strategies in second part. The numerical simulation in the third part demonstrates the effectiveness of the optimal control method that has been proved in Section 5. We constructed a BA (Barab a ´ si-Albert) scale-free network [48], which satisfies a power-law degree distribution P ( k ) ∼ C k − 3 , the network size N is set as 1000, n = k m a x =80. This network evolved from the initial network with size of m 0 = 3 and during each time step, new nodes with m = 3 edges are added to the network. Without loss of generality, we note λ ( k ) = λ k .
(I) Firstly, we perform some simulations in Figure 2 to verify the important results of global stability of equilibria. We denote
φ ( k ) = k , k ≤ 30 ; 30 , k > 30 .
Figure 2(a) shows the relationship between I ( t ) and infectious rate λ on some different networks. Based on the basic reproduction number R 0 , we can acquire the epidemic threshold of the disease is λ c = 〈 k 〉 ∖ ∑ i = 1 n φ ( i ) p ( i ) i N i * ( 1 − δ i ) β i + γ + d , where b = 0.2 , d = 0.16 , β k = 0.17 , η = 0.3 , δ k = 0.2 , γ = 0.36 . One can see that the epidemic threshold is consistent with our theoretical results very well. Figure 2(b) depicts that the disease-free equilibrium cannot undergo a Hopf bifurcation, i.e., if R 0 < 1 , the disease free equilibrium is global stability, and if R 0 > 1 , then the endemic equilibrium is persist and global stability, where b = 0.2 , d = 0.1 , β k = 0.2 , η = 0.3 , δ k = 0.2 , λ =0.01, 0.038, 0.055, 0.21, 0.28, 0.35 and γ =0.36, 0.36, 0.36, 0.18, 0.18, 0.18.
(II) Secondly, we depicts the effectiveness of the immune and quarantining control strategies in Figure 3 to Figure 4. In this part, we also discuss the SIQS model (1) on the network with various immunization (proportional immune strategy δ ˜ , target immune strategy δ k t , acquaintance immune strategy δ k a c ) schemes based on [49] and define quarantine schemes of infected individual (proportional quarantine strategy β k , target quarantine strategy β k t , acquaintance quarantining strategy β k a c ) according to various immunization schemes. Then, we define the heterogeneous quarantine rate β k as follows,
Proportional quarantine strategy: Denote the average quarantine rate of proportional quarantine β ˜ , 0 < β ˜ < 1 . Randomly selecting one infected node for isolation, the quarantine rate is independent of the degree of node, which is also a situation discussed in many papers.
Target quarantine strategy: we can devise a quarantine strategy for the infected nodes according to the definition of immunization [49]. Introduce an upper threshold κ , such that all infected nodes with connectivity k > κ are prioritize quarantined, i.e., we defined the quarantine rate β k t by
β k t = 1 , k > κ ; c , k = κ ; 0 , k < κ .
where 0 < c ≤ 1 , and ∑ k β k t P ( k ) = β k t ˜ , where β k t ˜ is the average quarantine rate of target quarantine.
Acquaintance quarantining strategy: Select a random portion p from the N nodes. The likelihood of quarantining a infected node with degree k is given by k P ( k ) N 〈 k 〉 , therefore β k a c = p k P ( k ) / 〈 k 〉 . We note that β k a c ˜ denote the average quarantine rate of acquaintance quarantine, where β k a c ˜ = ∑ k β k a c P ( k ) .
Figure 3(a) shows the I ( t ) under different quarantining control strategies, the target quarantine strategy is the most effective in controlling disease. Figure 3(b) compares the effectiveness of different quarantine strategies. We get that the target quarantine strategy has better effectiveness than others. Figure 3(c) shows the effectiveness of different immunity strategies, it shows that all three immunization schemes are effective compared to the case without any immunization; the targeted immunization scheme is more efficient than the proportional scheme discussed.
Figure 4(a) depicts the average infectious density with respect to quarantine rate under different immunity strategies. It also shows that the target strategy is better than proportional and acquaintance. We further show the average infectious density with respect to infected rate for the immunization schemes and quarantine strategies targeted, and acquaintance in Figure 4(b). We get that the targeted immunity and the target quarantine strategy have better effectiveness than others.
(III) Thirdly, we analyze and illustrate the optimal control and various quarantine schemes by numerical simulations in Figure 5 to Figure 6. In Figure 5, we depict I ( t ) under different control strategies. In order to provide a clearer representation of the findings in Figure 5(a), we additionally computed the objective function J ( μ ) values for diverse control approaches, as shown in Table 2. In the absence of any control strategy (i.e., u k = 0 ), the infection ultimately breaks out and reaches a stable level of infection. We also set a fixed control strategy compared with the optimal control strategy, which can find that if we want to obtain better results than the optimal control strategy, it will usually lead to a significant increase in control costs (i.e., u k m a x = 0.9 ). In Figure 5(b), we demonstrate the comparative effects of optimal control, without control, and acquaintance immunity combining with multiple quarantine strategies on infectious disease control. Compared with other strategies, the optimal control strategy has the best control effect.
Figure 6(a) illustrates the I ( t ) under optimal control under three cases: Low-cost at B k = 0.01 , moderate-cost at B k = 1 , and high-cost at B k = 100 . Even under high costs, as seen in the third scenario, the scale of infection can be notably curtailed through optimal control. Figure 6(b) displays the fluctuation of μ k across varying degrees under optimal regulation. It is evident that μ k tends to escalate as the degree rises. This indicates a higher level of infection, resulting in a higher value of μ k .

7. Conclusion

We propose an SIQS epidemic model with heterogeneous immune and quarantine measures on heterogeneous networks. We have performed a detailed mathematical analysis of our system, which deduces that the basic reproduction number R 0 , is collectively determined by the infection rate and the effectiveness of disease control measures. Specifically, when R 0 < 1 , the disease-free equilibrium E 0 exhibits global asymptotic stability. When R 0 > 1 , the endemic equilibrium E * demonstrates both local and global asymptotic stability. At the same time, we conducted an in-depth theoretical examination on system (1) to tackle the optimal quarantine control issue, confirming the presence of optimal solutions. We define different forms of quarantine measures and numerically simulated the effectiveness of a combination of different quarantine strategies and immune schemes in controlling diseases. Our findings indicate that the implementation of any control strategy can have a favorable impact on the magnitude of an epidemic outbreak, with the optimal control being particularly effective. Among them, the effect of target quarantine scheme can be comparable to the effect of optimal control. However, target isolation requires knowing the degree of all nodes in the network, which is a significant cost and workload.
A variety of control strategies, such as quarantine and immune schemes, can be employed for the effective management, mitigation, and potential eradication of infectious diseases. We expect that this paper can contributes to a understanding of the dynamics of infectious disease with the control measures. However, our paper is not based on a specific infectious disease, so there are still certain limitations in providing a specific basis for public health prevention measures. Studying the control measures for a specific disease based on infectious disease data will be a very meaningful work.

Author Contributions

Conceptualization, S.C. and K.S.; methodology, S.C., Y.W. and L.L.; software, S.C., Y.W. and L.L.; validation, S.C. and Y.W.; formal analysis, S.C. and K.S.; writing—original draft preparation, Y.W. and S.C.; writing—review and editing, Y.W., S.C., D.Y. and K.S.; visualization, Y.W., S.C. and K.S.; supervision, K.S.; funding acquisition, D.Y.

Funding

This work is supported by the National Social Science Funds of China (Grant No. 22BSH025), National Natural Science Foundation of China (Grant No.62303303 and Grant No. 61803047), Major Project of The National Social Science Foundation of China (19ZDA149, 19ZDA324) and Fundamental Research Funds for the Central Universities (14370119, 14390110). Ke-ke Shang is supported by Jiangsu Qing Lan Project.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

Theoretical Physics of Complex Systems Center (Nanjing University).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Xie, Y.K.; Wang, Z. A ratio-dependent impulsive control of an SIQS epidemic model with non-linear incidence. Applied Mathematics and Computation 2022, 423, 127018. [Google Scholar] [CrossRef]
  2. Hamou, A.A.; Rasul, R.R.; Hammouch, Z.; Özdemir, N. Analysis and dynamics of a mathematical model to predict unreported cases of COVID-19 epidemic in Morocco. Computational and Applied Mathematics 2022, 41, 289. [Google Scholar] [CrossRef]
  3. Bin, Y.; Ke-ke, S.; Michael, S.; Naipeng, C. Information overload: How hot topics distract from news—COVID-19 spread in the US. National Science Open 2023, 2, 20220051. [Google Scholar]
  4. Peter, O.J.; Afolabi, O.A.; Victor, A.A.; Akpan, C.E.; Oguntolu, F.A. Mathematical model for the control of measles. Journal of Applied Sciences and Environmental Management 2018, 22, 571–576. [Google Scholar] [CrossRef]
  5. Fraser, C.; Donnelly, C.A.; Cauchemez, S.; Hanage, W.P.; Van Kerkhove, M.D.; Hollingsworth, T.D.; Griffin, J.; Baggaley, R.F.; Jenkins, H.E.; Lyons, E.J.; et al. Pandemic potential of a strain of influenza A (H1N1): early findings. Science 2009, 324, 1557–1561. [Google Scholar] [CrossRef] [PubMed]
  6. Lipsitch, M.; Cohen, T.; Cooper, B.; Robins, J.M.; Ma, S.; James, L.; Gopalakrishna, G.; Chew, S.K.; Tan, C.C.; Samore, M.H.; et al. Transmission dynamics and control of severe acute respiratory syndrome. Science 2003, 300, 1966–1970. [Google Scholar] [CrossRef] [PubMed]
  7. Cai, L.M.; Li, Z.Q.; Song, X.Y. Global analysis of an epidemic model with vaccination. Journal of Applied Mathematics and Computing 2018, 57, 605–628. [Google Scholar] [CrossRef]
  8. Li, X.G.; Zou, X.; Cai, L.M.; Chen, Y.M. Global dynamics of a vector-borne disease model with direct transmission and differential susceptibility. Journal of Applied Mathematics and Computing 2023, 69, 381–402. [Google Scholar] [CrossRef]
  9. Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proceedings of the royal society of london. Series A, Containing papers of a mathematical and physical character 1927, 115, 700–721. [Google Scholar] [CrossRef]
  10. Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics. II.The problem of endemicity. Proceedings of the Royal Society of London. Series A, containing papers of a mathematical and physical character 1932, 138, 55–83. [Google Scholar] [CrossRef]
  11. Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics. III.Further studies of the problem of endemicity. Proceedings of the Royal Society of London. Series A, Containing papers of a mathematical and physical character 1933, 141, 94–122. [Google Scholar] [CrossRef]
  12. Chen, S.S.; Small, M.; Fu, X.C. Global stability of epidemic models with imperfect vaccination and quarantine on scale-free networks. IEEE Transactions on Network Science and Engineering 2019, 7, 1583–1596. [Google Scholar] [CrossRef]
  13. Peter, O.J.; Adebisi, A.F.; Ajisope, M.O.; Ajibade, F.O.; Abioye, A.I.; Oguntolu, F.A. Global stability analysis of typhoid fever model. Advances in Systems Science and Applications 2020, 20, 20–31. [Google Scholar] [CrossRef]
  14. Hethcote, H.; Zhi En, M.; Sheng Bing, L. Effects of quarantine in six endemic models for infectious diseases. Mathematical biosciences 2002, 180, 141–160. [Google Scholar] [CrossRef] [PubMed]
  15. Suo, Y.H. Asymptotical Stability of an SIQS Epidemic Model with Age Dependence and Generally Nonlinear Contact Rate. Applied Mechanics and Materials 2011, 58, 292–297. [Google Scholar] [CrossRef]
  16. Wei, F.Y.; Chen, F.X. Stochastic permanence of an SIQS epidemic model with saturated incidence and independent random perturbations. Physica A: Statistical Mechanics and its Applications 2016, 453, 99–107. [Google Scholar] [CrossRef]
  17. Zhang, X.B.; Liu, R.J. The stationary distribution of a stochastic SIQS epidemic model with varying total population size. Applied Mathematics Letters 2021, 116, 106974. [Google Scholar] [CrossRef]
  18. Li, T.; Wang, Y.M.; Guan, Z.H. Spreading dynamics of a SIQRS epidemic model on scale-free networks. Communications in Nonlinear Science and Numerical Simulation 2014, 19, 686–692. [Google Scholar] [CrossRef]
  19. Kang, H.Y.; Liu, K.H.; Fu, X.C. Dynamics of an epidemic model with quarantine on scale-free networks. Physics Letters A 2017, 381, 3945–3951. [Google Scholar] [CrossRef]
  20. Cheng, X.X.; Wang, Y.; Huang, G. Global dynamics of a network-based SIQS epidemic model with nonmonotone incidence rate. Chaos, Solitons and Fractals 2021, 153, 111502. [Google Scholar] [CrossRef]
  21. Zhao, R.D.; Liu, Q.M.; Sun, M.C. Dynamical behavior of a stochastic SIQS epidemic model on scale-free networks. Journal of Applied Mathematics and Computing 2022, 68, 813–838. [Google Scholar] [CrossRef]
  22. Iacoviello, D.; Stasio, N. Optimal control for SIRC epidemic outbreak. Computer methods and programs in biomedicine 2013, 110, 333–342. [Google Scholar] [CrossRef] [PubMed]
  23. Buonomo, B.; Lacitignola, D.; Vargas-De-León, C. Qualitative analysis and optimal control of an epidemic model with vaccination and treatment. Mathematics and Computers in Simulation 2014, 100, 88–102. [Google Scholar] [CrossRef]
  24. Kandhway, K.; Kuri, J. How to run a campaign: Optimal control of SIS and SIR information epidemics. Applied Mathematics and Computation 2014, 231, 79–92. [Google Scholar] [CrossRef]
  25. Kandhway, K.; Kuri, J. Optimal control of information epidemics modeled as Maki Thompson rumors. Communications in Nonlinear Science and Numerical Simulation 2014, 19, 4135–4147. [Google Scholar] [CrossRef]
  26. Jang, J.; Kwon, H.D.; Lee, J. Optimal control problem of an SIR reaction–diffusion model with inequality constraints. Mathematics and Computers in Simulation 2020, 171, 136–151. [Google Scholar] [CrossRef]
  27. Wang, B.; Tian, X.H.; Xu, R.; Song, C.W. Threshold dynamics and optimal control of a dengue epidemic model with time delay and saturated incidence. Journal of Applied Mathematics and Computing 2023, 69, 871–893. [Google Scholar] [CrossRef]
  28. Chen, L.J.; Sun, J.T. Global stability and optimal control of an SIRS epidemic model on heterogeneous networks. Physica A: Statistical Mechanics and its Applications 2014, 410, 196–204. [Google Scholar] [CrossRef]
  29. Chen, L.J.; Sun, J.T. Optimal vaccination and treatment of an epidemic network model. Physics Letters A 2014, 378, 3028–3036. [Google Scholar] [CrossRef]
  30. Xu, D.G.; Xu, X.Y.; Xie, Y.F.; Yang, C.H. Optimal control of an SIVRS epidemic spreading model with virus variation based on complex networks. Communications in Nonlinear Science and Numerical Simulation 2017, 48, 200–210. [Google Scholar] [CrossRef]
  31. Jia, N.; Ding, L.; Liu, Y.J.; Hu, P. Global stability and optimal control of epidemic spreading on multiplex networks with nonlinear mutual interaction. Physica A: Statistical Mechanics and its Applications 2018, 502, 93–105. [Google Scholar] [CrossRef]
  32. Li, K.Z.; Zhu, G.H.; Ma, Z.J.; Chen, L.J. Dynamic stability of an SIQS epidemic network and its optimal control. Communications in Nonlinear Science and Numerical Simulation 2019, 66, 84–95. [Google Scholar] [CrossRef]
  33. Wei, X.D.; Xu, G.C.; Zhou, W.S. Global stability of endemic equilibrium for a SIQRS epidemic model on complex networks. Physica A: Statistical Mechanics and its Applications 2018, 512, 203–214. [Google Scholar] [CrossRef]
  34. Zhang, L.; Liu, M.X.; Xie, B.L. Optimal control of an SIQRS epidemic model with three measures on networks. Nonlinear Dynamics 2021, 103, 2097–2107. [Google Scholar] [CrossRef]
  35. Yang, P.; Jia, J.B.; Shi, W.; Feng, J.W.; Fu, X.C. Stability analysis and optimal control in an epidemic model on directed complex networks with nonlinear incidence. Communications in Nonlinear Science and Numerical Simulation 2023, 121, 107206. [Google Scholar] [CrossRef]
  36. Pastor-Satorras, R.; Vespignani, A. Epidemic dynamics in finite size scale-free networks. Physical Review E 2002, 65, 035108. [Google Scholar] [CrossRef] [PubMed]
  37. Moreno, Y.; Pastor-Satorras, R.; Vespignani, A. Epidemic outbreaks in complex heterogeneous networks. The European Physical Journal B-Condensed Matter and Complex Systems 2002, 26, 521–529. [Google Scholar] [CrossRef]
  38. Wang, L.; Dai, G.Z. Global stability of virus spreading in complex heterogeneous networks. SIAM Journal on Applied Mathematics 2008, 68, 1495–1502. [Google Scholar] [CrossRef]
  39. Yang, R.; Wang, B.H.; Ren, J.; Bai, W.J.; Shi, Z.W.; Wang, W.X.; Zhou, T. Epidemic spreading on heterogeneous networks with identical infectivity. Physics Letters A 2007, 364, 189–193. [Google Scholar] [CrossRef]
  40. Chu, X.W.; Zhang, Z.Z.; Guan, J.H.; Zhou, S.G. Epidemic spreading with nonlinear infectivity in weighted scale-free networks. Physica A: Statistical Mechanics and its Applications 2011, 390, 471–481. [Google Scholar] [CrossRef]
  41. Zhang, H.F.; Fu, X.C. Spreading of epidemics on scale-free networks with nonlinear infectivity. Nonlinear Analysis: Theory, Methods & Applications 2009, 70, 3273–3278. [Google Scholar] [CrossRef]
  42. Zhu, G.H.; Chen, G.R.; Xu, X.J.; Fu, X.C. Epidemic spreading on contact networks with adaptive weights. Journal of Theoretical Biology 2013, 317, 133–139. [Google Scholar] [CrossRef]
  43. Liu, X.N.; Takeuchi, Y.; Iwami, S. SVIR epidemic models with vaccination strategies. Journal of Theoretical biology 2008, 253, 1–11. [Google Scholar] [CrossRef]
  44. Culshaw, R.V.; Ruan, S.; Spiteri, R.J. Optimal HIV treatment by maximising immune response. Journal of mathematical biology 2004, 48, 545–562. [Google Scholar] [CrossRef] [PubMed]
  45. Chen, P.Y.; Cheng, S.M.; Chen, K.C. Optimal control of epidemic information dissemination over networks. IEEE transactions on cybernetics 2014, 44, 2316–2328. [Google Scholar] [CrossRef] [PubMed]
  46. Abboubakar, H.; Guidzavai, A.K.; Yangla, J.; Damakoa, I.; Mouangue, R. Mathematical modeling and projections of a vector-borne disease with optimal control strategies: A case study of the Chikungunya in Chad. Chaos, Solitons and Fractals 2021, 150, 111197. [Google Scholar] [CrossRef]
  47. Fleming, W.H.; Rishel, R.W. Deterministic and stochastic optimal control; Vol. 1, 2012.
  48. Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
  49. Fu, X.C.; Small, M.; Walker, D.M.; Zhang, H.F. Epidemic dynamics on scale-free networks with piecewise linear infectivity and immunization. Physical Review E 2008, 77, 036113. [Google Scholar] [CrossRef]
1
The heterogeneous control strategies refer that the quarantine rate of infected node is not the constant, but related to the degree of node, and the immunize rates of susceptible nodes also are related to degree of node, the nodes with the same degree have the same control strategy. In other words, in the contact network, the control strategy for the nodes in the network is not uniform, but different control strategies are formulated based on the degree of the nodes.
Preprints 89539 g001
Figure 1. Flow chart of the SIQS model. Here S, I, Q represent susceptible, infected and quarantined state.
Figure 1. Flow chart of the SIQS model. Here S, I, Q represent susceptible, infected and quarantined state.
Preprints 89539 g001
Preprints 89539 g002
Figure 2. (a) The I ( t ) with respect to λ and the structure of network with different parameters m and m 0 . λ c denotes the theoretical epidemic threshold. Other parameter settings are as follows: b = 0.2 , d = 0.16 , β k = 0.17 , η = 0.3 , δ k = 0.2 γ = 0.36 ; (b) The average infected density I ( t ) under different parameters: λ = 0.01,0.038,0.055,0.21,0.28,0.3, γ =0.36,0.36,0.36,0.18,0.18,0.18, b = 0.2 , d = 0.1 , β k = 0.2 , η = 0.3 , δ k = 0.2 , which are corresponding to R 0 =0.1734, 0.6590, 0.9538<1; R 0 =5.3671,7.1561,8.9451> 1.
Figure 2. (a) The I ( t ) with respect to λ and the structure of network with different parameters m and m 0 . λ c denotes the theoretical epidemic threshold. Other parameter settings are as follows: b = 0.2 , d = 0.16 , β k = 0.17 , η = 0.3 , δ k = 0.2 γ = 0.36 ; (b) The average infected density I ( t ) under different parameters: λ = 0.01,0.038,0.055,0.21,0.28,0.3, γ =0.36,0.36,0.36,0.18,0.18,0.18, b = 0.2 , d = 0.1 , β k = 0.2 , η = 0.3 , δ k = 0.2 , which are corresponding to R 0 =0.1734, 0.6590, 0.9538<1; R 0 =5.3671,7.1561,8.9451> 1.
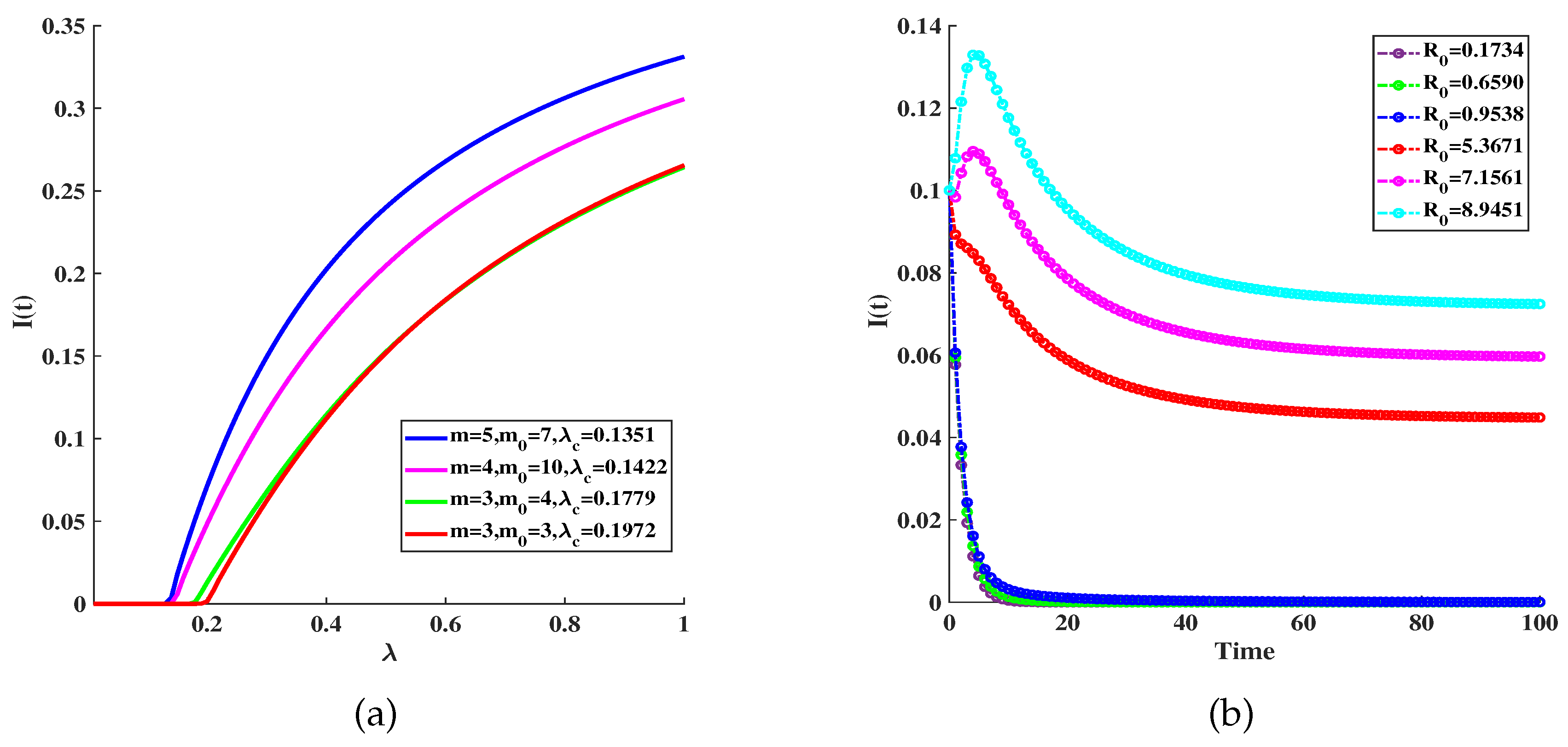
Preprints 89539 g002
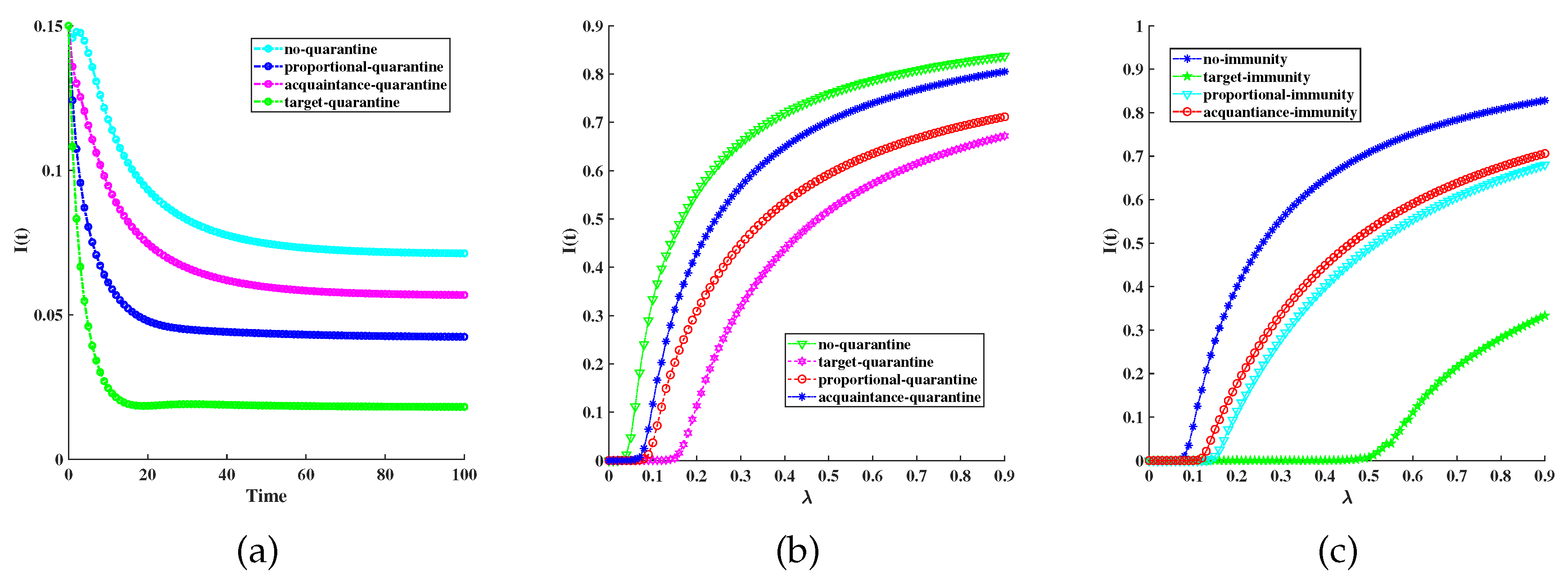
Preprints 89539 g003
Figure 3. (a) The I ( t ) under different quarantining control strategies, no-quarantine(cyan line), acquaintance-quarantine(prune line), proportional-quarantine(blue line), target-quarantine(green line): b = 0.2 , d = 0.08 , η = 0.3 , λ = 0.28 , δ k = 0.2 , γ = 0.18 , c = 0.8 , κ = 15 , p = 0.386 , β k = β k a c ˜ = β k t ˜ = β ˜ = 0.0499 . (b) The epidemic threshold λ c under different quarantine control strategies, no-quarantine(green line); target-quarantine(prune line); acquaintance-quarantine(blue line); proportional-quarantine(red line): b = 0.2 , d = 0.18 , δ k = 0.2 , γ = 0.5 , η = 0.35 , c = 0.8 , κ = 10 , p = 0.8946 , β k = β k a c ˜ = β k t ˜ = β ˜ = 0.1150 . (c) The epidemic threshold λ c under different immunize strategies, no-immunity(blue line); target-immunity(green line); proportional-immunity(cyan line); acquaintance-immunity(red line): b = 0.2 , d = 0.18 , γ = 0.5 , η = 0.35 , β k = 0.21 , c = 1 , κ = 7 , p = 0.9836 , δ k = δ k a c ˜ = δ k t ˜ = δ ˜ = 0.218 .
Figure 3. (a) The I ( t ) under different quarantining control strategies, no-quarantine(cyan line), acquaintance-quarantine(prune line), proportional-quarantine(blue line), target-quarantine(green line): b = 0.2 , d = 0.08 , η = 0.3 , λ = 0.28 , δ k = 0.2 , γ = 0.18 , c = 0.8 , κ = 15 , p = 0.386 , β k = β k a c ˜ = β k t ˜ = β ˜ = 0.0499 . (b) The epidemic threshold λ c under different quarantine control strategies, no-quarantine(green line); target-quarantine(prune line); acquaintance-quarantine(blue line); proportional-quarantine(red line): b = 0.2 , d = 0.18 , δ k = 0.2 , γ = 0.5 , η = 0.35 , c = 0.8 , κ = 10 , p = 0.8946 , β k = β k a c ˜ = β k t ˜ = β ˜ = 0.1150 . (c) The epidemic threshold λ c under different immunize strategies, no-immunity(blue line); target-immunity(green line); proportional-immunity(cyan line); acquaintance-immunity(red line): b = 0.2 , d = 0.18 , γ = 0.5 , η = 0.35 , β k = 0.21 , c = 1 , κ = 7 , p = 0.9836 , δ k = δ k a c ˜ = δ k t ˜ = δ ˜ = 0.218 .
Preprints 89539 g003
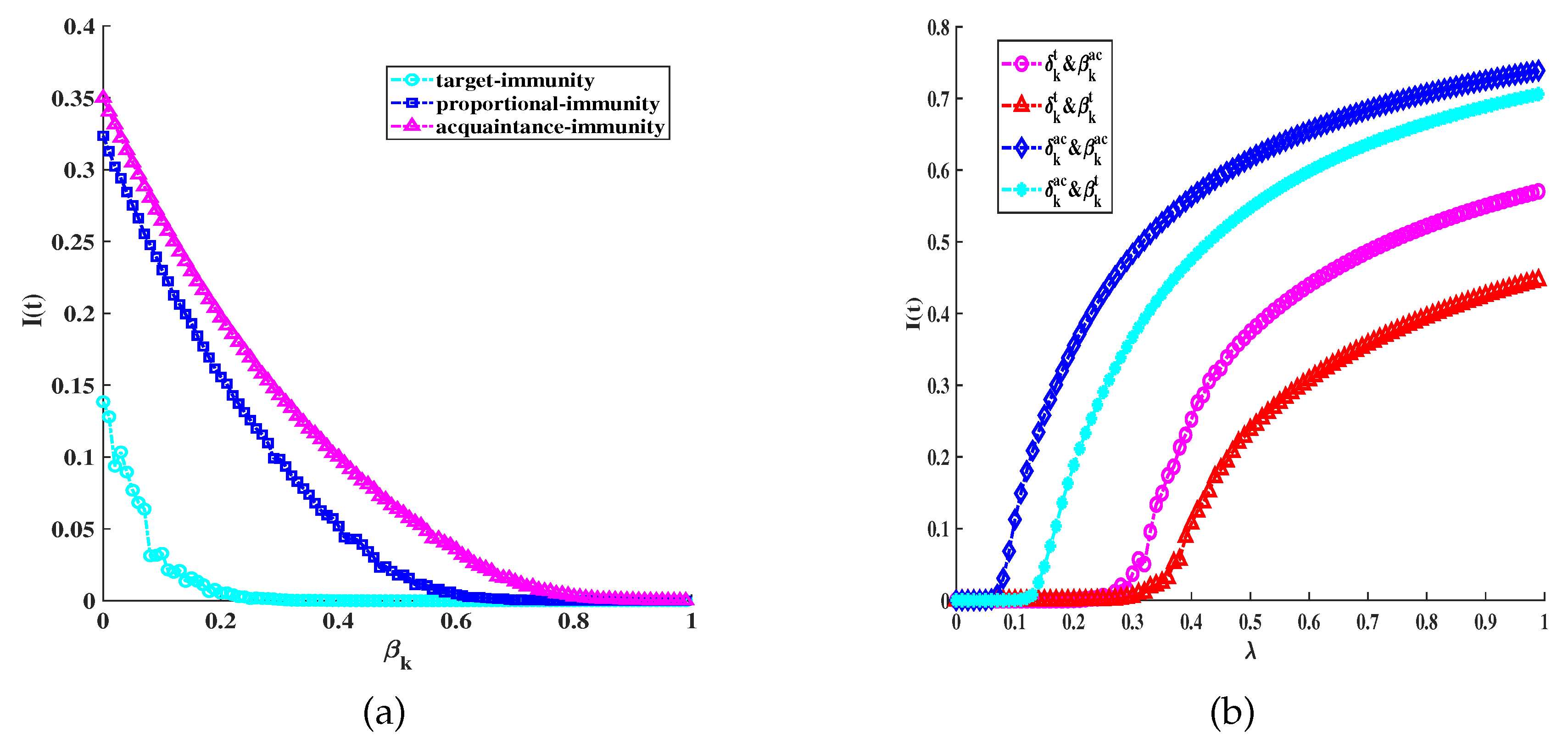
Preprints 89539 g004
Figure 4. The effectiveness of combination immune and quarantining control strategies: b = 0.2 , d = 0.18 , c = 1 , κ = 7 , p = 0.9836 , δ k = δ k a c ˜ = δ k t ˜ = δ ˜ = 0.218 . (a) Different immunity strategies with respect to quarantine rate: λ = 0.2 , γ = 0.38 , η = 0.3 , acquaintance-immunity (prune line), proportional-immunity (blue line), target-immunity(cyan line). (b) Comparison of different combination control strategies: γ = 0.5 , η = 0.35 , c = 0.8 , κ = 10 , p = 0.8946 , β k a c ˜ ( δ k a c ˜ ) = β k t ˜ ( δ k t ˜ ) = β ˜ ( δ ˜ ) = 0.1150 , target-immunity and target-quarantine(red line), target-immunity and acquaintance-quarantine(prune line), acquaintance-immunity and target-quarantine(cyan line), acquaintance-immunity and acquaintance-quarantine(blue line).
Figure 4. The effectiveness of combination immune and quarantining control strategies: b = 0.2 , d = 0.18 , c = 1 , κ = 7 , p = 0.9836 , δ k = δ k a c ˜ = δ k t ˜ = δ ˜ = 0.218 . (a) Different immunity strategies with respect to quarantine rate: λ = 0.2 , γ = 0.38 , η = 0.3 , acquaintance-immunity (prune line), proportional-immunity (blue line), target-immunity(cyan line). (b) Comparison of different combination control strategies: γ = 0.5 , η = 0.35 , c = 0.8 , κ = 10 , p = 0.8946 , β k a c ˜ ( δ k a c ˜ ) = β k t ˜ ( δ k t ˜ ) = β ˜ ( δ ˜ ) = 0.1150 , target-immunity and target-quarantine(red line), target-immunity and acquaintance-quarantine(prune line), acquaintance-immunity and target-quarantine(cyan line), acquaintance-immunity and acquaintance-quarantine(blue line).
Preprints 89539 g004
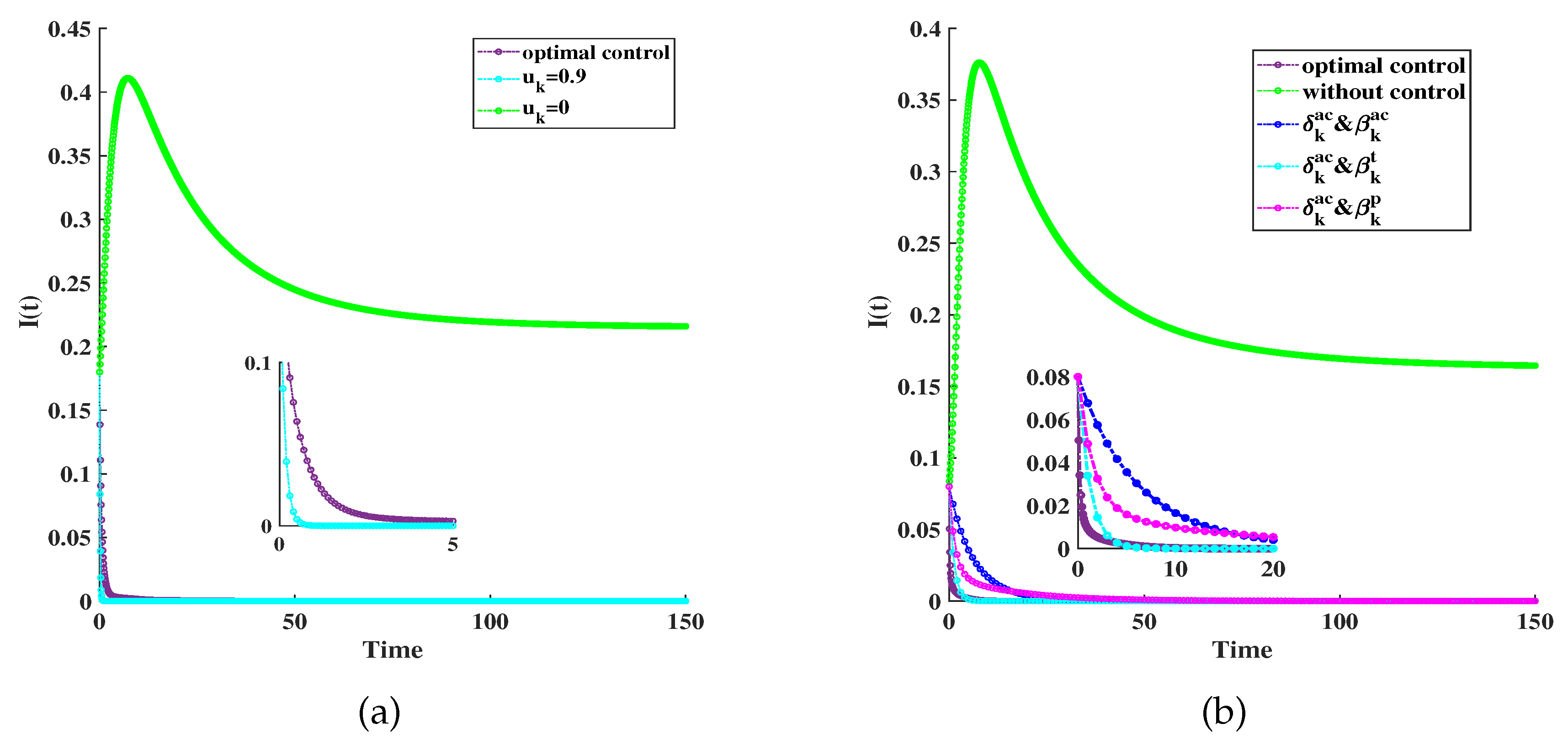
Preprints 89539 g005
Figure 5. (a) The average density I ( t ) under different control strategies, the lines with different colors corresponding to different optimal control: u k ( t ) = optimal control(purple line); u k ( t ) = 0.9 (cyan line); u k ( t ) = 0 (green line). Other parameter settings are as follows: b = 0.09 , d = 0.012 , λ = 0.3 , γ = 0.01 , η = 0.03 , δ k = 0.1 ; (b) Comparison of optimal control and combined heterogeneous control strategies, without control (green line); acquaintance immunization and acquaintance quarantine(blue line); acquaintance immunization and proportional quarantine(prune line); acquaintance immunization and target quarantine(cyan line); optimal control (purple line): b = 0.09 , d = 0.012 , λ = 0.3 , γ = 0.01 , δ = 0.218 , c = 1 , κ = 7 , p = 0.9836 , β k = β k a c ˜ = β k t ˜ = β ˜ = 0.218 .
Figure 5. (a) The average density I ( t ) under different control strategies, the lines with different colors corresponding to different optimal control: u k ( t ) = optimal control(purple line); u k ( t ) = 0.9 (cyan line); u k ( t ) = 0 (green line). Other parameter settings are as follows: b = 0.09 , d = 0.012 , λ = 0.3 , γ = 0.01 , η = 0.03 , δ k = 0.1 ; (b) Comparison of optimal control and combined heterogeneous control strategies, without control (green line); acquaintance immunization and acquaintance quarantine(blue line); acquaintance immunization and proportional quarantine(prune line); acquaintance immunization and target quarantine(cyan line); optimal control (purple line): b = 0.09 , d = 0.012 , λ = 0.3 , γ = 0.01 , δ = 0.218 , c = 1 , κ = 7 , p = 0.9836 , β k = β k a c ˜ = β k t ˜ = β ˜ = 0.218 .
Preprints 89539 g005
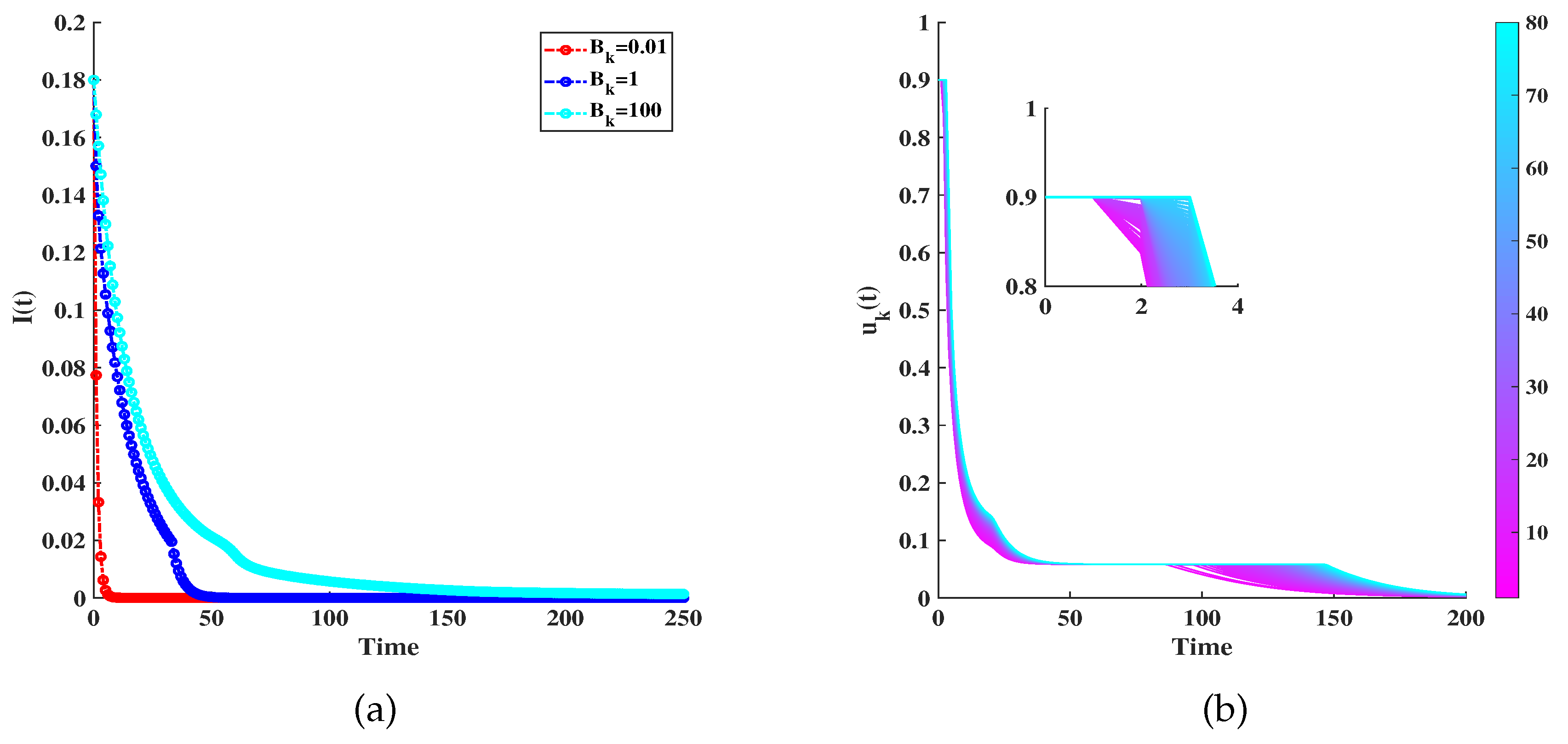
Preprints 89539 g006
Figure 6. (a) The I ( t ) under optimal control with varying weights. Low costs: B k = 0.01 (red line); Moderate costs: B k = 1 (blue line); High costs: B k = 100 (cyan line). Other parameters are fixed as b = 0.09 , d = 0.012 , λ = 0.3 , γ = 0.008 , η = 0.03 , δ k = 0.1 . (b) The quarantine rates u k ( t ) for any degree. Other parameters are fixed as b = 0.09 , d = 0.02 , λ = 0.3 , γ = 0.01 , η = 0.03 , δ k = 0.1 .
Figure 6. (a) The I ( t ) under optimal control with varying weights. Low costs: B k = 0.01 (red line); Moderate costs: B k = 1 (blue line); High costs: B k = 100 (cyan line). Other parameters are fixed as b = 0.09 , d = 0.012 , λ = 0.3 , γ = 0.008 , η = 0.03 , δ k = 0.1 . (b) The quarantine rates u k ( t ) for any degree. Other parameters are fixed as b = 0.09 , d = 0.02 , λ = 0.3 , γ = 0.01 , η = 0.03 , δ k = 0.1 .
Preprints 89539 g006
Table 1. Symbols Employed in Models.
Table 1. Symbols Employed in Models.
Symbols Description
p ( k ) Proportion of nodes with degree k.
〈 k 〉 Average degree   〈 k 〉 = ∑ k k p ( k ) .
n The max degree.
b Birth rate.
d Natural death rate.
Ψ k ( t ) The fertile contact probability between a node with degree k and its neighbors.
λ ( k ) Transmission rate of infected nodes with degree k.
δ k Vaccination rate of susceptible nodes with degree k.
β k Quarantine rate of infected nodes with degree k.
γ Recovery rate of infected nodes.
η Recovery rate of quarantined nodes.
Table 2. The values of J ( μ ) under different control strategies.
Table 2. The values of J ( μ ) under different control strategies.
Optimal control Max control No control
J ≈ 1.7817 e + 03 J ≈ 6.5164 e + 04 J ≈ 5.1127 e + 03
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated