Prerpints.org logo
Preprint
Article

Application of Gradient Optimization Methodsin Defining Neural Dynamics

Altmetrics

Downloads

88

Views

120

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

03 November 2023

Posted:

06 November 2023

You are already at the latest version

Alerts
Abstract
Applications of gradient method for nonlinear optimization in development of Gradient Neural Network (GNN) and Zhang Neural Network (ZNN) are investigated. Particularly, the solution of the matrix equation AXB=D which changes over time is studied using the novel GNN model, termed as GGNN(A,B,D). The GGNN model is developed applying GNN dynamics on the gradient of the error matrix used in the development of the GNN model. The convergence analysis shows that the neural state matrix of the GGNN(A,B,D) design converges asymptotically to the solution of the matrix equation AXB=D, for any initial state matrix. It is also shown that the convergence result is the least square solution which is defined depending on the selected initial matrix. A hybridization of GGNN with analogous modification GZNN of the ZNN dynamics is considered. The Simulink implementation of presented GGNN models is carried out on the set of real matrices.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

1. Introduction and background

Recurrent neural networks (RNNs) are important class of algorithms for computing matrix (generalized) inverses. These algorithms are used to find the solutions of the matrix equations or to minimize certain nonlinear matrix functions. RNNs are divided into 2 subgroups: Gradient Neural Networks (GNN) and Zhang Neural Networks (ZNN). The GNN design is explicit and mostly applicable to time-invariant problems, which means that coefficients of the equations which are addressed are constant matrices. ZNN models can be implicit and capable to solve time-varying problems where coefficients of the equations depend on the variable t ∈ R , t > 0 , representing the time [31].
GNN neural design models for computing the inverse or the Moore-Penrose inverse and linear matrix equations were proposed in [6,25,26,27]. Further, various dynamical systems aimed to approximating the pseudo-inverse of rank-deficient matrices were originated in [6]. Wei in [28] proposed three RNN models for approximation of the weighted Moore-Penrose inverse. Cichocki in [29] proposed a feed-forward neural network for approximating the Drazin inverse. Online matrix inversion in complex matrix case was considered in [30].
Applications of this type of inverses can be found in important areas such as modeling of electrical circuits [10], estimation of DNA sequences [22,23], balancing chemical equations [11,12] and in other important research domains related to robotics [13] and statistics [14].
In the following sections we will focus on GNN and ZNN dynamic systems based on gradient of the objective function and their implementation. The main goal of this research is the analysis of convergence and the study of analytic solutions. In this study we are concerned with solving the matrix equation A X B = D [20,21] in real time using the GNN model, denoted by GNN ( A , B , D ) [3,4,5,6,7,8,9], and the novel gradient-based GGNN model, termed as GGNN ( A , B , D ) . The proposed GGNN model is defined evolving the standard GNN dynamics along the gradient of the standard error matrix. The convergence analysis reveals the global asymptotic convergence of GGNN ( A , B , D ) without restrictions, while the output belongs to the set of general solutions to the matrix equation A X B = D . The implementation is performed in MATLAB Simulink and numerical experiments are developed with simulations of GNN and GGNN models.
The GNN used to solve the general linear matrix equation A X B = D is defined over the error matrix E ( t ) = D − A V ( t ) B , where t ∈ [ 0 , + ∞ ) is the time and V ( t ) is an unknown state-variable matrix that approximates the unknown matrix X in A X B = D . The goal function is ε ( t ) = | | D − A V ( t ) B | | F 2 / 2 and its gradient is equal to
∂ ε ( t ) ∂ V = ∇ ε = 1 2 ∂ | | D − A V ( t ) B | | F 2 ∂ V = − A T ( D − A V ( t ) B ) B T .
The GNN evolutionary design is defined by the dynamic system
V ˙ ( t ) = d V ( t ) d t = − γ ∂ ε ( t ) ∂ V , V ( 0 ) = V 0 ,
where γ > 0 is real parameter used to speed up the convergence. Thus, the linear GNN aimed at solving A X B = D is given by the following dynamics:
V ˙ ( t ) = γ A T ( D − A V ( t ) B ) B T .
The dynamical flow (2) is denoted as as GNN ( A , B , D ) . The nonlinear GNN ( A , B , D ) for solving A X B = D is defined by
V ˙ ( t ) = γ A T F ( D − A V ( t ) B ) B T .
The function array F ( C ) is based on appropriate odd and monotonically increasing activation function, which is applicable to elements of a real matrix C = ( c i j ) ∈ R m × n , i.e. F ( C ) = ( f ( c i j ) ) , i = 1 , … , m , j = 1 , … , n , .
Proposition 1 restates restrictions about the solvability of A X B = D and its general solution.
Proposition 1.
[1,18] If A ∈ R m × n , B ∈ R p × q and D ∈ R m × q then fulfillment of the condition
A A † D B † B = D
is necessary and sufficient for solvability of the linear matrix equation A X B = D . In this case, the set of all solutions is given by
X = A † D B † + Y − A † A Y B B † | Y ∈ R n × p .
The following results from [15] describe the conditions of convergence and the limit of the unknown matrix V ( t ) from (3) as t → + ∞ .
Proposition 2.
[15] Suppose the matrices A ∈ R m × n , B ∈ R p × q and D ∈ R m × q satisfy (4). Then the unknown matrix V ( t ) from (3) converges as t → + ∞ with the equilibrium state
V ( t ) → V ˜ = A † D B † + V ( 0 ) − A † A V ( 0 ) B B †
for any initial state variable matrix V ( 0 ) ∈ R n × p .
The research in [24] investigated various ZNN models based on optimization methods. The goal of current research is to develop the GNN model based on the gradient E G ( t ) of ∥ E ( t ) ∥ F 2 instead of the original goal function E ( t ) .
Obtained results are summarized as follows.
  • A novel error function E G ( t ) is proposed for development of the GNN dynamical evolution.
  • GNN design evolved upon the error function E G ( t ) is developed and analyzed theoretically and numerically.
  • A hybridization of GNN and ZNN dynamical systems based on the error matrix E G is proposed and investigated.
Global organization of section is as follows. Motivation and derivation of GGNN and GZNN models are presented in Section 2. Section 3 is aimed to convergence analysis of the GGNN dynamics. Numerical comparison on GNN and GGNN dynamics are given in Section 4, in which SubSection 4.1 investigates a practical application of GGNN to electrical networks. Neural dynamics based on the hybridization of GGNN and GZNN model for solving matrix equations are considered in Section 6. Numerical examples on hybrid models model are analysed in Section 6. Finally, the last section presents some concluding remarks and vision of further research.

2. Motivation and derivation of the GGNN and GZNN models

The standard GNN design (2) solves the GLME A X B = D under the constraint (4). Our goal is to resolve this restriction and propose dynamic evolutions based on the error functions that tend to zero without restrictions.
Our goal is to define the GNN design for solving the GLME A X B = D based on the error function
E G ( t ) : = ∇ ε ( t ) = A T D − A V ( t ) B B T = A T E ( t ) B T .
The equilibria points of (7) satisfy
E G ( t ) : = ∇ ε ( t ) = 0 .
We continue investigation from [24]. More precisely, we will develop the GNN model based on the error function E G ( t ) instead of the error function E ( t ) . In this way, new neural dynamics is aimed to force the gradient E G to zero instead of the standard goal function E ( t ) . It is reasonable to call such RNN model as gradient-based GNN (GGNN shortly).
Proposition 3 gives conditions for solvability of the matrix equations E ( t ) = 0 and E G ( t ) = 0 and general solutions to these systems.
Proposition 3.
[24] Consider arbitrary matrices A ∈ R m × n , B ∈ R k × h and D ∈ R m × h . The next statements are true.
(a) The equation E ( t ) = 0 is solvable if and only if (4) is satisfied and the general solution to E ( t ) = 0 is given by (5).
(b) The equation E G ( t ) = 0 is always solvable and its general solution coincides with (5).
In this way, the matrix equation E ( t ) = 0 is solvable under the condition (4), while the equation E G ( t ) = 0 is always consistent. In addition, the general solutions to equations E ( t ) = 0 and E G ( t ) = 0 are identical [24].
The next step is to define the GGNN dynamics using the error matrix E G ( t ) . Let us define the objective function ε G = | | E G | | F 2 / 2 , whose gradient is equal to
∂ ε G ( V ( t ) ) ∂ V = ∂ | | A T ( D − A V ( t ) B ) B T | | F 2 ∂ V = − A T A A T ( D − A V ( t ) B ) B T B B T .
The dynamical system for the GGNN formula is obtained applying the GNN evolution along the gradient of ε G ( V ( t ) ) based on E G ( t ) , as follows
V ˙ ( t ) = − γ ∂ ε G ∂ V = γ A T A A T D − A V ( t ) B B T B B T .
The nonlinear GGNN dynamics is defined as
V ˙ ( t ) = γ A T A F ( A T D − A V ( t ) B B T ) B B T ,
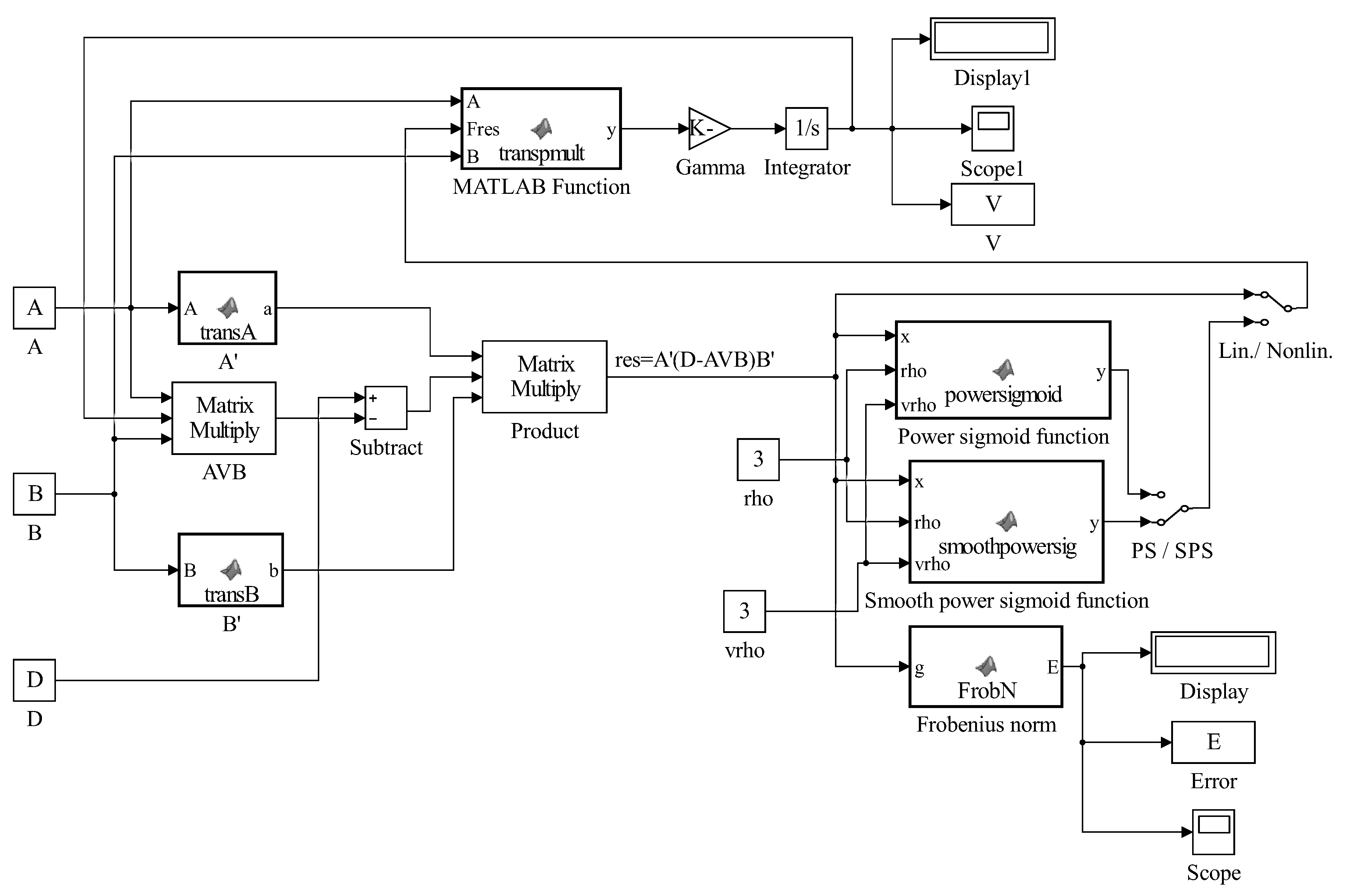
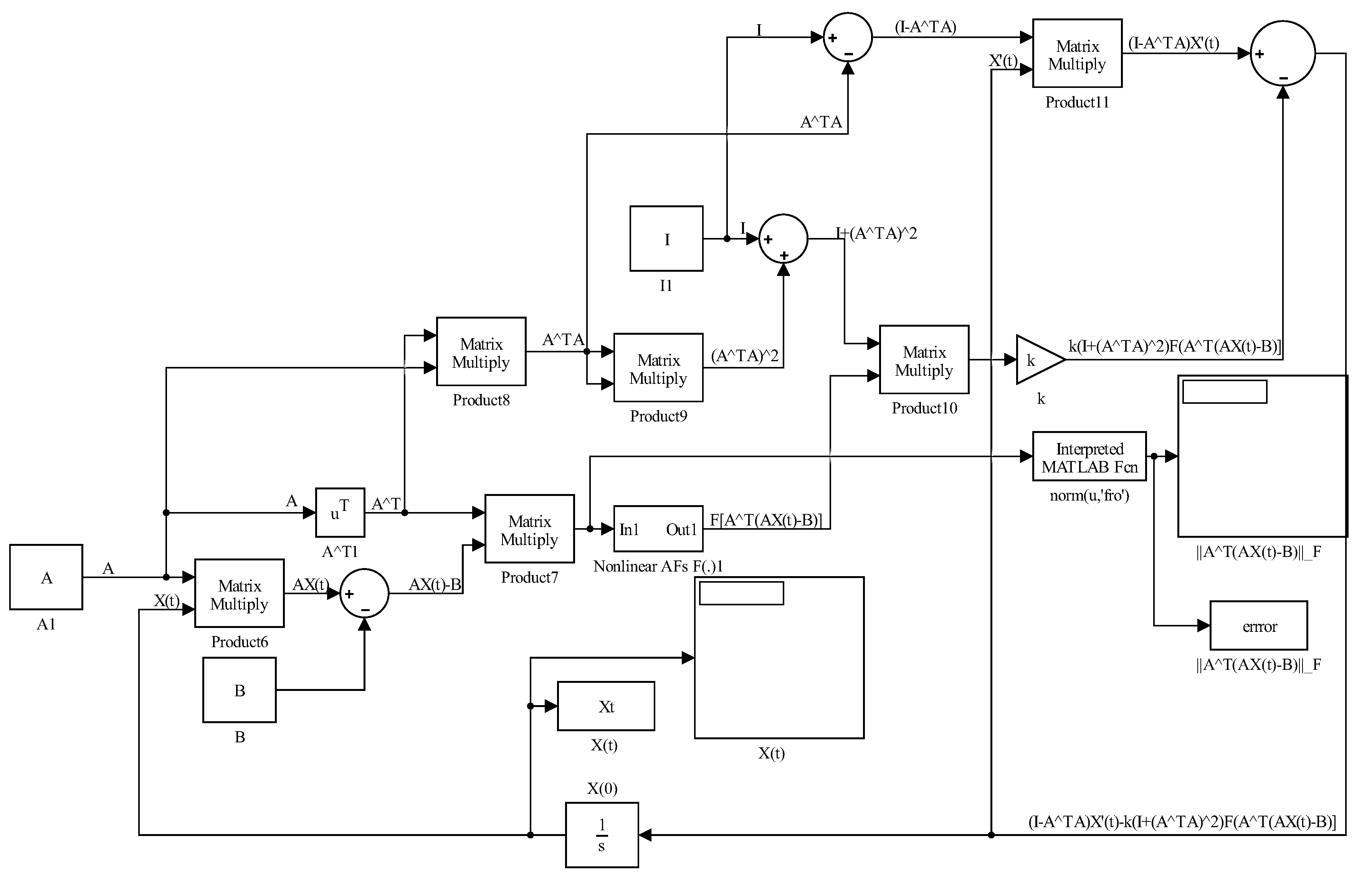
in which F ( C ) denotes an odd and monotonically increasing function array, as mentioned in previous section for the GNN model (3). An arbitrary monotonically increasing odd activation function f ( · ) is used for the construction of the GNN neural design. The model (9) is termed as GGNN ( A , B , D ) . Figure 1 represents the Simulink implementation of GGNN ( A , B , D ) dynamics (9).
On the other hand, the GZNN model defined upon the Zhangian matrix E G ( t ) is defined in [24] by the general evolution design
E ˙ G ( t ) = d E G ( t ) d t = − γ F ( E G ( t ) ) .

3. Convergence analysis of GGNN dynamics

In this section, we will analyze convergence properties of GGNN model given by dynamics (9).
Theorem 1.
Consider matrices A ∈ R m × n , B ∈ R p × q and D ∈ R m × q . If an odd and monotonically increasing array activation function F ( · ) based on an elementwise function f ( · ) is used, then the neural state matrix V ( t ) ∈ R n × p of the GGNN ( A , B , D ) model (9) asymptotically converges to the solution of the matrix equation A X B = D , i.e., A T A V ( t ) B B T → A T D B T as t → + ∞ , for an arbitrary initial state matrix V ( 0 ) .
Proof. 
From the statement b) of Proposition 3, the solvability of A T A V B B T = A T D B T is ensured. The substitution V ( t ) = V ¯ ( t ) + A † D B † transforms the dynamics (9) into
d V ¯ ( t ) d t = d V ( t ) d t = γ A T A F A T D − A V ( t ) B B T B B T = γ A T A F A T D − A V ¯ ( t ) B − A A † D B † B B T B B T = ( 4 ) γ A T A F A T D − A V ¯ ( t ) B − D B T B B T = − γ A T A F A T A V ¯ ( t ) B B T B B T .
Lyapunov function candidate which measures the convergence performance is defined by
L V ¯ ( t ) , t = 1 2 | | V ¯ ( t ) | | F 2 = 1 2 Tr V ¯ ( t ) T V ¯ ( t ) .
The conclusion is L ( V ¯ ( t ) , t ) ≥ 0 . According to (12), assuming (11) and using d Tr ( X T X ) = 2 Tr ( X T d X ) in conjunction with basic properties of the matrix trace function, one can express the time derivative of L ( V ¯ ( t ) , t ) as in the following
d L ( V ¯ ( t ) , t ) d t = 1 2 d Tr V ¯ ( t ) T V ¯ ( t ) d t = 1 2 · 2 · Tr V ¯ ( t ) T d V ¯ ( t ) d t = Tr V ¯ ( t ) T − γ A T A F A T A V ¯ ( t ) B B T B B T = − γ Tr V ¯ ( t ) T A T A F A T A V ¯ ( t ) B B T B B T = − γ Tr B B T V ¯ ( t ) T A T A F A T A V ¯ ( t ) B B T = − γ Tr A T A V ¯ ( t ) B B T T F A T A V ¯ ( t ) B B T .
Since the scalar-valued function f ( · ) is an odd and monotonically increasing, it follow for W ( t ) = A T A V ¯ ( t ) B B T
d L ( V ¯ ( t ) , t ) d t = − γ Tr ( W T F ( W ) ) = − γ ∑ i = 1 m ∑ j = 1 n w i j f ( w i j ) < 0 if W ( t ) : = A T A V ¯ ( t ) B B T ≠ 0 = 0 if W ( t ) : = A T A V ¯ ( t ) B B T = 0 ,
which implies
d L ( V ¯ ( t ) , t ) d t < 0 if W ( t ) ≠ 0 = 0 if W ( t ) = 0 .
Observing the identity
W ( t ) = A T A V ¯ ( t ) B B T = A T A V ( t ) − A † D B † B B T = A T A V ( t ) B B T − A T D B T = A T A V ( t ) B − D B T ,
and using the Lyapunov stability theory, W ( t ) : = A T A V ( t ) B − D B T globally converges to the zero matrix, from arbitrary initial value V ( 0 ) . □
Theorem 2.
The activation state variables matrix V ( t ) of the model GGNN ( A , B , D ) , defined by (9), is convergent as t → + ∞ and its equilibrium state is
V ( t ) → V ˜ ( t ) = A † D B † + V ( 0 ) − A † A V ( 0 ) B B †
for every initial state matrix V ( 0 ) ∈ R n × p .
Proof. 
From (9), the matrix V 1 ( t ) = ( A T A ) † A T A V ( t ) B B T ( B B T ) † satisfies
d V 1 ( t ) d t = ( A T A ) † A T A d V ( t ) d t B B T ( B B T ) † = γ ( A T A ) † A T A A T A A T ( D − A V ( t ) B ) B T B B T B B T ( B B T ) † .
According to the basic properties of the Moore–Penrose inverse [18,19], it follows
( B B T ) T B B T ( B B T ) † = ( B B T ) T = B B T , ( A T A ) † A T A ( A T A ) T = ( A T A ) T = A T A
which further implies
d V 1 ( t ) d t = γ A T A A T ( D − A V ( t ) B ) B T B B T = d V ( t ) d t .
Consequently, V 2 ( t ) = V ( t ) − V 1 ( t ) satisfies d V 2 ( t ) d t = d V ( t ) d t − d V 1 ( t ) d t = 0 , which implies
V 2 ( t ) = V 2 ( 0 ) = V ( 0 ) − V 1 ( 0 ) = V ( 0 ) − ( A T A ) † A T A V ( 0 ) B B T ( B B T ) † = V ( 0 ) − A † A V ( 0 ) B B † , t ≥ 0 .
Furthermore, from Theorem 1, A T A V ( t ) B B T → A T D B T and V 1 ( t ) converges to
V 1 ( t ) = ( A T A ) † A T A V ( t ) B B T ( B B T ) † → ( A T A ) † A T D B T ( B B T ) † = A † D B †
as t → + ∞ . Therefore, V ( t ) = V 1 ( t ) + V 2 ( t ) converges to the equilibrium state
V ˜ ( t ) = A † D B † + V 2 ( t ) = A † D B † + V ( 0 ) − A † A V ( 0 ) B B † .
The proof is finished. □

4. Numerical experiments on GNN and GGNN dynamics

Numerical examples in this section are represented based on the Simulink implementation of GGNN formula in Figure 1. Three activation functions f ( · ) are used in numerical experiments:
1. linear function
f l i n ( x ) = x ;
2. power-sigmoid activation function
f p s ( x , ρ , ϱ ) = x ρ if | x | ≥ 1 1 + e − ϱ 1 − e − ϱ · 1 + e − ϱ x 1 − e − ϱ x if | x | < 1
where ϱ > 2 and ρ ≥ 3 is odd integer.
3. smooth power-sigmoid function
f s p s ( x , ρ , ϱ ) = 1 2 x ρ + 1 + e − ϱ 1 − e − ϱ · 1 + e − ϱ x 1 − e − ϱ x ,
where ϱ > 2 and ρ ≥ 3 is odd integer.
The parameter γ , initial state V ( 0 ) and parameters ρ and ϱ of the nonlinear activation functions (19) and (20), are entered directly in the model, while matrices A, B and D are defined from the workspace. It is assumed ρ = ϱ = 3 in all examples. The ode15s differential equation solver is used in configuration parameters.
The blocks powersig, smoothpowersig and transpmult include the codes described in [15].
Example 4.1.
Let us consider the idempotent matrix A from [32,33]
A = 1 0 1 1 0 1 1 2 0 0 0 0 0 0 0 0
with the theoretical Moore-Penrose inverse
V * = A † = 1 3 2 − 1 0 0 − 1 1 0 0 1 0 0 0 0 1 0 0
under the input parameters γ = 10 8 , B = D = I 4 , V ( 0 ) = O 4 , where I 4 and O 4 denote the identity and zero 4 × 4 matrix, respectively. The Simulink implementation from Figure 1 exports the graphical results in Figure 2 and Figure 3 which display the behavior of | | A T ( D − A V ( t ) B ) B T | | F and | | V ( t ) − V * | | F respectively. It is observable that the norms generated by the application of GGNN formula vanish faster to zero against corresponding norms in the GNN model. 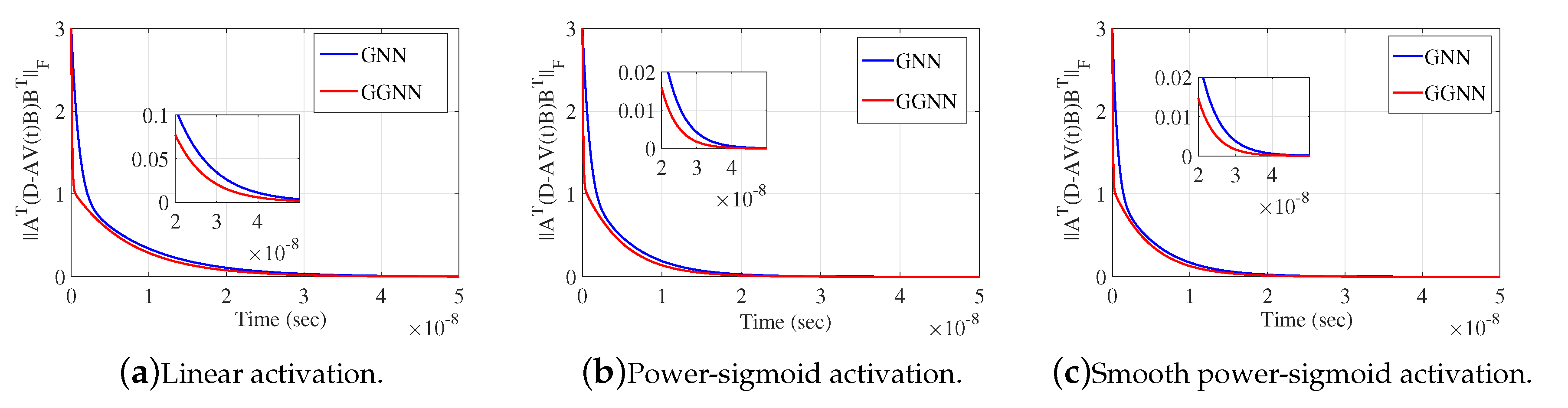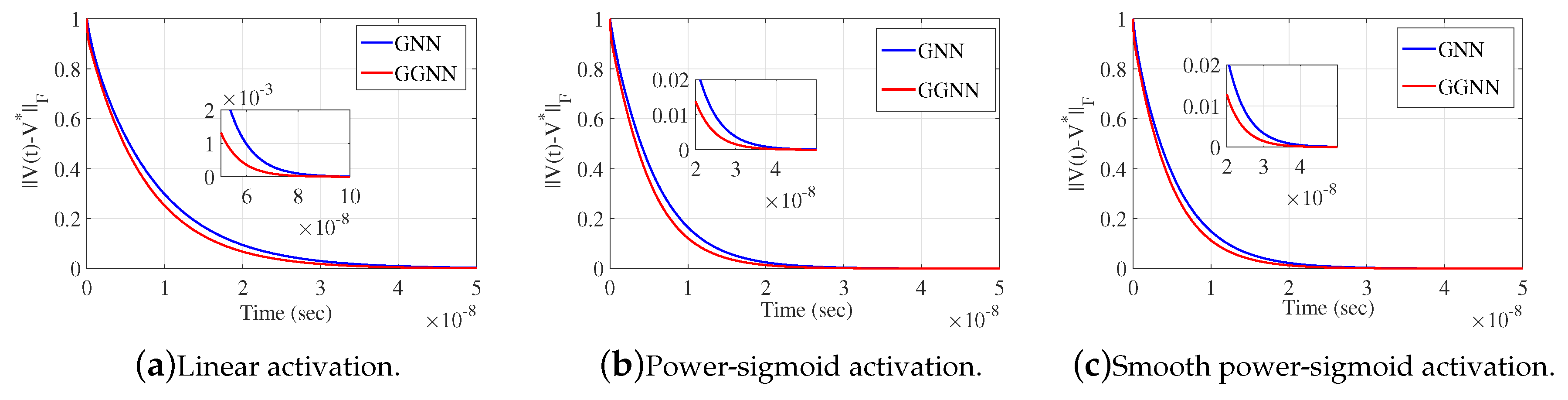Graphs in presented figures strengthen the fast convergence of the GGNN dynamical system and the important role which can include the application of this specific model (9) to problems that require the computation of the Moore-Penrose inverse.
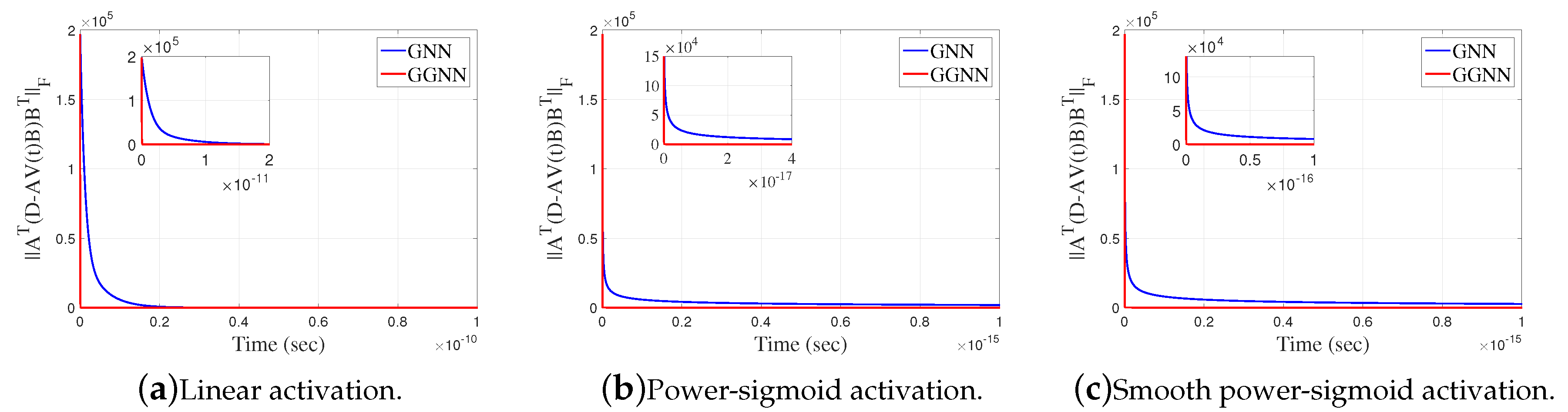
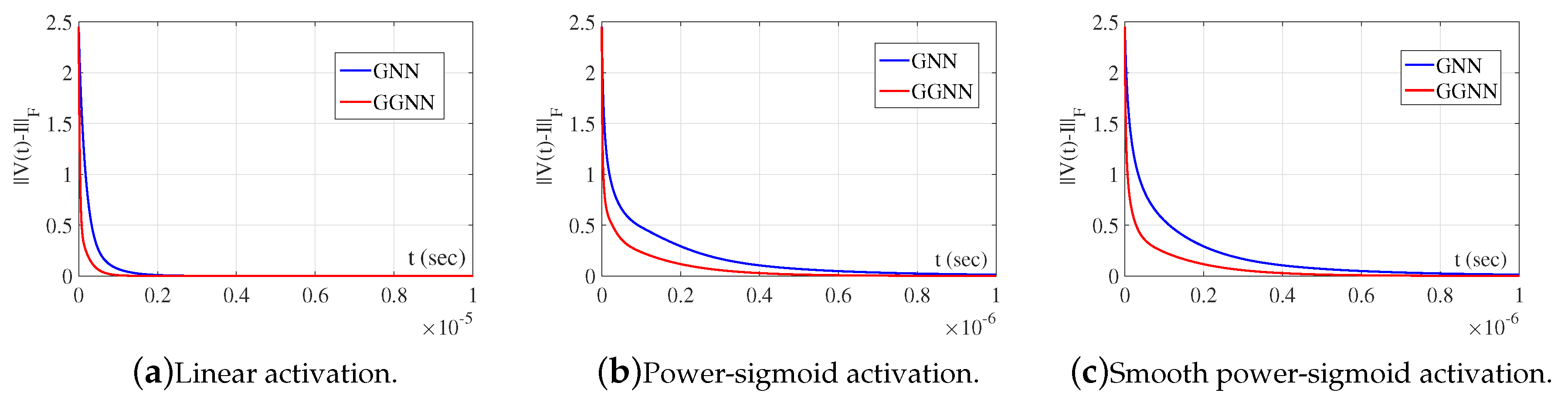
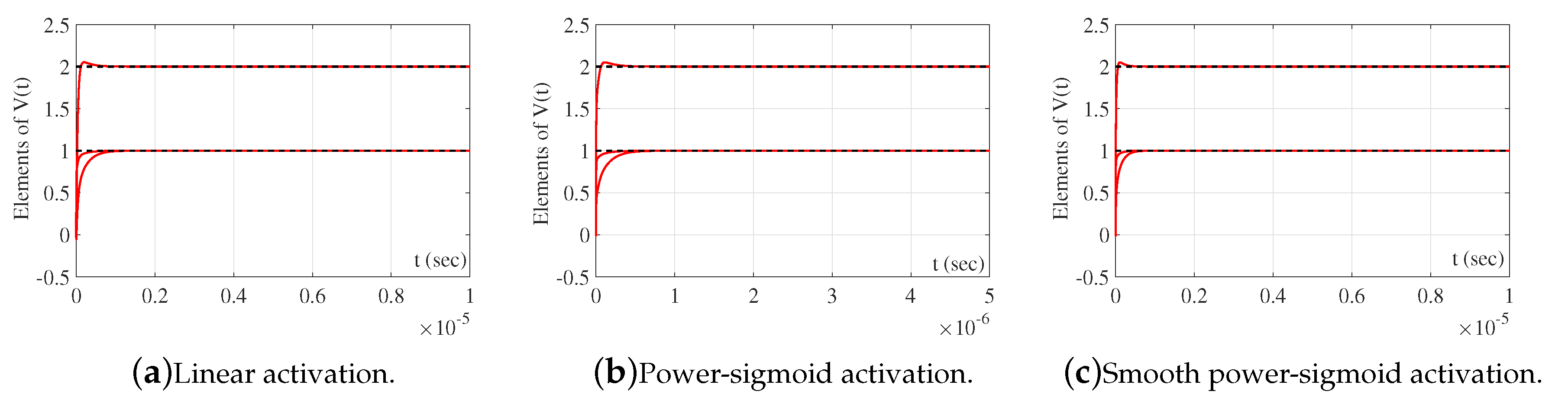
Example 4.2.
Let us consider the matrices
A = − 8 8 − 4 11 4 − 7 1 − 4 3 0 12 − 10 6 12 − 12 , B = 1 0 0 0 1 0 0 0 1 0 0 0 , D = − 84 2524 304 − 2252 − 623 2897 484 − 885 − 701 − 1894 2278 2652 − 2778 1524 3750 .
Ranks of input matrices are equal to r = rank ( A ) = 2 , rank ( D ) = 2 and rank ( B ) = 3 . The linear GGNN formula GGNN ( A , B , D ) (9) is applied to solve the matrix equation A X B = D , which gives in the case V ( 0 ) = 0
X = A † D B † = − 113.9846 − 147.1385 137.7385 0 − 74.4615 136.1538 107.8462 0 100.0462 − 64.4154 − 135.7846 0 .
The gain parameter of the model is γ = 10 9 , V ( 0 ) = 0 and the final time is t = 0.00001 .
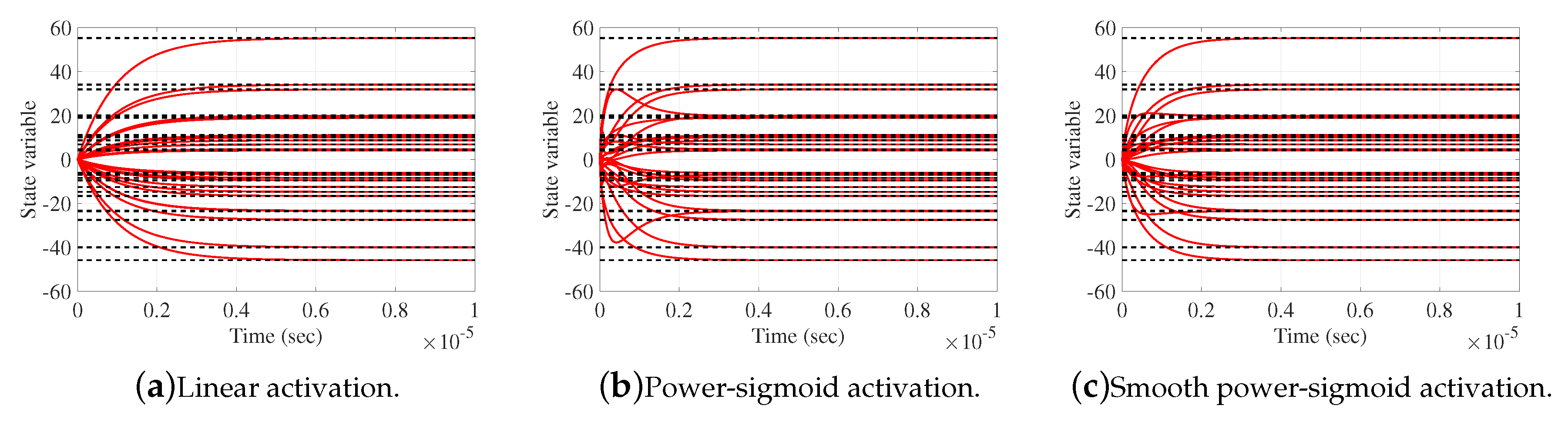
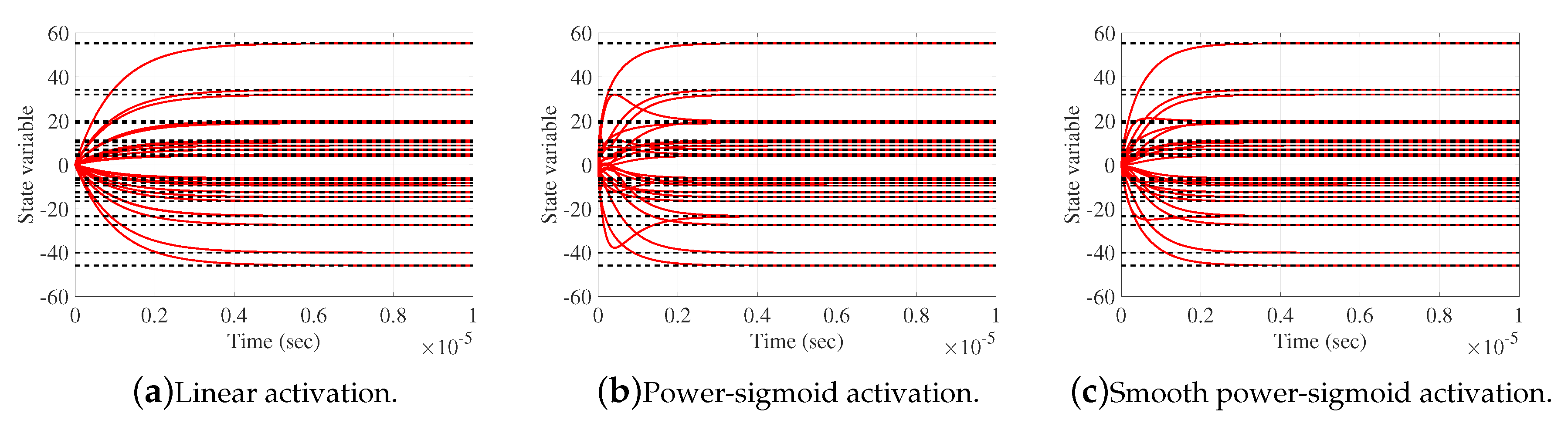
Elementwise trajectories of the variable state matrix V ( t ) with red lines are shown in Figure 4a–c, for linear, power-sigmoid and smooth power-sigmoid activation functions, respectively. It is observable the convergence of elementwise trajectories to the black dashed lines of the theoretical solution X. The trajectories in figures indicate a usual convergence behaviour, so the system is globally asymptotically stable. The norm of the error matrix E G of both model for linear and non-linear activation function are shown on Figure 5a–c. The nonlinear activation function shows superiority in the convergence speed, comparing with the linear activation function. On each graph, Frobenius norm of the error from GGNN formula vanish faster to zero than GNN model which strengthens the fact that the proposed dynamical system (9) includes accelerated convergence property against (3).
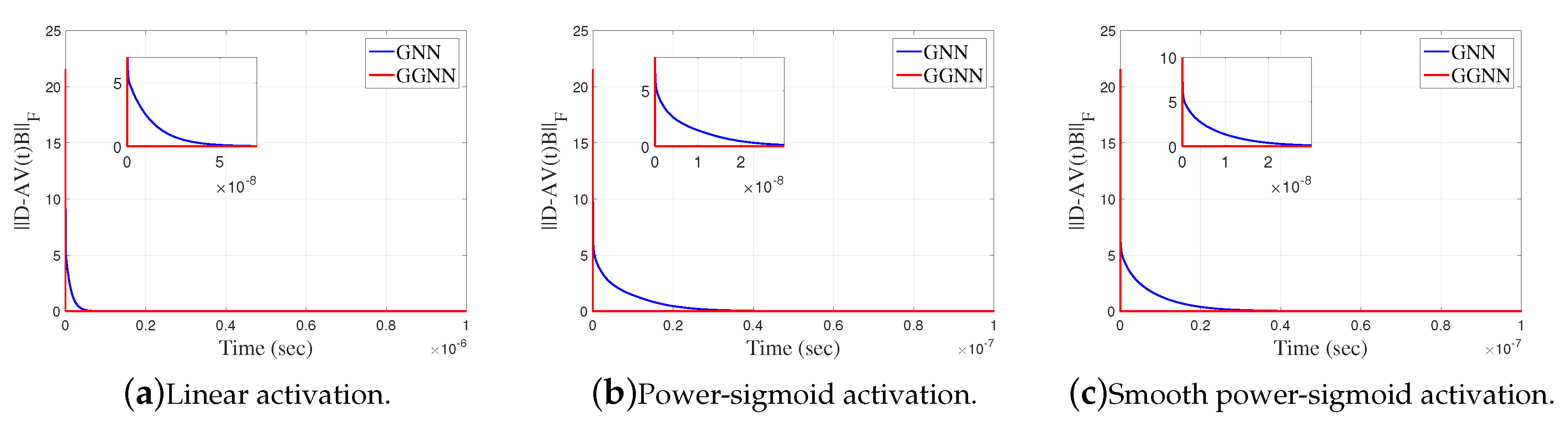
Example 4.3.
Let us explore behavior of GGNN ( A A T , A T A , A ) for computing the Moore-Penrose inverse. We consider matrix:
A = 9 3 − 3 − 1 1 0 4 7 2 2 4 − 4 13 5 8 .
The error matrix E ( t ) = A T ( I − A V ) initiates the GNN ( A T A , I , A T ) dynamics for computing A † . Corresponding error matrix for GGNN ( ( A T A ) 2 , I , A T A A T ) is
E G ( t ) = A T A A T − A T A V = A T A A T I − A V .
Rank of the input matrix is equal to r = rank ( A ) = 3 . The gain parameter of the model is γ = 100 , initial state is V ( 0 ) = 0 with stop time t = 0.00001 . The Moore–Penrose inverse of A is given by
A † ≈ 0.0775 − 0.0235 − 0.0538 − 0.0069 0.0390 − 0.0445 0.0376 0.1310 0.0655 − 0.0167 − 0.0826 0.0077 0.0252 − 0.0577 0.0589
The error matrix E ( t ) = D − A V ( t ) B of GNN and GGNN model for both linear and non-linear activation functions are shown on Figure 6a–c, and E G of both model for linear and non-linear activation function are shown on Figure 7a–c. Like in previously example, we can conclude that GGNN converges faster compared to the GNN model.
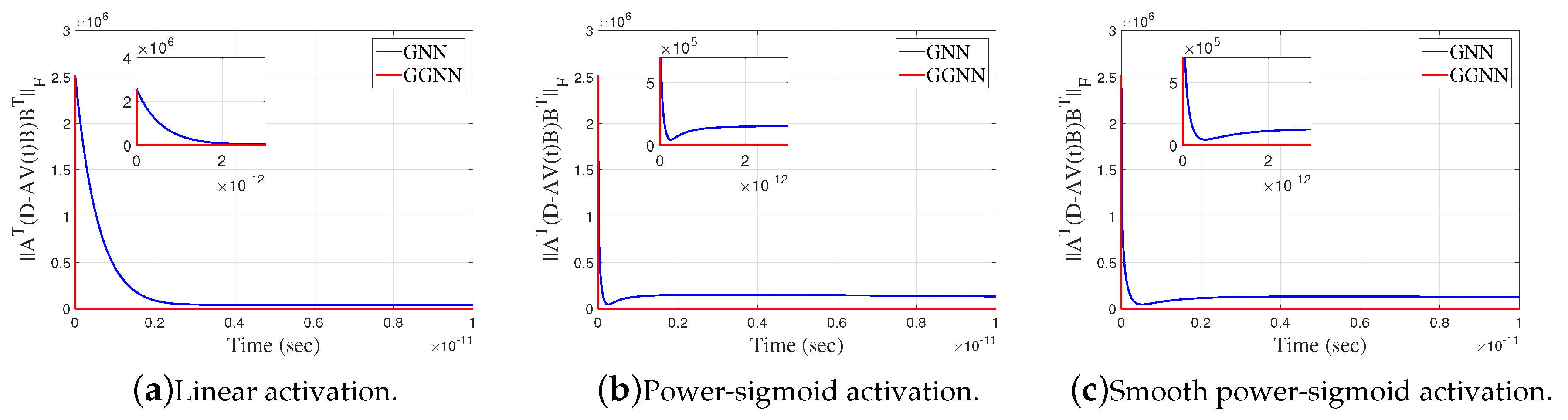
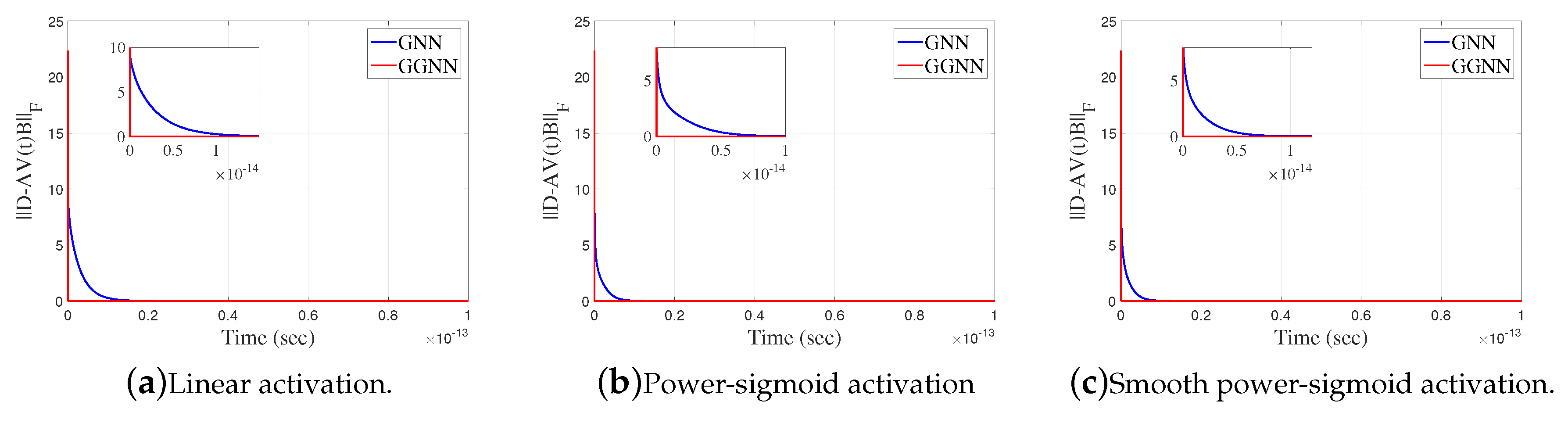
Example 4.4.
Consider the matrices
A = 15 − 352 − 45 − 238 42 − 5 14 8 132 − 65 235 − 65 44 350 − 73 , D = − 4 4 16 3 1 − 9 1 − 7 2 2 2 − 4 4 1 − 5 , A 1 = D A ,
that dissatisfy rank ( A 1 ) = rank ( D ) = 3 . Now, we apply GGNN formula to solve the matrix equation A 1 X = D . Notice, if we look at GGNN ( A , B , D ) in this example, we actually operate with A = A 1 and B = I 3 . So, we consider GNN ( A 1 , I 3 , D ) . The error matrix for the corresponding GGNN model is
E G ( t ) = A 1 T D − A 1 V I 3 I 3 T = A 1 T D − A 1 V .
The gain parameter of the model is γ = 10 9 and the final time is t = 0.00001 . The zero initial state V ( 0 ) = 0 generates the best approximate solution X = A 1 † D = ( D A ) † D of the matrix equation A 1 X = D , given by
X = A 1 † D = − 0.000742151758732906 − 0.00913940509710217 0.00337604725603635 − 0.00281859443979587 − 0.00383668701022646 − 0.000268348265455338 − 0.000377755170367094 − 0.00134463893719598 0.000458599151069315 − 0.000177073414005706 0.00403153859974667 0.000743238210989296 − 0.000956081467310272 − 0.00748631706136413 0.00124829423173208 .
The Frobenius norm of the error matrix D − A V ( t ) B in GNN and GGNN models for both linear and non-linear activation functions are shown on Figure 8a–c, and error matrix E G in both models for linear and non-linear activation function are shown on Figure 9a–c. It is observable that GGNN converges faster than GNN.
Example 4.5.
Table 2 shows the results obtained during experiments we conducted with nonsquared matrices, where m × n is dimension of matrix. Table 1 is the input data in the Simulink model which are used to perform experiments that generate results in Table 2. Best cases in Table 2 are marked in bold text.
Numerical results arranged in Table 2 are divided into two parts by a horizontal line. The upper part corresponds to test matrices of dimensions ≤ 10 while the lower part corresponds to the dimensions m , n ≥ 10 . Considering first two columns, it is observable from the upper part that GGNN generates smaller values | | E ( t ) | | F compared to GGNN. Values | | E ( t ) | | F in the lower part generated by GNN and GGNN are equal. Considering the third and fourth columns, it is observable from the upper part that GGNN generates smaller values | | E G ( t ) | | F compared to GGNN. On the other hand, values | | E G ( t ) | | F in the lower part, generated by GGNN, are smaller than corresponding values generated by GNN. Last two columns show that the GGNN requires smaller CPU time compared to GNN. General conclusion is that GGNN model is more efficient on rank deficient test matrices of larger order m , n ≥ 10 .

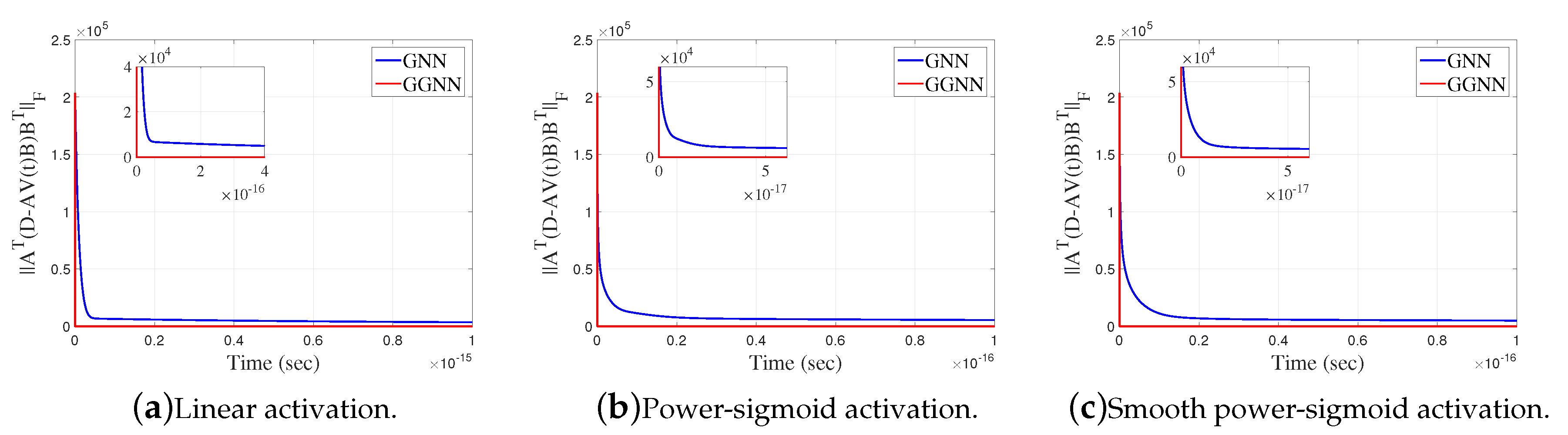
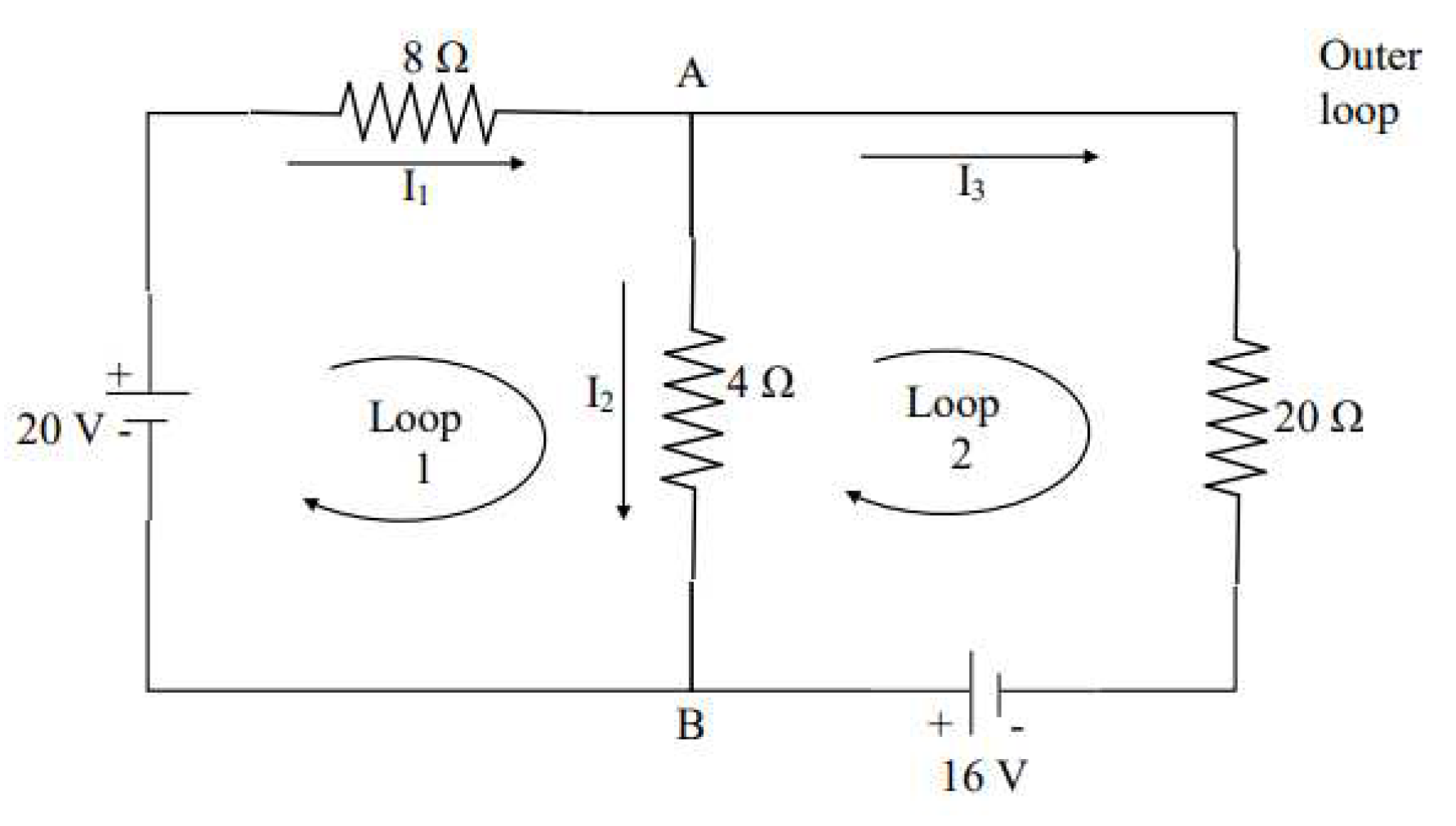
4.1. Application of GGNN to electrical networks

It is really interesting to apply the novel GGNN formula (9) for the calculation and study of different parameters related to electrical networks. For this reason the following circuit in Figure 10 from [34] is considered.
Our goal is to estimate the currents I 1 , I 2 , I 3 in amperes ( A ) while electrical potential E is measured in volts ( V ) and resistors with resistance R is measured in ohms ( Ω ) . Applying the current law in the points A , B , relationships I 1 = I 2 + I 3 and 8 I 1 + 4 I 2 = 20 obtained respectively and from the voltage law the relationship 20 I 3 − 4 I 2 = 16 which lead to the following system A I = D in matrix form
1 − 1 − 1 2 1 0 0 1 5 . I 1 I 2 I 3 = 0 5 − 4 .
with theoretical solution I 1 = 2 , I 2 = I 3 = 1 . For the parameters γ = 10 6 and the zero initial condition simulink implementation from Figure 1 extracts Figure 11 and Figure 12.
It is observable from Figure 11 that GGNN ( A , 1 , D ) initiates a faster convergence than GNN ( A , 1 , D ) formula for the same parameter γ as error | | V ( t ) − I | | F vanishes faster to zero. Figure 12 presents state trajectories of I 1 , I 2 , I 3 obtained by the exact solution with the trajectories resulting from the GGNN formula for γ = 10 6 and V ( 0 ) = 0 . These observations indicate that the proposed GGNN formula for solving general linear matrix equations is usable in solving electrical networks, which is an interesting engineering problem.

5. Mixed GGNN-GZNN model for solving matrix equations

Let us define gradient error matrix of the matrix equation A X = B by
E A , I , B ( t ) = A T A V ( t ) − B .
The GZNN design (10) corresponding to the error matrix E A , I , B , marked with GZNN ( A , I , B ) , is of the form:
E ˙ A , I , B ( t ) = − γ 1 F A T A V ( t ) − B .
Now, the scalar-valued norm-based error function corresponding to E A , I , B ( t ) is given by
ε ( t ) = ε V ( t ) = 1 2 | | E A , I , B ( t ) | | F = | | A T A V ( t ) − B | | F 2 .
The following dynamic state equation can be derived using the GGNN ( A , I , B ) design formula derived from (9):
V ˙ ( t ) = − γ 2 A T A F A T A V ( t ) − B .
Further, it follows
E ˙ A , I , B ( t ) = A T A V ˙ ( t ) = − γ 2 A T A A T A F A T A V ( t ) − B .
Next step is to define new hybrid model based on the summation of (21) and (23) in the case γ 1 = γ 2 = 1 2 γ , as follows:
E ˙ A , I , B ( t ) = A T A V ˙ ( t ) = − γ A T A 2 + I F A T A V ( t ) − B = − γ A T A 2 + I F E A , I , B ( t ) .
The model (24) is derived as a combination of the model GGNN ( A , I , B ) and the model GZNN ( A , I , B ) . Hence, it is equally justified to use the term Hybrid GGNN (HGGNN shortly) or Hybrid GZNN (HGZNN shortly) model. But, the model (24) is implicit, so that it is not a kind of GGNN dynamics. On the other hand, it is designed for time-invariant matrices, which is not in accordance with the common nature of GZNN models, because usually GZNN is used for the time-varying case. A formal comparison of (24) and GZNN ( A , I , B ) reveals that both these methods possess identical left hand sides and the right hand side of (24) can be derived multiplying the right hand side of GZNN ( A , I , B ) by the term A T A 2 + I .
Formally, (24) is closer to the GZNN dynamics, so, we will denote the model (2.4) by HGZNN ( A , I , B ) , considering that this model is not the exact GZNN neural dynamics and it is applicable in time-invariant case. This is the case of constant coefficient matrices A, I, B. Figure 13 represents the Simulink implementation of HGZNN ( A , I , B ) dynamics (24).
Now, we will take into account solving the matrix equation X C = D . The error matrix for this equation is defined by
E I , C , D ( t ) = V ( t ) C − D C T .
The GZNN design (10) corresponding to the error matrix E I , C , D , marked with GZNN ( I , C , D ) , is of the form:
E ˙ I , C , D ( t ) = V ˙ C C T = − γ 1 F V ( t ) C − D C T .
On the other hand, the GGNN design formula (9) produces the following dynamic state equation:
V ˙ ( t ) = − γ 2 F ( V ( t ) C − D ) C T C C T , V ( 0 ) = V 0 .
The GGNN model (26) is denoted by GGNN ( I , C , D ) . It implies
E ˙ I , C , D ( t ) = V ˙ ( t ) C C T = − γ 2 F ( V ( t ) C − D ) C T C C T C C T .
A new hybrid model based on the summation of (25) and (27) in the case γ = 2 γ 1 = 2 γ 2 can be proposed as follows
E ˙ I , C , D ( t ) = V ˙ ( t ) C C T = − γ F ( V ( t ) C − D ) C T I + C C T 2 = − γ F E I , C , D ( t ) I + C C T 2 .
The model (28) will be denoted by HGZNN ( I , C , D ) . This is the case of constant coefficient matrices I, C, D.
For the purposes of the proof of the following results, we will denote by E C R ( M ) the exponential convergence rate of the model M . With λ m i n ( K ) and λ m a x ( K ) , we denote the smallest and largest eigenvalue of a matrix K, respectively. In the continuation of the work we use three types of activation functions F : linear, power-sigmoid and smooth power-sigmoid.
Next theorem determines the equilibrium state of HGZNN ( A , I , B ) and defines its global exponential convergence.
Theorem 3.
Let A ∈ R k × n , B ∈ R k × m be given and satisfy A A † B = B and V ( t ) ∈ R n × m be the state matrix of (24), where F is defined by f l i n , f p s or f s p s .
a) Then V ( t ) achieves global convergence and satisfies A V ( t ) → B when t → + ∞ , starting from any initial state X ( 0 ) ∈ R n × m . The state matrix V ( t ) ∈ R n × m of HGZNN  ( A , I , B ) is stable in the sense of Lyapunov.
b) The exponential convergence rate of the  HGZNN  ( A , I , B ) model (24) in the linear case is equal to
E C R ( HGZNN ( A , I , B ) ) = γ 1 + λ m i n A T A 2 .
c) The activation state variables matrix V ( t ) of the model HGZNN  ( A , I , B ) is convergent when t → + ∞ with the equilibrium state matrix
V ( t ) → V ˜ V ( 0 ) = A † B + ( I − A † A ) V ( 0 ) .
Proof. 
a) With the assumption A A † B = B we have solvability of the matrix equation A X = B .
We can define the Lyapunov function as
L ( t ) = 1 2 | | E A , I , B ( t ) | | F 2 = 1 2 Tr E A , I , B ( t ) T E A , I , B ( t ) .
Hence, from (24) and d Tr ( V T V ) = 2 Tr ( V T d V ) , it holds that
L ˙ ( t ) = 1 2 d Tr E A , I , B ( t ) T E A , I , B ( t ) = 1 2 2 Tr E A , I , B ( t ) T d E A , I , B ( t ) = Tr E A , I , B ( t ) T E ˙ A , I , B ( t ) = Tr E A , I , B ( t ) T − γ A T A 2 + I F E A , I , B ( t ) = − γ Tr A T A 2 + I F E A , I , B ( t ) E A , I , B ( t ) T .
In the linear case it follows
L ˙ ( t ) = − γ Tr A T A 2 + I E A , I , B ( t ) E A , I , B ( t ) T .
We also consider next inequality [35], which is valid for a real symmetric matrix K and a real symmetric positive-semidefinite matrix L of the same size:
λ min ( K ) T r ( L ) ≤ Tr ( K L ) ≤ λ max ( K ) Tr ( L ) .
Now, it can be chosen: K = A T A 2 + I and L = E A , I , B ( t ) E A , I , B ( t ) T . Let λ min A T A 2 ≥ 0 be the minimal eigenvalue of A T A 2 . Then 1 + λ min A T A 2 ≥ 1 is the minimal nonzero eigenvalue of A T A 2 + I , which implies
L ˙ ( t ) ≤ − γ 1 + λ min A T A 2 Tr E A , I , B ( t ) E A , I , B ( t ) T .
From (31), it can be concluded
L ˙ ( t ) = < 0 if E A , I , B ( t ) ≠ 0 = 0 if E A , I , B ( t ) = 0 .
According to (32), the Lyapunov stability theory confirms that E A , I , B ( t ) = A V ( t ) − B = 0 is a globally asymptotically stable equilibrium point of the HGZNN ( A , I , B ) model (24). So, E A , I , B ( t ) converges to the zero matrix, i.e. A V ( t ) → B from any initial state X ( 0 ) .
b) From a) it follows that
L ˙ ≤ − γ 1 + λ min A T A 2 Tr E A , I , B ( t ) T E A , I , B ( t ) = − γ 1 + λ min A T A 2 | | E A , I , B ( t ) | | F 2 = − 2 γ 1 + λ min A T A 2 L ( t ) .
This implies
L ≤ L ( 0 ) e − 2 γ 1 + λ min A T A 2 t ⟺ | | E A , I , B ( t ) | | F 2 ≤ | | E A , I , B ( 0 ) | | F 2 e − 2 γ 1 + λ min A T A 2 ⟺ | | E A , I , B ( t ) | | F ≤ | | E A , I , B ( 0 ) | | F e − γ 1 + λ min A T A 2 ,
which confirms the convergence rate (29) of HGZNN ( A , I , B ) .
c) This part of the proof can be verified by following an analogous result from [17]. □
Theorem 4.
Let C ∈ R m × l , D ∈ R n × l be given and satisfy D C † C = D and V ( t ) ∈ R n × m be the state matrix of (28), where F is defined by f l i n , f p s or f s p s .
a) Then V ( t ) achieves global convergence V ( t ) C → D when t → + ∞ , starting from any initial state V ( 0 ) ∈ R n × m . The state matrix V ( t ) ∈ R n × m of HGZNN  ( I , C , D ) is stable in the sense of Lyapunov.
b) The exponential convergence rate of the  HGZNN  ( I , C , D ) model (28) in the linear case is equal to
E C R ( HGZNN ( I , C , D ) ) = γ 1 + λ m i n C C T 2 .
c) The activation state variables matrix V ( t ) of the model HGZNN  ( I , C , D ) is convergent when t → + ∞ with the equilibrium state matrix
V ( t ) → V ˜ V ( 0 ) = D C † + V ( 0 ) ( I − C C † ) .
Proof. 
a) With the assumption D C † C = D we have solvability of the matrix equation X C = D .
Lets define the Lyapunov function with
L ( t ) = 1 2 | | E I , C , D ( t ) | | F 2 = 1 2 Tr E I , C , D ( t ) T E I , C , D ( t ) .
Hence, from (28) and d Tr ( X T X ) = 2 Tr ( X T d X ) , it holds that
L ˙ ( t ) = 1 2 d Tr E I , C , D ( t ) T E I , C , D ( t ) = Tr E I , C , D ( t ) T E ˙ I , C , D ( t ) = Tr E I , C , D ( t ) T − γ C C T 2 + I F E I , C , D ( t ) = − γ Tr C C T 2 + I F E I , C , D ( t ) E I , C , D ( t ) T .
According to similar results from [36], one can verify the following inequality
L ˙ ( t ) = − γ Tr C C T 2 + I E I , C , D ( t ) E I , C , D ( t ) T .
We also consider next inequality [35], which is valid for a real symmetric matrix K and a real symmetric positive-semidefinite matrix L of the same size:
λ min ( K ) Tr ( L ) ≤ Tr ( K L ) ≤ λ max ( K ) Tr ( L ) .
Now, it can be chosen: K = C C T 2 + I and L = E I , C , D ( t ) E I , C , D ( t ) T .
Let λ min C C T 2 ≥ 0 be the minimal eigenvalue of C C T 2 . Then 1 + λ min C C T 2 ≥ 1 is the minimal nonzero eigenvalue of C C T 2 + I . This implies
L ˙ ( t ) = − γ 1 + λ min C C T 2 Tr E I , C , D ( t ) E I , C , D ( t ) T .
From (35), it can be concluded
L ˙ ( t ) = < 0 if E I , C , D ( t ) ≠ 0 = 0 if E I , C , D ( t ) = 0 .
According to (36), the Lyapunov stability theory confirms that E I , C , D ( t ) = V ( t ) C − D = 0 is a globally asymptotically stable equilibrium point of the HGZNN ( A , I , B ) model (28). So, E I , C , D ( t ) converges to the zero matrix, i.e. V ( t ) C → D from any initial state V ( 0 ) .
b) From a) it follows
L ˙ ≤ − γ 1 + λ min C C T 2 T r E I , C , D ( t ) T E I , C , D ( t ) = − γ 1 + λ min C C T 2 | | E I , C , D ( t ) | | F 2 = − 2 γ 1 + λ min C C T 2 L ( t ) .
This implies
L ≤ L ( 0 ) e − 2 γ 1 + λ min C C T 2 t ⟺ | | E I , C , D ( t ) | | F 2 ≤ | | E I , C , D ( 0 ) | | F 2 e − 2 γ 1 + λ min C C T 2 ⟺ | | E I , C , D ( t ) | | F ≤ | | E I , C , D ( 0 ) | | F e − γ 1 + λ min C C T 2 ,
which confirms that the convergence rate of HGZNN ( I , C , D ) is
E C R ( HGZNN ( I , C , D ) ) = γ 1 + λ min C C T 2 .
c) This part of the proof can be verified by following an analogous result from [17]. □
Corollary 5.1.
a) Let the matrices A ∈ R k × n , B ∈ R k × m be given and satisfy A A † B = B and V ( t ) ∈ R n × m be the state matrix of (24), with an arbitrary nonlinear activation F . Then E C R ( GZNN ( A , I , B ) ) = γ .
b) Let the matrices C ∈ R m × l , D ∈ R n × l be given and satisfy D C † C = D and V ( t ) ∈ R n × m be the state matrix of (28) with an arbitrary nonlinear activation F . Then E C R ( GZNN ( I , C , D ) ) = γ .

5.1. Regularized HGZNN model for solving matrix equations

From Theorem 3 and Corollary 5.1 (a), it follows
E C R ( HGZNN ( A , I , B ) ) E C R ( GZNN ( A , I , B ) ) = 1 + λ min A T A 2 ≥ 1 .
Similarly, according to Theorem 4 and Corollary 5.1 (b), it can be concluded that
E C R ( HGZNN ( I , C , D ) ) E C R ( GZNN ( I , C , D ) ) = 1 + λ min C C T 2 ≥ 1 .
Convergence of HGZNN ( A , I , B ) (resp. HGZNN ( I , C , D ) ) can be improved in the case λ min A T A 2 > 0 (resp. λ min C C T 2 > 0 ). There exist two possible situations when the acceleration terms A T A and C C T improve the convergence. The first case assumes invertibility of A (resp. C), and the second case assumes left invertibility of A (resp. right invertibility of C). Still, in some situations the matrices A and C could be rank deficient. Hence, in the case when A and C are square and singular, it is useful to use the invertible matrices A + λ I and C + λ I , λ > 0 instead of A and C, and consider the models HGZNN ( A + λ I , I , B ) and HGZNN ( I , C + λ I , D ) . In below are presented the convergence results considering nonsingularity of A + λ I and C + λ I .
Corollary 5.2.
Let A ∈ R n × n , B ∈ R n × m be given and V ( t ) ∈ R n × m be the state matrix of (24), where F is defined by f l i n , f p s or f s p s . Let λ > 0 be a selected real number. Then the following statements are valid:
a) The state matrix V ( t ) ∈ R r n × m of the model HGZNN  ( A + λ I , I , B ) converges globally to
V ˜ V ( 0 ) = ( A + λ I ) − 1 B ,
when t → + ∞ , starting from any initial state X ( 0 ) ∈ R n × m and the solution is stable in the sense of Lyapunov.
b) The minimal exponential convergence rate of HGZNN  ( A + λ I , I , B ) in the case F = I is equal to
E C R HGZNN ( A + λ I , I , B ) = γ 1 + λ min A + λ I T A + λ I 2 .
c) Let V ˜ V ( 0 ) be the limiting value of V ( t ) when t → + ∞ . Then
lim λ → 0 V ˜ V ( 0 ) = lim λ → 0 A + λ I − 1 B .
Proof. 
Since A + λ I is invertible, it follows V = A + λ I − 1 B .
From (30) and invertibility of A + λ I we can get validity of a). In this case, it follows
V ˜ V ( 0 ) = ( A + λ I ) − 1 B + ( I − ( A + λ I ) − 1 ( A + λ I ) ) V ( 0 ) = ( A + λ I ) − 1 B + ( I − I ) V ( 0 ) = ( A + λ I ) − 1 B .
Part b) is proved analogously as in Theorem 3. Last part c) follows from a). □
Corollary 5.3.
Let C ∈ R m × m , D ∈ R n × m be given and V ( t ) ∈ R n × m be the state matrix of (28), where F = I , F = F p s or F = F s p s . Let λ > 0 be a selected real number. Then the following statements are valid:
a) The state matrix V ( t ) ∈ R r n × m of HGZNN  ( I , C + λ I , D ) converges globally to
V ˜ V ( 0 ) = D ( C + λ I ) − 1 ,
when t → + ∞ , starting from any initial state X ( 0 ) ∈ R n × m and the solution is stable in the sense of Lyapunov.
b) The minimal exponential convergence rate of HGZNN  ( I , C + λ I , D ) in the case F = I is equal to
E C R HGZNN ( I , C + λ I , D ) = γ 1 + λ min C + λ I C + λ I T 2 .
c) Let V ˜ V ( 0 ) be the limiting value of V ( t ) when t → + ∞ . Then
lim λ → 0 V ˜ V ( 0 ) = lim λ → 0 D C + λ I − 1 .
Proof. 
It can be proved analogously to Corollary 5.2. □
Remark 1.
The notation A 1 = A + λ I and C 1 = C + λ I will be used. Main observations about the convergence properties of HGZNN  ( A , I , B ) and HGZNN  ( I , C , D ) are highlighted as follows.
  1 . Hybrid neural dynamics HGZNN  ( A , I , B ) (resp. HGZNN  ( I , C , D ) ) converge faster than GZNN  ( A , I , B ) (resp. GZNN  ( I , C , D ) ). The accelerated convergence rate is equal to 1 + λ min A T A 2 > 1 (resp. 1 + λ min C C T 2 > 1 ).
  2 . Regularized hybrid dynamics HGZNN  ( A 1 , I , B ) and HGZNN  ( I , C 1 , D ) are applicable even in the case if A and C are singular matrices.
  3 .  HGZNN  ( A 1 , I , B ) (resp. HGZNN  ( I , C 1 , D ) ) always faster converge than GZNN  ( A 1 , I , B ) (resp. GZNN  ( I , C 1 , D ) ). The accelerated convergence rate is 1 + λ min A 1 T A 1 2 > 1 (resp. 1 + λ min C 1 C 1 T 2 > 1 ).

6. Numerical examples on hybrid models model

In this section the numerical examples are represented based on the Simulink implementation of HGZNN formula. The previously mentioned three types of activation functions f ( · ) in (18), (19) and (20) will be used in the following examples. The parameters γ , initial state V ( 0 ) and parameters ρ and ϱ of the nonlinear activation functions (19) and (20), are entered directly in the model, while matrices A, B, C and D are defined from the workspace. We assume that ρ = ϱ = 3 in all examples. The ordinary differential equation solver in configuration paremeters is the ode15s. The blocks powersig, smoothpowersig and transpmult include the codes described in [16].
We present numerical examples in which we compare Frobenius norms | | E G | | F and | | A − 1 B − V ( t ) | | F which are generated by HGZNN, GZNN and GGNN.
Example 6.1.
Consider the matrix
A = 0.49 0.276 0.498 0.751 0.959 0.446 0.68 0.96 0.255 0.547 0.646 0.655 0.34 0.506 0.139 0.71 0.163 0.585 0.699 0.149 0.755 0.119 0.224 0.891 0.258 .
In this example we compare HGZNN ( A , I , I ) model with GZNN ( A , I , I ) and GGNN ( A , I , I ) considering all three types of activation functions. The gain parameter of the model is γ = 10 6 , initial state V ( 0 ) = 0 and the final time is t = 0.00001 .
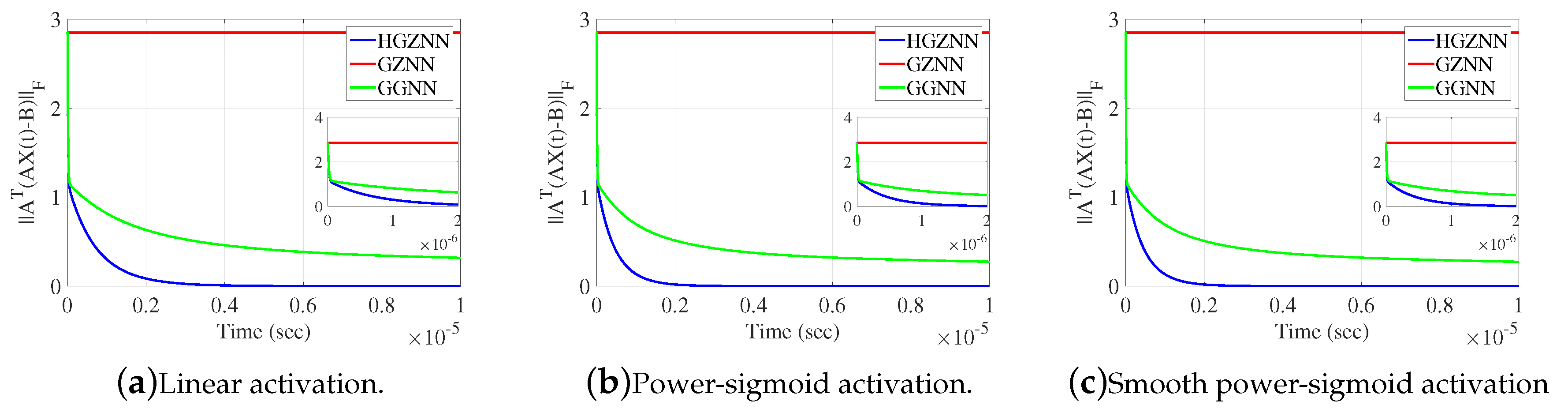
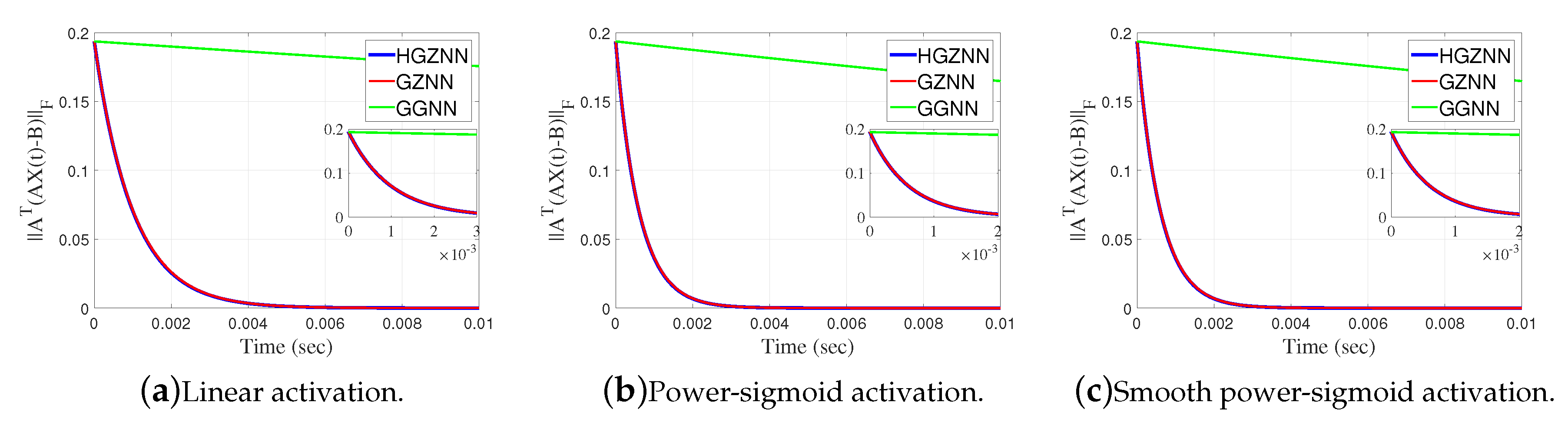
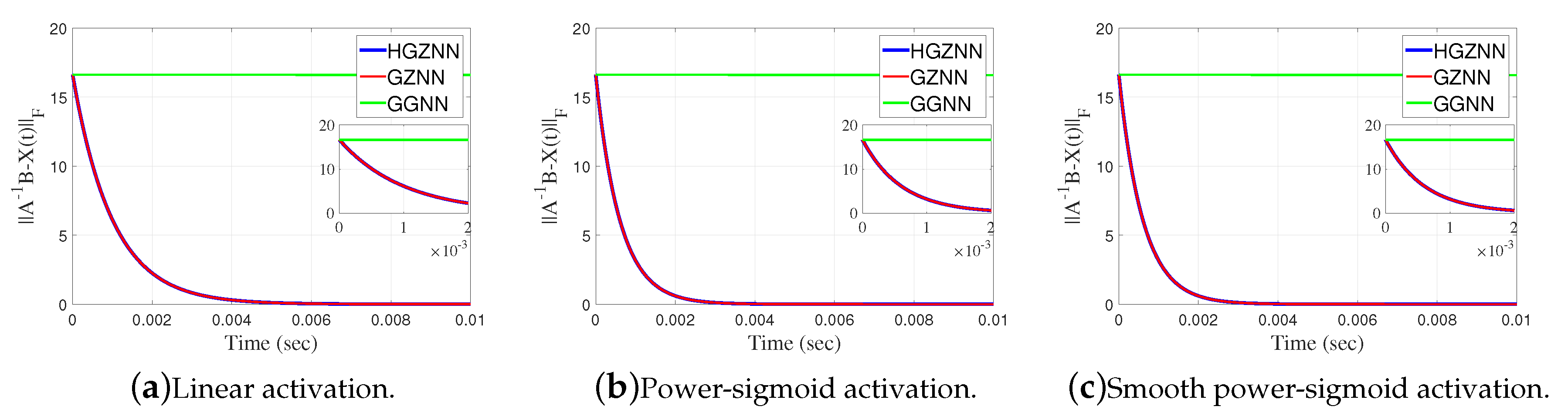
Elementwise trajectories of the state variable with red lines are shown in Figure 14a–c, for linear, power-sigmoid and smooth power-sigmoid activation functions, respectively, and is observable the converge to the black dashed lines of the theoretical solution X. Trajectories indicate a usual convergence behaviour, so the system is globally asymptotically stable. Error matrix E G of HGZNN, GZNN and GGNN model for both linear and non-linear activation functions are shown on Figure 15a–c, and error matrix A − 1 B − V ( t ) of both model for linear and non-linear activation function are shown on Figure 16a–c. On each graph, Frobenius norm of error from HGZNN formula vanish faster to zero than GZNN and GGNN model.
Example 6.2.
Consider the matrices
A = 0.0818 0.0973 0.0083 0.0060 0.0292 0.0372 0.0818 0.0649 0.0133 0.0399 0.0432 0.0198 0.0722 0.0800 0.0173 0.0527 0.0015 0.0490 0.0150 0.0454 0.0391 0.0417 0.0984 0.0339 0.0660 0.0432 0.0831 0.0657 0.0167 0.0952 0.0519 0.0825 0.0803 0.0628 0.0106 0.0920 , B = 0.1649 0.1813 0.0851 0.1197 0.0138 0.1437 0.1558 0.1965 0.1759 0.0625 0.0942 0.0639 0.1937 0.0847 0.1460 0.1636 0.0323 0.1392 0.1062 0.1063 0.0182 0.0688 0.0521 0.0358 0.1400 0.1309 0.0650 0.0533 0.1168 0.1189 0.0846 0.1277 0.0815 0.0211 0.0307 0.0216 0.0045 0.0188 0.0067 0.1640 0.1222 0.0562 .
In this example, we compare HGZNN ( A , I , B ) model with GZNN ( A , I , B ) and GGNN ( A , I , B ) considering all three types of activation functions. The gain parameter of the model is γ = 1000 , initial state V ( 0 ) = 0 and the final time is t = 0.01 .
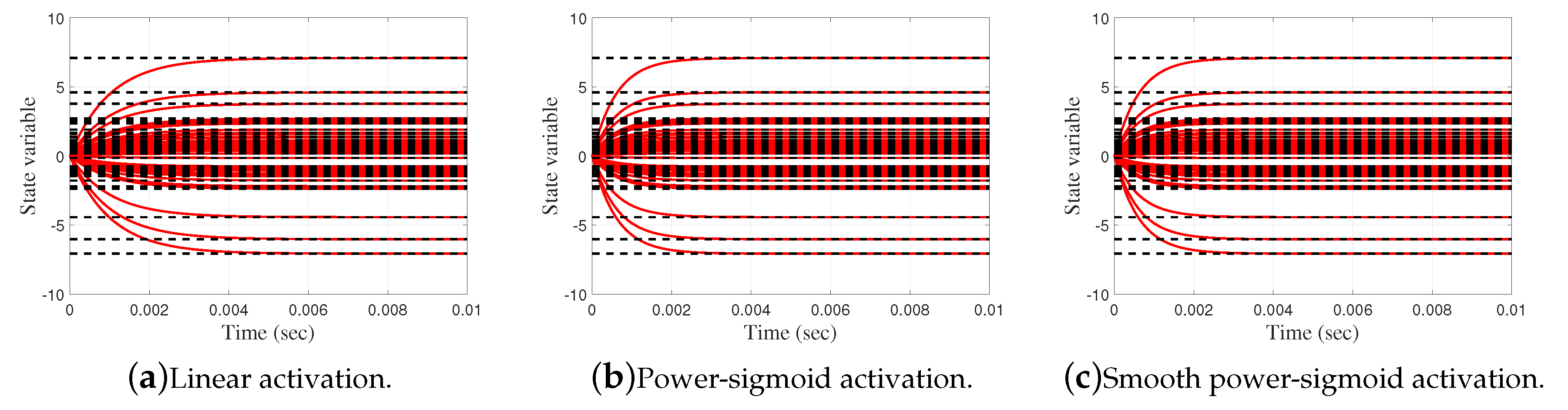
Elementwise trajectories of the state variable with red lines are shown in Figure 17a–c, for linear, power-sigmoid and smooth power-sigmoid activation functions, respectively, and is observable the converge to the black dashed lines of the theoretical solution X. We can see that trajectories indicate a usual convergence behaviour, so the system is globally asymptotically stable. The error matrix E G of HGZNN, GZNN and GGNN model for both linear and non-linear activation functions are shown on Figure 18a–c, and the residual matrix A − 1 B − X ( t ) of both models for linear and non-linear activation function are shown on Figure 19a–c. On each graph, for both error cases, the Frobenius norm of error HGZNN formula is similar to the Frobenius norm of error of GZNN model, and they both converges faster to zero than GGNN model.

7. Conclusions

We show that the error function lying in the basement of GNN and ZNN dynamical evolutions can be defined using the gradient of the Frobenius norm of the traditional error function E ( t ) . The result of this intention is usage of an original error function E G ( t ) for the basis of GNN dynamics which results in the proposed GGNN model. The results related to the GNN model (called GNN ( A , B , D ) ) for solving the general matrix equation A X B = D are extended on GGNN model (called GGNN ( A , B , D ) ) in both theoretical and computational directions. In theoretical sense, the convergence of defined GGNN model is considered. It is shown that the neural state matrix V ( t ) of the GGNN ( A , B , D ) model asymptotically converges to the solution of the matrix equation A X B = D , for an arbitrary initial state matrix V ( 0 ) , and coincides with the general solution of the linear matrix equation. A number of applications of GNN(A, B, D) are considered. All applications are globally convergent. Several particular appearances of the general matrix equation are observed and applied in computing various classes of generalized inverses. Illustrative numerical examples and simulation results are obtained using Matlab Simulink implementation and presented to demonstrate validity of the derived theoretical results. The influence of various nonlinear activations on the GNN models is considered in both the theoretical and the computational direction. In the presented examples it can be concluded that GGNN model is faster and has smaller error compared to the GNN model.
Further research can be oriented to definition of finite-time convergent GGNN or GZNN models as well as definition of noise-tolerant GGNN or GZNN design.

Author Contributions

Conceptualization, P.S. and G.V.M.; methodology, P.S., N.T., D.G. and V.S.; software, D.G., V.K. and N.T.; validation, G.V.M., M.P. and P.S.; formal analysis, M.P., N.T. and D.G. ; investigation, M.P., G.V.M. and P.S.; resources, D.G., N.T., V.K., V.S.; data curation, M.P., V.K., V.S., D.G. and N.T.; writing—original draft preparation, P.S., D.G., N.T.; writing—review and editing, M.P. and G.V.M.; visualization, D.G. and N.T.; supervision, G.V.M.; project administration, M.P.; funding acquisition, G.V.M., M.P. and P.S.. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Ministry of Science and Higher Education of the Russian Federation (Grant No. 075-15-2022-1121).

Data Availability Statement

Data results are available on readers request.

Acknowledgments

Predrag Stanimirović is supported by the Science Fund of the Republic of Serbia, (No. 7750185, Quantitative Automata Models: Fundamental Problems and Applications - QUAM). Dimitrios Gerontitis is supported by financial support of the “Savas Parastatidis” named scholarship granted by the Bodossaki Foundation.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

Abbreviations

The following abbreviations are used in this manuscript:
MDPI Multidisciplinary Digital Publishing Institute
DOAJ Directory of open access journals
TLA Three letter acronym
LD Linear dichroism

References

  1. Ben-Israel, A.; Greville, T. N. E.Generalized Inverses: Theory and Applications; CMS Books in Mathematics, Springer, New York, NY, second ed., 2003.
  2. Nocedal, J.; Wright, S. Numerical Optimization; Springer-Verlag New York, Inc., 1999.
  3. Wang, J. Electronic realisation of recurrent neural network for solving simultaneous linear equations; Electronics Letters, 1992, 28, pp. 493–495.
  4. Wang, J. A recurrent neural network for real-time matrix inversion. Applied Mathematics and Computation, 1993, 55, pp. 89–100.
  5. Zhang, Y.; Chen, K.; Tan, H.Z. Performance analysis of gradient neural network exploited for online time-varying matrix inversion. IEEE Transactions on Automatic Control, 54, pp. 1940–1945, 2009.
  6. Wang, J. Recurrent neural networks for computing pseudoinverses of rank-deficient matrices. SIAM Journal on Scientific Computing, 1997, 18, pp. 1479–1493.
  7. Wei, Y. Recurrent neural networks for computing weighted Moore–Penrose inverse. Applied Mathematics and Computation, 2000, 116, pp. 279–287.
  8. Wang, J.; Li,H. Solving simultaneous linear equations using recurrent neural networks. Information Sciences, 1994, 76, pp. 255–277.
  9. Ding, F.; Chen, T. Gradient based iterative algorithms for solving a class of matrix equations. IEEE Transactions on Automatic Control, 2005, 50, pp. 1216–1221.
  10. Dash, P.; Zohora, F.T.; Rahaman, M.; Hasan, M.M.; Arifuzzaman, M. Usage of Mathematics Tools with Example in Electrical and Electronic Engineering. American Scientific Research Journal for Engineering, Technology, and Sciences (ASRJETS), 2018, 46, pp. 178–188.
  11. Soleimani, F.; Stanimirović, P.S.; Soleimani, F. Some matrix iterations for computing generalized inverses and balancing chemical equations. Algorithms, 2015, 8, pp: 982-998.
  12. Udawat, B.; Begani, J.; Mansinghka, M.; Bhatia, N.; Sharma, H.; Hadap, A. Gauss Jordan method for balancing chemical equation for different materials. Materials Today: Proceedings, 2022, 51 pp: 451-454.
  13. Doty, K.L.; Melchiorri, C.; Bonivento, C. A theory of generalized inverses applied to robotics. The International Journal of Robotics Research, 1993, 12, pp: 1-19.
  14. Li, L.; Hu, J. An efficient second-order neural network model for computing the Moore–Penrose inverse of matrices. IET Signal Processing, 2022, 16, pp: 1106-1117.
  15. Stanimirović, P.S.; Petković, M.D. Gradient neural dynamics for solving matrix equations and their applications. Neurocomputing, 2018, 306, pp. 200–212.
  16. Stanimirović, P.S.; Petković, M.D.; Gerontitis, D. Gradient neural network with nonlinear activation for computing inner inverses and the Drazin inverse. Neural Processing Letters, 2017, 48, pp: 109-133.
  17. Stanimirović, P.S.; Cirić, M.; Stojanović, I.; Gerontitis, D. Conditions for existence, representations and computation of matrix generalized inverses. Complexity, Volume 2017, Article ID 6429725, 27 pages. [CrossRef]
  18. Wang, G.; Wei, Y.; Qiao, S. Generalized Inverses: Theory and Computations. Science Press, 2003.
  19. Wang, G.; Wei, Y.; Qiao, S., Lin, P.; Chen, Y. Generalized inverses: theory and computations. Singapore: Springer, 2018, 10.
  20. Zhang, Y.; Chen, K. Comparison on Zhang neural network and gradient neural network for time-varying linear matrix equation AXB = C solving, IEEE International Conference on Industrial Technology, 2008.
  21. Wang, X.; Tang, B.; Gao, X.G.; Wu, W.H. Finite iterative algorithms for the generalized reflexive and anti-reflexive solutions of the linear matrix equation AXB = C, Filomat 2017, 31, 2151–2162.
  22. Qin, F.; Lee, J. Dynamic methods for missing value estimation for DNA sequences. In: 2010 International Conference on Computational and Information Sciences. IEEE, 2010.
  23. Qin, F.; Collins, J.; Lee, J. Robust SVD Method for Missing Value Estimation of DNA Microarrays. In Proceedings of the International Conference on Bioinformatics & Computational Biology (BIOCOMP) (p. 1). The Steering Committee of The World Congress in Computer Science, Computer Engineering and Applied Computing (WorldComp), 2011.
  24. Stanimirović, P.S.; Mourtas, S.D.; Katsikis, V.N.; Kazakovtsev, L.A. Krutikov, V.N. Recurrent neural network models based on optimization methods, Mathematics, 2022, 10.
  25. Fa-Long, L.; Zheng, B. Neural network approach to computing matrix inversion, Appl. Math. Comput. 1992, 47, 109–120.
  26. Wang, J. A recurrent neural network for real-time matrix inversion, Appl. Math. Comput., 1993, 55, 89–100.
  27. Wang, J. Recurrent neural networks for solving linear matrix equations, Comput. Math. Appl., 1993, 26, 23–34.
  28. Wei, Y. Recurrent neural networks for computing weighted Moore-Penrose inverse, Appl. Math. Comput., 2000, 116, 279–287.
  29. Cichocki, A.; Kaczorek, T. Stajniak, A. Computation of the Drazin inverse of a singular matrix making use of neural networks, Bulletin of the Polish Academy of Sciences Technical Sciences, 1992, 40, 387–394.
  30. Xiao, L.; Zhang, Y.; Li, K.; Liao, B.; Tan, Z. FA novel recurrent neural network and its finite-time solution to time-varying complex matrix inversion, Neurocomputing, 2019, 331, 483–492.
  31. Zhang, Y.; Yi, C.; Guo, D.; Zheng, J. Comparison on Zhang neural dynamics and gradient-based neural dynamics for online solution of nonlinear time-varying equation, Neural Computing and Applications, 2011, 20, 1–7.
  32. Smoktunowicz, A.; Smoktunowicz, A. Set-theoretic solutions of the Yang–Baxter equation and new classes of R-matrices, Linear Algebra and its Applications, 2018, 546, 86–114.
  33. Baksalary, O. M.; Trenkler, G. On matrices whose Moore–Penrose inverse is idempotent, Linear and Multilinear Algebra, 2022, 70, 2014–2026.
  34. Siddiki, A. M. The solution of large system of linear equations by using several methods and its applications, IJISET - International Journal of Innovative Science, Engineering & Technology, 2015, 2, 2.
  35. Wang, S.D.; Kuo, T.S.; Hsu, C.F. Trace bounds on the solution of the algebraic matrix Riccati and Lyapunov equation, IEEE Transactions on Automatic Control, 1986, 31.
  36. Wang, X.Z.; Ma, H.; Stanimirović, P.S. Nonlinearly activated recurrent neural network for computing the Drazin inverse, Neural Processing Letters, 2017, 46, pp. 195–217.
Preprints 89603 g001
Figure 1. Simulink implementation of GGNN ( A , B , D ) evolution (9).
Figure 1. Simulink implementation of GGNN ( A , B , D ) evolution (9).
Preprints 89603 g001
Preprints 89603 g002
Figure 2. Frobenius norm of error matrix A T ( D − A V ( t ) B ) B T of GGNN ( A , B , D ) against GNN ( A , B , D ) in Example 4.1.
Figure 2. Frobenius norm of error matrix A T ( D − A V ( t ) B ) B T of GGNN ( A , B , D ) against GNN ( A , B , D ) in Example 4.1.
Preprints 89603 g002
Preprints 89603 g003
Figure 3. Frobenius norm of error matrix V ( t ) − V * of GGNN ( A , B , D ) against GNN ( A , B , D ) in Example 4.1.
Figure 3. Frobenius norm of error matrix V ( t ) − V * of GGNN ( A , B , D ) against GNN ( A , B , D ) in Example 4.1.
Preprints 89603 g003
Preprints 89603 g004
Figure 4. Elementwise convergence trajectories of the GGNN ( A , B , D ) network in Example 4.2.
Figure 4. Elementwise convergence trajectories of the GGNN ( A , B , D ) network in Example 4.2.
Preprints 89603 g004
Preprints 89603 g005
Figure 5. Frobenius norm of error matrix E G of GGNN ( A , B , D ) against GNN ( A , B , D ) in Example 4.2.
Figure 5. Frobenius norm of error matrix E G of GGNN ( A , B , D ) against GNN ( A , B , D ) in Example 4.2.
Preprints 89603 g005
Preprints 89603 g006
Figure 6. Frobenius norm of D − A V ( t ) B in GGNN ( ( A T A ) 2 , I , A T A A T ) against GNN ( A T A , I , A T ) in Example 4.3.
Figure 6. Frobenius norm of D − A V ( t ) B in GGNN ( ( A T A ) 2 , I , A T A A T ) against GNN ( A T A , I , A T ) in Example 4.3.
Preprints 89603 g006
Preprints 89603 g007
Figure 7. Frobenius norm of E G in GGNN ( ( A T A ) 2 , I , A T A A T ) against GNN ( A T A , I , A T ) in Example 4.3.
Figure 7. Frobenius norm of E G in GGNN ( ( A T A ) 2 , I , A T A A T ) against GNN ( A T A , I , A T ) in Example 4.3.
Preprints 89603 g007
Preprints 89603 g008
Figure 8. Frobenius norm of error matrix D − A V ( t ) B of GGNN ( A 1 T A 1 , I 3 , A 1 T D ) against GNN ( A 1 , I 3 , D ) in Example 4.4.
Figure 8. Frobenius norm of error matrix D − A V ( t ) B of GGNN ( A 1 T A 1 , I 3 , A 1 T D ) against GNN ( A 1 , I 3 , D ) in Example 4.4.
Preprints 89603 g008
Preprints 89603 g009
Figure 9. Frobenius norm of error matrix E G of GGNN ( A 1 T A 1 , I 3 , A 1 T D ) against GNN ( A 1 , I 3 , D ) in Example 4.4.
Figure 9. Frobenius norm of error matrix E G of GGNN ( A 1 T A 1 , I 3 , A 1 T D ) against GNN ( A 1 , I 3 , D ) in Example 4.4.
Preprints 89603 g009
Preprints 89603 g010
Figure 10. Electrical Network.
Figure 10. Electrical Network.
Preprints 89603 g010
Preprints 89603 g011
Figure 11. Frobenius norm of error | | V ( t ) − I | | F of GGNN ( A , 1 , D ) against GNN ( A , 1 , D ) for the electrical network application.
Figure 11. Frobenius norm of error | | V ( t ) − I | | F of GGNN ( A , 1 , D ) against GNN ( A , 1 , D ) for the electrical network application.
Preprints 89603 g011
Preprints 89603 g012
Figure 12. Elementwise convergence trajectories of the GGNN ( A , 1 , D ) network in electrical network application.
Figure 12. Elementwise convergence trajectories of the GGNN ( A , 1 , D ) network in electrical network application.
Preprints 89603 g012
Preprints 89603 g013
Figure 13. Simulink implementation of (24).
Figure 13. Simulink implementation of (24).
Preprints 89603 g013
Preprints 89603 g014
Figure 14. Elementwise convergence trajectories of the HGZNN ( A , I , I ) network in Example 6.1.
Figure 14. Elementwise convergence trajectories of the HGZNN ( A , I , I ) network in Example 6.1.
Preprints 89603 g014
Preprints 89603 g015
Figure 15. Frobenius norm of error matrix E A , I , B of HGZNN ( A , I , I ) against GGNN ( A , I , I ) and GZNN ( A , I , I ) in Example 6.1.
Figure 15. Frobenius norm of error matrix E A , I , B of HGZNN ( A , I , I ) against GGNN ( A , I , I ) and GZNN ( A , I , I ) in Example 6.1.
Preprints 89603 g015
Preprints 89603 g016
Figure 16. Frobenius norm of the residual matrix A − 1 B − V ( t ) of HGZNN ( A , I , I ) against GGNN ( A , I , I ) and GZNN ( A , I , I ) in Example 6.1.
Figure 16. Frobenius norm of the residual matrix A − 1 B − V ( t ) of HGZNN ( A , I , I ) against GGNN ( A , I , I ) and GZNN ( A , I , I ) in Example 6.1.
Preprints 89603 g016
Preprints 89603 g017
Figure 17. Elementwise convergence trajectories of the HGZNN ( A , I , B ) network in Example 6.2.
Figure 17. Elementwise convergence trajectories of the HGZNN ( A , I , B ) network in Example 6.2.
Preprints 89603 g017
Preprints 89603 g018
Figure 18. Frobenius norm of error matrix E A , I , B of HGZNN ( A , I , B ) against GGNN ( A , I , B ) and GZNN ( A , I , B ) in Example 6.2.
Figure 18. Frobenius norm of error matrix E A , I , B of HGZNN ( A , I , B ) against GGNN ( A , I , B ) and GZNN ( A , I , B ) in Example 6.2.
Preprints 89603 g018
Preprints 89603 g019
Figure 19. Frobenius norm of error matrix A − 1 B − X ( t ) of HGZNN ( A , I , B ) against GGNN ( A , I , B ) and GZNN ( A , I , B ) in Example 6.2.
Figure 19. Frobenius norm of error matrix A − 1 B − X ( t ) of HGZNN ( A , I , B ) against GGNN ( A , I , B ) and GZNN ( A , I , B ) in Example 6.2.
Preprints 89603 g019
Table 1. Input data.
Table 1. Input data.
Matrix A Matrix B Matrix D Input and residual norm
m n rank ( A ) p q rank ( B ) m q rank ( D ) γ t f Å † D B † B − D _ F
10 8 8 9 7 7 10 7 7 10 4 0.5 1.051
10 8 6 9 7 7 10 7 7 10 4 0.5 1.318
10 8 6 9 7 5 10 7 7 10 4 0.5 1.81
10 8 6 9 7 5 10 7 5 10 4 5 2.048
10 8 1 9 7 2 10 7 1 10 4 5 2.372
20 10 10 8 5 5 20 5 5 10 6 5 1.984
20 10 5 8 5 5 20 5 5 10 6 5 2.455
20 10 5 8 5 2 20 5 5 10 6 1 3.769
20 10 2 8 5 2 20 5 2 10 6 1 2.71
20 15 15 5 2 2 20 2 2 10 8 1 1.1
20 15 10 5 2 2 20 2 2 10 8 1 1.158
20 15 10 5 2 1 20 2 2 10 8 1 2.211
20 15 5 5 2 1 20 2 2 10 8 1 1.726
Table 2. Experimental results based on data presented in Table 1
Table 2. Experimental results based on data presented in Table 1
E ( t ) F (GNN) E ( t ) F (GGNN) E G ( t ) F (GNN) E G ( t ) F (GGNN) CPU(GNN) CPU(GGNN)
1 . 051 1.094 2 . 52 e − 09 0.02524 5 . 017148 13.470995
1 . 318 1.393 3 . 122 e − 07 0.03661 22.753954 10 . 734163
1 . 811 1.899 0 . 0008711 0.03947 15.754537 15 . 547785
2 . 048 2.082 1 . 96 e − 10 0.00964 9 . 435709 17.137916
2 . 372 2 . 372 2 1 . 7422 e − 15 2.003e-15 21.645386 13 . 255210
1 . 984 1 . 984 2.288e-14 9.978e-15 21.645386 13.255210
2.455 2.455 1.657e-11 1.693e-14 50.846893 19.059385
3.769 3.769 6.991e-11 4.071e-14 42.184748 13.722390
2.71 2.71 1.429e-14 1.176e-14 148.484258 13.527065
1.1 1.1 1.766e-13 5.949e-15 218.169376 17.5666568
1.158 1.158 2.747e-10 2.981e-13 45.505618 12.441782
2.211 2.211 7.942e-12 8.963e-14 194.605133 14.117241
1.726 1.726 8.042e-15 3.207e-15 22.340501 11.650829
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated