Prerpints.org logo
Preprint
Article

Sparse Mix-Attention Transformer for Multispectral Image and Hyperspectral Image Fusion

Altmetrics

Downloads

120

Views

49

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

03 November 2023

Posted:

06 November 2023

You are already at the latest version

Alerts
Abstract
Multispectral image (MSI) and hyperspectral image (HSI) fusion (MHIF) aims to address the challenge of acquiring high-resolution (HR) HSI images. This field combines a low-resolution (LR) HSI with an HR-MSI to reconstruct HR-HSI. Existing methods directly utilize transformers to perform feature extraction and fusion. Despite the demonstrated success, there exist two limitations: 1) Employing the entire transformer model for feature extraction and fusion fails to fully harness the transformer’s potential in integrating the spectral of the HSI and spatial information of the MSI. 2) HSI has a strong spectral correlation and exhibits sparsity in the spatial domain. Existing transformer-based models do not optimize this physical property, which makes their methods prone to spectral distortion. To accomplish these issues, this paper introduces a novel framework for MHIF called Sparse Mix-Attention Transformer (SAMformer). Specifically, to fully harness the advantages of the Transformer architecture, we propose a Spectral Mix Attention Block (SMAB), which concatenates the keys and values extracted from LR-HSI and HR-MSI to create a new multi-head attention module. This design facilitates the extraction of detailed long-range information across spatial and spectral dimensions. Besides, to address the spatial sparsity inherent in HSI, we incorporated a sparse mechanism within the core of SMAB called Sparse Spectral Mix Attention Block (SSMAB). In the SSMAB, we compute attention maps from queries and keys and select the K highly correlated values as the sparse attention map. This approach enables us to achieve a sparse representation of spatial information while eliminating spatially disruptive noise. Extensive experiments conducted on three benchmark datasets, namely Cave, Harvard, and Pavia Center, demonstrate the SMAformer method outperforms state-of-the-art methods.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

Multispectral image (MSI) and hyperspectral image (HSI) fusion (MHIF) aims to obtain a high-resolution (HR) HSI by fusing a low-resolution (LR) HSI and an HR-MSI in the same scene. Compared to traditional images containing only a few bands (such as RGB), HSI offers the advantage of capturing more spectral information about the same scene. Research has demonstrated the significant benefits of HSI in various vision tasks, including tracking [1], segmentation[2], and classification[3].
Early methods of MHIF drew inspiration from pan-sharpening techniques used in remote sensing images. These methods, such as component substitution (CS)[4,5] and multiresolution analysis (MRA)[6,7,8], were computationally efficient. However, they face challenges in fusion quality and easily lead to spectral distortion. This can be attributed to the fact that a single panchromatic image inherently contains less spectral information compared to HSI. The subsequent model-based techniques, e.g., bayesian-based[9,10], tensor-based[11,12], and matrix factorization-based methods[13,14]. These methods rely on prior knowledge of HSI to address this issue. They have made some progress to a certain extent due to the availability of more accurate prior knowledge. However, it’s important to note that these prior knowledge sources are artificially designed and may not encompass all the characteristics of real data. As a result, the model’s ability to generalize is significantly constrained.
In recent years, deep learning methods have shown remarkable advancements in various domains of computer vision, including SR tasks[19,20]. The field of MHIF has also witnessed significant exploration in applying deep learning methods. One of the earliest deep learning approaches in this field is based on a 3D convolutional neural network (CNN)[21], which has achieved impressive results. 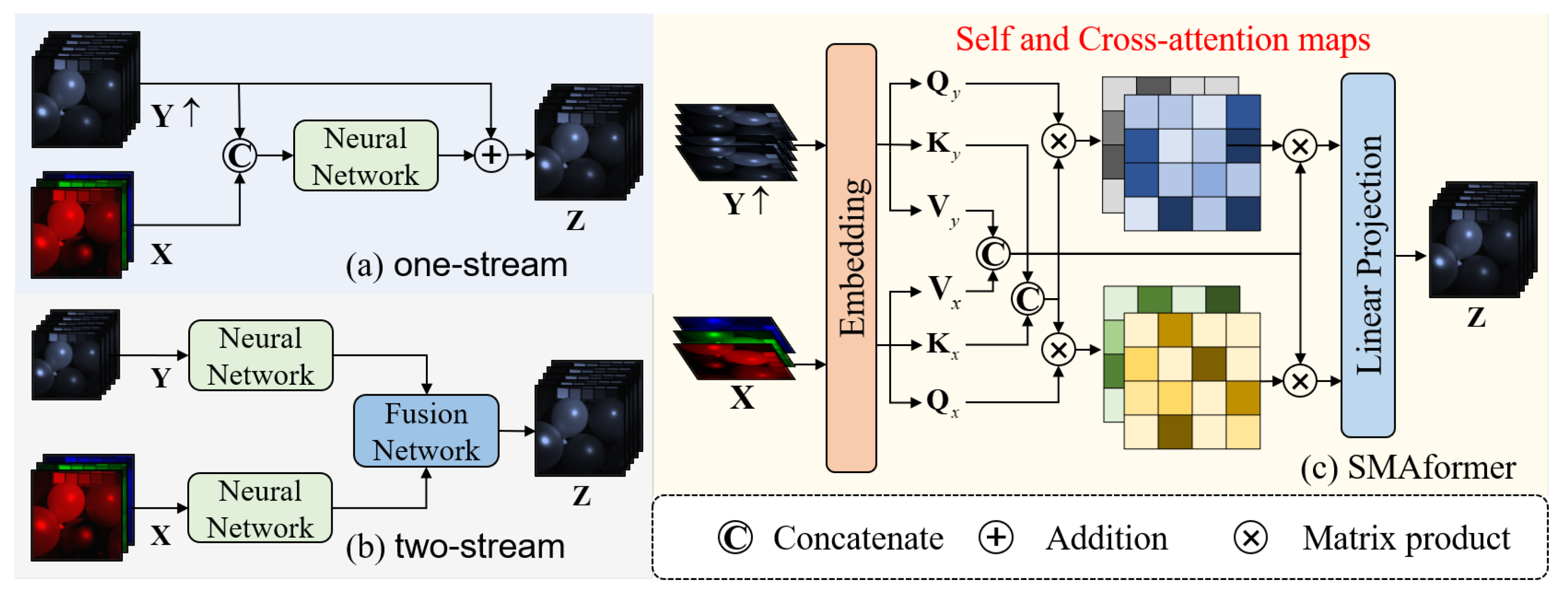Xie et al.[22] have successfully combined deep learning algorithms with optimization algorithms to enhance interpretability. These methods can be broadly categorized into two types, as shown in Figure 1. The first type (see Figure 1 (a)) directly concatenates the upsampled HSI and MSI as input and passes them through a neural network to obtain the reconstructed image[15,16]. The second type (see Figure 1 (b)) employs two independent neural networks to extract features from the HSI and MSI separately, a fusion module is then utilized to generate the final output[17,18]. Although these methods have shown advancements compared to traditional approaches, they still exhibit certain limitations. The restricted receptive field of CNNs hinders the effective capture of global information, resulting in constraints on the final fusion outcomes.
In order to address the aforementioned issues, researchers have applied the Transformer model to the MHIF. The Transformer model proves to be capable of capturing global information from the images, effectively solving long-range dependencies and accurately capturing fine details between HSI and MSI. Hu et al.[23]were among the first to adopt the Transformer model for MHIF. Their framework resembles the first type of CNN architecture, where the HSI and MSI images are merged, and the self-attention mechanism is employed to establish relationships between the two images. Following this, Jia et al. [24]proposed a two-stream network, which is similar to the second type of CNN network. This approach involves extracting spectral features from HSI and spatial features from MSI separately. Both of these methods show improvement over CNN models, nonetheless, they still have two main problems. Firstly, they remain constrained by conventional frameworks and do not fully harness the Transformer model’s potential to establish a comprehensive mapping relationship between HSI and MSI. Secondly, the earlier Transformer models include all pixels in the image in the computation process, resulting in a dense calculation process. However, HSI data exhibits sparsity in spatial distribution, with low correlations among certain pixels. Merely employing a primitive transformer not only escalates computational complexity but also introduces potential system noise interference.
To overcome the limitations of previous methods, we propose a novel MHIF framework named SMAformer. There are two main technologies included in the framework. Firstly, in order to fully utilize the flexibility of the attention mechanism in the Transformer model, we combine feature extraction and feature fusion to generate a unified framework called Spectral Mix Attention Block (SMAB). Specifically, as illustrated in Figure 1(c), we expand both the upsampled LR-HSI and MSI in the channel dimension, treating each channel as a token. Subsequently, we concatenate the K and V of the two images and perform attention operations separately, combining self-attention and cross-attention. By treating channels as tokens, we are able to emphasize the close relationship between the spectra of the HSI. The use of two attention mechanisms allows us to pay attention to both the intrinsic information of the HSI and the reference information from the MSI. During this process, the extracted feature information can be more efficiently integrated. Secondly, in the past, transformers utilized all available information in their calculations. Nonetheless, the spatial sparsity inherent in HSI often results in significant computational inefficiency when following these approaches. To mitigate unnecessary computational overhead, we introduced a sparse attention mechanism to replace the original self-attention. More specifically, after calculating the self-attention for the MSI image at a high-resolution stage, we select the K ones with the highest correlation for subsequent computations, while setting the rest to zero. In lower resolutions, we employ a conventional transformer. This approach allows information from the MSI to selectively complement the HSI, rather than being entirely combined with it. This not only aligns with the physical characteristics of the HSI but also minimizes the impact of irrelevant information from the MSI on the restored image. The main contributions of this article can be summarized as the following three points:
  • We introduce a novel transformer-based network called SMAformer, it takes advantage of the flexibility of the attention mechanism in the transformer to effectively extract intricate long-range information in both spatial and spectral dimensions.
  • We use the sparse attention mechanism to replace the self-attention mechanism. This enables us to achieve a sparse representation of spatial information while eliminating interfering noise in space.
  • Extensive experiments on three benchmark datasets, Cave, Harvard, and Pavia Center, show that SMAformer outperforms state-of-the-art methods.

2. Related Work

We divide existing MHIF methods into two categories, traditional and deep learning-based methods. In the following, we review them in detail.

2.1. Traditional Work

Early methods were based on the principle of linear transformations: Principal Component Analysis(PCA) and Wavelet Transformation. For example, Nunez et al. [25] proposed two wavelet decomposition-based MSI pan-sharpening methods: an additive method and a replacement method. Matrix factorization-based methods assume that each spectrum can be linearly represented by a few spectral atoms. Naoto et al.[26] decomposed the HSI and the MSI alternately into an endmember matrix and an abundance matrix, then built the sensor observation model related to these two data into the initialization matrix of each nonnegative matrix factorization (NMF) unmixing process. Finally, get HR-HSI. Spatial sparsity of hyperspectral input by Kawakami et al.[13], who unmix hyperspectral input and combine it with RGB input to produce the desired result, which treats the unmixing problem as decomposing the input into a basis and a search for a set of maximally sparse coefficients. Another important method of HSI super-resolution is based on tensor factorization. Tensor factorization technology can convert traditional 2D matrix images into 4D or even higher-order tensors without losing information. Zhang et al.[27] regularized the low-rank tensor decomposition based on the spatial spectrogram, derived the spatial domain map using MSI, derived the spectral domain map using HSI, and finally fused the two parts. Xu et al.[28]proposed a coupled tensor ring(TR) representation model to fuse HSI and MSI, while introducing graph Laplacian regularization into the spectral kernel tensor to preserve spectral information.
Although the above traditional methods are successful to a certain extent, they are all based on certain priors or assumptions, which may not match the complex display environment, thus causing many negative effects, such as spectral distortion.

2.2. Deep Learning Based Work

Due to the powerful representation ability of CNN, the method of deep learning has also been applied to the super-resolution task of HSI. Dian et al.[29] use a deep residual network to directly learn image priors, and finally use an optimization algorithm to reconstruct the HSI. Considering the rich spectral information of HSI, Palsson[21] uses a 3D convolutional network to fuse MSI and HSI. In order to reduce the amount of calculation, it uses principal component analysis(PCA) to reduce the dimension of the HSI image and input it. This method realizes end-to-end training and has achieved Very good results. Yang et al.[18] designed a dual-branch network, one branch extracts MSI spatial information, the other extracts HSI spectral information, and finally fuses to obtain ideal results. Considering the spatial and spectral degradation of the HSI image, Xie et al.[22] established a deep model and used an optimization algorithm to iteratively solve it. Due to the inherent defects of convolution, the above CNN-based deep learning method is limited by the receptive field, and cannot fully mine the correlation between MSI and HSI, resulting in the loss of some structural details.
Transformer can solve the shortcomings of CNN due to its ability to perceive full image information and establish long-range details. Hu et al.[23] first applied it to the field of MHIF called Fusformer, which can use Transformer to globally explore the internal relationship within the feature. Jia et al.[24] used the transformer to establish a dual-branch fusion network, one network extracts spectral information, and the other branch extracts spatial information. Although the above methods have made significant improvements, their fusion framework still complies with the previous CNN network and does not use the flexibility of the Transformer network to establish the connection between HSI and MSI. We directly establish the relationship between the two within the transformer to fully obtain the relevant information of the two.

3. Method

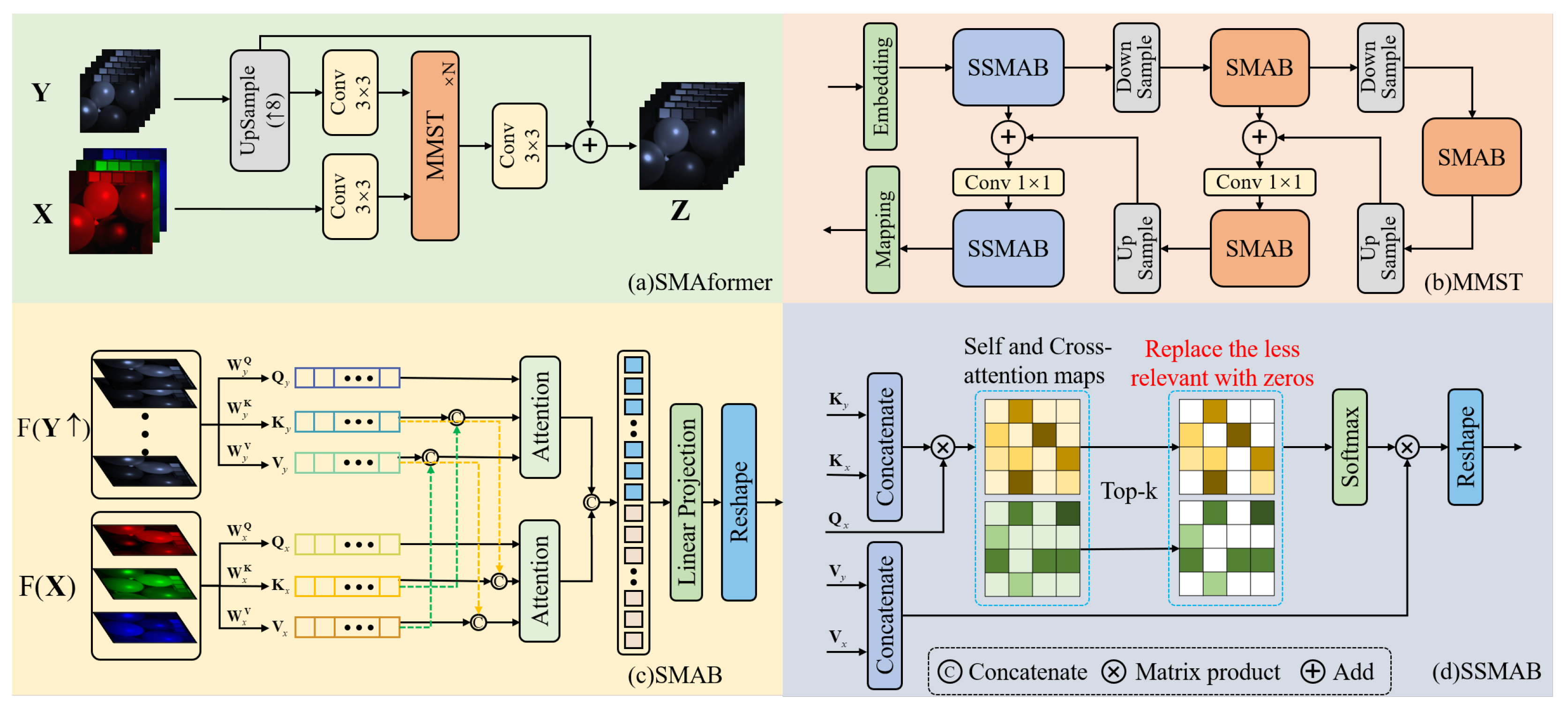
3.1. Network Architecture

Figure 2(a) illustrates our overall framework. Given a pair of HR-MSI and LR-HSI, represented by X ∈ R H × W × c and Y ∈ R h × w × C , where H and h represent the height of MSI and HSI respectively, W and w represent the width, C and c represent the number of channels. The network takes the upsampled HSI Y ↑ and X as inputs and generates the corresponding reconstructed HR-HSI( Z ∈ R H × W × C ). First, feed Y ↑ and X into separate 3 × 3 convolutional layers to obtain initial feature matrices F ( Y ↑ ) and F ( X ) , these two initial feature matrices have the same shape. Subsequently, input these two feature matrices into N Multi-stage Mixed Spectral-wise Transformer (MMST) modules. The output of the MMST is further processed through a 3 × 3 convolution to yield a feature matrix with the same dimensions as Y ↑ . Ultimately, this feature matrix is summed with Y ↑ to produce the final HR-HSI. The overall network structure can be expressed as the following formula:
Y ↑ = U p s a m p l e × 8 ( Y ) , F ( Y ↑ ) = conv 3 × 3 Y ↑ , F ( X ) = conv 3 × 3 X , Z = c o n v 3 × 3 MMST × N F ( Y ↑ ) , F ( X ) + Y ↑ ,
where c o n v 3 × 3 represents 3 × 3 convolution, and NMST×N indicates N Multi-stage MMST module. The specific structure of the MMST module is shown in Figure 2(b), where it adopts a U-shaped structure consisting of encoders, decoders, and bottlenecks. Considering the spatially sparse nature of HSI, the first stage of the encoder utilizes Sparse Spectral Mix Attention Blocks (SSMAB) at high resolution, while SMAB is used in the subsequent low-resolution stages and bottlenecks. The same strategy is employed in the decoder. Both the Embedding and Mapping layers employ c o n v 3 × 3 while downsampling uses c o n v 4 × 4 with a stride of 2. To minimize information loss during downsampling, skip connections are utilized between the encoder and decoder. Specifically, after upsampling through d e c o n v 2 × 2 convolution, the feature of the same resolution as in the encoding stage is concatenated along the channels, and c o n v 1 × 1 convolution is employed for dimensionality reduction as the input for the subsequent stage. We will provide a more detailed explanation of SMAB and the sparse attention in SSMAB in the next two sections.

3.2. Spectral Mix Attention Block

Different from the previous use of one-stream and two-stream, our network uses a completely new architecture. The spatial mix attention block, as shown in Figure 2(c), plays a crucial role in the system. It takes inputs features of Y ↑ and X , then extracts their own long-range features simultaneously and fuses the interactive information between them. This module differs from the traditional transformer multi-head self-attention in two key ways. First, considering the spatial sparseness and inter-spectral correlation in HSI, we perform the attention operation on the image channels. This approach not only reduces computational complexity but also proves to be more suitable for the current task. Second, we employ two parallel attention modules: self-attention and cross-attention. These modules not only focus on their own long-range information but also capture the cross-information between the two inputs. Specifically, we expand Y ↑ and X along the channel dimension and apply linear transformations to obtain Q y , K y , V y for Y ↑ and Q x , K x , V x for X . This enables us to capture both the intrinsic relationships between Y ↑ and X and the information exchange between them. By concatenating the K y and K x , as well as the V y and V x , we perform the attention operation using their respective Q . The following formula illustrates this process:
Q y , K y , V y = Y ↑ W y Q , W y K , W y V , Q x , K x , V x = X W x Q , W x K , W x V , K c = C o n c a t ( K x , K y ) , V c = C o n c a t ( V x , V y ) , Attention y = Softmax ( Q y K c T d ) V c , Attention x = Softmax ( Q x K c T d ) V c ,
where W y Q , W y K , W y V and W x Q , W x K , W x V ∈ R n × n denote the learnable parameters of Q , K and V of Y ↑ and X respectively, Attention x and Attention x denote the attention maps of Y ↑ and X respectively, which include self-attention and cross-attention. Finally, the two are seamlessly Concatenated together. Subsequently, a projection mapping and reshape operation is applied, resulting in the generation of feature maps that match the size of the inputs.

3.3. Sparse Spectral Mix Attention Block

The global self-attention of the transformer is not well-suited for MHIF. This is primarily due to two reasons. Firstly, HSI exhibits spatial sparsity, making dense self-attention unsuitable for capturing their physical characteristics. Secondly, the spectral correlation in HSI is stronger than the spatial correlation. Therefore, it is necessary to reduce the proportion of spatial reference information branches to mitigate the interference of irrelevant features and noise.
To overcome these limitations, We introduce a sparse attention[30] module that leverages the sparsity inherent in neural networks, as shown in Figure 2(d). This module is applied to the branch of MSI and integrated into the overall framework. The initial feature extraction stage remains consistent with the spectral mix transformer. However, after calculating the Q × K ⊤ , we select only the Top-K elements with the largest attention coefficients in the attention map. The objective of this step is to retain the most important components and discard redundant or irrelevant ones. Here, the value of k is an adjustable dynamic parameter, and by varying it, we can sparsify the attention coefficients to different degrees. The final formulation for sparse attention will take the following form:
SparseAtt = softmax T k Q K ⊤ d V ,
where T k is an operator that selects the Top-K values, it can be represented by the following formula :
T k ( M ) i j = M i j M i j ≥ t i 0 otherwise .
After applying this method in the high-resolution step, the rest of the process is always the same as the previous method. Figure 3 illustrates the impact of employing various Multi-Head Self-Attention(MSA) techniques. It is evident that the heat map generated through our utilization strategy exhibits the highest resemblance to the Ground Truth(GT).

3.4. Loss Function

After obtaining the reconstructed HR-HSI, we proceed to train the network using the following loss function formula:
L = L 1 + λ L s s i m ,
The loss function comprises two components: the first component is the L 1 loss function, aimed at enhancing the clarity of the recovered edges and details. The formula is as follows:
L 1 = Z ^ − Z 1 ,
where Z ^ and Z denote the GT and the fusion result respectively.
The second component is the L s s i m loss function[31], which contributes to overall image performance improvements. It is defined as:
L s s i m = 1 − S S I M ( Z ^ − Z ) , = 1 − 1 S ∑ k = 1 S 2 μ Z ^ k μ Z k + c 1 2 σ Z ^ k Z k + c 2 μ Z ^ k 2 + μ Z k 2 + c 1 σ Z ^ k 2 + σ Z k 2 + c 1 ,
where k represents different bands from 1 to S, and S represents the number of channels of the image. μ Z ^ k and μ Z k represent the average values of the GT and the fusion result respectively, while σ Z ^ k and σ Z k signify the standard deviation of the image pixel values. σ Z ^ k Z k represents covariance, and c 1 and c 2 are two constants introduced to prevent a denominator of 0.
The parameter λ in the middle serves as a coefficient used to balance the two components, and in this paper, a value of 0.1 is employed.

4. Experiments

In this section, to demonstrate the effectiveness of the method presented in this paper, we carried out a series of experiments. Firstly, we introduce the experimental environment and configuration, as well as present three datasets and various evaluation metrics. Following this, a comprehensive comparative analysis is performed to assess the performance of the method proposed in this paper in comparison to several advanced methods on these datasets. Finally, in order to validate the efficacy of our proposed module, we conducted ablation experiments

4.1. Experimental Settings

This method utilizes PyTorch 1.10.1 and Python 3.6.15 for training on a single NVIDIA GPU GeForce GTX 2080Ti. The Adam optimizer is employed to minimize the loss function, and the training is carried out for 2000 epochs. For the learning rate, a dynamic approach is adopted. Initially, the learning rate is set to 1×10-4 and then decreased by a factor of 0.8 every 100 epochs.

4.2. Datasets

To fully validate the effectiveness of the method proposed in this paper, we conducted a comparison using three datasets, including two real-world datasets: CAVE[32] and Harvard[33], and a remote sensing dataset Pavia Center. The characteristics of these datasets are as follows:
CAVE: Captured by Apogee Alta U260 CCD camera, this dataset comprises spectral bands ranging from 400nm to 700nm with 10nm intervals, representing real-world objects. It consists of a total of 32 scenes, categorized into five groups: Stuff, Skin and Hair, Paints, Food and Drinks, Real and Fake. Each scene contains 512×512 pixels and 31 spectral bands. Additionally, RGB images corresponding to these scenes are also provided. For our experiments, we selected the first 20 scenes as the training set and the remaining 12 scenes as the test set.
Harvard: Captured using Nuance FX, CRI Inc., this dataset comprises both indoor and outdoor real scenes captured under sunlight. It contains the same 31 spectral bands as the CAVE dataset, but the spectral band ranges from 420nm to 720nm. The resolution of each scene is 1392×1040 pixels. We designated the last 12 scenes as the test set and used the remaining scenes for training.
Pavia Center: The Pavia Center dataset was obtained through satellite remote sensing using ROSIS sensors, capturing imagery from the heart of Pavia, Italy. Pavia is a small city encompassing urban regions, agricultural land, and diverse geographic features, the scene is even more intricate. This dataset comprises 102 spectral bands, and the images have a resolution of 1096 x 1096 pixels.
Data Simulation: For the CAVE and Harvard datasets, to train the network, paired LR-HSI and HR-MSI data are required. However, the dataset only provides one HSI image, necessitating data simulation. In this process, the original image serves as the GT. The HR-MSI image is calculated using the response function of the Nikon D700 camera and the original HSI image. For LR-HSI, a Gaussian convolution kernel with size r×r is applied to blur the original HSI image. The resulting image is then downsampled by a factor of 8, yielding the final LR-HSI. Due to the Pavia Center dataset consisting of only a single image, it was divided into two segments. The 512×216 pixel block located in the lower left corner serves as the test set, while the remaining sections are allocated for training. The HR-MSI was generated by utilizing the spectral response functions of the IKONOS satellite and raw images. The method used to generate the LR-HSI remains consistent with the previous two methods.

4.3. Evaluation Metrics

To comprehensively assess the efficacy of our method, we have chosen five evaluation metrics to appraise the images restored by our approach. These metrics include Peak Signal-to-Noise Ratio(PSNR)[34], Structural Similarity Index Metric(SSIM)[31], Spectral Angle Mapper(SAM)[35], Erreur Relative Global Adimensionnelle Synthese(ERGAS)[36], and Universal Image Quality Index(UIQI)[37]. Subsequently, we will introduce each of these evaluation indicators individually.

4.3.1. PSNR

PSNR calculates the peak error between the corresponding pixels of the generated image and the reference image. The formula for this calculation is as follows:
PSNR Z ^ , Z = 10 S ∑ k = 1 S l o g 10 M A X Z k 2 MSE Z ^ k , Z k ,
where k represents different bands from 1 to S, and S represents the number of channels of the image. M A X Z k represents the maximum pixel value of the two input images, with the maximum value for the images in this paper being 1. MSE Z ^ k , Z k stands for Mean Square Error between the GT and the fusion result, and its formula is as follows:
MSE Z k ^ , Z k = 1 H W ∑ i = 0 H − 1 ∑ j = 0 W − 1 Z ^ k i , j − Z k i , j 2 ,
where H and W represent the height and width of the image, respectively. A higher PSNR value indicates a smaller error between the generated image and the real image, indicating better image quality.

4.3.2. SSIM

SSIM measures the similarity between two images, focusing on improved image quality in terms of brightness, contrast, and structure. The calculation formula is as follows:
SSIM Z ^ , Z = 1 S ∑ k = 1 S 2 μ Z ^ k μ Z k + c 1 2 σ Z ^ k Z k + c 2 μ Z ^ k 2 + μ Z k 2 + c 1 σ Z ^ k 2 + σ Z k 2 + c 1 ,
where μ Z ^ k and μ Z k represent the average values of image pixels, serving to quantify image brightness, while σ Z ^ k and σ Z k signify the standard deviation of the image pixel values, used to gauge image contrast. σ Z ^ k Z k represents covariance, indicating the similarity in image structure, and c 1 and c 2 are two constants introduced to prevent a denominator of 0. This metric aligns more closely with human visual perception characteristics than PSNR. A larger SSIM value corresponds to a better human visual perception effect and a smaller disparity between the enhanced image and the original image.

4.3.3. SAM

The SAM treats the spectrum of each pixel within the image as a high-dimensional vector and quantifies the similarity between these spectra by determining the angle between the two vectors. A smaller angle indicates a higher degree of similarity between the two spectra. The formula for SAM is expressed as follows:
SAM Z ^ , Z = 1 H W ∑ j = 1 H W arccos Z j ⊤ Z ^ j Z j 2 Z ^ j 2 ,
where Z ^ j and Z j represent the j-th spectral band of Z ^ and Z , respectively, and · 2 represents the l 2 norm.

4.3.4. ERGAS

ERGAS is a metric used to assess the quality of remote-sensing images. It is typically employed to compare the quality difference between two remote-sensing images. A lower ERGAS value indicates a smaller difference between the reconstructed image and the original image, indicating higher image quality. Defined as follows:
ERGAS ( Z ^ , Z ) = 100 r 1 S ∑ k = 1 S MSE Z ^ k , Z k μ Z ^ k 2 ,
where r represents the magnification of the image, the value of r is set to 8 in this paper. μ Z ^ k 2 represents the square of the mean-value of the pixel value in the k-th spectral dimension of the image.

4.3.5. UIQI

The UIQI is a metric used to assess the quality of an image by comparing it to a reference or original image. It measures the similarity between the two images in terms of three key factors: correlation loss, brightness distortion, and contrast distortion. UIQI is a mathematical metric and does not explicitly consider the human visual system. However, it has been found to be consistent with subjective quality assessments for a wide range of image distortions. It is defined as follows:
UIQI ( Z ^ , Z ) = 1 S ∑ k = 1 S 4 μ Z ^ k μ Z k σ Z k μ Z ^ k 2 + μ Z k 2 σ Z ^ k 2 + σ Z k 2 .
The greater the UIQI value, the higher the quality of the corresponding image.

4.4. Quantitative Analysis

To demonstrate the effectiveness of our approach in this study, we conducted comprehensive experiments on two datasets. Furthermore, we compared our method with several state-of-the-art approaches, encompassing a variety of research methods, including matrix factorization-based LTTR[38], CNN-based MHF-Net[22], DBIN[39], ADMM-HFNet[15], Spf-Net[16], GuidedNet[40], and transformer-based Fusformer[23].
Table 1 provides an overview of the average quality metrics for our method and other methods on the CAVE dataset. It is evident that our method consistently claims the top position across all performance indicators. Specifically, in terms of the PSNR metric, we outperform the second-ranked method by 0.3 dB, signifying a more robust noise suppression capability in our approach. Furthermore, in the SSIM metric, we also maintain a lead, indicating superior perceptual quality in the images generated by our method. In the realm of spectral recovery, our SAM (Spectral Angle Mapper) score significantly surpasses that of the second-ranked method, resulting in minimal spectral distortion. Lastly, when considering the two comprehensive evaluation metrics, ERGAS and UIQI, we maintain a substantial lead, underlining that the images restored by our method exhibit superior overall quality, closely resembling real-world images.
Similarly, Table 2 presents the performance metrics for our method and other methods on the Harvard dataset, where our method also excels across various indicators. Although we rank slightly lower than the first-place method in the SSIM and ERGAS metrics, we still maintain a significant lead over the third-place method. In all other metrics, we significantly outperform other methods.
In summary, our method showcases exceptional performance in image quality restoration, as demonstrated through evaluations on the CAVE and Harvard datasets. Whether it’s noise reduction, perceptual quality, spectral recovery, or overall image quality assessment, our method consistently emerges as the leader in these domains, underscoring its remarkable potential in the field of MHIF.

4.5. Qualitative Analysis

To better exhibit the effectiveness of our method, we conducted comparisons with four other four methods. In Figure 4, We chose three representative images from CAVE, each displaying its pseudo-RGB representation, utilizing the 3rd, 13th, and 2nd dimensions. The error maps below their corresponding images, in the error map, a stronger blue color indicates that the image has fewer errors, while a stronger red color indicates that the image has more errors. From the figures, it is evident that MHF-net and Fusformer exhibit noticeable color deviations in their restored images, indicating significant spectral errors in the recovered HSI. This discrepancy is also apparent in their respective error maps when compared to the GT. LTTR performs better compared to the first two methods, yet still shows pronounced distortions in challenging areas, such as the colored spheres in the image. SPF-net method yields relatively favorable results with overall minimal distortions and relatively realistic details.
In contrast, our method demonstrates the smallest difference when compared to the GT. In terms of color, our images exhibit no discernible differences, suggesting that our method preserves spectral information with minimal distortion. Furthermore, in terms of details, our method accurately restores object structures, even in areas where other methods struggle to provide clear representations.
To provide a more comprehensive display of our restoration results, we conducted experiments using the Harvard dataset. Figure 5 showcases the images restored by our method and the results of the other methods. It can be observed that MHF-net performs similarly to the CAVE dataset, with better overall performance, but still exhibits notable spectral distortions in some images. The other three methods produce images with fewer distortions, although some deficiencies remain in certain details. Our method clearly outperforms the others both globally and locally, with hardly any evident errors in the error maps.
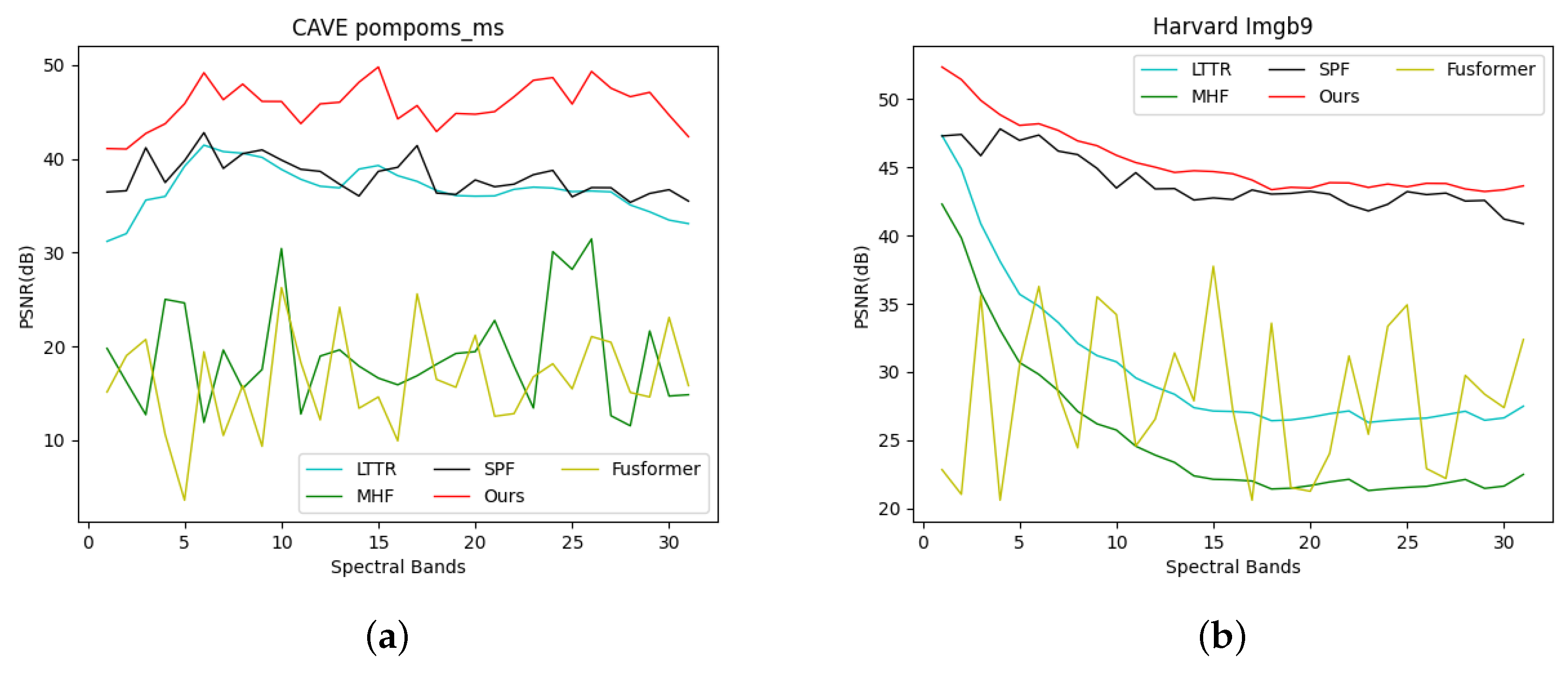
To showcase the superior performance of our method, we selected an image from both the CAVE and Harvard datasets. We then computed the PSNR values for each spectral dimension and visualized them in Figure 6. As Figure 6 demonstrates, our SMAformer method (depicted by the red curve) consistently outperforms other methods, clearly leading the pack. This indicates that our method not only excels in overall image recovery quality but also surpasses others in every spectral dimension.
Furthermore, to validate the practicality of our approach, we conducted comparative experiments on real remote sensing imagery from Pavia Center. The resulting image depicts a 216×216 pixel section situated on top of the test set. We assigned the 65th band to red, the 30th band to green, and the 15th band to blue, creating a pseudo-RGB representation. To highlight details, we applied a 3 x magnification factor to a specific area using a red box within the image. Additionally, error maps were generated and displayed beneath the respective pseudo-RGB image.
After a thorough image analysis, it is evident that the other four methods have indeed produced satisfactory results, effectively revitalizing the original visual fidelity. Nevertheless, upon meticulous scrutiny of the magnified image, it becomes apparent that certain fine details have not been fully restored. Common issues such as chromatic aberration and blurred edges persist in their results. In stark contrast, our method excels in the meticulous restoration of these intricate details. From the error map, it is evident that there is virtually no distinction between our method and the actual image. Our approach adeptly and precisely rejuvenates the true appearance, achieving the highest scores across various performance indicators.
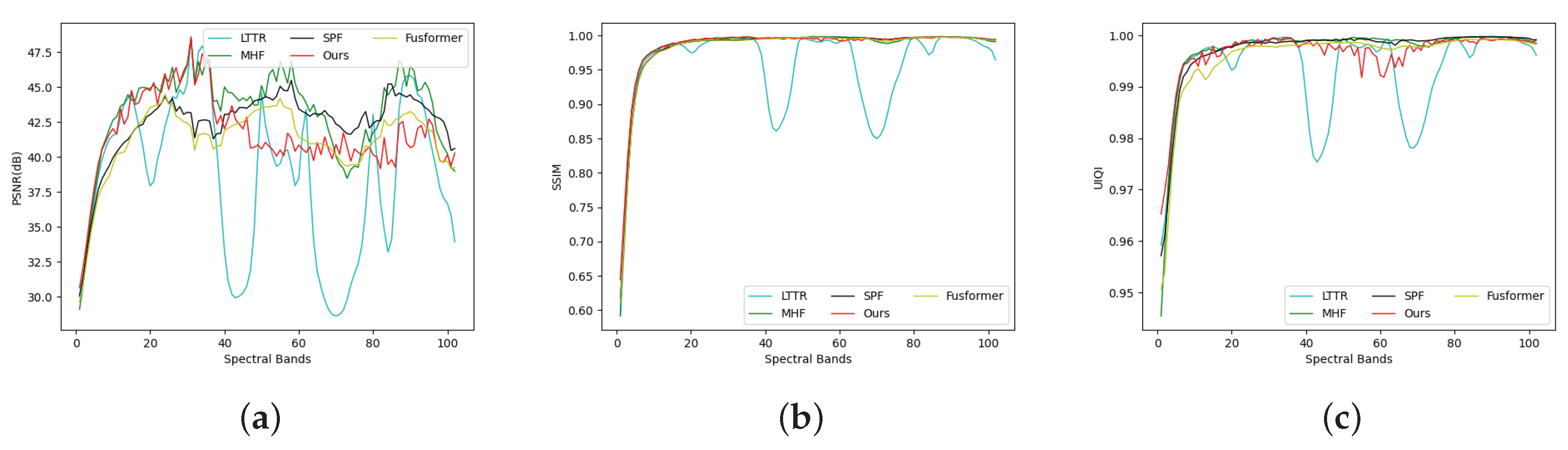
In Figure 8, we present the index curves representing images generated by different methods alongside the GT in each spectral band. Figure 8(a) illustrates the PSNR values. It is evident that our method excels in lower spectral bands and still delivers strong performance in higher dimensions, even though there is a slight decline. This demonstrates that images produced by our method exhibit reduced noise levels. Figure 8(b) showcases the performance based on SSIM values. With the exception of the LTTR method, which exhibits significant fluctuations, the other methods maintain relatively consistent performance.In Figure 8(c), we observe the UIQI indicator. Our method lags slightly behind in the middle band but consistently leads in other bands. This underlines the effectiveness of our approach in preserving image quality across different spectral bands.
In summary, based on the performance on these three datasets, our method not only excels in terms of metrics but also produces more realistic images with richer detailed information.

4.6. Ablation Study

To validate the effectiveness of our proposed method, we conducted ablation studies using the CAVE dataset.
Our primary module, MMST, incorporates a total of three stages. To determine the most suitable stage, we conducted experiments separately on each of the four stages, including one stage, two stages, four stages, and the three stages used in this paper. The experimental results on the CAVE dataset for different stage counts are presented in Table 3. The table reveals that increasing the number of stages enhances the performance of the model to a certain extent. The SSIM and SAM indicators achieve their peak results when utilizing four stages. However, the PSNR, ERGAS, and UIQI indicators exhibit superior performance with three stages. Simultaneously, with the escalation of the number of stages, the parameters of the model increase, and the time required for image generation significantly extends. Hence, to strike a balance between metrics and time, we opted for the utilization of three stages.
We proposed two modules: SMAB and SSMAB. SMAB leverages the flexibility of the transformer to establish self-generated and mutual correlations between HR-MSI and LR-HSI within the module. SSMAB builds upon SMAB by incorporating a sparse attention module to better accommodate the spatial sparse characteristics of HSI. To assess the effectiveness of our proposed modules, we conducted experiments. We replaced SMAB with residual convolutional blocks in the original module to obtain w/o SMAB method and replaced SSMAB with SMAB to create the w/o SSMAB method. While keeping other parameters constant, the final results are presented in Table 3.
Table 4 reveals that substituting SMAB with residual convolutional blocks led to a notable drop in PSNR by 2.18dB. This suggests that our module excels in extracting crucial information from both images compared to its predecessors. When SSMAB was omitted, the PSNR decreased by 1.54dB, underscoring the idea that sparsity is better suited for handling HSI.

5. Conclusions

In this paper, we have proposed a novel model for the MHIF task, called SMAformer. Different from previous fusion methods, we have focused on fusion super-resolution tasks and have given full play to the flexibility of the Transformer model. We have designed a multi-stage fusion module that can effectively capture the information between space and the spectrum to improve the fusion effect. In addition, considering the characteristics of HSI, we have performed sparse processing inside the model to make the generated images more realistic. Extensive experimental results on three benchmark datasets have demonstrated that our SMAformer has surpassed the state-of-the-art methods.

Author Contributions

“Conceptualization, Shihai Yu; methodology, Shihai Yu; software, Shihai Yu; validation, Shihai Yu; formal analysis, Xu Zhang; investigation, Xu Zhang; resources, Huihui Song; data curation, Shihai Yu; writing—original draft preparation, Shihai Yu; writing—review and editing, Huihui Song and Xu Zhang; visualization, Shihai Yu; supervision, Huihui Song; project administration, Xu Zhang; funding acquisition, Xu Zhang and Huihui Song. All authors have read and agreed to the published version of the manuscript.”, please turn to the CRediT taxonomy for the term explanation. Authorship must be limited to those who have contributed substantially to the work reported.

Funding

This work is supported in part by The Seventh Batch of Science and Technology Development Plan (Agriculture) Project of Suzhou (SNG2023007), in part by NSFC under Grant Nos. 61872189.

Acknowledgments

In this section you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

Conflicts of Interest

Declare conflicts of interest or state “The authors declare no conflict of interest.” Authors must identify and declare any personal circumstances or interest that may be perceived as inappropriately influencing the representation or interpretation of reported research results. Any role of the funders in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript, or in the decision to publish the results must be declared in this section. If there is no role, please state “The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results”.

References

  1. Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–spatial feature tokenization transformer for hyperspectral image classification. IEEE Transactions on Geoscience and Remote Sensing 2022, 60, 1–14. [Google Scholar] [CrossRef]
  2. Uzkent, B.; Hoffman, M.J.; Vodacek, A. Real-time vehicle tracking in aerial video using hyperspectral features. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, 2016, pp. 36–44.
  3. Hong, D.; Yao, J.; Meng, D.; Xu, Z.; Chanussot, J. Multimodal GANs: Toward crossmodal hyperspectral–multispectral image segmentation. IEEE Transactions on Geoscience and Remote Sensing 2020, 59, 5103–5113. [Google Scholar] [CrossRef]
  4. Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS + Pan data. IEEE Transactions on Geoscience and Remote Sensing 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
  5. Chavez, P.; Sides, S.C.; Anderson, J.A.; others. Comparison of three different methods to merge multiresolution and multispectral data- Landsat TM and SPOT panchromatic. Photogrammetric Engineering and remote sensing 1991, 57, 295–303. [Google Scholar]
  6. Burt, P.J.; Adelson, E.H. The Laplacian pyramid as a compact image code. In Readings in computer vision; Elsevier, 1987; pp. 671–679.
  7. Loncan, L.; De Almeida, L.B.; Bioucas-Dias, J.M.; Briottet, X.; Chanussot, J.; Dobigeon, N.; Fabre, S.; Liao, W.; Licciardi, G.A.; Simoes, M.; others. Hyperspectral pansharpening: A review. IEEE Geoscience and remote sensing magazine 2015, 3, 27–46. [Google Scholar] [CrossRef]
  8. Starck, J.L.; Fadili, J.; Murtagh, F. The undecimated wavelet decomposition and its reconstruction. IEEE transactions on image processing 2007, 16, 297–309. [Google Scholar] [CrossRef]
  9. Bungert, L.; Coomes, D.A.; Ehrhardt, M.J.; Rasch, J.; Reisenhofer, R.; Schönlieb, C.B. Blind image fusion for hyperspectral imaging with the directional total variation. Inverse Problems 2018, 34, 044003. [Google Scholar] [CrossRef]
  10. Akhtar, N.; Shafait, F.; Mian, A. Bayesian sparse representation for hyperspectral image super resolution. Proceedings of the IEEE conference on computer vision and pattern recognition, 2015, pp. 3631–3640.
  11. Dian, R.; Fang, L.; Li, S. Hyperspectral image super-resolution via non-local sparse tensor factorization. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2017, pp. 5344–5353.
  12. Li, S.; Dian, R.; Fang, L.; Bioucas-Dias, J.M. Fusing hyperspectral and multispectral images via coupled sparse tensor factorization. IEEE Transactions on Image Processing 2018, 27, 4118–4130. [Google Scholar] [CrossRef]
  13. Kawakami, R.; Matsushita, Y.; Wright, J.; Ben-Ezra, M.; Tai, Y.W.; Ikeuchi, K. High-resolution hyperspectral imaging via matrix factorization. CVPR 2011. IEEE, 2011, pp. 2329–2336.
  14. Akhtar, N.; Shafait, F.; Mian, A. Sparse spatio-spectral representation for hyperspectral image super-resolution. Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6-12 September 2014, Proceedings, Part VII 13. Springer, 2014, pp. 63–78.
  15. Shen, D.; Liu, J.; Wu, Z.; Yang, J.; Xiao, L. ADMM-HFNet: A matrix decomposition-based deep approach for hyperspectral image fusion. IEEE Transactions on Geoscience and Remote Sensing 2021, 60, 1–17. [Google Scholar] [CrossRef]
  16. Liu, J.; Shen, D.; Wu, Z.; Xiao, L.; Sun, J.; Yan, H. Patch-aware deep hyperspectral and multispectral image fusion by unfolding subspace-based optimization model. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2022, 15, 1024–1038. [Google Scholar] [CrossRef]
  17. Yao, J.; Hong, D.; Chanussot, J.; Meng, D.; Zhu, X.; Xu, Z. Cross-attention in coupled unmixing nets for unsupervised hyperspectral super-resolution. Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part XXIX 16. Springer, 2020, pp. 208–224.
  18. Yang, J.; Zhao, Y.Q.; Chan, J.C.W. Hyperspectral and multispectral image fusion via deep two-branches convolutional neural network. Remote Sensing 2018, 10, 800. [Google Scholar] [CrossRef]
  19. Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, September 6-12, 2014, Proceedings, Part IV 13. Springer, 2014, pp. 184–199.
  20. Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, October 11-14, 2016, Proceedings, Part II 14. Springer, 2016, pp. 391–407.
  21. Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. Multispectral and hyperspectral image fusion using a 3-D-convolutional neural network. IEEE Geoscience and Remote Sensing Letters 2017, 14, 639–643. [Google Scholar] [CrossRef]
  22. Xie, Q.; Zhou, M.; Zhao, Q.; Xu, Z.; Meng, D. MHF-Net: An interpretable deep network for multispectral and hyperspectral image fusion. IEEE Transactions on Pattern Analysis and Machine Intelligence 2020, 44, 1457–1473. [Google Scholar] [CrossRef]
  23. Hu, J.F.; Huang, T.Z.; Deng, L.J.; Dou, H.X.; Hong, D.; Vivone, G. Fusformer: A transformer-based fusion network for hyperspectral image super-resolution. IEEE Geoscience and Remote Sensing Letters 2022, 19, 1–5. [Google Scholar] [CrossRef]
  24. Jia, S.; Min, Z.; Fu, X. Multiscale spatial–spectral transformer network for hyperspectral and multispectral image fusion. Information Fusion 2023, 96, 117–129. [Google Scholar] [CrossRef]
  25. Nunez, J.; Otazu, X.; Fors, O.; Prades, A.; Pala, V.; Arbiol, R. Multiresolution-based image fusion with additive wavelet decomposition. IEEE Transactions on Geoscience and Remote sensing 1999, 37, 1204–1211. [Google Scholar] [CrossRef]
  26. Yokoya, N.; Yairi, T.; Iwasaki, A. Coupled nonnegative matrix factorization unmixing for hyperspectral and multispectral data fusion. IEEE Transactions on Geoscience and Remote Sensing 2011, 50, 528–537. [Google Scholar] [CrossRef]
  27. Zhang, K.; Wang, M.; Yang, S.; Jiao, L. Spatial–spectral-graph-regularized low-rank tensor decomposition for multispectral and hyperspectral image fusion. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2018, 11, 1030–1040. [Google Scholar] [CrossRef]
  28. Xu, Y.; Wu, Z.; Chanussot, J.; Wei, Z. Hyperspectral images super-resolution via learning high-order coupled tensor ring representation. IEEE transactions on neural networks and learning systems 2020, 31, 4747–4760. [Google Scholar] [CrossRef]
  29. Dian, R.; Li, S.; Guo, A.; Fang, L. Deep hyperspectral image sharpening. IEEE transactions on neural networks and learning systems 2018, 29, 5345–5355. [Google Scholar] [CrossRef]
  30. Chen, X.; Li, H.; Li, M.; Pan, J. Learning A Sparse Transformer Network for Effective Image Deraining. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2023, pp. 5896–5905.
  31. Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: from error visibility to structural similarity. IEEE transactions on image processing 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
  32. Yasuma, F.; Mitsunaga, T.; Iso, D.; Nayar, S.K. Generalized assorted pixel camera: postcapture control of resolution, dynamic range, and spectrum. IEEE transactions on image processing 2010, 19, 2241–2253. [Google Scholar] [CrossRef] [PubMed]
  33. Chakrabarti, A.; Zickler, T. Statistics of real-world hyperspectral images. CVPR 2011. IEEE, 2011, pp. 193–200.
  34. Yuanji, W.; Jianhua, L.; Yi, L.; Yao, F.; Qinzhong, J. Image quality evaluation based on image weighted separating block peak signal to noise ratio. International Conference on Neural Networks and Signal Processing, 2003. Proceedings of the 2003. IEEE, 2003, Vol. 2, pp. 994–997.
  35. Yuhas, R.H.; Goetz, A.F.; Boardman, J.W. Discrimination among semi-arid landscape endmembers using the spectral angle mapper (SAM) algorithm. JPL, Summaries of the Third Annual JPL Airborne Geoscience Workshop. Volume 1: AVIRIS Workshop, 1992.
  36. Wald, L. Quality of high resolution synthesised images: Is there a simple criterion? Third conference" Fusion of Earth data: merging point measurements, raster maps and remotely sensed images". SEE/URISCA, 2000, pp. 99–103.
  37. Wang, Z.; Bovik, A.C. A universal image quality index. IEEE signal processing letters 2002, 9, 81–84. [Google Scholar] [CrossRef]
  38. Dian, R.; Li, S.; Fang, L. Learning a low tensor-train rank representation for hyperspectral image super-resolution. IEEE transactions on neural networks and learning systems 2019, 30, 2672–2683. [Google Scholar] [CrossRef]
  39. Wang, W.; Zeng, W.; Huang, Y.; Ding, X.; Paisley, J. Deep blind hyperspectral image fusion. Proceedings of the IEEE/CVF International Conference on Computer Vision, 2019, pp. 4150–4159.
  40. Ran, R.; Deng, L.J.; Jiang, T.X.; Hu, J.F.; Chanussot, J.; Vivone, G. GuidedNet: A general CNN fusion framework via high-resolution guidance for hyperspectral image super-resolution. IEEE Transactions on Cybernetics 2023. [Google Scholar] [CrossRef]
Preprints 89594 g001
Figure 1. Comparing two existing deep learning frameworks[15,16,17,18] with our SMAformer. The previous methods (a), (b) solely focused on either spatial or spectral fusion, neglecting the spatial sparsity in HSI images. In contrast, our SMAformer fully integrates both spatial and spectral information and incorporates sparse representation in spatial domains.
Figure 1. Comparing two existing deep learning frameworks[15,16,17,18] with our SMAformer. The previous methods (a), (b) solely focused on either spatial or spectral fusion, neglecting the spatial sparsity in HSI images. In contrast, our SMAformer fully integrates both spatial and spectral information and incorporates sparse representation in spatial domains.
Preprints 89594 g001
Preprints 89594 g002
Figure 2. Illustration of the proposed method. (a) The network architecture of our work, and (b) the specific structure of the MMST. (c) A detailed description of the SMAB. (d) Detailed description of the SSMAB.
Figure 2. Illustration of the proposed method. (a) The network architecture of our work, and (b) the specific structure of the MMST. (c) A detailed description of the SMAB. (d) Detailed description of the SSMAB.
Preprints 89594 g002
Preprints 89594 g003
Figure 3. The image illustrates the correlation coefficients of the twentieth dimension in images generated with different MSA techniques. It is evident that the MSA strategy employed in our approach yields a correlation coefficient map that closely aligns with those of the GT.
Figure 3. The image illustrates the correlation coefficients of the twentieth dimension in images generated with different MSA techniques. It is evident that the MSA strategy employed in our approach yields a correlation coefficient map that closely aligns with those of the GT.
Preprints 89594 g003
Preprints 89594 g004
Figure 4. The results of three images from the CAVE dataset are displayed, namely superballs in the first and second rows, pompoms in the third and fourth rows, and photo and face in the fifth and sixth rows. In each group of photos, the first column: the top/bottom image indicates the GT/corresponding LR-HSI in pseudo-color (R-3, G-13, B-2), and the 2nd-6th columns: are the visualization images and the corresponding error maps of all compared models.
Figure 4. The results of three images from the CAVE dataset are displayed, namely superballs in the first and second rows, pompoms in the third and fourth rows, and photo and face in the fifth and sixth rows. In each group of photos, the first column: the top/bottom image indicates the GT/corresponding LR-HSI in pseudo-color (R-3, G-13, B-2), and the 2nd-6th columns: are the visualization images and the corresponding error maps of all compared models.
Preprints 89594 g004
Preprints 89594 g005
Figure 5. The results of three images from the Harvard dataset in pseudo-color(R-29, G-21, B-28).
Figure 5. The results of three images from the Harvard dataset in pseudo-color(R-29, G-21, B-28).
Preprints 89594 g005
Preprints 89594 g006
Figure 6. The figure illustrates the the PSNR values of each spectral band for images restored using various methods, in comparison to real images.(a) Illustrates the results for pompoms_ms in the CAVE dataset, while (b) presents the results for Imageb9 in the Harvard dataset.
Figure 6. The figure illustrates the the PSNR values of each spectral band for images restored using various methods, in comparison to real images.(a) Illustrates the results for pompoms_ms in the CAVE dataset, while (b) presents the results for Imageb9 in the Harvard dataset.
Preprints 89594 g006
Preprints 89594 g007
Figure 7. First column: the top/bottom image indicates the GT/corresponding LR-HSI of the top 216 × 216-pixel test image from the Pavia Center dataset in pseudo-color (R-65, G-30, B-15). The 2nd-6th columns: the visualization images and the corresponding error maps of all compared models. In the pseudo-color images, a red-marked region has been triple magnified to assist the visual analysis.
Figure 7. First column: the top/bottom image indicates the GT/corresponding LR-HSI of the top 216 × 216-pixel test image from the Pavia Center dataset in pseudo-color (R-65, G-30, B-15). The 2nd-6th columns: the visualization images and the corresponding error maps of all compared models. In the pseudo-color images, a red-marked region has been triple magnified to assist the visual analysis.
Preprints 89594 g007
Preprints 89594 g008
Figure 8. Index curves for various spectral bands compared to the GT are depicted. (a) The PSNR curve, (b) the SSIM curve, and (c) the UIQI curve.
Figure 8. Index curves for various spectral bands compared to the GT are depicted. (a) The PSNR curve, (b) the SSIM curve, and (c) the UIQI curve.
Preprints 89594 g008
Table 1. Average quantitative results by all the compared methods on the CAVE dataset.
Table 1. Average quantitative results by all the compared methods on the CAVE dataset.
Title PSNR↑ SSIM ↑ SAM↓ ERGAS↓ UIQI↑
LTTR[38] 41.20 0.980 4.25 1.90 0.984
MHFnet[22] 45.23 0.988 4.88 0.71 0.981
DBIN[39] 45.02 0.981 3.38 0.71 0.992
ADMM-HFNet[15] 45.48 0.992 3.39 0.71 0.992
SpfNet[16] 46.29 0.990 4.24 1.46 0.980
Fusformer[23] 42.18 0.993 3.07 1.25 0.992
GuidedNet[40] 45.41 0.991 4.03 0.97 -
Ours 46.56 0.994 2.92 0.64 0.995
1 The best values are highlighted, and the second-best values are underlined.
Table 2. Average quantitative results by all the compared methods on the Harvard dataset.
Table 2. Average quantitative results by all the compared methods on the Harvard dataset.
Title PSNR↑ SSIM ↑ SAM↓ ERGAS↓ UIQI↑
LTTR[38] 40.06 0.999 4.69 1.29 0.993
MHFnet[22] 44.50 0.981 3.68 1.21 0.991
DBIN[39] 45.33 0.983 3.04 1.09 0.995
ADMM-HFNet[15] 45.53 0.983 3.04 1.08 0.995
SpfNet[16] 45.09 0.984 2.31 0.65 0.997
Fusformer[23] 41.96 0.995 3.33 2.86 0.995
GuidedNet[40] 41.64 0.981 2.85 1.20 -
Ours 47.86 0.995 2.25 0.75 0.997
Table 3. Average quantitative results by different stages
Table 3. Average quantitative results by different stages
STGAES PSNR↑ SSIM ↑ SAM↓ ERGAS↓ UIQI↑ Time↓
1-stage 43.06 0.986 3.69 1.19 0.993 0.45
2-stages 45.38 0.990 3.20 0.97 0.991 0.51
3-stages 46.56 0.994 2.92 0.64 0.995 0.55
4-stages 46.01 0.995 2.91 0.78 0.993 0.68
Table 4. Average quantitative results by different modules.
Table 4. Average quantitative results by different modules.
Method PSNR↑ SSIM ↑ SAM↓ ERGAS↓ UIQI↑
w/o SMAB 44.38 0.991 3.24 0.96 0.990
w/o SSMAB 45.02 0.990 2.96 0.77 0.992
Ours 46.56 0.994 2.92 0.64 0.995
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated