Prerpints.org logo
Preprint
Review

Turbomachinery Noise Review

Altmetrics

Downloads

233

Views

91

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

03 November 2023

Posted:

06 November 2023

You are already at the latest version

Alerts
Abstract
The present paper is aimed at presenting an updated review of prediction methods for the aerodynamic noise of ducted rotor-stator stages. Indeed, ducted rotating-blade technologies are in continuous evolution and increasingly used, for both aeronautical propulsion units, power generation and air conditioning systems. Different needs are faced, from the early design stage to the final definition of a machine. Fast-running, approximate analytical approaches and high-fidelity numerical simulations are considered as the best suited tools for each, respectively. Recent advances are discussed, with emphasis on their pros and cons.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

1. Introduction

Periodically reviewing advances in aeroacoustic prediction methods makes sense for both young and senior engineers in charge of developing noise mitigation strategies. Indeed, the range of possible actions is regularly reconsidered, in view of the rapidly growing capabilities in terms of numerical predictions and, to some extent, of advances in the capabilities of analytical techniques. Furthermore, existing technological options are pushed beyond their previously defined limits, and new technologies emerge. In both cases, a status of simulations and/or modeling approaches and of their performances may need to be re-addressed. In this context, the present review, dedicated to ducted axial-flow turbomachinery, is aimed at updating previous recent reviews on rotating-blade noise by the authors [1,2,3,4].
Current ducted axial-flow rotating machines involve both high-speed High By-pass Ratio (HBR) turboengines, short-duct propulsion systems envisioned for instance in certain future Urban Air Mobility (UAM) vehicles, and low speed ventilators used in ventilation systems for buildings, mines or transportation systems. This covers a large range of geometrical parameters and flow conditions that are first recalled in the next section. This will in turn motivate the adequate analytical and numerical strategies used to tackle the noise generated by these machines.
This paper reviews analytical and numerical approaches, that can be applied at various stages of a low-noise design procedure, ensuring noise mitigation with regards to aerodynamic and acoustic installation effects. On the one hand, low-cost, fast-running analytical tools, informed by Reynolds-Averaged Navier-Stokes simulations to be more physically consistent, allow exploring a wide range of parameters, and identifying promising or detrimental configurations. They can then be embedded in multi-disciplinary, multi-objective optimization algorithms [5,6], in a preliminary design step. On the other hand, high-fidelity numerical simulations provide accurate descriptions of the underlying mechanisms, at the price of considerably higher computational time and cost. For this reason, they can be dedicated to the final, more accurate investigation of already selected candidates, for final design. Experimental studies remain of primary interest. Comparisons with a couple of them are also included in the present review, for validation purpose.

2. Context

Before reviewing analytical and numerical methods for ducted rotating machines, it is useful to position these machines with respect to their geometrical features and flow conditions. Indeed, the latter affect the unsteady aerodynamics generating the sound, and the in-duct transmission of that sound. Furthermore, different simplifications leading to analytical formulations can be either justified or abusive, depending on the addressed configuration. Dimensional analysis, based on the identification of key parameters, provides guidelines for this positioning.
Following the classification of Moreau & Roger [1], Moving/stationary blade/vane rows can be characterized by several geometrical parameters. Based on the unwrapped representation of a blade/vane row with B blades/vanes at a given radius R between the inner and outer radii of the duct, say R 1 and R 2 , the main dimensions are the chord length c, the inter-blade/vane spacing defining the solidity σ = c B / ( 2 π R ) , the inter-blade/vane channel width h and the overlap d. The latter is related to other parameters by the stagger angle γ , defined here as the blade/vane angle with respect to the cascade-front direction. As noise mitigation is concerned, the radial stacking of the blade/vane cross-sections, not detailed here, can also have some significant effect. Both angles characterizing the blade skew in the rotational and the meridian planes, defining lean and sweep, should be considered [7,8,9], more specifically when addressing the tonal noise of non-compact blade/vane rows, for which they have significant effects on the interference between sources. Finally, the rotor-stator distance, say D, also needs to be considered to complete the description of a typical turbomachinery stage.
Similarly, moving/stationary blade/vane rows can also be characterized by different flow conditions, in terms of characteristic axial velocity U a , rotational speed Ω , air density ρ 0 and speed of sound c 0 .
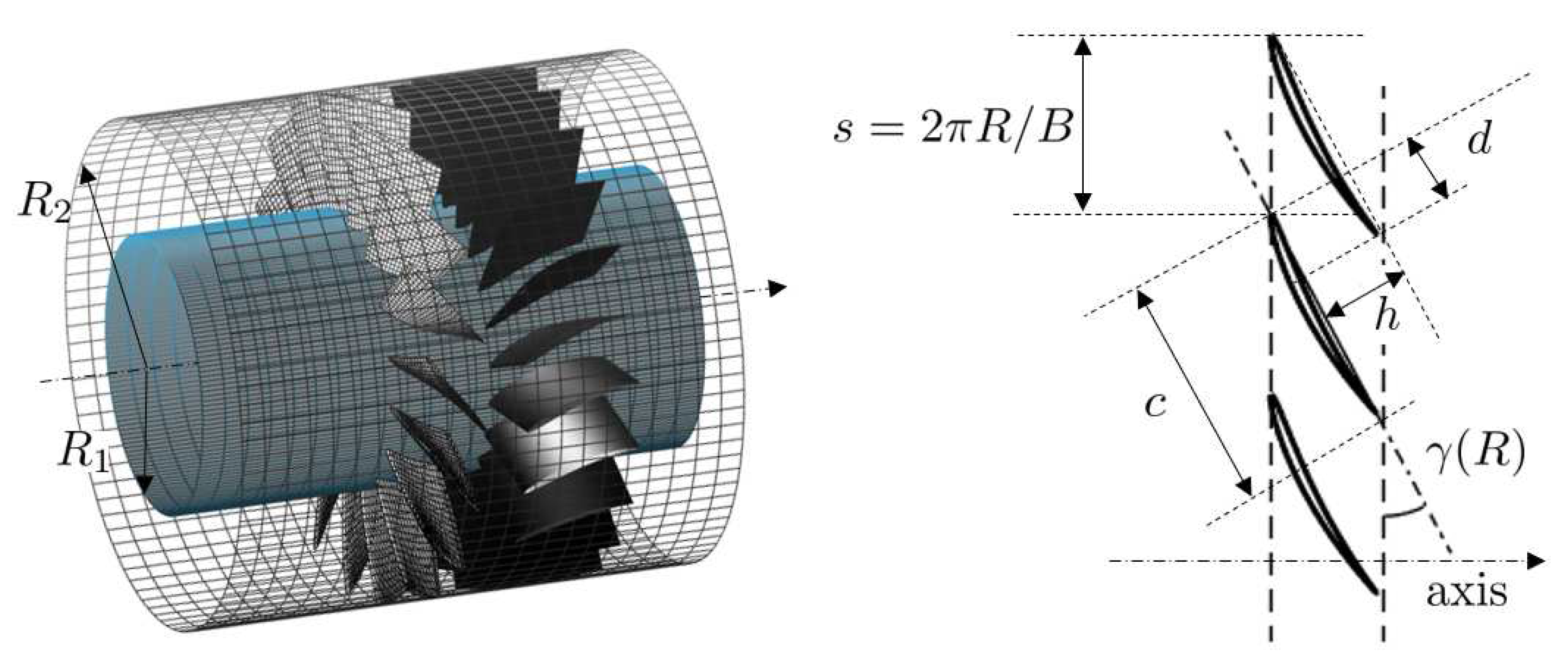
Preprints 89640 g001
Figure 1. Definition of a rotor-stator stage in annular duct (left) and main parameters of an unwrapped cascade representation of a rotor (right).
Figure 1. Definition of a rotor-stator stage in annular duct (left) and main parameters of an unwrapped cascade representation of a rotor (right).
Preprints 89640 g001
Once the geometrical and aerodynamic quantities are identified, any noise indicator built on the sound pressure p at some point is a function of the dimensionless ratios built on them, in the form
p ρ 0 c 0 2 / 2 = F M t , R e c , σ , R 1 R 2 , D R 2 , k R 2 , . . . ,
involving the tip Mach number, M t = Ω R 2 / c 0 , and the chord-based Reynolds number, R e c = U c / ν , where U stands for the relative velocity on a typical blade/vane cross-section. Defining characteristic ranges of the dimensionless parameters entering the functional form F , in which approximations make sense, is a key step, in particular in the development of relevant analytical methods. The set of parameters might need to be increased to integrate more realistic design features in the future. The values of characteristic Mach and Reynolds numbers may help to define best-suited numerical approaches, for instance. The hub-to-tip ratio R 1 / R 2 is another parameter of crucial importance. Small hub-to-tip ratios, such as in the bypass duct of a modern turbofan engine, require a non-compact and fully three-dimensional formulation, whereas large ones, representative of narrow annuli, make some assumptions justified, typically two-dimensional reductions. Large values of D / R 2 correspond to extended axial regions of mean swirl, known to have a significant effect on the cutoff properties of sound waves [10]. Oppositely, the effect of swirl can be ignored for short separations D / R 2 . Finally, the solidity and the stagger angle are key parameters, related to blade-to-blade or vane-to-vane interactions. Isolated airfoil-response functions are acceptable for moderate solidity, and as long as the overlap of adjacent blades/vanes is small. Otherwise, a cascade-response function, or any equivalent, is necessary.
Several fan/Outlet Guide Vane (OGV) configurations typical of high or ultra-high by-pass ratio (HBR or UHBR) turboengines similar to the CFM56 or the LEAP engines have now been considered: this constitutes a major update compared to the most recent reviews in [2,3]. First, a major focus will still be on the NASA Source Diagnostic Test (SDT) turbofan, the geometry of which has been made available through an AIAA Fan Broadband Noise Prediction benchmark that started in 2014. The SDT rotor has 22 blades, whereas the OGV can be varied from 54 straight vanes (the reference configuration) to 26 low-noise swept vanes, and 26 low-count radial vanes. The rotor-stator distance is greater than one and a half rotor axial chord length for all configurations. It constitutes the largest aero-acoustic data base for turbofans [11,12,13,14]. Secondly, a new turbofan benchmark has been unveiled in the European project TurboNoiseBB, the ACAT1 fan/OGV, which consists of 20 fan blades and 44 stator vanes. Two rotor-stator gaps have been considered in AneCom AeroTest [15,16]: one with a short fan-OGV gap, less than a fan axial chord length, and a longer rotor–stator gap, larger than two axial chord lengths. Finally, a recent scaled UHBR designed at Ecole Centrale de Lyon (ECL) to fit into the test facility PHARE-2 for aeroelasticity and aeroacoustic investigations, termed ECL5, has been considered. Its fan has 16 rotor blades and its OGV 31 vanes. The fan/OGV distance is greater than a rotor axial chord length. Additional details on this configuration are provided by Brandstetter et al. [17]. One common feature of all these rotor blades and stator vanes is the use of modern Controlled-Diffusion (CD) airfoils for the blade and vane rows (see figure 6 in [17] for the ECL5 for instance).

3. Analytical models

As mentioned in [1], most analytical methods resort to the so-called strip theory to account for both geometrical and aerodynamic radial variations. The blade span is decomposed into a number of strips, on which the flow conditions are assumed uniform. The best suited number of strips is mostly a matter of combined hub-to-tip ratio R 1 / R 2 and typical aspect ratio ( R 2 − R 1 ) / c . Moreover, in subsonic flows, the fluctuating aerodynamic forces on blades and vanes are the dominant sources, acting as equivalent dipoles, as stated by the acoustic analogy [18,19]. In this case, as described in [3], noise modeling can be split into three main steps. The first step is the definition of velocity disturbances impinging on blade/vane rows, responsible for the fluctuating forces. The second step is formulating the blade/vane response to this excitation. It typically requires that the blades and vanes are assimilated to thin flat plates, and relies on linearized unsteady-aerodynamics theories, based on either isolated-airfoil or cascade response functions. The third step is calculating the sound transmission along the duct and to the external far field. It is usually achieved with the in-duct formulation of the analogy (group A in the classification in [20]). This paradigm is followed in the code OPTIBRUI developed at Université de Sherbrooke for different noise generating mechanisms (flow distortion, wake interaction, potential interaction, vortex interaction etc.), and used in [20,21] for the rotor-stator interaction (RSI) only. At higher Mach numbers, additional quadrupole sources, related to the mean gradients and fluctuations of velocity in the flow, as well as the monopole-like thickness noise, should also be considered. This is usually discarded from in-duct analytical formulations.
An alternative to the above strip theory is the mode-matching approach in bifurcated waveguides (MMBW), according to which the blade/vane rows are considered as periodic bifurcated channels, instead of cascades of plates. It has been recently re-addressed from works initiated in the seventies. Its essentials and a review are found in [22]. An attractive aspect of MMBW is that it may alleviate some of the drawbacks of the strip-theory approach, mostly caused by the inherent lack of communication between strips. Indeed, in principle, it can be extended to three-dimensional annular spaces without resorting to strips, and therefore include the proper radial scattering effects, at the price of a suitable description of the aerodynamic excitation. The edge-dipole formalism proposed in [23] to model the trailing-edge noise of an annular cascade is an example of such a dedicated description. Details on the method can also be found in [1].
It must be noted that both the strip theory and the MMBW assume the framework of linear acoustics, and that sound predictions for different noise mechanisms are performed separately; they can be either summed up, for a complete sound estimate, or considered independently, which provides fundamental physical insight into the mechanisms. This advantage also allows to develop clear parametric investigations of basic mechanisms.

3.1. Tonal noise

Advances with the mode-matching approach are discussed in this section. Reported comparisons with other analytical and numerical methods on the noise propagation through a two-dimensional turbofan OGV cascade, extracted from the SDT case and used as an aeroacoustic benchmark, showed some limitations of the approach, presented in Moreau & Roger [1]. The limitations are inherent to the flat-plate assumption, not compatible with the necessary change of mean-flow angle from upstream to downstream of the vanes (swirl recovery), and are also a matter of concern for other analytical approaches. In particular, the reflected and transmitted waves were found very sensitive to the ’equivalent’ stagger angle chosen for the flat-plate vanes, making the method questionable. This is why the method has been extended in two dimensions to staggered and curved vanes, which allows reproducing the swirl recovery with neither ambiguity nor artificial action [24].
Another advantage of the MMBW is that it can be applied to multiple cascades, via an iterative procedure, in particular to model the complete behavior of a rotor-stator stage. The procedure has been recently described and implemented by Girier et al [25]. It requires multiple changes of reference frame, going from the stationary, OGV-attached frame to the moving, rotor-attached frame, to formulate the matching equations on interfaces of the stationary and moving cascades, respectively. The preliminary implementation described in the reference considers a rotor of zero-stagger blades, thus assumes a non-zero pre-swirl; the next step is the extension to inclined blades, for a proper representation of the complete stage, including the aforementioned realistic swirl recovery, with axial mean flow upstream and downstream of the stage. It is worth noting that, in the blade-tip region, assimilating the blades to inclined flat plates is rather representative of real designs. A typical result is reported in Figure 2. The plotted quantity is the instantaneous acoustic pressure generated by a row of cambered OGV because of impinging rotor wakes. The trace of the wakes cannot be seen, because they are described as a vortical, pressure-free excitation. The sources of the sound field are on the vane leading edges. The radiated field is computed, accounting for the scattering of stator noise by the rotor blades (Figure 2-a) or not (Figure 2-b). In this example, the downstream sound field is nearly the same in both computations. In contrast, the upstream sound field has a much lower amplitude as rotor scattering is included, with different modal contents resulting in different interference patterns. Some of the scattered waves are obviously trapped in the interstage. The test suggests that, more generally, a relevant prediction of stator noise must include rotor scattering. It is worth noting that several multiples of the BPF are considered in parallel in this MMBW implementation. Any mode of order n 0 at angular frequency m B Ω emitted by the stator, B denoting the number of rotor blades, is scattered as the modes n = n 0 − s B at frequencies ( m + s ) B Ω , where s is an arbitrary integer. This capability of the method is one of its key advantages.
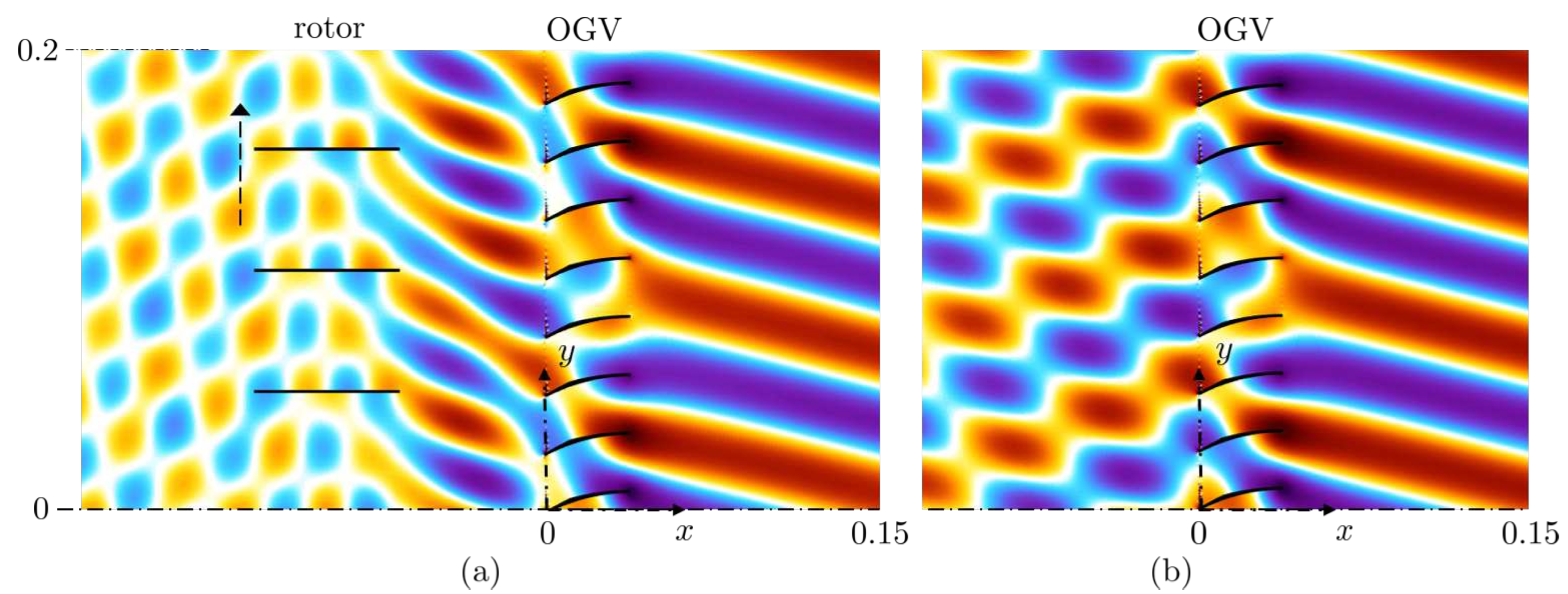
Preprints 89640 g002
Figure 2. Two-dimensional predictions of the instantaneous sound-pressure map produced by rotor wakes impinging on stator vanes, accounting for rotor scattering (a), and only considering the free-field stator response (b). The arrow indicates the vertical relative motion of the (zero-stagger) rotor blades. Paramaters: blade/vane counts 26/54, unwrapped radius = 0.2235 m, axial and tangential Mach numbers 0.36 and 0.19, upstream flow angle 28° Helmholtz number based on vane pitch 2.88, incident disturbance mode order 5.
Figure 2. Two-dimensional predictions of the instantaneous sound-pressure map produced by rotor wakes impinging on stator vanes, accounting for rotor scattering (a), and only considering the free-field stator response (b). The arrow indicates the vertical relative motion of the (zero-stagger) rotor blades. Paramaters: blade/vane counts 26/54, unwrapped radius = 0.2235 m, axial and tangential Mach numbers 0.36 and 0.19, upstream flow angle 28° Helmholtz number based on vane pitch 2.88, incident disturbance mode order 5.
Preprints 89640 g002

3.2. Broadband noise

All analytical broadband noise models presented in this section are dedicated to the RSI only and neither rotor shielding nor possible multiple reflections in the fan/OGV interstage are accounted for. Rotor-blade trailing-edge noise is also ignored. Contrarily to empirical models, they are physically based and rely on mean flow data provided by Reynolds-Averaged Navier-Stokes simulations used to predict overall performances of a given turbomachine.
Recently, Lewis et al. [21] performed a very detailed comparison of different analytical models with the NASA SDT data base, namely Ventres’ [26], Hanson’s [27] , Posson’s [28,29] and Masson’s [10] models. As already mentioned in [2], a thorough validation of the model implementation was achieved. A consistency check was first achieved between the three-dimensional rectilinear cascade response of Posson [30] and Ventres’s two-dimensional one. A second verification has been to properly reproduce Nallasamy and Envia’s results [31] with Ventres’ cascade response and a Gaussian spectrum for the upwash velocity (see figure 11 in [2]). A third assessment [32] has been to properly converge the numerical collocation method involved in Ventres’ model and to compare with additional test cases [30,33]. As in [34,35,36], all models are found to be sensitive to the RANS solution and the equivalent flat plate stagger angle. Yet, accounting for swirl as in Masson’s model limits the effect of the latter geometrical parameter to high frequencies because of its modification on the amplitude of the cut-on modes. Another key parameter describing the excitation is the turbulence spectrum that has a substantial impact on the acoustic power prediction [29,36]. Posson et al. showed that a Gaussian spectrum would increase both upstream and downstream sound power levels (SWL), whereas an axisymmetric turbulence spectrum with realistic length scales would significantly decrease them compared to isotropic models such as von Kàrmàn and Liepmann spectra (Figure 11 and 12 in [29]), which provide the best comparison with hot-wire measurements. Using such more realistic turbulence spectra with Ventres’s two-dimensional cascade response yields an underestimate of both upstream and downstream SWL by more than 10 dB over the whole frequency range, stressing the crucial role of the spanwise wave number and obliques gusts. Moreover, accounting for subcritical gusts improves the low-frequency predictions as was found previously by Moreau & Roger [37,38] for isolated airfoils, Roger for an annular airfoil [39] and Posson & Roger [40] for rectilinear cascades. Lewis et al. [21] also compared the three-dimensional cascade response with Amiet’s isolated airfoil response, and showed that both vane responses do not agree for high-solidity configurations, even at high frequency, contrarily to what was found before in 2D [41] and consistently with what Grace found by introducing the spanwise wave number in her RSI code [42]. In summary, only full three-dimensional models give results that are consistent with experimental data, confirming that both a proper three-dimensional flow description and the use of three-dimensional cascade response are mandatory to carry out analytically based acoustic predictions. Accounting for all supercritical and subcritical gusts also improves the predictions.
In another recent review summarizing all findings of the European project TurboNoiseBB, Kissner et al. [43] and Guerin et al. [20] also compared different analytical and numerical models for the prediction of the broadband noise of the ACAT1 turbofan that was tested at AneCom AeroTest [15]. Twelve different approaches implemented in seven different acoustic solvers were tested, including analytical methods derived originally from the works of Amiet [44] and Hanson[27] relying on a description of the OGV in terms of strips. Details on the considered models can be found in [20] (specifically the classification in Figure 8 and tables A1 and A2 in [20]). Additionally, it should be emphasized that Amiet’s model for isolated airfoils [44] relies on the iterative application of Schwarzchild’s solution [45] at each vane edge to yield its unsteady response. For the turbulence-interaction noise (TIN) mechanism two iterations including the trailing-edge back-scattering are enough to converge, and Moreau & Roger [37] showed that including all supercritical and subcritical gusts allows retrieving a blade response similar to Sears’one [46] at low frequencies. Note that similar conclusions have also been drawn for the other airfoil/blade noise mechanism: trailing-edge noise (TEN) or self-noise [38,47,48]. As also noted in [2,3], Schwarzschild’s technique [45] applied to a wave equation with two boundary conditions imposed in two half planes is equivalent to the Wiener-Hopf method. Recent extensions of the latter to finite chord (section 2.1.7 in [49]) is also based on the notion of iterative corrections for back scattering [50]. Some conclusions from the studies of Kissner et al. [43] and Guerin et al. [20] corroborate the above findings on SDT. First, both the RANS turbulence model and the selected analytical approach for the noise were also found to have a significant impact on the predictions of RSI broadband noise. On the other hand, replacing the actual geometry by an infinitely thin flat plate yielded minor differences in power levels. Similarly, using different isotropic turbulence spectra (von Kármán or Liepmann) did not change the noise levels significantly. Differences between models at low frequencies were also attributed to the account of subcritical gusts in the prediction. The choice of the Green’s function and the cascade response (2D or 3D) were also identified to yield different noise levels in different frequency ranges. Yet, different combinations of both are not always consistent, and some mismatch between the source model and the Green’s function prevented drawing definite conclusions. Moreover, contrarily to SDT predictions, all noise predictions had levels usually lower than those measured by some decibels, even though the turbulent intensity was overestimated by the RANS simulations. The closest prediction to experiment was provided by the model that considered the incompressible Sears’ isolated flat plate response [46] and only parallel gusts with free-field propagation, whereas the lowest levels were obtained with the more realistic three-dimensional rectilinear flat plate response combined with the in-duct Green’s function. In fact, the comparison still relied on the conventional assumption that rotor-wake interaction was the only dominant noise mechanism at stake. However, Guerin et al. noted that other noise sources could be involved and the best comparison with the simplest analytical model could be still fortuitous. Finally, another interesting result of this study was the comparison of computational times between all methods: all analytical models excluding the cascade response provided results with a large number of strips in a matter of minutes, those including the cascade response in a matter of hours and the full numerical method based on the linearized Euler equations on a limited number of strips in a matter of days.

4. High-fidelity simulations

As recently noted by Moreau [4], Computational AeraAcoustics (CAA) is now entering a third golden age, in which the development of high-order Navier-Stokes solvers on hybrid unstructured grids [51,52,53,54] and the emergence of new methods, such as the Lattice Boltzmann Method (LBM) on Cartesian octree-grids [55,56] in which solid bodies are immersed, have allowed to compute complex geometries such as turboengines in a much more efficient way. The latter method by its inherent low dissipation-low dispersion properties on regular Cartesian grids [4,57] and its computational efficiency (about an order of magnitude faster [58,59]) even allow directly computing the far-field noise at the microphone positions. Details on the numerical schemes and parameters (notably the boundary conditions) can be found in [4] and the associated references, and the first applications to other ducted blade rows in turboengines, such as the low-pressure compressor CME2 and the high-pressure turbine MT1, can be found in [2,3]. Low speed cases, such as the NASA-ANCF stage or typical automotive fan systems and modules, can also be found in [3,58]. Only the fan-OGV configuration is considered here, as it represents the greatest numerical challenge by its size and flow parameters (tip Mach and Reynolds numbers).

4.1. Tonal noise

As already shown in [3] unsteady RANS (uRANS) simulations are shown to yield accurate tonal noise predictions of most complex turbomachinery configurations. A good alternative is also to move to the frequency domain and to use harmonic balance techniques for wake-interaction problems [60], which can now be applied in multiple blade rows [61]. As also foreseen in [3], more and more simulations involve the full annulus at different operating conditions as in [62,63] to assess the noise generated by inlet distortion, this noise mechanism becoming more sensitive in UHBR engine with shorter nacelles. For instance in [64], Daroukh et al. studied a full-scale UHBR engine with inflow distortion at transonic conditions. They showed that the inflow distortion not only modifies the shock amplitudes along the circumferential direction (shock wave generation), but also creates azimuthal modes in addition to the rotor-locked mode present without distortion (shock wave radiation). More recently, the same methodology was used to study the noise impact of boundary layer ingestion in new aircraft architectures, such as the Airbus Nautilius engine integration concept [65,66].

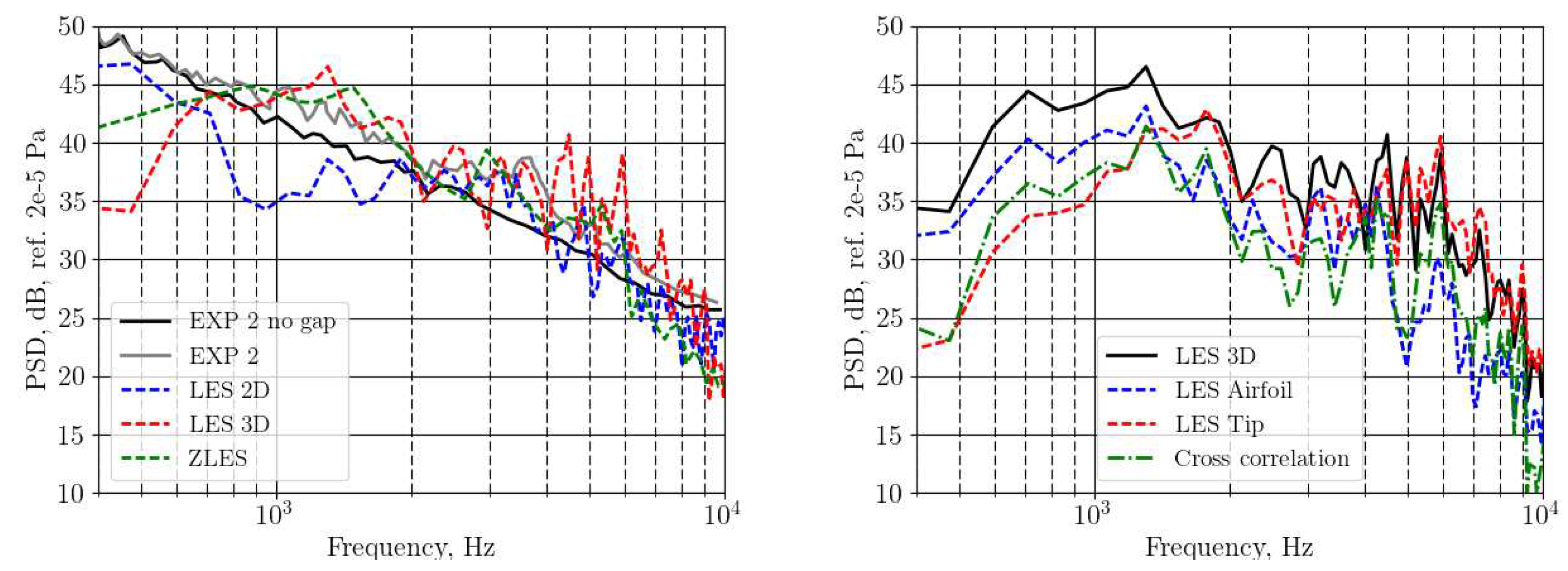
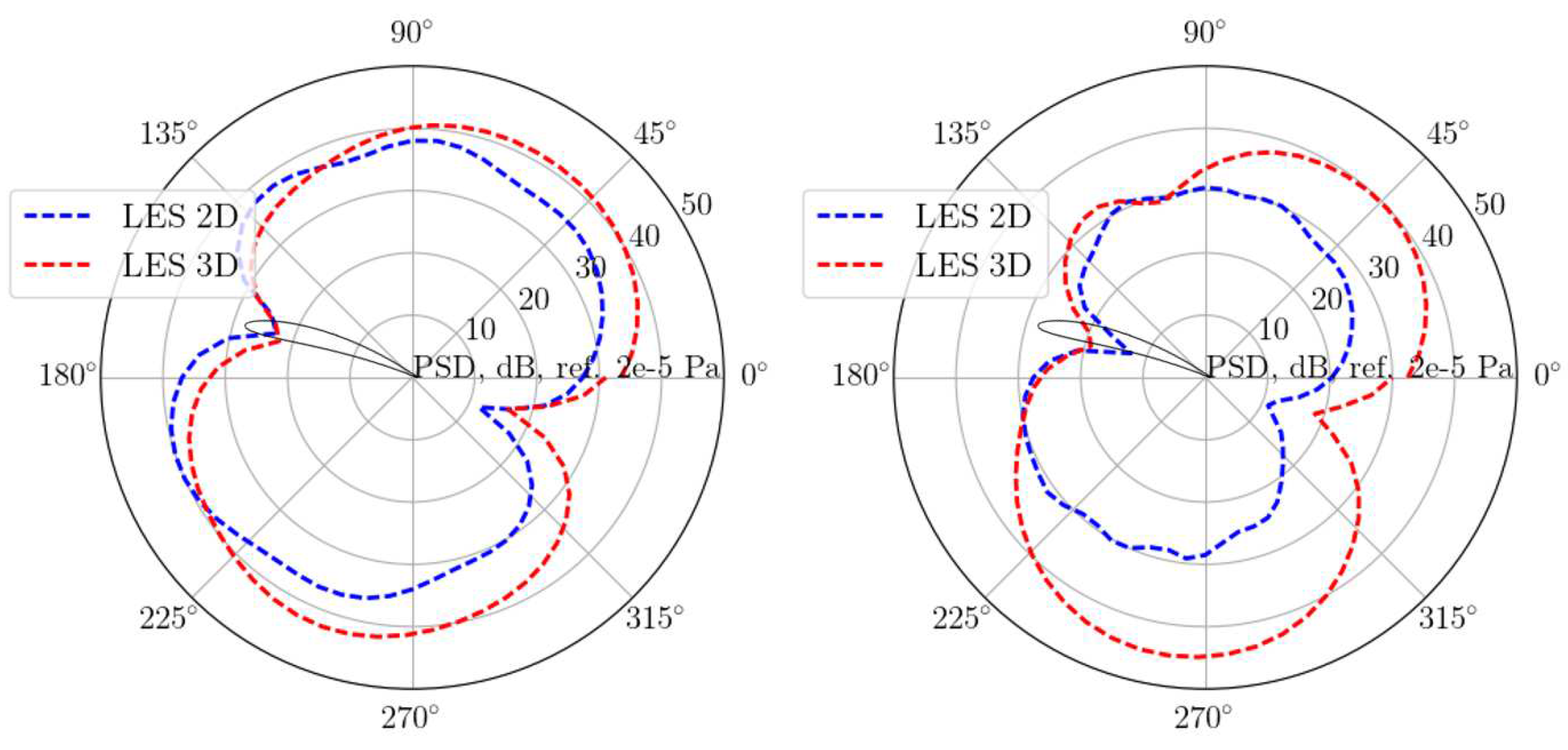
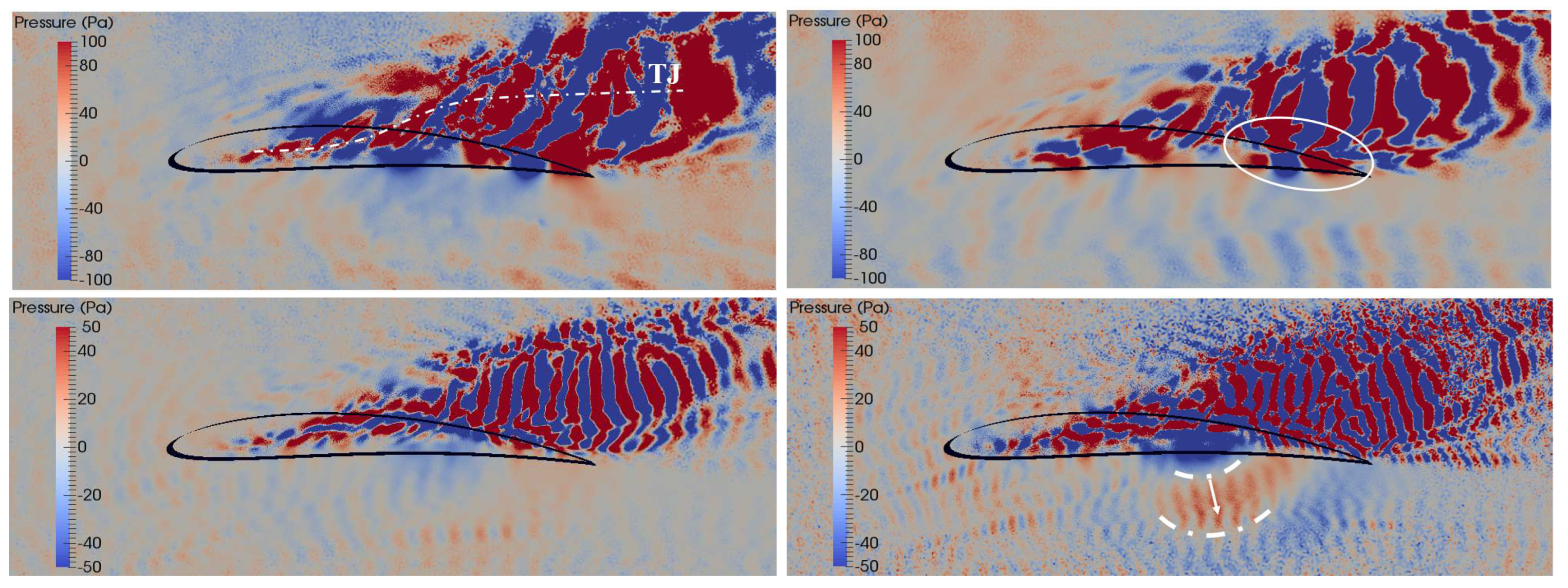
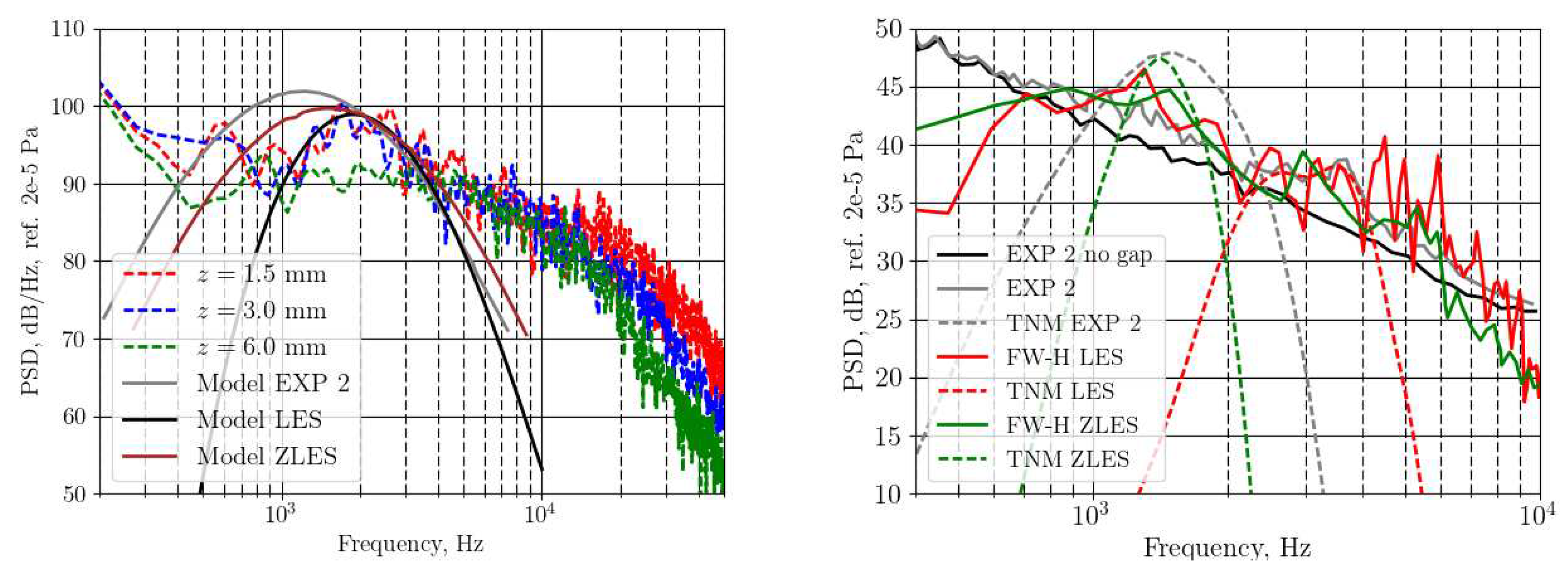
4.2. Broadband noise

Thanks to the recent progress in CAA [4], several turboengine fan/OGV configurations described in Section 2 have now been simulated by high-fidelity methods, such as compressible Large Eddy Simulations (LES) that resolve a significant amount of the flow turbulent scales to yield broadband noise predictions. The latter are obtained either directly at the microphone positions, as shown with LBM by Casalino et al. [67], or using a hybrid methodology combining the near-field noise sources with an acoustic analogy. The latter can again be in free-field using the Ffowcs Williams and Hawkings’ analogy (FWH) [18], or in a infinite duct using Goldstein’s analogy in a cylindrical duct [19] or its extension in an annular duct [29,68]. These analogies can be applied either on the blade surface (solid FWH or Goldstein) or on a de-localized control surface away from the blade (permeable FWH or Goldstein). Note that, if the surfaces enclose all aforementioned quadrupolar sources, the difference between these two formulations can be a more efficient way to estimate their strength than the implementation of the volume integral.
As already mentioned in [2,3], the most intensively simulated configuration so far has been the NASA SDT turbofan, in its versions with 22 rotor blades, and mostly the reference stator case (54 vanes) at approach condition. Both wall-modeled Navier-Stokes LES [68] or hybrid LB-VLES [67] have been achieved on this fan-OGV configuration. Yet, the former involves an OGV rescaling to have 55 vanes ( 2 π / 11 periodicity), whereas the latter considers the full annulus. Note also that similar tip resolution is found between the N-S LES performed with the unstructured LES code AVBP developed by Cerfacs [69] and the finest LBM simulation with PowerFLOW developed by 3DS [70]. Additional rotor-only configurations have now been simulated with quasi wall-resolved simulations (WR-LES) achieved by Kholodov & Moreau [71] that can serve as a reference simulation. Comparisons with the previous wall-modelled LES [72,73] using two different numerical schemes (Lax-Wendroff and TTG4A) show little differences on the blade and in the wake: noticeably similar overall global performances within 1% of measurements and good comparison with the hot-wire mean and root-mean-square (rms) velocity components downstream of the rotor. Only the tip vortices are better resolved as shown in Figure 3. In the mean flow (Figure 3 right), the tip leakage vortex (TLV) is thinner because better resolved, and accompanied with two induced counter-rotating vortices (TCR). The instantaneous flow inspection (Figure 3 right) still reveals a strong interaction between the radial leading-edge vortex (LEV) and the TLV, which breaks down in the blade passage. In both plots, the tip separation vortex (TS) presents multiple fingers similarly to what Koch et al. observed on both tip flows of the single airfoil tested at ECL and the Virginia Tech cascade [74,75]. This better resolved vortical structure in turn yields sharper LEV trace at the suction-side leading edge over the entire blade span (L), and lower wall-pressure fluctuations locally at the tip, as shown in the rms pressure contours on the rotor blade in Figure 4. Furthermore, coherence of wall-pressure fluctuations between two probes at the blade leading edge on the suction side within the LEV (1 and 3) and two probes at the trailing edge (2 and 4) at two different blade height ( l / L ) exhibits a hump around 30 kHz, which suggests that the LEV contributes to the trailing-edge scattering in this frequency range. This is quite similar to what Shubham et al. [76] reported on the CD airfoil with increasing different Mach numbers, noticeably the increasing noise contribution of the LSB formed at the leading edge to airfoil self-noise. Actually, blade-to-blade dilatation fields above 75% span [77] already show some significant acoustic radiation from the LEV, consistently with what Deuse & Sandberg [78] found on the CD airfoil.
Preprints 89640 g003
Figure 3. NASA-SDT (WR-LES [71]): tip vortices visualized by the Q-criterion; left: instantaneous field, right: mean field; TLV: Tip-Leakage Vortex, TS: Tip Separation vortex, TCR: Tip Counter-Rotating vortex.
Figure 3. NASA-SDT (WR-LES [71]): tip vortices visualized by the Q-criterion; left: instantaneous field, right: mean field; TLV: Tip-Leakage Vortex, TS: Tip Separation vortex, TCR: Tip Counter-Rotating vortex.
Preprints 89640 g003
The lower wall-pressure fluctuations at the tip also trigger lower predicted far-field noise sound power levels (SWL) at low frequencies, much closer to the NASA experimental data both upstream and downstream (Figure 6), as suspected in [68]. To further identify the main noise sources and their localization, the rotor blade is divided into different areas, as shown by the red lines in Figure 4. The 20% tip portion is first separated from the remaining 80% part (Figure 4 right). Figure 6 shows the corresponding sound power level contributions. The additional cross-correlation term (grey dashed line) stresses that these two areas are hardly correlated, which infers that both contributions should add up to yield the full blade SWL (red line). In the upstream direction (Figure 6 left), the airfoil contribution (green dashed line) is the largest, except at low and high frequencies. Downstream (Figure 6 right), the tip contribution is dominant, except at mid-frequencies where both contributions are similar. An additional split of the rotor blade leading edge as shown in Figure 4 (left) emphasizes that the tip region where the LEV and TLV collide is the largest contributor over the whole frequency range [77]. Further modal decomposition of the pressure fluctuations on the blade and in the tip gap at different frequencies have confirmed the importance of these additional noise sources, mainly at the blade tip, and the previous findings of Kholodov & Moreau in the corresponding wall-modelled LES [79]. Further analysis of tip noise is also provided in Section 5. Note that other simulations on this NASA/SDT configuration have involved chorochronic boundary conditions and mixed uRANS/detached-eddy simulations [80,81,82,83]. In [83], Suzuki et al. even suggested that there is a potential amplification mechanism of RSI noise via spiral-Poiseuille-flow instability.
Preprints 89640 g004
Figure 4. NASA-SDT (WR-LES [71]): rms wall-pressure; left: suction side, right: pressure side.
Figure 4. NASA-SDT (WR-LES [71]): rms wall-pressure; left: suction side, right: pressure side.
Preprints 89640 g004
Preprints 89640 g005
Figure 5. NASA-SDT (WR-LES [71]): wall-pressure coherence between leading-edge (1 and 3) and trailing-edge (2 and 4) probes at two spanwise locations l / L ; ; left: suction side, right: pressure side.
Figure 5. NASA-SDT (WR-LES [71]): wall-pressure coherence between leading-edge (1 and 3) and trailing-edge (2 and 4) probes at two spanwise locations l / L ; ; left: suction side, right: pressure side.
Preprints 89640 g005
Preprints 89640 g006
Figure 6. NASA-SDT (WR-LES [71]): Upstream (left) and downstream (right) sound power levels. "RO" stands for Rotor Only; "Airfoil" and "Tip" refers to the split of the full blade shown in Figure 4.
Figure 6. NASA-SDT (WR-LES [71]): Upstream (left) and downstream (right) sound power levels. "RO" stands for Rotor Only; "Airfoil" and "Tip" refers to the split of the full blade shown in Figure 4.
Preprints 89640 g006
Similarly, within the European project TurboNoiseBB, several wall-modelled LES of the ACAT1 turbofan with the shortest fan-OGV gap have been achieved with the high-order unstructured LES code AVBP [84,85]. As for the SDT case, to reduce the computational time the OGV has been rescaled to yield a 1 rotor blade–2 stator vanes configuration ( 2 π / 20 periodicity), but the by-pass has been introduced for the first time and a grid sensitivity has also been achieved for the first time, at approach conditions. The two LES meet wall-modelled criteria [86], but the finer one has more grid points in the streamwise and spanwise directions, yielding a twice as large grid (210 versus 95 million cells respectively). Both RANS simulations and LES predict overall performances (mass-flow rate and fan pressure ratio) accurately, within 1% of measurements. The LES and RANS flow topologies are quite similar on the rotor, while the LES show much more radial flow on the stator vanes (with even a flow separation in the coarser LES) [85]. Yet, the rotor LEV is much bigger and more two-dimensional, similar to a laminar separation bubble (LSB), in the RANS case. The finer LES also provides profiles of rms velocity components in the wake much closer to the hot-wire measurements within the experimental uncertainty [84]. In [84,85], two types of acoustic predictions have been performed, the above hybrid predictions by combining direct wall-pressure fields with free-field FWH and in-duct Goldstein analogies, and semi-analytical broadband noise predictions by combining the simulated excitations with the models described in Section 3. Note that when the results of the predictions of the above analytical models are compared with both the RANS and the mean LES flow fields, the latter yields significantly closer results to the experiment (see Figure 27 and 28 in [85] for Posson’s and Hanson’s models respectively), consistently with the wake velocity profiles. A 5–10 dB noise difference over the whole frequency range is also observed between the two analogies, similar to what was found in SDT [68]. Again splitting the OGV into two parts, consisting of the first 40% of the vane maximum axial chord over the entire vane span, and the 60% left aft part, shows in both LES that the trailing-edge noise may exceed that of the RSI mechanism. A significant broadband noise contribution of the rotor sources is also highlighted, especially at medium and high frequencies, for which it compares with the stator contribution. Such a result is consistent with what Kholodov & Moreau [71] and Koch [77] found on the SDT reference case with both the wall-modelled and wall-resolved LES. This also confirms the above presumption of Guerin et al. [20]. On this fan-OGV configuration, rotor shielding has also been assessed with a frequency domain linearized Navier-Stokes solver (LNS) by Blàsquez & Corral [87]. They estimate a decrease in the upstream emitted noise of about 2.5 dB at approach, which is consistent with measurements [16] and previous estimates by Posson & Moreau [88] and Envia on the NASA-SDT at similar flow regime. Another recent numerical investigation of the rotor blockage effect on an ideal NACA0012 cascade noise by Ying et al. [89] also yields about 3 dB reduction of the upstream SWL with a similar 3 dB increase of the downstream SWL. They also confirm Posson & Moreau’s result that the upstream SWL decrease is at low and mid-frequencies, whereas there is an increase at high frequencies, which can be attributed to energy transfer between frequencies and modes (from counter-rotating to co-rotating modes). In [87] (Figure 17), noise propagation is also found to be even more affected by the fan rotor blockage at high-rate operating conditions, such as cutback and sideline. Because of the presence of shocks and supersonic pockets in the fan flow-field, as found in another UHBR configuration [64], the flat-plate models cannot reproduce the more exact LNS as closely in that cases. This study also shows that the by-pass inlet guide vane or engine section stator contributes slightly to the upstream noise at approach, but significantly at other operating conditions. Thus, this is an additional potential noise source to be considered besides RSI, especially for cutback and sideline conditions.
On the ECL5 turbofan case, Al Am and co-workers have considered three different configurations using the same high-order unstructured LES approach with AVBP [90,91]. They have first simulated a radial–slice sector centered around 80% of the actual blade span, as was done previously by de Laborderie et al. on the CME2 compressor [32,92]; then they have computed a full–span sector as shown above on the other turbofans; and finally, they have achieved the first aero-acoustic prediction of a full–annulus turbofan. Note that Pérez Arroyo et al [93] had already achieved a full LES of the complete DGEN engine including the fan, but without considering noise. For the radial slice and the full–span sector, the OGV has again been rescaled to yield a 1 rotor blade–2 stator vanes configuration ( 2 π / 16 periodicity). The radial–slice sector has been simulated at four different mass flow rates corresponding to four fan blade angles-of-attack, to illustrate how the flow topology and noise generation evolve around the approach condition [90]. Three competing noise mechanisms have been observed: a first one coming from the LSB also found near the rotor leading edge in this ECL5 configuration, a second one at the rotor trailing-edge and a final one on the stator leading-edge caused by the rotor wake interaction. The first rotor noise source gets more intense as the mass flow rate is decreased, as the LSB gets larger and more unsteady. It also appears as high-frequency tones, which have been related to the LSB unsteady coherent shedding by applying a dynamic mode tracking technique: this is actually very similar to the tonal noise generated by the large rollers created by Kelvin-Helmholtz instabilities of the LSB shear layer observed on the CD airfoil at 5 ° geometrical incidence [94,95]. An additional simulation without the stator row showed the two identical noise sources on the rotor, but reduced broadband levels only beyond 3-4 kHz, which suggests a dominant rotor noise source at low and mid-frequencies, and a RSI noise at higher frequencies. For the full–span sector, the mass-flow rate has been unfortunately increased to minimize the leading-edge separation, compared to the radial–slice sector and to previous approach simulations (SDT and ACAT1). Yet, a more limited LEV can still be observed in the top part of the blade starting at 60% span (Figure 6 in [96]).
Another noticeable difference with the previous SDT and ACAT1 cases is the loading close to the tip induced by a very different transonic DCA-type airfoil with a strong aft camber at the blade tip, which triggers a strong aft loading. Consequently, several strong tip vortices are formed and they leave the tip gap after mid-chord, yielding a strong tip noise mostly at high frequencies caused by two noise mechanisms: the interaction of the tip leakage vortex with the next blade trailing edge (hump between 2 and 9 kHz) and the interaction of the tip separation and induced vortices with the same blade trailing edge (hump between 10 and 25 kHz). The interaction between the LEV and the tip vortices is also minimized. At midspan, as shown with the dilatation field in the blade row in Figure 7, the dominant noise sources are the RSI and the blade and vane trailing-edge noise. Finally, Al Am also performed a full–annulus LES shown in Figure 8. Similar mean flow as for the full–span sector case is found but smaller rms fluctuation fields and lower upstream and downstream SWL by a couple of dB, mostly caused by both lower grid resolution and larger artificial viscosity. Yet, no significant effect of the periodicity can be noticed on either the unsteady flow field and the radiated noise.
Preprints 89640 g007
Figure 7. ECL5 (sector WM-LES [96]): Instantaneous dilatation field at 80% blade span.
Figure 7. ECL5 (sector WM-LES [96]): Instantaneous dilatation field at 80% blade span.
Preprints 89640 g007
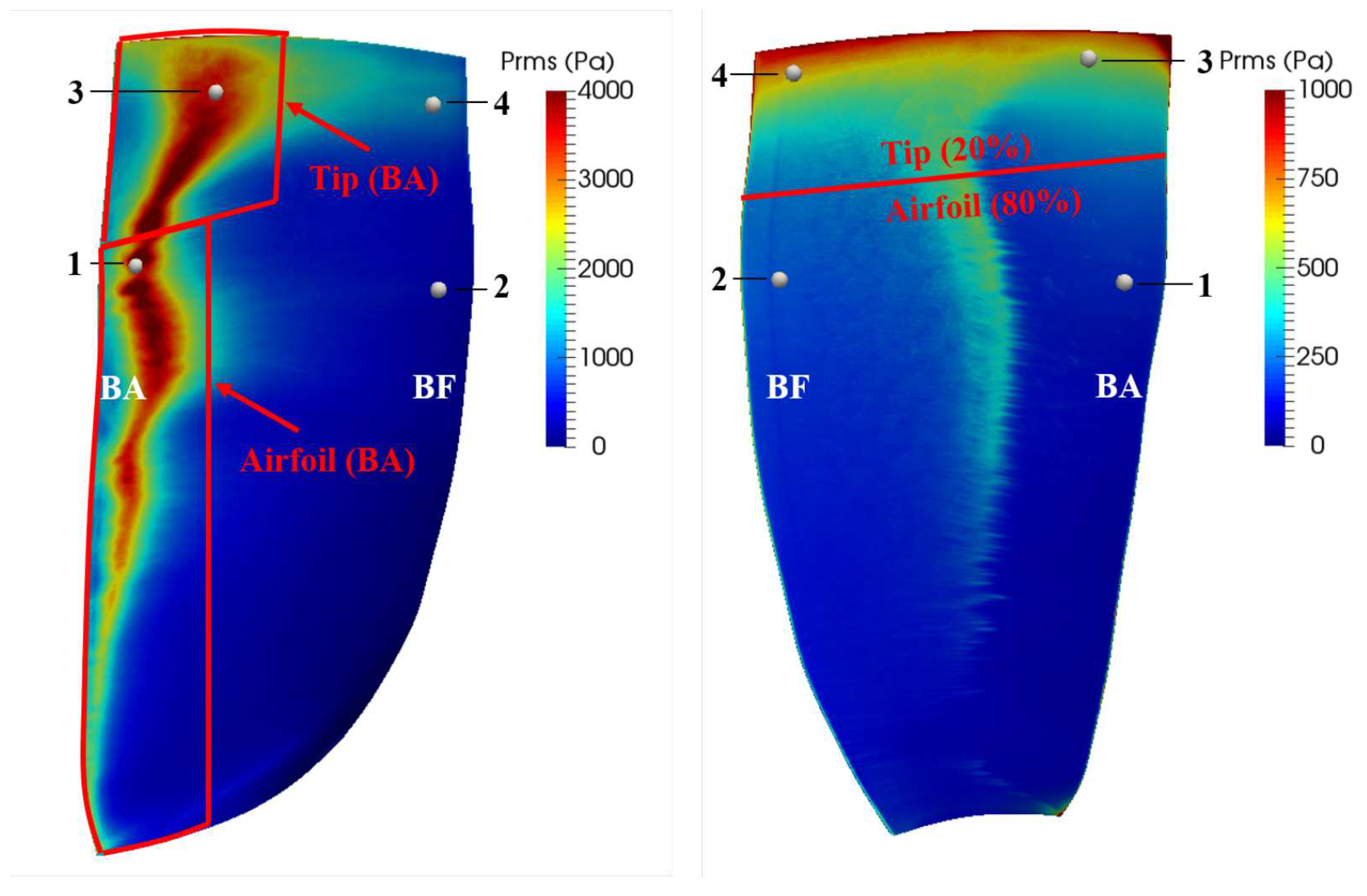
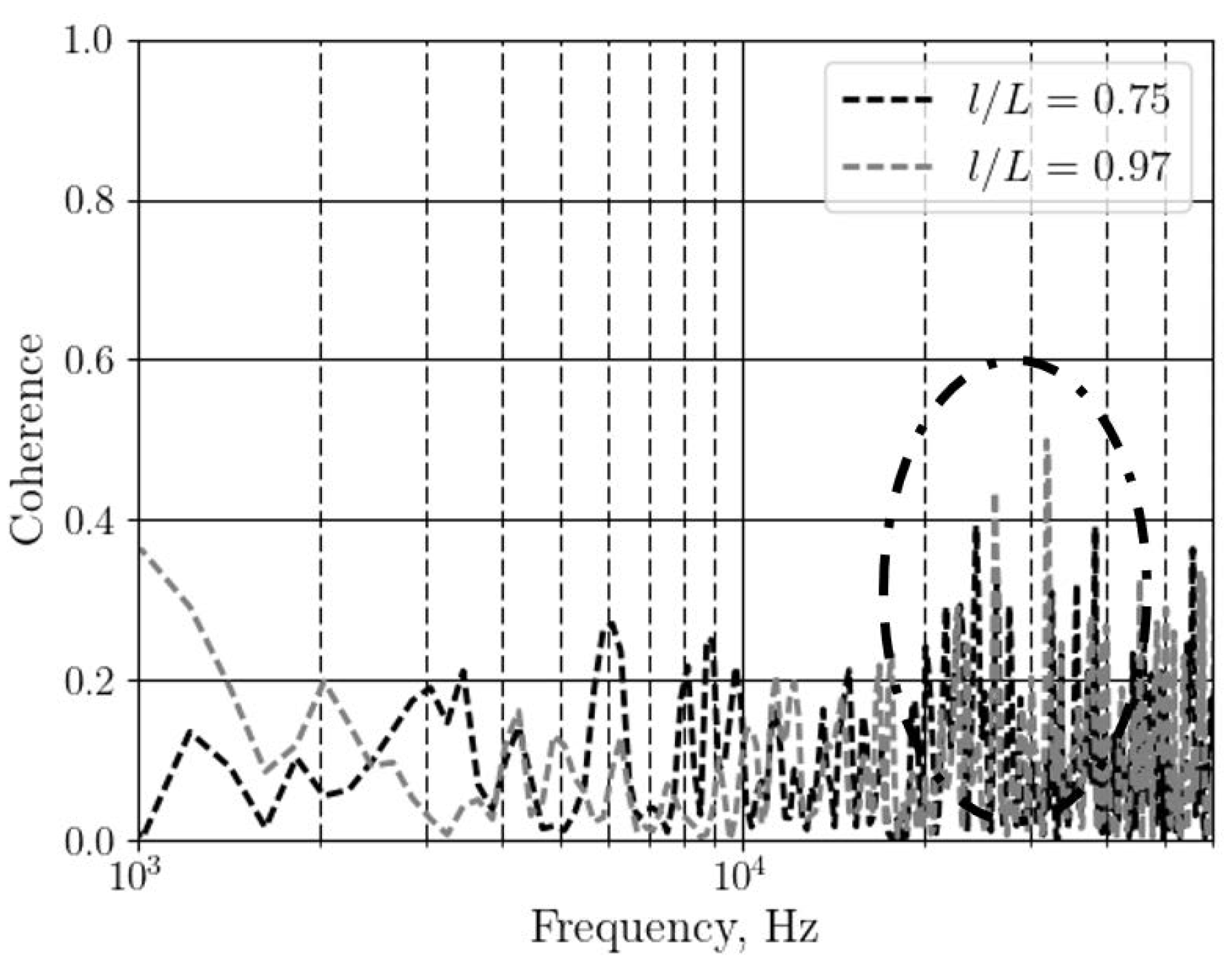
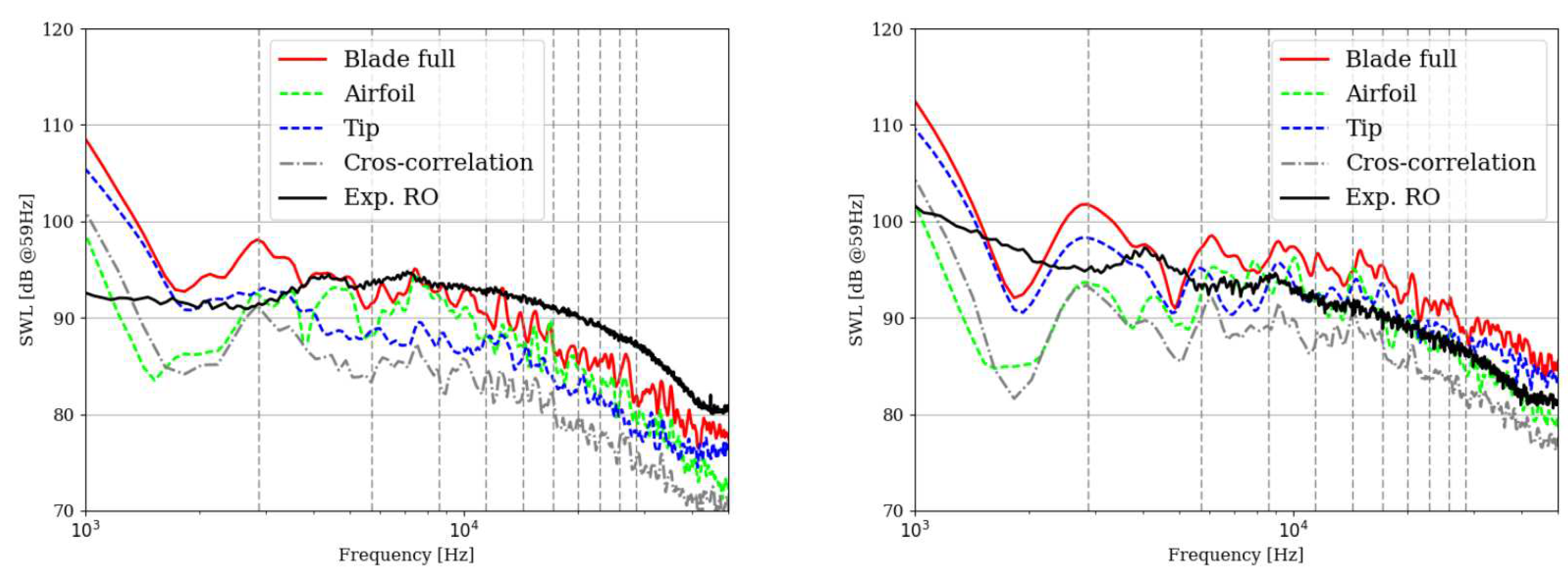
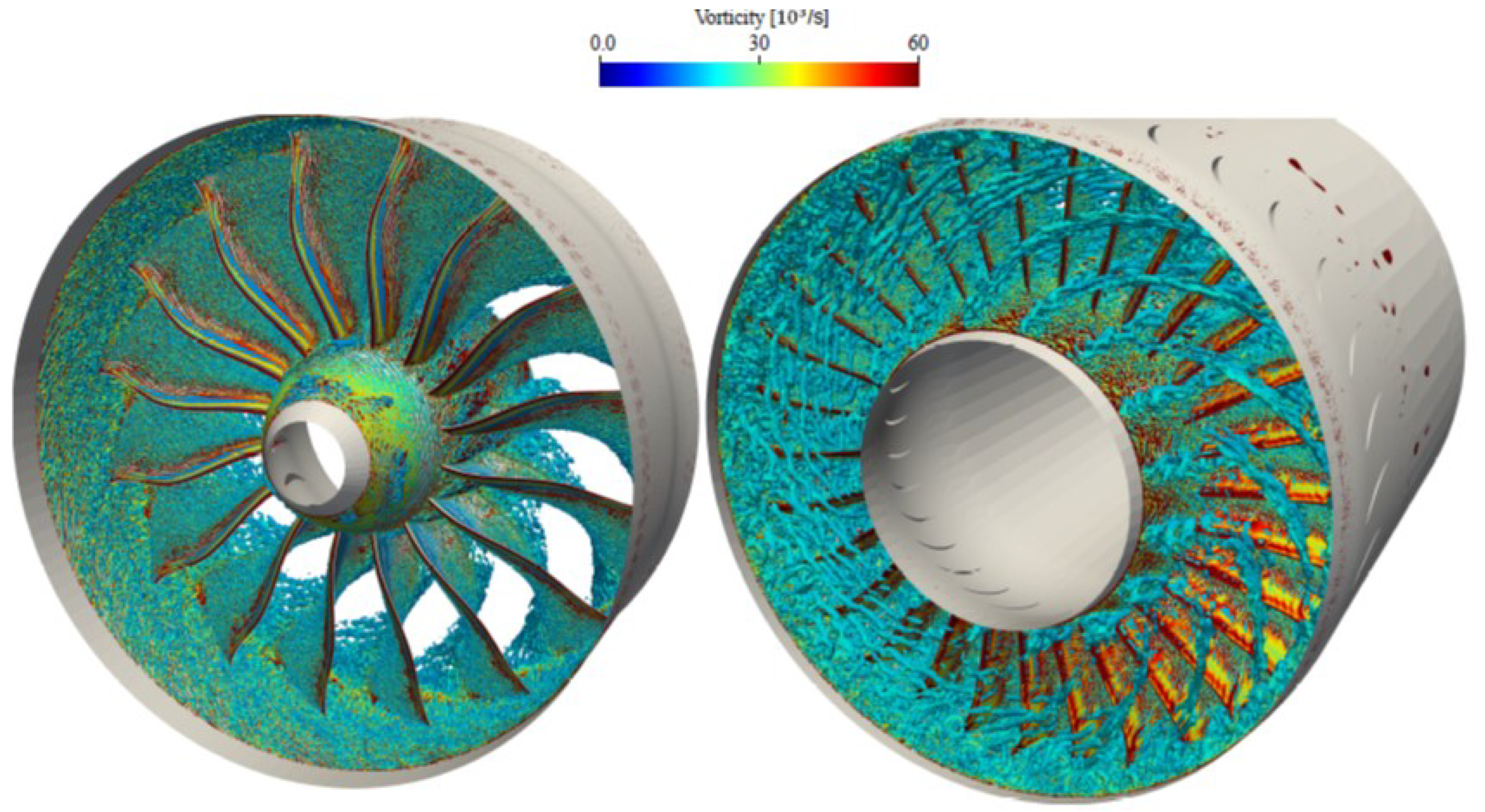
Preprints 89640 g008
Figure 8. ECL5 (full annulus WM-LES [91]): Iso-surface of Q-criterion colored by the vorticity magnitude; upstream view (left); downstream view (right). Courtesy of Al Am [91].
Figure 8. ECL5 (full annulus WM-LES [91]): Iso-surface of Q-criterion colored by the vorticity magnitude; upstream view (left); downstream view (right). Courtesy of Al Am [91].
Preprints 89640 g008
The interesting conclusions from these three independent studies on three different high by-pass ratio turbofans in approach conditins are the following. Firstly, all LES show some similar flow topology within the fan/OGV system. The classical rotor usually presents a strong LEV that spirals toward the blade tip and strongly interacts with the tip leakage vortices that possibly get totally dislocated. The LEV can be seen as the three-dimensional generalization of the LSB that was previously observed at similar loading on the isolated CD airfoil [78,97,98,99], and more recently on the small-span CD blade row, which corresponds to 80% blade span of the ECL5 configuration [90]). The tip leakage vortices and the wakes then impinge on the stator vanes without immediate transition to turbulence at the vane leading edge. This is turn may trigger additional LSB on the stator vanes around mid-chord [85]. All these vortical flow features are potential candidates for additional rotor and stator noise sources, as suggested by the recent analysis of Kholodov & Moreau [79] and Lewis [84], similarly to what was found on the CD airfoil at all simulated Mach numbers [76,78,99] and on the small-span ECL5 CD blade row [90]. For instance, all three cases showed some high-frequency contribution for the LSB or LEV with quasi-tones in the case of the radial–slice cascade caused by the highly coherent rollers formed in the small-span; this noise radiation is clearly seen in the dilatation field or in a modal analysis filtered at high frequencies. Note that Koch et al. [75] also reported a similar noise source in the LES of the Virginia Tech CD cascade (Figure 18), even though the more adapted loading of this configuration is quite different, yielding a LSB on the pressure side. Secondly, all hybrid noise predictions provide satisfactory comparisons with far-field noise measurements, with a clear improvement when using the more realistic in-duct annular acoustic analogy [68,85]. The comparison with the FWH free-field analogy also suggests that the latter overpredicts the levels at all frequencies, confirming some of the trends seen in the analytical models [20]. Finally, another common conclusion from all these studies is that the rotor wake turbulence is quasi-isotropic upstream of the stator vanes over most of the vane span, which justifies the use of analytical isotropic turbulence spectra, such as von Kármán’s or Liepmann’s [68]. Yet, as noted in [20], the ACAT1 hot-wire measurements in the shortest interstage indicate that this assumption might be dubious near the casing wall because of the rotor tip vortex and the boundary layer in this region, and a different approach should be applied locally.

5. Future in turbomachinery noise predictions

As already hinted at in [3], to address more accurate noise predictions of turbomachines and to further improve their designs, the above two different approaches need to be tackled and combined: fast-running analytical models to enter the design cycle early enough and provide multi-disciplinary optimization [5], and high-fidelity simulations to provide detailed analysis and physical insight into the noise generating mechanisms. Two examples of such an interplay are discussed below: one on tonal noise for a subsonic rotor-stator test-case and one on broadband tip noise with the examples already shown in previous sections.

5.1. Tonal noise

A subsonic ducted-fan test case (termed LP3), reported by Pestana et al [100] and recently re-addressed [101,102], is considered in this section, to illustrate the benefit of associating various approaches. The test is a good example of how advanced, high-order simulations can be used jointly with low-order, analytical modeling and dedicated experiments, in a cross-validation process, for a better understanding of sound generating mechanisms. The fan, of diameter 170 mm, is typical of aircraft air-conditioning and avionics-cooling applications. It is made of a 17-bladed rotor and of a stator of 23 outlet guide vanes. It operates at a blade-tip Mach number of about 0.3, in conditions for which the first two BPF tones attributable to rotor-stator interactions are theoretically cut-off. Indeed, by virtue of classical Tyler & Sofrin’s rule in the ( B = 17 , V = 23 ) arrangement, with identical and regularly spaced blades and vanes, only the mode orders n = m B − s V are selected at the harmonic of order m of the BPF, s being any relative integer. More precisely, at the BPF, the lowest order is n = − 6 , already cut-off. At twice the BPF, again the selected mode orders n = − 11 , 12 are cut-off, so that the first cut-on BPF tone is the third one, for which the lowest-order n = 5 corresponds to cut-on modes ( n , j ) = ( 5 , 0 ) , ( 5 , 1 ) , ( 5 , 2 ) . However, the fan on its test bench at ECL was found to radiate the first two BPF tones at high levels, in contradiction with expectations. The thicker practical manufacturing of 3 from the 23 stator vanes, for structural constraints, was suspected at the origin of this unexpected transmission through the duct. The first reason is that, from isolated-airfoil noise studies, increased thickness at leading edge is known to reduce the unsteady-lift response to incident velocity disturbances. Furthermore, a thicker vane generates higher localized potential distortion, able to extend farther upstream. Therefore, a higher potential-interaction noise, on the one hand, and some vane-to-vane variation of wake-impingement noise, on the other hand, are expected. For both mechanisms, the periodicity of period 2 π / 23 of the ideal stator is lost. This imposes to reconsider the modal structure of the tonal noise. Furthermore, the complete fan annulus must be retained for a relevant analysis, also stressing how advanced designs turn to be much more demanding in terms of computational resources.
LBM simulations have been performed twice on the complete test bench configuration, one assuming a perfectly homogeneous rotor-stator arrangement, and the other one considering the real stator with 3 modified vanes. The predicted sound spectra inside the duct were found to indeed exhibit high tones at the first two BPF in the heterogeneous case, as in the experiment, whereas these tones had only residual levels in the homogeneous case. One of the outcomes of the simulations is that the effect on potential-interaction noise was minor, and that the heterogeneous response to wake impingement was probably the dominant cause of sound regeneration. For validation purpose, another stator with 23 identical vanes has been manufactured and mounted in the modular setup, in place of the production stator. Measurements have been repeated. Typical averaged in-duct sound spectra are shown in Figure 9. The first two tones where found to strongly decrease, confirming the significant role of the heterogeneity [101], in spite of the very minor vane modification. It is worth noting that the effect of thicker vanes is strong on tonal noise, whereas the broadband noise remains unaffected.
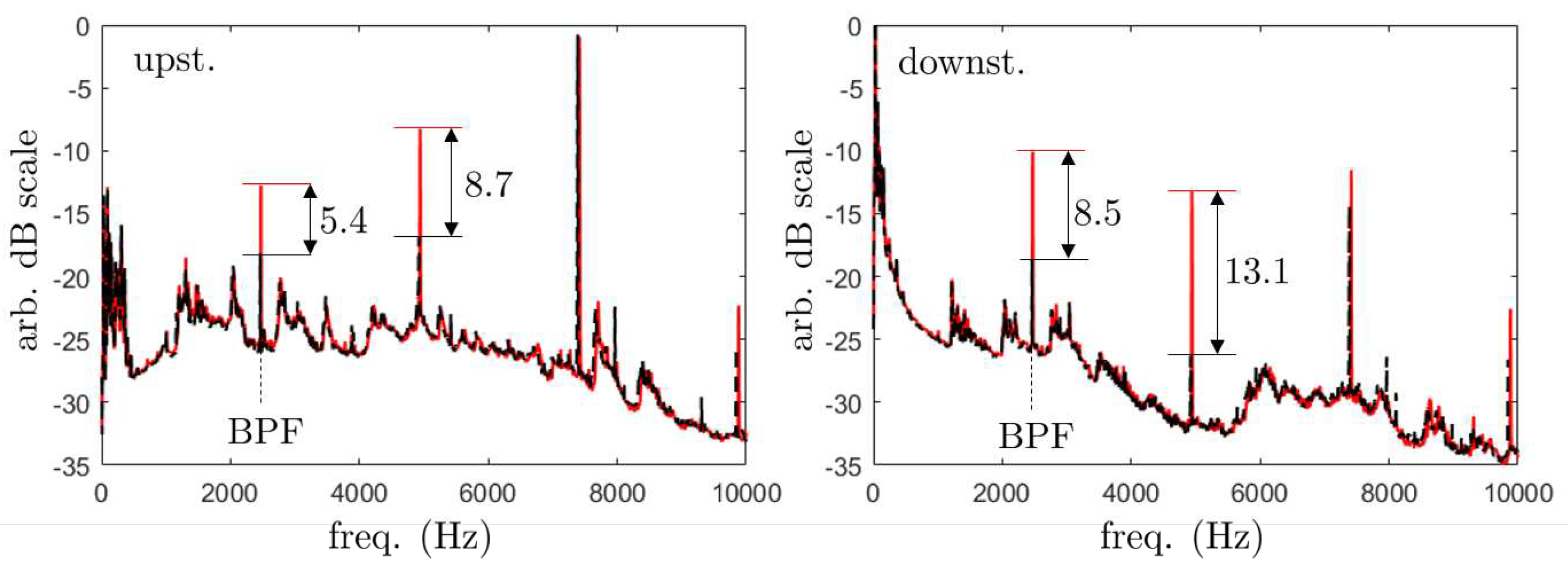
Preprints 89640 g009
Figure 9. In-duct sound-pressure spectra measured on the fan test-bench of ECL. Production fan with 3 thicker vanes (red), fan with homogeneous stator (black dashed). .
Figure 9. In-duct sound-pressure spectra measured on the fan test-bench of ECL. Production fan with 3 thicker vanes (red), fan with homogeneous stator (black dashed). .
Preprints 89640 g009
Blind tonal-noise predictions of the same fan have been attempted, based on simple analytical arguments [102]. The aim was twofold: explaining the fundamental features of the tonal-noise regeneration due to stator heterogeneity, on the one hand, and assessing the ability of analytical approaches to predict the possible detrimental effect of heterogeneous design, from the early design stage, on the other hand. Classical Goldstein’s analogy in a hard-walled annular duct was used, together with Amiet’s model, for the sound-propagation and sound-generation steps, respectively. The modified response of thicker vanes to oncoming wakes was approximated, using an empirical noise-reduction formula established for thick airfoils embedded in a turbulent stream. Introducing the heterogeneity in the analytical model has been performed by relying on a linear-superposition principle: the sound from the heterogeneous stator is assumed the sum of that of the homogeneous stator of 23 vanes, and of the sound of a virtual ’error’ stator of 3 vanes or dipoles. The strength of these dipoles is the response difference between the thicker and baseline vanes. Results are summarized in Figure 10, for upstream propagation in the fan inlet duct. According to the predictions, shown as empty black bars, the modes − 3 , 0 and + 3 emerge at the BPF and the mode + 5 dominates at 2BPF, with lower amplitudes at all other cut-on modes. An even more complex modal structure is found at 3BPF, with the emergence of modes of positive (co-rotating) orders 2, 5, 8, 11. The measurements, performed by post-processing signals from a wall-mounted microphone-array, are plotted as grey bars, for the heterogeneous stator (production fan). The predictions are in a fairly good qualitative agreement with the actually measured trends, but with some overall underestimate. This is partly attributable to lacking information about input data in the model, but also to some probable remaining, unidentified, source of distortion in the experiment. A remarkable point is the very good agreement obtained at 3BPF on the Tyler & Sofrin’s mode n = 5 , in spite of the crude assumptions made. For this already cut-on mode in homogeneous configuration, slight modifications of some vanes do not result in significant changes, as confirmed by the experimental result in Figure 9. The main effect of heterogeneity is to make modes, that should cancel out to zero by virtue of destructive interference between vanes, re-emerge, because the cancellation is deactivated.
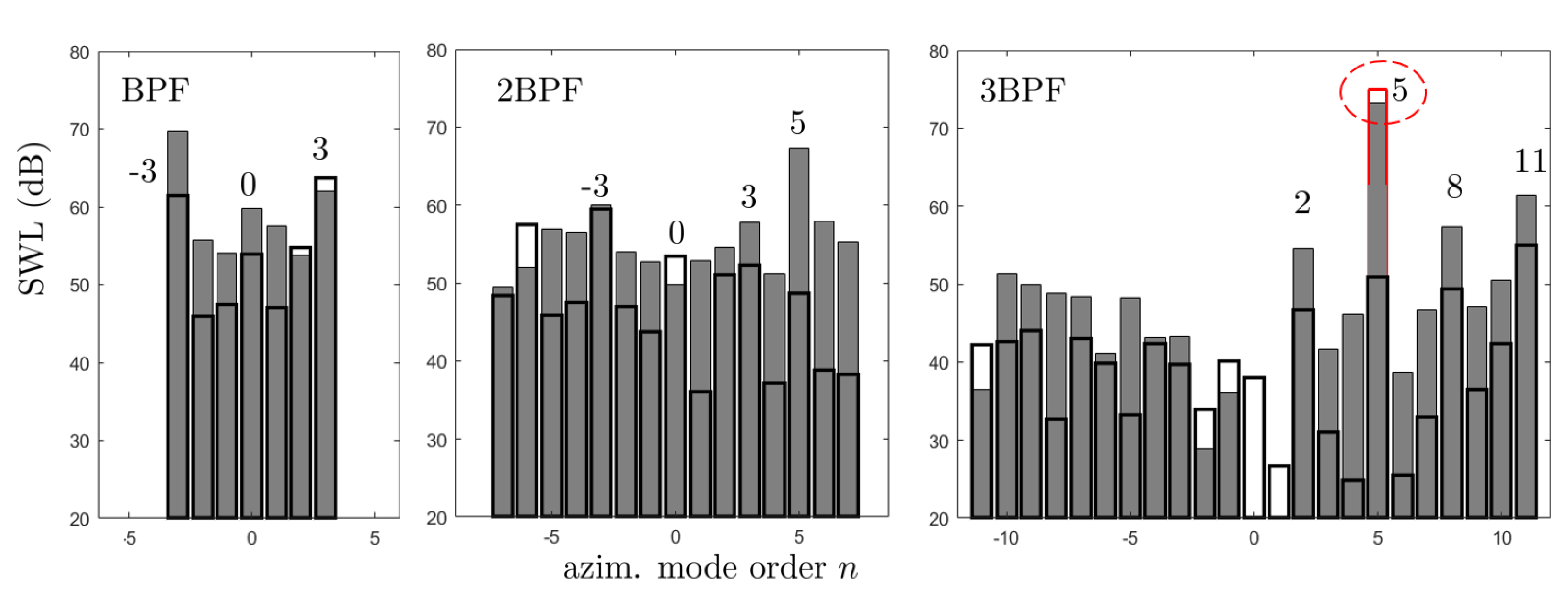
Preprints 89640 g010
Figure 10. Modal spectra of the ECL fan, for upstream in-duct radiation at the first 3 BPF tones; azimuthal modes only, all radial modes combined. Gray bars: measurements for the production fan with thicker vanes; empty back bars: blind analytical predictions. Red: analytical prediction of the homogeneous stator at 3BPF. .
Figure 10. Modal spectra of the ECL fan, for upstream in-duct radiation at the first 3 BPF tones; azimuthal modes only, all radial modes combined. Gray bars: measurements for the production fan with thicker vanes; empty back bars: blind analytical predictions. Red: analytical prediction of the homogeneous stator at 3BPF. .
Preprints 89640 g010
The same modal expansion was applied to the in-duct numerical results. It evidenced the modes n = − 3 and + 3 upstream at the BPF, and the dominant mode n = 5 at 2BPF [103]. In the analytical modeling, the true amplitude of the equivalent ’error’ dipoles is the key missing information; in a future step, it could be provided by inspection of the unsteady lift forces reconstructed from the LBM on various vanes. It appears that the numerical simulation is also a way to improve the analytical model. This illustrates a possible synergy. On the one hand, the analytical formulation is used to interpret the results of the simulations. On the other hand, the simulation fills a gap of the analytical model, making it upgraded for further fast-running calculations. It is worth mentioning that, as soon as heterogeneous blade/vane rows are considered in analytical models, both cascade-response functions and the MMBW must be abandoned, because only isolated-airfoil response functions are able to individualize blades or vanes [104,105].

5.2. Broadband noise

As noted in [2], the previous noise comparisons on both the SDT and ACAT1 configurations suggested that the remaining overprediction at low frequencies was caused by insufficiently resolved tip flow and consequently too large a tip noise contribution. In turn, it also meant that this noise contribution is significant and needed to be modeled. To illustrate the possible strong interplay between experiment, detailed numerical simulations and analytical modeling for tip noise, we will focus on the single airfoil with tip gap tested at ECL [106,107] and more recently at the Institute of Sound and Vibration Research (ISVR). As already mentioned in Sec. 4.2, the flow in the tip gap involves several large coherent structures, mainly a detached TLV and a TSV in form of several fingers, as shown in Figure 3.
In Figure 11 (left), the PSD of the far-field acoustic pressure predicted by the Zonal LES (ZLES) of Boudet et al. [108] (green dashed line) and the wall-resolved LES of Koch et al. [74] (red and blue dashed lines corresponding to with and without tip gap respectively) are compared with the acoustic measurements of the second experimental campaign at ECL [107] termed EXP2 (grey and black solid lines corresponding to with and without tip gap respectively), in which spurious noise sources coming from the side plates and the boundary-layer suction system have been mitigated. The compressible LES wall-pressure statistics are coupled with a solid Ffowcs Williams and Hawkings’ analogy. Note that the LES 2D corresponds to an extruded airfoil without tip gap and periodic boundary conditions in the spanwise directions. All results show that two additional noise sources are seen, a first one around 1.5 kHz and another one around 4 kHz. A decomposition of the different contributions on the blade in Figure 11 (right) similar to Figure 4 (right) on the SDT blade (see also Figure20 in [74]) suggests that the two frequency ranges correspond to tip noise sources. Moreover, very similar flow and wall-pressure statistics have also been observed close to the trailing edge at midspan between the two LES configurations suggesting similar blade trailing-edge noise away from the tip. The additional sources can then be attributed to the flow in the tip gap only.
Preprints 89640 g011
Figure 11. ECL-NACA5510 airfoil: far-field acoustic pressure at 90° 2 m from trailing edge; (left) comparison with experiment and other simulations and (right) decomposition of noise sources.
Figure 11. ECL-NACA5510 airfoil: far-field acoustic pressure at 90° 2 m from trailing edge; (left) comparison with experiment and other simulations and (right) decomposition of noise sources.
Preprints 89640 g011
The directivity plots from the wall-resolved LES of Koch et al. [74], 2 m away from the airfoil trailing edge at 2 and 4 kHz respectively are shown in Figure 12. They exhibit the typical dipolar radiation with two lobes in both cases. Extra lobes are seen in the LES 2D as the airfoil becomes non-compact. In the LES 3D the directivity lobes are bigger and more toward downstream because of the additional noise source at the tip trailing edge. Similar observations with higher levels on the pressure side can be made at 5 kHz (not shown).
Preprints 89640 g012
Figure 12. ECL-NACA5510 airfoil (WR-LES [74]): directivity of far-field acoustic pressure 2 m from trailing edge; (left) at 2 kHz and (right) at 4 kHz.
Figure 12. ECL-NACA5510 airfoil (WR-LES [74]): directivity of far-field acoustic pressure 2 m from trailing edge; (left) at 2 kHz and (right) at 4 kHz.
Preprints 89640 g012
A dynamic mode decomposition (DMD) has then been performed on the pressure field in the tip gap of the wall-resolved LES of Koch et al. [74], over 600 instantaneous snapshots. Figure 13 show the results at selected frequencies corresponding to the above two identified tip noise sources. At 1 and 2 kHz (top left and right plots respectively), a clear modal structure appears close to the trailing edge (white circle), whereas at 5 and 6 kHz (bottom left and right plots respectively), another modal structure appears more at mid-chord yielding radiation fronts (dashed white lines) mostly on the pressure side and the extra levels seen in Figure 12 (right). Additional DMD on the airfoil wall-pressure field at the same frequencies confirms these two noise sources and emphasize that the latter are concentrated in the tip region.
Preprints 89640 g013
Figure 13. ECL-NACA5510 airfoil (WR-LES [74]): dynamic mode decomposition of pressure field in tip gap; (top left) 1 kHz, (top right) 2 kHz, (bottom left) 4 kHz and (bottom right) 6 kHz.
Figure 13. ECL-NACA5510 airfoil (WR-LES [74]): dynamic mode decomposition of pressure field in tip gap; (top left) 1 kHz, (top right) 2 kHz, (bottom left) 4 kHz and (bottom right) 6 kHz.
Preprints 89640 g013
The above numerical results therefore clearly suggest a first tip dipolar noise source near the tip trailing edge, which was also identified by the wavelet analysis of the first ECL experimental data of Camussi et al. [109]. In [110], Grillat et al. then proposed to modify Amiet’s dipolar trailing-edge noise model by accounting for the presence of the stationary wall as a perfect acoustic reflector, and for the concentrated noise source at the tip by considering exponentially decaying incident gusts in the spanwise direction. The wall-pressure statistics from the high-fidelity simulations (ZLES and wall-resolved LES) are fit to Gaussian and exponential models to yield the wall-pressure PSD near the trailing edge shown in Figure 14 (left) for instance. The corresponding far-field acoustic pressure PSD predicted by the Tip Noise Model (TNM) show a fair agreement with the experimental extra tip noise contribution (labelled EXP2) and the direct FWH predictions in Figure 14 (right). This emphasizes that the model is physically consistent and reproduces the proper transfer function from the pressure near field to the acoustic far field. Yet, the observed frequency shift in the TNM LES case caused by an inaccurate estimate of the convection velocity first shows that the model is highly sensitive to all three main parameters of the noise sources, the wall-pressure PSD, the spanwise correlation length and the convection velocity. Secondly, the model is still hardly predictable as it strongly relies on detailed and well converged high-fidelity simulations to provide these parameters.
The additional experimental data recently collected at ISVR corroborates such a tip noise decomposition and analysis [111]. Note however that such a decomposition with strong coherent structures with 3 main fingers of the tip separation vortex may not be fully representative of turbofans, even at approach condition, as the tip gap and the blade tip loading in this case induced by the high angle-of-attack are much higher than in the SDT case for instance (see Figure 6.38 in [77]). These additional parameters, tip gap size and blade loading, should therefore be introduced in tip noise modeling. By varying both gap size and angle-of-attack in the ISVR set-up, Saraceno et al. [111,112] have already confirmed and assessed the impact of such parameters, providing valuable information for future analytical noise modeling.
Preprints 89640 g014
Figure 14. ECL-NACA5510 airfoil: tip noise modeling; (left) wall-pressure spectrum close to the trailing edge; (right) far-field acoustic spectrum at 90° 2 m from trailing edge.
Figure 14. ECL-NACA5510 airfoil: tip noise modeling; (left) wall-pressure spectrum close to the trailing edge; (right) far-field acoustic spectrum at 90° 2 m from trailing edge.
Preprints 89640 g014

6. Conclusions

The present review provides an update on the noise identification and prediction from ducted high-speed turbomachines both from analytical and numerical points of view.
On the analytical side, progress in tonal noise predictions has been mostly achieved with the mode matching approach. The latter has been extended in two dimensions to staggered and curved vanes, which allows reproducing the swirl recovery. It has also been extended to rotor-stator configurations, which has allowed capturing trapped modes in the interstage for the first time. Moreover, detailed comparisons of various RSI broadband noise models with measurements have now been achieved, on both the NASA-SDT and ACAT1 fan-OGV benchmarks. In both configurations at approach, the underprediction of the most accurate models including a 3D blade response and an annular acoustic analogy suggests that additional noise sources are present. For the RSI broadband noise mechanism, the high-fidelity simulations have also confirmed that the assumption of isotropic turbulence is mostly valid, except close to the tip in the shortest fan-OGV distances. The only remaining critical parameter is the turbulence integral length scale, which is still hard to predict accurately from RANS simulations.
On the numerical side, more and more complete uRANS simulations have allowed computing tonal noise on full annulus and installed configurations. Moreover, several LES meeting at least the wall-modeled requirements have been successfully achieved on three different high by-pass ratio fan-OGV configurations (NASA-SDT, ACAT1 and ECL5). All show the same overall flow topology at approach, despite the sensitivity to grid resolution shown in the ACAT1 case. Because of the off-design incidence on the rotor blades made of CD airfoils, a strong radially-spiralling LEV is formed at the rotor leading edge; it interacts with the strong TLV and possibly multiple fingers of the TS in the tip region. These unsteady coherent vortical structures yield additional acoustic waves that propagate both upstream and downstream of the rotor. Rotor trailing-edge noise is also seen to contribute significantly, notably at high frequencies. The wall-resolved LES of the SDT rotor confirms that these noise sources have levels similar to RSI. Moreover, the ECL5 full-annulus simulations that capture the full acoustic modal structure show no significant blade to blade correlation at approach. The first LES results at cutback and sideline also suggest that the unsteady interaction of the shock with the tip flow is another additional noise source. This should motivate further analytical modeling beyond the existing ones. In all cases, hybrid noise predictions coupling compressible LES results with an in-duct annular acoustic analogy reproduce the measured spectra more closely than the free-field FWH one, stressing again the importance of accounting for the cut-off duct modes.
Finally, two examples of joint experimental, numerical and analytical studies on both tonal and broadband noise predictions have shown how complex noise sources can be deciphered and modeled. On the one hand, the detailed analysis of the LP3 rotor-stator configuration has allowed explaining the re-generation of strong tones mainly by asymmetric stator-vane distribution (stator heterogeneity) and possibly by residual inlet distortion. The associated physically-based analytical models have again been able to reproduce both the experimental and numerical trends at a marginal cost. On the other hand, the isolated NACA5510 airfoil with tip gap configuration has provided some first evidence of the actual tip noise sources and yielded a first physically-consistent analytical noise model for one of the identified noise mechanisms.
It is worth noting that new emerging architectures of commercial aircraft are presently investigated in the aeronautical community, in particular based on the technology of half-buried engines, to meet the needs of coming decades. Special installation effects, including boundary-layer ingestion, will be faced, which implies modifications in the ranking of noise sources and continued interest in efficient and robust noise prediction strategies. The advanced approaches reviewed in the present work will probably be intensively used in the future to maintain aircraft noise at acceptable levels. New high-fidelity simulations on turbofans, covering the full annulus, should be achieved at different operating conditions and provide additional evidence to the additional noise sources, besides wake interaction noise. The interplay between reduced models and complete geometries, and between analytical models and high-fidelity simulations should also unveil additional flow and noise features, with emphasis on the relationship between vortex dynamics and sound.

Author Contributions

Conceptualization, methodology, software, validation, formal analysis, investigation, resources, data curation, writing—original draft preparation, writing—review and editing, visualization, project administration, funding acquisition: S. Moreau & M. Roger. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding

Acknowledgments

This work was performed within the framework of the LABEX CeLyA (ANR-10-LABX-0060) of Université de Lyon, within the program ’Investissements d’Avenir’ (ANR-11-IDEX-0007) operated by the French National Research Agency (ANR). It was also partly supported by the French-Canadian Associate Laboratory, IRP CNRS CAC (Centre Acoustique Jacques Cartier).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Moreau, S.; Roger, M. Advanced noise modeling for future propulsion systems. Int. J. of Aeroacoustics 2018, 17, 576–599. [Google Scholar] [CrossRef]
  2. Moreau, S. Turbomachinery Noise Predictions: Present and Future. Acoustics 2019, 92–116. [Google Scholar] [CrossRef]
  3. Moreau, S. A Review of Turbomachinery Noise: From Analytical Models to High-Fidelity Simulations. Fundamentals of High-Lift for Future Civil Aircraft, Chap.10; R. Radespliel & R. Semaan, S., Ed., 2021.
  4. Moreau, S. The third golden age of aeroacoustics. Phys. Fluids 2022, 34, 031301. [Google Scholar] [CrossRef]
  5. Grasso, G.; Moreau, S.; Christophe, J.; Schram, C. Multi-disciplinary optimization of a contra-rotating fan. Int. J. of Aeroacoustics 2018, 17, 655–686. [Google Scholar] [CrossRef]
  6. Lallier-Daniels, D.; Bolduc-Teasdale, F.; Rancourt, D.; Moreau, S. Fast Multi-Objective Aeroacoustic Optimization of Propeller Blades. Vertical Flight Society’s 77th Annual Forum & Technology Display, 2021.
  7. Envia, E.; Nallasamy, M. Design selection and analysis of a swept and leaned stator concept. J. Sound & Vib. 1999, 228, 793–836. [Google Scholar]
  8. de Laborderie, J.; Moreau, S. Prediction of tonal ducted fan noise. J. Sound & Vib. 2016, 372, 105–132. [Google Scholar]
  9. Krömer, F.; Moreau, S.; Becker, S. Experimental investigation of the interplay between the sound field and the flow field in skewed low-pressure axial fans. J. Sound & Vib. 2019, 442, 220–236. [Google Scholar]
  10. Masson, V.; Posson, H.; Sanjosé, M.; Moreau, S.; Roger, M. Fan-OGV interaction broadband noise prediction in a rigid annular duct with swirling and sheared mean flow. 22nd AIAA/CEAS Aeroacoustics Conference. American Institute of Aeronautics and Astronautics, 2016, AIAA Paper 2016-2944.
  11. Hughes, C. Aerodynamic performance of scale-model turbofan outlet guide vanes designed for low noise. 40th AIAA Aerospace Sciences Meeting & Exhibit; AIAA Papers: Reno, NV, USA, 2002. [Google Scholar]
  12. Hughes, C.; Jeracki, R.; Woodward, R.; Miller, C. Fan Noise Source Diagnostic Test - Rotor Alone Aerodynamic Performance Results. 8th AIAA/CEAS Aeroacoustics Conference & Exhibit; AIAA papers: Breckenridge, CO, USA, 2002; AIAA-2002-2426. [Google Scholar]
  13. Podboy, G.; Krupar, M.; Helland, S.; Hughes, C. Steady and unsteady flow field measurements within a NASA 22 inch fan model. 40th AIAA Aerospace Sciences Meeting & Exhibit, 2002, p. 1033.
  14. Woodward, R.P.; Hughes, C.E.; Jeracki, R.J.; Miller, C.J. Fan Noise Source Diagnostic Test - Far-Field Acoustic Results. Technical Memorandum TM-2002-211591, 2002.
  15. Tapken, U.; Behn, M.; Spitalny, M.; Pardowitz, B. Radial mode breakdown of the ACAT1 fan broadband872 noise generation in the bypass duct using a sparse sensor array. 25th AIAA/CEAS Aeroacoustics Conference, Delft, Netherlands, 2019, paper 2019-2400.
  16. Behn, M.; Tapken, U. Investigation of sound generation and transmission effects through the ACAT1 fan stage using compressed sensing-based mode analysis. 25th AIAA/CEAS Aeroacoustics Conference, Delft, Netherlands, 2019, paper 2019-2502.
  17. Brandstetter, C.; Pagès, V.; Duquesne, P.; Ottavy, X.; Ferrand, P.; Aubert, S.; Blanc, L. UHBR open-test-case fan ECL5/catana Part 1: Geometry and aerodynamic performance. 14th European Turbomachinery Conference, Gdansk, Poland, 2021.
  18. Ffowcs Williams, J.; Hawkings, D. Sound generation by turbulence and surfaces in arbitrary motion. Phil. Trans. Roy. Soc. 1969, A 264. [Google Scholar]
  19. Goldstein, M. Aeroacoustics; McGraw-Hill, NY, 1976.
  20. Guérin, S.; Kissner, C.; Seeler, P.; Blázquez, R.; Carrasco Laraña, P.; de Laborderie, H.; Lewis, D.; Chaitanya, P.; Polacsek, C.; Thisse, J. ACAT1 Benchmark of RANS-informed Analytical Methods for Fan Broadband Noise Prediction: Part II -Influence of the Acoustic Models. Acoustics 2020, 3, 617–649. [Google Scholar] [CrossRef]
  21. Lewis, D.; de Laborderie, J.; Sanjosé, M.; Moreau, S.; Jacob, M.C.; Masson, V. Parametric study on state-of-the-art analytical models for fan broadband interaction noise predictions. J. Sound & Vib. 2021, 514, 116423. [Google Scholar]
  22. Bouley, S.; François, B.; Roger, M.; Posson, H.; Moreau, S. On a two-dimensional mode-matching technique for sound generation and transmission in axial-flow outlet guide vanes. J. Sound & Vib. 2017, 403, 190–213. [Google Scholar]
  23. Roger, M.; François, B.; Moreau, S. Cascade trailing-edge noise modeling using a mode-matching technique and the edge-dipole theory. J. Sound & Vib. 2016, 382, 310–327. [Google Scholar]
  24. Roger, M.; François, B. Combined analytical models for sound generation and transmission in cambered axial-flow outlet guide vanes. European J. of Mechanics, B/Fluids 2017, 61, 218–225. [Google Scholar] [CrossRef]
  25. Girier, L.; Roger, M.; Lafitte, A. A Two-Dimensional Mode-Matching Technique for Wake-Interaction Tonal Noise Including Rotor-Stator Coupling. AIAA Aviation Forum; 2023; Paper 2023-4189.
  26. Ventres, C.S.; Theobald, M.A.; Mark, W.D. Turbofan Noise Generation, Volume 1 : Analysis. Contractor Report CR-167952, 1982.
  27. Hanson, D.B. Theory for broadband noise of rotor and stator cascades with inhomogeneous inflow turbulence including effects of lean and sweep. Contractor Report NASA-CR-210762, 2001.
  28. Posson, H.; Moreau, S.; Roger, M. On the use of a uniformly valid analytical cascade response function for fan broadband noise predictions. J. Sound & Vib. 2010, 329, 3721–3743. [Google Scholar]
  29. Posson, H.; Moreau, S.; Roger, M. Broadband noise prediction of fan outlet guide vanes using a cascade response function. J. Sound & Vib. 2011, 330, 6153–6183. [Google Scholar]
  30. Posson, H.; Roger, M.; Moreau, S. On a uniformly valid analytical rectilinear cascade response function. J. Fluid Mech. 2010, 663, 22–52. [Google Scholar] [CrossRef]
  31. Nallasamy, M.; Envia, E. Computation of rotor wake turbulence noise. J. Sound & Vib. 2005, 282, 649–678. [Google Scholar]
  32. de Laborderie, J. Approches analytiques et numériques pour la prédiction du bruit tonal et large bande de soufflantes de turboréacteurs. PhD thesis, Université de Sherbrooke, Sherbrooke, QC, CANADA, 2013.
  33. Verdon, J.M.; Hall, K.C. Development of a linearized unsteady aerodynamic analysis for cascade gust response predictions. Contractor Report CR-4308, 1990.
  34. Maunus, J.; Grace, S.M.; Sondak, D.L. Effect of Rotor Wake Structure on Fan Interaction Noise. 16th AIAA/CEAS Aeroacoustics Conference; 2010; AIAA2010–3746 paper.
  35. Grace, S.M.; Maunus, J.; Sondak, D.L. Effect of CFD Wake Prediction in a Hybrid Simulation of Fan Broadband Interaction Noise. 17th AIAA/CEAS Aeroacoustics Conference; 2011; AIAA2011–2875 paper.
  36. Grace, S.M. Fan broadband interaction noise modeling using a low-order method. J. Sound & Vib. 2015, 346, 402–423. [Google Scholar]
  37. Moreau, S.; Roger, M. Competing Broadband Noise Mechanisms in Low-Speed Axial Fans. AIAA Journal 2007, 45, 48–57. [Google Scholar] [CrossRef]
  38. Moreau, S.; Roger, M. Back-scattering correction and further extensions of Amiet’s trailing-edge noise model. Part II: Application. J. Sound & Vib. 2009, 323, 397–425. [Google Scholar]
  39. Roger, M. On broadband jet–ring interaction noise and aerofoil turbulence-interaction noise predictions. J. Fluid Mech. 2010, 653, 337–364. [Google Scholar] [CrossRef]
  40. Posson, H.; Roger, M. Experimental Validation of a Cascade Response Function for Fan Broadband Noise Predictions. AIAA journal 2011, 49(9), 1907–1918. [Google Scholar] [CrossRef]
  41. Cheong, C.; Joseph, P.; Lee, S. High frequency formulation for the acoustic power spectrum due to cascade-turbulence interaction. J. Acous. Soc. Amer. 2006, 119, 108–122. [Google Scholar] [CrossRef]
  42. Grace, S.M. Influence of model parameters and the vane response method on a low-order prediction of fan broadband noise. Int. J. Aeroacoust. 2016, 15, 131–143. [Google Scholar] [CrossRef]
  43. Kissner, C.; Guérin, S.; Seeler, P.; Billson, M.; Paruchuri, C.; Carrasco Laraña, P.; de Laborderie, H.; François, B.; Lefarth, K.; Lewis, D.; Montero Villar, G.; Nodé-Langlois, T. ACAT1 Benchmark of RANS-informed Analytical Methods for Fan Broadband Noise Prediction: Part I -Influence of the RANS Simulation. Acoustics 2020, 3, 539–578. [Google Scholar] [CrossRef]
  44. Amiet, R.K. Acoustic Radiation From an Airfoil in a Turbulent Stream. J. Sound & Vib. 1975, 41, 407–420. [Google Scholar]
  45. Schwarzschild, K. Die Beugung und Polarisation des Lichts durch einen Spalt. I. Mathematische Annalen 1902, 55, 177–247. [Google Scholar] [CrossRef]
  46. Sears, W.R. Some aspects of non-stationary airfoil theory and its practical application. Journal of the Aeronautical Sciences 1941, 8, 104–108. [Google Scholar] [CrossRef]
  47. Roger, M.; Moreau, S. Back-scattering correction and further extensions of Amiet’s trailing edge noise model. Part 1: theory. J. Sound Vib. 2005, 286, 477–506. [Google Scholar] [CrossRef]
  48. Roger, M.; Moreau, S. Addendum to the back-scattering correction of Amiet’s trailing-edge noise model. J. Sound & Vib. 2012, 331, 5383–5385. [Google Scholar] [CrossRef]
  49. Lee, S.; Ayton, L.; Bertagnolio, F.; Moreau, S.; Chong, T.P.; Joseph, P. Turbulent boundary layer trailing-edge noise: Theory, computation, experiment,and application. Progress in Aerospace Sciences 2021, 126, 100737:1–56. [Google Scholar] [CrossRef]
  50. Priddin, M.J.; Kisil, A.V.; Ayton, L.J. Applying an iterative method numerically to solve n×n matrix Wiener–Hopf equations with exponential factors. Proc. Roy. Soc. London. Series A. Mathematical and Physical Sciences 2020, 378, 20190241:1–18. [Google Scholar] [CrossRef]
  51. Quartapelle, L.; Selmin, V. High-order Taylor-Galerkin methods for nonlinear multidimensional problems. Finite Elements in Fluids; Pineridge Press: Swansea, UK, 1993; pp. 1374–84. [Google Scholar]
  52. Liu, L.; Li, X.; Hu, F.Q. Nonuniform time-step Runge–Kutta discontinuous Galerkin method for Computational Aeroacoustics. J. Comp. Phys. 2010, 229, 6874–6897. [Google Scholar] [CrossRef]
  53. Léger, R.; Peyret, C.; Piperno, S. Coupled Discontinuous Galerkin/Finite Difference Solver on Hybrid Meshes for Computational Aeroacoustics. AIAA J. 2012, 50, 338–349. [Google Scholar] [CrossRef]
  54. Brès, G.A.; Ham, F.E.; Nichols, J.W.; Lele, S.K. Unstructured Large-Eddy Simulations of Supersonic Jets. AIAA J. 2017, 55, 1164–1184. [Google Scholar] [CrossRef]
  55. Chen, H. Volumetric formulation of the lattice Boltzmann method for fluid dynamics: Basic concept. Phys. Rev. E 1998, 58, 3955–3963. [Google Scholar] [CrossRef]
  56. Chen, H.; Orszag, S.A.; Staroselsky, I.; Succi, S. Expanded analogy between Boltzmann kinetic theory of fluids and turbulence. J. Fluid Mech. 2004, 519, 301–314. [Google Scholar] [CrossRef]
  57. Brès, G.; Pérot, F.; Freed, D. Properties of the Lattice-Boltzmann Method for Acoustics. 15th AIAA/CEAS Aeroacoustics Conference; 2009; AIAA 2009-3395 paper.
  58. Moreau, S. Direct Noise Computation of Low-speed Ring Fans. Acta Acustica united with Acustica 2019, 105, 1–13. [Google Scholar] [CrossRef]
  59. Astoul, T. Towards improved lattice Boltzmann aeroacoustic simulations with non-uniform grids: applicationto landing gears noise prediction. PhD thesis, Université Aix-Marseille Université Marseille, France, 2021.
  60. Gomar, A.; Bouvy, Q.; Sicot, F.; Dufour, G.; Cinnella, P.; François, B. Non-uniform time sampling for multiple-frequency harmonic balance computations. J. Comp. Phys. 2014, 278, 229–256. [Google Scholar] [CrossRef]
  61. Guédeney, T.; Gomar, A.; Gallard, F.; Sicot, F.; Dufour, G.; Puigt, G. Non-uniform time sampling for multiple-frequency harmonic balance computations. J. Comp. Phys. 2013, 236, 317–345. [Google Scholar] [CrossRef]
  62. Daroukh, M.; Moreau, S.; Gourdain, N.; Boussuge, J.F.; Sensiau, C. Effect of Distortion on Turbofan Tonal Noise at Cutback with Hybrid Methods. Int. J. Turbomach. Propuls. Power 2017, 2, 1–22. [Google Scholar] [CrossRef]
  63. Daroukh, M.; Moreau, S.; Gourdain, N.; Boussuge, J.F.; Sensiau, C. Tonal Noise Prediction of a Modern Turbofan Engine With Large Upstream and Downstream Distortion. J. Turbomach. 2019, 141, 021010. [Google Scholar] [CrossRef]
  64. Daroukh, M.; Polacsek, C.; Chelius, A. Shock Wave Generation and Radiation from a Turbofan Engine Under Flow Distortion. AIAA J. 2020, 58, 787–801. [Google Scholar] [CrossRef]
  65. Daroukh, M.; Polacsek, C.; Carini, M. Acoustic Assessment of BLI Effects on Airbus Nautilius EngineIntegration Concept - Part I: Noise Generation. 28th AIAA/CEAS Aeroacoustics Conference; 2022; AIAA paper 2022-2943.
  66. Lorteau, M.; Le Garrec, T.; Daroukh, M.; Polacsek, C. Acoustic Assessment of BLI Effects on Airbus Nautilius EngineIntegration Concept - Part II: Noise Propagation. 28th AIAA/CEAS Aeroacoustics Conference; 2022; AIAA 2022-2992 paper.
  67. Casalino, D.; Hazir, A.; Mann, A. Turbofan Broadband Noise Prediction Using the Lattice Boltzmann Method. AIAA J. 2018, 56(2), 609–628. [Google Scholar] [CrossRef]
  68. Pérez Arroyo, C.; Leonard, T.; Sanjosé, M.; Moreau, S.; Duchaine, F. Large Eddy Simulation of a Scale-model Turbofan for Fan Noise Source Diagnostic. J. Sound & Vib. 2019, 445, 64–76. [Google Scholar]
  69. AVBP. AVBP Code: www.cerfacs.fr/cfd/avbp_code.php and www.cerfacs.fr/cfd/CFDPublications.html.
  70. Dassault-Systèmes. SIMULIA PowerFLOW User’s Guide, 2020.
  71. Kholodov, P.; Moreau, S. Wall-Resolved Large Eddy Simulation of a Realistic Turbofan Rotor for Noise Prediction. 27th AIAA/CEAS Aeroacoustics Conference; 2021; AIAA 2021-2256 paper.
  72. Pérez Arroyo, C.; Kholodov, P.; Sanjosé, M.; Moreau, S. CFD Modeling of a Realistic Turbofan for Noise Prediction. Part 1: Aerodynamics. Proceedings of Global Power and Propulsion Society; 2019; GPPS-BJ-2019-126 paper.
  73. Sanjosé, M.; Kholodov, P.; Pérez Arroyo, C.; Moreau, S. CFD Modeling of a Realistic Turbofan for Noise Prediction. Part 2: Analytical Acoustic Predictions. Proceedings of Global Power and Propulsion Society; 2019; GPPS-BJ-2019-224 paper.
  74. Koch, R.; Sanjose, M.; Moreau, S. Large-Eddy Simulation of a Single Airfoil Tip-Leakage Flow. AIAA J. 2021, 59, 2546–2557. [Google Scholar] [CrossRef]
  75. Koch, R.; Sanjosé, M.; Moreau, S. Numerical Aeroacoustic Analysis of a Linear Compressor Cascade with Tip Gap. AIAA J. 2022, 60, 4840–4854. [Google Scholar] [CrossRef]
  76. Shubham, S.; Sandberg, R.; Moreau, S.; Wu, H. Surface pressure spectrum variation with Mach number on a CD airfoil. J. Sound & Vib. 2022, 526, 116762:1–15. [Google Scholar]
  77. Koch, R. Identification des sources de bruit aérodynamique liées aux écoulements de jeu en tête de pale de soufflante de turboréacteur. PhD thesis, Université de Sherbrooke, Sherbrooke, QC, CANADA, 2021.
  78. Deuse, M.; Sandberg, R. Different noise generation mechanisms of a controlled diffusion aerofoil and their dependence on Mach number. J. Sound & Vib. 2020, 476, 1–18. [Google Scholar]
  79. Kholodov, P.; Moreau, S. Identification of noise sources in a realistic turbofan rotor using Large Eddy Simulation. Acoustics 2020, 2, 691–706. [Google Scholar] [CrossRef]
  80. François, B.; Polacsek, C.; Daroukh, M.; Barrier, R. Zonal Detached Eddy Simulation of the Fan-Outlet Guide Vanes Stage of a Turbofan Engine. Part I – Methodology, Numerical Setup, and Aerodynamic Analysis. J. Turbomachinery 2022, 144, 111004. [Google Scholar] [CrossRef]
  81. Polacsek, C.; Daroukh, M.; François, B.; Barrier, R. Zonal Detached Eddy Simulation of the Fan-Outlet Guide Vanes Stage of a Turbofan Engine. Part II – Broadband Noise Predictions. J. Turbomachinery 2022, 144, 111005. [Google Scholar] [CrossRef]
  82. Suzuki, T.; Spalart, P.; Shur, M.; Strelets, M.; Travin, A. Unsteady Simulations of a Fan Outlet-Guide-Vane System Broadband-Noise Computation. AIAA J. 2019, 57, 5168–5181. [Google Scholar] [CrossRef]
  83. Suzuki, T.; Shur, M.; Strelets, M.; Travin, A. Potential Amplification Mechanism of Rotor–Stator-Interaction Noise via Spiral-Poiseuille-Flow Instability. AIAA J. 2022, 60, 2441–2457. [Google Scholar] [CrossRef]
  84. Lewis, D. From analytical to fully numerical predictions of the broadband noise radiated by a full fan-OGV. PhD thesis, Ecole Centrale de Lyon, Lyon, France, 2020.
  85. Lewis, D.; Moreau, S.; Jacob, M.C.; Sanjosé, M. ACAT1 fan stage broadband noise prediction using large-eddy simulation and analytical models. AIAA Journal 2022, 60, 360–380. [Google Scholar]
  86. Piomelli, U. Large eddy simulations in 2030 and beyond. Phil. Trans. R. Soc. London, Ser. A 2014, 372, 1–13. [Google Scholar] [CrossRef] [PubMed]
  87. Blàzquez-Navarro, R.; Corral, R. Prediction of fan acoustic blockage on fan/outlet guide vane broadband interaction noise using frequency domain linearised Navier–Stokes solvers. J. Sound & Vib. 2021, 500, 116033. [Google Scholar]
  88. Posson, H.; Moreau, S. Effect of Rotor Shielding on Fan-Outlet Guide Vanes Broadband Noise Prediction. AIAA J. 2013, 51, 1576–1592. [Google Scholar] [CrossRef]
  89. Ying, W.; Fattah, R.; Zhong, Z.; Zhang, X.; Gea-Aguilera, F. A numerical investigation of the rotor blockage effect on cascade noise using a sliding mesh method. J. Sound & Vib. 2021, 502, 116030. [Google Scholar]
  90. Al Am, J.; Clair, V.; Giauque, A.; Boudet, J.; Gea-Aguilera, F. On the effects of a separation bubble on fan noise. J. Sound & Vib. 2022, 537, 117180:1–19. [Google Scholar]
  91. Al Am, J. Broadband noise predictions of a fan stage using large eddy simulations. PhD thesis, Université de Lyon, Ecole Centrale de Lyon, Ecully, FRANCE, 2022.
  92. de Laborderie, J.; Moreau, S.; Berry, A. Compressor Stage Broadband Noise Prediction using a Large-Eddy Simulation and Comparisons with a Cascade Response Model. 19th AIAA/CEAS Aeroacoustics Conference; 2013; AIAA 2013-2042 paper.
  93. Pérez Arroyo, C.; Dombard, J.; Duchaine, F.; Gicquel, L.; Odier, N.; Exilard, G.; Richard, S.; Buffaz, N.; Démolis, J. Large-Eddy Simulation of an Integrated High-Pressure Compressor and Combustion Chamber of a Typical Turbine Engine Architecture. ASME Turbo Expo 2020; 2020; ASME GT2020-16288 paper.
  94. Sanjosé, M.; Towne, A.; Jaiswal, P.; Moreau, S.; Lele, S. Modal analysis of the laminar boundary layer instability and tonal noise of an airfoil at Reynolds number 150,000. Int. J. of Aeroacoustics 2019, 18, 317–350. [Google Scholar] [CrossRef]
  95. Jaiswal, P.; Yakhina, G.; Pasco, Y.; Moreau, S. Experimental investigation of aerofoil tonal noise at low Mach number. J. Fluid Mech. 2022, 932, A37. [Google Scholar] [CrossRef]
  96. Al Am, J.; Clair, V.; Giauque, A.; Boudet, J.; Gea-Aguilera, F. Direct noise predictions of fan broadband noise using LES and analytical models. 28th AIAA/CEAS Aeroacoustics Conference; 2022; AIAA paper 2022-2882.
  97. Sanjosé, M.; Moreau, S.; Kim, M.S.; Pérot, F. Direct Self-noise Simulation of the Installed Controlled Diffusion Airfoil. 17th AIAA/CEAS Aeroacoustics Conference; 2011; AIAA 2011-2716 paper. AIAA-2011-2716.
  98. Wu, H.; Moreau, S.; Sandberg, R. Effects of pressure gradient on the evolution of velocity-gradient tensor invariant dynamics on a controlled-diffusion aerofoil at Rec=150000. J. Fluid Mech. 2019, 868, 584–610. [Google Scholar] [CrossRef]
  99. Wu, H.; Sandberg, R.; Moreau, S. Stability characteristics of different aerofoil flows at Rec=1.5×105 and the implications for aerofoil self-noise. J. Sound & Vib. 2021, 487, 115620. [Google Scholar] [CrossRef]
  100. Pestana, M.; Sanjosé, M.; Roger, M.; Moreau, S.; Gruber, M. Assessment of the Impact of a Heterogeneous Stator on the Noise of an Axial-Flow Low Mach-Number Stage. 25th AIAA/CEAS Aeroacoustics Conference; 2019; paper 2019-2589.
  101. Pereira, A.; Roger, M. A modular low-Mach number, axial-flow fan test bench: impact of outlet-guide-vane heterogeneity on the radiated noise. ICSV 29; 2023; paper 396.
  102. Roger, M.; Pereira, A. Regeneration of ducted rotor-stator wake-interaction tonal noise because of vane-to-vane irregularities. ICSV 29; 2023; paper 347.
  103. Pestana, M. Impact of a heterogeneous stator on the rotor-stator interaction-noise: an analytical, experimental and numerical investigation. PhD thesis, École Centrale de Lyon, 2020LYSEC03, 2020.
  104. Sanjosé, M.; Daroukh, M.; Magnet, W.; De Laborderie, J.; Moreau, S.; Mann, A. Tonal fan noise prediction and validation on the ANCF configuration. Noise Control Eng. J. 2015, 63, 552–561. [Google Scholar] [CrossRef]
  105. Sanjose, M.; Moreau, S.; Pestana, M.; Roger, M. Effect of Weak Outlet-Guide-Vane Heterogeneity on Rotor–Stator Tonal Noise. AIAA J. 2017, 55, 3440–3457. [Google Scholar] [CrossRef]
  106. Jacob, M.C.; Grilliat, J.; Camussi, R.; Caputi Gennaro, G. Aeroacoustic investigation of a single airfoil tip leakage flow. Int. J. of Aeroacoustics 2010, 9, 253–272. [Google Scholar] [CrossRef]
  107. Jacob, M.C.; Jondeau, E.; Li, B. Time-resolved PIV measurements of a tip leakage flow. Int. J. of Aeroacoustics 2016, 15, 662–685. [Google Scholar] [CrossRef]
  108. Boudet, J.; Caro, J.; Li, B.; Jondeau, E.; Jacob, M.C. Zonal large-eddy simulation of a tip leakage flow. Int. J. of Aeroacoustics 2016, 15, 646–661. [Google Scholar] [CrossRef]
  109. Camussi, R.; Grilliat, J.; Caputi-Gennaro, G.; Jacob, M.C. Experimental study of a tip leakage flow: wavelet analysis of pressure fluctuations. J. Fluid Mech. 2010, 660, 87–113. [Google Scholar] [CrossRef]
  110. Grilliat, J.; Jacob, M.; Jondeau, E.; Roger, M.; Camussi, R. Broaband noise prediction models and measurements of tip leakage flows. 14th AIAA/CEAS Aeroacoustics Conference (29th AIAA Aeroacoustics Conference) Vancouver, Canada, May, 2008, AIAA2008-2845 paper.
  111. Saraceno, I.; Palleja-Cabre, S.; Paruchuri, C. On the tip leakage noise generating mechanisms of single-fixed aerofoil. 28th AIAA/CEAS Aeroacoustics Conference; 2022; AIAA 2022-2881 paper.
  112. Saraceno, I.; Palleja-Cabre, S.; Paruchuri, C.; Ganapathisubramani, B. Influence of non-dimensional parameters on the tip leakage noise. 29th AIAA/CEAS Aeroacoustics Conference; 2023; AIAA 2023-3838 paper.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated