Prerpints.org logo
Preprint
Article

Total Edge Irregularity Strength of Star Snake Graphs

Altmetrics

Downloads

90

Views

35

Comments

0

This version is not peer-reviewed

Mathematical Modeling

Submitted:

04 November 2023

Posted:

06 November 2023

You are already at the latest version

Alerts
Abstract
In different fields in our life, like physics, coding theory and computer science, graph labeling dramas an vital role and appears in many applications. A labeling of a graph is a map which assign each element in with a positive integer number. An edge irregular total -labeling is a function such that where and are weights for any two distinct edges. In this case, has total edge irregularity strength (TEIS) if is minimum. In our paper, we defined a new type of graphs called a triple star snake graph and star snake graph . Also, we investigated TEIS for a triple star snake graph . After that, we generalized the results for star snake graph .
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematics

1. Introduction

For a graph M V , E , which is connected and simple, an edge irregular total ᵹ -labeling was introduced by Baca et al. in [1] as a map Ʊ : V M ∪ E M → 1,2 , 3 , . . . . ,   ᵹ such that W Ʊ h ≠ W Ʊ z where W Ʊ h and W Ʊ z are weights for any two distinct edges. Also, the inequality of TEIS a graph G , with the maximum degree of vertices ∆ G , was deduced in the form
t e s ( M ) ≥ m a x E ( M ) + 2 3 , ∆ M + 1 2
Since then, many authors have begun to find TEIS for many families of graphs. Ivanĉo and Jendroî in [2] determined TEIS for a tree as
t e s T = m a x k + 1 3 , ∆ M + 1 2 .
Ahmad et al. [3,4,5,6,7,8,9] have investigated TEIS for zigzag graphs, helm and sun graphs, the categorical product of two cycles, the categorical product of two paths, the generalized Petersen graph, certain families of graphs and some classes of plane graphs. Therefore, TEIS has been determined for hexagonal grid graphs in Al-Mushayt and Ahmad [10], planar graphs in Yang et al. [11], for some classes of plane graphs in Tarawneh et al. [12], for fan, wheel, triangular book, and friendship graphs in Tilukay et al. [13], for subdivision of star in Siddiqui [14], for some Cartesian product graphs in Ramdan and Salman [15], for trees in Amar and Togn [16], for generalized web graphs and related graphs in Indriat et al. [17], for generalized prism in Bača and Siddiqui [18], for complete graph and complete bipartite graphs in Jendroî et al. [19], for the disjoint union of wheel graphs in Jeyanth and Sudhai [20], for dense graphs in Majersk et al. [21], for the grids in Miškuf and Jendroî [22], for, disjoint union of isomorphic copies of generalized Petersen graph in Naeem and Siddiqui [23], for large graphs in Pfender [24], for centralized uniform theta graphs in Putra and Susanti [25], for series parallel graphs in Rajasingh et al. [26].
Salama [27,28,29,30,31] has determined TEIS for polar grid graph, special families of graphs, heptagonal snake graph, uniform theta snake graphs and quintet snake graph.
In our paper, we defined new types of graphs called a triple star snake graph P S 3 , n and m − star snake graph P S m , n . Also, we investigated TEIS for a triple star snake graph P S 3 , n . After that, we generalized the results for m − star snake graph P S m , n .

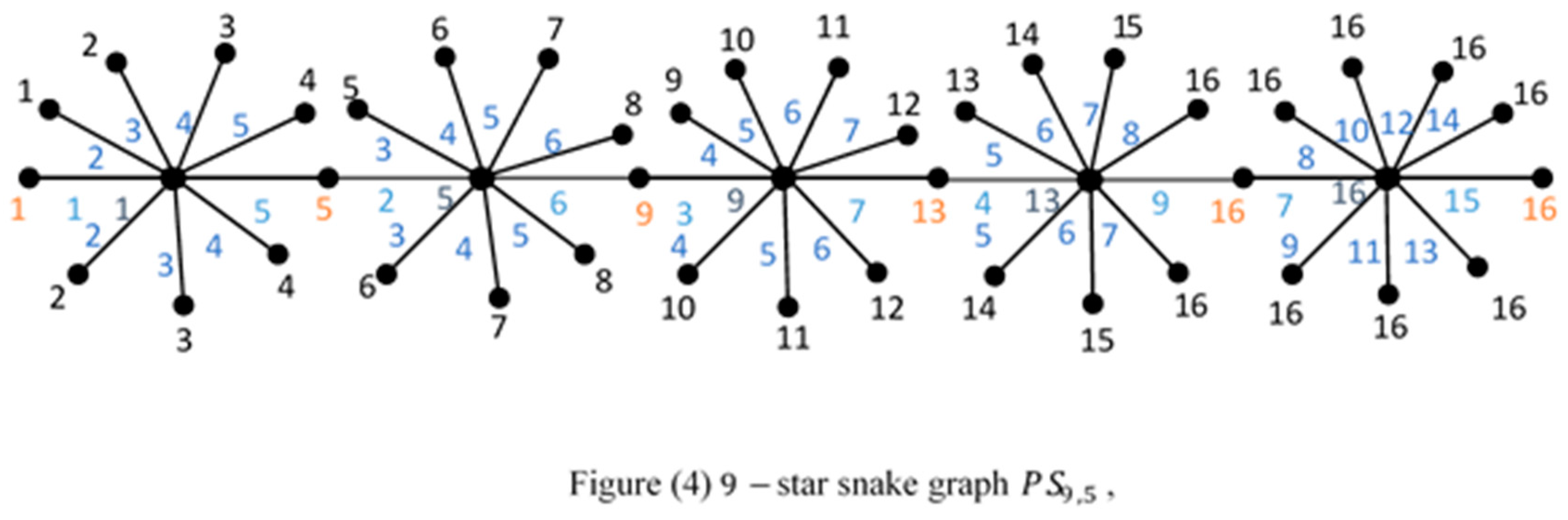
2. Main results:

In this section, we will define a star snake graph and some related graphs and determine TEIS for these graphs.
Definition1. 
In a path P n if we replace every edge in it with a star S 3 then have a new graph called a triple star snake graph, denoted P S 3 , n , see Figure (1).
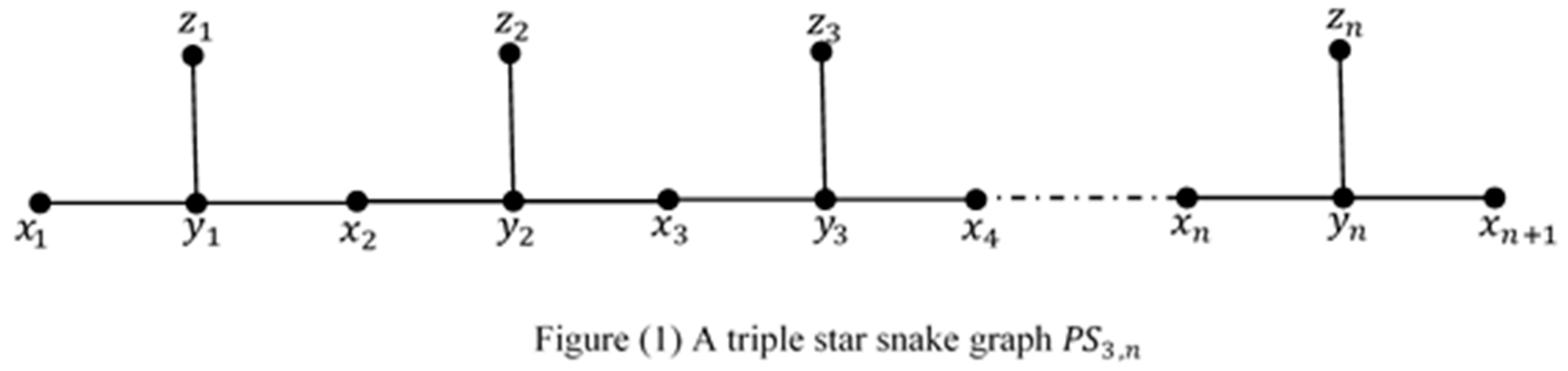
Preprints 89677 g001
Preprints 89677 g001
Theorem1. 
If P S 3 , n is a triple star snake graph with 3 n + 1 vertices, then TEIS is:
t e s P S 3 , n = n + 1
Proof. 
Since E P S 3 , n = 3 n   a n d   Δ P S 3 , n = 3 . Then inequality (1) becomes:
t e s P S 3 , n ≥ n + 1
To complete the proof, we will prove the inverse inequality. Let ᵹ = n + 1 and Ʊ : V P S 3 , n ∪ E P S 3 , n → 1,2 , 3,4 , . . . , ᵹ is a total ᵹ -labeling defined as:
Ʊ x ƍ = ƍ   f o r   ƍ ∈ 1,2 , 3,4 . . . , n + 1
Ʊ y ƍ = Ʊ z ƍ = ƍ   f o r   ƍ ∈ 1,2 , 3,4 , . . . , n
Ʊ x ъ y ƍ = ƍ   f o r   ƍ ∈ 1,2 , 3,4 , . . . , n
Ʊ y ƍ x ƍ + 1 = Ʊ y ƍ z ƍ = ƍ + 1   f o r   ƍ ∈ 1,2 , 3,4 , . . . , n
the above equations means that ᵹ = n + 1 is the greatest label of edges and vertices. The weights of edges are given by:
ⱳ Ʊ x ƍ y ƍ = 3 ƍ   f o r   ƍ ∈ 1,2 , 3,4 , . . . , n
ⱳ Ʊ y ƍ x ƍ + 1 = 3 ƍ + 2   f o r   ƍ ∈ 1,2 , 3,4 , . . . , n
ⱳ Ʊ y ƍ z ƍ = 3 ƍ + 1   f o r   ƍ ∈ 1,2 , 3,4 , . . . , n
It is clear that: the edges weights are dissimilar. Then
t e s P S 3 , n = n + 1
Definition2. 
An m − star snake graph P S m , n is a path P n in which we replace each edge with a star S m , see Figure (2-a), (2-b).
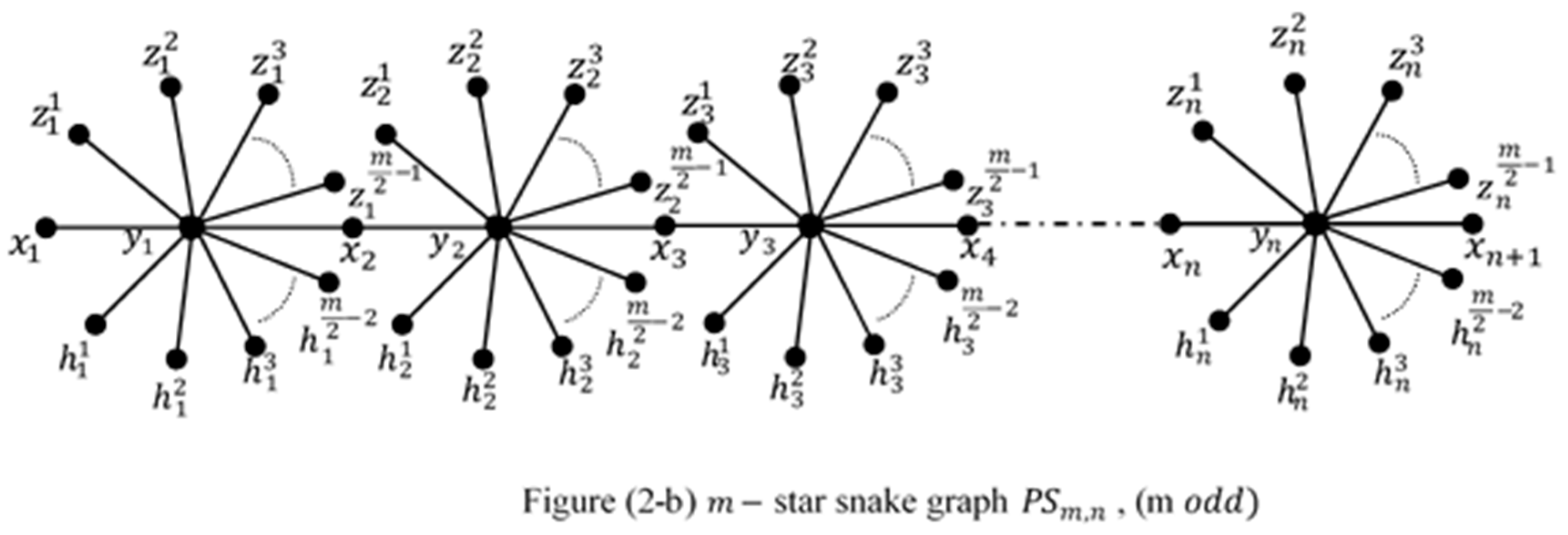
Preprints 89677 g002
Preprints 89677 g002
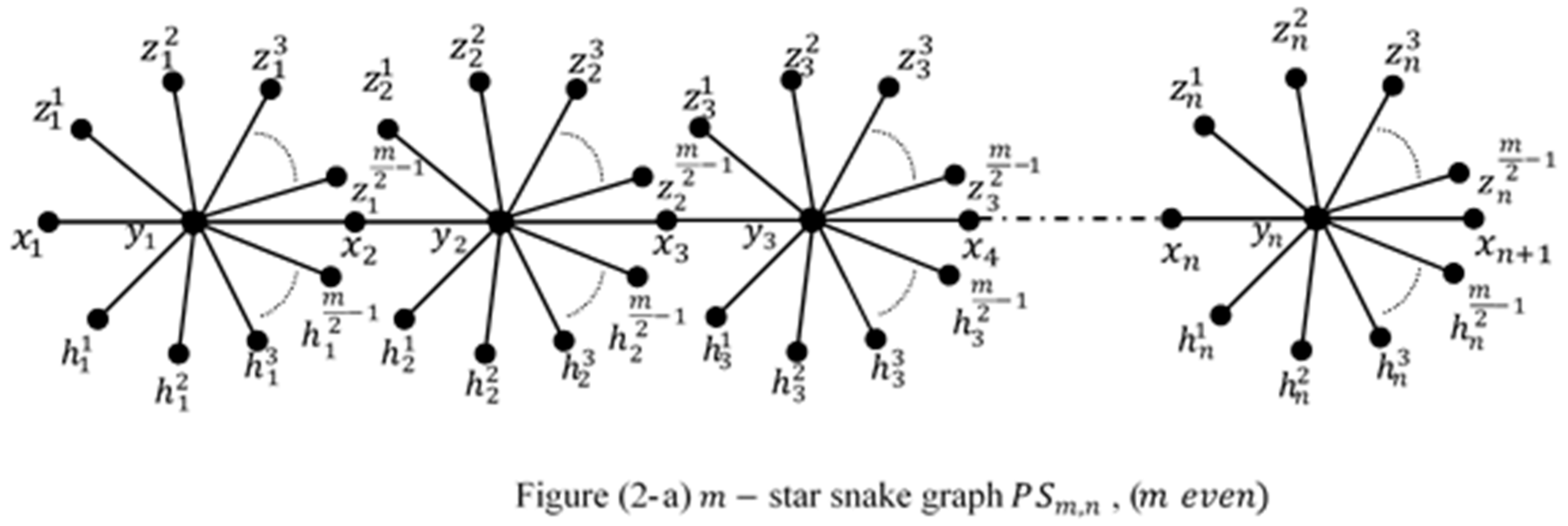
Preprints 89677 g003
Preprints 89677 g003
Theorem2. 
An m − star snake graph P S m , n with m n + 1 vertices n ≻ 3 , has TEIS given by:
t e s P S m , n = m n + 2 3
Proof. 
By substituting with E P S 4 , n = m n   a n d   Δ P S m , n = m in inequality(2) we find
t e s P S m , n ≥ m n + 2 3 .
An edge irregular total ᵹ -labeling will be shown assuming that a map Ʊ : E P S m , n ∪ V P S m , n → 1,2 , 3,4 , . . . , ᵹ   is a total ᵹ -labeling defines in two cases:
Case 1: 
m is even Ʊ is defined as:
Ʊ x ƍ = m 2 ƍ − 1 + 1   f o r   ƍ ∈ 1,2 , 3 , . . . , ᵹ − 1 m 2 + 1 ᵹ   f o r   ƍ ∈ ᵹ − 1 m 2 + 2 , . . . , n + 1
y ƍ = m 2 ƍ − 1 + 1   f o r   ƍ ∈ 1,2 , 3 . . . , ᵹ − 1 m 2 + 1 ᵹ   f o r   ƍ ∈ ᵹ − 1 m 2 + 2 , . . . , n
Ʊ h ƍ s = Ʊ z ƍ s = m 2 − 1 ƍ − 1 + s   f o r   ƍ ∈ 1,2 , 3 , . . . , ᵹ − 1 m 2 + 1 m 2 − 1 ƍ − 1 + s   f o r ƍ = ᵹ − 1 m 2 + 2 s = 1,2 , 3 , . . . , ᵹ − m 2 − 1 ƍ − 1 ᵹ   f o r ƍ = ᵹ − 1 m 2 + 2 s = ᵹ − m 2 − 1 ƍ − 1 + 1 , . . . , m 2 − 1 ᵹ   f o r   ƍ ∈ ᵹ − 1 m 2 + 3 , . . . , n
Ʊ x ƍ y ƍ = 1   f o r   ƍ ∈ 1,2 , 3 , . . . , ᵹ − 1 m 2 + 1 ƍ − 1 m − 2 ᵹ + 3   f o r   ƍ ∈ ᵹ − 1 m 2 + 2 , . . . , n
Ʊ y ƍ x ƍ + 1 = m 2   f o r   ƍ ∈ 1,2 , 3 , . . . , ᵹ − 1 m 2 m 2 ƍ + 1 − ᵹ + 1   f o r   ƍ = ᵹ − 1 m 2 + 1 ƍ m − 2 ᵹ + 2   f o r   ƍ ∈ ᵹ − 1 m 2 + 2 , . . . , n
Ʊ y ƍ z ƍ s = ƍ + s   f o r   ƍ ∈ 1,2 , 3 , . . . , ᵹ − 1 m 2 + 1 m 2 ƍ − 1 − ᵹ + ƍ + s + 1   f o r   ƍ = ᵹ − 1 m 2 + 2 s = 1,2 , 3 , . . . , ᵹ − m 2 − 1 ƍ − 1 ƍ − 1 m − 2 ᵹ + 2 s + 2   f o r   ƍ = ᵹ − 1 m 2 + 2 s = ᵹ − m 2 − 1 ƍ − 1 + 1 , . . . , m 2 − 1 ƍ − 1 m − 2 ᵹ + 2 s + 2   f o r   ƍ ∈ ᵹ − 1 m 2 + 3 , . . . , n
Ʊ y ƍ h ƍ s = ƍ + s + 1   f o r   ƍ ∈ 1 , . . . , ᵹ − 1 m 2 + 1 m 2 ƍ − 1 − ᵹ + ƍ + s + 2   f o r   ƍ = ᵹ − 1 m 2 + 2 s = 1,2 , 3 , . . . , ᵹ − m 2 − 1 ƍ − 1 ƍ − 1 m − 2 ᵹ + 2 s + 3   f o r   ƍ = ᵹ − 1 m 2 + 2 s = ᵹ − m 2 − 1 ƍ − 1 + 1 , . . . , m 2 − 1 ƍ − 1 m − 2 ᵹ + 2 s + 3   f o r   ƍ ∈ ᵹ − 1 m 2 + 3 , . . . , n
From the previous equations, we can say ᵹ is the maximum number which labels vertices and edges. The edges weights of P S m , n are given by:
ⱳ Ʊ x ƍ y ƍ = ƍ − 1 m + 3
ⱳ Ʊ y ƍ x ƍ + 1 = m ƍ + 2
ⱳ Ʊ y ƍ z ƍ s = m ƍ − 1 + 2 s + 1
ⱳ Ʊ y ƍ h ƍ s = m ƍ − 1 + 2 s + 3
We can say that from the previous equations, the weights are distinct for any two edges so
t e s P S m , n = m n + 2 3 .
Case 2: 
m is odd Ʊ is defined as:
Ʊ x ƍ = 1   +   m 2 ƍ − 1   f o r   ƍ ∈ 1,2 , 3 , . . . , ᵹ − 1 m 2 + 1 ᵹ   f o r   ƍ   ∈ ᵹ − 1 m 2 + 2 , . . . , n
Ʊ y ƍ = 1 +   m 2 ƍ − 1   f o r   ƍ ∈ 1,2 , 3 , . . . , ᵹ − 1 m 2 + 1 ᵹ   f o r   ƍ ∈ ᵹ − 1 m 2 + 2 , . . . , n + 1
Ʊ z ƍ s = s +   m 2 ƍ − 1   f o r   ƍ ∈ 1,2 , 3 , . . . , ᵹ − 1 m 2 s +   m 2 ƍ − 1   f o r ƍ = ᵹ − 1 m 2 + 1 s = 1,2 , 3 , . . . , ᵹ − m 2 ƍ − 1 ᵹ   f o r ƍ = ᵹ − 1 m 2 + 1 s = ᵹ − m 2 ƍ − 1 + 1 , . . . , m 2 ᵹ   f o r   ƍ ∈ ᵹ − 1 m 2 + 2 , . . . , n
Ʊ h ƍ s = s +   m 2 ƍ − 1 + 1   f o r   ƍ ∈ 1,2 , 3 , . . . , ᵹ − 1 m 2 s +   m 2 ƍ − 1 + 1   f o r ƍ = ᵹ − 1 m 2 + 1 s = 1,2 , 3 , . . . , ᵹ − m 2 ƍ − 1 − 1 ᵹ   f o r ƍ = ᵹ − 1 m 2 + 1 s = ᵹ − m 2 ƍ − 1 , . . . , m 2 − 1 ᵹ   f o r   ƍ ∈ ᵹ − 1 m 2 + 2 , . . . , n
Ʊ x ƍ y ƍ = ƍ   f o r   ƍ ∈ 1,2 , 3 , . . . , ᵹ − 1 m 2 + 1 ƍ − 1 m − 2 ᵹ + 3   f o r   ƍ ∈ ᵹ − 1 m 2 + 2 , . . . , n
Ʊ y ƍ x ƍ + 1 = m 2 + ƍ   f o r   ƍ ∈ 1,2 , 3 , . . . , ᵹ − 1 m 2 ƍ m + 1 − ᵹ − m 2 ƍ − 1   f o r   ƍ = ᵹ − 1 m 2 + 1 ƍ m − 2 ᵹ + 2   f o r   ƍ ∈ ᵹ − 1 m 2 + 2 , . . . , n
Ʊ y ƍ z ƍ s = ƍ + s   f o r   ƍ ∈ 1,2 , 3 , . . . , ᵹ − 1 m 2 ƍ + s   f o r   ƍ = ᵹ − 1 m 2 + 1   s = 1,2 , 3 , . . . , ᵹ − m 2 ƍ − 1 m 2 ƍ − 1 − ᵹ + 2   s + ƍ   f o r   ƍ = ᵹ − 1 m 2 + 1   s = ᵹ − m 2 ƍ − 1 + 1 , . . . , m 2 ƍ − 1 m − 2 ᵹ + 2   s + 2   f o r   ƍ ∈ ᵹ − 1 m 2 + 2 , . . . , n
Ʊ y ƍ h ƍ s = ƍ + s + 1   f o r   ƍ ∈ 1 , . . . , ᵹ − 1 m 2 ƍ + s + 1   f o r   ƍ = ᵹ − 1 m 2 + 1 s = 1,2 , 3 , . . . , ᵹ − m 2 ƍ − 1 − 1 m 2 ƍ − 1 − ᵹ + 2 s + ƍ + 1   f o r   ƍ = ᵹ − 1 m 2 + 1 s = ᵹ − m 2 ƍ − 1 , . . . , m 2 − 1 ƍ − 1 m − 2 ᵹ + 2 s + 3   f o r   ƍ ∈ ᵹ − 1 m 2 + 2 , . . . , n
From the previous formulas, we can deduce that ᵹ is the greatest label of edges and vertices. After calculating the weights of the edges of the graph P S m , n we find:
ⱳ Ʊ x ƍ y ƍ = ƍ − 1 m + 3
ⱳ Ʊ y ƍ x ƍ + 1 = m ƍ + 2
ⱳ Ʊ y ƍ z ƍ s = m ƍ − 1 + 2 s + 1
ⱳ Ʊ y ƍ h ƍ s = m ƍ − 1 + 2 s + 3
From the equations of weights of edges we find them different, so Ʊ is an edge irregular total ᵹ labeling. Then:
t e s P S m , n = m n + 2 3 .
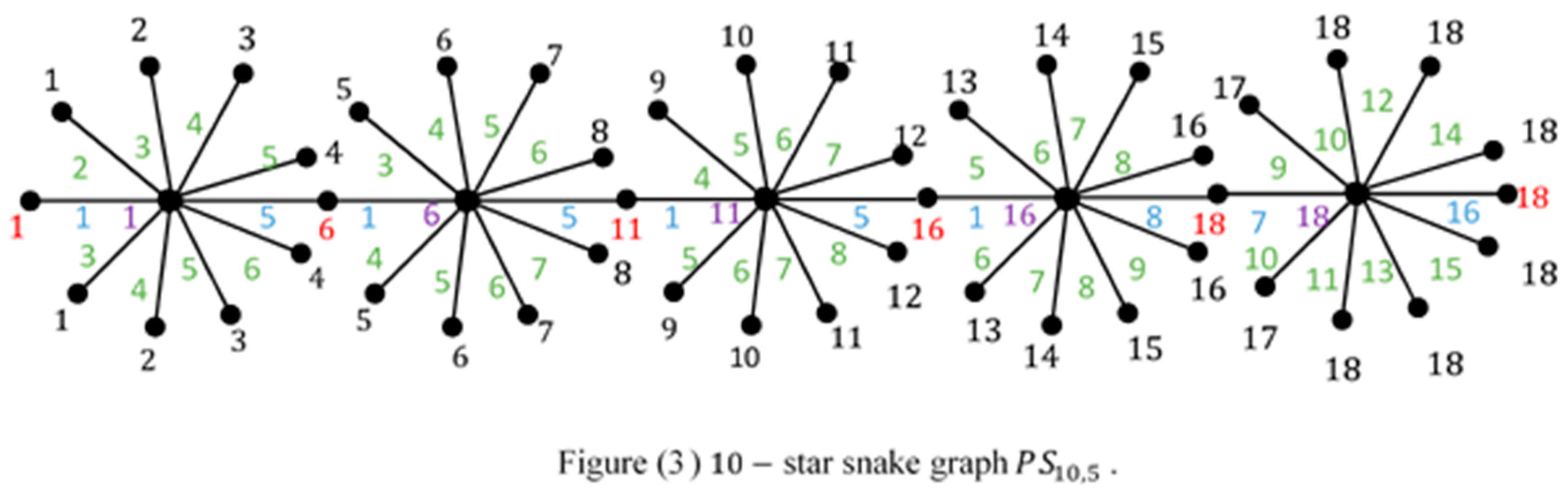
Preprints 89677 g004
Preprints 89677 g004
Preprints 89677 g005
Preprints 89677 g005

3. Conclusions

In our paper, new types of graphs called a triple star snake graph P S 3 , n and m − star snake graph P S m , n were defied . Also, we have investigated TEIS for a triple star snake graph P S 3 , n ,
t e s P S 3 , n = n + 1 .
After that, we have generalized the results for m − star snake graph P S m , n ,
t e s P S m , n = m n + 2 3 .

Acknowledgment

The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number 445-9-526.

Conflict of Interest

All authors declare no conflict of interest in this paper.

References

  1. Bača, M.; Jendroî, S.; Miller, M.; Ryan, J. On irregular total labellings, Discrete Math., 307 (2007), 1378–1388. [CrossRef]
  2. Ivanĉo, J. ; Jendroî, S.Total edge irregularity strength of trees, Discussiones Math. Graph Theory, 26 (2006), 449–456. [CrossRef]
  3. Ahmad, A.; Siddiqui, M. K. ; Afzal, D. On the total edge irregularity strength of zigzag graphs, Australas. J. Comb., 54 (2012), 141–149.
  4. Ahmad, A. ; Arshad, M.; Ižaríková, G. Irregular labelings of helm and sun graphs, AKCE Int. J. Graphs Combinatorics, 12 (2015), 161–168. [CrossRef]
  5. Ahmad, A.; Bača, M.; Siddiqui, M. K. On edge irregular total labeling of categorical product of two cycles, Theory Comput. Syst., 54 (2014), 1–12. [CrossRef]
  6. Ahmad, A.; Bača, M. Total edge irregularity strength of a categorical product of two paths, Ars Comb., 114 (2014), 203–212.
  7. Ahmad, A. ; Al-Mushayt, O. B. S. ; Bača, M.On edge irregularity strength of graphs, Appl. Math. Comput., 243 (2014), 607–610.
  8. Ahmad, A.; Siddiqui, M. K. ; Ibrahim, M.; Asif, M.On the total irregularity strength of generalized Petersen graph, Math. Rep., 18 (2016), 197–204.
  9. A. Ahmad, M. Bača, Edge irregular total labeling of certain family of graphs, AKCE Int. J. Graphs. Combinatorics, 6 (2009), 21–29.
  10. Al-Mushayt, O. ; Ahmad, A.; Siddiqui, M. K. On the total edge irregularity strength of hexagonal grid graphs, Australas. J. Comb., 53 (2012), 263–271.
  11. Yang, H.; Siddiqui, M. K. ; Ibrahim, M.; Ahmad, S.; Ahmad, A.Computing the irregularity strength of planar graphs, Mathematics, 6 (2018), 150. [CrossRef]
  12. Tarawneh, I. ; Hasni, R.; Ahmad, A.; Asim, M. A. On the edge irregularity strength for some classes of plane graphs, AIMS Math., 6 (2021), 2724–2731. [CrossRef]
  13. Tilukay, M. I. ; Salman, A. N. M. ; Persulessy, E. R. On the total irregularity strength of fan, wheel, triangular book, and friendship graphs, Procedia Comput. Sci., 74 (2015), 124–131. [CrossRef]
  14. Siddiqui, M. K. On edge irregularity strength of subdivision of star , Int. J. Math. Soft Comput., 2 (2012), 75–82. [CrossRef]
  15. Ramdani, R. ; Salman, A. N. M. On the total irregularity strength of some Cartesian product graphs, AKCE Int. J. Graphs Combinatorics, 10 (2013), 199–209.
  16. D. Amar, O. Togni, Irregularity strength of trees, Discrete Math., 190 (1998), 15–38. [CrossRef]
  17. Indriati, D. ; Widodo; Wijayanti, I. E. ; Sugeng, K. A. ; Bača, M. On total edge irregularity strength of generalized web graphs and related graphs, Math. Comput. Sci., 9 (2015), 161–167. [CrossRef]
  18. Bača, M.; Siddiqui, M. K. Total edge irregularity strength of generalized prism, Appl. Math. Comput., 235 (2014), 168–173. [CrossRef]
  19. Jendroî, S.; Miŝkuf, J.; Soták, R. Total edge irregularity strength of complete graph and complete bipartite graphs, Electron. Notes Discrete Math., 28 (2007), 281–285. [CrossRef]
  20. Jeyanthi, P.; Sudha, A. Total edge irregularity strength of disjoint union of wheel graphs, Electron. Notes Discrete Math., 48 (2015), 175–182. [CrossRef]
  21. Majerski, P. ; Przybylo, J. On the irregularity strength of dense graphs, SIAM J. Discrete Math., 28 (2014), 197–205. [CrossRef]
  22. Miškuf, J.; Jendroî, S. On total edge irregularity strength of the grids, Tatra Mt. Math. Publ., 36 (2007), 147–151.
  23. Naeem, M.; Siddiqui, M. K. Total irregularity strength of disjoint union of isomorphic copies of generalized Petersen graph, Discrete Math. Algorithms Appl., 9 (2017), 1750071. [CrossRef]
  24. Pfender, F. Total edge irregularity strength of large graphs, Discrete Math., 312 (2012), 229–237. [CrossRef]
  25. Putra, R. W.; Susanti, Y. On total edge irregularity strength of centralized uniform theta graphs, AKCE Int. J. Graphs Combinatorics, 15 (2018), 7–13. [CrossRef]
  26. Rajasingh, I.; Arockiamary, S. T. Total edge irregularity strength of series parallel graphs, Int. J. Pure Appl. Math., 99 (2015), 11–21. [CrossRef]
  27. Salama, F. On total edge irregularity strength of polar grid graph, J. Taibah Univ. Sci., 13 (2019), 912–916. [CrossRef]
  28. Salama, F. Exact value of total edge irregularity strength for special families of graphs, An. Univ. Oradea, Fasc. Math., 26 (2020), 123–130.
  29. Salama, F. Computing total edge irregularity strength for heptagonal snake graph and related graphs, Soft Computing ,2022, 26:155–164. [CrossRef]
  30. Salama, F,; Abo Elanin, R.M. On total edge irregularity strength for some special types of uniform theta snake graphs, AIMS Mathematics, 2021,6(8): 8127–8148. [CrossRef]
  31. Salama, F. Computing the total edge irregularity strength for quintet snake graph and related graphs, J. Discrete Math. Sci. Cryptography, (2021), 1–14. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated