Preprint
Article
SO(3)-Irreducible Geometry in Complex Dimension Five and Ternary Generalization of Pauli Exclusion Principle
Altmetrics
Downloads
77
Views
26
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
06 November 2023
Posted:
07 November 2023
You are already at the latest version
Alerts
Abstract
We propose a notion of a ternary skew-symmetric covariant tensor of 3rd order, consider it as a 3-dimensional matrix and study a ten-dimensional complex space of these tensors. We split this space into a direct sum of two five-dimensional subspaces and in each subspace there is an irreducible representation of the rotation group SO(3)↪SO(5). We find two independent SO(3)-invariants of ternary skew-symmetric tensors, where one of them is the Hermitian metric and the other is the quadratic form. We find the stabilizer of this quadratic form and its invariant properties. Making use of these invariant properties we define a SO(3)-irreducible geometric structure on a five-dimensional complex Hermitian manifold. We study a connection on a five-dimensional complex Hermitian manifold with a SO(3)-irreducible geometric structure, find its curvature and torsion. The structures proposed in this paper and their study are motivated by a ternary generalization of the Pauli’s principle proposed by R. Kerner.
Keywords:
Subject: Computer Science and Mathematics - Geometry and Topology
MSC: 17A40; 20N10; 53C07
1. Introduction
The concept of skew symmetry underlies many structures of modern algebra and geometry. The following structures can serve as examples of such structures: Lie algebras, Grassmann algebras, algebras of differential forms on a manifold, Clifford algebras. In the case of a Lie algebra its Lie bracket is skew-symmetric with respect to a permutation of arguments of this bracket. A Grassmann algebra can be constructed by means of covariant skew-symmetric tensors of some finite dimensional vector space. In this case the skew symmetry of a tensor means that the rearrangement of any two subscripts leads to the change of the sign of a tensor, and the exterior multiplication of two such tensors is defined with the help of the alternation of the tensor product of these tensors. At the end of the last century and the beginning of this century, we witnessed the emergence of interest towards an n-ary generalization of Lie algebra, that is, a generalization in which a Lie bracket contains n arguments. The concept of skew symmetry can be easily extended to n-ary multiplications if we require that any inversion of two arguments in an n-ary product results in a change in sign. An n-ary bracket of n-Lie algebra is skew-symmetric precisely in this classical sense. However, when moving from a binary law of multiplication to an n-ary one, where n>2, we can pose an interesting question of possible analogues of the classical concept of skew symmetry. In order to formulate the concept of skew symmetry of an algebraic operation we use permutations of factors in the product. In the case of binary multiplication we have only one permutation of variables in this multiplication and, consequently, we have only one notion of skew-symmetric binary product. By requiring that an n-ary product of elements () be equal to zero whenever any two elements in this product are equal, we obtain an equivalent form of the concept of skew symmetry (an n-ary product is assumed to be linear in each argument). This formulation of skew symmetry explains why the concept of skew symmetry plays an important role in theoretical physics. Recall the Pauli exclusion principle, which states that two fermions in a quantum system cannot co-exist if they have identically equal sets of quantum numbers. It follows then that a wave function of a quantum system containing identical sets of quantum numbers of two fermions must vanish. Now the skew-symmetry of a wave function with respect to permutation of quantum states of any two fermions follows from the linearity of a wave function.
If we consider a ternary multiplication then in a ternary product we have six possible permutations of arguments, where three of them are inversions (non-cyclic permutations), and three are cyclic.It is natural to use non-cyclic permutations to extend binary skew-symmetry to ternary multiplication laws, that is, we call a ternary multiplication totally skew-symmetric if it is skew-symmetric with respect to any pair of arguments. It is precisely this notion of skew symmetry that is used in 3-Lie algebras, that is, any non-cyclic permutation of arguments in a ternary Lie bracket of 3-Lie algebra changes a sign of this bracket. Equivalently, if among the three elements of a ternary Lie bracket there are two equal ones, then regardless of where in the bracket these equal elements appear, the ternary bracket is equal to zero. In this formulation we see a direct connection with the classical Pauli exclusion principle.
But in the case of ternary multiplication, unlike the binary one, we have three more cyclic permutations, and these permutations can be used to construct a ternary analogue of skew symmetry, different from the one indicated above. Let V be a finite dimensional vector space with a skew-symmetric binary law of multiplication . Then the skew-symmetry can be expressed in two equivalent ways
Let be a complex finite dimensional vector space equipped with a ternary trilinear law of multiplication
Since we use cyclic permutations a ternary analog of (1) is
It is natural to raise the question of what could serve as a ternary analogue of relation (). The answer to this question is the relations
or their conjugate version
where is the primitive 3rd order root of unity. It is important to note that there is a significant difference between binary relations (1), () and ternary relations (3),(4). In the binary case, the relations (1) and () are equivalent, one immediately follows from the other. This is not true in the case of a ternary law of multiplication. Relations (3) and (4) are not equivalent. Due to the well-known property of cubic roots of unity , the relations (3) follow from the relations (4), but not vice-versa. By other words (3) is a more general condition than (4).
Thus, an analogue of the notion of skew symmetry in the case of ternary multiplication can be one of the conditions (3), (4), (5) with (4), (5) being particular cases of (3). But in any case, no matter which of the conditions (3), (4), (5) we take as a ternary analogue of the concept of skew symmetry, for any we will have , and generally , where . Consequently, a ternary analogue of skew symmetry defined either by (3) or (4) or (5) is significantly different from the classical concept of skew symmetry in the sense that in the case of classical skew symmetry, the presence of two equal elements in a product leads to zero, and in the case of ternary skew symmetry defined by one of the conditions (3), (4), (5) the presence of two equal elements in a ternary product in general does not imply that this product is equal to zero. But at the same time, if all three elements in a ternary product are equal, that is , then the product is equal to zero .
An analogue of the Pauli exclusion principle, which is based on a ternary skew symmetry, defined by one of conditions (3)-(5), could be formulated as follows: Three particles cannot coexist in a quantum system if these three particles are in the same quantum state, but two such particles can. It is in this form that an analogue of the Pauli exclusion principle was proposed by Richard Kerner, who calls it a ternary generalization of the Pauli exclusion principle. Richard Kerner argues that the ternary generalization of the Pauli exclusion principle applies to quarks. In the quark model, quarks are considered as fermions, and three quarks or three anti-quarks form a baryon. The ternary generalization of the Pauli exclusion principle can in this case be formulated as: Three quarks in the same quantum state cannot form a stable configuration, observed as one of strongly interacting particles, but at the same time, the coexistence of two quarks with the same isospin value is possible.
Relations (3)-(5) can be used to construct an analogue of Grassmann algebra, that is, we can consider an algebra over the field of complex numbers generated by a system of generators that obey one of the relations (3)-(5). The properties, structure and possible applications of such algebras were studied in papers [1,4,13]. These algebras can be applied to construct a generalization of exterior calculus with exterior differential d satisfying [2]. A generalization of the Dirac operator based on the mentioned above algebras and relation to a ternary generalization of Pauli exclusion principle can be found in [12,13,14,15] to In this article, the main object of study is the subspace of an algebra whose generators obey relations (3), spanned by the triple products of the generators. This subspace can be identified with the space of complex-valued covariant third-order tensors in three-dimensional space which have the following property
If we impose an additional condition on the tensors of this space, which is
i.e. the trace of a tensor over any pair of subscripts is equal to zero, we obtain the space of tensors known in the theory of representations of the rotation group [11]. More precisely, the space of tensors satisfying conditions (6), (7) is ten-dimensional and in this space we have a twofold irreducible tensor representation of the rotation group. Let us denote this ten-dimensional complex vector space by . A twofold irreducible tensor representation of the rotation group in splits into two irreducible tensor representations if we decompose the ten-dimensional representation space into a direct sum of two five-dimensional subspaces in a way invariant under the action of the rotation group. A decomposition into two subspaces can be made with the help of the relations (4), (5), that is, we define the subspace by imposing the additional condition
It is easy to see that in this case the condition (6) follows from (8). Hence we have
and analogously
Then and in each of subspaces we have an irreducible representation of the rotation group. It is known that every representation of the rotation group can be made unitary if we endow a representation space with an appropriate Hermitian metric. We endow the space with the Hermitian metric
and show that the irreducible representation of the rotation group in is an inclusion . We find the orthonormal basis (here are complex-valued 3rd order covariant tensors satisfying (7), (8)) for the Hermitian space and identify the space with the Hermitian vector space of tensors by putting
Then the irreducible representation R of the rotation group can be written in the form
where . We calculate all -invariants of the representation R and this calculation shows that there are only two non-trivial independent invariants. Obviously one of them is the canonical Hermitian metric and the other is the quadratic form
We study the properties of the quadratic form . Particularly we show that the matrix of the quadratic form is symmetric, unitary and its determinant is the 6th order primitive root of unity . These properties are invariant under action of the unitary group in the five-dimensional complex space . Then we find the subgroup of the group which is a stabilizer of the quadratic from in the five-dimensional complex vector space . In analogy with approach proposed in [9] and developed in [7] we define a -irreducible geometric structure in complex dimension 5 and study its geometry.
2. Five-dimensional complex space of -irreducible representation
The aim of this section is to describe an irreducible tensor representation of the rotation group. In what follows we consider complex-valued covariant tensors defined in 3-dimensional Euclidean space . Let be a tensor of rank p. In what follows, we will use the Einstein convention of summation over repeated indices. Then the formula
where is a rotation in , defines a linear transformation in a vector space of covariant tensors of rank p, i.e. it defines a representation of the rotation group, which is called a tensor representation. A linear transformation (14) will be denoted by , that is, . In this section we give an explicit description of an irreducible 5-dimensional tensor representation of the rotation group in the complex vector space of covariant tensors of rank 3.
Let be the vector space of tensors of rank 3 which satisfy the following conditions:
- T1.
- A contraction of a tensor over any pair of subscripts (trace) is zero, that is, for any it holds
- T2.
- For any combination of integers (each running from 1 to 3) the sum of the components of tensor , obtained by cyclic permutation of its subscripts, is equal to zero, that is,
It can be easily verified that the conditions are invariant under the action of the rotation group (14). Hence for any rotation we have . It is shown in [11] that the vector space is 10-dimensional and the formula (14) defines a two-fold irreducible tensor representation of the rotation group in this vector space. If we split the 10-dimensional vector space into a direct sum of two 5-dimensional subspaces in a way invariant with respect to the action of the rotation group (14) then in each 5-dimensional subspace of we will have an irreducible tensor representation of the rotation group.
One can split the 10-dimensional vector space into a direct sum of two 5-dimensional subspaces, which are invariant with respect to a tensor representation of the rotation group, by making use of a linear operator induced by a substitution. Let us denote by the cyclic substitution of first three integers . Then one can define the operator acting on the tensors of rank 3 as follows
and extend it by linearity to the vector space of all tensors of rank three. Obviously and
where is the identity mapping. Thus the equation (15) can be written in the form
Now it is easy to show that the vector space is invariant under the action of the operator , that is, . Assume that a tensor satisfies the condition or, equivalently, the equation (17). Denote . Then
and also satisfies the equation (17). Similarly one can verify that the operator preserves the condition .
Generally the property of the linear operator implies that it has three eigenvalues in the vector space of all tensors of rank 3. Here is the primitive third order root of unity and is its complex conjugate. Another general formula is based on the property of the third order roots of unity . Indeed it is easy to see that due to the mentioned property of the third order roots of unity any tensor of rank 3 can be decomposed into the sum of three tensors
where
Obviously the tensors are the eigenvectors of the linear operator corresponding to the eigenvalues respectively. Thus we have
or, equivalently,
It is worth to mention that the components and of a tensors T satisfy the condition . Restricting (18) to the vector space , we see that due to the condition the first term at the right-hand side vanishes, i.e. and (18) takes on the form , where . Hence we can decompose the vector space into the direct sum of two subspaces, which will be denoted by and . Here is the subspace of the eigenvectors of the linear operator with eigenvalue q and is the subspace of the eigenvectors of the linear operator with eigenvalue . Thus .
The subspaces play a basic role in what follows and it is useful to give here their exact description. is a vector space of complex-valued tensors of rank 3 which satisfy the condition (trace over any pair of subscripts is zero) and they are eigenvectors of the linear operator with eigenvalue q, that is, they satisfy or . Similarly is a vector space of complex-valued tensors of rank 3 which satisfy and they are the eigenvectors of the linear operator with eigenvalue , i.e. or . Hence
The important role of these subspaces is that they are spaces of a 5-dimensional irreducible representation of the rotation group.
A tensor of the third rank is a quantity with three subscripts . Therefore, in what follows, it will be convenient for us to represent tensors of the third rank in the form of 3-dimensional matrices, which are also called hypermatrices. By a 3-dimensional matrix, we mean a 3-dimensional cube with components of a tensor located on the sections of this cube. Here by section we mean a section of a cube by plane perpendicular to its edges. We assume that a cube is located in space so that the first subscript i of a tensor enumerates sections of a cube parallel to the plane of this page and the numbering starts from the section closest to us () and then takes values 2,3 as the distance from us increases (see figure). 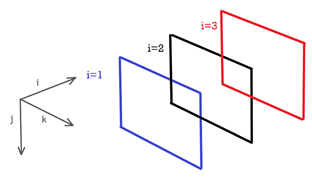

We will map a 3-dimensional matrix onto the plane of page of this paper by placing the numbered sections of a cube (which are the usual third-order matrices) from left to right, that is, on the left there will be the section with , in the center with and on the right with . Thus a 3-dimensional matrix of a third order tensor can be represented as follows
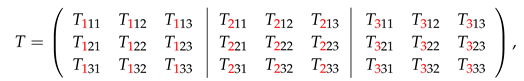 where a number of a section i is indicated by red color. If a 3-dimensional matrix T is represented in the form (20) then we will say that is written in the direction i. Analogously we can define j-directional and k-directional representations of a 3-dimensional matrix.
where a number of a section i is indicated by red color. If a 3-dimensional matrix T is represented in the form (20) then we will say that is written in the direction i. Analogously we can define j-directional and k-directional representations of a 3-dimensional matrix.
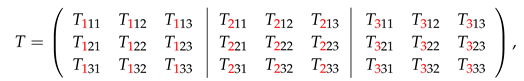
Now we consider the 5-dimensional complex vector space endowed with the canonical Hermitian metric h. The coordinates of this space will be denoted by , where A runs from 1 to 5. Then . We will identify this 5-dimensional complex vector space with the complex vector space of the third-rank covariant tensors (or 3-dimensional matrices) by identifying a point with the 3-dimensional matrix , i.e.
where
It is easy to verify that satisfies the condition , that is, the trace over any pair of subscripts is zero, and Thus, in what follows we will consider the 5-dimensional complex vector space whose points are identified with 3-dimensional complex matrices .
The formula (14) defines an action of the rotation group on our 5-dimensional complex vector space and this action yields an irreducible tensor representation of the rotation group [11]. Now our aim is to find and study the invariants of this representation, which we will use to construct an irreducible special geometry.
In this paper, we use the classification of invariants of third-order tensors that transform according to formula (14), that is, under the action of the rotation group . If we do not assume that a tensor has any symmetries, then there is only one linear invariant
where is the Levi-Civita tensor in 3-dimensional Euclidean space. Since we consider the space of tensors that satisfy the property , that is, the sum of the components obtained by cyclic permutations of subscripts is equal to zero, the linear invariant vanishes.
The complete set of quadratic -invariants of a third-order real-valued tensor T (no symmetries) includes eleven invariants. Six of eleven invariants contain the trace of a tensor T with respect to some pair of subscripts, and, due to property , these invariants vanish when restricted to the space . This leaves us with five -invariants of a real-valued tensor, and these invariants are on the left side of the table shown below. Due to the fact that we are considering complex-valued tensors, this list of five invariants should be extended by supplementing it with additional invariants. These additional invariants are constructed from those in the left side of the table by replacing one of the factors in a product of tensor components with the complex conjugate and the additional invariants are shown in the right side of the table. Direct calculation leads to the following table of invariants
The table of invariants shows that we have two independent quadratic invariants , where the first one is the canonical Hermitian metric of the complex five-dimensional space . Hence each rotation of the 3-dimensional space induces a unitary transformation of the complex five-dimensional Hermitian space , that is, we have a representation . Obviously the homomorphism R from the rotation group into the group of unitary matrices of order 5 is injective. At the infinitesimal level, the representation R generates the representation of the Lie algebra of the rotation group . Our next goal is to find an explicit form of this representation using the basis of the 5-dimensional complex Hermitian space of 3-dimensional matrices (21). By other words, given a skew-symmetric third-order matrix we will calculate a fifth-order skew-Hermitian traceless matrix . We will see that the form of a skew-Hermitian matrix is determined by the second invariant , and this matrix is surprisingly similar to the matrix used in the Georgie-Glashow model for unification of elementary particles.
In order to calculate the infinitesimal part of the representation , we use the exponential map from the Lie algebra to the rotation group , taking only the linear part of the corresponding expansion , where is a skew-symmetric matrix. We can write
Hence the infinitesimal part of the action (up to the terms of the second order and higher) defines the linear operator , where
It will be convenient for us to pass to a parameterization of matrix with the help of parameters containing one index. Let us define . Then
Now we can calculate a matrix of this operator (we will use the same notation for the matrix of the operator) by means of the following basis in 5-dimensional complex space of 3-dimensional matrices (21)
Let us enumerate the 3-dimensional matrices of this basis (starting from the left in the first row and moving from left to right and then from top to bottom) as follows , where . By straightforward calculation we find
Hence the matrix of the operator has the form
Due to the fact that the irreducible representation of the rotation group in the complex space of three-dimensional matrices (21) is unitary (as we mentioned above one of the invariants of this representation is the Hermitian metric of the 5-dimensional complex space), the matrix of the representation of the Lie algebra of the rotation group must be skew-Hermitian, and this is indeed the case, because the matrix satisfies the relation , where . It is easy to see that is a traceless matrix. Hence belongs to the Lie algebra of the group , that is, . Hence we can express this matrix in terms of generators of denoted in physics papers by , where , and are Hermitian traceless matrices of 5th order normalized by . In this paper we use the following numbering of the generators of :
- The first eight generators correspond to , that is,where are Gell-Mann matrices,
- the next four generators have the formwhere and are Pauli matrices,
- the next twelve generators (sometimes called broken matrices) are of the formwhere and is a matrix with only one non-zero element, which is at the intersection of ith row with kth column.
Then the matrix can be written in the terms of -generators as follows
It should be noted here that the matrix is not only skew-Hermitian and traceless, it also satisfies some additional conditions that follow from the fact that the irreducible representation of the rotation group has one more quadratic invariant (22). We will denote the quadratic form in the 5-dimensional complex vector space induced by this invariant as follows
The matrix of this quadratic form
can be considered as a covariant second-order tensor in the 5-dimensional complex vector space and the properties of this tensor will be studied in the next section. Here we only note that the matrix is symmetric and unitary, i.e.
where is the identity matrix.
The infinitesimal action (28) generates the following vector fields in 5-dimensional complex space
These vector fields span the Lie algebra isomorphic to the Lie algebra of matrices (29). Due to the fact that the Hermitian metric and the quadratic form are invariants of the irreducible representation of the rotation group , the vector fields vanish on the Hermitian form and the quadratic form .
Now our goal is to show that, in fact, the irreducible representation of the rotation group has the form , that is, each rotation generates a special (with determinant equal to 1) unitary transformation in the 5-dimensional complex vector space. For this purpose, we will find a parameterization of the irreducible representation using Euler angles. Let us consider two one-parameter subgroups of the rotation group
The one-parameter subgroups of unitary transformations in 5-dimensional complex vector space generated by the irreducible representation of and have the following form respectively
Direct calculation shows that the determinants of these matrices are equal to 1. Since any rotation can be written as a composition , where are Euler angles, we conclude that each rotation generates a unitary transformation with determinant 1, that is, the irreducible representation has the form of inclusion and we will denote the image of the rotation group with respect to this inclusion by . Hence .
3. -irreducible geometric structure on a five-dimensional Hermitian manifold
The purpose of this section is to study the properties of the quadratic form
which is invariant under the irreducible representation R of the rotation group, where . In the previous section we denoted the image of this inclusion by and, according to the formulas (34), (), any element of the group can be written as a product , where are real parameters. Hence is a stabilizer of the quadratic form in . Assume that , where is a regular complex -matrix, is a linear transformation in the five-dimensional complex space . Then the matrix of the quadratic form
transforms under this transformation as follows
or in the matrix form
where are matrices of the form in different bases of the Hermitian space and is the transposed matrix of U. The set of all matrices obtained with the help of (39) will be referred to as an orbit of the quadratic form with an indication of a group of transformations. For example, the set of all matrices obtained by means of unitary transformations will be referred to as a -orbit of . Obviously, we can consider the matrix as a second-order covariant tensor in a five-dimensional vector space and in this case we will talk about the -orbit of the tensor . Our aim in this section is to find properties of the quadratic form (or of the corresponding tensor ) such that they will uniquely determine the orbit of this quadratic form.
First of all, it is easy to see that the tensor K is symmetric and unitary and these properties are invariant with respect to the group of unitary transformations . Indeed for any we have
and
where is the complex conjugate matrix of U and E is the unit matrix. Hence the -orbit of the tensor is an orbit of symmetric and unitary tensor.
We recall that determinant of the matrix of a quadratic form is referred to as a discriminant of a quadratic form. It is easy to find that the discriminant of the quadratic form is , where is the primitive sixth-order root of unity. But the discriminant of the quadratic form is invariant with respect to the action of the group . Indeed we have
Hence the -orbit of the second order covariant tensor is an orbit of the tensor with determinant equal to .
The -invariant properties of the tensor found above do not yet uniquely determine the -orbit of this tensor in the space of -orbits of all second order covariant tensors. In order to find additional invariant conditions we use the following fact from the matrix calculus. It is known [10] that a symmetric and unitary complex matrix X, that is,
can be written in the exponential form , where Y is the real symmetric matrix. The tensor is symmetric, unitary, and these properties are -invariant. Thus in any orthonormal basis for the five-dimensional complex space or, by other words, at any point of -orbit this tensor considered as a matrix can be written in the exponential form , where S is a real symmetric matrix. Particularly in the case of the matrix (37) a straightforward computation gives the block form of the 5th order real symmetric matrix S
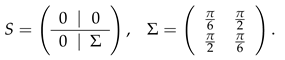
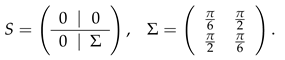
In particular case when is a real unitary transformation, that is , we can easily find a transformation law of the matrix S. Indeed in the case of a real unitary matrix U we have
and implies . But a real unitary matrix is an orthogonal real matrix and, making use of a transformation , the real symmetric matrix S can be put into a diagonal form. Straightforward computation gives the diagonal forms of matrices
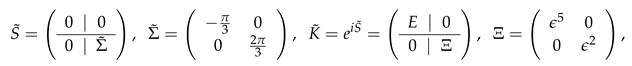 where and E is the 3rd order unit matrix. It is easy to verify that the sixth power of the matrix K of the quadratic form is equal to the identity matrix, that is, , and this relation is invariant under real unitary transformations of the five-dimensional complex space. It is well known that if the nth power of a matrix is equal to the identity matrix, then the eigenvalues of such a matrix are the nth roots of unity. Thus, the diagonal form of the matrix K in (41) with the sixth order roots of unity on the main diagonal, is a consequence of the fact that K or to the sixth power is equal to the identity matrix. We proved the following statement
where and E is the 3rd order unit matrix. It is easy to verify that the sixth power of the matrix K of the quadratic form is equal to the identity matrix, that is, , and this relation is invariant under real unitary transformations of the five-dimensional complex space. It is well known that if the nth power of a matrix is equal to the identity matrix, then the eigenvalues of such a matrix are the nth roots of unity. Thus, the diagonal form of the matrix K in (41) with the sixth order roots of unity on the main diagonal, is a consequence of the fact that K or to the sixth power is equal to the identity matrix. We proved the following statement
Proposition 3.1.
For any orthonormal basis , where , for the five-dimensional complex Hermitian space the second order covariant tensor determined by the quadratic form has the following -invariant properties:
- (symmetric),
- (unitary),
- , where is the sixth order root of unity.
It also has the following properties, which are invariant with respect to real unitary transformations:
- , where the tensor is considered as a matrix,
- the eigenvalues of the tensor are , where is the cubic root of unity.
This statement provides a basis for studying five-dimensional complex manifolds with a structure determined by the tensor . Let be a five-dimensional Hermitian manifold, where h is a Hermitian metric. A Hermitian metric h makes it possible to reduce the group of non-degenerate linear transformations of a tangent space of a manifold M to the group of unitary transformations . In other words, we can consider the principal bundle of orthonormal frames over a manifold M with the structure group . Thus, by a tensor field on a manifold M we mean a tensor defined at each point of a manifold M and transformed under the action of the structure group . If is the subgroup of real unitary matrices then we can consider the sub-orbit of a -tensor field, that is, the tensor field transforming according to the action of the subgroup and this sub-orbit will be referred to as a -tensor.
Definition 3.2.
An -irreducible geometric structure on a five-dimensional complex Hermitian manifold is a 2nd order covariant symmetric, unitary tensor field whose determinant is equal to the primitive sixth order root of unity Moreover, the tensor field considered as a -tensor field has the eigenvalues , where the multiplicity of the eigenvalue 1 is 3, and q is the primitive cubic root of unity .
From this definition it follows that an -irreducible geometric structure on a five-dimensional Hermitian manifold M can be considered as a triple , where h is a Hermitian metric of M and K is a 2nd order covariant tensor field defined on M or the corresponding quadratic form. Two triples and will be referred to as equivalent -irreducible geometric structures on Hermitian manifolds respectively if there exists a diffeomorphism such that
where are tangent vectors to a manifold M, is the differential of a diffeomorphism and are quadratic forms induced by the tensors respectively.
Let us study a local structure of a manifold M. It follows from Proposition 3.1 and Definition 3.2 that locally we can choose a frame of vector fields and its dual coframe of complex-valued 1-forms, i.e. , such that
- is an orthonormal frame, that is, and
- the components of the tensor form the following matrixand the quadratic form induced by these components is
It is clear that the subgroup (isomorphic to the rotation group) studied at the end of the previous section is the stabilizer of the quadratic form (42). Hence we can reduce the gauge group to this subgroup and consider a -connection 1-form on a manifold M, where is the Lie algebra of . We can write this -valued connection 1-form as follows
where are real-valued 1-forms. It is easy to see that a connection 1-form is a skew-Hermitian, that is, . Then the torsion 2-form and the curvature 2-form of a connection can be expressed as follows
Straightforward calculation gives for the torsion
and for the curvature
where is a 2-form defined by , where is a cyclic permutation of integers . It can be proved that a connection is consistent with a Hermitian metric h and it preserves the tensor , that is,
where is the covariant derivative of tensor fields induced by a connection .
4. Discussion
In this paper, we study a ternary generalization of the concept of skew-symmetry, which is different from the classical one. This ternary analogue of skew-symmetry is defined by means of a faithful representation of the cyclic group by the cubic roots of unity . A ternary generalization of skew-symmetry considered in the present paper is motivated by the ternary generalization of the Pauli’s exclusion principle proposed by R. Kerner in connection with quantum properties of quarks. The algebraic aspect of ternary generalization of skew-symmetry was studied in a number of scientific papers, where this generalization was used to construct ternary algebras with generators. Then these algebras were used to construct a generalization of the Dirac operator and of the calculus of differential forms. In this article we study a ternary generalization of the notion of skew-symmetry from the point of view of geometric structures. We consider the space of 3rd order covariant tensors, which are ternary skew-symmetric, that is, the sum of the tensor components obtained by cyclic permutations of subscripts is equal to zero. Moreover, the trace of a tensor over any pair of subscripts must be equal to zero. We think that this requirement is a ternary analogue of the fact that in the case of a 2nd order skew-symmetric (in the classical sense) covariant tensor, all diagonal elements (with equal subscripts) are equal to zero (and hence the sum, that is, the trace will be equal to zero). Tensors of 3rd order with the properties described above are known in the representation theory of the rotation group. They form a ten-dimensional space and in this space there is a twofold irreducible representation of the rotation group. In order to split this twofold representation into two irreducible representations we decompose this ten-dimensional space into a direct sum of two five-dimensional spaces with the help of the primitive cubic roots of unity . This decomposition can be considered as some kind of duality, which is possibly related to the duality quark-anti-quark. We construct the five-dimensional complex Hermitian space whose points are identified with ternary skew-symmetric covariant 3rd order tensors. If we consider a 3rd order tensor as a 3-dimensional matrix, then we have a five-dimensional complex space whose points can be identified with 3-dimensional matrices. Figuratively speaking, we have a five-dimensional complex space, whose points are 3-dimensional lattices and the components of 3rd order ternary skew-symmetric covariant tensors are located at the nodes of these lattices. It is possible that a geometry of this five-dimensional complex Hermitian space is an appropriate geometric model for a space of our Universe at distances comparable with the sizes of quarks.
Author Contributions
Conceptualization, V.A. and O.L.; methodology, V.A.; software and computation, O.L.; writing—original draft preparation, V.A.; writing—review and editing, O.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
References
- Abramov, V. , Kerner, R. , and Le Roy, B. Hypersymmetry: A Z3-generalization of supersymmetry, J. Math. Phys. 1997, 38(3), 1650–1669. [Google Scholar]
- Abramov, V. , Kerner, R. Exterior differentials of higher order and their covariant generalization, J. Math. Phys. 2000, 41(8), 5598–5614. [Google Scholar]
- Abramov, V., Kerner, R., and Liivapuu, O. Algebras with Ternary Composition Law Combining Z2 and Z3 Gradings, Algebraic Structures and Applications, Springer Proceedings in Mathematics & Statistics, Springer Nature Switzerland, 2020.
- Abramov, V. Ternary algebras associated with irreducible tensor representations of SO(3) and the quark model, Int. Journal of Geometric Methods in Modern Physics 2023, 20(5). [Google Scholar]
- Abramov, V., Groote, S., Lätt, P. Algebra with ternary cyclic relations, representations and quark model, Proceedings of the Estonian Academy of Sciences, 72 (1), 61–67.
- Ahmad, F. Invariants of a Cartesian tensor of rank 3. Arch. Mech. 2011, 63(10), 383–392. [Google Scholar]
- Bobienski, M. , Nurowski, P. Irreducible SO(3) geometry in dimension five, J. reine angew. Math. 2007, 605, 51–93. [Google Scholar]
- Croon, D. , Gonzalo, T. E., Graf, L., Košnik, N., and White, G. GUT Physics in the Era of the LHC, Front. Phys. 2019, 7, doi. [Google Scholar]
- Friedrich, Th. On types of non-integrable geometries, Rend. Circ. Mat. Palermo 2003, Serie II, Suppl. Circ. Mat. Palermo 2003, Suppl. 71, 99–113. [Google Scholar]
- Gantmacher, F. R. The Theory of Matrices, 3rd ed. Chelsea Publishing Company, 1984.
- Gelfand, I. M.; Minlos, R. A.; Shapiro, Z. Ya. Representations of the Rotation and Lorentz Groups and Their Applications, Dover Publications, Ins.: Mineola, New York, 2018.
- Kerner, R. Graduation Z3 et la racine cubique de l’opérateur de Dirac, C. R. Acad. Sci. Paris 1991, 312, 191–196. [Google Scholar]
- Kerner, R. Z3 graded algebras and the cubic root of the supersymmetry translations, J. Math. Phys. 1992, 33, 403–411. [Google Scholar] [CrossRef]
- Kerner, R. Ternary Generalization of Pauli’s Principle and the Z6-Graded Algebras, Phys. At. Nucl. 2017, 80, 522–534. [Google Scholar]
- Kerner, R. The Quantum Nature of Lorentz Invariance, Universe 2019, 5, no. 1.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






