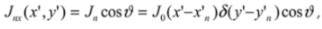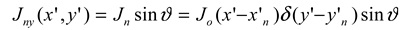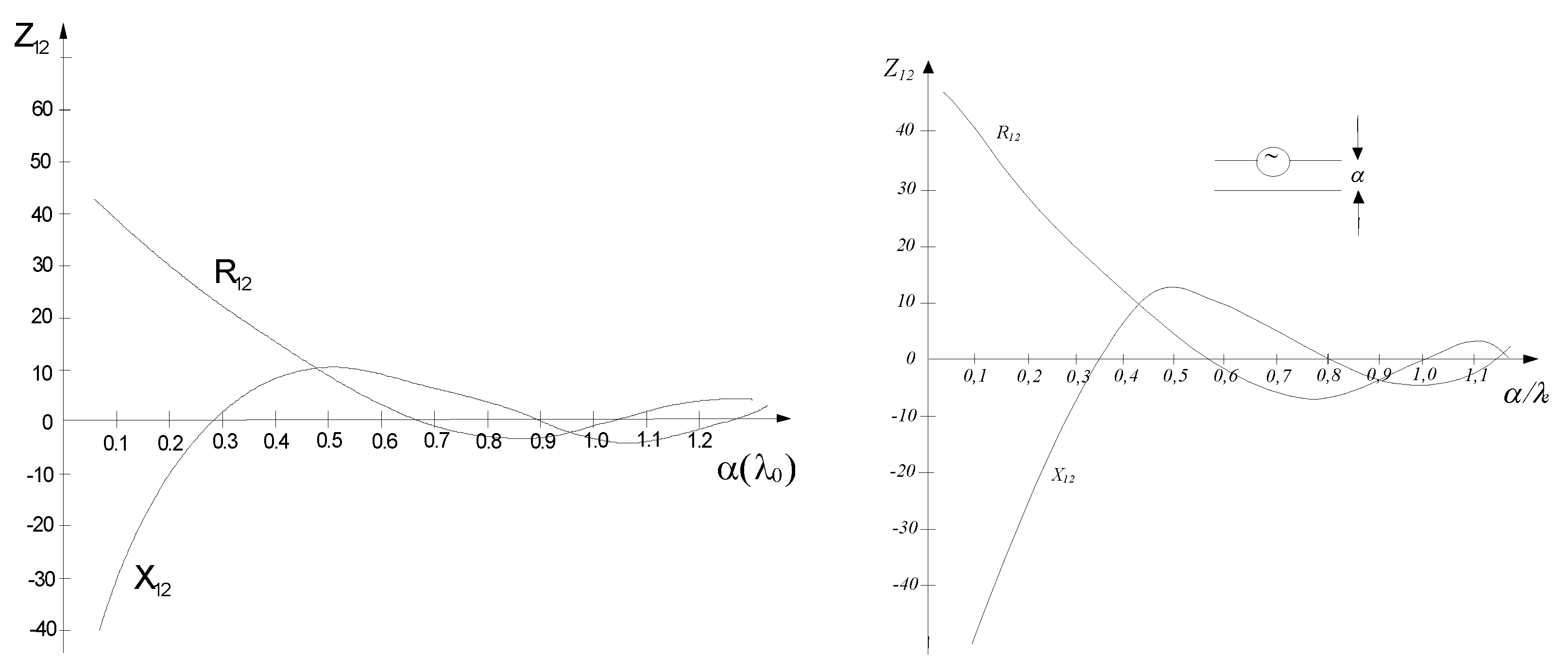Mutual Impedance of Antennas Placed on a Multilayer Dielectric

Preprint

Article

Mutual Impedance of Antennas Placed on a Multilayer Dielectric

Altmetrics

Downloads

Views

Comments

Marian Wnuk^*

This version is not peer-reviewed

Submitted:

07 November 2023

Posted:

07 November 2023

You are already at the latest version

Alerts

Abstract

The paper presents a method for determining the mutual impedance of two dipoles located on a multilayer dielectric structure. Determining the mutual impedance of linear antennas is a complex issue and we are unable to obtain an exact solution, it is influenced by many elements (location, dimensions, electrical parameters of the earth, thickness of the substrate, thickness and antenna conductivity, etc.) In the case of antennas on a dielectric substrate, the coupling analysis is even more complicated, because the operation of these antennas is significantly influenced by the occurrence of surface waves conducted through an open dielectric structure. The problem was solved by the method of moments using the Galerkin method as its special case. The work uses a method developed by Richmond for obtaining the elements of the impedance matrix, based on the concept of reaction between sections of the base and testing functions. Their mutual interaction was described by the reaction of the electric field caused by the current flowing through one dipole with the current flowing through the other dipole. Based on this analysis, the mutual impedance of two arbitrarily oriented dipoles located on a multilayer dielectric was determined, where the current distribution and antenna lengths are arbitrary. A computer program was developed that allowed to determine the mutual impedance for freely oriented dipoles.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Printed antennas have been one of the most innovative fields of antenna technology for over a dozen years. In the early 1950s, radiation from strip lines and microstrip lines was observed. However, from the point of view of the use of transmission lines, it was an undesirable phenomenon, so apart from a few articles suggesting its use in the construction of antennas, it did not arouse much interest. Only Munson's article [L-1] showed that microstrip antennas can have practical applications. Until 1971, however, most of the published works were only presentations of experimental results. It was only in the 1970s that rapid development began in theoretical and experimental work on this type of antennas. In 1979, the first international conference was held in La Cruses, devoted to a comprehensive approach to antennas on dielectric substrates, i.e., materials, construction plans, configuration systems and theoretical foundations.

Microstrip antennas have many interesting features, such as [L-2]:

accurate representation on the surface,
low manufacturing cost,
high repeatability of workmanship,
insignificant volume,
masking of operating frequency,
simplicity of production provided that relatively advanced technologies are used,
flat shape and low weight allow the use of dielectric-based antennas on fast flying objects without fear of deterioration of their aerodynamic properties.
theory of propagation modes
method of integral equations

However, the dielectric substrate used favors the excitation of surface waves [L-3], which propagate along the dielectric plane and disturb the normal operation of the antenna. Other disadvantages of microstrip antennas are [L-4]: narrow operating bandwidth, limited power load.

These antennas allow for miniaturization of the antenna system, thus increasing its density. This causes mutual couplings that change the field distributions on aperture antennas and current distributions in linear antennas [L-5]. This situation, in turn, causes a change in the spatial characteristics of the antenna radiation and their input impedance.

Determining the mutual impedance of linear antennas is a complex issue and we are unable to obtain an exact solution, it is influenced by many elements (location, dimensions, electrical parameters of the earth, thickness of the substrate, thickness, and antenna conductivity, etc.) [L-6 ]. In the case of antennas on a dielectric substrate, the coupling analysis is even more complicated because, as previously mentioned, the operation of these antennas is significantly influenced by the occurrence of surface waves conducted through an open dielectric structure.

Historically developed methods of analyzing such systems can be divided into two basic groups:

methods in which a specific form of functions describing current distributions along wires is assumed a priori, [L-7]:
methods of searching for current distributions (directly or indirectly) [L-8].

The first group includes: the induced emf method and the Poyting vector method. They lead to identical final results and can therefore be considered as two variants of the so-called asymptotic method.

In the methods forming the second group, three fundamentally different approaches to the problem can be distinguished:

resonance theory;
theory of propagation modes [L-9];
the method of integral equations [L-10];

The first two methods are of historical importance. However, the integral equation method allows to determine the mutual impedance only for a narrow group of antenna systems. This is caused by difficulties in solving integral equations using analytical methods [L-11 ]. The exact solutions obtained by this method are basically limited to the self-impedance. Therefore, the issue of determining mutual impedance is still relevant and is even gaining in importance.

2. Mutual Impedance of Two Arbitrarily Oriented Antennas Placed on a Dielectric Layered Substrate

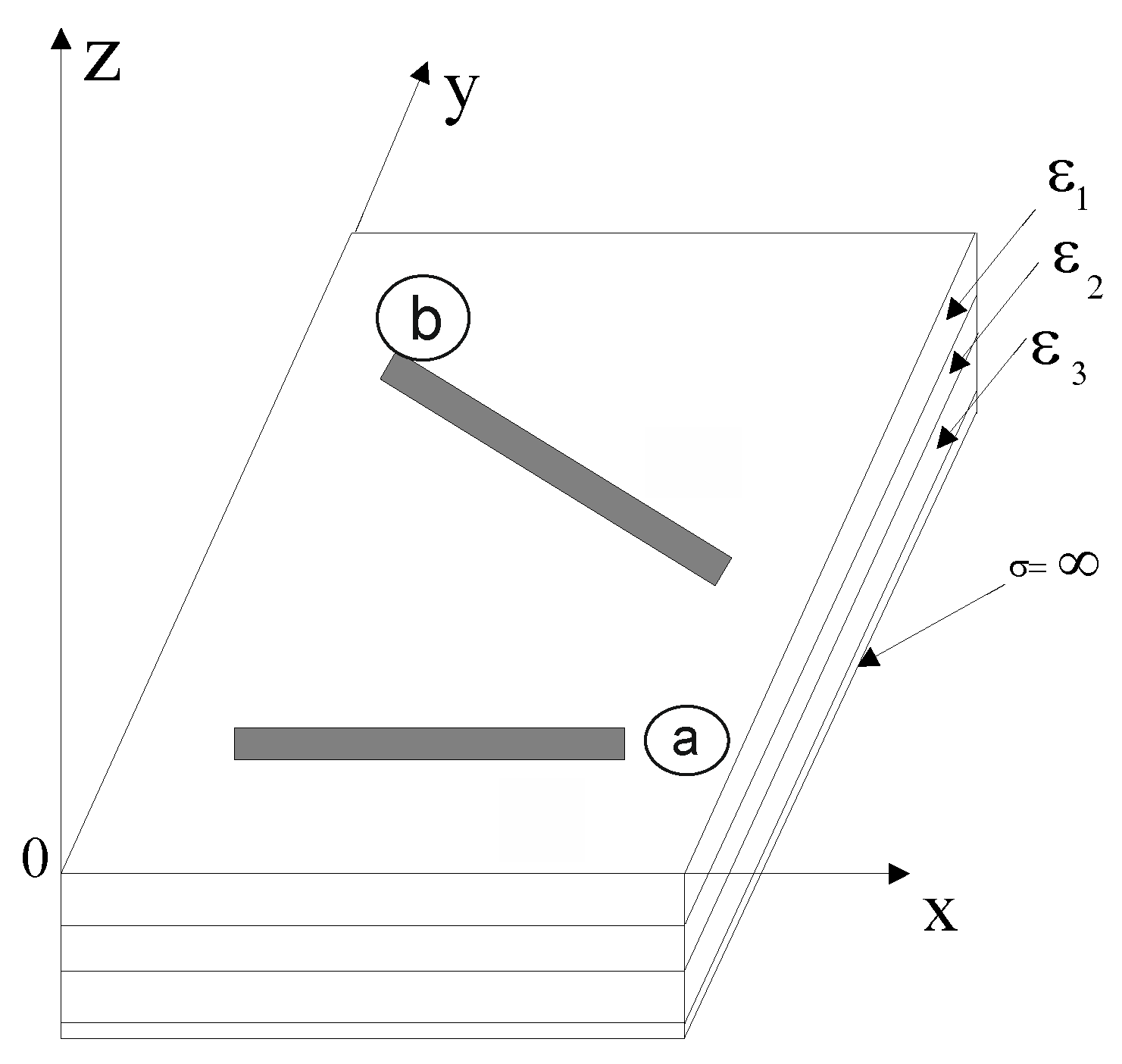
We consider an arrangement of two freely oriented microstrip antennas lying on the plane, which is also the upper surface of the multilayer dielectric substrate see Fig. 1; we are looking for expressions for:

mutual impedance,
current distribution along the analyzed antennas
radiation characteristics
self-impedance

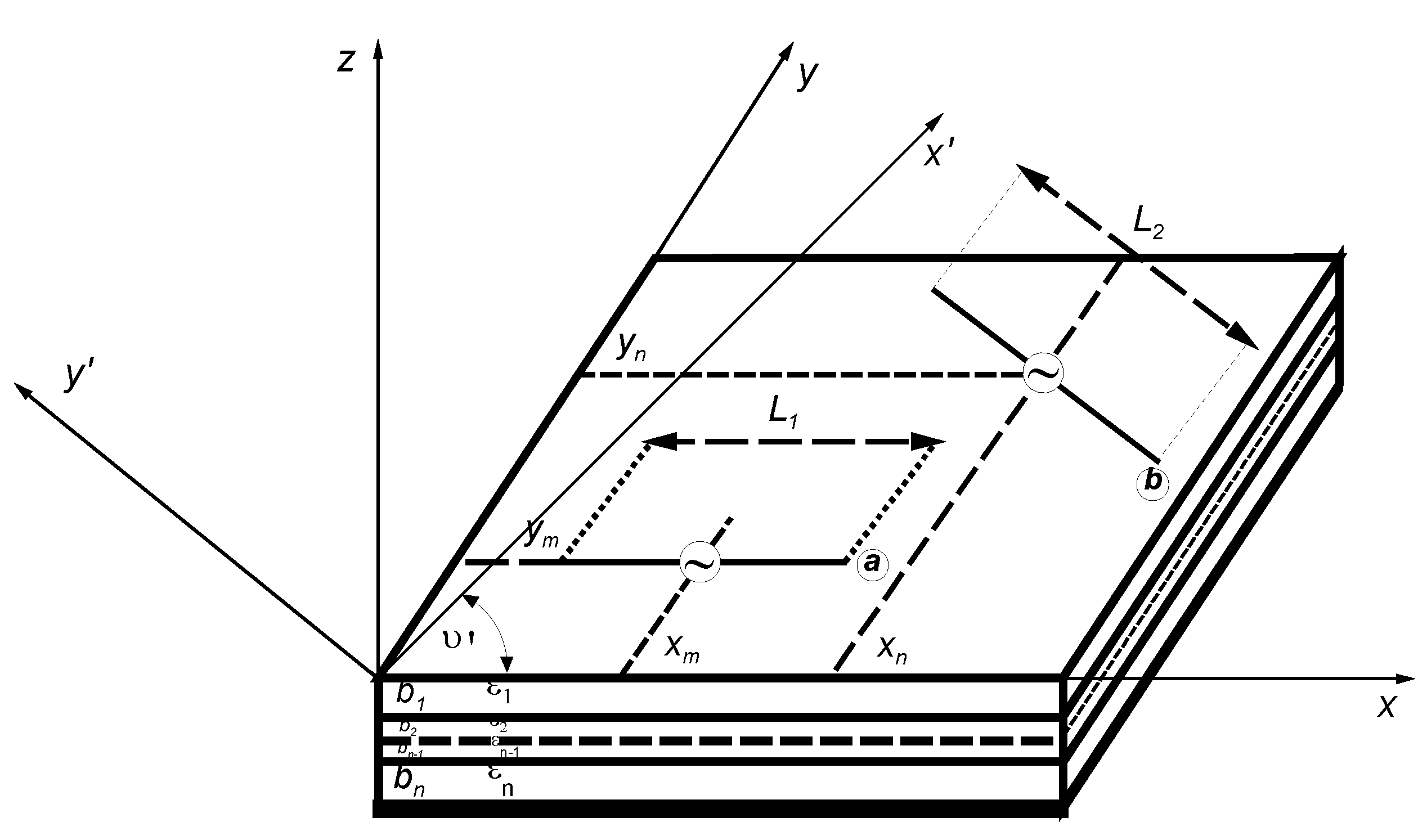
The mathematical model of this antenna system adopted for consideration is presented in: Fig. 2. Let's define the mutual impedance of two antennas, freely oriented ⓐ i ⓑ in the plane constituting the upper boundary of the dielectric layered medium.

Figure 1. Arrangement of linear antennas on a multilayer dielectric substrate [L-2].

We can treat the system presented in Fig. 2 as a four-circuit and define an impedance matrix for it.

[\begin{matrix} V_{a} \\ V_{b} \end{matrix}] = [\begin{matrix} z_{a a} & z_{a b} \\ z_{b a} & z_{b b} \end{matrix}] \cdot [\begin{matrix} i_{a} \\ i_{b} \end{matrix}]

(1)

Figure 2. Mathematical model of the antenna system shown in Fig. 1.

We consider two cases at the antenna feed point ⓑ:

antenna ⓑ shorted

V_{b} = 0

antenna ⓑ open

i_{b} = 0

this will allow us to determine the self-impedance of the antenna ⓐ, and after substituting it into the matrix equation (1) and solving it with respect to it

z_{a b}

, we obtain the mutual impedance:

z_{a b} = \frac{V_{a}}{i_{b} \cdot i_{a 0}} (i_{a 0} - i_{a}) .

(2)

We see that in order to determine the mutual impedance value, it is necessary to know the currents

i_{a}, i_{b}, i_{a 0}

for the same value of the applied voltage.

3. Application of the Method of Moments to Determine the Current Distribution along Dipoles.

We use the method of moments to determine these currents. Using the method of obtaining the elements of the impedance matrix developed by Richmond [L-13], based on the concept of reaction between sections of the base and testing functions. We assume that currents flow through the dipoles

{\underline{J}}_{m}

and

{\underline{J}}_{n}

, respectively. Their mutual interaction is described by the reaction of the electric field caused by the current flowing through one dipole with the current flowing through the other dipole. The reaction of arbitrarily oriented electric currents

{\underline{J}}_{m}

and

{\underline{J}}_{n}

takes the form of the scalar product of the electric field produced by the current

{\underline{J}}_{m}

and

{\underline{J}}_{n}

the current:

< {\underline{J}}_{m}, {\underline{J}}_{n >} > = \iint {\underline{E}}_{m} (\underline{r}) \circ {\underline{J}}_{n} (\underline{r}) d \underline{r} .

(2)

Assume that we know the Green's function

\underline{G}

for the electric field

\underline{E}

excited by a pulse (Dirac delta type) of current located in the plane

(x, y)

.Then the field

{\underline{E}}_{m} (\underline{r}) = \underline{E} ({\underline{J}}_{m}) (\underline{r})

is expressed as follows [L-14]:

{\underline{E}}_{m} (x, y) = (\underline{G} * {\underline{J}}_{m}) (x, y) = \iint \underline{G} (x - X, y - Y) {\underline{J}}_{m} (X, Y) d X d Y,

(3)

which completes the definition of the reaction described by equation (2). Using the concept of reaction and convolution functions, the mutual impedance of two dipoles ⓜ and ⓝ is defined as follows:

z_{m n} = - < {\underline{J}}_{m}, {\underline{J}}_{n} > .

(4)

We assume that one of the considered dipoles

{\underline{J}}_{m}

is directed along the x axis, its central point has coordinates

(x_{m}, y_{m})

and the electric current distribution on it has a given the form of the base function

J_{0} (x)

from above:

{\underline{J}}_{m} (x, y) = [J_{m x} (x, y), J_{m y} (x, y)] = [J_{m} (x, y), 0],

(5)

J_{m x} (x, y) \bar{=} J_{m} (x, y) = J_{o} (x - x_{m}) δ (y - y_{m})

(6)

The second dipole

{\underline{J}}_{n}

is generally directed along another axis

x^{'}

making an angleϑ with the x axis. In an orthogonal coordinate system

(x^{'}, y^{'})

, the center of the dipole is shifted by a vector

({x^{'}}_{n}, {y^{'}}_{n})

relative to the center of the system

(x^{'}, y^{'})

. We also assume, due to the Galerkin method [L-15], used later, that the current distribution on this dipole also takes the form of the J₀ function:

(7)

(8)

We assume that the coordinate system

(x^{'}, y^{'})

is a shifted replica of the system

(x, y)

by a vector

(X, Y)

and rotated by an angle ϑ::

x^{'} = (x - X) \cos ϑ - (y - Y) \sin ϑ,

(9)

y^{'} = (x - X) \sin ϑ + (y - Y) \cos ϑ .

(10)

We obtain analogous expressions for the dipole shift vector (n):

{x^{'}}_{n} = (x_{n} - X) \cos ϑ - (y_{n} - Y) \sin ϑ .

(11)

{y^{'}}_{n} = (x_{n} - X) \sin ϑ + (y_{n} - Y) \cos ϑ,

(12)

and for the wave vectors

(k_{x}, k_{y})

and

({k^{'}}_{x}, {k^{'}}_{y})

(x, y)

(x^{'}, y^{'})

:, associated with these coordinate systems:

{k^{'}}_{x} = k_{x} \cos ϑ - k_{y} \sin ϑ,

(13)

{k^{'}}_{y} = k_{x} \sin ϑ + k_{y} \cos ϑ

(14)

For further calculations, we express the quantities associated with the system

(x, y)

in terms of quantities associated with the system

(x^{'}, y^{'})

Below, until further notice, we assume the common location of the means of the arrangements:

(x, y)

(x^{'}, y^{'})

Deriving the equation for mutual impedance therefore comes down to calculating the expression:

z_{m n} = - < {\underline{J}}_{m}, {\underline{J}}_{n} > = - {\iint (\underline{E}}_{m} \circ {\underline{J}}_{n}) d x d y = - \iint (E_{m x} J_{n x} + E_{m y} J_{n y}) d x d y

(15)

integral function in the form of a scalar product of two components

E_{m}

and

J_{n}

with components reduced to the inverse Fourier transform from specific expressions [L-16]:

E_{m x} (\underline{r}) = (G_{x x} * J_{m x} + G_{x y} * J_{m y}) (\underline{r}) = (G_{x x} * J_{m}) (\underline{r}) = {(2 π)}^{2} F^{- 1} \{[F (G_{x x}) F (J_{m})]\} (\underline{r})

(16)

E_{m y} (\underline{r}) = (G_{y x} * J_{m x} + G_{y y} * J_{m y}) (\underline{r}) = (G_{y x} * J_{m}) (\underline{r}) = {(2 π)}^{2} F^{- 1} \{[F (G_{y x}) F (J_{m})]\} (\underline{r})

(17)

From the properties of the Fourier transform, we obtain the explicit form of the integrand function in (15) expressed in terms of the rotation angle ϑ and the Fourier transform [L-17]:of the components

G_{x x}

and

G_{y x}

Green's function

J_{m}

and

J_{n}

currents and:

\begin{array}{l} {\underline{E}}_{m} (\underline{r}) \circ {\underline{J}}_{n} (r) = {(2 π)}^{2} F^{- 1} \{[F (G_{x x}) F (J_{m})] * F (J_{n})\} (\underline{r}) \cos ϑ + \\ - {(2 π)}^{2} F^{- 1} \{[F (G_{y x}) F (J_{m})] * F (J_{n})\} (\underline{r}) \sin ϑ . \end{array}

(18)

For currents

{\underline{J}}_{m}

and

{\underline{J}}_{n}

, formulas (5) and (6) apply. Hence:

F (J_{m}) (k_{x}, k_{y}) = F (J_{0}) (k_{x}, k_{y}) e^{[- i (k_{x} x_{m} + k_{y} y_{m})]},

(19)

\begin{array}{l} F (J_{n}) ({k^{'}}_{x}, {k^{'}}_{y}) = F (J_{0}) ({k^{'}}_{x}, {k^{'}}_{y}) e^{[- i ({k^{'}}_{x} {x^{'}}_{m} + {k^{'}}_{y} {y^{'}}_{m})]} = \\ = F (J_{0}) (k_{x} \cos ϑ - k_{y} \sin ϑ, k_{x} \sin ϑ + k_{y} \cos ϑ) e^{[- i (k_{x} x_{n} + k_{y} y_{n})]} . \end{array}

(20)

Since we are considering an isotropic medium, the Green's function and its Fourier transform are symmetric with respect to the coordinate inversion[L-18]. We also assume that the basis functions are symmetric. From formulas (18) ÷ (19) we finally obtain the integral expression for the mutual impedance of two freely oriented base dipoles:

\begin{array}{l} z_{m n} = - \iint {\underline{E}}_{m} (x, y) \circ {\underline{J}}_{n} (x, y) d x d y = \\ - {(2 π)}^{- 2} \iint \{F (G_{x x}) (k_{x}, k_{y}) F (J_{0}) (k_{x}, k_{y}) F (J_{0}) ({k^{'}}_{x}, {k^{'}}_{y}) \cos ϑ \times e^{[i k_{x} (x_{m} - x_{n})]} e^{[i k_{y} (y_{m} - y_{n})]} + \\ - F (G_{y x}) (k_{x}, k_{y}) F (J_{0}) (k_{x}, k_{y}) F (J_{0}) ({k^{'}}_{x}, {k^{'}}_{y}) \sin ϑ \times e^{[i k_{x} (x_{m} - x_{n})]} e^{[i k_{y} (y_{m} - y_{n})]}\} d k_{x} d k_{y} \end{array}

(21)

To effectively determine the mutual impedance

z_{m n}

, the form of the J₀ basis functions [L-19] must be optimally selected and the components of the Green's function must be derived. For a sinusoidal symmetrical distribution of the base current J₀ we get:

J_{0} (x, y) = \frac{\sin k_{e f} (L_{N} - |x|)}{\sin k_{e f} L_{N}} Θ (L_{N} - |x|) δ (y)

(22)

F (J_{0}) (k_{x}, k_{y}) = - 2 k_{e f} (2 π)^{- 2} \frac{1}{\sin k_{e f} d} \frac{\cos k_{x} L_{N} - \cos k_{e f} L_{N}}{k_{x}^{2} - {k_{e f}}^{2}}

(23)

where:

d - length of the base (testing) section,

k_{e f}

- the parameter (in particular

k_{e f} = k \sqrt{\frac{ε_{r} + 1}{2}}

) determines the convergence of the integral,

k - wavenumber,

2 π / λ

ε- electrical permittivity of the medium,

Θ- is the Heaviside function

Θ (x) = \{\begin{matrix} 1, f o r x \geq 0 \\ 0, f o r x < 0 . \end{matrix}

(24)

The J₀ function has a unit value on the x-axis and a unit impulse on the y-axis, and its carrier lies on the x-axis along the section

- d < x < d

and on the y-axis at the point

y = 0

4. Mutual Impedance of Two Antennas of Any Length and Current Distribution

The above-derived relationships for the mutual impedance of two arbitrarily oriented dipoles assume the same current distribution on both dipoles. In general, however, the current distribution and antenna lengths are arbitrary and solving the problem of coupling such antennas requires the use of the method of moments [L-20] or the Galerkin method as its special case. The basic relationships necessary to solve the general case of antenna coupling using the Galerkin method will be presented below. The expression (21) for the mutual impedance of two dipoles with a given current distribution covers both the case of their location on two separate antennas, as well as in different places of the same antenna. In a special case, for the identical position of both dipoles, we obtain formulas for the self-impedance of the dipole. Let us consider the case of two infinitely thin linear antennas ⓐ end ⓑ (Fig. 2) placed on a dielectric layered substrate. Without loss of generality, we assume that the antenna ⓐ is parallel to the x axis and the antenna ⓑ is directed at an angle ϑ to the x axis. We model the flow of current induced in the antenna ⓐ by the distribution of base currents

{\underline{J}}_{m}

(5) and (6). The distribution of current induced in the antenna ⓐ then takes the form (

y_{m} = c o n s t

J_{a} (x) = \sum_{m} i_{m} J_{m} (x, y_{m}) = \sum_{m} i_{m} J_{0} (x - x_{m}),

(25)

and the electric field induced by this current is

E_{a} (x, y) \equiv E (J_{a}) (x, y) = \sum_{m} i_{m} E_{m} (x, y)

(26)

Similarly, the distribution of the induced current

J_{b} (x^{'})

in the antenna ⓑ and the electric field

E_{b} (x, y)

generated by this current are expressed as follows:

J_{b} (x) = \sum_{n} i_{n} J_{n} (x, y) = \sum_{n} i_{n} J_{0} (x n - x_{n}^{n}),

(27)

E_{b} (x, y) \equiv E (J_{b}) (x, y) = \sum_{n} i_{n} E_{n} (x, y),

(28)

Let the number of base dipoles on antennas ⓐ and ⓑ be 2M+1, respectively and 2N+1. The center of the base dipole coincides with the end of the adjacent base dipole. So the centers of the antenna ⓐ base dipoles are located at the points:

x_{\pm m} = x_{a} \pm m L_{N}; y = y_{m} = c o n s t,

(29)

and the base dipoles ⓑ of the antenna are located at the following points:

x_{\pm n} = x_{b} \pm n L_{N} \cos ϑ; y_{\pm n} = y_{b} \pm n L_{N} \sin ϑ,

(30)

where x_a and x_b denote the central points of antennas ⓐ and ⓑ. Let us create a vector of induced currents on both antennas from the quantities defined in this way:

J \equiv {[J_{k}]}^{T} = {[J_{- M}, ... J_{a 0}, ..., J_{M}, J_{- N}, ..., J_{b 0}, ..., J_{+ N}]}^{T},

(31)

where the symbol "T" means transposition, the indicators a₀ and b are the central points of the antenna ⓐ and antenna ⓑ, k=1,..,2M+2N+2, the first 2M+1 terms mean the base currents in the antenna ⓑ and the remaining 2N+1 terms mean the base currents in the antenna ⓑ. In a similar way, we create a vector of electromagnetic fields

E_{k}

generated by induced currents

J = [J_{k}]

and a vector of amplitudes of the

I_{k} = [i_{k}]

base currents. So we can write expressions for the current induced in the antennas ⓐ and ⓑ.

J (x, y) = \sum_{k} i_{k} J_{k} (x_{k}, y_{k}) = \sum_{k} i_{k} J_{0} (x - x_{k}) δ (y - y_{k})

(32)

and to the electric field induced by this current

E (x, y) \equiv E (J) (x, y) = \sum_{k} i_{k} E_{k} (x, y)

(33)

We assume that both antennas are made of perfect conductors

(σ \to \infty)

and the excitation of these antennas is modeled with the delta gap generator approximation [L-21]. This means that on the surface of both antennas the total electric field disappears, i.e.:

E^{(i)} (x, y) \equiv E (J^{(i)}) (x, y) = - E (J) (x, y)

(34)

where:

J^{(i)} = [J_{k}^{(i)}]

means the vector of currents stimulating the antenna, analogous to the previously defined vectors.

So we can write:

J = \sum_{k} i_{k} J_{k}

(35)

E = - E^{(i)} = \sum_{k} i_{k} E_{k} .

(36)

The above equation means that the reaction between excitation currents

J^{(i)}

and induced J is:

< J^{(i)}, J_{l} > = - \sum_{k} i_{k} < J_{k}, J_{l} > .

(37)

Using the reciprocity theorem we get[M1] :

< J_{l}, J^{(i)} > = < J^{(i)}, J_{l} > = - \sum_{k} i_{k} < J_{l}, J_{k} >

(38)

Based on the above relation, let us define generalized stress vectors

[V]

and generalized currents

[I]

[V] = [\begin{matrix} V_{1} \\ \cdot \\ \cdot \\ V_{2 M + 2 N + 1} \end{matrix}] [I] = [\begin{matrix} I_{1} \\ \cdot \\ \cdot \\ I_{2 M + 2 N + 1} \end{matrix}]

(39)

where:

V_{k} = < J_{k}, J^{(i)} > = < J^{(i)}, J_{k} >

(40)

The relationship between the vector of generalized voltages

[V]

and the vector of generalized currents

[I]

takes the form for components

V_{l} = \sum_{k} Z_{l k} I_{k}

(41)

and is expressed by the generalized impedance matrix [Z]

[Z] = [\begin{matrix} Z_{1, 1} & Z_{1, 2 M + 2 N + 2} \\ \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot \\ Z_{2 M + 2 N + 2, 1} & Z_{2 M + 2 N + 2, 2 M + 2 N + 2} \end{matrix}] \begin{matrix} , \end{matrix}

(42)

between the individual currents induced on both antennas. The elements of the generalized impedance matrix are therefore expressed through the reactions of the corresponding currents induced in the antennas:

Z_{k, l} = - 〈J_{k}, J_{l}〉 .

(43)

Depending on the location of the current elements J_k, and J_l we get: for the current J_k located on the antenna ⓐ, and the current J_l on the antenna ⓐ

where:

k = 1, ..., 2 M + 1, l = 2 M + 2, ..., 2 M + 2 N + 2

for the current located on the antenna ⓐ, and the current

J_{k}

on the antenna ⓑ:

k = 1, ..., 2 N + 1, l = 2 N + 2, ..., 2 N + 2 M + 2

(see formula (21)

\begin{array}{l} z_{k l} = - \iint {\underline{E}}_{k} (x, y) \circ {\underline{J}}_{l} (x, y) d x d y = \\ - {(2 π)}^{- 2} \iint \{F (G_{x x}) (k_{x}, k_{y}) F (J_{0}) (k_{x}, k_{y}) F (J_{0}) ({k^{'}}_{x}, {k^{'}}_{y}) \cos ϑ \times e^{[i k_{x} (x_{k} - x_{l})]} e^{[i k_{y} (y_{k} - y_{l})]} + \\ - F (G_{y x}) (k_{x}, k_{y}) F (J_{0}) (k_{x}, k_{y}) F (J_{0}) ({k^{'}}_{x}, {k^{'}}_{y}) \sin ϑ \times e^{[i k_{x} (x_{k} - x_{l})]} e^{[i k_{y} (y_{k} - y_{l})]}\} d k_{x} d k_{y}, \end{array}

(44)

for both currents located on the antenna ⓐ:

k = 1, ..., 2 M + 1, l = 1, ..., 2 M + 1

\begin{array}{l} z_{k l} = - \iint {\underline{E}}_{k} (x, y) \circ {\underline{J}}_{l} (x, y) d x d y = \\ - {(2 π)}^{- 2} \iint \{- F (G_{x x}) (k_{x}, k_{y}) F (J_{0}) (k_{x}, k_{y}) F (J_{0}) (k_{x}, k_{y}) \times e^{[i k_{x} (x_{k} - x_{l})]} e^{[i k_{y} (x_{y} - x_{l})]}\} d k_{x} d k_{y}, \end{array}

(45)

for both currents located on the antenna ⓑ:

k = 1, ..., 2 N + 1, l = 1, ...2 N + 1

we repeat the construction analogous to the construction of formula 21,

(k = m, l = n)

Deriving the equation for mutual impedance comes down to calculating the expression:

z_{m n} = - < {\underline{J}}_{m}, {\underline{J}}_{n} > = - {\iint (\underline{E}}_{m} \circ {\underline{J}}_{n}) d x d y = - \iint (E_{m x} J_{n x} + E_{m y} J_{n y}) d x d y

(46)

integral function in the form of a scalar product of two components

E_{m}

and

J_{n}

with components reduced to the inverse Fourier transform from specific expressions:

\begin{array}{l} E_{n x} (\underline{r}) = (G_{x x} * J_{n x} + G_{x y} * J_{n y}) (\underline{r}) = \\ = {(2 π)}^{2} \cos ϑ F^{- 1} \{[F (G_{x x}) F (J_{n})]\} (\underline{r}) - {(2 π)}^{2} \sin ϑ F^{- 1} \{[F (G_{x y}) F (J_{n})]\} (\underline{r}), \end{array}

(47)

\begin{array}{l} E_{n y} (\underline{r}) = (G_{y x} * J_{n x} + G_{y y} * J_{n y}) (\underline{r}) = \\ = {(2 π)}^{2} \cos ϑ F^{- 1} \{[F (G_{y x}) F (J_{n})]\} (\underline{r}) - {(2 π)}^{2} \sin ϑ F^{- 1} \{[F (G_{y y}) F (J_{n})]\} (\underline{r}), \end{array}

(48)

From the properties of the Fourier transform we obtain the explicit form of the integrand function in expressed in terms of the rotation angle ϑ and Fourier transforms of components

G_{x x}

and

G_{y x}

Green's functions and currents

J_{m}

and

J_{n}

\begin{array}{l} {\underline{E}}_{n} (\underline{r}) \circ {\underline{J}}_{n} (\underline{r}) = {(2 π)}^{2} F^{- 1} \{[F (G_{x x}) F (J_{n})] * F (J_{n})\} (\underline{r}) \cos^{2} ϑ + \\ - {(2 π)}^{2} F^{- 1} \{[F (G_{y x}) F (J_{n})] * F (J_{n})\} (\underline{r}) \cos ϑ \sin ϑ + \\ - {(2 π)}^{2} F^{- 1} \{[F (G_{x y}) F (J_{n})] * F (J_{n})\} (\underline{r}) \sin ϑ \cos ϑ + \\ + {(2 π)}^{2} F^{- 1} \{[F (G_{y y}) F (J_{n})] * F (J_{n}) * F (J_{n})\} (\underline{r}) \sin^{2} ϑ . \end{array}

(49)

For currents

{\underline{J}}_{m}

and

{\underline{J}}_{n}

, formulas (5) and (6) apply. Hence:

F (J_{m}) (k_{x}, k_{y}) = F (J_{0}) (k_{x}, k_{y}) \exp [- i (k_{x} x_{m} + k_{y} y_{m})]

\begin{array}{l} F (J_{n}) (k_{x} n, k_{y} n) = F (J_{0}) (k_{x} n, k_{y} n) \exp [- i (k_{x} n x_{m} n + k_{y} n y_{m} n)] \\ = F (J_{0}) (k_{x} \cos ϑ - k_{y} \sin ϑ, k_{x} \sin ϑ + k_{y} \cos ϑ) \exp (- i (k_{x} x_{n} + k_{y} y_{n})) \end{array}

(51)

Since we are considering an isotropic medium, the Green's function and its Fourier transform are symmetric with respect to the coordinate inversion [L-22]. We also assume symmetric basis functions.

From formulas 46 ÷ 51 we finally obtain the integral expression for the mutual impedance of two base dipoles located on the antenna ⓑ

(k = m, l = n)

\begin{array}{l} z_{m n} = - \iint {\underline{E}}_{m} (x, y) \circ {\underline{J}}_{n} (x, y) d x d y = \\ - {(2 π)}^{- 2} \iint \{F (G_{x x}) (k_{x}, k_{y}) F (J_{0}) ({k^{'}}_{x}, {k^{'}}_{y}) F (J_{0}) ({k^{'}}_{x}, {k^{'}}_{y}) \cos^{2} ϑ \times e^{[i k_{x} (x_{m} - x_{n})]} e^{[i k_{y} (y_{m} - y_{n})]} \\ - F (G_{y x}) (k_{x}, k_{y}) F (J_{0}) ({k^{'}}_{x}, {k^{'}}_{y}) F (J_{0}) ({k^{'}}_{x}, {k^{'}}_{y}) \cos ϑ \sin ϑ \times e^{[i k_{x} (x_{m} - x_{n})]} e^{[i k_{y} (y_{m} - y_{n})]} + \\ - F (G_{x y}) (k_{x}, k_{y}) F (J_{0}) ({k^{'}}_{x}, {k^{'}}_{y}) F (J_{0}) ({k^{'}}_{x}, {k^{'}}_{y}) \cos ϑ \sin ϑ \times e^{[i k_{x} (x_{m} - x_{n})]} e^{[i k_{y} (y_{m} - y_{n})]} + \\ + F (G_{y y}) (k_{x}, k_{y}) F (J_{0}) ({k^{'}}_{x}, {k^{'}}_{y}) F (J_{0}) ({k^{'}}_{x}, {k^{'}}_{y}) \sin^{2} ϑ \times e^{[i k_{x} (x_{m} - x_{n})]} e^{[i k_{y} (y_{m} - y_{n})]}\} d k_{x} d k_{y} . \end{array}

(52)

In this way, all elements of the generalized impedance matrix

[Z]

, as well as the elements of the generalized admittance matrix, are determined

[Y]

[Y] = {[Z]}^{- 1}

(53)

By multiplying both sides of equation (41) by the matrix

[Y]

we get:

[Y] [V] = [I]

(54)

which determines the currents

[V]

induced on them for a given excitation of the antennas:

J = \sum_{k} \sum_{l} Y_{k l} J_{k} V_{l}

(55)

5. Determination of Currents i_a, i_b, i_a0

As follows from relation (55), the method of moments provides a solution for induced currents

{\underline{J}}_{s}

when, in the case of impedance calculation, knowledge of the current value

{\underline{J}}_{i}

(induced at the short-circuited antenna input ⓑ) is needed. However, within the adopted model of feeding the delta-gap generator antenna ⓐ, the V = 1 supply current

{\underline{J}}_{i} = {\underline{J}}_{s}

, i.e., the current thread (source) in the gap, has a limit value of the current induced at the break boundary points [L-23]. Hence, the determination

{\underline{J}}_{s}

also determines the total current. For an exact solution, an infinite sequence of basic functions is necessary. We limit the number of basic functions to 2M+1, so we obtain an approximate solution. For the power supply model adopted

v_{a} = V_{M + 1}

in this way, it is the only non-zero component of the vector

[V] = [\begin{matrix} 0 \\ V_{M + 1} \\ 0 \\ 0 \\ 0 \end{matrix}] \begin{matrix} . \end{matrix}

(56)

current values are:

J = \sum_{k = 1}^{2 M + 2 N + 2} Y_{k, M + 1} J_{k} V_{M + 1}

(57)

in case (I) the antenna ⓑ is short-circuited

V_{b} = 0

(i_b=0) we determine the current i_a0

in the case (II) of an open antenna ⓑ, we determine the currents i_a and i_b.

Case (I):

For the current vector, the currents induced in the antennas are expressed by:

[\begin{matrix} I_{1} \\ I_{M + 1} = i_{10} \\ . \\ 0. \\ I_{2 M + 2 N + 2} \end{matrix}] = [\begin{matrix} Y_{1, 1} & . & . & . & Y_{2 M + 2 N + 2, 1} \\ . & . \\ . & . \\ . & . \\ Y_{1, 2 M + 2 N + 2} & . & . & . & Y_{2 M + 2 N + 2, 2 M + 2 N + 2} \end{matrix}] [\begin{matrix} 0 \\ V_{M + 1} \\ 0 \\ 0 \\ 0 \end{matrix}]

(58)

which leads to the equation for current

i_{a 0}

i_{a 0} = I_{M + 1} J_{M + 1} = J_{M + 1} Y_{M + 1, M + 1} V_{M + 1}

(59)

Case (II):

For the current vector, the currents induced in the antennas are expressed by:

[\begin{matrix} I_{1} \\ I_{M + 1} = i_{1} \\ . \\ I_{2 M + N + 1} = i_{2} \\ I_{2 M + 2 N + 2} \end{matrix}] = [\begin{matrix} Y_{1, 1} & . & . & . & Y_{2 M + 2 N + 2, 1} \\ . & . \\ . & . \\ . & . \\ Y_{1, 2 M + 2 N + 2} & . & . & . & Y_{2 M + 2 N + 2, 2 M + 2 N + 2} \end{matrix}] [\begin{matrix} 0 \\ V_{M + 1} \\ 0 \\ 0 \\ 0 \end{matrix}] \begin{matrix} , \end{matrix}

(60)

which leads to the equations for currents

i_{a}

i_{b}

i_{a} = I_{M + 1} J_{M + 1} = J_{M + 1} Y_{M + 1, M + 1} V_{M + 1}

(61)

i_{b} = I_{2 M + N + 1} J_{2 M + N + 1} = J_{2 M + N + 1} Y_{2 M + N + 1, M + 1} V_{M + 1} .

(62)

As a result, equations (1), (59), (61), (62) give the value of the mutual impedance

z_{a b}

of two arbitrarily oriented, infinitely thin antennas placed on a dielectric layered substrate.

6. Expression of Generalized Impedance z_mn in Integral Form

Having determined the Green's functions and the assumed form of the base current [L-24] further considerations will be reduced to presenting the generalized impedance zmm written in equations (44, 45, 52) as a double integral, where the integral function will be presented in an explicit form. And after substituting, for example, into expression (44) and after transformations, we obtain the following expression describing the generalized impedance

\begin{array}{l} z_{m n} = - {(2 π)}^{- 4} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} \{F [G (k_{x} - k_{x}^{'}; k_{y} - k_{y}^{'})] F [J_{o} (k_{x} - k_{x}^{'})] \cdot \\ \cdot F [J_{o} (k_{x} - k_{x}^{'})] \cdot F [J_{o} (k_{x})] e^{- i (k_{x} - k_{x}^{'}) x_{m} - k_{x}^{'} x_{n} - i (k_{y} - k_{y}^{'}) y_{m} - i k_{y}^{'} y_{n} + i k_{x} x + i k_{y} y} d k_{y}^{'} d k_{x}^{'} d k_{y} d k_{x} d y d x \end{array}

(63)

The integral described by expression (63) converges slowly, moreover, it contains poles related to the occurrence of a surface wave and requires great caution when calculating in the vicinity of the source. There are two ways to calculate the integral. When calculating in the spatial domain, the spectral variables k_x and k_y are converted into variables in the polar coordinate system ϕ and K. Using the properties of the spectral Green's functions, integration over the variable ϕ is performed analytically. The integral (63) therefore reduces to the form:

\int_{x} \int_{y} \int_{x_{0}} \int_{y_{0}} \int_{0}^{\infty} J_{m} (x) G (x, y, x_{0}, y_{0}, K) J_{n} (x_{0}, y_{0}) d K d y_{0} d x_{0} d y d x

(64)

By integrating the function G over the variable K, we obtain the field at point (x,y) produced by the source placed at point (x_o, y_o), hence the method is similar to the standard method of moments used to solve linear antennas and can be used in calculations previously learned and developed techniques (e.g. use of Toeplitz matrix symmetry). The main inconvenience of this method, which makes the calculation of antennas with very thin substrates very difficult or even impossible, is the singularity that occurs when the point (x,y) approaches the source in the integration process. Despite this, it is used by some authors.

The second approach to calculating the integral requires moving to the spectral domain. The integration over the spatial variables in (63) can then be performed analytically. Occurrence. exponential factors means the Fourier transform of the functions J_m and J_n. These transforms can usually be written using simple formulas. Then the integral (63) reduces to

\int_{- \infty}^{\infty} \int_{- \infty}^{\infty} F_{m} (k_{x}, k_{y}) \underline{G} (k_{x}, k_{y}) F_{n} (k_{x}, k_{y}) d k_{y} d k_{x}

(65)

where F_m and F_n are the Fourier transforms of the basis and test functions, respectively.

This integral is calculated numerically, but it is the most time-consuming process due to the slow convergence of the integral. Slow convergence is caused by the fact that the singularities of the integral in the spatial domain have been removed by converting the domain into a spectral domain and have become "scattered" in this domain. Calculating the integral (63) in the spectral domain allows it to be easily extended to the case of an infinite array of antennas. Further analysis is carried out in the spectral domain.

7. Results of calculations and measurements

The analysis was carried out, the singularities occurring in the integrand expressions were determined and examined, which allowed the development of a computer program to determine the sought quantities. In the process of theoretical analysis and experimental antennas made on a dielectric substrate with an electric permittivity of ε₁= 4.6 were tested in the following systems:

a. ε₁=4.6, b=1.5mm, tanδ=10^-3 , ε₂=ε₀, b₁=0mm,

b. ε₁=4.6, b=1.5mm, tanδ=10^-3, ε₂=ε₀,, b₁=3mm.

The Fig. shows the results of calculations of the mutual impedance components, i.e. R₁₂(α) and X₁₂(α) for two antennas oriented in parallel, for array a and b.

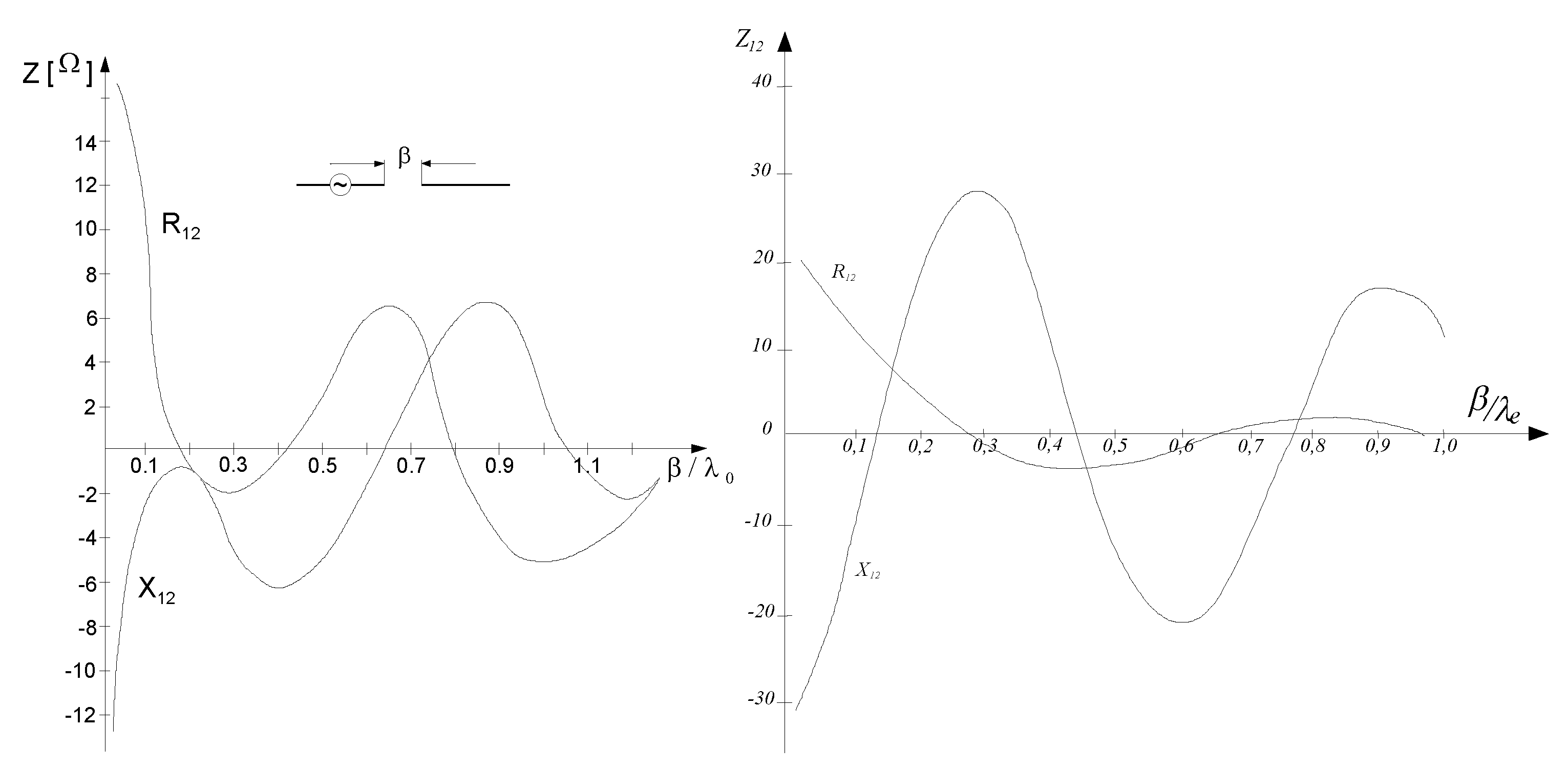
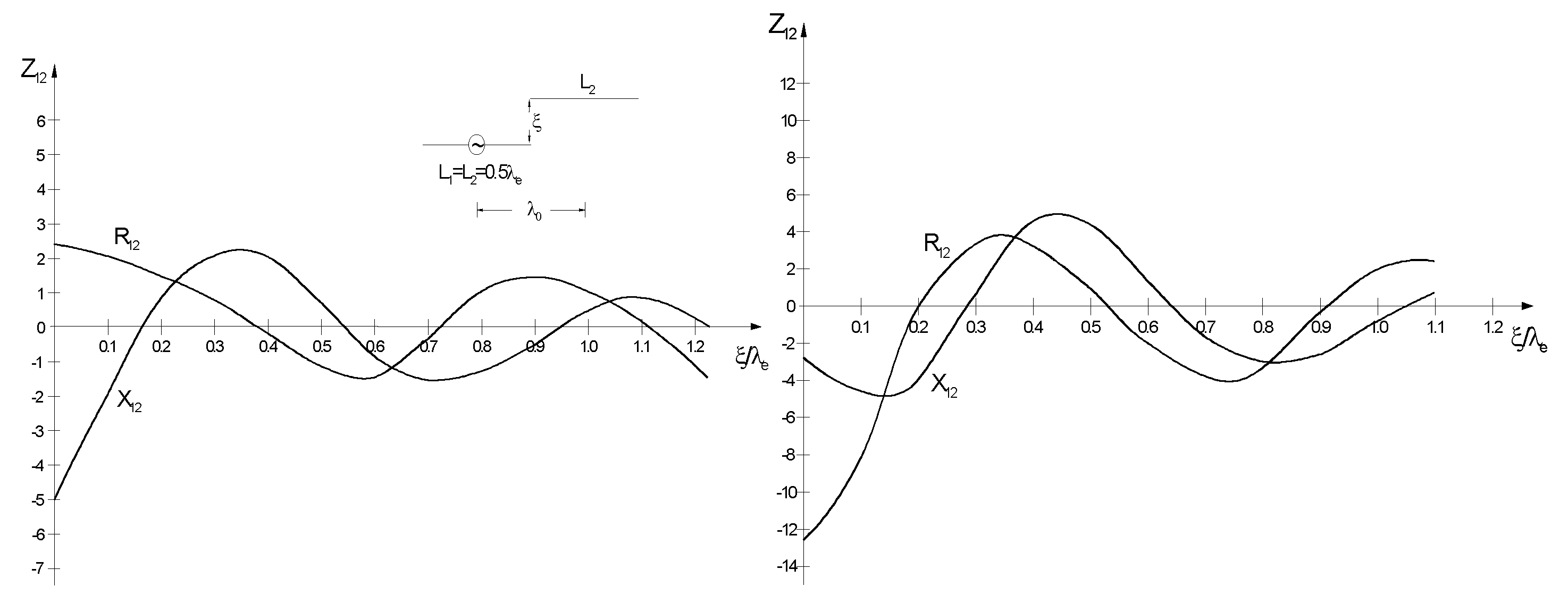
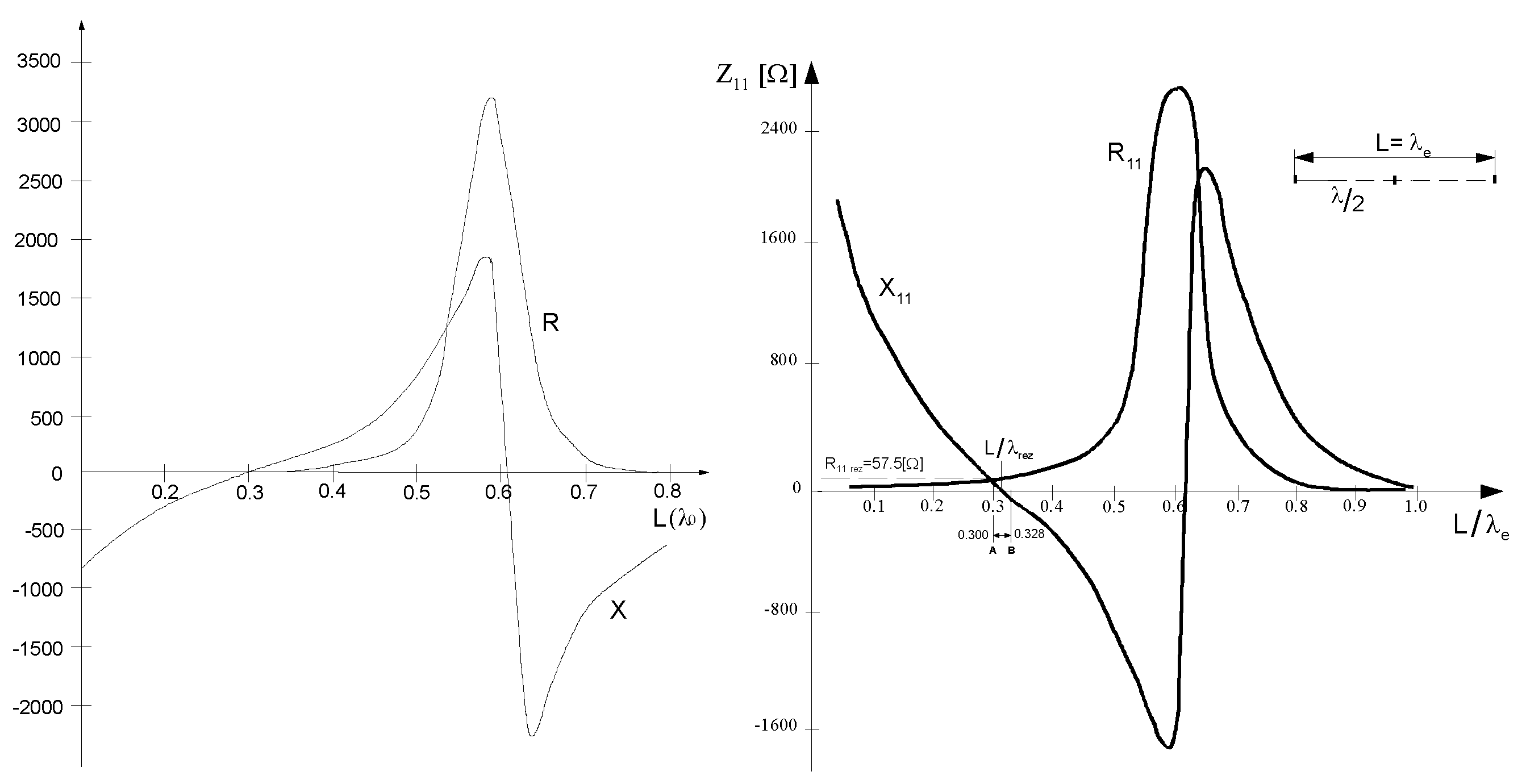
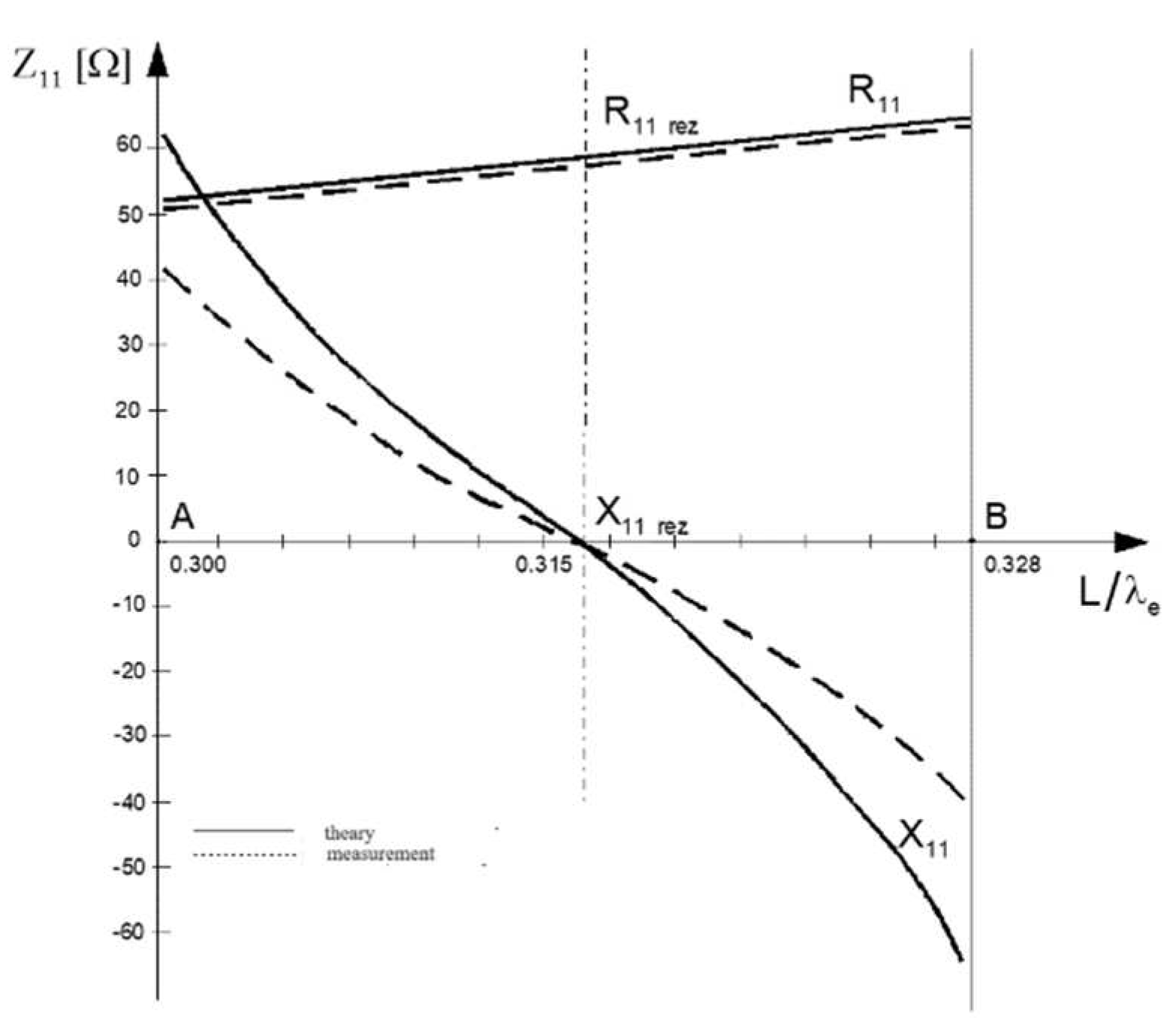
Fig. 4 shows similar impedance components obtained for two antennas lying along the same straight line. Fig. 5 shows the mutual impedance for a typical mutual arrangement of dipoles used in wall antennas. Fig. 6 shows the input impedance of the antenna as a function of its geometric length. Measurements were made at the resonance frequency and compared with the appropriate calculations, see Fig. 7. Good agreement of the results was obtained.

Figure 3. Mutual impedance of dipoles as a function of the mutual distance α.

Figure 4. Mutual impedance of dipoles as a function of their mutual distance β.

Figure 5. Mutual impedance of dipoles as a function of their mutual distance ξ.

Figure 6. Input impedance of the dipole as a function of its length (calculated).

Figure 7. Measured and calculated antenna input impedance (for the resonant frequency).

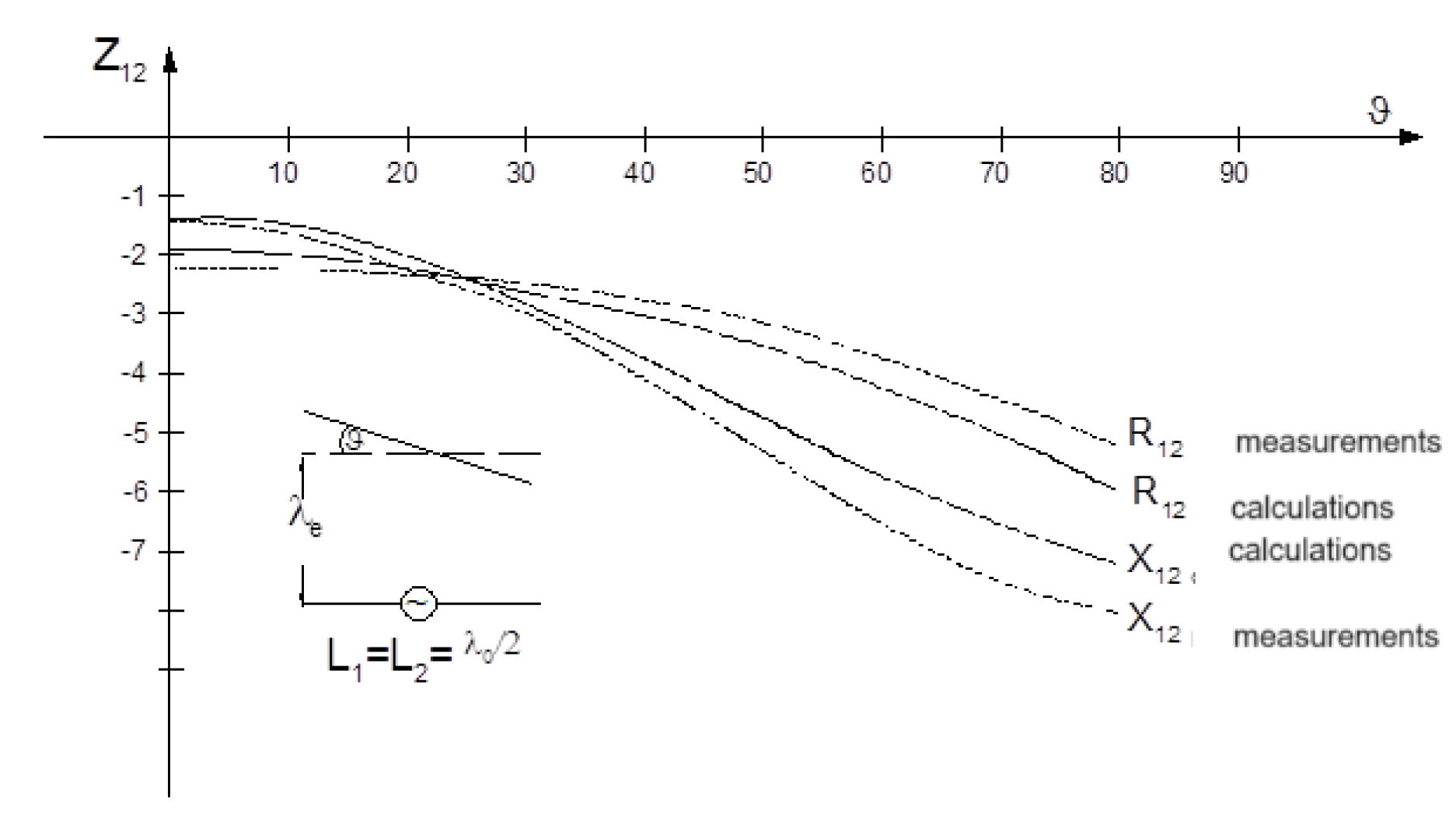
The results of calculations and measurements for any mutual position of the antennas as a function of the rotation angle are presented in Fig. 8.

Figure 8. Mutual impedance of dipoles as a function of rotation angle

ϑ

Figure 8. Mutual impedance of dipoles as a function of rotation angle

ϑ

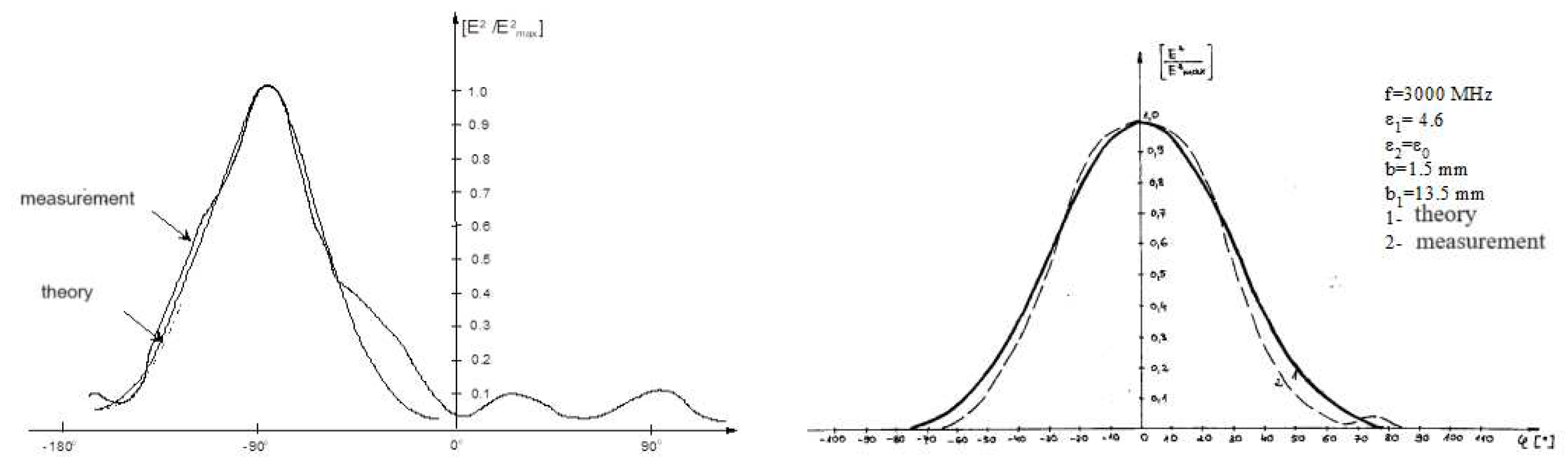
Using this method, we can also determine the radiation characteristics of antennas by summing the field generated by individual base (test) sections. This possibility is illustrated in Figure 9.

Figure 9. Radiation characteristics of the antenna.

Comparing the results of the obtained calculations with the experimental results, a good agreement is visible. The obtained results are of great practical importance because they serve to better understand the couplings in antenna systems and can be used to design antenna arrays on multilayer substrates.

8. Conclusions

Microstrip antennas combine field and peripheral issues and require the use of analytical methods with a high degree of complexity. Therefore, at present, there are no standard methods that can be used in engineering practice. The work is a step towards filling these gaps. It covers all issues related to the analysis of couplings of arbitrarily placed linear antennas on a multilayer dielectric and generalizes the obtained results to antenna arrays.

The first part of the work presents a general analytical method for determining the mutual impedance of linear antennas placed on a multilayer dielectric substrate with a perfectly conductive screen, assuming any orientation of the antennas located on the dielectric plane, taking into account the influence of the substrate.

The use of the method of moments allowed, in the course of numerical calculation of mutual impedance, to determine the current distribution along the analyzed structure, the self-impedance of the active antenna and the radiation characteristics. The problem was reduced to an exact solution of the Hertzian dipole radiation for a layered system. The obtained solution was used to synthesize a solution for the case of finite dimensions of the antenna, using the standard formalism of Green's functions, representing the field coming from a point source.

These functions satisfy the inhomogeneous Helmholtz equation, the Sommerfeld radiation condition and the appropriate boundary conditions. Using Fourier transforms and their properties, an analytical expression for the generalized impedance was determined in the form of a double integral. Due to the fact that there are singular points in the integrand function, the behavior of this function was examined. The conditions for the generation of surface waves were determined. The analysis carried out allows for the numerical determination of the generalized impedance and thus:

mutual impedance
self-impedance
current distribution along the analyzed structure
radiation characteristics

The analytical model and computer program is only an image and an incomplete representation of reality. You should always be aware of the limitations of approximations and model imperfections. The ultimate test of the correctness of a theory is the construction and measurement of physical models of a given device. Only by comparing the results obtained during the simulation and the measurement results and making any corrections can the design process be considered completed. Therefore, the obtained calculation results were compared with the experimental results, and good agreement was obtained.

References

Munson, R. Conformal microstrip antennas and microstrip phased arrays. IEEE Trans. Antennas Propag. 1974, 22, 74–78. [Google Scholar] [CrossRef]
Wnuk, M. Multilayer dielectric periodic antenna structure in a cascade view. Appl. Sci. 2022, 12, 1–14. [Google Scholar] [CrossRef]
Minatti, G.; Faenzi, M.; Martini, E.; Caminita, F.; de Vita, P.; Gonz’alez-Ovejero, D.; Sabbadini, M.; Maci, S. Modulated metasurface antennas for space: Synthesis, analysis and realizations. IEEE Trans. Antennas Propag. 2014, 63, 1288–1300. [Google Scholar] [CrossRef]
Sharawi, S.M. Printed Multi-Band MIMO Antenna Systems and Their Performance Metrics. IEEE Antennas Propag. Mag. 2013, 55, 218–232. [Google Scholar] [CrossRef]
Oltman, G.H. Electromagnetically coupled microstrip dipoles. IEEE Trans. Antennas Propag. 1981, 29, 151–157. [Google Scholar] [CrossRef]
Sadiku, M.N. Elements of electromagnetics. Oxford University Press, 2014.
Malaisamy, K.; Haridoss Pandian, A.; Rima, S. Design of Crossed Dipole Yagi–Uda MIMO Antenna for Radar Applications Internationa. J. Antennas Propag. 2022, 2022, 8157541. [Google Scholar] [CrossRef]
Haobo, Y.; Hongguang, Z.; Hongwei, L.; Xiaojie, D.; Xi, C. Computing Mutual Impedance of Antennas by Spherical Harmonic Transform. IEEE Trans. Antennas Propag. 2019, 67, 4377. [Google Scholar] [CrossRef]
Aourik, S.; Erkik, A.; Oukaira, A.; Dhaou SJamal, Z.; Lakhssassi, A. An Advanced Array Configuration Antenna Based on Mutual Coupling Reduction. Electronics 2023, 12, 170. [Google Scholar] [CrossRef]
Alexopoulos, N.G.; Rana, I.E. Mutual impedance computation between printed dipoles. IEEE Trans. Antennas Propag. 1981, 29, 106–111. [Google Scholar] [CrossRef]
Liu, S.; Sun, S.; Chew, W.C. A potential-based integral equation method for low-frequency electromagnetic problems. IEEE Trans. Antennas Propag. 2018, 66, 1413–1426. [Google Scholar] [CrossRef]
Gao, X.; Han, X.; Cao, W.-P.; Li, H.O.; Ma, H.F.; Cui, T.J. Ultrawideband and high-efficiency linear polarization converter based on double v-shaped metasurface. IEEE Trans. Antennas Propag. 2015, 63, 3522–3530. [Google Scholar] [CrossRef]
Cao, Y.F.; Zhang, X.Y.; Xue, Q. Compact Shared-Aperture Dual-Band Dual-Polarized Array Using Filtering Slot Antenna and Dual-Function Metasurface. IEEE Trans. Antennas Propag. Publ. 2022, 4, 1120–1131. [Google Scholar] [CrossRef]
Liu, Q.S.; Sun, S.; Chew, W.C. A potential-based integral equation method for low-frequency electromagnetic problems. IEEE Trans. Antennas Propag. 2018, 66, 1413–1426. [Google Scholar] [CrossRef]
Yaghjian, A.D. Reflections on Maxwell’s treatise. Prog. Electromagnetic. Res. 2014, 149, 217–249. [Google Scholar] [CrossRef]
Khaleghi, S.S.M.; Moradi, G.; Jafargholi, R.S.S.A. Microstrip Line Impedance Matching Using ENZ Metamaterials. Des. Appl. Trans. Antennas Propag. 2019, 67, 2243. [Google Scholar] [CrossRef]
Kong, J.A. Electromagnetic Wave Theory; EMW Publishing: Cambridge, MA, USA, 2008. [Google Scholar]
Radavaram, S.; Pour, M. Wideband Radiation Reconfigurable Microstrip Patch Antenna Loaded With Two Inverted. IEEE Trans. Antennas Propag. 2019, 67, 1501–1505. [Google Scholar] [CrossRef]
Sadiku, M.N. Elements of Electromagnetics; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
Bender, C.M.; Orszag, S.A. Advanced Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
. Balanis, C.A. Antenna Theory: Analysis and Design; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
Oppenheim, A.V.; Schafer, R.W. Electromagnetic Field Theory Discrete-Time Signal Processing; Pearson Education: London, UK, 2014. [Google Scholar]
Lancaster, T.; Blundell, S.J. Quantum Field Theory for the Gifted Amateur; OUP Oxford: Oxford, UK, 2014. [Google Scholar]
Oppenheim A., V. and Schafer R. W. Electromagnetic Field Theory Discrete-time signal processing, 2014. [Google Scholar]
Balanis C., A. Antenna theory: analysis and design. John Wiley & Sons, 2016.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Mutual Impedance of Antennas Placed on a Multilayer Dielectric

Abstract

1. Introduction

2. Mutual Impedance of Two Arbitrarily Oriented Antennas Placed on a Dielectric Layered Substrate

3. Application of the Method of Moments to Determine the Current Distribution along Dipoles.

4. Mutual Impedance of Two Antennas of Any Length and Current Distribution

5. Determination of Currents ia, ib, ia0

6. Expression of Generalized Impedance zmn in Integral Form

7. Results of calculations and measurements

8. Conclusions

References

MDPI Initiatives

Important Links

Subscribe

5. Determination of Currents i_a, i_b, i_a0

6. Expression of Generalized Impedance z_mn in Integral Form