Prerpints.org logo
Preprint
Article

Research on Specific Scenario Generation Methods for Autonomous Driving Simulation Tests

Altmetrics

Downloads

109

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

07 November 2023

Posted:

07 November 2023

You are already at the latest version

Alerts
Abstract
In this paper, we propose a method for the generation of simulation test scenarios for autonomous driving. Based on the requirements of standard regulatory test scenarios, we can generate virtual simulation scenarios and functional scenario libraries for autonomous driving, which can be used for simulation verification of different ADAS functions. Firstly, the design operation domain (ODD) of the functional scenario is selected and the weight values of the ODD elements taken are calculated; then a combination test algorithm based on parameter weights is improved to generate autonomous driving virtual simulation test cases for the ODD elements, which can effectively reduce the number of generated test cases compared with the traditional combination test algorithm; then the traffic participant elements under each test case are Then, the values of the subelements under the traffic participant element in each test case are sampled and clustered to obtain hazard specific scenarios. Finally, the specific scenarios are applied to the automatic emergency braking (AEB) system on the model-in-the-loop (MIL) testbed to verify the effectiveness of this scenario generation method.
Keywords: 
Subject: Engineering  -   Automotive Engineering

1. Introduction

As the level of autonomous driving increases, the driving body of the vehicle gradually changes from a human to a computer or machine, which requires a large number of tests to prove that driving a car by a machine is safe enough. Automated driving test is divided into three stages, including virtual simulation test, closed-field test and open-road test, of which both closed-field test and open-road test are real-road test. In the early stage of autonomous driving testing, real road testing faces a large number of problems, such as longer road testing time, higher cost, lower efficiency, single scenario, test safety cannot be guaranteed, etc. According to relevant studies, If 100 cars are tested at 40 km per hour, 24 hours a day, it will take more than 200 years to test the algorithm of self-driving cars to the same level as human drivers [1]. It is difficult to accept.
Nowadays, with the help of virtual simulation software, virtual simulation testing with reference to the standardized process of testing has become an important part of self-driving car testing. With the development of simulation technology, simulation testing is required to account for more than 90% of the self-driving test, closed-field testing accounts for 9%, and open-road testing completes the last 1% of the test volume, and the three methods complement each other to accelerate the commercialization of self-driving to the ground.
Several test scenarios can be formed into a test scenario library, and the construction of the simulation test scenario library is one of the focuses of the construction of the virtual simulation test for autonomous driving. The construction of the scenario library includes the generation of scenarios in the scenario library and the evaluation of the scenario library. There are two methods of scenario generation, one is to describe the physical mechanism through expert experience and formulas, parse and reorganize the elements in the scenario, and generate the test scenario through mathematical methods for different test function requirements, while expressing the dynamic interaction problem in the scenario as an optimization solution problem and generating the scenario through the optimization solution method. bagschik et al [2]. studied the highway scenario and proposed They proposed an ontology-based scenario generation method, divided the high-speed scenario into five levels, and used class and logical semantics to realize the modeling and generation of the scenario. Chen et a [3]. studied the ramp convergence and convergence scenario, and proposed an ontology-based scenario test case generation method, described the scenario into three ontologies of road, weather and vehicle and realized the generation. Kluck et al [4]. combined ontology with combinatorial testing and proposed an algorithm to map ontology to combinatorial testing, which has been applied to the process of simulation system development. Gao et a [5]. combined combinatorial testing method with test matrix to design automatic scenario generation method and proposed a scenario complexity index to evaluate scenario implementation. Duan et al [6]. proposed a scenario complexity-based combinatorial testing method that uses Bayesian networks to find the balance between scenario complexity and testing cost, which can find system faults faster and improve testing efficiency. Lee et al [7]. first proposed an adaptive stress test scenario generation method by applying a tree-based reinforcement learning algorithm to solve the problem, using sampling and forward simulation to progressively build a search tree, modeling the subject as a reinforcement learning training environment that can effectively search for the most likely trajectory leading to an accident by interacting with the environment in real time. It was subsequently also improved and introduced to collision avoidance scenario generation for autonomous driving by Koren et al [8]. The problem is described as a Markov decision process and Monte Carlo Tree Search (MCTS) and feedforward neural networks are used to find collision scenarios.
The other is to take the collected real natural driving data, accident scenario data, and generate scenarios for simulation testing through transformation methods. The U.S. Department of Transportation, in cooperation with the University of Michigan, selected 16 vehicles for a 12-month naturalistic driving data collection effort to study truck tailgating problem [9]. The US NGSIM dataset, which uses high-definition cameras set up next to highways to collect highway vehicle data, has collected more than 10,000 data for the study of high-speed tailgating behavio. Accident scene datasets are generally used for the generation of hazard scenes, and Demetriou et al [10]. used RC-GAN method to establish a deep learning framework based on the driving trajectory data in real accident data to realize the extension of vehicle driving trajectories, so as to generate a hazard scene library. Ding et al [11]. proposed a multi-vehicle trajectory generator consisting of a bidirectional encoder and a multi-branch decoder, and the multi-vehicle scenes of interactions are encoded and sampled to find hazardous scenes. Bolted et al [12]. find the definition of boundaries in hazard scene data and predict relevant objects at relevant locations, which can identify hazard scenes that have not occurred. Ries et al [13]. introduce a method to efficiently train scene feature extractors using autoencoders, which can identify boundary scenes in a large natural driving dataset. Zhang et al [14]. propose a Markov chain and Monte Carlo based method for subset simulation sampling, which solves the problem of difficulty in modeling importance functions in high-dimensional complex scenes.
Based on the analysis of the automatic driving simulation test scenario generation method and evaluation system, this paper proposes an automatic driving virtual simulation scenario generation method that can meet the generated scenario library covering the realistic standard regulatory test scenarios and small probability hazardous accident scenarios. Firstly, it is determined that the simulation test scenarios generated in this paper take functional test as the demand, introduce design operation domain (ODD), establish the ODD element structure for different functional tests, take the values of the third layer elements in the ODD element structure as the input conditions of the autonomous driving virtual simulation test, and at the same time propose a method to assign weights to the ODD element values to get the weight values of the ODD element values. Then, an improved test case set generation method is used to improve the existing combination test algorithm by introducing the weight of ODD element values, and the improved ES(a,b) algorithm is obtained to optimize the number of test cases in the test case set generated by the improved algorithm. Then the Monte Carlo method is used to sample the successive elements of the test cases to take values, and the clustering algorithm is used to cluster the sampling results to obtain specific scenarios. Finally, the generated specific scenarios are tested with PreScan and matlab/simulink for autonomous driving MIL, which proves the effectiveness of the virtual simulation scenario generation method for autonomous driving based on this paper.
This paper is organized as follows: Section 2 describes the construction of a functional test ODD element structure. Section 3 introduces an improved algorithm for generating test cases for combinatorial testing. Section 4 describes the steps to achieve specific danger scenario generation by Monte Carlo and clustering algorithms. In Section 5, the effectiveness of the method is verified by applying it to an automatic emergency braking (AEB) system. Finally, Section 6 concludes the paper.

2. Methods to Describe Functional Test Scenarios

Generating an autonomous driving virtual simulation test scenario requires determining the input conditions of the scenario, i.e., the values taken by the elements in the scenario. This section introduces the design operation domain (ODD) for the scenario elements based on functional testing. It also proposes an ODD element assignment method, including subjective assignment method, objective assignment method, subjective-objective integrated assignment method and absolute weight calculation method in four steps, to get the final weight value of the ODD element taking values.

2.1. Scene Element Design

According to its testing requirements, autonomous driving testing is divided into functional testing, scenario testing and task testing [15], and this paper selects function as the testing requirement. Functional testing is a test method to verify whether an autonomous vehicle achieves a certain function. The test first determines the function to be tested, and then designs a test scenario according to the function. Compared with scenario testing and task testing, functional testing is more targeted for functional verification.
The Operational Design Domain (ODD) refers to the external environmental conditions and the self-vehicle state of the autonomous driving function as determined at design time. The German PEGASUS project identified six layers of ODD-related elements in the scenario, including a road layer, an infrastructure layer, a temporary operational layer, a target object layer, a natural environment layer, and a digital information layer. the Society of Automotive Engineers (SAE) established a generic ODD terminology and framework consisting of seven dimensions, including weather-related The Association of Standardization of Automation and Measuring Systems (ASAM)’s OpenODD is the openX family of safety standards for the design of operational domains classifies ODDs into three categories: scenarios, environments, and dynamic elements. Scenarios include areas where vehicles travel, intersections or ramps, fixed common road structures, special road structures, and temporary road structures; environments include weather, airborne particulate matter, and lighting conditions; and dynamic elements include traffic participants and their own vehicles.
In summary, the simulation test scenarios generated in this paper are based on functional tests, and for different functional tests, their ODDs are analyzed, and the ODD elements are used as the scene elements in the generated simulation scenarios, and the classification of ODDs in the OpenODD and PEGASUS projects are used as the main criteria to design the elements in the ODDs, as shown in Figure 1.
Since the subelements contained under the traffic participant element are mostly the motion states of vehicles, such as: self-vehicle speed, target vehicle speed, target vehicle acceleration, etc., the values of these elements have the characteristics of continuous and unbounded, so the values of the elements need to be discretized. Take the main vehicle speed as an example, the result of discretization processing is shown in Figure 2.

2.2. Calculation of Scene Element Taking Weight Value

According to Figure 2, the values of the elements at the bottom of the ODD are used as the values of the scenario elements in the virtual simulation test scenario of autonomous driving. Since the different values of each element at the bottom of the ODD have different weight and importance in the autonomous driving test, it is necessary to quantify the importance of the elements in the autonomous driving test by assigning weights to their values.
Weight assignment methods are generally divided into subjective weight assignment method and objective weight assignment method [16]. Subjective weight assignment method is a method in which the evaluator compares the importance of each element based on his or her subjective judgment and calculates the corresponding weight of each element [17]. The advantage of subjective weighting method is that the relative importance of the elements will not violate people’s common sense; the disadvantage is that the results obtained are more arbitrary. The objective weighting method is a method to determine the weights by calculation based on the objective information of the elements obtained without relying on the subjective attitude of the evaluator [18]. The advantage of the objective weighting method is that the calculation results are based on real data and do not depend on people’s subjective judgment; the disadvantage is that it lacks the complement of subjective consciousness, which will lead to one-sided and single judgment results.
In order to combine the advantages and disadvantages of subjective assignment method and objective assignment method, this paper adopts both subjective assignment method and objective assignment method to assign the values of ODD elements. The objective assignment method is used to assign the values of the elements in the ODD that can be obtained from the real distribution by means of published statistics, such as the speed of the vehicle and the weather, while the subjective assignment method is used to assign the values of the remaining elements at the bottom of the ODD.
In this paper, the CRITIC method is selected to subjectively assign the values of the bottom elements of ODD. This method is an objective assignment method based on data volatility, which determines the objective weight values of indicators by comparing the intensity and evaluating the conflicting nature between indicators [19].
If there are m rows of the original data set for n values of some third level element of the ODD, the matrix X is formed:
X = x 11 ⋯ x 1 n ⋮ ⋱ ⋮ x m 1 ⋯ x m n
where x i j denotes the value of the j-th taken value of some third level element of the ODD in the data set of the x-th row, x ∈ 1 , m , j ∈ 1 , n .
The standard deviation x j ¯ of the j-th value of the element is calculated as:
x j ¯ = 1 m ∑ i = 1 m x i j
The variability S j of the j-th value of the element is calculated as:
S j = ∑ i = 1 m ( x i j − x j ¯ ) 2 m − 1
Calculate the conflict of the j-th value of the element R j , denoted by the correlation coefficient r i j :
R j = ∑ i = 1 m ( 1 − r i j )
r i j represents the conflict of the matrix, X.; is inversely related to the conflict. the larger the r i j , the stronger the correlation between the value of the element and the value of the other elements, the less the conflict, the more information is repeated with the value of the other elements, and therefore the less important information is reflected in the value of the element, and the weight assigned to the value of the element should be reduced [20].
The amount of information C j for calculating the j-th value of the element taken is:
C j = S j × R j = S j ∑ i = 1 m 1 − r i j
Finally, the objective relative weight value of the j-th taken value of the ODD element is calculated as:
w j = C j ∑ j = 1 n C j
In this paper, the Analytic Hierarchy Process (AHP) is selected to subjectively assign weights to the values of the lowest element of the ODD. The AHP method is a hierarchical weighting decision analysis method for solving complex multi-objective problems and is widely used in the fields of aerospace and electric power systems [21]. The steps of the AHP are to first take the values of any two elements belonging to the same ODD element a i and a j are assigned a quantitative scale a i j to the relative influence degree of the function to be measured, and the scale a i j is taken using the 9-quantile scale in the scale method [22].
Assuming that an element of ODD has m taken values, the scale matrix A is obtained according to the proportional scale table as:
A = a 11 a 12 ⋯ a 1 m a 21 a 22 ⋯ a 2 m ⋮ ⋮ ⋱ ⋮ a m 1 a m 2 ⋯ a m m
The eigenvector corresponding to the largest eigenvalue of the scalar matrix A is calculated , as the subjective relative weight value of these m taken values.
To make the calculated results more reasonable, it is necessary to check the consistency of the feature vectors W i , which is expressed by the Random consistency ratio ( C R ). According to the relevant studies, when C R ≤ 0.1 , the consistency of the scale matrix A is considered to meet the requirements, and the feature vector calculated by the matrix A can be used as the subjective relative weight of the values taken by the elements of ODD. When C R ≥ 0.1 , it is necessary to reassign the scaling to the m taken values of the elements and to recalculate the scaling matrix A and the eigenvector W i .
The stochastic consistency ratio CR is calculated as:
C R = C I R I
where the Consistency index (CI) is calculated as:
C I = λ max − m m − 1
where λ max is the maximum characteristic root of matrix A, which is calculated as:
λ max = 1 m ∑ i = 1 m A i W i W i
where A i is the i-th row of matrix A.
In Equation (8), the value of Average random consistency index (RI) varies with the order m of the scale matrix A, as shown in Table 1.
The weight values of all the element fetches of the next layer directly subordinated to the elements contained in any layer are calculated by the above-mentioned weight value calculation method. For a multi-level element structure, the absolute weight value of each element in the bottommost level for the values taken by the first level of the target level is obtained by multiplying the weight values of the values taken by each element in each level from the top to the bottom.
In an n-layer system, let there be at most m values taken for an element in any layer, then the absolute weight value W i , j for each value taken for the j-th element in the i-th layer is calculated by the formula:
W i , j = W i , j ∏ a = 1 i w a , Ψ j
where i ∈ [ 1 , n ] , j ∈ [ 1 , m ] , Ψ j is the set of subscripts of all elements in the j-th element in the i-th layer with the first layer element backtracking path.

3. Improved Combination Testing Methods Based on Parameter Weights

After obtaining the values of functional test ODD elements and their weight values, they are used as the input conditions of the virtual simulation test of autonomous driving for the generation of simulation test scenarios. The traditional scenario generation method mostly adopts the Exhaustive Testing (ET) method in the test case generation method, and the number of generated test cases num is:
n u m = ∏ i = 1 N F i
where N is the number of influencing factors in the input conditions of the test case, and F i is the number of values of each influencing factor. When the number of influencing factors and the number of values of each influencing factor are too many, the number of test cases generated by ET algorithm will be greatly increased, so the Combinatorial Testing (CT) method is often used to generate test cases to reduce the number of test cases generated. In software testing, the failure of a system is generally caused by its own factors and the interaction between factors, so full coverage testing of the combination of factors is required.
In the autonomous driving function test, Zhang et al [23]. investigated the Lane Departure Warning (LDW) function in autonomous driving, and tested it and found that the faults of the tested functional system were all caused by a single element such as road shape, lane line blurring and missing conditions, changing conditions of light, and weather conditions. Gao et al [8]. tested the functionality of the body controller system and found that the system produced a total of 21 system defects, of which 16 defects were triggered by specific values of single system elements and 5 system defects were caused by different values of three system elements. Due to the analogy between the ODD elements of the autonomous driving functional test and the system fault factors in software testing, the CT approach in the field of software testing was used to implement the test cases in the generation of the virtual simulation test of autonomous driving.

3.1. Basic Principle of CT Combination Test Algorithm

At present, there are three main combinatorial testing algorithms: mathematical construction method, greedy algorithm and metaheuristic search algorithm [24]. The greedy algorithm generates the test case set by first establishing an initial empty set or a set T with partial test cases, and then extending the test cases row by row or column by column, so that each extended test case can cover as many combinations in the uncovered combination set as possible until the combinations in the uncovered combination set are fully covered. The greedy algorithm is divided into two types of algorithms according to the expansion method: one-test-at-a-time test case generation algorithm and in-parameter-order test case generation algorithm. According to the related research, in the combination test with low-dimensional coverage, especially the combination test with two-dimensional coverage, the number of generated test case sets based on one-test-at-a-time algorithm is better than the number of generated test case sets based on in-parameter-order algorithm. Therefore, in this paper, the greedy algorithm is used as the design basis for improving the one-test-at-a-time algorithm to optimize the number of test cases generated in low-dimensional coverage and improve the efficiency of simulation testing.
To facilitate the introduction of the proposed improved CT algorithm, some definitions and basic concepts of the CT method are given.
The basic idea of the combined test generation test case approach: for a Soft Under Testing (SUT) with N input parameters, the set of parameters is X = { x 1 , x 2 , x 3 , ⋯ , x N } , where the set of values of x i is denoted by Y i and the k-th value in Y i is denoted by y i , k . A number of test cases are generated to form a test case set T such that for any n (n is a positive integer, n ≤ N ) parameters in the SUT of the system to be tested, the combination of all values of these n parameters is covered by at least one test case in T [25].
Definition 1
(n-dimensional combined coverage test case set). Assume that the set T = { t 1 , t 2 , t 3 , ⋯ , t s } is a test case set of the SUT, and if for any combination ( y 1 , k 1 , y 2 , k 2 , ⋯ , y n , k n ) of any n values of the input parameters x 1 ∈ X , x 2 ∈ X , ⋯ , x n ∈ X ( n ≤ N ) , at least one test case t i can be found in T satisfying y 1 , k 1 , y 2 , k 2 , ⋯ , y n , k n ∈ t i . Then, we call the set T a n-dimensional combined coverage test case set of the SUT of the system to be tested, and n is also called the coverage dimension.

3.2. Improved ES Algorithm Based on Parameter Weights

At present, depending on the way of generating test case sets, One-test-at-a-time algorithms are AETG, TCG, DDA, ES, etc. In this paper, ES algorithm is chosen as the improved base algorithm.
The design idea of the iterative search algorithm (ES) is: first, calculate the N-dimensional combinations of all parameters, generate the test case set UT, determine the coverage dimension n and generate the initial n-dimensional uncovered combination set UC and the initial empty test case set T; then iterate through UT, find the test case that can cover the most combinations in UC, add it to the test case set T, and the next test case added to T can also cover as many combinations in UC, and output the test case set T when the combinations in UC are fully covered by the test cases in T.
The ES(a,b) algorithm introduces the weights of the parameter fetch values for test case generation when considering the multiple coverage of the current test case and the multiple coverage of the next test case. The sum of the weight values corresponding to all covered parameter fetches in the current test case set T, denoted as a, and the sum of the weight values corresponding to all uncovered parameter fetches, denoted as b, is a+b=1, where a ≥ 0 and b ≥ 0 . The a and b values in the traditional ES(a,b) algorithm are fixed values, which are generally taken as (a=1, b=0), (a=0.75, b=0.25), (a=0.5, b=0.5), (a=0.25, b=0.75), (a=0, b=1), and several other cases for test case generation. The values of a and b in this paper will change as the set of test cases T increases, which requires that the values of parameters a and b are dynamically updated when traversing the set of combinations of values of parameters, making the values of weights used for each calculation different.
In the process of expanding the test case set, it is necessary to consider that the next test case added to the test case set can also cover as many uncovered combinations as possible, which requires that the parameters in the uncovered combinations should be spread out as much as possible to avoid the existence of multiple values of a parameter that are not covered. Suppose there are two cases. In the first case, the current uncovered two-dimensional combination set of test cases T is U C 1 = { ( a 1 , b 1 ) , ( b 1 , c 2 ) , ( a 1 , c 1 ) } . At this time, a test case ( a 1 , b 1 , c 2 ) is found to cover two combinations of ( a 1 , b 1 ) , ( b 1 , c 2 ) in U C 1 . Then, as long as another test case, such as ( a 1 , b 2 , c 1 ) , is used to cover ( a 1 , c 1 ) , the full coverage of U C 1 is achieved, thus completing the generation of the test case set. In the second case, the set of test cases T is not yet covered by the two-dimensional combination set U C 2 = ( a 1 , b 1 ) , ( a 2 , b 1 ) , ( b 2 , c 2 ) . At this time, it is impossible to find a test case that can cover any two or more combinations, so three test cases, such as ( a 1 , b 1 , c 1 ) , ( a 2 , b 1 , c 1 ) and ( a 2 , b 2 , c 2 ) , are needed to achieve full coverage and complete the generation of the test case set. Comparing U C 1 and U C 2 , we can see that there are 4 values for 3 parameters in U C 1 , which is less, making it possible to increase the selection margin, and a test case can cover two two-dimensional combinations; while U C 2 contains 5 values for 3 parameters, which is more than one parameter, resulting in each test case can only cover one two-dimensional combination.
In the following, the ES(a,b) algorithm is designed and n=2 is chosen to cover the test case generation in two dimensions, and all the parameter variables designed by the algorithm and their meanings are shown in Table 2.
The specific step-by-step flow of the designed ES(a,b) algorithm is shown in Figure 3.
Finally, the pseudo-code form of the ES(a,b) algorithm implementation is given, as shown in Algorithm 1.
Algorithm 1 ES(a,b) algorithm pseudocode
1:
Input: UT, UC
2:
Output: T
3:
T = [ ] .
4:
while  U C ≠ ϕ  do
5:
     t max = t 1 , t 1 ∈ U T ∖ T .
6:
     a = C o v e r _ o v e r ( T ) , b = C o v e r _ n o t ( T ) .
7:
     f max = a × g ( t max ) − b × h ( t max ) .
8:
    for  t 1 in U T ∖ T  do
9:
           f = a × g ( t i ) − b × h ( t i ) .
10:
        if  f max ≤ f  then
11:
            f max = f .
12:
            t max = t i .
13:
        end if
14:
    end for
15:
     T = T ∪ { t max } .
16:
     U C = U C ∖ C ( t max ) .
17:
end while
18:
return T

4. Methods for Generating Functional Test Scenarios

From the discrete processing of the self-vehicle speed values in Figure 2, it can be seen that the test case set generated by the ES(a,b) algorithm has continuous values for the subelements under the traffic participant element in each test case, for example, the self-vehicle speed value of 40 represents the self-vehicle speed value interval of (30m/h, 40km/h), so the generated test cases cannot be used as scenarios for automatic driving simulation tests Therefore, the generated test case cannot be used as a scenario for the simulation test of autonomous driving, and it is necessary to conduct secondary sampling of these elements to generate specific values and obtain specific scenarios before conducting the simulation test.

4.1. Monte Carlo Method

Monte Carlo Simulation (MC) is a stochastic simulation method that uses repetitive random sampling to derive numerical results [26]. MC methods include constructing or describing probabilistic processes, sampling from known probability distributions, and obtaining results through computation or simulation. Constructing or describing a probabilistic process means randomizing the parameters, for example, describing the values of the four elements under the ODD “elements in vehicle operation” as a probability distribution in the above section. After constructing the probability model, sampling from the known probability distribution is required, and the usual sampling methods include receive-reject sampling, importance sampling, Markov Monte Carlo sampling, etc. The results are obtained by performing calculations or simulations after sampling the distribution [27].
The focus of the Monte Carlo method is to calculate the expectation of a random variable [28]. Assuming that X represents a random variable that obeys the probability distribution p ( x ) , then to calculate the mathematical expectation of function f ( x ) , it is necessary to take consecutive samples x i from p ( x ) , and then take the average of these samples of function f ( x i ) to approximate the mathematical expectation of f ( x ) , as expressed in Equation (13).
E p ( f ( x ) ) = 1 n ∑ i = 1 n f x i , x i ∼ p ( x )
where x i is the sample, f ( x i ) is the function of the sample, n is the number of samples, and E p ( f ( x ) ) is the mathematical expectation of f ( x ) obtained by estimating the sample.
For all possible test scenarios of the autopilot function, with Ω denoting the sample space, ε denoting a hazardous scenario that occurs less frequently but triggers the autopilot function, and ε ⊂ Ω , then the function describing whether scenario ε occurs can be defined as:
f ( x ) = 1 x ∈ ε 0 e l s e
The probability of occurrence of scenario ε needs to be estimated, that is, to find E ε ( f ( x ) ) . For such hazardous scenarios, which are usually located at both ends of the probability distribution p ( x ) of the functional test scenario parameters, the sampling yields very few hazardous accident scenarios with large variance in E ε ( f ( x ) ) . This requires more sampling to reduce the variance and leads to computational overload [29].

4.2. Dangerous Scenario Clustering

Most of the sub-element fetches under the traffic participant elements generated using the Monte Carlo method are similar, which will result in a more repetitive and less efficient test if they are directly used as fetches for specific scenarios. Therefore, the group of element fetches needs to be filtered again to find out the most representative fetches, so as to improve the efficiency of the test. In this paper, a clustering algorithm is used for screening.
Clustering algorithm is an unsupervised machine learning algorithm, mainly used for data partitioning and data grouping in data mining, the purpose of clustering is to group similar objects in the data into one group. k-means algorithm belongs to division clustering algorithm, by clustering an n-dimensional vector of data point set D = x i | i = 1 , 2 , ⋯ , n , where x i denotes the i-th data point in the data point set, and finally dividing this data point set D into k class clusters [30]. The main basis for dividing the class clusters is the similarity of objects in the point set and the gap between objects, using Euclidean distance as the similarity measure and the error sum of squares as the objective function, and the data points are finally divided into k clusters by minimizing the objective function. The final cluster center coordinates obtained in this paper are the values taken for the subelements under the traffic participant element in the specific scenario generated by each test case.
The Euclidean distance between point x and point y in the data set is:
d ( x , y ) = ∑ i = 1 n ( x i − y i ) 2
The basic steps of K-means algorithm are: the first step is to select k data as the initial cluster centers; the second step is to classify the data points, calculate the Euclidean distance of each point to the initial cluster center, find the cluster center with the closest Euclidean distance to each point, and divide the point under this cluster center; the third step is to check whether the cluster center to which the data points belong has changed, if not, then the clustering is finished, otherwise go to the fourth step; the fourth step is to update the cluster center coordinates, calculate the mean value of all data points under each cluster center as the new cluster center, and then skip to the second step [31].

5. Automatic Driving Function Test Scenario Generation and Simulation Test Analysis

In this paper, the function to be tested for autonomous driving is selected, and the functional test scenario generation method introduced above is used to generate simulation scenarios, and simulation software is used to conduct simulation tests, thus proving the effectiveness of the scenarios obtained based on the generation method in this paper.

5.1. Functional Test Specific Scenario Generation

Advanced Driving Assistance System (ADAS) is an intelligent system that uses a variety of on-board sensors to collect environmental information, road network information, road facilities and road participants while the vehicle is in motion, and then realizes the alert of impending danger through system calculation and analysis. ADAS has been widely cited at the L1 and L2 levels of autonomous driving.
Autonomous Emergency Braking (AEB), is one of the most widely used ADAS functions on L2 autonomous vehicles. In this paper, we take AEB function as an example to generate a specific scenario for simulation testing of AEB function. Firstly, it is necessary to construct an ODD that complies with the test regulations of AEB function.
In 2014, Euro-NCAP released a test standard for AEB systems, which specifies two test methods and evaluation criteria for automatic emergency braking, including automatic emergency braking for vehicle-to-vehicle (C2C) and automatic emergency braking for vehicles and vulnerable road users such as pedestrians, autonomous vehicles, and VRU [32]. Among them, the evaluation criteria of AEB testing for vehicle-to-vehicle (C2C) mainly focus on the scenario where the test vehicle is rear-ended with the target vehicle, i.e., the front vehicle. There are three scenarios, Car-to-Car Stationary (CCRs), Car-to-Car Moving (CCRm) and Car-to-Car Braking (CCRb), depending on the movement state of the vehicle in front.
According to relevant statistics [33], the car shop rear-end scenario is one of the most dominant scenarios in current traffic accidents, so this paper selects the car shop automatic emergency braking scenario in AEB function for design.
The AEB function test ODD is shown in Table 3. The sub-element values under the traffic participant element are discretized for continuous values and each value represents an interval, for example, the self- driving speed value of 40 represents a value interval of (30km/h,40km/h).
The weight values of ODD elements are obtained by the calculation method of scene element fetching weight values in Section 2, as shown in Table 4.
The AEB function ODD element values and their weight values are used as the input parameters and their weight values of the improved combination testing algorithm, and the ES(a,b) algorithm is used to generate test case sets covering dimension n=2, n=3, n=4, n=5. In order to show the generation effect of ES(a,b) algorithm, this paper selects currently available combination testing tools or combination testing open source code, such as PICT, AllPairs, AETG [34], and uses the same AEB function ODD elements as input parameters of the algorithm to generate test case sets. The number of test cases in the test case set generated by different algorithms is shown in Table 5.
From Table 4, it can be seen that the ES(a,b) algorithm can effectively reduce the effect of test case generation at both lower coverage dimensions and higher coverage dimensions, so the optimization effect of ES(a,b) algorithm for test case generation has been verified.
The specific scenario generation method is used to sample the four sub-element value intervals under each test case traffic participant element in the set of test cases with different coverage dimensions obtained by the ES(a,b) algorithm to obtain specific scenarios.
Take one test case in the two-dimensional combined coverage test case set generated by the ES(a,b) algorithm as an example, the four subelements under the traffic participant element of this test case take the values shown in Table 6.
Using Monte Carlo method and clustering algorithm, the obtained post-clustering elements take values as shown in Table 7.

5.2. Automatic Driving MIL Test Based on AEB Function

As can be seen from the above, the automatic driving simulation test is divided into four types according to the test method: SIL, MIL, HIL and HIL, and the MIL test method is chosen in this paper.
The automated driving simulation test relies on simulation software, and the automated driving virtual simulation software is a three-dimensional graphics processing software developed based on virtual reality technology [35]. The automated driving simulation test platform established based on the simulation software needs to have the ability to truly restore standard regulatory test scenes and transform the road collection data of real vehicles to generate simulation scenes, while the simulation test platform should realize that vehicles can be carried out in the platform cloud At the same time, the simulation test platform should realize the ability of large batch and parallel simulation of vehicles in the platform cloud, so that the simulation test can realize the closed-loop test of the full-stack algorithm of automatic driving perception, planning, decision making and control.
This paper uses PreScan, a simulation software for driver assistance system and safety system development and validation, whose main functions include scenario building, sensor modeling, developing control algorithms and running simulation [36]. Compared with VTD, CarSim, Carla and other simulation software, the advantages of PreScan are simple scenario modeling process, perfect sensor and vehicle dynamics model, and PreScan is equipped with an interface for joint simulation with Matlab/Simulink, through which control and decision making algorithms in Matlab/Simulink can be imported. algorithms, and also in Matlab/Simulink to modify the vehicle dynamics model and demo algorithms that come with PreScan [37]. In this paper, the specific scenario of Table 7 is selected for simulation testing, and the ODD elements of the specific scenario of Table 7 are taken as shown in Table 8.
The simulation scenario generated by PreScan is shown in Figure 4.
Add long-range millimeter wave radar for self-vehicle in PreScan, set FoV as pyramidal, single beam, scanning frequency 25Hz, detection distance 150m, lateral FoV opening angle 9 degrees, maximum number of detected targets 32, and the rest parameters as default parameters.
Add short-range millimeter wave radar, set FoV as pyramidal, single beam, scanning frequency 25Hz, detection distance 30m, lateral FoV opening angle 90 degrees, maximum number of detected targets 32, and the rest parameters as default parameters.
Click build to compile, and after compiling, open the corresponding .slx file in simulink and complete the connection of each module input and output. In this paper, we choose Prescan’s own AEB control algorithm, which uses the time to collision (TTC) as the judgment criterion. When TTC < 2.6s, the control algorithm gives an alarm signal; when TTC < 1.6s, the control algorithm gives about 40% of the half braking signal; when TTC < 0.6s, the control algorithm gives about 100% of the full braking signal.
The added sensor model, dynamics model, and AEB control algorithm are the same for both scenarios. When you click Run Simulation, you can see the two windows added with the vehicle view, the real-time motion status window of the vehicle, and the window showing the sensing results of the millimeter wave radar, as shown in Figure 5.
At the end of the simulation run, the graphs of the change of the speed of the self-vehicle and the relative distance between the self-vehicle and the target vehicle can be obtained, as shown in Figure 6. The horizontal coordinate in the graph represents the simulation running time, the red curve represents the relative distance between two vehicles, and the blue curve represents the speed of the self-vehicle.
As can be seen from Figure 6, Scenario 1 at the beginning of the simulation, the two cars are 74.43m apart, the self-car monitors the target car, and the self-car travels straight at a constant speed of 43.63km/h or 12.12m/s; when the two cars are about 18m apart, the AEB system gives a full brake and the self-car brakes to stop; after the brakes stop the two cars are about 1m apart and the self-car braking time is 2.7s.
Scenario 2 At the beginning of the simulation, the two cars are 65.21m apart, the self-car monitors the target car, the self-car goes straight at a constant speed of 47.40km/h or 13.17m/s; when the distance between the two cars is about 19m, the AEB system gives a full brake and the self-car brakes to stop; the distance between the two cars after braking is about 1.5m, and the braking time of the self-car is 2.2s.
From the simulation results, it can be seen that the AEB control algorithm and the millimeter wave radar used in the simulation test performed well under the bad weather conditions of sand and haze, when the speed range of the self-car was (40km/h,60km/h), and the self-car braked at about 1-2m distance between the two cars to avoid the accident.
To test the effect of the AEB function when the speed of the self-car is high under the same sandy haze weather conditions, this paper selects another test case in the two-dimensional combined coverage test case set generated by the ES(a,b) algorithm for testing. The specific scenario generated by this test case is shown in Table 9.
Add the sensor model, vehicle dynamics model and AEB control algorithm consistent with the above. Run the simulation and get the variation graphs of self-vehicle speed, relative distance between self-vehicle and target vehicle and self-vehicle braking force parameters, as shown in Figure 7.
At the beginning of simulation scenario 1, the speed of the self-car is 99.29km/h or 27.58m/s, and the distance between the self-car and the target car is 67.89m; when the distance between the two cars is about 40m, the AEB control algorithm controls the self-car to give about 40% braking force; when the distance between the two cars is about 10m, the AEB control algorithm controls the self-car to give 100% full braking force; when the distance between the two cars is 0m, the self-car When the distance between two cars is 0m, the speed is about 16m/s, the self-car is not braked, and the two cars collide. Since the collision animation effect is not set, the animation shown is that the target car passes through the self-car, and then the self-car brakes to stop.
At the beginning of simulation scenario 2, the speed of the self-car is 67.26km/h or 18.68m/s, and the distance between the self-car and the target car is 69.30m; when the distance between the two cars is about 38m, the AEB control algorithm controls the self-car to give about 40% braking force; when the distance between the two cars is about 10m, the AEB control algorithm controls the self-car to give 100% full braking force; when the distance between the two cars is 0m, the self-car The speed is about 15m/s, the self-car is not braked, and the two cars collide.
At the beginning of simulation scenario 3, the speed of the self-car is 83.07km/h or 23.08m/s, and the distance between the self-car and the target car is 67.84m; when the distance between the two cars is about 32m, the AEB control algorithm controls the self-car to give about 40% braking force; when the distance between the two cars is about 9m, the AEB control algorithm controls the self-car to give 100% full braking force; when the distance between the two cars is 0m, the speed of the self-car is When the distance between the two cars is 0m, the speed of the self-car is about 11m/s, the self-car is not braked, and the two cars collide.
At the beginning of simulation scenario 4, the speed of the self-car is 113.87km/h or 31.63m/s, and the distance between the self-car and the target car is 73.13m; when the distance between the two cars is about 42m, the AEB control algorithm controls the self-car to give about 40% braking force; when the distance between the two cars is about 13m, the AEB control algorithm controls the self-car to give 100% full braking force; when the distance between the two cars is 0m, the self-car When the distance between the two cars is 0m, the speed is about 18m/s, the self-car is not braked, and the two cars collide.
From the simulation results, it can be seen that under the bad weather conditions of sand and haze, the AEB control algorithm and the millimeter wave radar used in the simulation test performed poorly when the speed range of the self-car was (60km/h,120km/h), and the AEB control algorithm did not give full braking directly when braking, but gave half braking first and then full braking, resulting in a collision between the two cars when they were 0m apart and the self-car did not brake.
In summary, the validity of the specific scenarios obtained above for MIL testing of AEB functions has been verified.

6. Conclusion

Aiming at the problems of lack of real data support, low generation efficiency and lack of dangerous scenes in the scene element parsing and reorganization of scene generation method in the autonomous driving virtual simulation test scene generation method, this paper proposes an autonomous driving virtual simulation scene generation method that can take into account the importance of scene elements in the real world, optimization of the number of scene generation and generation of dangerous specific scenes. Based on this, an autonomous driving MIL test platform is built with PreScan and matlab/simulink to verify the effectiveness of the scenario generation method through simulation testing of ADAS functions. The method can be used to generate test scenarios for all functions of L2-level ADAS for autonomous driving, and can also generate simulation scenarios required for scenario testing and task testing. In the future, when the laws and regulations for L3 and above autonomous driving tests are perfected, the scenario generation method proposed in this paper only needs to improve the structure of ODD elements and more detailed division, and can be used for the generation of L3 and above autonomous driving simulation test scenarios.
However, the method still has certain limitations and problems, which need further research and improvement. The main areas include the following:
(1) The method of scene element analysis and scene reorganization is used to generate scenes, and although the weight values of ODD element values are calculated by referring to real statistics, the support of traffic accident data is lacking. Therefore, in the future, traffic accident data should be introduced into the calculation of the weight value of the ODD elements, and the distribution of the elements under the road conditions, environmental conditions and vehicle operation state when the real accident scenes occur should be analyzed to assign weights to the ODD elements, so as to improve the realism of the generated scenes.
(2) The improved combination test algorithm based on the weight values of ODD element taking values has longer generation time and lower efficiency at higher coverage dimensions. Therefore, future research should consider introducing machine learning and reinforcement learning methods into scene generation methods to design optimized objective functions to generate scenes; in addition, subsequent research can use optimization algorithms, such as random number search algorithms, particle swarm optimization algorithms, simulated annealing algorithms, and other algorithms to quickly converge to the global optimal solution and find dangerous scenarios.

References

  1. Kalra, N.; Paddock, S.M. Driving to safety: How many miles of driving would it take to demonstrate autonomous vehicle reliability? Transportation Research Part A: Policy and Practice 2016, 94, 182–193. [Google Scholar] [CrossRef]
  2. Menzel, T.; Bagschik, G.; Maurer, M. Scenarios for Development, Test and Validation of Automated Vehicles. In: 2018 IEEE Intelligent Vehicles Symposium (IV) 26-30 June 2018 2018, pp.1821-1827.
  3. Chen, W.; Kloul L. An Ontology-based Approach to Generate the Advanced Driver Assistance Use Cases of Highway Traffic. 2018, p.75-83.
  4. Klueck, F.; Li, Y.; Nica, M.; et al. Using Ontologies for Test Suites Generation for Automated and Autonomous Driving Functions. In: 2018 IEEE International Symposium on Software Reliability Engineering Workshops (ISSREW) 15-18 Oct. 2018 2018, pp.118-123.
  5. Gao, F.; Duan, J.; He, Y.; et al. A Test Scenario Automatic Generation Strategy for Intelligent Driving Systems. Mathematical Problems in Engineering 2019, 2019, 1–10. [Google Scholar] [CrossRef]
  6. Gao, F.; Duan, J.; Han, Z.; et al. Automatic Virtual Test Technology for Intelligent Driving Systems Considering Both Coverage and Efficiency. IEEE Transactions on Vehicular Technology 2020; PP: 1-1. [CrossRef]
  7. Lee, R.; Kochenderfer, M.; Mengshoel, O.; et al. Adaptive stress testing of airborne collision avoidance systems. 2015, p.1-24.
  8. Koren M, Alsaif S, Lee R, et al. Adaptive Stress Testing for Autonomous Vehicles. In: 2018 IEEE Intelligent Vehicles Symposium (IV) 26-30 June 2018 2018, pp.1-7.
  9. Alexiadis, V.; Colyar, J.; Halkias, J.; et al. The next generation simulation program. ITE Journal (Institute of Transportation Engineers) 2004, 74, 22–26. [Google Scholar]
  10. Demetriou, A.; Alfsvåg, H.; Rahrovani, S.; et al. A Deep Learning Framework for Generation and Analysis of Driving Scenario Trajectories. SN Computer Science 2023, 4. [Google Scholar] [CrossRef]
  11. Ding, W.; Wang, W.; Zhao, D. A Multi-Vehicle Trajectories Generator to Simulate Vehicle-to-Vehicle Encountering Scenarios. 2019, p.4255-4261.
  12. Termöhlen J-A, Bär, A.; Lipinski, D.; et al. Towards Corner Case Detection for Autonomous Driving. 2019, p.438-445.
  13. Ries, L.; Langner, J.; Otten, S.; et al. A Driving Scenario Representation for Scalable Real-Data Analytics with Neural Networks. 2019.
  14. Zhang, S.; Peng, H.; Zhao, D.; et al. Accelerated Evaluation of Autonomous Vehicles in the Lane Change Scenario Based on Subset Simulation Technique. In: 2018 21st International Conference on Intelligent Transportation Systems (ITSC) 4-7 Nov. 2018 2018, pp.3935-3940.
  15. Li, L.; Yilun, L.; Zheng, N.-N.; et al. Artificial intelligence test: a case study of intelligent vehicles. Artificial Intelligence Review 2018, 50. [Google Scholar] [CrossRef]
  16. Zimmerman M. Empowerment Theory. 2012. [CrossRef]
  17. Ye, F.-F.; Yang, L.-H.; Wang, Y.-M. A new environmental governance cost prediction method based on indicator synthesis and different risk coefficients. Journal of Cleaner Production 2019, 212, 548–566. [Google Scholar] [CrossRef]
  18. Cattaneo, L.; Chapman, A. The Process of Empowerment A Model for Use in Research and Practice. The American psychologist 2010, 65, 646–659. [Google Scholar] [CrossRef]
  19. Krishnan, A.; Mat Kasim, M.; Hamid, R.; et al. A Modified CRITIC Method to Estimate the Objective Weights of Decision Criteria. Symmetry 2021, 13. [Google Scholar] [CrossRef]
  20. Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Computers & Operations Research 1995, 22, 763–770. [Google Scholar] [CrossRef]
  21. Pedrycz, W.; Song, M. Analytic Hierarchy Process (AHP) in Group Decision Making and its Optimization With an Allocation of Information Granularity. IEEE Transactions on Fuzzy Systems 2011, 19, 527–539. [Google Scholar] [CrossRef]
  22. Ahmed, F.; Kilic, K. Fuzzy Analytic Hierarchy Process: A performance analysis of various algorithms. Fuzzy Sets and Systems 2019, 362, 110–128. [Google Scholar] [CrossRef]
  23. Zhang, Q.; Chen, D.; Li, Y.; et al. Research on Performance Test Method of Lane Departure Warning System with PreScan. 2015, pp.445-453.
  24. Ahmed, B.S.; Zamli, K.Z. A variable strength interaction test suites generation strategy using Particle Swarm Optimization. Journal of Systems and Software 2011, 84, 2171–2185. [Google Scholar] [CrossRef]
  25. Calò, A.; Arcaini, P.; Ali, S.; et al. Generating Avoidable Collision Scenarios for Testing Autonomous Driving Systems. 2020.
  26. Drews, T. Monte Carlo Simulation of Kinetically Limited Electrodeposition on a Surface with Metal Seed Clusters. Zeitschrift Fur Physikalische Chemie-international Journal of Research in Physical Chemistry & Chemical Physics - Z PHYS CHEM 2007, 221, 1287–1305. [Google Scholar] [CrossRef]
  27. Sarrut, D.; Etxebeste, A.; Muñoz, E.; et al. Artificial Intelligence for Monte Carlo Simulation in Medical Physics. Frontiers in Physics 2021, 9. [Google Scholar] [CrossRef]
  28. Qazi, A.; Shamayleh, A.; El-Sayegh, S.; et al. Prioritizing risks in sustainable construction projects using a risk matrix-based Monte Carlo Simulation approach. Sustainable Cities and Society 2020, 65, 102576. [Google Scholar] [CrossRef]
  29. Mallongi, A.; Rauf, A.; Daud, A.; et al. Health risk assessment of potentially toxic elements in Maros karst groundwater: a Monte Carlo simulation approach. Geomatics, Natural Hazards and Risk 2022, 13, 338–363. [Google Scholar] [CrossRef]
  30. Sinaga, K.; Yang, M.-S. Unsupervised K-Means Clustering Algorithm. IEEE Access 2020; PP: 1-1. [CrossRef]
  31. Ahmed, M.; Seraj, R.; Islam, S. The k-means Algorithm: A Comprehensive Survey and Performance Evaluation. Electronics 2020, 9, 1295. [Google Scholar] [CrossRef]
  32. Dollorenzo, M.; Dodde, V.; Giannoccaro, N.; et al. Simulation and Post-Processing for Advanced Driver Assistance System (ADAS). Machines 2022, 10, 867. [Google Scholar] [CrossRef]
  33. Pal, C.; Sangolla, N.; Vimalathithan, K.; et al. Real World Accident Analysis of Driver Car-to-Car Intersection Near-Side Impacts: Focus on Impact Location, Impact Angle and Lateral Delta-V. 2018.
  34. Cohen, D.M.; Dalal, S.R.; Fredman, M.L.; et al. The AETG system: an approach to testing based on combinatorial design. IEEE Transactions on Software Engineering 1997, 23, 437–444. [Google Scholar] [CrossRef]
  35. Nalić, Đ.; Pandrevic, A.; Eichberger, A.; et al. Design and Implementation of a Co-Simulation Framework for Testing of Automated Driving Systems. Sustainability 2020, 12. [Google Scholar] [CrossRef]
  36. Ortega Ortega, J.; Lengyel, H.; Szalay, Z. Overtaking maneuver scenario building for autonomous vehicles with PreScan software. Transportation Engineering 2020, 2, 100029. [Google Scholar] [CrossRef]
  37. Wang, C.-S.; Liu, D.-y.; Hsu, K.-S. Simulation and application of cooperative driving sense systems using prescan software. Microsystem Technologies 2021, 27. [Google Scholar] [CrossRef]
Preprints 89855 g001
Figure 1. Autonomous driving function test ODD element structure
Figure 1. Autonomous driving function test ODD element structure
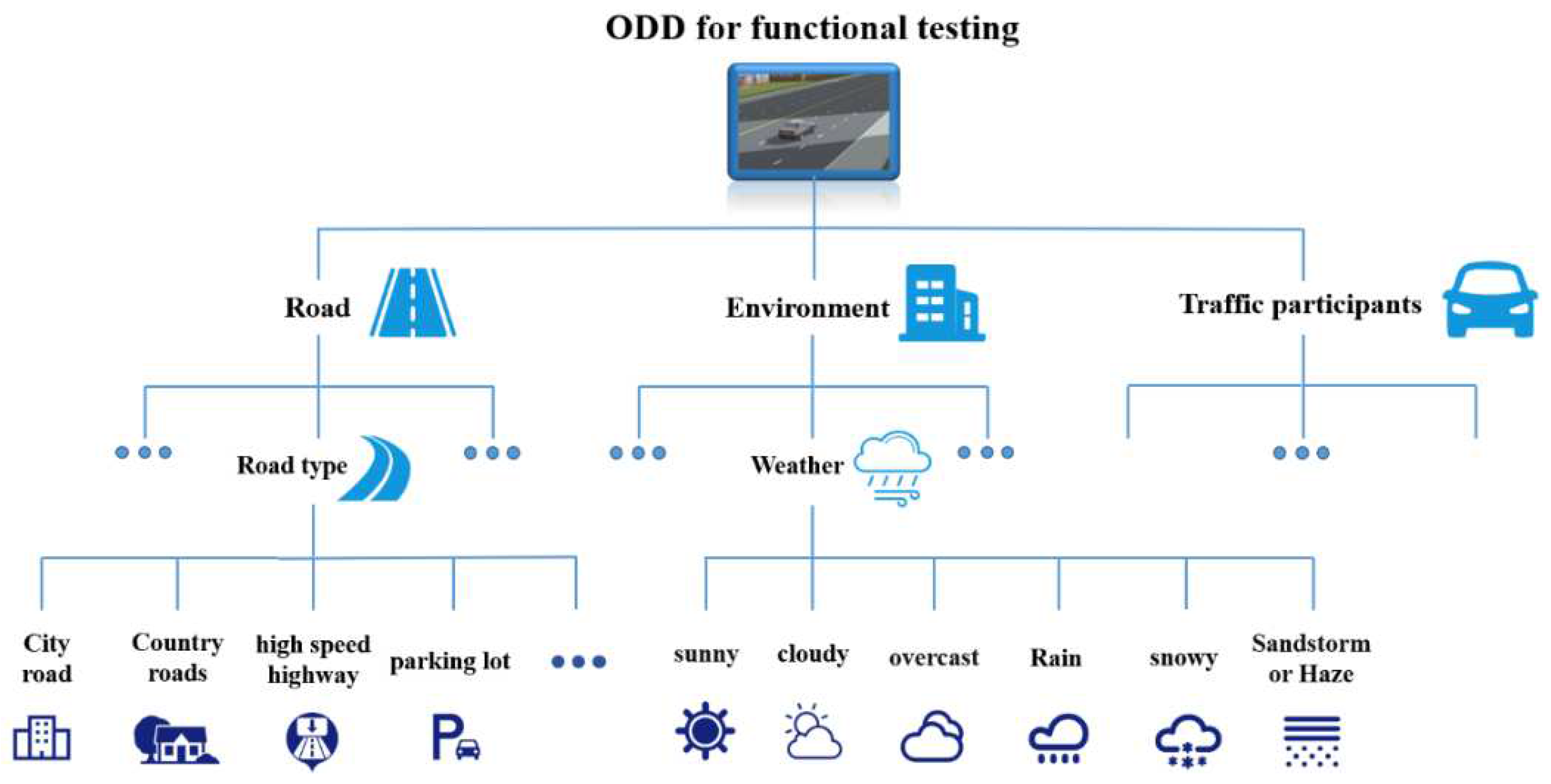
Preprints 89855 g001
Preprints 89855 g002
Figure 2. Discretization of self-driving speed
Figure 2. Discretization of self-driving speed
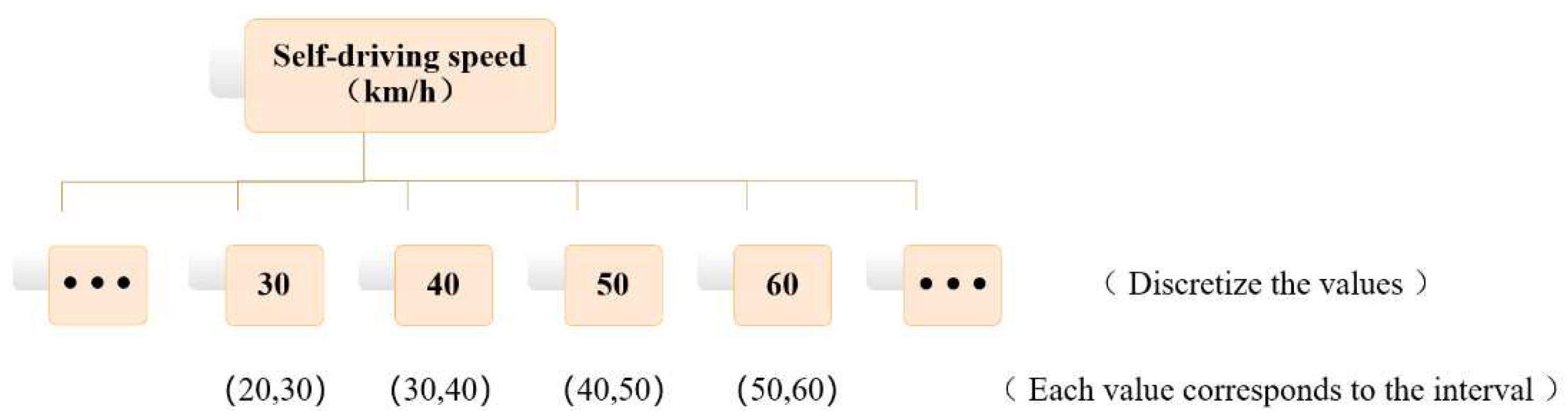
Preprints 89855 g002
Preprints 89855 g003
Figure 3. The ES(a,b) algorithm generates a methodological flowchart of the test case process
Figure 3. The ES(a,b) algorithm generates a methodological flowchart of the test case process
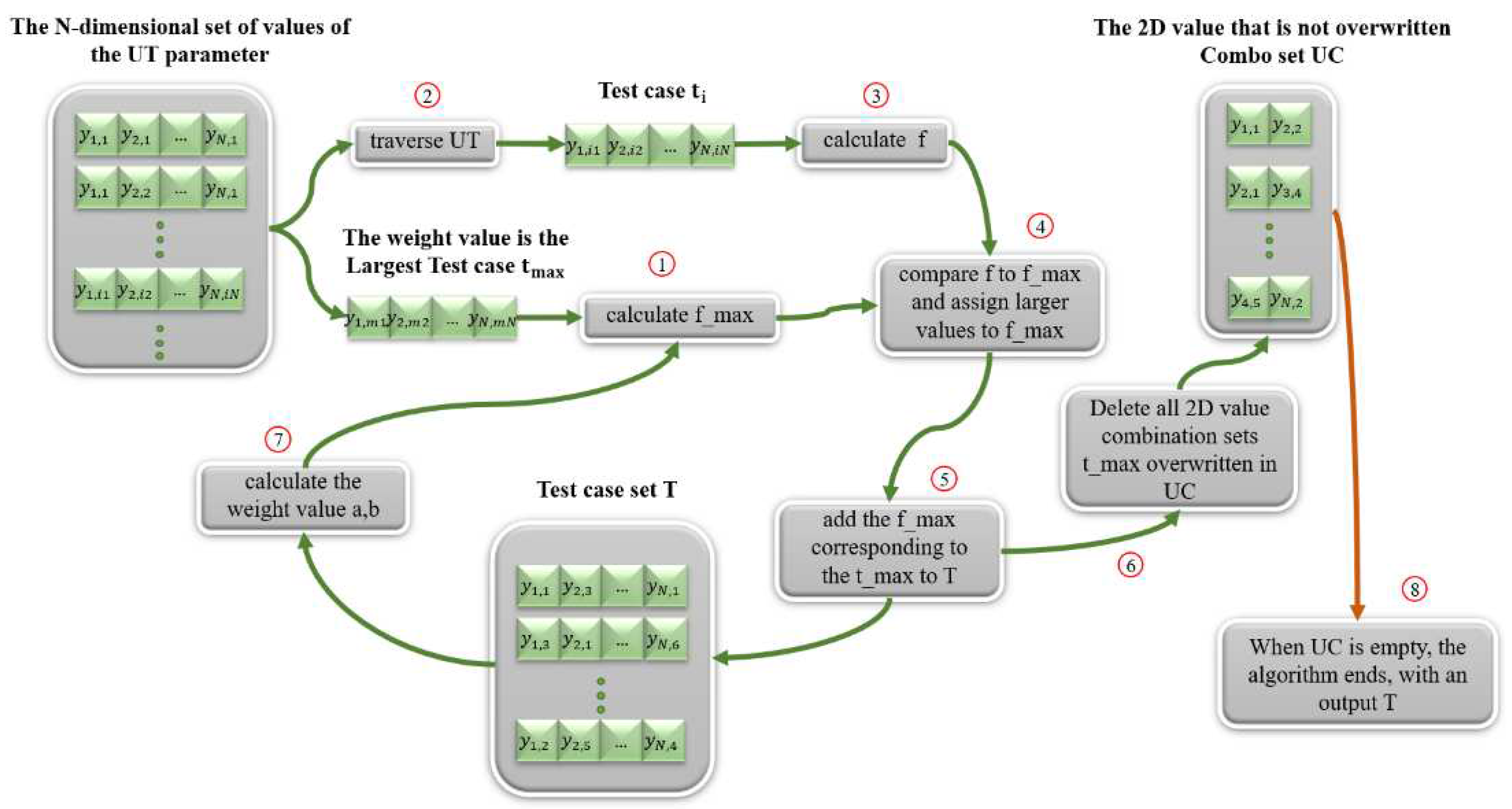
Preprints 89855 g003
Preprints 89855 g004
Figure 4. AEB simulation tests scenarios
Figure 4. AEB simulation tests scenarios
Preprints 89855 g004
Preprints 89855 g005
Figure 5. PreScan simulation runs each window interface
Figure 5. PreScan simulation runs each window interface
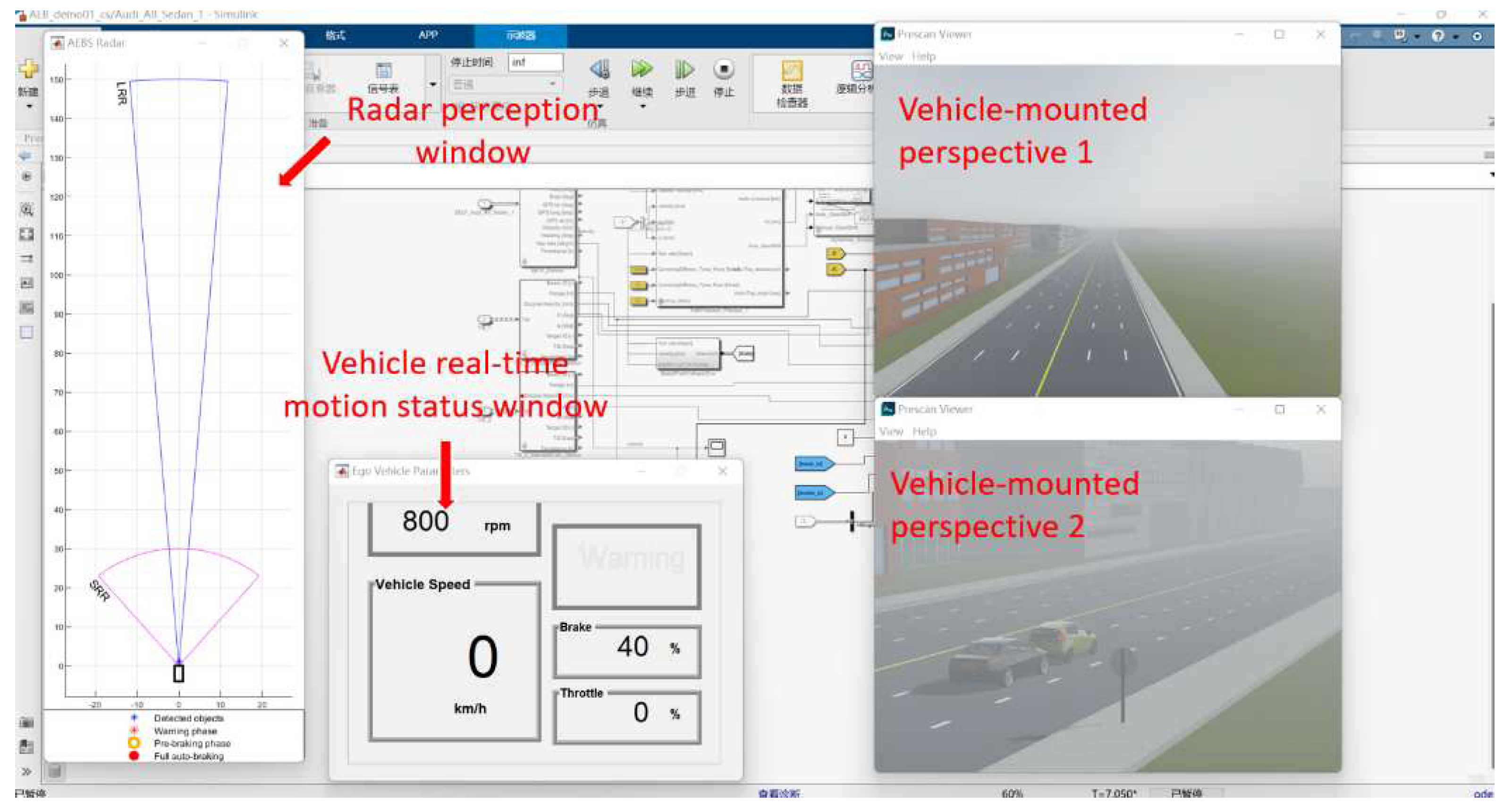
Preprints 89855 g005
Preprints 89855 g006
Figure 6. Simulate and test the results of each indicator parameter
Figure 6. Simulate and test the results of each indicator parameter
Preprints 89855 g006
Preprints 89855 g007
Figure 7. Simulate and test the results of each indicator parameter
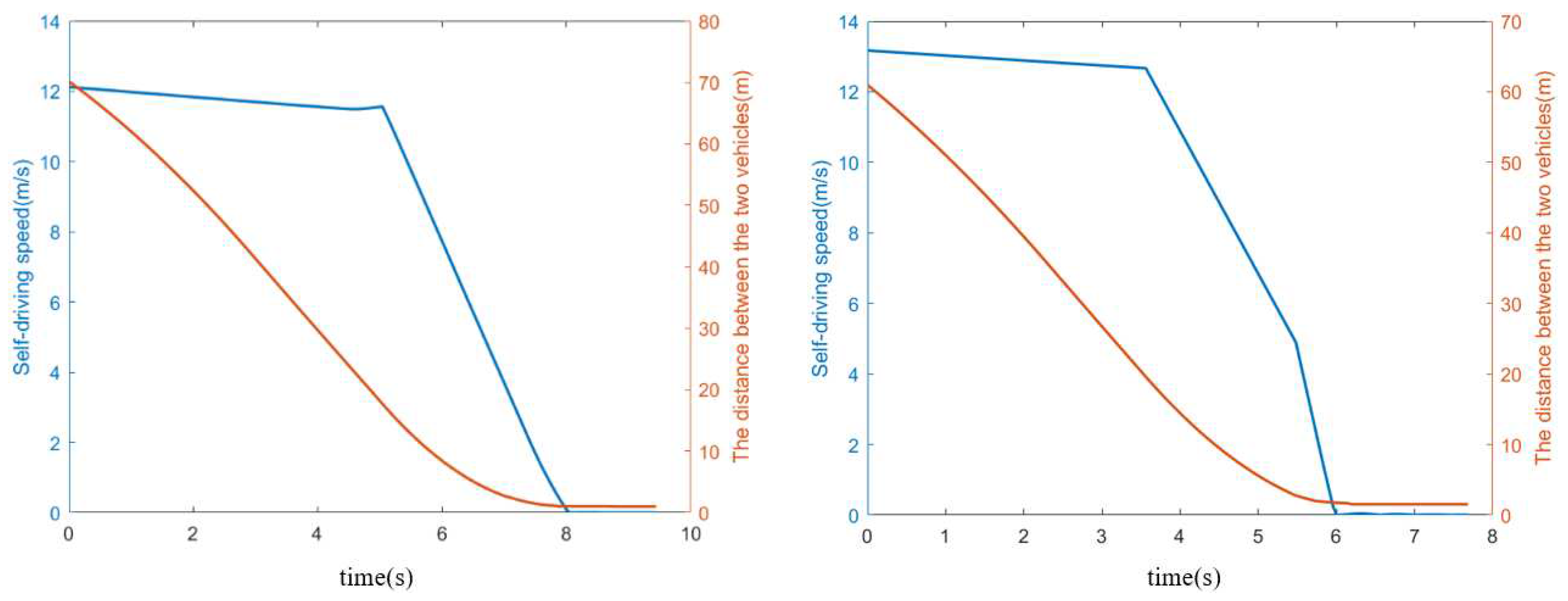
Figure 7. Simulate and test the results of each indicator parameter
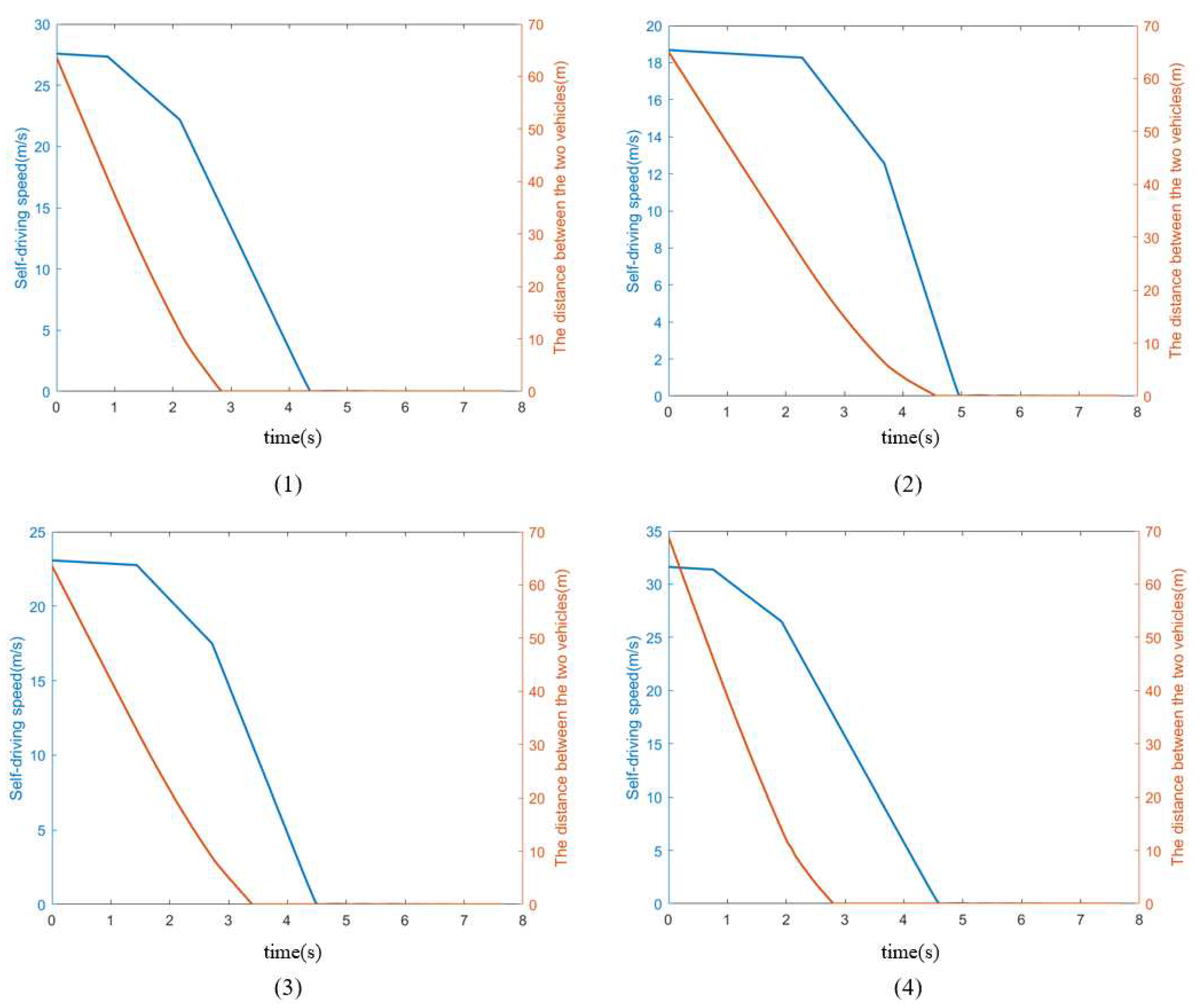
Preprints 89855 g007
Table 1. The Stochastic Consistency Indicator RI takes the value
Table 1. The Stochastic Consistency Indicator RI takes the value
m 1 2 3 4 5 6 7 8 9 10 11 12
R I 0 0 0.58 0.9 1.12 1.24 1.32 1.41 1.45 1.49 1.51 1.54
Table 2. Variables involved in ES(a,b) algorithms
Table 2. Variables involved in ES(a,b) algorithms
Variables Variable Meaning
UT N-dimensional set of combinations of values for all parameters
UC The set of all uncovered two-dimensional combinations of values
T Generated test case set
t One test case
C(t) The set of combinations of fetch values in UC covered by t
g(t) Number of elements in C(t)
h(t) The maximum number of parameters of the combinatorial set in which UC does not cover C(t)
Cover_over(T) Sum of the weight values of all currently covered parameter values of the test case set T
Cover_not(T) Sum of the weight values of all the currently uncovered parameter values of the test case set T
Table 3. The values of each element of the ODD of the AEB function
Table 3. The values of each element of the ODD of the AEB function
ODD Element The value of the element
Road Road type city roads, country roads, highways
Road surface asphalt pavement, concrete pavement, other pavement
Road shape straights, curves (1/250), curves (1/500), curves (1/750), intersections/ramps
Road slope uphill, downhill, no slope
Number of lanes 1, 2, 3, 4
Environment Weather sunny, cloudy, overcast, rain, snow, sand haze
Time daylight, dawn/dusk, night
Traffic sign traffic signs, traffic lights
Traffic participants Self-driving speed (km/h) 20, 30, 40, 50, 60, >60
Target vehicle speed (km/h) 0, 10, 20, 30, 40,>40
Target vehicle acceleration (m/s2) −10, −6, −3, 0, 3, 6
The distance between the two vehicles (m) 40, 60, 80, 100
Table 4. AEB function ODD weight value index of all elements and their values
Table 4. AEB function ODD weight value index of all elements and their values
ODD Element Value of the element Weight value
AEB function ODD Road Road type city roads 0.0115
highways 0.0061
country roads 0.0044
Road surface asphalt pavement 0.0126
concrete pavement 0.0243
other pavement 0.0117
Road shape straights 0.0641
curves (1/250) 0.0102
curves (1/500) 0.0271
curves (1/750) 0.0271
intersections/ramps 0.0102
Road slope uphill 0.0084
downhill 0.0084
No slope 0.0318
Number of lanes 1 0.0017
2 0.0044
3 0.0115
4 0.0044
Environment Weather sunny 0.0694
cloudy 0.0371
overcast 0.0249
rain 0.0575
snow 0.0128
sand haze 0.0096
Time daylight 0.0496
dawn/dusk 0.0204
night 0.0083
Traffic sign traffic signs 0.0141
traffic lights 0.0077
Traffic participants Self-driving speed (km/h) 20 0.0162
30 0.0426
40 0.0655
50 0.0221
60 0.0149
>60 0.0053
Target vehicle speed (km/h) 0 0.0644
10 0.0118
20 0.0284
30 0.0284
40 0.0118
>40 0.0052
Target vehicle acceleration (m/s2) −10 0.0018
−6 0.0040
−3 0.0096
0 0.0210
3 0.0096
6 0.0040
The distance between the two vehicles (m) 40 0.0048
60 0.0199
80 0.0126
100 0.0048
Table 5. Number of use cases generated by different combined testing algorithm in different coverage dimensions
Table 5. Number of use cases generated by different combined testing algorithm in different coverage dimensions
PICT AllPairs AETG ES(a,b)
n=2 49 55 53 47
n=3 321 352 318 306
n=4 1759 1857 1766 1717
n=5 8283 10036 8184 8179
Table 6. Elements compare of the wheel and body acceleration
Table 6. Elements compare of the wheel and body acceleration
Self-driving speed (km/h) Target vehicle speed (km/h) Target vehicle acceleration (m/s2) Distance between the two vehicles (m)
Min 40 10 −3 60
Max 50 20 0 80
Table 7. Grouping of values for clustered elements
Table 7. Grouping of values for clustered elements
Self-driving speed (km/h) Target vehicle speed (km/h) Target vehicle acceleration (m/s2) The distance between the two vehicles (m)
1 43.63 16.82 −1.59 74.43
2 47.40 14.45 −1.74 65.21
Table 8. In Table 7, the ODD road and environment elements are selected for specific scenarios
Table 8. In Table 7, the ODD road and environment elements are selected for specific scenarios
id Road type Road surface Road shape Road shope Lanes number Weather Time Traffic sign Selfdriving speed (km/h) Target vehicle speed (km/h) Target vehicle acceleration (m/s2) The distance between the two vehicles (m)
1 country roads other pavement straights down hill 3 sand haze daylight traffic signs 43.63 16.82 −1.59 74.43
2 country roads other pavement straights down hill 3 sand haze daylight traffic signs 47.40 14.45 −1.74 65.21
Table 9. Specific scenarios generated by the test cases
Table 9. Specific scenarios generated by the test cases
id Road type Road surface Road shape Road shope Lanes number Weather Time Traffic sign Selfdriving speed (km/h) Target vehicle speed (km/h) Target vehicle acceleration (m/s2) The distance between the two vehicles (m)
1 highways other pavement straights no slope 1 sand haze dawn/ dusk traffic lights 99.29 4.39 0 67.89
2 highways other pavement straights no slope 1 sand haze dawn/ dusk traffic lights 67.26 4.87 0 69.30
3 highways other pavement straights no slope 1 sand haze dawn/ dusk traffic lights 83.07 5.35 0 67.84
4 highways other pavement straights no slope 1 sand haze dawn/ dusk traffic lights 113.87 4.91 0 73.13
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated