Prerpints.org logo
Preprint
Article

Fuzzy Logic, Neural Network and ANFIS in Delegation of Standard Concrete Beam Calculations

Altmetrics

Downloads

78

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

06 November 2023

Posted:

07 November 2023

You are already at the latest version

Alerts
Abstract
Machine Learning (ML) has proved its capabilities in different scientific and industrial fields, but it needs to be further investigated in the construction industry for practical utilization. One of the use cases of ML is delegating the structural calculation process. In this study, to discuss ML’s capabilities in performing the work of a structural designer, calculations of concrete sections based on ACI (American Concrete Institute) as a case study were selected. At first, all manual design steps and standard considerations for a concrete beam section were coded parametrically in MATLAB. After comparing with structural design references to prove the accuracy of codes in calculating shear and bending capacities, the parametric results were used as initial data (Look−up table) for training the ML operators. Regarding different types of ML techniques and as a comparison between them, in the next steps, all essential codes for Fuzzy Logic (FL), Neural Network (NN) and Adaptive Neuro-Fuzzy Inference System (ANFIS) were coded in the same platform. The performance of the three coded ML operators to replace (delegate) standard calculations compared to direct calculations was individually investigated and displayed through parametric examples. After initial examples, the influences of the number of parameters and size of the Look−up table on the accuracy of each operator were discussed. The study concluded that although all three operators can delegate the standard calculation, the precision of the results differs considerably. In case of the desirable size of the Look−up table, ANFIS operators can represent the standard calculations with a different number of parameters and entirely high precision.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Artificial intelligence (AI) and Machine Learning (ML) are two related terms in computer science and technology. Although they are related, their definitions are not interchangeable. While AI refers to creating machines that perform tasks that typically require human intelligence, such as perception, reasoning, learning, and decision-making, ML is only a subset of AI that involves training algorithms to learn patterns in data and make predictions or decisions based on them. AI is, therefore, a much broader concept encompassing various fields of study, such as computer vision, natural language processing, robotics, and more. Additionally, Machine Learning focuses on developing algorithms and statistical models that can analyze data and predict, interpret or decide [1]. AI typically uses a rule-based approach, where systems are programmed with a set of rules and instructions to follow. Machine Learning, on the other hand, uses a data-driven approach, where algorithms learn from data to identify patterns and make predictions. AI systems are typically designed and programmed by humans, while Machine Learning algorithms are trained on data [2]. Machine Learning algorithms require large amounts of data to be trained effectively, whereas AI systems can be designed with a smaller set of rules and instructions [1].
There are three main types of Machine Learning: supervised learning, unsupervised learning, and reinforcement learning. In supervised learning, the algorithm is trained on a labelled dataset to predict an output given an input [3]. In unsupervised learning, the algorithm identifies patterns and structures in an unlabeled dataset. In semi-supervised learning, the algorithm is trained on a combination of labelled and unlabeled data. Finally, in reinforcement learning, the algorithm learns to make decisions by interacting with an environment and receiving feedback in the form of rewards or penalties [4]. Each type of Machine Learning has its strengths and weaknesses, and the choice of which type to use depends on the nature of the problem and the available data [5]. Neural Networks ( N N ) and Adaptive Neuro-Fuzzy Inference Systems (ANFIS) are two types of supervised ML. A Fuzzy approach can be applied in supervised and unsupervised classifications as a mathematical framework [6,7].
Fuzzy Logic (FL), developed by Zadeh [8], is an approach for dealing with imprecise or uncertain data often encountered in real-world applications. FL provides a way to handle linguistic variables and Fuzzy sets, delegating and manipulating imprecise or ambiguous data. It provides a set of rules for making decisions or predictions based on this data and allows for more flexible and nuanced reasoning than traditional Boolean logic [9]. FL has been used in various fields, including control systems, pattern recognition, and decision-making. For example, FL has been used to control the speed of electric motors in industrial processes, to diagnose medical conditions based on symptoms, and to make decisions in financial forecasting [10].
FL has been used in various fields, including structural studies. FL provides a framework for dealing with imprecise or uncertain data, often encountered in structural studies. FL allows for more flexible and nuanced reasoning, making it an attractive tool for analyzing complex structural systems. FL has been applied in structural studies in assessing seismic hazards and estimating earthquake probability and potential consequences. FL combined data from multiple sources, such as seismic data, geological information, and historical earthquake data, to generate a comprehensive seismic hazard assessment [11]. FL was also utilized to design and analyze structural systems to model the performance of complex systems, such as buildings, bridges, and other infrastructure, including optimizing the design of reinforced concrete structures [12]. FL can be used to analyze data from multiple sensors, such as strain gauges and accelerometers, to detect changes in the structural performance that may indicate damage or deterioration [13]. Another type of utilization was for parametric evaluation of dry concrete joints to continuously evaluate the joints with different parameter ratios. At the same time, the limited number of the tests can be generally managed, which will, without ML, end to discrete data [14].
Neural Networks ( N N ), a supervised technique, has been increasingly used in various fields, including structural studies. Using Neural Networks in structural studies can lead to more accurate and reliable analyses and help ensure the safety and reliability of critical infrastructure. Structural health assessment is one area where Neural Networks have been applied in structural studies. Structural health assessment involves monitoring the condition of structures, such as bridges and buildings, to detect any defects or damage. Neural Networks can be used to analyze data from multiple sensors, such as strain gauges and accelerometers, to detect changes in the structural performance that may indicate damage or deterioration [15]. Neural Networks have also been used to design and optimize structural systems. It was utilized to model the performance of complex systems, such as buildings, bridges, and other infrastructure, and to optimize their design based on performance criteria. For example, Neural Networks were utilized to optimize the design of steel-concrete composite structures [16]. Another application of N N in structural studies is in predicting structural performance under various loading conditions, trained on data from physical experiments or numerical simulations to predict the response of structural systems to different loads. Likewise, N N to predict the deflection and stress of steel-concrete composite [17].
Adaptive Neuro-Fuzzy Inference System (ANFIS) is another supervised ML approach, which is a type of ML algorithm that combines the strengths of Neural Networks and FL used in various fields, including structural studies such as in predicting the dynamic performance of structures under seismic loads. ANFIS can be trained on data from physical experiments or numerical simulations to predict the response of structural systems to seismic loads and the displacement and acceleration response of steel frame structures [18]. ANFIS was also employed in the assessment of structural health. It can be used to analyze data from sensors, such as accelerometers and strain gauges, to detect structural defects or damage. For example, ANFIS has been used to detect damage in reinforced concrete structures based on data from acoustic emissions [19]. Another application in structural studies is in the design and optimization of structural systems. ANFIS can model the performance of complex systems, such as buildings and bridges, and optimize their design based on performance criteria. For example, ANFIS was used to optimize the design of steel-concrete composite beams [20].
Reinforced concrete is a widely used construction material in structural engineering due to its strength and durability. However, predicting the performance of reinforced concrete structures is a complex task, as it depends on various factors such as material properties, geometry, and loading conditions. FL, Neural Network, and ANFIS are three Machine Learning techniques that can be used in reinforced concrete research to accurately predict these structures’ behaviour. For instance - FL is utilized to model the mechanical behaviour of concrete structures under different loading conditions and predict the deflection of reinforced concrete beams [21]. - Neural Networks can be trained on large datasets to identify complex patterns and relationships between input and output variables, predicting the compressive strength of concrete based on various input parameters [22]. - ANFIS has been used in reinforced concrete research to predict various properties of concrete structures, such as the compressive strength, flexural performance, and shear strength, along with predicting the performance of reinforced concrete beams with different reinforcement [23,24].
Despite their potential, several challenges must be addressed to apply the ML approach practically. Some primary challenges can be mentioned: 1. Lack of engineers’ familiarity with this method and difficulty in modelling complex relationships; 2- Lack of awareness about the differences in performance of different ML techniques to a wise tool selection. 3- Sensitivity of these techniques to the size of a L o o k − u p table, number of parameters and type of relation between the input and outputs (linear and nonlinear). 4- Machine Learning models are often called "black boxes" because they can produce complex and non-intuitive results. This makes it challenging for engineers to interpret and explain the outputs of the models; in other words, the designers do not know up to which stand these methods are trustworthy. 5- the studies in which the ML approaches were used are mainly based on the researches and experimental data, while direct comparisons between the standard known calculations and ML’s results are needed.
In this regard, the current paper aims to discuss the three types of Machine Learning, including Fuzzy, N N and ANFIS, to re-introduce and compare their performances in one example. In the case study, the Standard calculation of a concrete beam was selected, which is known to the engineer. This discussion discussed the sensitivity of the methods to the number of parameters and the size of the L o o k − u p table. Additionally, the accuracy of all methods with each other and routine calculations was compared.

2. Discussion

2.1. Initialization

Coding, Standard Beam Section Calculation

This paper aims to evaluate the performance of ML operators in delegating the standard structural computing process. As the case study, a wide range of structural subjects and Standards can be selected for analyzing or designing steel and concrete elements. Here, the known designing process of concrete beams (Figure 1) was chosen as the subject of interest, and in particular, the calculations of the beams’ bending and shear capacity were defined as the output (referring to A C I 318 − 14 [25] standard), whereas features of the section were the adjustable parameters (Figure 1) in the codes. In these calculations, after initialization and some basic calculations such as section area (A), amount of compressive and tensile re-bars, A s , A s ′ , and their percentages ρ c , ρ t , along with beam re-bar balance percentage ρ b , were calculated.
Simple algorithmic codes were developed in MATLAB to calculate ACI and parametrically calculate the capacities. The shear calculation regarding steel (stirrups) and concrete capacities was managed in one step. The shear capacity ( V c ) is 75 % of the steel and concrete capacities summation. The bending performance of the section was divided into three different steps. Figure 1 shows that the bending performances based on the comparison between ρ b , ρ t and availability of compressive re-bar get divided into three different performance types ( P 1 . , P 2 . , P 3 . ).
In the following process, comparison with available and minimum allowed re-bar categorizes the section to other subcategories P ( 1 . , 2 . , 3 . ) ( 1 , 2 ) . This category indicates the type of Standard formulas for calculating neutral lines and capacities of each type of section. Finally, a comparison between the amounts of the calculated strains indicates some coefficients which, based on the standard, should be multiplied by the bending results. Numbers showed this last step of calculations as ( P ( 1 . , 2 . , 3 . ) ( 1 , 2 ) ( 1 , 2 ) ). Finally, the following discussions interfaced the standard codes as a MATLAB function to all ML operations.
The results of several series of parametric calculations will produce different databases ( L o o k − u p table) to be inferred with operators, and the operators’ results will be compared to the direct ACI coding. The aim of the study is not to discuss the performance of the beams, and the accuracy of the parametric calculations results is not decisive. Nonetheless, to have a practical example, the accuracy of the coded ACI function was compared to other references. Table 1 compares the codes’ results and calculated amounts in references. Although not all of the references use ACI, the results displayed similar results for shear and bending capacities, proving the accuracy of the coded ACI and the similarity between the referenced standards.
The selection properties, including the Height ( H e ) and Width ( W i ), besides concrete and steel properties along with the steel mounts, are shown in the first row of Table 1. The N r in this Table shows the depth of the neutral line, calculated by codes and references for bending calculations. In selection, examples with different performance types were selected. For instance, the bending capacity of the first section (No.1 Table, Table 1), by the codes and in the reference, are 7.1e08N.mm and 7.08e08N.mm. Likewise, the comparison of shear capacities in example 6 shows 3.53N and 3.5N. Generally, it was shown that the maximum difference between the results of the codes and references is 2 % , proving the accuracy of the codes.

Coding, the Machine Learning Operators

Despite the different parameters for tuning, Machine Learning operators can be selected due to the limitation of the size of the paper, and the focus of the current study does not intensely discuss other possible variants of Coding. The codes were initially developed by other researchers/engineers and, alone as a possibility, were selected to prepare an overview for the structural engineers. This study aims to give an outline to the structural engineer for finding the solution for the desirable interpretation of their numerical and experimental results and does not aim to propose the best commands; the developed codes in this study can further researchers be replaced by other programming languages or can be optimized for promoting their performances. Alone, some parts of the developed MATLAB codes to give an overview will be briefly mentioned in each section.

2.2. Problem Definitions (Preparation of Look-up Table)

For discussing different ML techniques, all following sections use the proved codes as a MATLAB function called P a r s S o l u t i o n . m . This function can para-metrically calculate different ranges of the variables based on ACI. It imports all of the section parameters, including Height( H e ( m m ) ), Width ( W i ( m m ) ), concrete compressive strength ( f c ( n / m m 2 ) , steel yield strength ( f y ( n / m m 2 )), Compressive re-bar ( A s ′ ( m m 2 )), tensile re-bar ( A s ( m m 2 )) and calculates the shear ( V c ( N . m / m ) and bending capacity ( M u ( n . m m ) ).
P a r s S o l u t i o n :
[ V c , M u , P ] = B e a m P a r s S o l u t i o n 1 ( L T S i , P a r N o , , A s , A s ′ , S T , F c , F y , H e , W i ) ;
Figure 2 shows a series of analyses, including the properties of 50 different beam sections. The input was produced randomly ( r a n d i ) but in a specific range for each variable (Table 2). The influences of these variables on the bending and shear capacities can be found in the last blue diagrams. The type of performance in the bar chart (P) is shown in blue, red and orange. For instance, the first section displayed 2 for the Height of blue and red also 1 for the orange part on top of the bar, which means the performance of it belongs to category (2.2.1). It displays the tensile re-bar yields, compressive does not yield, and the strain is higher than 0.004 (Chart in Figure 1).
In addition to the parameter and the ranges, P a r s S o l t i o n demands two other criteria. The first criterion informs P a r s S o l u t i o n about the number of parameters selected in each calculation series ( P a r N o ). It means all different features of the section can be selected parametrically (i.e. A s , A s ′ , S T , f c , F y , H e , W i ( P a r N o = 7 ) ) or just some (e.g. A s , A s ′ , S T ( P a r N o = 3 ) ). The second criterion is the size of the L o o k − u p table ( L T S i ) or, in other words, the number of calculated sections. The number of parameters ( P a r N o ) and the size of the L o o k − u p table ( L T S i ) as the primary measure was regarded for dissecting the performances of ML Operator ( M L O ) in the following sections. An MLO, which can delegate the results with higher accuracy and a lower amount of initial data (low L T S i ), has a more desirable performance. It would show its considerable importance when the difficulties in data production are considered. Indifferent filed, the data can be collected by quaternary (asking from experts), numerical analysis or experimental test, while in structural engineering, increasing the L T S i , especially in experimental studies, is complex and costly.

2.3. Parametric Evaluation of the Beams

In this study, beam capacity was selected as one of the easy structural calculations to evaluate the MLO. Likewise, P a r s S o l t i o n can be used for independent parametric evaluations. It could also be connected to an optimization algorithm. Such a function, similar to software (e.g. SAP2000 Section Designer), can easily calculate the capacity of sections with different parameters. Hence, different operators can use it for multi-analysis to regard different aspects of the section’s performances and perform statistical evaluations and sensitivity analysis by MATLAB Simulink.
One simple evaluation without coding Sensitivity Analysis is evaluating the influence of each parameter on M u & V c . Table 3, shows the influence of increasing the parameters twice (2.00) on this range’s bending and shear capacities. This evaluation showed that increasing the amount of all parameters twice increases the shear and bending capacity 7.18 times and 8.14 times. It means that bending capacity is more sensitive (No.1). That is, if the influences of stirrups are ignored despite no changes in increasing of M u , the changes in V c were reduced to 4.74 (No.2). It means in the selected range (Table 2), distances between the stirrups influence the shear capacity up to 34 % . The distance between the stirrups can not be due to the standard’s limitations (e.g. for keeping the ductility of beams) limitless changed, but the range was accepted as a parametric study.
In this range, Height has a similar influence on shear and bending and has a linear relation (No.3). Width has a higher effect on shear rather than bending (No.4). The changes in bending are not linear, and the width effect on bending in one step gets higher (due to changes in P). F c also shows a similar low influence on the V c and M u ; it means increasing the concrete properties regarding the C o s t s in comparison to the changes in other parameters, such as high is not economical (No.5). Generally, the lowest influence was shown by compressive re-bar (No.7) and higher by Height and tensile re-bars (No.8).

3. Machine LEARNING Operatos (MLO)

To discuss the performance of the following MLO, the specific range is based on the expected dimensions and properties of the material used in all following investigations (Table 2). In the prepared L o o k − u p table, the parameters linearly increased. Based on the ACI calculation, the first section selects Fuzzy Logic for delegating, interpreting, and using data ( L o o k − u p table). Likewise, the Neural Network and ANFIS will repeat the same process. Additionally, their sensitivity to the size of L T S i and P a r N o will be investigated. Finally, their performances regarding the different sizes of the L o o k − u p table and the number of parameters will be compared.

3.1. Fuzzy Log (FL)

Since MATLAB GUI ca N N ot generate codes to accept different ‘input’ and ‘output’ parameters, codes for making the interpreter of the L o o k − u p table and M e m b e r s h i p F o u n c t i o n s were developed. In the membership function, two types of functions were regarded, including (‘trimf’ and ‘gaussmf’) to be adjusted by the operator ( F a c ∈ 1 , 2 ). Assigning the inputs to outputs for such a range of data was not effortless for making the rules. Hence, a ‘for’ loop based on the L o o k − u p table was developed to develop adaptable codes for all essential parameters in designing the beams. In which the ‘1’ as the Variables and Weight for all rows of the Rule table was regarded. Then, the lookup table and ‘mamdani’ was used to make the ‘fis’ ( f i s = n e w f i s ( ′ L o o k u p T a b l e F I S ′ , ′ m a m d a n i ′ ) . Furthermore, ‘input’, ‘output’ etc., by a d d v a r assigned to the ‘fis’, and finalized by adding the rules.
Figure 3 displays an example of the series of section calculations. In this example, H e , f y , A S as the variables were selected, and 250 sections were calculated to make the L o o k − u p table ( L T S i = 250 ). This Figure shows how the parameters change linearly to increase the bending and shear capacity based on ACI. The same input in Fuzzy, the L o o k − u p table, is used, and the two diagrams show the Fuzzy delegating results. In these diagrams, the flat parameters indicate the not chosen variable, which means the P a r N o = 3 . The shown parameter in the last two diagrams, in blue, is the shear and bending capacity based on ACI. Likewise, red diagrams display the results of the Fuzzy operator. In these diagrams, the yellow bars are the difference between the targets (diversity between input from ACI codes and Fuzzy outputs). A similar example was made, utilizing randomized input and, accordingly, chaotic results of Fuzzy and ACI. This example shows the capacity of FL to interpret the not-sorted input. This capability shows its importance when several results of the studies against the current study regarding the type of the input parameters ca N N ot be sorted, Figure 4.
In another example in which just H e as the variable and ( L T S i = 500 ) as the table size was selected, the maximum Error (Differences between Fuzzy and Standard happened divided by the ACI capacities in each section), was limited to 16 & 17 % . In this example, with three parameters, Error raised to ′ 50 ′ % and ′ 59 ′ % for the calculation of shear and bending, respectively, displaying a considerably low accuracy. In Figure 3, the wave format of these Fuzzy diagrams and Errors shows that the error amount is not the same in different sections. The changes in Error are not related to beam section performance but come from the nature of Fuzzy. In another example with ′ 1 ′ parameter and ′ 100 ′ L o o k − u p table size, the Error in shear and bending capacity was ′ 17 & 19 ′ % , compared to the previous example with ′ 500 ′ L o o k − u p table size is just ′ 1 % ′ percent less accurate. It means up to some limits; despite its positive influence, increasing the size considerably raises the analyzing C o s t s , ca N N ot significantly improve the accuracy. Nonetheless, adjusting the Fuzzy codes and changes in several parameters or the L o o k − u p table size can influence the results more. The influences of these adjusting components should be evaluated para-metrically.
Two more loops were added to the codes to evaluate the capability of adjusting the MLO. The first ′ f o r ′ loop operates the MLO by a different range of initial data in the L o o k − u p table. It means if the L T S i is for instance 1208, ParsolutionSolution function, in the specific range calculates 1208, beam sections to be referenced by Fuzzy operator L T S i ∈ [ 20 , 416 , 812 , 1208 , 1604 , 2000 ] . This evaluation shows how much data (including all parameters) is needed for the selected beam example. The other parameters, such as a nest (loop), were also regarded. This loop, in five different steps, changes the number of parameters. This additional ′ f o r ′ loop (PARA) in five different steps selects different parameters, decided based on the results of parametric evaluations (efficient of the parameter on the capacity), Table 3. It was written by a s w i t c h c a s e o r function, demanding 5 × 6 = 30 , general operations, while each one may have up to 2000, beam calculations.
P A R A ∈ [ 1 , 2 , 3 , 5 , 7 ] ≡ [ ( H e ) , ( H e , A s ) , ( H e , A s , F y ) , ( H e , A s , F y , W i , S T ) , ( H e , A s , F y , W i , S T , F c , A s ′ ) ] .
The shear and bending Errors and the Standard deviation results are shown in Figure 5. Since the C o s t s of analysis is an important factor for evaluating the desirability of an operator’s performance, the duration of the process was also measured and documented in these diagrams. In Figure 5, all analyses with any ′ P a r N o ′ reduced the Error by increasing the L T S i , indicating the capability of them in case of suitable size of L o o k − u p Table. The sensitivity of Error to the amount of L T S i , by increasing that reduced. In all of the Errors and standard deviation, disregarding the P a r N o , the accuracy is considerably low when the L T S i < 250 . Increasing the ′ P a r N o ′ increases the analysis C o s t s , but the influence of increasing the P a r N o on the Errors is not linear. For instance, P a r N o = 4 has higher accuracy than P a r N o = 3 . This influence might be related to the value of P a r N o and the type of the membership functions. Despite the high probability of low accuracy in using FL in delegating the ACI codes, it can operate more stable (with less scattery results) with suitable adjustment and input.

3.2. Neural Network ( N N )

To compare N N and FL, Figure 6 displays the same examples solved and delegated by Neural Network codes. The codes of Neural Networks were developed in MATLAB. In order to fit the Network, as the activation operators, Sigmoid activation ( ′ s i g m o i d ′ ) and Hyperbolic tangent Sigmoid ( ′ t a n s i g ′ ), along with Linear function ( ′ p u r e l i n ′ ) for transferring the input were selected. In addition to inputs, targets and the number of the hidden layer (NHL), these operators were (by ′ n e w f f ′ command) assigned to the Network. For choosing, ’in/out-put’ and ’re/post-processing’ functions were coded. Likewise, operators were coded for removing rows with constant values ( ′ r e m o v e c o n s t a n t r o w s ′ ) and mapping rows with minimum and maximum values ( ′ m a p m i n m a x ′ ). Furthermore, ′ d i v i d e r a n d ′ for random division of data and every sample ( ′ s a m p l e ′ ) was picked, in which 70 % of the data for training and equal percent for validation and tests of the Network selected ( 30 % ). Additionally, for choosing and helping the train function, Levenberg-Marquardt ( ′ t r a i n l m ′ ) and Mean squared Error ( ′ m s e ′ ) were assigned to the Network performance function. In the codes, the number of the hidden layer ( N H L ) as an adjustable parameter was regarded (e.g. N H L = 5 ).
The same types of L o o k − u p tables as the input imported by Fuzzy were prepared in this section to be interpreted by N N . Figure 6 illustrates the results of these two examples with sorted and randomized input types. In this example, the size of the Table and parameters’ number are 250 & 3 respectively, ( L T S i = 250 , P a r N o = 3 ). Likewise, the red and blue diagrams show the N N and ACI results, while the differences between N N and ACI are shown in the yellow bar. The remarkably higher accuracy of N N compared to FL in both delegated results is visible. Generally, bending capacity ( M u ), compared to shear ( V c ), has a higher number of effective parameters, which causes the relation between feature and output to be more nonlinear. The Error results in these two examples show that N N can present a more exact bending capacity in sorted inputs. Despite this, randomized input bending diagrams show less exact. The N N operator also calculated several other examples based on and in compression to FL; it can be calculated that the capability of the Nural Network for delegating the ACI calculation is considerably higher.
One of the main components of the Nural Network is the number of the hidden layer (NHL). In a series of example same problem ( L T S i = 250 , P a r N o = 3 ) with different number of hidden layer ( N H L = [ 1 − 10 ] ) was repeated, Figure 7. It can be seen that compared to the chaotic nature of the coded N N , the NHL cannot show a strong influence on the results of this example. Based on multiple examples tested by the current study, it can be concluded that increasing the number of layers for more than three layers has more influence on the analysis C o s t s than the amount of Errors.
Nonetheless, the main highlight of using N N is the chaotic amount of accuracy. In other words, despite the input parameters, in a series of examples were increased gradually, the Error amounts in some were almost zero, and in some, they were several times higher than the maximum amounts of bending and shear capacity. To illustrate, a repetition of the same problem was documented in Figure 7. In these examples ( L T S i = 100 , P a r N o = 3 , N H L = 10 ), the Error of delegating the shear and bending beside the Errors Standard deviation was displayed. It can be seen that the Error in examples 1 & 6 is almost zero while, in example 2, shear is 30, times higher than ACI calculations. Despite FL showing, in general, lower accuracy, such an issue (chaotic results) was not detected. Some examples have acceptable performance in bending Error and are high in shear. Hence, in an operator like N N with low robustness, the Error amounts in objects may differ considerably. The high probability of facing low accuracy in the results of FL and, despite high capability, chaotic results of N N indicates the necessity of developing a method using the potentials of Fuzzy and N N while solving their issues.
It should be remembered that in all MLO in this study against other Multi-Objective optimization algorithms, the objects (here V c & M u ) are calculated separately in two different parallel interpreting processes.

3.3. Adaptive Neuro-Fuzzy-Inference System (ANFIS)

Adaptive Neuro-Fuzzy Inference System is a hybrid artificial intelligence model that combines the strengths of FL and Neural Networks. This operator was similarly developed in MATLAB, regarding the same feature coded for Fuzzy and N N . As the T r a i n D a t a , features of the beam section and the capacity of the beams calculated by ACI codes were selected. Inputs by Gaussian membership function ′ g a u s s m f ′ and linear output types in ′ 5 ′ layers were selected ( ′ l i n e a r ′ ). To remove and generate the system, subtractive clustering was chosen ( S u b . C l u s t e r i n g ). The options by ′ i n p u t d l g ′ were assigned to create dialogue box ′ P A R A M S ′ . The data, including the inputs, outputs and training data, were assigned to the ′ f i s ′ , by ′ g e n f i s 2 ′ , selected FIS generation approach. During the initial investigations, ′ S u b . C l u s t e r i n g ′ with ′ g e n f i s 2 ′ and ′ g e n f i s 3 ′ , both tried and due to this study’s low influence and concentration, ′ g e n f i s 3 ′ were in preparation for the results used. The cluster number was ′ 10 ′ , and the Exponent matric was partitioned to ′ 2 ′ . The number of maximum iterations and the number of Epochs was ′ 100 ′ , and the minimum improvement was ’ 1 e − 5 ’. In these studies, the initial step was 0.01 and the step size was 0.9, while 1.1 was the step size increasing rate and 0 as the error target was assigned.
Like the previous section, as the first examples, three parameters and the sorted and randomized inputs were selected to compare directly. Figure 8 shows the results of ANFIS in the delegation of beam calculations. It can be seen that the Error in the calculation of bending and shear capacities is deficient (approaching zeros). Generally, ANFIS has a robust homogeneous performance. The range of examples made by ANFIS displayed higher accuracy in calculating the bending in all examples with different L T S i and P a r N o , was repeated in average the bending Error is less than shear Error. The shear Error increases, especially with a low number of L T S i and P a r N o . In this investigation, different example series were solved by ANFIS. Based on an example with L T S i = 2400 when the number of parameters is 7, the calculation accuracy is ≈ 6 × 10 4 times lower than the same operation with a 1 parameter. Despite this, the Error range in both is less than 1.3 % and ignorable, Figure 9.
Similar results were experienced for the Standards deviation V C & M u . It might be concluded that the capability of this operator is more suitable for complex structural issues. If the duration of the process as the analyzing C o s t s is regarded, increasing the L T S i is the main factor for raising the C o s t s . Likewise, increasing the P a r N o , from 1 to 7, when L T S i = 800 in average increased the analyzing C o s t s to 450 % . ANFIS, in repeating the same problem, had the same results, proving its analytical stability. Additionally, increasing the size of L T S i in sorted input type proved its low positive influence on reducing the Error, but randomized input increased the Error.

3.4. Comparison between the Three MLO

Figure 10 (Left) displays a series of examples based on a randomized L o o k − u p table, in which L T S i range increases up to 1000. The Error of V C & M u , in addition to the analyzing duration by increasing the L T S i increases, is entirely visible in N N diagrams. ANFIS, in addition to having higher accuracy, has a robust performance; it did not indicate significant changes in V C & M u capacity representation of the ACI bending and shear capacity with less than 1 % differences. In this range, the analyzing C o s t s of Fuzzy and Neural Networks are similar and for the same problems are almost 66 % of ANFIS. The other examples showed higher differences between the C o s t s of FL and N N compared to ANFIS by increasing the L T S i , P a r N o & N H L .
Likewise, the duration of Fuzzy has an exponential relation with P a r N o and L T S i . It means that in representing the small problem, FL performs faster than N N and ANFIS. As mentioned, this study just selected MATLAB as a proper platform, and rewriting the codes in primary programming languages (e.g. C + + ) can considerably reduce the analyzing C o s t s . It should be mentioned that the time for preparing the L o o k − u p table was not considered when discussing the analyzing C o s t s . Accuracy (Error), duration (time) and robustness of the operator are the three selected. Hence, Figure 10 (Right) contrasts the MLO operations’ robustness by running the same problem with times to compare directly.
A general contrast between the performance of the MLO was made by fitting 3D surfaces to the results. This surface is also fitting managed in MATLAB, while the size of the L o o k − u p table ( L T S i ) and parameter Number ( P a r N o ), along with the average amount of shear and bending amounts, were separately selected. Figure 11 displays the accuracy of all three coded Machine Learning operators (including FL, N N and ANFIS). The top diagrams of Figure 11 illustrate the bending and shear errors in the down row. The results of various analyses were shown next to each other in these diagrams. The average amounts of shear and bending differences (Error between ACI and MLO), regarding the range of L T S i = [ 15 − 2400 ] , P a r N o = [ 1 − 5 ] , by fitting surfaces on them were plotted in MATLAB. Generally, one of the main usages of the MLO is curve fitting. Despite the higher power of MLO for fitting continuous surfaces to the discrete data and synergy between curve fitting and all discussed MLO, due to simpleness, in this diagram, simple codes in MATLAB were used.
FL has the lowest accuracy despite the highest stability in the calculations and results. The amount of Error in the calculation of the bending capacity gets lower by reducing the size of the L o o k − u p Table and increasing the number of parameters. On average, the bending calculated by FL and ACI in this range maximum differ ± 53.8 % , while for shear, this difference increases to ± 119.8 % . Generally, FL initial coding starts with defining the Linguistic Variables. Linguistic Variables include 1- The name of the variable (e.g. A s H e i g h t W i d t h ), 2- Amount of variables for each group (e.g. A s in [0.2,0.5,0]), 3- Range of the changes in variables (e.g. Height of a beam), and 4-Fuzzy set. Hence, each Linguistic Variable can be defined. It enables the FL to convert the initial digits to Fuzzy parameters (called Fuzzification) and, after the operation, to digits (called Defuzzification). This will be continued by developing the Rules for the logical implications needed. The conversion of the digits to logical and Linguistic variables enables the FL to import different types of data (e.g. Verbal information of a questionary form) but can be the reason for reducing the accuracy of the results (increasing the Error).
The results of N N on the average show ( ± 15.7 , ± 7.52 % ) Error for shear and bending, respectively, which is considerably lower than FL. Likewise, increasing the size of the L o o k − u p Table or, in other words, preparation of more initial data (e.g. from numerical or experimental structural analyses) can reduce the Error and scattered results faced more in calculating bending capacities.
Due to the issues of FL and N N (i.e. low accuracy and analyzing stability), this study also developed ANFIS codes. The results of this operator, which has the advantages of FL and N N , are shown in the last column of Figure 11. Against FL and N N , enlarging the L o o k − u p table can considerably increase the analysis C o s t s and does not enhance the accuracy. Increasing the number of parameters (beams sections feature) also reduces accuracy. Additionally, its performance in the calculation of shear compared to bending calculation is more accurate. ANFIS, with all sizes of inputs, should have entirely acceptable performance while, on average, the differences between the ACI direct calculation and ANFIS for bending and shear are ( ± 0.83 , ± 0.11 % ). The maximum experienced average Error, in general, is less than 1.5 % , which indicates the capability of ANFIS for delegating standard designs.

4. Conclusions

This study discussed the capability of different Machine Learning techniques in delegating conventional structural calculations. In other words, the study wants to investigate the possibility of replacing a design engineer with a Machine Learning operator. For such an evaluation and further practical utilization, different structural problems can be addressed, including structural analysis and design. Likewise, different Machine Learning methods can be selected. In the current study, as the structural problem, the Standard calculation of reinforced concrete beam section based on ACI was chosen. A wide range of computational operators was in the past decades developed (e.g. for deep learning and optimizations). The selected operators by this study, which might be regarded as a part of Machine Learning techniques, are Fuzzy Logic (FL), Neural Network ( N N ) and (Adaptive Neuro-Fuzzy Inference System) ANFIS, which were separated and entirely coded in MATLAB. After proving the accuracy of the coded standard by comparing it to references, since the operators need training data, L o o k − u p tables based on Standard parametric calculations were prepared. The relation between the Errors of each operator (i.e. comparison to direct ACI-based calculations), besides the number of parameters and size of the L o o k − u p tables, was also discussed.
Some highlighted results:
  • All coded three operators are adaptable and capable of delegating the standard parametric calculation.
  • The performance of all three operators depends on the number of parameters and size of training data.
  • Fuzzy Logic has the lowest accuracy and most stable operation, shown by repetition of the same problems.
  • The accuracy of the N N compared to FL is considerably higher, and the speed of the operation (analyzing C o s t s ) is slightly lower.
  • Despite the high capacity of the Neural Network, the results of its operation on the same problem are less stable.
  • Increasing the size of a L o o k − u p table and reducing the number of parameters can significantly improve the accuracy of the FL and N N results. The scatter performance of N N in bending calculation is considerably higher.
  • High probability of facing low accuracy in the results of FL and, despite high capability, chaotic results of N N indicates the necessity of developing a method using the potentials of Fuzzy and N N while solving their issues.
  • Overall, ANFIS provides a robust framework for modelling systems for calculating beam capacities, indicating the ability to handle uncertainty and learn from structural studies data.
  • ANFIS can delegate the ACI calculation, with, on average, less than ± 1 % difference.
  • More complex subjects, such as larger input size or parameter number, can slightly reduce the precision of ANFIS.
Some highlighted Out Look:
  • Developing Parsolutions, like what in this study was for preparation of the L o o k − u p table coded for other structural subjects and proper parametric evaluation (e.g. by sensitivity analyses), assist the engineers in the industry to design optimally.
  • To increase the accuracy and reduce the analyzing C o s t s , the developed FL, N N and ANFIS codes should be developed in other platforms and primary Coding languages for preparing software.
  • The developed MLO was used with the most common adjustments and parameters. The Coding options and parameters should be tuned in the next step for more desirable operation.

Author Contributions

Conceptualization, AB and HK; methodology, AB and NB; software; writing article-title draft preparation, AB; writing review and editing, NB and AB; visualization, NB; supervision, HK, NB and AB; project administration, HK; All authors have read and agreed to the published version of the manuscript.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
F L Fuzzy Logic
N N
Nural Network
A N F I S Adaptive Neuro-Fuzzy Inference System
M L O Machine Learning Operators
N H L the number of the hidden layer
W i Width of the concrete Section
H e Height of the concrete Section
S t Distance between stirrups (mm)
M u Bending capacity (N.mm)
V c Shear capacity
F y Steel Yield Stress (N=mm2)
f ′ c Concrete compressive Strength (N=mm2)
A s ′ Number of Compressive re-bar
A s Number of Tensile re-bar
N r Neutral Axis of the concrete Section
ρ t , b , m i n tensile, balance and minimum re-bar percentage in the section
ξ t Tensile strain in the concrete section
P a r N o Number of the parameters used in each operation
L T S i Size of the L o o k − u p table (number of the calculated section in each operation)

References

  1. Burnham, K. Artificial Intelligence vs. Machine Learning: What’s the Difference? Northeastern University 2020.
  2. Goldenberg, S.L.; Nir, G.; Salcudean, S.E. A new era: Artificial intelligence and machine learning in prostate cancer. Nature Reviews Urology 2019, 16, 391–403. [CrossRef]
  3. Brownlee, J. A tour of machine learning algorithms. 2019. URL https://machinelearningmastery.com/a-tour-of-machine-learning-algorithms 2020.
  4. Weidman, S. Deep Learning from Scratch: Building with Python from First Principles; O’Reilly Media, 2019.
  5. Makrynioti, N.; Vasiloglou, N.; Pasalic, E.; Vassalos, V. Modelling machine learning algorithms on relational data with datalog. In Proceedings of the Second Workshop on Data Management for End-To-End Machine Learning, 2018, pp. 1–4. [CrossRef]
  6. Aksjonov, A.; Nedoma, P.; Vodovozov, V.; Petlenkov, E.; Herrmann, M. Detection and evaluation of driver distraction using machine learning and fuzzy logic. IEEE Transactions on Intelligent Transportation Systems 2018, 20, 2048–2059. [CrossRef]
  7. Thomas, A. An introduction to neural networks for beginners. Technical report, Technical report in Adventures in Machine Learning, 2017.
  8. Zadeh, L.A. The role of fuzzy logic in modeling, identification and control. In Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers by Lotfi A Zadeh; World Scientific, 1996; pp. 783–795. [CrossRef]
  9. Klir, G.; Yuan, B. Fuzzy sets and fuzzy logic; Vol. 4, Prentice hall New Jersey, 1995.
  10. Ross, T.J. Fuzzy logic with engineering applications; John Wiley & Sons, 2009. [CrossRef]
  11. Frangopol, D.M.; Hong, K. A Probabilistic-Fuzzy Model for Seismic Hazard. Reliability and Safety Analyses under Fuzziness. Springer, 1995, pp. 302–325. [CrossRef]
  12. Khatibinia, M.; Gharehbagh, S.; Moustafa, A. Seismic reliability-based design optimization of reinforced concrete structures including soil-structure interaction effects. Earthquake Engineering-From Engineering Seismology to Optimal Seismic Design of Engineering Structures 2015, pp. 267–304. [CrossRef]
  13. Sahu, S.; Kumar, P.B.; Parhi, D.R. Intelligent hybrid fuzzy logic system for damage detection of beam-like structural elements. Journal of Theoretical and Applied Mechanics 2017, 55, 509–521. [CrossRef]
  14. Baghdadi, A.; Meshkini, A.; Kloft, H. Parametric design of in-plane concrete dry joints by FE method and Fuzzy logic toward utilising additive manufacturing technique. Proceedings of IASS Annual Symposia. International Association for Shell and Spatial Structures (IASS), 2020, Vol. 2014, pp. 1–12.
  15. Yu, Y.; Rashidi, M.; Samali, B.; Mohammadi, M.; Nguyen, T.N.; Zhou, X. Crack detection of concrete structures using deep convolutional neural networks optimized by enhanced chicken swarm algorithm. Structural Health Monitoring 2022, 21, 2244–2263. [CrossRef]
  16. Behnam, A.; Esfahani, M.R. Prediction of biaxial bending behavior of steel-concrete composite beam-columns by artificial neural network. Int. J. Optim. Civil Eng 2018, 8, 381–399.
  17. İpek, S.; Güneyisi, E.M.; Mermerdaş, K.; Algın, Z. Optimization and modeling of axial strength of concrete-filled double skin steel tubular columns using response surface and neural-network methods. Journal of Building Engineering 2021, 43, 103128. [CrossRef]
  18. Fathali, M.; Asgarian, B. Seismic response prediction of steel frame structures using adaptive neuro-fuzzy inference system. Structural Engineering and Mechanics 2019, 69(5), 547–556. [CrossRef]
  19. Bastami, A., K.A.; P., F. Acoustic emission-based damage detection in reinforced concrete structures using adaptive neuro-fuzzy inference system. Construction and Building Materials 2020, 262, 120918.
  20. Bazargan-Lari, R.; A., H. Optimization of steel-concrete composite beams using ANFIS algorithm. Journal of Constructional Steel Research 2019, 155, 47–60.
  21. Darain, K.; Hossain, M.; Jumaat, M.; Arifuzzaman, M. Prediction of Deflection Behavior of NSM Strengthened Reinforced Concrete Beam Using Fuzzy Logic. Selected Scientific Papers-Journal of Civil Engineering 2022, 17, 1–10. [CrossRef]
  22. Chopra, P.; Sharma, R.K.; Kumar, M. Prediction of compressive strength of concrete using artificial neural network and genetic programming. Advances in Materials Science and Engineering 2016, 2016. [CrossRef]
  23. Amani, J.; Moeini, R. Prediction of shear strength of reinforced concrete beams using adaptive neuro-fuzzy inference system and artificial neural network. Scientia Iranica 2012, 19, 242–248. [CrossRef]
  24. Toghroli, A.; Mohammadhassani, M.; Suhatril, M.; Shariati, M.; Ibrahim, Z. Prediction of shear capacity of channel shear connectors using the ANFIS model. Steel Compos Struct 2014, 17, 623–639. [CrossRef]
  25. by ACI Committee 318, R. Building Code Requirements for Structural Concrete (ACI 318-14), Commentary on Building Code Requirements for Structural Concrete (ACI 318R-14). An ACI Standard and Report. American Concrete Institute, 2014, Vol. ISBN: 978-0-87031-930-3.
  26. Mostofinejad, D. Rainforced concrete Structures, Based on ACI 318-05 and Iranian Concrete Code; Vol. II, Arkan Scince, ISBN:964-2591-04-9, 2008. [CrossRef]
  27. Developers, E.S.; Diagram.com, B.M. Free Bending Moment and Shear Force. Link: https://bendingmomentdiagram.com/free-calculator/reinforced-concrete-beam-calculator/ SkyeCiV.
  28. Tahouni, S. Design of reinforced concrete buildings; University of Tehran, ISBN:978-964-03-6363-8, 2010.
  29. Kainia, A. Analysis and design of concrete structures; Industrial University of Isfahan, ISBN:964-6122-08-6, 2010.
Preprints 89825 g001
Figure 1. Section’s Calculation Chart.
Figure 1. Section’s Calculation Chart.
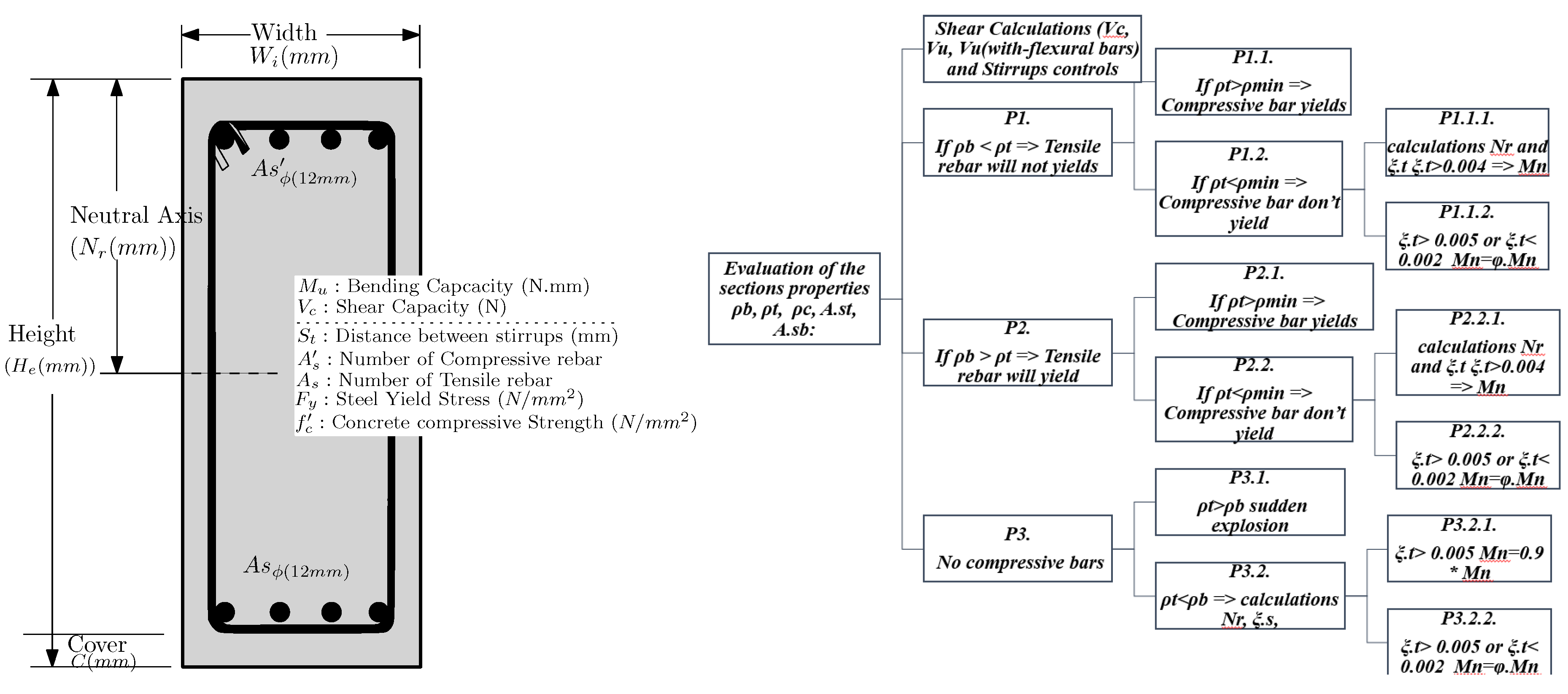
Preprints 89825 g001
Preprints 89825 g002
Figure 2. Random features of the 50 beam sections and the capacity based on ACI.
Figure 2. Random features of the 50 beam sections and the capacity based on ACI.
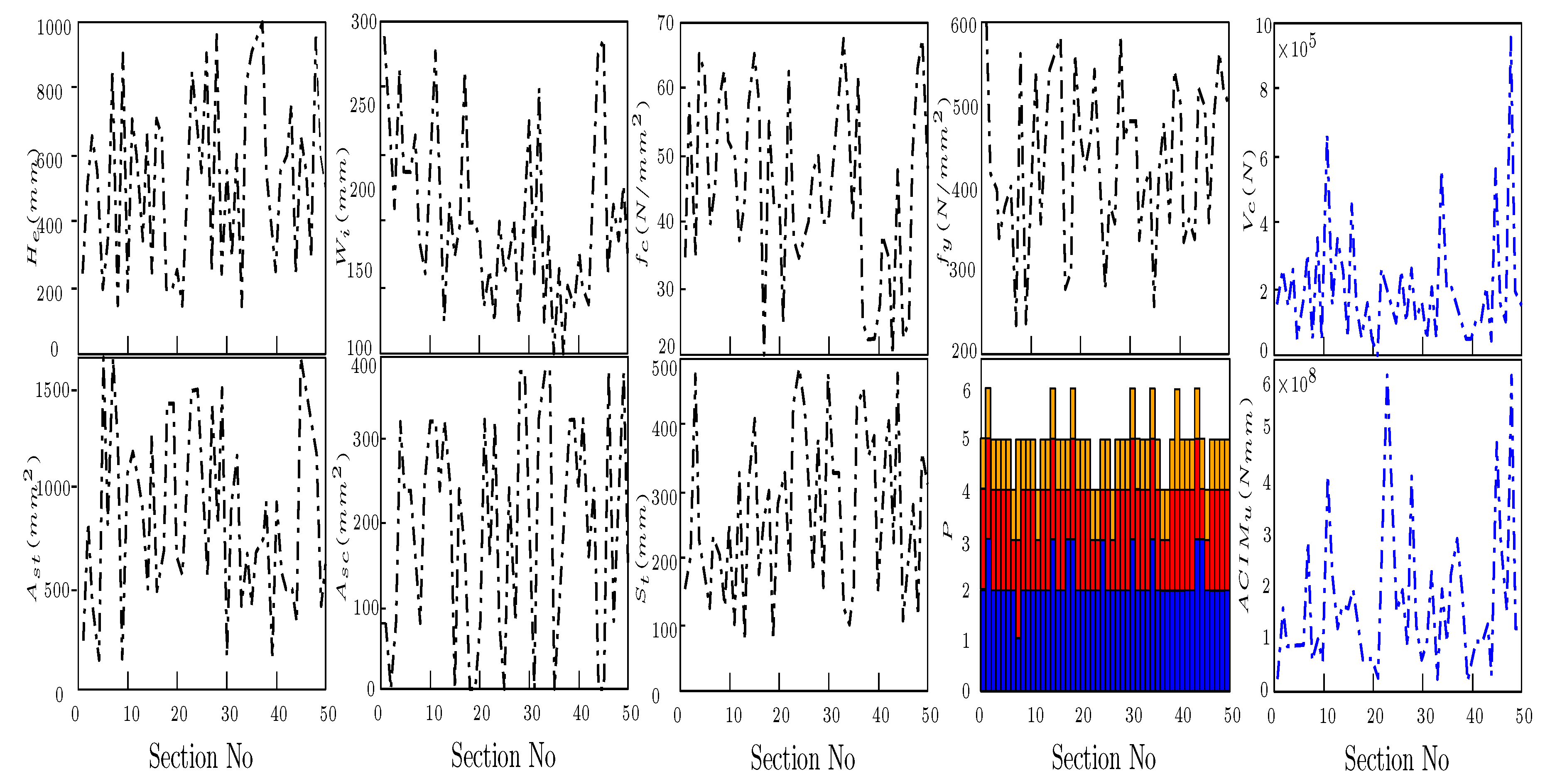
Preprints 89825 g002
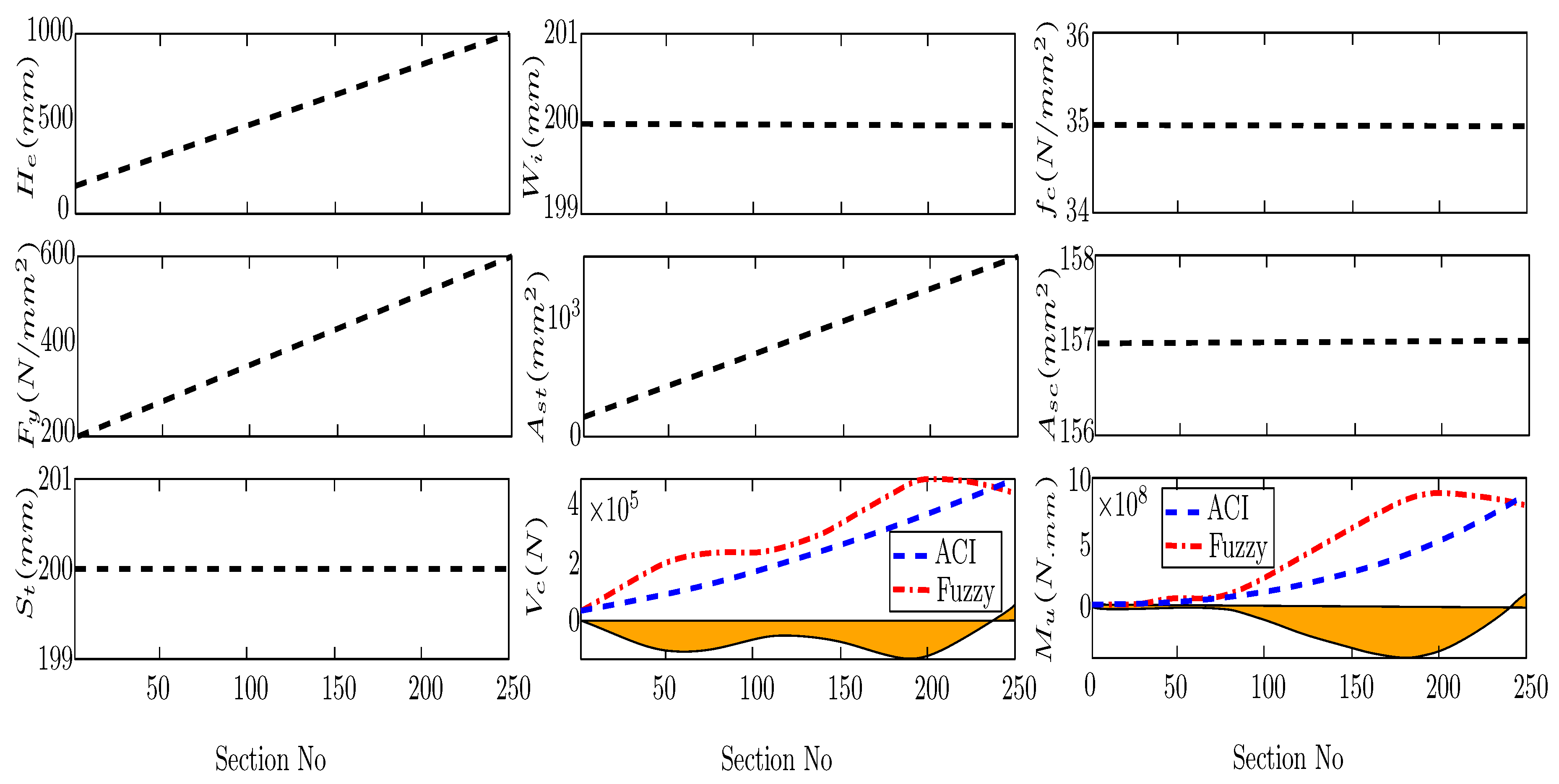
Preprints 89825 g003
Figure 3. Results of Fuzzy operation with 250, table size and three variables and ’gaussmf’.
Figure 3. Results of Fuzzy operation with 250, table size and three variables and ’gaussmf’.
Preprints 89825 g003
Preprints 89825 g004
Figure 4. Results of Fuzzy operation with ’250’, table size and ’3’ variables and ’gaussmf’.
Figure 4. Results of Fuzzy operation with ’250’, table size and ’3’ variables and ’gaussmf’.
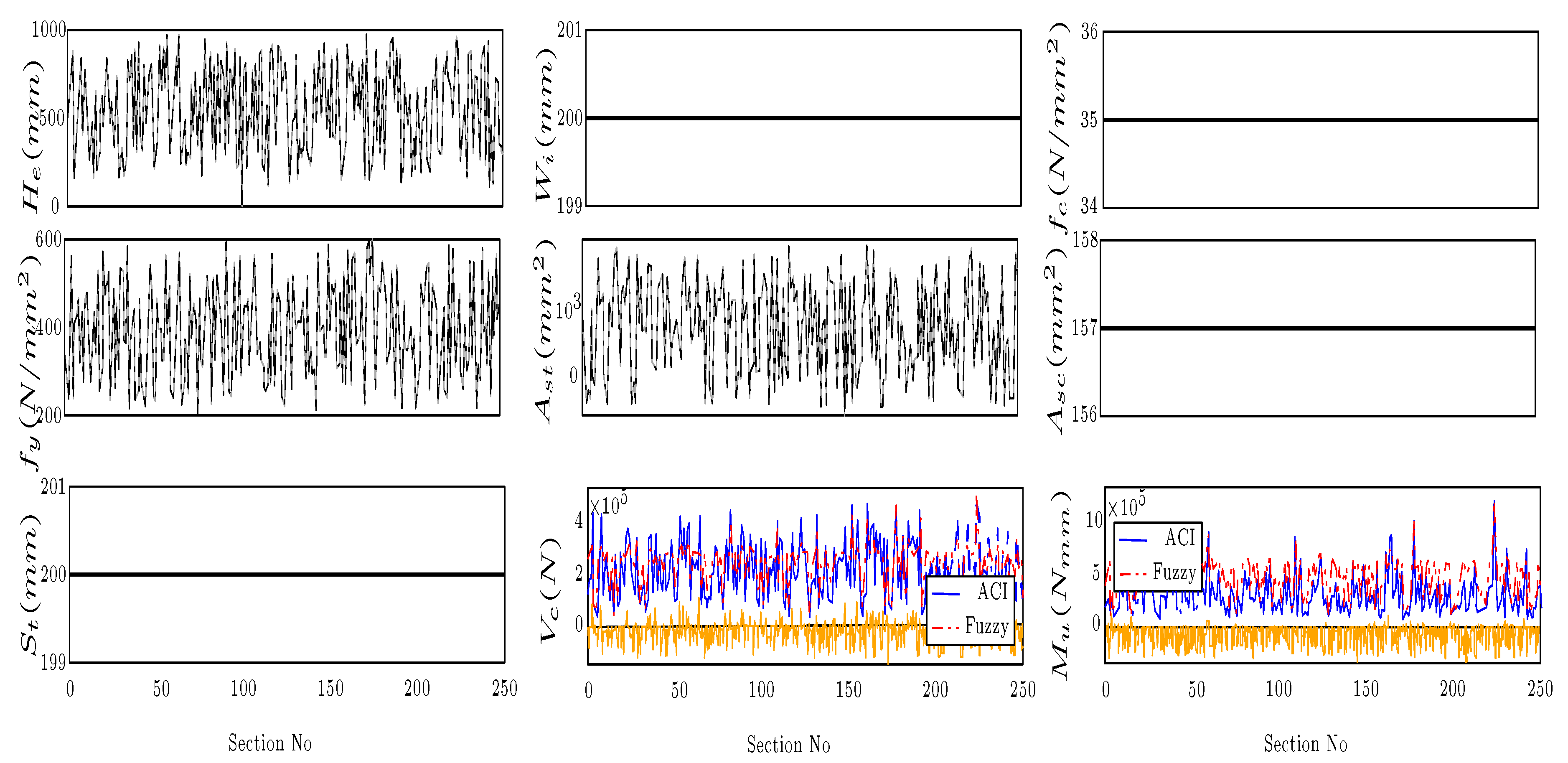
Preprints 89825 g004
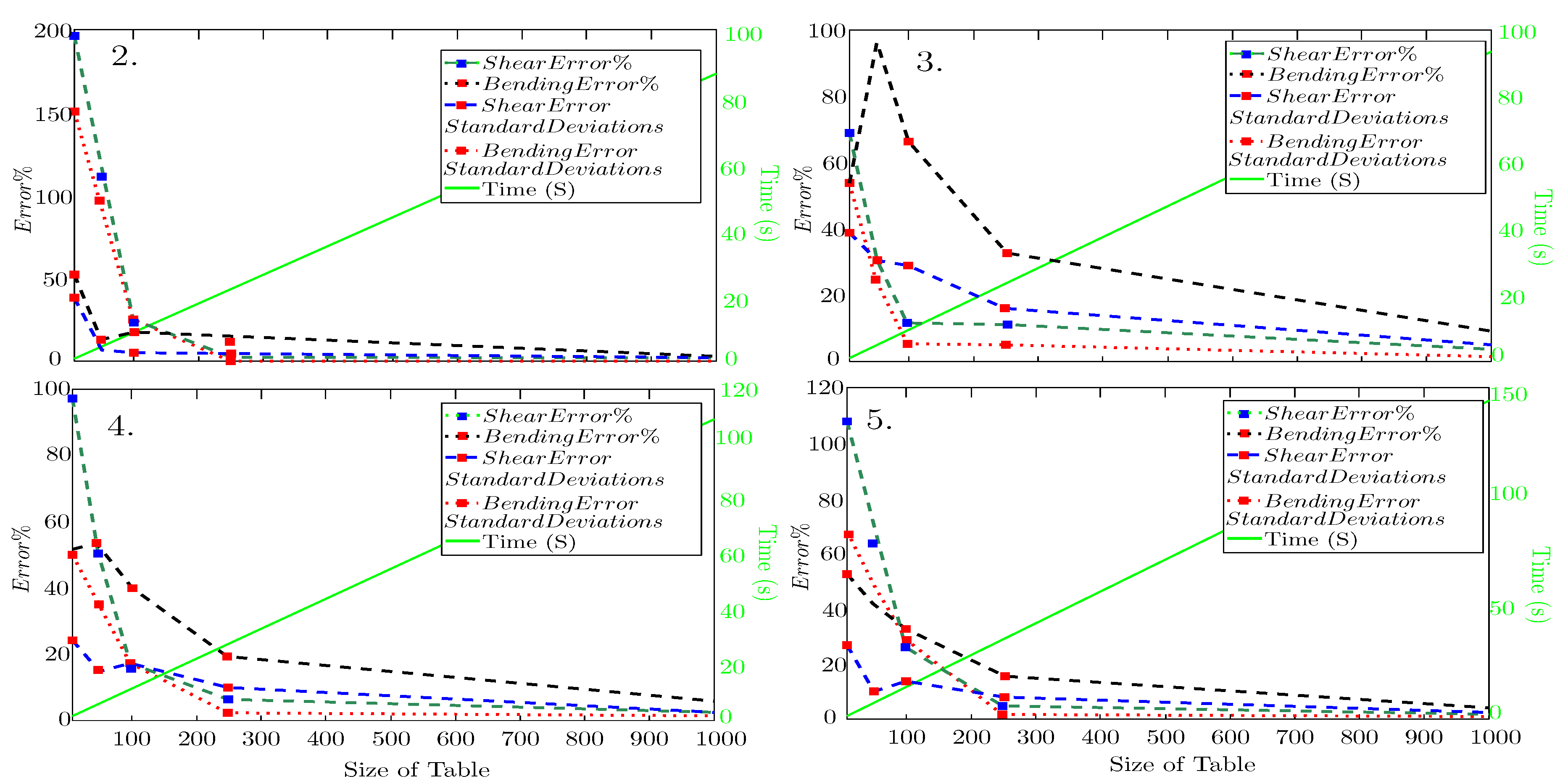
Preprints 89825 g005
Figure 5. Results of parametric adjustment of Fuzzy operator, P a r N o = [ 2 , 3 , 4 , 5 ] , L T S i = [ 20 − 1000 ] .
Figure 5. Results of parametric adjustment of Fuzzy operator, P a r N o = [ 2 , 3 , 4 , 5 ] , L T S i = [ 20 − 1000 ] .
Preprints 89825 g005
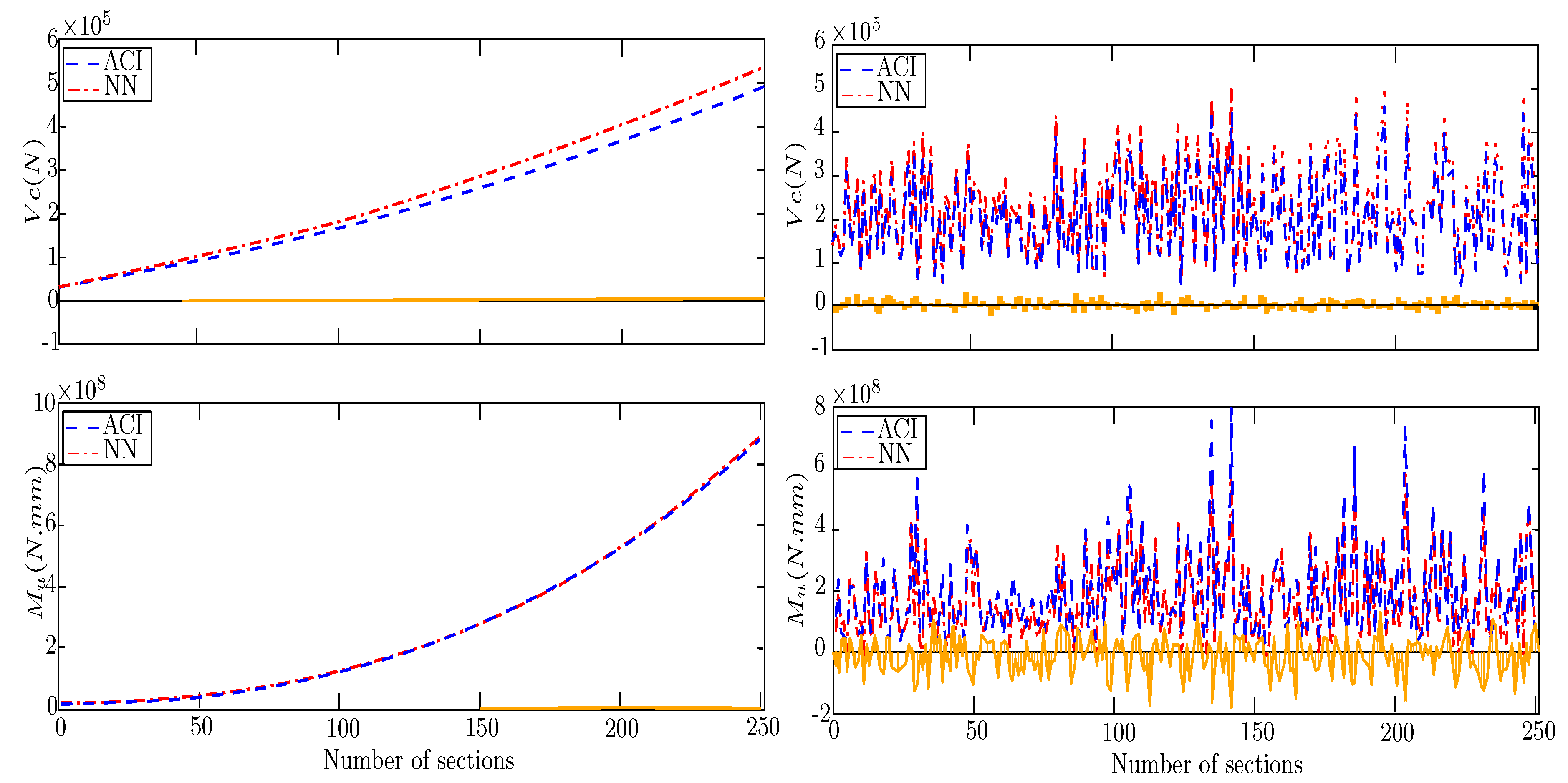
Preprints 89825 g006
Figure 6. Neural Network Results of sorted (left) and randomize (right) inputs, L T S i = 250 , P a r N o = 3 .
Figure 6. Neural Network Results of sorted (left) and randomize (right) inputs, L T S i = 250 , P a r N o = 3 .
Preprints 89825 g006
Preprints 89825 g007
Figure 7. Neural Network Results, for (right) discussing the influence of NHL and (left) robustness of the results in repetition of an exact problem.
Figure 7. Neural Network Results, for (right) discussing the influence of NHL and (left) robustness of the results in repetition of an exact problem.
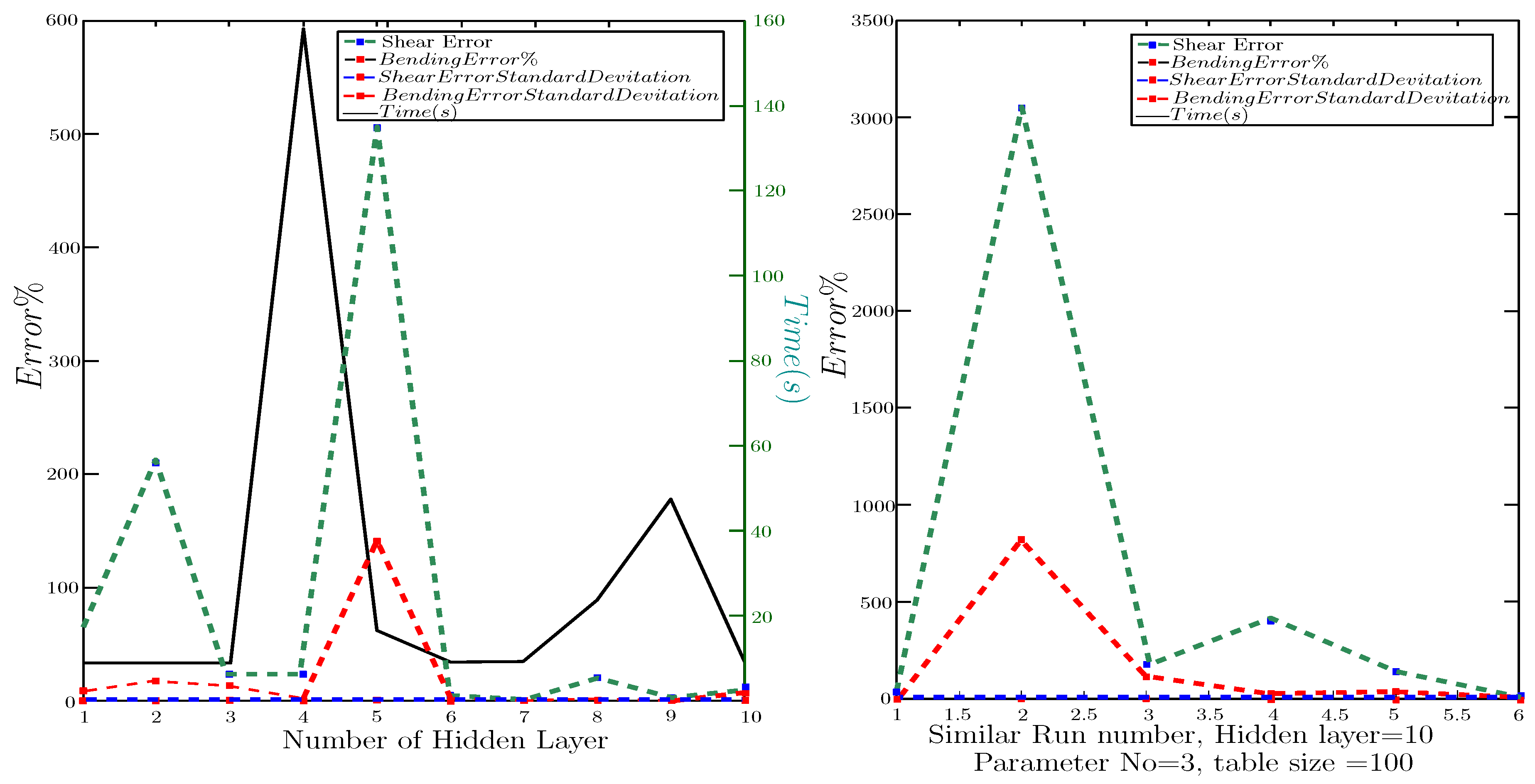
Preprints 89825 g007
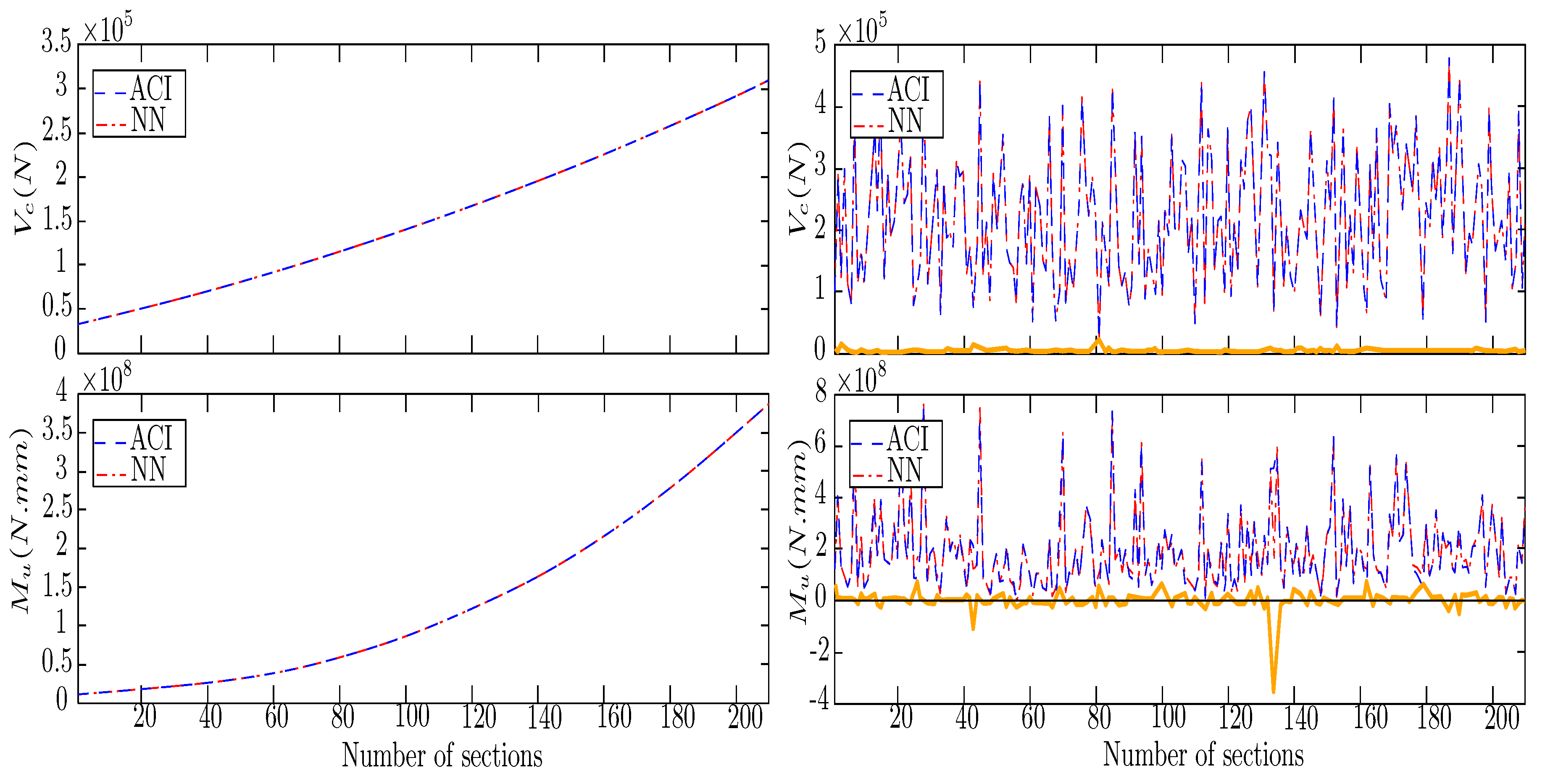
Preprints 89825 g008
Figure 8. ANFIS results of sorted (left) and randomize (right) inputs, L T S i = 220 , P a r N o = 3
Figure 8. ANFIS results of sorted (left) and randomize (right) inputs, L T S i = 220 , P a r N o = 3
Preprints 89825 g008
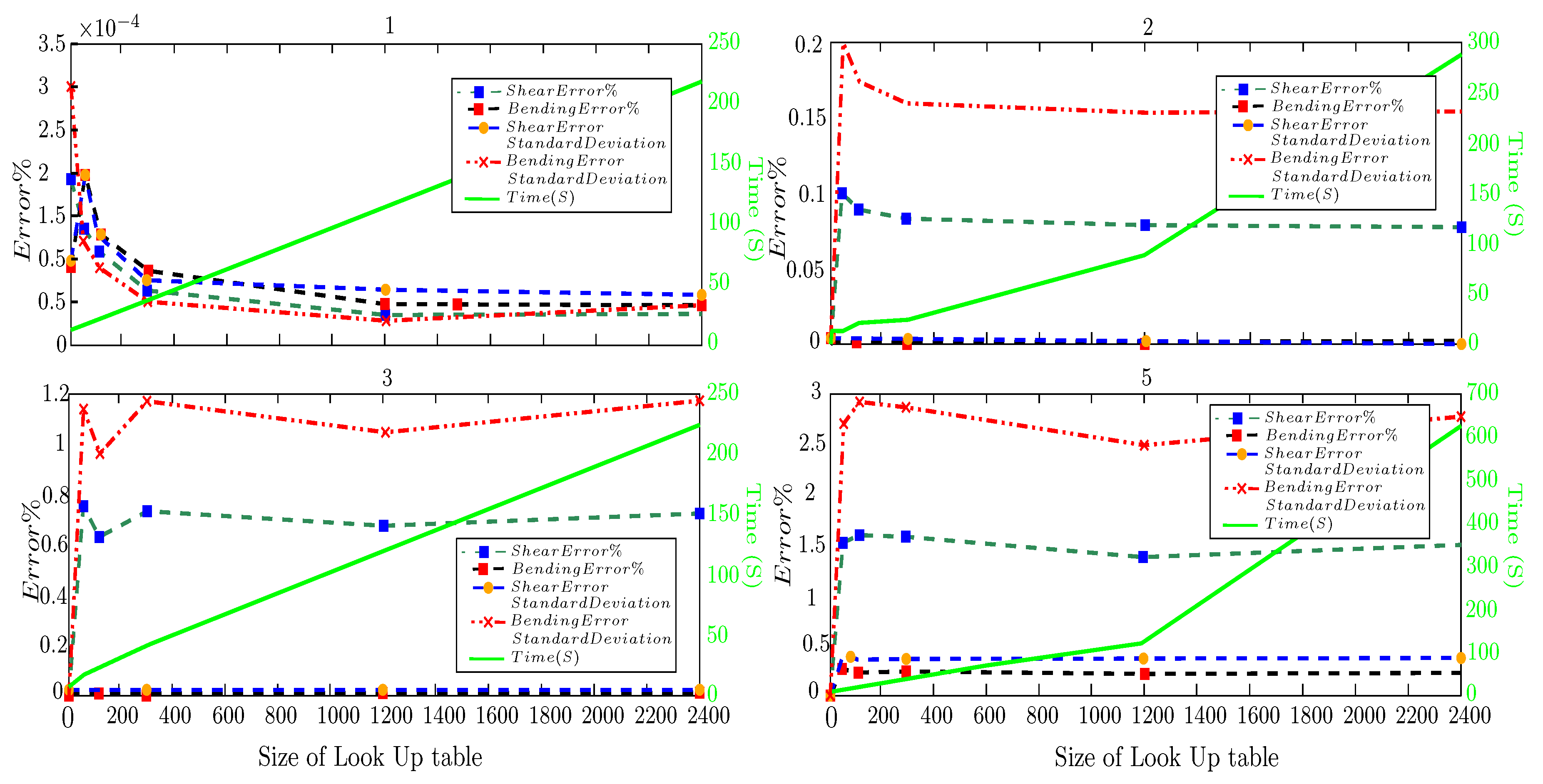
Preprints 89825 g009
Figure 9. Performance of ANFIS L T S i = [ 15 − 2400 ] , P a r N o = [ 1 − 5 ] .
Figure 9. Performance of ANFIS L T S i = [ 15 − 2400 ] , P a r N o = [ 1 − 5 ] .
Preprints 89825 g009
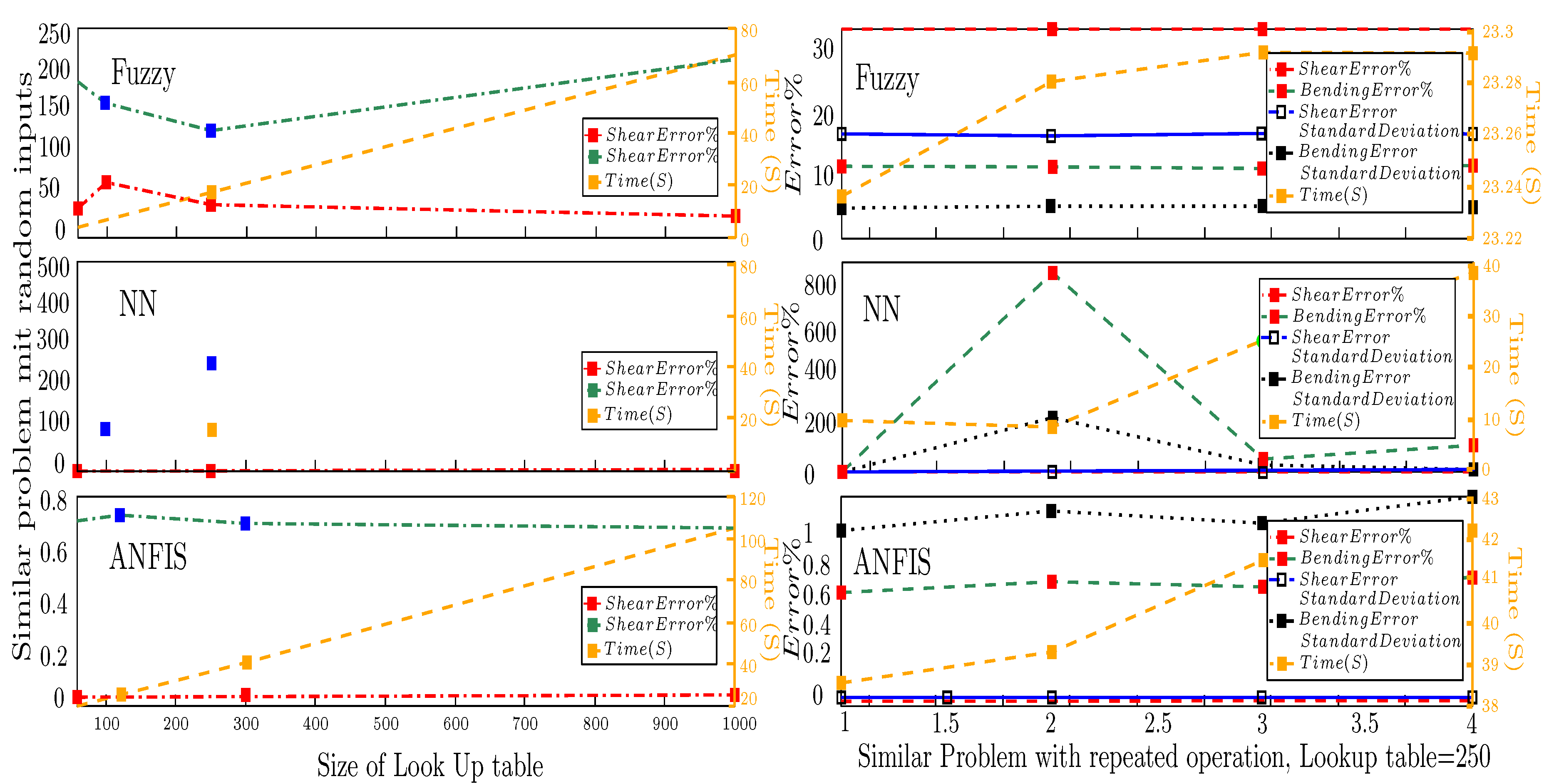
Preprints 89825 g010
Figure 10. Time comparison as the C o s t s for regarding different MLO, number of parameters and size of the L o o k − u p table, without the duration of time needed for the production of the L o o k − u p table and stability of the results on repetition of the similar problems.
Figure 10. Time comparison as the C o s t s for regarding different MLO, number of parameters and size of the L o o k − u p table, without the duration of time needed for the production of the L o o k − u p table and stability of the results on repetition of the similar problems.
Preprints 89825 g010
Preprints 89825 g011
Figure 11. Comparison between the performances of the discussed MLO, by fitting surfaces to shear and bending Errors, while L T S i = [ 15 − 2000 ] , P a r N o = [ 1 − 5 ] as the parameter ranges were regarded.
Figure 11. Comparison between the performances of the discussed MLO, by fitting surfaces to shear and bending Errors, while L T S i = [ 15 − 2000 ] , P a r N o = [ 1 − 5 ] as the parameter ranges were regarded.
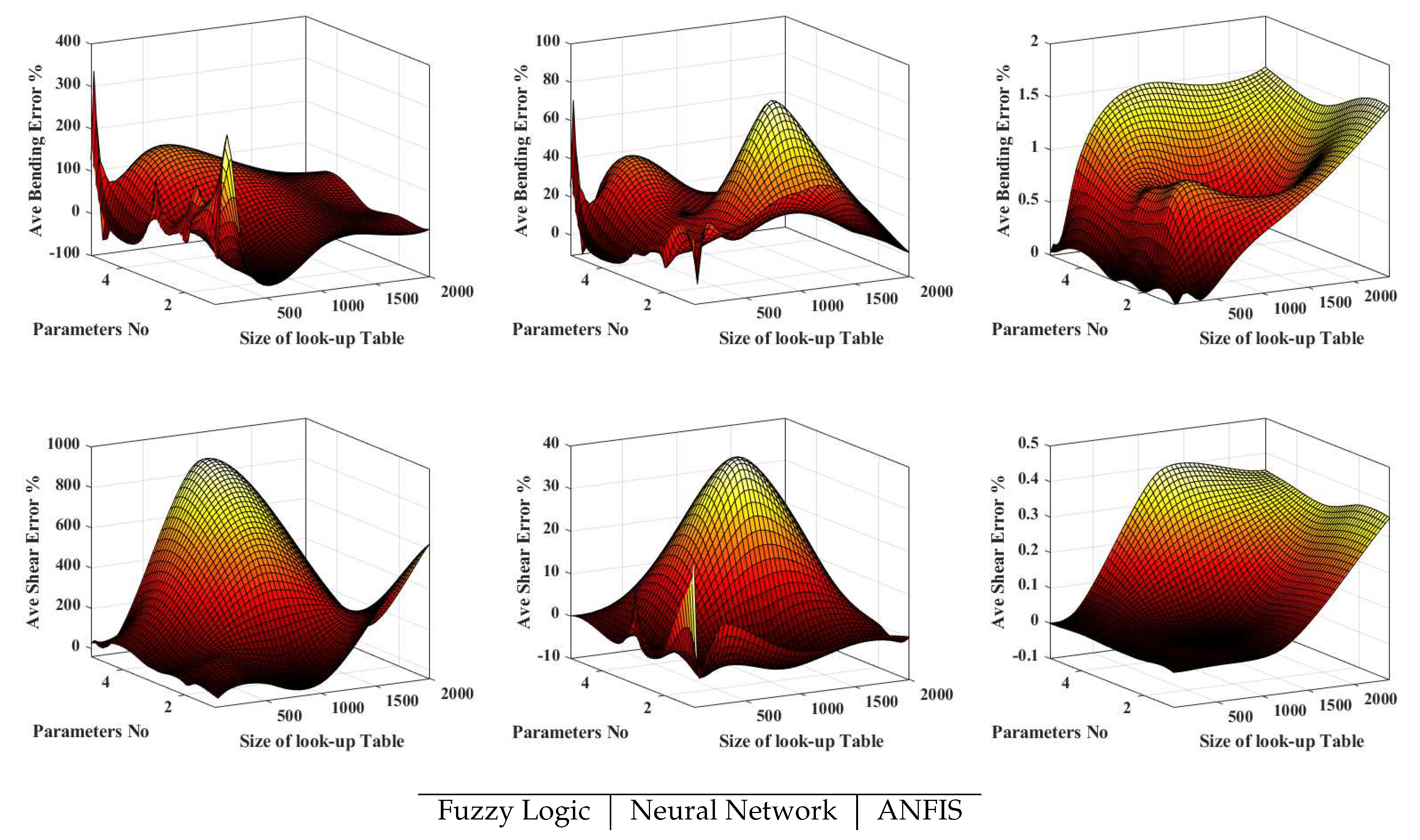
Preprints 89825 g011
Table 1. Verification of the accuracy of the coded beam calculations in comparison to the references.
Table 1. Verification of the accuracy of the coded beam calculations in comparison to the references.
He Wi fc fy As’ As St Perf N r Mu Vu Ref
No mm mm N/ m m 2 N/ m m 2 m m m m mm name mm N.mm N Name Amount
1 500 350 30 400 942 4825 - 2.1.2 174-174 7.1e08 - 11-5 [26] Mu:7.1e08
2 300 350 21 400 942 3217 - 1.1.2 149-145 2.1e08 - 12-5 [26] Mu:1.9e08
3 500 400 35 400 - 1357 - 3.2.1 47 2.6e08 - 5-5 [26] Mu:2.4e08
4 350 200 32 500 - 804.2 3.2.1 75-74 1.3e08 - [27] Mu:1.2e08
5 3500 2000 32 500 - 8040 - 3.2.1 75-74 1.4e10 - [27] Mu:1.4e10
6 500 300 35 400 - - ϕ 10@80 - - - 3.53e05 1-7 [1] Vu:3.5e05
7 520 350 21 300 - - ϕ 12@125 - - - 2.92e05 3-7 [26] Vu:2.8e05
8 500 300 30 400 1231 2412 - 2.2.1 72 - 3.95e8 3-8 [28] Mu:3.9e08
9 500 450 25 400 - - ϕ 12@100 - - - 3.97e05 [29] Vu:4.1e05
10 650 300 21 275 - 3220 3.1.1 5.0e08 [27] Mu:4.8e08
Table 2. Selected Range of Changes in the Variables.
Table 2. Selected Range of Changes in the Variables.
H e W i f c f y A s ’ A s S t
No mm mm N / m m 2 N / m m 2 m m 2 m m 2 mm
Range [150-1000] [100-300] [20-70] [200-600] [0-393] [158-1570] [500-50]
Table 3. Influence of parameters changes on the beam capacities (all numbers are percentages).
Table 3. Influence of parameters changes on the beam capacities (all numbers are percentages).
No H e ( % ) W i ( % ) f c ( % ) f y ( % ) A s ′ ( % ) A s ( % ) S t ( % ) M u ( % ) V c ( % )
1. 2,00 2,00 2,00 2,00 2,00 2,00 2,00 8,15 7,18
2. 2,00 2,00 2,00 2,00 2,00 2,00 1,00 8,15 4,74
3. 2,00 1,00 1,00 1,00 1,00 1,00 1,00 2.03 2,07
4. 1,00 2,00 1,00 1,00 1,00 1,00 1,00 1,08 1,32
5. 1,00 1,00 2,00 1,00 1,00 1,00 1,00 1,07 1,14
6. 1,00 1,00 1,00 2,00 1,00 1,00 1,00 1,95 1,54
7. 1,00 1,00 1,00 1,00 2,00 1,00 1,00 1,00 1,00
8. 1,00 1,00 1,00 1,00 1,00 2,00 1,00 1,95 1,00
9. 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated