Prerpints.org logo
Preprint
Article

A Generalised Series Model for LES of Premixed and Non-Premixed Turbulent Combustion

Altmetrics

Downloads

118

Views

56

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

08 November 2023

Posted:

08 November 2023

You are already at the latest version

Alerts
Abstract
In this study, the generality and prediction accuracy of a generalised series model for large eddy simulation of premixed and non-premixed turbulent combustion is explored. The model is based on Taylor series expansion of the chemical source term in scalar space and implemented into OpenFOAM. The mathematical model does not depend on the combustion regimes, and has the correct limiting behaviour. The numerical error sources are outlined and analysed. The model is first applied to a piloted methane/air non-premixed jet flame (Sandia Flame D). The statistical (time-averaged and RMS) results agree well with experimental measurements, particularly with regard to the mixture fraction, velocity, temperature, and concentrations of major species CH4, CO2, H2O, and O2. The concentrations of intermediates CO and H2 are over-predicted, due to the limitations of the reduced reaction mechanism employed. Then, a Bunsen piloted flame is simulated. Most of the statistical properties of both reactive species and progress variable are well reproduced. The only major discrepancy evident is in the temperature, which is attributed to the experimental uncertainties of temperature fields in the pilot stream. These findings have demonstrated the model`s generality for both premixed and non-premixed combustion simulation, as well as the accuracy of prediction of reactive species distribution.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

A challenge in the development of turbulent reacting models is the broad spectrum of length and temporal scales introduced by large Reynolds (Re) and Damköhler (Da) numbers in modern combustors [1,2,3]. Compromising between the practicality of Reynolds Averaged Navier-Stokes (RANS) for industrial scale applications and the accuracy of Direct Numerical Simulations (DNS), Large Eddy Simulation (LES) has proven itself a promising technique for the simulation of propulsion and energy systems, if appropriate sub-grid-scale (SGS) models are employed. The vast majority of established reactive SGS models are “borrowed” from those in RANS, and can be classified into three categories [2,4]: a) geometric approaches, such as flamelet [5], flame wrinkling [6], and thickened flame [7], b) statistical methods, including presumed [8] and transported PDF [9] and Conditional Moment Closures [10]/Multiple Mapping Closures [11], c) models based on turbulent mixing description, like, eddy break up [12], and eddy dissipation assumption [13]. Extensive reviews can be found in [14,15,16].
While these models offer satisfactory predictions, if combined with fine grid resolutions, they rely heavily on assumptions related to specific combustion regimes or they are too expensive (such as the PDF transport model). Formerly, mathematical approaches [2,17,18] based on series expansion were attempted within the RANS framework, and were limited to conditions like supersonic combustion [17] and atmospheric boundary layers [2,18]. In RANS, the high-order series of the chemical source may partake larger contributions beyond the first-order one and thus nonnegligible truncation errors, due to the substantial temporal oscillations of the temperature and specie fraction. This gives rise to the challenging task of modelling accurately the involved scalar gradient ( Y F ″ Y O ″ ¯ , Y F ″ T ″ ¯ ). Nevertheless, the same challenge does not exist in LES since filtering is operated in physical space (rather than temporal averaging of RANS), so that the higher-order contribution becomes less given a relatively well-resolved mesh and short time-stepping. This is evident in the research [19,20] of LES of non-reactive flows, in which a Taylor expansion on the filtered velocity field operates to close the SGS Reynolds stress in the Navier-Stokes equations. The simulation is validated against DNS and obtain satisfactory precision [21]. The model is later applied to modelling a neutral boundary layer flowing over a rough wall and the velocities coincide with theoretic solutions very well, ameliorating against standard eddy-viscosity approaches [19].
Similar mathematical methods [22,23] have also been proven feasible in the premixed turbulent combustion context, where series expansion is acted upon the reactive scalar field to determine the F factor in an artificially thickened flame (ATF) model. LES of a turbulent Bunsen flame is conducted, then accurate predictions regarding velocities and scalars are achieved [22,23]. For turbulent scalar signals, fourth order terms are found not to play a major role [22].
Based on the above work, we have presented a novel series model for turbulent combustion in the previous research [24]. Taylor series expansion is performed in scalar space to avoid the highly spatial non-linearity of the chemical source term; meanwhile, the method is generalised for non-premixed and premixed combustion, owing to its mathematical derivation. This model was previously validated on premixed bluff-body stablised flames [24]. Due to the experimental limitation of species information [25], we only briefly examined the predictive capability of combustion dynamics, velocity and temperature profiles (but not species) in the premixed context, in addition to the grid resolution dependence [24].
In this paper we build upon our previous work in order to provide a more detailed and well-rounded model evaluation. We extend the analysis of the model in the premixed regime with a new case (Bunsen jet flame F3 [26]) which benefits from a wider range of experimental data for validation. We also present results for non-premixed cases (Sandia Flame D [27]). The suitability of the model in non-premixed combustion has not been presented before. The objectives of this study are twofold: exploring the model’s generality for both premixed and non-premixed combustion simulation, and assessing the predicting accuracy for reactive species distribution simulations. In the next sections, the derivation of the series model and the numerical implementation into OpenFOAM is demonstrated, followed by the error analysis. Subsequently, LESs of the two widely-used validation benchmarks are presented. The results are analysed along with experimental data and data from previous relevant publications. Finally, major conclusions and suggestions for future work are presented.

2. Methodology

2.1. Mathematical formulation

The Mathematical formulation is identical to that in the study [24]. In the LES governing equations [2], the SGS stress tensor is computed by the dynamic one equation eddy model [28], although other approaches can be in principle be used. For the closure of reaction rates, a Taylor series expansion is operated in scalar domain, averting the high nonlinearity in physical space (regarding the source term as a function of spatial coordinates). The chemical source term is first expanded in a single scalar form.
ω ˙ c = ω ˙ c ¯ + ∂ ω ˙ ∂ c c = c ¯ ∂ c ∂ x i δ x i + 1 2 ∂ 2 ω ˙ ∂ c 2 c = c ¯ ∂ c ∂ x i δ x i 2 + …
Note that index notation is employed. Then an isotropic filter is practiced to relation (1). All terms with odd powers of x, y, and z vanish by means of symmetry elimination [24]. For detailed process, one can refer to the study [24] and the similar manipulations in the publications [19,20,21,22,23].
ω ˙ c ¯ = ω ˙ c ¯ + Δ 2 24 ∂ 2 ω ˙ ∂ c 2 c = c ¯ ∂ c ∂ x i 2 ¯ + O ( Δ 4 )
The same processes are executed on the chemical source, a function of multiple scalars φ k , including chemical species, temperature and pressure:
ω α ˙ φ 1 ,   φ 2 ,   … , φ k ¯ = ω α ˙ φ 1 ¯ ,   φ 2 ¯ ,   … , φ k ¯ + Δ 2 24 ∂ 2 ω α ˙ φ 1 ,   φ 2 ,   … , φ k ∂ φ m ∂ φ n φ 1 ,   φ 2 ,   … , φ k = φ 1 ¯ ,   φ 2 ¯ ,   … , φ k ¯ ∂ φ m ∂ x i ∂ φ n ∂ x i ¯ + O ( Δ 4 )
The unclosed scalar gradient term within, treated as the pseudo-scalar-dissipation form[2,17,18,24], is approximated by an algebraic expression approach [29]:
∂ φ m ∂ x i ∂ φ n ∂ x i ¯ = ∂ φ m ¯ ∂ x i ∂ φ n ¯ ∂ x i + χ sgs ≈   ( 1 + C sgs ) ∂ φ m ¯ ∂ x i ∂ φ n ¯ ∂ x i
For non-premixed combustion, C sgs is adopted as 0.1 following [30,31]. Otherwise, C sgs can be provided by transport equation models at the cost of high computational demands, which remains to be explored in future.
Finally, the model explicitly turns out to be:
ω α ˙ φ 1 ,   φ 2 ,   … , φ k ¯ = ω α ˙ φ 1 ¯ ,   φ 2 ¯ ,   … , φ k ¯ + Δ 2 24 ∂ 2 ω α ˙ φ 1 ,   φ 2 ,   … , φ n ∂ φ m ∂ φ n φ 1 ,   φ 2 ,   … , φ k = φ 1 ¯ ,   φ 2 ¯ ,   … , φ k ¯ ( 1 +   C sgs ) ∂ φ m ¯ ∂ x i ∂ φ n ¯ ∂ x i + O Δ 4
The final closure in expression (5) takes no presumption with respect to the combustion regime and, a-priori, it is applicable for premixed, non-premixed, and partially premixed combustion. Besides, accuracy is explicitly determined by the series truncation order. Finally, the approach preserves the reasonable restricting properties, where the SGS contribution decreases with the square of the filter width, see Relation (5), approaching DNS as  reaches Kolmogorov scales. For more details, one can refer to the study [24].

2.2. Numerical Implementation and Error Analysis

The series model is implemented on OpenFOAM platform [32]. In practice, the approach is incorporated in the reactingFoam solver through the manipulation on the chemical source in scalar balance equations. Besides, the library combustionModel is customised to import the sub-grid part of the series model into the source term interface. In order to utilise the information of Arrhenius reaction rate, the library chemicalModel is called. Then, the series model is coupled through the scalar transport equation with LES equations in the formation of a new reactingFoam-based solver. The PIMPLE algorithm is employed to deal with iterative procedures for coupling equations of momentum and mass conservation.
Despite the series model is derived mathematically, computational errors inevitably will occur, like any other sub-grid combustion models. The sources of error can potentially stem from:
First, high-order terms. The accuracy of the model is mainly determined by the order of Taylor series. In application, terms of the fourth and higher order are neglected, as they are not discovered to act a major role [23]. Nevertheless, under some extreme conditions, for example in modelling deflagration and detonation transition, these higher order contributions can significantly affect the flow field and lead to inaccuracy of predicting the sub-grid influence.
Second, the chemical mechanism. The series model requires the 2nd-derivative of the chemical source, which may become noisy under certain conditions. The choice of a well-established chemical scheme is crucial.
Thirdly, the scalar gradient term. The approximation in Equation (4) could be inaccurate in poorly resolved flames, where scalar gradients are large in the periphery of the reaction zones. This can be improved by employing a better refined/adaptive mesh.

3. Results and discussion

3.1. Non-premixed combustion simulation

The case under consideration is Sandia Flame D, an ideal experimental benchmark for non-premixed combustion, broadly utilised for model verification in past studies due to the large set of experimental data available. Experimentally, this jet flame has been studied on a piloted burner at Sydney University [33] by Barlow [34] who measured the temperature and species field, and Schneider [27] who provided LDV velocity details. The burner has an inner nozzle with a diameter D = 7.2 mm, where a mixture of 25% methane and 75% air by volume is injected at different bulk velocities 49.5m/s, resulting in Re = 22400. The pilot nozzle expands to a diameter of 18.2mm, coaxial to the main jet. From it exits a lean (Φ = 0.77, T = 1880K) mixture of C2H2, H2, air, CO2, and N2. Surrounding the pilot nozzle air streams at a velocity of 0.9m/s. The burner exit is positioned approximately 15 cm above the exit of the vertical wind tunnel [34]
The details of modelling parameters are exhibited in Table 1, along with comparisons with previous studies. According to it, the radial domain widely chosen ranged from 8 to 40D in the radial direction, while the axial part from 35 to 150D. In our work, the domain extends 70D in axial directions. Previous studies [35,36] suggest that clapping the grids to 50D does not affect the results, and in the radial direction it has an increase from 15 to 30D to capture the downstream flame/temperature expansion. The mesh is aligned with polar coordinates, but in the centre, a square section (or o-grid) is applied to avoid very fine meshes in the centreline. Two resolutions are employed under the Pope criterion [37]: a fine grid of 71 points in the tangential direction, 48 points in the azimuthal direction and 210 points in the axial direction, with an o-grid area of 12×12; a coarse one, which is approximately downscaled with a factor of 1.5 in each direction (52, 36, 139), with an o-grid zone of 9×9. Both grids stretch along the axial and tangential directions to handle the inlet variance and the strong gradients in shear layers. The sketch of simulation domain and grid allocation is depicted in Figure 1.
Snapshots of the simulated instantaneous fully-developed fields are shown in Figure 2. From the temperature and CO2 distribution, the predicted flame structure displays the conventional characteristics of non-premixed combustion [2] as expected: a preliminary area close to the inlet nozzle where flames are thin and a subsequent zone beside which hot products fill the majority of the downstream realm.
Statistical collection is performed over 16 burner flow-through times based on the jet bulk velocity. In addition, 10 flow-through times are initially computed to guarantee the flows fully developed. To compare, published Flame D predictions by [43] in Table 1 are imported in the following result plots. The main reason is that it adopts the same 4-step chemistry mechanism and uses the sophisticated Eulerian stochastic field method for combustion modelling. This will allow us to evaluate the performance of the series method against a well-established and reliable model avoiding complexities associated with the chemical mechanism. The results (fine-grid set) presented are carried with a similar resolution to the fine mesh employed in this study.
Figure 3 displays the mean and root-mean-square (RMS) trends of mixture fraction, temperature, axial velocity and species along the centreline, and Figure 4 show the radial distributions. The mixture fraction is defined following Bilger [34]. Along the centreline, the series model shows good prediction with mixture fraction experimental data in the fine grid, with slight over-prediction from z/D=10 to 40, illustrating that the flame shape is replicated reasonably. For the coarse resolution, the result shows a reasonable trend, but diverges off the fine grid prediction from z/D = 15. This is largely due to the grid insufficiency of the coarse mesh in the downstream part. However, the situation is opposite in the reference case [43], where over-prediction is observed in the immediate vicinity of the inlet. The authors attributed it for the limited grid resolution of the mixing layers evolving between the jet and pilot close to the nozzle. Switching to the radial distributions in Figure 4, the mixture fraction profiles are well reproduced by the series model, although small over-predictions of the peak values are found at z/D =30 and 45 in the coarse grid simulation. It is consistent with the centreline observations. The results from the stochastic fields method [37] are comparable in terms of accuracy with the series results although some under-prediction in the inner (fuel-rich side) regions at z/D =7.5 and 15 is noticed, which is not observed in the series model.
The axial profile of mean and RMS temperature is also displayed in Figure 3. Along the centreline, the mean temperature, the flame location accordingly, is well reproduced for the series model, and the fine grid prediction behaves better than the coarse one as expected. The temperature RMS keeps the same level as the experimental data, although small over-prediction appears in the upstream locations before z/D =25. This evidences that the temperature fluctuation is sufficiently resolved by the series model with a simplified chemical mechanism. Besides, the RMS trend duplicates the observations in the experiments that the minimum arises around the location of the maximum mean profile. For the radial profiles in Figure 4, the statistical distributions agree well with the experiments, albeit with slight over-predictions of the mean values at z/D =15 and 30. The over-predictions are also spotted in the reference case [43] and the discrepancies may originate from the thermal radiation that is not considered in both LES simulations. Besides, it should be noticed that the series model performs relatively better than the PDF method [43] at predicting the location of the mean peak at the near-nozzle positions z/D=7.5 and 15. This is related to the under-prediction of mixture fraction profiles in the stochastic field simulation[43]. The centreline distribution of velocities is displayed in Figure 3 as well. Clearly, those quantities are decently reproduced by the series model, in spite of some acceleration after 15D in the coarse grid simulation. For the stochastic field model [43], it predicts a relatively better trend.
Figure 3 also exhibits the axial profiles of reactive species. Observing the series model results, the reactants CH4 and O2 tend to consume faster than the experimental data, consistent with the slightly over-predicted temperature trend. The predictions of CO2 and H2O agree well with the measurements, though coarse grid results are less accurate. Nevertheless, the prediction of CO and H2 is significantly over-predicted. The discrepancies as well as the accelerated CH4 decay rate are like those observed in the simulation [43] and it can be attributed to the limitations of the simplified mechanism [42]. The findings[43,59] suggest that the C1 scheme in the mechanism[42] gives rise to an over-prediction of reaction rates on the fuel-rich side of the non-premixed flames. It is evidenced in the radial distribution of CH4 in Figure 4. Besides, the reduced reaction mechanism suffers from the shortcomings of predicting intermediates like H2 and CO as it is susceptible to diffusive transport [42]. This accounts for the inferior distributions of the same intermediate species in Figure 3. In spite, good radial agreement is achieved for both the series model and stochastic fields method [43], regarding the mean and RMS of CO2 and H2O. The peak locations near the nozzle exit are slightly under-predicted in the reference case [43], owing to the same reason of the temperature distribution.
Overall, both the mean and RMS behaviours of the non-premixed flame are well captured by the series model. Improvements are obtained with grid refinement, especially in terms of reproducing the temperature, mixture fraction and major species distributions. In contrast to the stochastic field approach using the same mechanism [43], the series model demonstrates comparatively good prediction in general, and even better at some occasions: like correctly capturing the radial distributions of mixture fractions and the peak locations of mean temperature and chemical species. This gives the series model a advantage to some extent since its formulation is simpler, the cost cheaper, and can be incorporated directly to the species transported equation.

3.2. Premixed combustion simulation

In this section, the methane/air turbulent Bunsen flame F3 experimented by Chen [26] is chosen. The configuration is a typical turbulent premixed flame with a wide range of available velocity, temperature and species experimental data provided in [25], and has been extensively applied for model validation in the combustion community. The burner has an inner nozzle with a diameter H = 12 mm, from which a stoichiometric mixture of methane and air is injected at different bulk velocities 30 m/s, leading to Re = 23,000. Surrounding the main fuel injection, a laminar stream (the burning products of stoichiometric methane and air) is piloted via a perforated plate for stabilising the turbulent flame [60], and the outer diameter is 68mm. Outward, the fresh air is entrained as a form of a low-velocity co-flow. In the diagram of the premixed regimes, the F3 flame lies in the thin reaction zone, more precisely near the flamelet regime.
Simulation details are presented in Table 2, along with the comparison with previous research. The simulated domain extends 30H downstream the nozzle, and 12H in the radial direction so as to capture the downstream flame/temperature expansion. As Table 2 summarises, the chosen domain is sufficient for the flame propagation. The grid used is aligned with polar coordinates, but in the centre, a square section (o-grid) is applied to avoid very fine meshes in the centreline as in Sandia Flame D. Two resolutions are employed following the Pope criterion [37]: a fine grid of 69 points in the tangential direction, 48 points in the azimuthal direction and 200 nodes in the axial direction; and a coarse one, which is approximately downscaled with a factor of 1.5 in each direction (49, 36, 134). Grids are stretched along the axial and tangential directions to seize the strong gradients stemming close to the nozzle and shear layers. The sketch of simulation domain and grid allocation is detailed in Figure 5.
On the inlet boundary, velocity is prescribed with the detailed flow field experimental data [26] above the nozzle exit. The inlet turbulence intensities are imposed using the same approach as the Sandia D flame. For the main jet species, flat profiles are specified using the measurements[26]. The composition of the pilot stream is following [60]. The pilot temperature is presumed as 1785K [60,73,74], corresponding to 20% heat loss. Free slip is used for the lateral boundary, while a non-reflecting outflow condition is used on the outflow plane. The numerical schemes, the time set-up and the chemistry mechanism are the same as in Sandia Flame D simulations.
Statistical collection is performed over 15 burner flow-through times based on the jet bulk velocity. Before it, 8 flow-through times are computed to guarantee the flows fully developed. As a comparison, a set of F3 flame predictions published by [22] in Table 2 are selected, since it adopts a similar mathematical approach based on Taylor series expansion on the scalar field to determine the F factor in the ATF model. The augmented reduced version of GRI 3.0 schemes is introduced to denote chemistry. Besides, the mesh resolution is higher than the fine grid in this work.
The radial profiles of mean temperature and reactive species at different streamwise locations are first depicted in Figure 6. In overall, the mean temperature is over-produced, especially near the nozzle. However, different researchers [60,64,66,67,69,75] reported the similar discrepancies related to experimental measurements (largely extending 10–25 % experimental uncertainties) using either reduced or detailed mechanisms. This discrepancy is largely due to the uncertainties of temperature fields in the pilot stream, where a large and unidentified portion (not reported in experiments [26]) of heat is lost to the burner exteriors [64,67]. Past studies in Table 2 indicate that the loss proportion varies between 0[64,65] and 34%[60,70]. On the other hand, the simulation domain starts just downstream the nozzle exit for computational cost reduction, and wall heat transfer is not considered.
The radial trends of species mass fraction are displayed in Figure 6. The profiles of CH4 and O2 are reasonably replicated; In spite of some minor under-predictions on the fuel-lean sides (r/H>0.5), the calculated reactants meet the measurements well at the fuel-rich side and keep the descending trend from upstream to downstream. This indicates that the consummation rates of CH4 and O2 are well reproduced along the centreline. On contrast, the reference results [22] are under-predicted on both the fuel-lean and fuel-rich sites.
The radial distributions of CO2 and H2O by the series model are in a reasonably decent consistence with experimental observations, despite of some under-predictions at z/H = 6.5. Meanwhile, improvements are obvious with the increase of grid resolutions. Compared with the reference case [22], the series model performs better on the fuel-rich sides. It is related with the situation that the profiles of the reactants CH4 and O2 are not well resolved in these areas [22]. Note that in ATF models, although the thickened flames are solved, the species transport equation is modified, the interaction between combustion and turbulence is transformed from a transport-dominant combustion regime to a chemistry-dominant one, and the impact of the heat release upon the flow field is not represented sufficiently. In contrast, the series model operates on the reaction rate term directly, without altering the formation of species balance equations. In terms of CO, the series model also obtains a good prediction, while the profiles are slightly under-predicted in the reference case[22]. On the other hand, the computed CO products are less sensitive to grid resolutions than major species, as less difference is found with grid refinement. The measurement error of major species varies from 8% to 15% and that of intermediate species reaches 25% [26]. The major and intermediate species predicted by the series model principally cater to the accuracy in both grid resolutions.
To further inspect the impact of the temperature discrepancies, a new progress variable is established by the definition of a linear combination of species concentration [76]:
c = Y CO 2 + Y CO ( Y CO 2 + Y CO ) pilot
The radial distribution is depicted in Figure 7 and compared with experimental measurements. In this regard, the progress variable based on species demonstrates a reasonable and much better agreement than the temperature profile. The trend is refined even in the vicinity of the nozzle exit, where substantial discrepancies in the mean temperature are detected.
Usually in non-premixed combustion where the flame is thick, one would eventually start resolving it as the mesh is refined. However, in premixed combustion, the reaction zones are very thin and they would always remain under the grid size in LES. In general, with the refinement of grid resolution, the series model improves at predicting the premixed Bunsen flame. Comparing the series model with the simulations of [22], which adopted a similar series approach to determine the F factor of the artificially thickened flame model, the predictions are as good, if not better. Considering that the reference simulation[22] employs a finer mesh and also more detailed chemistry, the series model shows the potential improvement if finer meshes are used or/and more detailed chemistry.

4. Conclusions

The generality and prediction accuracy of the generalised series model for LES of premixed and non-premixed turbulent combustion is presented. It is based on Taylor series expansion of the chemical source term in scalar space around the filtered value and implemented into OpenFOAM. The mathematical model does not depend on the combustion regimes, has the correct limiting behaviour, and determines the order of accuracy explicitly.
The model is first applied to a piloted methane/air non-premixed jet flame (Sandia Flame D) with two mesh resolutions. Overall, the statistical (time-averaged and RMS) results agree well with experimental measurements, particularly with regard to the mixture fraction, velocity, temperature, and the concentrations of major reactive species CH4, CO2, H2O, and O2. The concentrations of intermediates CO and H2 are over-predicted, due to the limitations of the reduced reaction mechanism employed. Then, a Bunsen piloted premixed flame is simulated. Most of the statistical properties of both reactive species and progress variable are also well reproduced by the series model. The only major discrepancy evident is in the temperature and it is attributed to the experimental uncertainties of temperature fields in the pilot stream.
Overall, the results have demonstrated the model’s generality for both premixed and non-premixed combustion simulation, and its accuracy of prediction of reactive species distribution. Future research will extend the present work to partially premixed flames with detailed chemistry.

Author Contributions

Conceptualization, K.L., K.V., and S.N.; methodology, K.L., K.V., and W.Z.; software, W.Z. and K.V.; validation, W.Z. and K.V.; formal analysis, W.Z.; investigation, W.Z.; resources, K.L., and X.W.; data curation, W.Z.; writing—original draft preparation, W.Z.; writing—review and editing, K.L., K.V., and X.W.; visualization, W.Z.; supervision, K.L.; project administration, K.L.; funding acquisition, K.L. and X.W. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by Guangdong Basic and Applied Basic Research Foundation (Grant No. 2020A1515110720), China Postdoctoral Science Foundation (Grant No. 2020M682178) and Natural Science Foundation of Shandong Province (Grant No. ZR2021QE144).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

c Species mass concentration α Chemical species
C sgs Sub-grid coefficient Δ Filter size
D Sandia flame D inlet diameter φ k Field scalar
Da Damköhler number χ Scalar dissipation rate
hrs Hours ω ˙ c Chemical source term
H Bunsen flame F3 inlet diameter
r Radial offset
Re Reynolds number
T Temperature
xj The spatial vector
Y Species mass fraction
z The spatial z-direction vector

References

  1. Taamallah, S.; Vogiatzaki, K.; Alzahrani, F.M.; Mokheimer, E.M.; Habib, M.; Ghoniem, A.F. Fuel flexibility, stability and emissions in premixed hydrogen-rich gas turbine combustion: Technology, fundamentals, and numerical simulations. Applied energy 2015, 154, 1020–1047. [Google Scholar] [CrossRef]
  2. T. Poinsot, D. Veynante, Theoretical and numerical combustion, RT Edwards, Inc.2005.
  3. Jiang, X.; Luo, K. Combustion-induced buoyancy effects of an axisymmetric reactive plume. Proceedings of the combustion institute 2000, 28, 1989–1995. [Google Scholar] [CrossRef]
  4. Giacomazzi, E.; Battaglia, V.; Bruno, C. The coupling of turbulence and chemistry in a premixed bluff-body flame as studied by LES. Combustion and Flame 2004, 138, 320–335. [Google Scholar] [CrossRef]
  5. Popp, S.; Hunger, F.; Hartl, S.; Messig, D.; Coriton, B.; Frank, J.H.; Fuest, F.; Hasse, C. LES flamelet-progress variable modeling and measurements of a turbulent partially-premixed dimethyl ether jet flame. Combustion and Flame 2015, 162, 3016–3029. [Google Scholar] [CrossRef]
  6. Volpiani, P.S.; Schmitt, T.; Vermorel, O.; Quillatre, P.; Veynante, D. Large eddy simulation of explosion deflagrating flames using a dynamic wrinkling formulation. Combustion and Flame 2017, 186, 17–31. [Google Scholar] [CrossRef]
  7. Sacomano Filho, F.L.; Kuenne, G.; Chrigui, M.; Sadiki, A.; Janicka, J. A consistent Artificially Thickened Flame approach for spray combustion using LES and the FGM chemistry reduction method: Validation in Lean Partially Pre-vaporized flames. Combustion and Flame 2017, 184, 68–89. [Google Scholar] [CrossRef]
  8. Malalasekera, W.; Ranga-Dinesh, K.; Ibrahim, S.S.; Masri, A.R. LES of recirculation and vortex breakdown in swirling flames. Combustion Science and Technology 2008, 180, 809–832. [Google Scholar] [CrossRef]
  9. Gallot-Lavallée, S.; Jones, W.; Marquis, A. Large Eddy Simulation of an ethanol spray flame under MILD combustion with the stochastic fields method. Proceedings of the Combustion Institute 2017, 36, 2577–2584. [Google Scholar] [CrossRef]
  10. Navarro-Martinez, S.; Kronenburg, A. Flame stabilization mechanisms in lifted flames. Flow, Turbulence and Combustion 2011, 87, 377–406. [Google Scholar] [CrossRef]
  11. Farrace, D.; Chung, K.; Pandurangi, S.S.; Wright, Y.M.; Boulouchos, K.; Swaminathan, N. Unstructured LES-CMC modelling of turbulent premixed bluff body flames close to blow-off. Proceedings of the Combustion Institute 2017, 36, 1977–1985. [Google Scholar] [CrossRef]
  12. D.B. Spalding. Development of the eddy-break-up model of turbulent combustion. In: editor^editors. Symposium (International) on Combustion; 1977: Elsevier. p. 1657-1663.
  13. Ertesvåg, I.S.; Magnussen, B.F. The eddy dissipation turbulence energy cascade model. Combustion science and technology 2000, 159, 213–235. [Google Scholar] [CrossRef]
  14. Gicquel, L.Y.; Staffelbach, G.; Poinsot, T. Large eddy simulations of gaseous flames in gas turbine combustion chambers. Progress in Energy and Combustion Science 2012, 38, 782–817. [Google Scholar] [CrossRef]
  15. Pitsch, H. Large-eddy simulation of turbulent combustion. Annu. Rev. Fluid Mech. 2006, 38, 453–482. [Google Scholar] [CrossRef]
  16. Janicka, J.; Sadiki, A. Large eddy simulation of turbulent combustion systems. Proceedings of the Combustion Institute 2005, 30, 537–547. [Google Scholar] [CrossRef]
  17. Villasenor, R.; Chen, J.-Y.; Pitz, R. Modeling ideally expanded supersonic turbulent jet flows with nonpremixed H2-air combustion. AIAA journal 1992, 30, 395–402. [Google Scholar] [CrossRef]
  18. F. Nieuwstadt, J. Meeder, Large-eddy simulation of air pollution dispersion: a review, New tools in turbulence modelling, Springer1997, pp. 265-280.
  19. Chow, F.K.; Street, R.L.; Xue, M.; Ferziger, J.H. Explicit filtering and reconstruction turbulence modeling for large-eddy simulation of neutral boundary layer flow. Journal of the Atmospheric Sciences 2005, 62, 2058–2077. [Google Scholar] [CrossRef]
  20. F.V. Katopodes, R. Street, J. Ferziger. Subfilter-scale scalar transport for large-eddy simulation. In: editor^editors. 14th Symposium on Boundary Layers and Turbulence; 2000: American Meteorologic Society Aspen (CO). p. 472-475.
  21. F.V. Katopodes, R.L. Street, J.H. Ferziger, A theory for the subfilter-scale model in large-eddy simulation, Environmental Fluid Mechanics Laboratory Tech. Rep, (2000) K1.
  22. Domingo, P.; Vervisch, L. Large Eddy Simulation of premixed turbulent combustion using approximate deconvolution and explicit flame filtering. Proceedings of the Combustion Institute 2015, 35, 1349–1357. [Google Scholar] [CrossRef]
  23. Domingo, P.; Vervisch, L. DNS and approximate deconvolution as a tool to analyse one-dimensional filtered flame sub-grid scale modelling. Combustion and Flame 2017, 177, 109–122. [Google Scholar] [CrossRef]
  24. W. Zeng, K. Vogiatzaki, S. Navarro-Martinez, K.H. Luo, Modelling of Sub-Grid Scale Reaction Rate Based on a Novel Series Model: Application to a Premixed Bluff-Body Stabilised Flame, Combustion Science and Technology, (2019) 1-16.
  25. Sjunnesson, A.; Nelsson, C.; Max, E. LDA measurements of velocities and turbulence in a bluff body stabilized flame. Laser Anemometry 1991, 3, 83–90. [Google Scholar]
  26. Chen, Y.-C.; Peters, N.; Schneemann, G.; Wruck, N.; Renz, U.; Mansour, M.S. The detailed flame structure of highly stretched turbulent premixed methane-air flames. Combustion and flame 1996, 107, 223–IN222. [Google Scholar] [CrossRef]
  27. Schneider, C.; Dreizler, A.; Janicka, J.; Hassel, E. Flow field measurements of stable and locally extinguishing hydrocarbon-fuelled jet flames. Combustion and Flame 2003, 135, 185–190. [Google Scholar] [CrossRef]
  28. Fureby, C.; Tabor, G.; Weller, H.; Gosman, A. A comparative study of subgrid scale models in homogeneous isotropic turbulence. Physics of fluids 1997, 9, 1416–1429. [Google Scholar] [CrossRef]
  29. Knudsen, E.; Richardson, E.; Doran, E.; Pitsch, H.; Chen, J. Modeling scalar dissipation and scalar variance in large eddy simulation: Algebraic and transport equation closures. Physics of Fluids 2012, 24, 055103. [Google Scholar] [CrossRef]
  30. Navarro-Martinez, S.; Kronenburg, A. LES-CMC simulations of a turbulent bluff-body flame. Proceedings of the Combustion Institute 2007, 31, 1721–1728. [Google Scholar] [CrossRef]
  31. Branley, N.; Jones, W. Large eddy simulation of a turbulent non-premixed flame. Combustion and Flame 2001, 127, 1914–1934. [Google Scholar] [CrossRef]
  32. Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Computers in physics 1998, 12, 620–631. [Google Scholar] [CrossRef]
  33. Masri, A.; Dibble, R.; Barlow, R. The structure of turbulent nonpremixed flames revealed by Raman-Rayleigh-LIF measurements. Progress in Energy and Combustion Science 1996, 22, 307–362. [Google Scholar] [CrossRef]
  34. R. Barlow, J. Frank. Effects of turbulence on species mass fractions in methane/air jet flames. In: editor^editors. Symposium (International) on Combustion; 1998: Elsevier. p. 1087-1095.
  35. Elbahloul, S.; Rigopoulos, S. Rate-Controlled Constrained Equilibrium (RCCE) simulations of turbulent partially premixed flames (Sandia D/E/F) and comparison with detailed chemistry. Combustion and Flame 2015, 162, 2256–2271. [Google Scholar] [CrossRef]
  36. Jones, W.; Prasad, V. Large Eddy Simulation of the Sandia Flame Series (D–F) using the Eulerian stochastic field method. Combustion and Flame 2010, 157, 1621–1636. [Google Scholar] [CrossRef]
  37. S.B. Pope, Turbulent flows, IOP Publishing2001.
  38. Kornev, N.; Hassel, E. Method of random spots for generation of synthetic inhomogeneous turbulent fields with prescribed autocorrelation functions. Communications in numerical methods in engineering 2007, 23, 35–43. [Google Scholar] [CrossRef]
  39. Kornev, N.; Hassel, E. Synthesis of homogeneous anisotropic divergence-free turbulent fields with prescribed second-order statistics by vortex dipoles. Physics of Fluids 2007, 19, 068101. [Google Scholar] [CrossRef]
  40. N. Kornev, H. Kröger, J. Turnow, E. Hassel. Synthesis of artificial turbulent fields with prescribed second-order statistics using the random-spot method. In: editor^editors. PAMM: Proceedings in Applied Mathematics and Mechanics; 2007: Wiley Online Library. p. 2100047-2100048.
  41. Zettervall, N.; Nordin-Bates, K.; Nilsson, E.; Fureby, C. Large Eddy Simulation of a premixed bluff body stabilized flame using global and skeletal reaction mechanisms. Combustion and Flame 2017, 179, 1–22. [Google Scholar] [CrossRef]
  42. Jones, W.; Lindstedt, R. Global reaction schemes for hydrocarbon combustion. Combustion and flame 1988, 73, 233–249. [Google Scholar] [CrossRef]
  43. Mustata, R.; Valiño, L.; Jiménez, C.; Jones, W.; Bondi, S. A probability density function Eulerian Monte Carlo field method for large eddy simulations: application to a turbulent piloted methane/air diffusion flame (Sandia D). Combustion and Flame 2006, 145, 88–104. [Google Scholar] [CrossRef]
  44. Jaravel, T.; Riber, E.; Cuenot, B.; Pepiot, P. Prediction of flame structure and pollutant formation of Sandia flame D using Large Eddy Simulation with direct integration of chemical kinetics. Combustion and Flame 2018, 188, 180–198. [Google Scholar] [CrossRef]
  45. Zhao, W. Large-eddy simulation of piloted diffusion flames using multi-environment probability density function models. Proceedings of the Combustion Institute 2017, 36, 1705–1712. [Google Scholar] [CrossRef]
  46. Vreman, A.; Albrecht, B.; Van Oijen, J.; De Goey, L.; Bastiaans, R. Premixed and nonpremixed generated manifolds in large-eddy simulation of Sandia flame D and F. Combustion and Flame 2008, 153, 394–416. [Google Scholar] [CrossRef]
  47. Vreman, A.; Van Oijen, J.; De Goey, L.; Bastiaans, R. Subgrid scale modeling in large-eddy simulation of turbulent combustion using premixed flamelet chemistry. Flow, Turbulence and Combustion 2009, 82, 511–535. [Google Scholar] [CrossRef]
  48. Ihme, M.; Pitsch, H. Prediction of extinction and reignition in nonpremixed turbulent flames using a flamelet/progress variable model: 2. Application in LES of Sandia flames D and E. Combustion and flame 2008, 155, 90–107. [Google Scholar] [CrossRef]
  49. Ihme, M.; Pitsch, H. Modeling of radiation and nitric oxide formation in turbulent nonpremixed flames using a flamelet/progress variable formulation. Physics of Fluids 2008, 20, 055110. [Google Scholar] [CrossRef]
  50. Raman, V.; Pitsch, H. A consistent LES/filtered-density function formulation for the simulation of turbulent flames with detailed chemistry. Proceedings of the Combustion Institute 2007, 31, 1711–1719. [Google Scholar] [CrossRef]
  51. Garmory, A.; Mastorakos, E. Capturing localised extinction in Sandia Flame F with LES–CMC. Proceedings of the Combustion Institute 2011, 33, 1673–1680. [Google Scholar] [CrossRef]
  52. Ge, Y.; Cleary, M.; Klimenko, A. Sparse-Lagrangian FDF simulations of Sandia Flame E with density coupling. Proceedings of the Combustion Institute 2011, 33, 1401–1409. [Google Scholar] [CrossRef]
  53. Ge, Y.; Cleary, M.; Klimenko, A. A comparative study of Sandia flame series (D–F) using sparse-Lagrangian MMC modelling. Proceedings of the Combustion Institute 2013, 34, 1325–1332. [Google Scholar] [CrossRef]
  54. Cleary, M.; Klimenko, A.; Janicka, J.; Pfitzner, M. A sparse-Lagrangian multiple mapping conditioning model for turbulent diffusion flames. Proceedings of the Combustion Institute 2009, 32, 1499–1507. [Google Scholar] [CrossRef]
  55. Lysenko, D.A.; Ertesvåg, I.S.; Rian, K.E. Numerical simulations of the sandia flame d using the eddy dissipation concept. Flow, turbulence and combustion 2014, 93, 665–687. [Google Scholar] [CrossRef]
  56. Pitsch, H.; Steiner, H. Large-eddy simulation of a turbulent piloted methane/air diffusion flame (Sandia flame D). Physics of fluids 2000, 12, 2541–2554. [Google Scholar] [CrossRef]
  57. Sheikhi, M.; Drozda, T.; Givi, P.; Jaberi, F.; Pope, S. Large eddy simulation of a turbulent nonpremixed piloted methane jet flame (Sandia Flame D). Proceedings of the Combustion Institute 2005, 30, 549–556. [Google Scholar] [CrossRef]
  58. Navarro-Martinez, S.; Kronenburg, A.; Di Mare, F. Conditional moment closure for large eddy simulations. Flow, Turbulence and Combustion 2005, 75, 245–274. [Google Scholar] [CrossRef]
  59. Roomina, M.; Bilger, R. Conditional moment closure (CMC) predictions of a turbulent methane-air jet flame. Combustion and Flame 2001, 125, 1176–1195. [Google Scholar] [CrossRef]
  60. Dodoulas, I.; Navarro-Martinez, S. Large eddy simulation of premixed turbulent flames using the probability density function approach. Flow, turbulence and combustion 2013, 90, 645–678. [Google Scholar] [CrossRef]
  61. Pitsch, H.; De Lageneste, L.D. Large-eddy simulation of premixed turbulent combustion using a level-set approach. Proceedings of the Combustion Institute 2002, 29, 2001–2008. [Google Scholar] [CrossRef]
  62. L.D. de Lageneste, H. Pitsch, A level-set approach to large eddy simulation of premixed turbulent combustion, CTR Annual Research Briefs, (2000).
  63. Knudsen, E.; Pitsch, H. A dynamic model for the turbulent burning velocity for large eddy simulation of premixed combustion. Combustion and flame 2008, 154, 740–760. [Google Scholar] [CrossRef]
  64. De, A.; Acharya, S. Large eddy simulation of a premixed Bunsen flame using a modified thickened-flame model at two Reynolds number. Combustion Science and Technology 2009, 181, 1231–1272. [Google Scholar] [CrossRef]
  65. De, A.; Acharya, S. Large eddy simulation of premixed combustion with a thickened-flame approach. Journal of Engineering for Gas Turbines and Power 2009, 131, 061501. [Google Scholar] [CrossRef]
  66. Langella, I.; Swaminathan, N.; Gao, Y.; Chakraborty, N. Assessment of dynamic closure for premixed combustion large eddy simulation. Combustion Theory and Modelling 2015, 19, 628–656. [Google Scholar] [CrossRef]
  67. Langella, I.; Swaminathan, N.; Gao, Y.; Chakraborty, N. Large eddy simulation of premixed combustion: Sensitivity to subgrid scale velocity modeling. Combustion Science and Technology 2017, 189, 43–78. [Google Scholar] [CrossRef]
  68. Langella, I.; Swaminathan, N. Unstrained and strained flamelets for LES of premixed combustion. Combustion Theory and Modelling 2016, 20, 410–440. [Google Scholar] [CrossRef]
  69. Wang, G.; Boileau, M.; Veynante, D. Implementation of a dynamic thickened flame model for large eddy simulations of turbulent premixed combustion. Combustion and Flame 2011, 158, 2199–2213. [Google Scholar] [CrossRef]
  70. Lindstedt, R.; Vaos, E. Transported PDF modeling of high-Reynolds-number premixed turbulent flames. Combustion and Flame 2006, 145, 495–511. [Google Scholar] [CrossRef]
  71. Stöllinger, M.; Heinz, S. PDF modeling and simulation of premixed turbulent combustion. Monte Carlo Methods and Applications 2008, 14, 343–377. [Google Scholar] [CrossRef]
  72. Schneider, E.; Sadiki, A.; Janicka, J. Modeling and 3D-simulation of the kinetic effects in the post-flame region of turbulent premixed flames based on the G-equation approach. Flow, turbulence and combustion 2005, 75, 191. [Google Scholar] [CrossRef]
  73. Lindstedt, R.; Milosavljevic, V.; Persson, M. Turbulent burning velocity predictions using transported PDF methods. Proceedings of the Combustion Institute 2011, 33, 1277–1284. [Google Scholar] [CrossRef]
  74. Knudsen, E.; Pitsch, H. Modeling partially premixed combustion behavior in multiphase LES. Combustion and Flame 2015, 162, 159–180. [Google Scholar] [CrossRef]
  75. Kolla, H.; Swaminathan, N. Strained flamelets for turbulent premixed flames II: Laboratory flame results. Combustion and Flame 2010, 157, 1274–1289. [Google Scholar] [CrossRef]
  76. Ihme, M.; Shunn, L.; Zhang, J. Regularization of reaction progress variable for application to flamelet-based combustion models. Journal of Computational Physics 2012, 231, 7715–7721. [Google Scholar] [CrossRef]
Preprints 89956 g001
Figure 1. A sketch of simulation domain and fine grid allocation. Blue area: main jet. Red area: pilot stream.
Figure 1. A sketch of simulation domain and fine grid allocation. Blue area: main jet. Red area: pilot stream.
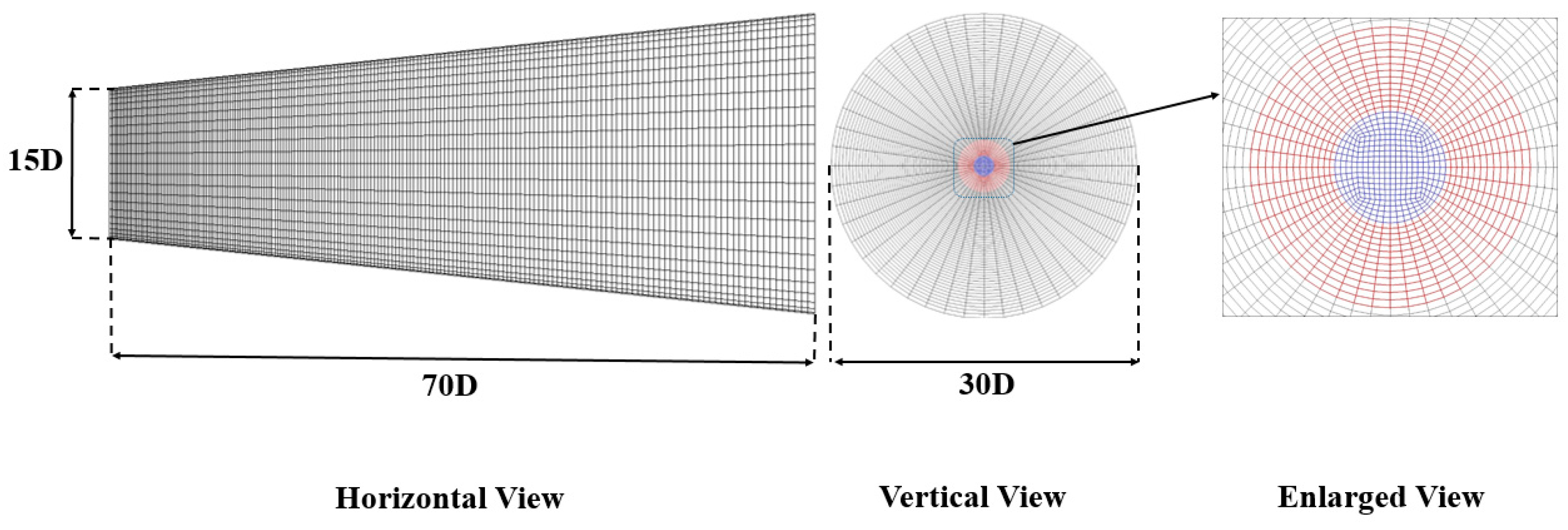
Preprints 89956 g001
Preprints 89956 g002
Figure 2. Instantaneous contour plots of temperature and CO2 mass fraction distribution.
Figure 2. Instantaneous contour plots of temperature and CO2 mass fraction distribution.
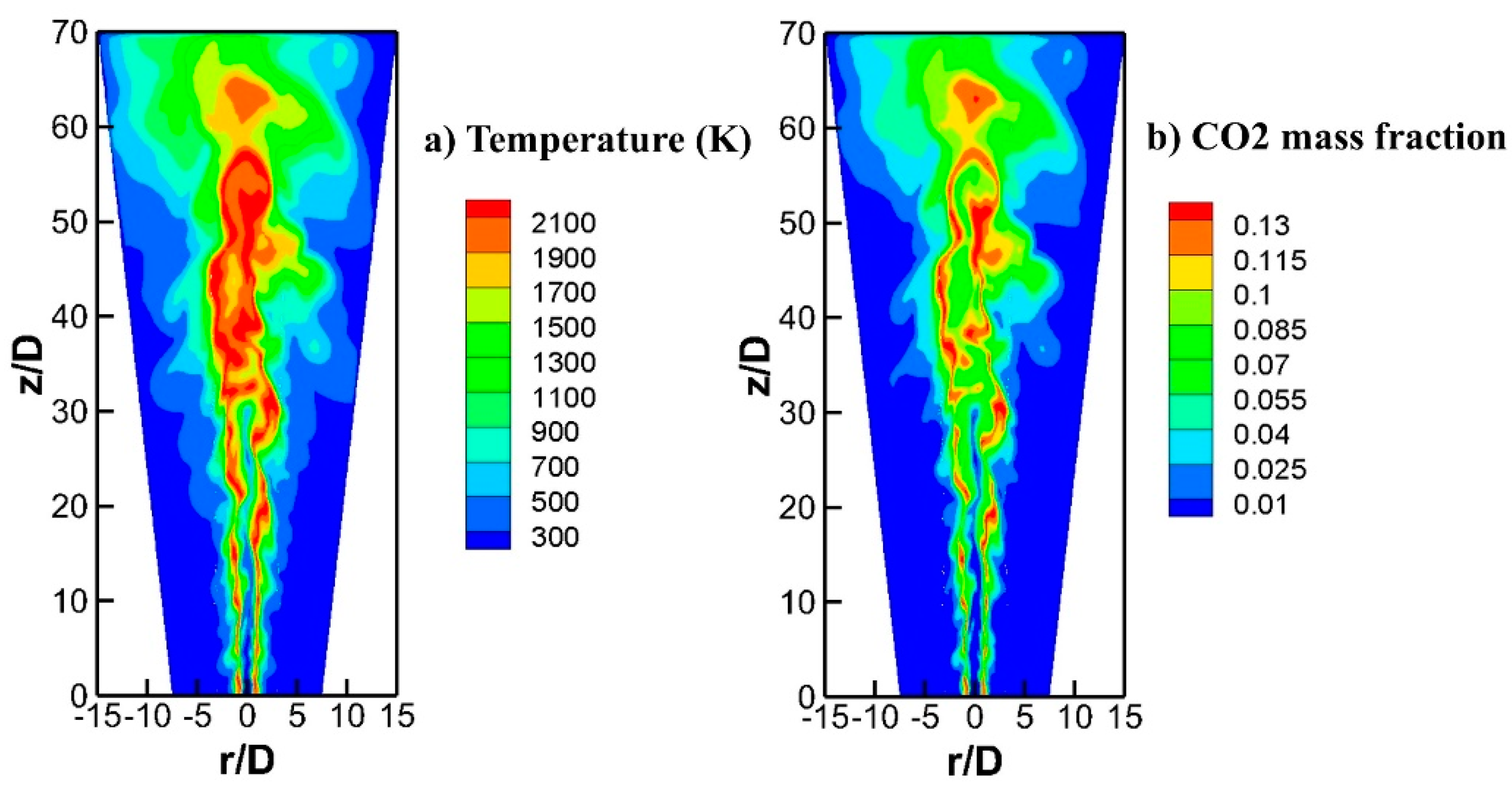
Preprints 89956 g002
Preprints 89956 g003
Figure 3. Centreline trends of mixture fraction, temperature, axial velocity and reactive species. Black solid line: mean value of series model in fine grid (i). Blue solid line: mean value of series model in coarse grid (ii). Square scatter: mean experimental data [34] (iii). Black dashed line: rms value of series model in fine grid (iv). Blue dashed line: rms value of series model in coarse grid (v). Round scatter: rms experimental data [34] (vi). Green solid line: mean value in reference [43] (vii). Green dashed line: rms value in reference [43] (viii).
Figure 3. Centreline trends of mixture fraction, temperature, axial velocity and reactive species. Black solid line: mean value of series model in fine grid (i). Blue solid line: mean value of series model in coarse grid (ii). Square scatter: mean experimental data [34] (iii). Black dashed line: rms value of series model in fine grid (iv). Blue dashed line: rms value of series model in coarse grid (v). Round scatter: rms experimental data [34] (vi). Green solid line: mean value in reference [43] (vii). Green dashed line: rms value in reference [43] (viii).
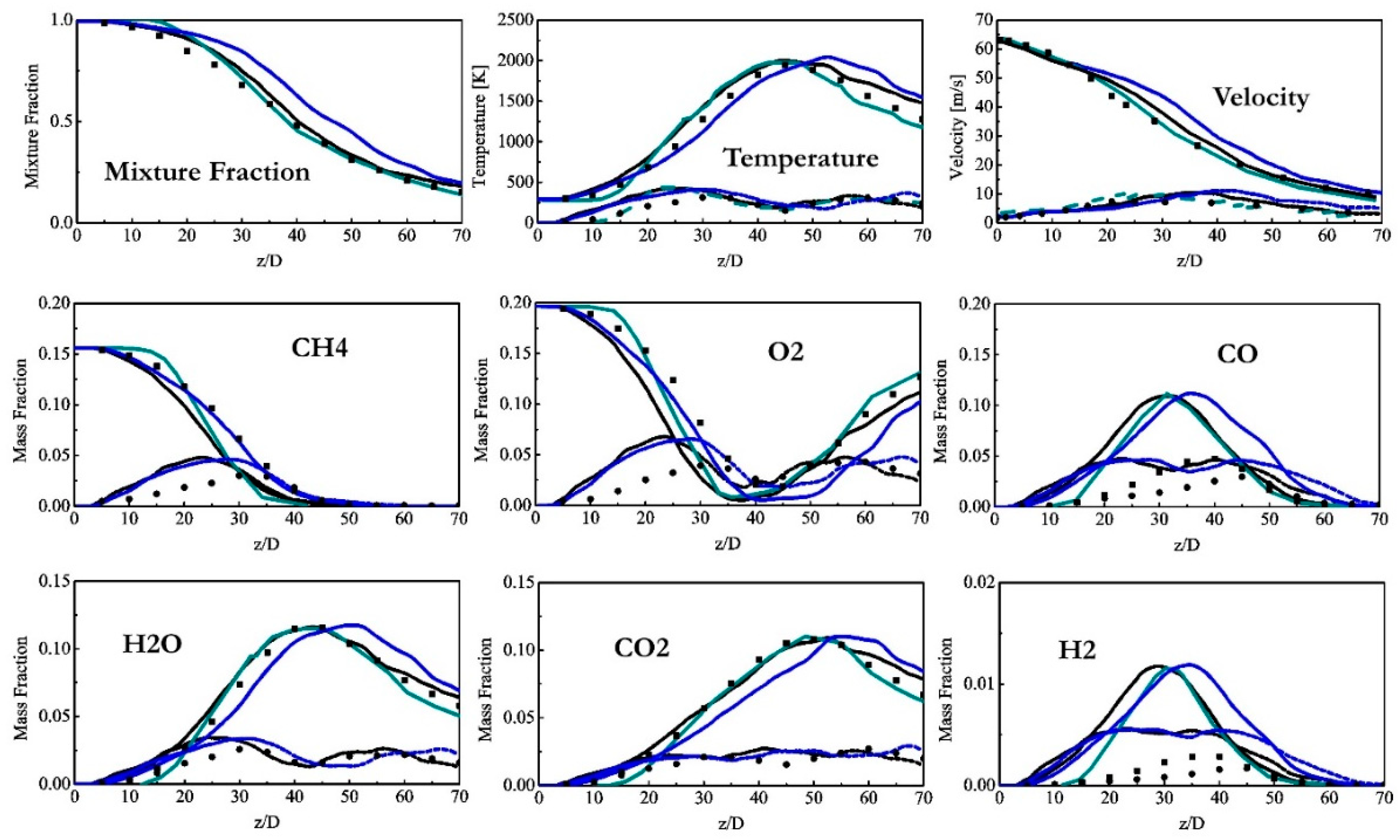
Preprints 89956 g003
Preprints 89956 g004
Figure 4. Radial distributions of mixture fraction, temperature as well as reactive species. Black solid line: mean value of series model in fine grid (i). Blue solid line: mean value of series model in coarse grid (ii). Square scatter: mean experimental data [34] (iii). Black dashed line: rms value of series model in fine grid (iv). Blue dashed line: rms value of series model in coarse grid (v). Round scatter: rms experimental data [34] (vi). Green solid line: mean value in reference [43] (vii).
Figure 4. Radial distributions of mixture fraction, temperature as well as reactive species. Black solid line: mean value of series model in fine grid (i). Blue solid line: mean value of series model in coarse grid (ii). Square scatter: mean experimental data [34] (iii). Black dashed line: rms value of series model in fine grid (iv). Blue dashed line: rms value of series model in coarse grid (v). Round scatter: rms experimental data [34] (vi). Green solid line: mean value in reference [43] (vii).
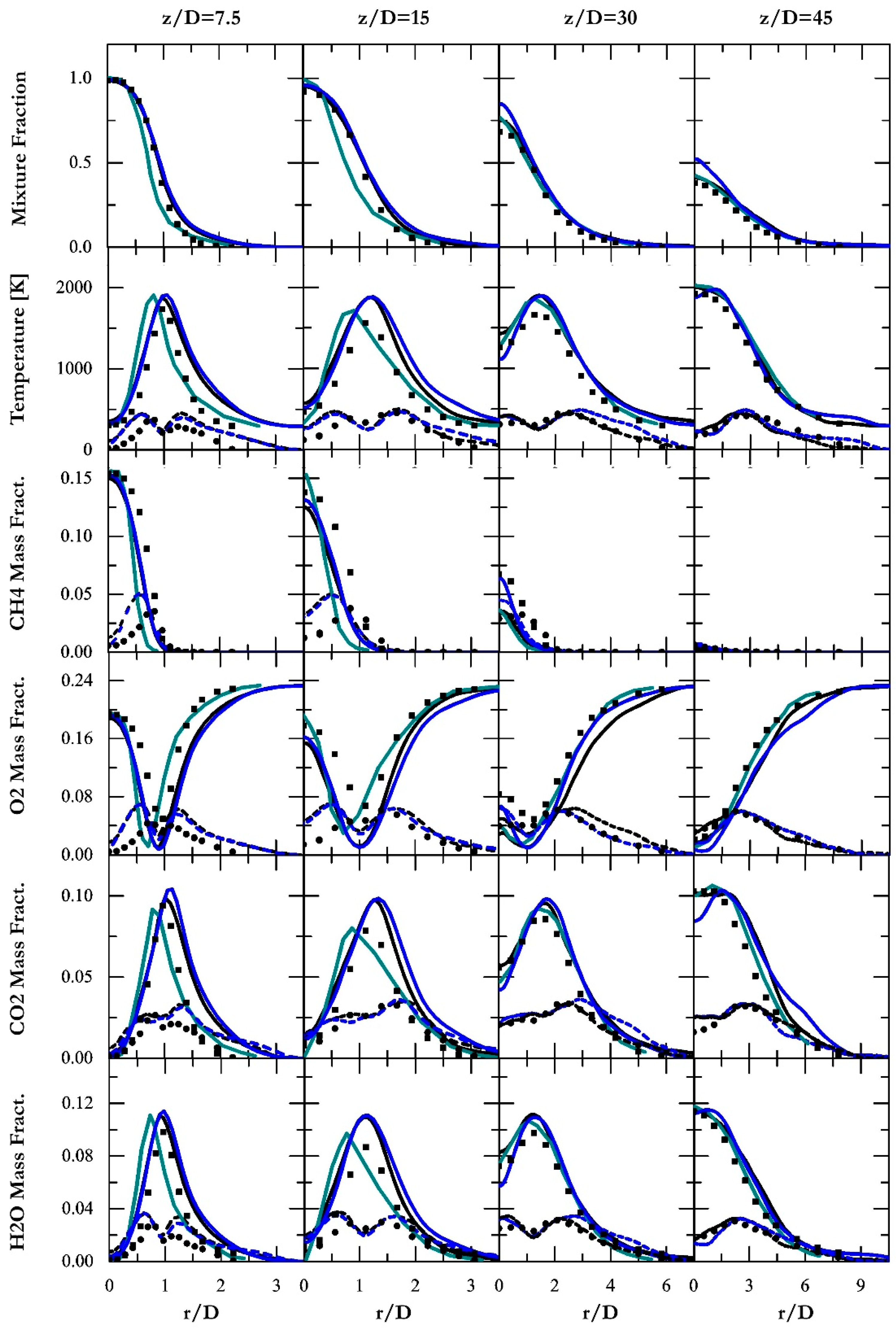
Preprints 89956 g004
Preprints 89956 g005
Figure 5. A sketch of the simulation domain and grid allocation. Blue area: main jet. Red area: pilot stream.
Figure 5. A sketch of the simulation domain and grid allocation. Blue area: main jet. Red area: pilot stream.
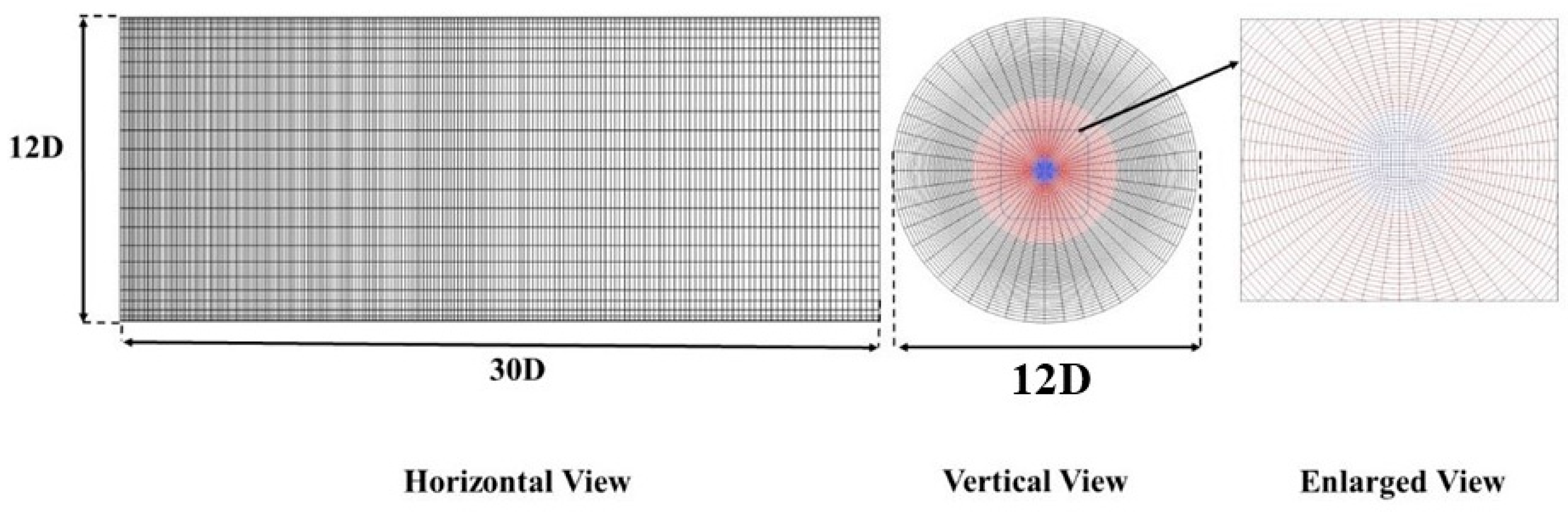
Preprints 89956 g005
Preprints 89956 g006
Figure 6. Radial trends of temperature and species mass fractions. Black solid line: series model in fine grid (i). Blue solid line: series model in coarse grid (ii). Square scatter: experimental data [26] (iii). Green solid line: the Domingo et al. simulation[22] (iv).
Figure 6. Radial trends of temperature and species mass fractions. Black solid line: series model in fine grid (i). Blue solid line: series model in coarse grid (ii). Square scatter: experimental data [26] (iii). Green solid line: the Domingo et al. simulation[22] (iv).
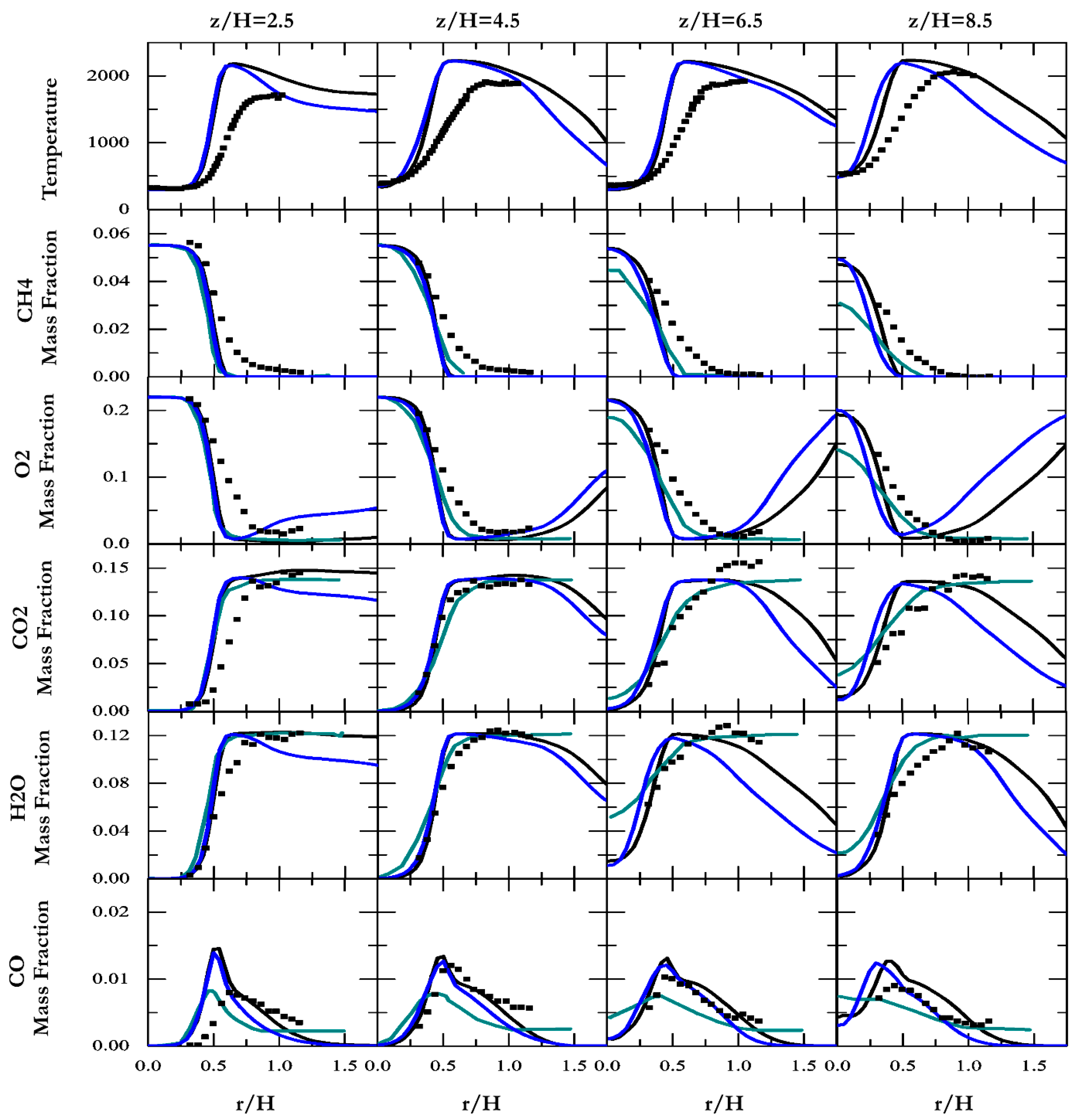
Preprints 89956 g006
Preprints 89956 g007
Figure 7. Progress variable radial profiles. Black solid line: series model in fine grid (i). Blue solid line: series model in coarse grid (ii). Square scatter: experimental data [26] (iii).
Figure 7. Progress variable radial profiles. Black solid line: series model in fine grid (i). Blue solid line: series model in coarse grid (ii). Square scatter: experimental data [26] (iii).
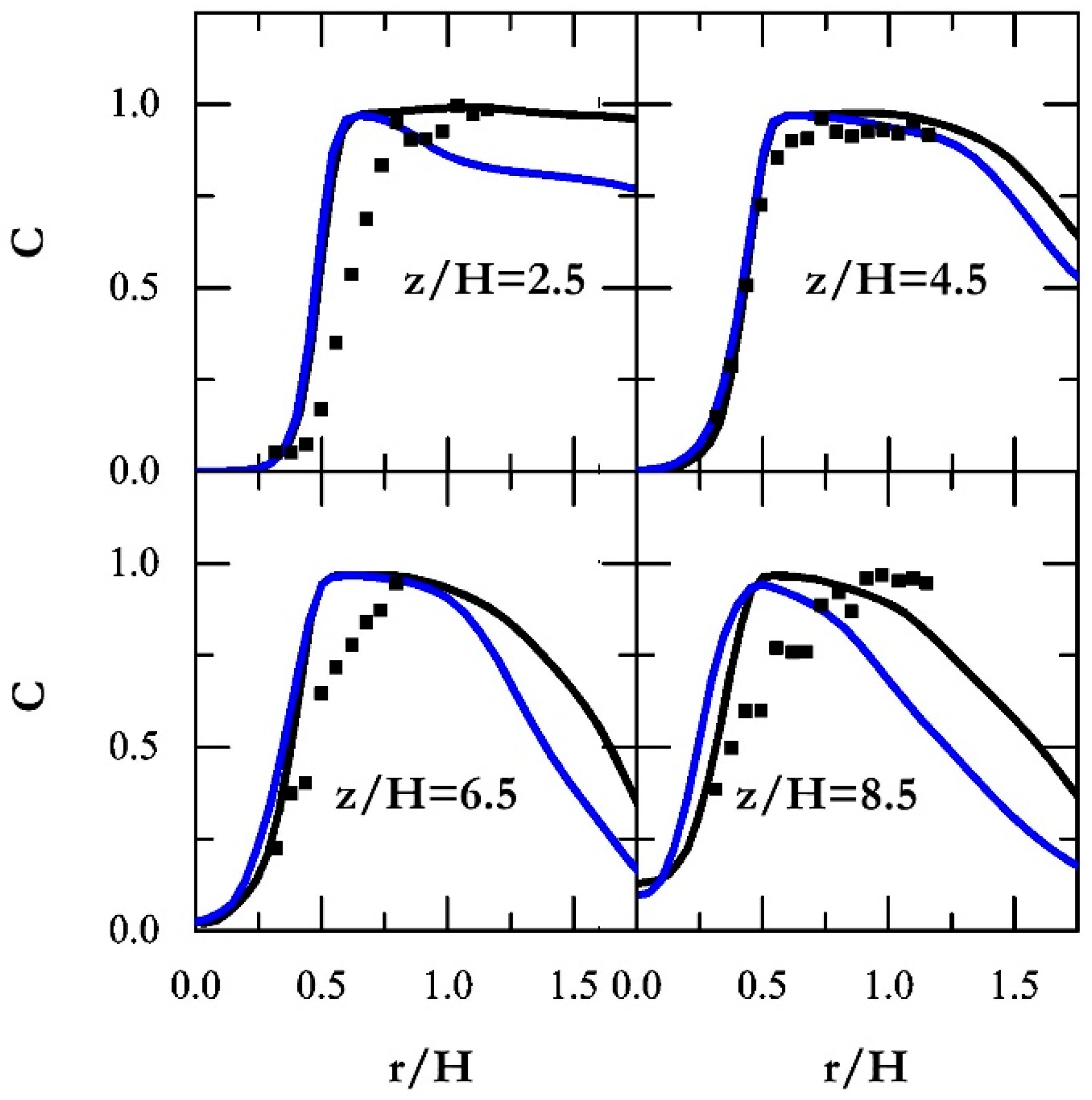
Preprints 89956 g007
Table 1. Simulation parameters and the comparison with previous studies.
Table 1. Simulation parameters and the comparison with previous studies.
Research Turbulent SGS closures Turbulent reacting LES closures Simulation domain Grid resolution Chemistry mechanism
Current study Dynamic Eddy viscosity model Series model (15~30D) × 2π× 70D Fine: 71 × 48 × 210 + 12 × 12 × 210 Coarse: 52 × 36 × 139+ 9 × 9 × 139 (Polar coordinates + o-grid) Jones- Lindstedt 4-step mechanism
[43] Eddy viscosity model Eulerian stochastic field method 40D× 40D× 84D 68 × 68 × 106 (Cartesian coordinates) Jones- Lindstedt 4-step mechanism
[44] SIGMA eddy viscosity model Direct integration of reduced chemical kinetics 40D× 40D× 138D 375 million tetrahedral elements (unstructured meshes) GRI 2.0 and 3.0
[45] Dynamic Smagorinsky Multi-environment PDF model (8~44D) × 2π× 80D 101 × 64 × 197 (cylindrical coordinates) Reduced GRI 3.0
[46,47] Eddy-viscosity model Presumed β-pdf and
Thickened flame approach 		40D× 40D× 150D 128 × 128 × 320 (Cartesian coordinates) GRI 3.0
[48,49] Dynamic Smagorinsky Extended flamelet/progress variable model 26.5D× 2π × 80D 160× 64× 256 (cylindrical coordinates) GRI 2.11
[36] Smagorinsky Eulerian stochastic field method 20D× 20D× 50D 81 × 81 × 160 (Cartesian coordinates) Augmented reduced Mechanism of GRI3.0
[50] Dynamic Smagorinsky Lagrangian filtered-density approach 20D× 2π × 80D 256 × 128 × 32 (cylindrical coordinates) GRI-2.11
[51] Dynamic Smagorinsky Conditional Moment Closure 20D× 20D× 80D 1.3M nodes (CMC grids) ARM2 chemistry
[52,53,54] Dynamic Smagorinksy Hybrid Eulerian LES/sparse-Lagrangian MMC model 35D× 2π × 35D 512 × 55 × 32 (cylindrical coordinates) GRI-3.0
[55] One equation eddy viscosity Eddy Dissipation Concept 21D× 2π × 73D 240 × 60 × 90 (cylindrical coordinates) GRI3.0 and Single Step mechanism
[56] Smagorinsky Lagrangian Flamelet Model 15D× 2π × 80D 110× 48× 192 (cylindrical coordinates) GRI
2.11
[57] Modified kinetic energy viscosity model Flamelet model 15D× 15D× 80D 101 × 101 × 91 (Cartesian coordinates) GRI
2.11
[58] Smagorinsky Conditional Moment Closure 8D× 8D× 80D 96 × 96 × 320 (Cartesian coordinates) Detailed mechanism by Meyer
Table 2. Simulation parameters and the comparison with previous studies.
Table 2. Simulation parameters and the comparison with previous studies.
Research Turbulent SGS closures Turbulent reacting LES closures Simulation domain Grid resolution Chemistry mechanism
Current Dynamic eddy viscosity model Series model 12H× 2π× 30H Fine: 69 × 48 × 200 +12 × 12 × 200 Coarse: 49 × 36 × 134+9 × 9 × 134
(Polar coordinates +o-grid)		 Jones and Lindstedt 4-step mechanism
[22,23] Vreman model Artificially thickened flame 8H×8H×16H 194 × 194 × 306 (Cartesian coordinates) GRI 3.0
[61,62] Smagorinsky G-field 4H×4H×20H 64×64 × 296 (Cartesian coordinates) GRI-MECH 2.11
[63] Germano model G-field and dynamic propagation model 6H×6H×30H 117 × 64 × 323 (cylindrical coordinates)
[60] Smagorinsky Eulerian stochastic fields 5H×5H×15H 56 × 36 × 112 (Cartesian coordinates) ARM for NO
[64,65] Dynamic Smagorinsky Artificially thickened flame 4H×2π ×20H 94× 64× 300 (cylindrical coordinates) A 2-step mechanism
[66,67,68] Smagorinsky Dynamic modelling and Assumed PDF 20H×20H×40H 1.5 minion cells (Cartesian coordinates) Augmented reduced of GRI3.0
[69] Dynamic Smagorinsky Dynamic thickened flame 40H×40H×120H Unstructured meshes A single-step mechanism
[6] Smagorinsky Dynamic thickened flame model 40H×40H×120H Unstructured meshes A 2-step mechanism
[70] Second momentclosures Transported pdf 4H×4H×12.5H (at least) Lagrangian particle grids Lindstedt reduced mechanism
[71] Linear stress model Pdf method 6.5H×20H 70 ×220 (2D simulation) Drm22
[72] Smagorinsky G-equation 6H×6H×45H 345,000 cells (cylindrical coordinates) Schmidt mechanism
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated